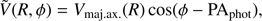| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 50 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201732473 | |
| Published online | 18 October 2018 | |
The extended Planetary Nebula Spectrograph (ePN.S) early-type galaxy survey: The kinematic diversity of stellar halos and the relation between halo transition scale and stellar mass
1
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
e-mail: cpulsoni@mpe.mpg.de
2
Excellence Cluster Universe, Boltzmannstraße 2, 85748 Garching, Germany
3
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
4
Kavli Institute for Astronomy and Astrophysics, Peking University, 5 Yiheyuan Road, Haidian District, 100871 Beijing, PR China
5
INAF – Astronomical Observatory of Capodimonte, Salita Moiariello, 16, 80131 Naples, Italy
6
School of Civil Engineering, The University of Sydney, NSW 2006, Australia
7
Department of Physics, Cornell University, Ithaca, 14853 New York, USA
8
University Observatory Munich, Scheinerstraße 1, 81679 Munich, Germany
9
University of Naples “Federico II”, Department of Physics “Ettore Pancini”, CU Monte Sant’Angelo, via Cinthia, 80126 Naples, Italy
10
Departamento de Astronomia, Instituto de Fisica, Universidade Federal do Rio Grande do Sul, Porto Alegre, RS 90040-060, Brazil
11
Departamento de Astronomia, Instituto de Astronomia, Geofisica e Ciencias Atmosfericas da USP, Cidade Universitaria, CEP:05508900 Sao Paulo, Brazil
12
Research School of Astronomy and Astrophysics, Mount Stromlo Observatory, Cotter Road, ACT 2611 Weston Creek, Australia
13 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
14
School of Physics and Astronomy, The University of Nottingham, University Park, NG7 2RD Nottingham, UK
15
Department of Physics and Astronomy, San Jose State University, One Washington Square, San Jose, CA 95192, USA
16
University of California Observatories, 1156 High Street, Santa Cruz, CA 95064, USA
17
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
Received:
15
December
2017
Accepted:
16
July
2018
Context. In the hierarchical two-phase formation scenario, the halos of early type galaxies (ETGs) are expected to have different physical properties from the galaxies’ central regions.
Aims. The ePN.S survey characterizes the kinematic properties of ETG halos using planetary nebulae (PNe) as tracers, overcoming the limitations of absorption line spectroscopy at low surface brightness.
Methods. We present two-dimensional velocity and velocity dispersion fields for 33 ETGs, including fast (FRs) and slow rotators (SRs). The velocity fields were reconstructed from the measured PN velocities using an adaptive kernel procedure validated with simulations, and extend to a median of 5.6 effective radii (Re). We complemented the PN kinematics with absorption line data from the literature, for a complete description of the kinematics from the center to the outskirts.
Results. ETGs typically show a kinematic transition between inner regions and halo. Estimated transition radii in units of Re anti-correlate with stellar mass. SRs have increased but still modest rotational support at large radii. Most of the FRs show a decrease in rotation, due to the fading of the inner disk in the outer, more slowly rotating spheroid. 30% of the FRs are dominated by rotation also at large radii. Most ETGs have flat or slightly falling halo velocity dispersion profiles, but 15% of the sample have steeply falling profiles. All of the SRs and 40% of the FRs show signatures of triaxial halos such as kinematic twists or misalignments. We show with illustrative photometric models that this is consistent with the distribution of isophote twists from extended photometry.
Conclusions. ETGs have more diverse kinematic properties in their halos than in the central regions. FRs do contain inner disk components but these frequently fade in outer spheroids which are often triaxial. The observed kinematic transition to the halo and its dependence on stellar mass is consistent with ΛCDM simulations and supports a two-phase formation scenario.
Key words: galaxies: elliptical and lenticular, cD / galaxies: general / galaxies: halos / galaxies: kinematics and dynamics / Galaxy: structure
© ESO 2018
1. Introduction
Observations (e.g., Trujillo et al. 2006; van Dokkum et al. 2010) as well as simulations (e.g., Oser et al. 2010; Rodriguez-Gomez et al. 2016; Qu et al. 2017) suggest a two phase scenario for the formation of early type galaxies (ETGs). An initial fast assembly stage, in which the ETGs grow through rapid star formation fueled by the infall of cold gas (z ≳ 1.5) or through major merger events (Wuyts et al. 2010; Sommer-Larsen & Toft 2010; Bournaud et al. 2011; Wellons et al. 2016), is followed by a series of merger episodes which enrich the galaxy halos of stars and make them grow efficiently in size (Oser et al. 2010; Gabor & Davé 2012; Lackner et al. 2012; Buitrago et al. 2017). The hierarchical accretion scenario finds its best evidence in the observations of a rapid growth of stellar halos at redshift z ≲ 2 with little or no star formation (e.g., Daddi et al. 2005; Trujillo et al. 2007; van Dokkum et al. 2010; Damjanov et al. 2011). In this context ETGs are layered structures in which the central regions are the remnant of the primordial stars formed in-situ, while the external halos are principally made of accreted material. The consequence is that the halos are expected to show significant variation with radius of properties such as light profiles (Huang et al. 2013; D’Souza et al. 2014; Iodice et al. 2016; Spavone et al. 2017), and kinematics (Coccato et al. 2009; Romanowsky & Fall 2012; Arnold et al. 2014; Foster et al. 2016).
Long slit spectroscopic observations of ETGs (e.g., Davies et al. 1983; Franx et al. 1989; Bender et al. 1994) revealed that this apparently homogeneous class of objects actually displays a kinematic diversity which also correlates with the isophote shape (Bender 1988b; Kormendy & Bender 1996). Disky ellipticals generally rotate fast, while slowly rotating ellipticals have a rather boxy shape. A remarkable step forward in the comprehension of the nature of ETGs was attained by the ATLAS3D project (Cappellari et al. 2011), which for the first time applied integral-field spectroscopy (IFS) over a statistically-significant sample, mapping kinematics, dynamics, and stellar population properties within one effective radius (Re). A new paradigm for ETGs was proposed, which distinguishes between fast (FRs) and slow rotators (SRs) according to the central projected specific angular momentum, λR (Emsellem et al. 2007). FRs include also S0 galaxies and represent the great majority (86%) of ETGs. These are apparently oblate systems with regular disk-like kinematics along the photometric major axis. SRs, on the other hand, often display kinematic features such as counter-rotating cores or twist of the kinematic position angle. They are relatively rounder systems, mildly triaxial, and tend to be massive (Cappellari et al. 2013a).
The two classes have been interpreted as the result of the variety of processes shaping galaxies, leading to a sequence of baryonic angular momentum (Emsellem et al. 2011; Naab et al. 2014; Wu et al. 2014). On-going surveys like MANGA (Bundy et al. 2015), CALIFA (Sánchez et al. 2012), SAMI (Croom et al. 2012; Bryant et al. 2015), and MASSIVE (Ma et al. 2014) are currently working on increasing the size of the sample of IFS mapped objects, and extending the study to a wider range of environment and mass.
However, a classification scheme based on the characteristics of the galaxies in the central regions (inside ∼1Re) may not be fully representative of the nature of these objects (e.g., Bellstedt et al. 2017b), raising the question of how complete our understanding is without a full knowledge of their properties on larger scales. The outer regions beyond Re in fact contain half of the galaxies’ stars and most of their dynamical mass. Dark matter is known to dominate there (e.g., Mandelbaum et al. 2006; Humphrey et al. 2006; Koopmans et al. 2009; Churazov et al. 2010) and dynamical modeling of the outskirts is essential to constrain its distribution at intermediate radii (e.g., Gerhard et al. 2001; Romanowsky et al. 2003; Thomas et al. 2009; Napolitano et al. 2011; Morganti et al. 2013). Stellar halos are predicted to host mostly accreted star material as shown by particle tagging simulations (Cooper et al. 2013) and hydro-dynamical simulations (Rodriguez-Gomez et al. 2016). In addition, these regions provide insight into the most recent dynamical phase of the galaxy. In the halos the settling times are of order 1 Gyr and so signatures of the most recent assembly events may still be apparent, providing a mine of information about their formation and evolution mechanisms (e.g., Bullock & Johnston 2005; Tal et al. 2009; Romanowsky et al. 2012; Coccato et al. 2013; Duc et al. 2015; Longobardi et al. 2015). Thus extending investigations to the outer halos is crucial for having a complete picture of ETGs.
However kinematic measurements are not easily obtained for ETG halos, which generally lack cold gas (and so the 21 cm HI emission) used to probe the outer parts of spiral galaxies. Since the continuum light from the stars quickly drops with radius, absorption line spectroscopy is challenging beyond 1−2Re. This limits the assessment of the complicated dynamics of ETGs which, because dominated by dispersion, necessitates a good knowledge of the higher moments of the line of sight velocity distribution (LOSVD) in order to alleviate the anisotropy-potential-degeneracy (e.g., Gerhard 1993; Rix et al. 1997; Thomas et al. 2009; de Lorenzi et al. 2009; Napolitano et al. 2009).
Kinematic studies of ETGs from integrated-light spectra out to large radii have been performed by Kelson et al. (2002), Weijmans et al. (2009), Coccato et al. (2010), Murphy et al. (2011), Barbosa et al. (2018) using long slit spectroscopy or IFS on individual objects. More recently the SLUGGS survey (Arnold et al. 2014; Foster et al. 2016; Bellstedt et al. 2017a), the MASSIVE survey (Raskutti et al. 2014; Veale et al. 2017), and Boardman et al. (2017) generated kinematic data from integral field spectrographs (IFSs) for larger samples of ETGs, but never reaching beyond 3−4Re 1.
The only possibility to probe the kinematics of a large sample of galaxies out to the very outskirts is through kinematic tracers that overcome the limit of the decreasing surface brightness, like globular clusters (e.g., Schuberth et al. 2010; Strader et al. 2011) or planetary nebulae.
Planetary nebulae (PNe) are established probes of the stellar population in ETG halos (e.g., Longobardi et al. 2013; Hartke et al. 2017). Their bright [OIII] line stands out against the faint galaxy background, making them relatively easy to detect. Since they are drawn from the main stellar population, their kinematics traces the bulk of the host-galaxy stars, and are directly comparable to integrated light measurements (Hui et al. 1995; Arnaboldi et al. 1996; Méndez et al. 2001; Coccato et al. 2009; Cortesi et al. 2013a). This makes PNe the ideal kinematic probes for the halos of ETGs. Globular clusters do not generally follow the surface brightness distribution of the stars and do not trace the stellar kinematics (e.g., Brodie & Strader 2006; Coccato et al. 2013; Veljanoski et al. 2014), and their color bimodality, suggesting two distinct formation mechanisms (Renaud et al. 2017, and references therein), complicates the interpretation of their use as kinematic tracers. The pioneering work of Coccato et al. (2009) studied the kinematics of 16 ETGs traced with PNe out to 8Re, finding evidence for kinematic transitions at large radii from the trends observed in the central regions (see also Arnold et al. 2014).
Planetary nebulae (PNe) are established probes of the stellar population in ETG halos (e.g., Longobardi et al. 2013; Hartke et al. 2017). Their bright [OIII] line stands out against the faint galaxy background, making them relatively easy to detect. Since they are drawn from the main stellar population, their kinematics traces the bulk of the host-galaxy stars, and are directly comparable to integrated light measurements (Hui et al. 1995; Arnaboldi et al. 1996; Méndez et al. 2001; Coccato et al. 2009; Cortesi et al. 2013a). This makes PNe the ideal kinematic probes for the halos of ETGs. Globular clusters do not generally follow the surface brightness distribution of the stars and do not trace the stellar kinematics (e.g., Brodie & Strader 2006; Coccato et al. 2013; Veljanoski et al. 2014), and their color bimodality, suggesting two distinct formation mechanisms (Renaud et al. 2017, and references therein), complicates the interpretation of their use as kinematic tracers. The pioneering work of Coccato et al. (2009) studied the kinematics of 16 ETGs traced with PNe out to 8Re, finding evidence for kinematic transitions at large radii from the trends observed in the central regions (see also Arnold et al. 2014).
The extended Planetary Nebula Spectrograph (ePN.S) survey in based on observation mostly done with the Planetary Nebula Spectrograph (PN.S), and consists of catalogs of PNe for 33 ETGs. This dataset is the largest survey to-date of extragalactic PNe identified in the halos of ETGs, complementing the absorption line kinematics of the central regions available in the literature. The rationale of the survey, the sample definition, and the construction of the catalogs are described in detail in Arnaboldi et al. (in prep.). Section 2 is a brief description of the ePN.S sample. Section 3 describes the general procedure adopted for extracting the mean velocity fields from the measured radial velocities of PNe, and reviews the adaptive kernel smoothing technique introduced by Coccato et al. (2009). In Sect. 4 we evaluate the systemic velocity of the galaxies. The point-symmetry of the smoothed velocity fields is studied in Sect. 5, while the trends of the kinematic parameters, such as rotational velocity, kinematic position angle, and velocity dispersion, are derived in Sect. 6. The results are described in Sect. 7 with a detailed analysis of SRs and FRs. A discussion of the results is presented in Sect. 8. In Sect. 9 we give a summary of the work and draw our conclusions.
2. Description of the sample, observations, and data reduction
This work is based mostly on data collected with the Planetary Nebula Spectrograph (PN.S) at the William Herschel Telescope in La Palma. The PN.S is a custom-built instrument designed for counter-dispersed imaging (Douglas et al. 2002). Arnaboldi et al. (in prep.) collected catalogs of PNe for 25 galaxies from PN.S, 11 of which new, to which they added six further catalogs from the literature and two additional new catalogs, for a total of 33 ETGs. This ePN.S sample is magnitude limited and covers a wide range of internal parameters, such as luminosity, central velocity dispersion, ellipticity, boxy and diskyness (Table 1 summarizes the properties of the sample and the origin of the catalogs). Our catalogs contain a total of 8636 PNe, with data covering 4, 6, and 8 effective radii (Re) for, respectively, 85%, 41%, and 17% of the sample, with median extension of 5.6Re (see Rmax values of the last radial bins in Table 1). This makes the ePN.S the largest kinematic survey to-date of extragalactic PNe in the outer halos of ETGs.
Properties of the ETG sample analyzed in this paper, and list of references.
Arnaboldi et al. (in prep.) give a full discussion of the extraction and validation of the catalogs; here we provide a brief description of the adopted procedures. All the datasets (the new catalogs, as well as the PN catalogs from the literature) are uniformly (re)analyzed, in order to obtain a homogeneous sample of ETG kinematics whose properties can be consistently compared. The new PN.S observations, the two additional new catalogs, and the reanalyzed catalogs will be described in Arnaboldi et al. (in prep.).
For each galaxy, after the raw catalog has been obtained, it is uniformly cleaned from possible spurious sources and from so-called velocity outliers. The first step for the removal of outliers among the PN candidates is the exclusion of all the detections with signal-to-noise ratio below a given threshold. We adopted S/N ≥ 2.5 as good compromise value between a reasonable S/N and the number of detections that satisfy this requirement.
Next we separate PNe belonging to any satellites from those in the hosts. For this we use the probability membership method from McNeil-Moylan et al. (2012), which uses both kinematic and photometric information to assign to each star a probability of belonging to the satellite or host. Membership to the host galaxy is assigned only if the probability is greater than 90%.
The last step is the removal of outliers in the remaining host PN velocity distribution. Such outliers could, for example, arise because of contamination from other narrow emission-line sources (i.e., background star-forming galaxies) that are not resolved and appear point-like in the counter-dispersed images, similar to the monochromatic [OIII] 5007 Å emission from a PN. We identify outliers using a robust sigma clipping procedure. The algorithm derives a robust mean velocity (vmean) and velocity dispersion σ, using a running average in a 2D phase space (coordinate, v) with a window of N data points (15 ≤ N ≤ 30, according to the number of tracers in each galaxy) and a three data points step. An iterative procedure clips the PN candidates whose |v − vmean| > 2σ, and evaluates vmean and σ until the number of clipped objects stabilizes. In each iteration σ is corrected by a factor 1.14 to account for the 2σ cut of the LOSVD tails. Finally, to the 95% of a galaxy’s PNe thus validated, the remaining 5% of the PNe are added back to the sample, using those clipped objects which are closest in v to the 2σ contours, so that the final PN sample also includes the objects expected in the approximately Gaussian tails of the LOSVD.
In the case of disk galaxies, dominated by rotation, a decomposition into disk and spheroid was performed following Cortesi et al. (2011): using both photometric data and kinematic information we assigned to each PN the probability of being associated with each photometric component. The tagging of the outliers from the disk and the spheroid separately allows us to account for their different kinematics when using the robust sigma clipping procedure. The disk is processed first, and its flagged PNe are added to the PNe of the bulge. Eventually the flagged bulge PNe are considered as outliers of the entire galaxy.
Finally, we estimated the number of background emitting galaxies, whose emission line might fall in the range of velocities determined in the procedure above. We employed the approach adopted in Longobardi et al. (2013), which uses the Lyman alpha (Lyα) luminosity function by Gronwall et al. (2007), and adapted it to the ePN.S survey. Given the limiting magnitude, the area coverage, and the filter band-passes of the PN.S, the number of expected background galaxies is 2. This is an upper limit, as the Gronwall et al. (2007) sample also includes [OII] emitters at z ≃ 0.34. These [OII] emitters are characterized by the oxygen doublet at 3726−3729 Å that is resolved in wavelength at the resolution of the PN.S, so the [OII] emitters have already been removed from the PN candidate sample because they are not monochromatic emission. We discuss the effect of the Lyα background contaminants on the kinematics in Sect. 3.2.2. The datasets processed in this way are the Bona Fide PNe catalogs used in the following analysis.
3. Kernel smoothing method
The measured line-of-sight (LOS) velocities of the PNe are random samplings of the galaxy LOSVD function at the position of the source. Therefore each velocity measurement randomly deviates from the local mean velocity by an amount that depends on the local LOS velocity dispersion.
In order to extract the mean LOS velocity and the LOS velocity dispersion fields from this discrete velocity field, we use an adaptive kernel smoothing technique, as described in Coccato et al. (2009), that performs a local average of the measured discrete LOS velocities. In the following section we briefly review the smoothing technique, while we refer to Coccato et al. (2009) for a more detailed discussion. In Appendix A we validated the adopted procedure on simulated data, in order to test the effects of different statistical realizations of a given sample of tracers, the dependency on the number of tracers, and different V/σ ratios on the estimated kinematic parameters.
3.1. Averaging the discrete velocity field with the adaptive kernel smoothing technique
The smoothing of the discrete velocity field is carried out by computing the velocity at each position (x, y) in the sky as a weighted mean ṽ(x, y) of all the PN LOS velocities v
while the velocity dispersion σ̃(x, y) is given by the square root of the variance of v with respect to ṽ![$ \begin{array}{*{20}{l}}{\tilde \sigma (x,y)}&{ = {{(\langle {v^2}\rangle - {{\langle v\rangle }^2} - \delta {v^2})}^{1/2}}}\\{}&{ = {{\left[ {\frac{{\mathop \sum \nolimits_i v_i^2{w_{i,p}}}}{{\mathop \sum \nolimits_i {w_{i,p}}}} - \tilde v{{(x,y)}^2} - \delta {v^2}} \right]}^{1/2}}.}\end{array}\ $](/articles/aa/full_html/2018/10/aa32473-17/aa32473-17-eq2.gif) (2)
(2)
The weight wi,p of each PN is defined using a Gaussian Kernel that depends on the distance of the PN from the position (x, y), normalized by a kernel width K
The latter controls the spatial scale of the region over which the smoothing is performed, and hence the spatial resolution of the kinematic study. Large values of K, in fact, lead to smoother profiles in the mean LOS velocity fields, highlighting the general trends, but also suppressing the small scale structures, while smaller values of K allow a better spatial resolution but may amplify any noise pattern. Hence the optimal K should be a compromise between spatial resolution and statistical noise smoothing.
The width K is therefore defined to be linearly dependent on the distance between the position (x, y) and the Mth closest PN, so that K is a function of the local density of tracers ρ(x, y). This allows K to be smaller in the innermost, dense regions of galaxies, and larger in the outskirts, where their density is usually lower. The optimal kernel parameters A and B are derived as described in Sect. 3.1.1. We chose M = 20, but Coccato et al. (2009) tested the procedure with 10 < M < 60 finding no significant differences in the results.
3.1.1. Deriving the optimal A and B kernel parameters
The parameters A and B in Eq. (3) are chosen so that the best compromise between spatial resolution and noise smoothing is achieved. We developed an iterative procedure in order to derive the optimal kernel parameters that realize this condition.
We first estimated the velocity gradient to be resolved by the smoothing procedure by performing a preliminary averaging with a fully adaptive kernel (A = 1 and B = 0). The derived mean velocity field, ṽA=1,B=0, is fitted with a cosine function, which, in general, approximately describes the velocity profiles of early type galaxies (see Cohen & Ryzhov 1997):
This interpolation function provides a measure of the position angle of the kinematic major axis (PAkin), along which the steepest velocity gradient dṽ is expected to lie. The gradient dṽ is obtained by fitting a straight line to the velocities ṽ of the PNe lying in a section along the PAkin direction, as a function of the radius.
The best kernel parameters that allow to resolve spatial substructures with typical velocity gradient dṽ are derived by building simulated sets of PNe (see Coccato et al. 2009). The stars are spatially distributed according to a given density ρ̄, while their velocities are assigned using the derived velocity gradient and adding a dispersion equal to the standard deviation of the observed radial velocities. The artificial sets are processed using different values of the kernel K until the simulated input velocity field is recovered: this provides the best K for this ρ̄. The procedure is repeated for different values of ρ̄, and the optimal A and B are the best fit values of Eq. (3) based on on the derived best K as a function of ρ̄.
3.1.2. Errors in the derived velocity fields
Errors on ṽ(x, y) and σ̃(x, y) are obtained using Monte Carlo simulations, as also discussed in Coccato et al. (2009). For each galaxy, 100 PN datasets are built with simulated radial velocities at the same positions as the observed PNe. The radial velocity for each simulated object is obtained from the two-dimensional smoothed velocity field, adding a random value from a Gaussian distribution centered at 0 and with dispersion  where δv is the velocity error. These simulated datasets are smoothed with the same kernel K as the real sample, and the standard deviations of the simulated velocity and velocity dispersion fields give the errors on ṽ and σ̃. This procedure is validated in Appendix A.2 with PN velocity distributions generated from a simulated merger remnant galaxy, which are analyzed in an identical manner as the real galaxy PN samples. As an additional test, we have also extracted and analyzed kinematic information from 1000 subsamples of the original PN sample for all our galaxies and found kinematic parameters consistent with our full-sample results, as described in Sect. 3.2.2.
where δv is the velocity error. These simulated datasets are smoothed with the same kernel K as the real sample, and the standard deviations of the simulated velocity and velocity dispersion fields give the errors on ṽ and σ̃. This procedure is validated in Appendix A.2 with PN velocity distributions generated from a simulated merger remnant galaxy, which are analyzed in an identical manner as the real galaxy PN samples. As an additional test, we have also extracted and analyzed kinematic information from 1000 subsamples of the original PN sample for all our galaxies and found kinematic parameters consistent with our full-sample results, as described in Sect. 3.2.2.
3.2. Fitting a rotation model
The mean velocity fields, derived from smoothing the discrete velocities, are divided into radial bins with equal numbers of PNe such that they contain at least 30 stars. If a galaxy contains less than 60 tracers, we divide the sample in two bins in order to study possible radial trends.
The bins are circular for galaxies either with small flattening, that is 10 × ϵ < 3, or whose PN spatial distribution has a rather square shape. For all the other galaxies we use elliptical bins oriented along the photometric major axis, with a flattening equal to a characteristic ellipticity of the isophotes of the galaxy (the adopted ellipticity, ϵ, and photometric position angle PAphot are given in Table 1). We found that the results of our analysis do not depend on the chosen flattening but, since the spatial distribution of the PNe follows the light, and so it may be rather flattened, elliptical bins help to sample the field homogeneously in an azimuthally-unbiased way.
In each radial bin, we fitted the PN velocities ṽi of position (Ri, ϕi) with a rotation model ṽ(ϕ, R) (see Sect. 3.2.1). Here ϕi is the eccentric anomaly of the PN in the bin of coordinates (xi, yi), ϕi(xi, yi) = arctan[yi/((1 − ϵ)xi)], and ϵ is the ellipticity. Ri is the major axis distance of each PN and R is the mean Ri of the PNe in each bin.
3.2.1. Point-symmetric rotation model
A velocity map ṽ(ϕ, R) is a periodic function in ϕ, so it can be expanded in a Fourier series and approximated by a finite number of harmonics:
Elliptical galaxies in dynamical equilibrium are triaxial systems (e.g., Statler 1994, and references therein), so the projection on the sky of the mean velocity field should be point-symmetric with respect to the systemic velocity a0 (see Krajnović et al. 2006; Coccato et al. 2013), that is symmetric positions have equal velocities with opposite sign (ṽ(ϕ) = −ṽ(ϕ + π)). Deviations from this behavior arise from perturbations from equilibrium that may be due to interaction or merger episodes. If one of these processes, which plays a role in the formation and evolution of early type galaxies, occurred relatively recently (a few Gyrs ago), it is likely that some signatures in the kinematics and orbital structure of the galaxy are still observable, especially in the halo where the dynamic time-scales are longer.
The requirement of point-symmetry on ṽ(R, ϕ), namely ṽ(R, ϕ) − a0 = −[ṽ(R, ϕ + π)], allows only odd values for n in Eq. (5). The expansion in Eq. (5) can be rewritten in a more direct way, as a rotation around the kinematic axis plus higher order modes. This is achieved through a rotation such that
with
The phase α can be chosen so that the amplitude of the first order sine term is 0: s1 = 0 if α = arctan(b1/a1). This implies that
and
In this notation α coincides with the position angle of the kinematic major axis, PAkin, a0 is the mean velocity of the PNe in the bin, and c1 is the amplitude of the projected rotation, Vrot. The amplitudes of the higher order harmonics, ck and sk, are corrections that account for deviations of the galaxy motion from the simple cosine rotation.
In practice the series in Eq. (9) can be truncated to the third order as the higher order harmonics are generally zero within the errors. The resulting function is fitted to the mean velocity estimates at all PN positions in each radial bin, with the position angle PAkin, the constant a0, and the amplitudes Vrot, s3, and c3, as free parameters. The fit of the parameter a0 gives an estimate of the systemic velocity Vsys in the halo (see Sect. 4). Once Vsys is subtracted from the velocity fields, their point-symmetry can be studied (Sect. 5) and used to produce the final mean velocity fields for the point symmetric galaxies (see Sect. 6.1). The final mean velocity fields, after subtracting Vsys, are eventually fitted with the function
where the only free parameters are PAkin, Vrot, s3, and c3 (see Sect. 6.2).
The kinematic quantities PAkin and Vrot obtained fitting the model in Eq. (10) on the smoothed velocity fields are comparable to the results from a kinemetry fit to IFS data (Krajnović et al. 2006, 2011; Foster et al. 2016). However, we do not apply kinemetry, because this would mean fitting ellipses to the PN smoothed velocity fields. Since these have been derived from small samples of discrete tracers which, by nature, have lower spatial resolution and S/N, a more straightforward approach, with fewer free parameters, is preferable.
3.2.2. Errors on the fitted parameters
The errors on the fitted parameters, a0(R), PAkin(R), Vrot(R), c3(R), and s3(R), are evaluated via Monte Carlo simulations: the 100 simulated datasets produced for deriving the errors on ṽ and σ̃ (see Sect. 3.1) are divided into radial bins and modeled with Eq. (9). The errors are the standard deviations on the fitted parameters.
We tested whether the mean velocity field extracted through the smoothing procedure is sensitive to the relatively large velocities of objects belonging to the tails of the LOSVD. For this we selected subsamples of the observed dataset, re-extracted the kinematics, and studied the distribution of the fitted kinematic parameters. For each galaxy we used 1000 subsamples built with 80% of the observed PNe each. (We do not use bootstrap with replacement as it would not be consistent with the constraint for the PNe to follow light.) Figure 1 shows the distributions of the fitted Vrot and PAkin in one radial bin for the PN subsamples extracted for NGC 0821 and NGC 3379. For all the ePN.S galaxies these distributions fall well within the statistical uncertainties of the fitted parameters from the full datasets. This shows that the values of Vrot and PAkin measured are not driven by a few high velocity objects, but are properties of the whole PN sample.
 |
Fig. 1. Distribution of the fitted Vrot and PAkin in one radial bin obtained from 1000 PN subsamples extracted for NGC 0821 and NGC 3379 (gray histograms). The red curves are Gaussians centered on the Vrot and PAkin fitted on the full dataset, and with dispersion given by the Monte Carlo simulations of the galaxy under study. The vertical solid lines show the position angle of the photometric major axis for the two galaxies; the dotted lines show the photometric minor axis. The values for PAphot are listed in Table 1. |
In addition, we simulated the effect of the contamination by background Lyα emitters by adding two random velocity measurements (see Sect. 2), uniformly drawn in velocity from the filter band-pass used for each individual galaxy in our sample. We then re-extracted all the kinematic observables, and found that they are well within the 1 sigma errors of the measurements without contaminants.
4. Systemic velocity subtraction
A measure of the systemic velocity of the galaxies is provided by the fit of the PN smoothed velocity field in radial bins with the harmonic expansion in Eq. (9). The bins are built as described in Sect. 3.2 and the adopted geometry for each galaxy (i.e. ellipticity, ϵ, and photometric position angle, PAphot) is listed in Table 1. The a0(R) parameter, in fact, represents the mean velocity of the tracers in the radial bin with radius R. When the galaxy does not display kinematic substructures (bulk motions), this mean velocity is an estimate of the systemic velocity of the galaxy which is constant with radius for a gravitationally bound system.
Since the PNe are not distributed uniformly on the sky, a0(R) gives actually a more precise evaluation of the systemic velocity than a straight average of the measured LOS velocities. The fit of Eq. (9) removes any contribution to the mean from rotation and is not sensitive to azimuthal completeness. Hence we can perform the fit leaving the parameter a0(R) free to vary in each bin. We find that a0(R) is generally constant with radius within the errors. Therefore we adopt, for each galaxy, a mean systemic velocity, Vsys, defined as a mean of the a0(R) values, weighted with the errors on the fit:
We conservatively consider as error on Vsys, ΔVsys, the mean of the errors Δa0(R), since the single measures of a0(R), coming from a smoothed velocity field, are not independent quantities.
We find that a0(R) does sometimes display a trend with radius within the errors. This is due to the interplay between spatial inhomogeneities and smoothing, which may result in a slight asymmetry of one side of the galaxy with respect to the other. This effect naturally disappears as soon as the catalogs are folded by point-symmetry transformation (see Sect. 5), but we keep track of it in the uncertainties, by adding in quadrature the scatter of the a0(R) values to the error ΔVsys.
NGC 1316 and NGC 5128 are treated separately with respect to the other galaxies. Their fitted a0(R) are constant in most radial bins, but they deviate in localized bins from this constant by more than twice the errors. At these radii the galaxies display important features in their velocity fields which cause an offset of the average velocity from the systemic value. We masked the most irregulars bins and use the fitted a0(R) on the others to compute the mean Vsys.
The measured values of Vsys for all the galaxies are reported in Table 2. We do not observe any systematic bias in the measured values, and they all agree within twice the error on Vsys with the literature. Hereafter we will refer to the barycentric velocities using V, and to the smoothed barycentric velocities using Ṽ.
Measured parameters and typical errors for the smoothed velocity and velocity dispersion fields.
5. Point symmetry analysis of the sample
In this section we investigate whether the galaxies in the ePN.S sample show any deviation from point-symmetry. We studied the point-symmetry of the velocity fields of the galaxies by comparing the velocities Ṽ(R, ϕ) with 0 ≤ ϕ < π with those with π ≤ ϕ < 2π, changed in sign, in each radial bin. Asymmetries in the velocity fields are visible where these quantities significantly differ from each other. Figure 2 shows a few examples of this analysis. NGC 4649 is point-symmetric, while the others show significant deviations. In the sample of 33 galaxies, five are found to be non-point-symmetric: NGC 1316, NGC 2768, NGC 4472, NGC 4594 and NGC 5128. The galaxies for which we find evidence for asymmetries are those with the richest PN catalogs. For these objects the kinematic details are best recovered.
 |
Fig. 2. Galaxies with deviations from point symmetry. Mean velocity Ṽ(R, ϕ) as a function of the PN eccentric anomaly ϕ, folded around ϕ = π, for each radial bin of NGC 1316, NGC 2768, NGC 4472, NGC 4594, NGC 4649, and NGC 5128. The black solid line is the fitted point-symmetric rotation model. The red points are the PN positions with 0 ≤ ϕi < π; the blue points are those located at π ≤ ϕi < 2π, with their velocity changed in sign and coordinate ϕ shifted by π, i.e. V(ϕ) are compared with −V(ϕ + π). The overlap of PNe of opposite sides shows possible asymmetries in the velocity fields. NGC 2768 and NGC 4594 show localized small scale deviations from point symmetry, that do not influence the kinematic analysis. NGC 1316, NGC 4472, and NGC 5128 have non-point-symmetric velocity fields. By comparison NGC 4649 is point-symmetric. |
The others galaxies are consistent with point-symmetry, so for these systems we used the folded catalogs to reconstruct the final velocity and velocity dispersion fields, as described in Sect. 6.1. Since the mean velocity fields are the result of a smoothing procedure, their point symmetry does not rule out kinematic asymmetries on smaller scales.
As first step, the PN smoothed velocities Ṽi are modeled with the harmonic expansion in Eq. (9), which also provides a good description of the galaxy velocity field where the spatial distribution of the tracers is not azimuthally complete. We consider as possible deviations from point-symmetry any groups of at least three tracers whose velocity Ṽi deviates more than twice the errors from the fitted point symmetric model.
We evaluate the significance of the observed deviations from point symmetry by using 100 models of the galaxies, constructed as described in Appendix A.3. These are built using the positions (xi,yi) of the PNe from the real dataset, and, by construction, have a point symmetric mean velocity field. If similar local deviations from point symmetry that we observe in the velocity field of the galaxy appear also in the smoothed velocity fields of the models, then we know that they are artifacts of the smoothing over that particular spatial distribution, and not properties of the intrinsic galaxy velocity field. Hence, for each feature in the galaxy, we select in the models the groups of PNe having the same coordinates as the feature, and compute the distribution of deviations of their velocities from the harmonic expansion fitted to each model. This distribution will give the probability of occurrence of the feature due to statistical fluctuations.
We found that the features in NGC 2768 and NGC 4594 have a probability <1% to happen in the symmetric models so they are likely real. Those in NGC 2768 might be related to asymmetries in light distribution clearly visible in deep optical images (e.g. the g and r maps of Duc et al. 2015)2. The features in NGC 4594 are more likely due to extinction effects from its dusty disk, which hampers the detection of a complete sample of PNe in that area. In both cases the deviations of the velocity fields from point symmetry are localized and do not influence the kinematic analysis.
For NGC 1316, NGC 4472, and NGC 5128 the velocity offsets and the phase-angle shifts of the Ṽ(R, ϕ) in (0 ≤ ϕ < π, red in Fig. 2) with respect to (π ≤ ϕ < 2π, blue in Fig. 2) cannot be reproduced by the point symmetric models. These galaxies are well known recent mergers. Their halos are dominated by the recently accreted component which is not yet in a phase-mixed equilibrium with the surroundings and hence it still maintains peculiar kinematics (see also Appendix C).
One may be tempted to identify the groups of PNe whose velocity significantly deviate from the model as those associated to the structure, but we need to keep in mind that their velocities are the result of an averaging procedure, and that the different kinematic components can only be separated by analyzing the full phase space (see e.g. the GMM modeling of Longobardi et al. 2015); such a study is beyond the scope of this paper.
6. The halo kinematics of ETGs
6.1. Velocity fields
A point symmetric system is, by definition, such that each point of the phase space (x, y, V) has a point-reflected counterpart (−x, −y, −V). For the galaxies that do not show any significant deviation from point symmetry (Sect. 5), we assume that point symmetry holds. In these cases we can double the number of data-points by adding to the observed dataset its mirror dataset, and creating in this way a folded catalog (e.g Arnaboldi et al. 1998; Napolitano et al. 2001; Peng et al. 2004; Coccato et al. 2009). This helps in reducing the fluctuations in the recovered velocity fields. The results obtained using the folded catalogs are consistent with those from the unfolded datasets within the errors. Therefore for the galaxies consistent with point symmetry we will use the folded catalogs to produce the final mean velocity fields; for the others (i.e. NGC 1316, NGC 2768, NGC 4472, NGC 4594 and NGC 5128) the original catalogs are used.
Figure 3 shows the result for two galaxies with a similar number of tracers, NGC 4494 and NGC 4552. Both are point symmetric, so the velocity fields in Fig. 3 are built using the folded catalogs. NGC 4494 is a FR showing some rotation also in the halo. Its velocity dispersion field reveals that σ decreases with radius. The SR NGC 4552, by contrast, displays increasing rotation velocity about two perpendicular axes, and increasing velocity dispersion with radius.
The smoothed velocity fields for all the galaxies of the ePN.S sample are shown in Appendix D. For a more immediate visualization we present interpolations of the velocity fields, based on computing Ṽ and σ̃ on a regular grid. The kinematics typically extends a median of 5.6Re, covering a minimum of 3Re to a maximum of 13Re. The adopted Re values are listed in Table 1. Table 1 also shows the mean radius of the last radial bins, in which we can statistically determine Ṽ and σ̃.
 |
Fig. 3. Top row: smoothed velocity fields of NGC 4494 and NGC 4552; bottom row: velocity dispersion fields. The fields are built using the folded catalogs, but only the positions of the actual PN data points are shown. The images in the background are from the Digitized Sky Survey (DSS); north is up, east is left. |
The typical errors on the mean velocities and on the velocity dispersions, evaluated with Monte Carlo simulations, range from 10 to 40 km s−1, being smaller for galaxies with a larger number of tracers and higher Ṽ/σ̃. These errors on the mean velocity fields, the mean errors on the radial velocity measurement, the kernel parameters A and B used in the smoothing procedure, and the systemic velocities subtracted are reported in Table 2.
A visual comparison with the kinematic maps published by the ATLAS3D (Krajnović et al. 2011) and SLUGGS (Arnold et al. 2014; Foster et al. 2016) surveys shows a general good agreement for all the galaxies in the regions of overlap. By consistency or good agreement we mean that the values and trends in Vrot, σ from either kinemetry (by Krajnović et al. 2008; Foster et al. 2016) or slit absorption line kinematics agree within the errors with the kinematics from the PNe in the regions of overlap, or the latter extend such radial trends to the outer regions. See the Appendix C for a detailed description of the individual objects.
6.2. Kinematic parameters
We quantify the properties of the reconstructed mean velocity fields by evaluating the amplitude of rotation Vrot, the variation of the PAkin with radius, and the possible misalignments with PAphot. Therefore we model the velocities in each elliptical bin as a function of the angle ϕ (positive angles are from north to east, with the zero at north) with the rotation model in Eq. (10), as described in Sect. 3.2.
Figure 4 shows the smoothed velocity field Ṽ(R, ϕ) in each elliptical radial bin for a subsample of galaxies: a SR, NGC 4552, and four FRs, NGC 4473, NGC 4494, NGC 5866, and NGC 7457. The solid lines are the rotation models that give the best fit to the data, and from which we derive the kinematic parameters. The errors on the fitted parameters are derived from Monte Carlo simulations as described in Sect. 3.2.2, and depend on the number of tracers and the ratio Ṽ/σ̃. In the case of the galaxies show in Fig. 4, they are largest for NGC 4473, which has very low rotation in the halo, and smallest for the lenticular galaxy NGC 7457, which is dominated by rotation up to large radii.
 |
Fig. 4. Point symmetric galaxies. Mean velocity field Ṽ(R, ϕ) in elliptical annuli as a function of the PN eccentric anomaly ϕ, folded around ϕ = π for the FRs NGC 4473, NGC 4494, NGC 5866 and NGC 7457, and the SR NGC 4552 (colors as in Fig. 2). Ṽ(R, ϕ) is reconstructed using the folded catalogs, and shown at the position (Ri,ϕi) of the actually observed PNe. The solid lines are the best rotation model (see Eq. (10)) fit to the velocity field. |
We divided the sample of ETGs into FRs and SRs according to the definition of Emsellem et al. (2011), see Table 1. In Fig. 5 we show separately for both families the fitted parameters Vrot, s3 and c3, as functions of the major axis distance R in units of Re. This is a reasonable choice in case of flattened systems rotating along the photometric major axis. In case of misalignment or twist of the PAkin, R does not correspond to the position of the peak in Ṽ but to the major axis of the elliptical bin in which the amplitude Ṽ is calculated. Figure 6 shows the misalignment Ψ of PAkin with respect to PAphot, Ψ = PAkin(R) − PAphot. If the difference PAkin(bin1) − PAphot (where PAkin(bin1) is the value measured in the first radial bin), is greater than 90 degrees, we define Ψ as PAkin(R) − PAphot − π. Since PAphot is a constant value for each galaxy, a variation of PAkin with radius corresponds to a variation of Ψ. We do not use the definition of Franx et al. (1991), sinΨ = sin(PAkin(R) − PAphot), as it does not allow the description of large position angle twists. The values and the references for the PAphot used are in Table 1.
 |
Fig. 5. Fitted rotation velocities Vrot(R) (full circles) and third order harmonics amplitudes, c3(R) in green and s3(R) in orange, as functions of the major axis distance for SRs and FRs. The comparison values for Vrot from absorption line data from the literature are shown with colored stars. Whenever available we show kinemetric profiles (light blue stars); for the other galaxies we show velocities from long slit spectroscopy along the photometric major axis (red stars) or minor axis (green stars). The references are in Table 1. For NGC 4594 we show in addition the stellar kinematics from a slit along PAphot, offset by 30 arcsec (purple stars). The dashed vertical lines for the FRs show the disk half light radius R1/2, see Sect. 7.3. The red dot-dashed vertical lines report the radial transition range RT ± ΔRT, see Sect. 8.6. |
 |
Fig. 6. Misalignments Ψ(R) (full circles) as function of the major axis distance for FRs and SRs. The horizontal solid line shows the Ψ = 0 axis. The light blue stars are the Ψ values calculated on PAkin from the kinemetry of Foster et al. (2016), Krajnović et al. (2008 and 2011); for the other galaxies the PAkin is not previously available in the literature. The red dot-dashed vertical lines report the radial transition range RT ± ΔRT, see Sect. 8.6. Signatures of triaxial halos are seen in NGC 0821, NGC 1344, NGC 1399, NGC 3377, NGC 3379, NGC 3608, NGC 3923, NGC 4365, NGC 4374, NGC 4472, NGC 4473, NGC 4494, NGC 4552, NGC 4636, NGC 4649, NGC 4742, NGC 5128, NGC 5846, and NGC 5866. |
Both Vrot and Ψ are compared with literature values in Figs. 5 and 6. When available, we show the profiles from the kinemetric analysis of Foster et al. (2016) on the SLUGGS+ATLAS3D data, or the kinemetric profiles from Krajnović et al. (2008). In these cases we rescale the radii of the profiles to major axis distances using the flattening qkin = qphot given by Foster et al. (2016), or ⟨qkin⟩ given by Krajnović et al. (2008). For the other galaxies we plot the corresponding quantities from the kinemetry of Krajnović et al. (2011,  and PAkin from their Table D1), or the kinematic profiles from long slit spectroscopy similarly rescaled (references in Table 1). While comparing with the literature, it is important to note the following effect. A kinematic measurement from a slit along the major axis of an edge-on fast rotating galaxy will give high velocities and low dispersions. On the other hand, the PN velocity fields are the results of a smoothing procedure, which averages together PNe belonging to the very flat disk with PN belonging to the spheroid. This might result in a systematically lower rotation and higher velocity dispersion (see Eq. (2)) in the PN velocity fields. A decomposition of the PNe into disk and spheroid components has already been performed by Cortesi et al. (2013b) for some ePN.S galaxies, and it is beyond the scope of this paper to extend this to the whole sample of fast rotators. In addition, if the number of tracers or the ratio V/σ is low, our kinematic analysis provides a lower limit for the rotation velocity and an upper limit for the velocity dispersion. This issue is addressed in Appendix A. In such cases, the kinematics traced by the PNe may show systematic differences from that in the integrated light as consequence of the discrete spatial sampling of the velocity field by the adopted tracers.
and PAkin from their Table D1), or the kinematic profiles from long slit spectroscopy similarly rescaled (references in Table 1). While comparing with the literature, it is important to note the following effect. A kinematic measurement from a slit along the major axis of an edge-on fast rotating galaxy will give high velocities and low dispersions. On the other hand, the PN velocity fields are the results of a smoothing procedure, which averages together PNe belonging to the very flat disk with PN belonging to the spheroid. This might result in a systematically lower rotation and higher velocity dispersion (see Eq. (2)) in the PN velocity fields. A decomposition of the PNe into disk and spheroid components has already been performed by Cortesi et al. (2013b) for some ePN.S galaxies, and it is beyond the scope of this paper to extend this to the whole sample of fast rotators. In addition, if the number of tracers or the ratio V/σ is low, our kinematic analysis provides a lower limit for the rotation velocity and an upper limit for the velocity dispersion. This issue is addressed in Appendix A. In such cases, the kinematics traced by the PNe may show systematic differences from that in the integrated light as consequence of the discrete spatial sampling of the velocity field by the adopted tracers.
The higher order harmonics amplitudes s3 and c3 differ from zero whenever the smoothed velocity field deviates from simple disk-like rotation. This happens for example when the velocity field is cylindrical (see the case of NGC 3115), or in correspondence to components rotating at different position angles (e.g. NGC 4649).
Misalignments and twists of the PAkin are typically displayed by triaxial galaxies, see Sect. 6.4. Figure 6 shows that both FRs and SRs can have radial variations of the PAkin or a constant non-negligible Ψ. These galaxies may have a triaxial halo. A few galaxies instead have kinematically decoupled halos with respect to the regions ≲2Re. Section 6.4 validates these results for each galaxy using models.
The asymmetric galaxies (i.e. NGC 1316, NGC 2768, NGC 4472, NGC 4594, and NGC 5128) are, by construction, not well represented by the point symmetric model and increasing the number of harmonics does not improve the quality of the fit. We can however still use the fitted parameters to obtain an approximate description of the shape of their velocity field.
6.3. Velocity dispersion profiles
Figure 7 shows the velocity dispersion profiles, azimuthally averaged in radial bins. These have been calculated using two different methods. In the first we used the interpolated velocity dispersion field σ̃(x, y) in elliptical annuli of growing radius, with position angle and ellipticity as in Table 1. The values shown in the plots (solid lines) are averages over each elliptical annulus, and the errors (dotted lines) are taken conservatively as the means of the Monte Carlo simulated errors in the elliptical annulus (Sect. 3.2.2). The second method is binning the measured radial velocities vi of the PNe in the radial bins built as described in Sect. 3.2. The PN catalogs are folded by point symmetry and the dispersion σbin with respect to the weighted mean velocity is computed in each bin. The weights are computed from the measurement errors. The errors on the dispersion are given by the expression: 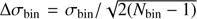 , where Nbin is the number of PNe in each bin. The values and the trends given by the two methods are generally in good agreement.
, where Nbin is the number of PNe in each bin. The values and the trends given by the two methods are generally in good agreement.
 |
Fig. 7. Azimuthally averaged velocity dispersion profiles as functions of the major axis distance in units of Re for SRs and FRs (full circles). The gray solid lines represent the profiles from the interpolated velocity fields with their errors (dashed lines, see text). The stars show dispersion from integrated light: when available we plot the kinemetric analysis of Foster et al. (2016) on the SLUGGS+ATLAS3D data in elliptical bins (light blue stars); for NGC 3384, NGC 3489, NGC 4339, NGC 4472, NGC 4552, and NGC 4636, we show azimuthally averaged profiles from ATLAS3D data (Cappellari et al. 2011; Emsellem et al. 2011); for the other galaxies we show data from long slit spectroscopy along PAphot (red stars, references in Table 1). For NGC 4594 we also plot the stellar velocity dispersion profile in a slit parallel to the major axis but 30 arcsec offset from the center (purple stars). |
The profiles obtained are compared with dispersion profiles from integrated light (red stars). For the galaxies in common with the SLUGGS survey, we show the profiles from the kinemetric analysis of Foster et al. (2016) on the SLUGGS+ATLAS3D data in elliptical radial bins. For NGC 3384, NGC 3489, NGC 4339, NGC 4552, and NGC 4636, we extracted the azimuthally averaged profiles from the ATLAS3D data (Cappellari et al. 2011; Emsellem et al. 2011) in elliptical bins (geometry in Table 1). For the other galaxies we show the velocity dispersion along the PAphot from long slit spectroscopy (references in Table 1). Our dispersion profiles generally compare well with the literature in the regions of overlap (typically R ≲ 2Re). The results are described in Sect. 7, separately for FRs and SRs.
We tested whether it is possible that the large scale trends in the velocity dispersion profiles are the result of statistical and smoothing effects, by using 100 models of the galaxies, built as described in Appendix A.3, created with a constant dispersion profile with radius. The velocity dispersion profiles are recovered with the same procedure as for the measured PN sample. We find that although artificial local structures may sometimes appear in the velocity dispersion maps, they are not such as to influence the trends with radius of the large scale velocity dispersion fields, and typically the error bars from Monte Carlo simulations give a good estimate of the uncertainties.
6.4. Triaxiality
Significant twists of the PAkin, as well as its departures from PAphot imply an intrinsic triaxial shape for the system. In an axisymmetric object both the projected photometric minor axis and the intrinsic angular momentum are aligned with the symmetry axis of the system, while in a triaxial galaxy the rotation axis can be in any direction in the plane containing both the short and long axis. This is because in a triaxial potential the main families of stable circulating orbits are tube orbits which loop around the minor (z-tube orbits) or the major axis (x-tube orbits; see e.g., de Zeeuw 1985; Statler 1987; Schwarzschild 1993). The relative number of z- and x-tube orbits determines the direction of the intrinsic angular momentum. Thus, depending on the variation of this ratio with radius we can have that
the measured PAkin shows a smooth radial twist (e.g. NGC 4552 in Fig. 6, see Sect. 6.4.1);
PAkin has a sudden change in direction (i.e. the galaxy has a kinematically decoupled halo, like NGC 1399, see Sect. 6.4.2);
PAkin has a constant misalignment with respect to the PAphot (e.g. NGC 3923, see Sect. 6.4.3).
Therefore we consider as triaxial galaxies the objects displaying at least one of these features in their velocity fields with statistical significance. We do not consider in this analysis galaxies that show significant variation of the kinematic position angle in the last radial bin only, as the geometrical shape of the survey area might prevent an azimuthally complete detection of PNe in the outermost bin. The statistical significance is determined by our MC modeling as described in Appendix A.3, which gives us the probability that a measured property of the smoothed velocity field is obtained in sequences of galaxy-specific simulated PN data sets without this feature. Table 3 provides a summary of the results, which are discussed in the following sections.
Results of the kinematic analysis.
6.4.1. Galaxies with radial variation in the kinematic position angle
Figure 6 shows that the fitted PAkin may show a smooth variation with radius. This happens in NGC 3377, NGC 3379, NGC 4494, NGC 4697, NGC 4649, NGC 5128, and NGC 5866, among the FRs, and in NGC 3608, NGC 4472, and NGC 4552 among the SRs.
We tested whether the variation with radius of the PAkin for a galaxy is an artifact of the combination of a small number of tracers and the smoothing procedure. We looked at the fitted PAkin in 100 models of each galaxy, built as described in Appendix A.3, which have by construction the PAkin of the mean velocity field aligned with PAphot. For each radial bin we computed the probability of obtaining the observed misalignment Ψ from the distribution of the misalignments in the models. We found that the probability of observing a twist of 48 ± 24 degrees in models of NGC 3377 is ∼4%; it is ∼3% for the twist of 71 ± 25 degrees in NGC 3379, ∼2% for the twist of 20±12 degrees in NGC 3608, and ∼4 for the twist 32±19 degrees in NGC 4494. For the other galaxies, none of the 100 models produces the observed trends of PAkin.
For NGC 4472 the determination of PAkin is influenced by the kinematics of the in-falling satellite UGC 7636. An inspection of its smoothed velocity field suggests that the main body of the galaxy has approximately major axis rotation, once the PNe of the satellite are excluded. Nevertheless we include this galaxy in the sample of potentially triaxial galaxies, and we refer to Hartke et al. (2018) for a more detailed study.
NGC 5128 shows non point-symmetric kinematics, and rotation along both the photometric major and minor axes. The high number of tracers available for this galaxy (1222 PNe) makes this kinematic signature unambiguous.
NGC 1316 shows a small but significant jump of the PAkin at ∼200−250 arcsec, that is related to the perturbed kinematics of this galaxy.
NGC 4697 has a constant PAkin profile consistent with the PAphot, with a sudden localized variation at ∼3Re. The study of Sambhus et al. (2006) on the same PN dataset showed evidence for a secondary PN population in this galaxy that is not in dynamical equilibrium with the main population, and which has not been excluded in this analysis. The presence of this population does not determine any significant deviation from point symmetry of its smoothed velocity field. However we refrain to include this galaxy in the sample of galaxies with triaxial halo.
Therefore, excluding NGC 1316 and NGC 4697 that have local and irregular variations of PAkin, there are nine galaxies in the sample showing significant kinematic twist, of which six are FRs and 3 SRs.
6.4.2. Galaxies with kinematically decoupled halos
Galaxies with kinematically decoupled halos are galaxies whose outskirts rotate about a different direction than their inner regions, hence PAkin shows a step function with radius. NGC 1399 and NGC 4365 both show this feature beyond 2Re.
NGC 1399 is found to be slowly rotating around its PAphot (i.e. Ψ ∼ 90 degrees) at ∼30 km s−1 inside 1Re, in very good agreement with the integral field spectroscopic data of Scott et al. (2014). The halo PAkin, by contrast, is almost aligned with the PAphot (i.e. Ψ = 0) degrees. We studied whether such a misalignment is an artifact of our procedure, using models that mimic the inner kinematics, that is with PAkin aligned with the photometric minor axis. The probability of measuring a misalignment of the halo similar to the observed one is 2%.
The PAkin of NGC 4365 is ill-constrained in the innermost regions where the kinematics is compatible with no rotation. At the center we do not recover the rolling about the minor axis visible in velocity fields from absorption line data (Emsellem et al. 2011; Arnold et al. 2014), because of smoothing over the inner velocity gradients. In these regions the bright background of the galaxy hampers the detection of PNe, and the resulting low number of tracers combined with the low V/σ leads to heavily smoothed velocities. We do detect a significant outer (R ≳ 3Re) rotation of ∼50 km s−1 along PAphot (Ψ ∼ 0 degrees), misaligned with respect to the inner kinematics reported in the literature. So we built mock models as described in Appendix A.3 but with PAkin given by IFS data up to 1Re (references are given in Table 1). We found that none of the models displays the observed step function in the PAkin values.
We therefore conclude that the signature of a kinematically decoupled halo has a high probability to be real in both galaxies.
6.4.3. Galaxies with constant offset between photometric and kinematic major axis
The galaxies showing an approximately constant misalignment of the PAkin with respect to the PAphot are NGC 0821, NGC 1344, NGC 3115, NGC 4473, and NGC 4742 among the FRs, and NGC 3923, NGC 4374, NGC 4636, and NGC 5846 among the SRs (see Fig. 6). In these cases we can define the PAkin using all the PNe, without radial binning. The derived quantities can be compared to the PAkin measured in mock models built as described in Appendix A.3.
For most of the listed galaxies none of the models reproduces the observed misalignments. NGC 0821 has a misalignment of 50 degrees with ∼4 probability in the Monte Carlo models, while the misalignment of 22 degrees of NGC 4742 has 1% probability. Because of the small number of tracers and the low V/σ ratio this probability is higher for NGC 5846 (9%). To these objects we add NGC 4473 whose PAkin is not well determined from the PN kinematics because of the very low V/σ ratio in its halo, but Foster et al. (2013) already detected a significant rotation along the minor axis using absorption line data, showing this object to be triaxial.
The PN velocity field of NGC 3115 shows a constant misalignment of ∼10 degrees with respect to PAphot. This misalignment is probably related to perturbations at the interface between the disk and the spheroid, visible as deviations from axisymmetry in the photometry of the disk component (Capaccioli et al. 1987, see also discussion in Appendix C). NGC 3115 is a complicated case, and is not included in the sample of galaxies with triaxial halo.
Therefore in the ePN.S sample a total of eight galaxies, four FRs and four SRs, show a significant constant misalignment of PAkin with PAphot.
6.4.4. Summary
We conclude that a total of 19 galaxies (∼60%) of the ePN.S sample show smoothed velocity fields that reveal their non-axisymmetric nature. Nine objects (6 FRs and three SRs) have significant kinematic twists, and eight (four FRs and four SRs) show a significant constant misalignment of PAkin with PAphot. In addition two SRs have a kinematically decoupled halo. The observed features are more than 2 sigma significant for most of the cases (1.7 sigma for NGC 5846), and they are not effects of the folding operation on the catalogs nor of the smoothing procedure.
All in all, we found that all the SRs and ten out of 24 FRs show indications of intrinsic triaxial morphology in the PN kinematics. We will discuss the signature of triaxiality in the photometry in Sect. 8.4.
7. Results per family
7.1. Slow rotators
In the sample of 33 galaxies nine are SRs. Figure 5 shows that they typically display some more pronounced rotation at large radii when compared to rotation in their central regions as measured from absorption line spectroscopy. The PN velocity fields show gently increasing profiles for the Vrot amplitude which, eventually, flatten around ∼50 km s−1. Twists or misalignments of the PAkin are commonly observed, so that all the SRs show signatures of a triaxial halo (see Fig. 6). In particular, we found that the halos of NGC 1399 and NGC 4365 are kinematically decoupled with respect to the innermost regions as mapped by Scott et al. (2014) and Arnold et al. (2014). NGC 4472 has a non point-symmetric velocity field, as a result of a recent accretion event. The complicated kinematics of the SRs is also reflected in the amplitudes of the third order harmonics, which describe the presence of additional kinematic components, and twists of the PAkin.
The velocity dispersion profiles, shown in Fig. 7, are generally flat in the halo. Some galaxies (e.g. NGC 1399, NGC 3608) reach such a constant value around ∼1−2Re. Others (e.g. NGC 4374, NGC 4552) flatten only beyond ∼4−5Re, after a small increase. NGC 4636 is the only SR showing a falling profile.
7.2. Fast rotators
In the ePN.S sample 24 galaxies are classified as FRs (Table 3). Figures 5 and 6 show that the majority of the objects have regular rotation along the photometric major axis. The comparison between inner and outer parts reveals that the rotation amplitudes Vrot show declining trends with more or less steep gradients for 14 out of 24 FRs: some galaxies show very small or no rotation in the outskirts (e.g. NGC 4278 and NGC 4473), while others reach a minimum, after which their rotation increases (e.g. NGC 4494 or NGC 4697). Among the remaining galaxies, three have fairly constant profiles (NGC 2768, NGC 4564, and NGC 5866), and 3 show increasing rotation (NGC 3384, NGC 4742, and NGC 7457). For NGC 0584, NGC 2974, NGC 3489 and NGC 4339, the limited number of tracers leads to heavy smoothing, allowing only an estimate of a lower limit for the rotation in the halo.
The PAkin is well aligned with the photometric major axis in the majority of cases, but ten out of 24 galaxies display a kinematic twist (NGC 3377, NGC 3379, NGC 4494, NGC 4649, NGC 5128, and NGC 5866) or a constant misalignment with PAphot (i.e. NGC 0821, NGC 1344, NGC 4473, and NGC 4742). The smoothed velocity fields of four galaxies (NGC 3379, NGC 4649, NGC 5128, and NGC 4494, see figures in Appendix D) show indications of additional components rotating along the minor axis of the system, while NGC 1344 has prolate rotation. All these features are generally interpreted as evidences of triaxiality of the systems (see Sect. 6.4) and 40% of the fast rotating galaxies of the sample display them in the halo.
The azimuthally averaged velocity dispersion profiles (Fig. 7) are found to be either constant (e.g. NGC 3377), or decreasing with radius. Some profiles decline gently (e.g. NGC 1344), while others decrease steeply in the halo (e.g. NGC 3379). This diversity between flat and falling profiles is also reflected in the variety of the Vrms profiles, as already observed by Coccato et al. (2009), and is the result of differences in the mass distributions (Gerhard et al. 2001; Romanowsky et al. 2003; Deason et al. 2012; Morganti et al. 2013; Cappellari et al. 2015; Alabi et al. 2016; Veale et al. 2018) or the presence of radial anisotropy in the orbits (Gerhard et al. 1998; de Lorenzi et al. 2009; Napolitano et al. 2009), which may contribute to a lower projected velocity dispersion. For some lenticular galaxies (e.g. NGC 1023 or NGC 3115), the two-dimensional velocity dispersion maps (see figures in Appendix D) reveal the presence of the colder disk along its major axis, while the dispersion is higher along the minor axes. For NGC 1023 the presence of the disk is evident also in the azimuthally averaged velocity dispersion profile, which increases with radius as the contribution of the disk to the light decreases.
Among the fast rotating galaxies there are two mergers, NGC 1316 and NGC 5128. Their velocity fields are highly disturbed by the recent accretion events and are not very well described by point-symmetric rotation models, see Appendix C for more details.
The comparison of the PN kinematics with integrated light data shows a general good agreement in the overlapping regions, confirming once again that the PNe are reliable tracers of the kinematics of the parent stellar population. The tension with the stellar kinematics in cases of high rotation and low dispersion (see e.g. NGC 1023, NGC 2768, NGC 4594) is primarily related to the presence of a known near edge-on very flat disk that dominates the major axis stellar kinematics but not that of the PNe. Because our velocity fields are the results of an averaging operation that does not distinguish the PNe from the disk from those belonging to the spheroid, the velocity gradients are underestimated. Likewise the discrepancy between the integrated light data of NGC 4494 and its PNe could be explained by a face on disk fading into the spheroid at radii beyond the coverage of the stellar kinematics, combined with the lower spatial resolution of the PN smoothed velocity field.
In addition, if the disk is obscured by dust, the fraction of observed disk PNe is reduced, causing a drop in the measured rotation and a higher dispersion. An example is the case of NGC 4594. This galaxy has a dusty disk which affects the detections of PNe in that region, leading to heavily absorbed light in this component and hence inhibit the PNe detections in that region where the rotation is highest. The rotational velocity and the dispersion profiles from PNe agree well with slit data along a direction slightly offset (30 arcsec) from the disk plane (purple stars in Figs. 5, 7 and 8), but are offset with respect to the major axis profiles. With this in mind, we shall consider the smoothed velocity fields as giving a global description of the halo kinematics, but not of their small-scale spatial structures, unless the number of tracers is very large (as, for example, in the case of NGC 1316).
 |
Fig. 8. Rotation velocity profiles for the FRs with highest number of tracers along the major axis. The full circles show the fitted amplitude Vmaj.ax. on the PN velocity fields (see Eq. (12)). The red stars are stellar kinematics along the photometric major axis from the literature (references in Table 1). The PN kinematics of NGC 4594 is compared with the stellar kinematics from a slit parallel to the major axis, offset by 30 arcsec (purple stars). The orange vertical lines mark the sizes of the photometric disks (see text). NGC 4494 shows a decrease in Vmaj.ax. but there is no photometric evidence for a stellar disk. When the disk fades in the slowly rotating spheroid, the rotation velocity decreases. In addition, the PN rotation velocity may be lower than the values from absorption line spectroscopy at the same radii because of the smoothing that averages disk and spheroid PNe for near edge-on disks. |
7.3. Embedded disks in fast rotators
The observed negative gradients of Vrot(R) observed for many FRs at large radii has been interpreted as signatures of a rotating disk component embedded in a dispersion dominated spheroid (Coccato et al. 2009; Arnold et al. 2014). Using a photometric disk-spheroid decomposition and maximum-likelihood fit, Cortesi et al. (2013b) reconstructed the kinematics of the disk and the spheroid separately in six of the ePN.S lenticular galaxies (NGC 1023, NGC 2768, NGC 3115, NGC 3384, NGC 3489 and NGC 7457). Arnold et al. (2014) reproduced the rotation profile of the E5-6 galaxy NGC 3377 also performing a disk-bulge decomposition. These works showed that the variation in rotation reflects the transition between disk and bulge dominance in light, and their different spatial contribution in each galaxy explains the variety in the observed λR profiles (the detailed study of the λR profiles for the ePN.S sample is the subject of a separate paper, Coccato et al., in prep.). In the following we use the term “disk component” for a highly flattened, but definitely three-dimensional, oblate rotating structure (see also Sect. 8.4).
Here we can verify the interpretation for the negative gradients of Vrot(R) by estimating and comparing the “size” of the disk components given by the photometry, and the radius at which we observe the decrease in rotation. Figure 8 shows a subsample of the galaxies with the highest number of tracers, in order to have the best possible statistics. Most of them show a decreasing rotation amplitude. We fitted their radially binned smoothed velocity fields with a cosine, whose position angle is aligned with the photometric major axis,
in order to extract the velocity profiles along the major axis. The fitted amplitudes are shown in Fig. 8. Overlaid in red is the stellar kinematics along the photometric major axis from literature slit data (references in Table 1). The orange vertical lines indicate the characteristic scale of the disks. For all the galaxies shown, the quantity plotted is the disk half light radius: R1/2 ≃ 1.67 Rh. Rh is the disk scale length from an exponential fit of the disk component (Rh from Burkhead 1986; Scorza et al. 1998; Pignatelli 1999; Laurikainen et al. 2010; Beletsky et al. 2011; Krajnović et al. 2013; Cortesi et al. 2013b, for Figs. 5 and 8).
We can see that the radial distance at which the decrease in the rotation occurs is consistent with the size of the disk. Therefore we interpret this behavior as the transition between a flat component that rotates fast and a dispersion dominated rounder spheroid. For NGC 4494 there is no photometric evidence for a disk component. In this case the stellar disk component might be absent or very faint if the galaxy is seen nearly face on (ϵ ∼ 0.14 for NGC 4494). In the other FRs that are not shown in Fig. 8, but displaying a drop in the amplitude of rotation, the comparison between slow rotating PN system and rapid rotation in the absorption line kinematics, suggests similar transition at smaller radii.
Figure 5 shows that the three galaxies with approximately constant Vrot profiles (NGC 2768, NGC 4564, and NGC 5866) do actually show a small decrease in rotation in correspondence to R1/2, when compared with the values from absorption line spectroscopy. At larger radii their fast-rotating spheroidal halo (NGC 2768, Cortesi et al. 2013b), or alternatively an unidentified outer disk component, dominates the kinematics. Among the remaining three galaxies in Fig. 5 with increasing Vrot profiles, two of them (NGC 3384 and NGC 7457) have an extended disk component, to which most of the PNe belong (Cortesi et al. 2013b). NGC 4742, by contrast, does not have any photometric evidence for a disk component, hence the high rotation at large radii is likely associated with the spheroid.
7.4. Summary
Our results show that the kinematics of ETGs at large radii can be substantially different from that in the inner regions. For the SRs we observe a growth in the amplitude of rotation. For the FRs, this variation in the kinematics manifests as a decrease in the amplitude of rotation or a twist in the PAkin. We interpreted this behavior as the transition from the inner disk component into the spheroidal halo, which is dispersion dominated and might deviate from axisymmetry.
Figure 9 illustrates this conclusion by comparing the V/σ ratio in the halo and in the inner regions (at 1Re). The V/σ(Re) values are derived by interpolating the Vrot and σ profiles from integrated light (shown in Figs. 5 and 7, see references in Table 1) at R = Re, while V/σ(halo) is the ratio of Vrot and σ estimated in the outermost radial bin of the PN velocity fields (see Table 1 for the outermost mean radius).
All the SRs fall below the 1:1 line, showing higher rotational support at large radii. The spread of the FRs in the diagram reflects their different intrinsic structure and kinematics. The halos of most FRs have V/σ ratio similar to the V/σ(halo) of SRs. Among these the scatter in V/σ(Re) is probably driven by the presence of a more or less prominent disk component seen at different inclinations, and embedded into the dispersion-dominated spheroid. The flattening of the ellipses in Fig. 9, in fact, shows that galaxies with higher ϵ also display higher V/σ(Re).
 |
Fig. 9. V/σ(Re) from absorption line data compared with V/σ(halo) from PN data. References for the absorption line data are in Table 1; for NGC 1399 and NGC 3923 data are available up to Re/2 and Re/4, respectively. The flattening of the ellipses used to plot the galaxies correspond to the ϵ values of Table 1. FRs and SRs are shown with different colors, as are the FR with triaxial halos. The gray open ellipses represent the galaxies (all FRs) with fewer tracers, for which our analysis provides a lower limit for V/σ(halo). The solid line traces equal values of V/σ(Re) and V/σ(halo). The orange circles shows the V/σ of simulated galaxies from Wu et al. (2014), divided by a factor 0.57 to rescale their two dimensional flux-weighted measurement to one-dimensional quantities (Cappellari et al. 2007). While the SRs show increased rotation in their halos, the majority of the FRs show a drop in rotation at large radii. |
A second group of FRs with high rotational support in the halo populate the diagram on the right of the 1:1 line. These galaxies are either dominated by disk rotation at all radii (NGC 3384 and NGC 7457), or have a rapidly rotating spheroid (NGC 2768, Cortesi et al. 2013b), or either of these (NGC 4564, NGC 4742).
The FRs with triaxial halos typically show equal values of V/σ(Re and V/σ(halo), spanning all values in V/σ(halo). It is possible that the group of galaxies near the 1:1 line but without signature of triaxiality in the current data could show such signatures with higher resolution in the kinematics. Therefore we cannot presently determine whether these last two subset of FRs are different or not.
The orange full circles in the V/σ plot show the inner-halo kinematics from Wu et al. (2014), who studied the kinematics of ETGs in cosmological zoom simulations (Oser et al. 2010; Naab et al. 2014) out to 5Re. Their V/σ(Re and V/σ(5Re) were divided by a factor 0.57 to rescale their two dimensional flux-weighted measurements to one-dimensional quantities (Cappellari et al. 2007). The comparison with the observations shows that these simulations do not adequately reproduce the observed properties of fast rotating galaxies, which span a much wider spectrum of kinematic properties at large radii.
8. Discussion
8.1. Halo rotation versus central rotation
The PN velocity fields show that ETGs may have very different kinematics at large radii compared to their inner regions. We found that SRs typically increase their rotation in the halo, while most of the FRs display a decrease of Vrot toward large radii.
The observed variety of radial trends for the rotation amplitudes is consistent with the different shapes of the λR parameter profiles observed in the smaller sample of Coccato et al. (2009), and confirmed by Arnold et al. (2014) and Foster et al. (2016). The study of the λR profiles for the current sample of galaxies is the subject of a future paper (Coccato et al. in prep.).
The existence of these radial trends was recently questioned by Raskutti et al. (2014) and Boardman et al. (2017), who found no evidence for a change in their stellar kinematics beyond Re. The divergence from our results may arise from the different radial coverage; their kinematics does not reach to the distances where the drop in rotation typically occurs, beyond ∼1Re. An example is the lenticular galaxy NGC 1023, in common between the two samples. For this galaxy Boardman et al. (2017) report a rising λR profile to almost 2Re, in agreement with our observation of a decrease in rotation only beyond ∼3Re.
The onset of rotation of the SRs at larger radii, often along directions that do not coincide with the major axis of the galaxy, may trace the accreted stellar component, which maintains a memory of the orbital angular momentum of the accreted progenitors. The decreased rotational support of the FRs is discussed in the next section.
8.2. Fast rotators with disks embedded in slowly rotating halos
The sharp drop in angular momentum in some FRs has been interpreted as the fading of an embedded disk structure of in-situ stars in a dispersion dominated spheroidal halo (Coccato et al. 2009; Arnold et al. 2014). We qualitatively verified this scenario in Sect. 7.3, where we observed that the radius at which the rotation along the major axis drops is consistent with the half light radius of the inner disk component.
Our results suggest that FRs contain a more or less extended rotating disk component, embedded in a more or less prominent halo with its own kinematic signature. This is reflected in the distribution of these objects in the V/σ plane (Fig. 9). We found that while a smaller group of FRs shows high rotation also in the halo, the halos of most FRs have rotational support comparable to that of the halos of SRs. This result is corroborated by the observation that the ePN.S FRs tend to become rounder at large radii (see Fig. 10).
 |
Fig. 10. Upper panel: ellipticity distribution for the FRs. The histogram of the maximum measured ellipticity at R > 0.5 Re is in green; the histogram of the outermost measured values is in blue. The distributions show that the FRs tend to have halos rounder than their central regions. Lower panel: maximum photometric twist versus mean projected ellipticity for a subsample of the ePN.S FRs with extended photometric data (gray triangles; see text and Appendix B.1, references in Table 2). The errors reflect the scatter between contiguous data points in the photometric profiles. For the galaxies with indications for ongoing interactions in the outermost photometry (see Appendices B.1 and C) we estimated the mean ellipticity and maximum position angle twist both from the complete profiles (open symbols) and considering only the regions with regular photometry (filled symbols). For NGC 1023 and NGC 3384 we show quantities derived excluding the regions where the bar dominates. The horizontal dashed line marks ΔPAphot = 10 degrees. The statistical distribution of points is consistent with simple photometric triaxial models, shown each with 100 random projections (solid circles as described in the legend; see text and Appendix B.2). |
This variety of kinematic properties is consistent with the variety of physical processes that may drive the evolution of these objects (minor mergers, major mergers that lead to a spin-up of the remnant, gas accretion, interactions with the environment, secular evolution; Duc et al. 2011; Naab et al. 2014; Penoyre et al. 2017; Smethurst et al. 2018) while preserving a rotating disk structure at the center. The comparison of our observations with simulated data from Wu et al. (2014) in Fig. 9 indicates, however, that those simulations do not yet reproduce the full diversity in the variety of these processes.
8.3. Signatures of triaxial halos in the kinematics
In Sect. 6.4 we studied the velocity fields and their kinematic position angle profiles PAkin(R), and linked the observed misalignments and twists with the triaxiality of the halos. SRs are known to be mildly triaxial in their central regions, while the FRs are predominantly oblate (Weijmans et al. 2014; Foster et al. 2017). Kinematic twists and misalignments for the FRs are rare and small in the central regions. By sampling the kinematics at more than twice the distances probed by previous studies, the PNe LOS velocities show that these features become more frequent and pronounced in the outskirts. Based on these signatures, we classified the halos of 40% of the FR galaxies as triaxial, while the remaining ones are still consistent with being axisymmetric at the resolution of the ePN.S survey. For these objects the triaxiality of the halos is not ruled out.
On the other hand, it is in principle possible that axisymmetric galaxies with a recent merger might display kinematic twists and misalignments because of the contribution of the unrelaxed accreted component to the PN velocity field. However, if the size of the accreted satellite is such as to significantly contribute to the PN population of the host halo, and so as to produce features in the PN velocity field, then the effect is short lived. This makes the probability of occurrence of such circumstance low. Deviations from a point-symmetric velocity field were found for 5/33 cases in Sect. 5, probably due to recent accretion or mergers in four cases and due to dust in one case. These galaxies are not included in the triaxial classification.
An examination of the smoothed velocity fields in Appendix D shows that for some galaxies the trends in PAkin with radius reflect a two-component velocity field in which rotation along one axis dominates at intermediate radii and rotation along the other axis dominates further out. This is the case for NGC 3379 and NGC 4649 among the FRs, and for NGC 4552 and NGC 4636 among the SRs. The velocity field of NGC 1344, instead, shows that this galaxy is a prolate rotator. Up to now there are not many observations of this phenomenon (Tsatsi et al. 2017, and references therein), which is probably related to a recent merger (Ebrová & Łokas 2017), as the shells of this galaxy attest. Our sample contains two other galaxies (NGC 3923 and NGC 4365) known to have prolate rotation at their centers, but their halos are decoupled with respect to the inner kinematics.
A previous study of the intrinsic shapes of ETG halos was performed by Foster et al. (2016) who, using the observed distribution of ellipticities and misalignments for the SLUGGS galaxies out to ∼2.5Re were unable to rule out triaxiality in the outskirts of FRs. The same authors had previously found strong evidence for minor axis rotation, hence a triaxial halo, in NGC 4473 (Foster et al. 2013). Viaene et al. (2018) recently observed a strong kinematic twist beyond 1.5Re for the massive FR NGC 5626. The extended PN kinematics allow us to generalize this result to a significant fraction of the FRs.
8.4. Signatures of triaxial halos in extended photometry
If the kinematic twists seen in the PN velocity fields for a significant fraction of ETGs indeed indicate triaxial halos in these systems, one expects additional evidence for triaxiality to come from observations of isophotal twists (Carter 1978; Leach 1981). Hence in this section we compare with photometric data from the literature, We do not expect to see a one-to-one correspondence between variations of PAkin and variations of PAphot (see also Foster et al. 2016), as the former are driven by the total potential of the galaxy, including dark matter, while the latter trace variations of the distribution of the light alone.
The isophotes of ETGs are well-described by ellipses, with deviations from perfect elliptical shape typically at the ∼0.5% level (e.g., Bender et al. 1988). Hence the constant luminosity surfaces of ETGs can be approximated by ellipsoids (for a review see Merritt 1992). The projection on the sky of a coaxial triaxial ellipsoidal distribution of stars can result in twisting isophotes only if their axial ratios varies with radius (Stark 1977; Benacchio & Galletta 1980). The effects of triaxiality on the PAphot profiles are model dependent (e.g., Benacchio & Galletta 1980; Franx 1988; Madejsky & Moellenhoff 1990). In general considerable twists (>10 degrees) can be produced by moderately triaxial models, but their relative frequency is low, ≲10%, as the effects on the PAphot are small whenever the systems are viewed close enough to one of their principal planes, and the magnitude of the twists depends on how much the axial ratios change.
Figure B.1 shows extended ellipticity and PAphot profiles from the literature for both FRs and SRs, for three quarters of the ePN.S sample. We chose to consider only galaxies with photometric data reaching at least 4Re. Twists of PAphot are observed for almost all the galaxies classified as triaxial in Sect. 6.4, and for several other FRs with no evidence for triaxiality at the spatial sampling of the PN kinematics. It is evident, however, that the variation of PAphot measured for the FRs is modest (<10 degrees) in 12/19 = 63% of the cases. Thus we verify whether the occurrence of small photometric twists is consistent with the presence of a triaxial halo. We do this by constructing illustrative, observationally motivated photometric models for triaxial FR galaxies, and comparing the statistical distribution of photometric twists in these models with that observed for the ePN.S sample of FR galaxies.
The models are built on the kinematic evidence found in the previous sections suggesting that centrally flat FRs are embedded in dispersion dominated spheroids, which can be triaxial. The intrinsic shape of the central regions of FRs were investigated by Weijmans et al. (2014, ATLAS3D survey) and Foster et al. (2017, SAMI survey), who found that these galaxies are close to oblate (p = 1)3 with mean flattening q ∼ 0.3. SRs are, instead, less flattened (q ∼ 0.6), and mildly triaxial but, because of the small number of these galaxies in the ATLAS3D and SAMI samples, their intrinsic shape distribution is not well constrained.
In our models, the central regions of the FRs have intrinsic shape in agreement with the previous results. In their halos, a significant fraction of the FRs has kinematics similar to the SRs (see Fig. 9). This is consistent with the expectation that the satellites accreted into the halo should be largely uncorrelated with the dynamics of the central galaxy. Thus for our first two halo models we assume outer halo axis ratios like those for the SRs, in which the accreted stars are expected to reach down to small radii (Cooper et al. 2013; Rodriguez-Gomez et al. 2016). This choice is supported by the evidence that the ellipticity profiles of FRs generally show decreasing trends at large radii (see Figs. 10 and B.1). However, some FRs in Fig. 9 rotate rapidly also in their halos; thus we also investigate triaxial halos with flatter isophotes. We parametrize the transition between inner and outer regions in different ways. The models are described in detail in Appendix B.2. In summary we use:
Model 1: a single component with a Sérsic n = 4 density distribution and variable flattening: q = 0.3 and p = 1 at the center, q = 0.6 and p = 0.9 in the outskirts. The transition between these regions happens at R = < RT > = 1.8Re, where RT is the kinematic transition radius defined in Sect. 8.6.
Model 2: a two-component model including a cored Sérsic n = 4 halo with intrinsic constant flattening q = 0.6 and p = 0.9 plus an embedded spheroidal-exponential disk with flattening q = 0.3 and p = 1. The scale length of the disk is taken to be such that 1.67 h = < RT >, as qualitatively observed in Sect. 7.3. Within r = RT the total luminosity of the disk in this model is ∼3.5 times that of the halo.
Model 3: as Model 2, but with a maximally triaxial halo with q = 0.6, p = 0.8.
Model 4: as Model 2, but with strongly flattened, slightly prolate-triaxial halo with q = 0.4, p = 0.8.
Figure 10 shows the maximum photometric twist and the mean projected ellipticity measured for the subsample of the ePN.S FRs with extended photometry (references in Table 2; the profiles are shown in Appendix B.1). The distribution of the galaxies in this diagram is compared with the same quantities from the four triaxial models, each observed at 100 random viewing angles. We find that:
- (1)
The fraction of twists larger than 10 degrees is of order 30% (45% for Model 3). Large twists occur for viewing angles θ ≲ 50 degrees for Models 1 and 2, and for θ ≲ 65 degrees for Models 3 and 4 (θ = 0 for face-on view).
- (2)
The comparison of the model prediction of twist angles with the data points for the ePN.S FRs in Fig. 10 shows that most of the model projections have low twists of the same magnitude as the majority (63%) of the galaxies. Within the statistical uncertainties, the models represent well the locations of the galaxies in Fig. 10: an average ∼35% of the models are above the 10 degrees threshold. From the models distribution ∼1−2 galaxies with photometric twists larger than 30 degrees and mean ellipticity ∼0.1 would be expected but are not observed. The missing ePN.S FRs in that region of the diagram could be a result of small number statistics, observational bias for near face-on systems, or model details.
- (3)
Since the photometric twists are thus expected to be small in most galaxies, the most obvious signature of a change in the intrinsic shape is the variation of the projected ellipticity with radius, as shown in Fig. B.2. The change in ellipticity observed in the majority of the FRs in Fig. B.1 (see also Appendix B.1) independently suggests the fading of the central disk component in a more spheroidal halo, as we previously inferred from rotation profiles.
This analysis based on illustrative oblate-triaxial photometric models shows that the presence of small photometric twists, as observed for the majority of the ePN.S FRs, is consistent with the presence of a triaxial halo. This means that it is likely that individual oblate-triaxial models for these galaxies can be constructed that are consistent with the measured photometric twist angles.
We infer that many of the ePN.S FRs show small photometric twists because of the highly flattened, oblate shape of their central regions and the gradual transition to a triaxial halo. The consequence is a near-alignment within ∼10 degrees between the inner kinematics and outer photometry of most these galaxies, as analogously observed for most of the FRs (Krajnović et al. 2011; Fogarty et al. 2015, however, this numerical value also depends on sample selection effects, see the following section). Hence extended kinematic studies that sample the outer regions of these FRs are important to unveil the kinematic transition and thus the change of the intrinsic shape.
Both PN kinematics and photometry are therefore consistent with a picture in which FRs have a central disk component embedded in a spheroidal dispersion dominated component. We found this component to be triaxial for at least 40% of the FRs in the ePN.S sample. The presence of photometric twists also for other FRs without evidence for a kinematic twist in the PN data, suggests that the fraction of galaxies with a triaxial halo might be higher. In the following sections we will see that the spheroidal component is most prominent in the most massive objects, and that the comparison with cosmological simulations suggests an ex-situ origin for it.
8.5. Comparison with the results of the ATLAS3D survey
The results discussed in the previous sections challenge a simple interpretation of the ATLAS3D survey results in terms of a dichotomy between disk FRs and triaxial SRs (see Cappellari 2016, for a review on the subject).
The ATLAS3D (A3D) survey carried out IFS and photometric observations of the central regions of a complete sample of 260 ETGs, morphologically selected from a volume-limited sample of galaxies brighter than MK < −21.5 (Cappellari et al. 2011). Their sample of ETGs spans luminosities −21.57 ≥ MK ≥ −25.78 and mostly contains lenticular galaxies, which means galaxies with T type T > −3.5: only 24% of their ETGs are ellipticals (T ≤ −3.5, Cappellari et al. 2011). The ePN.S sample is, on average, 1 mag more luminous in the K band (−22.38 ≥ MK ≥ −26.02), and the majority of the galaxies (73%) are ellipticals, according to their T type from HyperLeda (see Arnaboldi et al. in prep. for more details on the sample selection). The A3D IFS kinematics covers typically radii up to ∼1Re (Emsellem et al. 2011). The fraction of Re covered is actually a decreasing function of galaxy luminosity, as Re depends on MK (Cappellari et al. 2011), hence, for the ePN.S galaxies in common with the A3D sample, the mean radial coverage is 0.49Re. Finally if one considers that the values adopted for Re may underestimate the half light radii for the brightest objects (see discussion in Sect. 8.6), this fraction is actually smaller: 0.35 Rhalflight, where Rhalflight is defined in Sect. 8.6.
 |
Fig. 11. EPN.S and ATLAS3D samples compared in the stellar mass versus ellipticity plane. The ATLAS3D sample of ETGs is displayed with gray open symbols (triangles for the FRs, circles for the SRs). For these galaxies we show the ellipticity values from Krajnović et al. (2011) and M* = MJAM = (M/L)JAM × Ltot,r from Cappellari et al. (2013b) as in their Eq. (28). The ePN.S galaxies are shown with full symbols: red circles for the SRs, blue triangles for the FRs, and green squares for the FRs with triaxial halos. For the ePN.S ETGs M* is the mean between MJAM (Cappellari et al. 2013b, when available), and the masses M*1 and M*2 reported in Table 2. The error bars on the mass show the rms scatter between these different mass determinations. The values for the ellipticity are listed in Table 1. |
Figure 11 shows the stellar mass versus ellipticity plane for both samples. The ePN.S galaxies are on average more massive and less flattened than the A3D ETGs. In particular, the ePN.S FRs with triaxial halos are among the most massive A3D FRs. For these galaxies the PNe kinematics generally show fairly large twists of the PAkin, as the limited spatial resolution of the survey prevents the measurement of small differences in angle. In the ePN.S sample 40% of the FRs show signatures of a triaxial halo. The comparison with the photometry in Sect. 8.4 and in Appendix B.1 suggests that the number of FRs with triaxial halos in the ePN.S sample might actually be higher.
Where the data overlap, the PN kinematics agrees well with the IFS observations of the central regions, where the rotating disk component dominates the kinematics of the FRs. At larger radii both kinematics and photometry suggest that these galaxies show a transition to a spheroidal component. If we interpret this component with different kinematics and flattening as mainly formed by accreted, ex-situ, stars, we find that for the most massive galaxies it dominates at smaller fractions of Re, in agreement with simulations (Rodriguez-Gomez et al. 2016, see Sect. 8.6). This dependence on mass, combined with the smaller radial coverage of the A3D kinematics, explains the different conclusions drawn by the two surveys: low mass FRs are dominated by the disk rotation up to large radii; the spheroid is more prominent in the most massive FRs, where the accreted envelope reaches smaller fractions of Re. Even so the radial coverage of the A3D kinematics does not reach the transition radius (see Sect. 8.6), since the fraction of Re observed also depends on mass, as discussed above.
The present work shows that the wider spatial coverage of the kinematics by the ePN.S survey delivers new informations about ETGs that extend the results of previous surveys. FRs do contain inner disk components, but many of them are not simply highly flattened oblate objects. The results presented in this paper point to a more complex scenario for ETGs than the simple fast and slow rotator dichotomy. As predicted by simulations (Naab et al. 2014; Rodriguez-Gomez et al. 2016), FR galaxies appear to be more diverse objects than previously thought.
8.6. Kinematic transition radius
We found that most of the galaxies in the sample show a transition in their kinematics, marked by a change in the rotation velocity Vrot or in the kinematic position angle PAkin. In the framework of the two-phase formation scenario, we can interpret such kinematic differences as tracing stellar components with different origins, such as the in- and the ex-situ components. From simulations (Rodriguez-Gomez et al. 2016, and references therein) it is predicted that the in-situ stars are concentrated in the central regions of galaxies, while the accreted stars dominate the halos, and that their relative contribution is related primarily to the total mass. Within this framework we can define a transition radius RT as the distance at which we observe the described transition in the kinematics, and compare it with the total stellar mass.
The radial range RT ± ΔRT is here quantified using
- (A)
in case of a declining Vrot profile, the interval between the radius at which Vrot is maximum and the radius at which it decreases by ∼50 km s−1;
- (B)
in case of an increasing Vrot profile, the radial range in which Vrot increases from ∼0 to ∼50 km s−1;
- (C)
in case of a kinematic twist, the radial range in which PAkin changes significantly.
Table 3 lists the RT ± ΔRT values measured, and specifies the criteria (A, B, C) used for deriving it. RT ± ΔRT is also plotted in Figs. 5 and 6 with vertical lines.
For each galaxy we estimate the stellar mass using two different approaches, designated by M*1 and M*2, to have also an estimate of the systematic uncertainties. The values for the masses are listed in Table 2, along with the description of the procedure used for calculating them.
Figure 12 shows the stellar mass of the galaxies versus RT/Re. The full circles show the same quantities in three bins of RT/Re; the error bars represent the standard deviation of the mass and of the RT/Re ratio in the bin. A clear correlation exists between total stellar mass and RT/Re, in the sense that the more massive galaxies tend to have transition radii at smaller fractions of Re. The shaded region in Fig. 12 shows the corresponding quantities from the N-body simulations of Cooper et al. (2013). Using their stellar mass surface density profiles in bins of dark halo virial mass (M200/M⊙; their Fig. 6), we estimated the transition radius in units of half mass radii as the distance at which the accreted component overcomes the in-situ component. The total masses M200 are converted to stellar masses via abundance matching, using the prescription given by Behroozi et al. (2010). Both data and simulation follow the same trend.
 |
Fig. 12. Transition radius in units of Re versus total stellar mass (open symbols: circles for SRs, triangles for FRs). The full symbols show the same quantities in bins of RT/Re. Different colors show the results of two different procedures for calculating the total stellar mass, see Table 2 for details. The shaded region shows the corresponding quantities from the simulations of Cooper et al. (2013), see text. |
 |
Fig. 13. Transition radius in units of Rhalflight versus total stellar mass (open symbols: circles for SRs, triangles for FRs). The full symbols show the same quantities in bins of RT/Rhalflight. Different colors show the results of two different procedures for calculating the total stellar mass, see Table 2 for details. |
We also observe a higher scatter in RT/Re for the lower mass galaxies, in agreement with the results of Rodriguez-Gomez et al. (2016) from the Illustris simulations. They defined a three-dimensional transition radius rT as the distance at which the accreted stellar mass fraction overcomes the in-situ, and normalized it by the stellar half mass radius rhalf,*. Their study shows an additional dependence of rT/rhalf,* on morphology, halo formation time, and recent merger history, and that rT/rhalf,* tightly correlates with the ex-situ stellar mass fraction.
We tested the dependence of the correlation found on the choice of the value of Re. The used values (listed in Table 1) derive mostly from a calibrated average between 2MASS and RC3 determinations (Cappellari et al. 2011). Deeper photometric data would deliver larger values for Re for the brightest galaxies (Kormendy et al. 2009). For this reason we carried out a simple photometric analysis, to be completed in a future study, with the goal of having a homogeneous determination of Re for all the sample galaxies which takes the shallower surface brightness profile of the brightest galaxies into account. Using the surface brightness profiles available in the literature (references in Table 2), we fitted a Sérsic law in the outermost regions of the galaxies and extrapolated the profiles up to very large radii to include all the stellar light. We then evaluated the half-light radius Rhalflight from the growth curves (see Table 2). Figure 13 shows that with these half-light radii, the relation between RT/Rhalflight and total stellar mass becomes steeper and agrees even better with the predicted trend from the simulations.
Spavone et al. (2017) quantified transition radii for a subsample of the ePN.S SRs using a parametrization of the light profiles with a multicomponents Sérsic fit. Their three-components model describes the superposition of an in-situ component dominating the central regions, a relaxed, phase-mixed accreted component, to which is associated the transition radius Rtr1, and an outer diffuse component of unrelaxed accreted material with transition radius Rtr2. The transition radius is defined there as the radius at which one component overcomes the other. The RT derived from the kinematics generally compares with Rtr1 for the same galaxies.
D’Souza et al. (2014), using image stacking of a large sample of galaxies, defined Racc as the radius at which the outer component of a double Sérsic model begins to dominate the integrated stellar light. They found a dependence of Racc on the stellar mass, and, at comparable masses, their photometric values Racc [kpc] are in the same range as our kinematic RT [kpc]. This is interesting considering the different approaches used to derive these quantities.
8.7. The diverse halo formation histories
Cosmological simulations (Naab et al. 2014; Penoyre et al. 2017) show that FRs, as well as SRs, are the result of different formation pathways, characterized by factors like the number of mergers, the merger mass ratio, the timing of mergers, and the gas fraction. We note, however, that the adopted star formation and AGN feedback models influence the resulting morphologies and kinematic properties, so that definitive statements about the origin of FRs and SRs cannot yet be made (see Naab & Ostriker 2017, for a recent review). In the two-phase scenario, if the formation history is dominated by dissipation, then it is likely that the system becomes a fast rotator. Dissipation is particularly important in the early stages of galaxy formation, when the in-situ component generally settles down in a flattened rotating disk component (Rodriguez-Gomez et al. 2016; Qu et al. 2017), so that before redshift ∼1 the progenitors of the FRs and SRs are nearly indistinguishable (Penoyre et al. 2017). Later on, the evolution of galaxies is determined by the stochasticity of merging events, which at low redshift are mostly gas-poor (e.g., Lee & Yi 2013). Major mergers contribute to the loss of spin of the remnant, while minor mergers are responsible for the growth in size and mass. The accretion of stars happens preferentially on radial orbits, and frequent mergers efficiently mix the in-situ and the accreted stellar populations while changing the intrinsic shape toward a more spheroidal form (e.g. Jesseit et al. 2005; Hilz et al. 2012, 2013; Röttgers et al. 2014). Fast rotating galaxies experience a lower number of mergers when compared to the more massive slowly rotating systems, so their in-situ component is preserved in the central regions, in an axisymmetric, rotationally supported disk (e.g., Naab et al. 2014; Penoyre et al. 2017). Their halos, which host most of the accreted component, are not necessarily axisymmetric.
9. Summary and conclusions
In this paper we reconstructed and analyzed the velocity fields of 33 ETGs into their outer halos using planetary nebulae (PNe) as tracers. For the total ePN.S sample, we combined 25 galaxies from the PN.S ETG survey with eight objects observed with counter-dispersed imaging or multi-object spectroscopy from other sources (Arnaboldi et al. in prep.). In the extended PN.S (ePN.S) sample, 24 galaxies are classified as FRs (following the definition by Emsellem et al. 2011), and nine are SRs. The kinematic information typically extends to 6 effective radii (Re), from a minimum of 3Re to a maximum of 13Re.
We derived kinematic quantities such as the amplitude of rotation, the kinematic position angle (PAkin), and the velocity dispersion, using an adaptive kernel smoothing technique validated with simulated velocity fields. In this process, we checked whether the galaxy velocity fields were point-symmetric as expected for triaxial galaxies in dynamical equilibrium, and whether the systemic velocity is unchanged in the outer halo.
We supplemented the PN kinematics with absorption line kinematic data from the literature (typically limited to the regions inside ∼1–2Re), in order to have a complete picture of the nature of the objects, and compared the results from different datasets in the regions of overlap. Highlights of the results are:
- (1)
Most FRs (70%) have decreasing rotation amplitudes with radius, while a minority shows constant (15%) or increasing (15%) trends. 60% have PAkin in their halos aligned with the photometric major axis at the spatial sampling of the ePN.S survey. The SRs display modest but significant rotation in their outskirts. Among the FRs, 10% have very weak or no rotation in their outskirts.
- (2)
SRs have approximately constant velocity dispersion profiles with radius, except for NGC 4636 which shows a steep drop in dispersion beyond 200 arcsec. The FRs display a variety of velocity dispersion profile shapes: some are approximately constant, others decrease steeply with radius (Fig. 7).
- (3)
From their velocity fields, all of the SRs and 40% of the FRs show signatures of a triaxial halo (Fig. 6). For these galaxies we observe either a twist in the PAkin or a constant misalignment with the photometric major axis. In addition, two SRs have halos that are decoupled in their PAkin.
- (4)
Five galaxies show deviations from point symmetry. For NGC 2768 and NGC 4594 these effects are small (probably related asymmetries in the light distribution, in the former, and to extinction effects in the latter) and do not influence our kinematic analysis. NGC 1316, NGC 4472, and NGC 5128 instead display strong features, that indicate halos not in dynamical equilibrium. NGC 5128 is a merger remnant with clear minor axis rotation, and hence it is a triaxial system. For NGC 4472 the determination of the PAkin is influenced by the presence of an in-falling satellite. While we included this SR among the triaxial objects, we note that the galaxy would have approximately major axis rotation once the PNe of the satellite are removed, and we refer to Hartke et al. (2018) for a more detailed study. NGC 1316 is a merger remnant with pronounced major axis rotation in the halo.
- 5)
In a V/σ(Re) versus V/σ(halo) diagram (Fig. 9), the previous results imply different locations for the slow and the FRs. The latter separate further between FRs with slowly rotating outer spheroid and FRs that rotate rapidly at large radii also. The high values of V/σ(halo) are either due to a dominating disk component (e.g. NGC 7457) or to a rapidly rotating outer spheroid (NGC 2768). The FRs with triaxial halos show approximately equal values of V/σ(Re) and V/σ(halo), and span all values of V/σ(halo).
- (6)
In the 11 FR galaxies with the largest number of PN tracers, we see a decrease in the rotation velocity profile. In 10 cases this occurs approximately at a transition radius RT similar to the scale radius of the known stellar disk component4, suggesting that the transition from rapid to slow rotation is due to the radial fading of the stellar disk in a slowly rotating outer spheroid. For NGC 4494 there is no photometric evidence for a disk. In the other FRs with fewer tracers that also show a decrease in rotation, the comparison between the slow rotation of the PN system and the rapid rotation in the absorption line kinematics, which is related to an inner disk, suggests a similar transition at smaller radii.
- (7)
In extended photometry, the ePN.S FRs with triaxial halos show small but significant isophote twists, typically of ∼5−15 degrees, lower than for the rounder SRs. The comparison with illustrative, observationally motivated, oblate-triaxial models shows that the distribution of observed photometric twists for the ePN.S FRs is consistent with the presence of a triaxial halo.
- (8)
For SRs, we estimate a kinematic transition radius RT from a variation in the rotation or in the PAkin profile. Combining with the transition radii of FRs, we find a relation between the ratio RT/Re and stellar mass, such that the most massive galaxies have the lowest RT/Re (Fig. 12). In the framework of the two-phase formation scenario we can interpret RT as marking the transition between the inner regions, dominated by the in-situ stellar component, and the halo, which is mostly accreted. The comparison with photometric studies (D’Souza et al. 2014) and cosmological simulations (Cooper et al. 2013; Rodriguez-Gomez et al. 2016) shows good agreement, in particular the prediction from simulations is quantitatively confirmed.
- (9)
In the mass-ellipticity plane (Fig. 11), the ePN.S FRs with triaxial halos are amongst the most massive of the FRs in the ATLAS3D survey. If we interpret the triaxial envelopes of these galaxies as mainly formed by accreted, ex-situ, stars, the observed mass dependence is in agreement with simulations (Rodriguez-Gomez et al. 2016) which predict that the accreted component dominates down to smaller fractions of Re for more massive galaxies (Fig. 13). The dependence on mass, combined with the fainter survey limit and smaller radial coverage of the ATLAS3D kinematics, explains the different conclusions drawn by the two surveys: low mass FRs are dominated by the disk rotation up to large radii; however, in the more massive FRs the spheroid is more prominent, where the accreted envelope reaches smaller fractions of Re. In the massive FRs, the inner disks frequently fade in slowly rotating outer spheroids which are often triaxial.
In the data presented here, we see
SRs;
FRs without apparent disks (NGC 4494 and NGC 4742);
FRs with only inner disks and slowly rotating spheroids (e.g. NGC 3377);
FRs with dominant disks all the way to their outermost regions (e.g. NGC 7457);
FRs with inner disks and rapidly rotating spheroids (e.g. NGC 2768);
FRs with triaxial halos that are dominated by dispersion (e.g. NGC 4649) or that rotate rapidly (NGC 4742 and NGC 5866).
Thus we conclude that ETGs show considerably more diversity in their halos than is apparent from their central bright regions. We also see clear signatures of the two-phase formation scenario: three galaxies show out of equilibrium kinematics in their halos, and more generally the inner and outer regions of ETGs often have different kinematic properties, where the transition radius depends on the stellar mass as predicted by cosmological simulations.
The values of Re used by most kinematic studies are measured in the bright central regions of galaxies, and may underestimate the half light radii (see discussion in Sect. 8.6).
Acknowledgments
We are grateful to Nigel G. Douglas for his fundamental contribution to the foundation of the Planetary Nebula Spectrograph instrument. We thank Luis Ho and Zhao-Yu Li for providing us with the Carnagie photometric data for the ePN.S ETG sample. We thank Peter Erwin for sharing his expertise with photometric modeling. C.P. thanks I. Soeldner-Rembold and J. Hartke for useful comments and discussions. C.P. is also grateful to F. Hofmann for advice and suggestions on the manuscript. AC would like to thank CNPq for the fellowship 4150977/2017-4. A.J.R. was supported by National Science Foundation grant AST-1616710, and as a Research Corporation for Science Advancement Cottrell Scholar. C.T. is supported through an NWO-VICI grant (project number 639.043.308). This research has made use of NASA’s Astrophysics Data System, of the data products from the Two Micron All Sky Survey (University of Massachusetts and the IPAC/CalTech), of the NASA/ IPAC Infrared Science Archive (Jet Propulsion Laboratory, CalTech), of the NASA/IPAC Extragalactic Database (NED), and of the VizieR catalog access tool, CDS, Strasbourg, France. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr) as well.
References
- Alabi, A. B., Forbes, D. A., Romanowsky, A. J., et al. 2016, MNRAS, 460, 3838 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Mendez, R. H., et al. 1996, ApJ, 472, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Gerhard, O., et al. 1998, ApJ, 507, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, J. A., Romanowsky, A. J., Brodie, J. P., et al. 2014, ApJ, 791, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni Battaia, F., Gavazzi, G., Fumagalli, M., et al. 2012, A&A, 543, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbon, R., & Capaccioli, M. 1975, A&A, 42, 103 [NASA ADS] [Google Scholar]
- Barbosa, C. E., Arnaboldi, M., Coccato, L., et al. 2018, A&A, 609, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedregal, A. G., Aragón-Salamanca, A., Merrifield, M. R., & Milvang-Jensen, B. 2006, MNRAS, 371, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Beletsky, Y., Gadotti, D. A., Moiseev, A., Alves, J., & Kniazev, A. 2011, MNRAS, 418, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bellstedt, S., Forbes, D. A., Foster, C., et al. 2017a, MNRAS, 467, 4540 [NASA ADS] [CrossRef] [Google Scholar]
- Bellstedt, S., Graham, A. W., Forbes, D. A., et al. 2017b, MNRAS, 470, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Benacchio, L., & Galletta, G. 1980, MNRAS, 193, 885 [NASA ADS] [Google Scholar]
- Bender, R. 1988a, A&A, 202, L5 [NASA ADS] [Google Scholar]
- Bender, R. 1988b, A&A, 193, L7 [Google Scholar]
- Bender, R., Doebereiner, S., & Moellenhoff, C. 1988, A&AS, 74, 385 [NASA ADS] [Google Scholar]
- Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Lucey, J. R., Barris, B. J., Hudson, M. J., & Tonry, J. L. 2001, MNRAS, 327, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, ApJ, 694, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Cantiello, M., Mei, S., et al. 2010, ApJ, 724, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Blom, C., Forbes, D. A., Brodie, J. P., et al. 2012, MNRAS, 426, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Boardman, N. F., Weijmans, A.-M., van den Bosch, R., et al. 2017, MNRAS, 471, 4005 [NASA ADS] [CrossRef] [Google Scholar]
- Bois, M., Emsellem, E., Bournaud, F., et al. 2011, MNRAS, 416, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bridges, T. J., Rhode, K. L., Zepf, S. E., & Freeman, K. C. 2007, ApJ, 658, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Brodie, J. P., & Strader, J. 2006, ARA&A, 44, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Brough, S., Forbes, D. A., Kilborn, V. A., & Couch, W. 2006, MNRAS, 370, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Bryant, J. J., Owers, M. S., Robotham, A. S. G., et al. 2015, MNRAS, 447, 2857 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Curtis-Lake, E., et al. 2017, MNRAS, 466, 4888 [NASA ADS] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhead, M. S. 1986, AJ, 91, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Capaccioli, M., & Rampazzo, R. 1990, A&AS, 86, 429 [NASA ADS] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1994, A&AS, 106, 199 [NASA ADS] [Google Scholar]
- Capaccioli, M., Held, E. V., & Nieto, J.-L. 1987, AJ, 94, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioli, M., Held, E. V., Lorenz, H., & Vietri, M. 1990, AJ, 99, 1813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappellari, M. 2016, ARA&A, 54, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013a, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013b, MNRAS, 432, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Romanowsky, A. J., Brodie, J. P., et al. 2015, ApJ, 804, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, D. 1978, MNRAS, 182, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, D., Thomson, R. C., & Hau, G. K. T. 1998, MNRAS, 294, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Tremaine, S., Forman, W., et al. 2010, MNRAS, 404, 1165 [NASA ADS] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., & Dejonghe, H. B. 1993, ApJ, 414, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Arnaboldi, M., Gerhard, O., et al. 2010, A&A, 519, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coccato, L., Arnaboldi, M., & Gerhard, O. 2013, MNRAS, 436, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., & Ryzhov, A. 1997, ApJ, 486, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [NASA ADS] [CrossRef] [Google Scholar]
- Cortesi, A., Merrifield, M. R., Arnaboldi, M., et al. 2011, MNRAS, 414, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Cortesi, A., Arnaboldi, M., Coccato, L., et al. 2013a, A&A, 549, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortesi, A., Merrifield, M. R., Coccato, L., et al. 2013b, MNRAS, 432, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Abraham, R. G., Glazebrook, K., et al. 2011, ApJ, 739, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., & Illingworth, G. 1983, ApJ, 266, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Efstathiou, G., Fall, S. M., Illingw orth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Kuntschner, H., Emsellem, E., et al. 2001, ApJ, 548, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Belokurov, V., Evans, N. W., & McCarth y, I. G. 2012, ApJ, 748, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., Corsini, E. M., & Aguerri, J. A. L. 2002, MNRAS, 332, 65 [NASA ADS] [CrossRef] [Google Scholar]
- De Bruyne, V., Dejonghe, H., Pizzella, A., Bernardi, M., & Zeilinger, W. W. 2001, ApJ, 546, 903 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Saglia, R. P., et al. 2008, MNRAS, 385, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- de Zeeuw, T. 1985, MNRAS, 216, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Arnaboldi, M., Freeman, K. C., et al. 2002, PASP, 114, 1234 [NASA ADS] [CrossRef] [Google Scholar]
- Dowell, J. L., Rhode, K. L., Bridges, T. J., et al. 2014, AJ, 147, 150 [NASA ADS] [CrossRef] [Google Scholar]
- D’Souza, R., Kauffman, G., Wang, J., & Vegetti, S. 2014, MNRAS, 443, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., Serra, P., et al. 2011, MNRAS, 417, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Duc, P.-A., Cuillandre, J.-C., Karabal, E., et al. 2015, MNRAS, 446, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrová, I., & Łokas, E. L. 2017, ApJ, 850, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Peletier, R. F., et al. 2004, MNRAS, 352, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Fogarty, L. M. R., Scott, N., Owers, M. S., et al. 2015, MNRAS, 454, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Romanowsky, A. J., Pastorello, N., et al. 2016, MNRAS, 457, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Forestell, A. D., & Gebhardt, K. 2010, ApJ, 716, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, C., Spitler, L. R., Romanowsky, A. J., et al. 2011, MNRAS, 415, 3393 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, C., Arnold, J. A., Forbes, D. A., et al. 2013, MNRAS, 435, 3587 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, C., Pastorello, N., Roediger, J., et al. 2016, MNRAS, 457, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, C., van de Sande, J., D’Eugenio, F., et al. 2017, MNRAS, 472, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Fouque, P., Gourgoulhon, E., Chamaraux, P., & Paturel, G. 1992, A&AS, 93, 211 [NASA ADS] [Google Scholar]
- Franx, M. 1988, MNRAS, 231, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., Illingworth, G., & Heckman, T. 1989, ApJ, 344, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Franx, M., Illingworth, G., & de Zeeuw, T. 1991, ApJ, 383, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Gabor, J. M., & Davé, R. 2012, MNRAS, 427, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A., & Sánchez-Janssen, R. 2012, MNRAS, 423, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, A. M. 1993, A&AS, 100, 47 [NASA ADS] [Google Scholar]
- Gebhardt, K., Richstone, D., Kormendy, J., et al. 2000, AJ, 119, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Jeske, G., Saglia, R. P., & Bender, R. 1998, MNRAS, 295, 197 [NASA ADS] [Google Scholar]
- Gerhard, O., Kronawitter, A., Saglia, R. P., & Bender, R. 2001, AJ, 121, 1936 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Hansen, L., Jorgensen, H. E., et al. 1994, A&AS, 104, 179 [NASA ADS] [Google Scholar]
- Graham, A. W., Colless, M. M., Busarello, G., Zaggia, S., & Longo, G. 1998, A&AS, 133, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gronwall, C., Ciardullo, R., Hickey, T., et al. 2007, ApJ, 667, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Guérou, A., Emsellem, E., Krajnović, D., et al. 2016, A&A, 591, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halliday, C., Davies, R. L., Kuntschner, H., et al. 2001, MNRAS, 326, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Hartke, J., Arnaboldi, M., Longobardi, A., et al. 2017, A&A, 603, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartke, J., Arnaboldi, M., Gerhard, O., et al. 2018, A&A, 616, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haynes, R. F., Cannon, R. D., & Ekers, R. D. 1983, Proc. Astron. Soc. Aus., 5, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Hilz, M., Naab, T., Ostriker, J. P., et al. 2012, MNRAS, 425, 3119 [NASA ADS] [CrossRef] [Google Scholar]
- Hilz, M., Naab, T., & Ostriker, J. P. 2013, MNRAS, 429, 2924 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2011, ApJS, 197, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2012, VizieR Online Data Catalog: J/ApJS/197/21 [Google Scholar]
- Hopkins, P. F., Cox, T. J., Dutta, S. N., et al. 2009, ApJS, 181, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Ho, L. C., Peng, C. Y., Li, Z.-Y., & Barth, A. J. 2013, ApJ, 768, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, X., Ford, H. C., Freeman, K. C., & Dopita, M. A. 1995, ApJ, 449, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, P. J., Buote, D. A., Gastaldello, F., et al. 2006, ApJ, 646, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Iodice, E., Capaccioli, M., Grado, A., et al. 2016, ApJ, 820, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Iodice, E., Spavone, M., Capaccioli, M., et al. 2017, ApJ, 839, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Janowiecki, S., Mihos, J. C., Harding, P., et al. 2010, ApJ, 715, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., Schneider, S. E., & Huchra, J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Jedrzejewski, R., & Schechter, P. L. 1988, ApJ, 330, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, J. B., Tonry, J. L., Barris, B. J., et al. 2003, ApJ, 583, 712 [Google Scholar]
- Jesseit, R., Naab, T., & Burkert, A. 2005, MNRAS, 360, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Zabludoff, A. I., Williams, K. A., et al. 2002, ApJ, 576, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Bender, R. 1996, ApJ, 464, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Illingworth, G. 1982, ApJ, 256, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Westpfahl, D. J. 1989, ApJ, 338, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Bacon, R., Cappellari, M., et al. 2008, MNRAS, 390, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Emsellem, E., Cappellari, M., et al. 2011, MNRAS, 414, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Alatalo, K., Blitz, L., et al. 2013, MNRAS, 432, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lackner, C. N., Cen, R., Ostriker, J. P., & Joung, M. R. 2012, MNRAS, 425, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Ajhar, E. A., Byun, Y.-I., et al. 1995, AJ, 110, 2622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lauer, T. R., Faber, S. M., Gebhardt, K., et al. 2005, AJ, 129, 2138 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., Knapen, J. H., & Comerón, S. 2010, MNRAS, 405, 1089 [NASA ADS] [Google Scholar]
- Leach, R. 1981, ApJ, 248, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., & Yi, S. K. 2013, ApJ, 766, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z.-Y., Ho, L. C., Barth, A. J., & Peng, C. Y. 2011, ApJS, 197, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Lima Neto, G. B., Gerbal, D., & Márquez, I. 1999, MNRAS, 309, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., et al. 2013, A&A, 558, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., & Mihos, J. C. 2015, A&A, 579, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loubser, S. I., Sansom, A. E., Sánchez-Blázquez, P., Soechting, I. K., & Bromage, G. E. 2008, MNRAS, 391, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-P., Greene, J. E., McConnell, N., et al. 2014, ApJ, 795, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Madejsky, R., & Moellenhoff, C. 1990, A&A, 234, 119 [NASA ADS] [Google Scholar]
- Madore, B. F., Freedman, W. L., & Bothun, G. D. 2004, ApJ, 607, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Malin, D. F., & Carter, D. 1980, Nature, 285, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Malin, D. F., Quinn, P. J., & Graham, J. A. 1983, ApJ, 272, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., Kauffmann, G., Hirata, C. M., & Brinkmann, J. 2006, MNRAS, 368, 715 [Google Scholar]
- Marcelin, M. 1983, in Internal Kinematics and Dynamics of Galaxies, ed. E. Athanassoula, IAU Symp., 100, 335 [NASA ADS] [Google Scholar]
- McNeil, E. K., Arnaboldi, M., Freeman, K. C., et al. 2010, A&A, 518, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McNeil-Moylan, E. K., Freeman, K. C., Arnaboldi, M., & Gerhard, O. E. 2012, A&A, 539, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez, R. H., Riffeser, A., Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Teodorescu, A. M., Kudritzki, R.-P., & Burkert, A. 2009, ApJ, 691, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1992, BAAS, 24, 522 [NASA ADS] [Google Scholar]
- Meusinger, H., & Ismail, H. A. 2007, Astron. Nachr., 328, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Michard, R., & Marchal, J. 1993, A&AS, 98, 29 [NASA ADS] [Google Scholar]
- Michard, R., & Marchal, J. 1994, A&AS, 105, 481 [NASA ADS] [Google Scholar]
- Morganti, L., Gerhard, O., Coccato, L., Martinez-Valpuesta, I., & Arnaboldi, M. 2013, MNRAS, 431, 3570 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, J. D., Gebhardt, K., & Adams, J. J. 2011, ApJ, 729, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2017, ARA&A, 55, 59 [Google Scholar]
- Naab, T., Oser, L., Emsellem, E., et al. 2014, MNRAS, 444, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Arnaboldi, M., Freeman, K. C., & Capaccioli, M. 2001, A&A, 377, 784 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Coccato, L., et al. 2009, MNRAS, 393, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., Capaccioli, M., et al. 2011, MNRAS, 411, 2035 [NASA ADS] [CrossRef] [Google Scholar]
- Neumayer, N. 2010, PASA, 27, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Noordermeer, E., Merrifield, M. R., Coccato, L., et al. 2008, MNRAS, 384, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., Sharples, R. M., & Kuntschner, H. 2006, MNRAS, 367, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., Gebhardt, K., Sharples, R. M., et al. 2012, MNRAS, 421, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Ostriker, J. P., Naab, T., Johansson, P. H., & Burkert, A. 2010, ApJ, 725, 2312 [NASA ADS] [CrossRef] [Google Scholar]
- Peletier, R. F., Davies, R. L., Illingworth, G. D., Davis, L. E., & Cawson, M. 1990, AJ, 100, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, E. W., Ford, H. C., Freeman, K. C., & White, R. L. 2002, AJ, 124, 3144 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, E. W., Ford, H. C., & Freeman, K. C. 2004, ApJ, 602, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Penoyre, Z., Moster, B. P., Sijacki, D., & Genel, S. 2017, MNRAS, 468, 3883 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatelli, E. 1999, ArXiv e-prints [arXiv:astro-ph/9906378] [Google Scholar]
- Pota, V., Forbes, D. A., Romanowsky, A. J., et al. 2013, MNRAS, 428, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Pota, V., Brodie, J. P., Bridges, T., et al. 2015, MNRAS, 450, 1962 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, R. N., Forbes, D. A., Romanowsky, A. J., et al. 2009, MNRAS, 398, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Pu, S.-B., & Han, Z.-W. 2011, Res. Astron. Astrophys., 11, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Qu, Y., Helly, J. C., Bower, R. G., et al. 2017, MNRAS, 464, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Raskutti, S., Greene, J. E., & Murphy, J. D. 2014, ApJ, 786, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Rejkuba, M., Minniti, D., Courbin, F., & Silva, D. R. 2002, ApJ, 564, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Agertz, O., & Gieles, M. 2017, MNRAS, 465, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Hilker, M., Kumar, B., et al. 2014, A&A, 569, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rix, H.-W., de Zeeuw, P. T., Cretton, N., van der Marel, R. P., & Carollo, C. M. 1997, ApJ, 488, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Gomez, V., Pillepich, A., Sales, L. V., et al. 2016, MNRAS, 458, 2371 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Romanowsky, A. J., Strader, J., Brodie, J. P., et al. 2012, ApJ, 748, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Röttgers, B., Naab, T., & Oser, L. 2014, MNRAS, 445, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Saglia, R. P., Kronawitter, A., Gerhard, O., & Bender, R. 2000, AJ, 119, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sambhus, N., Gerhard, O., & Méndez, R. H. 2006, AJ, 131, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sancisi, R., vanWoerden, H., Davies, R. D., & Hart, L. 1984, MNRAS, 210, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Visvanathan, N. 1978, ApJ, 223, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2012, A&A, 544, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild, M. 1993, ApJ, 409, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Schweizer, F. 1980, ApJ, 237, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Scorza, C., Bender, R., Winkelmann, C., Capaccioli, M., & Macchetto, D. F. 1998, A&AS, 131, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, N., Graham, A. W., & Schombert, J. 2013, ApJ, 768, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, N., Davies, R. L., Houghton, R. C. W., et al. 2014, MNRAS, 441, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Sengupta, C., & Balasubramanyam, R. 2006, MNRAS, 369, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Sikkema, G., Carter, D., Peletier, R. F., et al. 2007, A&A, 467, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simien, F., & Prugniel, P. 1997a, A&AS, 122, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simien, F., & Prugniel, P. 1997b, A&AS, 126, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simien, F., & Prugniel, P. 1997c, A&AS, 126, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sluis, A. P. N., & Williams, T. B. 2006, AJ, 131, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Smethurst, R. J., Masters, K. L., Lintott, C. J., et al. 2018, MNRAS, 473, 2679 [NASA ADS] [CrossRef] [Google Scholar]
- Sommer-Larsen, J., & Toft, S. 2010, ApJ, 721, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Spavone, M., Capaccioli, M., Napolitano, N. R., et al. 2017, A&A, 603, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spiniello, C., Napolitano, N. R., Coccato, L., et al. 2015, MNRAS, 452, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, A. A. 1977, ApJ, 213, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S. 1987, ApJ, 321, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S. 1994, ApJ, 425, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S., & Smecker-Hane, T. 1999, AJ, 117, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Strader, J., Romanowsky, A. J., Brodie, J. P., et al. 2011, ApJS, 197, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tal, T., van Dokkum, P. G., Nelan, J., & Bezanson, R. 2009, AJ, 138, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Saglia, R. P., et al. 2005, ApJ, 635, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Bernardi, F., et al. 2011, ApJ, 736, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J., Jesseit, R., Saglia, R. P., et al. 2009, MNRAS, 393, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. Hanisch, R. J. Brissenden, R. J. V., & Barnes, J., ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Förster Schreiber, N. M., Rudnick, G., et al. 2006, ApJ, 650, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Tsatsi, A., Lyubenova, M., van de Ven, G., et al. 2017, A&A, 606, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bergh, S. 1961, AJ, 66, 562 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., Rix, H. W., Carter, D., et al. 1994, MNRAS, 268, 521 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Whitaker, K. E., Brammer, G., et al. 2010, ApJ, 709, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Thomas, J., et al. 2017, MNRAS, 464, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Greene, J. E., et al. 2018, MNRAS, 473, 5446 [NASA ADS] [CrossRef] [Google Scholar]
- Veljanoski, J., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Viaene, S., Sarzi, M., Baes, M., & Puerari, I. 2018, MNRAS, 474, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. R., Rejkuba, M., & Walton, N. A. 2015, A&A, 574, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weijmans, A.-M., Cappellari, M., Bacon, R., et al. 2009, MNRAS, 398, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Weijmans, A.-M., de Zeeuw, P. T., Emsellem, E., et al. 2014, MNRAS, 444, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Wellons, S., Torrey, P., Ma, C.-P., et al. 2016, MNRAS, 456, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Gerhard, O., Naab, T., et al. 2014, MNRAS, 438, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Cox, T. J., Hayward, C. C., et al. 2010, ApJ, 722, 1666 [NASA ADS] [CrossRef] [Google Scholar]
- Young, L. M., Rosolowsky, E., van Gorkom, J. H., & Lamb, S. A. 2006, ApJ, 650, 166 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Testing the adaptive kernel smoothing procedure on simulated data
Our procedure for the measurement of the mean velocity and velocity dispersion fields from the observed LOS velocities of the PNe is based on performing a weighted local average, where the weights depend on the local density of tracers. The derived quantities depend on how well the detected PNe statistically sample the parent galaxy in the phase space. In particular the spatial distribution of the PNe plays an important role, as the smoothing averages over objects that are close together on the sky. Appendix A.1 describes what determines the observed PN spatial distribution and how this, combined with a smoothing procedure, may affect the results. Appendices A.2 and A.3 study and quantify these effects on a simulated galaxy (with variable number of tracers and V/σ ratio) and on simulated velocity fields, with the same spatial distribution as the observed galaxies. We found that the smoothing procedure does not create artifacts in the velocity fields above the 1σ level; any features above this threshold are probably real.
A.1. PN spatial distribution and completeness
The observed PN spatial distribution depends on several factors. The most evident one is the incompleteness in the central high surface brightness regions because of the difficulty in detecting faint point sources against a bright background (Arnaboldi et al., in prep.; Coccato et al. 2009). This is a strong function of the radius and it is quantified by the completeness function, the fraction of detected objects in different radial ranges.
In addition, the PN number density is proportional to the local surface brightness of the galaxy. This means that the number of tracers decreases with radius following the steep decrease of the surface brightness, and features in the surface brightness distribution may generate under- or over-densities of PNe. Of course at our typical number of tracers (∼200) these features in density are barely distinguishable from statistical effects.
The adopted smoothing procedure takes the natural non-uniformity of the PNe distribution into account through the use of an adaptive kernel technique, which optimizes the size of the kernel to the local density of tracers. Nevertheless a local average of the velocities over a non-uniform spatial distribution, combined with the statistics in the LOSVD sampling, may in principle generate features in the kinematic maps or biases in the estimate of the kinematic parameters. On the other hand, averaging over voids or over sparsely distributed tracers unavoidably leads to over-smoothed velocity amplitudes and to under-resolved velocity gradients. The residual velocities from the unresolved gradients may artificially boost the dispersion, creating local maxima in the velocity dispersion maps. In Appendices A.2 and A.3 we assess the impact of such biases using simulated data.
 |
Fig. A.1. Smoothed velocity and velocity dispersion fields in the ePN.S field of view for a simulated ETG, traced by 10 000 particles, 400, and 200 stars after the convolution with a completeness function. For the 200 particle case, we show two typical statistical realizations (A and B) of the extracted sample, to illustrate the effects of the limited statistics on the smoothed quantities. The global features of the simulation are preserved in the different fields but, as expected, the spatial and velocity resolution of the local gradients is downgraded when the number of tracers decreases. The lower right panels display the fitted kinematic position angle PA, the rotation velocity Vrot, and the azimuthally averaged velocity dispersion σ in circular radial bins as function of radius. It is evident that the radial gradients are less resolved with fewer tracers, and that the amplitude of rotation for the case with 200 stars is oversmoothed. This happens because the kernel width is larger than the real spatial scale of the velocity gradients due to the sparse distribution of the tracers. The blue full circles show a simulation with higher V/σ ratio and two of its typical statistical realizations sampled by 200 objects to illustrate how of the accuracy of the reconstructed velocity amplitudes depends on the statistical noise. Errors for the kinematic profiles are determined from Monte Carlo simulations using the smoothed velocity and velocity dispersion fields as described in Sect. 3.2.2. |
A.2. Tests with data from a simulated galaxy
We used a simulated major merger remnant, sampled by 10 000 particles. We reproduced a realistic observed dataset by locating the simulated galaxy at a distance of 20 Mpc, and applying to it a completeness function similar to those observed (see Arnaboldi et al. in prep.). We observed the galaxy in a field of view similar to that of the ePN.S, 800 × 800 arcsec2 wide centered on to the galaxy. At this point, the simulated galaxy can be used as a test case for the procedure: we can explore how the results change by varying the number of tracers at our disposal, by selecting randomly typical numbers of observed PNe; different random extractions of tracers give us different statistical realizations of the system, and different projections of the galaxy on the sky plane give us different V/σ ratios.
Figure A.1 shows an example of such an experiment. The smoothed velocity and velocity dispersion fields are plotted for the 10 000 particle simulation, together with the maps for 400 stars and 200 stars. For the 200 particles case we show two typical statistical realizations (A and B) in order to illustrate the effects of limited statistics on the kinematic quantities. The panels at the bottom right show the fitted kinematic position angles, the amplitudes of the rotational velocity, and the azimuthally averaged velocity dispersion profiles in circular bins. The kinematic quantities are in general well recovered within the errors. The simulation is point symmetric in the region selected, and so are the limited statistical realizations. The statistical fluctuations that appear in the smoothed fields usually do not cause a deviation from point symmetry nor a variation of the kinematic position angle larger than the error bars. The velocity dispersion may be marginally boosted at the center of the galaxy, associated with the lack of detections, (see the case of 200 stars in Fig. A.1), but the dispersion profile is recovered within the errors. So we conclude that the procedure to calibrate the smoothing parameters through Monte Carlo simulations (Sect. 3.1.1) works very well in reconstructing the mean properties of the velocity and velocity dispersion fields. Even though the smoothing procedure may create artificial peaks or deeps in the velocity maps, all these features are generally within the 1σ level. Any radial trends can therefore be considered significant only if it is outside the statistical uncertainties.
However, we can notice that as the number of tracers drops or the ratio V/σ decreases, the amplitude of rotation is systematically underestimated, while the velocity dispersion is systematically higher (see also Napolitano et al. 2001). This happens because lower numbers of stars or higher statistical noise require larger smoothing scales, which eventually become larger than the actual spatial scales of the velocity gradients. Oversmoothed velocity amplitudes (i.e. lower ⟨v⟩), imply higher σ̃ in Eq. (2). There is no way to estimate this offsets unless the mean velocity and velocity dispersion fields of the galaxy are known from independent data, since the effects of the smoothing jointly depend on the local density of tracers, on the V/σ ratio, and on the particular statistical realization (e.g. A and B in Fig. A.1), hence they vary from case to case. It is however safe to say that for the galaxies with limited statistics the recovered kinematics provides a lower limit to the amplitude of rotation and an upper limit for the velocity dispersion in the halos.
A.3. Statistical tests with simulated velocity fields on real galaxies
Simulated velocity fields were used to verify the results obtained for the ePN.S sample of galaxies, such as assessing the significance of deviations from point symmetry or the radial trends of the kinematic parameters. These simulated velocity fields are featureless and trend-less (fixed kinematic position angle and constant velocity dispersion) and are built for each galaxy using the positions of the observed PNe. This means that the incompleteness function is already built into the simulated catalogs and is identical to that for the real galaxy under study. In this way we can check how the smoothing procedure correlates spatially close PNe, as the degree of spatial correlation in the models will be identical to that of the real datasets.
The simulated velocity field at the positions (xi, yi) of the ith PNe, from the real datasets, is interpolated with the simple function
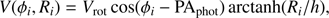 A.1
where ϕi is the position angle of the ith PN with coordinates (xi, yi), Ri its distance from the center, and h is a scale-length that defines the steepness of the central velocity radial gradient. Vrot is chosen to be equal to the maximum fitted rotational amplitude for the galaxy in consideration, while h has the dimension of the central void of the detections (∼50 arcsec). We choose to align the rotation of the simulated velocity field with the real photometric position angle of the galaxy, in order to simulate the velocity field of a regular, point-symmetric disk. The model velocity field V(xi, yi) is sampled with a constant dispersion σ, which is equal to the mean velocity dispersion of the galaxy under study. This is done by extracting random values from a Gaussian distribution centered at 0 and with dispersion σ, and adding them to V(xi, yi). The assumption of constant dispersion is certainly unrealistic for the central regions of the galaxies, but it is reasonable at large radii. We produced 100 statistical realizations for each galaxy, and each of those is treated as a real dataset for obtaining a total of 100 smoothed velocity fields.
A.1
where ϕi is the position angle of the ith PN with coordinates (xi, yi), Ri its distance from the center, and h is a scale-length that defines the steepness of the central velocity radial gradient. Vrot is chosen to be equal to the maximum fitted rotational amplitude for the galaxy in consideration, while h has the dimension of the central void of the detections (∼50 arcsec). We choose to align the rotation of the simulated velocity field with the real photometric position angle of the galaxy, in order to simulate the velocity field of a regular, point-symmetric disk. The model velocity field V(xi, yi) is sampled with a constant dispersion σ, which is equal to the mean velocity dispersion of the galaxy under study. This is done by extracting random values from a Gaussian distribution centered at 0 and with dispersion σ, and adding them to V(xi, yi). The assumption of constant dispersion is certainly unrealistic for the central regions of the galaxies, but it is reasonable at large radii. We produced 100 statistical realizations for each galaxy, and each of those is treated as a real dataset for obtaining a total of 100 smoothed velocity fields.
The smoothed velocity fields obtained in this way were used to assess whether an observed feature in the galaxy velocity or velocity dispersion field is real, by studying whether it can be produced by statistical effects in a featureless velocity field, and how typically this happens (see Sects. 5 and 6.3). Also, the 100 models can provide a statistic for the fitted kinematic parameters (Eq. (9)) to check the probability that statistical noise combined with the smoothing procedure artificially produce effects like twists of the kinematic position angle or misalignments with the photometric axes (Sect. 6.4).
Appendix B: Photometric profiles and models
In this appendix we report extended photometric data from the literature for three quarters of the ePN.S galaxies to compare with the PN kinematic analysis of this paper, as discussed in Sect. 8.4. Furthermore we present illustrative photometric models which reproduce the main trends seen in the photometric profiles of the galaxies.
B.1. Photometric profiles from the literature
Figure B.1 shows ellipticity and PAphot profiles from the literature for the subsample of the ePN.S galaxies (references in Table 2) with photometric data reaching at least 4 Re, excluding the merger remnants NGC 1316, NGC 4472, and NGC 5128. For three galaxies, NGC 0584, NGC 2768, and NGC 5866, we marked the outermost photometric measurements that may be affected by perturbations from ongoing interactions (see Appendix C). For NGC 1023 and NGC 3384 the presence of multiple components, like for example the bar, affect the PAphot and ellipticity profiles. Therefore for these galaxies we flagged the corresponding regions, as described in Appendix C. These regions are highlighted with open symbols and black vertical lines in Fig. B.1.
The PAphot profiles in Fig. B.1 show more or less pronounced variations with radius for most of the galaxies. All SRs have isophote twists, typically ∼10−40 degrees with a very large twist in NGC 4374. For the fast rotating galaxies classified as triaxial in Sect. 6.4 photometric twists range from ∼3 to 20 degrees with the largest twist in NGC 4494 (∼22 degrees). For the other FRs the photometric twists range from ∼0−28 degrees, with two galaxies NGC 4278 and NGC 0584 having twists of ∼28 degrees. The latter objects are consistent with axisymmetry at the resolution of the kinematic survey, but the photometry suggests that some of them might be triaxial as well.
The ellipticity profiles show that while most of the SRs become flatter in the outskirts, the opposite is true for the FRs. Most of the FRs shown in Fig. B.1 have decreasing ellipticity profiles at large radii, approximately at the distance where Vrot is observed to drop. The vertical lines indicate the radial range of the kinematic transition discussed in Sect. 8.6. This is also evident from the distribution of the maximum ellipticity and of the outermost measured values in Fig. 10, and it is consistent with a picture where the FRs are dominated by a disk component in the central regions, embedded in a rounder, dispersion dominated outer component which is triaxial for a fraction of the sample. The exceptions to the decreasing trend in ellipticity at large radii are NGC 1344, a prolate rotator in the halo, NGC 3379 and NGC 4494 which are both very round at all radii, and NGC 2974, NGC 3384 and NGC 4339 for which the small number of tracers does not allow us to resolve any kinematic transition.
 |
Fig. B.1. Position angle (red triangles, y axis on the left) and ellipticity profiles (dark blue squares, y axis on the right) for the subsample of the ePN.S galaxies with literature photometry reaching at least 4Re (references in Table 2). The NGCnumbers of the galaxies are shown in red for the SRs, in blue for the FRs, and in green for the FRs with triaxial halos. The open symbols and the black vertical line for NGC0584, 2768, 5866 mark regions that are probably affected by ongoing interactions, and for NGC1023 and NGC3384 the regions affected by the presence of other photometric components, e.g. the bar (see Appendix C). For NGC4594 we excluded the data beyond 350″ where the small ellipticity corresponds to large uncertainties in the PAphot measurements. The horizontal lines report the PAphot (solid line) and ⋴ (dotted line) with values listed in Table 1. The red dot-dashed vertical lines show the kinematic transition range RT ± ΔRT from Sect. 8.6. |
B.2. Photometric models of a FR with triaxial halo
Here we describe triaxial photometric models for FR galaxies which explain the magnitude of the photometric twists seen in Fig. 10, and which are used in the discussion in Sect. 8.4. These simple models are not meant to provide an exact description of the intrinsic shape of a galaxy. Their purpose is to obtain a reasonable representation of the structure of FRs with triaxial halos, to derive what is the maximum isophotal twist expected, and compare it with the observations.
To build these models we use the results of previous studies on the intrinsic shapes of FRs that constrain their central regions. Weijmans et al. (2014) and Foster et al. (2017) found that FRs are close to oblate (p ∼ 1), and rather flat (q ∼ 0:3). Guided by the PN kinematic results, we assume that the intrinsic shape of the FR model changes from flat and oblate in the innermost regions, to rounder and mildly triaxial beyond the transition radius in the outer regions, as discussed in Sect. 8.4. Weijmans et al. (2014) and Foster et al. (2017) found that SRs have q ∼ 0.6, but the p value is not well constrained (their analysis failed to converge). The main reason for this is the rather small number of SRs in the ATLAS3D and in the SAMI samples. In addition, as argued by Foster et al. (2017), the family of SRs comprises both truly spheroidal pressure dominated systems and flattened non-regular rotators, which might prevent the analysis to converge.
To build these models we use the results of previous studies on the intrinsic shapes of FRs that constrain their central regions. Weijmans et al. (2014) and Foster et al. (2017) found that FRs are close to oblate (p ∼ 1), and rather flat (q ∼ 0.3). Guided by the PN kinematic results, we assume that the intrinsic shape of the FR model changes from flat and oblate in the innermost regions, to rounder and mildly triaxial beyond the transition radius in the outer regions, as discussed in Sect. 8.4. Weijmans et al. (2014) and Foster et al. (2017) found that SRs have q ∼ 0.6, but the p value is not well constrained (their analysis failed to converge). The main reason for this is the rather small number of SRs in the ATLAS3D and in the SAMI samples. In addition, as argued by Foster et al. (2017), the family of SRs comprises both truly spheroidal pressure dominated systems and flattened non-regular rotators, which might prevent the analysis to converge.
We present here four different photometric models, that have similar axis ratios in the central regions but different halos intrinsic shapes, as well as different realizations in how the transition between central-oblate regions and triaxial halos occurs:
The Sérsic model (Model 1) is a one component model built using the three-dimensional Sérsic deprojection proposed by Lima et al. (1999) with Sérsic index n = 4 and variable flattening. The effective radius of the two-dimensional profile is set equal to the average of the observed Re = 50 arcsec. The transition radius is also the average of the measured values for the FRs: RT = 1.8 Re. We used (q = 0.3, p = 1) for the inner axis ratios, as measured by Weijmans et al. (2014) and Foster et al. (2017). For the outer regions we choose (q = 0.6, p = 0.9), close to values found by Weijmans et al. (2014) for the SRs. The variation between inner and outer values of flattening is modeled by an arctangent function; the width of the radial transition is chosen to be 50 arcsec (mean ΔRT, Sect. 8.6).
The cored Sérsic halo plus disk model (Model 2) is a two component model built from the sum of deprojections of an n = 4 spheroid and n = 1 spheroidal-exponential disk as in Lima et al. (1999), but we added a core with radius Rcore = RT = 1.8 × 50 arcsec to the deprojected n = 4 profile. Both the spheroid and the disk have constant flattening: (q = 0.6, p = 0.9) for the former, (q = 0.3, p = 1) for the latter. The horizontal scale-height of the disk is such that 1.67 h = RT, which means that the transition radius is equal to the half-light radius of the disk, as qualitatively observed in Sect. 7.3. The effective radius of the two-dimensional profile of the spheroid is Re = 150 arcsec. The luminosity density of the disk is scaled so that it equals the luminosity density of the spheroid at r = RT, hence in this model the disk component dominates the luminosity density from the center out to RT. This choice makes the total integrated light of the disk inside r = RT circa 3.5 times the total luminosity of the spheroidal component inside RT. The intrinsic axis ratios of the spheroid are (q = 0.6, p = 0.9), those of the disk are (q = 0.3, p = 1).
The maximally triaxial cored Sérsic halo plus disk model (Model 3) is built as Model 2 but with axis ratios (q = 0.6, p = 0.8) for the halo.
Model 4 has a strongly flattened triaxial halo plus disk. The model is built as Model 2 with a cored Sérsic halo, but the axis ratios are (q = 0.4, p = 0.8).
Each model is observed at 100 random viewing angles. We chose a coordinate system with axes (x, y, z) aligned, respectively, with the major, the intermediate, and the minor axis of model ellipsoids, and called ϕ and θ the azimuthal and polar angles that define the direction of the LOS. We choose the LOS by random samplings of the solid angle centered on the center of the ellipsoids dΩ = sin θdθdϕ. This makes the probability of observing the galaxy face-on (i.e. θ = 0) lower with respect to edge-on (θ = 90). The models, projected on a plane orthogonal to the LOS, are fitted with ellipses using the IRAF task ELLIPSE (Tody 1993), to derive surface brightness, ellipticity and position angle profiles.
Figure B.2 shows the result of this analysis on three models for six different values of θ in bins of 15 degrees. The shapes of the model ellipticity and position angle profiles are qualitatively similar to the observed profiles in Fig. B.1. Large photometric twists (> 10 degrees) are observed for viewing angles θ ≲ 50 degrees for Models 1 and 2, and for θ ≲ 65 degrees for Models 3 and 4. The rate of occurrence of large twists is of order ∼30% for our models (45% for Model 3), as shown also in Fig. 10 in Sect. 8.4 where we report the maximum twist versus the mean ellipticity. The distribution of the models in this diagram represent well the location of the ePN.S FRs, for which we observe a fraction 37% having photometric twists larger than 10 degrees. This analysis based on simple triaxial photometric models shows that the presence of small photometric twists, as typically observed for most of the FRs, is consistent with the presence of a triaxial halo. This means that it is likely that detailed individual models of these galaxies can be constructed that are consistent with the measured kinematic and photometric twist angles.
 |
Fig. B.2. Surface brightness, position angle, and ellipticity profiles for three photometric models described in this Appendix B.2, at different inclinations θ (θ = 0 for face-on, θ = 90 edge-on). For each photometric model, we show one random projection in each of six intervals Δθ = 15 degrees, starting from near face-on (Δθ = 0−15 degrees, darkest color profile), through Δθ = 15–30 degrees, etc., to near edge-on (Δθ = 75–90 degrees, lightest profile). These Δθ intervals represent 3%, 10%, 20%, 19%, 21%, 27% of 100 random directions, from face-on (darkest) to edge-on (lightest profiles). |
Appendix C: Notes on single galaxies and comparison with the literature
C.1. Fast rotators
NGC 0584. This is the brightest member of a small cluster containing mostly E galaxies (van den Bergh 1961). It is classified as a E4 in the NED catalog, but seems to contain a disk structure (Michard & Marchal 1994). Our PN kinematic data show that the galaxy halo rotates with at least ∼50 km s−1 along the photometric major axis, and has a velocity dispersion of ∼100 km s−1. The galaxy has central ellipticity ϵ ∼ 0.4 which falls to ∼0.1 at 150″ ∼5Re from whereon ϵ increases again. The photometry shows pronounced isophote twist starting at ∼1Re, which steepens beyond 5Re. Both the outer increase in ellipticity and the rapid outer isophote twist may be related to the nearby companion galaxy, NGC 0586; therefore we consider only the region where the ellipticity decreases as intrinsic to the galaxy.
NGC 0821. This is a field E6 galaxy. The ATLAS3D velocity field (Emsellem et al. 2004) maps the inner regions of the galaxy where it behaves like a regular rotator along the photometric major axis. The PNe sample, instead, probes the kinematics from 1 to 5Re and show a sustained rotation along the photometric minor axis with a maximum amplitude of 51 ± 16 km s−1, suggesting the triaxiality of the object. No rotation is detected along the major axis. The long-slit data from Proctor et al. (2009) and the integral field map of Arnold et al. (2014) agree in detecting rotation along the photometric major axis, with decreasing amplitude (80 km s−1 at 0.3Re to very slow rotation at R < 2Re). They do not detect any rotation along the minor axis, but their data do not extend far beyond 1.5Re along that axis. The kinemetry of Foster et al. (2016), based on the same data used by Arnold et al. (2014) but with a more careful treatment of outliers, shows a radial twist of the PAkin between 40 and 60 arcsec toward the same position angle measured from the PNe. Long slit data from Weijmans et al. (2009) and Forestell & Gebhardt (2010) also show some minor axis rotation at large radii. PN data are consistent with the kinematics of the blue GCs (see Pota et al. 2013), which are found to rotate at ∼85 km s−1 along a direction consistent with the photometric minor axis. The red GCs instead appear to faintly counter-rotate with respect to the host galaxy stars. The outer gradient of the velocity dispersion radial profile has been debated in the literature, with implications on the inferred dark matter content of the galaxy. The PN data combined with the long slit stellar kinematics show a decrease of the velocity dispersion as a function of radius, consistently as both red and blue GCs show, while Proctor et al. (2009) and Forestell & Gebhardt (2010) found a flat profile within 100 arcsec.
NGC 1023. This is a barred lenticular galaxy (SB0), brightest member of a group of 13 galaxies (Tonry et al. 2001). It has a small companion NGC 1023A, which is probably interacting with the main galaxy (Sancisi et al. 1984), but it is likely too small to cause significant disruptions in the dynamical state of the main galaxy (Noordermeer et al. 2008). The ATLAS3D velocity map (Emsellem et al. 2004) covers the innermost regions of the galaxy, up to half effective radii, and displays rotation with maximum amplitude of ∼120 km s−1 and strong twist of the zero-velocity line. The stellar kinematics along the major axis of Debattista et al. (2002) and Boardman et al. (2017) show that the rotation continues to increase mildly in the outer regions exceeding 200 km s−1 beyond 2Re. Both the PN and SLUGGS (Arnold et al. 2014) velocity maps show decreasing rotation beyond 3Re, (see also Noordermeer et al. 2008; Coccato et al. 2009; Cortesi et al. 2013b). The galaxy does not show any twist of the kinematic position angle or any misalignment with the photometric axis. The non zero third order harmonics amplitudes describe a rather cylindrical velocity field. The velocity dispersion map shows minimum values (σ∼40 km s−1) at the location of the disk, while the outermost (bulge) PNe are hotter (σ∼120 km s−1). The photometric position angle profile is influenced by the presence of the bar at R < 100″ (Barbon & Capaccioli 1975), therefore we excluded these regions from our discussion of the photometric twists.
NGC 1316. This is a giant elliptical (also classified as a peculiar S0), member of the Fornax cluster (Fornax A). NGC 1316 is a known merger remnant. Its photometric substructures were mapped for the first time by Schweizer (1980), and were recently studied by Iodice et al. (2017). The PN velocity field is highly asymmetric, showing that the galaxy is in a non-equilibrium phase. The modeling with a point-symmetric rotation model gives an approximate description of the properties of the galaxy. The fit of the a0(R) parameter of the rotation model (see Eq. (10)) in radial bins shows the presence of peculiar bulk motions in groups of PNe. There is no kinematics from integral field spectroscopy in literature, and the comparison with the long-slit observations from Bedregal et al. (2006) shows general good agreement with our data in the regions of overlap. The PNe in the halo of NGC 1316 (Fig. C.1) reveal that the galaxy rotates along the major axis with an amplitude of ∼65 km s−1, as already observed by Arnaboldi et al. (1998), McNeil-Moylan et al. (2012). The structures in the velocity field can be spatially associated with corresponding surface brightness features in the same location. There is an overdensity of PNe on the north-eastern part, co-located spatially with the ripple R4 (the designations of the photometric features are from Schweizer 1980, and their positions are indicated in black in Fig. C.1), with velocities that do not have a point symmetric counterpart. Other groups of PNe that result in non-point-symmetric velocities are those possibly related with the loop L1, on the south-west side, and to the plume P in the north-west. Figure 2 shows that the PNe of NGC 1316 in the innermost radial bin (∼100 arcsec) have a velocity offset of ∼150 km s−1 with respect to the systemic velocity. This is produced by a group of relatively slower PNe with mean velocity ∼1325 km s−1 and dispersion ∼60 km s−1 (highlighted in Fig. C.1 with white circles, along with the photometric feature O1 found by Richtler et al. 2014, in red). These PNe are not associated with any substructures in the light, and the fact that they are very localized in the phase space challenges (but does not rule out) the possibility that they could be contaminants. More likely this kinematic feature is the result of a combination of spatial incompleteness and differential absorption from localized dust in the galaxy, producing local lacks of detections in the phase space and so more negative smoothed velocities Ṽ A more detailed study is beyond the scope of this paper.
NGC 1344. This galaxy, also known as NGC 1340, is an E5 elliptical belonging to the Fornax cluster. It is characterized by the presence of internal and external concentric shells (Malin & Carter 1980), as consequences of a recent merger activity. The smoothed velocity field does not deviate from point symmetry, however it shows that the galaxy in the outskirts rolls around the photometric major axis. The velocity dispersion field shows a gently decreasing profile. Unfortunately there is no integral field stellar kinematics available for a comparison with the PNe kinematics. The long slit stellar kinematics (Teodorescu et al. 2005) show sustained rotation along the photometric major axis that reaches ∼100 km s−1 at 1.3Re and a decreasing velocity dispersion. The σ values from the spectroscopy are in agreement with those found with the PN data. We do not detect such an strong rotation, probably because of the different radial coverage of the PN data.
NGC 2768. This S0 is a field galaxy (Madore et al. 2004) or member of a poor group (Fouque et al. 1992). NGC 2768 has a cylindrical velocity field (Emsellem et al. 2004) whose amplitude remains constant at around ∼130 km s−1 from the innermost regions (Emsellem et al. 2004) to the outskirts (see Proctor et al. 2009; Pota et al. 2013). Our velocity map is in good agreement with that presented by Arnold et al. (2014) and extends it beyond 6Re. There is some discrepancy between the PN Vrot and the kinemetry fit from Foster et al. (2016) in the innermost radial bins where the disk strongly dominates. This is due to the fact that the smoothed PN velocity field in these bins is an average over the fast rotating PNe in the disk and the more slowly rotating PNe from the spheroid. A kinematic study of the different components of this galaxy was published by Cortesi et al. (2013b). At larger radii (r ≳ 3Re) the contribution of the disk weakens and the PN kinematics trace the spheroid. In this region we find a constant sustained (V ∼ 130 km s−1) rotation along the photometric major axis. The velocity dispersion profile is flat at ∼140 km s−1. The PN smoothed velocity field of NGC 2768 shows localized, small scale deviations from point symmetry. These asymmetries do not influence the kinematic analysis, but we used the unfolded catalog to build the velocity fields. The light distribution shows asymmetries beyond ∼20 kpc radius (Duc et al. 2015) which cause an increased isophote twist beyond 3Re = 186″ ∼ 20 kpc. The PN velocity field is aligned with the major axis except in the last bin which could be related to these asymmetries. Therefore the galaxy is classified as consistent with axisymmetry. The PN kinematics agrees with that of GCs. Pota et al. (2013) found significant rotation only for the red GCs along the photometric major axis and with constant amplitude. Their velocity dispersion decreases with radius.
NGC 2974. This is an elliptical (E4) field galaxy. Its kinematics was mapped by the SAURON survey (Emsellem et al. 2004), showing that the galaxy is rotating at ∼120 km s−1 along the photometric major axis, while the velocity dispersion has a steep decreasing profile. PN kinematic data show that the galaxy halo rotates at least at ∼70 km s−1 along the photometric major axis, and has a velocity dispersion of 150 km s−1.
NGC 3115. This is an S0 associated with a loose group of galaxies (Fouque et al. 1992). It has a nearly edge-on disk (i = 86 degrees) which flares outward (Capaccioli et al. 1987). The long slit spectroscopy from Norris et al. (2006) and the IFS observations of Guérou et al. (2016) show that the rotation velocity increases steeply from the innermost regions to ∼230 km s−1 around ∼1Re = 93″. The major axis profile from Guérou et al. (2016) offset by 20 arcsec along the minor axis show that also the spheroidal component has pronounced rotation. The velocity dispersion field is colder (σ ∼ 120 km s−1) in the region dominated by the disk, and hotter along the minor axis (σ∼ 220 km s−1). The kinemetry of Foster et al. (2016) on SLUGGS data show that the amplitude of rotation decreases from ∼1Re outward. The PN data show a cylindrical velocity field with gently decreasing rotation amplitude reaching ∼120 km s−1 at ∼3Re, where the spheroid dominates. The PAkin has a constant misalignment of ∼10 ± 5 degrees with respect to PAphot. By comparison the kinemetry from Foster et al. (2016) in Fig. 6 has ∼ 5 ± 10 degrees misalignment at 200″ major axis radius, slightly offset from the PAphot in the same direction as the PNe, showing that both datasets agree within the errors. This misalignment is probably related to perturbations at the interface between the disk and the spheroid, visible as deviations from axisymmetry in the photometry of the disk component. Capaccioli et al. (1987) found that the spheroidal component of this galaxy shows a photometric twist of ∼4 degrees, from ∼45 degrees at 10 arcsec to ∼41 degrees at 350 arcsec. The disk instead flares (Fig. 23 from Capaccioli et al. 1987) and has a warp of few degrees (their Fig. 24) in the same direction of the PN velocity field. The same features are visible in the photometry of Guérou et al. (2016; their Fig. 11) and in new observations with the VST telescope (VEGAS survey, Iodice private communication). This shows that NGC 3115 is indeed a complicated case, and we therefore do not include it in the sample of galaxies with triaxial halo.
NGC 3377. It is an E6 galaxy in the Leo I group. The absorption line kinematics (Coccato et al. 2009; Emsellem et al. 2004; Foster et al. 2016) shows that the galaxy displays a disk-like rotation in the inner regions, which starts to decrease at ∼1.5Re. Our analysis of the PN kinematics shows that the decreasing trend continues out to large radii, where it becomes 16 ± 8 km s−1 at ∼4 Re and 11 ± 7 km s−1 beyond ∼7 Re. The kinematic major axis position angle twists with radius in the outskirts in agreement with Foster et al. (2016). The velocity dispersion at large radii decreases very gently with radius, from ∼80 km s−1 at 1 Re and to ≲60 km s−1 at 8 Re. This is consistent with the GC study of Pota et al. (2013), whose kinematics reaches ∼8 Re. While the red GCs show a constant rotation of ∼50 km s−1, the blue ones do not rotate significantly in agreement with the PNe. The velocity dispersion of the whole GC sample is consistent with that from PNe.
NGC 3379. This is the largest galaxy in the Leo I group, classified as an E1. The PN system of this galaxy is has been widely studied in literature (Ciardullo et al. 1993; Romanowsky et al. 2003; Sluis & Williams 2006). The velocity maps from Emsellem et al. (2004) reveal that the galaxy rotates regularly along its photometric major axis (
 ), while the velocity dispersion has a central peak of ∼220 km s−1 and it decreases to 180 km s−1 around 0.25 Re. Then, the long slit data of Statler & Smecker-Hane (1999) and Weijmans et al. (2009) show that the profile gently declines to ∼120 km s−1 at ∼2 Re. The PN smoothed velocity field is in good agreement with the inner kinematics and extends it to 6 Re. We find that the galaxy has a rotation along an axis that twists from the photometric major axis position angle (∼70° at ∼15 arcsec) toward higher values at large radii. We observe the onset of a rotation along the minor axis at ∼2.5 Re. This is reflected in the trend of the fitted kinematic position angle and in the amplitudes of the third order harmonics. The amplitude of this additional rotation is ∼30 km s−1. At the moment there are no integral field kinematic data covering these large distances from the center of the galaxy. The velocity dispersion map shows that the decline continues up to 6 Re where it reaches values around 70 km s−1.
), while the velocity dispersion has a central peak of ∼220 km s−1 and it decreases to 180 km s−1 around 0.25 Re. Then, the long slit data of Statler & Smecker-Hane (1999) and Weijmans et al. (2009) show that the profile gently declines to ∼120 km s−1 at ∼2 Re. The PN smoothed velocity field is in good agreement with the inner kinematics and extends it to 6 Re. We find that the galaxy has a rotation along an axis that twists from the photometric major axis position angle (∼70° at ∼15 arcsec) toward higher values at large radii. We observe the onset of a rotation along the minor axis at ∼2.5 Re. This is reflected in the trend of the fitted kinematic position angle and in the amplitudes of the third order harmonics. The amplitude of this additional rotation is ∼30 km s−1. At the moment there are no integral field kinematic data covering these large distances from the center of the galaxy. The velocity dispersion map shows that the decline continues up to 6 Re where it reaches values around 70 km s−1.NGC 3384. This lenticular galaxy is a member of the Leo I group (Fouque et al. 1992). We find a rotation velocity of 160 ± 7 km s−1 at ∼7 Re, consistent with the rotation amplitude published by Krajnović et al. (2011). We do not observe any twist of the kinematic position angle or any misalignment with the photometric one, and the motion is that of a regular rotator. The velocity dispersion map in Emsellem et al. (2004) shows that the σ has a double peak at the center (σ∼155 km s−1), and a declining profile that reaches ∼80 km s−1 at ∼0.5 Re. The PN data show a velocity dispersion of ∼80 km s−1. Cortesi et al. (2013b) performed a kinematic analysis of the disk and spheroid component separately. The photometric study of Meusinger & Ismail (2007) showed the presence of an “inner component” and “elongated” component, visible in the PAphot profiles as a local minimum at R = 3″ and a local maximum at R = 15″. Therefore we considered only the regions at R > 30″ in our discussion in Sect. 8.4.
NGC 3489. This S0 galaxy belongs to the Leo I group. The ATLAS3D kinematic map (Krajnović et al. 2011) shows a fast rotation along the photometric major axis, whose amplitude reaches ∼115 km s−1 at ∼1 Re. PN data show that the halo of this galaxy is also rotating at >40 km s−1. The dispersion is around 80 km s−1, consistent with Cappellari et al. (2011). We refer to Cortesi et al. (2013b) for a kinematic analysis of the disk and spheroid component separately.
NGC 4278. This a rather round elliptical galaxy (E1-2), member of the Coma I group. The ATLAS3D kinematic map Krajnović et al. (2011) shows that stars are regularly rotating only within 0.5 Re along a direction slightly offset from the photometric major axis, while there is very weak or no rotation farther out. The kinemetry of Foster et al. (2016) shows that the galaxy does not significantly rotate beyond 1 Re. The PN velocity field does not show any significant rotation, hence also the kinematic position angle is not very well defined. Pota et al. (2013) do not find any evidence of rotation for the metal rich GCs, while the blue metal poor GCs display a weak rotation in the outer regions, along a direction between the major and the minor axes. The velocity dispersion falls rapidly with radius from a central value of ∼270 km s−1 to ∼120 km s−1 at ∼2 Re (Bender et al. 1994; Emsellem et al. 2004; Foster et al. 2016). Our map shows values of σ almost constant at 130 km s−1, in good agreement with the literature.
NGC 4339. This is a member of the Virgo cluster, classified as intermediate type between E0 and S0. It is regular FR, showing no misalignment between the photometric and kinematic major axis (Cappellari et al. 2011). The PN motion agrees with the stellar kinematics showing a rotation of >20 km s−1 and a dispersion of 30 km s−1.
NGC 4473. This Virgo galaxy is an E5 disky elliptical. It is well known for its multicomponent central kinematics (Emsellem et al. 2004): it is a fast but non-regular rotator (
 , along the photometric major axis) and the velocity dispersion map displays a double peak, which have been interpreted as the presence of a counter-rotating disk (Cappellari et al. 2007), maybe formed in binary disk major mergers (Bois et al. 2011). We detect a low amplitude rotation of ∼30 km s−1 along a direction tilted with respect to the photometric major axis. The kinematics from integrated light of Foster et al. (2013) already proved this object to be triaxial. Our velocity dispersion map does show the double peaked structure along the major axis, where σ∼ 160 km s−1. The velocity dispersion decreases to ∼100 km s−1 at 10 Re.
, along the photometric major axis) and the velocity dispersion map displays a double peak, which have been interpreted as the presence of a counter-rotating disk (Cappellari et al. 2007), maybe formed in binary disk major mergers (Bois et al. 2011). We detect a low amplitude rotation of ∼30 km s−1 along a direction tilted with respect to the photometric major axis. The kinematics from integrated light of Foster et al. (2013) already proved this object to be triaxial. Our velocity dispersion map does show the double peaked structure along the major axis, where σ∼ 160 km s−1. The velocity dispersion decreases to ∼100 km s−1 at 10 Re.NGC 4494. This is an E1 galaxy in the NGC 4565 group. The velocity map from Krajnović et al. (2011) shows a kinematically distinct core. The galaxy rotates almost constantly at ∼60 km s−1 up to 2 Re (Napolitano et al. 2009; Foster et al. 2016). In the halo we find that this amplitude decreases with radius. There is evidence for an additional component rotating along the photometric minor axis at ∼25 km s−1, as also shown by the twist of the PAkin. The velocity dispersion field shows a peak at the center (σ∼150 km s−1), and then decreases to ∼80 km s−1 at R ≳ 5 Re, in very good agreement with the stellar kinematics. The four-fold structure that appears in the σ map is a result from smoothing procedure, and reflects some unresolved gradient in the velocity field. The trend of the rotation amplitude from PN kinematics seems to be confirmed by the kinematic map from Arnold et al. (2014), but their data do not extend out in radii enough to show any rotation along the minor axis. The kinematics of GCs is studied by Foster et al. (2011) out to ∼3.5 Re. They found that the metal poor GCs rotate with similar amplitude as the galaxy stars, while the metal-rich GCs show marginal rotation. The velocity dispersion profile of the global GC sample is consistent with that of the stars.
NGC 4564. NGC 4564 is an E4 galaxy in the Virgo cluster. It shows a prominent stellar disk along the apparent major axis, so that it has also been referred as an S0 (Michard & Marchal 1994). We agree with the stellar kinematic from Foster et al. (2016) and we extend it beyond 6 Re, where the galaxy is still clearly rotating along its photometric major axis (Vrot ∼ 95 km s−1). The velocity dispersion profile is decreasing, from the central peak of 180 km s−1 (Emsellem et al. 2004) to ∼70 km s−1 at 6 Re.
NGC 4594. NGC 4594, also known as “the Sombrero” (M 104), is an SAa galaxy in the Virgo cluster. It has an extremely bright bulge, while its disk contributes only 10% of the light (Burkhead 1986) and has pronounced dust lanes. Kinematics from line-profile measurements show that the galaxy rotates along its major axis reaching ∼250 km s−1 at ∼1 Re, where the rotation curve flattens to a constant amplitude (Kormendy & Illingworth 1982; van der Marel et al. 1994). The velocity dispersion declines from the central value of ∼ 280 km s−1 to values close to 100 km s−1 where the disk component dominates. The bulge, instead, has a dispersion remarkably constant at 210 km s−1. Our PN data extend beyond 4 Re, but there is a void in the detections along the major axis because of the dust lane. For this reason the PNe do not trace the fast rotating disk, and their kinematics is in very good agreement with the integrated light kinematics of Kormendy & Westpfahl (1989) from a slit parallel to the major axis, offset by 30 arcsec. Extinction effects are probably also responsible for the slight asymmetry of the smoothed velocity field, so the kinematic analysis is performed on the unfolded catalog. These asymmetries are localized and do not significantly influence the kinematic results. The only studies of the kinematics of this galaxy at large radii is from Bridges et al. (2007) and Dowell et al. (2014) using GCs. The latter sample distances out to 24′ with 360 tracers, finding little or no evidence of rotation in the GC system as a whole, and within the red and blue subpopulations. The photometry shows ellipticity less than 0.1 and a correspondingly uncertain large isophote twist beyond 350″ which we do not include in the photometric analysis.
NGC 4649. Also known as M 60, it is an E2 galaxy in the Virgo cluster. It forms a close optical pair with NGC 4647, but the lack of evidence of strong tidal interaction features (e.g., Young et al. 2006) suggests that the galaxies are at different distances. The ATLAS3D velocity map shows a regular, cylindrical rotation of ∼95 km s−1 (Krajnović et al. 2011), while the dispersion has a central peak of ∼370 km s−1 and it decreases to ∼260 km s−1 at 0.5 Re. The kinematic maps from Arnold et al. (2014) shows that the cylindrical rotation extends up to 2 Re, while there the dispersion is ∼120 km s−1. The PN data extend out to 5 Re. The smoothed PN velocity field shows that the amplitude of the rotation along the photometric major axis decreases with radius, and no rotation along the major axis is detected beyond 2 Re. In the outer regions, instead, the system rotates along a nearly orthogonal direction, suggesting a triaxial halo. The velocity dispersion is roughly constant at ∼200 km s−1 from 1 to 5 Re. We see a slight bump in the dispersion profile at 3Re, but it may be associated to an unresolved velocity gradient. There are several studies of the GC kinematics in NGC 4649. The most recent, with the largest sample is from Pota et al. (2015). The red GCs display a nearly constant rotation with radius along the photometric major axis. Interestingly they observe a dip in rotation velocity between 100 and 200 arcsec, where we observe the inner rotation decreasing also. The blue GCs also show hints of rotation at all radii, with lower amplitude, and generally along the major axis of the galaxy. Blue GCs also appear to have a minor axis rotating component at 300 arcsec, coinciding with the one found with the PNe. The velocity dispersion of GCs is constant at σ = 240 ± 30 km s−1.
NGC 4697. This is an E6 galaxy in the Virgo southern extension, belonging to a group of 18 galaxies (Garcia 1993). This galaxy has 535 PN detections by Méndez et al. (2001). In this dataset Sambhus et al. (2006) found evidence for two separate PN populations, with different luminosity functions, spatial distributions, and radial velocities. In particular the secondary population of PNe is found to be azimuthally unmixed and not in dynamical equilibrium. The velocity field shows a rotation along the photometric major axis with amplitude decreasing with radius from the maximum ∼90 km s−1 at 1 Re to ∼15 km s−1 at 2.5. There is a hint for an increase in the amplitude of rotation at larger distances (∼40 km s−1 at 4.5 Re). The kinematic position angle is constant, aligned with the photometric major axis. There is a variation of the PAkin profile at ∼3 Re, but we did not interpreted it as signature of a triaxial halo, as the present dataset still includes the secondary not-in-equilibrium population of PNe. The velocity dispersion steady declines with radius, from ∼180 km s−1 at 0.5 Re to ∼100 km s−1 at 4.5 Re. The kinematic maps from Krajnović et al. (2011) and Spiniello et al. (2015) show a regular disk-like rotation with a maximum amplitude of 111 km s−1, confirming the trend for the rotation amplitudes that we find. Arnold et al. (2014) also observes a clear decline of the rotation and of the velocity dispersion, in agreement with PN data.
NGC 4742. This is a field E4 galaxy. It is a faint object, so the number of PN detections is relatively low. We detect a rotation of at least ∼74 km s−1, in agreement with the stellar kinematics of Davies et al. (1983). The direction of rotation is along a direction misaligned with respect to the photometric position angle. The dispersion decreases from 100 km s−1 at 1.5 arcsec (Davies et al. 1983) to below 50 km s−1 in the outskirts. The photometric PA profile from Li et al. (2011) shows a jump inside ∼40″ which is in disagreement with Lauer et al. (1995) based on HST data. Because the PA from Lauer et al. (1995) agrees with the outer profile from Li et al. (2011) we therefore use combined ellipticity and PA profiles from both sources.
NGC 5128. Also known as Centaurus A, it is a giant elliptical (often classified as a peculiar lenticular) in the Centaurus group. It shows clear signs of its accretion history in tidal streams and shells (Malin et al. 1983; Peng et al. 2002; Crnojević et al. 2016), evidences of major nuclear activity (see e.g. Neumayer 2010), and jet-induced star forming regions (e.g., Rejkuba et al. 2002). Its kinematics probed by PNe reflects the presence of regions which are not in equilibrium, showing a highly asymmetric and rich in subcomponents velocity field. The fit of the a0(R) parameter of the rotation model (10) in radial bins shows the presence of peculiar bulk motions in groups of PNe. The galaxy shows a rotation along the photometric major axis (NE direction) with increasing amplitude, from ∼50 km s−1 at ∼200 arcsec (∼1.5 Re) till at least ∼150 km s−1 at 800 arcsec (∼5 Re). The system also displays strong rotation (∼100 km s−1) along the minor axis, revealing its triaxiality (see also Peng et al. 2004). The deviation from point-symmetry of the kinematics in almost all the radial bins is accompanied by several features in the light. In particular the outermost regions, from 700 arcsec outward, show the most important kinematic features (Coccato et al. 2013), in correspondence to the elongated structure (sketched with black contours in Fig. C.2) in light extending roughly along the radio jets (Haynes et al. 1983).
NGC 5866. NGC 5866 is an SA0 galaxy belonging to a loose group (Sengupta & Balasubramanyam 2006). It has a narrow, clear-cut dark lane, running along the disk at an angle with respect to the photometric major axis. It is a regular, disk-like rotator (Krajnović et al. 2011) with a maximum amplitude of ∼150–180 km s−1 Foster et al. (2016) at ∼2 Re, beyond which the rotation decreases to 110 km s−1 at ∼3 Re. Our velocity map shows that the galaxy keeps rotating at approximately constant speed (∼85 km s−1) at large radii (up to 9 Re), with a progressive twist of the kinematic position angle. The PN velocity dispersion map and velocity dispersion profile have values around 90 km s−1 that are constant within the errors from 2 up to 9 Re. We refer to Cortesi et al. (in prep.) for a kinematic study of the disk and spheroid components. The photometric position angle is constant from 30″ to 80″, then decreasing by ∼2 degrees until 160″ = 4.5 Re (Michard & Marchal 1993). Beyond 160″ the profile becomes more irregular which coincides with a flare or X-like structure on the deep image by Duc et al. (2015) that could be due to tidal debris along a radial orbit nearly aligned with the disk.
NGC 7457. This is a field S0. The velocity maps from Emsellem et al. (2004) and Arnold et al. (2014) show that this galaxy is a regular rotator along the major axis. Our PN velocity map shows that the rotation velocity is growing with radius, reaching 100 km s−1 at ∼3.5 Re. No twisting of the kinematic major axis is observed. The velocity dispersion is relatively low, around ∼60 km s−1 at 1 Re, ∼40 km s−1 at ∼3 Re. There is good agreement between the PN kinematics and the kinemetry from Foster et al. (2016).
 |
Fig. C.1. Smoothed velocity field and velocity dispersion field of NGC1316 shown on the DSS image; north is up, east is left. The circles highlight the PNe belonging to a structure in the phase space, discussed in the text. The black contours trace features in the surface brightness distribution (designations from Schweizer 1980). In red is marked the position of the feature O1 observed by Richtler et al. (2014). The arrow at the bottom right shows the direction of the PAphot. |
C.2. Slow rotators
NGC 1399. It is a CD galaxy in the Fornax I cluster. We observe a very low amplitude (30 ± 15 km s−1) rotation inside 1Re along the photometric minor axis, and a slow rotation also in the halo (R ∼ 4 Re), which almost counter-rotates with respect to the inner regions. The rotation velocity is also very low in the innermost regions as reported by integral light kinematics studies (e.g., Graham et al. 1998; Saglia et al. 2000; Loubser et al. 2008; Scott et al. 2014), which are in good agreement with the PN data. In particular the integral field map from Scott et al. (2014) shows that NGC 1399 does not display important ordered motions in the central regions, while at a radius of ∼30″ it rotates along the minor axis (∼45 km s−1). The velocity dispersion, instead, is relatively high: it rises steeply in the inner 10 arcsec, reaching ∼370 km s−1 at the center (e.g., Saglia et al. 2000), while at large radii (from ∼1 Re) the PN σ flattens at ≲200 km s−1. McNeil et al. (2010) showed that kinematics of the red GCs of NGC 1399 is in excellent agreement with the PNe.
NGC 3608. This is an E2 galaxy in the Leo II group. It is known to have a counter-rotating core (Jedrzejewski & Schechter 1988) in the central 0.27 Re, aligned with the photometric major axis and rotating at ∼20 km s−1 (Halliday et al. 2001; Emsellem et al. 2004). From ∼Re galaxy starts to rotate at approximately along the photometric major axis (Foster et al. 2016). The PN kinematics shows that the growing trend continues at larger radii, where the amplitude of rotation reaches ∼65 km s−1. The twist of the PAkin reveals that the system is triaxial. The velocity dispersion decreases from the central value of ∼220 km s−1 to 100 km s−1 at ∼1 Re (Halliday et al. 2001). We find a constant velocity dispersion profile in the halo (∼90 km s−1).
NGC 3923. This an E4-5 galaxy in a group of eight galaxies (Brough et al. 2006). We detect a cylindrical velocity field along an intermediate direction between the minor and the major axes, which rotate at ∼75 km s−1. The velocity dispersion is constant around 235 km s−1. Long-slit kinematics from Carter et al. (1998) inside ∼1 Re shows that NGC 3923 does not rotate significantly along the photometric major axis for R ≲ 0.5 Re, but it displays a weak rotation (∼20 km s−1) along the photometric minor axis. They also found a falling dispersion profile, from the central value of ∼285 km s−1 to ∼240 km s−1 at 0.7 Re. Norris et al. (2012) studied the kinematics of 79 GC/UCD extended to more than 6 Re. They do not show appreciable rotation, and their velocity dispersion seem constant with radius.
NGC 4365. It is an E3 galaxy, one of the brightest member of the Virgo cluster. It has a complex kinematic structure with a counter-rotating core (Bender 1988a), aligned with the photometric major axis, and a prolate rotation of ∼61 km s−1 (Davies et al. 2001), which indicates a triaxial potential. Our PN velocity field extends to 6 Re. The inner kinematics (R ≲ 2 Re) is compatible with no rotation. We do not detect the rolling about the minor axis that Arnold et al. (2014) report, probably because of the smoothing over the inner velocity gradients. We do measure a significant outer (R ≳ 3 Re) rotation of ∼50 km s−1 along the major axis, counter-rotating with respect to the kinematically decoupled core. The velocity dispersion map has almost constant values, around ∼150 km s−1, with slightly lower values in the region along the major axis (∼140 km s−1). The velocity dispersion measured by Davies et al. (2001) shows a inner value of >250 km s−1 which decreases to ∼185 km s−1 at 0.5 Re. Arnold et al. (2014) measure a σ∼ 150 km s−1 at 2 Re, consistent with the values found with PNe. Blom et al. (2012), studying the GC kinematics, found that the intermediate metallicity subpopulation (green) rotates along the photometric minor axis, as the stellar population at intermediate radii, while the red GCs rotate only at large radii along the photometric major axis in the opposite direction of the core of the galaxy, in agreement with the PN kinematics at large radii.
NGC 4374. Also known as M84, it is a bright E1 galaxy in the Virgo cluster. The galaxy does not show significant rotation in the innermost ∼0.4 Re, as reported by Emsellem et al. (2004) and Foster et al. (2016), while the velocity dispersion steeply decreases from 310 km s−1 at the center to ∼200 km s−1 at ∼1 Re. The PN velocity field shows evidence for rotation only at large radii (R ≳ 2 Re), with constant amplitude ∼60 km s−1 and along a direction compatible with the minor axis. The velocity dispersion is rather constant around ∼220 km s−1 up to 6 Re. Our kinematics is in agreement with that from the SLUGGS velocity maps (Arnold et al. 2014; Foster et al. 2016), but their data extend only to ∼2 Re. The long slit kinematics of Coccato et al. (2009) reaches almost 3 Re and agrees in showing no signs of rotation along the major axis, the onset of rotation along the minor, and constant velocity dispersion in the outer regions around ∼230 km s−1.
NGC 4472. NGC 4472 (M 49) is an E2 galaxy, the brightest object in the Virgo cluster. It is surrounded by a complex system of diffuse shells and other features in light which are evidences of its recent and still ongoing accretion activity (see Janowiecki et al. 2010; Arrigoni Battaia et al. 2012; Hartke et al. 2018). It is classified as a non regular rotator by Krajnović et al. (2011), who also found evidence for a counter-rotating core. From R ∼ 0.2 Re the galaxy rotates at ∼60 km s−1 (Cappellari et al. 2011; Veale et al. 2017). Beyond ∼3 Re the PN data show a complicated and out of equilibrium kinematics. The halo rotates along a direction compatible with the galaxy minor axis. This motion is neither point- nor axi-symmetric, and is dominated by the kinematics of the in-falling satellite, the dwarf UGC 7636. A visual inspection of the smoothed velocity field reveals that the main body of the galaxy would show major axis rotation once the PNe belonging to the satellite are excluded (see Hartke et al. 2018, for a detailed study). While the velocity dispersion profile is flat over 4 Re at ∼250 km s−1, we notice a high dispersion feature with σ ∼ 350 km s−1 in a position corresponding to the coordinates of UGC 7636.
NGC 4552. NGC 4552 (M 89) is an E0-1 galaxy in Virgo. It known to possess a kinematically distinct core, with the innermost region rotating at ∼30 km s−1, and the region outside 0.3 Re having very weak rotation (Simien & Prugniel 1997b; Emsellem et al. 2004). Our PN smoothed velocity field shows that the galaxy start rotating beyond 3 Re. The smoothed velocity field reveal that the rotation is about two perpendicular directions. This is reflected in the twist of the kinematic position angle with radius. The velocity dispersion map from the data is consistent with the one from the integrated light (Emsellem et al. 2004), and it shows constant values with radius, around 180 km s−1.
NGC 4636. This is an E0-1 galaxy in the Virgo cluster. The velocity map from Krajnović et al. (2011) does not show significant rotation in the innermost region (R < 0.25 Re). The velocity dispersion, instead, has a central value of ∼240 km s−1 and it decreases to 190 km s−1 at 0.25 Re. The long slit kinematics from Pu & Han (2011) show that the galaxy starts rotating along the minor axis at ∼40 arcsec (0.2 Re), and along the major axis at ∼85 arcsec (∼1 Re). The σ profile is gently decreasing along the minor axis, reaching ∼100 km s−1 at 0.5 Re, while it is rather flat along the major, around 190 km s−1, then it decreases to ∼150 km s−1 where the rotation starts. We detect a weak rotation (40 ± 15 km s−1) along a direction compatible with the minor axis. In addition, in the smoothed velocity map there is evidence for a rotation of comparable magnitude at larger radii (R ∼ 1 Re) around the major axis, in very good agreement with Pu & Han (2011). The PN velocity dispersion profile decreases abruptly from ∼180 km s−1 at R < 2 Re to ∼110 km s−1 at 3 Re. Schuberth et al. (2012) find a strong rotation signature for the blue GCs (V ∼ 88 km s−1 along the major axis, but in opposite direction with respect to the outermost PNe). The red GCs have a weaker rotation (V ∼ 30 km s−1)} along an axis that changes with being aligned with the minor axis to the photometric major axis, in agreement with the PN kinematics. For radii beyond 1.5 Re the axis of rotation remains constant along the direction of the major axis. The dispersion profile of the blue GC declines with radius, while the red GCs show values of σ∼135 km s−1.
NGC 5846. This is an E0 galaxy, the brightest member in a group of ten. Emsellem et al. (2004) detect a low rotation of ≲ 30 km s−1 and a high central dispersion of 255 km s−1. PN smoothed velocity field is consistent with low amplitude rotation. We find constant values for the velocity dispersion around 180 km s−1. The SLUGGS kinematic maps Arnold et al. (2014), Foster et al. (2016) are consistent with PN data. Pota et al. (2013) showed that neither the GC subpopulations show significant rotation. The velocity dispersion of the red GCs has a flat profile, around values comparable with those found for the PNe. The blue GCs have systematically higher σ∼260 km s−1.
 |
Fig. C.2. Smoothed velocity field and velocity dispersion field of NGC 5128 shown on the DSS image; north is up, east is left. Features in the surface brightness distribution spatially consistent with features in the PN kinematics are contoured in black. The arrow at the bottom left shows the direction of the PAphot. |
 |
Fig. C.3. Smoothed velocity field and velocity dispersion field of NGC 4472 shown on the DSS image; north is up, east is left. The black cross marks the position of the in-falling dwarf UGC 7636. The arrow at the bottom right shows the direction of the PAphot. |
Appendix D: Velocity and Velocity Dispersion Fields
Smoothed velocity and velocity dispersion fields. The maps are interpolated on a regular grid of coordinates, as described in Sect. 6.1. The fields are rotated such that the photometric major axis is horizontal (PAphot values are listed in Table 1); the orientation is specified by the direction of the arrows indicating north and east. The X and Y axes units are arc seconds. The elliptical contours displayed on the velocity fields are ellipses of constant ellipticity ϵ as given in Table 1, and of major axes radii equal to even multiples of Re (Table 1).
 |
Fig. D.1. Smoothed velocity and velocity dispersion fields. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
 |
Fig. D.1. continued. |
All Tables
Measured parameters and typical errors for the smoothed velocity and velocity dispersion fields.
All Figures
 |
Fig. 1. Distribution of the fitted Vrot and PAkin in one radial bin obtained from 1000 PN subsamples extracted for NGC 0821 and NGC 3379 (gray histograms). The red curves are Gaussians centered on the Vrot and PAkin fitted on the full dataset, and with dispersion given by the Monte Carlo simulations of the galaxy under study. The vertical solid lines show the position angle of the photometric major axis for the two galaxies; the dotted lines show the photometric minor axis. The values for PAphot are listed in Table 1. |
| In the text | |
 |
Fig. 2. Galaxies with deviations from point symmetry. Mean velocity Ṽ(R, ϕ) as a function of the PN eccentric anomaly ϕ, folded around ϕ = π, for each radial bin of NGC 1316, NGC 2768, NGC 4472, NGC 4594, NGC 4649, and NGC 5128. The black solid line is the fitted point-symmetric rotation model. The red points are the PN positions with 0 ≤ ϕi < π; the blue points are those located at π ≤ ϕi < 2π, with their velocity changed in sign and coordinate ϕ shifted by π, i.e. V(ϕ) are compared with −V(ϕ + π). The overlap of PNe of opposite sides shows possible asymmetries in the velocity fields. NGC 2768 and NGC 4594 show localized small scale deviations from point symmetry, that do not influence the kinematic analysis. NGC 1316, NGC 4472, and NGC 5128 have non-point-symmetric velocity fields. By comparison NGC 4649 is point-symmetric. |
| In the text | |
 |
Fig. 3. Top row: smoothed velocity fields of NGC 4494 and NGC 4552; bottom row: velocity dispersion fields. The fields are built using the folded catalogs, but only the positions of the actual PN data points are shown. The images in the background are from the Digitized Sky Survey (DSS); north is up, east is left. |
| In the text | |
 |
Fig. 4. Point symmetric galaxies. Mean velocity field Ṽ(R, ϕ) in elliptical annuli as a function of the PN eccentric anomaly ϕ, folded around ϕ = π for the FRs NGC 4473, NGC 4494, NGC 5866 and NGC 7457, and the SR NGC 4552 (colors as in Fig. 2). Ṽ(R, ϕ) is reconstructed using the folded catalogs, and shown at the position (Ri,ϕi) of the actually observed PNe. The solid lines are the best rotation model (see Eq. (10)) fit to the velocity field. |
| In the text | |
 |
Fig. 5. Fitted rotation velocities Vrot(R) (full circles) and third order harmonics amplitudes, c3(R) in green and s3(R) in orange, as functions of the major axis distance for SRs and FRs. The comparison values for Vrot from absorption line data from the literature are shown with colored stars. Whenever available we show kinemetric profiles (light blue stars); for the other galaxies we show velocities from long slit spectroscopy along the photometric major axis (red stars) or minor axis (green stars). The references are in Table 1. For NGC 4594 we show in addition the stellar kinematics from a slit along PAphot, offset by 30 arcsec (purple stars). The dashed vertical lines for the FRs show the disk half light radius R1/2, see Sect. 7.3. The red dot-dashed vertical lines report the radial transition range RT ± ΔRT, see Sect. 8.6. |
| In the text | |
 |
Fig. 6. Misalignments Ψ(R) (full circles) as function of the major axis distance for FRs and SRs. The horizontal solid line shows the Ψ = 0 axis. The light blue stars are the Ψ values calculated on PAkin from the kinemetry of Foster et al. (2016), Krajnović et al. (2008 and 2011); for the other galaxies the PAkin is not previously available in the literature. The red dot-dashed vertical lines report the radial transition range RT ± ΔRT, see Sect. 8.6. Signatures of triaxial halos are seen in NGC 0821, NGC 1344, NGC 1399, NGC 3377, NGC 3379, NGC 3608, NGC 3923, NGC 4365, NGC 4374, NGC 4472, NGC 4473, NGC 4494, NGC 4552, NGC 4636, NGC 4649, NGC 4742, NGC 5128, NGC 5846, and NGC 5866. |
| In the text | |
 |
Fig. 7. Azimuthally averaged velocity dispersion profiles as functions of the major axis distance in units of Re for SRs and FRs (full circles). The gray solid lines represent the profiles from the interpolated velocity fields with their errors (dashed lines, see text). The stars show dispersion from integrated light: when available we plot the kinemetric analysis of Foster et al. (2016) on the SLUGGS+ATLAS3D data in elliptical bins (light blue stars); for NGC 3384, NGC 3489, NGC 4339, NGC 4472, NGC 4552, and NGC 4636, we show azimuthally averaged profiles from ATLAS3D data (Cappellari et al. 2011; Emsellem et al. 2011); for the other galaxies we show data from long slit spectroscopy along PAphot (red stars, references in Table 1). For NGC 4594 we also plot the stellar velocity dispersion profile in a slit parallel to the major axis but 30 arcsec offset from the center (purple stars). |
| In the text | |
 |
Fig. 8. Rotation velocity profiles for the FRs with highest number of tracers along the major axis. The full circles show the fitted amplitude Vmaj.ax. on the PN velocity fields (see Eq. (12)). The red stars are stellar kinematics along the photometric major axis from the literature (references in Table 1). The PN kinematics of NGC 4594 is compared with the stellar kinematics from a slit parallel to the major axis, offset by 30 arcsec (purple stars). The orange vertical lines mark the sizes of the photometric disks (see text). NGC 4494 shows a decrease in Vmaj.ax. but there is no photometric evidence for a stellar disk. When the disk fades in the slowly rotating spheroid, the rotation velocity decreases. In addition, the PN rotation velocity may be lower than the values from absorption line spectroscopy at the same radii because of the smoothing that averages disk and spheroid PNe for near edge-on disks. |
| In the text | |
 |
Fig. 9. V/σ(Re) from absorption line data compared with V/σ(halo) from PN data. References for the absorption line data are in Table 1; for NGC 1399 and NGC 3923 data are available up to Re/2 and Re/4, respectively. The flattening of the ellipses used to plot the galaxies correspond to the ϵ values of Table 1. FRs and SRs are shown with different colors, as are the FR with triaxial halos. The gray open ellipses represent the galaxies (all FRs) with fewer tracers, for which our analysis provides a lower limit for V/σ(halo). The solid line traces equal values of V/σ(Re) and V/σ(halo). The orange circles shows the V/σ of simulated galaxies from Wu et al. (2014), divided by a factor 0.57 to rescale their two dimensional flux-weighted measurement to one-dimensional quantities (Cappellari et al. 2007). While the SRs show increased rotation in their halos, the majority of the FRs show a drop in rotation at large radii. |
| In the text | |
 |
Fig. 10. Upper panel: ellipticity distribution for the FRs. The histogram of the maximum measured ellipticity at R > 0.5 Re is in green; the histogram of the outermost measured values is in blue. The distributions show that the FRs tend to have halos rounder than their central regions. Lower panel: maximum photometric twist versus mean projected ellipticity for a subsample of the ePN.S FRs with extended photometric data (gray triangles; see text and Appendix B.1, references in Table 2). The errors reflect the scatter between contiguous data points in the photometric profiles. For the galaxies with indications for ongoing interactions in the outermost photometry (see Appendices B.1 and C) we estimated the mean ellipticity and maximum position angle twist both from the complete profiles (open symbols) and considering only the regions with regular photometry (filled symbols). For NGC 1023 and NGC 3384 we show quantities derived excluding the regions where the bar dominates. The horizontal dashed line marks ΔPAphot = 10 degrees. The statistical distribution of points is consistent with simple photometric triaxial models, shown each with 100 random projections (solid circles as described in the legend; see text and Appendix B.2). |
| In the text | |
 |
Fig. 11. EPN.S and ATLAS3D samples compared in the stellar mass versus ellipticity plane. The ATLAS3D sample of ETGs is displayed with gray open symbols (triangles for the FRs, circles for the SRs). For these galaxies we show the ellipticity values from Krajnović et al. (2011) and M* = MJAM = (M/L)JAM × Ltot,r from Cappellari et al. (2013b) as in their Eq. (28). The ePN.S galaxies are shown with full symbols: red circles for the SRs, blue triangles for the FRs, and green squares for the FRs with triaxial halos. For the ePN.S ETGs M* is the mean between MJAM (Cappellari et al. 2013b, when available), and the masses M*1 and M*2 reported in Table 2. The error bars on the mass show the rms scatter between these different mass determinations. The values for the ellipticity are listed in Table 1. |
| In the text | |
 |
Fig. 12. Transition radius in units of Re versus total stellar mass (open symbols: circles for SRs, triangles for FRs). The full symbols show the same quantities in bins of RT/Re. Different colors show the results of two different procedures for calculating the total stellar mass, see Table 2 for details. The shaded region shows the corresponding quantities from the simulations of Cooper et al. (2013), see text. |
| In the text | |
 |
Fig. 13. Transition radius in units of Rhalflight versus total stellar mass (open symbols: circles for SRs, triangles for FRs). The full symbols show the same quantities in bins of RT/Rhalflight. Different colors show the results of two different procedures for calculating the total stellar mass, see Table 2 for details. |
| In the text | |
 |
Fig. A.1. Smoothed velocity and velocity dispersion fields in the ePN.S field of view for a simulated ETG, traced by 10 000 particles, 400, and 200 stars after the convolution with a completeness function. For the 200 particle case, we show two typical statistical realizations (A and B) of the extracted sample, to illustrate the effects of the limited statistics on the smoothed quantities. The global features of the simulation are preserved in the different fields but, as expected, the spatial and velocity resolution of the local gradients is downgraded when the number of tracers decreases. The lower right panels display the fitted kinematic position angle PA, the rotation velocity Vrot, and the azimuthally averaged velocity dispersion σ in circular radial bins as function of radius. It is evident that the radial gradients are less resolved with fewer tracers, and that the amplitude of rotation for the case with 200 stars is oversmoothed. This happens because the kernel width is larger than the real spatial scale of the velocity gradients due to the sparse distribution of the tracers. The blue full circles show a simulation with higher V/σ ratio and two of its typical statistical realizations sampled by 200 objects to illustrate how of the accuracy of the reconstructed velocity amplitudes depends on the statistical noise. Errors for the kinematic profiles are determined from Monte Carlo simulations using the smoothed velocity and velocity dispersion fields as described in Sect. 3.2.2. |
| In the text | |
 |
Fig. B.1. Position angle (red triangles, y axis on the left) and ellipticity profiles (dark blue squares, y axis on the right) for the subsample of the ePN.S galaxies with literature photometry reaching at least 4Re (references in Table 2). The NGCnumbers of the galaxies are shown in red for the SRs, in blue for the FRs, and in green for the FRs with triaxial halos. The open symbols and the black vertical line for NGC0584, 2768, 5866 mark regions that are probably affected by ongoing interactions, and for NGC1023 and NGC3384 the regions affected by the presence of other photometric components, e.g. the bar (see Appendix C). For NGC4594 we excluded the data beyond 350″ where the small ellipticity corresponds to large uncertainties in the PAphot measurements. The horizontal lines report the PAphot (solid line) and ⋴ (dotted line) with values listed in Table 1. The red dot-dashed vertical lines show the kinematic transition range RT ± ΔRT from Sect. 8.6. |
| In the text | |
 |
Fig. B.2. Surface brightness, position angle, and ellipticity profiles for three photometric models described in this Appendix B.2, at different inclinations θ (θ = 0 for face-on, θ = 90 edge-on). For each photometric model, we show one random projection in each of six intervals Δθ = 15 degrees, starting from near face-on (Δθ = 0−15 degrees, darkest color profile), through Δθ = 15–30 degrees, etc., to near edge-on (Δθ = 75–90 degrees, lightest profile). These Δθ intervals represent 3%, 10%, 20%, 19%, 21%, 27% of 100 random directions, from face-on (darkest) to edge-on (lightest profiles). |
| In the text | |
 |
Fig. C.1. Smoothed velocity field and velocity dispersion field of NGC1316 shown on the DSS image; north is up, east is left. The circles highlight the PNe belonging to a structure in the phase space, discussed in the text. The black contours trace features in the surface brightness distribution (designations from Schweizer 1980). In red is marked the position of the feature O1 observed by Richtler et al. (2014). The arrow at the bottom right shows the direction of the PAphot. |
| In the text | |
 |
Fig. C.2. Smoothed velocity field and velocity dispersion field of NGC 5128 shown on the DSS image; north is up, east is left. Features in the surface brightness distribution spatially consistent with features in the PN kinematics are contoured in black. The arrow at the bottom left shows the direction of the PAphot. |
| In the text | |
 |
Fig. C.3. Smoothed velocity field and velocity dispersion field of NGC 4472 shown on the DSS image; north is up, east is left. The black cross marks the position of the in-falling dwarf UGC 7636. The arrow at the bottom right shows the direction of the PAphot. |
| In the text | |
 |
Fig. D.1. Smoothed velocity and velocity dispersion fields. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
 |
Fig. D.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.