| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 62 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201731449 | |
| Published online | 18 January 2018 | |
Observational properties of massive black hole binary progenitors
1 Institut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Str. 24/25, 14476 Potsdam, Germany
e-mail: rhainich@astro.physik.uni-potsdam.de
2 Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
3 Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA) and Department of Physics and Astronomy, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA
4 Department of Physics, University of Auckland, Private Bag 92019, Auckland, New Zealand
Received: 25 June 2017
Accepted: 26 October 2017
Context. The first directly detected gravitational waves (GW 150914) were emitted by two coalescing black holes (BHs) with masses of ≈ 36 M⊙ and ≈ 29 M⊙. Several scenarios have been proposed to put this detection into an astrophysical context. The evolution of an isolated massive binary system is among commonly considered models.
Aims. Various groups have performed detailed binary-evolution calculations that lead to BH merger events. However, the question remains open as to whether binary systems with the predicted properties really exist. The aim of this paper is to help observers to close this gap by providing spectral characteristics of massive binary BH progenitors during a phase where at least one of the companions is still non-degenerate.
Methods. Stellar evolution models predict fundamental stellar parameters. Using these as input for our stellar atmosphere code (Potsdam Wolf-Rayet), we compute a set of models for selected evolutionary stages of massive merging BH progenitors at different metallicities.
Results. The synthetic spectra obtained from our atmosphere calculations reveal that progenitors of massive BH merger events start their lives as O2-3V stars that evolve to early-type blue supergiants before they undergo core-collapse during the Wolf-Rayet phase. When the primary has collapsed, the remaining system will appear as a wind-fed high-mass X-ray binary. Based on our atmosphere models, we provide feedback parameters, broad band magnitudes, and spectral templates that should help to identify such binaries in the future.
Conclusions. While the predicted parameter space for massive BH binary progenitors is partly realized in nature, none of the known massive binaries match our synthetic spectra of massive BH binary progenitors exactly. Comparisons of empirically determined mass-loss rates with those assumed by evolution calculations reveal significant differences. The consideration of the empirical mass-loss rates in evolution calculations will possibly entail a shift of the maximum in the predicted binary-BH merger rate to higher metallicities, that is, more candidates should be expected in our cosmic neighborhood than previously assumed.
Key words: gravitational waves / binaries: close / stars: early-type / stars: atmospheres / stars: winds, outflows / stars: mass-loss
© ESO, 2018
1. Introduction
The first direct detection of gravitational waves (GW), GW 150914, proved to be the echo of two coalescing black holes (BH) with unexpectedly high masses of ≈ 29 M⊙ and ≈ 36 M⊙ (Abbott et al. 2016c). The luminosity distance of the event, ≈ 400 Mpc, showed that such massive BHs are present in our cosmic neighborhood. The most recent GW event GW170104 was due to merging BHs with masses of ≈ 32 M⊙ and ≈ 19 M⊙ at a luminosity distance of ≈ 900 Mpc (Abbott et al. 2017). Yet, the masses of accreting BHs in X-ray binaries in ours and neighboring galaxies are much smaller (Özel et al. 2010) – they are compatible to those measured in the second reported GW event, GW 151226 with ≈ 14 M⊙ and ≈ 8 M⊙ (Abbott et al. 2016b). At present, it is unclear if the massive BHs detected by GW observatories are remnants of massive stars analogous to the BHs residing in stellar X-ray binaries.
Hence, among the most urgent questions in the new field of gravitational wave astrophysics is to establish whether massive stars, as we presently know and understand them, could be the progenitors of massive BHs. Answering this question could help to discriminating among the families of models put forward to explain the first GW detections.
A large theoretical work is underway to explain GW observations. The majority of the proposed models invoke massive star evolution. Fast evolutionary channels leading to massive BH mergers are related to massive star binaries and could explain either of the detected GW events (e.g., Mennekens & Vanbeveren 2014; Abbott et al. 2016a; Belczynski et al. 2016a,b; Marchant et al. 2016; Mandel & de Mink 2016; Stevenson et al. 2017). In this case, the evolutionary time scale from the stellar binary formation until the double BH merger is about one billion years. If GW events are the result of this fast channel, potential progenitors of massive BHs must be present among observed stellar populations.
Slow evolutionary channels require a time period one order of magnitude longer for the BH merger. These channels also commonly invoke massive star progenitors of BHs, such as wide and eccentric massive star binaries (Eldridge & Stanway 2016) or dynamic interactions in dense star clusters (e.g., Rodriguez et al. 2015). In this case one can also expect that the progenitor stars could, in principle, be identified among present-day massive stars.
Alternative models include Population III stars (Inayoshi et al. 2017) and primordial BHs (e.g., Bird et al. 2016). These models do not require the existence of Population I massive stars capable of collapsing into massive BHs.
The prevalence of stellar versus cosmological origin could be distinguished using conventional observations. We need to search and find massive BH progenitors or rule out their current presence.
The primary goal of this paper is to predict what the potential massive BH and GW event progenitor stars should look like and how they could be identified. On this basis, the expected massive BH progenitor properties can be compared to those of known massive stars. If actual stars with the predicted stellar parameters are found, this will provide strong empirical validation for the corresponding evolutionary channel.
To achieve this goal, we use the theoretical predictions of the progenitor properties as input for state-of-the-art stellar atmosphere models and compute synthetic spectra. We provide photometric fluxes, spectral types, stellar and feedback parameters that can be used to identify such objects and to evaluate their impact on the Galactic ecology. Based on our templates, we discuss whether stars with such properties are already known. In this paper, we focus on progenitors of GW 150914-like events.
The paper is structured as follows: in Sects. 2 and 3, we describe the stellar atmosphere models, the stellar evolution calculations used in this study, and the calculated sets of synthetic spectra. Section 4 constitutes a thorough comparison of the parameters and templates obtained in this study with observations. The X-ray properties of the binary BH progenitors are discussed in Sect. 5, while the feedback provided by those objects is described in Sect. 6. The summary and the conclusions are given in Sect. 7. Additional tables and synthetic spectra are presented in Appendices A and B, respectively.
2. The stellar atmosphere models
The synthetic spectra presented in this paper are calculated with the state-of-the-art Potsdam Wolf-Rayet (PoWR) code for expanding stellar atmospheres1. This code assumes a star with a spherically stationary symmetric outflow and fully accounts for deviations from the local thermodynamic equilibrium (non-LTE), wind inhomogeneities, and iron line blanketing. The code solves the radiative transfer equation in the co-moving frame consistently with the rate equations for statistical equilibrium, while ensuring energy conservation. Detailed information on the assumptions and numerical methods used in the code can be found in Gräfener et al. (2002), Hamann & Gräfener (2003, 2004), and Sander et al. (2015).
The stellar radius R∗ is the input parameter that sets the inner boundary of the model. It is defined as the radius where the Rosseland continuum optical depth reaches τross = 20. This radius is – to a good approximation – coincident with the radius of the star in hydrostatic equilibrium, enabling us to use the output from evolution models as input in our atmosphere models. The outer atmosphere boundary is set to Rmax = 100 R∗ for O-type models and 1000 R∗ for WR models, which proved to be sufficient. The stellar temperature T∗ is the effective temperature, corresponding to R∗, and the luminosity L via the Stefan-Boltzmann law 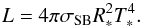 (1)In the main model iteration, we account for the random motion within the stellar atmosphere by assuming Gaussian line profiles with a Doppler width of 30 km s-1 and 100 km s-1 for the O and WR stars, respectively. This velocity is disassembled in its components, a depth-dependent thermal motion and a micro turbulence velocity ξ, during the final calculation of the emergent spectrum. The latter is assumed to grow with the wind velocity up to a value of ξ(Rmax) = 0.1 v∞, while it is set to ξ(R∗) = 20 km s-1 and ξ(R∗) = 100 km s-1 at the inner boundary for the models that resemble O and WR stars, respectively.
(1)In the main model iteration, we account for the random motion within the stellar atmosphere by assuming Gaussian line profiles with a Doppler width of 30 km s-1 and 100 km s-1 for the O and WR stars, respectively. This velocity is disassembled in its components, a depth-dependent thermal motion and a micro turbulence velocity ξ, during the final calculation of the emergent spectrum. The latter is assumed to grow with the wind velocity up to a value of ξ(Rmax) = 0.1 v∞, while it is set to ξ(R∗) = 20 km s-1 and ξ(R∗) = 100 km s-1 at the inner boundary for the models that resemble O and WR stars, respectively.
In O-type models, the quasi-hydrostatic part of the atmosphere is calculated self-consistently to fulfill the hydrostatic equation (Sander et al. 2015). In the supersonic part, corresponding to the stellar wind, v(r) is prescribed by the so-called β-law (Castor & Lamers 1979; Pauldrach et al. 1986). For O-type stars, the finite disk corrected CAK theory (Castor et al. 1975; Pauldrach et al. 1986) predicts a β exponent of about 0.8 (e.g., Kudritzki et al. 1989), which is consistent with the results obtained from the propagation of clumps in O-type star winds (e.g., Eversberg et al. 1998). This value is therefore assumed in the calculation of the O-type star models. For WR stars, different estimates of the β exponent are available in the literature. While empirical studies suggest a velocity law with β = 1.0 for hydrogen rich WR stars and a β in excess of four for more evolved WR stars (Lépine & Moffat 1999; Dessart & Owocki 2005), theoretical predictions based on hydrodynamic consistent stellar atmosphere models point to a more complex velocity law in the form of a double-β law (Hillier & Miller 1999; Gräfener & Hamann 2005). Therefore, models that resemble hydrogen-rich WN stars are calculated with β = 1.0, while models of more evolved WR stars are calculated with a double-β law in the form as presented in Todt et al. (2015).
PoWR model atmospheres account for wind inhomogeneities in the form of the so-called “microclumping” approximation, assuming optically thin clumps that fill a volume fraction fV, with a void interclump medium (Hillier 1991; Hamann & Koesterke 1998). The clumping factor 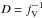 describes the density contrast between the clumps and a homogeneous model with the same mass-loss rate Ṁ. The clumping factor can have a radial dependency, that is, D(r). For all models presented in this paper, we assume that clumping starts at the sonic point, increases outwards, and reaches its maximum with D = 10 (fV = 0.1) at a radius of 10 R∗ (Runacres & Owocki 2002). This choice of the maximum clumping factor is motivated by theoretical simulations (e.g., Feldmeier et al. 1997) as well as spectral analyses (e.g., Hainich et al. 2014, 2015), although larger values, especially for O-type stars, are sometimes claimed in the literature (e.g., Bouret et al. 2012).
describes the density contrast between the clumps and a homogeneous model with the same mass-loss rate Ṁ. The clumping factor can have a radial dependency, that is, D(r). For all models presented in this paper, we assume that clumping starts at the sonic point, increases outwards, and reaches its maximum with D = 10 (fV = 0.1) at a radius of 10 R∗ (Runacres & Owocki 2002). This choice of the maximum clumping factor is motivated by theoretical simulations (e.g., Feldmeier et al. 1997) as well as spectral analyses (e.g., Hainich et al. 2014, 2015), although larger values, especially for O-type stars, are sometimes claimed in the literature (e.g., Bouret et al. 2012).
For the non-LTE calculations, detailed model atoms of H, He, C, N, O, Mg, Si, P, and S are used (see Table A.1 for details). For the iron group elements Fe, Sc, Ti, V, Cr, Mn, Co, and Ni, a “superlevel approach” is applied where thousands of levels and millions of line transitions are grouped into superlevels with pre-calculated, complex functions for the transition cross-sections (see Gräfener et al. 2002).
One output of binary evolution models are tracks on the Hertzsprung-Russell Diagram (HRD) that describe the changes in fundamental stellar parameters, T∗, R∗, and L, in the course of stellar evolution. These parameters are used as an input for our PoWR atmosphere calculations. The mass-loss rates and chemical abundances for each element are also adopted from the stellar evolution models. Since the BPASS models do not consider the elements Mg, Si, P, and S, the corresponding solar abundances (Asplund et al. 2009) are used and scaled according to the metallicity of the stellar evolution tracks.
Model spectra of the binary systems are computed by adding up the absolute line spectra of the individual binary components. Afterwards, this combined spectrum is normalized with the composite continuum. We neglect all asymmetries that can occur in close binary systems or during Roche lobe overflow (RLOF), such as wind-wind collision zones or accretion flows.
3. Binary evolution models
In this paper, we make use of the binary-evolution tracks computed by two independent groups and codes, Marchant et al. (2016) and Eldridge & Stanway (2016). Both models predict evolutionary paths leading to binary BHs that would merge producing an event similar to GW 150914. The choice of these two models is primarily motivated by their detailed predictions of the fundamental stellar parameters at different evolutionary stages, which are required for the computations of synthetic spectra and comparisons with observed stellar populations.
Any massive star evolution-model depends on a number of input parameters, some of the most important being the initial metallicity Z and stellar wind mass-loss rate Ṁ(Z) at the various phases of stellar evolution. The mass loss largely determines whether the star will maintain its fast rotation and undergo chemical mixing, when and how its core will collapse, how the orbit evolves, and what the final BH mass will be.
Fast rotating massive stars experience strong internal mixing that can lead to quasi-chemically homogeneous evolution (QCHE; Heger & Langer 2000; Yoon & Langer 2005), but see Vink & Harries (2017). Such stars do not significantly expand during their evolution. Even in close binary systems, they typically do not fill their Roche lobes and avoid mass transfer onto their companions. Thus, the components may remain very massive and have a small orbital separation at the moment of collapse.
Hot star winds are mainly driven by scattering of UV photons in metal lines (Lucy & Solomon 1970; Castor et al. 1975). Hence, stellar winds are generally weaker at low metallicity environments, and remove less mass and angular momentum. Thus, a metal-poor star will undergo its core collapse at a higher mass and at faster rotation than a star with initially the same mass but higher metallicity.
For a given initial stellar mass, the mass of the immediate BH progenitor is a function of the mass-loss rate. Both sets of evolution models considered in this study rely on recipes prescribing Ṁ(Z) at different evolutionary stages. Marchant et al. (2016) adopted the scaling of the mass-loss rate with metallicity as Ṁ(Z) ∝ (Z/Z⊙)0.85 for stars at all evolutionary stages. Eldridge & Stanway (2016) use Ṁ(Z) ∝ (Z/Z⊙)0.69 for hydrogen-rich O-type stars and (Z/Z⊙)0.5 for more evolved, hydrogen-poor stars. For more details on the mass-loss recipes applied in the individual evolution calculations, we refer the reader to Marchant et al. (2016), Eldridge & Stanway (2016), and the references therein.
 |
Fig. 1 Hertzsprung-Russell diagram showing the two stellar evolution tracks calculated by Marchant et al. (2016) that are used in this paper. Only the evolution path of the primary is shown, since the evolution of the secondary is virtually identical after the initial mass transfer. The blue filled asterisks mark the positions at which stellar atmosphere models where calculated. The labels near these asterisks are the atmosphere-model identifiers used throughout the text and Tables 1 and A.2. The highlighted and color-coded parts of the tracks refer to different WR phases and the period where the Roche lobe volume is filled, respectively (see inlet). |
Recent theoretical work and empirical measurements of mass-loss rates from massive stars show that the Ṁ(Z) ∝ (Z/Z⊙)0.7−0.9 scaling adopted in evolution calculations is reasonably accurate for O-type stars (Mokiem et al. 2007; Lucy 2012). On the other hand, for the more evolved WR stars, which represent massive stars during a late evolutionary stage prior to core collapse, the metallicity dependence of the mass-loss rate is steeper than assumed in evolution models. For example, Hainich et al. (2015) showed that the mass-loss rates of WR stars of the nitrogen sequence (WN stars) scale with metallicity as Ṁ ∝ Z1.2. This scaling was later confirmed by Tramper et al. (2016).
In this work, we calculate synthetic stellar spectra of O stars adopting the same Ṁ(Z) and other wind parameters as used in the evolution calculations. For WN stars, however, we use two alternative prescriptions for the mass-loss rate metallicity scaling – the one adopted in the evolution calculations, and the empirical one.
3.1. Progenitors of GW 150914-like systems in the quasi-chemically homogeneous evolution channel
The stellar evolution calculations by Marchant et al. (2016) focus on the QCHE in close binary systems. This scenario involves a very tight binary consisting of two massive stars that remain fully mixed during the course of their evolution as a result of their tidally induced high spin. The models account for detailed effects of tidal interactions and differential rotation.
The binary components start their lives with a mass ratio q so close to unity that exchange of mass during core hydrogen burning leads to a quick equalization of the component masses. After this, the components stay in contact with each other for some time, before the system subsequently evolves as a detached binary. These tracks are shown in Fig. 1 for two metallicities. The tracks reflect the evolutionary paths of the primaries only. The secondaries have virtually identical tracks because of the mass equalization early in their evolution (see Fig. 1 of Marchant et al. 2016).
Parameters of the stellar atmosphere models calculated for the 60 M⊙ track with Z = 1/10 Z⊙ (Marchant et al. 2016, see track I in Fig. 1).
One of the two tracks displayed in Fig. 1 is calculated for a star with an initial mass of 60 M⊙ at a metallicity2 of 0.1 Z⊙, while the other one shows the evolution of a star with an initial mass of 50 M⊙ at a lower metallicity (Z = 0.05 Z⊙). These metallicities roughly correspond to dwarf galaxies in the Local Group, like Leo I, IC 1613, Phoenix, WLM, or Sextans A and B (Kniazev et al. 2005; Leaman et al. 2013; Ross et al. 2015).
After leaving the zero-age main sequence (ZAMS), the tracks always stay in the blue part of the HRD, given their high surface temperatures in excess of 50 kK. This is a consequence of the rotationally induced QCHE. While constantly evolving to higher luminosities and higher temperatures, the stellar mass drops, mainly because of wind-mass loss, to about 34 M⊙ and 35 M⊙ shortly before core collapse for the Z = 0.1 Z⊙ and Z = 0.05 Z⊙ models, respectively.
For both tracks shown in Fig. 1, stellar atmosphere models and corresponding synthetic spectra have been calculated at five selected evolutionary stages. For each track, the first atmosphere model (marked by No. 1 in Fig. 1) is computed at the evolutionary stage shortly after the mass ratio of the binary components has reached unity following the initial RLOF phase. The next atmosphere model is calculated for the point No. 2 when the binary components are well detached from each other and continue to evolve quasi-homogeneously. When the track turns to the left (No. 3), that is, the star evolves to significantly higher surface temperatures, the third atmosphere model is calculated. An atmosphere model corresponding to the evolutionary stage characterized by a reduced hydrogen abundance, as observed in WN stars, is calculated next (No. 4). The final model (No. 5) is calculated at the stage when the hydrogen abundance has dropped below 5% (mass fraction) – roughly corresponding to the detection limit for hydrogen in the atmospheres of WR stars. In the track for the higher metallicity, this evolutionary stage corresponds to the WR stars of carbon/oxygen spectral type (WC/WO stars). The model parameters and the results of our calculations for Z = 0.1 Z⊙ and 0.05 Z⊙ are summarized in Tables 1 and A.2.
3.2. The GW-event progenitors as predicted by BPASS stellar evolution models
 |
Fig. 2 Same as Fig. 1 but showing the BPASS binary evolution tracks. Since the BPASS binary-calculations are stopped after the first core collapse event, the track of the secondary is split in two parts, leaving a gap between the positions E4 and E5 (dashed line, see text for details). |
The Binary Population and Spectral Synthesis (BPASS) models3 consider a general population of binaries with a distribution of masses, mass ratios, and orbits. The code follows the evolution of both the primary and the secondary star (Eldridge et al. 2008). In contrast to the Marchant et al. (2016) models discussed above, the evolution channels presented by Eldridge & Stanway (2016) do not require initially very tight binaries and quick equalization of binary component masses to produce massive BH binaries. The BPASS models in principle also account for common-envelope phases. However, this poorly understood evolutionary stage, where a nearly arbitrary amount of mass could be removed from the system, is avoided in the models presented in this paper.
The population synthesis conducted by Eldridge & Stanway (2016) shows that the formation of GW progenitor binaries is most likely at low metallicities. According to this study, the occurrence of the GW progenitor systems is highest at Z = 0.005 Z⊙, while mergers similar to GW 150914 are predicted up to metallicities of Z = 0.5 Z⊙. At a metallicity of Z = 10-4Z⊙, Eldridge & Stanway (2016) predict that more than a quarter of all expected BH mergers would have masses similar to those measured in the GW 150914 event.
Tracks for both components of a binary evolution model leading to the formation of a GW 150914-like binary are shown in Fig. 2. In contrast to the scenarios developed by Marchant et al. (2016), in the BPASS models the binary components do not experience mass transfer before core hydrogen exhaustion. Both components evolve like single stars until the mass transfer sets in, which then lasts for about 3 × 105 yr. At the end of this phase, the primary explodes as a supernova (SN), and leaves a remnant BH with a mass of about 35 M⊙. A probability is assigned to the SN kick and for the system to remain bound after a SN.
Due to the mass gain, the secondary increases its mass from 32 M⊙ on the ZAMS to about 50 M⊙ at the end of the mass transfer. The track of the secondary star in Fig. 2 has a gap between positions E 4 and E 5 (dashed line). This gap is because of the approximate treatment by the BPASS model of the secondary evolution during the fast RLOF mass-accretion stage.
Initially, the evolution of the secondary star is conventional. However, the secondary is significantly spun up by the mass and angular momentum transfer during the primary RLOF phase. The newly acquired high rotational velocity makes the secondary evolve quasi-homogeneously after the first BH formation. Therefore, the secondary star remains compact during its subsequent evolution. Hence, a common envelope phase between the secondary and the BH, which could potentially lead to a BH in-spiral, is avoided.
During all phases of the binary evolution prior to the primary collapse, the total luminosity of the system is dominated by the primary – the contribution of the secondary to the overall flux is only a few percent.
Stellar atmosphere models were calculated at characteristic points on the BPASS tracks as highlighted by the numbers in Fig. 2. The key difference compared to the approach used in Sect. 3.1 is that we now have to compute two separate sets of synthetic spectra, one for the primary and one for the secondary star.
 |
Fig. 3 Sequence of synthetic spectra at five different evolutionary stages (marked by the identifiers also used in Fig. 1 and Table 1) of a massive star with initial mass 60 M⊙ evolving quasi-homogeneously at Z = 0.1 Z⊙ (Marchant track I). The continuum levels and the zero lines are indicated by horizontal thin gray lines. The time series starts at the bottom with the spectrum of the model at the ZAMS. To facilitate a comparison with observed spectra, the model spectra are convolved with a Gaussian profile with a FWHM of 1.0 Å. |
The first two spectral models correspond to the phase when both binary components are on the ZAMS (E 1 in Fig. 2). The next stage at which synthetic spectra are computed is immediately before the mass-transfer starts (E 2). The following atmosphere models refer to a phase during which the primary looses its outer hydrogen-rich envelope and contracts (E 3). The last atmosphere model for the primary was calculated for the short phase between the end of mass transfer and the core collapse of the primary (E 4).
After the primary has collapsed, we compute spectral models only for the secondary star. The secondary now evolves quasi-homogeneously as a single star (E 5, 6, and 7 in Fig. 2). We note that the BPASS models account for rotational mixing in a somewhat simplified way. Furthermore, it is assumed that the fast rotation required for the QCHE is the result of mass transfer only. Throughout the QCHE, the temperature and the luminosity increase, while the hydrogen abundance drops. Eventually, the star starts to display WR-type abundances (E 8). The star ends its evolution with a low surface hydrogen abundance (E 9 and 10), leaving the second BH remnant upon core collapse. The BH merger is expected within 10 Gyr.
3.3. Predicted spectral sequence of potential GW-progenitors
An exemplary sequence of synthetic UV and optical spectra at different evolutionary stages is shown in Fig. 3. These figures illustrate the stellar atmosphere models calculated for the 60 M⊙ track (Z = 0.1 Z⊙) published by Marchant et al. (2016). Corresponding Fures for the 50 M⊙ track (Z = 0.05 Z⊙) can be found in Appendix B and spectra of a binary system evolving according to the BPASS tracks (Eldridge et al. 2008) are shown in Fig. 4.
In each of those plots, the time series starts at the bottom of each figure with the spectrum of the model at the ZAMS. The spectra of the subsequent evolution steps are shifted upwards by one flux unit each for clarity.
For illustration, the spectra of the binary components are shifted according to the maximum velocity amplitude of the orbital motion, assuming the statistically most probable inclination of i ≈ 57deg. The spectra are also convolved with a rotational profile accounting for the rotational velocity predicted by the evolution models. To facilitate a comparison with observations, the model spectra are degraded to a medium resolution by convolving them with a Gaussian profile with a FWHM of 1.0 Å. Moreover, the spectra account for a macroturbulence velocity of 20 km s-1. In Appendix B, we also present plots for the different stages in the evolution of the investigated binary system, showing the complete normalized spectrum together with the spectral energy distribution (SED) for the different evolution phases. These spectral templates can be used to identify such binaries in low-metallicity stellar populations.
We derived spectral types for all synthetic spectra presented in this work (see Tables 1, A.2, and A.3) using the classification criteria published by Crowther et al. (1998), van der Hucht (2001), Walborn et al. (2002), Evans et al. (2004), and Sota et al. (2011). As one would expect for homogeneously evolving stars, the derived spectral types reflect the high surface temperatures, resulting in early-type spectra throughout their evolution. In contrast, the BPASS models (Eldridge et al. 2008) also exhibit later spectral types, which is especially evident during the WR phase of the primary, permitting a WN9 classification. This highlights that binary BH progenitors can come in very different shapes, while eventually leading to similar massive BH systems.
The SED from the extreme UV to the infrared (IR) spectral range and for the different evolution phases are shown in Figs. B.3, B.2, and B.4, revealing significant differences in the stellar fluxes depending on T∗, Ṁ, and Z. This has a strong influence on observable properties like broad band magnitudes as well as feedback parameters (see Sect. 6 for details).
Comparing the evolutionary sequence of spectral types at different metallicities as shown in Figs. 3 and B.1 (see also Tables 1 and A.2), one can notice the differences arising from the reduction of the wind strength at lower Z. At a metallicity of Z = 0.1 Z⊙, the mass-loss rate is high enough that the star passes through the WN phase and is evolving further, exhibiting optical spectra with prominent metal lines, representative for WC/WO stars (see e.g., Fig. 3). This stage directly precedes the gravitational collapse into a BH. On the other hand, at the lower metallicity Z = 0.05 Z⊙, the stellar wind is not sufficiently strong enough to remove a significant part of the helium-rich outer envelope. At such low metallicity, the model predicts that massive QCHE stars will end their lives as WN-type stars.
Reflecting a metal-poor chemical composition, the synthetic spectra calculated for our exemplary binary system are characterized by the weakness or even absence of metal lines. The spectra of the main sequence stars, for example, basically show only hydrogen and helium lines in the optical and infrared range. However, already very early in their evolution, the QCHE leaves its footprint in a significant nitrogen self-enrichment (see Tables A.2 and 1). This increase in the nitrogen abundance results in the appearance of weak but noticeable nitrogen lines in the optical spectra. The strength of the nitrogen lines is steadily decreasing with the increasing effective temperature (see Fig. B.1) due to the shift in the ionization balance towards higher ions that, in the case of nitrogen, do not have noticeable lines in the optical.
Hence, at low metallicities, a spectral classification and analysis can be troublesome. In particular, spectral classification criteria in the optical for Of and WN stars lose significance with reduced metallicities. However, even at Z = 0.005 Z⊙, some metal lines are present in the near and far UV (see Fig. 4). Moreover, since the winds of massive stars are significantly decreasing with metallicity, observational constraints on the mass-loss rates at low metallicity are scarce. UV spectra often provide the only diagnostics to determine mass-loss rates at these metallicities. Consequently, the access to the UV spectral range is essential for a detailed spectral classification and robust spectral analysis of those objects.
A key for identifying GW progenitor systems in our neighborhood is the detection of their binary nature. All of the prototypical GW progenitor systems presented here exhibit substantial radial velocity (RV) amplitudes throughout their evolution. Assuming an average inclination of i = ⟨i⟩ = 57°, the models from Marchant et al. (2016) predict projected RVs with amplitudes in excess of 400 km s-1 in the initial phase of their evolution. The RV amplitudes drop as the systems evolve, but remain in excess of ≈ 200 km s-1. Since the primary and secondary are essentially equally massive throughout the system’s evolution, their RV amplitudes are virtually identical. Moreover, the stars are almost equally bright, making the spectrum of the system easily detectable as SB2. This applies for both for the Z = 0.01 Z⊙ as well as the Z = 0.05 Z⊙ scenarios. We conclude that GW progenitor systems undergoing QCHE should be easily detectable as SB2 binaries even with low spectral resolution (R ≈ 2000) and a modest signal-to-noise ratio (S/N).
GW progenitors that do not evolve as very tight binary systems (the slow evolution channel), such as those modeled by the BPASS code, which are generally harder to identify as binaries. The reason for this is two fold: first, this scenario typically entails systems with mass ratios that significantly differ from unity. Thus the primary, the more massive star, strongly dominates the spectrum. For example, in the prototypical BPASS scenario presented here, the primary is brighter than the secondary in the optical by a factor of ten or more throughout the evolution of the system. Secondly, the RV amplitudes in those systems are generally much smaller compared to those in systems undergoing QCHE, since the components are not necessarily as close. In the BPASS model used here, the projected RV amplitudes are rather large: The primary’s RV amplitude ranges from initially ≈ 300 km s-1 to ≈ 200 km s-1 shortly before its core collapse. The secondary’s projected RV amplitude increases in the same time from ≈ 100 km s-1 initially to ≈ 200 km s-1. However, in the framework of the BPASS models (Eldridge & Stanway 2016) one may also expect GW progenitor systems with initially low RV amplitudes that might be identified at best as SB1 binaries. To identify both components and properly analyze such systems, spectra with a S/N of at least ≈ 150 and a resolving power of R ≳ 10 000 would be needed.
The binary systems discussed in this work are hot and very luminous (log L/L⊙ = 5.5–6.2), and thus could in principle be observed in galaxies beyond the Local Group (see, e.g., Kudritzki et al. 2014, 2016). However, spectroscopy of those objects with a modern instrument mounted to a 8 m class telescope would still be restricted to a low spectral resolution on the order of R ≈ 1000 to obtain a useful S/N. This restriction makes the detection of the investigated systems outside the Local Group very difficult.
4. Comparison with observations
4.1. Early O-type stars
Stellar and wind parameters of the GW progenitor models on the main sequence, compared to the earliest-type main sequence stars observed in the SMC and IC 1613 (see the original publications for details).
In both sets of evolution models considered here, the progenitor stars settle on the main sequence as a very early O-type star and evolve through the WN spectral type towards a WC/WO type. Stars with similar spectral types are known in local low-metallicity galaxies, thus enabling a comparison between model predictions and observations.
In general, very massive O-type stars are scarce. In Table 2, we compare the model predictions and the properties of the earliest O-type stars in the Small Magellanic Could (SMC) and IC 1613. In the whole SMC, only four O stars with spectral types earlier than O4 are known (Evans et al. 2012). The earliest-type O dwarfs in the SMC occupy positions on the HRD that agree well with the predictions of those massive BH progenitor models that evolve quasi-homogeneously. Supporting QCHE, significant nitrogen enrichment compared to the baseline SMC value was measured in Sk 183 (Evans et al. 2012). The enhanced nitrogen abundance in the most massive O-stars in the SMC, such as Cl* NGC 346 MPG 324, was discussed in Bouret et al. (2003). They noted that standard evolution models do not predict a nitrogen surface enrichment during the main-sequence phase, but fast rotation induces mixing and can lead to the observed abundance pattern (Maeder 1987). Thus, analyses of observations support the idea that the stars may indeed evolve quasi-chemically homogeneously. Since the measured projected rotational velocity of the earliest O-stars in the SMC is quite significant, it is plausible to invoke rotational mixing to explain the abundance patterns.
Another, indirect evidence for quasi-homogeneous evolution of massive stars in the SMC is that, except for one object, the red supergiant (RSG) stars in the SMC have luminosities below log L/L⊙< 5.8 (Massey & Olsen 2003). This suggests that while the less massive stars in the SMC may follow the standard evolution channels, the stars initially more massive than 40 M⊙ are evolving quasi-homogeneously and do not become RGSs (Hamann et al. 2017).
The binary status of the earliest metal poor O stars is not well known. The spectral analysis of Sk 183 lead Evans et al. (2012) to suggest that this star is a binary with a less massive OB-type companion; binarity of Cl* NGC 346 MPG 324 and MPG 355 could not be ruled out either (Bouret et al. 2003).
The stellar masses of stars in the SMC and IC 1613 listed in Table 2 are spectroscopically determined. They are lower than those predicted by the evolution models for massive BH progenitors. However, the typical uncertainty in spectroscopically derived surface gravities log g is 0.2 dex, implying an error in the spectroscopic masses of about 60 %. Systematic discrepancies between spectroscopic and evolution masses are notoriously found for yet unknown reasons (Herrero et al. 1992; Repolust et al. 2004; Massey et al. 2012).
O-type stars with stellar parameters similar to those given in Tables 1, A.2, and A.3 can also be found at metallicities that are significantly higher than the metallicity range explored in this paper. An intriguing example is the LMC star VFTS 755 (Bestenlehner et al. 2014) that closely resembles our model MI 1, albeit the mass-loss rate and the stellar temperature of VFTS 755 are a bit lower. The same can be concluded for HD 93128, a Galactic O3 V((f)) star (Repolust et al. 2004). Therefore, we state that the parameter range investigated in this work is also partly realized at super-SMC metallicities.
Overall, we conclude that, nonetheless rare, stars with properties similar to those expected for a massive BH progenitor do exists in our neighboring galaxies.
4.2. Metallicity, clumping, and mass-loss rate
Comparing the empirical and model stellar properties shown in Table 2, it is obvious that the empirical mass-loss rates at SMC metallicity are already much lower than those adopted in the evolution models for Z = 0.1 Z⊙. Only at even lower metallicities (Z ≲ 0.05 Z⊙) are the mass-loss rates assumed in the evolution calculations comparable or lower than those empirically derived for unevolved early O-type stars in the SMC. For example, the empirical mass-loss rate of an O3V star at Z = 0.2 Z⊙ is only six times higher than the mass-loss rate assumed for a forty times smaller metallicity (Z = 0.005 Z⊙), while it is an order of magnitude lower than the one assumed for Z = 0.1 Z⊙.
How justified is the comparison between the GW progenitor models and real massive O stars, given the different metallicities adopted in the models and the one observed in local dwarf galaxies, like the SMC? The metallicity requirements in evolution models are set by the model parametrization of mass loss via stellar winds. Mass-loss rates for O stars may not exceed certain limits Ṁ ≲ 10-6 to not significantly lose angular momentum and maintain the fast rotation necessary for the quasi-homogeneous evolution. These low Ṁ values are also necessary to limit the orbit widening and to retain a stellar mass high enough for the production of a massive BH. As can be seen in Table 2, the evolution models assume that stellar winds are sufficiently weak only at very low metallicities. The adopted mass-loss rates in evolution calculations are significantly too large for early-type O dwarfs, and consequently the corresponding models underestimate the metallicity needed for the production of massive BHs.
Nevertheless, when comparing theoretical and empirical mass-loss rates, one must be well aware of the problems with empirical mass-loss rate determinations. One caveat regarding the mass-loss diagnostic based on UV, optical, and IR data is that some of the stellar wind might be in a hot shock-heated phase and therefore not be detectable in the UV and optical. This scenario was considered by Oskinova et al. (2011) and Huenemoerder et al. (2012) as a solution for the so-called weak-wind problem. This phenomenon is based on the finding that the mass-loss rates inferred from spectral analyses of OB-dwarfs with low luminosity (log Lbol/L⊙< 5.2) are significantly lower than predicted by standard mass-loss recipes (Bouret et al. 2003; Martins et al. 2005; Marcolino et al. 2009).
Arguably, the most serious problem affecting mass-loss diagnostics is stellar wind clumping (see Hamann et al. 2008 for an overview). Depending on the assumption on clumping properties, the empirically determined mass-loss rates are drastically different.
Wind clumping on small scales (micro clumping) reduces mass-loss rates empirically measured from fitting recombination lines in the stellar spectrum (usually the Hα line) by a factor 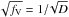 (Fullerton et al. 2006). Mass-loss rates measured by modeling of resonance lines in the UV spectra are affected by wind clumping in the opposite way – namely neglecting for optically thick wind clumping in spectral modeling can lead to an underestimation of mass-loss rates (Oskinova et al. 2007). The question of real mass-loss rates is not yet firmly settled. The spectral analyses of Galactic early O-type stars show that the standard mass-loss recipe (Vink et al. 2001) most likely gives overly large values, while the true mass-loss rates are a factor of between 1.3 and 3 lower (Sundqvist et al. 2011; Bouret et al. 2012; Šurlan et al. 2013; Shenar et al. 2015).
(Fullerton et al. 2006). Mass-loss rates measured by modeling of resonance lines in the UV spectra are affected by wind clumping in the opposite way – namely neglecting for optically thick wind clumping in spectral modeling can lead to an underestimation of mass-loss rates (Oskinova et al. 2007). The question of real mass-loss rates is not yet firmly settled. The spectral analyses of Galactic early O-type stars show that the standard mass-loss recipe (Vink et al. 2001) most likely gives overly large values, while the true mass-loss rates are a factor of between 1.3 and 3 lower (Sundqvist et al. 2011; Bouret et al. 2012; Šurlan et al. 2013; Shenar et al. 2015).
Yet, while the existence of stellar wind inhomogeneities is indisputable, robust clumping diagnostics are scarce. Clear demonstrations of wind clumping were provided by the detection of stochastic variability in the He ii λ4686 Å emission line in the spectrum of an O supergiant (Eversberg et al. 1998). Markova et al. (2005) concluded that the Hα-line variability observed for a large sample of O-type supergiants could be explained by a structured wind consisting of shell fragments. Using spectral diagnostics, Prinja & Massa (2010) showed that the winds of B-type supergiants are clumped. In a recent study, Martins et al. (2015) found that spectral lines formed in the winds of all OB supergiants in their sample are variable on various time scales. Lépine & Moffat (2008) monitored the line-profile variations in a sample of O stars and explained their observations using a phenomenological model that depicts winds as being made up of a large number of clumps. Brown et al. (2000) and Davies et al. (2007) modeled polarimetric variability arising in a clumped wind. All these studies are largely restricted to supergiants (see, e.g., Puls et al. 2006; Najarro et al. 2011). The knowledge of clumping in the winds of O dwarfs is still limited; its improvement requires quite sophisticated approaches, such as three-dimensional (3D) wind simulations (Šurlan et al. 2013).
Studies confirm that massive star winds are also clumped at low metallicities (Marchenko et al. 2007). This implies that empirically derived mass-loss rates corrected for clumping would be lower than those obtained using the standard recipe. Moreover, clumping may not be the sole reason for the low mass-loss rates empirically measured from O stars in low-metallicity galaxies. Recent models using a different approach than Vink et al. (2001) predict lower mass-loss rates at low metallicities (Lucy 2015). For an extensive discussion, we refer the reader to Bouret et al. (2015, and references therein).
The lower mass-loss rates are corroborated by the trends seen in Fig. 5, where we compile the ratio between empirically determined mass-loss rates and those predicted by the standard mass-loss recipe derived by Vink et al. (2001) for a sample of 16 massive dwarfs with spectral types earlier than O4V, residing in four galaxies with different metallicities.
 |
Fig. 5 Difference between empirical mass-loss rates and those predicted by the mass-loss recipe proposed by Vink et al. (2001). The sample consists of 14 early O-dwarfs with spectral types earlier than O4V (see text for the references and discussion) in the Galaxy (Z = 1 Z⊙), the LMC (Z = 0.5 Z⊙), the SMC (Z = 0.2 Z⊙), and IC 1613 (Z = 0.14 Z⊙). |
Among the stars in the sample shown in Fig. 5 are four Galactic early O stars, HD 93128 (O3V((f))), HD 93250 (O3V((f))), and HD 303308 (O4V((f+))), that were analyzed by Repolust et al. (2004). The mass-loss rates from their Table 4 were reduced by a factor of three to account for the effect of wind clumping adopting fV = 0.1. The clumped (fV = 0.1) mass-loss rate of HD 46223 (O4V((f))) is from Martins et al. (2012). The mass-loss rates for the eight early LMC O-stars are from the analyses by Bestenlehner et al. (2014) and Ramachandran et al. (2018), who also adopted fV = 0.1. We note that the metallicity of the stars in the LMC sub-sample is likely slightly higher than Z = 0.5 Z⊙. Concerning the sub-sample of the SMC stars, the clumped mass-loss rates of Cl* NGC 346 MPG 324 (O4 V((f)), fV = 0.1) and Cl* NGC 346 MPG 368 (O4-5 V((f)), fV = 0.05) are from Bouret et al. (2003). The unclumped mass-loss rate for Sk 183 (O3((f))) from Evans et al. (2012) was corrected for clumping with fV = 0.1. The clumped (fV = 0.03) mass-loss rate of [BUG2007] A 13 (O3V((f))) is from Bouret et al. (2015), who notes that a higher, SMC-like, metallicity cannot be ruled out for this star in IC 1613.
In Fig. 6, we show the modified wind momentum of these stars as a function of their luminosity. The modified wind momentum is a measure for the strength of the stellar wind (Kudritzki et al. 1995, 1999; Puls et al. 1996) that is defined as 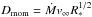 . The line-driven wind theory predicts a distinct relation of the form Dmom ∝ Lα, the so-called wind-momentum luminosity relation (WLR; Kudritzki et al. 1999), which is expected to show a metallicity dependence. To illustrate the deviations between empirical derived values and what is predicted by a mass-loss recipe applied in most stellar evolution calculations, we also plot the WLRs predicted by Vink et al. (2001) in Fig. 6. Only for the primary in the binary system N206-FS 180 (Ramachandran et al. 2018) is the mass-loss rate predicted by the standard mass-loss recipe of Vink et al. (2001) in agreement with the empirically derived value (see also Fig. 5). However, the spectral analysis of this object is complicated by its binarity. Figures 5 and 6 demonstrate that the standard mass-loss recipe severely overestimates the mass-loss rates of massive stars at early stages of their evolution.
. The line-driven wind theory predicts a distinct relation of the form Dmom ∝ Lα, the so-called wind-momentum luminosity relation (WLR; Kudritzki et al. 1999), which is expected to show a metallicity dependence. To illustrate the deviations between empirical derived values and what is predicted by a mass-loss recipe applied in most stellar evolution calculations, we also plot the WLRs predicted by Vink et al. (2001) in Fig. 6. Only for the primary in the binary system N206-FS 180 (Ramachandran et al. 2018) is the mass-loss rate predicted by the standard mass-loss recipe of Vink et al. (2001) in agreement with the empirically derived value (see also Fig. 5). However, the spectral analysis of this object is complicated by its binarity. Figures 5 and 6 demonstrate that the standard mass-loss recipe severely overestimates the mass-loss rates of massive stars at early stages of their evolution.
 |
Fig. 6 Modified wind momentum ( |
The available sample of low-metallicity massive stars with empirically established mass-loss rates is currently very limited, but nevertheless some trends are apparent (see Fig. 5). Based on this small sample of very early-type O dwarfs (with Teff> 40 kK and log L∗/L⊙> 5.5), we suggest an empirically calibrated Ṁ relation of the form 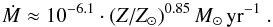 (2)The uncertainty in this correlation is on the order of a factor 2−3. A thorough investigation of the mass-loss rates of very early O-stars, including the derivation of a detailed mass-loss recipe, will be the subject of a forthcoming paper.
(2)The uncertainty in this correlation is on the order of a factor 2−3. A thorough investigation of the mass-loss rates of very early O-stars, including the derivation of a detailed mass-loss recipe, will be the subject of a forthcoming paper.
4.3. Wolf-Rayet stars
Comparison between the stellar and wind parameters of the GW model progenitors during the WR phase and the earliest WR stars observed at low metallicity (see the original publicationsa for details).
The comprehensive empirical analyses of the Galactic WR star population show that WN stars form two distinct sub-classes (Hamann et al. 2006). The descendants of stars with initial masses in the range 20–40 M⊙ become WN early (WNE) stars, that are typically hydrogen-free. Such WNE stars are hotter and less luminous than the stars of the WN late (WNL) type. The latter stem directly from O-stars with masses exceeding ~ 40 M⊙. WNL stars have high luminosities (log L/L⊙> 6), are somewhat cooler than WNEs, and usually contain a significant amount of hydrogen in their atmospheres.
This dichotomy, however, does not hold for the WN populations in the LMC (Hainich et al. 2014) and SMC (Hainich et al. 2015). For the latter, Hainich et al. (2015) found that the evolutionary origin of the SMC WN stars can be explained by QCHE. In this case, even those WN stars that originate from very massive O stars remain compact and hot during their evolution, while still containing hydrogen in their atmosphere. However, Hainich et al. (2015) noticed that lower mass-loss rates during the WN phase need to be used in the QCHE models to bring the predicted hydrogen surface abundance in SMC WN stars in accordance with observations.
These suggestions are in line with the predictions of the GW progenitor models investigated in this paper. Let us first consider the spectral evolutionary sequence in the case of quasi-homogeneous evolution as presented by Marchant et al. (2016) and as illustrated in Fig. 1 and Table 1. As one can see, the O-star stage is directly followed by a very early WN-type stage. The star contracts and becomes hotter, while retaining hydrogen in its atmosphere.
The BPASS models (Eldridge & Stanway 2016) predict a different evolution of the spectral types (see Fig. 4 and Table A.3). In this case, the primary does not evolve quasi-homogeneously. Therefore, following the O-star stage and directly preceding its core collapse, the star becomes a very luminous and rather cool WNL star of a late subtype with a sizable amount of hydrogen in its atmosphere.
On the other hand, the secondary, spun up after the primary’s SN explosion, evolves quasi-homogeneously and becomes a much hotter but still very luminous WN star of an early sub-type. Such stars can evolve further and become early-type carbon/oxygen rich (WO/WC) stars that collapse into a BH.
The population of WR stars in the SMC is considered to be fully known. The complete sample of SMC WR stars was analyzed in Martins et al. (2009), Hainich et al. (2015), and Shenar et al. (2016). The former two papers presented support for QCHE of the most massive SMC single stars. The latter, concentrating on the WR binaries, found no evidence of QCHE in those systems, which might avoid full mixing because their rotation is slowed down by tidal interactions in wide binaries.
As shown in Table 3, the observed WR stars in local galaxies have properties similar to the model predictions. Two of these stars, namely SMC AB 1 & 9, closely resemble some of the stellar atmosphere models presented in this paper (model MII 3 and model MI 4, respectively) in terms of stellar temperature, luminosity, and mass. This shows that the stellar parameter range predicted for the massive BH progenitors is, to our current knowledge, quite valid.
Interestingly, the empirical masses of WN stars are even higher than expected for the GW progenitor, with the exception being the WO-type stars that obviously cannot produce a BH with more than ≈ 20 M⊙. SMC AB 1 & 9 have current masses in a range where pair-instability supernovae (PISNe) are expected to occur. If these stars continue to evolve quasi-homogeneously and if their mass-loss rates do not significantly change during the rest of their evolution, the cores of these objects might become susceptible to PISNe (Heger & Woosley 2002; Chatzopoulos & Wheeler 2012), leading to the total disruption of the stars rather than the formation of BHs. However, the uncertainty of empirical WR masses are high because they are solely based on luminosities and mass-luminosity relations. Unfortunately, no direct observational handle on the mass or surface gravity is available for those stars (see discussion in Shenar et al. 2016).
As in the case of O stars, the evolution models adopt overly large mass-loss rates during the WN evolutionary phase and, consequently, underestimate the metallicity domain where massive BH binaries can be found. In comparison to O-type stars, an even steeper relationship between the mass-loss rate and the metallicity is observed for WN stars. Hainich et al. (2015) found a relation of the form 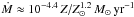 . For a more thorough derivation and discussion of this dependency, we refer the reader to Hainich et al. (2015).
. For a more thorough derivation and discussion of this dependency, we refer the reader to Hainich et al. (2015).
Among the binary WR stars in the SMC is AB 8 (see Table 3), the only one that contains a WO type star known in this galaxy (while no WC-type stars are identified in the SMC). This system (WO4 + O4I, 20 + 60 M⊙) is in a relatively tight orbit, P = 16.6 d, only slightly larger than the orbits expected for a GW progenitor system. However, this is already sufficient to reduce the spin because of tidal interactions hampering QCHE and preventing the formation of a tight BH binary. SMC AB 8 can thus be considered as a binary BH progenitor, but most likely it would not follow the fast evolution channel. Similar conclusions can be drawn for SMC AB 5 (HD 5980), which is a hierarchical quadrupole system containing a WN6h+WN6-7 (61 + 66 M⊙) binary with a 19.3 d orbital period.
All of the most massive O and WR binaries observed so far in the SMC have wider orbits than required for either of the GW progenitor models. It remains to be seen whether sufficiently close and massive binary systems will be identified in future surveys of low-metallicity galaxies.
4.4. Implications
The above findings have some implications for the metallicity dependence of the BH merger rate. Belczynski et al. (2016a) predicted massive BH mergers for metallicities up to Z ≤ 0.1 Z⊙, similar to what Marchant et al. (2016) obtained. Eldridge & Stanway (2016) found an upper metallicity limit of 0.5 Z⊙, while predicting that the BH merger rate peaks at metallicities as low as Z ≤ 0.005 Z⊙.
However, as shown above, overly large mass-loss rates were adopted in evolution calculations of massive stars at early stages of their evolution and in the WN stage, especially at low metallicities. This is one reason why evolution models predict massive BH progenitors preferentially at low metallicities. Stellar evolution models that account for realistic mass-loss rates might lead not only to larger BH masses but also less orbital widening in the course of the stellar evolution due to angular momentum loss. Potentially giving rise to a larger fraction of stars evolving quasi homogeneously, this reinforces the importance of the evolution channels discussed in this paper for the formation of binary BHs that will merge within a Hubble time. Moreover, we suspect that the discussed evolution channels would occur already at higher metallicities, if a steep Ṁ(Z) relation for the WN phase and lower mass-loss rates for massive main sequence stars (see Sect. 4.2) are used in stellar evolution calculations.
A population synthesis study evaluating the binary BH merger rates and the rates of expected LIGO events is beyond the scope of this paper. Such studies have been performed by various authors (e.g., Dominik et al. 2015; Belczynski et al. 2016a; Mandel & de Mink 2016; Marchant et al. 2016; Eldridge & Stanway 2016), but should be repeated with more realistic mass-loss rates as discussed above. We speculate that this will shift the peak of the binary BH merger rate to higher metallicities than predicted hitherto.
Apart from the wind mass-loss rates, further important uncertainties affect the BH masses predicted by evolution models. Episodic mass loss associated with luminous blue variable (LBV) phases might contribute significantly to the total mass lost over the lifetime of a massive star and hence substantially influence its final mass. The LBV phenomenon is generally attributed to the proximity of these stars to the Eddington limit, at which the surface gravity is balanced by the radiative acceleration, while additional mechanisms were proposed to explain the different variabilities associated with this transient state (see review by Vink 2012). An LBV-like mass-loss episode might also be related to unstable late nuclear burning phases or to the onset of a pulsational PISN (Woosley et al. 2007; Chatzopoulos & Wheeler 2012), as was proposed for the supernova imposter SN 2009ip (Mauerhan et al. 2013). However, despite intensive research on LBVs, their eruptions and the underlying mechanisms are still not understood.
In recent years, growing evidence has been provided that massive stars in a certain mass range might not explode, but end as a failed SN or directly collapse to form a BH (see, e.g., O’Connor & Ott 2011; Kochanek 2015; Sukhbold et al. 2016; Adams et al. 2017). Albeit failed SNe can eject a substantial amount of mass (Nadezhin 1980; Lovegrove & Woosley 2013), the remaining BH masses can be significantly higher compared to those from an energetic SN (see also Woosley 2016). The direct collapse scenario also avoids large kicks as expected for SNe that form neutron stars (NSs) or BHs (Fryer et al. 2012; Mirabel 2017). This entails that multiple systems where at least one of the components directly collapses to a BH have a lower probability of becoming disrupted compared to those systems where all components exhibit a SN. Another consequence of the direct collapse scenario is the increased importance of stellar winds, since, in this scenario, only the winds chemically enrich the surrounding interstellar medium (ISM) and inject kinetic energy into it.
Nevetheless, we only consider binaries in this work; an interesting possibility to form close pairs is via triple systems. A hierarchical triple system might experience an orbital tightening of the inner pair due to the Lidov-Kozai mechanism (e.g., Shappee & Thompson 2013).
5. X-ray properties of massive binary BH progenitors
X-rays provide one of the best observational windows for the identification of binaries among the general massive star population. Massive binary components drive strong supersonic stellar winds that collide, shock, and thereby power X-ray emission. During a later evolutionary phase, when one of the binary components has already collapsed into a BH, stellar wind accretion leads to characteristically strong X-ray emission. Therefore, observations in X-rays are pivotal for finding potential binary BH progenitors.
5.1. Colliding wind binaries
Both components in a massive binary drive stellar winds. When the binary orbital parameters and wind strengths are favorable, the two winds collide and power strong X-ray emission (see recent review by Rauw & Nazé 2016). As a result, the X-ray luminosity of the binary system can be significantly higher than that of the components. Such a situation is realized in the Marchant et al. (2016) models. In these models, both binary components have the same spectral type during their evolutionary paths, drive strong winds, and are at favorable separations to facilitate a significant X-ray emission from their colliding winds. Therefore, X-ray observations are potentially effective for identifying binaries, such as those predicted by the Marchant et al. (2016) evolutionary scenario.
Stevens et al. (1992) showed that the efficiency of radiative cooling in a colliding wind binary can be estimated based on the parameter χ ≈ v4d/Ṁ, where v is the wind velocity in 1000 km s-1, Ṁ is the mass-loss rate for each binary component in 10-7M⊙ yr-1, and d is the distance to the shock zone in 107 km. In the case of identical components, this distance is half of the orbital separation. We stress that the above equation was derived for solar abundances and that the cooling efficiency will be slightly different at sub-solar metallicities. Therefore, we only use this equation for an order of magnitude estimate. When χ> 1, the cooling is adiabatic, and for χ ≪ 1 the cooling is radiative. For models shown in Tables 1 and A.2, the cooling is adiabatic only for the models MI 1, MII I, MI 5b, and MII 5b. In all other cases, the cooling is radiative. The models based on Eldridge & Stanway (2016) evolutionary tracks are characterized by larger orbital separation compared to the Marchant et al. (2016) tracks. For all binary parameters shown in Table A.3 the cooling in the colliding wind zone is adiabatic.
With the help of Eq. (10) from Stevens et al. (1992), we can roughly estimate the X-ray luminosities assuming adiabatic cooling. For this purpose, we use the model binary separations and wind parameters given in Tables 1 and A.2, but note that these models do not include effects of radiative braking, which may act to reduce the derived X-ray luminosity (Gayley et al. 1997). Our models show that the winds would collide when their velocity is about 75 % of v∞, that is, already very high. For an O3V+O3V binary (model MI 1 and MII 1), the expected X-ray luminosity is LX,CWB ≈ 1034 erg s-1, while for an WO+WO binary (model MI 5b), X-ray luminosities up to LX,CWB ≲ 1036 erg s-1 might occur. Hence, if an apparently single O3 V star has an X-ray luminosity exceeding 1034 erg s-1, this would be a strong indication for a colliding wind binary. However, if an early-type star is X-ray dim, this does not exclude its binary nature, because, for example, the binary separation might be just too large to facilitate a substantial X-ray emission.
Binary systems with parameters shown in Table A.3 are expected to generate moderately strong X-ray emission before the primary’s core collapse. The highest X-ray luminosity is predicted for the WN7-9+O5V systems (models E 3 and E 4), but does not exceed ≈ 1034 erg s-1 for all models in this table.
In order to estimate the X-ray luminosity for the cases where the shocked plasma cools radiatively, we consider the semi-analytical models presented by Antokhin et al. (2004). These models predict upper limits to the X-ray luminosity of colliding wind binaries. For none of the binary models considered in this work, do the upper limits exceed LX,CWB ≈ 1034 erg s-1. This upper limit is in agreement with observations. In the Galaxy, X-ray luminosities of massive O+O binaries, in general, do not exceed 1034 erg s-1, while some WR+O binaries can be an order of magnitude brighter (Oskinova 2005; Nazé et al. 2011; Gagné et al. 2012).
The known colliding wind binaries in the SMC are not especially X-ray bright. The X-ray brightest system is the quadrupole star AB 5 (WN6h+WN6-7, HD 5980) with LX,CWB ≈ 2 × 1034 erg s-1 (Nazé et al. 2007; Shenar et al. 2016). The putatively single O-type stars have lower X-ray luminosities – none of them was so far detected in X-rays, putting the upper limit on their X-ray emission at about 1033 erg s-1 (Oskinova et al. 2013). Therefore, it appears safe to conclude that, in general, O-type and WR stars with X-ray luminosities exceeding 1033 erg s-1 are most likely colliding wind massive binaries.
Yet, it is important to realize that, while X-ray luminosities in the range 1033−1035 erg s-1 for O and WR-type stars may be a sufficient criterion to identify them as colliding wind binaries, it is not a necessary condition. For example, the WO4 + O4 binary AB 8 in the SMC is not detected in X-rays with an upper limit <5 × 1032 erg s-1. Orbital geometry, wind structure and opacity, as well as radiative braking are among the factors that are capable of significantly reducing the emergent X-ray flux. Hence, even very massive binaries may be X-ray faint.
5.2. High-mass X-ray binaries
At some point in the evolution of a massive binary, the primary might be already collapsed to a BH, while the secondary is still a normal non-degenerate star. The accretion of matter from the secondary into the BH will power strong X-ray emission. Such systems are known as high-mass X-ray binaries (HMXBs). The GW progenitor models predict the orbital configuration, the BH mass, and the parameters of the donor star. With this information at hand, one can calculate the expected X-ray luminosities of HMXBs during an immediate phase before the formation of a binary black hole.
An upper limit to the luminosity of a BH is set by the Eddington luminosity. This is the luminosity at which the radiative acceleration from the scattering of photons by electrons equals the inward gravitational force, LEdd = 4πGMBHcκ-1, where κ is the mass-absorption coefficient, and other notations have their usual meaning. Assuming that the plasma is fully ionized and that it only consists of hydrogen and helium, the Eddington luminosity can be written as 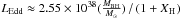 erg s-1, with XH being the hydrogen mass fraction (solar value: XH = 0.7). For example, a 36 M⊙ mass BH accreting matter with a solar hydrogen abundance, this limit becomes 5.4 × 1039 erg s-1.
erg s-1, with XH being the hydrogen mass fraction (solar value: XH = 0.7). For example, a 36 M⊙ mass BH accreting matter with a solar hydrogen abundance, this limit becomes 5.4 × 1039 erg s-1.
This classical Eddington X-ray luminosity is comparable to that of ultra-luminous X-ray sources (ULXs). The latter are usually defined as non-nuclear, point-like X-ray sources with an apparent isotropic X-ray luminosity exceeding 1039 erg s-1 in the 0.3–10.0 keV band (see Kaaret et al. 2017, and references therein).
The X-ray luminosity of an accreting BH is related to the accretion rate, Saccr, via the accretion efficiency constant ϵ that depends on the detailed physics of accretion: LX = ϵSaccrc2. We can define the Eddington accretion rate such that SEdd ≡ LEddc-2. Then, the dimensionless accretion rate and luminosity may be written as  (3)Hence, the luminosity of an accreting BH can be expressed in dimensionless units as
(3)Hence, the luminosity of an accreting BH can be expressed in dimensionless units as 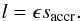 (4)In both sets of evolution models that we consider in this work, the systems remain detached after the formation of the first black hole. Therefore, the X-ray emission of the BH is powered only by stellar wind accretion. The stellar wind accretion rate can be estimated using the Bondi-Hoyle-Lyttleton formalism (e.g., Davidson & Ostriker 1973; Martínez-Núñez et al. 2017) as
(4)In both sets of evolution models that we consider in this work, the systems remain detached after the formation of the first black hole. Therefore, the X-ray emission of the BH is powered only by stellar wind accretion. The stellar wind accretion rate can be estimated using the Bondi-Hoyle-Lyttleton formalism (e.g., Davidson & Ostriker 1973; Martínez-Núñez et al. 2017) as 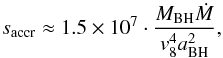 (5)where MBH is in M⊙, Ṁ is the stellar wind mass-loss rate in units of M⊙ yr-1, v8 is the stellar wind velocity in 108 cm s-1, and aBH is the orbital separation in R⊙.
(5)where MBH is in M⊙, Ṁ is the stellar wind mass-loss rate in units of M⊙ yr-1, v8 is the stellar wind velocity in 108 cm s-1, and aBH is the orbital separation in R⊙.
The Bondi accretion rate (Eq. (5)) gives an upper limit on the accretion rate from stellar winds, since it does not account for radiative feedback effects. On the other hand, the Eddington rate SEdd gives the maximum accretion rate limited by the radiative pressure feedback close to the BH. While detailed numeric simulations are required to obtain robust estimates of accretion rates (Park & Ricotti 2011), one can more readily estimate the accretion efficiency ϵ. In the standard Shakura-Sunyaev disk model (Shakura & Sunyaev 1973), accretion occurs via a geometrically thin but optically thick disk. For such disks, ϵ ≈ 0.1 is a constant (e.g., Shapiro 1973). On the other hand, in case of advection-dominated disks or spherical accretion, ϵ ∝ saccr ≲ 10-4 (see Fig. 2 in Park & Ostriker 2001). For saccr> 1, the super-Eddington accretion regime is realized and the system appears as an ULX characterized by a high X-ray luminosity and powerful outflows (Poutanen et al. 2007).
The predicted accretion rates based on Eq. (5) and X-ray luminosities for the QCHE GW progenitor models are given in Tables 1 and A.2, assuming ϵ ≈ 0.1 and a 36 M⊙ BH. As an example, let us consider the progenitor models given in Table 1. For the given orbital parameters and masses, super-Eddington accretion rates are predicted only for the WN stages. Thus, ULXs with a WR-type donor may be expected. Based on existing observations, only five WR stars with relativistic companions are suspected. The Galactic system Cyg X-3 is strongly obscured, revealing only little information about its donor star, even though its identification as a WR star seems to be secure (Zdziarski et al. 2013). The BH mass in Cyg X-3 seems to be quite low, (≈ 2 M⊙). The extragalactic systems IC 10 X-1 and NGC 300 X-1 may host WN-type donors (Crowther et al. 2007). The mass of the compact object in IC 10 X-1 was recently reassessed and also found to be quite low (≈ 2 M⊙) (Laycock et al. 2015). In the case of NGC 300 X-1, Binder et al. (2015) showed that a low-mass donor star is not excluded and that the BH mass measurements are not reliable. The WR-type features observed in M101 ULX-1 are likely not from the donor star, but from a disk wind instead (Soria & Kong 2016). The nature of CXOUJ123030.3+413853 is still controversial (Esposito et al. 2015). Hence, it appears that no WN HMXB hosting a massive BH (as expected for a GW progenitor system) is firmly detected yet.
According to the models by Marchant et al. (2016), the first BH is formed when the secondary is already an evolved WR-type star. For a GW 150914-like progenitor, the first BH is born when the secondary is a WO star and thus the lifetime of the HMXB would be very short. At this stage, the accretion rate is approximately a few percent of the Eddington rate. Such systems would be observed as HMXBs, but would not manifest themselves as ULXs. Moreover, WC/WO winds are optically very thick for X-rays (Oskinova et al. 2009). As a consequence, the observable X-ray luminosity might be significantly lower than the intrinsic one. HMXBs with WC/WO-type donors are not known.
The evolutionary models by Eldridge & Stanway (2016) predict orbital parameters only up to the first core collapse (see Table A.3). To estimate the X-ray luminosity of the HMXB formed after the primary’s collapse into a BH, we assumed that the orbital separation remains the same as in the moment of the BH formation, that is, 64 R⊙. The X-ray luminosities powered by direct accretion shown in Table A.3 are modest, so no ULX formation is predicted for these models.
6. Feedback parameters of massive BH progenitors
The massive black hole progenitor models predict their formation in a low Z environment. This requirement is to reduce the amount of matter lost by the massive star via its wind before collapse.
Since the stellar winds are weaker at low Z, such massive stars inject less mechanical energy and momentum into the ISM. The exception could be WR stars that exhibit a significant self-enrichment with nuclear burning products, like WC and WO stars. However, the 50 M⊙ track based on Marchant et al. (2016) models for a metallicity of 0.05 Z⊙ shows that self enrichment is quite limited even for the stars evolving quasi-homogeneously during a significant fraction of their life. Moreover, more massive stars may directly collapse into BHs avoiding a SN explosion, further reducing the massive star feedback at low Z.
While mechanical energy input from massive stars at low Z may be reduced compared to solar metallicity, the radiative energy feedback is very significant. A salient characteristic of the QCHE binary models shown in Fig. 1 (and partly also those shown in Fig. 2) is that these stars evolve to very high stellar temperatures even at very low metallicities, in strong contrast to the standard non-homogeneous models. Consequently, the radiative feedback from a homogeneously evolving star of a certain initial mass is significantly higher than its counterpart that follows a classical, non homogeneous evolution path (see e.g., Stanway et al. 2016 for the effect of QCHE on stellar populations). Therefore, just a few very hot and luminous WN stars resulting from QCHE can, in principle, dominate the entire ionizing radiation budget of a low metallicity dwarf galaxy.
An intriguing example of such a galaxy is I Zw 18, which is characterized by a metallicity of Z ≈ 1/32 Z⊙ (Vílchez & Iglesias-Páramo 1998). Kehrig et al. (2015) determined the rate of He ii ionizing photons necessary to power the observed He ii nebular emission to be 1.33 × 1050 s-1. For comparison, model MII 5 calculated for the 50 M⊙ track (Z = 0.05 Z⊙) provided by Marchant et al. (2016) emits a He ii ionizing photon flux of log QHe ii = 49.31 photons s-1. Thus, only six of these stars (three binary systems) would be able to provide the necessary ionizing radiation to explain the observed He ii nebular emission in I Zw 18.
Homogeneously evolving massive and very massive stars at the metallicity of I Zw 18 were studied by Szécsi et al. (2015). The authors investigated the radiative feedback provided by their models, assuming blackbody fluxes. In comparison to those results, our sophisticated stellar atmosphere models give similar hydrogen ionizing fluxes, but the predicted He ii ionizing fluxes are an order of magnitude lower.
As shown above, the mass-loss rates assumed by evolution models seem to be overestimated, which is partly attributable to the Z scaling (see Sect. 3). It remains to be seen how a steeper Ṁ-Z prescription will affect the outcome of the evolution calculations. Here we only explore the effect of different mass-loss rates in the WN phase on the number of ionizing photons and other observable quantities, such as broad-band magnitudes. For this purpose, we have calculated synthetic spectra with different Ṁ, according to the two Ṁ(Z) prescriptions given in Sect. 3. The comparison between these two model sets is presented in Tables 1 and A.2.
The most severe effect is seen in the atmosphere models with Z = 0.1 Z⊙. The number of He ii ionizing photons of those models using the steep Ṁ(Z) prescription (Hainich et al. 2015) can be several orders of magnitude higher compared to the models that follow the shallower dependence of Ṁ(Z) (e.g., see model MI 3 in Table 1). In contrast, at lower metallicities (Z = 0.05 Z⊙) the number of He ii ionizing photons is slightly higher in those models that assume higher mass-loss rates.
Most of the potential progenitor systems investigated in this work are characterized by high luminosities and high surface temperatures, entailing hard flux distributions (see Figs. B.2, B.3, and B.4). Consequently, those stars are much brighter in the UV and optical in comparison to the IR (see Tables 1, A.2, and A.3). Moreover, the low-metallicity massive stars are significantly fainter in the IR compared to similar stars at higher metallicities (see also Crowther & Hadfield 2006), because of the lower mass-loss rates at low Z. It is informative to compare, for example, model MI 4 with MII 4 calculated for the 0.1 Z⊙ and 0.05 Z⊙ tracks, respectively (see Tables 1 and A.2). In latter case, the K-band magnitude is more than 4 mag lower than in the former case, which is mainly attributable to the significantly lower Ṁ. This hardening of the massive star SED at lower metallicities needs to be taken into account in an IR-based census of massive stars in low Z galaxies.
7. Summary and conclusions
The GW observatories have discovered BHs with large masses, well above those previously known from observations of X-ray binaries. Elaborate models have been proposed showing that such massive BHs can be a natural result of stellar binary evolution.
In this paper, we consider two independent model sets presented by Marchant et al. (2016) and Eldridge & Stanway (2016). Both models provide detailed stellar evolution tracks for massive BH progenitors that eventually lead to a BH merger event similar to GW 150914. QCHE is realized in both sets of evolution models, while the common envelope evolution is avoided and mass removal by stellar winds is an important factor in the evolution towards the BH binary system.
On the basis of these evolution models and using advanced non-LTE stellar atmosphere PoWR models, we compute synthetic stellar spectra of massive BH progenitors at key evolutionary stages to provide spectral templates. Their spectral classification, photometry, and stellar feedback parameters are established. This allows direct comparison between model predictions and empirical parameters of massive stars. Our main conclusions are:
-
1)
The range of stellar parameters predicted for massive BHprogenitors is realized in nature.
-
2)
The massive BH progenitors evolve from O3V through WN towards WO spectral types, while the latter is only reached for the highest metallicity (Z = 0.1 Z⊙) considered in this work.
-
3)
Existing evolution models adopt stellar mass-loss rates, which are significantly too large. Empirically derived mass-loss rates are up to an order of magnitude lower. For early O-type dwarfs (with Teff> 40 kK and log L∗/L⊙> 5.5), empirical measurements suggest a Ṁ relation of the form Ṁ ≈ 10-6.1 (Z/Z⊙)0.85M⊙ yr-1, resulting in significantly lower mass-loss rates compared to standard prescriptions. The corresponding relation for WN stars is Ṁ ≈ 10-4.4 (Z/Z⊙)1.2M⊙ yr-1.
-
4)
We suspect that the metallicity at which the massive binary-BH merger rate peaks as predicted by population synthesis studies will be higher, if mass-loss rates in agreement with the empirical values are used in stellar evolution calculations. A significant number of massive BHs may be formed already at SMC-like metallicities (≲0.2 Z⊙).
-
5)
There is no one-to-one correspondence between GW progenitor prediction models and already known objects. This conclusion holds for both known massive binaries and HMXBs.
-
6)
We provide spectral templates and broad band magnitudes that should help to identify progenitors of massive BH merger events.
Comprehensive grids of stellar atmosphere models for O-type and WR stars, calculated for different metallicities, can be found at the PoWR website: www.astro.physik.uni-potsdam.de/PoWR
Marchant et al. (2016) define solar metallicity is Z⊙ = 0.017, while Eldridge & Stanway (2016) adopt Z⊙ = 0.02.
Acknowledgments
We thank our anonymous referee for their constructive comments. A. A. C. S. is supported by the Deutsche Forschungsgemeinschaft (DFG) under grant HA 1455/26. T. S. is grateful for financial support from the Leibniz Graduate School for Quantitative Spectroscopy in Astrophysics, a joint project of the Leibniz Institute for Astrophysics Potsdam (AIP) and the Institute of Physics and Astronomy of the University of Potsdam. This research has made use of the VizieR catalogue access tool, Strasbourg, France. The original description of the VizieR service was published in A&AS 143, 23.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, ApJ, 818, L22 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 241103 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016c, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 118, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Adams, S. M., Kochanek, C. S., Gerke, J. R., Stanek, K. Z., & Dai, X. 2017, MNRAS, 468, 4968 [NASA ADS] [CrossRef] [Google Scholar]
- Antokhin, I. I., Owocki, S. P., & Brown, J. C. 2004, ApJ, 611, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016a, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Repetto, S., Holz, D. E., et al. 2016b, ApJ, 819, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binder, B., Gross, J., Williams, B. F., & Simons, D. 2015, MNRAS, 451, 4471 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, S., Cholis, I., Muñoz, J. B., et al. 2016, Phys. Rev. Lett., 116, 201301 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Hillier, D. J., Lanz, T., & Fullerton, A. W. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2015, MNRAS, 449, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Ignace, R., & Cassinelli, J. P. 2000, A&A, 356, 619 [NASA ADS] [Google Scholar]
- Castor, J. I., & Lamers, H. J. G. L. M. 1979, ApJS, 39, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chatzopoulos, E., & Wheeler, J. C. 2012, ApJ, 748, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., & Hadfield, L. J. 2006, A&A, 449, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., De Marco, O., & Barlow, M. J. 1998, MNRAS, 296, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Carpano, S., Hadfield, L. J., & Pollock, A. M. T. 2007, A&A, 469, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Vink, J. S., & Oudmaijer, R. D. 2007, A&A, 469, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessart, L., & Owocki, S. P. 2005, A&A, 432, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, M., Berti, E., O’Shaughnessy, R., et al. 2015, ApJ, 806, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, P., Israel, G. L., Milisavljevic, D., et al. 2015, MNRAS, 452, 1112 [CrossRef] [Google Scholar]
- Evans, C. J., Howarth, I. D., Irwin, M. J., Burnley, A. W., & Harries, T. J. 2004, MNRAS, 353, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Hainich, R., Oskinova, L. M., et al. 2012, ApJ, 753, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Eversberg, T., Lépine, S., & Moffat, A. F. J. 1998, ApJ, 494, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gagné, M., Fehon, G., Savoy, M. R., et al. 2012, in Proc. Scientific Meeting in Honor of Anthony F. J. Moffat, eds. L. Drissen, C. Robert, N. St-Louis, & A. F. J. Moffat, ASP Conf. Ser., 465, 301 [Google Scholar]
- Garcia, M., Herrero, A., Najarro, F., Lennon, D. J., & Alejandro Urbaneja, M. 2014, ApJ, 788, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gayley, K. G., Owocki, S. P., & Cranmer, S. R. 1997, ApJ, 475, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2005, A&A, 432, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., Koesterke, L., & Hamann, W.-R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hainich, R., Rühling, U., Todt, H., et al. 2014, A&A, 565, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hainich, R., Pasemann, D., Todt, H., et al. 2015, A&A, 581, A21 [Google Scholar]
- Hamann, W.-R., & Gräfener, G. 2003, A&A, 410, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Gräfener, G. 2004, A&A, 427, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS] [Google Scholar]
- Hamann, W.-R., Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., Feldmeier, A., & Oskinova, L. M., eds. 2008, Clumping in hot-star winds [Google Scholar]
- Hamann, W.-R., Oskinova, L., Todt, H., et al. 2017, IAU Symp., 329, submitted [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1999, ApJ, 519, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Huenemoerder, D. P., Oskinova, L. M., Ignace, R., et al. 2012, ApJ, 756, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., Hirai, R., Kinugawa, T., & Hotokezaka, K. 2017, MNRAS, 468, 5020 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kehrig, C., Vílchez, J. M., Pérez-Montero, E., et al. 2015, ApJ, 801, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Kniazev, A. Y., Grebel, E. K., Pustilnik, S. A., Pramskij, A. G., & Zucker, D. B. 2005, AJ, 130, 1558 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2015, MNRAS, 446, 1213 [CrossRef] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989, A&A, 219, 205 [NASA ADS] [Google Scholar]
- Kudritzki, R.-P., Lennon, D. J., & Puls, J. 1995, in Science with the VLT, eds. J. R. Walsh, & I. J. Danziger, 246 [Google Scholar]
- Kudritzki, R. P., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., Hosek, Jr., M. W., & Przybilla, N. 2014, ApJ, 788, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., Castro, N., Urbaneja, M. A., et al. 2016, ApJ, 829, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Laycock, S. G. T., Maccarone, T. J., & Christodoulou, D. M. 2015, MNRAS, 452, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Leaman, R., Venn, K. A., Brooks, A. M., et al. 2013, ApJ, 767, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Moffat, A. F. J. 1999, ApJ, 514, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Moffat, A. F. J. 2008, AJ, 136, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Lovegrove, E., & Woosley, S. E. 2013, ApJ, 769, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 2012, A&A, 543, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2015, A&A, 582, A108 [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1987, A&A, 178, 159 [NASA ADS] [Google Scholar]
- Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchenko, S. V., Foellmi, C., Moffat, A. F. J., et al. 2007, ApJ, 656, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolino, W. L. F., Bouret, J.-C., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., Puls, J., Scuderi, S., & Markov, H. 2005, A&A, 440, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Núñez, S., Kretschmar, P., Bozzo, E., et al. 2017, Space Sci. Rev., 212, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Hillier, D. J., Bouret, J. C., et al. 2009, A&A, 495, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Mahy, L., Hillier, D. J., & Rauw, G. 2012, A&A, 538, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Marcolino, W., Hillier, D. J., Donati, J.-F., & Bouret, J.-C. 2015, A&A, 574, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P., & Olsen, K. A. G. 2003, AJ, 126, 2867 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Morrell, N. I., Neugent, K. F., et al. 2012, ApJ, 748, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Mauerhan, J. C., Smith, N., Filippenko, A. V., et al. 2013, MNRAS, 430, 1801 [NASA ADS] [CrossRef] [Google Scholar]
- Mennekens, N., & Vanbeveren, D. 2014, A&A, 564, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mirabel, I. F. 2017, in IAU Symp., 324, 303 [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nadezhin, D. K. 1980, Ap&SS, 69, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Najarro, F., Hanson, M. M., & Puls, J. 2011, A&A, 535, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., Corcoran, M. F., Koenigsberger, G., & Moffat, A. F. J. 2007, ApJ, 658, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Nazé, Y., Broos, P. S., Oskinova, L., et al. 2011, ApJS, 194, 7 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connor, E., & Ott, C. D. 2011, ApJ, 730, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M. 2005, MNRAS, 361, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., Feldmeier, A., Ignace, R., & Chu, Y.-H. 2009, ApJ, 693, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Todt, H., Ignace, R., et al. 2011, MNRAS, 416, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Steinke, M., Hamann, W.-R., et al. 2013, MNRAS, 436, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918 [NASA ADS] [CrossRef] [Google Scholar]
- Park, K., & Ricotti, M. 2011, ApJ, 739, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Park, M.-G., & Ostriker, J. P. 2001, ApJ, 549, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Prinja, R. K., & Massa, D. L. 2010, A&A, 521, L55 [Google Scholar]
- Puls, J., Kudritzki, R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramachandran, V., Hainich, R., Hamann, W.-R., et al. 2018, A&A, 609, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G., & Nazé, Y. 2016, Adv. Space Res., 58, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, C. L., Morscher, M., Pattabiraman, B., et al. 2015, Phys. Rev. Lett., 115, 051101 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, T. L., Holtzman, J., Saha, A., & Anthony-Twarog, B. J. 2015, AJ, 149, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sander, A., Shenar, T., Hainich, R., et al. 2015, A&A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shapiro, S. L. 1973, ApJ, 180, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., & Thompson, T. A. 2013, ApJ, 766, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Oskinova, L., Hamann, W.-R., et al. 2015, ApJ, 809, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Hainich, R., Todt, H., et al. 2016, A&A, 591, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soria, R., & Kong, A. 2016, MNRAS, 456, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Eldridge, J. J., & Becker, G. D. 2016, MNRAS, 456, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Sundqvist, J. O., Puls, J., Feldmeier, A., & Owocki, S. P. 2011, A&A, 528, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szécsi, D., Langer, N., Yoon, S.-C., et al. 2015, A&A, 581, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Todt, H., Sander, A., Hainich, R., et al. 2015, A&A, accepted [Google Scholar]
- Tramper, F., Gräfener, G., Hartoog, O. E., et al. 2013, A&A, 559, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramper, F., Sana, H., & de Koter, A. 2016, ApJ, 833, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Aret, A., et al. 2013, A&A, 559, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Hucht, K. A. 2001, New Astron. Rev., 45, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Vílchez, J. M., & Iglesias-Páramo, J. 1998, ApJ, 508, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S. 2012, in Eta Carinae and the Supernova Impostors, eds. K. Davidson, & R. M. Humphreys, Astrophys. Space Sci. Lib., 384, 221 [Google Scholar]
- Vink, J. S., & Harries, T. J. 2017, A&A, 603, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 2016, ApJ, 824, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Mikołajewska, J., & Belczyński, K. 2013, MNRAS, 429, L104 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Atomic models used in the stellar atmosphere calculations.
Parameters of the stellar atmosphere models calculated for the 50 M⊙ track with Z = 0.05 Z⊙ (Marchant et al. 2016).
Parameters of the stellar atmosphere models calculated for the BPASS stellar evolution tracks.
Appendix B: Synthetic spectra
 |
Fig. B.1 Same as Fig. 3 but for the 50 M⊙ track provided by Marchant et al. (2016) for a metallicity of 0.05 Z⊙. |
 |
Fig. B.2 Sequence of model SEDs calculated at characteristic points of the stellar evolution track provided by Marchant et al. (2016) for a metallicity of 0.1 Z⊙. The model SEDs are convolved with a Gaussian profile of 8 Å to increase lucidity. |
 |
Fig. B.4 Same as Fig. B.3 but for the BPASS evolution models (Eldridge & Stanway 2016). |
 |
Fig. B.5 Synthetic binary spectrum (red straight line) of model MI 1 for the 60 M⊙ track calculated by Marchant et al. (2016) for a metallicity of 0.1 Z⊙ (see Fig. 1 and Table 1). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The continuum level is indicated by a thin black line. |
 |
Fig. B.5 continued. |
 |
Fig. B.6 continued. |
 |
Fig. B.7 continued. |
 |
Fig. B.8 continued. |
 |
Fig. B.9 continued. |
 |
Fig. B.10 Synthetic binary spectrum (red straight line) of model MII 1 for the 50 M⊙ track calculated by Marchant et al. (2016) for a metallicity of 0.05 Z⊙ (see Fig. 1 and Table A.2). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The continuum level is indicated by a thin black line. |
 |
Fig. B.10 continued. |
 |
Fig. B.11 continued. |
 |
Fig. B.12 continued. |
 |
Fig. B.13 continued. |
 |
Fig. B.14 continued. |
 |
Fig. B.15 Synthetic binary spectrum (red straight line) of model E 1 for the BPASS evolution track calculate by Eldridge & Stanway (2016) (see Fig. 2 and Table A.3). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The offsets between the spectra refers to the wavelength dependent light ratio of the components. The continuum level is indicated by a thin black line. |
 |
Fig. B.15 continued. |
 |
Fig. B.16 continued. |
 |
Fig. B.17 continued. |
 |
Fig. B.18 continued. |
 |
Fig. B.19 Synthetic spectrum (red straight line) of model E 5 for the BPASS evolution track (see Fig. 2 and Table A.3), referring to the secondary after the primary collapsed into a BH. |
 |
Fig. B.19 continued. |
 |
Fig. B.20 continued. |
 |
Fig. B.21 continued. |
 |
Fig. B.22 continued. |
 |
Fig. B.23 continued. |
 |
Fig. B.24 continued. |
All Tables
Parameters of the stellar atmosphere models calculated for the 60 M⊙ track with Z = 1/10 Z⊙ (Marchant et al. 2016, see track I in Fig. 1).
Stellar and wind parameters of the GW progenitor models on the main sequence, compared to the earliest-type main sequence stars observed in the SMC and IC 1613 (see the original publications for details).
Comparison between the stellar and wind parameters of the GW model progenitors during the WR phase and the earliest WR stars observed at low metallicity (see the original publicationsa for details).
Parameters of the stellar atmosphere models calculated for the 50 M⊙ track with Z = 0.05 Z⊙ (Marchant et al. 2016).
Parameters of the stellar atmosphere models calculated for the BPASS stellar evolution tracks.
All Figures
 |
Fig. 1 Hertzsprung-Russell diagram showing the two stellar evolution tracks calculated by Marchant et al. (2016) that are used in this paper. Only the evolution path of the primary is shown, since the evolution of the secondary is virtually identical after the initial mass transfer. The blue filled asterisks mark the positions at which stellar atmosphere models where calculated. The labels near these asterisks are the atmosphere-model identifiers used throughout the text and Tables 1 and A.2. The highlighted and color-coded parts of the tracks refer to different WR phases and the period where the Roche lobe volume is filled, respectively (see inlet). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but showing the BPASS binary evolution tracks. Since the BPASS binary-calculations are stopped after the first core collapse event, the track of the secondary is split in two parts, leaving a gap between the positions E4 and E5 (dashed line, see text for details). |
| In the text | |
 |
Fig. 3 Sequence of synthetic spectra at five different evolutionary stages (marked by the identifiers also used in Fig. 1 and Table 1) of a massive star with initial mass 60 M⊙ evolving quasi-homogeneously at Z = 0.1 Z⊙ (Marchant track I). The continuum levels and the zero lines are indicated by horizontal thin gray lines. The time series starts at the bottom with the spectrum of the model at the ZAMS. To facilitate a comparison with observed spectra, the model spectra are convolved with a Gaussian profile with a FWHM of 1.0 Å. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but for the BPASS stellar evolution tracks and a metallicity of 0.005 Z⊙. |
| In the text | |
 |
Fig. 5 Difference between empirical mass-loss rates and those predicted by the mass-loss recipe proposed by Vink et al. (2001). The sample consists of 14 early O-dwarfs with spectral types earlier than O4V (see text for the references and discussion) in the Galaxy (Z = 1 Z⊙), the LMC (Z = 0.5 Z⊙), the SMC (Z = 0.2 Z⊙), and IC 1613 (Z = 0.14 Z⊙). |
| In the text | |
 |
Fig. 6 Modified wind momentum ( |
| In the text | |
 |
Fig. B.1 Same as Fig. 3 but for the 50 M⊙ track provided by Marchant et al. (2016) for a metallicity of 0.05 Z⊙. |
| In the text | |
 |
Fig. B.2 Sequence of model SEDs calculated at characteristic points of the stellar evolution track provided by Marchant et al. (2016) for a metallicity of 0.1 Z⊙. The model SEDs are convolved with a Gaussian profile of 8 Å to increase lucidity. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.2 but for a metallicity of 0.05 Z⊙. |
| In the text | |
 |
Fig. B.4 Same as Fig. B.3 but for the BPASS evolution models (Eldridge & Stanway 2016). |
| In the text | |
 |
Fig. B.5 Synthetic binary spectrum (red straight line) of model MI 1 for the 60 M⊙ track calculated by Marchant et al. (2016) for a metallicity of 0.1 Z⊙ (see Fig. 1 and Table 1). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The continuum level is indicated by a thin black line. |
| In the text | |
 |
Fig. B.5 continued. |
| In the text | |
 |
Fig. B.6 Same as Fig. B.5 but for model MI 2. |
| In the text | |
 |
Fig. B.6 continued. |
| In the text | |
 |
Fig. B.7 Same as Fig. B.5 but for model MI 3. |
| In the text | |
 |
Fig. B.7 continued. |
| In the text | |
 |
Fig. B.8 Same as Fig. B.5 but for model MI 4. |
| In the text | |
 |
Fig. B.8 continued. |
| In the text | |
 |
Fig. B.9 Same as Fig. B.5 but for model MI 5. |
| In the text | |
 |
Fig. B.9 continued. |
| In the text | |
 |
Fig. B.10 Synthetic binary spectrum (red straight line) of model MII 1 for the 50 M⊙ track calculated by Marchant et al. (2016) for a metallicity of 0.05 Z⊙ (see Fig. 1 and Table A.2). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The continuum level is indicated by a thin black line. |
| In the text | |
 |
Fig. B.10 continued. |
| In the text | |
 |
Fig. B.11 Same as Fig. B.10 but for model MI 2. |
| In the text | |
 |
Fig. B.11 continued. |
| In the text | |
 |
Fig. B.12 Same as Fig. B.10 but for model MI 3. |
| In the text | |
 |
Fig. B.12 continued. |
| In the text | |
 |
Fig. B.13 Same as Fig. B.10 but for model MI 4. |
| In the text | |
 |
Fig. B.13 continued. |
| In the text | |
 |
Fig. B.14 Same as Fig. B.10 but for model MI 5. |
| In the text | |
 |
Fig. B.14 continued. |
| In the text | |
 |
Fig. B.15 Synthetic binary spectrum (red straight line) of model E 1 for the BPASS evolution track calculate by Eldridge & Stanway (2016) (see Fig. 2 and Table A.3). The composite spectrum is the sum of the primary spectrum (brown dashed line) and the secondary spectrum (green dotted line). The offsets between the spectra refers to the wavelength dependent light ratio of the components. The continuum level is indicated by a thin black line. |
| In the text | |
 |
Fig. B.15 continued. |
| In the text | |
 |
Fig. B.16 Same as Fig. B.15 but for model E 2. |
| In the text | |
 |
Fig. B.16 continued. |
| In the text | |
 |
Fig. B.17 Same as Fig. B.15 but for model E 3. |
| In the text | |
 |
Fig. B.17 continued. |
| In the text | |
 |
Fig. B.18 Same as Fig. B.15 but for model E 4. |
| In the text | |
 |
Fig. B.18 continued. |
| In the text | |
 |
Fig. B.19 Synthetic spectrum (red straight line) of model E 5 for the BPASS evolution track (see Fig. 2 and Table A.3), referring to the secondary after the primary collapsed into a BH. |
| In the text | |
 |
Fig. B.19 continued. |
| In the text | |
 |
Fig. B.20 Same as Fig. B.19 but for model E 6. |
| In the text | |
 |
Fig. B.20 continued. |
| In the text | |
 |
Fig. B.21 Same as Fig. B.19 but for model E 7. |
| In the text | |
 |
Fig. B.21 continued. |
| In the text | |
 |
Fig. B.22 Same as Fig. B.19 but for model E 8. |
| In the text | |
 |
Fig. B.22 continued. |
| In the text | |
 |
Fig. B.23 Same as Fig. B.19 but for model E 9. |
| In the text | |
 |
Fig. B.23 continued. |
| In the text | |
 |
Fig. B.24 Same as Fig. B.19 but for model E 10. |
| In the text | |
 |
Fig. B.24 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


