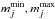© ESO, 2017

1. Introduction

While the nature of global magnetic fields in late-type stars with convective envelopes seems to be – at least in principle – understood as a consequence of the dynamo mechanism, the origin of organized magnetic fields detected in some O and B stars is less obvious. Given the large progress in the instrumentation allowing the detection of even weak magnetic fields, it is understandable that a very systematic search for the presence of magnetic fields among WR, O, B, and Be stars has recently been conducted by a large team of collaborators. This project, known as MiMES (Magnetism in MassivE Stars), was conducted between 2008 and 2013, and the first summary report was published by Wade et al. (2016). These authors report that unlike the magnetic fields of late-type stars, the magnetic fields of hot stars do not show any clear correlations with basic stellar properties such as their mass or rotation rate. We note that the realisation has grown in recent years that a large portion of O and B stars are binaries or even multiple systems, which must have significant impact on the understanding of their properties (see, e.g. Chini et al. 2012; de Mink et al. 2013). The role of multiplicity in the magnetism of hot stars is worth consideration. Recently, Neiner et al. (2014) reported one preliminary result of the MiMES survey: the discovery of a magnetic field of the triple system V746 Cas. Since the properties of this system were not well known, we were motivated to this study.

V746 Cas (HD 1976, HR 91, BD+51°62, HIP 1921, Boss 67) is a bright (V = 5$\mathit{.}{}^{\mathrm{m}}$6) B5 IV star. Its radial-velocity (RV) variations were discovered by Adams (1912) and confirmed by Plaskett & Pearce (1931). Blaauw & van Albada (1963) derived RVs from a new series of McDonald spectra and published the first orbital elements; see Table 1. In addition to their spectra, they also used the Dominion Astrophysical Observatory (DAO) spectra. Abt (1970) published six previous Mt. Wilson RVs, which partly overlap with those published by Adams (1912). Abt et al. (1990) measured RVs of 20 new KPNO spectra and published another set of elements, deriving a period of 25$\mathit{.}{}^{\mathrm{d}}$44 ± 0$\mathit{.}{}^{\mathrm{d}}$03. Their solution is based solely on the KPNO RVs, but the authors claim that it also fits the previous Mt. Wilson, DAO, and McDonald RVs. McSwain et al. (2007) analysed their 15 new KPNO RVs along with earlier published data and found two comparable periods near 25$\mathit{.}{}^{\mathrm{d}}$4 and 27$\mathit{.}{}^{\mathrm{d}}$6. We note that these two periods are 1 yr aliases of each other. McSwain et al. (2007) preferred the shorter period and obtained another solution, this time based on most of previously published RVs, which is also given in Table 1.

The first attempt to detect the spectral lines of the secondary was reported by Gómez & Abt (1982). They studied 160 Å long CCD spectra in two wavelength regions: one containing He i 5876 Å and the Na i doublet at 5889 and 5895 Å, and the other containing the Si ii doublet at 6347 and 6371 Å, the Ne i 6402 Å line, and several Fe ii, Fe i, and Ca i lines, to be able to restrict the possible spectral class of the secondary. They did not show the actual line profiles and published only a few comments. They concluded that the spectral type of the secondary must be earlier than F6, and suspected a possible weak secondary component in the He i 5876 Å line.

V746 Cas is also the brighter member of the visual system ADS 328. Doboco & Andrade (in Doboco & Ling 2005) derived the orbit of the wide pair with a period of 169.29 yr (61 832 d), semimajor axis 0.̋214, eccentricity 0.163, inclination , argument of periastron and periastron passage at 1955.06 (JD 2 435 130). The distant component B is by some 0$\mathit{.}{}^{\mathrm{m}}$9 fainter than V746 Cas.

The light variability of V746 Cas in the range from 5$\mathit{.}{}^{\mathrm{m}}$54 to 5$\mathit{.}{}^{\mathrm{m}}$56 was discovered by the Hipparcos team (Perryman & ESA 1997), and several investigators reported the presence of two principal periods, 1$\mathit{.}{}^{\mathrm{d}}$065 and 2$\mathit{.}{}^{\mathrm{d}}$504, and alternatively a few additional periods as well (for instance Waelkens et al. 1998; Andrews & Dukes 2000; De Cat et al. 2007; Dukes et al. 2009, see Sect. 4 for a more detailed account). They all classified the object as a slowly pulsating B-type star (SPB). Before the light variability was discovered, Glushneva et al. (1992) published spectrophotometry of V746 Cas and several other stars and suggested that V746 Cas could serve as a secondary spectrophotometric standard.

Neiner et al. (2014) reported the discovery that the line spectra of V746 Cas are composed of a narrow component, for which they found clear signatures of a magnetic field, and a broad component that is much more variable in RV. They identified the narrow lines and the magnetic field with the primary and the broad-line component with the secondary of the 25$\mathit{.}{}^{\mathrm{d}}$4 binary, concluding that the lines of the distant tertiary are not seen in the spectra. They allowed, however, that the narrow-lined star might also be the visual tertiary or a combination of the primary and tertiary.

Our initial motivation for this study was to resolve the remaining ambiguity in the value of the orbital period. We started to collect new CCD spectra in the red spectral region. Their subsequent analysis led us to a more complex investigation and hopefully to a better understanding of this remarkable triple system, which we report here.

2. Available observational data and their reductions

2.1. Spectroscopy

Our observational material consists of 41 Ondřejov CCD spectra secured in 2014–2015 (S/N 160–300; three underexposed spectra with 27, 37, and 100), 17 OHP Aurelie spectra with an S/N of 130–230, the first one of 36 only (Gillet et al. 1994), which were obtained and studied by Mathias et al. (2001), 3 archival OHP Elodie spectra with S/N 270–280 in the red parts of the spectra (Moultaka et al. 2004), and 13 publicly available echelle spectra from the Bernard Lyot telescope with an S/N greater than 200 in the red parts of the spectra (Petit et al. 2014). The initial reduction of all Ondřejov spectra (bias subtraction, flat-fielding, creation of 1D spectra, and wavelength calibration) was carried out in IRAF. For the Bernard Lyot and OHP Elodie spectra, extracted from public databases, we adopted the original reductions, verifying that the zero-point of the wavelength scale was corrected via telluric lines, as was the case for the Ondřejov spectra. This was more complicated with the Aurelie spectra, which are not available from public archives. P. Mathias kindly provided us with the old DAT tapes, which were reconstructed in Prague. Their new reduction was carried out with the help of simple dedicated programs, the wavelength calibration being carried out with the program SPEFO (Horn et al. 1996; Škoda 1996), namely the latest version 2.63 developed by J. Krpata. Median values of each corresponding sets of offsets and flat spectra were used.

Rectification and removal of residual cosmics and flaws for all sets of spectra were carried out in SPEFO.

We first extracted the red parts of the Elodie and Bernard Lyot spectra (~6360–6740 Å) to have the same spectral region as is covered by the Ondřejov spectra. One Ondřejov spectrum is shown in Fig. 1. As was previously noted by Neiner et al. (2014), the line profiles are not symmetric but contain broad and narrow components, the broad component varying in RV over a wide velocity range. The profiles might also be affected by subfeatures that are related to rapid light and line-profile variations and move across the line profiles as a result of stellar rotation. For all Elodie and Bernard Lyot spectra, we also extracted the blue, green, and yellow parts of the spectra over the wavelength range from 4000 to 6360 Å. We also extracted the Aurelie spectra, which cover the wavelength range from 4095 to 4155 Å.

Finally, we also collected RV measurements obtained by several investigators and published in the literature. The journal of all available RVs is listed in Table 2 and all individual RVs are presented in Table A.1 for the data from the literature. When they were not available in the original source, we converted the observation dates into HJDs. For brevity, we use reduced Julian dates

$\mathrm{RJD}\mathrm{=}\mathrm{HJD}\hspace{0.17em}\mathrm{-}\hspace{0.17em}\mathrm{2}\hspace{0.17em}\mathrm{400}\hspace{0.17em}\mathrm{000.0}$throughout. Abt (1970) published six RVs from Mount Wilson secured between December 1910 and November 1921. They include RVs published by Adams (1912), with the exception of the very first observation, which was secured on 1910 December 21. We therefore adopted the first RV from Adams (1912) and all remaining Mount Wilson RVs (spg. 1) from Abt (1970).

2.2. Standard RV measurements

To resolve the problem of the true orbital period and to obtain reliable orbital elements, we first tested several techniques of RV measurements. For the most numerous set of the red spectra, we measured the two strongest lines, Hα and He i 6678 Å, in SPEFO. This program displays direct and flipped traces of the line profiles superimposed on the computer screen that the user can slide to achieve a precise overlapping of the parts of the profile whose RV is to be measured. We separately measured the line cores and outer line wings. We note that two of the Ondřejov spectra (RJDs 56 920 and 57 228) are underexposed and we were only able to measure the RVs of the wings of Hα. These RV measurements are listed in Table A.2. For the Aurelie spectra, we also measured RVs of the broad wings of the He i 4144 Å line, and these measurements are listed in Table A.3 in Appendix A.

While the uncertainty of the SPEFO measuring procedure alone seems small (of the order of a few km s^-1), as determined from three independent measurements, there are three additional sources of uncertainties: photon noise, systematics arising from the rectification, and systematics from line blending. The latter is probably not critical for RVs of a particular spectral line, but they may dominate the uncertainty budget for a mean RV from several spectral lines (as discussed below). In any case, the total uncertainty is higher than the formal rms errors and might reach up to 10 km s^-1 in the least favourable cases.

For the Elodie and Bernard Lyot spectra, we also measured RVs of the following stronger lines in SPEFO: He i 4009, 4143, 4471, 4713, 4922, 5016, 5047, and 5876 Å, C ii 4267 Å, and Mg ii 4481 Å. We did not use the He i 4026 Å, 4120 Å, and 4387 Å lines, since the first is affected by an inter-order jump in all Bernard Lyot spectra, while the profiles of the other two lines are affected by strong blends in their neighbourhood. Finally, for the Aurelie spectra we measured RVs of Hδ and He i 4143 Å.

2.3. Photoelectric observations and their homogenisation

There are three principal sets of photoelectric observations suitable for period analyses:

• 1.

  The Hipparcos H_p observations (Perryman &ESA 1997);

• 2.

  the uvby observations from the Four-College APT secured by one of us; a subset of these observations has previously been analysed by Dukes et al. (2009); and

• 3.

  the Geneva 7-C observations obtained and studied by De Cat et al. (2004) and De Cat et al. (2007).

One of us, R.J. Dukes, was able to recover the APT uvby observations, or more precisely, a more numerous data set than was used in his published studies. It was deemed useful to repeat the period analysis with a complete and homogenised set of the data. The yellow-band observations (H_p and Geneva V magnitudes converted into Johnson V, and Strömgren y) are the most numerous and represent the best set for the analysis. More details on the data processing and their homogenisation can be found in Appendix C, where the journal of these observations is also listed in Table C.1. After the removal of data from non-photometric nights, we are left with 2060 individual yellow-band observations spanning an interval of nearly 9800 d.

3. Towards true orbital periods of the system

Figure 2 shows dynamical spectra for the Hα and He i 6678 Å line versus phase of the 25$\mathit{.}{}^{\mathrm{d}}$416 period. The orbital motion in the line wings of both lines is clearly visible. In contrast, the line cores do not exhibit clear RV variations with the same amplitude. We also note that there is no indication of an antiphase RV variation expected for the secondary in the 25$\mathit{.}{}^{\mathrm{d}}$416 orbit. This means that the bulk of the line cores is not associated with the primary, as suggested by Neiner et al. (2014), but with the tertiary of the visual orbit.

As explained above, we measured RVs separately for the broad and narrow parts of the Hα and He i 6678 Å lines. We immediately noted, in accord with Neiner et al. (2014), that the range of RV variations is much smaller for the narrow parts of the lines, and we verified that the RVs of the wide parts of the lines vary with the known ~ 25.4 d period.

The SPEFO RVs of the line cores of the Balmer lines seemingly follow the 25.4 d RV curve of the wide parts of the lines, in phase with the wide wings, but with a strongly reduced amplitude. This implies that they do not belong to the secondary in the 25.4 d orbit but to the distant tertiary, with a nearly constant RV. Their apparent RV changes are caused only by the strong line blending of the lines of the primary and tertiary.

3.1. Period analysis of RVs

To resolve the question of the true value of the orbital period of the closer pair, we calculated PDM periodograms (Stellingwerf 1978) for individual data subsets. They are shown in Fig. 3. It is immediately seen that neither the Blaauw & van Albada (1963) nor the McSwain et al. (2007) RVs alone are able to restrict the value of the orbital period. Blaauw & van Albada (1963) were obviously aware of the limitations of their data set since they estimated the uncertainty of the 27$\mathit{.}{}^{\mathrm{d}}$8 period to be as much as one day. The time interval covered by their own observations is shorter than two orbital periods. We also note that the first data set from spectrograph 1, although it spans a long time interval, is probably of limited accuracy and cannot be used to determine a unique period.

Only observations by Abt (1970) and our new RVs are numerous enough to identify the true orbital period. Their periodograms are mutually similar. The dominant period of 25$\mathit{.}{}^{\mathrm{d}}$416 (f = 0.0393 c d^-1) and its first harmonics are clearly visible. A smaller minimum at 0.0360 c d^-1 corresponds to a 1 yr alias of the 25$\mathit{.}{}^{\mathrm{d}}$416 period.

3.2. Linear ephemeris for the inner-orbit period

To obtain as precise a value of the orbital period P₁ of the inner binary as possible, we derived some trial orbital solutions with the program FOTEL (Hadrava 1990, 2004a). We first calculated an orbital solution based on our new SPEFO RVs. The semiamplitude for the He i 6678 Å RVs is higher than that obtained from the Hα RVs. It is a well-known effect for early-type stars that the lines with appreciably Stark-broadened wings like the Balmer lines give lower RV amplitudes and are not suitable for the determination of true orbital elements (e.g. Andersen 1975; Andersen et al. 1983). This clearly represents another complication on the way to obtaining realistic binary properties.

Since our first task is, however, to derive the correct value of the orbital period, we adopted the SPEFO Hα RVs and Hδ RVs for the Aurelie spectra, which give a semiamplitude closer to those found by previous investigators; see Table 1. We combined them with all RVs from the literature and ran a solution in which we allowed the calculation of individual systemic velocities (γs) for individual data sets. Using the rms errors of individual sets, we derived their weights inversely proportional to the squares of the corresponding rms errors. Investigating the phase plots, we found that the RVs of spectrograph 1 (Mt. Wilson) probably refer to a combination of the broad and narrow parts of the line profiles and cannot contribute meaningfully to constrain the orbital period.

We then calculated a joint solution for all weighted RVs from spgs. 2–8 (see the first solution in Table 3), and we adopted the orbital period from this solution ${\mathit{T}}_{\mathrm{super}\mathit{.}\mathrm{conj}\mathit{.}}\mathrm{=}\mathrm{HJD}\mathrm{2}\hspace{0.17em}\mathrm{454}\hspace{0.17em}\mathrm{384.65}\mathrm{\left(}\mathrm{44}\mathrm{\right)}\mathrm{+}\mathrm{25}\stackrel{\mathrm{d}}{.}\mathrm{41569}\mathrm{\left(}\mathrm{42}\mathrm{\right)}\hspace{0.17em}\mathit{.}$(1)Phase plots for this joint solution are shown in Fig. 4, separately for the RVs from the literature and for our new Hα and Hδ RVs.

Keeping the orbital period fixed, we then derived two other solutions, this time based on our new He i 6678 Å RVs from spgs. 6–9 and using alternatively the RV set based on the Gaussian fits and on the SPEFO RVs. The results are also listed in Table 3. The elements show that it is not easy to choose the correct value of K₁ and the mass function. The semiamplitude and eccentricity differ for the individual solutions, depending on the line(s) measured and also on the measuring technique. A part of the problem is the fact that almost all spectral lines are to some extent affected by neighbouring blends.

We also tried to disentangle the lines of the system components using the KOREL program (Hadrava 1995, 1997, 2004b). However, since the spectra at our disposal cover only one-tenth of the visual orbit for the He i 4143 Å line and even less for the other spectral lines, the semiamplitudes of the bodies in the outer orbit could not be meaningfully converged and we have no firm clue how to fix them. We only verified that no trace of the secondary could be found. In our experience, this implies that the secondary must be for more than three magnitudes fainter than the combined light of the primary and tertiary.

3.3. Speckle-interferometry and the visual orbit

Adding one speckle-interferometric observation from 2007 (Mason et al. 2009) to the existing set of 37 observations of V746 Cas, we were able to derive a new visual orbit of the third body, but our preliminary solution confirmed the orbit published by Docobo and Andrade (see Doboco & Ling 2005). For reference, it is summarised in Table 4. The reported uncertainties are the nominal ones, corresponding to a single local minimum of the respective χ². However, the values of P₂ and e₂ seem to be strongly correlated. Moreover, they strongly depend on the five previous astrometric observations from the beginning of the 20th century. Their real uncertainty can probably be greater than 0.02 arcsec, which we assumed for them.

4. Nature of the rapid photometric variations

4.1. Overview and analysis of previous results

Table 5 provides an overview of various frequencies of light variations of V746 Cas reported by several investigators. There seems to be no doubt about the two principal frequencies, detected by all investigators, 0.939 and 0.399 c d^-1. Notably, Mathias et al. (2001) were unable to find any spectroscopic signatures of these two frequencies in their Aurelie spectra covering the wavelength interval from 4085 to 4155 Å. The authors state, however, that all their spectra have S/Ns lower than 140. Two groups, De Cat et al. (2004) and Dukes et al. (2009), reported another frequency, 0.799 c d^-1. De Cat et al. (2004) denoted it as a possible alias. We note that it is an exact harmonics of the 0.399 c d^-1 frequency. In our opinion, this indicates that the light curve with the 0.399 c d^-1 frequency deviates from a sinusoidal shape. Therefore, the 0.799 c d^-1 frequency is not an independent frequency. Another weak frequency of 1.20346 c d^-1 reported by De Cat et al. (2007, which in our opinion could be the second harmonics of 0.399 c d^-1 could not be confirmed by Dukes et al. (2009), who analysed their own Strömgen uvby photometry from the Four College Automatic Photoelectric telescope (APT) along with the H_p and Geneva 7-C photometries. They found a frequency of 0.9309 c d^-1, however, which is quite close to f₁ = 0.939 c d^-1. We note that 0.9390 and 0.9309 c d^-1 mutually differ for one-third of the frequency of a sidereal year, so we suspect that the 0.9309 cd^-1 frequency is an alias. The above facts led us to suspect that the light changes of V746 Cas are modulated only by two independent periods.

4.2. New period analysis of available photometry

For the purpose of the period analysis, we subtracted seasonal mean values from all data to remove possible slight secular variations of either instrumental systems of the telescopes or true small secular changes (see Appendix C for details). We used the programs PERIOD04 (Lenz & Breger 2005) and FOTEL for the modelling and fits. We found that the longer, non-sinusoidal period of 2.5 d has larger amplitudes for the second and fifth harmonics as well (periods 1$\mathit{.}{}^{\mathrm{d}}$25 194, and 0$\mathit{.}{}^{\mathrm{d}}$50 077), which were then included into fits. Inspecting cases with more observations within short time-intervals like 0.03 d, we conclude that in all three data sets there are cases when the rms error of single observations exceeds 0$\mathit{.}{}^{\mathrm{m}}$007. The rms error of the fit is only slowly decreasing when more frequencies are added, and it remains on the 0$\mathit{.}{}^{\mathrm{m}}$007 level.

We arrive at the following ephemerides for the 1$\mathit{.}{}^{\mathrm{d}}$065, and 2$\mathit{.}{}^{\mathrm{d}}$504 periods: $\begin{array}{ccc}{\mathit{T}}_{\max \mathit{.}\mathrm{light}}& \mathrm{=}& \\ {\mathit{T}}_{\max \mathit{.}\mathrm{light}}& \mathrm{=}& \end{array}$Binary eclipses can also be safely excluded from the available photometry (see Fig. 5). Our simulations of the light curve for the 25$\mathit{.}{}^{\mathrm{d}}$4 orbit with the program PHOEBE 1 (Prša & Zwitter 2005) for plausible values of the stellar radii (see below) then show there is a rather strict upper limit for the orbital inclination, i₁ ≤ 85°.

4.3. Periodic variations of the magnetic field

We tried to determine whether the observed variations of the magnetic field found by Neiner et al. (2014) might not be related to the known photometric changes. We quickly found that the magnetic field indeed varies with the longer of the photometric periods, 2$\mathit{.}{}^{\mathrm{d}}$50 387; see Fig. 6.

A sinusoidal variation of the magnetic field intensity is commonly interpreted as a dipole field inclined to the rotational axis of the star and varying with the stellar rotational period. Neiner et al. (2014) associated the magnetic field with the narrow-line component, which they considered to be the primary, but which is – as we have shown here – the distant tertiary component moving in the long orbit with the 25$\mathit{.}{}^{\mathrm{d}}$4 binary.

In the bottom panel of Fig. 6 we also plot the Gaussian-fit RVs of the narrow component of He i 6678 Å (i.e. RVs of the magnetic-field tertiary) line vs. phase of the 2$\mathit{.}{}^{\mathrm{d}}$504 period. The scatter is rather large, but the RV variations clearly show some similarity to the light changes. This could be due to the corotating structures related to the magnetic field of the tertiary. We mention this to alert future observers that it might be rewarding to obtain systematic whole-night series of spectra at high resolution to verify the reality of the phenomenon and possibly to apply techniques such as Doppler imaging if the phenomenon is confirmed to be real.

4.4. Rapid line-profile changes of the primary?

If some rapid line-profile changes are also present in the spectra of the primary, they could manifest themselves as additional RV disturbances, overlapped over the orbital RV changes. While the technique of the settings on the outer line wings in SPEFO might tend to mask such changes (while affecting the true RV amplitude), such disturbances should be best detected in the Gaussian fits, which use two fixed Gaussian line profiles, mutually moved only in RV. We therefore inspected the O–C RV residuals from the 25$\mathit{.}{}^{\mathrm{d}}$4 orbit for the Gaussian He i 6678 Å RVs based on repeated measurements. In Fig. 7 we compare the plot of these RV residuals with the plot of yellow-band photometry prewhitened for the 2$\mathit{.}{}^{\mathrm{d}}$50 387 period. There is some indication of sinusoidal residual RV changes with the photometric period of 1$\mathit{.}{}^{\mathrm{d}}$065, especially for RVs with lower rms errors. The modulation is nicely seen in the subset of Aurelie high-S/N and high-resolution spectra. While it is clear that the ultimate confirmation may only come from new whole-night series of high-resolution spectra, we do believe there is a reason to identify the 1$\mathit{.}{}^{\mathrm{d}}$065 period with the rotational period of the primary. The modulation of measured RVs could be caused by some structures on the surface of the primary, moving across the stellar disk as the star rotates. We note that there is growing evidence for rotational modulation for a number of B stars from the photometry obtained by the Kepler satellite and by ground-based surveys (see, e.g. McNamara et al. 2012; Nielsen et al. 2013; Kourniotis et al. 2014; Balona et al. 2015, 2016).

5. Initial estimates of the basic physical elements of the system

5.1. Radiative properties of the primary and tetriary

To determine the radiative properties of the two dominant components, we used the Python program PYTERPOL, which interpolates in a pre-calculated grid of synthetic spectra. Using a set of observed spectra, it tries to find the optimal fit between the observed and interpolated model spectra with the help of a simplex minimization technique. It returns the radiative properties of the system components such as T_eff, v sin i or log  g, but also the relative luminosities of the stars and RVs of individual spectra¹. The function of the program is described in detail in Nemravová et al. (2016).

In our particular application, two grids of synthetic spectra, Lanz & Hubený (2007) for T_eff > 15 000 K, and Palacios et al. (2010) for T_eff  < 15 000 K, were used to estimate basic properties of the primary and tertiary for all 16 Aurelie, 3 Elodie, and 13 Bernard Lyot high-S/N spectra. The following spectral regions containing numerous spectral lines, but avoiding the inter-order transitions and regions with stronger telluric lines, were modelled simultaneously:

Relative component luminosities were fitted separately in four spectral bands: 4000–4280 Å, 4308–4490 Å, 4700–5025 Å, and 6670–6690 Å. Uncertainties of radiative properties were obtained through Markov chain Monte Carlo (MCMC) simulation implemented within emcee² Python library by Foreman-Mackey et al. (2013). They are summarised in Table 6. We note that in contrast to the N-body model, which we use below for the final estimate of the most probable properties of the system, PYTERPOL derives the RV from individual spectra without any assumption about orbital motion. It is therefore reassuring that when we allowed for a free convergence of the orbital period in a trial solution based on the PYTERPOL RVs, we arrived at a value of 25$\mathit{.}{}^{\mathrm{d}}$4156(13), in excellent agreement with the value of ephemeris (1) based on all available RVs.

5.2. Additional properties of the primary

All available MKK spectral classifications of V746 Cas summarized in the SIMBAD bibliography, including a recent one by Tamazian et al. (2006) based on high-resolution spectra, agree on the spectral type B5 IV. Dereddening of the mean all-sky standard UBV magnitudes from Hvar (see Table C.1) gives V₀ =5$\mathit{.}{}^{\mathrm{m}}$43, (B−V)₀ = −0$\mathit{.}{}^{\mathrm{m}}$170, (U–B)₀ = −0$\mathit{.}{}^{\mathrm{m}}$635, and E(B−V) = 0$\mathit{.}{}^{\mathrm{m}}$055, which corresponds to a B4-5IV star after the calibration by Golay (1974).

We can then use the observed Hipparcos parallax p of V746 Cas to further constrain the primary. According to the improved reduction (van Leeuwen 2007a,b), . Assuming the above mentioned V₀ = 5$\mathit{.}{}^{\mathrm{m}}$43 for the whole system, the observed magnitude difference between the primary and tertiary and neglecting the light contribution from the unseen secondary, we arrive at ${\mathit{V}}_{\mathrm{0}}^{\mathrm{1}}\mathrm{=}\mathrm{5}$$\mathit{.}{}^{\mathrm{m}}$82 for the primary. Using the above-mentioned range of the possible values of the parallax, 0.̋00263 to 0.̋00394, we obtain ${\mathit{M}}_{\mathrm{V}}^{\mathrm{1}}\mathrm{=}\mathrm{-}\mathrm{2}$$\mathit{.}{}^{\mathrm{m}}$08 and −1$\mathit{.}{}^{\mathrm{m}}$20, respectively. The bolometric corrections for the considered range of the effective temperature of the primary are from −1$\mathit{.}{}^{\mathrm{m}}$433 to −1$\mathit{.}{}^{\mathrm{m}}$557 so that the extreme allowed values of the bolometric magnitude of the primary ${\mathit{M}}_{\mathrm{bol}}^{\mathrm{1}}$ are −2$\mathit{.}{}^{\mathrm{m}}$63 to −3$\mathit{.}{}^{\mathrm{m}}$64.

If 1$\mathit{.}{}^{\mathrm{d}}$065 is the rotational period of the primary, then for v sini₁ = 179 km s^-1, derived from the PYTERPOL solution for the primary, R₁ ≥ 2πvsini/P = 3.77 R_⊙. For instance, if i₁ = 70°, we obtain R₁ = 4.01 R_⊙. For the expected range of the primary mass, this would imply log g  = 3.98 to 4.04 [cgs] for the primary, which is slightly offset at the 2.5σ level with respect to the range deduced from the fit by synthetic spectra (Table 6). We note, however, that the log g values are very sensitive to an accurate placement of the continuum, which is especially difficult for Balmer lines from the echelle spectra. On the other hand, if the true rotational period is a photometric double-wave curve with a period twice longer, that is, 2$\mathit{.}{}^{\mathrm{d}}$130, we would obtain log g  = 3.38 to 3.44 [cgs]; again offset from the nominal range. This would also correspond to significantly larger radius R₁ = 8.02 R_⊙ and an even lower upper limit of i. Given all the uncertainties involved, however, both possibilities need to be kept in mind.

5.3. Tertiary component

The more recent estimates of the magnitude difference between the close binary and tertiary from astrometry (Perryman & ESA 1997; Mason et al. 2009) agree on ${\mathit{m}}_{\mathrm{3}\hspace{0.17em}\mathrm{V}}\mathrm{-}{\mathit{m}}_{\mathrm{(}\mathrm{1}\mathrm{+}\mathrm{2}\mathrm{)}\hspace{0.17em}\mathrm{V}}\mathrm{~}\mathrm{0}\stackrel{\mathrm{m}}{.}\mathrm{9}$. The relative luminosities of the primary and tertiary estimated with PYTERPOL (see Table 6) imply ${\mathit{m}}_{\mathrm{3}\hspace{0.17em}\mathrm{V}}\mathrm{-}{\mathit{m}}_{\mathrm{(}\mathrm{1}\mathrm{+}\mathrm{2}\mathrm{)}\hspace{0.17em}\mathrm{V}}\mathrm{=}\mathrm{0}\stackrel{\mathrm{m}}{.}\mathrm{92}$, in remarkable agreement with the astrometric estimates. This once more confirms our identification of the narrow-line component seen in the spectra with the tertiary.

Using the v sini₃ = 72 km s^-1 estimated from the PYTERPOL solution for the tertiary and adopting the 2$\mathit{.}{}^{\mathrm{d}}$504 period as its period of rotation, we can similarly estimate the radius of the tertiary R₃ ≥ 3.56 R_⊙. Assuming that the inclination of the rotational axis of the tertiary is identical with the orbital inclination of the outer orbit 64°, we estimate log g from 3.90 to 4.01 for it. This agrees quite well with the observed range of log g from the line-profile modelling.

5.4. Component masses

In order to preliminarily estimate the component masses, we calculated evolutionary tracks using the Mesastar program (Paxton et al. 2015) and compared them with the observed range of the values of T_eff and log g, deduced from the line-profile fits, in Table 6. In all cases we assumed a helium abundance Y = 0.274, metallicity Z = 0.0195 (i.e. very close to the standard values of Caughlan & Fowler 1988), and mixing length parameter α = 2.1. We also accounted for element diffusion, Reimers red giant branch (RGB) wind with η = 0.6, Blocker AGB wind with η = 0.1, even though neither is very relevant on the zero-age main sequence (ZAMS). Semiconvection and convective overshooting were both switched off. The maximum output time step was Δt = 10⁵ yr to resolve the terminal main sequence (TAMS). Mesastar program, rev. 8845 (Paxton et al. 2015), was used for these computations.

From the comparison presented in Fig. 8, we can estimate the mass of the primary to be from m₁ = 5.6 to 6.7 M_⊙ (1σ range). We verified that the evolutionary tracks in the considered region close to the TAMS are not overly sensitive to the value of metallicity. For Z = 0.04, the corresponding mass range changes by as much as 0.1 M_⊙; lower metallicities are not likely for relatively young stars. The same is true for the mixing-length parameter α or the semiconvection parameter α_sc, since both stars are in a radiative equilibrium. For instance, α = 1.6 or α_sc = 0.01 lead to essentially the same results. For the overshooting parameters f_ov = 0.014 and f₀ = 0.004 (i.e. within the range discussed in Herwig 2000), the evolution around the TAMS is notably different, nevertheless, the range of masses would be shifted only slightly upwards, by less than 0.1 M_⊙,

A similar analysis for the tertiary component led to the mass m₃ = 4.6 to 6.0 M_⊙. Within the uncertainties, the primary and tertiary stars can even be equally massive and have very similar effective temperatures. The similarity of the primary and tertiary is also supported by the fact that their relative luminosities over the whole optical range seem to be the same; see Table 6.

6. N-body model of the V746 Cas system

6.1. Formulation

To analyse all available observational data in the most consistent way, we attempted to use the N-body model of Brož (2017), which was recently developed and successfully applied to the ξ Tauri quadruple system (Nemravová et al. 2016). Here, we used a significantly extended version of it. While a detailed technical description is given in the latter paper, we repeat here a subset of equations relevant for our problem:

$\begin{array}{ccc}& & {\begin{array}{c}\mathrm{¨}\\ {r}\end{array}}_{\mathrm{b}\mathit{i}}\mathrm{=}\mathrm{-}\sum _{\mathit{j}\ne \mathit{i}}^{{\mathit{N}}_{\mathrm{bod}}}\frac{\mathit{G}{\mathit{m}}_{\mathit{j}}}{{\mathit{r}}_{\mathit{ji}}^{\mathrm{3}}}\hspace{0.17em}{{r}}_{\mathit{ji}}\mathrm{+}{{f}}_{\mathrm{tidal}}\mathrm{+}{{f}}_{\mathrm{oblat}}\mathrm{+}{{f}}_{\mathrm{ppn}}\mathit{,}\\ & & {\mathit{I}}_{\mathit{\lambda }}^{\mathrm{\prime }}\mathrm{=}\sum _{\mathit{j}\mathrm{=}\mathrm{1}}^{{\mathit{N}}_{\mathrm{bod}}}\frac{{\mathit{L}}_{\mathit{j}}}{{\mathit{L}}_{\mathrm{tot}}}\hspace{0.17em}{\mathit{I}}_{\mathrm{syn}}\left[\mathit{\lambda }\left(\mathrm{1}\mathrm{-}\frac{{\mathit{v}}_{\mathit{z}\mathrm{b}\mathit{j}\mathrm{+}\mathit{\gamma }}}{\mathit{c}}\right)\mathit{,}{\mathit{T}}_{\mathrm{eff}\hspace{0.17em}\mathit{j}}\mathit{,}\log {\mathit{g}}_{\mathit{j}}\mathit{,}{\mathit{v}}_{\mathrm{rot}\hspace{0.17em}\mathit{j}}\mathit{,}{\mathrm{𝒵}}_{\mathit{j}}\right]\mathit{,}\\ & & {\mathit{F}}_{\mathit{V}}^{\mathrm{\prime }}\mathrm{=}\sum _{\mathit{j}\mathrm{=}\mathrm{1}}^{{\mathit{N}}_{\mathrm{bod}}}{\left(\frac{{\mathit{R}}_{\mathit{j}}}{\mathit{d}}\right)}^{\mathrm{2}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}{\mathit{F}}_{\mathrm{syn}}\mathrm{[}\mathit{\lambda ,}{\mathit{T}}_{\mathrm{eff}\hspace{0.17em}\mathit{j}}\mathit{,}\log {\mathit{g}}_{\mathit{j}}\mathit{,}{\mathit{v}}_{\mathrm{rot}\hspace{0.17em}\mathit{j}}\mathit{,}{\mathrm{𝒵}}_{\mathit{j}}\mathrm{]}{\mathit{f}}_{\mathit{V}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{d}\mathit{\lambda ,}\\ & & {\mathit{m}}_{\mathit{V}}^{\mathrm{\prime }}\mathrm{=}\mathrm{-}\mathrm{2.5}{\log }_{\mathrm{10}}\frac{{\mathit{F}}_{\mathit{V}}^{\mathrm{\prime }}}{{\mathit{F}}_{\mathit{V}\mathrm{calib}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}{\mathit{f}}_{\mathit{V}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{d}\mathit{\lambda }}\hspace{0.17em}\mathit{,}\end{array}$

where the notation is as follows. The index i always corresponds to observational data, j to individual bodies, N_bod = 3 is the number of bodies, r_b barycentric coordinates, m component mass, f_tidal, f_oblat and f_ppn contributions from tidal, oblateness, and parametrized post-Newtonian (PPN) accelerations, which are included for the sake of completeness, even though they are negligible in the V746 Cas system; I_λ, I_syn normalized synthetic spectrum (intensity) of the whole system and component, with appropriate Doppler shifts, L,L_tot component luminosity and the total luminosity, T_eff effective temperature, log g surface gravity [in cgs], v_rot projected rotational velocity, metallicity, F_syn absolute monochromatic flux (in erg s^-1 cm^-2 cm^-1 units) for any of the standard UBVRIJHK or non-standard bands, F_Vcalib calibration flux, and f_V(λ) filter transmission function. Both normalized and absolute synthetic spectra were interpolated on-the-fly by PYTERPOL, as described in Nemravová et al. (2016). For the absolute spectra, the grids BSTAR (Lanz & Hubený 2007) and PHOENIX (Husser et al. 2013) were used.

Synthetic data and observation are compared by means of a combined χ² metric 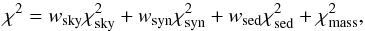${\mathit{\chi }}^{\mathrm{2}}\mathrm{=}{\mathit{w}}_{\mathrm{sky}}{\mathit{\chi }}_{\mathrm{sky}}^{\mathrm{2}}\mathrm{+}{\mathit{w}}_{\mathrm{syn}}{\mathit{\chi }}_{\mathrm{syn}}^{\mathrm{2}}\mathrm{+}{\mathit{w}}_{\mathrm{sed}}{\mathit{\chi }}_{\mathrm{sed}}^{\mathrm{2}}\mathrm{+}{\mathit{\chi }}_{\mathrm{mass}}^{\mathrm{2}}\mathit{,}$(8)with individual contributions defined as

$\begin{array}{ccc}& & \\ & & \mathrm{\left(}\mathrm{\Delta }{\mathit{x}}_{\mathit{ji}}\mathit{,}\mathrm{\Delta }{\mathit{y}}_{\mathit{ji}}\mathrm{\right)}\mathrm{=}{R}\left(\mathrm{-}{\mathit{\phi }}_{\mathrm{ellipse}}\mathrm{-}\frac{\mathit{\pi }}{\mathrm{2}}\right)\mathrm{\times }\left(\begin{array}{c}\\ \\ \end{array}\right)\mathit{,}\\ & & \\ & & \\ & & \end{array}$

where x_p,y_p denote 1 + 2 photocentric sky-plane coordinates, σ_{sky major, minor} uncertainty of the astrometric position, φ_ellipse position angle of the respective ellipse, R(... ) the corresponding 2 × 2 rotation matrix, σ_syn uncertainty of the normalized intensity, σ_sed uncertainty of the spectral-energy distribution, and ${\mathit{m}}_{\mathit{j}}^{\min }\mathit{,}{\mathit{m}}_{\mathit{j}}^{\max }$ minimum and maximum allowed masses. The last term is an artificial function with a sufficiently steep and smooth behaviour; the high exponent prevents the simplex from drifting away. Optionally, we can use weights w to enforce a convergence for selected less-numerous data sets (e.g. with w_sky = 10).

6.2. Application to V746 Cas

The number of free parameters in our model is L_free = 26; namely the masses m_j, orbital elements of the two orbits P_j, e_j, i_j, Ω_j, ω_j, M_j, systemic velocity γ, distance d, gravitational acceleration log g_j, effective temperatures T_{eff j}, and projected rotational velocities v_{rot j}. Radii are thus dependent quantities computed as ${\mathit{R}}_{\mathit{j}}\mathrm{=}\sqrt{\mathit{G}{\mathit{m}}_{\mathit{j}}\mathit{/}{\mathit{g}}_{\mathit{j}}}$. As usual, the parameter space is very extended and we can expect a number of local minima. As reasonable starting points, we used the results of previous observation-specific models. We then employed a simplex algorithm for the minimisation, with various starting points and several restarts. We also verified the results by simulated annealing, even though neither of the algorithms can guarantee that the true global minimum was found.

We used a complete observational data set: (i) 37 speckle-interferometric and astrometric observations of the third body, including some older and rather uncertain ones; (ii) 72 spectra from the Elodie, Aurelie, Lyot, and Ondřejov datasets; this would represent 184 666 individual data points, but for our analysis we used 21 506 mean points in order to have a faster computation with a comparable resolution of all spectra; (iii) 93 spectral-energy distribution measurements from Hvar, Geneva and Glushneva et al. (1992). For the last data set we had to perform dereddening, assuming A_V = 3.1 E(B−V) relation, E(B−V) = 0.055, and the wavelength dependence from Scheffler & Elsaesser (1987), Table 4.1.

On the other hand, we did not use radial velocities, as these are derived quantities possibly affected by some systematics, but rather the rectified spectra directly. We incorporated the same spectral regions, unaffected by any stronger telluric lines as in Sect. 5.1. Our approach is even better than using Pyterpol alone (which fits a single spectrum at a time), because the orbital motion is simulated by the N-body model, which links the spectra observed at different times. As a consequence, we are more sensitive to uncertainties and systematics of the rectification procedure, which would otherwise be hidden.

We encountered two serious problems, which required some modifications of the program. First, the secondary is practically unconstrained, except for the radial motion of the primary. Its convergence is thus impossible and we used the Harmanec (1988) relations instead, that is to say, we used only its effective temperature T_{eff 2} as a free parameter and computed the remaining ones, as log m₂(X), log R₂(X), log g₂(X), where X ≡ log T_{eff 2}, to constrain the secondary as a main-sequence star. If the secondary becomes too hot in the course of convergence, it will become visible in the synthetic spectra, of course.

Another problem arises from missing direct estimates of the radii R₁ and R₃ (there are no eclipses, no spectro-interferometry). We experienced a tendency to converge towards unrealistic hot subdwarfs and therefore had to use a mass constraint inferred from Mesastar modelling, in particular ${\mathit{m}}_{\mathrm{1}}^{\min }\mathrm{=}\mathrm{4.6}\hspace{0.17em}{\mathit{M}}_{\mathrm{\odot }}$, which corresponds to a 3σ lower limit.

Finally, a technical note: we prefer to inspect first the χ₂ values, which are not reduced, that is, not divided by the respective number of degrees of freedom ν. This gives a better chance to search for possible reasons of systematic errors (or model deficiencies).

We also prefer to use the nominal uncertainties in our modelling (not directly the “realistic” ones) because otherwise we would not be sensitive to any systematics at all; they would be completely hidden in large σs and we might be falsely satisfied with the model.

6.3. Nominal model

The nominal model is presented in Table 7 and Fig. 9. Its total χ² value seems too high, χ² = 157 756, that is, much higher than the corresponding number of degrees of freedom ν ≡ N_data−L_free = 21 647, the reduced ${\mathit{\chi }}_{\mathrm{R}}^{\mathrm{2}}\mathrm{\equiv }{\mathit{\chi }}^{\mathrm{2}}\mathit{/}\mathit{\nu }\mathrm{=}\mathrm{7.3}$  and the resulting probability is thus essentially zero. However, we explain the mismatch as follows. While the ${\mathit{\chi }}_{\mathrm{sky}}^{\mathrm{2}}$ contribution seems perfectly reasonable and it is indeed not difficult to reach the value as low as N_sky, it may become larger in the course of fitting because the other data sets are much more numerous and are likely affected by systematics.

The systematics in ${\mathit{\chi }}_{\mathrm{syn}}^{\mathrm{2}}$ are probably caused by the rectification procedure, even though it was performed as carefully as possible. For example, we sometimes see differences for a given spectrum that is surrounded by two or more spectra that are fitted well enough. The same is true for individual lines in a single spectrum, for instance, we have a good fit of the C ii and Mg ii lines, while H_γ (with its extended wings) and He i are somewhat offset. In principle, we cannot exclude the presence of rapid line-profile variations, but a self-consistent model would be needed for them, otherwise such unconstrained variations could explain any departures from the model (including any systematics).

The value of 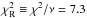${\mathit{\chi }}_{\mathrm{sed}}^{\mathrm{2}}$ seems also higher than expected. This is probably caused by systematics in calibrations of the absolute fluxes (even the Hvar and Geneva photometry from Table C1 differ by more than 3σ). Alternatively, a significant systematic uncertainty can be hidden in the dereddening procedure (see below). If we accept the arguments above and the high value of the nominal χ², then 1σ probability level would correspond to an increase of up to 158 659, and 3σ to 162 201.

Parameter uncertainties can be obtained by a bootstrap or χ² mapping. In this case, we used the latter method, with the notion that the respective uncertainties correspond to a local minimum only. Several correlations are still present in the model, however. In particular, a lower inclination i₁ usually requires a higher m_tot. A similar correlation exists between the distance d and m_tot. Moreover, there is a non-zero possibility of a long orbit of the tertiary, with P₂ ≃ 211 000 d, a high eccentricity e₂ ≃ 0.65, and small d, with only marginally worse ${\mathit{\chi }}_{\mathrm{sky}}^{\mathrm{2}}\mathrm{=}\mathrm{124}$, but the total χ² is then relatively large.

We emphasize that the results can differ from previous observation-specific models. In Table 7, we use osculating elements corresponding to the epoch T₀ = 2 454 384.65, which differ from fixed elements. In particular, P₁ is different from Eq. (1) because the very definition of osculation is “without any perturbation”, that is to say without the third body; the period perceived by an observer is close to that in Eq. (1). We note, however, that for the period P₂ of the long orbit, the difference between the osculating and the sidereal value is negligible. Moreover, we realized that at least several Aurelie spectra (RJD between 51 005.6 and 51 010.6) were affected by the rectification systematics (overcorrection), since the spectra do not cover the blue H_δ wing completely, and this made the K₁ estimates too large. The true K₁ value seems closer to 30 km s^-1 according to the N-body model. In a similar way, these systematics can increase (or decrease) the value of e₁.

Mirror solutions.

Obviously, there are several mirror solutions that cannot be easily resolved with the current limited data set (no eclipses, no spectro-interferometry). In particular, we have ${\mathit{i}}_{\mathrm{1}}^{\mathrm{\prime }}\mathrm{=}{\mathrm{180}}^{\mathrm{◦}}\mathrm{-}{\mathit{i}}_{\mathrm{1}}\mathrm{=}{\mathrm{95}}^{\mathrm{◦}}$, which gives the same χ² = 157 757. Unfortunately, with the current data set, Ω₁ is unconstrained, but we can expect a mirror solution ${\mathrm{\Omega }}_{\mathrm{1}}^{\mathrm{\prime }}\mathrm{=}{\mathrm{\Omega }}_{\mathrm{1}}\mathrm{+}{\mathrm{180}}^{\mathrm{◦}}$ anyway. Finally, the third body can have ${\mathit{i}}_{\mathrm{2}}^{\mathrm{\prime }}\mathrm{=}\mathrm{-}{\mathit{i}}_{\mathrm{2}}\mathrm{=}\mathrm{-}{\mathrm{57}}^{\mathrm{◦}}$, resulting in χ² = 157 815, which is again statistically the same.

Higher reddening.

We also tried to assume the reddening E(B − V) = 0.101, that is, at a typical 1σ uncertainty. This would allow for higher luminosities of the primary and tertiary. Indeed, the value of ${\mathit{\chi }}_{\mathrm{sed}}^{\mathrm{2}}\mathrm{=}\mathrm{3797}$ is somewhat lower, but the total value χ² = 156 777 is neither significantly higher nor lower. We therefore conclude that increasing the reddening alone is not a definitive solution. There might be additional systematics related to the wavelength dependence of extinction A_λ, in other words, a presence of additional interstellar matter with different κ_λ in the direction towards V746 Cas.

The complex interplay among the various types of observational data.

Finally, we explain that the N-body model is strongly constrained by the SED data: high masses m₁, m₃, with log g₁, log g₃ fixed by the line spectra, lead to large radii R₁, R₃, which would result in too bright stars, or a large distance d. At the same time, we fit both the speckle-interferometric data (astrometry of the third body) and the spectra (also known as RVs), where large d inevitably requires high m_tot, and this would contradict the former set of constraints. It may seem that making hot stars cooler is an option, but significantly lower T_{eff j} are incompatible with the observed (rectified) spectra. These sometimes unexpected but inevitable relationships are the main reasons why some of the parameters may be different from observation-specific models.

On the other hand, it is obvious that the result in terms of surprisingly low stellar masses is not satisfactory. Upon closer inspection, we concluded that the problem lies in a strong sensitivity of the result to the exact values of the surface gravities, which might be affected mainly by the instrumental problems of the Balmer lines from the echelle spectra. For this reason, we derived another model that we discuss below.

6.4. Model with the H_α line, but without other Balmer lines

Further examinations of the rectification procedure confirmed that the corrections of a slowly varying atmospheric extinction, instrument response, and sharp inter-order jumps in the echelle spectra at the same time are difficult to deal with. Consequently, we decided to also compute a model without the H_β, H_γ, and H_δ Balmer lines, which are especially prone to such effects. On the other hand, using no hydrogen lines at all would mean to loose the most sensitive indicator of the gravity acceleration. Therefore, we decided to use H_α from the Ondřejov (spg. 9) linear spectra, for which the rectification is straightforward. However, it was necessary to remove a number of regions affected by the water vapour telluric lines. Specifically, we included the following spectral regions: 4125–4155, 4260–4280, 4380–4405, 4450–4490, 4700–4725, 4912–4935, 5008–5025, 6500.6–6501.6, 6509.9–6511.4, 6520.5–6522.3, 6525.3–6530.0, 6538.2–6541.7, 6546.2–6547.2, 6549.7–6552.3, 6554.7–6557.1, 6559.2–6563.8, 6565.1–6571.7, 6573.2–6574.3, 6576.0–6580.5, 6588.0–6598.7, and 6603.5–6690 Å.

The resulting model is presented in Table 8 and Figs. 10 to 12. After several simplex runs we reached χ² as low as 97 733, which should be compared with the larger number of degrees of freedom, ν = 30 614. The differences with respect to the previous Table 7 seem to be acceptable and within uncertainties, except for m₁, m₃, e₂, log g₁, log g₃, R₁, and R₃. The substantially higher and more realistic masses are allowed for higher log g values, enforced by the H_α line. The differences in radii simply correspond to relatively higher T₁ and lower T₃, in order to fit the same SED. The mass of the tertiary m₃ is now in better agreement with the high T_{eff 3}, and R₃ fulfils the condition from Sect. 5.3, which makes our model more self-consistent. The e₂ value reflects more freedom given to the outer orbit due to higher m_tot. Last but not least, the reduced ${\mathit{\chi }}_{\mathrm{R}}^{\mathrm{2}}$ decreased from 7.3 down to 3.2, which indicates that we succeeded to remove a substantial part of the systematic uncertainties. We thus consider this model to be the preferred one.

7. Conclusions

Using several approaches to the analysis of the rich set of spectral, photometric, spectro-photometric, and astrometric observations available to us, we attempted to provide a new interpretation of the interesting massive triple system V746 Cas with a tertiary, which possesses a measurable magnetic field. The existing principal geometric limitations, such as that there are no eclipses and the flux of the secondary component was not detected, prevented us from deriving unique physical properties for all the components of the system. However, by combining all types of observations and bounding them mutually with the help of the N-body model, we were able to present a reasonably self-consistent picture of the system.

Our main findings are summarised below.

• 1.

  The rapidly rotating B4-B5 primary moves in the orbit with anunseen secondary. The fact that the secondary could not bedetected in the optical spectra, even when using the spectradisentangling and the observed mass function imply that itprobably is an A or F star. A direct detection of itsspectrum by standard observing techniques is probablyimpossible.

• 2.

  The bipolar magnetic field, discovered by Neiner et al. (2014), varies with the photometric period of 2$\mathit{.}{}^{\mathrm{d}}$50 387. It is associated with the tertiary, which is in a wide orbit with the 25$\mathit{.}{}^{\mathrm{d}}$4 binary. The tertiary is a ~B5-6IV star, which contributes 30% of the light in the optical region.

• 3.

  The photometric period of 2$\mathit{.}{}^{\mathrm{d}}$504 can almost certainly be identified with the rotational period of the tertiary. We note that for the radius and the projected rotational velocity of the tertiary from Table 8, this assumption leads to an inclination of the rotational axis identical (within the error limits) with the orbital inclination of the wide orbit.

• 4.

  The photometric period 1$\mathit{.}{}^{\mathrm{d}}$065 is tentatively identified with the rotational period of the primary, but this identification is much less certain and needs to be proved or disproved by future high S/N whole-night series of spectra. (At the moment, the radius and the projected rotational velocity of the primary from Table 8 would require an inclination of the rotational axis as low as ~44°.) The ultimate proof of line-profile variations with the 1$\mathit{.}{}^{\mathrm{d}}$065 period and a reliable and more accurate determination of log  g of the primary with the help of several Balmer lines are both needed.

• 5.

  Very accurate systematic photometric observations relative to some truly constant comparison star and new spectral observations consisting of whole-night series, which would constrain putative rapid line-profile variations, are also needed to progress in the understanding of this system.

• 6.

  The classification of V746 Cas as an SPB variable should be critically re-examined.

---

Acknowledgments

We profited from the use of 13 echelle spectra from the Bernard Lyot telescope, made publicly available via the Polar Base web service and Geneva 7-C photometry made available via HELAS service, to which we were kindly directed by C. Aerts. P. Mathias kindly provided us with old archival DAT tapes with the original Aurelie spectra of ten B stars and some advice about their content and structure. The spectra were reconstructed from the tapes with the help of R. Veselý. H. Božić, K. Hoňková, and D. Vršnjak kindly obtained some of the calibrated UBV observations of V746 Cas and its comparison stars for us. We acknowledge the use of the public versions of programs FOTEL and KOREL, written by P. Hadrava and PHOEBE 1.0 written by A. Prša. The research of P.H., M.B., P.M., and J.N. was supported by the grant P209/10/0715 of the Czech Science Foundation. J.N. and P.H. were also supported by the grants GA15-02112S of the Czech Science Foundation and No. 250015 of the Grant Agency of the Charles University in Prague. Research of D.K. was supported by a grant GA17-00871S of the Czech Science Foundation. Our thanks are due to M. Wolf, who obtained one Ondřejov spectrum used here and who provided a few useful comments to this paper. A persistent but constructive criticism by an anonymous referee helped us to re-think the whole study, present our arguments and analyses more clearly and convincingly, and to improve the layout of the text and figures as well. The use of the NASA/ADS bibliographical service and SIMBAD electronic database are gratefully acknowledged.

References

Appendix A: Details of the spectral data reduction and measurements

All RVs collected from the astronomical literature are provided in Table A.1. Whenever necessary, we derived heliocentric Julian dates (HJDs) for them. The RVs derived by us are provided in Tables A.2 and A.3.

Appendix B: Fitting the spectra with interpolated synthetic spectra

Using the Python program PYTERPOL and two grids of synthetic spectra, Lanz & Hubený (2007) for T_eff > 15 000 K, and Palacios et al. (2010) for T_eff  < 15 000 K, we estimated the properties of the primary and tertiary, which are summarised in Table 6. Figures B.1–B.3 show some examples of the comparison of the observed and the best interpolated synthetic spectra in detail for several different spectrograms and spectral regions.

Appendix C: Details of the photometric data reduction and homogenisation

In an effort to bring at least all yellow-band photometric observations of V746 Cas on a comparable scale, we used several UBV observations of V746 Cas and its comparison stars HR 96 and HD 567 secured with the 0.65 m reflector and photoelectric photometer at Hvar. These observations were reduced to the standard Johnson system with the help of the program HEC22, based on non-linear transformation formulae (Harmanec et al. 1994). Extinction and its variations during observing nights were taken into account during the data reduction³. We then used the mean all-sky Hvar values of HD 96 and added them to the magnitude differences y−y_{HR 96} for both V746 Cas and HD 567 Strömgren APT observations of data set 12.

Hipparcos H_p observations (data set 11) were transformed into the standard Johnson V magnitude after Harmanec (1998), using the all-sky B−V   and U–B indices of all three stars derived at Hvar.

Finally, the Geneva 7-C all-sky observations (data set 13) were transformed into the standard UBV system using the transformation formulæ devised by Harmanec & Božić (2001). All mean UBV values for individual data sets thus obtained are summarised in Table C.1 to illustrate the accuracy with which the conversion into one system was possible.

In Fig. C.1 we also plot all homogenised yellow-band observations versus time. There are probably still some minor zero-point differences between individual data sets (APT photometry in on the instrumental system, which, however, seems to be rather stable in time; Guinan, priv. com.). The plot in the bottom panel of Fig. C.1 is indicative of some small secular variations, but such a statement would require verification through differential observations relative to some other comparison than HR 96.

The reason for the above statement is that the primary comparison HR 96 = HD 2054 is suspected to be a CP star and it was found to be a spectroscopic binary with a 48$\mathit{.}{}^{\mathrm{d}}$2905 period (Hube 1983). Using the program FOTEL, we re-analysed available radial velocities, namely 2 RVs from the David Dunlap Observatory (DDO) prismatic 33 Å mm^-1 spectra (Hube 1983), 4 RVs from the DDO 40 Å mm^-1 grating-spectrograph spectra (Hube 1970), 5 RVs from Herstmonceux (HRM) Yapp-reflector prismatic 70–173 Å mm^-1 spectra (Palmer et al. 1968), and 25 RVs from the Dominion Astrophysical Observatory (DAO) 15 Å mm^-1grating spectra (Hube 1983). We weighted individual RVs by the weights inversely proportional to their rms errors and then also applied similar external weights for individual spectrographs. Unlike Hube (1983), we allowed for the determination of individual systemic γ velocities for the four individual spectrographs. Our solution is compared with that of Hube (1983) in Table C.2

In Fig. C.2 we show a plot of the Hipparcos H_p photometry transformed into Johnson V magnitude versus phase of the 48$\mathit{.}{}^{\mathrm{d}}$29 orbital period of HR 96. A small-amplitude variation with a minimum near the superior conjunction of the binary is detected. This can naturally further complicate the period analysis of the photometry of V746 Cas.

All Tables

All Figures