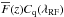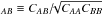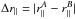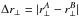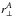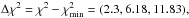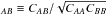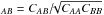| Issue |
A&A
Volume 608, December 2017
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201731731 | |
| Published online | 15 December 2017 | |
Baryon acoustic oscillations from the complete SDSS-III Lyα-quasar cross-correlation function at z = 2.4
1 IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
e-mail: rich@hep.saclay.cea.fr
2 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
3 APC, Université Paris Diderot-Paris 7, CNRS/IN2P3, CEA, Observatoire de Paris, 10 rue A. Domon & L. Duquet, 75014 Paris, France
4 LPNHE, CNRS/IN2P3, Université Pierre et Marie Curie Paris 6, Université Denis Diderot Paris 7, 4 place Jussieu, 75252 Paris Cedex, France
5 Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
6 Department of Physics and Astronomy, University of Utah, 115 S 1400 E, Salt Lake City, UT 84112, USA
7 Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
8 Department of Physics and Astronomy, University College London, Gower Street, London, UK
9 Department of Physics and Astronomy, University of California, Irvine, CA 92697, USA
10 Institució Catalana de Recerca i Estudis Avançats, 08010 Barcelona, Catalonia, Spain
11 Institució de Ciències del Cosmos, Universitat de Barcelona (UB-IEEC), 080028 Barcelona, Catalonia, Spain
12 Université Paris 6 et CNRS, Institut d’Astrophysique de Paris, 98 bis Blvd. Arago, 75014 Paris, France
13 SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
14 Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
15 Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
16 Brookhaven National Laboratory, 2 Center Road, Upton, NY 11973, USA
17 Department of Astronomy, Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
Received: 7 August 2017
Accepted: 25 September 2017
We present a measurement of baryon acoustic oscillations (BAO) in the cross-correlation of quasars with the Lyα-forest flux transmission at a mean redshift of z = 2.40. The measurement uses the complete Sloan Digital Sky Survey (SDSS-III) data sample: 168 889 forests and 234 367 quasars from the SDSS data release DR12. In addition to the statistical improvement on our previous study using DR11, we have implemented numerous improvements at the analysis level enabling a more accurate measurement of this cross-correlation. We have also developed the first simulations of the cross-correlation that allow us to test different aspects of our data analysis and to search for potential systematic errors in the determination of the BAO peak position. We measure the two ratios DH(z = 2.40) /rd = 9.01 ± 0.36 and DM(z = 2.40) /rd = 35.7 ± 1.7, where the errors include marginalization over the non-linear velocity of quasars and the cross-correlation of metals and quasars, among other effects. These results are within 1.8σ of the prediction of the flat-ΛCDM model describing the observed cosmic microwave background anisotropies. We combine this study with the Lyα-forest auto-correlation function, yielding DH(z = 2.40) /rd = 8.94 ± 0.22 and DM(z = 2.40) /rd = 36.6 ± 1.2, within 2.3σ of the same flat-ΛCDM model.
Key words: cosmological parameters / dark energy / large-scale structure of Universe
© ESO, 2017
1. Introduction
Baryon acoustic oscillations (BAO) in the pre-recombination universe (Peebles & Yu 1970; Sunyaev & Zeldovich 1970) left their imprint on the anisotropy spectrum of the cosmic microwave background (CMB) and on late-time correlations of the matter density. These two effects provide a well-understood tool for studying cosmological models. The CMB anisotropy spectrum (Planck Collaboration XIII 2016) provides percent-level measurements of the matter and baryon densities relative to the known photon density and thereby precisely fixes the parameters of the flat-Λ cold dark matter (CMD) cosmological model. The position of the BAO peak in the late-time correlation function determines the angular and Hubble distances at the observed redshift, both relative to the sound horizon, rd. Such measurements allow one to constrain more complicated cosmological models that include non-zero curvature and/or evolving dark energy (Planck Collaboration XIII 2016; Aubourg et al. 2015).
The original studies of the BAO peak (Eisenstein et al. 2005; Cole et al. 2005), and most of those that followed, have used galaxies as mass tracers. The most precise measurements were in the redshift range 0.35 <z< 0.65 from the Baryon Oscillation Spectroscopy Survey (BOSS) of the Sloan Digital Sky Survey (SDSS-III; Anderson et al. 2012, 2014b,a; Alam et al. 2017). Other measurements using galaxies (Percival et al. 2007, 2010; Beutler et al. 2011; Blake et al. 2011; Padmanabhan et al. 2012; Mehta et al. 2012; Chuang & Wang 2012; Xu et al. 2013; Ross et al. 2015) map distances and expansion rates for z< 0.8. The first observations of the BAO peak in the range 0.8 <z< 2.2 using the eBOSS quasars as tracers have recently been reported (Ata et al. 2018). There is an impressive agreement between the results of these studies and the expectations of flat-ΛCDM models based on CMB data, as emphasized by Planck Collaboration XIII (2016).
BAO correlations can be studied at redshift near z ~ 2.4 by using the flux transmission in Lyα forests as a mass tracer (McDonald & Eisenstein 2007). The BAO peak has been detected in the transmission auto-correlation of SDSS Lyα forests (Busca et al. 2013; Slosar et al. 2013; Kirkby et al. 2013; Delubac et al. 2015; Bautista et al. 2017). Complementary to the auto-correlation, BAO can also be studied using the cross-correlation of quasars and the flux in Lyα forests. Such correlations were first detected in SDSS DR9 (Font-Ribera et al. 2013), and the first BAO detection was presented in Font-Ribera et al. (2014) using SDSS DR11.
 |
Fig. 1 Mollweide projection of the BOSS DR12 footprint in equatorial coordinates used in this study. The light gray points represent the position of the Galactic plane. The blue points are the positions of the forests from DR12 used here zforest ∈ [2,6]. The light blue points are the positions of the new forests not included in the DR11 study of Font-Ribera et al. (2014). |
This paper presents the DR12 study of the quasar-forest cross-correlation and derives joint cosmological constraints using the Lyα-forest auto-correlation of DR12 (Bautista et al. 2017). In addition to the use of an increased number of quasar-forest pairs, the analysis presented here includes three important improvements on the analysis of Font-Ribera et al. (2014), the first two of which were also used in the auto-correlation analysis of Bautista et al. (2017):
-
We use a new data reduction pipeline whose most importantfeatures are described in Sect. 2. The new pipelinehas improved linearity for the small fluxes characteristic of the Lyαforest resulting in a better understanding of the effects ofimperfect modeling of the calibration stars.
-
We model the distortion of the correlation function due to the continuum fitting in the forest. This procedure, described in Sect. 4.2, allows us to fit the observed correlation function without the addition of arbitrary power-law “broadband” terms.
-
We test the analysis procedure with the mock data sets described in Sect. 6 that contain correlated quasars and forests. The mock data sets previously used to test the auto-correlation analysis contained correlated forests but no physical correlation with the associated quasars. The lack of mock data sets was the major limitation of the analysis of Font-Ribera et al. (2014).
This paper is organized as follows. Section 2 describes the DR12 data set used in this study. Section 3 summarizes the measurement of the flux-transmission field and Sect. 4 describes its correlation with quasars. Section 5 describes our theoretical model of the cross-correlation and the fits to the observed correlation function. The mock data sets used to validate the analysis procedure are presented in Sect. 6. Section 7 summarizes the cosmological implications of these and other BAO measurements. Section 8 presents our conclusions.
2. Quasar and forest samples and data reduction
The results presented here are based on data collected by the SDSS (York et al. 2000). Most of the quasars and the entirety of the Lyα forests were gathered over a five-year period by the SDSS-III Collaboration (Eisenstein et al. 2011; Gunn et al. 1998, 2006; Smee et al. 2013). This data is publicly available in the twelfth data release (DR12) of SDSS as presented in Alam et al. (2015). The DR12 celestial footprint covering ~π sr ~ 104 deg2 is displayed in Fig. 1.
The DR12 quasar catalog is described in Pâris et al. (2017). Most of the quasar spectra were obtained by the Baryon Oscillation Spectroscopic Survey, BOSS (Dawson et al. 2013). However, DR12 also includes six months of data from SEQUELS (Myers et al. 2015; Alam et al. 2015), the pilot survey for the eBOSS survey. We have also used quasars, but not forests, from the SDSS DR7 quasar catalog (Schneider et al. 2010). Figure 2 displays a typical quasar spectrum in the forest wavelength range where the BOSS spectrograph resolution is ~0.2 nm.
The quasar target selection used in BOSS, summarized in Ross et al. (2012), combines different targeting methods described in Yèche et al. (2010), Kirkpatrick et al. (2011), and Bovy et al. (2011). The selection algorithms use SDSS photometry and, when available, data from the GALEX survey (Martin et al. 2005) in the UV, the UKIDSS survey (Lawrence et al. 2007) in the NIR, and the FIRST survey (Becker et al. 1995) in the radio.
As described in Bautista et al. (2017), the DR12 data were processed using a new software package that differs from the standard DR12 SDSS-III pipeline (Bolton et al. 2012) and which has become the standard pipeline for SDSS DR13 (SDSS Collaboration et al. 2016). For this study, the most important difference with respect to the DR12 pipeline is that pixels on the CCD image are combined to give a flux with pixel-weights determined only by the CCD readout noise. While this method is sub-optimal because it ignores photo-electron Poisson noise, compared to the DR12 method it yields an unbiased flux estimate since the weights do not depend on the observed CCD counts, which are needed to estimate Poisson noise. A more detailed description of the changes to the extraction pipeline is given in Appendix A of Bautista et al. (2017).
 |
Fig. 2 Example of a BOSS quasar spectrum of at z = 2.91. The spectrograph resolution at λ ~ 400 nm is ~0.2 nm. The red and blue lines cover the forest region used here, λRF ∈ [104,120] nm. This region is sandwiched between the quasar’s Lyβ and Lyα emission lines at 102.572 nm and 121.567 nm respectively. The blue line is the model of the continuum for this particular quasar, Cq(λRF), and the red line is the product of the continuum and the mean absorption, |
For each object, the pipeline provides a flux calibrated spectrum, f(λ), errors, and an object classification (galaxy, quasar, star). A model spectrum is fit to f(λ), providing a redshift estimate. For this study, we use the “coadded” spectra constructed from typically four exposures of 15 minutes resampled at wavelength pixels of width Δlog 10λ = 10-4 (cΔλ/λ ~ 69 km s-1). Unlike the auto-correlation measurement of Bautista et al. (2017), we use these pixels directly, not combining them into wider analysis pixels. Approximately 10% of the quasars have repeated observations widely separated in time, in which case we use the observation with the best signal-to-noise ratio.
The mean ratio, R(λ), of model and observed fluxes as a function of observed wavelength have small (~1%) deviations from unity caused by imperfect modeling of the spectra of calibration stars. As described in Bautista et al. (2017), the fluxes were given a global correction for these imperfections by dividing them by R(λ) estimated in the weakly absorbed range (141 <λRF < 153 nm).
The spectra of all quasar targets were visually inspected (Pâris et al. 2012, 2014, 2017) to correct for misidentifications, to flag broad absorption lines (BALs), and to determine the quasar redshift used in the analysis. Damped Lyα troughs (DLAs; Wolfe et al. 1986) were visually flagged, but also identified and characterized automatically (Noterdaeme et al. 2012). The visual inspection of DR12 confirmed 216 579 quasars in the redshift range 1.7 <zq < 5.8 to which we add 17 788 DR7 quasars that are not included in DR12, producing a total of 234 367 quasars. Their redshift distribution is shown in Fig. 3. The forest sample is taken from 198 357 DR12 quasars in the range 2.0 <zq< 6.0 (Fig. 3). Elimination of spectra with identified BALs leaves 174 726 forests. Requiring 50 or more pixels in the Lyα forest regions then leaves 171 579 forests. Finally, 2690 forests failed the continuum fitting procedure, producing a total of 168 889 forests for this study.
Because of the very low number of observed quasars at z> 3.5 and the requirement that a sufficient range of forest be within the spectral range of SDSS, the quasar-forest pixel pairs actually used for the calculation of the cross-correlation function involved mostly quasars in the range 1.8 <zq< 3.5 and forests with quasars in the range 2.0 <zq< 3.5. In these ranges, our sample includes 217 780 quasars and 157 845 forests, to be compared with 164 017 and 130 825 for the study of Font-Ribera et al. (2014).
 |
Fig. 3 Left panel: distribution of the redshift of quasars (blue) and forest pixels (green) with the redshift for the latter calculated assuming Lyα absorption. The pixels are weighted as described in Sect. 4.1. Right panel: weighted distribution of the redshift of the 1.8 × 109 pixel-quasar pairs in the BAO region: rpair ∈ [80,120] h-1 Mpc. The redshift of a pair is defined by: zpair = (zpixel + zQSO)/2. The weighted mean redshift of the pairs (dashed black line) defines the mean redshift, zeff = 2.40, of the measurement of the BAO peak position. |
For the measurement of the flux transmission, we adopt the rest-frame wavelength interval 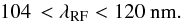 (1)As illustrated in Fig. 2, this range is bracketed by the emission lines λLyβ = 102.572 nm and λLyα = 121.567 nm. This region was chosen as the maximum range that avoids the large pixel variances on the wings of the two lines due to quasar-to-quasar diversity of line-emission strengths and profiles. The observed wavelength range is
(1)As illustrated in Fig. 2, this range is bracketed by the emission lines λLyβ = 102.572 nm and λLyα = 121.567 nm. This region was chosen as the maximum range that avoids the large pixel variances on the wings of the two lines due to quasar-to-quasar diversity of line-emission strengths and profiles. The observed wavelength range is 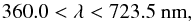 (2)corresponding to the redshift range 1.96 <z< 4.96 for Lyα absorption. The lower limit is set by the requirement that the system throughput be greater than 10% of its peak value. The upper limit on λ is, in fact, of no importance because there are few quasar-pixel pairs beyond z = 3.5 (λ = 547 nm). The distribution of the redshift of Lyα-absorber-quasar pairs contributing to the BAO peak is shown in the righthand panel of Fig. 3. The pixels are weighted as described in Sect. 4.1. The distribution has a weighted mean of zeff = 2.40, which defines the effective redshift of our measurement of the BAO peak position.
(2)corresponding to the redshift range 1.96 <z< 4.96 for Lyα absorption. The lower limit is set by the requirement that the system throughput be greater than 10% of its peak value. The upper limit on λ is, in fact, of no importance because there are few quasar-pixel pairs beyond z = 3.5 (λ = 547 nm). The distribution of the redshift of Lyα-absorber-quasar pairs contributing to the BAO peak is shown in the righthand panel of Fig. 3. The pixels are weighted as described in Sect. 4.1. The distribution has a weighted mean of zeff = 2.40, which defines the effective redshift of our measurement of the BAO peak position.
3. Measurement of the transmission field
Fluctuations in the flux transmission fraction are defined by 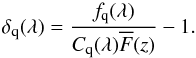 (3)Here, fq(λ) is the observed flux density for quasar q at observed wavelength λ, Cq(λ) is the unabsorbed flux density (the so-called “continuum”), and
(3)Here, fq(λ) is the observed flux density for quasar q at observed wavelength λ, Cq(λ) is the unabsorbed flux density (the so-called “continuum”), and 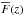 is the mean transmitted fraction at the absorber redshift, z(λ) = λ/λLyα−1. Measurement of the flux-transmission field δq(λ) requires estimates of the product
is the mean transmitted fraction at the absorber redshift, z(λ) = λ/λLyα−1. Measurement of the flux-transmission field δq(λ) requires estimates of the product 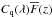 for each quasar. We closely follow the procedure used for the auto-correlation measurement (Bautista et al. 2017). We assume the quasar continuum, Cq(λ), is the product of a universal function of the rest-frame wavelength, λRF = λ/ (1 + zq) and a quasar-dependent linear function of λRF, included to account for quasar spectral diversity:
for each quasar. We closely follow the procedure used for the auto-correlation measurement (Bautista et al. 2017). We assume the quasar continuum, Cq(λ), is the product of a universal function of the rest-frame wavelength, λRF = λ/ (1 + zq) and a quasar-dependent linear function of λRF, included to account for quasar spectral diversity: ![\begin{equation} C_{\rm q}(\lambda) = C(\lamrf) \left[a_{\rm q} + b_{\rm q}(\lamrf-\overline{\lamrf})\right], \label{templatewarpeq} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq61.png) (4)where
(4)where  is the weighted mean for each forest and where C(λRF) is normalized so that its integral over the forest is equal to unity. The (aq,bq) and C(λRF) are determined by maximizing the likelihood function given by
is the weighted mean for each forest and where C(λRF) is normalized so that its integral over the forest is equal to unity. The (aq,bq) and C(λRF) are determined by maximizing the likelihood function given by 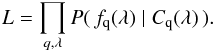 (5)Here P(fq(λ) | Cq(λ)) is the probability to observe a flux fq(λ) for a given continuum found by convolving the intrinsic probability, D(F = fq(λ) /Cq(λ),z), with the observational resolution assumed to be Gaussian:
(5)Here P(fq(λ) | Cq(λ)) is the probability to observe a flux fq(λ) for a given continuum found by convolving the intrinsic probability, D(F = fq(λ) /Cq(λ),z), with the observational resolution assumed to be Gaussian: ![\begin{equation} P(\, \fqlam\;|\;C_{\rm q}(\lambda)\,) \propto \int_0^1 {\rm d}F D(F,z)\exp\left[ \frac{-(C_{\rm q}F-\fqlam)^2}{2\sigma_{\rm q}^2(\lambda)} \right], \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq68.png) (6)where
(6)where 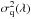 is the variance due to readout noise and photon statistics. The function D(F,z) is taken to be the log-normal model of absorption used to generate the mock data of Bautista et al. (2015).
is the variance due to readout noise and photon statistics. The function D(F,z) is taken to be the log-normal model of absorption used to generate the mock data of Bautista et al. (2015).
As emphasized in Bautista et al. (2017), the use of forest data to determine the quasar continuum necessarily produces biased estimates of δq(λ) because of two effects. The most important is that fitting an amplitude and slope (aq,bq) for each forest biases the mean δq(λ) and its first moment toward vanishing values within a given forest. Since this bias is only approximate, we find it convenient to make it exact by explicitly subtracting from each δq(λ) (defined by Eq. (3)) the mean and first moments: 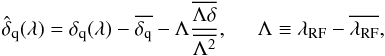 (7)where the over-bars refer to weighted averages over individual forests. The resulting values of
(7)where the over-bars refer to weighted averages over individual forests. The resulting values of 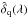 are thus linear combinations of the originals:
are thus linear combinations of the originals: 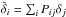 with the projection matrix given by
with the projection matrix given by 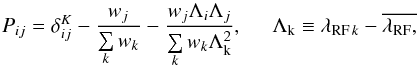 (8)where
(8)where 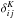 is the Kroeneker delta and the wj are weights used in the calculation of the correlation function (Eq. (10)).
is the Kroeneker delta and the wj are weights used in the calculation of the correlation function (Eq. (10)).
The second effect is that fitting 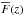 biases toward zero the mean δ at each observed wavelength,
biases toward zero the mean δ at each observed wavelength, 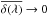 , where the over-bar means the average at fixed λ. As the last step, we therefore explicitly transform the
, where the over-bar means the average at fixed λ. As the last step, we therefore explicitly transform the 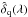 of Eq. (7):
of Eq. (7): 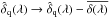 . Because of the large number of forests, this transformation has much less effect than the intra-forest subtraction (7).
. Because of the large number of forests, this transformation has much less effect than the intra-forest subtraction (7).
4. The Lyα-forest-quasar cross-correlation
The flux-transmission field is sampled at points in a space defined by observed wavelength and position on the sky. It is therefore natural to measure the cross-correlation with quasars as a function of angular and redshift separation, ξ(Δθ,Δz), where Δz is the difference between the quasar redshift and the forest-pixel redshift calculated assuming Lyα absorption. In the approximation that Lyα absorption dominates in the forest, the BAO peak in these coordinates would be at Δz = rd/DH(z) in the radial direction and at Δθ = rd/DM(z) in the transverse direction, where DH(z) = c/H(z) and DM(z) are the Hubble and comoving-angular distances. While this formulation has the advantage of remaining close to the directly observed quantities, it has the disadvantage that both DH and DM vary significantly over the redshift range of BOSS. This would lead to significant broadening of the peak unless several wavelength bins were used.
To avoid this complication we transform (Δθ,Δz) to Cartesian coordinates, (r⊥,r∥) using the distances, Dq = DM(zq) and DLyα = DM(zLyα), calculated according to a flat “fiducial” cosmological model: 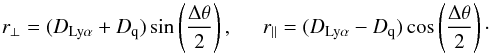 (9)To the extent that Lyα-absorption dominates the absorption field, and if the fiducial cosmology is the true cosmology, the function ξ(r⊥,r∥) will be the expected biased version of the mass correlation function and the BAO peak will be at the predicted position. Absorption by metals and the high column-density systems (HCDs) complicates this simple picture, and therefore the fits of Sect. 5 must take these and other effects into account.
(9)To the extent that Lyα-absorption dominates the absorption field, and if the fiducial cosmology is the true cosmology, the function ξ(r⊥,r∥) will be the expected biased version of the mass correlation function and the BAO peak will be at the predicted position. Absorption by metals and the high column-density systems (HCDs) complicates this simple picture, and therefore the fits of Sect. 5 must take these and other effects into account.
Parameters of the flat-ΛCDM cosmological model used for the production and analysis of the mock spectra and for the analysis of the data.
The fiducial cosmology used for the analysis of the data is the best-fit flat-ΛCDM model of Planck Collaboration XIII (2016). The parameters of this model are given in the second column of Table 1. The mock spectra were produced using a different cosmology (Col. 1 of the table) and we use this cosmology to analyze the mock data.
4.1. The correlation function
The correlation between the transmission field in the Lyα forest and the quasar distribution is estimated using a simple weighted mean of 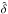 at a given distance of a quasar:
at a given distance of a quasar: 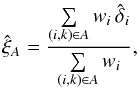 (10)where wi is the weight given to a measurement
(10)where wi is the weight given to a measurement 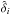 (see below). The sum runs over all possible pixel-quasar pairs (i,k) falling inside the bin A. This bin is defined in separation space A = (r∥,r⊥)A, but in this paper we will also refer to (r,μ), with
(see below). The sum runs over all possible pixel-quasar pairs (i,k) falling inside the bin A. This bin is defined in separation space A = (r∥,r⊥)A, but in this paper we will also refer to (r,μ), with 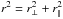 and μ = r∥/r, the cosine of the angle formed by the line of sight and the vector r. Following Eq. (9), positive values of r∥ correspond to an absorber distance greater than the quasar distance. The bins are squares in (r⊥,r∥)-space of size 4 h-1 Mpc. We calculate the correlation for separations r∥ ∈ [−200,200] h-1 Mpc and for r⊥ ∈ [0,200] h-1 Mpc. We thus have 100 bins in the r∥ direction and 50 in the r⊥ direction, with a total number of bins, Nbin = 100 × 50 = 5000.
and μ = r∥/r, the cosine of the angle formed by the line of sight and the vector r. Following Eq. (9), positive values of r∥ correspond to an absorber distance greater than the quasar distance. The bins are squares in (r⊥,r∥)-space of size 4 h-1 Mpc. We calculate the correlation for separations r∥ ∈ [−200,200] h-1 Mpc and for r⊥ ∈ [0,200] h-1 Mpc. We thus have 100 bins in the r∥ direction and 50 in the r⊥ direction, with a total number of bins, Nbin = 100 × 50 = 5000.
Because of the continuum fit and the projection of pixels (Eq. (7)) the pixel-quasar correlation vanishes on all scales for pixels of a quasar’s own forest. For this reason, we do not use such pairs. As described in Delubac et al. (2015), the weights, wi, are chosen so as to account for both Poisson noise in the flux measurement and for the intrinsic fluctuations in δi due to cosmological large-scale structure. The weights are set to zero for pixels flagged by the pipeline as having problems due, for example, to sky emission lines or cosmic rays.
4.2. The distortion matrix
The transformation (7) mixes pixels so that the correlation between a quasar and a pixel is equal to the original quasar-pixel correlation plus a linear combination of the correlations between the quasar and the other pixels of the forest. This statement means that the measured correlation function is a “distorted” version of the true correlation function. Since the transformation (7) is linear, the relation between measured,  , and true, ξ, correlation functions is given by a distortion matrix DAA′:
, and true, ξ, correlation functions is given by a distortion matrix DAA′: 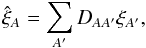 (11)where
(11)where 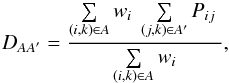 (12)where i and j refer to pixels from the same forest, k refers to a quasar, and Pij is the projection matrix (Eq. (8)).
(12)where i and j refer to pixels from the same forest, k refers to a quasar, and Pij is the projection matrix (Eq. (8)).
The matrix DAA′ depends only on the geometry and weights of the survey. Its effect is illustrated on the mocks by Fig. 11. The diagonal elements of the matrix are close to one, DAA ≈ 0.97, and the non-diagonal elements are small, | DAA′ | ≲ 0.01. Since the continuum fitting only mixes pixels from the same forest, all matrix elements DAA′ with 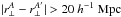 are negligible.
are negligible.
 |
Fig. 4 Mean normalized covariance matrix, Corr |
4.3. The covariance matrix
The covariance associated with the measured correlation function 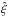 for two bins A and B is given by:
for two bins A and B is given by: 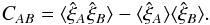 (13)We estimated the covariance matrix of the data using two independent approaches.
(13)We estimated the covariance matrix of the data using two independent approaches.
The first technique involves writing the covariance matrix as a function of the known flux auto-correlation function. Combining Eqs. (10)and (13), we have: 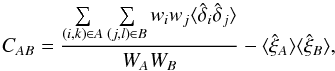 (14)where (i,k) is a pixel-quasar pair falling in the bin A and (j,l) a pixel-quasar pair falling in the bin B. The sums of weights, WA and WB, are for the bins A and B respectively. This expression of the covariance matrix depends on the correlation between two pixels,
(14)where (i,k) is a pixel-quasar pair falling in the bin A and (j,l) a pixel-quasar pair falling in the bin B. The sums of weights, WA and WB, are for the bins A and B respectively. This expression of the covariance matrix depends on the correlation between two pixels, 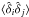 . Intra-forest correlations, ξff,1D, are generally larger than inter-forest correlations so the largest off-diagonal elements of the covariance matrix are due to the terms where k and l are the same quasar and i and j are in the same forest. This behavior implies that the largest elements have r⊥ A = r⊥ B. The other terms involving inter-forest correlations can be described by “diagrams” of increasing complexity, as discussed in Appendix A.
. Intra-forest correlations, ξff,1D, are generally larger than inter-forest correlations so the largest off-diagonal elements of the covariance matrix are due to the terms where k and l are the same quasar and i and j are in the same forest. This behavior implies that the largest elements have r⊥ A = r⊥ B. The other terms involving inter-forest correlations can be described by “diagrams” of increasing complexity, as discussed in Appendix A.
The second technique uses sub-samples of the data. We divide the BOSS footprint of Fig. 1 into sub-samples and measure 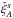 and
and 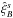 in each sub-sample s. Neglecting the small correlations between sub-samples, the covariance (13) is given by:
in each sub-sample s. Neglecting the small correlations between sub-samples, the covariance (13) is given by: ![\begin{equation} C_{AB} = \frac{1}{W_{A} W_{B}} \sum\limits_{s} W_{A}^{s} W_{B}^{s} \left[ \xihat^{s}_{A} \xihat^{s}_{B} - \xihat_{A} \xihat_{B} \right] , \label{equation::covar_xi_estimator_subsampling} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq167.png) (15)where
(15)where 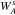 is the sum of weights in the sub-sample s for the bin A. We used 80 sub-samples of similar statistical sizes and shapes. We tested with 1000 sub-samples and observed no significant changes of χ2 of the fit and the value and precision of the BAO-peak parameters.
is the sum of weights in the sub-sample s for the bin A. We used 80 sub-samples of similar statistical sizes and shapes. We tested with 1000 sub-samples and observed no significant changes of χ2 of the fit and the value and precision of the BAO-peak parameters.
Although more accurate, the calculation of the diagram expansion is time consuming, and therefore not practical for the analysis of the mock data sets. We thus fit the data and the mocks using the covariance from the 80 sub-samplings. To limit the noise of this estimate, we use the normalized covariance matrix (hereafter “correlation matrix”), 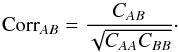 (16)To good approximation, CorrAB is a function only of (Δr⊥,Δr∥) where Δr⊥ = | r⊥ A−r⊥ B | and Δr∥ = | r∥ A−r∥ B |. We therefore average the correlation matrix to determine CorrAB(Δr⊥,Δr∥), which is then used to calculate CAB(Δr⊥,Δr∥). This procedure is validated with a fit of the data and of a subset of the mocks using the covariance matrix from the diagram expansion (Eq. (14)).
(16)To good approximation, CorrAB is a function only of (Δr⊥,Δr∥) where Δr⊥ = | r⊥ A−r⊥ B | and Δr∥ = | r∥ A−r∥ B |. We therefore average the correlation matrix to determine CorrAB(Δr⊥,Δr∥), which is then used to calculate CAB(Δr⊥,Δr∥). This procedure is validated with a fit of the data and of a subset of the mocks using the covariance matrix from the diagram expansion (Eq. (14)).
As a partial check of the first two methods, we used a third technique based on a shuffle of the positions on the sky of the forests. We keep the values of pixels but change the position of each forest to the position of another forest of the survey. We then produce a large number of realizations of shuffles, r, and measure for each of them the cross-correlation 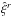 . We then measure the covariance matrix of these nearly independent cross-correlations with Eq. (15)(replacing s with r). The shuffling procedure removes inter-forest and quasar-forest correlations but retains the intra-forest correlations. As such, we expect that the shuffle technique will correctly calculate the important Δr⊥ = 0 elements of the covariance matrix.
. We then measure the covariance matrix of these nearly independent cross-correlations with Eq. (15)(replacing s with r). The shuffling procedure removes inter-forest and quasar-forest correlations but retains the intra-forest correlations. As such, we expect that the shuffle technique will correctly calculate the important Δr⊥ = 0 elements of the covariance matrix.
A fourth technique can be applied only to mock data sets where the covariance is given directly by the mock-to-mock variations of the correlation function. The results of this technique, presented in Sect. 6.2, agree with the other techniques and confirm their validity.
The 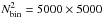 elements of matrix CAB have a relatively simple structure. By far the most important elements are on the diagonal. They are, to a good approximation, inversely proportional to the number of pixel-quasar pairs,
elements of matrix CAB have a relatively simple structure. By far the most important elements are on the diagonal. They are, to a good approximation, inversely proportional to the number of pixel-quasar pairs, 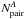 , used in the calculation of the correlation function in the bin A:
, used in the calculation of the correlation function in the bin A: 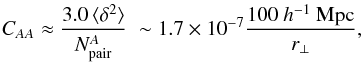 (17)where ⟨ δ2 ⟩ ≈ 0.2 is the variance of BOSS pixels in the Lyα forest and where the second form uses the fact that
(17)where ⟨ δ2 ⟩ ≈ 0.2 is the variance of BOSS pixels in the Lyα forest and where the second form uses the fact that 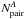 is approximately proportional to r⊥. The variance, CAA, is about three times what one would calculate assuming all pixels are independent. This decrease in the effective number of pixels is due to the correlations between neighboring pixels in a given forest.
is approximately proportional to r⊥. The variance, CAA, is about three times what one would calculate assuming all pixels are independent. This decrease in the effective number of pixels is due to the correlations between neighboring pixels in a given forest.
To display the off-diagonal elements it is convenient to use the correlation matrix (16). The off-diagonal elements of the correlation matrix have a simple structure. The correlation is primarily due to pairs of pixel-quasar pairs sharing the same quasar and the same forest (T2 in Fig. A.2). As a result, the largest elements have Δr⊥ = 0. The elements of the correlation matrix as a function of 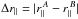 for the smallest values of
for the smallest values of 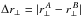 are presented in Fig. 4. Its four panels show the good agreement between the correlation matrix from the sub-sampling and the diagram expansion. As expected, the shuffle technique works well for Δr⊥ = 0 but not for Δr⊥> 0. The top panels present CorrAB for Δr⊥ = 0. These two panels are the reflection of the ξff,1D shown in Fig. 10. The Lyα metal peaks listed in Table 3 are visible. The bottom left and right panels give the correlation matrix for Δr⊥ = 4 h-1 Mpc and for Δr⊥ = 8 h-1 Mpc where the correlation is very small.
are presented in Fig. 4. Its four panels show the good agreement between the correlation matrix from the sub-sampling and the diagram expansion. As expected, the shuffle technique works well for Δr⊥ = 0 but not for Δr⊥> 0. The top panels present CorrAB for Δr⊥ = 0. These two panels are the reflection of the ξff,1D shown in Fig. 10. The Lyα metal peaks listed in Table 3 are visible. The bottom left and right panels give the correlation matrix for Δr⊥ = 4 h-1 Mpc and for Δr⊥ = 8 h-1 Mpc where the correlation is very small.
Parameters of the fits of the Lyα-forest-quasar cross-correlation.
5. Fits for the peak position
To determine the position of the BAO peak, we fit the measured forest-quasar cross-correlations, shown in the left panel of Fig. 5, to a model that describes the underlying physical correlations and possible systematics. We use the model of Lyα correlations introduced by Bautista et al. (2017), and generalized here to include quasars. Its parameters are described in Table 2 and the best fit model is shown in the right panel of Fig. 5. The best fit parameters are listed in Table 4. We use the fitting package “picca”1, which evolved from the baofit package (Kirkby et al. 2013; Blomqvist et al. 2015).
 |
Fig. 5 Measured (left) and the best fit model (right) of the Lyα-forest-quasar cross-correlation. The distortion matrix (12) has been applied to the model. The correlation is multiplied by a factor r. The BAO scale appears here as a half ring of radius r ≈ 100 h-1 Mpc. The color code is saturated for clarity. |
5.1. Model of the cross-correlation
Major metal transitions seen in the intergalactic medium (IGM) and present in the forest-quasar cross-correlation for r∥ ∈ [−200,200] h-1 Mpc.
Fit results for the cross-correlation (this study), the auto-correlation (Bautista et al. 2017) extrapolated to z = 2.40, and the combined fit.
The expected value of the measured cross-correlation, 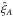 , in the (r⊥,r∥) bin A is related to the theoretical cross-correlation, ξqf,th, by:
, in the (r⊥,r∥) bin A is related to the theoretical cross-correlation, ξqf,th, by: ![\begin{equation} \xihat_A = \sum\limits_{A^\prime} D_{AA^\prime} \left[ \xiqfth_{A^\prime} + \xibb_{A^\prime} \right], \label{equation::xi_complete} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq310.png) (18)where DAA′ is the distortion matrix (Sect. 4.2). The broadband term,
(18)where DAA′ is the distortion matrix (Sect. 4.2). The broadband term, 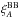 , is an optional function used to test for imperfections in the model and for systematic errors.
, is an optional function used to test for imperfections in the model and for systematic errors.
The cosmological cross-correlation is the sum of several contributions: 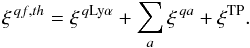 (19)The first term represents the correlation between quasars, q, and Lyα absorption in the IGM. The second term is the sum over all other absorbers: the metals of Table 3 and unidentifed HCDs. All absorbers trace the underlying matter fluctuations, but we separate out the Lyα absorbers because Lyα absorption is assumed in the calculation of the quasar-pixel separation, (r⊥,r∥), therefore requiring a special treatment for metals. The third term, ξTP, is the correlation between a quasar and a neighboring forest due to the effect of the quasar’s radiation on the ionized fraction of the IGM. This effect of a quasar on its own forest is generally referred to as the “proximity effect” (Murdoch et al. 1986; Bajtlik et al. 1988). In the general case studied here, we use the term “transverse proximity effect”, ξTP.
(19)The first term represents the correlation between quasars, q, and Lyα absorption in the IGM. The second term is the sum over all other absorbers: the metals of Table 3 and unidentifed HCDs. All absorbers trace the underlying matter fluctuations, but we separate out the Lyα absorbers because Lyα absorption is assumed in the calculation of the quasar-pixel separation, (r⊥,r∥), therefore requiring a special treatment for metals. The third term, ξTP, is the correlation between a quasar and a neighboring forest due to the effect of the quasar’s radiation on the ionized fraction of the IGM. This effect of a quasar on its own forest is generally referred to as the “proximity effect” (Murdoch et al. 1986; Bajtlik et al. 1988). In the general case studied here, we use the term “transverse proximity effect”, ξTP.
The physical component of the model is dominated by the cross-correlation due to Lyα absorption in the IGM. It is assumed to be a biased version of the total matter auto-correlation of the appropriate flat-ΛCDM model modified to free the position of the BAO peak: 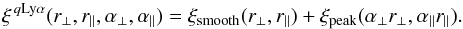 (20)The BAO peak position parameters to be fit are
(20)The BAO peak position parameters to be fit are ![\begin{equation} \aparMath = \frac { \left[\DHh(\zeff)/r_{\rm d}\right] } {\left[\DHh(\zeff )/r_{\rm d}\right]_{\rm fid}} \hspace*{3mm}{\rm and}\hspace*{5mm} \aperpMath = \frac { \left[\DMm(\zeff)/r_{\rm d}\right] } {\left[\DMm(\zeff)/r_{\rm d}\right]_{\rm fid}} , \label{equation::alpha} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq315.png) (21)where the subscript “fid” refers to the fiducial cosmological model from Table 1 used to transform angle differences and redshift differences to (r⊥,r∥).
(21)where the subscript “fid” refers to the fiducial cosmological model from Table 1 used to transform angle differences and redshift differences to (r⊥,r∥).
The nominal correlation function, ξqLyα(r⊥,r∥,α⊥ = α∥ = 1), is derived from its Fourier transform: 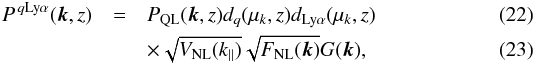 where k = (k∥,k⊥) is the wavenumber of modulus k and μk = k∥/k, with k∥ being the component along the line of sight and k⊥ across. As described in more detail below, PQL is the (quasi) linear matter spectrum, dq and dLyα are the standard factors (Kaiser 1987) describing redshift-space distortion, VNL and FNL describe non-linear corrections, and G(k) gives the effects of (r⊥,r∥) binning on the measurement. Calculation of ξqLyα for a given (r⊥,r∥) bin uses the weighted mean (r⊥,r∥) of pixel pairs in the bin and, for PqLyα(k,z), the weighted mean redshift of the bin. From bin to bin, this redshift varies in the range 2.38 to 2.43 about the mean redshift of the survey, zeff = 2.40.
where k = (k∥,k⊥) is the wavenumber of modulus k and μk = k∥/k, with k∥ being the component along the line of sight and k⊥ across. As described in more detail below, PQL is the (quasi) linear matter spectrum, dq and dLyα are the standard factors (Kaiser 1987) describing redshift-space distortion, VNL and FNL describe non-linear corrections, and G(k) gives the effects of (r⊥,r∥) binning on the measurement. Calculation of ξqLyα for a given (r⊥,r∥) bin uses the weighted mean (r⊥,r∥) of pixel pairs in the bin and, for PqLyα(k,z), the weighted mean redshift of the bin. From bin to bin, this redshift varies in the range 2.38 to 2.43 about the mean redshift of the survey, zeff = 2.40.
The first term in (23) provides for the aforementioned separation of the peak and smooth contributions to the correlation function (Eq. (20)): ![\begin{equation} \PQL(\vec{k},z) = \Psmooth(k,z) + \Apeak {\rm e}^{ -\left[ ( k_{\parallel}\Sigma_{\parallel} )^{2} + ( k_{\perp}\Sigma_{\perp} )^{2} \right]/2 } \Ppeak(k,z), \label{equation::pk_p_nl} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq331.png) (24)where the smooth component, Psm, is derived from the linear power spectrum, PL(k,z), via the side-band technique (Kirkby et al. 2013) and Ppeak = PL−Psm. The redshift-dependent linear power spectrum is obtained from CAMB (Lewis et al. 2000) with the appropriate cosmology for data or mocks (Table 1). The peak amplitude parameter, Apeak, is normally set to unity but can be fit in non-standard analyses. The correction for non-linear broadening of the BAO peak is parameterized by Σ = (Σ∥,Σ⊥), set equal to (6.41,3.26) h-1 Mpc in the standard fit (Eisenstein et al. 2007).
(24)where the smooth component, Psm, is derived from the linear power spectrum, PL(k,z), via the side-band technique (Kirkby et al. 2013) and Ppeak = PL−Psm. The redshift-dependent linear power spectrum is obtained from CAMB (Lewis et al. 2000) with the appropriate cosmology for data or mocks (Table 1). The peak amplitude parameter, Apeak, is normally set to unity but can be fit in non-standard analyses. The correction for non-linear broadening of the BAO peak is parameterized by Σ = (Σ∥,Σ⊥), set equal to (6.41,3.26) h-1 Mpc in the standard fit (Eisenstein et al. 2007).
The second and third terms in (23) are the quasar and Lyα Kaiser factors describing redshift-space distortions: 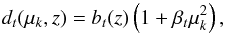 (25)where bt(z) is the bias and βt is the redshift space distortion (RSD) parameter for the tracer t( =Lyα,quasar). The fit of the cross-correlation is clearly only sensitive to the product of the quasar and Lyα biases, so by convention we set bQSO = 3.87 as measured by Laurent et al. (2016) and assume a redshift dependence given by Eq. (15) of Croom et al. (2005):
(25)where bt(z) is the bias and βt is the redshift space distortion (RSD) parameter for the tracer t( =Lyα,quasar). The fit of the cross-correlation is clearly only sensitive to the product of the quasar and Lyα biases, so by convention we set bQSO = 3.87 as measured by Laurent et al. (2016) and assume a redshift dependence given by Eq. (15) of Croom et al. (2005): 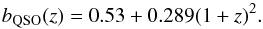 (26)For Lyα absorption we assume
(26)For Lyα absorption we assume ![\begin{equation} \blya(z) = \blya(2.4)[(1+z)/(1+2.4)]^{\alpha_{\LyaMath}}, \label{equation::bias_absorber_evolution_definition} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq343.png) (27)where αLyα = 2.9 as observed in measurements of the flux-correlation, ξff,1D, within individual forests (McDonald et al. 2006).
(27)where αLyα = 2.9 as observed in measurements of the flux-correlation, ξff,1D, within individual forests (McDonald et al. 2006).
Fluctuations of ionizing UV radiation (Pontzen 2014; Gontcho A Gontcho et al. 2014) lead to a scale-dependence of bLyα given by Eq. (12) of Gontcho A Gontcho et al. (2014). The effect of the fluctuations is to increase bLyα from its nominal value at small scale to a different value at large scale. The transition scale is determined by the UV photon mean free path, which we set to a comoving value of λUV = 300 h-1 Mpc (Rudie et al. 2013). We then fit for one parameter, bΓ corresponding to the bΓ(bs−ba) of Gontcho A Gontcho et al. (2014); it determines the change in bLyα between large and small scales. A second bias, 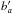 , that determines the precise dependence of the bias on scale, is set to the nominal value of −2/3 used by Gontcho A Gontcho et al. (2014).
, that determines the precise dependence of the bias on scale, is set to the nominal value of −2/3 used by Gontcho A Gontcho et al. (2014).
The Lyα RSD parameter, βLyα, is expected to have a redshift dependence that is somewhat weaker than that for the bias bLyα, varying between z = 2.25 and z = 3.0 by a factor ~1.2 in the simulations of Arinyo-i-Prats et al. (2015) compared to a factor ~1.8 for bLyα (Eq. (27)). Because of the narrow range of mean redshifts of (r⊥,r∥) bins, we neglect the variation of βLyα, fitting only its value at zeff. For quasars, the RSD parameter, βq, is directly linked to the bias bQSO and to f, the linear growth rate of structure: 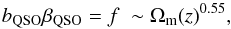 (28)where f = f(zeff) is given in Table 1.
(28)where f = f(zeff) is given in Table 1.
The term VNL(k∥) is the effect on the power spectrum of non-linear quasar velocities and the precision of quasar redshift measurements. Following Eq. (18) of Percival & White (2009), we use a Lorentz-damping form: 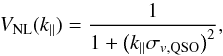 (29)where σv,QSO [h-1 Mpc] is a free parameter. Alternative fits use a Gaussian form.
(29)where σv,QSO [h-1 Mpc] is a free parameter. Alternative fits use a Gaussian form.
The term FNL(k) is a correction for non-linear effects in Lyα absorption at large k due to the isotropic enhancement of power due to non-linear growth, the isotropic suppression of power due to gas pressure, and the suppression of power due to line-of-sight non-linear peculiar velocity and thermal broadening. It can be chosen to be of one of the two forms given by Eq. (21) of (McDonald 2003) or as presented in Arinyo-i-Prats et al. (2015). Our standard fit uses the former.
The last term in (23), G(k), accounts for smoothing due to the binning of the measurement of ξ qf. Following Bautista et al. (2017), we use ![\begin{equation} G(\vec{k}) = \left[ \sinc{\left( \frac{R_{\parallel}k_{\parallel}}{2}\right)} \sinc{\left( \frac{R_{\perp}k_{\perp}}{2}\right)} \right]^{2}, \label{equation::pk_binning_term} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq363.png) (30)where R∥ and R⊥ are the scales of the smoothing. For standard fits, we fix both to the bin width, R∥ = R⊥ = 4 h-1 Mpc.
(30)where R∥ and R⊥ are the scales of the smoothing. For standard fits, we fix both to the bin width, R∥ = R⊥ = 4 h-1 Mpc.
The second contribution to ξqf,th in Eq. (19) is the sum over non-Lyα absorbers. Because there is little absorption by metals, the treatment of metal components is simplified without the separation into peak and smooth components. The fiducial correlation function is directly used to calculate the metal-quasar correlation, although with individual (b,β) for each species.
Absorption by metals is complicated by the fact that the (r⊥,r∥) bins A corresponding to an observed (Δθ,Δλ) are calculated assuming absorption due to the Lyα transition (Eq. (9)). This (r⊥,r∥) does not correspond to the physical quasar-absorber separation if the absorption is not due to Lyα. The model correlation function 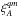 must be evaluated at a different (r⊥,r∥) found by replacing DLyα in (9) with the distance calculated from the redshift zm = λ/λm−1 and taking the weighted average for pixel-quasar pairs in the bin A.
must be evaluated at a different (r⊥,r∥) found by replacing DLyα in (9) with the distance calculated from the redshift zm = λ/λm−1 and taking the weighted average for pixel-quasar pairs in the bin A.
The contribution of each absorber to the cross-correlation is maximized in the (r⊥,r∥) bin that corresponds to vanishing physical separation. For the Lyα contribution, this bin corresponds to (r⊥,r∥) = (0,0). For the other species, it corresponds to r⊥ = 0 and to r∥ ~ (1 + z)DH(z)(λm−λLyα) /λLyα as given in Table 3. Because amplitudes for SiII and SiIII are mostly determined by the excess correlation at (r⊥ ~ 0,r∥ ≠ 0), the β for each metal is poorly determined. We therefore fix their value to β = 0.5 corresponding to host halos with bias of two, the value found for DLAs (Font-Ribera & Miralda-Escudé 2012), which is also typical of star-forming galaxies. The redshift dependence of the biases is assumed to be the same as that for bLyα as given by Eq. (27). Because all (r⊥,r∥) bins have nearly the same mean redshift, this assumption has very little impact on the fits.
The standard fit also takes into account the correlation between the quasar distribution and absorption by unidentified HCD systems. This new absorber is modeled with a modified Kaiser factor (Bautista et al. 2017) defined as: 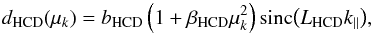 (31)where bHCD,βHCD are the traditional bias and beta parameters of the absorption, and LHCD is the associated smoothing scale. Because of degeneracies, we add a Gaussian prior for βHCD, of mean 0.5 and standard deviation 0.2.
(31)where bHCD,βHCD are the traditional bias and beta parameters of the absorption, and LHCD is the associated smoothing scale. Because of degeneracies, we add a Gaussian prior for βHCD, of mean 0.5 and standard deviation 0.2.
The final term in (19), ξTP, represents the contribution to the Lyα-quasar cross-correlation from radiation effects. In the vicinity of a quasar, the radiation emitted from the quasar dominates over the UV background, increasing the ionization fraction of the surrounding gas. This increase makes it more transparent to the quasar Lyα photons. Therefore, this effect introduces an extra term in the correlation between the quasars and the Lyα forest (Font-Ribera et al. 2013). We use the form ![\begin{equation} \xitp= \frac{\xitp_0}{r^2} \exp\left[\frac{-r}{\lambdauv}\right] [1-\auv(1-\mu^2)] \exp\left[\frac{-r(1+\mu)}{\tuv}\right] , \label{equation::qso_lya_radiation_contribution} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq384.png) (32)where r is the comoving separation in units of h-1 Mpc, λUV = 300 h-1 Mpc (Rudie et al. 2013), and
(32)where r is the comoving separation in units of h-1 Mpc, λUV = 300 h-1 Mpc (Rudie et al. 2013), and 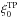 is an amplitude to be fitted. The parameters
is an amplitude to be fitted. The parameters 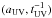 describe anisotropic and time-dependent emission. They are set to zero in the standard fit. Leaving them free in the fit gives a slight preference for anisotropy: aUV = 1.27 ± 0.56 (Table B.1).
describe anisotropic and time-dependent emission. They are set to zero in the standard fit. Leaving them free in the fit gives a slight preference for anisotropy: aUV = 1.27 ± 0.56 (Table B.1).
 |
Fig. 6 Cross-correlation function in four ranges of μ = r∥/r. The data are the black points and the red curves give the standard fit (10 <r< 160 h-1 Mpc) used to measure the BAO parameters. The cross-correlation is multiplied by r2 to show the BAO scale. |
The optional 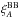 term of (18) is a “broadband function” that is a slowly varying function of (r∥,r⊥):
term of (18) is a “broadband function” that is a slowly varying function of (r∥,r⊥): 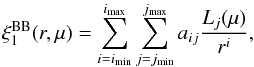 (33)where Lj is the Legendre polynomial of degree j. The standard form, (imin,imax,jmin,jmax) = (0,2,0,6), corresponds to parabolas in r2ξ(r,μ) for seven independent μ ranges. We have also used functions of the form (see Appendix B):
(33)where Lj is the Legendre polynomial of degree j. The standard form, (imin,imax,jmin,jmax) = (0,2,0,6), corresponds to parabolas in r2ξ(r,μ) for seven independent μ ranges. We have also used functions of the form (see Appendix B): 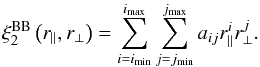 (34)In previous studies, broadband functions were of central importance since we did not attempt to model the distortion from the continuum fitting. In this study this effect is modeled with the distortion matrix DAA′. The purpose of the broadband functions is now only to search for systematic errors due to hypothetical correlations between the peak position and the sidebands. Its function is also to account for unknown physical, instrumental, or analytical effects missing in the model. The standard fit, used to measure the BAO parameters, has no broadband functions: aij = 0.
(34)In previous studies, broadband functions were of central importance since we did not attempt to model the distortion from the continuum fitting. In this study this effect is modeled with the distortion matrix DAA′. The purpose of the broadband functions is now only to search for systematic errors due to hypothetical correlations between the peak position and the sidebands. Its function is also to account for unknown physical, instrumental, or analytical effects missing in the model. The standard fit, used to measure the BAO parameters, has no broadband functions: aij = 0.
When estimating the model on the grid of separation coordinate, we allow for a mean shift of the absorber-quasar separation along the r∥ direction: 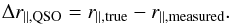 (35)The shift, described by the fit parameter Δr∥ ,QSO, is mostly due to systematic errors in the measurement of the redshift of the quasar. Indeed, the different emission lines of the quasars have different relative velocities (Gaskell 1982; Shen et al. 2016).
(35)The shift, described by the fit parameter Δr∥ ,QSO, is mostly due to systematic errors in the measurement of the redshift of the quasar. Indeed, the different emission lines of the quasars have different relative velocities (Gaskell 1982; Shen et al. 2016).
The model of the correlation function is not r∥-symmetric because of the contribution of metal absorption and the variation of the mean redshifts with r∥. Further asymmetry is introduced by the continuum-fitting distortion. The mean of any residual r∥-asymmetry is absorbed by the quasar-redshift parameter (35). The fits do not reveal any significant additional asymmetries but a complete study of such effects (Bonvin et al. 2014; Iršič et al. 2016) is not included here.
 |
Fig. 7 Correlation function for two ranges of |
5.2. Fits of the cross-correlation
Our “standard” fit of the cross-correlation function uses the 15 parameters in the first group of Table 2. The best-fit values are shown in the column “cross alone” of Table 4. Instead of fitting the bias of the Lyα absorber, bLyα, we fit the combination bLyα(1 + βLyα), which is less correlated with βLyα and better constrained. We limit the fit to separations r ∈ [10,160] h-1 Mpc and fit all directions μ ∈ [−1,1]. As we will see below, these choices have no significant impact on the values and precision of the two BAO-peak parameters.
The best fit is shown in Fig. 6 for four ranges of μ and in Fig. 7 for the two lowest r⊥ bins. The best-fit values of the BAO peak position are (α⊥,α∥) = (0.898, 1.077) with constant χ2 contours indicated in red in Fig. 8. The dashed contours for 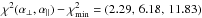 correspond to the nominal (68.27,95.45,99.73%) limits on (α⊥,α∥). This correspondence is, however, not expected to be exact because even if ξ has Gaussian errors, the model is not a linear function of (α⊥,α∥). In the analysis of the 100 mock data sets (Sect. 6), the number of sets yielding
correspond to the nominal (68.27,95.45,99.73%) limits on (α⊥,α∥). This correspondence is, however, not expected to be exact because even if ξ has Gaussian errors, the model is not a linear function of (α⊥,α∥). In the analysis of the 100 mock data sets (Sect. 6), the number of sets yielding 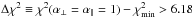 was greater than the expected 4.5% (Table 5, last column). This result suggests that the confidence level corresponding to Δχ2 = 6.18 is overestimated. To make a more precise estimate of the relation between Δχ2 and confidence level, we generated a large number of simulated correlation functions using the fiducial cosmological model and the best fit values of non-BAO parameters, randomized using the covariance matrix measured with the data. Based on these studies, described in detail in Appendix C and summarized in Table C.1, we adopt Δχ2 = (2.62,7.25) as confidence levels of (68.27, 95.45%). These levels are the solid red lines in Fig. 8. The best-fit values of (α⊥, α∥) are 1.8σ from the CMB-inspired flat-ΛCDM model (Planck Collaboration XIII 2016), which has a χ2 that is 6.27 greater than the best fit.
was greater than the expected 4.5% (Table 5, last column). This result suggests that the confidence level corresponding to Δχ2 = 6.18 is overestimated. To make a more precise estimate of the relation between Δχ2 and confidence level, we generated a large number of simulated correlation functions using the fiducial cosmological model and the best fit values of non-BAO parameters, randomized using the covariance matrix measured with the data. Based on these studies, described in detail in Appendix C and summarized in Table C.1, we adopt Δχ2 = (2.62,7.25) as confidence levels of (68.27, 95.45%). These levels are the solid red lines in Fig. 8. The best-fit values of (α⊥, α∥) are 1.8σ from the CMB-inspired flat-ΛCDM model (Planck Collaboration XIII 2016), which has a χ2 that is 6.27 greater than the best fit.
The best-fit values and confidence level (68.27,95.45%) ranges for the BAO parameters are: ![\begin{eqnarray} \aperpMath&=& 0.898~_{- 0.041 }^{+ 0.043 }\;_{- 0.084 }^{+ 0.098 } \label{equation::measure_alpha_perp},\\[2pt] \aparMath&=& 1.077~_{ -0.041 }^{ +0.043 }\;_{ -0.084 }^{ +0.090 } \label{equation::measure_alpha_parallel}, \end{eqnarray}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq418.png) corresponding to
corresponding to ![\begin{eqnarray} \frac{\DMm(z=\MEANZ)}{r_{\rm d}}&=& 35.7~_{- 1.6 }^{+ 1.7 }\;_{ -3.3 }^{ +3.9 } \label{equation::measure_DA_over_rd},\\[2pt] \frac{\DHh(z=\MEANZ)}{r_{\rm d}}&=& 9.01~_{- 0.35 }^{+ 0.36 }\;_{- 0.71 }^{+ 0.75 } \label{equation::measure_Dh_over_rd}. \end{eqnarray}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq419.png) The two BAO parameters are −38% correlated with one another. Following the results of Table C.1, the (1σ,2σ) errors correspond to Δχ2 = (1.17,4.94) for DM/rd and to Δχ2 = (1.19,4.87) for DH/rd.
The two BAO parameters are −38% correlated with one another. Following the results of Table C.1, the (1σ,2σ) errors correspond to Δχ2 = (1.17,4.94) for DM/rd and to Δχ2 = (1.19,4.87) for DH/rd.
Font-Ribera et al. (2014) measured DH(z = 2.36) /rd = 9.0 ± 0.3 and DM(z = 2.36) /rd = 36.3 ± 1.4. Scaling DM(2.36) and DH(2.36) to z = 2.4 (using the fiducial cosmology) results in DH(z = 2.4) /rd = 8.85 ± 0.3 and DM(z = 2.4) /rd = 35.7 ± 1.4. The prior DM measurement agrees well with the present result, while DH has shifted by 0.5σ. As discussed in Bautista et al. (2017), this shift is typical of what can be expected due to the statistical difference between the DR11 and DR12 samples.
 |
Fig. 8 Constraints on (α∥,α⊥) from the standard fit (red) and fit with a broadband term (33) (blue). The dashed red lines correspond to |
The best fit values for the bias and the RSD parameters of the Lyα field are bLyα(1 + βLyα) = −0.350 ± 0.019 and βLyα = 1.90 ± 0.34. They are compatible with the values of Bautista et al. (2017) found using the auto-correlation function, reported here in the column “auto alone” of Table 4.
The effect of metals is visible in the lowest r⊥ bins (Fig. 7). The measured bias of SiIII(120.7), bSiIII(120.7) = −0.0070 ± 0.0017, is incompatible with zero at more than 4 sigma. We thus have evidence of a large-scale cross-correlation between metals and quasars. The three other metals are detected with less significance or not at all.
While the metal parameters found in the cross-correlation are broadly consistent with those found in the auto-correlation, this is not the case for the HCD parameters. The best-fit value of bHCD even has the opposite sign of that found in the auto-correlation. This suggests that the HCD parameters model non-HCD effects, as noted by Bautista et al. (2017). Fortunately, the BAO parameters are insensitive to the HCD modeling. Fixing the HCD parameters to those found in the auto-correlation results in no significant change in (α⊥, α∥) (Line “HCD fixed” of Table B.1).
The uncertainties in Eqs. (36) through (39) are purely statistical. In the Lyα auto-correlation measurement of Bautista et al. (2017), possible systematic uncertainties in the correlation function related to correlated flux-calibration errors were studied in detail. For the quasar-flux cross-correlation, these errors are not relevant. The primary identified systematic error here is in the measurement of quasar redshifts, but this issue leads to an asymmetry in ξ(r∥), which is parameterized by Δr∥ ,QSO and included in the fit. As such, the error is included in the statistical error.
To search for unexpected systematic errors in the determination of the BAO-peak position, we performed fits with modified models. These fits are described in Appendix B and summarized in Table B.1. No obvious discrepancies with the standard fit were found. Of special interest are fits that included a broadband component of the form (33). This fit provides constraints on (α⊥, α∥) that are very similar to the standard fit, as seen in Fig. 8. This insensitivity to the addition of a broadband term differs from the result for the auto-correlation (Bautista et al. 2017) where, because of the very weak BAO signal in the transverse direction, such terms significantly degraded constraints on α⊥. We also performed fits on subsamples of the data as described in Appendix B and summarized in Table B.2. No obvious discrepancies were found.
 |
Fig. 9 Constraints on (α∥,α⊥) corresponding to CL = 68.27 and 95.45% for the cross-correlation (red) and the auto-correlation (Bautista et al. 2017) with a unconstrained broadband (blue). The black lines show the CL = 68.27, 95.45% and 99.7% limits for the combined fit. The black point (α∥,α⊥) = (1,1) indicates the value for the Planck 2016 flat-ΛCDM cosmology. |
5.3. Combination with the auto-correlation
This analysis of the Lyα-quasar cross-correlation in DR12 quasars can be combined with the results of the Lyα auto-correlation in DR12 (Bautista et al. 2017). This study can be done by simply combining the (α⊥, α∥) likelihood contours for the two correlation functions, or by performing a joint fit of the two correlation functions. In the first case we need to estimate the covariance between the two values of (α⊥, α∥). The second case requires the full covariance matrix between the two correlation functions. This problem was studied in Delubac et al. (2015), who showed that the covariance was sufficiently small to be ignored. The studies with the mock data sets discussed in Sect. 6.3 confirm this conclusion and demonstrate that, as expected, the (α⊥, α∥) derived from the auto- and cross-correlations are largely uncorrelated.
We first combine the two measurements by performing a joint fit of the two correlation functions. This fit has 17 free parameters: the 15 from the cross-correlation model and the biases of the CIV forest, bCIV, and of quasars, bQSO. The best-fit results are presented in Table 4. Figure 9 gives (in black) the 68.27%, 95.45%, and 99.7% CL contours (using Δχ2 = (2.5,6.5,13.0) from Table C.1). The results differ from the prediction of the Planck 2016 flat ΛCDM cosmology by 2.3σ. The figure also displays the contours for the auto-correlation in blue (Bautista et al. 2017) and the cross-correlation in red (this study).
The best-fit values for the BAO parameters are: ![\begin{eqnarray} \aperpMath&= & 0.920~_{- 0.030 }^{+ 0.033 }\;_{- 0.062 }^{+ 0.072 } \label{equation::measure_alpha_perp_combined},\\[2pt] \aparMath&=~ & 1.069~_{- 0.026 }^{+ 0.027 }\;_{- 0.052 }^{+ 0.055 } \label{equation::measure_alpha_parallel_combined}, \end{eqnarray}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq449.png) corresponding to:
corresponding to: ![\begin{eqnarray} \frac{\DMm(z=\MEANZ)}{r_{\rm d}}&= & 36.6~_{ -1.3 }^{ +1.4 }\;_{ -2.4 }^{ +2.8 } \label{equation::measure_DA_over_rd_combined},\\[2pt] \frac{\DHh(z=\MEANZ)}{r_{\rm d}}&= & 8.94~_{- 0.22 }^{+ 0.23 }\;_{- 0.43 }^{+ 0.46 } \label{equation::measure_Dh_over_rd_combined}. \end{eqnarray}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq450.png) The combined fit of the auto- and cross-correlations breaks the degeneracy between bLyα and bQSO and we find:
The combined fit of the auto- and cross-correlations breaks the degeneracy between bLyα and bQSO and we find: 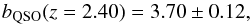 (44)where the error is statistical. This result is in agreement with the results of Croom et al. (2005) and of Laurent et al. (2016), but a study of possible systematic errors will not be presented here.
(44)where the error is statistical. This result is in agreement with the results of Croom et al. (2005) and of Laurent et al. (2016), but a study of possible systematic errors will not be presented here.
The second method of performing the joint fit consists of simply summing the χ2(α⊥,α∥) of the cross-correlation measurement (Fig. 8) and the auto-correlation measurement of Bautista et al. (2017). The measurement of the auto-correlation depends on whether or not one includes a broadband term in the fitting, as seen in Table 6 and Fig. 15 of Bautista et al. (2017). The broadband does not improve the quality of the fit so we adopt the broadband-free result as our primary result. The summed χ2 broadband-free fit gives a result hardly different from (40) and (41): α⊥ = 0.925 ± 0.035 ± 0.075 and α∥ = 1.066 ± 0.028 ± 0.059, corresponding to a shift of ~0.15σ. Use of a broadband (“no additional priors” of Table 6 of Bautista et al. 2017) results in α⊥ = 0.935 ± 0.038 ± 0.082 and α∥ = 1.063 ± 0.028 ± 0.058, corresponding to a shift of ~0.4σ.
6. Validation of the analysis with mocks
At the time of the cross-correlation analysis of Font-Ribera et al. (2014), the only mock data sets that were available (Font-Ribera et al. 2012; Bautista et al. 2015) contained Lyα forests where the underlying density field was traced by the transmission field but not by the associated quasars. The forest-quasar cross-correlation therefore vanishes for these mock data sets. Because of this property, essential features of the cross-correlation analysis could not be checked with the analysis of the mock data.
For the analysis presented in this paper, we have produced a new set of mock spectra where the Lyα forests are properly correlated with the quasars. This correlation is done using the technique of Le Goff et al. (2011) where quasars are placed at peaks of a Gaussian-random field. The transmission field generated with the same Gaussian field is thus correctly correlated with the quasars. These simulations are the first to include the four measured correlations: the 1D correlation of two pixels in the same forest, ξff,1D, the 3D auto-correlation of pixels in different forests, ξff, the 3D auto-correlation of two quasars, ξqq, and, most importantly for this study, the 3D cross-correlation of pixel-quasar on different forests, ξ qf. A disadvantage of this approach is that the quasars and forests are not at the same positions and redshifts as those in the real data. However, this technique should still allow us to test the estimation of the covariance matrix and of the precision of the fit parameters, and to search for systematic errors.
 |
Fig. 10 Correlation function for two pixels from the same forest, ξff,1D, as a function of wavelength ratio for the data and for the mocks, respectively, in red and blue. Prominent peaks due to Lyα-metal correlations are indicated. The metal transitions relevant to this study are given in Table 3. The differences in ξff,1D for data and mocks lead to differences in the covariance matrix for data and mocks. |
6.1. Description of the mock data sets
The production of the mock data sets proceeded as follows. A Gaussian random field of density fluctuations is generated in a cubical volume of 79 (h-1 Gpc)3 with the linear matter power-spectrum of CAMB (Lewis et al. 2000). We adopted a flat ΛCDM fiducial cosmology with parameters given in Table 1. The corresponding box of line-of-sight velocities is generated at the same time. This density field, δLR, has a low resolution since the cubic cells of the box have a side of 3.15 h-1 Mpc. We set the center of the box at z = 2.5, compute the resulting redshift in each cell, and multiply δLR by the corresponding linear growth factor. The velocities are also evolved to the redshift of the cell. The size of the box along the line of sight corresponds to the redshift range 1.71 <z< 3.66 and the box covers 9078 deg2 at z = 2.5.
We draw quasar positions randomly within cells where the field is above a threshold. This threshold is set such as to get a bias of 3.6 relative to matter distribution at z = 2.5, which is consistent with the results of Croom et al. (2005). We do not vary the threshold with the redshift, resulting in a real-space quasar correlation function that does not evolve with redshift within the box. This approach is a significantly better approximation than a constant bias. A random selection of these cells is rejected in order to reproduce the variation of the quasar number density with redshift. Finally, the quasar redshifts are shifted according to the line-of-sight velocity of their cell. The simulations up to the generation of the transmission are then essentially as in Le Goff et al. (2011). One limitation is that the generated lines of sight are parallel. We analyze the mock spectra accordingly, so in a slightly different way than the real data.
Results of the fits of the 100 mocks of each of the three sets of spectra: Lyα absorption only; Lyα absorption superimposed on a quasar continuum; and including metal absorption.
 |
Fig. 11 Cross-correlation of the stack of the 100 mocks in four bins of μ = r∥/r, with the points representing the reconstructed correlation function and the lines representing the fit correlation function (over the range 10 <r< 160 h-1 Mpc). Green and blue represent the Lyα and Lyα+Continuum types, respectively. The agreement between lines and points indicates that the distortion due to continuum fitting is well modeled by the distortion matrix DAA′ (12). The cross-correlation is multiplied by a factor r2 to show the BAO scale. |
 |
Fig. 12 Stack of the 100 mocks cross-correlation for two different ranges of r⊥ with the points representing the reconstructed correlation function and the lines representing the fit correlation function (over the range 10 <r< 160 h-1 Mpc). Blue and red represent the Lyα+Continuum type and Lyα+Continuum+Metals types, respectively. The four black dashed lines indicate the positions of the four peaks of the metal-quasar correlations. The trough at r∥ ≈ −60 h-1 Mpc is due to the SiII(119.3)- and SiII(119.0)-quasar cross-correlations, at r∥ ≈ −21 h-1 Mpc to the SiIII(120.7)-quasar cross-correlation, and at r∥ ≈ + 103 h-1 Mpc to the SiIII(126.0)-quasar cross-correlation. |
 |
Fig. 13 Mean normalized covariance matrix of the mocks, Corr |
Our simulations average over a scale of 3.15 h-1 Mpc and therefore miss a significant amount of transverse small-scale power in true forests, which are smoothed at the Jeans length, ~100 kpc. To compensate for this lack of power, 20 high-resolution simulations with 163 cells of size ~0.2 h-1 Mpc were performed. The delta field from a randomly chosen high-resolution simulation was added to the delta of each large cell to provide the missing small-scale power.
The transmission, F, was computed as ![\begin{equation} F = \exp \left[ -a(z) \exp \left( b g(z) \delta \right) \right], \label{equation::gunn_peterson} \end{equation}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq535.png) (45)where δ is the Gaussian field, g(z) is the linear growth factor, b = 1.58 (Hui & Gnedin 1997), and a(z) is set to reproduce the measured 1D power spectrum (McDonald et al. 2006).
(45)where δ is the Gaussian field, g(z) is the linear growth factor, b = 1.58 (Hui & Gnedin 1997), and a(z) is set to reproduce the measured 1D power spectrum (McDonald et al. 2006).
The next step is to take into account the effect of velocity field. The transmission in each pixel of a spectrum is transformed to the optical depth, τ = −lnF, the pixel is moved in wavelength according to the value of the velocity, and the value of the optical depth is modified according to the gradient of the velocity. Finally, the optical depth is transformed back to the transmission. The resulting field follows the Kaiser formula (Eq. (25)) in the range k< 0.2 (h-1 Mpc)-1 relevant for BAO, with a value of β ≈ 1.2.
The mock expander, described in Bautista et al. (2015), transforms the transmission, F, to a flux, f. This process takes into account the resolution of the SDSS-III BOSS spectrograph, the continuum and magnitude properties of the BOSS quasars, and the level of noise of the data.
We also add absorption due to metal transitions near the Lyα transition: SiII(126.0), SiIII(120.7), SiII(119.3), and SiII(119.0) (Table 3). Absorption due to transitions far from the Lyα transition, such as CIV(154.9), are due to matter at low redshift, and are nearly uncorrelated with the quasars in this study. We use the “procedure 1” of Bautista et al. (2017) to generate absorption by metals. Parameters of the metal transmission field are set in order to reproduce their presence in the observed ξff,1D, the correlation between pixels of the same forest, shown in Fig. 10. The peaks in the figure are due to correlations in absorption by two different transitions at the same physical position. The peaks present in the data but not in the mocks are due to metal1-metal2 correlations that are not correctly modeled in the procedure. These correlations have no effect on the quasar-forest cross-correlation.
Ten Gaussian-random-field boxes of 79 (h-1 Gpc)3 volume were produced. For each of them we use ten different random seeds to define the quasar positions, which provides ten mock quasar catalogs. This approach is reasonable since the quasars occupy only 1.1% of the total number of cells above threshold. When producing the Lyα spectra corresponding to the resulting 100 mock quasar catalogs, different random seeds were used for each quasar catalog, both for the noise and for the quasar continua. Since our quasar and Lyα forest samples are strongly shot-noise limited, the 100 sets of mock catalog and spectra are essentially uncorrelated.
For each of the 100 mock data sets, three types of spectra were produced and analyzed. This procedure allows us to understand the impact of the different physical aspects and physical parameters introduced along the mock production. The results of the fits on the three types are summarized in Table 5. The three types, in order of increasing realism, are:
-
1.
Lyα: the forest pixel values are the transmission field of the Lyα in theIGM. The quasar continuum, the metals absorption of the IGM,and the BOSS spectrograph resolution and noise are notintroduced. When analyzing this type, the distortion matrix is setto the unit matrix.
-
2.
Lyα+Continuum: the quasar continuum, and the BOSS spectrograph resolution and noise are added to the Lyα mocks. This type allows us to understand and test our ability to model the distortion introduced by the lack of knowledge of the true continuum of the quasar.
-
3.
Lyα+Continuum+Metals: this type adds metals of Table 3 to the Lyα+Continuum mocks.
Figures 11 and 12 show stacks of the 100 mock sets for the three types. Figure 11 illustrates how the distortion matrix DAA′ accounts for the change in the correlation function due to continuum fitting. Figure 12 shows the presence of the metals in the low r⊥ bins.
6.2. Fits of individual mock sets
Individual mocks sets were analyzed with the aim of validating the techniques used to analyze the data. In particular, we wished to verify the accuracy of the covariance matrix and search for biases in the determination of the BAO peak position.
The covariance matrix for the data was calculated using the two methods described in Sect. 4.3. One of the goals of the analysis of the mock spectra was to confirm the validity of these methods by observing directly the mock-to-mock variation of the correlation function. The comparison of the covariance determined by this direct method with the two methods used for the data is shown in Fig. 13.
The procedure for fitting the mock correlation function was the same as that for the data with the following exceptions. Because only the linear power spectrum was used to generate the mock spectra, we have FNL(k) = 1 and VNL(k∥) = 1 for the mocks. As stated previously, because of the size of the cells of the mocks, we let free the two parameters R = (R∥,R⊥).
The results of the fits of the 100 mocks are summarized in Table 5, which shows the weighted mean of the best-fit values of α∥,α⊥,bLyα(1 + βLyα) and βLyα. Most importantly, the mean values of α⊥ and α∥ are within 1% of the expected value of unity, indicating no significant bias in the determination of the BAO peak position. The table gives the mean of the one-sigma errors of the four parameters. These means are not far from those observed for fits of the data (Table 4). The mean χ2 for the mock fits are near unity per degree of freedom, confirming that the covariance matrix of ξ(r⊥,r∥) is well estimated. The last column of the table lists the number of mocks sets with values 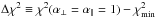 that exceed 6.18. This number is generally greater than 4.5, the number expected for Gaussian errors on (α⊥, α∥). This result, confirmed by the Monte Carlo simulations of Appendix C, is unsurprising because the model is not a linear function of these variables.
that exceed 6.18. This number is generally greater than 4.5, the number expected for Gaussian errors on (α⊥, α∥). This result, confirmed by the Monte Carlo simulations of Appendix C, is unsurprising because the model is not a linear function of these variables.
 |
Fig. 14 Mean normalized covariance, Corr |
6.3. Combined fits of the cross- and auto-correlation
As with the data, the cross- and auto-correlation functions of the mocks can be combined either by performing a joint fit of the two functions, or by combining the values of (α⊥,α∥) measured separately with the two functions. The former requires the covariance matrix between the cross- and auto-correlations while the latter requires the covariance of the two measurements of (α⊥,α∥). The mock-to-mock variations of the auto- and cross-correlations shown in Fig. 14 indicate that the covariance of the two correlation functions is negligible. The correlation of the auto and cross measurements of (α⊥,α∥) are presented in Fig. 15 and Table 6. As expected, they are consistent with zero.
 |
Fig. 15 Scatter plot of the BAO peak position parameters measured with the cross-correlation versus those measured with the auto-correlation for the 100 Lyα+Continuum+Metal mocks. |
Correlations between the (α⊥,α∥) measured by the cross- and auto-correlation functions derived from the mock-to-mock variations of best-fit values for the 100 mocks.
7. Cosmological interpretation
The measurements of the BAO peak with the Lyα auto-correlation and the quasar-Lyα cross-correlation yield the constraints on DM(z ~ 2.4) /rd and DH(z ~ 2.4) /rd that are presented in Fig. 9. The auto-correlation measurement of Bautista et al. (2017) produced a value of 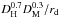 about one standard deviation from the flat-ΛCDM model that yields the CMB anisotropy spectrum measured by Planck Collaboration XIII (2016). The cross-correlation measurement presented here is 1.8 standard deviations from the CMB prediction, and the combined measurement differs by 2.3 standard deviations from this prediction.
about one standard deviation from the flat-ΛCDM model that yields the CMB anisotropy spectrum measured by Planck Collaboration XIII (2016). The cross-correlation measurement presented here is 1.8 standard deviations from the CMB prediction, and the combined measurement differs by 2.3 standard deviations from this prediction.
While the results presented here represent “tension” with CMB-inspired flat ΛCDM model, the complete set of BAO measurements presented in Fig. 16 are in good agreement with this model. The CMB model has χ2 = 14.8 for 12 data points. The contributions to this χ2 from the two low-redshift DV/rd measurements are Δχ2 = 0.12 (Beutler et al. 2011) and Δχ2 = 0.82 (Ross et al. 2015). The measurements of (DM/rd,DH/rd) at 0.2 <z< 0.8 contribute 5.40/6 points (Alam et al. (2017), “BAO-only”) while the Lyα auto-correlation at z = 2.33 contributes 2.18/2 points (Bautista et al. 2017). The cross-correlation measurement presented here contributes 6.27/2 points, corresponding to a 1.8σ deviation from the ΛCDM values. This tension has no simple, well-motivated solution (Aubourg et al. 2015), which suggests that it results from a statistical fluctuation.
The BAO measurements by themselves yield the constraints on the ΛCDM parameters (Ωm,ΩΛ) shown in Fig. 17. The flat-ΛCDM CMB-inspired model is about one standard deviation from the best fit, which has χ2 = 12.5 for (12−3) degrees of freedom and the best-fit parameters: 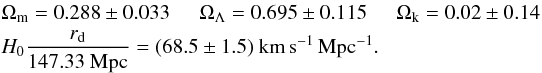 (46)Imposing Ωk = 0 results in Ωm = 0.292 ± 0.019, in good agreement with the CMB value Ωm = 0.315 ± 0.017 (Planck Collaboration XIII 2016).
(46)Imposing Ωk = 0 results in Ωm = 0.292 ± 0.019, in good agreement with the CMB value Ωm = 0.315 ± 0.017 (Planck Collaboration XIII 2016).
The BAO best-fit values (46) use the primary Lyα auto-correlation result without a broadband added to the correlation function. Inclusion of a broadband for the auto-correlation changes the best-fit values by ~0.3σ: Ωm = 0.275 ± 0.034, ΩΛ = 0.657 ± 0.125, and Ωk = 0.07 ± 0.15.
 |
Fig. 16 BAO measurement of DM(z) /rd and DH(z) /rd and combinations thereof, compared to the prediction the flat-ΛCDM model favored by CMB-anisotropy measurements (Planck Collaboration XIII 2016). The BAO measurements come from the 6dFGS (Beutler et al. 2011), SDSS-MGS (Ross et al. 2015), BOSS Galaxies (Alam et al. (2017), “BAO-only”), eBOSS quasars (Ata et al. 2018), the Lyα forest flux auto-correlation (Bautista et al. 2017), and the Lyα-quasar cross-correlation (this work). |
 |
Fig. 17 Constraints on (ΩM,ΩΛ). The red contours give the one, two, and three standard deviation constraints from the DV/rd measurements of Beutler et al. (2011) and Ross et al. (2015) and the (DM/rd,DH/rd) measurements of Alam et al. (2017), Bautista et al. (2017), and this work. The blue contours give the SNIa constraints of Betoule et al. (2014). The black point indicates the Planck flat-ΛCDM value of (ΩM,ΩΛ). This point has χ2 = 14.8 for d.o.f. = 12. |
While the result (46) strongly disfavors matter-only models (i.e., ΩΛ = 0), it does not strongly imply that the expansion is accelerating at the present epoch. This is because we have used data at z> 1 where the expansion was decelerating, so any statement about present-day acceleration is model-dependent. A recent report (Nielsen et al. 2016) that low redshift measurements require acceleration only at <3σ significance stimulated a re-examination of the evidence. The general conclusion is that, in the absence of unidentified luminosity evolution, the SNIa data (Betoule et al. 2014) do support acceleration at >4σ significance (Rubin & Hayden 2016; Haridasu et al. 2017; Tutusaus et al. 2017). The BAO data do not provide such precision because at low redshift the number of available galaxies to measure the correlation function is small. If one uses the four BAO data points in Fig. 16 with z< 0.4, one finds that the best non-accelerating model (q0 = Ωm/ 2−ΩΛ> 0) has (Ωm,ΩΛ) = (0,0) with χ2 = 8.1. This can be compared with χ2 = 0.7 for the best-fit model and χ2 = 2.1 for the Planck-2016 model. Acceleration is preferred at the 2.5σ level.
8. Summary and conclusions
Using the entirety of the BOSS data set, this paper has presented a measurement of the cross-correlation of quasars and the Lyα flux transmission at redshift 2.4. Apart from the improved statistical precision over our previous measurement, we have benefited from an improved pipeline and better modeling of the effects of continuum fitting. The availability of mock data sets with quasar-forest correlations was essential for verifying the reliability of the analysis.
The modeling of continuum-fitting distortions done here opens up the possibility of constraining cosmology with the full correlation function, in addition to the BAO peak. However, this would require further studies to determine the sensitivity of such constraints to poorly constrained astrophysics: DLA absorption, UV fluctuations, and the transverse proximity effect. These studies would probably require an analysis of the data with multiple redshift bins. Relativistic effects (Bonvin et al. 2014; Iršič et al. 2016) should also be included in the model. Further improvement on these results will be forthcoming from the ongoing eBOSS project (Dawson et al. 2016) and the upcoming DESI (DESI Collaboration et al. 2016), HETDEX (Hill et al. 2008) and WEAVE (Pieri et al. 2016) projects.
The position of the BAO peak is 1.8σ from the flat-ΛCDM model favored by CMB anisotropy measurements (Planck Collaboration XIII 2016). Combined with the Lyα-flux-transmission auto-correlation measurement of Bautista et al. (2017), the BAO peak at z = 2.4 is 2.3σ from the expected value. Despite this tension, the ensemble of BAO measurements is in good agreement with the CMB-inspired flat-ΛCDM model. The measured auto- and cross-correlation, the best-fit results, and χ2 scan are publicly available2.
Acknowledgments
We thank Christophe Magneville for help in the production of the mock data sets. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max-Planck-Institute for Astrophysics, Max-Planck-Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
The French Participation Group of SDSS-III was supported by the Agence Nationale de la Recherche under contracts ANR-08-BLAN-0222 and ANR-12-BS05-0015-01. M.B., M.M.P., and I.P. were supported by the A*MIDEX project (ANR- 11-IDEX-0001-02) funded by the “Investissements d’Avenir” French Government program, managed by the French National Research Agency (ANR), and by ANR under contract ANR-14-ACHN-0021”. A.F.R. and N.P.R. acknowledge support from the STFC and the Ernest Rutherford Fellowship scheme.
References
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014a, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2014b, MNRAS, 439, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Arinyo-i-Prats, A., Miralda-Escudé, J., Viel, M., & Cen, R. 2015, J. Cosmol. Astropart. Phys., 12, 017 [NASA ADS] [CrossRef] [Google Scholar]
- Ata, M., Baumgarten, F., Bautista, J., et al. 2018, MNRAS, 473, 4773 [NASA ADS] [CrossRef] [Google Scholar]
- Aubourg, É., Bailey, S., Bautista, J. E., et al. 2015, Phys. Rev. D, 92, 123516 [NASA ADS] [CrossRef] [Google Scholar]
- Bajtlik, S., Duncan, R. C., & Ostriker, J. P. 1988, ApJ, 327, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Bailey, S., Font-Ribera, A., et al. 2015, J. Cosmol. Astropart. Phys., 5, 60 [Google Scholar]
- Bautista, J. E., Busca, N. G., Guy, J., et al. 2017, A&A, 603, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Davis, T., Poole, G. B., et al. 2011, MNRAS, 415, 2892 [NASA ADS] [CrossRef] [Google Scholar]
- Blomqvist, M., Kirkby, D., Bautista, J. E., et al. 2015, J. Cosmol. Astropart. Phys., 11, 034 [Google Scholar]
- Bolton, A. S., Schlegel, D. J., Aubourg, É., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Bonvin, C., Hui, L., & Gaztañaga, E. 2014, Phys. Rev. D, 89, 083535 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Hennawi, J. F., Hogg, D. W., et al. 2011, ApJ, 729, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Busca, N. G., Delubac, T., Rich, J., et al. 2013, A&A, 552, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chuang, C.-H., & Wang, Y. 2012, MNRAS, 426, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Boyle, B. J., Shanks, T., et al. 2005, MNRAS, 356, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Delubac, T., Bautista, J. E., Busca, N. G., et al. 2015, A&A, 574, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Seo, H.-J., & White, M. 2007, ApJ, 664, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Font-Ribera, A., & Miralda-Escudé, J. 2012, J. Cosmol. Astropart. Phys., 7, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., McDonald, P., & Miralda-Escudé, J. 2012, J. Cosmol. Astropart. Phys., 1, 001 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., Arnau, E., Miralda-Escudé, J., et al. 2013, J. Cosmol. Astropart. Phys., 5, 018 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., Kirkby, D., Busca, N., et al. 2014, J. Cosmol. Astropart. Phys., 5, 27 [Google Scholar]
- Gaskell, C. M. 1982, ApJ, 263, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcho A Gontcho, S., Miralda-Escudé, J., & Busca, N. G. 2014, MNRAS, 442, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Haridasu, B. S., Luković, V. V., D’Agostino, R., & Vittorio, N. 2017, A&A, 600, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, G. J., Gebhardt, K., Komatsu, E., et al. 2008, in Panoramic Views of Galaxy Formation and Evolution, eds. T. Kodama, T. Yamada, & K. Aoki, ASP Conf. Ser., 399, 115 [Google Scholar]
- Hui, L., & Gnedin, N. Y. 1997, MNRAS, 292, 27 [Google Scholar]
- Iršič, V., Di Dio, E., & Viel, M. 2016, J. Cosmol. Astropart. Phys., 2, 051 [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkby, D., Margala, D., Slosar, A., et al. 2013, J. Cosmol. Astropart. Phys., 3, 024 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. A., Schlegel, D. J., Ross, N. P., et al. 2011, ApJ, 743, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., Le Goff, J.-M., Burtin, E., et al. 2016, J. Cosmol. Astropart. Phys., 11, 060 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Le Goff, J. M., Magneville, C., Rollinde, E., et al. 2011, A&A, 534, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- Linder, E. V., & Cahn, R. N. 2007, Astropart. Phys., 28, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- McDonald, P. 2003, ApJ, 585, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., & Eisenstein, D. J. 2007, Phys. Rev. D, 76, 063009 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Seljak, U., Burles, S., et al. 2006, ApJS, 163, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Mehta, K. T., Cuesta, A. J., Xu, X., Eisenstein, D. J., & Padmanabhan, N. 2012, MNRAS, 427, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Murdoch, H. S., Hunstead, R. W., Pettini, M., & Blades, J. C. 1986, ApJ, 309, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, A. D., Palanque-Delabrouille, N., Prakash, A., et al. 2015, ApJS, 221, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, J. T., Guffanti, A., & Sarkar, S. 2016, Sci. Rep., 6, 35596 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Carithers, W. C., et al. 2012, A&A, 547, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padmanabhan, N., Xu, X., Eisenstein, D. J., et al. 2012, MNRAS, 427, 2132 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2012, A&A, 548, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2014, A&A, 563, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Ross, N. P., et al. 2017, A&A, 597, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peebles, P. J. E., & Yu, J. T. 1970, ApJ, 162, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., & White, M. 2009, MNRAS, 393, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, M. M., Bonoli, S., Chaves-Montero, J., et al. 2016, in SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, J. Richard, L. Cambrésy, M. Deleuil, E. Pécontal, L. Tresse, & I. Vauglin, 259 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A. 2014, Phys. Rev. D, 89, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, N. P., Myers, A. D., Sheldon, E. S., et al. 2012, ApJS, 199, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, D., & Hayden, B. 2016, ApJ, 833, L30 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rudie, G. C., Steidel, C. C., Shapley, A. E., & Pettini, M. 2013, ApJ, 769, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- SDSS Collaboration (Albareti, F. D., et al.) 2016, ApJS, submitted [arXiv:1608.02013] [Google Scholar]
- Shen, Y., Brandt, W. N., Richards, G. T., et al. 2016, ApJ, 831, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Slosar, A., Iršič, V., Kirkby, D., et al. 2013, J. Cosmol. Astropart. Phys., 4, 26 [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970, Ap&SS, 7, 3 [NASA ADS] [Google Scholar]
- Tutusaus, I., Lamine, B., Dupays, A., & Blanchard, A. 2017, A&A, 602, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfe, A. M., Turnshek, D. A., Smith, H. E., & Cohen, R. D. 1986, ApJS, 61, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., Cuesta, A. J., Padmanabhan, N., Eisenstein, D. J., & McBride, C. K. 2013, MNRAS, 431, 2834 [NASA ADS] [CrossRef] [Google Scholar]
- Yèche, C., Petitjean, P., Rich, J., et al. 2010, A&A, 523, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
Appendix A: Covariance matrix
The calculation of CAB via Eq. (14)can be decomposed into six different diagrams, presented in Fig. A.1. In the six diagrams of this figure, the dashed lines indicate the Lyα-forests and the crosses indicate the quasars. In Diagrams T1 and T3, the two pixel-quasar pairs share the same pixel, i = j. In these cases the pixel-pixel correlation is given by the variance of pixels at its observed wavelength: ⟨ δiδi ⟩ = ξff,1D(λi,λi). In Diagrams T2 and T4, the two pixels from the two pairs belong to the same forest. Here the pixel-pixel correlation is given by the 1D correlation: ⟨ δiδj ⟩ = ξff,1D(λi,λj/λi). This correlation is presented for the simulations and for the data in Fig. 10. In Diagrams T5 and T6, the two pixels belong to different forests, and the pixel-pixel correlation is given by the 3D Lyα-forest auto-correlation: ⟨ δiδj ⟩ = ξff(rij). This correlation is studied in Bautista et al. (2017).
Figure A.2 presents the contribution to the correlation matrix (Eq. (16)) of the six diagrams and their sum. The elements of 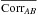 are given as a function of
are given as a function of 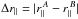 for the smallest values of
for the smallest values of 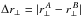 . The top left panel shows the correlation matrix for Δr⊥ = 0, and the top right panel displays an expanded image. These two panels are the reflection of the ξff,1D presented in Fig. 10. Some of the Lyα-metal lines are visible. The bottom left and right panels display the correlation matrix for Δr⊥ = 4 h-1 Mpc and for Δr⊥ = 8 h-1 Mpc. As expected, these correlations are very small.
. The top left panel shows the correlation matrix for Δr⊥ = 0, and the top right panel displays an expanded image. These two panels are the reflection of the ξff,1D presented in Fig. 10. Some of the Lyα-metal lines are visible. The bottom left and right panels display the correlation matrix for Δr⊥ = 4 h-1 Mpc and for Δr⊥ = 8 h-1 Mpc. As expected, these correlations are very small.
Diagrams T1 and T2 dominate the variance CAA and T2 the covariance CAB when the bins A and B have similar transverse separation r⊥. T2 vanishes for very different r⊥.
 |
Fig. A.1 Six different diagrams of pairs of pixel-quasar pairs. The dashed lines refer to the forests, the crosses refer to the quasar position. The variance is dominated by T1 and T2. The off-diagonal terms of the covariance are dominated by T2. The diagrams T3 and T4 cancel out at large scale, the diagram T5 has a small contribution at small scales and T6 is negligible. |
Due to the projection of the δ (Sect. 3), Diagrams T3 and T4 have only a maximum sub-percent contribution to the correlation matrix and cancel out at large scale. T5 has a small contribution at small scales and T6 is negligible.
 |
Fig. A.2 Mean normalized covariance matrix of the data, Corr |
 |
Fig. A.3 As in Fig. 6 but showing three models fit to the data. Red lines indicate the standard fit used to measure the BAO parameters (Sect. 5.2), blue lines the standard fit if the velocity distribution of quasars was null, and green lines the standard fit with the addition of a broadband defined by (33) with (imin,imax,jmin,jmax) = (0,2,0,6). The cross-correlation is multiplied by a factor r2 to show the BAO scale. |
Appendix B: Non-standard fits of the correlation function
In order to test the robustness of our measurement of (α⊥, α∥), we performed fits in which the standard model was modified. All fits yield compatible values and precision of the two BAO parameters, and provide confidence in the validity of our measurement.
For all of these models, Table B.1 lists the best-fit values of the four main parameters: α∥, α⊥, bLyα(1 + βLyα), and βLyα, as well as the 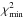 of the fit. The first group of fits gives the results for increasingly complicated physical models, starting with a model with only Lyα absorption and including successively metals, HCDs, UV fluctuations, and the transverse proximity effect. The last of this group, Lyα+Metals+zq+HCD+UV+TP, corresponds to the standard fit of Sect. 5.2. The first two fits (“Lyα” and “Lyα + Metals”), which do not take into account the velocity dispersion of quasars, have a high
of the fit. The first group of fits gives the results for increasingly complicated physical models, starting with a model with only Lyα absorption and including successively metals, HCDs, UV fluctuations, and the transverse proximity effect. The last of this group, Lyα+Metals+zq+HCD+UV+TP, corresponds to the standard fit of Sect. 5.2. The first two fits (“Lyα” and “Lyα + Metals”), which do not take into account the velocity dispersion of quasars, have a high 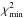 . Adding this effect (zq in Table B.1) reduces significantly
. Adding this effect (zq in Table B.1) reduces significantly 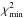 , but the best-fit values and precision of the two BAO parameters do not change significantly with successive models. However, due to correlations and degeneracies, the values and the precision of the bias and RSD parameters of the Lyα field change significantly when adding the velocity dispersion of the quasars.
, but the best-fit values and precision of the two BAO parameters do not change significantly with successive models. However, due to correlations and degeneracies, the values and the precision of the bias and RSD parameters of the Lyα field change significantly when adding the velocity dispersion of the quasars.
The second section of Table B.1 presents the results with different fitting ranges. The third section gives results for fits where normally unfit parameters are fit. Finally, the fourth section includes fits with additional constraints: the absence of a BAO peak (Apeak = 0), an isotropic BAO peak (α⊥ = α∥), or imposing the fiducial cosmology (α⊥ = α∥ = 1)
Figure A.3 shows the measured cross-correlation for the data in four bins of μ. Also shown are three of the fits listed in Table B.1: the standard fit (Sect. 5.2), the standard fit if the velocity distribution of quasars was null, and finally the fit with the broadband function (33).
In our earlier studies of the cross-correlation (Font-Ribera et al. 2014) and of the auto-correlation (Delubac et al. 2015) we did not attempt to measure the distortion of the correlations by the fit of the quasar continuum. This distortion was modeled by the broadband function (33). We now take this effect into account with the distortion matrix (12), so we use these broadband functions to test for any systematic errors in the determination of the BAO parameters’ values and precision. These potential errors could be induced by any correlations between the sidebands and the BAO peak position (smooth and peak components in Eq. (24)). In this study, we tested a large number of broadband functions modeled by Eq. (33), keeping (i,j) within reasonable values: (imin,imax) ∈ [−4,3] and (jmin,jmax) ∈ [0,6]. In a similar way, for the broadband functions modeled by Eq. (34), we tested reasonable values of (i,j): (imin,imax,jmin,jmax) ∈ [−4,3]. These choices allowed an investigation of a wide range of broadbands without introducing an excessive number of parameters and unrealistic features in the cross-correlation. All of these different broadband functions do not change the values of the two BAO parameters by more than 0.5σ. The precision of the two BAO parameters is also not significantly degraded by the presence of broadbands. This behavior is in contrast to the auto-correlation function (Bautista et al. 2017) where the broadband terms over the range 40 <r< 180 h-1 Mpc degraded significantly the precision on α⊥.
Results of non-standard fits.
Best-fit results for the four most important parameters for different data splits as described in the text.
Values of Δχ2 corresponding to CL = (68.27, 95.45, 99.7%) as derived from the Monte-Carlo simulation of correlation functions.
In addition to the changes in the fitting procedure described in the previous section, we also tested the robustness of the BAO peak position determination by dividing the data into roughly equal subsamples that would be expected to yield compatible peak positions. The results of these “data splits” are listed in Table B.2. The splits divide the data according to the relative distances of the quasar and forest pixel (r∥< 0, ≥0), the pair redshift (zpair), the Galactic hemisphere (NGC, SGC), the quasar position on the observing plates (fiber Id < 500, ≥500), quasar target sample (CORE, notCORE; Ross et al. 2012), and quasar emission-line strength (Amp. CIV). The last three data splits in the table use indicators of the quality of the quasar spectrum: the quasar magnitude (iq) and the signal-to-noise ratio in the forest (SNRLyα) and redward of Lyα emission (SNR1700). None of these data splits indicate an unexpected shift in the BAO peak.
Appendix C: Monte-Carlo determination of the statistical errors of fit parameters
To make a precise estimate of the relation between Δχ2 and confidence level, we generated a large number of simulated correlation functions using the fiducial cosmological model and the best-fit values of non-BAO parameters, randomized using the covariance matrix measured with the data. Two types of simulated correlation functions were produced: one with only Lyα-absorption and one “complete” simulation that included metals, UV fluctuations, and quasar (QSO) radiation. Each simulated correlation function was then fit for the model parameters and the χ2 for the best-fit parameters compared with the best χ2 with one or more parameters set to the known input values. The Δχ2 corresponding to a given fraction of simulated correlation functions could then be determined.
The results are summarized in Table C.1 for fits of the cross- and auto-correlation functions and for combined fits. For the cross-correlation, the parameters bLyα(1 + βLyα) and βLyα have an associated Δχ2 for CL = (68.27,95.45,99.7)% that is consistent with the expected values of (1,4,9). The values for the BAO peak parameters (α⊥, α∥) are somewhat higher: Δχ2 ~ (1.18,4.8,11.) suggesting that the nominal “1σ” errors should be increased by a factor 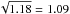 . This is true for both the Lyα-only and complete simulations. For the pair (α⊥, α∥), the results indicate Δχ2 ~ (2.62,7.25) corresponds to confidence levels of (68.27,95.45%). We have adopted these values of Δχ2 for the errors reported in Eqs. (36) through (39) and the contours in Fig. 8.
. This is true for both the Lyα-only and complete simulations. For the pair (α⊥, α∥), the results indicate Δχ2 ~ (2.62,7.25) corresponds to confidence levels of (68.27,95.45%). We have adopted these values of Δχ2 for the errors reported in Eqs. (36) through (39) and the contours in Fig. 8.
The values for Δχ2 for the auto-correlation are similar to those for the cross-correlation. An exception is the value for the parameter βLyα , which has Δχ2 = 1.09 ± 0.02, significantly higher than the expected value of unity. For the pair (α⊥, α∥), we have adopted the values Δχ2 = (2.6,7.1) for the auto-correlation contours in Fig. 9.
For the combined fits, the Δχ2 are closer to the nominal values. This is to be expected because the peak position is better determined, so the model is closer to being a linear function of (α⊥, α∥) in the limited range around (1, 1). For the combined-fit contours in Fig. 9. we have adopted the values Δχ2 = 2.45,6.4,14.) for CL = (68.27,95.45,99.7)%.
The “frequentist” intervals reported in this paper are renormalized using the Δχ2 found with the simulation presented in this section. Bayesian “credible intervals” require no such renormalization since they use directly the measured χ2 as a function of model parameters. The Bayesian analogs of our results (36) and (37) for a uniform prior on (α⊥, α∥) are ![\appendix \setcounter{section}{3} \begin{eqnarray} \aperpMath = 0.906 \pm 0.0424\, (68.27\%) \pm 0.0917\, (95.45\%) \\[3mm] \aparMath = 1.077 \pm 0.0405\, (68.27\%) \pm 0.0841\, (95.45\%) . \end{eqnarray}](/articles/aa/full_html/2017/12/aa31731-17/aa31731-17-eq953.png)
All Tables
Parameters of the flat-ΛCDM cosmological model used for the production and analysis of the mock spectra and for the analysis of the data.
Major metal transitions seen in the intergalactic medium (IGM) and present in the forest-quasar cross-correlation for r∥ ∈ [−200,200] h-1 Mpc.
Fit results for the cross-correlation (this study), the auto-correlation (Bautista et al. 2017) extrapolated to z = 2.40, and the combined fit.
Results of the fits of the 100 mocks of each of the three sets of spectra: Lyα absorption only; Lyα absorption superimposed on a quasar continuum; and including metal absorption.
Correlations between the (α⊥,α∥) measured by the cross- and auto-correlation functions derived from the mock-to-mock variations of best-fit values for the 100 mocks.
Best-fit results for the four most important parameters for different data splits as described in the text.
Values of Δχ2 corresponding to CL = (68.27, 95.45, 99.7%) as derived from the Monte-Carlo simulation of correlation functions.
All Figures
 |
Fig. 1 Mollweide projection of the BOSS DR12 footprint in equatorial coordinates used in this study. The light gray points represent the position of the Galactic plane. The blue points are the positions of the forests from DR12 used here zforest ∈ [2,6]. The light blue points are the positions of the new forests not included in the DR11 study of Font-Ribera et al. (2014). |
| In the text | |
 |
Fig. 2 Example of a BOSS quasar spectrum of at z = 2.91. The spectrograph resolution at λ ~ 400 nm is ~0.2 nm. The red and blue lines cover the forest region used here, λRF ∈ [104,120] nm. This region is sandwiched between the quasar’s Lyβ and Lyα emission lines at 102.572 nm and 121.567 nm respectively. The blue line is the model of the continuum for this particular quasar, Cq(λRF), and the red line is the product of the continuum and the mean absorption, |
| In the text | |
 |
Fig. 3 Left panel: distribution of the redshift of quasars (blue) and forest pixels (green) with the redshift for the latter calculated assuming Lyα absorption. The pixels are weighted as described in Sect. 4.1. Right panel: weighted distribution of the redshift of the 1.8 × 109 pixel-quasar pairs in the BAO region: rpair ∈ [80,120] h-1 Mpc. The redshift of a pair is defined by: zpair = (zpixel + zQSO)/2. The weighted mean redshift of the pairs (dashed black line) defines the mean redshift, zeff = 2.40, of the measurement of the BAO peak position. |
| In the text | |
 |
Fig. 4 Mean normalized covariance matrix, Corr |
| In the text | |
 |
Fig. 5 Measured (left) and the best fit model (right) of the Lyα-forest-quasar cross-correlation. The distortion matrix (12) has been applied to the model. The correlation is multiplied by a factor r. The BAO scale appears here as a half ring of radius r ≈ 100 h-1 Mpc. The color code is saturated for clarity. |
| In the text | |
 |
Fig. 6 Cross-correlation function in four ranges of μ = r∥/r. The data are the black points and the red curves give the standard fit (10 <r< 160 h-1 Mpc) used to measure the BAO parameters. The cross-correlation is multiplied by r2 to show the BAO scale. |
| In the text | |
 |
Fig. 7 Correlation function for two ranges of |
| In the text | |
 |
Fig. 8 Constraints on (α∥,α⊥) from the standard fit (red) and fit with a broadband term (33) (blue). The dashed red lines correspond to |
| In the text | |
 |
Fig. 9 Constraints on (α∥,α⊥) corresponding to CL = 68.27 and 95.45% for the cross-correlation (red) and the auto-correlation (Bautista et al. 2017) with a unconstrained broadband (blue). The black lines show the CL = 68.27, 95.45% and 99.7% limits for the combined fit. The black point (α∥,α⊥) = (1,1) indicates the value for the Planck 2016 flat-ΛCDM cosmology. |
| In the text | |
 |
Fig. 10 Correlation function for two pixels from the same forest, ξff,1D, as a function of wavelength ratio for the data and for the mocks, respectively, in red and blue. Prominent peaks due to Lyα-metal correlations are indicated. The metal transitions relevant to this study are given in Table 3. The differences in ξff,1D for data and mocks lead to differences in the covariance matrix for data and mocks. |
| In the text | |
 |
Fig. 11 Cross-correlation of the stack of the 100 mocks in four bins of μ = r∥/r, with the points representing the reconstructed correlation function and the lines representing the fit correlation function (over the range 10 <r< 160 h-1 Mpc). Green and blue represent the Lyα and Lyα+Continuum types, respectively. The agreement between lines and points indicates that the distortion due to continuum fitting is well modeled by the distortion matrix DAA′ (12). The cross-correlation is multiplied by a factor r2 to show the BAO scale. |
| In the text | |
 |
Fig. 12 Stack of the 100 mocks cross-correlation for two different ranges of r⊥ with the points representing the reconstructed correlation function and the lines representing the fit correlation function (over the range 10 <r< 160 h-1 Mpc). Blue and red represent the Lyα+Continuum type and Lyα+Continuum+Metals types, respectively. The four black dashed lines indicate the positions of the four peaks of the metal-quasar correlations. The trough at r∥ ≈ −60 h-1 Mpc is due to the SiII(119.3)- and SiII(119.0)-quasar cross-correlations, at r∥ ≈ −21 h-1 Mpc to the SiIII(120.7)-quasar cross-correlation, and at r∥ ≈ + 103 h-1 Mpc to the SiIII(126.0)-quasar cross-correlation. |
| In the text | |
 |
Fig. 13 Mean normalized covariance matrix of the mocks, Corr |
| In the text | |
 |
Fig. 14 Mean normalized covariance, Corr |
| In the text | |
 |
Fig. 15 Scatter plot of the BAO peak position parameters measured with the cross-correlation versus those measured with the auto-correlation for the 100 Lyα+Continuum+Metal mocks. |
| In the text | |
 |
Fig. 16 BAO measurement of DM(z) /rd and DH(z) /rd and combinations thereof, compared to the prediction the flat-ΛCDM model favored by CMB-anisotropy measurements (Planck Collaboration XIII 2016). The BAO measurements come from the 6dFGS (Beutler et al. 2011), SDSS-MGS (Ross et al. 2015), BOSS Galaxies (Alam et al. (2017), “BAO-only”), eBOSS quasars (Ata et al. 2018), the Lyα forest flux auto-correlation (Bautista et al. 2017), and the Lyα-quasar cross-correlation (this work). |
| In the text | |
 |
Fig. 17 Constraints on (ΩM,ΩΛ). The red contours give the one, two, and three standard deviation constraints from the DV/rd measurements of Beutler et al. (2011) and Ross et al. (2015) and the (DM/rd,DH/rd) measurements of Alam et al. (2017), Bautista et al. (2017), and this work. The blue contours give the SNIa constraints of Betoule et al. (2014). The black point indicates the Planck flat-ΛCDM value of (ΩM,ΩΛ). This point has χ2 = 14.8 for d.o.f. = 12. |
| In the text | |
 |
Fig. A.1 Six different diagrams of pairs of pixel-quasar pairs. The dashed lines refer to the forests, the crosses refer to the quasar position. The variance is dominated by T1 and T2. The off-diagonal terms of the covariance are dominated by T2. The diagrams T3 and T4 cancel out at large scale, the diagram T5 has a small contribution at small scales and T6 is negligible. |
| In the text | |
 |
Fig. A.2 Mean normalized covariance matrix of the data, Corr |
| In the text | |
 |
Fig. A.3 As in Fig. 6 but showing three models fit to the data. Red lines indicate the standard fit used to measure the BAO parameters (Sect. 5.2), blue lines the standard fit if the velocity distribution of quasars was null, and green lines the standard fit with the addition of a broadband defined by (33) with (imin,imax,jmin,jmax) = (0,2,0,6). The cross-correlation is multiplied by a factor r2 to show the BAO scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.