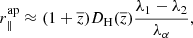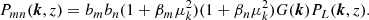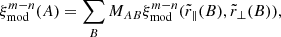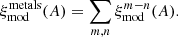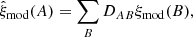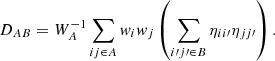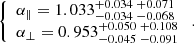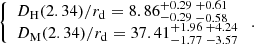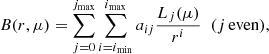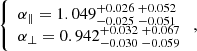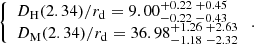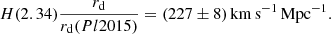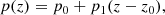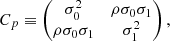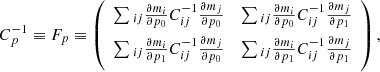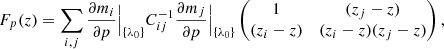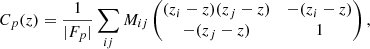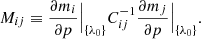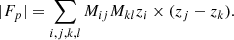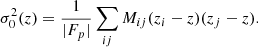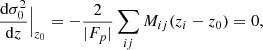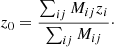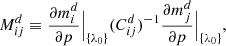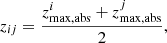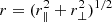| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935638 | |
| Published online | 10 September 2019 | |
Baryon acoustic oscillations at z = 2.34 from the correlations of Lyα absorption in eBOSS DR14
1
Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies, LPNHE, 4 Place Jussieu, 75252 Paris, France
e-mail: victoria.de.sainte.agathe@lpnhe.in2p3.fr
2
Department of Physics and Astronomy, University of Utah, 115 S. 1400 E., Salt Lake City, UT 84112
USA
3
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
4
Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
5
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
6
University College London, Gower St, Kings Cross, London WC1E 6BT, UK
7
Institute of Cosmology & Gravitation, University of Portsmouth, Dennis Sciama Building, Portsmouth PO1 3FX, UK
8
Instituto de Astronomía, Universidad Nacional Autónoma de México, A.P. 70-264, DF 04510 México, Mexico
9
Department of Physics and Astronomy, University of Waterloo, 200 University Ave. W., Waterloo, ON N2L 3G1, Canada
10
Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA, 16802, USA
11
Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA, 16802, USA
12
Brookhaven National Laboratory, 2 Center Road, Upton, NY 11973, USA
Received:
8
April
2019
Accepted:
8
July
2019
We measure the imprint of primordial baryon acoustic oscillations (BAOs) in the correlation function of Lyα absorption in quasar spectra from the Baryon Oscillation Spectroscopic Survey (BOSS) and the extended BOSS (eBOSS) in Data Release 14 (DR14) of the Sloan Digital Sky Survey (SDSS)-IV. In addition to 179 965 spectra with absorption in the Lyman-α (Lyα) region, we use Lyα absorption in the Lyman-β region of 56 154 spectra for the first time. We measure the Hubble distance, DH, and the comoving angular diameter distance, DM, relative to the sound horizon at the drag epoch rd at an effective redshift z = 2.34. Using a physical model of the correlation function outside the BAO peak, we find DH(2.34)/rd = 8.86 ± 0.29 and DM(2.34)/rd = 37.41 ± 1.86, within 1σ from the flat-ΛCDM model consistent with CMB anisotropy measurements. With the addition of polynomial “broadband” terms, the results remain within one standard deviation of the CMB-inspired model. Combined with the quasar-Lyα cross-correlation measurement presented in a companion paper, the BAO measurements at z = 2.35 are within 1.7σ of the predictions of this model.
Key words: cosmology: observations / cosmological parameters / dark energy
© V. de Sainte Agathe et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Since the first observations of the imprint of primordial baryonic acoustic oscillations (BAOs) as a peak in the galaxy correlation function (Eisenstein et al. 2005) or as a periodic modulation in the corresponding power spectrum (Cole et al. 2005), the BAO signal has led to significant constraints on cosmological parameters. The BAO peak in the radial direction at a redshift z yields DH(z)/rd = c/(rdH(z)), where H(z) is the Hubble parameter and rd is the sound horizon at the drag epoch (Eisenstein & Hu 1998). The transverse measurement constrains the quantity DM(z)/rd = (1 + z)DA(z)/rd, where DA(z) is the angular diameter distance. Because of its sensitivity to both the distance and the expansion rate, the ensemble of BAO measurements yields tight constraints on Λ cold dark matter (ΛCDM) parameters (Aubourg et al. 2015) even without the use of cosmic microwave background (CMB) data.
Most BAO measurements have employed discrete objects like galaxies (Percival et al. 2010; Reid et al. 2010; Beutler et al. 2011; Blake et al. 2011; Anderson et al. 2012, 2014a,b; Ross et al. 2015; Alam et al. 2017; Bautista et al. 2018) or quasars (Ata et al. 2018; Gil-Marín et al. 2018; Hou et al. 2018; Zarrouk et al. 2018). An alternative tracer of the density is the intergalactic medium (IGM), itself traced by Lyα absorption in quasar spectra. Such measurements at z ≈ 2.4 were suggested by McDonald (2003) and McDonald & Eisenstein (2007). The first detections of a BAO peak in the Lyα auto-correlation function (Busca et al. 2013; Slosar et al. 2013) used data from the Baryon Oscillation Spectroscopic Survey (BOSS) in the Sloan Digital Sky Survey (SDSS) data-release 9 (DR9), at an effective redshift of z = 2.3. Delubac et al. (2015), using BOSS in SDSS-DR11, confirmed the detection of a BAO acoustic peak in the Lyα auto-correlation function at the 5σ level. Most recently, Bautista et al. (2017; B17 hereafter) used Lyα forests from BOSS DR12 data and provided a measurement of DH/rd at 3.4% precision level (or of the optimal combination 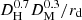 at the 2.5% level). The results were within 1σ of the prediction of the flat ΛCDM model favored by CMB anisotropies (Planck Collaboration XIII 2016). However, when combined with the BAO imprint on the cross-correlation of the Lyα forest with BOSS DR12 quasars (du Mas des Bourboux et al. 2017), the values of DH/rd and DM/rd at z ∼ 2.3 differ by 2.3σ from this model. This mild tension was already present in the combined constraints of the cross-correlation measurement of Font-Ribera et al. (2014) and the auto-correlation of Delubac et al. (2015).
at the 2.5% level). The results were within 1σ of the prediction of the flat ΛCDM model favored by CMB anisotropies (Planck Collaboration XIII 2016). However, when combined with the BAO imprint on the cross-correlation of the Lyα forest with BOSS DR12 quasars (du Mas des Bourboux et al. 2017), the values of DH/rd and DM/rd at z ∼ 2.3 differ by 2.3σ from this model. This mild tension was already present in the combined constraints of the cross-correlation measurement of Font-Ribera et al. (2014) and the auto-correlation of Delubac et al. (2015).
In the present paper, we use quasar spectra from the BOSS survey and from its extended version eBOSS in the SDSS DR14 to study BAO in the Lyα auto-correlation function. The quasar-Lyα cross-correlation is studied in a companion paper (Blomqvist et al. 2019). As in previous measurements, we use Lyα absorption in the “Lyα region” of quasar spectra, that is, quasar rest-frame wavelengths in the range 104 < λRF < 120 nm. We refer to the auto-correlation function using only this region as the Lyα(Lyα) × Lyα(Lyα) correlation1. To increase the statistical power, we also include Lyα absorption in the Lyβ regions of quasars, 97.4 < λRF < 102 nm, correlated with the Lyα absorption in Lyα regions, and refer to this as the Lyα(Lyα) × Lyα(Lyβ) correlation function. The Lyβ region was previously used by Iršič et al. (2013) to investigate the flux transmission power spectrum within individual spectra.
Besides the use of the Lyβ region, the analysis presented here differs in several ways from that of Bautista et al. (2017) based on DR12 data. For each quasar, we now use all observations instead of just the best one and we analyze ∼15% more Lyα regions. We have refined the modeling of the weights (Sect. 3.2), thereby taking into account the effect of unmasked high-column-density (HCD) systems, and the modeling of nonlinearities in the power spectrum (Sect. 4.1). We have not developed new mock spectra beyond those used in the DR12 analysis though this is being done for the final eBOSS analysis.
The layout of the paper is the following. In Sect. 2, we present the Lyα and Lyβ spectral region samples used in the present study. We compute correlation function of Lyα absorption for the DR14 data in Sect. 3 and present our physical model for this function in Sect. 4. The results of fitting the data are presented and discussed in Sect. 5. We draw cosmological conclusions in Sect. 6 and summarize our results in Sect. 7.
The computations of the correlation functions presented in this paper have been performed using a dedicated software package: Package for Igm Cosmological-Correlations Analyses (picca), developed by our team2.
2. Data sample and reduction
The extended Baryon Oscillation Spectroscopic Survey (eBOSS; Dawson et al. 2016) is the extension of the BOSS experiment (Dawson et al. 2013) which aims to measure cosmology with BAO using optical spectra from quasars, emission line galaxies, and luminous red galaxies. It is one of the four projects of the fourth stage of the Sloan Digital Sky Survey (SDSS-IV; Blanton et al. 2017).
The optical spectra are collected from 1000 fibers, attached to the focal plane of a 2.5 m telescope in Apache Point Observatory (Gunn et al. 2006), by two spectrographs in the wavelength range [360, 1000] nm (Smee et al. 2013). The spectral resolution of the spectrographs is ≈2000.
In this paper, we use the forests of the high-redshift quasar sample from the SDSS Data Release 14 (DR14; Abolfathi et al. 2018). This sample contains the first two years of eBOSS data and the five years of BOSS observations reprocessed using the eBOSS pipeline. It also includes data from the ancillary programs Time-Domain Spectroscopic Survey (TDSS) and SPectroscopic IDentification of ERosita Sources (SPIDERS). The quasar target selection is presented in Myers et al. (2015). We note that eBOSS also targets quasars at low redshifts (where the Lyα region is not observable) to be used in other programs (Ata et al. 2018; Wang et al. 2018; Blomqvist et al. 2018; Zhao et al. 2019; du Mas des Bourboux et al. 2019).
The automated data reduction is organized in two steps (Dawson et al. 2016). The pipeline initially extracts the two-dimensional raw data into a one-dimensional flux-calibrated spectrum. During this procedure, the spectra are wavelength and flux calibrated and the individual exposures of one object are coadded into a rebinned spectrum with Δ log(λ) = 10−4. The spectra are then classified as STAR or GALAXY or QSO, and their redshift is estimated. Objects that cannot be automatically classified are visually inspected (Pâris et al. 2018) and a quasar catalog is produced, which contains 526 356 quasar spectra with redshift 0 < z < 7. Among these objects, 144 046 were not in DR12. The coverage footprint of DR14 quasars is presented in Fig. 1.
 |
Fig. 1. Sky distribution of the 216 163 quasars with redshift in the [2.0, 3.5] range in the DR14 footprint of the BOSS and eBOSS surveys. The high-density regions are the eBOSS and SEQUELS observations (for the highest declinations in the two Galactic caps) and SDSS-stripe 82 (on the celestial equator in the south Galactic cap). |
In this study, we examine both Lyα and Lyβ regions (see Fig. 2). The Lyα region in the quasar spectrum lies between the Lyα and the Lyβ emission peaks. We limit its coverage to the rest-frame wavelength range [104, 120] nm in order to exclude the emission peaks, whose shape depends on the environment of the quasar. This approach minimizes the variance of the flux-transmission field defined in Sect. 3.1. Similarly, we define the Lyβ region as the rest-frame wavelength range [97.4, 102] nm (Table 1, Fig. 2).
Definitions of the Lyα and Lyβ regions in terms of restframe wavelength range.
In the DR14 quasar catalog, selecting quasar redshifts in the range [2.0, 3.5] yields 216 162 spectra containing, at least partially, the Lyα region, and selecting quasar redshifts in the range zq ∈ [2.53, 3.5] yields 86 245 spectra containing the Lyβ region. We choose zq = 3.5 as an upper limit, as beyond this redshift the quasar density is insufficient to measure correlations and the rate of redshift misidentification is large (Busca & Balland 2018). The requirement that the observed wavelength must be greater than 360 nm is due to the low CCD response and atmospheric transmission in the UV region.
In order to mask damped Lyα systems (DLAs), we use the updated DR14 DLA catalog of Noterdaeme et al. (2009, 2012), which contains 34 541 DLAs in 27 212 forests. The absorption of the identified DLAs is modeled with a Voigt profile and the regions with more than 20% of absorbed flux are masked. For the Lyβ regions, we apply this procedure both for Lyα and Lyβ strong absorbers. We also mask the sky emission and absorption lines listed on the SDSS website3. The broad absorption line (BAL) quasars are automatically identified (Pâris et al. 2018) and excluded from the data, leaving a sample of 201 286 objects for the Lyα regions and 80 443 for the Lyβ regions.
For the determination of the correlation function, we divide spectra into “analysis pixels” that are the inverse-variance-weighted flux average over three adjacent pipeline pixels. Throughout the rest of this paper, “pixels” refers to analysis pixels unless otherwise stated. Spectral regions with < 50 such pixels or regions which have failed the continuum-fitting procedure (Sect. 3.1) are discarded. These selection criteria produce 179 965 Lyα regions (compared to 157 783 in B17) and 56 154 Lyβ regions (see Table 1).
The analysis procedure described in the following section assigns redshifts to the observed pixel wavelengths by assuming that flux decrements in both the Lyα and Lyβ regions are due to Lyα absorption. The effect of non-Lyα absorption is taken into account in the correlation-function model presented in Sect. 4. The weighted distribution of the redshifts of pairs of pixels used to measure Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlations are presented in Fig. 3. The mean redshift of the combined set of pixel pairs is 2.34.
 |
Fig. 3. Weighted distribution of the redshift of pairs used to measure the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions. The mean redshift of the combined sample is ⟨zpairs⟩=2.34. |
3. Computing the Lyα correlation function from the data
This section describes the measurement of the flux-transmission field and then its correlation function and associated covariance matrix.
3.1. Flux-transmission field δq(λ)
The computation of the correlation function requires an estimation of the transmission field along the line of sight (LOS) towards surveyed quasars. This field arises due to the presence along the LOS of intergalactic gas. More precisely, for the correlation calculation, we only need to know the flux fluctuations around the average transmitted flux spectrum in the forests of quasars q at wavelength λ. We thus define the field δq(λ), for each quasar q under investigation, as:
where fq(λ) denotes the observed flux of quasar q at observed wavelength λ, Cq(λ) is the continuum flux, and 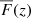 is the mean transmission at the absorber redshift z.
is the mean transmission at the absorber redshift z.
We estimate the quantity 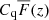 from the average of the transmitted flux of all forest spectra in the sample:
from the average of the transmitted flux of all forest spectra in the sample:
where λRF is the rest-frame wavelength and wq is a weight (see Sect. 3.2). For each quasar, 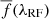 is then multiplied by a linear polynomial function of Λ ≡ log(λ) to account for the diversity of quasar luminosity and spectral shape:
is then multiplied by a linear polynomial function of Λ ≡ log(λ) to account for the diversity of quasar luminosity and spectral shape:
There are thus two adjustable parameters per quasar, aq and bq.
Those forests with identified DLAs are given special treatment. All pixels where the absorption due to the DLA is > 20% are not used. The absorption in the wings is corrected using a Voigt profile following the procedure of Noterdaeme et al. (2012).
The fitting procedure to determine (aq, bq) forces the mean and spectral slope of δq(λ) for each quasar to zero, thus introducing spurious correlations in the measured field. To make it easier to deal with this distortion in the analysis, we follow B17 by transforming the measured δq(λ) to 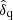 :
:
where
where 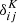 denotes the Kronecker symbol. The advantage of this transformation is that it makes the distortion of the true field introduced by the continuum fit procedure explicit, and as a consequence simplifies the link between the true correlation function and the measured, distorted one (see Sect. 4.3).
denotes the Kronecker symbol. The advantage of this transformation is that it makes the distortion of the true field introduced by the continuum fit procedure explicit, and as a consequence simplifies the link between the true correlation function and the measured, distorted one (see Sect. 4.3).
The statistics of 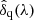 within individual forests are described (in part) by the so-called one-dimensional correlation function,
within individual forests are described (in part) by the so-called one-dimensional correlation function, 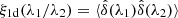 . Figure 4 presents this function for the Lyα and Lyβ forests. The peaks are due to absorption by different transitions at the same physical position. Table 3 lists the important observed transition pairs (see also Pieri et al. 2014).
. Figure 4 presents this function for the Lyα and Lyβ forests. The peaks are due to absorption by different transitions at the same physical position. Table 3 lists the important observed transition pairs (see also Pieri et al. 2014).
 |
Fig. 4. One-dimensional correlation functions, ξ1d, in the Lyα (red curve) and Lyβ (blue curve) regions as a function of the ratio of transition wavelengths. Peaks are due to absorption by the two labeled elements at zero physical separation (Table 3). |
3.2. Pixel weights
The pixel weights are proportional to the inverse of the variance of δq(λ). Following Blomqvist et al. (2018), the variance is modeled as the sum of three terms:
The noise pixel variance is 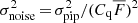 where
where 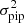 is the pipeline estimate of the pixel variance. The intrinsic, redshift-dependent contribution of the density fluctuations underlying Lyα regions is
is the pipeline estimate of the pixel variance. The intrinsic, redshift-dependent contribution of the density fluctuations underlying Lyα regions is 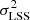 . The third term,
. The third term, 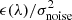 , takes into account differences between the fitted quasar spectrum and the individual spectrum of quasar q (these differences appear at high signal-to-noise ratios). The functions η(λ) and ϵ(λ) correct for imperfections of the pipeline estimates and differences between the average and individual spectra, respectively.
, takes into account differences between the fitted quasar spectrum and the individual spectrum of quasar q (these differences appear at high signal-to-noise ratios). The functions η(λ) and ϵ(λ) correct for imperfections of the pipeline estimates and differences between the average and individual spectra, respectively.
Following Busca et al. (2013), the weights are corrected to take into account the expected redshift dependence of the correlation function amplitude:
where the Lyα bias redshift-evolution parameter, γα = 2.9 (McDonald et al. 2006) and λα is the Lyα restframe wavelength.
In practice, one starts with an initial estimate of the weights, allowing a first estimate of the mean spectrum 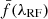 (Eq. (2)) and the quasar parameters aq and bq (Eq. (3)). The functions η(λ), ϵ(λ), and σLSS(λ) are then fit and the mean spectrum is then recalculated with the new weights. This process is repeated until stable values are obtained after about five iterations.
(Eq. (2)) and the quasar parameters aq and bq (Eq. (3)). The functions η(λ), ϵ(λ), and σLSS(λ) are then fit and the mean spectrum is then recalculated with the new weights. This process is repeated until stable values are obtained after about five iterations.
3.3. Correlation function
To compute the correlation function, we correlate absorption at an observed wavelength λi in the LOS of a given quasar q, with absorption at an observed wavelength λj in the LOS of another quasar q′. Assuming the absorption is due to the Lyα transition, one can compute, from the values of λi and λj, the redshifts zi and zj of the matter absorbing these lines. Each pair of absorbers (z, q) entering the computation defines a “pixel” in real space and we use rij to refer to the physical separation between two such pixels i and j (see Fig. 5). This distance is calculated assuming the Pl2015 cosmology (Table 2). The distance rij can be projected on the radial and the transverse directions, leading to two components r∥, ij and r⊥, ij. These components can be expressed in terms of the comoving distances D(zi) and D(zj) from us to absorbers i and j and the subtended angle between the two LOSs, θij, as:
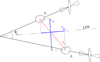 |
Fig. 5. Definition of the coordinates of pixels used in the computation of the correlation function. Absorbers i and j have angular separation θij and distance separation rij. The radial separation r∥, ij is the projection of rij on the median LOS, and the transverse separation r⊥, ij is the LOS perpendicular component of rij, assuming the flat Pl2015 model (Table 2). |
Parameters of the “Pl2015 model”, i.e. the flat ΛCDM model of Planck Collaboration XIII (2016) that we use here to transform redshifts and angular separations into radial and transverse separations.
We then define bins of (r∥, ij, r⊥, ij) on a 2D grid. In practice, the grid uses 2500 bins of dimensions 4 h−1 Mpc × 4 h−1 Mpc over 0 < r⊥ < 200 h−1 Mpc and 0 < r∥ < 200 h−1 Mpc. For a given bin in this grid, A, we consider each pair of pixels (i,j) whose r∥ and r⊥ coordinates fall on this bin. The measured correlation function in bin A reads:
with wk ≡ wqk(λk) and 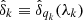 .
.
We discard from the computation all pixel pairs belonging to the same LOS, since two pixels belonging to the same quasar spectrum are affected in a correlated way by the fitting procedure described in Sect. 3.1. Likewise, pixels belonging to the same half plate at the same wavelength are excluded to avoid unphysical correlations induced by the extraction pipeline.
3.4. Covariance matrix
The covariance between two bins A and B is defined as:
where ⟨…⟩ denotes an ensemble average. Following Delubac et al. (2015) and B17, we estimate Eq. (10) by dividing the eBOSS footprint in Nh = 876 sky pixels using the HEALPix tessellation scheme (see Górski et al. 2005) and by equating the ensemble averages of Eq. (10) with the weighted mean over these sky pixels:
and
with 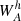 being the sum of the weights of pairs in sky pixels h contributing to bin A. Similarly,
being the sum of the weights of pairs in sky pixels h contributing to bin A. Similarly, 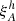 is the correlation function of pairs in sky pixels h that contribute to bin A.
is the correlation function of pairs in sky pixels h that contribute to bin A.
In practice, for the computation of the correlation function, a pair (i, j) is attributed to the sky pixel of the first quasar of the pair, and the pair (j, i) is never considered, insuring that a pair is not counted twice in the calculation.
In this approximation, we assume that each sky pixel provides an independent realization of the δ field. This statement is not exactly true as correlations do exist between pairs in different sky pixels, but these correlations are small (e.g., Delubac et al. 2015).
We subsequently compute the covariance matrix defined in Eq. (10) using the following expression:
where 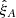 is given by (9). Due to the finite number of sky pixels, the estimate (13) is noisy and must be smoothed before it can be used in fits. We perform the smoothing by approximating the correlation, Corr
is given by (9). Due to the finite number of sky pixels, the estimate (13) is noisy and must be smoothed before it can be used in fits. We perform the smoothing by approximating the correlation, Corr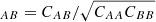 , as a function of
, as a function of 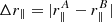 and
and 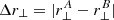 only, ignoring the small dependence on r∥ and r⊥.
only, ignoring the small dependence on r∥ and r⊥.
As a check of the subsampling method, the covariance can also be estimated by neglecting inter-forest correlations, in which case the four-point function vanishes unless the four pixels are drawn from just two spectra:
where ξ1d is the intra-forest correlation function shown in Fig. 4. The sum can then be estimated from a random sample of forest pairs. Because neighboring forests are nearly parallel, the sum necessarily produces CAB = 0 unless 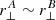 .
.
Because the Lyα and Lyβ forests have different ξ1d, we expect differences between the covariances for Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlations. These differences are illustrated in Fig. 6, which shows, for the two lowest values of Δr⊥, the correlation CorrAB. For Δr⊥ = 0, there is good agreement between the subsampling (13) and independent-forest (14) calculations.
 |
Fig. 6. Averaged correlations, CorrAB = CAB/ |
Figure 7 displays the CorrAB between the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions. The CorrAB are < 1%, and will be ignored in the fits of the correlation functions.
 |
Fig. 7. Averaged correlations, CorrAB = CAB/ |
4. Modeling the correlation function
This section details the model of the Lyα auto-correlation function that is fitted against the estimator 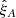 of Eq. (9). Table 4 lists the different parameters of the model. The model includes two components: one is the Lyα-only correlation function computed from Lyα absorption only; the other component incorporates the contribution to the correlation function of absorption by metals, for which the nominal separation for the pixel is not the true separation (see Sect. 4.2). We thus write
of Eq. (9). Table 4 lists the different parameters of the model. The model includes two components: one is the Lyα-only correlation function computed from Lyα absorption only; the other component incorporates the contribution to the correlation function of absorption by metals, for which the nominal separation for the pixel is not the true separation (see Sect. 4.2). We thus write
The following sections describe these two components. Section 4.3 explains how the model is “distorted” to fit the data.
4.1. Baseline model for 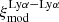
We start from the CAMB linear power spectrum (Lewis et al. 2000) which is decomposed into a smooth component and a peak component, following the side-band technique described by Kirkby et al. (2013). This allows one to constrain the position of the BAO peak independently of the correlation function at scales much smaller or much larger than the BAO distance scale. We thus model the matter power spectrum as the sum of two terms corresponding to the smooth and the peak terms in the correlation function. Moreover, in order to incorporate the effects of the nonlinear growth of matter that lead to broadening of the BAO peak, the peak term is corrected by a Gaussian factor (Eisenstein et al. 2007). The “quasi-linear” power spectrum hence reads
where Psmooth(k, z) and Ppeak(k, z) are the power spectra of the smooth and peak components, and Σ∥ and Σ⊥ represent the rms displacements in the parallel and transverse directions, respectively. We adopt the values of Kirkby et al. (2013) for these parameters: Σ∥ = 6.41 h−1 Mpc and Σ⊥ = 3.26 h−1 Mpc.
The power spectrum is obtained from PQL as
where dLyα is the Kaiser factor (Kaiser 1987) for the Lyα absorption and DNL(k) takes into account nonlinear effects. The function G(k) models the effect of binning of the correlation function on the separation grid.
The Kaiser factor can be written as
where 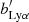 is the effective bias of Lyα absorbers with respect to the underlying matter density field,
is the effective bias of Lyα absorbers with respect to the underlying matter density field, 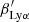 is the effective redshift space distortion (RSD) parameter, and μk = k∥/k. The two effective parameters (
is the effective redshift space distortion (RSD) parameter, and μk = k∥/k. The two effective parameters (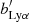 and
and 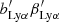 ) combine Lyα absorption in the IGM and in unmasked HCD systems, i.e., HI absorbers with column densities NHI > 1017.2 cm−2:
) combine Lyα absorption in the IGM and in unmasked HCD systems, i.e., HI absorbers with column densities NHI > 1017.2 cm−2:
where (bLyα, βLyα) and (bHCD, βHCD) are the bias parameters associated with the IGM and HCD systems and FHCD is a function defined below.
Following McDonald et al. (2006), we assume that the product of bLyα and the growth factor of structures varies with redshift as (1 + z)γα − 1, with γα = 2.9, while we make use of the approximation that βLyα does not depend on redshift.
HCD absorbers are expected to trace the underlying density field and their effect on the flux-transmission field depends on whether or not they are identified and given the special treatment described in Sect. 2. If they are correctly identified with the total absorption region masked and the wings correctly modeled, they can be expected to have no significant effect on the field. Conversely, if they are not identified, the measured correlation function will be modified because their absorption is spread along the radial direction. This broadening effect introduces a k∥ dependence of the effective bias (Font-Ribera & Miralda-Escudé 2012). Following the study of Rogers et al. (2018), we adopt a simple exponential form, FHCD = exp(−LHCDk∥), where LHCD is a typical length scale for these systems. DLA identification is possible if the width (wavelength interval for absorption greater than 20%) of the system(s) is above ∼2.0 nm, corresponding to ∼14 h−1 Mpc in our sample. Based on results from Rogers et al. (2018), we impose LHCD ∼ 10 h−1 Mpc while fitting for the bias parameters bHCD and βHCD. Fixing LHCD is necessary because otherwise the model becomes too unconstrained. We have verified that setting LHCD in the range 7 < LHCD < 13 h−1 Mpc does not significantly change the inferred BAO peak position.
We focus on the minimal model able to reproduce the data, designated the “baseline model”. This baseline model does not include the correction of the UV background fluctuations (Pontzen et al. 2014; Gontcho A Gontcho et al. 2014) used in B17. In Sect. 5 we discuss the improvement of the fit when this UV correction is added.
The function DNL(k) accounts for nonlinear effects such as thermal broadening, peculiar velocities, and nonlinear structure growth. A fitting formula for DNL is given by Eq. (21) of McDonald (2003) and has been extensively used in previous studies. More recently, Arinyo-i-Prats et al. (2015) proposed a new fitting formula involving six free parameters given by their Eq. (3.6). Besides reducing the number of free parameters with respect to McDonald (2003), it has the correct behavior at small wavenumber k and an explicit dependence on PQL(k), whereas this dependence is only implicit in the McDonald (2003) formula. In practice, the two approaches yield similar results but for the above reasons we adopt the formula of Arinyo-i-Prats et al. (2015) in the present work and linearly interpolate the parameter values from their Table 7 at the effective redshift z = 2.34.
To account for the effect of the binning of the correlation function on the separation grid, we assume the distribution to be homogeneous on each bin4 and compute the function G(k) as the product of the Fourier transforms of the rectangle functions that model a uniform square bin:
where R∥ and R⊥ are the radial and transverse widths of the bins, respectively.
The two terms in PQL(k, z) (Eq. (16)) are Fourier transformed to the smooth and peak components of the correlation function:
The amplitude of the peak, Apeak, is fixed to unity in the standard fit. In the peak component we have introduced the parameters (α∥, α⊥) which allow us to fit for the peak position independently of the smooth component:
where 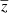 is the effective redshift of the measurement and the suffix “fid” denotes the Pl2015 cosmology from Table 2.
is the effective redshift of the measurement and the suffix “fid” denotes the Pl2015 cosmology from Table 2.
4.2. Contamination by metals
The second term in the model correlation function (Eq. (15)) accounts for absorption by metals along the quasar LOS. Such absorption is correlated with Lyα absorption (Pieri et al. 2014) and can be used as a tracer of the density field (Blomqvist et al. 2018; du Mas des Bourboux et al. 2019). Here, it is a complicating factor in the analysis because the redshifts of pixels are calculated assuming Lyα absorption.
The important metals can be seen in the 1D correlation function, ξ1d(λ1/λ2), shown in Fig. 4. Column 2 of Table 3 lists the wavelength ratios for the main metal/metal and metal/Lyα absorption correlations, relevant for the Lyα auto-correlation function computation. The corresponding apparent radial separation at vanishing physical separation is
Lyα/metal and metal/metal pairs contributing to the flux correlation function.
where 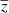 is the mean redshift of the pair. Values are given in Table 3 for
is the mean redshift of the pair. Values are given in Table 3 for 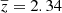 .
.
We model the power spectrum of each pair of absorbers, (m, n), with the same form as that for Lyα–Lyα absorption (17) except that HCD effects are neglected:
Since the bm and βm are mostly determined near 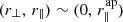 , they cannot be determined separately. We therefore fix βCIV(eff) = 0.27 (Blomqvist et al. 2018). For the other metal species we keep the value β = 0.50 used in Bautista et al. (2017) which comes from DLA measurements (Font-Ribera & Miralda-Escudé 2012).
, they cannot be determined separately. We therefore fix βCIV(eff) = 0.27 (Blomqvist et al. 2018). For the other metal species we keep the value β = 0.50 used in Bautista et al. (2017) which comes from DLA measurements (Font-Ribera & Miralda-Escudé 2012).
The Fourier transform of Pmn(k, z) is then the model correlation function of the pair (m, n): 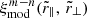 , where
, where 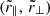 are the separations calculated using the correct restframe wavelengths, (λm, λn).
are the separations calculated using the correct restframe wavelengths, (λm, λn).
Since we assign a redshift, zα, assuming Lyα absorption, the rest-frame wavelength we ascribe to a metal transition m observed at wavelength λi is not equal to the true rest-frame wavelength λi/(1 + zm), where zm is the true redshift of the metal absorber. This misidentification results in a shift of the model contaminant correlation function. For each pair (m, n) of contaminants, we compute the shifted model correlation function with respect to the unshifted model metal correlation function 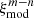 by introducing a metal matrix MAB (Blomqvist et al. 2018), such that:
by introducing a metal matrix MAB (Blomqvist et al. 2018), such that:
where
and (m, n)∈A refers to pixel separation computed assuming zα, and (m, n)∈B to pixel separation computed using the redshifts of the m and n absorbers, zm and zn. We take into account the redshift dependence of the weights (Eq. (7)) in the computation of wm and wn.
The total metal contaminant correlation function, 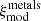 , is the sum of all the
, is the sum of all the 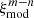 contributions, where (m, n) runs over all the involved transition pairs for the Lyα auto-correlation function; see Table 3:
contributions, where (m, n) runs over all the involved transition pairs for the Lyα auto-correlation function; see Table 3:
4.3. Distorted model
The model correlation function, ξmod of Eq. (15) cannot be fit directly to the estimated correlation function (9) because the measured 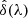 are only related to the true δ(λ) through the transformation (4). Following B17, we can account for this effect in the fit by using a distorted model:
are only related to the true δ(λ) through the transformation (4). Following B17, we can account for this effect in the fit by using a distorted model:
where DAB is the distortion matrix which, following Eq. (5), is given by
The accuracy of this method of accounting for the distortion of the correlation function was tested with mock data sets by Bautista et al. (2017).
In practice, to avoid prohibitive computational time, the distortion matrix is computed using only a random 5% portion of the total number of pairs.
5. Fitting the BAO peak position
Table 5 presents the best-fit parameters for the Lyα(Lyα) × Lyα(Lyα) correlation function alone and those including the Lyβ region, that is, the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation function. Figure 8 displays data for the latter in four ranges of μ along with the best fits. The BAO peak is apparent for μ > 0.8 and is suggested for 0.5 < μ < 0.8.
 |
Fig. 8. Weighted combination between measured Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions along with the model best fits in four ranges of μ = r∥/r. The curves show the standard fit and the two fits with broadband terms defined by Eq. (32) with (imin, imax, jmax)=(0, 2, 6) with and without additional priors, as described in the text. |
The BAO parameters for the fit using both Lyα and Lyβ regions are
Using the D/rd values for the Pl2015 cosmology in Table 2, these values yield
These results can be compared with those of B17, who found α∥ = 1.053 ± 0.036 and α⊥ = 0.965 ± 0.055 at z = 2.33 using only the Lyα region. These values are very near the present results using only the Lyα region: α∥ = 1.047 ± 0.035 and α⊥ = 0.960 ± 0.041. Our use of the Lyβ region produces consistent results, given the increase in the data set; the main improvement is that on the precision on DM/rd by ∼25%.
Constraints on the BAO parameters (α∥, α⊥) are presented in Fig. 9. Following the method introduced and described in detail in du Mas des Bourboux et al. (2017), we estimate the relation between 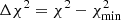 and confidence levels (CLs) for the BAO parameters using a large number of simulated correlation functions generated from the best-fit model and the covariance matrix measured with the data. The results of the study, summarized in Table D.1, indicate that the (68.27, 95.45%) confidence levels for (α∥, α⊥) correspond to Δχ2 = (2.74, 7.41); instead of the nominal values Δχ2 = (2.3, 6.18). These levels are shown as the red contours in Fig. 9 for the Lyα(Lyα) × Lyα(Lyα + Lyβ) fit. The best fit is within one standard deviation of the Pl2015 model.
and confidence levels (CLs) for the BAO parameters using a large number of simulated correlation functions generated from the best-fit model and the covariance matrix measured with the data. The results of the study, summarized in Table D.1, indicate that the (68.27, 95.45%) confidence levels for (α∥, α⊥) correspond to Δχ2 = (2.74, 7.41); instead of the nominal values Δχ2 = (2.3, 6.18). These levels are shown as the red contours in Fig. 9 for the Lyα(Lyα) × Lyα(Lyα + Lyβ) fit. The best fit is within one standard deviation of the Pl2015 model.
 |
Fig. 9. Left panel: 68% and 95% confidence level contours in the (α∥, α⊥) plane from the Lyα(Lyα) × Lyα(Lyα + Lyβ) auto-correlation function for the standard fit and for fits with polynomial broadband terms with and without additional priors, as described in the text. Right panel: contours for Lyα(Lyα) × Lyα(Lyα + Lyβ) auto-correlation standard fit and those from the combined fit of the auto-correlation and the quasar-Lyα cross-correlation of Blomqvist et al. (2019). In both panels the value for the Pl2015 model (Planck Collaboration XIII 2016) is shown as a black point. |
In addition to the baseline fits, we performed a variety of nonstandard fits to verify that our BAO results are robust and independent of the model. The results of this exercise are given in Table 6. The first group of fits starts with the simple Kaiser redshift-space model and then includes progressively metals, HCD absorption, and UV background fluctuations. Including HCD absorption is necessary to obtain a good χ2 but adding UV fluctuations such as those characterized in Gontcho A Gontcho et al. (2014) does not improve the fit, justifying our choice of ignoring the UV issue in the baseline fit. In the standard fit, the physical parameters (LHCD, Σ⊥, Σ∥, βm) are fixed (see Table 4) in order to avoid degeneracies with other parameters and nonphysical values. We verified that letting them free has no impact on the α∥ and α⊥ parameters.
Parameters of the model of the correlation function.
Parameters of the model of the correlation function and the best-fit values of the Lyα(Lyα) × Lyα(Lyα) data (third column) and those of the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) data (fourth column).
An important test of systematic effects in the position of the BAO peak is performed by adding polynomial “broadband” terms to the correlation function (before distortion). We follow the procedure and choice of broadband forms used by B17 and adopt the form
where the Lj are Legendre polynomials.
We want to ensure that the power-law terms model variations of the slowly varying part of the correlation function under the BAO peak. We therefore perform these fits only over the restricted range 40 < r < 180 h−1 Mpc, avoiding the introduction of undue influence of the 10 < r < 40 h−1 Mpc range on the amplitudes of the power laws. Following B17, we fit with (imin, imax) = (0, 2) corresponding to a parabola in r2ξsmooth underneath the BAO peak. We set jmax = 6, giving four values of j corresponding to approximately independent broadbands in each of the four angular ranges in Fig. 8.
We performed the broadband fits in two ways. The first placed “physical priors” on (bLyα, βLyα, bHCD) in the form of a Gaussian with the same mean and width as those of the fit without broadband terms. Such priors ensured that the broadband terms were relatively small perturbations to the physical model. The second type of fit placed no priors on (bLyα, βLyα, bHCD).
The results of these fits are given in Table 6 and Fig. 9. We see that the addition of such terms does not change α∥ significantly but does shift α⊥ by 0.5σ or 0.7σ for fits with and without physical priors, respectively. This effect was already seen in B17 but with less significance. Figure 9 shows that in all cases the BAO peak position is within one standard deviation of the prediction of the Pl2015 model.
Best-fit values of (α∥, α⊥) for the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation function fit with various models.
The fits of the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions described above are the primary results of this paper. We also performed fits with two redshift bins, as described in Appendix B. Each of the two redshifts yielded values of (α∥, α⊥) that are within 1.2σ of the Pl2015 model (Fig. B.2). We also fit the Lyα(Lyα) × Lyβ(Lyβ) correlation as described in Appendix C. Adding the Lyβ absorption data does not add a significant signal to the BAO peak, but it does allow us to measure the Lyβ bias parameters.
Finally, we combine the measurement of Lyα auto-correlation function of the present analysis with the Lyα – quasar cross-correlation measurement of Blomqvist et al. (2019) by performing a joint fit of the two correlation functions. We use the baseline models of the two analyses and consider the errors to be independent. The joint fit has 18 free parameters and the effective redshift is z = 2.34. The results are given in the column four of Table 7 and the constraints on (α⊥, α∥) in the right panel of Fig. 9. From this combined fit, we obtain:
Best-fit results of the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation function (second column), of the QSO × Lyα(Lyα + Lyβ) correlation function given by Blomqvist et al. (2019) (third column), and of the two correlation functions (fourth column).
corresponding to
The value of χ2 for (α∥ = 1, α⊥ = 1) is 4.99 greater than the best fit. Using the confidence levels of Table D.1, we conclude that the results of the combined fit are 1.7σ from the predictions of the Pl2015 model (Planck Collaboration XIII 2016).
6. Cosmological constraints
Baryon acoustic oscillation data over the redshift range 0.1 < z < 2.4 is in overall good agreement with the predictions of the flat ΛCDM models consistent with CMB anisotropies, as illustrated in Fig. 10. A striking illustration of the expansion history can be made by transforming DH(z)/rd to H(z)rd. The measurement presented here gives
 |
Fig. 10. Baryon acoustic oscillation measurement of DH/rd and DM/rd using BOSS galaxies (Alam et al. 2017), Lyα absorption in BOSS-eBOSS quasars (this work), and correlation between BOSS-eBOSS quasars and Lyα absorption (Blomqvist et al. 2019). Other measurements give DV/rd, with |
Figure 11 plots this value along with other measurements. The data are consistent with the expected behavior of deceleration at high redshift followed by acceleration at low redshift.
 |
Fig. 11. Baryon acoustic oscillation measurement of the comoving expansion rate, H(z)/(1 + z), measured with BAO with rd = 147.3 Mpc. The red square is the present measurement at z = 2.34. The measurement by Blomqvist et al. (2019) is the blue dot. The other points are computed using galaxy measurements (Beutler et al. 2011; Ross et al. 2015; Alam et al. 2017). The points at z = 0.106 (Beutler et al. 2011) and z = 0.15 (Ross et al. 2015) are converted from DV to H(z) using the SNIa measurement of q0 given by Betoule et al. (2014). Solid black line shows the Pl2015 values (Planck Collaboration XIII 2016). |
Independent of CMB data and without assuming flatness, the BAO data by themselves constrain the parameters (Ωm, ΩΛ, H0rd) of the (o)ΛCDM model. Using the combined fit (Eq. (34)), the galaxy data of Beutler et al. (2011), Ross et al. (2015), Alam et al. (2017), and Bautista et al. (2018) and the quasar data of Ata et al. (2018) yield
corresponding to Ωk = 0.032 ± 0.117. The best fit gives (c/H0)/rd = 29.78 ± 0.55, corresponding to hrd = (0.683 ± 0.013)×147.33 Mpc. The Pl2015 model has χ2 = 13.76 for 12° of freedom and is within one standard deviation of the best fit, as illustrated in Fig. 12.
 |
Fig. 12. One and two standard deviation constraints on (Ωm, ΩΛ). The red contours use BAO measurements of DM/rd and DH/rd of this work, those of Blomqvist et al. (2019) and Alam et al. (2017), and the measurements of DV/rd of Beutler et al. (2011), Ross et al. (2015), Ata et al. (2018) and Bautista et al. (2018). The gray contours do not use the Lyα-quasar cross-correlation measurement of Blomqvist et al. (2019). The green contours show the constraints from SN Ia Pantheon sample (Scolnic et al. 2018). The black point indicates the values for the Planck Collaboration XIII (2016) best-fit flat ΛCDM cosmology. |
7. Conclusions
We used Lyα and Lyβ spectral regions from the BOSS and eBOSS DR14 data sample to study BAO. Following B17, we built a model for the Lyα auto-correlation function that we then fit to the data. Our model incorporates the effects of redshift space distortions, the nonlinear growth of matter, the contamination by metals, and the modeling of HCD systems along the LOS to quasars. Including UV fluctuations has only a minor impact on the fit results. We measure the ratios DH/rd and DM/rd at the average redshift of pixel pairs, z = 2.34. We also performed a measurement of these ratios from the Lyα auto-correlation function in two redshift bins, at z = 2.19 and z = 2.49.
The DH/rd ratio is measured with a precision of ∼3.3%, a slight improvement over the precision obtained by B17 for this ratio. The DM/rd ratio is measured with a precision of ∼4.4%, which represents an improvement of about 25% with respect to B17. The cosmological measurements obtained in this analysis are in agreement with the predictions of the flat ΛCDM model (Pl2015) favored by the measurement of CMB anisotropies by Planck.
We also combined the measurements of the present analysis with those obtained from the cross-correlation of Lyα absorption and quasars by Blomqvist et al. (2019). The latter alone favor a value of the DH/rd ratio ∼3% higher than the one favored by the Lyα auto-correlation. As a result, the best-fit value of DH/rd for the combined fit is shifted towards a higher value than the best-fit from the Lyα auto-correlation alone. Combining the measurement of Lyα auto-correlation (this paper) with the quasar–Lyα cross-correlation of Blomqvist et al. (2019), the BAO measurements at z = 2.34 are within 1.7σ of the predictions of the Pl2015 model.
The ensemble of BAO measurements is in good agreement with the Pl2015 model (Planck Collaboration XIII 2016). They provide an independent way of determining cosmological parameters that is based only on low-redshift measurements. As illustrated in Fig. 12, the BAO results are also consistent with the recent Pantheon SNIa results (Scolnic et al. 2018).
The present measurements will be much improved by the greater statistical power of the upcoming DESI (DESI Collaboration 2016) and WEAVE-QSO (Pieri et al. 2016) projects. The challenge will be to improve the physical modeling of the correlation function in order to fully profit from the improved data.
Available at https://github.com/igmhub/picca
Acknowledgments
We thank Pasquier Noterdaeme for providing the DLA catalog for eBOSS DR14 quasar. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is http://www.sdss.org/. MB, MP and IPR were supported by the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French Government program, managed by the French National Research Agency (ANR), and by ANR under contract ANR-14-ACHN-0021 SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.
References
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014a, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2014b, MNRAS, 439, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Arinyo-i-Prats, A., Miralda-Escudé, J., Viel, M., & Cen, R. 2015, J. Cosmol. Astropart. Phys., 12, 017 [NASA ADS] [CrossRef] [Google Scholar]
- Ata, M., Baumgarten, F., Bautista, J., et al. 2018, MNRAS, 473, 4773 [NASA ADS] [CrossRef] [Google Scholar]
- Aubourg, É., Bailey, S., Bautista, J. E., et al. 2015, Phys. Rev. D, 92, 123516 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Busca, N. G., Guy, J., et al. 2017, A&A, 603, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, J. E., Vargas-Magaña, M., Dawson, K. S., et al. 2018, ApJ, 863, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Blomqvist, M., Pieri, M. M., du Mas des Bourboux, H., et al. 2018, J. Cosmol. Astropart. Phys., 5, 029 [Google Scholar]
- Blomqvist, M., du Mas des Bourboux, H., Busca, N. G., et al. 2019, A&A, 629, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busca, N., & Balland, C. 2018, MNRAS, submitted [arXiv:1808.09955] [Google Scholar]
- Busca, N. G., Delubac, T., Rich, J., et al. 2013, A&A, 552, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Delubac, T., Bautista, J. E., Busca, N. G., et al. 2015, A&A, 574, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Dijkstra, M., Lidz, A., & Hui, L. 2004, ApJ, 605, 7 [NASA ADS] [CrossRef] [Google Scholar]
- du Mas des Bourboux, H., Le Goff, J. M., Blomqvist, M., et al. 2017, A&A, 608, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- du Mas des Bourboux, H., Dawson, K. S., Busca, N. G., et al. 2019, ApJ, 878, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Seo, H.-J., & White, M. 2007, ApJ, 664, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., & Miralda-Escudé, J. 2012, J. Cosmol. Astropart. Phys., 7, 028 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., Kirkby, D., Busca, N., et al. 2014, J. Cosmol. Astropart. Phys., 5, 027 [Google Scholar]
- Gil-Marín, H., Guy, J., Zarrouk, P., et al. 2018, MNRAS, 477, 1604 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcho A Gontcho, S., Miralda-Escudé, J., & Busca, N. G. 2014, MNRAS, 442, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, J., Sánchez, A. G., Scoccimarro, R., et al. 2018, MNRAS, 480, 2521 [Google Scholar]
- Iršič, V., & Viel, M. 2014, J. Cosmol. Astropart. Phys., 12, 024 [NASA ADS] [Google Scholar]
- Iršič, V., Slosar, A., Bailey, S., et al. 2013, J. Cosmol. Astropart. Phys., 9, 016 [NASA ADS] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkby, D., Margala, D., Slosar, A., et al. 2013, J. Cosmol. Astropart. Phys., 3, 024 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P. 2003, ApJ, 585, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., & Eisenstein, D. J. 2007, Phys. Rev. D, 76, 063009 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Seljak, U., Burles, S., et al. 2006, ApJS, 163, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, A. D., Palanque-Delabrouille, N., Prakash, A., et al. 2015, ApJS, 221, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Ledoux, C., & Srianand, R. 2009, A&A, 505, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Carithers, W. C., et al. 2012, A&A, 547, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, E., et al. 2018, A&A, 613, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, M. M., Mortonson, M. J., Frank, S., et al. 2014, MNRAS, 441, 1718 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, M. M., Bonoli, S., Chaves-Montero, J., et al. 2016, in SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, J. Richard, L. Cambrésy, et al., 259 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A., Bird, S., Peiris, H., & Verde, L. 2014, ApJ, 792, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, B. A., Percival, W. J., Eisenstein, D. J., et al. 2010, MNRAS, 404, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, K. K., Bird, S., Peiris, H. V., et al. 2018, MNRAS, 476, 3716 [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Slosar, A., Iršič, V., Kirkby, D., et al. 2013, J. Cosmol. Astropart. Phys., 4, 26 [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Wang, D., Zhao, G.-B., Wang, Y., et al. 2018, MNRAS, 477, 1528 [NASA ADS] [Google Scholar]
- Zarrouk, P., Burtin, E., Gil-Marín, H., et al. 2018, MNRAS, 477, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G.-B., Wang, Y., Saito, S., et al. 2019, MNRAS, 482, 3497 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effective redshift of the fitted parameters
In this section we present a method to determine the region in (r⊥, r∥, z) space that is most constraining for the various parameters in the fits of the correlation function. We can expect that the parameters (α⊥, α∥) are mostly determined by (r⊥, r∥) bins near the BAO peak and at a redshift near the mean redshift of the pixel pairs used in the BAO region. Previous studies (B17, Busca et al. 2013; Delubac et al. 2015) defined the effective redshift of the BAO measurement in this way. Here, we make this intuitive conclusion more precise by using a Fisher matrix analysis.
We use the Fisher matrix formalism as follows: given a parameter p varying linearly with redshift, we define the effective redshift z0 at which it is measured by
where p0 is the value given by the fit at z = z0. The covariance matrix Cp between two parameters p0 and p1 is given by
where 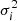 is the variance of the parameter pi, and ρ is the correlation coefficient between p0 and p1. By definition, Cp is the inverse of the Fisher matrix Fp :
is the variance of the parameter pi, and ρ is the correlation coefficient between p0 and p1. By definition, Cp is the inverse of the Fisher matrix Fp :
with mi the model at bin i. In the case of the linear redshift dependency (A.1), the Fisher matrix Fp at redshift z, computed using the set of all the fitted parameter values, {λ0}, is given by
with zi the mean redshift of the pairs in bin i.
We represent the quantities 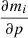 for 4 of the 12 fitted parameters of the Lyα auto-correlation function in Fig. A.1. The covariance matrix Cp(z) then reads
for 4 of the 12 fitted parameters of the Lyα auto-correlation function in Fig. A.1. The covariance matrix Cp(z) then reads
 |
Fig. A.1. Quantity ∂m/∂p in the (r⊥, r∥) plane for the fitted parameters p ∈ [α∥, α⊥, bLyα, bSiIII(1207)], where m is the baseline model of the Lyα auto-correlation function. The graphs show which pixels contribute the most to the constraints on the considered parameter. BAO parameters α∥ and α⊥ are constrained by the bins around the location of the BAO peak, while the Lyα bias is mostly constrained by the bins at approximately zero separation. We also note that the Si III(1207) bias is mostly constrained by the bins r⊥ ∼ 0, r∥ ∼ 21 h−1 Mpc, in agreement with the |
with
Since Mij is symmetric, the determinant of the Fisher matrix, |Fp|, does not depend on redshift and is given by
The variance of p0 at redshift z becomes:
The effective redshift z0 is the value which minimizes the error on p0 :
that is,
In the case of a combined fit, we compute one matrix Md for each correlation function entering the fit:
where 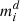 is the model for the correlation function d at bin i. In this case, z0 reads
is the model for the correlation function d at bin i. In this case, z0 reads
Table A.1 presents the effective redshifts at which the α∥ and α⊥ parameters are measured for the different correlation functions computed in this paper. The effective redshift values differ by < 0.5% for α∥ and α⊥. Figure A.1 shows the quantities ∂m/∂p in the (r⊥, r∥) plane for the fitted parameters p ∈ [α∥, α⊥, bLyα, bSiIII(1207)]. m is the baseline model for the Lyα auto-correlation.
Effective redshifts at which the α∥ and α⊥ parameters are measured.
Appendix B: Fits in two redshift bins
The present data set is large enough to constrain the BAO parameters in two independent redshift bins, in a way similar to what will be done in forthcoming cosmological surveys, such as the DESI project (DESI Collaboration 2016). To simplify the analysis, we consider only the Lyα(Lyα) × Lyα(Lyα) correlation function.
A straightforward way of defining a high- and low-redshift sample of pixel pairs would be to simply use pixel pairs of mean redshift less than or greater than an appropriately chosen value, zcut. The drawback of such an approach is that a given pair of forests could belong to both bins, as some pixels in a given forest would be associated with some pixels in the other forest, either in pixel pairs with mean redshift less than zcut, or in pixel pairs with mean redshift greater than zcut. The fact that some pairs of forests belong to both redshift bins introduces unwanted correlations when correcting for the distortions introduced by our continuum fitting procedure. To circumvent this problem, we choose to assign forest pairs to the high- or low-redshift sample by cutting on the mean of the maximum z of the two forests.
We thus evaluate, for all pairs of forests (i, j), the following quantity:
where 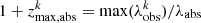 , with max
, with max 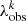 the last pixel of forest k, and λabs the rest-frame wavelength of the considered transition. The condition zij < zcut defines the low-redshift bin, while the opposite condition defines the high-redshift one.
the last pixel of forest k, and λabs the rest-frame wavelength of the considered transition. The condition zij < zcut defines the low-redshift bin, while the opposite condition defines the high-redshift one.
The value of zcut is tuned so that the sum of the weights of all absorber pairs in the high-redshift correlation function equals the one of all pairs in the low-redshift correlation function. This ensures the two bins have a comparable statistical power. This process leads us to select zcut = 2.5. The redshift distribution of absorber pairs obtained in this way are shown on Fig. B.1. The average pair redshift is 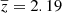 and
and 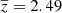 for the low- and high-redshift bin, respectively.
for the low- and high-redshift bin, respectively.
 |
Fig. B.1. Pixel pair redshift distribution of the subsamples used in the present analysis: full Lyα auto-correlation function (gray), low-redshift Lyα auto-correlation function (blue), high-redshift Lyα auto-correlation function (red). The two latter subsamples are used to produce a measurement of H(z) at z = 2.19 and z = 2.49. |
Figure B.3 presents the result of fitting the Lyα(Lyα) × Lyα(Lyα) correlation baseline model to the data in the low- (blue points) and high-redshift (red points) bins in the usual four μ wedges.
Table B.1 shows the associated best-fit parameters. From the table, we note that βLyα is notably different at low and high redshift. When fitting the full sample, we assumed βLyα to be constant, following Kirkby et al. (2013). A redshift-dependent βLyα could therefore be an improvement in future analyses.
Results in two redshift bins from fitting the baseline model to the Lyα(Lyα) × Lyα(Lyα) correlation function.
From the lower right panel of Fig. B.3, we see that the amplitude of the high-redshift correlation function is higher than the amplitude of the low-redshift one. This is expected, as bLyα increases with redshift (Kirkby et al. 2013).
Figure B.2 presents the constraints obtained, in the (α⊥, α∥) parameter space, from fitting the Lyα auto-correlation Lyα(Lyα) × Lyα(Lyα) in the low-(blue contours) and high-redshift (red contours) bins. The values of Δχ2 corresponding to a given confidence level were taken from Table D.1. Both the high- and low-redshift measurements are within 1.2σ of the Pl1015 model.
 |
Fig. B.2. 68% and 95% confidence level contours in the (α∥, α⊥) plane from the Lyα(Lyα) × Lyα(Lyα) computed with the low- and high-redshift bins. The Δχ2 values corresponding to confidence levels are taken from Table D.1. The black dot corresponds to the Pl2015 model. |
 |
Fig. B.3. Lyα(Lyα) × Lyα(Lyα) function in four ranges of μ = r∥/r values, computed in a low-redshift (blue dots) and in a high-redshift (red dots) bin obtained by splitting our sample so that the two bins have equivalent statistical power. The dashed lines correspond to the simple fits to the data of the Lyα(Lyα) × Lyα(Lyα) correlation function, the solid line to the combining fits to the data of the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions. |
Appendix C: The Lyα(Lyα) × Lyβ(Lyβ) cross correlation
As an extension of our main analysis, we compute the Lyα(Lyα) × Lyβ(Lyβ) correlation function, following the procedure previously described. We computed the 1D correlation function in the Lyβ region (Fig. C.1) to identify the contaminating metals (see Table C.1).
 |
Fig. C.1. Same as Fig. 4 but for cross-correlation function of Lyα with Lyβ regions, as a function of the ratio of transition wavelengths. |
Same as Table 3 for the main metal/metal, metal/Lyβ, and Lyα/metal correlations relevant to the computation of the Lyα(Lyα) × Lyβ(Lyβ) correlation function.
The results of this analysis are presented in Table C.2. The Lyβ absorption signal is clearly detected as bLyβ is nonzero at the 2.9σ level. We also see the signal due to O VI(1032) and O VI(1036). We note that the correlation between Lyβ and Si II(1260) occurs near the BAO peak (last line of Table C.1). Due to the small Lyβ absorption cross-section and to the small wavelength extent of the Lyβ region, it is harder to detect the BAO peak than for the Lyα auto-correlation function. Moreover, the Lyβ-Si II correlation further overlaps the BAO signal at small r⊥, hampering its detection in our data.
Results of the combining fit on Lyα(Lyα) × Lyα(Lyα), Lyα(Lyα) × Lyα(Lyβ) and Lyα(Lyα) × Lyβ(Lyβ) correlation functions with the BAO parameters (α∥, α⊥) fixed to 1.
Figure C.2 presents for the first time the 2D Lyα(Lyα) × Lyβ(Lyβ) correlation function. It is shown in the usual four wedges of μ values, as a function of r = 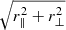 multiplied by the sign of r∥. We note that the model is not symmetric around zero separation.
multiplied by the sign of r∥. We note that the model is not symmetric around zero separation.
 |
Fig. C.2. Measured Lyα(Lyα) × Lyβ(Lyβ) correlation function in four ranges of μ. In order to see the asymmetry of this correlation function, |
The oscillator strength of Lyβ absorption is a fifth of that of Lyα, and consequently there are far fewer Lyβ HCD systems than Lyα HCD systems. On the other hand Lyβ absorption in our analysis occurs at a systematically higher redshift. Overall we find that 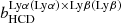 is consistent with zero.
is consistent with zero.
In summary, there are not enough data at present to constrain the BAO peak position with Lyβ absorption only. However, Lyβ absorption could be used to access to physical IGM parameters at redshifts for which the Lyα absorption is saturated (Dijkstra et al. 2004; Iršič & Viel 2014).
Appendix D: Confidence levels
To make a precise estimate of the relation between Δχ2 and confidence level, we closely followed the procedure of du Mas des Bourboux et al. (2017). We generated a large number of simulated correlation functions using the fiducial cosmological model and the best-fit values of nonBAO parameters, randomized using the covariance matrix measured with the data. Each simulated correlation function was then fit for the model parameters and the χ2 for the best-fit parameters compared with the best χ2 with one or more parameters set to the known input values. Confidence levels are the fractions of the generated data sets that have best fits below the Δχ2 limit. The uncertainties are estimated using a bootstrap technique.
The analysis of du Mas des Bourboux et al. (2017) followed this procedure using models that incorporated only Lyα absorption and models that incorporated also HCDs and metals. Since no significant differences were seen in the two methods, we use here only Lyα absorption, simplifying the analysis considerably.
The results are summarized in Table D.1 for various correlation functions. In all cases the Δχ2 values corresponding to a given confidence level are increased above the standard values. For example, for the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation, the one- and two-standard deviation contours for (α∥, α⊥) correspond to Δχ2 = 2.77 and Δχ2 = 7.33, to be compared with the standard values of 2.29 and 6.18.
Values of Δχ2 corresponding to confidence levels (CLs) (68.27, 95.45%).
All Tables
Parameters of the “Pl2015 model”, i.e. the flat ΛCDM model of Planck Collaboration XIII (2016) that we use here to transform redshifts and angular separations into radial and transverse separations.
Parameters of the model of the correlation function and the best-fit values of the Lyα(Lyα) × Lyα(Lyα) data (third column) and those of the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) data (fourth column).
Best-fit values of (α∥, α⊥) for the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation function fit with various models.
Best-fit results of the Lyα(Lyα) × Lyα(Lyα + Lyβ) correlation function (second column), of the QSO × Lyα(Lyα + Lyβ) correlation function given by Blomqvist et al. (2019) (third column), and of the two correlation functions (fourth column).
Results in two redshift bins from fitting the baseline model to the Lyα(Lyα) × Lyα(Lyα) correlation function.
Same as Table 3 for the main metal/metal, metal/Lyβ, and Lyα/metal correlations relevant to the computation of the Lyα(Lyα) × Lyβ(Lyβ) correlation function.
Results of the combining fit on Lyα(Lyα) × Lyα(Lyα), Lyα(Lyα) × Lyα(Lyβ) and Lyα(Lyα) × Lyβ(Lyβ) correlation functions with the BAO parameters (α∥, α⊥) fixed to 1.
All Figures
 |
Fig. 1. Sky distribution of the 216 163 quasars with redshift in the [2.0, 3.5] range in the DR14 footprint of the BOSS and eBOSS surveys. The high-density regions are the eBOSS and SEQUELS observations (for the highest declinations in the two Galactic caps) and SDSS-stripe 82 (on the celestial equator in the south Galactic cap). |
| In the text | |
 |
Fig. 2. Lyα and Lyβ spectral regions defined in Table 1. |
| In the text | |
 |
Fig. 3. Weighted distribution of the redshift of pairs used to measure the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions. The mean redshift of the combined sample is ⟨zpairs⟩=2.34. |
| In the text | |
 |
Fig. 4. One-dimensional correlation functions, ξ1d, in the Lyα (red curve) and Lyβ (blue curve) regions as a function of the ratio of transition wavelengths. Peaks are due to absorption by the two labeled elements at zero physical separation (Table 3). |
| In the text | |
 |
Fig. 5. Definition of the coordinates of pixels used in the computation of the correlation function. Absorbers i and j have angular separation θij and distance separation rij. The radial separation r∥, ij is the projection of rij on the median LOS, and the transverse separation r⊥, ij is the LOS perpendicular component of rij, assuming the flat Pl2015 model (Table 2). |
| In the text | |
 |
Fig. 6. Averaged correlations, CorrAB = CAB/ |
| In the text | |
 |
Fig. 7. Averaged correlations, CorrAB = CAB/ |
| In the text | |
 |
Fig. 8. Weighted combination between measured Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions along with the model best fits in four ranges of μ = r∥/r. The curves show the standard fit and the two fits with broadband terms defined by Eq. (32) with (imin, imax, jmax)=(0, 2, 6) with and without additional priors, as described in the text. |
| In the text | |
 |
Fig. 9. Left panel: 68% and 95% confidence level contours in the (α∥, α⊥) plane from the Lyα(Lyα) × Lyα(Lyα + Lyβ) auto-correlation function for the standard fit and for fits with polynomial broadband terms with and without additional priors, as described in the text. Right panel: contours for Lyα(Lyα) × Lyα(Lyα + Lyβ) auto-correlation standard fit and those from the combined fit of the auto-correlation and the quasar-Lyα cross-correlation of Blomqvist et al. (2019). In both panels the value for the Pl2015 model (Planck Collaboration XIII 2016) is shown as a black point. |
| In the text | |
 |
Fig. 10. Baryon acoustic oscillation measurement of DH/rd and DM/rd using BOSS galaxies (Alam et al. 2017), Lyα absorption in BOSS-eBOSS quasars (this work), and correlation between BOSS-eBOSS quasars and Lyα absorption (Blomqvist et al. 2019). Other measurements give DV/rd, with |
| In the text | |
 |
Fig. 11. Baryon acoustic oscillation measurement of the comoving expansion rate, H(z)/(1 + z), measured with BAO with rd = 147.3 Mpc. The red square is the present measurement at z = 2.34. The measurement by Blomqvist et al. (2019) is the blue dot. The other points are computed using galaxy measurements (Beutler et al. 2011; Ross et al. 2015; Alam et al. 2017). The points at z = 0.106 (Beutler et al. 2011) and z = 0.15 (Ross et al. 2015) are converted from DV to H(z) using the SNIa measurement of q0 given by Betoule et al. (2014). Solid black line shows the Pl2015 values (Planck Collaboration XIII 2016). |
| In the text | |
 |
Fig. 12. One and two standard deviation constraints on (Ωm, ΩΛ). The red contours use BAO measurements of DM/rd and DH/rd of this work, those of Blomqvist et al. (2019) and Alam et al. (2017), and the measurements of DV/rd of Beutler et al. (2011), Ross et al. (2015), Ata et al. (2018) and Bautista et al. (2018). The gray contours do not use the Lyα-quasar cross-correlation measurement of Blomqvist et al. (2019). The green contours show the constraints from SN Ia Pantheon sample (Scolnic et al. 2018). The black point indicates the values for the Planck Collaboration XIII (2016) best-fit flat ΛCDM cosmology. |
| In the text | |
 |
Fig. A.1. Quantity ∂m/∂p in the (r⊥, r∥) plane for the fitted parameters p ∈ [α∥, α⊥, bLyα, bSiIII(1207)], where m is the baseline model of the Lyα auto-correlation function. The graphs show which pixels contribute the most to the constraints on the considered parameter. BAO parameters α∥ and α⊥ are constrained by the bins around the location of the BAO peak, while the Lyα bias is mostly constrained by the bins at approximately zero separation. We also note that the Si III(1207) bias is mostly constrained by the bins r⊥ ∼ 0, r∥ ∼ 21 h−1 Mpc, in agreement with the |
| In the text | |
 |
Fig. B.1. Pixel pair redshift distribution of the subsamples used in the present analysis: full Lyα auto-correlation function (gray), low-redshift Lyα auto-correlation function (blue), high-redshift Lyα auto-correlation function (red). The two latter subsamples are used to produce a measurement of H(z) at z = 2.19 and z = 2.49. |
| In the text | |
 |
Fig. B.2. 68% and 95% confidence level contours in the (α∥, α⊥) plane from the Lyα(Lyα) × Lyα(Lyα) computed with the low- and high-redshift bins. The Δχ2 values corresponding to confidence levels are taken from Table D.1. The black dot corresponds to the Pl2015 model. |
| In the text | |
 |
Fig. B.3. Lyα(Lyα) × Lyα(Lyα) function in four ranges of μ = r∥/r values, computed in a low-redshift (blue dots) and in a high-redshift (red dots) bin obtained by splitting our sample so that the two bins have equivalent statistical power. The dashed lines correspond to the simple fits to the data of the Lyα(Lyα) × Lyα(Lyα) correlation function, the solid line to the combining fits to the data of the Lyα(Lyα) × Lyα(Lyα) and Lyα(Lyα) × Lyα(Lyβ) correlation functions. |
| In the text | |
 |
Fig. C.1. Same as Fig. 4 but for cross-correlation function of Lyα with Lyβ regions, as a function of the ratio of transition wavelengths. |
| In the text | |
 |
Fig. C.2. Measured Lyα(Lyα) × Lyβ(Lyβ) correlation function in four ranges of μ. In order to see the asymmetry of this correlation function, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



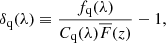
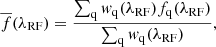
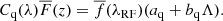
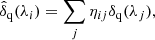
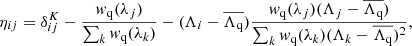
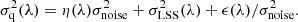
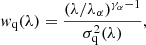
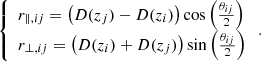
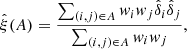
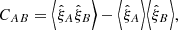
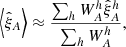
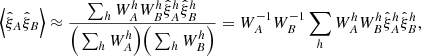
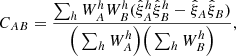
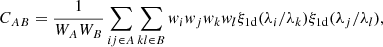
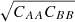
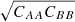
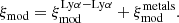
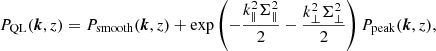
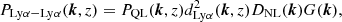
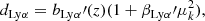
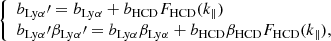
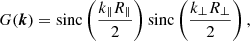
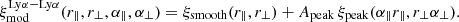
![$$ \begin{aligned} \alpha _\parallel = \frac{D_{\rm H}(\overline{z})/r_{\rm d}}{[D_{\rm H}(\overline{z})/r_{\rm d}]_{\mathrm{fid} }},\quad \alpha _\perp = \frac{D_{\rm M}(\bar{z})/r_{\rm d}}{[D_{\rm M}(\bar{z})/r_{\rm d}]_{\mathrm{fid} }}, \end{aligned} $$](/articles/aa/full_html/2019/09/aa35638-19/aa35638-19-eq51.gif)