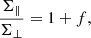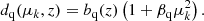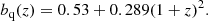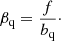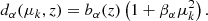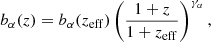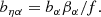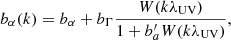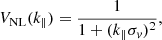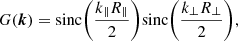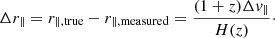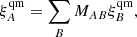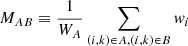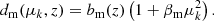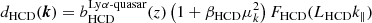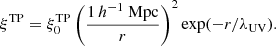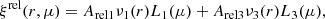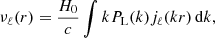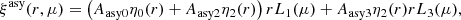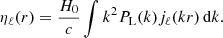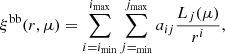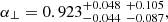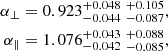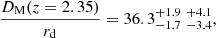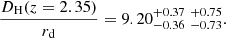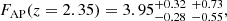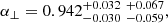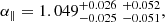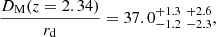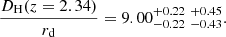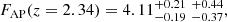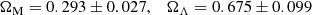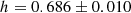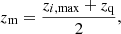| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935641 | |
| Published online | 10 September 2019 | |
Baryon acoustic oscillations from the cross-correlation of Lyα absorption and quasars in eBOSS DR14
1
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
e-mail: michael.blomqvist@lam.fr
2
Department of Physics and Astronomy, University of Utah, 115 S. 1400 E., Salt Lake City, UT 84112, USA
3
Sorbonne Université, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies, LPNHE, 4 Place Jussieu, 75252 Paris, France
4
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
5
Institute of Cosmology & Gravitation, University of Portsmouth, Dennis Sciama Building, Portsmouth PO1 3FX, UK
6
University College London, Gower St, Kings Cross, WC1E 6BT London, UK
7
Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA
8
Department of Physics and Astronomy, University of Waterloo, 200 University Ave. W., Waterloo, ON N2L 3G1, Canada
9
Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
10
Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA
11
Brookhaven National Laboratory, 2 Center Road, Upton, NY 11973, USA
Received:
8
April
2019
Accepted:
22
July
2019
We present a measurement of the baryon acoustic oscillation (BAO) scale at redshift z = 2.35 from the three-dimensional correlation of Lyman-α (Lyα) forest absorption and quasars. The study uses 266 590 quasars in the redshift range 1.77 < z < 3.5 from the Sloan Digital Sky Survey (SDSS) Data Release 14 (DR14). The sample includes the first two years of observations by the SDSS-IV extended Baryon Oscillation Spectroscopic Survey (eBOSS), providing new quasars and re-observations of BOSS quasars for improved statistical precision. Statistics are further improved by including Lyα absorption occurring in the Lyβ wavelength band of the spectra. From the measured BAO peak position along and across the line of sight, we determined the Hubble distance DH and the comoving angular diameter distance DM relative to the sound horizon at the drag epoch rd: DH(z = 2.35)/rd = 9.20 ± 0.36 and DM(z = 2.35)/rd = 36.3 ± 1.8. These results are consistent at 1.5σ with the prediction of the best-fit spatially-flat cosmological model with the cosmological constant reported for the Planck (2016) analysis of cosmic microwave background anisotropies. Combined with the Lyα auto-correlation measurement presented in a companion paper, the BAO measurements at z = 2.34 are within 1.7σ of the predictions of this model.
Key words: large-scale structure of Universe / dark energy / cosmological parameters / cosmology: observations / quasars: absorption lines
© M. Blomqvist et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The baryon acoustic oscillation (BAO) peak in the cosmological matter correlation function at a distance corresponding to the sound horizon, rd ∼ 100 h−1 Mpc, has been seen at several redshifts using a variety of tracers. Following the original measurements (Eisenstein et al. 2005; Cole et al. 2005), the most precise results have been obtained using bright galaxies in the redshift range 0.35 < z < 0.65 (Anderson et al. 2014a,b, 2012; Alam et al. 2017) from the Baryon Oscillation Spectroscopy Survey (BOSS; Dawson et al. 2013) of the Sloan Digital Sky Survey-III (SDSS-III; Eisenstein et al. 2011). Other measurements using galaxies cover the range 0.1 < z < 0.8 (Percival et al. 2007, 2010; Beutler et al. 2011; Blake et al. 2011; Padmanabhan et al. 2012; Mehta et al. 2012; Chuang & Wang 2012; Xu et al. 2013; Ross et al. 2015; Bautista et al. 2018). At higher redshift, the peak has been seen in the correlation function of quasars at a mean redshift z ∼ 1.5 (Ata et al. 2018; Gil-Marín et al. 2018; Hou et al. 2018; Zarrouk et al. 2018) and in the flux-transmission correlation function in Lyman-α (Lyα) forests at z ∼ 2.3 (Busca et al. 2013; Slosar et al. 2013; Kirkby et al. 2013; Delubac et al. 2015; Bautista et al. 2017) and in the forest cross-correlation with quasars (Font-Ribera et al. 2014; du Mas des Bourboux et al. 2017). These observations all yield measurements of comoving angular-diameter distances and Hubble distances at the corresponding redshift, DM(z)/rd and DH(z)/rd = c/(H(z)rd), relative to the sound horizon.
BAO measurements have found an important role in testing the robustness of the spatially-flat cosmology with cold dark matter and the cosmological constant (ΛCDM) that is consistent with observed cosmic microwave background (CMB) anisotropies (Planck Collaboration XIII 2016). While the parameters of this model are precisely determined by the CMB data by itself, more general models are not constrained as well. Most significantly, adding BAO data improves constraints on curvature (Planck Collaboration XIII 2016). The addition of BAO and type Ia supernova (SN Ia) data (Betoule et al. 2014) generalizes the “CMB” measurement of H0, which assumes flatness, to give an “inverse-ladder” measurement of H0 (Aubourg et al. 2015) that can be compared with distance-ladder measurements (Riess et al. 2016, 2018a,b). Here, the inverse-ladder method uses the CMB-determined value of rd to define BAO-determined absolute distances to intermediate redshifts, z ∼ 0.5, which can then be used to calibrate SN Ia luminosities. The usual distance ladder calibrates the SN Ia luminosity using Cepheid luminosities, themselves calibrated through geometrical distance determinations.
A third use of BAO data is to determine ΛCDM parameters in a CMB-independent way. The Lyα forest auto- and cross-correlations that BOSS has pioneered are critical when gathering such measurements. It is striking that the oΛCDM parameters (ΩM, ΩΛ) determined by this method are in good agreement with the CMB values determined by assuming flat ΛCDM (Aubourg et al. 2015).
The individual BAO measurements of DM(z)/rd and DH(z)/rd are generally in good agreement with the CMB flat ΛCDM model. The largest single discrepancy, 1.8 standard deviations, is that of the BOSS (SDSS Data Release 12) measurement of the Lyα forest–quasar cross-correlation of du Mas des Bourboux et al. (2017, hereafter dMdB17). In this paper, we update this analysis with new quasars and forests from the SDSS Data Release 14 (DR14; Abolfathi et al. 2018; Pâris et al. 2018) obtained in the extended Baryon Oscillation Spectroscopy Survey (eBOSS) program (Dawson et al. 2016) of SDSS-IV (Blanton et al. 2017). This data set has been previously used to measure the cross-correlation between quasars and the flux in the “CIV forest” due to absorption by triply-ionized carbon (Blomqvist et al. 2018).
Besides the addition of new quasars and forests, our analysis differs in a few ways with that of dMdB17. Most importantly, we expand the wavelength range of the forest from the nominal Lyα forest, 104.0 < λrf < 120.0 nm, to include Lyα absorption (λα = 121.567 nm) in the Lyβ region of the spectra, 97.4 < λrf < 102.0 nm, thus increasing the statistical power of the sample. The procedure for fitting the correlation function is also slightly modified by including relativistic corrections (Bonvin et al. 2014; Iršič et al. 2016). Furthermore, we divide the data to report BAO measurements for two redshift bins. We have not developed new sets of mock spectra beyond those used in dMdB17. We refer to Sect. 6 of dMdB17 for the analysis of those mocks and the tests used to justify the analysis procedure.
The organization of this paper follows closely that of dMdB17. Section 2 describes the DR14 data set used in this study. Section 3 summarizes the measurement of the flux-transmission field. Section 4 describes the measurement of the cross-correlation of the transmission field with quasars and the associated covariance matrix. We also derive the “distortion matrix” that describes how the measured cross-correlation is related to the underlying physical cross-correlation. Section 5 describes our theoretical model of the cross-correlation. Section 6 presents the fits to the observed correlation function and Sect. 7 combines these results with those from the Lyα auto-correlation function presented in a companion paper (de Sainte Agathe et al. 2019). Section 8 summarizes the constraints on cosmological parameters derived from these results and those from de Sainte Agathe et al. (2019). Our conclusions are presented in Sect. 9. The measurements presented in this paper were made using the publicly available Python package picca1 developed by our team.
2. Data sample and reduction
The quasars and forests used in this study are drawn from SDSS DR14. This release includes data from DR12 taken in the first two generations SDSS-I/II, in the BOSS program of SDSS-III and in the eBOSS pilot program SEQUELS (Myers et al. 2015). These data were used in the measurement of the quasar–forest cross-correlation of dMdB17. Here, we use in addition data from the first two years of the eBOSS program and the completed SEQUELS.
The quasar target selection for BOSS, summarized in Ross et al. (2012), combines different targeting methods described in Yèche et al. (2010), Kirkpatrick et al. (2011), and Bovy et al. (2011). The methods employed for eBOSS quasar target selection are described in Myers et al. (2015) and Palanque-Delabrouille et al. (2016).
The catalog of identified quasars, DR14Q (Pâris et al. 2018), includes 266 590 quasars2 in the redshift range 1.77 < zq < 3.5. The distribution on the sky of these quasars is shown in Fig. 1 and the redshift distribution in Fig. 2.
 |
Fig. 1. Sky distribution for sample of 266 590 tracer quasars (1.77 < zq < 3.5) from DR14Q in J2000 equatorial coordinates. The solid black curve is the Galactic plane. The high-density regions are the eBOSS and SEQUELS observations (for the northern regions of the two Galactic hemispheres) and SDSS-stripe 82 (for declination δ ∼ 0). The discontiguous small areas contain only SDSS DR7 quasars. |
 |
Fig. 2. Normalized redshift distributions for tracer quasars (black) and Lyα forest absorption pixels of Lyα region (blue) and Lyβ region (red). The histograms include 266 590 tracer quasars, 30.2 × 106 pixels in the Lyα region, and 4.0 × 106 pixels in the Lyβ region. The vertical dashed lines show the mean value of each distribution: |
All spectra used for this analysis were obtained using the BOSS spectrograph (Smee et al. 2013) on the 2.5 m SDSS telescope (Gunn et al. 2006) at Apache Point Observatory (APO). The spectrograph covers observed wavelengths 360.0 ≲ λ ≲ 1040.0 nm, with a resolving power R ≡ λ/ΔλFWHM increasing from ∼1300 to ∼2600 across the wavelength range. The data were processed by the eBOSS pipeline, the same (but a marginally updated version) as that used for the cross-correlation measurement of dMdB17. The pipeline performs wavelength calibration, flux calibration and sky subtraction of the spectra. The individual exposures (typically four of 15 min) of a given object are combined into a coadded spectrum that is rebinned onto pixels on a uniform grid with Δ log10(λ) = 10−4 (velocity width Δv ≈ 69 km s−1). The pipeline additionally provides an automatic classification into object type (galaxy, quasar or star) and a redshift estimate by fitting a model spectrum (Bolton et al. 2012).
Visual inspection of quasar spectra was an important procedure during the first three generations of SDSS to correct for mis-classifications of object type and inaccurate redshift determinations by the pipeline (Schneider et al. 2010; Pâris et al. 2017). Starting in SDSS-IV, most of the objects are securely classified by the pipeline, with less than 10% of the spectra requiring visual inspection (Dawson et al. 2016). The visual-inspection redshifts, when available, are taken as the definitive quasar redshifts, while the remaining quasars have redshifts estimated by the pipeline.
The cross-correlation analysis presented here involves the selection of three quasar samples from DR14Q: tracer quasars (for which we only need the redshifts and positions on the sky), quasars providing Lyα forest absorption in the Lyα region, and quasars providing Lyα forest absorption in the Lyβ region. The selected sample of tracer quasars contains 266 590 quasars in the range 1.77 < zq < 3.5. It includes 13 406 SDSS DR7 quasars (Schneider et al. 2010) and 18 418 broad absorption line (BAL) quasars, the latter identified as having a CIV balnicity index (Weymann et al. 1991) BI_CIV> 0 in DR14Q. Quasars with redshifts less than 1.77 are excluded because they are necessarily separated from observable forest pixels (see below) by more than 200 h−1 Mpc, the maximum distance where the correlation function is measured. The upper limit of zq = 3.5 is adopted because of the low number of higher-redshift quasars that both limits their usefulness for correlation measurements and make them subject to contamination due to redshift errors of the much more numerous low-redshift quasars (Busca & Balland 2018). Such contaminations would be expected to add noise (but not signal) to the cross-correlation.
The summary of the Lyα forest data covering the Lyα or Lyβ region of the quasar spectrum is given in Table 1. Both samples exclude SDSS DR7 quasars and BAL quasars. The Lyα sample is derived from a super set consisting of 194,166 quasars in the redshift range 2.05 < zq < 3.5, whereas the Lyβ sample is taken from a super set containing 76,650 quasars with 2.55 < zq < 3.5. The lower redshift limits are a consequence of the forests exiting the wavelength coverage of the spectrograph for quasars with zq < 2 and zq < 2.53, respectively. Spectra with the same object identification THING_ID (re-observed quasars) are coadded using inverse-variance weighting. For the selected forest samples, 17% of the quasars have duplicate spectra (less than 2% have more than one reobservation) taken with the BOSS spectrograph.
Definition of Lyα and Lyβ regions of quasar spectrum in which we measured Lyα forest absorption.
The forest spectra are prepared for analysis by discarding pixels which were flagged as problematic in the flux calibration or sky subtraction by the pipeline. We mask pixels around bright sky lines using the condition |104log10(λ/λsky)| ≤ 1.5, where λsky is the wavelength at the pixel center of the sky line where the pipeline sky subtraction is found to be inaccurate. Finally, we double the mask width to remove pixels around the observed CaII H&K lines arising from absorption by the interstellar medium of the Milky Way.
Forests featuring identified damped Lyα systems (DLAs) are given a special treatment. We use an updated (DR14) version of the DLA catalog of DR9 (Noterdaeme et al. 2012). The DLA detection and estimation of the neutral-hydrogen column density NHI was based on correlating observed spectra with synthetic spectra. The effective threshold for DLA detection depends on the signal-to-noise ratio (and therefore on redshift) but is typically log10NHI ≈ 20.3 for spectra with S/N > 3 for which the efficiency and purity are ≈95%. For the purposes of the measurement of the correlation function, all pixels in the DLA where the transmission is less than 20% are masked and the absorption in the wings is corrected using a Voigt profile following the procedure of Lee et al. (2013). The effect on the correlation function of undetected DLAs or more generally of high-column-density (HCD) systems with log10NHI > 17.2 are modeled in the theoretical power spectrum, as described in Sect. 5.3.
To facilitate the computation of the cross-correlation, we follow the approach in Bautista et al. (2017) to combine three adjacent pipeline pixels into wider “analysis pixels” defined as the inverse-variance-weighted flux average. Requiring a minimum of 20 analysis pixels in each spectrum discards 2447 (6155) forests for the Lyα (Lyβ) region. Lastly, 3087 (1882) forests failed the continuum-fitting procedure (see Sect. 3) for the Lyα (Lyβ) region by having negative continua due to their low spectral signal-to-noise ratios. The final samples include 188 632 forests for the Lyα region and 68 613 forests for the Lyβ region. Figure 2 shows the redshift distributions for the tracer quasars and the Lyα absorption pixels. Our samples can be compared to those of dMdB17, which included 234 367 quasars (217 780 with 1.8 < zq < 3.5) and 168 889 forests (157 845 with 2.0 < zq < 3.5) over a wider redshift range.
3. The Lyα forest flux-transmission field
The transmitted flux fraction F in a pixel of the forest region of quasar q is defined as the ratio of the observed flux density fq with the continuum flux Cq (the flux density that would be observed in the absence of absorption). We will be studying the transmission relative to the mean value at the observed wavelength 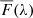 , and refer to this quantity as the “delta-field”:
, and refer to this quantity as the “delta-field”:
We employ a similar method to the one established by previous Lyα forest BAO analyses (Busca et al. 2013; Delubac et al. 2015) in which the delta-field is derived by estimating the product 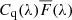 for each quasar. Each spectrum is modeled assuming a uniform forest spectral template which is multiplied by a quasar-dependent linear function, setting the overall amplitude and slope, to account for the diversity of quasar luminosity and spectral shape:
for each quasar. Each spectrum is modeled assuming a uniform forest spectral template which is multiplied by a quasar-dependent linear function, setting the overall amplitude and slope, to account for the diversity of quasar luminosity and spectral shape:
where aq and bq are free parameters fit to the observed flux of the quasar. The forest spectral template 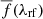 is derived from the data as a weighted mean normalized flux, obtained by stacking the spectra in the quasar rest-frame. The continuum fitting procedure is handled separately for the Lyα and Lyβ regions.
is derived from the data as a weighted mean normalized flux, obtained by stacking the spectra in the quasar rest-frame. The continuum fitting procedure is handled separately for the Lyα and Lyβ regions.
The total variance of the delta-field is modeled as
where the noise variance 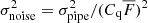 . The first term represents the pipeline estimate of the flux variance, corrected by a function η(λ) that accounts for possible misestimation. The second term gives the contribution due to the large-scale structure (LSS) and acts as a lower limit on the variance at high signal-to-noise ratio. Lastly, the third term absorbs additional variance from quasar diversity apparent at high signal-to-noise ratio. In bins of
. The first term represents the pipeline estimate of the flux variance, corrected by a function η(λ) that accounts for possible misestimation. The second term gives the contribution due to the large-scale structure (LSS) and acts as a lower limit on the variance at high signal-to-noise ratio. Lastly, the third term absorbs additional variance from quasar diversity apparent at high signal-to-noise ratio. In bins of 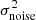 and observed wavelength, we measure the variance of the delta-field and fit for the values of η,
and observed wavelength, we measure the variance of the delta-field and fit for the values of η, 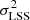 and ϵ as a function of observed wavelength. These three functions are different for the Lyα and Lyβ regions. The procedure of stacking the spectra, fitting the continua and measuring the variance of δ is iterated, until the three functions converge. We find that five iterations is sufficient. Figure 3 presents an example spectrum and the best-fit model
and ϵ as a function of observed wavelength. These three functions are different for the Lyα and Lyβ regions. The procedure of stacking the spectra, fitting the continua and measuring the variance of δ is iterated, until the three functions converge. We find that five iterations is sufficient. Figure 3 presents an example spectrum and the best-fit model 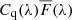 for the Lyα and Lyβ regions.
for the Lyα and Lyβ regions.
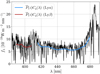 |
Fig. 3. Example spectrum of DR14Q quasar identified by (Plate, MJD, FiberID)=(7305, 56 991, 570) at zq = 3.0. The blue line indicates the best-fit model |
As detailed in Bautista et al. (2017), the delta-field can be redefined in two steps to make exact the biases introduced by the continuum fitting procedure. In the first step, we define
where the over-bars refer to weighted averages over individual forests. Next, we transform the 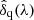 by subtracting the weighted average at each observed wavelength:
by subtracting the weighted average at each observed wavelength:
4. The Lyα forest–quasar cross-correlation
The three-dimensional positions of the quasars and the Lyα forest delta-field are determined by their redshifts and angular positions on the sky. We transform the observed angular and redshift separations (Δθ, Δz) of the quasar–Lyα absorption pixel pairs into Cartesian coordinates (r⊥, r∥) assuming a spatially flat fiducial cosmology. The comoving separations along the line of sight r∥ (parallel direction) and transverse to the line of sight r⊥ (perpendicular direction) are calculated as
where Dα ≡ Dc(zα) and Dq ≡ Dc(zq) are the comoving distances to the Lyα absorption pixel and the quasar, respectively. Line of sight separations r∥ > 0 (< 0) thus correspond to background (foreground) absorption with respect to the tracer quasar position. In this paper, we will also refer to the coordinates (r, μ), where 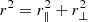 and μ = r∥/r, the cosine of the angle of the vector r from the line of sight. The pair redshift is defined as zpair = (zα + zq)/2. A histogram of the pair redshifts is displayed in Fig. 4. We do not include pairs involving a quasar and pixels from its own forest in the cross-correlation analysis, because the correlation of such pairs vanishes due to the continuum fit and delta-field redefinition (Eq. (4)).
and μ = r∥/r, the cosine of the angle of the vector r from the line of sight. The pair redshift is defined as zpair = (zα + zq)/2. A histogram of the pair redshifts is displayed in Fig. 4. We do not include pairs involving a quasar and pixels from its own forest in the cross-correlation analysis, because the correlation of such pairs vanishes due to the continuum fit and delta-field redefinition (Eq. (4)).
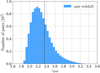 |
Fig. 4. Redshift distribution of 9.7 × 109 correlation pairs. The dashed vertical black line indicates the effective redshift of the BAO measurement, zeff = 2.35, calculated as the weighted mean of the pair redshifts for separations in the range 80 < r < 120 h−1 Mpc. |
The fiducial cosmology used in the analysis is a flat ΛCDM model with parameter values taken from the Planck (2016) result for the TT+lowP combination (Planck Collaboration XIII 2016) described in Table 2. It is the same fiducial cosmology employed by dMdB17.
Parameters of flat ΛCDM fiducial cosmological model (Planck Collaboration XIII 2016).
4.1. Cross-correlation
We estimate the cross-correlation at a separation bin A, ξA, as the weighted mean of the delta-field in pairs of pixel i and quasar k at a separation within the bin A (Font-Ribera et al. 2012):
The weights wi are defined as the inverse of the total pixel variance (see Eq. (3)), multiplied by redshift evolution factors for the forest and quasar, so as to approximately minimize the relative error on 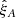 (Busca et al. 2013):
(Busca et al. 2013):
where γα = 2.9 (McDonald et al. 2006) and γq = 1.44 (du Mas des Bourboux et al. 2019). The validity of the correlation estimator, as well as the accuracy of the distortion matrix (Sect. 4.2) and covariance matrix estimation (Sect. 4.3) were tested and confirmed on simulated data in dMdB17.
Our separation grid consists of 100 bins of 4 h−1 Mpc for separations r∥ ∈ [ − 200, 200] h−1 Mpc in the parallel direction and 50 bins of 4 h−1 Mpc for separations r⊥ ∈ [0, 200] h−1 Mpc in the perpendicular direction; the total number of bins is Nbin = 5000. Each bin is defined by the weighted mean (r⊥, r∥) of the quasar-pixel pairs of that bin, and its redshift by the weighted mean pair redshift. The mean redshifts range from z = 2.29 to z = 2.40. The effective redshift of the cross-correlation measurement is defined to be the inverse-variance-weighted mean of the redshifts of the bins with separations in the range 80 < r < 120 h−1 Mpc around the BAO scale. Its value is zeff = 2.35.
Because the Lyβ transition is sufficiently separated in wavelength from the Lyα transition, corresponding to large physical separations > 441 h−1 Mpc for the wavelength range of the analysis, we neglect the contamination from Lyβ absorption interpreted as Lyα absorption. The total number of pairs of the cross-correlation measurement is 9.7 × 109. The Lyα absorption in the Lyβ region contributes 1.2 × 109 pairs (13%) and reduces the mean variance of the correlation function by 9% compared to the Lyα region-only measurement. Our cross-correlation measurement has 39% lower mean variance than the measurement of dMdB17.
4.2. Distortion matrix
The procedure used to estimate the delta-field (Sect. 3) suppresses fluctuations of characteristic scales corresponding to the forest length, since the estimate of the product 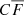 (Eq. (1)) would typically erase such a fluctuation. The result is a suppression of the power spectrum in the radial direction on large scales (low k∥). As illustrated in Fig. 11 of dMdB17, this induces a significant but smooth distortion of the correlation function on all relevant scales while leaving the BAO peak visually intact. As first noted in Slosar et al. (2011) and further investigated in Blomqvist et al. (2015), the distortion effect can be modeled in Fourier space as a multiplicative function of the radial component k∥ on the Lyα forest transmission power spectrum.
(Eq. (1)) would typically erase such a fluctuation. The result is a suppression of the power spectrum in the radial direction on large scales (low k∥). As illustrated in Fig. 11 of dMdB17, this induces a significant but smooth distortion of the correlation function on all relevant scales while leaving the BAO peak visually intact. As first noted in Slosar et al. (2011) and further investigated in Blomqvist et al. (2015), the distortion effect can be modeled in Fourier space as a multiplicative function of the radial component k∥ on the Lyα forest transmission power spectrum.
Here, we use the method introduced by Bautista et al. (2017) for the Lyα auto-correlation and adapted to the cross-correlation by dMdB17 which allows one to encode the effect of this distortion on the correlation function in a distortion matrix. This approach, extensively validated in these publications using simulated data, uses the fact that that Eqs. (4) and (5) are linear in δ. This fact allows one to describe the measured correlation function for a separation bin A as a linear combination of the true correlation function for bins A′:
The distortion matrix DAA′ depends only on the geometry of the survey, the lengths of the forests and the pixel weights,
where the projection matrix
and δK is the Kronecker delta. The indices i and j in Eq. (11) refer to pixels from the same forest, k refers to a quasar, and the sums run over all pixel-quasar pairs that contribute to the separation bins A and A′. The diagonal elements dominate the distortion matrix and are close to unity, DAA ≈ 0.97, whereas the off-diagonal elements are small, |DAA′| ≲ 0.03. We use the distortion matrix when performing fits of the measured cross-correlation function (see Eq. (16)).
4.3. Covariance matrix
We estimate the covariance matrix of the cross-correlation from the data by using the subsampling technique introduced by Busca et al. (2013) and adapted to the cross-correlation by dMdB17. We divide the DR14 footprint of Fig. 1 into subsamples and measure the covariance from the variability across the subsamples. Such estimates of the covariance matrix are unbiased, but the noise due to the finite number of subsamples leads to biases in the inverse of the covariance (Joachimi et al. 2014). As was done in dMdB17, we smooth the noise by assuming, to good approximation, that the covariance between separation bins A and B depends only on the absolute difference 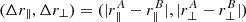 .
.
We define the subsamples through a HEALPix (Górski et al. 2005) pixelization of the sky. A quasar-absorption pixel pair is assigned to a subsample s if the forest that contains the absorption belongs to that HEALPix pixel. We use HEALPix parameter nside=32, resulting in 3262 subsamples. Using fewer but larger HEALPix pixels (nside = 16; 876 subsamples) has no significant impact on the covariance matrix or the BAO peak position measurement.
The (noisy) covariance matrix is calculated as
where the sum runs over all subsamples and WA is the sum of the pair weights w belonging to bin A,
From the covariance, we calculate the correlation matrix:
The smoothing procedure is applied to this correlation matrix by averaging as a function of (Δr∥, Δr⊥). The final covariance used in the fits is obtained by multiplying the smoothed correlation matrix by the diagonal elements of the original covariance matrix. Figure 5 displays the smoothed correlation matrix as a function of Δr∥ for the three lowest values of Δr⊥.
 |
Fig. 5. Smoothed correlation matrix from sub-sampling as a function of Δr∥ = |r∥, A − r∥, B|. The curves are for constant Δr⊥ = |r⊥, A − r⊥, B| for the three lowest values Δr⊥ = [0,4,8] h−1 Mpc. The right panel shows an expansion of the region Δr∥ < 140 h−1 Mpc. |
5. Model of the cross-correlation
We fit the measured cross-correlation function, 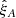 , in the (r⊥, r∥) bin A, to a cosmological correlation function
, in the (r⊥, r∥) bin A, to a cosmological correlation function 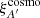 :
:
where DAA′ is the distortion matrix (Eq. (11)). The broadband term, 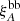 , is an optional function used to test for imperfections in the model and for systematic errors. The set of parameters for the model is summarized in Table 3. The model is calculated at the weighted mean (r⊥, r∥) and redshift of each bin of the correlation function. Because of the relatively narrow redshift distribution of the bins (Δz = 0.11), most model parameters can be assumed as redshift independent to good accuracy.
, is an optional function used to test for imperfections in the model and for systematic errors. The set of parameters for the model is summarized in Table 3. The model is calculated at the weighted mean (r⊥, r∥) and redshift of each bin of the correlation function. Because of the relatively narrow redshift distribution of the bins (Δz = 0.11), most model parameters can be assumed as redshift independent to good accuracy.
Parameters of cross-correlation model.
The cosmological cross-correlation function is the sum of several contributions
The first term represents the standard correlation between quasars, q, and Lyα absorption in the IGM. It is the most important part of the correlation function and, used by itself, would lead to an accurate determination of the BAO peak position (see results in Sect. 6).
The remaining terms in Eq. (17) represent subdominant effects but contribute toward improving the fit of the correlation function outside the BAO peak. The second term is the sum over correlations from metal absorbers in the IGM. The third term represents Lyα absorption by high column density systems (HCDs). The fourth term is the correlation from the effect of a quasar’s radiation on a neighboring forest (“transverse proximity effect”). The fifth term is a relativistic correction leading to odd-ℓ multipoles in the correlation function, and the final term includes other sources of odd-ℓ multipoles (Bonvin et al. 2014). These terms will be described in detail below.
5.1. Quasar–Lyα correlation term
The quasar–Lyα cross-correlation, ξqα, is the dominant contribution to the cosmological cross-correlation. It is assumed to be a biased version of the total matter auto-correlation of the appropriate flat ΛCDM model, separated into a smooth component and a peak component to free the position of the BAO peak:
where Apeak is the BAO peak amplitude. The anisotropic shift of the observed BAO peak position relative to the peak position of the fiducial cosmological model from Table 2 is described by the line-of-sight and transverse scale parameters
The nominal correlation function, ξqα(r⊥, r∥, α⊥ = α∥ = 1), is the Fourier transform of the quasar–Lyα cross-power spectrum:
where k = (k‖, k⊥) is the wavenumber of modulus k with components k∥ along the line of sight and k⊥ across, and μk = k∥/k is the cosine of the angle of the wavenumber from the line of sight. As described in detail below, PQL is the (quasi) linear matter spectrum, dq and dLyα are the standard linear-theory factors describing the tracer bias and redshift-space distortion (Kaiser 1987), VNL describes further nonlinear corrections not included in PQL, and G(k) gives the effects of (r⊥, r∥) binning on the measurement.
The first term in ((20)) provides for the aforementioned decoupling of the peak component (Eq. (18)):
where the smooth component, Psm, is derived from the linear power spectrum, PL(k, z), via the side-band technique (Kirkby et al. 2013) and Ppeak = PL − Psm. The redshift-dependent linear power spectrum is obtained from CAMB (Lewis et al. 2000) with the fiducial cosmology.
The correction for nonlinear broadening of the BAO peak is parameterized by Σ = (Σ‖, Σ⊥), with Σ⊥ = 3.26 h−1 Mpc and
where 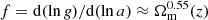 is the linear growth rate of structure.
is the linear growth rate of structure.
The second term in (20) describes the quasar bias and redshift-space distortion
Because the fit of the cross-correlation is only sensitive to the product of the quasar and Lyα biases, we set bq ≡ bq(zeff) = 3.77 and assume a redshift dependence of the quasar bias given by (Croom et al. 2005)
The quasar redshift-space distortion, assumed to be redshift independent, is
Setting f = 0.969 for our fiducial cosmology yields βq = 0.257.
The third term in (20) is the Lyα forest factor,
We assume that the transmission bias evolves with redshift as
with γα = 2.9 (McDonald et al. 2006), while βα is assumed to be redshift independent. We choose to fit for βα and the velocity gradient bias of the Lyα forest:
Beyond our standard treatment of the Lyα transmission bias, we also consider the effect of fluctuations of ionizing UV radiation which lead to a scale-dependence of bα (Pontzen 2014; Gontcho A Gontcho et al. 2014):
where W(x)=arctan(x)/x (following the parameterization of Gontcho A Gontcho et al. 2014). Our standard fit does not include the effect of UV fluctuations due to its minor contribution to the fit quality. A fit that includes the UV modeling is presented in Table A.1 for which we fix the UV photon mean free path λUV = 300 h−1 Mpc (Rudie et al. 2013) and 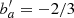 (Gontcho A Gontcho et al. 2014), and fit for bΓ, as was done in dMdB17.
(Gontcho A Gontcho et al. 2014), and fit for bΓ, as was done in dMdB17.
The effect of quasar nonlinear velocities and statistical redshift errors on the power spectrum is modeled as a Lorentz damping (Percival & White 2009),
where σv is a free parameter.
The last term in (20), G(k), accounts for smoothing due to the binning of the measurement of the correlation function (Bautista et al. 2017). We use
where R∥ and R⊥ are the scales of the smoothing. In the transverse direction, this form is not exact, but we have verified that it generates a sufficiently accurate correlation function. We fix both to the bin width, R∥ = R⊥ = 4 h−1 Mpc.
Systematic errors in the quasar redshift estimates lead to a shift of the cross-correlation along the line of sight which is accounted for in the fit using the free parameter
5.2. Quasar–metal correlation terms
Absorption by metals in the intergalactic medium (e.g., Pieri et al. 2014) with similar rest-frame wavelengths to Lyα yields a sub-dominant contribution to the measured cross-correlation. Assuming that these contaminant absorptions have redshifts corresponding to Lyα absorption results in an apparent shift of the quasar–metal cross-correlations along the line of sight in the observed cross-correlation. Following Blomqvist et al. (2018), metal correlations are modeled as
where
is a “metal distortion matrix” that allows us to calculate the shifted quasar–metal cross-correlation function for a given non-shifted quasar–metal cross-correlation function. The condition (i, k)∈A refers to pixel distances calculated using zα, but (i, k)∈B refers to pixel distances calculated using zm. For each metal absorption line, the (non-shifted) quasar–metal correlation is modeled using (20) with dα replaced by
The metal absorption lines included in the fit are listed in Table 4. Because the redshift-space distortion parameter of each metal is poorly determined in the fit, we fix βm = 0.5, the value derived for DLA host halos (Font-Ribera et al. 2012; Pérez-Ràfols et al. 2018). Transmission biases are assumed to evolve with redshift as a power-law with exponent γm = 1, similar to the measured evolution of the CIV bias (Blomqvist et al. 2018), but our results are not sensitive to this choice.
Most important metal absorptions of intergalactic medium that imprint correlations observed in Lyα–quasar cross-correlation for r∥ ∈ [ − 200, 200] h−1 Mpc.
5.3. Other correlation terms
The presence of HCDs in the absorption spectra modifies the expected correlation function. The flux transmission of spectra with identified DLAs are estimated by masking the strong absorption regions (transmission less than 20%) and correcting the wings using a Voigt profile following the procedure of Lee et al. (2013). If this procedure worked perfectly, we would expect no strong modification of the power spectrum. However, it does not operate for HCDs below the nominal threshold of log NHI ≈ 20, and even above this threshold the detection efficiency depends on the signal-to-noise ratio of the spectrum. These imperfections modify the expected power spectrum.
We model the correlations due to absorption by unidentified HCD systems by adding to the power spectrum a term with the same form as the usual Lyα correlations (Eq. (20)) but with dα replaced by
where the bias 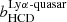 and the redshift-space distortion βHCD are free parameters in the fit. The function FHCD(LHCDk∥) describes the suppression of power at large k∥ due to unidentified HCDs of typical extent LHCD. The studies of mock data sets by Bautista et al. (2017) tried several functional forms and F = sinc(LHCDk∥) was adopted by them and by dMdB17, though other forms gave similar results. Following the more detailed studies of Rogers et al. (2018), we choose to use the form F = exp(−LHCDk∥).
and the redshift-space distortion βHCD are free parameters in the fit. The function FHCD(LHCDk∥) describes the suppression of power at large k∥ due to unidentified HCDs of typical extent LHCD. The studies of mock data sets by Bautista et al. (2017) tried several functional forms and F = sinc(LHCDk∥) was adopted by them and by dMdB17, though other forms gave similar results. Following the more detailed studies of Rogers et al. (2018), we choose to use the form F = exp(−LHCDk∥).
Our DLA-identification procedure requires their width (wavelength interval for absorption greater than 20% ) to be above ∼2.0 nm, corresponding to ∼14 h−1 Mpc. Following the study of Rogers et al. (2018), the corresponding unidentified HCD systems are well-modeled with LHCD = 10 h−1 Mpc and we fix LHCD to this value in the fits. We have verified that varying this parameter over the range 5 < LHCD < 15 h−1 Mpc does not change the fit position of the BAO peak. Due to degeneracies, we add a Gaussian prior on βHCD of mean 0.5 and standard deviation 0.2.
The term in Eq. (17) representing the transverse proximity effect takes the form (Font-Ribera et al. 2013):
This form supposes isotropic emission from the quasars. We fix λUV = 300 h−1 Mpc (Rudie et al. 2013) and fit for the amplitude 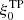 .
.
In addition to accounting for asymmetries in the cross-correlation introduced by metal absorptions, continuum-fitting distortion and systematic redshift errors, the standard fit includes modeling of relativistic effects (Bonvin et al. 2014). The relativistic correction in (17) is the sum of two components describing a dipole and an octupole,
where L1 and L3 are the Legendre polynomial of degree 1 and 3 respectively, Arel1 and Arel3 are the amplitudes, and
where jℓ is the spherical Bessel function. The relativistic dipole is expected to be the dominant contribution of odd-ℓ asymmetry and our standard fit therefore neglects the relativistic octupole (Arel3 = 0).
Dipole and octupole asymmetries also arise in the “standard” correlation function due to the evolution of the tracer biases and growth factor, as well as from the wide-angle correction (Bonvin et al. 2014):
where
Here, the two amplitudes Aasy0 and Aasy2 determine the dipole contribution, while Aasy3 is the octupole amplitude. The ξasy term is neglected in the standard fit, but we check the robustness of the BAO measurement with respect to the odd-ℓ multipoles in Table A.1.
5.4. Broadband function
The optional ξbb term of (16) is a “broadband function” that is a slowly varying function of (r∥, r⊥):
where Lj is the Legendre polynomial of degree j. Its purpose is to account for unknown physical, instrumental or analytical effects missing in the model that could potentially impact the BAO measurement. The standard fit features no broadband function. The result of adding a broadband function of the form (imin, imax, jmin, jmax) = (0, 2, 0, 6) is presented in Table A.1.
6. Fits of the cross-correlation
Our standard fit of the cross-correlation function uses the 14 parameters in the first group of Table 3. The fit includes 3180 data bins in the range 10 < r < 180 h−1 Mpc. The best-fit values are presented in the column “Lyα–quasar” of Table 5. Figure 6 shows the best fit for four ranges of μ and Fig. 7 for the two lowest r⊥ bins.
 |
Fig. 6. Cross-correlation function averaged in four ranges of μ = r∥/r. The red curves show the best-fit model of the standard fit obtained for the fitting range 10 < r < 180 h−1 Mpc. The curves have been extrapolated outside this range. |
 |
Fig. 7. Cross-correlation function as a function of r∥ for two lowest values r⊥ = [2, 6] h−1 Mpc. The red curves indicate the best-fit model of the standard fit obtained for the fitting range 10 < r < 180 h−1 Mpc. The curves have been extrapolated outside this range. The imprints of quasar–metal correlations are visible as peaks indicated by the dashed black lines at r∥ ≈ −21 h−1 Mpc (SiIII(120.7)), r∥ ≈ −53 h−1 Mpc (SiII(119.0)), r∥ ≈ −59 h−1 Mpc (SiII(119.3)), and r∥ ≈ +103 h−1 Mpc (SiII(126.0)). |
Fit results for cross-correlation, auto-correlation of de Sainte Agathe et al. (2019), and combined fit.
Constraints on the BAO parameters (α⊥, α∥) are presented in Fig. 8. Following the method introduced and described in detail in dMdB17, we estimate the relation between 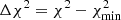 and confidence levels for the BAO parameters using a large number of simulated correlation functions generated from the best-fit model and the covariance matrix measured with the data. The results of the study, summarized in Table 6, indicate that the (68.27,95.45%) confidence levels for (α⊥, α∥) correspond to Δχ2 = (2.51, 6.67) (instead of the nominal values Δχ2 = (2.3, 6.18)). These levels are shown as contours in Fig. 8. The best-fit values and confidence level (68.27,95.45%) ranges are:
and confidence levels for the BAO parameters using a large number of simulated correlation functions generated from the best-fit model and the covariance matrix measured with the data. The results of the study, summarized in Table 6, indicate that the (68.27,95.45%) confidence levels for (α⊥, α∥) correspond to Δχ2 = (2.51, 6.67) (instead of the nominal values Δχ2 = (2.3, 6.18)). These levels are shown as contours in Fig. 8. The best-fit values and confidence level (68.27,95.45%) ranges are:
 |
Fig. 8. Constraints on (α∥, α⊥) for cross-correlation (red) and combination with auto-correlation (black). Contours correspond to confidence levels of (68.27%,95.45%). The black point at (α∥, α⊥)=(1, 1) indicates the prediction of the Planck (2016) best-fit flat ΛCDM cosmology. The effective redshift of the combined fit is zeff = 2.34 where the fiducial distance ratios are (DM/rd, DH/rd)=(39.26, 8.58). |
Values of Δχ2 corresponding to CL = (68.27, 95.45%).
corresponding to
These results are consistent at 1.5 standard deviations with the prediction of the Planck (2016) best-fit flat ΛCDM model. Using a model without the BAO peak (Apeak = 0) degrades the quality of the fit by Δχ2 = 22.48.
Our BAO constraints can be compared with the DR12 measurement of dMdB17 at a slightly higher redshift: DM(2.40)/rd = 35.7 ± 1.7 and DH(2.40)=9.01 ± 0.36 corresponding to α⊥ = 0.898 ± 0.042 and α∥ = 1.077 ± 0.042, relative to the same Planck model. The results (43) and (44) thus represent a movement of ∼0.3σ toward the Planck-inspired model through a shift in α⊥. As a cross-check of the results, we apply our analysis to the DR12 data set of dMdB17, without including the absorption in the Lyβ region. The best-fit values are α⊥ = 0.889 ± 0.040 and α∥ = 1.080 ± 0.039 (errors correspond to Δχ2 = 1), in good agreement with the measurement of dMdB17. This result indicates that the movement toward the fiducial model in DR14 is driven by the data.
Model predictions for DM/rd and DH/rd depend both on pre-recombination physics, which determine rd, and on late-time physics, which determine DM and DH. Taking the ratio, yielding the Alcock–Paczyński parameter FAP = DM/DH (Alcock & Paczynski 1979), isolates the late-time effects which, in the ΛCDM model depend only on (Ωm, ΩΛ). We find
where the Δχ2 curve is shown in Fig. 9 and we have adopted that the (68.27,95.45%) confidence levels correspond to Δχ2 = (1.13, 4.74) (instead of the nominal values Δχ2 = (1, 4)). This result is 1.8 standard deviations from the prediction of the Planck-inspired model, FAP(z = 2.35) = 4.60.
 |
Fig. 9. Constraints on Alcock–Paczyński parameter FAP for cross-correlation (red) and combination with auto-correlation (black). Confidence levels of (68.27%,95.45%) are indicated with the horizontal dotted lines for the cross-correlation and dashed lines for the combined fit. The prediction of the Planck (2016) best-fit flat ΛCDM cosmology is indicated with the vertical dotted line at FAP(z = 2.35)=4.60 for the cross-correlation and dashed line at FAP(z = 2.34)=4.57 for the combined fit. |
The fit values of the Lyα bias parameters, bηα = −0.267 ± 0.014 and βα = 2.28 ± 0.31 are consistent with those found by dMdB17, bηα = −0.23 ± 0.02 and βα = 1.90 ± 0.34. These parameters can also be determined from the Lyα auto-correlation and our value of βα is consistent with that found with the auto-correlation function, βα = 1.93 ± 0.10 (de Sainte Agathe et al. 2019). However, these values are not in good agreement with the value βα = 1.656 ± 0.086 found earlier by Bautista et al. (2017). The auto- and cross-correlations values of bηα also differ by ∼20%: −0.267 ± 0.014 for the cross correlation and −0.211 ± 0.004 for the auto-correlation. Furthermore, the bias parameters are not in good agreement with recent simulations (Arinyo-i-Prats et al. 2015) which predict βα ≈ 1.4 and |bηα| in the range 0.14 to 0.20. Since our quoted uncertainties on the bias parameters (not on BAO parameters) come from approximating the likelihood as Gaussian, they might be underestimated in the presence of non-trivial correlations between the parameters. A dedicated study would be necessary to further investigate the consistency between the measured and predicted values. Fortunately, the bias parameters describe mostly the smooth component of the correlation function and do not significantly influence the BAO parameters (α⊥, α∥), as indicated by the non-standard fits discussed below and summarized in Table A.1.
The fit of the cross-correlation prefers a vanishing contribution from the quasar–HCD correlation term (bHCD ≈ 0). This preference is in contrast to the Lyα auto-correlation of de Sainte Agathe et al. (2019) where the HCD model is a crucial element to obtain a good fit (but does not affect the BAO peak position measurement). The best-fit radial coordinate shift Δr∥ is consistent with zero systematic redshift error, but the parameter is strongly correlated with the amplitude of the relativistic dipole. Setting Arel1 = 0 in the fit yields Δr∥ = −0.92 ± 0.12, in good agreement with the value reported in dMdB17. The best fit suggests marginal support for a non-zero value of Arel1, and the combined fit increases the significance of this result. However, even with sufficient statistical significance, its correlation with Δr∥ (as well as other potential systematic errors on Arel1) prevents claims of a discovery of relativistic effects. The parameters σv and 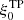 have best-fit values in agreement with the result of dMdB17.
have best-fit values in agreement with the result of dMdB17.
Among the metals, only SiIII(120.7) has a bias parameter significantly different from zero (> 4σ) to show evidence for large-scale correlations with quasars. The imprints of the metal correlations are visible in the line-of-sight direction in Fig. 7.
Besides the standard approach, we have also performed non-standard analyses, described in Appendix A, to search for unexpected systematic errors in the BAO peak-position measurement. The results for the non-standard fits of the cross-correlation are summarized in Table A.1. No significant changes of the best-fit values of (α⊥, α∥) are observed. We have also divided the data to perform fits of the cross-correlation for a low- and a high-redshift bin as described in Appendix B. These fits are summarized in Table B.1 and yield consistent best-fit BAO parameters for the two bins.
7. Combination with the Lyα auto-correlation
We combine our measurement of the Lyα–quasar cross-correlation with the DR14 Lyα auto-correlation of de Sainte Agathe et al. (2019) by performing a combined fit of the correlation functions. For the auto-correlation, we use the combination Lyα(Lyα) × Lyα(Lyα) + Lyα(Lyα) × Lyα(Lyβ) described in de Sainte Agathe et al. (2019). Because the covariance between the auto- and cross-correlation is sufficiently small to be ignored, as studied in Delubac et al. (2015) and dMdB17, we treat their errors as independent. The combined fit uses the standard fit model of each analysis. In addition to the 14 free parameters in Table 3, we let free the redshift-space distortion of quasars, βq, and the auto-correlation fit introduces three additional bias parameters (bCIV(154.9), 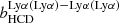 ,
, 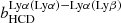 ), for a total of 18 free parameters. The effective redshift of the combined fit is zeff = 2.34.
), for a total of 18 free parameters. The effective redshift of the combined fit is zeff = 2.34.
The best-fit results are presented in the column “combined” of Table 5. Figure 8 displays the constraints on (α⊥, α∥) from the combined measurement as black contours indicating the (68.27,95.45%) confidence levels (corresponding to Δχ2 = (2.47, 6.71); see Table 6). The combined constraints on the BAO parameters are:
corresponding to
These results are within 1.7 standard deviations of the prediction of the Planck (2016) best-fit flat ΛCDM model. This movement of ∼0.6σ toward the Planck prediction compared to the DR12 combined-fit result of dMdB17 is a consequence of the auto- and cross-correlation results individually moving toward the fiducial model.
Figure 9 shows the Δχ2 curve for the Alcock–Paczyński parameter from the combined fit, for which the (68.27,95.45%) confidence levels correspond to Δχ2 = (1.11, 4.39). The combined constraint is
within 2.1 standard deviations of the value FAP(z = 2.34)=4.57 expected in the Planck-inspired model.
8. Implications for cosmological parameters
The combined-fit measurement of (DM/rd, DH/rd) at z = 2.34 presented here is within 1.7 standard deviations of the predictions of the flat ΛCDM model favored by the measurement of CMB anisotropies (Planck Collaboration XIII 2016). This result thus does not constitute statistically significant evidence for new physics or unidentified systematic errors in the measurement. Figure 10 illustrates the agreement with the Planck prediction for the ensemble of BAO measurements.
 |
Fig. 10. Measurements of DM/rd, DH/rd and DV/rd at various redshifts: 6dFGS (Beutler et al. 2011), SDSS MGS (Ross et al. 2015), BOSS galaxies (Alam et al. 2017), eBOSS Galaxies (Bautista et al. 2018), eBOSS quasars (Ata et al. 2018), eBOSS Lyα–Lyα (de Sainte Agathe et al. 2019), and eBOSS Lyα–quasars (this work). For clarity, the Lyα–Lyα results at z = 2.34 and the Lyα–quasar results at z = 2.35 have been separated slightly in the horizontal direction. Error bars represent 1σ uncertainties. |
Independent of CMB data and without assuming flatness, the BAO data by themselves constrain the parameters (Ωm, ΩΛ, H0rd) of the (o)ΛCDM model. Using the combined fit (Eqs. (50) and (51)), the galaxy data of Alam et al. (2017), Beutler et al. (2011) Ross et al. (2015) and Bautista et al. (2018) and the quasar data of Ata et al. (2018) yields
corresponding to Ωk = 0.032 ± 0.117. The best fit gives (c/H0)/rd = 29.78 ± 0.56 corresponding to hrd = (0.683 ± 0.013)×147.33 Mpc. The CMB inspired flat ΛCDM model has χ2 = 13.76 for 12 degrees of freedom and is within one standard deviation of the best fit, as illustrated in Fig. 11.
 |
Fig. 11. One and two standard deviation constraints on (Ωm, ΩΛ). The red contours use BAO measurements of DM/rd and DH/rd of this work, of de Sainte Agathe et al. (2019) and Alam et al. (2017), and the measurements of DV/rd of Beutler et al. (2011), Ross et al. (2015), Ata et al. (2018), and Bautista et al. (2018). The blue contours do not use the Lyα auto-correlation measurement of de Sainte Agathe et al. (2019). The green contours show the constraints from SN-Ia Pantheon sample (Scolnic et al. 2018). The black point indicates the values for the Planck (2016) best-fit flat ΛCDM cosmology. |
A value of H0 can be obtained either by using the CMB measurement of rd or by using the Primordial-Nucleosynethsis value of Ωbh2 to constrain rd. Adopting the value 100Ωbh2 = 2.260 ± 0.034 derived from the deuterium abundance measurement of Cooke et al. (2018) and assuming flat ΛCDM, we derive the constraints on (H0, Ωmh2) shown in Fig. 12 with
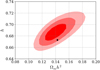 |
Fig. 12. One and two standard deviation constraints on H0 and Ωmh2 derived from BAO data used in Fig. 11 and from Big-Bang Nucleosynthesis. This figure assumes a flat universe and a Gaussian prior 100Ωbh2 = 2.260 ± 0.034 derived from the deuterium abundance measurement of Cooke et al. (2018). |
or h < 0.706 at 95% CL The limit degrades to h < 0.724 (95% CL) if one adopts a more conservative uncertainty on the baryon density: 100Ωbh2 = 2.26 ± 0.20. Nevertheless, as previously noted (Aubourg et al. 2015; Addison et al. 2018), the combination of BAO and nucleosynthsis provides a CMB-free confirmation of the tension with the distance-ladder determinations of H0 (Riess et al. 2016, 2018a,b).
9. Conclusions
Using the entirety of BOSS and the first two years of eBOSS observations from SDSS DR14, this paper has presented a measurement of the cross-correlation of quasars and the Lyα flux transmission at redshift 2.35. In addition to the new and reobserved quasars provided in DR14, we have improved statistics further by extending the Lyα forest to include Lyα absorption in the Lyβ region of the spectra.
The position of the BAO peak is 1.5σ from the flat ΛCDM model favored by CMB anisotropy measurements (Planck Collaboration XIII 2016). We emphasize that the measured peak position shows no significant variation when adding astrophysical elements to the fit model. The basic Lyα-only model on its own provides an accurate determination of the peak position, while still yielding an acceptable fit to the data. Compared to the BAO measurement for the DR12 data set reported by dMdB17, our result represents a movement of ∼0.3σ toward the Planck-cosmology prediction through a shift in the transverse BAO parameter α⊥. This change is driven by the data and not by differences in the analyses. The inclusion of Lyα absorption in the Lyβ region has no impact on the best-fit value of α⊥. Combined with the Lyα–flux-transmission auto-correlation measurement presented in a companion paper (de Sainte Agathe et al. 2019), the BAO peak at z = 2.34 is 1.7σ from the expected value.
The ensemble of BAO measurements is in good agreement with the CMB-inspired flat ΛCDM model. By themselves, the BAO data provide a good confirmation of this model. The use of SNIa to measure cosmological distances (Scolnic et al. 2018) provides independent measurements of the model parameters. As can be seen in Fig. 11 they are in agreement with the BAO measurements.
The BAO measurements presented here will be improved by the upcoming DESI (DESI Collaboration 2016) and WEAVE-QSO (Pieri et al. 2016) projects both by increasing the number of quasars and improving the spectral resolution.
The best-fit results and the χ2 scans for the cross-correlation by itself and the combination with the auto-correlation are publicly available3.
Package for Igm Cosmological-Correlations Analyses (picca) is available at https://github.com/igmhub/picca/
Acknowledgments
We thank Pasquier Noterdaeme for providing the DLA catalog for eBOSS DR14 quasars. This work was supported by the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French Government program, managed by the French National Research Agency (ANR), and by ANR under contract ANR-14-ACHN-0021. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is http://www.sdss.org/. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. A.F.R. was supported by an STFC Ernest Rutherford Fellowship, grant reference ST/N003853/1, and by STFC Consolidated Grant no ST/R000476/1.
References
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Addison, G. E., Watts, D. J., Bennett, C. L., et al. 2018, ApJ, 853, 119 [Google Scholar]
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., & Paczynski, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2014a, MNRAS, 439, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014b, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Arinyo-i-Prats, A., Miralda-Escudé, J., Viel, M., & Cen, R. 2015, JCAP, 12, 017 [Google Scholar]
- Ata, M., Baumgarten, F., Bautista, J., et al. 2018, MNRAS, 473, 4773 [NASA ADS] [CrossRef] [Google Scholar]
- Aubourg, É., Bailey, S., Bautista, J. E., et al. 2015, Phys. Rev. D, 92, 123516 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, J. E., Busca, N. G., Guy, J., et al. 2017, A&A, 603, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, J. E., Vargas-Magaña, M., Dawson, K. S., et al. 2018, ApJ, 863, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Davis, T., Poole, G. B., et al. 2011, MNRAS, 415, 2892 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Blomqvist, M., Kirkby, D., Bautista, J. E., et al. 2015, JCAP, 11, 034 [NASA ADS] [CrossRef] [Google Scholar]
- Blomqvist, M., Pieri, M. M., du Mas des Bourboux, H., et al. 2018, JCAP, 5, 029 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., Schlegel, D. J., Aubourg, É., et al. 2012, AJ, 144, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Bonvin, C., Hui, L., & Gaztañaga, E. 2014, Phys. Rev. D, 89, 083535 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Hennawi, J. F., Hogg, D. W., et al. 2011, ApJ, 729, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Busca, N., & Balland, C. 2018, MNRAS, submitted [arXiv:1808.09955] [Google Scholar]
- Busca, N. G., Delubac, T., Rich, J., et al. 2013, A&A, 552, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chuang, C.-H., & Wang, Y. 2012, MNRAS, 426, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Cooke, R. J., Pettini, M., & Steidel, C. C. 2018, ApJ, 855, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Boyle, B. J., Shanks, T., et al. 2005, MNRAS, 356, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Delubac, T., Bautista, J. E., Busca, N. G., et al. 2015, A&A, 574, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Sainte Agathe, V., Balland, C., du Mas des Bourboux, H., et al. 2019, A&A, 629, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- du Mas des Bourboux, H., Le Goff, J.-M., Blomqvist, M., et al. 2017, A&A, 608, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- du Mas des Bourboux, H., Dawson, K. S., Busca, N. G., et al. 2019, ApJ, 878, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Font-Ribera, A., Miralda-Escudé, J., Arnau, E., et al. 2012, JCAP, 11, 059 [NASA ADS] [CrossRef] [Google Scholar]
- Font-Ribera, A., Arnau, E., Miralda-Escudé, J., et al. 2013, JCAP, 5, 018 [Google Scholar]
- Font-Ribera, A., Kirkby, D., Busca, N., et al. 2014, JCAP, 5, 27 [Google Scholar]
- Gil-Marín, H., Guy, J., Zarrouk, P., et al. 2018, MNRAS, 477, 1604 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcho A Gontcho, S., Miralda-Escudé, J., & Busca, N. G. 2014, MNRAS, 442, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, J., Sánchez, A. G., Scoccimarro, R., et al. 2018, MNRAS, 480, 2521 [Google Scholar]
- Iršič, V., Di Dio, E., & Viel, M. 2016, JCAP, 2, 051 [NASA ADS] [Google Scholar]
- Joachimi, B., & Taylor, A. 2014, in Statistical Challenges in 21st Century Cosmology, eds. A. Heavens, J. L. Starck, & A. Krone-Martins, IAU Symp., 306, 99 [NASA ADS] [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkby, D., Margala, D., Slosar, A., et al. 2013, JCAP, 3, 024 [Google Scholar]
- Kirkpatrick, J. A., Schlegel, D. J., Ross, N. P., et al. 2011, ApJ, 743, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K.-G., Bailey, S., Bartsch, L. E., et al. 2013, AJ, 145, 69 [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- McDonald, P., Seljak, U., Burles, S., et al. 2006, ApJS, 163, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Mehta, K. T., Cuesta, A. J., Xu, X., Eisenstein, D. J., & Padmanabhan, N. 2012, MNRAS, 427, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, A. D., Palanque-Delabrouille, N., Prakash, A., et al. 2015, ApJS, 221, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Carithers, W. C., et al. 2012, A&A, 547, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padmanabhan, N., Xu, X., Eisenstein, D. J., et al. 2012, MNRAS, 427, 2132 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Palanque-Delabrouille, N., Magneville, C., Yèche, C., et al. 2016, A&A, 587, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Ross, N. P., et al. 2017, A&A, 597, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2018, A&A, 613, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Percival, W. J., & White, M. 2009, MNRAS, 393, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Ràfols, I., Font-Ribera, A., Miralda-Escudé, J., et al. 2018, MNRAS, 473, 3019 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, M. M., Mortonson, M. J., Frank, S., et al. 2014, MNRAS, 441, 1718 [NASA ADS] [CrossRef] [Google Scholar]
- Pieri, M. M., Bonoli, S., Chaves-Montero, J., et al. 2016, in SF2A-2016: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, J. Richard, L. Cambrésy, et al., 259 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A. 2014, Phys. Rev. D, 89, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018a, ApJ, 855, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018b, ApJ, 861, 126 [Google Scholar]
- Rogers, K. K., Bird, S., Peiris, H. V., et al. 2018, MNRAS, 476, 3716 [Google Scholar]
- Ross, N. P., Myers, A. D., Sheldon, E. S., et al. 2012, ApJS, 199, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Rudie, G. C., Steidel, C. C., Shapley, A. E., & Pettini, M. 2013, ApJ, 769, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Slosar, A., Font-Ribera, A., Pieri, M. M., et al. 2011, JCAP, 9, 1 [NASA ADS] [Google Scholar]
- Slosar, A., Iršič, V., Kirkby, D., et al. 2013, JCAP, 4, 26 [Google Scholar]
- Smee, S. A., Gunn, J. E., Uomoto, A., et al. 2013, AJ, 146, 32 [Google Scholar]
- Weymann, R. J., Morris, S. L., Foltz, C. B., & Hewett, P. C. 1991, ApJ, 373, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., Cuesta, A. J., Padmanabhan, N., Eisenstein, D. J., & McBride, C. K. 2013, MNRAS, 431, 2834 [NASA ADS] [CrossRef] [Google Scholar]
- Yèche, C., Petitjean, P., Rich, J., et al. 2010, A&A, 523, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarrouk, P., Burtin, E., Gil-Marín, H., et al. 2018, MNRAS, 477, 1639 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Non-standard fits of the cross-correlation
The results of performing non-standard fits of the cross-correlation are summarized in Table A.1. The first group reports results obtained by successively adding elements to the model, starting with a model with only the standard Lyα correlation function and ending with the complete model of Table 5. Adding elements does not significantly change the best-fit values of (α⊥, α∥) while gradually improving the quality of the fit.
Results of non-standard fits.
The second group of fits in Table A.1 adds elements to the standard fit in the form of fluctuations of the UV background radiation (Eq. (29)), the Arel3 term (Eq. (38)) and the other odd-ℓ terms from Eq. (40), or the broadband function (Eq. (42)). For these fits, we set ξqHCD = 0 to facilitate the parameter error estimation with no impact on the best fits. No significant changes of the BAO parameters are observed.
The third group of fits concern non-standard data samples that either omits the correlation pairs from the Lyβ region (“no Lyβ”) or leaves the DLAs uncorrected in the spectra (“keep DLAs”). Even for these modified data samples the best-fit values of (α⊥, α∥) do not deviate significantly from those of our standard analysis.
Figure A.1 shows the measured cross-correlation for four ranges of μ and three of the fits listed in Table A.1: the standard fit used to measure the BAO parameters, the basic Lyα-only fit, and the fit with the broadband function.
 |
Fig. A.1. Same as Fig. 6 but showing three models fit to data. Red curves indicate the standard fit, blue curves the basic Lyα-only model, and green curves the standard fit (with ξqHCD = 0) with the addition of the broadband function (Eq. (42)) of the form (imin, imax, jmin, jmax)=(0, 2, 0, 6). The curves have been extrapolated outside the fitting range 10 < r < 180 h−1 Mpc. |
Appendix B: Redshift split
The statistical limitations of the present data set are such that it is not possible to usefully measure the expected redshift-variation of DM(z)/rd and DH(z)/rd. However, to search for unexpected effects, we perform an analysis that independently treats a low- and a high-redshift bin.
A quasar and entire forest pair is assigned to either bin depending on their mean redshift:
where zi, max is the pixel with the highest absorption redshift in the forest. As the data split is defined, individual forests and quasars can contribute to both redshift bins. The limiting value of zm is chosen so as to approximately equalize the correlation signal-to-noise ratio (as determined by the best-fit fiducial correlation model) on BAO scales for the two redshift bins. This approach ensures that the redshift bins have similar statistical power for determining the BAO peak position. We set the limit at zm = 2.48. After identifying which quasar–forest pairs contribute to each redshift bin, we rederive the delta fields for each bin separately to ensure that the mean deltas vanish. The effective redshifts are zeff = 2.21 and zeff = 2.58 for the low-z and high-z bin, respectively. The pair redshift distribution for the low-z bin extends up to z = 2.48 (by definition) and its overlap with the distribution for the high-z bin is Δz ≈ 0.25. Correlations between the redshift bins are at the per cent level.
The result of the data split is summarized in Table B.1. Figure B.1 shows the correlation functions and the best-fit models for four ranges of μ. The best-fit values of (α⊥, α∥) for the two bins are consistent, with similar BAO errors of ∼6%. The bias parameter bηα changes between the two redshifts by a factor 1.57 ± 0.15 consistent with the expected factor (3.58/3.21)2.9 = 1.37. The parameter βα increases by a factor 1.6 ± 0.4, within two standard deviations of the predicted decrease of 6% from simulations of Arinyo-i-Prats et al. (2015).
Fit results for two redshift bins.
 |
Fig. B.1. Cross-correlation function averaged in four ranges of μ = r∥/r for the fitting range 10 < r < 180 h−1 Mpc. The blue points are the data for the low-z bin (zm < 2.48) and the blue curve the best-fit model. The red points are the data for the high-z bin (zm > 2.48) and the red curve the best-fit model. |
All Tables
Definition of Lyα and Lyβ regions of quasar spectrum in which we measured Lyα forest absorption.
Parameters of flat ΛCDM fiducial cosmological model (Planck Collaboration XIII 2016).
Most important metal absorptions of intergalactic medium that imprint correlations observed in Lyα–quasar cross-correlation for r∥ ∈ [ − 200, 200] h−1 Mpc.
Fit results for cross-correlation, auto-correlation of de Sainte Agathe et al. (2019), and combined fit.
All Figures
 |
Fig. 1. Sky distribution for sample of 266 590 tracer quasars (1.77 < zq < 3.5) from DR14Q in J2000 equatorial coordinates. The solid black curve is the Galactic plane. The high-density regions are the eBOSS and SEQUELS observations (for the northern regions of the two Galactic hemispheres) and SDSS-stripe 82 (for declination δ ∼ 0). The discontiguous small areas contain only SDSS DR7 quasars. |
| In the text | |
 |
Fig. 2. Normalized redshift distributions for tracer quasars (black) and Lyα forest absorption pixels of Lyα region (blue) and Lyβ region (red). The histograms include 266 590 tracer quasars, 30.2 × 106 pixels in the Lyα region, and 4.0 × 106 pixels in the Lyβ region. The vertical dashed lines show the mean value of each distribution: |
| In the text | |
 |
Fig. 3. Example spectrum of DR14Q quasar identified by (Plate, MJD, FiberID)=(7305, 56 991, 570) at zq = 3.0. The blue line indicates the best-fit model |
| In the text | |
 |
Fig. 4. Redshift distribution of 9.7 × 109 correlation pairs. The dashed vertical black line indicates the effective redshift of the BAO measurement, zeff = 2.35, calculated as the weighted mean of the pair redshifts for separations in the range 80 < r < 120 h−1 Mpc. |
| In the text | |
 |
Fig. 5. Smoothed correlation matrix from sub-sampling as a function of Δr∥ = |r∥, A − r∥, B|. The curves are for constant Δr⊥ = |r⊥, A − r⊥, B| for the three lowest values Δr⊥ = [0,4,8] h−1 Mpc. The right panel shows an expansion of the region Δr∥ < 140 h−1 Mpc. |
| In the text | |
 |
Fig. 6. Cross-correlation function averaged in four ranges of μ = r∥/r. The red curves show the best-fit model of the standard fit obtained for the fitting range 10 < r < 180 h−1 Mpc. The curves have been extrapolated outside this range. |
| In the text | |
 |
Fig. 7. Cross-correlation function as a function of r∥ for two lowest values r⊥ = [2, 6] h−1 Mpc. The red curves indicate the best-fit model of the standard fit obtained for the fitting range 10 < r < 180 h−1 Mpc. The curves have been extrapolated outside this range. The imprints of quasar–metal correlations are visible as peaks indicated by the dashed black lines at r∥ ≈ −21 h−1 Mpc (SiIII(120.7)), r∥ ≈ −53 h−1 Mpc (SiII(119.0)), r∥ ≈ −59 h−1 Mpc (SiII(119.3)), and r∥ ≈ +103 h−1 Mpc (SiII(126.0)). |
| In the text | |
 |
Fig. 8. Constraints on (α∥, α⊥) for cross-correlation (red) and combination with auto-correlation (black). Contours correspond to confidence levels of (68.27%,95.45%). The black point at (α∥, α⊥)=(1, 1) indicates the prediction of the Planck (2016) best-fit flat ΛCDM cosmology. The effective redshift of the combined fit is zeff = 2.34 where the fiducial distance ratios are (DM/rd, DH/rd)=(39.26, 8.58). |
| In the text | |
 |
Fig. 9. Constraints on Alcock–Paczyński parameter FAP for cross-correlation (red) and combination with auto-correlation (black). Confidence levels of (68.27%,95.45%) are indicated with the horizontal dotted lines for the cross-correlation and dashed lines for the combined fit. The prediction of the Planck (2016) best-fit flat ΛCDM cosmology is indicated with the vertical dotted line at FAP(z = 2.35)=4.60 for the cross-correlation and dashed line at FAP(z = 2.34)=4.57 for the combined fit. |
| In the text | |
 |
Fig. 10. Measurements of DM/rd, DH/rd and DV/rd at various redshifts: 6dFGS (Beutler et al. 2011), SDSS MGS (Ross et al. 2015), BOSS galaxies (Alam et al. 2017), eBOSS Galaxies (Bautista et al. 2018), eBOSS quasars (Ata et al. 2018), eBOSS Lyα–Lyα (de Sainte Agathe et al. 2019), and eBOSS Lyα–quasars (this work). For clarity, the Lyα–Lyα results at z = 2.34 and the Lyα–quasar results at z = 2.35 have been separated slightly in the horizontal direction. Error bars represent 1σ uncertainties. |
| In the text | |
 |
Fig. 11. One and two standard deviation constraints on (Ωm, ΩΛ). The red contours use BAO measurements of DM/rd and DH/rd of this work, of de Sainte Agathe et al. (2019) and Alam et al. (2017), and the measurements of DV/rd of Beutler et al. (2011), Ross et al. (2015), Ata et al. (2018), and Bautista et al. (2018). The blue contours do not use the Lyα auto-correlation measurement of de Sainte Agathe et al. (2019). The green contours show the constraints from SN-Ia Pantheon sample (Scolnic et al. 2018). The black point indicates the values for the Planck (2016) best-fit flat ΛCDM cosmology. |
| In the text | |
 |
Fig. 12. One and two standard deviation constraints on H0 and Ωmh2 derived from BAO data used in Fig. 11 and from Big-Bang Nucleosynthesis. This figure assumes a flat universe and a Gaussian prior 100Ωbh2 = 2.260 ± 0.034 derived from the deuterium abundance measurement of Cooke et al. (2018). |
| In the text | |
 |
Fig. A.1. Same as Fig. 6 but showing three models fit to data. Red curves indicate the standard fit, blue curves the basic Lyα-only model, and green curves the standard fit (with ξqHCD = 0) with the addition of the broadband function (Eq. (42)) of the form (imin, imax, jmin, jmax)=(0, 2, 0, 6). The curves have been extrapolated outside the fitting range 10 < r < 180 h−1 Mpc. |
| In the text | |
 |
Fig. B.1. Cross-correlation function averaged in four ranges of μ = r∥/r for the fitting range 10 < r < 180 h−1 Mpc. The blue points are the data for the low-z bin (zm < 2.48) and the blue curve the best-fit model. The red points are the data for the high-z bin (zm > 2.48) and the red curve the best-fit model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



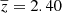
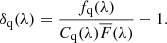
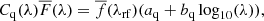
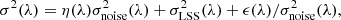
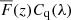
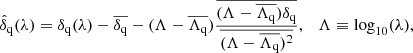
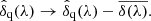
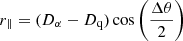
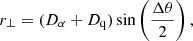
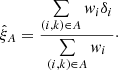
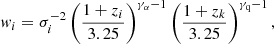
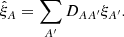
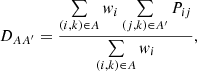
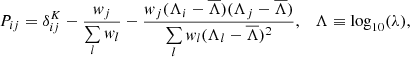
![$$ \begin{aligned} C_{AB} = \frac{1}{W_{A}W_{B}}\sum \limits _{s}W_{A}^{s}W_{B}^{s}\left[\xi _{A}^{s}\xi _{B}^{s}-\xi _{A}\xi _{B}\right], \end{aligned} $$](/articles/aa/full_html/2019/09/aa35641-19/aa35641-19-eq27.gif)
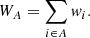
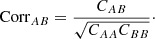
![$$ \begin{aligned} \hat{\xi }_A = \sum \limits _{A^\prime } D_{AA^\prime }\left[ \xi _{A^\prime }^\mathrm{cosmo} + \xi _{A^\prime }^\mathrm{bb} \right], \end{aligned} $$](/articles/aa/full_html/2019/09/aa35641-19/aa35641-19-eq32.gif)
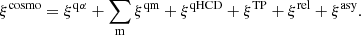
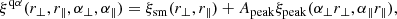
![$$ \begin{aligned} \alpha _{\parallel } = \frac{\left[D_{\rm H}(z_{\rm eff})/r_{\rm d}\right]}{\left[D_{\rm H}(z_{\rm eff})/r_{\rm d}\right]_{\rm fid}} \quad \mathrm{and}\quad \alpha _{\perp } = \frac{\left[D_{\rm M}(z_{\rm eff})/r_{\rm d}\right]}{\left[D_{\rm M}(z_{\rm eff})/r_{\rm d}\right]_{\rm fid}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/09/aa35641-19/aa35641-19-eq38.gif)
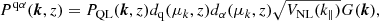
![$$ \begin{aligned} P_{\rm QL}(\boldsymbol{k},z) = P_{\rm sm}(k,z) + \exp \left[-(k_{\parallel }^2\Sigma _{\parallel }^2+k_{\perp }^2\Sigma _{\perp }^2)/2\right]P_{\rm peak}(k,z), \end{aligned} $$](/articles/aa/full_html/2019/09/aa35641-19/aa35641-19-eq40.gif)