| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 42 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629929 | |
| Published online | 21 March 2017 | |
X-shooter spectroscopy of young stellar objects in Lupus
Accretion properties of class II and transitional objects⋆
1 INAF-Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
e-mail: alcala@oacn.inaf.it
2 Scientific Support Office, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
3 INAF-Osservatorio Astrofisico di Arcetri, via Moiariello 16, Largo E. Fermi 5, 50125 Firenze, Italy
4 DIAS/School of Cosmic Physics, Dublin Institute for Advanced Studies, 31 Fitzwilliams Place, Dublin 2, Ireland
5 INAF-Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
6 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
7 Excellence Cluster Universe, Boltzmannstr. 2, 85748 Garching, Germany
8 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00078 Monte Porzio Catone, Italy
9 INAF–Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
10 Institute for Astronomy, University of Hawaii at Manoa, Honolulu, HI 96822, USA
11 INAF–Osservatorio Astornomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
Received: 19 October 2016
Accepted: 15 December 2016
The mass accretion rate, Ṁacc, is a key quantity for the understanding of the physical processes governing the evolution of accretion discs around young low-mass (M⋆ ≲ 2.0 M⊙) stars and substellar objects (YSOs). We present here the results of a study of the stellar and accretion properties of the (almost) complete sample of class II and transitional YSOs in the Lupus I, II, III and IV clouds, based on spectroscopic data acquired with the VLT/X-shooter spectrograph. Our study combines the dataset from our previous work with new observations of 55 additional objects. We have investigated 92 YSO candidates in total, 11 of which have been definitely identified with giant stars unrelated to Lupus. The stellar and accretion properties of the 81 bona fide YSOs, which represent more than 90% of the whole class II and transition disc YSO population in the aforementioned Lupus clouds, have been homogeneously and self-consistently derived, allowing for an unbiased study of accretion and its relationship with stellar parameters. The accretion luminosity, Lacc, increases with the stellar luminosity, L⋆, with an overall slope of ~1.6, similar but with a smaller scatter than in previous studies. There is a significant lack of strong accretors below L⋆ ≈ 0.1 L⊙, where Lacc is always lower than 0.01 L⋆. We argue that the Lacc − L⋆ slope is not due to observational biases, but is a true property of the Lupus YSOs. The log Ṁacc – log M⋆ correlation shows a statistically significant evidence of a break, with a steeper relation for M⋆ ≲ 0.2 M⊙ and a flatter slope for higher masses. The bimodality of the Ṁacc – M⋆ relation is confirmed with four different evolutionary models used to derive the stellar mass. The bimodal behaviour of the observed relationship supports the importance of modelling self-gravity in the early evolution of the more massive discs, but other processes, such as photo-evaporation and planet formation during the YSO’s lifetime, may also lead to disc dispersal on different timescales depending on the stellar mass. The sample studied here more than doubles the number of YSOs with homogeneously and simultaneously determined Lacc and luminosity, Lline, of many permitted emission lines. Hence, we also refined the empirical relationships between Lacc and Lline on a more solid statistical basis.
Key words: stars: pre-main sequence / stars: low-mass / accretion, accretion disks / open clusters and associations: individual: Lupus
© ESO, 2017
1. Introduction
The mass accretion rate, Ṁacc, is a crucial parameter for the study of the evolution of accretion discs around young low-mass (M⋆ ≲ 2.0 M⊙) stellar and substellar objects (YSOs). It sets important constraints for disc evolution models (Hartmann et al. 1998) and disc clearing mechanisms (Alexander et al. 2014, and references therein), and is a key quantity for the studies of pre-main sequence (PMS) stellar evolution and planet formation. Observationally, Ṁacc can be derived by measuring the flux in excess to the photospheric one due to the release of the accretion energy in the form of continuum emission and lines (accretion luminosity Lacc) and using the stellar properties (see Gullbring et al. 1998; Hartmann 1998). Continuum excess luminosity has been measured in a number of objects from spectroscopy at different resolutions (e.g., Gullbring et al. 1998; Herczeg & Hillenbrand 2008; Rigliaco et al. 2012; Ingleby et al. 2013, 2014; Alcalá et al. 2014; Manara et al. 2014, 2016a). More often, Lacc has been computed from empirical relations between line luminosity, Lline, and Lacc (e.g. Natta et al. 2006; Fang et al. 2013a; Biazzo et al. 2012; Antoniucci et al. 2014; Manara et al. 2015, and reference therein). The results of these works showed that Ṁacc shows up to three orders of magnitude of unexplained spread for stars of similar mass and age and over the mass spectrum.
During the class II phase – after the protostar has almost entirely dispersed its envelope but is still actively accreting from the optically thick accretion disc – the stellar mass undergoes negligible changes. Therefore, the Ṁacc vs. M⋆ relation represents a diagnostic tool for the evolution of Ṁacc (Clarke & Pringle 2006) and for the process driving disc evolution (Ercolano et al. 2014). The distribution of class II YSOs in the Ṁacc – M⋆ plane has been obtained for a number of different star-forming regions (SFRs); in all regions studied so far (e.g. ρ-Oph, Taurus, σ-Ori, ONC, Tr37, NGC 2264) it has been found that, while there is a positive correlation of Ṁacc with the stellar mass, Ṁacc has a very large scatter, sometimes more than 3 dex for objects with the same M⋆ (Muzerolle et al. 2005; Natta et al. 2006; Biazzo et al. 2012; Antoniucci et al. 2014,and references therein).
Theoretically, both the steep dependence of Ṁacc on M⋆ and the large scatter of Ṁacc values are a somewhat surprising finding, in that it appears to indicate that the accretion processes scale not just with M⋆ (Natta et al. 2006). Effects such as variability, or the natural decline of Ṁacc with age in viscous disc evolution have been ruled out as possible source of the large spread within individual SFRs (Natta et al. 2006; Costigan et al. 2014; Venuti et al. 2014). It appears more likely to be related to a spread in the properties of the parental cores, their angular momentum in particular (e.g. Dullemond et al. 2006, and references therein), and the disc mass. The scatter of Ṁacc may be also related to a spread of stellar properties, such as X-ray and EUV emission (Clarke & Pringle 2006; Ercolano et al. 2014), or on the competition between different accretion mechanisms, such as viscosity and gravitational instabilities at different stellar masses (Vorobyov & Basu 2008, 2009; DeSouza & Basu 2017). These latter authors suggested that two different exponents for the power-law relation Ṁacc∝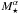 , at different mass regimes, can better describe the data than a single power-law. On the other hand, Stamatellos & Herczeg (2015) claim that very low-mass brown dwarfs and planetary-mass objects may follow a different Ṁacc – Mobject scaling relationship than stars, with their accretion rate being almost independent of the central object mass.
, at different mass regimes, can better describe the data than a single power-law. On the other hand, Stamatellos & Herczeg (2015) claim that very low-mass brown dwarfs and planetary-mass objects may follow a different Ṁacc – Mobject scaling relationship than stars, with their accretion rate being almost independent of the central object mass.
A third quantity, namely the disc mass, is likely to play an important role, as it is predicted that both M⋆ and Ṁacc should scale with the disc mass Mdisc in viscously evolving discs (Hartmann et al. 1998). However, the efforts to observationally confirm such scaling relations have failed in the past mainly because of the limited sensitivity of the interferometers used for measuring the bulk of dust and gas mass of protoplanetary discs, and because different methodologies to measure the stellar and accretion properties produce a large scatter in the relationships. A robust Mdisc–M⋆ correlation for Taurus class II YSOs has been confirmed by Andrews et al. (2013), and we are now in a position that allows us to study the relationship between these three fundamental quantities in a statistically meaningful way for a number of star-forming regions. On one hand, VLT/X-shooter is delivering homogeneous and precise determinations of both accretion and stellar properties (e.g. Rigliaco et al. 2012; Manara et al. 2013a, 2014, 2015, 2016a; Alcalá et al. 2014). On the other hand, the Atacama Large Millimeter Array (ALMA) now provides sufficient sensitivity and resolution at sub-mm wavelengths to detect and measure the mass of protoplanetary discs around YSOs with a mass down to 0.1 M⊙ (Ansdell et al. 2016; Pascucci et al. 2016; Barenfeld et al. 2016).
In a previous work (Alcalá et al. 2014, henceforth A14) we studied the stellar and accretion properties of 36 accreting YSOs mainly in the Lupus I and III clouds, spanning a range in mass from ~0.03 to ~1.2 M⊙, but mostly with 0.1 M⊙<M⋆< 0.5 M⊙. The analysis was based on spectroscopic data acquired with the VLT/X-shooter spectrograph. We used the continuum UV-excess emission as a measure of the accretion luminosity, Lacc, hence of Ṁacc, and provided improved relationships between Lacc and the luminosity, Lline, for a large number of emission lines. In A14 we found that the log Ṁacc – log M⋆ correlation has a slope 1.8 ± 0.2, but a more important result was that the relationship has a much smaller dispersion (~0.4 dex) with respect to previous studies. Although the level of accretion was not a criterion for the target selection, the YSOs analysed by A14 represent a sub-sample of the total class II population in Lupus. Therefore, in order to confirm or disprove the result avoiding any type of bias, it was necessary to expand our analysis to a sample as complete as possible, by including as many class II sources as possible and using the same methodologies as in A14 with X-shooter to derive the stellar and accretion properties.
In this paper we present a synthesis of the accretion properties of an almost complete sample of class II YSOs in Lupus. Our study combines our previous sample in A14 with new X-shooter observations of 55 additional objects classified as class II and transition disc YSOs based mainly on the analysis of their spectral energy distribution (SED; e.g. Merín et al. 2008; Evans et al. 2009, and references therein) and/or the presence of strong emission lines in spectra with limited resolution and wavelength coverage (Comerón 2008). The stellar and accretion properties of the combined sample have been homogeneously and self-consistently derived here, allowing an unbiased study of accretion and its relationship with the stellar parameters. The results on the stellar parameters and Ṁacc presented here were combined with those of the ALMA survey of Lupus protoplanetary discs to study the Mdisc–M⋆ and Mdisc–Ṁacc relationships in the papers by Ansdell et al. (2016) and Manara et al. (2016b), respectively.
The new sample, the observations, and data processing are presented in Sect. 2. In Sect. 3 the newly observed sample is characterised in terms of its stellar and accretion properties and the results are compared with those in A14. The total sample is characterised in Sect. 4 in terms of stellar masses and mass accretion rates, while the accretion properties are examined in relation with the stellar parameters in Sect. 5. The results are then discussed in Sect. 6. Our main conclusions are summarised in Sect. 7. The relationships between Lacc and Lline presented in A14 are revisited in Appendix B using the total sample.
2. Sample, observations, and data reduction
All the data used in this paper were acquired with the X-shooter spectrograph (Vernet et al. 2011) at the VLT. The capabilities of X-shooter in terms of wide spectral coverage (310−2500 nm), resolution and limiting magnitudes allow us to assess simultaneously the mass accretion and outflow, and disc diagnostics, from the UV and optical to the near IR.
2.1. Sample
The complete class II sample in the Lupus I, II, III and IV clouds, as selected from the Spitzer c2d survey (Merín et al. 2008) and from the previous literature (e.g. Hughes et al. 1994; Comerón 2008), contains ~101 objects. Several of these were only candidate YSOs.
The sample studied in this paper consists mainly of two sets of low-mass class II YSOs in the aforementioned Lupus clouds. The first one comprises the 36 objects published in A14, observed within the context of the X-shooter INAF/GTO (Alcalá et al. 2011) project; for simplicity we will refer to it as the “GTO sample” throughout the paper. One additional source namely Sz105, was investigated with X-shooter during the GTO, but rejected as a legitimate YSO (see below). The second sample consists of 49 objects observed during ESO periods 95 and 97 (1 April−30 September 2015 and 1 April−30 September 2016, respectively). In addition, we include here six objects observed with X-shooter in other programmes taken from the ESO archive. In total, 55 objects were newly analysed here and we will refer to them as the “new sample”. The main goal of these new observations was to expand our previous analysis in A14 to a more complete sample. Among the 101 YSO candidates, there are seven young brown dwarf candidates by Nakajima et al. (2000) which were not observed by us because they are too faint (J> 17 mag) for X-shooter. We also stress that sources with flat SEDs are not considered in our study (however see Appendix C), and that we do not include objects of the Lupus V and VI clouds.
In total, we have investigated 92 Lupus YSO candidates with X-shooter. The 92 spectroscopically studied stars comprise the 36 YSOs and Sz105 investigated in A14 and the 55 objects studied here. As will be shown in Sect. 3.1, 11 of the 92 are confirmed to be giants unrelated to the Lupus star forming region. Therefore, the total sample of this paper, reported in Table A.2, includes 81 legitimate YSOs. An additional YSO candidate (SSTc2d J155945.3-415457), not included in our X-shooter observations, was confirmed to be an asymptotic giant branch (AGB) star in a previous work (Mortier et al. 2011). Thus, assuming that the seven Nakajima et al. (2000) brown dwarf candidates are also legitimate YSOs, the total sample of bona fide class II YSOs in the Lupus I, II, III and IV clouds would comprise 89 (= 101−12) objects. Therefore, our 81 YSOs (36 of A14 plus 45 of this paper) represent more than 90% of the total. We note that 12 out of the 81 YSOs have been identified with transitional discs based on mid and far IR (Merín et al. 2008; Romero et al. 2012; Bustamante et al. 2015) and/or sub-millimeter observations (Tsukagoshi et al. 2014; Ansdell et al. 2016; van der Marel et al. 2016). The study of transitional discs is important for the understanding of disc evolution in general and of the mechanisms regulating the disc dispersal in particular (e.g. Espaillat et al. 2014). High levels of accretion have been detected in some YSOs with transitional discs in the past (Espaillat et al. 2014; Alcalá et al. 2014; Manara et al. 2014, and references therein). It is thus important to also investigate the accretion properties of the Lupus YSOs with transitional discs in comparison with those with full discs. Finally, we adopted a distance of 150 pc for objects in the Lupus I, II and IV clouds, and 200 pc for those in the Lup III cloud (see Comerón 2008, for a discussion on the distance of the Lupus clouds).
2.2. Observations
As in the GTO, most of the targets in the new sample were observed using the 1.̋0/0.̋9/0.̋9 slits in the UVB/VIS/NIR arms, respectively, yielding resolving powers of 5100/8800/5600. Only Sz102 was observed through the 0.̋5/0.̋4/0.̋4 slits in the UVB/VIS/NIR arms, respectively, yielding resolving powers of 9100/17400/10500. In Frasca et al. (2017) we have measured the resolution using several exposures of the ThAr calibration lamp and found that it remained basically unchanged in the period between 2011 to 2015. The high resolution mode for the later target was chosen in order to be able to study the outflows by measuring the gas kinematics more accurately (Whelan et al., in prep.). Table 1 presents the observing log for the new targets. In order to achieve the best possible accuracy in flux calibration and account for slit losses, short exposures (of ~10% the science exposures) were performed using the wide slit of 5.̋0 right before the science observations. These were part of the same observing block for each target, minimising overheads and allowing accurate spectrophotometry of the targets.
Most of the targets were observed in one cycle using the A-B nodding mode, while five (AKC2006-18, 2MASS J16081497-3857145, Lup 607, 2MASS J16085373-3914367, and Sz 108B) were observed in two cycles using the A-B-B-A nodding mode. All the 5.̋0-slit observations were performed in stare mode. For one target (2MASS J16085373-3914367) there was no detection in the UVB arm.
During the observations, the star Sz 81 showed up in the acquisition image as a visual binary with a separation of 1.̋9 and PA = 20°. Except for Sz 102 and the visual binary Sz 81, all targets were observed at parallactic angle in order to minimise the atmospheric dispersion. Sz102 was observed both with the slit along the known outflow (PA = 95°, Comerón & Fernández 2011) and perpendicular to it (PA = 5°), while the components of the visual binary Sz 81 were observed both by aligning the slit at PA = 20°.
The data gathered from the ESO archive were acquired using the 0.̋5/0.̋4/0.̋4 slits in the UVB/VIS/NIR arms, respectively, and adopting the same AB nodding strategy as explained above, but with different number of cycles as indicated in Table 1. These data were not taken using the wide slit prior to the narrow slit observations. Thus, their flux calibration is more uncertain.
Several telluric standard stars were observed with the same instrumental set-up and at similar airmass as the targets. Typically, two flux standards per night were observed through a 5 arcsec slit to calibrate the flux.
Observing log for the new sample.
2.3. Data reduction
The data processing was done using the same methods as for the GTO sample described in A14. Here we summarise the procedures. The basic processing of bias- or dark subtraction, flat-fielding, optimal extraction, wavelength calibration, and sky subtraction, and correction for instrumental response was performed using the X-shooter pipeline v.2.3.0 (Modigliani et al. 2010). The nodding mode of the pipeline was used for the reduction of the nodding observations, while the wide-slit observations were reduced using the stare mode. Post-pipeline processing was done using IRAF1. The telluric correction was performed independently in the VIS and NIR spectra, as explained in Appendix A of A14. The X-shooter scale of ~0.16 arcsec/pix along the slit direction allowed us to resolve the components of the binary Sz81, which in turn enabled us to extract the spectra of the individual components without any light contamination. The flux-calibrated spectra observed with the wide slit were used to correct the spectra acquired with the narrow slits for slit losses. The correction factors, which depend mainly on seeing variations, are in the ranges 1–2.9, 1–3.2 and 1–2.7 for the UVB, VIS and NIR arms respectively. Since all the targets were observed at low airmass, no wavelength dependence was found in these correction factors.
Finally, photometric data from the literature were used to compare the spectroscopic fluxes with the photometric ones. The spectra follow the corresponding SED shape very well, with most of them matching the photometric fluxes at the 10% level. In a few objects (SSTc2dJ154508.9-341734, MY Lup, Sz131, Sz133 and Sz98) we found that the flux ratio may be up to a factor 2, meaning 0.3 dex in log scale, which is well within the expected range of variability for class II YSOs (see Venuti et al. 2014, and references therein).
In order to estimate the flux losses of the archive data, observed with the narrow slits, we compared the flux of the spectra with NIR photometric fluxes from 2MASS, where the variability effects are minimised. The correction factors are consistent with those based on the spectrophotometry. However, since photometry is not symultaneous with the X-shooter observations, the spectroscopic flux may be uncertain by a factor of about two. In addition, EX Lup is the well known prototype of EXors (Comerón 2008; Sipos et al. 2009; Lorenzetti et al. 2012; Sicilia-Aguilar et al. 2015) hence, large variations may be expected. However, we find good agreement between the flux of the spectrum after correction for slit losses and the photometric flux in the V-band, gathered from the AAVSO database and quasi-simultaneous to the X-shooter observation (see Appendix D).
3. Results
3.1. Non-members
Nine objects of the new sample (see Table 1), without appropriate spectroscopy in the past but previously classified as class II YSOs, lack the Li i λ670.8 nm absorption line and show narrow photospheric lines, with their spectrum resembling more that of a giant than of a PMS star. A detailed analysis of the radial velocity, combined with determinations of the surface gravity based on our X-shooter spectra (Frasca et al. 2017), demonstrated that these objects are indeed background giants. Likewise, one additional object (SSTc2dJ161045.4-385455) for which the Li i line has been detected, was found to be a background Li-rich giant based on discrepant surface gravity and radial velocity with respect to the Lupus YSOs. Another object namely Sz105, previously classified as class II YSO candidate based on the Spitzer survey, has been rejected as YSO in A14 and confirmed to be a background giant in Frasca et al. (2017).
Thus, including SSTc2d J155945.3-415457 classified as an AGB star by Mortier et al. (2011) and not observed by us, there are 12 objects previously classified as class II YSO candidates, which are unrelated to Lupus. It is also worth mentioning that 10 of these were included in the 95% complete ALMA survey of Lupus protoplanetary discs by Ansdell et al. (2016) and none were detected. That survey detected ~70% of the observed objects in 890 μm continuum emission. This highlights the importance of combining ALMA discs surveys with detailed optical/IR classification of the host star (see also Pascucci et al. 2016; and Manara et al. 2017).
The new sample then consists of the 45 legitimate YSOs listed in Table 1. The objects rejected by us as class II YSOs are listed in the bottom of this table and their properties will be discussed in detail in the parallel paper by Frasca et al. (2017). The physical parameters and accretion properties of the 45 confirmed YSOs are derived next and compared with those of the GTO sample. The complete list of 81 confirmed class II and transitional YSOs of this work is reported in Table A.2.
3.2. Accretion luminosity
The continuum excess emission in YSOs is most easily detected as Balmer continuum emission (see Valenti et al. 1993; Gullbring et al. 1998; Herczeg & Hillenbrand 2008; Rigliaco et al. 2012; Manara et al. 2016a, A14 and references therein). In A14, Balmer continuum emission was evident in all the YSOs of the GTO sample. In the new sample the results are the following: one object (2MASSJ16085373-3914367) lacks information in the UVB (see Sect. 2.2). Balmer continuum emission is seen in 38 objects. All of them, but the K2-type star Sz102, are later than K4. Other 3 M-type objects (Lup607, SSTc2dJ154508.9-341734, 2MASSJ16085324-3914401) have noisy UVB spectra. In three objects (MY Lup, Sz68, and SSTc2dJ160830.7-382827), all earlier than K3, the Balmer continuum emission is not evident from the spectra. This is because the Balmer continuum emission is more easily seen in the spectra of late-type (>K5) YSOs than in the early types due to the higher contrast between photospheric emission and continuum emission.
To derive the accretion luminosity, Lacc, of the new sample we have followed the methods described by A14, but using the procedures of Manara et al. (2013b). Briefly, the spectrum of each class II YSO was fitted as the sum of the photospheric spectrum of a class III template and the emission of a slab of hydrogen; the accretion luminosity is given by the luminosity emitted by the slab. The stellar and accretion parameters are self-consistently derived by finding the best fit among a grid of slab models and using the continuum UV-excess emission and the broad wavelength range covered by the X-shooter spectra (330−2500 nm) to constrain both the spectral type of the target and the interstellar extinction toward it. The best fit is found by minimizing a 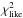 distribution. The stellar parameters are reported in Table A.2 and the complete set of plots showing the fits for the 44 targets detected in the UVB arm are provided in figures from E.7 to E.11. For consistency with the literature and homogeneity with our previous work we did not attempt to fit the hydrogen emission lines, but only the continuum emission. The adopted class III templates and Lacc values corresponding to each YSO are reported in Table A.3. For completeness, the Lacc values for the GTO sample are also included in this table. From our analysis in A14 we estimate that in general the uncertainty on Lacc in log scale is ~0.25 dex.
distribution. The stellar parameters are reported in Table A.2 and the complete set of plots showing the fits for the 44 targets detected in the UVB arm are provided in figures from E.7 to E.11. For consistency with the literature and homogeneity with our previous work we did not attempt to fit the hydrogen emission lines, but only the continuum emission. The adopted class III templates and Lacc values corresponding to each YSO are reported in Table A.3. For completeness, the Lacc values for the GTO sample are also included in this table. From our analysis in A14 we estimate that in general the uncertainty on Lacc in log scale is ~0.25 dex.
For all the objects we also calculated an average Lacc from the luminosity of several emission lines (see Sect. 3.4) and using the log Lacc vs. log Lline relationships reported in A14. In all cases Lacc calculated from the slab modelling is in very good agreement with the average Lacc calculated from the lines. This check was particularly useful for some cases where the low-S/N in the UVB spectrograph arm made the slab modelling difficult.
Based on the slab modelling, UVB excess emission ascribable to accretion is barely evident in five objects (Lup 607, MY Lup, Sz65, Sz68, and SST c2dJ160830.7-382827). The analysis of the emission lines in these objects in Sect. B.1 shows that their excess emission is close to the chromospheric level. Thus, in the following we consider these objects as weak accretors, and distinguish them in the plots. We do not expect that their Lacc and Ṁacc values are higher than what we measured. In principle one could consider them as upper limits, but our results are not affected if we assume them as such (see Sect. 5).
Two objects, namely Lup 607 and SSTc2dJ160703.9-391112, have a rather low accretion luminosity (Lacc≈ 10-5 L⊙). The former is a weak accretor (cf. Sect. B.1), while the other one is sub-luminous, hence also sub-luminous in Lacc (see Sect. 7.4 in A14). Finally, in the case of the target 2MASS J16085373-3914367, which lacks UVB data (see Sect. 2.2), Lacc was calculated from the luminosity of 7 permitted emission lines detected in the VIS and NIR and using the Lacc – Lline relationships revisited in Appendix B. The width and intensity of the emission lines in the VIS and NIR, as well as the computed Lacc and Lacc/L⋆ values confirm that the object is accreting.
3.3. Spectral type, extinction and luminosity of the new sample
We focus here on the determination of the parameters which are necessary for studying the accretion properties, namely spectral type and extinction, effective temperature, stellar luminosity, and radius, with the mass determination being deferred to Sect. 4. Other properties like radial velocity, surface gravity, as well as lithium and other elemental abundances for the whole X-shooter sample will be analysed in parallel papers by Frasca et al. (2017) and Biazzo, et al. (in prep.).
In addition to the self-consistent methods described in Sect. 3.2, we have also used the methods of our previous study in A14 to derive spectral type and extinction for the new sample. For the late type (M0 or later) stars spectral types were calculated using the spectral indices by Riddick et al. (2007) and the H2O-K2 index from Rojas-Ayala et al. (2012) for the NIR spectra. For the K-type objects we derived spectral types by direct comparison of class III templates after artificially reddening the templates, until the best match with the class II YSOs is found. Several class III YSOs, indistinctly quoted here as class III YSOs or class III templates, were observed throughout the various Italian-GTO star formation runs, and their properties were published in separate papers (Manara et al. 2013a; Stelzer et al. 2013b). A few other class III templates, filling-in the gaps of spectral type distribution of the previous templates, were used here and will be published in Manara et al. (in prep.). The use of templates to derive spectral types for the M-type objects provides basically the same results as when using spectral indices (see Frasca et al. 2017). Both the A14 methods and those described in Sect. 3.2 provide consistent results within errors hence, for homogeneity we adopted the results of the self-consistent methods. The spectral types and extinction values are reported in Table A.2. The uncertainties in spectral type are ±0.5 sub-class for the M-type objects and ±1 sub-class for the earlier type stars. The estimated uncertainty in extinction is ≤0.5 mag.
The spectral types of the new sample range from K0 to M7, with an overabundance of M4-M5 objects (see Fig. 1 upper panel). While the GTO sample did not include objects with spectral type earlier than K7, the new sample contains 11 objects earlier than that. Our spectral types and extinction values are generally consistent within errors with those in the literature.
 |
Fig. 1 Distributions of spectral type (upper panel), effective temperature (middle panel) and luminosity (lower panel) of the GTO (red histograms) and total (blue histograms) samples. |
As in A14, the effective temperature, Teff, was derived using the temperature scales given by Kenyon & Hartmann (1995) for the K-type stars, and by Luhman et al. (2003) for the M-type YSOs. These Teff values, as well as those in the GTO in A14, are in very good agreement with those determined using the ROTFIT code (see Frasca et al. 2017). The stellar luminosity was derived using our flux calibrated X-shooter spectra in the same way as described in Manara et al. (2013b), that is, by direct integration of the spectra and using the synthetic BT-Settl spectra (Allard et al. 2012), of the same Teff as the objects, to extrapolate the X-shooter spectra to wavelengths shorter than 310 nm and longer than 2500 nm. The error in YSO luminosity was estimated from the signal-to-noise (S/N) of the spectra and the error in visual extinction. The details are given in Appendix A. The error in extinction dominates the overall uncertainty in all cases, although for some targets with a low S/N spectrum the contribution of photon noise to the error becomes important. The stellar radius was calculated from the effective temperature and stellar luminosity. All the physical stellar parameters are listed in Table A.2, which includes the parameters of the GTO sample for completeness.
In comparison with the GTO sample, the new sample extends to Teff values as high as 5100 K, but about 70% are cooler than 4000 K (see Fig. 1, middle panel). Likewise, most of the objects have a luminosity lower than 0.5 L⊙, with 11 exceeding 1 L⊙ (see Fig. 1, lower panel).
3.4. Emission lines
A large number of permitted and forbidden emission lines displaying a variety of profiles were detected. The analysis of forbidden emission lines for the GTO sample has been published by Natta et al. (2014), and for the total sample in a parallel paper by Nisini et al. (in prep.).
The permitted emission lines studied here are the same as those in Table 4 of A14, except for the He i λ1082.9 nm line. Because its complexity both in terms of line profile and interpretation as accretion or wind diagnostic (see Edwards et al. 2006) we decided not to include this line here, but defer its analysis to a future paper. Note also that the line appears blended with the Si iλ1082.7091 nm photospheric line, which is very strong in late-type stars. The number of detections of each line is given in column five of Table B.1. For consistency with A14, our analysis is restricted to Balmer lines up to H15, Paschen lines up to Pa 10, and the Brγ line, as well as the helium, calcium, sodium, and oxygen lines.
The flux at the Earth in permitted lines was computed by directly integrating the flux-calibrated spectra using the splot package under IRAF, and following the procedures described in A14, including estimates of upper limits for non-detections. The observed fluxes, equivalent widths, and their errors are reported in several tables provided in Tables E.1 to E.9. The flux errors are those resulting from the uncertainty in continuum placement. The estimated ~10% uncertainty of flux calibration (see Sect. 2.3) should be added in quadrature. The contribution of the photospheric absorption lines of the Hα, Na i D lines and the Ca ii IR triplet lines (IRT), strongest in the K and early-to-mid M-type objects, were removed in all spectra as described by Frasca et al. (2017). The luminosity of the different emission lines was computed as Lline= 4πd2·fline, where d is the YSO distance listed in Table A.2 and fline is the extinction-corrected flux of the lines.
Together, the GTO and new sample more than double the number of YSOs in our previous work, and have homogeneously and simultaneously determined Lacc and Lline values. Therefore, it is worth revisiting the Lacc– Lline relationships given in Sect. 5 of A14. This is reported in Appendix B.
4. The total sample
The new objects, combined with the GTO targets constitutes our total sample of 81 YSOs for the study of accretion in this paper. This sample is complete at more than the 90% level (see Sect. 2.1) and is presented in Table A.2. In this section we characterise it by deriving masses, and mass accretion rates in a homogeneous and self-consistent way.
4.1. Stellar masses
We estimated masses by interpolating PMS evolutionary models (see Appendix A). In A14 we have used the Baraffe et al. (1998) tracks, which were suited for deriving the mass of all the YSOs because they cover well the range in Teff and L⋆ of the GTO sample. As shown in Sect. 3.3 the new sample extends to higher values of Teff and L⋆ than those of the GTO, i.e. to masses not covered by the Baraffe et al. (1998) tracks. The Baraffe et al. (1998) models have been updated by Baraffe et al. (2015), but as the previous models, they are for masses ≤1.4 M⊙. The Siess et al. (2000) tracks include higher masses, but their lowest mass is 0.1 M⊙.
The Hertzsprung-Russell diagram for the total sample is shown in Fig. 2 with the PMS evolutionary tracks by Siess et al. (2000) overplotted. Only three objects of the total sample have a mass significantly lower than 0.1 M⊙ on these tracks. In Appendix A we describe how we compared the resulting masses of the total sample when adopting four different models. The Baraffe et al. (2015) and the Siess et al. (2000) tracks yield very similar results in the overlapping mass range. Therefore, for our analysis of accretion in Sect. 5 we adopted the Siess et al. (2000) tracks to derive masses ≥0.1 M⊙ and those of Baraffe et al. (2015) for the three objects with lower values. The derived masses are given in Table A.2. More details on the mass determination and its error are provided in that Appendix, where the D’Antona & Mazzitelli (1997) models are additionally used.
 |
Fig. 2 Hertzsprung-Russell diagram for the total sample. The GTO and new samples are represented with the black symbols. The seven sub-luminous objects described in the text are represented with open circles. The dashed lines show the isochrones, reported by Siess et al. (2000), while the continuous lines show the low-mass Pre-Main Sequence evolutionary tracks by the same authors as labelled. |
We note that there are seven sub-luminous objects, namely Par-Lup3-4, Lup706, Sz 123B, Sz 106, Sz 102, Sz 133, and SSTc2dJ160703.9-391112. The first four were part of the GTO, while the latter three are from the new sample. Both Sz 102 and Sz 133 fall below the Zero-Age Main Sequence hence we cannot estimate their mass. These two objects were previously known to be sub-luminous, with their disc most likely seen edge-on (Hughes et al. 1994). Sz 102 (also known as Krautter’s star) is one of the most famous YSOs in Lupus known to host a strong outflow (see, Krautter 1986; Whelan et al., in prep., for details). The seven sub-luminous objects are represented with open symbols in Fig. 2 and are flagged in Table A.2. MY Lup, the hottest object in the sample, appears rather sub-luminous with respect to YSOs of similar spectral type. Based on ALMA data, its disc inclination angle has been measured at 73° (Ansdell et al. 2016). Thus, we cannot exclude that the star is at least partially obscured by the disc. As a consequence, the mass of MY Lup may be underestimated.
The distribution of M⋆ for the total sample, according to the Siess et al. (2000) tracks, is shown in Fig. 3. All YSOs have masses lower than 2.2 M⊙, with only six having a mass higher than 1 M⊙, and about 76% have a mass lower than 0.5 M⊙. We note that these numbers do not account for the sub-luminous YSOs Sz 102 and Sz 133. Apart from the six objects with a mass higher than 1 M⊙, both the M⋆ distributions of the GTO and new samples are similar, peaking at ~0.2 M⊙. With a mass of 0.02 M⊙, that is, close to the planetary mass regime, 2MASS J16085953-3856275 is the lowest mass object in the total sample.
 |
Fig. 3 Histograms of M⋆. The GTO sample is shown with the red histogram, while the total sample is shown with the blue one. |
The distribution of the Lupus stars on the HR diagram suggests an age of ~3 Myr. We note that stars with M⋆≈ 0.1 M⊙ have a very large dispersion in L⋆, with about 1/2 apparently older than 10 Myr. This effect is seen in many star forming regions, and has been interpreted by Herczeg & Hillenbrand (2015) as an indication that the theoretical isochrones for the lowest mass stars are in reality much steeper than what the current models predict.
4.2. Mass accretion rate of the total sample
The accretion luminosities of the total sample given in Table A.3 were converted into mass accretion rates, Ṁacc, using the relation 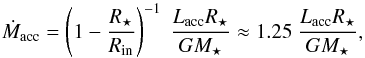 (1)where R⋆ and Rin are the YSO radius and inner-disc radius, respectively (Gullbring et al. 1998; Hartmann 1998). For consistency with previous studies (e.g. Gullbring et al. 1998; Herczeg & Hillenbrand 2008; Rigliaco et al. 2012; Manara et al. 2016a, and A14), here we also assumed Rin to be 5 R⋆. The R⋆ and M⋆ values were taken from Table A.2. The results on Ṁacc are listed in Table A.3. As in A14, we estimate that the cumulative relative uncertainty in Ṁacc in log scale is about 0.42 dex. The four Ṁacc values reported in Table A.2 for each YSO correspond to the four evolutionary models adopted to derive the mass. The differences on Ṁacc when adopting different models are well within the errors.
(1)where R⋆ and Rin are the YSO radius and inner-disc radius, respectively (Gullbring et al. 1998; Hartmann 1998). For consistency with previous studies (e.g. Gullbring et al. 1998; Herczeg & Hillenbrand 2008; Rigliaco et al. 2012; Manara et al. 2016a, and A14), here we also assumed Rin to be 5 R⋆. The R⋆ and M⋆ values were taken from Table A.2. The results on Ṁacc are listed in Table A.3. As in A14, we estimate that the cumulative relative uncertainty in Ṁacc in log scale is about 0.42 dex. The four Ṁacc values reported in Table A.2 for each YSO correspond to the four evolutionary models adopted to derive the mass. The differences on Ṁacc when adopting different models are well within the errors.
We derived mass accretion rates in the range from ~ 5 × 10-12 M⊙ yr-1 to ~ 6 × 10-8 M⊙ yr-1, that is, similar to the Ṁacc range of the GTO sample. With a Ṁacc~ 6 × 10-8 M⊙ yr-1 the strongest accretors in the total sample are the ~0.8 M⊙ YSOs Sz 83, Sz 98, and GQ Lup. We note that these numbers do not account for the sub-luminous objects. When corrected for disk obscuration Sz 102 may be among the strongest accretors. The weakest accretor is the ~0.07 M⊙ object AKC2006-18 with Ṁacc of 5.8×10-12 M⊙ yr-1. With M⋆ = 0.02 M⊙, 2MASS J16085953-3856275 is close to the planetary mass regime, but its mass accretion rate of 2.4 × 1-11 M⊙ yr-1 is similar or higher than that of objects with a mass ≈0.1 M⊙.
5. Accretion properties of the total sample
In this section we present the results of the accretion properties of the total sample in relationship with the YSOs stellar parameters.
5.1. Accretion luminosity versus YSO luminosity
The accretion luminosity as a function of stellar luminosity is shown in Fig. 4. There is no significant difference between the distribution of points of the new sample in the diagram with respect to the GTO sample, although the global dispersion of the Lacc – L⋆ relationship slightly increased and the trend seems less steep than for the GTO alone. Yet, the data points are apparently less scattered than those of previous samples of other star forming regions like ρ-Oph or σ-Ori (e.g. Natta et al. 2006; Rigliaco et al. 2011; Manara et al. 2015, 2016a,and references therein), where the scatter may be more than 2 dex at a given stellar luminosity.
 |
Fig. 4 Accretion luminosity as a function of stellar luminosity. The transitional discs are shown with crossed squares, while the sub-luminous objects with open circles. The five weak accretors are shown with red symbols. The continuous lines represent the three Lacc vs. L⋆ relations as labelled. Average error bars are shown in the upper left. |
All the Lupus YSOs analysed here fall below the Lacc = L⋆ boundary, with a small fraction of objects (~12%) between 0.1 and 1 L⊙, and many with Lacc/L⋆< 0.01. The fact that our sample lacks YSOs with Lacc > 1 L⋆ is interesting because in other star forming regions like Chamaeleon and Taurus there are class II sources with Lacc≥L⋆ (see Manara et al. 2016a, for Chamaeleon I). This is rather peculiar for class II sources because it is expected that Lacc>L⋆ only in class I sources in which the level of accretion rate is very high. In fact, the luminosity of class I protostars is mainly driven by accretion and not by a photosphere. The point closest to the Lacc = L⋆ boundary corresponds to the sub-luminous YSO Sz 102, whereas the (non sub-luminous) object with the lowest log Lacc value is Lup 607, but its accretion rate is low and comparable with the chromospheric level. The YSOs with transitional discs follow the same trend as the objects with full discs. A linear fit to the data in Fig. 4 using ASURV (Feigelson & Nelson 1985), excluding sub-luminous objects and considering the five weak accretors as upper limits (see Sect. B.1), yields: 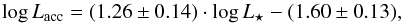 (2)with a standard deviation of 0.7, while considering the five weak accretors as detections the fit yields:
(2)with a standard deviation of 0.7, while considering the five weak accretors as detections the fit yields: 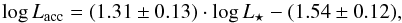 (3)with a standard deviation of 0.7. Therefore, considering the five values as upper limits or real detections has no significant effect on the fits. In the following, we consider the values for the weak accretors as detections. The tool of robust regression analysis based on the least median of squares (LMS; see Rousseuw 1984; Rousseuw & Leroy 1987) implemented in ESO-MIDAS2 yields a slope of 1.55 ± 0.11. Thus, the log Lacc – log L⋆ relationship for the total sample in Lupus is steeper than the Lacc/L⋆= constant lines, as found in previous works for YSOs in other star forming regions (e.g. Natta et al. 2006; Rigliaco et al. 2011).
(3)with a standard deviation of 0.7. Therefore, considering the five values as upper limits or real detections has no significant effect on the fits. In the following, we consider the values for the weak accretors as detections. The tool of robust regression analysis based on the least median of squares (LMS; see Rousseuw 1984; Rousseuw & Leroy 1987) implemented in ESO-MIDAS2 yields a slope of 1.55 ± 0.11. Thus, the log Lacc – log L⋆ relationship for the total sample in Lupus is steeper than the Lacc/L⋆= constant lines, as found in previous works for YSOs in other star forming regions (e.g. Natta et al. 2006; Rigliaco et al. 2011).
 |
Fig. 5 Median values of accretion luminosity as a function of binned stellar luminosities. Each point represents the median of 5 Lacc values with similar L⋆. The horizontal bars show the intervals of log L⋆. |
Interestingly, the distribution of points in the Lacc – L⋆ plane in Fig. 4 shows some evidence of a break at log L⋆ values between −1.2 and −1.0, which corresponds to a mass between 0.1 M⊙ and 0.2 M⊙ at the 3 Myr isochrone (see Fig. 2). There are basically no strong accretors at low stellar luminosities; the vast majority of the (non sub-luminous) objects with L⋆ lower than a tenth of a solar luminosity fall below the Lacc/L⋆= 0.01 line, with only three having Lacc/L⋆ values between 0.1 and 1, and six between 0.01 and 0.1. To further investigate the behaviour of the log Lacc–log L⋆ relationship we calculated median values of Lacc as function of L⋆ (Fig. 5). The width of each of the 15 bins has been chosen to have a similar number of stars in each bin (5). The binning was done over the total sample, but excluding the sub-luminous objects. The plotting errors were estimated as 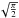 σmean/
σmean/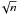 (see Kendall & Stuart 1977), where σmean is the standard deviation over the mean and n is the sample size in each bin (five). The binned log Lacc–log L⋆ relationship rises rapidly with a slope 1.7 ± 0.2 for −1.6 ≲log (L⋆/L⊙) ≲−0.4 and flattens at L⋆≳−0.4 (slope ≈ 1.0), while remaining more or less flat for log L⋆ values below −1.6. However, we stress that the latter behaviour is affected by incompleteness of the sample at very low L⋆ values, that is, in the sub-stellar regime.
(see Kendall & Stuart 1977), where σmean is the standard deviation over the mean and n is the sample size in each bin (five). The binned log Lacc–log L⋆ relationship rises rapidly with a slope 1.7 ± 0.2 for −1.6 ≲log (L⋆/L⊙) ≲−0.4 and flattens at L⋆≳−0.4 (slope ≈ 1.0), while remaining more or less flat for log L⋆ values below −1.6. However, we stress that the latter behaviour is affected by incompleteness of the sample at very low L⋆ values, that is, in the sub-stellar regime.
5.2. Accretion rate versus mass
In Fig. 6 the mass accretion rate is shown as a function of the stellar mass. When including the new sample, the scatter of the Ṁacc−M⋆ relationship increases with respect to the scatter of the GTO sample alone (see also Fig. 8 in A14). A linear fit to all the data taking into account upper limits, but excluding the sub-luminous objects, yields a slope 1.8 ± 0.2, with a dispersion of 0.7 (see Table A.1). Although increased with respect to the value for the GTO sample alone (0.3 using the Siess et al. 2000, tracks), the dispersion of the Ṁacc−M⋆ relationship is still less than in previous investigations in the literature (Muzerolle et al. 2003; Mohanty et al. 2005; Natta et al. 2006; Herczeg & Hillenbrand 2008; Rigliaco et al. 2011; Antoniucci et al. 2011; Biazzo et al. 2012, and references therein). Therefore, at first approximation, we can conclude that for the class II and transitional YSOs in Lupus Ṁacc∝M⋆1.8(±0.2), in agreement with the results of a number of previous studies of other star forming regions (Natta et al. 2006; Muzerolle et al. 2005; Herczeg & Hillenbrand 2008; Rigliaco et al. 2011; Antoniucci et al. 2011; Biazzo et al. 2012; Manara et al. 2016a). Using other evolutionary models to derive M⋆ and Ṁacc yields similar results for the slope of the relationship, although the Baraffe et al. (1998) tracks tend to provide a slightly less steep (slope 1.6 ± 0.2) relationship and the scatter varies significantly depending on the adopted evolutionary tracks (see Appendix A).
 |
Fig. 6 Mass accretion rate Ṁacc as a function of mass for the total sample in log scale. Plotting symbols are the same as in Fig. 4. The average errors in log M⋆ and log Ṁacc are shown in the upper left. The black dashed line shows the double power-law theoretically predicted by Vorobyov & Basu (2009). The continuous magenta lines represent the fits to the data as in Eqs. (4) and (5). The long-dashed blue line shows the robust double-linear fit following the prescription by Manara et al. (2017) as explained in the text. |
The distribution of points in Fig. 6 also shows some evidence of a break at log M⋆ values between −1 and −0.7 (i.e. 0.1 M⊙ and 0.2 M⊙). More interesting, the range of Ṁacc in log scale for the sub-sample with M⋆< 0.2 M⊙ covers about 3.5 dex in less than about 1 dex in M⋆, whereas in comparison the higher-mass sub-sample covers a narrower range of Ṁacc (~2.7 dex) in a wider range of mass (>1 dex). The larger range in log Ṁacc in the low-mass sub-sample in comparison with the range for the high-mass sub-sample is confirmed by the Kaplan-Meier (K-M; Kaplan & Meier 1958) distributions shown in Fig. 7. The difference between the Ṁacc distribution of the sub-samples can be indeed quantified by the K-M distributions. The slope (−0.43 ± 0.01) of the K-M distribution for the high-mass sub-sample is slightly steeper than for the low-mass subsample (slope =−0.38 ± 0.01), and significantly steeper than the K-M distribution of the objects with log Ṁacc≤−10.0 (slope = −0.28 ± 0.02). All these arguments suggest that the distribution of Ṁacc as a function of mass for the high-mass subsample remains flatter than for the low-mass sub-sample, meaning a bi-modal behaviour of the log Ṁacc – log M⋆ relationship.
 |
Fig. 7 Kaplan-Meier distribution of log Ṁacc for the low-mass (M⋆≤ 0.2 M⊙) and high-mass (M⋆>0.2 M⊙) sub-samples are shown in red and blue, respectively. |
The suggestion by Vorobyov & Basu (2008) that the Ṁacc∝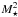 relationship can be explained on the basis of self-regulated accretion by gravitational torques in self-gravitating discs led these authors to conclude that the relationship is better described as a double power-law, with the break occurring at M⋆≈ 0.2 M⊙, (Vorobyov & Basu 2009). The double power-law suggested by these authors is shown in Fig. 6 with the black dashed line. Although the theoretically predicted Ṁacc values are generally higher than the measured ones, they are rather consistent with the upper envelope of the Lupus relationship. As pointed out by Vorobyov & Basu (2009), the theoretical Ṁacc values may be somewhat overestimated with respect to the observed ones. They explained this effect in terms of the adopted values of viscosity in the models. The objects in Fig. 6 falling above the modelled values are the strongest accretors at a given mass and are also among the more luminous on the HR diagram. Separate linear fits to the data, setting 0.2 M⊙ as dividing line, and using the tool of robust regression analysis based on the LMS method (see Rousseuw 1984; Rousseuw & Leroy 1987) yield the following results:
relationship can be explained on the basis of self-regulated accretion by gravitational torques in self-gravitating discs led these authors to conclude that the relationship is better described as a double power-law, with the break occurring at M⋆≈ 0.2 M⊙, (Vorobyov & Basu 2009). The double power-law suggested by these authors is shown in Fig. 6 with the black dashed line. Although the theoretically predicted Ṁacc values are generally higher than the measured ones, they are rather consistent with the upper envelope of the Lupus relationship. As pointed out by Vorobyov & Basu (2009), the theoretical Ṁacc values may be somewhat overestimated with respect to the observed ones. They explained this effect in terms of the adopted values of viscosity in the models. The objects in Fig. 6 falling above the modelled values are the strongest accretors at a given mass and are also among the more luminous on the HR diagram. Separate linear fits to the data, setting 0.2 M⊙ as dividing line, and using the tool of robust regression analysis based on the LMS method (see Rousseuw 1984; Rousseuw & Leroy 1987) yield the following results: 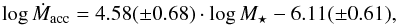 (4)and
(4)and 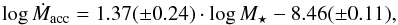 (5)
(5)
for the low and high mass regimes, respectively. These fits, shown as magenta lines in Fig. 6, still resemble the theoretical behaviour, but with a steeper slope for the low-mass regime and the measured values being about 1 dex below the predicted ones. We have performed a further fit setting the breakpoint of the relationship as a free parameter and following the prescription outlined in Manara et al. (2017). These authors performed a statistical test to demonstrate that a double-power law is a slightly better description of the log Ṁacc – log M⋆ relationship than a single-power law. The break point of the robust double-linear fit is at M⋆= 0.29 M⊙, and the slopes for the low and high mass regimes are 3.64 and 1.35, respectively. The double-linear fit is shown with the long-dashed blue line in Fig. 6. As shown in Appendix A the break of the Ṁacc – M⋆ relationship is evident independently of the PMS evolutionary track used to derive M⋆ and Ṁacc. Thus, we conclude that at high masses the relationship is flatter than at low masses.
The steeper slope for the low-mass regime might be biased by the small number statistics at M⋆≲ 0.2 M⊙. A similar binning approach as for the log Lacc–log L⋆ relationship in the previous section, yields the binned log Ṁacc – log M⋆ relationship shown in Fig. 8. In this figure the two-slope relationship by Vorobyov & Basu (2009) is overplotted with a dashed line, but shifted by −1 dex in Ṁacc. Although the predicted Ṁacc values are higher than our measurements, the Lupus results are qualitatively consistent with those models.
 |
Fig. 8 Median values of accretion rate as a function of binned stellar mass. Each point is the median of 5 Ṁacc values with similar M⋆. The plotting errors were computed in the same way as in Fig. 5. The horizontal bars represent the intervals in log M⋆. The dashed line shows the two power-law relationship by Vorobyov & Basu (2009), vertically shifted by −1 dex. |
Finally, another interesting result is that most of the YSOs with transitional discs are well mixed with those of full discs in the log Ṁacc – log M⋆ plot, suggesting that their accretion properties are in general similar to those of YSOs with full discs, in agreement with previous results (Manara et al. 2014; Espaillat et al. 2014). We note, however, that there are no transitional YSOs exhibiting levels of accretion as high as those displayed by some YSOs with full discs and at a given mass some of them (e.g. MY Lup and SSTc2dJ160830.7-382827) are among the weakest accretors in the total sample.
6. Discussion
A detailed observational study of accretion and its evolution requires complete and homogeneous samples of YSOs. The sample of class II and transitional YSOs studied here is complete at a level of more than 90% with respect to the total sample of this type of objects in the Lupus I, II, III and IV clouds. The stellar and accretion properties of the sample have been self-consistently derived, allowing an unbiased study of the accretion and its relationship with the stellar parameters. We have shown that the accretion luminosity and stellar luminosity of the Lupus class II and transitional YSOs are correlated with a lower scatter in comparison with previous studies of YSOs in other star forming regions (e.g. Natta et al. 2006; Rigliaco et al. 2011,and references therein). A similar low scatter has been found recently for the Lacc–L⋆ relationship of the Chamaeleon I YSOs (Manara et al. 2016a), analysed with similar methodologies as here.
The Lupus correlation between Lacc and L⋆, when fitted with a single power-law, is similar within the errors to that found in previous work (e.g. Natta et al. 2006). Clarke & Pringle (2006) pointed out that the distribution of points in the Lacc – L⋆ plane more or less fills a region that is bounded by the Lacc= L⋆ relation at high Lacc, and claimed that the relation is the result of a combination of detection biases at low values of Lacc, roughly following a power-law Lacc∝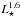 . The Lupus results suggest that the relation is real, as argued, for example, by Ercolano et al. (2014). The relation Lacc – L⋆ in Lupus, however, shows that a single power-law may not the best description of the data, which show evidence of a break, with the relationship being steeper at low L⋆ values than at high L⋆ values. This effect was not seen in other regions, but is also observed in the Chamaeleon I X-shooter survey by Manara et al. (2017).
. The Lupus results suggest that the relation is real, as argued, for example, by Ercolano et al. (2014). The relation Lacc – L⋆ in Lupus, however, shows that a single power-law may not the best description of the data, which show evidence of a break, with the relationship being steeper at low L⋆ values than at high L⋆ values. This effect was not seen in other regions, but is also observed in the Chamaeleon I X-shooter survey by Manara et al. (2017).
The approximation Ṁacc∝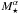 , with α ≈ + 2 for the Lupus YSOs is consistent with the previous results for YSOs in other star forming regions. The steep relation and sread of the Ṁacc−M⋆ correlation has been interpreted as the imprints of the initial angular momentum of the parental cores where the star-disc systems were formed (e.g. Dullemond et al. 2006). The spread of the relationship has also been ascribed to a spread of stellar properties, such as X-ray and EUV emission (Muzerolle et al. 2003; Ercolano et al. 2014). These latter authors in particular conclude that the observed Ṁacc – M⋆ relation in YSOs is consistent with being a simple consequence of disc dispersal by X-ray photoevaporation. Variability is another possible source of spread in the Ṁacc values. Costigan et al. (2012) have shown that the typical variability of Ṁacc in Chamaeleon I targets is generally ≤0.4 dex. Independent studies in other star forming regions confirm similar values (e.g. Biazzo et al. 2012; Venuti et al. 2014). Therefore, this effect can be relevant to explain some of the observed spread of Ṁacc values. In fact the average size of the error bars of the binned log Ṁacc – log M⋆ relationship shown in Fig. 8 is also on the order of 0.3−0.4 dex. The level of variability, however, may be different depending on the evolutionary status of the YSO populations. This may contribute explaining a different spread of Ṁacc among YSOs of the same mass in star forming regions of different age.
, with α ≈ + 2 for the Lupus YSOs is consistent with the previous results for YSOs in other star forming regions. The steep relation and sread of the Ṁacc−M⋆ correlation has been interpreted as the imprints of the initial angular momentum of the parental cores where the star-disc systems were formed (e.g. Dullemond et al. 2006). The spread of the relationship has also been ascribed to a spread of stellar properties, such as X-ray and EUV emission (Muzerolle et al. 2003; Ercolano et al. 2014). These latter authors in particular conclude that the observed Ṁacc – M⋆ relation in YSOs is consistent with being a simple consequence of disc dispersal by X-ray photoevaporation. Variability is another possible source of spread in the Ṁacc values. Costigan et al. (2012) have shown that the typical variability of Ṁacc in Chamaeleon I targets is generally ≤0.4 dex. Independent studies in other star forming regions confirm similar values (e.g. Biazzo et al. 2012; Venuti et al. 2014). Therefore, this effect can be relevant to explain some of the observed spread of Ṁacc values. In fact the average size of the error bars of the binned log Ṁacc – log M⋆ relationship shown in Fig. 8 is also on the order of 0.3−0.4 dex. The level of variability, however, may be different depending on the evolutionary status of the YSO populations. This may contribute explaining a different spread of Ṁacc among YSOs of the same mass in star forming regions of different age.
However, the new result from our analysis is that there is evidence of a break of the scaling relations at low M⋆ and L⋆ values. The homogeneous methods used here and the completeness of the sample allow us to conclude that the bi-modality of the Ṁacc – M⋆ relation of Lupus is real, regardless of the evolutionary models used to derive the stellar mass. It is worth noting that a similar behavior has been confirmed for the young stellar population in the L1641 region (Fang et al. 2013b) and in Chamaeleon I (Manara et al. 2017).
The break of the empirical relationship in Lupus resembles the theoretical prediction by Vorobyov & Basu (2009). In these models the gravitational instability due to the self-gravity of the discs in the early phase of disc evolution limits the disc mass in the higher mass (M⋆≳ 0.2 M⊙) objects, effectively setting an upper limit on the mass accretion rates in the late evolution, hence flattening the Ṁacc−M⋆ relation in this mass regime. The gravitational instability has little effect in the low-mass regime, where viscous evolution dominates at basically all times. Therefore, our result that the Ṁacc – M⋆ relation flattens at the high mass regime supports the importance of modelling self-gravity in the early evolution of the more massive systems, as suggested in Hartmann et al. (2006). However, as pointed out in Rigliaco et al. (2011), other physical processes, such as photo-evaporation and planet formation, may also occur during YSOs lifetime leading to disc dissipation on different timescales depending on the stellar mass.
Interestingly, a break of the Ṁacc – M⋆ relation at the very low-mass regime (M⋆≲ 0.1 M⊙) has also been predicted by Stamatellos & Herczeg (2015). To explain the very high levels of accretion observed in substellar and planetary-mass companions to some T Tauri stars (Zhou et al. 2014), Stamatellos & Herczeg (2015) model the accretion onto very low-mass objects that formed by the fragmentation of the disc around the more massive star. During the early evolution the individual discs of substellar companions -including those at the planetary-mass regime- accrete additional material from the gas-rich parent disc, hence, their discs are more massive and their accretion rates are higher than if they were formed in isolation. Therefore, these very low-mass objects have disc masses and accretion rates that are independent of the mass of the central object and are higher than expected from the scaling relations of more massive YSOs. These models predict that Ṁacc is basically independent of M⋆. Our data show a hint for a flattening of both Lacc–L⋆ and Ṁacc – M⋆ relationships at the very low L⋆/M⋆ end, but the sample lacks a statistically significant number of low-mass substellar objects to establish the trend. It is, however, interesting that our target close to the planetary-mass regime has a relatively high Ṁacc in comparison with the value measured in the lowest mass YSOs in our sample.
Although the scatter of the Lupus relationship increased with respect to our previous result in A14, it is still less than for other samples and its upper envelope follows the same steep trend, in contrast to the Taurus YSOs, where the upper envelope of the relationship is flatter (see Fig. 1 in Hartmann et al. 2006). The steeper slope of the upper envelope may lead to the idea of a faster disc evolution of the Lupus low-mass stars than those in Taurus, suggesting that the Lupus YSO population might be different from the population in Taurus or other regions. Hughes et al. (1994) concluded that Lupus may be a region of sub-critical star formation where magnetic fields slow the collapse of the clouds, leading to low mass accretion rates with the consequence that the lowest mass stars in Lupus are less active than similar objects in other regions. On the other hand, Galli et al. (2015) provided evidence that the disc lifetimes may be shorter in Lupus in comparison with those in Taurus.
A crucial aspect of the models regarding viscously evolving discs is the presence of the correlations of Mdisc with M⋆ and Ṁacc (e.g. Lynden-Bell & Pringle 1974; Hartmann et al. 2006; Dullemond et al. 2006; Tilling et al. 2008, and references therein). On the observational side, these scaling relationships have been discussed in the reviews by Natta et al. (2007) and Williams & Cieza (2011). Despite the strong efforts on detecting such correlations, previous works (e.g. Ricci et al. 2010; Andrews et al. 2010; Olofsson et al. 2013) failed on finding a scaling between the disc mass and the stellar mass, or the mass accretion rate, within the uncertainties of the measurements. Later investigations confirmed a robust Mdisc−M⋆ correlation for the class II YSOs in Taurus Andrews et al. (2013) and in the Upper Scorpius OB Association Barenfeld et al. (2016), and more recently the synergy between the ALMA and X-shooter projects has also been successful in confirming it for YSOs in Chamaeleon I (Pascucci et al. 2016). The combination of the data presented here with those reported in the ALMA survey of Lupus protoplanetary discs have shown significant correlations between Mdisc and M⋆ (Ansdell et al. 2016) and Mdisc and Ṁacc (Manara et al. 2016b). The ALMA survey did not include, however, YSOs with M⋆≤ 0.1 M⊙, preventing us from investigating whether the scaling relationships are different for low-mass substellar objects than for stars. The characterisation of the physical and accretion properties of candidates to very low-mass substellar objects, using future facilities with higher performance than X-shooter, and high-sensitivity observations with ALMA of these objects will provide important clues for their formation mechanisms.
7. Summary and conclusions
We have used X-shooter@VLT to investigate 93 YSOs previously classified as class II sources in the Lupus star forming region. The capabilities of X-shooter in terms of wide spectral coverage, resolution and accurate flux allowed us to characterise the sample in terms of stellar and accretion properties in a homogeneous and self-consistent way and to accomplish an unbiased study of accretion and its relationship with stellar parameters.
Our observations confirm that one of the most important sources of contamination of the samples of YSO candidates drawn from photometric surveys are background giants, in agreement with previous works (e.g. Oliveira et al. 2009; Alcalá et al. 2011; Mortier et al. 2011; Comerón et al. 2013). We have found that about 10% of the YSOs previously classified as class II candidates are indeed unrelated to the Lupus star forming region, with an important impact on the disc demography of the star forming region. Without the knowledge of this contaminating component the detection rate of the 95% complete ALMA survey of Lupus protoplanetary discs by Ansdell et al. (2016) would have resulted in ~60% instead of ~70%, highlighting the need for optical/infrared spectroscopic complementary data to ALMA.
Our study of the 81 confirmed Lupus YSOs allowed us to accomplish a synthesis of the accretion properties of the almost (>90%) complete sample. The accretion luminosity and stellar luminosity of the Lupus YSOs are correlated with a lower scatter in comparison with previous studies of YSOs in other star forming regions. The slope of the Lacc–L⋆ relationship is not driven by selection biases and there is a lack of strong accretors at the low YSO luminosity regime, suggesting a break of the relationship at L⋆≈ 0.1 L⊙.
For the Lupus YSOs we conclude that Ṁacc∝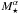 , with α = + 1.8 ± 0.2, but we found evidence of a break of the scaling relations at low M⋆ and L⋆ values. The homogeneous methods used here and the completeness of the sample allow us to confirm the bi-modality of the Ṁacc – M⋆ relation of Lupus YSOs, independently of the evolutionary models used to derive the stellar mass. The bimodal behaviour of the observed relationship supports the importance of modelling self-gravity in the early evolution of the more massive discs, but other processes such as photo-evaporation and planet formation during YSOs lifetime, may also lead to disc dissipation on different timescales depending on the stellar mass. Our data show tantalising evidence of relatively constant Ṁacc below 0.1 M⊙, possibly indicating that some of the very low-mass substellar objects may have formed as companions of stars by the fragmentation of the circumstellar disc. However, our sample lacks a statistically significant number of low-mass substellar objects to confirm the result.
, with α = + 1.8 ± 0.2, but we found evidence of a break of the scaling relations at low M⋆ and L⋆ values. The homogeneous methods used here and the completeness of the sample allow us to confirm the bi-modality of the Ṁacc – M⋆ relation of Lupus YSOs, independently of the evolutionary models used to derive the stellar mass. The bimodal behaviour of the observed relationship supports the importance of modelling self-gravity in the early evolution of the more massive discs, but other processes such as photo-evaporation and planet formation during YSOs lifetime, may also lead to disc dissipation on different timescales depending on the stellar mass. Our data show tantalising evidence of relatively constant Ṁacc below 0.1 M⊙, possibly indicating that some of the very low-mass substellar objects may have formed as companions of stars by the fragmentation of the circumstellar disc. However, our sample lacks a statistically significant number of low-mass substellar objects to confirm the result.
The accretion properties of most transitional YSOs are in general similar to those of objects with full discs, with a minority of them having accretion rates an order of magnitude lower than objects with full discs. However, the highest accretion rates are only seen in objects with full discs.
Acknowledgments
We thank the anonymous referee for her/his comments and suggestions. CFM gratefully acknowledges an ESA Research Fellowship. A.N. acknowledges funding from Science Foundation Ireland (Grant 13/ERC/I2907). We thank M. Tazzari and M. Ansdell for discussions on ALMA data. We also thank the ESO staff, in particular Markus Wittkowski and Giacomo Beccari for their excellent support during phase-2 proposal preparation, and the Paranal staff for their support during the observations. We thank G. Cupani, V. D’Odorico, P. Goldoni and A. Modigliani for their help with the X-shooter pipeline. Financial support from INAF under the program PRIN2013 “Disk jets and the dawn of planets” is also acknowledged. This work was partly supported by the Gothenburg Centre for Advanced Studies in Science and Technology as part of the GoCAS program Origins of Habitable Planets and by the Italian Min- istero dell’Istruzione, Universitá e Ricerca through the grant Progetti Premiali 2012-iALMA (CUP C52I13000140001). This research made use of the SIMBAD database, operated at the CDS (Strasbourg, France).
References
- Alcalá, J. M., Stelzer, B., Covino, E., et al. 2011, Astron. Nachr., 332, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalá, J. M., Natta, A., Manara, C., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, R. D., Pascucci, I., Andrews, S., Armitage, P., & Cieza, L. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (University of Arizona Press), 475 [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, ASP Conf. Ser., 448, 91 [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., van der Marel, N., et al. 2016, ApJ, 828, 46 [Google Scholar]
- Antoniucci, S., García López, R., Nisini, B., et al. 2011, A&A, 534, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoniucci, S., García López, R., Nisini, B., et al. 2014, A&A, 572, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Haschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barenfeld, S. A., Carpenter, J. M., Ricci, L., Isella, A. 2016, ApJ, 827,142 [NASA ADS] [CrossRef] [Google Scholar]
- Biazzo, K., Alcalá, J. M., Covino, et al. 2012, A&A, 547, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biazzo, K., Alcalá, J. M., Frasca, A., et al. 2014, A&A, 572, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bustamante, I., Merín, B., Ribas, Á., et al. 2015, A&A, 578, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., Hartmann, L., Kenyon, S. J., & Whitney, B. A. 1994, ApJ, 434, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., & Pringle, J. E. 2006, MNRAS, 370, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, F. 2008, Handbook of Star Forming Regions, Volume II: The Southern Sky ASP Monograph Publications, ed. B. Reipurth, 5, 295 [Google Scholar]
- Comerón, F., & Fernández, M. 2011, A&A, 528, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, F., Spezzi, L., & López-Martí, B. 2009, A&A, 500, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, F., Spezzi, L., López-Martí, B., & Merín, B. 2013, A&A, 554, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costigan, G., Scholz, A., Stelzer, B., et al. 2012, MNRAS, 427, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Costigan, G., Vink, J. S., Jorick, S., et al. 2014, MNRAS, 440, 3444 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1997, Mem. Soc. Astron. It., 68, 807 [Google Scholar]
- DeSouza, A. L., & Basu, S. 2017, New Astron., 51, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Natta, A., & Testi, L. 2006, ApJ, 645, 69 [Google Scholar]
- Edwards, S., Fischer, W., Hillenbrand, L., & Kwan, J. 2006, ApJ, 646, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Mayr, D., Owen, J. E., Rosotti, G., & Manara, C. F. 2014, MNRAS, 439, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (University of Arizona Press), 497 [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., Jinyoung, S., van Boekel, R., et al. 2013a, ApJS, 207, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, M., Kim, J. S., van Boekel, R., et al. 2013b, ApJS, 207, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., Biazzo, K., Lanzafame, A. C., et al. 2015, A&A, 575, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., & Alcalá, J. M., 2017, A&A, in press DOI: 10.1051/0004-6361/2201630108 [Google Scholar]
- Gahm, G. F., Walter, F. M., Stempels, H. C., Petrov, P. P., & Herczeg, G. 2008, A&A, 482, 35 [Google Scholar]
- Galli, P. A. B., Bertout, C., Teixeira, R., & Ducourant, C. 2015, A&A, 580, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceño, C., & Calvet, N. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. 1998, in Accretion Processes in Star Formation (Cambridge University Press) [Google Scholar]
- Hartmann, L. E., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., D’Alessio, P., Calvet, N., & Muzerolle, J. 2006, ApJ, 648, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G., & Hillenbrand, L. A. 2008, ApJ, 681, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G., & Hillenbrand, L. A. 2015, ApJ, 808, 23 [Google Scholar]
- Herczeg, G., Cruz, K. L., & Hillenbrand, L. A. 2009, ApJ, 696, 1589 [Google Scholar]
- Hughes, J., Hartigan, P., Krautter, J., & Kelemen, J. 1994, AJ, 108, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Ingleby, L., Calvet, N., Bergin, E., et al. 2011, ApJ, 743, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Ingleby, L., Calvet, N., Herczeg, G., et al. 2013, ApJ, 767,112 [NASA ADS] [CrossRef] [Google Scholar]
- Ingleby, L., Calvet, N., Hernández, J., et al. 2014, ApJ, 790, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, E. L., & Meier, P. 1958, J. Amer. Statist. Asso., 53, 282 [Google Scholar]
- Kendall, S. M., & Stuart, A. 1977, Book The advanced theory of statistics (London, Great Britain: Charles Griffin & Company Limited), 4, 1 [Google Scholar]
- Kenyon, S., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Krautter, J. 1986, A&A, 161, 195 [NASA ADS] [Google Scholar]
- Lorenzetti, D., Antoniucci, S., Giannini, T., et al. 2012, ApJ, 749, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., Muench, A. A., et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C. F., Testi, L., Rigliaco, E., et al. 2013a, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Beccari, G., Da Rio, N., et al. 2013b, A&A, 558, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Testi, L., Natta, A., et al. 2014, A&A, 568, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Testi, L., Natta, A., & Alcalá, J. M. 2015, A&A, 579, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Fedele, D., Herczeg, G. J., & Teixeira, P. S. 2016a, A&A, 585, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Rosotti, G., Testi, L., et al. 2016b, A&A, 591, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Testi, L., Herczeg, G., et al. 2017, A&A, submitted [Google Scholar]
- Mendigutía, I., Oudmaijer, R. D., Rigliaco, E., et al. 2015, MNRAS, 452, 2837 [NASA ADS] [CrossRef] [Google Scholar]
- Merín, B., Jørgensen, J. K., Spezzi, L., et al. 2008, ApJS, 177, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in Observatory Operations: Strategies, Processes, and Systems III, SPIE, eds. D. R. Silva, A. B. Peck, & B. T. Soifer [Google Scholar]
- Mohanty, S., Jayawardhana, R., & Basri, G. 2005, ApJ, 626, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Mortier, A., Oliveira, I., & van Dishoeck, E. F. 2011, MNRAS, 418, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Hillenbrand, L., Calvet, N., Briceño, C., & Hartmann, L. 2003, ApJ, 592, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Luhman, K., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Mužić, K., Scholz, A., Geers, V. C., Jayawardhana, R., & López Martí, B. 2014, ApJ, 785, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Strom, S. E., & Muzerolle, J. 2007, MNRAS, 378, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, Y., Tamura, M., Oasa, Y., & Nakajima, T. 2000, AJ, 119, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 452, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (University of Arizona Press), 767 [Google Scholar]
- Natta, A., Testi, L., Alcalá, J. M., et al. 2014, A&A, 569, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliveira, I., Merín, B., Pontoppidan, K. M., et al. 2009, ApJ, 691, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Szücs, L., Henning, Th., et al. 2013, A&A, 560, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riddick, F. C., Roche, P. F., & Lucas, P. W. 2007, MNRAS, 381, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Rigliaco, E., Natta, A., Randich, S., et al. 2011, A&A, 525, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. A., Schreiber, M. R., Cieza, L. A., et al. 2012, ApJ, 749, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseeuw, P. J. 1984, in J. Amer. Statist. Asso., 79, 871 [Google Scholar]
- Rousseeuw, P. J., & Leroy, A. M. 1987, in Robust Regression and Outlier Detection (New York: Wiley) [Google Scholar]
- Sicilia-Aguilar, A., Kim, J. S., Sobolev, A., et al. 2013, A&A, 551, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicilia-Aguilar, A., Fang, M., Roccatagliata, V., et al. 2015, A&A, 580, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipos, N., Ábrahám, P., Acosta-Pulido, J., et al. 2009, A&A, 507, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Stamatellos, D., & Herczeg, G. J. 2015, MNRAS, 449, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Alcalá, J. M., Scholz, A., et al. 2013a, A&A, 551, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stelzer, B., Frasca, A., Alcalá, J. M., et al. 2013b, A&A, 558, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tilling, I., Clarke, C. J., Pringle, J. E., & Tout, C. A. 2008, MNRAS, 385, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Tsukagoshi, T., Momose, M., Hashimoto, J., et al. 2014, ApJ, 783, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., Basri, G., & Johns, C. M. 1993, ApJ, 106, 2024 [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2008, ApJ, 676, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2009, ApJ, 703, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., Verhaar, B. W., van Terwisga, S., et al. 2016, A&A, 592, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, Y., Herczeg, G. J., Kraus, A. L., Metchev, S., & Cruz, K. L. 2014, ApJ, 783, L17 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Physical parameters and accretion properties of the total sample adopting different models
The complete list of the 81 confirmed YSOs and the synthesis of their physical parameters are given in Table A.2. The quantities have been consistently derived as explained in A14 for the GTO sample (first 36 raws) and Sect. 3.3 for the new sample, respectively. The ±0.5 subclass and ±1 subclass uncertainties for the M-type and earlier type objects translate into uncertainties of 0.01 dex and 0.02 dex in log Teff, respectively. The error in YSO luminosity in log scale is proportional to the error in flux in log scale. The error in log L⋆ was then estimated by taking into account the contribution of both the signal-to-noise (S/N) of the flux-calibrated spectra and the error in visual extinction, which for the purpose of error estimates we assume to be 0.5 mag for all objects (see also A14). The rms of the continuum of the spectra was estimated in four spectral regions adjacent to the Hα, H6, H13 and H15 lines; this was taken as the 1σ error on the flux at the four wavelengths. The uncertainty due to extinction at the corresponding spectral regions was computed as ln10·0.4·RV·ΔAV, where RV is the extinction curve. The relative errors due to the flux and extinction were then combined in quadratures, yielding a relative error in flux ΔF/F at each spectral region. A weighted average was then computed providing Δlog L⋆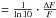 . The error in luminosity was then computed as ln10·L⋆·Δlog L⋆.
. The error in luminosity was then computed as ln10·L⋆·Δlog L⋆.
One of our main goals here is the study of the Ṁacc vs. M⋆ relation and how it depends on the adopted PMS evolutionary models. Therefore, we have used the tracks by D’Antona & Mazzitelli (1997), Baraffe et al. (1998), Siess et al. (2000) and Baraffe et al. (2015), hereafter DM97, BA98, S00 and B15, respectively to derive masses. The errors in the mass were calculated with a Monte Carlo procedure considering the errors in Teff and L⋆ on the HR diagram. In each realisation, the value of Teff and L⋆ was randomly selected in a Gaussian distribution centered on the measured value and with a σ equivalent to the uncertainty. With these values, the mass was measured using the different evolutionary models. A total of 1000 realisations were obtained, and the standard deviation of the derived stellar masses is then taken as the error on the mass estimate. The resulting masses with their errors are listed in Table A.2.
The accretion luminosity for each YSO in the total sample is given in column three of Table A.3. Using the data in Table A.2, and Eq. (1), these Lacc’s were converted into the four Ṁacc values listed in the last four columns of Table A.3. Uncertainties on Ṁacc were derived by error propagation using
Eq. (1) in logarithmic form, i.e. log Ṁacc= log (1.25 ∗ G) +log Lacc+log R⋆−log M⋆. Typical errors 0.25 dex, 0.1 dex, and 0.1 dex in Lacc, R⋆ and M⋆, respectively, yield an uncertainty of ~0.3 dex in Ṁacc. The uncertainty on the Lupus YSOs distance is estimated to be ~23% (see Comerón 2008, and references therein), yielding a relative uncertainty of about 0.3 dex in the mass accretion rate3. Therefore we estimate the cumulative relative uncertainty in log Ṁacc to be about 0.42 dex. Within errors, the mass accretion rates for each object, derived using the mass drawn from the different evolutionary models, are practically the same.
Appendix A.1: The Macc vs. M⋆ relation with different PMS evolutionary models
Figure A.1 shows the log Ṁacc – log M⋆ plots for our total sample of class II YSOs and transitional discs in Lupus when adopting the four evolutionary models discussed in the previous subsection. For a given object the Ṁacc values are practically the same hence, the differences in the diagrams are mainly induced by the different M⋆ values derived from the different models. We found similar results in a previous work (Biazzo et al. 2014) for a sample of YSOs in the L 1615/L 1616 cometary cloud in Orion. The fit corresponding to each model is given in Table A.1. The fits take into account weak accretors, but exclude the sub-luminous objects. For the three YSOs with M⋆< 0.1 M⊙ in the Siess et al. (2000) tracks, we used the mass derived from the Baraffe et al. (2015) models to perform the fit. The most and less scattered relationships are those drawn form the DM97 and B98 models, respectively, but the four fits are similar within errors. Importantly, the break of the relationship discussed in Sect. 5.2 is evident independently of the evolutionary model adopted to derive the mass and mass accretion rate.
Fits to the log Ṁacc – log M⋆ relationship adopting different PMS models to derive M⋆ and Ṁacc. The fits are of the form log Ṁacc = m·log M⋆+ c.
Confirmed YSOs of the total sample with spectral types, extinction, and physical parameters.
Accretion properties of the total sample.
 |
Fig. A.1 Mass accretion rate Ṁacc as a function of M⋆ in log scale as determined using the four different PMS evolutionary models described in Section A. The YSOs with transitional discs are distinguished with crossed squares, while the sub-luminous objects are shown with open circles. The low accretors are shown with red symbols (see Sect. B.1). The arrows show upper or lower limits on the mass according to the availability of the tracks in each model. Average errors are shown in the upper left of each panel. The purple dashed lines represent the corresponding linear fits as in Table A.1. |
Appendix B: Accretion luminosity versus line luminosity relationships revisited
In this paper we more than double the number of YSOs in Lupus with accurately and homogeneously determined values of accretion luminosity and line luminosity. The latter was measured for large number of permitted emission lines simultaneously observed in a wide spectral range from the UVB to the NIR. It is then worth to revisit the relationships between the continuum excess emission and the emission in the individual permitted lines that we have derived in A14, on a more statistically significant basis by using the total sample.
Revisited Lacc– Lline linear fits.
Figures E.1 to E.6 show the relationships between Lacc and the luminosity of the permitted emission lines discussed in A14 for the GTO sample. Overplotted in these figures are the data corresponding to the new sample. The line luminosities were calculated as explained in Sect. 3.4. For the reasons discussed in that Section, the He i λ1082.9 nm line is not included in our analysis here. In order to avoid confusion we do not include the data from the literature on the plots.
A comparison of the results shown in Table 4 of A14 and those in Table B.1 shows that the linear fits of the GTO sample and those presented here for the total sample are in very good agreement for all the lines. The linear fits of the log Lacc vs. log Lline relationships were then recalculated using the package ASURV (Feigelson & Nelson 1985), which includes censoring of upper or lower limits in the fits. The results of the new fits (cf. Table B.1) including and excluding upper limits are consistent within the errors, but given the good number statistics the fits were done with detections only. The total number of points and the standard deviation of the fits are given in the fifth and sixth columns of Table B.1, respectively. For the reasons discussed in A14 no fits were calculated for the Br 8 (Brδ) relation.
The new relationships are very similar to those in A14 with the only difference that the errors on the parameters of the linear fits are reduced by about 30%, although the standard deviation from the fits has generally increased by about 15% on the average. The latter is a natural consequence of the larger number of points included here with respect to A14. The recommended relationships to calculate Lacc from Lline are indicated in the notes of Table B.1. All the conclusions regarding the physical interpretations on these relationships given in A14 are confirmed here with the total sample.
Mendigutía et al. (2015) suggest that all the Lacc–Lline relationships are a direct consequence of the Lacc–L⋆ correlation and not necessarily related with the physical origin of the lines. Whatever the case, these relationships are a useful tool to derive estimates of the accretion luminosity hence, accretion rate. The relations computed here have in general a lower dispersion than those found in the literature by applying similar methodologies of fitting the UV excess emission, and in general continuum excess emission (e.g. Herczeg & Hillenbrand 2008; Rigliaco et al. 2012; Ingleby et al. 2013). However, one must keep in mind that each point in the relationships represents an instantaneous snapshot of Lacc and Lline. Note that the results of temporal monitoring of several YSOs indicate variability in optically thick line fluxes, without significant changes in the corresponding continuum accretion rate (e.g. Gahm et al. 2008; Herczeg et al. 2009), so that some dispersion may still arise from variability even when the observations are simultaneous.
 |
Fig. B.1 Average accretion luminosity ⟨Lacc(lines)⟩ derived from emission lines as described in the text (upper panel) and the ⟨Lacc(lines)/L⋆⟩ ratio (lower panel) in logarithmic scale as a function of effective temperature for the total sample. The objects with transitional discs are distinguished with crossed squares, while the sub-luminous objects are shown with open circles. The dashed lines in both panels mark the locus below which chromospheric emission is important in comparison with Lacc. The vertical error bars represent the standard deviation over the average. The weak accretors and RY Lup are labelled. |
Appendix B.1: Accretion versus chromospheric emission
An important aspect to be considered when determining the accretion and line luminosity is the contribution of chromospheric emission. The relative importance of (hydrogen) line emission with respect to Lacc is higher for low Lacc values, and chromospheric emission may be the dominant process in the lines (Ingleby et al 2011; Rigliaco et al. 2012; Manara et al. 2013a; Frasca et al. 2015). Based on the luminosity of several chromospheric emission lines in the class III templates, Manara et al. (2013a) determined a threshold below which chromospheric emission dominates line luminosities. The threshold depends on YSO effective temperature and age.
To investigate the possible effects of chromospheric line emission in the new sample, we have compared the threshold derived by Manara et al. (2013a) with the accretion luminosity, Lacc(lines), derived by using emission line diagnostics and the revisited Lacc–Lline relations. In Fig. B.1 the ⟨Lacc(lines)⟩ values and the ⟨Lacc(lines)/L⋆⟩ ratio (as suggested in Manara et al. 2013a; Mendigutía et al. 2015) are plotted in logarithmic scale as a function of Teff. The dashed lines in the figure show the level of chromospheric noise as determined by Manara et al. (2013a). The lines represent the locus below which the contribution of chromospheric emission starts to be important in comparison with energy losses due to accretion.
Except for a sub-luminous object, the accretion level of all the YSOs shown in Fig. B.1 is above the chromospheric noise in the Lacc vs. Teff diagram, but some of the new sample are scattered towards lower Lacc values than those of the GTO. When normalising to the stellar luminosity, six objects namely RY Lup, MY Lup, Sz65, Sz68, SST c2dJ160830.7-382827, and the M6.5 type star Lup607, fall on the locus of chromospheric noise in the Lacc/L⋆ vs. Teff diagram. Note that these are the objects for which Balmer continuum emission is not evident after the slab modelling analysis of Sect. 3.2. Of these, RY Lup, MY Lup, and SST c2dJ160830.7-382827 have transitional discs, whereas the classification of Lup 607 as a class II YSO is dubious because based on an uncertain SED (Merín et al. 2008). On the other hand, the results of the ALMA survey of Lupus by Ansdell et al. (2016) show that their resolved transition discs have much higher disc gas masses than the disc gas mass in Sz65 and Sz68. Therefore, except for RY Lup, where the Paβ and Brγ lines are clearly detected in emission, the other five objects are considered as weak (or dubious) accretors. These objects are flagged in Table A.3 and are distinguished in the plots.
Appendix C: The flat source SSTc2d J160708.6-391408
This source is interesting because it is probably one of the brightest and least extincted (AV = 3.0 ± 0.5 mag as determined by Muzic et al. 2014) YSOs with a flat SED (Merín et al. 2008; Evans et al. 2009). This makes possible the acquisition of a X-shooter spectrum with sufficient S/N in the three spectrograph arms allowing us to perform the same analysis as for the class II sources. We have thus observed SSTc2d J160708.6-391408 in 2016-06-05 following the same observational strategy as for the class II sources. The data reduction procedures, as well as the analysis to determine the stellar and accretion properties was the same as for the class II sources.
The X-shooter spectrum of SSTc2d J160708.6-391408 is very rich in permitted and forbidden emission lines, and shows a strong continuum UV-excess emission (see Fig. C.1). The extinction corrected flux and equivalent width of permitted lines are reported in the Tables E.1 to E.9. We classify the star as M5, but noticed that the results of the slab modelling are also consistent with a M3 type. The reason for this uncertainty is related to the fact that this object is strongly accreting, and thus strongly veiled, while having a relatively high extinction due to a still partially optically thick envelope. This represents an extreme case which can hardly be reproduced by a model including only the photospheric and the accretion emission. Assuming a M5 type, a distance of 200 pc and the Siess et al. (2000) tracks, we derived the following stellar and accretion properties: Teff = 3125 ± 72 K. AV = 3.60 mag ; L⋆= 0.0107 ± 0.0061 L⊙ ; M⋆= 0.13 ± 0.03 M⊙, Lacc= 6.31 × 10-3 L⊙ and Ṁacc= 5.89 × 10-10 M⊙ yr-1. Adopting M3, yields basically the same results on the accretion properties, but increases L⋆ and M⋆ by a factor of about 2. Our results place SSTc2d J160708.6-391408 in a rather anomalous position on the log Lacc–log L⋆ plot with respect to other YSOs, with a quite high Lacc/L⋆ ratio of 0.6, but L⋆ may be underestimated (see below).
 |
Fig. C.1 Extinction-corrected X-shooter spectrum of the flat source SSTc2d J160708.6-391408 (red). The continuum is fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab. The total fit is represented with the blue line. |
Based on their VIMOS@VLT data, Muzic et al. (2014) classify the star as M1.75, in agreement with the result by Frasca et al. (2017) after applying the ROTFIT code, which classifies the object as M2. Although these results would be more in line with our M3 estimate, we worn that it is not straightforward to calculate and include veiling in these analyses. Determinations of L⋆ by these and other authors (e.g. Comerón et al. 2009) are similar to our result. All these estimates make the object rather under-luminous with respect to other YSOs of similar spectral type.
Flat sources may be interpreted as YSOs with infalling envelopes (Calvet et al. 1994) hence, SSTc2d J160708.6-391408 may still be on a stage of accretion from an envelope of gas and dust in which part of the stellar radiation is reprocessed. The above calculations of L⋆ do not account for these effects hence, may underestimate the luminosity of the YSO. The bolometric luminosity of 0.18 L⊙, as derived by Evans et al. (2009) for this source, would imply a Lacc/Lbol ratio of 0.04, i.e. quite consistent with the value for YSOs of similar mass.
Further results on the analysis of the X-shooter spectrum of this object will be presented in the papers by Frasca et al. (2017) for the stellar parameters and by Nisini et al. (in prep.) for the analysis of forbidden emission lines.
Appendix D: EX Lup
The X-shooter spectrum of EX Lup is very rich in emission lines and displays strong UVB continuum emission (see Fig. E.11). The spectrum shows narrower emission lines in comparison with other spectra of the same object acquired during burst (e.g. Sicilia-Aguilar et al. 2015). Thus, it is most likely that the object was not in burst during the X-shooter observation.
Our Ṁacc determination of 3.6 × 10-8 M⊙/yr is much higher than the one estimated by Sicilia-Aguilar et al. (2015): these authors used the same X-shooter data as us, but they analysed the reduced 1D spectra gathered from the ESO Phase-3 data release and to our knowledge did not correct for slit losses, despite the narrow slits used during the observations. Two main reasons may explain the large discrepancy. First, Sicilia-Aguilar et al. (2015) adopt AV = 0 mag, while our best fit to the spectrum yields AV = 1.1 mag. Second, we have applied a factor of 2.5 to correct for slit losses, and since the object is quite variable, we may overestimate the absolute flux of the spectrum. In order to investigate this, we have used the AAVSO database to check for photometric observations closest in time to the date of the X-shooter acquisition. We found that the V magnitude of EX Lup was 13.7 mag and 13.4 mag, in JD 2 455 307.9 0278 and JD 2 455 331.98 958, respectively, i.e. 13.5 mag when interpolating to the observing date May 4, 2010 (or JD 2 455 320.164 155). This can be converted into a fluxe of 1.6 × 10-13 erg s-1 cm-2 nm-1, which is in agreement whithin less than a factor 1.5 with the flux of the X-shooter spectrum, after our correction for slit losses. Likewise, calculating the “synthetic” V magnitude from the spectrum with the Johnson V passband we derived a V = 13.03 mag.
It is worth noting that the log Ṁacc≈−9.4 estimate by Sicilia-Aguilar et al. (2015) would imply a log (Lacc/L⋆)=−2.3, and given the Teff= 3850 K, would place EX Lup very close to the chromospheric noise level (see Sect. B.1) and among the lowest accretors in Lupus, with a position on the log Ṁacc – log M⋆ diagram comparable to the one of our weakest (or dubious) accretors. All this is at odds with the strong Balmer continuum emission detected in the X-shooter spectrum (see Fig. E.11) an with the substantial veling of 0.43 and 0.36 that we measured at 580 nm and 670 nm, respectively. In addition, the log Lacc(lines) =−0.98 ± 0.18 we calculated from the luminosity of 34 emission lines and the Lacc–Lline relationships in A14, is in good agreement with the log Lacc(slab) = −0.70 ± 0.25 derived from our slab modelling. Assuming that our extinction estimate is wrong and fixing AV = 0 mag would drop our log Ṁacc estimate only by about 0.5 dex.
Therefore, we think that the flux of the emission lines, measured by Sicilia-Aguilar et al. (2015) in the ESO Phase-3 1D spectrum to calculate Lacc, was underestimated.
It has been shown that EX Lup may reach Ṁacc values as high as 10-7 M⊙/yr during busrts (Sicilia-Aguilar et al. 2015, and references there in). Our Ṁacc estimate is thus consistent with the fact that the object was not in a burst stage during the X-shooter acquisition.
Appendix E: Additional material
 |
Fig. E.1 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The YSOs of the GTO and new samples are represented as black and blue dots, respectively. |
 |
Fig. E.2 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
 |
Fig. E.3 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
 |
Fig. E.4 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
 |
Fig. E.5 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
 |
Fig. E.6 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
 |
Fig. E.7 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
 |
Fig. E.8 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
 |
Fig. E.9 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
 |
Fig. E.10 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
 |
Fig. E.11 Extinction-corrected spectra of the objects drawn form the ESO archive (red), fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
Extinction-corrected fluxes and equivalent widths of Balmer lines for the new sample: Hα to Hϵ.
Extinction-corrected fluxes and equivalent widths of Balmer lines: H8 to H11.
Extinction-corrected fluxes and equivalent widths of Balmer lines: H12 to H15.
Extinction-corrected fluxes and equivalent widths of Paschen lines: Paβ to Pa8.
Extinction-corrected fluxes and equivalent widths of Pa9, Pa10, and Brγ.
Extinction-corrected fluxes and equivalent widths of helium lines.
Extinction-corrected fluxes and equivalent widths of helium lines.
Extinction-corrected fluxes and equivalent widths of Ca ii H and K and IRT lines.
Extinction-corrected fluxes and equivalent widths of the Na i D lines
All Tables
Fits to the log Ṁacc – log M⋆ relationship adopting different PMS models to derive M⋆ and Ṁacc. The fits are of the form log Ṁacc = m·log M⋆+ c.
Confirmed YSOs of the total sample with spectral types, extinction, and physical parameters.
Extinction-corrected fluxes and equivalent widths of Balmer lines for the new sample: Hα to Hϵ.
Extinction-corrected fluxes and equivalent widths of Balmer lines: H12 to H15.
Extinction-corrected fluxes and equivalent widths of Paschen lines: Paβ to Pa8.
Extinction-corrected fluxes and equivalent widths of Ca ii H and K and IRT lines.
All Figures
 |
Fig. 1 Distributions of spectral type (upper panel), effective temperature (middle panel) and luminosity (lower panel) of the GTO (red histograms) and total (blue histograms) samples. |
| In the text | |
 |
Fig. 2 Hertzsprung-Russell diagram for the total sample. The GTO and new samples are represented with the black symbols. The seven sub-luminous objects described in the text are represented with open circles. The dashed lines show the isochrones, reported by Siess et al. (2000), while the continuous lines show the low-mass Pre-Main Sequence evolutionary tracks by the same authors as labelled. |
| In the text | |
 |
Fig. 3 Histograms of M⋆. The GTO sample is shown with the red histogram, while the total sample is shown with the blue one. |
| In the text | |
 |
Fig. 4 Accretion luminosity as a function of stellar luminosity. The transitional discs are shown with crossed squares, while the sub-luminous objects with open circles. The five weak accretors are shown with red symbols. The continuous lines represent the three Lacc vs. L⋆ relations as labelled. Average error bars are shown in the upper left. |
| In the text | |
 |
Fig. 5 Median values of accretion luminosity as a function of binned stellar luminosities. Each point represents the median of 5 Lacc values with similar L⋆. The horizontal bars show the intervals of log L⋆. |
| In the text | |
 |
Fig. 6 Mass accretion rate Ṁacc as a function of mass for the total sample in log scale. Plotting symbols are the same as in Fig. 4. The average errors in log M⋆ and log Ṁacc are shown in the upper left. The black dashed line shows the double power-law theoretically predicted by Vorobyov & Basu (2009). The continuous magenta lines represent the fits to the data as in Eqs. (4) and (5). The long-dashed blue line shows the robust double-linear fit following the prescription by Manara et al. (2017) as explained in the text. |
| In the text | |
 |
Fig. 7 Kaplan-Meier distribution of log Ṁacc for the low-mass (M⋆≤ 0.2 M⊙) and high-mass (M⋆>0.2 M⊙) sub-samples are shown in red and blue, respectively. |
| In the text | |
 |
Fig. 8 Median values of accretion rate as a function of binned stellar mass. Each point is the median of 5 Ṁacc values with similar M⋆. The plotting errors were computed in the same way as in Fig. 5. The horizontal bars represent the intervals in log M⋆. The dashed line shows the two power-law relationship by Vorobyov & Basu (2009), vertically shifted by −1 dex. |
| In the text | |
 |
Fig. A.1 Mass accretion rate Ṁacc as a function of M⋆ in log scale as determined using the four different PMS evolutionary models described in Section A. The YSOs with transitional discs are distinguished with crossed squares, while the sub-luminous objects are shown with open circles. The low accretors are shown with red symbols (see Sect. B.1). The arrows show upper or lower limits on the mass according to the availability of the tracks in each model. Average errors are shown in the upper left of each panel. The purple dashed lines represent the corresponding linear fits as in Table A.1. |
| In the text | |
 |
Fig. B.1 Average accretion luminosity ⟨Lacc(lines)⟩ derived from emission lines as described in the text (upper panel) and the ⟨Lacc(lines)/L⋆⟩ ratio (lower panel) in logarithmic scale as a function of effective temperature for the total sample. The objects with transitional discs are distinguished with crossed squares, while the sub-luminous objects are shown with open circles. The dashed lines in both panels mark the locus below which chromospheric emission is important in comparison with Lacc. The vertical error bars represent the standard deviation over the average. The weak accretors and RY Lup are labelled. |
| In the text | |
 |
Fig. C.1 Extinction-corrected X-shooter spectrum of the flat source SSTc2d J160708.6-391408 (red). The continuum is fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab. The total fit is represented with the blue line. |
| In the text | |
 |
Fig. E.1 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. The YSOs of the GTO and new samples are represented as black and blue dots, respectively. |
| In the text | |
 |
Fig. E.2 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
| In the text | |
 |
Fig. E.3 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
| In the text | |
 |
Fig. E.4 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
| In the text | |
 |
Fig. E.5 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
| In the text | |
 |
Fig. E.6 Relationships between accretion luminosity and line luminosity for the several diagnostics as labelled in each panel. Plotting symbols are as in Fig. E.1. |
| In the text | |
 |
Fig. E.7 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| In the text | |
 |
Fig. E.8 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| In the text | |
 |
Fig. E.9 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| In the text | |
 |
Fig. E.10 Extinction-corrected spectra (red) fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| In the text | |
 |
Fig. E.11 Extinction-corrected spectra of the objects drawn form the ESO archive (red), fitted with a combination of a photospheric template (green) and the synthetic continuum spectrum from a hydrogen slab (black). The total fit is represented with the blue line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


