| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 35 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628597 | |
| Published online | 17 March 2017 | |
Hydrogen in diffuse molecular clouds in the Milky Way
Atomic column densities and molecular fraction along prominent lines of sight⋆
1 Max-Planck-Institut für Radioastronomie (MPIfR), Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: bwinkel@mpifr.de
2 Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD 21218, USA
3 LERMA, Observatoire de Paris, PSL Research University, CNRS, UMR 8112, 75014 Paris, France
4 Sorbonne Universités, UPMC Univ. Paris 06, UMR 8112, LERMA, 75005 Paris, France
5 Department of Astronomy, University of Michigan, Ann Arbor, MI 48109, USA
Received: 27 March 2016
Accepted: 30 December 2016
Context. Recent submillimeter and far-infrared wavelength observations of absorption in the rotational ground-state lines of various simple molecules against distant Galactic continuum sources have opened the possibility of studying the chemistry of diffuse molecular clouds throughout the Milky Way. In order to calculate abundances, the column densities of molecular and atomic hydrogen, H i, must be known.
Aims. We aim at determining the atomic hydrogen column densities for diffuse clouds located on the sight lines toward a sample of prominent high-mass star-forming regions that were intensely studied with the HIFI instrument onboard Herschel.
Methods. Based on Jansky Very Large Array data, we employ the 21 cm H i absorption-line technique to construct profiles of the H i opacity versus radial velocity toward our target sources. These profiles are combined with lower resolution archival data of extended H i emission to calculate the H i column densities of the individual clouds along the sight lines. We employ Bayesian inference to estimate the uncertainties of the derived quantities.
Results. Our study delivers reliable estimates of the atomic hydrogen column density for a large number of diffuse molecular clouds at various Galactocentric distances. Together with column densities of molecular hydrogen derived from its surrogates observed with HIFI, the measurements can be used to characterize the clouds and investigate the dependence of their chemistry on the molecular fraction, for example.
Key words: astrochemistry / ISM: abundances / ISM: molecules
The data sets are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/600/A2
© ESO, 2017
1. Introduction
Between 2009 and 2013, absorption-line measurements with the Heterodyne Instrument for the Far Infrared (HIFI; de Graauw et al. de Graauw et al. 2010) onboard Herschel1 have revolutionized our view of chemistry in the diffuse interstellar medium (ISM). Studies with HIFI have targeted the ground-state rotational transitions of a variety of (mostly) di- and triatomic molecules. For earth-bound astronomy, these are very difficult or impossible to observe as a result of the absorption from H2O vapor and dry constituents of the atmosphere. With excellent spectral resolution (~0.1 km s-1), in particular the Guaranteed Time Observing Programs PRISMAS (Gerin et al. 2012) and HEXOS (Bergin et al. 2010) have delivered a whole series of remarkable results that address H2O itself (Lis et al. 2010; van Dishoeck et al. 2013), for instance, but also the other reactants leading to its formation, that is, OH+, H2O+, and H3O+ (Gerin et al. 2010a; Indriolo et al. 2015; Gerin et al. 2016). Now that Herschel has ceased operations, the HIFI instrument finds its continuation and extension in the GREAT receiver (Heyminck et al. 2012) flown on the Stratospheric Observatory for Infrared Astronomy (SOFIA). For example, to the H2/oxygen chemistry path, observations with GREAT have added data with high spectral resolution on the 2.5 THz ground-state transition of OH and the 63 μm [OI] fine-structure line (Wiesemeyer et al. 2012, 2016). The basic pathways of nitrogen and carbon chemistry have been similarly explored through observations of CH, CH+, and C3 (Gerin et al. 2010b; Falgarone et al. 2010; Mookerjea et al. 2012), and of NH, NH2, and NH3, respectively (Persson et al. 2010, 2012). It should be added that the rotational ground-state transitions of several hydrides species lie in favorable atmospheric windows and can be explored from the ground, for example with the Atacama Pathfinder Experiment telescope (APEX). These include NH2 (van Dishoeck et al. 1993), OH+ (Wyrowski et al. 2010), SH+, HCl, and 13CH+ (all Menten et al. 2011).
In optical and UV observations of absorption lines the background sources must be bright stars, which limits these studies mostly to diffuse clouds within 1–2 kpc (Snow & McCall 2006). In contrast, at submillimeter and far-infrared wavelengths, rotational lines observed with HIFI, GREAT, or APEX appear in absorption against the bright continuum radiation from warm dust associated with the hot cores of high-mass star-forming regions. The rotational lines of the aforementioned and many other species are easily excited inside hot molecular cores so that they may appear in emission. In lower density diffuse clouds and the dilute envelopes of hot-core-containing regions, however, these molecules basically remain in their ground state and are seen in absorption at the radial velocities of the spiral arms crossing the sight line, determined by Galactic rotation. The brightest high-mass star-forming regions can be seen in dust and ionized gas throughout the galaxy, therefore sight lines longer than that to the Galactic center can be studied, for instance, to W 49 at 11 kpc.
To build a picture of the physics and chemistry of the ISM in the diverse clouds along the sight lines, chemical networks are constructed that predict the abundances of various molecules. These theoretical calculations must then be constrained by abundances that are derived from observations. In the low-density ISM of diffuse clouds, the distribution of the rotational levels is generally determined by the temperature of the cosmic microwave background (2.728 K). Thus, it is straightforward to calculate the column densities of the observed species. We note, that the excitation temperature of hydrides can be slightly higher than 2.728 K as a consequence of the far-infrared background. This effect has been described by Flagey et al. (2013) for o-H2O.
For the derivation of abundances we also need the column densities of atomic and molecular hydrogen, NH i and NH2, respectively, whose relative ratio varies with the cloud density (Snow & McCall 2006). The molecular fraction, that is, the fraction of hydrogen nuclei bound in H2, is given by fH2 ≡ 2NH2/ (NH i + 2NH2). It is a key parameter for understanding cloud chemistry thanks to the stable 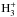 ion, which initializes the chemistry of oxygen-bearing species and that of carbon-bearing species in dense clouds.
ion, which initializes the chemistry of oxygen-bearing species and that of carbon-bearing species in dense clouds.
The electric quadrupole transitions of the homo-nuclear molecule H2 are excited in warm clouds and shocks, but not in diffuse and dense gas. The first detection in diffuse gas was made on the sight line to ζ Persei in the Lyman resonance absorption bands (Carruthers 1970). Follow-up work was done with the far-ultraviolet satellites Copernicus (Savage et al. 1977) and FUSE (Shull et al. 2000; Rachford et al. 2002, 2009) on sight lines toward extragalactic background sources. On longer path lengths, where far-ultraviolet observations are not possible anymore because of high reddening, direct measurements of NH2 are very difficult. CH and HF have been proposed as surrogates (Gerin et al. 2010b; Qin et al. 2010; Sonnentrucker et al. 2010). As discussed by Neufeld et al. (1997) and Monje et al. (2011), HF is a good proxy for the H2 column density because fluorine is the only atom that can react exothermically with H2 to form a diatomic hydride and HF is destroyed very slowly. Hence it is expected to be the dominant reservoir of gas-phase fluorine when H2 and HF are the dominant reservoirs of gas-phase H and F nuclei, as shown by Neufeld et al. (2005). For more details we refer to Godard et al. (2012, their Appendix C), Indriolo et al. (2013, HF abundance from ro-vibrational spectroscopy) and Wiesemeyer et al. (2016, Appendix E), and to the recent review article by Gerin et al. (2016). Recently, the abundance of HF has been constrained by Sonnentrucker et al. (2015) to values in the range from 0.9 to 3.3 × 10-8 at the low densities of cloud surfaces and, respectively, in the centers of dense translucent clouds. These models, which use recent measurements of the F+H2 reaction rate (Tizniti et al. 2014), describe the abundance found by Indriolo et al. (2013), who compared the column densities deduced from ro-vibrational near-infrared absorption profiles of HF at λ2.5 μm to directly determined H2 column densities from the far-ultraviolet and near-infrared lines.
In contrast, direct determinations of the atomic hydrogen (H i) column density, NH i, from the famous 21 cm line are relatively straightforward, and the main subject of this paper. In the optically thin limit, NH i can be inferred from emission spectra alone, ![\begin{equation} N_\ion{H}{i}\left[\mathrm{cm}^{-2}\right] = 1.823\times10^{18}\int~\mathrm{d}\varv\,T_\mathrm{B}(\varv)\,\left[\mathrm{K\,km\,s}^{-1}\right],\label{eq:coldens} \end{equation}](/articles/aa/full_html/2017/04/aa28597-16/aa28597-16-eq16.png) (1)where TB(ν) is the brightness temperature profile of the H i gas and ν is the radial velocity. However, especially in the Milky Way (MW) disk, the opacity of the gas is usually non-negligible (e.g., Radhakrishnan 1960; Gibson et al. 2005a; Braun et al. 2009; Martin et al. 2015). In such cases, H i absorption spectroscopy is a great tool to measure the optical depth, which in combination with TB can be used to estimate the true column density of the H i gas and its spin temperature, a method pioneered by Lazareff (1975).
(1)where TB(ν) is the brightness temperature profile of the H i gas and ν is the radial velocity. However, especially in the Milky Way (MW) disk, the opacity of the gas is usually non-negligible (e.g., Radhakrishnan 1960; Gibson et al. 2005a; Braun et al. 2009; Martin et al. 2015). In such cases, H i absorption spectroscopy is a great tool to measure the optical depth, which in combination with TB can be used to estimate the true column density of the H i gas and its spin temperature, a method pioneered by Lazareff (1975).
Interferometric observations of H i absorption allow us to study the MW ISM with fantastic angular resolution and sensitivity. In particular, the Canadian Galactic Plane Survey (CGPS, Taylor et al. 2003), the Southern Galactic Plane Survey (SGPS, McClure-Griffiths et al. 2005), and the VLA Galactic Plane Survey (VGPS, Stil et al. 2006) provide an extremely useful database. For example, the structure of the MW is well traced, as discussed in Strasser et al. (2007), Dickey et al. (2009, outer spiral arms), and Dickey et al. (2003, inner Galaxy). With the observation of so-called H i self-absorption (HISA) features, we can reveal small-scale fluctuations such as filaments, which are not visible in emission data (Gibson et al. 2000, 2005b; McClure-Griffiths et al. 2006). With the Millennium Arecibo 21 cm absorption-line survey (Heiles & Troland 2003a), the solar neighborhood was studied in detail (Heiles & Troland 2003b). Not only Galactic con- tinuum sources are used, but also extra-galactic sources (Strasser & Taylor 2004; Stanimirović et al. 2014; Lee et al. 2015). This has the great advantage that blending of different features along the lines of sight is much better under control (see also Sect. 4.1). It is even possible to detect H i absorption with Very Long Baseline Interferometry (VLBI). With this, extremely small-scale features have been discovered, the so-called tiny-scale atomic structure (TSAS; Heiles 1997, and references therein), with characteristic sizes of a few tens of AU.
The main motivation for the study we present here was to provide an H i data set, corrected for optical-depth effects, as a complement for previous studies of ISM chemistry: in combination with HF measurements, the total hydrogen column density as well as the ratio between atomic and molecular gas can be inferred, which is a valuable ingredient in the analysis of the complex processes in the ISM, such as hydrogen abstraction reactions in the pathways of diffuse cloud chemistry (Gerin et al. 2016, further references therein). Therefore we performed VLA observations of selected sight lines through the Milky Way disk, mostly targeting sources from the PRISMAS and HEXOS samples, as well as toward G 31.41+0.31. Preliminary results derived from our observations of H i along these sight lines have been used in several studies based on PRISMAS, HEXOS, and SOFIA data (e.g., Schilke et al. 2014; Gerin et al. 2015; Indriolo et al. 2015; Neufeld et al. 2015b,a; Wiesemeyer et al. 2016). They are essential in allowing column densities of species prevalent in primarily atomic gas, including ArH+, C+, OH+, and H2O+, to be converted into relative abundances that can be compared with model predictions. Such comparisons can provide unique information of general importance to our understanding of diffuse interstellar gas, including estimates of the cosmic-ray ionization rate (e.g., Indriolo et al. 2015), the gas pressure (Gerin et al. 2015), and the distribution of cloud sizes (e.g., Neufeld & Wolfire 2016). Such investigations will need to be combined with theoretical studies and simulations (e.g., Dobbs et al. 2012; Valdivia et al. 2016) to build a consistent picture of the Galactic ISM. In the following we provide a detailed discussion of the derivation of opacity-corrected H i column densities, to be used as reference for these and similar future studies.
H i absorption toward some of our targets has been investigated previously. Koo (1997) used the VLA in its D configuration and the Arecibo 305 m telescope to infer opacities for the W 51 complex. Brogan & Troland (2001) showed VLA B and D array data of W 49. Sgr B2 was observed by Liszt et al. (1983) (VLA, only nine antennas) and recently, in much greater detail, by Lang et al. (2010). Roberts et al. (1997) used the VLA in B configuration to map DR 21. Except for DR 21 and Sgr B2, the cited studies have a spectral resolution that is too low to be of use here. The latter two have even much more sensitive data. Nevertheless, for this work we make use of our own data, for the following reasons:
-
The different sight lines should have been observed andprocessed in the same way, to allow direct comparison.
-
Not all of the previous studies have calculated column density profiles, which is what we are interested in. This is usually because no suitable H i emission line data are available.
Furthermore, we like to explore the uncertainty of the derived opacity and of the corrected column density spectra. None of the previous studies did this.
It should also be noted here that a VLA C-array survey is currently under way, the H i/OH/Recombination line survey (THOR, P.I.: H. Beuther). First data products have just been released (Beuther et al. 2016). Furthermore, a pilot study that analyzes the W 43 star-forming region was recently published (Bihr et al. 2015). THOR will produce H i absorption data for many Galactic lines of sight, but as a large-scale on-the-fly survey, THOR is much less sensitive than pointed observations.
In Sect. 2 we present the formalism for deriving the atomic hydrogen column density by combining emission and absorption profiles of H i line observations. The data sets we used are described in Sect. 3, along with some details about data processing. Section 4 presents the derivation of NH i and discusses systematic uncertainties. Section 5 deals with the analysis of the molecular hydrogen fraction, and with its interpretation in terms of Galactic spiral structure. We conclude this work with a summary in Sect. 6.
2. Deriving opacity-corrected H i column densities through absorption spectroscopy
As discussed in the introduction, deriving H i opacities and corrected column densities has been the topic of many studies for several decades. The method itself and relevant equations are also covered in textbooks. Nevertheless, we here briefly repeat the basics.
We start by considering the simplest case of a single (isothermal) cloud in front of a continuum source. Recording two spectra, one in the direction of the background source, the other one offset but nearby, we find 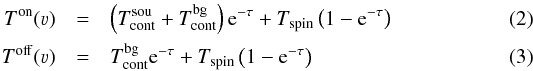 with the continuum flux density of the background source,
with the continuum flux density of the background source, 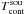 , and the larger-scale continuum sky background in the area,
, and the larger-scale continuum sky background in the area, 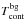 . It is explicitly assumed that the contribution of the foreground cloud is identical for both sight lines, while the Toff spectrum contains none of the background source’s continuum. The brightness temperature TB = Tspin(1−e− τ) of the foreground cloud is a function of the spin temperature, Tspin, and of the optical depth, τ, of the cloud.
. It is explicitly assumed that the contribution of the foreground cloud is identical for both sight lines, while the Toff spectrum contains none of the background source’s continuum. The brightness temperature TB = Tspin(1−e− τ) of the foreground cloud is a function of the spin temperature, Tspin, and of the optical depth, τ, of the cloud.
We left out in Eq. (2) the potential effects of (1) a non-uniform coverage of the continuum emission by the absorbing foreground medium and (2) beam filling, that is, the background source being unresolved by the telescope beam. When the background source is smaller than the observing beam, the measured (i.e., beam weighted) 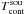 contribution is smaller than the true background source’s brightness temperature. Likewise, when the foreground cloud is not a sheet with uniform physical and chemical conditions but varies across the beam, we would need to correct for this as well. In general, it will even be the case that relevant structures in fore- and background are completely mismatched because they are not physically related. As a consequence, the correction for the filling factors is non-trivial and often complex (Wilson et al. 2013). We return to this in Sect. 4.
contribution is smaller than the true background source’s brightness temperature. Likewise, when the foreground cloud is not a sheet with uniform physical and chemical conditions but varies across the beam, we would need to correct for this as well. In general, it will even be the case that relevant structures in fore- and background are completely mismatched because they are not physically related. As a consequence, the correction for the filling factors is non-trivial and often complex (Wilson et al. 2013). We return to this in Sect. 4.
One important step to lessen the impact of structure of the absorber is to place the Off position as close as possible to the On sight line. Data with high angular resolution are obviously preferable for this and also provide a better match to the pencil-beam absorption spectrum. Further improvement can be obtained by means of interpolation, where we try to estimate the Toff spectrum from the surrounding as it would appear at the spatial position of the On sight line if no absorption was present. For sensitive single-dish observations, where only targeted spectra are measured, Heiles & Troland (2003a) proposed a scheme consisting of 16 Off positions, which makes it possible to correct for side-lobe contamination. Their interpolation is based on Taylor expansion. When we have access to a full spectral data cube (a map of spectra), as in the case of radio interferometry data, we can apply a larger variety of interpolation methods (see, e.g., Sect. 3.2). For convenience, we introduce the baseline (continuum) level for each of the two spectra,  In principle, one problem can be that the sky continuum background not necessarily originates from behind the cloud; the cloud may even be located within the diffuse ionized gas that emits the continuum background. However, for the sight lines in this work,
In principle, one problem can be that the sky continuum background not necessarily originates from behind the cloud; the cloud may even be located within the diffuse ionized gas that emits the continuum background. However, for the sight lines in this work, 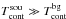 , such that we can safely ignore this issue.
, such that we can safely ignore this issue.
We note that for the optically thick case (τ ≫ 1), we find TB = Tspin, while for τ ≪ 1, we have TB = τTspin. Generally, TB ≤ Tspin for all τ. As a consequence, if source- and beam-filling effects can be neglected, Ton(ν) ≥ Toff(ν).
From Eqs. (2) and (3) the optical depth, 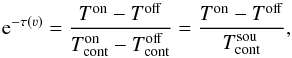 (6)can be calculated. From the opacity, τ, we can easily infer the spin temperature,
(6)can be calculated. From the opacity, τ, we can easily infer the spin temperature, 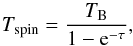 (7)and the H i column density
(7)and the H i column density ![\begin{equation} N_\ion{H}{i}\left[\mathrm{cm}^{-2}\right]=1.823\times10^{18} \int\mathrm{d} \varv\, \tau(\varv)T_\mathrm{spin}(\varv) \left[\mathrm{K\,km\,s}^{-1}\right]. \end{equation}](/articles/aa/full_html/2017/04/aa28597-16/aa28597-16-eq39.png) (8)While the basic idea and equations are very simple, many problems can arise. In addition to the filling factor issues, the numerical stability of the results is affected by the nonlinearity of Eq. (6). For very high opacities, the measured on-source spectral intensity is very close to the lowest possible value. Then, even small calibration errors or noise can lead to “unphysical” situations, that is, technically, the numerator in Eq. (6) can become negative. Furthermore, when estimating errors, we cannot assume Normal distributions for several of the quantities. The opacity and the derived column densities in particular have highly asymmetric uncertainty distributions.
(8)While the basic idea and equations are very simple, many problems can arise. In addition to the filling factor issues, the numerical stability of the results is affected by the nonlinearity of Eq. (6). For very high opacities, the measured on-source spectral intensity is very close to the lowest possible value. Then, even small calibration errors or noise can lead to “unphysical” situations, that is, technically, the numerator in Eq. (6) can become negative. Furthermore, when estimating errors, we cannot assume Normal distributions for several of the quantities. The opacity and the derived column densities in particular have highly asymmetric uncertainty distributions.
Program sources and JVLA continuum images summary.
Furthermore, in most circumstances we do not simply deal with one single isothermal cloud per sight line, but rather with an ensemble of clouds, sheets, or filaments, all having different physical properties (Tspin, τ) and being located at different distances with different radial velocities. Distance and radial velocity can even be uncorrelated. If two clouds at different distances (partly) share radial velocities, then the cloud in front will absorb a certain fraction of the radiation, leaving the cloud in the back. In the extreme case, the continuum source itself might be embedded in absorbing material. In fact, the latter is the case for all of the sight lines in our sample, but as we are mostly interested in the foreground clouds, this is not a major problem since the objects have different radial velocities.
There have been several attempts to correct for these effects. For this, a two-component gas is assumed, the so-called cold and warm neutral medium (CNM, WNM). The former is thought to produce the bulk of the absorption features, while the latter is considered to be diffuse and optically thin. Nevertheless, its higher spin temperature leads to considerable contributions to the total NH i (compare, e.g., Heiles & Troland 2003a; Stanimirović et al. 2014). The measured brightness temperatures are then separated, accounting for contributions by the CNM and the WNM. For the WNM, a distinction is made for clouds in front and behind each absorber. First attempts by Mebold et al. (1997) and Dickey et al. (2000) plotted TB vs. 1−e− τ to estimate spin temperatures for different velocity intervals in a spectrum. Later, Heiles & Troland (2003a) significantly improved on this idea by performing a least-squares fit of all CNM and WNM components and their physical parameters, by means of a Gaussian decomposition.
In our case, however, the continuum emitters are within the Milky Way disk. Hence, for most of our sight lines, the Galactic rotation leads to superposition of features from before and behind the continuum source in the emission spectrum. The method discussed above allows WNM components this freedom, but it assumes that high-opacity features are all accounted for in the absorption spectrum. This was the case for previous studies, which used extra-galactic background sources, but it is certainly not the case for our sight lines.
The two effects, blending of CNM/WNM features from the farther fraction of the sight line and neglecting the WNM components situated in front of the continuum emitter, act independently: consider (1) CNM and WNM with one component each, covering the same radial velocities. By associating the complete brightness temperature spectrum with the CNM alone, the inferred spin temperature will be too high, as is also true of NH i; (2) two CNM components, in front and behind the continuum source. Again, Tspin will be overestimated (because the brightness temperature falsely associated with the absorber is overestimated). NH i can either be over- or underestimated, however, depending entirely on the ratio of the opacities of the two components. If the component in front of the continuum source has higher τ, then NH i will be overpredicted, if its τ is smaller, NH i will be underestimated.
Lacking any further information, we can only treat each sight line as if the absorbing material in each spectral channel were associated to a single isothermal cloud, and introduce the concept of efficient spin temperature and total optical depth (see Chengalur et al. 2013, and references therein). This approach usually leads to estimates close to the true value by a factor of ≲2, as was shown by Chengalur et al. (2013) using Monte Carlo simulations.
3. H i absorption and emission line data
3.1. JVLA observations and data reduction
We observed the H i absorption line at 21 cm (at a rest frequency of 1420.405752 MHz) toward eight high-mass star-forming regions in the Galaxy (Sgr B2, G 10.62−0.39 (W 31C), W 33, G 31.41+0.31, G 34.3+0.1, W 49N, W 51, and DR 21) on January 20, 2012, using the National Radio Astronomy Observatory (NRAO) Karl G. Jansky Very Large Array (JVLA) in DnC configuration (program 11B-236). The phase center coordinates, which are identical to the positions Herschel was pointed at in the PRISMAS and HEXOS projects, for each of the maps are given in Table 1.
During the total observing time of 3 h, we first observed flux calibrators (e.g., 3C 286) for 30 min, and then placed two observing blocks of about 1 h duration each. Each 1-h block consisted of three repetitions of 22-min groups, each consisting of ~5-min scans toward four target sources and a 3-min scan toward the phase calibrator 1751−2524. We employed a frequency band of 2 MHz bandwidth in both right- and left-circular polarizations. The 2-MHz band was split into 4096 spectral channels, yielding a channel separation of 0.49 kHz and a velocity resolution of 0.10 km s-1 for the H i rest frequency.
The data calibration was performed using the NRAO Astronomical Image Processing System (AIPS) in the standard manner. Bandpass amplitude and phase corrections were determined from the calibrator 3C 286 and applied to all sources. We removed instrumental delay and phase offsets using the primary flux calibrator 3C 286 and the phase calibrator 1751−2524 and corrected the target source data for these offsets. Spectral-line image cubes were then made with the AIPS task IMAGR, and the images were cleaned subsequently.
 |
Fig. 1 Continuum maps at 1.4 GHz of the regions Sgr B2, G 10.62−0.39, W 33 A, and G 31.41+0.31 as observed with JVLA. The sight lines extracted for our analysis are annotated. The spatial coordinates of the sight lines are compiled in Table 2 for reference. Contour lines are in multiples of the RMS noise level as stated in the title of each panel. Negative contour lines are dotted, positive contours have solid line style. The beam size is indicated by the green ellipse in the lower left corner of each map. Inside graticules display Galactic coordinates. All maps were primary-beam corrected. Note that for the sake of better visualization only the central part of each map is displayed (about half the size of the primary beam). The blue crosses mark the phase centers of the JVLA observations. PRISMAS/HEXOS program positions are labeled with “P39”, and the PRISMAS/HEXOS 550-GHz beam size of ~ 39″ is indicated by red circles. For Sgr B2 two sight lines were observed within the HEXOS program, which we annotate “P39M” and “P39N”. Note that the JVLA phase centers do not necessarily match the highest continuum intensity positions. |
 |
Fig. 2 As Fig. 1, showing the regions G 34.3+0.1, W 49N, W 51, and DR 21. For W 51 the P39 position coincides with the ultra-compact H ii regions W 51 e1 to e4. |
In Figs. 1 and 2 we show 1.4-GHz continuum maps as observed with JVLA. For all sources, data for one or more (sufficiently bright) sight lines are extracted for subsequent analysis. The spatial coordinates for each of the extracted sight lines are compiled in Table 2. The continuum root-mean-square (RMS) was calculated following an iterative approach, masking values in excess of 3σRMS in each step. The RMS estimate converged after few iterations. The derived continuum RMS values are given in Table 1.
In contrast to common practice, we did not subtract the continuum from the spectral-line data, neither before nor after imaging the visibilities. This has the advantage that planes in the produced data cube that are most affected by absorption need the least amount of cleaning, while the continuum contribution of the background emitter appears as a (strong) positive feature in absorption-free planes. If we had subtracted the continuum in the first place, it would be the opposite way. Then the results in the most interesting parts of the spectrum would need extremely careful cleaning. The JVLA data are corrected for the primary-beam response before the relevant data are extracted.
We were unable to clean the continuum maps down to the thermal noise level. For the Sgr B2, W 49N, and W 51 maps in particular, residual artifacts appear (this is reflected by the apparent high noise levels). Since much effort was invested in calibration and deconvolution of the data, we suspect that the poor uv-coverage of our snapshot data is simply not sufficient for the relatively complex (and very bright) sources. We can still use the derived continuum maps for our analysis, but the nominally higher noise level leads to larger uncertainties in the derived opacity and column density spectra.
For each of the reduced data sets we extracted one or more absorption spectra from the final data cube for sight lines containing sufficient background continuum to warrant good signal-to-noise ratio for further analyses. These sight lines are annotated in Figs. 1 and 2. For four targets (G 10.62−0.39, G 34.3+0.1, W 49N, and W 51), continuum intensities at the exact PRISMAS program positions are high enough to study the associated profiles in detail. These sight lines are labeled P39, and the PRISMAS 550-GHz beam size of ~39″ is indicated by a red circle. For SGR B2 two positions (M and N) were observed within the HEXOS project. The associated sight lines are annotated P39M and P39N, respectively.
Lacking sufficient 21 cm continuum emission, no meaningful H i column density could be determined toward the strong far-infrared source W 33 A, but only toward the H ii region W 33 (Main); compare Fig. 1 (we refer to Immer et al. 2013 for a definition of the subregions of the W 33 complex). In addition, DR 21 (OH) shows only very weak radio continuum, and H i absorption data are retrieved toward the strong radio emission of the compact H ii region DR 21. This is shown in Fig. 2, where the centroid position is ~3′ south of the position given in Table 1; the centroid position has also been a Herschel/HIFI target (see, e.g., the first detection of H2O+ by Ossenkopf et al. 2010).
3.2. Using archival data to infer emission spectra
While the JVLA data cubes have high angular and spectral resolution, they are unfortunately not suitable to obtain an H i emission spectrum. This is because our JVLA data suffer severely from a lack of short spacings. In fact, there is little H i emission visible in the data cubes.
Since all observed sight lines are located within the Galactic plane, emission line data can be extracted from the three Galactic plane surveys. These data sets are publicly available and have been combined with single-dish data to incorporate short spacings. In our case, the sight lines of W 51, W 49N, G 31.41+0.31, and G 34.3+0.1 are contained in VGPS, DR 21 is from CGPS, while W 33 and G 10.62−0.39 sight lines were taken from SGPS. The Galactic center region needed for Sgr B2 is included in the ATCA H i Galactic Center Survey (McClure-Griffiths et al. 2012). In Table 3 basic survey parameters have been compiled.
 |
Fig. 3 Visualization of the moving-ring filter operation used to estimate the emission spectrum, TB(ν), at the positions affected by absorption features. The left panel shows a single plane (νlsr = 45.5 km s-1) of the VGPS data cube of W 51 located in the center of the map. In the middle panel the filtered plane is shown. The size of the ring filter is marked with the two black circles in the upper left. The right panel contains the residual image. It is used to estimate the error of the emission spectrum by calculating the RMS. To improve the RMS calculation, a mask was applied (see text). The mask is indicated by the black contours. |
Summary of the main observational parameters of the Galactic Plane surveys used to obtain emission spectra.
Of course, the Galactic plane surveys also exhibit H i absorption features toward bright continuum sources, and in our case these can be quite extended. Therefore, special treatment is necessary to construct a suitable emission spectrum, TB. We applied a moving-ring filter to each plane in the data cube: each pixel pi,j is replaced by the median value of all pixels in a ring around pi,j. The inner and outer radii of this ring were set to ri = 4′ and ro = 5′ for all sources except for Sgr B2, where we used ri = 7′ and ro = 9′ to account for the larger extent of the background continuum source. The aim of the ring filter is to replace pixels affected by absorption with an average of the surrounding material. In principle, this would be necessary only for the pixels/sight lines of interest. However, applying the filter operation to the full map allowed us to estimate the residual scatter in regions around the sight lines, which is useful for subsequent error estimation. To further improve the filter operation we blanked pixels showing substantial absorption, T < −25 K ≈ −10σRMS, at any radial velocity prior to filtering. The unphysical negative brightness temperature values are merely a result of the Galactic plane survey data reduction, where the continuum levels were subtracted from the spectral line data cube. We note that the ri and ro values were made as low as possible to yield a minimal RMS level in the residual map, but under the constraint that spurious signs of the relevant absorption features must not be visible in the filtered maps.
The filtered cube was subsequently subtracted from the original data, yielding a residual data cube containing only small-scale fluctuations. For each plane in the residual cube, the RMS noise was calculated within a circle of radius 20′ (30′ for Sgr B2) around the JVLA phase centers. This results in a “noise spectrum” ΔTB associated with each data set. The previously constructed blank mask was used again, after a dilation operator (five pixels in size) had been applied to it.
As an example, in Fig. 3 the result of such filtering is shown for one plane of the W 51 data cube (νlsr = 45.5 km s-1). The left panel displays the original data, the middle panel shows the ring-filtered data, and the right panel contains the residual. Except for a few regions in the map, mostly those exhibiting strong absorption, the residual is relatively homogeneous.
3.3. Correcting systematic errors
For the derivation of the opacity and column densities formulas in Sect. 2, we made several simplifying assumptions, which may in principle lead to systematic errors in our results. In the following, we briefly discuss the two main sources of potential uncertainty, and how to correct for them or lessen their impact.
3.3.1. Short-spacings correction
 |
Fig. 4 Comparison between Galactic plane survey (top panel) and JVLA emission (bottom panel) data. The missing short-spacings in the latter cause a significant lack of (diffuse) emission. The example displays DR 21 data at νlsr = 10.1 km s-1. Note the different intensity scales. |
As mentioned at the beginning of Sect. 3.2, the JVLA absorption data cubes are severely affected by the lack of short spacings. In Fig. 4 we show an example for the sight line to DR 21. The top panel shows a plane of the CGPS data cube at νlsr = 10.1 km s-1. The bottom panel contains the respective data from our JVLA data set. The former has a much higher base level of about 100 K, while in case of the JVLA, the mean is ~0 K.
 |
Fig. 5 Short-spacings correction for the JVLA absorption data. As an example, sight line 1 of the DR 21 source is shown. The black line is the original HI4PI spectrum, the red line is the JVLA data smoothed to HI4PI resolution, and the green line is the resulting short-spacings contribution. For comparison the result of the ring-filter operation, applied to the Galactic plane survey data cube, is displayed in blue (with 1σ uncertainties). |
To add the missing spacings, we made use of the recently published HI4PI data (HI4PI Collaboration et al. 2016). HI4PI is an all-sky single-dish H i survey combined from observations with the 64 m Parkes/Australia and 100 m Effelsberg/Germany radio telescopes. In principle, we could also use the Galactic plane survey data sets, but HI4PI is more sensitive. There are various techniques to correct for missing spacings (see, e.g., Stanimirovic 2002). Here, we chose combination in the image domain. First, we obtained suitable HI4PI data cubes of size 1° × 1° centered on the JVLA phase centers for each of our sources. Then, the JVLA data cubes were spatially and spectrally smoothed to the HI4PI resolution and resampled to the HI4PI voxel (volume pixel) grid, using the Python gridding software cygrid (Winkel et al. 2016). This gives the brightness temperatures, 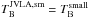 , that would have been observed by HI4PI if only the small angular scales, accessible to JVLA, were present. Of course, HI4PI, being a single-dish survey, observed all angular scales (i.e.,
, that would have been observed by HI4PI if only the small angular scales, accessible to JVLA, were present. Of course, HI4PI, being a single-dish survey, observed all angular scales (i.e., 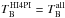 ). Therefore, the larger angular scales, which are missing in the JVLA data, can be computed as
). Therefore, the larger angular scales, which are missing in the JVLA data, can be computed as 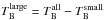 and subsequently be used to correct the JVLA absorption spectra for each sight line.
and subsequently be used to correct the JVLA absorption spectra for each sight line.
As an example, we display the three quantities in Fig. 5. The black line is the original HI4PI spectrum, 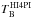 , on the position of sight line 1 of the DR 21 source. From the smoothed JVLA data cube we extract
, on the position of sight line 1 of the DR 21 source. From the smoothed JVLA data cube we extract 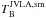 (red line). The result,
(red line). The result, 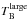 , is plotted in green. For comparison, we also show the result from the ring-filtered Galactic plane survey data set (blue line, with 1σ errors). We also find for all other sources and sight lines that the short-spacings contribution is very similar to the GPS (ring-filtered), which means that no significant contribution stems from angular scales larger than the size of the ring-filter aperture. We note that this effectively means that the nominator in Eq. (6) reduces to the originally measured JVLA absorption spectrum, and the opacity spectrum is therefore almost exclusively determined by the JVLA absorption data alone. However, the interpolated brightness temperature spectrum, Toff, is still mandatory for deriving spin temperatures and column densities.
, is plotted in green. For comparison, we also show the result from the ring-filtered Galactic plane survey data set (blue line, with 1σ errors). We also find for all other sources and sight lines that the short-spacings contribution is very similar to the GPS (ring-filtered), which means that no significant contribution stems from angular scales larger than the size of the ring-filter aperture. We note that this effectively means that the nominator in Eq. (6) reduces to the originally measured JVLA absorption spectrum, and the opacity spectrum is therefore almost exclusively determined by the JVLA absorption data alone. However, the interpolated brightness temperature spectrum, Toff, is still mandatory for deriving spin temperatures and column densities.
3.3.2. Beam-filling considerations
We have discussed in Sect. 2 that the effect of beam filling can usually not be neglected. Its consequence is a reduction of the observed intensity, 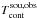 , by a factor fB, that is,
, by a factor fB, that is, 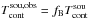 . Likewise, the observed On spectrum is modified
. Likewise, the observed On spectrum is modified 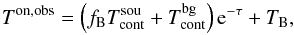 (9)and we can show that
(9)and we can show that 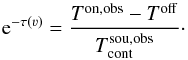 (10)Hereafter, we use the superscript “obs” to mark a quantity that is affected by beam filling (with respect to the continuum-emitting background source, only). Equation (10) shows that it is not necessary to incorporate the beam-filling factor in the opacity calculations; we can just work with the observed quantities. However, the absorption profile itself is changed indeed: fB effectively acts a weighting factor between emission and absorption in Eq. (9). This also explains why absorption features in low-angular resolution data are often much less pronounced. The relative strength of the absorption line (with respect to TB) is suppressed. If no other filling factor effects were to play a role, however, we could infer the opacity equally well from such data. In practice, however, in lower-angular resolution single-dish observations, the structure of the absorbing source cannot be neglected, which makes an analysis much more challenging.
(10)Hereafter, we use the superscript “obs” to mark a quantity that is affected by beam filling (with respect to the continuum-emitting background source, only). Equation (10) shows that it is not necessary to incorporate the beam-filling factor in the opacity calculations; we can just work with the observed quantities. However, the absorption profile itself is changed indeed: fB effectively acts a weighting factor between emission and absorption in Eq. (9). This also explains why absorption features in low-angular resolution data are often much less pronounced. The relative strength of the absorption line (with respect to TB) is suppressed. If no other filling factor effects were to play a role, however, we could infer the opacity equally well from such data. In practice, however, in lower-angular resolution single-dish observations, the structure of the absorbing source cannot be neglected, which makes an analysis much more challenging.
Although fB does not play a role for estimating τ, we still determined it for each sight line and quote the values (Sect. 4, Fig. B.14, and Appendix B) because it may be useful when comparing the absorption profiles.
The continuum maps (Figs. 1 and 2) show that most of the extracted sight lines are toward unresolved sources. Assuming the sources can be described by an elliptical Gaussian, the angular size of the beam and the intrinsic size of each source add quadratically. Thus, it is possible to obtain a rough estimate on fB by fitting (elliptical) Gaussians to the sight lines. In several cases blending of features complicates the fitting, however. Stable results could be achieved by using an iterative approach, applying a clip mask (neglecting values above 3σRMS) and increasing the fit aperture in steps from two to three beam widths. With the determined source sizes we calculated the beam-filling factors through numerical integration.
Unfortunately, we can only estimate the beam-filling effects for the background continuum emitter, but not for the absorbing material. As a consequence, a correction for the source covering factors is not possible. All our derived opacity and column density profiles will therefore include the implicit assumption that absorbing material is a constant sheet of gas (across the beam). However, we show below that in the derived opacity and column density spectra relatively strong spatial variations are detected, which casts doubts on the validity of this assumption.
4. Computing H i opacities and column densities
In the following we describe how the two complementary data sets are used to compute optical depth, spin temperature, and column density spectra. To estimate reasonable error bars, we employed Bayesian inference using the pymc framework (version 3), which is a library module available for the Python programming language. If provided with a list of stochastic variables and their relationship, the pymc framework can automatically calculate the joint likelihood distribution. Given a start parameter vector, pymc can then sample the complex parameter space using Markov-chain Monte Carlo (MCMC) calculations. From the resulting chains, it is possible to marginalize over individual parameters, which allows us to compute the expected value of each parameter and its error distribution.
In our case, we have four observed quantities (per spectral channel). For each we can estimate its uncertainty:
-
For the absorption noise spectrum, we first smoothed the VLAdata cube in velocity (using a Gaussian filter with a kernel width ofeight spectral channels, FWHM) to approximately match thespectral resolution of the emission spectrum. For each sight line,we extracted the spectrum
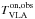 . Furthermore, in the resulting data cube we iteratively inferred the RMS, σRMS, per velocity plane in a robust manner, by blanking 4σRMS outliers in each step. This typically converged after three iterations and results in an estimate for
. Furthermore, in the resulting data cube we iteratively inferred the RMS, σRMS, per velocity plane in a robust manner, by blanking 4σRMS outliers in each step. This typically converged after three iterations and results in an estimate for 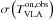 .
. -
For the emission spectrum, inferred from the Galactic plane surveys, the method described in Sect. 3.2 delivers not only the
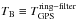 estimate, but also its frequency-dependent uncertainty spectrum,
estimate, but also its frequency-dependent uncertainty spectrum, 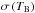 , for each target data set. For subsequent calculations, the resulting emission spectra were interpolated to the spectral grid defined by the VLA absorption data sets.
, for each target data set. For subsequent calculations, the resulting emission spectra were interpolated to the spectral grid defined by the VLA absorption data sets. -
The continuum levels,
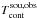 , for each sight line were extracted from the continuum maps (Figs. 1 and 2). The associated errors
, for each sight line were extracted from the continuum maps (Figs. 1 and 2). The associated errors 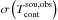 , were already quoted in Sect. 3.1, Table 1.
, were already quoted in Sect. 3.1, Table 1. -
For the sky background,
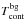 , and its uncertainty,
, and its uncertainty, 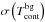 , we took rough estimates from the Stockert 21 cm survey (Reich 1982; Reich & Reich 1986). However, the contribution of
, we took rough estimates from the Stockert 21 cm survey (Reich 1982; Reich & Reich 1986). However, the contribution of 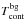 to the JVLA continuum flux is smaller than 1% in all cases and can safely be ignored, compared to the magnitude of all other uncertainties.
to the JVLA continuum flux is smaller than 1% in all cases and can safely be ignored, compared to the magnitude of all other uncertainties.
We note that all these estimates account for spatial variations and not only for the noise in one sight line. This means that potential errors caused by improper cleaning and short-spacings correction or the ring-filtering are included.
Before we processed the data in pymc, we calculated the effectively observed On and Off profiles 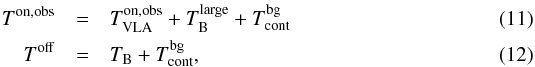 where we added
where we added 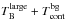 to the VLA H i absorption spectrum,
to the VLA H i absorption spectrum,  , to account for short-spacings (see Sect. 3.3.1). Because the errors of the inputs are approximately Normal-distributed, we can directly calculate the resulting uncertainties
, to account for short-spacings (see Sect. 3.3.1). Because the errors of the inputs are approximately Normal-distributed, we can directly calculate the resulting uncertainties 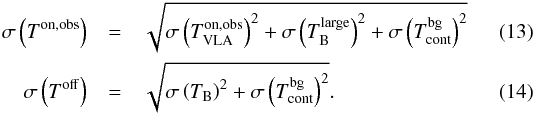 For the four variables, Ton,obs, Toff,
For the four variables, Ton,obs, Toff, 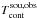 , and
, and 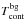 we assigned Normal distributions in pymc with the according standard deviations. We note that technically we have to provide pymc a Normal-distribution object with an observed keyword argument along with the mean and standard deviation of the distribution if we wish to define observables. For Ton,obs and Toff we inserted the two model equations, Eqs. (9) and (3), for the mean, and the inferred errors for the standard deviation. However, in case of
we assigned Normal distributions in pymc with the according standard deviations. We note that technically we have to provide pymc a Normal-distribution object with an observed keyword argument along with the mean and standard deviation of the distribution if we wish to define observables. For Ton,obs and Toff we inserted the two model equations, Eqs. (9) and (3), for the mean, and the inferred errors for the standard deviation. However, in case of 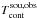 and
and 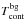 we do not know the true mean of the distribution (our measurement is one draw from it, and pymc cannot calculate it from other quantities). The solution is to define the mean as another random variable with a flat prior (i.e., using a uniform distribution).
we do not know the true mean of the distribution (our measurement is one draw from it, and pymc cannot calculate it from other quantities). The solution is to define the mean as another random variable with a flat prior (i.e., using a uniform distribution).
Furthermore, we have two unknown variables, the opacity, τ and the spin temperature, Tspin. For τ, which certainly has an asymmetric distribution, we used a lognormal prior with μ = 0 and σ = 2. Having no better prior information, we work with a flat prior for the spin temperature.
These six distributions are linked through Eqs. (2) and (3), and pymc automatically computes the resulting likelihood function. For the posteriors of τ and Tspin we can then calculate distribution percentiles to quantify 1σ and 3σ confidence levels (CL). The 1σ interval is defined by the 15.87% and 84.13% percentiles, while the 3σ interval is given by the 0.13% and 99.87% percentiles. Furthermore, we determine the 50% percentile (i.e., the median); this is the most likely result.
 |
Fig. 6 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the PRISMAS program source W 51, sight line P39. For a detailed description see text. The labels CL 1 and CL 3 refer to the 1σ and 3σ confidence intervals, i.e., the 68% and 99.7% distribution percentiles (see also text). |
Figure 6 shows the results of our absorption analysis for the example of the PRISMAS program source W 51 (sight line P39). Other PRISMAS/HEXOS sight lines are contained in Appendix A, Figs. A.1 to A.3, and all remaining spectra are compiled in Appendix B, Figs. B.1 to B.14 (compare Figs. 1 and 2 for the spatial position of the sight lines). The top panel displays the normalized on-source spectrum, 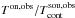 . The black solid line is the spectrally smoothed profile, which matches the resolution of the emission data. The blue interval visualizes the 1σ interval. The continuum flux density,
. The black solid line is the spectrally smoothed profile, which matches the resolution of the emission data. The blue interval visualizes the 1σ interval. The continuum flux density, 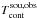 , of the background point source, as inferred from the continuum maps, is denoted in the upper panel.
, of the background point source, as inferred from the continuum maps, is denoted in the upper panel.
The second panel contains the interpolated brightness temperature spectrum, Toff (black solid line), including 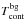 . The blue interval again shows the 1σ interval. The value of
. The blue interval again shows the 1σ interval. The value of 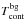 is annotated in the plot.
is annotated in the plot.
The remaining three panels show the optical depth, spin temperature, and H i column density. In each panel, the blue and gray intervals refer to the 1σ (68% percentile) and 3σ (99.7% percentile) confidence levels, as discussed above, while the black solid line is the median of the resulting distributions (50% percentile). In the temperature panel, we also show the brightness temperature for comparison (blue solid line). By design, it provides a lower limit to the spin temperature because we added the emission spectrum to the H i absorption profile for an approximate short-spacings correction. The bottom panel also displays the uncorrected column density spectrum, 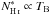 (blue solid line).
(blue solid line).
4.1. Discussion
Similar to Fish et al. (2003), we have plotted a distance indicator in each of the figures (upper panels). It is based on a very simple model of disk rotation of the Milky Way (flat rotation curve with R0 = 8.34 kpc and Θ0 = 240 km s-1 (A5 model); see Reid et al. 2014) calculated for each of the sight lines. The bend in the bar refers to the terminal velocity (tangent point), and the black circle marks the distance to the PRISMAS/HEXOS program sources on the respective sight lines (compare Table 1). The associated LSR velocity of this black circle is in most cases inconsistent with observations; compare Table 1. This is either caused by peculiar velocities or by the applied MW rotation model being incorrect. Therefore, we also draw a black arrow in the top panel to indicate the approximate source velocity of the continuum-emitting PRISMAS/HEXOS source, as inferred from observations. It is not possible to plot a distance indicator for the sight line to Sgr B2 since there is no radial velocity component toward the Galactic center in a simple disk-rotation model. According to Levine et al. (2006), the H i surface density has considerable values out to galactocentric radii of R ~ 20 kpc. We can therefore calculate a maximum distance for each sight line out to which H i emission can be expected. This is reflected by the length of the distance indicators in the plots. The emission spectrum covers the possible range of distances quite well in all cases.
This also clearly illustrates our discussion of blending issues in Sect. 2: the velocity-distance relation is degenerate. H i features from the far end of the MW disk are folded into the velocity range covered by the absorbing material. In all sight lines the “background” continuum source is at much shorter distances than the full length of the sight line through the MW H i gas. This additional contribution to the emission spectrum, Toff, is unaccounted for when calculating spin temperatures and opacity-corrected column densities because we cannot separate the near- and far-side components. For the On–Off technique, only the near-side contribution would be relevant. This issue introduces a systematic error, which is not incorporated into the Bayesian uncertainty calculation, and leads to overestimation of Tspin and NH i. Because the received H i emission from a thin sheet of gas at distance [d,d + Δd] decreases with d2 but at the same time the observed volume increases with d2, the contribution of a near- and far-side component with identical radial velocity will be similar, given homogeneous density. In reality, however, the radial velocities and the H i distribution along the sight lines are too complex for a simple estimation of the size of the overall effect.
For several of the targets we were able to extract more than one absorption profile. In some cases there is considerable small-scale variation in the absorbing material that is unrelated to the background objects: the absorption features differ significantly in the sight lines toward G 10.62−0.39 and W 51. As an example, for G 10.62−0.39 the two analyzed sight lines are only 90′′ apart, and absorption features differ significantly on radial distances smaller than 2 to 3 kpc. This converts into spatial scales of about 1 pc. Fluctuations on even smaller scales (several AU) were detected with VLBI experiments (e.g., Faison et al. 1998; Brogan et al. 2005; Lazio et al. 2009), which used as background sources the bright continuum emission of the jets of the active galactic nuclei of 3C 138, 3C 147 and other galaxies. For W 33 and G 34.3+0.1, the JVLA profiles seem to have much less variation. The remaining targets do not permit such an analysis.
4.2. Comparison with previous studies
As noted in the introduction, for several of our targets there exist other studies, which calculated H i opacities and in some cases also NH i values.
4.2.1. Sgr B2
H i absorption in the Galactic center region has been studied in great detail in Lang et al. (2010). Their Sgr B2 sight line was also part of their analyses. The derived opacity spectrum is consistent with our findings, although the spectral resolution of δν = 2.5 km s-1 is lower. Based on consistency arguments, Lang et al. (2010) assumed a spin temperature of 60 K, which is close to our findings for a good fraction of the absorbers along the sight line.
4.2.2. G 31.41+0.31 and G 34.3+0.1
For G 31.41+0.31 and G 34.3+0.1 we are not aware of dedicated H i absorption measurements. However, Dickey et al. (1983) presented a spectrum toward the extragalactic source 1849+005, (l,b) = (33.5°,0.19°, which is in close vicinity. The sensitivity and spectral resolution is much poorer, but nevertheless, the τ spectrum seems consistent, with one exception: in our G 34.3+0.1 data, the absorption is only visible below ν≲ 70 km s-1, while in 1849+005 and G 31.41+0.31 absorption occurs out to ν≲ 120 km s-1. This is not surprising because G 34.3+0.1 is located at much smaller distance.
4.2.3. W 49
The source W 49 was also observed by Brogan & Troland (2001, their sight line L equals our sight line 4). Their opacity spectrum only covers −20 < νlsr< 20 km s-1 and is, in this interval, consistent with our findings. They did not measure Tspin, but estimated it to be in the range of 20 to 150 K, which is compatible with our findings, if not a very strict limit.
4.2.4. W 51
The whole W 51 complex has been studied by Koo (1997), while we only observed a smaller region in the northwestern part of W 51 (their sight line G 49.5−0.4 e corresponds to our PRISMAS sight line P39). Their spectra have relatively coarse resolution, but the opacities and integrated H i column densities are very consistent, ours being only about 20% higher. To derive NH i, Koo (1997) assumed a constant spin temperature of 160 K, which is compatible with our findings at local velocities, but for 40 ≲ νlsr ≲ 70 km s-1 we find significantly lower values of Tspin ≲ 100 K (which is probably even overestimated; see Sect. 2).
4.2.5. DR 21
The source DR 21 is interesting because it features a molecular outflow (Roberts et al. 1997) that is visible as a broad wing in the absorption spectrum (−30 < νlsr< −6 km s-1). The opacities, derived in Roberts et al. (1997), are slightly higher than our values, and their assumed Tspin of 20 K is significantly below the ~100 K from our calculation.
5. Molecular hydrogen fraction on the observed sight lines
With the H i column densities at hand, we can derive the molecular hydrogen fraction fH2≡ 2NH2/ (NH i + 2NH2) in a relatively straightforward way. As already stated in the introduction, the direct measurement of NH2 is excluded on sight lines that are mainly populated with translucent clouds (Rachford et al. 2002), and where possible, it has a limited spectral resolution (typically 20 km s-1). We therefore used the HF absorption spectra from HIFI (key projects PRISMAS, Gerin et al. 2012, and for Sgr B2, HEXOS; Bergin et al. 2010) as a proxy for H2. Data analysis was performed with the CLASS software2. We did not consider the sight lines to DR 21 (OH) and W 33 A because their radio continuum is too weak to allow for a reliable estimate of fH2.
5.1. Computing HF column densities
As described in the introduction, HF and CH can be used as surrogates for H2. The rotational ground-state line of CH has a relatively large hyperfine splitting of ~20 km s-1. At the radial velocities of the hot cores, illuminating the diffuse gas on the sight line, the CH lines easily turn into emission. Both circumstances lead to complications that we prefer to avoid here. The correspondence between HF and CH column densities has been discussed by Godard et al. (2012, and references therein). Wiesemeyer et al. (2016) have confirmed this correspondence on the sight line to W 49N. Within 15%, the conversion factor deduced from the HIFI/PRISMAS absorption spectrum is in agreement with an abundance of HF of 1.4 × 10-8, which agrees with recent findings by Sonnentrucker et al. (2015), who in turn confirmed the measurements of Indriolo et al. (2013) in the v = 1−0,R(0) ro-vibrational transition of HF using recent measurements of the HF+H2 reaction rate (Tizniti et al. 2014).
The HF molecule, which was first discovered on the sight line to Sgr B2 (Neufeld et al. 1997), owes its usefulness as proxy for H2 to the reaction F(H2, H)HF (fluorine is the only element capable of such an exothermic reaction with H2). Light hydrides, such as HF and CH, have large Einstein A-coefficients, which is why it is difficult to excite them collisionally in diffuse clouds. In the radiative equilibrium with the Galactic interstellar radiation field, we can safely assume that basically all HF molecules are in the ground state.
 |
Fig. 7 Molecular hydrogen fraction fH2≡ 2NH2/ (NH i + 2NH2) on the sight lines toward G 10.62−0.39 (W 31C) and G 34.3+0.1. |
This allows us to directly determine the H2 column density, dN/ dν, from the measured optical depth τ by means of the equation (e.g., Cannon 2012) ![\begin{equation} \tau = \frac{A_\mathrm{E}c^3}{8\pi \nu^3} \left[1-\exp{\left(-\frac{E_\mathrm{u}}{k_\mathrm{b}T}\right)}\right] \frac{g_{\mathrm{u}}}{Q(T)}\frac{{\rm d}N}{{\rm d}\varv}, \end{equation}](/articles/aa/full_html/2017/04/aa28597-16/aa28597-16-eq366.png) (15)where AE is the spontaneous emission Einstein coefficient of the transition of frequency ν, Eu is the energy of the upper level with degeneracy gu, and Q(T) is the partition function at temperature T. For thermalization of the level population at temperatures of up to ~ 10 K (e.g., for radiative equilibrium with the cosmic microwave background, Tcmb = 2.728 K), the factor
(15)where AE is the spontaneous emission Einstein coefficient of the transition of frequency ν, Eu is the energy of the upper level with degeneracy gu, and Q(T) is the partition function at temperature T. For thermalization of the level population at temperatures of up to ~ 10 K (e.g., for radiative equilibrium with the cosmic microwave background, Tcmb = 2.728 K), the factor ![\hbox{$\left[1-\exp\left(-\frac{E_\mathrm{u}}{k_\mathrm{b}T}\right)\right]/Q(T) \simeq 0.99$}](/articles/aa/full_html/2017/04/aa28597-16/aa28597-16-eq375.png) , and the total column density per unit velocity can be directly determined from the measured opacity. For the HF J = 1−0 transition, the underlying parameters are ν = 1232.47627 GHz, AE = 0.024234 s-1, Eu = 59.14919 K, gu = 2Ju + 1 = 3, and Q(9.375 K)= 1.006 (Pickett et al. 1998, further references therein). The resulting column density profiles are shown in Fig. 7 for sight lines to G 10.62−0.39 (W 31C) and G 34.3+0.1, in Fig. 8 for sight lines to W 49N and W 51e4, and in Fig. 9 for the sight line to Sgr B2.
, and the total column density per unit velocity can be directly determined from the measured opacity. For the HF J = 1−0 transition, the underlying parameters are ν = 1232.47627 GHz, AE = 0.024234 s-1, Eu = 59.14919 K, gu = 2Ju + 1 = 3, and Q(9.375 K)= 1.006 (Pickett et al. 1998, further references therein). The resulting column density profiles are shown in Fig. 7 for sight lines to G 10.62−0.39 (W 31C) and G 34.3+0.1, in Fig. 8 for sight lines to W 49N and W 51e4, and in Fig. 9 for the sight line to Sgr B2.
Associated opacity and spin temperature profiles are presented in Appendix A, Figs. A.1 to A.3. The evaluation of confidence levels follows the method described in Sect. 4. Again, large errors are apparent where the sight line absorption turns to saturation either in H i or in HF, or both. This is systematically the case toward the illuminating background sources, where our assumption of a complete ground-state occupation breaks down, and where the chemistry is very different from that in diffuse clouds (for the chemistry of light hydrides in hot cores see, e.g., Bruderer et al. 2010). Another reason for the large errors is that we derive fH2 from ratios of column density velocity profiles, not from quantities averaged across a given velocity interval (allowing for a cutoff at velocities where fH2 is fraught with large uncertainties), thought to represent a spiral arm crossing, for instance. Both approaches have their conveniences and caveats, which are briefly discussed in Wiesemeyer et al. (2016, their Appendix B). Table 4 summarizes the molecular hydrogen fraction toward the five investigated sight lines. The reported velocity intervals correspond to peaks in the column density distributions of H i and/or HF. The intervals are taken large enough so that the uncertainties in fH2 are not dominated by velocity components with large errors, and at the same time small enough to avoid a blend of spiral arm crossings.
5.2. Discussion
Despite the relatively large errors in fH2, it is possible to identify some spiral arm crossings. In the following we briefly discuss their fingerprints, which are detected in the velocity profiles of the molecular hydrogen fraction. This overview is based on the kinematic model of the Galaxy of Reid et al. (2014, for further references see Table 1. The velocity-averaged molecular hydrogen densities mentioned in the following are listed in Table 4. We recall that even at a given velocity (i.e., spiral arm crossing) the derived fH2 represents an average of individual clouds with varying physical and chemical properties.
5.2.1. Sgr B2
The sight line toward Sgr B2 (M) and (N) crosses the Sagittarius spiral arm, the Scutum/Crux arm and the 3 kpc expanding ring before it enters the Galactic center. While the absorption off the HF ground state is saturated in the environment of Sgr B2, near νlsr ~ 62 km s-1, we obtained the fH2 profile for the intervening spiral arms and the 3 kpc ring. The result shows that the diffuse gas is mainly molecular, which does not preclude entities of diffuse, mainly atomic gas, such as clouds or envelopes of cloud cores. Our results confirm another analysis of this sightline by Menten et al. (2011), who studied the absorption observed in 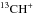 and SH+. Moreover, in the inner Galaxy the molecular fraction in the interarm gas contrasts only moderately with that in the spiral arms (~20% Koda et al. 2016). While the detailed analysis of this sight line will be postponed to future work, here we comment on the slight differences in the molecular hydrogen fraction fH2 toward Sgr B2 M and Sgr B2 N that appear in Fig. 9. The two components are separated by an apparent distance of 45″, which at a distance of 7.8 kpc (Reid et al. 2014) corresponds to a length scale of 1.7 pc. The varying molecular hydrogen fractions are therefore due to diffuse or translucent cloud entities of at most such a size scale. This upper limit holds for the local environment of Sgr B2. For the near side of the expanding 3 kpc arm, the upper limit to the length scale of the absorbing cloud entities would drop to 1 pc and correspondingly less for the Scutum/Crux spiral arm and the near side of the Sagittarius spiral arm.
and SH+. Moreover, in the inner Galaxy the molecular fraction in the interarm gas contrasts only moderately with that in the spiral arms (~20% Koda et al. 2016). While the detailed analysis of this sight line will be postponed to future work, here we comment on the slight differences in the molecular hydrogen fraction fH2 toward Sgr B2 M and Sgr B2 N that appear in Fig. 9. The two components are separated by an apparent distance of 45″, which at a distance of 7.8 kpc (Reid et al. 2014) corresponds to a length scale of 1.7 pc. The varying molecular hydrogen fractions are therefore due to diffuse or translucent cloud entities of at most such a size scale. This upper limit holds for the local environment of Sgr B2. For the near side of the expanding 3 kpc arm, the upper limit to the length scale of the absorbing cloud entities would drop to 1 pc and correspondingly less for the Scutum/Crux spiral arm and the near side of the Sagittarius spiral arm.
5.2.2. G 10.62−0.39
The background source is located in the 3 kpc arm, at 4.95 ± 0.47 kpc distance (Sanna et al. 2014). The crossings of the Scutum and Sagittarius arms are clearly visible at around 40 and 0 km s-1, respectively, while the velocity of G 10.62−0.39 is identical to that of the Sagittarius arm crossing (i.e., coincides in velocity with local gas). A further interpretation of the corresponding velocity interval is therefore impossible. At the spiral arm crossings, the molecular hydrogen fractions fH2 are close to unity. Liszt & Gerin (2016) estimate a typical clump size of 5.5 pc. At the distance of the Scutum arm (4 kpc), this corresponds to an angular extent of 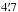 , which is well above the expected far-infrared size of G 10.62−0.39.
, which is well above the expected far-infrared size of G 10.62−0.39.
5.2.3. G 34.3+0.1
With 1.56 ± 0.12 kpc (Kurayama et al. 2011), this is a relatively short sight line, grazing the Sagittarius arm almost tangentially. The HF column densities show a stronger arm-to-interarm contrast than those seen in H i. Although it is short, this sight line contains clouds of markedly different fH2, which may have several reasons: The variations may be of truly intrinsic origin, since on a short sight line we have a better chance to separate individual foreground clouds with different fH2, whereas on longer distances the chances for blends are higher, simply owing to sight-line crowding. The other reason could be the misinterpretation of the data. As we have stated before, H i emission from the rear part of the sight line may lead to a significant contamination of the derived column density profile. This caveat holds for all derived fH2 profiles, not only for this one.
5.2.4. W 49N
This 11.11 ± 0.86 kpc long sight line (Zhang et al. 2013) contains three groups of diffuse clouds, both in H i and in HF. Their velocity intervals are 0 to 20 km s-1, 30 to 45 km s-1, and 45 to 70 km s-1, corresponding to the Perseus arm (where W 49N is located), and the near- and far-side crossings of the Sagittarius arm, respectively (cf. Vallée 2008). In the recent literature, the far-side crossing of the Sagittarius arm is instead assigned to a crossing of the molecular ring, as modeled by Dobbs & Burkert (2012). Different from Vallée (2008), the authors assume that the Scutum-Centaurus arm starts immediately at the bar, not at the Sagittarius–Carina arm. Li et al. (2016) modeled the molecular ring as an ensemble formed by two bar-driven spiral arms and the Scutum arm. In the framework of either model it seems fair to say that the velocities around 50 km s-1 are also assigned to interarm gas. By consequence, the corresponding molecular hydrogen fractions are significantly different: typically 20% in the interarm gas, and above 50% in the spiral arms. Such an arm-to-interarm contrast compares to that found in the outer Galaxy (Koda et al. 2016). The sightline to W 49, located at a galactocentric distance of 7.6 kpc (Table 1), crosses a larger fraction of atomic gas than the sightlines toward targets in the inner Galaxy.
5.2.5. W 51e4
The sight line to W 51e4, which is at 5.41 ± 0.21 kpc distance (Sato et al. 2010), follows the Sagittarius spiral arm. As in the case of W 49N, the contrast between the interarm region and the near-side crossing of the Sagittarius spiral arm is higher in HF than in H i.
6. Summary
Based on JVLA 21 cm absorption profiles combined with H i emission line data of the interferometric galactic plane surveys, we were able to infer the optical depth, spin temperatures, and H i column densities toward eight continuum-bright galactic targets, which allowed us to study the total hydrogen content of absorbing clouds in the foreground.
We employed Bayesian inference using the pymc Python module to estimate the error distributions of the resulting profiles, which are highly asymmetric. Despite a careful study of the statistical uncertainties, there are several systematic effects that we were unable to account for with the observational data and the tools available to us. Especially the blending of H i emission originating from behind the continuum source into the velocity range of interest can potentially cause a strong bias to the inferred spin temperatures and H i column densities.
Using archival Herschel data from the PRISMAS and HEXOS key projects (Gerin et al. 2012; Bergin et al. 2010, respectively), we have determined the molecular hydrogen fraction fH2 in the spiral arm crossings located on the sight lines toward the background sources Sgr B2, G 10.62−0.39 (W 31C), G 34.3+0.1, W 49N, and W 51e4. Despite the large errors in the dN/ dν profile, the data strongly suggest that the majority of the diffuse clouds crossed in the spiral arms is predominantly molecular and not mainly atomic. By consequence, the contrast between the column densities in the spiral arms and interarm regions is significantly higher in H i than in HF. Toward W 49N a similar contrast was found between CO and H i (Heyer & Terebey 1998) and between OH+ and OH (Wiesemeyer et al. 2016). With the results derived here, we expect to provide a good basis for a broad range of investigations studying the chemical and physical conditions along prominent sight lines through the Milky Way disk.
Acknowledgments
We are grateful to Arnaud Belloche for careful proof-reading of the manuscript. We also thank the anonymous referee for a very constructive report and Lars Flöer for useful hints regarding pymc. The research presented in this paper has used data from the Canadian Galactic Plane Survey, a Canadian project with international partners, supported by the Natural Sciences and Engineering Research Council. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. HI4PI is based on observations with the 100 m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg and the Parkes Radio Telescope, which is part of the Australia Telescope, funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. M.G. would like to thank CNES for financial support. We would like to express our gratitude to the developers of the many C/C++ and Python libraries, made available as open-source software, that we have used: most importantly, NumPy (van der Walt et al. 2011), SciPy (Jones et al. 2001), and Astropy (Astropy Collaboration et al. 2013). The Bayesian inferences were derived using the pymc3 package (Patil et al. 2010). Figures have been prepared using matplotlib (Hunter 2007) and in part using the Kapteyn Package (Terlouw & Vogelaar 2015).
References
- Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Bihr, S., Rugel, M., et al. 2016, A&A, 595, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bihr, S., Beuther, H., Ott, J., et al. 2015, A&A, 580, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R., Thilker, D. A., Walterbos, R. A. M., & Corbelli, E. 2009, ApJ, 695, 937 [Google Scholar]
- Brogan, C. L., & Troland, T. H. 2001, ApJ, 550, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Zauderer, B. A., Lazio, T. J., et al. 2005, AJ, 130, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Bronfman, L., Nyman, L.-A., & May, J. 1996, A&AS, 115, 81 [NASA ADS] [Google Scholar]
- Bruderer, S., Benz, A. O., Stäuber, P., & Doty, S. D. 2010, ApJ, 720, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, C. J. 2012, The Transfer of Spectral Line Radiation (Cambridge University Press) [Google Scholar]
- Carruthers, G. R. 1970, ApJ, 161, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Chengalur, J. N., Kanekar, N., & Roy, N. 2013, MNRAS, 432, 3074 [NASA ADS] [CrossRef] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickey, J. M., Kulkarni, S. R., van Gorkom, J. H., & Heiles, C. E. 1983, ApJS, 53, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., Mebold, U., Stanimirovic, S., & Staveley-Smith, L. 2000, ApJ, 536, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., McClure-Griffiths, N. M., Gaensler, B. M., & Green, A. J. 2003, ApJ, 585, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., Strasser, S., Gaensler, B. M., et al. 2009, ApJ, 693, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., & Burkert, A. 2012, MNRAS, 421, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Pringle, J. E., & Burkert, A. 2012, MNRAS, 425, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Faison, M. D., Goss, W. M., Diamond, P. J., & Taylor, G. B. 1998, AJ, 116, 2916 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Godard, B., Cernicharo, J., et al. 2010, A&A, 521, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fish, V. L., Reid, M. J., Wilner, D. J., & Churchwell, E. 2003, ApJ, 587, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Flagey, N., Goldsmith, P. F., Lis, D. C., et al. 2013, ApJ, 762, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., de Luca, M., Black, J., et al. 2010a, A&A, 518, L110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., de Luca, M., Goicoechea, J. R., et al. 2010b, A&A, 521, L16 [Google Scholar]
- Gerin, M., Levrier, F., Falgarone, E., et al. 2012, Philosophical Transactions of the Royal Society of London Series A, 370, 5174 [Google Scholar]
- Gerin, M., Ruaud, M., Goicoechea, J. R., et al. 2015, A&A, 573, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. J., Taylor, A. R., Higgs, L. A., & Dewdney, P. E. 2000, ApJ, 540, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. J., Taylor, A. R., Higgs, L. A., Brunt, C. M., & Dewdney, P. E. 2005a, ApJ, 626, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. J., Taylor, A. R., Higgs, L. A., Brunt, C. M., & Dewdney, P. E. 2005b, ApJ, 626, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., et al. 2012, A&A, 540, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C. 1997, ApJ, 481, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003a, ApJS, 145, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003b, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H., & Terebey, S. 1998, ApJ, 502, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Heyminck, S., Graf, U. U., Güsten, R., et al. 2012, A&A, 542, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- HI4PI Collaboration, Ben Bekhti, N., Flöer, L., et al. 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Immer, K., Reid, M. J., Menten, K. M., Brunthaler, A., & Dame, T. M. 2013, A&A, 553, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Seifahrt, A., & Richter, M. J. 2013, ApJ, 764, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Online; accessed 2015-06-27] [Google Scholar]
- Koda, J., Scoville, N., & Heyer, M. 2016, ApJ, 823, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Koo, B.-C. 1997, ApJS, 108, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Kurayama, T., Nakagawa, A., Sawada-Satoh, S., et al. 2011, PASJ, 63, 513 [NASA ADS] [Google Scholar]
- Lang, C. C., Goss, W. M., Cyganowski, C., & Clubb, K. I. 2010, ApJS, 191, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Lazareff, B. 1975, A&A, 42, 25 [NASA ADS] [Google Scholar]
- Lazio, T. J. W., Brogan, C. L., Goss, W. M., & Stanimirović, S. 2009, AJ, 137, 4526 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M.-Y., Stanimirović, S., Murray, C. E., Heiles, C., & Miller, J. 2015, ApJ, 809, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, E. S., Blitz, L., & Heiles, C. 2006, Science, 312, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Gerhard, O., Shen, J., Portail, M., & Wegg, C. 2016, ApJ, 824, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Phillips, T. G., Goldsmith, P. F., et al. 2010, A&A, 521, L26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., & Gerin, M. 2016, A&A, 585, A80 [Google Scholar]
- Liszt, H. S., van der Hulst, J. M., Burton, W. B., & Ondrechen, M. P. 1983, A&A, 126, 341 [NASA ADS] [Google Scholar]
- Martin, P. G., Blagrave, K. P. M., Lockman, F. J., et al. 2015, ApJ, 809, 153 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2005, ApJS, 158, 178 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., Green, A. J., & Haverkorn, M. 2006, ApJ, 652, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2012, ApJS, 199, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Mebold, U., Düsterberg, C., Dickey, J. M., Staveley-Smith, L., & Kalberla, P. 1997, ApJ, 490, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Wyrowski, F., Belloche, A., et al. 2011, A&A, 525, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monje, R. R., Emprechtinger, M., Phillips, T. G., et al. 2011, ApJ, 734, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mookerjea, B., Hassel, G. E., Gerin, M., et al. 2012, A&A, 546, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2016, ApJ, 826, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Zmuidzinas, J., Schilke, P., & Phillips, T. G. 1997, ApJ, 488, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Black, J. H., Gerin, M., et al. 2015a, ApJ, 807, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Godard, B., Gerin, M., et al. 2015b, A&A, 577, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., Müller, H. S. P., Lis, D. C., et al. 2010, A&A, 518, L111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. 2010, J. Stat. Software, 35, 1 [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A&A, 543, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Qin, S.-L., Schilke, P., Comito, C., et al. 2010, A&A, 521, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Destree, J. D., et al. 2009, ApJS, 180, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V. 1960, PASP, 72, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W. 1982, A&AS, 48, 219 [NASA ADS] [Google Scholar]
- Reich, P., & Reich, W. 1986, A&AS, 63, 205 [NASA ADS] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Reid, M. J., Dame, T. M., Menten, K. M., & Brunthaler, A. 2017, ApJ, submitted [Google Scholar]
- Roberts, D. A., Dickel, H. R., & Goss, W. M. 1997, ApJ, 476, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Rygl, K. L. J., Brunthaler, A., Sanna, A., et al. 2012, A&A, 539, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Reid, M. J., Menten, K. M., et al. 2014, ApJ, 781, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Reid, M. J., Brunthaler, A., & Menten, K. M. 2010, ApJ, 720, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Neufeld, D. A., Müller, H. S. P., et al. 2014, A&A, 566, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shull, J. M., Tumlinson, J., Jenkins, E. B., et al. 2000, ApJ, 538, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnentrucker, P., Neufeld, D. A., Phillips, T. G., et al. 2010, A&A, 521, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sonnentrucker, P., Wolfire, M., Neufeld, D. A., et al. 2015, ApJ, 806, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirovic, S. 2002, in Single-Dish Radio Astronomy: Techniques and Applications, eds. S. Stanimirovic, D. Altschuler, P. Goldsmith, & C. Salter, ASP Conf. Ser., 278, 375 [Google Scholar]
- Stanimirović, S., Murray, C. E., Lee, M.-Y., Heiles, C., & Miller, J. 2014, ApJ, 793, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Stil, J. M., Taylor, A. R., Dickey, J. M., et al. 2006, AJ, 132, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Strasser, S., & Taylor, A. R. 2004, ApJ, 603, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Strasser, S. T., Dickey, J. M., Taylor, A. R., et al. 2007, AJ, 134, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Terlouw, J. P., & Vogelaar, M. G. R. 2015, Kapteyn Package, version 2.3, Kapteyn Astronomical Institute, Groningen, available from http://www.astro.rug.nl/software/kapteyn/ [Google Scholar]
- Tizniti, M., Le Picard, S. D., Lique, F., et al. 2014, Nat. Chem., 6, 141 [Google Scholar]
- Valdivia, V., Hennebelle, P., Gérin, M., & Lesaffre, P. 2016, A&A, 587, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vallée, J. P. 2008, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S., & Varoquaux, G. 2011, Computing in Science Engineering, 13, 22 [Google Scholar]
- van Dishoeck, E. F., Jansen, D. J., Schilke, P., & Phillips, T. G. 1993, ApJ, 416, L83 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wiesemeyer, H., Güsten, R., Heyminck, S., et al. 2012, A&A, 542, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiesemeyer, H., Güsten, R., Heyminck, S., et al. 2016, A&A, 585, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2013, Tools of Radio Astronomy (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Winkel, B., Lenz, D., & Flöer, L. 2016, A&A, 591, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyrowski, F., Menten, K. M., Güsten, R., & Belloche, A. 2010, A&A, 518, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyrowski, F., Güsten, R., Menten, K. M., Wiesemeyer, H., & Klein, B. 2012, A&A, 542, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, B., Reid, M. J., Menten, K. M., et al. 2013, ApJ, 775, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Moscadelli, L., Sato, M., et al. 2014, ApJ, 781, 89 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Prismas sight lines
 |
Fig. A.1 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the HEXOS program sources Sgr B2 (M) and Sgr B2 (N). For a detailed description see text. |
 |
Fig. A.2 As Fig. A.1 for the PRISMAS program sources G 10.62−0.39 and G 34.3+0.1. |
Appendix B: Other sight lines
 |
Fig. B.1 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the source Sgr B2, sight lines (1) and (2). For a detailed description see text. |
 |
Fig. B.3 As Fig. B.1 for source G 10.62−0.39, sight lines (1) and (2). |
 |
Fig. B.5 As Fig. B.1 for source G 31.41+0.31, sight line (1). |
 |
Fig. B.6 As Fig. B.1 for source G 34.3+0.1, sight lines (1) and (2). |
All Tables
Summary of the main observational parameters of the Galactic Plane surveys used to obtain emission spectra.
All Figures
 |
Fig. 1 Continuum maps at 1.4 GHz of the regions Sgr B2, G 10.62−0.39, W 33 A, and G 31.41+0.31 as observed with JVLA. The sight lines extracted for our analysis are annotated. The spatial coordinates of the sight lines are compiled in Table 2 for reference. Contour lines are in multiples of the RMS noise level as stated in the title of each panel. Negative contour lines are dotted, positive contours have solid line style. The beam size is indicated by the green ellipse in the lower left corner of each map. Inside graticules display Galactic coordinates. All maps were primary-beam corrected. Note that for the sake of better visualization only the central part of each map is displayed (about half the size of the primary beam). The blue crosses mark the phase centers of the JVLA observations. PRISMAS/HEXOS program positions are labeled with “P39”, and the PRISMAS/HEXOS 550-GHz beam size of ~ 39″ is indicated by red circles. For Sgr B2 two sight lines were observed within the HEXOS program, which we annotate “P39M” and “P39N”. Note that the JVLA phase centers do not necessarily match the highest continuum intensity positions. |
| In the text | |
 |
Fig. 2 As Fig. 1, showing the regions G 34.3+0.1, W 49N, W 51, and DR 21. For W 51 the P39 position coincides with the ultra-compact H ii regions W 51 e1 to e4. |
| In the text | |
 |
Fig. 3 Visualization of the moving-ring filter operation used to estimate the emission spectrum, TB(ν), at the positions affected by absorption features. The left panel shows a single plane (νlsr = 45.5 km s-1) of the VGPS data cube of W 51 located in the center of the map. In the middle panel the filtered plane is shown. The size of the ring filter is marked with the two black circles in the upper left. The right panel contains the residual image. It is used to estimate the error of the emission spectrum by calculating the RMS. To improve the RMS calculation, a mask was applied (see text). The mask is indicated by the black contours. |
| In the text | |
 |
Fig. 4 Comparison between Galactic plane survey (top panel) and JVLA emission (bottom panel) data. The missing short-spacings in the latter cause a significant lack of (diffuse) emission. The example displays DR 21 data at νlsr = 10.1 km s-1. Note the different intensity scales. |
| In the text | |
 |
Fig. 5 Short-spacings correction for the JVLA absorption data. As an example, sight line 1 of the DR 21 source is shown. The black line is the original HI4PI spectrum, the red line is the JVLA data smoothed to HI4PI resolution, and the green line is the resulting short-spacings contribution. For comparison the result of the ring-filter operation, applied to the Galactic plane survey data cube, is displayed in blue (with 1σ uncertainties). |
| In the text | |
 |
Fig. 6 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the PRISMAS program source W 51, sight line P39. For a detailed description see text. The labels CL 1 and CL 3 refer to the 1σ and 3σ confidence intervals, i.e., the 68% and 99.7% distribution percentiles (see also text). |
| In the text | |
 |
Fig. 7 Molecular hydrogen fraction fH2≡ 2NH2/ (NH i + 2NH2) on the sight lines toward G 10.62−0.39 (W 31C) and G 34.3+0.1. |
| In the text | |
 |
Fig. A.1 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the HEXOS program sources Sgr B2 (M) and Sgr B2 (N). For a detailed description see text. |
| In the text | |
 |
Fig. A.2 As Fig. A.1 for the PRISMAS program sources G 10.62−0.39 and G 34.3+0.1. |
| In the text | |
 |
Fig. B.1 Measured absorption and emission spectra, Ton and Toff, with their respective errors, and derived quantities, optical depth, spin temperature, and H i column density for the source Sgr B2, sight lines (1) and (2). For a detailed description see text. |
| In the text | |
 |
Fig. B.2 As Fig. B.1 for sight line (3). |
| In the text | |
 |
Fig. B.3 As Fig. B.1 for source G 10.62−0.39, sight lines (1) and (2). |
| In the text | |
 |
Fig. B.5 As Fig. B.1 for source G 31.41+0.31, sight line (1). |
| In the text | |
 |
Fig. B.6 As Fig. B.1 for source G 34.3+0.1, sight lines (1) and (2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.














