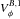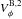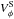| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526749 | |
| Published online | 06 January 2017 | |
Interactions of the Galactic bar and spiral arm in NGC 3627⋆,⋆⋆
1 Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: name@mpia.de
2 Dipartimento di Fisica e Astronomia, University of Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
3 INAF – Istituto di Radioastronomia & Italian ALMA Regional Centre, via P. Gobetti 101, 40129 Bologna, Italy
4 Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
5 National Radio Astronomy Observatory, Charlottesville, VA 22903, USA
Received: 15 June 2015
Accepted: 20 September 2016
Aims. To gain insight into the expected gas dynamics at the interface of the Galactic bar and spiral arms in our own Milky Way galaxy, we examine as an extragalactic counterpart the evidence of multiple distinct velocity components in the cold dense molecular gas that populates a similar region at the end of the bar in the nearby galaxy NGC 3627.
Methods. We assembled a high-resolution view of molecular gas kinematics traced by CO(2−1) emission and extracted line-of-sight velocity profiles from regions of high and low gas velocity dispersion.
Results. The high velocity dispersions arise with often double-peaked or multiple line-profiles. We compare the centroids of the different velocity components to expectations based on orbital dynamics in the presence of bar and spiral potential perturbations. A model of the region as the interface of two gas-populated orbits families supporting the bar and the independently rotating spiral arms provides an overall good match to the data. An extent of the bar to the corotation radius of the galaxy is favored.
Conclusions. Using NGC 3627 as an extragalactic example, we expect situations like this to favor strong star formation events such as are observed in our own Milky Way since gas can pile up where the orbit families cross. The relative motions of the material following these orbits is most likely even more important for the build-up of high density in the region. The surface densities in NGC 3627 are also so high that shear at the bar end is unlikely to significantly weaken the star formation activity. We speculate that scenarios in which the bar and spiral rotate at two different pattern speeds may be the most favorable for intense star formation at such interfaces.
Key words: stars: formation / galaxies: individual: NGC 3627 / stars: massive / ISM: clouds / ISM: structure
The reduced images (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/597/A85
© ESO, 2017
1. Introduction
The interfaces of galactic bars and outer spiral arms represent some of most active star-forming environments in the local Universe. In our own Milky Way, the overlap between the end of the Galactic bar and the inner Scutum-Centaurus spiral arm at longitudes of ~30 degrees hosts the W43 mini-starburst with an approximate luminosity of L ~ 3 × 106 L⊙ (e.g., Blum et al. 1999; Motte et al. 2003; Bally et al. 2010; Nguyen Luong et al. 2011). Questions about the nature of star formation in such bar-spiral interface regions remain puzzling. Is it possible, for instance, that clouds at different relative velocities physically interact and maybe even induce the star formation process in this way? Nguyen Luong et al. (2011) estimated a star formation rate (SFR) of between 0.01 and 0.1 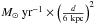 (with d the distance) over the approximate diameter of the W43 cloud complex of ~140 pc. One of the observational difficulties lies in the fact that gas kinematics are hard to constrain at these locations, both in our own Milky Way and in external galaxies.
(with d the distance) over the approximate diameter of the W43 cloud complex of ~140 pc. One of the observational difficulties lies in the fact that gas kinematics are hard to constrain at these locations, both in our own Milky Way and in external galaxies.
In W43, several lines of evidence reveal the dynamics of the bar-spiral interaction and its effect on gas motions as the source of burst of star formation, which is thought to be the site of converging flows (e.g., Benjamin et al. 2005; López-Corredoira et al. 2007; Rodriguez-Fernandez & Combes 2008; Nguyen Luong et al. 2011; Carlhoff et al. 2013; Motte et al. 2014). This region contains various evolutionary stages, from young infrared dark clouds to active star-forming clouds and a Wolf-Rayet cluster (Blum et al. 1999; Beuther et al. 2012).
A peculiar aspect of the W43 region are the two prominent gas velocity components along the line of sight, the principle component at ~100 km s-1, and a secondary at ~50 km s-1. Motte et al. (2014) discussed several converging gas flows in that region which are associated with kinematic CO and HI gas components between approximately 60 and 120 km s-1. In their picture, the 50 km s-1 component is not considered further because they did not identify associated converging velocity structures towards W43. Similarly, Nguyen Luong et al. (2011) and Carlhoff et al. (2013) argued that the more prominent ~100 km s-1 peak is dominant for the on-going star formation in the region, corresponding to the W43 complex, whereas the ~50 km s-1 component may only be a chance alignment that could be attributed to the Perseus spiral arm. In contrast to this, Beuther et al. (2012) found both components in the 13CO(2–1) emission not just along the same sidelines, but the two components appear in projection spatially connected. Furthermore, both components are also detected in dense gas tracers like N2H+, and again, they appear in mapping studies as connected gas structures (Beuther et al. 2012). While this may still be a chance alignment, it nevertheless suggests that the two components may emerge from the same region. This part of our Galaxy is also almost the only region in the Milky Way that exhibits multiple velocity components in the ionized gas tracer through radio recombination lines (Anderson et al. 2011). This can be interpreted as additional evidence of potentially interacting gas clouds.
Our position in the Galaxy means, however, that it is currently not possible to accurately determine the distance of the two components, and therefore to unambiguously determine whether the two gas components in W43 are either in fact interacting or just chance alignments in different parts of the Galaxy. Unambiguous proof will most likely depend on future exact distance measurements through maser parallaxes of the Bessel project of the two velocity components (Brunthaler et al. 2011). While the 100 km s-1 component has recently been determined to be at a distance of ~5.5 kpc through maser parallax measurements (Zhang et al. 2014), the comparable measurement for the 50 km s-1 component is still lacking.
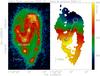 |
Fig. 1 Herschel 70 μm (Kennicutt et al. 2011) and HERACLES CO(2–1) data of NGC 3627 (Leroy et al. 2009). The left panel presents in color the 70 μm emission (logarithmic stretch from 0.0001 to 0.1 Jy pixel-1), while the contours shows the integrated CO(2–1) emission from 5 to 55 K km s-1 in 5 K km s-1 steps. In the right panel, the color scale presents the first moment map (intensity-weighted velocities), the contours again show the integrated CO(2–1) emission. Circles mark the locations and areas of the PdBI(2−1) primary beams for NGC 3627N and NGC 3627S. The central star and white line indicate the bar location following Casasola et al. (2011). A linear scale bar assuming 11.1 Mpc distance is shown in the bottom left corner. |
Hence, while proofing the spatial (dis)association of velocity components 50 km s-1 apart is currently not possible for the interface of bar and spiral arm in the Milky Way, we wish to test whether the scenario is in principle possible by means of studying a nearby galaxy with more favorable almost face-on geometry. Comparable regions in nearby galaxies can provide critical insight into the nature of Galactic environments such as that of W43. Much of our understanding in this context derives from the study of Kenney & Lord (1991), who first linked star formation at the end of the bar in M 83 to the molecular gas reservoir traced by CO. Their detailed examination of the properties and kinematics of the molecular gas at the time, although limited to rather coarse resolution, suggested that the change in orbit structure from the bar to the spiral may lead to the observed local build-up of gas, which might then favor a burst of star formation. Soon thereafter, Rand (1992) found supporting evidence for this picture, showing that the intense star formation observed at the end of the bar in M 51 is linked to locally high (molecular) gas surface densities. Since then, numerous observational and theoretical studies have dealt with galactic bars and their dynamical importance for star formation as well as galactic dynamics (e.g., Martin & Friedli 1997; Jogee et al. 2005; Verley et al. 2007; Athanassoula et al. 2013; Zhou et al. 2015).
It is still unclear, however, how frequently star formation of this type occurs, which types of bars and spirals may be most conducive, or whether it can explain environments such as that of W43 in our own Milky Way. To develop this picture further requires an in-depth study of the gas kinematics at more such interfaces, which are still poorly constrained in our Milky Way, as well as in external galaxies.
In this paper, we seek to explore potential interactions of bar and spiral arm in an exemplary external galaxy that allows a better identification of associated velocity components because of a geometry that is near to face-on. As a starting point we used the HERACLES database, which provides sensitive CO(2–1) images of several tens of nearby galaxies (Leroy et al. 2009). Additionally, all HERACLES galaxies have extensive multi-wavelength coverage from the X-ray to the radio regime from the SINGS (Kennicutt et al. 2003) and KINGFISH (Kennicutt et al. 2011) efforts. Of the barred galaxies in the HERACLES sample, only two galaxies show the desired geometry, that is, a stellar bar with strong spiral arms emanating from the bar ends and associated massive star formation. NGC 3627 is one of these two galaxies and has high-quality published molecular gas observations available (Paladino et al. 2008; Leroy et al. 2009). The well-known barred spiral galaxy NGC 3627 exhibits strong burst signatures at the two interfaces of bar and arm in the north and south, as is visible, for example, in the 70 μm Herschel map (Fig. 1 left panel, Kennicutt et al. 2011). These active interaction zones of bar and arm closely resemble the structures found in W43 in our Milky Way. Furthermore, the location of NGC 3627 is very favorable for our study: the orientation is almost face-on (inclination angle of 65 deg with a position angle θPA = 170°, Chemin et al. 2003), the object is relatively nearby at a distance of 11.1 Mpc (e.g., Saha et al. 1999), where spatial resolution elements of 1′′ correspond to linear scales of ~54 pc, and the systemic velocity is Vsys = 744 km s-1 (Casasola et al. 2011). More details are given in Sect. 4. Although these linear scales are obviously much larger than what can be achieved within our Milky Way, the almost face-on nature of this galaxy facilitates the interpretation of the data tremendously.
Using near-infrared imaging from the Spitzer Survey for Stellar Structure (S4G, Sheth et al. 2010), Buta et al. (2015) classified NGC 3627 as a SBx(s)bpec, that is, as a strongly barred galaxy with a boxy or peanut bulge. NGC 3627 has a stellar mass of log (M⋆(M⊙)) ≈ 10.8 and a specific SFR (sSFR = SFR/M⋆) of log (sSFR(yr-1)) ≈ −10.3, meaning that it lies on the local main sequence of star-forming galaxies (Salim et al. 2007). As we are interested in a qualitative comparison of signatures for the stellar bar and spiral arm region, an exact match in properties between NGC 3627 and the Milky Way is not necessary.
 |
Fig. 2 Combined PdBI+30 m CO(2−1) data toward NGC 3627 north and south (top and bottom panels, respectively). The colors show in the left and right panels the first (intensity-weighted peak velocities) and second moments (intensity-weighted line widths), respectively. The contours present the integrated intensities in the velocity regimes indicated above each panel from 5 to 95% of the peak intensities (in 10% steps). The stars in the right panels show the positions for spectrum extraction. Example spectra are shown in Fig. 3, and fit results are presented in Tables A.1 and A.2. |
The two interface regions between the bar and inner spiral arms at the northern and southern ends of the stellar bar of NGC 3627 have been observed with the Plateau de Bure Interferometer (PdBI) in the CO(1–0) and CO(2–1) emission by Paladino et al. (2008). While the authors concentrated on the connection between radio continuum, CO and 8 μm emission, we now analyze the kinematics of the gas. We recalibrate and reimage these data (see next section), and in particular we added the CO(2–1) short-spacing information from the HERACLES data (Leroy et al. 2009) to minimize flux and imaging artifacts. Figure 1 (right panel) presents the single-dish HERACLES CO(2–1) data as a first-moment map (intensity-weighted velocities) with the integrated intensity contours. This image shows the bar and spiral structure as well as the rotational velocities of the gas. The primary beams of the PdBI observations are also marked.
Using the PACS 70 μm image from KINGFISH (Kennicutt et al. 2011), we assess the SFR of the NGC 3627 southeast bar end region. To do this, we convolve the PACS image to have a round Gaussian beam of FWHM 8″. At this resolution (~350 pc) the star-forming region is largely unresolved. For the 70 μm-to-SFR conversion quoted by Kennicutt & Evans (2012), the bar end has an SFR of ≈0.23 M⊙ yr-1 inside the 8″ Gaussian beam. This compares relatively well to the ≈0.01−0.1 M⊙ yr-1 for W43 (Nguyen Luong et al. 2011) given the degree of uncertainty in extragalactic SFR estimates, especially for individual regions.
With the goal to better understand the interface dynamics of bar and arm in an external galaxy and set this into context to our Milky Way, we here study the nearby galaxy NGC 3627 as an excellent example case with a comparable configuration to the Milky Way. This paper is structured as follows: Sect. 2 describes the combination of the Plateau de Bure Interferometer and 30 single-dish data. Section 3 then outlines the basic morphological and spectral signatures of the spectral line data. Section 4 reports the dynamical interpretation of the multiple velocity components at the interface of bar and arm in the framework of crossing orbit families corresponding to the bar and arm. Finally, Sect. 5 discusses these results as potential reasons for enhanced star formation activities at interfaces of bar and arm, and also sets it into context with our Milky Way and particularly W43. Section 6 then summarizes our results.
2. Observations
 |
Fig. 3 PdBI+30 m CO(2−1) example spectra toward NGC 3627N (left) and NGC 3627S (right). The offsets of the positions are marked (see also Fig. 2). The green lines present the Gaussian fits to the data. The corresponding FWHM and peak positions are reported in Tables A.1 and A.2. The blue and red lines at the bottom of each panel indicate mean values of the velocities for the bar 1 scenario and the spiral described in Sect. 4. The corresponding full velocity ranges are shown in Figs. 5 and 6. |
Paladino et al. (2008) presented the PdBI for the first time, however, they focused on the CO(1–0) observations and did not complement the data with short-spacing information. The PdBI observations were carried out on March 20, 2005 with six antennas in the C configuration. At that time, 1.3 and 2.6 mm data could be taken simultaneously, and the observations targeted the CO(1–0) and (2–1) lines, respectively. The two frequencies were centered on 114.997 and 229.88 GHz, which are the transition rest frequencies at an assumed vlsr of ~712.6 km s-1. With four overlapping 160 MHz spectral units, the correlator covered 580 MHz for each line (corresponding to 1512 and 756 km s-1 for the (1–0) and (2–1) lines, respectively). Bandpass and flux calibration were conducted with 1055+018 and MWC349, and the gains were calibrated with regular observations of 1116+128.
To complement the PdBI CO(2–1) data with the lacking short-spacing information, we used the IRAM 30 m single-dish observations from the HERACLES survey (Leroy et al. 2009)1. The HERACLES CO(2–1) data were further processed in GILDAS/CLASS and finally combined and imaged with the PdBI data within the mapping part of the GILDAS package.
In the following, we only use the combined PdBI+30 m CO(2–1) data. The phase reference centers for NGC 3627N and NGC 3727S are RA(J2000.0) 11:20:13.50, Dec(J2000.0) 13:00:17.70 and RA(J2000.0) 11:20:16.60, Dec(J2000.0) 12:58:44.50., respectively. The final channel spacing of the used data product is 5 km s-1. The 1σ rms and synthesized beam values for the merged PdBI+30 m CO(2–1) data are ~6 mJy beam-1 and 1.66′′ × 0.87′′ (PA 22 deg). At the given distance of 11.1 Mpc, this corresponds to an approximate linear resolution of ~68 pc.
3. Results
3.1. Morphological and spectral structures
Figure 2 present the first and second moment maps (intensity-weighted peak velocities and line width) of the combined PdBI+30 m CO(2–1) data toward the two target regions at the northern and southern ends of the galactic bar in NGC 3627. In the following, we refer to the two regions as NGC 3627N and NGC 3627S. Both regions are detected at high significance in the CO(2–1) emission, and the moment maps already reveal a wealth of kinematic structure. Toward the northern end of the bar, we find an intensity-weighted peak velocity spread between ~550 and ~660 km s-1, which it is even higher in the southern region between ~760 and ~915 km s-1. While we see velocity gradients across both regions, the second-moment maps also show that most of the broadest lines are found toward the integrated intensity peaks, that is, toward the highest column density positions.
A different way to look at the kinematic properties of the gas is by inspecting the spectra toward selected points in the fields. To do this, we extracted the combined PdBI+30 m CO(2–1) spectra toward regularly spaced grids in NGC 3627N and NGC 3627S that are separated by the approximate beam size of 1.7′′ as marked in Fig. 2. Figure 3 presents example spectra and Gaussian fits to them, the fit results are listed in Tables A.1 and A.2. To fit the Gaussians, we averaged spectra over an area slightly larger than the beam size. We included all spectra with offsets ± 0.5′′ from the respective position, which then results in a fitted area corresponding to a ~1.6′′ beam size, a factor of 1.625 larger in area than for the nominal resolution. This reduces the average rms in the fitted spectra to ~4.5 mJy beam-1. The number of Gaussian components to be fitted was visually identified individually for each spectrum. In most cases, the selection of the number of components was unambiguous and straightforward (Fig. 3), but for some positions other solutions might be found: for example, the spectrum at position 0.2′′/ −1.7′′ in NGC 3627N may indicate more than two components (Fig. 3, second panel to the left), however, the Gaussian fitting algorithm did not converge with more than two components. Therefore, we restricted ourselves to the lowest number of reasonable components in such cases. While very broad components (Tables A.1 and A.2) may in reality consist of more components, for our interpretation and analysis this is less important because we are mainly interested in the dominating components that may stem from the bar and/or spiral. Multiple and blended components are also discussed in Sect. 4.2.
The only adjusted parameter for each fit is the number of Gaussian components, all other parameters, in particular the peak velocities vpeak and the full-width at half-maximum (FWHM) line widths Δv for each component are free parameters. In general, we fit Gaussians only to peak flux densities above the 3σ level of 13.5 mJy beam-1. In a few cases (~8% out of 207 features in total) we also allowed slightly lower peak flux densities with the lowest value at 9.2 mJy beam. However, in all these cases, visual inspection of the spectra confirmed the reality of the features because they were detected in several contiguous channels. The strongest peaks exhibit peak flux densities >100 mJy beam-1 (maximum 142 mJy beam-1), and we can detect peak-to-peak flux density differences between neighboring features of around a factor 10. The smallest identified separation between adjacent peaks is ~20 km s-1 (Tables A.1 and A.2).
We find a variety of features: Some spectra are single-peaked, but many also exhibit clearly spectrally resolved multiple peaks toward individual positions. The derived FWHM (or Δv) values for the different spectra also cover a relatively broad range of FWHM values between ~5 km s-1 at the narrow end (which is also our spectral resolution limit), and values up to 100 km s-1. While the broadest lines most likely consist of multiple components that are difficult to separate, the narrow end with several values between 10 and 20 km s-1 is approximately in agreement with what would be expected from Larson’s line-width Δv size L relation 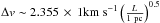 , where Δv is the velocity FWHM and L the root-mean-square size (Solomon et al. 1987). Using the average synthesized beam FWHM of 1.3′′ as an estimate for the size L ~ 1.3′′/ 2.355, this results in a linear L of ~70/2.355 pc or an approximate δv of 12.8 km s-1. Taking into account that the size estimated in this way is most likely a lower limit since the peak regions are no point sources but extended (see Fig. 2), we conclude that the narrower lines observed in NGC 3627 are broadly consistent with Larson’s relation and hence resemble typical molecular clouds.
, where Δv is the velocity FWHM and L the root-mean-square size (Solomon et al. 1987). Using the average synthesized beam FWHM of 1.3′′ as an estimate for the size L ~ 1.3′′/ 2.355, this results in a linear L of ~70/2.355 pc or an approximate δv of 12.8 km s-1. Taking into account that the size estimated in this way is most likely a lower limit since the peak regions are no point sources but extended (see Fig. 2), we conclude that the narrower lines observed in NGC 3627 are broadly consistent with Larson’s relation and hence resemble typical molecular clouds.
4. Dynamical interpretation
In this section we examine whether the observed velocity components are consistent with expected streaming motions in the presence of the stellar bar and spiral arms. Potential implications for enhanced star formation activity and the connection to our Milky Way will be drawn in Sect. 5.
At each position (x,y) relative to the galaxy center, we assume that the centroid of the line profile reflects both radial and azimuthal components vr and vφ in projection, that is, ![\begin{equation} V_{\rm los}=V_{\rm sys}+\left[v_r\sin{(\theta-\theta_{\rm PA})}+v_\phi \cos{(\theta-\theta_{\rm PA})}\right]\sin{i} \label{eq:los} , \end{equation}](/articles/aa/full_html/2017/01/aa26749-15/aa26749-15-eq50.png) (1)where θ = arctan(y/x) measures the offset from the kinematic major axis position angle θPA (by convention measured in the anti-clockwise direction with respect to the major axis of the receding half of the galaxy) and vφ includes the circular velocity Vc. We adopted the inclination i = 65circ, θPA = 170circ and the kinematic center as determined by Chemin et al. (2003) and took the systemic velocity Vsys = 744 km s-1 following Casasola et al. (2011).
(1)where θ = arctan(y/x) measures the offset from the kinematic major axis position angle θPA (by convention measured in the anti-clockwise direction with respect to the major axis of the receding half of the galaxy) and vφ includes the circular velocity Vc. We adopted the inclination i = 65circ, θPA = 170circ and the kinematic center as determined by Chemin et al. (2003) and took the systemic velocity Vsys = 744 km s-1 following Casasola et al. (2011).
Our goal in what follows is to develop a model for vr and vφ at the end of the bar that we can compare with the observations. In this particular galaxy, given the alignment of the bar morphological major axis with the disk kinematic major axis (so that θ ~ θPA), the comparison of a model for vr and vφ at the end of the bar with observations is considerably simplified. Typically, this orientation can inhibit the extraction of kinematic information related to the bar strength and pattern speed (i.e., Rand & Wallin 2004), since characteristic strong radial motions directed along x1 orbits in the bar potential are directed almost entirely out of the line of sight. For studying the bar end, however, this is in fact ideal: here the orbits of stars and gas are characterized by primarily azimuthal motions (and negligible radial motions). In this favorable set-up, the line-of-sight velocity therefore captures almost entirely the full picture of azimuthal motions in the bar potential.
 |
Fig. 4 Angular frequency curves in NGC 3627: Ω (thick black), Ω ± κ/ 2 (light gray), and Ω−κ/ 4 (dashed). The vertical line marks the end of the bar (Chemin & Hernandez 2009) with length aB = 49′′. The red horizontal box shows the range in spiral speeds as measured from gas kinematics (see text). The blue horizontal box indicates the range of bar speeds in scenario 1, suggested by Chemin & Hernandez (2009), while the green box shows the bar speed in scenario 2 (same speed as the spiral). The different bar and spiral scenarios are labeled in the plot. |
The dominant contribution to the line-of-sight velocity originates from circular motion about the galaxy center, projected on the plane of the sky. We adopted the rotation curve model of Chemin et al. (2003), which extends out to ~90′′, beyond which it closely matches the circular velocities modeled by Trachternach et al. (2008). Figure 4 shows the angular frequency curves Ω = Vc/R, Ω ± κ/ 2 and Ω−κ/ 4, where the radial orbital oscillation frequency κ is defined by 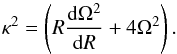 (2)These curves are shown together with two models for the relation between the bar and spiral pattern described in more detail below. These two models correspond to different azimuthal streaming near the end of the bar, which we assume to additionally contribute to the observed line-of-sight velocity.
(2)These curves are shown together with two models for the relation between the bar and spiral pattern described in more detail below. These two models correspond to different azimuthal streaming near the end of the bar, which we assume to additionally contribute to the observed line-of-sight velocity.
4.1. Combined system of bar and spiral
Depending on position, the line-of-sight velocity profiles near the bar end will contain information related to azimuthal motions directed along orbits in the presence of either the bar or spiral, or both. When gas populates intersecting bar and spiral orbits, two velocity components will emerge (although they may not be spatially resolvable). The locations of the individual bar and spiral components, and their relation to each other, depend on the relation between the bar and spiral pattern speeds. We considered two possibilities, one in which the bar and spiral rotate with the same speed (bar 2 scenario), and a second, in which the bar and spiral rotate with distinct speeds (although they may be dynamically coupled, bar 1 scenario). As described below, the latter corresponds to a scenario in which the bar extends out to its corotation radius Rc, the location where the bar pattern speed Ωp is equal to the disk angular rotation Ω. In the former scenario, the bar ends well inside corotation.
Constraints on the likelihood of one or the other scenario in this particular galaxy are varied, mostly as a result of the orientation of the bar, which leads to ambiguous results with kinematics-based techniques. The direct, model-independent Tremaine-Weinberg method (TW; Tremaine & Weinberg 1984) uses departures from axisymmetry traced by a continuity-obeying kinematic tracer (e.g., HI or CO) along the line of sight to measure the pattern speed, and thus provides little constraint on the speed of the bar. The pattern speed ΩP,s = 50 km s-1 kpc-1 measured by Rand & Wallin (2004), however, provides an estimate for the spiral speed.
Although we cannot rule out that the bar drives a spiral with the same speed based on the TW method, we have other reasons to expect that the bar may rotate with a much higher speed. Stellar orbit theory predicts that bars end at or near their corotation radii (e.g., Contopoulos & Papayannopoulos 1980), which is the location where the pattern speed Ωp is equal to the disk angular rotation Ω. We can estimate the speed that would be necessary for the bar length aB to fall within the predicted range, that is, 1 < aB/Rc < 1.4, by inspection of the angular rotation curve Ω as shown in Fig. 4.
Chemin et al. (2003) previously suggested a pattern speed Ωp,B in the range 56−72 km s-1 kpc-1, based on the requirement that 1 < aB/Rc< 1.4. Corotation at this location in the disk was later confirmed from an analysis of gravitational torques by Casasola et al. (2011). Meanwhile, the spiral appears to rotate at a lower speed, most likely in the range 40 < ΩP,s < 50 km s-1, according to the results of the TW method (Rand & Wallin 2004) and the harmonic decomposition of the HI velocity field by Trachternach et al. (2008), which clearly shows the signature of corotation at ~100′′.
This set of bar and spiral speeds is consistent with the mode-coupling scenario (Masset & Tagger 1997), in which the overlap of two patterns at resonance leads to the efficient transfer of energy and angular momentum between them. Figure 4 shows that the bar corotation (where the blue lines intersect with the black curve, at the bar end) overlaps with the radius of the inner 4:1 resonance of the spiral (where the spiral pattern speed Ωp = Ω−κ/ 4, i.e., the red band intersects the dark gray curve), which arrangement has been found previously in nearby observed galaxies (e.g., Meidt et al. 2009; Rautiainen et al. 2005).
4.1.1. Bar streaming motions
Whether or not the bar extends to its corotation radius has implications for the line-of-sight velocity expected for gas motions directed along orbits supporting the bar.
Bar 1 scenario: Bar ends at corotation. When the bar extends to its corotation, we can describe streaming using the equations of motion specifically at the corotation resonance of a weak bar perturbation (i.e., Binney & Tremaine 1987, Eqs. (3)−(123)). These imply that the radial and azimuthal streaming motions are (nearly) identically zero and the azimuthal component of the velocity equals the circular velocity in the disk, that is, 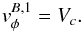 (3)For libration at the bar end (instead of circulation about the galaxy center; i.e., Binney & Tremaine 1987), the trapped stars or gas still overall rotate with the bar. Thus, even with the (small) additional component Ωϵ for a libration of size ϵ, Eq. (3) remains a good approximation.
(3)For libration at the bar end (instead of circulation about the galaxy center; i.e., Binney & Tremaine 1987), the trapped stars or gas still overall rotate with the bar. Thus, even with the (small) additional component Ωϵ for a libration of size ϵ, Eq. (3) remains a good approximation.
Bar 2 scenario: Bar ends inside corotation. In the alternate scenario, in which the bar ends well inside its corotation radius, we can gain insight into gas flow characteristics at the bar end by considering the case of a weak bar (e.g., Sellwood & Evans 2001). Although the bar in NGC 3627 is more accurately a strong bar, motions at the bar end are qualitatively similar to those in the weak case.
We followed Sellwood & Sánchez (2010) to estimate the magnitude of azimuthal streaming adopting the (weak) bar perturbation to the gravitational potential 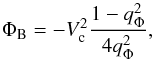 (4)where qΦ is the axial ratio of the bar potential, which is related to the axial ratio of the density distribution as
(4)where qΦ is the axial ratio of the bar potential, which is related to the axial ratio of the density distribution as 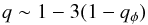 (5)(Binney & Tremaine 1987). We estimated q as (1−ϵbar) using the bar ellipticity ϵbar = 0.69 measured from the S4G 3.6 μm image tracing the stellar mass (Cisternas et al. 2013).
(5)(Binney & Tremaine 1987). We estimated q as (1−ϵbar) using the bar ellipticity ϵbar = 0.69 measured from the S4G 3.6 μm image tracing the stellar mass (Cisternas et al. 2013).
In this case, the azimuthal component of the velocity away from corotation (i.e., Sellwood & Sánchez 2010) is reduced to 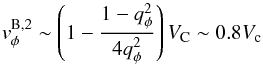 (6)at the bar end. Although there are non-negligible radial motions
(6)at the bar end. Although there are non-negligible radial motions 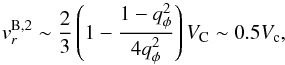 (7)they go to zero at azimuths aligned with the bar major axis.
(7)they go to zero at azimuths aligned with the bar major axis.
4.1.2. Spiral streaming motions
Spiral density wave theory provides the basis for estimating the magnitude of spiral streaming motions, which we assumed are the same in the two scenarios (since the spiral pattern speed is the same in both). Following Binney & Tremaine (1987), the azimuthal velocity component associated with the spiral in the tight-winding approximation is 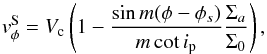 (8)and the radial component is
(8)and the radial component is 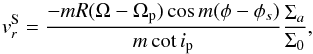 (9)where the circular velocity is Vc = RΩ, Ωp is the spiral pattern speed, ip = 34circ is the spiral arm pitch angle (La Vigne et al. 2006), m = 2 since there are two spiral arms, and Σa/ Σ0 is the ratio of the perturbed to unperturbed surface mass density. We estimate Σa/ Σ0 using the arm-interarm contrast, which we expect to fall between 2−3 (so that Σa/ Σ0 ~ 1−2) given this galaxy’s SABb classification, using the 3.6 μm contrast for this type measured by Elmegreen et al. (2011) and assuming a constant 3.6 μm mass-to-light ratio (e.g., Meidt et al. 2014). We have confirmed that this is consistent with the arm contrast that is directly measurable from the stellar mass map for this galaxy derived by Querejeta et al. (2015) from its S4G Spitzer/IRAC 3.6 μm image.
(9)where the circular velocity is Vc = RΩ, Ωp is the spiral pattern speed, ip = 34circ is the spiral arm pitch angle (La Vigne et al. 2006), m = 2 since there are two spiral arms, and Σa/ Σ0 is the ratio of the perturbed to unperturbed surface mass density. We estimate Σa/ Σ0 using the arm-interarm contrast, which we expect to fall between 2−3 (so that Σa/ Σ0 ~ 1−2) given this galaxy’s SABb classification, using the 3.6 μm contrast for this type measured by Elmegreen et al. (2011) and assuming a constant 3.6 μm mass-to-light ratio (e.g., Meidt et al. 2014). We have confirmed that this is consistent with the arm contrast that is directly measurable from the stellar mass map for this galaxy derived by Querejeta et al. (2015) from its S4G Spitzer/IRAC 3.6 μm image.
Because of the alignment (zero phase offset) between the end of the bar and the start of the spiral arms, we considered motions near the spiral arm potential minimum where φ ≈ φs. According to Eq. (8), azimuthal streaming motions should go to zero. However, the gas response can be complex, with shocking and viscous and gravitational torques that introduce non-zero azimuthal motions in close proximity to the spiral minimum, such as are observed in M 51 (Shetty et al. 2007). Models of gas streaming in the presence of a density wave qualitatively predict that vφ varies rapidly as gas encounters the arm, passing through zero on switching from negative (in the interarm) to positive immediately upon exiting the arm (e.g., Roberts & Stewart 1987; Shetty et al. 2007). In the slightly upstream position at which the observed line profiles are extracted (see Figs. 2 and 1), we expect a maximum of 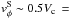 and
and 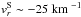 .
.
We note that radial streaming motions would be considerably stronger for a lower spiral pattern speed, whereas azimuthal motions would be unchanged. As we are most sensitive to the latter along the line of sight with this particular set of disk and bar orientations, we cannot distinguish the proposed scenario, in which the spiral pattern speed is Ωp ~ 50 km s-1 kpc-1, from one in which it is closer to Ωp ~ 25 km s-1 kpc-1. Such a low value has been suggested by Reuter et al. (1996), taking the corotation Rc = 216′′ identified with the Canzian (1993) method, and it is also consistent with the value measured by Rand & Wallin (2004) specifically for the southern extension of the western arm, which appears to lie off the plane of the rest of the disk. We do not consider streaming motions predicted in the case of this low speed further because they are most likely applicable only at larger galactocentric radius and would further be identical to those predicted in the azimuthal direction in our nominal scenario.
4.2. Comparison to observations
As argued in the previous section, the line-of-sight velocity at the bar end in NGC 3627 is dominated by azimuthal motions, and we expect two distinct kinematic components when gas populates bar and spiral orbits. Thus, in our bar 1 scenario, in which the bar ends at its corotation radius, we expect one component from the bar to be centered on ~Vsys ± Vc(aB)sini. This component should exhibit as much as 80 km s-1 offset from a second component associated with the spiral, at ~Vsys ± 0.5Vc(aB)sini.
 |
Fig. 5 Histogram showing the relative frequency of the centroid velocities of all fitted velocity components (PdBI+30 m CO(2−1) data). Velocities measured in the north and south are shown as gray dashed and solid lines, respectively, while the solid black line takes all components into consideration. The centroid velocity is shown transformed into the galaxy-plane (Eq. (1)). Overlaid rectangles represent the different predictions of the models described in Sect. 4. Two predictions for the bar are shown: the blue rectangle shows |
Figures 5 and 6 show the measured centroid velocity in comparison to the different bar 1, bar 2, and spiral model introduced in the previous section. NGC 3627S frequently shows two velocity components (21 out of 42). The lower-velocity component arises from within a range ~100−150 km s-1, while the higher-velocity component is more regularly found near an average of 200±10 km s-1. The single-peak profiles (17 out of 42) consistently arise near the high 200 km s-1 value and tend to be located offset from the region of brightest CO emission. Figure 7 visualizes the number of components with respect to the location, confirming that the single-peaked profiles avoid the zone of strongest interaction and trace mainly bar orbits (see right panel of Fig. 7). More statistical properties of the kinematic gas properties are shown in Fig. B.1 and are referred to below.
 |
Fig. 6 Histograms of the centroid velocity of each fitted component extracted in the north (right) and south (left). The line style indicates the number of velocity components fitted along each line of sight: single (solid), double (dashed), and triple or more (dotted). The centroid velocity is shown transformed into the galaxy-plane as in Fig. 5. Overlaid colored rectangles show the predictions of the model for the spiral, the bar in scenario 1, and the bar in scenario 2 as in Fig. 5. |
 |
Fig. 7 Map of the locations of the different velocity profiles in the south (left) and north (right) where spectra are fit with single (open circle), double (filled circle), triple (triangle), or more (square) components (see for comparison Fig. 2). The size of the symbol is scaled to the integrated CO intensity, while the gray scaling indicates the effective velocity width of the profile shown by the scale bar to the right (estimated by summing the ΔV measured for each individual component in quadrature). The same scaling is adopted for the northern and southern bar ends. |
These features are remarkably consistent with the predictions of our simple model. Based on the higher velocity components in Fig. 6, which are close to the circular velocity Vc ≈ 200 km s-1 at these radii, we can rule out the bar 2 scenario (the green rectangles in Figs. 5 and 6) in which the maximum velocity does not exceed 0.8 Vc. In contrast to this, we find good agreement between the observations and our model for velocities at the end of the bar in scenario 1 (the blue rectangles in Figs. 5 and 6). The width of the blue and green rectangle illustrating the predicted bar velocity is set by the range in Vc corresponding to the range in galactocentric radii spaned by the mapped regions.
The prediction for the spiral (red rectangle in Figs. 5 and 6), which also agrees well with the observations, spans a wider range to demonstrate the effect of variation in the strength of the spiral and/or in the exact (azimuthal) location at which the profile is extracted relative to the spiral potential minimum. Figures 5 and 6 illustrate the range of velocities corresponding to an increase in the strength of the spiral arm from Σa/ Σ0 = 0.5 to 1.5. This range of spiral strengths yields azimuthal streaming motions that vary from low (Vs = 33 km s-1) to high (Vs = 100 km s-1). This reduces the azimuthal velocity 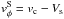 (Eq. (8), plotted in Figs. 5 and 6) at these spatial locations to 91−172 km s-1 (Sect. 4.1.2).
(Eq. (8), plotted in Figs. 5 and 6) at these spatial locations to 91−172 km s-1 (Sect. 4.1.2).
In comparison to the south, spectra in NGC 3627N still show double-peaked profiles (33 out of 80), but regularly also exhibit single components centered on a location near the spiral velocity of ~150 km s-1 (27 out of 80; Figs. 5 and 6). Although the bar 2 model could be consistent with the lower grouping of velocities near 150 km s-1 (Fig. 6), measurements in NGC 3627S make this scenario unlikely. We therefore associate the lower-velocity component in the north with the spiral. The lower-velocity component is more frequent than the higher-velocity component around 200 km s-1 (expected for the bar, Fig. 5). In contrast to the south, where single peaks are mostly associated with the higher- velocity bar component, in the north many single-peaked profiles are centered on a spot close to the lower-velocity spiral component. All profiles in the north lie farther beyond the bar end than in the south, by 10′′ ~ 0.5 kpc on average (top row of Fig. B.1). They may also arise from a different location in the spiral potential than the profiles extracted in the south, which are found 10 degrees further downstream on average (middle row of Fig. B.1). According to the model, in both circumstances the magnitude of the spiral streaming motions might be qualitatively reduced compared to the south, where profiles appear to arise consistently throughout the interaction zone of bar and spiral. This could explain why the lower of the two primary velocities observed in the north is nearer to the circular velocity, implying weaker spiral streaming motions.
The northern bar end probed by the observations might also be influenced by interaction with the companion galaxy NGC 3628. This galaxy has an evident effect on the morphology and kinematics of the spiral emerging from the northern bar end at large galactocentric radius (R = 90′′, Chemin et al. 2003). These signs of interaction suggest that the spiral arm dynamics are more complex, even at galactocentric radii R ~ 50′′, and deviate from our simple model.
The number and the widths of velocity peaks along each line of sight contain additional information to support the idea of interacting clouds on overlapping bar and spiral orbits. For example, at either bar end a small fraction of spectra shows more than two velocity peaks (3 out of 42 in the south and 14 out of 80 in the north). On average, these are narrower (Δv ~ 20 km s-1, Fig. B.1 bottom row) than either of the two primary components characteristic of the double- or single-peaked profiles (typical Δv ~ 40−80 km s-1) and closer to the value expected from the size-linewidth relation (Sect. 3.1). In all cases, at least two of the velocities are consistent with the bar-spiral model, while other additional components fall near one or the other of the two primary velocities and accordingly appear to belong to either the bar or spiral components.
5. Discussion
5.1. Enhanced star formation at interfaces of bar and spiral?
In the previous section, we presented a simple model of intersecting gas-populated orbits supporting the bar and spiral arms that can explain the double-peaked line of sight velocity profiles observed in CO(2–1) emission at the end of the bar in NGC 3627. These two velocity components most regularly appear at the southern bar end. Kinematics to the north, on the other hand, appear to deviate from the simple model expectation, which might be due, for instance, either to the influence of the interaction evident at larger radii or to a genuine underpopulation of one set of orbits. Regardless of the nature of gas motions in the north, it is clear that over similarly sized areas at the end of the bar, the frequency of two distinct components is higher in the south than in the north. At the same time, the south shows enhanced rates of star formation per unit gas mass relative to the north (e.g., Paladino et al. 2008). It therefore appears that the existence of double-peaked profiles is connected to enhanced star formation, presumably through an increase in collisions within the gas.
Here we discuss the mechanisms by which our model of gas motions at the intersection of the bar and spiral arms can lead to intense star formation, focusing only on the role of streaming motions in increasing the likelihood of collisions in the region. As first argued by Kenney & Lord (1991), orbit crossing between orbit families alone would seem to be insufficient for building high gas densities and triggering star formation. The region of potential crossing within the gas is spatially extended and unlikely to explain the highly localized bursts of star formation that are observed. Instead, collisions could be enhanced with the help of streaming motions that specifically transport the gas into the orbit-crossing region.
Streaming motions at the bar-spiral interface in NGC 3627.
Table 1 summarizes the velocities expected in the two different scenarios considered so far. As discussed in the previous section, our comparison rules out the second scenario, which predicts much lower velocities at the bar end in NGC 3627 than exhibited by the observed profiles. We still include it here because it is thought to apply in the prototype case of M 83. (Kenney & Lord 1991, argued that the bar corotation radius RCR in M 83 lies well beyond the bar end, and thus the bar and spiral patterns have the same angular speed at the interface of bar and spiral).
In both scenarios, radial streaming is expected to be minimal at the interface, of ~25 km s-1 as a result of motion associated with the spiral. The primary difference between scenarios 1 and 2 is the relative azimuthal velocity between the bar and spiral. In the first scenario, the bar and spiral exhibit a difference of 80 km s-1, whereas we expect the bar and spiral to have very little relative azimuthal velocity at the interface in scenario 2. This is qualitatively different from what was described by Kenney & Lord (1991) at the end of the bar in M 83, where it is suggested that streaming is observed to enhance collision in exactly scenario 2.
The difference arises from the interpretation of the observations. With only ~400 pc resolution, the interferometric CO(1−0) observations analyzed by Kenney & Lord (1991) were not resolved well enough to reveal multiple velocity components along the line of sight. To estimate the angular velocities at the interface, they therefore measured single isolated components that sampled the bar and spiral individually from neighboring positions. However, according to the previous section, we do not expect the angular velocities exhibited by gas populating either set of bar or spiral orbits to necessarily persist at the actual orbit interface. For bars that end at corotation, bar streaming will be on the order of −Vcϵ at a small distance ϵ from corotation, but then go to zero at the interface with the spiral. This means that although Kenney & Lord (1991) inferred a velocity difference in the gas populating bar and spiral orbits at the interface in their presumed scenario 2, we suspect that this may not be evident upon closer inspection. (The bar-spiral interface in M 83 may even be found to better resemble scenario 1 if the bar and spiral exhibit genuinely different speeds, unlike what was assumed by Kenney & Lord 1991.)
In contrast to the conclusion of Kenney & Lord (1991), we therefore argue that the likelihood of collision is quite low in scenario 2, when the bar and spiral rotate with the same pattern speed. Instead, the large azimuthal velocity difference characteristic of scenario 1, when the bar and spiral have different speeds, probably enhances collision. We note that even if the spiral arms were to rotate with the same high pattern speed as the bar, the likelihood of collision in such a scenario would still be reduced. In this case, the spiral arms would sit entirely outside corotation, which would lead to azimuthal streaming motions directed in the opposite sense to that described above (even as they approach zero near corotation).
Numerical simulations by Renaud et al. (2013, 2015) and Emsellem et al. (2015) have modeled a Milky Way-like galaxy at sub-pc resolution to study various aspects of ISM interactions from large spiral and bar scales down to the fueling of central black holes. Recently, Renaud et al. (2015) investigated the effect of bars on triggering and/or regulating star formation. In their study, they also found that the leading edges of bars are favorable for converging gas flows and large-scale shocks (see also Athanassoula 1992). While the gas circulates fast along the bar, it slows down and accumulates at both bar ends. Hence, orbital crowding at the edge of the bar can then lead to cloud-cloud interactions.
Shear motions may act destructively on the star formation process. However, in the case of NGC 3627, gas surface densities at the bar end exceed the critical density for stabilization from shear or Coriolis forces. We have estimated the shear at the bar end by adopting the rotation curve in Fig. 4. Only background shear due to differential rotation of the disk material is important at the end of the bar because shear due to gradients in the motions within the bar potential goes to zero at the bar end, where streaming motions are reduced (e.g., Athanassoula et al. 2013, and as described by the analytical model here). Following Elmegreen (1993; and see Meidt et al. 2013), we can estimate the shear critical surface density as 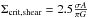 where the Oort parameter A = 1/2(vc/R−dvc/ dR) measures the shear rate and σ is the gas velocity dispersion. At the end of the bar, R = 49′′, we find the shear critical surface density to be 85 M⊙ pc-2. We compare this to the observed surface densities in the two mapped regions: the average integrated intensities of the maps in Fig. 2 are 1.88 Jy km s-1 and 2.44 Jy km s-1 for NGC 3727N and NGC 3627S, respectively. Assuming the Rayleigh-Jeans approximation, this converts into 25.6 K km s-1 and 33.2 K km s-1 for the northern and southern region. This is equivalent to 113 and 146 M⊙ pc-2, adopting a standard Galactic CO-to-H2 conversion factor (e.g., Hughes et al. 2013), which is well above the shear critical density estimated above. Since these are only average values, the peak surface densities are even higher. It therefore seems unlikely that shear at the bar end in NGC 3627 greatly weakens the ability of gas to form stars.
where the Oort parameter A = 1/2(vc/R−dvc/ dR) measures the shear rate and σ is the gas velocity dispersion. At the end of the bar, R = 49′′, we find the shear critical surface density to be 85 M⊙ pc-2. We compare this to the observed surface densities in the two mapped regions: the average integrated intensities of the maps in Fig. 2 are 1.88 Jy km s-1 and 2.44 Jy km s-1 for NGC 3727N and NGC 3627S, respectively. Assuming the Rayleigh-Jeans approximation, this converts into 25.6 K km s-1 and 33.2 K km s-1 for the northern and southern region. This is equivalent to 113 and 146 M⊙ pc-2, adopting a standard Galactic CO-to-H2 conversion factor (e.g., Hughes et al. 2013), which is well above the shear critical density estimated above. Since these are only average values, the peak surface densities are even higher. It therefore seems unlikely that shear at the bar end in NGC 3627 greatly weakens the ability of gas to form stars.
Based on our findings in NGC 3627, we therefore conclude that the strength of the interaction between gas populating bar and spiral orbits may be more sensitive to the relative azimuthal speeds of the two components, rather than the difference in radial motions. Bursts of star formation may therefore occur preferentially when the bar and spiral have two different pattern speeds.
We emphasize that the likelihood of collision is probably further enhanced given gravitational torquing on the gas (due to the bar and spiral). When both the bar and spiral sit inside their own corotation radii, the torques they exert will lead to continual gas inflow. Radially inward motions along the spiral supporting orbits might be particularly conducive to collision. We note that this would occur in either scenario.
5.2. Comparison with the Galactic bar-arm interaction region around W43
One of the goals of this investigation is to provide a comparison to Milky Way studies of the bar-arm interaction regions that are hampered by Galactic projection and line-of-sight contamination problems. As outlined in the Introduction, the interface of bar and arm in the Milky Way around W43 exhibits several velocity components, a very broad one between 60 and 120 km s-1 consisting of several sub-components, and a separate one roughly between 30 and 55 km s-1. Several indicators described in Sect. 1 support a picture of two physically related clouds at the location of W43, but this evidence is only circumstantial and simple projection effects of clouds in different spiral arms are also capable of explaining the results (Nguyen Luong et al. 2011; Beuther et al. 2012; Carlhoff et al. 2013; Motte et al. 2014).
Several parameters can be compared between the W43 complex and the clouds in the interface of bar and arm of NGC 3627. These are the velocity differences between several cloud components, the line widths, and the peak flux densities of different velocity components. For W43, Nguyen Luong et al. (2011) reported a ratio of peak flux densities between the 100 and 50 km s-1 components between 3 and 4 (their Fig. 2). These are typical ratios that we also found in NGC 3627. Furthermore, for W43, the velocity difference between the two components is ~50 km s-1, and Nguyen Luong et al. (2011) reported a FWHM of the 13CO(1–0) line averaged over an extent of ~140 pc of ~22.3 km s-1. A direct comparison between the numbers for W43 and those reported in Sect. 3.1 is tricky because of several reasons: first, the 13CO(1–0) line in W43 traces partly different gas components than the 12CO(2–1) line analysis presented in the current paper. Furthermore, W43 in our Milky Way is observed along the line of sight, whereas the NGC 3627 clouds are seen almost face-on. Nevertheless, the measured line widths and velocity separations approximately agree and are comparable between NGC 3627 and the Milky Way. While cloud-cloud collisions in theoretical simulations without Galactic bar effects typically take place at lower velocity-separations (≤20 km s-1, e.g., Dobbs et al. 2015; but see also Renaud et al. 2015, who reported larger velocity separations, including a bar potential), and Motte et al. (2014) concentrated on velocity components in that regime for their converging gas flow stduy in W43, bar-spiral interface regions are special in that regard because they pile up much more material than in other regions of a galaxy. Since velocity separations are similar in NGC 3627 and the Milky Way W43 region, even if shear motions are strong, physical associations of clouds at velocity differences on the order of 50 km s-1 appear reasonable. Although this does not allow a conclusive answer to whether the two clouds in W43 are indeed physically related, the data in NGC 3627 of several clouds with similar spectral parameters make the cloud-cloud interface interpretation for W43 at least plausible.
6. Conclusions
With the aim to gain insight into the nature of the Galactic bar and spiral arm interface region W43 in our Milky Way, we investigated as an extragalactic counterpart example region the kinematic properties of the molecular gas in the interface region of the bar and spiral arm of the nearby almost face-on galaxy NGC 3627. Similar to the situation in our Milky Way, we also found several independent spectral velocity components in many spectra toward the interface in NGC 3627. Modeling these velocity components as being caused by different orbit families that independently populate the bar and spiral of NGC 3627, we found that solutions with the bar extending to the corotation radius give a reasonable fit to our data.
The implications of this are various. The similarity of the spectral signatures at the Milky Way interface of bar and spiral to that of NGC 3627 make it plausible that the multiple velocity components found toward W43 may indeed stem from interacting molecular clouds in this region and are not located in different spiral arms. Furthermore, the extremely active star formation processes at the interface of bar and spiral may be caused by exactly such crossing gas orbits and interacting or colliding gas clouds. The crossing gas streams may pile up significant amounts of dense gas, which can then collapse and undergo intense star formation activity. Furthermore, the gas surface densities in NGC 3627 are so high that shear motions are probably incapable of significantly reducing the star formation activity. While this scenario is intriguing, further investigations of more regions with respect to their gas kinematics as well as star formation activity are needed to investigate the importance of these cloud-collision processes in more detail.
These data are available for download at www.mpia.de/HERACLES
Acknowledgments
We would like to thank Fabian Walter for feedback and discussions during the process of this work. We are also grateful to the HERACLES team for making the single-dish data available. Furthermore, we thank the referee for commenting on the draft with great care. H.B. acknowledges support from the European Research Council under the Horizon 2020 Framework Program via the ERC Consolidator Grant CSF-648505.
References
- Anderson, L. D., Bania, T. M., Balser, D. S., & Rood, R. T. 2011, ApJS, 194, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Machado, R. E. G., & Rodionov, S. A. 2013, MNRAS, 429, 1949 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Anderson, L. D., Battersby, C., et al. 2010, A&A, 518, L90 [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Tackenberg, J., Linz, H., et al. 2012, A&A, 538, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics, Princeton Series in Astrophysics [Google Scholar]
- Blum, R. D., Damineli, A., & Conti, P. S. 1999, AJ, 117, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Brunthaler, A., Reid, M. J., Menten, K. M., et al. 2011, Astron. Nachr., 332, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., Sheth, K., Athanassoula, E., et al. 2015, ApJS, 217, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Canzian, B. 1993, ApJ, 414, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Carlhoff, P., Nguyen Luong, Q., Schilke, P., et al. 2013, A&A, 560, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasola, V., Hunt, L. K., Combes, F., García-Burillo, S., & Neri, R. 2011, A&A, 527, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chemin, L., & Hernandez, O. 2009, A&A, 499, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chemin, L., Cayatte, V., Balkowski, C., et al. 2003, A&A, 405, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cisternas, M., Gadotti, D. A., Knapen, J. H., et al. 2013, ApJ, 776, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G., & Papayannopoulos, T. 1980, A&A, 92, 33 [NASA ADS] [Google Scholar]
- Dobbs, C. L., Pringle, J. E., & Duarte-Cabral, A. 2015, MNRAS, 446, 3608 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M. 1993, in Star Formation, Galaxies and the Interstellar Medium, eds. J. Franco, F. Ferrini, & G. Tenorio-Tagle [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Yau, A., et al. 2011, ApJ, 737, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Renaud, F., Bournaud, F., et al. 2015, MNRAS, 446, 2468 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A., Meidt, S. E., Colombo, D., et al. 2013, ApJ, 779, 46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jogee, S., Scoville, N., & Kenney, J. D. P. 2005, ApJ, 630, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Kenney, J. D. P., & Lord, S. D. 1991, ApJ, 381, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- La Vigne, M. A., Vogel, S. N., & Ostriker, E. C. 2006, ApJ, 650, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- López-Corredoira, M., Cabrera-Lavers, A., Mahoney, T. J., et al. 2007, AJ, 133, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., & Friedli, D. 1997, A&A, 326, 449 [NASA ADS] [Google Scholar]
- Masset, F., & Tagger, M. 1997, A&A, 322, 442 [NASA ADS] [Google Scholar]
- Meidt, S. E., Rand, R. J., & Merrifield, M. R. 2009, ApJ, 702, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., García-Burillo, S., et al. 2013, ApJ, 779, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., van de Ven, G., et al. 2014, ApJ, 788, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Schilke, P., & Lis, D. C. 2003, ApJ, 582, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Nguyên Luong, Q., Schneider, N., et al. 2014, A&A, 571, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nguyen Luong, Q., Motte, F., Schuller, F., et al. 2011, A&A, 529, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladino, R., Murgia, M., Tarchi, A., Moscadelli, L., & Comito, C. 2008, A&A, 485, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Querejeta, M., Meidt, S. E., Schinnerer, E., et al. 2015, ApJS, 219, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J. 1992, AJ, 103, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J., & Wallin, J. F. 2004, ApJ, 614, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Rautiainen, P., Salo, H., & Laurikainen, E. 2005, ApJ, 631, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2013, MNRAS, 436, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Bournaud, F., Emsellem, E., et al. 2015, MNRAS, 454, 3299 [NASA ADS] [CrossRef] [Google Scholar]
- Reuter, H.-P., Sievers, A. W., Pohl, M., Lesch, H., & Wielebinski, R. 1996, A&A, 306, 721 [NASA ADS] [Google Scholar]
- Roberts, Jr., W. W., & Stewart, G. R. 1987, ApJ, 314, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Fernandez, N. J., & Combes, F. 2008, A&A, 489, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saha, A., Sandage, A., Tammann, G. A., et al. 1999, ApJ, 522, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Evans, N. W. 2001, ApJ, 546, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Sánchez, R. Z. 2010, MNRAS, 404, 1733 [NASA ADS] [Google Scholar]
- Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Vogel, S. N., Ostriker, E. C., & Teuben, P. J. 2007, ApJ, 665, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Trachternach, C., de Blok, W. J. G., Walter, F., Brinks, E., & Kennicutt, Jr., R. C. 2008, AJ, 136, 2720 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, ApJ, 282, L5 [Google Scholar]
- Verley, S., Combes, F., Verdes-Montenegro, L., Bergond, G., & Leon, S. 2007, A&A, 474, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, B., Moscadelli, L., Sato, M., et al. 2014, ApJ, 781, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, Z.-M., Cao, C., & Wu, H. 2015, AJ, 149, 1 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fit results
Gaussian fit results for NGC 3727N.
Gaussian fit results for NGC 3727S.
Appendix B: Additionnal figure
 |
Fig. B.1 Histograms of galactocentric radius (top) and azimuthal angle (relative to the bar major axis; middle) at which spectra are extracted toward the north (right) and south (left) ends of the bar in NGC 3627. The bar end is located at aB = 49′′ according to Chemin & Hernandez (2009). The line style indicates the number of velocity components that are fit along each line of sight: single (solid), double (dashed), and triple or more (dotted). Histograms of the FWHMΔv of each fit component are shown in the bottom row. |
All Tables
All Figures
 |
Fig. 1 Herschel 70 μm (Kennicutt et al. 2011) and HERACLES CO(2–1) data of NGC 3627 (Leroy et al. 2009). The left panel presents in color the 70 μm emission (logarithmic stretch from 0.0001 to 0.1 Jy pixel-1), while the contours shows the integrated CO(2–1) emission from 5 to 55 K km s-1 in 5 K km s-1 steps. In the right panel, the color scale presents the first moment map (intensity-weighted velocities), the contours again show the integrated CO(2–1) emission. Circles mark the locations and areas of the PdBI(2−1) primary beams for NGC 3627N and NGC 3627S. The central star and white line indicate the bar location following Casasola et al. (2011). A linear scale bar assuming 11.1 Mpc distance is shown in the bottom left corner. |
| In the text | |
 |
Fig. 2 Combined PdBI+30 m CO(2−1) data toward NGC 3627 north and south (top and bottom panels, respectively). The colors show in the left and right panels the first (intensity-weighted peak velocities) and second moments (intensity-weighted line widths), respectively. The contours present the integrated intensities in the velocity regimes indicated above each panel from 5 to 95% of the peak intensities (in 10% steps). The stars in the right panels show the positions for spectrum extraction. Example spectra are shown in Fig. 3, and fit results are presented in Tables A.1 and A.2. |
| In the text | |
 |
Fig. 3 PdBI+30 m CO(2−1) example spectra toward NGC 3627N (left) and NGC 3627S (right). The offsets of the positions are marked (see also Fig. 2). The green lines present the Gaussian fits to the data. The corresponding FWHM and peak positions are reported in Tables A.1 and A.2. The blue and red lines at the bottom of each panel indicate mean values of the velocities for the bar 1 scenario and the spiral described in Sect. 4. The corresponding full velocity ranges are shown in Figs. 5 and 6. |
| In the text | |
 |
Fig. 4 Angular frequency curves in NGC 3627: Ω (thick black), Ω ± κ/ 2 (light gray), and Ω−κ/ 4 (dashed). The vertical line marks the end of the bar (Chemin & Hernandez 2009) with length aB = 49′′. The red horizontal box shows the range in spiral speeds as measured from gas kinematics (see text). The blue horizontal box indicates the range of bar speeds in scenario 1, suggested by Chemin & Hernandez (2009), while the green box shows the bar speed in scenario 2 (same speed as the spiral). The different bar and spiral scenarios are labeled in the plot. |
| In the text | |
 |
Fig. 5 Histogram showing the relative frequency of the centroid velocities of all fitted velocity components (PdBI+30 m CO(2−1) data). Velocities measured in the north and south are shown as gray dashed and solid lines, respectively, while the solid black line takes all components into consideration. The centroid velocity is shown transformed into the galaxy-plane (Eq. (1)). Overlaid rectangles represent the different predictions of the models described in Sect. 4. Two predictions for the bar are shown: the blue rectangle shows |
| In the text | |
 |
Fig. 6 Histograms of the centroid velocity of each fitted component extracted in the north (right) and south (left). The line style indicates the number of velocity components fitted along each line of sight: single (solid), double (dashed), and triple or more (dotted). The centroid velocity is shown transformed into the galaxy-plane as in Fig. 5. Overlaid colored rectangles show the predictions of the model for the spiral, the bar in scenario 1, and the bar in scenario 2 as in Fig. 5. |
| In the text | |
 |
Fig. 7 Map of the locations of the different velocity profiles in the south (left) and north (right) where spectra are fit with single (open circle), double (filled circle), triple (triangle), or more (square) components (see for comparison Fig. 2). The size of the symbol is scaled to the integrated CO intensity, while the gray scaling indicates the effective velocity width of the profile shown by the scale bar to the right (estimated by summing the ΔV measured for each individual component in quadrature). The same scaling is adopted for the northern and southern bar ends. |
| In the text | |
 |
Fig. B.1 Histograms of galactocentric radius (top) and azimuthal angle (relative to the bar major axis; middle) at which spectra are extracted toward the north (right) and south (left) ends of the bar in NGC 3627. The bar end is located at aB = 49′′ according to Chemin & Hernandez (2009). The line style indicates the number of velocity components that are fit along each line of sight: single (solid), double (dashed), and triple or more (dotted). Histograms of the FWHMΔv of each fit component are shown in the bottom row. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.