| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201629012 | |
| Published online | 01 November 2016 | |
Velocity segregation effects in galaxy clusters at 0.4 ≲ z ≲ 1.5
1 Dipartimento di Fisica, Università degli Studi di Trieste, via Tiepolo 11, 34143 Trieste, Italy
e-mail: stefania.jess@gmail.com
2 INAF–Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11, 34133 Trieste, Italy
3 INFN–Sezione di Trieste, via Valerio 2, 34127 Trieste, Italy
Received: 27 May 2016
Accepted: 11 August 2016
Aims. Our study is meant to extend our knowledge of the galaxy color and luminosity segregation in velocity space (VCS and VLS, respectively), to clusters at intermediate and high redshift.
Methods. Our sample is a collection of 41 clusters in the 0.4 ≲ z ≲ 1.5 redshift range for a total of 4172 galaxies, 1674 of which are member galaxies of the clusters within 2R200 with photometric or spectroscopic information, as taken from the literature. We perform homogeneous procedures to select cluster members, compute global cluster properties, in particular the line-of-sight (LOS) velocity dispersion σV, and separate blue from red galaxies.
Results. We find evidence of VCS in clusters out to z ≃ 0.8 (at the 97−99.99% confidence level, depending on the test), in the sense that the blue galaxy population has a 10−20% larger σV than the red galaxy population. Poor or no VCS is found in the high-z sample at z ≥ 0.8. For the first time, we detect VLS in non-local clusters and confirm that VLS only affects the very luminous galaxies; brighter galaxies have lower velocities. The threshold magnitude of VLS is ~ m3 + 0.5, where m3 is the magnitude of the third brightest cluster galaxy. Current data suggest that the threshold value moves to fainter magnitudes at higher redshift. We also detect (marginal) evidence of VLS for blue galaxies.
Conclusions. We conclude that segregation effects can be important tracers of the galaxy evolution and cluster assembly when they are studied up to distant clusters. We also discuss the evidence of VCS at high redshift, which is poor or absent.
Key words: galaxies: clusters: general / galaxies: kinematics and dynamics / galaxies: evolution / cosmology: observations
© ESO, 2016
1. Introduction
It is well established that the properties of cluster galaxies differ from those of field galaxies and that clusters are characterized by radial gradients. Galaxies in denser, central regions are typically of earlier morphological type, redder color, and have a lower star formation rate. This is the well-known phenomenon of the spatial segregation between blue spiral and red elliptical galaxies in local and distant clusters (e.g., Melnick & Sargent 1977; Dressler 1980; Whitmore et al. 1993; Abraham et al. 1996; Dressler et al. 1999; Gerken et al. 2004). More recently, this effect has only been questioned at very high redshift where some authors have detected an inversion of the star formation rate vs. galaxy density (Tran et al. 2010; Santos et al. 2015; but see Ziparo et al. 2014). The spatial segregation is a basic observable in the framework of galaxy evolution and, in particular, of the connection between galaxy evolution and cluster environment.
A related phenomenon is the segregation of galaxies of different color and type in velocity space (VCS). It requires much observational effort to measure galaxy redshifts, therefore this effect is unfortunately far less well known than the spatial segregation. Since the pioneering works of Tammann (1972) and Moss & Dickens (1977), several studies have reported significant differences in the velocity distributions of different galaxy populations. The velocity dispersion of the population of blue star-forming galaxies is found to be larger than that of the population of red passive galaxies (e.g., Sodré et al. 1989; Biviano et al. 1992, 1996, 1997; Scodeggio et al. 1995; Colless & Dunn 1996; Mohr et al. 1996; Adami et al. 1998; Dressler et al. 1999; Goto 2005).
Moss & Dickens (1977) suggested that VCS is evidence of an infalling population of field galaxies into the clusters. Large data samples, obtained by stacking galaxies of several clusters, have allowed tracing the velocity dispersion profiles (VDPs) and obtaining new insights into this problem. Biviano et al. (1997) analyzed the ESO Nearby Abell Cluster Survey (ENACS – 107 clusters, see Katgert et al. 1996) and inferred that the kinematical segregation of the emission line galaxies (ELGs) with respect to the passive galaxy population reflects the time of infall and not the virialized condition. They found that the VDP of ELGs is consistent with the fact that ELGs are on more radial orbits than passive galaxies. Carlberg et al. (1997) analyzed the Canadian Network for Observational Cosmology cluster sample (CNOC – 16 clusters at medium redshift z ~ 0.3, see Yee et al. 1996), finding that the blue galaxy population is characterized by a higher value of the global velocity dispersion than the red galaxy population and a different VDP. The difference in the VDP is an expected consequence of the fact that both populations trace the same cluster potential with different spatial density profiles. Biviano & Katgert (2004) have shown that early and late spectroscopic type galaxies of ENACS clusters are in equilibrium in the cluster potential and that late-type galaxies have more radially elongated orbits. Some interesting papers have started to analyze cluster numerical simulations in the attempt to trace galaxies during their infall into clusters and relate galaxy properties to their position in the projected phase space or to the kinematical properties of the galaxy population, that is, velocity distribution and velocity dispersion (e.g., Mahajan et al. 2011; Hernández-Fernández et al. 2014; Haines et al. 2015). In this context, VCS is therefore an important observational feature related to galaxy evolution during cluster assembly.
The presence of VCS has been questioned in a few past and recent studies. Analyzing a sample of six clusters, Zabludoff & Franx (1993) found that early- and late-type galaxies have no different velocity dispersions. The analysis of the Cluster and Infall Region Nearby Survey (CAIRNS – 8 clusters at z< 0.05, see Rines et al. 2003) have shown that the kinematics of star-forming galaxies in the infall region closely matches that of absorption-dominated galaxies (Rines et al. 2005). Hwang & Lee (2008) investigated the orbital difference between early-type and late-type galaxies in ten clusters using data extracted from SDSS and 2dFGRS data; in four of these they did not find any difference. Rines et al. (2013) analyzed the Hectospec Cluster Survey (HeCS – 58 clusters with 0.1 ≤ z ≤ 0.3) and reported that the determination of velocity dispersion and dynamical mass is insensitive to the inclusion of bluer members and that the velocity dispersion of the ensemble cluster of all galaxies is only 0.8% larger than that of the red-sequence galaxies.
These discrepancies can probably be understood by taking into account that the analysis of VCS implies several difficulties and possible sources of confusion. The member selection is particularly critical since the effect of including typically blue field galaxies can bias the velocity dispersion of the blue population toward higher values. Another difficulty is that the amount of VCS detected so far is small; it accounts for ~ 10 − 20% (30% at most) of the value of the velocity dispersion. For a small velocity segregation, there is a strong spatial segregation and a decreasing trend of the VDP, in particular in star-forming galaxies (Biviano & Katgert 2004). The last two effects combine in such a way as to hide the VCS effect when global values of the velocity dispersion are computed, in spite of the positive detection in the VDP (e.g., Girardi et al. 2015). Most of the existing positive detections of VCS have been derived from analyzing the VDPs of ensemble clusters obtained by stacking together galaxies of many clusters. The price to be paid for the large gain in statistics when using ensemble clusters is that possible individual behaviors are averaged out, which might explain the reported discrepancies. Recent and ongoing cluster catalogs, based on hundreds of member galaxies per cluster (e.g., Owers et al. 2011), will allow us to study the VDP and VCS of individual clusters. MACS J1206.2−0847 is the first cluster of the CLASH-VLT survey (Rosati et al. 2014) for which the VCS has been analyzed (Girardi et al. 2015).
Moreover, to date, little is known about the velocity segregation in relation to cluster properties. For instance, the relation between the VCS and cluster dynamical status has been explored in very few studies (Ribeiro et al. 2010, 2013). The member selection might be particularly critical in very active clusters, and the scenario is made more complex by the fact that cluster mergers might also enhance star formation in galaxies (e.g., Caldwell & Rose 1997; Ferrari et al. 2005; Owen et al. 2005). The dependence of VCS on redshift is also only rarely investigated. The pioneering study of Biviano & Poggianti (2009), based on 18 clusters of the ESO Distant Cluster Survey (EDisCS – z ~ 0.4 − 0.8, see White et al. 2005), indicates that VCS is not as pronounced as in local ENACS clusters. Crawford et al. (2014) analyzed five distant clusters (0.5 <z< 0.9), finding that red sequence, blue cloud, and green valley galaxies have similar velocity distributions. To probe the VCS in distant clusters is also of interest in view of the spectroscopic survey to be provided by the ESA Euclid mission (Laureijs et al. 2011). Euclid will provide spectroscopic data for distant clusters at 0.8 <z< 1.8, but only for galaxies with Hα lines (Sartoris et al. 2016, and references therein). This raises the question as to how velocity dispersions measured using star-forming galaxies compare with those usually measured with red galaxies. Understanding possible biases in the measurements of velocity dispersions using different galaxy populations has implications for cosmological applications of the distribution function of velocity dispersions (e.g., Borgani et al. 1997).
This paper is devoted to the study of the VCS in distant clusters (0.4 ≲ z ≲ 1.5) and is based on data of 41 clusters collected from the literature. To obtain further insights into the physical processes involved in the velocity segregation, we also analyzed the possible presence of luminosity segregation in velocity space (VLS), which is reported in the literature as a minor effect with respect to VCS (Chincarini & Rood 1977; Biviano et al. 1992, and references therein). In particular, Biviano et al. (1992) have found that only the most luminous galaxies are segregated in velocity, with brighter galaxies having lower velocities. This result has been confirmed in more recent papers (Adami et al. 1998; Goto 2005; Ribeiro et al. 2013) and in poor group environments (Girardi et al. 2003; Ribeiro et al. 2010). The observed phenomenon has been explained by physical processes that transfers kinetic energy from more massive galaxies to less massive ones. In particular, the dynamical friction (Sarazin 1986) is the most probable mechanism (Biviano et al. 1992; Mahajan et al. 2011).
The paper is organized as follows. We present our cluster catalog in Sect. 2. Sections 3 and 4 are devoted to the presentation of member selection, main cluster properties, and separation between red and blue galaxy populations. Section 5 concentrates on the analysis of the VCS and VLS effects, which are discussed in the following Sect. 6. We summarize our results and conclude in Sect. 7.
Unless otherwise stated, we give errors at the 68% confidence level (hereafter c.l.). Throughout this paper, we use H0 = 70 km s-1 Mpc-1 in a flat cosmology with Ω0 = 0.3 and ΩΛ = 0.7.
2. Data sample
We collected data for clusters with redshift z ≳ 0.4 and sampled by at least 20 galaxies with measured z in the cluster field. To separate blue star-forming late-type galaxies from red passive early-type galaxies, we also required color or spectral information. In most cases we used the color information, and in the following, we refer to the two above classes of galaxies as blue and red galaxies. In the data collection we also made use of NED1 to search for cluster data until 2015 June 5. We only considered clusters with homogeneous data samples, clusters reported by one author or one collaboration. Table A.1 lists the 41 clusters that met our requirements (see the end of Sect. 4). The cluster catalog samples the redshift range 0.39−1.46 with a median redshift of 0.58 (see Fig. 1) and is a collection of 4172 galaxies, 100 galaxies per cluster (median value).
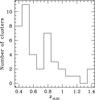 |
Fig. 1 Distribution of redshifts for the 41 clusters of the sample. |
For each cluster, Table A.1 lists the name of the cluster (Col. 1), the redshift as listed in the literature (Col. 2), the available magnitude information (Col. 3), the number of galaxies with measured redshift in the field, Nz (Col. 4), the sampling radius, Rsam, in units of R200 (Col. 5), and the redshift and magnitude references (Col. 6). The sampling radius, which is based on the estimates of the cluster center and the R200 radius computed in Sect. 3, is listed here to show the radial extension of the original cluster data sample. The radius R200 is the radius of a sphere with mass overdensity 200 times the critical density at the redshift of the galaxy system. Correspondingly, M200 is the total mass contained within this radius.
Our cluster sample results from a collection of data from several sources, which results in different sampling criteria related to the strategy used by the different observers to select spectroscopic targets. As a result, the data samples we use differ in their photometric properties and completeness limits. This is not expected to affect our results, which are based on kinematics and relative comparisons, but we suggest to be cautious in drawing other conclusions. For instance, we report the numbers of cluster galaxies only to stress the relative statistical weights of the different samples. Since these numbers are dependent on the different (and often poorly known) selection functions of the original data sources, they are not representative of the intrinsic relative fractions of the different cluster populations.
3. Member selection and global cluster properties
To select cluster members, we applied the two-step procedure introduced by Fadda et al. (1996) that is called peak+gap (P+G) in more recent studies (Biviano et al. 2013; Girardi et al. 2015). The method is a combination of the 1D adaptive-kernel method DEDICA (Pisani 1993; see also the Appendix of Girardi et al. 1996) and the shifting gapper method, which uses both position and velocity information (Fadda et al. 1996). The 1D-DEDICA method is a non-parametric adaptive method of density reconstruction, optimized as described in Pisani (1993). It is used to detect the cluster peak in the redshift distribution and to assign the respective galaxies. For each cluster, we detected a peak at the cluster redshift reported by the literature, that is, with a difference Δz< 0.003, with high significant c.l. (i.e., ≥ 99%, with the exception of RX J1716.6+6708 at the 98% c.l.). In the few cases where secondary peaks are also detected, we considered as belonging to the cluster peaks that are less distant than 2500 km s-1from the main peak and that had at least ≥ 25% overlap with the main peak. For each cluster, the preliminary cluster members were used to compute the center as the mean position in RA and Dec of the galaxies using the biweight estimator (ROSTAT software, Beers et al. 1990). The shifting gapper procedure rejects galaxies that are too far in velocity from the main body of galaxies and within a fixed radial bin that shifts along the distance from the cluster center. The procedure is iterated until the number of cluster members converges to the final value. Following Fadda et al. (1996), we used a gap of 1000 km s-1in the cluster rest-frame and a bin of 0.6 Mpc, or large enough to include 15 galaxies.
For each cluster, we computed the global properties through a recursive procedure. First, we estimated the mean cluster redshift, using the biweight estimator, and the robust estimate of the LOS velocity dispersion. For robust estimate we mean that we used the biweight estimator and the gapper estimator for samples with ≥ or < 15 member galaxies, respectively, following the suggestions of Beers et al. (1990) and Girardi et al. (1993). When we computed velocity dispersions we also applied the cosmological correction and the standard correction for velocity errors (Danese et al. 1980). To obtain a first estimate of the radius R200 and the cluster mass M200 contained therein, we used the theoretical relation between mass and velocity dispersion of Munari et al. (2013; Eq. (1)), which those authors verified on simulated clusters. We considered the galaxies within this first estimate of R200 to recompute the galaxy properties and in particular the final estimate of R200 and M200. Using galaxies within this fiducial estimate of R200, we estimated the final cluster properties, which are the cluster center, the mean redshift zcl, and the velocity dispersion σV, as listed in Table A.2. We do not list the errors on R200 (M200) since its relative error is nominally equal to (three times) that on σV considering the scaling relation, R200 ∝ σV (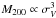 ). An additional ~ 10% uncertainty on M200 arises from the intrinsic scatter between M200 and σV, as indicated by numerical simulations (Munari et al. 2013).
). An additional ~ 10% uncertainty on M200 arises from the intrinsic scatter between M200 and σV, as indicated by numerical simulations (Munari et al. 2013).
Twenty-three clusters are not sampled out to R200 (see Table A.1). We used the other 18 well-sampled clusters to verify that this undersampling does not introduce any bias in our estimate of the velocity dispersion and, consequently, of R200 and M200. For these 18 clusters, we compared the distribution of the velocity dispersions computed within 0.5R200 and that within R200. We obtained no significant evidence of a difference according to the Kolmogorov-Smirnov test (hereafter KS-test; see, e.g., Lederman 1984), and according to two more sensitive tests, the Sign and Wilcoxon signed-rank tests (hereafter S- and W-tests, e.g., Siegel 1956).
4. Populations of red and blue galaxies
To separate red passive from blue star-forming galaxies, we used a color-based procedure. We considered the two magnitude bands in such a way that the Balmer break at the cluster redshift was located roughly between the two filters (see Fig. 18 of Westra et al. 2010). The color distribution was analyzed using the Kaye mixture model (KMM) method, as implemented by Ashman et al. (1994), to detect the color bimodality and define the respective group partition and, consequently, the value of the color cut (see Fig. 2 as an example).
 |
Fig. 2 Separation between red and blue galaxies in the MS 1054.4−0321 cluster. Left panel: color−magnitude diagram. The horizontal dashed line indicates the color cut obtained using the V − i colors for member galaxies. For this well-sampled cluster we also show the red sequence line fitted with a two-sigma procedure applied to the red galaxies (black solid line). Larger sizes of the symbols for larger EW[OII] show the good agreement between the photometric and spectroscopic methods to separate red passive from blue star-forming galaxy populations. Right panel: distribution of V − i colors for member galaxies. The two Gaussians are obtained through the KMM method and allow us to define the color cut in the left panel. |
The KMM procedure fails in detecting a significant bimodality in eight clusters, typically those with very few available data, and we used alternative procedures. To define the color cut in four clusters, we adopted the intermediate value between the typical color of red and blue galaxies at z = 0 (Fukugita et al. 1995), conveniently shifted at the cluster redshift using the k- and evolutionary corrections by Poggianti (1997). In the four distant clusters for which the magnitude corrections are less reliable, we preferred to use spectroscopic features to separate red passive from blue star-forming galaxies. We defined as star-forming galaxies those with the [OII] emission line in their spectrum. When EW[OII] measures were available, we defined as star-forming galaxies those with EW[OII] ≥15 Å (see, e.g., Postman et al. 1998; Hammer et al. 1997). For the eleven clusters for which both good magnitude and spectroscopic information are available, the location of ELGs in the color−magnitude diagram supports the good agreement of the photometric- and spectroscopic-based methods (see Fig. 2, left panel, for an example). For each cluster, Table A.3 lists the number of member galaxies with measured magnitudes, Nm (Col. 2), the color and magnitude used in our analysis (Cols. 3 and 4), and the adopted color cut (Col. 5). In the case of the spectroscopic-based separation, Nm refers to the number of galaxies with available EW[OII] information. The relevant information about the reference sources of the magnitudes is listed in Table A.1.
We considered the cluster regions within 2R200. Out to 2R200, the cluster density and mass profiles are a reasonable extrapolation of those determined within R200 (Biviano & Girardi 2003). A requirement of our catalog is that each cluster is sampled at least with four red and four blue galaxy members within 2R200. Generally, the clusters in our catalog are much better sampled (see Cols. 6 and 8 in Table A.3), with 20 red galaxies and 14 blue galaxies per cluster (median values). Table A.3 lists the velocity dispersions of the red and blue galaxies within 2R200. The values of σV,red and σV,blue correlate at the > 99.99% c.l. according to the Spearman test (coefficient value of 0.70, see Fig. 3).
 |
Fig. 3 Velocity dispersion of the red galaxy population vs. velocity dispersion of the blue galaxy population for all clusters of our sample. The filled symbols highlight the clusters where the two values are different according to the F-test (at a c.l. ≥ 90%, see Table 1). The inset shows the number of clusters with σV,blue/σV,red> 1 (blue shaded bar) and the number of clusters with σV,blue/σV,red< 1 (red solid bar). |
5. Analysis and results
5.1. Galaxy color segregation in velocity space
To investigate the relative kinematics of red and blue galaxy populations, we applied a set of tests. As for the individual clusters, we checked for different values of velocity dispersions of the two galaxy populations by applying the standard F-test (Press et al. 1992). We found that only 6 (9) of the 41 clusters show evidence of a kinematical difference at the 95% (90%) c.l. In most of these cases, that is, 5 (7) clusters, we found σV,blue>σV,red (see Table 1).
Clusters where σV,red ≠ σV,blue.
We compared the σV,red distribution and the σV,blue distribution. According to the KS-test, the probability that the two distributions are drawn from the same parent distribution is ~ 24%, which means that there is no evidence of a significant difference. The cumulative distributions are compared in Fig. 4 and the separation between the two distribution median values is 75 km s-1, that is ~ 11% of the median value of global σV. The availability of two measures, σV,red and σV,blue, for each cluster, allows us to also apply the S- and W-tests, which are more sensitive tests than the KS-test, and to look for a possible systematic, even if small difference. According to the S- and W-tests, σV,blue is larger than σV,red at the 97.02% and 99.45% c.ls., respectively. Out of 41 clusters, the number of those with σV,blue > σV,red is 27 (see inset in Fig. 3).
 |
Fig. 4 Cumulative distributions of the velocity dispersions of red and blue galaxies. |
As a final test, we considered the projected phase space, that is, the rest-frame velocities Vrf = (V − ⟨ V ⟩ )/(1 + z) vs. clustercentric distance R, of two ensemble clusters, one for red and one for blue galaxies. These two ensemble cluster data were obtained by stacking the red (or blue) galaxies of each cluster, normalizing the velocity and the clustercentric distance of each galaxy with the σV and R200 values of the parent cluster. The result is shown in Fig. 5 (upper panel), where we also trace the limits that are due to the escape velocity in the cluster, assuming a typical cluster mass distribution described by a Navarro-Frenk-White (NFW) density profile with a concentration parameter c = 3.8, which is typical for halos of mass M = 3 × 1014M⊙ at z = 0.6, the median values in our sample (Dolag et al. 2004). The trumpet shape of the projected phase space data distribution and the good agreement with the escape velocity curves should be considered as a posteriori sanity check of the member selection procedure, which we made completely independent of the model used. In principle, the projection of possible non-member galaxies, most likely blue field galaxies, onto the trumpet shape cannot be excluded. However, according to the analysis of N-body cosmological simulations (Biviano et al. 2006), their effect should be that of slightly decreasing the value of the velocity dispersion, that is, an opposite effect with respect to the segregation effect reported in the present and previous studies.
The respective VDPs for red and blue galaxies are shown in the lower panel of Fig. 5. The VDPs are shown to decline, as expected, at least out to ≳ R200. In the outer regions, the uncertainties are very large and the fraction of possible interlopers, that is, galaxies outside the theoretical escape velocity curves, that passed our member selection procedure, increases (see the upper panel of Fig. 5). Within R200 the VDP of blue galaxies is higher than that of red galaxies and the difference is significant at the > 99.99% c.l. according to the χ2-test applied to the values of the four bins, which combine a total of 936 red and 532 blue galaxies. Table 2 summarizes the results of all the tests we applied.
 |
Fig. 5 Upper panel: rest-frame LOS velocity vs. projected clustercentric distance for the galaxies of the ensemble cluster. Small red dots indicate red galaxies and blue triangles indicate blue galaxies. Black curves show the limits that are due to the escape velocity assuming a NFW mass profile (see text). Lower panel: velocity dispersion profiles (VDPs) for red and blue galaxies of the ensemble cluster (solid red circles and blue open triangles). Data are binned in intervals of 0.25 Mpc in the 0–2R200 range. The point abscissae are set to the averages of the R/R200 values of each sample within the bins. The error bars are determined by a bootstrap resampling procedure. |
Statistical results about the relative kinematics of red and blue populations.
To investigate the variation of the kinematical difference between red and blue galaxy populations at different redshifts, we divided the cluster sample into three subsamples, low-z sample with z< 0.5, medium-z with 0.5 ≤ z< 0.8, high-z with z ≥ 0.8, having a roughly comparable number of clusters and galaxies. We applied the above-described set of tests to the three subsamples. Figure 6 points out the relation between σV,blue and σV,red separately for the three subsamples and shows that clusters of the high-z sample are equally split by σV,blue>σV,red and σV,blue<σV,red values. Figure 7 shows the variation of the normalized σV,blue (and σV,red) values with redshift, no difference is found for the high-z sample. To apply the VDP χ2-test, we considered data binned in three intervals within 1.2R200 (see Fig. 8) for a total of 349 red and 224 blue galaxies in the low-z sample, 247 red and 160 blue galaxies in the medium-z sample, 369 red and 193 blue galaxies in the high-z sample. The results of the whole set of tests are listed in Table 2. We find that in the high-z sample there is no or poorer evidence of kinematical segregation than in the other two samples, in particular with respect to the low-z sample.
 |
Fig. 6 Velocity dispersion of the blue galaxy population vs. velocity dispersion of the red galaxy population for the three subsamples: low-z (open circles), medium-z (crosses), and high-z (solid squares). |
 |
Fig. 7 Normalized velocity dispersion of the red galaxy population vs. normalized velocity dispersion of the blue galaxy population for the three subsamples: low-z, medium-z, and high-z. |
 |
Fig. 8 Same as in Fig. 5, but for the ensemble clusters of the low-z, medium-z, and high-z subsamples (top, middle, and bottom panels). Data are binned in intervals of 0.4 Mpc in the 0–1.2R200 range. |
5.2. Galaxy luminosity segregation in velocity space
As in previous studies of VLS, our analysis is based on the ensemble cluster. We restricted our analysis to galaxies within R200. Because of the non-homogeneity of the photometric data of the different clusters in our sample, we adopted the same approach as Biviano et al. (1992) and normalized the magnitude of each galaxy with the magnitude of the third brightest galaxy (m3). We used one of the magnitude bands listed in Table A.1, preferring red or NIR bands. We analyzed the behavior of | Vrf | vs. m − m3, and Fig. 9 highlights the main results. (i) The red galaxies have lower | Vrf | than the blue galaxies, independent of their magnitudes; and (ii) both red and blue galaxies show evidence of velocity segregation. To statistically evaluate VLS, we also considered the correlation between | Vrf | /σV and m − m3 for galaxies with m − m3 ≤ 0.5 or m − m3 > 0.5, where m − m3 = 0.5 mag is the threshold value suggested from inspection of Fig. 9. For the red (blue) galaxies with m − m3 ≤ 0.5 we find that | Vrf | and m − m3 correlate at the ~ 94% c.l. (~ 90%) according to the Spearman test. No significant correlation is found for red and blue galaxies with m − m3 > 0.5.
 |
Fig. 9 Normalized velocities of red and blue galaxies (solid red circles and blue open triangles) vs. m − m3, where m3 is the magnitude of the third brightest galaxy in each cluster. Data are binned in intervals of 0.5 mag. The error bars are obtained by a bootstrap resampling procedure. Points without error bars indicate the values based on only three galaxies. The dashed line represents our fit for red galaxies in the m − m3 ≤ 0.5 region. The results of Biviano et al. (1992) are shown for comparison (small black squares). |
To investigate a possible dependence of VLS on redshift, we also show the results for the three redshift subsamples. Although current data are not sufficient to obtain firm conclusions, the visual inspection of Fig. 10 suggests that the segregation threshold value in the low-z sample lies at brighter magnitudes than the values in the medium-z and high-z samples.
 |
Fig. 10 Same as in Fig. 9, but for all red+blue galaxies and analyzing low-z, medium-z, and high-z subsamples separately (polygons, asterisks, and stars, respectively). |
6. Discussion
We found evidence of VCS in our sample of clusters. In our analysis, VCS was detected over the whole sampled galaxy luminosity range (see Fig. 9). In particular, when we analyzed the clusters in three redshift ranges separately, we found that the amount of VCS decreases with increasing redshift and that very poor or no evidence of segregation is found in the high-z sample (Table 2). Qualitatively, this agrees with the results of Biviano & Poggianti (2009) in EDisCS clusters at z ~ 0.4−0.8 (our low-z+medium-z samples), for which there is much less evidence of VCS than in local clusters. Crawford et al. (2014) found no evidence of VCS between red sequence and blue cloud galaxies in five distant cluster (0.5 < z < 0.9), but they did not analyze a local sample for comparison.
We confirm that the effect of VCS is quantitatively small and, therefore, difficult to detect. For instance, according to the KS-test, the σV distributions of red and blue galaxies might derive from the same parent distribution. We had to resort to very sensitive tests such as the S- and W-tests to detect a significant difference in the σV distributions. As in most previous positive detections in the literature, our most significant detection was obtained by stacking galaxies of all clusters. Quantitatively, the estimates of the difference in σV reported in the literature are of about 10−20%, 30% at most (Biviano et al. 1997; Carlberg et al. 1997; Adami et al. 1998; de Theije & Katgert 1999; Haines et al. 2015) and vary according to the selection of the two populations. In fact, when the population is selected according to higher values of star formation rate, its σV is higher (Haines et al. 2015). The values we obtained in our study are comparable with those reported in the literature. We estimated that σV of red and blue galaxies differ for ΔσV/σV ~ 20% and 10% in the low-z and medium-z samples, and the median value of the ratios of the VDP binned values for blue and red galaxies is 1.2 (within R200, see Fig. 5).
Taking the difficulties related to the detection and measure of VCS into account, any result is more reliable when obtained through a homogeneous analysis than by comparing results from different authors. In this context, it is interesting that our results are in line with that of Biviano & Poggianti (2009) on a decreasing amount of VCS at higher redshifts, although their claim holds for clusters at z ~ 0.4−0.8, while ours was obtained for clusters in the 0.8 ≤ z ≤ 1.5 range. The poor evidence of VCS in high-redshift clusters can be explained in a scenario where the segregation develops as the result of a continuous regular smooth accretion of field blue galaxies, then possibly evolving into red galaxies, into the cluster. VCS is erased when cluster-cluster mergers drive violent relaxation, and the frequency of such mergers is expected to be higher at higher redshift.
Since our cluster sample spans a wide range of masses, of about two orders of magnitudes (see Table A.2), we also checked for a possible dependence of VCS on mass. We found no significant correlation of σV,blue/σV,red vs. cluster mass. This agrees with the fact that the evidence of VCS, which is well known in clusters, is also detected in groups (Girardi et al. 2003; Ribeiro et al. 2010).
To our knowledge, this is the first study in which VLS is detected in non-local clusters. The | Vrf | vs. m − m3 relation we detected is similar to that originally shown by Biviano et al. (1992). Assuming the mass-follows-light hypothesis, the faint galaxies can be described by a regime of velocity equipartition, while the bright galaxies can be better described by a regime of energy equipartition, with more massive objects being slower. Since we used red or NIR magnitude bands, the luminosity is a good indicator of the stellar mass, but the mass-follows-light assumption is needed to extrapolate our interpretation to the whole halo galaxy mass. As has been discussed by other authors (Biviano et al. 1992; Mahajan et al. 2011), the most likely cause for the observed VLS is the dynamical friction process, whose characteristic time-scale is inversely proportional to mass.
We confirm that VLS holds for red galaxies and find for the first time evidence that the same segregation also applies to the population of blue galaxies. Adami et al. (1998) and Ribeiro et al. (2013) both found VLS for ellipticals and passive galaxies, but no (or even opposite) effect is reported for galaxies of other types. However, the inspection of Fig. 2b of Adami et al. (1998) suggests that their non-detection might instead be due to the large uncertainties involved. The presence of the VLS for blue galaxies indicates that the kinematical relaxation time-scale is shorter than the transformation time-scale or that massive blue galaxies are robust against environmental effects and possible transformation to S0 (e.g., Moore et al. 1996; Bekki & Couch 2011).
A more detailed comparison of our results with those of Biviano et al. (1992, see also our Fig. 9) shows two differences. As a first difference, our | Vrf | and m − m3 relation is steeper than their relation. The fit of the logarithm of | Vrf | vs. m − m3 gives a slope of 0.52 ± 0.05 for red galaxies only, and 0.48 ± 0.04 for all galaxies. For comparison, Biviano et al. (1992) obtained a value of 0.2, which is that expected for energy equipartition (assuming a constant mass-to-light ratio). Adami et al. (1998) also claimed that a 0.2 slope is consistent with their results, but large uncertainties are shown in their Fig. 1a and the inspection of their Fig. 2a for ellipticals instead suggests a steeper slope. The second difference concerns the threshold value between the two kinematic regimes. Biviano et al. (1992) indicated a threshold value around m3 and Adami et al. (1998) reported that VLS concerns about four galaxies per cluster. In the whole sample, our results instead suggest m3 + 0.5 (Fig. 9), and we found that VLS concerns seven galaxies per cluster, computed as the median value of the numbers of galaxies with m − m3 ≤ 0.5 in each cluster. However, Biviano et al. (1992) and Adami et al. (1998) both analyzed local clusters and the inspection of Fig. 10 indicates that the threshold value of VLS in the low-z sample lies at brighter magnitudes than the values in the medium-z and high-z samples. Present data do not allow a precise quantitative conclusion, but suggest that the dependence of the segregation threshold should be taken into account. In particular, the possible explanation for a fainter threshold at higher redshifts might be that clusters at higher redshift have higher density. Per given galaxy mass, the greater the density of the surrounding medium, the stronger the effect of dynamical friction.
7. Summary and conclusions
We presented our results about color and luminosity segregation in velocity space (VCS and VLS, respectively) for a sample of 41 clusters at intermediate and high redshifts (0.4 ≲ z ≲ 1.5) for a total of 4172 galaxies. The data were taken from different sources in the literature, with the constraint that data for each single cluster come from one single source. Moreover, we applied homogeneous preliminary procedures to select cluster members, compute global cluster properties, in particular the LOS velocity dispersions σV, and separate blue from red galaxies. We restricted our analysis to the 1674 member galaxies within 2R200 with photometric or spectroscopic information, 1023 red and 651 blue galaxies. We applied a set of different tests to study VCS and VLS. We used the estimates of velocity dispersion for each individual cluster and the properties of an ensemble cluster obtained by stacking together galaxies of many clusters.
The main results of our analysis are summarized as follows.
-
From the analysis of the whole sample we detect evidence of VCS according to several tests (S-, W-, and VDP χ2-tests), with the blue galaxy population having a larger σV than the red galaxy population.
-
When analyzing three subsamples at different redshifts (low-z with z < 0.5, medium-z with 0.5 ≤ z < 0.8, high-z with z ≥ 0.8), we found very poor or no evidence of VCS in the high-z sample. That VCS is weaker at higher redshifts has been pointed out by Biviano & Poggianti (2009), although our threshold of no detection is at higher z than theirs. The disappearance of the VCS for distant clusters can be explained when considering that our high-z sample is very close to the epoch of cluster formation, with major mergers driving violent relaxation, which leads to the velocity equipartition regime.
-
In agreement with previous studies, we confirm that the effect of VCS is quantitatively small (10 − 20% in the σV estimate) and requires sensitive tests or the VDP analysis based on many galaxies. We conclude that VCS is an elusive effect, which might partly explain the discrepant claims reported in the literature on this issue.
-
VCS concerns the whole magnitude range that we covered, ~ 4 mag down to m3; more clusters are needed to sample the bright end to obtain firm conclusions.
-
We detect evidence of VLS for galaxies more luminous than m3 + 0.5, brighter galaxies having lower velocities. Qualitatively, this result is similar to that found for local clusters, but we noted and discussed minor differences, for instance, in the threshold value of the segregation.
-
VLS concerns both red and blue galaxies. The latter finding has not been reported in the literature, not even for local clusters.
Acknowledgments
We thank the referee for useful comments. We thank P. Rosati for providing us data on XMMU J2235.3−2557. M.A., A.B., and M.N. acknowledge financial support from PRIN-INAF 2014 1.05.01.94.02. M.G. acknowledges financial support from the University of Trieste through the program “Finanziamento di Ateneo per progetti di ricerca scientifica – FRA 2015”. S.B. acknowledges financial support from the PRIN-MIUR 201278X4FL grant and from the “InDark” INFN Grant. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Abraham, R. G., Smecker-Hane, T. A., Hutchings, J. B., et al. 1996, ApJ, 471, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Adami, C., Biviano, A., & Mazure, A. 1998, A&A, 331, 439 [NASA ADS] [Google Scholar]
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Couch, W. J. 2011, MNRAS, 415, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Girardi, M. 2003, ApJ, 585, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Katgert, P. 2004, A&A, 424, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., & Poggianti, B. M. 2009, A&A, 501, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1992, ApJ, 396, 35 [CrossRef] [Google Scholar]
- Biviano, A., Durret, F., Gerbal, D., et al. 1996, A&A, 311, 95 [NASA ADS] [Google Scholar]
- Biviano, A., Katgert, P., Mazure, A., et al. 1997, A&A, 321, 84 [NASA ADS] [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al. 2006, A&A, 456, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borgani, S., Gardini, A., Girardi, M., & Gottlöber, S. 1997, New Astron., 2, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N., & Rose, J. A. 1997, AJ, 113, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Ellingson, E., et al. 1997, ApJ, 476, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco, E. R., Cypriano, E. S., Neto, G. B. L., et al. 2007, ApJ, 664, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., & Rood, H. J. 1977, ApJ, 214, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., & Dunn, A. M. 1996, ApJ, 458, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, S. M., Wirth, G. D., & Bershady, M. A. 2014, ApJ, 786, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Danese, L., de Zotti, G., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] [Google Scholar]
- Demarco, R., Rosati, P., Lidman, C., et al. 2007, ApJ, 663, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Demarco, R., Gobat, R., Rosati, P., et al. 2010, ApJ, 725, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- de Theije, P. A. M., & Katgert, P. 1999, A&A, 341, 371 [NASA ADS] [Google Scholar]
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Ellingson, E., Yee, H. K. C., Abraham, R. G., et al. 1997, ApJS, 113, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ellingson, E., Yee, H. K. C., Abraham, R. G., Morris, S. L., & Carlberg, R. G. 1998, ApJS, 116, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D. G., Bautz, M. W., & McClintock, J. E. 1994, AJ, 107, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Fassbender, R., Böhringer, H., Santos, J. S., et al. 2011, A&A, 527, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrari, C., Benoist, C., Maurogordato, S., Cappi, A., & Slezak, E. 2005, A&A, 430, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gerken, B., Ziegler, B., Balogh, M., et al. 2004, A&A, 421, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gioia, I. M., Henry, J. P., Mullis, C. R., Ebeling, H., & Wolter, A. 1999, AJ, 117, 2608 [Google Scholar]
- Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1993, ApJ, 404, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Fadda, D., Giuricin, G., et al. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Rigoni, E., Mardirossian, F., & Mezzetti, M. 2003, A&A, 406, 403 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Girardi, M., Mercurio, A., Balestra, I., et al. 2015, A&A, 579, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, T. 2005, MNRAS, 359, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Pereira, M. J., Smith, G. P., et al. 2015, ApJ, 806, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Halliday, C., Milvang-Jensen, B., Poirier, S., et al. 2004, A&A, 427, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Flores, H., Lilly, S. J., et al. 1997, ApJ, 481, 49 [CrossRef] [Google Scholar]
- Hernández-Fernández, J. D., Haines, C. P., Diaferio, A., et al. 2014, MNRAS, 438, 2186 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Lloyd-Davies, E., Stanford, S. A., et al. 2010, ApJ, 718, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, H. S., & Lee, M. G. 2008, ApJ, 676, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., & Chiboucas, K. 2013, AJ, 145, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Katgert, P., Mazure, A., Perea, J., et al. 1996, A&A, 310, 8 [NASA ADS] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lederman, W. 1984, Handbook of applicable mathematics, Vol. 6, A: Statistics; B: Statistics (Chichester: Wiley-Interscience Publication) [Google Scholar]
- Lerchster, M., Seitz, S., Brimioulle, F., et al. 2011, MNRAS, 411, 2667 [NASA ADS] [CrossRef] [Google Scholar]
- Lubin, L. M., Oke, J. B., & Postman, M. 2002, AJ, 124, 1905 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S., Mamon, G. A., & Raychaudhury, S. 2011, MNRAS, 416, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, J., & Sargent, W. L. W. 1977, ApJ, 215, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Milvang-Jensen, B., Noll, S., Halliday, C., et al. 2008, A&A, 482, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohr, J. J., Geller, M. J., & Wegner, G. 1996, AJ, 112, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, C., & Dickens, R. J. 1977, MNRAS, 178, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Biviano, A., Borgani, S., Murante, G., & Fabjan, D. 2013, MNRAS, 430, 2638 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N., Ledlow, M. J., Keel, W. C., Wang, Q. D., & Morrison, G. E. 2005, AJ, 129, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Owers, M. S., Nulsen, P. E. J., & Couch, W. J. 2011, ApJ, 741, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] [Google Scholar]
- Poggianti, B. M. 1997, A&AS, 122 399 [Google Scholar]
- Postman, M., Lubin, L. M., & Oke, J. B. 1998, AJ, 116, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Lubin, L. M., & Oke, J. B. 2001, AJ, 122, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing (Cambridge: Cambridge University Press) [Google Scholar]
- Ribeiro, A. L. B., Lopes, P. A. A., & Trevisan, M. 2010, MNRAS, 409, L124 [NASA ADS] [Google Scholar]
- Ribeiro, A. L. B., Lopes, P. A. A., & Rembold, S. B. 2013, A&A, 556, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rines, K., Geller, M. J., Kurtz, M. J., & Diaferio, A. 2003, AJ, 126, 2152 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Kurtz, M. J., & Diaferio, A. 2005, AJ, 130, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., & Kurtz, M. J. 2013, ApJ, 767, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Tozzi, P., Gobat, R., et al. 2009, A&A, 508, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosati, P., Balestra, I., Grillo, C., et al. 2014, The Messenger, 158, 48 [NASA ADS] [Google Scholar]
- Santos, J. S., Altieri, B., Valtchanov, I., et al. 2015, MNRAS, 447, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoris, B., Biviano, A., Fedeli, C., et al. 2016, MNRAS, 459, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Solanes, J. M., Giovanelli, R., & Haynes, M. P. 1995, ApJ, 444, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, S. 1956, Nonparametric statistics for the behavioral sciences (Tokyo: McGraw-Hill Kogakusha) [Google Scholar]
- Sodré, Jr., L., Capelato, H. V., Steiner, J. E., & Mazure, A. 1989, AJ, 97, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A. 1972, A&A, 21, 355 [NASA ADS] [Google Scholar]
- Tanaka, M., Finoguenov, A., Kodama, T., et al. 2008, A&A, 489, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tran, K.-V. H., Franx, M., Illingworth, G. D., et al. 2007, ApJ, 661, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, K.-V. H., Papovich, C., Saintonge, A., et al. 2010, ApJ, 719, L126 [CrossRef] [Google Scholar]
- Vulcani, B., Aragón-Salamanca, A., Poggianti, B. M., et al. 2012, A&A, 544, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westra, E., Geller, M. J., Kurtz, M. J., Fabricant, D. G., & Dell’Antonio, I. 2010, PASP, 122, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Clowe, D. I., Simard, L., et al. 2005, A&A, 444, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitmore, B. C., Gilmore, D. M., & Jones, C. 1993, ApJ, 407, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C., Ellingson, E., & Carlberg, R. G. 1996, ApJS, 102, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., & Franx, M. 1993, AJ, 106, 1314 [NASA ADS] [CrossRef] [Google Scholar]
- Ziparo, F., Popesso, P., Finoguenov, A., et al. 2014, MNRAS, 437, 458 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Cluster sample.
Cluster properties.
Color cuts and velocity dispersions of red and blue populations.
All Tables
All Figures
 |
Fig. 1 Distribution of redshifts for the 41 clusters of the sample. |
| In the text | |
 |
Fig. 2 Separation between red and blue galaxies in the MS 1054.4−0321 cluster. Left panel: color−magnitude diagram. The horizontal dashed line indicates the color cut obtained using the V − i colors for member galaxies. For this well-sampled cluster we also show the red sequence line fitted with a two-sigma procedure applied to the red galaxies (black solid line). Larger sizes of the symbols for larger EW[OII] show the good agreement between the photometric and spectroscopic methods to separate red passive from blue star-forming galaxy populations. Right panel: distribution of V − i colors for member galaxies. The two Gaussians are obtained through the KMM method and allow us to define the color cut in the left panel. |
| In the text | |
 |
Fig. 3 Velocity dispersion of the red galaxy population vs. velocity dispersion of the blue galaxy population for all clusters of our sample. The filled symbols highlight the clusters where the two values are different according to the F-test (at a c.l. ≥ 90%, see Table 1). The inset shows the number of clusters with σV,blue/σV,red> 1 (blue shaded bar) and the number of clusters with σV,blue/σV,red< 1 (red solid bar). |
| In the text | |
 |
Fig. 4 Cumulative distributions of the velocity dispersions of red and blue galaxies. |
| In the text | |
 |
Fig. 5 Upper panel: rest-frame LOS velocity vs. projected clustercentric distance for the galaxies of the ensemble cluster. Small red dots indicate red galaxies and blue triangles indicate blue galaxies. Black curves show the limits that are due to the escape velocity assuming a NFW mass profile (see text). Lower panel: velocity dispersion profiles (VDPs) for red and blue galaxies of the ensemble cluster (solid red circles and blue open triangles). Data are binned in intervals of 0.25 Mpc in the 0–2R200 range. The point abscissae are set to the averages of the R/R200 values of each sample within the bins. The error bars are determined by a bootstrap resampling procedure. |
| In the text | |
 |
Fig. 6 Velocity dispersion of the blue galaxy population vs. velocity dispersion of the red galaxy population for the three subsamples: low-z (open circles), medium-z (crosses), and high-z (solid squares). |
| In the text | |
 |
Fig. 7 Normalized velocity dispersion of the red galaxy population vs. normalized velocity dispersion of the blue galaxy population for the three subsamples: low-z, medium-z, and high-z. |
| In the text | |
 |
Fig. 8 Same as in Fig. 5, but for the ensemble clusters of the low-z, medium-z, and high-z subsamples (top, middle, and bottom panels). Data are binned in intervals of 0.4 Mpc in the 0–1.2R200 range. |
| In the text | |
 |
Fig. 9 Normalized velocities of red and blue galaxies (solid red circles and blue open triangles) vs. m − m3, where m3 is the magnitude of the third brightest galaxy in each cluster. Data are binned in intervals of 0.5 mag. The error bars are obtained by a bootstrap resampling procedure. Points without error bars indicate the values based on only three galaxies. The dashed line represents our fit for red galaxies in the m − m3 ≤ 0.5 region. The results of Biviano et al. (1992) are shown for comparison (small black squares). |
| In the text | |
 |
Fig. 10 Same as in Fig. 9, but for all red+blue galaxies and analyzing low-z, medium-z, and high-z subsamples separately (polygons, asterisks, and stars, respectively). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


