| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628519 | |
| Published online | 13 October 2016 | |
The segregation of starless and protostellar clumps in the Hi-GAL ℓ = 224° region⋆
1 INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: olmi.luca@gmail.com
2 University of Puerto Rico, Rio Piedras Campus, Physics Dept., Box 23343, UPR station, San Juan, Puerto Rico, USA
3 School of Physics, University of New South Wales, 2052 Sydney, Australia
4 INAF, Istituto di Astrofisica e Planetologia Spaziali, via Fosso del Cavaliere 100, 00133 Roma, Italy
Received: 15 March 2016
Accepted: 16 July 2016
Context. Stars form in dense, dusty structures, which are embedded in larger clumps of molecular clouds often showing a clear filamentary structure on large scales (≳1 pc). The origin (e.g., turbulence or gravitational instabilities) and evolution of these filaments, as well as their relation to clump and core formation, are not yet fully understood. A large sample of both starless and protostellar clumps can now be found in the Herschel Infrared GALactic Plane Survey (Hi-GAL) key project, which also provides striking images of the filamentary structure of the parent molecular clouds. Recent results indicate that populations of clumps on and off filaments may differ.
Aims. One of the best-studied regions in the Hi-GAL survey can be observed toward the ℓ = 224° field. Here, a filamentary region has been studied and it has been found that protostellar clumps are mostly located along the main filament, whereas starless clumps are detected off this filament and are instead found on secondary, less prominent filaments. We want to investigate this segregation effect and how it may affect the clumps properties.
Methods. We mapped the 12CO (1−0) line and its main three isotopologues toward the two most prominent filaments observed toward the ℓ = 224° field using the Mopra radio telescope, in order to set observational constraints on the dynamics of these structures and the associated starless and protostellar clumps.
Results. Compared to the starless clumps, the protostellar clumps are more luminous, more turbulent and lie in regions where the filamentary ambient gas shows larger linewidths. We see evidence of gas flowing along the main filament, but we do not find any signs of accretion flow from the filament onto the Hi-GAL clumps. We analyze the radial column density profile of the filaments and their gravitational stability.
Conclusions. The more massive and highly fragmented main filament appears to be thermally supercritical and gravitationally bound, assuming that all of the non-thermal motion is contributing thermal-like support, suggesting a later stage of evolution compared to the secondary filament. The status and evolutionary phase of the Hi-GAL clumps would then appear to correlate with that of the host filament.
Key words: stars: formation / ISM: clouds / ISM: molecules
Mopra data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/594/A58
© ESO, 2016
1. Introduction
Stars form in dense, dusty structures, which are embedded in larger clumps of molecular clouds. Here, the term clump refers to any compact density enhancement (with size ~ 0.1−1 pc and density ~ 104−105cm-3), as identified by source-extraction algorithms, and core (size ≲ 0.01−0.1 pc and density ≳ 105cm-3) refers to the clump sub-structures which are going to form stars. A large sample of both starless (i.e., with no sign of active star formation, and not necessarily gravitationally bound) and protostellar clumps can now be found in the Herschel Infrared GALactic Plane Survey (Hi-GAL) key project (Molinari et al. 2010). The Hi-GAL survey also provides striking images of the filamentary structure of the parent molecular clouds on large scales (≳ 1 pc), which now allow to study the physical connection between the clumps/cores and the filaments. Filamentary structures were known to be present in molecular clouds even before the recent large scale star-formation surveys at far-infrared wavelengths. The origin (e.g., turbulence or gravitational instabilities) and evolution of these filaments, as well as their relation to star formation, are not yet fully understood.
Observationally, filaments show complex structures with multiple branches and hubs, where the dense clumps/cores detected in the Hi-GAL survey are more frequently found. The observed similarity between the mass distribution of the clumps and the stellar initial mass function (IMF) supports the accepted idea that clumps may fragment into sub-structures (cores or fragments) which then form stars or even clusters of stars. Therefore, in order to draw a more complete picture of star formation it is fundamental to study the transition phase from the observed clump mass function (CMF) to the IMF, and to understand how the presence of filaments affects the formation of clumps and their mass distribution.
 |
Fig. 1 SPIRE 250 μm emission observed toward the ℓ = 224° region, with a (logarithmic) color-scale in MJy sr-1 (Elia et al. 2013). Blue star symbols represent protostellar clumps while the red empty circles represent starless clumps. The dashed, black contour shows the region mapped with the Mopra telescope. The yellow and blue solid contours correspond to about 100 and 200 MJy sr-1, respectively, and approximately trace the secondary filament toward the north (besides to low-level emission from the main filament) and the main filament. |
Two interesting recent results have been published as part of the Herschel Gould Belt Survey (HGBS, André et al. 2010). Polychroni et al. (2013) studied the L 1641 molecular clouds in Orion A and found that most (≃ 70%) of the starless clumps were located on filaments. They also found that the two clump populations (on and off the identified filaments) had distinctly different CMF. In a separate work, Arzoumanian et al. (2013) investigated the gas velocity dispersions of a sample of filaments, also detected as part of the HGBS in the IC 5146, Aquila, and Polaris interstellar clouds. They found that these filaments could be divided into two regimes: (i) thermally subcritical filaments, gravitationally unbound; and (ii) thermally supercritical filaments, which have higher velocity dispersions and are self-gravitating. These authors propose that, as they contract and accrete material from the background cloud, supercritical filaments are expected to fragment into clumps and form (proto)stars (as supported by some theoretical models, e.g., Pon et al. 2011). On the other hand, Schneider et al. (2010) analyzed the dynamics of the DR21 high-mass star-forming region and found that its filamentary morphology, and the existence of sub-filaments, can be explained if the DR21 filament was formed by the convergence of gas flows on large scales.
In their works, Polychroni et al. (2013) completely ignore the protostellar clumps, while Arzoumanian et al. (2013) and Schneider et al. (2010) do not correlate the study of the filament dynamics with the presence of starless and protostellar clumps. In addition, the massive DR21 region is quite different from the molecular clouds studied in the HGBS, and thus the question arises of whether different filament dynamics may lead to different (low- and high-mass) star formation. Molecular line mapping of a larger sample of filaments is thus required, in order to set stronger observational constraints on the dynamics of these structures.
2. Observations
2.1. Hi-GAL observations
The Hi-GAL survey offers the best opportunity to look at large clump populations in various clouds with different physical conditions, while using self-consistent analysis to derive their physical parameters (see, e.g., Elia et al. 2010, 2013; Olmi et al. 2013). Mass and other physical parameters of the Hi-GAL clumps were derived from a single-temperature spectral energy distribution (SED) model applied to suitable candidates in the Hi-GAL catalog. To extract candidate sources, a first catalog based on image photometry was compiled in each of the observed Hi-GAL fields, identifying the sources detected in the five different bands based on simple positional association.
 |
Fig. 2 Maps of the line integrated intensity, |
One of the best-studied regions in the Hi-GAL survey is found in the ℓ = 217°−224° field. The filamentary structure in this field has been studied by Schisano et al. (2014), while Elia et al. (2013) identified a well-defined and isolated filamentary cloud, at ℓ ≃ 224° and a distance of about 1.0 kpc, with clear signs of star formation (see Fig. 1). The most peculiar property of this cloud is the segregation observed between starless and protostellar clumps. In fact, protostellar clumps are mostly found along the main filament (filament here is used qualitatively to indicate an elongated or threadlike structure, and we do not use a specific operational definition; see also Sect. 5.1), whereas starless clumps are detected off this filament and are instead found on secondary, less prominent filaments (see Fig. 1). Therefore, also in this region most clumps are indeed located on filaments, as already noted by Polychroni et al. (2013), but the segregation in terms of clump type observed here has not yet been reported.
2.2. Mopra
Our observations were carried out with the ATNF Mopra 22-m telescope1 in Australia, in June 2014. We observed the 12CO (1−0) (115.271202 GHz), 13CO (1−0) (110.201353 GHz), C18O (1−0) (109.782173 GHz) and C17O (1−0) (112.359280 GHz) spectral lines. The 12CO (1−0) line is known to be optically thick, and thus the other three isotopologues were also observed to provide optical depth and line profile information. Unfortunately, except for 13CO(1−0), their intensity was in general too weak to allow derivation of column densities throughout the map and other useful physical and kinematical parameters, and thus most of our analysis will be based on 13CO(1−0) and partly on C18O(1−0) (from now on the (1−0) will be omitted for simplicity when referring to any of the observed transitions).
We used the single pixel broadband spectrometer, MOPS, which allows for multiple spectral windows to be observed simultaneously. Specifically, MOPS was used in its zoom mode, which allowed to split the 8.3 GHz instantaneous band in up to 16 zoom bands to focus on different molecules of interest. Each sub-band in zoom mode was 137.5 MHz wide and had 2 × 4096 channels, and the spectral resolution was ≃ 0.09 km s-1 for the 90 GHz receiver. During our observations the system temperature was typically comprised in the range ≃ 240−450 K (13CO and C18O), ≃ 280−500 K (C17O) and ≃ 520−920 K (12CO). We reached a RMS sensitivity in 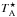 units of about ~ 0.12−0.18 K (13CO, C18O and C17O) and ~ 0.25−0.40 K (12CO) after rebinning to a 0.20 km s-1 velocity resolution. The beam full width at half maximum (FWHM) was about 38 arcsec and the pointing was checked every hour by using a SiO maser as a reference source (Indermuehle et al. 2013). Typically, pointing errors were found to be ~ 5−10 arcsec. The parameter ηmb to convert from antenna temperature to main-beam brightness temperature has been assumed to be 0.44 at 100 GHz and 0.49 at 86 GHz (Ladd et al. 2005).
units of about ~ 0.12−0.18 K (13CO, C18O and C17O) and ~ 0.25−0.40 K (12CO) after rebinning to a 0.20 km s-1 velocity resolution. The beam full width at half maximum (FWHM) was about 38 arcsec and the pointing was checked every hour by using a SiO maser as a reference source (Indermuehle et al. 2013). Typically, pointing errors were found to be ~ 5−10 arcsec. The parameter ηmb to convert from antenna temperature to main-beam brightness temperature has been assumed to be 0.44 at 100 GHz and 0.49 at 86 GHz (Ladd et al. 2005).
The single-point observations were performed in position-switching mode, whereas the spectral line maps, composed of individual tiles of size mostly 5 × 5 arcmin2, were obtained using the Mopra on-the-fly mapping mode, scanning in both right ascension and declination. A total of 8 tiles were observed (see Figs. 1 and 2): seven tiles are mostly contiguous, while an additional tile was observed off the main and secondary filaments and covers an isolated group of Hi-GAL clumps. The data were reduced with livedata and gridzilla for the bandpass correction and gridding2. The fits cubes were taken into miriad3 for a 3-pt hanning smoothing and an additional first-order correction to the baselines. The data were then analyzed with the xs4 package of the Onsala Space Observatory, and they were also imported into CLASS5 and IDL6 for line parameter measurement and further analysis.
3. Results
3.1. Physical properties of the Hi-GAL clumps
Before analysing the results of the spectral line observations we first show in Fig. 3 a plot of the bolometric luminosities versus the masses of the Hi-GAL clumps (see also Elia et al. 2013). In this plot starless and protostellar sources are represented by the red empty circles and blue star signs, respectively, and one can note immediately that they populate quite different regions of the diagram. The regions occupied by the starless and protostellar sources can be characterized by using the evolutionary tracks discussed by Molinari et al. (2008), who proposed an evolutionary sequence for protostars in terms of two parameters: the envelope mass and the bolometric luminosity. These authors suggest an evolutionary sequence which is concentrated in two main phases: protostars first accrete mass from their envelopes, and later disperse their envelopes by winds and/or radiation. In Fig. 3 the calculated evolutionary tracks thus rise upward in luminosity (almost vertically in the case of high-mass protostars) during the accretion phase, and then proceed horizontally to the left (to lower masses) during the envelope dispersal phase.
 |
Fig. 3 Clump bolometric luminosity vs. mass, as derived from the Hi-GAL observations. Symbols for starless and protostellar sources are as in Fig. 1. The dotted lines represent loci of constant 250μm flux density, ranging from 0.1 to 500 Jy, assuming a modified blackbody spectral energy distribution with β = 1.5 and a fixed distance of ~ 1 kpc. Roughly orthogonal to these are loci (dashed lines) at constant temperature, for the same modified blackbody. The green solid lines and small green filled circles represent the evolutionary tracks for the low- and high-mass regimes, respectively, taken from Molinari et al. (2008). |
As already noted by Elia et al. (2013) protostellar and starless sources populate quite different regions of the diagram, corresponding to the accreting core phase in the first case, and to a quiescent or collapsing core in the second, respectively. In fact, the protostellar sources occupy regions of the diagram at higher temperature, as shown by the loci at constant temperature of a modified blackbody (dashed lines). Although this plot cannot be used to obtain a classical single-YSO classification (see Elia et al. 2013 for a discussion of this point), it suggests as expected an additional type of evolutionary segregation between starless and protostellar clumps, besides to the observed positional segregation discussed in Sect. 2.1.
 |
Fig. 4 Positionally averaged spectra of 13CO (red), C18O (green) and C17O(1−0) (blue) lines. The regions considered (from left to right) are: a ~ 4 × 4 arcmin2 region around positions (RA ~07h11m18s, Dec ~− 10°36′; corresponding to the isolated individual region in the SE); a ~ 4 × 2 arcmin2 region around position (RA ~07h10m42s, Dec ~− 10°23′), at the NE end of the secondary filament; and a ~ 8 × 3 arcmin2 region around the bright region of emission toward the NW along the main filament. These last two regions are shown as black boxes in Fig. 2. The dashed vertical line corresponds to the velocity, 15.6 km s-1 obtained with a Gaussian fit to the C18O(1−0) line of the first region. |
3.2. Basic cloud structure: integrated intensity
We present maps of the integrated intensity of the CO isotopologues in Fig. 2. These maps were meant to cover most of the emission from the main and secondary filaments shown in Fig. 1. The main filament is visible as a strip of intense emission from the NW to SE. A secondary, less intense filament, can be observed running from the NE toward the center of the map where it meets the main filament. Although our coverage across the ℓ = 224° region is not complete, the observed spectral line maps cover most of the warm dust emission from both main and secondary filaments, as shown in Fig. 1. As mentioned in Sect. 2.2 we also mapped a smaller region, visible in the SE corner of the maps and relatively off the main filament, which contains a small group of starless clumps. However, this isolated tile will not be shown on subsequent maps, for the sake of clarity.
Both 13CO and C18O have a good signal-to-noise ratio (S/N) along the main filament. However, the secondary filament is better traced by 12CO and 13CO. One can see that in general the 13CO and C18O emission closely follows the dust continuum emission, whereas the optically thick 12CO shows significant deviations, as expected. The most intense region of extended emission, located along the main filament in the NW of the Hi-GAL map (at approximately RA ~07h09m19s and Dec ~− 10°27′), is clearly visible in the less optically thick 13CO and C18O tracers. However, we note a lack of correspondence between the C18O emission and the dust continuum peaks which are visible near the center of the Hi-GAL map (at RA ~07h10m05.8s and Dec ~− 10°31′30′′). C18O and submillimeter dust continuum emission are both tracers of column density, but they have different dependences on temperature. Therefore, temperature variations, more likely to be observed toward dense clumps, may affect the relative distributions of these two column density tracers (see, e.g., Wilson et al. 1986). In addition, this departure between the C18O and dust continuum emission coincides with the location of several dense clumps and thus another alternative (or additional) explanation for the lack of C18O emission is that that this molecule has depleted from the dense gas (see, e.g., Hacar et al. 2013, and references therein).
3.3. Basic velocity structure: channel maps
The area that we mapped with the Mopra telescope has already been covered by the lower angular resolution (2.7 arcmin) survey of molecular clouds in the Monoceros and Canis Major regions carried out with the NANTEN telescope in the 13CO (1−0) line (Kim et al. 2004), spanning an area of 560 deg2. The NANTEN observations were also much less sensitive, with a typical RMS noise of ~ 0.5 K. However, although the NANTEN data can be used to estimate the kinematic distances needed to derive masses and luminosities (Elia et al. 2013), higher angular resolution and more sensitive maps are necessary to analyze the column density distribution in the ℓ = 224° region.
We show the channel maps of the 13CO and C18O lines in Figs. A.1 and A.2. The distribution of bulk emission in the NW part of the cloud between ~ 13.5 and 16 km s-1 is similar in both tracers. As mentioned above, the emission toward the center of the field is better detected in the 13CO map. Extended emission from 13CO in both the main and secondary filaments is better viewed at Vlsr ~ 14.2−14.6 km s-1. Emission from the secondary filament appears to be concentrated on a narrower velocity range, compared to emission from the main filament. Along the latter a velocity gradient (see Sect. 4.2.1) is also visible, with emission slowly shifting from the NW (at low velocities) to the SE (at higher velocities). A similar velocity gradient is also observed in the C18O channel map.
The averaged spectra of 13CO, C18O and C17O are shown in Fig. 4. The minor deviations from a Gaussian shape and the relatively large velocity range of emission (≳ 5 km s-1 for 13CO) are a consequence of the velocity gradients in the region. The 13CO emission from two of the regions considered is clearly double-peaked (see also Figs. A.1 and A.3). This appears to be the consequence of two separate cloud components at different velocities (14.4 and 16.2 km s-1), rather than a dip due to self-absorption. In fact, the average C18O(1−0) spectra from the same regions show weak emission to be present at the lower-velocity component, which also appears to be the most intense. However, the limited extent of our maps does not allow us to investigate whether this 13CO double-peaked profile actually corresponds to two entirely different filaments that overlap in projection, as for example observed by Hacar et al. (2013).
An interesting feature is the double-peaked profile of the C17O spectrum toward the main clump of emission. The more intense, high-velocity component corresponds to the same emission as from 13CO and C18O. However, the lower-velocity component, peaking at about 12 km s-1, has no correspondence in the spectra of the more abundant isotopologues, and a clump of emission at this velocity can be clearly seen in Fig. A.5. Given the difference in the typical optical depth of C17O and the other isotopologues, one possibility to explain these data is that the lower-velocity clump is behind the presumably more massive, high-velocity component, thus preventing detection of the less massive clump in the optically thicker 13CO and C18O lines. Figure A.5 also shows another interesting feature, namely, C17O emission along the main filament is clearly detected at different velocities, peaking for example in the 13.6 km s-1 channel and then rising again near 16 km s-1. This suggests that these filaments may indeed be characterized by a more complex velocity structure, as observed by Hacar et al. (2013).
4. Analysis
In this section we will discuss the derivation of various physical parameters such as column density, mass and kinetic temperature, that are fundamental for the analysis of the sources. We will also analyse the kinematics of the sources, determining velocity gradients and line asymmetries. The estimate of the virial masses will also allow us to determine which sources are currently gravitationally bound and which are not.
4.1. Opacity, excitation temperature and column density
4.1.1. Results from the 13CO and C18O data
Column densities were derived from the 13CO and C18O data by assuming a filled beam and a uniform excitation temperature (equal for both tracers) within the beam. We follow the standard procedure of deriving the opacity in both lines at each position in the maps, from the ratio, R, of 13CO to C18O main-beam brightness temperatures: ![\begin{equation} R = \frac{T_{\rm mb}[^{13}{\rm CO}]} { T_{\rm mb}[{\rm C}^{18}{\rm O}] } = \frac{ 1 - \exp(-\tau_{13}) } { 1 - \exp(-\tau_{18})}\cdot \label{eq:tau} \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq58.png) (1)To reduce the effects of noise, the spectra were binned to a velocity resolution of 0.3 km s-1, and the brightness ratio was only computed when the S/N was > 3 in the C18O data. If we assume an abundance ratio [13CO]/[C18O] ≃7.4 (Wilson & Rood 1994) then τ13 ≃ 7τ18 and Eq. (1) can thus be solved for τ18. We calculate the opacity of the two CO isotopologues at the peak of the C18O spectrum at each position in the map.
(1)To reduce the effects of noise, the spectra were binned to a velocity resolution of 0.3 km s-1, and the brightness ratio was only computed when the S/N was > 3 in the C18O data. If we assume an abundance ratio [13CO]/[C18O] ≃7.4 (Wilson & Rood 1994) then τ13 ≃ 7τ18 and Eq. (1) can thus be solved for τ18. We calculate the opacity of the two CO isotopologues at the peak of the C18O spectrum at each position in the map.
If the optical depth is known, the excitation temperature Tex can then be derived easily from the equation of radiative transfer: ![\begin{equation} T_{\rm mb} = [ J_\nu(T_{\rm ex}) - J_\nu(T_{\rm bg}) ] \, [ 1 - \exp(-\tau) ], \label{eq:radtransf} \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq65.png) (2)where we assumed a unity filling factor and Tbg = 2.7 K. In Eq. (2) we also used Jν(T) ≡ To/ [ exp(To/T)−1 ], with To = hν/k, where h and k represent the Planck and Boltzmann constants, respectively.
(2)where we assumed a unity filling factor and Tbg = 2.7 K. In Eq. (2) we also used Jν(T) ≡ To/ [ exp(To/T)−1 ], with To = hν/k, where h and k represent the Planck and Boltzmann constants, respectively.
Given Tex and τ13 for the J = 1−0 transition, the total column density, Nmol, of 13CO can be derived using the following formula (see, e.g., Lis & Goldsmith 1991): ![\begin{eqnarray} N_{\rm mol} \, [{\rm cm}^{-2}] &=& \frac{4.0\times 10^{12}} {J^2\mu^2[{\rm D}] \,B [{\rm K}] } Z \exp\left( \frac{E_{\rm J}}{T_{\rm ex}} \right ) \nonumber \\ && \quad \times\, \frac{1}{\eta_{\rm mb}} \frac{\tau}{1-{\rm e}^{-\tau}} \int \, T_{\rm A}^{\star} \, {\rm d}v \, [{\rm K~ km~ s}^{-1}], \label{eq:cd} \end{eqnarray}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq74.png) (3)where B denotes the rotational constant, EJ is the upper state energy, μ is the dipole moment (in Debye) and we used the escape probability τ/ [ 1−exp(−τ) ] to account for first-order optical depth effects. With Z we have indicated the partition function of a linear molecule which, for kTex ≫ hB, is given by:
(3)where B denotes the rotational constant, EJ is the upper state energy, μ is the dipole moment (in Debye) and we used the escape probability τ/ [ 1−exp(−τ) ] to account for first-order optical depth effects. With Z we have indicated the partition function of a linear molecule which, for kTex ≫ hB, is given by: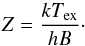 (4)The molecular hydrogen column density, N(H2), was then calculated assuming a [13CO]/[H2] ≃1.4 × 10-6 abundance ratio (Frerking et al. 1982) and thus we obtain [C18O]/[H2] ≃2 × 10-7. The top panel of Fig. 5 shows the resulting column density map at all positions where both Tex and τ13 could be reliably calculated. The column density and Hi-GAL 250 μm emission maps look quite similar, with the notable exception of the enhanced 250 μm emission at position (RA, Dec) ≃ (07:10:05, −10:32:00) which has no corresponding clump in the N(H2) map. This may be a consequence of C18O not tracing closely the dust emission at this position (see Sect. 3.2) and also because of the partially missing data near this position as well (see Figs. 2 and A.2). The missing data near the peaks of N(H2) are due to the 13CO line becoming self-absorbed and the ratio R becoming < 1. The typical values for excitation temperature and opacity across the measured region are Tex ~ 5−9 K and τ13 ~ 2−10. This suggests that the 13CO line is mostly optically thick, but also the C18O line could be moderately optically thick at some positions.
(4)The molecular hydrogen column density, N(H2), was then calculated assuming a [13CO]/[H2] ≃1.4 × 10-6 abundance ratio (Frerking et al. 1982) and thus we obtain [C18O]/[H2] ≃2 × 10-7. The top panel of Fig. 5 shows the resulting column density map at all positions where both Tex and τ13 could be reliably calculated. The column density and Hi-GAL 250 μm emission maps look quite similar, with the notable exception of the enhanced 250 μm emission at position (RA, Dec) ≃ (07:10:05, −10:32:00) which has no corresponding clump in the N(H2) map. This may be a consequence of C18O not tracing closely the dust emission at this position (see Sect. 3.2) and also because of the partially missing data near this position as well (see Figs. 2 and A.2). The missing data near the peaks of N(H2) are due to the 13CO line becoming self-absorbed and the ratio R becoming < 1. The typical values for excitation temperature and opacity across the measured region are Tex ~ 5−9 K and τ13 ~ 2−10. This suggests that the 13CO line is mostly optically thick, but also the C18O line could be moderately optically thick at some positions.
4.1.2. Results from the 12CO and 13CO data
The 13CO and C18O data are effective in deriving excitation temperature, opacity and column density along the main filament. However, as shown by Fig. 5, there are regions in the map where the physical parameters of the gas could not be determined, mainly because the C18O spectra were not good enough. We then decided to use 12CO and 13CO to extend the derivation of the physical parameters to most of the field area mapped with the Mopra telescope.
Then, assuming that the 12CO transition is optically thick and that Tpk [ 12CO] is the main beam brightness temperature at the peak of 12CO(1−0), we can derive the excitation temperature using Eq. (2): ![\begin{equation} T_{\rm ex} = \frac{ T_o[^{12}{\rm CO}] } { \ln[ 1 + T_o[^{12}{\rm CO}]/( T_{\rm pk}[^{12}{\rm CO}] + 0.86{\rm K} ) ] }, \label{eq:tex} \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq92.png) (5)where To [ 12CO] = hν [ 12CO] /k = 5.5 K.
(5)where To [ 12CO] = hν [ 12CO] /k = 5.5 K.
Then, assuming that the excitation temperatures of the 12CO and 13CO lines are the same, the optical depth of 13CO can also be derived from Eq. (2): ![\begin{equation} \tau[^{13}{\rm CO}] = - \ln \left [ 1 - \frac{ T_{\rm pk}[^{13}{\rm CO}]/T_o[^{13}{\rm CO}] } { 1/(\exp(T_o[^{13}{\rm CO}]/T_{\rm ex}) -1) - 0.16 } \right ], \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq96.png) (6)where To [ 13CO] = hν [ 13CO] /k = 5.3 K and Tpk [ 13CO ] is the main beam brightness temperature at the peak of 13CO. The main caveat of this method is that the most dense regions will not be accurately probed by 12CO, whose emission is restricted to outer cloud material due to its higher opacity. The bottom panel of Fig. 5 shows the resulting column density. The discrepancies with respect to the column density map obtained as described in Sect. 4.1.1 are clearly visible, and they are likely a consequence of the assumptions made for each method, in particular regarding the molecular abundances. We also note that the values for the H2 column density obtained by Elia et al. (2013) using the dust continuum emission are typically intermediate between those shown in the lower and upper panels of Fig. 5, indicating an overall internal consistency.
(6)where To [ 13CO] = hν [ 13CO] /k = 5.3 K and Tpk [ 13CO ] is the main beam brightness temperature at the peak of 13CO. The main caveat of this method is that the most dense regions will not be accurately probed by 12CO, whose emission is restricted to outer cloud material due to its higher opacity. The bottom panel of Fig. 5 shows the resulting column density. The discrepancies with respect to the column density map obtained as described in Sect. 4.1.1 are clearly visible, and they are likely a consequence of the assumptions made for each method, in particular regarding the molecular abundances. We also note that the values for the H2 column density obtained by Elia et al. (2013) using the dust continuum emission are typically intermediate between those shown in the lower and upper panels of Fig. 5, indicating an overall internal consistency.
4.2. Gas kinematics
4.2.1. Velocity gradients
Systematic variations in the 13CO and C18O line center velocity are apparent across the mapped region. In fact, it can be seen in Figs. 6 to 8 that the velocity gradually increases along a particular direction.
 |
Fig. 5 H2 column density map as derived from the 13CO and C18O(1−0) data, regridded with the program xs to a 80 arcsec grid size and 40 arcsec spacing (top panel), and from the 13CO and 12CO(1−0) data (bottom panel). Overlaid are the contours of the column density as derived by Elia et al. (2013) (with first contour corresponding to 2.8 × 1021cm-2 and subsequent contours equally spaced on a logarithmic scale, with Log(ΔN [ cm-2 ] ) = 0.2), which are also regridded in the top panel. Abundance ratios of [13CO]/[C18O] ≃7 and [C18O]/[H2] ≃10-7 were assumed (see text). |
Results of velocity gradient fitting.
We measure the velocity gradient across the whole mapped region following the procedure outlined in Goodman et al. (1993). We assume the centroid velocities of the spectral lines follow a simple linear form and fit the function: 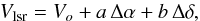 (7)to the peak velocity of a Gaussian fit to the emission profile of the 13CO and C18O lines. Here, Δα and Δδ represent offsets in right ascension and declination, expressed in radians, a and b are the projections of the gradient per radian on the α and δ axes, respectively, and Vo is the LSR systemic velocity of the cloud.
(7)to the peak velocity of a Gaussian fit to the emission profile of the 13CO and C18O lines. Here, Δα and Δδ represent offsets in right ascension and declination, expressed in radians, a and b are the projections of the gradient per radian on the α and δ axes, respectively, and Vo is the LSR systemic velocity of the cloud.
We found the best-fitting values to the constants a and b using MPFIT (Markwardt 2009), and then converted all of the angular velocity gradients to physical scale assuming a distance of 1 kpc. This yields the overall velocity gradients listed in Table 1. Since in the Gaussian fitting procedure only spectra with a S/N≥4 are considered, the velocity gradient estimated from C18O is mainly sensitive to systematic variations along the main filament, while the velocity gradient estimated from 13CO is sensitive to velocity variations across the whole mapped region. This may explain the higher value of dV/ dr derived from C18O. In Table 1 the velocity gradient from C18O along the secondary filament has not been estimated because we have few spectra with S/N≥4.
The Vo and θv parameters of the best-fit velocity gradients are quite similar for both molecular tracers. The values estimated from 13CO show that the directions of the velocity gradient along the main and secondary filament are clearly different, by more than 30 deg. In particular, the velocity gradient along the main filament is oriented almost parallel to the filament itself, with velocity increasing roughly from the NE to the SE, as also shown by Figs. 6 and 7. The velocity gradient associated with the secondary filament appears instead almost perpendicular to the filament itself. However, this result is less reliable because of the limited extent of the mapped region, especially in the direction orthogonal to the filament.
 |
Fig. 6 Kinematics toward the ℓ = 224° region. The top panel shows the line center velocity from the 13CO(1−0) data, while the bottom panel shows the line width. The black arrows represent the direction and relative magnitude of the velocity gradients along the main and secondary filaments (see Sect. 4.2.1), while the black filled circle at the bottom left (top panel) indicates the Mopra beam FWHM. Symbols in the lower panel are as in Fig. 1. The overlaid contours of the SPIRE 250 μm emission are as in Fig. 5. The line centers and line widths have been computed by fitting a 1- or 2-component Gaussian to the spectrum at each point (see text). |
 |
Fig. 7 Same as Fig. 6 for C18O(1−0). The line centers and line widths have been computed by fitting a 1-component Gaussian to the spectrum at each point (see text). |
 |
Fig. 8 Line center velocities (left column) and line widths (right column) after convolving (from top to bottom) the 13CO, C18O and C17O(1−0) Mopra maps to 80′′ and regridding with a 40′′ spacing. The smaller red areas are map artifacts. |
In Sect. 5.3 we suggest that a possible physical cause for the observed velocity gradients is the presence of accretion flows. However, at present we cannot exclude that the observed velocity gradients are produced by other motions. For example, the velocity gradients could be interpreted as rotation, though our limited and irregular mapped area makes this interpretation more difficult. Then following Goodman et al. (1993) we can calculate the parameter β, defined as the ratio of rotational kinetic energy to gravitational energy for a sphere of uniform density δ°: 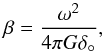 (8)where ω is the angular velocity and G is the gravitational constant. For the most intense region of emission in the NW section of the main filament (shown as a black box in Fig. 2) we find β ≃ 0.08, suggesting that if this interpretation were correct then the rotational energy would be a negligible fraction of the gravitational energy.
(8)where ω is the angular velocity and G is the gravitational constant. For the most intense region of emission in the NW section of the main filament (shown as a black box in Fig. 2) we find β ≃ 0.08, suggesting that if this interpretation were correct then the rotational energy would be a negligible fraction of the gravitational energy.
At present, we do not have data indicating the presence of protostellar outflows in the mapped region. However, while outflows could be a plausible physical explanation for velocity gradients observed at the clumps scale, it is unlikely that a single outflow or multiply oriented outflows could explain the observed large-scale velocity gradients.
4.2.2. Line profile and line widths
Figures 1 and 5 show a reasonable agreement between the distributions of dust emission and gas column density. Figure 1 also shows that the Hi-GAL compact clumps concentrate in regions of higher column density relative to the surrounding regions, as expected. Figures 6 and 7 then show that on the main filament the column density roughly correlates also with the C18O and 13CO velocity dispersion. However, Fig. 6 shows that on the secondary filament such a correlation is much less evident, and actually looks like an anti-correlation at some positions.
Likewise, Figs. 6 to 8 show that starless clumps are preferentially located at positions where the line widths are generally lower than those observed at the positions of the protostellar clumps. This is confirmed by extracting the C18O line width at the nominal position of each Hi-GAL clump, if the line was detected. Table 2 then shows the average line widths as measured from the C18O spectral line cube at the original angular resolution (column “Clump center”), and also the average values after the cube has been spatially convolved (regridded with the program xs to a 80 arcsec grid size and 40 arcsec spacing). The latter values (column “Ambient gas”) are more representative of the molecular gas surrounding the clump, and should give a better estimate of the kinematical status of the ambient gas immediately around the Hi-GAL clump. Table 2 shows that in both case the C18O line widths are larger toward the protostellar clumps, though they are marginally consistent within the errors. The location of starless clumps in regions of lower velocity dispersion is further confirmed by the small linewidths measured in the isolated tile at the SE (see Fig. 8), which hosts a small cluster of starless clumps.
Our analysis shows evidence of gas flow along the main filament. However, we do not find any signs of accretion flow from the filament onto the Hi-GAL clumps. In fact, as mentioned in Sect. 3.3 the line profiles of our emission lines are mostly Gaussian and double-peaked in some cases, and we do not observe clear signs of self-absorption. The lack of (detectable) self-absorption means that we do not see any sign of infall or gas accretion across the filaments. Self-absorbed line profiles in filamentary regions were instead observed, for example, toward the Serpens South cluster and filament (Kirk et al. 2013) and also toward the high-mass star-forming region DR21 (Schneider et al. 2010), where evidence for material radially contracting onto the filaments has been found. In these two regions the authors used the HCO+ (1−0) line to detect and analyze the self-absorption. However, Arzoumanian et al. (2013) did not detect any sign of self-absorption in their observations of C18O (1−0), (2−1) and 13CO (2−1) toward several filaments. Clearly, the exact line profiles of HCO+, C18O and 13CO depend on the velocity and density structure of both the ambient gas and the molecular clumps. Carrying out a detailed comparison of the line profiles of these different molecular tracers is beyond the scope of this paper. However, even without using complex radiative transfer codes, it is possible to analyze the effects of various source and telescope parameters on the hypothetical blue-asymmetric infall line profile using an analytical model, such as the one discussed by De Vries & Myers (2005).
 |
Fig. 9 Top panel: non-thermal component of the velocity line width of the C18O (1−0) transition, vs. the total clump mass, Mclump = MHiGAL (see text). Stars represent protostellar clumps and the empty circles represent starless clumps. Bottom panel: non-thermal velocity dispersion, from C18O (1−0), to sound speed ratio, fturb, vs. the total clump mass, Mclump. The green solid line represents the linear fit to all points (see text); the Spearman rank coefficient is 0.66. |
Another parameter of interest for the analysis of the Hi-GAL clumps is the non-thermal (turbulent) component of the velocity line widths. If we take a clump’s observed velocity line width, ΔVC18O, to be the quadrature sum of its thermal and non-thermal line widths (assuming that the two contributions are independent of each other), ΔVT and ΔVNT, respectively: 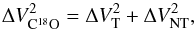 (9)then in order to find ΔVNT we must determine ΔVT:
(9)then in order to find ΔVNT we must determine ΔVT: 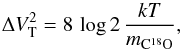 (10)where mC18O is the mass of the C18O molecule. The clump temperature, T = Td, is taken from the dust-determined Hi-GAL physical parameters. The top panel of Fig. 9 shows ΔVNT, estimated for all Hi-GAL clumps with a reliable C18O detection, vs. the total clump mass, Mclump = MHiGAL, also derived from the Hi-GAL data. This figure shows a tentative trend of increasing ΔVNT with Mclump and, despite the low number of starless clumps in this plot, it also shows that ΔVNT tends to be higher toward protostellar clumps. The average values of ΔVNT are 1.2 ± 0.3 km s-1 and 1.7 ± 0.6 km s-1 for starless and protostellar clumps, respectively.
(10)where mC18O is the mass of the C18O molecule. The clump temperature, T = Td, is taken from the dust-determined Hi-GAL physical parameters. The top panel of Fig. 9 shows ΔVNT, estimated for all Hi-GAL clumps with a reliable C18O detection, vs. the total clump mass, Mclump = MHiGAL, also derived from the Hi-GAL data. This figure shows a tentative trend of increasing ΔVNT with Mclump and, despite the low number of starless clumps in this plot, it also shows that ΔVNT tends to be higher toward protostellar clumps. The average values of ΔVNT are 1.2 ± 0.3 km s-1 and 1.7 ± 0.6 km s-1 for starless and protostellar clumps, respectively.
However, because of the difference in temperature, the physically significant parameter is the non-thermal velocity dispersion, σNT, to thermal sound speed, cs, ratio which we call fturb = σNT/cs following Curtis & Richer (2011). 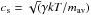 is the isothermal sound speed in the bulk of the gas of mean molecular weight mav = 2.3 amu (with respect to the total number of particles), assuming a mass fraction for He of 25%. The parameter γ is the adiabatic index (≃ 7 / 5 for a diatomic molecular gas). In the bottom panel of Fig. 9 we then plot fturb vs. Mclump, and we note that the trend of increasing fturb with mass is still visible. We also note that for similar ranges of mass the fturb parameter of the starless clumps is typically lower compared to that of protostellar clumps, though their (full range) average values are 2.46 ± 0.73 and 2.96 ± 1.02, respectively. In the bottom panel of Fig. 9 we also show the result of a linear regression to find the slope of the best fit line, using the Bayesian IDL routine LINMIX_ERR.
is the isothermal sound speed in the bulk of the gas of mean molecular weight mav = 2.3 amu (with respect to the total number of particles), assuming a mass fraction for He of 25%. The parameter γ is the adiabatic index (≃ 7 / 5 for a diatomic molecular gas). In the bottom panel of Fig. 9 we then plot fturb vs. Mclump, and we note that the trend of increasing fturb with mass is still visible. We also note that for similar ranges of mass the fturb parameter of the starless clumps is typically lower compared to that of protostellar clumps, though their (full range) average values are 2.46 ± 0.73 and 2.96 ± 1.02, respectively. In the bottom panel of Fig. 9 we also show the result of a linear regression to find the slope of the best fit line, using the Bayesian IDL routine LINMIX_ERR.
Our results clearly indicate that the line widths toward the Hi-GAL clumps are supersonic. In addition, since stars can inject significant energy into their surroundings, it is not surprising that protostellar clumps display somewhat larger non-thermal velocity dispersion compared to starless clumps, within similar mass ranges. Instead, Curtis & Richer (2011) do not find a significant difference between the distributions of fturb of the starless and protostellar subsets. Clearly, we need similar samples of starless and protostellar clumps in order for these differences to be statistically significant.
4.3. Derivation of masses
4.3.1. Mass of the filaments derived from column density
The calculation of the filaments mass from the column density assumes LTE and we determine the molecular gas mass integrating the molecule column density over a given extent of the molecular cloud. Then we can write: 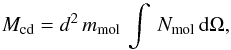 (11)where ∫Nmol dΩ is the molecule column density integrated over the region enclosed by the chosen contour level, mmol is the mass of the specific molecule being considered, and d is the distance to the source. Equation (11) is actually implemented by writing:
(11)where ∫Nmol dΩ is the molecule column density integrated over the region enclosed by the chosen contour level, mmol is the mass of the specific molecule being considered, and d is the distance to the source. Equation (11) is actually implemented by writing: 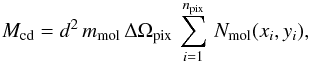 (12)where Nmol(xi,yi) represents the column density in a single pixel (xi,yi) of the map, with npix representing the total number of pixels, and ΔΩpix represents the solid angle covered by a single pixel. The map pixels selected are those that have an integrated intensity I ≥ 3σmap, where the RMS integrated intensity, σmap ≃ 0.2 K km s-1, has been estimated directly from the map, averaging pixels where no emission is detected.
(12)where Nmol(xi,yi) represents the column density in a single pixel (xi,yi) of the map, with npix representing the total number of pixels, and ΔΩpix represents the solid angle covered by a single pixel. The map pixels selected are those that have an integrated intensity I ≥ 3σmap, where the RMS integrated intensity, σmap ≃ 0.2 K km s-1, has been estimated directly from the map, averaging pixels where no emission is detected.
Using the H2 column density derived from the 13CO and 12CO(1−0) lines (shown in the bottom panel of Fig. 5) the total gas mass calculated is ~ 2.5 × 103M⊙, including the isolated tile shown in Fig. 1, using the relative molecular abundances described in Sect. 4.1. Specifically, we obtain ≃ 1.8 × 103M⊙ and ≃ 6.0 × 102M⊙ for the main and secondary filaments, respectively. For comparison, if we use the H2 column density derived from the 13CO and C18O(1−0) lines (shown in the top panel of Fig. 5) the total gas mass calculated would be ~ 4.4 × 103M⊙.
4.3.2. Clumps virial mass
 |
Fig. 10 Total clump mass, Mclump = MHiGAL, vs. the virial mass, Mvir, calculated using the velocity line widths of the C18O (1−0) transition (see text). The solid line indicates the minimum Mclump = 0.5 Mvir for which the clump should be self-gravitating. Symbols are as in Fig. 9. |
The question of whether molecular clumps and their sub-structures are bound is of great importance in understanding star and cluster formation. The virial mass estimate, in combination with other mass estimates, may allow to determine whether or not a specific clump is bound and virialized. We estimate the virial mass of the clumps assuming they are simple spherical systems with uniform density (MacLaren et al. 1988): ![\begin{equation} M_{\rm vir}{[M_\odot]} = 210 \, R_{\rm dec}{\rm [pc]} \, (\Delta V_{\rm av} {\rm [km~s^{-1}]})^2, \label{eq:mvir} \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq171.png) (13)where Rdec is the deconvolved source radius and ΔVav represents the line FWHM of the molecule of mean mass, calculated as the sum of the thermal and turbulent components (see Sect. 4.2.2):
(13)where Rdec is the deconvolved source radius and ΔVav represents the line FWHM of the molecule of mean mass, calculated as the sum of the thermal and turbulent components (see Sect. 4.2.2): 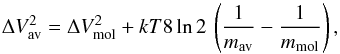 (14)where ΔVmol is the line FWHM of the molecular transition being considered. We note that according to MacLaren et al. (1988), Eq. (13) may lead to a mass overestimate if the density distribution is not uniform. For example, in the case of a sphere with a density distribution ρ ∝ r-2 the numerical factor in Eq. (13) should be replaced by 126.
(14)where ΔVmol is the line FWHM of the molecular transition being considered. We note that according to MacLaren et al. (1988), Eq. (13) may lead to a mass overestimate if the density distribution is not uniform. For example, in the case of a sphere with a density distribution ρ ∝ r-2 the numerical factor in Eq. (13) should be replaced by 126.
As described in Sect. 4.2.2 the line FWHM is calculated from the C18O spectrum observed at the nominal position of each Hi-GAL clump. Since even C18O may not trace the denser molecular gas and may be affected by the ambient, less dense material, we have corrected its line width for the average ratio of the C17O to C18O line width ratio, which is 0.84 toward the bright region of emission in the NW section of the main filament (shown as a black box in Fig. 2). In addition, we have used the numerical factor 126 in Eq. (13), since for the density profiles of molecular clumps power-laws have been put forward by various studies (see, e.g., Fontani et al. 2002 where they find n ~ rp with an average p = −2.59).
The plot of the total clump mass, MHiGAL, as derived from Hi-GAL, vs. the virial mass is shown in Fig. 10. We note that all of the starless clumps where the C18O line has been detected lie above the self-gravitating line, indicating that they are likely to be gravitationally bound. The protostellar clumps, much more numerous, are almost equally divided between those above and below the self-gravitating line. In interpreting this plot, however, one should consider that the line widths we measure are from a region (determined by the Mopra telescope beam) that is generally different than the virial radius we assign to it, which is instead determined from the source-extraction procedure used for the Hi-GAL maps. Whether the continuum emission is more extended or not than the dense molecular gas emitting volume depends on the specific excitation conditions of the gas and the molecular tracer. Therefore, given the uncertainties in both the virial and Hi-GAL dust mass estimates, it is not possible to draw unequivocal conclusions about the stability of individual clumps.
4.3.3. Dust continuum masses
Obtaining mass estimates of molecular clouds with molecular lines may be problematic due to high column densities and also molecular freezeout onto dust grains in some cases. Alternatively, the cold dust emission, as observed in the (sub)millimeter, can be used to provide more reliable mass estimates as it is optically thin and does not deplete.
We use the 250 μm dust continuum emission from Hi-GAL, to achieve isothermal mass estimates using the expression: 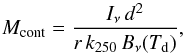 (15)where Iν is the source surface brightness (or specific intensity) in the Hi-GAL map at 250 μm (MJy sr-1), d is the distance (cm), rk250 is the dust mass absorption coefficient (cm2 g-1), often called the opacity, corrected for the dust-to-gas ratio, r, at λ° = 250 μm, and Bν(Td) is the Planck function at dust temperature, Td. We adopt a value of rk250 = 0.11 cm2 g-1 from Martin et al. (2012).
(15)where Iν is the source surface brightness (or specific intensity) in the Hi-GAL map at 250 μm (MJy sr-1), d is the distance (cm), rk250 is the dust mass absorption coefficient (cm2 g-1), often called the opacity, corrected for the dust-to-gas ratio, r, at λ° = 250 μm, and Bν(Td) is the Planck function at dust temperature, Td. We adopt a value of rk250 = 0.11 cm2 g-1 from Martin et al. (2012).
We integrate Iν in the same area as mapped at Mopra, as shown in Fig. 1, and also assume that Td can vary in the same range analyzed by Martin et al. (2012), that is, ≃ 12−17 K. We then obtain Mcont ~ 2 × 103M⊙ (Td = 12 K) and Mcont ~ 5 × 102M⊙ (Td = 17 K). If we use a typical intermediate value of Td = 14 K, the total mass is Mcont ~ 103M⊙ and specifically, Mcont ~ 7.6 × 102 and ~ 1.9 × 102M⊙ for the main and secondary filaments, respectively. Given all uncertainties in both molecular abundances and dust parameters, the dust continuum masses agree reasonably well with the column density masses derived in Sect. 4.3.1. Also the main to secondary filament mass ratios estimated from molecular lines and dust continuum are very similar (Mmain/Msec ≃ 3−4), showing that the secondary filament has about 1/3 of the mass of the main filament. The good agreement of the mass ratio, Mmain/Msec, derived with these two methods, suggests that the difference between the absolute mass values, Mmain and Msec, derived from the molecular lines and the dust continuum depends on the choice of parameters such as molecular abundances and dust mass absorption coefficient.
 |
Fig. 11 Radial column density profile of the main (left column) and secondary (right column) filaments. The dots, connected by the red solid line, show the mean profile across the filaments, while the shaded area indicates the standard deviation. In the top row the average profiles were estimated from the 13CO and C18O(1−0) derived column density (Fig. 5, top panel), while in the bottom row we used the column density estimated by Elia et al. (2013). The black solid line represents the best fit profile, following the formulation in Arzoumanian et al. (2011). |
5. Discussion
The results presented in Sects. 3 and 4 can be used to discuss the physical properties and evolutionary state of the two filaments.
5.1. Column density profiles
In this section, we analyze the radial column density profile of the filaments using both molecular line emission and dust submillimeter continuum emission. To construct the mean radial density profile of each filament we used the following procedure. First, we searched for the location of peak emission along every cut in declination through each filament. A simple scanning in declination allowed us to unambiguously find the peak emission because the main axis of each filament make a large (> 45°) angle to the declination axis. Second, we constructed the midline of each filament by joining all peak ridge points. We then measured a radial column density profile perpendicular to the midline at each position. Finally, we derived the mean radial profile by averaging all profiles along each filament. The mean profiles and standard deviations, at each radial separation, are shown in Fig. 11.
In order to characterize each observed column density profile, following Arzoumanian et al. (2011) we adopt the model of a cylindrical filament with radial column density profile (as a function of cylindrical radius r) of the form: ![\begin{equation} N_{{\rm H}_2}(r) = A_{\rm p} \, \frac{ \rho_{\rm c} R_{\rm flat} } { [1 + (r/R_{\rm flat})^2 ]^\frac{p-1}{2} }, \label{eq:cdprofile} \end{equation}](/articles/aa/full_html/2016/10/aa28519-16/aa28519-16-eq206.png) (16)where NH2(r) is the column density at radial separation r, ρc is the number density at the center of the filament, Rflat is the characteristic radius of the flat inner portion of the density profile, and the parameter Ap, for p> 1, is calculated as:
(16)where NH2(r) is the column density at radial separation r, ρc is the number density at the center of the filament, Rflat is the characteristic radius of the flat inner portion of the density profile, and the parameter Ap, for p> 1, is calculated as: 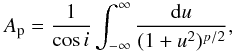 (17)where the inclination angle along the line of sight, i, is assumed to be 0 for simplicity. Allowing all three parameters, p, ρc and Rflat to vary, we find the values listed in Table 3, while the best fit profiles are shown in Fig. 11. For the dust continuum emission we used the column density map derived by Elia et al. (2013) for better accuracy. In fact, they obtained the column density after performing a fit to the SED at each point in the Hi-GAL maps, thus deriving the dust temperature at the same time.
(17)where the inclination angle along the line of sight, i, is assumed to be 0 for simplicity. Allowing all three parameters, p, ρc and Rflat to vary, we find the values listed in Table 3, while the best fit profiles are shown in Fig. 11. For the dust continuum emission we used the column density map derived by Elia et al. (2013) for better accuracy. In fact, they obtained the column density after performing a fit to the SED at each point in the Hi-GAL maps, thus deriving the dust temperature at the same time.
Comparing the best-fit values of Table 3 with those in the literature, we find that the values of p are similar to those found by Arzoumanian et al. (2011) and André et al. (2016, who used dust derived column density maps), and also by Kirk et al. (2013, who used molecular lines). However, Nutter et al. (2008) found a value of p somewhat higher (p = 3) toward TMC1. Instead, the best fit values of the other two free parameters, ρc and Rflat, significantly differ from those of Kirk et al. (2013), Arzoumanian et al. (2011, who do not list their ρc values) and André et al. (2016), particularly when the values derived from the molecular lines are considered. However, our best-fit values for all three parameters are quite similar to those found by Juvela et al. (2012b), who in addition analyzed sources with a range of distances more similar to that of the ℓ = 224° region, and hence with similar distance-related effects.
The differences found in the literature are certainly caused, at least in part, by the way the analyzed structures are selected and by the analysis methods themselves (see for example the discussion in Juvela et al. 2012b). Specifically, although both of the filaments studied here have been identified by Schisano et al. (2014), they are not as well defined (e.g., with a sharper central peak in the column density average profile) as those mapped by Kirk et al. (2013) and Arzoumanian et al. (2011), which also lie at quite a different distance, or also simulated (see, e.g., Juvela et al. 2012a). It is not thus entirely surprising that we obtain lower values of the filament central density and a higher value of Rflat.
In Table 3 and Fig. 11, comparing the column density profiles obtained from the molecular lines and from the dust continuum emission, the observed discrepancies are likely caused in part by the different radial extent measurable in the Mopra and Hi-GAL maps. In fact, when using the column density derived from molecular line emission the reliability of our fit is limited by the fact that we were able to measure the radial column density profile only relatively close to the central ridge. For the specific case of the secondary filament, the radial column density profile from the Mopra data is more uncertain due to the lower S/N in this region of the map, particularly at the edges of the filament, and thus the best-fit parameters are not shown in Table 3. The main filament should be less affected by S/N problems and the different radial profiles shown in Fig. 11 must thus be caused also by the method used to retrieve the column density and/or the intrinsic distribution of the material detected with each technique. The shallow or flat radial column density profile derived from the Mopra spectral line data suggests that we are probably sensitive to some amount of large-scale structures, that is, diffuse material not directly associated with the star-forming regions along the filament, which is more reliably traced by the optically thin dust emission.
5.2. Gravitational stability of the filaments
The properties of interstellar filaments and possible scenarios for their formation and evolution have already been discussed in many papers, both theoretically (e.g., Ostriker 1964; Inutsuka & Miyama 1997; Inutsuka & Tsuribe 2001; Fiege & Pudritz 2000) and observationally (e.g., André et al. 2010; Arzoumanian et al. 2011, 2013; Kirk et al. 2013). A proposed scenario, especially supported by the results of the HGBS, is that large-scale turbulence, rather than large-scale gravity, plays the dominant role in forming interstellar filaments. However, gravity would appear to be the major driver in the subsequent evolution of the filaments, which may contract and accrete material from the background cloud, thus causing filaments to fragment into clumps and form (proto)stars under certain physical conditions.
Observationally, the gravitational fragmentation of filaments can be analyzed by comparing our Hi-GAL maps to existing models of filamentary cloud fragmentation. Inutsuka & Miyama (1997, and references therein) showed that an unmagnetized isothermal filament is unstable to axisymmetric perturbations if the line mass or mass per unit length, Mline, of the filament is larger than the critical value required for equilibrium, 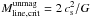 , where G is the gravitational constant. As shown by Ostriker (1964), the critical line mass depends on gas temperature only and, following Kirk et al. (2013),
, where G is the gravitational constant. As shown by Ostriker (1964), the critical line mass depends on gas temperature only and, following Kirk et al. (2013), 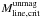 can also be written in more convenient units as:
can also be written in more convenient units as: 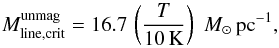 (18)therefore if T is in the range of ≃ 10 to 15 K, then
(18)therefore if T is in the range of ≃ 10 to 15 K, then 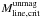 is between ≃ 17 and 25 M⊙ pc-1. To derive the filament masses per unit length from our Hi-GAL maps, we used the radial column density profiles discussed in Sect. 5.1. The observed mass per unit length, Mline, of the main and secondary filaments was then derived by integrating the measured average column density profile (as shown in Fig. 11) over radius, i.e., Mline = μH2mH∫ ⟨ NH2(r) ⟩ dr, where μH2 = 2.8 is the molecular weight per hydrogen molecule (Kauffmann et al. 2008) and mH is the H-atom mass.
is between ≃ 17 and 25 M⊙ pc-1. To derive the filament masses per unit length from our Hi-GAL maps, we used the radial column density profiles discussed in Sect. 5.1. The observed mass per unit length, Mline, of the main and secondary filaments was then derived by integrating the measured average column density profile (as shown in Fig. 11) over radius, i.e., Mline = μH2mH∫ ⟨ NH2(r) ⟩ dr, where μH2 = 2.8 is the molecular weight per hydrogen molecule (Kauffmann et al. 2008) and mH is the H-atom mass.
Because it is difficult to exactly define the edges of a filament, we decided to limit the range of integration to the 50% level of the peak value. If we use the 250 μm radial column density profile we obtain Mline ≃ 230 and ≃ 50 M⊙ pc-1 for the main and secondary filaments7, respectively. Both filaments would then appear to be supercritical, that is, gravitationally unstable with 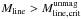 . As a comparison, the values of Mline found in the literature vary in a wide range, from a few M⊙ pc-1 (e.g., Arzoumanian et al. 2013; Juvela et al. 2012b; Schisano et al. 2014) to as much as several 100s of M⊙ pc-1 (e.g., Contreras et al. 2013; Li et al. 2016; Schisano et al. 2014).
. As a comparison, the values of Mline found in the literature vary in a wide range, from a few M⊙ pc-1 (e.g., Arzoumanian et al. 2013; Juvela et al. 2012b; Schisano et al. 2014) to as much as several 100s of M⊙ pc-1 (e.g., Contreras et al. 2013; Li et al. 2016; Schisano et al. 2014).
We note that while the main filament is highly supercritical, with Mline roughly ten times larger than the critical value, the secondary filament has a much lower Mline value. The total amount of support available in the main filament is therefore likely insufficient to keep the filament in equilibrium, implying that it should be radially contracting. This scenario assumes that unstable filaments would accrete additional mass from their surroundings and increase in mass per unit length while contracting with time. At the same time as they contract and accrete material from the background cloud, supercritical filaments are expected to fragment into clumps and form (proto)stars, giving rise to the morphology of the main filament and clumps shown in Fig. 1. However, as we noted in Sect. 4.2.2, we find no observational evidence showing that the gas is globally and radially infalling in either filament. This is either due to observational effects, related to the spectral lines used, or the radially contracting phase has already slowed down or stopped (or possibly not started yet, in the case of the secondary filament), thus being effectively undetectable.
Another alternative to explain the non-detection of radial infall toward the main filament is that all of the non-thermal motion is contributing thermal-like support. In this case one must consider the virial mass per unit length, 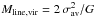 (Fiege & Pudritz 2000), where σav is the velocity dispersion of the molecule of mean mass (see Sect. 4.3.2):
(Fiege & Pudritz 2000), where σav is the velocity dispersion of the molecule of mean mass (see Sect. 4.3.2): 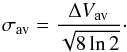 (19)We note that Mline,vir is analogous to the virial mass and thus the dividing value between gravitationally unbound and bound filaments is defined by Mline,vir = 2 Mline. Figures 7 and 8 can be used to estimate a typical velocity dispersion for the main filament, σav ~ 0.6 km s-1, and the secondary filament, σav ~ 0.4 km s-1. Thus we estimate Mline,vir~ 70 and ~ 160 M⊙ pc-1 for the main and secondary filaments, respectively. Therefore, the thermally supercritical main filament is found to be a self-gravitating structure. The dynamical state of the secondary filament is instead much less defined, due to the uncertainty in the actual value used for σav, and is thus at the edge of being in virial equilibrium or gravitationally unbound.
(19)We note that Mline,vir is analogous to the virial mass and thus the dividing value between gravitationally unbound and bound filaments is defined by Mline,vir = 2 Mline. Figures 7 and 8 can be used to estimate a typical velocity dispersion for the main filament, σav ~ 0.6 km s-1, and the secondary filament, σav ~ 0.4 km s-1. Thus we estimate Mline,vir~ 70 and ~ 160 M⊙ pc-1 for the main and secondary filaments, respectively. Therefore, the thermally supercritical main filament is found to be a self-gravitating structure. The dynamical state of the secondary filament is instead much less defined, due to the uncertainty in the actual value used for σav, and is thus at the edge of being in virial equilibrium or gravitationally unbound.
5.3. A possible evolutionary scenario
The noticeable separation between the (less evolved, younger; see Fig. 3) starless clumps and the (more evolved, older) protostellar clumps on the secondary and main filament, respectively, and the fact that the more massive and highly fragmented main filament is thermally supercritical and gravitationally bound, suggest a later stage of evolution of the main filament. In the main filament clumps have accreted enough mass to become mostly protostellar, and the molecular gas surrounding them appears to be more turbulent compared to starless clumps, as shown in Sect. 4.2.2. Also, the more diffuse gas in the main filament shows a higher degree of turbulence compared to the secondary filament. A trend of increasing σav with Mline has in fact been discussed by Arzoumanian et al. (2013).
As mentioned in Sect. 4.2.1 we observe a velocity gradient along the main axis of the filament, and we have discussed several possible interpretations for this gradient. It is however interesting to discuss in greater details the explanation of this velocity gradient in terms of a possible accretion flow from the filament onto the central cluster. A similar scenario has indeed been proposed for the case of the Serpens South filament and cluster, though with a higher value of dV/ dr (Kirk et al. 2013). A difficulty with this interpretation is that in our main filament the protostellar clumps are actually distributed along the entire length of the structure (see Figs. 1 and 6), though there is a main cluster of clumps in the NW section of the filament.
The much less massive secondary filament, which is also marginally supercritical, appears to have a smoother and regular profile (as confirmed by the narrow shaded area, indicating the standard deviation, in Fig. 11). As we mentioned already it contains only starless clumps, and the less turbulent ambient gas and its dynamical state (gravitationally unbound or near to virial equilibrium) suggest that this structure could be in an earlier evolutionary phase. Alternatively, this low-density filament may have evolved differently from the main filament, and its current dynamical state may prevent any further accretion. However, our spectral line maps are not extended enough to determine whether molecular gas is actually flowing from the ambient gas also toward the secondary filament, and whether it could eventually follow the same evolutionary path of its main counterpart.
If this low-density filament is indeed unbound it may be expected to disperse on a turbulent crossing time, unless it is confined by some external pressure. Arzoumanian et al. (2013) also suggest that low-density filaments, observed roughly perpendicular to the main supercritical filaments, could be feeding them contributing to their accretion process and growth in mass per unit length. The velocity gradient measured along the secondary filament and shown in Fig. 6 is roughly directed toward the main filament, and appears to point toward the bright region located at the center-south (RA ~07h10m, Dec ~− 10°30′) of both Hi-GAL and spectral line maps (see Figs. 1, 2 and 5), which also corresponds to a higher concentration of protostellar clumps. However, as noted in Sect. 4.2.1, this velocity gradient is less reliable compared to that measured along the main filament.
Therefore, if we use the simple method discussed by Kirk et al. (2013) to estimate the mass accretion rate implied by the velocity gradient along the main filament, we obtain an accretion rate along the filament onto the two main clusters of protostellar clumps of ~ 100 M⊙/Myr, assuming the inclination of the filament to the plane of the sky is exactly 0, and also assuming that the observed velocity gradient has not an entirely different kinematical origin (e.g., rotation). We can compare this estimate of the accretion rate with the star-formation rate (SFR), ≃ 260 M⊙/Myr, found by Elia et al. (2013) for the ℓ = 224° region. Thus we can see that our estimate of the mass accretion rate is comparable with the mass supply required to form the current generation of YSOs along the main filament. This result suggests that filamentary accretion may significantly affect the formation and evolution of stars along the main filament.
6. Conclusions
Using the Hi-GAL dust continuum information and analyzing the Mopra spectral line maps, we study the distribution of starless and protostellar clumps as well as the dynamics of the two filaments observed toward the ℓ = 224° region. The protostellar clumps are more luminous and more turbulent compared to the starless clumps, and also lie in regions where the filamentary ambient gas shows larger linewidths. The more massive and highly fragmented main filament appears to be thermally supercritical and gravitationally bound, suggesting a later stage of evolution compared to the secondary filament, which is gravitationally unbound (or near to virial equilibrium) and hosts less turbulent ambient gas. Therefore, the low-density secondary filament is either in an earlier evolutionary phase, or it may have evolved differently from the main filament, and its current dynamical state may prevent any further accretion. The status and evolutionary phase of the Hi-GAL clumps would then appear to correlate with that of the host filament.
Our observations show a velocity gradient along the main filament. If this gradient is indeed associated with a mass flow along the filament, possibly feeding the main two clusters of protostellar objects, then the estimated mass accretion rate would be high enough to lead to the formation of several tens of YSOs (of mean mass 0.5 M⊙) in a few Myr. Our observations also indicate that there might be gas flow from the secondary filament onto the two main clusters of protostellar clumps located on the main filament. To assess the reliability of this tentative scenario as well as to investigate the presence of infalling gas from the filament onto the clusters, the area covered by our Mopra maps would need to be extended and different spectral lines, such as HCO+ and H13CO+ (1−0), should be used.
Acknowledgments
The Mopra radio telescope is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. The University of New South Wales Digital Filter Bank used for the observations with the Mopra Telescope was provided with support from the Australian Research Council. The authors wish to thank the staff of the Mopra Observatory for the support provided before and during the observations. D.E.’s research activity is supported by the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 607380 (VIALACTEA: the Milky Way as a star-formation engine).
References
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Revéret, V., Könyves, V., et al. 2016, A&A, 592, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Arzoumanian, D., André, P., Peretto, N., & Könyves, V. 2013, A&A, 553, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contreras, Y., Rathborne, J., & Garay, G. 2013, MNRAS, 433, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Curtis, E. I., & Richer, J. S. 2011, MNRAS, 410, 75 [NASA ADS] [CrossRef] [Google Scholar]
- De Vries, C. H., & Myers, P. C. 2005, ApJ, 620, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Schisano, E., Molinari, S., et al. 2010, A&A, 518, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elia, D., Molinari, S., Fukui, Y., et al. 2013, ApJ, 772, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000, MNRAS, 311, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Cesaroni, R., Caselli, P., & Olmi, L. 2002, A&A, 389, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Indermuehle, B., Edwards, P., Brooks, K., & Urquhart, J. 2013, in CSIRO Data Archive, DOI: 10.4225/08/521A8EF38E042 [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., & Tsuribe, T. 2001, in The Formation of Binary Stars, eds. H. Zinnecker, & R. Mathieu, IAU Symp., 200, 391 [Google Scholar]
- Juvela, M., Malinen, J., & Lunttila, T. 2012a, A&A, 544, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pagani, L., et al. 2012b, A&A, 541, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, II, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, B. G., Kawamura, A., Yonekura, Y., & Fukui, Y. 2004, PASJ, 56, 313 [NASA ADS] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Ladd, N., Purcell, C., Wong, T., & Robertson, S. 2005, PASA, 22, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G.-X., Urquhart, J. S., Leurini, S., et al. 2016, A&A, 591, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., & Goldsmith, P. F. 1991, ApJ, 369, 157 [NASA ADS] [CrossRef] [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Nutter, D., Kirk, J. M., Stamatellos, D., & Ward-Thompson, D. 2008, MNRAS, 384, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Olmi, L., Anglés-Alcázar, D., Elia, D., et al. 2013, A&A, 551, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Polychroni, D., Schisano, E., Elia, D., et al. 2013, ApJ, 777, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Johnstone, D., & Heitsch, F. 2011, ApJ, 740, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Schisano, E., Rygl, K. L. J., Molinari, S., et al. 2014, ApJ, 791, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., Serabyn, E., Henkel, C., & Walmsley, C. M. 1986, A&A, 158, L1 [NASA ADS] [Google Scholar]
Appendix A: Channel maps
 |
Fig. A.1 Channel maps of 13CO(1−0), between 13 and 16.6 km s-1 (as shown in the top-left corner of each panel). The isolated individual region, centered at (RA, Dec) ~ (07:11:18, −10:36:00), has been dropped from this figure to increase visibility of the main regions of emission. |
 |
Fig. A.3 Same as Fig. A.1, after convolving the map with a 80 arcsec beam and re-gridding the map on a 40 arcsec step. |
All Tables
All Figures
 |
Fig. 1 SPIRE 250 μm emission observed toward the ℓ = 224° region, with a (logarithmic) color-scale in MJy sr-1 (Elia et al. 2013). Blue star symbols represent protostellar clumps while the red empty circles represent starless clumps. The dashed, black contour shows the region mapped with the Mopra telescope. The yellow and blue solid contours correspond to about 100 and 200 MJy sr-1, respectively, and approximately trace the secondary filament toward the north (besides to low-level emission from the main filament) and the main filament. |
| In the text | |
 |
Fig. 2 Maps of the line integrated intensity, |
| In the text | |
 |
Fig. 3 Clump bolometric luminosity vs. mass, as derived from the Hi-GAL observations. Symbols for starless and protostellar sources are as in Fig. 1. The dotted lines represent loci of constant 250μm flux density, ranging from 0.1 to 500 Jy, assuming a modified blackbody spectral energy distribution with β = 1.5 and a fixed distance of ~ 1 kpc. Roughly orthogonal to these are loci (dashed lines) at constant temperature, for the same modified blackbody. The green solid lines and small green filled circles represent the evolutionary tracks for the low- and high-mass regimes, respectively, taken from Molinari et al. (2008). |
| In the text | |
 |
Fig. 4 Positionally averaged spectra of 13CO (red), C18O (green) and C17O(1−0) (blue) lines. The regions considered (from left to right) are: a ~ 4 × 4 arcmin2 region around positions (RA ~07h11m18s, Dec ~− 10°36′; corresponding to the isolated individual region in the SE); a ~ 4 × 2 arcmin2 region around position (RA ~07h10m42s, Dec ~− 10°23′), at the NE end of the secondary filament; and a ~ 8 × 3 arcmin2 region around the bright region of emission toward the NW along the main filament. These last two regions are shown as black boxes in Fig. 2. The dashed vertical line corresponds to the velocity, 15.6 km s-1 obtained with a Gaussian fit to the C18O(1−0) line of the first region. |
| In the text | |
 |
Fig. 5 H2 column density map as derived from the 13CO and C18O(1−0) data, regridded with the program xs to a 80 arcsec grid size and 40 arcsec spacing (top panel), and from the 13CO and 12CO(1−0) data (bottom panel). Overlaid are the contours of the column density as derived by Elia et al. (2013) (with first contour corresponding to 2.8 × 1021cm-2 and subsequent contours equally spaced on a logarithmic scale, with Log(ΔN [ cm-2 ] ) = 0.2), which are also regridded in the top panel. Abundance ratios of [13CO]/[C18O] ≃7 and [C18O]/[H2] ≃10-7 were assumed (see text). |
| In the text | |
 |
Fig. 6 Kinematics toward the ℓ = 224° region. The top panel shows the line center velocity from the 13CO(1−0) data, while the bottom panel shows the line width. The black arrows represent the direction and relative magnitude of the velocity gradients along the main and secondary filaments (see Sect. 4.2.1), while the black filled circle at the bottom left (top panel) indicates the Mopra beam FWHM. Symbols in the lower panel are as in Fig. 1. The overlaid contours of the SPIRE 250 μm emission are as in Fig. 5. The line centers and line widths have been computed by fitting a 1- or 2-component Gaussian to the spectrum at each point (see text). |
| In the text | |
 |
Fig. 7 Same as Fig. 6 for C18O(1−0). The line centers and line widths have been computed by fitting a 1-component Gaussian to the spectrum at each point (see text). |
| In the text | |
 |
Fig. 8 Line center velocities (left column) and line widths (right column) after convolving (from top to bottom) the 13CO, C18O and C17O(1−0) Mopra maps to 80′′ and regridding with a 40′′ spacing. The smaller red areas are map artifacts. |
| In the text | |
 |
Fig. 9 Top panel: non-thermal component of the velocity line width of the C18O (1−0) transition, vs. the total clump mass, Mclump = MHiGAL (see text). Stars represent protostellar clumps and the empty circles represent starless clumps. Bottom panel: non-thermal velocity dispersion, from C18O (1−0), to sound speed ratio, fturb, vs. the total clump mass, Mclump. The green solid line represents the linear fit to all points (see text); the Spearman rank coefficient is 0.66. |
| In the text | |
 |
Fig. 10 Total clump mass, Mclump = MHiGAL, vs. the virial mass, Mvir, calculated using the velocity line widths of the C18O (1−0) transition (see text). The solid line indicates the minimum Mclump = 0.5 Mvir for which the clump should be self-gravitating. Symbols are as in Fig. 9. |
| In the text | |
 |
Fig. 11 Radial column density profile of the main (left column) and secondary (right column) filaments. The dots, connected by the red solid line, show the mean profile across the filaments, while the shaded area indicates the standard deviation. In the top row the average profiles were estimated from the 13CO and C18O(1−0) derived column density (Fig. 5, top panel), while in the bottom row we used the column density estimated by Elia et al. (2013). The black solid line represents the best fit profile, following the formulation in Arzoumanian et al. (2011). |
| In the text | |
 |
Fig. A.1 Channel maps of 13CO(1−0), between 13 and 16.6 km s-1 (as shown in the top-left corner of each panel). The isolated individual region, centered at (RA, Dec) ~ (07:11:18, −10:36:00), has been dropped from this figure to increase visibility of the main regions of emission. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 for C18O(1−0). |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1, after convolving the map with a 80 arcsec beam and re-gridding the map on a 40 arcsec step. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.3 for C18O(1−0). |
| In the text | |
 |
Fig. A.5 Same as Fig. A.3 for C17O(1−0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.