| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527783 | |
| Published online | 05 February 2016 | |
A rotating helical filament in the L1251 dark cloud⋆
1
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112, 21029
Hamburg,
Germany
2
Ioffe Physical-Technical Institute, Polytekhnicheskaya Str. 26, 194021
St. Petersburg,
Russia
3
St. Petersburg Electrotechnical University LETI,
Prof. Popov Str. 5,
197376
St. Petersburg,
Russia
e-mail: lev@astro.ioffe.rssi.ru
4
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
5
Astronomy Department, King Abdulaziz University,
PO Box 80203, 21589
Jeddah, Saudi
Arabia
Received: 18 November 2015
Accepted: 22 December 2015
Aims. We derive the physical properties of a filament discovered in the dark cometary-shaped cloud L1251.
Methods. Mapping observations in the NH3(1, 1) and (2, 2) inversion lines, encompassing 300 positions toward L1251, were performed with the Effelsberg 100-m telescope at a spatial resolution of 40′′ and a spectral resolution of 0.045 km s-1.
Results. The filament L1251A consists of three condensations (α, β, and γ) of elongated morphology, which are combined in a long and narrow structure covering a 38′ × 3′ angular range (∼3.3 pc × 0.3 pc). Comparing the kinematics with the more extended envelope (∼61′ × 33′) emitting in 13CO, we find that: (1) the angular velocity of the envelope around the horizontal axis E → W is ΩEWCO ≈−2 × 10-14 rad s-1 (the line-of-sight velocity is more negative to the north); (2) approximately one half of the filament (combined α and β condensations) exhibits counter-rotation with ΩEWαβ ≈2 × 10-14 rad s-1; (3) one third of the filament (the γ condensation) co-rotates with ΩEWγ ≈−2 × 10-14 rad s-1; (4) the central part of the filament between these two kinematically distinct regions does not show any rotation around this axis; (5) the whole filament revolves slowly around the vertical axis S → N with ΩSNtot ≈7 × 10-15 rad s-1.
The opposite chirality (dextral and sinistral) of the αβ and γ condensations indicates magnetic field helicities of two types, negative and positive, which were most probably caused by dynamo mechanisms. We estimated the magnetic Reynolds number Rm ≳ 600 and the Rossby number ℛ < 1, which means that dynamo action is important.
Key words: ISM: clouds / ISM: molecules / ISM: kinematics and dynamics / radio lines: ISM / techniques: spectroscopic / line: profiles
FITS cube is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/586/A126
© ESO, 2016
1. Introduction
Observations show that magnetic fields are ubiquitous in the local universe and are often associated with filamentary structures (e.g., André et al. 2014, and references cited therein). Filamentary molecular clouds play an important role in star formation since star-forming cores appear primarily along dense elongated blocks. Thus to derive their physical parameters is a crucial issue for understanding star formation (e.g., Konyves et al. 2015). Magnetic fields support and form the morphology of filaments, and there is evidence that some filaments are wrapped by helical fields (Matthews et al. 2001; Hily-Blant et al. 2004; Carlqvist et al. 2003; Poidevin et al. 2010).
In the present paper we describe a filament detected within the molecular cloud L1251 by means of spectral observations of NH3 emission lines. L1251 is a star-forming dark cloud of the opacity class 5 (the second highest, see Lynds 1962), elongated E-W inside the molecular ring in the Cepheus flare (Hubble 1934; Lebrun 1986) at a distance of D = 300 ± 50 pc (Kun & Prusti 1993). With the coordinates ℓ ≈ 115°, b ≈ 15°, its distance from the galactic midplane is about 100 pc. 13CO observations show a cometary distribution of gas with a U-shaped dense “head” turned toward the center of the Cep – Cas void created by a 4 × 104 yr-old Type I supernova (McCammon et al. 1983; Grenier et al. 1989). Supernova shock fronts have probably triggered the formation of stars in L1215 and affected the cloud morphology.
The detailed distribution of molecular gas in L1251 was studied by Grenier et al. (1989), Sato & Fukui (1989), and later on at higher angular resolutions by Sato et al. (1994, hereafter S94). S94 revealed five C18O dense cores embedded in the 13CO cloud. The cores, designated as “A” to “E” with increasing RA, exhibit an elongated structure with a major axis of ~5 pc (E → W) and a minor axis of ~3 pc (S → N).
Figure 1 shows schematically cloud morphology with ellipses representing locations and angular sizes of the five C18O dense cores. The boundary of the cloud (shown by a gray line) is set by the integrated 13CO(1–0) emission at the lowest level of 1.5 K km s-1 (see Fig. 2b in S94). The (0, 0) map position is RA = 22:31:02.3, Dec = 75:13:39 (J2000), which is fixed throughout the present paper.
 |
Fig. 1 Morphology of a cometary-shaped cloud L1251 as revealed in Sato et al. 1994. The contour shows the integrated 13CO(1–0) emission at the lowest level of 1.5 K km s-1 (Fig. 2b in Sato et al. 1994). Five ellipses represent locations and angular sizes of five C18O dense cores (Tables 1 and 2 in S94). The rotation of the individual cores is shown by small-sized gray arc arrows. The global rotation of the 13CO cloud is indicated by the large-sized arc arrow. For each arc arrow, denser gray color indicates the outer near side of the surface of the arc. The dashed lines are the rotation axes. The (0, 0) map position is RA = 22:31:02.3, Dec = 75:13:39 (J2000). The adopted distance to the cloud is 300 pc. |
The kinematic structure of the radial velocity field of L1251 reveals a number of peculiar features. The 13CO(1–0) and C18O(1–0) emission lines show a
highly ordered velocity gradient of 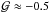 km s-1 pc-1 in the direction parallel to
the minor axis of the cloud in the head of the cloud east of the offset RA ~0′ in Fig. 1. Since it is interpreted as a solid body rotation, this gradient corresponds to
an angular velocity of ΩCO ≈ −2 ×
10-14 rad s-1. The negative sign means that the radial velocity is
more negative to the north; i.e., the velocity gradient is directed N → S across the head. This global motion is
indicated in Fig. 1 by a large-sized arc arrow around
the horizontal E–W axis (dashed line). In this respect L1251 resembles rotating elephant trunks found in star formation regions
(Pound et al. 2003; Hily-Blant et al. 2005; Gahm et al. 2006). The cores A, B, and E disposed along this axis have approximately the same
radial velocity VLSR≈−4.0 km s-1, whereas for the northern core C and the southern core D
VLSR(C) ≈ −4.6 km s-1, and VLSR(D)
≈−3.8 km s-1. (A typical uncertainty of
VLSR is ~0.1 km s-1, S94.)
km s-1 pc-1 in the direction parallel to
the minor axis of the cloud in the head of the cloud east of the offset RA ~0′ in Fig. 1. Since it is interpreted as a solid body rotation, this gradient corresponds to
an angular velocity of ΩCO ≈ −2 ×
10-14 rad s-1. The negative sign means that the radial velocity is
more negative to the north; i.e., the velocity gradient is directed N → S across the head. This global motion is
indicated in Fig. 1 by a large-sized arc arrow around
the horizontal E–W axis (dashed line). In this respect L1251 resembles rotating elephant trunks found in star formation regions
(Pound et al. 2003; Hily-Blant et al. 2005; Gahm et al. 2006). The cores A, B, and E disposed along this axis have approximately the same
radial velocity VLSR≈−4.0 km s-1, whereas for the northern core C and the southern core D
VLSR(C) ≈ −4.6 km s-1, and VLSR(D)
≈−3.8 km s-1. (A typical uncertainty of
VLSR is ~0.1 km s-1, S94.)
However, observations in NH3(1,1) revealed that despite the N → S global velocity gradient, the northern
core C exhibits a counter-rotation characterized by a highly ordered velocity gradient with
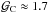 km s-1 pc-1, and position angle PA
~ 30° (E of N), corresponding to the angular
velocity of ΩNH3 ≈ 4 ×
10-14 rad s-1 (see Fig. 6 in Levshakov et al. 2014). Taking into account that C-bearing molecules are usually
distributed in the outer parts of the cores (e.g., Tafalla et al. 2004), we conclude that the denser interior of this core traced by
ammonia emission moves in a direction opposite to the global motion of the CO envelope.
km s-1 pc-1, and position angle PA
~ 30° (E of N), corresponding to the angular
velocity of ΩNH3 ≈ 4 ×
10-14 rad s-1 (see Fig. 6 in Levshakov et al. 2014). Taking into account that C-bearing molecules are usually
distributed in the outer parts of the cores (e.g., Tafalla et al. 2004), we conclude that the denser interior of this core traced by
ammonia emission moves in a direction opposite to the global motion of the CO envelope.
For core A, Goodman et al. (1993) reported an
approximately east-west velocity gradient in NH3 (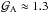 km s-1 pc-1, and PA ≈ −77°) with the rotation axis oriented almost
perpendicular to the horizontal (E–W) rotation axis of the dark cloud L1251 (also Tóth & Walmsley 1996, hereafter TW96).
km s-1 pc-1, and PA ≈ −77°) with the rotation axis oriented almost
perpendicular to the horizontal (E–W) rotation axis of the dark cloud L1251 (also Tóth & Walmsley 1996, hereafter TW96).
A more complex gas motion is observed in core E. According to Goodman et al. (1993), who used spectral-line maps from Benson &
Myers (1989), the velocity gradient direction in E is
nearly orthogonal to the gradient direction in A (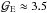 km s-1 pc-1, and PA ≈ −156°). However, Caselli et al. (2002) mapped this core in N2H+(1–0) with an angular resolution
of 54′′ (1.5 times the angular
resolution of Benson & Myers) and found reverse velocity gradients in the eastern and
western parts of the core suggestive of two counter-rotating adjacent clumps. For these
clumps taken together, the N2H+ tracer shows
km s-1 pc-1, and PA ≈ −156°). However, Caselli et al. (2002) mapped this core in N2H+(1–0) with an angular resolution
of 54′′ (1.5 times the angular
resolution of Benson & Myers) and found reverse velocity gradients in the eastern and
western parts of the core suggestive of two counter-rotating adjacent clumps. For these
clumps taken together, the N2H+ tracer shows 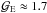 km s-1 pc-1and PA ≈ −130° (Caselli et al. 2002), meaning that the directions of increasing velocity for both
NH3 and
N2H+ are significantly correlated.
Further single-dish and interferometric studies supported very complex kinematics, including
rapid rotation, infall, and outflow motions in the dense core E (Lee et al. 2007). The directions of rotation and related rotation
axes inferred from these studies are depicted in Fig. 1. No information exists on kinematic processes in cores B and D, except for radial
velocities and linewidths of the 13CO(1–0) and C18O(1–0) lines measured in S94.
km s-1 pc-1and PA ≈ −130° (Caselli et al. 2002), meaning that the directions of increasing velocity for both
NH3 and
N2H+ are significantly correlated.
Further single-dish and interferometric studies supported very complex kinematics, including
rapid rotation, infall, and outflow motions in the dense core E (Lee et al. 2007). The directions of rotation and related rotation
axes inferred from these studies are depicted in Fig. 1. No information exists on kinematic processes in cores B and D, except for radial
velocities and linewidths of the 13CO(1–0) and C18O(1–0) lines measured in S94.
Here we continue our investigations of dense cores of the dark cloud L1251 in the NH3(1, 1) and (2, 2) inversion transitions with the Effelsberg 100-m telescope1. In a previous paper (Levshakov et al. 2014), we mapped core C. The present target is core A, which is one of the ammonia emitters exhibiting some of the narrowest (Δv≲0.2 km s-1)2 lines ever observed (Jijina et al. 1999). For this reason L1251 was included in our list of targets used to validate the Einstein equivalence principle – local position invariance (Levshakov et al. 2010, 2013b).
2. Observations
The ammonia observations were carried out with the Effelsberg 100-m telescope in one session on April 22–27, 2014. The measurements were performed in the position-switching mode with the backend eXtended bandwidth FFTS (XFFTS) operating at 100 MHz bandwidth and providing 32 768 channels for each polarization. The resulting channel width was Δch = 0.039 km s-1, but the true velocity resolution is 1.16 times coarser (Klein et al. 2012). The NH3 lines were measured with a K-band high-electron mobility transistor (HEMT) dual channel receiver, yielding spectra with a spatial resolution of 40′′ (FWHP) in two orthogonally oriented linear polarizations at the rest frequency of the (J,K) = (1, 1) and (2, 2) lines, f1,1 = 23 694.495487 MHz and f2,2 = 23 722.633644 MHz (Kukolich 1967). Averaging the emission from both channels, the typical system temperature (receiver noise and atmosphere) is 100 K on a main beam brightness temperature scale.
The mapping was done on a 40′′ grid. The pointing was checked every hour by continuum cross scans of nearby continuum sources. The pointing accuracy was better than 5′′. The spectral line data were calibrated by means of continuum sources with a known flux density. We mainly used G29.96–0.02 (Churchwell et al. 1990). With this calibration source, a main beam brightness temperature scale, TMB, can be established. Since the main beam size (40′′) is smaller than most core radii (>50′′) of our target, the ammonia emission couples well to the main beam so that the TMB scale is appropriate. Compensations for differences in elevation between the calibrator and the source were ≲20% and have not been taken into account. Similar uncertainties of the main beam brightness temperature were found from a comparison of spectra toward the same position taken on different dates.
The typical rms noise in our observations was 0.3 K per channel in main-beam brightness temperature units (150s ON and 150s OFF positions for one scan). Some points were observed several times resulting in rms ~0.15 K. For a characteristic line width of 0.2 km s-1 (see below), this yields typical rms values of 0.05 K km s-1, so that we choose 0.2 K km s-1 as the lowest contour in the following.
3. Results
The ammonia spectra were analyzed in the same way as in Levshakov et al. (2014). There are no features with two velocity components. The radial velocity, VLSR, the linewidth Δv, the optical depths τ11 and τ22, the integrated ammonia emission ∫TMBdv, and the kinetic temperature Tkin are all well-determined physical parameters, whereas the excitation temperature Tex, the ammonia column density N(NH3), and the gas density nH2 are less certain since they depend on the beam filling factor η, which is not known for unresolved clumps. Assuming that η ranges between ηmin and 1, one can estimate limits for Tex, N(NH3), and nH2, where a minimum value of nH2 is obtained by the choice of η = 1. The corresponding equations are given in Appendix A in Levshakov et al. (2013a, hereafter L13).
The errors of the model parameters were estimated from the diagonal elements of the covariance matrix calculated for the minimum of χ2. The error in VLSR was also estimated independently by the Δχ2 method (Press et al. 1992). When the two estimates differed, the larger error was adopted. Table 1 illustrates that a typical uncertainty of VLSR and Δv at peak intensities of NH3(1, 1) is ~0.01 km s-1 (1σ confidence level, C.L.). Below we describe the obtained results in detail.
 |
Fig. 2 a) NH3(1, 1) integrated intensity map (∫TMBdv in units of K km s-1) of the molecular core L1251A. Each color box has a size of 40′′ × 40′′, and its bottom left corner corresponds to the telescope pointing. The parameters of the NH3 peaks α,β, and γ are given in Table 1. The core exhibits a filamentary structure that can be enveloped by an ellipse (dashed line) with principal axes of 1140′′ and 89′′. b) Schematic configuration of the filament and peak positions of the ammonia cores T1–T4. The gray contours restrict ammonia emission to the lowest level of the integrated NH3(1, 1) emission as in Fig. 3 in Tóth & Walmsley (1996). The location of the IRS sources are from Lee et al. (2010). The red star is the IR source detected by IRAS. The filled blue and red circles outline areas of the narrowest ammonia lines with FWHP line widths of, respectively, Δv ~ 0.2 km s-1, and ~0.1 km s-1; their offsets are listed in Table 1. c) The sum over the integrated intensities for a given RA, ∑ ΔδIΔα(Δδ). The (0, 0) map position and the distance to the source are as in Fig. 1. |
 |
Fig. 3 Distributions of the measured parameters in L1251A: a) the gas volume density, nH2; b) the NH3 column density, NNH3; c) the kinetic temperature, Tkin; and (d) the excitation temperature, Tex. Three parameters nH2, NNH3, and Tkin were measured at the 54 positions where both the NH3(1, 1) and (2, 2) lines were observed, whereas Tex was estimated from the NH3(1, 1) lines, which are not very weak. Each color box has a size of 40′′×40′′ and its bottom left corner corresponds to the telescope pointing. The contours are the NH3(1, 1) integrated intensity map. The starting point for the contour levels is 0.2 K km s-1; the increment is 1.0 K km s-1. The (0, 0) map position is as in Fig. 1. We note that for the beam filling factor η< 1, certain parameters could be larger (see Sects. 3 and 3.1 for details). |
3.1. Global gas morphology from NH3
Our NH3 observations cover the whole molecular core A and part of core B of L1251 and consist of 300 measured positions, each of which is represented by a color box in the NH3(1, 1) integrated intensity map in Fig. 2a. The NH3 map clearly reveals three peaks that are labeled by α, β, and γ. Their parameters are given in Table 1. In Fig. 2a, the peak positions of cores B and A have offsets (Δα,Δδ) = (362″, −76″) and (− 474″,38″), respectively. Thus, the ammonia β peak coincides with the C18O peak A, whereas the C18O peak B is slightly shifted from the ammonia α peak to the southeast. For this reason we will call the whole structure traced by NH3 emission as L1251A.
As mentioned above, the ammonia map was sampled at intervals of 40′′, which is half the grid size of 80′′ in TW96. The denser sampling resulted in a different apparent morphology of the NH3 distribution. For instance, TW96 identified four ammonia cores dubbed as “T1” to “T4” in decreasing RA direction. The first three T1–T3 have a common envelope, whereas T4 is separated (see Fig. 2b). However, our results show that these two zones of ammonia emission are not separated, but, in fact, all four cores belong to a central part of a continuous elongated structure that is much larger than the area of the NH3 emission mapped by TW96. The peak positions of cores T1–T4 are marked by black stars in Fig. 2b for comparison with our observations. The known infrared sources are indicated as well.
The shape of the filament at the lowest level of 0.2 K km s-1 can be approximated by an ellipse with the angular sizes of the major (E-W) and minor (S-N) axes on the plane of the sky of about 38′ and 3′. The projected linear sizes of these axes are ℓ1 ≈ 3.3 pc and ℓ2 ≈ 0.3 pc; i.e., the aspect ratio is ε ≈ 11.
The NH3(1, 1)
integrated intensities 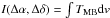 form three condensations around the
α,
β, and
γ peaks,
which are clearly seen in Fig. 2c where we plot the
sum over Δδ
values, ∑
ΔδIΔα(Δδ),
at each fixed Δα as a function of RA. The shape of this function,
shown by gray in Fig. 2c, allows us to formally
assign the boundaries for these condensations: −160″ ≲ Δα ≤ 600″ for α, −880″ ≲ Δα ≲ −160″ for
β, and
−1640″ ≤ Δα ≲ −
880″ for γ.
form three condensations around the
α,
β, and
γ peaks,
which are clearly seen in Fig. 2c where we plot the
sum over Δδ
values, ∑
ΔδIΔα(Δδ),
at each fixed Δα as a function of RA. The shape of this function,
shown by gray in Fig. 2c, allows us to formally
assign the boundaries for these condensations: −160″ ≲ Δα ≤ 600″ for α, −880″ ≲ Δα ≲ −160″ for
β, and
−1640″ ≤ Δα ≲ −
880″ for γ.
The thickness of the filament along the line of sight (the third axis ℓ3) can be
estimated from the measured ammonia column density, NNH3,
and the gas number density, nH2, assuming a mean
abundance ratio [ NH3 ]/[
H2 ] = (4.6 ± 0.3) × 10-8 found in dark clouds
(Dunham et al. 2011). The measured values of
nH2 and NNH3
over the ammonia map are shown in panels (a) and (b) in Fig. 3. Along the major axis ℓ1, we observed both the
NH3(1, 1) and (2,
2) transitions at 54 positions between the offsets Δα = 440″ and
−1280″, except for a gap
−1040″ ≤ Δα ≤ −
640″. Averaging this dataset we obtain ⟨ N ⟩ NH3 = (1.03 ±
0.05) × 1015 cm-2 (1σ C.L.)3 and
⟨ n ⟩
H2 = (3.9 ± 1.3) × 104
cm-3 under the
assumption that the beam filling factor η = 1 (Eqs. (A.19) and (A.21) in L13); i.e., we
observe a rather small (~5%)
fluctuation in column densities along with a significant variation (≳30%) in gas number densities. For instance, a twofold variation is
found between α peak where 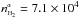 cm-3 and other peaks with
cm-3 and other peaks with
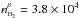 cm-3 and
cm-3 and
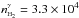 cm-3. Besides this, a sharp change
in nH2 is measured between the
offsets (0′′, 0′′) and (0″, −40″) showing nH2 = 6.8 ×
104 cm-3 and 1.7 ×
104 cm-3, respectively.
cm-3. Besides this, a sharp change
in nH2 is measured between the
offsets (0′′, 0′′) and (0″, −40″) showing nH2 = 6.8 ×
104 cm-3 and 1.7 ×
104 cm-3, respectively.
The reason for such a high density fluctuation is not clear. It might be due to the used filling factor η = 1 and the presence of small clumps with linear sizes less than 0.05 pc that are unresolved in our observations4. Shown in Fig. 3d, the excitation temperature Tex, also estimated at η = 1 (Eq. (A.10) in L13), may be inaccurate as well, since Tex then corresponds to a minimum value. With increasing Tex (i.e., decreasing η) and, as a result, decreasing difference (Tkin − Tex), the estimate of nH2 loses stability (Ho & Townes 1983). In this difference, Tkin is actually a fixed quantity since the kinetic temperature is found to be almost constant over the whole filament (see Fig. 3c). Its mean value is ⟨ Tkin ⟩ = 10.12 ± 0.08 K.
 |
Fig. 4 Thickness along the line of sight through the core L1251A estimated from the measured column densities NNH3 and number densities nH2 shown in Fig. 3. The mean abundance ratio of [ NH3 ]/[ H2 ] = 4.6 × 10-8 (Dunham et al. 2011) is fixed for the whole filament. The (0, 0) map position is as in Fig. 1. We note that for the beam filling factor η< 1, the thickness is smaller (see Sects. 3 and 3.1 for details). |
For the mean abundance [ NH3 ]/[ H2 ] = 4.6 × 10-8, the ratio of ⟨ N ⟩ NH3 and ⟨ n ⟩ H2 gives the mean thickness of the filament of ⟨ ℓ3 ⟩ ~ 0.2 pc, which is comparable to ℓ2. We note that for η< 1, ⟨ ℓ3 ⟩ would become smaller. Thus, if we use the sample means, then the filamentary structure traced by ammonia emission resembles a prolate ellipsoid of revolution (rod-like) with ℓ1 ≫ ℓ2 ≳ ℓ3.
However, the ammonia filament may have a more complex morphology if one compares individual gas densities at each point. Following this approach, we obtained local thickness at different positions as displayed in Fig. 4. It is seen that the linear dimension ℓ3 within the area occupied by the α and β condensations is ~0.2 pc, whereas it is two times larger, ~0.4 pc, at the position of the γ condensation.
It has to be noted that such calculations of ℓ3 are only legitimate at gas densities below or near the critical density, nH2 ≤ ncr, since otherwise the observed line intensity is no longer unambiguously related to the gas density because the collisionally induced transitions produce no photons. For NH3(1, 1), the critical density at Tkin = 10 K is ncr = 3.90 × 103 cm-3 (Maret et al. 2009), which is an order of magnitude lower than the measured mean value of ⟨ n ⟩ H2. Therefore, the estimates of ℓ3 must be taken with some caution. Nevertheless, a sheet-like geometry of L1251A with ℓ3 ~ ℓ1 may be excluded since it would produce too low a gas number density, nH2 ~ 2 × 103 cm-3 – an order of magnitude lower than the measured values of nH2. An η< 1 would make ℓ3 even shorter.
 |
Fig. 5 Portion of Fig. 17 from Kirk et al. (2009) with extended structure toward L1251A and L1247. The gray scale shows the distribution of visual extinction as derived from the Digitized Sky Survey (Dobashi et al. 2005), and the superimposed higher resolution extinction maps (outlined by solid straight black lines) observed with the Spitzer Infrared Array Camera (IRAC; 3.6–8.0 μm) and Multiband Imaging Photometer (MIPS; 24–160 μm). Two dashed lines refer to Dobashi AV = 1 mag and Spitzer AV = 5 mag. The colored markers show the location and spectral type of the young stellar object (YSO) candidates: red/green/blue for Class I/Flat/Class II. The black stars are the same markers as in Fig. 2b. The NH3(1, 1) integrated intensity map, as in Fig. 4, is denoted by the red contours. The approximate orientation and linear size of a jet extending about 10′ and a small bipolar nebula to the east of the jet (solid green lines) are copied from Fig. 1 in Lee et al. (2010). |
In what follows, we assume that the filament has a rod-like geometry consisting of two cylinders with different cross-sections: a circular one with diameter 0.2 pc for α and β, and an elliptical cylinder with the major and minor axes of 0.4 pc and 0.2 pc for γ. Their corresponding linear sizes are 2.2 pc and 1.1 pc. The mean gas number densities are ⟨ n ⟩ αβ = (4 ± 2) × 104 cm-3 (sample size = 48), and ⟨ n ⟩ γ = (2.6 ± 0.4) × 104 cm-3 (sample size = 6).
It is interesting to compare our results with previous ones. According to TW96, the angular size (E-W) of the combined cores T1–T3 is ~7′, which is in line with the ammonia map of Goodman et al. (1993). Together with T4, the total size of the T1–T4 complex in the E-W direction is about 15′, which is more than two times shorter as compared with ℓ1. In the orthogonal direction (S-N), we observe the same extension of the ammonia map as reported by Goodman et al. and TW96.
The previous ammonia observations did not reveal the γ condensation which is partly overlapping the nearby dark cloud L1247 (Fig. 5). The maximum of the NH3(1, 1) integrated intensity lies in the region with minimum visual extinction just between L1251A and L1247. Thus, approximately three fourths of the ammonia map coincides with the most prominent filament evident in the dust emission (dark gray area with AV ≳ 5 mag in Fig. 5), whereas one fourth follows a weaker dust emission with AV ~ 1 mag.
The question then arises as to how it is possible that in the γ region the maximum of the ammonia emission originates in areas with minimal visual extinction. This is perhaps due to small scale clumping with the NH3 gas providing high visual extinction but not covering the entire area, hinting at an η< 1 for this region. Possibly, η is smaller in the γ fragment than in αβ. In Sect. 3.3, we discuss that the average H2 density is well below what is deduced from NH3. This is also consistent with small scale clumping.
The comparison with the C18O(1–0) map, which has the major (E → W) and minor (S → N) axes of 17′× 7′ (Fig. 2 in S94), shows that in general both NH3 and C18O trace each other, but the former is more concentrated on the horizontal E–W axis. This is not surprising since the C18O(1–0) transition becomes excited at densities an order of magnitude lower than needed for NH3(1, 1). However, an unexpected result is that a rather large area of ammonia emission from the western part of L1251A (γ condensation in Fig. 2a) is not seen in C18O: this part of L1251 was mapped only in 13CO(1–0) (Fig. 1) and in dust emission (Fig. 5). The 13CO “tail” of L1251 west of the offset RA ~0′ in Fig. 1 has an angular size of ~27′ × 20′, which is much larger than regions with visual extinction AV ~ 5 mag and the similarly extended C18O emission.
Considering the spatial distributions of these emitters, we see that the tail of L1251A has a cocoon-like morphology with radial stratification from the outer to the innermost layers seen in 13CO, C18O, dust emission, and NH3. The radius of the first region projected on the plane of the sky is R1 ~ 0.9 pc (13CO), the second R2 ~ 0.3 pc (C18O and dust), and the third R3 ~ 0.13 pc (NH3). The ambient medium traced by 12CO emission (the outermost envelope) has a very large angular size and irregular morphology as displayed in Fig. 1 in Grenier et al. (1989).
In the next section, we show that all three ammonia condensations α, β, and γ are involved in a common global motion of the filamentary structure with some intrinsic peculiarities.
3.2. Global gas kinematics from NH3
The NH3 radial
velocity map is shown in Fig. 6. In our analysis of
ammonia spectra, all hyperfine structure (hfs) components of the NH3(1, 1) and (2, 2) transitions
were fitted simultaneously to determine the total optical depth, τtot, in the
respective inversion transition, the LSR velocity of the line, VLSR, the
intrinsic full-width at half power linewidth, Δv (FWHP), for individual hf components, and the
amplitude, 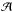 (see Appendix A in L13). For unsaturated lines (τhf ≲ 1), the velocity VLSR represents
an intensity-weighted average centroid velocity along the line of sight through the cloud.
(see Appendix A in L13). For unsaturated lines (τhf ≲ 1), the velocity VLSR represents
an intensity-weighted average centroid velocity along the line of sight through the cloud.
If the cloud rotates as a solid body, VLSR is independent of distance along
the line of sight, and linearly dependent on the coordinates in the plane of the sky
(e.g., Goodman et al. 1993; Belloche 2013). Then, the cloud rotation velocity field is
defined by the equation 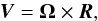 (1)where Ω is the angular velocity, and
R the
distance to the rotation axis. This means that a cloud in solid-body rotation should
demonstrate a linear gradient, ∇VLSR, across the surface of a map,
orthogonal to the rotation axis Ω. This is just the case of L1251A where the velocity gradient in the direction E → W along the major axis can be easily
identified by eye (Fig. 6).
(1)where Ω is the angular velocity, and
R the
distance to the rotation axis. This means that a cloud in solid-body rotation should
demonstrate a linear gradient, ∇VLSR, across the surface of a map,
orthogonal to the rotation axis Ω. This is just the case of L1251A where the velocity gradient in the direction E → W along the major axis can be easily
identified by eye (Fig. 6).
3.2.1. The whole filament, –1640″≤Δα ≤ 600″
The VLSR values are systematically increasing with decreasing RA (E → W) on the total linear scale of the filament ℓ1 ≈ 3.3 pc. As it follows from Fig. 6, the velocity difference between the eastern and western edges of the filament is ΔV ≈ 0.7 km s-1, meaning that the gradient becomes ∇VLSR≈0.2 km s-1 pc-1.
The same gradient can be found from the regression analysis shown in Fig. 7, where a functional dependence of spatial averages of
⟨VLSR⟩ on RA is depicted. At each offset
Δα, the
weighted mean value of ⟨VLSR⟩ was found from averaging along the S
→ N direction with weights
inversely proportional to the uncertainties of the measured line-of-sight velocities.
The regression line (shown by red) is defined by 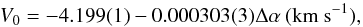 (2)which corresponds to ∇VLSR= 0.208 ± 0.003 km s-1 pc-1. Here, the numbers in
parentheses are 1σ errors on the last digit, and Δα is counted in arcsec.
(2)which corresponds to ∇VLSR= 0.208 ± 0.003 km s-1 pc-1. Here, the numbers in
parentheses are 1σ errors on the last digit, and Δα is counted in arcsec.
It follows from Eqs. (1) and (2) that the angular velocity of the whole
filament around the vertical axis (S → N) is 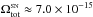 rad s-1, and the period for a
complete rotation
rad s-1, and the period for a
complete rotation 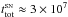 yr.
yr.
3.2.2. The α and β kinematic fragments, –480″≤ Δα ≤ 600″
Figure 7 demonstrates that radial velocities
increase gradually with RA over the area occupied by the α and β condensations from the
offset Δα =
600″ to Δα ~ −480″. The regression line for this
kinematic fragment is practically the same as for the whole filament: 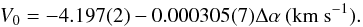 (3)Its angular velocity around the vertical
axis (S → N) is
(3)Its angular velocity around the vertical
axis (S → N) is
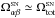 .
.
It is noteworthy that the gas in this area exhibits an additional spinning around the horizontal axis (E → W), which is revealed in a systematic difference between the radial velocities toward the northern and southern ridges of the filament. To specify this effect numerically, we considered the probability density function (pdf) of line centroid velocity fluctuations ΔV = VLSR −V0 calculated at each offset position on the map of the αβ fragment. Here, V0 is a local systemic velocity at a given Δα, which is defined by (3). The obtained pdf is shown by the blue histogram (approximated by a Gaussian) in Fig. 8a. It consists of three peaks: the central component with ΔV = 0 km s-1, and the two lateral components with ΔVN,S ≈ ± 0.11 km s-1. In this case, the positive northern component ΔVN indicates that the line-of-sight velocity is higher to the north, whereas the negative southern component ΔVS shows that VLSR is predominantly directed to the observer.
The velocity difference between these two filament ridges is ~0.22 km s-1, which gives the gradient
∇VLSR~ 0.7 km s-1 pc-1 in the direction S
→ N. The corresponding
angular velocity 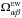 has the opposite sign to the rotation of
the CO envelope (ΩCO ≈ −2 ×
10-14 rad s-1) and equals
has the opposite sign to the rotation of
the CO envelope (ΩCO ≈ −2 ×
10-14 rad s-1) and equals 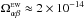 rad s-1
(
rad s-1
(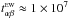 yr).
yr).
 |
Fig. 7 Position-velocity diagram of NH3(1, 1) along the direction of the velocity gradient (E → W). At each offset Δα, the measured centroid velocities (VLSR) are averaged across the filament in the direction S → N. The error bars (the standard deviation of the mean) result from this averaging. The different positions were weighted inversely proportional to the variance. The linear regression for the total range is shown by red: V0 = −4.199(1)−0.000303(3)Δα (km s-1) (here Δα is in arcsec). For the αβ condensation (−480″ ≤ Δα ≤ 600″), the regression line is practically the same. For the γ condensation (−1640″ ≤ Δα ≤ −800″), it is shown by a blue line with V0 = − 4.38(1) −0.00046(1)Δα (km s-1). The number in parentheses is the one-sigma (1σ) uncertainty in the last digit of the given value. The (0, 0) map position is as in Fig. 1. |
3.2.3. The bar, –800″≤ Δα ≤ –480″
Figure 7 shows that near the geometric center of the filament in the range −800″ ≤ Δα ≤ −480″, the mean radial velocity between the adjoining points is held constant: ⟨ VLSR ⟩ = −3.997 ± 0.004 km s-1. This kinematic fragment is also characterized by an extremely low linewidth of ammonia lines, Δv~ 0.1–0.2 km s-1 (blue and red filled circles in Fig. 2b), and decreasing gas density nH2 from 4 × 104 cm-3 to 2 × 104 cm-3 with changing Δα from −480″ to −600″ along the cut Δδ = 0″. Beyond this interval, between Δα = −640″ and −1040″, we did not detect the second ammonia transition NH3(2, 2), and, therefore, the gas number density was not estimated. The same tendency is observed for the ammonia column density: N(NH3) decreases from 1.5 × 1015 cm-2 to 0.5 × 1015 cm-2 within the interval −600″ ≤ Δα ≤ − 480″.
In what follows, we refer to this fragment of the filament as a “bar”. Figure 2a shows that it starts at the western edge of the β condensation and its projected linear size is ℓbar ≈ 0.5 pc.
3.2.4. The γ kinematic fragment, –1640″≤ Δα ≤ –800″
The regression line of the γ kinematic fragment, ranging from
Δα = −
800″ to −1640″ (shown by blue in Fig. 7), is defined by 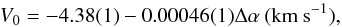 (4)i.e., ∇VLSR= 0.316 ± 0.007 km s-1 pc-1. Thus, the western part of
the filament rotates around the vertical axis (S → N) with a slightly higher angular
velocity
(4)i.e., ∇VLSR= 0.316 ± 0.007 km s-1 pc-1. Thus, the western part of
the filament rotates around the vertical axis (S → N) with a slightly higher angular
velocity 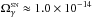 rad s-1 than
rad s-1 than
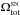 .
.
 |
Fig. 8 Histograms are the probability density functions (pdfs) of line centroid velocity fluctuations ΔV = VLSR − V0, and the smooth curves are their approximations by Gaussians. Here V0 is the systemic velocity component defined by the regression lines shown in Fig. 7. Panels a) and b) represent the αβ (red regression line in Fig. 7) and γ (blue regression line in Fig. 7) condensations. The lateral peaks labeled by the letters “N” and “S” correspond to the northern and southern ridges of the filament. Note the opposite chirality of the angular rotation around the horizontal axis E → W (see Sects. 3.2.2 and 3.2.4 for details). |
Toward the γ condensation, we also reveal an additional systemic motion around the axis E → W: the radial velocity is more negative to the north than what is observed from the global rotation of the CO envelope. Applying the same procedure as for the αβ fragment, we calculated pdfs of the residuals ΔV using the two definitions of the systemic velocity V0 given by Eqs. (2) and (4). The resulting distribution functions are shown by the cyan and blue histograms in Fig. 8b, respectively. It is seen that the definition (2) based on the total dataset provides unresolved lateral peaks and a broad central component, whereas the regression line (4) allows us to partly resolve the lateral peaks.
It is remarkable that in this case we observe spinning with opposite chirality (dextral
vs. sinistral): the northern peak is shifted to negative line-of-sight velocities, and
the southern – to positive velocities. Because of an asymmetric shape of the northern
peak, it was approximated by a convolution of two Gaussians shown by the dotted curve in
Fig. 8b. Their barycenter is ΔVN ≈ −0.089
km s-1, whereas
the center of the southern component is ΔVS ≈ 0.056 km s-1. This leads to a velocity
difference between the northern and southern ridges of the filament of ~−0.15 km s-1and a gradient
∇VLSR~−0.5 km s-1 pc-1. The corresponding angular
velocity of the γ fragment around the axis E → W is
 rad s-1
(
rad s-1
(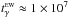 yr).
yr).
Thus, here we find two kinematic fragments of opposite chirality when the filament is viewed from the eastern footpoint along the axis E → W: the fragment γ spins clockwise, whereas the fragment αβ rotates counterclockwise. The filament chirality directly indicates the magnetic field helicity of two types, negative and positive (e.g., Martin 1998).
It should be emphasized that all measured periods exceed the age of the supernova remnant considerably, tSNR ~ 4 × 104 yr, mentioned in Sect. 1. Since dark clouds evolve slowly, this may imply that the dynamical stage of L1251A was triggered by another supernova exploded in the past 106−7 yr in this region, as suggested in S94. A similar lifetime of ~106 yr for starless cores with average volume density n ~ 104 cm-3 was estimated by Lee & Myers (1999), among others.
3.2.5. Smoothness of the velocity field
The distribution of the centroid velocities over the map of the filament (Fig. 6) reveals only one offset position (Δα,Δδ) = (−200″, − 40″) (blue square) with a peculiar velocity VLSR = −4.84(3) km s-1 which deviates noticeably from velocities measured at the neighboring positions. For instance, VLSR(−200″, −80″) = −4.32(3) km s-1, VLSR(−200″,0″) = −4.019(7) km s-1, or VLSR(−240″,0″) = −3.961(7) km s-1, which gives a break of | ΔV | ~ 0.5 −0.9 km s-1 on a scale ~0.05 pc. The nature of the outlier at (−200′′, −40′′) is not clear and requires further exploration. We note that this peculiar velocity is not a product of measurement errors but is connected with other peculiarities outlined further below in the same section.
At all other offsets, VLSR changes smoothly from point to
point. The variance of centroid velocity fluctuations at a given spatial lag can be
estimated from velocity differences between neighboring positions. The histogram in Fig.
9 shows the pdf of such differences at the lags
40″ and
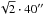 for the whole filament L1251A except for the outlier at the offset
(−200′′, −40′′). For a given position i,j (shown by red on the
grid in the top lefthand corner of Fig. 9), the
velocity differences ΔVi,j are
calculated between each blue point on the grid and the central red point. The total
sample size consists of p =
680 pairs of these neighboring points. The velocity difference pdf
was approximated by Gauss (black curve) and Lorentz (red curve) functions with the
widths (FWHP) of ΔvG ≈ 0.22 km s-1 and ΔvL ≈ 0.11 km
s-1. The rms
turbulent velocity at a lag ~0.05 −
0.08 pc is equal to σG ≈ 0.096 km s-1. The value of
σG depends weakly on the lag size. For
instance, two times and three times larger lags provide σG ≈ 0.129 km
s-1(p = 524) and σG ≈ 0.131 km
s-1(p = 381), respectively. A similar weak
dependence of the non-thermal velocity ΔvNT on radius, ΔvNT ∝
R0.09 ± 0.05, was noted by Goodman et
al. (1998) for ammonia gas in L1251A.
for the whole filament L1251A except for the outlier at the offset
(−200′′, −40′′). For a given position i,j (shown by red on the
grid in the top lefthand corner of Fig. 9), the
velocity differences ΔVi,j are
calculated between each blue point on the grid and the central red point. The total
sample size consists of p =
680 pairs of these neighboring points. The velocity difference pdf
was approximated by Gauss (black curve) and Lorentz (red curve) functions with the
widths (FWHP) of ΔvG ≈ 0.22 km s-1 and ΔvL ≈ 0.11 km
s-1. The rms
turbulent velocity at a lag ~0.05 −
0.08 pc is equal to σG ≈ 0.096 km s-1. The value of
σG depends weakly on the lag size. For
instance, two times and three times larger lags provide σG ≈ 0.129 km
s-1(p = 524) and σG ≈ 0.131 km
s-1(p = 381), respectively. A similar weak
dependence of the non-thermal velocity ΔvNT on radius, ΔvNT ∝
R0.09 ± 0.05, was noted by Goodman et
al. (1998) for ammonia gas in L1251A.
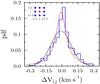 |
Fig. 9 Histogram is the probability density function (pdf) of line centroid velocity fluctuations between neighboring positions over the whole NH3 map of the filament L1251A except for the outlier at the offset (Δα,Δδ) = ( − 200′′, −40′′). In the upper left hand corner, the grid with color points illustrates the calculation of ΔVi,j: for a current position (i,j) (marked by red), the velocity differences are calculated between each blue point and the central red point. The total number of different pairs is 680. The histogram is approximated by a Gauss (black) and a Lorentz (red) function with the widths (FWHP) of ΔvG = 0.22 km s-1 and ΔvL = 0.11 km s-1. |
 |
Fig. 10 a) Linewidths, Δv, of the ammonia (1, 1) lines (FWHP) measured toward the core L1251A. b) Mach numbers, Ms, of non-thermal motions at the 54 positions where Tkin was measured directly from the relative population of the (1, 1) and (2, 2) energy levels of NH3. The contours are as in Fig. 3. The (0, 0) map position is as in Fig. 1. |
It is noteworthy that the Lorentz distribution in Fig. 9 is in better concordance with the histogram, and its width is narrower than that of the Gaussian. This may mean that the central part of the filament is organized into a coherent structure akin those found in some star-forming dense cores (e.g., Goodman et al. 1998; Caselli et al. 2002; Pineda et al. 2010). The size scale at which turbulent motions become coherent, the “coherence length”, is usually deduced from the “cutoff” wavelength below which Alfvén waves cannot propagate because of the neutral medium opacity depending on the magnetic field strength, B, the ionization fraction, xe, and the gas volume density, n. For the typical values observed in dark clouds (B ~ 10μG, xe ~ 10-8, n ~ 105 cm-3), the coherence length is about 0.01 pc (e.g., Caselli et al. 2002). Given the values of ℓ1,ℓ2, and ℓ3, there must be a large number of coherent cells along each axis of the filament L1251A, which may result in a non-Gaussian shape of the general velocity pdf (Fig. 9).
The coherence also leads to the nearly thermal NH3 linewidths, which do not vary
much in the interior of ammonia maps (and which are usually narrower than the linewidths
of the surrounding C18O and 13CO gas), and transonic to subsonic velocity
dispersions (e.g., Smith et al. 2009). We explore
these issues in Fig. 10. Panel (a) shows a
dominant linewidth Δv ~
0.2 km s-1, which is very close to the thermal broadening of
NH3 at a
kinetic temperature Tkin = 10 K: Δvth ≈ 0.16 km
s-1 (Eq. (A.6)
in L13). The hyperfine structure fit to the NH3(1, 1) multiplet yields a maximum optical depth of
~1 for the isolated
hfs component 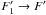 , F′ → F = 0 → 1,1/2 → 3
/2 at the offset (120′′, −40′′),
suggesting negligible (<20%)
optical depth broadening. Thus, the non-thermal motions do not dominate the thermal
motions along the main axis E → W of the filament.
, F′ → F = 0 → 1,1/2 → 3
/2 at the offset (120′′, −40′′),
suggesting negligible (<20%)
optical depth broadening. Thus, the non-thermal motions do not dominate the thermal
motions along the main axis E → W of the filament.
However, approximately five times larger linewidths Δv ~ 1 km s-1 were detected at a few points spread over the northern and southern ridges of the filament and in the vicinity of the outlier at the offset (−200″, −40″) with a maximum Δv = 1.0(1) km s-1 at (Δα,Δδ) = ( −240″, −40″). The increasing contribution of the non-thermal motions to the NH3 linewidths at the filament bounds correlates with the dynamics of the surrounding C18O and 13CO gas, showing Δv(C18O) = 1.3 km s-1 and Δv(13CO) = 1.9 km s-1 at a mean excitation temperature of 10 K (S94). At this temperature, the thermal width of the carbon monoxide molecules is Δvth ~ 0.12 km s-1, i.e., non-thermal motions such as infall, outflow, or turbulence dominate over the thermal motions in the outskirts of the filament. Therefore, the internal (C18O) and external (13CO) gas envelopes have a dynamical behavior that differs from that of the central ammonia string.
We also note that there are no visible correlations between the distribution of the NH3 linewidths on the ammonia map in Fig. 10a and the directions of the jet and bipolar nebula outflows that are shown in Fig. 5. This can be understood if the axes of both jet and bipolar nebula were almost orthogonal to the line of sight.
Another way of looking at velocity coherence is to consider distributions of the Mach
number defined locally as 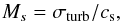 (5)where σturb is the
non-thermal velocity dispersion derived from the apparent line width (Eq. (A.7) in L13),
and cs is the thermal sound speed
(5)where σturb is the
non-thermal velocity dispersion derived from the apparent line width (Eq. (A.7) in L13),
and cs is the thermal sound speed
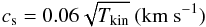 (6)for an isothermal gas (Eq. (A.8) in L13).
(6)for an isothermal gas (Eq. (A.8) in L13).
Figure 10b shows the distribution of the calculated Mach numbers at the 54 positions where Tkin was measured directly from the relative population of the NH3(1, 1) and (2, 2) energy levels. Panel (10b) demonstrates that the ratio of the non-thermal velocity dispersion to the sound speed along the main axis E → W lies in the interval 0.3 ≲ Ms ≲ 0.8; i.e., the filament has subsonic internal velocity dispersion in the coherent velocity region embedded in a generally supersonic turbulent envelope characterized by Ms(C18O) ~ 3 and Ms(13CO) ~ 4.
Finally, we conclude that the filament consists of at least three kinematically distinguished fragments with respect to their motion around the horizontal E → W axis (αβ, bar, and γ fragments), while all of them are involved in a common rotation around the vertical axis S → N. The αβ and γ fragments spin around the E → W axis in opposite directions that can be ascribed to dextral and sinistral chiralities. The bar shows no revolution, whereas the motion of the whole ammonia filament around the S → N axis resembles a simple solid-body rotation. All these properties imply that the filament is kinematically detached from the outer layer traced by 13CO emission. The revealed coherence in the spatial and velocity distributions may, as usually supposed, be the manifestation of the intermittency of turbulent dissipation in molecular clouds connected with processes of star formation (e.g., Hennebelle & Falgarone 2012). The opposite chirality of the substructures in L1251A puts it in a list of fascinating objects that show a filamentary structure of a complex helix-like geometry (Carlqvist 2005).
3.3. Mass of the filament
The mass of NH3
gas can be estimated from the dynamical characteristics and linear scale of the filament.
If the cloud rotates as a solid body, the total mass of the ammonia filament stems from
equilibrium of the centrifugal and gravitational forces: 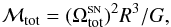 (7)where G is the gravitational
constant, and R is the radius along the major axis at which the
linear velocity V =
ΩR is measured. For
(7)where G is the gravitational
constant, and R is the radius along the major axis at which the
linear velocity V =
ΩR is measured. For
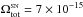 rad s-1 and R ≈ 1.65 pc, one finds
ℳtot ≈ 45
ℳ⊙. A two times higher mass was derived from the
C18O data in S94
for cores A and B: ℳA ≈ 56
ℳ⊙, and ℳB ≈ 38 ℳ⊙.
rad s-1 and R ≈ 1.65 pc, one finds
ℳtot ≈ 45
ℳ⊙. A two times higher mass was derived from the
C18O data in S94
for cores A and B: ℳA ≈ 56
ℳ⊙, and ℳB ≈ 38 ℳ⊙.
If the considered object is an ellipsoid of revolution with axes ℓ1,ℓ2,ℓ3,
then its volume is 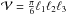 , and for a uniform medium of mean density
⟨ ρ ⟩, its
mass is
, and for a uniform medium of mean density
⟨ ρ ⟩, its
mass is 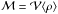 . Substituting
numerical values for ℓ1,ℓ2,ℓ3
and for ℳ = ℳtot,
and using a mean molecular weight μ = 2.33, we find the mean gas number density
⟨ n ⟩ H = ⟨
ρ ⟩ /μmH = 5.5 ×
103 cm-3, where mH is the mass of the hydrogen atom. A
similar estimate, ⟨ n ⟩ = 6.0
× 103 cm-3, is obtained if we adopt the rod-like geometry
introduced in Sect. 3.1.
. Substituting
numerical values for ℓ1,ℓ2,ℓ3
and for ℳ = ℳtot,
and using a mean molecular weight μ = 2.33, we find the mean gas number density
⟨ n ⟩ H = ⟨
ρ ⟩ /μmH = 5.5 ×
103 cm-3, where mH is the mass of the hydrogen atom. A
similar estimate, ⟨ n ⟩ = 6.0
× 103 cm-3, is obtained if we adopt the rod-like geometry
introduced in Sect. 3.1.
These gas densities are almost an order of magnitude lower than the ⟨ n ⟩ H2 ~ 4 ×
104 cm-3 derived from ammonia emission along the major axis – a
fact suggesting that there should be a gas number density gradient along the minor axes.
Usually, the shape of a filament radial profile is described by a Plummer-like function of
the form: ![\begin{equation} \rho(r) = {\rho_c}/{\left[ 1 + (r/r_0)^2 \right]^{\kappa/2}} , \label{Eq8} \end{equation}](/articles/aa/full_html/2016/02/aa27783-15/aa27783-15-eq320.png) (8)where ρc is the central density
of the filament, and r0 is the radius in the plane orthogonal
to the major axis (André et al. 2014).
(8)where ρc is the central density
of the filament, and r0 is the radius in the plane orthogonal
to the major axis (André et al. 2014).
For an isothermal gas cylinder in hydrostatic equilibrium, the power-law exponent of the density profile is κ = 4 and n(r) ∝ r-4 (Ostriker 1964). However, observed filaments often show n(r) ∝ r-2, i.e., κ ≈ 2 (e.g., Lada et al. 1999), suggesting that dense filaments may not be strictly isothermal but better described by a polytropic equation of state, P(r) ∝ ρ(r)γ or T(r) ∝ ρ(r)γ − 1 with γ ≲ 1 (Palmeirim et al. 2013).
It is easy to show that our case also requires κ ≈ 2 to match the aforementioned estimates of the gas number densities ⟨ n ⟩ H and ⟨ n ⟩ H2. Thus, the filament L1251A is centrally condensed along its major axis, the NH3 substructure is the densest part of it, its density profile is close to the Plummer model with κ ≈ 2, and the total mass of the ammonia substructure is about 45 ℳ⊙.
3.4. Gravitational equilibrium
The bound prestellar filaments are usually gravitationally unstable and prone to forming
fragments (e.g., André et al. 2014). A
self-gravitating cylinder will be in hydrostatic equilibrium only when its mass per unit
length, 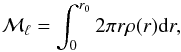 (9)has the special critical value (Ostriker
1964):
(9)has the special critical value (Ostriker
1964): 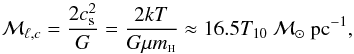 (10)where cs is the
isothermal sound speed, and T10 the gas temperature in units of 10
K. Since the mean molecular weight μ = 2.33 is expected to be almost constant in the
interstellar molecular clouds, the critical line mass ℳℓ,c is
independent of the gas density and determined only by the kinetic temperature
Tkin.
(10)where cs is the
isothermal sound speed, and T10 the gas temperature in units of 10
K. Since the mean molecular weight μ = 2.33 is expected to be almost constant in the
interstellar molecular clouds, the critical line mass ℳℓ,c is
independent of the gas density and determined only by the kinetic temperature
Tkin.
If the mass per unit length ℳℓ is equal to ℳℓ,c, then the self-gravitational force per unit mass and the pressure gradient force per unit mass are equal5. If ℳℓ< ℳℓ,c, then a filament expands until it is supported by external pressure. Otherwise, when ℳℓ> ℳℓ,c, the filamentary structure is gravitationally unstable, and self-gravity dominates the pressure force. In this case, if ℳℓ ≫ ℳℓ,c, perturbations do not grow much and the filament collapses toward the major axis without fragmentation (Inutsuka & Miyama 1992; Inutsuka & Miyama 1997).
Adopting ⟨ T ⟩ kin
≈ 10 K (Sect. 3.1), one finds a
critical mass per unit length for the ammonia filament of ℳℓ,c ≈ 17 ℳ⊙
pc-1. Taking into account that the volumes of
condensations 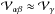 ,
their mean gas densities ⟨ n ⟩
αβ ≈ 2 ⟨ n ⟩
γ, and the projected lengths
ℓαβ ≈ 2.2 pc,
ℓγ ≈ 1.1 pc (Sect.
3.1), the masses of the αβ and γ condensations are equal
to ℳαβ ~ 30
M⊙ and ℳγ ~ 15
M⊙. This gives the line masses of
ℳℓ,αβ =
ℳℓ,γ ~ 14 ℳ⊙
pc-1. Thus, the masses per unit length are less than or
comparable to ℳℓ,c which is expected for gas in
hydrostatic equilibrium.
,
their mean gas densities ⟨ n ⟩
αβ ≈ 2 ⟨ n ⟩
γ, and the projected lengths
ℓαβ ≈ 2.2 pc,
ℓγ ≈ 1.1 pc (Sect.
3.1), the masses of the αβ and γ condensations are equal
to ℳαβ ~ 30
M⊙ and ℳγ ~ 15
M⊙. This gives the line masses of
ℳℓ,αβ =
ℳℓ,γ ~ 14 ℳ⊙
pc-1. Thus, the masses per unit length are less than or
comparable to ℳℓ,c which is expected for gas in
hydrostatic equilibrium.
4. Discussion
From the analysis of the dynamical stability of dark cloud L1251, Sato et al. (1994) concluded that all five C18O cores embedded in molecular gas (see Fig. 1) are gravitationally stable. The present observations in NH3 inversion lines revealed that two of them, the cores A and B, have an elongated filament-like morphology and a complex velocity field. The filament exists for about 107 yr and exhibits two types of global motions: (i) it rotates as a whole around the minor S–N axis, and (ii) its eastern and western fragments revolve around the major E–W axis in opposite directions of dextral and sinistral chirality. By analogy with the α-ω geodynamo mechanism with broken symmetry (see, e.g., Fig. 2 in Love 1999), we suggest that these kinds of motions in L1251A may be maintained by helical magnetic fields threaded through the cloud.
Dynamo is a mechanism that converts kinetic energy into electromagnetic energy. The motion of an electrical conductor through a magnetic field induces electrical currents that can generate secondary induced magnetic fields that are sustained as long as energy is supplied. A self-exciting dynamo requires no external fields or currents to sustain the dynamo, aside from a weak seed magnetic field to get started. The ω-effect is a conversion of poloidal field to toroidal that is caused by differential rotation (shear) of toroidal flows on the cloud surface. The α-effect is a regeneration of the poloidal field from toroidal field due to upwelling poloidal flows possessing vorticity.
In this picture, the central region of L1251A (the bar between the eastern and western fragments), which shows no revolution, is the place where the helical magnetic field wrapped around the filament changes polarity from negative and positive. As a result we observe the eastern and western fragments revolving in opposite directions.
The physical parameters measured in L1251A allow
us to evaluate the efficiency of the α-ω dynamo mechanism. The importance of magnetic
induction relative to magnetic diffusion is characterized by the magnetic Reynolds number
(e.g., Brandenburg & Subramanian 2005):
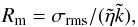 (11)where σrms is the
typical rms velocity,
(11)where σrms is the
typical rms velocity, 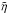 the resistivity (cm2 s-1 in cgs units), and
the resistivity (cm2 s-1 in cgs units), and
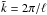 is the wavenumber. If, for numerical
estimate, we take for
is the wavenumber. If, for numerical
estimate, we take for 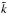 a lower limit on the size of eddies close to
the molecular mean free path in a dense core,
a lower limit on the size of eddies close to
the molecular mean free path in a dense core, 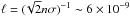 pc (the effective cross section
σ ~
10-15 cm2, the gas density n ~ 4 × 104
cm-3), then
pc (the effective cross section
σ ~
10-15 cm2, the gas density n ~ 4 × 104
cm-3), then
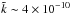 cm-1.
cm-1.
In dark clouds the gas is mostly neutral with low kinetic temperatures. In this case, the
resistivity is given by (e.g., Balbus & Terquem 2001): 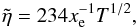 (12)where xe =
ne/n is the ionization
fraction, and n
the number density of neutral particles.
(12)where xe =
ne/n is the ionization
fraction, and n
the number density of neutral particles.
If gas is shielded well from the external incident radiation, the gas temperature mainly comes from the heating by cosmic rays. Then the value of temperature is determined by the balance between heating and cooling. If the only source of heating are the cosmic rays and the cooling comes from the line radiation, then a lower bound on the kinetic temperature is about 8 K (Goldsmith & Langer 1978).
The ionization fraction xe at the ionization-recombination
equilibrium is approximately given by (e.g., Draine et al. 1983):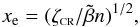 (13)where ζCR is the
ionization rate by cosmic rays, and
(13)where ζCR is the
ionization rate by cosmic rays, and 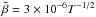 cm3 s-1 is the dissociative recombination rate. Adopting the
midplane value of ζCR
≈ 10-17 s-1 (e.g., Sano & Stone 2002) and the measured mean temperature Tkin≈ 10 K for the ionization rate due to cosmic
rays, we find xe
~ 2 × 10-8, so that
cm3 s-1 is the dissociative recombination rate. Adopting the
midplane value of ζCR
≈ 10-17 s-1 (e.g., Sano & Stone 2002) and the measured mean temperature Tkin≈ 10 K for the ionization rate due to cosmic
rays, we find xe
~ 2 × 10-8, so that
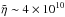 cm2 s-1. Then for σrms ~ 0.1 km s-1, we estimate the magnetic
Reynolds number Rm ≳
600.
cm2 s-1. Then for σrms ~ 0.1 km s-1, we estimate the magnetic
Reynolds number Rm ≳
600.
To control bulk motions, magnetic and non-thermal energy densities should be comparable,
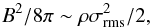 (14)where ρ is the gas density, and
σrms the rms non-thermal (turbulent)
velocity. With σrms
~ 0.1 km s-1 and ρ =
μmHnH ~ 3
× 10-19 g cm-3, the mean equipartition strength of the magnetic field
for the filament L1251A is expected to be
⟨ B ⟩ ~
20μG, which is a typical value of B measured in dark clouds
(e.g., Crutcher 2012).
(14)where ρ is the gas density, and
σrms the rms non-thermal (turbulent)
velocity. With σrms
~ 0.1 km s-1 and ρ =
μmHnH ~ 3
× 10-19 g cm-3, the mean equipartition strength of the magnetic field
for the filament L1251A is expected to be
⟨ B ⟩ ~
20μG, which is a typical value of B measured in dark clouds
(e.g., Crutcher 2012).
To amplify a dynamically significant magnetic field from a background initially weak seed
field in a self-gravitating system, the gas must persist for a number of free-fall times,
which is (e.g., McKee & Ostriker 2007)
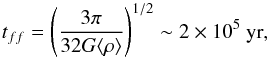 (15)for L1251A. The value of tff, together with the
estimated periods of the filament spinning (t ~ 107 yr) and the age of the
supernova remnants (t ~
106−7 yr), indicates that there has been plenty of time
for the magnetic field to build up in the filament.
(15)for L1251A. The value of tff, together with the
estimated periods of the filament spinning (t ~ 107 yr) and the age of the
supernova remnants (t ~
106−7 yr), indicates that there has been plenty of time
for the magnetic field to build up in the filament.
Theoretically, it has been suggested that a number of processes induce and maintain magnetic fields in dark clouds. Among them, mechanisms of a linear growth with time of the interstellar seed field from B ~ 1μG to a typical B ~ 20μG inside dark clouds are associated with a winding-up of frozen-in fields. Their efficiency is proportional to the number of rotations. Since the period for a complete rotation of the filament L1251A is comparable to its lifetime, which should be near the age of the supernova remnants, this type of mechanism can be excluded.
Other processes are based on an exponential growth that is realized in a dynamo
amplification due to shear flows, turbulent, and Coriolis motions. The exponential growth
can, in principle, strengthen the magnetic field on a timescale that resembles the filament
rotation period. In case L1251A, different stages
of the filament formation may be characterized by different types of magnetic field growth.
In the first stages, when supernovae shock waves hit the cloud and caused strong turbulence,
weak seed magnetic fields were exponentially amplified by the small-scale turbulent dynamo
(e.g., Beresnyak & Lazarian 2015). At present,
turbulent motions in the centrally condensed gas along the major axis are subsonic so that
the turbulent dynamo is less effective. On the other hand, complex kinematics of L1251A and differential rotation may cause the Coriolis
forces that tend to organize gas motions and electric currents into large scale Taylor
columns (Taylor 1923) aligned with the rotation axis
that, in turn, lead to induction of a magnetic field similar to the ω-dynamo effect. The Taylor
columns are formed when the Coriolis force is far more significant than the inertia force.
The ratio between these two forces is characterized by the Rossby number, which is a
dimensionless ratio of the inertia force over the Coriolis force: 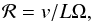 (16)where v is the velocity of a parcel
of fluid (a small amount of higher density fluid), L is its scale (diameter),
and Ω is the angular rotation.
If the filament rotates more quickly than the parcel moves through it (i.e., ℛ < 1), the gas flow is dragged across the
filament at right angles to the spin axis and, thus, lifts and twists magnetic field lines,
which is a similar process to the α-dynamo effect. Both α- and ω-dynamo can maintain the
strength of the magnetic field close to the equilibrium value given by Eq. (14).
(16)where v is the velocity of a parcel
of fluid (a small amount of higher density fluid), L is its scale (diameter),
and Ω is the angular rotation.
If the filament rotates more quickly than the parcel moves through it (i.e., ℛ < 1), the gas flow is dragged across the
filament at right angles to the spin axis and, thus, lifts and twists magnetic field lines,
which is a similar process to the α-dynamo effect. Both α- and ω-dynamo can maintain the
strength of the magnetic field close to the equilibrium value given by Eq. (14).
5. Conclusions
Three hundred positions toward the C18O cores A and B within the dark cometary-shaped cloud L1251 were observed in the NH3(1, 1) and (2, 2) inversion lines with the Effelsberg 100-m telescope at a spectral resolution of 0.045 km s-1 and a spatial resolution of 40′′. The main results are summarized as follows.
-
1.
For the first time, we detect in L1251 a long and narrow structurecovering a38′ × 3′ angular range (~3.3 pc × 0.3 pc) in the E–W direction. The integrated ammonia intensity distribution is not homogeneous but concentrated in three condensations (α, β, and γ) which form a rod-like filament. All of them are involved in a common rotation around the vertical S–N axis with angular velocity
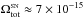 rad s-1.
rad s-1. -
2.
The condensations exhibit a complex dynamical behavior: combined α and β fragments are counter-rotating around the major E–W axis with respect to the 13CO envelope of the filament, whereas the γ fragment co-rotates with this envelope. For both of them, the angular velocity is | ΩEW | ≈ 2 × 10-14 rad s-1. The central part of the filament between these two kinematically distinct regions does not show any rotation around the E–W axis.
-
3.
The dextral and sinistral chirality of the αβ and γ condensations indicates the presence of magnetic field helicity of two types, negative and positive, supported by dynamo action.
-
4.
An exclusive feature of the filament is extremely narrow ammonia lines observed at several “quiet zones” where the linewidths are Δv ~ 0.1 km s-1, meaning that they reveal almost purely thermal broadening at kinetic temperatures as low as ~8 K.
-
5.
Along the major E–W axis, we observed both the NH3(1, 1) and (2, 2) transitions at 54 positions and found the mean ammonia column density ⟨ N ⟩ NH3 = (1.03 ± 0.05) × 1015 cm-2 and the gas number density ⟨ n ⟩ H2 = (3.9 ± 1.3) × 104 cm-3 under the assumption that the beam filling factor η = 1. The mean kinetic temperature is ⟨ Tkin ⟩ = 10.12 ± 0.08 K.
-
6.
The central part of the filament is organized into a coherent structure akin to those found in some other star-forming dense cores.
-
7.
The Mach numbers calculated at the 54 positions within the coherent velocity region range between 0.3 and 0.8, which means that the filament shows subsonic internal velocity dispersion. The coherent velocity region is embedded in a generally supersonic turbulent envelope with Mach numbers ~3–4 as derived from observations of C18O and 13CO lines.
-
8.
The filament L1251A is centrally condensed along the E–W axis, the NH3 substructure is the densest part of it, the density profile is close to the Plummer model with the power-law exponent κ ≈ 2, and the total mass of the ammonia substructure is ℳ ~ 45 ℳ⊙.
-
9.
The line masses ℳℓ of the αβ and γ condensations ℳℓ,αβ = ℳℓ,γ ~ 14 ℳ⊙ pc-1 are less than or comparable to the critical value of ℳℓ,c ~ 17 ℳ⊙ pc-1 which is expected for gas in hydrostatic equilibrium.
Helical magnetic fields aligned with the spin E–W axis play an important role in the evolution of the filament. The magnetic Reynolds number Rm ≳ 600 means that magnetic induction dominates magnetic diffusion, a condition required for ω-dynamos. The Rossby number ℛ < 1 indicates that the Taylor columns are dragged across the filament leading to the α-dynamo effect. The joint action of both the ω- and α-dynamo mechanisms can provide a large scale magnetic field of positive and negative helicity that, in turn, results in the observed gas motions of opposite chirality.
Acknowledgments
We thank the staff of the Effelsberg 100-m telescope for their assistance in observations, and we appreciate Vadim Urpin’s comments on an early version of the manuscript. We also thank our referee Gösta Gahm for suggestions that led to improvements in the paper. S.A.L. is grateful for the kind hospitality of the Max-Planck-Institut für Radioastronomie and Hamburger Sternwarte where this work was prepared. This work was supported in part by the grant DFG Sonderforschungsbereich SFB 676 Teilprojekt C4, and by the RFBR grant No. 14-02-00241.
References
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: Univ. Arizona Press), 27 [Google Scholar]
- Balbus, S. A., & Terquem, C. 2001, ApJ, 552, 235 [Google Scholar]
- Belloche, A. 2013, EAS, 62, 25 [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Beresnyak, A., & Lazarian, A. 2015, Astrophys. Space Sci. Lib., 407, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Carlqvist, P. 2005, A&A, 436, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlqvist, P., Gahm, G. F., & Kristen, H. 2003, A&A, 403, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Walmsley, C. M., & Cesaroni, R. 1990, A&AS, 83, 119 [NASA ADS] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, 1 [Google Scholar]
- Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. K., Rosolowsky, E., Evans, N. J., II,Cyganowski, C., & Urquhart, J. S. 2011, ApJ, 741, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Gahm, G. F., Carlqvist, P., Johansson, L. E. B., & Nikolić, S., 2006, A&A, 454, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1978, ApJ, 222, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., Lebrun, F., Arnaud, M., Dame, T. M., & Thaddeus, P. 1989, ApJ, 347, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&AR, 20, 55 [Google Scholar]
- Hily-Blant, P., Falgarone, E., Pineau des Forêts, G., & Phillips, T. G. 2004, Astrophys. Space Sci., 292, 285 [Google Scholar]
- Hily-Blant, P., Teyssier, D., Philipp, S., & Güsten, R. 2005, A&A, 440, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1934, ApJ, 79, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Jijina, J., Hyers, P. C., & Adams, F. C. 1999, ApJS, 125, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, N. J., II, & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., Di Francesco, J., et al. 2009, ApJS, 185, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Konyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kukolich, S. G. 1967,Phys. Rev., 156, 83 [Google Scholar]
- Kun, M., & Prusti, T. 1993, A&A, 272, 235 [NASA ADS] [Google Scholar]
- Lada, C. J., Alves, J., & Lada, E. A. 1999, ApJ, 512, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrun, F. 1986, ApJ, 306, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Di Francesco, J. D., Bourke, T. L., Evans, N. J., II, & Wu, J. 2007, ApJ, 671, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Lee, H.-G., Shinn, J.-H., et al. 2010, ApJ, 709, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Levshakov, S. A., Molaro, P., Lapinov, A. V., et al. 2010, A&A, 512, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Henkel, C., Reimers, D., et al. 2013a, A&A, 553, A58 (L13) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Reimers, D., Henkel, C., et al. 2013b, A&A, 559, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Henkel, C., Reimers, D., & Wang, M. 2014, A&A, 567, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Love, J. J. 1999, Astron. Geophys., 40, 14 [CrossRef] [Google Scholar]
- Lynds, B. T. 1962, ApJS, 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Faure, A., Scifoni, E., & Wiesenfeld, L. 2009, MNRAS, 399, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 1998, Sol. Phys., 182, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. C., Wilson, C. D., & Fiege, J. D. 2001, ApJ, 562, 400 [NASA ADS] [CrossRef] [Google Scholar]
- McCammon, D., Burrows, D. N., Sanders, W. T., & Kraushaar, W. L. 1983, ApJ, 269, 107 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., Fuller, G. A., Goodman, A. A., & Benson, P. J. 1991, ApJ, 376, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Goodman, A. A., Arce, H. G., et al. 2010, ApJ, 712, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Poidevin, F., Bastien, P., & Matthews, B. C. 2010, ApJ, 716, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Pound, M. W., Reipurth, B., & Bally, J. 2003, AJ, 125, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C (Cambridge: Cambridge Uni. Press) [Google Scholar]
- Ryden, B. S. 1996, ApJ, 471, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Sano, T., & Stone, J. M. 2002, ApJ, 570, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, F., & Fukui, Y. 1989, ApJ, 343, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, F., Mizuno, A., Nagahama, T., & Onishi, T. 1994, ApJ, 435, 279 (S94) [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Clark, P. C., & Bonnell, I. A. 2009, MNRAS, 396, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, G. I., 1923, Proc. Roy. Soc. (Londona), A104, 213 [NASA ADS] [Google Scholar]
- Tóth, L. V., & Walmsley, C. M. 1996, A&A, 311, 981 (TW96) [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Morphology of a cometary-shaped cloud L1251 as revealed in Sato et al. 1994. The contour shows the integrated 13CO(1–0) emission at the lowest level of 1.5 K km s-1 (Fig. 2b in Sato et al. 1994). Five ellipses represent locations and angular sizes of five C18O dense cores (Tables 1 and 2 in S94). The rotation of the individual cores is shown by small-sized gray arc arrows. The global rotation of the 13CO cloud is indicated by the large-sized arc arrow. For each arc arrow, denser gray color indicates the outer near side of the surface of the arc. The dashed lines are the rotation axes. The (0, 0) map position is RA = 22:31:02.3, Dec = 75:13:39 (J2000). The adopted distance to the cloud is 300 pc. |
| In the text | |
 |
Fig. 2 a) NH3(1, 1) integrated intensity map (∫TMBdv in units of K km s-1) of the molecular core L1251A. Each color box has a size of 40′′ × 40′′, and its bottom left corner corresponds to the telescope pointing. The parameters of the NH3 peaks α,β, and γ are given in Table 1. The core exhibits a filamentary structure that can be enveloped by an ellipse (dashed line) with principal axes of 1140′′ and 89′′. b) Schematic configuration of the filament and peak positions of the ammonia cores T1–T4. The gray contours restrict ammonia emission to the lowest level of the integrated NH3(1, 1) emission as in Fig. 3 in Tóth & Walmsley (1996). The location of the IRS sources are from Lee et al. (2010). The red star is the IR source detected by IRAS. The filled blue and red circles outline areas of the narrowest ammonia lines with FWHP line widths of, respectively, Δv ~ 0.2 km s-1, and ~0.1 km s-1; their offsets are listed in Table 1. c) The sum over the integrated intensities for a given RA, ∑ ΔδIΔα(Δδ). The (0, 0) map position and the distance to the source are as in Fig. 1. |
| In the text | |
 |
Fig. 3 Distributions of the measured parameters in L1251A: a) the gas volume density, nH2; b) the NH3 column density, NNH3; c) the kinetic temperature, Tkin; and (d) the excitation temperature, Tex. Three parameters nH2, NNH3, and Tkin were measured at the 54 positions where both the NH3(1, 1) and (2, 2) lines were observed, whereas Tex was estimated from the NH3(1, 1) lines, which are not very weak. Each color box has a size of 40′′×40′′ and its bottom left corner corresponds to the telescope pointing. The contours are the NH3(1, 1) integrated intensity map. The starting point for the contour levels is 0.2 K km s-1; the increment is 1.0 K km s-1. The (0, 0) map position is as in Fig. 1. We note that for the beam filling factor η< 1, certain parameters could be larger (see Sects. 3 and 3.1 for details). |
| In the text | |
 |
Fig. 4 Thickness along the line of sight through the core L1251A estimated from the measured column densities NNH3 and number densities nH2 shown in Fig. 3. The mean abundance ratio of [ NH3 ]/[ H2 ] = 4.6 × 10-8 (Dunham et al. 2011) is fixed for the whole filament. The (0, 0) map position is as in Fig. 1. We note that for the beam filling factor η< 1, the thickness is smaller (see Sects. 3 and 3.1 for details). |
| In the text | |
 |
Fig. 5 Portion of Fig. 17 from Kirk et al. (2009) with extended structure toward L1251A and L1247. The gray scale shows the distribution of visual extinction as derived from the Digitized Sky Survey (Dobashi et al. 2005), and the superimposed higher resolution extinction maps (outlined by solid straight black lines) observed with the Spitzer Infrared Array Camera (IRAC; 3.6–8.0 μm) and Multiband Imaging Photometer (MIPS; 24–160 μm). Two dashed lines refer to Dobashi AV = 1 mag and Spitzer AV = 5 mag. The colored markers show the location and spectral type of the young stellar object (YSO) candidates: red/green/blue for Class I/Flat/Class II. The black stars are the same markers as in Fig. 2b. The NH3(1, 1) integrated intensity map, as in Fig. 4, is denoted by the red contours. The approximate orientation and linear size of a jet extending about 10′ and a small bipolar nebula to the east of the jet (solid green lines) are copied from Fig. 1 in Lee et al. (2010). |
| In the text | |
 |
Fig. 6 Same as Fig. 4 but for the NH3(1, 1) radial velocity field (VLSR). |
| In the text | |
 |
Fig. 7 Position-velocity diagram of NH3(1, 1) along the direction of the velocity gradient (E → W). At each offset Δα, the measured centroid velocities (VLSR) are averaged across the filament in the direction S → N. The error bars (the standard deviation of the mean) result from this averaging. The different positions were weighted inversely proportional to the variance. The linear regression for the total range is shown by red: V0 = −4.199(1)−0.000303(3)Δα (km s-1) (here Δα is in arcsec). For the αβ condensation (−480″ ≤ Δα ≤ 600″), the regression line is practically the same. For the γ condensation (−1640″ ≤ Δα ≤ −800″), it is shown by a blue line with V0 = − 4.38(1) −0.00046(1)Δα (km s-1). The number in parentheses is the one-sigma (1σ) uncertainty in the last digit of the given value. The (0, 0) map position is as in Fig. 1. |
| In the text | |
 |
Fig. 8 Histograms are the probability density functions (pdfs) of line centroid velocity fluctuations ΔV = VLSR − V0, and the smooth curves are their approximations by Gaussians. Here V0 is the systemic velocity component defined by the regression lines shown in Fig. 7. Panels a) and b) represent the αβ (red regression line in Fig. 7) and γ (blue regression line in Fig. 7) condensations. The lateral peaks labeled by the letters “N” and “S” correspond to the northern and southern ridges of the filament. Note the opposite chirality of the angular rotation around the horizontal axis E → W (see Sects. 3.2.2 and 3.2.4 for details). |
| In the text | |
 |
Fig. 9 Histogram is the probability density function (pdf) of line centroid velocity fluctuations between neighboring positions over the whole NH3 map of the filament L1251A except for the outlier at the offset (Δα,Δδ) = ( − 200′′, −40′′). In the upper left hand corner, the grid with color points illustrates the calculation of ΔVi,j: for a current position (i,j) (marked by red), the velocity differences are calculated between each blue point and the central red point. The total number of different pairs is 680. The histogram is approximated by a Gauss (black) and a Lorentz (red) function with the widths (FWHP) of ΔvG = 0.22 km s-1 and ΔvL = 0.11 km s-1. |
| In the text | |
 |
Fig. 10 a) Linewidths, Δv, of the ammonia (1, 1) lines (FWHP) measured toward the core L1251A. b) Mach numbers, Ms, of non-thermal motions at the 54 positions where Tkin was measured directly from the relative population of the (1, 1) and (2, 2) energy levels of NH3. The contours are as in Fig. 3. The (0, 0) map position is as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


