| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201526704 | |
| Published online | 23 December 2015 | |
COSMOGRAIL: the COSmological MOnitoring of GRAvItational Lenses
XV. Assessing the achievability and precision of time-delay measurements
1 Laboratoire d’astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
e-mail: vivien.bonvin@epfl.ch
2 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
3 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, B5c, 4000 Liège, Belgium
Received: 9 June 2015
Accepted: 28 September 2015
COSMOGRAIL is a long-term photometric monitoring of gravitationally lensed quasars aimed at implementing Refsdal’s time-delay method to measure cosmological parameters, in particular H0. Given the long and well sampled light curves of strongly lensed quasars, time-delay measurements require numerical techniques whose quality must be assessed. To this end, and also in view of future monitoring programs or surveys such as the LSST, a blind signal processing competition named Time Delay Challenge 1 (TDC1) was held in 2014. The aim of the present paper, which is based on the simulated light curves from the TDC1, is double. First, we test the performance of the time-delay measurement techniques currently used in COSMOGRAIL. Second, we analyse the quantity and quality of the harvest of time delays obtained from the TDC1 simulations. To achieve these goals, we first discover time delays through a careful inspection of the light curves via a dedicated visual interface. Our measurement algorithms can then be applied to the data in an automated way. We show that our techniques have no significant biases, and yield adequate uncertainty estimates resulting in reduced χ2 values between 0.5 and 1.0. We provide estimates for the number and precision of time-delay measurements that can be expected from future time-delay monitoring campaigns as a function of the photometric signal-to-noise ratio and of the true time delay. We make our blind measurements on the TDC1 data publicly available.
Key words: methods: data analysis / gravitational lensing: strong / cosmological parameters
© ESO, 2015
1. Introduction
The methods used to constrain current cosmological models all benefit from independent measurements of the local value of the Hubble parameter, H0 (see e.g. Fig. 48 of Weinberg et al. 2013). One way of achieving a measurement of H0 is based on time delays in strong gravitational lens systems. The method, first suggested by Refsdal (1964), proposes measuring the differences in the travel time of photons coming from multiple images of a distant source, such as a quasar. This time delay, Δt, is connected to the overall matter distribution responsible for the lensing effect, and to the time-delay distance DΔt to the lens, i.e. H0, with some sensitivity to curvature and dark energy as well (e.g., Suyu et al. 2014).
Exploiting this relationship to constrain H0 and cosmology in general requires both an accurate mass model for the lens and accurate time delay measurements (see e.g., Suyu et al. 2012; Linder 2011; Moustakas et al. 2009). Modelling the lens mass in an unbiased way is difficult and prone to degeneracies known as the mass-sheet degeneracy (e.g., Schneider & Sluse 2013) and, more generally, the source plane transformation described in Schneider & Sluse (2014). The effect of lens model degeneracies can be mitigated by combining astrometric information from high resolution imaging, measurements of the lens dynamics, priors on the mass density profile of the lens, and an analysis of structures along the line of sight (e.g., Suyu et al. 2014; Greene et al. 2013; Fadely et al. 2010; Treu & Koopmans 2002; Falco et al. 1997; Keeton & Kochanek 1997). Integral field spectroscopy coupled with the adaptive optics that is becoming available on the VLT and at the Keck observatory will be essential in this respect. One of the key ingredient for the method to work at all is, however, the quality of the time-delay measurements, which is the focus of the present work.
In practice, measuring time delays is achievable if the lensed source is photometrically variable. Gravitationally lensed quasars are ideal targets: the quasars can show variability accessible by moderately sized ground-based optical telescopes on timescales of a few days, while the time delays resulting from galaxy-scale lenses are typically of the order of weeks to months (see, e.g., Oguri & Marshall 2010). The intrinsic light curve of the quasar is seen shifted by the relative time delays in the different lensed images. However, this simple situation is often contaminated: microlensing by stars in the lensing galaxy introduces extrinsic variability in the individual light curves with an amplitude sometimes comparable with that of the intrinsic variability of the quasar. To yield competitive cosmological constraints, reliable time-delay measurements with percent-level precision are needed (Treu 2010). An efficient implementation of these measurements has long been hampered by how difficult it is to obtain photometric data for periods of many years at a desirable cadence, which must be close to 1 epoch per few days (Eigenbrod et al. 2005).
COSMOGRAIL is a monitoring program targeting more than 30 strongly lensed quasars using meter-class telescopes, with a cadence of 3 days for the most interesting systems. Recent results include light curves and time-delay measurements that are accurate to within a few percent points in HE 0435−1223 (Courbin et al. 2011), SDSS J1001+5027 (Rathna Kumar et al. 2013) and in RX J1131−1231 (Tewes et al. 2013b). To measure these time delays, we developed and implemented several algorithms in the form of a COSMOGRAIL curve-shifting toolbox named PyCS, described in Tewes et al. (2013a).
In the fall of 2013, a first blind time-delay measurement competition named Time Delay Challenge 1 (TDC1) was proposed to the community by Dobler et al. (2015). The two main goals of this open challenge were (1) to homogeneously assess the quality of time-delay measurement algorithms on a common set of realistic synthetic light curves, and (2) to obtain some quantitative informations on the impact of observing strategy (cadence, season length, campaign length) on time-delay measurements. We took part in this challenge and submitted time-delay estimates using the team name PyCS. Liao et al. (2015) give a summary of the results from all TDC1 participating teams, as well as some general conclusions. The present paper is complementary to Liao et al. (2015). It focuses on the PyCS methods that we also apply to real light curves, and hence assesses the quality and reliability of the COSMOGRAIL time-delay measurements.
To evaluate our existing techniques with the thousands of light curves of TDC1 under conditions similar to the analysis of COSMOGRAIL data, we separated the problem of time-delay measurement of a light curve pair into two successive stages.
-
Stage I:
we first attempt to discover a plausible time delay, withouttrying to measuring it precisely. We also evaluated how confidentwe were that the proposed approximate solution is close to the truetime delay and not a catastrophic failure. Owing to the limitedlength of the monitoring seasons, the randomness of quasarvariability, noise and microlensing, this was not possible forevery light curve pair of TDC1 or a real monitoring campaign. Wenote that in the case of TDC1 we had no prior information on thetime delay to look for, as we had no knowledge of the massdistribution in the lensing galaxy. Only the light curvesthemselves were used.
-
Stage II:
for those systems for which Stage I was successful, we then focused on accurately estimating the time delay and associated uncertainty with the PyCS techniques, constraining the algorithms to a delay range around the solution from Stage I. As the PyCS Stage II methods did not rely on a physical model of the light curves, they would not be able to deal adequately with comparing odds among very different solutions.
This two-stage structure is of general interest beyond PyCS, as the stages concern discernible aspects of the time-delay measurement problem. Stage I deals with the quantity and the purity of time-delay measurements, while Stage II deals with their actual accuracy.
The paper is structured as follows. Section 2 summarizes the data from the TDC1 and the metrics used to evaluate techniques. In Sect. 3, we present the approaches we took to address Stage I, while Sect. 4 presents the Stage II algorithms. In Sect. 5 we discuss the results, expanding on the analysis of Liao et al. (2015), and we conclude in Sect. 6.
2. Time Delay Challenge 1
The mock data used in this work are synthetic quasar light curves made publicly available in the context of the TDC1 proposed by Dobler et al. (2015). These data mimic the photometric variations seen in real gravitationally lensed quasars, with different time sampling, number of seasons, and season length. The curves are generated with simple yet plausible noise properties, and include microlensing variability. The dataset is split into five “rungs” or stages that simulate different observational strategies, each rung consisting of 1024 pairs of light curves. The rungs randomly mix microlensing, noise properties, and variability but differ in time sampling, number of seasons, and season length. These differences are listed in Table 1 of Liao et al. (2015, hereafter TDC1 paper).
Participants to the TDC1 were asked to provide their best point estimate 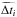 and associated 1σ uncertainty δi for as many pairs of curves as possible. The submitted entries to the challenge were then compared to the true input delays, and evaluated using simple metrics probing different properties of the estimates. The details of how the simulations were set up, as well as a discussion of these metrics are given in Dobler et al. (2015). Results obtained by the blind submissions of the different participating teams are summarized in the TDC1 paper, including our submissions denoted “PyCS”. For completeness, we briefly summarize the four main metrics:
and associated 1σ uncertainty δi for as many pairs of curves as possible. The submitted entries to the challenge were then compared to the true input delays, and evaluated using simple metrics probing different properties of the estimates. The details of how the simulations were set up, as well as a discussion of these metrics are given in Dobler et al. (2015). Results obtained by the blind submissions of the different participating teams are summarized in the TDC1 paper, including our submissions denoted “PyCS”. For completeness, we briefly summarize the four main metrics:
- 1.
the fraction f of submitted time delay estimates,
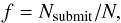 (1)where Nsubmit is the number of measured time delays and N is the total number of curves.
(1)where Nsubmit is the number of measured time delays and N is the total number of curves. - 2.
the mean χ2 between the measured time delay
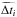 and the true value Δti weighted using the estimated uncertainties δi,
and the true value Δti weighted using the estimated uncertainties δi, 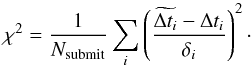 (2)
(2) - 3.
the mean “claimed” precision P of the time-delay measurements, computed from the estimated uncertainties δi,
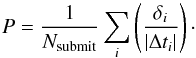 (3)
(3) - 4.
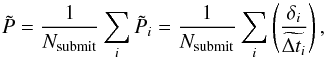 (5)where we replace in Eq. (3) the true value of Δti by its estimation
(5)where we replace in Eq. (3) the true value of Δti by its estimation 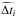 . This metric can be computed without knowing of the true time delays; its summation terms are useful, for instance to sort light curve pairs of a real monitoring survey. Second, we introduce a variant of the accuracy
. This metric can be computed without knowing of the true time delays; its summation terms are useful, for instance to sort light curve pairs of a real monitoring survey. Second, we introduce a variant of the accuracy 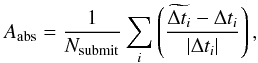 (6)where we replace the Δti in the denominator of Eq. (4) by its absolute value. While A is sensitive to a bias on the amplitude of
(6)where we replace the Δti in the denominator of Eq. (4) by its absolute value. While A is sensitive to a bias on the amplitude of 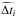 (i.e., over- or underestimation of delays), Aabs responds to signed biases.
(i.e., over- or underestimation of delays), Aabs responds to signed biases.
Statistical uncertainties on these metrics are computed following 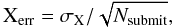 (7)where σX is the sample standard deviation of the summation terms of X = χ2, P, and A.
(7)where σX is the sample standard deviation of the summation terms of X = χ2, P, and A.
3. Stage I: discovering time delays
To apply any of the PyCS time-delay measurement algorithms (Tewes et al. 2013a) to a pair of light curves, a prior estimate of the time delay is required. Depending on the considered light curves, identifying this delay from the data might be difficult or even impossible. In the following, we describe two approaches to discover rough time-delay estimates (Stage I). Both methods rely solely on the light curves without considering the configuration of the lens system. The first method is based on a visual inspection of the light curves and is the method we used to blindly prepare submissions for the TDC1 (Liao et al. 2015). We developed the second method after the TDC1 results were released. We use the data from the challenge to evaluate the relative merits and drawbacks of each method.
3.1. D3CS: D3 visual curve shifting
This method is based on visual inspection of the light curves, in the spirit of citizen science projects (e.g., see the review by Marshall et al. 2015). To ease this process, we developed a dedicated browser-based visualization interface, using the D3.js JavaScript library1 by Bostock et al. (2011). We have made this interface public2.
The main motivations behind this time-costly yet simple approach were (1) to obtain rough initial estimates for the time delays and their associated uncertainties, and (2) to estimate how confident one can be that the time-delay estimations are not catastrophic outliers. Clearly, visual curve-shifting allows for more freedom than any automated procedure. It also permits dealing in a more flexible way with unusual behaviour of light curves, such as highly variable signal-to-noise from one season to the next, extreme microlensing, or even when the time delays are comparable in length to the visibility period of the object.
 |
Fig. 1 Left panel: stacked histogram of the errors made by the visual time-delay estimation, for the secure and plausible D3CS samples. All the secure estimations are within the displayed range of errors of ± 20 days. Only 2.6% of the time delays in the plausible sample have an absolute error larger than 20 days. Right panel: absolute time-delay error made by D3CS as a function of the true delay for both samples. |
Our interface allows users to interactively shift the light curves in time, magnitude, and flux, and to zoom in on sections of the data. It permits the visual estimation of the time delay and of an associated uncertainty. Importantly, the interface also asks to pick one of four choices of confidence category for the proposed solution:
-
1.
secure: if a catastrophic error can be excluded with a very highconfidence3;
-
2.
plausible: if the solution yields a good fit and no other solutions are seen;
-
3.
multimodal: if the proposed solution is only one among two or more possible solutions that are equally satisfactory;
-
4.
uninformative: if the data does not allow the estimate of any time delay.
Unlike massive crowdsourcing programs (e.g. Galaxy Zoo;Lintott et al. 2008), only four scientists participated in the visual inspection of TDC1 and each pair of curves was measured by at least two independent scientists. The behaviour of different users in terms of time spent per time-delay measurement span a broad range. Fast users spend on average 25 s per object, while slower users spend more than 60 s per object. This includes the time taken to measure a delay, to estimate a 1σ uncertainty, and to allocate one of the four confidence levels described above.
To obtain a single Stage I estimation for each light curve pair, we reduce the results obtained by all four scientists in a very conservative way. We systematically downgrade to multimodal the confidence category of pairs with conflicting time-delay estimates.
We define samples combining the four confidence categories as follows: sec stands for secure only, secpla stands for secure + plausible, and secplamul for secure + plausible + multimodal. The combination of all estimations is labelled all.
Figure 1 shows the distribution of the error on the time-delay estimation versus the true time delay for the secure and plausible D3CS subsamples. Table 1 summarizes the results of the D3CS classification and displays the fraction of catastrophic outliers ϵ, i.e. time-delay estimations more than 20 days away from the truth. Notably, the secure sample contains 1623 time-delay estimates free of any catastrophic outliers.
D3CS classification of the TDC1 light curve pairs.
Through this simple experiment, we have demonstrated that such an approach is easily manageable for about 5000 light curves. In total the four scientists involved in the visual estimation of the time delays spent 150 h measuring the 5120 delays. We note that 30% of the time delays were measured by three or more users.
3.2. Attempt to design an automated Stage I procedure
Visual inspection of the light curves is a time-consuming process that cannot be repeated many times. Designing an automated method whose efficiency approaches that of D3CS is therefore complementary and would help to minimize the time spent on the visual inspection. We developed such a method after the end of TDC1. The concept of the method is to estimate a time delay by fitting a spline on one of the two light curves, and computing the residual signal of the second light curve relative to the spline after applying time and magnitude shifts. The details of the method are described in Appendix A; the present section evaluates its performance and compares this estimation to the visual time-delay values.
We characterize the efficiency of the automated Stage I procedure by comparing its fraction of catastrophic outliers ϵ with that of D3CS. We define catastrophic outliers as time-delay estimations deviating from the truth by more than 20 days, i.e. with 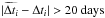 . The time-delay and confidence estimation evaluated by the automated procedure are reduced to two numbers: the depth of the absolute minimum μ and the interseason variations of the microlensing ξ. Figure 2 shows the evolution of the fraction of catastrophic outliers ϵ as a function of the cumulative number of time-delay estimations, sorted by increasing μ. The larger μ is, the more confident the automated procedure in the time-delay estimation is. We study the impact of the automated procedure parameters μ and ξ by introducing three subsamples of automated estimations:
. The time-delay and confidence estimation evaluated by the automated procedure are reduced to two numbers: the depth of the absolute minimum μ and the interseason variations of the microlensing ξ. Figure 2 shows the evolution of the fraction of catastrophic outliers ϵ as a function of the cumulative number of time-delay estimations, sorted by increasing μ. The larger μ is, the more confident the automated procedure in the time-delay estimation is. We study the impact of the automated procedure parameters μ and ξ by introducing three subsamples of automated estimations:
-
the Crude-all subsample contains all the estimations;
-
the Crude-1min subsample contains only the estimations for which the procedure finds a unique local minimum with a depth μ<1;
-
the Crude-1.5ξ subsample contains only the estimations with a magnitude shift deviation ξ< 1.5 at the location of the absolute minimum μ.
Figure 2 shows the fraction of outliers ϵ in the three subsamples and compares them to the value obtained visually with D3CS, which are shown as four diamond-shaped symbols corresponding to the combination of the four confidence categories of D3CS described in Sect. 3.1. We note that the uninformative D3CS estimations are systematically considered as catastrophic outliers here.
The selection criteria applied to the Crude-1min and Crude-1.5ξ subsamples are not able to decrease the fraction of outliers. This highlights how difficult it is to find efficient selection criteria for the automated procedure parameters, although no exhaustive exploration of the parameters space has been conducted. As expected, all the D3CS subsamples contain fewer outliers than the corresponding automated procedure subsamples. However, the efficiency of the latter are of the same order as the other automated methods presented in the TDC1 paper, which have ϵ = 2−3% when half of the TDC1 data, i.e. 2500 light curve pairs, are measured.
In conclusion, although the automated procedure presented here is less complete and reliable than D3CS, it yields candidates that can be evaluated by eye in a second phase. Such a combined approach would benefit both from the speed of the automated method and from the flexibility of the human eye estimate when dealing with a broad variety of properties in the light curves. We note, however, that in the rest of the paper, we only use the results obtained via D3CS as our Stage I estimates.
 |
Fig. 2 Cumulative evolution of the fraction of catastrophic outliers ϵ (in percentage points) as a function of the number of time-delay estimations. To produce the plot, the curves are first sorted according to the depth of their absolute minimum μ, indicated in the colour bar. Each black line (solid, dashed and dotted) represents a different subsample (see text for details). The coloured diamonds show the value of ϵ for the D3CS combined samples; the corresponding number of estimations are indicated in parenthesis. |
4. Stage II: measuring time delays
Using the Stage I results as initial estimates, we proceed in this section by running our PyCS time-delay measurement techniques on the simulated TDC1 light curves. In Tewes et al. (2013a), three different algorithms were proposed: the simultaneous fit of the light curves using free-knot splines, the regression difference technique, and an approach based on a dispersion measurement of which the free-knot splines and the regression difference technique yielded the most accurate and precise results when applied to simulated COSMOGRAIL data (in Courbin et al. 2011; Tewes et al. 2013b; Eulaers et al. 2013; Rathna Kumar et al. 2013). To analyse the TDC1 simulations, we have therefore focused on adapting only these two most promising methods for an automated use.
We note again that our Stage II methods cannot be asked to judge the plausibility of a proposed delay. This step belongs to the Stage I method, i.e. to the visual inspection with D3CS to prevent or at least reduce catastrophic outliers. In practice, despite a correct Stage I estimate, any automated Stage II method may fail to converge, or it may yield a time-delay measurement that is incompatible with the initial approximation. To prevent these failures from contaminating our measurements we systematically discard any Stage II result that does not lie within 1.5 D3CS uncertainty estimate of the D3CS point estimate. This threshold acknowledges that the uncertainty estimates obtained from D3CS are typically overestimated by a factor of 2 to 3, which has been confirmed by Liao et al. (2015). We note that this rejection affects less than 1% of the light curve pairs and has no significant influence on the f metric.
4.1. Free-knot spline technique
In the free-knot spline technique (spl), each light curve in a pair is modelled as the sum of a spline representing the intrinsic variability of the quasar, common to both images of the pair, and an independent spline representing the extrinsic variability due to microlensing. The intrinsic spline has a higher density of knots and is therefore more flexible accomodating the quasar variability, which is assumed to be faster than the microlensing variability. During the iterative fitting process, the light curves are shifted in time so as to optimize the χ2 between the data and the model light curve. To analyse a TDC1 light curve pair, we repeat this fit 20 times, starting form different initial conditions covering the Stage I uncertainty. This tests the robustness of the optimization procedure. The best model fit is then used to generate 40 simulated noisy light curves with a range of true time delays around the best-fit solution and using the temporal sampling of the original light curves. By blindly rerunning the spline fit on these simulated data, and comparing the resulting delays with the true input time delays, the delay measurement uncertainty is estimated.
We simplified and automated the spl algorithm for TDC1 with respect to the description of the free-knot spline method given in (Tewes et al. 2013a) and its applications to real COSMOGRAIL data. The main adaptations are the following:
-
1.
The temporal density of spline knots controlling the flexibilityof the intrinsic spline was computed from the signal-to-noiseratios measured on the two light curves, using an empiricalcalibration. The signal-to-noise ratios were obtained from astructure function, by comparing the typical amplitude of thelight curve variability observed on a timescale of 50 to 75 dayswith the scatter between temporally adjacent observing epochs.For the microlensing spline, the knot density was fixed to be thesame for all TDC1 pairs.
-
2.
When generating our mock light curves, we did not inject any fast microlensing signal to mimic correlated noise. Only plain white noise was added to the generative model.
-
3.
We did not analyse the time-delay measurement errors on the simulated curves as a function of true time delay. Instead, only the RMS error of these time-delay measurements was used as our total uncertainty estimate.
-
4.
Finally, we did not manually fine-tune any parameters or correct for problematic model fits.
As a result, the entire spl analysis took about 5 CPU-minutes per TDC1 pair.
 |
Fig. 3 Quantitative analysis of the discoverability of time delays through the extensive visual search with D3CS (Stage I) in the case of four-month observing seasons and a cadence of 3 days. The coloured tiles show the fraction of discovered delays as a function of the photometric precision of the fainter quasar image and the true time delay of the system. Left panel shows results from the very conservative sec sample, and central panel shows the less pure secpla sample that includes delay candidates considered as plausible (see text). Right panel, also for secpla, doubles the number of observing seasons. In each panel, only tiles covering more than three light curve pairs are shown. |
4.2. Regression difference with splines
Our second Stage II method, sdi (for spline difference), is based on the regression difference technique of Tewes et al. (2013a). To speed up the analysis, we replace the Gaussian process regressions by spline fits. In summary, the method independently fits a different spline to each of the two light curves, and then minimizes the variability of the difference between these two splines by shifting them in time with respect to each other. The advantage of this approach is that it does not require an explicit microlensing model. To estimate the uncertainty, the sdi method is run on the same simulated light curves provided by the spl technique. The sdi method has an even lower computational cost than spl.
 |
Fig. 4 Summary of metrics obtained with the Stage II algorithms spl and sdi, without any a posteriori clipping of the outliers. Bottom row presents enlargements taken from the panels on the upper row. The shaded regions represent the somewhat arbitrary target areas that were defined in the TDC1 paper. |
 |
Fig. 5 Quantitative analysis of the precision achieved for the Stage II time-delay measurement as a function of the photometric precision of the fainter quasar image and as a function of the true time delay. All panels show results from the bias-free spl technique for the secure + plausible selection of rungs 2 and 3 after rejection of the catastrophic outliers (see text). Top left panel shows the metric P as computed using the uncertainty estimates δi without using |
5. Results on the TDC1 data
In this section, we separately analyse results from the Stage I and Stage II measurement processes as obtained on the simulated light curves of TDC1. General results from Liao et al. (2015) regarding submissions prepared with our methods include the following:
-
1.
The Stage II methods spl and sdi show no significantdeviations of the accuracy A from zero, and can thus be considered as inherently unbiased, given the statistical limits due to the finite challenge size.
-
2.
The claimed precisions P of spl and sdi are very good, with χ2 values of the order of
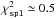 and
and 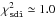 .
. -
3.
Based on results from the spl method simple power-law models for the dependence of A, P, and f on monitoring cadence, season length, and campaign length were adjusted. These relations attempt to capture general trends regarding the behaviour of all methods used in the context of TDC1, including our spl technique.
In the present paper, we focus on aspects that are complementary to the discussion of Liao et al. (2015).
5.1. Efficiency of time-delay discovery (Stage I)
We start by analysing the fraction of light curve pairs for which a time delay can be discovered with visual inspection, as a function of time delay and image brightness. This analysis relates only to the first stage of the time-delay measurement process.
Aside from the time delay and the quasar image brightness, the question of discoverability depends on observational conditions (e.g. monitoring cadence and duration) and on astrophysical characteristics (e.g. amount of quasar variability and microlensing perturbations). In the following, we select a given observing strategy and average over the astrophysical parameters of the TDC1 simulations, which follow clearly motivated distributions (Dobler et al. 2015). A large sample of light curve pairs with almost identical observing conditions can be obtained by merging rungs 2 and 3. These rungs share the fiducial three-day monitoring cadence for five seasons of four months each. The differing cadence dispersion of 0.0 days for rung 2 and 1.0 days for rung 3 (Table 1 of Liao et al. 2015) do not have a significant impact on the discoverability of time delays.
In practice, time delays can be measured accurately in pairs of light curves if the quality of both light curves is sufficient. In the following we consider as a relevant observable the photometric precision achieved in the fainter image of a pair. This is computed for each pair of light curves, as the median of the photometric error bars across the epochs of the TDC1 simulations. This is made legitimate by their overall effectiveness in representing the amplitude of the simulated noise, except for very few “evil” epochs of some systems (see Sect. 2.5 of Liao et al. 2015). However, when analysing real light curves, using the photometric scatter between the points might be a better choice than using potentially mis-estimated photometric error bars.
Figure 3 presents the distribution of the fraction of light curve pairs for which time delays could be identified via a meticulous D3CS visual inspection for two different monitoring strategies. In the left panel, only time delays categorized as secure through the visual inspection are considered as discovered. This is very conservative because in a real survey, simple lens models will help to identify the correct time delay for almost all of the plausible systems as well. For this reason we also consider the combined secpla sample, shown in the central panel.
Some of the cases categorized as multimodal could certainly also be resolved using simple lens model considerations, but in practice the vast majority of these light curve pairs contain too few clear common features to estimate a reliable time delay, even if an approximate value would be known from the modelling. We therefore consider the discoverability of the secpla selection shown in the central panel of Fig. 3 as roughly representative of the fraction of potentially helpful delays that can be reliably measured from a real monitoring campaign or survey. It can be seen as an approximate lower limit for the fraction of time delays that can be observationally constrained in the absence of prior from a lens model, provided the properties of the microlensing signal are similar to those of the simulated light curves used here. Finally, the right panel shows the evolution of this discoverability if the same monitoring strategy is carried out for five more seasons, i.e., for a total of ten years.
We observe that after five years of monitoring, light curve pairs with a photometric precision in the fainter image better than σ = 0.1 mag and a true time delay shorter than Δt = 80 days (2/3 of the season length) are very likely to yield a time-delay measurement. Pursuing the monitoring for five more years significantly increases the average chances that longer delays up to ~90% of the season length become measurable.
 |
Fig. 6 Evolution of the TDC1 metrics per rung as a function of the fraction of estimations f for the spl-sec and sdi-sec samples. The plots are sorted by increasing values of the blind precision |
5.2. Precision of time-delay measurement (Stage II)
We now turn to the analysis of the time-delay measurements (Stage II) for all systems where the time delay is successfully discovered (Stage I).
Figure 4 summarizes the results of the spl and sdi methods in terms of the metrics A (accuracy), P (claimed precision), and χ2, as defined in Sect. 2. The figure follows the same conventions as Table 4 of Liao et al. (2015), but also includes measurements obtained on the secpla samples of each rung. As expected, the results for these secpla samples are more scattered than for the sec samples. The reason for these significant offsets in A and χ2 with respect to the sec results is the stronger impact of outliers on the non-robust metrics.
To characterize the achievable precision of the Stage II measurements without being influenced by catastrophic outliers but still benefiting from a large number of light curve pairs, we now focus on the secpla sample from which we remove systems with estimated delays that are off by more than 20 days. This rejects about 1% of the secpla sample. We also note that catastrophic outliers are errors of the Stage I estimate, not Stage II.
Figure 5 presents metrics related to the Stage II time-delay measurement precision as a function of the photometric quality of the fainter quasar light curve and the time delay. In each tile the top left panel shows the average claimed precision P for the spl technique, for a five-year monitoring with four-month seasons and a cadence of three days. We find that the cadence dispersion plays no significant role in this analysis, and we therefore merge rungs 2 and 3 to obtain this larger sample.
In contrast, each tile of the top right panel shows the root mean square (rms) of the relative error of the time-delay estimates 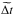 . The observed structure is inevitably noisier because this rms is computed from the actual point estimates, while the precision P is based on the corresponding claimed uncertainty estimates. We observe both a qualitative and a quantitative similarity between these plots, suggesting that the time-delay uncertainty estimates, δi (Eq. (2)), from the PyCS techniques correctly capture trends related to the photometric quality and to the amount of temporal overlap in the light curves.
. The observed structure is inevitably noisier because this rms is computed from the actual point estimates, while the precision P is based on the corresponding claimed uncertainty estimates. We observe both a qualitative and a quantitative similarity between these plots, suggesting that the time-delay uncertainty estimates, δi (Eq. (2)), from the PyCS techniques correctly capture trends related to the photometric quality and to the amount of temporal overlap in the light curves.
In the lower right panel of Fig. 5, the map of χ2 metrics for the spl technique shows no strong evolution across the well-sampled regions of the parameter space. It does however indicate that the uncertainty estimates δi from spl are too conservative by a small factor of (χ2)− 1/2 ≃ 0.5− 1/2 ≃ 1.4. This is particularly visible for the high quality light curves with small time delays, i.e. with large temporal overlaps. Finally, the bottom left panel shows the average P metric computed using only the best half of light curve pairs in each tile, where the quality of a system is judged via the blind relative precision 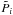 (see Eq. (5)). This operation, aimed at increasing the precision, divides by two the usable fraction of systems as given in Fig. 3. We consider such a selection in more detail in Sect. 5.3.
(see Eq. (5)). This operation, aimed at increasing the precision, divides by two the usable fraction of systems as given in Fig. 3. We consider such a selection in more detail in Sect. 5.3.
We observe in Fig. 5 that the best average relative precision in time-delay measurements seems to be achieved for time delays in the range 40−80 days for this particular monitoring strategy. This corresponds to about half of the season length, and results from the trade-off between absolute delay length and amount of overlap in the light curves.
Given the observed general aptitude of our time-delay uncertainty estimates, and thus P, to describe the actual point estimate errors committed by the spl technique, and the excellent competitiveness of spl compared to other time delay measurement techniques (see, e.g., Fig. 13 of Liao et al. 2015), we see the left panels of Fig. 5 as roughly representative of the precision that can be achieved by a state-of-the-art time-delay measurement method.
5.3. Effect on the overall metrics of selecting the best systems
In Fig. 6 we show the evolution of the overall average metrics as a function of the fraction of estimations f for the spl-sec and sdi-sec samples. The five columns represent the five rungs and the estimations are sorted according to their blind precision 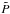 , i.e the precision estimate from the TDC1 data prior to the unblinding of the true values. The non-cumulative median value of the true delays (bottom row) is computed on consecutive bins of ten estimations. The shaded regions represent the statistical uncertainties of the metrics Xerr defined in Eq. (7). These uncertainties are too small in the top row to be distinguished from the curves.
, i.e the precision estimate from the TDC1 data prior to the unblinding of the true values. The non-cumulative median value of the true delays (bottom row) is computed on consecutive bins of ten estimations. The shaded regions represent the statistical uncertainties of the metrics Xerr defined in Eq. (7). These uncertainties are too small in the top row to be distinguished from the curves.
In the top row, P increases monotonically with f. This is expected since the estimations are sorted according to 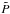 and since the D3CS sec sample is free of any outliers. The metrics χ2, A, and Aabs, respectively in the second, third and fourth rows stabilize around a mean value once a significant fraction of estimations is considered. The variations around the mean such as the jump in χ2 at f ~ 0.05 in rung 2 are due to non-catastrophic outliers, i.e. time delays that deviate significantly from the truth but by less than 20 days. These outliers are the result of a non-optimal convergence of the Stage II methods for the curves with the lowest signal-to-noise.
and since the D3CS sec sample is free of any outliers. The metrics χ2, A, and Aabs, respectively in the second, third and fourth rows stabilize around a mean value once a significant fraction of estimations is considered. The variations around the mean such as the jump in χ2 at f ~ 0.05 in rung 2 are due to non-catastrophic outliers, i.e. time delays that deviate significantly from the truth but by less than 20 days. These outliers are the result of a non-optimal convergence of the Stage II methods for the curves with the lowest signal-to-noise.
The high-f end of A and Aabs are subject to strong variations in all rungs. These variations occur for small absolute values of the true time delay | Δt |. Similarly, the high-f end of P increases strongly. A small error on the time-delay estimation particularly affects P, A, and Aabs if the true time delay is small.
This correlation between the loss in precision and accuracy means that for the corresponding light curves, our algorithms estimate the time delays less accurately, but do provide larger error bars. We observe that the χ2 remains constant as f increases. In conclusion, sorting the measurements in 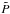 and rejecting a small fraction of the least precise estimations allows an optimal accuracy to be maintained without affecting the χ2.
and rejecting a small fraction of the least precise estimations allows an optimal accuracy to be maintained without affecting the χ2.
 |
Fig. 7 Evolution of the TDC1 metrics with the fraction of estimations sorted by increasing blind precision |
Figure 7 shows the evolution of the TDC1 metrics with the fraction of estimations, f, sorted by increasing order of 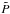 , for the spl-sec and spl-secpla sample. The few catastrophic outliers result in striking discontinuities in the curves. Quantifying the accuracy and precision of Stage II methods is different from avoiding such catastrophic outliers, and to address the former question, we also display in Fig. 7 a new subsample, spl-secpla-cut, where the 29 time-delay estimates with an absolute time-delay error larger than 20 days are a posteriori removed. Similarly, the impact of outliers can be reduced by considering the median of the individual metrics instead of their mean. This is not surprising, but nevertheless it reflects the need either to use metrics that can cope with outliers or, as in our Stage I approach, to make sure that no outliers contaminate the time-delay samples used for subsequent cosmological application.
, for the spl-sec and spl-secpla sample. The few catastrophic outliers result in striking discontinuities in the curves. Quantifying the accuracy and precision of Stage II methods is different from avoiding such catastrophic outliers, and to address the former question, we also display in Fig. 7 a new subsample, spl-secpla-cut, where the 29 time-delay estimates with an absolute time-delay error larger than 20 days are a posteriori removed. Similarly, the impact of outliers can be reduced by considering the median of the individual metrics instead of their mean. This is not surprising, but nevertheless it reflects the need either to use metrics that can cope with outliers or, as in our Stage I approach, to make sure that no outliers contaminate the time-delay samples used for subsequent cosmological application.
6. Summary and conclusions
In this work, we used the simulated light curves of the TDC1 proposed by Dobler et al. (2015) to test the performance of the PyCS numerical techniques currently in use in COSMOGRAIL to measure time delays. These methods are fully data-driven, in the sense that they do not attempt to include any physical model for microlensing or for the intrinsic variations of quasars. This choice was deliberate and considers an empirical representation of the data that minimizes the risk of bias due to choosing the wrong physical model. The price to pay is that error bars on the measurements must be estimated from mocks and that we cannot use prior knowledge from external observations of quasars in a direct formal way. Using the same simulated light curves, we also assessed the quantity and quality of the time-delay measurements from future monitoring campaigns or surveys. We have made public our six main TDC1 submissions, obtained using the D3CS, spl, and sdi methods for the high purity secure and the less conservative plausible samples. These data are available on the COSMOGRAIL website4. Our results can be summarized as follows:
-
1.
The visual estimation of time delays (Stage I) is extremely efficient in spotting catastrophic outliers and in providing useful time-delay estimates to be refined with subsequent numerical techniques (Stage II).
-
2.
We attempted to build a simple automated time-delay estimation procedure that we can apply to the TDC1 data. While useful, this automated procedure does not achieve as good purity in the time-delay sample as the visual estimation. We note that we did not use this automated procedure for any of our submissions to the TDC1.
-
3.
We provide a general analysis of the achievability of time-delay measurements as a function of the photometric precision of the light curves. In particular we show that almost all time delays shorter than two-thirds of the season length can be measured in five years of monitoring with four-month seasons and realistic photometric quality.
-
4.
Our Stage II methods spl and sdi can be considered unbiased given the statistical limits due to the finite challenge size. The χ2 values are close to unity. These good results emphasize the reliability of COSMOGRAIL time-delay measurements in general.
-
5.
We quantify the average precision on the time-delay measurements as a function of photometric quality of the light curves. We find that the best average precision seems to be obtained for pairs whose time delay is approximately half of the monitoring season length.
-
6.
We show that we can reliably evaluate the individual precision of our time-delay estimates. This may enable us, for any sample of light curves, to identify which are the most valuable objects to be followed up for cosmological purposes. We note, however, that any selection on the time delays in a quasar sample may also result in biases on the cosmological inference.
Data-Driven Documents, http://www.d3js.org/
http://www.astro.uni-bonn.de/~mtewes/d3cs/tdc1/ (See “Read me first” for help).
This same category was named doubtless in Liao et al. (2015).
Acknowledgments
The authors would like to thank the organizers of the Time Delay Challenge, as well as Peter Schneider for useful discussions and the anonymous referee for his/her useful comments. This work is supported by the Swiss National Science Foundation (SNSF). Malte Tewes acknowledges support by a fellowship of the Alexander von Humboldt Foundation and the DFG grant Hi 1495/2-1. Dominique Sluse acknowledges support from a Back to Belgium grant from the Belgian Federal Science Policy (BELSPO).
References
- Bostock, M., Ogievetsky, V., & Heer, J. 2011, IEEE Trans. Visualization & Comp. Graphics (Proc. InfoVis) [Google Scholar]
- Courbin, F., Chantry, V., Revaz, Y., et al. 2011, A&A, 536, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobler, G., Fassnacht, C. D., Treu, T., et al. 2015, ApJ, 799, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Eigenbrod, A., Courbin, F., Vuissoz, C., et al. 2005, A&A, 436, 25 [Google Scholar]
- Eulaers, E., Tewes, M., Magain, P., et al. 2013, A&A, 553, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fadely, R., Keeton, C. R., Nakajima, R., & Bernstein, G. M. 2010, ApJ, 711, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Falco, E. E., Shapiro, I. I., Moustakas, L. A., & Davis, M. 1997, ApJ, 484, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, Z. S., Suyu, S. H., Treu, T., et al. 2013, ApJ, 768, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R., & Kochanek, C. S. 1997, ApJ, 487, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, K., Treu, T., Marshall, P., et al. 2015, ApJ, 800, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. V. 2011, Phys. Rev. D, 84, 123529 [NASA ADS] [CrossRef] [Google Scholar]
- Lintott, C. J., Schawinski, K., Slosar, A., et al. 2008, MNRAS, 389, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, P. J., Lintott, C. J., & Fletcher, L. N. 2015, ARA&A, 53, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, N., Durand, J., & Sabatier, R. 2004, Comput. Stat. Data Analys., 45, 159 [Google Scholar]
- Moustakas, L. A., Abazajian, K., Benson, A., et al. 2009, ArXiv e-prints [arXiv:0902.3219] [Google Scholar]
- Oguri, M., & Marshall, P. J. 2010, MNRAS, 405, 2579 [NASA ADS] [Google Scholar]
- Rathna Kumar, S., Tewes, M., Stalin, C. S., et al. 2013, A&A, 557, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Sluse, D. 2013, A&A, 559, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., & Sluse, D. 2014, A&A, 564, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suyu, S. H., Treu, T., Blandford, R. D., et al. 2012, ArXiv e-prints [arXiv:1202.4459] [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Tewes, M., Courbin, F., & Meylan, G. 2013a, A&A, 553, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tewes, M., Courbin, F., Meylan, G., et al. 2013b, A&A, 556, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T. 2010, ARA&A, 48, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2002, MNRAS, 337, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, D. H., Mortonson, M. J., Eisenstein, D. J., et al. 2013, Phys. Rep., 530, 87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Appendix A: Automated Stage I procedure
 |
Fig. A.1 Example of time-delay estimations and confidence level from the automated procedure. The vertical grey dashed line represents the true value of the time delay. The blue diamonds correspond to the smallest absolute average residuals ri returned by the automated procedure. The depth of the two minima μi are represented by the number below each minimum. The colour bar indicates the microlensing variability ξ (see text). |
If more time had been devoted to the visual inspection, we expect that more correctly estimated plausible time-delay estimations would have been classified as secure. After the TDC1, we developed an automated Stage I procedure. Its goal is to speed up and possibly improve the quality of the D3CS output by providing a range of reasonable initial time delays and associated confidence estimation. The following section describes technically how the time-delay and confidence estimation for this automated procedure are computed.
Appendix A.1: Time-delay estimation
For each pair of curves, a bounded-optimal-knot spline (Molinari et al. 2004; Tewes et al. 2013a) s(t) is fitted to one of the two light curves. The second light curve l(t) is then shifted by an amount δt in time and δm in magnitude. Thus, for a given observing epoch t, the value of the shifted light curve can be written as l(t−δt)δm. For every value of the time and magnitude shifts, we select all the N points in the second light curve that overlap in time with the spline. For these points, we compute the residuals resn relative to the spline, i.e. the difference in magnitude between the points and the spline. The residual resn for point n is ![\appendix \setcounter{section}{1} \begin{equation} {\rm res}_{n} = [s(t) - l(t-\delta t)_{\delta m}]_{n}. \end{equation}](/articles/aa/full_html/2016/01/aa26704-15/aa26704-15-eq67.png) (A.1)We then compute the average absolute residual r(δt,δm) for every time and magnitude shift, i.e.
(A.1)We then compute the average absolute residual r(δt,δm) for every time and magnitude shift, i.e. 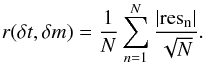 (A.2)\newpage\noindentThe possible presence of microlensing, assumed to be constant over an observing season, is handled in a very simple way. For each time shift δti, we apply independent magnitude shifts δmj(δti) to each season j. We define the residual curve r = {r1,...,ri,...,rT} as the sum of the smallest average absolute residuals for each season j. The i index runs from 1 to T and denotes the different time-delay values δti we want to test. This translates into
(A.2)\newpage\noindentThe possible presence of microlensing, assumed to be constant over an observing season, is handled in a very simple way. For each time shift δti, we apply independent magnitude shifts δmj(δti) to each season j. We define the residual curve r = {r1,...,ri,...,rT} as the sum of the smallest average absolute residuals for each season j. The i index runs from 1 to T and denotes the different time-delay values δti we want to test. This translates into ![\appendix \setcounter{section}{1} \begin{equation} r_{i} = \sum_{{j}}\min_{{j}}{\big{[}r(\delta t_{{i}}, \delta m_{{j}})\big{]}}. \end{equation}](/articles/aa/full_html/2016/01/aa26704-15/aa26704-15-eq77.png) (A.3)We define ri as a local minimum in r if
(A.3)We define ri as a local minimum in r if 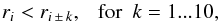 (A.4)where we keep the absolute minimum in r as the final time-delay estimation. The k index running from 1 to 10 spans a range of ±20 days around each tested value ri. Figure A.1 shows a typical residual curve r with the absolute minimum indicated as a coloured diamond and the true time delay indicated as a vertical dashed grey line.
(A.4)where we keep the absolute minimum in r as the final time-delay estimation. The k index running from 1 to 10 spans a range of ±20 days around each tested value ri. Figure A.1 shows a typical residual curve r with the absolute minimum indicated as a coloured diamond and the true time delay indicated as a vertical dashed grey line.
Appendix A.2: Confidence estimation
For each pair of curves, we compute three parameters related to the shape of the residual curve r that can be used to estimate the quality of the time-delay estimations:
-
1.
The number of local minima in r.
-
2.
The depth of each minimum μi and the absolute (i.e. the deepest) minimum μ,
![\appendix \setcounter{section}{1} \begin{equation} \mu_{{i}} = \frac{\bar{\vec{r}}-r_{{i}}}{\sigma_{\vec{r}}} \ \ \ \ , \ \ \ \mu=\min_{\delta t_{{i}}}{[\mu_{{i}}]}, \end{equation}](/articles/aa/full_html/2016/01/aa26704-15/aa26704-15-eq82.png) (A.5)where σr is the standard deviation between the elements in r. Examples of values for μi are indicated in Fig. A.1 below the minima for time shifts δt ≃ −120 days and δt ≃ + 80 days.
(A.5)where σr is the standard deviation between the elements in r. Examples of values for μi are indicated in Fig. A.1 below the minima for time shifts δt ≃ −120 days and δt ≃ + 80 days. -
3.
The total magnitude shift δm = {δm1,...,δmT} and the microlensing variability ξ(δti,δm), where we use the per season magnitude shifts δmj(δti) minimizing the average absolute residual ri at each time shift δti,
![\appendix \setcounter{section}{1} \begin{equation} \delta m_{{i}} = \sum_{{j}} \delta m_{{j}}(\delta t_{{i}}) \ \ \ \ , \ \ \ \ \xi(\delta t_{{i}},\vec{\delta m}) = \frac{\min{[\vec{\delta m}]} - \delta m_{{i}}}{\sigma_{\vec{\delta m}}}, \end{equation}](/articles/aa/full_html/2016/01/aa26704-15/aa26704-15-eq88.png) (A.6)where σδm is the standard deviation between the elements in δm. In other words the quantity ξ(δti,δm) is the difference between the sum of the magnitude shifts applied to each season at a given time shift δti and the minimum of this sum on all time shifts. This quantity follows the colour code in the sidebar of Fig. A.1 and is equivalent to the season-to-season microlensing variations minimizing the residuals for a given time shift. The lower this quantity is, the smaller the impact of microlensing is.
(A.6)where σδm is the standard deviation between the elements in δm. In other words the quantity ξ(δti,δm) is the difference between the sum of the magnitude shifts applied to each season at a given time shift δti and the minimum of this sum on all time shifts. This quantity follows the colour code in the sidebar of Fig. A.1 and is equivalent to the season-to-season microlensing variations minimizing the residuals for a given time shift. The lower this quantity is, the smaller the impact of microlensing is.
All Tables
All Figures
 |
Fig. 1 Left panel: stacked histogram of the errors made by the visual time-delay estimation, for the secure and plausible D3CS samples. All the secure estimations are within the displayed range of errors of ± 20 days. Only 2.6% of the time delays in the plausible sample have an absolute error larger than 20 days. Right panel: absolute time-delay error made by D3CS as a function of the true delay for both samples. |
| In the text | |
 |
Fig. 2 Cumulative evolution of the fraction of catastrophic outliers ϵ (in percentage points) as a function of the number of time-delay estimations. To produce the plot, the curves are first sorted according to the depth of their absolute minimum μ, indicated in the colour bar. Each black line (solid, dashed and dotted) represents a different subsample (see text for details). The coloured diamonds show the value of ϵ for the D3CS combined samples; the corresponding number of estimations are indicated in parenthesis. |
| In the text | |
 |
Fig. 3 Quantitative analysis of the discoverability of time delays through the extensive visual search with D3CS (Stage I) in the case of four-month observing seasons and a cadence of 3 days. The coloured tiles show the fraction of discovered delays as a function of the photometric precision of the fainter quasar image and the true time delay of the system. Left panel shows results from the very conservative sec sample, and central panel shows the less pure secpla sample that includes delay candidates considered as plausible (see text). Right panel, also for secpla, doubles the number of observing seasons. In each panel, only tiles covering more than three light curve pairs are shown. |
| In the text | |
 |
Fig. 4 Summary of metrics obtained with the Stage II algorithms spl and sdi, without any a posteriori clipping of the outliers. Bottom row presents enlargements taken from the panels on the upper row. The shaded regions represent the somewhat arbitrary target areas that were defined in the TDC1 paper. |
| In the text | |
 |
Fig. 5 Quantitative analysis of the precision achieved for the Stage II time-delay measurement as a function of the photometric precision of the fainter quasar image and as a function of the true time delay. All panels show results from the bias-free spl technique for the secure + plausible selection of rungs 2 and 3 after rejection of the catastrophic outliers (see text). Top left panel shows the metric P as computed using the uncertainty estimates δi without using |
| In the text | |
 |
Fig. 6 Evolution of the TDC1 metrics per rung as a function of the fraction of estimations f for the spl-sec and sdi-sec samples. The plots are sorted by increasing values of the blind precision |
| In the text | |
 |
Fig. 7 Evolution of the TDC1 metrics with the fraction of estimations sorted by increasing blind precision |
| In the text | |
 |
Fig. A.1 Example of time-delay estimations and confidence level from the automated procedure. The vertical grey dashed line represents the true value of the time delay. The blue diamonds correspond to the smallest absolute average residuals ri returned by the automated procedure. The depth of the two minima μi are represented by the number below each minimum. The colour bar indicates the microlensing variability ξ (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.