| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526203 | |
| Published online | 02 December 2015 | |
The evolution of streams in a time-dependent potential⋆
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: buist@astro.rug.nl
Received: 27 March 2015
Accepted: 17 June 2015
We study the evolution of streams in a time-dependent spherical gravitational potential. Our goal is to establish what are the imprints of this time evolution on the properties of streams as well as their observability. To this end, we have performed a suite of test-particle experiments for a host system that doubles its mass during the integration time and for a variety of initial conditions. In these experiments we found that the most striking imprint is a misalignment of ~10° in the angular location of the apocentres of the streams compared to the static case (and to the orbit of the centre of mass), which only becomes apparent for sufficiently long streams. We have also developed an analytic model using action-angle variables which allows us to explain this behaviour and to identify the most important signature of time evolution, namely a difference in the slope defined by the distribution of particles along a stream in frequency and in angle space. Although a difference in slope can arise when the present-day potential is not correctly modelled, this shortcoming can be by-passed because in this case, streams are no longer straight lines in angle space, but depict a wiggly appearance and an implausible energy gradient. The difference in slope due to time evolution is small, typically ~10-2 and its amplitude depends on the growth rate of the potential, but nonetheless we find that it could be observable if accurate full-space information for nearby long streams is available. On the other hand, disregarding this effect may bias the determination of the present-day characteristics of the potential.
Key words: dark matter / Galaxy: halo / Galaxy: kinematics and dynamics / Galaxy: structure / galaxies: evolution
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Throughout the history of the Milky Way and in the context of the Λ cold dark matter cosmogony, many dwarf galaxies must have been disrupted, leaving behind stellar streams (Helmi & White 1999). Especially the Galactic halo probably contains many such relics of this assembly history (Helmi 2008).
Tidal streams were predicted for the first time in the seminal work of Toomre & Toomre (1972) who simulated the interactions of two galaxies. Lynden-Bell & Lynden-Bell (1995) and Johnston et al. (1996) put forward the idea of tidal streams lurking in the Galactic halo, merely a few years after the discovery of the Sagittarius dSph by Ibata et al. (1994). Streams and debris from the Sagittarius stream were found several years later by Ivezić et al. (2000), Yanny et al. (2000), Ibata et al. (2001b), and a full-sky view of the Sagittarius stream was provided by Majewski et al. (2003). Other examples are the globular cluster streams (Grillmair et al. 1995), such as Palomar 5 (Odenkirchen et al. 2001) and NGC 5466 (Grillmair & Johnson 2006). A wealth of new streams have been found in the Sloan Digital Sky Survey (see e.g. Grillmair & Dionatos 2006), in the “Field of Streams” (Belokurov et al. 2006). Streams have also been found with other galaxies (Martínez-Delgado et al. 2010; Martin et al. 2014), most notably around M31 (Ibata et al. 2001a).
On the modelling side, much effort has been put into understanding the dynamics of streams and using these to infer the Galactic potential. Stream stars follow trajectories that are very similar to those of their progenitors (Jin & Lynden-Bell 2007; Binney 2008), albeit slightly offset. The evolution of streams is relatively simple in action-angle coordinates (Helmi & White 1999; Tremaine 1999). Furthermore, streams appear as distinct clumps in integrals of motion space (Helmi et al. 1999; Helmi & de Zeeuw 2000), and they show the highest coherence in the true (underlying) potential. This can be used to constrain its characteristic parameters (Peñarrubia et al. 2012; Sanderson et al. 2014). The alignment of the angles and orbital frequencies can aid in determining the potential, as proposed by Sanders & Binney (2013a).
The current cosmological model predicts significant evolution in the mass content of galaxies and of their dark matter haloes through cosmic time (Springel et al. 2005). This evolution may be directly measurable using stellar streams, given their sensitivity to the gravitational potential in which they are embedded (Johnston et al. 1999; Eyre & Binney 2009; Price-Whelan et al. 2014; Bonaca et al. 2014). A first study was presented by Peñarrubia et al. (2006), who concluded that there are no discernible effects of evolution on the distribution of streams in the space of angular momenta and energy because they only reflect the potential at the present day. However, Gómez & Helmi (2010) found that the structure of streams in frequency space does depict long-lasting signatures of time evolution. Bonaca et al. (2014) also found several biases when they attempted to derive the characteristic parameters of a time dependent potential using streams. They attributed these biases partly to the time evolution of the potential in their simulations.
In the coming decade, the Gaia satellite (Perryman et al. 2001), successfully launched in 2013, will provide an unprecedented vast and detailed view of our Galaxy. With the correct understanding of streams, Gaia will allow us to address the assembly history of our Milky Way. This is the main motivation of this paper. Our goal is to establish what kinds of observable imprints remain on the stream properties and how to use them in recovering the evolutionary path of the Galactic potential. To this end we use the cosmologically motivated growth model of a spherical halo by Buist & Helmi (2014) and follow the evolution of streams both numerically and using the action-angle formalism.
This paper is organised as follows. In Sect. 2 we explain the simulations of streams in a time-dependent potential. We analyse the simulations in Sect. 3 and develop an analytic model based on action-angles in the adiabatic regime. This allows us to identify the signature of time evolution on a stream in Sect. 4. In Sect. 5 we explore the prospects of observing this effect. We conclude in Sect. 6.
2. Methodology
To understand the behaviour of streams in time-dependent potentials, we take two complementary approaches. We first numerically study the evolution of groups of test particles that initially resemble a satellite galaxy. We then attempt to model this evolution using a formalism based on action-angle variables. In Sect. 2.1 we describe the set-up of our numerical experiments, and in Sect. 2.2 we briefly introduce the action-angle variables and their properties.
2.1. Simulation set-up
2.1.1. Evolution of the gravitational potential
We modelled the evolution of a time-dependent Navarro-Frenk-White potential (Navarro et al. 1997, NFW) using the prescription models from Buist & Helmi (2014). This model gives rise to an inside-out smooth growth that well reproduces the average mass accretion history of the Milky-Way-sized haloes from the Aquarius simulations (Springel et al. 2008; Wang et al. 2011). An important characteristic of this model is that mass growth is positive at each radius (i.e. there is no inward flow of mass between neighbouring mass shells). The scale radius rs and the scale mass Ms (mass enclosed within rs) of such a halo vary according to 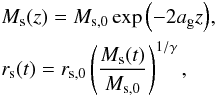 (1)where z is the redshift, and Ms,0 and rs,0 the scale mass and scale radius at the final time (z = 0, in a cosmology with Ωm = 0.29 and h100 = 0.71). We used γ = 2 to grow inside-out for an NFW potential (Buist & Helmi 2014). The parameter ag determines the formation epoch, and higher values correspond to more recent formation. We here explore a range of values of ag up to ag = 0.8, which would represent a quite recent formation epoch.
(1)where z is the redshift, and Ms,0 and rs,0 the scale mass and scale radius at the final time (z = 0, in a cosmology with Ωm = 0.29 and h100 = 0.71). We used γ = 2 to grow inside-out for an NFW potential (Buist & Helmi 2014). The parameter ag determines the formation epoch, and higher values correspond to more recent formation. We here explore a range of values of ag up to ag = 0.8, which would represent a quite recent formation epoch.
We modelled the evolution of streams in this time-dependent potential, but we also studied their behaviour in the static case. To make a fair comparison, we fixed the scale mass and scale radius at the final time to Ms = 5 × 1011M⊙ and rs = 12 kpc for all our experiments, independent of their time evolution.
2.1.2. Orbits
Orbital properties at the final time.
 |
Fig. 1 Increase of the enclosed mass for several orbits for our time-dependent potential with a growth factor of ag = 0.8. The dashed lines show the enclosed mass within the final value of their apocentre. Since the apocentric distances shrink with time, we show the mass enclosed within the time-dependent apocentre values with solid lines. The integration time span for the streams is t ~ 7–8 Gyr, and the enclosed mass approximately doubles over this timescale. |
We placed the satellites on 15 different orbits as listed in Table 1. We chose this number to have a variety in distances, orbital timescales (and hence the degree of adiabaticity), and eccentricity of the streams. The apo- and pericentres at the final time were chosen such that the particles spend most of their time in the outer halo and beyond the scale radius of the potential. For a fair comparison of each experiment the final 6D position of the satellite’s centre of mass is the same for the static and time-dependent cases. We then integrated the orbits backwards in time for about 7–8 Gyr and the more circular orbits for 6–7 Gyr. This range was chosen to ensure that all orbits are bound at early times in the time-dependent case.
We chose to start our orbital integrations when the satellite’s centre of mass was at its first pericentre to represent the first interaction with the Galaxy. This implies that the various orbits have slightly different total integration times, but these only differ up to a maximum of 0.5 Gyr. Within this integration time, the enclosed mass within a fixed radius increases on average with more than a factor 2 in our halo, as seen in Fig. 1. The actual orbits experience a somewhat smaller increase in enclosed mass because they respond to the halo growth by shrinking slowly.
2.1.3. Progenitors
We distributed the particles in the satellites assuming they follow an isotropic Gaussian in position and in velocity space, characterised by dispersions σpos and σvel. We used 10 000 particles centred on the centre of mass of the satellite, which was placed on the orbits described previously. We did not include self-gravity in our simulations. We considered three different progenitors, which we called “Carina”, “Sculptor” and “Sagittarius” because they have properties reminiscent of these dwarf spheroidal satellites of the Milky Way (see e.g. Martin et al. 2008; Wolf et al. 2010, see Table 2).
2.2. Action-angle coordinates
2.2.1. Generalities
A particularly useful description of the evolution of streams may be obtained using action-angle coordinates (Goldstein 1950; Helmi & White 1999; Tremaine 1999). In action-angle coordinates, the actions are the momenta and the angles are the coordinates. The actions are integrals of motion that are adiabatic, or in other words, invariant under slow changes of the host potential.
In this section, we only work with a time-independent potential. For a single star, the actions can be found from 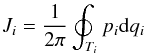 (2)with pi the conjugate momentum of coordinate qi, and
(2)with pi the conjugate momentum of coordinate qi, and 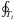 to indicate that we integrate over a full period of coordinate qi. In a spherically symmetric system the actions are the radial, latitudinal and azimuthal actions (Jr, Jθ, and Jφ respectively), and the angles are θr, θθ, and θφ, and represent the phase of the orbit in the r, θ, and φ coordinates, respectively.
to indicate that we integrate over a full period of coordinate qi. In a spherically symmetric system the actions are the radial, latitudinal and azimuthal actions (Jr, Jθ, and Jφ respectively), and the angles are θr, θθ, and θφ, and represent the phase of the orbit in the r, θ, and φ coordinates, respectively.
For only a few potentials algebraic expressions of the actions can be derived, such as for the isochrone potential (of which the Kepler potential and harmonic oscillator are limiting cases). Typically numerical methods are therefore required to find the actions (Binney & Tremaine 2008). Furthermore, actions are only directly available when the Hamilton-Jacobi equations are separable, as in the case of spherical and Staeckel potentials (Goldstein 1950; de Zeeuw 1985). In more general axisymmetric and triaxial potentials, approximations to the actions and angles must be used (see e.g. Kaasalainen & Binney 1994; Binney & McMillan 2011; Binney 2012; Sanders & Binney 2014, 2015; Bovy 2014).
Progenitor properties.
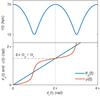 |
Fig. 2 Relation between the coordinates and the angles in the plane of the orbit. The top panel shows that the radial angle θr increases by 2π in one radial oscillation. In the bottom panel we have plotted φ (red) and θφ (blue) as functions of θr. After one radial period, both angles reach the same value 2πΩφ/ Ωr. |
Hamilton’s equations for the Ji and θi are 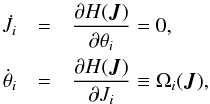 (3)and H = H(J) only because the actions are invariant. The Ωi are constants that correspond to the orbital frequencies and also only depend on the Ji. The resulting equations of motion for the θi are
(3)and H = H(J) only because the actions are invariant. The Ωi are constants that correspond to the orbital frequencies and also only depend on the Ji. The resulting equations of motion for the θi are 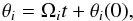 (4)with θi(0) the initial phase of ith coordinate.
(4)with θi(0) the initial phase of ith coordinate.
To determine the angles, we used a canonical transformation of the second kind W(q,J) (Goldstein 1950; Binney & Tremaine 2008), such that 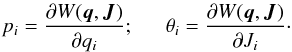 (5)The generating function for the transformation in a spherical potential is given by (adapted from Binney & Tremaine 2008)
(5)The generating function for the transformation in a spherical potential is given by (adapted from Binney & Tremaine 2008) 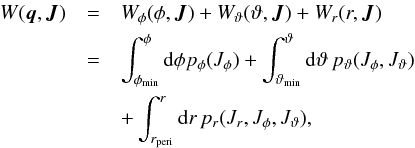 (6)where the integration is along the trajectory of a particle in phase space. We note that the three parts of the generating function are indefinite versions of the action integrals without a factor of 2π, and each increases therefore by 2πJi in their corresponding periods 2π/ Ωi. This equation has an algebraic expression in the case of an isochrone potential and has to be solved numerically otherwise. For the full integrals needed to compute θi in a spherical potential we refer to Appendix A.
(6)where the integration is along the trajectory of a particle in phase space. We note that the three parts of the generating function are indefinite versions of the action integrals without a factor of 2π, and each increases therefore by 2πJi in their corresponding periods 2π/ Ωi. This equation has an algebraic expression in the case of an isochrone potential and has to be solved numerically otherwise. For the full integrals needed to compute θi in a spherical potential we refer to Appendix A.
 |
Fig. 3 Distribution in action (left), frequency (second panel) and angle space (right) for particles in a stream, and centred on the centre of mass of the progenitor system. The colours represent the energy gradient, where red is for the trailing and green for the leading arms. |
In Fig. 2 we show an example of how the radial and azimuthal angles (θr and θφ) are related to the radial and azimuthal coordinates (r and φ) in the orbital plane. Since Wφ = φJφ and using Eqs. (5) and (6)1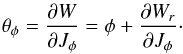 (7)The term
(7)The term 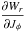 has a non-secular oscillation with frequency Ωr and vanishes at apo- and pericentre (θr = {0, ± π}). The secular behaviour of φ and θφ with time is therefore the same, as can also be seen in Fig. 2.
has a non-secular oscillation with frequency Ωr and vanishes at apo- and pericentre (θr = {0, ± π}). The secular behaviour of φ and θφ with time is therefore the same, as can also be seen in Fig. 2.
2.2.2. Streams in action-angle coordinates: time-independent case
A stream is created when particles drift away from the progenitor, which means we should look at the relative phase with respect to the progenitor centre of mass. For example, the relative azimuthal phase of the kth particle is 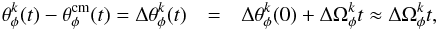 (8)where
(8)where 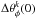 is the separation in angles at the initial time, and where the second line corresponds to the case in which the progenitor is small and the stream has evolved for a sufficiently long time.
is the separation in angles at the initial time, and where the second line corresponds to the case in which the progenitor is small and the stream has evolved for a sufficiently long time.
The 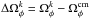 depends on the distribution in action space
depends on the distribution in action space 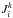 , such that a broad action spread results in a wide range of frequencies. This implies that larger progenitors generate longer streams than smaller ones if integrated for the same amount of time.
, such that a broad action spread results in a wide range of frequencies. This implies that larger progenitors generate longer streams than smaller ones if integrated for the same amount of time.
In Fig. 3 we show the structure of a stream in action-angle coordinates for the time-independent case. The colours represent the energy gradient, such that green represents the leading tail and red the trailing tail. The left panel shows the action distribution, which depends both on the initial conditions σpos and σvel and on the initial orbit2. This distribution also remains invariant in time in an adiabatically evolving potential. The second-left panel of shows the structure in frequency space, while the third corresponds to angle space. Since angles are 2π periodic variables, in the right most panel we show the angles modulo 2π. The different streaks signify the number of radial and azimuthal wraps the stream has. We note that the slope of the lines in frequency and in angle space are the same in this time-independent potential (Sanders & Binney 2013a) when the initial spread in angles can be neglected3: 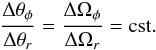 (9)This directly shows why all particles are distributed along straight lines with the same slope in angle and in frequency space.
(9)This directly shows why all particles are distributed along straight lines with the same slope in angle and in frequency space.
3. Analysis of the test-particle simulations
 |
Fig. 4 Streams from three progenitor sizes for each of the 15 orbits evolved in the time-dependent ag = 0.8 potential. The left, middle, and right panels correspond to the “Carina”, “Sculptor”, and “Sagittarius”-like progenitors, respectively (see Table 2 for their properties). Particles in green are more bound to the host galaxy (leading arm), while those in red are less bound (trailing arm) than the progenitor. The dashed curves are the progenitor orbits evolved in today’s potential, with the green integrated forward in time for the leading arm and red backwards for the trailing arm. The current position of the progenitor is indicated with a red cross. |
 |
Fig. 5 Radial vs. angular distribution of particles in the orbital plane for experiment O7 for the different progenitors in the time-dependent case. The dashed curves show the orbit of the centre of mass of the system integrated long enough to roughly reproduce the lengths of the streams. The variations in the apocentric distances are a reflection both of time evolution and of the energy gradient present along a stream. The difference in angular location of the apocentre, on the other hand, is a clear imprint of time evolution, as can be seen by comparing to e.g. Fig. 7. |
 |
Fig. 6 Streams from the Carina progenitor in the evolving and in the non-evolving potential. The streams in the left and centre have the same initial distribution in configuration and velocity space. Those in the right panels have the same initial action-angle distribution as the time-evolving potential (middle panel), but are evolved in a static potential. The colour coding is the same as in the previous figure. The stream-orbit misalignment can be seen by looking at the azimuthal angle of the petals starting from one radial period away from the progenitor, whose position is indicated with a red cross. |
 |
Fig. 7 Radial vs. angular distribution of particles in the orbital plane for experiment O7 for the Carina-like progenitor in the static case (left), time-dependent case (middle), and static case with the same initial action-angle distribution as in the middle panel. The dashed curves show the orbit of the centre of mass of the system integrated in the present-day potential for the left and right panels, and in the evolving potential for the middle panel. For the static cases, the variations in the apocentric distances are a reflection of the energy gradient present along the stream, while a second effect is present in the middle panel because of time evolution. In this case, the difference in angular location of the apocentre is also much more pronounced and systematically increases for older wraps. |
 |
Fig. 8 Action-space distributions for a sample of four streams from Fig. 6, measured with respect to the centre of mass of the progenitor at the final time. The colours of the particles represent the energy gradient, such that green is the leading arm and red the trailing arm. In the static cases, the initial and final distributions coincide exactly, but in the time-dependent case there can be small deviations if the orbit is not in the adiabatic regime, as can be seen by comparing the middle and right panels for orbits O11 and O15. The left panels show a smaller spread because the time-dependent cases start farther outwards and in an initially much lighter potential. |
The results of the simulations for the three progenitors on the various orbits for the time-dependent potential with growth factor ag = 0.8 are shown in Fig. 4. The colour coding indicates the leading (green) and trailing (red) arms of the stream. For comparison we have over-plotted the orbit of the progenitor integrated forward and backwards in time in the present-day potential. The time of integration for that orbit is between 1 to 3 Gyr and is chosen to roughly match the length of the corresponding stream. Note that this is much shorter than the time of integration of the particles that form the stream, which is approximately 8 Gyr.
Figure 4 clearly shows that larger progenitors give rise to longer and wider streams. The smaller (Carina) progenitor generates thin, short streams, which makes the separate loops of the stream easily recognizable by eye, while the streams from the larger progenitors, depending on the specific orbit considered, are wider and longer, much more phase mixed, and sometimes difficult to discern. As we show below, a clear imprint of the time evolution of the potential is apparent in the angular location and in the variation of the maximum distance of each “petal” of a stream (the latter being related to both the shrinking of the progenitor’s orbit because of mass growth and to the energy gradient along a stream). This effect is more easily discernible for heavier progenitors since they produce more loops, that is, longer streams, as can be seen in Fig. 5. On the other hand, thinner streams have the advantage that they depict their mean orbit much more clearly, which is the reason we mainly focus on the “Carina” progenitor in what follows.
The differences in the evolution for time-dependent and static potentials are shown in Figs. 6 and 7 for the Carina-like progenitor, depicted as before on the orbital plane of the progenitor. We note that in all cases the stream in the time-dependent potential is longer than in the static case, as can be seen by comparing the left and middle panels.
The length of a stream depends both on the orbital period and on the initial extent in phase- and configuration space of the progenitor. In the time-dependent potential the enclosed mass at initial times is lower, and the progenitor starts farther out. This results in lower orbital frequencies, or longer periods. Since the rate of divergence of particles in a stream in a spherical potential is proportional to (t/P)2 ∝ (Ωt)2 (Helmi & White 1999), this would imply that streams should actually be shorter for a fixed integration time t. However, in a time-dependent potential the spread in actions (or integrals of motion such as the energy) is broader for given initial σpos and σvel (see Fig. 8).
For an initially “compact” ensemble of particles, we may use a linear transformation between action-angle coordinates and Cartesian coordinates to derive the initial spread in action-angle space: ![\begin{eqnarray} \renewcommand\arraystretch{1.2} \left[\begin{matrix} \Delta \boldsymbol\theta \\ \Delta {\vec J} \end{matrix}\right] = \left[ \renewcommand\arraystretch{2.2}\begin{matrix} \dfrac{\partial\boldsymbol\theta}{\partial{\vec q}} & \dfrac{\partial\boldsymbol\theta}{\partial{\vec p}} \\ \dfrac{\partial{\vec J}}{\partial{\vec q}} & \dfrac{\partial{\vec J}}{\partial{\vec p}} \end{matrix} \right] \cdot \left[ \renewcommand\arraystretch{1.2} \begin{matrix} \Delta {\vec q} \\ \Delta {\vec p} \end{matrix}\right] \equiv {\bf T} \cdot \left[ \renewcommand\arraystretch{1.2} \begin{matrix} \Delta {\vec q} \\ \Delta {\vec p} \end{matrix}\right] , \label{eq:lintransformation} \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq70.png) (10)where the elements of the transformation matrix T will depend on second derivatives of the generating function evaluated at the centre of mass of the progenitor (Helmi & White 1999), as described in detail in Appendix B. We see that many of the terms depend on 1/Ωr, which is larger in a shallower potential and farther out in the potential, confirming that the initial spread in actions is greater. Therefore the particles in the progenitor integrated in the evolving potential can spread more and give rise to longer and wider streams.
(10)where the elements of the transformation matrix T will depend on second derivatives of the generating function evaluated at the centre of mass of the progenitor (Helmi & White 1999), as described in detail in Appendix B. We see that many of the terms depend on 1/Ωr, which is larger in a shallower potential and farther out in the potential, confirming that the initial spread in actions is greater. Therefore the particles in the progenitor integrated in the evolving potential can spread more and give rise to longer and wider streams.
In our initial set-up we took the progenitors to have the same σpos and σvel. However, their initial distribution in action-angle space is different for the static and time-dependent potentials, as discussed above. This implies that their final distribution in action (or energy) space will also be different. This is shown for the progenitor placed on two of our orbits in Fig. 8. Here we have plotted the distribution at the final time of ΔJr and ΔL in the top panels for the static (left) and time-dependent (middle) potentials for the “Carina”-like progenitor.
An alternative is to consider that the particles have the same initial ΔJr and ΔL, whether they are evolved in a static or time-dependent gravitational potential. To establish the effect of such a change in the initial configuration, we set up progenitors with these properties and evolved them in the static potential. The right panels of Fig. 8 show the distribution of particles evolved in the static potential, but set up with the same initial conditions in action-angle space as in the time-dependent case. If all orbits were in the adiabatic regime, the middle and right panels should give identical results. However, some of the orbits are not, which can be seen in the streams from orbits O11 and O15, where the action distributions are not exactly the same.
The streams resulting from these different initial conditions evolved in the time-independent potential are shown in the right panels of Fig. 6 for each of the orbits. As anticipated, the streams in the time-dependent potential (middle panels) are now shorter than the streams in the time-independent potential starting from the new initial conditions. This characteristic is now solely due to the evolution of the potential.
An interesting feature visible in Figs. 6 and 7 that was mentioned earlier is that the stream-orbit misalignment differs in the static and evolving cases. For example, as can be seen for experiment O7, the mean orbit traces the stream in the time-independent case relatively well. On the other hand, it is clear that the angular position of the rosette petal of the stream and the progenitor orbit at one radial period behind (or ahead) are offset from each other. This is apparent in all experiments, to a lesser or greater degree. This offset is systematic, can be as large as 10 degrees, and is a first direct indication of the effect of time evolution on the gravitational potential.
4. Analytic models
4.1. Action-angle coordinates in an adiabatically evolving potential
In this section our aim is to extend the use of action-angles to an adiabatically changing spherical potential. The action-angles are still a valid canonical coordinate system in a time-dependent system, but the equations of motion in action-angle coordinates are more complicated, as we show below.
In the models we have considered so far, the gravitational potential is made time dependent by making its characteristic parameters, such as mass and scale, a function of time. Its overall shape or functional form remain the same. Therefore angular momentum is still conserved because of the assumed spherical symmetry, but the radial action Jr may vary with time.
For a time-dependent potential, the generating function that allows the transformation between Cartesian and action-angle spaces is an explicit function of time 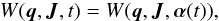 (11)where the parameters of the potential are in the vector α. The appropriate Hamiltonian in action-angle coordinates then becomes
(11)where the parameters of the potential are in the vector α. The appropriate Hamiltonian in action-angle coordinates then becomes 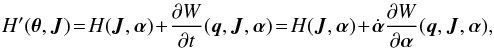 (12)which is the original Hamiltonian perturbed by the partial time derivative of the generating function (Goldstein 1950, Sects. 11–7). This extra term naturally vanishes in the time-independent case. The new equations of motion are
(12)which is the original Hamiltonian perturbed by the partial time derivative of the generating function (Goldstein 1950, Sects. 11–7). This extra term naturally vanishes in the time-independent case. The new equations of motion are 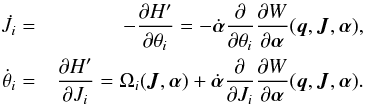 (13)Compared to the original equations of motion given in Eq. (3), there are a few correction terms that depend on the rate of change of the characteristic parameters of the potential
(13)Compared to the original equations of motion given in Eq. (3), there are a few correction terms that depend on the rate of change of the characteristic parameters of the potential 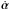 .
.
Since in general we are interested in the mean increase in the actions and angles, we take an average over one period, where we assume that α changes little over one period (Goldstein 1950; Vandervoort 1961) 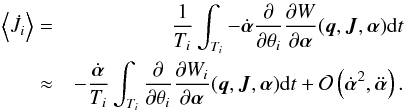 (14)The three parts of the generating function (Wr, Wθ and Wφ) increase by 2πJi in the corresponding period Ti. This means that each of the Wi is a periodic function, and we can do a Fourier expansion
(14)The three parts of the generating function (Wr, Wθ and Wφ) increase by 2πJi in the corresponding period Ti. This means that each of the Wi is a periodic function, and we can do a Fourier expansion 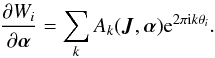 (15)However, the whole first term in Eq. (14) vanishes since
(15)However, the whole first term in Eq. (14) vanishes since 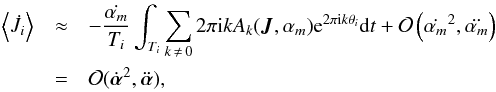 (16)where we use the Einstein summation convention for the parameters αm. The actions are therefore invariant up to second order. Vandervoort (1961) showed that the actual condition for adiabatic evolution for each of the αm and each of the orbital periods Ti is
(16)where we use the Einstein summation convention for the parameters αm. The actions are therefore invariant up to second order. Vandervoort (1961) showed that the actual condition for adiabatic evolution for each of the αm and each of the orbital periods Ti is 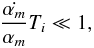 (17)which states that the timescale of change should be much longer than the orbital period.
(17)which states that the timescale of change should be much longer than the orbital period.
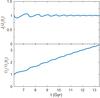 |
Fig. 9 Response of the radial action and the radial frequency to a time-dependent potential for orbit O7 (Table 1). For this orbit, the action shows a non-secular oscillation that decreases in amplitude as the rate of change of the potential decreases. The value of Ωr changes significantly with time, and here there are also oscillations that become smaller as the change rate of the potential decreases. The period of the oscillations corresponds with the radial period. The evolution of Jr has been quite adiabatic because it oscillates around a limiting value, which is the starting value when the particles were released at pericentre. |
On short timescales, Jr shows a periodic oscillation that decreases in amplitude when the changes in the parameters become smaller, as shown in Fig. 9 for one of our orbits. The final time value of Jr returns to the initial value, indicating we are in the adiabatic regime4. In the case of non-adiabaticity, full integration of Eq. (13) is needed to model the behaviour of the system in action-angle space.
In an analogous way as for the actions, we compute the effect for the mean change in the angles 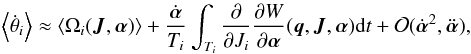 (18)where we can exchange the order of the derivatives
(18)where we can exchange the order of the derivatives 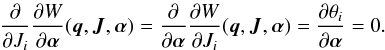 (19)The result is that only the term dependent on the (evolving) frequency remains
(19)The result is that only the term dependent on the (evolving) frequency remains 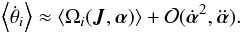 (20)The angles as a function of time may be computed from
(20)The angles as a function of time may be computed from 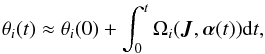 (21)where like in the time-independent case, θi(0) is the phase at the initial time. The frequencies Ωi(t) are understood to be the instantaneous frequencies at every time step. Equivalently, we can numerically integrate the orbit in Cartesian coordinates and find θi(t) from the instantaneous coordinate transformation at all times t using the generating function. The advantage of the action-angle description is that it stresses that the phase angles (modulo 2π) depend on how the frequencies have changed with time.
(21)where like in the time-independent case, θi(0) is the phase at the initial time. The frequencies Ωi(t) are understood to be the instantaneous frequencies at every time step. Equivalently, we can numerically integrate the orbit in Cartesian coordinates and find θi(t) from the instantaneous coordinate transformation at all times t using the generating function. The advantage of the action-angle description is that it stresses that the phase angles (modulo 2π) depend on how the frequencies have changed with time.
4.2. Streams in action-angle space
4.2.1. Sensitivity to the gravitational potential
 |
Fig. 10 Angle space of stream O7 (see Table 1) evolved in a time-dependent potential, but where the angles have been computed with different (incorrect) parameters. The central panel shows the correct parameters, while rs is changed vertically and Ms horizontally by 10% and 30%. The colour coding indicates the energies, with green representing the leading arm (more bound) and red the trailing arm (less bound). |
 |
Fig. 11 Angle space of streams O11 (top) and stream O1 (bottom) evolved in a time-dependent potential, but where the angles have been computed with different (incorrect) parameters. We note that although the distortions in angle space are less pronounced for the more radial orbit O1, the energy gradient (indicated by the colour gradient and coding used before) is not preserved. |
We have mentioned that if the initial spread in angles is negligible, then the slopes in the angle and frequency spaces should be equal for a static potential (Sanders & Binney 2013b,a), as can be seen from Eq. (8), if computed in the true potential. An example of the distortion in angle space for a stream now evolved in a time-dependent potential where the angles (and the energy) were computed using incorrect parameters is shown in Fig. 10 for experiment O7. The central panel corresponds to the parameters in the true (final) potential, while we varied rs in the vertical and Ms in the horizontal direction. The parameters in the eight panels around the central panel were changed by only 10%, and even in this case, some deviations from the expected straight lines are visible. When the parameters were changed by as much as 30%, as in the outer panels, the deviations become much more pronounced and are very strong. We note that similar results are found when the stream is evolved in a static potential.
The more incorrect the potential, the more we see wiggles in angle space. Similar distortions are also present in the frequency spaces and action spaces. Furthermore, the energy gradient along the stream is no longer preserved as the parameters of the potential are varied, which implies that the most bound (least bound) particles in the specific trial potential are no longer “found” at the end of the leading tail (trailing tail). Although the streams have a normal appearance in physical space, the coordinate transformation to action-angle space and the computation of the energy are incorrect when the wrong gravitational potential is assumed. This leads to the distorted appearance and broken energy gradient seen in Fig. 10. Clearly, these imprints will only be obvious for sufficiently long streams, that is, those more extended than 2π in angle space.
We note that the distortions in angle space are less pronounced for the panels located along the diagonal that runs from bottom left to top right in Fig. 10, for which the enclosed mass within the orbit is the same for the given Ms and rs.
The degree to which these distortions and broken energy gradients manifest also depends on the type of orbit the stream progenitor has followed. This is shown in Fig. 11 for a scale radius that is 70% of the true value and for different scale masses Ms. The top panels correspond to experiment O11, which is on a relatively circular orbit of apocentre-to-pericentre ratio of 2, while the experiment in the bottom O1 has a relatively radial orbit, with apocentre-to-pericentre ratio of 18.
4.2.2. Sensitivity to time-dependence
In the time-dependent potential the exact correspondence between the slopes of the spreads in the frequencies and in the angles is broken, meaning that Eq. (9) is no longer valid. This is because the evolution of Δθφ and Δθr depends on integrals over time, that is,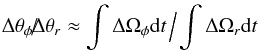 (22)(assuming the initial angle spreads are negligible).
(22)(assuming the initial angle spreads are negligible).
In Fig. 12 we compare the lines fitted to the frequency and angle spaces for the stream from orbit O7 in the time-dependent and static cases for the correct final potential. The top panel shows that for the time-dependent case, the initial slope in frequency space (grey line) is steeper than at the end of the simulation (blue line). This is because the orbit shrinks as the mass increases5. In the time-independent case we see, as expected, that both lines coincide. Another difference between the static and evolving case is that the stream-orbit misalignment changes (compare the green and red dashed lines), which is only caused by the changes in the angle space due to time evolution. The behaviour in angle space (indicated by the red dashed line) may be understood from the fact that the angles’ slope is like a time average of the frequencies’ slope, and is therefore expected to lie between the initial and the final frequency slope as observed. Therefore, a clear signature of time evolution is a difference in the slope derived for the angles and that derived for the frequencies, even if they are computed using the present-day gravitational potential.
We now explore an analytic model to describe the behaviour of the frequency and angle slopes more generally. We may derive the slope in frequency space S(ΔΩ) by making a Taylor expansion in the actions near the centre of mass of the progenitor (Helmi & White 1999) 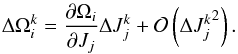 (23)The expansion is done for the kth particle, all terms are evaluated at time t. The derivative is evaluated for the progenitor orbit and we used the Einstein summation convention on the subscript indices. We recall that
(23)The expansion is done for the kth particle, all terms are evaluated at time t. The derivative is evaluated for the progenitor orbit and we used the Einstein summation convention on the subscript indices. We recall that 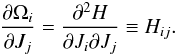 (24)Working out the frequency spreads, we find
(24)Working out the frequency spreads, we find ![\begin{eqnarray*} \Delta \Omega_r^k(t) &\approx& H_{rr}(t) \Delta J_r^k + H_{r\theta}(t) \Delta J_\theta^k + H_{r\phi}(t) \Delta J_\phi^k,\\[2mm] \Delta \Omega_\phi^k(t) &\approx& H_{\phi r}(t) \Delta J_r^k + H_{\phi\theta}(t) \Delta J_\theta^k + H_{\phi\phi}(t) \Delta J_\phi^k. \end{eqnarray*}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq101.png) The cross terms are second derivatives of the Hamiltonian and therefore symmetric, Hij = Hji. Furthermore, in a spherical potential, the Hamiltonian is only a function of E and L, so that for all j, Hθj = Hφj6. The evolution of the slope of S(ΔΩ) can then be found from
The cross terms are second derivatives of the Hamiltonian and therefore symmetric, Hij = Hji. Furthermore, in a spherical potential, the Hamiltonian is only a function of E and L, so that for all j, Hθj = Hφj6. The evolution of the slope of S(ΔΩ) can then be found from 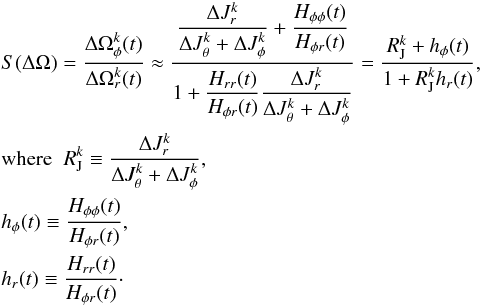 (25)Here
(25)Here 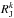 is the ratio of the actions and hi the ratio of the Hessians. The Hessians Hij and the Hessian ratios hi are shown in Fig. 13 and are ranked as | Hrr | > | Hφr | > | Hφφ |. But most importantly, the resulting ratio hr increases with time, while hφ decreases with time. Assuming that the action ratio
is the ratio of the actions and hi the ratio of the Hessians. The Hessians Hij and the Hessian ratios hi are shown in Fig. 13 and are ranked as | Hrr | > | Hφr | > | Hφφ |. But most importantly, the resulting ratio hr increases with time, while hφ decreases with time. Assuming that the action ratio 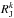 remains constant (adiabatic limit), we find from this equation that the slope in frequency space S(ΔΩ) decreases with time.
remains constant (adiabatic limit), we find from this equation that the slope in frequency space S(ΔΩ) decreases with time.
For the angles of the kth particle we can use the following approximation 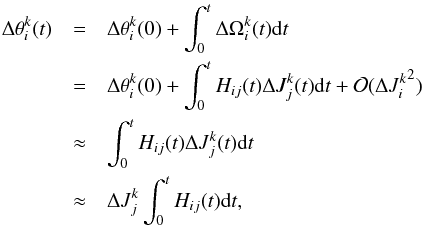 (26)where we have neglected the initial angle spread and in the last approximation assumed adiabaticity of the actions. Therefore
(26)where we have neglected the initial angle spread and in the last approximation assumed adiabaticity of the actions. Therefore 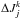 may be evaluated at any time step, although we typically use the values at the final time in our computations.
may be evaluated at any time step, although we typically use the values at the final time in our computations.
 |
Fig. 12 Lines fitted to the angle space (red dashed line) and the frequency space (blue line) of stream O7 evolved in a time-dependent (top) and static potential (bottom) using the same (correct) final potential. Additionally, the green line shows the track of the progenitor assuming the potential is static (i.e. θcm(t) = Ωcm(tf)t), and the grey line shows the line fitted to the frequency space at the beginning of the simulation. The inset labels show the numerical values of the aperture angle (misalignment) between the stream and the (static) progenitor orbit ΨS, O, and between the stream in angle and in frequency space ΨΔθ, ΔΩ (see Eqs. (34) and (35)). |
We now focus on the slope in angle space. If we define 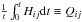 (the time-averaged Hessian), then
(the time-averaged Hessian), then 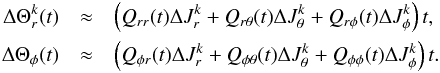 The slope in the angles can then be found from
The slope in the angles can then be found from 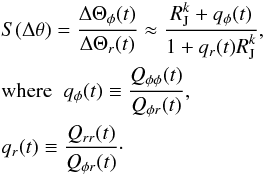 (27)Here the qi are the ratios of the Qij. The ranking of the Qij and the qi behaves very similarly to that of the Hij and hi, as shown in Fig. 13. In the same manner as for the frequency slope, we infer that S(Δθ) is also a decreasing function of time.
(27)Here the qi are the ratios of the Qij. The ranking of the Qij and the qi behaves very similarly to that of the Hij and hi, as shown in Fig. 13. In the same manner as for the frequency slope, we infer that S(Δθ) is also a decreasing function of time.
We are now ready to compute the difference between S(Δθ) and S(ΔΩ) by using that the difference between the qi and the hi is small:  where the appropriate sign was chosen such that the ϵi are always positive. We define for computational ease
where the appropriate sign was chosen such that the ϵi are always positive. We define for computational ease  We may expand the inverse of the angle slope T(Δθ)
We may expand the inverse of the angle slope T(Δθ)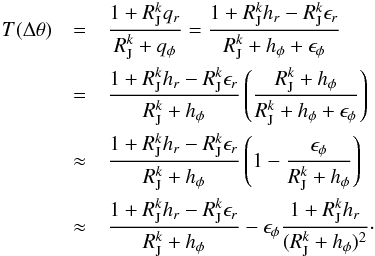 (32)Using Eq. (25) to compute T(Δθ), we can derive the difference of the inverse slopes
(32)Using Eq. (25) to compute T(Δθ), we can derive the difference of the inverse slopes 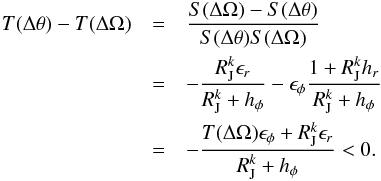 (33)All the terms in the fraction are positive, and T(ΔΩ) is therefore always greater than T(Δθ). This means that S(Δθ) is always larger than S(ΔΩ), and this difference will increase with time. The longer the system is evolved in a time-dependent potential, the larger the difference in slopes becomes with respect to the same final static potential. This also means that streams that fell in at early times will show a stronger signature of the separation between the angle and frequency relations than streams that fell in more recently.
(33)All the terms in the fraction are positive, and T(ΔΩ) is therefore always greater than T(Δθ). This means that S(Δθ) is always larger than S(ΔΩ), and this difference will increase with time. The longer the system is evolved in a time-dependent potential, the larger the difference in slopes becomes with respect to the same final static potential. This also means that streams that fell in at early times will show a stronger signature of the separation between the angle and frequency relations than streams that fell in more recently.
 |
Fig. 13 Hessians Hij, time-averaged Hessians Qij (both in units of 10-3 kpc-2), and their ratios hi and qi for orbit O7. Left panel: the dash-dotted lines show Hij in the static potential, the solid lines the Hij in the time-dependent potential, and the dashed lines Qij in the time-dependent potential. We note that | Hrr | > | Hrφ | > | Hφφ |, and similarly for Qij. The middle panel shows that hφ>qφ at all times and that both increase with time. On the other hand, hr<qr at all t, and both decrease with time. Right panel: the ranking of the hi for the different orbits. Both hφ and hr are ranked by the ratio Ωφ/ Ωr, indicating the dependence on the type of orbit. The qi are ranked in the same way. |
In Fig. 14 we show the predictions of the slope differences for the angle and frequency spaces for the orbits in Table 1. With increasing amount of time evolution by changing the growth parameter ag, the difference in slope also becomes larger. Another interesting prediction is that the more circular orbits have a larger slope difference, although this is at a small level. We gauge the magnitude of the angle-frequency misalignment by using the aperture angle ΨΔθ, ΔΩ between the fitted lines in the angle and frequency space (as also used by Sanders & Binney 2013b,a) 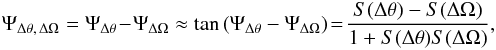 (34)where S(i) = tan(Ψi), and we have used that the difference in slopes is small7. With this definition of the angle-frequency misalignment, typical values of ΨΔθ, ΔΩ are around 1.5° for ag = 0.8.
(34)where S(i) = tan(Ψi), and we have used that the difference in slopes is small7. With this definition of the angle-frequency misalignment, typical values of ΨΔθ, ΔΩ are around 1.5° for ag = 0.8.
It has been discussed earlier that a stream does not exactly follow an orbit, and the small difference between these two trajectories is known as the stream-orbit misalignment. The characteristic magnitude of this can be found from 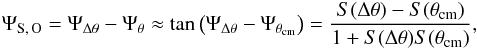 (35)where S(θcm) = tanΨθcm is the slope of the straight line traced by the centre of the mass of the progenitor in angle space for a static potential (see also Fig. 12). The typical order of magnitude of ΨS, O for the Carina progenitor is about 1 degree, similar to what was found in Sanders & Binney (2013b) for a static logarithmic axisymmetric potential, and also similar to values of the stream-orbit misalignment in the isochrone potential of Eyre & Binney (2011). We note that the angle-frequency differences in slope that we find are of the same order of magnitude as the stream-orbit misalignment.
(35)where S(θcm) = tanΨθcm is the slope of the straight line traced by the centre of the mass of the progenitor in angle space for a static potential (see also Fig. 12). The typical order of magnitude of ΨS, O for the Carina progenitor is about 1 degree, similar to what was found in Sanders & Binney (2013b) for a static logarithmic axisymmetric potential, and also similar to values of the stream-orbit misalignment in the isochrone potential of Eyre & Binney (2011). We note that the angle-frequency differences in slope that we find are of the same order of magnitude as the stream-orbit misalignment.
 |
Fig. 14 Slope differences between the streams in angle and in frequency space as a function of growth parameter ag, as predicted by our analytic model using Eqs. (23) and (26) for our experiments. |
When comparing simulations with and without time evolution, the stream-orbit misalignment can also be used as an indicator of time evolution. In Fig. 6 we saw that the angular position of the stream and progenitor orbit petals one radial period away from the current progenitor location are different for the time-dependent case. This angular separation can be derived as follows. For the progenitor, the location of the petal is simply the precession of the orbit in one radial period, that is, ψcm = 2πS(θcm) = 2πΩφ/ Ωr. For the stream, this difference in radial angle from the progenitor is ΔΘr = 2π, and therefore the angle of the petal of the stream is ψstream = 2πS(Δθ). Therefore the stream-orbit misalignment in azimuthal angle is 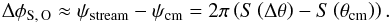 (36)Increasingly higher growth rates of the potential will yield also larger angular stream-orbit separations because S(Δθ) changes by the amount in Fig. 14 (S(ΔΩ) and S(θcm) are by construction the same at the final time). By multiplying this by 360° to find the difference at the first petals next to the progenitor, we find that these differences can reach up to 10 degrees in our experiments.
(36)Increasingly higher growth rates of the potential will yield also larger angular stream-orbit separations because S(Δθ) changes by the amount in Fig. 14 (S(ΔΩ) and S(θcm) are by construction the same at the final time). By multiplying this by 360° to find the difference at the first petals next to the progenitor, we find that these differences can reach up to 10 degrees in our experiments.
In summary, stream particles are distributed following straight lines in angle space when computed using the correct potential and otherwise show a wiggly behaviour and a broken energy gradient. These straight lines have the same slope in frequency space in the static case. If the potential has evolved in time, then the slope in frequency space is typically shallower than in angle space, to an extent that depends on the growth of the gravitational potential.
4.2.3. Validation of the analytic model
We expect our analytic model to faithfully reproduce the behaviour of the test-particle simulations except in some cases. We neglected two effects that can modify these slopes in the derivations above. The first appears when the initial angle spread of the progenitor is comparable to its current extent, in which case the former needs to be taken into account. Since the initial extent typically is unknown, it is better to use very extended streams to derive the evolution in time of the host potential. The second effect is when the time evolution of the potential is non-adiabatic. In this case, the higher order terms of Eq. (13) have to be taken into account.
To confirm this, we used three simulations with different growth factors ag = {0.0,0.4,0.8}, but with the same initial action distribution as in the ag = 0.8 case by using the transformation described in Eq. (10).
 |
Fig. 15 Examples of the slope differences between the angle and frequency distributions (top panels) and histograms of the spread of Δθr(0)/Δθr(tf) (bottom panels). In the top panels, the blue crosses indicate values from the full simulation, while the green lines are the predictions from our analytic model. The red crosses are the slopes measured when the initial spreads from the simulations are removed. All orbits now align with the model when ag = 0. For large ag the more circular orbits such as orbit O15 deviate strongly from the model because of non-adiabaticity. |
 |
Fig. 16 Angle and frequency space plots and residuals of the frequency space fits of all 15 streams for 1% distance (and proper motion) errors in the time-dependent potential. The streams are centred on the position of the centre of mass of the progenitor in the error-free case. The black points are error-convolved, while those in yellow are error-free and only shown in the bottom row. The residuals were computed by subtracting the best-fit straight line to the error-free frequency distribution (green line) from ΔΩφ. The text in the panels shows the relative difference in the slopes for the error-convolved and error-free cases derived in angle space Eθ and in frequency space EΩ (i.e. using the red vs. green straight lines, respectively). The panels for which Ei< 0.005 are marked with a green box. The difference in slope in angle space clearly is generally far below this value, while the frequencies are much more strongly affected by the errors. |
Figure 15 shows the difference between the slopes in angle and in frequency spaces for our analytic model. In this figure, the green line shows the prediction of our model using Eqs. (25) and (27), and the actual measured slope differences from the test-particle simulations are shown as blue crosses. This comparison shows that the agreement is excellent, as exemplified for Orbit O7 in the left panel, and this is true for most of the orbits we explored. However, there are a few cases, such as those shown in the panels on the right, where the model fails.
 |
Fig. 17 Selection of the seven best orbits of Fig. 16, but now with 10% parallax (and proper motion) errors. The colours, lines, and insets are the same as in Fig. 16. With these 10× larger distance errors, the angle slopes of the streams are still well measured for most orbits, while the frequency slopes generally are not. |
 |
Fig. 18 Selection of the orbits of Fig. 16 with 10% parallax errors, but now with two cuts: σd ≤ 2 kpc and | Ωr−⟨Ωr⟩ | ≤ SDΩr. The colours are the same as in Fig. 17, with the addition that green points represent the particles that remain after the cuts. The grey vertical dashed lines indicate ⟨Ωr⟩ and ⟨Ωr⟩ ± SDΩr applied after the distance cut. The insets in the top panels show the number of remaining particles after the cuts Ncut, while those in the bottom panels are the number of particles within a distance of 20 kpc from the Sun N (d< 20 kpc). |
For these two cases, the initial extent of the progenitor in angle space cannot be neglected, as can be seen from the bottom panels. This can either be because the streams are relatively short or because the initial spread in angles is large. When the initial angle spreads as given by Eqs. (8) and (26) are removed, the simulations match the model significantly better, as indicated by the red crosses.
The rightmost panel still shows some disagreement, especially for higher values of the growth factor ag. This behaviour stems from the non-adiabatic evolution of the orbit, so that higher terms in Eq. (12), and the last approximation in Eq. (26), fail. An indication that these orbits evolved non-adiabatically is for example that Jr(0) /Jr(tf)−1 ≈ 0.18 for orbit O15. The orbits that are more circular typically suffer more strongly from this effect. This implies that radial orbits may be preferred to obtain the amount of time evolution for a stream that evolved in a smoothly growing potential such as ours.
5. Observational prospects
Now that we have determined the signature of time evolution of a gravitational potential through the difference in slopes in the angle and frequency spaces, we are interested in establishing whether this effect is measurable. This is particularly relevant in the context of the upcoming catalogues from the Gaia satellite.
We therefore convolved our simulated data in observable space with errors. The largest uncertainties typically come from the errors in distance and proper motion. We investigated two cases for the errors in the parallax: 1% (σπ/π = 0.01) and 10% (σπ/π = 0.1), while the proper motion errors are set to be σμ = 0.5σπ), as given by the Gaia mission error estimates. We assumed radial velocity errors of 1 km s-1, which is the level obtainable from follow-up surveys of the Gaia satellite such as 4MOST (de Jong et al. 2012) and WEAVE (Dalton et al. 2012). Although this error may be seen as small, we have found no significant dependence on the radial velocity error, even if this was as large as 10 km s-1. After applying error convolution, we converted the data back to Cartesian coordinates.
In Fig. 16 we show the structure in angle (top row) and in frequency (middle row) space for the 1% distance errors for all 15 orbits evolved in the time-dependent potential. The bottom row panels show the residuals in frequency space after subtracting the fitted slope from the error-free case (green line). Here the black points correspond to the error-convolved case, while the yellow points are error free.
We define the relative difference in slope in the frequency EΩ and angle Eθ spaces after error convolution as 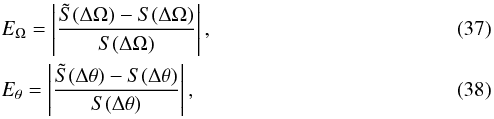 with the
with the 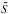 representing the slopes derived by fitting the distributions with errors. The various panels in Fig. 16 show that this relative difference typically varies from 10-5 up to 6 × 10-4 for Eθ and between 3 × 10-4 up to 10-2 for EΩ, indicating that errors affect the distribution of frequencies more severely than that of angles.
representing the slopes derived by fitting the distributions with errors. The various panels in Fig. 16 show that this relative difference typically varies from 10-5 up to 6 × 10-4 for Eθ and between 3 × 10-4 up to 10-2 for EΩ, indicating that errors affect the distribution of frequencies more severely than that of angles.
An estimate of tolerable errors may be derived from the following arguments. If ΔS is the slope difference between frequency and angle space (typically a few %), then we can tolerate 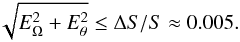 (39)The panels that satisfy this requirement are highlighted with a green box. The very radial orbits that have small pericentres are mostly selected in this way. These streams have many stars relatively near the Sun (which is positioned at 8 kpc from the Galactic centre along the x axis). The more radial streams also have a much broader spread in Jr, which is slightly less affected by the errors than the more circular orbits, which have a broader spread in angular momentum. We conclude that the 1% distance errors allow us to uncover the time evolution for at least half of our orbits when the growth factor is ag = 0.8. However, if we were to consider a growth factor ag = 0.4, the misalignment between angle and frequency space would typically be reduced by a factor 2, and the errors would considerably hinder measuring the time evolution for more slowly evolving potentials.
(39)The panels that satisfy this requirement are highlighted with a green box. The very radial orbits that have small pericentres are mostly selected in this way. These streams have many stars relatively near the Sun (which is positioned at 8 kpc from the Galactic centre along the x axis). The more radial streams also have a much broader spread in Jr, which is slightly less affected by the errors than the more circular orbits, which have a broader spread in angular momentum. We conclude that the 1% distance errors allow us to uncover the time evolution for at least half of our orbits when the growth factor is ag = 0.8. However, if we were to consider a growth factor ag = 0.4, the misalignment between angle and frequency space would typically be reduced by a factor 2, and the errors would considerably hinder measuring the time evolution for more slowly evolving potentials.
In Fig. 17 we show the seven best orbits from Fig. 16, but now with 10% distance errors. The colours and insets are the same as in Fig. 16. As the insets and green boxes show, the angles are still quite well measured, but the frequency slope is not. Only one very radial orbit (that comes close to the Sun) presents an acceptable level of uncertainty. There is significant structure in the bottom panels, which depict the residuals between the distribution in frequency space before and after error convolution. For each experiment this is a result of superposing individual wraps with varying distance gradients, and this, after a distance-dependent error convolution, causes different frequency distributions. The bow-tie-like structure is thus the result of the overlap of multiple wraps that are differently distorted in frequency space. The more circular orbits O15 and O9 only show one leg of these bow-tie-like structures because basically just slightly more than one wrap is present for these experiments.
Given that the 10% errors make it challenging to fit a slope in frequency space, but less so in angle space, we investigated methods for cutting the data and retaining the highest quality measurements. Figure 18 shows the result of combining a distance cut and a frequency cut for the same seven orbits as in Fig. 17. The cuts are given by 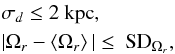 (40)
(40)
with ⟨Ωr⟩ the mean frequency from the data and SDΩr the standard deviation of Ωr, both computed after the distance cut. The distance error cut improves both the tangential velocities and the distances, and its effect is to mainly select particles at pericentre, as seen in the top panels of this figure. Our cut at 2 kpc essentially removes particles with errors larger than 10% at 20 kpc. The motivation for imposing a frequency cut is to remove outliers. The vertical dashed lines in the frequency space of Fig. 18 show the mean and standard deviation of ΔΩr with errors, and they encompass the error-free ΔΩr distribution indicated in yellow quite well. The combination of these cuts still leaves many particles in the stream, as indicated by the insets in the figure, except for orbits O15 and O9, which basically have no or too few particles closer than 20 kpc, and hence have distance errors larger than 2 kpc. In conclusion, a cut in frequency and distance leads to satisfactory improvements, except when there are too few particles and for a few pathological cases. Such a cut might therefore be used to measure the slope in frequency space, but is not necessary in angle space.
6. Discussion and conclusions
We have investigated the effect of an adiabatically growing time-dependent potential on streams. To this end we used the inside-out growing spherical NFW potential from Buist & Helmi (2014) as a background for modelling the evolution of a set of 15 test-particle streams.
We performed a series of numerical experiments starting from different initial conditions that were mostly ran in a quite strongly growing model in which the enclosed mass within the orbits that we explored approximately doubled. These experiments showed that the precession rate of streams, that is, the angular location of the “apocentres” of streams in the orbital plane, is significantly different when the potential has evolved in time. Time evolution typically leads to a misalignment or angular difference of ~10° in comparison to the static case, and this is roughly independent of the progenitor size. To be able to detect this effect, however, streams need to be sufficiently long, meaning that they need to have wrapped around more than once.
We then analysed the behaviour of streams in action-angle coordinates. Streams typically appear as extended linear structures in angle and frequency space, also in the time-dependent case. We found that time evolution causes these distributions to differ in slope, unlike what is expected for a static potential. To explain these findings, we developed an analytic description of a stream in an adiabatically changing time-dependent potential. This allowed us to predict that the difference in slopes in angle and in frequency space is of order ~0.005–0.025, that is, 0.3°–1.5°, for potentials with a growth factor ranging from 0.2 to 0.8. Experiments for which the time evolution signal is most reliably recovered were those that initially had a small size and evolved in an adiabatic way. This condition is most easily satisfied for the more radial orbits.
Although the predicted effect is small, we explored whether it would be observable with the next-generation facilities for mapping the Galaxy, such as the Gaia satellite mission (Prusti 2012) and the follow-up surveys 4MOST (de Jong et al. 2012) and WEAVE (Dalton et al. 2012). When assuming an error in parallax of 1% (and half of that in the proper motion), we found that for about half of the streams the time-dependence signature is expected to be measurable. When the errors in parallax (and consequently in proper motion) are increased to 10%, only 1 of our 15 streams can be used to determine the time evolution. Reasonable additional cuts in distance errors and in frequency space (because this is most strongly affected by errors), allowed the time evolution to be determined for an additional four streams. The best results were obtained for streams that are very radial and have small pericentres (inside the solar circle). This is predominantly because these streams have many stars close to the Sun and therefore have smaller observational uncertainties. There is no guarantee that streams with such characteristics will be present in the Gaia dataset, of course, both because of the requirement on their orbital properties and on the rather optimistic assumptions on the distance and proper motion errors.
Another important issue is that the correct potential is necessary to derive the correct angle and frequency space distributions. Fortunately, an incorrect potential distorts the distribution in angle and in frequency spaces in such a manner that each space can be used independently to improve the estimation of the potential for sufficiently long streams. For short streams (e.g. with only one wrap), the misalignment observed might be confused with time evolution instead of the incorrect assumptions about the potential. The use of short streams might therefore induce a bias in the derived values of the characteristic parameters of the potential or its time dependence.
By construction, we neglected the effect of self-gravity in our experiments. Self-gravity would create a gap in the action space between (the progenitor and) the leading and trailing streams (Gibbons et al. 2014), because the particles released at specific points along the orbit (rather than continuously) are offset in energy (Johnston 1998). This structure will most likely also be apparent in the angle and frequency distributions of the particles that make up the stream (Eyre & Binney 2011). Moreover, when close to the progenitor, released particles still experience a gravitational pull by the progenitor (Choi et al. 2009), and epicyclic oscillations are seen in streams in N-body simulations (Küpper et al. 2010, 2012). These effects may complicate fitting a straight line to the distribution and determining its slope accurately, but after the particles become unbound, the dynamics is essentially the same as in our test-particle integrations (Sanders & Binney 2013b).
Other interesting time-dependent effects may be involved in shaping streams and complicate interpretations. Interactions with dark subhaloes orbiting the Galactic halo will affect the structure of streams and create gaps, for example (Yoon et al. 2011; Carlberg 2013; Ngan & Carlberg 2014). Dwarf galaxies as massive as the Large and Small Magellanic Clouds are able to significantly perturb the potential (Vera-Ciro & Helmi 2013), and might induce non-adiabatic changes in the stream orbits (Gómez et al. 2015). It therefore seems important to try and understand these less secular effects on the dynamical evolution of streams.
We have presented here the first steps towards understanding the imprints of time evolution. More explorations are necessary because we did not study other density profiles or deviations from spherical symmetry, nor did we take into account the effects of a live halo or a (growing) disk. It may be possible to extend our method to any potential for which action-angle coordinates can be derived or approximated, and we do expect the general behaviour to be similar when the potential is growing adiabatically. Overall, we expect the imprint of the smooth mass growth of the Galactic dark halo to be present in streams and to a have a small but non-negligible magnitude.
Online material
Appendix A: Computing the angles
The angles result from the derivatives of the generating function W(x,J) w.r.t. the actions 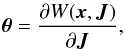 (A.1)(Binney & Tremaine 2008, Eq. (3.204)). The complete generating function for a spherical system is given by (modified from Eq. (3.220), Binney & Tremaine 2008)
(A.1)(Binney & Tremaine 2008, Eq. (3.204)). The complete generating function for a spherical system is given by (modified from Eq. (3.220), Binney & Tremaine 2008) 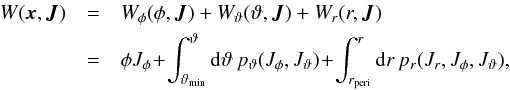 (A.2)where we integrate over the particles trajectory in phase space, which means for example that during a whole radial period, the particle transverses twice the branch from pericentre to apocentre, but once in reversed direction. The latitudinal momentum pϑ is
(A.2)where we integrate over the particles trajectory in phase space, which means for example that during a whole radial period, the particle transverses twice the branch from pericentre to apocentre, but once in reversed direction. The latitudinal momentum pϑ is 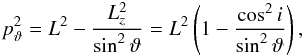 (A.3)where cosi = Lz/L. The radial momentum pr is
(A.3)where cosi = Lz/L. The radial momentum pr is 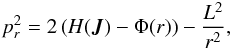 (A.4)where L = Jθ + | Jφ | and Jφ ≥ 0 is assumed8.
(A.4)where L = Jθ + | Jφ | and Jφ ≥ 0 is assumed8.
We find the radial angle as 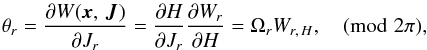 (A.5)where we note that the angles are always defined modulo 2π because there is no information on how many loops a particle made around the Galactic centre. The derivative of the generating function is given by
(A.5)where we note that the angles are always defined modulo 2π because there is no information on how many loops a particle made around the Galactic centre. The derivative of the generating function is given by ![\appendix \setcounter{section}{1} \begin{eqnarray} &&W_{r,\,H} = \int \frac{{\rm d}r}{p_r} = \begin{cases} f_1(r) & \text{if } p_r \geq 0, \\ 2 f_1(r_\text{apo}) - f_1(r) & \text{if } p_r < 0, \end{cases} \nonumber \nonumber\\[4pt] &&\hspace*{4.1cm}\nonumber f_1(r) = \int_{r_\text{peri}}^r \frac{{\rm d}r}{p_r}, \\ &&\hspace*{4.1cm} f_1(r_\text{apo}) = \frac{\pi}{\Omega_r}, \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq199.png) (A.6)where the conditions on pr are necessary to take the right branch of f1. After one full period, we find θr = 2π as expected.
(A.6)where the conditions on pr are necessary to take the right branch of f1. After one full period, we find θr = 2π as expected.
For the azimuthal angle we find 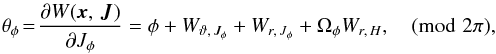 (A.7)where we find φ using the (quadrant-aware) arctangent
(A.7)where we find φ using the (quadrant-aware) arctangent 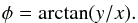 (A.8)The derivative Wr,H has already been worked out for θr, and the other derivatives are
(A.8)The derivative Wr,H has already been worked out for θr, and the other derivatives are
The function Wϑ,Jφ is oscillatory in nature (w.r.t. ϑ), while the combination Wr,Jφ + ΩφWr,H is also oscillatory (w.r.t. r): after one radial period it evaluates to −2Lf2(rapo) + 2Ωφf1(rapo) = 0.
The latitudinal angle is given by 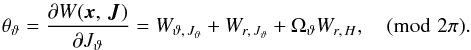 (A.11)Because we assume Jφ ≥ 0, we find Wr,Jϑ = Wr,Jφ and Ωϑ = Ωφ. The remaining derivative of the generating function is
(A.11)Because we assume Jφ ≥ 0, we find Wr,Jϑ = Wr,Jφ and Ωϑ = Ωφ. The remaining derivative of the generating function is ![\appendix \setcounter{section}{1} \begin{eqnarray} &&W_{\vartheta,\,J_\vartheta} = \int \frac{{\rm d}\vartheta}{p_\vartheta} L = \int {\rm d}\vartheta \frac{ 1 }{\sqrt{1 - \frac{\cos^2 i }{\sin^2 \vartheta}}} \nonumber\\ &&\hspace*{2.5cm}= \begin{cases} f_4(\vartheta) & \text{if } p_\vartheta \geq 0 , \\[4pt] 2\pi-f_4(\vartheta) & \text{if } p_\vartheta < 0 , \end{cases} \nonumber \\[4pt] &&\hspace*{3cm} f_4(\vartheta) = \int_{\vartheta_\text{min}}^\vartheta {\rm d}\vartheta \frac{ 1 }{\sqrt{1 - \frac{\cos^2 i }{\sin^2 \vartheta}}} , \nonumber\\[4pt] &&\hspace*{3cm}f_4(\vartheta_\text{max}) = \pi , \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq213.png) (A.12)where the term Wr,Jϑ + ΩϑWr,H vanishes after one radial period, while the term Wϑ,Jϑ contains the dependence on ϑ and increases by 2π after one period in ϑ.
(A.12)where the term Wr,Jϑ + ΩϑWr,H vanishes after one radial period, while the term Wϑ,Jϑ contains the dependence on ϑ and increases by 2π after one period in ϑ.
Appendix B: Transformation equations
The linearised transformation between action-angle coordinates and Cartesian coordinates is ![\appendix \setcounter{section}{2} \begin{eqnarray} {\bf T} = \left[ \renewcommand\arraystretch{2.2}\begin{matrix} \dfrac{\partial^2 W}{\partial {\vec J} \partial {\vec J}} \dfrac{\partial {\vec J}}{\partial {\vec q}} + \dfrac{\partial^2 W}{\partial {\vec J} \partial {\vec q}} & \dfrac{\partial^2 W}{\partial {\vec J} \partial {\vec J}} \dfrac{\partial {\vec J}}{\partial {\vec p}} \\ \dfrac{\partial {\vec J}}{\partial {\vec q}} & \dfrac{\partial {\vec J}}{\partial {\vec p}} \end{matrix} \right] . \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq216.png) (B.1)For simplicity, we provide here the matrix for the 2D case (i.e. when the orbit is in the plane). In that case, Jθ = 0 and Jφ = L = Lz, so that we find
(B.1)For simplicity, we provide here the matrix for the 2D case (i.e. when the orbit is in the plane). In that case, Jθ = 0 and Jφ = L = Lz, so that we find ![\appendix \setcounter{section}{2} \begin{eqnarray} {\bf T} = \left[ \renewcommand\arraystretch{2.2}\begin{matrix} 1 & t_{\theta_\phi,\,r} & t_{\theta_\phi,\,p_\phi} & t_{\theta_\phi,\,p_r} \\ 0 & t_{\theta_r,\,r} & t_{\theta_r,\,p_\phi} & t_{\theta_r,\,p_r} \\ 0 & 0 & 1 & 0 \end{matrix} \right] , \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq219.png) (B.2)where the above terms are given by
(B.2)where the above terms are given by 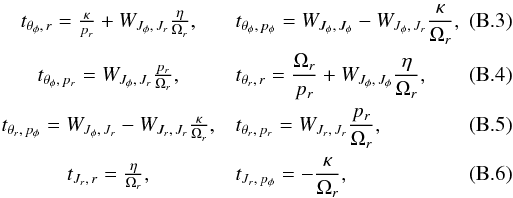
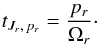 (B.7)The functions κ and η are
(B.7)The functions κ and η are  and the WJi,Jj are found by differentiating the generating function
and the WJi,Jj are found by differentiating the generating function 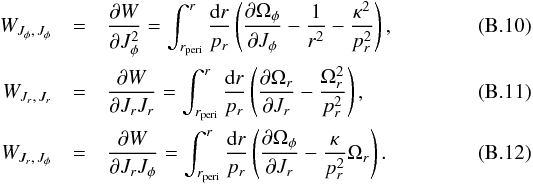
We recall that the ratio of angular to radial frequencies for any gravitational potential is limited by the homogeneous sphere case, for which Ωφ/ Ωr = 1/2 and the Kepler case, for which Ωφ/ Ωr = 1. As mass increases and the orbit shrinks, we may say, effectively, that the stream moves farther away from experiencing a Kepler potential (and hence a steeper slope) and closer to the homogeneous sphere (a shallower slope, as also seen in Gómez & Helmi 2010), although the NFW potential is neither of these limiting cases.
Acknowledgments
H.J.T.B. and A.H. gratefully acknowledge financial support from ERC-Starting Grant GALACTICA-240271. We thank the anonymous referee for a constructive report that helped improve this manuscript. H.J.T.B. thanks Robyn E. Sanderson for the many interesting and useful discussions.
References
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2008, MNRAS, 386, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2012, MNRAS, 426, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & McMillan, P. 2011, MNRAS, 413, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press) [Google Scholar]
- Bonaca, A., Geha, M., Küpper, A. H. W., et al. 2014, ApJ, 795, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J. 2014, ApJ, 795, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Buist, H. J. T., & Helmi, A. 2014, A&A, 563, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlberg, R. G. 2013, ApJ, 775, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J.-H., Weinberg, M. D., & Katz, N. 2009, MNRAS, 400, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
- de Zeeuw, T. 1985, MNRAS, 216, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Eyre, A., & Binney, J. 2009, MNRAS, 400, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Eyre, A., & Binney, J. 2011, MNRAS, 413, 1852 [NASA ADS] [CrossRef] [Google Scholar]
- Gibbons, S. L. J., Belokurov, V., & Evans, N. W. 2014, MNRAS, 445, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1950, Classical mechanics (Addison-Wesley Publishing Company) [Google Scholar]
- Gómez, F. A., & Helmi, A. 2010, MNRAS, 401, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, F. A., Besla, G., Carpintero, D. D., et al. 2015, ApJ, 802, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006, ApJ, 643, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Johnson, R. 2006, ApJ, 639, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., Freeman, K. C., Irwin, M., & Quinn, P. J. 1995, AJ, 109, 2553 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2008, A&ARv, 15, 145 [CrossRef] [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., & White, S. D. M. 1999, MNRAS, 307, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Zhao, H., & de Zeeuw, T. 1999, in The Third Stromlo Symp.: The Galactic Halo, eds. B. K. Gibson, R. S. Axelrod, & M. E. Putman, ASP Conf. Ser., 165, 125 [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001a, Nature, 412, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ibata, R., Irwin, M., Lewis, G. F., & Stolte, A. 2001b, ApJ, 547, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Goldston, J., Finlator, K., et al. 2000, AJ, 120, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, S., & Lynden-Bell, D. 2007, MNRAS, 378, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V. 1998, ApJ, 495, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Hernquist, L., & Bolte, M. 1996, ApJ, 465, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, K. V., Zhao, H., Spergel, D. N., & Hernquist, L. 1999, ApJ, 512, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Binney, J. 1994, MNRAS, 268, 1033 [NASA ADS] [Google Scholar]
- Küpper, A. H. W., Kroupa, P., Baumgardt, H., & Heggie, D. C. 2010, MNRAS, 401, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Küpper, A. H. W., Lane, R. R., & Heggie, D. C. 2012, MNRAS, 420, 2700 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Lynden-Bell, R. M. 1995, MNRAS, 275, 429 [NASA ADS] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Ibata, R. A., Rich, R. M., et al. 2014, ApJ, 787, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Ngan, W. H. W., & Carlberg, R. G. 2014, ApJ, 788, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Odenkirchen, M., Grebel, E. K., Rockosi, C. M., et al. 2001, ApJ, 548, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J., Benson, A. J., Martínez-Delgado, D., & Rix, H. W. 2006, ApJ, 645, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J., Koposov, S. E., & Walker, M. G. 2012, ApJ, 760, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price-Whelan, A. M., Hogg, D. W., Johnston, K. V., & Hendel, D. 2014, ApJ, 794, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Prusti, T. 2012, Astron. Nachr., 333, 453 [NASA ADS] [Google Scholar]
- Sanders, J. L., & Binney, J. 2013a, MNRAS, 433, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., & Binney, J. 2013b, MNRAS, 433, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., & Binney, J. 2014, MNRAS, 441, 3284 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. L., & Binney, J. 2015, MNRAS, 447, 2479 [NASA ADS] [CrossRef] [Google Scholar]
- Sanderson, R. E., Helmi, A., & Hogg, D. W. 2014, in IAU Symp. 298, eds. S. Feltzing, G. Zhao, N. A. Walton, & P. Whitelock, 207 [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S. 1999, MNRAS, 307, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Vandervoort, P. O. 1961, Ann. Phys., 12, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Vera-Ciro, C., & Helmi, A. 2013, ApJ, 773, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Navarro, J. F., Frenk, C. S., et al. 2011, MNRAS, 413, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
- Yanny, B., Newberg, H. J., Kent, S., et al. 2000, ApJ, 540, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, J. H., Johnston, K. V., & Hogg, D. W. 2011, ApJ, 731, 58 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Increase of the enclosed mass for several orbits for our time-dependent potential with a growth factor of ag = 0.8. The dashed lines show the enclosed mass within the final value of their apocentre. Since the apocentric distances shrink with time, we show the mass enclosed within the time-dependent apocentre values with solid lines. The integration time span for the streams is t ~ 7–8 Gyr, and the enclosed mass approximately doubles over this timescale. |
| In the text | |
 |
Fig. 2 Relation between the coordinates and the angles in the plane of the orbit. The top panel shows that the radial angle θr increases by 2π in one radial oscillation. In the bottom panel we have plotted φ (red) and θφ (blue) as functions of θr. After one radial period, both angles reach the same value 2πΩφ/ Ωr. |
| In the text | |
 |
Fig. 3 Distribution in action (left), frequency (second panel) and angle space (right) for particles in a stream, and centred on the centre of mass of the progenitor system. The colours represent the energy gradient, where red is for the trailing and green for the leading arms. |
| In the text | |
 |
Fig. 4 Streams from three progenitor sizes for each of the 15 orbits evolved in the time-dependent ag = 0.8 potential. The left, middle, and right panels correspond to the “Carina”, “Sculptor”, and “Sagittarius”-like progenitors, respectively (see Table 2 for their properties). Particles in green are more bound to the host galaxy (leading arm), while those in red are less bound (trailing arm) than the progenitor. The dashed curves are the progenitor orbits evolved in today’s potential, with the green integrated forward in time for the leading arm and red backwards for the trailing arm. The current position of the progenitor is indicated with a red cross. |
| In the text | |
 |
Fig. 5 Radial vs. angular distribution of particles in the orbital plane for experiment O7 for the different progenitors in the time-dependent case. The dashed curves show the orbit of the centre of mass of the system integrated long enough to roughly reproduce the lengths of the streams. The variations in the apocentric distances are a reflection both of time evolution and of the energy gradient present along a stream. The difference in angular location of the apocentre, on the other hand, is a clear imprint of time evolution, as can be seen by comparing to e.g. Fig. 7. |
| In the text | |
 |
Fig. 6 Streams from the Carina progenitor in the evolving and in the non-evolving potential. The streams in the left and centre have the same initial distribution in configuration and velocity space. Those in the right panels have the same initial action-angle distribution as the time-evolving potential (middle panel), but are evolved in a static potential. The colour coding is the same as in the previous figure. The stream-orbit misalignment can be seen by looking at the azimuthal angle of the petals starting from one radial period away from the progenitor, whose position is indicated with a red cross. |
| In the text | |
 |
Fig. 7 Radial vs. angular distribution of particles in the orbital plane for experiment O7 for the Carina-like progenitor in the static case (left), time-dependent case (middle), and static case with the same initial action-angle distribution as in the middle panel. The dashed curves show the orbit of the centre of mass of the system integrated in the present-day potential for the left and right panels, and in the evolving potential for the middle panel. For the static cases, the variations in the apocentric distances are a reflection of the energy gradient present along the stream, while a second effect is present in the middle panel because of time evolution. In this case, the difference in angular location of the apocentre is also much more pronounced and systematically increases for older wraps. |
| In the text | |
 |
Fig. 8 Action-space distributions for a sample of four streams from Fig. 6, measured with respect to the centre of mass of the progenitor at the final time. The colours of the particles represent the energy gradient, such that green is the leading arm and red the trailing arm. In the static cases, the initial and final distributions coincide exactly, but in the time-dependent case there can be small deviations if the orbit is not in the adiabatic regime, as can be seen by comparing the middle and right panels for orbits O11 and O15. The left panels show a smaller spread because the time-dependent cases start farther outwards and in an initially much lighter potential. |
| In the text | |
 |
Fig. 9 Response of the radial action and the radial frequency to a time-dependent potential for orbit O7 (Table 1). For this orbit, the action shows a non-secular oscillation that decreases in amplitude as the rate of change of the potential decreases. The value of Ωr changes significantly with time, and here there are also oscillations that become smaller as the change rate of the potential decreases. The period of the oscillations corresponds with the radial period. The evolution of Jr has been quite adiabatic because it oscillates around a limiting value, which is the starting value when the particles were released at pericentre. |
| In the text | |
 |
Fig. 10 Angle space of stream O7 (see Table 1) evolved in a time-dependent potential, but where the angles have been computed with different (incorrect) parameters. The central panel shows the correct parameters, while rs is changed vertically and Ms horizontally by 10% and 30%. The colour coding indicates the energies, with green representing the leading arm (more bound) and red the trailing arm (less bound). |
| In the text | |
 |
Fig. 11 Angle space of streams O11 (top) and stream O1 (bottom) evolved in a time-dependent potential, but where the angles have been computed with different (incorrect) parameters. We note that although the distortions in angle space are less pronounced for the more radial orbit O1, the energy gradient (indicated by the colour gradient and coding used before) is not preserved. |
| In the text | |
 |
Fig. 12 Lines fitted to the angle space (red dashed line) and the frequency space (blue line) of stream O7 evolved in a time-dependent (top) and static potential (bottom) using the same (correct) final potential. Additionally, the green line shows the track of the progenitor assuming the potential is static (i.e. θcm(t) = Ωcm(tf)t), and the grey line shows the line fitted to the frequency space at the beginning of the simulation. The inset labels show the numerical values of the aperture angle (misalignment) between the stream and the (static) progenitor orbit ΨS, O, and between the stream in angle and in frequency space ΨΔθ, ΔΩ (see Eqs. (34) and (35)). |
| In the text | |
 |
Fig. 13 Hessians Hij, time-averaged Hessians Qij (both in units of 10-3 kpc-2), and their ratios hi and qi for orbit O7. Left panel: the dash-dotted lines show Hij in the static potential, the solid lines the Hij in the time-dependent potential, and the dashed lines Qij in the time-dependent potential. We note that | Hrr | > | Hrφ | > | Hφφ |, and similarly for Qij. The middle panel shows that hφ>qφ at all times and that both increase with time. On the other hand, hr<qr at all t, and both decrease with time. Right panel: the ranking of the hi for the different orbits. Both hφ and hr are ranked by the ratio Ωφ/ Ωr, indicating the dependence on the type of orbit. The qi are ranked in the same way. |
| In the text | |
 |
Fig. 14 Slope differences between the streams in angle and in frequency space as a function of growth parameter ag, as predicted by our analytic model using Eqs. (23) and (26) for our experiments. |
| In the text | |
 |
Fig. 15 Examples of the slope differences between the angle and frequency distributions (top panels) and histograms of the spread of Δθr(0)/Δθr(tf) (bottom panels). In the top panels, the blue crosses indicate values from the full simulation, while the green lines are the predictions from our analytic model. The red crosses are the slopes measured when the initial spreads from the simulations are removed. All orbits now align with the model when ag = 0. For large ag the more circular orbits such as orbit O15 deviate strongly from the model because of non-adiabaticity. |
| In the text | |
 |
Fig. 16 Angle and frequency space plots and residuals of the frequency space fits of all 15 streams for 1% distance (and proper motion) errors in the time-dependent potential. The streams are centred on the position of the centre of mass of the progenitor in the error-free case. The black points are error-convolved, while those in yellow are error-free and only shown in the bottom row. The residuals were computed by subtracting the best-fit straight line to the error-free frequency distribution (green line) from ΔΩφ. The text in the panels shows the relative difference in the slopes for the error-convolved and error-free cases derived in angle space Eθ and in frequency space EΩ (i.e. using the red vs. green straight lines, respectively). The panels for which Ei< 0.005 are marked with a green box. The difference in slope in angle space clearly is generally far below this value, while the frequencies are much more strongly affected by the errors. |
| In the text | |
 |
Fig. 17 Selection of the seven best orbits of Fig. 16, but now with 10% parallax (and proper motion) errors. The colours, lines, and insets are the same as in Fig. 16. With these 10× larger distance errors, the angle slopes of the streams are still well measured for most orbits, while the frequency slopes generally are not. |
| In the text | |
 |
Fig. 18 Selection of the orbits of Fig. 16 with 10% parallax errors, but now with two cuts: σd ≤ 2 kpc and | Ωr−⟨Ωr⟩ | ≤ SDΩr. The colours are the same as in Fig. 17, with the addition that green points represent the particles that remain after the cuts. The grey vertical dashed lines indicate ⟨Ωr⟩ and ⟨Ωr⟩ ± SDΩr applied after the distance cut. The insets in the top panels show the number of remaining particles after the cuts Ncut, while those in the bottom panels are the number of particles within a distance of 20 kpc from the Sun N (d< 20 kpc). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\appendix \setcounter{section}{1} \begin{eqnarray} &&W_{r,\,J_\phi} = - L \int \frac{{\rm d}r} {p_r \, r^2} = - L \begin{cases} f_2(r) & \text{if } p_r \geq 0 , \\[4pt] 2 f_2(r_\text{apo}) - f_2(r) & \text{if } p_r < 0 , \end{cases}\nonumber\\[4pt] &&\hspace*{5.5cm}\nonumber f_2(r) = \int_{r_\textrm{peri}}^r \frac{{\rm d}r} {p_r \, r^2} , \nonumber\\[4pt] &&\hspace*{5.5cm}f_2({r_\textrm{apo}}) = \frac{\Omega_\phi}{L} f_1(r_\text{apo}) , \nonumber\\ \\ &&\nonumber W_{\vartheta,\,J_\phi} = \int \frac{{\rm d}\vartheta}{p_\vartheta} \left[ L - \frac{J_\phi}{\sin^2\vartheta} \right] = \int {\rm d}\vartheta \frac{ 1 - \frac{\cos i}{\sin^2\vartheta}}{\sqrt{1 - \frac{\cos^2 i }{\sin^2 \vartheta}}} \nonumber\\ &&\hspace*{4.07cm} = \begin{cases} f_3(\vartheta) & \text{if } p_\vartheta \geq 0 , \nonumber\\[4pt] -f_3(\vartheta) & \text{if } p_\vartheta < 0 , \end{cases} \\[4pt] &&\hspace*{4.6cm} \nonumber f_3(\vartheta) = \int_{\vartheta_\text{min}}^\vartheta {\rm d}\vartheta \frac{ 1 - \frac{\cos i}{\sin^2\vartheta}}{\sqrt{1 - \frac{\cos^2 i }{\sin^2 \vartheta}}} , \\[4pt] &&\hspace*{4.6cm}f_3(\vartheta_\text{max}) = 0. \end{eqnarray}](/articles/aa/full_html/2015/12/aa26203-15/aa26203-15-eq205.png)