| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 20 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526203 | |
| Published online | 02 December 2015 | |
Online material
Appendix A: Computing the angles
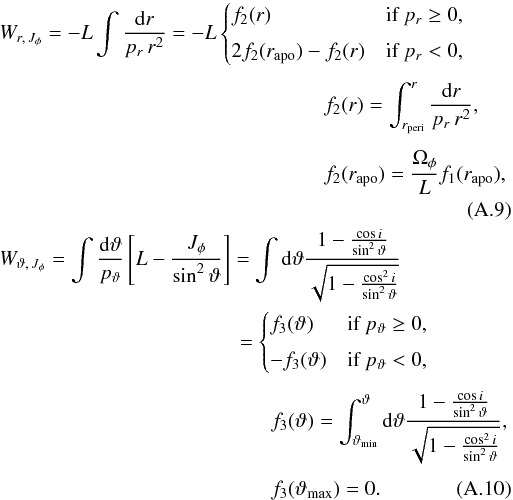
The angles result from the derivatives of the generating function W(x,J) w.r.t. the actions 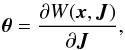 (A.1)(Binney & Tremaine 2008, Eq. (3.204)). The complete generating function for a spherical system is given by (modified from Eq. (3.220), Binney & Tremaine 2008)
(A.1)(Binney & Tremaine 2008, Eq. (3.204)). The complete generating function for a spherical system is given by (modified from Eq. (3.220), Binney & Tremaine 2008) 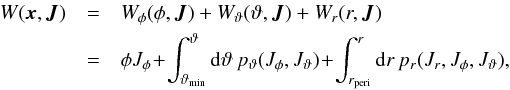 (A.2)where we integrate over the particles trajectory in phase space, which means for example that during a whole radial period, the particle transverses twice the branch from pericentre to apocentre, but once in reversed direction. The latitudinal momentum pϑ is
(A.2)where we integrate over the particles trajectory in phase space, which means for example that during a whole radial period, the particle transverses twice the branch from pericentre to apocentre, but once in reversed direction. The latitudinal momentum pϑ is 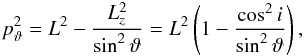 (A.3)where cosi = Lz/L. The radial momentum pr is
(A.3)where cosi = Lz/L. The radial momentum pr is ![]() (A.4)where L = Jθ + | Jφ | and Jφ ≥ 0 is assumed8.
(A.4)where L = Jθ + | Jφ | and Jφ ≥ 0 is assumed8.
We find the radial angle as  (A.5)where we note that the angles are always defined modulo 2π because there is no information on how many loops a particle made around the Galactic centre. The derivative of the generating function is given by
(A.5)where we note that the angles are always defined modulo 2π because there is no information on how many loops a particle made around the Galactic centre. The derivative of the generating function is given by  (A.6)where the conditions on pr are necessary to take the right branch of f1. After one full period, we find θr = 2π as expected.
(A.6)where the conditions on pr are necessary to take the right branch of f1. After one full period, we find θr = 2π as expected.
For the azimuthal angle we find 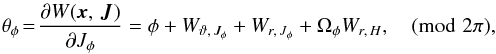 (A.7)where we find φ using the (quadrant-aware) arctangent
(A.7)where we find φ using the (quadrant-aware) arctangent ![]() (A.8)The derivative Wr,H has already been worked out for θr, and the other derivatives are
(A.8)The derivative Wr,H has already been worked out for θr, and the other derivatives are
The function Wϑ,Jφ is oscillatory in nature (w.r.t. ϑ), while the combination Wr,Jφ + ΩφWr,H is also oscillatory (w.r.t. r): after one radial period it evaluates to −2Lf2(rapo) + 2Ωφf1(rapo) = 0.
The latitudinal angle is given by  (A.11)Because we assume Jφ ≥ 0, we find Wr,Jϑ = Wr,Jφ and Ωϑ = Ωφ. The remaining derivative of the generating function is
(A.11)Because we assume Jφ ≥ 0, we find Wr,Jϑ = Wr,Jφ and Ωϑ = Ωφ. The remaining derivative of the generating function is 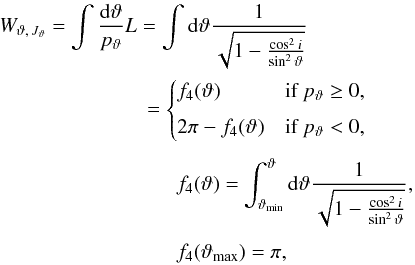 (A.12)where the term Wr,Jϑ + ΩϑWr,H vanishes after one radial period, while the term Wϑ,Jϑ contains the dependence on ϑ and increases by 2π after one period in ϑ.
(A.12)where the term Wr,Jϑ + ΩϑWr,H vanishes after one radial period, while the term Wϑ,Jϑ contains the dependence on ϑ and increases by 2π after one period in ϑ.
Appendix B: Transformation equations
The linearised transformation between action-angle coordinates and Cartesian coordinates is 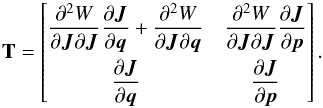 (B.1)For simplicity, we provide here the matrix for the 2D case (i.e. when the orbit is in the plane). In that case, Jθ = 0 and Jφ = L = Lz, so that we find
(B.1)For simplicity, we provide here the matrix for the 2D case (i.e. when the orbit is in the plane). In that case, Jθ = 0 and Jφ = L = Lz, so that we find 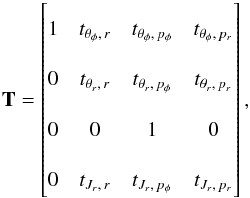 (B.2)where the above terms are given by
(B.2)where the above terms are given by 
![]() (B.7)The functions κ and η are
(B.7)The functions κ and η are  and the WJi,Jj are found by differentiating the generating function
and the WJi,Jj are found by differentiating the generating function 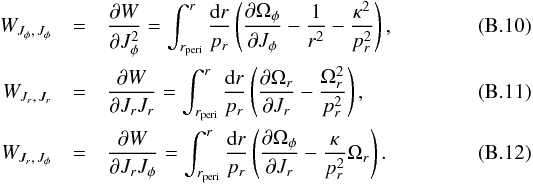
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.