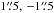| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424850 | |
| Published online | 02 November 2015 | |
The nuclear gas disk of NGC 1566 dissected by SINFONI and ALMA ⋆, ⋆⋆
1 I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
e-mail: smajic@ph1.uni-koeln.de
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 Observatoire de Paris, LERMA, PSL, CNRS, Sorbonne Univ. UPMC and College de France, 75014 Paris, France
4 Observatorio Astronómico Nacional (OAN) – Observatorio de Madrid, Alfonso XII 3, 28014 Madrid, Spain
Received: 22 August 2014
Accepted: 10 August 2015
We present the results of near-infrared (NIR) H- and K-band European Southern Observatory SINFONI integral field spectroscopy (IFS) of the Seyfert galaxy NGC 1566. We investigate the central kpc of this nearby galaxy, concentrating on excitation conditions, morphology, and stellar content. NGC 1566 was selected from our NUGA (-south) sample and is a ringed, spiral galaxy with a stellar bar in north-south direction (PA ~ 5°). The galaxy inhibits a very active Seyfert 1 nucleus but narrow line ratios from optical observations in the nuclear region are similar to Seyfert 2 galaxies. The recent strong activity phase, as inferred from strong variablity in X-ray to IR wavelengths, makes NGC 1566 an ideal candidate to look for feeding and feedback of a supermassive black hole. We present emission and absorption line measurements in the central kpc of NGC 1566. Broad and narrow Brγ lines were detected. The detection of a broad Brγ component is a clear sign of a supermassive black hole in the center. Blackbody emission temperatures of ~1000 K are indicative of a hot dust component, the torus, in the nuclear region. The molecular hydrogen lines, hydrogen recombination lines, and [Fe ii] indicate that the excitation at the center is coming from an AGN. The central region is predominantly inhabited by molecular gas, dust, and an old K-M type giant stellar population. The molecular gas and stellar velocity maps both show a rotation pattern. The molecular gas velocity field shows a perturbation toward the center that is typical for bars or spiral density waves. The molecular gas species of warm H2(1−0)S(1) and cold 12CO(3−2) gas trace a nuclear gas disk of about 3″ in radius with a nuclear spiral reaching toward the nucleus. From the equivalent width of H2(1−0)S(1) a molecular ring with r ≲ 3″ can be inferred. This spiral seems to be an instrument that allows gas to fall toward the nucleus down to <50 pc scales. The excitation of molecular hydrogen in the nuclear gas disk is not clear, but diagnostic diagrams show a distinction between the nuclear region and a <9 Myr old star-forming region at the southwestern spiral arm. Gas that might be shocked is detected ≈2″ from the center, which is visible in dispersion maps of H2(1−0)S(1) and 12CO(3−2) and in the 0.87 mm continuum.
Key words: galaxies: active / galaxies: individual: NGC 1566 / galaxies: ISM / galaxies: nuclei / infrared: galaxies / galaxies: kinematics and dynamics
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The NUclei of GAlaxies (NUGA) project (García-Burillo et al. 2003) started with the IRAM Plateau de Bure Interferometer (PdBI) and 30 m single-dish survey of nearby low-luminosity active galactic nuclei (LLAGN) in the northern hemisphere. The project is ideally suited to map the distribution and dynamics of (cool) molecular gas in the inner kpc of LLAGN and to study the possible mechanisms for gas fueling at a high angular resolution (≈0.̋5−2′′) and high sensitivity. The ongoing implementation of the Atacama Large Millimeter/submillimeter Array (ALMA) in the Atacama desert in Chile finally allows the NUGA project to expand to the southern hemisphere (Combes et al. 2013, 2014) at an even higher angular resolution (~6−37 mas, assuming the full array is used) and sensitivity. The Spectrograph for INtegral Field Observations in the Near Infrared (SINFONI) adds complementary information to the NUGA goal in the near-infrared (NIR, Smajić et al. 2014). By maping (hot) gas and the mass dominating stellar population we investigate star formation and the feeding and feedback of nearby LLAGN in the NIR.
1.1. Feeding and feedback in AGN
Unresolved, powerful, and highly ionizing emission detected in the centers of galaxies is thought to stem from accretion events onto a supermassive black hole (SMBH). These galaxies are said to have an active galactic nucleus (AGN). According to the unified model of AGN this active nucleus consists of a SMBH surrounded by an accretion disk at scales of up to a few lightdays which ionizes the surrounding gas on scales from several lightdays, in Seyfert galaxies, up to lightyears, in Quasars, (e.g., broad line region − BLR) to several hundred parsecs (e.g., narrow line region − NLR) and up to even larger scales via jets. The torus, a mantle of dust and gas, surrounds the AGN on parsec to tens of parsec scales and is thought to be responsible for Seyfert 1 (torus almost face-on toward the observer) and Seyfert 2 (torus almost edge-on) classifications of AGN. The existence of the torus can be inferred from high column densities toward Seyfert 2 AGN and dust blackbody emission in Seyfert 1 AGN with temperatures up to the sublimation temperature of dust (≈1300 K).
The host galaxy and its SMBH have been found to exhibit close correlations. These correlations mostly apply to the stellar bulge (e.g., Magorrian et al. 1998; Ferrarese & Merritt 2000; Marconi & Hunt 2003). The correlations connect the mass of the central SMBH with the mass, luminosity, and kinematics of the bulge. The latest studies show that these correlations may depend on the galaxy classification (e.g., barred galaxies, Graham & Scott 2013) and that several galaxies show an over-luminous bulge or an under-massive SMBH (Busch et al. 2014). Läsker et al. (2014) show that the total luminosity of the host galaxy seems a more robust tracer of the SMBH mass than the bulge luminosity. The distribution of the gas in the host is essential to understand these correlations, since gas is the progenitor of stars which mainly contribute to the mass, luminosity, and kinematics of the bulge. Gravitational torques are one of the strongest forms of force to act on the distribution of the gas on these scales. Gravitational mechanisms that exert gravitational torques such as galaxy-galaxy interactions (e.g., galaxy merger) or non-axisymmetries within the galaxy potential (e.g., spiral density waves or stellar bars on large scales) can lead to loss of angular momentum in the gas. Hydrodynamical mechanisms such as shocks and viscosity torques introduced by turbulences in the interstellar medium (ISM) can remove angular momentum from gas, too. The original NUGA (north) project has already studied the gaseous distribution in more than ten nearby galaxies (≈4−40 Mpc) with results that show a variety of morphologies in nuclear regions, including bars and spirals (García-Burillo et al. 2005, 2009; Boone et al. 2007; Hunt et al. 2008; Lindt-Krieg et al. 2008), rings (Combes et al. 2004, 2009; Casasola et al. 2008) and lopsided disks (García-Burillo et al. 2003; Krips et al. 2005; Casasola et al. 2010).
On large scales, hundreds to thousands of parsecs, gravitational torques are the strongest mechanism to successfully transport gas close to the nucleus, whereas viscosity torques can take over on smaller scales (<200 pc, e.g., Combes et al. 2004; van der Laan et al. 2011). Therefore, large-scale stellar bars are an important feature to transport gas toward the inner Lindblad resonance (ILR, e.g., Sheth et al. 2005) where the formation of nuclear spirals and rings is induced.
The NUGA sample studies the cold gas distribution. We can use the cold gas distribution as a complement to our SINFONI NIR observations and compare it to the sites of hot molecular and ionized gas (Combes et al. 2013, 2014; Smajić et al. 2014). This enables us to identify ongoing star formation sites and regions ionized by shocks (i.e., super novae (SN) or outflows). Furthermore, we are able to compare the distribution of cold (e.g., CO, HCN) and hot (e.g., H2) molecular gas that will give us a more clear insight on feeding and feedback of the AGN through its ambient gas reservoir. Riffel et al. (2013, and references therein) assume that molecular gas (e.g., H2) traces the ambient disk structure and in some cases the streaming motions, i.e., the feeding of the SMBH, whereas ionized gas often traces outflowing material that is above the galaxy disk plane, i.e., the feedback from the SMBH. However, molecular emission lines in the NIR (e.g., H2(1−0)S(1) emission) are known shock tracer that are found in regions shocked by jets or outflows (e.g., Riffel et al. 2014; Davies et al. 2014, and references therein). Lately, García-Burillo et al. (2014) find that cold molecular gas (e.g., 12CO(3−2) emission) can be found in outflows.
Here, we analyze the interactions of nuclear star formation sites and the AGN with regard to fueling and feedback, of both participants. Using the differently excited H2 lines (e.g., H2λ2.12 μm, 1.957 μm, 2.247 μm) and the hydrogen recombination line Brγ in K-band and the forbidden transition [Fe ii] λ1.644μm in H-band we are able to constrain the excitation type (e.g., thermal, non-thermal) of the warm gas and the excitation temperature (Mouri 1994; Rodríguez-Ardila et al. 2004; Zuther et al. 2007). The cold gas information can then be compared to our results.
We will use the stellar absorption features (e.g., Si i, CO(6−3), Mg i, Na i, CO(2−0)) to get insight into the star formation history of the nuclear region (e.g., Davies et al. 2007). Star formation, recent or ongoing, on scales of 0.1−1 kpc around the nucleus is an important process which is frequently found in all types of AGN in contrast to quiescent galaxies (e.g., Cid Fernandes et al. 2004; Davies et al. 2006; Busch et al. 2015). The debate if outflows from the AGN quench or initiate star formation is still going on, but it is most probable that outflows can show both effects.
1.2. NGC 1566
NGC 1566 is a barred, ringed, spiral SAB(s)bc galaxy in the Dorado group (Mulchaey & Regan 1997; Reunanen et al. 2002) harboring a low-luminosity AGN (LLAGN) at a redshift of z ≈ 0.005017 (Koribalski et al. 2004). The bar is oriented in the north-south direction (PA ~ 5°) and the ring has a diameter of 1.7 kpc (see Fig. 1). Alloin et al. (1985) detect broad Balmer lines with widths of FWHMHβ = 2400 ± 300 km s-1. They also measure an increase in flux of the broad Hβ line by a factor of 4−5 within 24 days. They find the narrow line ratio of Hα/Hβ to be ≈3.1, which is typical for Seyfert 2 galaxies, however, the broad line flux variation and the broad to narrow line ratio Hβ(b)/Hβ(n) ≈ 10 shows that NGC 1566 is in a high activity state typical for Seyfert 1.2 galaxies. The light crossing time of the NLR is about 102−103 years, hence, the NLR line ratios suggest that in the past few 100 years NGC 1566 has shown more the characteristics of a Seyfert 2 galaxy than that of a Seyfert 1. Kriss et al. (1991) measure a redshift of the broad emission lines of 200−1000 km s-1. This might result from gravitational redshift (Netzer 1977) but can also be induced by an outflow of optically thick clouds at the far side or an infall of clouds at the near side of the BLR where the far side is obscured from our view.
NGC 1566 shows variability from the X-ray to IR wavelengths. Baribaud et al. (1992) conclude that X-ray flickering should occur on time scales of 5 × 103 s. They also note that the NIR flux variation (heated dust reacting to UV flux changes) happens within the central 450 pc from the center at time scales similar to the broad Hα variability time scale. The extinction toward the nuclear region of NGC 1566 from NLR and BLR line ratios seems to be negligible. Baribaud et al. (1992) also calculate a dust mass Mdust ≈ 7 × 10-4M⊙ and a dust evaporation radius of about 47 light-days. Reunanen et al. (2002) used slit spectroscopy on the nucleus of NGC 1566. They detect [Fe ii] in the H-band and the H2λ2.122 μm line in the K-band. They note that the lines and the continuum appear weaker along the NLR cone than perpendicular to it. They do not detect narrow Brγ emission, only a broad Brγ component with an FWHMBrγ = 2100 km s-1.
 |
Fig. 1 An HST image of NGC 1566 taken with the WFC3 UVIS2 F438W filter at a pivot wavelength of 4326Å. North is up and east is left. The white rectangle marks our 10″ × 10″ field of view (FOV). |
NGC 1566 is an interesting candidate to investigate the feeding and feedback of the nuclear region and the AGN since the galaxy seems to be waking up from a low activity state in the past few hundred years (low ionization level in the NLR) and shows signs of high activity with strong variability and high ionization on scales smaller than the NLR. Combes et al. (2014) find from ALMA 12CO(3−2) and HST data that gravitational torques are a very likely cause to drive gas infall in NGC 1566. They derive negative torques from 300 pc down to 50 pc. From this point dynamical friction can drive the gas to the nucleus.
We will investigate the central 10″ × 10″ to find if the hot gas distribution and kinematics are similar to the cold gas observed with ALMA. Are there any signs of a feeding of the SMBH (e.g., strong ionization of the nuclear region, streaming gas motion)? How strongly is it accreting? Is any strong feedback (e.g., jets) visible in the hot gas? Is gas infall accompanied by star formation or is star formation rather hindered by the torque budget found by Combes et al. (2014)?
This paper is structured as follows: in Sect. 2 we present the observation and the data reduction. Section 3 states the results of our study and how these were derived. Section 4 discusses the results and compares them with literature. In Sect. 5 a summary of the results is given and the conclusions we take from our study are phrased.
Throughout the paper we adopt a systemic velocity of 1504 km s-1 and a distance of 10 Mpc for NGC 1566, following Alloin et al. (1985); Combes et al. (2014).
2. Observation and data reduction
In this paper we present the results of our ESO SINFONI (Eisenhauer et al. 2003; Bonnet et al. 2004) observation of NGC 1566 with the Unit Telescope 4 of the Very Large Telescope in Chile. The 0.̋25 plate scale with an 8″ × 8″ FOV without adaptive optics assistance was used. The average seeing was ≈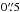 . To increase the FOV to 12″ × 12″ and minimize the overlap of dead pixels in critical areas a dithering sequence of the FOV by ± 2″ was introduced. However, the outer 2″ have data of insufficient quality, hence for the analysis a FOV of 10″× 10″ was used. The dithering was done at 9 positions where the central 4″ × 4″ were observed with the full integration time. The gratings used are the H-band grating at a spectral resolution of R ≈ 3000 and the K-band grating at a resolution of R ≈ 4000. Both bands were observed at a digital integration time of 150 s and an TST ... nodding sequence (T: target, S: sky), to increase on-source time. The overall integration time on the target source in H-band is 2550 s and in K-band 3000 s with an additional 1200 s in H-band and 1500 s in K-band on sky. The G2V star HIP 33144 was observed in H-band and in K-band within the respective science target observation. The observing strategy was to observe it twice (star in opposite corners of the FOV) with an integration time of 2 s. The ESO SINFONI pipeline was used for data reduction except for atmospheric OH line correction and final cube creation which were done manually. Detector specific corrections were performed manually, as well. For more details on the reduction see Smajić et al. (2014). The standard star was used to correct for telluric absorption in the atmosphere and to perform a flux calibration of the target. A high signal-to-noise ratio solar spectrum was used to correct for the blackbody and intrinsic spectral features of an G2V star (Maiolino et al. 1996). The solar spectrum was convolved with a Gaussian to adapt its resolution to the resolution of the standard star spectrum. The solar spectrum edges were interpolated by a blackbody with a temperature of T = 5800 K. The telluric standard star spectrum was extracted by taking the total of all pixels within the radius of 3 × FWHMPSF of the point spread function (PSF; Howell 2000), centered on the peak of a two-dimensional Gaussian fit. The flux calibration of the target source was performed during the telluric correction procedure. We referenced the standard star counts at λ1.662 μm and λ2.159 μm in H- and K-band respectively to the flux given by the 2MASS All-sky Point Source Catalogue1.
. To increase the FOV to 12″ × 12″ and minimize the overlap of dead pixels in critical areas a dithering sequence of the FOV by ± 2″ was introduced. However, the outer 2″ have data of insufficient quality, hence for the analysis a FOV of 10″× 10″ was used. The dithering was done at 9 positions where the central 4″ × 4″ were observed with the full integration time. The gratings used are the H-band grating at a spectral resolution of R ≈ 3000 and the K-band grating at a resolution of R ≈ 4000. Both bands were observed at a digital integration time of 150 s and an TST ... nodding sequence (T: target, S: sky), to increase on-source time. The overall integration time on the target source in H-band is 2550 s and in K-band 3000 s with an additional 1200 s in H-band and 1500 s in K-band on sky. The G2V star HIP 33144 was observed in H-band and in K-band within the respective science target observation. The observing strategy was to observe it twice (star in opposite corners of the FOV) with an integration time of 2 s. The ESO SINFONI pipeline was used for data reduction except for atmospheric OH line correction and final cube creation which were done manually. Detector specific corrections were performed manually, as well. For more details on the reduction see Smajić et al. (2014). The standard star was used to correct for telluric absorption in the atmosphere and to perform a flux calibration of the target. A high signal-to-noise ratio solar spectrum was used to correct for the blackbody and intrinsic spectral features of an G2V star (Maiolino et al. 1996). The solar spectrum was convolved with a Gaussian to adapt its resolution to the resolution of the standard star spectrum. The solar spectrum edges were interpolated by a blackbody with a temperature of T = 5800 K. The telluric standard star spectrum was extracted by taking the total of all pixels within the radius of 3 × FWHMPSF of the point spread function (PSF; Howell 2000), centered on the peak of a two-dimensional Gaussian fit. The flux calibration of the target source was performed during the telluric correction procedure. We referenced the standard star counts at λ1.662 μm and λ2.159 μm in H- and K-band respectively to the flux given by the 2MASS All-sky Point Source Catalogue1.
To determine the spatial resolution of our observation we looked at the radial profiles of the telluric star, the continuum emission in H- and K-band, and at the radial profiles of the emission lines [Fe ii], narrow Brγ, and broad Brγ (see Fig. 2). We use the broad component of the hydrogen recombination line Brγ to determine an accurate value of the FWHM of the PSF for the K-band because we can measure this value from the science data itself. Figure 2 shows that the narrow component of Brγ and [Fe ii] as well as the telluric stars in H- and K-band show about the same spatial extent. From this we infer that the spatial resolution in H- and K-band is similar. We measure a FWHM of the broad Brγ component of ~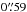 which corresponds to ~29 pc. Spatially the PSF shows an elongation in the east-west direction slightly rotated by 10° (Fig. 3).
which corresponds to ~29 pc. Spatially the PSF shows an elongation in the east-west direction slightly rotated by 10° (Fig. 3).
 |
Fig. 2 Radial profiles of the telluric star in K- and H-band, the K- and H-band galaxy continuum, [Fe ii], narrow Brγ and broad Brγ. |
The correction of the OH lines, the cube alignment, the final cube creation, the linemap and spectra extraction was conducted using our own IDL routines.
We use calibrated 350 GHz ALMA data and compare these with our NIR results. The final product data is publicly available from the ALMA archive under project ID 2011.0.00208.S (PI: Combes). Details on observational setup, calibration, imaging and quality can be found in Combes et al. (2014) and in the project reports in the ALMA archive. The line cube comprises 50 channels of 10 km s-1 width and a beam of 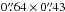 at an PA of 123°. The rms achieved is 0.05 mJy beam-1 in the continuum and ~1.3 mJy beam-1 in the line cubes. Imaging and parts of the analysis have been conducted with the CASA software (v3.3 McMullin et al. 2007).
at an PA of 123°. The rms achieved is 0.05 mJy beam-1 in the continuum and ~1.3 mJy beam-1 in the line cubes. Imaging and parts of the analysis have been conducted with the CASA software (v3.3 McMullin et al. 2007).
3. Results and discussion
We resolve the central 485 pc of NGC 1566 at a seeing limited spatial resolution of 29 pc using the integral field spectrograph SINFONI at the VLT. Narrow and broad components of the hydrogen recombination line Brγλ2.166 μm and several rovibrational molecular hydrogen lines (e.g., H2(1−0)S(1) λ2.12μm) are identified. Additionally, several stellar absorption features in K-band (e.g., CO(2−0) λ2.29 μm, NaD λ2.207 μm, CaT λ2.266 μm) are detected. The H-band shows a variety of stellar absorption features (e.g., Si iλ 1.59 μm, CO(6−3) λ1.62 μm) and it harbors the [Fe ii] λ1.644 μm line, which is important for NIR line diagnostics. The flux and the FWHM of all detected emission lines are summarized in Table 1 for the regions: center r = 1″, center r = 5″, center r = PSF, star formation region (SFr), star formation region at PSF sized aperture (SF PSF), and center at PSF sized aperture (cPSF), see Fig. 3 for more detail. The emission line FWHMa presented in this paper are corrected for instrumental broadening. The cold molecular gas tracer 12CO(3−2) and 0.87 mm emission observed with ALMA are used to compare hot NIR gas and dust with cold gas and dust in the sub-mm.
3.1. The distribution of gas
We describe and compare the distribution of the observed gas, i.e., ionized [Fe ii] and Brγ gas and molecular H2(1−0)S(1) and 12CO(3−2) gas.
3.1.1. Ionized gas
Ionized gas is detected in the [Fe ii] λ1.644 μm, Brγ, and He iλ2.06 μm emission lines in the NIR.
The forbidden transition [Fe ii] λ1.644 μm is slightly blended by the CO(7−4) λ1.641 μm absorption feature in H-band but is very strong. With an FWHM of 350 km s-1 it is the broadest narrow emission line at the center (Figs. 3a and b). The line map of the [Fe ii] emission shows a triangular shape pointing in north, east, and southwest directions. The FWHM and equivalent width (EW) maps both show elongated features in the east-west direction. Toward the north the FWHM decreases quickly to about 100 km s-1. To the southwest it stays for about one arcsecond above 300 km s-1 before it drops to ~150 km s-1. The eastern part extends to about 1.̋5 with an FWHM of about 250 km s-1. The [Fe ii] emission is point-like on the nucleus with a stronger eastern wing and a weaker southwestern wing best seen in the EW map (Fig. 3c). The EW is 6.8Å on the nucleus and only 0.6 Å in the southwest. A small plateau is detected to the east with an EW of ~0.9 Å.
The Brγ line shows, spatially and spectrally, two components. We detect a narrow and a broad Brγ emission at the center. The broad component shows an FWHM of about 2000 km s-1 and is redshifted by 340 km s-1. From the spatial distribution of the BLR emission a reliable value for the PSF of ~29 pc is determined (Sect. 2). The broad component is a clear indicator for a SMBH. The narrow component at the center has an FWHM of about 230 km s-1 and suggests a region size of 13.5 pc, after deconvolution with the PSF width.
We also detect a spatially resolved strong narrow Brγ emission about 1″ southwest from the nucleus (Fig. 3j). The off-nuclear Brγ emission shows a rather elliptical shape in the southeast to northwest direction. The FWHM in this region is ~100 km s-1 with a maximum of 150 km s-1 in the southeast and a minimum of 70 km s-1 in the northwest. The EW of the narrow Brγ line at the nucleus is about 1.0 Å. At the off-nuclear region it is about 2.6 Å in the brightest spot and falls to about 2 Å along the ellipse.
 |
Fig. 3 From left to right: flux [10-20 W m-2], FWHM (corrected for instrumental broadening) [km s-1] and EW [Å] maps of, from top to bottom: [Fe ii], He i, H2(1−0)S(1), and narrow Brγ emission lines. The regions discussed in this paper are marked in the flux maps a), g) and i). |
In addition, the He iλ2.06 μm emission line is detected. The emission is strongest at the center but is also very prominent in the southwestern region where the strong narrow Brγ emission is detected. The FWHM peaks on the center with 250 km s-1 whereas the southwestern region shows a broadness ~120 km s-1 similar to that of the Brγ. The flux distribution and with it the EW of both lines is not as similar. The southwestern emission region shows a peak in Brγ in its lower part, whereas He i is uniformly distributed over the whole ellipse. The EW of He i is up to 0.8 Å at the nucleus and up to 1.3 Å at the southwestern emission region.
 |
Fig. 4 Panels a) and d): 12CO(3−2) and continuum at 0.87 mm flux maps in [Jy beam-1 km s-1] and [Jy beam-1], respectively, overlayed with H2(1−0)S(1) EW contours. Panels b) and c): 12CO(3−2) first and second moment maps in [km s-1] overlayed with H2(1−0)S(1) LOSV and FWHM contours, respectively. |
3.1.2. Molecular gas
The most prominent molecular hydrogen lines that we detect in K-band are the H2(1−0)S(1) λ2.12 μm and H2(1−0)S(3) λ1.96 μm lines. Other detected molecular hydrogen lines are the H2(1−0)S(2) λ2.03 μm, H2(1−0)S(0) λ2.22 μm, H2 (2−1)S(1) λ2.248 μm, H2(1−0)Q(1) λ2.41 μm H2(1−0)Q(3) λ2.42 μm lines.
The molecular emission line H2(1−0)S(1) shows strong emission on the nucleus and reveals a nuclear spiral structure within an r = 3″ nuclear disk (Figs. 3g, i). The EW map reveals the full extent of the nuclear structure. The arms are clearly visible, with the eastern arm having a higher EW than the western, which is visible in the flux map as well. In EW the center looks like a gaseous bar. The spiral does not seem to become narrow here, however, this might be a resolution effect. The strong off-nuclear Brγ emission is situated along the southern edge of the western arm, where the EW is lower. Both arms are oriented at a PA of ~90° and point counter-clockwise. The eastern arm and the nuclear region both show the maximum in EW of about 3.4 Å, outside these regions the EW drops to ~1.75Å. Both arms show concentrated cigar-shaped emission in the parts connected to the nucleus and then turn over by about ~90° into more diffuse emission. The arms do not look like a geometrical spiral close to the center. Inferred from the EW map a bar seems to connect the spiral arms toward the nucleus. In the outer part the two-arm spiral becomes flocculate and forms a ring-like structure at a 2″ radius. This ring might correspond to an inner ILR due to a secondary nuclear bar (Sect. 3.4.2) or is rather created by gas falling in from the 200−300 pc scales toward the lower angular momentum transport region at ≤150 pc scales (Combes et al. 2014).
The line of sight velocity (LOSV) shows a rotation at a PA of ~45° that reaches velocities of about ±150 km s-1 at a radius of about 2.̋5 (for more details see Sect. 3.6.2). In addition, there is a strong gradient in the central region with the line of nodes at a PA ~ 0°. This change in the PA is indicative of a bar or spiral density wave. The FWHM reaches a velocity of 200 km s-1 at the center and in regions ~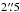 to the northeast and to the southwest of the nucleus. Along the spiral arms the FWHM is ~130 km s-1. Along the minor axis of the galactic rotation the FWHM does not fall to the width of the spiral arms but stays at about 160 km s-1. In the northwest and southeast the FWHM drops down to 70 km s-1 (Fig. 3h).
to the northeast and to the southwest of the nucleus. Along the spiral arms the FWHM is ~130 km s-1. Along the minor axis of the galactic rotation the FWHM does not fall to the width of the spiral arms but stays at about 160 km s-1. In the northwest and southeast the FWHM drops down to 70 km s-1 (Fig. 3h).
H2(1−0)S(3) and all other detected molecular hydrogen emission lines look very similar to H2(1−0)S(1) in shape and value (e.g., similar velocities, similar flux distribution, see Figs. A.2 and A.3). Therefore, we use the H2(1−0)S(1) emission line as the general description of all molecular hydrogen lines.
In the mm-regime we use the 12CO(3−2) line to compare the cold molecular gas distribution to our hot molecular gas distribution derived from ro-vibrational H2 line emission described above. In general, the 12CO(3−2) emission is very similar to the H2(1−0)S(1) emission. In both lines an r = 3″ disk with a nuclear spiral is detected. The nuclear spiral looks almost identical when comparing the 12CO(3−2) emission and the H2(1−0)S(1) EW maps (Fig. 3i and 4a). The difference lies in the location of the emission maxima. The emission line 12CO(3−2) peaks at connection points of the spiral arms to the center.
The LOSV-field is identical in shape, i.e., maxima and disturbances, and value, i.e., both gases show max/min velocities of ±150 km s-1, see Figs. 4b and 13d. The dispersion of the 12CO(3−2) gas is similar in distribution but differs in value, i.e., the NIR H2 dispersion is lower by ~30 km s-1.
Emission lines.
3.2. Gas masses
From the detected molecular hydrogen lines the warm H2 gas mass can be determined using the luminosity of the H2(1−0)S(1), LH2(1−−0)S(1), and the equation 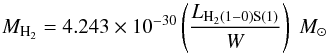 (1)following Turner & Ostriker (1977); Scoville et al. (1982); Wolniewicz et al. (1998); Riffel et al. (2008). The warm H2 gas mass in a 5″ radius aperture, which is all of the warm H2 in our FOV, is derived to 57 M⊙. To estimate the cold gas mass we use the conversion factor derived by Mazzalay et al. (2013)
(1)following Turner & Ostriker (1977); Scoville et al. (1982); Wolniewicz et al. (1998); Riffel et al. (2008). The warm H2 gas mass in a 5″ radius aperture, which is all of the warm H2 in our FOV, is derived to 57 M⊙. To estimate the cold gas mass we use the conversion factor derived by Mazzalay et al. (2013)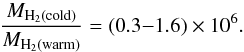 (2)We find a cold H2 gas mass in the central 10″ × 10″ of (1.7−9.1) × 107M⊙. Combes et al. (2014) detect 7 × 107M⊙ in their r = 18″ FOV from CO(3−2) observations with ALMA. The values are in good agreement since the bulk of the molecular mass in NGC 1566 is located in the inner 6″ (Figs. 3, 4 and Combes et al. 2014,and their Fig. 3).
(2)We find a cold H2 gas mass in the central 10″ × 10″ of (1.7−9.1) × 107M⊙. Combes et al. (2014) detect 7 × 107M⊙ in their r = 18″ FOV from CO(3−2) observations with ALMA. The values are in good agreement since the bulk of the molecular mass in NGC 1566 is located in the inner 6″ (Figs. 3, 4 and Combes et al. 2014,and their Fig. 3).
The cold gas masses of the central r = 3″ disk and the cPSF region are estimated from H2(1−0)S(1) and 12CO(3−2) emission (see Fig. 3g and 4a). We measure a 12CO(3−2) flux of ~570 Jy km s-1 for the central r = 3″ gas disk and ~12 Jy km s-1 for the cPSF region. Furthermore, we estimate masses of ~6.6 × 107M⊙ and ~1.4 × 106M⊙ respectively, using the Milky Way conversion values from Bolatto et al. (2013). Using H2(1−0)S(1) luminosities we estimate cold gas masses for the central r = 3″ gas disk and cPSF region of (1.4−7.5) × 107M⊙ and (1.5−7.8) × 106M⊙ respectively.
3.3. Emission line regions
The detection of several narrow emission lines gives us the opportunity to analyze the emission at the center of NGC 1566. We analyze the ratios of the narrow ionized and molecular emission lines with the goal of finding the nature of their excitation. We investigate apertures centered on the nucleus and on the ionization region situated ~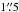 southwest of the nucleus.
southwest of the nucleus.
3.3.1. Emission line ratios
The narrow Brγ emission line as well as [Fe ii] and H2(1−0)S(1) transitions can be used in a diagnostic diagram to disentangle photoionization by young, bright stars and shock ionization (e.g., supernovae). Young and bright stars can be found in systems with recent and strong star formation like starburst galaxies. LINER galaxies exhibit high [Fe ii] and H2(1−0)S(1) fluxes. These species are good shock tracer as they are often found in regions of supernovae or outflows/jets.
We find that the nuclear regions cPSF, r = PSF, and r = 1″ lie on the linear transition relation from SB over AGN to LINER (see Fig. 5). The r = PSF region is well situated in the AGN regime indicating mixed ionization mechanisms, typical for AGN.
 |
Fig. 5 Diagnostic diagram of log [Fe ii] /Paβ and log H2/ Brγ for the central r = PSF, r = 1″ and the star formation region (SFr). The conversion factor of 0.744 was used for [Fe ii]λ1.644μm over [Fe ii]λ1.257μm (Nussbaumer & Storey 1988). For the conversion of Brγ to Paβ the case B ratio of 0.17 was used. Open symbols correspond to literature values from Larkin et al. (1998, LINER), Dale et al. (2004, SB), Rodríguez-Ardila et al. (2004, 2005, Sy1, Sy2). |
The region SFr lies off the linear correlation seen in Fig. 5. It is situated in the AGN regime, but under the relation where the Seyfert galaxies reside. The ratio log [Fe ii] /Paβ puts SFr into the H ii galaxy region, however, the ratio log H2/ Brγ shifts it to the AGN regime. This behavior can be explained by an H2 overabundance. As mentioned above, the high H2 fluxes shift the central r = 1″ aperture toward the LINER like excitation regime. This is the case for SFr as well. The high H2 flux shifts the SFr region from the photo ionization or star formation regime toward the mixed ionization or AGN regime. The H2 over Brγ ratio is five to ten times higher than in typical H ii galaxies.
The rich molecular gas disk in the central r = 3″ shows a variety of H2 transitions in the NIR (see Table 1). There are three main excitation mechanisms for molecular hydrogen in the NIR (Mouri 1994; Rodríguez-Ardila et al. 2005) which can be discriminated with the detected H2 species:
- i)
UV fluorescence (non-thermal) can occur in warm high-density gas where highly energetic UV photons from the Lyman-Werner band (912−1108Å) are re-emitted by the H2 molecules. To distinguish the UV pumping (non-thermal) from collisional excitation (thermal) higher level transitions need to be detected since the lower levels are populated by collisions.
- ii)
X-ray heating (thermal) is responsible for H2 excitation in regions with temperatures of <1000 K. At higher temperatures collisional excitation populates the lower levels.
- iii)
Shocks (thermal) can collisionaly populate the electronic ground levels of H2 molecules. The rovibrational transitions are populated following a Boltzmann distribution where kinetic temperatures can be higher than 2000 K (Draine & McKee 1993).
 |
Fig. 6 Molecular hydrogen line ratio diagrams. The ratios of H2(2−1)S(1)/H2(1−0)S(1) versus H2(1−0)S(2)/H2(1−0)S(0) are shown in a). The ratios of H2(2−1)S(1)/H2(1−0)S(1) versus H2(1−0)S(3)/H2(1−0)S(1) are shown in b). The curves represent the thermal emission at 1000−3000 K. Vertical stripes represent the region where models by Black & van Dishoeck (1987) predict non-thermal UV excitation. Horizontal stripes are thermal UV excitation models by Sternberg & Dalgarno (1989). The open, magenta triangle represents thermal X-ray models by Draine & Woods (1990) and the open, turquoise circle represents a shock model from Brand et al. (1989). The filled dark bullets connected with a dotted line in a) are the predicted line ratios from a mixture of thermal and low-density fluorescence models of Black & van Dishoeck (1987). The first bullet from the left represents 10% non-thermal and 90% thermal UV-fluorescence, the second 20% non-thermal and 80% thermal UV-fluorescence and so on. |
3.3.2. Level population of the H2 gas
The ro-vibrational levels will be populated according to the Boltzmann equation when we assume thermal excitation. Then the excitation temperature Texc can be derived from the inverse of the gradient of the line fitted to the thermalized levels in the graph shown in Fig. 7. These will be on a linear relation if the excitation is thermal. The estimate of the population density can be inferred from the observed column density (Lester et al. 1988) 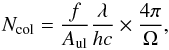 (3)with flux f in W m-2, Aul the transition probability (Wolniewicz et al. 1998), λ the rest frame line wavelength, h the Planck constant, c the speed of light, and Ω the aperture size in radian. In thermal equilibrium the ratio of two levels can be written as
(3)with flux f in W m-2, Aul the transition probability (Wolniewicz et al. 1998), λ the rest frame line wavelength, h the Planck constant, c the speed of light, and Ω the aperture size in radian. In thermal equilibrium the ratio of two levels can be written as 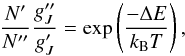 (4)with column densities N′ and N′′, statistical weights
(4)with column densities N′ and N′′, statistical weights 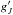 and
and 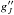 , Boltzmann constant kB, and the temperature of the thermal equilibrium T.
, Boltzmann constant kB, and the temperature of the thermal equilibrium T.
The level population diagram in Fig. 7 compares our measured level population of the H2 emission lines to UV-excitation models derived by Davies et al. (2003).
Model 1 is a low-density model (nH = 103 cm-3) with cool T = 100 K gas and a relatively weak FUV field. In model 2 density and UV field are increased by one order of magnitude and a thermal profile is adopted for the temperature with Tmax = 1000 K. Model 3 is the same as model 2 but with a maximum temperature of Tmax = 2000 K. Model 4 is the same as model 2 but the FUV field is increased by a factor of 100. And model 5 is the high-density model with an nH = 106 cm-3 and temperature and FUV field as in model 4. For more details on the models see Davies et al. (2003).
3.3.3. Line emission at the nuclear region
The nuclear line emssion is well situated in the AGN regime in the diagnostic diagram in Fig. 5. Interestingly, the r = 1″ region with its slightly bigger aperture moves farther toward the LINER regime. This trend is caused by aperture effects alone. The Brγ flux at the center stems from a deconvolved region of 13.5 pc, whereas the H2 emission stems as well from the extended r = 3″ molecular gas disk. The Brγ emission at r = 1″ is the flux in the wings of the PSF whereas the H2 emission is present in the central gas disk of up to r< 3″ distance from the center. Hence, larger apertures will shift the H2 over Brγ ratio toward higher H2 fluxes and in this case toward the LINER domain.
The diagrams in Fig. 6 infer that the central regions move with smaller aperture toward the shock model at ~2000 K indicating a stronger thermal ionization close to the nucleus. However, dense gas ionized by UV-fluorescence can show similar emission. The v = 1 transitions are thermalized by collisions and with higher density of the gas the v = 2 transitions are thermalized as well and hence underpredicted with respect to lower density gas excited by UV-fluorescence (e.g., Sternberg & Dalgarno 1989, 1995; Sternberg & Neufeld 1999; Davies et al. 2003, 2005). Therefore we compare the level population of H2 to models from Davies et al. (2003). The v = 1 transitions in the central regions, e.g., cPSF, seem to be thermalized with an excitation temperature of Texc ~ 1800 K (Fig. 7). However, none of the apertures taken from the center exhibit values of purely thermalized gas. This is shown by the v = 2, J = 3 level which lies off the excitation temperature line fitted to the v = 1 levels. This should not be the case for a thermal ionization process. Hence, other ionization processes, e.g., UV-fluorescence, have to be taken into account. The v = 2, J = 5 level seems suppressed with regard to the v = 2, J = 3 level and fits the thermal equilibrium fit. This effect is seen in the X-ray models of Draine & Woods (1990) which predict a decrement in the v = 2, J = 5 level.
We are not able to disentangle ionization and excitation of the gas by the AGN or by stars.
 |
Fig. 7 Molecular hydrogen level population diagram relative to the H2(1−0)S(1) transition. The column density N is given in [m-2]. The center r = 1″ region marks the energy of the level, the other regions are shifted for a better presentation in the plot. The models are for dense UV-excited gas taken from Davies et al. (2003). The linear fit is to the v = 1 levels of region cPSF which yields a kinetic excitation temperature of Texc ~ 1800 K. |
3.3.4. Star formation
The star formation history of the central 10″ × 10″ of NGC 1566 does not seem to have been involved in recent star formation due to the lack of H ii regions. In fact, Brγ emission is only detected on the nucleus and in one off nuclear region. The luminosity of Brγ, LBrγ, is proportional to the Lyman continuum flux and can be used as a measure for the star formation rate (SFR; Panuzzo et al. 2003; Valencia-S. et al. 2012) in the emitting region 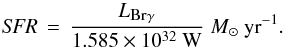 (5)The two regions of interest are at the nucleus with an 1″ radius and a luminosity of LBrγ = 8.45 × 1029 W and the lenticular region 1
(5)The two regions of interest are at the nucleus with an 1″ radius and a luminosity of LBrγ = 8.45 × 1029 W and the lenticular region 1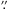 5 southwest from the center with a luminosity of LBrγ = 4.15 × 1029 W over an area of ~1.33 arcsec2. We derive a SFR of ~5.3 × 10-3M⊙ yr-1 at the center and SFR ~ 2.6 × 10-3M⊙ yr-1 at the southwestern region. Additionally, we can estimate the supernova rate (SNR) in this region using the [Fe ii] emission. We follow Bedregal et al. (2009) and use two different calibrations
5 southwest from the center with a luminosity of LBrγ = 4.15 × 1029 W over an area of ~1.33 arcsec2. We derive a SFR of ~5.3 × 10-3M⊙ yr-1 at the center and SFR ~ 2.6 × 10-3M⊙ yr-1 at the southwestern region. Additionally, we can estimate the supernova rate (SNR) in this region using the [Fe ii] emission. We follow Bedregal et al. (2009) and use two different calibrations ![\begin{equation} \mbox{SNR}_{\mbox{\tiny Cal97}}=5.38\;\frac{L_{\mbox{\tiny[\ion{Fe}{ii}]}}}{10^{35}~\mbox{W}}\;\mbox{yr}^{-1} \end{equation}](/articles/aa/full_html/2015/11/aa24850-14/aa24850-14-eq265.png) (6)after Calzetti (1997) and
(6)after Calzetti (1997) and ![\begin{equation} \mbox{SNR}_{\mbox{\tiny AlH03}}=8.08\;\frac{L_{\mbox{\tiny[\ion{Fe}{ii}]}}}{10^{35}~\mbox{W}}\;\mbox{yr}^{-1} \end{equation}](/articles/aa/full_html/2015/11/aa24850-14/aa24850-14-eq266.png) (7)after Alonso-Herrero et al. (2003). The luminosity of [Fe ii] is measured to be L[Fe ii] = 7.1 × 1030 W at the center and L[Fe ii] = 2.51 × 1029 W at the southwest. The SNRs are ~3.82 × 10-4 yr-1, and ~5.74 × 10-4 yr-1, respectively, at the center and ~1.35 × 10-5 yr-1, and ~2.03 × 10-5 yr-1, respectively, in the southwest. The estimates at the central region are upper limits since star formation and the AGN are responsible for the excitation of Brγ and [Fe ii] and their respective contributions cannot be distinguished.
(7)after Alonso-Herrero et al. (2003). The luminosity of [Fe ii] is measured to be L[Fe ii] = 7.1 × 1030 W at the center and L[Fe ii] = 2.51 × 1029 W at the southwest. The SNRs are ~3.82 × 10-4 yr-1, and ~5.74 × 10-4 yr-1, respectively, at the center and ~1.35 × 10-5 yr-1, and ~2.03 × 10-5 yr-1, respectively, in the southwest. The estimates at the central region are upper limits since star formation and the AGN are responsible for the excitation of Brγ and [Fe ii] and their respective contributions cannot be distinguished.
The off-nuclear Brγ emission in region SFr is a strong indicator for star formation. The EW of Brγ is relatively high here. The H2(1−0)S(1) EW in that region goes down with respect to the same region in the eastern spiral arm indicating additional continuum emission, e.g., young star formation. The diagnostic diagram in Fig. 5 places this region into the AGN regime, however, it is off the linear correlation. This is an aperture effect. PSF smearing due to the earlier mentioned H ii deficiency at the center of NGC 1566 will introduce the shift in the diagnostic diagram of this region. The log H2/ Brγ line ratio has values of down to −0.2 at the position of the brightest spots in the HST images (Figs. 1a, 8). These at least three distinct bright emission regions in the HST image are probably the brightest or least attenuated star formation regions. However, the elongated shape of the Brγ emission there indicates more star formation behind the dust and molecular gas of the nuclear spiral.
 |
Fig. 8 Brγ contours plotted over the HST image at 4326 Å. We note the bright emission spots at the SFr emission region at (−1, −1). |
In the molecular line ratio diagrams the estimated ratios are close to the predicted ratios of Black & van Dishoeck (1987) for a mixture of thermal and low-density fluorescence models (Fig. 6a). The two off nuclear regions, SFr and SF PSF, lie clearly off the thermal excitation curve with a tendency toward non-thermal UV excitation at smaller apertures. The estimated ratio of non-thermal to thermal excitation for the region SFr would imply a contribution of ~30%. This is a strong hint at young star formation taking place at regions SFr and SF PSF. Since strong Brγ emission is detected in the SF PSF region and the [Fe ii] emission is low here, and therefore the SFR to SNR ratio is high with >102, it is probable that the star formation here is very young, e.g., <9 Myr.
The contribution of non-thermal excitation for the central regions is about 10−20% (cPSF, r = PSF and r = 1″). This is lower than in regions SF PSF and SFr but still a significant value that might hint at star formation at the nucleus.
The H2 level population shows that the v = 1 transitions scatter around the higher density models (models 2−5). The region SFr tends toward lower density gas, e.g., model 1, and indicates the characteristic ortho-to-para shift of fluorescent excitation (Sternberg & Neufeld 1999). The v = 2 transitions show a similar effect but the differences in the models are here more evident than for the v = 1 transitions.
3.4. Continuum
We analyze the emission of the 0.87 mm continuum observed with ALMA and the NIR continuum observed with SINFONI.
3.4.1. The millimeter continuum
The mm-continuum at 0.87 mm (Fig. 4d) peaks in the same region as the NIR continuum but the distribution is different compared to the NIR (see Sect. 3.4.2). The 0.87 mm emission is distributed similar to the molecular lines. Apart from the peak in the center, 0.87 mm emission is detected in the southwestern spiral arm at the position of narrow Brγ emission and in the northeast coinciding with the regions that show an increased width in the molecular lines (Fig. 4c). Combes et al. (2014) find that the 0.87 mm continuum is dominated by dust emission in the full 18″ × 18″ FOV. To decide on the dominating mechanism in local emission regions is not possible due to the lack of high-resolution radio data at other frequencies.
3.4.2. The NIR continuum
In the NIR the H- and the K-band emission was observed. The continuum flux density is stronger in H- than in K-band. Towards the center the continuum becomes redder, as is expected in a Seyfert 1 galaxy, hence the slope becomes flatter but it is not inverted. The H−K map (Fig. 9) shows a clear reddening toward the center with an H−K value of >0.8 mag at the very center. This implies that we see warm to hot dust emission in the galaxy center (Fischer et al. 2006; Busch et al. 2014). Since we see a broad Brγ component we assume that we as well see the inner edge of the dust torus surrounding the AGN.
 |
Fig. 9 H−K color diagram in magnitudes of the central 4″ × 4″ of NGC 1566. The red ellipse at ( |
To analyze the NIR continuum further a decomposition was performed. The continuum components: stellar template, hot dust blackbody, power-law and an overlaying extinction component were used to determine the continuum composition. The stellar component was fitted using resolution adapted template stars from Winge et al. (2009). Since these stars are only available in K-band from 2.2 μm to 2.4 μm the decomposition had to be performed in this wavelength range. For more details on the decomposition see Smajić et al. (2012 and 2014).
 |
Fig. 10 Continuum decomposition for six different regions. The axes are flux density [10-18 W m-2μm-1] versus wavelength [μm]. The components are: red curve: hot dust component; Yellow curve: power-law component; full blue curve: total stellar component; lined blue curve: M0III star; Line-dot blue curve: K3III star; triple-dot-lined blue curve: G5III star. The combined components curve is in green and the original input spectrum is in black. The dotted black curve around zero is the residual of spectrum minus combined curve. We note that the emission lines at λ2.223 μm and λ2.247 μm were masked. |
The decomposition provides two interesting results, see Figs. 10a, c, f. The blackbody, responsible for fitting hot dust, returns a hot ~1000 K component with a significant contribution at the very center. The stellar component produces best results when HD2490, an M0III star, representing the old stellar population, and HD1737, a G5III star are used. The contribution of G5III-like stellar emission becomes apparent at the center.
In the NIR, the continuum emission of NGC 1566 in the central 10″ × 10″ is mainly produced by stars. The continuum decomposition, however, reveals a hot dust component at the nucleus. The fits at the center, r = 1″ (Fig. 10a), r = PSF (Fig. 10c), and center PSF (cPSF) (Fig. 10f), need a hot dust component. The hot dust exhibits only 4% of the flux density in the r = 1″ region, whereas the r = PSF region exhibits 7% of the flux density and the cPSF region exhibits even 16% flux density as hot dust emission at a temperature of ~1000 K. The hot dust emission is not strong enough to create a steep red continuum in K-band. The difference in percentage here is caused by the aperture size of the central regions. All regions exhibit a hot dust flux density of ~500 × 10-18 W m-1μm-1 (Fig. 10). This hot dust emission at the nucleus is visible in the H−K map as well (Fig. 9). The nucleus of NGC 1566 shows characteristics of Seyfert 1 nuclei on smaller scales, i.e., broad hydrogen lines, and hot dust continuum emission. The effect of aperture on the features is essential. Apertures of more than 100 pc or 2″ would probably not be able to detect and measure the hot dust component. NGC 1566 would then show the characteristics of a quiescent galaxy without any narrow H ii emission at the nuclear region, the broad Brγ emission might be detected farther out, depending on its strength (e.g., Reunanen et al. 2002).
The stellar continuum in our FOV is best fitted by an M0III star, a giant. The central r ~ 1″ needs a G5III giant as well for the fit. The G-type star contributes one third of the flux in the central r = 1″ region. Outside this region the G-type star is not needed. The differences between the two stars are the temperature, i.e., the spectral slope, and the depth of the absorption features, e.g., CO(2−0). The G5III stellar contribution indicates a need for bluer continuum emission or for shallower features in the continuum emission at the center of NGC 1566. The need for bluer continuum emission might stem from uncertainties in the hot dust contribution, however, the hot dust flux stays constant over several apertures. The main argument for a G-type star here is the EW of the CO absorption feature. The EW in CO(2−0) of the M0III star is too high, i.e., the CO absorption feature is too deep, although a hot dust contribution is taken into account. A higher hot dust contribution can be excluded since the spectral shape of the residual galaxy spectrum, after subtraction of the hot dust blackbody emission, becomes too blue for an K- or M-type star to fit. Star formation at the center of Seyfert galaxies and in the torus itself is not unusual (e.g., Davies et al. 2007) and can account for additional featureless continuum.
 |
Fig. 11 From left to right: K-band continuum [10-18 W m-2μm-1], the fitted stellar continuum [arbitrary units] and the SVD [km s-1] obtained from the continuum decomposition. For more details, see Sect. 3.4. |
The spatial shape of the continuum emission is roundish with a slight elongation at a PA of 34°. This is the same PA as the line-of-nodes of the stellar velocity field. Hence, the stars in the center do not follow the main stellar bar distribution, which is at a PA of ~0°. The 34° that we measure are either created by a small nuclear bar within the 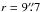 pseudo-ring (Comerón et al. 2010) or the angle stems from the bulge population and is affected by projection effects. However, to disentangle this a sophisticated decomposition of the galaxy structure using high-resolution imaging in the NIR is required (e.g., Busch et al. 2014).
pseudo-ring (Comerón et al. 2010) or the angle stems from the bulge population and is affected by projection effects. However, to disentangle this a sophisticated decomposition of the galaxy structure using high-resolution imaging in the NIR is required (e.g., Busch et al. 2014).
The stellar velocity dispersion, LOSV, and intensity distribution are shown in Figs. 11−13. The stellar LOSV shows a rather regular rotational field with a PA of 214° at velocities of ±60 km s-1 with a boxy redshifted side. The stellar velocity dispersion shows velocities of 90 to 125 km s-1 with the very center being at 100 km s-1 and does not show signs of kinematically decoupled regions.
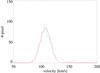 |
Fig. 12 Stellar velocity dispersion histogram. The X-axis shows the fitted dispersion in 5 km s-1 bins. The Y-axis shows the total number of spatial pixels that correspond to the dispersion bin. The red curve is a Gaussian fit to the distribution. |
3.5. The active nucleus
The AGN of NGC 1566 is a Seyfert 1 nucleus that exhibits broad hydrogen emission lines and is showing variability across the whole wavelength range.
3.5.1. Mass of the SMBH
The broad Brγ line flux and FWHM are used to estimate the mass of the central SMBH of NGC 1566. A conversion factor of Paα/Brγ~ 12 is used to translate the Brγ to Paα flux and be able to use the equation 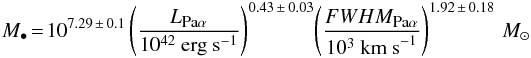 (8)derived by Kim et al. (2010). We estimate a black hole mass of M• = (3.0 ± 0.9) × 106M⊙ using a luminosity of LBrγ = 5 × 1038 erg s-1 and a FWHMBrγ = 2000 km s-1. This value is less than a factor of two smaller than the 5 × 106M⊙ estimated from optical broad line measurements (Kriss et al. 1991). This difference might be introduced by variations in the activity of the AGN. A flux increase in the broad Hβ line was measured by a factor of four to five within only 24 days (Alloin et al. 1985). Assuming a low activity state during our observation, an increase of a factor of four in luminosity will increase the BH mass derived from the Brγ broad line to (5.5 ± 1.7) × 106M⊙, a factor of two. Hence, the derived value of (3.0 ± 0.9) × 106M⊙ is in good agreement with the literature value.
(8)derived by Kim et al. (2010). We estimate a black hole mass of M• = (3.0 ± 0.9) × 106M⊙ using a luminosity of LBrγ = 5 × 1038 erg s-1 and a FWHMBrγ = 2000 km s-1. This value is less than a factor of two smaller than the 5 × 106M⊙ estimated from optical broad line measurements (Kriss et al. 1991). This difference might be introduced by variations in the activity of the AGN. A flux increase in the broad Hβ line was measured by a factor of four to five within only 24 days (Alloin et al. 1985). Assuming a low activity state during our observation, an increase of a factor of four in luminosity will increase the BH mass derived from the Brγ broad line to (5.5 ± 1.7) × 106M⊙, a factor of two. Hence, the derived value of (3.0 ± 0.9) × 106M⊙ is in good agreement with the literature value.
To use the M−σ∗ relation and estimate the mass of the SMBH the dispersion of the bulge is needed. To determine the bulge dispersion a Gaussian fit was performed on the distribution of the stellar velocity dispersion values (Fig. 12). The fit yields a dispersion of 105 ± 10 km s-1. Following Gültekin et al. (2009)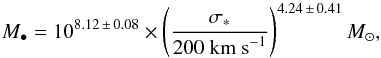 (9)the mass of the SMBH is then estimated to M• = 8.6 ± 4.4 × 106M⊙. This value is similar to the 8.3 × 106M⊙ from Woo & Urry (2002) but a factor of two to three higher than the BH mass estimate from the broad emission lines.
(9)the mass of the SMBH is then estimated to M• = 8.6 ± 4.4 × 106M⊙. This value is similar to the 8.3 × 106M⊙ from Woo & Urry (2002) but a factor of two to three higher than the BH mass estimate from the broad emission lines.
Graham & Scott (2013) have investigated the M−σ∗ relation for barred galaxies. They find that barred galaxies follow a slightly different M−σ∗ relation than non-barred galaxies. Their best fit 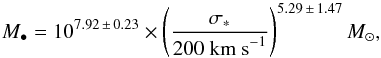 (10)returns an upper limit for the BH mass of M• = 6 × 106M⊙. When we use their fit with the least root-mean-square scatter
(10)returns an upper limit for the BH mass of M• = 6 × 106M⊙. When we use their fit with the least root-mean-square scatter 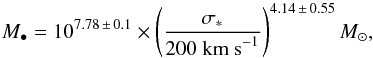 (11)the result is a BH mass of M• = (4.2 ± 2.4) × 106M⊙. The latter two results agree within the errors with mass estimates using the broad emission lines, i.e., broad Brγ (see Sect. 3.1.1), broad Hα (Kriss et al. 1991).
(11)the result is a BH mass of M• = (4.2 ± 2.4) × 106M⊙. The latter two results agree within the errors with mass estimates using the broad emission lines, i.e., broad Brγ (see Sect. 3.1.1), broad Hα (Kriss et al. 1991).
The scatter of the individually estimated BH masses is higher than their uncertainties. Therefore, we derive a mean BH mass from the four relations used in this paper to estimate the BH mass of NGC 1566. The mean BH mass is (5.3 ± 2.9) × 106M⊙. All individual BH mass values are within the standard deviation of the mean BH mass.
3.5.2. Activity of the SMBH
NGC 1566 is actively accreting mass as can be inferred from the observed variabilities. The 2−10 keV X-ray luminosity of the AGN was measured by Levenson et al. (2009) to LX,D20 = 1041.5 erg s-1 for a distance of 21.2 Mpc, hence we estimate an LX = 7.0 × 1040 erg s-1 for 10 Mpc. From the derived mean BH mass an Eddington luminosity of LEdd = (6.6 ± 3.7) × 1044 erg s-1 can be determined. Using the relation Lbol ≈ 16 × LX = (1.1 ± 0.4) × 1042 erg s-1 for LLAGN (Ho 2008, 2009) the Eddington ratio of the active nucleus in NGC 1566 can be estimated to λEdd = (2 ± 1) × 10-3. This is a typical value for Seyfert 1 LLAGN (Ho 2008). Although Kawamuro et al. (2013) use different parameters, e.g., BH mass, distance, LX conversion factor, they find a similar value of 3.2 × 10-3.
 |
Fig. 13 Top: stellar LOSV, fitted LOSV model and the subtracted residual in units of [km s-1]. Bottom: H2(1−0)S(1) LOSV, fitted LOSV model and the subtracted residual overlayed with contours of the EW map of H2(1−0)S(1) in units of [km s-1]. The EW map was overlayed to display the nuclear spiral onto the residual velocity field of the gas. The straight lines denote the orientation of the major and minor rotation axis as determined by the LOSV model. For more details, see Sect. 3.6. |
The mass accretion onto the SMBH can then be estimated with 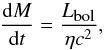 (12)where η is an efficiency factor which is usually on the order of 0.1. We calculate a mass accretion rate of (2.0 ± 0.7) × 10-4M⊙ yr-1 using Lbol from above. The cold H2 gas mass in the 10″ × 10″ FOV was measured to be ~5.4 × 107M⊙. This mass is enclosed in the central r = 3″ gas disk (see Fig. 3g) which then has a column density of ~1.9 × 106M⊙ arcsec-2 or ~7.7 × 102M⊙ pc-2. We derive a gas mass density of 3.6 × 102M⊙ pc-3 from the H2 cPSF flux measurement by assuming that the emission stems from a spherical region 29 pc in diameter. Hence, the black hole of NGC 1566 has enough mass enclosed in its central few parcsecs to accrete at the current rate for a few Myrs.
(12)where η is an efficiency factor which is usually on the order of 0.1. We calculate a mass accretion rate of (2.0 ± 0.7) × 10-4M⊙ yr-1 using Lbol from above. The cold H2 gas mass in the 10″ × 10″ FOV was measured to be ~5.4 × 107M⊙. This mass is enclosed in the central r = 3″ gas disk (see Fig. 3g) which then has a column density of ~1.9 × 106M⊙ arcsec-2 or ~7.7 × 102M⊙ pc-2. We derive a gas mass density of 3.6 × 102M⊙ pc-3 from the H2 cPSF flux measurement by assuming that the emission stems from a spherical region 29 pc in diameter. Hence, the black hole of NGC 1566 has enough mass enclosed in its central few parcsecs to accrete at the current rate for a few Myrs.
Because of the narrow line ratio of Hα/Hβ ~ 3.1 ± 0.3, which are typical for Seyfert 2 galaxies, Alloin et al. (1985) conclude that NGC 1566 might be a waking up Seyfert 1, which was in a low ionization state in the past few hundred years as inferred from emission line ratios in the NLR, beginning the harder ionization of the nuclear region. The AGN would have enough fuel to do so and start ionizing hydrogen outside the ~13.5 pc at the center (see Sect. 3.1.1). However, on the one hand, the line ratio from Alloin et al. (1985) might have been created by an aperture effect and the H ii deficiency in the central region of NGC 1566 (Comte & Duquennoy 1982). On the other hand, the H ii deficiency might result from the low activity state in the past of NGC 1566 since there is hydrogen in the nuclear region but in molecular form mainly. The activity of NGC 1566 over the last ~20 yr is a variable one (e.g., Alloin et al. 1985; Kriss et al. 1991; Baribaud et al. 1992; Levenson et al. 2009) without a specific trend of in- or decrease. Hence, we can confirm that NGC 1566 hosts a Seyfert 1 nucleus at its center and it has a gas reservoir in the central few pc to keep the central engine fueled for several Myrs.
3.6. Kinematics
The kinematics in the center of NGC 1566 show rotations at a PA of ~214° for the stellar kinematics (Fig. 13a) and at a PA of ~222.5° for the molecular gas (e.g., H2(1−0)S(1), Fig. 13d). The observed velocity field of the molecular gas shows strong deviations from rotation at the center.
The orientation of the galaxy toward the observer can be inferred from considerations of the winding sense of the spiral arms (Fig. 1). These kind of spiral arms are always seen to be trailing. Hence, the near side has to be in the northwest when the arms are trailing because there is blueshifted motion in the northeast and the arms are oriented as seen in Fig. 1.
3.6.1. Stellar kinematics
The line of nodes of the stellar rotation is aligned with the stellar continuum major axis at a PA of 34°. We derive a PA from the H2(1−0)S(1) line of 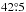 in good agreement with Agüero et al. (2004). They find a PA of 44° ± 8° from optical emission lines. The stellar LOSV map shows a smooth rotation field. We fit a model to the observed velocity using the Plummer potential to represent the bulge gravitational potential (Barbosa et al. 2006). The model subtracted map shows low residuals (Fig. 13c). The stellar velocity dispersion shows a slight drop at the very center (Sect. 3.4). This is often an indication for a stellar disk (e.g., Emsellem et al. 2001; Falcón-Barroso et al. 2006) at scales <100 pc. However, there are no features in the stellar residual LOSV map (Fig. 13c) that would support a stellar disk at these scales.
in good agreement with Agüero et al. (2004). They find a PA of 44° ± 8° from optical emission lines. The stellar LOSV map shows a smooth rotation field. We fit a model to the observed velocity using the Plummer potential to represent the bulge gravitational potential (Barbosa et al. 2006). The model subtracted map shows low residuals (Fig. 13c). The stellar velocity dispersion shows a slight drop at the very center (Sect. 3.4). This is often an indication for a stellar disk (e.g., Emsellem et al. 2001; Falcón-Barroso et al. 2006) at scales <100 pc. However, there are no features in the stellar residual LOSV map (Fig. 13c) that would support a stellar disk at these scales.
The difference in stellar and gaseous PA might be explained by streaming motions of the gas related to a strong spiral wave, but the gaseous PA over the central 8″ × 8″ is in agreement with measurements at larger scales, hence the effect has to stem from larger scale spiral density waves rather than the nuclear spiral discussed here. To substantiate any misalignment between gaseous and stellar disk, however, a much better estimate of the PAs is needed. Hence, we find that gaseous and stellar disk are oriented very similar but might be misaligned.
3.6.2. Gas kinematics
On scales of 200−300 pc Combes et al. (2014) showed that the gravitational torques are able to transport almost half of the angular momentum of the gas in one rotation period. Here gas is able to move in spiral arms that connect the ILR of the nuclear bar with the central ≤200 pc. On smaller scales the angular momentum transport is smaller per rotation period, but the period becomes smaller as well. The inner 200 pc show the molecular nuclear gas disk which exhibits a clear two-arm spiral structure (Figs. 3g, i, and 4a).
The nuclear spiral disturbs the velocity field of the molecular gas and creates a strong S-shaped feature at the center. To remove the rotational part from the spiral disturbance we again fit a model to the observed velocity using the Plummer potential to represent the bulge gravitational potential. The residual of the fit (Fig. 13f) highlights the difference in the observed LOSV (Fig. 13d) and the model (Fig. 13e). The center of the residual map shows blueshifted residuals to the west and redshifted residuals to the east of the nuceleus. The nucleus is situated at 0 km s-1. Contrary to the case of NGC 1068, discussed by García-Burillo et al. (2014), where non-virial outflow motions are required to explain the residual velocity field derived for the nuclear 200 pc gas disk of that Seyfert 2 galaxy, in NGC 1566 residuals shown in Fig. 13f can be accounted for by streaming motions produced by the spiral/bar structure. The S-shape shows non-circular motion in one surface as it is the case for bars or warps. Non-circular orbits, e.g., a closed elliptical orbit with axes not parallel to one of the symmetry axis (minor or major), can produce residual velocities as observed in Fig. 13f.
There are no signs for an outflow from the center. Schmitt & Kinney (1996) detect a faint one-sided cone in [O iii] pointing toward the southeast. The cone is smaller than  and can probably be associated with the NLR of NGC 1566. The increase of the FWHM of H2 along the minor axis is in the same direction as the [O iii] cone but is probably caused by beam smearing along the 0 km s-1 velocity gradient. At a size of
and can probably be associated with the NLR of NGC 1566. The increase of the FWHM of H2 along the minor axis is in the same direction as the [O iii] cone but is probably caused by beam smearing along the 0 km s-1 velocity gradient. At a size of 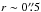 the [O iii] cone occupies spatially the nuclear Brγ and [Fe ii] emission region, i.e., these lines originate from the same region. However, we do not detect one-sided emission on the nucleus from any emission line (Fig. 3). The [Fe ii] emission has a triangular shape but is centered on the nucleus. There is extended flux toward the southeast and also a broadening of the [Fe ii] line. These are only hints at a possible weak outflow from the nuclear region of NGC 1566 and can as well be associated with the NLR. The LOSV residuals up to 1″ from the center in Fig. 13f fit an outflow along the minor axis, but these residuals are easily explained due to deviations introduced by the density waves of the nuclear spiral. Higher angular resolution observations are needed to be able to compare the [O iii] emission with shock tracers in the NIR (e.g., H2(1−0)S(1) and [Fe ii]) and look for signs of outflowing gas in the LOSV and FWHM.
the [O iii] cone occupies spatially the nuclear Brγ and [Fe ii] emission region, i.e., these lines originate from the same region. However, we do not detect one-sided emission on the nucleus from any emission line (Fig. 3). The [Fe ii] emission has a triangular shape but is centered on the nucleus. There is extended flux toward the southeast and also a broadening of the [Fe ii] line. These are only hints at a possible weak outflow from the nuclear region of NGC 1566 and can as well be associated with the NLR. The LOSV residuals up to 1″ from the center in Fig. 13f fit an outflow along the minor axis, but these residuals are easily explained due to deviations introduced by the density waves of the nuclear spiral. Higher angular resolution observations are needed to be able to compare the [O iii] emission with shock tracers in the NIR (e.g., H2(1−0)S(1) and [Fe ii]) and look for signs of outflowing gas in the LOSV and FWHM.
At 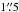 east and 1″ north the dispersion increases over the nuclear disk average in both investigated molecular species, i.e., H2(1−0)S(1) and 12CO(3−2), see Fig. 4. No increase in line flux can be measured here, but the 0.87 mm continuum shows some substantial emission. Combes et al. (2014) find that in their full 18″ × 18″ FOV the 0.87 mm continuum is dominated by dust. Hence, it is most probable that heated dust, rather than synchrotron emission from supernovae or free-free emission, is creating the 0.87 mm continuum emission. In combination with the higher dispersion in these regions it must be turbulences in the gas that warm up the dust. What is creating this turbulence is not clear. As mentioned above an outflow from the nucleus is rather improbable as the only signs for an outflow are hinting toward the southeast. Other possibilities are interactions of nuclear disk and spiral arms, e.g., the nuclear spiral. However, these are only speculations since our data is not giving any substantial hints toward the origin of this turbulence.
east and 1″ north the dispersion increases over the nuclear disk average in both investigated molecular species, i.e., H2(1−0)S(1) and 12CO(3−2), see Fig. 4. No increase in line flux can be measured here, but the 0.87 mm continuum shows some substantial emission. Combes et al. (2014) find that in their full 18″ × 18″ FOV the 0.87 mm continuum is dominated by dust. Hence, it is most probable that heated dust, rather than synchrotron emission from supernovae or free-free emission, is creating the 0.87 mm continuum emission. In combination with the higher dispersion in these regions it must be turbulences in the gas that warm up the dust. What is creating this turbulence is not clear. As mentioned above an outflow from the nucleus is rather improbable as the only signs for an outflow are hinting toward the southeast. Other possibilities are interactions of nuclear disk and spiral arms, e.g., the nuclear spiral. However, these are only speculations since our data is not giving any substantial hints toward the origin of this turbulence.
4. Conclusion and summary
We have analyzed NIR IFS data of the central 10″ × 10″ of the Seyfert 1 galaxy NGC 1566. The H ii deficiency reported by Comte & Duquennoy (1982) is confirmed. We make a first detection of narrow Brγ emission at the center and at one region offset to the southwest, in contrast to Reunanen et al. (2002). They probably were not able to detect the narrow Brγ emission due to the width of their aperture since the slit positions do coincide with the positions of narrow Brγ emission.
From the detection of a broad Brγ component we estimate a BH mass of (3.0 ± 0.9) × 106M⊙ similar to other BH mass measurements from broad lines (Kriss et al. 1991). From our continuum decomposition we derive the mass dominating stellar distribution and its velocities. Using the velocity dispersion of the stars in the bulge we estimate the BH mass independently from broad emission lines. We find a BH mass of (4.2 ± 2.4) × 106M⊙, in excellent agreement with the BH estimate from broad emission lines. We find a BH mass of (5.3 ± 2.9) × 106M⊙ as a mean value from all methods and relations used in this paper. Furthermore, the Seyfert 1 classification is verified due to hot dust blackbody emission of ~1000 K at the nuclear position, which indicates that the hot inner edge of the torus structure is visible.
The accretion onto the SMBH is typical for LLAGN with Eddington ratios of λEdd = (2 ± 1) × 10-3. The estimated accretion rate is ~10-4 and therefore 102 to 104 times higher than for SgrA* (Bower et al. 2003; Nayakshin 2005), which has a similar SMBH mass.
Molecular hydrogen is very strong in the observed FOV particularly in an r = 3″ disk and in a spiral structure within this disk. Disk and spiral are both detected as well in the warm H2 emission lines with SINFONI as in cold H2 gas from the 12CO(3−2) emission with ALMA. The shape of the spiral looks similar when comparing the EW of H2(1−0)S(1) with the flux map of 12CO(3−2). However, H2(1−0)S(1) shows the strongest emission on the nucleus whereas 12CO(3−2) shows several strong emission spots. The southwestern emission spot of 12CO(3−2) coincides with the Brγ emission seen in the SF region. From our H2 emission we determine a cold H2 gas mass of (1.7−9.1) × 107M⊙ which is in agreement with results based on the ALMA observation by Combes et al. (2014). The molecular gas seems to form a ring-like structure at r ~ 2″ best seen in the EW map in Fig. 3i and the 12CO(3−2) emission line map (see Fig. 4a).
Along the southern spiral arm a star-forming region is detected at a distance of ~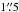 from the center. The measured SFR over a surface area of ~1.33 arcsec2 is 2.6 × 10-3M⊙ yr-1. Comparing this to the global Schmidt law (Kennicutt 1998) we find that our data point for SFr lies very close to the relation. However, the value for the nuclear 3″×3″ disk is situated below the relation with an SFR of 8.0 × 10-3M⊙ yr-1 over a surface area of π × 9 arcsec2. The nuclear region of NGC 1566 has a large molecular gas reservoir which it is not using efficiently for star formation.
from the center. The measured SFR over a surface area of ~1.33 arcsec2 is 2.6 × 10-3M⊙ yr-1. Comparing this to the global Schmidt law (Kennicutt 1998) we find that our data point for SFr lies very close to the relation. However, the value for the nuclear 3″×3″ disk is situated below the relation with an SFR of 8.0 × 10-3M⊙ yr-1 over a surface area of π × 9 arcsec2. The nuclear region of NGC 1566 has a large molecular gas reservoir which it is not using efficiently for star formation.
The excitation mechanism of the molecular gas is partly due to thermal processes (e.g., shocks) and partly due to non-thermal excitation (e.g., UV fluorescence). The diagnostic diagrams in Figs. 5 and 6 show a clear distinction between the nuclear region and the star-forming region. The apertures taken from the nuclear region are situated in the AGN regime in the diagnostic diagram in Fig. 5. The SF region is situated right of the starburst region due to the above mentioned H2 overabundance. The H2 line ratios (Fig. 6) imply young star formation at regions SFr and SF PSF due to a non-thermal excitation fraction of up to 30%. From the strong Brγ but very low [Fe ii] emission a young starburst of <9 Myr is suggested. Therefore we find that gas infall is accompanied by young star formation that can be associated with the nuclear spiral arms.
The central regions are closer to the shock models but show a non-thermal component as well (Fig. 6). The level population diagram (Fig. 7) shows that the v = 2 levels are not thermalized with the v = 1 levels indicating that the region is excited by a combination of thermal and non-thermal processes in dense gas, i.e., shocked gas and gas ionized by UV-fluorescence from young newly formed bright stars. Both methods hint to star formation at the nucleus which we are not able to distinguish from ionizing emission of the AGN.
A region of high dispersion is found in the molecular lines with increased 0.87 mm continuum emission at a distance of ≈2″ from the center. The gas here seems to be shocked, however, what produces the shock is not clear, an outflow or a spiral arm interaction are possible explanations.
Strong feedback cannot be confirmed in the center of NGC 1566. Residual velocities that might indicate an outflow and which coincide with higher velocity dispersion in molecular gas are detected. However, these features are aligned with the minor axis which can explain the higher dispersion. The LOSV residuals might be explained by other means, e.g., streaming motions introduced by the nuclear spiral. These might be signs of a feeding of the SMBH. The central ~1″ harbors possible nuclear star formation as inferred from non-thermal excitation (e.g., UV photons from young bright stars) on the nucleus. High angular resolution measurements with SINFONI are needed to identify possible feedback and star formation in the central arcsecond of the seemingly waking up Seyfert 1 nucleus. The lack of strong feedback could be a reason for the lack of strong star formation in the nuclear disk if the nuclear spiral is not able to condense gas strong enough to enable star formation.
In the case of NGC 1566 the distribution and velocities of warm and cold molecular gas are very similar. In our first simultaneous observation of NUGA sources in the NIR and sub-mm in NGC 1433 (Smajić et al. 2014) the similarities were not as high. The distribution was similar but 12CO(3−2) seemed to be a better tracer of the pseudo-ring in NGC 1433. In NGC 1566 the r = 3″ disk is detected in 12CO(3−2) and H2(1−0)S(1), which indicates that the central r ≈ 200 pc are warmer than the central region of NGC 1433. Additionally, in NGC 1433 the LOSV differed in value over the full FOV and in distinct regions in LOSV and dispersion. This is not the case for NGC 1566 where hot and cold gas show similar LOSVs.
Online material
Appendix A: Figures
We have attached the line maps to all important emission lines that were detected except for the H2 Q-branch. The Q-branch is situated at the end of K-band and therefore the maps show noise features as well. However, the flux and FWHM of these lines is given in Table 1 for the regions discussed here. Additionally, several line ratio maps are presented in Fig. A.1
Figure A.2 shows the flux, FWHM, and EW of all other detected H2 lines detected up to 2.3μm. The flux distribution is very similar in all H2 lines and peaks on the nucleus. The FWHM is increased in the center along the minor axis and H2(1−0)S(3) shows an increased width in the northeast and a decreased width in the northwest, similar to H2(1−0)S(1). The nuclear spiral is detected in all EW maps which show an increased EW at the position of the spiral density wave.
Figure A.3 shows the LOSV of all H2 lines from A.2 and additionally the LOSV maps of the detected ionized gas. The LOSV in the molecular lines is very similar, as are flux and EW, indicating that they all originate from the same region, i.e. the nuclear molecular gas disk. For the ionized lines it is hard to tell because the region in which they are detected is not large enough to give information about the spatial velocity distribution. However, the LOSV fields do not look very different from the molecular LOSV fields (e.g., Brγ).
 |
Fig. A.1 Logarithmic line ratios of H2(1−0)S(1) over Brγ and [Fe ii] over Brγ in a) and b). Panel c): logarithmic H2(1−0)S(1) over He i ratio. Panels d), e), f): H2(2−1)S(1) over H2(1−0)S(1), H2(1−0)S(2) over H2(1−0)S(0) and H2(1−0)S(3) over H2(1−0)S(1). |
 |
Fig. A.2 Molecular hydrogen emission lines. From left to right: flux [10-20 W m-2], FWHM (corrected for instrumental broadening) [km s-1] and EW [Å] maps of, from top to bottom: H2(1−0)S(3), H2(1−0)S(2), H2(1−0)S(0), and H2(2−1)S(1). |
 |
Fig. A.3 Presented are the LOSV [km s-1] maps of, from left to right and top to bottom: [Fe ii], He i, narrow Brγ, H2(1−0)S(3), H2(1−0)S(2), H2(1−0)S(0), H2(2−1)S(1). |
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
Acknowledgments
The authors kindly thank the staff at the Observatory Paranal for their assistance during the observation. Additionally, the authors thank the anonymous referees and the editor for fruitful comments and suggestions. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00208.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We use data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We used observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Institute. STScI is operated by the association of Universities for Research in Astronomy, Inc. under the NASA contract NAS 5-26555. We used observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA), and the Canadian Astronomy Data Centre (CADC/NRC/CSA). This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) via the Bonn Cologne Graduate School (BCGS), and via grant SFB 956, as well as by the Max Planck Society and the University of Cologne through the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics and by the German federal department for education and research (BMBF) under the project number 50OS1101. We had fruitful discussions with members of the European Union funded COST Action MP0905: Black Holes in a violent Universe and the COST Action MP1104: Polarization as a tool to study the Solar System and beyond. We received funding from the European Union Seventh Framework Programme (FP7/2007−2013) under grant agreement No. 312789. F.C. acknowledges the European Research Council for the Advanced Grant Program Num 267399-Momentum.
References
- Agüero, E. L., Dìaz, R. J., & Bajaja, E. 2004, A&A, 414, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alloin, D., Pelat, D., Phillips, M., & Whittle, M. 1985, ApJ, 288, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Kelly, D. M. 2003, AJ, 125, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Barbosa, F. K. B., Storchi-Bergmann, T., Cid Fernandes, R., Winge, C., & Schmitt, H. 2006, MNRAS, 371, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Baribaud, T., Alloin, D., Glass, I., & Pelat, D. 1992, A&A, 256, 375 [NASA ADS] [Google Scholar]
- Bedregal, A. G., Colina, L., Alonso-Herrero, A., & Arribas, S. 2009, ApJ, 698, 1852 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bonnet, H., Abuter, R., Baker, A., et al. 2004, The Messenger, 117, 17 [NASA ADS] [Google Scholar]
- Boone, F., Baker, A. J., Schinnerer, E., et al. 2007, A&A, 471, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2003, ApJ, 588, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Brand, P. W. J. L., Toner, M. P., Geballe, T. R., et al. 1989, MNRAS, 236, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Busch, G., Zuther, J., Valencia-S. M., et al. 2014, A&A, 561, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busch, G., Smajić, S., Scharwächter, J., et al. 2015, A&A, 575, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 1997, AJ, 113, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Casasola, V., Combes, F., García-Burillo, S., et al. 2008, A&A, 490, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casasola, V., Hunt, L. K., Combes, F., et al. 2010, A&A, 510, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cid Fernandes, R., Gu, Q., Melnick, J., et al. 2004, MNRAS, 355, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., García-Burillo, S., Boone, F., et al. 2004, A&A, 414, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., Baker, A. J., Schinnerer, E., et al. 2009, A&A, 503, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S., Knapen, J. H., Beckman, J. E., et al. 2010, MNRAS, 402, 2462 [NASA ADS] [CrossRef] [Google Scholar]
- Comte, G., & Duquennoy, A. 1982, A&A, 114, 7 [NASA ADS] [Google Scholar]
- Dale, D. A., Roussel, H., Contursi, A., et al. 2004, ApJ, 601, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Sternberg, A., Lehnert, M., & Tacconi-Garman, L. E. 2003, ApJ, 597, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Sternberg, A., Lehnert, M. D., & Tacconi-Garman, L. E. 2005, ApJ, 633, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Thomas, J., Genzel, R., et al. 2006, ApJ, 646, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Müller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Maciejewski, W., Hicks, E. K. S., et al. 2014, ApJ, 792, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Woods, D. T. 1990, ApJ, 363, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1548 [Google Scholar]
- Emsellem, E., Greusard, D., Combes, F., et al. 2001, A&A, 368, 52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., Bacon, R., Bureau, M., et al. 2006, MNRAS, 369, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, S., Iserlohe, C., Zuther, J., et al. 2006, A&A, 452, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Hunt, L. K., et al. 2003, A&A, 407, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Fernández-García, S., Combes, F., et al. 2009, A&A, 496, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, A. W., & Scott, N. 2013, ApJ, 764, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 2008, ARA&A, 46, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 2009, ApJ, 699, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2000, Handbook of CCD Astronomy (Cambridge, UK, New York: Cambridge University Press) [Google Scholar]
- Hunt, L. K., Combes, F., García-Burillo, S., et al. 2008, A&A, 482, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawamuro, T., Ueda, Y., Tazaki, F., & Terashima, Y. 2013, ApJ, 770, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., & Kim, M. 2010, ApJ, 724, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Koribalski, B. S., Staveley-Smith, L., Kilborn, V. A., et al. 2004, AJ, 128, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Eckart, A., Neri, R., et al. 2005, A&A, 442, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kriss, G. A., Hartig, G. F., Armus, L., et al. 1991, ApJ, 377, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Larkin, J. E., Armus, L., Knop, R. A., Soifer, B. T., & Matthews, K. 1998, ApJS, 114, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lester, D. F., Harvey, P. M., & Carr, J. 1988, ApJ, 329, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Levenson, N. A., Radomski, J. T., Packham, C., et al. 2009, ApJ, 703, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Lindt-Krieg, E., Eckart, A., Neri, R., et al. 2008, A&A, 479, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Läsker, R., Ferrarese, L., van de Ven, G., & Shankar, F. 2014, ApJ, 780, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Rieke, G. H., & Rieke, M. J. 1996, AJ, 111, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzalay, X., Saglia, R. P., Erwin, P., et al. 2013, MNRAS, 428, 2389 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and systems XVI, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mouri, H. 1994, ApJ, 427, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Mulchaey, J. S., & Regan, M. W. 1997, ApJ, 482, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S. 2005, A&A, 429, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H. 1977, MNRAS, 181, 89 [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1988, A&A, 193, 327 [NASA ADS] [Google Scholar]
- Panuzzo, P., Bressan, A., Granato, G. L., Silva, L., & Danese, L. 2003, A&A, 409, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reunanen, J., Kotilainen, J. K., & Prieto, M. A. 2002, MNRAS, 331, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R. A., Storchi-Bergmann, T., Winge, C., et al. 2008, MNRAS, 385, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R. A., Storchi-Bergmann, T., & Winge, C. 2013, MNRAS, 430, 2249 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R. A., Vale, T. B., Storchi-Bergmann, T., & McGregor, P. J. 2014, MNRAS, 442, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Ardila, A., Pastoriza, M. G., Viegas, S., Sigut, T. A. A., & Pradhan, A. K. 2004, A&A, 425, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez-Ardila, A., Riffel, R., & Pastoriza, M. G. 2005, MNRAS, 364, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., & Kinney, A. L. 1996, ApJ, 463, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Hall, D. N. B., Ridgway, S. T., & Kleinmann, S. G. 1982, ApJ, 253, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, K., Vogel, S. N., Regan, M. W., Thornley, M. D., & Teuben, P. J. 2005, ApJ, 632, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Smajić, S., Moser, L., Eckart, A., et al. 2014, A&A, 567, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smajić, S., Fischer, S., Zuther, J., & Eckart, A. 2012, A&A, 544, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Neufeld, D. A. 1999, ApJ, 516, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, E. L., & Ostriker, J. P. 1977, ApJ, 217, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia-S., M., Zuther, J., Eckart, A., et al. 2012, A&A, 544, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Laan, T. P. R., Schinnerer, E., Boone, F., et al. 2011, A&A, 529, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winge, C., Riffel, R. A., & Storchi-Bergmann, T. 2009, ApJS, 185, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Wolniewicz, L., Simbotin, I., & Dalgarno, A. 1998, ApJS, 115, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., & Urry, C. M. 2002, ApJ, 579, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Zuther, J., Iserlohe, C., Pott, J.-U., et al. 2007, A&A, 466, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 An HST image of NGC 1566 taken with the WFC3 UVIS2 F438W filter at a pivot wavelength of 4326Å. North is up and east is left. The white rectangle marks our 10″ × 10″ field of view (FOV). |
| In the text | |
 |
Fig. 2 Radial profiles of the telluric star in K- and H-band, the K- and H-band galaxy continuum, [Fe ii], narrow Brγ and broad Brγ. |
| In the text | |
 |
Fig. 3 From left to right: flux [10-20 W m-2], FWHM (corrected for instrumental broadening) [km s-1] and EW [Å] maps of, from top to bottom: [Fe ii], He i, H2(1−0)S(1), and narrow Brγ emission lines. The regions discussed in this paper are marked in the flux maps a), g) and i). |
| In the text | |
 |
Fig. 4 Panels a) and d): 12CO(3−2) and continuum at 0.87 mm flux maps in [Jy beam-1 km s-1] and [Jy beam-1], respectively, overlayed with H2(1−0)S(1) EW contours. Panels b) and c): 12CO(3−2) first and second moment maps in [km s-1] overlayed with H2(1−0)S(1) LOSV and FWHM contours, respectively. |
| In the text | |
 |
Fig. 5 Diagnostic diagram of log [Fe ii] /Paβ and log H2/ Brγ for the central r = PSF, r = 1″ and the star formation region (SFr). The conversion factor of 0.744 was used for [Fe ii]λ1.644μm over [Fe ii]λ1.257μm (Nussbaumer & Storey 1988). For the conversion of Brγ to Paβ the case B ratio of 0.17 was used. Open symbols correspond to literature values from Larkin et al. (1998, LINER), Dale et al. (2004, SB), Rodríguez-Ardila et al. (2004, 2005, Sy1, Sy2). |
| In the text | |
 |
Fig. 6 Molecular hydrogen line ratio diagrams. The ratios of H2(2−1)S(1)/H2(1−0)S(1) versus H2(1−0)S(2)/H2(1−0)S(0) are shown in a). The ratios of H2(2−1)S(1)/H2(1−0)S(1) versus H2(1−0)S(3)/H2(1−0)S(1) are shown in b). The curves represent the thermal emission at 1000−3000 K. Vertical stripes represent the region where models by Black & van Dishoeck (1987) predict non-thermal UV excitation. Horizontal stripes are thermal UV excitation models by Sternberg & Dalgarno (1989). The open, magenta triangle represents thermal X-ray models by Draine & Woods (1990) and the open, turquoise circle represents a shock model from Brand et al. (1989). The filled dark bullets connected with a dotted line in a) are the predicted line ratios from a mixture of thermal and low-density fluorescence models of Black & van Dishoeck (1987). The first bullet from the left represents 10% non-thermal and 90% thermal UV-fluorescence, the second 20% non-thermal and 80% thermal UV-fluorescence and so on. |
| In the text | |
 |
Fig. 7 Molecular hydrogen level population diagram relative to the H2(1−0)S(1) transition. The column density N is given in [m-2]. The center r = 1″ region marks the energy of the level, the other regions are shifted for a better presentation in the plot. The models are for dense UV-excited gas taken from Davies et al. (2003). The linear fit is to the v = 1 levels of region cPSF which yields a kinetic excitation temperature of Texc ~ 1800 K. |
| In the text | |
 |
Fig. 8 Brγ contours plotted over the HST image at 4326 Å. We note the bright emission spots at the SFr emission region at (−1, −1). |
| In the text | |
 |
Fig. 9 H−K color diagram in magnitudes of the central 4″ × 4″ of NGC 1566. The red ellipse at ( |
| In the text | |
 |
Fig. 10 Continuum decomposition for six different regions. The axes are flux density [10-18 W m-2μm-1] versus wavelength [μm]. The components are: red curve: hot dust component; Yellow curve: power-law component; full blue curve: total stellar component; lined blue curve: M0III star; Line-dot blue curve: K3III star; triple-dot-lined blue curve: G5III star. The combined components curve is in green and the original input spectrum is in black. The dotted black curve around zero is the residual of spectrum minus combined curve. We note that the emission lines at λ2.223 μm and λ2.247 μm were masked. |
| In the text | |
 |
Fig. 11 From left to right: K-band continuum [10-18 W m-2μm-1], the fitted stellar continuum [arbitrary units] and the SVD [km s-1] obtained from the continuum decomposition. For more details, see Sect. 3.4. |
| In the text | |
 |
Fig. 12 Stellar velocity dispersion histogram. The X-axis shows the fitted dispersion in 5 km s-1 bins. The Y-axis shows the total number of spatial pixels that correspond to the dispersion bin. The red curve is a Gaussian fit to the distribution. |
| In the text | |
 |
Fig. 13 Top: stellar LOSV, fitted LOSV model and the subtracted residual in units of [km s-1]. Bottom: H2(1−0)S(1) LOSV, fitted LOSV model and the subtracted residual overlayed with contours of the EW map of H2(1−0)S(1) in units of [km s-1]. The EW map was overlayed to display the nuclear spiral onto the residual velocity field of the gas. The straight lines denote the orientation of the major and minor rotation axis as determined by the LOSV model. For more details, see Sect. 3.6. |
| In the text | |
 |
Fig. A.1 Logarithmic line ratios of H2(1−0)S(1) over Brγ and [Fe ii] over Brγ in a) and b). Panel c): logarithmic H2(1−0)S(1) over He i ratio. Panels d), e), f): H2(2−1)S(1) over H2(1−0)S(1), H2(1−0)S(2) over H2(1−0)S(0) and H2(1−0)S(3) over H2(1−0)S(1). |
| In the text | |
 |
Fig. A.2 Molecular hydrogen emission lines. From left to right: flux [10-20 W m-2], FWHM (corrected for instrumental broadening) [km s-1] and EW [Å] maps of, from top to bottom: H2(1−0)S(3), H2(1−0)S(2), H2(1−0)S(0), and H2(2−1)S(1). |
| In the text | |
 |
Fig. A.3 Presented are the LOSV [km s-1] maps of, from left to right and top to bottom: [Fe ii], He i, narrow Brγ, H2(1−0)S(3), H2(1−0)S(2), H2(1−0)S(0), H2(2−1)S(1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.