| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201425525 | |
| Published online | 19 October 2015 | |
Accretion of Uranus and Neptune from inward-migrating planetary embryos blocked by Jupiter and Saturn
1
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux, UMR
5804,
33270
Floirac,
France
e-mail:
izidoro.costa@gmail.com
2
Laboratoire Lagrange, Université Côte d’Azur, Observatoire de la
Côte d’Azur, CNRS, Blvd de l’Observatoire, CS 34229, 06304
Nice Cedex 4,
France
3
Capes Foundation, Ministry of Education of Brazil,
Brasília/DF
70040-020,
Brazil
4
CNRS and Université de Bordeaux, Laboratoire d’Astrophysique de
Bordeaux, UMR 5804, 33270
Floirac,
France
Received: 16 December 2014
Accepted: 9 June 2015
Reproducing Uranus and Neptune remains a challenge for simulations of solar system formation. The ice giants’ peculiar obliquities suggest that they both suffered giant collisions during their formation. Thus, there must have been an epoch of accretion dominated by collisions among large planetary embryos in the primordial outer solar system. We test this idea using N-body numerical simulations including the effects of a gaseous protoplanetary disk. One strong constraint is that the masses of the ice giants are very similar – the Neptune and Uranus mass ratio is ~1.18. We show that similar-sized ice giants do indeed form by collisions between planetary embryos beyond Saturn. The fraction of successful simulations varies depending on the initial number of planetary embryos in the system, their individual and total masses. Similar-sized ice giants are consistently reproduced in simulations starting with five to ten planetary embryos with initial masses of ~3–6 M⊕. We conclude that accretion from a population of planetary embryos is a plausible scenario for the origin of Uranus and Neptune.
Key words: planets and satellites: formation / protoplanetary disks / planet-disk interactions
© ESO, 2015
1. Introduction
The formation of Uranus and Neptune is one of the longest-standing problems in solar system formation (Safronov 1972; Levison & Stewart 2001; Thommes et al. 1999, 2002; Goldreich et al. 2004a,b; Morbidelli et al. 2012; Jakubik et al. 2012). The accretion timescale is strongly dependent on the amount of solid material available (i.e., the density of solids) and on the dynamical timescales (related to the orbital period) in the region of formation (e.g., Safronov 1972). At their current positions, Uranus and Neptune’s calculated accretion timescales are implausibly long (Levison & Stewart 2001; Thommes et al. 2003) because of the low density in the protoplanetary disk (e.g., Weidschelling 1977; Hayashi 1981) and long dynamical timescales beyond ~20 AU. Goldreich et al. (2004a,b) claimed to have solved the problem by assuming that Uranus and Neptune formed from a highly collisional disk of small particles, but Levison & Morbidelli (2007) later showed that the simulated evolution of the system is very different from what they envisioned analytically.
Studies of the formation and dynamical evolution of giant planets in our solar system (see a review by Morbidelli et al. 2012) as well as the discoveries of extrasolar hot-Jupiters (Cumming et al. 2008; Mayor et al. 2011; Howard et al. 2012; Batalha et al. 2013; Fressin et al. 2013) and hot super-Earths (Mayor et al. 2009, 2011; Howard et al. 2010; 2012) have destroyed the belief that planets formed where they are now observed. Planetary migration seems to be a generic process of planetary formation. During the gas-disk phase planets exchange angular momentum with their natal protoplanetary disk and migrate in a regime that depends on the planet mass (Ward 1986; 1997). After gas disk dissipation, planet migration is also possible due to other mechanisms, such as tidal interaction of the planet with its host star (e.g., Rasio et al. 1996; Jackson et al. 2008), gravitational scattering of planetesimals by the planet (e.g., Fernandez & Ip 1984; Hahn & Malhotra 1999; Gomes 2003), or mutual scattering between planets (Thommes et al. 1999; Tsiganis et al. 2005; Nagasawa et al. 2008; Naoz et al. 2011).
The orbital structure of small-body populations firmly supports the hypothesis that Saturn, Uranus, and Neptune migrated outward after the gas-disk dispersed by interactions with a leftover disk of planetesimal (e.g., Fernandez & Ip 1984; Hahn & Malhotra 1999; Gomes 2003). In the Nice model (Gomes et al. 2005; Morbidelli et al. 2005; 2007; Tsiganis et al. 2005; Levison et al. 2008; 2011; Nesvorny 2011; Nesvorny & Morbidelli 2012; Batygin et al. 2010; 2012) all giant planets would have formed inside 15 AU. This may partially alleviate the accretion timescale problem. However, even in these more propitious conditions, the accretion of multiple ~10 M⊕ planetary cores from planetesimals during the gas disk lifetime remains unlikely (Levison et al. 2010).
In fact, Levison et al. (2010) were unable to repeatedly form giant planet cores by accretion of planetesimals via runaway (e.g., Wetherill & Stewart 1989; Kokubo & Ida 1996) and oligarch growth (e.g., Ida & Makino 1993; Kokubo & Ida 1998; 2000). Planetary embryos and cores stir up neighboring planetesimals and increase their velocity dispersions. Cores open gaps in the distribution of planetesimals around their orbits (Ida & Makino 1993; Tanaka & Ida 1997), and this drastically reduces their rate of growth long before reaching masses similar to those of the real ice giants (Levison et al. 2010).
A new model for the formation of planetary cores called pebble accretion may help solve this problem (Johansen 2009; Lambrechts & Johansen 2012; Morbidelli & Nesvorny 2012; Chambers 2014; Kretke & Levison 2014). In the pebble-accretion model, planetary cores grow from a population of seed planetesimals. Planetesimals accrete pebbles spiralling towards the star due to gas drag (Johansen et al. 2009). The formation of multi-Earth-mass planetary cores can be extremely fast even in traditional disks such as the minimum mass solar nebula (Weidenschilling 1977; Hayashi et al. 2011). The timescale accretion problem disappears even if Uranus and Neptune formed at their current locations (Lambrechts & Johansen 2014; Lambrechts et al. 2014).
It is unlikely, however, that Uranus and Neptune formed solely by pebble accretion. The ice giants have high obliquities (spin axis inclinations relative to their orbital planes): about 90 degrees for Uranus and about 30 degrees for Neptune. A planet accreting only small bodies should have a null obliquity (Dones & Tremaine 1993; Johansen & Lacerda 2010). Yet Jupiter is the only giant planet with a low obliquity. Saturn has a 26-degree obliquity, but this is probably due to a spin-orbit resonance with Neptune (Ward & Hamilton 2004; Hamilton & Ward 2004; Boue et al. 2009). The terrestrial planets have a quasi-random obliquity distribution due to the giant impacts that they suffered during their formation (Agnor et al. 1999; Chambers 2001; Kokubo & Ida 2007). Similarly, no process other than giant impacts has been shown to be able to successfully tilt the obliquities of Uranus and Neptune (Lee et al. 2007; Morbidelli et al. 2012). Thus, one possibility is that a system of planetary embryos formed by pebble accretion, and that these embryos then collided with each other to form the cores of Uranus and Neptune.
The number of planetary embryos that form by pebble accretion depends on the number of sufficiently massive seed planetesimals originally in the disk. Kretke et al. (2014) performed global simulations of pebble accretion assuming a system of ~100 seed planetesimals. In their simulations, ~100 Mars- to Earth-mass planetary embryos form, in a process similar to oligarchic growth. However, the authors observed that these embryos do not merge with each other to form just a few large planetary cores. Instead, they scatter off one another and create a dispersed system of many planets, most of which have a lower mass than the cores of the giant planets. Moreover, in many of their simulations the system becomes dynamically unstable. Some of the embryos end up in the inner solar system or in the Kuiper belt, which is inconsistent with the current structure of the solar system in these regions.
In a previous publication (Izidoro et al. 2015) we showed that the dynamical evolution of a system of planetary embryos changes if the innermost embryo grows into a gas giant planet. As it transitions from the type I to the type II regime, the giant planet’s migration drastically slows, such that more distant embryos, also migrating inward, catch up with the giant planet. The gas giant acts as an efficient dynamical barrier to the other embryos’ inward migration. The giant planet prevents them from penetrating into the inner system. Instead, the embryos pile up exterior to the gas giant.
We envision the following scenario. It takes place in a gaseous protoplanetary disk with considerable mass in pebbles. There is also a population of seed planetesimals. The two innermost seed planetesimals quickly grew into giant planet cores, achieved a critical mass (Lambrechts et al. 2014), and accreted massive gaseous atmospheres to become Jupiter and Saturn. Jupiter and Saturn do not migrate inward but rather migrate outward (Masset & Snellgrove 2001; Morbidelli & Crida 2007; Pierens & Nelson 2008; Pierens & Raymond 2011; Pierens et al. 2014). Farther out a number of planetesimals grew more slowly in an oligarchic fashion and generated a system of planetary embryos with similar masses. The embryos migrated inward until they reached the dynamical barrier posed by the gas giants. Their mutual accretion produced Uranus and Neptune through a series of mutual giant impacts (and possibly an additional ice giant; see Nesvorny & Morbidelli 2012), which issued random obliquities for the final planets.
The goal of this paper is to simulate the late phases of this scenario. We wish to test whether the dynamical barrier offered by Jupiter and Saturn does in fact promote the mutual accretion of these embryos to form a few planet cores.
A similar study was performed by Jakubík et al. (2012). In our model we explore a different set of parameters than those considered there. Here, we perform simulations from a wide range of initial numbers and masses of planetary embryos and adopt different dissipation timescales for the protoplanetary disk. Jakubík et al. (2012) instead restricted the initial planetary embryos to be 3 M⊕ or lower.
For simplicity, they also used a surface density of the gas that did not evolve with time in their simulations, which covered a time span of 5 Myr. Thus, our study differs from the previous one by exploring a distinct and more realistic set of parameters.
1.1. Previous study: Jakubík et al. (2012)
Before presenting our methods and the results of our simulations, we summarize the most important results found in Jakubík et al. (2012). We use them below as a reference for comparison with our results. Using exclusively planetary embryos with initial masses equal to 3 M⊕ (or lower), 2012 systematically explored the effects of reduced type I migration rates for the planetary embryos, enhanced surface density of the gas, the presence of a planet trap at the edge of Saturn’s gap, and of turbulence in the disk.
In the simulations that considered no planet trap, but only a reduced type I migration speed for planetary embryos (with a reduction factor relative to the nominal rate varying between 1 and 6), Jakubík et al. found no significant trends of the results concerning the formation of Uranus and Neptune analogs. They also explored the effects of considering enhanced gas surface densities (scale by a factor up to 6), but despite all considered parameters, these simulations still failed systematically in producing good Uranus and Neptune analogs. They usually were able to produce a massive planetary core, with mass higher than 10 M⊕, beyond Saturn; but the second-largest core on average reached only 6 Earth masses or less. This trend was observed in their entire set of simulations, containing 14 or even 28 planetary embryos of 3 M⊕ each (or lower). Moreover, the simulations showed that high values for these parameters usually produce massive planets in the inner solar system. However, this high probability of planets crossing the orbit of Jupiter and Saturn and surviving in the inner solar system was most likely overestimated. This result was presumably a direct consequence of the high gas surface density assumed for the protoplanetary disks, which, in addition, was assumed to remain constant during the 5 Myr integrations (see also Izidoro et al. 2015).
The simulations of Jakubík et al. that considered a planet trap at the edge of Saturn’s gap (see also Podlewska-Gaca et al. 2012) marginally increased the mean mass of the largest core. This trend was also observed when enhancing the surface density of the gas. However, in general, the low mass for the second core remained a problem for the simulations without a planet trap. Only one simulation produced two planetary cores of 15 Earth masses each beyond Saturn and no other bodies in the inner solar system or on distant orbits.
The simulations of Jakubík et al. that considered a turbulent disk (e.g., Nelson 2000; Ogihara et al. 2007) typically produced only one planetary core instead of two. This is because a turbulent gaseous disk prevents cores from achieving a stable resonant configuration. Instead, the cores tend to suffer mutual scattering events until they all collide with each other and produce a single object.
All these results were important to help defining the set-up of our simulations. For example, given the weak dependence of the results of Jakubík et al. on many of the considered parameters, we assumed in this study the nominal isothermal type I migration rate for the planetary embryos and a gas surface density in the protoplanetary disk equivalent to that of the minimum mass solar nebula (see Morbidelli & Crida 2007; Pierens & Raymond 2011).
The structure of this paper is as follows: in Sect. 2 we detail our model. In Sect. 3 we describe our simulations. In Sect. 4 we present our results, and in Sect. 5 we highlight our main results and conclusions.
2. Methods
Our study used N-body simulations including the effects of a gaseous protoplanetary disk with a surface density modeled in one dimension (the radial direction; this approach is similar to that of 2012; and Izidoro et al. 2015). Although real hydrodynamical simulations would be ideal to study the problem in consideration, there are at two important reasons for our choice. First, hydrodynamical calculations considering multiple and mutual interacting planets embedded in a gaseous disk are extremely expensive computationally (e.g., Morbidelli et al. 2008; Pierens et al. 2013). It would be impractical to perform this study using hydrodynamical simulations given the multi-Myr timescale that the simulations need to cover. Second, the method of implementing in a N-body calculation synthetic forces computed from a 1D disk model is qualitatively reliable. It has been widely tested and used in similar studies, where it was shown to mimic the important gas effects on planets observed in genuine hydrodynamical simulations (e.g., Cresswell & Nelson 2006; 2008; Morbidelli et al. 2008).
Our simulations started with fully formed Jupiter and Saturn orbiting at 3.5 AU and 4.58 AU, respectively. This corresponds to the approximate formation location of the gas giants in the Grand Tack model (Walsh et al. 2011; Pierens & Raymond 2011; O’Brien et al. 2014; Jacobson & Morbidelli 2014; Raymond & Morbidelli 2014). In practice, the resulting dynamics involved would be only weakly dependent on the orbital radius, and the actual range of formation locations for the assumed gas giants is relatively narrow (between roughly 3–6 AU for the core of Jupiter). Therefore we did not chose to test different locations for giant planets.
Beyond the orbit of these giant planets, we considered a population of planetary embryos embedded in the gas disk. We performed simulations considering different numbers and masses for the planetary embryos. Here we present simulations considering 2, 3, 5, 10, and 20 planetary embryos. To set the mass of these bodies, we defined the mass in solids beyond the giant planets, which we call the solid disk mass for simplicity. We tested two different values for this parameter: 30 and 60 M⊕. This mass was equally divided between the 2–20 migrating planetary embryos. For example, setting the number of migrating planetary embryos equal to 10 and assuming 30 M⊕ in solids, the simulation started with ten planetary embryos of 3 M⊕ each. These bodies were randomly distributed beyond the orbits of the giant planets, separated from each other by 5 to 10 mutual Hill radii (e.g. Kokubo & Ida 2000). The eccentricities and inclinations of the embryos were initially set to be randomly chosen between 10-3 and 10-2 degrees. Their argument of pericenter and longitude of ascending node were randomly selected between 0 and 360 degrees. The bulk density of the planetary embryos was set at 3 g/cm3.
In our simulations we assumed the locally isothermal approximation to describe the disk thermodynamics. Thus, the gas temperature was set to be a simple power law given by T ~ r− β, where r is the heliocentric distance and β is the temperature profile index (e.g., Hayashi et al. 1981). We are aware that the direction of type I migration is extremely sensitive to the disk thermodynamics and to the planet mass (e.g., Kley & Nelson 2012; Baruteau et al. 2014). Combination of different torques acting on the planet from the gas disk may result in inward or outward migration (Paardekooper & Mellema 2006; Baruteau & Masset 2008; Paardekooper & Papaloizou 2008b; Kley & Crida 2008; Bitsch & Kley 2011; Kretke & Lin 2012; Bitsch et al. 2013, 2014). Outward migration is only possible in specific regions of a non-isothermal disk (Kley & Crida 2008; Kley et al. 2009; Bitsch et al. 2014). As the disk evolves outward, migration must eventually cease. This is because the disk irradiates efficiently and behaves like an isothermal disk when it becomes optically thin (Paardekooper & Mellema 2008a). When this occurs, type I migrating planets simply migrate inward at the type I isothermal rate (Bitsch et al. 2013, 2014; Cossou et al. 2014). Because we assumed that Jupiter and Saturn are already fully formed, we considered for simplicity that the disk has evolved sufficiently to behave as an isothermal disk.
2.1. Gaseous protoplanetary disk
To represent the gas disk we read the 1D radial density distribution obtained from hydrodynamical simulations into our N-body code. We assumed a minimum mass solar nebula disk as traditionally used in simulations of the formation of our solar system (Masset et al. 2006; Morbidelli & Crida 2007; Walsh et al. 2011; Pierens & Raymond 2011). When performing the hydrodynamical simulations, Jupiter and Saturn were kept on non-migrating orbits and allowed to open a gap in the disk until an equilibrium gas distribution was achieved (e.g., Masset & Snellgrove 2001b). We then averaged the resulting radial profile over the azimuthal direction. Our fiducial profile is shown in Fig. 1. In this case, Jupiter is assumed to be at 3.5 AU (its preferred initial location in the model of Walsh et al. 2011) but, as we said above, this is not really important for the results. In Sect. 4.5 we perform simulations with different gap profiles to discuss the effects of considering different initial surface density profiles.
In all our simulations the gas disk dissipation due to viscous accretion and photoevaporation was mimicked by an exponential decay of the surface density as Exp(−t/τgas), where t is the time and τgas is the gas dissipation timescale. Simulations were carried out considering values for τgas equal to 1 Myr and 3 Myr. At 3 and 9 Myr, respectively, the remaining gas is removed instantaneously.
In all our simulations the gas disk aspect ratio is given by 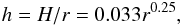 (1)where r is the heliocentric distance and H is the disk scale height.
(1)where r is the heliocentric distance and H is the disk scale height.
 |
Fig. 1 Surface density profile generated from a hydrodynamical simulation considering a mininum mass solar nebula and Jupiter and Saturn on fixed orbits. Two variations of the minimum mass solar nebula disk are shown for comparison (Weidenschilling 1977; Hayashi 1981). |
Still in the hydrodynamical simulation that provides the gas-disk profile, the disk viscous stress was modeled using the standard “alpha” prescription for the disk viscosity ν = αcsH (Shakura & Sunyaev 1973), where cs is the isothermal sound speed. In our simulation α = 0.002.
2.1.1. Tidal interaction of planetary embryos with the gas
Our simulations started with planetary embryos of a few M⊕ distributed beyond the orbit of Saturn. These embryos launched spiral waves in the disk, and the back-reaction of these waves torqued the embryo orbits and caused them to migrate (Goldreich & Tremaine 1980; Ward 1986; Tanaka et al. 2002; Tanaka & Ward 2004). At the same time, apsidal and bending waves damped the embryo orbital eccentricities and inclinations (Papaloizou & Larwood 2000; Tanaka & Ward 2004).
To include the effects of type I migration, we followed Pardekooper et al. (2011) and invoked the locally isothermal approximation to describe the disk thermodynamics. The disk temperature varies as the heliocentric distance as T ~ r-0.5, and the adiabatic index was set to be γ = 1. In this case, normalized unsaturated torques can be written purely as function of the negative of the local (at the location of the planet) gas surface density and temperature gradients, 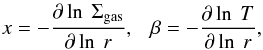 (2)where r is the heliocentric distance and Σgas and T are the local surface density and disk temperature. We note that the shape of the gas surface density (and consequently the local x) in the region near to but beyond Saturn will play a very important role in the migration timescale of planetary embryos entering in this region. Using our surface density profile, x (as in Eq. (2)) is dominantly a negative value inside ~10 AU. Beyond 10 AU, however, the gas surface density decreases monotonically and x is always positive. Given our disk temperature profile (or aspect ratio) β = 0.5.
(2)where r is the heliocentric distance and Σgas and T are the local surface density and disk temperature. We note that the shape of the gas surface density (and consequently the local x) in the region near to but beyond Saturn will play a very important role in the migration timescale of planetary embryos entering in this region. Using our surface density profile, x (as in Eq. (2)) is dominantly a negative value inside ~10 AU. Beyond 10 AU, however, the gas surface density decreases monotonically and x is always positive. Given our disk temperature profile (or aspect ratio) β = 0.5.
In the locally isothermal limit, the total torque experienced by a low-mass planets may be represented by 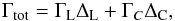 (3)where ΓL is the Lindblad torque and ΓC represents the coorbital torque contribution. ΔL and ΔC are rescaling functions that account for the reduction of the Lindblad and coorbital torques due to the planet eccentricity and orbital inclination (Bitsch & Kley 2010; 2011; Fendyke & Nelson 2014). To implement these reductions factors in our simulations, we followed Cresswell et al. (2008) and Coleman et al. (2014). The reduction factor ΔL is given as
(3)where ΓL is the Lindblad torque and ΓC represents the coorbital torque contribution. ΔL and ΔC are rescaling functions that account for the reduction of the Lindblad and coorbital torques due to the planet eccentricity and orbital inclination (Bitsch & Kley 2010; 2011; Fendyke & Nelson 2014). To implement these reductions factors in our simulations, we followed Cresswell et al. (2008) and Coleman et al. (2014). The reduction factor ΔL is given as ![\begin{eqnarray} {\Delta_{\rm L} \!= \!\left[ P_{\rm e}\! +\! \frac{P_{\rm e}}{|P_{\rm e}|} \times \left\lbrace 0.07 \left( \frac{i}{h}\right) \! +\! 0.085\left( \frac{i}{h}\right)^4\! -\! 0.08\left( \frac{e}{h} \right) \left( \frac{i}{h} \right)^2 \right \rbrace \right] ^{-1} } , \end{eqnarray}](/articles/aa/full_html/2015/10/aa25525-14/aa25525-14-eq35.png) (4)where
(4)where 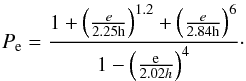 (5)The reduction factor ΔC may be written as
(5)The reduction factor ΔC may be written as 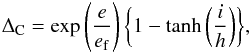 (6)where e is the planet eccentricity, i is the planet orbital inclination, and ef is defined as
(6)where e is the planet eccentricity, i is the planet orbital inclination, and ef is defined as 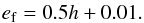 (7)Accounting for the effects of torque saturation due to viscous diffusion, the coorbital torque may be expressed as the sum of the barotropic part of the horseshoed drag, the barotropic part of the linear corotation torque, and the entropy-related part of the linear corotation torque:
(7)Accounting for the effects of torque saturation due to viscous diffusion, the coorbital torque may be expressed as the sum of the barotropic part of the horseshoed drag, the barotropic part of the linear corotation torque, and the entropy-related part of the linear corotation torque: 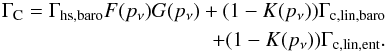 (8)The formulae for ΓL, Γhs,baro, Γc,lin,baro, and Γc,lin,ent are
(8)The formulae for ΓL, Γhs,baro, Γc,lin,baro, and Γc,lin,ent are 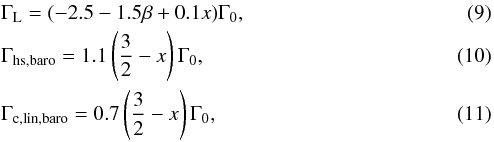
and 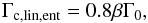 (12)where
(12)where 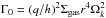 is calculated at the location of the planet. Still, we recall that q is the planet-star mass ratio, h is the disk aspect ratio, Σgas is the local surface density and Ωk is the planet’s Keplerian frequency.
is calculated at the location of the planet. Still, we recall that q is the planet-star mass ratio, h is the disk aspect ratio, Σgas is the local surface density and Ωk is the planet’s Keplerian frequency.
The functions F,G, and K are given in Pardekooper et al. (2011; see their Eqs. (23), (30), and (31)). pν is the parameter governing saturation at the location of the planet and is given by 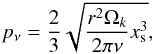 (13)where xs is the non-dimensional half-width of the horseshoe region,
(13)where xs is the non-dimensional half-width of the horseshoe region, 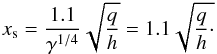 (14)We stress that when calculating these torques, we assumed a gravitational smoothing length for the planet potential equal to b = 0.4 h.
(14)We stress that when calculating these torques, we assumed a gravitational smoothing length for the planet potential equal to b = 0.4 h.
Following Papaloizou et al. (2000), we defined the migration timescale as 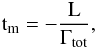 (15)where L is the planet angular momentum and Γ is the torque felt by the planet gravitationally interacting with the gas disk as given by Eq. (3). Thus, for constant eccentricity, the timescale for the planet to reach the star is given by 0.5tm.
(15)where L is the planet angular momentum and Γ is the torque felt by the planet gravitationally interacting with the gas disk as given by Eq. (3). Thus, for constant eccentricity, the timescale for the planet to reach the star is given by 0.5tm.
Thus, as in our previous studies (Izidoro et al. 2014, 2015), the effects of eccentricity and inclination damping were included in our simulations following the formalism of Tanaka et al. (2004), modified by Papaloizou & Larwood (2000), and Cresswell & Nelson (2006, 2008) to cover the case of high eccentricities. The timescales for eccentricity and inclination damping are given by te and ti, respectively. Their values are 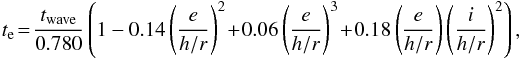 (16)and
(16)and 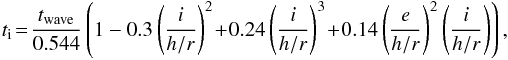 (17)where
(17)where 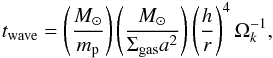 (18)and M⊙, ap, mp, i, and e are the solar mass and the embryo semimajor axis, mass, orbital inclination, and eccentricity, respectively.
(18)and M⊙, ap, mp, i, and e are the solar mass and the embryo semimajor axis, mass, orbital inclination, and eccentricity, respectively.
To model the damping of semimajor axis, eccentricities, and inclinations over the corresponding timescales defined above, we included in the equations of motion of the planetary embryos the synthetic accelerations defined in Cresswell & Cresswell & Nelson (2008), namely  where k is the unit vector in the z-direction.
where k is the unit vector in the z-direction.
All our simulations were performed using the type I migration, inclination, and eccentricity damping timescales defined above.
3. Numerical simulations
We performed 2000 simulations using the Symba integrator (Duncan et al. 1998) using a three-day integration timestep. The code was modified to include type I migration, eccentricity, and inclination damping of the planetary embryos as explained above. Physical collisions were considered to be inelastic, resulting in a merging event that conserves linear momentum. During the simulations planetary embryos that reached heliocentric distances smaller than 0.1 AU were assumed to collide with the central body. Planetary embryos were removed from the system if they were ejected beyond 100 AU of the central star.
Our simulations represent 20 different setups. They were obtained by combining different solid disk masses, initial numbers of planetary embryos, and gas dissipation timescales. For each set, we performed 100 simulations with slightly different initial conditions for the planetary embryos. That means, we used different randomly generated values for the initial mutual orbital distance between these objects, chosen between 5 to 10 mutual Hill radii.
We performed simulations considering the giant planets on non-migrating orbits and simulations considering Jupiter and Saturn migrating outward in a Grand Tack-like scenario. Simulations considering Jupiter and Saturn migrating outwards are presented in Sect. 4.7. During the evolution of the giant planets their orbital eccentricities can increase in both scenarios up to significantly high values because of their interaction with an inward-migrating planetary embryo trapped in an exterior resonance. Counterbalancing this effect, in our simulations, the eccentricities of the giant planets are artificially damped. The eccentricity of Jupiter (and the orbital inclinations) is damped on a timescale ej/ (dej/ dt) ≃ 104 years (ij/ (dij/ dt) ≃ 105 years). This is consistent with the expected damping force felt by Jupiter-mass planets as a consequence of their gravitational interaction with the gaseous disk, calculated in hydrodynamical simulations (e.g. Crida et al. 2008). The eccentricity (orbital inclinations) of Saturn is damped on a shorter timescale, es/ (des/ dt) ~ 103 years (is/ (dis/ dt) ~ 104 years). We consider these to be reasonable values since only a partial gap is opened by Saturn in the disk (see Fig. 1). Thus, this planet should feel a powerful tidal damping similar to that experienced by type I migrating planets (see Eqs. (16) and (17)). In simulations where Jupiter and Saturn are on non-migrating orbits, the eccentricity and inclination damping on these giant planets combined with the pushing from planetary embryos migrating inwards tend to move the giant planets artificially inward. Thus, we restored the initial position of the giant planets on a timescale of ~1 Myr. Our code also rescales the surface density of the gas according to the location of Jupiter and as it migrates (see Sect. 4.7).
4. Results
In this section we present the results of simulations considering Jupiter and Saturn on non-migrating orbits. Here, we recall that as in Izidoro et al. (2015), most of surviving planetary cores and embryos in our simulations stay beyond the orbit of Saturn. In other words, in general, it is rare for planetary embryos or cores to cross the orbit of Jupiter and Saturn, have their orbits dynamically cooled down by the gas effects and survive in the inner regions. We call these protoplanetary embryos the “jumpers” (Izidoro et al. 2015). This result is very different from that of Jakubík et al. where most of the simulations showed objects penetrating and surviving in the inner solar system (see discussion in Sect. 1). However, as mentioned before, this latter result is obviously inconsistent with our planetary system. Thus, in our analysis we rejected those simulations that produced jumper planets. After applying this filtering process in our simulations, for each set of simulations (20 in total) consisting of 100 simulations we are still left with at least ~60% of the simulations. In other words, the production rate of jumper planets in all our simulations has an upper limit of ~40% (see also Izidoro et al. 2015).
4.1. Dynamical evolution
Figure 2 shows the results of two simulations that illustrate the typical dynamical evolution of populations of inward-migrating planetary embryos. In these simulations we initially considered 3 and 20 planetary embryos. These objects migrated toward Saturn and were captured in mean-motion resonances with the giant planets. Migrating planetary cores pile up into resonant chains (Thommes et al. 2005; Morbidelli et al. 2008; Liu et al. 2015). In systems with many migrating embryos, the resonant configurations are eventually broken due to the mutual gravitational interaction among the embryos. When this happens, the system becomes dynamically unstable. During this period, planetary embryos are scattered by mutual encounters and by the encounters with the giant planets. Some objects are ejected from the system (or collide with the giant planets), while others undergo mutual collisions and build more massive cores.
 |
Fig. 2 Typical dynamical evolution of a population of planetary embryos in two different simulations. In both plots, the horizontal axis represents the time and the vertical one shows the semimajor axis. The upper panel shows the dynamical evolution of three planetary embryos or cores of 10 M⊕ each. The lower panel shows the dynamical evolution of a numerous population of 20 planetary embryos of 1.5 M⊕ each. In both simulations the gas lasts 9 Myr. |
The upper panel (Fig. 2) shows a system with just three planetary embryos of 10 M⊕ each. The lower plot shows a system containing 20 planetary embryos of 1.5 M⊕ each. In the simulation with three embryos the system quickly reaches a resonant stable configuration. However, in the system with 20 planetary embryos initially, a continuous stream of inward-migrating embryos generates a long-lived period of instability that lasts to the end of the gas disk phase. The dynamical evolution of simulations considering an intermediate number of planetary embryos is shown in Sect. 4.4.
4.2. Initial and final number of planetary embryos or cores
Figure 3 shows the number of surviving embryos or cores as a function of the initial number. Each dot represents the mean of the results of the 100 simulations in a given series, and the vertical error bar represents the highest and lowest values within the sample over which the mean value was calculated. As expected, there is a clear trend: the more initial embryos, the more survivors. When comparing sets of simulations with the same initial number of planets, but different disk masses or gas disk dissipation timescales, we do not find a clear trend. This is because the initial total mass in protoplanetary embryos considered in our simulations is only different by a factor of 2 (30 and 60 Earth masses). In our case, in all setups, the simulations that started with five planetary embryos ended with a mean of two to three survivors. In general, the statistics for the various series of simulations illustrated in Fig. 3 are similar. Perhaps the clearest difference is observed for the simulations with 20 initial embryos. In this case, the final number of objects decreases for longer gas dissipation timescales. This is because, when the system starts with as many as 20 objects, 3 Myr (gas lifetime) is not long enough for the system of embryos to reach a final stable configuration with just a few objects (see Fig. 2). Even 9 Myr is not long enough, and this is why there are still typically more than five to ten cores in the end. If there are that many initial embryos, the disk dissipation timescale has to be longer than we considered here.
 |
Fig. 3 Statistical analysis of the results of all simulations. The x-axis shows the initial number of planetary embryos in the simulations. The y-axis shows the final number of cores surviving beyond the orbit of Saturn. The filled circles shows the mean values calculated over those simulations that did not produce jumper planets. The vertical error bar shows the highest and lowest values within the sample over which the mean value was calculated. The total initial mass of the disk and the gas dissipation timescale is shown in each panel. |
For a given setup to be consistent with the solar system, there need to be only a few final cores or embryos: at least two, but probably no more than three or four. This is because numerical models of the dynamical evolution of the outer solar system show that the current architecture could be produced in simulations initially with Jupiter and Saturn plus three or four ice giants, that is, Uranus, Neptune, and a third (possibly fourth) object, all in a compact, resonant configuration (like those we produce here). The rogue planet(s) was eventually ejected from our solar system during the dynamical instability that characterizes the transition from the initial to the current configuration (Nesvorny 2011; Nesvorny & Morbidelli 2012). Thus, just on the basis of the final number of surviving protoplanetary cores (we consider the question of mass ratio below), Fig. 3 indicates that the best scenarios are those considering between three to ten planetary cores. Consistent with our results, the simulations of 2012 that initially considered 14 planetary embryos also produced on average between two and three protoplanetary cores.
The simulations that initially considered two or three planetary objects of 10 M⊕ or higher demonstrate that it is possible to preserve the initial number of cores if they are not numerous. In this case, however, there would be no giant impacts to explain the high spin tilt that characterizes Uranus and Neptune, as discussed in the Introduction.
4.3. Initial and final masses of the planetary embryos or cores
Figure 4 shows the final masses of the innermost and second-innermost cores formed in our simulations (outside the orbit of Saturn). In our setup, the initial individual masses of the planetary embryos decrease when we increase the number of these objects. Figure 4 shows that, as expected, this property reflects on the final masses of the planets beyond the orbit of Saturn. When more than two planetary embryos or cores survived beyond Saturn, the two largest are in general the innermost ones. For more than two final planetary objects beyond Saturn, the additional objects are, in general, leftover objects that did not grow. Some simulations also produced coorbital systems (mainly when the gas lasts longer). In these cases, the 1:1 resonant configuration tends to be observed between the innermost object (in general, the largest planetary core) and a planetary embryo that did not grow. However, this latter object is not counted as the second innermost in our analysis (see discussion in Sect. 5).
The masses of Uranus and Neptune are 14.5 and 17.2 M⊕, respectively. Figure 4 suggests that it is more likely to produce an innermost planet with about 17 M⊕ in simulations with five or ten planetary embryos initially. However, the second innermost planet is, in general, smaller than the innermost one. This has also been observed in simulations by 2012. In our simulations, nonetheless, the innermost planetary core is on average ~1.5–2 times more massive than the second one (simulations with five or ten planetary embryos initially), while in Jakubík et al. this number is in general slightly larger, about two or three. The difference with their results is due to three reasons. First because we used a more sophisticated and realistic prescription for the gas tidal damping and migration of protoplanetary embryos. Second, because in our case the gaseous disk dissipates exponentially instead of being kept constant over all time. Third, because we initially used different numbers and masses for planetary embryos (see how the mass ratio changes depending on these parameters in Fig. 4).
 |
Fig. 4 Masses of the innermost and second innermost core surviving beyond Saturn for our different sets of simulations. The filled circles and squares show the mean mass for the innermost and second innermost cores, respectively; the vertical bars range from the highest to the lowest values. |
4.4. Some of our best results
We now highlight simulations that formed reasonable Uranus and Neptune “analogs”. Of course, none of the simulations produced planets with masses identical to that of the ice giants in our solar system. We do not consider this is a drawback of this scenario, but rather a limitation imposed by our simple initial conditions (e.g., all embryos having identical masses). We present the results of simulations that initially considered planetary embryos with different masses in Sect. 4.8. It is also possible that if fragmentation or erosion caused by embryo-embryo collisions were incorporated in the simulations, it could alleviate this issue and lead to better results. But we do not expect these effects to qualitatively change the main trends observed in our results.
We calculated the fraction of the simulations that produced planets similar to Uranus and Neptune. Motivated by the results presented in Sects. 4.2 and 4.3, we limited our analysis to those simulations starting with five or ten planetary embryos with individual masses ranging between 3 to 6 M⊕. This selected eight different sets totaling 800 simulations. We generously tagged a system as a good Uranus-Neptune analog using the following combination of parameters: (1) both planets beyond the orbit of Saturn (innermost and second innermost ones), have masses equal to or high than 12 M⊕ (i.e., experienced at least one collision each); and (2) their mass ratio1 is 1 ≤ M1/M2 ≤ 1.5 (the mass ratio between Neptune and Uranus is about 1.18). We note that Neptune is more massive than Uranus, but these planets might have switched position during the dynamical instability phase (Tsiganis et al. 2005).
Fraction of success in producing Uranus and Neptune analogs in two sets of our simulations.
Simulations that satisfied these two conditions produced up to six planetary embryos or cores beyond Saturn, but in most cases only three or four objects. In a very small fraction of our simulations that produce Uranus and Neptune analogs (<10%) we did observe the formation of two planetary cores where the second innermost one (beyond Saturn) is larger than the innermost one.
 |
Fig. 5 Evolution of planetary embryos leading to the formation of Uranus and Neptune “analogs” in six different simulations. Six panels are shown and labeled from a) to f). Each panel refers to a different simulation and is composed of two sticking plots. The upper panel shows the time evolution of the semimajor axis of all migrating planetary embryos (gray) and giant planets (black). The lower panel shows the time evolution of the mass of those planetary embryos or cores surviving until the end of our integrations. |
About 0–43% of our simulations satisfied the two conditions simultaneously (on mass ratio and individual mass). This clearly shows that the fraction of successful simulations varies depending on the initial number of planetary embryos in the system, their individual and total masses. This may also explain, at least partially, why 2012 produced Uranus and Neptune analogs in only one simulation. As discussed before, we explored in this work a much broader set of parameters of this problem.
Figure 5 shows the dynamical evolution of some of the most successful cases. Most of the collisions tend to occur during the first Myr of integration. Moreover, in general about two to three collisions occur for each planet, which may explain the observed obliquities of Uranus and Neptune (Morbidelli et al. 2012).
In all the simulations illustrated in Fig. 5 the accretion of planetary cores is fairly efficient in the sense that the final mass retained in the surviving largest cores is in general about 50% (or more) of the initial solid disk mass. For example, in the simulation from Fig. 5a the accretion efficiency was 100%. In this case, 30 M⊕ in embryos was converted into two cores of 18 and 12 M⊕. All other simulations of Fig. 5 show either the ejection of at least one object from the system, collisions with the giant planets, or leftover planetary embryos in the system.
Figure 5b shows a simulation that formed two planetary cores of 24 M⊕. In this case, each planetary core was formed through two collisions instead of three, as might be expected given their initial individual masses. First, they hit two planetary embryos growing to 12 Earth masses. Between 0.2 and 0.3 Myr, each of these larger bodies hit another two 12 Earth-mass bodies and reached their final masses. We note that in this simulation there are two leftover planetary embryos beyond the two largest cores that did not experience any collision.
Figure 5c shows one of our best results compared to the architecture of the solar system. In this case, ten planetary embryos of 6 M⊕ formed two planetary cores of 18 M⊕. Figure 5d shows one simulation that also started with ten planetary embryos of 6 Earth masses. This case also formed two planetary cores with 18 M⊕. However, the third body here was no leftover planetary embryo since it has experienced one collision. This is a very atypical result, however. In this case, the gas lasts for 9 Myr and the system retained the same dynamical architecture for 9 Myr of integration.
Figure 5e shows another very interesting case where three objects survived beyond the orbit of Saturn. The two innermost objects have masses of 24 and 18 M⊕, while the third one is a stranded planetary core that did not suffer any collision. In this case, the gas lasted for 3 Myr. Figure 5f shows a simulation that initially contained five planetary embryos of 12 Earth masses each. Even in this case, where the planetary embryos are initially very massive (12 Earth masses), we note that two of them suffered one giant collision each.
Figure 5 also shows that most of our simulations ended with more than two planets beyond Saturn, typically about three (see also Fig. 3). Even though Fig. 5 shows only a sample of our results, it may be considered, in this sense, representative of our results. Importantly, we stress that although the number of final bodies beyond Saturn seems to support the five-planet version of the Nice model proposed by Nesvorny (2011) and Nesvorny et al. (2012), our results do not directly support that scenario. In fact, in the five-planet version of the Nice model, the rogue planets have a similar mass to those of Uranus and Neptune (but see Fig. 5d). Here the mass of this extra planet is, in general, much lower. There are successful six-planet version of the Nice model with two rogue planets of about half the mass of Uranus and Neptune, but they need to be initially placed in between the orbits of Saturn and those of Uranus and Neptune. In our results, instead, the surviving small-mass embryos are always exterior to the two grown cores. It will be interesting to try new multiplanet Nice-model simulations in the future, with initial conditions similar to those we built here.
4.5. Effect of the initial gas surface density profile
We also performed simulations considering different initial gas surface density profiles. For simplicity, we investigated this scenario by rescaling the fiducial gas surface density shown in Fig. 1 (Σgas) by a factor ϵ. We assumed values for ϵ equal to 0.4, 0.75, 1.2, 1.5, and 3. Results of these simulations are summarized in Table 2.
Our results show that a relatively gas-depleted disk is less successful in forming Uranus and Neptune analogs than our simulations with our fiducial gas disk. In a more depleted gaseous disk, planetary embryos migrate more slowly (towards Saturn) and more often reach and retain mutual stable resonant configurations during their gas disk lifetime. Consequently, these simulations tend to have more planetary embryos in the end (at the time the gas is gone). For example, our simulations that initially considered ten planetary embryos with six Earth masses each and a reduction in the gas surface density given by 60% (0.4Σgas) produced on average five planets per system (compare with Fig. 3). This is also indirectly shown by the mean mass of the innermost and second innermost planetary cores beyond Saturn in Table 2. We note that these objects are systematically smaller when the disk is more depleted. The fraction of success in forming good Uranus-Neptune analogs in these simulations is about 22%. This shows that the success rate in forming Uranus-Neptune analogs dropped significantly compared to our fiducial model (42%). In fact, none of our simulations in this scenario produced two planets beyond Saturn with masses higher than 12 Earth masses, where at least one of them suffered two collisions and their mass ratio is between 1 and 1.35. In this case, we also note that the mean mass of the innermost and second innermost planets beyond Saturn are both lower than 11 Earth masses.
On the other hand, a disk richer in gas than our fiducial disk causes the planets to migrate faster, and this also critically affects the mass ratio between the two innermost planets beyond Saturn. If they migrate inward too fast, it is as if these objects were strongly “all together” crunched toward Saturn. This favors that the first innermost planetary core beyond Saturn becomes much more massive than the second innermost one. This, for example, tends to reduce the final number of objects in the system. But, consequently, the mass ratio between the first innermost cores beyond Saturn objects tend to increase, as is also shown in Table 2. This also reduces the success fraction of forming Uranus-Neptune analogs.
The results presented here show that the migration timescale of planetary embryos, particularly in the region very close Saturn where most of the collisions occur, plays a very important role for the formation of planetary cores with similar masses to those of Uranus and Neptune (or their almost unitary mass ratio).
Effects of the initial gas surface density
4.6. Obliquity distribution of planets in our simulations
We tracked the spin angular momentum and obliquity (the angle between rotational and orbital angular momentum of the planet) of the protoplanetary embryos in our simulations assuming that at the beginning of our simulations each planetary embryo had no spin angular momentum. When collisions occurred, the spin angular momentum of the target planet was incremented by summing the spin angular momenta of the two bodies involved in the collision (in the beginning of our simulations they are zero) to the relative orbital angular momentum of the two bodies assuming a two-body approximation (e.g., Lissauer & Safronov 1991; Chambers 2001). Obviously, this approach assumes that all planetary collisions are purely inelastic and that the star gravitational perturbation may be neglected during the very close approach between colliding bodies.
Figure 6 shows the obliquity distribution of the final planets formed in our simulations. The histogram was computed considering only those objects that have suffered at least one collision during the course of our simulations. In this figure, there is clearly a remarkable pile-up of bodies either with obliquities near 0 or 180 degrees (we note that this is a generic trend observed in our results regardless of the initial number of planetary embryos in the system). However, as also shown in this figure, another significant fraction of this population shows a random distribution between 0 and 180 degrees. This is a very interesting result. The expected distribution of planet obliquities during giant collisions is an isotropic distribution with both prograde and retrograde rotations (Agnor et al. 1999; Chambers 2001; Kokubo & Ida 2007). But different from these previous studies, in our simulations we have the effects of gas tidal damping acting on the planetary embryos, which may eventually damp their orbital inclinations to very low values.
We recall that to tilt (significantly) a planet (target), the projectile needs to hit near the pole of the target. The condition for this to occur is that at the instant of the physical collision, a × i>Rtarget, where a is the semimajor axis (target and/or projectile), i (radians) is the mutual orbital inclination between projectile and target and Rtarget is the radius of the target2. If we assume for simplicity that (i) 10 AU is the typical location where our collision occurs; (ii) that a representative mass of our colliding bodies is about 5 Earth masses; (iii) and that these objects have a bulk density of ~3 g/cm3 and therefore a radius of ~14 000 km, we are in three dimensional collision regime if i> 10-5 radians (~6 × 10-4 degrees). In other words, for planets with mutual orbital inclinations below ~6 × 10-4 degrees we preferentially expect obliquities near 0 or 180 degrees. Figure 7 shows the obliquity distribution versus orbital inclination and confirm this analysis. The horizontal dashed line in this figure marks the location where i = 6 × 10-4 degrees. The orbital inclinations of bodies below this line with obliquities significantly different from 0 or 180 were significantly damped by the gas after the giant collisions.
Given our results and because both Uranus and Neptune have high obliquities, either the tidal damping of the inclinations by the gas-disk was not as strong as in our simulations (e.g., the collisions occurred when the disk was old and mass starving), or the system was quite crowded by protoplanets (so that there was not enough time to damp the inclinations between mutual encounters), or the disk was turbulent, so that very low inclinations could never be achieved (Nelson 2005). Of these three alternatives, the last one seems to be the most compelling. The results of our simulations considering a more depleted gas disk (0.4Σgas) did not show this remarkably pile-up of objects with obliquities around 0 and 180 degrees (Fig. 6). But as our results showed, a gas-depleted disk tends to decrease the success of forming good Uranus-Neptune analogs. Moreover, in this scenario, the final systems usually host many planetary objects (five on average). A very numerous population of planetary cores beyond Saturn would probably make the system dynamically unstable after the gas disk dissipation. Thus, a turbulent disk could be the most elegant solution for this problem (see also Sect. 5).
 |
Fig. 6 Obliquity distribution of all planetary embryos and planets that suffered at least one collision in all our simulations (initial number of planetary embryos = 2, 3, 5, 10, and 20) where the disk total mass is equal to 60 M⊕ and the gas exponentially dissipates in 3 Myr. The vertical axes shows the number of planets, and the horizontal axes show the obliquity. |
 |
Fig. 7 Obliquity vs. orbital inclination of all planetary embryos and planets that suffered at least one collision in all our simulations (initial number of planetary embryos = 2, 3, 5, 10, and 20) where the disk total mass is equal to 60 M⊕ and the gas exponentially dissipates in 3 Myr. The dashed line shows i = 6e–4 degrees. |
4.7. Effect of the outward migration of Jupiter and Saturn
Up to now, we have assumed that Jupiter and Saturn are on non-migrating orbits. The orbital radii of the giant planets were chosen to be consistent with models of the later evolution of the solar system, specifically the Grand Tack model (Walsh et al. 2011). But in the Grand Tack model Jupiter and Saturn migrate outward during the late phases of the disk lifetime. Outward migration is driven by an imbalance in disk torques that occurs due to the specific mass ratio of Jupiter and Saturn and their narrow orbital spacing (Masset & Snellgrove 2001; Morbidelli & Crida 2007; Pierens & Nelson 2008; Pierens & Raymond 2011; Pierens et al. 2014). The question then arises about the effect of the outward migration of the gas giants on the accretion of the ice giants.
We performed additional simulations similar to those presented in Sect. 4, but imposing outward migration of Jupiter and Saturn. Jupiter and Saturn started at 1.5 and ~2 AU, respectively. As in Walsh et al. (2011), we applied additional accelerations to the planet orbits to force them to migrate outward. The gas disk was exponentially dissipated. For the outward migration of Jupiter and Saturn and gas disk dissipation timescales we assumed values consistent with those in Walsh et al. (2011), that is, τgas ≃ τmig ≃ 0.5–1 Myr.
 |
Fig. 8 Same as Fig. 5, but in simulations where Jupiter and Saturn migrate outward. The migration and gas dissipation timescales are 0.5 Myr and 1 Myr, respectively. The lower panel shows simulations with a jumper planet. In the lower panel, one of the objects suffered a collision before 0.01 Myr. |
Figure 8 shows the evolution of one simulation with migrating gas giants. As in previous simulations, embryos migrate inward, undergo multiple episodes of instability, and pile up in a resonant chain exterior to Saturn. The upper panel in Fig. 8 shows a case without a jumper planet. In contrast, the lower panel shows a case where a planet is scattered inward and survives inside the orbit of Jupiter. This certainly makes this simulation inconsistent with the current architecture of our solar system.
In general, the main trends observed in simulations where Jupiter and Saturn are on non-migrating orbits were also observed in simulations considering Jupiter and Saturn to migrate outward. Importantly, we stress that in this scenario it is also relatively challenging to produce two planets with masses similar to those of Uranus and Neptune. However, simulations with migrating Jupiter and Saturn present some modest differences relative to those with non-migrating giant planets.
Simulations where Jupiter and Saturn migrate outward tend to produce, on average, fewer planets than those where Jupiter and Saturn are on non-migrating orbits. For example, in simulations with Jupiter and Saturn migrating outward and starting with ten planetary embryos of 6 Earth masses, the final mean number of planetary objects beyond Saturn is around 2.6 (see Fig. 3 for comparison). This is because the outward migration of Jupiter and Saturn combined with the inward migration of the protoplanetary embryos tend to quickly crunch the system into a small region (see Fig. 8). During this phase, resonant configurations among these objects and giant planets (or other planetary embryos) tend to be easily broken down. As a result, planetary embryos become dynamically unstable, are ejected, scattered inward, or suffer mutual accretion. This process is repeated until the migration of Jupiter and Saturn is completed. Consequently, the mutual accretion among protoplanetary cores tends to be accelerated and generally occurs very early (≲0.1–0.5 Myr – e.g., Fig. 8).
We also observed that the rate of jumpers was higher with migrating giant planets (see Izidoro et al. 2015). For example, for τgas ≃ τmig ≃ 0.5−1 Myr and simulations that initially considered ten planetary embryos with 6 Earth masses each show a rate of jumpers of about ~50–80% (depending on the combination between the parameters τgas and τmig). This makes sense for two reasons. First, because a higher relative migration rate between the gas giants and embryos should produce stronger instabilities (see Izidoro et al. 2014). Second, in simulations where Jupiter and Saturn migrate outward, they start closer to the star (Jupiter starts at ~1.5 AU and Saturn at ~2.0 AU). Our code rescales the surface density of the gas according to the location of Jupiter and as it migrates. Thus, the closer Jupiter is to the star, the higher is the gas surface density inside its orbit (Walsh et al. 2011) and Izidoro et al. (2015) found that the probability that a planetary embryo jumps across giant planet orbits increases with the gas density. However, the fraction of simulations that produced ice giant analogs with similar masses is similar in the cases with migrating and non-migrating giant planets. In fact, the fraction of Uranus and Neptune analogs is 12% in simulations that initially considered five planetary embryos of 6 Earth masses each. In simulations that initially considered ten planetary embryos of 6 Earth masses each this number is about 12% (4%). Thus the difference in success rates between the simulations with and without migrating giants is not critically different. The values shown in brackets show the fraction of our simulations where at least one of the planetary cores experienced two collisions, both have masses higher than or equal to 12 M⊕ and the mass ratio between them is between 1 and 1.35.
4.8. Simulations with different initial mass for planetary embryos
We also performed 600 simulations that initially considered planetary embryos with different masses. To set the mass of these bodies, we kept the total mass of disk fixed (30 or 60 Earth masses as in our fiducial model) and continued to insert planetary embryos into the system until the set mass limit was reached. We performed two sets of simulations varying the width of the distribution of mass of individual planetary embryos. In the first one (hereafter called V1) we allowed a very wide range of masses, where the initial mass of the embryos was randomly chosen to be between 1 and 10 Earth masses. In the second one (hereafter called V2), the individual mass of the planetary embryos was randomly chosen in a narrower range of between 3 and 6 Earth masses.
 |
Fig. 9 Same as Fig. 5, but in simulations where planetary embryos initially have different masses. In both simulations the gas dissipates in 3 Myr, and the initial total mass carried by planetary embryos is about 60 Earth masses. |
Figure 9 shows two examples of these simulations. The initial masses of the protoplanetary embryos are different. In both cases, two Uranus and Neptune analogs are formed where the mass of the two largest planetary cores are very similar to those of the real planets. Figure 9a represents a simulation of setup V1, while Fig. 9b corresponds to setup V2.
 |
Fig. 10 Similar to Fig. 3, but for simulations initially considering a different mass for the planetary embryos. The horizontal axis show the initial (mean) number of planetary embryos. The points show the mean final number of planetary cores beyond Saturn for V1 and V2. The horizontal error bars show the range of values over which the mean initial number of planetary embryos is calculated. The vertical bars show the range of values over which the mean final number of planets is calculated. |
Figure 10 shows that the mean initial number of planetary embryos in our simulation of set V1 is about 10.5 planets, while in set V2 this number is about 13. The horizontal error bars show the range over which the mean initial number of planetary embryos is calculated. In the vertical axis, Fig. 10 also shows the mean final number of planetary cores and the range over which this value is calculated (vertical error bars).
 |
Fig. 11 Similar to Fig. 4, but for simulations initially considering different masses for the planetary embryos. In this case, we plot the initial mean number of planetary embryos (the range over which this number is calculated is shown by the horizontal error bars in Fig. 10) against the mean mass of the innermost and second innermost planetary cores formed beyond Saturn. The range over which this mean value is calculated is shown by the vertical error bars. |
Figure 11 shows the mean mass of the first innermost and second innermost planets formed beyond Saturn. The mass ratio between the mean mass of the first innermost core and second one beyond Saturn is 1.6 for V1 and 1.7 for V2. Compared with our other results, this suggests that allowing a varied mass distribution may be almost equally good as simulations that initially considered a population of planetary embryos with identical masses. In fact, the fractions of good Uranus-Neptune analogs, as defined previously, produced in these simulations are 20% (9%) and 6% (5%) for set V1 and V2, respectively. As before, the values shown in brackets show the fraction of our simulations where at least one of the planetary cores experienced two collisions, both have masses higher than or equal to 12 M⊕ and the mass ratio between the two analogs is between 1 and 1.35. However, we cannot fail to notice that simulations that successfully produced Uranus and Neptune analogs initially had massive planetary embryos in the system (e.g., Fig. 9), similar to the mass of planetary embryos in simulations starting with a single-mass component (≳6 M⊕).
5. Discussion
Our simulations confirm that producing planet analogs to Uranus and Neptune – with high and similar masses – from a set of planetary embryos is indeed a difficult task. The main challenge are not the individual masses of the simulated planets, but their mass ratio. This is consistent with what 2012 found.
But unlike Jakubík et al. we also found that planetary embryos usually remain beyond the orbits of Jupiter and Saturn. The giant planets act as an efficient dynamical barrier (see Izidoro et al. 2015) that prevents embryos from jumping across their orbits. The reason for this main difference with respect to the results of Jakubík et al. is our use of a more realistic surface density profile of the gaseous disk, as well as more realistic migration and damping forces. The low probability of penetration of an embryo into the inner solar system is a positive aspect of our results, because Izidoro et al. (2014) showed that the migration of a super-Earth through 1 AU would have prevented the formation of the Earth, unless its migration occurred very rapidly.
According to our scenario, the success rate in producing Uranus and Neptune analogs varies significantly depending on the initial number of planetary embryos in the system, their initial and total masses. Our best results in terms of mass ratio were obtained in simulations that initially considered planetary cores with masses equal to or higher than 3 M⊕. In fact, 6 M⊕ seems to be the best initial mass for coming close to the real masses and mass ratio of Uranus and Neptune. However, as observed for our simulations considering an initial distribution of planetary embryos with different masses, an initial distribution of planetary embryos with different masses in a mass range between 3 and 6 M⊕ or 1 and 10 M⊕ may be similarly good.
The requirement that the initial embryos had a mass of the order of 5 M⊕ may make the interest of our result seem doubtful. In fact, producing multiple ~5 M⊕ embryos may be equally unlikely as directly forming two embryos with Uranus or Neptune masses. This may not be possible by planetesimal accretion (Levison et al. 2010), but may be feasible by pebble accretion (Lambrechts & Johansen 2012; 2014). The advantage of forming Uranus and Neptune from a set of smaller (although massive) embryos probably is that one can explain the origin of the high obliquities of Uranus and Neptune by giant impacts. In a significant fraction of our simulations (Tables 1 and 2) the final planets indeed suffered at least one giant collision.
It is quite interesting that the best scenario for the formation of Uranus and Neptune requires a population of planetary embryos of about ~5 M⊕ (between 3 and 6 M⊕). Recent studies (Youdin 2011; Fressin et al. 2013; Petigura et al. 2013; Weiss & Marcy 2014; Marcy et al. 2014; Silburt et al. 2015; Rogers 2015) have shown that the size distribution of extrasolar planets peaks at about ~2 Earth radii (between 1.5 and <3.0). This same pattern is clearly present in the current planet candidate population (Burke et al. 2014). In fact, using the mean of the observed mass-density relation, a 2.0 Earth radii planet is equivalent to a ~5 Earth mass planet (Weiss & Marcy 2014; Hasegawa & Pudritz 2014). Thus, it may be tempting to conjecture that ~5 M⊕ is the typical mass of planetary embryos formed in the protoplanetary disk.
The typical dynamical evolution of our simulations shows that a few embryos are scattered beyond 100 AU. In our simulations we removed these objects. In reality, if the solar system formed within a stellar cluster, with a significant probability (a few to 15%) these planets could be decoupled by stellar perturbations from Jupiter and Saturn and remain trapped on orbits with semimajor axes of a few 100 to few 1000 AU (Brasser et al. 2006; 2012). Thus, if Uranus and Neptune were formed from a system of multi-Earth-mass planetary embryos, our simulations may explain the existence today of a primordial scattered planetary embryo on a distant orbit. The existence of such an object has been invoked to explain the observed orbital properties of the most distant trans-Neptunian objects (e.g., Gomes et al. 2006; Lykawka & Mukai 2008; Trujillo & Sheppard 2014).
As in Jakubík et al. some of our simulations produced planetary cores in orbital resonance 1:1 with another planetary embryo. This was observed in about 5–20% of our simulations that produced good Uranus and Neptune analogs. This kind of orbital configuration is generally formed by the innermost planetary core beyond Saturn, which typically is the largest one, and a non-grown or partially grown planetary embryo, but in a smaller fraction of cases we do observe the formation of a coorbital system with the second innermost planetary core beyond Saturn. This planetary arrangement is in contrast with the actual state of our solar system. However, as discussed in Jakubík et al. the smaller coorbital body would probably be removed during a later dynamical instability between the giant planets.
Most of our simulations that successfully produced Uranus-Neptune analogs formed more than two objects beyond Saturn (see, for example, Fig. 5). This is because, as shown in Fig. 3, simulations with five or ten planetary embryos initially tend on average to end with three planetary objects beyond Saturn. In our model, the extra bodies are in general leftover planetary embryos that did not grow. This is partially consistent with models of the evolution of the solar system that consider that the solar system lost one or more ice giants (Nesvorny 2011; Nesvorny & Morbidelli 2012). The main difference is that in our case the additional planets are in most cases original embryos, so they are smaller than Uranus and Neptune, unlike what is considered in those works. Moreover, in our simulations the additional planets tend to be beyond Uranus and Neptune, while they are placed in between them in the best simulations of Nesvorny & Morbidelli (2012).
One caveat of our results is that about ~35% of the bodies that suffered at least one collision in our simulations have an obliquity either near zero (<10 degrees) or 180 degrees (between 170 and 180 degrees). The remaining ~65% of our planetary cores, however, show an isotropic obliquity distribution. This is a consequence of the tidal inclination damping (Eq. (17)) felt by the planetary embryos in our simulations. In our model, planetary embryos or cores may have their orbital inclinations damped to very low values, which favors subsequent collisions with other objects to occur near the equator (between two bodies with low mutual orbital inclination). The latter results in a low tilt to the final planet. Although this is important, we do not consider that this issue invalidates our model. This drawback could be easily eliminated if in reality the gaseous disk was turbulent (e.g., Nelson 2000). The intensity of this turbulence only needs to be strong enough to keep planetary embryos or cores around 10 AU with inclinations higher than ~6 × 10-4 degrees (see Fig. 8). Thus, the necessary stirring mechanism could be weak enough to not affect the other properties of the dynamics or the process of pebble accretion, because the velocity dispersion it would need to generate could be very low, about two orders of magnitude lower than the deviation of the orbital velocity of the gas from Keplerian velocity.
6. Conclusions
It remains a challenge to directly simulate the formation of Uranus and Neptune. Their growth by planetesimal accretion seems impossible both on their current orbits (Levison & Stewart 2001) and on orbits at ~10 AU (Levison et al. 2010). The process of pebble accretion seems to be more efficient and is a promising mechanism for forming massive objects within the protoplanetary disk lifetime (Lambrechts & Johansen 2012; 2014). However, it is unlikely that Uranus and Neptune formed purely by pebble accretion. Instead, the high obliquities of Uranus and Neptune suggest that both planets suffered giant impacts during their growth history (e.g., Slattery 1992; Morbidelli et al. 2012).
In this paper we investigated the accretion of Uranus and Neptune by mutual collisions between multi-Earth-mass planetary embryos formed originally beyond the orbit of Saturn. These simulations correspond to the phase where the gaseous protoplanetary disk was still present, but disappearing. Our simulations were performed using an N-body code adapted to take into account the effects of gas on the planetary embryos. Our protoplanetary disk was represented by a 1D (radial) gas surface density profile, obtained by averaging the result of a hydrodynamical simulation accounting from the presence of Jupiter and Saturn over the azimuthal direction. The effects of type I migration, eccentricity, and inclination damping on the orbits of the protoplanetary cores were incorporated in our code in a way that had been previously calibrated to match the effects observed in hydrodynamical simulations and account for the shape of the density distribution of the gas-disk sculpted by the giant planets. We performed simulations considering Jupiter and Saturn on non-migrating orbits and simulations considering that these two giant planets migrate outward (Walsh et al. 2011).
Our best results regarding the formation of analogs of Uranus and Neptune were obtained by initially considering five or ten planetary embryos with masses between 3 and 6 M⊕. We tend to exclude the possibility of forming Uranus and Neptune from a system of more numerous (~20) but much smaller planetary embryos because in all our simulation starting with 20 planetary embryos of 3 M⊕ or smaller, there are finally more than five objects on average, and in many cases even ten. In addition, the innermost planet formed in these simulations is usually very small.
With the exception of the simulations starting with 20 embryos and a total mass in planetary embryos equal to 30 M⊕, we produce in general at least one planet with a mass similar to or higher than those of Uranus and Neptune. Most of our simulations do not show the scattering of an embryo into the inner solar system, which is consistent with the observed structure of the terrestrial planet system (Izidoro et al. 2014). The most challenging property to match is the mass ratio between Uranus and Neptune. In a significant fraction of the cases, however, we produce two planets with a mass ratio between 1 and 1.5 (or even between 1 and 1.35), suggesting that the actual Uranus/Neptune mass configuration, although not typical, does have a significant probability to occur within this scenario.
Acknowledgments
We are very grateful to an anonymous referee for comments that helped us to substantially improve an earlier version of this paper. A.I. thanks for financial support from the CAPES Foundation (Grant: 18489-12-5). A.M., S.R, F.H., and A.P. thank the Agence Nationale pour la Recherche for support via grant ANR-13-BS05-0003-01 (project MOJO). We also thank the CRIMSON team for managing the mesocentre SIGAMM of the OCA, where these simulations were performed.
References
- Agnor, C. B., Canup, R. M., & Levison, H. F. 1999, Icarus, 142, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Masset, F. 2008, ApJ, 678, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S.-J., et al. 2014, Protostars and Planets VI, 667 [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Brown, M. E. 2010, ApJ, 716, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Brown, M. E., & Betts, H. 2012, ApJ, 744, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Kley, W. 2011, A&A, 536, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Lega, E., & Crida, A. 2014, A&A, 564, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., Duncan, M. J., & Levison, H. F. 2006, Icarus, 184, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., Duncan, M. J., Levison, H. F., Schwamb, M. E., & Brown, M. E. 2012, Icarus, 217, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Boué, G., Laskar, J., & Kuchynka, P. 2009, ApJ, 702, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, C. J., Bryson, S. T., Mullally, F., et al. 2014, ApJS, 210, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2001, Icarus, 152, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2014, Icarus, 233, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. A. L., & Nelson, R. P. 2014, MNRAS, 445, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., Sándor, Z., & Kley, W. 2008, A&A, 483, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Dones, L., & Tremaine, S. 1993, Science, 259, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fendyke, S. M., & Nelson, R. P. 2014, MNRAS, 437, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, J. A., & Ip, W.-H. 1984, Icarus, 58, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldreich, P., Lithwick, Y., & Sari, R. 2004a, ApJ, 614, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., Lithwick, Y., & Sari, R. 2004b, ARA&A, 42, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R. S. 2003, Icarus, 161, 404 [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gomes, R. S., Matese, J. J., & Lissauer, J. J. 2006, Icarus, 184, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, J. M., & Malhotra, R. 1999, AJ, 117, 3041 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, D. P., & Ward, W. R. 2004, AJ, 128, 2510 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, Y., & Pudritz, R. E. 2014, ApJ, 794, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Izidoro, A., Morbidelli, A., & Raymond, S. N. 2014, ApJ, 794, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., Hersant, F., & Pierens, A. 2015, ApJ, 800, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, B., Greenberg, R., & Barnes, R. 2008, ApJ, 681, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, S. A., & Morbidelli, A. 2014, Roy. Soc. London Phil. Trans. Ser. A, 372, 0174 [Google Scholar]
- Jakubík, M., Morbidelli, A., Neslušan, L., & Brasser, R. 2012, A&A, 540, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Johansen, A., Youdin, A., & Mac Low, M.-M. 2009, ApJ, 704, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Levison, H. F. 2014, AJ, 148, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2012, ApJ, 755, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Crida, A. 2008, A&A, 487, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokubo, E., & Ida, S. 1996, Icarus, 123, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2000, Icarus, 143, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2007, ApJ, 671, 2082 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H., Peale, S. J., Pfahl, E., & Ward, W. R. 2007, Icarus, 190, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Morbidelli, A. 2007, Icarus, 189, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., & Stewart, G. R. 2001, Icarus, 153, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Van Laerhoven, C., Gomes, R., & Tsiganis, K. 2008, Icarus, 196, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Morbidelli, A., Tsiganis, K., Nesvorný, D., & Gomes, R. 2011, AJ, 142, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Zhang, X., Lin, D. N. C., & Aarseth, S. J. 2015, ApJ, 798, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Lykawka, P. S., & Mukai, T. 2008, AJ, 135, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., & Kary, D. M. 1991, Icarus, 94, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Isaacson, H., Howard, A. W., et al. 2014, ApJS, 210, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F., & Snellgrove, M. 2001, MNRAS, 320, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Morbidelli, A., & Crida, A. 2007, Icarus, 191, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Crida, A., Levison, H. F., & Gomes, R. 2007, AJ, 134, 1790 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Crida, A., Masset, F., & Nelson, R. P. 2008, A&A, 478, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Batygin, K., Crida, A., & Gomes, R. 2012, Icarus, 219, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., Papaloizou, J. C. B., Masset, F., & Kley, W. 2000, MNRAS, 318, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D. 2011, ApJ, 742, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2012, AJ, 144, 117 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, D. P., Walsh, K. J., Morbidelli, A., Raymond, S. N., & Mandell, A. M. 2014, Icarus, 239, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., Ida, S., & Morbidelli, A. 2007, Icarus, 188, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2008a, A&A, 478, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2008b, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petigura, E. A., Howard, A. W., & Marcy, G. W. 2013, Proc. Nat. Acad. Sci., 110, 19273 [Google Scholar]
- Pierens, A., & Nelson, R. P. 2008, A&A, 483, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., & Raymond, S. N. 2011, A&A, 533, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., Cossou, C., & Raymond, S. N. 2013, A&A, 558, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierens, A., Raymond, S. N., Nesvorny, D., & Morbidelli, A. 2014, ApJ, 795, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Podlewska-Gaca, E., Papaloizou, J. C. B., & Szuszkiewicz, E. 2012, MNRAS, 421, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Raymond, S. N., & Morbidelli, A. 2014, IAU Symp., 310, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, L. A. 2015, ApJ, 801, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1972, Evolution of the protoplanetary cloud and formation of the Earth and planets, ed. V. S. Safronov, Translated from Russian. Jerusalem (Israel): Israel Program for Scientific Translations (Keter Publishing House), 212 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Silburt, A., Gaidos, E., & Wu, Y. 2015, ApJ, 799, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Slattery, W. L. 1992, Icarus, 99, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., & Ida, S. 1997, Icarus, 125, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W. 2005, ApJ, 626, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 1999, Nature, 402, 635 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2002, AJ, 123, 2862 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2003, Icarus, 161, 431 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Trujillo, C. A., & Sheppard, S. S. 2014, Nature, 507, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Youdin, A. N. 2011, ApJ, 742, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ward, W. R. 1986, Icarus, 67, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R. 1997, Icarus, 126, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R., & Hamilton, D. P. 2004, AJ, 128, 2501 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W., & Stewart, G. R. 1989, Icarus, 77, 330 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fraction of success in producing Uranus and Neptune analogs in two sets of our simulations.
All Figures
 |
Fig. 1 Surface density profile generated from a hydrodynamical simulation considering a mininum mass solar nebula and Jupiter and Saturn on fixed orbits. Two variations of the minimum mass solar nebula disk are shown for comparison (Weidenschilling 1977; Hayashi 1981). |
| In the text | |
 |
Fig. 2 Typical dynamical evolution of a population of planetary embryos in two different simulations. In both plots, the horizontal axis represents the time and the vertical one shows the semimajor axis. The upper panel shows the dynamical evolution of three planetary embryos or cores of 10 M⊕ each. The lower panel shows the dynamical evolution of a numerous population of 20 planetary embryos of 1.5 M⊕ each. In both simulations the gas lasts 9 Myr. |
| In the text | |
 |
Fig. 3 Statistical analysis of the results of all simulations. The x-axis shows the initial number of planetary embryos in the simulations. The y-axis shows the final number of cores surviving beyond the orbit of Saturn. The filled circles shows the mean values calculated over those simulations that did not produce jumper planets. The vertical error bar shows the highest and lowest values within the sample over which the mean value was calculated. The total initial mass of the disk and the gas dissipation timescale is shown in each panel. |
| In the text | |
 |
Fig. 4 Masses of the innermost and second innermost core surviving beyond Saturn for our different sets of simulations. The filled circles and squares show the mean mass for the innermost and second innermost cores, respectively; the vertical bars range from the highest to the lowest values. |
| In the text | |
 |
Fig. 5 Evolution of planetary embryos leading to the formation of Uranus and Neptune “analogs” in six different simulations. Six panels are shown and labeled from a) to f). Each panel refers to a different simulation and is composed of two sticking plots. The upper panel shows the time evolution of the semimajor axis of all migrating planetary embryos (gray) and giant planets (black). The lower panel shows the time evolution of the mass of those planetary embryos or cores surviving until the end of our integrations. |
| In the text | |
 |
Fig. 6 Obliquity distribution of all planetary embryos and planets that suffered at least one collision in all our simulations (initial number of planetary embryos = 2, 3, 5, 10, and 20) where the disk total mass is equal to 60 M⊕ and the gas exponentially dissipates in 3 Myr. The vertical axes shows the number of planets, and the horizontal axes show the obliquity. |
| In the text | |
 |
Fig. 7 Obliquity vs. orbital inclination of all planetary embryos and planets that suffered at least one collision in all our simulations (initial number of planetary embryos = 2, 3, 5, 10, and 20) where the disk total mass is equal to 60 M⊕ and the gas exponentially dissipates in 3 Myr. The dashed line shows i = 6e–4 degrees. |
| In the text | |
 |
Fig. 8 Same as Fig. 5, but in simulations where Jupiter and Saturn migrate outward. The migration and gas dissipation timescales are 0.5 Myr and 1 Myr, respectively. The lower panel shows simulations with a jumper planet. In the lower panel, one of the objects suffered a collision before 0.01 Myr. |
| In the text | |
 |
Fig. 9 Same as Fig. 5, but in simulations where planetary embryos initially have different masses. In both simulations the gas dissipates in 3 Myr, and the initial total mass carried by planetary embryos is about 60 Earth masses. |
| In the text | |
 |
Fig. 10 Similar to Fig. 3, but for simulations initially considering a different mass for the planetary embryos. The horizontal axis show the initial (mean) number of planetary embryos. The points show the mean final number of planetary cores beyond Saturn for V1 and V2. The horizontal error bars show the range of values over which the mean initial number of planetary embryos is calculated. The vertical bars show the range of values over which the mean final number of planets is calculated. |
| In the text | |
 |
Fig. 11 Similar to Fig. 4, but for simulations initially considering different masses for the planetary embryos. In this case, we plot the initial mean number of planetary embryos (the range over which this number is calculated is shown by the horizontal error bars in Fig. 10) against the mean mass of the innermost and second innermost planetary cores formed beyond Saturn. The range over which this mean value is calculated is shown by the vertical error bars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


