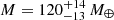EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 675 (July 2023) A&A, 675 (2023) L8 Full HTML
Highlight
Open Access
Issue
A&A
Volume 675, July 2023
Article Number L8
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202346850
Published online 10 July 2023

© ESO 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Understanding the origin of the outer planets in the Solar System, and giant planet formation in general, is a key objective of planetary science (e.g., Helled & Morbidelli 2021; Helled et al. 2014, and references therein). The exploration of the giant planets in the Solar System by the Juno and Cassini spacecraft provided new and exciting data about the interiors of Jupiter and Saturn, respectively (e.g., Wahl et al. 2017; Mankovich & Fuller 2021; Helled et al. 2022a; Miguel et al. 2022). The new measurements have challenged giant planet formation theory and have led to the construction of new formation and internal structure models. It is now more accepted that both planets have fuzzy cores, with the core extending out to as much as 60% of the planetary radius. While the exact composition of the planets is not well determined due to the degenerate nature of structure models, Saturn is known to be more metal-rich than Jupiter (e.g., Nettelmann et al. 2021)1.

Saturn is often treated as simply a smaller version of Jupiter in terms of formation and interior structure. However, the two planets differ significantly in terms of their inferred bulk composition and the extension of their cores. In addition, giant planet formation theory predicts that gap formation typically occurs at Jupiter’s mass (Dong & Fung 2017), which raises the question of what prevented Saturn from growing further in mass. This could be explained if the gas disk disappeared exactly at the time when Saturn reached its current mass, but this is a fine-tuning argument that is rather unsatisfying.

Traditionally, giant planet formation theory separated the formation of Jupiter and Saturn (the so-called gas giants) from that of Uranus and Neptune (the so-called ice giants), as it is assumed that Uranus and Neptune grew too slowly to reach the phase of runaway gas accretion and are therefore “failed giant planets”. Here we suggest that the transition to hydrogen and helium (H–He) dominated planets, which is associated with undergoing runaway gas accretion during formation, occurs at a mass of ∼100 Earth masses (M⊕). In that case, Saturn, like Uranus and Neptune, never reached runaway accretion and is also a failed giant planet. The transition to runaway gas accretion at this mass offers interesting explanations for some of the observed features of Jupiter and Saturn and the mass–radius (M–R) relation of exoplanets.

2. Slow giant planet formation and delayed runaway gas accretion

In the standard model for giant planet formation, a heavy-element core forms, followed by gradual solid and gas accretion until runway gas accretion is reached, leading to rapid gas accretion (Pollack et al. 1996). For a while, giant planet formation models had to accelerate the formation timescale since accretion rates were too low, and the disk’s lifetime was assumed to be ∼3 Myr (e.g., Alibert et al. 2005; Movshovitz et al. 2010) in order to be consistent with the estimated average disk lifetime at the time (Mamajek 2009). The possibility of rapid core formation via pebble accretion (Lambrechts & Johansen 2014), and the fact that recent disk observations imply that gaseous disks can have lifetimes beyond 3 Myr (e.g., Michel et al. 2021), relaxes the need for the rapid formation of giant planets. It is now known that giant planets are less common than small planets (e.g., Fulton et al. 2021), and this could be a result of a relatively slow growth of giant planets in comparison to standard disk lifetimes. In addition, more traditional formation models suggest that runaway gas accretion occurs at the crossover mass (i.e., when the heavy-element mass is comparable to the H–He mass), which occurs at a planetary mass of ∼30 M⊕, though the exact mass is strongly dependent on the specific model.

Recent formation models of Jupiter suggest important modifications to the old picture of giant planet formation: (i) cores are formed more efficiently via pebble accretion (e.g., Lambrechts & Johansen 2014; Johansen & Lambrechts 2017), (ii) the accretion of solids (heavies) and gas (H–He) leads to a gradual distribution of heavy elements within the planetary deep interior (e.g., Helled & Stevenson 2017), (iii) additional enrichment of heavies is required to explain the estimated heavy-element masses in Jupiter and Saturn (e.g., Li et al. 2010; Shibata & Ikoma 2019; Shibata & Helled 2022), and (iv) the formation of Jupiter within a few million years can explain the existence of two reservoirs of small bodies in the early Solar System (Kruijer et al. 2017).

Alibert et al. (2018) suggested that Jupiter’s formation was characterized by core formation dominated by pebble accretion followed by planetesimal accretion, and that Jupiter reached its final mass ∼3-Myr after the formation of the Solar System. It was later shown more systematically that Jupiter’s formation timescale could have indeed been a few million years if runaway gas accretion was delayed by planetesimal accretion for a large range of initial formation locations and planetesimal sizes (Venturini & Helled 2020).

Efficient heavy-element accretion, on the order of 10−5 M⊕ yr−1, provides enough energy to hinder runaway gas accretion since it prolongs the cooling of the planet (e.g., Alibert et al. 2018; Venturini & Helled 2020; Kessler & Alibert 2023). Such a formation path includes: (i) core formation that is dominated by heavy-element accretion (and a very low level of gas accretion), (ii) an intermediate phase of accretion of solids, (iii) and a steadily increasing accretion of H–He gas until the protoplanet is massive enough (∼100 M⊕) to initiate a rapid accretion of H–He gas (e.g., Helled et al. 2022b). During the intermediate phase, the planetary envelope remains in hydrostatic and thermal equilibrium, with the accreted solids providing all of the radiative luminosity. In that case, the formation timescale of giant planets can be significantly longer (a few million years), and, in addition, the planetary mass associated with the initiation of runaway accretion would be significantly higher.

The required intermediate phase of heavy-element accretion with a rate on the order of ∼10−5 M⊕ yr−1 lasting for a couple million years is not only required to delay gas accretion, but also provides a mechanism for heavy-element enrichment in gas giant planets. While the required accretion rate for this model to work can be estimated, the source of the solid accretion is yet to be determined.

There are various ways to delay the onset of runaway accretion. For the sake of argument, we hereafter simply assume that, after core formation, further solids can be accreted without specifying the sizes and origin of the solids (i.e., whether the source is pebbles and/or planetesimals; see Sect. 3 for further discussion). Finally, the nature of the so-called runaway accretion phase is not fully understood either and is still a topic of intensive investigation. This phase could be a rapid hydrodynamic collapse of the envelope or a quasi-hydrostatic equilibrium contraction occurring on a Kelvin-Helmholtz timescale.

Figure 1 (top panel) shows a sketch of the expected planetary growth and the expected associated timescales of the different phases. The bottom panel shows the planetary composition (heavy-element mass fraction) as a function of planetary mass (until a Jupiter mass is reached) in this formation scenario. This figure should be taken as a qualitative demonstration of the formation scenario, and it includes a shaded region that represents the large modeling uncertainty. However, the figure shows that a longer formation timescale due to an extended second phase can explain the extension of Jupiter’s fuzzy core that stops at ∼100 M⊕ as predicted from structure models. In addition, it naturally explains why Saturn has a higher metallicity (heavy-element mass fraction) than Jupiter. It should be noted that this mass is significantly higher than the crossover mass of ∼20−30 M⊕ traditionally assumed in giant planet formation models (e.g., Stevenson 1982; Bodenheimer & Pollack 1986; Pollack et al. 1996; Piso & Youdin 2014; Helled et al. 2014, and references therein).

thumbnail Fig. 1.

Planetary growth and expected composition. Top: planetary mass as a function of time. The dotted and dashed lines correspond to the heavy-element and H–He mass, respectively. The curve is based on formation calculations (see Helled et al. 2022b for details). Bottom: planetary bulk metallicity (represented by the heavy-element mass fraction) as a function of planetary mass until a Jupiter mass is reached. A large shaded area is included to indicate the large uncertainties associated with the details of the formation models. Interestingly, the expected bulk compositions of the outer planets are consistent with this curve. This model includes planetesimal accretion after core formation, which delays cooling and, therefore, rapid gas accretion (Alibert et al. 2018; Venturini & Helled 2020). Also indicated is the mass where gas accretion is initiated after a few million years of growth (approximately Saturn’s mass) and the order of magnitude of the expected formation timescales. The plots clearly show that low-mass planets are expected to be heavy-element dominated in composition, while planets more massive than ∼100 M⊕ are H–He-rich.

A formation scenario in which the initiation of runaway gas accretion takes place at planetary masses of ∼100 M⊕ implies that Saturn might be a failed giant planet, that is, a planet that has never undergone runaway accretion. In this case, no gap opening is required to explain Saturn’s final mass. Instead, it suggests that Saturn’s growth took a few million years and that the gas disk disappeared before it could enter the phase of rapid gas accretion that leads to the formation of a gas giant planet. It should be noted that the exact planetary mass at which runaway accretion begins depends on the assumed parameters and therefore has a non-negligible uncertainty. The uncertainty was estimated based on different formation models (e.g., Venturini & Helled 2020; Valletta & Helled 2020) but in fact could be larger since the exact composition of the planet and the mass at which runaway accretion is initiated can vary depending on local formation conditions, such as the type of the accreted solids and their distribution within the disk, the planetary formation location and potential migration, and the disk’s physical parameters (such as temperature, pressure, and viscosity).

If Saturn never reached the runaway gas accretion phase, it means that the enrichment of its envelope is a result of heavy-element accretion during the second prolonged phase of accretion and/or the mixing of primordial composition gradients, which can enrich the outer envelope (e.g., Vazan et al. 2018; Müller et al. 2020). Indeed, Saturn interior models imply that Saturn has an extended fuzzy core (e.g., Mankovich & Fuller 2021; Nettelmann et al. 2021). The delay of gas accretion by a few million years and the transition to a gas giant planet at a higher mass also naturally explain why Uranus and Neptune are heavy-element dominated in composition (e.g., Valletta & Helled 2022; Helled & Bodenheimer 2014) – as indicated by Fig. 1 (bottom panel), at a planetary mass of ∼15 M⊕, the H–He mass fraction is about 10%.

2.1. Giant exoplanets

From a different point of view, we can use the M–R relation of exoplanets and their characterization to better understand the nature of giant planets. In the case of warm Jupiters, which are not highly irradiated, we can estimate the planetary bulk composition (e.g., Thorngren et al. 2016; Thorngren & Fortney 2019; Müller & Helled 2023, and references therein). If planets undergo runaway gas accretion, their compositions are expected to be H–He dominated. Interestingly, exoplanet data imply that there is a transition in the M–R relation of exoplanets at a mass of ∼100 M⊕, which could be associated with the transition to gas giant planets. Beyond this mass, the planets are expected to be H–He dominated, which changes the relation between the planetary mass and radius. This is demonstrated in Fig. 2, which shows the M–R relation of planets from the PlanetS Catalog2, which only includes exoplanets with measurement uncertainties smaller than 25% in mass and 8% in radius (Otegi et al. 2020). The top panel shows that the M–R relation follows a power law up to the transition mass to a gas giant planet, around Saturn’s mass, where the M–R relation becomes flat. We note that the M–R relation of planets that are highly irradiated by their host star (F* > 2 × 108 erg s−1 cm2) is less reliable because their radii are affected by an unknown mechanism and by an unknown magnitude. As a result, these highly irradiated planets are shown in gray. The M–R relation and transition point follow the result of Chen & Kipping (2017), although an estimated transition mass of ∼120 M⊕ has been inferred by other studies (see, e.g., Weiss et al. 2013; Hatzes & Rauer 2015; Bashi et al. 2017)3. All these previous statistical analyses identified a transition in the M–R relation of exoplanets occurring at around Saturn’s mass and, depending on the study, was estimated to occur at a mass of ∼95−150 M⊕ (see Weiss et al. 2013; Hatzes & Rauer 2015; Chen & Kipping 2017; Bashi et al. 2017 for details).

thumbnail Fig. 2.

M–R relation of exoplanets from the PlanetS Catalog (https://dace.unige.ch/exoplanets/). Planets that are highly irradiated by their host star (F* > 2 × 108 erg s−1 cm2) are shown in gray as their radii are inflated. Top: planets shown with the M–R relation fit from Chen & Kipping (2017) and the associated uncertainly in the M–R relation slope. The change in the M–R relation is found to occur at a mass of ∼120 M⊕. Bottom: planets shown with composition curves of H–He in a proto-solar ratio (black) and water (blue) assuming an effective temperature of 1500 K. It is clear that planets around or below Saturn’s mass are much more compact than planets with a composition that is dominated by H–He.

The bottom panel shows the same data with compositional curves of a H–He mixture in a proto-solar ratio for an assumed effective temperature of 1500 K at an age of 4.5 Gyr (Howard & Guillot 2023) and pure water with a similar effective temperature (Haldemann et al. 2020). One can clearly see that below about Saturn’s mass, most of the planets are significantly more compact than predicted for a planet whose composition is dominated by H–He. One can also see that the M–R relation of intermediate-mass exoplanets is more diverse, indicating a range of metallicities (i.e., mass ratios between heavy elements and H–He) that would be a natural outcome of different accretion rates and formation locations.

The mass associated with the transition of the M–R relation above Saturn’s mass, and the flattening of the M–R relation, are caused by the onset of electron degeneracy in hydrogen and are, therefore, linked to the planetary bulk composition: the data suggest that beyond this mass the dominating planetary composition is H–He, which is consistent with the initiation of runaway gas accretion. Intermediate-mass planets have radii well below the H–He mixture, suggesting that they are composed of other (heavier) elements. In addition, the spread in radii is significantly larger, implying a larger variety in bulk composition.

While the conclusion that the compositions of planets more massive than Saturn are H–He dominated is robust, it is yet to be shown that planets below this mass never reach the stage of runaway gas accretion. However, the expected timescale of runaway gas accretion is rather short (≪1 Myr). Therefore, in order to explain the composition of the intermediate-mass planets, which is not dominated by H–He, a mechanism to limit gas accretion during the runaway stage would be required (e.g., gas dissipated at the time of gas accretion); alternatively, one must invoke a post-formation mechanism that results in significant loss of the H–He envelope, such as photoevaporation, tidal disruption, core-powered mass loss, and giant impacts (e.g., Owen & Jackson 2012; Owen & Lai 2018; Ginzburg et al. 2018; Ogihara et al. 2021).

A higher transition mass to giant planets also explains the existence of relatively massive exoplanets (whose masses are below that of Saturn) that are highly enriched with heavy elements (e.g., Brahm et al. 2020). In addition, delaying the stage of runaway gas accretion by a few million years means that giant planets generally form relatively slowly, on timescales comparable to the disks’ lifetime. This makes the formation of giant planets less likely, which is consistent with the relatively low occurrence rate of giant exoplanets (e.g., Reffert et al. 2015; Fulton et al. 2021). It is clear that each individual planet has a unique formation path that depends on exact formation conditions, such as formation location, metallicity, disk lifetime, and so on. However, to the first order, a delayed gas accretion offers a simple solution for some key challenges in giant planet theory.

3. Discussion and conclusions

The picture presented here is clearly oversimplified. First, giant planets form at different locations, which affects both the pebble isolation mass and the pebble and planetesimal accretion rates. Therefore, the final composition and structure of giant planets would depend on the exact accretion rates as well as the disk’s metallicity and lifetime. It should also be noted that the heavy-element mass in a planet and the extension of its core depends on the local conditions during the formation process. In addition, the mutual growth of planets could affect accretion rates and the formation timescale.

Second, our arguments are very general, and the suggested formation path (and relation between planetary metallicity and mass) is based on Jupiter formation models. In reality, each planet would have a formation path that is unique, although qualitatively similar to that presented here. For example, since Saturn formed at a larger radial distance than Jupiter, the accretion rates would change accordingly, resulting in a different final heavy-element to H–He ratio as well as a different formation timescale. Since the solid surface density decreases with increasing radial distance, lower accretion rates and therefore longer formation timescales are expected at larger radial distances. In the case of Uranus and Neptune, their growth could easily take a few million years, unless their formation process was dominated by pebble accretion. Nevertheless, low H–He masses for Uranus and Neptune are predicted in both cases of planetesimal and pebble accretion – this is because (i) the pebble isolation mass increases with radial distance, making runaway gas accretion less likely, and (ii) in the case of planetesimals, the accretion rate is lower due to the lower solid surface density of planetesimals with increasing radial distance. Clearly, detailed investigations of the growth of Uranus and Neptune are still required.

Third, the source (and likelihood) of solid (heavy-element) accretion at the required rate of ∼10−5 M⊕ yr−1 is rather uncertain, and more research on this topic is needed. The heavy elements could come in the form of pebbles, planetesimals, and their combination. At the moment, both solely pebble accretion and solely planetesimal accretion have shortcomings. In reality, both types of solids are expected to play a role in giant planet formation. Pebble accretion is thought to be inefficient prior to a gap opening due to radial pumps (e.g., Bitsch et al. 2018) and therefore is unlikely to be the dominant mechanism. In terms of core formation, pebble accretion is efficient only once a small core (more massive than Mars) has already been formed (e.g., Ormel & Klahr 2010). In addition, recent results from fluid-dynamic simulations suggest that pebble accretion is not effective for cores more massive than 1 Earth mass due to the gas flow around the core (Okamura & Kobayashi 2021). Instead, the collisional growth of pebbles produces planetesimals, which accelerate the core’s growth (Kobayashi & Tanaka 2021). As a result, it is likely that, also during the early stages of planet formation, when the core is formed, the heavy-element accretion is determined from a combination of pebble and planetesimal accretion.

Planetesimals can be accreted during migration in a unperturbed planetesimal disk. Shibata & Helled (2022) show that efficient planetesimal accretion can occur during migration in a massive planetesimal disk with a heavy-element accretion rate on the order of ∼10−5M⊕ yr−1. This rate, however, corresponds to a case of an unperturbed planetesimal disk, and it would decrease with increasing inclination excitation. At the same time, the growing giant planet is unlikely to increase the planetesimals’ inclination before rapid gas accretion (e.g., Tanaka & Ida 1999). Instead, the embryos around the growing planet are expected to control the inclination of the planetesimal disk. Nevertheless, even if the inclination is increased by orders of magnitude, the planetesimal accretion rate is expected to decrease only by a factor of a few (Shibata et al. 2023). Each of the simulations mentioned, however, correspond to different conditions. It is therefore clear that a more systematic investigation of the conditions that lead to the required accretion rates needed to delay runaway gas accretion is desirable, and we hope to address this in future research.

Fourth, our suggested scenario does not explain the low metallicities of intermediate-mass planets or the very high metallicities of planets more massive than Jupiter. These planets, however, are less common and could be a result of additional mechanisms that affect the planetary composition and structure, such as inflation, atmospheric loss, and giant impacts.

Finally, the suggested transition mass of ∼100 M⊕ to become a giant planet (H–He-dominated in composition) is also not set in stone and is expected to vary depending on the exact formation conditions. Therefore, in the case of giant exoplanets, it would depend on the formation environment. Nevertheless, this formation path predicts a change in composition for masses greater than that of Saturn; below this mass, the planetary metallicity is more diverse and can be up to 50%, consistent with exoplanetary data.

To summarize, we suggest that the onset of rapid gas accretion occurs at at around Saturn’s mass, and that this mass defines the transition to gas giant planets. If true, this would explain:

  1. The difference in the relative enrichment of the outer planets in the Solar System.

  2. The fuzzy cores of Jupiter and Saturn.

  3. The transition of the M–R relation of exoplanets at ∼100 M⊕ and why above this mass the planetary composition is dominated by H–He.

  4. The relatively low occurrence rate of giant planets.

The origin and internal structure of the outer planets in the Solar System are still being investigated. At the same time, with the available exoplanetary data, we can better characterize giant exoplanets and put our Solar System in perspective. While many questions remain open, this is a golden era for giant planet exploration. The upcoming characterization of many giant planets around other stars based on James Webb Space Telescope, Plato, and Ariel data, the continuous and future exploration of the outer planets in the Solar System, and ongoing theoretical efforts will provide new insights into the nature of gas giant planets.

1

This can also be seen from the mass–radius (M–R) relation of the planets (e.g., Helled et al. 2020).

3

Using these data, we find that the break point in the M–R relation occurs at M = 120 − 13 + 14 M ⊕ $ M = 120^{+14}_{-13}\,M_{\oplus} $.

Acknowledgments

I thank S. Müller for great support. I also thank S. Shibata, D. Stevenson, K. Batygin, and C. Valletta for interesting and useful comments as well as an anonymous referee for valuable corrections and suggestions. Finally, I acknowledge support from the Swiss National Science Foundation (SNSF) via grant 200020_188460.

References

  1. Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alibert, Y., Venturini, J., Helled, R., et al. 2018, Nat. Astron., 2, 873 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bashi, D., Helled, R., Zucker, S., & Mordasini, C. 2017, A&A, 604, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bodenheimer, P., & Pollack, J. B. 1986, Icarus, 67, 391 [Google Scholar]
  6. Brahm, R., Nielsen, L. D., Wittenmyer, R. A., et al. 2020, AJ, 160, 235 [Google Scholar]
  7. Chen, J., & Kipping, D. 2017, ApJ, 834, 17 [Google Scholar]
  8. Dong, R., & Fung, J. 2017, ApJ, 835, 146 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fulton, B. J., Rosenthal, L. J., Hirsch, L. A., et al. 2021, ApJS, 255, 14 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ginzburg, S., Schlichting, H. E., & Sari, R. 2018, MNRAS, 476, 759 [Google Scholar]
  11. Haldemann, J., Alibert, Y., Mordasini, C., & Benz, W. 2020, A&A, 643, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Hatzes, A. P., & Rauer, H. 2015, ApJ, 810, L25 [Google Scholar]
  13. Helled, R., & Bodenheimer, P. 2014, ApJ, 789, 69 [NASA ADS] [CrossRef] [Google Scholar]
  14. Helled, R., & Morbidelli, A. 2021, in ExoFrontiers; Big Questions in Exoplanetary Science, ed. N. Madhusudhan, 12 [Google Scholar]
  15. Helled, R., & Stevenson, D. 2017, ApJ, 840, L4 [NASA ADS] [CrossRef] [Google Scholar]
  16. Helled, R., Bodenheimer, P., Podolak, M., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 643 [Google Scholar]
  17. Helled, R., Mazzola, G., & Redmer, R. 2020, Nat. Rev. Phys., 2, 562 [NASA ADS] [CrossRef] [Google Scholar]
  18. Helled, R., Werner, S., Dorn, C., et al. 2022a, Exp. Astron., 53, 323 [NASA ADS] [CrossRef] [Google Scholar]
  19. Helled, R., Stevenson, D. J., Lunine, J. I., et al. 2022b, Icarus, 378, 114937 [NASA ADS] [CrossRef] [Google Scholar]
  20. Howard, S., & Guillot, T. 2023, A&A, 672, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Johansen, A., & Lambrechts, M. 2017, Annu. Rev. Earth Planet. Sci., 45, 359 [Google Scholar]
  22. Kessler, A., & Alibert, Y. 2023, A&A, 674, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kobayashi, H., & Tanaka, H. 2021, ApJ, 922, 16 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kruijer, T. S., Burkhardt, C., Budde, G., & Kleine, T. 2017, Proc. Natl. Acad. Sci., 114, 6712 [Google Scholar]
  25. Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Li, S. L., Agnor, C. B., & Lin, D. N. C. 2010, ApJ, 720, 1161 [NASA ADS] [CrossRef] [Google Scholar]
  27. Mamajek, E. E. 2009, in Exoplanets and Disks: Their Formation and Diversity, eds. T. Usuda, M. Tamura, & M. Ishii, AIP Conf. Ser., 1158, 3 [NASA ADS] [CrossRef] [Google Scholar]
  28. Mankovich, C. R., & Fuller, J. 2021, Nat. Astron., 5, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  29. Michel, A., van der Marel, N., & Matthews, B. C. 2021, ApJ, 921, 72 [CrossRef] [Google Scholar]
  30. Miguel, Y., Bazot, M., Guillot, T., et al. 2022, A&A, 662, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Movshovitz, N., Bodenheimer, P., Podolak, M., & Lissauer, J. J. 2010, Icarus, 209, 616 [Google Scholar]
  32. Müller, S., & Helled, R. 2023, A&A, 669, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Müller, S., Helled, R., & Cumming, A. 2020, A&A, 638, A121 [Google Scholar]
  34. Nettelmann, N., Movshovitz, N., Ni, D., et al. 2021, Planet. Sci. J., 2, 241 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ogihara, M., Hori, Y., Kunitomo, M., & Kurosaki, K. 2021, A&A, 648, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Okamura, T., & Kobayashi, H. 2021, ApJ, 916, 109 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Otegi, J. F., Bouchy, F., & Helled, R. 2020, A&A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Owen, J. E., & Jackson, A. P. 2012, MNRAS, 425, 2931 [Google Scholar]
  40. Owen, J. E., & Lai, D. 2018, MNRAS, 479, 5012 [Google Scholar]
  41. Piso, A.-M. A., & Youdin, A. N. 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  43. Reffert, S., Bergmann, C., Quirrenbach, A., Trifonov, T., & Künstler, A. 2015, A&A, 574, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Shibata, S., & Helled, R. 2022, ApJ, 926, L37 [NASA ADS] [CrossRef] [Google Scholar]
  45. Shibata, S., & Ikoma, M. 2019, MNRAS, 487, 4510 [NASA ADS] [CrossRef] [Google Scholar]
  46. Shibata, S., Helled, R., & Kobayashi, H. 2023, MNRAS, 519, 1713 [Google Scholar]
  47. Stevenson, D. J. 1982, Annu. Rev. Earth Planet. Sci., 10, 257 [CrossRef] [Google Scholar]
  48. Tanaka, H., & Ida, S. 1999, Icarus, 139, 350 [NASA ADS] [CrossRef] [Google Scholar]
  49. Thorngren, D., & Fortney, J. J. 2019, ApJ, 874, L31 [Google Scholar]
  50. Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
  51. Valletta, C., & Helled, R. 2020, ApJ, 900, 133 [NASA ADS] [CrossRef] [Google Scholar]
  52. Valletta, C., & Helled, R. 2022, ApJ, 931, 21 [NASA ADS] [CrossRef] [Google Scholar]
  53. Vazan, A., Helled, R., & Guillot, T. 2018, A&A, 610, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Venturini, J., & Helled, R. 2020, A&A, 634, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Wahl, S., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [CrossRef] [Google Scholar]
  56. Weiss, L. M., Marcy, G. W., Rowe, J. F., et al. 2013, ApJ, 768, 14 [Google Scholar]

All Figures

thumbnail Fig. 1.

Planetary growth and expected composition. Top: planetary mass as a function of time. The dotted and dashed lines correspond to the heavy-element and H–He mass, respectively. The curve is based on formation calculations (see Helled et al. 2022b for details). Bottom: planetary bulk metallicity (represented by the heavy-element mass fraction) as a function of planetary mass until a Jupiter mass is reached. A large shaded area is included to indicate the large uncertainties associated with the details of the formation models. Interestingly, the expected bulk compositions of the outer planets are consistent with this curve. This model includes planetesimal accretion after core formation, which delays cooling and, therefore, rapid gas accretion (Alibert et al. 2018; Venturini & Helled 2020). Also indicated is the mass where gas accretion is initiated after a few million years of growth (approximately Saturn’s mass) and the order of magnitude of the expected formation timescales. The plots clearly show that low-mass planets are expected to be heavy-element dominated in composition, while planets more massive than ∼100 M⊕ are H–He-rich.
In the text
thumbnail Fig. 2.

M–R relation of exoplanets from the PlanetS Catalog (https://dace.unige.ch/exoplanets/). Planets that are highly irradiated by their host star (F* > 2 × 108 erg s−1 cm2) are shown in gray as their radii are inflated. Top: planets shown with the M–R relation fit from Chen & Kipping (2017) and the associated uncertainly in the M–R relation slope. The change in the M–R relation is found to occur at a mass of ∼120 M⊕. Bottom: planets shown with composition curves of H–He in a proto-solar ratio (black) and water (blue) assuming an effective temperature of 1500 K. It is clear that planets around or below Saturn’s mass are much more compact than planets with a composition that is dominated by H–He.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.