| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424375 | |
| Published online | 27 May 2015 | |
Understanding star formation in molecular clouds
II. Signatures of gravitational collapse of IRDCs⋆
1
Université Bordeaux, LAB, UMR 5804, 33270
Floirac, France
e-mail:
nschneid@cea.fr
2
CNRS, LAB, UMR 5804, 33270
Floirac,
France
3
Max-Planck Institut für Radioastronomie,
Auf dem Hügel, 53121
Bonn,
Germany
4
Zentrum für Astronomie der Universität Heidelberg,
Inst. für Theor. Astrophysik, Albert-Ueberle Str.
2, 69120
Heidelberg,
Germany
5
Department of Astronomy and Astrophysics, University of
California, Santa
Cruz, CA
95064,
USA
6
Kavli Institute for Particle Astrophysics and Cosmology, Stanford
University, SLAC National Accelerator Laboratory, Menlo Park, CA
94025,
USA
7
Astrophysics Group, University of Exeter,
EX4 4 QL Exeter, UK
8
Maison de la Simulation, CEA-CNRS-INRIA-UPS-UVSQ, USR 3441, CEA
Saclay, 91191
Gif-sur-Yvette,
France
9
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Straße 77,
50937
Köln,
Germany
10
School of Physics and Astronomy, Cardiff University, Queens
Buildings, Cardiff
CF24 3AA, UK17
11 Monash Centre for Astrophysics, School of Mathematical
Sciences, Monash University, VIC 3800, Australia
12
Research School of Astronomy&Astrophysics, The Australian
National University, Canberra, ACT
2611,
Australia
Received: 11 June 2014
Accepted: 11 March 2015
We analyse column density and temperature maps derived from Herschel dust continuum observations of a sample of prominent, massive infrared dark clouds (IRDCs) i.e. G11.11-0.12, G18.82-0.28, G28.37+0.07, and G28.53-0.25. We disentangle the velocity structure of the clouds using 13CO 1→0 and 12CO 3→2 data, showing that these IRDCs are the densest regions in massive giant molecular clouds (GMCs) and not isolated features. The probability distribution function (PDF) of column densities for all clouds have a power-law distribution over all (high) column densities, regardless of the evolutionary stage of the cloud: G11.11-0.12, G18.82-0.28, and G28.37+0.07 contain (proto)-stars, while G28.53-0.25 shows no signs of star formation. This is in contrast to the purely log-normal PDFs reported for near and/or mid-IR extinction maps. We only find a log-normal distribution for lower column densities, if we perform PDFs of the column density maps of the whole GMC in which the IRDCs are embedded. By comparing the PDF slope and the radial column density profile of three of our clouds, we attribute the power law to the effect of large-scale gravitational collapse and to local free-fall collapse of pre- and protostellar cores for the highest column densities. A significant impact on the cloud properties from radiative feedback is unlikely because the clouds are mostly devoid of star formation. Independent from the PDF analysis, we find infall signatures in the spectral profiles of 12CO for G28.37+0.07 and G11.11-0.12, supporting the scenario of gravitational collapse. Our results are in line with earlier interpretations that see massive IRDCs as the densest regions within GMCs, which may be the progenitors of massive stars or clusters. At least some of the IRDCs are probably the same features as ridges (high column density regions with N> 1023 cm-2 over small areas), which were defined for nearby IR-bright GMCs. Because IRDCs are only confined to the densest (gravity dominated) cloud regions, the PDF constructed from this kind of a clipped image does not represent the (turbulence dominated) low column density regime of the cloud.
Key words: ISM: clouds / dust, extinction
The column density maps (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A29
© ESO, 2015
1. Introduction
Infrared dark clouds (IRDCs) were detected as dark, cold (<25 K) absorption features with high column density (N> 1022−1023 cm-2; e.g. Carey et al. 1998; Peretto & Fuller 2010) against the Galactic background at mid-IR wavelengths (Egan et al. 1998). Simon et al. (2006a), Teyssier et al. (2002), and Kainulainen et al. (2011a) showed that some IRDCs are embedded in giant molecular clouds (GMCs), and thus are not isolated features as originally suggested by Egan et al. (1998). Peretto & Fuller (2010) demonstrated on the basis of a large sample (>10 000 clouds) that IRDCs span a large range of mass and size, with and without star formation activity. The most massive and largest IRDCs are proposed to represent the earliest stage of massive star formation (e.g. Rathborne et al. 2006; Nguyen-Luong et al. 2011; Beuther et al. 2013) because they are thought to have not yet started to form stars or are at the verge of star formation. On the other hand, an increasing number of studies (e.g. Carey et al. 2000; Rathborne et al. 2011; Sakai et al. 2013) now reveal that many of the massive IRDCs show signatures of active and ongoing (massive) star formation such as hot core and outflow emission and IR hot spots.
Coordinates, distance D, and physical parameters of IRDCs, obtained from Herschel far-IR data, CO data, and near-IR/mid-IR extinction.
How do these observations fit together? Are IRDCs a special category of molecular clouds/clumps that are dominated by turbulence during their earliest stages of evolution? Or are they only the densest condensations in massive star-forming clouds and then dominated by gravity as IR-bright clouds? To address these questions, it is crucial to start with studying the gas reservoir of IRDCs, i.e. the column density structure as the most convenient observable. In particular the probability distribution function (PDF) of column density serves as a key property in characterising various physical processes that shape the structure of molecular clouds (see e.g. Federrath & Klessen 2013, and references therein). Observational studies, based on near-IR extinction or Herschel dust column density maps, showed that the PDF of star-forming clouds has a log-normal distribution for low column densities and a power-law tail for higher column densities, where the power-law tail is either interpreted as due to external pressure (Kainulainen et al. 2011b), self-gravity (Froebrich & Rowles 2010; Schneider et al. 2013, 2015), or a combination of both (Tremblin et al. 2014). Numerical simulations (e.g. Padoan et al. 1997; Kritsuk et al. 2007; Federrath et al. 2008a) have shown that supersonic turbulence in isothermal gas (without self-gravity) can reproduce a log-normal distribution. When self-gravity is switched on in the models, a power-law tail develops on the end of the PDF with high column density (Klessen 2000; Vazquez-Semadeni et al. 2008; Kritsuk et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014). The only PDFs reported for IRDCs were either constructed from ALMA dust continuum (G0.253+0.016, Rathborne et al. 2014) or from extinction maps obtained from near- and mid-IR data (Kainulainen & Tan 2013; and Butler et al. 2014, called KT and BTK in the following). The latter are best fitted by log-normal distributions.
In this paper we investigate a sample of four well-known IRDCs from the catalogue of Simon et al. (2006b). The IRDC G11.11-0.12 (the “snake”) lies at a distance of 3.6 kpc and has a linear extent of ~30 pc. G18.82-0.28, G28.37+0.07, and G28.53-0.25 are smaller (size of a few pc) and further away (Table 1), and were studied by KT and BTK, who named them Cloud A, C, and D, respectively. The objective of this paper is to show that these IRDCs, which are amongst the most massive in the Galaxy, are dominated by gravity and show the same properties (e.g. average column density, PDF shape, spectral line profiles) as the central cloud regions, called ridges (Schneider et al. 2010; Hill et al. 2011; Hennemann et al. 2012), in IR-bright GMCs.
 |
Fig. 1 Top: Spitzer 8 μm (~2.5′′ resolution) and PACS 70 μm maps (~11′′ resolution). The Spitzer/IRAC data were taken from the public available GLIMPSE archive. Bottom: SPIRE 500 μm map (36′′ resolution) and ATLASGAL 870 μm maps (23′′ resolution) of G28.37+0.07. The central dark feature in the Spitzer and PACS images is the IRDC, appearing bright at longer wavelengths (SPIRE and ATLASGAL). |
2. Observations and data analysis
Column density maps from Herschel
We use Herschel1 (Pilbratt et al. 2010) archive data from the Herschel Infrared GALactic plane survey (Hi-GAL), Molinari et al. 2010) program. The PACS (Poglitsch et al. 2010) data were reduced using scanamorphos v23 (Roussel 2013). The SPIRE (Griffin et al. 2010) data were reduced employing the HIPE10 pipeline and not the ROMAGAL software (Traficante et al. 2011) that was developed for the Hi-Gal project. We preferred to use the Herschel interactive processing environment (HIPE; Ott et al. 2011) because it is the officially developed and well-documented data reduction software for the Herschel satellite. The column density and temperature maps are determined from a pixel-to-pixel grey-body fit to the 160 μm (PACS), and 250, 350, 500 μm (SPIRE) wavelengths. These maps have an angular resolution of ~36′′, corresponding to the nominal Gaussian full width at half maximum (FWHM) value of 36.4′′ for the 500 μm map given in the SPIRE Handbook (v2.5, 2014). To perform the spectral energy distribution (SED) fit, all lower wavelengths maps with high angular resolution were smoothed to 36′′. All Herschel maps have an absolute flux calibration, using Planck-corrections from the zeropointcorrection task in HIPE10 for SPIRE and IRAS maps for PACS. For the SED fit, we fix the specific dust opacity per unit mass (dust+gas) approximated by the power law κν = 0.1 (ν/ 1000 GHz)β cm2/g and β = 2, and leave the dust temperature and column density as free parameters (see Schneider et al. 2015, for further details). We estimate the final uncertainties in the column density maps to be around ~30−50%, mainly arising from the uncertainty in the assumed form of the opacity law and possible temperature gradients along the line-of-sight (Russeil et al. 2013; Roy et al. 2013).
Molecular
line data:
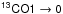 and
and
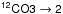
Data cubes of 13CO 1→0 (110.2 GHz) emission were taken from the Galactic Ring Survey archive (GRS), a survey covering the first Galactic quadrant (Jackson et al. 2006), obtained with the Five Colleges Radio Astronomy Observatory (FCRAO). The angular resolution is ~45′′ at a velocity resolution of 0.21 km s-1. We obtained 12CO 3→2 (345.8 GHz) data (angular resolution of 14′′ and velocity resolution of 1 km s-1) from the JCMT/COHRS archive (Dempsey et al. 2013). Both CO data sets are given on a main beam brightness temperature scale.
 |
Fig. 2 Left: H2-column density map from an SED fit to Herschel fluxes at 160−500 μm. The black contours indicate the levels Ndust = 4 to 7 × 1022 cm-2 in steps of 1022 cm-2, the white-dashed contour outlines the approximate completeness level (~3 × 1022 cm-2), and the white ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: temperature map of G28.37+0.07. |
 |
Fig. 3 Left: line integrated 13CO 1→0 emission in colour scale between v = 72 and 84 km s-1, the velocity range of the bulk emission of the IRDC, and the associated GMC. The white contour indicates the 3.5 K kms-1 level, corresponding to Av = 2, which defines the extent of the GMC and was used for mass estimation. The Herschel column density is overlaid as black contours (levels 2 to 6 × 1022 cm-2 in steps of 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). Right: H2-column density map of the centre region of the GMC, obtained from 13CO 1→0. The white-dashed contour indicates a column density of 1.25 × 1022 cm-2, the remaining black contours the levels 1.5, 1.75, and 2 × 1022 cm-2. |
ATLASGAL
The ATLASGAL survey (Schuller et al. 2009) imaged 420 deg2 of the Galactic plane (l = ± 60°, b = ± 1.5°) at a 19.2′′ spatial resolution at 870 μm with the LABOCA camera (Siringo et al. 2009) on the APEX Telescope. The data, together with the catalogue of compact sources, is presented in Csengeri et al. (2014). Here, we make use of the publicly available ATLASGAL data2. The sensitivity of the data is dominated by the noise level of the ATLASGAL survey, which in these regions is ~60 mJy/beam. Ground-based bolometer observations intrinsically filter emission from larger scales when removing the correlated noise during data reduction. In the original LABOCA observations the low-level emission is therefore filtered out above ~2.5′ angular scales, and only the densest regions are visible. The more extended emission has been recovered using the high sensitivity all-sky survey of the Planck/HFI instrument at 353 GHz, following the method of Weiss et al. (2001), and presented in more detail in Csengeri et al. (in prep.). As shown in the figures presenting the ATLASGAL data, the combined data set is sensitive to the cold dust at all spatial scales. For display reasons, we smoothed the data slightly to 23′′ angular resolution. We only display the maps to show the large scale distribution of dense and cold gas. We do not use the ATLASGAL data to determine the column density. This will be done in a future work in which we produce column density maps at higher angular resolution using ATLASGAL and selected Herschel bands.
3. Results and discussion
In this section we show as a representative case all continuum and molecular line data for G28.37+0.07 (Cloud C), which was studied in Simon et al. (2006b), KT, and BTK. Maps for the other three clouds are shown in Appendix A.
3.1. G28.37+0.07 with Herschel and ATLASGAL
Figure 1 displays G28.37+0.07 as an extended dark feature in the 8 μm Spitzer/IRAC3 and 70 μm PACS maps except with an emission peak at l = 28.396°, b = 0.081°. The cloud is overall bright at 500 μm and 870 μm, but also at 8 μm (Carey et al. 2000, BTK). It corresponds to an IRAS source (IRAS 18402-403), and contains massive protostellar cores (Zhang et al. 2009), and is thus most likely a protocluster. Because this peak is also prominent at longer wavelengths, the protocluster is still embedded in a dense, cold, molecular envelope. In particular, the 500 and 870 μm maps, tracing the large-scale distribution of cold, molecular gas, show that the IRDC is not an isolated feature. This also becomes obvious in the column density and temperature maps (Fig. 2), where this central region is outlined by low temperatures of approximately 16 to 19 K, except for the locally heated protostellar environment, and column densities of 6 × 1022 cm-2 to a few 1023 cm-2. Comparing our column density maps with those of KT and BTK shows that the highest column densities above a column density of few 1023 cm-2 (BTK give a threshold of Av ~ 200) are missing in the BTK studies because (i) there is extinction saturation i.e. mid-IR foreground emission is as bright as the emission towards the cloud; and (ii) it is a bright 8 μm region: the densest part of G28.37+0.07 is emitting strongly at 8 μm, so it does not appear as an extinction feature. Therefore recovering the column density structure from an extinction map at these positions is impossible (Peretto & Fuller 2010).
3.2. G28.37+0.07 in 13CO 1–0 emission
3.2.1. The IRDC as part of a GMC
To identify the exact velocity range of G28.37+0.07, we followed the method outlined in Simon et al. (2006b) using the GRS 13CO 1→0 data to establish a morphological match between the Herschel column density map and 13CO emission. Simon et al. (2006b) already listed this source with a velocity (vlsr) of 78.6 km s-1 and a velocity dispersion of 8.3 km s-1. Figure 3 (left) shows the large-scale velocity integrated (72 to 84 km s-1) 13CO map with the dust column density overlaid as contours. We define the “border” of the GMC by the Av = 2 level (see Sect. 3.2.2). The right panel of Fig. 3 shows a zoom into one of the cloud peak emission regions that include the IRDC. This map is given in H2-column density, determined from the 13CO 1→0 map, and can be compared to the Herschel H2-map calculated from dust emission (Fig. 2).
The overall correspondence on the GMC scale between 13CO and dust emission is good. The two most prominent peaks in 13CO emission correlate well with contours of dust column density, indicating that most of the dust seen with Herschel indeed comes from gas of the molecular cloud at that velocity range i.e. the bulk emission of the cloud. All 13CO emission outside this velocity range is due to diffuse emission and/or clouds along the line-of-sight. We estimate this contribution to sum up to a column density of ~7 × 1021 cm-2 (Sect. 3.2.3). On the IRDC scale, a one-to-one correspondence between H2 from 13CO and dust is not expected because 13CO can become optically thick and no longer traces the coldest and highest density regions. However, the maps agree well and the prominent peak, which is also seen at 500 and 870 μm emission and column density (Fig. 1), shows up as a peak in 13CO (and H2) in Fig. 3. This correlation, and the fact that this peak has the same velocity as seen in N2H+ 1→0 (Tackenberg et al. 2014), provides evidence that this high column density clump is clearly an intrinsic part of the IRDC.
A more quantitative comparison between the H2-maps from 13CO and dust shows that both maps display a gradient of decreasing columm density, down to Av ~ 15 for the map obtained from 13CO and Av ~ 30 for the Herschel map. Considering a line-of-sight confusion for the Herschel map of around Av = 7 (Sect. 3.2.3), and the large uncertainties for both methods in determining H2 column density maps, the agreement is rather good. However, this finding is in contrast with the extinction map of BTK, which shows a much steeper gradient in extinction going down to values of Av = 3. In our map (H2 from 13CO), this low value is only found at the borders of the whole GMC.
In summary, we have shown, using the 13CO map, that G28.37+0.07 is a part of a much larger molecular cloud complex. It constitutes the cloud centre region with highest (column) densities. We obtain the same results for the other clouds in this study. Appendix A shows a 12CO 3→2 map of G11.11-0.12 and 13CO 1→0 maps of G18.82-00.28 and G28.53-00.25. Because of the spatial limit of the COHRS 12CO survey, the GMC associated with G11.11-0.12 (Fig. A.2) is not fully covered towards lower galactic latitudes. However, G11.11-0.12 is clearly not an isolated feature but forms a dense region within this GMC that has a mass of at least 0.5 × 105M⊙ (Table 1). The IRDCs G18.82-00.28 and G28.53-00.25 (Figs. A.4 and A.6) are part of more massive clouds (~1.5 × 105M⊙) that were fully included in the GRS 13CO survey. Our results are thus in line with earlier findings (e.g. Carey et al. 2000; Simon et al. 2006a; Teyssier et al. 2002), which see many IRDCs as an intrinsic part of a larger molecular cloud.
3.2.2. Mass determination and link to IR-bright GMCs
For the mass determination from 13CO, we define the extent of the GMC above an Av level of 2 mag. This threshold is commonly used (e.g. Lada et al. 2010; Heiderman et al. 2010). To be consistent with Simon et al. (2001, 2006a), we employ an N(H2)/N(13CO) conversion factor of 4.92 × 105 (see Simon et al. 2001 for further details). For the excitation temperature, we take a value of 15 K. This is a compromise between the average dust temperature of 21 K, determined from the map shown in Fig. 2, and the excitation temperature obtained from the 12CO 3→2 data4. From 12CO, we derive Tex = 11 (16, 22) K for an observed main beam temperature of Tmb = 4 (6, 8) K (see Fig. 8). The dust temperature is most likely overestimated by a few degrees (Peretto et al. 2013), and it is not clear how well the dust is mixed with the gas. Taking Tex = 15 K seem to be reasonable choice and leads to a value of ~3.5 K kms-1 for the line integrated 13CO emission for Av = 2. The total mass of the GMC above this level (indicated by a white contour in Fig. 3) is then 9.0 × 106M⊙, and the equivalent radius ~40 pc.
The IRDC G28.37+0.07 occupies only a small spatial fraction within the GMC. From the 13CO measurements, we are consistent with Simon et al. (2006a) and find a peak H2 column density of 16(21) × 1021 cm-2 for Tex = 15(20) K, and a mass of 6.3 × 104M⊙. From the dust continuum, we obtain higher values of average and peak column density i.e. ⟨ Ndust ⟩ ~ 4 × 1022 cm-2 and Npeak ~ 3 × 1023 cm-2, respectively, and a high surface density (Σdust ~ 740M⊙ pc-2). The surface density (Σdust = Mdust/A) refers to the area A within the ellipse defining the IRDC.
The values of column densities and surface densities for the other IRDCs of our sample are also high i.e. ⟨ Ndust ⟩ ~ 2.5 × 1022 cm-2 and Σdust> 400M⊙ pc-2. These massive IRDCs may thus correspond to ridges that were defined as the central regions within a GMC with column densities above ~1022−23 cm-2 at temperatures below 20 K for the IR-bright cloud Vela C (Hill et al. 2011) and the DR21 ridge5 (Schneider et al. 2010; Hennemann et al. 2012).
 |
Fig. 4 PDFs of G28.37+0.07 and its associated GMC, derived from the Herschel column density map. The upper panel shows the PDF of the IRDC, only from the pixels inside the ellipse shown in Fig. 2. The lower panel shows the PDF obtained for the whole GMC (all pixels inside the contour indicated in Fig. 3, right). The error bars were calculated using Poisson statistics. The left y-axis gives the normalised probability p(η) and the right y-axis indicates the number of pixels per log bin. The upper x-axis is the visual extinction and the lower x-axis is the logarithm of the normalised column density. The green curve shows a log-normal fit to the PDF from the GMC. The red line indicates a power-law fit to the high column density tail with the slope s together with its error and the reduced X2 goodness-of-fit. The exponent α of an equivalent spherical density distribution ρ(r) ∝ r− α is also indicated in the panel. The dashed line in the upper panel indicates the completeness level; the PDF left of this line is incomplete. |
3.2.3. Line-of-sight confusion towards G28.37+0.07
We estimate the 13CO emission along the line-of-sight to assess how much of H2 column density may arise from clouds and diffuse emission not related to our target cloud. The average H2-column density, using the same conversion factor N(H2)/N(13CO) of 4.92 × 105 as for the determination of the masses of the GMC, in the velocity ranges outside the bulk emission of the IRDC and within the ellipse is ⟨ Ncont ⟩ = 7 × 1021 cm-2. The H2 column density ⟨ Ndust ⟩ determined from the Herschel map is ~40 × 1021 cm-2 and that from 13CO is ⟨ Nbulk ⟩ ~ 16 × 1021 cm-2. However, if 13CO becomes optically thick and/or freezes out in the highest density regions, it underestimates the H2 column density. On the other hand, the Herschel column density map is affected by line-of-sight contamination and thus overestimates the H2 column density. Considering these effects and the uncertainties of the methods, a factor of 2 disagreement between the column density determined from CO and dust is acceptable.
4. Probability distribution functions of IRDCs
4.1. Do IRDCs have a log-normal or power-law PDF?
4.1.1. PDFs from dust continuum
The PDFs6 of dust column density for the IRDC G28.37+0.07 and its associated GMC are shown in Fig. 4, those for G11.11-0.12, G18.82-0.28, and G28.53-0.25 are listed in Appendix B. To be consistent with other studies, we express the PDF in visual extinction Av using the conversion N(H2) /Av = 0.94 × 1021 cm-2 mag-1 (Bohlin et al. 1978).
All PDFs are sampled with a bin size of 0.15 (in η) using maps of a grid of 14′′. In Schneider et al. (2015), we investigated the effect of different bin sizes on the PDF and found that the PDF properties, and in particular the slope, do not change significantly using different bins. As shown in their Fig. A.1, the best compromise between high sampling and resolution lies for bin sizes of 0.1 to 0.2. We thus decided to adopt a bin size of 0.15. The PDFs are constructed from pixels above the approximate completeness limit within the ellipses defining the IRDC. This level was obtained from the column density maps (e.g., Fig. 2) where we determined the lowest contour level (indicated by a white dashed line) that is still continuous. That implies that above this contour, the majority of pixels is still found within the ellipse defining the IRDC, and below this contour, the map is incomplete. Accordingly, for lower column densities, the pixel distribution is also not complete and can create an artificial fall-off of the PDF, which should not be confused with a log-normal PDF. The PDF of the IRDC alone obtained in this way, as well as the PDFs for the other IRDC clouds (see Fig. B.1), is consistent with a pure power-law distribution. In contrast, the PDF of the whole GMC (Fig. 4, bottom) in which the IRDC is embedded indeed shows a log-normal part plus a power-law tail, similar to what was found for star-forming clouds (e.g. Kainulainen et al. 2011b; Schneider et al. 2013).
To exclude a possible log-normal distribution for our observed PDF of the IRDC, we performed a two-sample Kolmogorow-Smirnov (KS)-test, comparing our distribution with a set of pure log-normal distributions with different widths (σ = 0.2 to 1.7) and normalisations (see Appendix C for details). The probabilities p in all cases of broad PDFs are very low so we exclude the possibility that our observed PDF is purely log-normal. We also made a KS-test using our PDF of the IRDC (Fig. 4, top), but including the data points left of the completeness level and ignoring the data points above Av ~ 100. The two-sample KS-test with the synthetic PDFs also shows small values for p (see Table C.1). The p-value for a PDF with σ = 1.7 (fitted by BTK) is 2.2 × 10-6 (or 4.7 × 10-4, depending on normalisation). The best-fitting log-normal has a width of σ = 0.4 (p-value = 0.25 (0.28)), which implies that the best-fit might be consistent at the 2-sigma level. However, the PDF is too narrow to be consistent with what was found in BTK.
We performed a linear regression fitting to the power-law part of the PDF. The starting point was chosen as the break point of the PDF between log-normal and power-law seen in the PDF of the GMC. For example, for G28.37+0.07 (Fig. 4), the break occurs at Av ~ 40 and we thus started the fitting for the IRDC at this value. The reduced χ2 values of the power-law fits scatter, but are all above one and thus indicate that the general assumption of a power-law dependence is justified.
In Appendix B, we show the PDFs of the other IRDCs (alone and including the embedding GMC). The result is the same as for G28.37+0.07 i.e. a log-normal plus power-law tail for the GMC and a power-law distribution for the IRDC. For G28.53-0.25, there is an indication for a log-normal distribution below Av ~ 30. However, the PDFs of the GMC are less reliable because effects of line-of-sight contamination become more important and can lead to a change in slope for the power-law tail (Schneider et al. 2015).
 |
Fig. 5 PDFs of the whole GMC including G28.37+0.07, obtained from H2 column density maps derived from 13CO emission. The blue PDF contains all emission along the line-of-sight (LOS) towards the GMC (v = 0 to 132 km s-1); the red PDF contains only emission coming from the bulk emission of the cloud (v = 72 to 84 km s-1). The long dashed line is the Av = 2 level outlining the GMC. |
4.1.2. Probability distribution functions from  CO
CO
Figure 5 shows PDFs obtained from the 13CO data. The red PDF is constructed from the map displayed in Fig. 3 and contains only emission from the GMC in the velocity range 72 to 84 km s-1. The PDF is similar to a log-normal but because it is cut-off at higher column densities (around Av = 10) most likely because of an increasing optical depth, we refrain from trying to fit the data. In addition, the highest column density range can not be traced by the 13CO line because its critical density is below the densities of the clumps or cores (around 104−6 cm-3) that populate the high Av-range. The blue PDF includes all emission along the line-of sight towards the GMC between velocities of 0 to 132 km s-1. This PDF is shifted by Av ~ 8−10 towards higher column density values compared to the red PDF. Though the 13CO line still saturates in each individual cloud along the sightline above Av ~ 10, the total H2-PDF can still go up to higher values. These findings confirm our direct calculation of the contaminating column density (Sect. 3.2.3). The blue PDF corresponds very well over the whole Av-range (10–40) with the PDF obtained from the dust column density (Fig. 4), indicating that the conversions H2 from 13CO and H2 from dust are rather consistent.
 |
Fig. 6 Top: H2 column density from dust continuum with the white contour, roughly outlining the GMC in which G28.37+0.07 is embedded. Bottom: PDFs of the GMC, derived from the dust column density map from the left above different Av-thresholds (indicated with different colours and given in the panel). |
5. Clipping effects and completeness level
Comparing the PDFs shown in Fig. 4 reveals that the PDF constructed only from the pixels defining the IRDC has no log-normal part in contrast to that obtained for the whole GMC. The reason is that the PDF of the IRDC alone is not sampled down to the lowest Av-ranges and a PDF from an image where the low column density pixels are ignored is just composed of a power-law distribution (Schneider et al. 2015).
To illustrate this cropping effect, we made PDFs from pixels above different Av-thresholds for the whole GMC (Fig. 3) using the Herschel dust column density map (see right panel of Fig. 3). Figure 6 shows how the PDF changes from a distribution that can be described by a log-normal plus power-law distribution (for pixels above Av = 12) into a purely power-law distribution (for pixels above Av = 20). Note that the curves “shift” due to different normalisations (the area/number of pixels decreases with increasing Av-level). We emphasise that the contour outlining the GMC still comprises higher column density gas (Av> 10), which is well above the threshold of typically Av = 1 or 2 (e.g. Lada et al. 2010) that is commonly used to “define” the extent of a molecular cloud. The dust continuum map, however, suffers from line-of-sight contamination on a high level of at least Av ~ 7−10 because (i) this is the value at the map borders outside of the GMC (Fig. 6); and (ii) it also corresponds to the H2 column density derived from 13CO adding all emission outside of the bulk emission of the GMC (Sect. 3.2).
In any case, the main point of this excercise is to demonstrate that the PDF of the IRDC (Fig. 4, top) can be fitted by a pure power law7 above Av-values of ~30. This PDF can be directly compared to that shown in BTK (their Fig. 3, left panel), which shows a broad PDF fitted by a log-normal distribution with a width of σ = 1.7. The two PDFs differ in the lowest and highest column density ranges. The authors BTK state a completeness limit of Av = 3, implying that their extinction map of the IRDC goes down to that value at the borders8. As outlined in Sect. 3.2, we show that the IRDC is the centre region of a GMC and the column density values remain high (at least on a level of Av ~ 10 to 20) at the borders. Though the higher angular resolution extinction map may resolve smaller spatial structures in which high and low column density regions are mixed, the border regions look homogeneous at a low Av value. In addition, the highest column density pixels (above Av ~ 100−200) are missing in BTK because they were masked out. However, if we compare only the Av range between ~30 to ~100 (which we find to be the column density range of the IRDC), the PDF of BTK could be well fit by a power-law distribution and our results would be consistent.
6. Global and local gravitational collapse of IRDCs
The power-law distribution we find for all PDFs of the IRDCs in our sample is in accordance with the power-law tails found for IR-bright clouds (Lombardi et al. 2008; Kainulainen et al. 2009; Hill et al. 2011; Schneider et al. 2012, 2013, 2015; Russeil et al. 2013; Tremblin et al. 2014; Alves de Oliveira et al. 2014). In these studies, a clear turnover from a log-normal distribution for low column densities (typically from Av< 1 up to Av of a few magnitudes) into a power-law tail was observed. Self-gravity as the dominating (over pressure and magnetic fields) process to form this power-law tail was advocated by numerical models (Klessen 2000; Federrath et al. 2008b; Kritsuk et al. 2011) and observationally supported by Froebrich & Rowles (2010) and Schneider et al. (2013). Recently, Rathborne et al. (2014) obtained a PDF from ALMA continuum data for the IRDC G0.253+0.016 in the central molecular zone (CMZ), which has a log-normal shape and some excess at highest column densities they attribute to self-gravity within the most massive cores. In the following, we will present additional evidence from radial column density profiles and molecular line observations that massive IRDCs can be in gravitational collapse, which is reflected in the power-law distribution of the column density.
6.1. The link between the PDF power-law tail and the column density profile
Provided that the power-law distribution of the PDF is only due to gravity, and if we assume spherical symmetry, the power-law slope s of the PDF is related to the exponent α of a radial density profile according to ρ(r) ∝ r− α and α = −2 /s + 1 (Federrath & Klessen 2013). For the PDFs of the IRDCs in our sample (Figs. 4 and B.1), we obtain values between ~1.5 and 2 for α 9. This is consistent with a structure dominated by self-gravity, i.e. local free-fall of individual cores and clumps and global collapse (Girichidis et al. 2014; Schneider et al. 2015). The extent to which the variations in the slope can be attributed to the evolutionary state of the cloud is not clear. As was shown in simulations (Ballesteros-Paredes et al. 2011; Federrath & Klessen 2013), the power-law flattens with time/increasing star formation efficiency. In our small sample of IRDCs, however, the low value of α points towards an early state in cloud evolution.
 |
Fig. 7 Radial column density profile for G28.37+0.07, G28.53-0.25, and G18.82-0.28. Each cross in the panels represents one pixel value in the map. The x-axis gives the distance to the centre of the ellipse (x-axis). The dashed orange line indicates the Herschel beam (Gaussian profile with a FWHM of 36′′ displayed in log-log format). The exponent α was deduced from fitting the column density profile (N ∝ r1−α). For the fit, we included only the pixels that were inside a radius of 3 pc. |
To derive a PDF-independent value for the exponent α, we fitted the radial column density profiles of G28.37+0.07, G28.53-0.25, and G18.82-0.28 (Fig. 7). From our sample, only these sources can roughly be approximated as “spherical”, G11.11-0.12 is too filamentary. Assuming again spherical geometry, the column density N can be expressed as N ∝ ρ(r) × r ∝ r1−α, thus the exponents α from the PDF and the column density profile should correspond. Within the error bars, this is approximately the case (see Table 2), we obtain from the column density profile α = 1.67,1.82,1.60 for G28.37+0.07, G28.53-0.25, and G18.82-0.28, respectively, compared to α = 1.58, 1.97, 1.54, deduced from the PDF. Figure 7 displays the column density of the pixels around the maximum column density as a function of their distance to this maximum. We only fitted the points within a circle of 3 pc around the maximum column density. The values of α between 1.6 and 1.8 determined from the column density profiles are consistent with gravitational collapse on large scales. In the next section, we demonstrate that complementary molecular line data indeed point towards this kind of a scenario for our IRDCs.
Exponents α and their errors Δα, assuming a spherical density distribution ρ(r) ∝ r− α, derived from the slope s of the power-law distribution from the PDF (Col. 2) and from the column density profiles (Col. 3).
 |
Fig. 8 Middle panel: line integrated 12CO 3→2 emission in K kms-1 on a main beam temperature scale (between 72 and 84 km s-1) of G28.37+0.07. The dust column density from Herschel is overlaid as black contours (levels 4,5,7 × 1022 cm-2). The dashed lines outline the area displayed in Fig. 9, and the numbering from 1 to 6 indicates the position of submm-continuum sources seen with ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). The 12CO 3→2 (black) and 13CO 1→0 (red) spectra at these positions are displayed in the panels around. Additionally, we show spectra from two positions (indicated by arrows) off the sources but still within the molecular cloud. The blue-dashed line denotes the centre velocity of the N2H+ line. |
6.2. Collapse signatures in molecular line profiles
The shape of molecular line profiles allows us to disentangle various dynamic processes, such as outflows, rotation, and infall, within a molecular cloud/clump/core. The inwards motion of gas caused by gravity in regions of star formation leads to a self-absorbed emission line profile (“double-peak” or “P-Cygni profile”) of an optically thick line. An optically thin line must then peak in the self-aborbed dip to exclude the possibility of several line components and rotation. Simple early models (see e.g. Myers et al. 1996, and references therein) are based on a gravitationally collapsing isothermal sphere and predict a “blue asymmetry” i.e. with increasing infall speed, the blue peak in the double-peak profile becomes brighter than the red peak. However, recently Smith et al. (2012, 2013) showed that collapsing embedded cores show more complex line profiles because of the contribution of the enclosing filament.
In any case, there are a number of examples where infall signatures in spectral profiles have been detected and successfully modelled, mostly for isolated low-mass cores (e.g. Walker et al. 1994; Tafalla et al. 2002) and high-mass cores (e.g. Csengeri et al. 2011). Gravitational collapse of a whole filament on a scale of a few pc was seen for the DR21 ridge (Schneider et al. 2010) and Serpens-South (Kirk et al. 2013). Global collapse of IRDCs was suggested for SDC335 (Peretto et al. 2013), G79.3+0.3 (Carey et al. 2000), and G32.03+0.05 (Battersby et al., priv. comm.).
 |
Fig. 9 Main beam brightness temperature spectra of 12CO 3 → 2 (black) and 13CO 1→0 (red) emission in the velocity range 55 to 95 km s-1 and temperature range −0.2 to 12 K. The area corresponds to the centre region of the IRDC G28.37+0.07, outlined in Fig. 8. The dust column density from Herschel is overlaid as blue contours (levels 4,5,7,10,16 × 1022 cm-2), and the numbering from 1 to 6 indicates the position of submm-continuum sources labelled using ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). |
For the IRDCs in our sample, we use the 12CO 3→2 line from the COHRS archive as an optically thick tracer, and 13CO 1→0 from the GRS as the optically thin line. For better comparison, we smoothed the 12CO data to the resolution of the 13CO data (45′′). Both CO data sets are only available for G28.37+0.07. For this source, we show in Fig. 8 the velocity integrated 12CO map and spectra from selected positions, i.e. the strongest submm-continuum sources from ATLASGAL (Contreras et al. 2013; Csengeri et al. 2014) and two positions off-source but within the cloud. The continuum sources were also observed in the optically thin N2H+ 1→0 line at 93.173 GHz with a velocity resolution of 0.2 km s-1 (Tackenberg et al. 2014), and the centre velocities reported in their Table 3 are indicated as a dashed blue line in Fig. 8. The same velocity of sources 2 and 6 are also derived by Shipman et al. (2014) based on pointed observations of optically thin lines, such as N2H+ and C17O, using Herschel and APEX.
The 13CO 1→0 line consists of several components, but there is no “double-peak” feature and the centre velocity of the main Gaussian corresponds very well to the velocities determined with N2H+, so that 13CO emission is optically thin or only moderately optically thick. Most importantly, the main 13CO line peaks in the gap of a double-peaked 12CO line, best visible for sources 1 and 4. This sort of 12CO profile seen for basically all spectra in the figure shows the classical infall signature profile with a brighter blue peak than the red peak. The optically thin 13CO line is blue shifted with respect to the self-absorption gap, clearly visible for positions 1 and 6 and those off the sources (offsets −720′′, 220′′ and −1000′′, 220′′), but less clearly for the remaining positions. Source 2 (most likely a protocluster, see Sect. 3.1) is more complex with several line components, associated with CH3OH and H2O masers (Pillai et al. 2006; Wang et al. 2008, 2014) and harbours a hot-core (Zhang et al. 2009). Some sources, in particular source 1 for velocities lower than ~70 km s-1, show broad wings that possibly indicate outflow emission from the protostellar object. This becomes more evident when the on-source 12CO spectra are compared to two spectra (indicated by offset –720′′, 220′′ and –1000′′, 220′′ in Fig. 8) that are located off source but still within the IRDC. These also show the self-absorption dip but no prominent wings. Though it is out of our scope to go into more detail for outflows, it is important to recognise those as indicators for star formation.
Though 12CO is not the best tracer for infall signatures, HCO+ or HCN are better suited because they show a clearer profile (Schneider et al. 2010), the general behaviour is the same. Since we can rather safely exclude the possibility that the double-peak profile of 12CO is due to several line components using the 13CO spectra and the N2H+ velocity information, the most likely explanation is that we observe inwards motion of gas.
There are several arguments as to why we think that the 12CO profile is not simply caused by a low-density, subthermally excited foreground cloud. First, we would not observe the blue asymmetry profile systematically, but the two apparant peaks of the 12CO line would be equally strong across the map. Outflows and rotation would also give rise to both a red and a blue asymmetric line. Second, the 13CO line may become optically thick at the positions with highest (column) density and should then also show self-absorption features (which is not the case). Third, the Herschel column density maps indicate that the IRDCs are cold, with an increase in excitation temperature into the cloud at least at the positions of protostellar sources. This contrasts with the requirement of a colder outer layer causing self-absorption.
Local infall on the pre-and protostellar sources is seen in H2O observations (Shipman et al. 2014) of source 2 and source 6 (labelled G28-MM and G28-NH3 in Shipman et al. 2014), where the water line appears in absorption and is systematically redshifted relative to the systemic velocity of the clump. However, comparing 12CO and 13CO spectra across the whole IRDC (the two off-source spectra in Figs. 8 and 9) shows that the double-peak profiles extend well beyond the source positions and are found basically everywhere inside the blue contours, outlining the IRDC. We thus propose that the whole IRDC is in global collapse.
In Appendix D, we show that infall 12CO profiles are also observed for G11.11-0.12. Because we have no complementary 13CO data, the global collapse scenario there is more tentative. However, single pointings in H2O in G11.11.-0.12 (Shipman et al. 2014) already show infall signatures similar to G28.37+0.07, so that we conclude that global collapse could probably be a feature shared by all massive IRDCs that are embedded in GMCs. Higher angular resolution molecular line observations using, e.g. HCO+ or HCN and the optically thin isotopologues H13CO+ or H13CN as line tracers, are required to investigate this scenario in more detail.
7. Summary and conclusions
Our study using Herschel, ATLASGAL, and 12CO and 13CO molecular data shows that massive IRDCs are embedded in more extended molecular clouds and have similar physical properties (peak and average column density, surface density) as ridges, i.e., the densest, central regions of GMCs. The PDFs for all four IRDCs obtained from Herschel dust column density maps show a power-law distribution, which we interpret as arising from gravitational contraction. There is no log-normal part in the PDF because the PDF is constructed from a cropped image, focussing on the densest region within the GMC. On the other hand, the PDF of the associated GMC shows a log-normal form for lower column densities and a power law for high densities.
We give two additional and independent arguments for the dominance of self-gravity for the IRDCs we present. First, fitting the radial column density profiles leads to similar exponents α = 1.70 ± 0.07 as derived from the slope of the PDF power-law distribution (α = 1.66 ± 0.18), and is consistent with self-gravity (α = 1.5 to 2 assuming a spherical density distribution). Second, molecular line profiles of the optically thick 12CO 3 → 2 line show self-absorption at the velocity of the bulk emission of the cloud, indicating locally infalling gas on proto- and prestellar cores and on the global IRDC scale.
The self-gravitating scenario on all scales is consistent with what is found in numerical models. Just to list a few, Ballesteros-Paredes et al. (2011), Kritsuk et al. (2011), Federrath & Klessen (2013), Girichidis et al. (2014), Ward et al. (2014) obtain a log-normal+power-law tail PDF (density or column density) for their simulations including self-gravity and turbulence, but without external pressure (such as radiative feedback). First, turbulence creates a self-similar structure of the gas that is well represented by a purely log-normal PDF. As soon as self-gravity is switched on and collapse proceeds for some time, the hierarchical structure in clouds is affected and the (column) density PDF departs from a log-normal and forms a power-law tail. Studies focussing on the spatial cloud structure, using power spectra or the Δ-variance (see Schneider et al. 2011, and references therein) also show that molecular clouds lose their hierarchical structure and show characteristic scales as soon as star formation sets in. Federrath & Klessen (2013, Fig. 4) link the change of the slope of the PDF to the star formation efficiency (SFE). Their simulations are consistent with our observations.
The PDFs of the IRDCs we present all show a power-law distribution with similar slopes, regardless of their evolutionary states: G18.82-0.28 and G28.37+0.07 show bright peaks at 70 μm, and in G11.11-0.12 the presence of IR-bright protostars was demonstrated (Henning et al. 2010). The IRDC G28.53-0.25 is in a very early stage because it contains no (F)IR-bright peaks. Despite its youth, this cloud shows a power-law distribution over all column densities. Given the uncertainties in the column-density PDFs, the slope differences are marginal and it is difficult to distinguish an SFE of 5% from 20% for most parameter sets of the simulations (note that the PDFs from simulations differ from those of observations, because they are averages over all three lines of sight from different directions). Given that the IRDCs of our sample are all in a collapsing state, and most of them have already started forming stars, they might well have local SFE of ~5% in agreement with the models shown in Federrath & Klessen (2013).
We define η ≡ ln(N/ ⟨ N ⟩) as the natural logarithm of the column density N, divided by the mean column density ⟨ N ⟩, and the quantity pη(η) then corresponds to the PDF of η with the normalisation 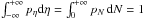 (see Schneider et al. 2015, for details).
(see Schneider et al. 2015, for details).
Note that fitting to binned data is not always statistically robust as discussed in Virkar & Clauset (2014). However, we make PDFs of η = ln(N/ ⟨ N ⟩) in linear binning with bin size dη = 0.15, while Virkar & Clauset use log-binning (of N/ ⟨ N ⟩ when applied to our case).
In Kainulainen & Tan (2013) the same map of G28.37+0.07 was produced with a slightly different method and a value of Av = 7 was given for the same completeness level, better fitting with our findings.
Note that these are lower limits for α because the power-law slope steepens because of line-of-sight contamination (Schneider et al. 2015).
Acknowledgments
We thank P. Girichidis for discussions on collapse scenarios. N.S. and S.B. acknowledge support by the ANR-11-BS56-010 “STARFICH”. N.S., V.O., and R.S.K. acknowledge funding from the DFG priority program SPP 1573 “Physics of the ISM” (project number OS177/2-1 and KL 1358/19-1). R.S.K. acknowledges subsidies from the collaborative research project SFB 881 (“The Milky Way System”, subprojects B1, B2, and B5), and support from the ERC Framework Programme FP7/2007-2013 via the ERC Advanced Grant STARLIGHT (project number 339177). R.S.K. thanks for the warm hospitality at the Department of Astronomy and Astrophysics at the University of California at Santa Cruz and the Kavli Institute for Particle Astrophysics and Cosmology at Stanford University during a sabbatical stay in 2014 and 2015. T.Cs. acknowledges financial support for the ERC Advanced Grant GLOSTAR under contract No. 247078.
References
- Alves de Oliveira, C., Schneider, N., Merin, B., et al. 2014, A&A, 568, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Gazol, A. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Linz, H., Tackenberg, J., et al. 2013, A&A, 553, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, M., Tan, J., & Kainulainen, J. 2014, ApJ, 782, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Feldman, P. A., Redman, R. O., et al. 2000, ApJ, 543, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, Y., Schuller, F., Urquhart, J. S., et al. 2013, A&A, 549, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Bontemps, S., Schneider, N., et al. 2011, A&A, 527, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dempsey, J. T., Thomas, H. S., & Currie, M. J. 2013, ApJS, 209, 13 [CrossRef] [Google Scholar]
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008a, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Glover, S., & Klessen, R. S. 2008b, Phys. Scr., 132, 014025 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., et al. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M., Abergel, A., Abreau, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Heiderman, A., Evans, N. J. E. II,Allen, L. E., et al. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Alves, J., Beuther, H., et al. 2011a, A&A, 536, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., et al. 2011b, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Myers, P. C., Bourke, T. L., et al. 2013, ApJ, 766, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., Padoan, P., & Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C., & Alves, J. 2008, A&A, 489, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marston, A. P., Reach, W. T., Noriega-Crespo, A., et al. 2004, ApJS, 154, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, P. C., Maradones, D., Tafalla, M., et al. 1996, ApJ, 465, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen-Luong, Q., Motte, F., Hennemann, M., et al. 2011, A&A, 535, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2011, ASP Conf. Ser. 442, eds. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, 347 [Google Scholar]
- Padoan, P., Jones, J. T., & Nordlund, A. A. 1997, ApJ, 474, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., & Fuller, G. 2010, ApJ, 723, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Fuller, G. A., Duarte-Cabral, A., et al. 2013, A&A, 555, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G., Riedinger, J., Passvogel, T., et al. 2010, A&A 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T,Wyrowski, F., Menten, K., et al. 2006, A&A, 447, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W., & Flannery, B. P. 1992, Numerical recipes in C. The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Garay, G., Jackson, J. M., et al. 2011, ApJ, 741, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Longmore, S., Jackson, J. M., et al. 2014, ApJ, 795, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roy, A., Martin, P., Polychroni, D., et al. 2013, ApJ, 763, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, T., Sakai, N., Foster, J. B., et al. 2013, ApJ, 775, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, Ph., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Menten, K., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shipman, R. F., van der Tak, F. F. S., Wyrowski, F., et al. 2014, A&A, 570, A51 [Google Scholar]
- Smith, R. J., Shetty, R., Stutz, A. M., & Klessen, R. S. 2012, ApJ, 750, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Shetty, R., Beuther, H., Klessen, R. S., & Bonnell, I. A. 2013, ApJ, 771, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., & Bania, T. M. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R., et al. 2006a, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Rathborne, J. M., et al. 2006b, ApJ, 639, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovacs, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strong, J., Bloemen, J., Dame, T., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
- Tackenberg, J., Beuther, H., Henning, T., et al. 2014, A&A, 565, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., et al. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, D., Hennebelle, P., & Perault, M. 2002, A&A, 624, A638 [Google Scholar]
- Traficante, A., Calzoletti, L., Veneziani, M., et al. 2011, MNRAS, 416, 2932 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazquez-Semadeni, E., Gonzales, R. F., Ballesteros-Paredes, J., et al. 2008, MNRAS, 390, 769 [NASA ADS] [Google Scholar]
- Vikar, Y., & Clauset, A. 2014, Ann. Appl. Stat., 8, 89 [CrossRef] [Google Scholar]
- Walker, C. K., Narayanan, G., & Boss, A. P. 1994, ApJ, 431, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Zhang, Q., Pillai, T., et al. 2008, ApJ, 672, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Zhang, Q., Testi, L., et al. 2014, MNRAS, 439, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Neininger, N., Hüttemeister, S., & Klein, U. 2001, A&A, 365, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Herschel maps of infrared dark clouds
In this section, we show the whole sample of far-IR-data from Herschel (70 μm and 500 μm data) and ATLASGAL (870 μm), and column density and temperature maps obtained from SED fits for the IRDCs G11.11-0.12 (“snake”), G18.82-0.28 (Cloud A), and G28.53-0.25 (Cloud D). In addition, molecular line data maps (13CO 1→0 for G18.82-0.28 and G28.53-0.25, and 12CO 3→2 for G11.11-0.12) of the associated GMC are shown.
 |
Fig. A.1 PACS 70 μm map, SPIRE 500 μm, and ATLASGAL 870 μm maps of G11.11-0.12 (the “snake”). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
 |
Fig. A.2 Left: column density map of G11.11-0.12, obtained from SED fit to Herschel 160, 250, 350, 500 μm data. The black contours indicate the levels Ndust = 2,3,5,7 × 1022 cm-2, the white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 12CO 3 → 2 emission in colour scale (in [K km s-1]) between v = 26 and 35 km s-1, the velocity range of the bulk emission of G11.11-0.12 and the associated GMC. The Herschel H2 column density is overlaid as black contours (levels 1.5,2,3,5,7 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
 |
Fig. A.3 PACS 70 μm map, SPIRE 500 μm, and ATLASGAL 870 μm maps of IRDC G18.82-0.28 (Cloud A). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
 |
Fig. A.4 Left: column density map of G18.82-0.28, obtained from SED-fit to Herschel 160, 250, 350, 500 μm data. Black contours indicate the levels Ndust = 2 to 5 × 1022 cm-2 in steps of 1022 cm-2, white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 13CO 1→0 emission in colour scale (in [K km s-1]) between v = 61 and 70 km s-1, the velocity range of the bulk emission of G18.82-0.28 and the associated GMC. Note that this GMC was already identified as a coherent cloud complex in Schuller et al. 2009. The Herschel H2 column density is overlaid as black contours (levels 1,2,3,4,5 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
 |
Fig. A.5 PACS 70 μm map (left), SPIRE 500 μm (middle) and ATLASGAL 870 μm maps of G28.53-0.25 (Cloud D). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
 |
Fig. A.6 Left: column density map of G28.53-0.25, obtained from SED fit to Herschel 160, 250, 350, 500 μm data. Black contours indicate the levels Ndust = 2.5,3,4,6 × 1022 cm-2, white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 13CO 1 → 0 emission in colour scale (in [K km s-1]) between v = 82 and 90 km s-1, the velocity range of the bulk emission of G28.53-0.25, and the associated GMC. The Herschel H2 column density is overlaid as black contours (levels 2,2.5,3,4,6 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
Appendix B: Probability distribution functions of column density for IRDCs
Probability distribution functions of column density, determined from Herschel data, for the IRDCs G11.11-0.12 (“snake”), G18.82-0.28 (Cloud A), and G28.53-0.25 (Cloud D) are shown. The assumption of a constant line-of-sight temperature for each pixel affects the accuracy of the column density maps in massive, UV-illuminated GMCs with internal embedded (proto)stars, and can lead to an underestimation of the column density map. We carefully checked each SED fit for each pixel and always found very good fitting results. In addition, the IRDC we study here are not strongly affected by radiation; G28.53-0.25 is even not correlated with any protostellar object, so we are confident in the validity of our column density maps.
 |
Fig. B.1 PDFs derived from Herschel column density maps (SED fit using only the Herschel wavelengths 160, 250, 350, and 500 μm) at 36′′ angular resolution. Left panel shows the PDFs of pixels comprising only the IRDC i.e. G18.82-0.28 (Cloud A), G28.53-0.25 (Cloud D), and G11.11-0.12. Right panel shows PDFs from associated GMC, including the IRDC. The left y-axis gives the normalised probability p(η), the right y-axis the number of pixels per log bin. The upper x-axis is the visual extinction and the lower x-axis the logarithm of the normalised column density. The dashed vertical line indicates the completeness level. The red line indicates a power-law fit to the high column density tail with the slope s together with its error and the reduced X2 goodness-of-fit. The exponent α of an equivalent spherical density distribution ρ(r) ∝ r− α is also indicated in the panel. The dashed line in the upper panel indicates the completeness level; the PDF left of this line is incomplete. |
Appendix C: KS-test
To verify if the column density distribution (PDF) we observed for G28.37+0.07 possibly arises from a log-normal distribution, we performed a two-sample KS-test. We first generated synthetic functions following a log-normal distribution ![\appendix \setcounter{section}{3} \begin{eqnarray} p_\eta\,{\rm d}\eta=\frac{1}{\sqrt{2\pi\sigma^2}}{\rm exp}\left[ -\frac{(\eta-\mu)^2}{2\sigma^2} \right]{\rm d}\eta, \end{eqnarray}](/articles/aa/full_html/2015/06/aa24375-14/aa24375-14-eq158.png) (C.1)where σ is the dispersion i.e. the width of the distribution, η the mean logarithmic column density, and μ the peak (in units of η). To have a larger parameter space to compare, we varied σ between 0.2 and 1.7 (the latter is the width stated in KT).
(C.1)where σ is the dispersion i.e. the width of the distribution, η the mean logarithmic column density, and μ the peak (in units of η). To have a larger parameter space to compare, we varied σ between 0.2 and 1.7 (the latter is the width stated in KT).
For the normalisation, we performed two approaches. First, we fixed the peak of all synthetic distributions to the observed value. The x-axis value for this peak at Av ~ 19 (μ = −0.23) was extracted from the PDF of the whole GMCs that revealed a log-normal + power-law tail distribution (Fig. 6). Because these distributions have the same peak value but not a normalisation to the same number of pixels, we also produced a second set of functions that have this kind of a normalisation (but different peaks). Both sets of resulting synthetic distributions together with our observed set are shown in Fig. C.1.
Eye inspection already shows that the observed PDF is not consistent with any log-normal distribution, in particular not with one of a large width (σ = 1.7 was found in KT). To quantify this result, we list in Table C.1 the results of the two-sample KS-test, which gives the statistic and associated probability that two data sets are drawn from the same distribution. We performed the test using the IDL-routine “ksto.pro” with the algorithm taken from procedure of the same name in “Numerical Recipes” by Press et al. (1992). The parameter D gives the maximum deviation between the cumulative distribution of the observed PDF and the assumed underlying statistic (the log-normal in our case), while p shows the significance level of the KS-statistic. Small values of p, which is the case for our test, indicate that the pairwise distributions are significantly different. The p-values below 0.3 show that we can exclude the scenario that our distribution can be fit with a log-normal distribution by more than one sigma. Note that though the pixel statstic is low and the binning is large, the general properties (width, peak, slope of power-law tail) of the PDF do not depend on binning in smaller or larger bins or varing the pixel size or resolution (Schneider et al. 2015).
 |
Fig. C.1 Synthetic distributions shown in various colours with different widths (indicated in the panel). The observed PDF for G28.37+0.07, constructed from Herschel data is indicated in bold black. Top panel shows distributions that are normalised to the peak; the bottom panel shows distributions that are normalised to the same number of pixels. |
Results of KS-test.
Appendix D: The 12CO 3→2 spectra of G11.11-0.12
Figure D.1 shows 12CO 3→2 spectra at the location of some of the continuum sources of the IRDC G11.11-0.12 (no 13CO data are available) in the velocity range where the emission is associated with the cloud. Similar as seen for G28.37+0.07, the optically thick 12CO line shows a self-absorbed dip close
to the velocity of the optically thin N2H+ line (indicated by a blue-dashed line). The velocity resolution of the CO data is only 1 km s-1 while that of N2H+ is 0.2 km s-1 so that resolution effects can play a role. The most straightforward explanation for the observed profile is infall, i.e. a line shape cause by the radial inwards motion of gas onto a central source.
 |
Fig. D.1 Middle panel: line integrated 12CO 3→2 emission (between 26 and 35 km s-1) of G11-0.12. The dust column density from Herschel is overlaid as black contours (levels 3,4,5,6 × 1022 cm-2). The numbering from 1 to 4 indicates the position of submm-continuum sources detected with ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). The 12CO 3→2 spectra at these positions are displayed in the panels. The blue-dashed line denotes the centre velocity of the N2H+ line. |
All Tables
Coordinates, distance D, and physical parameters of IRDCs, obtained from Herschel far-IR data, CO data, and near-IR/mid-IR extinction.
Exponents α and their errors Δα, assuming a spherical density distribution ρ(r) ∝ r− α, derived from the slope s of the power-law distribution from the PDF (Col. 2) and from the column density profiles (Col. 3).
All Figures
 |
Fig. 1 Top: Spitzer 8 μm (~2.5′′ resolution) and PACS 70 μm maps (~11′′ resolution). The Spitzer/IRAC data were taken from the public available GLIMPSE archive. Bottom: SPIRE 500 μm map (36′′ resolution) and ATLASGAL 870 μm maps (23′′ resolution) of G28.37+0.07. The central dark feature in the Spitzer and PACS images is the IRDC, appearing bright at longer wavelengths (SPIRE and ATLASGAL). |
| In the text | |
 |
Fig. 2 Left: H2-column density map from an SED fit to Herschel fluxes at 160−500 μm. The black contours indicate the levels Ndust = 4 to 7 × 1022 cm-2 in steps of 1022 cm-2, the white-dashed contour outlines the approximate completeness level (~3 × 1022 cm-2), and the white ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: temperature map of G28.37+0.07. |
| In the text | |
 |
Fig. 3 Left: line integrated 13CO 1→0 emission in colour scale between v = 72 and 84 km s-1, the velocity range of the bulk emission of the IRDC, and the associated GMC. The white contour indicates the 3.5 K kms-1 level, corresponding to Av = 2, which defines the extent of the GMC and was used for mass estimation. The Herschel column density is overlaid as black contours (levels 2 to 6 × 1022 cm-2 in steps of 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). Right: H2-column density map of the centre region of the GMC, obtained from 13CO 1→0. The white-dashed contour indicates a column density of 1.25 × 1022 cm-2, the remaining black contours the levels 1.5, 1.75, and 2 × 1022 cm-2. |
| In the text | |
 |
Fig. 4 PDFs of G28.37+0.07 and its associated GMC, derived from the Herschel column density map. The upper panel shows the PDF of the IRDC, only from the pixels inside the ellipse shown in Fig. 2. The lower panel shows the PDF obtained for the whole GMC (all pixels inside the contour indicated in Fig. 3, right). The error bars were calculated using Poisson statistics. The left y-axis gives the normalised probability p(η) and the right y-axis indicates the number of pixels per log bin. The upper x-axis is the visual extinction and the lower x-axis is the logarithm of the normalised column density. The green curve shows a log-normal fit to the PDF from the GMC. The red line indicates a power-law fit to the high column density tail with the slope s together with its error and the reduced X2 goodness-of-fit. The exponent α of an equivalent spherical density distribution ρ(r) ∝ r− α is also indicated in the panel. The dashed line in the upper panel indicates the completeness level; the PDF left of this line is incomplete. |
| In the text | |
 |
Fig. 5 PDFs of the whole GMC including G28.37+0.07, obtained from H2 column density maps derived from 13CO emission. The blue PDF contains all emission along the line-of-sight (LOS) towards the GMC (v = 0 to 132 km s-1); the red PDF contains only emission coming from the bulk emission of the cloud (v = 72 to 84 km s-1). The long dashed line is the Av = 2 level outlining the GMC. |
| In the text | |
 |
Fig. 6 Top: H2 column density from dust continuum with the white contour, roughly outlining the GMC in which G28.37+0.07 is embedded. Bottom: PDFs of the GMC, derived from the dust column density map from the left above different Av-thresholds (indicated with different colours and given in the panel). |
| In the text | |
 |
Fig. 7 Radial column density profile for G28.37+0.07, G28.53-0.25, and G18.82-0.28. Each cross in the panels represents one pixel value in the map. The x-axis gives the distance to the centre of the ellipse (x-axis). The dashed orange line indicates the Herschel beam (Gaussian profile with a FWHM of 36′′ displayed in log-log format). The exponent α was deduced from fitting the column density profile (N ∝ r1−α). For the fit, we included only the pixels that were inside a radius of 3 pc. |
| In the text | |
 |
Fig. 8 Middle panel: line integrated 12CO 3→2 emission in K kms-1 on a main beam temperature scale (between 72 and 84 km s-1) of G28.37+0.07. The dust column density from Herschel is overlaid as black contours (levels 4,5,7 × 1022 cm-2). The dashed lines outline the area displayed in Fig. 9, and the numbering from 1 to 6 indicates the position of submm-continuum sources seen with ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). The 12CO 3→2 (black) and 13CO 1→0 (red) spectra at these positions are displayed in the panels around. Additionally, we show spectra from two positions (indicated by arrows) off the sources but still within the molecular cloud. The blue-dashed line denotes the centre velocity of the N2H+ line. |
| In the text | |
 |
Fig. 9 Main beam brightness temperature spectra of 12CO 3 → 2 (black) and 13CO 1→0 (red) emission in the velocity range 55 to 95 km s-1 and temperature range −0.2 to 12 K. The area corresponds to the centre region of the IRDC G28.37+0.07, outlined in Fig. 8. The dust column density from Herschel is overlaid as blue contours (levels 4,5,7,10,16 × 1022 cm-2), and the numbering from 1 to 6 indicates the position of submm-continuum sources labelled using ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). |
| In the text | |
 |
Fig. A.1 PACS 70 μm map, SPIRE 500 μm, and ATLASGAL 870 μm maps of G11.11-0.12 (the “snake”). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
| In the text | |
 |
Fig. A.2 Left: column density map of G11.11-0.12, obtained from SED fit to Herschel 160, 250, 350, 500 μm data. The black contours indicate the levels Ndust = 2,3,5,7 × 1022 cm-2, the white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 12CO 3 → 2 emission in colour scale (in [K km s-1]) between v = 26 and 35 km s-1, the velocity range of the bulk emission of G11.11-0.12 and the associated GMC. The Herschel H2 column density is overlaid as black contours (levels 1.5,2,3,5,7 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
| In the text | |
 |
Fig. A.3 PACS 70 μm map, SPIRE 500 μm, and ATLASGAL 870 μm maps of IRDC G18.82-0.28 (Cloud A). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
| In the text | |
 |
Fig. A.4 Left: column density map of G18.82-0.28, obtained from SED-fit to Herschel 160, 250, 350, 500 μm data. Black contours indicate the levels Ndust = 2 to 5 × 1022 cm-2 in steps of 1022 cm-2, white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 13CO 1→0 emission in colour scale (in [K km s-1]) between v = 61 and 70 km s-1, the velocity range of the bulk emission of G18.82-0.28 and the associated GMC. Note that this GMC was already identified as a coherent cloud complex in Schuller et al. 2009. The Herschel H2 column density is overlaid as black contours (levels 1,2,3,4,5 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
| In the text | |
 |
Fig. A.5 PACS 70 μm map (left), SPIRE 500 μm (middle) and ATLASGAL 870 μm maps of G28.53-0.25 (Cloud D). The long filamentary structure is well visible as a dark (bright) feature in the 70 μm (500, 870 μm) maps. Bottom right: temperature map from SED fit 160−500 μm. |
| In the text | |
 |
Fig. A.6 Left: column density map of G28.53-0.25, obtained from SED fit to Herschel 160, 250, 350, 500 μm data. Black contours indicate the levels Ndust = 2.5,3,4,6 × 1022 cm-2, white-dashed contour outlines the approximate completeness level, and ellipse is taken from Simon et al. (2006b), defining the IRDC. Right: line integrated 13CO 1 → 0 emission in colour scale (in [K km s-1]) between v = 82 and 90 km s-1, the velocity range of the bulk emission of G28.53-0.25, and the associated GMC. The Herschel H2 column density is overlaid as black contours (levels 2,2.5,3,4,6 × 1022 cm-2) and the IRDC is outlined by an ellipse (Simon et al. 2006b). |
| In the text | |
 |
Fig. B.1 PDFs derived from Herschel column density maps (SED fit using only the Herschel wavelengths 160, 250, 350, and 500 μm) at 36′′ angular resolution. Left panel shows the PDFs of pixels comprising only the IRDC i.e. G18.82-0.28 (Cloud A), G28.53-0.25 (Cloud D), and G11.11-0.12. Right panel shows PDFs from associated GMC, including the IRDC. The left y-axis gives the normalised probability p(η), the right y-axis the number of pixels per log bin. The upper x-axis is the visual extinction and the lower x-axis the logarithm of the normalised column density. The dashed vertical line indicates the completeness level. The red line indicates a power-law fit to the high column density tail with the slope s together with its error and the reduced X2 goodness-of-fit. The exponent α of an equivalent spherical density distribution ρ(r) ∝ r− α is also indicated in the panel. The dashed line in the upper panel indicates the completeness level; the PDF left of this line is incomplete. |
| In the text | |
 |
Fig. C.1 Synthetic distributions shown in various colours with different widths (indicated in the panel). The observed PDF for G28.37+0.07, constructed from Herschel data is indicated in bold black. Top panel shows distributions that are normalised to the peak; the bottom panel shows distributions that are normalised to the same number of pixels. |
| In the text | |
 |
Fig. D.1 Middle panel: line integrated 12CO 3→2 emission (between 26 and 35 km s-1) of G11-0.12. The dust column density from Herschel is overlaid as black contours (levels 3,4,5,6 × 1022 cm-2). The numbering from 1 to 4 indicates the position of submm-continuum sources detected with ATLASGAL and subsequently observed in N2H+ (Tackenberg et al. 2014). The 12CO 3→2 spectra at these positions are displayed in the panels. The blue-dashed line denotes the centre velocity of the N2H+ line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


