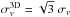| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424030 | |
| Published online | 11 June 2015 | |
G-virial: Gravity-based structure analysis of molecular clouds ⋆,⋆⋆
1
Max-Planck Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail:
gxli@mpifr-bonn.mpg.de
2
University of Toledo, Ritter Astrophysical Observatory, Department
of Physics and Astronomy, Toledo
OH
43606,
USA
3
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Straße 1, 85740
Garching bei München,
Germany
Received: 18 April 2014
Accepted: 24 February 2015
We present the G-virial method which aims to quantify (1) the importance of gravity in molecular clouds in the position-position-velocity (PPV) space; and (2) properties of the gas condensations in molecular clouds. Different from previous approaches that calculate the virial parameter for different regions, our new method takes gravitational interactions between all the voxels in 3D PPV data cubes into account, and generates maps of the importance of gravity. This map can be combined with the original data cube to derive relations such as the mass-radius relation. Our method is important for several reasons. First, it offers the ability to quantify the centrally condensed structures in the 3D PPV data cubes, and enables us to compare them in an uniform framework. Second, it allows us to understand the importance of gravity at different locations in the data cube, and provides a global picture of gravity in clouds. Third, it offers a robust approach to decomposing the data into different regions which are gravitationally coherent. To demonstrate the application of our method we identified regions from the Perseus and Ophiuchus molecular clouds, and analyzed their properties. We found an increase in the importance of gravity towards the centers of the individual molecular condensations. We also quantified the properties of the regions in terms of mass-radius and mass-velocity relations. Through evaluating the virial parameters based on the G-virial, we found that all our regions are almost gravitationally bound. Cluster-forming regions appear are more centrally condensed.
Key words: gravitation / ISM: structure / ISM: kinematics and dynamics / stars: formation / methods: numerical / ISM: clouds
Appendices and movie are available in electronic form at http://www.aanda.org
Available at http://gxli.github.io/G-virial/
© ESO, 2015
1. Introduction
Star formation takes place in the dense and shielded parts of the interstellar medium. Observations show that the interstellar medium exhibits complicated, irregular, and filamentary structures (Schneider & Elmegreen 1979; Williams et al. 2000; Goldsmith et al. 2008; Men’shchikov et al. 2010). Theoretically, such structures are created by various physical processes such as turbulence, gravity, magnetic field, and radiation.
To understand star formation it is necessary to understand how various physical processes affect it. Gravity is a long-range interaction, and plays important roles in most astrophysical processes at a multiple of physical scales. This is particularly true for turbulent molecular clouds (e.g., Heyer et al. 2009; Kauffmann et al. 2013). However, characterizing the role of gravity on a cloud at various physical scales is not straightforward.
In observations, the structure of molecular gas can be traced by spectral lines in the 3D position-position-velocity (PPV) space where molecular gas exhibits complicated structures. However, given the rich information obtained observationally, few constraints on the role of gravity in the clouds have been obtained so far. One major difficulty is to properly quantify the irregular structure of the gas. The virial parameter αvir = 5σ2R/GM1 is commonly used to quantify the importance of gravity, and to calculate it we must define a region in which σ and M can be evaluated2. As a result, the virial parameter is only suitable for the cases where the structures are well defined. The morphology of the molecular interstellar medium is generally so complicated that in many cases it is difficult to separate individual objects from a continuous distribution of material. This has been further complicated by the fact that we observe the structures of the sky plane, and the structures identified from the observations are biased by various projection effects (Pichardo et al. 2000; Dib et al. 2006; Shetty et al. 2010; Beaumont et al. 2013).
Another difficulty with the virial parameter is that it is localized. To define the virial parameter we need to define the region, and by evaluating the virial parameter of that region, we automatically neglect the gravitational interaction between the region and its surroundings. As a result, the virial parameter can be used to quantify the importance of gravity for the individual structures, but it cannot be used to understand the importance of gravity for a cloud as a whole. Gravity is a long-range interaction, and to understand its importance, we need to understand how it works not it one region on one particular physical scale, but on a multiple of physical scales.
One case where such an understanding is required is the cluster-forming region. In observations, such regions are found to be centrally condensed in both the position-position space and the PPV space, and physically we expect that gravity is important at the centers of the cluster-forming regions and should become less important if we move from the centers to the outskirts. This stratification, which is of crucial importance for understanding stellar clustering, awaits to be quantified.
In this paper we introduce a new method called G-virial to quantify the importance of gravity in a variety of situations where mass is traced in the 3D PPV space. Instead of dividing the molecular cloud into regions based on iso-intensity contours in the 3D data cube (e.g., Williams et al. 1994), the method takes the gravitational interactions between all the voxels in the 3D PPV data cube into account, and generates maps of the importance of gravity in 3D. As a result, it provides constraints on the global importance of gravity. This is complementary to methods that calculate the self-gravity such as the virial parameter. Such a map of the importance of gravity also enables us to identify gravitationally coherent regions in molecular clouds and to quantify the structures of the regions.
In this paper, we introduce the G-virial method (Sects. 2–5), and explore its usage in quantifying the importance of gravity and the structures of the molecular condensations seen in simulations (Sect. 5) and observations (Sect. 6). We conclude in Sect. 7.
2. Problem formulation
Observationally, molecular gas can be mapped by rotational transitions of molecules such as CO. Through proper modeling of the emission, it is possible to construct the distribution of the molecular gas in the form of a 3D PPV data cube which covers a continuous (x,y,v) space 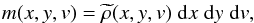 (1)where m represents the mass, x and y represent the spatial dimensions, and v represents the velocity dimension. Here
(1)where m represents the mass, x and y represent the spatial dimensions, and v represents the velocity dimension. Here 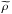 has a dimension of ML-3T, and represents the amount of mass per unit area per unit velocity. The distribution of
has a dimension of ML-3T, and represents the amount of mass per unit area per unit velocity. The distribution of 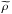 in the v dimension represents the distribution of gas at different velocities along the same line of sight.
in the v dimension represents the distribution of gas at different velocities along the same line of sight.
We start with a mass distribution in a 3D PPV data cube (Fig. 1). We aim to understand how a particle at voxel i is bound by mass from all the voxels j (not excluding i). To achieve this, we split our task into two subtasks. First, we need to estimate the gravitational boundedness of voxel i by another voxel j in the 3D PPV data cube. Second, we need to estimate the gravitational boundedness of a voxel i based on the information we have about all the other voxels j.
2.1. Boundedness of a voxel pair in a 3D data cube
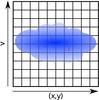 |
Fig. 1 Setup of the problem. We consider a mass distribution in a 3D PPV data cube. This is represented as the black grid. x–y represents the spatial dimensions and v represents the velocity dimension. The mass distribution is represented in blue. For each voxel i, its G-virial can be determined by taking its interactions with all the voxels j (not excluding i) into account. See Sect. 2 for details. |
We start by defining the gravitational boundedness between a pair of voxels (i,j). We are interested in the extent to which a particle i is bound to another voxel j. For our purpose, i can be treated as a massless test particle, and the boundedness of particle i is determined by the mass of the voxel j.
The available measurable quantities in 3D PPV data cube include the mass mj, the spatial separation δrij and the velocity separation δvij. We expect the boundedness to increase with mj and decrease with δrij since gravitational attraction increases with the mass and decreases with the distance.
The remaining question is how to make use of the information contained in the velocity direction. We expect that voxels with large velocity differences are not likely to be bound to each other, for two reasons. First, a larger velocity separation implies higher kinetic energy, which consequently decreases the likelihood of it being gravitationally bound. Second, it has been found that the molecular gas follows the Larson’s relation (Larson 1981)3 where the spatial length and velocity dispersion are related by 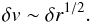 (2)As a result, a larger velocity separation implies a larger spatial separation, which implies a lower gravitationally boundedness.
(2)As a result, a larger velocity separation implies a larger spatial separation, which implies a lower gravitationally boundedness.
Here, we define the gravitational boundedness contributed from voxel j to voxel i as 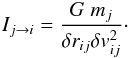 (3)The boundedness Ij → i increases with mass and decreases with spatial and velocity separation.
(3)The boundedness Ij → i increases with mass and decreases with spatial and velocity separation.
Apparent similarities exist between Eq. (3) and the virial parameter. The virial parameter is defined as (Bertoldi & McKee 1992)4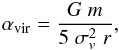 (4)where m, r, and σv are the mass, radius, and velocity dispersion of the clumps. The virial parameter is a measurement of the gravitational boundedness of an object. The quantity Ij → i defined by Eq. (3) has a dimension of G Mass/Radius Velocity2, which is the same as that of the virial parameter. Therefore, Eq. (3) can be viewed as a generalization of the virial parameter to a voxel pair, and a larger Ij → i is related to a larger chance for voxel i to be bounded by voxel j.
(4)where m, r, and σv are the mass, radius, and velocity dispersion of the clumps. The virial parameter is a measurement of the gravitational boundedness of an object. The quantity Ij → i defined by Eq. (3) has a dimension of G Mass/Radius Velocity2, which is the same as that of the virial parameter. Therefore, Eq. (3) can be viewed as a generalization of the virial parameter to a voxel pair, and a larger Ij → i is related to a larger chance for voxel i to be bounded by voxel j.
2.2. The G-virial
We define the G-virial of a voxel i as the sum of the gravitational boundedness contributed from all the voxels j (not excluding i). To be more precise, 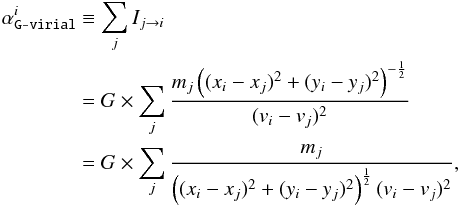 (5)where Ij → i comes from Eq. (3), and in the second step we take into account that the G-virial is measured in the 3D PPV space. The physical meaning of Eq. (5) can be understood as follows. For one voxel i, its G-virial is determined by summing up its boundedness with all the other voxels j.
(5)where Ij → i comes from Eq. (3), and in the second step we take into account that the G-virial is measured in the 3D PPV space. The physical meaning of Eq. (5) can be understood as follows. For one voxel i, its G-virial is determined by summing up its boundedness with all the other voxels j.
In Eq. (5), if j is close to i in both the spatial and the velocity direction, it contributes more to the G-virial. The contribution is proportional to the mass mj, and inversely proportional to δrij and 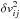 .
.
For a continuous distribution of material, Eq. (5) can be written as 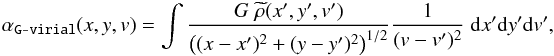 (6)where the integration is carried out over the whole data cube. Here
(6)where the integration is carried out over the whole data cube. Here 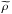 has a dimension of ML-2V-1 where M is mass, L is size, and V is velocity.
has a dimension of ML-2V-1 where M is mass, L is size, and V is velocity.
If the separation between i and j becomes small, the denominator of Eq. (6) approaches zero and the integrand can become large. If the density distribution is smooth, the term 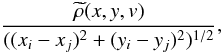 is still finite and does not induce a singularity. However, the term
is still finite and does not induce a singularity. However, the term 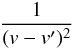 is singular. In our calculations, we change it to
is singular. In our calculations, we change it to 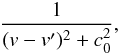 (7)which means we suppress the contribution to the G-virial when the velocity separation is smaller than c0, and in our case, c0 is comparable to the sound speed. We introduce this cutoff in order to make the integrand convergent. Nevertheless, there is a physical reason behind this. In a molecular cloud, the velocity dispersion that we observe comes from two parts: one from the thermal motion, and the other from the large-scale streaming motion of the gas. The first part is almost scale-independent, and the second part increases with the physical size. We are mainly interested in the balance between gravity and the large-scale streaming motion, and as a result, it is reasonable to discard the contributions where δv ≲ c0. In our calculations, c0 is chosen to be 1kms-1, which is comparable to the sound speed. The effect of changing c0 influences the absolute values of the G-virial; however, the relative values of the G-virial stay unchanged (Appendix B). Therefore, the G-virial is a relative measure of the gravitational boundedness. In the case where the G-virial map of several observations needs to be compared, a single value of c0 needs to be chosen in advance.
(7)which means we suppress the contribution to the G-virial when the velocity separation is smaller than c0, and in our case, c0 is comparable to the sound speed. We introduce this cutoff in order to make the integrand convergent. Nevertheless, there is a physical reason behind this. In a molecular cloud, the velocity dispersion that we observe comes from two parts: one from the thermal motion, and the other from the large-scale streaming motion of the gas. The first part is almost scale-independent, and the second part increases with the physical size. We are mainly interested in the balance between gravity and the large-scale streaming motion, and as a result, it is reasonable to discard the contributions where δv ≲ c0. In our calculations, c0 is chosen to be 1kms-1, which is comparable to the sound speed. The effect of changing c0 influences the absolute values of the G-virial; however, the relative values of the G-virial stay unchanged (Appendix B). Therefore, the G-virial is a relative measure of the gravitational boundedness. In the case where the G-virial map of several observations needs to be compared, a single value of c0 needs to be chosen in advance.
The reasons for the name G-virial in Eq. (5) include the following: first, we named it G-virial to emphasize its connection with the commonly used virial parameter; second, we added the letter G to emphasize that our virial parameter is a generalized version of the virial parameter and that it is global. Different from the case of Bertoldi & McKee (1992) and Goodman et al. (2009) where the virial parameter is used to quantify self-gravity, our G-virial takes all the gravitational interactions between gas in the data cube into account. More clarifications concerning the concept of the G-virial can be found in Appendix A.
3. Separating components with different velocities
One difficulty that we need to deal with is the line-of-sight confusion. When calculating the G-virial, different components along the same line of sight are distinguished through their velocities. If two components happen to have the same velocity, the G-virial will be over-estimated, since physically unassociated components will be treated as one single component in the calculations.
We argue that in many cases, the separation in the velocity axis provides information so that we can separate different components based on the velocity difference or at least alleviate the problem. We consider two cases; the first is the line-of-sight confusion in a given molecular cloud, and the second is the line-of-sight confusion in our Milky Way disk.
In a molecular cloud, the line-of-sight confusion problem can be alleviated if the molecular gas follows the Larson’s relation (Larson 1981; Roman-Duval et al. 2011) because the boundedness is proportional to 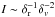 (Eq. (3)) where δr and δv are the separations in position and velocity direction, respectively. We consider two points along the same line of sight separated by δz. According to the Larson’s relation, the velocity dispersion (which is a width of the statistical distribution velocity separation between the two points) is
(Eq. (3)) where δr and δv are the separations in position and velocity direction, respectively. We consider two points along the same line of sight separated by δz. According to the Larson’s relation, the velocity dispersion (which is a width of the statistical distribution velocity separation between the two points) is 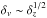 . Therefore, the boundedness related to δz by
. Therefore, the boundedness related to δz by 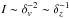 . In other words, the contribution is not likely to be large since the velocity is likely to be different in an averaged sense.
. In other words, the contribution is not likely to be large since the velocity is likely to be different in an averaged sense.
In the case of the Milky Way disk, different spiral arms usually have different velocities, they will be separated easily in our calculations. We note that in Eq. (3) the interaction is proportional to δr-1 and δv-2. Therefore, a small separation in velocity will lead to a much bigger decrease in interaction and finally make the contribution to the total G-virial negligible. Since the method uses velocity difference to deal with line-of-sight confusion, it is more accurate for the cases where the velocity increases with distance (e.g., including systematic expansion and contraction where velocity increases with distance).
4. Numerical procedure
In the case of a 3D PPV data cube, for a voxel (x,y,v), the G-virial is defined as (see Eqs. (6) and (7)) 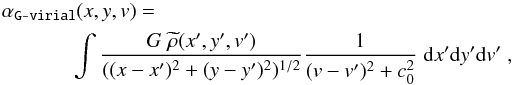 (8)where the integration is carried out over the whole data cube. With an observationally constructed distribution of mass in the 3D PPV data cube, we can easily construct the G-virial using Eq. (8).
(8)where the integration is carried out over the whole data cube. With an observationally constructed distribution of mass in the 3D PPV data cube, we can easily construct the G-virial using Eq. (8).
Equation (8) takes the form of a convolution, and can be conveniently calculated in Fourier space. In real space, the kernel is 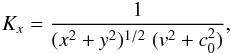 (9)and in Fourier space it can be shown that5
(9)and in Fourier space it can be shown that5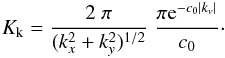 (10)Equation (10) enables us to calculate the G-virial map efficiently. In our calculations, we first make a 3D fast Fourier transform (FFT) to the observationally constructed mass distribution
(10)Equation (10) enables us to calculate the G-virial map efficiently. In our calculations, we first make a 3D fast Fourier transform (FFT) to the observationally constructed mass distribution 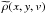 and obtain
and obtain 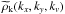 . Then we calculate the G-virial in the Fourier space
. Then we calculate the G-virial in the Fourier space 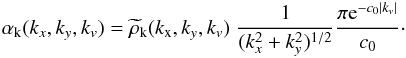 (11)In the last step the G-virial map is obtained by a inverse FFT of αk.
(11)In the last step the G-virial map is obtained by a inverse FFT of αk.
We found that the absolute values of the G-virial are dependent on c0 (see Appendix B); however, the relative values of the G-virial are insensitive to c0. As a result, the G-virial is a relative measurement of gravitational boundedness rather than an absolute one. In order for the G-virial maps from different regions to be comparable, a unique value of c0 has to be chosen; c0 also needs to be larger than the velocity resolution of the observations.
5. Quantifying the structure of molecular gas with G-virial
We present applications of the G-virial to quantify gravity and the structure of molecular gas. To begin with, we apply the method to the models where both the 3D density and 3D velocity structure are available. We focus on two aspects: first, we present the use of G-virial in quantifying the importance of gravity in the 3D PPV data cube; second, we quantify the structures of molecular condensations bases on the G-virial.
5.1. Defining G-virial in the PPP space
To properly evaluate the accuracy of the G-virial method, we first define the G-virialmodel in the PPP space where all the position and velocity information are available, and then compare it with the observationally reconstructed values of the G-virial in the PPV space. Following Eqs. (3) and (5), we define the model G-virial as 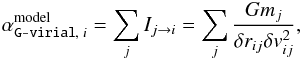 (12)where
(12)where 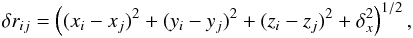 (13)and
(13)and 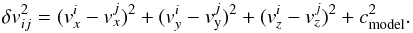 (14)Here the voxel pair (i,j) has positions ((xi,yi,zi),(xj,yj,zj)) and velocities
(14)Here the voxel pair (i,j) has positions ((xi,yi,zi),(xj,yj,zj)) and velocities 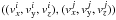 . The parameter δx is the spatial resolution of the simulation. Writing Eq. (12) in its integral form, we have
. The parameter δx is the spatial resolution of the simulation. Writing Eq. (12) in its integral form, we have ![\begin{eqnarray} \label{eq:gvirial:3d} \alpha_{\texttt{G-virial},\; i}^{\rm model}& =& \int \frac{G\; \rho(x', y', z')}{\left((x-x')^2 + (y-y')^2 + (z-z')^2 + \delta_{\rm x}^2\right)^{1/2}} \nonumber \\ && \times \frac{1}{\dfrac{ \Big(v_x(p) - v_x(p'))^2 + \left(v_y(p) - v_y(p')\right)^2 }{ +\Big(v_{z}(p) - v_{z}(p'))^2 + c_{\rm model }^2\Big)}}\nonumber\\[1mm] &&\times {\rm d}x' \;{\rm d}y'\; {\rm d}z', \end{eqnarray}](/articles/aa/full_html/2015/06/aa24030-14/aa24030-14-eq63.png) (15)where p stand for (x,y,z) and p′ stand for (x′,y′,z′). Here we choose cmodel = 3 × c0 since the denominator of Eq. (15) is composed of a sum of the velocity difference from the three dimensions. Since the G-virial is a relative measure of the gravitational boundedness (Appendix B), our results are not affected by this.
(15)where p stand for (x,y,z) and p′ stand for (x′,y′,z′). Here we choose cmodel = 3 × c0 since the denominator of Eq. (15) is composed of a sum of the velocity difference from the three dimensions. Since the G-virial is a relative measure of the gravitational boundedness (Appendix B), our results are not affected by this.
5.2. Quantifying the importance of gravity
We study how the importance of gravity traced in the G-virial inferred from the simulated observations is related to the G-virial theoretically defined in the models.
We consider two models. The first (hydrodynamic simulation model) was taken from a numerical simulation of turbulent gas. The simulation used here was carried out under periodical boundary conditions, and turbulence is injected through compressive forcing mode (Federrath et al. 2008), and no self-gravity is included. The details of the simulations are described in Federrath et al. (2010), Roman-Duval et al. (2011)6. Since self-gravity is not included in the simulation, the line-of-sight confusion effect is probably over-estimated because, as was found in Beaumont et al. (2013), in the simulations without gravity structures will overlap more in the PPV space. In this work, we make use of the density and velocity cubes from the simulations.
We make a cutout of a size of 4.8pc × 4.8pc × 4.8 pc from the snapshot at t = 5 T where T is the crossing timescale of the simulation. The computation of Eq. (15) is computationally expensive (o(N2)). To save computational time, we choose a portion of the simulation with a relatively large gas condensation and relatively complicated internal structures (Fig. 2).
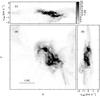 |
Fig. 2 a) Map of the peak brightness temperature of the simulated 13CO(1–0) emission along the velocity axis. b) Position-velocity map of peak brightness temperatures of 13CO(1–0) along the Y-axis. c) Position-velocity map of peak brightness temperatures of 13CO(1–0)) along the X-axis. |
The second model (the analytical model) is constructed to resemble a typical molecular condensation (e.g., McKee & Tan 2003). It is defined within rin<r<rout where r is the radius, rin = 1 pc, and rout = 10pc. The density structure is 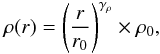 (16)where r0 = 1pc; ρ0 = 103 × mH2, where mH2 is the mass of the H2 molecule; and γρ are chosen to vary from − 1.8 to − 2.2. The velocity structure is parametrized as
(16)where r0 = 1pc; ρ0 = 103 × mH2, where mH2 is the mass of the H2 molecule; and γρ are chosen to vary from − 1.8 to − 2.2. The velocity structure is parametrized as  (17)where r0 = 1 pc, γv is chosen to vary from 0.35 to 0.6, and v0 = 1 kms-1. It can be viewed as an expanding sphere. At a given radius, the magnitude of velocity is distributed uniformly between 0.9v(r) and 1.1v(r), and the direction of the velocity is distributed uniformly in 3D. The model is sampled through a total of 3 × 105 particles, and then turned into a 3D PPV data cube.
(17)where r0 = 1 pc, γv is chosen to vary from 0.35 to 0.6, and v0 = 1 kms-1. It can be viewed as an expanding sphere. At a given radius, the magnitude of velocity is distributed uniformly between 0.9v(r) and 1.1v(r), and the direction of the velocity is distributed uniformly in 3D. The model is sampled through a total of 3 × 105 particles, and then turned into a 3D PPV data cube.
We chose the two models because they represent two typical situations. In the first case (the hydrodynamic simulation model), the model exhibits a high degree of physical complexity. In the second case (the analytical model), the density distribution is centrally condensed, and the model has well-defined mass-radius and velocity-radius structures. We will study the behavior of the G-virial in both cases.
The models are turned into a 3D PPV data cube using a simple radiative transfer model (Sect. 3.3 of Roman-Duval et al. 2011). It is assumed that the 13CO(1–0) emission is optically thin and n(13CO)/n(H2) = 1.7 × 10-6 (Langer & Penzias 1990; Blake et al. 1987). The excitation temperature is assumed to be 10 K. In reality, the 13CO(1–0) emission can be optically thick and both the abundance and excitation conditions can vary, and these can lead to inaccuracies. However, in testing our method, we are interested in the cases where mass can be reliably traced in the PPV data cube, and observationally this can be achieved by modeling several transitions of CO or using more reliable tracers.
In our calculation of the model G-virial (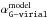 ), we choose cmodel = 1 km s-1, and in our calculation of the G-virial reconstructed from the simulated map (
), we choose cmodel = 1 km s-1, and in our calculation of the G-virial reconstructed from the simulated map (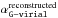 ), we choose c0 = 0.3 km s-1. We make this choice because in Eq. (15) all three velocity components are considered, and in Eq. (6) only one velocity component is considered. Since G-virial is a relative measure of the gravitational boundedness (Appendix B), the conclusions are not dependent on this.
), we choose c0 = 0.3 km s-1. We make this choice because in Eq. (15) all three velocity components are considered, and in Eq. (6) only one velocity component is considered. Since G-virial is a relative measure of the gravitational boundedness (Appendix B), the conclusions are not dependent on this.
 |
Fig. 3 Comparison between the G-virialmodel calculated from the model and the G-virialreconstructed, which is reconstructed from the simulated observations in the PPV space. Panel a) shows the result for the hydrodynamic simulation; and panel b) shows the result for the analytical model with γρ = −2.2 and γv = 0.5. The colors stand for the amount of mass in a given interval. |
In Fig. 3 we compare the G-virialmodel calculated from the model with the G-virialreconstructed reconstructed from the simulated observations in the PPV space. The first thing to be noticed is that the absolute values of the G-virial differ because the G-virial is only a relative measure of the gravitational boundedness, rather than an absolute one.
In general, a larger G-virialmodel is related to a larger G-virialreconstructed. The reconstructed G-virial exhibits a higher uncertainty in the hydrodynamic simulation model since its flow has complicated structures.
 |
Fig. 4 Comparison between between G-virialmodel and G-virialreconstructed in the PPV space for the hydrodynamical model described in Sect. 5.2. In the model, turbulence is injected through compressible forcing, and no self-gravity is included (Federrath et al. 2008). The G-virialmodel in the PPV space is defined as the mass-weighted average of the G-virialmodel in the PPP space, which is defined in 12. Here, the grayscale image is the simulated 13CO(1–0) emission from the model. The red contours stand for the G-virialmodel, and the contour levels are (6, 5, 10). The blue contours stand for the G-virialreconstructed, and the contour levels are (3, 6). It worth noting that the G-virialmodel and the G-virialreconstructed agrees better at regions where mass is traced. This can be seen in the v = −0.2 km s-1 channel. They agree better at the regions where mass is traced (e.g., the red arrow), but does not agree well at the region without mass (e.g., the blue arrow). |
To look further into the relation between G-virialmodel and G-virialreconstructed, we convert the G-virialmodel from the PPP space into the PPV space, and study the connection between the two (Fig. 4). At a given velocity interval, the G-virialmodel in the PPV space is defined as the mass-weighted average of the G-virialmodel in the PPP space, and the average is carried over the entire line of sight. There are some significant differences between the iso- G-virialmodel contours (isosurfaces where the G-virial takes constant values) and iso- G-virialreconstructed contours: the iso- G-virialmodel exhibit more structures and iso- G-virialreconstructed is smoother because the G-virialmodel is unaffected by the line-of-sight confusion. Thus, the G-virial map constructed in the PPV space is better suited to studying the effect of gravity at large scale, but is not suitable for the study of the importance of gravity at small scale (e.g., individual cores). Although the iso- G-virialmodel and the iso- G-virialreconstructed does not agree completely, they agree better at positions where emission is enhanced and mass is traced, and tends to differ more where there is little emission. Since we are interested in the gravitational boundedness of the gas, this disagreement at regions where little mass is present is not as important as it might appear.
 |
Fig. 5 Comparison between the structure of the model and the structure reconstructed through the G-virial for different sets of model parameters. The upper panels show the results where the analytical model is constructed with different γρ, and the lower panels show the results where the analytical model is constructed with different γv. The left panels are the mass-radius relations and the right panels are the velocity dispersion-radius relations. Here the radius is scaled up by a factor of 1.4 and the velocity dispersion is scaled up by a factor of 1.45 for an easy comparison. |
Since the hydrodynamic simulation model exhibit complicated structures, the line-of-sight confusion has a larger impact on the results than the case of the analytical model. However, in the gravity-free hydrodynamic simulation model the confusion probably has been over-estimated. According to Beaumont et al. (2013), structures tend to overlap more without self-gravity.
5.3. Quantifying the internal structures
For a given region, its G-virial map is centrally concentrated, and if we divide the region based on different isosurfaces of G-virial values, we get a set of regions that nest inside one another. We propose to quantify the structures of the gas condensations in the PPV space with the mass-radius relation and velocity dispersion-radius relation derived with the help of the isosurfaces of the G-virial.
Inside a closed region where the G-virial of the voxels is larger than a given threshold, we can evaluate parameters such as mass, radius, and velocity dispersion. Using a map of mass distribution m(x,y,v) and a map of the G-virial αG-virial(x,y,v), the corresponding parameters are evaluated by taking all the voxels inside a given contour of the αG-virial(x,y,v) map into account. The mass of a region is defined as 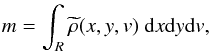 (18)where R denotes a coherent region that satisfies αG-virial(x,y,v)>αmin and the central velocity of a region is defined as
(18)where R denotes a coherent region that satisfies αG-virial(x,y,v)>αmin and the central velocity of a region is defined as 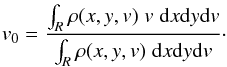 (19)The velocity dispersion is defined as
(19)The velocity dispersion is defined as 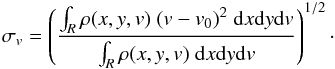 (20)The radius of the region is defined by diagonalizing the tensor of second moments of the position coordinates weighted by the intensity (Goodman et al. 2009), and is defined as
(20)The radius of the region is defined by diagonalizing the tensor of second moments of the position coordinates weighted by the intensity (Goodman et al. 2009), and is defined as 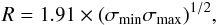 (21)where σmin and σmax are the dispersions along the major and minor axes.
(21)where σmin and σmax are the dispersions along the major and minor axes.
This set of definitions enables us to quantify the structure of molecular condensations observed in the PPV space in terms of mass-radius and velocity dispersion-radius relations. If the molecular gas has a relatively diffuse morphology, we expect to see a steeper dependence of the enclosed mass M with the radius r; if the molecular gas is centrally condensed, we expect to see a shallower M-r dependence. Similar arguments can be applied to the dependence of velocity dispersion on radius σv-r.
If the molecular gas is centrally condensed, the M-r and σv-r relations of the gas condensations are well defined in the PPP (position-position-position) space. It is expected that we can reconstruct these relations observationally with the help of the G-virial. If a molecular gas condensation has a diffuse and irregular morphology, these G-virial-derived relations can still represent the morphology of the gas condensations. The difference between different regions can be represented in the M-r and σv-r planes.
To demonstrate the diagnostic power of the M-r and σv-r relations, we generated a set of models with different density and velocity structures, and compare them with the M-r and σv-r relations reconstructed with the G-virial (Fig. 5). The differences in structure among different regions can be accurately reconstructed with the help of the G-virial. Furthermore, the slope of the M-r and σv-r relations are accurately reconstructed with the G-virial7.
We also plot the dependence of G-virial as a function of radius for various models (Fig. 6). For all the models, we found an increase of G-virial towards the centers of the regions. Larger G-virial are found for the models with more condensed structure and lower velocity dispersion.
5.4. Short summary
In this section we demonstrated the usage of G-virial to quantify the structure of molecular gas condensations. We summarize our findings and remind the reader of the caveats.
We found that the G-virial can be used to quantify the importance of gravity and to quantify the structures of the gas condensations.
-
1.
The G-virial measured from the PPV data cube is positivelyrelated to the G-virial found in the model(PPP space), and a larger G-virial is related to alarger probability of being gravitationally bound by the ambientgas.
-
2.
The G-virial map can be used to derive mass-radius and velocity dispersion-radius relations. The G-virial-derived relations are good reconstructions of the structures of the models when the models are symmetric, and can also provide good representations of the structures if the models are irregular.
Several caveats need to be noted. First, the G-virial is a relative measure of the gravitational boundedness. A larger G-virial means a larger change of being gravitationally bound. The absolute values of the G-virial cannot be directly used to tell if a region is gravitationally bound or not. The absolute values of the G-virial are dependent on c0. Therefore, in order for the values of G-virial from several maps to be comparable, a unique value of c0 needs to be chosen in advance. This value should be comparable to the sound speed of the medium, and in this work we have chosen it to be c0 = 1 km s-1. We also note that the G-virial is reconstructed from the PPV space where the projection effect tends to smear out structures; it is more suitable for the study of the gravitational boundedness of the structures larger than the individual gas condensations.
Second, the G-virial method can be used to derive the mass-radius and velocity dispersion-radius relations for molecular condensations. However, the results need to be properly interpreted. If the structures of the gas condensations are regular and are close to being spherically symmetric, the G-virial-derived mass-radius and velocity dispersion-radius relations should be good reconstructions of the real 3D structure. If the structure of the gas condensations are irregular, the G-virial can be used to derive these relations. However, in this case, the G-virial-derived relations should be viewed as representations of the compactness of the structures in the PPV space, and are not necessarily related the compactness of the structures in the PPP space.
 |
Fig. 6 G-virial as a function of radii for models with different γρ and γv. |
Finally, we would like to emphasize that the G-virial methods works in the PPV space, and like other methods, its accuracy is limited by line-of-sight contamination. The method relies on using the velocity difference to alleviate the line-of-sight confusion. This requires different gas components to have different velocities, which is satisfied in many cases. For a single object, this requires the velocity separation to increase with radius. Whereas this generally holds for individual molecular clouds and clumps, it does not hold for some cores or disks where the velocity decreases with radius (e.g., collapsing cores).
6. Applications to molecular clouds
In this section we present applications of our method to several molecular clouds. Our method requires a map of the distribution of molecular gas in the 3D PPV space. Observationally, this can be conveniently achieved using rotational transitions of the CO molecule.
In the simplest case, this can be achieved by observing the 13CO(1–0) transition alone. Assuming an excitation temperature of 10 K, a 12CO abundance of X(12CO/H2) = 8 × 10-5, and a 12CO to 13CO ratio of R(12CO/13CO) = 45, the column density can be estimated as (Simon et al. 2001; Roman-Duval et al. 2010) 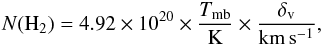 (22)where Tmb is measured in K and δv is the velocity resolution of the data cube measured in kms-1. Changing the excitation temperature to 20 or 30 K decreases the derived mass by 40% and 92%, respectively (Simon et al. 2001). For an observed 13CO(1–0) data cube Tmb(x,y,v), the mass distribution m(x,y,v) can be obtained as
(22)where Tmb is measured in K and δv is the velocity resolution of the data cube measured in kms-1. Changing the excitation temperature to 20 or 30 K decreases the derived mass by 40% and 92%, respectively (Simon et al. 2001). For an observed 13CO(1–0) data cube Tmb(x,y,v), the mass distribution m(x,y,v) can be obtained as 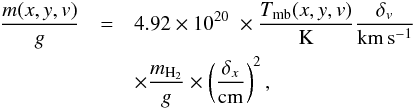 (23)where δx is the voxel size of the spatial dimension in cm and δv is the channel width in kms-1. The values of m and
(23)where δx is the voxel size of the spatial dimension in cm and δv is the channel width in kms-1. The values of m and 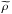 in Eq. (6) are related by
in Eq. (6) are related by 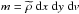 .
.
We apply our G-virial method to the publicly available data from the COMPLETE survey (Ridge et al. 2006). The observations have a spatial resolution of 46″ and a velocity resolution of 0.067 km s-1, the mean RMS per channel is ~0.33 K in terms of 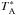 , and the beam efficiency is ~0.5.
, and the beam efficiency is ~0.5.
With a distance of 250 ± 50 pc and a total mass of 104M⊙ (Enoch et al. 2006), the Perseus molecular cloud is among the best-studied molecular clouds in the Milky Way. It is composed of several distinct regions: B1, B3, NGC 1333, and IC 348. The Ophiuchus molecular cloud has a distance of 125 pc and a mass of 7 × 103M⊙ (de Geus et al. 1989) and contains clouds L1688 and L1689. In particular, L1688 and NGC 1333 are cluster-bearing regions. IC 348 also hosts a star cluster; however, it is generally considered older than the other regions in Perseus (Gutermuth et al. 2009).
In this section, we provide a study of the structure of the Perseus and Ophiuchus molecular clouds with our G-virial method. We present maps of the G-virial, together with an analysis of the structure of the regions in the clouds based on the G-virial method.
 |
Fig. 7 Channel maps of the 13CO(1–0) emission and the corresponding G-virial. The upper panel shows the results from the Perseus molecular cloud and the lower panel shows the results from the Ophiuchus molecular cloud. Grayscale images stand for 13CO(1–0) emission and the red contours represents the G-virial. Contour levels start from 1.2 in steps of 0.8. |
6.1. Maps of the G-virial
In Fig. 7 we channel maps of the G-virial in the 3D PPV space. Three-dimensional renderings of the maps are presented in Appendix C. For both clouds, the 13CO(1–0) maps contain complicated and filamentary structure, whereas the G-virial maps are smooth and contain fewer structures. Interestingly, higher values of G-virial are reached only at cluster-bearing regions such as NGC 1333, IC 348, and L1688, and this highlights the importance of gravity in such regions. Different regions are indicated in Fig. 8.
6.2. Identification of regions
The G-virial offers a new way to divide the molecular cloud into regions. Previously, this has been done either by visual inspection, or with contour-based algorithms such as clumpfind (Williams et al. 1994). It is worth mentioning that other region-finding algorithms are available, such as dendrogram (Rosolowsky et al. 2008) and dochamp (Whiting 2012).
Many of the algorithms (e.g., clumpfind and dendrogram) are contour-based, and they tend to assign voxels to regions based on iso-column-density contours in the 2D case or on iso-intensity contours in the case of a 3D PPV data cube. Molecular clouds are characterized by a set of complicated hierarchical structures, and a naive application of the clumpfind tends to produce hundreds of clumps for one single molecular cloud. It has also been pointed out recently that contour-based methods suffer from superposition and confusion when the volume filling factor of emitting material is large (Beaumont et al. 2013).
In our analysis we are interested in finding gravitationally coherent regions. This can be achieved by applying the dendrogram8 to the G-virial map, which is a measurement of the gravitational boundedness. Figure 8 shows the regions identified by applying the dendrogram algorithm to our G-virial map. The identified regions correspond to the “leaves” of the dendrogram. In the dendrogram calculations, the minimum difference between different contours is set to 0.4, and the regions correspond to the leaves of the dendrogram. Each identified region consists of a continuous list of voxels in the 3D PPV space. In Fig. 8 the projected boundaries of the regions are plotted9.
Compared to clumpfind, a combination of the G-virial method and the Dendrogram method tends to identify regions that are coherent while the clumpfind tends to break up those regions. The reason is that ourG-virial maps are much smoother than the original map10. Since the G-virial maps are much smoother, the results obtained with the G-virial maps are much less sensitive to the technical parameters (e.g., the minimum separation of the contours) used in the computations compared to the case with the intensity maps. Therefore, the G-virial offers a more robust definition of regions. With G-virial we can study the structure of molecular gas in terms of these gravitationally coherent regions. In the 2D case, our method is similar to the gridcore code which is based on 2D projected gravitational potential (Gong & Ostriker 2011).
6.3. Internal structure of the regions
 |
Fig. 8 Regions identified by applying the dendrogram algorithm to our G-virial map. The results from the Perseus molecular cloud (upper panel) and Ophiuchus molecular cloud (lower panel) are presented. The grayscale images correspond to the velocity-integrated 13CO(1–0) emission and the contours correspond to the projected boundaries of the identified regions. These regions correspond to the “leaves” of the dendrogram. The conventional names of the regions are labeled. |
In this section we study the internal structure of the molecular gas in the individual regions. Previously, the structure of molecular gas was studied in terms of the clumps, and quantified using parameters that are evaluated for the whole clumps. While these methods do provide constraints on the role of gravity inside the regions, the role of gravity on scales larger than the individual gas condensations is neglected. The spatial structure of molecular gas larger than the clump scale can be quantified using the dendrogram algorithm. However, the dendrogram method is contour-based, and only the connection between the adjacent regions in the tree diagram are preserved. This makes it difficult to use dendrogram to quantify the structure of molecular gas on the large scale.
 |
Fig. 9 Dependence of velocity and velocity dispersion as a function of radius. Here the solid lines represent the velocities of the regions, and the bars represent the velocity dispersions of the regions at given radii. The vertical extent of the errorbars are the 3D velocity dispersion |
 |
Fig. 10 Amount of molecular gas enclosed in regions with different thresholds of the G-virial. The x-axis is the threshold of G-virial which we take to define the region, and the y-axis is the amount of gas that is enclosed in the region. |
 |
Fig. 11 G-virial as a function of radius for different regions. |
 |
Fig. 12 Enclosed mass as a function of radius for different regions. The scaling relation from Larson (1981) and Kauffmann et al. (2010b) are added. For all the curves, the G-virial decreases with increasing radii. |
Here we provide an analysis of the structure of the individual regions with the G-virial method. As we have shown in Sect. 5.3, the intrinsic mass-radius and velocity-radius relations in the model can be reconstructed with our G-virial method to a good accuracy if the velocity dispersion increases with the size.
In Fig. 9 we plot the dependence of velocity v0 and velocity dispersion σv on the radii of the regions. The inner parts of the regions are clearly at the center of the outer part of the regions in velocity space. This means the central part of the regions remains quiescent with respect to the outer parts, and this is consistent with the findings by Kirk et al. (2010), Walsh et al. (2004) and André et al. (2007).
We assess the importance of gravity in these regions with the G-virial method. In our method, a larger G-virial is related to a larger importance of gravity, and as a result the importance of gravity at a given region can be quantified by measuring the amount of gas at different thresholds of the G-virial parameter. In Fig. 10, we plot the dependence of gas mass on the G-virial threshold for different regions, and in Fig. 11 we plot the dependence of the G-virial on the radius. For all the regions, the G-virial increases towards the centers. For cluster-bearing regions such as NGC 1333 in Perseus and L1688 in Ophiuchus, much higher G-virial values have been reached at their centers. This implies that gravity is more important for the clustered mode of star formation.
With our method it is straightforward to derive relations such as the mass-radius and velocity-size relation. Recently, there has been growing interest in quantifying cloud structure in terms of various mass-size relations (e.g., Kauffmann et al. 2010a,b). In Fig. 12 we plot the mass-size relation obtained using our G-virial method (see Sect. 5). Our mass-size relation is different from that of Kauffmann et al. (2010b) since we use the G-virial contours to define our regions, and mass is evaluated within a given region where the G-virial is larger than the threshold. In Kauffmann et al. (2010b) the mass in evaluated within a region where the column density is larger than a given threshold. In our case, along one single line of sight, only the gas that stays within a given surface of a constant value of the G-virial is taken into account while in Kauffmann et al. (2010b) all the mass along the line of sight is taken into account. Similar to Kauffmann et al. (2010b), we also found that cluster-bearing regions such as L1688 and NGC 1333 are more massive in terms of molecular gas than the regions devoid of clusters at a give radius. In Fig. 12 we also plot the scaling relations proposed in Larson (1981, m(r) = 460 M⊙(r/ pc)1.9, and Kauffmann et al. (2010b, m(r) = 400 M⊙(r/ pc)1.7 , and found that both provide approximate descriptions of the structure of the regions.
Molecular clouds are believed to be turbulence-dominated, and this is mainly inferred from the fact that the clouds obey the velocity-linewidth relation (Larson 1981). In Fig. 13 we plot the 3D velocity dispersion of our regions as a function of radius. Here the 3D velocity dispersion is 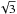 times the velocity dispersion evaluated in Eq. (20). The scaling relation from Larson (1981) is also plotted (L/ pc ~ 1.01 × (σv/ kms-1)0.38). In our case, the velocity-linewidth relation is evaluated for centrally condensed objects, and a smaller physical scale is related to the inner part of a gas condensation, whereas in Larson (1981) a smaller physical scale is related to a smaller size of a subregion in a cloud11. For our centrally condensed objects, the scaling relation from Larson (1981) seems to be valid. We also note that cluster-bearing regions such as NGC 1333 and L1688 have much larger velocity dispersions at large radii.
times the velocity dispersion evaluated in Eq. (20). The scaling relation from Larson (1981) is also plotted (L/ pc ~ 1.01 × (σv/ kms-1)0.38). In our case, the velocity-linewidth relation is evaluated for centrally condensed objects, and a smaller physical scale is related to the inner part of a gas condensation, whereas in Larson (1981) a smaller physical scale is related to a smaller size of a subregion in a cloud11. For our centrally condensed objects, the scaling relation from Larson (1981) seems to be valid. We also note that cluster-bearing regions such as NGC 1333 and L1688 have much larger velocity dispersions at large radii.
Heyer et al. (2009) found a dependence of the scaling coefficient σv/r1 / 2 of Larson’s relation on the column density, and attributed this to the fact that the clouds are in self-gravitational equilibrium. We plot σv/r1 / 2 as a function of column density Σ ≡ M/πr2, where M is the mass and r is the radius of our regions (Fig. 14). Since we decompose one region into a set of nested subregions based on the G-virial, one single region will appear as a curve in Fig. 14. All our regions are quite close to being gravitationally bound, and the scatter around the y-axis is much smaller than what is found for Milky Way molecular clouds as studied in Heyer et al. (2009). This difference arises mainly from the fact that the G-virial method tends to identify regions that are gravitationally coherent.
 |
Fig. 13 3D velocity dispersion as a function of radius for different regions. The velocity-linewidth relation from Larson (1981) is also plotted. |
 |
Fig. 14 σv/r1 / 2 as a function of column density σ for the regions. In order to be consistent with Heyer et al. (2009), σv is the 1D velocity dispersion as defined in Eq. (20) and Σ ≡ M/πr2 where M is the mass r is the radius. The solid straight line shows the boundary below which the structures are gravitationally bound. It is defined as σv/r1 / 2 = (πG/ 5)1 / 2Σ1 / 2. The gray crosses come from the catalogue of giant molecular clouds studied in Roman-Duval et al. (2010). |
7. Conclusion
7.1. Results and perspectives
In this paper we proposed a general method (G-virial) for studying the structure molecular clouds. Different from the previous methods which decompose molecular clouds based on contours in the 2D plane or 3D PPV data cubes, in this method a map is generated by taking all the gravitational interactions between all the voxels in the 3D data cubes into account.
The generated 3D G-virial maps have a dimensionless unit that is the same as that of the virial parameter, and a larger G-virial is related to a larger chance of being gravitationally bound. Therefore, the method provides a global picture of gravity in the PPV space. Using a hydrodynamical simulation model and a simple spherical-symmetric model, we demonstrate the connection between G-virial calculated in the observed PPV data cube and the G-virial calculated from the model. We found that the two are positively related. A larger G-virial is therefore linked to a larger chance of being gravitationally bound. Different from the virial parameter which quantifies self-gravity, the G-virial quantifies the effect of global gravity on the gas where all the interactions between all the particles in the 3D data cubes have been taken into account.
A map of this kind enables us to to identify regions in molecular clouds in terms of gravitationally coherent regions. Compared with previous ways of defining regions based on emission, the regions identified from the G-virial maps more coherent and are less dependent on the technical parameters. Another advantage of such a definition is that the regions identified are coherent under gravity and are likely to collapse on their own.
We also demonstrated how to use the G-virial maps to quantify the structures of the identified gas condensations in terms of mass-radius and velocity dispersion-radius relations. We found that both the mass-radius relation and the velocity-dispersion relation of the model can be reconstructed with the help of the G-virial with a good fidelity when the model is symmetric. If the model is not symmetric, the G-virial map can used to quantify the structures of the gas condensations, and it allows us to compare different structures.
As examples, we analyzed the 13CO(1–0) emission from the Perseus and Ophiuchus molecular clouds, and found that both can be decomposed into several regions which are gravitationally coherent (Fig. 8). Moreover, the cluster-bearing regions show higher values of G-virial at the centers which implies that gravity plays a more prominent role in these parts (Fig. 11). We carried out an analysis of a total of five regions identified in the Perseus and Ophiuchus molecular cloud, and derived mass-size relations and velocity dispersion-size relations for the regions. We also found that cluster-bearing regions are more massive at a given radius than those which do not bear a cluster (Fig. 12), and the cluster-bearing regions have a higher velocity dispersion at the outer parts (Fig. 13).
The method is general and can be applied to a variety of objects observed in 3D PPV space where gravity is supposed to play a role, and from the observations the method offers ways to quantify and compare these structures. We leave these possibilities for further explorations.
The importance of gravity in molecular clouds remains unclear. The effect of gravity as compared to kinetic motion is usually quantified using the virial parameter. The major uncertainty of the virial parameter comes from the definition of boundaries the regions. With the G-virial method, we can eliminate this uncertainty by focusing on the regions that are gravitationally coherent. As shown in Fig. 14, the G-virial-defined regions are much closer to being gravitationally bound than the giant molecular clouds studied in Heyer et al. (2009). A study of a larger sample of molecular clouds can potentially tell if gravity is important throughout the Milky Way molecular clouds, and we leave this for a further study.
7.2. Caveats
Like all the other methods that quantify the ISM structures, our method is influenced by the line-of-sight confusion. One advantage of our method is that the line-of-sight confusion can be reduced by taking the velocity information into account. For a single object, if the velocity dispersion increases with radius, the G-virial method can take this into account and reduce the line-of-sight confusion effect. If different objects have different velocities, they will be separated easily. If different objects with comparable mass velocity are found on the same line of sight, the G-virial method becomes inaccurate.
The G-virial is a relative measure of the gravitational boundedness. As a result, it is not possible to tell whether a region is gravitationally bound based on the G-virial. However, a larger G-virial value means a region is more likely to be gravitationally bound. It is also possible to derive the virial parameter afterwards based on the iso-G-virial contours.
Online material
Movie 1 Access here
Appendix A: Relation between G-virial and the virial parameter
The relative importance between gravitational and kinetic energy is usually characterized with the virial parameter, which is introduced in Bertoldi & McKee (1992). To evaluate the virial parameter, it is necessary to define a structure on which the virial parameter is calculated.
One difference between G-virial and the virial parameter is that to evaluate the G-virial no such boundary is needed. Therefore the G-virial can be viewed as a generalization of the virial parameter to a continuous distribution of mass.
To illustrate the physical meaning of the G-virial, we define a quantity called particle virial, p-virial, which is the ratio between the gravitational energy of a particle to its kinetic energy αp−virial = Ep/ 2Ek. The potential energy Ep is determined by m × φ where m is the mass of the particle and φ is the gravitation potential, and Ek is determined as 1 / 2 × m(v − vc)2. To define the kinetic energy, the velocity of the center of mass vc is needed. Therefore p-virial is only suitable in the cases where a center of mass can be easily found. In the case of a molecular cloud, this is not straightforward because inside a molecular cloud the condensations can move at different velocities. The velocity of the center of mass depends on which clumps are included in the calculation, which is not unique. This difficulty is illustrated in Fig. A.1.
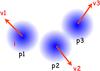 |
Fig. A.1 The difficulty of finding a proper center of mass. We consider three clumps p1, p2, p3 moving at velocities v1, v2, v3. If we are interested in whether i is gravitationally bound, since the majority of attraction comes from p1, physically the center of mass should be the center of mass of p1 instead of the center of mass of the three clumps p1, p2, p3, since p2 and p3 do not contribute much gravitational attraction to i compared to p1. Therefore to estimate the gravitational boundedness, a naive calculation of the center of mass where all the mass in the whole cloud is included is not appropriate. In the case of a complicated distribution of gas, finding the center of mass is not straightforward. |
One major advantage of the G-virial over the p-virial is that no center of mass is needed. The G-virial is the sum of the gravitational boundedness, and to evaluate it we do not need to introduce the center of mass. Therefore, the G-virial can provide estimates of the importance of gravity when the geometry of the object is complicated and the center of mass is not well defined.
Appendix B: Dependence on of G-virial the smoothing velocity c0
The only free parameter in our method is the smoothing velocity c0 in Eq. (6). We added this parameter to avoid the divergence of Eq. (6) when the separation of velocity is zero.
Physically, if the velocity separation is zero, and if two gas particles spatially coincide with each other, the gravitational interaction will cause them to collide. However, the velocity separation cannot be zero since the gas also has velocity dispersions that have either thermal or non-thermal origin (Larson 1981). A physically lower limit of c0 should be the sound speed.
In reality, this is also affected by the superposition along the line of sight, since different gases that are physically unassociated can stay along the same line of sight and therefore appear to be gravitationally bound. Therefore, it is difficult to find a unique value of c0 based on first principles. In our case, we choose c0 to be 1 km s-1, which is larger than and still comparable to the sound speed.
Here we investigate how our results can be affected by the parameter c0. First, we made a G-virial map by assuming c0 = 1 km s-1 and then we made another map by assuming c0 = 2 km s-1. Finally, we made a voxel-by-voxel comparison of the maps (Fig. B.1). We found the major effect of changing c0 on the absolute values of G-virial: if we change c0 to 2 km s-1 the G-virial decreases by a factor of ~2. However, there is good correspondence between the old and new G-virial values. Therefore, changing c0 affects the absolute values of the G-virial; however, the relative values are unaffected. Therefore, all our figures should be unaffected by a change of c0 and the G-virial axes of Figs. 10 and 11 will change accordingly.
In the case where the G-virial is applied to different data cubes, in order for the results to be comparable, a unique choice of c0 is necessary.
 |
Fig. B.1 Comparison of G-virial map of the Ophiuchus molecular cloud under different c0. The horizontal axis is the G-virial calculated assuming c0 = 1 km s-1 and the vertical axis is the G-virial calculated assuming c0 = 2 km s-1. The grayscale image stands for the number of voxels that fall into each bin. |
Appendix C: 3D renderings of G-virial of the Perseus and Ophiuchus molecular clouds
 |
Fig. C.1 Volume rending representations of the 13CO(1–0) emission and the corresponding G-virial map. The upper panel shows the result from the Perseus molecular cloud and the lower panel shows the result from the Ophiuchus molecular cloud. Blue stands for 13CO(1–0) emission and red and orange stand for G-virial. Both clouds are projected along the velocity direction. For the Perseus molecular cloud, the iso-surfaces of 13CO(1–0) emission start from 0.3 K and increase in steps of 0.64 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. For the Ophiuchus molecular cloud, the contours of 13CO(1–0) emission start from 0.3 K and increase in steps of 1.24 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. |
In order to provide intuitive representations of our G-virial maps, we present volume renderings of the 3D PPV data cubes with yt (Turk et al. 2011)12 in Fig. 7. A movie can be found in the electronic edition of the journal.
Appendix D: Comparison with other methods
The previous methods to quantify the structure of molecular condensations such as Clumpfind and Dendrogram focus on the structure traced by the intensity map. The Clumpfind method tends to produces isolated structures. The Dendrogram produces hierarchical representations of the nested isosurfaces in 3D molecular line data cubes, and offers multi-scale decompositions. It can be applied to a much larger variety of situations. Both methods work in 2D (position-position) and 3D (PPV) space and both methods decompose the data to some extent.
The G-virial method presented in this paper is also based on a map of intensity in 3D PPV space. However, its output is neither a list of structures (as in the case of the Clumpfind) nor a tree representation of a hierarchy of structures (as in the gas of the Dendrogram). Instead, it produces a map of the importance of gravity in the 3D PPV. The output is also a map 3D PPV space. The G-virial map itself does not provide a decomposition of the data. To decompose the cloud into regions and to analyze their properties, other methods are needed.
In this work, we use the Dendrogram to identify gravitationally coherent regions from the G-virial map, and use the iso-G-virial contours to quantify the properties of the regions in the M-r and σv-r plane. The G-virial method is not a replacement of the other methods, but it provides a new map on which those methods could be applied.
Here σ is the velocity dispersion and M is the mass (Bertoldi & McKee 1992). The surface terms and the magnetic terms are neglected. See Ballesteros-Paredes (2006) for a thorough discussion.
Such regions have been defined with the clumpfind (Williams et al. 1994) and the dendrogram (Rosolowsky et al. 2008) programs in the past.
In Larson (1981) the index is 0.38. In Roman-Duval et al. (2011) the index is found to be 0.51.
Here our virial parameter is Ep/ 2Ek, and in Bertoldi & McKee (1992) the virial parameter is 2Ek/Ep.
The simulations are available at http://starformat.obspm.fr/starformat/documentation.jsp
To make the G-virial-derived relations overlap with the model values, we scaled the estimated radius by a factor of 1.4 and the estimated velocity dispersion by a factor of 1.45. This adjustment is made in order to make it easier to compare different curves. In practice, the radii of the estimated regions are based on the tensor of second moments of the position coordinates, and the radii do not necessarily coincide with the radii defined in the model. A similar argument also applies to the estimation of the velocity dispersion.
Avaliable at https://dendrograms.readthedocs.org/en/latest/
This is similar to the case of Smith et al. (2009) where they identified structures form a simulation in the 3D position-position-position space based on gravitational potential.
The physical scale here can have different meanings (see Lazarian & Pogosyan 2004; Heyer & Brunt 2004; Roman-Duval et al. 2011).
Available at http://yt-project.org/
Acknowledgments
Guang-Xing Li is supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. Guang-Xing Li thanks Dr. Ke-Jia Lee for helping with the calculations and thanks Dr. Arnaud Belloche for discussions. We thank Eve Ostriker and Hao Gong for email exchanges. This study makes use of data from the COMPLETE survey. We also thank the yt and astrodendro teams for making their codes available, and would like to thank Thomas Robitaille for email exchanges. Dr. James Urquhart and Rosie Chen are acknowledged for careful readings of the draft and for their helpful comments. We thank the anonymous referee for several thorough and careful reviews of the paper and his/her insightful comments, and thank Malcolm Walmsley for his efforts.
References
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J. 2006, MNRAS, 372, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Beaumont, C. N., Offner, S. S. R., Shetty, R., Glover, S. C. O., & Goodman, A. A. 2013, ApJ, 777, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- de Geus, E. J., de Zeeuw, P. T., & Lub, J. 1989, A&A, 216, 44 [NASA ADS] [Google Scholar]
- Dib, S., Bell, E., & Burkert, A. 2006, ApJ, 638, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, H., & Ostriker, E. C. 2011, ApJ, 729, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Rosolowsky, E. W., Borkin, M. A., et al. 2009, Nature, 457, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gutermuth, R. A., Megeath, S. T., Myers, P. C., et al. 2009, ApJS, 184, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M. H., & Brunt, C. M. 2004, ApJ, 615, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Shetty, R., Myers, P. C., & Goodman, A. A. 2010a, ApJ, 712, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Shetty, R., Myers, P. C., & Goodman, A. A. 2010b, ApJ, 716, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., & Goldsmith, P. F. 2013, ApJ, 779, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, H., Pineda, J. E., Johnstone, D., & Goodman, A. 2010, ApJ, 723, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Pogosyan, D. 2004, ApJ, 616, 943 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pichardo, B., Vázquez-Semadeni, E., Gazol, A., Passot, T., & Ballesteros-Paredes, J. 2000, ApJ, 532, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Ridge, N. A., Di Francesco, J., Kirk, H., et al. 2006, AJ, 131, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., Rathborne, J., & Simon, R. 2010, ApJ, 723, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Federrath, C., Brunt, C., et al. 2011, ApJ, 740, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Collins, D. C., Kauffmann, J., et al. 2010, ApJ, 712, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., Bania, T. M., & Heyer, M. H. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Clark, P. C., & Bonnell, I. A. 2009, MNRAS, 396, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, A. J., Myers, P. C., & Burton, M. G. 2004, ApJ, 614, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Whiting, M. T. 2012, MNRAS, 421, 3242 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, Protostars and Planets IV, 97 [Google Scholar]
All Figures
 |
Fig. 1 Setup of the problem. We consider a mass distribution in a 3D PPV data cube. This is represented as the black grid. x–y represents the spatial dimensions and v represents the velocity dimension. The mass distribution is represented in blue. For each voxel i, its G-virial can be determined by taking its interactions with all the voxels j (not excluding i) into account. See Sect. 2 for details. |
| In the text | |
 |
Fig. 2 a) Map of the peak brightness temperature of the simulated 13CO(1–0) emission along the velocity axis. b) Position-velocity map of peak brightness temperatures of 13CO(1–0) along the Y-axis. c) Position-velocity map of peak brightness temperatures of 13CO(1–0)) along the X-axis. |
| In the text | |
 |
Fig. 3 Comparison between the G-virialmodel calculated from the model and the G-virialreconstructed, which is reconstructed from the simulated observations in the PPV space. Panel a) shows the result for the hydrodynamic simulation; and panel b) shows the result for the analytical model with γρ = −2.2 and γv = 0.5. The colors stand for the amount of mass in a given interval. |
| In the text | |
 |
Fig. 4 Comparison between between G-virialmodel and G-virialreconstructed in the PPV space for the hydrodynamical model described in Sect. 5.2. In the model, turbulence is injected through compressible forcing, and no self-gravity is included (Federrath et al. 2008). The G-virialmodel in the PPV space is defined as the mass-weighted average of the G-virialmodel in the PPP space, which is defined in 12. Here, the grayscale image is the simulated 13CO(1–0) emission from the model. The red contours stand for the G-virialmodel, and the contour levels are (6, 5, 10). The blue contours stand for the G-virialreconstructed, and the contour levels are (3, 6). It worth noting that the G-virialmodel and the G-virialreconstructed agrees better at regions where mass is traced. This can be seen in the v = −0.2 km s-1 channel. They agree better at the regions where mass is traced (e.g., the red arrow), but does not agree well at the region without mass (e.g., the blue arrow). |
| In the text | |
 |
Fig. 5 Comparison between the structure of the model and the structure reconstructed through the G-virial for different sets of model parameters. The upper panels show the results where the analytical model is constructed with different γρ, and the lower panels show the results where the analytical model is constructed with different γv. The left panels are the mass-radius relations and the right panels are the velocity dispersion-radius relations. Here the radius is scaled up by a factor of 1.4 and the velocity dispersion is scaled up by a factor of 1.45 for an easy comparison. |
| In the text | |
 |
Fig. 6 G-virial as a function of radii for models with different γρ and γv. |
| In the text | |
 |
Fig. 7 Channel maps of the 13CO(1–0) emission and the corresponding G-virial. The upper panel shows the results from the Perseus molecular cloud and the lower panel shows the results from the Ophiuchus molecular cloud. Grayscale images stand for 13CO(1–0) emission and the red contours represents the G-virial. Contour levels start from 1.2 in steps of 0.8. |
| In the text | |
 |
Fig. 8 Regions identified by applying the dendrogram algorithm to our G-virial map. The results from the Perseus molecular cloud (upper panel) and Ophiuchus molecular cloud (lower panel) are presented. The grayscale images correspond to the velocity-integrated 13CO(1–0) emission and the contours correspond to the projected boundaries of the identified regions. These regions correspond to the “leaves” of the dendrogram. The conventional names of the regions are labeled. |
| In the text | |
 |
Fig. 9 Dependence of velocity and velocity dispersion as a function of radius. Here the solid lines represent the velocities of the regions, and the bars represent the velocity dispersions of the regions at given radii. The vertical extent of the errorbars are the 3D velocity dispersion |
| In the text | |
 |
Fig. 10 Amount of molecular gas enclosed in regions with different thresholds of the G-virial. The x-axis is the threshold of G-virial which we take to define the region, and the y-axis is the amount of gas that is enclosed in the region. |
| In the text | |
 |
Fig. 11 G-virial as a function of radius for different regions. |
| In the text | |
 |
Fig. 12 Enclosed mass as a function of radius for different regions. The scaling relation from Larson (1981) and Kauffmann et al. (2010b) are added. For all the curves, the G-virial decreases with increasing radii. |
| In the text | |
 |
Fig. 13 3D velocity dispersion as a function of radius for different regions. The velocity-linewidth relation from Larson (1981) is also plotted. |
| In the text | |
 |
Fig. 14 σv/r1 / 2 as a function of column density σ for the regions. In order to be consistent with Heyer et al. (2009), σv is the 1D velocity dispersion as defined in Eq. (20) and Σ ≡ M/πr2 where M is the mass r is the radius. The solid straight line shows the boundary below which the structures are gravitationally bound. It is defined as σv/r1 / 2 = (πG/ 5)1 / 2Σ1 / 2. The gray crosses come from the catalogue of giant molecular clouds studied in Roman-Duval et al. (2010). |
| In the text | |
 |
Fig. A.1 The difficulty of finding a proper center of mass. We consider three clumps p1, p2, p3 moving at velocities v1, v2, v3. If we are interested in whether i is gravitationally bound, since the majority of attraction comes from p1, physically the center of mass should be the center of mass of p1 instead of the center of mass of the three clumps p1, p2, p3, since p2 and p3 do not contribute much gravitational attraction to i compared to p1. Therefore to estimate the gravitational boundedness, a naive calculation of the center of mass where all the mass in the whole cloud is included is not appropriate. In the case of a complicated distribution of gas, finding the center of mass is not straightforward. |
| In the text | |
 |
Fig. B.1 Comparison of G-virial map of the Ophiuchus molecular cloud under different c0. The horizontal axis is the G-virial calculated assuming c0 = 1 km s-1 and the vertical axis is the G-virial calculated assuming c0 = 2 km s-1. The grayscale image stands for the number of voxels that fall into each bin. |
| In the text | |
 |
Fig. C.1 Volume rending representations of the 13CO(1–0) emission and the corresponding G-virial map. The upper panel shows the result from the Perseus molecular cloud and the lower panel shows the result from the Ophiuchus molecular cloud. Blue stands for 13CO(1–0) emission and red and orange stand for G-virial. Both clouds are projected along the velocity direction. For the Perseus molecular cloud, the iso-surfaces of 13CO(1–0) emission start from 0.3 K and increase in steps of 0.64 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. For the Ophiuchus molecular cloud, the contours of 13CO(1–0) emission start from 0.3 K and increase in steps of 1.24 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.