| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424030 | |
| Published online | 11 June 2015 | |
Online material
Movie 1
Download Video: Formats: mp4 (772.2 KB) | webm (299.9 KB) | ogg (1.1 MB) | Original mp4 (772.2 KB)
Appendix A: Relation between G-virial and the virial parameter
The relative importance between gravitational and kinetic energy is usually characterized with the virial parameter, which is introduced in Bertoldi & McKee (1992). To evaluate the virial parameter, it is necessary to define a structure on which the virial parameter is calculated.
One difference between G-virial and the virial parameter is that to evaluate the G-virial no such boundary is needed. Therefore the G-virial can be viewed as a generalization of the virial parameter to a continuous distribution of mass.
To illustrate the physical meaning of the G-virial, we define a quantity called particle virial, p-virial, which is the ratio between the gravitational energy of a particle to its kinetic energy αp−virial = Ep/ 2Ek. The potential energy Ep is determined by m × φ where m is the mass of the particle and φ is the gravitation potential, and Ek is determined as 1 / 2 × m(v − vc)2. To define the kinetic energy, the velocity of the center of mass vc is needed. Therefore p-virial is only suitable in the cases where a center of mass can be easily found. In the case of a molecular cloud, this is not straightforward because inside a molecular cloud the condensations can move at different velocities. The velocity of the center of mass depends on which clumps are included in the calculation, which is not unique. This difficulty is illustrated in Fig. A.1.
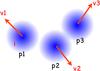 |
Fig. A.1
The difficulty of finding a proper center of mass. We consider three clumps p1, p2, p3 moving at velocities v1, v2, v3. If we are interested in whether i is gravitationally bound, since the majority of attraction comes from p1, physically the center of mass should be the center of mass of p1 instead of the center of mass of the three clumps p1, p2, p3, since p2 and p3 do not contribute much gravitational attraction to i compared to p1. Therefore to estimate the gravitational boundedness, a naive calculation of the center of mass where all the mass in the whole cloud is included is not appropriate. In the case of a complicated distribution of gas, finding the center of mass is not straightforward. |
| Open with DEXTER | |
One major advantage of the G-virial over the p-virial is that no center of mass is needed. The G-virial is the sum of the gravitational boundedness, and to evaluate it we do not need to introduce the center of mass. Therefore, the G-virial can provide estimates of the importance of gravity when the geometry of the object is complicated and the center of mass is not well defined.
Appendix B: Dependence on of G-virial the smoothing velocity c0
The only free parameter in our method is the smoothing velocity c0 in Eq. (6). We added this parameter to avoid the divergence of Eq. (6) when the separation of velocity is zero.
Physically, if the velocity separation is zero, and if two gas particles spatially coincide with each other, the gravitational interaction will cause them to collide. However, the velocity separation cannot be zero since the gas also has velocity dispersions that have either thermal or non-thermal origin (Larson 1981). A physically lower limit of c0 should be the sound speed.
In reality, this is also affected by the superposition along the line of sight, since different gases that are physically unassociated can stay along the same line of sight and therefore appear to be gravitationally bound. Therefore, it is difficult to find a unique value of c0 based on first principles. In our case, we choose c0 to be 1 km s-1, which is larger than and still comparable to the sound speed.
Here we investigate how our results can be affected by the parameter c0. First, we made a G-virial map by assuming c0 = 1 km s-1 and then we made another map by assuming c0 = 2 km s-1. Finally, we made a voxel-by-voxel comparison of the maps (Fig. B.1). We found the major effect of changing c0 on the absolute values of G-virial: if we change c0 to 2 km s-1 the G-virial decreases by a factor of ~2. However, there is good correspondence between the old and new G-virial values. Therefore, changing c0 affects the absolute values of the G-virial; however, the relative values are unaffected. Therefore, all our figures should be unaffected by a change of c0 and the G-virial axes of Figs. 10 and 11 will change accordingly.
In the case where the G-virial is applied to different data cubes, in order for the results to be comparable, a unique choice of c0 is necessary.
 |
Fig. B.1
Comparison of G-virial map of the Ophiuchus molecular cloud under different c0. The horizontal axis is the G-virial calculated assuming c0 = 1 km s-1 and the vertical axis is the G-virial calculated assuming c0 = 2 km s-1. The grayscale image stands for the number of voxels that fall into each bin. |
| Open with DEXTER | |
Appendix C: 3D renderings of G-virial of the Perseus and Ophiuchus molecular clouds
 |
Fig. C.1
Volume rending representations of the 13CO(1–0) emission and the corresponding G-virial map. The upper panel shows the result from the Perseus molecular cloud and the lower panel shows the result from the Ophiuchus molecular cloud. Blue stands for 13CO(1–0) emission and red and orange stand for G-virial. Both clouds are projected along the velocity direction. For the Perseus molecular cloud, the iso-surfaces of 13CO(1–0) emission start from 0.3 K and increase in steps of 0.64 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. For the Ophiuchus molecular cloud, the contours of 13CO(1–0) emission start from 0.3 K and increase in steps of 1.24 K. The contours of the G-virial starts from 1.2 and increase in steps of 0.8. |
| Open with DEXTER | |
In order to provide intuitive representations of our G-virial maps, we present volume renderings of the 3D PPV data cubes with yt (Turk et al. 2011)12 in Fig. 7. A movie can be found in the electronic edition of the journal.
Appendix D: Comparison with other methods
The previous methods to quantify the structure of molecular condensations such as Clumpfind and Dendrogram focus on the structure traced by the intensity map. The Clumpfind method tends to produces isolated structures. The Dendrogram produces hierarchical representations of the nested isosurfaces in 3D molecular line data cubes, and offers multi-scale decompositions. It can be applied to a much larger variety of situations. Both methods work in 2D (position-position) and 3D (PPV) space and both methods decompose the data to some extent.
The G-virial method presented in this paper is also based on a map of intensity in 3D PPV space. However, its output is neither a list of structures (as in the case of the Clumpfind) nor a tree representation of a hierarchy of structures (as in the gas of the Dendrogram). Instead, it produces a map of the importance of gravity in the 3D PPV. The output is also a map 3D PPV space. The G-virial map itself does not provide a decomposition of the data. To decompose the cloud into regions and to analyze their properties, other methods are needed.
In this work, we use the Dendrogram to identify gravitationally coherent regions from the G-virial map, and use the iso-G-virial contours to quantify the properties of the regions in the M-r and σv-r plane. The G-virial method is not a replacement of the other methods, but it provides a new map on which those methods could be applied.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


