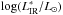| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425399 | |
| Published online | 20 May 2015 | |
Dust attenuation up to z ≃ 2 in the AKARI North Ecliptic Pole Deep Field
1
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326, 13388
Marseille, France
e-mail:
veronique.buat@lam.fr
2
Institute of Space and Astronautical Science,
Japan Aerospace Exploration Agency,
Sagamihara, 229-8510
Kanagawa,
Japan
3
Department of Astronomy CSS Bldg., Rm. 1204, Stadium Dr. University of Maryland College
Park, MD
20742-2421, USA
4
University of Crete, Department of Physics and Institute of
Theoretical & Computational Physics, 71003
Heraklion,
Greece
5
Division of Particle and Astrophysical Science, Nagoya
University, Furo-cho, Chikusa-ku,
464-8602
Nagoya,
Japan
6
National Centre for Nuclear Research, ul. Hoza 69,
00-681
Warszawa,
Poland
7 Institute of Astronomy, National Tsing Hua University, No.
101, Sect. 2, Kuang-Fu Road, Hsinchu, Taiwan 30013, R.O.C.
8
University of California, Los Angeles, CA
90095-1547,
USA
9 Academia Sinica, Institute of Astronomy and Astrophysics,
No.1, Sect. 4, Roosevelt Rd, Taipei 10617, Taiwan, R.O.C.
10
RAL Space, CCLRC Rutherford Appleton Laboratory,
Chilton, Didcot, Oxfordshire
OX11 0QX,
UK
11
The Open University, Milton Keynes, MK7 6AA, UK
12
Oxford Astrophysics, Denys Wilkinson Building, University of
Oxford, Keble Rd,
Oxford
OX1 3RH,
UK
13
Instituto de Astronomía sede Ensenada, UNAM,
Km 103, Carret.
Tijuana-Ensenada, Ensenada, 22860, Mexico
14
University of California, San Diego, Center for Astrophysics and Space Sciences, 9500
Gilman Dr., La
Jolla, CA
92093-0424,
USA
15
European Southern Observatory, ESO Headquarters, Karl-Schwarzschild-Str. 2,
85748
Garching bei München,
Germany
16
Max-Planck-Institut für extraterrestische Physik,
Postfach 1312, 85741
Garching,
Germany
Received: 24 November 2014
Accepted: 8 March 2015
Aims. We aim to study the evolution of dust attenuation in galaxies selected in the infrared (IR) in the redshift range in which they are known to dominate the star formation activity in the universe. The comparison with other measurements of dust attenuation in samples selected using different criteria will give us a global picture of the attenuation at work in star-forming galaxies and its evolution with redshift.
Methods. We selected galaxies in the mid-IR from the deep survey of the North Ecliptic Field performed by the AKARI satellite. Using multiple filters of IRC instrument, we selected more than 4000 galaxies from their rest-frame emission at 8 μm, from z ≃ 0.2 to ~2. We built spectral energy distributions from the rest-frame ultraviolet (UV) to the far-IR by adding ancillary data in the optical-near IR and from GALEX and Herschel surveys. We fit spectral energy distributions with the physically-motivated code CIGALE. We test different templates for active galactic nuclei (AGNs) and recipes for dust attenuation and estimate stellar masses, star formation rates, amount of dust attenuation, and AGN contribution to the total IR luminosity. We discuss the uncertainties affecting these estimates on a subsample of galaxies with spectroscopic redshifts. We also define a subsample of galaxies with an IR luminosity close to the characteristic IR luminosity at each redshift and study the evolution of dust attenuation of this selection representative of the bulk of the IR emission.
Results. The AGN contribution to the total IR luminosity is found to be on average approximately 10%, with a slight increase with redshift. The determination of AGN contribution does not depend significantly on the assumed AGN templates except for galaxies detected in X-ray. The choice of attenuation law has a marginal impact on the determination of stellar masses and star formation rates. Dust attenuation in galaxies dominating the IR luminosity function is found to increase from z = 0 to z = 1 and to remain almost constant from z = 1 to z = 1.5. Conversely, when galaxies are selected at a fixed IR luminosity, their dust attenuation slightly decreases as redshift increases but with a large dispersion, confirming previous results obtained at lower redshift.The attenuation in our mid-IR selected sample is found ~2 mag higher than that found globally in the universe or in UV and Hα line selections in the same redshift range. This difference is well explained by an increase of dust attenuation with the stellar mass, in global agreement with other recent studies. Starbursting galaxies do not systematically exhibit a high attenuation. We conclude that the galaxies selected in IR and dominating the star formation exhibit a higher attenuation than those measured on average in the universe because they are massive systems. Conversely UV selected galaxies exhibit a large range of stellar masses leading in a lower average attenuation than that found in an IR selection.
Key words: galaxies: photometry / surveys / infrared: galaxies / ultraviolet: galaxies / galaxies: evolution / galaxies: ISM
© ESO, 2015
1. Introduction
One of the most complex processes in galaxies is star formation and understanding it and its evolution with time remains a challenge for modern astronomy. The evolution of dark matter is now modeled with high accuracy and is shaping the large scale structures in the universe. The physics of baryons, including star formation, is much more difficult to understand and to implement in models of galaxy formation and evolution. The first natural step is to find constrains from observations by measuring a reliable star formation rate (SFR) at various scales and redshifts and studying the main drivers of its variations.
Major progress has been made in the measure of the SFR inside the disk of nearby galaxies with strong relation found between SFR and molecular gas content (e.g., Bigiel et al. 2008; Leroy et al. 2008; Kennicutt & Evans 2012, for a review), and the measure of the star formation efficiency in galaxies is now possible up to large redshifts (e.g., Daddi et al. 2010; Tacconi et al. 2010, 2013; Santini et al. 2014). Besides these studies aimed to understand the process of star formation, the global amount of star formation in the universe is measured by building statistical samples with observables related to the recent star formation. The rest-frame UV emission is frequently privileged. The observations of the GALEX satellite up to z = 1 and the numerous optical surveys give very sensitive UV rest-frame measurements from the nearby universe to high redshifts and for large samples of galaxies (e.g., Salim et al. 2006; Cucciati et al. 2012; Finkelstein et al. 2012). However, UV emission suffers from a major issue, which is dust attenuation. In the nearby universe and within galaxies like the Milky Way, about half of the stellar light is absorbed and re-emitted by dust at wavelengths larger than ~5 μm, and that fraction can increase to more than 90% in starbursting objects. Therefore measuring the IR emission of galaxies has been identified as mandatory for measuring the total SFR, and adding both UV and IR emissions is now recognized as a very robust method to measure the SFR. The development of IR facilities allows the building of statistical samples of galaxies detected in IR, although the lower sensitivity of IR detectors combined with poor spatial resolution makes comparison with UV-optical surveys still difficult. The Spitzer and Herschel deep observations combined with ground-based optical surveys give us a complete view of the star formation up to z ~ 2 (e.g., Reddy et al. 2008, 2012; Buat et al. 2012; Oteo et al. 2014) although selection biases are recognized to be complex (Bernhard et al. 2014; Heinis et al. 2014). The very high redshifts (z ≫ 2) remain almost unexplored in IR even with Herschel Madau & Dickinson (2014) and stacking methods are intensively used to find the average IR emission of optically faint objects not detected individually (e.g., Reddy et al. 2012; Ibar et al. 2013; Heinis et al. 2013, 2014; Pannella et al. 2014; Whitaker et al. 2014).
To complement the analysis of galaxy samples, the comparison of UV and IR luminosity functions gives the global energy budget of the universe. Takeuchi et al. (2005) first compare the UV and IR luminosity functions from z = 0 to z = 1, and Burgarella et al. (2013) extend the analysis up to z = 4 taking advantage of the most recent Herschel measurements. Both studies measure the evolution with redshift of the global dust attenuation by comparing the UV and IR luminosity densities: they found it increases from z = 0 to z = 1.2 and then declining up to z = 4 with a similar amount of dust attenuation at z = 0 and z = 4. Although these results depend on the exact shape of the IR luminosity function, which remains uncertain especially at high redshift (Casey et al. 2014a, for a review), they are found to be very consistent with those obtained by Cucciati et al. (2012) for a large sample of UV selected galaxies in the same redshift range.
Sample selection.
UV and IR luminosity functions exhibit very different shapes (Burgarella et al. 2013, and references therein): bright objects are much more numerous in IR than in UV and the luminosity evolution with redshift is stronger in IR than in UV. The faint end of the IR luminosity function is not well constrained but may be considerably flatter than that measured for the UV luminosity function (Gruppioni et al. 2013). These very different distributions imply that UV or IR selected samples are expected to be composed of different galaxy populations, in terms of luminosity and dust attenuation (Buat et al. 2007a).
The strong impact of dust attenuation and the need to estimate it as accurately as possible when UV data are used has led to numerous investigations of samples of star-forming galaxies. Quite naturally these studies focus on galaxies selected either in their UV rest-frame or from their emission in gas recombination lines. A correlation is found between the amount of dust attenuation and the stellar mass of these galaxies at low and high redshift (Garn & Best 2010; Sawicki 2012; Buat et al. 2012; Ibar et al. 2013; Kashino et al. 2013). Heinis et al. (2014) study the IR properties of UV selected galaxies in the COSMOS field by stacking Herschel/SPIRE images at redshift 1.5, 3 and 4. They find that the average amount of dust attenuation correlates well with the stellar mass in their sample whereas it remains roughly constant when the observed UV luminosity (LUV) varies. For a given LUV, the galaxies exhibit a very large range of masses and thus dust attenuation.
The aim of the present work is to select galaxies in the IR to investigate the impact of this kind of selection on the dust attenuation properties and to compare our results to the ones obtained from UV rest-frame selections or globally in the universe. It is of particular importance since most of the star formation in the universe can be securely measured in IR up to redshift ~2 since the stellar emission reprocessed by dust dominates the unattenuated emission from stars. Numerous studies were already devoted to characterize dust attenuation in IR selected galaxies (e.g., Goldader et al. 2002; Burgarella et al. 2005; Buat et al. 2005; Howell et al. 2010; Takeuchi et al. 2010). A major result of these studies is the deviation of the sources detected in IR surveys from the relation found between the ratio of IR to UV luminosity and the slope of the UV continuum for local starburst galaxies with bluer colors than expected (but see also Murphy et al. 2011). Recently Casey et al. (2014b) attributed this departure to a patchy geometry.
The infrared space telescope AKARI carried out a deep survey of the North Ecliptic Pole (hereafter NEP-deep) with all the filters of the InfraRedCamera (IRC). We take advantage of the continuous filter coverage in the mid-IR to build a 8 μm rest-frame selection following the strategy of Goto et al. (2010). A 8 μm selection is relevant to select dusty galaxies active in star formation since it focuses on the emission of polycyclic aromatic hydrocarbons. Main sequence galaxies defined to have a normal mode of star formation and a tight relation between their SFR and their stellar mass are found to have similar ratios of 8 μm rest-frame to total IR luminosities (Elbaz et al. 2011; Nordon et al. 2012; Murata et al. 2014). For these galaxies, a 8 μm selection is similar to a selection based on their total IR emission. Using the S11, L15, L18W, and L24 filters, we can select galaxies properly on a large range of redshift from z = 0.15 to z = 2.05. Combining the near to mid-IR catalog of Murata et al. (2013) with the optical data of Oi et al. (2014) and with GALEX and Herschel/PACS detections, we are able to build the UV to IR spectral energy distributions (SED) of our selected sources. These SEDs are analyzed with the code CIGALE to measure physical parameters such as dust attenuation, SFR, or stellar masses. We first optimize the SED fitting process on a subsample of galaxies with a full wavelength coverage and spectroscopic redshifts and then we run CIGALE on the whole sample of 4077 galaxies. The amount of dust attenuation and its evolution in redshift is measured and compared to the results found with other selections.
The paper is organized as follows: the sample selection is described in Sect. 2, and the SED fitting process and its optimization on a subsample of galaxies is detailed in Sect. 3. The main result of this work, the measure of dust attenuation and its evolution with redshift, is presented in Sect. 4. In Sect. 5, we compare our results to other measures of dust attenuation for different sample selections and propose the stellar mass as the main driver for dust attenuation. Our conclusions are presented in Sect. 6.
Throughout the paper we use the WMAP7 cosmological parameters. The parameter LIR corresponds to the total luminosity emitted by dust as defined in Sect. 3, and the UV luminosity LUV is defined as νLν at 150 nm. All luminosities are expressed in solar units (L⊙ = 3.83 × 1033 erg s-1).
2. Sample selection
Our aim is to combine data at different wavelengths for galaxies primarily selected at 8 μm in their rest frame. We start with the Murata et al. (2013) catalog of the AKARI-NEP deep survey, which contains 27 770 sources over 0.5 deg2. We cross-matched this catalog with the optical-near-IR catalog of Oi et al. (2014) for which photometric redshift are calculated. We found 23 345 sources in common within a tolerance radius of 1 arcsec on the coordinates. MegaCam (u⋆,g′,r′,i′,z′) and WIRCam (Y,J,Ks) data are available for these sources. The 5σ detection limits correspond to u⋆ = 24.6, g′ = 26.5, r′ = 25.7, i′ = 24.9, z′ = 23.9, Y = 23.2, J = 22.8, and Ks = 22.5 mag (AB scale). The photometric redshifts are estimated using Le Phare software (Ilbert et al. 2006). The redshift accuracy (σΔz/ (1 + z)) is found to be equal to 0.032 at z< 1 and 0.117 at z> 1. We refer to Oi et al. (2014) for a more detailed description.
We perform our 8 μm rest-frame selection following the same strategy as Goto et al. (2010). We consider the four AKARI filters S11, L15, L18 and L24 and define redshift bins so that the observed wavelength of the 8 μm feature corresponds to a transmission of the filters larger than 0.8. We then check that the detection rate in the photometric catalog of Oi et al. (2014) is similar for each subsample of sources detected in one of these these filters (85% for sources detected in the S11 filter, 80% for the L15 and L18 filters, and 78% for the L24 filter), which ensures us that we do not have any systematic bias between our bins. The L18 filter has a very broad bandpass, which largely overlaps those of the L15 and L24 filters. We first define the redshift range reachable with the L15 filter, and then the redshift bin of the L18 filter starts at z = 1.34 in order not to overlap the one defined with the L15 filter. The L24 band has a low sensitivity and we prefer to use it only when the 8 μm rest-frame comes out of the L18 filter (z> 1.85). We define a sample of 4077 alaxies. The redshift distribution is described in Table 1 together with the number of galaxies per bin of redshift defined with each filter.
The AKARI-NEP field was also observed by GALEX for 89 450 s (Program GI4-057001-AKARI-NEP, P.I. M. Malkan). When available we add the GALEX/NUV data for galaxies with redshift lower than 0.925, corresponding to a rest-frame wavelength larger than 1200 Å. The near-UV (NUV) fluxes were measured from the images taken on the MAST database, the flux extraction is performed with DAOPHOT (Mazyed et al., in prep.) and the detected sources are cross-matched with the optical coordinates of the sources within a matching radius of 2 arcsec. NUV fluxes are added to the SED of 1207 sources with z< 0.925.
The AKARI-NEP field was also observed by Herschel with the PACS and SPIRE instruments for 73.5 h (Program OT1-sserj01-1, P.I. S. Serjeant). Given the small number of sources detected with SPIRE in the field studied in this work, we only consider PACS data. Fluxes at 100 and 160 μm from the PACS images were also measured with DAOPHOT (Mazyed et al., in prep.) the match with our selected sources catalog is made with a matching radius of 3.5 arcsec, we keep only sources with a single match within this radius. We find that 599 sources are detected with PACS at 100 μm and 270, both at 100 and 160 μm (Table 1).
We are interested in studying dust attenuation in these galaxies. To this aim, data in the UV range bring information very complementary to those in the IR range. Therefore we check the number of sources for which rest-frame UV data are available. In Table 1 we report the number of sources in each redshift bin with a least one detection at a wavelength lower than 0.25 μm in the rest frame of the galaxy. Approximately 90% of the sources are observed in UV except for the first redshift bin for which only 62% of the selected sources are detected with GALEX.
The AKARI-NEP Deep Field was observed with Chandra with a detection limit of ~10-15 erg s-1 cm-2 in the 0.5−2 keV band. The X-ray source catalog is presented in Krumpe et al. (2015). We used the V1.0 version of the catalog. Unfortunately X-ray observations cover only approximately half of our field. We cross-matched the catalog of X-ray sources from Krumpe et al. (2015) with our selection following their prescription (separation lower than the match radius) and found 147 matches. It corresponds to 6% of our initial sample. We can expect the same low contribution of such X-ray sources for the whole field.
Last, we also define a subsample of our 8 μm selected galaxies with a spectroscopic redshift from the compilation of Oi et al. (2014) and detected with PACS as well as in most of the other bands: 106 galaxies are thus selected, 7 are classified active galactic nucleus (AGN) type 1, and 1 is classified AGN type 2. The field where spectroscopic redshifts are available is entirely covered by the X-ray observations. Fifteen sources are detected, and four out of the seven AGN type 1 and AGN type 2 are also detected in X-ray. This catalog is called SPECZ sample in the following and is used to optimize the SED fitting process. The redshift distribution of the sources included in each sample is shown in Fig. 1.
 |
Fig. 1 Redshift distribution of the whole sample (black solid line) of galaxies detected with PACS (black dotted line) and with a spectroscopic redshift (SPECZ sample: green-filled histogram). |
3. Fitting the spectral energy distributions
The SED fitting is performed with the version v0.3 of the CIGALE code (Code Investigating GALaxy Emission)1 developed with PYTHON. CIGALE combines a UV-optical stellar SED with a dust component emitting in the IR and fully conserves the energy balance between dust absorbed emission and its re-emission in the IR. This energy balance is also observed for the AGN emission absorbed and re-emitted by the dusty torus (see below). The total IR luminosity LIR is defined as the sum of luminosities coming from stellar and AGN light re-processed by dust. Star formation history as well as dust attenuation characteristics, including the attenuation law, are input parameters that can be either taken free or fixed according to the available data or the specific aims. The main characteristics of the code are described in Noll et al. (2009). We refer to Burgarella et al. (in prep.) and Boquien et al. (in prep.) for a detailed description of the new version of the code. Here we only describe the assumptions and choices specific to the current study. The main parameters and range of input values are reported in Table 2. The output values parameters are estimated by building the probability distribution function (PDF) and by taking the mean and standard deviation of the PDF.
Range of values of the input parameters for dust and stellar emission, used for the SED fitting with CIGALE.
3.1. Star formation history
Different scenarios of star formation history are implemented in CIGALE: exponentially declining or rising SFR, delayed SFR, and a declining SFR with an overimposed burst. It is possible to study any SFR by adding a file. As shown in several studies (e.g., Pforr et al. 2012; Buat et al. 2014; Conroy 2013, and references therein), it is difficult to disentangle the different scenarios because of the degeneracy of the fits. As long as IR data are available and we are dealing with galaxies that are actively forming stars, the measure of dust attenuation is not affected by the detailed star formation history (Meurer et al. 1999; Buat et al. 2005, 2011; Cortese et al. 2008; Hao et al. 2011). We adopt a model with two stellar populations: a recent stellar population with a constant SFR on top of an older stellar population created with an exponentially declining SFR. Ages of the older stellar population and young component (tf and tySP respectively) are free parameters (Noll et al. 2009). The initial mass function of Chabrier (2003) is adopted with the stellar synthesis models of Bruzual & Charlot (2003). Compared to the widely used, simple exponentially decreasing SFR, this type of bimodal star formation history is able to better reproduce real systems with several phases of star formation known and to give more realistic stellar ages (Buat et al. 2014, and references therein).
3.2. Dust attenuation recipe and dust re-emission
Since we are fitting the SED of galaxies selected in the IR, the treatment of dust attenuation and re-emission is critical. In CIGALE, dust attenuation is controled by the choice of the attenuation curve. The light re-processed by dust and re-emitted in IR is modeled using IR SED templates.
3.2.1. Attenuation curves
To model the attenuation by dust, the code uses the attenuation law of Calzetti et al. (2000, hereafter C00), and offers the possibility of varying the steepness of this law and adding a bump centered at 2175 Å. We refer to Noll et al. (2009) for a complete description of the dust attenuation prescription, which still holds in the new version of the code. In brief, the dust attenuation is described as 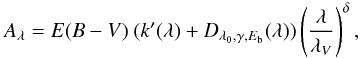 (1)where λV = 5500 Å, k′(λ) comes from Calzetti et al. (2000, Eq. (4)) and Dλ0,γ,Eb(λ), the Lorentzian-like Drude profile commonly used to describe the UV bump (Fitzpatrick & Massa 1990), is defined as
(1)where λV = 5500 Å, k′(λ) comes from Calzetti et al. (2000, Eq. (4)) and Dλ0,γ,Eb(λ), the Lorentzian-like Drude profile commonly used to describe the UV bump (Fitzpatrick & Massa 1990), is defined as 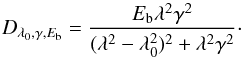 (2)The coarse wavelength coverage in the UV rest frame does not allow us to measure the dust attenuation curve for every galaxy. Instead we can run CIGALE with different predefined attenuation curves and compare the results. We obtained our fiducial attenuation curve by studying high redshift galaxies Buat et al. (2012, hereafter B12), corresponding to Eb = 1.6 and δ = −0.27, which is close to the LMC2 extinction curve with a UV bump of moderate amplitude. We also consider the C00 attenuation law (Eb = 0,δ = 0). Ilbert et al. (2009) found that considering an SMC extinction curve and a screen geometry could help to measure photometric redshifts. The curve corresponding to δ = −0.5 and Eb = 0 is similar to the SMC curve of Gordon et al. (2003) (Boquien et al. 2012) and is added for comparison (hereafter SMC-like). We introduce a differential attenuation for young and old stars, the color excess is reduced by a factor 2 for stars older than 107 years (Calzetti 1997; Charlot & Fall 2000; Panuzzo et al. 2007).
(2)The coarse wavelength coverage in the UV rest frame does not allow us to measure the dust attenuation curve for every galaxy. Instead we can run CIGALE with different predefined attenuation curves and compare the results. We obtained our fiducial attenuation curve by studying high redshift galaxies Buat et al. (2012, hereafter B12), corresponding to Eb = 1.6 and δ = −0.27, which is close to the LMC2 extinction curve with a UV bump of moderate amplitude. We also consider the C00 attenuation law (Eb = 0,δ = 0). Ilbert et al. (2009) found that considering an SMC extinction curve and a screen geometry could help to measure photometric redshifts. The curve corresponding to δ = −0.5 and Eb = 0 is similar to the SMC curve of Gordon et al. (2003) (Boquien et al. 2012) and is added for comparison (hereafter SMC-like). We introduce a differential attenuation for young and old stars, the color excess is reduced by a factor 2 for stars older than 107 years (Calzetti 1997; Charlot & Fall 2000; Panuzzo et al. 2007).
3.2.2. Dust emission templates
The stellar emission absorbed by dust is re-emitted in IR. This emission is generated using different empirical templates. Draine & Li (2007), Casey (2012), and Dale et al. (2014) models are implemented in CIGALE. The templates used in this work are those of Dale et al. (2014). They are updated templates from the Dale & Helou (2002) library, which provides good fits of Herschel data (e.g., Wuyts et al. 2011; Magnelli et al. 2013). Dale et al. (2014) also add a quasar component. Here we use these templates without this quasar contribution since the AGN contribution is defined separately in CIGALE, as described below.
3.3. AGN component
With CIGALE, it is possible to add the contribution of an AGN to the SED. The adopted templates are those of Fritz et al. (2006) based on two components: the emission of the central source and the radiation from the dusty torus in the vicinity heated by the central source. Fritz et al. (2006) introduce a set of six parameters in their model, describing the geometrical configuration of the torus and the properties of the dust and solving the radiation transfer equation. The dust distribution inside the torus is assumed to be smooth. The different parameters are described in Hatziminaoglou et al. (2008). When one accounts for this component in CIGALE, all the free parameters related to this AGN contribution are added to the already numerous parameters related to stellar (direct and re-processed) emission. With only photometric data we are confronted by the well-known degeneracy of SED fitting processes induced by the limited number of data points compared to the number of parameters used to build the SED templates. From simulated composite SEDs with an AGN and a stellar component, Ciesla et al. (2015) find that only extreme values of the angle between the AGN axis and the line of sight, characterizing the nature of the AGN (type 1 or 2), can be estimated. Thus we choose to fix several parameters to average values: from Hatziminaoglou et al. (2008) the ratio of the outer to inner radius is fixed to 60, the dust density parameters β and γ are fixed to − 0.5 and 0, respectively, and the opening angle of the torus is equal to 100°. The remaining free parameters are the optical depth at 9.7 μm (τ9.7) and the angle ψ between the AGN axis and the line of sight.
CIGALE calculates the relative contribution of the dusty torus of the AGN to the total IR luminosity that is called the AGN fraction (fracAGN). We explore several combinations of the three parameters: τ9.7, ψ, and fracAGN. A large number of AGN fractions is introduced since it is the main parameter relevant to the AGN component that we want to retrieve: we consider eight values of fracAGN linearly spaced between 0 and 0.5 (cf. Table 2). Following the prescription of Ciesla et al. (2015), we consider only two extreme values for the angle ψ, ψ = 0° and 80° to reproduce an AGN type 2 and type 1, respectively2. After several trade-offs we also consider a low (τ9.7 = 1) and a high (τ9.7 = 6) optical depth model. Hatziminaoglou et al. (2008) have also introduced models corresponding to low optical depth tori to improve the fits of their SWIRE/SDSS quasars. Our four selected templates are plotted in Fig. 2. We can see that τ9.7 = 6 and ψ = 0° corresponds to a hidden AGN with a strong silicate absorption. The two templates corresponding to ψ = 80° are very similar and correspond to a quasar emission with a strong UV/optical emission. Combining this kind of an SED with a stellar component, even with a low AGN fraction, will induce a high contribution of the AGN. The template corresponding to τ9.7 = 1 and ψ = 0° exhibits a smooth distribution in the mid-IR, not very different from the cases with ψ = 80°, if we ignore the small silicate emission of these templates, which does not affect broadband measurements. However, in this case, the UV-optical part is obscured since crossing the torus leads to a much lower flux than in the case ψ = 80°. The AGN models with a smooth dust distribution are known to produce sudden jumps in the SEDs, and whether the line of sight intercepts the torus or not, a clumpy dust distribution will produce a smoother transition (Feltre et al. 2012). So as not to introduce an overly large contribution of the AGN in the UV-optical, but to allow for a silicate absorption or a smoother distribution in the mid-IR, our fits will be based on two configurations: τ9.7 = 1,6 and ψ = 0° for scenario 1, τ9.7 = 6 and ψ = 0,80° for scenario 23.
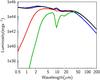 |
Fig. 2 SED templates for AGNs considered in this work and defined from the Fritz et al. (2006) library with different values of the optical depths τ9.7 and viewing angle ψ. The other parameters are fixed as described in the text. Green line: τ9.7 = 6, ψ = 0; red line: τ9.7 = 1, ψ = 0; blue line: τ9.7 = 1, ψ = 80; black line: τ9.7 = 6, ψ = 80. The fiducial models correspond to τ9.7 = 1,6 and ψ = 0. The models represented here correspond to a bolometric luminosity of 1046 erg s-1. |
 |
Fig. 3 Examples of fits for the SPECZ sample with various redshifts, |
 |
Fig. 4 Comparison of |
3.4. Fitting sources with spectroscopic redshifts
The quality of the fitting process is checked on the SPECZ sample for which spectroscopic redshifts are available. The fits are very good, 99 out of the 106 SEDs fitted with a reduced 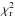 lower than 3 and
lower than 3 and 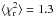 . Some examples are given in Fig. 3.
. Some examples are given in Fig. 3.
3.4.1. AGN templates
The SPECZ sample is well suited to check the influence of the choice of the AGN templates. We explore the two combinations of parameters presented above (scenario 1 and 2). In Fig. 4 we compare the reduced 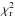 and AGN fractions found with these two configurations, and X-ray sources are checked separately. In the majority of cases a good agreement is found for the
and AGN fractions found with these two configurations, and X-ray sources are checked separately. In the majority of cases a good agreement is found for the 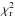 and AGN fraction values. Only two values of τ9.7 or ψ are introduced in both scenarios and the PDF of these parameters cannot be built: for the current discussion, we consider the values of τ9.7 and ψ corresponding to the best model. When two input values of τ9.7 are considered (scenario 1, τ9.7 = 1,6 ), the best model corresponds to τ9.7 = 1 for 85 galaxies (80% of the cases). When two values of ψ are allowed (scenario 2, ψ = 0, 80°), ψ is found equal to 0° (AGN type 2) for the best model of 70 sources (66% of the cases). Eight galaxies exhibit a difference between their
and AGN fraction values. Only two values of τ9.7 or ψ are introduced in both scenarios and the PDF of these parameters cannot be built: for the current discussion, we consider the values of τ9.7 and ψ corresponding to the best model. When two input values of τ9.7 are considered (scenario 1, τ9.7 = 1,6 ), the best model corresponds to τ9.7 = 1 for 85 galaxies (80% of the cases). When two values of ψ are allowed (scenario 2, ψ = 0, 80°), ψ is found equal to 0° (AGN type 2) for the best model of 70 sources (66% of the cases). Eight galaxies exhibit a difference between their 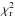 larger than 0.5. All of these galaxies are detected in X-ray and three are classified as AGN type 1 from their spectra. Their AGN fractions are also found to be more dispersed than for the other galaxies. In all but one case
larger than 0.5. All of these galaxies are detected in X-ray and three are classified as AGN type 1 from their spectra. Their AGN fractions are also found to be more dispersed than for the other galaxies. In all but one case 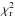 is significantly lower with scenario 1. Hereafter we adopt scenario 1, corresponding to AGN type 2 models with either a high silicate absorption or an almost flat mid-IR continuum, as our fiducial scenario for the AGN component.
is significantly lower with scenario 1. Hereafter we adopt scenario 1, corresponding to AGN type 2 models with either a high silicate absorption or an almost flat mid-IR continuum, as our fiducial scenario for the AGN component.
It is worth noting that the choice of the AGN template substantially modifies its contribution to the UV-optical SED as shown in Fig. 2, and we expect some impact on the determination of the attenuation. This impact is illustrated in Fig. 5 with two examples: a galaxy detected in X-ray and a galaxy defined as “typical” (without any X-ray emission or spectral classification). Their SEDs are fitted with the two scenarios inducing very different dust attenuations: 1.4 mag versus 6.4 mag for the X-ray source and 5.2 mag versus 6.8 mag for the “typical” galaxy. AGN fractions are similar and a low 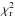 value is obtained for both scenarios. The two corresponding best models are shown: when only AGN type 2 templates are considered (left panels, scenario 1) the UV-optical SED is dominated by the stellar emission, whereas the quasar emission is found to dominate when the best model corresponds to an AGN type 1 (right panels, scenario 2). Finally, we would like to emphasize the difficulty of fitting SEDs with multiple components. As shown in Fig. 5, both fits are satisfactory with
value is obtained for both scenarios. The two corresponding best models are shown: when only AGN type 2 templates are considered (left panels, scenario 1) the UV-optical SED is dominated by the stellar emission, whereas the quasar emission is found to dominate when the best model corresponds to an AGN type 1 (right panels, scenario 2). Finally, we would like to emphasize the difficulty of fitting SEDs with multiple components. As shown in Fig. 5, both fits are satisfactory with 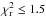 whereas the nature of the AGN component found for each best model (type 1 or 2) differs.
whereas the nature of the AGN component found for each best model (type 1 or 2) differs.
3.4.2. Attenuation curves
Here we analyze the impact of changing the attenuation curve on the estimation of attenuation, SFR, and stellar masses. The code was run with the three different attenuation curves described in Sect. 3.2.1 (B12, C00 and SMC-like). We adopt scenario 1 as our fiducial scenario for the AGN component (τ9.7 = 1,6 and ψ = 0) and check that the results do not depend on the assumed AGN templates (scenario 1 or 2). The fits are very good for the three attenuations curves: in all cases more than 90% of the fits correspond to 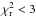 . The SMC-like curve is chosen as the best choice for 25 sources against 38 and 43 for C00 and B12, respectively, implying a slightly lower pertinence for the SMC-like curve as compared to the two others. Systematic differences are found for AUV and AV as shown in Fig. 6. These differences occur because of the limited amount of data (if any) in the UV rest-frame range. Using the B12 curve as the reference, a larger attenuation is found in the V band for C00 together with a lower attenuation in the UV, and inverse trends are found for the SMC-like curve. Opposite variations found for the UV and V bands are explained by the shape of the attenuation curve. The C00 slope is flatter than the B12 and SMC-like slopes: for the same amount of IR emission, the attenuation is lower in UV and higher in the V band. The SMC-like curve is the steepest, giving the highest attenuation in the V band and the lowest in the UV.
. The SMC-like curve is chosen as the best choice for 25 sources against 38 and 43 for C00 and B12, respectively, implying a slightly lower pertinence for the SMC-like curve as compared to the two others. Systematic differences are found for AUV and AV as shown in Fig. 6. These differences occur because of the limited amount of data (if any) in the UV rest-frame range. Using the B12 curve as the reference, a larger attenuation is found in the V band for C00 together with a lower attenuation in the UV, and inverse trends are found for the SMC-like curve. Opposite variations found for the UV and V bands are explained by the shape of the attenuation curve. The C00 slope is flatter than the B12 and SMC-like slopes: for the same amount of IR emission, the attenuation is lower in UV and higher in the V band. The SMC-like curve is the steepest, giving the highest attenuation in the V band and the lowest in the UV.
 |
Fig. 5 Examples of fits with the two scenarios for the AGN component. Symbols and lines are the same as in Fig. 3. Galaxy 1 (upper panels) is detected in X-ray and identified as an AGN type 1, galaxy 2 (lower panels) is a “typical” galaxy of our sample, without any X-ray detection or spectral classification. The left panels correspond to best models obtained with scenario 1 (τ9.7 = 1,6, ψ = 0° ) and right panels correspond to best models obtained with scenario 2 (τ9.7 = 6 and ψ = 0,80°). All fits are good with consistent AGN fractions but the amount of dust attenuation varies according to the adopted scenario. |
Linear regressions between the different estimations yield 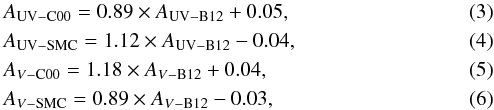 where the values obtained with the B12 curve (AV − B12 and AUV − B12) are taken as independent values for the regression.
where the values obtained with the B12 curve (AV − B12 and AUV − B12) are taken as independent values for the regression.
The SFR is mainly constrained by the IR emission, so we do not expect strong differences and only small variations are found. The variation of SFR is plotted against AUV in Fig. 7. ⟨ Δ(log (SFR) ⟩ = −0.04 dex and + 0.02 dex between C00 and B12, and SMC-like and B12, respectively. The discrepancy increases with attenuation as expected: the difference in attenuation increases with the attenuation itself. With the C00 curve the UV attenuation is found to be lower, so is the SFR, the inverse holds for the SMC-like curve.
The estimations of stellar masses are unaffected by changing the attenuation curve as long as AV< ~ 1.4 mag. For higher attenuations, when compared to the reference chosen here (B12 law), the C00 law gives larger stellar masses (corresponding to a larger dust correction in the V band) and the SMC-like curve lower masses (corresponding to a lower correction). The differences remain lower than 0.1 dex on average (Fig. 7).
 |
Fig. 6 Comparison of attenuation factors in the UV (upper panel) and in the V band (lower panel) for the different attenuation curves. The values found for the B12 attenuation curve are plotted on the x-axis, and those found for the C00 (filled red circles) and SMC-like (blue empty circles) attenuation curves are plotted on the y-axis. The dispersion of the measures is reported as an error bar. |
 |
Fig. 7 Comparison of SFR and stellar mass (Mstar) estimations for different attenuations curves. The attenuation (in the UV (resp. V band) for the SFR (resp. Mstar) estimations) is plotted on the x-axis. The difference (expressed with a logarithmic scale) between SFR and Mstar estimations with the C00 and the SMC-like attenuation curves and the B12 attenuation curve is plotted on the y-axis. The symbols are the same as in Fig. 6. |
 |
Fig. 8 Redshift and luminosity distributions of the sources. The total IR luminosity LIR, plotted on the y-axis, is an output of the SED fitting. The small dots represent the whole sample and the filled circles the subsample of galaxies selected around |
4. Evolution of dust attenuation
4.1. Definition of representative samples
Our aim is to measure dust attenuation in galaxies selected with similar criteria at different redshifts. The combination of the different IRC filters led us to perform a 8 μm rest-frame selection. In Fig. 8 is reported the IR luminosity (obtained with CIGALE) against redshift for our sample. We estimated the detection limit at 5σ using the flux limits of Murata et al. (2013) for each IRC filter used to define the sample (cf. Table 1), and the average ratio between LIR (found by SED fitting) and the monochromatic luminosity in the IRC filter corresponding to the redshift selection. Clearly, we cannot study galaxies with a similar LIR over the full redshift range since the limit in luminosity increases sharply with z. We adopt two strategies:
-
1.
studying galaxies sampling the same domain of the luminosityfunction at different redshifts,
-
2.
selecting galaxies of similar luminosity on a reduced range of redshift.
In the first case, we must select the galaxies dominating the luminosity function and the luminosity density at a given redshift. To this aim, we take the total IR luminosity functions of Magnelli et al. (2013), who fitted a double power-law function originally defined by Sanders et al. (2003). In each redshift bin, we select galaxies with an IR luminosity inside a bin of 0.6 dex centered on the characteristic IR luminosity 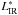 corresponding to the transition luminosity of the double power-law function. The luminosity
corresponding to the transition luminosity of the double power-law function. The luminosity 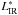 is calculated with relations given by Magnelli et al. (2013). The selection is represented in Fig. 8, and we split the bin 2 in two parts (z< 1 and z> 1). The selected sources lie above the 5σ detection limit for the first three bins, except for a small overlap at the end of the second redshift bin. The detection limit in bin 4 does not allow us to sample the luminosity function well, and we drop this bin for this selection.
is calculated with relations given by Magnelli et al. (2013). The selection is represented in Fig. 8, and we split the bin 2 in two parts (z< 1 and z> 1). The selected sources lie above the 5σ detection limit for the first three bins, except for a small overlap at the end of the second redshift bin. The detection limit in bin 4 does not allow us to sample the luminosity function well, and we drop this bin for this selection.
Evolution of dust attenuation at UV wavelength with redshift for the fiducial model (B12 attenuation curve and AGN 2) and galaxies with a luminosity close to 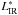 .
.
The average values of the stellar mass found for each redshift bin are reported in Table 3. They are close to the specific values found by Ilbert et al. (2010) for galaxies at similar redshift and with an intermediate star formation activity. These values are also in the range of values found by Karim et al. (2011) for the galaxies dominating the SFR density up to z = 3.
In the second approach, we want to measure the evolution of galaxies of similar LIR. We define a first luminosity bin, 11 < log (LIR/L⊙) < 11.4, for galaxies with z< 1 corresponding to the bin 1 and a part of bin 2 (Fig. 8). At higher redshift, galaxies with LIR ≥ 1011.7L⊙ can be observed in the redshift bins 2 and 3, and we select galaxies in these bins with 11.7 < log (LIR/L⊙) < 12.1.
4.2. SED fitting
CIGALE is run on the whole set of data (4077 sources) with a fiducial configuration (cf. Sect. 3). The reduced 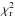 distributions are very good: for 93% of the sources the minimum value of
distributions are very good: for 93% of the sources the minimum value of 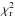 is lower than 5, with a similar result for each redshift bin and for galaxies detected with or without PACS. We are studying dust attenuation in the UV with a sampling of this wavelength range that changes with redshift. We must check that our results are not biased by varying wavelength coverage. We have also considered the subsample of galaxies with available UV rest-frame data that we defined in Sect. 2 and Table 1. The results for this subsample are very similar to those found for the whole sample.
is lower than 5, with a similar result for each redshift bin and for galaxies detected with or without PACS. We are studying dust attenuation in the UV with a sampling of this wavelength range that changes with redshift. We must check that our results are not biased by varying wavelength coverage. We have also considered the subsample of galaxies with available UV rest-frame data that we defined in Sect. 2 and Table 1. The results for this subsample are very similar to those found for the whole sample.
The AGN fraction is on average approximately 10% for the whole sample and is found to globally increase with z (Fig. 9). Our spectral coverage varies with redshift and, for most of the sources, we do not have PACS data. With only mind-IR data, the decomposition of the IR emission in a stellar and a nonthermal component is difficult. We checked that the same trend is found when only galaxies detected with PACS are considered as shown in Fig. 9 (as well as for our SPECZ sample, not shown here). The average value of fracAGN is 6 ± 5, 9 ± 7, 11 ± 8,14 ± 8, and 21 ± 10% from bin 1 to bin 4. Scenario 2 (τ9.7 = 6 and ψ = 0,80°) yields slightly lower AGN fractions but also increases with redshift (6, 9, 11, and 15% from bin 1 to bin 4 with similar dispersions). Our results are in global agreement with those of Goto et al. (2011), who isolated AGN galaxies in their AKARI/SDSS sample using emission line ratios and also found a very moderate contribution of AGNs to the global IR emission.
 |
Fig. 9 AGN fractions measured with CIGALE plotted versus the redshift of the sources: the whole sample is plotted with grey points, the measures for galaxies detected with PACS are represented with red points. The average values and dispersion for each redshift bin are over plotted (black filled circles for the whole sample, red filled circles for the PACS detections). The AGN fractions are always larger than 0 since they are measured as the mean of the PDF. The last redshift bin is not considered for the PACS detections since it contains only 7 sources. |
4.3. Dust attenuation
4.3.1. Evolution of the amount of dust attenuation with redshift for L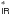 galaxies
galaxies
To study the average attenuation as a function of redshift, we first consider the subsample of galaxies with luminosities around 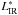 . The average values of AUV for this selection are reported in Table 3.
. The average values of AUV for this selection are reported in Table 3.
We show in Sect. 3 that the measure of the attenuation depends on the choice of the attenuation curve. We can calculate the average values of the attenuation in each redshift bin for the different attenuation curves that we consider by applying regression relations (Eqs. (3) and (4)). The variation with redshift of the different estimations of the attenuation is shown in Fig. 10.
We must check that the definition of 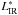 as well as the expected increase of the uncertainty on the measure of AUV with the AGN fraction do not affect our results. To this aim, we also consider the whole galaxy sample in each redshift bin and the sources with an AGN fraction lower than 10%. With the whole galaxy sample the average values of AUV are found 0.2 mag lower than for the subsample of galaxies with luminosities around
as well as the expected increase of the uncertainty on the measure of AUV with the AGN fraction do not affect our results. To this aim, we also consider the whole galaxy sample in each redshift bin and the sources with an AGN fraction lower than 10%. With the whole galaxy sample the average values of AUV are found 0.2 mag lower than for the subsample of galaxies with luminosities around 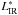 except for the first bin for which the difference reaches 0.3 mag (as expected since we add a large number of fainter galaxies). When only galaxies with an AGN fraction lower than 10% are considered, the difference never exceeds 0.2 mag. These variations are lower than the difference induced for example by changing of the attenuation law (Fig. 10).
except for the first bin for which the difference reaches 0.3 mag (as expected since we add a large number of fainter galaxies). When only galaxies with an AGN fraction lower than 10% are considered, the difference never exceeds 0.2 mag. These variations are lower than the difference induced for example by changing of the attenuation law (Fig. 10).
We can add other measures of attenuation, already obtained for IR selected galaxies, to our analysis. At z = 0, Buat et al. (2007a) combined GALEX and IRAS data and derived volume averaged measures of the attenuation. For a luminosity 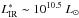 (Sanders et al. 2003), the average UV attenuation AUV = 2.4 ± 0.7 mag. Buat et al. (2007b) measured the attenuation of luminous IR Galaxies (LIRGs, LIR> 1011L⊙) at z = 0.7 by combining Spitzer and GALEX data and found a mean attenuation of 3.33 mag with a dispersion similar to that found at z = 0. Choi et al. (2006) also measured dust attenuation in mid-IR selected galaxies of the Spitzer First Look Survey at z = 0.8 by comparing SFR measured with the strength of emission lines and LIR. We apply their relation between AV and LIR to the average value of LIR for the redshift bin 2 (Table 3) and get AV = 2.33 mag. The visual extinction can then be translated to an attenuation in the UV continuum as explained in Buat et al. (2007b) giving AUV = 3.4 mag. The dispersion is directly measured on Fig. 12 of Choi et al. (2006). Oi et al. (in prep.) observe the Hα emission line of a sample of mid-IR bright sources at z = 0.9 with the Subaru/FMOS spectrograph. We consider their 25 confirmed detections: the average attenuation AHα = 1.5 ± 0.60 mag, which translates to AUV = 3.4 ± 1.3 mag (using the relations detailed in Sect. 5.2).
(Sanders et al. 2003), the average UV attenuation AUV = 2.4 ± 0.7 mag. Buat et al. (2007b) measured the attenuation of luminous IR Galaxies (LIRGs, LIR> 1011L⊙) at z = 0.7 by combining Spitzer and GALEX data and found a mean attenuation of 3.33 mag with a dispersion similar to that found at z = 0. Choi et al. (2006) also measured dust attenuation in mid-IR selected galaxies of the Spitzer First Look Survey at z = 0.8 by comparing SFR measured with the strength of emission lines and LIR. We apply their relation between AV and LIR to the average value of LIR for the redshift bin 2 (Table 3) and get AV = 2.33 mag. The visual extinction can then be translated to an attenuation in the UV continuum as explained in Buat et al. (2007b) giving AUV = 3.4 mag. The dispersion is directly measured on Fig. 12 of Choi et al. (2006). Oi et al. (in prep.) observe the Hα emission line of a sample of mid-IR bright sources at z = 0.9 with the Subaru/FMOS spectrograph. We consider their 25 confirmed detections: the average attenuation AHα = 1.5 ± 0.60 mag, which translates to AUV = 3.4 ± 1.3 mag (using the relations detailed in Sect. 5.2).
All these measures are overplotted on Fig. 10. Given the different methods applied to measure AUV they are found to be consistent and our obtained values extend the analysis up to z ~ 1.5. The attenuation in UV for 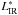 galaxies is found to increase with redshift from ~2.5 mag at z = 0 to ~4 mag at z ≃ 1 and then to remain almost constant up to z = 1.5.
galaxies is found to increase with redshift from ~2.5 mag at z = 0 to ~4 mag at z ≃ 1 and then to remain almost constant up to z = 1.5.
4.3.2. Evolution of the amount of dust attenuation with redshift for galaxies of fixed LIR
We also have access to the amount of dust attenuation in galaxies of similar LIR on limited ranges of redshifts. For galaxies with 11 < log (LIR/L⊙) < 11.4 and z< 1, we find ⟨ AUV ⟩ = 4 mag at ⟨ z ⟩ = 0.4 (bin 1) and ⟨ AUV ⟩ = 3.6 mag at ⟨ z ⟩ = 0.9 (bin 2 with z< 1). The dispersion in both cases reaches 1.3 mag. For comparison, we can add the results of Buat et al. (2007b) for LIRGs with ⟨ AUV ⟩ = 3.8 mag at z = 0 and 3.3 mag at z = 0.7 with a dispersion about 0.7 mag. The results are consistent given the dispersion of the measurements and both show a slight decrease of the attenuation when z increases.
In the redshift bins 2 and 3, we select galaxies with 11.7 < log (LIR/L⊙) < 12.1. The variation of AUV with z for these objects is plotted on Fig. 11. Despite a very large dispersion, a decrease of attenuation with z is found, the trend is also clearly found when only galaxies detected in their UV rest frame are considered.
 |
Fig. 10 Average values of the attenuation factor, AUV, versus redshift. The red symbols refer to IR selected samples. The results of the present study are plotted with red-filled circles for the fiducial modeling, empty circles and squares are used for the C00 and SMC-like attenuation laws. Measurements from Buat et al. (2007a,b) are plotted with red-filled triangles, those from Choi et al. (2006) and Oi et al. with a filled red square and a filled red triangle. The blue symbols and lines refer to UV and Hα line selections discussed in Sect. 5. Cucciati et al. (2012) results are reported with a blue-dashed line. The blue squares refer to measurements from Heinis et al. (2014) based on a stacking analysis: the empty square for the whole UV selection and the filled square for galaxies with Mstar = 1010.9M⊙. The blue circles refer to measurements from Ibar et al. (2013) for Hα emitters: the empty circle is for the whole selection and filled circle for galaxies with Mstar = 1010.9M⊙. The blue empty triangle refers to measurements from Reddy et al. (2008). The black line and crosses correspond to the global estimates of Burgarella et al. (2013) based on luminosity functions. Their analytical relation is plotted as a solid line and crosses correspond to their measurements at different redshifts. The dispersion of each measurement is reported with a vertical bar. The measure of the dispersion for the Heinis et al. (2014) values are based on a stacking analysis whereas the others are estimated based on individual detections. The green empty squares are the average values of the attenuation found with the model of Bernhard et al. (2014), discussed in Sect. 5. |
4.3.3. Variation of the amount of dust attenuation with LIR and Mstar
Many previous studies have concluded that dust attenuation increases with SFR or bolometric emission of young stars (e.g., Hopkins et al. 2001; Martin et al. 2005; Choi et al. 2006; Xu et al. 2007; Buat et al. 2007a; Zheng et al. 2007) and stellar mass (e.g., Brinchmann et al. 2004; Martin et al. 2007; Iglesias-Pàramo et al. 2007; Pannella et al. 2009; Garn & Best 2010; Buat et al. 2012, and reference therein). Recent studies find that the relation between attenuation and stellar mass (Mstar) should not evolve with redshift (Ibar et al. 2013; Heinis et al. 2014; Pannella et al. 2014). In Fig. 12, AUV is plotted versus LIR and Mstar for our complete galaxy sample since there is no need here to restrict the analysis to any subsample. A general increase of AUV with LIR is found that explains the increase of the average attenuation with redshift for galaxies close to 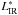 . The very large dispersion leaves room for the slight decrease found with z for galaxies with a fixed LIR.
. The very large dispersion leaves room for the slight decrease found with z for galaxies with a fixed LIR.
When AUV is plotted against Mstar the redshift bins appear to overlap, except in the case of the first bin, which samples much lower masses than the others. No clear trend is found with z in agreement with a nonevolution with redshift at least for z> 0.5. There is a global increase of AUV with Mstar with a very large dispersion. In Fig. 12 we overplot the relation between AUV and Mstar found by Heinis et al. (2014) with a dispersion of 1 mag measured by Pannella et al. (2014) using Herschel detections. Half of the sample, lying between the limits of the relation at ± 1σ and 35%, are found above the upper limit, which roughly correspond to an excess of 20% of galaxies above the AUV − Mstar relation of Heinis et al. (2014) and Pannella et al. (2014).
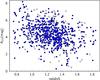 |
Fig. 11 Attenuation factor, AUV, versus redshift for individual galaxies with 11.7 < log (LIR/L⊙) < 12.1. Measurements for galaxies detected in their UV rest-frame are plotted with blue filled circles, the empty black circles correspond to galaxies without UV rest-frame data. |
 |
Fig. 12 Attenuation factor, AUV, versus LIR (upper panel) and Mstar (lower panel). The color coding is the same as in Fig. 8, larger symbols are used for bins 3 and 4 to improve their visibility. In the lower panel, the relation of Heinis et al. (2014) is plotted with a black solid line, the dotted line is the 1σ dispersion of the relation (see text for details). |
5. Discussion
We now compare the redshift evolution of the attenuation measured with different methods and in samples selected with different criteria. We consider the global measure of Burgarella et al. (2013) based on luminosity densities as well as measurements performed in large samples of star-forming galaxies selected to be either UV or Hα emitters. We begin by a discussion of these measurements and then we compare them to our results for our mid-IR selection.
5.1. Average dust attenuation in the universe and in UV selected samples
Burgarella et al. (2013) measured the global attenuation in the universe by comparing the IR and UV luminosity densities. Their result is plotted in Fig. 10 (black line and crosses). This measure is not related to individual objects and can be considered as a measure of the attenuation averaged over all the galaxy populations. This measure is much lower than the one we measure in our sample selected in IR. The difference is on the order of 2 mag (1.6 mag for bin 1).
Cucciati et al. (2012) selected galaxies in their UV rest frame in the VVDS-0226-04 field up to z = 4.5. They derived dust attenuation for each galaxy of their UV selection through SED fitting (without IR data), the variation they found is in close agreement with the results of Burgarella et al. (2013) as shown in Fig. 10. Heinis et al. (2013) measured the average attenuation of a UV selection at z ~ 1.5 in the COSMOS field by stacking Herschel/SPIRE images. The average value found for their whole selection is reported in Fig. 10 and is consistent with that derived by Cucciati et al. (2012) at the same redshift. In Fig. 10 we also report the measure of Reddy et al. (2008) at z ~ 2 for a sample of galaxies selected on their UV rest-frame colors, which also agree with the other measurements. The amount of attenuation found for our IR selection is much higher than the values found either in a UV selection or globally in the universe.
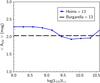 |
Fig. 13 Prediction of the average amount of attenuation in a UV selected sample at z = 1.5 from the model of Heinis et al. (2013). The threshold in LUV (observed) is plotted on the x-axis and the corresponding average amount of dust attenuation AUV is plotted on the y-axis with a blue line (see text for details). The dotted black horizontal line is the measure of Burgarella et al. (2013) at the same redshift. |
At first glance the agreement between Burgarella et al. (2013) and Cucciati et al. (2012) or Reddy et al. (2008) measurements may be surprising since they are obtained using very different approaches. Cucciati et al. measured the attenuation in individual galaxies whereas the values reported by Burgarella et al. (2013) and based on luminosity functions are averaged over the galaxy populations and cannot be directly compared to individual measurements.
These similar results can be explained by the lack of correlation between the average attenuation and LUV observed, obtained by Heinis et al. (2013). We use their simulated catalog built to reproduce the IR properties of their UV selected sample at z = 1.5: we cut it at different values of LUV and calculate the luminosity density in UV and in IR of the selected objects. The ratio of these luminosity densities is then translated in AUV as in Burgarella et al. (2013) for comparison purposes. The resulting attenuation is plotted against the threshold in LUV in Fig. 13 and compared to the value found by Burgarella et al. (2013) at the same redshift. It is clearly seen that the cut in LUV has no significant impact on the average measure of the attenuation. Therefore a galaxy sample selected in UV, as in Cucciati et al. (2012) or Reddy et al. (2008), can be representative of the average attenuation in the universe, without systematic bias due to a limiting UV luminosity.
5.2. Dust attenuation of Hα emitters
Ibar et al. (2013) analyzed the IR properties of galaxies detected in their Hα line (HIZELS project) at z = 1.46. From a stacking analysis of Spitzer, Herschel, and AzTEC images they derived the average total IR luminosity of their sample. Using a local calibration between Hα line and IR continuum emissions from Kennicutt et al. (2009) they obtained a median attenuation AHα = 1.2 ± 0.2 mag. This attenuation can be translated in UV using the recipe of Calzetti (1997). The attenuation AHα is related to the color excess of the ionized gas by applying a standard extinction curve, i.e., 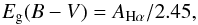 (7)adopting a Galactic extinction curve (Pei 1992) and a screen geometry.
(7)adopting a Galactic extinction curve (Pei 1992) and a screen geometry.
The color excess of the stellar continuum E(B − V) is related to the color excess of the gas (Calzetti 1997), i.e., 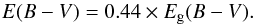 (8)The attenuation in UV is then calculated with the adopted attenuation law. To be consistent with our analysis, we use the B12 attenuation curve,
(8)The attenuation in UV is then calculated with the adopted attenuation law. To be consistent with our analysis, we use the B12 attenuation curve, 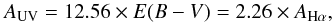 (9)(AUV = 10.33 E(B − V) = 1.86 AHα if the C00 law is used).
(9)(AUV = 10.33 E(B − V) = 1.86 AHα if the C00 law is used).
The corresponding value, AUV = 2.7 ± 0.4 mag (2.23 ± 0.4 for C00), is plotted in Fig. 10 and is marginally consistent with the other measures performed in a UV selection or globally with the luminosity functions (and fully consistent if the C00 attenuation law is used). Kashino et al. (2013) found a larger value for the ratio E(B − V) /Eg(B − V) reaching 0.7−0.8. Using this value for the color excess would lead to an attenuation of 4.6 mag, close to the values found for our IR selected samples, we do not favor this a high value as discussed below.
5.3. Comparing dust attenuation in IR and UV or Hα selected samples
We have to explain why the attenuation found in IR selections is much higher than those found in UV or emission lines selected samples and on average in the universe. With our IR selection, we select galaxies dominating the star formation at the redshifts considered. We find these galaxies experience a dust attenuation that is much higher than the average attenuation in the universe or that is found in UV selected samples: the galaxies dominating the star formation are not representative of the average attenuation in the universe.
Dust attenuation is found to depend on the stellar mass without a strong evolution with redshift (see references above). We can try to use the relation linking these two quantities to account for the stellar mass distributions when we compare dust attenuation from different selections.
Let us consider the measure of Heinis et al. (2013) at z ~ 1.5: the average stellar mass for our IR selection in the redshift bin 3 is 1010.9M⊙. Using the relation found by Heinis et al. (2014) between dust attenuation and Mstar, we find that the average attenuation increases from 1.8 to 3.8 mag if we only consider UV selected galaxies with an average stellar mass of 1010.9M⊙, leading to a value consistent with the measures obtained in IR samples at the same redshift.
The same exercise can be performed for the Hα selected sample of Ibar et al. (2013) at the same redshift. Using their relation between attenuation in the Hα line and Mstar for Mstar = 1010.9M⊙, we find AHα = 1.6 mag, which translates to 3.6 mag in UV a result again consistent with what is found for our IR selected samples of similar mass. These new values, which account for the stellar mass distribution, are also reported in Fig. 10. Using the calibration of stellar and gas color excess of Kashino et al. (2013) gives an attenuation of 5.8 mag (and 4.7 mag for the C00 law), much higher than that found in our IR selection. The value found by Kashino et al. (2013) may apply to galaxies experiencing a phase of intense star formation, but it seems to overestimate the UV attenuation in our sample of galaxies. However an intermediate value between 0.44 and 0.7−0.8 would also be consistent with our results.
We find that considering the relation between dust attenuation and stellar mass helps at reconciling measures of dust attenuation in UV, Hα, and IR selections. The phenomenological model proposed by Bernhard et al. (2014) to explain the evolution of UV and IR luminosity functions with redshift is a good framework to go ahead in our analysis. Starting from stellar mass distributions at different redshifts, they assume a SFR-Mstar relation (the so-called main sequence) and the relation between attenuation and stellar mass found by Heinis et al. (2014) with a significant dispersion (σ = 1 mag, see Fig. 12) to predict LIR and LUV for each object. They are able to reproduce the average trends found in the UV selections of Heinis et al. (2014) and their model is well suited to simulate an IR selection. We apply the same selection to their simulated sample as the selection we performed in Fig. 8 and Table 3. The average attenuation we get is equal respectively to 2.89, 3.93, 3.81, and 4.05 mag for the 4 bins defined in Table 3, with a dispersion on the order of 1 mag. It is in good agreement with our measurements as shown in Fig. 10.
 |
Fig. 14 AUV versus Mstar for starburst galaxies defined with a sSFR 0.6 dex higher than the average value found in each redshift bin. The color coding is the same as in Fig. 8. The AUV–Mstar relation assumed by Bernhard et al. (2014) is plotted with a solid black line, and the 1σ dispersion with dotted lines. |
A major assumption of the model of Bernhard et al. (2014), which we can try to check, is their recipe for dust attenuation. In their model they distinguish between galaxies on the main sequence and starbursting objects. The galaxies on the main sequence follow the AUV − Mstar relation described above and plotted in our Fig. 12. They are defined as starbursts sources with a specific SFR (sSFR defined as SFR/Mstar) 0.6 dex above the average value of the main sequence. The attenuation of these starbursting objects is assumed to be higher than that of galaxies on the main sequence and the fraction of star formation attributed to the starburst is completely obscured in their model. We can check if starbursting galaxies from our sample exhibit a larger attenuation than the other galaxies. We adopt a similar definition to define starbursts in each redshift bin by selecting sources with a sSFR 0.6 dex above the average value of the sSFR found in the bin. Our aim is is not to fully study the relation between SFR and Mstar in our sample, and moreover our 8 μm selection is likely to miss starbursting systems with an IR luminosity close to the detection limit since these objects exhibit a lower 8 μm rest frame to total IR luminosity (Murata et al. 2014). The stellar mass and dust attenuation of these galaxies with a large sSFR are reported in Fig. 14. We find that the starburst galaxies are preferentially located above the average relation, thus exhibiting a large attenuation, but the effect is not systematic. These galaxies are neither numerous nor attenuated enough to explain the “excess” of ~20% of galaxies found in Sect. 4.3.3 to show an attenuation larger than that expected from the average AUV − Mstar relation: in our sample, galaxies with a more moderate star formation activity can also experience a large dust attenuation.
6. Conclusions
We have studied the evolution of the amount of dust attenuation in a sample of 4077 galaxies selected in their rest-frame 8 μm in the AKARI-NEP Deep Field observed with the IRC instrument. To complement optical and near-IR data, GALEX and Herschel/PACS data are also added to the set of data.
Dust attenuation is measured from the fit of the UV-to-IR SED of each galaxy with the CIGALE code. An AGN component is introduced from the Fritz et al. (2006) library. We use different attenuation laws. The method of SED fitting is optimized on a subsample of 106 galaxies with spectroscopic redshift. The choice of the attenuation law is found to affect only marginally the measure of stellar mass and of SFR, the latter being essentially measured with the IR emission. Conversely, the amount of dust attenuation in the UV rest frame at 150 nm varies with the choice of the attenuation curve: adopting the Buat et al. (2012) law as a reference, a higher attenuation is found with a SMC extinction law and a lower attenuation with the Calzetti et al. (2000) recipe, and inverse trends are found for the attenuation in the rest-frame V band. We find that the AGN contribution to the total IR emission is low, but the introduction of AGN type 1 or type 2 templates in the fitting process affects the estimation of dust attenuation. The dust attenuation is systematically higher with an AGN type 1 contribution.
Dust attenuation is found to increase with redshift up to z = 1 and the measurements are consistent with a constant attenuation in the redshift range 1−1.5, in agreement with previous measurements on a smaller range of redshift. Dust attenuation increases with both LIR and Mstar. No trend with redshift is found when AUV is plotted against Mstar. For a given LIR, we find the dust attenuation decreases slightly when redshift increases in consistency with the large dispersion found when the attenuation is plotted against LIR. We find that the dust attenuation is larger than that measured in UV selected samples or samples selected in the Hα line at similar redshift, and that the dust attenuation is larger than the global attenuation in the universe measured with the IR and UV luminosity densities, the difference reaching ~2 mag. This large difference is well explained when considering the average relation between dust attenuation and stellar mass: an IR selection is biased toward massive galaxies whereas UV selected galaxies exhibit a large range of stellar mass. Starbursting galaxies do not systematically exhibit a large attenuation. The phenomenological model of Bernhard et al. (2014) is able to very well reproduce the average measure of dust attenuation at different redshifts, but we find that the relation between Mstar and AUV more dispersed in our sample than is assumed in their model.
The definition of ψ used in the grid of AGN models implemented in the current version of CIGALE (V0.3) is different from the one used in the paper of Fritz et al. (2006). If we note ψ0 the value used by Fritz et al. (2006) then ψ = 90 − ψ0. For the sake of consistency, we use the CIGALE convention.
Acknowledgments
We thank Matthieu Béthermin for fruitful discussions and to have given us the opportunity to work with the simulated sample of Bernhard et al. (2014). We also thank Kazumi Murata for his help during the definition of the samples. We are grateful to Jacopo Fritz for his useful comments about our treatment of the AGN contribution and to Médéric Boquien for his help in running CIGALE. V. Buat and D. Burgarella acknowledge the support of the Institute of Space and Astronautical Science. V. Buat is also supported by the Institut Universitaire de France. Kasia Malek has been supported by the National Science Centre (grant UMO-2013/09/D/ST9/04030), and by the JSPS Strategic Young Researcher Overseas Visits Program for Accelerating Brain Circulation. Youichi Ohyama is supported by a MOST grant (100-2112-M-001-001-MY3). Laure Ciesla acknowledges financial support from the Thales project 383549 that is jointly funded by the European Union and the Greek Government in the framework of the program “Education and lifelong learning”
References
- Bernhard, E., Béthermin, M., Sargent, M., et al. 2014, MNRAS, 442, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Buat, V., Boselli, A., et al. 2012, A&A, 539, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Iglesias-Páramo, J., Seibert, M., et al. 2005, ApJ, 619, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Takeuchi, T. T., Iglesias-Páramo, J., et al. 2007a, ApJS, 173, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Marcillac, D., Burgarella, D., et al. 2007b, A&A, 469, 19 [Google Scholar]
- Buat, V., Giovannoli, E., Heinis, S., et al. 2011, A&A, 533, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Noll, S., Heinis, S., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Heinis, S., Boquien, M., et al. 2014, A&A, 561, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D. 1997, AIP Conf. Ser., 408, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M. 2012, MNRAS, 425, 3094 [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014a, Phys. Rep., 541, A45 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Scoville, N. Z., Sanders, D. B., et al. 2014b, ApJ, 796, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, P. I., Yan, L., Im, M., et al. 2006, ApJ, 637, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Charmandaris, V., Georgakakis, A., et al. 2015, A&A, 576, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Boselli, A., Franzetti, P., et al. 2008, MNRAS, 386, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, F. S., Papovich, C., Salmon, B., et al. 2012, ApJ, 756, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1990, ApJS, 72, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Garn, T., & Best, P. N. 2010, MNRAS, 409, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Goldader, J. D., Meurer, G., Heckman, T. M., et al. 2002, ApJ, 568, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, T., Takagi, T., Matsuhara, H., et al. 2010, A&A, 514, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, T., Arnouts, S., Malkan, M., et al. 2011, MNRAS, 414, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, MNRAS, 432, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kenniccutt, R. C., Jonhson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Fritz, J., Franceschini, A., et al. 2008, MNRAS, 386, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Heinis, S., Buat, V., Bethermin, M., et al. 2013, MNRAS, 429, 1113 [Google Scholar]
- Heinis, S., Buat, V., Bethermin, M., et al. 2014, MNRAS, 437, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Connolly, A. J., Haarsma, D. B., & Cram, L. E. 2001, AJ, 122, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, J. H., Armus, L., Mazzarella, J. M., et al. 2010, ApJ, 715, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Ibar, E., Sobral, D., Best, P. N., et al. 2013, MNRAS, 434, 3218 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Pàramo, J., Buat, V., Hernandez-Fernandez, J., et al. 2007, ApJ, 670, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kashino, D., Silverman, J. D., Rodighiero, G., et al. 2013, ApJ, 777, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Krumpe, M., Miyaji, T., Brunner, H., et al. 2015, MNRAS, 446, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Popesso, P., Berta, S., et al. 2013, A&A, 553, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. C., Seibert, M., Buat, V., et al. 2005, ApJ, 619, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Small, T., Schiminovich, D., et al. 2007, ApJS, 173, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Murata, K., Matsuhara, H., Wada, T., et al. 2013, A&A, 559, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murata, K., Matsuhara, H., Inami, H., et al. 2014, A&A, 566, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J., Chary, R.-R., Dickinson, M., et al. 2011, ApJ, 732, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordon, R., Lutz, D., Genzel, R., et al. 2012, ApJ, 745, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Oi, N., Matsuhara, H., Murata, K., et al. 2014, A&A, 566, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oteo, I., Bongiovanni, Á., Magdis, G., et al. 2014, MNRAS, 439, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Pannella, M., Carilli, C. L., Daddi, E., et al. 2009, ApJ, 698, L116 [Google Scholar]
- Pannella, M., Elbaz, D., Daddi, E., et al. 2014, ApJ, submitted [arXiv:1407.5072] [Google Scholar]
- Panuzzo, P., Granato, G. L., Buat, V., et al. 2007, MNRAS, 375, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Pforr, J., Maraston, C., & Tonini, C. 2012, MNRAS, 422, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., et al. 2008, ApJS, 175, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N., Dickinson, M., Elbaz, D., et al. 2012, ApJ, 744, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2014, A&A, 562, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sawicki, M. 2012, MNRAS, 421, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Takeuchi, T. T., Buat, V., & Burgarella, D. 2005, A&A, 440, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeuchi, T. T., Buat, V., Heinis, S., et al. 2010, A&A, 514, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, C. K., Shupe, D., Buat, V., et al. 2007, ApJS, 173, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wuyts, S., Forster-Schreiber, N., Lutz, D., et al. 2011, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, X. Z., Dole, H., Bell, E. F., et al. 2007, ApJ, 670, 301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Range of values of the input parameters for dust and stellar emission, used for the SED fitting with CIGALE.
Evolution of dust attenuation at UV wavelength with redshift for the fiducial model (B12 attenuation curve and AGN 2) and galaxies with a luminosity close to  .
.
All Figures
 |
Fig. 1 Redshift distribution of the whole sample (black solid line) of galaxies detected with PACS (black dotted line) and with a spectroscopic redshift (SPECZ sample: green-filled histogram). |
| In the text | |
 |
Fig. 2 SED templates for AGNs considered in this work and defined from the Fritz et al. (2006) library with different values of the optical depths τ9.7 and viewing angle ψ. The other parameters are fixed as described in the text. Green line: τ9.7 = 6, ψ = 0; red line: τ9.7 = 1, ψ = 0; blue line: τ9.7 = 1, ψ = 80; black line: τ9.7 = 6, ψ = 80. The fiducial models correspond to τ9.7 = 1,6 and ψ = 0. The models represented here correspond to a bolometric luminosity of 1046 erg s-1. |
| In the text | |
 |
Fig. 3 Examples of fits for the SPECZ sample with various redshifts, |
| In the text | |
 |
Fig. 4 Comparison of |
| In the text | |
 |
Fig. 5 Examples of fits with the two scenarios for the AGN component. Symbols and lines are the same as in Fig. 3. Galaxy 1 (upper panels) is detected in X-ray and identified as an AGN type 1, galaxy 2 (lower panels) is a “typical” galaxy of our sample, without any X-ray detection or spectral classification. The left panels correspond to best models obtained with scenario 1 (τ9.7 = 1,6, ψ = 0° ) and right panels correspond to best models obtained with scenario 2 (τ9.7 = 6 and ψ = 0,80°). All fits are good with consistent AGN fractions but the amount of dust attenuation varies according to the adopted scenario. |
| In the text | |
 |
Fig. 6 Comparison of attenuation factors in the UV (upper panel) and in the V band (lower panel) for the different attenuation curves. The values found for the B12 attenuation curve are plotted on the x-axis, and those found for the C00 (filled red circles) and SMC-like (blue empty circles) attenuation curves are plotted on the y-axis. The dispersion of the measures is reported as an error bar. |
| In the text | |
 |
Fig. 7 Comparison of SFR and stellar mass (Mstar) estimations for different attenuations curves. The attenuation (in the UV (resp. V band) for the SFR (resp. Mstar) estimations) is plotted on the x-axis. The difference (expressed with a logarithmic scale) between SFR and Mstar estimations with the C00 and the SMC-like attenuation curves and the B12 attenuation curve is plotted on the y-axis. The symbols are the same as in Fig. 6. |
| In the text | |
 |
Fig. 8 Redshift and luminosity distributions of the sources. The total IR luminosity LIR, plotted on the y-axis, is an output of the SED fitting. The small dots represent the whole sample and the filled circles the subsample of galaxies selected around |
| In the text | |
 |
Fig. 9 AGN fractions measured with CIGALE plotted versus the redshift of the sources: the whole sample is plotted with grey points, the measures for galaxies detected with PACS are represented with red points. The average values and dispersion for each redshift bin are over plotted (black filled circles for the whole sample, red filled circles for the PACS detections). The AGN fractions are always larger than 0 since they are measured as the mean of the PDF. The last redshift bin is not considered for the PACS detections since it contains only 7 sources. |
| In the text | |
 |
Fig. 10 Average values of the attenuation factor, AUV, versus redshift. The red symbols refer to IR selected samples. The results of the present study are plotted with red-filled circles for the fiducial modeling, empty circles and squares are used for the C00 and SMC-like attenuation laws. Measurements from Buat et al. (2007a,b) are plotted with red-filled triangles, those from Choi et al. (2006) and Oi et al. with a filled red square and a filled red triangle. The blue symbols and lines refer to UV and Hα line selections discussed in Sect. 5. Cucciati et al. (2012) results are reported with a blue-dashed line. The blue squares refer to measurements from Heinis et al. (2014) based on a stacking analysis: the empty square for the whole UV selection and the filled square for galaxies with Mstar = 1010.9M⊙. The blue circles refer to measurements from Ibar et al. (2013) for Hα emitters: the empty circle is for the whole selection and filled circle for galaxies with Mstar = 1010.9M⊙. The blue empty triangle refers to measurements from Reddy et al. (2008). The black line and crosses correspond to the global estimates of Burgarella et al. (2013) based on luminosity functions. Their analytical relation is plotted as a solid line and crosses correspond to their measurements at different redshifts. The dispersion of each measurement is reported with a vertical bar. The measure of the dispersion for the Heinis et al. (2014) values are based on a stacking analysis whereas the others are estimated based on individual detections. The green empty squares are the average values of the attenuation found with the model of Bernhard et al. (2014), discussed in Sect. 5. |
| In the text | |
 |
Fig. 11 Attenuation factor, AUV, versus redshift for individual galaxies with 11.7 < log (LIR/L⊙) < 12.1. Measurements for galaxies detected in their UV rest-frame are plotted with blue filled circles, the empty black circles correspond to galaxies without UV rest-frame data. |
| In the text | |
 |
Fig. 12 Attenuation factor, AUV, versus LIR (upper panel) and Mstar (lower panel). The color coding is the same as in Fig. 8, larger symbols are used for bins 3 and 4 to improve their visibility. In the lower panel, the relation of Heinis et al. (2014) is plotted with a black solid line, the dotted line is the 1σ dispersion of the relation (see text for details). |
| In the text | |
 |
Fig. 13 Prediction of the average amount of attenuation in a UV selected sample at z = 1.5 from the model of Heinis et al. (2013). The threshold in LUV (observed) is plotted on the x-axis and the corresponding average amount of dust attenuation AUV is plotted on the y-axis with a blue line (see text for details). The dotted black horizontal line is the measure of Burgarella et al. (2013) at the same redshift. |
| In the text | |
 |
Fig. 14 AUV versus Mstar for starburst galaxies defined with a sSFR 0.6 dex higher than the average value found in each redshift bin. The color coding is the same as in Fig. 8. The AUV–Mstar relation assumed by Bernhard et al. (2014) is plotted with a solid black line, and the 1σ dispersion with dotted lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.