| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424772 | |
| Published online | 01 May 2015 | |
Non-conservative evolution in Algols: where is the matter?⋆
1
European Southern Observatory, Alonso de Cordova 3107, 19001 Casilla,
Santiago, Chile
2
Institut d’Astronomie et d’Astrophysique, Université Libre de
Bruxelles, ULB, CP
226, 1050
Brussels,
Belgium
e-mail: Romain.Deschamps@ulb.ac.be
3
Sterrenkundig Observatorium, Universiteit Gent,
Krijgslaan 281 S9, 9000
Gent,
Belgium
Received: 7 August 2014
Accepted: 15 February 2015
Context. There is indirect evidence of non-conservative evolutions in Algols. However, the systemic mass-loss rate is poorly constrained by observations and generally set as a free parameter in binary-star evolution simulations. Moreover, systemic mass loss may lead to observational signatures that still need to be found.
Aims. Within the “hotspot” ejection mechanism, some of the material that is initially transferred from the companion star via an accretion stream is expelled from the system due to the radiative energy released on the gainer’s surface by the impacting material. The objective of this paper is to retrieve observable quantities from this process and to compare them with observations.
Methods. We investigate the impact of the outflowing gas and the possible presence of dust grains on the spectral energy distribution (SED). We used the 1D plasma code Cloudy and compared the results with the 3D Monte-Carlo radiative transfer code Skirt for dusty simulations. The circumbinary mass-distribution and binary parameters were computed with state-of-the-art binary calculations done with the Binstar evolution code.
Results. The outflowing material reduces the continuum flux level of the stellar SED in the optical and UV. Because of the time-dependence of this effect, it may help to distinguish between different ejection mechanisms. If present, dust leads to observable infrared excesses, even with low dust-to-gas ratios, and traces the cold material at large distances from the star. By searching for this dust emission in the WISE catalogue, we found a small number of Algols showing infrared excesses, among which the two rather surprising objects SX Aur and CZ Vel. We find that some binary B[e] stars show the same strong Balmer continuum as we predict with our models. However, direct evidence of systemic mass loss is probably not observable in genuine Algols, since these systems no longer eject mass through the hotspot mechanism. Furthermore, owing to its high velocity, the outflowing material dissipates in a few hundred years. If hot enough, the hotspot may produce highly ionised species, such as Si iv, and observable characteristics that are typical of W Ser systems.
Conclusions. If present, systemic mass loss leads to clear observational imprints. These signatures are not to be found in genuine Algols but in the closely related β Lyraes, W Serpentis stars, double periodic variables, symbiotic Algols, and binary B[e] stars. We emphasise the need for further observations of such objects where systemic mass loss is most likely to occur.
Key words: binaries: general / radiative transfer / circumstellar matter / methods: numerical
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Algol systems are short-period, semi-detached binary systems (with orbital periods from several hours to tens of days) generally composed of a hot (B-A) main-sequence star and a less massive but more evolved companion overfilling its Roche lobe and transferring mass via Roche lobe overflow (RLOF; Kopal 1955; Giuricin et al. 1983).
Although Algol systems have been studied since the 18th century (Goodricke 1783) and seem to be rather simple objects within the zoo of binary systems, it is still unclear whether the mass transfer can be fully conservative or if systemic mass loss is a universal feature of Algols as has already been inferred by Crawford (1955), among others. It has been shown that systemic angular-momentum losses (and thus mass losses) must be involved to reproduce the current state of some observed Algols. For example, Refsdal et al. (1974) found that only a non-conservative evolution can reproduce the system AS Eridani. Massevitch & Yungelson (1975) noticed that Algol models must lose at least 40% of their mass in order to reproduce the observed properties. Then, Sarna (1993) concluded that the Algol prototype β Per must have lost 15% of its initial total mass during its evolution and 30% of its total angular momentum. Statistically, Chaubey (1979) found that semi-detached binaries have lower orbital angular momentum than detached systems of the same total mass. Finally, many other clues (e.g., comparison of grid of models with observations or population synthesis analysis; Mezzetti et al. 1980; Nelson & Eggleton 2001; van Rensbergen et al. 2011) converge in favour of non-conservative evolution.
Different mechanisms have been proposed to explain systemic mass loss. They may be classified into four groups: bipolar jets (Umana et al. 2000, 2002; Ak et al. 2007; Lomax & Hoffman 2011), enhanced winds (Chap. 4 of Maeder 2009; Tout & Pringle 1992), losses through the outer Lagrangian point ℒ3 (Sytov et al. 2007), and “hotspot”. The last mechanism appears to be the most promising, because the mass-loss rates derived from the first three mechanisms are too low to account for the inferred systemic mass loss of some Algols. In this scenario, the mass loss is driven by the radiation pressure of a hotspot (van Rensbergen et al. 2008, 2010; Deschamps et al. 2013, hereafter Paper I) that forms when the stream of material coming from the donor via RLOF hits the accreting star and releases energy to heat the stellar surface and increase the luminosity locally. This hotspot is observed in some Algol-like stars (e.g., Banks et al. 1990; Weiland et al. 1995; Richards & Albright 1999, in case of direct accretion on the stellar surface and Harmanec 2002; Soydugan et al. 2007 in case of accretion on the edge of a disc).
In the line of van Rensbergen et al. (2008), Deschamps et al. (2013) derived another model for
systemic mass loss via hotspot based on energy conservation at the impact location and shows
that for a typical initial 3.6 M⊙ + 6 M⊙
system with an initial orbital period P = 2
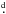 5, a large amount of matter (of the order of 1.4 M⊙, i.e. 15% of
the initial total mass of the system) can be lost during the short-lasting (2 × 105 years), rapid
(ṀRLOF = 1 ×
10-5−1 × 10-4M⊙
yr-1) mass-transfer
phase. This total amount of mass lost is in good agreement with the value inferred by Sarna (1993) to reconcile Algol models with observations.
Using the mass-loss history, and assuming that the wind follow the prescription of Castor et al. (1975) for line-driven winds, a density
profile for the material surrounding the system was derived.
5, a large amount of matter (of the order of 1.4 M⊙, i.e. 15% of
the initial total mass of the system) can be lost during the short-lasting (2 × 105 years), rapid
(ṀRLOF = 1 ×
10-5−1 × 10-4M⊙
yr-1) mass-transfer
phase. This total amount of mass lost is in good agreement with the value inferred by Sarna (1993) to reconcile Algol models with observations.
Using the mass-loss history, and assuming that the wind follow the prescription of Castor et al. (1975) for line-driven winds, a density
profile for the material surrounding the system was derived.
In this paper, we compare this prediction of systemic mass loss to observations by converting the density profile into observable quantities. We thus analyse light emission and absorption by this material using the codes Cloudy (Ferland et al. 2013) and Skirt (Baes et al. 2003, 2011; Camps & Baes 2015). Section 2 briefly summarises and discusses the assumptions made to obtain the density profile and presents the characteristics of the model system and the set-up of the two codes. The results are presented in Sect. 3. We then compare our findings to Algol observations and broaden our study to promising Algol-related objects in Sect. 4 before concluding in Sect. 5.
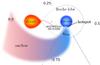 |
Fig. 1 Schematic overview of an Algol system undergoing systemic mass loss due to a hotspot on the surface of the gainer. The ticks and numbers indicate the different phases (0.0: primary eclipse). |
2. The model system
2.1. Density profile of the out-flowing matter
We follow the ballistic trajectory (RLOF-stream) and thus the specific kinetic energy of the material escaping from the donor star via Roche-lobe overflow through the Lagrangian point ℒ1 and accreting onto the gainer star by direct impact (Paper I). When impacting onto the stellar surface, a fraction of this energy heats up the perturbed stellar surface, forming a hotspot (see Fig. 1), and the remainder is radiated away. Mass loss is assumed to occur whenever the total luminosity at the impact location (stellar + hotspot luminosity) exceeds the local Eddington luminosity. The latter is computed using the gainer upper layers’ opacity.
We assume that the wind (hereafter outflow) emitted by the hotspot is line-driven and follow the Castor et al. (1975) prescription to compute the outflow speed vflow. Owing to the orbital motion, the outflow will exhibit a spiral shape (Fig. 1; see Sect. 2.2). The acceleration of the particles moving in this spiral outflow will be considerably reduced once the matter leaves the “irradiation” cone defined by the opening angle θflow (whose estimate is provided in Appendix A). It is important to stress that a mass element ejected from the hotspot will escape the system, even if the outflowing material is not constantly lit up by the hotspot, because it exceeds its escape velocity after a small portion of the orbital period1 (0.038 × Porb at the beginning of the mass-transfer phase, 0.011 × Porb at the end of the non-conservative phase), during which the change of the orientation of the hotspot is negligible.
The density of the material surrounding the system at a given time t and distance
r is
calculated using the continuity equation (see Paper I for a complete description):
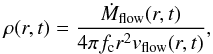 (1)where Ṁflow is the
systemic mass-loss rate calculated with the Binstar code (Siess et al. 2013, Paper I), 4πfc is the solid angle
into which the material is ejected, and fc is the covering factor defined by Eq.
(A.9). It is related to the opening
angle θflow of the outflow (see Fig. 1). The possibility that the outflowing matter is blocked
by the infalling material from the RLOF stream has not been considered, because the
hotspot will be elongated as a consequence of stellar rotation. (The accreting star is
spun up and no longer synchronised, as observed by Mukherjee et al. 1996.) It is therefore very likely that there is only a small
overlap between the stream and the outflow.
(1)where Ṁflow is the
systemic mass-loss rate calculated with the Binstar code (Siess et al. 2013, Paper I), 4πfc is the solid angle
into which the material is ejected, and fc is the covering factor defined by Eq.
(A.9). It is related to the opening
angle θflow of the outflow (see Fig. 1). The possibility that the outflowing matter is blocked
by the infalling material from the RLOF stream has not been considered, because the
hotspot will be elongated as a consequence of stellar rotation. (The accreting star is
spun up and no longer synchronised, as observed by Mukherjee et al. 1996.) It is therefore very likely that there is only a small
overlap between the stream and the outflow.
By computing the density profile of the circumstellar material at different stages during the evolution, we can estimate the total amount of mass that is potentially detectable. Figure 2 shows the evolution of this quantity during the non-conservative phase. We see that the total amount of detectable mass surrounding the binary is at its maximum before the reversal of the mass ratio (mass ratio q = 1 at t ~ 75 000 yr: the beginning of the Algol phase). The gainer surface temperature mainly evolves during the rapid phase of mass transfer and reaches a plateau when the mass ratio is reversed.
 |
Fig. 2 Red crosses: evolution of the mass surrounding the system (integrated up to the radius where the density of the outflow equals the ISM density; see text). The cyan circles (labelled with the model name) indicate the models selected for the simulations presented in this work. Long-dashed green line (right-hand scale): evolution of the gainer-star surface temperature. Magenta dotted line and dashed blue line: evolution of the masses of the donor and gainer (in unit of M⊙/ 500). |
For our radiative-transfer simulations, we selected three configurations (see Table 1): (i) right after the mass-ratio reversal (t = 80 000 yr; hereafter model A); (ii) at t = 120 000 yr (model B); (iii) at the end of the non-conservative phase (t = 162 000 yr; model C, our default configuration). In the density profiles of models A and B, the densities in the ionised region close to the system become so high that an increasing amount of the starlight is transformed into recombination lines and continua that are not explicitly calculated by Cloudy. Indeed, the model atoms used by Cloudy account for a finite number of energy levels, and emission from recombinations to higher levels cannot be included in the spectrum. As a result, a significant fraction of the energy released in these recombinations and in the subsequent cascades to the corresponding ground states are missing in the emergent spectrum. In these conditions, it is difficult to predict observable quantities, so we decided to use the density profile of the model C for the models A and B while keeping the hotspot and stellar parameters given by the evolutionary model. Therefore, the simulations corresponding to cases A and B should be considered as exploring the sensitivity of our results to the luminosity of the hotspot, which is the property differing the most between cases A, B, and C (Table 1). The sensitivity to the circumstellar shell mass (which was the initial goal for considering cases A, B, and C – but which could not be fulfilled for the reason explained above) – may instead be probed by varying the dust-to-gas ratio Φ. As discussed in Sect. 2.3, a simulation for case C has been run with 200 times more dust than standard (model labelled “C_hd_0.71” in Table 2). This case thus mimics a situation with a thicker dust shell.
Figure 3 shows the density profile of the outflow for different covering factors (fc) for model C. The profile is cut at the distance rcut, where the density drops below the interstellar medium (ISM) value. This occurs at 6.08 × 1017 cm (≈40 600 AU or 2.5 × 105Aorb, where Aorb is the orbital separation) from the gainer for fc = 0.71. We do not take any bow-shock formation at this location into account. When the systemic mass loss stops, within 300 years the material disperses and the density profile drops everywhere below the ISM density (≈10-24 g cm-3) because of the very high velocity of the line-driven outflow (Fig. 3).
 |
Fig. 3 Density (left-hand scale, solid lines) and velocity (right-hand scale, dashed line) profiles of the outflowing material (similar – but with different parameters – to Fig. 9 of Paper I). Blue line: spherically-symmetric and isotropic outflow corresponding to a covering factor of fc = 1 (see text, Sect. 2.1); green lines: ejection confined in a disc of opening angle 90° (fc = 0.71); red line: ejection confined in a disc of opening angle 74°(fc = 0.6); The solid light-grey lines are the density profiles for fc = 0.71 at 100 different times uniformly distributed during the non-conservative phase. |
Parameters for the three models; Model A: mass ratio reversal; Model B: intermediate case; Model C: end of non-conservative mass transfer. (For this case, three hotspot temperatures are investigated.)
Parameters of the simulations performed with the Cloudy and Skirt codes.
2.2. Spiral structure
Owing to the orbital motion and the fact that the outflow comes from a small area on the star, we must expect a spiral structure to form close to the star. The width of the spiral arm increases as a function of the distance from the star (Fig. 1), and eventually the spiral arm will overlap itself so that the spiral structure fades, giving rise to a disc instead. Using an opening angle for the outflow of 90° (standard θflow configuration corresponding to fc = 0.71) and the velocity profile shown in Fig. 3, we estimate the distance at which the spiral fades to be ≈3.6 AU (22 Aorb). This distance is reached by the outflow on the time scale of an orbital period. At greater distances, our assumption of a smooth density profile is thus sufficiently accurate. At shorter distances, we expect deviations due to the spiral structure. In these regions, the density will be the highest when the line of sight points towards the hotspot and will decrease as the orbital motion moves the hotspot out of sight. Ultimately, right before the hotspot points again towards the observer, the density close to the star reaches a minimum because only the material that has been launched orbital periods ago is seen far away from the star.
To mimic this effect and investigate any variability due to the orbital motion, we
performed some simulations with a reduced, constant density profile close to the star (in
the following, we call these simulations “plateau” and label them with a “p” in the name).
Considering the orbital motion (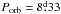 at the end of the non-conservative phase),
we can estimate the density of the outflow ahead of the hotspot. Given the travel time
(one orbital period) and the flow velocity, we can estimate the distance travelled by the
material, rpl, as well as the density at that
location, ρpl. As a first approximation, we adopt a
density profile where the density is equal to ρpl up to rpl and then
follow the standard (unmodified) density profile. For the model with fc = 0.71, we
retrieve a radius of rpl = 6.05 × 1013 cm
(≈4.05 AU or 25
Aorb) and a corresponding density of
ρpl = 9.44 ×
10-17 g cm-3.
at the end of the non-conservative phase),
we can estimate the density of the outflow ahead of the hotspot. Given the travel time
(one orbital period) and the flow velocity, we can estimate the distance travelled by the
material, rpl, as well as the density at that
location, ρpl. As a first approximation, we adopt a
density profile where the density is equal to ρpl up to rpl and then
follow the standard (unmodified) density profile. For the model with fc = 0.71, we
retrieve a radius of rpl = 6.05 × 1013 cm
(≈4.05 AU or 25
Aorb) and a corresponding density of
ρpl = 9.44 ×
10-17 g cm-3.
2.3. Chemistry of the outflow: gas composition and dust formation
One important point for the radiative-transfer analysis is the composition of the gas, which we assume to be that of the donor as listed in Table D.1. The main signature is the depletion of carbon and enhancement of nitrogen during the non-conservative phase (since the mass transfer reveals the inner layers of the giant star).
Although grains can be useful tracers of the cool outermost regions of the outflow, it is not clear whether they can form. Indeed, the escaping material cools as it leaves the gainer’s vicinity. Eventually, the temperature drops below the condensation temperature, allowing for the formation of grains. However, UV and X-ray photons from the hotspot and star (e.g., Ignace et al. 2008) may prevent grain formation. Surprisingly, grains are found in the surroundings of Wolf-Rayet stars (Barniske et al. 2008), which are also emitters of hard radiation.
Since there are no observational constraints on the chemical composition and optical
properties of (hypothetical) dust grains around Algol systems, we use the standard ISM
model implemented in Cloudy. However, we exclude carbonaceous grains, because the
evolutionary stages of both stars imply C/O < 1 (see Table D.1) so that
we can assume that most carbon atoms in the outflow are locked up in CO molecules. For the
slope of the size distribution of the remaining silicate grains, we use the expression
suggested by Mathis et al. (1977), 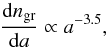 (2)where ngr is the
number density of grains and a the grain size. The size distribution is
discretised in ten bins, which is the maximum number of size bins allowed by Cloudy,
ranging from 0.005 to 0.25 μm, with a ratio amax/amin ≈
1.48 in each bin, where amax and amin are the
upper and lower size limits of the bins, respectively. Within each bin, the optical
properties of the dust grains are averaged over the respective size interval. For our
simulations, the chosen number of bins and their width and location have very little
impact on the results. Varying the number and size of the bins only results in a deviation
of ≲2% in the flux ratios and
magnitudes. Barniske et al. (2008) evaluate the
impact of the lower cut-off on the grain size (0.005 μm in our case) and find
that only the flux bluewards of 8.3 μm is altered, which has no influence on WISE bands
3 and 4 (>10
μm) that
will be used in Sect. 4.2.2. Similarly, we ran
simulations with different grain sizes and found that the region of the spectra below
~6 μm does not depend on grain
size so that 2MASS fluxes (<5 μm) are not affected.
(2)where ngr is the
number density of grains and a the grain size. The size distribution is
discretised in ten bins, which is the maximum number of size bins allowed by Cloudy,
ranging from 0.005 to 0.25 μm, with a ratio amax/amin ≈
1.48 in each bin, where amax and amin are the
upper and lower size limits of the bins, respectively. Within each bin, the optical
properties of the dust grains are averaged over the respective size interval. For our
simulations, the chosen number of bins and their width and location have very little
impact on the results. Varying the number and size of the bins only results in a deviation
of ≲2% in the flux ratios and
magnitudes. Barniske et al. (2008) evaluate the
impact of the lower cut-off on the grain size (0.005 μm in our case) and find
that only the flux bluewards of 8.3 μm is altered, which has no influence on WISE bands
3 and 4 (>10
μm) that
will be used in Sect. 4.2.2. Similarly, we ran
simulations with different grain sizes and found that the region of the spectra below
~6 μm does not depend on grain
size so that 2MASS fluxes (<5 μm) are not affected.
The optical properties of the grains are calculated by using the Mie theory as described by van Hoof et al. (2004). Because the gainer star has spectral type B, its radiation will probably interfere with the formation of dust grains, and we cannot expect the dust-to-gas ratio (Φ) to be as high as in the ISM. Instead, we use the results of Barniske et al. (2008), who find dust in the surroundings of WN stars. From their best-fit models, we derive values of Φ up to 2 × 10-5, which we adopt in this work for our standard dusty configuration (models labelled “ld” for low-dust). To investigate the impact of the dust-to-gas ratio, we also computed a model with Φ = 4 × 10-3 (model labelled “hd” for high-dust).
We do not explicitly calculate the destruction of dust grains caused by the high temperatures close to the star. Instead, we use the Cloudy code to derive a temperature profile for a pure-gas model (models labelled “df” for dust-free) and then define a dust-free region around the star where the temperature exceeds the dust sublimation temperature (≈1400 K for silicate dust, see Martin & Rouleau 1991; Laor & Draine 1993). The circumstellar material will be dust-free up to a transition radius rtr (radius at which the temperature goes below the condensation temperature).
2.4. Stellar parameters
2.4.1. Luminosities
The system is composed of the donor star (a late G-type red giant), the gainer star (a B-type dwarf), the hotspot and the material escaping from the hotspot (Fig. 1). The properties of the system (masses, radii, stellar and hotspot luminosities, stellar temperatures; Deschamps et al. 2013) are computed with the Binstar code and given in Table 1 for the three selected models.
We can estimate the size of the hotspot (rhs) as being identical to the size of
the impacting stream (rstream), which can in turn be
identified with the size of the stream at the Lagrangian point ℒ1. According to Pringle & Wade (1985), it can be approximated by
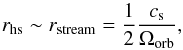 (3)where cs is the
sound speed of the material leaving the donor star at ℒ1, and Ωorb is the orbital angular
velocity.
(3)where cs is the
sound speed of the material leaving the donor star at ℒ1, and Ωorb is the orbital angular
velocity.
The effective luminosity felt by the material escaping the system depends on its
location along the spiral. In the cone with opening θflow above
the hotspot (Fig. 1), the escaping material is
irradiated by both the gainer and the hotspot2. But
outside this cone, the hotspot luminosity no longer contributes. We account for this
effect by using an effective hotspot luminosity that corresponds to the actual value
reduced by a geometrical factor γ. This geometrical factor is obtained (Appendix
B) by assuming that the hotspot luminosity is
diluted over a strip-shaped surface encircling the star (blue band in Fig. B.1). The effective flux from that surface reads
as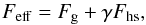 (4)where
(4)where
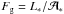 and
and 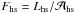 are the surface fluxes of the gainer star and the hotspot, respectively (see Appendix
B for details on the calculation of the factor
γ). With
the quantities given in Table 1, we find
γ ~
0.05 for model C.
are the surface fluxes of the gainer star and the hotspot, respectively (see Appendix
B for details on the calculation of the factor
γ). With
the quantities given in Table 1, we find
γ ~
0.05 for model C.
The use of a time-independent configuration, with an effective flux that constantly
irradiates all the surrounding material, is justified by the fact that the cooling time
scale (as computed by Cloudy; see Fig. 5)
becomes longer than the orbital period at distances r ≈ 3.8 × 1012
cm (0.25 au) for model C. Owing to the high outflow velocity (up to 900
km s-1; Fig.
3), the time needed for the flow to reach that
distance is short (≈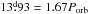 at the end of the non-conservative
phase). Therefore, the outflow properties (such as temperature or emission spectrum)
will not change too much over one orbital period, and several phases of irradiation (as
the material passes in front of the hotspot) can be averaged into a constant
irradiation.
at the end of the non-conservative
phase). Therefore, the outflow properties (such as temperature or emission spectrum)
will not change too much over one orbital period, and several phases of irradiation (as
the material passes in front of the hotspot) can be averaged into a constant
irradiation.
The spectrum of the gainer star is obtained by interpolating in the “TLUSTY” grid of Lanz & Hubeny (2007) to match the effective temperature given in the first column of Table 1. The donor-star spectrum is taken as a black-body spectrum (see upper panel of Fig. 7). For all the components constituting the total incident spectrum (donor, gainer, hotspot), we use the metallicities listed in Table D.1. The donor has by definition the same abundances as the material ejected, and for the selected models, the gainer star is entirely covered by the donor’s material.
 |
Fig. 4 Distance distribution for observed Algols. The sample of Algols is from Budding et al. (2004). Parallaxes are from the Hipparcos catalogue (ESA 1997). The dashed green curve represents the flux at 25 μm (right-hand scale) as a function of distance for the dusty simulation C_ld_0.71_inter. The flux is integrated over the whole nebula. The dotted blue line is the IRAS 5σ limit at 25 μm. The WISE 5σ limit for band W4 is 2600 μJy and is always below the dashed green curve. |
2.4.2. Distance
To relate absolute fluxes (from the models) with predicted apparent magnitudes for, e.g., the infrared excesses, the distance to the system needs to be fixed. We chose a typical distance from the distribution of measured parallaxes for Algols. In Fig. 4, we present the distance distribution for 152 objects (joint entries in the Budding et al. (2004) and Hipparcos (ESA 1997) catalogues), which correspond to about 10% of all Algols in the Budding et al. (2004) catalogue.
To evaluate which among these systems might be detectable by IRAS, Fig. 4 also presents the 25 μm flux of the dusty simulation C_ld_0.71_inter, integrated over the whole nebula, as a function of distance. Only the infrared sources with a flux larger than the IRAS 5σ detection limit at 25 μm can be detected, so that a system with the same IR emission as our model C_ld_0.71_inter must be within 400 pc of the Sun for its IR excess to be detected, and this includes most of the Algols with a known parallax. Based on this result, a typical distance of 300 pc is adopted to convert model fluxes into apparent fluxes and magnitudes, as listed in Sects. 3 and 4.2.2. To give an idea, β Lyrae is located at a distance of 294 pc, while W Ser is estimated to lie at 1428 pc (Hipparcos catalogue, van Leeuwen 2007). Of course, the apparent fluxes of the model spectral energy distributions (SEDs) can be easily rescaled for comparison with a system at a different distance.
 |
Fig. 5 Temperature profile (solid red line) and cooling time scale (dotted blue line; see text) of the material surrounding the star as a function of distance to the star (model C_df_0.71_inter). The dot-dashed cyan line represents the dust condensation temperature (1400 K). |
2.4.3. The temperature of the hotspot
To assess the dependence of our results on the SED of the hotspot, we used three different hotspot temperatures Ths in model C with fc = 0.71 (see Tables 1 and 2). In the first model (C_xx_0.71_cold), we assumed that the hotspot emits with a B-star spectrum at a temperature of 30 000 K3. In the second model (C_xx_0.71_inter), we assumed a temperature of 35 000 K and use an O-star spectrum (also interpolated from the TLUSTY grid). In the third model (C_xx_0.71_hot), we used an O-star spectrum with a temperature of 40 000 K. These three temperatures are based on observed hotspot values in Algols with similar properties (stellar masses and orbital periods; van Rensbergen et al. 2011), and the corresponding results are presented in Sect. 3.3. These three models allow the effect of the hotspot properties on the emergent SED to be clearly disentangled.
To satisfy the Stefan-Boltzmann law 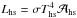 (cf. Eq. (B.2)), the radius of the hotspot is treated as a free parameter
(Lhs and Ths are fixed)
and compared to the estimate given by Eq. (3) (see Table 1). Although Eq. (3) can only give a rough approximation of the
radius of the hotspot, we see a good match between this value and the one imposed by the
Stefan-Boltzmann law.
(cf. Eq. (B.2)), the radius of the hotspot is treated as a free parameter
(Lhs and Ths are fixed)
and compared to the estimate given by Eq. (3) (see Table 1). Although Eq. (3) can only give a rough approximation of the
radius of the hotspot, we see a good match between this value and the one imposed by the
Stefan-Boltzmann law.
2.5. Setup of CLOUDY and SKIRT
We used version 13.02 of Cloudy, last described by Ferland et al. (2013), to calculate the ionisation of the gas close to the gainer star and the emission from the dust grains in the outflow at longer distances. Cloudy calculates the thermal and ionisation balance with a simultaneous treatment of radiative transfer. For the latter, an escape probability formalism is used. In our simulations, the photon energy scale was discretised with a resolution of λ/ Δλ = 2000 down to λ = 0.152 nm4. Cloudy calculates the strengths of ≳105 spectral lines. We found that the number of energy levels that are used for the Fe ii ion can have a strong impact on the resulting temperature profile and thus on the transition radius rtr, and also on the emitted spectrum. Therefore, we used the detailed Fe ii model that was developed by Verner et al. (1999) and implemented in Cloudy. To define the spatial step size, Cloudy uses adaptive logic. However, for the models C_df_0.71_hot, C_ld_0.71_hot, C_df_1.00_inter, and C_ld_1.00_inter, we had to define a lower limit for the step size, of the order of 108 cm, to reach convergence.
The ejection of matter triggered by the hotspot is assumed to occur primarily in the orbital plane and is assumed to be seen edge-on. In our spherical 1D simulations with Cloudy, we take that into account by adjusting the covering factor (equivalent to the factor fc introduced in Sect. 2.1, Eq. (1)). In Appendix A, we estimate the covering factor (or, equivalently, the opening angle) based on the assumption of isotropic radiation from the hotspot. To study the effect of the choice of opening angle on the results, we performed simulations with different covering factors (the three digits in the label of each simulation: “x.xx”).
When assessing the systematic uncertainties due to the 1D geometry and the simplified approach used by Cloudy for the radiative transfer, we use the Skirt code, which simulates the general 3D continuum transfer for dust, including absorption, multiple anisotropic scattering, and thermal emission (Baes et al. 2003, 2011; Camps & Baes 2015). The 3D dust-distribution is represented by a disc that is centred on the gainer star and truncated at its inner edge at the dust condensation radius. The thickness of the disc increases linearly with distance as defined by the opening angle θflow (see Appendix A), and the density inside the disc is assumed to be a function of distance only (see Fig. 3).
The spatial grid consists of 200 concentric shells. The density is set to zero in the
directions where the polar angle is outside the range π/ 2−θflow/ 2 ≤
θ ≤ π/ 2 + θflow/
2, and the extent of the grid cells is adapted accordingly. The
positions ri of the grid cells
along the radial coordinate follow a power-law distribution in the form 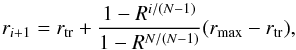 (5)where N>i ≥ 0
and r0 =
0, rtr is the dust formation radius (212 AU
for the model C_ld_0.71_inter; Sect. 3.1),
N = 200 the
number of grid points, and rmax is chosen in such a way that the
density drops below the ISM density at the outer edge of the grid. Here, R = 800 is approximately
the ratio of the sizes of the outermost and innermost grid cells, (rN −
rN − 1) / (r2
− r1).
(5)where N>i ≥ 0
and r0 =
0, rtr is the dust formation radius (212 AU
for the model C_ld_0.71_inter; Sect. 3.1),
N = 200 the
number of grid points, and rmax is chosen in such a way that the
density drops below the ISM density at the outer edge of the grid. Here, R = 800 is approximately
the ratio of the sizes of the outermost and innermost grid cells, (rN −
rN − 1) / (r2
− r1).
The functional form of Eq. (5) is motivated by the steeply decreasing density profile. The ratio of the widths of two adjacent grid cells is held constant. This implies that the width of the grid cells increases from the centre towards the outer edge. Therefore, the high-density regions close to the centre are covered by more cells than the outer low-density regions. This allows us to save computing time. The first term on the right-hand side of Eq. (5) is introduced because there is a dust-free region around the centre, which does not have to be resolved in the SSkirt simulations. The composition and size distribution of the dust are the same as in the CCloudy models. In the radiative-transfer Monte-Carlo method used in SSkirt, the radiation field is represented by discrete photon packages. We used 106 photon packages per wavelength in our simulations. Our wavelength grid consists of 1000 wavelength points with logarithmic spacing between 1 nm and 500 μm, which allows convergence within a reasonable computation time. The different parameters used in the simulations performed with Cloudy and Skirt are summarised in Table 2.
3. Results
3.1. Temperature and emissivity profiles
The first quantity of interest is the outflow-temperature profile, because dust can only form if it falls below the condensation temperature. Figure 5 shows the temperature profile for the model C_df_0.71_inter (see Table 2). The temperature drops below the dust condensation temperature at rtr = 3.2 × 1015 cm (≈212 AU), which is low compared to the extent of the outflow rcut ≈ 6.1 × 1017 cm (see Sect. 2.1). Of course, this value depends on the covering factor and incident spectrum.
The temperature profile shown in Fig. 5 is a decreasing function of distance in the inner regions, with temperatures dropping from ≈17 000 K to ≈180 K in the first ≈1 × 1017 cm (≈6700 AU) from the star’s centre. Then, owing to the steeply decreasing density, the temperature again increases up to about 300 K.
Two other interesting quantities to follow are the profiles of the volume emissivity at some specific wavelengths (especially for the investigation of dust), such as the central wavelengths for some widely-used IR-photometry systems (2MASS, WISE; Cutri et al. 2003, 2012) and the ionisation fraction profiles of some ions that are observed in the emission-line spectra of many Algol-related systems (Fe ii, Si iv, etc.). The ionisation fraction for an ion X z is defined as wX z = nX z/nX,total, where nX,total is the total number density of element X . These profiles tell us where most of the flux comes from.
 |
Fig. 6 Top panel: emissivity profiles (solid lines) and relative ionisation (dashed lines) for the simulation C_ld_0.71_inter (blue solid line: 2MASS Ks; green and red solid: WISE W2 and W4, respectively; green dashed: H ii fraction; blue dashed: Fe ii fraction). The vertical cyan line represents the Roche lobe radius for the gainer star. Bottom panel: Si iv (solid lines) and Fe ii fraction (dashed lines) for the high-temperature hotspot simulations (blue: model C_df_0.71_inter; red: C_df_0.71_hot). |
The top panel of Fig. 6 shows the emissivity profiles of the 2MASS Ks, WISE W2, and W4 bands for the dusty simulation with fc = 0.71 and Φ = 2 × 10-5 (model C_ld_0.71_inter). Most of the flux comes from the inner part of the system, but the infrared excess in these specific bands comes from the outer dusty regions at r ≳ 2 × 1015 cm. We indeed clearly see that W4 dominates W2 and 2MASS Ks in this outer region, which is not the case at smaller radii. In the outer region, the emissivity is low (of the order of 10-15 erg cm-3 s-1), but the total emission, which is the integral over the volume, remains large. The infrared excess in the W4 band is therefore visible as a “bump” in the infrared part of the SED from ~10 μm towards longer wavelengths (Fig. 9). Owing to the rapidly decreasing density profile, only the dust that is closest to the star contributes to the infrared excess, especially at the lowest wavelengths. For this simulation, as well as for the dust-free one, the inner part is totally ionised (H ii, Fe iii, and higher). Although Fe ii is mainly present in the outer part of the system, the formation of Fe ii lines may partially happen close to the star and present some line variability there (see Sect. 3.3 and bottom panel of Fig. 6). In contrast, the contribution from Fe ii in the outer parts comes from a smooth, roughly time-steady density distribution and is probably not variable. The resulting observed line will be the sum of the two contributions (variable inner part, steady outer part).
3.2. Synthetic SEDs
In this section, we inspect the output spectra in the different regimes, from ultraviolet to infrared, and the impact of the different parameters.
 |
Fig. 7 Top: synthetic SEDs of the dust-free Cloudy models in the UV-optical regime. The input spectrum is the sum of the spectra of the gainer star, donor star, and hot spot with a temperature of 35 000 K (the last diluted according to the prescriptions of Appendix B). The fluxes are computed for a system distance of 300 pc. Bottom: same as top panel but for the different models A, B, and C (at different evolutionary times). The input spectra are in black from bottom to top (A, B, C). |
3.2.1. Optical-UV
The top panel of Fig. 7 shows the emergent SEDs for the dust-free models C_df_0.60_inter, C_df_0.71_inter, C_df_0.71_cold, and C_df_1.00_inter (the corresponding SEDs for models that contain dust are nearly identical in this spectral region and are therefore not shown). They all show pronounced Balmer and Paschen recombination continua. The Balmer jump in emission leads to observable diagnostics, as further discussed in Sect. 4.3.
In the SEDs of the models C_df_0.71, we notice a slight absorption in the UV up to a wavelength of ~0.2 μm (also seen in Fig. 8 for the same model), which is mainly attributable to photoionisation close to the star, where the density is high. This has two consequences: i) this absorption will quickly disappear when the non-conservative phase stops, because the outflowing material will rapidly dissipate (see Sect. 2.1); ii) the UV absorption should show a phase dependence owing to the spiral structure of the outflow. (This prediction is compared to observations of W Ser in Appendix C.)
The bottom panel of Fig. 7 presents the SED for the different models (A, B, C) with a covering factor fc = 0.71 (corresponding to θflow = 90°) and Ths = 35 000 K. Model C exhibits the strongest Balmer and Paschen recombination continua and model A the most prominent UV absorption. As discussed in Sect. 4.3, The presence of the recombination continuum and emission lines and the absence of stellar absorption lines are not typical of Algols, but are a common feature of symbiotic systems or planetary nebulae (Kenyon 1986).
 |
Fig. 8 Synthetic SEDs of dust-free models in the UV regime. The solid black line in the upper panel represents the input stellar spectrum. The lower panel shows the difference between the output and input spectra for the two models identified by the line labels. |
3.2.2. Far UV-continuum orbital modulation
The comparison of the results from the model C_df_0.71_inter and the corresponding “plateau” model C_df_p_0.71 (the latter having a lower density in the inner region around the system) allows us to evaluate the impact of the azimuthal dependence of the outflow density, since the line of sight probes different parts of the outflow spiral structure. As discussed in Sect. 2.2, the “plateau” model mimics situations that correspond to orbital phases where the line of sight does not enter the cone of opening θflow (Fig. 1), so when the density close to the star is low. Figure 8, which presents the SED in the UV regime for these two models, reveals that the “plateau” model has no far-UV absorption, whereas the non-plateau models have. Thus, one expects an orbital modulation of the far-UV continuum as a consequence of the azimuthal distribution of the outflowing material close to the star. A comparison with far-UV spectro-photometric observations could thus possibly provide insight into the spatial structure of the outflow.
3.2.3. Emission lines from weakly ionised species
Figure 7 reveals the presence of many Fe ii emission lines for the different models considered, which are best seen in the range 0.2–0.3 μm but are also present in the optical. Figure 6 reveals that these lines mainly form in the outer part of the outflow, outside the Roche lobe. Detecting these lines may help to prove that some material is indeed escaping from the binary system. The absence of such lines in the spectra of genuine Algols may thus be considered as an argument against the presence of outflowing matter in these systems.
 |
Fig. 9 Same as Fig. 7 but for the IR region, including the Skirt model C_SK_ld. For clarity, spectral lines have been removed from the Cloudy SEDs. The red arrows are 5 σ IRAS upper limits (in the faint-source catalogue): 0.2 Jy for the 12 and 25 μm bands and 0.28 Jy for the 60 μm band. |
3.2.4. Infrared
Figure 9 shows the characteristic silicate feature that is produced by the dust grains in the outer part of the outflow in our models. All models produce infrared excesses above the 5σ IRAS detection limit at 12 and 25 μm, but only the simulation with the highest dust-to-gas ratio has a 60 μm flux detectable by IRAS (for systems located as usual at a distance of 300 pc). In the “plateau” simulation (C_ld_p_0.71, not shown in the figure), there is no dust emission, because the temperature falls below the condensation temperature at a location where the density is too low to produce any detectable infrared excesses.
3.2.5. Synthetic photometry
To ease the comparison of our models with observations, Table 3 presents, for all our models, the magnitudes in the Strömgren
uvby
system and the corresponding colour indices, using the passbands and zero points of
Bessell (2011) and assuming that the models are
located 300 pc away from the Sun. As expected, the systems with a strong Balmer
continuum emission appear with a negative value of c1 = (u −
v) − (v − b).
Figure 10 presents our models in the
[m1,0; c1,0] diagram
compared with data from the Long-Term Photometry of Variables project (Manfroid et al. 1991). Only comparison stars
(labelled A, B, or C in their catalogue) have been retained to define the main sequence.
The c1,0 and m1,0 indices
are not affected by interstellar reddening and are defined by (Strömgren 1966) ![\begin{eqnarray} c_{1,0}& =& c_1 - 0.2(b-y) = \left[(u-v)-(v-b)\right] - 0.2(b-y)\\ m_{1,0}& =& m_1 + 0.18(b-y) = \left[(v-b)-(b-y)\right] + 0.18(b-y). \end{eqnarray}](/articles/aa/full_html/2015/05/aa24772-14/aa24772-14-eq132.png) While our input spectrum falls within the
main-sequence population (Strömgren 1966), our
models deviate considerably towards lower c1,0. Deviations in m1,0 are also
observed for some models. In addition to the Strömgren photometry, Table 4 shows the SDSS magnitudes and two colour indices,
which we calculated using the passbands provided by Moro
& Munari (2000) and the zero points from Fukugita et al. (1996). In Table 5, we
also present the 2MASS and WISE band magnitudes that will be used in Sect. 4.2.2. WISE magnitudes are computed according to Tokunaga & Vacca (2005), based on transmission
curves from the Explanatory Supplement to the WISE All-Sky Data Release Products (Cutri et al. 2012)5. The 2MASS response curves are set up according to ADPS6 (See also the “Explanatory Supplement to the 2MASS All Sky Data
Release and Extended Mission Products”7).
While our input spectrum falls within the
main-sequence population (Strömgren 1966), our
models deviate considerably towards lower c1,0. Deviations in m1,0 are also
observed for some models. In addition to the Strömgren photometry, Table 4 shows the SDSS magnitudes and two colour indices,
which we calculated using the passbands provided by Moro
& Munari (2000) and the zero points from Fukugita et al. (1996). In Table 5, we
also present the 2MASS and WISE band magnitudes that will be used in Sect. 4.2.2. WISE magnitudes are computed according to Tokunaga & Vacca (2005), based on transmission
curves from the Explanatory Supplement to the WISE All-Sky Data Release Products (Cutri et al. 2012)5. The 2MASS response curves are set up according to ADPS6 (See also the “Explanatory Supplement to the 2MASS All Sky Data
Release and Extended Mission Products”7).
 |
Fig. 10 Strömgren photometry [m10; c10] diagram for our models (crosses) and for comparison, normal main-sequence stars (red dots) from the Long-Term Photometry of Variables project (Manfroid et al. 1991, to be discussed in Sect. 4.3). From the latter, only data obtained with the Danish telescope (system 7) were retained. For clarity, the models are not labelled, and only their general properties are indicated in blue. We refer to Table 3 for the values. We added observations of W Ser, B[e], and Be stars for comparison (green dots). The blue dots are the average values for the latter objects when several observations are available. |
Magnitudes in Strömgren (uvby) bands and corresponding colour indices.
Magnitudes in SDSS bands and corresponding colour indices.
3.2.6. Radio emission: H i-21 cm and rotational CO lines
The 21 cm line of neutral hydrogen (H i-21 cm) and molecular rotational lines, such as CO1−0λ = 2.6806 mm and CO2−1λ = 1.3004 mm, may help to map the cold (neutral) outer regions of the outflow. Although the 21 cm line may be completely blended with ISM lines, the high speed of the ejected material (with terminal velocities up to ≈900 km s-1) may help to distinguish between the circumstellar and ISM contributions. In our models, the CO abundance is very small and does not lead to any observable lines. The H i-21 cm line is also very weak, possibly because of the low densities far from the star in the neutral hydrogen region. The H i-21 cm line luminosity does not exceed a few 1020 erg s-1 for both the dust-free and dusty simulations, which corresponds to a few μJy at a resolving power of 2000 and a distance of 300 pc. The outer part of the outflow is therefore probably not detectable in these radio bands.
3.3. Models with strong ionisation
In this section, we investigate the impact of the hotspot temperature and SED on the emergent SED, as well as on the formation of dust and emission lines. A hotspot SED corresponding to a higher temperature implies more ionising photons and thus larger abundances of species, such as Si iv, N v, or C iv. Figure 11 shows the [Si iv] doublet at 139.4 nm and 140.3 nm. There is no difference between the incident and emerging SEDs for the model with Ths = 30 000 K (“C_df_0.71_low”). With a hotter hotspot and star, emission lines from strongly ionised elements can form (although still only barely noticeable for Ths = 35 000 K; model “C_df_0.71_inter”).
The bottom panel of Fig. 6 shows the relative abundance of Si iv and Fe ii for the models C_df_0.71_inter and C_df_0.71_hot. We find that Si iv is restricted to the Roche volume around the gainer star. We therefore expect a strong line-profile variability due to the orbital motion, as well as eclipses by the donor and the gainer stars as observed in some W Ser systems (see Appendix C). Unfortunately, we cannot simulate these effects in our models, which do not resolve the inner binary system. Owing to the short cooling time scale close to the star (Fig. 5), only the material above the hotspot (within the cone of opening angle θflow in Fig. 1) may contain highly ionised species. The low hotspot-temperature models produce much less Si iv, but more Fe ii than the high-temperature ones.
The observed presence of [Si iv] emission in the Algol-related systems W Ser (Sect. 4.1 and Appendix C) does not necessarily imply systemic mass loss, however, because it probes the inner part of the nebula, which may still be gravitationally bound. However, if present, the variability of lines from such highly ionised species may help to understand the ejection mechanism (Guinan 1989). Indeed, since the ionised elements form close to the hot region (the ejection point in the hotspot paradigm), we should be able to constrain the position of the UV source and check whether it is compatible with the location of the accretion point. On top of that, radial-velocity measurements may constrain the global motion of this material (expelled from the accretion region or revolving around the accreting star, etc.).
With increasing hotspot temperatures, only the outermost regions contain dust. Thus the following dichotomy is expected: (dust/weak ionisation) or (no dust/strongly ionised elements), which is supported by observations as discussed in Sect. 4.2.
 |
Fig. 11 [Si iv] 1394 and 1403 Å doublet for three different configurations. |
Magnitudes in 2MASS and WISE bands assuming the models are located 300 pc away from the Sun.
 |
Fig. 12 Skirt intensity map at 12 μm (top), 25 μm (middle), and 60 μm (bottom) for Φ = 2 × 10-5 (model C_SK_ld). To ease the comparison, the same limits are used for the three bands for the “x” and “y” axes. The angular size and intensity are given for a system at 300 pc. The figure is zoomed on a box 12 000 × 8516 AU2 wide. |
3.4. Parameter study: geometry – SKIRT simulations – dust-to-gas ratio
In this section, we compare 1D results from Cloudy with results from the 3D dust radiative-transfer code Skirt. When the codes are applied to the same environment (as described by the stellar parameters, the opening angle of the stream, etc.), very good agreement between the 1D and 3D results is found (see Fig. 9: compare the dashed green line and dotted long-dashed cyan line). This agreement validates the results obtained with Cloudy and described so far.
As described in Sect. 2.5, we calculated models with different covering factors fc representing different outflow geometries. Figure 7 shows the impact of the covering factor for three configurations: the spherical emission case (fc = 1) and two cases of a disc-like emission (fc = 0.71 and fc = 0.6). For each covering factor, we recomputed the density profile according to Eq. (1) so that the total mass in the outflow is conserved. The UV/optical absorption increases with decreasing covering factor, because the densities increase, but the effect is modest. With the higher covering factors, the IR flux is significantly reduced because the dust condensation radius being larger, and less dust contributes to the infrared emission (Fig. 9).
Figure 12 shows a 2D map of the edge-on system at
three different wavelengths (12, 25, and 60 μm) produced with Skirt using the same
physical properties as in model C_ld_0.71_inter (same opening angle and dust-to-gas ratio
Φ = 2 × 10-5;
model C_SK_ld). We restrained our investigation to regions where the flux is close to the
actual detection limits, set at 0.1 mJy arcsec-2 (≈1/10 of current observational thresholds in the mid- to near-IR for
the VLT/VISIR instrument; Lagage et al. 2004). We
do not expect a strong contribution from the cosmic infrared background (CIB) at the
selected wavelengths. Schlegel et al. (1998) show
that at 100 μm (their lowest wavelength), the CIB value is only
≈3.3 mJy
arcsec-2 in the
galactic plane and not as close to the galactic pole and at shorter wavelengths. The
speckle effect (coarseness observed especially far from the centre of the box) seen in
Fig. 12 is due to the smaller number of photon
packages sent from the outer regions compared to the inner regions, so it is numerical
noise. The edges of the disc-like outflow are too cold to be seen at 12 μm, and only the longer
wavelengths can probe these outer regions. However, the flux decreases at longer
wavelengths and drops below the adopted detection limit. The “X” shape is due to the
opening angle of the disc-like outflow, seen through the optically thin outer part. We
recall that, in our models, there is no material outside the opening angle θflow, whereas
in a real system we expect a much smoother transition, with the highest density on the
binary plane and a lower density at higher latitudes. Therefore, the “X” will be less
marked. The inner hot region, where dust cannot form, has a diameter of ≈425 AU corresponding to ≈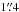 (18 pixels) in Fig. 12. For comparison, the binary system has a separation
of less than 1 AU and is thus far from being resolved.
(18 pixels) in Fig. 12. For comparison, the binary system has a separation
of less than 1 AU and is thus far from being resolved.
For the models (C_hd_0.71 and C_SK_hd) with a higher dust-to-gas ratio (Φ = 4 × 10-3, typical of the ISM) and a covering factor fc = 0.71, the 12 μm peak rises to ≈60 Jy in both the Cloudy and the Skirt simulations, as compared to 0.6 Jy for the model C_ld_0.71_inter displayed in Figs. 9 and 12. A ratio of 100 between the 12 μm fluxes of models differing by a factor of 200 in their dust-to-gas ratios may seem surprising when the dust shell is optically thin, as is the case here. However, one should first subtract the stellar contribution from the observed 12 μm flux of model C_ld_0.71_inter and then take the ratio with the flux from model C_hd_0.71. The expected ratio of 200 is found then. Clearly, the uncertainty on the dust-to-gas ratio in the Algol environment has a strong impact on the present predictions.
4. Comparison to observations
4.1. Stellar samples
In this section, we present the samples of objects investigated for the presence of systemic mass loss as predicted by the models. The observable diagnostics extracted from the models and discussed in Sect. 3 are not typical of Algol systems, but instead share similarities with the properties of Algol-related systems, such as W Serpentis and β Lyrae stars, B[e] and Be stars, symbiotic Algols, and double periodic variables.
Algols
are defined by the Simbad database8 as “detached eclipsing binaries showing the Algol paradox (the more massive component of the system is the less evolved)”. However, many among the systems considered as Algols in the literature are actually semi-detached systems.. In the present study, we call “genuine Algols” those systems that are detached or semi-detached, showing the Algol paradox in the absence of UV emission lines (that are used as a property of W Ser systems as discussed next). We created our own sample of Algols based on the catalogues of Brancewicz & Dworak (1980) containing 701 Algols9 and (Budding et al. 2004) containing 435 Algols10. In these two catalogues, the classification “Algol” is based on the individual mass ratio.
W Serpentis and β Lyrae
are the prototypes of two subsets of Class-II11 Algol systems. The accreting star in these objects may be obscured by a thick accretion disc (see the review of Guinan 1989). They correspond to rapid mass-transfer systems most likely during case B, or BB for β Lyr itself (second phase of mass transfer following the case-B mass-transfer phase). The main property of W Ser systems is the presence of strong ultraviolet emission lines ([C iv], [C ii], [He ii], [N v], [Si iv], etc.; see Appendix C) seen at every phase (Plavec 1980, 1982, 1988, 1989; Guinan 1989). Our sample of W Ser is built on the catalogue of 31 peculiar emission-line Algols (PELAs; Gudel & Elias 1996) after removing those systems from that list that show no evidence of these UV emission lines. The strong ultraviolet emission lines from highly ionised species observed in W Ser systems may be identified with those appearing in our model with the highest-temperature hotspot (C_df_0.71_hot). However, these spectral signatures cannot confirm the presence of material escaping the system since they form inside the Roche lobe of the star (see Sect. 3.3). Moreover, in W Ser systems, there are two contributions to the strongly ionised emission lines (Weiland et al. 1995, see Appendix C): the boundary layer between the disc and the star, responsible for the broad emission seen at every phase; and the hotspot, responsible for the highly phase-dependent narrow emission. There have also been reports of infrared emission that we will further investigate. Taranova & Shenavrin (1997) report infrared excesses at 3.5 and 5 μm possibly attributable to dusty material. Similarly, RY Sct possesses an extended dusty nebula (2000 AU wide; Grundstrom et al. 2007).
Be stars
are rapidly rotating (v> 300 km s -1 ), non-supergiant B stars showing strong Balmer emission lines or evidence of an ionised shell (see Rivinius et al. 2013 for a recent review). These stars form a dust-free, outwardly diffusing disc. In single Be stars, the formation mechanism of these decretion discs is related to the rapid rotation of the star, but some Be stars are interacting binaries, likely Algols. In this case, the formation of the disc and the star’s rapid rotation could result from the RLOF accretion stream (Paczynski 1991; Colpi et al. 1991; Deschamps et al. 2013). Although there is no catalogue of truly Algol-like Be stars available yet, Harmanec (2001) has compiled an extensive list of Be stars in binary systems that may serve as an interesting starting point. In that list, we identified five Algol-like systems of particular interest because it will be apparent from our subsequent analysis: φ Per (Gies et al. 1998), SX Aur (Linnell et al. 1988), HR 2142 (Peters 1983; Waters et al. 1991), π Aqr (Bjorkman et al. 2002) and CX Dra (Berdyugin & Piirola 2002).
 |
Fig. 13 Top panel: WISE FW4/FW1 against 2MASS J/Ks flux ratios for Algols from the catalogue of Budding et al. (2004), and for W Ser from the list of Gudel & Elias (1996). The symbiotic Algol SS Lep and a few Be and B[e] systems have been considered as well (as discussed in Sect. 4.1). The black filled triangles (linked by the dashed line) are black bodies of given temperatures (labels in Kelvin). The red filled squares represent the simulations (STAR: input spectrum). For clarity, only extreme models are labelled, and we refer to Table 5 for unlabelled models. The filled circles correspond to Algols with a S/N > 3.2. The size of the circle is proportional to the S/N for band W4 (except for SS Lep which has a S/N of 962 and for which we limit the size of the symbol), and the symbol colour relates to the χ2 for the same band. Bottom panel: same as top panel but for FW3/FW1 with S/N and χ2 relative to W3. |
B[e] stars
are B stars that show strong forbidden emission lines, Balmer emission lines, and infrared excesses due to hot circumstellar dust (Lamers et al. 1998). However, this class contains several poorly understood systems and includes young and evolved, single, and binary stars. Therefore, different mechanisms at the origin of the gas surrounding B[e] stars may be involved, among which some may be related to mass transfer across the B[e] binary systems (see, e.g., Dunstall et al. 2012). There is no specific catalogue of binary B[e] stars.
Symbiotic Algols
are a subtype of symbiotic stars. Although most symbiotic stars are assumed to host an
accreting white dwarf (e.g., Mikołajewska 2007),
it is not necessarily the case for all of them. For example, SS Lep (Blind et al. 2011) is a non-eclipsing symbiotic,
showing the Algol paradox, composed of a red-giant donor and a main-sequence accreting
star. This system shows the presence of a dusty circumbinary disc or envelope (Jura et al. 2001). The main difference with standard
Algols lies in the mass transfer scheme, which is believed to be wind Roche-lobe
overflow (WRLOF; Mohamed & Podsiadlowski
2007) instead of standard RLOF. Owing to the long period of the system (260
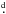 3), mass accretion onto the gainer is supposed to occur via an
accretion disc. Unfortunately, the properties of the hotspot on the edge of an accretion
disc are badly constrained, which makes it difficult to predict systemic mass-loss rates
and to compare with observational data. Moreover, it is not clear whether the hotspot
mechanism can work with WRLOF, because of the lower mass-transfer rates.
3), mass accretion onto the gainer is supposed to occur via an
accretion disc. Unfortunately, the properties of the hotspot on the edge of an accretion
disc are badly constrained, which makes it difficult to predict systemic mass-loss rates
and to compare with observational data. Moreover, it is not clear whether the hotspot
mechanism can work with WRLOF, because of the lower mass-transfer rates.
Double periodic variables
(DPVs) are interacting binaries exhibiting two closely linked periodic variations, the shortest one being the orbital period (Mennickent et al. 2003, 2005, 2008) and the second one of unknown nature but probably linked to the variations in the strength of the disc wind (Mennickent et al. 2012). They are considered as one specific evolutionary step for the more massive Algols. An interesting property of these objects is the surprising constancy of their orbital period, which is not expected in Algols undergoing RLOF mass transfer with a mass ratio different from 1 (Garrido et al. 2013). An explanation could be that systemic mass loss compensates for the period increase caused by mass transfer from a less massive star to its more massive companion. Mennickent et al. (2008) has already emphasised the need for further investigation of these systems. Some DPVs (the Galactic ones) already appear in our Algol or W Ser catalogues, but most of these objects have been found thanks to surveys in the Small Magellanic Cloud and are therefore too far away to allow any clear detection of an infrared excess. We therefore do not include them in this study.
4.2. Constraint on the dust formation: IR diagnostics
In this section, we search for systems that exhibit the infrared colours typical of dust emission. We select Class II and III objects (flaring and quiescent Algols, respectively, with a mass ratio already reversed, according to the nomenclature of Paper I), for which we expect most of the mass to have been ejected and dust to have formed. Class III objects should no longer show any signature of systemic mass loss, though, because of the short-lived outflow, but they were nevertheless considered for completeness. We extracted the IR data from the IRAS, 2MASS, and WISE catalogues. The use of the IRAS catalogues is motivated by their completeness in the 12 to 60 μm range. On the other hand, the choice of the WISE and 2MASS databases has been motivated by their better detection limits as compared to IRAS (IRAS sensitivities: 0.5 Jy at 12, 25, and 60 μm; WISE 5σ sensitivities: 120, 160, 650, and 2600 μJy at 3.3, 4.7, 12, and 23 μm, respectively; 2MASS 10σ at J< 15.0 mag, H< 14.2 mag, Ks< 13.5 mag).
4.2.1. IRAS data
We selected the data from the IRAS (InfraRed All-sky Survey) point12 (Helou & Walker 1988)
and faint13 (Moshir & et al. 1990) source catalogues. We retrieved 241 Algol entries
with a matching IRAS source within a 2′ positional tolerance. We searched for IR excesses using the colour
indices ![\begin{equation} [i]-[j] = -2.5 \log \left( \frac{F_{i}}{F_{j}} \frac{F_{j,0}}{F_{i,0}}\right), \end{equation}](/articles/aa/full_html/2015/05/aa24772-14/aa24772-14-eq181.png) (8)where i and j correspond to the IRAS
bands at 12, 25, or 60 μm, and Fj,0 and
Fi,0 are the
zero-magnitude fluxes. After rejecting spurious detections (contaminated by a nearby
infrared source), we did not find any systems presenting a deviation larger than 0.5 mag
above the black-body line in the ([12]−[25], [12]−[60]) plane.
(8)where i and j correspond to the IRAS
bands at 12, 25, or 60 μm, and Fj,0 and
Fi,0 are the
zero-magnitude fluxes. After rejecting spurious detections (contaminated by a nearby
infrared source), we did not find any systems presenting a deviation larger than 0.5 mag
above the black-body line in the ([12]−[25], [12]−[60]) plane.
4.2.2. WISE data
2MASS14 and WISE15 data are provided by Cutri et al. (2003) and Cutri et al. (2012), respectively. Figure 13 shows the flux ratios [WISE FW4 (22.1 μm)/FW1 (3.35 μm)] and [WISE FW3 (11.6 μm)/FW1 (3.35 μm)] as functions of [2MASS FJ (1.25 μm)/FKs (2.17 μm)] for 79 Algols having positional matches with both 2MASS and WISE within less than 3′′. (31 objects have matches better than 0.̋12 and 15 better than 0.̋06.) Spurious detections due to a diffraction spike from a close bright star, the persistence from a bright star scanned immediately before the target, and halo scattering from a close source or optical ghost have all been discarded. We retained systems having a signal-to-noise ratio (S/N) in band W4 higher than 3.2. In addition, we note that the variability labels range from “not variable” (about 45 objects; this number depends on the band considered) to “high probability of being true variable” (34 objects). This variability observed by WISE could be attributed to an outflow, but it could also simply result from the eclipse of the donor by the gainer (in our model, the donor is three times brighter than the gainer in the W4 band). A more precise analysis of variability with WISE data is beyond the scope of this study.
Figure 13 includes observed systems and our models. The circle colour codes the χ2 (which measures the deviation from the point-spread function-PSF; it is larger than 1 for extended sources) for bands W4 and W3. The circle size is proportional to the S/N in bands W3 and W4. The J and Ks bands are not affected by dust emission (see Fig. 9) and only depend on the stellar temperatures and on the covering factor. Since our simulations are based on one specific Algol system at three different stages of its evolution (see details in Table 1), the range in FJ/FKs values covered by the models is limited compared to observations. In the adopted Algol model system, the donor star dominates the spectrum at longer wavelengths beyond the J band (Figs. 9 and 12).
On the other hand, FW4/FW1 directly traces the presence of IR emission from dust grains (Fig. 9), and FW3/FW1 probes the silicate emission around 12 μm. The models distribute along three horizontal sequences in the upper panel of Fig. 13, dust-free models corresponding to the lowest FW4/FW1 value (close to the stellar locus), followed by low-dust models at an intermediate FW4/FW1 value, and finally the high-dust model “C_hd_0.71_inter” falling above the limit of the figure.
Figure 13 reveals that several Algols and a few W Ser and β Lyr in our sample have FW4/FW1 ratios falling above the black-body sequence, thus hinting at the presence of dust emission. The same holds true for the FW4/FW2 ratio, which has not been displayed, though, because the W2 flux may reach (close to) saturation for bright systems. For four Algols (CZ Vel, UZ Nor, DM Pup and V509 Mon), one β Lyr (RY Sct), and the symbiotic Algol SS Lep, FW4/FW1 is close to or larger than 1, well above our model predictions for a dust-to-gas ratio of Φ = 2 × 10-5. The S/Ns of the WISE measurements for these systems are among the highest in our sample (see Table 6). The WISE and 2MASS data for these systems16 and others with moderate excesses are collected in Table 6. Amongst these, not much is known (apart from their eclipsing light curve) for DM Pup, V509 Mon, CZ Vel, UZ Nor, V442 Cas, and DH Her, but given the interesting nature of all the other stars picked up by the FW4/FW1 criterion, a dedicated study of this short list of not well-studied stars will certainly pay off. RY Sct is a very interesting contact binary consisting of two seemingly O-type supergiants (but the 11 d orbital period makes it unlikely that the components are really as extended as supergiants are), with dust forming in an ionising radiation field and with a radiation-driven nebular wind with a kinematic age of 120 yr (e.g., Smith et al. 2001).
 |
Fig. 14 WISE band-4 images for the genuine Algol CZ Vel (left) and the Be star SX Aur (right). The images are centred on the objects, with north up and east to the left. The flux scale goes from the background level to background plus 150 times the background scatter σ, and the first thin (green) contour line corresponds to the background level plus 3 times its fluctuation, the next intermediate (blue) contour curve to 5σ, and the inermost thick black contour line to 10σ. |
Finally, three more systems have FW4/FW1 ratios close to the value expected for Φ = 2 × 10-5: the Be systems V696 Mon (=HR 2142), φ Per, and SX Aur. SX Aur shows an extended shell in the W4 band as can be seen in Fig. 14. This is an interesting result in view of the controversy regarding the exact evolutionary status of that system: from the light curve analysis, Chambliss & Leung (1979) obtained a semi-detached configuration with the secondary filling its Roche lobe and endorse an earlier suggestion by Stothers (1973) that the system is undergoing case-A mass transfer and that mass reversal has occurred. In contrast, based on a new light curve analysis, Linnell et al. (1988) concluded that the system is made of two unevolved B stars, the primary being, however, on the verge of filling its Roche lobe. Our discovery of an extended infrared shell around SX Aur (Fig. 14) seems to suggest that some mass was lost from the system in the recent past, even though mass transfer is not currently occurring. This result confirms the interest of also considering Be stars when looking for evidence of systemic mass loss from Algols (see Sect. 4.1). Concerning HR 2142, it must be noted that the target lies close to a star-forming region (Monoceros R2 at 56′), and it is likely that the infrared emission does not originate in the binary system itself but rather in the rich sky background.
Amongst the systems with the highest FW4/FW1
ratios, we note that CZ Vel is the only genuine Algol system with an extended nebula
detected by WISE (Fig. 14), as could be inferred
by its high 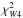 . Its largest angular size is about
180′′. Unfortunately, the
parallax of CZ Vel is unknown, as is therefore the linear size of the nebula. The nebula
is very asymmetric and does not resemble our predictions (Fig. 12).
. Its largest angular size is about
180′′. Unfortunately, the
parallax of CZ Vel is unknown, as is therefore the linear size of the nebula. The nebula
is very asymmetric and does not resemble our predictions (Fig. 12).
There is something else to notice from Fig. 13.
Systems like W Ser or V930 Oph (having the lowest FJ/FKs
= 0.4 and 0.71, respectively) exhibit very low equivalent black-body
temperatures (T<
3000 K); in fact, they are well below the components’ effective
temperatures. These low temperatures thus indicate that the system light is, at those
infrared wavelengths, dominated by a very cool object, possibly an accretion disc that
obscures the gainer star, as in W Ser. The very short period
(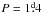 ; Malkov
1993) of V930 Oph does not support,
however, the presence of an accretion disc; direct impact of the accreting stream is
expected instead (Lubow & Shu 1975). The
low-temperature black body detected is therefore likely to originate in a substantial
amount of cool dust far from the system, which is indicative of systemic mass loss.
; Malkov
1993) of V930 Oph does not support,
however, the presence of an accretion disc; direct impact of the accreting stream is
expected instead (Lubow & Shu 1975). The
low-temperature black body detected is therefore likely to originate in a substantial
amount of cool dust far from the system, which is indicative of systemic mass loss.
Figure 13 shows that a typical ISM dust-to-gas ratio (Φ = 4 × 10-3, model C_hd_0.71) produces FW4/FW1 ratios that are higher than those observed with WISE in Algols with an infrared excess. Thus, observations favour a lower dust-to-gas ratio in the stellar nebula than in the ISM. This conclusion is consistent with dust being destroyed by high-energy photons from both the B star and the hotspot. For the same reason, it is likely that so few genuine Algols exhibit infrared excesses caused by dust. Moreover, in the framework of the hotspot mechanism (Paper I), systemic mass loss occurs in the early stage of mass transfer. Since the circumstellar shell dissipates very quickly (within 300 years) after the cessation of the non-conservative evolution, this is another reason that infrared excesses are expected to be rare around genuine Algols.
Similarly, W Ser systems rarely show the signature of dust emission. This is compatible with our finding that the presence of highly ionised species (as seen in W Ser systems) is exclusive of the presence of dust (see Sect. 3.3).
Strömgren m1,0 and c1,0 for our sample of W Ser and Be stars.
4.3. Constraint on Strömgren photometry and weakly ionised emission lines
As mentioned in Sect. 3.2.1, the presence of a strong Balmer continuum in emission and the forest of metallic-line emission in the emergent spectrum are not typical of Algols. Through its c1 index (Sect. 3.2.5 and Fig. 10), Strömgren photometry offers an easy way to check for the presence of Balmer emission continuum. Usually, as concluded before, IR excesses and emission lines or continua are mutually exclusive. There are three interesting exceptions, though: the β Lyr system RY Sct, consisting of two stars with O-type spectra (Smith et al. 2001) and dust formation in the circumstellar nebula despite ionising radiation (Gehrz et al. 1995). We confirm the finding of Gehrz et al. (1995), since RY Sct is the system with the highest FW4/FW1 ratio (Table 6) and at the same time the smallest c1,0 index (Table 7), which is indicative of a strong Balmer continuum in emission. The system clearly has all the features that indicate systematic mass loss. The Be stars φ Per and π Aqr also present negative c1,0, indicating a strong Balmer continuum. This property thus reveals once more the interest of Be binary systems in the search for Algol-like systems with systemic mass loss.
In Table 7, there are three other objects with negative c1,0 values: the W Ser stars, AX Mon and V644 Mon, and the Be star HR 2142. All the other systems are located in a region of the m1,0 – c1,0 diagram that is not typical of Balmer-continuum emission. On the contrary, the W Ser star V367 Cyg has large c1,0 and deviates considerably from the main sequence locus. Young & Snyder (1982) presented a dedicated study off uvby photometry of V367 Cyg (along with a few other W Ser systems) and found the same peculiar Strömgren colours as those reported here, which imply either excess flux longwards of 400 nm or a strong absorption in the u band, due for instance to improperly corrected interstellar absorption. The latter interpretation is made likely by V367 Cyg being a remote object in the Cygnus dust clouds. Therefore, Young & Snyder (1982) conclude that “there is reason to question the reddening correction” in such a peculiar environment. Of course, one cannot firmly exclude an alternative reason related to the physics of the binary system, even though the (m1,0, c1,0) colours of V367 Cyg are not typical of the other W Ser systems studied here and by Young & Snyder (1982).
5. Conclusions
We performed photoionisation and radiative-transfer simulations of the material surrounding an Algol system that is losing mass via the hotspot mechanism. We calculated models with various configurations (different hotspot temperatures, with or without dust, different opening angles for the disc-like outflow), and found that the resulting IR excesses produced by dust in the outer parts of the outflow are consistent with WISE observations for a small number of Algols, especially the systems CZ Vel, UZ Nor, and V509 Mon. We also reported infrared excess in the Be system SX Aur, in the β Lyrae system RY Sct, and in the symbiotic Algol SS Lep (already known for the last two). As expected, most genuine Algols do not exhibit strong infrared excesses since the systemic mass loss occurred in an earlier phase, and the material has dissipated since. Our models also predict strong Balmer continua that are not observed in Algols but are visible in some Be systems.
The outflowing gas can significantly reduce the observed UV continuum-flux level. We suspect that this absorption disappears quickly after the end of the non-conservative phase owing to the high outflow speed of the line-driven wind and shows some phase dependency because the matter is launched from the hotspot. This variability may help to identify systems undergoing systemic mass loss due to the hotspot mechanism.
Our simulations indicate that the geometry of the outflow has an impact on the emergent SEDs, especially in the IR range for dusty models, where the fluxes decrease with increasing opening angle of the outflow.
In the SEDs computed from our models with a hotspot temperature Ths ≳ 35 000 K, we find strong emission lines of highly ionised species such as Si iv that arise close to the stellar surface, inside the Roche lobe of the gainer star, and they are typical of W Ser systems. We emphasise the need for further observations of the extended family of Algols, which includes DPVs, symbiotic Algols, Be and B[e] binaries, W Ser, and β Lyr systems. These types of objects can be related to different steps in the evolution of Algols or to different initial configurations (masses, periods). The search for signatures of a non-conservative evolution should not focus specifically on Algols, since they are older Class III systems (Paper I), but more generally on Algol-related systems where systemic mass loss can potentially occur. We also hope that this first study of the hotspot-outflow formation will motivate a more precise analysis of the stream/star or stream/disc interaction, preferably by using 3D models including radiation-hydrodynamics (see Bisikalo et al. 2000; Nazarenko & Glazunova 2013, for β Lyr).
Online material
Appendix A: Estimation of the opening angle of the outflow
 |
Fig. A.1 Geometry of the hotspot emission. |
The geometry of the escaping stream may be complex, forming a disc-like geometry, and possibly creating a spiral-like structure close to the star (see Sect. 2.2). The geometrical thickness of the disc structure is determined by the opening angle of the outflow. Since the outflow is driven by the radiative flux of momentum pν, we can estimate the geometrical thickness of the outflow by using the dependence of pν on the direction given by θn (angle measured with respect to the direction perpendicular to the hotspot surface; see Fig. A.1).
The total momentum flux, which is normal to an element of surface
d that is parallel to the hotspot, is given by (Fig. A.1)
that is parallel to the hotspot, is given by (Fig. A.1) 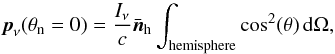 (A.1)where Iν is the specific
intensity (assumed to be isotropic) originating in the hotspot,
(A.1)where Iν is the specific
intensity (assumed to be isotropic) originating in the hotspot,
 is the unit vector normal to the
hotspot, c
is the speed of light, and dΩ =
sinθdθdφ.
is the unit vector normal to the
hotspot, c
is the speed of light, and dΩ =
sinθdθdφ.
To calculate the momentum flux towards an arbitrary angle θn<π/
2, we introduce the reference frame
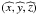 , where the
, where the
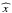 axis lies in the plane of the hotspot,
the
axis lies in the plane of the hotspot,
the 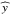 axis lies in the plane
axis lies in the plane
 ,
and
,
and 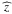 is collinear with
is collinear with
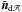 , the normal to
, the normal to
 .
We note that θ is measured with respect to
.
We note that θ is measured with respect to
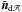 . The general expression of Eq. (A.1) for arbitrary angles θn reads
. The general expression of Eq. (A.1) for arbitrary angles θn reads
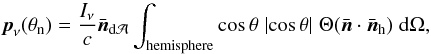 (A.2)where
(A.2)where
 is the unit vector pointing in the
direction (θ,φ). The absolute value in the second factor of
the integrand ensures that radiation traversing the surface
is the unit vector pointing in the
direction (θ,φ). The absolute value in the second factor of
the integrand ensures that radiation traversing the surface
 from above adds a negative contribution to the total momentum flux. The Heavyside step
function
from above adds a negative contribution to the total momentum flux. The Heavyside step
function  accounts for the fact that the hotspot
only radiates upwards.
accounts for the fact that the hotspot
only radiates upwards.
For a fixed angle θn, the vector
 normal to the hotspot has coordinates
(0, −
sinθn,cosθn),
so that an evaluation of the dot product gives the limits of integration in
φ:
normal to the hotspot has coordinates
(0, −
sinθn,cosθn),
so that an evaluation of the dot product gives the limits of integration in
φ:
![\appendix \setcounter{section}{1} \begin{eqnarray} \phi_{\mathrm{lim,1}}& = \begin{cases} \arcsin{[1/(\tan{\theta}\tan{\theta_\mathrm{n}})]} \\ 0 \end{cases} & \begin{array}{l} \theta>\pi/2-\theta_\mathrm{n} \\ \mathrm{otherwise,} \end{array} \\ \phi_{\mathrm{lim,2}}& = \begin{cases} \pi-\arcsin{[1/(\tan{\theta}\tan{\theta_\mathrm{n}})]} \\ 2\pi \end{cases} & \begin{array}{l} \theta>\pi/2-\theta_\mathrm{n} \\ \mathrm{otherwise,} \end{array} \end{eqnarray}](/articles/aa/full_html/2015/05/aa24772-14/aa24772-14-eq257.png) where the latter expression for
φlim,2 results from the symmetry of the
problem (the angle φ is 0 above the
where the latter expression for
φlim,2 results from the symmetry of the
problem (the angle φ is 0 above the
 axis). With these limits, Eq. (A.1) can be expressed as
axis). With these limits, Eq. (A.1) can be expressed as  where the first integral (Eq. (A.5)) corresponds to the hemisphere over the
surface element
where the first integral (Eq. (A.5)) corresponds to the hemisphere over the
surface element 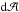 in Fig. A.1, and the second integral (Eq. (A.6)) corresponds to the two green parts.
The first of the two green parts is subtracted because it lies below the hotspot surface
and does not contribute, and the second one makes a negative contribution to the
momentum flux because it is below the surface element
d
in Fig. A.1, and the second integral (Eq. (A.6)) corresponds to the two green parts.
The first of the two green parts is subtracted because it lies below the hotspot surface
and does not contribute, and the second one makes a negative contribution to the
momentum flux because it is below the surface element
d .
These two regions are identical by symmetry, and they allow us to use the same limits of
integration in φ and θ.
.
These two regions are identical by symmetry, and they allow us to use the same limits of
integration in φ and θ.
Our estimate of the opening angle θflow of the outflow is based on the
integral of the momentum flux pν
over θn. We define it as the angle that
corresponds to a fraction of 0.68 (arbitrarily set; standard 1σ as for a Gaussian
distribution) of the total integral, i.e.,
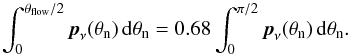 (A.8)This gives an opening angle of
θflow ~
90°. The “effective” solid angle in which the disc-like outflow
spreads is given by:
(A.8)This gives an opening angle of
θflow ~
90°. The “effective” solid angle in which the disc-like outflow
spreads is given by: 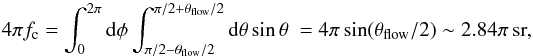 (A.9)where fc is the
covering factor that is defined as the fraction of the spherical domain that is covered
by gas (Sect. 2.1). This is different from the
geometry adopted in Paper I, where the outflow was arbitrarily assumed to be confined in
a quarter of a sphere (solid angle equal to π).
(A.9)where fc is the
covering factor that is defined as the fraction of the spherical domain that is covered
by gas (Sect. 2.1). This is different from the
geometry adopted in Paper I, where the outflow was arbitrarily assumed to be confined in
a quarter of a sphere (solid angle equal to π).
Appendix B: Calculation of the effective flux
 |
Fig. B.1 Representation of the effective surface of the hotspot over a full orbital period. See text for description. |
In our simulations, the effective radiative flux Feff is given
by  (B.1)where
(B.1)where
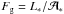 and
and 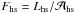 are the gainer star and hotspot fluxes, respectively;
are the gainer star and hotspot fluxes, respectively;
 is the surface area of the star; and
is the surface area of the star; and  is the surface area of the hotspot, i.e. the surface of a calotte with the radius of the
base equivalent to the radius of the impacting stream,
is the surface area of the hotspot, i.e. the surface of a calotte with the radius of the
base equivalent to the radius of the impacting stream, 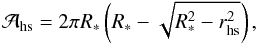 (B.2)where R∗ and
rhs are the star and hotspot radius.
Here,
(B.2)where R∗ and
rhs are the star and hotspot radius.
Here, 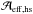 is the area of the strip at the equator of the star of height 2rhs (Fig.
B.1),
is the area of the strip at the equator of the star of height 2rhs (Fig.
B.1),
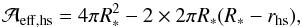 (B.3)over which the hotspot flux is averaged.
Therefore, the effective flux reads
as
(B.3)over which the hotspot flux is averaged.
Therefore, the effective flux reads
as![\appendix \setcounter{section}{2} \begin{equation} F_{\mathrm{eff}} = F_{\mathrm{g}} + \frac{R_{*}}{2 r_{\mathrm{hs}}} \left[1 - \sqrt{1 - \left(\frac{r_{\mathrm{hs}}}{R_{*}} \right)^{2}} \right] F_{\mathrm{hs}} . \end{equation}](/articles/aa/full_html/2015/05/aa24772-14/aa24772-14-eq272.png) (B.4)The net flux from the hotspot is thus
reduced by the factor
(B.4)The net flux from the hotspot is thus
reduced by the factor ![\appendix \setcounter{section}{2} \begin{equation} \gamma = \frac{R_{*}}{2 r_{\mathrm{hs}}} \left[1 - \sqrt{1 - \left(\frac{r_{\mathrm{hs}}}{R_{*}} \right)^{2}} \right]\cdot \end{equation}](/articles/aa/full_html/2015/05/aa24772-14/aa24772-14-eq273.png) (B.5)In our simulations, the source of radiation
emits isotropically, so that the total effective luminosity will be
(B.5)In our simulations, the source of radiation
emits isotropically, so that the total effective luminosity will be
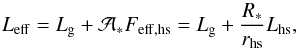 (B.6)where
(B.6)where
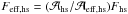 .
.
Appendix C: UV continuum and line variability in W Ser
 |
Fig. C.1 Top: continuum in the UV band for W Ser observed with IUE. Black: SWP47439 observation made on 1993-04-07 (20:02:16) at phase Φ = 0.84; red: SWP47457 observation made on 1993-04-10 (21:40:17) at phase Φ = 0.06. Bottom: difference of the two spectra. |
 |
Fig. C.2 HST/GHRS spectra of the [Si iv] 1393.76 and 1402.77 Å lines of W Ser at two distinct phases (black: z0lu5108t observation made on 1991-07-12 (05:32:25) at phase Φ = 0.00, primary eclipse; red: z0lu0308t observation made on 1991-07-19 (03:29:13) at phase Φ = 0.5, secondary eclipse). |
W Ser systems are known to show strong line variability in the UV (especially for highly ionised species; see the review by Plavec 1982). In this appendix, we investigate the observed UV spectra for the prototypical system W Ser in the search for variations in the continuum as presented in Sect. 3.2. We also demonstrate the variability of [Si iv] lines for this object.
Figure C.1 shows low-dispersion, large aperture spectra of W Ser in the UV as observed by the International Ultraviolet Explorer (IUE) at two distinct phases. (These phases are estimated thanks to the improved ephemeris of Piirola et al. 2005.) The two spectra have been taken only three days apart, thus limiting the effect of intrinsic variability. The red spectrum is taken between the secondary and the primary eclipses at phase 0.8 and the black one at phase 0.1 during the primary eclipse. We note that at phase 0.1, the absorption in the longer wavelength region of the spectra (λ> 1400 Å) and the Lyman α emission are stronger than during the secondary eclipse, possibly indicating a hot ionised region.
Figure C.2 presents the profiles of the [Si iv] 1393.76 and 1402.77 Å lines as observed with HST/GHRS for W Ser at two different phases: primary eclipse (Φ = 0.0), and secondary eclipse (Φ = 0.5). The same ephemeris has been used. We clearly see an excess of flux in the blue wing at phase Φ = 0.5. The total extent of the wings of both lines reaches 600 km s-1, which is comparable to the escape velocity at the surface of the star (643 km s-1 considering a main sequence gainer star of 1.51 M⊙ according to Budding et al. 2004, and following a mass-radius relation for main-sequence stars of the form R ∝ M0.8) and with the outflow terminal velocity in our model (850 km s-1). In their attempt to model this line variability, Weiland et al. (1995) found two components, a broad one likely due to the boundary layer of an accretion disc, and a narrow one possibly due to the formation of a hotspot. Further
investigation, especially at different phases, may shed new light on the origin of the [Si iv] emission.
Appendix D: Chemical composition of the outflow
Table D.1 presents the chemical composition of the donor star atmosphere that will be transferred by RLOF onto the accretor’s surface and eventually ejected by the hotspot.
Chemical composition of the outflowing material for the three models computed.
As presented in Fig. 3, the escape velocity is reached at a fixed distance from the star, hence after a fixed amount of time.
We assume that the donor star does not contribute to the irradiation of the outflowing material, because its luminosity is much lower than that of the gainer (see Table 1). This, however, may not remain true in Algols with a fainter gainer of spectral type A.
http://wise2.ipac.caltech.edu/docs/release/allsky/expsup/index.html, 2014-02-27, Sect. IV.4.h, Fig. 5a and Table 3.
http://www.ipac.caltech.edu/2mass/releases/allsky/doc/explsup.html, 2014-03-05, Sect. VI.4.a.
Rapid mass transfer systems with mass ratio reversed (Deschamps et al. 2013).
We thus do not confirm the conclusion of Taranova & Shenavrin (1997), who seemingly found evidence of dust around the W Ser system RX Cas, though at shorter wavelengths (in the LM bands at 3−5 μm). For this system, we found no significant infrared excesses from WISE (FW4/FW1 = 0.056). Therefore, the excess found by Taranova & Shenavrin (1997) in the LM bands cannot come from dust.
Acknowledgments
R.D. acknowledges support from the Communauté française de Belgique – Actions de Recherche Concertées and benefits from a European Southern Observatory studentship. K.B. is an F.R.S.-FNRS post-doctoral fellow and acknowledges support from contract 2.4501.12. L.S. is an FNRS Researcher. P.C. is supported by the CHARM network, part of the phase VII Interuniversity Attraction Pole (IAP) programme organised by the Belgian Science Policy Office (BELSPO). This research has made use of the VizieR catalogue access tool and SIMBAD database, CDS, Strasbourg, France. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration, as well as of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Ak, H., Chadima, P., Harmanec, P., et al. 2007, A&A, 463, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen de Prieto, C., Lambert, D. L., & Asplund, M. 2001, ApJ, 556, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Lambert, D. L., & Asplund, M. 2002, ApJ, 573, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Davies, J. I., Dejonghe, H., et al. 2003, MNRAS, 343, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Verstappen, J., De Looze, I., et al. 2011, ApJS, 196, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Banks, T., Sullivan, D. J., & Budding, E. 1990, Ap&SS, 173, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Barniske, A., Oskinova, L. M., & Hamann, W.-R. 2008, A&A, 486, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugin, A., & Piirola, V. 2002, A&A, 394, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 2011, PASP, 123, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Bisikalo, D. V., Harmanec, P., Boyarchuk, A. A., Kuznetsov, O. A., & Hadrava, P. 2000, A&A, 353, 1009 [NASA ADS] [Google Scholar]
- Bjorkman, K. S., Miroshnichenko, A. S., McDavid, D., & Pogrosheva, T. M. 2002, ApJ, 573, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Blind, N., Boffin, H. M. J., Berger, J.-P., et al. 2011, A&A, 536, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brancewicz, H. K., & Dworak, T. Z. 1980, Acta Astron., 30, 501 [Google Scholar]
- Budding, E., Erdem, A., Çiçek, C., et al. 2004, A&A, 417, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. C. 1966, Georgetown Obs. Monogram, 21, [Google Scholar]
- Camps, P., & Baes, M. 2015, Astron. Comput., 9, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Chambliss, C. R., & Leung, K.-C. 1979, ApJ, 228, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Chaubey, U. S. 1979, Ap&SS, 64, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Nannurelli, M., & Calvani, M. 1991, MNRAS, 253, 55 [NASA ADS] [Google Scholar]
- Crawford, J. A. 1955, ApJ, 121, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., Barnes, J. V., & Golson, J. C. 1971, AJ, 76, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
- Deschamps, R., Siess, L., Davis, P. J., & Jorissen, A. 2013, A&A, 557, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunstall, P. R., Fraser, M., Clark, J. S., et al. 2012, A&A, 542, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA 1997, The Hipparcos and TYCHO catalogues, Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Garrido, H. E., Mennickent, R. E., Djurašević, G., et al. 2013, MNRAS, 428, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrz, R. D., Hayward, T. L., Houck, J. R., et al. 1995, ApJ, 439, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Bagnuolo, Jr., W. G., Ferrara, E. C., et al. 1998, ApJ, 493, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Giuricin, G., Mardirossian, F., & Mezzetti, M. 1983, ApJS, 52, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Goodricke, J. 1783, Roy. Soc. London Phil. Trans. Ser. I, 73, 474 [Google Scholar]
- Gray, R. O., & Olsen, E. H. 1991, A&AS, 87, 541 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grønbech, B., & Olsen, E. H. 1976, A&AS, 25, 213 [NASA ADS] [Google Scholar]
- Grundstrom, E. D., Gies, D. R., Hillwig, T. C., et al. 2007, ApJ, 667, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Gudel, M., & Elias, II, N. M. 1996, in Radio Emission from the Stars and the Sun, eds. A. R. Taylor, & J. M. Paredes, ASP Conf. Ser., 93, 312 [Google Scholar]
- Guinan, E. F. 1989, Space Sci. Rev., 50, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Harmanec, P. 2001, Pub. Astron. Inst. Czechoslovak Academy of Sciences, 89, 9 [Google Scholar]
- Harmanec, P. 2002, Astron. Nachr., 323, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1980, A&AS, 40, 1 [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hegedus, T. 1988, Bull. Inf. Centre de Données Stellaires, 35, 15 [Google Scholar]
- Helou, G., & Walker, D. W. 1988, Infrared astronomical satellite (IRAS) catalogs and atlases, Vol. 7: The small scale structure catalog [Google Scholar]
- Holweger, H. 2001, in Joint SOHO/ACE workshop, Solar and Galactic Composition, ed. R. F. Wimmer-Schweingruber, AIP Conf. Ser., 598, 23 [Google Scholar]
- Hummel, W., & Štefl, S. 2001, A&A, 368, 471 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ignace, R., Oskinova, L. M., Waldron, W. L., Hoffman, J. L., & Hamann, W.-R. 2008, A&A, 477, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jura, M., Webb, R. A., & Kahane, C. 2001, ApJ, 550, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J. 1986, The symbiotic stars (Cambridge, New York: Cambridge University Press) [Google Scholar]
- Kilkenny, D., Whittet, D. C. B., Davies, J. K., et al. 1985, South African Astron. Obs. Circ., 9, 55 [Google Scholar]
- Knude, J. 1992, A&AS, 92, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Kopal, Z. 1955, Ann. Astrophys., 18, 379 [Google Scholar]
- Kreiner, J. M. 2004, Acta Astron., 54, 207 [NASA ADS] [Google Scholar]
- Lagage, P. O., Pel, J. W., Authier, M., et al. 2004, The Messenger, 117, 12 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Zickgraf, F.-J., de Winter, D., Houziaux, L., & Zorec, J. 1998, A&A, 340, 117 [NASA ADS] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Linnell, A. P., Peters, G. J., & Polidan, R. S. 1988, ApJ, 327, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Lomax, J. R., & Hoffman, J. L. 2011, Bull. Soc. Roy. Sci. Liège, 80, 689 [NASA ADS] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [Google Scholar]
- Malkov, O. Y. 1993, Bull. Inf. Centre de Données Stellaires, 42, 27 [NASA ADS] [Google Scholar]
- Manfroid, J., Sterken, C., Bruch, A., et al. 1991, A&AS, 87, 481 [NASA ADS] [Google Scholar]
- Martin, P. G., & Rouleau, F. 1991, in Extreme Ultraviolet Astronomy, eds. R. F. Malina, & S. Bowyer, 341 [Google Scholar]
- Massevitch, A., & Yungelson, L. 1975, Mem. Soc. Astron. It., 46, 217 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Pietrzyński, G., Diaz, M., & Gieren, W. 2003, A&A, 399, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennickent, R. E., Cidale, L., Díaz, M., et al. 2005, MNRAS, 357, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., Kołaczkowski, Z., Michalska, G., et al. 2008, MNRAS, 389, 1605 [Google Scholar]
- Mennickent, R. E., Kołaczkowski, Z., Djurasevic, G., et al. 2012, MNRAS, 427, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Mezzetti, M., Giuricin, G., & Mardirossian, F. 1980, A&A, 83, 217 [NASA ADS] [Google Scholar]
- Mikołajewska, J. 2007, Balt. Astron., 16, 1 [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [Google Scholar]
- Moro, D., & Munari, U. 2000, A&AS, 147, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moshir, M., et al. 1990, in IRAS Faint Source Catalogue, version 2.0 [Google Scholar]
- Mukherjee, J., Peters, G. J., & Wilson, R. E. 1996, MNRAS, 283, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Nazarenko, V. V., & Glazunova, L. V. 2013, Astron. Rep., 57, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, E. H. 1983, A&AS, 54, 55 [NASA ADS] [Google Scholar]
- Olsen, E. H. 1993, A&AS, 102, 89 [NASA ADS] [Google Scholar]
- Paczynski, B. 1991, ApJ, 370, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Perry, C. L. 1969, AJ, 74, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, G. J. 1983, PASP, 95, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Piirola, V., Berdyugin, A., Mikkola, S., & Coyne, G. V. 2005, ApJ, 632, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Plavec, M. J. 1980, Highlights of Astronomy, 5, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Plavec, M. J. 1982, in NASA Conf. Pub. 2338, ed. Y. Kondo, 526 [Google Scholar]
- Plavec, M. J. 1988, ESA SP, 281, 221 [NASA ADS] [Google Scholar]
- Plavec, M. J. 1989, Space Sci. Rev., 50, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Wade, R. A. 1985, Interacting binary stars, Cambridge Astrophysics Series (Cambridge: Cambridge University Press) [Google Scholar]
- Refsdal, S., Roth, M. L., & Weigert, A. 1974, A&A, 36, 113 [NASA ADS] [Google Scholar]
- Richards, M. T., & Albright, G. E. 1999, ApJS, 123, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Sarna, M. J. 1993, MNRAS, 262, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Izzard, R. G., Davis, P. J., & Deschamps, R. 2013, A&A, 550, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, N., Gehrz, R. D., & Goss, W. M. 2001, AJ, 122, 2700 [NASA ADS] [CrossRef] [Google Scholar]
- Soydugan, F., Frasca, A., Soydugan, E., et al. 2007, MNRAS, 379, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Stothers, R. 1973, PASP, 85, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Strömgren, B. 1966, ARA&A, 4, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Sytov, A. Y., Kaigorodov, P. V., Bisikalo, D. V., Kuznetsov, O. A., & Boyarchuk, A. A. 2007, Astron. Rep., 51, 836 [Google Scholar]
- Taranova, O. G., & Shenavrin, V. I. 1997, Astron. Lett., 23, 698 [NASA ADS] [Google Scholar]
- Tokunaga, A. T., & Vacca, W. D. 2005, PASP, 117, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., & Pringle, J. E. 1992, MNRAS, 256, 269 [NASA ADS] [Google Scholar]
- Umana, G., Maxted, P. F. L., Trigilio, C., et al. 2000, A&A, 358, 229 [NASA ADS] [Google Scholar]
- Umana, G., Leone, F., & Trigilio, C. 2002, A&A, 391, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Hoof, P. A. M., Weingartner, J. C., Martin, P. G., Volk, K., & Ferland, G. J. 2004, MNRAS, 350, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., De Greve, J. P., De Loore, C., & Mennekens, N. 2008, A&A, 487, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., De Greve, J. P., Mennekens, N., Jansen, K., & De Loore, C. 2010, A&A, 510, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., de Greve, J. P., Mennekens, N., Jansen, K., & de Loore, C. 2011, A&A, 528, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, E. M., Verner, D. A., Korista, K. T., et al. 1999, ApJS, 120, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1982, AJ, 87, 1300 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, L. B. F. M., Cote, J., & Pols, O. R. 1991, A&A, 250, 437 [NASA ADS] [Google Scholar]
- Weiland, J. L., Shore, S. N., Beaver, E. A., Lyons, R. W., & Rosenblatt, E. I. 1995, ApJ, 447, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Westin, T. N. G. 1982, A&AS, 49, 561 [NASA ADS] [Google Scholar]
- Wolf, G. W., & Kern, J. T. 1983, ApJS, 52, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Young, A., & Snyder, J. A. 1982, ApJ, 262, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P. 2009, New Astron., 14, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P. 2011, New Astron., 16, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Zoła, S., & Ogłoza, W. 2001, A&A, 368, 932 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters for the three models; Model A: mass ratio reversal; Model B: intermediate case; Model C: end of non-conservative mass transfer. (For this case, three hotspot temperatures are investigated.)
Magnitudes in 2MASS and WISE bands assuming the models are located 300 pc away from the Sun.
All Figures
 |
Fig. 1 Schematic overview of an Algol system undergoing systemic mass loss due to a hotspot on the surface of the gainer. The ticks and numbers indicate the different phases (0.0: primary eclipse). |
| In the text | |
 |
Fig. 2 Red crosses: evolution of the mass surrounding the system (integrated up to the radius where the density of the outflow equals the ISM density; see text). The cyan circles (labelled with the model name) indicate the models selected for the simulations presented in this work. Long-dashed green line (right-hand scale): evolution of the gainer-star surface temperature. Magenta dotted line and dashed blue line: evolution of the masses of the donor and gainer (in unit of M⊙/ 500). |
| In the text | |
 |
Fig. 3 Density (left-hand scale, solid lines) and velocity (right-hand scale, dashed line) profiles of the outflowing material (similar – but with different parameters – to Fig. 9 of Paper I). Blue line: spherically-symmetric and isotropic outflow corresponding to a covering factor of fc = 1 (see text, Sect. 2.1); green lines: ejection confined in a disc of opening angle 90° (fc = 0.71); red line: ejection confined in a disc of opening angle 74°(fc = 0.6); The solid light-grey lines are the density profiles for fc = 0.71 at 100 different times uniformly distributed during the non-conservative phase. |
| In the text | |
 |
Fig. 4 Distance distribution for observed Algols. The sample of Algols is from Budding et al. (2004). Parallaxes are from the Hipparcos catalogue (ESA 1997). The dashed green curve represents the flux at 25 μm (right-hand scale) as a function of distance for the dusty simulation C_ld_0.71_inter. The flux is integrated over the whole nebula. The dotted blue line is the IRAS 5σ limit at 25 μm. The WISE 5σ limit for band W4 is 2600 μJy and is always below the dashed green curve. |
| In the text | |
 |
Fig. 5 Temperature profile (solid red line) and cooling time scale (dotted blue line; see text) of the material surrounding the star as a function of distance to the star (model C_df_0.71_inter). The dot-dashed cyan line represents the dust condensation temperature (1400 K). |
| In the text | |
 |
Fig. 6 Top panel: emissivity profiles (solid lines) and relative ionisation (dashed lines) for the simulation C_ld_0.71_inter (blue solid line: 2MASS Ks; green and red solid: WISE W2 and W4, respectively; green dashed: H ii fraction; blue dashed: Fe ii fraction). The vertical cyan line represents the Roche lobe radius for the gainer star. Bottom panel: Si iv (solid lines) and Fe ii fraction (dashed lines) for the high-temperature hotspot simulations (blue: model C_df_0.71_inter; red: C_df_0.71_hot). |
| In the text | |
 |
Fig. 7 Top: synthetic SEDs of the dust-free Cloudy models in the UV-optical regime. The input spectrum is the sum of the spectra of the gainer star, donor star, and hot spot with a temperature of 35 000 K (the last diluted according to the prescriptions of Appendix B). The fluxes are computed for a system distance of 300 pc. Bottom: same as top panel but for the different models A, B, and C (at different evolutionary times). The input spectra are in black from bottom to top (A, B, C). |
| In the text | |
 |
Fig. 8 Synthetic SEDs of dust-free models in the UV regime. The solid black line in the upper panel represents the input stellar spectrum. The lower panel shows the difference between the output and input spectra for the two models identified by the line labels. |
| In the text | |
 |
Fig. 9 Same as Fig. 7 but for the IR region, including the Skirt model C_SK_ld. For clarity, spectral lines have been removed from the Cloudy SEDs. The red arrows are 5 σ IRAS upper limits (in the faint-source catalogue): 0.2 Jy for the 12 and 25 μm bands and 0.28 Jy for the 60 μm band. |
| In the text | |
 |
Fig. 10 Strömgren photometry [m10; c10] diagram for our models (crosses) and for comparison, normal main-sequence stars (red dots) from the Long-Term Photometry of Variables project (Manfroid et al. 1991, to be discussed in Sect. 4.3). From the latter, only data obtained with the Danish telescope (system 7) were retained. For clarity, the models are not labelled, and only their general properties are indicated in blue. We refer to Table 3 for the values. We added observations of W Ser, B[e], and Be stars for comparison (green dots). The blue dots are the average values for the latter objects when several observations are available. |
| In the text | |
 |
Fig. 11 [Si iv] 1394 and 1403 Å doublet for three different configurations. |
| In the text | |
 |
Fig. 12 Skirt intensity map at 12 μm (top), 25 μm (middle), and 60 μm (bottom) for Φ = 2 × 10-5 (model C_SK_ld). To ease the comparison, the same limits are used for the three bands for the “x” and “y” axes. The angular size and intensity are given for a system at 300 pc. The figure is zoomed on a box 12 000 × 8516 AU2 wide. |
| In the text | |
 |
Fig. 13 Top panel: WISE FW4/FW1 against 2MASS J/Ks flux ratios for Algols from the catalogue of Budding et al. (2004), and for W Ser from the list of Gudel & Elias (1996). The symbiotic Algol SS Lep and a few Be and B[e] systems have been considered as well (as discussed in Sect. 4.1). The black filled triangles (linked by the dashed line) are black bodies of given temperatures (labels in Kelvin). The red filled squares represent the simulations (STAR: input spectrum). For clarity, only extreme models are labelled, and we refer to Table 5 for unlabelled models. The filled circles correspond to Algols with a S/N > 3.2. The size of the circle is proportional to the S/N for band W4 (except for SS Lep which has a S/N of 962 and for which we limit the size of the symbol), and the symbol colour relates to the χ2 for the same band. Bottom panel: same as top panel but for FW3/FW1 with S/N and χ2 relative to W3. |
| In the text | |
 |
Fig. 14 WISE band-4 images for the genuine Algol CZ Vel (left) and the Be star SX Aur (right). The images are centred on the objects, with north up and east to the left. The flux scale goes from the background level to background plus 150 times the background scatter σ, and the first thin (green) contour line corresponds to the background level plus 3 times its fluctuation, the next intermediate (blue) contour curve to 5σ, and the inermost thick black contour line to 10σ. |
| In the text | |
 |
Fig. A.1 Geometry of the hotspot emission. |
| In the text | |
 |
Fig. B.1 Representation of the effective surface of the hotspot over a full orbital period. See text for description. |
| In the text | |
 |
Fig. C.1 Top: continuum in the UV band for W Ser observed with IUE. Black: SWP47439 observation made on 1993-04-07 (20:02:16) at phase Φ = 0.84; red: SWP47457 observation made on 1993-04-10 (21:40:17) at phase Φ = 0.06. Bottom: difference of the two spectra. |
| In the text | |
 |
Fig. C.2 HST/GHRS spectra of the [Si iv] 1393.76 and 1402.77 Å lines of W Ser at two distinct phases (black: z0lu5108t observation made on 1991-07-12 (05:32:25) at phase Φ = 0.00, primary eclipse; red: z0lu0308t observation made on 1991-07-19 (03:29:13) at phase Φ = 0.5, secondary eclipse). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.