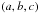| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425140 | |
| Published online | 13 March 2015 | |
Pressure distribution of the high-redshift cluster of galaxies CL J1226.9+3332 with NIKA ⋆
1 Laboratoire de Physique Subatomique et de Cosmologie (LPSC), Université Grenoble-Alpes, CNRS/IN2P3, 53 avenue des Martyrs, 38026 Grenoble, France
e-mail: adam@lpsc.in2p3.fr
2 Institut de RadioAstronomie Millimétrique (IRAM), 38406 Grenoble, France
3 Astronomy Instrumentation Group, University of Cardiff, UK
4 Laboratoire AIM, CEA/IRFU, CNRS/INSU, Université Paris Diderot, CEA-Saclay, 91191 Gif-Sur-Yvette, France
5 Institut d’Astrophysique Spatiale (IAS), CNRS and Université Paris Sud, 91405 Orsay, France
6 Institut d’Electronique Fondamentale (IEF), Université Paris Sud, 91405 Orsay, France
7 Institut Néel, CNRS and Université de Grenoble, 38000 Grenoble, France
8 Institut de RadioAstronomie Millimétrique (IRAM), Granada, Spain
9 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
10 CNRS, IPAG, 38000 Grenoble, France
11 Université de Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse, France
12 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
13 University College London, Department of Physics and Astronomy, Gower Street, London WC1E 6BT, UK
14 School of Earth and Space Exploration and Department of Physics, Arizona State University, Tempe, AZ 85287, USA
15 Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
Received: 10 October 2014
Accepted: 28 November 2014
The thermal Sunyaev-Zel’dovich (tSZ) effect is expected to provide a low scatter mass proxy for galaxy clusters since it is directly proportional to the cluster thermal energy. The tSZ observations have proven to be a powerful tool for detecting and studying them, but high angular resolution observations are now needed to push their investigation to a higher redshift. In this paper, we report high angular (<20 arcsec) resolution tSZ observations of the high-redshift cluster CL J1226.9+3332 (z = 0.89). It was imaged at 150 and 260 GHz using the NIKA camera at the IRAM 30-m telescope. The 150 GHz map shows that CL J1226.9+3332 is morphologically relaxed on large scales with evidence of a disturbed core, while the 260 GHz channel is used mostly to identify point source contamination. NIKA data are combined with those of Planck and X-ray from Chandra to infer the cluster’s radial pressure, density, temperature, and entropy distributions. The total mass profile of the cluster is derived, and we find M500 = 5.96+1.02-0.79 × 1014M⊙ within the radius R500 = 930+50-43 kpc, at a 68% confidence level. (R500 is the radius within which the average density is 500 times the critical density at the cluster’s redshift.) NIKA is the prototype camera of NIKA2, a KIDs (kinetic inductance detectors) based instrument to be installed at the end of 2015. This work is, therefore, part of a pilot study aiming at optimizing tSZ NIKA2 large programs.
Key words: techniques: high angular resolution / galaxies: clusters: individual: CL J1226.9+3332
The FITS file of the published maps is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/576/A12
© ESO, 2015
1. Introduction
Galaxy clusters are the largest gravitationally bound objects in the Universe. They arise from the collapse of primordial matter fluctuations, forming overdensity peaks at the intersection of filamentary structures. They offer a unique tracer of the matter distribution and a powerful probe for cosmology because they form across the expansion of the Universe. (See, for example, Allen et al. 2011 and references therein for a detailed review.)
Clusters are mainly made of dark matter (about 85% of their total masses), but also of hot ionized gas (about 12%) and of the stars and interstellar medium within galaxies (a few percent), representing the baryonic component that can be used to detect and study them. Optical observations have been historically used to measure their total mass (Zwicky 1933) – typically around 1014M⊙ – from galaxy velocity dispersion and, more recently, from lensing measurements of background objects (see Bartelmann 2010, for a review). Since galaxy clusters form by accreting of surrounding material (dark matter, galaxies, and gas) and by merging with other clusters, they can be the source of a significant amount of non-thermal emission. Radio measurements around 1 GHz are used to explore such processes (e.g., Feretti et al. 2011). The hot gas contained in the intracluster medium (ICM) – a few keV – emits X-ray photons due to the bremsstrahlung of energetic electrons (see Sarazin 1988). Therefore, X-ray imaging can be used to study the electronic density distribution in galaxy clusters (with a weak dependence on the temperature). In addition, X-ray spectroscopy provides the possibility of measuring the ICM temperature (see, for example, Böhringer & Werner 2010).
To be used for cosmology, galaxy clusters observables need to be related in some way to their total mass. The precise calibration of such scaling relations requires to use as many available probes (that are complementary to each other) as possible. The thermal Sunyaev-Zel’dovich (tSZ, Sunyaev & Zel’dovich 1972, 1980) effect provides such a probe. It is due to the inverse Compton scattering of cosmic microwave background (CMB) photons with high-energy electrons in the ICM. The photons are shifted to higher frequencies providing a characteristic spectral distortion of the CMB, observable at millimeter wavelengths. Since the observable is not the cluster itself but the CMB, tSZ offers a key advantage because it does not suffer from cosmological dimming as do other probes. Its amplitude is directly proportional to the pressure distribution in clusters and is therefore expected to provide a low scatter mass proxy when assuming hydrostatic equilibrium (e.g., Nagai 2006). Together with X-ray observations, the tSZ effect allows for a detailed characterization of the ICM thermodynamics. See Birkinshaw (1999), Carlstrom et al. (2002), and Kitayama (2014) for detailed reviews on the tSZ effect.
The Planck satellite (Planck Collaboration XXIX 2014), the South Pole Telescope (SPT, Reichardt et al. 2013; Bleem et al. 2015), and the Atacama Cosmology Telescope (ACT, Hasselfield et al. 2013) have produced, and will continue to improve, large tSZ selected cluster samples. However, as the high-redshift end of these samples is reached, clusters are not resolved owing to insufficient available angular resolution (larger than 1 arcmin). High angular resolution follow-up observations of these objects are needed to precisely calibrate the tSZ cluster observable versus their total mass, through their pressure profiles. The universality of such pressure distributions (Planck Collaboration Int. V 2013; Arnaud et al. 2010), taken as a standard candle, also has to be tested against redshift.
The object CL J1226.9+3332 is a high-redshift, hot and massive cluster of galaxies at z = 0.89. It was discovered in the WARPS survey (Wide Angle ROSAT Pointed Survey, Ebeling et al. 2001) and has been the object of multiwavelength studies. Owing to difficulty of X-ray spectroscopy at high-redshift, the first temperature estimates were made from SZA (Sunyaev-Zel’dovich Array) observations (Joy et al. 2001, 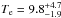 keV), providing the first confirmation that it is indeed a massive system. A detailed X-ray analysis of XMM-Newton observations by Maughan et al. (2004) reports a consistent temperature,
keV), providing the first confirmation that it is indeed a massive system. A detailed X-ray analysis of XMM-Newton observations by Maughan et al. (2004) reports a consistent temperature, 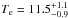 keV. They also measured CL J1226.9+3332 to show evidence of a relaxed X-ray morphology, in agreement with ROSAT first observations, and provided a total mass of (1.4 ± 0.5) × 1015M⊙. More recent Chandra observations also agree that CL J1226.9+3332 is a hot system (Bonamente et al. 2006,
keV. They also measured CL J1226.9+3332 to show evidence of a relaxed X-ray morphology, in agreement with ROSAT first observations, and provided a total mass of (1.4 ± 0.5) × 1015M⊙. More recent Chandra observations also agree that CL J1226.9+3332 is a hot system (Bonamente et al. 2006, 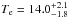 keV). The pressure profile of the cluster was measured at arcmin angular scales using the interferometric SZA observations at 30 and 90 GHz (Muchovej et al. 2007; Mroczkowski et al. 2009; Mroczkowski 2011), providing a detailed picture of the ICM on these scales. First indications of a disturbed core were made by an XMM/Chandra analysis, showing an asymmetry in the temperature map with a hotter southwest region (Maughan et al. 2007). Lensing observations by the Hubble Space Telescope (HST Jee & Tyson 2009) found a relaxed morphology on large scales and agree on the presence of a disturbed core on smaller scales, with the presence of a subclump 40 arcsec toward the southwest. This is consistent with the hotter region and highly correlated with the cluster galaxy distribution. They propose a scenario in which a less massive system has passed through the main cluster and the gas has been stripped during this passage. The mass inferred within the radius1rΔ = 200 is (1.4 ± 0.2) × 1015M⊙. Finally, MUSTANG tSZ observations at 90 GHz on ~8−45 arcsec scales (Korngut et al. 2011) have revealed a narrow 20 arcsec long ridge 10 arcsec southwest of the X-ray peak, in addition to another peak coincident with X-ray and the brightest cluster galaxy.
keV). The pressure profile of the cluster was measured at arcmin angular scales using the interferometric SZA observations at 30 and 90 GHz (Muchovej et al. 2007; Mroczkowski et al. 2009; Mroczkowski 2011), providing a detailed picture of the ICM on these scales. First indications of a disturbed core were made by an XMM/Chandra analysis, showing an asymmetry in the temperature map with a hotter southwest region (Maughan et al. 2007). Lensing observations by the Hubble Space Telescope (HST Jee & Tyson 2009) found a relaxed morphology on large scales and agree on the presence of a disturbed core on smaller scales, with the presence of a subclump 40 arcsec toward the southwest. This is consistent with the hotter region and highly correlated with the cluster galaxy distribution. They propose a scenario in which a less massive system has passed through the main cluster and the gas has been stripped during this passage. The mass inferred within the radius1rΔ = 200 is (1.4 ± 0.2) × 1015M⊙. Finally, MUSTANG tSZ observations at 90 GHz on ~8−45 arcsec scales (Korngut et al. 2011) have revealed a narrow 20 arcsec long ridge 10 arcsec southwest of the X-ray peak, in addition to another peak coincident with X-ray and the brightest cluster galaxy.
In this paper, we report 150 and 260 GHz tSZ observations of CL J1226.9+3332, using the New IRAM KIDs Array (NIKA, see Monfardini et al. 2010, 2011; Bourrion et al. 2011; Calvo et al. 2013; Adam et al. 2014; Catalano et al. 2014, for more details on the NIKA camera) at the IRAM (Institut de Radio Astronomie Millimétrique) 30-m telescope. The reconstructed tSZ map of the cluster is used to constrain its pressure distribution, as well as the thermodynamics of the ICM gas by combining it with X-ray data. Since NIKA is the prototype of the future NIKA2 camera, these observations are part of a pilot study that aims at showing the potential of NIKA2 for follow-ups of unresolved Planck and ACT clusters.
The paper is organized as follows. The observations of CL J1226.9+3332 are presented in Sect. 2, including the reduction of NIKA data. In Sect. 3, we present the analysis performed to recover the thermodynamical properties of the cluster. The results are provided in Sect. 4 and compared to data of other observatories and previous observations. The conclusions and NIKA2 perspectives are given in Sect. 5. Throughout this paper we assume a flat ΛCDM cosmology according to the latest Planck results (Planck Collaboration XVI 2014) with H0 = 67.11 km s-1 Mpc-1, ΩM = 0.3175, and ΩΛ = 0.6825.
2. High resolution thermal Sunyaev-Zel’dovich observations
2.1. Observations of CL J1226.9+3332
The NIKA camera was used at the IRAM 30-m telescope (Pico Veleta, Spain) to image CL J1226.9+3332 at 150 and 260 GHz during the first NIKA open pool of February 2014. The cluster was mapped using on-the-fly raster scans made of constant azimuth – resp. elevation – subscans. Scans were made of 19 subscans of 6 arcmin length, separated by 10 arcsec elevation – resp. azimuth – steps. The subscan duration was fixed to ten seconds, giving a scanning speed of 36 arcsec per second and a total time of 3.3 minutes per scan. The pointing center was chosen to be (RA, Dec) = (12h 26m 58s, 33o32′40′′) based on MUSTANG tSZ observations (Korngut et al. 2011). All coordinates in this paper are given in equinox 2000.
The data collected were taken with an opacity, at 150 GHz (respectively 260 GHz), in the range 0.06–0.23 (respectively 0.06–0.29) and a mean value of 0.13 (respectively 0.16), corresponding to average winter conditions. The observations were mostly carried out during night time. A small fraction of the scans were flagged due to bad weather conditions and some others were lost because of missing data streams with the telescope position. The overall effective observing time on the cluster is 7.8 h.
The overall final pointing residual errors were obtained with a precision of less than 3 arcsec using the observations of nearby quasars, 1308+326 and 1156+295, every hour. Uranus was taken as our primary calibrator, and we used its frequency-dependent brightness temperature model as given by Moreno (2010), assumed to be accurate at the level of 5%, as shown by Planck Collaboration VIII (2014). Within the NIKA bandpasses of the February 2014 campaign, we obtain a mean brightness temperature of 112.7 and 92.8 K at 150 and 260 GHz, respectively. Uncertainties on the calibration were measured to be 5% and 11% at 150 and 260 GHz, respectively, using the dispersion of the recovered flux on Uranus maps. This corresponds to 7% and 12% overall calibration uncertainties when including the model error. The focus of the telescope was checked on Uranus or other bright point sources every two to three hours and systematically after sunset and sunrise. The effective FWHM was measured to be 18.2 and 12.0 arcsec at 150 and 260 GHz, respectively, by fitting a Gaussian model on the planet. The opacity was measured and corrected for by using NIKA total power data as a tau-meter as described in Catalano et al. (2014). The Compton y to surface brightness (measured in Jy/beam) conversions were computed by integrating the tSZ spectrum (see Sect. 3) within the NIKA bandpasses transmissions and accounting for the beam angular coverage, as described in more detail in Adam et al. (2014). For this campaign, the conversions are −10.9 ± 0.8 and 3.5 ± 0.5 Jy/beam per unit of y at 150 and 260 GHz, respectively, including the overall calibration error and the 2% error arising from the bandpasses uncertainties.
In Table 1, we summarize the instrumental properties of the NIKA camera as it was used during CL J1226.9+332 observation.
Instrumental characteristics of NIKA for the February 2014 campaign.
2.2. Data reduction
The details of the NIKA data reduction are available in Adam et al. (2014) and Catalano et al. (2014). Here, the main procedure is briefly summarized for the reader’s convenience. Invalid detectors were removed based on the statistical properties of their noise and their optical response. Cosmic ray impacts on the arrays were flagged and removed from the data. To remove the low-frequency atmospheric emission from the data, a common-mode template was built by averaging the detector time stream across each array. This was done by flagging the source in signal-to-noise in an iterative manner to avoid ringing and reduce signal filtering effects. This data reduction was preferred for CL J1226.9+3332, with respect to the spectral dual-band noise decorrelation described in Adam et al. (2014). The latter allows more extended emission to be recovered but is noisier. Moreover, the cluster is sufficiently compact for any filtering effect to be weak enough, allowing the recovery of cluster maps at both wavelengths simultaneously. Frequency lines produced by the pulse tube of the cryostat were notch-filtered in the Fourier domain. Data were finally projected onto 2-arcsec pixel grid maps using inverse variance weighting and a nearest grid projection.
 |
Fig. 1 NIKA raw maps of CL J1226.9+3332 at 150 GHz (left) and 260 GHz (right). Contours are multiples of 3σ, excluding the zero level, which is not shown. The effective beams FWHM (12.0 and 18.2 arcsec native resolution) are shown as the bottom left white circles, although the display images are smoothed with an extra 10 arcsec FWHM Gaussian. The position of the X-ray center is shown as a white cross in both maps and that of the point source is shown as a red star in the 150 GHz map. |
The raw (direct output of the pipeline) 150 and 260 GHz NIKA maps of CL J1226.9+3332 are presented in Fig. 1. They are centered on the X-ray peak coordinates (taken from Cavagnolo et al. 2009), (RA, Dec) = (12h 26m 58.37s, 33o32′47.4′′), and have been smoothed with a 10 arcsec Gaussian filter for display purposes. The 150 GHz map shows a strong tSZ decrement reaching 18σ per beam at the peak. Because the noise is higher at 260 GHz, and the tSZ signal weaker by a factor of about one third, the map does not show a very significant tSZ detection, even if diffuse positive emission is seen at about 3σ on the map at the cluster position. However, the 260 GHz channel reveals the presence of a point source (referred to as PS260 in the following) located about 30 arcsec southeast of the X-ray center, detected at about 10σ. The source is not clearly detected at 150 GHz due to the strong tSZ signal, but it is visible as a lack of tSZ at its corresponding location. In Sect. 2.4, we discuss the implications of point source contamination on our tSZ observation.
In Fig. 2, we provide the flux density profile corresponding to the 150 GHz map. It is computed by averaging the signal in concentric annuli with the X-ray center taken as the origin. The profile appears to be smooth and peaks at the center.
2.3. Transfer function
The data reduction described above induces an attenuation of the astrophysical signal in the recovered maps of Fig. 1, since detectors are combined to remove the correlated noise. The characterization of this effective transfer function as a function of the angular scales was done by using noise plus input signal simulations. To do so, the map of an input known simulated astrophysical signal (see below) was compared to the output signal after processing.
The simulated input signal was the one expected for clusters of galaxies, as described in detail in Adam et al. (2014). It was computed using a generalized Navarro, Frenk & White (gNFW) pressure profile (see Sect. 3.2.1, Nagai et al. 2007b) integrated along the line of sight to produce a tSZ flux density map. The typical amplitude and angular size of the simulated clusters were similar to the one in Fig. 1, but the result transfer function was checked to see that it did not depend on the radial size and amplitude of the input signal.
To simulate the atmospheric and intrinsic correlated and uncorrelated noise, we used the NIKA data themselves. The real data used for the simulations were those of our other projects taken during the first NIKA open pool of February 2014, for which the scanning strategy was similar to that of CL J1226.9+3332. These scans were taken with atmospheric conditions comparable to those during which the data presented in this paper were taken. The astrophysical signal within the data was checked to be faint enough that it did not affect the reduction, i.e. negligible compared to the noise.
To deal with the residual noise contribution in the final processed maps, we considered the simulated data with and without including the known input signal. In this way we obtained estimates of both the processed noisy signal and of the noise itself, which we could subtract from the processed signal-plus-noise map to produce an output signal-only map. The transfer function was then computed as the ratio of the power spectra of the output signal, free of noise, and the input one. However, small noise residuals are observed because of the differences in the processing introduced by the signal itself.
The estimated transfer function is given in Fig. 3. The uncertainties were calculated from the dispersion of the transfer function obtained for all the scans used to compute it, and are mostly due to residual noise. As we can see, it is approximately flat and close to one, with ~5% attenuation, on scales smaller than the NIKA field of view. On larger scales, the recovered flux vanishes smoothly with decreasing wave number. In Sec. 3.4, we use this transfer function when comparing a model to the NIKA map.
 |
Fig. 2 Flux density profile of CL J1226.9+3332 as measured by NIKA at 150 GHz, i.e., the radial average within concentric annuli. The point source has been fitted and subtracted (see Sect. 3.4) before computing the profile. Error bars are only statistical. |
 |
Fig. 3 NIKA data reduction transfer function as a function of angular frequency. Uncertainties were computed using the dispersion of the results over the different noise realizations. The 150 GHz beam cutoff and size of the NIKA field of view are also represented by green dashed lines for illustration, i.e. (18.2 arcsec)-1 and (1.9 arcmin)-1. The black horizontal dashed line corresponds to 5% filtering. |
2.4. Point source contamination
The SZA data were used to search for radio sources around CL J1226.9+3332 (Muchovej et al. 2007). From their observations, no such objects are present within the NIKA field. From the residual between the MUSTANG map and the SZA pressure model of Mroczkowski et al. (2009), Korngut et al. (2011) have inferred the presence of a possible submillimeter source 10 arcsec north of the X-ray peak. Using the NIKA 260 GHz frequency band, we searched for such a contaminant and do not observe any point source within a 1.5 arcmin radius around the map center, apart from PS260. This is done by fitting PS260 and the tSZ signal simultaneously, as described in detail in Sect. 3.4. The root-mean-squared between the best-fit model and the data allows us to set a 2σ flux upper limit of 1.5 mJy at this frequency. Therefore, the feature seen by Korngut et al. (2011) is unlikely to be a real submillimeter source. The flux distribution of the detected point source, PS260, is fitted using a Gaussian model with FWHM fixed to the NIKA 260 GHz beam. Its flux is measured to be 6.8 ± 0.7 (stat.) ± 1.0 (cal.) mJy and its position (RA, Dec.) = (12h 27m0.01s, 33o32′42.0′′), with statistical and calibration error quoted as stat and cal. We note that the source possibly coincides with two known optically detected galaxies J12265995+3332405 and J12265923+3332405 (Holden et al. 2009). They are located 1.7 and 9.8 arcsec away from the best-fit position obtained, respectively. We conclude that no additional point sources, wether radio or submillimeter, affect the 150 GHz map of NIKA. The detected source is accounted for in the analysis described hereafter.
3. Characterization of the intracluster medium
3.1. SZ and X-ray observables
3.1.1. Thermal SZ
The tSZ effect results in a distortion of the CMB black-body spectrum whose frequency dependence is given by (Birkinshaw 1999) 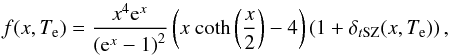 (1)where
(1)where 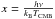 is the dimensionless frequency, h the Planck constant, kB the Boltzmann constant, ν the observation frequency, and TCMB the temperature of the CMB. We use the Itoh et al. (1998) relativistic corrections to compute δtSZ(x,Te), where Te is the electrons temperature. The induced change in intensity relative to the primary CMB intensity I0 reads as
is the dimensionless frequency, h the Planck constant, kB the Boltzmann constant, ν the observation frequency, and TCMB the temperature of the CMB. We use the Itoh et al. (1998) relativistic corrections to compute δtSZ(x,Te), where Te is the electrons temperature. The induced change in intensity relative to the primary CMB intensity I0 reads as 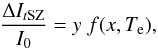 (2)where y is the Compton parameter, which measures the integrated electronic pressure Pe along the line of sight, dl, written as
(2)where y is the Compton parameter, which measures the integrated electronic pressure Pe along the line of sight, dl, written as 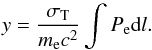 (3)The parameter σT is the Thomson cross section, me is the electron rest mass, and c the speed of light. Neglecting the relativistic corrections, the tSZ spectral distortion is nil around 217 GHz, negative below and positive above.
(3)The parameter σT is the Thomson cross section, me is the electron rest mass, and c the speed of light. Neglecting the relativistic corrections, the tSZ spectral distortion is nil around 217 GHz, negative below and positive above.
3.1.2. Kinetic SZ
In addition to the tSZ effect, the kinetic Sunyaev-Zel’dovich (kSZ) is caused by the motion of the intracluster gas and its electrons relative to the CMB. This motion leads to a Doppler shift of the CMB photons that are scattered via the Compton effect. It can be expressed as (Birkinshaw 1999) 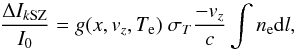 (4)where vz is the line-of-sight peculiar velocity of the cluster with respect to the Hubble flow, which is positive (negative) for a cluster receding from (coming towards) the observer, and ne the electronic density. The function g(x,vz,Te) provides the spectral dependence of the kSZ effect as
(4)where vz is the line-of-sight peculiar velocity of the cluster with respect to the Hubble flow, which is positive (negative) for a cluster receding from (coming towards) the observer, and ne the electronic density. The function g(x,vz,Te) provides the spectral dependence of the kSZ effect as 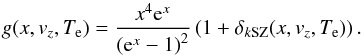 (5)Again, we use Itoh et al. (1998) to account for the relativistic corrections δkSZ and neglect the velocity dependance as it is expected to be less than 1%. By writing ΔI(ν) = AtSZΔItSZ(ν) + AkSZΔIkSZ(ν) where AtSZ,kSZ stand for dimensionless amplitudes (see Eqs. (2) and (4)), and assuming the observed region to be isothermal, one can deduce the line-of-sight velocity as
(5)Again, we use Itoh et al. (1998) to account for the relativistic corrections δkSZ and neglect the velocity dependance as it is expected to be less than 1%. By writing ΔI(ν) = AtSZΔItSZ(ν) + AkSZΔIkSZ(ν) where AtSZ,kSZ stand for dimensionless amplitudes (see Eqs. (2) and (4)), and assuming the observed region to be isothermal, one can deduce the line-of-sight velocity as 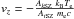 .
.
3.1.3. X-ray emission
The X-ray surface brightness, in units of counts cm-2 s-1 sr-1, is related to the electronic density as 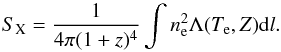 (6)The parameter z is the redshift, Λ(Te,Z) is the cooling function that is proportional to
(6)The parameter z is the redshift, Λ(Te,Z) is the cooling function that is proportional to 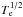 , and Z is the metallicity. Additionally, the gas temperature can be estimated from X-ray spectroscopy.
, and Z is the metallicity. Additionally, the gas temperature can be estimated from X-ray spectroscopy.
3.2. Intracluster medium modeling
3.2.1. Pressure profile
The cluster electronic pressure distribution is modeled by a spherical gNFW profile (Nagai et al. 2007b), described by 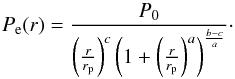 (7)The parameter P0 is a normalizing constant; rp is a characteristic radius; and a, b, and c set the slopes at intermediate, large, and small radii, respectively. We can also write P0 = PΔ × P0 and rΔ = cΔrp, where PΔ is the average pressure within rΔ, P0 is a normalizing constant, and cΔ the concentration parameter (Arnaud et al. 2010). The mass enclosed within rΔ, M(r = rΔ), is then related to PΔ by a scaling law. One can finally define θp,Δ = rp,Δ/DA, where DA is the angular distance of the cluster.
(7)The parameter P0 is a normalizing constant; rp is a characteristic radius; and a, b, and c set the slopes at intermediate, large, and small radii, respectively. We can also write P0 = PΔ × P0 and rΔ = cΔrp, where PΔ is the average pressure within rΔ, P0 is a normalizing constant, and cΔ the concentration parameter (Arnaud et al. 2010). The mass enclosed within rΔ, M(r = rΔ), is then related to PΔ by a scaling law. One can finally define θp,Δ = rp,Δ/DA, where DA is the angular distance of the cluster.
In the following, we use three different choices to fix the slope parameters (see Table 2). 1) We fix c to the value obtained by Comis et al. (2011) for this cluster and fix a and b to the one obtained by Planck Collaboration Int. V (2013) when stacking the tSZ signal of 62 nearby clusters. This choice is used as the baseline since the two outer slope parameters have been obtained directly from tSZ data and are expected to provide a good description of most clusters. The parameter c was not fitted by Planck Collaboration Int. V (2013) so we rely on Chandra X-ray data that are specific to CL J1226.9+3332. This set of parameters is referred to PPC in the following. 2) We fix a, b, and c to the values obtained by Nagai et al. (2007a) based on X-ray Chandra clusters and numerical simulations. This set of parameters allows us to directly compare our results to that of Mroczkowski et al. (2009), who used them in their modeling. It is referred to as NNN. 3) We fix b and c to values similar to those of PPC, but fit for the parameter a since it corresponds to scales at which NIKA is the most sensitive for this cluster. This choice is referred to as FPC.
Pressure profile parameters for the three models presented in this paper.
The parameters P0 and rp are always allowed to vary. Since the pressure profile parameters are highly degenerate, in particular a, P0, and rp, the main difference between the three models relies on the choice of the core slope parameter c and the outer slope parameter b, which cannot be constrained directly with the NIKA data. As discussed in Sect. 4, the core slope parameter is related to the thermodynamics of the cluster core but does not affect the overall mass determination. By contrast, the outer slope is associated to the steepness of the mass profile at outer radii. Therefore it controls the cluster overall mass at large radii and can lead to a bias in the mass estimate for radii above those constrained directly from the data. By using these three models, we test the impact of the choice of the model in the regions of the ICM profiles for which NIKA is not directly sensitive.
3.2.2. Density profile
Following Mroczkowski et al. (2009) and since we use the work of Comis et al. (2011), the electron density profile is described by a simplified version (SVM) of the model suggested by Vikhlinin et al. (2006)![\begin{equation} n_{\rm e}(r) = n_{\rm e0} \left[1+\left(\frac{r}{r_{\rm c}}\right)^2 \right]^{-3 \beta /2} \left[1+\left(\frac{r}{r_{\rm s}}\right)^{\gamma} \right]^{-\epsilon/2 \gamma}, \label{eq:SVM} \end{equation}](/articles/aa/full_html/2015/04/aa25140-14/aa25140-14-eq79.png) (8)which is an extension of the β model (Cavaliere & Fusco-Femiano 1978) with an additional steepening freedom at radii larger than ~ rs, for which the slope parameter is ϵ. The core radius is still given by rc, and γ accounts for the width of the transition between the two profiles. In the case of ϵ = 0, this model is equivalent to the standard β model. Similar to Mroczkowski et al. (2009) and Comis et al. (2011), we fix the parameter γ = 3 because it is a good fit to all the clusters considered by Vikhlinin et al. (2006), and leave the other ones as free parameters.
(8)which is an extension of the β model (Cavaliere & Fusco-Femiano 1978) with an additional steepening freedom at radii larger than ~ rs, for which the slope parameter is ϵ. The core radius is still given by rc, and γ accounts for the width of the transition between the two profiles. In the case of ϵ = 0, this model is equivalent to the standard β model. Similar to Mroczkowski et al. (2009) and Comis et al. (2011), we fix the parameter γ = 3 because it is a good fit to all the clusters considered by Vikhlinin et al. (2006), and leave the other ones as free parameters.
3.2.3. Temperature and entropy
Assuming the ideal gas law, the temperature of the electron population can simply be computed as 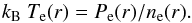 (9)It is implicitly modeled as the ratio of the distributions given by the gNFW and SVM models of Eqs. (7) and (8). The ICM entropy is defined as (see review from Voit 2005)
(9)It is implicitly modeled as the ratio of the distributions given by the gNFW and SVM models of Eqs. (7) and (8). The ICM entropy is defined as (see review from Voit 2005) 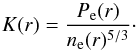 (10)
(10)
3.2.4. Mass distribution
When assuming CL J1227.9+3332 to be in hydrostatic equilibrium, its total mass enclosed within r, Mtot(r), is related to the electronic density and pressure profiles through 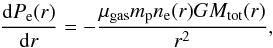 (11)where mp is the proton mass and G the Newton’s constant. We assume in this paper a mean molecular weight μe = 1.15 for the electrons and μgas = 0.61 for the gas. By directly integrating the electronic density profile up to a radius R, we obtain the gas mass enclosed within R,
(11)where mp is the proton mass and G the Newton’s constant. We assume in this paper a mean molecular weight μe = 1.15 for the electrons and μgas = 0.61 for the gas. By directly integrating the electronic density profile up to a radius R, we obtain the gas mass enclosed within R, 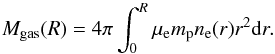 (12)It is straightforward to deduce the gas fraction profile, defined as the ratio at a given radius between the gas mass and the total mass enclosed within r, as
(12)It is straightforward to deduce the gas fraction profile, defined as the ratio at a given radius between the gas mass and the total mass enclosed within r, as 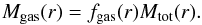 (13)Finally, the total mass is directly related to RΔ from its definition as
(13)Finally, the total mass is directly related to RΔ from its definition as 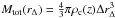 , where ρc(z) is the critical density of the Universe at redshift z. Combining the value of RΔ and rp, directly related to the pressure profile, we can therefore measure the concentration parameter cΔ.
, where ρc(z) is the critical density of the Universe at redshift z. Combining the value of RΔ and rp, directly related to the pressure profile, we can therefore measure the concentration parameter cΔ.
3.3. Extra datasets
In addition to the NIKA data we consider the ACCEPT and Planck datasets.
3.3.1. ACCEPT density profile
We make use of the ACCEPT catalog (Archive of Chandra Cluster Entropy Profile Tables2, Cavagnolo et al. 2009). We only consider the deprojected X-ray density profile of CL J1226.9+3332, which is computed from the publicly available Chandra data. The angular resolution of Chandra, ~ 0.5 arcsec, is negligible compared to that of NIKA. As fully explained in Cavagnolo et al. (2009), the flux measured in the energy range 0.7–2.0 keV is a good diagnosis of the ICM density (Eq. (6)). The high angular resolution surface brightness profile is therefore converted into a deprojected electron density profile using normalization and count rates taken from the spectral analysis. The profile extends up to 835 kpc, which corresponds approximately to R500 (see Sect. 4).
3.3.2. Planck integrated compton parameter
The cluster CL J1226.9+3332 is not in the Planck tSZ cluster catalog (Planck Collaboration XXIX 2014) since its flux is diluted by the Planck beam, and it is therefore not detected with high enough signal-to-noise. Nevertheless, in addition to NIKA tSZ observations, we use the Planck maps to produce a Compton y parameter map as described in Planck Collaboration XXI (2014; see Hurier et al. 2013 for the method). Its angular resolution is 7.5 arcmin, limited by the lowest Planck frequency channel used to construct it. This map is used to measure the integrated Compton parameter of CL J1226.9+3332 within θmax, defined as 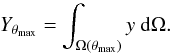 (14)The uncertainty on this quantity is obtained by applying the same integration on the map at positions around the cluster, where the noise is homogeneous and the map is free of emission. We also check on the jackknife (half-ring half-difference, see Planck Collaboration I 2014) map that the error is consistent with the expected noise. We obtain YΩ(15′) = (0.94 ± 0.36) × 10-3 arcmin2.
(14)The uncertainty on this quantity is obtained by applying the same integration on the map at positions around the cluster, where the noise is homogeneous and the map is free of emission. We also check on the jackknife (half-ring half-difference, see Planck Collaboration I 2014) map that the error is consistent with the expected noise. We obtain YΩ(15′) = (0.94 ± 0.36) × 10-3 arcmin2.
3.4. Maximum likelihood analysis
We aim at recovering the three-dimensional electronic pressure and electronic density profiles of CL J1226.9+3332. To do so, we use an approach in which input models are processed similarly to the measured tSZ signal such that they can be compared to it. Best-fit values of the electronic pressure and density model parameters are jointly obtained from a Markov Chain Monte Carlo (MCMC) approach, using a Metropolis-Hasting algorithm (Chib & Greenberg 1995). A set of chains of tested models samples the multidimensional likelihood parameter space. At each step of the chains, a model map is computed by integrating the tested pressure model along the line of sight. The map is then convolved with the NIKA beam and the pipeline transfer function. The model is converted into surface brightness using the Jy/beam to y conversion factors given in Sect. 2.2. A radial temperature model is inferred from the pressure and the density models, and used to account for relativistic corrections (Itoh et al. 1998) on the tSZ map model. We also use the Planck integrated flux to add an extra constraint on the overall flux. The flux and the position of PS260 are simultaneously fitted. We only impose a Gaussian prior on its position based on the fit at 260 GHz, assuming a 3 arcsec uncertainty. We include a set of nuisance parameters in the fit, such as calibration uncertainties, map zero level, and the pointing position, which are randomly sampled within their error bars at each step.
The χ2 used in the Metropolis-Hasting acceptance (or rejection) process of the chain samples is defined as 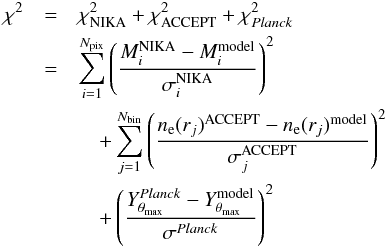 (15)where the sums are made over the number of pixels in the NIKA map (Npix) and the number of radial bins of the ACCEPT density profile (Nbin). The quantity M represents the 150 GHz only tSZ surface-brightness-plus-point-source map. The parameters σNIKA, σACCEPT and σPlanck are the respective errors, assumed to be Gaussian. While X-ray counts follow Poisson statistics, the deprojected density profile is computed by combining a set of random variables; therefore, assuming that the central limit theorem applies in this process, we expect the error statistics followed by the ACCEPT deprojected density profile to be Gaussian. It is also naturally the case for Planck and NIKA errors.
(15)where the sums are made over the number of pixels in the NIKA map (Npix) and the number of radial bins of the ACCEPT density profile (Nbin). The quantity M represents the 150 GHz only tSZ surface-brightness-plus-point-source map. The parameters σNIKA, σACCEPT and σPlanck are the respective errors, assumed to be Gaussian. While X-ray counts follow Poisson statistics, the deprojected density profile is computed by combining a set of random variables; therefore, assuming that the central limit theorem applies in this process, we expect the error statistics followed by the ACCEPT deprojected density profile to be Gaussian. It is also naturally the case for Planck and NIKA errors.
The convergence of the MCMC is ensured by the Gelman & Rubin (1992) test. Once reached, the histogram of the chains along the considered parameter is marginalized over all other dimensions (including nuisance parameters) providing the posterior probability distribution for each fitted parameter. The integrated posterior probability distribution up to 68% probability gives the quoted errors.
To estimate the uncertainties on the derived cluster physical properties for each radial bin, we fully propagate the information contained in the MCMC parameter chains to the given quantity. For each set of parameters tested against the data (i.e., a model), we compute all derived physical quantities as a function of the radial distance. Therefore, for each radius, we obtain a probability distribution function for the considered quantity. We then compute the reference value of the given quantity as the median of the distribution and its error by integrating the distributions up to the requested confidence limit, for each radial bin.
4. Results and discussions
4.1. NIKA dual-band detection and mapping of the tSZ signal
 |
Fig. 4 Compton parameter profile y of CL J1226.9+3332 at 150 GHz (red) and 260 GHz (green). The point source has been subtracted before extracting the profile. Statistical uncertainties are shown as error bars, and systematic uncertainties are given as a dashed-line envelope. |
From the MCMC analysis we obtain a flux of 1.9 ± 0.2 (stat.) mJy at 150 GHz for PS260. With these results, PS260 is subtracted from the maps in the following analysis. The Compton parameter profile is computed by averaging the signal within radial bins and accounting for the conversion between flux density and Compton parameter. Figure 4 shows the Compton parameter radial profile, computed from the X-ray center for both 150 and 260 GHz. The signal is detected on the profile up to about 1 arcmin at 150 GHz. Error bars are only statistical uncertainties; calibration uncertainties would result in an overall multiplicative factor to apply to the entire profile. The two profiles are compatible over the whole radial range. Nevertheless, we notice the presence of a few distinct peaks in the 260 GHz profile. These peaks might indicate the presence of additional contamination from submillimeter sources, which are most probably below the noise in the 260 GHz map. Assuming a dust-like spectrum, we expect the contribution from these sources to be negligible at 150 GHz. By fitting the 260 GHz profile to the 150 GHz one, taken as the model, we obtain a 7σ tSZ detection at 260 GHz. We obtain a reduced χ2 of 0.95 with 24 degrees of freedom.
 |
Fig. 5 Top left: NIKA 150 GHz raw map of CL J1226.9+3332. Top right: MCMC maximum likelihood tSZ + point source model. Bottom left: point-source-subtracted map. Bottom right: tSZ + point-source-subtracted residual map. The contours are spaced by 0.5 mJy/beam, and the maps have been smoothed with a 10 arcsec Gaussian filter. The effective beam is shown in the bottom left corner of each map. |
Figure 5 provides the raw, best-fit, point source subtracted and residual maps obtained from the maximum likelihood analysis. After subtracting PS260 the cluster appears circular at the NIKA resolution and is aligned with the X-ray peak on which the maps are centered. The signal is extended and clearly detected at the map level up to 1 arcmin scales. The NIKA map is morphologically consistent with previous interferometric observations by SZA (Joy et al. 2001; Muchovej et al. 2007; Mroczkowski et al. 2009) and does not show any evidence of being disturbed on large angular scales. However, the cluster core is slightly elongated toward the southwest at scales close to our our beam (and smaller). Using MUSTANG 90 GHz observations, at an effective resolution of 11 arcsec, Korngut et al. (2011) have indeed detected a narrow ridge ~ 20 arcsec long located about 10 arcsec from the X-ray center towards the southwest. This is consistent with the hotter region found by Maughan et al. (2007) using Chandra and XMM X-ray data. Additional lensing observations from HST (Jee & Tyson 2009) also reveals the presence of a secondary peak in the surface mass distribution in this region.
The NIKA observations agree with CL J1226.9+3332 being relaxed on large scales with a disturbed core, the origin of the latter being probably due to the merger of a smaller subcluster. Since NIKA probes scales between ~ 20 arcsec to a few arcmin, these observations complement the ones by MUSTANG on small scales (~10−50 arcsec) and by SZA interferometric data that are the most sensitive on scales of a few arcmin. Finally, we notice that the NIKA residual map is well correlated with the temperature map presented in Maughan et al. (2007), i.e. the tSZ signal appears to be slightly stronger on the north (being under estimated by our spherically symmetric model), where the gas is hotter than it is in the south (respectively, overestimated), where the gas is cooler.
 |
Fig. 6 Constraints on the kSZ and tSZ spectra computed within 50 arcsec of the X-ray center. The green, yellow, and red swaths give the tSZ, kSZ, and tSZ+kSZ contributions, respectively. The two data points are the NIKA measurements. |
 |
Fig. 7 Density profile as a function of physical distance from the cluster center. The data correspond to those from the ACCEPT database (Cavagnolo et al. 2009) discussed in the text. The solid line represents the best-fit density model. The 1σ uncertainties are represented by the gray contours. The difference between the data and the best-fit model normalized by the 1σ uncertainties (χ) is also shown. |
By measuring the integrated flux toward the cluster within a 50 arcsec radius circle centered on the X-ray peak at both NIKA wavelengths, it is possible to set constraints on the kSZ contribution (see Sect. 3.1.2). As shown in Fig. 6, the kSZ spectrum amplitude is compatible with zero within 1σ. Assuming the cluster average temperature within the region considered to be Te = 10 ± 1 keV, we infer a limit on the line-of-sight velocity of vz = −445 ± 461 km s-1 at 1σ including calibration uncertainties.
4.2. Intracluster medium radial distribution
The best-fit density profile is represented in Fig. 7 with the data points of the ACCEPT catalog used to fit it. As shown in the bottom residual profile (χ, the difference between data points and the best-fit model normalized by the data point errors), the model fits the data over the full radial range for the purpose of this paper. Since the best-fit density profile depends on the choice of the pressure profile slope only through the relativistic correction (see Sect. 3.4), we show the result only for the first case, our baseline PPC pressure profile, and the differences between models are insignificant.
In Fig. 8 we present the radial distributions of the pressure, temperature, and entropy of the ICM of CL J1226.9+3332 derived using NIKA data. Uncertainties are given at 68% confidence level and account for both statistical and NIKA overall calibration errors. The profiles corresponding to the different pressure profile models, PPC, NNN, and FPC (see Sect. 3.2.1) are given.
The pressure (left) is characterized well by NIKA, with less than 10% uncertainty below 500 kpc and up to 25% at 1500 kpc for PPC. The profile is best constrained around 250 kpc, corresponding to ~30 arcsec when projected onto the sky, where NIKA is most sensitive. The PPC profile is in qualitative agreement with the one obtained by Mroczkowski et al. (2009), despite a different choice of slope parameter. When using the same modeling, NNN, we find a good agreement, particularly on small scales. As expected, when loosening the constraints on parameter a, as in the case of the FPC profile, uncertainties increase by a factor of about 1.5. Thanks to the degeneracy between the pressure profile parameters, the different models agree well in the region where NIKA is sensitive. At both larger and smaller scales, the models tend to deviate from one another up to more than 1σ, in particular NNN versus PPC and FPC, which directly propagates onto the other derived profiles, as discussed below.
The temperature profile, derived from the pressure and the density, presents a core value of about 15 keV and decreases toward the outskirts of the cluster, reaching about 5 keV around 1500 kpc. For the PPC model we find uncertainties of about 10−15%. The profile is slightly higher, but compatible within errors to those measured by Mroczkowski et al. (2009) with SZA and Maughan et al. (2007) with a detailed X-ray (Chandra + XMM) analysis. All three tested pressure profile models give compatible temperature results. Nevertheless, we notice that the core slope, c, obtained by Comis et al. (2011) tends to indicate a cooler core below 200 kpc, while it is not the case for NNN. This is because the core temperature, which is the ratio between the pressure and the density, is directly related to the core pressure slope c. The flatter core of PPC and FPC, with respect to NNN, leads to a cooler core for the same density profile. Higher angular resolution tSZ observations would be necessary to provide constraints on the core slope pressure parameter c.
 |
Fig. 8 Pressure (left), temperature (middle) and entropy (right) profiles as a function of physical distance from the cluster center. The green, yellow, and red swaths provide the 68% confidence limit, accounting for both calibration and statistical uncertainties. They correspond to modeling of the pressure profile with different choices for slope parameters |
The entropy profile is generally described well by 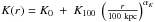 (e.g., Pratt et al. 2010; Cavagnolo et al. 2009), where K0 is called the core entropy, K100 is a normalization, and αK provides the slope of the profile. Large core entropies are expected for clusters with disturbed core such as CL J1226.9+3332. The obtained entropy profile (right), shown on a logarithmic scale for both axes, is described well by a simple power law in the range directly probed by NIKA (≳100 kpc). As we fixed the pressure profile parameter c = 0.014 (Comis et al. 2011) in our baseline pressure model, which is expected to truly extrapolate the pressure parametrization on small scales, we expect the entropy profile to be accurate below100 kpc but limit ourselves to a qualitative discussion. The entropy profile shows signs of flattening below this scale with a core entropy above 100 keV cm2, which would indicate that CL J1226.9+3332 is disturbed on small scales. At large radii, the slope seems to change but the error bars are too large for this effect to be measured. This discussion is also valid in the case of the NNN model, even if the core entropy tends to deviate by more than 1σ between the two. Our baseline model, PPC, is fully compatible with the one obtained by Maughan et al. (2007). At large radii, however, the NNN profile is in better agreement with this X-ray analysis, with the main differences coming from the choice of the slope parameters at the core and the outer radii of the pressure profile.
(e.g., Pratt et al. 2010; Cavagnolo et al. 2009), where K0 is called the core entropy, K100 is a normalization, and αK provides the slope of the profile. Large core entropies are expected for clusters with disturbed core such as CL J1226.9+3332. The obtained entropy profile (right), shown on a logarithmic scale for both axes, is described well by a simple power law in the range directly probed by NIKA (≳100 kpc). As we fixed the pressure profile parameter c = 0.014 (Comis et al. 2011) in our baseline pressure model, which is expected to truly extrapolate the pressure parametrization on small scales, we expect the entropy profile to be accurate below100 kpc but limit ourselves to a qualitative discussion. The entropy profile shows signs of flattening below this scale with a core entropy above 100 keV cm2, which would indicate that CL J1226.9+3332 is disturbed on small scales. At large radii, the slope seems to change but the error bars are too large for this effect to be measured. This discussion is also valid in the case of the NNN model, even if the core entropy tends to deviate by more than 1σ between the two. Our baseline model, PPC, is fully compatible with the one obtained by Maughan et al. (2007). At large radii, however, the NNN profile is in better agreement with this X-ray analysis, with the main differences coming from the choice of the slope parameters at the core and the outer radii of the pressure profile.
 |
Fig. 9 NIKA best-fit derived radial profiles for hydrostatic equilibrium (HSE) total mass (left) and the gas fraction (right). The color code is the same as in Fig. 8. |
The total mass and the gas fraction profiles are presented in Fig. 9. From the total mass profile we extract 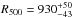 kpc, which in turn gives
kpc, which in turn gives 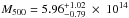 M⊙, compatible with previous measurements (e.g., Mroczkowski et al. 2009; Maughan et al. 2007). We obtain a gas fraction within R500 of
M⊙, compatible with previous measurements (e.g., Mroczkowski et al. 2009; Maughan et al. 2007). We obtain a gas fraction within R500 of 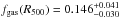 . The total mass PPC and NNN profiles give compatible results over the full radial range. Small differences between the two are most noticeable in the range where NIKA is not very sensitive, i.e., on scales below 100 kpc where NNN is higher than PPC, mainly due to the difference in the pressure profile. The FPC model is fully compatible with the two other ones, and it presents larger error contours. The results are similar for the gas fraction, for which PPC presents a flattening below 200 kpc, while NNN keeps decreasing. Assuming the gas fraction of CL J1226.9+3332 within R500 to be a good representation of the matter content in the Universe, we compare it to its expected gas fraction using Planck Collaboration XVI (2014) cold dark matter, Ωc, and baryon density, Ωb, as
. The total mass PPC and NNN profiles give compatible results over the full radial range. Small differences between the two are most noticeable in the range where NIKA is not very sensitive, i.e., on scales below 100 kpc where NNN is higher than PPC, mainly due to the difference in the pressure profile. The FPC model is fully compatible with the two other ones, and it presents larger error contours. The results are similar for the gas fraction, for which PPC presents a flattening below 200 kpc, while NNN keeps decreasing. Assuming the gas fraction of CL J1226.9+3332 within R500 to be a good representation of the matter content in the Universe, we compare it to its expected gas fraction using Planck Collaboration XVI (2014) cold dark matter, Ωc, and baryon density, Ωb, as 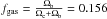 . We find that it is compatible with our result within error bars.
. We find that it is compatible with our result within error bars.
Main results of the MCMC analysis.
The posterior ICM distribution is compatible in all cases with the integrated tSZ flux measured by Planck. The main outcomes of our analysis are summarized in Table 3.
4.3. CL J1226.9+3332 and the tSZ–Mass scaling relations
 |
Fig. 10 Left: Planck universal pressure profile (black line), together with the best-fit profile obtained for CL J1226.9+3332 in green with the 1σ error as a light green shadow accounting for all PPC, FPC, and NNN profile’s. The Planck average of the individual pressure profiles across the 62 nearby cluster sample is given as red data points and the stacked pressure profile derived from the XMM data for the same sample is also given as purple dots (Planck Collaboration Int. V 2013). The dispersion about the respective tSZ and X-ray profiles are shown by shaded area with similar (lighter) colors. The scale corresponding to the one at which the NIKA data start to be affected by filtering is also given as a vertical dashed line. Right: Planck Y500–M500 calibration (Planck Collaboration XX 2014), together with the NIKA value obtained for CL J1226.9+3332 in the case of the PPC pressure profile parameterization. The Planck scaling law is represented as a black line, and the data points of the clusters used for its calibration are given as black dots. The NIKA data point is given by the red star. |
Clusters of galaxies are usually used for cosmological studies assuming a self-similar scenario because they are expected to be a scaled version of one another. In practice, non-gravitational processes can induce dispersion in the general trend and biases. The Planck satellite has recently released the largest tSZ selected cluster sample (1227 objects, Planck Collaboration XXIX 2014). To use this catalog for cosmology, Planck Collaboration XX (2014) have calibrated the relation between Yθ500 ≡ Y500 and M500![\begin{equation} E(z)^{-2/3} \left[\frac{D_{\rm A}^2 Y_{500}}{10^{-4}~{\rm Mpc}^2}\right] = 10^{-0.19 \pm 0.02} \left[\frac{(1-b) M_{500}}{6 \times 10^{14}~M_{\sun}}\right]^{1.79\, \pm\, 0.08}, \label{eq:Y500M500} \end{equation}](/articles/aa/full_html/2015/04/aa25140-14/aa25140-14-eq156.png) (16)where
(16)where 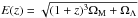 . The extra bias term, (1 − b), corresponds to the expectation that the hydrostatic equilibrium (HSE) mass underestimates the true mass due to non-thermal pressure, so that
. The extra bias term, (1 − b), corresponds to the expectation that the hydrostatic equilibrium (HSE) mass underestimates the true mass due to non-thermal pressure, so that 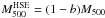 . In this paper we set b = 0.2, because it was the baseline for Planck Collaboration XX (2014).
. In this paper we set b = 0.2, because it was the baseline for Planck Collaboration XX (2014).
As a demonstration of the potential of future NIKA2 tSZ dedicated large programs, we present a comparison of the recovered characteristics for CL J1226.9+3332 in terms of pressure profile and tSZ–mass scaling relation, to the Planck 2013 results (Planck Collaboration Int. V 2013; Planck Collaboration XX 2014). The left panel of Fig. 10 provides a comparison between the pressure profile of CL J1226.9+3332, at high-redshift, and the average profile over 62 nearby clusters obtained by Planck Collaboration Int. V (2013). Both have been normalized to account for the mass and redshift dependance by 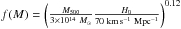 as detailed in Planck Collaboration Int. V (2013). The NIKA data show that the normalized pressure profile of CL J1226.9+3332 is among the highest ones, but does not show any significant evidence of non-standard redshift evolution, within error bars. In addition we notice that our error bars are model dependent and do not reflect the full uncertainty of the data. The evolution of the pressure profile with redshift has been statistically tested recently using a Chandra X-ray analysis of 80 SPT clusters (McDonald et al. 2014) with a highest bin at a mean redshift z = 0.82. They find no significant evolution, apart from the cluster’s cores, and agree with a standard redshift evolution of the pressure distribution among clusters. In the right hand panel of Fig. 10, we present Y500 as a function of M500 for CL J1226.9+3332. For comparison we also show the best-fit Planck Collaboration XX (2014) scaling law and the data corresponding to the 71 clusters used for its calibration. The mean redshift of this cluster sample is 0.195 with a maximum redshift of 0.447. The cluster CL J1226.9+3332, at z = 0.89, is consistent with the Planck Collaboration XX (2014) scaling relation. This single data point does not allow us to draw any conclusion on the evolution with redshift. However, our results illustrate the strength of such measurements based on a sample of a few tens of clusters with future NIKA2 observations. This will indeed allow us to precisely constrain the redshift evolution of scaling relations, on the basis of individual measurements.
as detailed in Planck Collaboration Int. V (2013). The NIKA data show that the normalized pressure profile of CL J1226.9+3332 is among the highest ones, but does not show any significant evidence of non-standard redshift evolution, within error bars. In addition we notice that our error bars are model dependent and do not reflect the full uncertainty of the data. The evolution of the pressure profile with redshift has been statistically tested recently using a Chandra X-ray analysis of 80 SPT clusters (McDonald et al. 2014) with a highest bin at a mean redshift z = 0.82. They find no significant evolution, apart from the cluster’s cores, and agree with a standard redshift evolution of the pressure distribution among clusters. In the right hand panel of Fig. 10, we present Y500 as a function of M500 for CL J1226.9+3332. For comparison we also show the best-fit Planck Collaboration XX (2014) scaling law and the data corresponding to the 71 clusters used for its calibration. The mean redshift of this cluster sample is 0.195 with a maximum redshift of 0.447. The cluster CL J1226.9+3332, at z = 0.89, is consistent with the Planck Collaboration XX (2014) scaling relation. This single data point does not allow us to draw any conclusion on the evolution with redshift. However, our results illustrate the strength of such measurements based on a sample of a few tens of clusters with future NIKA2 observations. This will indeed allow us to precisely constrain the redshift evolution of scaling relations, on the basis of individual measurements.
5. Summary and conclusions
The NIKA camera at the IRAM 30-m telescope was used to image the cluster of galaxies CL J1226.9+3332 via the tSZ effect at 150 and 260 GHz with 18.2 and 12.0 arcsec angular resolution, respectively. It provides the first resolved observation of this cluster at these frequencies. The cluster signal is detected in the two bands, but our tSZ analysis focuses on the 150 GHz map since the signal-to-noise is higher at this frequency. A submillimeter point source is detected at 260 GHz, 30 arcsec away from the cluster center, showing the interest of the dual-band capabilities of NIKA to account for such contaminant. These observations, on scales ~20−200 arcsec, complement previous single-dish 90 GHz MUSTANG observations on scales in the range ~10−50 arcsec and interferometric SZA data at 30 and 90 GHz, which are the most sensitive at arcmin scales. The ICM morphology of the cluster agrees with these previous measurements. CL J1226.9+3332 appears relaxed on large scales and shows evidence of a disturbed core, most likely due to the merger of a subcluster to the southwest. It is also consistent with X-ray and lensing observations.
We used maximum likelihood analysis to constrain the pressure profile of the cluster via Markov Chain Monte Carlo sampling. The NIKA maps were combined with Chandra X-ray data using the ACCEPT data, to jointly derive ICM thermodynamic quantities (pressure, density, temperature, and entropy profiles). Planck tSZ data were also used to cross-check the overall flux of CL J1226.9+3332. The inferred temperature profile of the cluster exhibits a core value of about 15 keV and decreases toward the outskirts, reaching about 5 keV around 1 Mpc. The entropy profile is described well by a simple power law in the range probed by NIKA but shows sign of flattening below 100 kpc with a core entropy above 100 keV cm2, agreeing with CL J1226.9+3332 being disturbed on small scales. Assuming that the hydrostatic equilibrium accurately applies to this cluster, we extracted the total mass and gas mass profile and derived the gas fraction profile. We measured 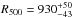 kpc and
kpc and 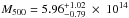 M⊙ at a 68% confidence level. We compared these results when assuming Planck tSZ-based pressure-profile slope parameters or X-ray/numerical simulation based ones and find that both choices give consistent results in general. These results are compatible within the uncertainties with previous tSZ and X-ray measurements.
M⊙ at a 68% confidence level. We compared these results when assuming Planck tSZ-based pressure-profile slope parameters or X-ray/numerical simulation based ones and find that both choices give consistent results in general. These results are compatible within the uncertainties with previous tSZ and X-ray measurements.
NIKA is the prototype of NIKA2, which will be permanently installed at the IRAM 30-m telescope at the end of 2015. NIKA2 will contain about 5000 detectors, i.e., 15 times more than NIKA, within the same frequency bands and similar angular resolution. Its instantaneous field of view will accordingly increase from 1.8 to 6.5 arcmin. With such characteristics, NIKA2 will be well adapted to mapping the tSZ signal in intermediate and distant clusters of galaxies. The observation of CL J1226.9+3332 is part of a pilot study that aims at characterizing the possible scientific outcomes of large observing campaigns with NIKA2. Future NIKA2 dedicated tSZ observations of a few tens of clusters would allow study of the evolution of scaling and structural properties of clusters of galaxies out to z ~ 1. Here, by comparing our results to the expected tSZ–mass Planck scaling relations for a single cluster, we have shown that with more objects, NIKA2 will be able to calibrate the tSZ-mass scaling relation and its eventual redshift dependence.
Acknowledgments
We are thankful to the anonymous referee for useful comments that helped improve the quality of the paper. We gratefully thank Marian Douspis and the Planck collaboration for providing the Planck data points shown in the right hand panel of Fig. 10. We thank Marco De Petris for useful comments. We would like to thank the IRAM staff for their support during the campaign. This work has been partially funded by the Foundation Nanoscience Grenoble, the ANR under the contracts “MKIDS” and “NIKA”. This work has been partially supported by the LabEx FOCUS ANR-11-LABX-0013. This work has benefited from the support of the European Research Council Advanced Grant ORISTARS under the European Union’s Seventh Framework Program (Grant Agreement No. 291294). The NIKA dilution cryostat was designed and built at the Institut Néel. In particular, we acknowledge the crucial contribution of the Cryogenics Group and, in particular Gregory Garde, Henri Rodenas, Jean Paul Leggeri, and Philippe Camus. R.A. would like to thank the ENIGMASS French LabEx for funding this work. B.C. acknowledges support from the CNES post-doctoral fellowship program. E.P. acknowledges support from grant ANR-11-BS56-015. A.R. would like to thank the FOCUS French LabEx for funding this work. A.R. acknowledges support from the CNES doctoral fellowship program.
References
- Adam, R., Comis, B., Macías-Pérez, J. F., et al. 2014, A&A, 569, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M. 2010, Class. Quant. Grav., 27, 233001 [CrossRef] [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bleem, L. E., Stalder, B., de Haan, T., et al. 2015, ApJS, 216, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv., 18, 127 [CrossRef] [Google Scholar]
- Bonamente, M., Joy, M. K., LaRoque, S. J., et al. 2006, ApJ, 647, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrion, O., Bideaud, A., Benoit, A., et al. 2011, J. Inst., 6, P06012 [Google Scholar]
- Calvo, M., Roesch, M., Désert, F. X., et al. 2013, A&A, 551, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlstrom, J. E., Holder, G. P., & Reese, E. D. 2002, ARA&A, 40, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Catalano, A., Calvo, M., Ponthieu, N., et al. 2014, A&A, 569, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1978, A&A, 70, 677 [NASA ADS] [Google Scholar]
- Chib, S., & Greenberg, E. 1995, Am. Statistician, 49, 327 [Google Scholar]
- Comis, B., de Petris, M., Conte, A., Lamagna, L., & de Gregori, S. 2011, MNRAS, 418, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Jones, L. R., Fairley, B. W., et al. 2001, ApJ, 548, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2011, in IAU Symp., 274, eds. A. Bonanno, E. de Gouveia Dal Pino, & A. G. Kosovichev, 340 [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Statistical Science, 7, 457 [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, J. Cosmol. Astropart. Phys., 7, 8 [Google Scholar]
- Holden, B. P., Franx, M., Illingworth, G. D., et al. 2009, ApJ, 693, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Itoh, N., Kohyama, Y., & Nozawa, S. 1998, ApJ, 502, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, M. J., & Tyson, J. A. 2009, ApJ, 691, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, M., LaRoque, S., Grego, L., et al. 2001, ApJ, 551, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T. 2014, Prog. Theor. Exp. Phys., 06B111 [Google Scholar]
- Korngut, P. M., Dicker, S. R., Reese, E. D., et al. 2011, ApJ, 734, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, L. R., Ebeling, H., & Scharf, C. 2004, MNRAS, 351, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, C., Jones, L. R., & Van Speybroeck, L. 2007, ApJ, 659, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Benson, B. A., Vikhlinin, A., et al. 2014, ApJ, 794, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Monfardini, A., Swenson, L. J., Bideaud, A., et al. 2010, A&A, 521, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monfardini, A., Benoit, A., Bideaud, A., et al. 2011, ApJS, 194, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, R. 2010, Neptune and Uranus planetary brightness temperature tabulation. Tech. Rep., ESA Herschel Science Center, available from ftp://ftp.sciops.esa.int/pub/hsc-calibration/PlanetaryModels/ESA2 [Google Scholar]
- Mroczkowski, T. 2011, ApJ, 728, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T., Bonamente, M., Carlstrom, J. E., et al. 2009, ApJ, 694, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Muchovej, S., Mroczkowski, T., Carlstrom, J. E., et al. 2007, ApJ, 663, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D. 2006, ApJ, 650, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007a, ApJ, 668, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007b, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2014, A&A, 571, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2014, A&A, 571, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1988, S&T, 76, 639 [NASA ADS] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Astrophys. Space Phys. Res., 4, 173 [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helvetica Phys. Acta, 6, 110 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 NIKA raw maps of CL J1226.9+3332 at 150 GHz (left) and 260 GHz (right). Contours are multiples of 3σ, excluding the zero level, which is not shown. The effective beams FWHM (12.0 and 18.2 arcsec native resolution) are shown as the bottom left white circles, although the display images are smoothed with an extra 10 arcsec FWHM Gaussian. The position of the X-ray center is shown as a white cross in both maps and that of the point source is shown as a red star in the 150 GHz map. |
| In the text | |
 |
Fig. 2 Flux density profile of CL J1226.9+3332 as measured by NIKA at 150 GHz, i.e., the radial average within concentric annuli. The point source has been fitted and subtracted (see Sect. 3.4) before computing the profile. Error bars are only statistical. |
| In the text | |
 |
Fig. 3 NIKA data reduction transfer function as a function of angular frequency. Uncertainties were computed using the dispersion of the results over the different noise realizations. The 150 GHz beam cutoff and size of the NIKA field of view are also represented by green dashed lines for illustration, i.e. (18.2 arcsec)-1 and (1.9 arcmin)-1. The black horizontal dashed line corresponds to 5% filtering. |
| In the text | |
 |
Fig. 4 Compton parameter profile y of CL J1226.9+3332 at 150 GHz (red) and 260 GHz (green). The point source has been subtracted before extracting the profile. Statistical uncertainties are shown as error bars, and systematic uncertainties are given as a dashed-line envelope. |
| In the text | |
 |
Fig. 5 Top left: NIKA 150 GHz raw map of CL J1226.9+3332. Top right: MCMC maximum likelihood tSZ + point source model. Bottom left: point-source-subtracted map. Bottom right: tSZ + point-source-subtracted residual map. The contours are spaced by 0.5 mJy/beam, and the maps have been smoothed with a 10 arcsec Gaussian filter. The effective beam is shown in the bottom left corner of each map. |
| In the text | |
 |
Fig. 6 Constraints on the kSZ and tSZ spectra computed within 50 arcsec of the X-ray center. The green, yellow, and red swaths give the tSZ, kSZ, and tSZ+kSZ contributions, respectively. The two data points are the NIKA measurements. |
| In the text | |
 |
Fig. 7 Density profile as a function of physical distance from the cluster center. The data correspond to those from the ACCEPT database (Cavagnolo et al. 2009) discussed in the text. The solid line represents the best-fit density model. The 1σ uncertainties are represented by the gray contours. The difference between the data and the best-fit model normalized by the 1σ uncertainties (χ) is also shown. |
| In the text | |
 |
Fig. 8 Pressure (left), temperature (middle) and entropy (right) profiles as a function of physical distance from the cluster center. The green, yellow, and red swaths provide the 68% confidence limit, accounting for both calibration and statistical uncertainties. They correspond to modeling of the pressure profile with different choices for slope parameters |
| In the text | |
 |
Fig. 9 NIKA best-fit derived radial profiles for hydrostatic equilibrium (HSE) total mass (left) and the gas fraction (right). The color code is the same as in Fig. 8. |
| In the text | |
 |
Fig. 10 Left: Planck universal pressure profile (black line), together with the best-fit profile obtained for CL J1226.9+3332 in green with the 1σ error as a light green shadow accounting for all PPC, FPC, and NNN profile’s. The Planck average of the individual pressure profiles across the 62 nearby cluster sample is given as red data points and the stacked pressure profile derived from the XMM data for the same sample is also given as purple dots (Planck Collaboration Int. V 2013). The dispersion about the respective tSZ and X-ray profiles are shown by shaded area with similar (lighter) colors. The scale corresponding to the one at which the NIKA data start to be affected by filtering is also given as a vertical dashed line. Right: Planck Y500–M500 calibration (Planck Collaboration XX 2014), together with the NIKA value obtained for CL J1226.9+3332 in the case of the PPC pressure profile parameterization. The Planck scaling law is represented as a black line, and the data points of the clusters used for its calibration are given as black dots. The NIKA data point is given by the red star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.