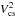| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424143 | |
| Published online | 19 December 2014 | |
A resolved, au-scale gas disk around the B[e] star HD 50138 ⋆, ⋆⋆
1
Anton Pannekoek Institute, University of Amsterdam,
Science Park 904,
1098 XH
Amsterdam,
The Netherlands
e-mail:
lucas.ellerbroek@gmail.com
2
Université Grenoble Alpes, IPAG, 38000
Grenoble,
France
3
CNRS, IPAG, 38000
Grenoble,
France
4
School of Physics, University of Exeter,
Stocker Road, Exeter
EX4 4QL,
UK
5
Observatório Nacional, Rua General José Cristino 77, 20921-400
São Cristovão, Rio de Janeiro,
Brazil
6
Laboratoire Lagrange, UMR 7293 UNS-CNRS-OCA, Boulevard de
l’Observatoire, CS
34229, 06304
Nice Cedex 4,
France
7
Leiden Observatory, Leiden University,
PO Box 9513, 2300 RA
Leiden, The
Netherlands
8
Université de Lyon, 69003
Lyon,
France
9 Université Lyon 1, Observatoire de Lyon, 9 avenue Charles
André, 69230 Saint Genis Laval, France
10
CNRS, UMR 5574, Centre de Recherche Astrophysique de Lyon; École Normale Supérieure,
69007
Lyon,
France
11
The CHARA Array of Georgia State University, Mount Wilson
Observatory, 91023
Mount Wilson
CA,
USA
12
Department of Physics, University of Cincinnati,
Cincinnati
OH
45221,
USA
13
Space Science Institute, 4750 Walnut Street, Boulder, CO
80303,
USA
14
The Aerospace Corporation, Los Angeles, CA
90009,
USA
15
Thule Scientific, Topanga, CA
90290,
USA
Received: 6 May 2014
Accepted: 17 September 2014
HD 50138 is a B[e] star surrounded by a large amount of circumstellar gas and dust. Its spectrum shows characteristics which may indicate either a pre- or a post-main-sequence system. Mapping the kinematics of the gas in the inner few au of the system contributes to a better understanding of its physical nature. We present the first high spatial and spectral resolution interferometric observations of the Brγ line of HD 50138, obtained with VLTI/AMBER. The line emission originates in a region more compact (up to 3 au) than the continuum-emitting region. Blue- and red-shifted emission originates from the two different hemispheres of an elongated structure perpendicular to the polarization angle. The velocity of the emitting medium decreases radially. An overall offset along the NW direction between the line- and continuum-emitting regions is observed. We compare the data with a geometric model of a thin Keplerian disk and a spherical halo on top of a Gaussian continuum. Most of the data are well reproduced by this model, except for the variability, the global offset and the visibility at the systemic velocity. The evolutionary state of the system is discussed; most diagnostics are ambiguous and may point either to a post-main-sequence or a pre-main-sequence nature.
Key words: stars: formation / stars: emission-line, Be / stars: variables: T Tauri, Herbig Ae/Be / circumstellar matter / stars: individual: HD 50138
Based on observations performed with X-Shooter (program 090.D-0212) and CRIRES (program 084.C-0668), mounted on the ESO Very Large Telescope, on Cerro Paranal, Chile, and AMBER mounted on the Very Large Telescope Interferometer (programs 082.C-0621, 082.C-0657, 083.C-0144, 084.C-0187, 084.C-0668, 084.C-0983, 384.D-0482, and 092.C-0376(B)).
Figure 4 and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
B[e] stars are an enigmatic class of stellar objects, the nature of which is in many cases unknown and strongly debated. They are defined as stars with spectral type B that show forbidden emission lines in their optical spectra, as well as strong near-infrared (NIR) excess (Slettebak 1976; Allen & Swings 1976; Zickgraf 1998). The forbidden lines originate in a tenuous circumstellar medium, while a dust envelope or a disk radiates in the infrared. The denomination “B[e] star” is phenomenological, where the defining characteristics can be produced by a heterogeneous set of astrophysical objects. Among its members are both young (pre-main-sequence stars) and evolved systems (e.g., supergiants, interacting binaries, and planetary nebulae). For many systems, determining their configuration and evolutionary state proves to be a difficult observational challenge (Lamers et al. 1998; Miroshnichenko 2007).
Lamers et al. (1998) formulated a classification scheme for B[e] stars of different natures based on their spectral lines, suspected luminosity and environment. For some objects, however, the diagnostics in Lamers’ scheme are inconclusive. These systems may be understood by combining observations with high resolution in the spectral, spatial, and temporal domains. In the last decade, a new generation of optical/NIR interferometers equipped with high spectral-resolution instruments have become available. With these, circumstellar gas dynamics can be mapped with unprecedented spatial (milli- to micro-arcsecond) and spectral (Δν ~ 25 km s-1) resolution. This has been a successful method of resolving some of the most intensely debated B[e] systems (Malbet et al. 2007; Domiciano de Souza et al. 2007; Millour et al. 2009; Weigelt et al. 2011; Kraus et al. 2008, 2012; Wang et al. 2012; Wheelwright et al. 2012b,c, 2013). In most of these cases, binary interaction is the most probable cause of the complex circumstellar environment. Gas disks are found to dominate the emission in the inner few astronomical units (au); however, only in a few cases a Keplerian velocity field could be resolved (e.g., Kraus et al. 2012).
In this paper, we present the first spectro-interferometric study employing high spectral resolution of the puzzling B[e] star HD 50138 (V743 Mon, MWC 158). Among the brightest B[e] stars in the sky, it is located at a distance of 500 ± 150 pc (van Leeuwen 2007) and has not been associated with a star-forming region. It may be part of the Orion-Monoceros molecular cloud complex (Maddalena et al. 1986), but because of the uncertainty in the distance, this cannot be confirmed.
Despite the ample amount of observations and literature, no definitive conclusion has been drawn regarding its evolutionary state. Arguments have been made to classify it as a pre-main-sequence object (Morrison & Beaver 1995) or a star on, or just evolving off, the main-sequence (Borges Fernandes et al. 2009, BF09). For more discussion of its evolutionary state, see, for example, Jaschek et al. (1993), Jaschek & Andrillat (1998), Lamers et al. (1998). The main property favoring a pre-main-sequence nature are spectral infall signatures. Conversely, the occurrence of shell phases have been interpreted as signs of a post-main-sequence nature. Many characteristics are ambiguous, such as the isolation of the object, its large infrared excess, and possible binarity (Cidale et al. 2001; Baines et al. 2006).
The circumstellar dust around the system is distributed in an aspherical geometry, which is represented well by a moderately inclined disk, i = 56 ± 4°, as determined by Borges Fernandes et al. (2011, BF11) based on near- (au-scale) and mid-infrared (10 au-scale) interferometry. The same authors find a position angle (from north through east) of the disk major axis, ψ = 71 ± 7°, perpendicular to the polarization angle (159 ± 4°, Bjorkman et al. 1998; Yudin & Evans 1998; Oudmaijer & Drew 1999). Signatures of outflowing and infalling gas are found in emission lines (Morrison & Beaver 1995; Grady et al. 1996; Pogodin 1997; BF09; Borges Fernandes et al. 2012, BF12). Spectropolarimetry by Bjorkman et al. (1998) suggests that a geometrically thin gas disk exists, where electron scattering dominates the polarization. Other polarimetry studies also find evidence of a circumstellar rotating disk or equatorial outflow (Oudmaijer & Drew 1999; Harrington & Kuhn 2007, 2009).
Spectro-astrometric measurements of the Hα line show a time-dependent shift in the photocenter and a decreasing spatial width across the line (Baines et al. 2006). This is interpreted by the authors as the sign of a binary companion on a wide orbit. The circumstellar material may be the result of the interaction with a much closer companion. Given the limited time sampling of monitoring campaigns to date, no evidence for any spectroscopic binary has been found (Corporon & Lagrange 1999; BF12). Photometric and spectroscopic variability is detected on timescales from days to years from as early as the 1930s. This has been attributed to shell phases and outbursts, during which the ejected material absorbs and scatters radiation in lines and in the continuum. This variability remains an actively discussed phenomenon (Merrill 1931; Merrill & Burwell 1933; Doazan 1965; Hutsemékers 1985; Andrillat & Houziaux 1991; Halbedel 1991; Bopp 1993; Pogodin 1997, BF09, BF12).
In this paper, we focus on the kinematics of the Brγ emission line tracing the circumstellar gas around HD 50138. We present a series of observations performed with the Astronomical Multi-Beam Combiner (AMBER) on the Very Large Telescope Interferometer (VLTI), with the VLT Cryogenic High-Resolution Infrared Echelle Spectrograph (CRIRES) and VLT/X-Shooter, all located on Cerro Paranal, Chile. We supplement the dataset with observations of the Hα line, taken with the Visible Spectrograph and Polarimeter (VEGA) on the CHARA array on Mount Wilson, California, USA. The observations are described in Sect. 2. We present the optical-to-infrared stellar and circumstellar spectra, and the most important trends and signatures found in the AMBER, CRIRES and VEGA data in Sect. 3. With baselines up to 120 m and a high spectral resolution (ν= 25 km s-1), we are able to trace photocenter shifts at a few micro-arcseconds of resolution in the line emission. In Sect. 4, the interferometric observations are compared to a geometric model, which consists of a Keplerian disk and halo. We discuss the validity of this and other possible model geometries in Sect. 5. The implications for the object’s evolutionary state are also considered. The main conclusions of this work are presented in Sect. 6.
Journal of the observations.
2. Observations and data reduction
A summary of the observations that are presented in this paper is given in Table 1.
2.1. VLTI/AMBER Spectro-interferometry
We observed HD 50138 between January 2009 and November 2013 during eleven nights. We used the NIR instrument AMBER on the VLTI (Schöller 2007; Haguenauer et al. 2010). AMBER enables the simultaneous combination of three beams in the K band (2.0−2.4 μm), with a spectral resolving power up to ℛ ~ 12 000 (Petrov et al. 2007).
Six measurements were obtained at medium spectral resolution (ℛ ~ 1500, Δν ~ 200 km s-1) and five at high resolution (ℛ ~ 12 000, Δν ~ 25 km s-1). We performed these observations using the relocatable 1.8 m auxiliary telescopes (ATs) and the 8.2 m unit telescopes (UTs), both arrays in two different configurations. The longest projected baseline is ~121 m. Figure 1 displays the (u,v)-plane coverage of the observations. The position angles (PA) of the baselines are color-coded in this image. The broadest range in spatial scales was intentionally achieved along a PA of ~ 71°, parallel to the disk major axis as found by BF11, where the object is most extended.
 |
Fig. 1 Coverage of the (u,v)-plane of the VLTI/AMBER-observations with ℛ ~ 12 000 (filled squares) and ℛ ~ 1500 (open squares). The two CHARA/VEGA-observations are also displayed (crosses). The dashed line is aligned with the major axis of the modeled disk ellipse (ψ = 71°). Colors indicate the baseline PA with respect to this line. |
Each measurement of HD 50138 was preceded and followed by observations of calibrator targets to measure the instrumental transfer function and to correct for instrumental effects. We used the following calibrators: HD 52938 (angular diameter θ ~ 0.87 ± 0.01 mas), HD 53267 (θ ~ 0.86 ± 0.01 mas), HD 44891 (θ ~ 1.41 ± 0.02 mas), and HD 59881 (θ ~ 0.44 ± 0.03 mas). The angular diameters were based on uniform disk models. The diameters of the first two calibrators were taken from Mérand et al. (2005), and the second two were directly computed by SearchCal (JSDC2 catalog, Bourgés et al. 2014). All the observations were performed using the fringe-tracker FINITO (Le Bouquin et al. 2008).
The data were reduced following standard procedures described in Tatulli et al. (2007b) and Chelli et al. (2009), using the amdlib package, release 3.0.6, and the yorick interface provided by the Jean-Marie Mariotti Center (JMMC)1. Raw spectral visibilities, differential phases, and closure phases were extracted for all the frames of each observing file. The frames of 5 to 15 consecutive observations were merged and a global selection of 80% of the highest quality frames was made to achieve higher accuracy on the visibilities and phases. The UV coverage did not change significantly during these sequences. The transfer function was obtained by averaging the calibrator measurements (from three to five observing blocks, depending on the night), over the entire sequence of observations, after correcting for their intrinsic diameters (uniform disk). The VLTI field of view is ~300 and ~60 mas for the AT and UT observations, respectively.
The wavelengths were converted to a velocity scale. The systemic velocity ν= 0 corresponds to the center of the Brγ line, determined from the spectrum by a single Gaussian fit. From the X-Shooter spectrum we determined that the Brγ line center is consistent with the systemic velocity as determined from the photospheric lines (BF09). The absolute value of the visibilities obtained with the UT baselines could not be determined because of vibrations of the telescopes. These vibrations randomly affect the observations with time, and do not necessarily alter the calibrator and science target observations in the same way. Unreliable calibration may also come from different FINITO locking performances on the calibrator and the science target. However, this issue affects all spectral channels in the same way, and does not modify our conclusions, most of which are based on differential quantities.
2.2. CHARA/VEGA Spectro-interferometry
We observed HD 50138 around the Hα line using the visible VEGA spectrograph (Mourard et al. (2009) at the CHARA array (ten Brummelaar et al. 2005). We observed in the medium resolution mode (ℛ = 5000), with the S1S2 baseline (Bp ~ 28 m). We operated VEGA in parallel with the CLIMB NIR beam combiner acting as a coherence sensor (Sturmann et al. 2010). We measured a typical residual jitter on the optical path difference on the order of 7 μm. We followed a sequence calibrator-target-calibrator, with 40 or 60 blocks of 1000 short exposures (of 25 ms) per star, using two calibrators: HD 46487 (θ ~ 0.178 ± 0.013 mas) and HD 59881 (θ ~ 0.42 ± 0.03 mas).
The spectra were extracted at ℛ = 5000, using a classical scheme of collapsing the 2D flux in one spectrum, calibrating the pixel-wavelength relation with a Thorium-Argon lamp, and normalizing the continuum by a polynomial fit. Because HD 50138 is close to the limiting magnitude of the VEGA instrument, we had to reduce the spectral binning to ℛ = 160 to compute differential visibilities and phases (Mourard et al. 2009). The errors on these quantities correspond to the root-mean-square variability in the continuum. The error values in the pixels containing the line emission were diminished by a factor 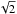 to account for the increased flux, which is around two times higher in the line with respect to the continuum.
to account for the increased flux, which is around two times higher in the line with respect to the continuum.
2.3. VLT/X-Shooter spectroscopy
Spectra of HD 50138 were obtained on 2013-02-14, UT 04:53, with X-Shooter on the VLT. X-Shooter covers the optical to NIR spectral region in three separate arms: ultraviolet (UVB, 290–590 nm), visible (VIS, 550–1010 nm) and NIR (1000−2480 nm; Vernet et al. 2011). Narrow slits were used: 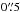 ,
, 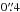 and
and 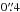 in the three spectrograph arms. This resulted in a spectral resolving power ℛ ≡ λ/ Δλ of 9100 in UVB, 17 400 in VIS and 11 300 in NIR. The signal-to-noise ratio (S/N) was 120 at 450 nm and 55 at 2150 nm.
in the three spectrograph arms. This resulted in a spectral resolving power ℛ ≡ λ/ Δλ of 9100 in UVB, 17 400 in VIS and 11 300 in NIR. The signal-to-noise ratio (S/N) was 120 at 450 nm and 55 at 2150 nm.
The frames were reduced using the X-Shooter pipeline (version 1.5.0, Modigliani et al. 2010) by employing the standard steps of data reduction, i.e. order extraction, flat fielding, wavelength calibration and sky subtraction. The wavelength calibration was verified by fitting selected OH lines in the sky spectrum. Flux calibration was performed using spectra of the spectrophotometric standard star GD0.653 (a DA white dwarf). The slit losses were estimated from measuring the seeing full width at half maximum (FWHM, 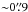 in V) from the spatial profile of the point source on the frame. These estimates were refined by comparing the obtained spectral energy distribution (SED) to the averaged photometry (Sitko et al. 2004, see Sect. A). This procedure introduces an uncertainty of about 10% in the absolute flux calibration, and the relative flux calibration is accurate to within 3%.
in V) from the spatial profile of the point source on the frame. These estimates were refined by comparing the obtained spectral energy distribution (SED) to the averaged photometry (Sitko et al. 2004, see Sect. A). This procedure introduces an uncertainty of about 10% in the absolute flux calibration, and the relative flux calibration is accurate to within 3%.
The wavelengths and velocities used throughout this paper are expressed in the systemic rest frame, for which we adopt 35 km s-1 with respect to the local standard of rest (BF09).
2.4. VLT/CRIRES spectro-astrometry
Spectra of HD 50138 were obtained in the K band with VLT/CRIRES, for the purpose of spectro-astrometry of the Brγ line. The data were taken on 2009 Nov. 5 at UT 06:15. A slit of 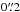 was used, resulting in a spectral resolving power ℛ = 100 000. The calibrator HD 60803 was observed directly afterwards. The rotator position angles were at 15°, 75° and 135°, and the respective counter-parallel angles. For a detailed description of the data reduction procedure, see Kraus et al. (2012).
was used, resulting in a spectral resolving power ℛ = 100 000. The calibrator HD 60803 was observed directly afterwards. The rotator position angles were at 15°, 75° and 135°, and the respective counter-parallel angles. For a detailed description of the data reduction procedure, see Kraus et al. (2012).
2.5. Supplementary data
Additional spectroscopic and photometric data from previous studies and data archives are used in this paper. An optical high-resolution (R ~ 80 000) spectrum was taken in March 2007 with the Narval spectropolarimeter at the telescope Bernard Lyot at the observatory of Pic du Midi, France. This spectrum was also presented in BF09.
Mid-infrared spectra were obtained on 1999 Dec. 24 and 2003 Jan. 08 with The Aerospace Corporation’s Broad-band Array Spectrograph System (BASS) at the Infrared Telescope Facility (Sitko et al. 2004). This instrument covers the 3−13 μm wavelength region. BASS is described more fully in Sitko et al. (2008). Magnitudes from the IRAS observatory are also used.
 |
Fig. 2 Spectra of the He iλ447.1 nm (left) and Hϵ (right) lines, obtained with X-Shooter (black line) and Narval (gray line). FASTWIND model profiles are overplotted for B6 and B7 giants and main-sequence stars. The inset in the right panel shows a detail of the line wing. The B7 III model provides the best fit with the observed profiles. The Ca ii H λ393 nm and Mg iiλ448 nm lines are also visible. |
3. Results
3.1. Spectroscopy
In this section, we present spectra obtained with VLT/X-Shooter and the AMBER Brγ spectra. We compare these to the Narval high-resolution optical spectrum obtained in 2007.
The spectral type of HD 50138 is difficult to constrain because of the temporal variability. Types in the range B5-A0 and luminosity classes I-V have been proposed in the literature; see references in BF09. The range in spectral types likely is the result of temporal variations (BF09, BF12). BF09 determine a spectral type of B6-B7 III-V based upon a detailed analysis of photometric and spectroscopic data. We check this estimate for consistency by comparing the X-Shooter spectra to model spectra of these subtypes. We adopt a similar by-eye fitting method to the one described in Ochsendorf et al. (2011), which is to qualitatively compare the observed profiles of selected lines to model spectra of B-type stars, varying over a range in temperature and surface gravity.
For mid- to late-B type spectra, the main temperature diagnostic is provided by the He iλ447 nm line, while the luminosity class is determined from the wings of the Hϵ line (Gray & Corbally 2009). Model profiles for these two lines are calculated for the subtypes B6-B7 III-V, using the non-LTE radiative transfer code FASTWIND (Puls et al. 2005). We adopt νsini = 100 km s-1 (BF12). The modeled spectra are compared to the observed profiles in Fig. 2. The B7 III model has the best overall fit, so we adopt this model in the remainder of the paper. The spectral type is consistent with the distance (d = 500 pc) and extinction (AV = 0.4 mag) of the source (see e.g. BF09).
 |
Fig. 3 Selection of spectral lines of HD 50138 obtained with X-Shooter, Narval (BF09), and AMBER. All lines show some degree of variability. Note the varying strength of double peaks and the component at ν~ 0 km s-1. The Narval and CRIRES spectra are rebinned to match the X-Shooter resolution (9100 in the optical, 17 400 in the NIR). |
The circumstellar gas environment produces many emission lines, with nearly 300 detected in the X-Shooter range. A selection representative of the different line morphologies seen across the X-Shooter range is displayed in Fig. 3. Additional spectra are also plotted to illustrate variability on timescales from days to years. These data are the AMBER spectra of Brγ (ℛ = 12 000), the CRIRES spectrum of Brγ (ℛ = 100 000) and the Narval optical spectrum. The resolution of the high-resulution spectra has been degraded to match the X-Shooter spectrum.
All profiles for which multiple observations are available show some degree of variability. The Hα profile is double-peaked, and the red-shifted peak is strongest. The blue-to-red peak intensity ratio is documented to vary between 0.3 and 0.9 (see BF09 and references therein). The other H i profiles also show double peaks. Their blue-to-red variability is not correlated with the Hα variability. The higher Paschen and Brackett transitions have relatively shallow profiles with pronounced peaks. The double peaks in the lower transitions, such as Hα and Paδ, are less pronounced and are “filled in” by an additional broad (Δν ~ 60 km s-1) and sharply peaked component at zero velocity. This is also seen in Brγ, where the profile changes from double- to single-peaked between the different AMBER and X-Shooter observations. An abrupt change from single- to double-peaked is also seen in the O iλ844 nm line.
The Fe ii lines have an emission component with a broad FWHM, as well as a narrow, variable absorption component close to zero velocity, which has been attributed to cold material in, e.g., a circumstellar shell or halo (see, e.g., Pogodin 1997, BF09). In the high-resolution data, it can be seen that the absorption is a blend of multiple narrow components (BF09). The He i lines (as well as optical Mg ii and Si ii lines, which are not shown) have a central absorption blended with blueshifted emission around − 100 km s-1. This could be an absorption profile combined with emission in a wind or outflow approaching the observer. It has also been interpreted as an inverse P-Cygni profile indicative of infall (Morrison & Beaver 1995; Pogodin 1997). Which of these two interpretations is correct depends on the value of the systemic velocity. With the adopted value from BF09 the first interpretation is favored.
The SED displayed in Fig. A.1 is compiled from the X-Shooter spectrum and infrared data from Sitko et al. (2004). A 13 000 K, log g = 3.5 atmospheric model (consistent with a B7 III spectral type Kurucz 1993) is overplotted, reddened with an AV = 0.4,RV = 3.1 extinction law (Cardelli et al. 1989). The resulting stellar radius and luminosity are R∗ = 7.0 ± 2.1R⊙ and L∗ = (1.2 ± 0.4) × 103L⊙. The stellar-to-total flux ratio f = F∗/Ftot in the K-band provides an important constraint for the analysis of the interferometric data (see Sects. 3.2 and 3.3). From the SED fit, we obtain f = 0.08 ± 0.01.
3.2. Size scales
In this section we give an overview of the interferometric data. The AMBER data, which are centered on the Brγ line, are displayed in Fig. 4. The error bars correspond to the root-mean-square variation in the continuum region at 500 < | ν | < 1000 km s-1. Two points are immediately apparent from the shape of the observed profiles. Firstly, the visibility is higher in the line than in the continuum for all baselines. This indicates that on the probed spatial scales, the Brγ emitting region (hot gas) is more compact than the region producing the NIR continuum emission (mostly from dust). Secondly, in most baselines the regions emitting at a projected velocity are spatially resolved, or indicate a spatial shift in the photocenter, as indicated by the “wiggle” in the differential phases, across the Brγ line.
 |
Fig. 5 Top to bottom: Hα spectrum, squared visibility and differential phase taken with CHARA/VEGA, taken on 2010-10-11 (left panels) and 2012-10-29 (right panels). |
Gaussian size estimates for the VEGA observations of Hα.
The VEGA data are displayed in Fig. 5. The visibility drop across the Hα line indicates that the Hα emitting region is more extended than the star, which we assume to be the only contributor to the continuum emission in the optical. The differential phases are, within the large error bars, consistent with zero. This indicates that the Hα and continuum photocenters are close.
We derive the size scales from the absolute visibilities. For VLTI observations carried out on the auxiliary telescopes, the absolute visibilities are well calibrated. We consider the three observations in the E0G0H0 configuration (1, 2 and 8, Table 1). These baselines are the shortest available (so the continuum is marginally resolved) and were aligned along PA = 72°−74° which coincides with the disk major axis found by BF11. The VEGA baselines are close to PA = 0°, more or less perpendicular to the disk major axis.
In the NIR, we assume that the brightness distribution of the source in the spectral window of interest (2159 <λ< 2173 nm, | ν | < 1000 km s-1) is made up of three sources: (i) the continuum emission from the star, denoted by subscript “∗”; (ii) the continuum emission from the circumstellar material, “cs” and (iii) the line emission from the circumstellar gas, “line”. To disentangle the different components in the data we use the same approach as described in Weigelt et al. (e.g., 2007). This method uses observed visibilities and phases to separate out the contributions of the line- and continuum-emitting regions, assuming their relative flux contributions as described in Sect. 4.1.
To derive absolute sizes, we compare the visibilities of the components to those of a simple Gaussian intensity distribution. This assumes that the continuum and line brightness distributions are approximated well by a Gaussian profile, and are furthermore centro-symmetric and not variable. Figure 6 shows the observed visibilities over a grid of Gaussian models as a function of baseline. The continuum squared visibilities 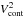 are measured as the mean value of V2 across the range 500 < | ν | < 1000 km s-1. For the high-resolution observations,
are measured as the mean value of V2 across the range 500 < | ν | < 1000 km s-1. For the high-resolution observations, 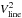 is computed and averaged over the central eight wavelength bins (| ν | < 50 km s-1, or two resolution elements). In the medium-resolution observations, no meaningful values of
is computed and averaged over the central eight wavelength bins (| ν | < 50 km s-1, or two resolution elements). In the medium-resolution observations, no meaningful values of 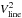 are retrieved, since the differential phase signal is very weak. The best-fitting models for
are retrieved, since the differential phase signal is very weak. The best-fitting models for 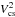 and
and 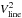 have an HWHM of θcs,mod = 3.4 mas (1.7 au;
have an HWHM of θcs,mod = 3.4 mas (1.7 au; 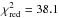 ) and θline,mod = 1.5 mas (0.8 au;
) and θline,mod = 1.5 mas (0.8 au; 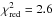 ), respectively. The high χ2-value of the
), respectively. The high χ2-value of the 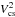 -fit results from a bad fit of the short-baseline visibilities. This indicates a probable additional contribution from an extended emission source (e.g. from an envelope or light scattered on outer disk layers), which could possibly be resolved by single-dish continuum observations. This model is corrected for the stellar flux and falls off to f2 instead of zero. These best-fit values are used as fiducial size parameters along the disk major axis in the model presented in Sect. 4.
-fit results from a bad fit of the short-baseline visibilities. This indicates a probable additional contribution from an extended emission source (e.g. from an envelope or light scattered on outer disk layers), which could possibly be resolved by single-dish continuum observations. This model is corrected for the stellar flux and falls off to f2 instead of zero. These best-fit values are used as fiducial size parameters along the disk major axis in the model presented in Sect. 4.
 |
Fig. 6 Average |
In the optical, the brightness distribution of the source is made up of only two components: the continuum emission from the star and the line emission from the circumstellar gas. The observed Hα visibilities (Fig. 5; Table 2) are converted to line visibilities Vline following the same approach as above. The visibilities correspond to a line-emitting region with Gaussian HWHM in the range θline,mod = 1.5−3.4 mas (~0.8–1.7 au. The position angles of the VEGA baselines have angles 60° and 87° to the disk major axis. The Hα-emitting region is thus probably slightly more extended than the Brγ-emitting region.
 |
Fig. 7 Top left: Brγ spectrum and differential phase measured over the three U2U3U4 baselines in three different observations with AMBER. Overplotted are the data rebinned on Δν = 20 km s-1 from –210 to 210 km s-1, color-coded with their velocity. The yellow lines correspond to the astrometric solution, P(λ), converted back to Δφ. Top right: two-dimensional representation of the photocenter displacement, P(λ), as a function of velocity across the Brγ line. North is up, east to the left. The (averaged) baselines of the U2U3U4 triplet are indicated in the bottom left. The dashed line corresponds to the orientation of the disk major axis (ψ = 71°) as derived by BF11. Bottom left: spectrum and spectro-astrometric signal detected by CRIRES; same colors as above. Bottom middle: photocenter displacement for CRIRES observations, continuum-corrected. Bottom right: photocenter displacement for CRIRES observations along the disk major axis (ψ = 71°). |
3.3. Photocenter shifts
The differential phase is related to the shift of the photocenter across the Brγ line. It can be used to perform spectro-astrometry if the baselines sufficiently cover the two dimensions in the (u,v)-plane. We use the three U2U3U4 observations (3, 4, and 5, Table 1), each with three baselines, which were taken with at most one month between observations. These observations are selected to reduce the effect of systematical errors. Eventually, we check the solution for consistency with other observations. To convert the Δφ-measurements to the photocenter displacement vector, P = { Px,Py }, we follow Lachaume (2003). We set P = 0 in the continuum, and implicitly assume that CP = 0 across the spectral range under scrutiny.
For marginally resolved objects (i.e., V2 ≳ 0.8) and for small displacements (B/λθ ≪ 1), the differential phase Δφi approximates a linear projection of P along the baseline vector B = −2π { ui,vi } /λ. We use this approximation even though our observations are not in the marginally resolved regime. We comment below on how this is justified.
From the nine measurements Δφ = { Δφ1,Δφ2,...,Δφ9 } the displacement is obtained by performing a weighted linear least square fit: 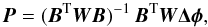 (1)where W is a 9 × 9 diagonal matrix containing the inverse squared errors on Δφ. We repeated this procedure for 21 velocity channels on the interval ν= (− 210,210) km s-1, rebinned with a width of 20 km s-1.
(1)where W is a 9 × 9 diagonal matrix containing the inverse squared errors on Δφ. We repeated this procedure for 21 velocity channels on the interval ν= (− 210,210) km s-1, rebinned with a width of 20 km s-1.
The result is plotted in Fig. 7 (top right). The line-emitting region is elongated NE to SW along PA ~ 70°, with an overall offset toward the NW with respect to the continuum. The position angle agrees with the disk major axis derived by BF11, which is perpendicular to the polarization angle. The blue-shifted and red-shifted parts of the line are clearly separated between the disk hemispheres. The largest spatial offsets are seen in the lowest velocity channels. This result suggests that the Brγ emission originates in a disk at ψ ~ 71° with a radially decreasing rotation around an axis of ~ 160°. The result is consistent with the Δφ measurements from the other AMBER datasets that were not included in the fit (Fig. A.2, bottom), indicating that no additional asymmetries are resolved at this angular resolution. Other rotation fields, e.g. rigid rotation or equatorial outflow, are not suggested as the velocity decreases with radius and the velocity gradient is parallel to the major disk axis.
The Brγ spectro-astrometric signal obtained with CRIRES (Fig. 7, bottom) is consistent with the AMBER differential phases. The differentially rotating disk-like structure and the offset to the NW are both seen in these data. The consistency of the AMBER and CRIRES results, as well as the agreement with the AMBER observations which were not included in the solution, justify the use of the Lachaume (2003) method, despite the low values of V2.
The solution P(λ) is a proxy for the first moment of the brightness map at wavelength λ. It is strictly a “center of gravity” of the line and continuum contributions to the brightness map, weighted by their respective fluxes. To obtain information on the absolute size and dynamics of the line emitting region, the contribution of the continuum emission must be subtracted from the solution. However, given the low S/N in V2, it is not feasible to derive channel-to-channel photocenter shifts in the line. Instead, we use the parameters derived in this section as an input for a geometric model (Sect. 4).
4. Geometric modeling
The results presented in Sect. 3 suggest the presence of an au-scale rotating gas disk around HD 50138. This interpretation is based on different subsets of the high-resolution AMBER data: Brγ size scale estimates are based on short-baseline observations (Sect. 3.2), while the spectro-astrometry is based on long-baseline observations in which the velocity field is resolved well (Sect. 3.3). In this section, we aim to interpret all the interferometric data in terms of a single, self-consistent physical interpretation. To this end, we construct a geometric model, whose predictions are compared to the data.
 |
Fig. 8 Selected channel maps of the geometric Keplerian disk plus spherical halo model (Model D0.6H; see text for description). The upper left panel shows the continuum map, and the white box denotes the plot region for the other panels. The brightness scaling is logarithmic; in the zoomed panels, the continuum was scaled down arbitrarily to emphasize the shape of the line emission. The width of the channels is 10 km s-1. Note the emission from the 3 au halo in the fourth to sixth panels (visible as the red circle that extends up to a radius of ~ 6′′). |
The model configuration is presented in Sect. 4.1. The number of parameters is kept as small as possible. Rather than obtaining the best-fit values by brute-force optimization, we choose a more intuitive approach. Most of the parameters are set to a priori estimated values based on independent results. Three representative models are presented to illustrate the effect of adding or changing some of the parameters. We justify these choices in Sect. 4.2. From this model, we calculate spectra, differential visibilities, and differential phases. We compare these to the data in Sect. 4.3, and discuss the constraints on and the degeneracies of the model parameters.
4.1. Model configuration
Our model consists of four physical components:
-
(i)
a star;
-
(ii)
a continuum-emitting disk;
-
(iii)
a line-emitting disk; and
-
(iv)
a line-emitting spherical halo.
The star (with mass M∗) is simulated as a point source at the grid origin at a distance d and with a fixed fraction f of the total flux in the modeled wavelength domain. For the circumstellar dust continuum emission, we adopt a single elliptical Gaussian distribution with as its parameters the HWHM along its major axis (acont), its orientation (ψ), and inclination (i). Both star and dust disk are centered at the origin. The gas disk is translated into a Brγ image in different velocity channels across the line. Directed by the results of Sect. 3.3, which indicate differential rotation, we assume that the gas is distributed in a geometrically thin rotating disk with a Keplerian velocity field (see also, e.g., Eisner et al. 2010; Kraus et al. 2012): 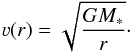 (2)The gas disk has inner and outer radii Rin and Rout, and has the same inclination and orientation as the continuum-emitting disk. We consider emission from the disk in the Brγ line at λ0 = 2166.167 nm in the optically thin limit. The emission measure depends on the local temperature and surface density. We parametrize the resulting radial surface brightness profile by a simple power law:
(2)The gas disk has inner and outer radii Rin and Rout, and has the same inclination and orientation as the continuum-emitting disk. We consider emission from the disk in the Brγ line at λ0 = 2166.167 nm in the optically thin limit. The emission measure depends on the local temperature and surface density. We parametrize the resulting radial surface brightness profile by a simple power law: 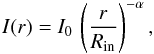 (3)where we fit I0 and α to match the observed Brγ spectrum.
(3)where we fit I0 and α to match the observed Brγ spectrum.
We also investigated the effect of adding a spherical halo of radius Rhalo to the line emission model, to explain the variable emission at the systemic velocity. The spectral line profile is uniform across the halo and centered on the systemic velocity. In reality, the observed line profile would be a result of various physical mechanisms (e.g., Doppler, temperature or pressure broadening). We simply assume a Gaussian profile, and set its HWHM, Δνhalo, and flux level by scaling it to fit the observed Brγ spectrum.
Summarizing, the model has nine parameters (d, ψ, i, acont, Rin, Rout, α, f, and M∗). Two more (Rhalo and Δνhalo) are added when a spherical halo is included.
The intensity at a physical radius r is given by ![\begin{equation} I(r,\lambda) = \frac{B(r)}{\sqrt{2\pi\sigma}} \exp\left[{-\frac{(\lambda-(\varv(r)/c) \lambda_0)^2}{2\sigma^2}}\right], \end{equation}](/articles/aa/full_html/2015/01/aa24143-14/aa24143-14-eq128.png) (4)where σ is:
(4)where σ is: 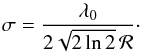 (5)The contribution of each pixel is calculated with high spectral resolution (Δν = 0.5 km s-1). Channel maps are created by summing all contributions with a spectral bin width of Δν = 10 km s-1. A selection of channel maps is displayed in Fig. 8. Each channel map is superposed on the continuum image. The two contributions are scaled to match the observed line peak to continuum ratio in the spectrum, which is close to 2 for the high-resolution observations and close to 1.5 for the medium-resolution observations.
(5)The contribution of each pixel is calculated with high spectral resolution (Δν = 0.5 km s-1). Channel maps are created by summing all contributions with a spectral bin width of Δν = 10 km s-1. A selection of channel maps is displayed in Fig. 8. Each channel map is superposed on the continuum image. The two contributions are scaled to match the observed line peak to continuum ratio in the spectrum, which is close to 2 for the high-resolution observations and close to 1.5 for the medium-resolution observations.
Model parameters.
Simulated observables are obtained from the model images, as follows. The spectrum is calculated as the integrated flux of the individual channel maps. For every baseline used in the observations, complex visibilities were extracted from the line and continuum maps. These were converted to observed quantities V2 and Δφ by taking the norm and argument of the Fourier transform at the (u,v) point corresponding to the observations. As the absolute calibration is uncertain, we compared squared differential visibilities 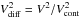 between models and observations.
between models and observations.
4.2. Model parameters
In this section we present the three sets of model parameters (see Table 3) which we use to interpret the data. We introduce three representative models, which differ in their value of the outer disk radius, Rout, and the presence of a gas halo. These representative models are a 0.6 au gas disk (D0.6), a 3.0 au gas disk (D3.0), and a 0.6 au gas disk plus 3.0 au halo (D0.6H). The disk’s outer radius Rout varies between models D0.6 and D3.0. Model D0.6H is the same as D0.6, but with the additional parameters Rhalo and Δνhalo. The other eight model parameters are the same in all three cases. These are the geometric parameters d, ψ, i; the stellar parameters f and M∗; the dust disk size, acont; and the gas disk parameters Rin and α. A priori estimates are based on the spectroscopy results (Sect. 3.1) and on previous studies.
The adopted distance to the system is d = 500 pc (van Leeuwen 2007). The dust continuum emission is modeled by an elliptical Gaussian. We adopt an orientation of the major axis, ψ = 71°, and an inclination angle, i = 56°, based on near- and mid-infrared continuum interferometry by BF11. The baselines used for the size estimates in Sect. 3.2 were almost parallel to ψ. The best-fit value for the HWHM of the Gaussian fit to Vcs is 3.4 mas (1.7 au), so we set acont to this value.
The parameter f = 0.08 was obtained from SED fitting (Sect. A.1). The stellar mass is estimated by comparing L∗ and Teff to pre- and post-main-sequence evolutionary models (BF09; see also Schaller et al. 1992; Hosokawa et al. 2010); we adopt M∗ = 6 M⊙. The highest velocities in the line profile trace the disk inner radius. No emission is detected at velocities | ν | > 230 km s-1, so we assume Rin = 0.1 au.
Two important physical features that are to be constrained by the model are the extent of the disk, and the presence of a halo. The (apparent) extent of the disk is determined by the combination of α and Rout. We adopt α = 2, which matches the observed Brγ spectrum, and is also a typical value for a (Herbig) Be star disk (Carciofi & Bjorkman 2008; Eisner et al. 2010). The results of Sect. 3.2 yield a size of ~ 3.1 mas for the line-emitting region along ψ, corresponding to a radius of 0.8 au. An independent estimate of the outer disk radius is derived from the double-peaked lines in the spectrum (Fig. 3). If these are a result of rotation, the peak-to-peak separation corresponds to the disk diameter (Horne & Marsh 1986). The average separation of ~ 200 km s-1 implies a disk outer radius of 0.5 au. Interpolating between these two estimates, we adopt Rout = 0.6 au. A model with Rout = 3 au is also calculated to show the effect of the disk size on the observables. These models are referred to as D0.6 (the 0.6 au disk) and D3.0 (the 3 au disk).
Motivated by the variable emission at the systemic velocity, a third model, D0.6H, is constructed with the same parameters as D0.6, but with the addition of a spherical halo. Its radius, Rhalo, is set to 3 au, because this radius most accurately reproduces the observed 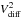 values. The width of the spectral line profile is set to Δνhalo = 60 km s-1 to fit the observed emission.
values. The width of the spectral line profile is set to Δνhalo = 60 km s-1 to fit the observed emission.
 |
Fig. 9 Two representative model fits. From top to bottom: spectrum, differential visibilities and differential phases observed with a compact (left) and extended (right) VLTI array. Overplotted are the observables calculated from models D0.6 (0.6 au disk, red line), D3.0 (3.0 au disk, blue line) and D0.6H (0.6 au disk + 3.0 au halo, green line). Figure A.3 compares the results of the same models with all the AMBER observations. |
4.3. Comparing observations with models
In Fig. 9 two representative observations (one with short AT baselines, one with long UT baselines) are shown. The D0.6, D3.0, and D0.6H modeled spectra, visibilities and phases are overplotted. Figure A.3 displays the same for all the observations. Model D0.6 correctly predicts the observed differential phase signatures (which was also suggested by Fig. 7, bottom). However, it produces a double-peaked spectral line profile, which is not observed. Moreover, the predicted differential visibilities are too high, implying that the emission is too bright and compact with respect to the continuum. Model D3.0 (with a larger outer gas disk radius) has a better fit to the spectra and visibilities, but too high an amplitude in the phase signal.
This discrepancy may be summarized as follows. The phases indicate Keplerian rotation at a compact (sub-au) scale, but the visibilities indicate a significant fraction of the emission comes from larger (several au) scales. Furthermore, the spectra suggest that the emission is not solely due to a rotating disk. This motivates the inclusion of a halo: model D0.6H. The discrepancies are partly resolved by this model. The double peaks of the line are filled in; the differential phase signal of model D0.6 is retained, and the visibilities are scaled down to the levels of model D3.0. A mismatch between this model and the observations is the visibility drop at zero velocity, an effect of the halo’s large size. The simple model does not reproduce the global offset of the emission in the NW direction.
Upon varying the eight fixed parameters, we conclude that these are reasonably well constrained. The effect of changing ψ, i and α has been investigated, leading us to conclude that no other choice of these parameters leads to a better match with the observations. A degeneracy exists between d, M∗ and the size parameters in the model. For example, a lower adopted stellar mass has an effect similar to a shorter observing distance, or a larger disk inner radius. However, the observations are best reproduced with the initial set of values for d, M∗, and Rin, which are consistent with the literature values (see Table 3). The size parameters Rout,Rhalo following from these are consistent with the absolute size scales derived in Sect. 3.2.
The differential visibilities observed with baselines exceeding 50 m are overpredicted by all the models. This indicates that at these size scales, the disk is more extended than is assumed by the (oversimplified) model. Alternatively, the very low S/N in Vcont (~0) may lead to a systematically underpredicted Vdiff. The substructure within the visibility peak, which is predicted by the models, is not observed in any of the baselines. Rather, the observed visibilities peak at zero velocity; this may point to a compact source of emission, like a binary companion. This is also a possible explanation for the photocenter offset between line and continuum (see Sect. 3.3), which is not predicted by our axisymmetric model. This is discussed further in Sect. 5.1.
In summary, the AMBER spectra, visibilities and phases are reproduced reasonably well by model D0.6H: a 0.6 au Keplerian disk and a 3 au halo. The parameters are constrained within a reasonable range, and consistent with independent observational results. However, the system shows signs of complexity that are not well constrained by the available observations (e.g., non-axisymmetry, variability) and that cannot be described with our simple model.
5. Discussion
In this section, we discuss the main constraints obtained from the analysis of the data and the modeling. We first discuss the kinematics of the circumstellar gas as derived from our analysis and modeling. We also comment on the properties of the circumstellar dust disk. We then briefly review the signatures of binarity obtained from ours and other observations. Finally, the implications of our results for the object’s evolutionary state are discussed.
5.1. Kinematics of the circumstellar gas
We find strong evidence of an au-scale Keplerian gas disk around HD 50138. The visibilities in the Brγ line imply that most of the emission originates within 4 mas, which corresponds to 2 au (Sect. 3.2). This is consistent with the NIR disk size estimates by BF11, as well as the size of the Hα-emitting region. Dust at the sublimation temperature (~ 1500 K) is a likely source of the K-band continuum emission. A picture where gas emission dominates within the dust sublimation radius is consistent with the observed 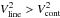 for all baselines. This is similar to what has been found in systems with a comparable dust SED (Kraus et al. 2008; Eisner et al. 2010).
for all baselines. This is similar to what has been found in systems with a comparable dust SED (Kraus et al. 2008; Eisner et al. 2010).
The differential phases and CRIRES spectro-astrometry show a signature of rotation around an axis of ~ 160° (Sect. 3.3). The decrease in velocity with the distance to the center is consistent with a central mass of ~ 6 M⊙ at a distance to the observer of 500 pc. Evidence of a gas disk with the same orientation was found in spectropolarimetry (Bjorkman et al. 1998; Oudmaijer & Drew 1999). The inclination and orientation are consistent with the mid- and NIR continuum-emitting disk found by BF11. Similar evidence of a Keplerian velocity field has been found in interferometric studies of other B[e] and pre-main-sequence systems of comparable mass (Kraus et al. 2012; Wheelwright et al. 2012c).
An additional, strongly variable emission peak at ν ~ 0 and with Δν ~ 60 km s-1 is seen in some lines (e.g., Brγ, O i). These lines alternate between double- and single-peaked profiles on timescales of days to years. This suggests variable emission from the disk or the presence of an additional star in the system, although current campaigns have not found periodicity in the spectroscopic variability. The ≲ 1.7-day period found in spectral lines by BF12 is attributed to stellar pulsations, that are reminiscent of pulsating late-type Be stars. Observations with temporal coverage at typical orbital timescales (i.e. weeks to months) are needed to constrain this possibility. We fit the emission component at the systemic velocity with a uniform line-emitting spherical halo, which could represent emission from a disk wind with a variable mass-loss rate.
Aside from a disk and halo, other possible geometries include line emission from infall or outflow, but are less likely. Infall is suggested by several He i, Mg ii and Si ii profiles, but the interpretation depends on the adopted systemic velocity. The spectral profile of the Brγ line does not show absorption components, nor does its velocity distribution resemble an infall geometry.
More commonly, however, this line traces outflow in a disk wind (Malbet et al. 2007; Tatulli et al. 2007a; Kraus et al. 2008; Benisty et al. 2010; Weigelt et al. 2011). The velocity is expected to increase as the material moves away from the source. In the case of HD 50138, a velocity decrease is observed. Also, asymmetries would exist between the red- and blue-shifted parts of the line emission, because the receding (red-shifted) jet lobe is blocked by the circumstellar disk (see, e.g., Ellerbroek et al. 2013b, 2014). These are not observed. Finally, the outflow axis would be perpendicular to the polarization angle, which is not likely in a disk-jet geometry (Maheswar et al. 2002). The combination of a single-peaked profile and a spectro-astrometric rotation signature has been found in the CO lines of some protoplanetary disks (Bast et al. 2011; Pontoppidan et al. 2011; Brown et al. 2013). In these cases, the single peak is fitted by including an equatorial outflow component in the disk velocity field. Excretion disks of Be stars are not seen to have a significant outward velocity component (Oudmaijer et al. 2011; Meilland et al. 2012; Wheelwright et al. 2012a).
Another important result is the offset of the Brγ line emission toward the NW with respect to the continuum photocenter (Fig. 7, top right). This may indicate that the line-emission disk geometry is more complicated; for example, a flaring inner disk (equivalent to the outer disk geometry described in Lagage et al. 2006) would naturally induce a photocenter offset. Alternative scenarios include an asymmetric inner disk structure or a close companion. An asymmetric distribution of the continuum emission would also influence the offset. The offset is in the polar direction, which would be a natural consequence of a disk rim; in the case of a binary this offset direction would be coincidental. Although the spatial extent of the Gaussian considered for the continuum is consistent with the estimated location of Rsub (Eq. (1) in Dullemond & Monnier 2010; 1.5−4 au (3−8 mas)), a more complicated spatial structure than a Gaussian is expected for the NIR emission. A Keplerian gas disk may exist whenever there is a close binary scenario as a result of mass exchange. Further indications of possible binarity are the ambiguous spectral classification and variability, although pulsations may cause the latter (BF09, BF12).
The photocenter offset in the Hα line found by Baines et al. (2006) is in the same NW direction as the Brγ shift. In this part of the spectrum, however, the continuum is dominated by photospheric emission; therefore, these authors interpret the offset as a signature of a (wide) binary. A more thorough investigation of the NIR continuum visibilities and phases will contribute to resolving possible companion(s) or an asymmetric disk (Kluska et al., in prep.). Close companions may also be found or excluded by a spectroscopic monitoring campaign.
To summarize, most observed signatures are consistent with the presence of an au-scale Keplerian disk plus gaseous halo. Signatures that have not been accounted for are the absolute level of the long-baseline visibilities, the variability of the emission and the photocenter offset. Additional sources of emission (e.g. a binary companion) and/or a more complicated disk geometry are required to obtain a satisfactory explanation for all the data.
5.2. Evolutionary state
The nature of HD 50138 is not clear. Is it a pre-main-sequence (i.e., Herbig B[e] star), main-sequence or post-main-sequence object? Most of the observed characteristics are consistent with all of these possibilities. In this section we will briefly review these explanations.
We find that the Brγ-emitting circumstellar gas has a rotation-dominated velocity field, most likely a disk, au-scale Keplerian gas disks are found around both pre-main-sequence (Acke et al. 2005; Bagnoli et al. 2010; Weigelt et al. 2011; Kraus et al. 2012) and post-main-sequence (Bujarrabal et al. 2007; Wheelwright et al. 2012c) early-type stars, some of which are known binaries. In pre-main-sequence stars, accretion columns and outflows more commonly dominate the Brγ emission (Eisner et al. 2010). The decretion disks of post-main-sequence systems are expected to have a strong outflow component (Lamers & Pauldrach 1991). In the case of HD 50138, rotation dominates the velocity field, which is consistent with both a pre- and a post-main-sequence nature.
The existence of a close binary companion, as suggested by various signatures (photocenter offset, ambiguous spectral type, variability), is also consistent with both scenarios. Close binary systems surrounded by dust disks are commonly seen in Herbig systems (Baines et al. 2006; Wheelwright et al. 2011; Garcia et al. 2013) and post-AGB systems (de Ruyter et al. 2006; Gielen et al. 2008; Kraus et al. 2013). In the former case, the close binary may have formed by disk fragmentation (Krumholz et al. 2009). In the latter, the dust disk is most likely a result of binary interaction, which would also give rise to shell phases. No signature of the companion star is seen in the spectral lines, which would indicate low mass with respect to the primary. The SED does not enable us to distinguish between these scenarios. Thermal pulses and thus a post-AGB phase are excluded given the system’s luminosity. Alternatively, the system could be a failed AGB star evolving into a subdwarf OB star (Heber 2009).
In other B[e] systems, high spatial and spectral resolution observations have yielded evidence of binarity and gas disks. Some of these are confirmed evolved systems, whose circumstellar gas and dust disk is a likely result of the interaction between the stellar companions (HD 87643, Millour et al. 2009; MWC 300, Wang et al. 2012; HD 327083, Wheelwright et al. 2012c). In a few cases, unambiguous evidence exists for an evolved evolutionary state (e.g., the 13CO abundance in HD 327083, Wheelwright et al. 2012b). Properties considered by some authors to be evidence of a pre-main-sequence nature are, for example, the absence of a binary companion (HD 85567, Wheelwright et al. 2013) or the absence of an outflow component in the disk (V 921 Sco, Kraus et al. 2012).
The emission component in Brγ and other spectral lines at ν~ 0 appears and disappears, indicating a highly variable circumstellar geometry. Apart from our interpretation as a gaseous halo in Sect. 4, the emission may arise as intrinsic emission from a companion star, from mass transfer columns in a close binary, or from slow-moving material in the accretion region close to the star. This component, as well as the many other detected variable signatures, may relate to shell phases and outbursts. These are also seen in both post- and pre-main-sequence objects (Crause et al. 2003; Kóspál et al. 2013; Ellerbroek et al. 2014). Peculiar spectral profiles (He i, Mg ii, Si ii) indicate either infall or outflow, and are thus inconclusive regarding the evolutionary state. The spectral variability is poorly constrained because of the limited time coverage of the observations.
Additional heuristic arguments prefer a post-main-sequence nature. The observed emission from high Paschen, Brackett and Pfund transitions are less commonly seen in young stars (Jaschek & Andrillat 1998; Lamers et al. 1998). The 2.3 μm CO emission is a common feature of young stellar objects in this mass range (Bik & Thi 2004; Ochsendorf et al. 2011; Ilee et al. 2013; Ellerbroek et al. 2013b,a), but is not observed in HD 50138. No clear signatures of accretion are seen, and the location of the object in the Hertzsprung-Russell diagram is inconclusive regarding its evolutionary state (BF09). Finally, the apparent isolation of the object from a star-forming region does not suggest a young age. Proper motion and distance measurements from the Gaia mission (Perryman et al. 2001) will constrain the formation history better.
In summary, in the case of HD 50138, a post-main-sequence and interacting binary nature is slightly favored over a pre-main-sequence nature, although many signatures are inconclusive. Given the extremely dynamical circumstellar environment, high-cadence spectroscopic and interferometric monitoring campaigns on timescales from days to years are the most promising strategy to unravel this system further.
6. Summary and conclusions
We have presented observations of the kinematics of the gaseous circumstellar environment of HD 50138. Our main conclusions are listed below:
-
Strong evidence is found that the Brγ emitting gas is distributed in a Keplerian rotating disk. This is suggested by the rotating and radially decreasing velocity field of the gas, which is distributed in an elongated structure aligned with independent estimates of the disk major axis.
-
The gas line emission originates in a smaller region (up to 3 au) than the continuum emission attributed to dust. This is consistent with the inner few au of the disk being too hot for dust to exist in equilibrium; in this region, the gas disk is expected to dominate the energy output.
-
The interferometric observables can be reproduced qualitatively with a model of a geometrically thin Keplerian disk surrounded by a low-velocity halo and a more extended source of continuum emission. Supporting evidence of these components is given by the spectrum of the source.
-
The strong variability of shell- or disk-dominated spectral line profiles indicates that significant changes take place in the system’s appearance on timescales as short as months, probably inhibiting a unified “fit” to all the datasets.
-
The absolute offset of the photocenter in the continuum may be caused by an asymmetric disk geometry that affects the line- and continuum-emitting regions differently (e.g., a puffed-up rim seen under an inclination angle). Alternatively, a binary companion may cause the offset.
-
No definitive conclusion could be reached for the evolutionary state. The system is possibly a binary, and it bears a strong resemblance to both Herbig B[e] and post-main-sequence systems. In view of mostly circumstantial evidence, the latter scenario is slightly favored.
After nearly a century of intensive research, HD 50138 continues to be an enigmatic object. In this study, we have mapped its inner environment for the first time and discovered a rotating gas disk. Observations at a higher temporal resolution are key toward a better understanding of the evolutionary state of this highly dynamical system. The combined forces of interferometry and spectroscopy on high spatial and spectral resolution, and a broad wavelength domain, proves to be a very insightful strategy. Complementary observations at high spatial and spectral resolution of different line and dust tracers (e.g. taken with the Atacama Large Millimeter Array) will help for resolving these elusive objects.
Online material
 |
Fig. 4 Spectra, squared visibilities, differential phases and closure phase of the Brγ line observed by AMBER. The top and bottom panels display the high- and medium-resolution data, respectively. Error bars are calculated as the 1σ noise level in the continuum. The array configurations, baseline lengths and position angles (N through E) are displayed in the top right corners of the panels. Colored squares in the bottom right corners connect properties of identical baselines. |
 |
Fig. 4 continued. |
Appendix A: Supplementary figures
 |
Fig. A.1 Spectral energy distribution; data from X-Shooter (black line), other data from Sitko et al. (2004, black symbols); model photosphere at 13 000 K (Kurucz 1993, gray line) and at d = 500 pc. The model is reddened with AV = 0.4 mag using the extinction law by Cardelli et al. (1989). The vertical dotted line corresponds to the stellar-to-total flux ratio in the K-band (λ = 2.16 μm), f = 0.08. |
 |
Fig. A.2 Astrometric solution, P(λ), (yellow line) overplotted on the differential phase observations which were not included in the fit. The error bars correspond to the 1σ spread in the continuum region. |
 |
Fig. A.3 Same as Fig. 4, but with
|
 |
Fig. A.3 continued. |
The calibrated data in the OI-FITS format (Pauls et al. 2005) will be included in the JMMC database http://www.jmmc.fr.
Available at http://www.jmmc.fr/amberdrs
Available at http://www.jmmc.fr/searchcal
Available at http://cdsweb.u-strasbg.fr/
Acknowledgments
The authors thank Olga Hartoog for providing the FASTWIND models. Jerome Bouvier, Alex Carciofi, Ewine van Dishoeck, Carsten Dominik, Alex de Koter, Henny Lamers, René Oudmaijer, Philippe Stee and Rens Waters are acknowledged for constructive discussions about the source. The ESO staff are acknowledged for technical support of the observations. The authors made use of the AMBER data reduction package of the Jean-Marie Mariotti Center2. We also used the SearchCal service3 codevelopped by Lagrange and IPAG, and of CDS Astronomical Databases SIMBAD and VIZIER4. The CHARA Array, operated by Georgia State University through the College of Arts and Sciences and NSF AST 12-11129, was built with funding provided by the National Science Foundation, Georgia State University, the W. M. Keck Foundation, and the David and Lucile Packard Foundation. LE and MB acknowledge a grant from the Fizeau Program, funded by WP14 OPTICON/FP7. ADS and MBF thank the CNRS-PICS program 2010−2012 for partial financial support.
References
- Acke, B., van den Ancker, M. E., & Dullemond, C. P. 2005, A&A, 436, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. A., & Swings, J. P. 1976, A&A, 47, 293 [NASA ADS] [Google Scholar]
- Andrillat, Y., & Houziaux, L. 1991, IAU Circ., 5164, 3 [Google Scholar]
- Bagnoli, T., van Lieshout, R., Waters, L. B. F. M., et al. 2010, ApJ, 724, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Baines, D., Oudmaijer, R. D., Porter, J. M., & Pozzo, M. 2006, MNRAS, 367, 737 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bast, J. E., Brown, J. M., Herczeg, G. J., van Dishoeck, E. F., & Pontoppidan, K. M. 2011, A&A, 527, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benisty, M., Malbet, F., Dougados, C., et al. 2010, A&A, 517, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bik, A., & Thi, W. F. 2004, A&A, 427, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjorkman, K. S., Miroshnichenko, A. S., Bjorkman, J. E., et al. 1998, ApJ, 509, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Bopp, B. W. 1993, Information Bulletin on Variable Stars, 3834, 1 [Google Scholar]
- Borges Fernandes, M., Kraus, M., Chesneau, O., et al. 2009, A&A, 508, 309 (BF09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borges Fernandes, M., Meilland, A., Bendjoya, P., et al. 2011, A&A, 528, A20 (BF11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borges Fernandes, M., Kraus, M., Nickeler, D. H., et al. 2012, A&A, 548, A13 (BF12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourgés, L., Lafrasse, S., Mella, G., et al. 2014, in ASP Conf. Ser. 485, eds. N. Manset, & P. Forshay, 223 [Google Scholar]
- Brown, L. R., Troutman, M. R., & Gibb, E. L. 2013, ApJ, 770, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V., van Winckel, H., Neri, R., et al. 2007, A&A, 468, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carciofi, A. C., & Bjorkman, J. E. 2008, ApJ, 684, 1374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chelli, A., Utrera, O. H., & Duvert, G. 2009, A&A, 502, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cidale, L., Zorec, J., & Tringaniello, L. 2001, A&A, 368, 160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corporon, P., & Lagrange, A.-M. 1999, A&AS, 136, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crause, L. A., Lawson, W. A., Kilkenny, D., et al. 2003, MNRAS, 341, 785 [NASA ADS] [CrossRef] [Google Scholar]
- de Ruyter, S., van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doazan, V. 1965, Ann. Astrophys., 28, 1 [Google Scholar]
- Domiciano de Souza, A., Driebe, T., Chesneau, O., et al. 2007, A&A, 464, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Monnier, J. D., Woillez, J., et al. 2010, ApJ, 718, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ellerbroek, L. E., Bik, A., Kaper, L., et al. 2013a, A&A, 558, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellerbroek, L. E., Podio, L., Kaper, L., et al. 2013b, A&A, 551, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellerbroek, L. E., Podio, L., Dougados, C., et al. 2014, A&A, 563, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, P. J. V., Benisty, M., Dougados, C., et al. 2013, MNRAS, 430, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Gielen, C., van Winckel, H., Min, M., Waters, L. B. F. M., & Lloyd Evans, T. 2008, A&A, 490, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Perez, M. R., Talavera, A., et al. 1996, A&AS, 120, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, R. O., & Corbally, J. C. 2009, Stellar Spectral Classification (Princeton University Press) [Google Scholar]
- Haguenauer, P., Alonso, J., Bourget, P., et al. 2010, in SPIE Conf. Ser. 7734 [Google Scholar]
- Halbedel, E. M. 1991, Information Bulletin on Variable Stars, 3585, 1 [Google Scholar]
- Harrington, D. M., & Kuhn, J. R. 2007, ApJ, 667, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, D. M., & Kuhn, J. R. 2009, ApJS, 180, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., & Marsh, T. R. 1986, MNRAS, 218, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Hutsemékers, D. 1985, A&AS, 60, 373 [NASA ADS] [Google Scholar]
- Ilee, J. D., Wheelwright, H. E., Oudmaijer, R. D., et al. 2013, MNRAS, 429, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Jaschek, C., & Andrillat, Y. 1998, A&AS, 128, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaschek, M., Jaschek, C., & Andrillat, Y. 1993, A&AS, 97, 781 [NASA ADS] [Google Scholar]
- Kóspál, Á., Ábrahám, P., Acosta-Pulido, J. A., et al. 2013, A&A, 551, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Hofmann, K.-H., Benisty, M., et al. 2008, A&A, 489, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, S., Calvet, N., Hartmann, L., et al. 2012, ApJ, 752, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, M., Oksala, M. E., Nickeler, D. H., et al. 2013, A&A, 549, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog: VI/39 [Google Scholar]
- Lachaume, R. 2003, A&A, 400, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagage, P.-O., Doucet, C., Pantin, E., et al. 2006, Science, 314, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lamers, H. J. G., & Pauldrach, A. W. A. 1991, A&A, 244, L5 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Zickgraf, F.-J., de Winter, D., Houziaux, L., & Zorec, J. 1998, A&A, 340, 117 [NASA ADS] [Google Scholar]
- Le Bouquin, J.-B., Bauvir, B., Haguenauer, P., et al. 2008, A&A, 481, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maddalena, R. J., Morris, M., Moscowitz, J., & Thaddeus, P. 1986, ApJ, 303, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Maheswar, G., Manoj, P., & Bhatt, H. C. 2002, A&A, 387, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malbet, F., Benisty, M., de Wit, W.-J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meilland, A., Millour, F., Kanaan, S., et al. 2012, A&A, 538, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merrill, P. W. 1931, ApJ, 73, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W., & Burwell, C. G. 1933, ApJ, 78, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Millour, F., Chesneau, O., Borges Fernandes, M., et al. 2009, A&A, 507, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miroshnichenko, A. S. 2007, ApJ, 667, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in SPIE Conf. Ser., 7737 [Google Scholar]
- Morrison, N. D., & Beaver, M. 1995, BAAS, 27, 825 [NASA ADS] [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ochsendorf, B. B., Ellerbroek, L. E., Chini, R., et al. 2011, A&A, 536, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oudmaijer, R. D., & Drew, J. E. 1999, MNRAS, 305, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Oudmaijer, R. D., Wheelwright, H. E., Carciofi, A. C., Bjorkman, J. E., & Bjorkman, K. S. 2011, in IAU Symp. 272, eds. C. Neiner, G. Wade, G. Meynet, & G. Peters, 418 [Google Scholar]
- Pauls, T. A., Young, J. S., Cotton, W. D., & Monnier, J. D. 2005, PASP, 117, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pogodin, M. A. 1997, A&A, 317, 185 [NASA ADS] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., & Smette, A. 2011, ApJ, 733, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schöller, M. 2007, New Astron. Rev., 51, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Sitko, M. L., Carpenter, W. J., Lynch, D. K., et al. 2004, BAAS, 36, 1363 [NASA ADS] [Google Scholar]
- Sitko, M. L., Carpenter, W. J., Kimes, R. L., et al. 2008, ApJ, 678, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Slettebak, A. 1976, Be and shell stars; Proceedings of the Merrill-McLaughlin Memorial Symposium, BASS River, Mass., September 15–18, IAU Symp, 70, 1975 [Google Scholar]
- Sturmann, J., Ten Brummelaar, T., Sturmann, L., & McAlister, H. A. 2010, SPIE Conf. Ser., 7734 [Google Scholar]
- Tatulli, E., Isella, A., Natta, A., et al. 2007a, A&A, 464, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007b, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Weigelt, G., Kreplin, A., et al. 2012, A&A, 545, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weigelt, G., Kraus, S., Driebe, T., et al. 2007, A&A, 464, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weigelt, G., Grinin, V. P., Groh, J. H., et al. 2011, A&A, 527, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheelwright, H. E., Vink, J. S., Oudmaijer, R. D., & Drew, J. E. 2011, A&A, 532, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheelwright, H. E., Bjorkman, J. E., Oudmaijer, R. D., et al. 2012a, MNRAS, 423, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Wheelwright, H. E., de Wit, W. J., Oudmaijer, R. D., & Vink, J. S. 2012b, A&A, 538, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheelwright, H. E., de Wit, W. J., Weigelt, G., Oudmaijer, R. D., & Ilee, J. D. 2012c, A&A, 543, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheelwright, H. E., Weigelt, G., Caratti o Garatti, A., & Garcia Lopez, R. 2013, A&A, 558, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yudin, R. V., & Evans, A. 1998, A&AS, 131, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zickgraf, F.-J. 1998, in B[e] stars, eds. A. M. Hubert, & C. Jaschek, Astrophysics and Space Science Library, 233, 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Coverage of the (u,v)-plane of the VLTI/AMBER-observations with ℛ ~ 12 000 (filled squares) and ℛ ~ 1500 (open squares). The two CHARA/VEGA-observations are also displayed (crosses). The dashed line is aligned with the major axis of the modeled disk ellipse (ψ = 71°). Colors indicate the baseline PA with respect to this line. |
| In the text | |
 |
Fig. 2 Spectra of the He iλ447.1 nm (left) and Hϵ (right) lines, obtained with X-Shooter (black line) and Narval (gray line). FASTWIND model profiles are overplotted for B6 and B7 giants and main-sequence stars. The inset in the right panel shows a detail of the line wing. The B7 III model provides the best fit with the observed profiles. The Ca ii H λ393 nm and Mg iiλ448 nm lines are also visible. |
| In the text | |
 |
Fig. 3 Selection of spectral lines of HD 50138 obtained with X-Shooter, Narval (BF09), and AMBER. All lines show some degree of variability. Note the varying strength of double peaks and the component at ν~ 0 km s-1. The Narval and CRIRES spectra are rebinned to match the X-Shooter resolution (9100 in the optical, 17 400 in the NIR). |
| In the text | |
 |
Fig. 5 Top to bottom: Hα spectrum, squared visibility and differential phase taken with CHARA/VEGA, taken on 2010-10-11 (left panels) and 2012-10-29 (right panels). |
| In the text | |
 |
Fig. 6 Average |
| In the text | |
 |
Fig. 7 Top left: Brγ spectrum and differential phase measured over the three U2U3U4 baselines in three different observations with AMBER. Overplotted are the data rebinned on Δν = 20 km s-1 from –210 to 210 km s-1, color-coded with their velocity. The yellow lines correspond to the astrometric solution, P(λ), converted back to Δφ. Top right: two-dimensional representation of the photocenter displacement, P(λ), as a function of velocity across the Brγ line. North is up, east to the left. The (averaged) baselines of the U2U3U4 triplet are indicated in the bottom left. The dashed line corresponds to the orientation of the disk major axis (ψ = 71°) as derived by BF11. Bottom left: spectrum and spectro-astrometric signal detected by CRIRES; same colors as above. Bottom middle: photocenter displacement for CRIRES observations, continuum-corrected. Bottom right: photocenter displacement for CRIRES observations along the disk major axis (ψ = 71°). |
| In the text | |
 |
Fig. 8 Selected channel maps of the geometric Keplerian disk plus spherical halo model (Model D0.6H; see text for description). The upper left panel shows the continuum map, and the white box denotes the plot region for the other panels. The brightness scaling is logarithmic; in the zoomed panels, the continuum was scaled down arbitrarily to emphasize the shape of the line emission. The width of the channels is 10 km s-1. Note the emission from the 3 au halo in the fourth to sixth panels (visible as the red circle that extends up to a radius of ~ 6′′). |
| In the text | |
 |
Fig. 9 Two representative model fits. From top to bottom: spectrum, differential visibilities and differential phases observed with a compact (left) and extended (right) VLTI array. Overplotted are the observables calculated from models D0.6 (0.6 au disk, red line), D3.0 (3.0 au disk, blue line) and D0.6H (0.6 au disk + 3.0 au halo, green line). Figure A.3 compares the results of the same models with all the AMBER observations. |
| In the text | |
 |
Fig. 4 Spectra, squared visibilities, differential phases and closure phase of the Brγ line observed by AMBER. The top and bottom panels display the high- and medium-resolution data, respectively. Error bars are calculated as the 1σ noise level in the continuum. The array configurations, baseline lengths and position angles (N through E) are displayed in the top right corners of the panels. Colored squares in the bottom right corners connect properties of identical baselines. |
| In the text | |
 |
Fig. 4 continued. |
| In the text | |
 |
Fig. A.1 Spectral energy distribution; data from X-Shooter (black line), other data from Sitko et al. (2004, black symbols); model photosphere at 13 000 K (Kurucz 1993, gray line) and at d = 500 pc. The model is reddened with AV = 0.4 mag using the extinction law by Cardelli et al. (1989). The vertical dotted line corresponds to the stellar-to-total flux ratio in the K-band (λ = 2.16 μm), f = 0.08. |
| In the text | |
 |
Fig. A.2 Astrometric solution, P(λ), (yellow line) overplotted on the differential phase observations which were not included in the fit. The error bars correspond to the 1σ spread in the continuum region. |
| In the text | |
 |
Fig. A.3 Same as Fig. 4, but with
|
| In the text | |
 |
Fig. A.3 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.