| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424425 | |
| Published online | 27 November 2014 | |
LOFAR observations of PSR B0943+10: profile evolution and discovery of a systematically changing profile delay in bright mode
1
Department of Astrophysics/IMAPPRadboud University Nijmegen,
PO Box 9010,
6500 GL
Nijmegen,
The Netherlands
e-mail:
a.bilous@science.ru.nl
2
ASTRON, the Netherlands Institute for Radio
Astronomy, Postbus
2, 7990 AA,
Dwingeloo, The
Netherlands
3
Anton Pannekoek Institute for Astronomy, University of
Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
4
Jodrell Bank Centre for Astrophysics, School of Physics and
Astronomy, University of Manchester, Manchester
M13 9PL,
UK
5
School of Physics and Astronomy, University of
Southampton, Southampton, SO17
1BJ, UK
6
Astro Space Centre of the Lebedev Physical
Institute, Profsoyuznaya str.
84/32, 117997
Moscow,
Russia
7
Centre for Astrophysics and Supercomputing, Swinburne University
of Technology, Mail H30, PO Box
218, VIC
3122,
Australia
8
ARC Centre of Excellence for All-sky Astrophysics (CAASTRO)
9
MPI für Radioastronomy, Auf dem Hügel 69,
53121
Bonn,
Germany
10
LPC2E - Université d’Orléans/CNRS,
France
11
SR de Nançay, Observatoire de Paris – CNRS/INSU, USR 704 – Univ. Orléans, OSUC,
route de
Souesmes, 18330
Nançay,
France
12
Department of Astrophysics, University of Oxford,
Denys Wilkinson Building, Keble
Road, Oxford
OX1 3RH,
UK
Received: 18 June 2014
Accepted: 29 August 2014
We present broadband, low-frequency (25−80 MHz and 110−190 MHz) LOFAR observations of PSR B0943+10, with the goal of better illuminating the nature of its enigmatic mode-switching behaviour. This pulsar shows two relatively stable states: a “bright” (B) and “quiet” (Q) mode, each with different characteristic brightness, profile morphology, and single-pulse properties. We model the average profile evolution both in frequency and time from the onset of each mode, and highlight the differences between the two modes. In both modes, the profile evolution can be explained well by radius-to-frequency mapping at altitudes within a few hundred kilometres of the stellar surface. If both B and Q-mode emissions originate at the same magnetic latitude, then we find that the change of emission height between the modes is less than 6%. We also find that, during B-mode, the average profile is gradually shifting towards later spin phase and then resets its position at the next Q-to-B transition. The observed B-mode profile delay is frequency-independent (at least from 25−80 MHz) and asymptotically changes towards a stable value of about 4 × 10-3 in spin phase by the end of mode instance, so much too high to be due to a changing spin-down rate. Such a delay can be interpreted as a gradual movement of the emission cone against the pulsar’s direction of rotation, with different field lines being illuminated over time. Another interesting explanation is a possible variation in the accelerating potential inside the polar gap. This explanation connects the observed profile delay to the gradually evolving subpulse drift rate, which depends on the gradient of the potential across the field lines.
Key words: pulsars: general / pulsars: individual: PSR B0943+10
© ESO, 2014
1. Introduction
PSR B0943+10, hereafter B0943, is an old (τc = 5 × 106 years), slow (P = 1.098 s) pulsar that has two distinct, recurring modes of radio emission. The modes show two distinct average pulse profiles and are named after their phase-integrated fluxes: in the “bright” (B) mode the pulsar is about two times brighter than in the “quiet” (Q) mode (at 62 and 102 MHz, Suleymanova & Izvekova 1984).
Summary of observations.
B0943 switches between B and Q-mode once in several hours (Suleymanova & Izvekova 1984). In both modes the average profile consists of two Gaussian-like components that merge towards higher frequencies. The modes differ in component separation, width, and ratio of the component peak amplitudes (Suleymanova et al. 1998). Such double-peaked profiles are traditionally explained by a hollow-cone emission model (Ruderman & Sutherland 1975; Rankin 1983, 1993). According to the radius-to-frequency mapping (RFM) model, the emission at a certain frequency originates at a fixed altitude above the stellar surface, with lower frequencies coming from higher in the magnetosphere (Cordes 1978). The emitting cone follows the diverging dipolar magnetic field lines, thus the opening angle of the cone is larger at lower frequencies and the profile components are farther apart. Deshpande & Rankin (2001) find that for B0943 our line of sight (LOS) cuts the emitting cone almost tangentially. In other words, the angle between the LOS and magnetic axis β is comparable to the opening angle of the cone ρ, with | β/ρ | at least 0.86 (in B-mode at 25 MHz). Above 300 MHz, the LOS no longer crosses the radial maximum-power point of the B-mode cone; for Q-mode, this should happen at even lower frequencies. Thus, at frequencies ≳300 MHz, only the periphery of the cone can be observed. This effect of viewing geometry can plausibly explain B0943’s particularly steep spectrum (S ∝ ν-2.9, Malofeev et al. 2000).
The two emission modes also have very different single-pulse properties. In the B-mode the emission is characterised by a series of coherently drifting sub-pulses, whereas in the Q-mode the emission consists of sporadic bright pulses, apparently chaotically distributed in phase within the average profile (Suleymanova et al. 1998).
The transition between modes happens nearly instantaneously, on a time scale of about one spin period (Suleymanova et al. 1998). Recently it has been discovered that this rapid change of radio emission is simultaneous with a mode switch in X-rays (Hermsen et al. 2013). Using data from the LOw-Frequency ARray (LOFAR, 120−160 MHz), the Giant Meterwave Radio Telescope (320 MHz), and XMM-Newton (0.2−10 keV), these authors show that B0943 emits bright pulsed thermal X-rays only during the radio Q-mode. This discovery demonstrates that the long-known radio mode switch is in fact a transformation of observed pulsar emission across a large part of the electromagnetic spectrum. Since different parts of the spectrum are produced by different mechanisms, this broadband switch is a manifestation of some global changes in the magnetosphere. These changes could, among other possibilities, be caused by some unknown, non-linear processes or an adjustment to the magnetospheric configuration (Timokhin 2010).
 |
Fig. 1 One-minute subintegrations versus rotational phase for five observing sessions. The top four panels show LBA (25−80 MHz) observations; the bottom one used the HBAs (110−190 MHz). Observation IDs are included on the right of each subplot. Mode transitions are marked with white ticks. Here and throughout the paper the three central LBA observations are aligned at the transition from Q-to-B, with the goal to facilitate visual comparison of time-dependent emission parameters. The B-mode of the observation L77924 was aligned relative to the others according to the ratio of component peak heights (see Fig. 6). The HBA observation was aligned by the Q-to-B transition in observation L169237. On the Y-axis, the pulsar’s zero spin phase was taken to match the midpoint between components at the start of the B-mode of that observation or at the beginning of the session if no Q-to-B transition was recorded. For L78450, the data from 60 to 80 minutes was cut out because of radio frequency interference (RFI). |
The mode switching phenomenon, as well as its relation to other variable emission behaviour like nulling, is still far from being well understood. Thus discovering new features in the portrait of mode-dependent pulsar emission can be helpful for deciphering the underlying physical processes. Very low radio frequencies provide an interesting diagnostic for studying B0943, because in both B and Q-mode the average profile morphology evolves rapidly with frequency below 100 MHz (Suleymanova et al. 1998); exploring this evolution may provide important clues to the shape and location of the emission regions in each mode. B0943 has been previously studied at very low frequencies with the Pushchino and Gauribidanur observatories (Suleymanova et al. 1998; Asgekar & Deshpande 2001). For both telescopes the observing bandwidth was less than 1 MHz and a single observing session was no longer than several minutes – i.e. not long enough to easily catch mode transitions or to follow the evolution of the emission characteristics during a multi-hour mode instance.
In contrast, LOFAR enables instantaneous frequency coverage from typically either 10−90 MHz or 110−190 MHz, and can track B0943 for up to 6 hours. The tremendous increase in bandwidth together with high sensitivity allow precise measurements of the profile evolution even in the faint Q-mode. Also, owing to the multi-hour observing sessions, for the first time it becomes possible to explore the gradual changes in the profile shape within a single mode instance (at these low frequencies). This gives us important information about dynamic changes in the pulsar magnetosphere within a single mode and can be a clue to the mode switching mystery itself.
2. Observations and timing
Depending on availability, we observed B0943 with either 19 or 21 LOFAR core stations. The signals from the stations were coherently added and the total intensity samples were recorded in a filterbank format (see van Haarlem et al. 2013 for an explanation of the telescope configurations; and Stappers et al. 2011 for a detailed description of LOFAR’s pulsar observing modes). There were five observing sessions with a total duration of about 20 hours. Four observations were conducted with the low-band antennas (LBAs), at a centre frequency of 53.8 MHz, and with 25 600 channels across a 78.1-MHz bandwidth. One observation was taken with the high-band antennas (HBAs): 152.24 MHz centre frequency, and 7808 channels over 95.3 MHz bandwidth. The time resolution of the raw data was 0.65 ms. The data were pre-processed with the standard LOFAR pulsar pipeline (Stappers et al. 2011), resulting in folded single-pulse archives with 512 phase bins per period and 512 channels per band. In this paper we describe uncalibrated total intensity, since flux/polarisation calibration was not fully developed at the time of data processing.
With the LBAs the pulsar was detected across the range of 25−80 MHz. With the HBAs, the pulsar was seen from 110−190 MHz, with 135−140 MHz cut out due to RFI. The one-minute frequency-integrated subintegrations for each session are plotted in Fig. 1 and the mode transitions are marked with white ticks.
Data were folded with the ephemerides from Shabanova et al. (2013).
 |
Fig. 2 Timing residuals from one full LBA observing session (L102418). TOAs from both Q and B modes are shown. The transition between Q and B mode happens in the middle of the observation. |
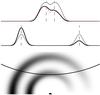 |
Fig. 3 A toy model of the average profile from two cone-like emission regions, centred on the magnetic axis. For the smaller cone, the LOS does not cut through the inner side of the cone. Gray profiles correspond to a uniformly illuminated cone (not shown); black profiles result from the cones with smooth variation of intensity with magnetic azimuth. The dotted line shows the merging component fit model. Vertical dashed lines mark the peaks of the uniformly illuminated cone profiles. On the upper subplot, note the slight change in apparent position of the leading component for the varying radial intensity case. |
Dedispersion was done with a more up-to-date and precise value of the dispersion measure (DM), obtained by measuring the ν-2 lag of the fiducial point in the B-mode profile (see Appendix B for details). In the work of Shabanova et al. (2013), B0943 was routinely observed during 1982−2012 at the Pushchino Observatory at frequencies close to 100 MHz. During this period, B0943 exhibited prominent timing noise, with a characteristic amplitude of 220 ms on a timescale of roughly 1500 days. Comparing the timing residuals from our LBA B-mode observations, we found that our residuals are in good agreement with the extrapolation of the timing noise curve from Shabanova et al. (2013), as they exhibited a long-term linear trend with a net pulse delay of 40 ms over 270 days.
We also found that within each observing session the times of arrival (TOAs) of the B-mode pulses exhibited a systematic delay with the time from the start of the mode. This delay (2 ms/h) is much longer than the expected lag due to the long-term timing noise (~0.006 ms/h) and is present in the B-mode only: the residuals from the pulsar’s Q-mode did not show any systematics (Fig. 2). In Fig. 2, residuals from the observation L102418 are shown. During this observation B0943 was in the Q-mode for the first half of the session and in the B-mode for the second half. TOAs were generated using separate templates for the band-integrated B and the Q-mode data. The templates used are derived from analytic fits using von Mises functions and the PSRCHIVE task paas1. In the B and Q-mode templates the width at 10% of the profile maximum was the same, and so we aligned the templates so that they overlap at this 10% width. As can be seen there is a significant offset in the arrival time of the first B-mode TOA and this offset decreases exponentially with time until the B-mode TOAs essentially align with those in the Q-mode2. This trend in the B-mode residuals can potentially be explained by a gradual change in profile shape with time: when cross-correlated with a fixed-shape template, it would result in a growing bias in the TOA determination (a similar bias, but for the frequency-dependent profile evolution, is investigated in Hassall et al. 2012, Ahuja et al. 2007). There is indeed evidence that the shape of B0943’s profile evolves within a B-mode: as was shown by Suleymanova & Rankin (2009), the ratio of component peaks in B-mode decreases with the time from the start of the mode.
The observed trend in B-mode residuals motivated us to do a time-resolved analysis of the profile shape and phase, in order to remove profile evolution bias from TOA measurements. The results of the analysis are presented in Sect. 3.2 and discussed in Sect. 4.3.
 |
Fig. 4 Frequency evolution of the average profile in B and Q-mode from observations L102418 in LBA and L78450 in HBA. The dashed line (green in the online version) shows the fit from the OC model (overlapping Gaussians) and the gray line (red in online version) is the MC model (merging Gaussians). For the LBA data within each model, both B and Q-mode were fit with two independent Gaussian components. For the HBA data, the separation between components, their width and ratio of the peaks were extrapolated from the frequency dependence within the LBA band and only the midpoint between components and S/N of the leading component were fit. LBA and HBA observations are aligned with respect to the midpoint between components in the OC model. |
3. Modelling the average profile
Here we give a phenomenological description of B0943’s average profile. We decompose the profile into two Gaussian components and analyse the evolution of the shape and phase of the components with time and frequency. Starting from some sufficiently high frequency (about 80 MHz for the B-mode and less than 30 MHz for the Q-mode), the two components come very close to each other in phase, and the values of the fitted parameters become dependent on the assumptions about the shape of the emitting region in the pulsar’s magnetosphere. In the following we made two such assumptions and thus fit the data with two separate models. The first model (“overlapping components”, or “OC model”) assumes that the components come from different parts of the magnetosphere3 and treats the profile as the sum of the individual components. The second model (“merging components” or “MC model”) assumes a cone-shaped emission region (Rankin 1993). For closely located components, the observer’s LOS does not cut through the inner part of the cone, thus the inner part does not contribute to the profile (Fig. 3). We approximated such profiles with two Gaussian components truncated on their inner sides. It should be noted that our MC model does not perfectly reproduce the profile from a cone-shaped emission region, as it slightly underestimates the intensity between closely located components (Fig. 3, dotted line). Nonetheless, we include the results from the MC model fitting. They serve as a check on how much the fitted model parameters are influenced by the OC model’s assumption that profile components are completely independent. In contrast, direct modelling of the average profile as an emission cone would require accounting for the unknown variation of intensity with magnetic azimuth, in order to model components at different emission heights (Fig. 3). That approach is not attempted here.
 |
Fig. 5 Frequency evolution of the fitted parameters for OC (lighter circles) and MC (darker circles) models for all LBA sessions. The signal was integrated in time within each session. Top row: B-mode. For most frequencies here the MC and OC measurements coincide within the point markers. Bottom row: Q-mode. Left: the midpoint between components φmid(ν). Phase 0 corresponds to frequency-averaged φmid for the OC model for each session. Middle: the separation between components φsep, fit with a power-law. Right: the FWHM of the components. Black and white markers indicate the FWHM corrected for intra-channel dispersive smearing (see text for details). |
 |
Fig. 6 Ratio of component amplitudes versus frequency and time for all observing sessions. In order to be able to plot both modes on the same scale, we give Ic2/Ic1 for B-mode and the inverse quantity, Ic1/Ic2 for the Q-mode. For the B-mode, Ic2/Ic1 changes with time and this evolution is similar for every mode instance. This makes it possible to estimate the time since the start of the B-mode for L77924 (top row), although we did not directly record the transition in this observation. The vertical black lines mark the transitions between the modes. |
For the profile analysis, we divided the data into several subbands in frequency (ν) and several subintegrations in time (t) and fit the average profile in each (ν,t) cell independently. The data from the B and Q-mode were analysed separately4, with the few-second region around the mode switch being removed. The subintegrations were at least 10 minutes long and the subbands at least 5 MHz wide. The number of subbands/subintegrations was reduced if the profile did not have a sufficient signal-to-noise ratio (S/N ~ 10). In each (ν,t) cell the I(φ) profile was fit with two Gaussians using the following parametrisation: ![\begin{equation} I_i(\phi) = I_{\rm c,i} \exp\left[\frac{(\phi-\phi_{\rm c,i})^2}{2\sigma_i^2}\right]\cdot \end{equation}](/articles/aa/full_html/2014/12/aa24425-14/aa24425-14-eq25.png) (1)Here i = 1,2 for the first (earlier in phase) and second component, respectively. Ic is the amplitude of the Gaussian and φc is the phase of its centre (in rotational phase). The full width at half maximum (FWHM) of the component is proportional to σ: FWHM ≈ 2.355σ. A preliminary fit to well-separated components (B-mode, ν< 80 MHz) showed that the widths of both components are consistent with being identical, σ1 = σ2. In what follows, we assumed that this equality extends for both modes at all frequencies and fitted both components with the same width σ (although still dependent on ν and t). Allowing these widths to be different gives the same quality of fit, but with larger uncertainty in fitted parameters due to covariance between them.
(1)Here i = 1,2 for the first (earlier in phase) and second component, respectively. Ic is the amplitude of the Gaussian and φc is the phase of its centre (in rotational phase). The full width at half maximum (FWHM) of the component is proportional to σ: FWHM ≈ 2.355σ. A preliminary fit to well-separated components (B-mode, ν< 80 MHz) showed that the widths of both components are consistent with being identical, σ1 = σ2. In what follows, we assumed that this equality extends for both modes at all frequencies and fitted both components with the same width σ (although still dependent on ν and t). Allowing these widths to be different gives the same quality of fit, but with larger uncertainty in fitted parameters due to covariance between them.
For the OC model the resulting profile was:  (2)For the MC model:
(2)For the MC model: 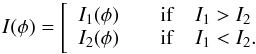 (3)For both B and Q-mode the profiles below 100 MHz are well described by both OC and MC models (Fig. 4). For both modes and models, the simple extension of the frequency dependent LBA fit results provides a reasonable match to the HBA data (Fig. 4). However, the direct fitting of HBA profiles with the OC and the MC models posed some difficulties. Above 100 MHz the components of the Q-mode profiles are almost completely merged, thus making the two-component fit meaningless. For the B-mode profiles, the HBA fit parameters appeared to be inconsistent with an extrapolation from the LBA data, both for the parameter values and their frequency dependence within the band. This may indicate that our simple MC and OC models can not be used to describe profiles with closely located components (see Appendix A for details). Thus, in this work we will not cite or discuss the fitted parameters for the HBA data, deferring the analysis to subsequent work with a better profile model.
(3)For both B and Q-mode the profiles below 100 MHz are well described by both OC and MC models (Fig. 4). For both modes and models, the simple extension of the frequency dependent LBA fit results provides a reasonable match to the HBA data (Fig. 4). However, the direct fitting of HBA profiles with the OC and the MC models posed some difficulties. Above 100 MHz the components of the Q-mode profiles are almost completely merged, thus making the two-component fit meaningless. For the B-mode profiles, the HBA fit parameters appeared to be inconsistent with an extrapolation from the LBA data, both for the parameter values and their frequency dependence within the band. This may indicate that our simple MC and OC models can not be used to describe profiles with closely located components (see Appendix A for details). Thus, in this work we will not cite or discuss the fitted parameters for the HBA data, deferring the analysis to subsequent work with a better profile model.
3.1. Spectral evolution of fit parameters
Figure 5 shows the frequency evolution of the fitted parameters, using B/Q profiles integrated over all LBA sessions5. For both modes above 30 MHz, the midpoint between components does not show any noticeable dependence on frequency. Judging from the leftmost subplots of Fig. 5, if there exist any frequency-dependent midpoint shifts, they must be less than 1 × 10-3 of the spin phase for the B-mode and 4 × 10-3 for the Q-mode.
For both modes, the separation between components is well described by a power-law:  (4)For both OC and MC models, the power-law index in the B-mode, η ≈ 0.57(1) agrees with η = 0.63(5), reported by Suleymanova et al. (1998). In the Q-mode, the separation between components has a steeper dependence on frequency: η ≈ 1.0(1) for the OC and 1.6(1) for the MC model. The frequency-dependent separation of the Q-mode profile components had not been investigated before, thus no direct comparison can be made with the results we present here.
(4)For both OC and MC models, the power-law index in the B-mode, η ≈ 0.57(1) agrees with η = 0.63(5), reported by Suleymanova et al. (1998). In the Q-mode, the separation between components has a steeper dependence on frequency: η ≈ 1.0(1) for the OC and 1.6(1) for the MC model. The frequency-dependent separation of the Q-mode profile components had not been investigated before, thus no direct comparison can be made with the results we present here.
 |
Fig. 7 Top: midpoint between profile components versus time for all LBA observing sessions. Bottom, from left to right: two average profiles of the Q-mode (at the start of observations and just before the mode transition) and the B-mode (right after mode transition and at the end of the observation). This is observing session L102418 and the profiles from Q-mode correspond to the first and third points on the upper plot. For B-mode, the profiles are from the first and last point of B-mode at the same subplot of the upper plot. The timing residuals from the same observations are plotted in Fig. 2. Noticeably, in addition to changes in relative intensity of the components and their width, the profile in B-mode shifts as a whole towards later spin phase. |
The width of the components remains roughly constant above 50 MHz, with the Q-mode FWHM being about 50% larger than that in B-mode. Below 50 MHz the B-mode FWHM grows from 20 × 10-3 of spin phase to about 30 × 10-3 at 24 MHz. However, at these low frequencies the measured FWHM is substantially affected by our observing setup, because interstellar dispersion was not compensated for within each 2.1-kHz wide channel, introducing additional smearing in time. To estimate the extra broadening we used Eq. (6.4) from Lorimer & Kramer (2005): 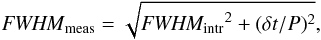 (5)where FWHMmeas is the measured FWHM of the profile, FWHMintr is the intrinsic FWHM and δt is the dispersive broadening within one channel. Both measured and intrinsic FWHMs are shown in Fig. 5, in the rightmost subplots. Since we are measuring FWHM in frequency bands, averaging the data from many channels, the resulting FWHM will depend on δt(ν) weighted with an unknown distribution of the uncalibrated peak intensity within each band. Two opposite assumptions: that all emission comes at the upper, or the lower, edge of subband are incorporated into the errorbars of the intrinsic FWHM values.
(5)where FWHMmeas is the measured FWHM of the profile, FWHMintr is the intrinsic FWHM and δt is the dispersive broadening within one channel. Both measured and intrinsic FWHMs are shown in Fig. 5, in the rightmost subplots. Since we are measuring FWHM in frequency bands, averaging the data from many channels, the resulting FWHM will depend on δt(ν) weighted with an unknown distribution of the uncalibrated peak intensity within each band. Two opposite assumptions: that all emission comes at the upper, or the lower, edge of subband are incorporated into the errorbars of the intrinsic FWHM values.
The incoherent dedispersion has little effect on the measured FWHMs of the Q-mode components, since the lower S/N of the data only allows measurements down to 35 MHz. For the B-mode, instrumental broadening can explain most of the rapid growth of FWHM below 30 MHz. Still, the B-mode components seem to have a slight intrinsic broadening towards lower frequencies, by about 1 × 10-3 of the spin phase between 80 and 40 MHz.
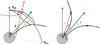 |
Fig. 8 Left: a toy model of the pulsar magnetosphere. The pulsar’s spin axis is vertical and the magnetic axis is inclined by the angle α. An example dipolar field line is shown by the thick black line. The position of the LOS vector (red in the online version) stays fixed in space while the pulsar rotates around its spin axis. The plot shows the moment when spin, magnetic and LOS vectors are lying in the same plane (the fiducial plane). At this moment the angle between observer and magnetic axis is β. Usually β is measured clockwise from the magnetic axis, so for the vectors here the value of β is negative. Here we assume that emission comes from a cone at fixed height above the pulsar surface (with respect to the magnetic axis). The opening angle of the cone is marked with a thick dotted gray line. All angles in this plot are identical to the ones in Lorimer & Kramer (2005, Fig. 3.4a). However, in order to make the relationship between the angles more clear, in their figure β and ρ are plotted as originating from the centre of the star. Such transformation does not affect Eq. (6), since w (φsep in our plot) stays the same for both cases. Right: relationship between the opening angle of the emission cone ρ and coordinates of the emitting point (r,θ). |
3.2. Time-resolved evolution of fit parameters
Earlier work on B0943 revealed slow changes of the B-mode profile shape during the mode. These changes were characterised by Ic2/Ic1(t) – the evolution of the ratio of component peaks with the time since mode onset. Here we confirm the result of Suleymanova & Rankin (2009), who carried out their analysis at similar observing frequencies. According to our observations, right after a Q-to-B transition, Ic2/Ic1 strongly depends on observing frequency, growing from 0.35 ± 0.05 at 34 MHz to 0.65 ± 0.05 at 66 MHz (Fig. 6). This tendency seems to hold true at higher observing frequencies: at 112 MHz the ratio is 1.2 ± 0.2 (Suleymanova & Rankin 2009) and at 327 MHz it reaches 1.75 ± 0.05 (Rankin & Suleymanova 2006). During the first 10−30 minutes from the start of the B-mode (hereafter “initial phase”), the Ic2/Ic1 below 100 MHz increases to about 0.5−0.6 (our data) and decreases above 100 MHz to 1 ± 0.2 (Rankin & Suleymanova 2006; Suleymanova & Rankin 2009). The duration of the initial phase seems to be smaller at higher frequencies (less than 10 min at 327 MHz and up to 30 min at 34 MHz). After the initial phase, Ic2/Ic1 starts gradually decreasing at all observing frequencies, reaching 0.3 ± 0.1 at 34 MHz (our data) and 0.2 ± 0.05 at 327 MHz (Rankin & Suleymanova 2006) by the next B-to-Q transition. Such behaviour of Ic2/Ic1 was similar for all B-mode instances and we used this fact to estimate the age (time from the start) of the B-mode for observing session L77924, where the Q-to-B transition happened before the observing session started. At the start of the observations Ic2/Ic1 at 34 and 66 MHz was the same and equal to 0.5, which corresponds to about 40 min from the start of the mode.
In the Q-mode the ratio of component peaks did not have any noticeable change with time. However, in the Q-mode the S/N is much lower, thus the ratio cannot be constrained as well as in the B-mode. The same applies to the FWHM: in Q-mode it did not have any temporal dependence. In the B-mode, the FWHM (not corrected for instrumental broadening) grew with the age of the mode: from 20 × 10-3 to 25 × 10-3 of the spin phase at 38 MHz (with typical error of measurement of 0.4 × 10-3) and from 19 × 10-3 to 20 × 10-3 at 69 MHz (with typical error of measurement of 0.2 × 10-3).
As was suggested by the observed changes in arrival time discussed in Sect. 2 and visible in Fig. 2, we also see a change in the B-mode profile midpoint as a function of time since the onset of each B-mode. In Fig. 7, the profile midpoint φmid(t) was obtained by weighted averaging of φmid(ν,t) in every (ν,t) cell. The error is the standard deviation of the weighted sample, about 0.3 × 10-3 of the spin phase. In B-mode the midpoint gradually moved towards later spin phases with an average rate of 2 ms (2 × 10-3 of spin phase) per hour. The shift was more rapid at the start of the B-mode and flattened out with time. In the Q-mode φmid(t) was constant with time within the error of a single measurement (2 × 10-3 of spin phase for the longest and highest S/N Q-mode observation, L102418). For both the OC and MC models, and for both of the observed Q-to-B transitions, the Q-mode midpoint seems to coincide with the initial B-mode midpoint within at most 4.5 errors of measurement. Based on the L169237 observation, the Q-mode midpoint is the same in every instance of the Q-mode, although more observations are needed before confirming this with certainty.
The size and rate of change of the B-mode midpoint location offset (Fig. 7) exactly matches that seen for the TOAs (Fig. 2). For the midpoint location, we also see a clear phase step at the transition between the B and Q-mode corresponding to about 4 milliseconds. Due to the TOAs and the profile variation models having different fiducial points in the two modes, this is seen as a step from B to Q and Q to B in the TOAs and profile variation models respectively.
We did not find any changes in separation between components throughout any of the B-modes we observed. At any given frequency, φsep(t) measurements did not have an obvious dependence on time and for the sessions with best S/N they had standard deviation of 0.4 × 10-3 of the spin phase.
4. Discussion
Here we give one possible interpretation of the frequency and time evolution of the average profile. We assume a purely dipolar field, with the magnetic axis inclined with respect to the spin axis by the angle obtained in Deshpande & Rankin (2001). We assume RFM, however we do not require the emission region to be cone-shaped. Our reasoning thus also applies to models where radio emission can come from multiple patches around field lines starting at different magnetic latitudes, as long as RFM holds within every single patch (Lyne & Manchester 1988; Karastergiou & Johnston 2007).
4.1. Verifying the basic geometry
The derivation of B0943’s geometry done by Deshpande & Rankin (2001, hereafter DR2001) was partially based on the frequency evolution of the width of the average profile. In this section we will examine if our measurements of average profile width agree with DR2001.
First, we review the derivation done by DR2001. The notation for angles is shown in Fig. 8. In the Figure, the case for negative β (LOS passes between spin and magnetic axis) is shown. This is called “inside traverse”. If β> 0, the LOS would be on the other side of the magnetic axis and this is an “outside traverse”. The relationship between profile width w(ν) and opening angle of the emission cone at that frequency can be established with spherical geometry (Gil et al. 1984): 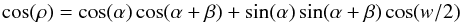 (6)DR2001 define w as the distance between the two half-maximum points in B-mode. Then, they assume that ρ(ν) obeys the empirical relation from Thorsett (1991), given here in the form adopted in DR2001:
(6)DR2001 define w as the distance between the two half-maximum points in B-mode. Then, they assume that ρ(ν) obeys the empirical relation from Thorsett (1991), given here in the form adopted in DR2001: 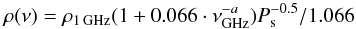 (7)Mitra & Deshpande (1999) analysed 37 non-recycled pulsars with conal profiles and showed that their opening angles at 1 GHz, ρ1 GHz, tend to group around the values of 4.3°, 4.5° and 5.7°, although the scatter within these groupings is comparable to their separation. The smallest and largest values are called “inner” and “outer” cones, after Rankin (1993).
(7)Mitra & Deshpande (1999) analysed 37 non-recycled pulsars with conal profiles and showed that their opening angles at 1 GHz, ρ1 GHz, tend to group around the values of 4.3°, 4.5° and 5.7°, although the scatter within these groupings is comparable to their separation. The smallest and largest values are called “inner” and “outer” cones, after Rankin (1993).
DR2001 use the observed w(ν) together with Eqs. (6) and (7) to fit for a, α and β. They fixed ρ1 GHz at the values for the inner and outer cone. This still left room for several solutions. The possibilities were narrowed down by drifting subpulse analysis, namely matching the predicted values for the longitude interval between drifting subpulses P2 and the rotation of position angle between subpulses. Only the inner traverse (β< 0) satisfied the observed data. In the case of an inner cone α = 11.58°, β = −4.29° and for an outer cone, α = 15.39°, β = −5.69°. These two models have identical predictions, and, as the authors note, any reasonable value of ρ1 GHz would behave similarly. That means that we do not really know α and β, but since most pulsars fall between inner and outer cones we can take these two sets of values as boundaries.
 |
Fig. 9 Width of the average profile in the B-mode between two half-maximum points, w ≡ φsep(ν) + FWHM(ν). The cyan diamonds are the measurements of profile width from Deshpande & Rankin (2001). The green and red circles are from our data (both LBA and HBA), fitted with the OC and MC models, respectively. At frequencies below 40 MHz the profile width is somewhat affected by intra-channel dispersive smearing. The most simple model is shown by the black line: it assumes φsep from the LBA fit and the FWHM derived from the LBA data above 40 MHz. |
In our notation, w(ν) ≡ φsep(ν) + FWHM(ν). Our values for w(ν) fall close to DR2001 (Fig. 9), with the discrepancy potentially being explained by the small fraction of the Q-mode data in their folded profiles (Deshpande & Rankin 2001). In Fig. 9 we also plot w(ν) for the independent fit in the HBA data. Although φsep and FWHM are covariant and do not match the extrapolated values from the LBA data (see Appendix A), their sum represents the actual width of the profile, which does not suffer so much from the complications of determining the individual phases and widths of the components. The small difference between the two models in the HBA data is due to discrepancy in estimating the peak S/N of the components, which affected the S/N of half-maximum and thus the value of FWHM6. Below 40 MHz the component widths are significantly affected by intra-channel dispersive smearing, although some hint that the components also broaden intrinsically does exist (see Fig. 5). For comparison, in Fig. 9 we plot wextrap(ν) = 0.384ν-0.567 + 0.0185, with the FWHM and component separation from the B-mode LBA data at 40−80 MHz.
Unfortunately, we cannot fully repeat the DR2001 derivation because it relies on polarimetric information, which we do not have. However, we checked if ρ(ν) determined from our data satisfies Eq. (7) at a given geometry. We converted w(ν) to ρ(ν) using Eq. (6) for the two possible sets of (α, β) and then fitted it with Eq. (7). We excluded ν< 40 MHz data from the fit due to intra-channel dispersive broadening. For both inner and outer cone geometries the widths from the OC/MC model can be reasonably fit with Eq. (7), with ρ1 GHz lying close to the implied values: 6.1°/6.0° for the outer cone and 4.6°/4.5° for the inner cone geometries. The power-law index a was −0.55/−0.58, somewhat higher than −0.396 from DR2001.
In summary, our measured w(ν) agrees with both the inner and the outer cone geometries from the DR2001 if one assumes a steeper frequency dependence of the profile width. Further discrimination between the two sets of angles will require polarimetric data.
4.2. Where does the emission originate?
B0943’s spin period of 1.098 s places its light cylinder at rLC = Pc/ (2π) = 5.24 × 104 km. The magnetic latitude of the last open field line is 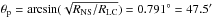 , assuming RNS = 10 km.
, assuming RNS = 10 km.
In the previous section, Eq. (6) was used to map the profile width to the opening angle of the emission cone. Note that this equation does not necessarily require the emission region to be cone-shaped; it simply sets the relation between a) the distance from a chosen profile component to the fiducial point and b) the angle between the corresponding emitting patch and magnetic axis. We use “fiducial point” here to describe the frequency-independent spin phase when the LOS passes the plane defined by magnetic and spin axes. In principle, emitting patches can be completely independent and components can have different φsep(ν) with respect to the fiducial point, as was indeed observed for PSR B0809+74 by Hassall et al. (2012).
For B0943, the components evolve symmetrically around a frequency-independent midpoint, making the latter an ideal candidate for the fiducial point. In this section we adopt the assumption that the emission region has circular symmetry around the magnetic axis and will refer to it as a cone, although all results obtained will also be valid for independent patches.
 |
Fig. 10 Emission heights (radial distance from the centre of the star) for a cone originating at the last open field line (magnetic latitude θp). For any other starting magnetic latitude θ0, r(θ0) ≈ r(θp) × (θp/θ0)2. The emission heights at frequencies above the LBA band were extrapolated from the parameters derived from the LBA data. |
The opening angle of the emission cone (found from Eq. (6) with w = φsep) can be related to the polar coordinates (r,θ) of the field line (Fig. 8, right). If the emission region is close to the magnetic axis (θ ≲ 20°, ρ ≲ 30°, true for all our data), then θ ≈ 2ρ/ 3. Combining this with the equation for a dipolar field line: 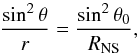 (8)we can obtain the coordinates of the centres of the emitting patches in the pulsar magnetosphere, (r(ν),θ(ν)). However, for each ν the coordinates are not unique, since we do not know the magnetic latitude of the foot of the field line, θ0. The upper limit on θ0 (and thus lowest possible emission height r(ν) for every ν) comes from the requirement that radio emission originates in the open-field-line region, thus θ0<θp. The lower limit on θ0 can be deduced from the absence of frequency-dependent arrival delays in the midpoint φmid(ν). For this, we use the derivations of Gangadhara & Gupta (2001). If frequencies ν1 and ν2 are emitted at radii r1 and r2 from the centre of the star, then the light travel time delay (retardation) between those two frequencies will be:
(8)we can obtain the coordinates of the centres of the emitting patches in the pulsar magnetosphere, (r(ν),θ(ν)). However, for each ν the coordinates are not unique, since we do not know the magnetic latitude of the foot of the field line, θ0. The upper limit on θ0 (and thus lowest possible emission height r(ν) for every ν) comes from the requirement that radio emission originates in the open-field-line region, thus θ0<θp. The lower limit on θ0 can be deduced from the absence of frequency-dependent arrival delays in the midpoint φmid(ν). For this, we use the derivations of Gangadhara & Gupta (2001). If frequencies ν1 and ν2 are emitted at radii r1 and r2 from the centre of the star, then the light travel time delay (retardation) between those two frequencies will be: 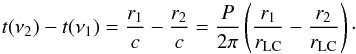 (9)The azimuthal corotation velocity 2πr/P is bending the emission beam in the direction of the pulsar rotation (aberration):
(9)The azimuthal corotation velocity 2πr/P is bending the emission beam in the direction of the pulsar rotation (aberration): ![\begin{equation} t(\nu_2)-t(\nu_1) = \frac{P}{2\pi}\left[ \sin^{-1}\left(\frac{r_1\sin(\alpha+\beta)}{r_\mathrm{LC}}\right)- \sin^{-1}\left(\frac{r_2\sin(\alpha+\beta)}{r_\mathrm{LC}}\right) \right]. \label{eq:aberr} \end{equation}](/articles/aa/full_html/2014/12/aa24425-14/aa24425-14-eq119.png) (10)Comparing the sum of the light travel and aberration delays7 with the observed φmid(ν) (Fig. 5, left), we conclude that the net delay must be less than 1 ms between 25 and 80 MHz in B-mode and at most 4 ms between 35 and 75 MHz in Q-mode. This places the minimum θ0 at about 0.1θp for the Q-mode and about 0.27θp for B-mode. The exact lower limits on θ0 for inner and outer cone and OC/MC models are given in Table 2.
(10)Comparing the sum of the light travel and aberration delays7 with the observed φmid(ν) (Fig. 5, left), we conclude that the net delay must be less than 1 ms between 25 and 80 MHz in B-mode and at most 4 ms between 35 and 75 MHz in Q-mode. This places the minimum θ0 at about 0.1θp for the Q-mode and about 0.27θp for B-mode. The exact lower limits on θ0 for inner and outer cone and OC/MC models are given in Table 2.
Figure 10 shows the emission heights for the last open field line, r(θp). For any other θ0, r(θ0) ≈ r(θp) × (θp/θ0)2. The heights for the B-mode and inner cone geometry are in good agreement with Deshpande & Rankin (2001). Note that if φsep derived from the LBA data does not change dramatically above the LBA band, then the emission at basically all frequencies above 20 MHz comes from quite a narrow range of heights: 13−300RNS, depending on the chosen (α,β) solution and θ0. At any given frequency above 20 MHz, the heights do not differ much between the modes, with 0.94 <rQ/rB< 1.04, assuming both modes come from the same θ0. Emission is much closer to the surface of the star than to the light cylinder: r/rLC< 0.06.
Minimum magnetic latitude θ0.
Although the MC model is only an approximation to the profile produced by a cone-shaped emission region, the results obtained within this model can still be used to estimate the width of the cone. At the surface of the star: 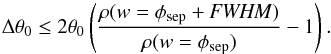 (11)The ≤ sign reflects the fact that the radial distribution of intensity within the cone is not symmetric around the maximum point, with the radial intensity dropping faster at the inner side of the cone8. Both allowed geometries give the same value for Δθ0. For B-mode at 30 MHz Δθ0 ≤ 4′ × θ0/θp, for the Q-mode Δθ0 ≤ 8′ × θ0/θp. At 80 MHz the width of the cone is about 2 times smaller.
(11)The ≤ sign reflects the fact that the radial distribution of intensity within the cone is not symmetric around the maximum point, with the radial intensity dropping faster at the inner side of the cone8. Both allowed geometries give the same value for Δθ0. For B-mode at 30 MHz Δθ0 ≤ 4′ × θ0/θp, for the Q-mode Δθ0 ≤ 8′ × θ0/θp. At 80 MHz the width of the cone is about 2 times smaller.
4.3. What causes the lag of the B-mode midpoint?
B0943’s average profile undergoes noticeable evolution during each B-mode. Both the ratio of the component peaks and their widths change in a frequency-dependent manner, and the midpoint between the two components, φmid, systematically shifts towards later spin phases in the LBA data. The cumulative midpoint lag per mode instance is Δφmid ≈ 4 ms, or 4 × 10-3 of the spin phase. Throughout the B-mode, φmid is independent of observing frequency down to the error of measurement of 0.3 ms. The frequency-dependent separation between components, φsep, also does not change during the B-mode: at any given frequency φsep is constant down to the typical error of measurement, 0.4 ms.
Our single HBA observation did not reveal any φmid drift within 2 ms, although we only recorded a 100-min part of the B-mode right before B-to-Q transition. The observed lag rate in the LBA data is not uniform, decreasing towards the end of the mode (Fig. 7), and the cumulative lag in the last 100 min is typically less than 2 ms. Also, at higher frequencies, where components are close to each other, it is important to develop better, more physically adequate profile models in order to avoid contamination of midpoint measurements by changing peak ratio (see Appendix A).
The LBA band Q-mode midpoint is constant within the uncertainties. However, uncertainties in the Q-mode are a few times larger than in the B-mode and the Q-mode is shorter, making it harder to detect any Q-mode lag. From the observing session with the highest S/N in the Q-mode (L102418), the cumulative Q-mode midpoint lag rate is less than 1 ms/h. Judging by the two available Q-to-B transitions, the midpoint in Q-mode coincides with the initial B-mode midpoint. On the other hand, at the B-to-Q (2 recorded) transitions there is a 4−6 ms jump to earlier rotational phase. We had only one observing session with two B-to-Q transitions (L169237) and on that day the midpoint was at the same phase at the end of both B-mode instances.
In what follows we propose several tentative explanations for the observed midpoint lag and discuss their plausibility.
4.3.1. Location of the emission regions
If the emitting region is gradually moving against the sense of the pulsar’s rotation (with different θ0 being illuminated over time), the pulse profile will appear to lag. However, in this case φmid and φsep will depend both on the frequency and time from the start of the mode (unless emission heights are adjusting themselves in a peculiar way that would keep φmid(ν) and φsep(t) constant). The 4 ms (86.4′) cumulative lag of the midpoint at the derived emission heights corresponds to a 0.57′ shift of the magnetic latitude of the centre of the emission cone at the pulsar’s surface. If at the beginning of a B-mode the magnetic latitude of the cone centre is 0.29′ and during the mode the cone gradually moves through the magnetic pole up to θ0 = 0.29′ on the other side of the fiducial plane, then φsep(t) will stay within the error of measurement and φmid(ν) within 2.5 measurement errors. Here we assumed that the emission heights do not change throughout the mode, however, some variation of emission heights is not excluded, as long as the net midpoint and separation stay within the measurement errors.
4.3.2. Variation of the cone intensity with magnetic azimuth
If the components are partially merging (the LOS does not cross the inner cone boundary), then the measurements of the midpoint position are biased if the components have different intensity (Fig. 3, compare the peak phases of partially merged profiles for the uniformly illuminated cone and the cone with the smooth variation of radial intensity with magnetic azimuth). The amount of bias depends on the ratio of the component peaks and thus will vary with time if the peak ratio varies. However, the direction of the midpoint shift caused by this effect should be opposite to that observed here: the midpoint shifts towards the brighter component, the leading one for the B-mode (which becomes only relatively brighter with the age of the mode, see Fig. 6). Also, this effect is frequency-dependent, being virtually zero for the lower frequencies, where components are well separated.
4.3.3. Spin-down rate
Lyne et al. (2010) showed that, for at least some pulsars, long-term variability in the radio profile shape is correlated with changes in the pulsar spin down rate. This may be true for B0943 as well, however the amplitude of this effect is too small to explain the observed midpoint lag of the B-mode profile. The delay of 2 ms/h corresponds to δṖ ≈ 10-9 s/s, 106 higher than the pulsar’s spin-down rate, Ṗ. That is, however, many orders-of-magnitude higher than the fractional changes in Ṗ found in PSRs B1931+24 (50%; Kramer et al. 2006), J1841−0500 (250%; Camilo et al. 2012) and 1832+0029 (77%; Lorimer et al. 2012). Furthermore, a spin-down rate change cannot explain the phase jump at B-to-Q transition. We thus conclude a different mechanism is likely in play.
4.3.4. Toroidal magnetic field
In a pulsar magnetosphere, radio waves are emitted in the direction of the magnetic field, thus any changes to the field lines at the emission heights will affect the direction of the beam. An observed shift of fiducial point towards later phases can be interpreted as evidence for a varying toroidal component of the magnetic field (field lines bending against the sense of rotation). A toroidal component can appear from the interaction between the rotating magnetic field and the frozen-in plasma. This effect was investigated by Michel (1969), who made a relativistic expansion to the Weber-Davis model of the solar wind. Using Eq. (8) from Michel (1969), the midpoint lag can be written as: ![\begin{equation} \Delta\phi_\mathrm{sep}=\frac{\Delta B_\phi}{B_r}=\frac{P c^3 r_\mathrm{em}^5\rho_\mathrm{GJ}}{B_\mathrm{NS}^2R_\mathrm{NS}^7}\Delta[(\rho/\rho_\mathrm{GJ})\times(\gamma-\gamma_0)]. \end{equation}](/articles/aa/full_html/2014/12/aa24425-14/aa24425-14-eq147.png) (12)Here γ0 is the gamma-factor of particles at their birth place (right above the polar gap) and γ is the gamma-factor at the emission height rem. At the heights dictated by RFM, (ρ/ρGJ) × (γ − γ0) must change by ~ 1019 in order to explain Δφ = 4 × 10-3. It does not seem plausible that such drastic change in particle energy and/or density at the emission height within the mode could happen without much more significant changes in the average profile.
(12)Here γ0 is the gamma-factor of particles at their birth place (right above the polar gap) and γ is the gamma-factor at the emission height rem. At the heights dictated by RFM, (ρ/ρGJ) × (γ − γ0) must change by ~ 1019 in order to explain Δφ = 4 × 10-3. It does not seem plausible that such drastic change in particle energy and/or density at the emission height within the mode could happen without much more significant changes in the average profile.
4.3.5. Polar gap height
According to Ruderman & Sutherland (1975), if there is a vacuum gap between the stellar surface and the plasma-filled magnetosphere of an aligned rotator, then the plasma above the gap will not co-rotate with the star itself, but will have a slightly larger spin period. The discrepancy between the plasma and pulsar spin periods is proportional to the height of the gap. Recently, Melrose & Yuen (2014) showed that non-corotating magnetospheres are also possible for the non-aligned rotators. Thus, the observed lag of the pulse profile’s fiducial point in the B-mode can be plausibly explained by a change in the spin period of plasma above the polar cap, caused by slow variations in gap height during the B-mode. As a first-order assumption, we estimate the necessary variation of the gap height by using a simple analytical equation from Appendix I in Ruderman & Sutherland (1975), derived for an aligned rotator with a spherical gap. To explain the phase difference between the beginning and the end of B-mode the plasma spin period must change by a fraction 5 × 10-7 and according to Eq. (A.6) from Ruderman & Sutherland (1975): 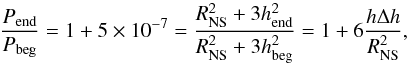 (13)giving that the relative change in gap height would be
(13)giving that the relative change in gap height would be 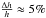 . Since the electric potential is proportional to h2, the relative change in potential between the surface of the pulsar and the start of the plasma-filled zone will be about 10%.
. Since the electric potential is proportional to h2, the relative change in potential between the surface of the pulsar and the start of the plasma-filled zone will be about 10%.
Interestingly, other evidence exists that the gap potential can vary within a B-mode instance. As was discovered before, the subpulse drift rate slowly changes during the B-mode (Suleymanova & Rankin 2009; Backus et al. 2011) and is directly proportional to the gradient of potential across the polar cap field lines (Ruderman & Sutherland 1975; van Leeuwen & Timokhin 2012). The morphology of subpulse drift rate change is similar to the fiducial point drift – more rapid at the beginning of the mode and slowing down towards B-to-Q transition (Suleymanova & Rankin 2009; Backus et al. 2011). To explain the observed change in subpulse drift rate, the gradient of the potential must change by −4%, which is close in magnitude to the 10% variation needed to explain the profile lag. We must stress though that the changing subpulse drift rate and the lag of the profile are caused by variation of the potential in orthogonal directions: across the field lines for the former and along the field lines for the latter.
The variation of subpulse drift rate could also, in principle, cause the apparent changes in the profile shape because of the redistribution of phases of individual subpulses within the on-pulse window. To investigate that, we simulated a sequence of profiles from a series of drifitng subpulses with the drift parameters taken from the single-pulse analysis of our data (Bilous et al., in prep.). We found that the varying drift rate influenced the shape of the average profile only if the integration time was less than about 30 spin periods. When integrated for at least 5 min, the average profile’s shape does not depend on the variation of the subpulse drift rate.
5. Summary and conclusions
LOFAR’s observations of B0943 provided a wealth of new information about this well-studied pulsar. The ultra-broad frequency coverage allowed us to place upper limits on the light-travel delays and thus to constrain the emission heights in both modes. The long observing sessions gave the opportunity to study the gradual changes in the average profile during the B-mode. Finally, the high sensitivity of the telescope allowed us to explore the frequency evolution of the faint Q-mode profile and to compare it to the B-mode.
We fit the pulsar’s average profile in B and Q-mode using two models. One of the models (“OC”) assumed that the radio emission comes from two independent patches in the pulsar’s magnetosphere, while the other (“MC”) served as an approximation to a cone-shaped emission region. For the LBA data both models worked well, resulting only in minor differences in the values of the fitted parameters. In the HBA frequency range both B and Q-mode profiles can be reasonably well approximated with the extension of the frequency-dependent LBA fit results.
The midpoint between profile components in the LBA B-mode data appeared to follow the ν-2 dispersion law down to 25 MHz, allowing us to measure DM independently of the profile evolution. The absence of aberration and retardation signatures in the profile midpoint φmid(ν) placed the emission region much closer to the stellar surface than to the light cylinder: r/rLC< 0.06. If the emission in both modes comes from the same magnetic field lines, then at any given frequency above 20 MHz radio emission heights do not differ much between the modes, with 0.94 <rQ/rB< 1.04.
In radio, B and Q-mode do not just have a different, static set of properties, they also differ in their dynamic behaviour during a mode. In Q-mode, the radio emission does not undergo any apparent changes with time, whereas in the B-mode both the average profile and single pulses evolve systematically during a mode instance (Rankin & Suleymanova 2006; Suleymanova & Rankin 2009). Thus, in addition to the rapid mode switch there exists some gradual build-up or relaxation in the B-mode, which, together with the unusual B-mode X-ray properties (namely the potential absence of thermal polar cap emission, Hermsen et al. 2013) might be a clue to deciphering the physical trigger of the mode change. Our observations discover one more feature of the B-mode profile evolution: at 20−80 MHz the midpoint between B-mode profile components is systematically shifting towards later spin phase with the time from the start of the mode. The observed lag is frequency-independent down to 0.3 ms and asymptotically changes towards a stable value of 4 ms (4 × 10-3 of spin phase). The lag rate is not uniform, being higher at the beginning of the mode. At the B-to-Q transition the profile midpoint jumps back to the earlier spin phase and remains constant throughout Q-mode until the next Q-to-B transition. The apparent lag of the midpoint can be interpreted as the gradual movement of the emission cone against the sense of pulsar rotation, with different field lines being illuminated over time. Another interesting explanation is the variation of accelerating potential between the surface of the pulsar and the start of the plasma-filled magnetosphere above the polar gap. This explanation connects the observed midpoint lag to the gradually evolving subpulse drift rate (Rankin & Suleymanova 2006). The subpulse drift rate is determined by the gradient of potential in orthogonal direction – across the field lines in the polar cap (Ruderman & Sutherland 1975; van Leeuwen & Timokhin 2012). Both the midpoint lag and subpulse drift rate evolve similarly with time from the mode start: faster right after the Q-to-B transition and gradually evening out with time. Observed magnitude of the midpoint lag points to about 10% variation in the accelerating potential throughout the mode. At the same time the gradient of the potential across the field lines changes by −4%.
At present, there is no clear understanding of the magnetospheric configurations during the two modes or what triggers the mode switching itself. Most probably, our picture of pulsar emission properties in each mode is also far from complete, being limited by how our LOS intersects the pulsar magnetosphere. Solving the mode-switching puzzle clearly requires much more work. One of the obvious problems to explore is the broadband low-frequency polarisation, both for single pulses and the average profile, as it can provide additional important clues to the structure of the magnetic field. Another interesting issue to be addressed is the transition region between the modes. Any information on the time-scale of mode switch, any special signatures found in B and Q-mode right around the transition will give us additional insight into the mystery of the mode switching. The ultimate goal remains to understand the connection, if any, between the variety of emission phenomena observed in radio pulsars.
As pointed out by the referee, a similar result has recently been obtained using many short snapshot observations taken as part of the long-term timing campaign on B0943 at the Pushchino observatory (to be published in Suleymanova & Rodin 2014).
For example, two separate patches located at different heights above the stellar surface on field lines originating at different magnetic latitudes in the polar cap (Karastergiou & Johnston 2007).
Here the folding ephemerides for the B-mode were adjusted in such a way that the drift of φmid(t) in the B-mode (see Sect. 3.2) was zero.
For the HBA data, profile components are so close to each other that in the OC model each component has a significant level of emission at the phase of the other component’s centre. Thus, the fitted S/N of the profile peak is smaller than in the MC model, which results in the lower half-maximum threshold and the larger fitted FWHM.
We did not include the magnetic sweepback delay (proportional to sin2α × ((r2 − r1) /rLC)3, Shitov 1983), because for our values of α and estimated emission heights it is much smaller than the aberration and retardation delays.
Note that ρ(w) from Eq. (6) is not a linear function of w. In order to reproduce an observed Gaussian-shaped component, the inner and outer half-widths of the cone must be different.
Acknowledgments
A.V.B. thanks T.T. Pennucci (University of Virginia) for useful discussions. J.W.T.H. acknowledges funding from an NWO Vidi fellowship and ERC Starting Grant “DRAGNET” (337062). LOFAR, the Low Frequency Array designed and constructed by ASTRON, has facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy.
References
- Ahuja, A. L., Mitra, D., & Gupta, Y. 2007, MNRAS, 377, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Asgekar, A., & Deshpande, A. 2001, MNRAS, 326, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Backus, I., Mitra, D., & Rankin, J. M. 2011, MNRAS, 418, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Bhat, N. D. R., Cordes, J. M., Camilo, F., Nice, D. J., & Lorimer, D. R. 2004, ApJ, 605, 759 [CrossRef] [Google Scholar]
- Camilo, F., Ransom, S. M., Chatterjee, S., Johnston, S., & Demorest, P. 2012, ApJ, 746, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 1978, ApJ, 222, 1006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
- Deshpande, A. A., & Rankin, J. M. 2001, MNRAS, 322, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Gangadhara, R. T., & Gupta, Y. 2001, ApJ, 555, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Gil, J., Gronkowski, P., & Rudnicki, W. 1984, A&A, 132, 312 [NASA ADS] [Google Scholar]
- Hassall, T. E., Stappers, B. W., Hessels, J. W. T., et al. 2012, A&A, 543, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hermsen, W., Hessels, J. W. T., Kuiper, L., et al. 2013, Science, 339, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Karastergiou, A., & Johnston, S. 2007, MNRAS, 380, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Lyne, A. G., O’Brien, J. T., Jordan, C. A., & Lorimer, D. R. 2006, Science, 312, 549 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy, eds. R. Ellis, J. Huchra, S. Kahn, G. Rieke, & P. B. Stetson [Google Scholar]
- Lorimer, D. R., Lyne, A. G., McLaughlin, M. A., et al. 2012, ApJ, 758, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., & Manchester, R. N. 1988, MNRAS, 234, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A., Hobbs, G., Kramer, M., Stairs, I., & Stappers, B. 2010, Science, 329, 408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Malofeev, V. M., Malov, O. I., & Shchegoleva, N. V. 2000, Astron. Rep., 44, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B., & Yuen, R. 2014, MNRAS, 437, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1969, ApJ, 158, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, D., & Deshpande, A. A. 1999, A&A, 346, 906 [NASA ADS] [Google Scholar]
- Rankin, J. M. 1983, ApJ, 274, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Rankin, J. M. 1993, ApJ, 405, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Rankin, J. M., & Suleymanova, S. A. 2006, A&A, 453, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shabanova, T. V., Pugachev, V. D., & Lapaev, K. A. 2013, ApJ, 775, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shitov, Y. P. 1983, AZh, 60, 541 [NASA ADS] [Google Scholar]
- Stappers, B. W., Hessels, J. W. T., Alexov, A., et al. 2011, A&A, 530, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleymanova, S. A., & Izvekova, V. A. 1984, Sov. Ast., 28, 32 [Google Scholar]
- Suleymanova, S. A., & Rankin, J. M. 2009, MNRAS, 396, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Suleymanova, S. A., & Rodin, A. 2014, Astron. Rep., 58, 11 [Google Scholar]
- Suleymanova, S. A., Izvekova, V. A., Rankin, J. M., & Rathnasree, N. 1998, J. Astrophys. Astron., 19, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsett, S. E. 1991, ApJ, 377, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Timokhin, A. N. 2010, MNRAS, 408, L41 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, J., & Timokhin, A. N. 2012, ApJ, 752, 155 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fitting and model applicability
 |
Fig. A.1 Left: an example high S/N average profile (B-mode, 2 hours of integration, 54−62 MHz), together with fit and residuals. The residuals show a small, but statistically significant discrepancy between the data and models. Right: two fits of HBA B-mode data. The upper subplot shows the LBA-like fit, with component positions, intensities and width being a priori unconstrained. On the lower subplot the FWHM, ratio of component peaks and their separation are extrapolated from the frequency dependence of corresponding LBA values. Only the midpoint, together with the S/N of the leading component, are fit. Neither of the fits and/or models describe the data perfectly and the fitted values from the unconstrained fit do not agree with fitted values extrapolated from LBA. |
All fits were done with the publicly available Markov-chain Monte Carlo software PyMC9. We assumed uniform priors on the parameters and implemented Gaussian likelihoods. The chains were run until they converged. The goodness of the fit was checked by using the fitted model to simulate datasets and then comparing the distribution of the simulated datasets to the actual data. For quantitative assessment we used the Bayesian p-value10 which uses Freeman-Tukey statistics to measure the discrepancy between the data (observed or simulated) and the value predicted by the fitted model. The Freeman-Tukey statistics are defined only for positive data, so we added a fixed arbitrary value to the profile, ensuring that all data points are positive. The p-value did not depend on the exact value of the offset added.
The Bayesian p-value is the proportion of simulated discrepancies (between the simulated data and expected value) that are larger than their corresponding observed discrepancies (between the observed data and expected value). If the model fits the data well, the p-value is around 0.5. If the p-value is too close to 1 or 0, that indicates an unreasonable fit. For our data, we found that the p-value depended on the S/N of the fitted profile. If the profile had S/N ≲ 80 (all Q-mode and part of B-mode), then the p-value was 0.5–0.8. When S/N was above 100, the p-value quickly reached 1.0, meaning that the model fit had residuals which were larger than the noise level. If we took the same observation of B-mode, and divided it into smaller chunks, reducing S/N in a single chunk, the fit in a single chunk had acceptable p-value. An example of a high-S/N profile fit, together with residuals, is shown in Fig. A.1, left. Note that the MC model gives a slightly worse fit, underestimating the intensity around the midpoint.
We also checked the covariances between the fitted parameters. Due to the finite length of the MCMC chains, the measured covariance is some random quantity around the true value (for the infinite chain), thus even for completely independent components we expect to get some small, but non-zero covariances between the fitting parameters. To check when our parameters become significantly more covariant than that, we performed the following simulation. We made two same-width Gaussians with separation between the peaks many times exceeding the FWHM, and fitted them in the same way as we fit our data. We ran the simulation 100 times, obtained a distribution for the correlation coefficients between fit parameters and compared these distributions to the real-data correlation coefficients. For the B-mode, below about 60 MHz the correlation coefficients are compatible with those of far-separated Gaussians. Above 60 MHz the absolute value of correlation coefficients starts slowly increasing and B-mode parameters become highly covariant in the HBA data.
In general, fitting B-mode profiles in the HBA band posed some difficulties. As in the LBA data, wherever the S/N of the average profile was above 80 the Bayesian p-value is close to 1 and the residuals were incompatible with noise (Fig. A.1, right, upper subplot). In addition, the fit parameters in the HBA data appeared to be inconsistent with an extrapolation from the LBA data, both for the parameter values and their frequency dependence within the band. The degree of inconsistency was smaller for the OC model than for the MC model. This discrepancy of fit results between the bands can mean that either there is a change in parameter behaviour somewhere between our bands, or that our model assumptions are not correct for higher frequencies. To investigate the latter we constructed an extrapolated profile, extending frequency dependence of the LBA data fit parameters to HBA frequencies. This extrapolated profile is shown in the bottom subplot of Fig. A.1, right. Both OC and MC models reproduce the position and width of components, but they underestimate the emission in the region between them. Since for the HBA data the unconstrained fit parameters are highly correlated, this underestimation will bias all fit parameters. Thus, in this work we will not cite or discuss the fitted parameters for the HBA B-mode data, deferring the analysis to subsequent work with a better profile model. To first order, the average profile in HBA B-mode can be approximated with an extrapolation of the frequency dependence of the LBA data fit parameters.
For the Q-mode, fitted parameters were covariant at all LBA frequencies, with correlation coefficients growing towards higher frequencies. For the HBA data the covariance between fitted parameters gets so large that no meaningful fit is possible without additionally constraining the ratio of components heights. Nevertheless, simple extrapolation of frequency dependence of LBA fit parameters works well (see Fig. A.1, right).
In this work we quote for the errors on the fit parameters the 68% posterior probability percentiles. When the sum, difference or ratio of parameters is given, the error bars include the covariances between parameters.
 |
Fig. A.2 Midpoint between components, φmid = 0.5(φc1 + φc2) versus ν-2 for one LBA B-mode observation, which was folded with some trial DM value. The midpoint closely follows ~ ν-2 down to 25 MHz and that allows one to determine the correction to the trial DM. The extra lag at the lowest frequency of 24.5 MHz can be explained by scattering delay. |
Appendix B: Dispersion measure
In the LBA B-mode the midpoint between the components, φmid = (φc1 + φc2)/2, is delayed with frequency in agreement with the dispersion law: 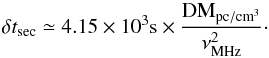 (B.1)In other words, increasing the DM used for folding the data by δDM shifts the midpoint between profile components by δφmid(ν) = (4.15 × 103/P) × δDMν-2. Such behaviour of the midpoint does not hold true for all pulsars (Hassall et al. 2012), but in our case it is fortunate because it allows us to separate interstellar medium (ISM) travel delay from the intrinsic profile evolution.
(B.1)In other words, increasing the DM used for folding the data by δDM shifts the midpoint between profile components by δφmid(ν) = (4.15 × 103/P) × δDMν-2. Such behaviour of the midpoint does not hold true for all pulsars (Hassall et al. 2012), but in our case it is fortunate because it allows us to separate interstellar medium (ISM) travel delay from the intrinsic profile evolution.
This dependence held true for all LBA B-mode sessions at frequencies down to 30 MHz. However, at frequencies of 24−28 MHz the midpoint was lagging the ν-2 fit by 1−2 ms (see Fig. A.2 and leftmost of Fig. 5). One of the plausible explanations for this lag is scattering of the radio waves on the inhomogeneities in the ISM. As the result of scattering (in its simplest form), the observer records a pulsar average profile convolved with a one-sided exponential, exp(−dt/τscatt). Scattering time strongly depends on observing frequency (τscatt ~ ν-4.4). In our data we did not notice any prominent asymmetry in the average profile shape, which indicates that even at the lowest frequencies τscatt is much smaller than the profile width. However, scattering would shift the peaks of the observed profile by an amount which is roughly (order of magnitude) comparable to the value of τscatt at that frequency. At the lowest frequencies the components are well separated, so scattering would shift the peaks of the both components by the same amount. The lowest frequency in Fig. A.2 is 24.5 MHz. If we take τscatt(24.5 MHz) = 1 ms, then scattering time at the centre of two next subbands, 28.4 and 32.3 MHz will be 0.5 and 0.3 ms, within the measurement error.
The few-minute intensity variations of the pulsar signal during the modes (see Fig. 1) can be well explained by diffractive scintillation if we adopt a scattering time of 1 ms at 24 MHz. Assuming the turbulence follows a Kolmogorov spectrum and taking the values for the distance to the pulsar and its transverse velocity from the ATNF catalogue v. 1.4811, the time scale for diffractive scintillation at the centre of the LBA band (50 MHz) is Δtdiff ~ 4 min.
We were unable to find published measurements of scattering time for B0943. The existing empirical recipes for scattering time give excessively large values: 26 ms for the empirical relationship between scattering time and DM from Bhat et al. (2004) and 280 ms from the NE2001 model of Cordes & Lazio (2002). Even τscatt = 26 ms is already comparable to the width of the average profile itself and would lead to evident distortions of the profile shape, which contradicts our observations. However, both of the empirical models are known to predict scattering time within one order-of-magnitude (Bhat et al. 2004; Cordes & Lazio 2002). Also, NE2001 gives the scattering time at 1 GHz and scaling it to our low frequencies becomes quite sensitive to the departure of turbulence from Kolmogorov frequency dependence. Thus we can safely conclude that our estimates of scattering time τscatt(25 MHz) ≈ 1 ms, although smaller than predicted by empirical models, do not obviously contradict them.
For all LBA observations we folded the data with the DM measured from the LBA B-mode midpoint, as described above, assuming that DM does not change in Q-mode (see Table 1 for DM values for each observing session). For the HBA observation, we used the DM from an LBA observation 2 days before. We also looked for changes in DM within a single observation. For all observing sessions we did not find any deviations in DM(t) down to an error of DM(t) measurement, 3 × 10-4 pc/cm3.
All Tables
All Figures
 |
Fig. 1 One-minute subintegrations versus rotational phase for five observing sessions. The top four panels show LBA (25−80 MHz) observations; the bottom one used the HBAs (110−190 MHz). Observation IDs are included on the right of each subplot. Mode transitions are marked with white ticks. Here and throughout the paper the three central LBA observations are aligned at the transition from Q-to-B, with the goal to facilitate visual comparison of time-dependent emission parameters. The B-mode of the observation L77924 was aligned relative to the others according to the ratio of component peak heights (see Fig. 6). The HBA observation was aligned by the Q-to-B transition in observation L169237. On the Y-axis, the pulsar’s zero spin phase was taken to match the midpoint between components at the start of the B-mode of that observation or at the beginning of the session if no Q-to-B transition was recorded. For L78450, the data from 60 to 80 minutes was cut out because of radio frequency interference (RFI). |
| In the text | |
 |
Fig. 2 Timing residuals from one full LBA observing session (L102418). TOAs from both Q and B modes are shown. The transition between Q and B mode happens in the middle of the observation. |
| In the text | |
 |
Fig. 3 A toy model of the average profile from two cone-like emission regions, centred on the magnetic axis. For the smaller cone, the LOS does not cut through the inner side of the cone. Gray profiles correspond to a uniformly illuminated cone (not shown); black profiles result from the cones with smooth variation of intensity with magnetic azimuth. The dotted line shows the merging component fit model. Vertical dashed lines mark the peaks of the uniformly illuminated cone profiles. On the upper subplot, note the slight change in apparent position of the leading component for the varying radial intensity case. |
| In the text | |
 |
Fig. 4 Frequency evolution of the average profile in B and Q-mode from observations L102418 in LBA and L78450 in HBA. The dashed line (green in the online version) shows the fit from the OC model (overlapping Gaussians) and the gray line (red in online version) is the MC model (merging Gaussians). For the LBA data within each model, both B and Q-mode were fit with two independent Gaussian components. For the HBA data, the separation between components, their width and ratio of the peaks were extrapolated from the frequency dependence within the LBA band and only the midpoint between components and S/N of the leading component were fit. LBA and HBA observations are aligned with respect to the midpoint between components in the OC model. |
| In the text | |
 |
Fig. 5 Frequency evolution of the fitted parameters for OC (lighter circles) and MC (darker circles) models for all LBA sessions. The signal was integrated in time within each session. Top row: B-mode. For most frequencies here the MC and OC measurements coincide within the point markers. Bottom row: Q-mode. Left: the midpoint between components φmid(ν). Phase 0 corresponds to frequency-averaged φmid for the OC model for each session. Middle: the separation between components φsep, fit with a power-law. Right: the FWHM of the components. Black and white markers indicate the FWHM corrected for intra-channel dispersive smearing (see text for details). |
| In the text | |
 |
Fig. 6 Ratio of component amplitudes versus frequency and time for all observing sessions. In order to be able to plot both modes on the same scale, we give Ic2/Ic1 for B-mode and the inverse quantity, Ic1/Ic2 for the Q-mode. For the B-mode, Ic2/Ic1 changes with time and this evolution is similar for every mode instance. This makes it possible to estimate the time since the start of the B-mode for L77924 (top row), although we did not directly record the transition in this observation. The vertical black lines mark the transitions between the modes. |
| In the text | |
 |
Fig. 7 Top: midpoint between profile components versus time for all LBA observing sessions. Bottom, from left to right: two average profiles of the Q-mode (at the start of observations and just before the mode transition) and the B-mode (right after mode transition and at the end of the observation). This is observing session L102418 and the profiles from Q-mode correspond to the first and third points on the upper plot. For B-mode, the profiles are from the first and last point of B-mode at the same subplot of the upper plot. The timing residuals from the same observations are plotted in Fig. 2. Noticeably, in addition to changes in relative intensity of the components and their width, the profile in B-mode shifts as a whole towards later spin phase. |
| In the text | |
 |
Fig. 8 Left: a toy model of the pulsar magnetosphere. The pulsar’s spin axis is vertical and the magnetic axis is inclined by the angle α. An example dipolar field line is shown by the thick black line. The position of the LOS vector (red in the online version) stays fixed in space while the pulsar rotates around its spin axis. The plot shows the moment when spin, magnetic and LOS vectors are lying in the same plane (the fiducial plane). At this moment the angle between observer and magnetic axis is β. Usually β is measured clockwise from the magnetic axis, so for the vectors here the value of β is negative. Here we assume that emission comes from a cone at fixed height above the pulsar surface (with respect to the magnetic axis). The opening angle of the cone is marked with a thick dotted gray line. All angles in this plot are identical to the ones in Lorimer & Kramer (2005, Fig. 3.4a). However, in order to make the relationship between the angles more clear, in their figure β and ρ are plotted as originating from the centre of the star. Such transformation does not affect Eq. (6), since w (φsep in our plot) stays the same for both cases. Right: relationship between the opening angle of the emission cone ρ and coordinates of the emitting point (r,θ). |
| In the text | |
 |
Fig. 9 Width of the average profile in the B-mode between two half-maximum points, w ≡ φsep(ν) + FWHM(ν). The cyan diamonds are the measurements of profile width from Deshpande & Rankin (2001). The green and red circles are from our data (both LBA and HBA), fitted with the OC and MC models, respectively. At frequencies below 40 MHz the profile width is somewhat affected by intra-channel dispersive smearing. The most simple model is shown by the black line: it assumes φsep from the LBA fit and the FWHM derived from the LBA data above 40 MHz. |
| In the text | |
 |
Fig. 10 Emission heights (radial distance from the centre of the star) for a cone originating at the last open field line (magnetic latitude θp). For any other starting magnetic latitude θ0, r(θ0) ≈ r(θp) × (θp/θ0)2. The emission heights at frequencies above the LBA band were extrapolated from the parameters derived from the LBA data. |
| In the text | |
 |
Fig. A.1 Left: an example high S/N average profile (B-mode, 2 hours of integration, 54−62 MHz), together with fit and residuals. The residuals show a small, but statistically significant discrepancy between the data and models. Right: two fits of HBA B-mode data. The upper subplot shows the LBA-like fit, with component positions, intensities and width being a priori unconstrained. On the lower subplot the FWHM, ratio of component peaks and their separation are extrapolated from the frequency dependence of corresponding LBA values. Only the midpoint, together with the S/N of the leading component, are fit. Neither of the fits and/or models describe the data perfectly and the fitted values from the unconstrained fit do not agree with fitted values extrapolated from LBA. |
| In the text | |
 |
Fig. A.2 Midpoint between components, φmid = 0.5(φc1 + φc2) versus ν-2 for one LBA B-mode observation, which was folded with some trial DM value. The midpoint closely follows ~ ν-2 down to 25 MHz and that allows one to determine the correction to the trial DM. The extra lag at the lowest frequency of 24.5 MHz can be explained by scattering delay. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


