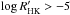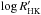| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 18 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201323086 | |
| Published online | 16 September 2014 | |
Variability of Sun-like stars: reproducing observed photometric trends⋆
1
Physikalisch-Meteorologishes Observatorium Davos,
World Radiation centre,
7260
Davos Dorf,
Switzerland
e-mail:
alexander.shapiro@pmodwrc.ch
2
Max-Planck-Institut fur Sonnensystemforschung,
37077
Goettingen,
Germany
3
School of Space Research, Kyung Hee University,
Yongin, 446-701
Gyeonggi,
Korea
4
Blackett Laboratory, Imperial College, London
SW7 2AZ,
UK
5
Hochschule fur Angewandte Wissenschaften, 8401
Winterthur, Zurich,
Switzerland
6
Institute for Atmospheric and Climate science, ETH, 8092
Zurich,
Switzerland
Received:
19
November
2013
Accepted:
29
May
2014
Context. The Sun and stars with low magnetic activity levels become photometrically brighter when their activity increases. Magnetically more active stars display the opposite behavior and become fainter when their activity increases.
Aims. We reproduce the observed photometric trends in stellar variations with a model thattreats stars as hypothetical suns with coverage by magnetic features different from that of the Sun.
Methods. The model attributes the variability of stellar spectra to the imbalance between the contributions from different components of the solar atmosphere, such as dark starspots and bright faculae. A stellar spectrum is calculated from spectra of the individual components by weighting them with corresponding disk-area coverages. The latter are obtained by extrapolating the solar dependences of spot and facular disk-area coverages on chromospheric activity to stars with different levels of mean chromospheric activity.
Results. We find that the contribution by starspots to the variability increases faster with chromospheric activity than the facular contribution. This causes the transition from faculae-dominated variability and direct activity-brightness correlation to spot-dominated variability and inverse activity-brightness correlation with increasing chromospheric activity level. We show that the regime of the variability also depends on the angle between the stellar rotation axis and the line-of-sight and on the latitudinal distribution of active regions on the stellar surface. Our model can be used as a tool for extrapolating the observed photometric variability of the Sun to Sun-like stars at different activity levels, which makes a direct comparison between solar and stellar irradiance data possible.
Key words: Sun: activity / stars: activity / stars: solar-type / stars: variables: general / solar-terrestrial relations / Sun: atmosphere
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The activity cycles in lower main-sequence stars were diskovered at the Mount Wilson Observatory by recording the emission in the cores of H and K lines of Ca II (Wilson 1978). The time-variable part of this emission mainly forms in the bright chromospheric areas that are heated by the magnetic field, and therefore is usually linked with stellar magnetic activity, which is also often referred to as chromospheric activity (see e.g. Baliunas et al. 1995; Hall 2008). The Mount Wilson program revealed that 60% of the lower main-sequence stars exhibit periodic variations in activity that is reminiscent of the solar 11 year cycle, 25% show fluctuations of activity without a clear periodicity (these stars are generally young and magnetically active), and 15% are the activity-flat stars whose activity is constant with time (Baliunas et al. 1998). This distribution was confirmed with the complementary synoptic Solar-Stellar Spectrograph program at the Lowell Observatory, which was more focused on nearly Sun-like stars (defined by Lockwood et al. 2007, as stars on or near the main sequence that have a color index 0.42 ≤ (B − V) ≤ 1.4, Hall et al. 2007b; Hall 2008).
Stellar photometric variations have been more difficult to detect, which, in fact, is also true in the case of the Sun. The solar S-index (which is a measure of the Ca II H and K emission) varies by more than 10% over the 11 year cycle (Radick et al. 1998), while the corresponding variability of the total solar irradiance (TSI, which is the spectrally integrated solar radiation at one Astronomical Unit from the Sun) is only about 0.1% (Fröhlich 2006). The first synoptic observations in the Strömgren filters b and v (centered at 467 and 411 nm) of dwarf stars close to the solar spectral type were unable to unambiguously confirm their variability (Jerzykiewicz & Serkowski 1966).
A considerable improvement in the precision of ground-based stellar photometry made it possible to establish the variability of the young main-sequence stars in the Hyades (Radick et al. 1995). Their photometric variations in the Strömgren b and y filters (centered at 467 and 547 nm) appeared to be in antiphase with variations of chromospheric activity (see also Lockwood et al. 2007).
A significant milestone was reached with the start of the synoptic observations of Sun-like stars at the Lowell observatory (Lockwood et al. 1992). Lockwood et al. (1997) selected 41 program stars bracketing the Sun in temperature and mean chromospheric activity (34 of these stars were also included in the Mount Wilson survey) and started the regular photometric monitoring of them in the Strömgren filters b and y. Most of the stars in the program were deemed variable on both the stellar rotation and the cycle timescales (Lockwood et al. 1997, 2007; Radick et al. 1998). While the solar 11 year variability in the Strömgren b and y filters is estimated to be around 0.0002 mag (Shapiro et al. 2013a), the variability of several stars was found to exceed 0.01 mag. Throughout this paper we calculate the variability in terms of root mean squares (rms), which is more appropriate for the analysis of the very broad variety of stellar light curves than the amplitude (Radick et al. 1998).
One of the most robust patterns of stellar variability established by the Lowell program
was a conspicuous division between less active (and consequently older, see e.g., Soderblom et al. 1991) and more active (younger) stars.
The former usually demonstrate a direct correlation between brightness and activity on the
activity-cycle timescale (an increase in activity is accompanied by an increase in the
photometric brightness). Conversely, the latter show an inverse correlation between
brightness and activity, meaning that these two quantities vary in antiphase. The threshold
between these two regimes occurs around an average chromospheric activity of
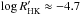 (see Radick et al. 1998, for a definition of
(see Radick et al. 1998, for a definition of
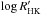 ), which
roughly corresponds to an age of 2 Gyr (Hall 2008).
We note that the mean level of solar chromospheric activity is
), which
roughly corresponds to an age of 2 Gyr (Hall 2008).
We note that the mean level of solar chromospheric activity is
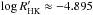 (Lockwood et al. 2007) and the Sun’s age is estimated to be around 4.5–5
Gyr (see e.g. Dziembowski et al. 1999, and references
therein). Thus, according to this classification, the Sun belongs to the group of older
stars with direct activity-brightness correlation.
(Lockwood et al. 2007) and the Sun’s age is estimated to be around 4.5–5
Gyr (see e.g. Dziembowski et al. 1999, and references
therein). Thus, according to this classification, the Sun belongs to the group of older
stars with direct activity-brightness correlation.
This result was later confirmed by Hall et al.
(2009) based on 14 years of combined photometric and Ca II measurements of 28
Sun-like stars taken with Automatic Photometric Telescopes at Fairborn Observatory and the
Solar-Stellar Spectrograph at Lowell Observatory. The Hall
et al. (2009) sample included all the brightest solar analogs with low activity,
seven of its stars were also members of the Lockwood et al.
(2007) sample. Hall et al. (2009) considered
the activity-brightness correlation in four-year moving boxcars and found that HD 140538
(ψ Ser with a
mean chromospheric activity of 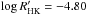 ) lies exactly at the threshold
between the two variability regimes and exhibits both direct and inverse activity-brightness
correlations on timescales of four years. They also found that in addition to the
chromospheric activity, there must be other factors that affect the variabiltiy regime. For
example, HD 82885 (
) lies exactly at the threshold
between the two variability regimes and exhibits both direct and inverse activity-brightness
correlations on timescales of four years. They also found that in addition to the
chromospheric activity, there must be other factors that affect the variabiltiy regime. For
example, HD 82885 (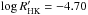 ) showed the most robust
inverse activity-brightness correlation among the entire Hall et al. (2009) sample, which is just slightly more active than HD 140538. Up
to now, there has been no good model to explain these observations.
) showed the most robust
inverse activity-brightness correlation among the entire Hall et al. (2009) sample, which is just slightly more active than HD 140538. Up
to now, there has been no good model to explain these observations.
The Lowell and Fairborn programs have also shown that stars with higher chromospheric
activity have, in general, a stronger photometric variability. Lockwood et al. (2007) and Hall et al.
(2009) presented empirical linear dependences of variability (expressed via
log (rms(b +
y)/2)) on activity (as traced by
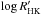 ). These
regressions have the same slopes, but the regression reported by Hall et al. (2009) is shifted by about 0.1 dex down in variability
relative to that found by Lockwood et al. (2007).
). These
regressions have the same slopes, but the regression reported by Hall et al. (2009) is shifted by about 0.1 dex down in variability
relative to that found by Lockwood et al. (2007).
One of the crucial questions in studies of the solar-stellar connection is understanding whether solar variability obeys the empirical patterns outlined above. Currently, there is no clear answer to this question. While the regime of the TSI variability over the 11 year cycle is well established – it varies in phase with solar activity (see, e.g., Fröhlich 2006; Ball et al. 2012; Solanki et al. 2013, and references therein) – the solar variability regime in the visible part of the spectrum is still under debate. The Sun is located so close to the threshold between direct and inverse correlations of visible irradiance (e.g., as measured in the Strömgren b and y filters) and activity, that there is evidence for both the direct (e.g., Lean et al. 2005; Krivova & Solanki 2008; Krivova et al. 2010; Ball et al. 2011) and inverse (Harder et al. 2009; Preminger et al. 2011) correlations. Lockwood et al. (2007) showed that while the solar 11 year cycle in chromospheric activity is more vigorous than the solar analogs, its photometric variability is significantly weaker than indicated by the stellar data (see also Shapiro et al. 2013a, and references therein). At the same time, Hall et al. (2007a, 2009) showed that both chromospheric and photometric variabilities of 18 Scorpii, which is believed to be the closest bright solar analog (Soubiran & Triaud 2004; Petit et al. 2008), are very similar to the solar values. Thus, even if the solar activity cycle is anomalous compared with the majority of stars (as proposed, for example, by Böhm-Vitense 2007), there are stars that exhibit solar-like chromospheric and photometric variabilities.
We note that the comparison of stellar and solar variabilities is not straightforward. The Sun-like stars have a broad range of chromospheric activities that bracket the solar value. The more rapidly rotating stars may also have different latitudinal distributions of active regions on their surfaces (Schüssler & Solanki 1992; Granzer 2002; Berdyugina 2005) and, unlike the Sun, which is observed from its near-equatorial plane, can be observed from arbitrary directions (Schatten 1993; Knaack et al. 2001; Vieira et al. 2012). All these factors affect the apparent variability of Sun-like stars and hinder the direct comparison of solar and stellar photometric and chromospheric data series.
In this paper we present a model that allows us to understand how the solar photometric variability would manifest itself if the Sun had a different level of chromospheric activity. It also allows us to study the dependence of the photometric and chromospheric variability on the angle between the stellar rotation axis and the line of sight, as well as on the latitudinal distribution of active regions on the surface. It thus provides a tool for comparing the Sun with solar analogs, which may help to better understand the physical mechanisms of solar and stellar variability.
Our model is based on a simplified version of the SATIRE (Spectral And Total Irradiance Reconstruction, see Fligge et al. 2000; Krivova et al. 2003) model of solar irradiance variability expanded from the Sun to stars with different activity levels (in particular, to more active stars). It allows us to understand whether the observed patterns of stellar variability are compatible with the solar paradigm and can be explained by a simple extrapolation from the Sun. Extrapolating from solar to stellar activity levels to explain the first observations of Lockwood et al. (1992) was proposed by Foukal (1994), although at a more qulitative level than we attempt in this paper.
In Sect. 2 we give a brief overview of our understanding of solar irradiance variability. In Sect. 3 we present empirical dependences of the solar spot and facular disk-area coverages on chromospheric activity and the datasets used to define them. In Sects. 4 and 5 we describe our model of stellar variability, based on the extrapolation of the empirical dependences introduced in Sect. 3. In Sect. 6 we employ this model to explain the observed patterns of stellar variability. Finally, we summarize our main results in Sect. 7.
2. Solar irradiance variability
It has been known since antiquity, when first naked-eye observations of sunspots were reported (see discussion in Usoskin 2008), that the solar surface is inhomogeneous in brightness. The cause of this inhomogeneity is the magnetic field on the solar surface, which gives rise to sunspots and facuale, convection (granulation), and oscillations (p-modes). Whereas convection and oscillations are the dominant contributors to solar irradiance variability on timescales shorter than a day (Seleznyov et al. 2011), the surface magnetic field is currently believed to be the main source of the solar irradiance variability over timescales ranging from days to decades and centuries (Domingo et al. 2009; Ermolli et al. 2013; Solanki et al. 2013). Modern models (e.g., Lean et al. 2005; Krivova & Solanki 2008; Shapiro et al. 2011; Fontenla et al. 2011) attribute the variability of the solar irradiance to the imbalance between the contributions from dark (e.g., sunspots or pores) and bright (e.g., faculae or network) magnetic features in the solar atmosphere. The rotation of the Sun causes the irradiance modulation with a 27 day period, while changes in the overall magnetic activity (and consequently in the surface-area coverage of active features) lead to the 11 year activity cycle and long-term changes in solar irradiance.
The variability of the solar irradiance affects the terrestrial climate (e.g., Haigh 2007; Gray et al. 2010; Ermolli et al. 2013) and therefore has been under close scrutiny since the beginning of regular space-borne measurements. The TSI has been measured almost continuously since the launch of the NIMBUS 7 mission in 1978 (Hoyt et al. 1992). Its variability on the 27 day and 11 year time scales is relatively well constrained (Fröhlich 2006; Ball et al. 2012; Solanki et al. 2013).
Measurements of the spectral solar irradiance (SSI) are not continuous, and the SSI variability is significantly less constrained than the TSI variability. Most of the available datasets yield similar amplitudes and spectral profiles of the SSI variability on the solar rotational timescale (Ball et al. 2011; Unruh et al. 2012; Lean & DeLand 2012; Ermolli et al. 2013). On longer timescales the accumulated uncertainty in the instrumental degradation corrections becomes larger and renders the interpretation of the SSI measurements very difficult. Thus analysing the 11 year activity cycle variability continues to produce surprises (Harder et al. 2009; Woods 2012; Wehrli et al. 2013), and the magnitude of the 11 year SSI variability is still uncertain (Deland & Cebula 2012; Ermolli et al. 2013).
The substantial disagreement between existing SSI datasets leads to different atmospheric responses when they are used in climate models (Oberländer et al. 2012; Thuillier et al. 2013; Shapiro et al. 2013b; Ermolli et al. 2013) and hinder understanding of the Sun-Earth connection.
An alternative way to improve and deepen our understanding of solar variability on all time scales is to test and validate the available SSI models and measurements against observations of Sun-like stars. This approach is starting to attract attention and has already been employed in the literature to constrain solar variability (Preminger et al. 2011; Judge et al. 2012; Shapiro et al. 2013a). The model presented below provides a quantitative basis for this comparison.
3. Disk-area coverage by active regions and chromospheric activity
During periods of high activity, a noticeable part of the solar disk is covered by faculae and spots. At the same time, during periods of low activity, the Sun can be completely spotless. For example, there were 265 spotless days in 2008 according to the Solar Influences Data Analysis center1. In this section we establish the connection between the fraction of the solar disk covered by active regions and the solar activity (characterized by the Ca II H and K emission, a widely used proxy in stellar activity research).
For this, we employed disk-area coverages from the SATIRE-S model (where “S” stands for the satellite era, see Krivova et al. 2011). SATIRE-S distinguishes three active components (together often referred to as active regions) representing spot umbra, spot penumbra, and faculae. The part of the solar disk that is not covered by these components is attributed to the quiet Sun. The disk-area coverages are calculated from the full-disk continuum images and magnetograms obtained by the 512-channel diode array and spectromagnetograph at the National Solar Observatory Kitt Peak Vacuum Tower (KP/512 and KP/SPM) and by the Michelson Doppler Imager onboard the Solar and Heliospheric Observatory (SOHO/MDI). The detailed description of the datasets and the homogenizing procedure are presented in Ball et al. (2012). To take into account that the small dark features, such as pores, are often not identifiable at the KP/512 continuum images, we followed Wenzler et al. (2006) and corrected the KP/512 spot coverages by multiplying them by the factor 1.127. Umbra and penumbra cannot be distinguished with the KP/512 data either, so that for all three instruments we obtained their sum (i.e., spot disk-area coverage) instead and assume a fixed umbra-to-penumbra area ratio 1:4 (Wenzler et al. 2006; Ball et al. 2012) for the rest of the paper.
The spot and facular disk-area coverages for the Sun are plotted in Fig. 1. They both show a clear 11 year activity modulation. While the annual spot disk-area coverage is close to zero during solar minimum periods, the annual facular disk-area coverage remains noticeably above the zero level even during solar minima.
 |
Fig. 1 Disk-area coverages by sunspots (upper panel) and solar faculae (middle panel) as well as the S-index (lower panel). The daily disk-area coverages are determined from the KP/512 (black dots), KP/SPM (red dots), and SOHO/MDI (blue dots) full-disk continuum images and magnetograms. The daily S-index (black dots in the lower panel) is calculated from the Sac Peak Ca II data. Magenta curves are the annually averaged data. |
The disk-integrated Ca II S-index of solar activity is proportional to the ratio between the summed flux in the Ca II H and K cores and the summed flux in two nearby continuum bands (see Radick et al. 1998, for a detailed discussion) and is often used as a proxy for solar and stellar chromospheric activity. However, the techniques employed for measurements of the solar and stellar Ca II indices are different. Additionally, there are multiple datasets of the solar Ca II index. Therefore various conversion factors are usually employed to connect different data. We used the daily Sac Peak K-index KSP (Keil et al. 1998), which can be transformed into the monthly Kitt Peak K-index KSP with the relationship KKP = − 0.01 + 1.1KSP (White et al. 1998). The Kitt Peak K-index can, in turn, be transformed into the S-index: S = 1.53KKP + 0.04 (White et al. 1992; Radick et al. 1998). The resulting solar S-index is plotted in the lower panel of Fig. 1.
To establish the dependence of the disk-area coverage by active regions on the S-index we considered all days for which simultaneous measurements of the S-index and disk-area coverages by spots and faculae are available. We sorted these days according to the S-index and split the resulting monotonous series of the S-index into bins containing 58 days. Then we calculated the mean value of the S-index and disk-area coverages for every bin.
Figure 2 illustrates the relationship between the
binned disk-area coverage and the S-index. While the facular disk-area
coverage increases linearly with the S-index, the spots instead display
rather a quadratic relationship (see also Foukal
1998; Solanki & Unruh 2013). This
means that the ratio between spot and facular disk-area coverages increases with activity.
By applying a least-squares fit and prescribing the value of the error of the mean disk-area
coverage to the standard deviation, we found the following dependence for the sunspot
disk-area coverage AS: 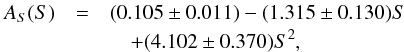 (1)and
for facular disk-area coverage AF:
(1)and
for facular disk-area coverage AF: 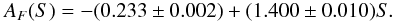 (2)Here
the errors correspond to 1σ uncertainty. Note that all terms are significant at
the 9σ level.
Conversely, if instead of the linear dependence in Eq. (2) we use a quadratic relationship, the quadratic term is insignificant
at the 2σ
level.
(2)Here
the errors correspond to 1σ uncertainty. Note that all terms are significant at
the 9σ level.
Conversely, if instead of the linear dependence in Eq. (2) we use a quadratic relationship, the quadratic term is insignificant
at the 2σ
level.
 |
Fig. 2 Dependence of the solar spot (upper panel) and facular (lower panel) disk-area coverages on the S-index of chromospheric activity. The crosses correspond to the binned values, the thick curves are the least-squares fit dependences (quadratic for spot disk-area coverages, and linear for facular disk-area coverages). |
We note that the S-index and the disk-area coverages are strongly variable on the 27 day solar rotation timescale. If instead of the binned values we use time averages (e.g., annual values), all information about the variability on the solar rotation timescale would be lost, and additionally, the uncertainty of the mean disk-area coverages would be larger. This would hinder our analysis.
The lowest annual value of the S-index based on the Sac Peak Ca II data over the last three solar activity cycles was reached in 1996 and equals 0.169. According to Eqs. (1), (2), this results in AS ≈ 0.003% and AF ≈ 0.36% at that time. The highest annual value of 0.188 was reached in 1991, which corresponds to AS ≈ 0.28% and AF ≈ 3%.
4. Model: calculating the photometric brightness and chromospheric activity
In this section we describe the model that allows us to establish the link between the stellar chromospheric activity (as traced by the S-index) and the photometric brightness and to explain the observed patterns of stellar variability.
Our model is conceptually an extrapolation of a simplified version of the SATIRE model for solar irradiance variability to stars with different levels of chromospheric activity and, consequently, different coverages by active regions. Following the SATIRE approach, we decomposed the stellar atmosphere into the four components: quiet regions, faculae, spot umbra, and spot penumbra. We also employed the SATIRE spectra of these components (see Unruh et al. 1999, for the detailed description), which are known to conform with the disk-area coverages described in Sect. 3 (see, e.g., Ball et al. 2011). This ensures the proper representation of the solar variability by our model (see also Solanki & Unruh 2013). We note that when applied to the Sun, our model leads to slightly different results than the model presented in Knaack et al. (2001), who studied the dependence of the spectral solar irradiance and the S-index on the angle between the direction to the observer and stellar rotational axis (hereafter stellar inclination). The reason for this is that Knaack et al. (2001) used a slightly different spot model atmosphere and employed a simplified approach to calculate the dependence of the S-index on inclination.
The main goal of our approach is to extrapolate the dependences established in Sect. 3 (Eqs. (1)–(2)) to higher activity levels and to use them to calculate stellar spot and facular disk-area coverages as functions of the S-index. This allows simulations of a magnetically active Sun by filling its surface with an increasing fraction of sunspots and faculae. By assuming a fixed umbra-to-penumbra area ratio (see Sect. 3), the spot disk-area coverage can be decomposed into umbral and penumbral coverages. The impact of the uncertainties in the extrapolation of disk-area coverages on our results is discussed in Appendix A.
We here focus on the variability on timescales of stellar activity cycles and only use the seasonally averaged stellar data. Thus we can assume that active regions are uniformly distributed over the activity belts whose positions on the stellar surface do not change with time, which is an additional simplification we made because of the unknown shape of the butterfly diagram in stars. This allows us to calculate the change of stellar photometric brightness due to active regions, using the full disk-area coverages given by Eqs. (1)–(2) and assuming that the contrasts between the active and quiet regions are the same as for the Sun. Our approach thus treats stars as hypothetical suns whose coverage by active regions may or may not differ from that of the Sun. The use of solar relationships (Eqs. (1)–(2)) means that we test how well the solar paradigm reproduces the behavior of more active stars. The use of solar model atmospheres implies that an accurate comparison can be carried out only with main-sequence stars of a similar spectral type.
 |
Fig. 3 Upper panels: visible projections of two bands between latitudes ± 5° and ± 30° on the stellar disk for three inclination values. The bands correspond to the solar distribution of spots employed here. The star sign indicates the position of the disk center. Lower panels: the fractional coverage of the stellar disk by spots plotted as functions of the impact parameter r/rstar (which is 0 at the disk centrer and 1 at the limb). The fractional coverage is calculated assuming that the two bands plotted in the upper panels are completely covered by spots. |
In general, the latitudinal distribution of active regions on the stellar disk might be different from that of the Sun. The situation is further complicated by the fact that while the Sun is basically observed from its equatorial plane (the angle between the solar equator and ecliptic is ~ 7.25° and is neglected in all further calculations), stellar inclinations may vary from 0° (the star is observed along the rotational axis) to 90° (the star is observed from its equatorial plane, which is similar to observing the Sun from the ecliptic) and is usually poorly known. This affects both the photometric brightness and the measured chromospheric activity.
Thus the connection between the photometric brightness and the observed S-index is additionally affected by the latitudinal distribution of active regions and the stellar inclination. In Sects. 4.1 and 4.2 we show how to calculate photometric and chromospheric variability assuming a solar distribution of active regions, that is, spot bands between 5° and 30° and facular bands between 5° and 40° (Knaack et al. 2001). The opposite case of a polar distribution of active regions is considered in Sect. 4.3.
4.1. Photometric brightness
The spectral flux can be decomposed into the quiet and active components: 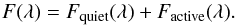 (3)The quiet component
Fquiet(λ) represents
the hypothetical case of a stellar disk without any magnetic features on the surface:
(3)The quiet component
Fquiet(λ) represents
the hypothetical case of a stellar disk without any magnetic features on the surface:
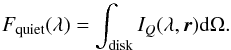 (4)Here the
integration is made over the visible stellar disk, IQ(λ,r)
is the intensity from the quiet stellar component along the direction r, and
dΩ is a differential of the
solid angle around the direction r. SATIRE employs 1D models of the
solar atmosphere so that the emerging intensity IQ(λ,r)
from a given component of the atmosphere only depends on the wavelength and the angle
between the direction to the disk center of the star and r.
(4)Here the
integration is made over the visible stellar disk, IQ(λ,r)
is the intensity from the quiet stellar component along the direction r, and
dΩ is a differential of the
solid angle around the direction r. SATIRE employs 1D models of the
solar atmosphere so that the emerging intensity IQ(λ,r)
from a given component of the atmosphere only depends on the wavelength and the angle
between the direction to the disk center of the star and r.
The emerging intensity is often written as a function of the cosine of the angle between
the direction to the observer and the local stellar radius, μ. Then Eq. (4) can be rewritten as 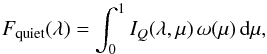 (5)where the
weighting function ω(μ) =
2πμ(rstar/dstar)2
(here rstar is the stellar radius and
dstar is the distance between the star and
the observer) represents the transformation between dΩ and dμ.
(5)where the
weighting function ω(μ) =
2πμ(rstar/dstar)2
(here rstar is the stellar radius and
dstar is the distance between the star and
the observer) represents the transformation between dΩ and dμ.
We note that starting from 1974 (when KP/512 became available, see Sect. 3) the solar irradiance was never equal to
Fquiet(λ) and was
affected by the active component, whose contribution is given by 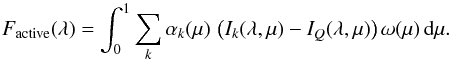 (6)Here
Ik(λ,μ) −
IQ(λ,μ)
is the wavelength- and angle-dependent contrast between the active component
k and quiet
stellar regions. In the ultraviolet and visible spectral ranges it is positive for faculae
(i.e., faculae cause a brightness excess) and negative for umbra and penumbra (i.e., spots
cause a brightness deficit). The functions αk(μ)
give the fractional coverage of the ring around the stellar disk center
with a radius corresponding to μ by the component k (e.g., αk(1) and αk(0) represent the
stellar disk center and limb). Integration over μ gives Ak, the fractional
coverage of the whole visible stellar disk by the component k:
(6)Here
Ik(λ,μ) −
IQ(λ,μ)
is the wavelength- and angle-dependent contrast between the active component
k and quiet
stellar regions. In the ultraviolet and visible spectral ranges it is positive for faculae
(i.e., faculae cause a brightness excess) and negative for umbra and penumbra (i.e., spots
cause a brightness deficit). The functions αk(μ)
give the fractional coverage of the ring around the stellar disk center
with a radius corresponding to μ by the component k (e.g., αk(1) and αk(0) represent the
stellar disk center and limb). Integration over μ gives Ak, the fractional
coverage of the whole visible stellar disk by the component k: 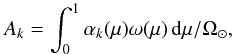 (7)where
(7)where
 is the solid angle
subtended by the star.
is the solid angle
subtended by the star.
While the stellar inclination does not directly enter Eqs. (6), (7), it affects the
area coverages αk(μ),
which depend on the inclination and latitudinal distribution of active regions. This is
illustrated in Fig. 3, which represents area
coverages of spots for three inclinations. Note that for convenience, the area coverages
are plotted in the lower panels as functions of the impact parameter
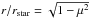 .
For all three cases the disk center is located outside of the visible activity belts, so
that αk = 0 for
r/rstar =
0 (or μ =
1). The value of αS becomes positive
when the corresponding ring starts to intersect the visible activity belts. The sudden
decrease of αS at r/rstar =
0.996 in the lower right panel of Fig. 3 is caused by the spot-free band between 0° and 5°. A similar figure for the
polar distribution of active regions (see Sect. 4.3)
is given in Fig. B.3. The change of the inclination
or latitudinal distribution of active regions might completely reshape the αk(r/rstar)
dependences and consequently the αk(μ)
dependences used in Eqs. (6), (7).
.
For all three cases the disk center is located outside of the visible activity belts, so
that αk = 0 for
r/rstar =
0 (or μ =
1). The value of αS becomes positive
when the corresponding ring starts to intersect the visible activity belts. The sudden
decrease of αS at r/rstar =
0.996 in the lower right panel of Fig. 3 is caused by the spot-free band between 0° and 5°. A similar figure for the
polar distribution of active regions (see Sect. 4.3)
is given in Fig. B.3. The change of the inclination
or latitudinal distribution of active regions might completely reshape the αk(r/rstar)
dependences and consequently the αk(μ)
dependences used in Eqs. (6), (7).
The contribution of a given ring with fixed μ value to Factive depends on the fractional coverages αk(μ), weighting coefficient ω(μ), and center-to-limb variations (CLV) of the intensity that emerges from different atmospheric components. The calculated CLVs of the spectral intensity averaged over the Strömgren (b + y)/2 profile are shown in the upper panel of Fig. 4 for the four atmospheric components employed in SATIRE. The contrast between the quiet regions and faculae increases steeply from the disk center toward the limb. This implies that enhancement of the irradiance caused by the faculae also increases from the disk center toward the limb. At the same time, the relative umbral and penumbral contrasts are barely affected by the CLV.
 |
Fig. 4 Upper panel: center-to-limb variation of the Strömgren (b + y)/2 intensity calculated for the quiet Sun, faculae, penumbra, and umbra models (black, red, magenta, and blue curves). Plotted are the ratios to the quiet-Sun intensity at the disk center. Lower panel: quadratic polynomial parameterization of the intensity center-to-limb variation at the Ca II K line and the nearby continuum (solid and dashed orange curves) according to Skumanich et al. (1984). Both intensities are normalized to unity at the disk center. |
For the solar distribution of active regions, Eqs. (1)–(2) define the disk-area coverages Ak (however, some caution is indicated because the S-index, which enters these equations, corresponds to observations from the equatorial plane and is, thus, different from the S-index measured on a star with another inclination of its rotation axis, see Sect. 4.2). Equation (7) makes it possible to convert Ak to fractional coverages αk(μ), which enter Eq. (6). Hence, the set of Eqs. (1)–(7) allows calculating the photometric brightness as a function of the S-index for an arbitrary stellar inclination.
4.2. Chromospheric activity
The S-index is proportional to the ratio of the flux in the cores of the
Ca II H and K lines to the flux in the nearby continuum. Skumanich et al. (1984) showed that the center-to-limb variation of the Ca II K
emission (which hereafter is used as a representation of the summed emission in the H and
K lines, see Radick et al. 1998) is the same for
the quiet Sun and faculae. This was confirmed by later measurements (see, e.g., Ermolli et al. 2007, 2010). Thus one can write
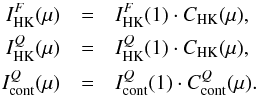 (8)Here
(8)Here
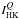 and
and
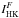 are the Ca II
H and K intensities (hereafter, HK intensity) from the quiet Sun and from faculae,
respectively, and
are the Ca II
H and K intensities (hereafter, HK intensity) from the quiet Sun and from faculae,
respectively, and 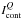 is the
quiet-Sun intensity in the nearby continuum. Functions CHK(μ) and
is the
quiet-Sun intensity in the nearby continuum. Functions CHK(μ) and
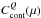 describe the CLV of the HK
and continuum fluxes. The HK flux and its CLV are strongly affected by the effects of
non-local thermodynamical equilibrium (see, e.g., Ermolli
et al. 2010), which are not taken into account in the spectra employed by the
SATIRE model (Unruh et al. 1999). Therefore,
instead of taking the theoretical CLV resulting from SATIRE, we employedquadratic
polynomial parameterizations (as a function of the heliocentric angle cosine
μ) of the
CLV from Skumanich et al. (1984), who employed
several observational datasets to define them. The parameterizations for the Ca II K line
core and the nearby continuum are shown in the lower panel of Fig. 4.
describe the CLV of the HK
and continuum fluxes. The HK flux and its CLV are strongly affected by the effects of
non-local thermodynamical equilibrium (see, e.g., Ermolli
et al. 2010), which are not taken into account in the spectra employed by the
SATIRE model (Unruh et al. 1999). Therefore,
instead of taking the theoretical CLV resulting from SATIRE, we employedquadratic
polynomial parameterizations (as a function of the heliocentric angle cosine
μ) of the
CLV from Skumanich et al. (1984), who employed
several observational datasets to define them. The parameterizations for the Ca II K line
core and the nearby continuum are shown in the lower panel of Fig. 4.
For a given inclination i, the S-index can be written as
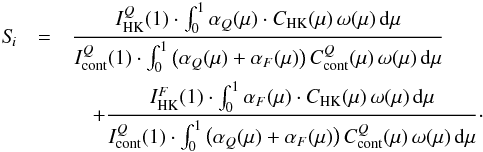 (9)The
first and second terms in Eq. (9) give the
contribution of the quiet stellar regions and faculae. The contrast between the quiet
regions and faculae in the continuum is small (unlike the contrast in the H and K lines,
see Fig. 1 from Skumanich et al. 1984), so that it
is neglected in the denominator of Eq. (9).
Additionally, we assumed for simplicity that both umbral and penumbral regions are
completely dark and simply diluted the continuum and HK fluxes.
(9)The
first and second terms in Eq. (9) give the
contribution of the quiet stellar regions and faculae. The contrast between the quiet
regions and faculae in the continuum is small (unlike the contrast in the H and K lines,
see Fig. 1 from Skumanich et al. 1984), so that it
is neglected in the denominator of Eq. (9).
Additionally, we assumed for simplicity that both umbral and penumbral regions are
completely dark and simply diluted the continuum and HK fluxes.
We note that the dependence of the S-index on inclination and latitudinal distribution of active regions enters Eq. (9) via the area coverages αQ(μ) and αF(μ), exactly in the same way as it enters Eq. (6) for Factive (see discussion in Sect. 4.1 as well as Figs. 3 and B.3). Therefore the measured S-index depends on the inclination, and the same star may have different S-indices if observed from different directions.
Using the fact that αS +
αF +
αQ = 1, Eq. (9) may be rewritten as follows: 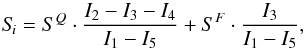 (10)where
(10)where ![\begin{eqnarray} I_1 &&\equiv \int_0^1 C_{\rm cont}^Q (\mu) \, \omega (\mu) \, {\rm{d}} \mu; \quad \quad I_2 \equiv \int_0^1 C_{\rm HK}(\mu) \, \omega (\mu) \, {\rm{d}} \mu \nonumber ; \\[1mm] I_3 &&\equiv \int_0^1 \alpha_F(\mu) \, C_{\rm HK}(\mu) \, \omega (\mu) \, {\rm{d}} \mu \nonumber ; \\[1mm] I_4 &&\equiv \int_0^1 \alpha_S(\mu) \cdot C_{\rm HK}(\mu) \, \omega (\mu) \, {\rm{d}} \mu \nonumber ; \\[1mm] I_5 &&\equiv \int_0^1 \alpha_S(\mu) \cdot C^Q_{\rm cont}(\mu) \, \omega (\mu) \, {\rm{d}} \mu, \label{eq:int} \end{eqnarray}](/articles/aa/full_html/2014/09/aa23086-13/aa23086-13-eq73.png) (11)and
(11)and
 (12)The
integrals I1 and I2 in Eq. (10) depend neither on inclination nor on
activity. Since AF is a linear
function of S90 (which is the S-index
observed from the equatorial plane, see Eq. (2)) and we assumed a fixed latitudinal distribution of active regions, the area
coverage αF(μ)
increases linearly with S90. Hence the integral I3 is a linear
function of S90.
(12)The
integrals I1 and I2 in Eq. (10) depend neither on inclination nor on
activity. Since AF is a linear
function of S90 (which is the S-index
observed from the equatorial plane, see Eq. (2)) and we assumed a fixed latitudinal distribution of active regions, the area
coverage αF(μ)
increases linearly with S90. Hence the integral I3 is a linear
function of S90.
We consider a star with a low level of mean chromospheric activity observed from its
equatorial plane (e.g., the Sun) with a measured S-index equal to
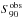 . For low
levels of magnetic activity the integrals I4 and I5 are
negligibly small so that the sunspots do not have any effect on the
S-index (see Knaack et al. 2001)
and Si is a linear function
of
. For low
levels of magnetic activity the integrals I4 and I5 are
negligibly small so that the sunspots do not have any effect on the
S-index (see Knaack et al. 2001)
and Si is a linear function
of 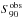 . The
. The
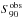 value can
be employed to calculate the disk-area coverages Ak (using Eqs. (1), (2)), which can then be converted into the area coverages αk(μ).
Knowing these, one can calculate the integral I3 (see Eq. (11)) and employ Eq. (10) to calculate
value can
be employed to calculate the disk-area coverages Ak (using Eqs. (1), (2)), which can then be converted into the area coverages αk(μ).
Knowing these, one can calculate the integral I3 (see Eq. (11)) and employ Eq. (10) to calculate
 . If our
approach is self-consistent, the calculated
. If our
approach is self-consistent, the calculated  value
must be equal to the
value
must be equal to the 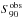 value
employed to drive our calculations. In other words, Eqs. (10)–(12) define the
dependence of the calculated Si-index on disk-area
coverages, while Eq. (2) defines the
inverse dependence of disk-area coverages on the S90-index. For a
star observed from its equatorial plane these dependences must agree with each other. As
discussed above, the right side of Eq. (10) is a linear function of
value
employed to drive our calculations. In other words, Eqs. (10)–(12) define the
dependence of the calculated Si-index on disk-area
coverages, while Eq. (2) defines the
inverse dependence of disk-area coverages on the S90-index. For a
star observed from its equatorial plane these dependences must agree with each other. As
discussed above, the right side of Eq. (10) is a linear function of 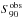 , so that
this equation expresses
, so that
this equation expresses  in terms
of
in terms
of 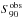 . Therefore,
the condition
. Therefore,
the condition 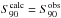 is
fulfilled if the parameters SQ and
SF take on a particular
set of values.
is
fulfilled if the parameters SQ and
SF take on a particular
set of values.
For the solar distribution of active regions this condition is fulfilled if SQ = 0.137 and SF = 0.711. These parameters are the values of the S-index from the quiet regions and the faculae observed at the disk center. The ratio between SQ and SF values agrees well with the Ca II K line profiles plotted in Fig. 1 of Skumanich et al. (1984). This means that the disk-area coverages given by Eqs. (1), (2) conform with the CLV of HK flux employed in our model. The linear dependence between facular disk-area coverage and activity (see Eq. (2)) implies that the SQ and SF parameters do not depend on the activity, meaning that the increase of the activity level affects the disk-area coverages, but not the structures of the individual components.
We note that the solar S-index of chromospheric activity that enters Eqs. (1), (2) is measured from the equatorial plane (hereafter S90). Consequently, these equations cannot be directly applied to calculate the disk-area coverages by active regions from the Si-index measured from an arbitrary inclination i, and the Si-index must first be converted into the the S90-index. Equation (10) provides a simple way to do this.
4.3. Different distributions of active regions
The first results of the Doppler imaging technique (see e.g. Berdyugina 2005, and references therein) already indicated that there are stellar spots at high latitudes, reaching even to the poles for stars with deep convection zones (in complete contrast to the solar case, where the spots are rarely observed above 30° latitude). To explain these high-latitude spots, Schüssler & Solanki (1992) suggested that while the rise of magnetic flux tubes through the convection zone in slowly rotating stars is controlled by the buoyancy force, the Coriolis force starts to be important for rapidly rotating stars. An alternative explanation, based on meridional flow, was later proposed by Schrijver & Title (2001). As a result, active features are distributed in the equatorial belts for the slowly rotating stars (like the Sun) and at higher latitudes for the rapidly rotating stars. The distribution of active features with latitude for the Sun-like stars considered in this paper is generally unknown.
As discussed above, the equations given in Sects. 4.1 and 4.2 are valid for an arbitrary latitudinal distribution of active regions. All geometrical information (i.e., inclination of the star and distribution of active regions) enters these equations via the area coverages αi(μ). The modification of the latitudinal distribution of active regions affects the area coverages, and consequently the contribution of the active regions to the photometric brightness (via the Factive term, see Eqs. (3)and (6)) and the S-index (via the I3 integral, see Eqs. (10)and (11)).
The main sophistication is that the S90-index, which is used to parameterize the spot and facular disk-area coverages in Sect. 3, corresponds to the solar distribution of active regions. The redistribution of the active regions affects S90 even if the disk-area coverages remain unchanged, so Eqs. (1)–(2) are only applicable for the solar distribution of active regions.
To take this into account we first considered a star with a solar distribution of active
regions. For such a star we can employ Eqs. (1), (2) and (7) to calculate the area coverages
αk(μ)
as functions of the parameter 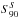 (hereafter,
the index S
represents the solar distribution of active regions) and equations from Sects. 4.1 and 4.2 to
calculate
(hereafter,
the index S
represents the solar distribution of active regions) and equations from Sects. 4.1 and 4.2 to
calculate 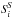 and
and 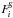 .
Then we rearranged the location of active regions according to the different distribution
and recalculated the area coverages αk(μ),
keeping the part of the stellar surface covered by each component
k (i.e.,
.
Then we rearranged the location of active regions according to the different distribution
and recalculated the area coverages αk(μ),
keeping the part of the stellar surface covered by each component
k (i.e., 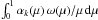 ) unaffected. These new area
coverages allowed us to recalculate the chromospheric activity Si and photometric
brightness Fi for an arbitrary
distribution of active regions.
) unaffected. These new area
coverages allowed us to recalculate the chromospheric activity Si and photometric
brightness Fi for an arbitrary
distribution of active regions.
In addition to the solar case, we also considered the homogeneous distribution of active regions on a stellar surface as well as the polar distribution when spots and faculae are gathered in two polar caps (north and south) with latitude >45°. The range of latitudes for the polar distribution is wider than for the solar distribution because a smaller area is covered by a ring of given latitude width at high latitudes than at low latitudes. Even when the polar caps reach so far down that they offer less surface area, they cover only 34% of the stellar surface compared with the 56% covered by the solar activity belts.
We expect that solar, polar, and homogeneous distributions of active regions encompass the behavior for most types of latitudinal distributions.
 |
Fig. 5 Simulated values of the S-index as they would be measured for inclinations of 90° (red curves), 57° (magenta curves), 0° (blue curves) vs. facular surface coverage for solar, polar, and homogeneous distributions of active regions. The maximum possible facular surface coverage (i.e., when faculae and spots fully cover the activity belts/caps or the entire stellar surface) is about 28%, 19%, and 47% for the adopted solar, polar, and homogeneous distributions. |
4.4. S-index as a proxy of stellar magnetic activity
In Fig. 5 we plot the S-index as a function of facular surface (i.e., hemispheric) coverage for a solar, polar, and homogeneous distributions of active regions and for three inclinations: i = 0, i = 57° (the mean inclination that is often used in the literature to characterize the intermediate case, see, e.g., Schatten 1993; Knaack et al. 2001), and i = 90°. For a homogeneous distribution of active regions, the S-index does not depend on the inclination so that the dependence is the same for different inclinations.
Integrals I4 and I5 are proportional to the spot surface coverage, which is a quadratic function of the facular surface coverage. Therefore the S-index is not a linear function of the facular surface coverage. The effect of spots on the S-index is equivalent to the reduction of the contribution of quiet regions to the continuum and HK emissions. This contribution is more important for the continuum emission because the HK emission is dominantly affected by the faculae. Thus, the spots diminish the continuum flux more strongly than the HK flux and lead to an increase of the S-index.
We note that the facular surface coverage is different from the facular
disk coverage AF. The former is
calculated for the visible part of the stellar surface (which is a hemisphere) and
proportional to 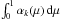 , while the latter is calculated
for the visible stellar disk and proportional to
, while the latter is calculated
for the visible stellar disk and proportional to 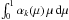 (see
Eq. (7)). All distributions of active
regions considered in this paper are centrally symmetric with respect to the center of the
star (which we deem to be a sphere). Thus the surface coverages of the visible front-side
of the star are equal to the surface coverages of the invisible far-side of the star.
(see
Eq. (7)). All distributions of active
regions considered in this paper are centrally symmetric with respect to the center of the
star (which we deem to be a sphere). Thus the surface coverages of the visible front-side
of the star are equal to the surface coverages of the invisible far-side of the star.
Stars with the same level of facular surface coverage are expected to have the same amount of magnetic flux emerging on the surface, but can have different facular disk coverages AF and measured S-indices (depending on the inclination and latitudinal distribution of active regions). Consequently, if two stars have the same S-indices, it does not necessarily mean that they have the same amount of magnetic flux. Thus, the S-index cannot be considered as an unequivocal proxy for stellar magnetic activity.
 |
Fig. 6 Simulated values of the photometric brightness change δ(b + y)/2 (upper panel) and S-index (lower panel) vs. stellar inclination i. Solid curves correspond to the solar distribution of active regions, dashed to polar distribution, and dotted to homogeneous distribution. The coverage by faculae and spots for all three distributions is chosen so that the S-index observed from the stellar equatorial plane (i = 90°) equals 0.19. |
5. Model: calculating the brightness-activity correlation
The magnetic field at the stellar surface affects the measured S-index and
photometric flux. In this section we apply the model described in Sect. 4 to establish the relationship between the observed
S-index and the alteration of the Strömgren (b + y)/2 flux caused by the magnetic activity. Hereafter the alteration of the
radiative flux is expressed in stellar magnitudes and defined as 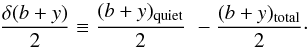 (13)The δ(b + y)/2 value corresponds to the Factive term in
Eq. (3) averaged over the spectral profiles
of Strömgren b and y filters. It is positive for a
brightness enhancement and negative for a brightness deficit.
(13)The δ(b + y)/2 value corresponds to the Factive term in
Eq. (3) averaged over the spectral profiles
of Strömgren b and y filters. It is positive for a
brightness enhancement and negative for a brightness deficit.
We note that not the δ(b + y)/2 value itself can be measured, but rather the change of this value
relative to some reference point (see Sect. 5.3):
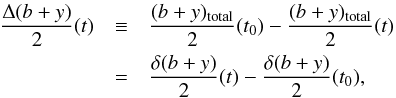 (14)where
t0
corresponds to the time of the reference measurement. The relative change Δ(b + y)/2 is defined such that a positive value corresponds to a flux increase
from t0 to t. In this section we
establish the dependence of δ(b + y)/2 on the S-index.
(14)where
t0
corresponds to the time of the reference measurement. The relative change Δ(b + y)/2 is defined such that a positive value corresponds to a flux increase
from t0 to t. In this section we
establish the dependence of δ(b + y)/2 on the S-index.
5.1. S-index and photometric brightness as functions of inclination
Figure 6 presents the dependences of the photometric brightness and S-index on the stellar inclination for solar, polar, and homogenous distributions of active regions. All three curves correspond to different degrees of coverage by faculae and spots and were chosen under the condition that S90 = 0.19, which is close to the maximum annual value of the solar S-index over three last cycles (0.188).
The dependence of δ(b + y)/2 and of S-index on inclination are oppositely
directed for solar and polar distributions of active regions (while, obviously, neither
δ(b +
y)/2 nor S-index
depend on the inclination for the homogeneous distribution of active regions). A decrease
of the inclination for a star with a solar distribution of active regions leads to their
apparent concentration near the limb (see Fig. 3).
While negative contrasts of spot umbra and penumbra slightly decrease toward the limb, the
positive facular contrast significantly increases (see upper panel of Fig. 4), so that the effect of the CLV tends to increase the
brightness of the star with a solar distribution of active regions when the observer moves
from the equatorial stellar plane to its pole. At the same time, the disk-area coverages
as seen by such an observer decrease toward the polar position because of the projection
effect (see Eq. (7)). For the considered
level of activity (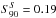 ),
the effect of the CLV in the Strömgren b and y filters outweighs the effect of projection, so
that the brightness of the star increases with decreasing inclination. The emission in the
Ca II K line decreases more slowly toward the limb than the emission in the nearby
continuum (see lower panel of Fig. 4), so that the
CLV effect also tends to amplify the S-index for a star observed along
its rotational axis. However, the projection effect now outweighs the CLV effect, and the
S-index grows slightly with inclination.
),
the effect of the CLV in the Strömgren b and y filters outweighs the effect of projection, so
that the brightness of the star increases with decreasing inclination. The emission in the
Ca II K line decreases more slowly toward the limb than the emission in the nearby
continuum (see lower panel of Fig. 4), so that the
CLV effect also tends to amplify the S-index for a star observed along
its rotational axis. However, the projection effect now outweighs the CLV effect, and the
S-index grows slightly with inclination.
The situation is different for stars with a polar distribution of active regions. For
such stars the projection effect amplifies the contribution of active regions when the
inclination decreases, so that the Si-index grows
significantly with decreasing inclination, reaching higher values at i = 0° than
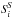 at any i.
This is because at the same total surface coverage by faculae (e.g., solid and dot-dashed
curves in Fig. 6) the polar distribution at
i = 0
corresponds to active regions more strongly concentrated at large μ (see Fig. B.3). The contribution of faculae to the photometric
brightness, however, diminishes with decreasing inclination. Therefore the contribution of
active regions changes from positive when the star is observed from the equatorial plane
to negative when it is observed from the rotational axis.
at any i.
This is because at the same total surface coverage by faculae (e.g., solid and dot-dashed
curves in Fig. 6) the polar distribution at
i = 0
corresponds to active regions more strongly concentrated at large μ (see Fig. B.3). The contribution of faculae to the photometric
brightness, however, diminishes with decreasing inclination. Therefore the contribution of
active regions changes from positive when the star is observed from the equatorial plane
to negative when it is observed from the rotational axis.
5.2. Simulated brightness-activity correlation for the Sun
To simulate the dependence of solar brightness on chromospheric activity over the solar cycle we considered the time series of the annually averaged solar S90-index for the period 1977–2011. A similar averaging was made by Lockwood et al. (2007). The S90 values were calculated from the Ca II Sac Peak data (see Sect. 3). The mean and rms variation values of the annual solar S90-index over this period are 0.177 and 0.006. We used this S90(t) time series to calculate the corresponding disk-area coverages AS(t) and AF(t) (see Sect. 3) and then, employing the technique described in Sect. 4, the δ(b + y)i(t)/2 and Si(t) time series. The self-consistent character of our approach implies that for the inclination i = 90° the S90(t) values calculated with our approach are equal to the observed S90(t) values used to calculate the disk-area coverages and drive the calculations (see Sect. 4.2).
 |
Fig. 7 Simulated values of the photometric brightness change δ(b + y)/2 vs. S-index for the Sun observed from three different directions. Plotted are the annual values as they would be measured from the equatorial plane (red crosses), a 57° inclination (magenta crosses), and from the solar rotational axis (blue crosses). |
Figure 7 shows the simulated dependences of the solar brightness on the S-index as they would be seen from three different inclinations. Independent of the inclination, active regions always increase the annually averaged solar photometric brightness relative to the quiet-Sun condition. The δ(b + y)/2 values are higher than zero even for solar minimum conditions, so that the Sun has not been completely quiet (i.e., free from apparent active regions) for the last three activity cycles. Decreasing the inclination simultaneously amplifies the amplitude of the δ(b + y)/2 variability and diminishes the amplitude of the S-index variability (see Fig. 6), so that it has a strong effect on the slope of the δ(b + y)/2 vs. S-index regression.
As solar activity rises, the sunspot area coverage grows faster than the facular area coverage (see Eqs. (1)–(2)), so that the relative contribution of sunspots to the solar photometric brightness increases with the S-index. This leads to the nonlinear profile of the photometric brightness vs. chromospheric activity and causes its saturation (for i = 90° and 57°) at high activity levels. The contribution of faculae increases with decreasing i so that this effect is most pronounced for the i = 90° case. For i = 0 the facular contribution is so strong that it completely dominates the spot contribution even for the highest solar activity level. As a result, the corresponding dependence of the photometric brightness on activity is almost linear.
 |
Fig. 8 Simulated values of the photometric brightness change δ(b + y)/2 as they would be measured from the equatorial plane (red crosses), at 57° inclination (magenta crosses), and from the stellar rotational axis (blue crosses) vs. S-index. Plotted are values for model stars with the activity level of HD 81809 (mean and rms variation values of S are equal to 0.1713 and 0.0080, left panel), of HD 10476 (0.1896 and 0.0136, middle panel), and of HD 82885 (0.2679 and 0.0186, right panel). The dashed lines correspond to the linear regressions calculated over the whole δ(b + y)/2 and S-index data sets. |
5.3. Spot- and facula-dominated regimes of variability
If the photometric brightness alteration δ(b + y)/2 is positive, the facular contribution to stellar brightness (or more specifically, to Factive, see Eq. (6)) outweighs the spot contribution. Conversely, negative values of δ(b + y)/2 imply that the spot contribution outweighs the facular contribution. Therefore, the sign of δ(b + y)/2 provides a clear indication of the relative role of faculae and spots in altering stellar brightness.
However, the level of irradiance from a star without any magnetic features on the surface ((b + y)quiet/2 in Eq. (13)) is unknown and may even be never reached (as for the Sun, where the calculated δ(b + y)/2 is always positive). Thus stellar observations do not allow one to measure δ(b + y)/2. Only the Δ(b + y)(t)/2 time series, which is different from the δ(b + y)(t)/2 time series by a constant term δ(b + y)(t0)/2 (see Eq. (14)), can be measured. Thus, the absolute values of δ(b + y)/2 are unimportant, so that the curves in Fig. 7 might be arbitrarily shifted up and down. Clearly, only the brightness-activity relationship can be compared with measurements and be used to determine the variability regime.
Consequently, we defined the variability of a star as facula-dominated when an increase of the observed S-index led to an increase of stellar brightness (i.e., the derivative of the photometric brightness with respect to the observed S-index is positive) and as spot-dominated when it led to a decrease of the photometric brightness. This definition follows that introduced by Lockwood et al. (1992). The same star can be observed as spot- or faculae-dominated at different levels of activity. For example, the Sun observed at i = 90° is faculae-dominated at low and intermediate activity, but it can become spot-dominated for a very short time around activity maximum (see Fig. 7).
5.4. Brightness-activity correlation for Sun-like stars
To model the brightness-activity relationships for Sun-like stars we linearly scaled the annual values of the solar S-index for the 1977–2011 period (which covers solar cycles 21–23 and the beginning of cycle 24) to reproduce the measured stellar mean and rms variation values of the S-index on various stars, where the mean and rms variation are taken over the whole period that the star is observed. We note that in reality, stellar cycles need not resemble the solar cycle and thus our approach is only an approximation.
Unlike the solar case, the observed stellar S-index corresponds to an arbitrary inclination i. Therefore, we first assumed that the star has a given inclination i and converted the observed mean and rms variation values of Si into the mean and rms variation values of S90, using the technique described in Sect. 4. Then we constructed the S90(t) time series as described in the above paragraph and used it to calculate δ(b + y)i/2 and Si (see Sect. 4). The self-consistent character of our approach guarantees that the Si values used to feed the model are identical to the values calculated in this final step. This procedure was repeated for a number of i values.
In Fig. 8 we plot the modeled brightness-activity dependences for HD 81809, which has a level of activity slightly lower than the solar value, for HD 10476, which is slightly more active than the Sun, and for HD 82885, which is significantly more active than the Sun. The mean and rms variation values of the observed S-index for these stars have been provided by Lockwood (2013, pers. comm.). The calculations were performed assuming a solar distribution of active regions. We note that unlike Fig. 7, where we considered the hypothetical case of the Sun observed out-of-ecliptic, the amplitude of the S-index (or rather Si-index) variability does not depend on the assumed inclination and always corresponds to the observed amplitude that is used to calculate the S90(t) time series.
The δ(b + y)/2 values of HD 81809 are always positive, independent of the inclination. This is not surprising, given its similar activity level to the Sun. The star is observed as faculae-dominated most of the time. However, for i = 57° and 90° starting from S ≃ 0.18, the dependence of the brightness on activity is saturated so that the further increase in activity has almost no effect on brightness. We note that the lowest value of the observed S-index for HD 81809 (≈ 0.166) is lower than the solar minimum value (≈ 0.169) so that, unlike the solar case, δ(b + y)/2 reaches zero. A relatively robust measure of whether the variability of a star is faculae- or spot-dominated during the period of observations is the slope of the brightness regression on activity calculated by employing the whole δ(b + y)/2 and S-index time series (dashed lines in Fig. 8).
The variability of HD 10476 is faculae-dominated for low values of the observed S-index and spot-dominated for high values at all i. The overall correlation is direct for i = 0°, and inverse for i = 57° and i = 90°. Thus HD 10476 presents a curious case of a star whose variabiltiy regime during the period of observations depends on the inclination. The activity of HD 82885 is so high that the facular contribution is negligibly small, and its variability is always spot-dominated.
 |
Fig. 9 Simulated values of the photometric brightness change δ(b + y)/2 as they would be measured from the equatorial plane (red curve), at 57° inclination (magenta curve), and from the stellar rotational axis (blue curve) vs. S-index. Unlike Fig. 8, the dependences are calculated over a broad range of stellar magnetic activity. The range bars designate the observed ranges of chromospheric activity variations of the Sun, HD 81809, HD 10476, and HD 82885. |
The discussion above was limited to the S-index and photometric time
series of specific stars. The approach presented in Sect. 4 also allows modeling the dependence of the photometric brightness on the
chromospheric activity over a broad range of S values. These dependences are plotted in Fig.
9 for three values of the inclination and assuming
a solar distribution of active regions. The chromospheric activity is characterized via
the 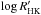 parameter,
which is a function of the S-index and B − V
color (see Radick et al. 1998, for a detailed
discussion). Hereafter, we use the solar value of the color (B − V =
0.65) to convert the S-index into
parameter,
which is a function of the S-index and B − V
color (see Radick et al. 1998, for a detailed
discussion). Hereafter, we use the solar value of the color (B − V =
0.65) to convert the S-index into
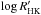 (e.g., the
range bars in Fig. 9 are also calculated assuming
solar B −
V value). This is equivalent to keeping the effective
temperature of the hypothetical sun unchanged while increasing its activity level.
(e.g., the
range bars in Fig. 9 are also calculated assuming
solar B −
V value). This is equivalent to keeping the effective
temperature of the hypothetical sun unchanged while increasing its activity level.
Figure 9 reveals that according to our model, low-activity values correspond to faculae-dominated variability, while high-activity values correspond to spot-dominated variability. For a solar distribution of active regions, the lower the inclination of the star, the stronger the amplification of the facular contribution by the CLV effect. Therefore the threshold activity that corresponds to the transition between the spot- and facuale-dominated regimes is higher for lower inclination values (blue vs. red curves in Fig. 9). Comparing Fig. 8 with Fig. 9 one can see that the individual stellar brightness-activity relationships presented in the three panels of Fig. 8 are different parts of the general dependence.
Up to this point we have established the connection between stellar brightness and activity and discussed different regimes of variability, refraining from a comparison with actual data. In the next section we show how our approach can be employed to model the general patterns of stellar variability obtained by the Lowell and Fairborn programs that were published by Radick et al. (1998); Lockwood et al. (2007).
6. Variability patterns: comparison of the model with observations
For every star from the Lowell and Fairborn programs, the two time series, (b + y)(t)/2 and S(t), are simultaneously available. In the literature the amplitude of the photometric variability is usually characterized via log (rms(b + y)/2) (expressed in stellar magnitudes). The connection between photometric brightness and chromospheric activity is expressed via the slope of the photometric brightness regression on the observed S-index Δ [ (b + y)/2 ]/ΔS (see the dashed lines in Fig. 8). Usually, the whole available time series are used to calculate these values, so that the variability of every star is described by the two numbers, log (rms(b + y)/2) and Δ [ (b + y)/2 ]/ΔS. Positive Δ [ (b + y)/2 ]/ΔS values correspond to the faculae-dominated regime of variability during the period of observations. The restriction to the particular period of variability is important since a given star may appear faculae- or spot-dominated at different times, so that having a long time-series is important. Negative Δ [ (b + y)/2 ]/ΔS values correspond to the spot-dominated variability.
The goal of this section is to establish the dependences of the log (rms(b + y)/2) and Δ
[ (b + y)/2 ]/ΔS values on the mean level of chromospheric activity
and compare them with the observed dependences. Lockwood
et al. (2007) found that the variability of the S-index increases
from less active to more active stars, and established an empirical linear relationship
between the variability of chromospheric activity 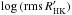 and mean activity
and mean activity
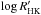 (see their
Fig. 6). This relationship may be used to connect the rms variation and the mean values of
the S-index (assuming the solar value for the color B-V, which is needed to convert
(see their
Fig. 6). This relationship may be used to connect the rms variation and the mean values of
the S-index (assuming the solar value for the color B-V, which is needed to convert
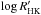 into the
S-index). The resulting relationship between the rms variation and the
mean values of S-index is established for a group of stars with random
distribution of inclinations and, thus, connects values that are averaged over all possible
inclinations (with a weighting factor sini, which is proportional to the probability that a
random star has an inclination i). Using the technique described in Sect. 4.2, we transformed this relationship into the relationship
that connects the rms variation and the mean values of the S-index expected
when observing in the equatorial plane.
into the
S-index). The resulting relationship between the rms variation and the
mean values of S-index is established for a group of stars with random
distribution of inclinations and, thus, connects values that are averaged over all possible
inclinations (with a weighting factor sini, which is proportional to the probability that a
random star has an inclination i). Using the technique described in Sect. 4.2, we transformed this relationship into the relationship
that connects the rms variation and the mean values of the S-index expected
when observing in the equatorial plane.
We considered a set of mean chromospheric activity ⟨ S90 ⟩ values
with a lowest value of 0.167
(which is the lowest annual value of the solar S-index) and a highest value
of 0.5. For each ⟨ S90 ⟩ value we
computed corresponding values of the rms variation assuming different distributions of
active regions and then generated the S-index time series by scaling the
solar S-index time series. Next, we employed these time series to calculate
log (rms(b +
y)/2), Δ [ (b + y)/2 ]/ΔS, and
⟨ S ⟩ values
for several inclinations and active regions distributions. The dependence of log (rms(b + y)/2) and of Δ [ (b + y)/2 ]/ΔS on mean chromospheric activity
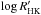 is presented
in Sect. 6.1 and Sect. 6.2.
is presented
in Sect. 6.1 and Sect. 6.2.
 |
Fig. 10 Comparison of the observed and modeled photometric variability. The modeled values of
the photometric variability are plotted vs. mean chromospheric activity for model
stars with solar (upper panel), polar (middle
panel), and homogeneous (lower panel) latitudinal
distributions of active regions. The asterisks and black lines indicate stars with
observed variability and the regression from Lockwood
et al. (2007). The dark (light) shaded areas indicate estimated
1σ
(2σ)
uncertainty in the Lockwood et al. (2007) data.
The diamond indicates 18 Scorpii (HD 146233) from Hall
et al. (2009). Colored curves result from our calculations for three values
of the stellar inclination: 90° (red curve), 57° (magenta curve),
0° (blue
curve). The dotted vertical lines denote the mean level of chromospheric activity of
stars with unconfirmed variability (only stars with
|
6.1. Photometric variability versus mean activity
In Fig. 10 we plot the stellar photometric
variability log (rms(b +
y)/2) vs. mean chromospheric
activity 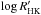 by
comparing the data of Lockwood et al. (2007, stars and regression line) with our
calculations (coloured curves). The shaded areas around the regression lines define the
uncertainty in stellar variability as a function of chromospheric activity. This was
estimated by accounting for the uncertainty in the variance measurements for the target
and the comparison stars. Most of the program stars in the Lockwood et al. (2007) sample have two suitable comparison stars. Lockwood et al. (2007) defined the variability of a
program star as the observed variance
by
comparing the data of Lockwood et al. (2007, stars and regression line) with our
calculations (coloured curves). The shaded areas around the regression lines define the
uncertainty in stellar variability as a function of chromospheric activity. This was
estimated by accounting for the uncertainty in the variance measurements for the target
and the comparison stars. Most of the program stars in the Lockwood et al. (2007) sample have two suitable comparison stars. Lockwood et al. (2007) defined the variability of a
program star as the observed variance 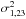 (relative to
the mean of the two comparison stars) minus one half of the observed variance of the
comparison star pair
(relative to
the mean of the two comparison stars) minus one half of the observed variance of the
comparison star pair 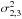 . Radick et al. (1998) adopted the uncertainty of the
variance ϵ =
0.0006 mag. This uncertainty is the same for the Lowell and Fairborn
observations and does not depend on the stellar magnitude (Lockwood et al. 2007). We used this value to estimate 1σ and 2σ uncertainties in the
observed photometric variability, assuming that both σ1,23 and σ2,3 values are known
with the uncertainty ϵ. We note that it is difficult to properly take the
variability of the comparison stars into account, especially for the low-activity program
stars with small photometric variability (several comparison stars appeared to be more
variable than the program stars). Thus our simple calculations provide a rather low
estimate of the uncertainty.
. Radick et al. (1998) adopted the uncertainty of the
variance ϵ =
0.0006 mag. This uncertainty is the same for the Lowell and Fairborn
observations and does not depend on the stellar magnitude (Lockwood et al. 2007). We used this value to estimate 1σ and 2σ uncertainties in the
observed photometric variability, assuming that both σ1,23 and σ2,3 values are known
with the uncertainty ϵ. We note that it is difficult to properly take the
variability of the comparison stars into account, especially for the low-activity program
stars with small photometric variability (several comparison stars appeared to be more
variable than the program stars). Thus our simple calculations provide a rather low
estimate of the uncertainty.
While our calculations agree reasonably well with the empirical regression for the high-activity stars, the variabilities of the low-activity stars given by our model are significantly below the observations. Interestingly, the variability of 18 Scorpii, which is arguably the closest bright solar analog (Hall et al. 2007a; Soubiran & Triaud 2004; Petit et al. 2008), is correctly reproduced by our model (see Fig. 10).
Models and measurements indicate that the solar irradiance variability on the 11 year cycle timescale is smaller than given by the Lockwood et al. (2007) empirical regression of the stellar variability vs. activity (see, e.g., Knaack et al. 2001; Judge et al. 2012; Shapiro et al. 2013a, and references therein). Because our model is based on SATIRE, which accurately reproduces the measured TSI variability, it is no surprise that it also leads to the same deviation.
One of the reasons for the disagreement between the values of the photometric variability of low-activity stars given by our model and obtained with the Lockwood et al. (2007) empirical regression comes from the uncertainties in the observational data. The Lockwood et al. (2007) regression may be affected by the short sample length (less than 20 years), small size (3 dozens stars), and possibly a selection effect (see e.g. Hall et al. 2009), so that the Sun-like stars with small variabilities are not included in the sample. Thus it would be important to repeat the comparison when more stellar data become available and the low end of the stellar activity sequence (which is the most difficult to study observationally) is better constrained.
The most conspicuous feature of our calculations is a strong decrease of the photometric
variability near 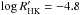 (hereafter called the
variability gap), which is absent from the data in Lockwood et al. (2007). In our calculations the variability gap is caused by the
compensation of the spot and facular contributions for the variability, and consequently,
the transition from the faculae-dominated (on the left side of the gap) to spot-dominated
(on the right side of the gap) variability regime. The level of activity (traced by
(hereafter called the
variability gap), which is absent from the data in Lockwood et al. (2007). In our calculations the variability gap is caused by the
compensation of the spot and facular contributions for the variability, and consequently,
the transition from the faculae-dominated (on the left side of the gap) to spot-dominated
(on the right side of the gap) variability regime. The level of activity (traced by
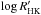 ) at which
the variability gap occurs depends on the inclination and latitudinal distribution of
active regions. For a solar distribution the decrease of the inclination shifts active
regions toward the limb (see Fig. 3) and amplifies
the facular contribution, shifting the variability gap to higher
) at which
the variability gap occurs depends on the inclination and latitudinal distribution of
active regions. For a solar distribution the decrease of the inclination shifts active
regions toward the limb (see Fig. 3) and amplifies
the facular contribution, shifting the variability gap to higher
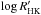 values. The
polar distribution displays the opposite behavior (see Fig. B.3), and the decrease of the inclination shifts the variability gap to lower
values. The
polar distribution displays the opposite behavior (see Fig. B.3), and the decrease of the inclination shifts the variability gap to lower
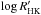 values.
values.
Interestingly, the chromospheric activity levels of the stars, whose variability Lockwood et al. (2007) were unable to confirm, cluster
around the variability gap predicted by our model (see Fig. 10). There are, however, also stars with confirmed variability located in the
variability gap.The variability of such stars cannot be reproduced by our model. We note
that these are exactly the stars that cause the deviation between the Lockwood et al. (2007) regression and our calculations
(here we ignore the four stars with 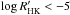 since their variability is
quite uncertain and our model cannot reproduce the variability of stars with such a low
magnetic activity, see Sect. 6.2). The absence of
the gap in the observational data and consequently the deviation between the empirical
regression reported by Lockwood et al. (2007) and
our model can be the result of one or more of the following:
since their variability is
quite uncertain and our model cannot reproduce the variability of stars with such a low
magnetic activity, see Sect. 6.2). The absence of
the gap in the observational data and consequently the deviation between the empirical
regression reported by Lockwood et al. (2007) and
our model can be the result of one or more of the following:
-
1.
The dependences of the spot and facular disk coverage on the S-index (Eqs. (1), (2)) employed in our model are ratherapproximate and may also vary from star to star. This may have astrong effect on the variability of stars around the gap. Indeed, thevariability of such stars is determined by the balance between spotand facular contributions. A small change of the ratio betweenspot and facular surface coverages (as well as between spot andfacular brightness contrasts, see point 3) may break this delicatebalance and thus strongly affect the variability of the stars aroundthe gap (see also Appendix B). In contrast, such a change onlymarginally affects the variability of stars far from the gap.
-
2.
Our model only accounts for the photometric variability on the activity timescale. The measured stellar variability may be affected by the long- and short-term variability on the timescale of stellar rotation, which may be not completely eliminated by the annual averaging performed by Lockwood et al. (2007). Since, unlike the case of the variability on the activity timescale, we do not expect any compensation effect in the rotational and long-term variabilities, they may significantly contribute to the total variability around the gap (see Shapiro et al. 2013a, for a more detailed discussion and estimates).
-
3.
The position of the gap very likely depends on B − V since the facular and sunspot contrasts are expected to depend on the effective temperature of the star. It is possible that while the Sun is located in the variability gap, other stars with similar levels of magnetic activity but higher photometric variabilities are located outside of the gap.
-
4.
The stellar variabilities may be affected by a not yet identified physical mechanism that is not taken into account by our simple extrapolation from the Sun.
6.2. Faculae- and spot-dominated stars
One quantity that allows distinguishing easily between stars whose photometric variability is dominated by faculae and those with spot-dominated photometric variability is the sign of the change in brightness with changing chromospheric activity. Lockwood et al. (1992) introduced the slope of the photometric brightness regression on the S-index Δ [ (b + y)/2 ]/ΔS as a measure of faculae- or spot-dominance. The zero value of Δ [ (b + y)/2 ]/ΔS corresponds to the threshold between faculae- and spot-dominated regimes of photometric variability.
 |
Fig. 11 Regression slope of the dependence of photometric brightness variation on HK
emission variation, plotted vs. mean chromospheric activity
|
In Fig. 11 we plot the Δ [ (b + y)/2 ]/ΔS values given by Lockwood et al. (2007) and similarly, those computed with our model. As in Fig. 10, the three panels differ only in the spatial distribution of active regions on the stellar surface assumed for the model (the observed data, asterisks, are the same in all panels). Most of the observed stars are located in between the synthetic curves, so our results agree well with the data of Lockwood et al. (2007). For the spot-dominated stars our model reproduces the increase of photometric variability relative to chromospheric variability with increasing activity level.
Interestingly, three stars in Fig. 11 appear to be spot-dominated despite the low level of their mean chromospheric activity. Our simple extrapolation from the Sun cannot reproduce such low values of the mean chromospheric activity (one would have to adjust the value of SQ for this; see Eq. (12)), which implies that the temperature structures of the quiet and magnetic regions of these stars are different from the respective solar temperature structures. At the same time, these stars are located in the light-gray shaded region in Fig. 11, which implies that their photometric variabilities are below the uncertainty level, and consequently, the Δ [ (b + y)/2 ]/ΔS values are quite uncertain. For example, one of these stars, HD 14376, was also observed by Hall et al. (2009), who found no activity-brightness correlation instead of the inverse activity-brightness correlation found by Lockwood et al. (2007).
If the observed stellar photometric brightness is affected by a systematic trend or noise (which may be stellar and/or instrumental in nature, see Sect. 6.1), it will have a stronger effect on the measured photometric variability than on the Δ [ (b + y)/2 ]/ΔS values. This may explain why the observed data and our model agree better in Fig. 11 than in Fig. 10.
Radick et al. (1998) suggested that the term Sun-like might be better applicable to the older and low-activity stars with faculae-dominated variability than for the stars with spot-dominated variability. Our results indicate that the qualitative behavior of the more active Sun-like stars can be reproduced using the Sun as a model star simply by extrapolation. Based on this, we conclude that even the younger stars with spot-dominated variability might be considered as Sun-like stars in the sense that their variability is defined by the same physical processes as the solar one.
We note that the Rossby number, which defines the efficiency of the stellar dynamo (Noyes et al. 1984), is supposed to increase with
stellar activity. At the same time, the latitudes of the magnetic field emergence depend
on the magnetic Rossby number (Schüssler & Solanki
1992). The actual latitudes of emergence of the field also depend on a number of
additional parameters, including the depth of the convection zone (i.e., on
B–V and on the evolutionary state of the star, see
Schüssler et al. 1996; Granzer 2002). In addition, meridional flows may move magnetic features
toward the poles even after emergence (Schrijver &
Title 2001). Therefore, while in general, one might expect that the solar
distribution of active regions is more representative for low-activity stars and the polar
distribution for high-activity stars, there are likely to be deviations from this
straightforward rule, and stars with the same 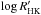 may have
different latitudinal distributions of active regions. The comparison of the slopes
calculated with different distributions allows one to estimate the scatter in the observed
values that might be attributed to different latitudinal distributions of active regions.
may have
different latitudinal distributions of active regions. The comparison of the slopes
calculated with different distributions allows one to estimate the scatter in the observed
values that might be attributed to different latitudinal distributions of active regions.
Our calculations indicate that the transition from the facula- to the spot-dominated
regime occurs somewhere between 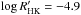 and
and
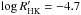 , which agrees well with the
observations of Lockwood et al. (2007) and Hall et al. (2009). The activity level of the
transition also depends on the inclination and latitudinal distribution of active regions
(and probably on B-V, which is beyond the scope of this study,
however), so that the variability regimes are not sharply defined, which is in line with
the observations of Hall et al. (2009). While
according to our calculations the solar variability is faculae-dominated (though see Harder et al. 2009; Preminger et al. 2011), the Sun is located very close to the threshold between
the regimes, so that stars that are slightly more active than the Sun might be observed as
spot-dominated.
, which agrees well with the
observations of Lockwood et al. (2007) and Hall et al. (2009). The activity level of the
transition also depends on the inclination and latitudinal distribution of active regions
(and probably on B-V, which is beyond the scope of this study,
however), so that the variability regimes are not sharply defined, which is in line with
the observations of Hall et al. (2009). While
according to our calculations the solar variability is faculae-dominated (though see Harder et al. 2009; Preminger et al. 2011), the Sun is located very close to the threshold between
the regimes, so that stars that are slightly more active than the Sun might be observed as
spot-dominated.
The mean and rms variation values of the chromospheric activity do not uniquely define the S-index time-series. This is an additional source of the scatter in Fig. 11 because the Δ [ (b + y)/2 ]/ΔS values might be affected by the specific form of the S-index time-variability. We note that the theoretical Δ [ (b + y)/2 ]/ΔS values presented here were calculated by employing the scaled solar S-index time-series (see Sect. 5.4), which is only an approximation. Additionally, the stellar observed time series may be too short to reveal a true variability regime. For example, if the Sun is observed for a short period of time around its activity maximum from its equatorial plane, it may be erroneously identified as spot-dominated (see Fig. 7). This effect may explain some part of the scatter in the observed slopes in Fig. 11 and points to the importance of having long time-series to accurately clarify such stars. The effect of the possible deviations in the stellar disk-area coverages by active regions from the dependences established in Sect. 3 is discussed in Appendices A and B.
If the varying stellar activity crosses the threshold between the facular- and
spot-dominated variability regimes, the star can appear to be facula-dominated over some
periods of time (when the activity is below the threshold), while it will be observed to
be spot-dominated over other intervals of time (when the activity is above the threshold).
In Fig. 11 we shaded the
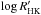 ranges that
correspond to such regimes of variability for both latitudinal distributions of active
regions. As expected, the Sun lies within the shaded area. Another interesting example of
a cross-over star is HD 140538 (ψ Ser), which demonstrates both direct and inverse
activity-brightness correlations on timescales of four years (Hall et al. 2009). We note, however, that the complete picture of its
variability might also be affected by many other factors, including the change of the
latitudinal distribution of active regions, change of faculae to spot coverage ratio, and
observational noise.
ranges that
correspond to such regimes of variability for both latitudinal distributions of active
regions. As expected, the Sun lies within the shaded area. Another interesting example of
a cross-over star is HD 140538 (ψ Ser), which demonstrates both direct and inverse
activity-brightness correlations on timescales of four years (Hall et al. 2009). We note, however, that the complete picture of its
variability might also be affected by many other factors, including the change of the
latitudinal distribution of active regions, change of faculae to spot coverage ratio, and
observational noise.
7. Conclusions
A long-standing puzzle in the study of stellar activity has been the observation that whereas on one hand stars with a relatively low level of activity become photometrically brighter (averaged over a year) as their activity level increases, on the other hand, more active stars display the opposite behavior, becoming darker with rising activity level. We reproduced this phenomenon based on the assumption that the solar paradigm is also valid for more active stars, that is, that we can qualitatively describe stellar behavior by extrapolating from solar activity and brightness variations.
We have expanded a simplified version of the SATIRE model of solar variability to Sun-like stars with different levels of magnetic activity. Our model attributes the variability of Sun-like stars to the spatial inhomogeneities (i.e., bright faculae and dark spots) on their surfaces, caused by the presence of a magnetic field at the solar/stellar surface. The key ingredient to the extrapolation is the finding that the area coverage by sunspots increases more rapidly with chromospheric activity than the coverage by faculae (see also Foukal 1998), although only the latter contribute strongly to the Ca II H and K line core emission, which determines the S-index.
We employed our model to study the dependences of the stellar photometric variability on the observed mean level of magnetic activity (as traced by the Ca II S-index), stellar inclination (i.e., the angle between the direction to the observer and stellar rotational axis) and, at a simple level, also on the latitudinal distribution of active regions on the stellar surface.
We found that our simple extrapolation from the Sun to higher activity stars reproduces the observed trend that while the variability of Sun-like stars with low magnetic activity is dominated by faculae (i.e., photometric brightness and magnetic activity are positively correlated), the variability of Sun-like stars with high magnetic activity is spot-dominated (photometric brightness and magnetic activity are negatively correlated). The switch between the regimes occurs around magnetic activity levels slightly higher than solar and depends on the inclination and latitudinal distribution of active regions. The slopes of the activity-brightness correlation, calculated with our model, agree well with the data reported by Lockwood et al. (2007). Our calculations indicate that the variability of a star with a solar level of magnetic activity is faculae-dominated, independently of the inclination and latitudinal distribution of active regions on the surface, although a too short time-series of solar activity, if caught at the right phase, may lead to the opposite conclusion.
The measured photometric variabilities of the high-activity stars agree reasonably well with our calculations. However, the variabilities of the low-activity stars calculated with our model are weaker than given by the empirical correlation between the stellar photometric variability and mean chromospheric activity level. This is probably caused by the limitations of our simple approach and by the uncertainties in the stellar measurements.
The general success of the model in reproducing the basic qualitative behavior of spot-dominated stars is an indication that the photometric variability of more active stars has the same fundamental causes as the variability of the Sun. Up until now, physics-based models of irradiance variability were solely applied to the solar case. Consequently, they could only be validated and constrained by solar data, which represent a single point in a wide parameter space of the possible magnetic activities, inclinations, latitudinal distribution of active regions, etc. The approach presented in this paper allows constraining the model over a much wider parameter space, and, thus, along with interpreting stellar data, it helps to better understand the mechanisms of solar variability.
As a next step, we plan to apply an extension of this model to study stellar variability on rotational timescales, as observed by the COROT (Baglin et al. 2006) and Kepler (Borucki et al. 2010) missions and as are in future to be measured by the PLATO mission (Rauer et al. 2013).
Online material
Appendix A: deviations in the disk-area coverages by active regions
 |
Fig. A.1 Photometric variability as a function of mean chromospheric activity calculated for α = 0 (original AS coverages given by Eq. (1), solid curve), α = 0.5 (increased AS coverages, dotted curve), α = − 0.5 (decreased AS coverages, dashed curve). The calculations are performed for the homogeneous distribution of active regions. |
 |
Fig. A.2 Regression slope of the dependence of photometric brightness variation on HK
emission variation, plotted vs. mean chromospheric activity
|
The relationships between disk-area coverages and chromospheric activity employed in the present study were established on the basis of solar data and then extrapolated to higher activity levels. While one might expect that the extrapolation works well for stars with activities similar to that of the Sun, the disk-area coverages of more active stars may deviate from the values given by Eqs. (1)–(2). To estimate the impact of such deviations on our results we recalculated the log (rms(b + y)/2) and Δ [ (b + y)/2 ]/ΔS values plotted in Figs. 10 and 11, first assuming that the coverage of the most active stars from the sample of Lockwood et al. (2007) is 50% larger then we expect from the extrapolation from the Sun and than that it is 50% smaller than we expect from solar extrapolation.
Namely, we applied following correction to the spot disk-area coverage:
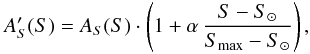 (A.1)where
(A.1)where
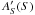 is the new spot disk-area
coverage, AS(S)
is the spot disk-area coverage given by Eq. (1), α is the coefficient that determines the amplitude
of the correction, S⊙ is the mean solar level of
chromospheric activity, and Smax was chosen to be equal to
0.5, which is the highest
mean chromospheric activity considered in the present study (see the description of the
algorithm employed to produce Figs. 10 and 11 in Sect. 6).
is the new spot disk-area
coverage, AS(S)
is the spot disk-area coverage given by Eq. (1), α is the coefficient that determines the amplitude
of the correction, S⊙ is the mean solar level of
chromospheric activity, and Smax was chosen to be equal to
0.5, which is the highest
mean chromospheric activity considered in the present study (see the description of the
algorithm employed to produce Figs. 10 and 11 in Sect. 6).
The resulting dependences of log (rms(b + y)/2) and Δ [ (b + y)/2 ]/ΔS on S are plotted in Figs. A.1 and A.2 for three values of α. One can see that the scatter in the surface coverages may lead to significant deviations in the theoretical curves plotted in Figs. A.1 and A.2. At the same time, the general success of our approach in modeling the stellar data implies that the simple extrapolation of solar disk-area coverages works remarkably well even for stars significantly more active than the Sun.
Appendix B: comparison with the SATIRE-S results
Our stellar variability model is based on the representation of the facular and spot disk-area coverages as functions of the S-index measured from a vantage point in the stellar equatorial plane (see Eqs. (1), (2)). For fixed inclination and distribution of active regions the change of the stellar brightness due to magnetic activity, δ(b + y)/2, is a single-value function of the observed S-index.
In reality, Eqs. (1), (2) are only approximate. For every particular observational season the disk-area coverages may differ from the values given by these equations, because they define the relation averaged over the longest time interval for which solar data are available (see Sect. 3). For example, a transit of a large spot may cause the stars deemed faculae-dominated by our analysis to be temporarily spot-dominated.
To estimate the importance of this effect we considered the solar S-index and photometric brightness (i.e. the Strömgren (b + y)/2 flux) time-series. The S-index was calculated from the Sac Peak K-index KSP (see Sect. 3). Because there are no long-term solar irradiance measurements equivalent to the Strömgren (b + y)/2 flux, we employed the SATIRE-S spectral irradiance time-series (see description in Ball et al. 2012, 2013, and references therein) convolved with the Strömgren (b + y)/2 spectral filter profile. From these data we calculated the slope of the photometric brightness regression on the observed S-index, Δ [ (b + y)/2 ]/ΔS, for 11 year time intervals (the value for the year X is the regression slope calculated for the [X–5, X + 5] dataset), offset by one year each.
 |
Fig. B.1 Annual values of the solar spectral flux in the Strömgren (b + y)/2 filters according to the SATIRE-S model (upper panel) and the S-index calculated from the Sac Peak measurements (middle panel) as well as the slopes of the activity-brightness correlation (lower panel). The solid line in the lower panel represents the slope calculated with the simplified model used in this paper, while the dashed line corresponds to the slope calculated with SATIRE-S data using the entire time series (1978–2010). |
The S-index, photometric time-series, and slopes are plotted in Fig. B.1. One can see that the photometric flux is not a single-value function of the S-index and the regression slope varies with time. For example, the increase of the slope after 2003 might be explained by the decrease of the ratio between spot and facular disk-area coverages.
The variations of the slope may explain some of the scatter in the observed stellar slopes (see Fig. 11). The effect increases if instead of the annual data we consider three-month averages (see Fig. B.2). The transit of large spots affects the photometric flux, but leaves the S-index unchanged (because for a star with a solar activity level the contribution of spots to the S-index is negligibly small). We note that the slopes calculated with our model using the entire time series (1978–2010) agree well with the more sophisticated and accurate SATIRE-S calculations.
Figures B.1 and B.2 reveal that according to the SATIRE-S model the variability of the solar Strömgren (b + y)/2 flux is always faculae-dominated if the Sun is observed for at least 11 years. This does not contradict with its position in the shaded band in Fig. 11 because if the Sun is observed for a shorter period of time around its activity maximum it can be erroneously identified as spot-dominated (see Fig. 7).
 |
Fig. B.3 The same as Fig. 3, but for the adopted polar distribution of spots (two caps with latitudes between ± 45° and ± 90°). |
Acknowledgments
We thank Wes Lockwood for useful discussions and for helping us to estimate the uncertainty in stellar data, and the referee Gibor Basri for constructive criticism and useful advise. The research leading to this paper was supported by the Swiss National Science Foundation under grant CRSI122-130642 (FUPSOL). It was also financially supported by the COST Action ES1005 TOSCA (http://www.tosca-cost.eu) and from the BK21 plus program through the National Research Foundation (NRF) funded by the Ministry of Education of Korea. W.T.B. and Y.C.U. acknowledge support through STFC grant ST/I001972/1. A.I.S. and W.K.S. acknowledge support from S.N.F. grant 100020_140573.
References
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR Meeting, 36, 36th COSPAR Scientific Assembly, 3749 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W., & Henry, G. W. 1998, in Conf. Ser., 154, Cool Stars, Stellar Systems, and the Sun, eds. R. A. Donahue, & J. A. Bookbinder, ASPs 153 [Google Scholar]
- Ball, W. T., Unruh, Y. C., Krivova, N. A., Solanki, S., & Harder, J. W. 2011, A&A., 530, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W. T., Unruh, Y. C., Krivova, N. A., et al. 2012, A&A., 541, A27 [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, W., Krivova, N., Unruh, Y., Haigh, J., & Solanki, S. 2013, J. Atmos. Sci., submitted [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deland, M. T., & Cebula, R. P. 2012, J. Atmos. Sol.-Terr. Phys., 77, 225 [Google Scholar]
- Domingo, V., Ermolli, I., Fox, P., et al. 2009, Space Sci. Rev., 145, 337 [Google Scholar]
- Dziembowski, W. A., Fiorentini, G., Ricci, B., & Sienkiewicz, R. 1999, A&A., 343, 990 [NASA ADS] [Google Scholar]
- Ermolli, I., Criscuoli, S., Centrone, M., Giorgi, F., & Penza, V. 2007, A&A., 465, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ermolli, I., Criscuoli, S., Uitenbroek, H., et al. 2010, A&A., 523, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ermolli, I., Matthes, K., Dudok de Wit, T., et al. 2013, Atm. Chem. & Phys., 13, 3945 [Google Scholar]
- Fligge, M., Solanki, S. K., & Unruh, Y. C. 2000, A&A., 353, 380 [NASA ADS] [Google Scholar]
- Fontenla, J. M., Harder, J., Livingston, W., Snow, M., & Woods, T. 2011, J. Geophys. Res., 116, 20108 [CrossRef] [Google Scholar]
- Foukal, P. 1994, Science, 264, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Foukal, P. 1998, ApJ, 500, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C. 2006, Space Sci. Rev., 125, 53 [Google Scholar]
- Granzer, T. 2002, Astron. Nachr., 323, 395 [Google Scholar]
- Gray, L. J., Beer, J., Geller, M., et al. 2010, Rev. Geophys., 48, 4001 [NASA ADS] [CrossRef] [Google Scholar]
- Haigh, J. D. 2007, Liv. Rev. Sol. Phys., 4, 2 [Google Scholar]
- Hall, J. C. 2008, Liv. Rev. Sol. Phys., 5, 2 [Google Scholar]
- Hall, J. C., Henry, G. W., & Lockwood, G. W. 2007a, AJ, 133, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., Lockwood, G. W., & Skiff, B. A. 2007b, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. C., Henry, G. W., Lockwood, G. W., Skiff, B. A., & Saar, S. H. 2009, AJ, 138, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C., & Woods, T. N. 2009, Geophys. Res. Lett., 36, 7801 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyt, D. V., Kyle, H. L., Hickey, J. R., & Maschhoff, R. H. 1992, J. Geophys. Res., 97, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Jerzykiewicz, M., & Serkowski, K. 1966, Lowell Observatory Bulletin, 6, 295 [NASA ADS] [Google Scholar]
- Judge, P. G., Lockwood, G. W., Radick, R. R., et al. 2012, A&A., 544, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keil, S. L., Henry, T. W., & Fleck, B. 1998, in ASP Conf. Ser., 140, Synoptic Solar Physics, eds. K. S. Balasubramaniam, J. Harvey, & D. Rabin, ASP, 301 [Google Scholar]
- Knaack, R., Fligge, M., Solanki, S. K., & Unruh, Y. C. 2001, A&A., 376, 1080 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., & Solanki, S. K. 2008, J. Astrophys. Astron., 29, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Krivova, N. A., Solanki, S. K., & Unruh, Y. C. 2011, J. Atmos. Sol. Terr. Phys., 73, 223 [Google Scholar]
- Krivova, N. A., Solanki, S. K., Fligge, M., & Unruh, Y. C. 2003, A&A., 399, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova, N. A., Vieira, L. E. A., & Solanki, S. K. 2010, J. Geophys. Res., 115, 12112 [CrossRef] [Google Scholar]
- Lean, J. L., & DeLand, M. T. 2012, J. Climate, 25, 2555 [NASA ADS] [CrossRef] [Google Scholar]
- Lean, J., Rottman, G., Harder, J., & Kopp, G. 2005, Sol. Phys., 230, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Baliunas, S. L., & Radick, R. R. 1992, Nature, 360, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., & Radick, R. R. 1997, ApJ, 485, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, G. W., Skiff, B. A., Henry, G. W., et al. 2007, ApJS, 171, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Oberländer, S., Langematz, U., Matthes, K., et al. 2012, Geophys. Res. Lett., 39, 1801 [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Preminger, D. G., Chapman, G. A., & Cookson, A. M. 2011, ApJ, 739, L45 [Google Scholar]
- Radick, R. R., Lockwood, G. W., Skiff, B. A., & Thompson, D. T. 1995, ApJ, 452, 332 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radick, R. R., Lockwood, G. W., Skiff, B. A., & Baliunas, S. L. 1998, ApJS, 118, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2013, Exp. Astron., submitted [arXiv:1310.0696] [Google Scholar]
- Schatten, K. H. 1993, J. Geophys. Res., 98, 18907 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2001, ApJ, 551, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M. & Solanki, S. K. 1992, A&A., 264, L13 [NASA ADS] [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., Solanki, S. K., & Stix, M. 1996, A&A., 314, 503 [NASA ADS] [Google Scholar]
- Seleznyov, A. D., Solanki, S. K., & Krivova, N. A. 2011, A&A., 532, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Schmutz, W., Rozanov, E., et al. 2011, A&A., 529, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Schmutz, W., Cessateur, G., & Rozanov, E. 2013a, A&A., 552, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. V., Rozanov, E. V., Shapiro, A. I., et al. 2013b, J. Geophys. Res., 118, 3781 [CrossRef] [Google Scholar]
- Skumanich, A., Lean, J. L., Livingston, W. C., & White, O. R. 1984, ApJ, 282, 776 [Google Scholar]
- Soderblom, D. R., Duncan, D. K., & Johnson, D. R. H. 1991, ApJ, 375, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Unruh, Y. C. 2013, Astron. Nachr., 334, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Haigh, J. D. 2013, ARA&A, 51, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., & Triaud, A. 2004, A&A., 418, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thuillier, G., Melo, S. M. L., Lean, J., et al. 2013, Sol. Phys., submitted [Google Scholar]
- Unruh, Y. C., Solanki, S. K., & Fligge, M. 1999, A&A., 345, 635 [NASA ADS] [Google Scholar]
- Unruh, Y. C., Ball, W. T., & Krivova, N. A. 2012, Surv. Geophys., 33, 475 [Google Scholar]
- Usoskin, I. G. 2008, Liv. Rev. Sol. Phys., 5, 3 [Google Scholar]
- Vieira, L. E. A., Norton, A., Dudok de Wit, T., et al. 2012, Geophys. Res. Lett., 39, 16104 [Google Scholar]
- Wehrli, C., Schmutz, W., & Shapiro, A. I. 2013, A&A., 556, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wenzler, T., Solanki, S. K., Krivova, N. A., & Fröhlich, C. 2006, A&A., 460, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, O. R., Skumanich, A., Lean, J., Livingston, W. C., & Keil, S. L. 1992, PASP, 104, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- White, O. R., Livingston, W. C., Keil, S. L., & Henry, T. W. 1998, in ASP Conf. Ser., 140, Synoptic Solar Physics, ed. K. S. Balasubramaniam, J. Harvey, & D. Rabin, 293 [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. 2012, in EGU General Assembly Conf. Abstracts, 14, eds. A. Abbasis, & N. Giesen, 14, 1520 [Google Scholar]
All Figures
 |
Fig. 1 Disk-area coverages by sunspots (upper panel) and solar faculae (middle panel) as well as the S-index (lower panel). The daily disk-area coverages are determined from the KP/512 (black dots), KP/SPM (red dots), and SOHO/MDI (blue dots) full-disk continuum images and magnetograms. The daily S-index (black dots in the lower panel) is calculated from the Sac Peak Ca II data. Magenta curves are the annually averaged data. |
| In the text | |
 |
Fig. 2 Dependence of the solar spot (upper panel) and facular (lower panel) disk-area coverages on the S-index of chromospheric activity. The crosses correspond to the binned values, the thick curves are the least-squares fit dependences (quadratic for spot disk-area coverages, and linear for facular disk-area coverages). |
| In the text | |
 |
Fig. 3 Upper panels: visible projections of two bands between latitudes ± 5° and ± 30° on the stellar disk for three inclination values. The bands correspond to the solar distribution of spots employed here. The star sign indicates the position of the disk center. Lower panels: the fractional coverage of the stellar disk by spots plotted as functions of the impact parameter r/rstar (which is 0 at the disk centrer and 1 at the limb). The fractional coverage is calculated assuming that the two bands plotted in the upper panels are completely covered by spots. |
| In the text | |
 |
Fig. 4 Upper panel: center-to-limb variation of the Strömgren (b + y)/2 intensity calculated for the quiet Sun, faculae, penumbra, and umbra models (black, red, magenta, and blue curves). Plotted are the ratios to the quiet-Sun intensity at the disk center. Lower panel: quadratic polynomial parameterization of the intensity center-to-limb variation at the Ca II K line and the nearby continuum (solid and dashed orange curves) according to Skumanich et al. (1984). Both intensities are normalized to unity at the disk center. |
| In the text | |
 |
Fig. 5 Simulated values of the S-index as they would be measured for inclinations of 90° (red curves), 57° (magenta curves), 0° (blue curves) vs. facular surface coverage for solar, polar, and homogeneous distributions of active regions. The maximum possible facular surface coverage (i.e., when faculae and spots fully cover the activity belts/caps or the entire stellar surface) is about 28%, 19%, and 47% for the adopted solar, polar, and homogeneous distributions. |
| In the text | |
 |
Fig. 6 Simulated values of the photometric brightness change δ(b + y)/2 (upper panel) and S-index (lower panel) vs. stellar inclination i. Solid curves correspond to the solar distribution of active regions, dashed to polar distribution, and dotted to homogeneous distribution. The coverage by faculae and spots for all three distributions is chosen so that the S-index observed from the stellar equatorial plane (i = 90°) equals 0.19. |
| In the text | |
 |
Fig. 7 Simulated values of the photometric brightness change δ(b + y)/2 vs. S-index for the Sun observed from three different directions. Plotted are the annual values as they would be measured from the equatorial plane (red crosses), a 57° inclination (magenta crosses), and from the solar rotational axis (blue crosses). |
| In the text | |
 |
Fig. 8 Simulated values of the photometric brightness change δ(b + y)/2 as they would be measured from the equatorial plane (red crosses), at 57° inclination (magenta crosses), and from the stellar rotational axis (blue crosses) vs. S-index. Plotted are values for model stars with the activity level of HD 81809 (mean and rms variation values of S are equal to 0.1713 and 0.0080, left panel), of HD 10476 (0.1896 and 0.0136, middle panel), and of HD 82885 (0.2679 and 0.0186, right panel). The dashed lines correspond to the linear regressions calculated over the whole δ(b + y)/2 and S-index data sets. |
| In the text | |
 |
Fig. 9 Simulated values of the photometric brightness change δ(b + y)/2 as they would be measured from the equatorial plane (red curve), at 57° inclination (magenta curve), and from the stellar rotational axis (blue curve) vs. S-index. Unlike Fig. 8, the dependences are calculated over a broad range of stellar magnetic activity. The range bars designate the observed ranges of chromospheric activity variations of the Sun, HD 81809, HD 10476, and HD 82885. |
| In the text | |
 |
Fig. 10 Comparison of the observed and modeled photometric variability. The modeled values of
the photometric variability are plotted vs. mean chromospheric activity for model
stars with solar (upper panel), polar (middle
panel), and homogeneous (lower panel) latitudinal
distributions of active regions. The asterisks and black lines indicate stars with
observed variability and the regression from Lockwood
et al. (2007). The dark (light) shaded areas indicate estimated
1σ
(2σ)
uncertainty in the Lockwood et al. (2007) data.
The diamond indicates 18 Scorpii (HD 146233) from Hall
et al. (2009). Colored curves result from our calculations for three values
of the stellar inclination: 90° (red curve), 57° (magenta curve),
0° (blue
curve). The dotted vertical lines denote the mean level of chromospheric activity of
stars with unconfirmed variability (only stars with
|
| In the text | |
 |
Fig. 11 Regression slope of the dependence of photometric brightness variation on HK
emission variation, plotted vs. mean chromospheric activity
|
| In the text | |
 |
Fig. A.1 Photometric variability as a function of mean chromospheric activity calculated for α = 0 (original AS coverages given by Eq. (1), solid curve), α = 0.5 (increased AS coverages, dotted curve), α = − 0.5 (decreased AS coverages, dashed curve). The calculations are performed for the homogeneous distribution of active regions. |
| In the text | |
 |
Fig. A.2 Regression slope of the dependence of photometric brightness variation on HK
emission variation, plotted vs. mean chromospheric activity
|
| In the text | |
 |
Fig. B.1 Annual values of the solar spectral flux in the Strömgren (b + y)/2 filters according to the SATIRE-S model (upper panel) and the S-index calculated from the Sac Peak measurements (middle panel) as well as the slopes of the activity-brightness correlation (lower panel). The solid line in the lower panel represents the slope calculated with the simplified model used in this paper, while the dashed line corresponds to the slope calculated with SATIRE-S data using the entire time series (1978–2010). |
| In the text | |
 |
Fig. B.2 The same as Fig. B.1, but for three-month averages. |
| In the text | |
 |
Fig. B.3 The same as Fig. 3, but for the adopted polar distribution of spots (two caps with latitudes between ± 45° and ± 90°). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.