| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 32 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201322505 | |
| Published online | 22 May 2014 | |
The X-shooter Spectral Library (XSL)
I. DR1: Near-ultraviolet through optical spectra from the first year of the survey⋆
1 Kapteyn Astronomical Institute, University of Groningen, PO BOX 800, 9700 AV Groningen, The Netherlands
e-mail: chenyp.astro@gmail.com; yanping@astro.rug.nl
2 Observatoire Astronomique, 11 rue de l’Université, 67000 Strasbourg, France
3 Instituto de Astrofísica de Canarias (IAC), 38200 La Laguna, Tenerife, Spain
4 Departamento de Astrofísica, Universidad de La Laguna, 38205 Tenerife, Spain
5 Université de Lyon, Université Lyon 1, 69622 Villeurbanne, France ;
CRAL, Observatoire de Lyon, CNRS UMR 5574, 69561 Saint-Genis Laval, France
6 National Optical Astronomy Observatory, 950 North Cherry Avenue, Tucson AZ 85719 USA
Received: 19 August 2013
Accepted: 10 March 2014
We present the first release of the X-shooter Spectral Library (XSL). This release contains 237 stars. The spectra in this release span a wavelength range of 3000–10 200 Å and have been observed at a resolving power of R ≡ λ/ Δλ ~ 10 000. The spectra were obtained at ESO’s 8-m Very Large Telescope (VLT). The sample contains O–M, long-period variable, C and S stars. The spectra are flux-calibrated and telluric-corrected. We describe a new technique for the telluric correction. The wavelength coverage, spectral resolution, and spectral type of this library make it well suited to stellar population synthesis of galaxies and clusters, kinematical investigation of stellar systems, and the study of the physics of cool stars.
Key words: stars: abundances / stars: fundamental parameters / stars: AGB and post-AGB / stars: atmospheres / galaxies: stellar content
Full Table 3 and Table A.1 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/565/A117
© ESO, 2014
1. Introduction
Spectral libraries play an important role in different fields of astrophysics. In particular they serve as a reference for the classification and automatic analysis of large stellar spectroscopic surveys and are fundamental ingredients for models of stellar populations used to study the evolution of galaxies.
Much of what we know about the formation, evolution, and current state of galaxies comes through studies of their starlight. In distant galaxies, where the ability to study their stellar populations star-by-star is compromised by crowding and blending due to poor resolution, we must resort to studying their integrated light. This typically means comparing colors or spectra to models of simple or composite stellar population models (e.g., Guiderdoni & Rocca-Volmerange 1987; Buzzoni et al. 1994; Worthey et al. 1994; Leitherer et al. 1996; Fioc & Rocca-Volmerange 1997; Leitherer et al. 1999; Bruzual & Charlot 2003; Le Borgne et al. 2004; González Delgado et al. 2005; Maraston 2005; Vazdekis et al. 2010; Conroy & van Dokkum 2012). These comparisons give insight into a galaxy’s evolution process: stellar population analysis can reveal the detailed chemical composition and star-formation history of a galaxy (e.g., González 1993; Davies et al. 1993; Trager et al. 2000; Thomas et al. 2005; Yamada et al. 2006; Koleva et al. 2013; Conroy et al. 2013).
Modern stellar population models consist of three primary ingredients (e.g., Vazdekis et al. 2010): stellar isochrones that represent the location in the luminosity–effective temperature plane (and, as a consequence, also surface gravity–effective temperature) of stars with different masses, the same initial chemical composition, and age; an initial mass function that populates the isochrones with a sensible number of stars; and a stellar library. A spectral library is a collection of stellar spectra that share similar wavelength coverage and spectral resolution. The spectra change as a function of effective temperature (Teff), surface gravity (log g), and metallicity ([Fe/H]). To reproduce galaxy spectra as precisely as possible, one requires a comprehensive stellar spectral library that covers the entire desired parameter space of Teff, log g, and [Fe/H]. Moreover, extended wavelength coverage is strongly desirable, because different stellar phases contribute their light in different bands. For instance, cool giants contribute more light than warmer faint giant stars in the near-infrared (NIR), while the situation is reversed in the optical (Frogel 1988; Maraston 2005). Asymptotic giant branch (AGB) stars dominate the light of intermediate-aged stellar populations in the NIR but are unimportant in the optical (Charlot & Bruzual 1991; Worthey et al. 1994; Maraston 1998). Detecting their presence requires broad wavelength coverage in both the target and model spectra.
Selection of previous empirical stellar libraries.
Stellar spectral libraries can be classified into empirical and theoretical libraries, depending on how libraries are obtained. Both theoretical and empirical libraries have improved in recent years. Widely used theoretical libraries in stellar population models include those of Kurucz (1993); Coelho et al. (2005); Martins et al. (2005); Munari et al. (2005); Coelho et al. (2007); Gustafsson et al. (2008), and Allard et al. (2011). Theoretical libraries have the advantage of (nearly) unlimited resolution and selectable abundance patterns, which include not only scaled-solar abundances but also non-solar patterns. Unfortunately, theoretical libraries suffer from systematic uncertainties, as they rely on model atmospheres and require a reliable list of atomic and molecular line wavelengths and opacities (Coelho et al. 2005). Empirical stellar libraries, on the other hand, have the advantage of being drawn from real, observed stars and therefore do not suffer this limitation. However, they frequently have relatively low resolution (with a few exceptions; see below) and are typically unable to reproduce the indices measured in giant elliptical galaxies, because they are based on local stars with Milky Way disk abundance patterns (Peletier 1989; Worthey et al. 1992). Table 1 lists several previous empirical stellar libraries and their principal features. In the optical, there are the (among others) Lick/IDS (Worthey & Ottaviani 1997), MILES (Sánchez-Blázquez et al. 2006), ELODIE (Prugniel & Soubiran 2001, 2004; Prugniel et al. 2007), STELIB (Le Borgne et al. 2003), NGSL (Gregg et al. 2006), and the Pickles (1998) libraries. Building stellar libraries in the NIR is a challenging task, but pioneering work has been done by Lançon & Rocca-Volmerange (1992); Lançon & Wood (2000, hereafter LW2000) and Lançon & Mouhcine (2002, hereafter LM2002); Mármol-Queraltó et al. (2008); and Rayner et al. (2009, IRTF-SpeX). However, spectral libraries with extended wavelength coverage at moderate resolution are still largely missing.
With the high-efficiency, broad-wavelength coverage and high/moderate resolution of the X-shooter spectrograph at ESO’s VLT (Vernet et al. 2011), we can now fill the gap between high-resolution theoretical stellar libraries and low-resolution empirical stellar libraries. To this end, we developed the X-shooter Spectral Library (XSL, PI: Trager), which is a survey of ≳700 stars that cover the entire Hertzsprung-Russell (HR) diagram, including both cool (M dwarfs, M giants, C stars, long-period variables, etc.) and hot stars (up to late O stars) with wavelength coverage from 300–2480 nm. This includes the entire near-ultraviolet (NUV) to NIR range at R ~ 8000–11 000.
Here, we present the first two of six periods of XSL data (from ESO Periods 84 and 85). We concentrate on the NUV–optical data (3000–10 200 Å) from the UVB and VIS arms of X-shooter in this paper and leave the NIR arm data for a forthcoming paper.
X-shooter observing modes for XSL in Periods 84 and 85.
2. Sample selection and observation
The targets of XSL are selected from several empirical stellar libraries and supplementary literature sources. We take stars from Lick/IDS, MILES, and NGSL to cover Teff, log g, and [Fe/H] as uniformly as possible. However, these libraries mostly lack the cool, bright stars, which are important in the NIR. For this purpose, we select AGB and long-period variable (LPV) stars from LW2000 and IRTF-SpeX with a declination <35° marked M, C or S-stars. LPV stars are also collected from Hughes & Wood (1990, for the Large Magellanic Cloud) and the Cioni et al. (2003, for the Small Magellanic Cloud). Red supergiant stars are taken from the lists of LW2000 and Levesque et al. (2005, 2007). To cover metal-rich stars with abundances similar to giant elliptical galaxies, we also include Galactic Bulge giants from the samples of Blanco et al. (1984) and Groenewegen & Blommaert (2005).
 |
Fig. 1 Distribution of spectral types in XSL observed in Periods 84 and 85 (excluding telluric calibrators). Spectral types were retrieved from SIMBAD or based on educated guesses from the source libraries or atmospheric parameters. |
As of the end of March 2011 (i.e., the completion of the Period 85 observing campaign), 258 observations of 237 individual stars from the XSL input catalog had been completed. Figure 1 shows the distribution of stellar types of these XSL stars. In Fig. 2 we show those sample stars with calculated stellar parameters in an HR diagram; these parameters were computed using ULySS (Koleva et al. 2009; Wu et al. 2011) and will be described in more detail in a forthcoming paper.
2.1. Observations
The observations described here were carried out in Periods 84 and 85 using X-shooter. The X-shooter spectrograph was built by a consortium of 11 institutes in Denmark, France, Italy and the Netherlands, and ESO. It is a single-target echelle spectrograph, which maximizes the sensitivity over a broad wavelength by splitting the spectra into three different arms (UVB, VIS, and NIR). Depending on wavelength and slit width, X-shooter yields a resolving power of R = 4000–14 000. A unique capability of X-shooter is that it collects spectra in the wavelength range from the NUV to the NIR through its three arms simultaneously. This property is extremely useful for observing variable stars, especially very cool stars, like AGB stars, whose spectra may vary substantially during their pulsation cycles.
 |
Fig. 2 HR diagram of the 219 XSL stars (O–M, LPV, S) with calculated Teff, log g and [Fe/H], where [Fe/H] is presented in different colors. |
X-shooter offers multiple spectroscopic observation modes; we used the longslit SLIT mode for all observations. Three observing strategies are supported in SLIT mode: classical “staring” observations, A–B “nodding” along the slit for improved sky subtraction, and on–off target–sky switching (“offset”). Almost all XSL stars were observed in nodding mode with a narrow slit, yielding an intermediate resolving power of ~10 000 and good sky subtraction; nearly all were also observed in staring mode with a wide slit for flux calibration. The observed modes used, slit widths, and CCD readout modes are given in Table 2. Wide-slit observations were carried out (except on the brightest stars, for which no wide-slit observations were made, since they would saturate the detectors) just before nodding observations. The CCD binning and readout speeds were altered depending on the brightness of a given target: faint stars (K ≥ 8 or V ≥ 10) were generally binned in the VIS arm and unbinned in the UVB arm with slow readout speeds in nodding mode. Fast readout speeds were used for brighter stars (Table 21).
Along with the program stars, we observed hot stars (mostly B-type) to be used as telluric standard stars. These were observed using the same narrow-slit setup to preserve the spectral resolution. Flux standard stars taken as part of the normal ESO X-shooter calibration program were collected from the archive; these were observed using a wide slit (5.0′′ × 11′′) to sample as much of the total flux as possible.
3. Data reduction
Basic data reduction was performed with the public release of the X-shooter pipeline version 1.5.0, following the standard steps described in the X-shooter pipeline manual2 up to the production of 2D spectra. This includes bias and/or dark correction, flat-fielding, geometric correction, wavelength calibration and sometimes sky subtraction. A master bias constructed from a set of at least five exposures was used to remove the bias level of the CCD and to correct for large-scale electronic noise patterns. A master flat field constructed from a set of at least five exposures was used to correct the pixel-to-pixel variations in the CCD response and the non-homogeneous illumination by the telescope. Wavelength and spatial scale calibration are performed with observations of a Th-Ar lamp in the UVB and VIS arm.
3.1. Difficulties encountered and proposed solutions
A number of issues were discovered during the pipeline reduction process, which required further processing steps. We give details about the most significant of these steps here.
3.1.1. Issues with nodding mode observations
 |
Fig. 3 Data observed in nodding mode in the VIS arm. Here, the star is sitting in the center of the slit in the first exposure (left panel), while the star is almost out of the slit in the second exposure (right panel). |
Most spectra were reduced using the pipeline recipes that correspond to the observation mode used: spectra observed in staring mode were reduced by the pipeline recipe “xsh_scired_slit_stare”, and spectra observed in nodding mode were reduced by the pipeline recipe “xsh_scired_slit_nod”. However, in the case of nodding-mode observations, the first exposure in an A–B pair was occasionally centered in the slit, and the “throw” to the B image (which is fixed angular difference plus a random extra “jitter”) was large enough to put the star at the end or even off of the slit in the B image. We show an example in Fig. 3. In these cases, we reduce the well centered slit in “offset” mode using the second frame as the “sky” frame. This does an excellent job of sky subtraction for these frames, but it means the effective exposure time for these stars is half that anticipated.
3.1.2. Background subtraction issues in UVB spectra
 |
Fig. 4 Example of background (“sky”) modeled by the pipeline from data observed in stare mode in the UVB arm, in which sky lines are nearly absent. Left panel: original raw frame. Right panel: sky frame generated by the pipeline scaled to the same intensity as the left panel. Note the very poor background model. |
When the sky lines are very weak in stare mode, which is often the case in short-exposure frames, such as in the UVB arm, the background model constructed by the pipeline can fail catastrophically, particularly if weak pattern noise is not properly subtracted by the master bias. This arises from electronic noise from the CCD readout amplifiers and varies in position (and amplitude) on each frame in an unpredictable manner. The derived master bias frame contains an average of the electronic noise features of each input bias frame, and neither the individual bias frames nor the average master bias frame had the same noise pattern as the science (star) frame. When the pipeline attempts to remove the background (“sky”) in the science (star) frame, it generates features in the “sky” that attempt to replicate the noise pattern of the image after corretion by the corrupted master bias frame. Figure 4 illustrates an extreme case of this: the left-hand panel is the observed star, and the right-hand panel is the background modeled by the pipeline, where the modeling has clearly failed. In such cases, we turn off sky subtraction in the pipeline. Instead, we estimate the sky using pixels on either side of the stellar spectrum in the rectified 2D spectra of each spectrograph order, as would be done for observations in stare mode.
The final sky-subtracted 1D spectrum is derived by subtracting the 1D sky spectrum from the 1D spectrum. In Fig. 5, we compare the two methods, showing that the in-place background estimation gives a clear improvement.
 |
Fig. 5 1D spectra extracted from the UVB arm, using the pipeline sky model (black) and a background extracted directly from the observation (red), when the sky emission lines are weak (or not observed). The blue spectrum shows the difference between the two methods. In the right panels, we zoom into three small wavelength regions, so that the sky modeling errors of the pipeline are clear. |
3.1.3. Extra cosmic ray cleaning
 |
Fig. 6 Panel a) black: 1D spectrum extracted from the pipeline; red: 1D spectra extracted after raw frames corrected using the algorithm of van Dokkum (2001). Panel b) raw image of “B” frame zoomed in on the CRH feature (red circle). Panel c) pipeline-corrected 2D spectrum zoomed in on the CRH feature (red circle). |
The X-shooter pipeline (ver. 1.5.0) removes the cosmic ray hits (CRHs) for multiple input images (n ≥ 3) in nodding and offset modes by computing a median of these images and applying a sigma-clipping. If only two raw images are used as input, as is the case for most of our nodding and offset mode exposures, proper CRH cleaning is not performed by the pipeline. This becomes an issue when a CRH in image “A" is sitting on the same position as the star in image “B”; this results in an artificial emission or absorption line in the final 1D spectrum. We present the case of exposures of the star [M2002] SMC 55188 in the VIS arm in Fig. 6a to illustrate the problem. We see an artificial feature around 1004 nm caused by the CRH in the original “B” frame, (Fig. 6b), which creates an artificial feature in the 2D image. To correct this problem, we use the algorithm of van Dokkum (2001, as implemented in the IDL code “la_cosmic.pro to clean the raw image before running the pipeline. The CRH-corrected images are then run through the pipeline before extracting the 1D spectrum (Fig. 6a). The CRH pre-cleaning is used whenever strong CRHs are found to corrupt the 1D spectra.
3.1.4. Bad columns
We have found that the bad pixel maps produced by and used in the pipeline reduction recipes do not always produce a complete list of bad pixels. In particular, a few bad columns in the VIS arm that are improperly mapped in the pipeline disrupt the object spectra in order 26 at 635–638 nm. Figure 7 shows these bad columns in the raw frame and the final 2D spectrum. These bad columns are difficult to correct effectively in the raw spectra and make it difficult to reconstruct the profile of the star in this region. Moreover, due to instrumental flexure, these bad columns can affect different exposures at slightly different wavelengths. In the current version of the spectral library, we have set the fluxes to zero from 635.1 nm to the end of order 26 in the final reduced 2D order-by-order frames.
3.1.5. Extraction of 1D spectra from pipeline-corrected 2D images
 |
Fig. 7 Upper panel: raw image of the telluric standard star Hip024505 zoomed into a region of bad columns in the VIS arm. Lower panel: corresponding final, pipeline-corrected 2D spectrum of this star. |
After the pipeline reduction and our modifications, we extract a one-dimensional spectrum from the pipeline-corrected, flat-fielded wavelength and geometrically corrected, single-order 2D spectra using our own weighted-extraction code in IDL, which is inspired by the prescription of Horne (1986). There are three extensions in total for each order in the pipeline-produced 2D spectra: the first is the flux in counts, the second is the error, and the third is the quality, which corresponds to the bad pixel mask. We make use of the third extension as the first guess for a bad pixel mask, and the second extension as the square root of each pixel’s variance. With 2 to 20 iterations, the bad pixel mask is improved, and most of the CRHs or bad pixels are masked. Spectra from each order are then extracted and merged using a variance-weighted mean of each wavelength in the overlapping regions.
The extraction aperture was set to a fixed width of 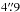 (in narrow-slit observations) or
(in narrow-slit observations) or 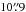 (in wide-slit observations) in the optimal-extraction code. However, if significant CRHs or other problems remain within the nominal extraction aperture of the final 2D frame, the extraction aperture was modified to exclude these regions.
(in wide-slit observations) in the optimal-extraction code. However, if significant CRHs or other problems remain within the nominal extraction aperture of the final 2D frame, the extraction aperture was modified to exclude these regions.
 |
Fig. 8 Order-by-order 1D spectrum extraction for the G2 star HD17072 in the UVB arm without flux calibration. Different colors correspond to different orders. The continuous black spectrum is the combined spectrum, which is offset for clarity. In the middle and bottom panels, we zoom in on two wavelength regions, 504–520 nm and 390–410 nm, where orders overlap to see the extraction and combination process in detail. |
We show a G2 star, HD17072, observed in the UVB arm in Fig. 8 to illustrate this process. We note that the orange order between 355 and 370 nm shows noisy features. However, the larger errors in this region yield lower weights compared with the green order in the overlap region. These features therefore do not appear in the final merged spectrum (thin black line).
3.2. Saturation
 |
Fig. 9 A saturated raw VIS arm frame after transformation of counts to a binary “good pixel”/“saturated pixel” basis, and summed along the wavelength direction. Note the sharp features with values in excess of 200, indicative of saturation due to overexposure. See text for details. |
In these first two periods, saturation was a common problem, as our sample contained variable stars near X-shooter’s bright target limit (and our exposure times were, in the absence of accurate light curves, determined for the mean stellar brightnesses). Given the large total number of frames in these periods (1847 for the 258 observations, including NIR arm spectra), an automated saturation-detection scheme was required. Uncorrected CRHs and bad pixels appear as nearly saturated pixels, so a scheme had to be developed to decide which frames were strongly saturated and had to be discarded. Every raw frame was transformed using the following rules. In the UVB and VIS arm images, pixels with counts ≥65 000 are set to “1”, which means “saturated”; all others are set to “0”, which means “good”3. Truly saturated frames typically have saturated pixels clustered together in individual orders. We sum each transformed binary “good”/“saturated” image along the wavelength direction for better visualization of the saturation. We show an example of this transformation for a typical saturated raw frame in Fig. 9. Here, saturated pixels are accumulated along the orders, showing sharp features. Raw frames with such features are considered to be “saturated” and removed from the library. In the end, 173 (9.3%) of 1847 extracted spectra were found to be “saturated” and removed.
4. Telluric correction
Ground-based spectroscopy is always subject to contamination from the Earth’s atmosphere. The sky subtraction described in Sect. 3.1 corrects for the additive component of this contamination, which leaves the multiplicative effect of absorption. In the visible and NIR portions of the spectrum, water vapor, molecular oxygen, carbon-dioxide, and methane generate strong absorption features. Absorption features that originate in the Earth’s atmosphere are referred to as telluric features. Correction for telluric contamination, therefore, is important for the XSL spectra in the VIS and NIR arms. The correction for the continuous component of atmospheric extinction is discussed in Sect. 5.1.
In general, if we knew how much light was absorbed by the Earth’s atmosphere in a certain wavelength region, we could “recover” the fluxes in that region by dividing the known absorbed fraction. This requires a telluric template, either determined by modeling the atmosphere by a radiative transfer code, such as ATRAN (Lord 1992) and LBLRTM4, or by observations of ideally featureless stars (in practice typically hot stars, whose only features are hydrogen and/or helium lines). Although radiative transfer codes have been shown to be promising (Seifahrt et al. 2010) to remove the atmospheric absorption, particularly at high spectral resolution in the NIR, this method requires a molecular line database and a model atmosphere based on meteorological data as input. Because we have thousands of spectra taken at different airmasses, pressures, and humidities, this method is currently computationally too expensive.
Instead, we use telluric standard star observations that are taken as part of the standard X-shooter calibration plan directly after each of our science observations as a basis for telluric correction of our data. The narrow-slit settings are used for the telluric standard observations to match the highest resolution of our science observations.
 |
Fig. 10 Ratio of counts between Cl* NGC 6522 ARP 4329 and the closest (in elapsed time) telluric standard star Hip094378, zoomed in the “A” band in the VIS arm. |
We find that the telluric absorption lines change strength on timescales shorter than the “long” exposure time (≥90 s) of faint XSL stars and the total overhead time of ~900 s, which results in an imperfect telluric correction. In addition, small changes in spectral resolution and wavelength zero-point occur even between successive observations. Figure 10 shows the ratio of counts between a science object (Cl* NGC 6522 ARP 4329, an M star in the Galactic bulge) and the telluric standard star (Hip094378, a B2V star) observed 37 min later. The ratio shows that the closest telluric standard spectrum does not give a satisfactory solution for the atmospheric transmission.
To optimize the telluric correction, we have built a library of telluric spectra, where the hot stars were first carefully wavelength-(re)calibrated. The final library is a large collection of different atmospheric transmissions used to correct the telluric absorption features in the XSL spectra, as described below. We note that we only discuss the correction of the VIS arm spectra in this paper, as the UVB spectra do not require telluric line correction, and we will discuss the NIR spectra in another paper.
4.1. The telluric library
Input stars for the VIS-arm telluric library.
We have collected 178 VIS arm spectra of telluric standard stars with spectral type A, B, and G in Periods 84 and 85. The data were reduced identically to the program spectra. As the G stars are much cooler and have more lines than A and B stars, we have not used them to build our telluric templates. Moreover, 22 out of 175 spectra of A and B had strong intrinsic emission lines and have not been used either. Full Table 3 lists the 152 telluric standard stars (and the airmass at which they were observed) used in the telluric library.
4.1.1. Identification of atmospheric transmission features
The goal of building the telluric library is to produce a collection of empirical atmospheric transmission spectra for use as a basis for correcting the telluric absorption in the science spectra. To accomplish this, the main telluric features in the observed telluric standard spectra must be separated from the intrinsic features of these hot stars.
To extract the atmospheric transmission from the 1D spectrum of a hot star, we need to identify the intrinsic spectral features of the star. We use synthetic spectra from model atmospheres drawn from the POLLUX database5 (Palacios et al. 2010) for stars with effective temperatures of 10 000–15 000 K and synthetic spectra from Munari et al. (2005) for stars with effective temperatures of 15 000–27 000 K. We use the full-spectrum-fitting program pPXF (Cappellari & Emsellem 2004) to fit the hot star’s intrinsic features with the synthetic spectra. We choose a subsample of templates from the collection of synthetic spectra, according to the spectral type of each telluric standard star.
 |
Fig. 11 Extraction of the telluric absorption from the B8V star Hip012389. The black spectrum is the original 1D spectrum (without telluric or flux calibration). This spectrum is fit by a synthetic LTE spectrum from a model atmosphere in the pixels outside of the vertical green lines. The red spectrum represents this fit. The lower part of the plot shows the residuals from the best fit: green points represent regions of intrinsic stellar absorption, while blue points are (almost) the telluric absorption spectrum. We note that the residual between the best fit and the data is scaled to the view level. It is, therefore, not surprising that some features are below zero. |
Pixels that are fit well by the model template are marked as intrinsic features of the hot stars, while any others are marked as contaminated by telluric features. It is not always straightforward to recognize which pixel belongs to the star itself or is affected by the atmosphere especially when the atmospheric features are superimposed on the hydrogen Paschen absorption lines of the hot stars, which is in the wavelength region ~8900–9800 Å. Furthermore, some lines affected by non-local thermodynamic equilibrium (NLTE) effects are not perfectly reproduced by the LTE POLLUX and Munari models. To separate the pixels containing telluric features from those containing intrinsic stellar features, at least two iterations are necessary. In the first iteration, we define strong hydrogen absorption regions uncontaminated by telluric absorption and fit these with the model synthetic spectrum and a moderate-order multiplicative polynomial. Because some parts of the Hα line (λ 6562.8 Å) are affected by NLTE (Thurl et al. 2006) and the core is occasionally filled by weak absorption, this line can be very hard to reproduce by the models based on LTE. We therefore mask the core of the Hα line, which is roughly ± 4 Å around the line center, and replace this region with the same wavelength region of the fitted model after the fit. Residuals from this first iteration are assumed to represent the noise of each pixel. Pixels deviating by more than 3–5 standard deviations from this first fit are mostly telluric absorption features and are masked from the fit in the next step.
In the second iteration, the fit is performed with a high-order multiplicative polynomial, and we are able to match the continuum of the hot star in detail. A B8V star is shown in Fig. 11 to illustrate the fitting process in this iteration. Subsequent iterations were occasionally necessary to improve the final fit. The telluric features were then extracted by dividing the original 1D telluric standard star spectrum by the best fit of the final iteration.
We call the telluric features extracted by this process the “raw transmission spectra”, as there are several steps required before the telluric library is ready to be used. The quality of the raw transmission spectra depends on the templates of the hot stars, the signal-to-noise of the original X-shooter spectra, and the multiplicative polynomial used in the fitting.
4.1.2. Absolute wavelength calibration and spectral cleaning
 |
Fig. 12 Two normalized telluric standard stars, Hip026545 (black line) and Hip012389 (dashed red line), zoomed into the wavelength region 9570–9620 Å, showing the impact of the flexure of the X-shooter backbone on the wavelength calibration. The wavelength shift is roughly 2 pixels between these two spectra, or ≈10 km s-1. |
To build the telluric library, all the telluric features in different standard stars must be at exactly the same wavelengths. We find that the wavelengths for the same telluric feature are slightly shifted in different spectra, due to the flexure and imperfect rotation of the X-shooter backbone. In Fig. 12, we show an example of this shift, which is equivalent to ≈10 km s-1 in this case. We therefore require an extra wavelength calibration step for each raw transmission spectrum.
Although we do not use theoretical atmospheric transmission spectra to correct our spectra for telluric absorption, we use them as references for the final wavelength calibration. We use a high-resolution (R ~ 60 000) model transmission spectrum computed for us by J. Vinther from the ESO Sky Model Calculator6 as a template to cross-correlate and correct the small residual wavelength offsets in the raw transmission spectra.
 |
Fig. 13 Extracted raw transmission spectrum from the B8V telluric standard star Hip012389 (black) and the shifted, cleaned “final” transmission spectrum from this star (red). The raw transmission spectrum has been offset for clarity. |
The extracted transmission spectra are inevitably influenced by the signal-to-noise ratios of the original spectra (and any remaining bad pixels). To reduce the influence on the final telluric-corrected spectra, especially those pixels which are not contaminated by telluric features, we “clean” the shifted transmission spectra based on the model transmission template. Pixels with values, which deviate more than 10 sigma from the template, are set to unity, so as not to introduce noise or artificial features into the telluric-corrected science spectra. Figure 13 shows the raw transmission spectrum and the shifted, cleaned transmission spectrum extracted from the telluric standard star Hip012389.
After carefully checking the quality of the output transmission spectra, the telluric library with 152 final transmission spectra is ready to be used.
4.2. Final telluric correction
Once the telluric library is available, we can perform the telluric correction on the science spectra. The simplest process would be to divide a science spectrum by the temporally-closest transmission spectrum. An improvement is obtained by exploiting the variety of telluric absorption properties present in our large telluric library. A combination of telluric templates can provide a better estimate of the telluric absorption in a given science exposure than the one telluric standard observed closest in time (Chen et al. 2011).
The key to our telluric correction method, which is similar to producing the telluric library itself, is the determination of the underlying stellar spectrum. A quick glance at the extracted 1D spectra shows that it is easier to define the continua of warm stars than cool stars, such as M-type giants and dwarfs, carbon stars, or LPVs. We therefore classify the science spectra according to their spectral types into two groups: those that have easily-determined continua, O to K stars, and the cooler stars, which do not. For warm stars, we estimate the atmospheric transmission using the optimization algorithm described below, which makes use of the original science spectra; for the cooler stars, we simply use the temporally-closest transmission spectrum from the telluric library.
4.2.1. Reconstructing telluric absorption with principal component analysis
Algorithms that estimate the telluric absorption by seeking the best linear combination of the 152 templates of the telluric library seemingly succeed (i.e., they produce a result that passes eye inspection), but they are dangerous: this linear problem is ill-conditioned. There are not 152 meaningful degrees of freedom in this problem. In more physical terms, there are not 152 fundamental Earth-atmospheric parameters that produce differences between transmission curves larger than the amplitude of the noise in the XSL data. The consequence is that the linear combination coefficients derived from a standard linear-optimization algorithm are determined to a large extent by the noise in the spectra rather than by the telluric features of interest (see Ocvirk et al. 2006, for further explanations in a conceptually similar context). Details of the science spectrum that are not telluric features may be erased. To avoid this issue, one needs to remove items from the telluric library until the linear problem is well behaved. We ask: but which ones? We use principal component analysis (PCA) to circumvent this problem.
Principal component analysis reveals the internal structure of a data set in a way that best explains the variance in the data. It is widely used in analyzing multidimensional data sets. In data reduction applications, PCA has been used for sky subtraction by Wild & Hewett (2005) and Sharp & Parkinson (2010). Inspired by this idea, we have developed a method to determine the telluric correction for our (warm) program stars. The algorithm (Wild & Hewett 2005) is to determine the basis vectors from those pixels, which vary most in the spectra of the telluric library. The amplitudes given by the projection of these basis vectors onto each science spectrum are used to reconstruct the telluric features in the science spectrum. Telluric correction is then a straightforward division of science spectrum by the projected telluric spectrum.
PCA components.
The telluric library contains 152 spectra, and each spectrum has a length of 43 615 pixels. Standard PCA analysis would require diagonalizing a 43 615 × 43 615 matrix, which is computationally expensive. Instead, we assume that X is the matrix that we built based on the telluric library with the mean subtracted from each individual spectrum. The covariance matrix C for computing the eigenvectors then can be written as 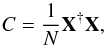 (1)where X† is the transpose of the matrix X and N is the number of objects, which is 152 here. The eigenvectors ui then can be solved from the equation
(1)where X† is the transpose of the matrix X and N is the number of objects, which is 152 here. The eigenvectors ui then can be solved from the equation 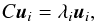 (2)where λi is the eigenvalue associated with ui. If we expand Eq. (2) and multiply by X on both sides, we have
(2)where λi is the eigenvalue associated with ui. If we expand Eq. (2) and multiply by X on both sides, we have 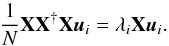 (3)Equation (3) has the same set of eigenvalues as Eq. (2) for the vector vi = Xui. The dimension of the array XX† at 152 × 152 is much smaller than in the standard formulation, dramatically reducing the computing time. When the temporary eigenvector vi is derived, we can derive the original eigenvector ui. We wrote our own IDL PCA code following the above algorithm and performed the PCA on our 152 telluric library spectra. The extracted 152 eigenvectors or principal components are then ready to be used to reconstruct the telluric features in the science objects.
(3)Equation (3) has the same set of eigenvalues as Eq. (2) for the vector vi = Xui. The dimension of the array XX† at 152 × 152 is much smaller than in the standard formulation, dramatically reducing the computing time. When the temporary eigenvector vi is derived, we can derive the original eigenvector ui. We wrote our own IDL PCA code following the above algorithm and performed the PCA on our 152 telluric library spectra. The extracted 152 eigenvectors or principal components are then ready to be used to reconstruct the telluric features in the science objects.
Figure 14 shows the first six principal components from the bottom to top. The first two components have a clear physical meaning: the first component shows the mean spectrum of the telluric library, while the second component appears to separate most of the water vapor features (seen “in absorption”) from O2 features (seen “in emission”).
 |
Fig. 14 The first six principal components of the telluric library. The eigenvalues decrease from the bottom to the top of this figure (i.e., the first and largest eigenvector is the lowest). The eigenvectors have been offset for display purposes. |
Reconstructing the telluric absorption spectra.
Two steps remain before we can obtain the final estimate of the telluric absorption in a science spectrum. First, we must normalize the science spectrum. Second, we have to correct the wavelength offset of the telluric features in the observed spectrum (due to instrument flexure) from the wavelengths of the telluric library spectra that are more accurate. The resulting telluric absorption spectrum is used to correct the science spectrum. In this procedure, any intrinsic absorption or emission features should not be removed from the science spectra. An accurate estimation of the stellar continuum is therefore required. We recall that we only perform the PCA reconstruction for the spectra of warm stars.
To normalize a science spectrum, we need to determine its continuum. We have developed an IDL code that determines an approximate continuum for a (warm) star. The code seeks the strong intrinsic features (e.g., Hα, Hβ, Caii triplet etc.) from a line list7, according to the radial velocity given by ULySS and defines them as nodes. We flag pixels between those nodes that have a second derivative greater than zero and replace them by a linear interpolation between the nearest unflagged pixels. By this process, weak and narrow lines are rejected, since we only care about a rough continuum. Usually around three to five iterations are used to find the local continuum between two nodes. Once the continuum of a spectrum has been found, the science spectrum is easily normalized by dividing the continuum before finding the PCA components.
We use pPXF to determine any residual wavelength shift in the telluric lines of the normalized science spectrum, taking the first principal component as a template. The shift is applied to the PCA components, thus avoiding unnecessary rebinning of the science spectrum.
For wide-slit observations, pPXF also determines an adequate broadening function for the lines of the telluric library. The principal components are then convolved with this function before they are used. We note that smoothed PCA components are not precisely the PCA components of a smoothed telluric library. After a few tests, smoothing first was judged to be too computationally expensive for our current purpose, considering that the wide-slit observations are used only to correct the high resolution observations for slit losses.
We finally project the mean-subtracted, normalized science spectrum onto the modified principal components and sum these projections. The final estimate of the transmission is derived by the combination of 40 principal components with the amplitudes that result from the projection. However, stars with weak emission lines or with a high density of lines present a challenge, and for these stars, we use only 20 components to avoid affecting their intrinsic features by mistake. Once the reconstructions have been constructed, the telluric correction can be performed by dividing the normalized spectra by the reconstructed transmission. The final telluric-corrected spectra are then derived by multiplying the resulting spectra by the continuum.
 |
Fig. 15 Spectrum of HD 164257 (A0) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. |
 |
Fig. 16 Spectrum of HD 193896 (G5IIIa) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. The spikes around 7600 Å are residuals after telluric correction. |
 |
Fig. 17 Spectrum of HD 79349 (K7IV) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. The spikes around 9350 Å are residuals after telluric correction. |
 |
Fig. 18 Telluric correction by two different methods for the cool bulge LPV star OGLEII DIA BUL-SC1 235. The black line is the original 1D spectrum extracted, and the blue and red lines are the spectrum after correction by the PCA reconstruction and the temporally-closest telluric absorption spectrum, respectively. The green spectrum is an M5III star with a similar temperature, HD175865, taken from NGSL as a comparison. |
We show the original 1D spectra of HD 164257 (A0V), HD 193896 (G5IIIa), and HD 79349 (K7IV) and their telluric-corrected versions in Figs. 15–17, respectively. We find that the telluric correction by the PCA reconstruction has done a reasonable job for both the early-type stars and some late-type stars. In general, this method works better for stars with simpler continua and high signal-to-noise ratios. Occasionally, division by almost zero produces artificial spikes, such as those seen at 7600 Å in Fig. 16 or at 9300–9400 Å in Fig. 17. When these occur, we flag the pixels that are incorrectly reconstructed and set them equal to zero in the final telluric-corrected spectra.
4.2.2. Telluric correction for cool stars
The PCA method requires an accurate representation of the stellar continuum to work correctly. It is difficult to trace the continua of cool stars. For instance, carbon stars have strong and sharp molecular bands. One therefore has to trace each absorption bandhead, which can be difficult because some molecular bands occur exactly at the same wavelengths as the telluric absorption regions. In this case, we use the temporally-closest transmission spectrum from the telluric library.
As in the warm stars, we must correct residual wavelength calibration errors and match the line-broadening of the science and the temporally-closest transmission spectra before dividing. We calculate these corrections as described above, using the wavelength range of the atmospheric “A” band of O2. The “A” band is chosen because it is the strongest telluric absorption feature in the VIS arm spectra and is easily distinguished from other molecular species. The telluric correction is then made by directly dividing the science spectrum by this modified transmission spectrum.
By using the closest telluric absorption spectrum, there is the risk that one may over- or underestimate the real telluric spectrum of the science object. In the case that the exposure time of the science object is short and the accompanying telluric standard star spectrum is therefore very close in time to the science object, this method does a better job to preserve the intrinsic features of the stars than the PCA method for cool stars. We show an example of the telluric correction made by both methods on an LPV star OGLEII DIA BUL-SC1 235 in Fig. 18. To make sure where the molecular bands should be, we use an NGSL star HD175865 with similar temperature as a comparison, which has no telluric contamination. The PCA reconstruction method, as shown in the blue spectrum, does not reproduce the molecular bands properly. The correction by the closest transmission spectrum, although not perfect, is closer to the intrinsic features of the star, as we can distinguish the molecular bands clearly.
We use this method on all carbon stars, LPV stars, and most of the cool M stars. We remind the reader that the method (using the closest transmission spectrum) for cool stars may not be the final, best solution for these stars, but we use it in the absence of accurate spectral models of these (molecule-rich and typically variable) stars.
4.2.3. Comparison of the two methods of telluric correction for warm stars
 |
Fig. 19 Telluric correction by the PCA reconstruction and temporally-closest telluric absorption methods on the G3V star G169-28. Symbols and wavelength ranges are the same as in Fig. 18. |
To test the PCA reconstruction method, we compare the results with a simple correction using the closest telluric absorption spectra on warm stars. In Fig. 19, we show the telluric correction achieved by our two methods for the G3V star G169-28. We zoom into the atmospheric “A” band for a fair comparison. It is clear that the PCA reconstruction does a better job than the temporally-closest telluric absorption spectrum in this warm star. Again, whether we use the PCA reconstruction method to perform the telluric correction depends on whether we can determine an accurate representation of a star’s continuum.
5. Flux calibration
To perform a reliable flux calibration, we observed several spectrophotometric standards (BD+17 4708, GD 71, GD 153, EG 274, Feige 110, LTT 3218, and LTT 7987) with a wide slit (5″ × 11″) in “stare” mode at different airmasses. All flux standard stars used here were observed with the readout mode “100k/1pt/hg”. The median signal-to-noise ratio of the flux standards (44 spectra in the UVB arm and 43 spectra in the VIS arm) spanned the range between 100 and 800.
5.1. Construction of the extinction curve
To reconstruct the intrinsic flux and spectral shape, it is important to correct the spectra for atmospheric extinction. We start from the basic assumption that the atmospheric (extinction curve) and instrumental (response curve) properties are uncorrelated. Determining the extinction curve then can be simply done by assuming the extinction curve does not change with time.
We reduced and extracted the spectra of flux standard stars with the same set of master bias and master flat-field frames in each arm. Telluric correction was performed in the VIS arm for each flux standard. The spectra of the standards were compared with the flux tables of the appropriate stars from the CALSPEC HST database8 (Bohlin 2007). By running IRAF.standard and using the Paranal extinction curve (Patat et al. 2011) as a first guess, we derived the extinction curve for our X-shooter observations in the UVB and VIS arms.
The extinction curve of the XSL in Period 84 and 85 is shown in Fig. 20, where the Paranal extinction curve (Patat et al. 2011) is shown as a reference. We find that the inferred extinction curve is very similar to that given by Patat et al. (2011) with a slightly steeper extinction coefficient in the red.
 |
Fig. 20 Extinction curve for XSL in the UVB arm (blue line) and the VIS arm (red line). The Paranal extinction curve of Patat et al. (2011) is shown as the black line for comparison. Lower panel shows the residual between XSL and Patat et al. (2011) calculated by the IRAF.standard procedure and applied to derive the XSL extinction. |
5.2. Construction of the response curve
We create our response curves as follows. First, for a given science spectrum, we reduce its flux-standard star with the same set of master bias and master flat-field frames as used for the science observation and extract the 1D spectrum. For the VIS arm spectra, we perform the telluric correction on the 1D spectrum of the flux standard. Second, the airmass of the flux standard is used to derive the atmospheric extinction using the XSL extinction curve. Third, the 1D spectrum of the flux standard is corrected by F′ = FADU/texp × AtmExt, where FADU is the original 1D spectrum, texp is the exposure time of the flux standard, and AtmExt is the derived extinction term. We compare this corrected 1D spectrum with its flux table from the CALSPEC HST database. The final response curve is derived by fitting a spline to the ratio between the reformed 1D flux standard spectrum and the corresponding flux table.
Because the flat field and bias of X-shooter are not stable, at least in Periods 84 and 85, the response curve derived from each flux standard can vary by around 5%. We show the averaged response curve in the UVB and VIS arm, respectively, in Fig. 21 to illustrate the overall response of the instrument. The sharp feature around 3700 Å in the top plot is due to the two flat field lamps used in the UVB arm. We note that there is a strong feature beyond λλ 5500 Å in the UVB arm (top panel). This is due to the dichroic used to split the beam between the UVB and VIS arms. This feature is also seen in the VIS arm before λλ 5800 Å (lower panel in Fig. 21).
 |
Fig. 21 Average response curves in the UVB (upper panel) and VIS arm (lower panel). The dotted line in the VIS arm indicates a low signal-to-noise region, interpolated for display purposes. Dichroic features are shown in both UVB and VIS arms around 5600–5800 Å. |
5.3. Flux calibration of individual frames
We note that the dichroic features do not always appear in the same position in the extracted 1D spectra, and therefore, it is difficult to completely remove those features in our final flux-calibrated spectra. To minimize the influence of the dichroic, we choose the observation closest in time for each science observation of a certain flux-standard star as the corresponding flux standard. The chosen flux standard is reduced and extracted as described above. If the binning of the science observation is different from the selected flux standard, we rebin the selected flux standard first.
For each science spectrum, we generated its response curve following the procedure described above. The flux-calibrated science spectrum is derived using the formula, 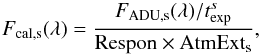 (4)where FADU,s is the 1D spectrum of the science object,
(4)where FADU,s is the 1D spectrum of the science object, 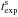 is the exposure time of the science object, Respon is the derived response curve, and AtmExts is the extinction term calculated from the airmass and the extinction curve of XSL. We perform the flux calibration process on both narrow slit and wide slit observations.
is the exposure time of the science object, Respon is the derived response curve, and AtmExts is the extinction term calculated from the airmass and the extinction curve of XSL. We perform the flux calibration process on both narrow slit and wide slit observations.
5.4. Final flux calibration
A final flux calibration is carried out on the narrow-slit observations using the shape of wide-slit observations to avoid flux losses. We use the wide-slit exposure paired with each flux-calibrated, narrow-slit spectrum to do this. If an unsaturated wide-slit observation is available, we run pPXF to shift and broaden the narrow-slit spectrum. The flux correction is performed by multiplying the narrow-slit spectrum by the second-order polynomial determined by pPXF. For the narrow-slit spectra whose corresponding wide-slit spectrum are saturated, we leave their flux as in the previous step (individual flux calibration). We note that stars without wide-slit flux correction may be missing flux, especially in the UVB arm.
5.5. ADC issue in the UVB arm
Some of our data, especially narrow-slit observations in the UVB arm that are observed from 18 July 2010 to 2 August 2010, are influenced by a failure of the atmospheric dispersion compensator (ADC). To correct for this ADC issue, we perform the following steps. First, we run pPXF to determine the possible shift and broadening between the narrow- and wide-slit observations. Second, we convolve the narrow-slit observation to the same resolution and wavelength range as the wide-slit exposure according to the first step. Third, we smooth the wide-slit observation and wide-slit-like narrow slit spectrum, respectively, with a boxcar size of 500 pixels to avoid possible noise features. The final compensation curve is given by the ratio of smoothed versions of the wide- and narrow-slit observations. Once the compensation curve is derived, we multiply it to the original narrow-slit spectrum to perform the flux calibration.
 |
Fig. 22 Average line-spread functions for the FGK stars (212 spectra) in the UVB (upper panel) and VIS (lower panel) arms. In each arm, the top panel shows the residual shift of the spectra (blue dots). The bottom panel shows the detected instrumental velocity dispersion. A simple first-order polynomial fit (red lines) of the line-spread function is marked in each panel. The error bars are the standard deviation in each wavelength bin. The three open circles show the region where two different flat field lamps are used in the UVB arm, which may result in larger uncertainties. |
6. Quality checks
6.1. Spectral resolution
We now determine the line-spread function (LSF) of our X-shooter spectra to accurately measure the spectral resolution and confirm the wavelength calibration of our observations. We fit the spectra of our F, G, and K stars (212 spectra) using the synthetic library of Coelho et al. (2005) as templates. To determine the LSF, we use the function ULY_LSF from ULySS, which minimizes the difference between the observed spectra and a parametric model by full-spectrum fitting (Koleva et al. 2008, 2009). The fit is performed in wavelength intervals of 200 Å spaced by 60 Å.
Figure 22 shows the LSF for the F, G, and K stars from XSL in the UVB (upper panels) and VIS (lower panels) arm, respectively. In each arm, we estimate the mean instrumental velocity dispersion (σ) and residual shift (v) using the IDL procedure BIWEIGHT_MEAN. The mean difference of the residual velocity in the UVB arm spans the range between −2.6 and + 2.3km s-1. This may be due to the imperfect wavelength calibration. We find that the wavelength solution is very good in the VIS arm (upper panel in the lower plot).
The instrumental velocity dispersion in the UVB arm ranges from 13.3 to 18.1km s-1, corresponding to a resolution R = 9584 − 7033. The fitted instrumental resolution in km s-1 is given by 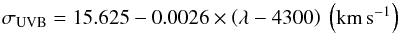 (5)with λ in Å. In the VIS arm, the instrumental variation is constant at σVIS = 11.62km s-1(i.e., R = 10 986), which is very close to the stated resolution R = 11 000.
(5)with λ in Å. In the VIS arm, the instrumental variation is constant at σVIS = 11.62km s-1(i.e., R = 10 986), which is very close to the stated resolution R = 11 000.
 |
Fig. 23 Root-mean-squared deviation of the ratio between the PCA-based and closest-in-time telluric corrections for 20-F stars from XSL. |
 |
Fig. 24 Upper panel: response functions of UBVRI filters (solid lines) and the Monitor Telescope u′,g′,r′,i′,z′ filters (dotted lines). Both systems are normalized to 1. Bottom panel: a typical XSL spectrum of HD82734 (K0III) for comparison. |
 |
Fig. 25 Comparison of synthetic (U − B), (B − V), (V − I), and (R − I) colors in XSL and NGSL. The residuals in each panel are calculated as colorXSL − colorNGSL. Blue squares indicate those stars that likely have flux losses, due to a lack of useful wide-slit observation. |
6.2. Arm combination
After carefully checking the resolution and flux calibration of our sample, we shift every spectra to zero velocity using the synthetic libraries of Coelho et al. (2005); Palacios et al. (2010), and Allard et al. (2011) as templates. The second wavelength calibration in the UVB arm is carefully performed to correct the small shifts shown in the upper panel of Fig. 22. Multiple observations of the same non-variable star are combined in the same arm. Multiple observations of the same variable star are kept as different spectra. We merge multiple UVB and VIS arm spectra of each star into a single spectrum using the overlapped region, mostly from 5420 to 5650 Å. Some of the spectra have the dichroic features slightly shifted in wavelength, and in this case, we shift the overlapped regions accordingly. The merged spectra of each star are carefully checked and evaluated to maintain the appropriate spectral shape.
6.3. Uncertainty of the PCA telluric correction
We have computed the root-mean-squared deviation of the ratio between the PCA-based and closest-in-time telluric corrections for 20 F stars from the sample. We plot this ratio in Fig. 23. We suggest that this is the maximum value of uncertainty that is likely in the PCA-based correction for any given warm star, as the closest-in-time telluric correction could be very different than the true telluric correction, if the closest-in-time calibrator in terms of the timescale of atmospheric changes in the molecular absorption lines was taken at a slightly different airmass at a time that is significantly after the program star.
6.4. Photometric comparison
We have calculated synthetic colors on the Johnson-Cousins UVBRI and Sloan Digital Sky Survey (SDSS) systems for our XSL stars and compared them with published values to check the reliability of our flux calibration.
A number of studies have discussed the response functions required to reproduce the standard Johnson-Cousins UVBRI photometric system (Johnson et al. 1966; Cousins 1971, 1973; Landolt 1973, 1983; Bessell 1990). Those which reproduce the observations most accurately are likely to be the work by Bessell (1990) and Fukugita et al. (1995). We therefore use the response functions from Bessell (1990) for the UVBRI system. The SDSS response functions (Fukugita et al. 1996) without the atmosphere are adopted here to calculate the colors through the u′g′r′i′z′ filters. We show the normalized UBVRI (solid lines) and SDSS (dotted lines) response functions in Fig. 24.
We have calculated the synthetic B − V, U − B, R − I, and V − I colors of the XSL sample. The synthetic magnitude of a filter X in the Johnson-Cousins system is given by ![\begin{equation} M_{X} = - 2.5\times \log_{10} \bigg[\frac{\int{\lambda f_{\lambda}(\lambda) R_{X}(\lambda) {\rm d} \lambda}} {\int \lambda f^{\rm Vega}_{\lambda}(\lambda) R_{X}(\lambda) {\rm d} \lambda}\bigg] + C_{X} , \end{equation}](/articles/aa/full_html/2014/05/aa22505-13/aa22505-13-eq92.png) (6)where X can be any of the filters UBVRI, RX(λ) is the response function of the filter X, CX is the X magnitude of Vega, and fλ and
(6)where X can be any of the filters UBVRI, RX(λ) is the response function of the filter X, CX is the X magnitude of Vega, and fλ and 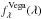 are the flux densities of the object and Vega, respectively.
are the flux densities of the object and Vega, respectively.
To check the colors, we compare our synthetic colors with synthetic colors from the NGSL library (Gregg et al. 2006) and observed colors from the Bright Star Catalogue by Hoffleit et al. (1983); Hoffleit & Jaschek (1991). There are a total of 77 stars in common with the NGSL library. Figure 25 illustrates the color comparison between NGSL and XSL. We calculate the mean offset and rms scatter for the (U − B), (B − V), (V − I), and (R − I) colors but avoiding stars which may have flux losses. The results are summarized in Table 4, where “XSL – NGSL” is the mean difference between colors of XSL and NGSL. We find an agreement at level of 2.4–7.1% between the XSL and NGSL synthetic colors.
 |
Fig. 26 Comparison of synthetic (B − V) and (U − B) colors of XSL and the Bright Star Catalogue. The residuals are calculated as in Fig. 25b. Blue squares indicate those stars that likely have flux losses due to a lack of useful wide-slit observation. |
Mean color difference and rms scatter between XSL and NGSL.
To further check the flux calibration, we also compare our colors with U − B and B − V colors from the Bright Star Catalogue. There are in total 54 stars in common. We show the comparison in Fig. 26. The XSL stars with flux losses are marked as blue squares. The star, which has a 0.3 mag difference between literature and measured U − B, is the variable star HD170756, which has a significant U − B scatter in the literature values (~0.5 mag) as well. The mean offsets and rms scatter measured from each color are summarized in Table 5. The large scatter in the U − B residual is partly due to variable stars and partly due to the low signal-to-noise region in the U band. The outliers in the B − V residual panel are mainly from the flux losses in the B band in the UVB arm, as discussed in Sect. 5.4.
Mean color difference and rms scatter between XSL and the Bright Star Catalogue (BSC).
 |
Fig. 27 Synthetic SDSS colors of the XSL sample (black dots) compared with synthetic model colors by Lenz et al. (1998). Only three metallicities are shown for the model colors: [M/H] = −2.0 (blue lines), 0.0 (red lines), and +1.0 (green lines). Solid lines indicate models with log g = 4.5 and dashed lines indicate models with log g = 2.5. |
 |
Fig. 28 Spectra of HD27295 from XSL (black), MILES (green), NGSL (red), and CaT (blue). The inset shows a zoomed-in region for a detailed comparison of the telluric corrections. |
 |
Fig. 31 Detailed spectral line comparison between XSL (black) and UVES-POP (red) of HD 102212 (M1III), where the UVES-POP spectrum is smoothed to the resolution of XSL. The XSL spectrum around 9350 Å is heavily contaminated by telluric features, and therefore the stellar features are difficult to recover. |
 |
Fig. 32 As for Fig. 31 but for HD 99648 (G8Iab). Telluric features are clearly seen in the UVES-POP spectrum, especially around 9300–9400 Å. |
 |
Fig. 33 Detailed spectral line comparison between XSL (black) and ELODIE (red) of HD 232078 (K3IIp), where the ELODIE spectrum is smoothed to the resolution of XSL. The gap in the two bottom panels represents bad pixels in ELODIE. |
 |
Fig. 35 Detailed spectral line comparison between XSL (black) and MIUSCAT (red) of HD 25329 (K1V), where the XSL spectrum is smoothed to the resolution of MIUSCAT. The gap in the third panel represents bad pixels in XSL. |
 |
Fig. 37 Detailed spectral line comparison between XSL (black) and NGSL (red) of HD 44007 (G5IV:w...), where the XSL spectrum is smoothed to the resolution of NGSL. The gap in the third panel represents bad pixels in XSL. |
The SDSS u′ − g′, g′ − r′, and r′ − i′ colors are calculated following the definition of AB magnitudes: ![\begin{equation} M_{\rm AB} = - 2.5\times \log_{10} [f_{\nu}^{\rm eff}]- 48.6, \end{equation}](/articles/aa/full_html/2014/05/aa22505-13/aa22505-13-eq106.png) (7)where
(7)where 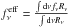 (see Fukugita et al. 1995, for details). Since there are few literature stars, which have the SDSS colors in common with our sample, we use the model colors computed by Lenz et al. (1998) as a rough check. Models with log g = 4.5 and log g = 2.5 are chosen to represent the main sequence and giants, respectively. Three metallicities [M/H] = −2.0,0, and 1.0 are used to cover the metallicity range of the XSL sample. Figure 27 shows the u′ − g′ vs g′ − r′ colors and r′ − i′ vs g′ − r′ colors for the XSL sample compared with the model colors. In general, the agreement between the models and data is very good. The coolest model from Lenz et al. has Teff = 3500 K, which is significantly warmer than the coolest XSL stars, and so the reddest model colors are not be as red as the reddest XSL stars.
(see Fukugita et al. 1995, for details). Since there are few literature stars, which have the SDSS colors in common with our sample, we use the model colors computed by Lenz et al. (1998) as a rough check. Models with log g = 4.5 and log g = 2.5 are chosen to represent the main sequence and giants, respectively. Three metallicities [M/H] = −2.0,0, and 1.0 are used to cover the metallicity range of the XSL sample. Figure 27 shows the u′ − g′ vs g′ − r′ colors and r′ − i′ vs g′ − r′ colors for the XSL sample compared with the model colors. In general, the agreement between the models and data is very good. The coolest model from Lenz et al. has Teff = 3500 K, which is significantly warmer than the coolest XSL stars, and so the reddest model colors are not be as red as the reddest XSL stars.
6.5. Comparison with literature spectra
Since our sample is selected from different literature sources, it is interesting to compare the XSL spectra with spectra of the same stars in other libraries. The first year of XSL has 77 stars in common with NGSL, 40 stars in common with MILES, 34 stars in common with ELODIE, 26 stars in common with IRTF, and 25 stars in common with CaT (Cenarro et al. 2001).
We show several examples of the spectral slope comparison between XSL, NGSL, MILES and CaT in Figs. 28–30. With the higher resolution data of XSL, we can resolve spectral features in detail. We see that the flux calibration of XSL agrees well with MILES and NGSL in general, with the occasional exception of the very red part of the MILES spectra for HD27295 due to the second-order problem of some MILES stars (see Fig. 28 and the discussion in Sect. 4.3 of Sánchez-Blázquez et al. 2006). Further, the comparison with the CaT library shows that library is not telluric corrected (Cenarro et al. 2001), as seen from the features around 9000 Å in Figs. 28 and 29.
As a further check on the quality of XSL, we compare our spectra with two higher-resolution spectral libraries: UVES-POP (Bagnulo et al. 2003) and ELODIE9 (Prugniel & Soubiran 2001, 2004; Prugniel et al. 2007). To make this comparison, we first smooth the UVES-POP and ELODIE spectra to the resolution of the XSL spectra and then use pPXF to match the continua and velocity zero points, masking bad pixels when necessary. Figures 31–34 show the results of these comparisons. The typical residual between XSL and UVES-POP is 2–4%; the typical residual between XSL and ELODIE is 2–6%. We find very good agreement in the line shapes and depths between XSL and the two higher-resolution libraries for both warm and cool stars. This gives us confidence that the XSL spectra will be a useful basis for moderate-resolution studies of both stars and composite stellar populations.
Comparison of XSL with the intermediate resolution spectral library MIUSCAT (Vazdekis et al. 2012) shows a good agreement for lines unaffected by telluric contamination. Figures 35 and 36 show the smoothed version of XSL and MIUSCAT for two stars in common, HD 25329 and HD 44007, over the wavelength range 3500 Å to 10000 Å. The typical rms flux residual between XSL and MIUSCAT is 2%. We note that the flux differences exist: for instance, a flux difference of ~7% over the wavelength range 3600–4200 Å is found in HD 44007. This may be due to the extinction used in MIUSCAT star, since comparison of XSL with NGSL for the same star shows excellent agreement (see Fig. 37). Flux differences of 2.3% are found in both stars over the wavelength range 8000–9400 Å, which likely arises from the joined libraries, which are CaT and INDO-US in MIUSCAT. To join the MILES with CaT spectral ranges, Vazdekis et al. (2012) used the (V − I) color–temperature–metallicity relations of Alonso et al. (1996, 1999). This matching is performed on the basis of these generic relations (see Vazdekis et al. 2012) according to the parameters of the stars. This might explain some of the difference in flux between the XSL and MIUSCAT in that specific spectral range, where the matching of the different libraries in MIUSCAT may cause slight flux calibration issues. Regions beyond ~9000 Å in MIUSCAT are contaminated by telluric absorption.
Comparison of XSL with the lower resolution spectral library NGSL also shows good agreement. Figures 37 and 38 show the smoothed version of XSL and NGSL for two stars in common HD 44007 and HD 82734 at wavelength range from 3200 Å to 10 000 Å. The typical rms flux residual between XSL and NGSL is 1%.
7. Summary
We are building a new, moderate-resolution stellar spectral library, the X-shooter Spectral Library (XSL). The pilot survey10 (this work) contains 237 unique stars covering the spectral range λλ 3100–10 185 Å at a resolution R ~ 10 000. We have identified a number of issues with the X-shooter pipeline and presented our solutions. A telluric library is built for telluric correction of the XSL data using a PCA-based method. Flux and wavelength calibrations are carefully performed and are shown to be consistent with published spectra. the X-shooter Spectral Library is still under construction, and the final database will contain more than 700 stars. This library will provide a vital tool for extragalactic astronomers to extract even more information from their observations than previously possible and will provide stellar astronomers with a unique empirical panchromatic spectral library for further studies of a wide range of stellar types.
For more information see http://www.hq.eso.org/sci /facilities/paranal/instruments/xshooter/doc/VLT-MAN-ESO-14650-4942_P91P92.pdf
Acknowledgments
We thank the referee, G. Worthey, for the careful review and helpful comments that improved the final manuscript. We thank our collaborators on XSL, S. Meneses-Goytia, A. J. Cenarro, J. Falcón-Barroso, E. Mármol-Queraltó, P. Sánchez-Blázquez, C. J. Walcher, P. Hauschildt and M. Koleva. We thank also B. Davies and G. Zhang for useful discussions. We would also like to extend our great thanks to V. Manieri, A. Modigliani, J. Vernet, and the ESO staff for their help during the XSL observations and reduction process. This research used the POLLUX database ( http://pollux.graal.univ-montp2.fr ) operated at LUPM (Université Montpellier II - CNRS, France with the support of the PNPS and INSU. This work has been supported by the Programa Nacional de Astronomía y Astrofísica of MINECO, under grant AYA2010-21322-C03-02.
References
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&AS, 117, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, V. M., McCarthy, M. F., & Blanco, B. M. 1984, AJ, 89, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 315 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buzzoni, A., Mantegazza, L., & Gariboldi, G. 1994, AJ, 107, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Cardiel, N., Gorgas, J., et al. 2001, MNRAS, 326, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Bruzual, A. G. 1991, ApJ, 367, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Trager, S., Peletier, R., & Lançon, A. 2011, J. Phys. Conf. Ser., 328, 2023 [Google Scholar]
- Cioni, M.-R. L., Blommaert, J. A. D. L., Groenewegen, M. A. T., et al. 2003, A&A, 406, 51 [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coelho, P., Bruzual, G., Charlot, S., et al. 2007, MNRAS, 382, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & van Dokkum, P. 2012, ApJ, 747, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., van Dokkum, P. G., & Graves, G. J. 2013, ApJ, 763, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cousins, A. W. J. 1971, Royal Observatory Annals, 7 [Google Scholar]
- Cousins, A. W. J. 1973, Mem. R. Astron. Soc., 77, 223 [NASA ADS] [Google Scholar]
- Davies, R. L., Sadler, E. M., & Peletier, R. F. 1993, MNRAS, 262, 650 [NASA ADS] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Frogel, J. A. 1988, ARA&A, 26, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- González, J. J. 1993, Ph.D. Thesis, Thesis (PH.D.)–University of California, USA, Dissertation Abstracts International, Volume: 54-05, Section: B, page: 2551 [Google Scholar]
- González Delgado, R. M., Cerviño, M., Martins, L. P., Leitherer, C., & Hauschildt, P. H. 2005, MNRAS, 357, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gregg, M. D., Silva, D., Rayner, J., et al. 2006, in The 2005 HST Calibration Workshop: Hubble After the Transition to Two-Gyro Mode, eds. A. M. Koekemoer, P. Goudfrooij, & L. L. Dressel, 209 [Google Scholar]
- Groenewegen, M. A. T., & Blommaert, J. A. D. L. 2005, A&A, 443, 143 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Guiderdoni, B., & Rocca-Volmerange, B. 1987, A&A, 186, 1 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoffleit, D., & Jaschek, C. . 1991, The Bright star catalogue (New Haven, USA: Yale University Observatory) [Google Scholar]
- Hoffleit, D., Saladyga, M., & Wlasuk, P. 1983, Bright star catalogue. Supplement (New Haven, USA: Yale University Observatory) [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, S. M. G., & Wood, P. R. 1990, AJ, 99, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Mitchell, R. I., Iriarte, B., & Wisniewski, W. Z. 1966, Communications of the Lunar and Planetary Laboratory, 4, 99 [Google Scholar]
- Koleva, M., Prugniel, P., Ocvirk, P., Le Borgne, D., & Soubiran, C. 2008, MNRAS, 385, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koleva, M., Bouchard, A., Prugniel, P., De Rijcke, S., & Vauglin, I. 2013, MNRAS, 428, 2949 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM (Cambridge, MA: Smithsonian Astrophysical Observatory), 13 [Google Scholar]
- Lançon, A., & Mouhcine, M. 2002, A&A, 393, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lançon, A., & Rocca-Volmerange, B. 1992, A&AS, 96, 593 [NASA ADS] [Google Scholar]
- Lançon, A., & Wood, P. R. 2000, A&AS, 146, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landolt, A. U. 1973, AJ, 78, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1983, AJ, 88, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, J.-F., Bruzual, G., Pelló, R., et al. 2003, A&A, 402, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Borgne, D., Rocca-Volmerange, B., Prugniel, P., et al. 2004, A&A, 425, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Alloin, D., Fritze-V., Alvensleben, U., et al. 1996, PASP, 108, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, D. D., Newberg, J., Rosner, R., Richards, G. T., & Stoughton, C. 1998, ApJS, 119, 121 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., et al. 2005, ApJ, 628, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Massey, P., Olsen, K. A. G., & Plez, B. 2007, ApJ, 667, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Lord, S. D. 1992, in NASA Technical Memorandum, 103957 [Google Scholar]
- Maraston, C. 1998, MNRAS, 300, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Mármol-Queraltó, E., Cardiel, N., Cenarro, A. J., et al. 2008, A&A, 489, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ocvirk, P., Pichon, C., Lançon, A., & Thiébaut, E. 2006, MNRAS, 365, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Palacios, A., Gebran, M., Josselin, E., et al. 2010, A&A, 516, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patat, F., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peletier, R. F. 1989, Ph.D. Thesis, University of Groningen, The Netherlands [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2004 [arXiv:0409214] [Google Scholar]
- Prugniel, P., Soubiran, C., Koleva, M., & Le Borgne, D. 2007 [arXiv:0703658] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Seifahrt, A., Käufl, H. U., Zängl, G., et al. 2010, A&A, 524, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharp, R., & Parkinson, H. 2010, MNRAS, 408, 2495 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thurl, C., Sackett, P. D., & Hauschildt, P. H. 2006, A&A, 455, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 119, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Vazdekis, A., Ricciardelli, E., Cenarro, A. J., et al. 2012, MNRAS, 424, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wild, V., & Hewett, P. C. 2005, MNRAS, 358, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., & Ottaviani, D. L. 1997, ApJS, 111, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., & González, J. J. 1992, ApJ, 398, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., González, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Singh, H. P., Prugniel, P., Gupta, R., & Koleva, M. 2011, A&A, 525, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamada, Y., Arimoto, N., Vazdekis, A., & Peletier, R. F. 2006, ApJ, 637, 200 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The first-year XSL sample
Our telluric-corrected, flux-calibrated, UVB- and VIS-arm-merged spectral library contains 246 spectra of 237 individual stars, which cover wavelengths from 3100–10 185 Å. Table A.1 (available at the CDS) lists the object name of XSL sample, the observation Modified Julian Date (MJD), the airmass of the observation, and the star’s spectral type. An asterisk (“*”) in column “Flux note” means that the star may have flux losses due to a missing wide-slit observation (see Sect. 5.4). When the merged spectrum of a certain star is combined from different observations, the MJD and airmass of the first observation are taken for this star.
Typical XSL spectra in the OBAFGKM sequence are shown in Fig. A.1. We show an M-star sequence in Fig. A.2 to illustrate our collection of these cool stars. Other cool stars, such as LPV, C, S, and L stars, are shown in Fig. A.3.
 |
Fig. A.1 OBAFGKM sequence of the XSL sample in log (Fλ). Gaps around 5700 Å indicate strong dichroic features between the UVB and VIS arms. |
 |
Fig. A.2 Sequence of M stars sorted by spectral type. Flat regions in the star GL644C indicate spectrum in very low signal-to-noise ratio regions. |
 |
Fig. A.3 A sample of LPV, C, S, and L stars in the XSL. |
All Tables
Mean color difference and rms scatter between XSL and the Bright Star Catalogue (BSC).
All Figures
 |
Fig. 1 Distribution of spectral types in XSL observed in Periods 84 and 85 (excluding telluric calibrators). Spectral types were retrieved from SIMBAD or based on educated guesses from the source libraries or atmospheric parameters. |
| In the text | |
 |
Fig. 2 HR diagram of the 219 XSL stars (O–M, LPV, S) with calculated Teff, log g and [Fe/H], where [Fe/H] is presented in different colors. |
| In the text | |
 |
Fig. 3 Data observed in nodding mode in the VIS arm. Here, the star is sitting in the center of the slit in the first exposure (left panel), while the star is almost out of the slit in the second exposure (right panel). |
| In the text | |
 |
Fig. 4 Example of background (“sky”) modeled by the pipeline from data observed in stare mode in the UVB arm, in which sky lines are nearly absent. Left panel: original raw frame. Right panel: sky frame generated by the pipeline scaled to the same intensity as the left panel. Note the very poor background model. |
| In the text | |
 |
Fig. 5 1D spectra extracted from the UVB arm, using the pipeline sky model (black) and a background extracted directly from the observation (red), when the sky emission lines are weak (or not observed). The blue spectrum shows the difference between the two methods. In the right panels, we zoom into three small wavelength regions, so that the sky modeling errors of the pipeline are clear. |
| In the text | |
 |
Fig. 6 Panel a) black: 1D spectrum extracted from the pipeline; red: 1D spectra extracted after raw frames corrected using the algorithm of van Dokkum (2001). Panel b) raw image of “B” frame zoomed in on the CRH feature (red circle). Panel c) pipeline-corrected 2D spectrum zoomed in on the CRH feature (red circle). |
| In the text | |
 |
Fig. 7 Upper panel: raw image of the telluric standard star Hip024505 zoomed into a region of bad columns in the VIS arm. Lower panel: corresponding final, pipeline-corrected 2D spectrum of this star. |
| In the text | |
 |
Fig. 8 Order-by-order 1D spectrum extraction for the G2 star HD17072 in the UVB arm without flux calibration. Different colors correspond to different orders. The continuous black spectrum is the combined spectrum, which is offset for clarity. In the middle and bottom panels, we zoom in on two wavelength regions, 504–520 nm and 390–410 nm, where orders overlap to see the extraction and combination process in detail. |
| In the text | |
 |
Fig. 9 A saturated raw VIS arm frame after transformation of counts to a binary “good pixel”/“saturated pixel” basis, and summed along the wavelength direction. Note the sharp features with values in excess of 200, indicative of saturation due to overexposure. See text for details. |
| In the text | |
 |
Fig. 10 Ratio of counts between Cl* NGC 6522 ARP 4329 and the closest (in elapsed time) telluric standard star Hip094378, zoomed in the “A” band in the VIS arm. |
| In the text | |
 |
Fig. 11 Extraction of the telluric absorption from the B8V star Hip012389. The black spectrum is the original 1D spectrum (without telluric or flux calibration). This spectrum is fit by a synthetic LTE spectrum from a model atmosphere in the pixels outside of the vertical green lines. The red spectrum represents this fit. The lower part of the plot shows the residuals from the best fit: green points represent regions of intrinsic stellar absorption, while blue points are (almost) the telluric absorption spectrum. We note that the residual between the best fit and the data is scaled to the view level. It is, therefore, not surprising that some features are below zero. |
| In the text | |
 |
Fig. 12 Two normalized telluric standard stars, Hip026545 (black line) and Hip012389 (dashed red line), zoomed into the wavelength region 9570–9620 Å, showing the impact of the flexure of the X-shooter backbone on the wavelength calibration. The wavelength shift is roughly 2 pixels between these two spectra, or ≈10 km s-1. |
| In the text | |
 |
Fig. 13 Extracted raw transmission spectrum from the B8V telluric standard star Hip012389 (black) and the shifted, cleaned “final” transmission spectrum from this star (red). The raw transmission spectrum has been offset for clarity. |
| In the text | |
 |
Fig. 14 The first six principal components of the telluric library. The eigenvalues decrease from the bottom to the top of this figure (i.e., the first and largest eigenvector is the lowest). The eigenvectors have been offset for display purposes. |
| In the text | |
 |
Fig. 15 Spectrum of HD 164257 (A0) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. |
| In the text | |
 |
Fig. 16 Spectrum of HD 193896 (G5IIIa) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. The spikes around 7600 Å are residuals after telluric correction. |
| In the text | |
 |
Fig. 17 Spectrum of HD 79349 (K7IV) before (black) and after (red) telluric correction in the VIS arm, using the PCA reconstruction method described in the text. The lower panel shows four zoomed-in regions to show the corrections in detail. The spikes around 9350 Å are residuals after telluric correction. |
| In the text | |
 |
Fig. 18 Telluric correction by two different methods for the cool bulge LPV star OGLEII DIA BUL-SC1 235. The black line is the original 1D spectrum extracted, and the blue and red lines are the spectrum after correction by the PCA reconstruction and the temporally-closest telluric absorption spectrum, respectively. The green spectrum is an M5III star with a similar temperature, HD175865, taken from NGSL as a comparison. |
| In the text | |
 |
Fig. 19 Telluric correction by the PCA reconstruction and temporally-closest telluric absorption methods on the G3V star G169-28. Symbols and wavelength ranges are the same as in Fig. 18. |
| In the text | |
 |
Fig. 20 Extinction curve for XSL in the UVB arm (blue line) and the VIS arm (red line). The Paranal extinction curve of Patat et al. (2011) is shown as the black line for comparison. Lower panel shows the residual between XSL and Patat et al. (2011) calculated by the IRAF.standard procedure and applied to derive the XSL extinction. |
| In the text | |
 |
Fig. 21 Average response curves in the UVB (upper panel) and VIS arm (lower panel). The dotted line in the VIS arm indicates a low signal-to-noise region, interpolated for display purposes. Dichroic features are shown in both UVB and VIS arms around 5600–5800 Å. |
| In the text | |
 |
Fig. 22 Average line-spread functions for the FGK stars (212 spectra) in the UVB (upper panel) and VIS (lower panel) arms. In each arm, the top panel shows the residual shift of the spectra (blue dots). The bottom panel shows the detected instrumental velocity dispersion. A simple first-order polynomial fit (red lines) of the line-spread function is marked in each panel. The error bars are the standard deviation in each wavelength bin. The three open circles show the region where two different flat field lamps are used in the UVB arm, which may result in larger uncertainties. |
| In the text | |
 |
Fig. 23 Root-mean-squared deviation of the ratio between the PCA-based and closest-in-time telluric corrections for 20-F stars from XSL. |
| In the text | |
 |
Fig. 24 Upper panel: response functions of UBVRI filters (solid lines) and the Monitor Telescope u′,g′,r′,i′,z′ filters (dotted lines). Both systems are normalized to 1. Bottom panel: a typical XSL spectrum of HD82734 (K0III) for comparison. |
| In the text | |
 |
Fig. 25 Comparison of synthetic (U − B), (B − V), (V − I), and (R − I) colors in XSL and NGSL. The residuals in each panel are calculated as colorXSL − colorNGSL. Blue squares indicate those stars that likely have flux losses, due to a lack of useful wide-slit observation. |
| In the text | |
 |
Fig. 26 Comparison of synthetic (B − V) and (U − B) colors of XSL and the Bright Star Catalogue. The residuals are calculated as in Fig. 25b. Blue squares indicate those stars that likely have flux losses due to a lack of useful wide-slit observation. |
| In the text | |
 |
Fig. 27 Synthetic SDSS colors of the XSL sample (black dots) compared with synthetic model colors by Lenz et al. (1998). Only three metallicities are shown for the model colors: [M/H] = −2.0 (blue lines), 0.0 (red lines), and +1.0 (green lines). Solid lines indicate models with log g = 4.5 and dashed lines indicate models with log g = 2.5. |
| In the text | |
 |
Fig. 28 Spectra of HD27295 from XSL (black), MILES (green), NGSL (red), and CaT (blue). The inset shows a zoomed-in region for a detailed comparison of the telluric corrections. |
| In the text | |
 |
Fig. 29 Spectra of HD 44007 from different spectral libraries. Colors are as in Fig. 28. |
| In the text | |
 |
Fig. 30 Spectra of HD 82734 from different spectral libraries. Colors are as in Fig. 28. |
| In the text | |
 |
Fig. 31 Detailed spectral line comparison between XSL (black) and UVES-POP (red) of HD 102212 (M1III), where the UVES-POP spectrum is smoothed to the resolution of XSL. The XSL spectrum around 9350 Å is heavily contaminated by telluric features, and therefore the stellar features are difficult to recover. |
| In the text | |
 |
Fig. 32 As for Fig. 31 but for HD 99648 (G8Iab). Telluric features are clearly seen in the UVES-POP spectrum, especially around 9300–9400 Å. |
| In the text | |
 |
Fig. 33 Detailed spectral line comparison between XSL (black) and ELODIE (red) of HD 232078 (K3IIp), where the ELODIE spectrum is smoothed to the resolution of XSL. The gap in the two bottom panels represents bad pixels in ELODIE. |
| In the text | |
 |
Fig. 34 As for Fig. 33 but for HD 4813 (F7IV-V). |
| In the text | |
 |
Fig. 35 Detailed spectral line comparison between XSL (black) and MIUSCAT (red) of HD 25329 (K1V), where the XSL spectrum is smoothed to the resolution of MIUSCAT. The gap in the third panel represents bad pixels in XSL. |
| In the text | |
 |
Fig. 36 As for Fig. 35 but for HD 44007 (G5IV:w...). |
| In the text | |
 |
Fig. 37 Detailed spectral line comparison between XSL (black) and NGSL (red) of HD 44007 (G5IV:w...), where the XSL spectrum is smoothed to the resolution of NGSL. The gap in the third panel represents bad pixels in XSL. |
| In the text | |
 |
Fig. 38 As for Fig. 37 but for HD 82734 (K0III). |
| In the text | |
 |
Fig. A.1 OBAFGKM sequence of the XSL sample in log (Fλ). Gaps around 5700 Å indicate strong dichroic features between the UVB and VIS arms. |
| In the text | |
 |
Fig. A.2 Sequence of M stars sorted by spectral type. Flat regions in the star GL644C indicate spectrum in very low signal-to-noise ratio regions. |
| In the text | |
 |
Fig. A.3 A sample of LPV, C, S, and L stars in the XSL. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


