| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201323209 | |
| Published online | 13 March 2014 | |
Mode identification based on time-series spectrophotometry for the bright rapid sdB pulsator EC 01541−1409⋆,⋆⋆
1 ESO, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
e-mail: srandall@eso.org
2 Département de Physique, Université de Montréal, CP 6128, Succ. Centre-Ville, Montréal QC H3C 3J7, Canada
3 Institut d’Astrophysique et de Géophysique de l’Université de Liège, allée du 6 Août 17, 4000 Liège, Belgium
4 Chargé de recherches, Fonds de la Recherche Scientifique, FNRS, rue d’Egmont 5, 1000 Bruxelles, Belgium
Received: 6 December 2013
Accepted: 28 January 2014
We present an analysis of time-resolved spectrophotometry gathered with FORS/VLT for the rapidly pulsating hot B subdwarf EC 01541−1409 with the aim of identifying the degree index ℓ of the larger amplitude modes. This mode identification can be extremely useful in detailed searches for viable asteroseismic models in parameter space, and can be crucial for testing the validity of a solution a posteriori. To achieve it, we exploit the ℓ-dependence of the monochromatic amplitude, phase, and velocity-to-amplitude ratio of a mode as a function of wavelength. We use the ℓ-sensitive phase lag between the flux perturbation and the radial velocity as an additional diagnostic tool. On this basis, we are able to unambiguously identify the dominant 140.5 s pulsation of our target as a radial mode, and the second-highest amplitude periodicity at 145.8 s as an ℓ = 2 mode. We further exploit the exceptionally high-sensitivity data that we gathered for the dominant mode to infer modal properties that are usually quite difficult to estimate in sdB pulsators, namely the physical values of the dimensionless radius, temperature, and surface gravity perturbations.
Key words: asteroseismology / techniques: imaging spectroscopy / stars: oscillations / stars: individual: EC 01541-1409 / stars: variables: general / stars: atmospheres
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile (proposal ID 087.D-0047).
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Among the many types of pulsating stars currently known, the pulsating hot B subdwarf (sdB) stars are turning out to be exceptional asteroseismological laboratories. There are two main categories of pulsating sdBs, the short-period p-mode oscillators of the V361 Hya type (or sdBVr) discovered in 1997 (Kilkenny et al. 1997), and the cooler, less compact long-period g-mode pulsators of the V1093 type (or sdBVs) discovered in 2003 (Green et al. 2003). These two families of pulsators show strong analogies with the β Cephei/slowly pulsating blue (SPB) stars on the main sequence. However, sdB stars lie well below the main sequence in the Hertzsprung-Russell diagram on the so-called extreme horizontal branch (EHB) and are hot (22 000 K ≤ Teff ≤ 42 000 K), compact (5.2 ≤ log g ≤ 6.2) core helium burning objects. Since the discovery that a significant fraction of them pulsate, tremendous progress has been made in terms of exploiting their asteroseismological potential (e.g. Charpinet et al. 2013). In the so-called forward approach to asteroseismology (Brassard et al. 2001), a detailed search in parameter space is carried out with the aim of finding an optimal model whose computed pulsation periods best match the observed periods. It is this method that was used to obtain the first view of the empirical mass distribution of sdB stars (Fontaine et al. 2012).
The asteroseismological determination of a unique solution in parameter space can be greatly aided by the independent identification of some of the properties of the pulsation modes observed. As part of the period fitting process the observed frequencies are associated with a computed mode of a given degree index ℓ and radial order k (the azimuthal order m is neglected unless there is evidence for rapid rotation). Any a priori information on the ℓ or k values of a given observed periodicity can therefore be used as an additional constraint and is, in practice, often required to discriminate between multiple models providing good solutions in terms of period fitting and atmospheric parameter ranges. It has become standard best practice to assume ℓ = 0,1,2 for the higher amplitude frequencies observed (see e.g. Van Grootel et al. 2013, for a recent analysis) because of their larger relative amplitude compared to higher degree modes when integrated over the visible disk of the star. However, more stringent constraints are sometimes required in order to find a unique solution, and can also be useful for testing the robustness of a derived solution retrospectively.
Attempts have been made over the past years to infer the degree indices of pulsation modes in sdBVr stars via the measurement of evenly spaced multiplets (only applicable to rapidly rotating stars; see e.g. Charpinet et al. 2005), the exploitation of line profile variations from high-resolution time-series spectroscopy (e.g. Telting et al. 2008), and the interpretation of radial velocity and equivalent width variations measured over the pulsation cycle (e.g. Telting & Østensen 2006). Meeting with rather limited success, these techniques have now largely been superceded by the analysis of the observed amplitude and phase variations of a pulsation mode as a function of wavelength. This method makes use of the imprint that the degree index leaves on the relative properties of a mode at different wavelengths as a result of the combination of its specific surface geometry and the effects of limb darkening. It has been applied very successfully to multi-colour photometry observations of sdBVr stars, yielding unique identifications of the degree index ℓ for a handful of modes based on their colour-amplitudes (Jeffery et al. 2004; Randall et al. 2005; Charpinet et al. 2008; Baran et al. 2008; Silvotti et al. 2010). The limiting factor for mode identification is quite clearly the signal-to-noise ratio (S/N) of the observations, in particular for low-degree (ℓ = 0,1,2) modes, which all show a very similar amplitude-wavelength behaviour. Given the short periods and comparatively low amplitudes of the pulsations observed in sdBVr stars coupled with the relative faintness of the targets, it is extremely challenging to determine the amplitudes and phases of individual modes to the required accuracy even using large telescopes. On the other hand, our modelling tools developed for the exploitation of multi-wavelength sdB pulsator amplitudes and phases (Randall et al. 2005) appear to work very well, as demonstrated by the almost perfect agreement with the observations in the cases where high-quality data do exist.
Using the same tools, we recently carried out an exploratory study attempting mode identification on the basis of the monochromatic rather than bandpass-integrated pulsation properties for the sdBVr star EC 20338−1925 (Randall et al. 2010). We obtained nearly 15 h of time-series spectrophotometry with the HIT-MS mode of FORS mounted at the VLT on Cerro Paranal, Chile. Despite the relative faintness of the target (V ~ 15.7), we were able to identify the dominant pulsation as a radial (ℓ = 0) mode from the monochromatic amplitude behaviour, while some of the lower amplitude modes could be constrained to ℓ = 0,1,2. Motivated by these encouraging results, we decided to repeat the exercise for another, brighter star.
The target EC 01541−1409 was first recognised as a bright (B ~ 12.1), rapid sdB pulsator by Kilkenny et al. (2009), who detected five periodicities between 110 s and 146 s and amplitudes up to 10 mmags on the basis of 14 h of time-series photometry gathered with the 1.0-m telescope at the South African Astronomical Observatory. A follow-up multi-site photometric campaign encompassing 210 h of time-series photometry yielded at least an additional 26 frequencies in a wider 64−164 s range, and revealed clear variations in pulsational amplitude over time for several of the frequencies (Reed et al. 2012a). While the dominant periodicity at 140.5 s was measured at a more or less constant amplitude over several years, others appeared to vary by as much as an order of magnitude, which is quite common for sdBVr stars. Radial velocity measurements have so far been able to recover only the main pulsation peak at an amplitude of ~4.5 km s-1 (Reed et al. 2012b). The star lies at the hot edge of the sdBVr instability strip with atmospheric parameters estimated at Teff = 37 100 K and log g = 5.71 by Østensen et al. (2010). It may be the hottest rapid sdB pulsator known.
2. Observations and data reduction
We observed EC 01541−1409 using the FORS HIT-MS mode at the VLT during four consecutive half-nights in September 2011 (see Table 1 for a log of the observations). The HIT-MS mode is ideal for fast time-series spectroscopy as it allows 41 observations per readout, achieved by exposing only a small part of the chip and successively shifting the exposed blocks of columns across the CCD while already integrating on the next spectrum. Given the brightness of our target and the good sensitivity in the blue of the E2V CCD used combined with the size of the telescope, we were able to cut down the exposure time per datapoint to 10 s, ideal for resolving the fast pulsations uncovered in this star. This resulted in continuous monitoring of EC 01541−1409 for 410 s interspersed with ~30 s gaps in the time series while the CCD was read out.
Employing the largest mask opening available in HIT-MS mode (5′′ × 5′′) allowed us to essentially obtain spectrophotometry, the average seeing being around 1.0″ on nights 1, 3, and 4 and around 1.25″ on night 2. Since the HIT-MS mode allows for two closely spaced targets to be observed, we also monitored the nearby bright (B ~ 11.65) early F-type main-sequence star BD-14 362 as a comparison star to be used for correcting atmospheric transparency fluctuations. Thus, we obtained a total of four spectra for each data point in time, one each for the red and the blue chip of the FORS E2V CCD for both our target EC 01541−1409 and the comparison star. The target spectra cover the wavelength range 3400–4790 Å (blue chip) and 4870−6440 Å (red chip), while the comparison star spectra are shifted redwards by ~600 Å. The wavelength resolution of the spectra is variable as it is determined by the seeing rather than a fixed slit width, and ranges from Δλ = 3.6–10.2 Å (corresponding to 0.6−1.7″ seeing).
Time-series spectroscopy obtained for EC 01541−1409.
Data reduction was performed using a custom-written IRAF script, which essentially treats the 41 spectra pairs in each image as echelle orders, and writes out the reduction products as individual FITS files with a time-stamp corresponding to the middle of the exposure. The steps performed are bias subtraction, bad pixel interpolation, cosmic ray cleaning, background fitting and subtraction, tracing and extraction of the spectra, and finally wavelength calibration. The extraction aperture was adjusted dynamically for each spectrum based on the FWHM of the spectrum cross-section in the centre of the chip in order to compensate for variations in seeing as far as possible. The wavelength calibration was slightly complicated because it is impossible to obtain useful arclamp spectra with the 5′′ × 5′′ slit cut into the science mask for FORS. Therefore, we had a special mask cut with narrow slits placed at the centre position of the science slits. This resulted in a wavelength calibration accurate to within less than 1 Å.
We show a typical single spectrum of EC 01541−1409 as well as the associated comparison star spectrum in Fig. 1. Thanks to the relative brightness of the targets, the quality of the individual science target spectra is quite high with a S/N of 150 and 60 in the central part of the blue and the red chip, respectively. The spectra cover the Balmer lines from Hγ upwards; owing to the unfortunate placement of the slit position on the mask, Hβ falls in the gap between the two chips and Hα is just off the edge of the red chip.
 |
Fig. 1 Typical individual spectra obtained with an exposure time of 10 s on 09 September 2011 for EC 01541−1409 (top) and the main-sequence comparison star (bottom). The spectra have been arbitrarily normalised for visualisation purposes, and are not flux calibrated. |
3. Data analysis
3.1. Atmospheric analysis
Given the importance of an accurate determination of the target star’s atmospheric parameters for the computation of the monochromatic quantities described in the following sections, we started our study with an atmospheric analysis of a combined time-averaged spectrum of EC 01541−1409. We combined all spectra obtained with a wavelength resolution of Δλ ≤ 4.8 Å (corresponding to a seeing of 0.8″) convolved to that resolution. This comprised 1680 spectra for the blue chip and 2796 for the red, and yielded a high S/N (>400 in the central parts of the chips) time-averaged spectrum containing several He I and He II lines as well as the hydrogen Balmer series from Hγ upwards.
We fit this averaged spectrum with our grids of synthetic sdB star spectra computed from NLTE model atmospheres using the public codes TLUSTY and SYNSPEC (Hubeny & Lanz 1995; Lanz & Hubeny 1995). As usual, we compared the best fit obtained for the observed H and He lines from model spectra containing only H and He in the atmospheric composition to that achieved by including metals with the representative abundances derived by Blanchette et al. (2008). Figure 2 shows the latter, and also gives the inferred values for the effective temperature, logarithmic surface gravity, and logarithmic fractional helium abundance. The parameters derived using only H and He in the model atmospheres are very similar, and are consistent within the formal errors, as is typical for hot sdBVr stars. Our values are also in agreement with those derived by Østensen et al. (2010). For the sake of completeness, we list the atmospheric parameters derived from all three analyses in Table 2.
 |
Fig. 2 Available H and He lines from the time-averaged FORS spectrum of EC 01541−1409, overplotted with the best model atmosphere fit including metals with the abundances indicated. The atmospheric parameters derived are also shown in the plot. |
Atmospheric parameters for EC 01541−1409.
Highest amplitude periodicities extracted from the continuum light-curve around 4600 Å.
3.2. Continuum Fourier analysis
The next step in our data analysis was to determine the periodicities present in the data through the Fourier analysis of a wavelength-averaged light curve. Given that very extensive time-series photometry observations had already been reported for our target by Reed et al. (2012a), the aim here was not to detect any new or even all of the already known periodicities, but to accurately measure the highest amplitude frequencies for the exact same data set as is used for the observed monochromatic amplitude and phase variations described in the following section.
With this in mind, we computed a light curve of the data set using only spectra with a wavelength resolution below 7.8 Å (corresponding to a seeing ≤1.3″) convolved to that wavelength resolution. This was deemed the best compromise between achieving a relatively good wavelength resolution and including a large fraction (91%) of the data points, 5654 in total. As the frequencies of pulsation are expected to be independent of wavelength for rapid sdB pulsators (see e.g. Randall et al. 2005), it should not matter which parts of the spectra obtained are used for the light curve in this initial analysis. After experimenting with different parts of the target and comparison star continuum spectrum, we found that the best differential light curve was obtained by using only the 4520−4670 Å portion of both spectra. This region is free of strong lines, and the flux is comparatively high for both targets. Using wider wavelength ranges tended to increase the effect of atmospheric variations on the light curve, even though we subtracted a second-order polynomial to correct for differential extinction as a function of airmass.
Unfortunately, even the best differential light curves we were able to obtain show significant low-frequency structure that appears to be associated with atmospheric variations, and that could not be fully corrected by the differential photometry approach used. While the flexible extraction width used for individual spectra during the data reduction process should have largely compensated for variations in seeing, it was impossible to accurately measure the sky background because of the very limited space between spectra on the CCD. Therefore, it is not surprising that the reduced data show some remnant signature of the atmospheric conditions encountered during the observations. Fortunately, the time scale of the atmospheric variations is an order of magnitude longer than the stellar pulsations, and as such does not significantly affect their measurement.
 |
Fig. 3 Fourier spectrum computed on the basis of the integrated continuum flux between 4520 Å and 4670 Å of all spectra obtained with a seeing of 7.8 Å or less. The lower-amplitude periodicities listed in Table 3 are marked by short vertical line segments. |
Figure 3 shows the Fourier spectrum of the combined differential light curve for all four nights. The strong aliasing corresponding to the ~2.3 mHz/440 s sampling pattern introduced by the HIT-MS mode is clearly noticeable, but low-level enough to pose no threat to accurate pre-whitening, at least for the stronger modes. Indeed, the dominant periodicity at ~140.5 s reported by both Kilkenny et al. (2009) and Reed et al. (2012a) is easily recovered at a relatively high amplitude of 1.36%, as are those at 117.0 s and 145.8 s, albeit at a much lower amplitude. Using standard pre-whitening techniques we extracted the periodicities present in the light curve down to a conservative 4.5σ level of 0.09% flux variation about the mean brightness of the star. Those believed to be credible harmonic oscillations are listed in Table 3. We explicitly exclude the lower amplitude peaks of multiplet structure with frequency spacings of the order of the resolution of the dataset (3.6 μHz), as these are likely to be due to either amplitude variability of the associated periodicities or unresolved frequency splitting (e.g. due to slow rotation). We also discarded a periodicity uncovered at 443.2 s together with its harmonics, as these are most likely due to the sampling particularities of the HIT-MS mode. We note that the formal least-squares fitting errors on the amplitudes measured are around 0.02%.
In order to place the periodicities detected into a broader context we also list the corresponding periods and amplitudes extracted from observations in late 2007 by Kilkenny et al. (2009) and in late 2008 and 2009 by Reed et al. (2012a) from white-light photometry. In most cases a clear match is achieved at least between the frequencies extracted here and those of Reed et al. (2012a); only the two periodicities encased in square brackets differ substantially. It is obvious that the observed frequency spectrum has changed quite significantly over the years in terms of amplitude, far beyond the small effects that may be expected due to the slightly different effective wavelength of the datasets considered. In particular, some of the stronger periodicities reported in the previous publications seem to have disappeared below the detection threshold (e.g. the 127 s peak earlier detected with an amplitude of up to 0.6%), while others have become stronger in relative terms (e.g. the 64.1 s and the 73.7 s peaks in our data compared to those reported by Reed et al.). This kind of amplitude variation is well-documented for many sdBVr stars and is thought to be inherent to the opacity mechanism driving the pulsations rather than the beating of unresolved multiplets in at least some cases (e.g. Randall et al. 2010). However, we currently lack the non-linear pulsation theory necessary to model the intrinsic amplitudes of different modes, and are therefore unable to quantitatively interpret absolute amplitudes or their variation. The relative pulsational amplitudes at different wavelengths, on the other hand, can be accurately modelled and ultimately used to constrain the internal parameters of the target star, as we will show in the following sections.
3.3. Observed monochromatic amplitudes and phases
We derived the observed monochromatic amplitudes and phases as a function of wavelength for the dominant periodicities listed in Table 3 using the exact same set of spectra as for the continuum Fourier analysis (i.e. all those with Δλ ≤ 7.8 Å convolved to that wavelength resolution). The first step was to compute normalised light curves for each of the 1867 1.5 Å wide wavelength bins between 3550 Å and 6350 Å, correcting for extinction using the integrated flux of the comparison star for the chip in question (4140−5370 Å for the blue chip, 5500−7000 Å for the red chip). For each of these light curves we then performed least-squares fitting to find the amplitude and phase for a sinusoid with a period fixed to P1 = 140.49 s. The resulting amplitude and phase as a function of wavelength is shown in Fig. 4 together with the total flux from the combined spectrum obtained.
 |
Fig. 4 Flux obtained from the combined time-averaged spectrum gathered for EC 01541−1409 across the two FORS chips (top panel) together with the wavelength-dependent amplitude (middle panel) and phase (bottom panel) extracted for the dominant 140.5 s mode. The flux and the amplitude spectra have been normalised to unity and are consequently dimensionless quantities, while the phase is plotted relative to its average value in the blue part of the spectrum in radians. The spectral lines identified are marked by vertical lines propagating across all plots: black continuous lines indicate hydrogen Balmer lines, dashed blue lines denote He I lines, and dotted red lines show He II lines. |
The high quality and large wavelength coverage of these data for the dominant mode are impressive, and far superior to the results obtained from the only other similar observing campaign on an sdBVr star to date (for the fainter target EC 20338−1925, cf. Fig. 7 from Randall et al. 2010). Both the amplitude and phase plots clearly trace the H/He spectral lines as well as the continuum behaviour as a function of wavelength. Quite interestingly, the continuum phase exhibits a very small (~0.7 s) but clear drift with wavelength, something that could not be detected for EC 20338−1925 because of the inferior data quality. This drift alone is sufficient to unambiguously identify the mode’s degree index, as will be shown in the following section.
After having pre-whitened each of the 1867 light curves of the 140.5 s mode, we attempted to repeat the least-squares fitting in amplitude and phase for the remaining periodicities extracted. Unfortunately, these are an order of magnitude weaker than the dominant mode, and thus the monochromatic amplitudes and phases inferred are very noisy. Only for P2 = 145.77 s were we finally able to exploit the wavelength dependent pulsation properties (see below).
3.4. Radial velocity variations
We attempted to detect radial velocity (RV) variations associated with the rapid p-mode pulsations using the exact same sample of spectra as in the luminosity variation study described above. The RVs were measured from the Doppler shift of the spectral lines with respect to their rest wavelengths by fitting a set of mathematical functions using the FITSB2 routine (Napiwotzki et al. 2004). We used a polynom to match the continuum, while the line wings were fit with a Lorentz profile and the line core with a Gaussian profile. Heliocentric corrections were then applied to the times and velocities.
We initially computed five separate RV curves based on Hδ, Hγ, He I (4026 Å and 4471 Å), and He II (4686 Å) in order to be able to check the extracted periodicities for consistency and possible systematic effects. All the original RV curves coming out of the cross-correlation are dominated by a large (~150 km s-1) variation reminiscent of the change in altitude of the star over the nightly observing period. This was attributed to an apparent movement of the target within the (wide) slit during the course of the night, and was corrected for by fitting and subtracting a spline function based on 20 time bins, which yielded nicely flattened RV curves for each of the nights. For each line, we then computed the Fourier spectrum on the basis of the combined flattened light curve. We found that the dominant 140.5 s periodicity was easily detected in all five datasets, and the derived amplitudes and phases were fully consistent within the formal errors. In order to reduce the noise level further we then averaged the five light curves into a combined, flattened RV curve.
Subjecting this combined RV curve to a standard Fourier analysis we recovered the dominant pulsation from photometry at the exact same period of 140.49 s with an amplitude of ~5.6 km s-1 and a high S/N of ~20. The largest of the lower amplitude periodicities from Table 3, P2, was also detected just above the 4σ level. Please see Fig. 5 for the RV Fourier spectrum, and Table 4 for details of the periodicities extracted. For comparison we also list the corresponding amplitudes and phases found for the continuum light curve around 4600 Å (see Sect. 3.2) and the phase shift of the flux compared to the radial velocity variability. The zeropoint for the phase is the mid-exposure time of the first datapoint. In the adiabatic approximation the radial velocity should lag behind the flux variability by exactly π/2, i.e. 0.25 of the actual period measured. As can be seen in the table, this is not the case, particularly for the dominant mode, implying measurable non-adiabatic effects. Also, the measured phase difference bears the signature of the ℓ index of the pulsation mode. This will be exploited below.
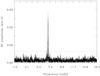 |
Fig. 5 Fourier spectrum of the combined radial velocity curve obtained from the five H and He lines observed for EC 01541−1409. The horizontal dotted line indicates the 4σ level adopted as the threshold for credible pulsations. |
Periodicities extracted from the combined RV curve for EC 01541−1409 together with the corresponding amplitudes and phases measured from the continuum light curve and the phase lag between the RV and flux variations.
Comparing the radial velocity amplitude of P1 to that published by Reed et al. (2012b) we find that our value is slightly higher (5.6 km s-1 compared to 4.5 km s-1), an effect that is linked in part to the shorter integration time that we used (10 s compared to 25 s). The longer the integration time, the more the incoming sinusoidal signal is smeared out in the data. However, this effect is small compared to the RV measurement uncertainties and in particular the intrinsic amplitude variations of the modes. Intrinsic amplitude variations are the reason why any quantitative comparisons of the pulsational properties must be based on data with the exact same temporal sampling. In the case presented here this is not an issue, as all our measurements are based on the same data set.
4. Partial mode identification from monochromatic amplitude and phase variations
We exploited the monochromatic amplitudes and phases for EC 01541−1409 following the approach developed by Randall et al. (2005) for the application to multi-colour photometry. It is the same method that was more recently adapted to time-series spectrophotometry and used to model the dominant pulsation in EC 20338−1925 (Randall et al. 2010). We refer the interested reader to these publications for more details on the underlying theory and the models and techniques used. Appendix A also provides a very brief account of the approach.
 |
Fig. 6 Top blocks: normalised observed amplitude for P1 (black curve) together with the theoretical monochromatic amplitudes (red curves) as calculated for a period P = 140.5 s and the atmospheric parameters determined for EC 01541−1409 for modes with degree of ℓ = 0−5 as indicated in the individual panels. Bottom blocks: the corresponding plots for the normalised monochromatic phase. Velocity fields were not included in our continuum phase calculations, which is why the observed phase jumps across spectral lines are not recovered by the models. |
In short, the method exploits the notion that, because of their different surface geometry, modes with different degree indices ℓ are affected differently by limb darkening. Since the limb darkening law is a function of wavelength, it becomes possible to constrain the degree index of a mode by comparing the amplitudes and phases measured at different wavelengths. Unknown parameters such as the inclination of the star and the intrinsic pulsational amplitude can be cancelled out by basing the analysis on amplitude ratios and phase differences rather than their absolute values. In this study, we normalise the amplitudes and phases to unity and zero, respectively, using the blue continuum (the Balmer continuum shortward of the Balmer jump) of the spectra as a reference.
The theoretical monochromatic amplitudes and phases were computed from full model atmospheres constructed specifically to mimic the atmospheric parameters of EC 01541−1409 as reported in Table 2. Non-adiabatic effects, known to be non-negligible for sdBVr stars (Randall et al. 2005), were incorporated using our standard second-generation seismic models (see e.g. Charpinet et al. 1997). These are static envelope structures, and as such are described not only by the values of log g and Teff derived from spectroscopy, but also assume a total stellar mass (set to 0.47 M⊙) and hydrogen envelope thickness (set to ![\hbox{$\log{q(\rm H)}\equiv\log{[1-\frac{M(\rm H)}{M_{\ast}}]} = -3.62$}](/articles/aa/full_html/2014/03/aa23209-13/aa23209-13-eq52.png) ). The values chosen for the mass and the envelope thickness are representative of a hot B subdwarf with the atmospheric parameters of EC 01541−1409 and were found by searching for a model that could reproduce the two main periodicities observed in terms of ℓ = 0 and 2 (i.e. the values inferred below). Unlike log g and Teff these two parameters influence only the non-adiabatic effects, and these only marginally, so their exact values are not critical.
). The values chosen for the mass and the envelope thickness are representative of a hot B subdwarf with the atmospheric parameters of EC 01541−1409 and were found by searching for a model that could reproduce the two main periodicities observed in terms of ℓ = 0 and 2 (i.e. the values inferred below). Unlike log g and Teff these two parameters influence only the non-adiabatic effects, and these only marginally, so their exact values are not critical.
The behaviour of the amplitude and phase as a function of wavelength was computed for the main periods observed for degree indices ℓ = 0 − 5 and normalised. In order to enable a quantitative comparison with the observational data, the computed quantities were convolved to the same effective spectral resolution (Δλ = 7.8 Å). In Fig. 6 we show the theoretical amplitudes and phases overplotted with the observed values for the dominant mode of pulsation at 140.5 s. For this representative model the values of log g and Teff were assumed to be those referred to as “with metals” in Table 2.
Examining first the amplitude plots (upper panels), it is clear from visual inspection alone that the observations are best fit by a mode with ℓ = 0, followed by one with ℓ = 1. Higher degree modes can be immediately rejected. Quantitatively speaking, and using the quality-of-fit parameter Q (Press et al. 1986) introduced by Randall et al. (2005) in conjunction with a standard χ2 approach, we find that only ℓ = 0 provides a formally acceptable solution with Q = 0.062 (0 free parameters, 1867 data points), while Q ~ 0 for the other degree indices (for values of Q < 0.001 the solution can be formally excluded in this nomenclature). The formal fitting errors on the individual amplitude points are typically 2−3% of the actual amplitude value, allowing the amplitude-wavelength behaviour to be characterised quite accurately.
In order to assess the robustness of the solution with respect to the atmospheric parameters inferred from spectroscopy, we recalculated the theoretical amplitudes and phases varying the values of log g and Teff within the uncertainties of the different solutions given in Table 2. We found that this did not change the results in a qualitative way. In this context, Fig. 7 provides a zoomed-in view of the ℓ = 0 fits obtained for the observed Fourier amplitude spectrum using models spanning a 2σ spread around our reference model in the log g-Teff plane.
The phase plots (lower panels of Fig. 6) confirm the radial nature of the main periodicity in a spectacular way. It is immediately obvious just from looking at the plots that ℓ = 0 provides by far the best fit thanks to the clear downward drift in relative continuum phase with increasing wavelength. This is only predicted for radial modes; a dipole mode should show practically no phase shift in the continuum, while the higher degree modes exhibit an upward drift. We note that for both the amplitude and phase, the modal discriminatory power rests with the contrast in behaviour between the Balmer continuum and the Paschen continuum. It would be extremely challenging to measure any such trend using spectra covering only wavelengths longer than 4000 Å since the continuum phase does not vary substantially at redder wavelengths. A quantitative analysis confirms the ℓ = 0 identification, again allowing all other degree indices to be formally excluded. We find a “perfect” Q value of 1.0 for the ℓ = 0 solution (0 free parameters, 1867 data points), while Q ~ 0 for all other values of ℓ considered. We also point out that neglecting non-adiabatic effects in our calculations would have made it impossible to exploit the phase data since in the adiabatic approximation the phase shift as a function of wavelength is always zero. The fact that we were able to account for the available continuum phase data in terms of our ℓ = 0 model (see again Fig. 6) demonstrates that our implementation of non-adiabatic effects in this sort of modelling is sound.
Having established without a doubt that the dominant 140.5 s pulsation in EC 01541−1409 is a radial mode, we can further exploit the available data to determine its intrinsic amplitude. Since radial modes have no particular symmetry axis, the real function 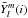 in Eq. (A.1) of Appendix A reduces to
in Eq. (A.1) of Appendix A reduces to 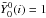 1. Given that
1. Given that 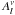 is calculated from the model atmospheres, one can then readily compare the observed (un-normalised) Fourier amplitude spectrum with its model equivalent
is calculated from the model atmospheres, one can then readily compare the observed (un-normalised) Fourier amplitude spectrum with its model equivalent 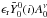 and solve for ϵr. We thus computed the average intrinsic amplitude on the basis of the 1867 observed data points available between 3550 Å and 6350 Å, and find that the intrinsic dimensionless radial amplitude of the 140.5 s mode is given by ϵr = 0.00107 ± 0.00003. We then exploited ϵr to estimate the dimensionless amplitude of the effective temperature perturbation ϵT = 0.0107, and that of the surface gravity perturbation ϵg = 0.0356, respectively using Eqs. (15) and (12) as given in Randall et al. (2005). We note that for ϵg, only 6% of the gravity perturbation is due to the change in the radius, the rest being due to the pulsational acceleration.
and solve for ϵr. We thus computed the average intrinsic amplitude on the basis of the 1867 observed data points available between 3550 Å and 6350 Å, and find that the intrinsic dimensionless radial amplitude of the 140.5 s mode is given by ϵr = 0.00107 ± 0.00003. We then exploited ϵr to estimate the dimensionless amplitude of the effective temperature perturbation ϵT = 0.0107, and that of the surface gravity perturbation ϵg = 0.0356, respectively using Eqs. (15) and (12) as given in Randall et al. (2005). We note that for ϵg, only 6% of the gravity perturbation is due to the change in the radius, the rest being due to the pulsational acceleration.
Derived properties of the dominant, ℓ = 0, 140.5 s pulsation mode in EC 01541−1409.
 |
Fig. 7 Normalised observed amplitude for P1 (black curve together with error bars for 1867 data points) compared with theoretical monochromatic amplitudes (five curves of different colours depicting the ℓ = 0 solution for our reference model and for four additional models spanning 2σ in the log g-Teff plane). |
 |
Fig. 8 Apparent variations in atmospheric parameters over the pulsation phase for the dominant period in EC 01541−1409. The points with error bars show the values of Teff (top panel), log g (middle panel), and log N(He)/N(H) (bottom panel) as derived from our model atmosphere fit to 10 spectra phase-binned to the 140.5 s periodicity (see text for details). Two pulsation cycles are shown for better visualisation. The dashed curves correspond to the phase-dependent Teff and log g as predicted from the respective amplitudes and equilibrium values listed in Table 5. The noticeable difference in phase between the Teff and the log g variations is due to non-adiabatic effects and corresponds to the departure from the adiabatic value (0.25 pulsation cycles) of the phase lag between the flux and RV variation reported in Table 4, i.e. 0.09 cycles. |
The dimensionless amplitudes are listed in Table 5 together with the equilibrium radius, effective temperature, and surface gravity determined from our seismic reference model and the resulting physical perturbation amplitudes. These represent the first reliable estimates of intrinsic pulsation amplitudes for a hot B subdwarf derived from the modelled emergent flux amplitude of a mode with known degree index ℓ. Previous determinations of intrinsic pulsational amplitudes in sdB stars (for the dominant radial modes in PG 1325+101 and Balloon 090100001, see Telting & Østensen 2004; Østensen et al. 2008) were mostly based on measurements of the apparent variations in Teff and log g from phase-binned spectra. In this method, model spectra are fit to observed spectra that have been averaged and phase-binned to the pulsation cycle of the periodicity in question, the atmospheric parameters are derived for each phased spectrum, and the apparent amplitudes of the variations are determined by fitting a sinusoid to the measurements. This technique works only if all of the following conditions are met: 1) the periodicity in question completely dominates the pulsation spectrum, implying that variations introduced by other periods are negligible in the phased spectra; 2) the mode is known to be radial. For non-radial modes, the emergent spectrum is distorted during a pulsation cycle and cannot be accurately fit with synthetic models that come from static, uniform, and homogeneous model atmospheres. On the other hand, for radial modes the instantaneous values of the atmospheric parameters are homogeneous across the visible disk of the star, and therefore the direct method of fitting makes physical sense; and 3) the amplitude of the mode in question is relatively small, i.e. no large non-linear effects (manifesting in harmonics in the Fourier spectrum) are present.
 |
Fig. 9 Left: observed relative amplitude behaviour as a function of wavelength for P2 = 145.8 s, depicted by the black points with error bars. Each point represents a 130 Å wide bin of the original monochromatic quantity, which was averaged in order to improve the S/N. The error bars indicate the rms deviation about the average value within the wavelength bin. The predicted monochromatic amplitudes for different degree indices are also shown and labelled. All quantities have been normalised. Right: similar to the left panel, but referring to the relative phase. |
Given that for the 140.5 s mode in EC 01541−1409 all these criteria are met, we computed average spectra for ten phase bins over the pulsation cycle. For each average spectrum we combined between 115 and 130 individual spectra taken from the first night of observations and the pool of spectra used for the estimation of the atmospheric parameters in Sect. 3.1, i.e. those that had a wavelength resolution better than 4.8 Å and were convolved to that resolution. Therefore, the phased spectra are internally consistent with the average spectrum and the same continuum normalisation could be applied. Each of the phased spectra was then fit using the same models as before. The atmospheric parameters derived are plotted as a function of pulsation phase together with the formal fitting errors in Fig. 8. The sinusoidal variation in both Teff and log g over the pulsation cycle is immediately evident, while the Helium abundance stays constant within the measurement uncertainties, as expected. Upon closer inspection, the measurements of log g show a phase shift compared to the Teff data, revealing the non-adiabatic lag of the radius compared to the temperature variations. Overplotted on the measurements are the Teff and log g as a function of pulsation phase as computed for a sinusoid characterised by the respective real amplitude and equilibrium value listed in Table 5. The two curves have been shifted relative to each other in phase by 0.09 cycles, which corresponds to the departure in adiabacity of the phase lag between the flux and the RV variation reported in Table 4. It can be seen that the agreement with the direct measurements is extremely good, and in particular both methods yield amplitudes that are fully consistent within the measurement uncertainties. From this we deduce that the dimensionless intrinsic amplitudes ϵT and ϵg inferred above are accurate. Since they are directly related to the dimensionless radial amplitude ϵr, which in turn is just the ratio of the observed flux amplitude to 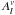 for a radial mode, we can infer that the modelled emergent flux amplitudes are reliable not just at the relative but also at the absolute level. This does not imply that our models are generally able to predict the intrinsic amplitudes of non-linear pulsations; these were derived from the observed amplitude only after the secure identification of the degree index of the pulsation mode, and constitute the average value over the time span of the observations.
for a radial mode, we can infer that the modelled emergent flux amplitudes are reliable not just at the relative but also at the absolute level. This does not imply that our models are generally able to predict the intrinsic amplitudes of non-linear pulsations; these were derived from the observed amplitude only after the secure identification of the degree index of the pulsation mode, and constitute the average value over the time span of the observations.
 |
Fig. 10 Left: diagnostic diagram based on the simultaneous use of the normalised amplitudes and normalised phases for the 145.8 s mode. The crosses refer to the observational data, while the curves refer to model predictions for ℓ = 0 (black), ℓ = 1 (red), and ℓ = 2 (blue). Right: similar to the left panel, but referring to the dominant 140.5 s mode. |
 |
Fig. 11 Left: relative χ2 values for the amplitude data alone (dotted red line), for the phase data alone (blue dotted line), and for the combination of amplitude and phase data (solid black line). Right: similar to the left panel, but referring to the dominant 140.5 s mode. |
Moving from the dominant periodicity to the lower amplitude pulsations listed in Table 3, we find that the S/N of the observed monochromatic amplitudes and phases is inferior by an order of magnitude. Only for P2 = 145.8 s, our second-highest amplitude mode, were we able to exploit the observed amplitudes and phases. In order to reduce the noise we binned the monochromatic observed quantities into 21 units with a width of 130 Å, and compared these to the theoretical values. The results are illustrated in Fig. 9. Here we normalised the data using the three bluest points in order to compensate for the relatively large measurement uncertainties. Formally speaking, and again using the Q-probability formalism (0 free parameters, 21 data points), none of the solutions shown in the left panel of Fig. 9 provide an acceptable fit to the amplitude data. The ℓ = 2 curve is the best of these bad fits. The situation is better for the phase data (Fig. 9, right panel), where we get a value of Q = 0.045 for a degree index ℓ = 2, Q = 0.004 for ℓ = 4, while all other possibilities can be formally excluded. These partial results are consistent with the constraint that P2 cannot be an ℓ = 0 mode given that its period, 145.8 s, is too close to that of the dominant ℓ = 0P1 mode at 140.5 s. Indeed, it is a basic mechanical property of hot B subdwarfs that the predicted theoretical period spacings should be ≳10 s for radial modes in these stars.
The discriminatory power of mode identification can be considerably enhanced by combining the amplitude and phase data, as was shown by Cugier & Daszyńska (2001) and Daszyńska-Daszkiewicz et al. (2005). Following these authors’ approach, we created the diagnostic diagrams shown in Fig. 10, the left panel of which demonstrates that the P2 mode is, in fact, an ℓ = 2 mode. Here we binned the theoretical monochromatic amplitudes and phases in the same way as the observational data (130 Å bin width) in order to reduce the spread of the theoretical points caused by the spectral lines in this diagram. The theoretical curves for ℓ = 3, 4, and 5 are not shown as they can be completely ruled out from the outset. The right panel of Fig. 10 provides an equivalent diagnostic diagram for the dominant mode P1 for illustration purposes. Of course, this mode was earlier identified as a radial mode on the basis of an independent analysis of both the amplitude and the phase data and the diagram quite unsurprisingly simply confirms this identification.
It is interesting to quantify the gain in modal discriminatory power achieved by combining amplitude and phase data compared to exploiting either of these individually. To do this, we computed the usual χ2 values for each assumed value of ℓ by comparing the 21 binned (normalised) observational data points with the corresponding 21 (normalised) theoretical bins for both the amplitude and the phase data. The resulting six values of χ2 (one for each ℓ) were then normalised by first dividing each by the lowest χ2 value and then subtracting 1 to obtain 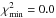 . Thus, the amplitude and phase results are placed in the same reference frame. We next added the χ2 values for the amplitude and phase together for each degree index ℓ. Finally, the results were converted to a logarithmic scale for better visualisation after again adding 1 to all the χ2 values of the three diagnostics considered (amplitudes only, phases only, amplitudes + phases). In this way, all data sets were normalised to log
. Thus, the amplitude and phase results are placed in the same reference frame. We next added the χ2 values for the amplitude and phase together for each degree index ℓ. Finally, the results were converted to a logarithmic scale for better visualisation after again adding 1 to all the χ2 values of the three diagnostics considered (amplitudes only, phases only, amplitudes + phases). In this way, all data sets were normalised to log 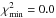 .
.
 |
Fig. 12 Left: observed monochromatic velocity-to-amplitude ratio (1867 data points with error bars superimposed on the heavy black curve) as a function of wavelength for P1 = 140.5 s. The predicted monochromatic ratios for different degree indices are also shown and labelled. The cgs unit convention is used for the y-axis. Right: similar to the left panel, but referring to the P2 mode with 21 wavelength bins. |
The results of this exercise are shown in Fig. 11 for the 145.8 s (left panel) and 140.5 s (right panel) pulsations. The red dotted lines illustrate the results from the amplitude data alone, while the blue dotted lines refer to the phase data alone. The solid black line is obtained by combining the amplitude and phase data and constitutes an improvement in modal discriminatory power for both pulsations. It is important to understand that, because of the way in which the data were normalised, these diagrams do not provide any indication of the absolute quality of the fits, but are instead designed to highlight the relative disriminatory power between different degree indices based on the three diagnostics. Any indication of whether one (or all) of the degree indices provide an acceptable fit to the observational data is lost in the normalisation, and therefore any such plots should always be combined with others (such as Fig. 6 or 10) that illustrate the quality of the best-fit and other possible solutions. In the case presented here, the dominant 140.5 s periodicity can be unambiguously identified from either the amplitude or phase data independently, while the lower amplitude pulsation cannot. Using only the amplitude data, even the best ℓ = 2 fit was not formally acceptable, while for the phase data both ℓ = 2 and 4 provided acceptable solutions. It is only by combining both the amplitude and phase data that we can conclude with confidence that the 145.8 s pulsation in EC 01541−1409 is an ℓ = 2 mode.
5. Exploitation of the radial velocity measurements
As described briefly in Appendix A, the velocity-to-amplitude ratio provides another potential diagnostic for inferring or constraining the degree index of a pulsation mode. In the left panel of Fig. 12 we compare the observed monochromatic velocity-to-amplitude ratio for the dominant mode P1 with the predictions of our reference model for different values of ℓ. The observational quantity was obtained by dividing the measured velocity from Table 4 (in cm/s) by the unnormalised spectrophotometric amplitudes (in fractional intensity units) for that mode and taking the logarithm. The distribution of the modelled velocity-to-amplitude ratios for different ℓ values implies that any ℓ = 3 or ℓ = 4 modes can be easily identified using this technique, while ℓ = 2 modes are more challenging but still show a fairly distinct signature. On the other hand, there is practically no discriminatory power in the diagram between the solutions with ℓ = 1 and ℓ = 0 for the seismic model of EC 01541−1409 as applied to the dominant mode. Indeed, using the amplitude and/or phase data as we did above provides far superior diagnostics to discriminate between these two ℓ values. A comparison of the observational data with the model curves indicates that the present results are at least consistent with our formal identification of the P1 mode above as a radial mode. However, the observational curve in Fig. 12 (left panel) falls below the ℓ = 0 curve by 14%, which is significant enough to formally rule out this identification (and all others) in the Q-probability formalism. Clearly, even the best solution for ℓ = 0 does not provide a good fit to the observations.
Diagnostic for ℓ identification based on the phase lag between the flux variation and the radial velocity.
The case is similar but less extreme for the P2 mode identified above as an ℓ = 2 pulsation (right panel of Fig. 12). Again, we find that the new results are consistent with our prior identification. The observational data points are now just above the ℓ = 2 curve in the plot, but thanks to the larger measurement uncertainties the fit is at least formally acceptable. We note for completeness that the theoretical velocity-to-amplitude ratios are slightly different for the two pulsations shown due to their slightly different periods.
Intrigued by our failure to quantitatively reproduce the monochromatic velocity-to-amplitude ratio, particularly for the dominant P1 mode, we carefully checked for and ruled out possible mistakes made in the implementation of the theoretical formulas associated with the radial velocity (see Appendix A) and in the measurement of the radial velocity itself. Unless we missed something significant in these checks, the most plausible explanation is that our radial velocity measurements do not reflect the pulsational behaviour of the atmospheric layers where the continuum originates very accurately. This is important because strictly speaking the underlying theory as developed in Randall et al. (2005) applies only to the emergent atmospheric continuum and not to spectral lines. We found a particularly interesting discussion on the difficulties of connecting actual radial velocity measurements with photospheric motions in Stamford & Watson (1981). These authors suggest that, ideally, only narrow and weak metal lines – by definition formed very near the continuum – should be used as velocity indicators. Unfortunately, the spectral resolution of our time-resolved spectrophotometry is insufficient to make use of such faint metal lines. Instead, we relied on measurements of the central wavelengths of the strong lines provided by Hδ, Hγ, He I 4026, He I 4471, and He II 4686, the cores of which are well-known to be formed much higher in the atmosphere than the continuum. In contrast, the observed flux amplitude is based on the continuum around 4600 Å, where our formalism is valid. Given that the modelled monochromatic amplitudes can reproduce not only the relative behaviour of the observed amplitudes as a function of wavelength but also the absolute variations measured in log g and Teff rather accurately, we believe them to be sound. Therefore, the discrepancy seen in the left panel of Fig. 12 is most likely related to the radial velocity amplitude. It would be eliminated if the radial velocity measured for P1 were just 0.8 km s-1 higher. This is certainly more than the formal measurement uncertainties (~0.2 km s-1); however, it should be kept in mind that these probably underestimate the true uncertainties and do not take into account possible systematic effects introduced by the choice of line profile during the RV fitting, for example. Searching the available literature for a precedent, we found just one example where radial velocity amplitudes were used in conjunction with amplitudes from photometry to derive the degree index for a pulsating sdB star (Baran et al. 2008). Unfortunately, no indication was given of the absolute quality-of-fit between the observed and the modelled quantities, so it is not clear to us whether these authors encountered similar difficulties.
The combination of flux and radial velocity measurements also leads to a second diagnostic tool which has the advantage of being insensitive to the depth of line formation in the atmosphere (see Appendix A). This second indicator is based on the comparison of the observed phase lag between the flux and the radial velocity and the computed phase difference, 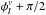 , for various assumed values of the degree index ℓ. The observed phase lags reported in Table 4 can be translated into phase shifts expressed in radians to give 2.13 ± 0.04 rad for the P1 mode, and 1.80 ± 0.20 rad for the P2 mode. These values are reported in Table 6, where they are compared to model predictions for different ℓ values based on the average of the monochromatic phase
, for various assumed values of the degree index ℓ. The observed phase lags reported in Table 4 can be translated into phase shifts expressed in radians to give 2.13 ± 0.04 rad for the P1 mode, and 1.80 ± 0.20 rad for the P2 mode. These values are reported in Table 6, where they are compared to model predictions for different ℓ values based on the average of the monochromatic phase 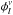 in the 4520−4670 Å bandwidth (the same that was used for the observed flux phases). Quite interestingly, the measurements for the P1 mode are sufficiently accurate to independently identify it as an ℓ = 0 pulsation, confirming the original identification once again. To our knowledge, this is the first time that mode identification has been achieved in a pulsating hot B subdwarf on the basis of this indicator. For the P2 mode the S/N is unfortunately insufficient to allow mode discrimination with that method (see Table 6), but we note that the modelled phase lag is consistent with our previous identification of ℓ = 2.
in the 4520−4670 Å bandwidth (the same that was used for the observed flux phases). Quite interestingly, the measurements for the P1 mode are sufficiently accurate to independently identify it as an ℓ = 0 pulsation, confirming the original identification once again. To our knowledge, this is the first time that mode identification has been achieved in a pulsating hot B subdwarf on the basis of this indicator. For the P2 mode the S/N is unfortunately insufficient to allow mode discrimination with that method (see Table 6), but we note that the modelled phase lag is consistent with our previous identification of ℓ = 2.
6. Conclusion
Our initial goal was to identify the degree index of one or more pulsation modes in the bright (B ~ 12.1) rapidly pulsating sdB star EC 01541−1409 using time-resolved spectrophotometry obtained using the unique HIT-MS mode on VLT/FORS. We had previously tested our technique using the same set-up, but for the much fainter target EC 20338−1925 (V ~ 15.7) for which we successfully identified the dominant pulsation as a radial mode based on the behaviour of its monochromatic amplitude as a function of wavelength (Randall et al. 2010). Having now chosen a much brighter target, we had hoped to analyse and identify the ℓ values for several modes. Such partial mode identification can be extremely useful input for detailed searches for viable seismic models in parameter space, and it can be crucial for testing the validity of a solution a posteriori.
We reached our goal in that we were able to unambiguously identify the ℓ index of the two highest amplitude modes, P1 and P2, in EC 01541−1409. We were hoping for more mode identifications, but unfortunately our target was not very cooperative and the light curve observed was dominated by a single pulsation mode with an amplitude more than an order of magnitude higher than for the other periodicities. On the positive side, the monochromatic amplitude and phase spectra that we gathered for the dominant mode are the very best data of this kind that have ever been obtained for pulsating hot B subdwarfs. Using the theoretical framework developed by Randall et al. (2005), we were able to model the wavelength-dependent amplitude and phase continuum spectra of that mode successfully and unambiguously identify it as a radial mode. Even the amplitude and phase data individually were sufficient to reach that conclusion, thanks to their sensitivity to the ℓ index in the wavelength range between the Paschen and the Balmer continuum. Had our observations been restricted to wavelengths higher than the Balmer jump, it would have been impossible to distinguish between the ℓ = 0, 1, 2, or even 4 possibilities for the dominant P1 mode. In the case of P2, which was detected at a much lower S/N, it was necessary to combine both the amplitude and phase data to derive an unequivocal value of ℓ = 2.
We were able to further exploit our time-resolved spectrophotometry by deriving radial velocity measurements for both the P1 and P2 modes. These were used to test two additional diagnostic tools to independently infer the ℓ values of the modes. First, a comparison between the observed monochromatic velocity-to-amplitude ratio with model values was used to confirm the P1 mode as a radial pulsation, and independently re-identify the P2 mode as an ℓ = 2 pulsation. However, the best fit for the velocity-to-amplitude ratio for the dominant mode, while consistent with the ℓ = 0 identification, did not provide a good match to the observations (see Fig. 12, left panel). We were not able to find a fully satisfying explanation for this, but suspect that deriving radial velocities on the basis of the central wavelengths of strong spectral lines (as we were forced to do) may not reflect the atmospheric motions near the region of continuum formation very accurately. We note that the basic theory (see e.g. Randall et al. 2005, and Appendix A) used for modelling the monochromatic amplitude, phase, and radial velocity strictly speaking only applies to the emergent flux in the continuum, not to spectral lines. The second diagnostic to emerge from the radial velocity measurements was the comparison of the observed difference in phase between the flux and the radial velocity with ℓ-sensitive model values. It led to an independent determination of ℓ = 0 for the P1 mode, while the lower S/N for P2 limited the diagnostic to a consistency check.
We would like to point out that our approach is completely homogeneous, since the amplitude, phase, and radial velocity spectra were derived from the same observational data set. Given that the pulsation amplitudes for sdB stars generally vary significantly throughout an observing season, this approach is the only way to ensure an internal consistency between the observables. Furthermore, we based our determination of the atmospheric parameters of EC 01541−1409 on a high S/N time-averaged spectrum that we extracted carefully from our time series, again maximizing the internal consistency. The values of the effective temperature and the surface gravity that we inferred from that time-averaged spectrum were essential inputs in the construction of the seismic structure used to model the observable quantities. The fact that we were able to account for both the high S/N amplitude and phase spectra of the dominant mode remarkably well is extremely encouraging and suggests that our treatment of the elusive non-adiabatic quantities in the atmospheric layers of pulsating sdB stars is accurate.
Given that the dominant mode was firmly established as a radial pulsation (with no particular symmetry axis), we were able to further exploit the unique high S/N data for that mode to obtain a precise estimate of its intrinsic (dimensionless) radius amplitude, ϵr = 0.00107 ± 0.00003. From that, we deduced intrinsic dimensionless amplitudes for both the temperature perturbation ϵT = 0.0107, and the surface gravity perturbation ϵg = 0.0356. In the latter case, about 94% of the perturbation comes from pulsational acceleration, and only a small fraction is caused by radius changes. Using our reference model for EC 01541−1409, we find that these perturbations amount to 1.07 × 107 cm, 396 K, and 2.24 × 104 cm s-2. These are very interesting modal properties that have so far mostly remained out of reach for pulsating sdB stars. We were able to confirm their accuracy using the apparent variations measured in log g and Teff over the main 140.5 s pulsation cycle on the basis of phase-folded spectra.
Finally, we note that our determinations of the ℓ index for two distinct pulsation modes in EC 01541−1409 add to a short but growing list of cases where mode identification has been possible for pulsating sdB stars. This is always dependent on the availability of very high S/N observational data that are extremely challenging to gather and require medium to large telescopes. On the basis of the theoretical framework developed by Randall et al. (2005), we have so far achieved formal and unambiguous ℓ identifications for the following pulsations: 1) Randall et al. (2005) used the high-quality WHT/ULTRACAM u′g′r′ multicolour photometry gathered on KPD 2109+4401 (Jeffery et al. 2004) to formally identify the largest amplitude 182.4 s mode detected in that pulsator at the time as a radial mode; 2) Charpinet et al. (2008b) presented an analysis of the exceptionally high S/N UBV photometry obtained with the CFHT/LAPOUNE combination on the bright target Balloon 090100001 to identify the dominant mode as a radial pulsation, and eight other modes with values of ℓ = 1 and 2; 3) Silvotti et al. (2010) used high S/N WHT/ULTRACAM photometry to associate the dominant 349.5 s mode detected in HS 2201+2610 with a radial mode and the second-highest amplitude mode at 354.1 s with an ℓ = 1 mode; 4) Randall et al. (2010) used time-resolved spectrophotometry gathered with the VLT/FORS combination to identify the dominant mode at 146.9 s as a radial mode in the relatively faint star EC 20338−1925, at the same time establishing the feasibility of the monochromatic approach; and 5) Using the same observational set-up, we demonstrated in this paper that the P1 mode in EC 01541−1409 is a radial mode, while the much lower amplitude P2 mode is an ℓ = 2 pulsation. Not surprisingly perhaps, the expected amplitude hierarchy seems to be well followed in pulsating sdB stars, and dominant pulsations generally correspond to radial modes.
Online material
Appendix A: Monochromatic amplitude, phase, and radial velocity of a pulsation mode
For a non-rotating star, linear theory leads to the following expression for the first-order perturbation to the emergent Eddington flux relative to the unperturbed flux in presence of a single pulsation mode, 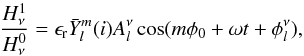 (A.1)where ϵr is the intrinsic dimensionless radial amplitude of the pulsation mode characterised by an angular frequency ω (=2π/P, P being the pulsation period), a degree index l, and an azimuthal order m, where
(A.1)where ϵr is the intrinsic dimensionless radial amplitude of the pulsation mode characterised by an angular frequency ω (=2π/P, P being the pulsation period), a degree index l, and an azimuthal order m, where  is a real function representing the viewing aspect (i is the inclination angle between the line of sight and the symmetry axis of the pulsation), where
is a real function representing the viewing aspect (i is the inclination angle between the line of sight and the symmetry axis of the pulsation), where 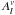 is a measure of the monochromatic amplitude of the relative flux, and where
is a measure of the monochromatic amplitude of the relative flux, and where 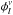 is the monochromatic phase of the relative flux with respect to an arbitrary zero point in time symbolised by the phase factor mφ0. This equation corresponds to Eq. (41) from Randall et al. (2005) using a slightly different notation, and the reader is referred to that publication for more details.
is the monochromatic phase of the relative flux with respect to an arbitrary zero point in time symbolised by the phase factor mφ0. This equation corresponds to Eq. (41) from Randall et al. (2005) using a slightly different notation, and the reader is referred to that publication for more details.
The term 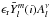 , which multiplies the cosine function in the previous equation, corresponds to the observable amplitude of the pulsation mode in the Fourier domain. However, given that the intrinsic radial amplitude ϵr and the viewing factor
, which multiplies the cosine function in the previous equation, corresponds to the observable amplitude of the pulsation mode in the Fourier domain. However, given that the intrinsic radial amplitude ϵr and the viewing factor 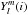 are unknown a priori, the Fourier amplitude does not reveal the details of the geometry of the mode. Hence, in order to exploit the l dependence of the amplitude as a function of wavelength (frequency), it is customary to compute the ratio of the amplitude at a given frequency ν with respect to the amplitude at some reference frequency ν′. By doing this, the monochromatic ratio
are unknown a priori, the Fourier amplitude does not reveal the details of the geometry of the mode. Hence, in order to exploit the l dependence of the amplitude as a function of wavelength (frequency), it is customary to compute the ratio of the amplitude at a given frequency ν with respect to the amplitude at some reference frequency ν′. By doing this, the monochromatic ratio 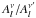 becomes independent of the unknown factors and still bears a wavelength-dependent signature of the degree index l of the mode. The phase difference
becomes independent of the unknown factors and still bears a wavelength-dependent signature of the degree index l of the mode. The phase difference 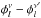 , which is independent of
, which is independent of 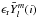 , also bears a similar, but distinct signature. We note that this signature is lost in the adiabatic approximation as no phase shift is then predicted. Given data of sufficiently high quality, amplitude ratios and phase differences can thus be exploited to infer or constrain the l index of a pulsation mode. This is a well-known method that we were fully able to make use of in this paper.
, also bears a similar, but distinct signature. We note that this signature is lost in the adiabatic approximation as no phase shift is then predicted. Given data of sufficiently high quality, amplitude ratios and phase differences can thus be exploited to infer or constrain the l index of a pulsation mode. This is a well-known method that we were fully able to make use of in this paper.
Mode discrimination between various l solutions can be improved, at least in principle, if radial velocity measurements can be obtained and combined with amplitude ratios and phase differences. This is described particularly well in Cugier & Daszyńska (2001), but we also refer the reader to the original paper of Dziembowski (1977) and to the review of Stamford & Watson (1981). According to these authors and others, the pulsational velocity projected along the line-of-sight and integrated over the visible disk of the star may be written as 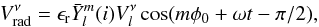 (A.2)\newpage
(A.2)\newpage
where 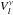 is given by
is given by 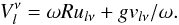 (A.3)In this expression, R is the (unperturbed) radius of the star, g is the (unperturbed) surface gravity, and ulν and vlν are l-dependent monochromatic quantities related to the disk-integrated quantity blν through the relations
(A.3)In this expression, R is the (unperturbed) radius of the star, g is the (unperturbed) surface gravity, and ulν and vlν are l-dependent monochromatic quantities related to the disk-integrated quantity blν through the relations ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:u} u_{l\nu} &=& (2l + 1)^{-1}[(l+1)b_{l+1\nu} + lb_{l-1\nu}], \\ \label{eq:v} v_{l\nu} &=& (2l + 1)^{-1}l(l+1)[b_{l-1\nu} - b_{l+1\nu}]. \end{eqnarray}](/articles/aa/full_html/2014/03/aa23209-13/aa23209-13-eq121.png) The disk-integrated quantity may be written as (see e.g. Eq. (25) of Randall et al. 2005),
The disk-integrated quantity may be written as (see e.g. Eq. (25) of Randall et al. 2005), 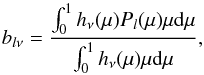 (A.6)where hν(μ) is the limb-darkening law, and Pl(μ) is a Legendre polynomial.
(A.6)where hν(μ) is the limb-darkening law, and Pl(μ) is a Legendre polynomial.
If one divides the term in front of the cosine term in Eq. (A.2) by its equivalent in Eq. (A.1), one eliminates the unknown factor 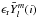 , and thus obtains another diagnostic tool to discriminate between l values, namely the monochromatic velocity-to-amplitude ratio,
, and thus obtains another diagnostic tool to discriminate between l values, namely the monochromatic velocity-to-amplitude ratio, 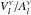 . It should be pointed out that the diagnostics based on amplitude ratios, phases differences, velocity-to-amplitude ratios, or combinations of the three work best when applied to the continuum part of the spectrum. This is because the theory was developed in this simpler framework, without having to add complicated velocity fields which are needed for a detailed description of the spectral lines, particularly the strong, dominant spectral lines. A potential difficulty with this approach in the particular case of EC 01541−1409, and more generally for pulsating hot subdwarf B stars, is that readily available radial velocity measurements – based on the central wavelengths of strong Balmer H I lines and strong He I and He II lines – cannot be easily connected with the pulsational behaviour of the continuum, which is formed significantly deeper in the atmosphere than the cores of these strong spectral features.
. It should be pointed out that the diagnostics based on amplitude ratios, phases differences, velocity-to-amplitude ratios, or combinations of the three work best when applied to the continuum part of the spectrum. This is because the theory was developed in this simpler framework, without having to add complicated velocity fields which are needed for a detailed description of the spectral lines, particularly the strong, dominant spectral lines. A potential difficulty with this approach in the particular case of EC 01541−1409, and more generally for pulsating hot subdwarf B stars, is that readily available radial velocity measurements – based on the central wavelengths of strong Balmer H I lines and strong He I and He II lines – cannot be easily connected with the pulsational behaviour of the continuum, which is formed significantly deeper in the atmosphere than the cores of these strong spectral features.
There is yet another potentially useful diagnostic that can be exploited by combining flux measurements with radial velocity measurements, and that is the predicted phase difference, 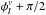 , between the flux and the velocity (see Eqs. (A.1) and (A.2)). This difference (to be measured in some suitable part of the continuum) is independent of the term
, between the flux and the velocity (see Eqs. (A.1) and (A.2)). This difference (to be measured in some suitable part of the continuum) is independent of the term 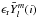 , and is also independent of the depth in the atmospheric layers since all moving parts must go through their equilibrium position at the same time during a modal cycle. The latter characteristic gives the phase lag technique the edge over the velocity-to-amplitude ratio diagnostic. If there is a pulsation node in the atmospheric layers – which is not the case for the pulsation modes of interest here – the phase could be off by a factor of π radian. Otherwise, the phase difference
, and is also independent of the depth in the atmospheric layers since all moving parts must go through their equilibrium position at the same time during a modal cycle. The latter characteristic gives the phase lag technique the edge over the velocity-to-amplitude ratio diagnostic. If there is a pulsation node in the atmospheric layers – which is not the case for the pulsation modes of interest here – the phase could be off by a factor of π radian. Otherwise, the phase difference 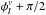 bears a signature of the degree index ℓ for a given mode.
bears a signature of the degree index ℓ for a given mode.
The real functions 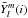 of interest here are related trivially to those introduced by Brassard et al. (1995) through a normalisation factor
of interest here are related trivially to those introduced by Brassard et al. (1995) through a normalisation factor 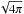 .
.
Acknowledgments
S.K.R. would like to thank the Paranal Science Operations, Engineering and Software staff, in particular Sylvain Guieu and Stéphane Brillant for their help with the observations. We also thank the anonymous referee for providing valuable comments and suggestions that helped to improve the quality of this paper. G.F. also wishes to acknowledge the contribution of the Canada Research Chair Program.
References
- Baran, A., Pigulski, A., & O’Toole, S. J. 2008, MNRAS, 385, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchette, J., Chayer, P., Wesemael, F., et al. 2008, ApJ, 678, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., & Wesemael, F. 1995, ApJS, 96, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Billères, M., et al. 2001, ApJ, 563, 1013 [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2005, A&A, 443, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 297 [Google Scholar]
- Charpinet, S., Van Grootel, V., Brassard, P., et al. 2013, in Eur. Phys. J. Web Conf., 43, 4005 [Google Scholar]
- Cugier, H., & Daszyńska, J. 2001, A&A, 377, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daszyńska-Daszkiewicz, J., Dziembowski, W. A., & Pamyatnykh, A. A. 2005, A&A, 441, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. 1977, Acta Astron., 27, 203 [NASA ADS] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2012, A&A, 539, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Jeffery, C. S., Dhillon, V. S., Marsh, T. R., & Ramachandran, B. 2004, MNRAS, 352, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Koen, C., O’Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285, 640 [Google Scholar]
- Kilkenny, D., O’Donoghue, D., Crause, L., et al. 2009, MNRAS, 396, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 1995, ApJ, 439, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Yungelson, L., Nelemans, G., et al. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 402 [Google Scholar]
- Østensen, R. H., Telting, J. H., Heber, U., & Jeffery, C. S. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 301 [Google Scholar]
- Østensen, R. H., Oreiro, R., Solheim, J.-E., et al. 2010, A&A, 513, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical recipes. The art of scientific computing (Cambridge University Press) [Google Scholar]
- Randall, S. K., Fontaine, G., Brassard, P., & Bergeron, P. 2005, ApJS, 161, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, S. K., Fontaine, G., Brassard, P., & Van Grootel, V. 2010, A&A, 522, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reed, M. D., Kilkenny, D., O’Toole, S., et al. 2012a, MNRAS, 421, 181 [NASA ADS] [Google Scholar]
- Reed, M. D., O’Toole, S. J., Telting, J. H., et al. 2012b, in Fifth Meeting on Hot Subdwarf Stars and Related Objects, eds. D. Kilkenny, C. S. Jeffery, & C. Koen, ASP Conf. Ser., 452, 193 [Google Scholar]
- Silvotti, R., Randall, S. K., Dhillon, V. S., et al. 2010, Astron. Nachr., 331, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Stamford, P. A., & Watson, R. D. 1981, Ap&SS, 77, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Telting, J. H., & Østensen, R. H. 2004, A&A, 419, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telting, J. H., & Østensen, R. H. 2006, A&A, 450, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telting, J. H., Geier, S., Østensen, R. H., et al. 2008, A&A, 492, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Grootel, V., Charpinet, S., Brassard, P., Fontaine, G., & Green, E. M. 2013, A&A, 553, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Highest amplitude periodicities extracted from the continuum light-curve around 4600 Å.
Periodicities extracted from the combined RV curve for EC 01541−1409 together with the corresponding amplitudes and phases measured from the continuum light curve and the phase lag between the RV and flux variations.
Derived properties of the dominant, ℓ = 0, 140.5 s pulsation mode in EC 01541−1409.
Diagnostic for ℓ identification based on the phase lag between the flux variation and the radial velocity.
All Figures
 |
Fig. 1 Typical individual spectra obtained with an exposure time of 10 s on 09 September 2011 for EC 01541−1409 (top) and the main-sequence comparison star (bottom). The spectra have been arbitrarily normalised for visualisation purposes, and are not flux calibrated. |
| In the text | |
 |
Fig. 2 Available H and He lines from the time-averaged FORS spectrum of EC 01541−1409, overplotted with the best model atmosphere fit including metals with the abundances indicated. The atmospheric parameters derived are also shown in the plot. |
| In the text | |
 |
Fig. 3 Fourier spectrum computed on the basis of the integrated continuum flux between 4520 Å and 4670 Å of all spectra obtained with a seeing of 7.8 Å or less. The lower-amplitude periodicities listed in Table 3 are marked by short vertical line segments. |
| In the text | |
 |
Fig. 4 Flux obtained from the combined time-averaged spectrum gathered for EC 01541−1409 across the two FORS chips (top panel) together with the wavelength-dependent amplitude (middle panel) and phase (bottom panel) extracted for the dominant 140.5 s mode. The flux and the amplitude spectra have been normalised to unity and are consequently dimensionless quantities, while the phase is plotted relative to its average value in the blue part of the spectrum in radians. The spectral lines identified are marked by vertical lines propagating across all plots: black continuous lines indicate hydrogen Balmer lines, dashed blue lines denote He I lines, and dotted red lines show He II lines. |
| In the text | |
 |
Fig. 5 Fourier spectrum of the combined radial velocity curve obtained from the five H and He lines observed for EC 01541−1409. The horizontal dotted line indicates the 4σ level adopted as the threshold for credible pulsations. |
| In the text | |
 |
Fig. 6 Top blocks: normalised observed amplitude for P1 (black curve) together with the theoretical monochromatic amplitudes (red curves) as calculated for a period P = 140.5 s and the atmospheric parameters determined for EC 01541−1409 for modes with degree of ℓ = 0−5 as indicated in the individual panels. Bottom blocks: the corresponding plots for the normalised monochromatic phase. Velocity fields were not included in our continuum phase calculations, which is why the observed phase jumps across spectral lines are not recovered by the models. |
| In the text | |
 |
Fig. 7 Normalised observed amplitude for P1 (black curve together with error bars for 1867 data points) compared with theoretical monochromatic amplitudes (five curves of different colours depicting the ℓ = 0 solution for our reference model and for four additional models spanning 2σ in the log g-Teff plane). |
| In the text | |
 |
Fig. 8 Apparent variations in atmospheric parameters over the pulsation phase for the dominant period in EC 01541−1409. The points with error bars show the values of Teff (top panel), log g (middle panel), and log N(He)/N(H) (bottom panel) as derived from our model atmosphere fit to 10 spectra phase-binned to the 140.5 s periodicity (see text for details). Two pulsation cycles are shown for better visualisation. The dashed curves correspond to the phase-dependent Teff and log g as predicted from the respective amplitudes and equilibrium values listed in Table 5. The noticeable difference in phase between the Teff and the log g variations is due to non-adiabatic effects and corresponds to the departure from the adiabatic value (0.25 pulsation cycles) of the phase lag between the flux and RV variation reported in Table 4, i.e. 0.09 cycles. |
| In the text | |
 |
Fig. 9 Left: observed relative amplitude behaviour as a function of wavelength for P2 = 145.8 s, depicted by the black points with error bars. Each point represents a 130 Å wide bin of the original monochromatic quantity, which was averaged in order to improve the S/N. The error bars indicate the rms deviation about the average value within the wavelength bin. The predicted monochromatic amplitudes for different degree indices are also shown and labelled. All quantities have been normalised. Right: similar to the left panel, but referring to the relative phase. |
| In the text | |
 |
Fig. 10 Left: diagnostic diagram based on the simultaneous use of the normalised amplitudes and normalised phases for the 145.8 s mode. The crosses refer to the observational data, while the curves refer to model predictions for ℓ = 0 (black), ℓ = 1 (red), and ℓ = 2 (blue). Right: similar to the left panel, but referring to the dominant 140.5 s mode. |
| In the text | |
 |
Fig. 11 Left: relative χ2 values for the amplitude data alone (dotted red line), for the phase data alone (blue dotted line), and for the combination of amplitude and phase data (solid black line). Right: similar to the left panel, but referring to the dominant 140.5 s mode. |
| In the text | |
 |
Fig. 12 Left: observed monochromatic velocity-to-amplitude ratio (1867 data points with error bars superimposed on the heavy black curve) as a function of wavelength for P1 = 140.5 s. The predicted monochromatic ratios for different degree indices are also shown and labelled. The cgs unit convention is used for the y-axis. Right: similar to the left panel, but referring to the P2 mode with 21 wavelength bins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


