| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322417 | |
| Published online | 14 March 2014 | |
The power spectrum of solar convection flows from high-resolution observations and 3D simulations
1
Instituto de Astrofísica de Canarias,
via Lactea, s/n, 38205
La Laguna, Tenerife,
Spain
e-mail:
fmi@iac.es
2
Dept. of Astrophysics, Universidad de La Laguna,
38200,
La Laguna, Tenerife,
Spain
Received:
31
July
2013
Accepted:
16
January
2014
Context. Understanding solar surface magnetoconvection requires the study of the Fourier spectra of the velocity fields. Nowadays, observations are available that resolve very small spatial scales, well into the subgranular range, almost reaching the scales routinely resolved in numerical magnetoconvection simulations. Comparison of numerical and observational data at present can provide an assessment of the validity of the observational proxies.
Aims. Our aims are: (1) to obtain Fourier spectra for the photospheric velocity fields using the spectropolarimetric observations with the highest spatial resolution so far (~120 km), thus reaching for the first time spatial scales well into the subgranular range; (2) to calculate corresponding Fourier spectra from realistic 3D numerical simulations of magnetoconvection and carry out a proper comparison with their observational counterparts considering the residual instrumental degradation in the observational data; and (3) to test the observational proxies on the basis of the numerical data alone, by comparing the actual velocity field in the simulations with synthetic observations obtained from the numerical boxes.
Methods. (a) For the observations, data from the SUNRISE/IMaX spectropolarimeter are used. (b) For the simulations, we use four series of runs obtained with the STAGGER code for different average signed vertical magnetic field values (0, 50, 100, and 200 G). Spectral line profiles are synthesized from the numerical boxes for the same line observed by IMaX (Fe I 5250.2 Å) and degraded to match the performance of the IMaX instrument. Proxies for the velocity field are obtained via Dopplergrams (vertical component) and local correlation tracking (LCT, for the horizontal component). Fourier power spectra are calculated and a comparison between the synthetic and observational data sets carried out. (c) For the internal comparison of the numerical data, velocity values on constant optical depth surfaces are used instead of on horizontal planes.
Results. A very good match between observational and simulated Fourier power spectra is obtained for the vertical velocity data for scales between 200 km and 6 Mm. Instead, a clear vertical shift is obtained when the synthetic observations are not degraded to emulate the degradation in the IMaX data. The match for the horizontal velocity data is much less impressive because of the inaccuracies of the LCT procedure. Concerning the internal comparison of the direct velocity values of the numerical boxes with those from the synthetic observations, a high correlation (0.96) is obtained for the vertical component when using the velocity values on the log τ500 = −1 surface in the box. The corresponding Fourier spectra are near each other. A lower maximum correlation (0.5) is reached (at log τ500 = 0) for the horizontal velocities as a result of the coarseness of the LCT procedure. Correspondingly, the Fourier spectra for the LCT-determined velocities is well below that from the actual velocity components.
Conclusions. As measured by the Fourier spectra, realistic numerical simulations of surface magnetoconvection provide a very good match to the observational proxies for the photospheric velocity fields at least on scales from several Mm down to around 200 km. Taking into account the spatial and spectral instrumental blurring is essential for the comparison between simulations and observations. Dopplergrams are an excellent proxy for the vertical velocities on constant-τ isosurfaces, while LCT is a much less reliable method of determining the horizontal velocities.
Key words: Sun: photosphere / Sun: granulation / convection / magnetohydrodynamics (MHD) / turbulence
© ESO, 2014
1. Introduction
The convective flows in the outermost layers of the solar interior and photosphere play an essential role in the dynamics and magnetism of the solar envelope and atmosphere. Their kinetic energy is distributed over a very wide range of space- and timescales (see, e.g., Nordlund et al. 2009), as results from (a) the strong stratification in the topmost tens of Megameters below the surface, leading to the appearance of convection cells from granular to supergranular size; and (b) the very high Reynolds numbers of those flows, which lead to turbulence and cascading of energy from the granular size downward to small scales before reaching the dissipation range. Solar convection provides a prime example of the need for interaction between observations and numerical simulations. The most recent advances in observational facilities now permit the observation of structures, flows, and fields with very high spatial resolution, down to ≈100 km. On the other hand, the numerical experiments and simulations of the past ten years, using the power of recent supercomputing installations, have reached high realism concerning the physical processes studied in the solar interior and photosphere (including material properties and detailed radiative transfer) with numerical grid spacing down to the order of 10 km (e.g., Stein & Nordlund 2006; Vögler & Schüssler 2007; Jacoutot et al. 2008). In addition, for the large scales, realistic simulations are now being produced on boxes with sides spanning several tens of Megameters in the horizontal directions, hence including a few supergranular cells in them (e.g., Stein et al. 2011). The simulations of convection with different numerical codes seem to agree reasonably well (Beeck et al. 2012).
A crucial tool to understanding the nature of the photospheric flows is their Fourier power spectrum. Application of this tool has been made along the years to both observational and numerical simulation data, mostly separately, but sometimes also comparing results from the two sources (e.g., Stein & Nordlund 1998; Georgobiani et al. 2006, 2007; Kitiashvili et al. 2012). For the observations, proxies have to be used for the velocity components, like Doppler shifts of spectral lines for the vertical velocity (e.g., Hathaway et al. 2000; Stein et al. 2006; Georgobiani et al. 2007; Rieutord et al. 2010; Kitiashvili et al. 2012; Katsukawa & Orozco Suárez 2012) or feature displacement on series of 2D continuum or Doppler maps (e.g., Rieutord et al. 2001, 2010; Stein et al. 2006; Georgobiani et al. 2006, 2007; Roudier et al. 2012; Goode et al. 2010; Abramenko et al. 2012; Kitiashvili et al. 2012). For the simulations, the velocity values on horizontal cuts in the numerical box have been Fourier-analyzed (Stein & Nordlund 1998; Rieutord et al. 2001; Stein et al. 2006; Georgobiani et al. 2006, 2007; Kitiashvili et al. 2012). In the current paper we would like to push the limits of the comparative analysis between simulations and observations in three directions:
-
(i)
by using Fourier spectra from observational proxies for the photospheric velocity field (Doppler, local correlation tracking) using as a basis recent observations with very high spatial resolution;
-
(ii)
by comparing them with Fourier spectra from numerical simulations but taking great care that the comparison is between homogeneous datasets, i.e., by first obtaining synthetic observations from the simulations and then modifying them to reproduce the instrumental degradation suffered by the real observations; and
-
(iii)
by checking the closeness of the synthetic observational proxies to the actual velocity vector components in the numerical box when using surfaces of constant optical depth (τ500 = const.) that correspond to the formation region of the spectral lines.
For the first aspect, observations with spatial resolution as high as one-tenth of the average granular size are available at present. Using Hinode/SOT data (spatial resolution: 200 km), Rieutord et al. (2010) have explored the power spectra of the vertical velocity down to scales of 400 km (and of the horizontal velocity in a range from 2.5 Mm to 76.3 Mm), but no comparison to numerical simulations was provided. Goode et al. (2010) obtained continuum images providing information down to very small scales of about 90 km using speckle-reconstruction techniques with the NST/BBSO telescope. From them, they could obtain horizontal-velocity maps using local correlation tracking (LCT) techniques. In the present paper we take advantage of the availability of time series of spectropolarimetric observations with unprecedented spatial resolution (near 120 km) obtained using the IMaX instrument aboard the SUNRISE balloon mission (Martínez Pillet et al. 2011; Solanki et al. 2010). These data allowed the determination of the line-of-sight velocity, continuum maps (used to compute the horizontal velocity by applying LCT) and of the full magnetic field vector with a field of view (FOV) of 32 × 32 Mm2 and for periods of half an hour with a 33.3-s cadence.
For the second aspect, comparisons so far have been done almost exclusively by using observational proxies, on the one hand, and 2D maps on horizontal planes in the numerical box, on the other. Yet, as done in the present paper, using spectral synthesis it is possible to obtain synthetic observations from the simulations that can then be subjected to the same sort of quality degradation that the solar spectrum suffers when going through the observational equipment: for that, one only needs to carry out a convolution of the synthetic spectra with a point spread function (PSF) in the spatial domain and with the monochromatic spectral response function (MSRF) in the spectral domain adequate to the specific equipment used to obtain the observations. In this way, the comparison can be carried out using the same kind of proxies on either side.
Finally, for the third aspect, the numerical datasets and techniques used in this paper allow us to approach the question of the closeness of the observational proxies (Dopplergrams and horizontal-velocity maps from feature tracking) to the actual velocity fields. So, it is of interest to check if the observational proxies are near the actual velocity field when both are obtained from the numerical results. The actual velocity field data have to be taken from a representative surface in the box, for which we choose an isosurface of the optical depth at 500 nm, τ500, which seems more appropriate than a horizontal plane in the numerical box. This is because, following basic spectral line formation theory (e.g., Gray 2005), the lines used for the Doppler velocity determination here are expected to be formed roughly in the same τ500-range for all vertical columns in the numerical box or in the observations (see further explanations in Sect. 8).
The layout of the paper is as follows: Sects. 2 and 3 describe the observational and numerical datasets, respectively, used in the paper. Section 4 details the procedure whereby we gain synthetic observations from the numerical boxes and the instrumental degradation that we have to apply to make these synthetic observations coherent with the observational data. The core of the paper are Sects. 6 through 8. Sections 6 and 7 discuss the Fourier power spectra obtained for the vertical and horizontal velocity distributions, respectively. Section 8 compares the observational proxies with the numerical data taken on τ500 isosurfaces. Sections 9 and 10 provide a discussion and conclusions.
2. Observations
 |
Fig. 1 Top: continuum intensity observed by the SUNRISE/IMaX instrument near the spectral line Fe I 5250.2 Å. Bottom: Doppler (vertical) velocity computed using the Stokes-I signal of the Fe I 5250.2 Å line. The velocity is expressed in km s-1. Details about granules and inter-granular lanes can be well appreciated. |
For this study we use sequences of images recorded with IMaX near the solar disk center on 2009 June 9. Images with pixel size 39.9 km were taken at five wavelengths along the profile of the magnetically sensitive FeI 5250.2 Å line, located at ±80 mÅ, ±40 mÅ from line center, and continuum at + 227 mÅ. The images were reconstructed considering the instrumental aberrations calibrated by the phase diversity method. The estimated circular polarization noise is 5 × 10-4 in units of the continuum wavelength for non-reconstructed data and three times larger for the reconstructed one. IMaX has a spectral resolution of 85 mÅ and a spatial resolution of 110–130 km (see Martínez Pillet et al. 2011, where further details about data acquisition and reduction procedures are given). We use two time series with a FOV of 32 × 32 Mm2 and cadence 33.3 s; the first series comprises 42 snapshots (23 min) and the second one 58 snapshots (32 min). The top panel of Fig. 1 displays a map of the normalized continuum intensity of one of the images. This map indicates that the contrast is particularly high thanks to the high resolution and the virtually seeing-free conditions of the IMaX instrument. The bottom panel of Fig. 1 shows the corresponding Doppler (vertical) velocity map. It shows downflows (positive values in the greyscale sidebar) associated with narrow inter-granular lanes, and upflows associated with the body of granules.
3. Simulations and spectral synthesis
For the simulations we use several series of (magneto)convection runs calculated with the Stagger code, a code developed by Å. Nordlund (see a description of the code in the paper by Beeck et al. 2012). This code includes a realistic equation of state with partial ionization effects; the radiation transfer problem is solved in the code using the frequency-binning method. In the particular runs in this paper, four frequency bins were used, and the transfer equation is solved along nine rays through each grid point.
The integration box has a size of 6 × 6 Mm2 in the horizontal directions and 2.5 Mm in the vertical direction. The photosphere, or, more precisely, the average τ500 = 1 level, is located some 430 km below the top lid of the box, with small variations of ± 10 km for the different time series described below. The numerical grid has 252 × 252 (horizontal) and 126 (vertical) points. The grid point separation in the horizontal directions is uniform and equal to 23.8 km, with periodic conditions on the side boundaries. A non-uniform grid is used in the vertical direction, with vertical grid spacing of 15 km near the photosphere. The dataset used in this paper consists of four time series each for a different value of the average signed vertical magnetic field strength ⟨Bz⟩ (with the averages taken on single horizontal cuts), namely 0 G (HD case) and 50 G, 100 G and 200 G (magnetoconvection cases). The convection runs were initially started with a uniform vertical magnetic field of the nominal strength for each series. Given the conservation of magnetic flux and the periodicity condition on the side boundaries, the average ⟨Bz⟩ is uniform across all heights and constant in time. The convective motions are pursued over a timespan of 30 solar minutes in each series; for the present paper we used snapshots stored with a 30-s cadence. In all cases, the 30 solar-min series used in the paper are extracted from the convection runs once a statistically-stationary state is obtained. These convection runs were developed in the framework of the solar abundance studies of Fabbian et al. (2010, 2012) and in the paper by Beck et al. (2013), where further details about the numerical model can be found.
A central role in this paper is played by the synthetic observations obtained from the numerical runs. To calculate them, we synthesize the electromagnetic spectrum for a few spectral lines emitted from the plasma in the individual columns of the numerical boxes. For the spectral synthesis we used the Nicole code (Socas-Navarro et al. 2011). For each vertical column in the box and for every snapshot in the series the outgoing spectrum is calculated for the Fe I 5250.20 Å line (the IMaX line) and for the Fe I 5576.09 Å line. To feed the Nicole code, a segment of each column stretching between log (τ500) = −4 and log (τ500) = 2 is selected and finely re-gridded in equal intervals of log τ. This allows an optimum opacity resolution and yields smooth continuum intensity maps in each box, a necessary condition for proper application of the LCT method (see Sect. 4). The columns are assumed to coincide with the LOS, i.e., the boxes are assumed to be placed at disc center. The lines are synthesized assuming LTE and using the following atomic parameters: for the 5250.20 Å line we took excitation potential χl = 0.121 eV and log(gf) = −4.94; for the 5576.09 Å line we used χl = 3.43 eV and log(gf) = −0.94. In either case we used the Unsöld collisional line broadening formalism with no enhancement. For a discussion of the synthetic spectra obtained from these snapshots and their closeness to the solar spectrum see the recent publications by Fabbian et al. (2010, 2012) and Beck et al. (2013).
4. Adjusting simulations to IMaX conditions
In order to compare the synthetic observations gained from the numerical simulations with the real observations from IMaX it is necessary to modify the former to take into account the residual instrumental degradation in the original data available from the SUNRISE mission. Therefore we have to apply the following steps to the simulated data:
-
(i)
The original IMaX data had been corrected for instrumentaloptical aberrations by deconvolving with a PSF derived fromphase diversity calibration thus achieving an effective resolutionlimit of 0.15–0.18 arcsec as reported by Martínez Pillet et al. (2011). However, this calibration does not model the effect of the stray light (far wings of the PSF). Thus, to render the synthetic observations comparable with the original IMaX data, the Stokes-I spectra coming out of the numerical box are convolved spatially with an additional PSF, called PSF′ in the following, to simulate the stray light contamination due to photons scattered by the various optical components of the instrument (Wedemeyer-Böhm 2008; Danilovic et al. 2008; Wedemeyer-Böhm & Rouppe van der Voort 2009; Scharmer et al. 2010; Beck et al. 2013). The mathematical expression we use to model this effect is a combination of a pulse (i.e., a Dirac-delta) and a Lorentzian function ℒ(A,r) with relative weight w,
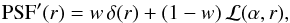 (1)where
α is
the parameter ruling the width of the Lorentzian. ℒ(α,r) is chosen so
that the area integral of PSF′ is unity. The values of w and α are tuned so that the
contrast of the synthetic continuum images matches the observed contrast of the IMaX
time series. Because of the presence of a Dirac-delta in the definition of
PSF′, the
cut-off wavenumber of its Fourier transform (the optical transfer function) is at
infinity. Consequently, the validity of the comparison between theoretical and
observational power spectra must be restricted to the range up to the effective
cut-off achieved by IMaX, i.e., to spatial scales of 110–130 km.
(1)where
α is
the parameter ruling the width of the Lorentzian. ℒ(α,r) is chosen so
that the area integral of PSF′ is unity. The values of w and α are tuned so that the
contrast of the synthetic continuum images matches the observed contrast of the IMaX
time series. Because of the presence of a Dirac-delta in the definition of
PSF′, the
cut-off wavenumber of its Fourier transform (the optical transfer function) is at
infinity. Consequently, the validity of the comparison between theoretical and
observational power spectra must be restricted to the range up to the effective
cut-off achieved by IMaX, i.e., to spatial scales of 110–130 km. -
(ii)
The synthetic spectra are convolved in the spectral dimension with a monochromatic response function (MSRF). A Gaussian profile is used here. It has a full width at half maximum FWHM = 85 mÅ in order to take into account the effect of the filter used to measure the spectra. For the sake of conciseness we will refer to the degradations described so far as the residual instrumental degradation.
-
(iii)
The resulting spectra are resampled spectrally at five wavelength positions corresponding to the location of the IMaX spectral sampling (see Sect. 2).
-
(iv)
The vertical velocity is determined by computing the Doppler shift of the spectral lines. To this end, a Gaussian fit is performed on the Stokes-I profiles, and the location of the minimum of the Gaussian curves with respect to the line center at rest is taken as the Doppler shift, which is then converted into a Doppler velocity. This procedure is used both for observations and simulations to make them comparable. In the case of the simulations, it is possible to compare the velocity determined by this method with the one obtained from the center of gravity of the full profile (before spectral resampling) with very high spectral resolution (7.5 mÅ). From the comparison we conclude that the two methods lead to quite similar velocities.
-
(v)
The horizontal velocity is computed using LCT applied to successive continuum images. The LCT routine (Welsch et al. 2004) is performed in local windows weighted by a Gaussian function with FWHM = 320 km and yields the two components of the horizontal velocity. Since no spectra are used in this case, to bring the simulated continuum images to observational conditions, we need only perform the step (i) described above. Specifically, we compute the continuum near the spectral line Fe I 5250.2 Å (the IMaX line) and convolve the resulting images with the PSF′ function introduced in (i).
-
(vi)
To complete the adjusting procedures between observations and simulations and to make the results comparable with other observations and simulations we use a p-mode filtering for both the vertical and the horizontal velocity components. Following the procedure indicated by Title et al. (1989), the p-modes are removed by applying a subsonic filter which removes modes located in the portion where ω/k > Vph in the (k,ω) diagram, with Vph being a chosen cut-off velocity. Here we use Vph = 4 km s-1 for most of the figures.
5. Fourier power spectrum and velocity spectrum: definitions
For a given component of the velocity, vi, in a given map, its
power spectrum Pi(k)
is defined via Parseval’s theorem as \right|^2}{A} \;{\rm d}\theta, \end{equation}](/articles/aa/full_html/2014/03/aa22417-13/aa22417-13-eq75.png) (2)with ℱ(vi) the two-dimensional
Fourier transform of vi, A the area of the spatial
domain, and k
and θ the
module and orientation angle, respectively, of the wavevector k. When speaking
of the power spectrum of the horizontal velocity below, we mean the sum of the spectra for
the two horizontal velocity components. To illustrate the physical meaning of the spectrum
(2), we recall that in a situation with
uniform density the kinetic energy spectrum of the map, E(k), is
given by
(2)with ℱ(vi) the two-dimensional
Fourier transform of vi, A the area of the spatial
domain, and k
and θ the
module and orientation angle, respectively, of the wavevector k. When speaking
of the power spectrum of the horizontal velocity below, we mean the sum of the spectra for
the two horizontal velocity components. To illustrate the physical meaning of the spectrum
(2), we recall that in a situation with
uniform density the kinetic energy spectrum of the map, E(k), is
given by ![\begin{equation} \label{eq:kinetic_energy_spectrum} E(k) = \frac{1}{2} \left[\strut P_x(k) + P_y(k) + P_z(k)\right] , \end{equation}](/articles/aa/full_html/2014/03/aa22417-13/aa22417-13-eq82.png) (3)so the total kinetic
energy per unit mass and area in the given map would be given by
(3)so the total kinetic
energy per unit mass and area in the given map would be given by
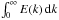 . In fact,
in the following, we will mostly use the so-called velocity spectrum which
is generically defined as
. In fact,
in the following, we will mostly use the so-called velocity spectrum which
is generically defined as ![\begin{equation} \label{eq:velocityspectrum} V(k) = [k\, P(k)]^{1/2}, \end{equation}](/articles/aa/full_html/2014/03/aa22417-13/aa22417-13-eq84.png) (4)where, depending on
the context, for P(k) the spectrum of a given
velocity component or of the horizontal velocity will be used. Trivially, the velocity
spectra V(k) have the dimension of a velocity
and fulfill
(4)where, depending on
the context, for P(k) the spectrum of a given
velocity component or of the horizontal velocity will be used. Trivially, the velocity
spectra V(k) have the dimension of a velocity
and fulfill ![\begin{equation} \label{eq:velocityspectrum_and_kineticenergy} \int_0^{\infty} E(k)\,{\rm d}k = \frac{1}{2}\,\int_0^{\infty} \left[\strut V_x^2(k) + V_y^2(k) + V_z^2(k)\right]\;{\rm d}\ln k , \end{equation}](/articles/aa/full_html/2014/03/aa22417-13/aa22417-13-eq87.png) (5)so they provide a
measure for the velocity amplitude corresponding to a given spatial scale (see also Nordlund et al. 2009). To characterize length scales we
will use the wavelength of the Fourier mode λ = 2π/k.
In the figures we will also use the spherical harmonic wavenumber, m = 2πR⊙/λ,
with R⊙ the solar radius. Following our use of
the Fast Fourier Transform algorithm on finite-domain data, we will be using summations over
a finite number of terms to calculate the spectra of Eq. (2) or the total kinetic energy in the box.
(5)so they provide a
measure for the velocity amplitude corresponding to a given spatial scale (see also Nordlund et al. 2009). To characterize length scales we
will use the wavelength of the Fourier mode λ = 2π/k.
In the figures we will also use the spherical harmonic wavenumber, m = 2πR⊙/λ,
with R⊙ the solar radius. Following our use of
the Fast Fourier Transform algorithm on finite-domain data, we will be using summations over
a finite number of terms to calculate the spectra of Eq. (2) or the total kinetic energy in the box.
 |
Fig. 2 Velocity spectra V(k) of the Doppler velocity computed from the shift of the Stokes-I signal of the Fe I 5250.2 Å line. In abscissas we use the spherical harmonic wavenumber (m, lower horizontal axis) or the corresponding wavelength λ (upper horizontal axis). Left panel: curves corresponding to the first IMaX time series (dashed black line); second IMaX time series (solid black line) and the HD simulation run (solid green line). Right: curves corresponding to the simulated HD/MHD time series (solid green: HD; solid red: MHD 50 G; dashed orange: MHD 100 G; dashed black: MHD 200 G). The curve corresponding to the second IMaX time series (solid black line) is added for comparison |
When calculating the Fourier spectra we compensate for the lack of periodicity of the real observations by zero-padding the outer rows and columns of the velocity map. To avoid the spurious high-frequency contributions caused by the strict application of a rectangle function with vertical walls for the zero-padding, we use a mesa-shaped profile with hangs smoothed via a cosine function. As usually done in the literature, we first subtract the average of the map, then apply the zero-padding and raise the result by the same amount we subtracted at the beginning. To comply with the condition of equal treatment of the real and synthetic observations, we apply the zero-padding to both kinds of datasets. The spectra obtained through this method have less total energy, since we have flattened the velocity maps at their rim. To correct for this, we calculate for each map the total energy before and after zero padding, and multiply the power spectra of the zero-padded map with the corresponding factor. This is akin to (and probably more accurate than) other k-independent corrections used in the literature (see, e.g., von der Luhe & Dunn 1987; Rieutord et al. 2010).
In the paper, in fact, averages over each time series (either observed or simulated) are
given instead of values for individual maps. To that end, we first compute the power
spectrum for each map, then calculate, for each k, the average over the whole time series,
⟨P(k)⟩. Finally, we calculate the
corresponding velocity spectrum through 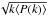 .
This averaging allows us to reduce the intermittence of individual spectra by having a large
statistical ensemble (for a discussion, see also Stein et
al. 2006). The kinetic energy spectrum for the statistical ensemble can then be
immediately obtained by averaging Eq. (3).
.
This averaging allows us to reduce the intermittence of individual spectra by having a large
statistical ensemble (for a discussion, see also Stein et
al. 2006). The kinetic energy spectrum for the statistical ensemble can then be
immediately obtained by averaging Eq. (3).
6. Fourier spectra for the vertical velocity
 |
Fig. 3 Power spectra P(k) of the Doppler velocity as a function of k. The curves here are for the same datasets as in Fig. 2 and with the same color and line style criteria. Left: spectra for the observational data and for the HD run. Right: the four simulated runs and the corresponding portion of the second IMaX time series (solid black line). The straight lines in the left panel show power laws ∝ k2 (dashed line), ∝ k−17/3 (dash-dotted) and ∝ k−29/3 (solid). |
6.1. The velocity spectra V(k)
The velocity spectra V(k) for the vertical velocity in the two observed IMaX time series are plotted in Fig. 2 (left panel) as a function of spherical harmonic wavenumber m (lower horizontal axis) or wavelength λ (upper horizontal axis). The dashed black line corresponds to the first time series, and the solid line is for the second series. Additionally, we plot as a solid green line the spectrum corresponding to the vertical velocity in the synthetic observation obtained from the purely hydrodynamic (HD, i.e., B = 0) numerical simulation. In the right panel, the spectra from the four numerical series are compared using the following color coding: ⟨Bz⟩ = 50 G (red, solid), ⟨Bz⟩ = 100 G (orange, dashed), ⟨Bz⟩ = 200 G (black, dashed), with, again, the HD case in green. In addition, the corresponding portion of the second IMaX time series (solid black line) is plotted for comparison.
All the simulated and observed curves are in good general agreement for scales ranging
from 200 km to 6 Mm, i.e., up to the horizontal extent of
the simulation boxes. In fact, looking at the left-hand panel of the figure (observations
vs. HD numerical simulations), the agreement can be said to be excellent, considering that
the two data sets have completely independent origins (observations and simulations,
respectively). There is a small apparent shift in wavenumber between the simulated and the
observational curves; a shift of this kind was already obtained by Georgobiani et al. (2007, see
their Fig. 5) for the spatial scales allowed by the MDI data they used in their work.
However, the total kinetic energy integral over all k
(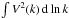 ) in the curves in Fig. 2 (left panel) is quite similar: the integral for the
simulated HD series is between the value of the integral for the two IMAX series, and the
mutual deviation between the latter is about 6%; that deviation is at any rate within the observational and
numerical errors of the curves.
) in the curves in Fig. 2 (left panel) is quite similar: the integral for the
simulated HD series is between the value of the integral for the two IMAX series, and the
mutual deviation between the latter is about 6%; that deviation is at any rate within the observational and
numerical errors of the curves.
6.1.1. The granular range and larger spatial scales
All velocity spectra show a broad maximum in the granulation range, which seems to be the only prominent scale in Fig. 2. For the spectrum of the observed data, for instance, the maximum has a value near 0.5 km s-1 and is located between λ = 1 and 1.2 Mm. For lengthscales larger than the granular one (smaller m), the spectra roughly follow a power-law as a function of m (see Sect. 6.2). None of the curves shows any prominent mesogranular bump; this is particularly interesting for the observational data, in spite of their large FOV. This fits well with the results of Yelles Chaouche et al. (2011). As for supergranular features, their absence in the observational spectra may be caused by the small horizontal extent of the sample: IMaX has a FOV of 32 × 32 Mm2, so the observations probably do not contain enough supergranules. The observations generally show higher power in the 1–3 Mm range than the simulations (see the right panel of Fig. 2), which may again be due to the limited horizontal size of the simulation box.
6.1.2. The subgranular range
In the subgranular scale range, the observed velocity spectra (black curves in the left panel of Fig. 2) also decrease following an approximate power law (Sect. 6.2) down to about 200 km, where the slope starts to become less negative. This change is probably due to the proximity of the effective spatial resolution limit (~120 km) and also because of numerical noise (arising, e.g., from the Doppler shift determination), which is particularly clear for scales λ < 120 km. A similar pattern is followed by the simulation curves (right panel): in that case, however, there is a clear inflection point located between λ ~ 120 and 140 km.
 |
Fig. 4 Similar to Fig. 2 with the simulated data not being convolved with any point spread function or spectral response function. |
6.1.3. Comparison of the different magnetic runs
The right panel shows that the differences between the HD, 50 G and 100 G simulation cases are not large, with the 200 G case showing the largest deviation. One can discern a clear trend in those curves: the curves have larger power in the subgranular range the larger the average vertical field ⟨Bz⟩; for scales larger than about 400 km, instead, the situation is reversed. The integral over all k in the figure reveals that the total kinetic energy diminishes with increasing ⟨Bz⟩: the normalized energy integral goes from 1 (HD) to 0.87 (50 G), 0.92 (100 G) and 0.68 (200 G), which indicates that there is less total kinetic energy in the height range of formation of the Fe I 5250.2 Å line the larger the vertical magnetic flux.
6.2. The power spectra P(k)
Figure 3 shows the power spectra of the Doppler
velocity, P(k), used in the calculation of
V(k) for Fig. 2. The curves of course have a similar morphology to those of Fig. 2 and their maximum occurs at a slightly larger
horizontal scale (≈1.5 Mm), as
follows from the 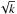 multiplication when going from P(k) to V(k) (see
Eq. (4)). The dashed straight line in the
left panel is a k2 power law for comparison with the
spectra on spatial scales above the granular one. This value has also been obtained
previously in the literature (see, e.g., Rieutord et al.
2010). The dash-dotted straight line corresponds to a power law, k−17/3, that fits the
observed spectra for scales below the granulation down to ≈200 km (about where the observed spectra
change their slope). Rieutord et al. (2010) have
found a similar value when using only two spectral wavelengths to calculate the Doppler
velocity for this Fe I line but for scales larger than ≈400 km. The tendency to find values for the
slope more negative than −5/3 has also been reported by, e.g., Katsukawa & Orozco Suárez (2012) using
Hinode/SP data and by Nordlund et al. (1997) using
3D MHD simulations. In fact the value −5/3 for the slope applies, strictly speaking,
to fully isotropic turbulence (Kolmogorov 1941;
Frisch 1996; Lesieur 2008), a condition that solar convection approaches to some extent only
when going to subphotospheric levels (Kitiashvili et al.
2012).
multiplication when going from P(k) to V(k) (see
Eq. (4)). The dashed straight line in the
left panel is a k2 power law for comparison with the
spectra on spatial scales above the granular one. This value has also been obtained
previously in the literature (see, e.g., Rieutord et al.
2010). The dash-dotted straight line corresponds to a power law, k−17/3, that fits the
observed spectra for scales below the granulation down to ≈200 km (about where the observed spectra
change their slope). Rieutord et al. (2010) have
found a similar value when using only two spectral wavelengths to calculate the Doppler
velocity for this Fe I line but for scales larger than ≈400 km. The tendency to find values for the
slope more negative than −5/3 has also been reported by, e.g., Katsukawa & Orozco Suárez (2012) using
Hinode/SP data and by Nordlund et al. (1997) using
3D MHD simulations. In fact the value −5/3 for the slope applies, strictly speaking,
to fully isotropic turbulence (Kolmogorov 1941;
Frisch 1996; Lesieur 2008), a condition that solar convection approaches to some extent only
when going to subphotospheric levels (Kitiashvili et al.
2012).
6.3. Fourier spectra without instrumental degradation
The quality of the match between observational and simulation curves apparent in Figs. 2 and 3 would be clearly affected if we had not taken care of the residual instrumental degradation. In Fig. 4 we show again the velocity spectra V(k), but now the simulation results have not been subjected to any degradation. There is a clear offset between the two sets of curves. The kinetic energy of the HD case, for instance, is 2.5 times larger than for the observations. Also: the maximum of the HD spectrum has now a value near 0.8 km s-1. Given the excellent match of the two sets when subjected to the same instrumental degradation, one can tentatively conclude that the actual velocity spectra in the Sun are possibly not far from the simulation ones in Fig. 4 down to sizes of at least about 100 km and for ⟨Bz⟩ in the range expected in the Sun, i.e., ⟨Bz⟩ ≲ 100 G.
6.4. Comparison with previous results based on Hinode data
For the particular case of the observed vertical velocities, Fourier spectra have already been presented in the literature based on Hinode data (Rieutord et al. 2010) and it can be interesting to check for similarities and differences with our results of Figs. 2 and 3. For the comparison, we have taken the spectrum those authors present in the left panel of their Fig. 6, which corresponds to the kinetic energy associated with the vertical component of the velocity, multiplied it by a factor 2, and obtained the corresponding velocity spectrum using our Eq. (4). The result is plotted in Fig. 5 as a dash-dotted black curve. The curve of Rieutord et al. (2010) had been treated by those authors to remove instrumental effects via deconvolution using a PSF that follows the prescription of Danilovic et al. (2008) for treating observations from SOT/Hinode. For the comparison, we include in Fig. 5 (black solid curve) the velocity spectrum corresponding to the second IMaX time series of Fig. 2 but now deconvolved with the PSF′ function introduced in Sect. 41. The comparison will be relevant if, as we expect, the degradation effect on the IMaX data represented by PSF′ is comparable to the defocusing effect considered by Danilovic et al. (2008). Furthermore, the Hinode data used by Rieutord et al. (2010) were based on Dopplergrams that used the Fe I 5576.09 Å line, instead of (like IMaX) the Fe I 5250.2 Å one. Then, to complete the comparison we have computed the velocity spectra from the simulated data (50-G MHD case) for those two Fe lines and plotted them as red and blue curves (for Fe I 5250.2 Å and Fe I 5576.09 Å, respectively), of course without applying any instrumental degradation to them.
 |
Fig. 5 Comparison with the Hinode-based Fourier spectrum of the Doppler velocity by Rieutord et al. (2010). Solid black: spectrum from our second IMaX time series deconvolved with the PSF′ function introduced in Sect. 4. Dash-dotted: velocity spectrum computed from a power spectrum in Fig. 6 of Rieutord et al. (2010), for a time series obtained from Hinode/NFI for the Fe I 5576.09 Å line. Red and blue curves: velocity spectra from our 50 G MHD simulation run with spectral synthesis carried out for the Fe I 5250.2 Å line and for the Fe I 5576.09 Å line, respectively. To obtain those curves, we have not applied any instrumental degradation (PSF′ and MSRF) to the simulated data. |
 |
Fig. 6 Velocity spectra for the horizontal velocity computed through local correlation tracking applied to continuum images near the Fe I 5250.2 Å line from the IMaX observations and from synthetic observations obtained from the simulation runs. Left panel: first (dashed black) and second (solid black) IMaX time series and the HD simulation run (solid green). Right panel: spectra from the four simulation runs (green: HD run; red: MHD 50 G run; dashed orange line: MHD 100 G run; dashed black line: MHD 200 G run). The corresponding portion of the second IMaX time series (solid black line) is added for comparison. |
Various features in this figure are worth commenting. In broad terms, the Hinode-based spectrum (dash-dotted curve) is quite similar to the other spectra in the figure, especially for spatial scales λ ≳ 1 Mm. Comparing the simulation curves (blue and red lines) among themselves, we see that the major difference between them is their amplitude near the maximum. This may be associated with the different height of formation of the FeI 5576.09 Å and FeI 5250.2 Å lines. Turning to the two curves in the figure that use the FeI 5576.09 Å spectral line (the Hinode dash-dotted one, and the blue curve for our simulated data) there seems to be a wavenumber shift between them. We assume that this feature may appear because the effects of the lack of spatial resolution in the Hinode data start to become apparent for λ much larger than in the case of the simulated data. Another possibility may be the different characteristics (e.g., average magnetic field) of the region of the Hinode data compared to those of the simulation. Comparing now the curves based on Hinode and IMaX observations (dash-dotted and solid black), we see how the latter provides useful information down to much smaller scales than the former: using, as a reference, the inflection points in the subgranular range, we note that they are located roughly around 700 km (Hinode) and 300 km (IMaX). Turning to scales above the granular one, the two curves show similar slopes, not far from ∝k2, and neither shows any prominent feature in that scale range (for the Hinode data, see discussion in Rieutord et al. 2010). A final remark concerning the comparison in Fig. 5: the p-mode filtering applied by Rieutord et al. (2010) used a cut-off at 6 km s-1 instead of at 4 km s-1 like in the present paper (as explained in Sect. 4). We have checked that using either one virtually makes no difference to the IMaX-based velocity spectrum (solid black curve) and to the MHD-based curves (red and blue curves).
7. Fourier spectra for the horizontal velocity
The horizontal velocity field for both the observed and simulated datasets was determined through LCT using 2D continuum maps for a wavelength near the FeI 5250.2 Å line (Sect. 4). As discussed in the previous section, for a proper comparison between observations and simulations, it is important that we use the same kind of input data for the Fourier analysis: hence the need to use synthetic observations from the simulated data (including instrumental degradation), and to use the LCT technique the same way as with the IMaX data. The extra advantage of having values for the actual velocity field in all grid points across the simulation box will be exploited in the next section (Sect. 8). The LCT procedure has often been applied in the literature to time-averaged data. The time averaging is used to smooth the transition between consecutive snapshots and reduce the noise. The averaging does not greatly affect the resulting large-scale velocity field and power spectra (e.g., supergranulation), but can considerably change the spectra in the small-scale (sub-granular) range (see examples and discussion in Rieutord et al. 2000, 2001, 2010; Stein et al. 2006; Kitiashvili et al. 2012). The IMaX observations have a high signal-to-noise ratio and a high spatial and temporal resolution and suffer very little from atmospheric distortion. These conditions make it possible to use LCT to determine instantaneous velocity maps with no temporal averaging. We can test the resulting velocity fields concerning their behavior also in the small-scale range. Like for the vertical component, to obtain the power and velocity spectra for the horizontal velocity field, we first compute the spectra of individual snapshots, and then make an average of the spectra over the whole time series.
The velocity spectra V(k) for the horizontal velocity are plotted in Fig. 6. The color and line-type coding is the same as the one employed in Fig. 2. The observed velocity spectra from the IMaX time series (left panel, solid and dashed black curves) exhibit a maximum of about 0.3 km s-1 corresponding to horizontal scales around 1.3–1.4 Mm. The location of the maximum is quite similar to that obtained for the vertical velocities. In the right panel we see that all curves have a similar shape but the observational ones exhibit less power as compared to the simulated ones. The green curve (HD case) is above all others, and reaches a peak value of about 0.4 km s-1; the 200 G MHD simulation shows the smallest values, with peak velocities of 0.3 km s-1. This confirms the tendency obtained for the vertical velocity (Sect. 6), namely, that the experiments with more magnetic flux exhibit less power, in this case at heights where the continuum is formed. Here, however, this is valid on all spatial scales (including the range below 300 km). In the large-scale range, say above 2 Mm, the observed and simulated spectra are rather featureless: the corresponding power spectra P(k) seem to follow a power law as k1. Again here, the only prominent scale in the whole range is the granular one, but the caveat explained in Sect. 6 still applies: the limitation in the FOV does not allow us to study properly the power on supergranulation scales. In the subgranular domain, the observed spectra decrease smoothly with m showing similar features as described for the vertical velocity spectra in Sect. 6: there is an inflection point for λ ~ 300 km (observations) and ~200 km (simulations). Beyond this value the results are surely contaminated by the remaining sources of noise. In this case, the corresponding power spectra P(k) (not shown here) follow a power law as k−11/3 down to horizontal scales of about 200 km. This power law is close to (but somewhat steeper than) that obtained from MHD simulations by Kitiashvili et al. (2012). The observed and simulated spectra have similar shapes, even if shifted with respect to each other. However, in Sect. 8, we will see that the slope of the power spectra of the LCT-determined horizontal velocity maps is strongly influenced by the LCT procedure itself rather than reflecting the spectra of the actual velocity field in the Sun.
 |
Fig. 7 Velocity spectra for the horizontal velocity computed from LCT eliminating the instrumental effects. The solid black curve corresponds to the first IMaX time series deconvolved with the PSF′ function introduced in Sect. 4. The green line corresponds to the HD simulation run without application of any instrumental degradation. |
In Fig. 7 we study the influence of the instrumental degradation on the spectra (as we did for Fig. 5, but now without external Hinode data). The black solid curve corresponds to the first IMaX time series deconvolved with the PSF′ function introduced in Sect. 4. It is very near the corresponding curve in Fig. 6. The green curve corresponds to the HD run; now, for coherence in the figure, the LCT procedure has been applied to continuum images that have not been convolved with PSF′. Also this curve is quite near the corresponding one plotted in Fig. 6. We conclude that in this scale range the LCT procedure is not very sensitive to the changes in the contrast of the continuum images: the convolution only modifies the amplitude of the features in the continuum images without obliterating them, so the tracking procedure yields similar velocity values. In the sub-granular range, the two curves have similar slopes down to ~200 km.
8. Comparing the velocities from the synthetic observations with the velocity grid of the simulation cubes
In the previous sections, we have seen that the power and velocity spectra from the simulations match those from the observations remarkably well in the case of the vertical velocity. The match is less good for the horizontal velocity. For the comparison, synthetic observations were obtained from the simulations and then subjected to the residual instrumental degradation of the IMaX maps. Since we have the full 3D grid of velocity vectors in the data cubes, it can be of interest to locate the positions in the cube where the velocities best match the synthetic observations, both concerning Doppler velocities as well as the LCT-determined horizontal velocities. The way in which the comparison is carried out has to be considered. In the literature, statistical studies directly based on the data grids in numerical simulations have often been carried out (e.g., Stein & Nordlund 1998; Rieutord et al. 2001; Stein et al. 2006; Georgobiani et al. 2007; Matloch et al. 2010; Kitiashvili et al. 2012), but those calculations use velocity distributions on horizontal planes in the box. For a comparison with observations (also with synthetic observations) it seems more adequate to use velocity values taken on constant-τ500 surfaces: the standard velocity response functions (VRFs) of the 5250.2 Å and 5576.09 Å lines are expected to have roughly the same dependence with τ500 in the different columns in the FOV (e.g., Gray 2005). In contrast, non-small vertical shifts of the VRFs are expected between the different regions in the FOV when seen as a function of the vertical coordinate, given the strong dependence of the individual opacities on density. The velocities in a Dopplergram are therefore expected to reflect the actual vertical velocity values on τ500 isosurfaces more closely than those on horizontal planes. The choice of the τ-isosurfaces for the horizontal velocity determination is less clear-cut, mostly because of the uncertainties in the LCT procedure, but the choice of horizontal planes is equally questionable in that case, so we have opted to use the same isosurfaces for both the vertical and horizontal velocities. In the following we first calculate the correlation between the Doppler (or LCT-determined) velocities, on the one hand, and the simulation data from individual τ500 = const. surfaces, on the other, so as to determine which τ better corresponds to the observations. The correlation is calculated for every individual snapshot in the series and then averaged over all snapshots. In the case of the horizontal velocity, we first convolve the velocity maps from constant τ500 surfaces with a Gaussian with FWHM equal to the LCT tracking window size. This allows us to have both horizontal velocity maps at a similar spatial resolution. As a second item, we compare the Fourier spectra from either source. For the sake of specificity, we use for this comparison the 100-G MHD series.
In the case of the vertical velocity, it is found that the Doppler and MHD velocities reach
a maximum correlation on the order of 0.96 near the log (τ500) ≈ −1 surface. This indicates
that the Doppler shift measures the vertical velocity in that surface with a high accuracy;
it also shows that the Fe I 5250.2 Å line is formed close to that optical depth. The
horizontal velocity field on const-τ surfaces and the LCT-determined one reach a maximum
correlation of close to 0.5 at
log (τ500) ≈ 0. This
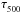 value is
concomitant with the fact that the LCT method applied here uses feature-tracking based on
continuum maps. On the other hand, the lower value of the correlation occurs because LCT as
a method is less accurate in determining the velocity than the Doppler procedure. A
precedent for this determination was provided by Rieutord et
al. (2001) who computed the correlation between LCT-determined horizontal velocity
fields and velocity data on horizontal surfaces from a numerical simulation
(they also used an alternative to LCT, the CST method). They subjected their velocity data
to time averages and concluded that longer averaging time results in higher correlations. In
our comparison, we use instantaneous velocity maps (with 33 s cadence) and do not average the velocity
data over time, which explains our lower value for the maximum correlation (similar to what
those authors obtain for 1000 s
averaging). We must use instantaneous determinations of the velocity since we want to study
the power/velocity spectra almost down to the diffraction limit of the telescope.
value is
concomitant with the fact that the LCT method applied here uses feature-tracking based on
continuum maps. On the other hand, the lower value of the correlation occurs because LCT as
a method is less accurate in determining the velocity than the Doppler procedure. A
precedent for this determination was provided by Rieutord et
al. (2001) who computed the correlation between LCT-determined horizontal velocity
fields and velocity data on horizontal surfaces from a numerical simulation
(they also used an alternative to LCT, the CST method). They subjected their velocity data
to time averages and concluded that longer averaging time results in higher correlations. In
our comparison, we use instantaneous velocity maps (with 33 s cadence) and do not average the velocity
data over time, which explains our lower value for the maximum correlation (similar to what
those authors obtain for 1000 s
averaging). We must use instantaneous determinations of the velocity since we want to study
the power/velocity spectra almost down to the diffraction limit of the telescope.
 |
Fig. 8 Comparison between Fourier spectra from Doppler-determined velocities and from vertical velocities on constant-τ500 surfaces, both obtained from the simulation data. Red: velocity spectra from the MHD 100 G data using Doppler shifts in the synthetic observation. The data have not been convolved spatially with a PSF nor, spectrally, with an MSRF. Black: velocity spectrum for the vertical component of the velocity taken directly from the MHD 100 G data cube on the log (τ500) = −1 surface. No p-mode filtering has been applied to obtain this figure. |
We now turn to the comparison of Fourier spectra for the data from the simulations obtained using either synthetic observations or data from constant-τ surfaces. Figure 8 shows velocity spectra for the vertical velocity from the 100G MHD run. The dashed curve corresponds to the synthetic observation, i.e., to the velocity measured through the Doppler shift of the Fe I 5250.2 Å line. The data used have not been subjected to the instrumental degradation or spectral rebinning described in Sect. 4, (i)–(iii). The solid curve is for the data taken directly from the MHD cube at the log (τ500) = −1 surface, where we found the maximum correlation earlier in this section. The two curves have a similar shape, with the one from the MHD cube exhibiting a little more power on all scales. The ratio of the integrated kinetic energy between the two datasets is 1.3. The agreement between the shape of the two curves indicates that the Doppler measurement of the velocity is quite reliably reproducing the velocity distribution over all spatial scales included in the study, and thereby can be used to study the properties of the photospheric turbulent flow in that range. For the spectra plotted in this section, no p-mode filtering has been applied to facilitate the comparison with the results from the data taken directly from the numerical box. Also, since the simulation data are strictly periodic, we could have dispensed with the zero-padding procedure explained in Sect. 5, which is mandatory for the observational data. However, the differences in the simulated spectra with or without it are very small (in other words: the correction explained in that section is quite accurate in this case), so we preferred to keep the zero padding and apodizing also here to maintain coherence among the figures in the paper.
 |
Fig. 9 Velocity spectra for the horizontal velocities. Dashed green: spectrum corresponding to the horizontal velocity determined via LCT on continuum maps in the synthetic observations obtained from the MHD 100 G simulation run. No instrumental degradation is applied to the synthetic observations. Solid black: spectrum for the horizontal component of the velocity taken directly from the MHD 100 G data cube on the log (τ500) = 0 surface. No p-mode filtering has been applied. The vertical velocity spectra from the synthetic observations (taken from Fig. 8) is plotted for comparison (dotted black line). |
The corresponding spectra for the horizontal velocity are shown in Fig. 9. The dashed curve is the velocity spectrum for the LCT-determined horizontal velocity on the basis of the synthetic observation. Like for the vertical velocity, no instrumental degradation has been applied to these synthetic observations. The solid curve corresponds to the spectra obtained from the ⟨Bz⟩ = 100 G MHD cubes at log (τ500) = 0, where the two data sets have the highest correlation. The latter curve shows much more power than the LCT-based case: the ratio of the total energy between the two horizontal velocity datasets is 5.4. This is in line with the concerns expressed in the literature that the LCT method can importantly underestimate the horizontal velocities (e.g., Strous 1995; Simon et al. 1995; Márquez et al. 2006). Apart from the global shift downward, the LCT curve has a less negative slope in the small-scale range, say for λ ≲ 300 km. In fact the FWHM of the window used here to determine the correlations in the LCT calculation is 320 km (Sect. 4), and this should be taken as a lower bound below which the method cannot be expected to determine the horizontal velocity field with any accuracy. Another related effect apparent in the figure is that the dashed curve has a narrower maximum, and its peak is at a larger horizontal scale (roughly λ ~ 1.5 Mm) than in the case of the spectrum for the actual velocity field on the τ500 = 1 isosurface. It is also of interest that the solid curves of Figs. 8 and 9 have similar shapes (to facilitate the comparison, we have reproduced the former as a dotted line in Fig. 9). We see that the two curves are very near each other. The coincidence, however, is of doubtful significance, since (a) the two curves correspond to different (even if not far removed) heights in the photosphere and (b) there need not be any vertical-horizontal isotropy in the convective flows in those heights.
9. Discussion
The availability in the past few years of very high resolution spectropolarimetric observations of the solar photosphere through the SUNRISE/IMaX mission has made it possible for us to explore the spectral properties of the photospheric velocity fields down to scales of a tenth of the average granular size, at the same time including large spatial scales, up to the supergranular range (FOV of 33 Mm). Simultaneously, we have used state-of-the-art, realistic models of solar magnetoconvection covering scales of up to 6 Mm to explore the level of agreement between the models and the observations. In particular, we have compared the Fourier power spectra of the velocity maps obtained from the IMaX time series with the ones obtained from the MHD simulations both for the vertical component (via Doppler shift determination) as well as for the horizontal component via LCT techniques. For the vertical velocity, when properly compared (i.e., when applying instrumental degradation to the simulations or, alternatively, cleaning the observations from PSF effects), we have found a very good agreement between observations and simulations (Figs. 2 and 3): the simulated spectra match the observed ones over a wide range of scales, namely from 200 km to 6 Mm. This lends additional credence to the claim that present-day numerical simulations of solar convection provide a faithful representation of the actual flows in the Sun down to the minimum observable scales. We have also found that the degradation of the electromagnetic spectrum caused by the instrumental effects (PSF and MSRF) can seriously modify the obtained kinetic energy of the flows (see Fig. 4). Still for the vertical velocity, we have compared the Fourier spectra of the simulation data when using synthetic observations to those obtained when using velocity values from τ500 = const. isosurfaces (Sect. 8). The excellent match between those two spectra allows us to conclude tentatively that the non-degraded spectra shown in Fig. 4 may already be nearing the real solar Fourier power spectrum for the vertical velocity in quiet Sun regions around the formation height of the IMaX line (roughly log τ500 ≈ −1, some 200 km above the nominal photosphere at log τ500 = 0) for spatial sizes above the resolution limit of the data. Additionally, from our spectra one can also tentatively conclude that the typical granulation velocity in those heights is around 0.8 km s-1.
Concerning the horizontal velocities, their determination in observations through feature- or correlation-tracking in 2D maps is fraught with a considerable uncertainty (see, e.g., Strous 1995; Simon et al. 1995; Márquez et al. 2006). With the tools developed for this research, we have been able to compare the LCT velocity from the synthetic observations in the MHD convection runs with the actual horizontal component of the velocity on constant-τ500 surfaces in those same simulations. We find that the maximum correlation between the LCT velocity and the actual MHD horizontal velocity occurs near the solar surface (τ500 ≈ 1), which is reasonable since continuum maps are being used for the LCT, and reaches comparatively low values of ≈0.5. Rieutord et al. (2001) showed that this kind of correlation (with vhor calculated on horizontal planes in their case) can be increased by carrying out a time-averaging in the LCT procedure with large time-windows of, e.g., 1 to 2 h, which reduces the small scale fluctuations. In our case we preferred to do without such time averaging not to dilute the high-resolution properties of the IMaX data.
Another symptom of the inaccuracy of the LCT velocities can be seen in the following: the velocity spectrum for the horizontal components of the velocity on the τ500 = 1 surface (Fig. 9, solid black curve) is well above the spectrum obtained from LCT-determined velocities on synthetic observations from the same set of numerical simulations. While the former, in fact, has a shape similar to the spectrum for the vertical velocities of Fig. 8, the latter shows a shift of its peak to larger scales and a low value for the total energy. This suggests that the Fourier spectra from horizontal velocities determined through tracking algorithms may not be fully representative of the solar reality in the range of length scales that can be studied with our numerical model.
A remarkable feature observed in Figs. 2–6, is the way the power spectra are affected by the average magnetic flux in the simulation boxes. The cases with more magnetic flux have less power around the maximum of the curves (Fig. 4, right panel). This behavior appears in the spectra for both the vertical and horizontal velocities (Figs. 2 and 6). An extension of this behavior toward the large-scale half of the plots is particularly clear for the case with average magnetic flux corresponding to a plage region (200 G case): it appears that the magnetic field is partially inhibiting the convective flow on those scales (see also the recent observational results by Katsukawa & Orozco Suárez 2012). In the small-scale half of the plots for the vertical velocity, say for scales λ ≲ 400 km, the situation is the opposite: the spectra (Fig. 2) show higher power the higher the average magnetic flux. Together with the results concerning the total kinetic energy associated with the velocity maps (Sect. 6.1.3), we tentatively conclude that a higher average vertical magnetic flux leads to less kinetic energy and to a shift in relative weight of the different scales toward the small-λ range. The behavior of the horizontal-velocity spectra in the small-scale end seems to be at variance with these results, but, as concluded in Sect. 8 (Figs. 8 and 9), the LCT-based results are not reliable enough in that part of the spectrum.
An important outcome of any calculation of Fourier power spectra of surface convection is the determination of the slope of the spectrum in the different wavenumber regions of interest. In the figures of the present paper approximate power laws can be discerned both on the large and small wavenumber ranges on either side of the granulation maximum. From Fig. 3, for instance, the power spectra for the vertical velocity in the scale range from about 1 Mm down to about 200 km can be approximated with a power law k−17/3 for the IMaX series, and, less accurately, for the HD simulation. The power spectra of the horizontal velocity, on the other hand, also follow a non-classical power law of approximately k−11/3 on scales ranging from ≈1 Mm down to 200 km. Both exponents clearly deviate from the classical Kolmogorov k−5/3 law valid for homogeneous and isotropic turbulence (Kolmogorov 1941; Frisch 1996; Lesieur 2008). Additionally to the comments provided when discussing Fig. 3, we note here that lack of spatial resolution may be affecting the slope of the spectra: the figures in the papers of Stein & Nordlund (1998, their Fig. 30) and Kitiashvili et al. (2012, their Fig. 2d) indicate that, for a grid spacing as we have in our paper (24 km), the vertical velocity power spectra show symptoms of nearing an inertial range with constant exponent at subgranular wavenumbers. The latter authors, in particular, obtain a quasi-inertial range for the velocities on a horizontal cut at the surface when using a grid spacing of 12.5 km, albeit with a slope clearly steeper than −5/3 (in fact, judging from their figure, probably between −2 and −3). The same authors show how an extended inertial range with slope much closer to −5/3 is obtained for the same resolution at much deeper levels (3 Mm below the solar surface), where isotropy should be more nearly reached.
10. Conclusions
As measured using Fourier power spectra, realistic numerical simulations of surface magnetoconvection provide an accurate picture of the photospheric vertical velocity fields in the range from a few 100 km to several Mm. This conclusion is based on a comparison of Dopplergrams obtained from real observations, on the one hand, and from synthetic observations calculated from the numerical data, on the other. Using as observational proxy for the horizontal velocities the LCT method, the match is worse due to the limitations of that technique.
Taking detailed care of spatial and spectral blurring caused by the observational equipment is necessary for a proper comparison between numerical and observational data: the instrumental degradation can seriously affect the Fourier power spectra of the LOS velocities (compare Fig. 2 with Fig. 4), leading to a much worse match of synthetic and real observations. Apodization of the observational data prior to Fourier processing is advisable but less crucial.
We have compared the vertical velocity proxy (Dopplergrams) in the synthetic observations with the actual velocity field on the individual τ500 = const. isosurfaces in the numerical box. The maximum correlation (0.96) is found for the log τ500 = −1 surface, which is ~200 km above the continuum-forming layer (log τ500 = 0). The corresponding Fourier spectra are very close to each other. The typical granulation velocity in those heights would be some 0.8–0.9 km s-1 (Fig. 8).
A similar comparison for the horizontal velocities leads to a smaller maximum correlation (0.5), which is reached at the τ500 = 1 isosurface, and to the spectrum for the actual velocity field on that isosurface being clearly above the spectrum for the LCT-determined velocity proxy (Fig. 9). Both problems can be ascribed to the limitations of the LCT technique particularly when dealing with small-scale features.
Comparing cases with different magnetic flux, we tentatively conclude that a higher average vertical flux leads to less kinetic energy and to a shift in relative weight of the different scales toward the small-λ range.
Acknowledgments
We gratefully acknowledge financial support from the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484) and from the Spanish Ministry of Research and Innovation through projects AYA2007-66502, CSD2007-00050, and AYA2011-24808. We acknowledge the computing time granted through the DEISA SolarAct and PRACE SunFlare projects and the corresponding use of the HLRS (Stuttgart, Germany) and FZJ-JSC (Jülich, Germany) supercomputer installations, as well as the computer resources and assistance provided at the MareNostrum (BSC/CNS/RES, Spain) and LaPalma (IAC/RES, Spain) supercomputers. IMaX, an instrument on board the SUNRISE mission, was funded by the Spanish MICINN under projects ESP2006-13030-C06 and AYA2009-14105-C06. The authors are grateful to Dr. H. Socas Navarro for providing the NICOLE spectral synthesis and inversion code and for his help in setting it up, to Dr Å. Nordlund for his encouragement to carry out this work, and to Dr. V. Martínez Pillet for useful clarifications concerning the capabilities of the IMaX instrument. We are also grateful to Drs B. Ruiz Cobo and D. Fabbian for clarifications concerning the formation region of the spectral lines used in this paper
References
- Abramenko, V., Yurchyshyn, V., & Goode, P. R. 2012, in 4th Hinode Science Meeting: Unsolved Problems and Recent Insights, eds. L. Bellot Rubio, F. Reale, & M. Carlsson, ASP Conf. Ser., 455, 17 [Google Scholar]
- Beck, C., Fabbian, D., Moreno-Insertis, F., Puschmann, K. G., & Rezaei, R. 2013, A&A, 557, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbian, D., Khomenko, E., Moreno-Insertis, F., & Nordlund, Å. 2010, ApJ, 724, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbian, D., Moreno-Insertis, F., Khomenko, E., & Nordlund, Å. 2012, A&A, 548, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, U. 1996, Turbulence. The legacy of A. N. Kolmogorov (Cambridge University Press) [Google Scholar]
- Georgobiani, D., Stein, R. F., & Nordlund, Å. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, eds. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 109 [Google Scholar]
- Georgobiani, D., Zhao, J., Kosovichev, A. G., et al. 2007, ApJ, 657, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Goode, P. R., Yurchyshyn, V., Cao, W., et al. 2010, ApJ, 714, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (UK: Cambridge University Press) [Google Scholar]
- Hathaway, D. H., Beck, J. G., Bogart, R. S., et al. 2000, Sol. Phys., 193, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoutot, L., Kosovichev, A. G., Wray, A., & Mansour, N. N. 2008, ApJ, 684, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Katsukawa, Y., & Orozco Suárez, D. 2012, ApJ, 758, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kitiashvili, I. N., Abramenko, V. I., Goode, P. R., et al. 2012, Phys. Scripta, submitted [arXiv:1206.5300] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Lesieur, M. 2008, Turbulence in Fluids (Berlin: Springer) [Google Scholar]
- Márquez, I., Sánchez Almeida, J., & Bonet, J. A. 2006, ApJ, 638, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Matloch, Ł., Cameron, R., Shelyag, S., Schmitt, D., & Schüssler, M. 2010, A&A, 519, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordlund, Å., Spruit, H. C., Ludwig, H.-G., & Trampedach, R. 1997, A&A, 328, 229 [NASA ADS] [Google Scholar]
- Nordlund, Å., Stein, R. F., & Asplund, M. 2009, Liv. Rev. Sol. Phys., 6, 2 [Google Scholar]
- Rieutord, M., Roudier, T., Malherbe, J. M., & Rincon, F. 2000, A&A, 357, 1063 [NASA ADS] [Google Scholar]
- Rieutord, M., Roudier, T., Ludwig, H., Nordlund, Å., & Stein, R. 2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Roudier, T., Rincon, F., et al. 2010, A&A, 512, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J. M., et al. 2012, A&A, 540, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Löfdahl, M. G., van Werkhoven, T. I. M., & de la Cruz Rodríguez, J. 2010, A&A, 521, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, G. W., Brandt, P. N., November, L. J., Shine, R. A., & Strous, L. H. 1995, in Helioseismology, ESA SP, 376, 223 [Google Scholar]
- Socas-Navarro, H., Asensio Ramos, A., & de la Cruz Rodríguez, J. 2011, NICOLE, A non-LTE Inversion Code using the Lorien engine (Instituto de Astrofísica de Canarias) [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2006, ApJ, 642, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., Benson, D., Georgobiani, D., & Nordlund, Å. 2006, in Proc. SOHO 18/GONG 2006/HELAS I, Beyond the spherical Sun, ESA SP, 624, 79 [Google Scholar]
- Stein, R. F., Lagerfjärd, A., Nordlund, Å., & Georgobiani, D. 2011, Sol. Phys., 268, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Strous, L. H. 1995, in Helioseismology, ESA SP, 376, 219 [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von der Luhe, O., & Dunn, R. B. 1987, A&A, 177, 265 [NASA ADS] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsch, B. T., Fisher, G. H., Abbett, W. P., & Regnier, S. 2004, ApJ, 610, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Yelles Chaouche, L., Moreno-Insertis, F., MartínezPillet, V., et al. 2011, ApJ, 727, L30 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Top: continuum intensity observed by the SUNRISE/IMaX instrument near the spectral line Fe I 5250.2 Å. Bottom: Doppler (vertical) velocity computed using the Stokes-I signal of the Fe I 5250.2 Å line. The velocity is expressed in km s-1. Details about granules and inter-granular lanes can be well appreciated. |
| In the text | |
 |
Fig. 2 Velocity spectra V(k) of the Doppler velocity computed from the shift of the Stokes-I signal of the Fe I 5250.2 Å line. In abscissas we use the spherical harmonic wavenumber (m, lower horizontal axis) or the corresponding wavelength λ (upper horizontal axis). Left panel: curves corresponding to the first IMaX time series (dashed black line); second IMaX time series (solid black line) and the HD simulation run (solid green line). Right: curves corresponding to the simulated HD/MHD time series (solid green: HD; solid red: MHD 50 G; dashed orange: MHD 100 G; dashed black: MHD 200 G). The curve corresponding to the second IMaX time series (solid black line) is added for comparison |
| In the text | |
 |
Fig. 3 Power spectra P(k) of the Doppler velocity as a function of k. The curves here are for the same datasets as in Fig. 2 and with the same color and line style criteria. Left: spectra for the observational data and for the HD run. Right: the four simulated runs and the corresponding portion of the second IMaX time series (solid black line). The straight lines in the left panel show power laws ∝ k2 (dashed line), ∝ k−17/3 (dash-dotted) and ∝ k−29/3 (solid). |
| In the text | |
 |
Fig. 4 Similar to Fig. 2 with the simulated data not being convolved with any point spread function or spectral response function. |
| In the text | |
 |
Fig. 5 Comparison with the Hinode-based Fourier spectrum of the Doppler velocity by Rieutord et al. (2010). Solid black: spectrum from our second IMaX time series deconvolved with the PSF′ function introduced in Sect. 4. Dash-dotted: velocity spectrum computed from a power spectrum in Fig. 6 of Rieutord et al. (2010), for a time series obtained from Hinode/NFI for the Fe I 5576.09 Å line. Red and blue curves: velocity spectra from our 50 G MHD simulation run with spectral synthesis carried out for the Fe I 5250.2 Å line and for the Fe I 5576.09 Å line, respectively. To obtain those curves, we have not applied any instrumental degradation (PSF′ and MSRF) to the simulated data. |
| In the text | |
 |
Fig. 6 Velocity spectra for the horizontal velocity computed through local correlation tracking applied to continuum images near the Fe I 5250.2 Å line from the IMaX observations and from synthetic observations obtained from the simulation runs. Left panel: first (dashed black) and second (solid black) IMaX time series and the HD simulation run (solid green). Right panel: spectra from the four simulation runs (green: HD run; red: MHD 50 G run; dashed orange line: MHD 100 G run; dashed black line: MHD 200 G run). The corresponding portion of the second IMaX time series (solid black line) is added for comparison. |
| In the text | |
 |
Fig. 7 Velocity spectra for the horizontal velocity computed from LCT eliminating the instrumental effects. The solid black curve corresponds to the first IMaX time series deconvolved with the PSF′ function introduced in Sect. 4. The green line corresponds to the HD simulation run without application of any instrumental degradation. |
| In the text | |
 |
Fig. 8 Comparison between Fourier spectra from Doppler-determined velocities and from vertical velocities on constant-τ500 surfaces, both obtained from the simulation data. Red: velocity spectra from the MHD 100 G data using Doppler shifts in the synthetic observation. The data have not been convolved spatially with a PSF nor, spectrally, with an MSRF. Black: velocity spectrum for the vertical component of the velocity taken directly from the MHD 100 G data cube on the log (τ500) = −1 surface. No p-mode filtering has been applied to obtain this figure. |
| In the text | |
 |
Fig. 9 Velocity spectra for the horizontal velocities. Dashed green: spectrum corresponding to the horizontal velocity determined via LCT on continuum maps in the synthetic observations obtained from the MHD 100 G simulation run. No instrumental degradation is applied to the synthetic observations. Solid black: spectrum for the horizontal component of the velocity taken directly from the MHD 100 G data cube on the log (τ500) = 0 surface. No p-mode filtering has been applied. The vertical velocity spectra from the synthetic observations (taken from Fig. 8) is plotted for comparison (dotted black line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


