| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322129 | |
| Published online | 02 December 2013 | |
Gas-phase CO depletion and N2H+ abundances in starless cores⋆,⋆⋆
1
Max-Planck-Institut für Astronomie (MPIA),
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail:
lippok@mpia.de
2
Institute of Astronomy, Russian Academy of Sciences,
Pyatnitskaya str.
48, 119017
Moscow,
Russia
3
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden, The
Netherlands
4
Universität zu Köln, Zülpicher Str. 77, 50937
Köln,
Germany
5
Department of Astronomy and Steward Observatory, University of
Arizona, Tucson
AZ
85721,
USA
Received:
24
June
2013
Accepted:
13
September
2013
Context. In the dense and cold interiors of starless molecular cloud cores, a number of chemical processes allow for the formation of complex molecules and the deposition of ice layers on dust grains. Dust density and temperature maps of starless cores derived from Herschel continuum observations constrain the physical structure of the cloud cores better than ever before. We use these to model the temporal chemical evolution of starless cores.
Aims. We derive molecular abundance profiles for a sample of starless cores. We then analyze these using chemical modeling based on dust temperature and hydrogen density maps derived from Herschel continuum observations.
Methods. We observed the 12CO (2–1), 13CO (2–1), C18O (2–1) and N2H+ (1–0) transitions towards seven isolated, nearby low-mass starless molecular cloud cores. Using far infrared (FIR) and submillimeter (submm) dust emission maps from the Herschel key program Earliest Phases of Star formation (EPoS) and by applying a ray-tracing technique, we derived the physical structure (density, dust temperature) of these cores. Based on these results we applied time-dependent chemical modeling of the molecular abundances. We modeled the molecular emission profiles with a line-radiative transfer code and compared them to the observed emission profiles.
Results. CO is frozen onto the grains in the center of all cores in our sample. The level of CO depletion increases with hydrogen density and ranges from 46% up to more than 95% in the core centers of the three cores with the highest hydrogen density. The average hydrogen density at which 50% of CO is frozen onto the grains is 1.1 ± 0.4 × 105 cm-3. At about this density, the cores typically have the highest relative abundance of N2H+. The cores with higher central densities show depletion of N2H+ at levels of 13% to 55%. The chemical ages for the individual species are on average (2 ± 1) × 105 yr for 13CO, (6 ± 3) × 104 yr for C18O, and (9 ± 2) × 104 yr for N2H+. Chemical modeling indirectly suggests that the gas and dust temperatures decouple in the envelopes and that the dust grains are not yet significantly coagulated.
Conclusions. We observationally confirm chemical models of CO-freezeout and nitrogen chemistry. We find clear correlations between the hydrogen density and CO depletion and the emergence of N2H+. The chemical ages indicate a core lifetime of less than 1 Myr.
Key words: astrochemistry / ISM: abundances / submillimeter: ISM / infrared: ISM / stars: formation / stars: low-mass
This work is partially based on observations by the Herschel Space Observatory. Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Stars form in cold cloud cores. In the prestellar phase, the centers of the cloud cores cool down to temperatures below 10 K and the hydrogen densities typically exceed 105 cm-3. In these conditions complex molecules are synthesized (Bacmann et al. 2012). At the same time, in the densest regions of the cores, many molecular species stick onto the dust grains (e.g., Bergin & Tafalla 2007). The evolution of the chemical composition influences the cooling rate of the clouds and changes the degree of ionization, both important properties that influence the star formation process.
The gas in the local interstellar medium (ISM) consists of 98% molecular hydrogen and helium. These species, however, do not emit at cold temperatures. Therefore, CO has become a popular tracer of the ISM. It is the second most abundant molecule and readily excited already at low temperatures. However, in the conditions in prestellar cores, CO freezes out onto the dust grains. This alters the chemical composition of the cloud cores and the dust properties. Nitrogen-bearing species like N2H+, which are otherwise destroyed by CO molecules, can now accumulate in the gas phase and trace these denser regions. N2H+ molecules form and deplete on longer time scales than does CO. Under reasonable assumptions of the initial abundances, physical conditions, and reaction rates, modeling both species together can therefore constrain the chemical age of the cores.
Source list.
While early studies had already detected CO mantles on dust grains from absorption features in the mid-infrared (e.g., Tielens et al. 1991), direct observational proof of molecular depletion from the gas phase in the centers of dense cores came only later. It requires the accurate determination of molecular abundances in the gas phase and of the total gas mass. One of the most robust ways to determine the total mass in dense clouds is to infer it via a presumably known gas-to-dust mass ratio from (column-) densities of the dust. They in turn can be derived from the black-body radiation of the dust grains (e.g., Launhardt et al. 2013) or the visual to mid-infrared extinction caused by the dust (e.g., Witt et al. 1990; Alves et al. 2001).
Several studies have been performed that quantify the CO depletion in starless cores on the basis of hydrogen masses deduced from dust measurements (e.g., Willacy et al. 1998; Caselli et al. 1999; Bacmann et al. 2002; Bergin et al. 2002; Tafalla et al. 2004; Pagani et al. 2005; Stutz et al. 2009; Ford & Shirley 2011). All of them find strong indications of a central freezeout of CO. So far, however, the observational studies of molecular depletion have only had weak constraints on the temperature distribution within molecular clouds or none at all. Knowledge of the dust temperature is, however, essential for both derivation of column densities from the dust emission and robust chemical modeling (Pavlyuchenkov et al. 2007). Uncertainties in the temperature also introduce large errors into the hydrogen densities derived from (sub-)mm dust emission.
Isolated Bok globules, which often contain only a single dense core and are devoid of larger envelopes, are the best suited objects for detailed studies of the physical and chemical structure of starless cores. We therefore observed seven globules containing a starless core as part of the Herschel guaranteed time key project Earliest Phases of Star formation (EPoS). The Herschel Space Observatory (Pilbratt et al. 2010) and its sensitive PACS (Poglitsch et al. 2010) and SPIRE (Griffin et al. 2010) bolometer arrays have made it possible to sample the peak of the thermal spectral energy distributions (SED) of cold molecular clouds with high sensitivity and spatial resolution for the first time. In Stutz et al. (2010); Launhardt et al. (2013) we presented dust temperature and hydrogen density maps of the starless cores in the globules derived by modified black-body fits to the continuum emission. We also developed a ray-tracing method to restore the full volume density and dust temperature structure of these cores. The results are presented in Nielbock et al. (2012) for B 68, for CB 17 in Schmalzl et al. (2013), and in this paper for the remaining five globules.
We also present maps of the 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0) transitions of the same seven globules. The maps of 12CO (J = 2−1) and 13CO (J = 2−1) of globules CB 17, CB 26, and CB 244 were previously presented in Stutz et al. (2009). Based on dust temperature and hydrogen density maps derived from the Herschel observations, and using time-dependent chemical modeling, we derive the molecular abundances. From the modeling results, we also constrain the chemical age of the cores and infer information on the dust grains in the globules.
The paper is structured as follows. In Sect. 2 we describe the observations and data reduction. In Sect. 3 we describe our modeling approaches. In Sect. 4 we present and discuss the results. We summarize our findings in Sect. 5. Maps of the observations and the derived dust density and hydrogen density maps are shown in Appendix B. We also present a simple local thermodynamical equilibrium (LTE) analysis of the molecular column densities in Appendix C.
List of observations.
2. Observations
2.1. Source selection
Within the EPoS project, 12 nearby Bok globules have been observed with the Herschel bolometers. The sample of globules has been selected based on results from previous studies (see Launhardt et al. 2013, and references therein) and was known to contain low-mass pre- and proto-stellar cores. Of particular importance for the selection was the criterion that the globules be very isolated and located outside the galactic plane. Their mean galactic latitude is 7.3 ± 3 degrees, with the closest one still 3.5 degrees away from the galactic plane, such that background levels and confusion from the galactic plane are minimized. Out of the 12 globules, seven globules contain starless cores. These globules are studied in this paper and are listed in Table 1. Three of the globules contain only a single starless core (CB 4, CB 27, and B 68), one contains an additional Class 0 core (CB 244), and two contain an additional Class I young stellar object (CB 17 and CB 26). CB 130 contains two additional cores (Class 0 and I).
2.2. Continuum observations
All globules were observed in the Herschel PACS bands at 100 and 160 μm and the Herschel SPIRE bands at 250 μm, 350 μm, and 500 μm. These observations were complemented with ground-based (sub-)mm observations ranging from 450 μm to 1.2 mm. The respective observations and data reduction are described in detail in Nielbock et al. (2012) and Launhardt et al. (2013), and references therein. The dust temperature and density maps presented in Sect. 4.1 were derived from this set of observations.
2.3. Molecular line observations
On-the-fly maps of the C18O (J = 2−1) line at 219.560 GHz and the N2H+ (J = 1−0) line complex around 93.174 GHz were taken at the IRAM 30m telescope between November 2010 and January 2011 of all starless cores except B 68. For this globule, we used data that were obtained before and published in Bergin et al. (2002). The observing parameters are compiled in Table 2. Map sizes are different for different sources and range from 3′ × 3′ to 6′ × 5′. The HPBWs were 12″ for C18O and 28″ for N2H+. The channel widths were 40 kHz for C18O and 20 kHz for N2H+, corresponding to 0.05 and 0.06 km s-1. Both molecular transitions were observed simultaneously using the EMIR receivers (Carter et al. 2012). Calibration was done using the standard chopper-wheel method every 15 min. The weather conditions were mixed during the course of the observations leading to mean system temperatures of 700 K for C18O and 180 K for N2H+. During the observations of CB 130, the weather was better, resulting in lower system temperatures of 300 K and 100 K.
To minimize scanning artifacts, the on-the-fly maps were taken with two orthogonal scan directions with two coverages each and a scanning speed of 6″/s. A reference position was observed approximately every 1.5 min. These positions were derived from IRIS 100 μm all-sky maps (Miville-Deschênes & Lagache 2005). They lie within extended regions of the lowest 100 μm continuum emission, preferably within 10′ from the source, and were expected to have no CO emission.
Molecular line maps of the 12CO and 13CO species at the J = 2−1 transition (230.538 GHz and 220.399 GHz) were obtained with the Heinrich Hertz Submilimeter Telescope (HHT) on Mt. Graham, Arizona, USA. The channel width was ~0.34 km s-1 and the angular resolution of the telescope was 32′′ (FWHM). For more details on the observations and data reduction, we refer the reader to Stutz et al. (2009).
Table 2 lists all molecular line observations used for this study. All maps were reprojected to the coordinate system of the corresponding dust temperature and density maps. They have also been smoothed to the same Gaussian beam size of 36.4″ (resolution of the SPIRE 500 μm maps and the dust temperature and density maps) and been regridded to the same pixel scale of 10′′ × 10′′.
3. Modeling
3.1. Dust temperature and density maps from ray-tracing models
The goal of the ray-tracing fitting of the continuum observations of the starless cores is to go beyond the line-of-sight (LoS) optical depth-averaged analysis presented in Launhardt et al. (2013) by also modeling the dust temperature variation along the LoS and deriving volume density distributions. The ray-tracing algorithm developed to derive the dust temperature and density structure of the cores from the Herschel and complementary ground-based continuum maps is described in Nielbock et al. (2012). Here, we only briefly summarize the hydrogen density and temperature profiles used by the algorithm and mention the formulae to illustrate the meaning of the profile parameters.
For all modeling steps we use the dust opacities
κd(ν) tabulated in Ossenkopf & Henning (1994)1 for mildly coagulated composite dust grains with thin ice mantles
(105 yrs coagulation time at gas density 105 cm-3)2. The density profiles of the cores have been modeled
assuming a “Plummer”-like shape (Plummer 1911),
which characterizes the radial density distribution of prestellar cores on the verge of
gravitational collapse (Whitworth & Ward-Thompson
2001): 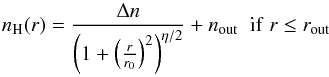 (1)where
nH = 2 × n(H2) + n(H)
is the total number density of hydrogen nuclei. The radius
rout sets the outer boundary of the model cloud. The density
beyond this radius is set to zero. We add a constant term to the profile to account for
the fact that the outer density and column density profiles in most globules do not drop
off like a power law, but turn over into a low-density envelope. This profile (i) accounts
for an inner flat density core inside r0 with a peak density
n0 = nout + Δn
(Δn ≫ nout), (ii) approaches modified
power-law behavior with an exponent η at
r ≫ r0, (iii) turns over into a
flat-density halo outside r1, where
(1)where
nH = 2 × n(H2) + n(H)
is the total number density of hydrogen nuclei. The radius
rout sets the outer boundary of the model cloud. The density
beyond this radius is set to zero. We add a constant term to the profile to account for
the fact that the outer density and column density profiles in most globules do not drop
off like a power law, but turn over into a low-density envelope. This profile (i) accounts
for an inner flat density core inside r0 with a peak density
n0 = nout + Δn
(Δn ≫ nout), (ii) approaches modified
power-law behavior with an exponent η at
r ≫ r0, (iii) turns over into a
flat-density halo outside r1, where 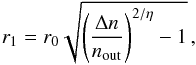 (2)and (iv) is cut off at
rout. The tenuous envelope is actually neither azimuthally
symmetric nor fully spatially recovered by our observations. Therefore, its real size
remains unconstrained, and rout cannot be considered a
reliable source property.
(2)and (iv) is cut off at
rout. The tenuous envelope is actually neither azimuthally
symmetric nor fully spatially recovered by our observations. Therefore, its real size
remains unconstrained, and rout cannot be considered a
reliable source property.
For the temperature profile of an externally heated cloud, we adopt the following
empirical prescription. It resembles the radiation transfer equation in coupling the local
temperature to the effective optical depth toward the outer “rim”, where the interstellar
radiation field (ISRF) affects 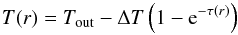 (3)with
ΔT = Tout−Tin
and the frequency-averaged effective optical depth
(3)with
ΔT = Tout−Tin
and the frequency-averaged effective optical depth 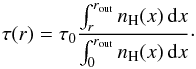 (4)Here,
τ0 is an empirical (i.e., free) scaling parameter that
accounts for the a priori unknown mean dust opacity and the SED of the UV radiation of the
ISRF, and Tin is the minimum, inner temperature and is
determined by IR and cosmic ray heating.
(4)Here,
τ0 is an empirical (i.e., free) scaling parameter that
accounts for the a priori unknown mean dust opacity and the SED of the UV radiation of the
ISRF, and Tin is the minimum, inner temperature and is
determined by IR and cosmic ray heating.
The results of this modeling approach are presented in Sect. 4.1. The uncertainties of the method have been discussed thoroughly in
Nielbock et al. (2012) and Launhardt et al. (2013). They come to the conclusion that the largest
uncertainty (up to a factor 3) in the derived density is introduced by the uncertainty in
the dust opacities. Additional uncertainties are introduced by the assumed distances, the
gas-to-dust ratio, the symmetry assumption (w.r.t. the plane-of-sky) for the LoS, and the
limited angular resolution. In particular, in the center of the cores, the density can be
systematically underestimated due to beam smoothing. We therefore estimate the overall
fitting uncertainty of the derived density maps to be ± 25%, plus a scaling uncertainty by
up to a factor 3 due to the not well-constrained dust opacity model. The accuracy of the
dust temperature is not as strongly affected by these effects and the modeled dust
temperature has an estimated uncertainty of 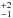 K.
K.
 |
Fig. 1 Azimuthally averaged profiles of the hydrogen density (left), hydrogen column density (center), and dust temperature (right) derived with the ray-tracing technique. |
3.2. Chemical modeling
On the basis of the dust temperature and the hydrogen density maps that were derived using the ray-tracing technique and that are presented in Sect. 4.1, we model the chemical evolution of the molecular gas in the cloud cores. The density and temperature profiles are kept constant during the chemical evolution of the cores. The gas is initially atomic, comprising 13 elements, and it evolves with time because of the processes described below. This approach of a chemical evolution under constant physical conditions is often called “pseudo time-dependent”. We call the time span during which the chemical models evolve “chemical age”. How this parameter is related to the “real” age of the cores is discussed in Sect. 4.4.4.
We act on the assumption that the gas temperature is equal to the dust temperature everywhere in the clouds. This simplifying assumption should hold to first order at hydrogen densities above 104 cm-3 where dust and gas are collisionally coupled (Galli et al. 2002) and where most of the molecular emission originates. However, the coupling might not be perfect even in the densest regions of our study (>106 cm-3): for example, for B 68, where we have derived a central hydrogen density of 4 × 105 cm-3 and central dust temperature of 8 K, Hotzel et al. (2002) and Lai et al. (2003) find a central gas temperature of 10−11 K from ammonia observations. On the other hand, ammonia might be depleted in the core center such that it instead traces a somewhat warmer inner layer of the envelope. In our model of B 68, the dust temperature in a shell of radius 5000 to 7000 AU is indeed 10−11 K. This could also explain at least part of this small discrepancy. The decoupling of gas and dust temperatures at lower densities affects our modeling results less than the chemical evolution, since the rotational transitions at low densities are subthermally excited. For instance, at a hydrogen density of 103 cm-3 and a gas temperature of 100 K, the J = 2−1 transition of CO would only be excited to about 9 K, while the same transition would be excited to 5 K at a gas temperature of 20 K3. Therefore, underestimating the gas temperature affects the modeled level populations and the molecular emission at low densities only weakly.
In the vicinity of the core centers, the majority of globules show almost circularly symmetric shapes. As we study these central cloud regions, the modeling is performed assuming 1D radial profiles. We obtain 1D profiles of the observed molecular emission and the dust temperature and density maps by azimuthal averaging. We cut out the segment of the circle in the direction of asymmetries for the averaging task. The regions that have been taken into account for deriving the 1D profiles are indicated in Figs. A.1–A.7. The resulting profiles of the dust temperature, hydrogen densities, and column densities are shown in Fig. 1.
We use the time-dependent gas-grain chemical model “ALCHEMIC” (see Semenov et al. 2010). A brief summary is given below. The chemical network is based on the 2007 version of the OSU network4. The reaction rates as of November 2010 are implemented (e.g., from the KIDA database5). We consider cosmic ray particles (CRP) and CRP-induced secondary UV photons as the only external ionizing sources. We adopt a CRP ionization rate of ζCR = 1.3 × 10-17 s-1 (Herbst & Klemperer 1973), although recent studies have revealed higher CRP ionization rates in translucent clouds (e.g., Indriolo et al. 2012). The dense molecular cloud cores studied here are embedded in extended envelopes that, despite their low density, effectively scatter the low energy particles of the cosmic rays and thereby reduce the luminosity of the cosmic rays in the shielded regions. Therefore the lower value of Herbst & Klemperer (1973) is expected to hold for dense and shielded clouds (e.g., Garrod 2013; Vasyunin & Herbst 2013). The UV dissociation and ionization photo rates are adopted from van Dishoeck et al. (2006)6. The self-shielding of H2 from photodissociation is calculated by Eq. (37) from Draine & Bertoldi (1996). The shielding of CO by dust grains, H2, and its self-shielding are calculated using the precomputed table of Lee et al. (1996, Table 11). As the chemical model does not include carbon isotopologues, the self-shielding factors for 12C18O are calculated by lowering the 12C16O abundances by an appropriate isotopic ratio (see below).
In addition to gas-phase chemistry, the chemical model includes the following gas-grain interaction processes. (We refer the reader to Sect. 2.3 in Semenov et al. 2010, for the corresponding equations.) Molecules accrete on and stick to dust grains by physisorption with 100% probability, except for H2, which is not allowed to stick. Chemisorption of surface molecules is not allowed. The surface molecules are released back to the gas phase by thermal, CRP-, and CRP-induced UV-photodesorption. All these processes are modeled with a first-order kinetics approach (Eq. (2) in Semenov et al. 2010). A UV photodesorption yield for surface species of 10-3 is assumed (e.g., Öberg et al. 2009a,b). The grain charging is modeled by dissociative recombination and radiative neutralization of ions on grains, and by electron sticking to grains. The synthesis of complex molecules is included, using a set of surface reactions and photoprocessing of ices from Garrod & Herbst (2006). We assume that each 0.1 μm spherical olivine grain provides ≈1.88 × 106 surface sites for accreting gaseous species (Biham et al. 2001). The surface recombination proceeds only via the Langmuir-Hinshelwood mechanism. Upon a surface recombination, the reaction products are assumed to remain on the grains. Following Katz et al. (1999), we use the standard rate equation approach to the surface chemistry and do not consider tunneling of H and H2 through the grain surface.
Overall, our chemical network consists of 656 species made of 13 elements and 7907 reactions. All chemical parameters are kept fixed during the iterative fitting of the observational data. With this model we calculate time-dependent CO and N2H+ abundances and use them for the line radiative transfer modeling and fitting of the observed spectral maps.
In the cloud 1D physical model, the density profiles are cut off at an outer radius where either no density could be derived because the continuum emission is too weak or where the morphology of the cloud becomes asymmetric. These radii are also the outer boundaries for the chemical modeling. At these radii the density has, however, not yet dropped to zero as the cores are further embedded in low-density extended envelopes. We therefore have to take into account that the external UV field is already attenuated at the outer edge of the cores. We derive the extinction level by converting the column density at the outer boundaries to an extinction level AV. We use a conversion factor Av/NH of 1 × 10-21 cm2. This is the average value estimated by comparing the NH maps derived from the dust emission to complementary near-infrared extinction maps (see Launhardt et al. 2013; Kainulainen et al. 2006), which will be presented and discussed in more detail in a forthcoming paper.
We want to compare models and observations of 13CO, C18O, and N2H+. Since the rare isotopologues are not explicitly taken into account in the chemical modeling, we proceed in two steps. In the first step, we calculate the chemical model for 12CO to get the N2H+ abundances accurately. The modeling itself also consists of two steps. First, the abundance of the molecules and the corresponding shielding factors are calculated using an analytic approximation. The shielding factors are subsequently used for the second step, the full time-dependent modeling. To calculate the profiles of 13CO and C18O, we artificially decrease the 12CO abundance by a factor in the analytic approximation and calculate the shielding-factor for these species. They are used for the time-dependent chemical modeling. The initial abundances are, however, taken to be the same as for the modeling of 12CO. To obtain the abundance of the rare isotopologues, the resulting abundances of the time-dependent modeling are divided by the corresponding fraction of these species with respect to their main isotopologue. This approach allows us to take the reduced self-shielding of 13CO and C18O into account with respect to 12CO without extending the chemical network to the rarer isotopologues. In the literature there is a spread of values mentioned for the ratios of the isotopologues. We use a fraction of 1/70 for 13CO with respect to 12CO and 1/490 for C18O (Wilson & Rood 1994; Lodders et al. 2009).
Since the temperature and abundances of the molecules vary along the LoS, the molecular emission could be partly subthermally excited or be optically thick. For these reasons, we calculate the rotational level populations and emission of the molecules from the synthetic abundance profiles using line-radiative transfer modeling. It is not our goal to model the kinematics of the cores. For the pure purpose of modeling the lineshape and the total intensity of the transitions, we can neglect variations of macroscopic and turbulent motions in the cores, since they are so weak that this simplification does not affect the results for the molecular abundances. We use the non-LTE line radiative transfer code “LIME” (Brinch & Hogerheijde 2010) and the molecular data files of the “Leiden Atomic and Molecular Database” (Schöier et al. 2005). The LIME code allows to take into account line-broadening due to micro turbulent motions. This is done by setting a scalar Doppler broadening parameter. Since the linewidths in the globules do not vary significantly over the globules, it is possible to set this parameter such that the linewidths of models and observations agree everywhere. The Doppler broadening parameter is taken as one free parameter in the modeling process. In this way we ensure that the optical depth of the emission is properly taken into account. The macroscopic velocity field in the modeling is set to zero. The velocity channel width is set to the value of the observed spectral cubes and the pixel spacing is set to 10″ to which all observational data are also regridded.
For the comparison of synthetic and observed spectra, the latter have been prepared as follows. We have removed line shifts from macroscopic motions in the observed spectra since we do not model the kinetics of the cores. For this task, the spectra have been fitted and shifted by the derived vLSR such that the centers of all spectra are located at vLSR = 0. They have also been rebinned such that vLSR = 0 lies in the center of a bin as is the case for the synthetic spectra. Finally, the spectra are azimuthally averaged. The resulting radially varying spectra build up the reference to which the modeled spectra can be compared directly.
During the course of the modeling, we vary four parameters. The chemical model has only one “true” free parameter, the chemical age, which is the time during which the gas evolves at constant physical conditions. In addition, we take into account uncertainties in the derived hydrogen densities of up to a factor 3 resulting from the uncertainties of the assumed dust properties (see Sect. 3.1). The relative initial abundances of the atomic species are kept constant when the hydrogen density is varied. We also need to consider that the hydrogen density has not dropped to zero at the outer boundaries of the model cores. Halos of dust particles around the globules with a mean extinction AV of typically 1−3 mag are detected in the SPIRE, as well as NIR extinction maps that are quite extended. Since these envelopes shield the globules from the UV-part of the ISRF, they need to be considered in the chemical modeling. The halos are not strictly spherically symmetric, either in extinction / column density or in extent, as pointed out in Launhardt et al. (2013). To account for this and other uncertainties discussed in Sect. 4.4.5, we consider the measured mean envelope extinction as a starting guess only and vary them during the modeling procedure.
We find the best model in the following way. The relative differences of observed and synthetic spectra are summed up for each velocity bin and at all radii. The model with the lowest value of this sum is taken as the best model. It reproduces not only the integrated emission well, but also the line shape such that the optical depth of the emission is taken into account properly.
4. Results and discussion
4.1. Dust temperature and density maps
The final parameters of the hydrogen number density and dust temperature profiles in the cores according to the formulae given in Sect. 3.1 are listed in Table 3. In Figs. B.1–B.7 we show the hydrogen density and dust temperature maps of all globules in the mid-plane across the sky as they were obtained from the continuum data with the ray-tracing technique described in Sect. 3.1. The central density of the starless cores ranges from 4 × 104 cm-3 to 4 × 105 cm-3. The cores are clearly non-isothermal, as already predicted by radiative transfer models (e.g., Evans et al. 2001). In all cores the dust temperature drops from the outer rims with 13−19 K to the core centers to 8−13 K. Compared to the temperatures derived from the modified black-body fitting technique in Launhardt et al. (2013), the central temperatures are lower by 1−3 K. The central column densities reach from 7 × 1021 to 6 × 1022 cm-2 in the maps derived with the ray tracing technique compared to the column densities of 7.5 × 1021 to 4.6 × 1022 cm-2 in Launhardt et al. (2013) which is on average 60% more. The lowest difference is found in the case of CB 17 with an increase of only 6% and the highest in the case of B 68 with an increase of 230%.
From the maps we have derived one-dimensional profiles by azimuthally averaging around the centers of the starless cores. The regions that were considered for deriving the radial profiles are indicated with thick white lines in the SPIRE 250 μm maps in Figs. A.1–A.7. Because of its strong asymmetry and the nearby protostellar core, the starless core in CB 130 is not well-suited for a 1D study. We therefore do not derive a radial profile of its density and temperature structure and will also not take it into account for the chemical modeling. The profiles of the hydrogen volume and column density, and dust temperature of the other globules are plotted in Fig. 1.
 |
Fig. 2 Stability of the cores. Same plot as Fig. 6 in Launhardt et al. (2013), but here for the results of the ray-tracing models. Top: ratio of gravitational potential to thermal kinetic energy vs. total gas mass (Mcore). The lower dashed horizontal line marks the bounding limit of −Egrav/Etherm = 1, while the upper line marks the state of virialization at −Egrav/Etherm = 2. Bottom: central density vs. total gas mass for the same cores. The dashed line marks the maximum stable density of a pressure-supported, self-gravitating modified (nonisothermal) BES as calculated by Keto & Caselli (2008, with their Fig. 14, model with photoelectric heating at the core boundary taken into account). The uncertainty resulting from the ray-tracing modeling is indicated by the error bars at CB 4. The arrows indicate the maximum systematic shift of the cores in the diagram if grain properties of ISM dust were used in the modeling. |
4.2. Sizes, masses, and stability of the cores.
We derived masses of the starless cores by integrating over the circularized 1D hydrogen
density profiles nH(r). We conservatively
estimate the mass by choosing r1 (Eq. (2)) as outer radii of the cores where the
profiles turn from a power-law like into a flat shape. These radii range from
27 × 103 to 57 × 103 AU and are listed in Table 3. We take into account that the total gas mass is
higher by a factor of μH = 1.36 than the hydrogen atom mass so
that the core masses are given by: 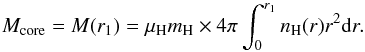 (5)The resulting core masses
range from 2 M⊙ to 10 M⊙ (see Fig.
2) and are well in agreement with those previously
estimated from modified black-body fits (see Stutz et al.
2010; Launhardt et al. 2013).
(5)The resulting core masses
range from 2 M⊙ to 10 M⊙ (see Fig.
2) and are well in agreement with those previously
estimated from modified black-body fits (see Stutz et al.
2010; Launhardt et al. 2013).
The stability of the cores was checked by comparing the gravitational potential with the thermal energy of the particles in the cores. We neglected turbulent pressure, rotational energy and magnetic fields. This is justified since the thermal energy is the strongest contributor to the stabilization. Assuming typical magnetic field strengths in Bok globules of a few 100 μG (Wolf et al. 2003), these three contributions are dominated by the turbulent pressure which we have estimated for all cores and typically adds only 10% to the thermal energy.
We estimated the gravitational potential by
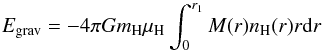 (6)where G
is the gravitational constant. The thermal energy of the molecules is calculated from
(6)where G
is the gravitational constant. The thermal energy of the molecules is calculated from
 (7)where
kB is the Boltzmann constant and
μHnH/μ
with μ/μH = 0.6 the mean
particle density for molecular gas. For the gas temperature, we adopt the dust
temperature. TGas might actually be higher than
TDust in the outer regions of the envelopes, so that we
probably underestimate Etherm.
(7)where
kB is the Boltzmann constant and
μHnH/μ
with μ/μH = 0.6 the mean
particle density for molecular gas. For the gas temperature, we adopt the dust
temperature. TGas might actually be higher than
TDust in the outer regions of the envelopes, so that we
probably underestimate Etherm.
In the top panel of Fig. 2, we plot the ratio of the total gravitational to thermal energy of all starless cores against their masses. The dashed horizontal line at a ratio of 2 indicates virial equilibrium while the dashed line at a ratio of 1 marks the bounding limit. The values for the cores indicate that only the starless core of CB 244 is clearly gravitationally unstable. In Fig. 2 (bottom) we plot the central density against the total mass of the cores. The dashed line indicates the maximum central density of a pressure-supported, self-gravitating modified (non-isothermal) Bonnor-Ebert sphere (BES; Bonnor 1956; Ebert 1955), calculated by Keto & Caselli (2008) for a core with photoelectric heating at the boundary. The comparison of the core properties to the theoretical curve strengthens the result that the starless core in CB 244 is prestellar. It also suggests that CB 17, CB 27, and B 68 are thermally super critical.
Spectral line parameters at the centers of the starless cores.
4.3. Spectra and molecular emission maps
In Figs. A.1–A.7, integrated emission maps of 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1) and N2H+ (J = 1−0) are presented. For the sake of comparison we also have included maps showing the same regions as observed with the SPIRE bolometer in the 250 μm band and from the Digitized Sky Survey 2 archive7. Because of their different abundances, the emission of three isotopologues becomes optically thick at different column densities. As the main CO isotopologue, 12CO traces the envelopes of the globules particularly well, while 13CO is best suited to tracing the outer parts of the cores. As the rarest isotopologue, C18O traces the dense regions of the cores up to hydrogen densities of ~1 × 105 cm-3. At these densities CO freezes out onto the dust grains. We therefore complemented our set of molecular line observations with maps of N2H+, which traces the densest parts of the cores where CO is frozen out. The time scales of build-up and depletion of N2H+ are longer than for CO so that both species in combination allow constraining the ages of the cores.
The 12CO and 13CO maps are smaller than the SPIRE 250 μm maps, but the molecular emission of 12CO is more extended than the continuum emission in some cases. This indicates that there are extended cold envelopes to which the continuum observations are less sensitive. C18O is the least abundant CO isotopologue used in this study. It is therefore the optically thinnest and best suited CO isotopologue for the dense regions of the cores where CO is not frozen out. While its emission is enhanced at the positions of some Class I objects, it does not show enhancement at the locations of the starless cores. In contrast, the N2H+ emission shows a positive gradient towards the core centers. In the two least dense starless cores, CB 4 and CB 26, N2H+ emission was only marginally detected.
The spectral line parameters at the centers of the starless cores are listed in Table 4. The spectra of all molecules toward the centers of the starless cores are also plotted in Fig. 3. C18O is single-peaked in all sources except CB 26, where two distinct peaks at a velocity separation of 0.33 km s-1 are observed. It is unlikely that the dip is due to self-absorption, since the line is quite weak. It is more likely caused by multiple velocity components. Almost no N2H+ emission is detected from the starless core in CB 26. At the position of the protostar in CB 26, the C18O line is also double peaked, with the dip at the same velocity as for the starless core. This is an indication of the protoplanetary disk seen edge-on (Launhardt & Sargent 2001). The peak main beam temperature TMB of the C18O (J = 1−0) transition ranges from 2 K to 6 K in the various globules.
The channel width of the 13CO observations is only 0.34 km s-1 compared to 0.05 km s-1 of the C18O spectra. If the 13CO line of CB 26 was double peaked as the C18O line, we could not resolve it. The 13CO line is single peaked in all cores except for CB 130 where it shows two peaks with a velocity separation of 0.53 km s-1. The dip of this line falls into the peak of the C18O emission and is thus probably a result of self-absorption.
 |
Fig. 3 Spectra of the 12CO (2−1), 13CO (2−1), C18O (2−1) and N2H+ (1−0) transitions in a 36.4″ HPB at the centers of the starless cores. |
The emission of the main isotopologue 12CO is optically thick towards the core centers but traces also the outskirts of the globules where the emission of the less abundant isotopes drops below the detection limit. Consequently, its linewidth is highest throughout the sample and ranges from 0.3 km s-1 to 0.7 km s-1 in the globules that only contain starless cores. In those globules that also inhabit protostellar cores, the linewidths are generally higher and reach values of up to 1.6 km s-1. CB 130 is an exceptional case with a very broad line emission, consistent with its location within a larger diffuse structure.
All globules show signs of slow large-scale motions. The linewidths are typically larger than the thermal linewidths and increase from the rare to the abundant CO isotopologues. The average linewidths of the spectra toward the core centers are 0.30 km s-1, 0.69 km s-1, and 1.0 km s-1 for C18O, 13CO, and 12CO, respectively. The thermal linewidths are typically around 0.15 km s-1, if one assumes that the gas temperature is equal to the dust temperature. The radiation of 13CO and 12CO emanate mainly from regions with nH ≲ 104 cm-3 where the gas is expected to be warmer than the dust, since the density is too low to couple both temperatures via collisions. Therefore, a fraction of the linewidth increase can be attributed to higher gas temperatures at the outskirts of the globules. Gas temperatures of 30 K to 50 K would, however, only result in a thermal line broadening of 0.22 km s-1 to 0.29 km s-1, respectively. The remaining broadening must be caused by turbulent or macroscopic motions, but is partly also mimicked by the optical thickness of the lines.
With the N2H+ observations we trace the inner part (r ≲ 104 AU) of the cores where large amounts of CO are expected to be frozen out onto the dust grains. The spectra at the position of the core centers are shown in Fig. 3 (right panels). The linewidths range from 0.08 km s-1 up to 0.37 km s-1. This range can only partially result from different temperatures and must have its origin in the different dynamics of the gas.
 |
Fig. 4 Profiles of the integrated emission that would result from the molecular abundances of the final models (solid line) compared to the observed profiles of the integrated emission for all modeled starless cores. (Left) 13CO (J = 2−1), (center) C18O (J = 2−1), (right) N2H+ (J = 1−0). |
 |
Fig. 5 To quantify the agreement of models and observations we compare the spectra over the full radius of the models. Here, an example of B 68 is shown. The solid lines represent observations, the dotted lines the synthetic spectra of the best models. On the left panels, we show the spectra of the 13CO (J = 2−1) (gray) and C18O (J = 2−1) (black) transitions. On the right panels, we show the spectra of the N2H+ (J = 1−0) transition. The top line shows the spectra at the position of the core center, the bottom line the spectra at a radial distance of 7000 AU. |
 |
Fig. 6 Relative abundances (absolute molecular density with respect to the hydrogen density) of gaseous C18O (black solid line), frozen-out C18O (dashed black line) and gaseous N2H+ (gray solid line) in the final models. At the outer radii of the emission profiles derived from the observations, the lines turn from a solid into a dotted line shape, indicating that these parts of the profiles are not constrained by observations. |
4.4. Core properties constrained from chemical modeling
On the basis of the dust temperature and hydrogen density profiles presented in Sect. 4.1, we have modeled the chemical evolution of the globules. The approach is explained in Sect. 3.2. The best fits of the modeled integrated emission to the observed profiles are presented in Fig. 4. In Fig. 5, we demonstrate the quality of the agreement between modeled and observed line shapes.
4.4.1. The individual globules
CB 4: while CB 4 is the most symmetric and isolated globule of our study (Fig. A.1), it is also the least dense one with a central hydrogen density of only 4 × 104 cm-3. It is the only core in the study for which the modeled 13CO emission is underestimated with all parameter sets. Owing to its low density, the coupling of gas and dust temperature is expected to be the weakest in this globule and the gas temperature might thus be significantly higher than the dust temperature. The emission of C18O and N2H+ is dominated by inner regions such that the gas temperature is closer to the dust temperature. We find that the chemical age of CB 4 is ~105 yr. The significance of the derived chemical ages is discussed in Sect. 4.4.4. To match the observations, we have to increase the hydrogen density by a factor of 3. We require AV, out to be set at a value of at least 4 mag, while a value of 0.6 mag has been derived from the NIR extinction maps.
CB 17: the 13CO emission of CB 17 can be reproduced assuming a chemical age of 7 × 104−105 yr and assuming that the hydrogen density is increased by a factor of 3. We only have a very small map of C18O emission for this source, such that the observational constraint to the model is limited. We find the best fit for an age of 5 × 104−105 yr. The best model for N2H+ is found at a chemical age of 105 yr. We find the best fits for an external visual extinction of 2 mag that is also found from the NIR extinction mapping, but the deviation is not strong for AV, out values ranging from 0 to 6 mag. Our finding of a low chemical age does not confirm the finding of Pavlyuchenkov et al. (2006) who found a chemical age of 2 Myr for the starless core in CB 17.
CB 26: we reproduce the 13CO emission from the starless core in CB 26 with a chemical age of 4 × 105 yr. The emission profile of C18O, however, is very steep and shows no signatures of freezeout. It is best described with chemical models at an age of only ~104 yr and by setting the external visual extinction at the model boundary to 0 (AV, out = 1 in the NIR extinction map). The parameters are consistent with the very weak observed emission of N2H+.
CB 27: the 13CO emission of CB 27 cannot be fit well. In particular, the emission coming from large radii is underestimated in all our models. This discrepancy can be overcome if an increased gas temperature in the envelope of this core is assumed. The range of chemical ages, for which the models fit the data similarly well within the uncertainties, is wide and reaches from 105 to 106 yr. For the C18O emission, we find the best models at AV, out values ranging from 2 to 6 mag (AV, out = 1 has been found in the NIR-extinction map) and an age between 5 × 104 and 105 yr. The hydrogen density needs to be multiplied by a factor of 3 with respect to the density profiles obtained from the EPoS project. The N2H+ emission is modeled best with the same age as the C18O emission but only a factor 2 in density.
B 68: this is the only core for which all three molecular emission profiles can be reproduced from our chemical models with the hydrogen density profile as derived in Sect. 4.1. If we increase the hydrogen density in the models, the resulting molecular emission profiles deviate significantly from the observed profiles. The best chemical age to match the 13CO observations is 2 × 105 yr, while we find that the C18O and N2H+ profiles are best explained by models with a chemical age between 7 × 104 and 105 yr. Bergin et al. (2006) found an chemical age of ~105 yr from chemical modeling and a comparison of the modeled and observed 13CO and C18O emission. This is well in agreement with our findings, and AV, out needs to be around 4−6 mag in the models while we derived a value of about 1 mag from the NIR extinction map.
CB 244: as for CB 27, all our models underestimate the 13CO emission at large radii, which could be explained by a decoupling of dust and gas temperatures at low densities. The chemical age that fits the data best is around 2 × 105 yr. In contrast, the C18O and N2H+ profiles are best fit with a chemical age of only 4 × 104 yr. Changing the external Av at the model boundaries does not have a significant impact on the goodness of the fits. The hydrogen density needs to be multiplied by 2 for the CO isotopologues and by a factor of 3 for N2H+.
That we obtain a discrepancy of a factor ~2−3 is an indication that the assumed dust model may be incorrect. This result is discussed in Sect. 4.4.6.
 |
Fig. 7 Top row: the ratio of icy-to-total C18O abundance of the best-fit models is plotted against the core radius, the hydrogen number density, the column density, and the dust temperature. Bottom row: the N2H+ abundance (relative to the hydrogen density) is plotted against the same quantities. The dashed lines indicate the results of the individual globules. Where the models cannot be compared to observations (because the line radiation is too weak), the dashed lines turn into dotted lines. The bold solid lines mark the mean values. The gray area indicates one standard deviation. |
Ratio of icy to total C18O abundance abundance in the core centers, radius, hydrogen column density, hydrogen density, and dust temperature at which 50% of the total C18O abundance is frozen onto the grains.
4.4.2. CO abundances
In Fig. 6, we plot the modeled relative abundance profiles of gaseous and frozen C18O of the final models that correspond to the emission profiles presented in Fig. 4. The abundance of gaseous C18O (X(C18O)≡ n(C18O)/nH) in molecular gas that is assumed to be shielded well and undepleted varies in the literature and ranges from 3.5 × 10-8 (Tafalla & Santiago 2004) to 2.4 × 10-7 (Lee et al. 2003). In the outer parts of all our cores, the C18O abundances X(C18O) reach the value of Tafalla & Santiago (2004). The highest abundance of 9 × 10-8 is reached in the envelope of the young and not that dense core CB 26. The hydrogen densities in the regions of maximum C18O abundances are typically between 104 and 5 × 104 cm-3. In the center of the cores, the gaseous C18O abundance drops because of freezeout onto the dust grains. There, the C18O abundance (relative to the peak abundance) drops by a factor of 2 in the least dense core (CB 4) and by a factor of 30 in the denser cores (CB 27, B 68, and CB 244). Towards the outer edges, CO is photodissociated by UV radiation, so that X(C18O) there also drops. The emission profiles of 13CO are not reproduced as well by the chemical models as for C18O (see Fig. 4). The reason for this is most likely that the emission of this molecule is dominated from the outer envelope, which is probably warmer than the dust in the same layers. Thus, the observed emission profiles are flatter and extended further towards larger radii than is the case in the models. The optical thickness of the lines becomes apparent, for, instance, in the modeled emission profile of CB 244 (Fig. 4). The density distribution of this model peaks at a radius of about 2 × 104 AU. The drop towards smaller radii is still indicated in the emission profile, but towards even smaller radii, it is dominated by the warm outer layer so that it even rises, thus explaining the double-peaked 13CO emission profiles in CB 27 and CB 244 (Fig. 4).
We also plot the profiles of icy C18O since they are predicted by the best-fit chemical models in Fig. 6. Its amount in the core center is in some cases greater than the amount of gaseous C18O at its peak position, since at high densities the CO production is faster than the freezeout of atomic C. If the abundances of icy C18O at the core centers are compared to the total C18O abundance there, the ratios range from 45% in CB 4 to more than 90% in those cores that have a central hydrogen density of more than 105 cm-3. In Fig. 7, we compare these ratios in all cores and correlate them to the core radius, the hydrogen volume and column densities, and the dust temperature. The freezeout increases towards the core centers and with increasing hydrogen densities. The total temperature range between Tin and Tout in the cores is less than 10 K, and the correlation of freezeout with the temperature is not as clear as for the other quantities. Typically, half of the total C18O molecules stick to the grains at a radius of ~104 AU, a hydrogen density of ~105 cm-3, and a temperature of 11 K. In Table 5 we list the maximum level of freezeout in the individual cores and the conditions at which half of the total C18O molecules are frozen onto the dust grains. The correlation of the freezeout level to the hydrogen densities is plotted for the conditions of the core centers in Fig. 8.
 |
Fig. 8 Correlation of C18O freezeout and hydrogen density in the core centers. The horizontal error bars on the hydrogen density represent the fitting uncertainty of the ray-tracing modeling (i.e., excluding systematic uncertainties from, e.g., the dust opacity model; see Sect. 3.1). The vertical error bars represent a 20% uncertainty in the amount of icy CO in the chemical model. |
Ratio of the N2H+ abundance in the core centers to the maximum abundance, corresponding radius, hydrogen density, and dust temperature.
4.4.3. N2H+ abundances
N2H+ forms and depletes on longer time scales than CO. We find that in four out of the six studied globules (those with a central density over 105 cm-3), N2H+ is strongly depleted in the core centers. For comparison, we show in Appendix C that a simple LoS, averaged LTE-analysis would not reveal depletion of N2H+, although the emission is optically thin (τ ≲ 0.5) in all cores as we have derived for calculating the molecular column densities in Appendix C. The ratios of the central to maximum abundance of N2H+ molecules are listed in Table 6. They range from 13% to 55%. The radii, hydrogen density, and dust temperature at which the N2H+ abundances reach their maximum are also given in Table 6. CB 4 and CB 26 do not show detectable depletion of N2H+. CB 4 is probably not dense enough and CB 26 might be too young to show depletion at its low central density (see Sect. 4.4.4). The correlation of X(N2H+) with core radii, hydrogen volume, and column density and with temperature are plotted for all cores in the bottom row of Fig. 7. X(N2H+) typically peaks at hydrogen densities of 105 cm-3 in cores at a chemical age of 105 yr. The mean radius of the peak X(N2H+) is (6800 ± 1000) AU. We resolve the regions of N2H+ depletion in all cores, since these radii are two to three times larger than the half beamwidth.
We find that the depletion of N2H+ is more restricted to the center as compared to the depletion of CO. It occurs at hydrogen densities ≳105 cm-3 and column densities >1022 cm-2, and requires a chemical age of ≳105 yr. This finding is consistent with the work of Bergin et al. (2002) on B 68, while other studies have claimed that depletion of N-bearing species would only occur at hydrogen densities ≳106 cm-3 (Tafalla et al. 2002; Pagani et al. 2005). The abundance quickly increases outwards and peaks where the majority of CO is still frozen onto the grains. Farther out, it drops where CO becomes abundant in the gas phase. In Fig. 9, we plot the relative gas phase C18O abundance against that of N2H+ for all globules. The N2H+ and C18O abundances are anticorrelated at C18O abundances above 10-8 (corresponding to X(CO) = 5 × 10-6 when assuming X(CO)/X(C18O) = 490), but the curves turn over to a positive gradient below this value. At this point, depletion of nitrogen mainly in form of N and N2 becomes the dominant reason for depletion of N2H+ compared to reactions with CO.
 |
Fig. 9 Relative gas phase abundance of C18O against that of N2H+. At X(C18O)≈ 2 × 10-8 the correlations turn into an anti-correlation. While at high X(C18O), the N2H+ molecules are destroyed by reactions with CO, at low X(C18O) (and high densities) freezeout of nitrogen is the dominant reason for depletion of N2H+. |
Chemical ages of the best fit models for 13CO, C18O, and N2H+.
4.4.4. Chemical age of the cores
“Chemical age” is a parameter in the modeling process. It sets the time span during which the gas develops starting from a state of purely atomic gas of 13 different elements. In this period complex molecules build up and deplete onto the grains. We find that the individual species are fitted best for models of different chemical ages. They are listed in Table 7. The average chemical age of the 13CO best-fit models is (2 ± 1) × 105 yr, for C18O (6 ± 3) × 104 yr, and for N2H+ (9 ± 2) × 104 yr. Up to an age of ~2 × 105 yr, the chemical models evolve quickly so that deviations of a few 104 yr already lead to significantly worse fits of the models to the data. Therefore, the difference in the chemical ages of the best-fit models between the individual species is significant. 13CO that mainly traces the outer envelope of the cores is modeled best with chemical ages that are on average more than 105 yr higher than those of the best-fit models of C18O and N2H+.
We interpret this finding as the result of core contraction and cooling during the chemical evolution. This would accelerate the freezeout of CO and the synthesis of N2H+ molecules. Since we assume a constant physical structure in the chemical modeling, we would thus systematically underestimate the chemical age of those species that trace the regions that have been contracting during the chemical evolution. Additional support for this hypothesis is provided by the analysis of the gravitational stability of the cores in Sect. 4.2. We found there that four cores are thermally supercritical and might be gravitationally unstable. This finding is less profound for the other two cores, but cannot be excluded.
Other effects that are not included in our model, such as nonthermal desorption processes like explosive desorption (Shalabiea & Greenberg 1994) or exothermic reactions in the grain mantles (Garrod et al. 2007), might also lead to underestimating the chemical ages. Also, turbulent diffusion (Xie et al. 1995; Willacy et al. 2002) of the gas and grains within the cores can decelerate the chemical aging. Coagulation of the dust grains in the dense part would also slow down the chemical evolution, since by this the grain surface area and thus the rate of grain surface reactions are reduced. In Sect. 4.4.6 we show, however, that the bulk of the dust in these globules cannot be significantly processed and coagulated. Accounting for these combined intrinsic uncertainties in the density structures of the cores, uncertainties associated with chemical reaction rates, and a range of grain sizes in the depletion zone of the cloud, we estimate that the best-fit chemical ages are between 105 and 106 years. This is consistent with a prestellar core lifetime of 0.3−1.6 Myr as derived by Lee & Myers (1999).
4.4.5. Strength of the impacting UV-field
Changing the parameter Av, out that accounts for the unconstrained extent of the dusty material around the globules in the chemical models has effects that cannot always be clearly distinguished from changing either the hydrogen density or the gas temperature. Nevertheless, the observations are modeled better if Av, out is increased for half of the globules by a few mag relative to the values that have been measured with NIR extinction mapping (which range from 0.2 to 2 mag for the different globules at the model boundaries). This is probably not a result of overestimating the ISRF in the chemical models. Launhardt et al. (2013) derived the total FIR/mm luminosity of the globules, and it is approximately equal for all of them to the luminosity of the “standard UV-field” (Draine 1978) impacting on spheres of the size of the globules. The same field is also adopted in the chemical modeling, so we do not overestimate its strength.
In the envelopes of the globules at hydrogen densities below 104 cm-3, gas and dust temperatures are expected to be decoupled. Since we assume equal gas and dust temperatures in the modeling, we introduce systematic errors in our analysis. In particular, the emission of the gas in the envelopes is underestimated. With a large Av, out we artificially compensate for this error. The additional shielding protects the molecules from being photodissociated and thus increases their abundance. This hypothesis is supported when comparing Av, out of the best models to Av, NIR, which are the values derived from the NIR extinction maps. Both values appear to be anticorrelated, and while we do not need to increase Av, out with respect to the observed values at Av, NIR ~ 2 mag, we have to increase it by more than 3 mag for the least shielded cores. Because of these uncertainties, we think that the need to increase Av, out is not convincing evidence that the globules are in fact shielded more strongly from UV-radiation than inferred from NIR-extinction maps.
 |
Fig. 10 We plot the parameters Av, out of the best models over the measured values of Av, NIR from the NIR extinction maps. The dashed line is a linear fit to the data points, which is only meant to illustrate the trend. The dotted line indicates Av, out = Av, NIR. We interpret the anti-correlation as an indication of increasing decoupling of gas and dust temperatures towards lower extinction. |
A direct measurement of the gas temperature in the envelopes would of course be desirable as a constraint for the chemical modeling. Furthermore, in comparison to the dust temperature it would allow distinguishing between shielding from extended envelopes and a weaker ISRF as the presumed Draine field, since the gas is only heated from the FUV component of the ISRF. Measuring the excitation of the gas in the envelopes is difficult, however, since the emission is weak, and most transitions are subthermally excited. The best-suited transition to study for this purpose might therefore be the 12CO (J = 1−0) line. Unfortunately, we do not have such data at hand. Another way to distinguish between both scenarios may be to study the distribution and emission of PAHs. All globules of this study have been mapped with Spitzer’s infrared array camera (IRAC). In particular the 5.8 μm and 8 μm bands are known to show PAH emission (e.g., Pagani et al. 2010). However, the maps are not extended enough to define a background level that would allow absolute values of the emission to be derived.
4.4.6. Constraints on the grain properties
To correctly model the observed molecular abundances, we must increase the molecular hydrogen density and, with it, the initial abundances of all species by a factor of 2 to 3 (except for B 68). We thus seem to systematically underestimate the hydrogen density in the dust-based modeling. This is understandable, at least in the envelopes of the cores, since we have assumed mildly coagulated grains, with a coagulation time of 105 yr at a gas density of 105 cm-3 (Ossenkopf & Henning 1994)8 over the entire globule. With the assumption of normal ISM dust (e.g., OH1), we would have derived hydrogen densities that are higher by a factor of 2.5. Increasing the density could also partly compensate for an underestimation of the gas temperature. However, we do not find any dependence on the observed AV. Moreover, the only core for which we do not have to increase the density is that of B 68 – one of the least shielded cores in our sample. Our molecular line observations and modeling thus suggest that in most regions of the cores that are resolved by our study, the grains are not yet significantly coagulated.
5. Conclusions
We observed a sample of seven globules containing starless cores in the 12CO (J = 2−1), the 13CO (J = 2−1), the C18O (J = 2−1) and the N2H+ (J = 1−0) transitions. The globules were also observed with the Herschel bolometers as part of the EPoS project (Launhardt et al. 2013). We presented dust temperature and hydrogen density maps of the globules that were obtained with a ray-tracing technique. Based on these dust-based temperature and density profiles, we analyzed the molecular emission assuming TDust = TGas. In the following we summarize the main results of this study.
-
1.
We confirm the findings of Launhardt et al. (2013) on the stability of the cores. Only one starless core (CB 244, see also Stutz et al. 2010) is clearly not supported against gravitational collapse by thermal pressure. CB 17, CB 27, and B 68 are probably also thermally supercritical. CB 4 and CB 26 are probably gravitationally stable.
-
2.
CO is depleted in the center of all studied cores to a level of at least 46%. CB 27, B 68, and CB 244 show a central CO depletion of more than 90%. The level of freezeout increases towards the core centers and with the hydrogen density. The average radius at which half of the CO is frozen to the grains is 9000 AU, and the average hydrogen density is 105 cm-3.
-
3.
N2H+ is depleted in the center of the cores with hydrogen densities exceeding 105 cm-3. The radius with maximum abundance of N2H+ is on average at 6800 AU. The degree of depletion in the center with respect to the maximum abundance ranges from 13% to 55%.
-
4.
The chemical age at which we find that the models match the data best is higher for 13CO than for C18O and N2H+. We find an average age of the six modeled cores of 2 ± 1 × 105 yr for 13CO and of 6 ± 3 × 104 yr for C18O, and 9 ± 2 × 104 yr for N2H+. The different ages of the dense gas tracers and 13CO suggest a central contraction of the cores during the chemical evolution. Considering the uncertainties, all cores have a chemical age of at most 106 yr and are probably younger.
-
5.
We generally need to increase the gas density that has been derived from the dust density, assuming mildly coagulated grains (OH5a) by a factor of 2−3 in order to model the observed molecular emission profiles correctly. We interpret this as a sign that the dust grains are not as heavily coagulated as assumed by our dust model in large parts of the globules and are better described by ISM dust models like OH1.
-
6.
We have to reduce the strength of the UV radiation field impacting at the globule boundaries with respect to the value predicted by Draine (1978) for half of the cores. However, we think that this does not indicate that the impacting UV-field is in fact weaker, but rather that we thereby compensate for the systematic error that is introduced by the underestimation of the gas temperature in the envelopes of these cores.
Online material
Appendix A: Observations
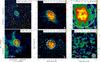 |
Fig. A.1 Observations of CB4. Digitized Sky Survey (DSS) red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2. The white circles indicate the regions of which 1D-profiles were obtained by azimuthally averaging. |
 |
Fig. A.2 Observations of CB17. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
 |
Fig. A.3 Observations of CB26. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
 |
Fig. A.4 Observations of CB27. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
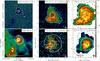 |
Fig. A.5 Observations of B68. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
 |
Fig. A.6 Observations of CB130: DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
 |
Fig. A.7 Observations of CB244: DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the center of the Class 0 protostellar core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
Appendix B: Hydrogen density and dust temperature maps
 |
Fig. B.1 Dust temperature map of CB4 overlaid with contours of the hydrogen density. They mark densities of 102, 103, and 104 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.2 Dust temperature map of CB17 overlaid with contours of the hydrogen density. They mark densities of 102, 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.3 Dust temperature map of CB26 overlaid with contours of the hydrogen density. They mark densities of 103, and 104 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.4 Dust temperature map of CB27 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.5 Dust temperature map of B68 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.6 Dust temperature map of CB130 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
 |
Fig. B.7 Dust temperature map of CB244 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
Appendix C: LTE Analysis
Appendix C.1: Model
We estimated the molecular column densities of 13CO, C18O, and N2H+ in a first step with a simple and well-established approach. For completeness, we briefy describe here this simplified approach and the results and discuss the differences and drawbacks with respect to the full chemical modeling.
We do not model the emission of the 12CO (J = 2−1) transition, since it becomes optically thick already at nH < 104 and therefore does not trace the regions of expected freezeout. At these low densities, gas and dust temperatures might also be decoupled (Galli et al. 2002), which is an additional obstacle for interpreting the 12CO emission.
The method is described in Stahler & Palla (2005). It assumes LTE and a constant gas temperature along the LoS. Since we do not have an independent measurement of the gas temperature, we make the simplifying assumption that the kinetic gas temperature is the same as the dust temperature we obtained from the LoS-averaged black-body-fitting of the continuum data in Launhardt et al. (2013). This is justified in the dense interiors of the starless cores, but may no longer be strictly valid in the outer parts at hydrogen densities below a few 104 cm-3.
To prepare the analysis, we obtain maps of the flux in the observed lines by
integrating over the velocity axis of the spectral cubes. Maps of the linewidths of
the CO isotopologues were derived from Gaussian fits to the spectra. For
N2H+ we use the hfs-fitting routine provided with the
CLASS package of GILDAS9. This routine allows fitting the full hyperfine structure of the
J = 1−0 transition and thus also derives the optical depth of the
lines. The frequency offsets and relative strengths of the individual lines are
adopted from Caselli et al. (1995). With these
intermediate results at hand we can derive the molecular column densities using
![\appendix \setcounter{section}{3} \begin{equation} N=\frac{8\pi\nu_0^2\Delta \nu Q \Delta \tau}{c^2 A_\mathrm{ul}}\left(\frac{g_\mathrm l}{g_\mathrm u}\right)\left[1-\exp\left(-\frac{T_0}{T_{\mathrm{ex}}}\right)\right]^{-1}, \end{equation}](/articles/aa/full_html/2013/12/aa22129-13/aa22129-13-eq325.png) (C.1)where
ν0 is the frequency of the transition,
Δν the observed linewidth, Q the partition
function of the rotational levels, Δτ the total optical thickness of
the line, Aul the Einstein parameter of the transition,
gi the relative statistical weights of
the upper and lower levels,
T0 = hν0/kB,
and Tex the excitation temperature of the molecules. Since
we assume LTE, we set
Tex = Tgas = Tdust, MBB.
The partition function Q is given by
(C.1)where
ν0 is the frequency of the transition,
Δν the observed linewidth, Q the partition
function of the rotational levels, Δτ the total optical thickness of
the line, Aul the Einstein parameter of the transition,
gi the relative statistical weights of
the upper and lower levels,
T0 = hν0/kB,
and Tex the excitation temperature of the molecules. Since
we assume LTE, we set
Tex = Tgas = Tdust, MBB.
The partition function Q is given by
![\appendix \setcounter{section}{3} \begin{equation} Q=\sum_J \left(2J+1\right)\exp\left[-\frac{h}{k_\mathrm BT_\mathrm{ex}}\left(BJ\left(J+1\right)\right)\right], \end{equation}](/articles/aa/full_html/2013/12/aa22129-13/aa22129-13-eq335.png) (C.2)where
B = 55 101.011 MHz is the rotational constant for
13CO, B = 54 891.420 MHz for C18O, and
B = 46 586.867 MHz for N2H+ (Pickett et al. 1998). While the optical depth of
N2H+ could be determined directly by comparing the strength of
the individual hyperfine components, we need to apply the “detection equation” in
order to derive the optical depth of the CO lines:
(C.2)where
B = 55 101.011 MHz is the rotational constant for
13CO, B = 54 891.420 MHz for C18O, and
B = 46 586.867 MHz for N2H+ (Pickett et al. 1998). While the optical depth of
N2H+ could be determined directly by comparing the strength of
the individual hyperfine components, we need to apply the “detection equation” in
order to derive the optical depth of the CO lines:
![\appendix \setcounter{section}{3} \begin{equation} T_B = T_0\left[f(T_\mathrm{ex})-f(T_\mathrm{bg})\right]\left[1-\mathrm e^{-\Delta \tau} \right], \end{equation}](/articles/aa/full_html/2013/12/aa22129-13/aa22129-13-eq339.png) (C.3)\newpagewhere
f(T) ≡ (exp(T0/T)−1)-1,
Tbg = 2.73 K, and
TB taken as the peak value of the
Gaussian fits.
(C.3)\newpagewhere
f(T) ≡ (exp(T0/T)−1)-1,
Tbg = 2.73 K, and
TB taken as the peak value of the
Gaussian fits.
One-dimensional profiles of the resulting maps were obtained by azimuthally averaging around the core centers. In case of asymmetries, a segment of the circle in this direction has been masked for the averaging task. The regions that have been taken into account for deriving the 1D-profiles are indicated in Figs. A.1–A.7.
Appendix C.2: Results
The derived radial profiles of the molecular column densities of 13CO, C18O ,and N2H+ are presented in Fig. C.1. We find signs of depletion of 13CO in all cores except for CB 4, which is the most tenuous core of the studied sample. The 13CO column density of the other cores decreases constantly with the increasing hydrogen column density. The results for 13CO are, however, affected by optical depth effects, as well as deviations of the gas temperature from the LoS-averaged dust temperature and sub-thermal rotational excitation.
The derivation of C18O column densities is less influenced by these effects since it is a rarer isotopologue (a factor of ~7 lower abundance as compared to 13CO) and since its emission comes from more restricted regions with higher gas densities. The plots of the 13CO column densities vs. visual extinction (top left panel of Fig. C.1) yield a remarkable difference to those of the C18O column densities. The relative abundance of 13CO drops continuously with increasing extinction, indicating central depletion of this species. While this behavior is also found for C18O, its relative abundance also drops toward low hydrogen column densities and peaks between an Av of 5 to 10 mag. The drop toward lower extinction can be explained by a weaker self-shielding of this rare isotopologue, which in turn leads to photodissociation of C18O in the envelopes where 13CO is already well shielded. The chemical modeling, however, suggests that the UV radiation is already attenuated by several magnitudes in these regions compared to the nominal strength of the ISRF (see Sect. 4.4.5). The difference in the profiles of both species becomes more obvious from the ratio of both column densities. The ratio N(13CO)/N(C18O) decreases continuously with increasing hydrogen column density in all starless cores. Interestingly, it even drops below the usually assumed ratio of 7 for the ISM. The change in the N(13CO)/N(C18O) ratio could thus not only be due to different self-shielding of both species but also partly due to reactions that increase the abundance of C18O with respect to 13CO due to ion-molecule exchange reactions in cold and dense environments (e.g., Langer et al. 1984).
Where the N2H+ emission is strong enough to fit the hyperfine structure, we also derive column densities for this molecule. We find that the ratio N(N2H+)/NH is roughly constant within the globules (see bottom row of Fig. C.1). This finding contrasts with the results of our advanced approach using chemical modeling and a subsequent line-radiative transfer. There we find depletion of N2H+ in the centers of the majority of the globules (see Sect. 4.4.3 and Fig. 6). This demonstrates the limitation of the often-used LOS-averaged analysis.
 |
Fig. C.1 Results from the LTE-analysis. Plotted are a) the relative column densities of 13CO against radius b) and against the hydrogen column density, c) the relative column densities of C18O against radius d) and against the hydrogen column density, e) the ratios of N(13CO)/N(C18O) are plotted against radius f) and against the hydrogen column density, g) the relative column densities of N2H+against radius, h) and against the hydrogen column density. The column densities of N2H+ in CB 4 and CB 26 could not be derived, since the emission in these globules is too weak and so are missing in the plots. |
This has been calculated using the online version of RADEX (van der Tak et al. 2007).
Acknowledgments
We thank the anonymous referee and the editor M. Walmsley for comments and suggestions that helped to improve the clarity and completeness of the paper. We wish to thank the IRAM Granada staff for the support at the 30 m telescope and T. Bergin for providing us with his line data of B 68. We also thank N. J. Evans II and E. Keto for interesting discussions that helped to improve the clarity of the paper. PACS has been developed by a consortium of institutes led by MPE (Germany), including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). The Heinrich Hertz Submillimeter Telescope is operated by Steward Observatory at the University of Arizona with partial support from the U.S. National Science Foundation through grant AST-1140030. D.S. acknowledges support by the Deutsche Forschungsgemeinschaft through SPP 1385: “The first ten million years of the solar system – a planetary materials approach” (SE 1962/1-1 and SE 1962/1-2). The work of A.M.S. was supported by the Deutsche Forschungsgemeinschaft priority program 1573 (“Physics of the Interstellar Medium”). Y.P. was supported by the Russian Foundation for Basic Research (project 13-02-00642). H.L., M.N., and Z.B. were funded by the Deutsches Zentrum für Luft- und Raumfahrt (DLR).
References
- Alves, F. O., & Franco, G. A. P. 2007, A&A, 470, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Maret, S., van der Tak, F. F. S., et al. 2006, ApJ, 645, 369 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Biham, O., Furman, I., Pirronello, V., & Vidali, G. 2001, ApJ, 553, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, M., Lazareff, B., Maier, D., et al. 2012, A&A, 538, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Myers, P. C., & Thaddeus, P. 1995, ApJ, 455, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- de Geus, E. J., de Zeeuw, P. T., & Lub, J. 1989, A&A, 216, 44 [NASA ADS] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebert, R. 1955, ZAp, 37, 217 [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, A. B., & Shirley, Y. L. 2011, ApJ, 728, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Herbst, E., & Klemperer, W. 1973, ApJ, 185, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Hotzel, S., Harju, J., Juvela, M., Mattila, K., & Haikala, L. K. 2002, A&A, 391, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2012, ApJ, 758, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Lehtinen, K., & Harju, J. 2006, A&A, 447, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Caselli, P. 2008, ApJ, 683, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Kun, M. 1998, ApJS, 115, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, S.-P., Velusamy, T., Langer, W. D., & Kuiper, T. B. H. 2003, AJ, 126, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., & Henning, T. 1997, A&A, 326, 329 [NASA ADS] [Google Scholar]
- Launhardt, R., & Sargent, A. I. 2001, ApJ, 562, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Nutter, D., Ward-Thompson, D., et al. 2010, ApJS, 188, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H.-H., Herbst, E., Pineau des Forets, G., Roueff, E., & LeBourlot, J. 1996, A&A, 311, 690 [NASA ADS] [Google Scholar]
- Lee, J.-E., Evans, II, N. J., Shirley, Y. L., & Tatematsu, K. 2003, ApJ, 583, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein, 44 [Google Scholar]
- Loinard, L., Mioduszewski, A. J., Torres, R. M., et al. 2011, Rev. Mex. Astron. Astrofis. Conf. Ser., 40, 205 [NASA ADS] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Linnartz, H., Visser, R., & van Dishoeck, E. F. 2009a, ApJ, 693, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., van Dishoeck, E. F., & Linnartz, H. 2009b, A&A, 496, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pagani, L., Pardo, J.-R., Apponi, A. J., Bacmann, A., & Cabrit, S. 2005, A&A, 429, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Steinacker, J., Bacmann, A., Stutz, A., & Henning, T. 2010, Science, 329, 1622 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pavlyuchenkov, Y., Wiebe, D., Launhardt, R., & Henning, T. 2006, ApJ, 645, 1212 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlyuchenkov, Y., Henning, T., & Wiebe, D. 2007, ApJ, 669, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Perrot, C. A., & Grenier, I. A. 2003, A&A, 404, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmalzl, M., Launhardt, R., Stutz, A. M., et al. 2013, A&A, submitted [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shalabiea, O. M., & Greenberg, J. M. 1994, A&A, 290, 266 [NASA ADS] [Google Scholar]
- Stahler, S. W., & Palla, F. 2005, The Formation of Stars (Wiley-VCH) [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 2003, A&A, 405, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A. M., Rieke, G. H., Bieging, J. H., et al. 2009, ApJ, 707, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Stutz, A., Launhardt, R., Linz, H., et al. 2010, A&A, 518, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., & Santiago, J. 2004, A&A, 414, L53 [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., Tokunaga, A. T., Geballe, T. R., & Baas, F. 1991, ApJ, 381, 181 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Chemical evolution of the Universe, Faraday discussions, 133, 231 [Google Scholar]
- Vasyunin, A. I., & Herbst, E. 2013, ApJ, 769, 34 [Google Scholar]
- Whitworth, A. P., & Ward-Thompson, D. 2001, ApJ, 547, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., Langer, W. D., & Velusamy, T. 1998, ApJ, 507, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., Langer, W. D., & Allen, M. 2002, ApJ, 573, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., Oliveri, M. V., & Schild, R. E. 1990, AJ, 99, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Launhardt, R., & Henning, T. 2003, ApJ, 592, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, T., Allen, M., & Langer, W. D. 1995, ApJ, 440, 674 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ratio of icy to total C18O abundance abundance in the core centers, radius, hydrogen column density, hydrogen density, and dust temperature at which 50% of the total C18O abundance is frozen onto the grains.
Ratio of the N2H+ abundance in the core centers to the maximum abundance, corresponding radius, hydrogen density, and dust temperature.
All Figures
 |
Fig. 1 Azimuthally averaged profiles of the hydrogen density (left), hydrogen column density (center), and dust temperature (right) derived with the ray-tracing technique. |
| In the text | |
 |
Fig. 2 Stability of the cores. Same plot as Fig. 6 in Launhardt et al. (2013), but here for the results of the ray-tracing models. Top: ratio of gravitational potential to thermal kinetic energy vs. total gas mass (Mcore). The lower dashed horizontal line marks the bounding limit of −Egrav/Etherm = 1, while the upper line marks the state of virialization at −Egrav/Etherm = 2. Bottom: central density vs. total gas mass for the same cores. The dashed line marks the maximum stable density of a pressure-supported, self-gravitating modified (nonisothermal) BES as calculated by Keto & Caselli (2008, with their Fig. 14, model with photoelectric heating at the core boundary taken into account). The uncertainty resulting from the ray-tracing modeling is indicated by the error bars at CB 4. The arrows indicate the maximum systematic shift of the cores in the diagram if grain properties of ISM dust were used in the modeling. |
| In the text | |
 |
Fig. 3 Spectra of the 12CO (2−1), 13CO (2−1), C18O (2−1) and N2H+ (1−0) transitions in a 36.4″ HPB at the centers of the starless cores. |
| In the text | |
 |
Fig. 4 Profiles of the integrated emission that would result from the molecular abundances of the final models (solid line) compared to the observed profiles of the integrated emission for all modeled starless cores. (Left) 13CO (J = 2−1), (center) C18O (J = 2−1), (right) N2H+ (J = 1−0). |
| In the text | |
 |
Fig. 5 To quantify the agreement of models and observations we compare the spectra over the full radius of the models. Here, an example of B 68 is shown. The solid lines represent observations, the dotted lines the synthetic spectra of the best models. On the left panels, we show the spectra of the 13CO (J = 2−1) (gray) and C18O (J = 2−1) (black) transitions. On the right panels, we show the spectra of the N2H+ (J = 1−0) transition. The top line shows the spectra at the position of the core center, the bottom line the spectra at a radial distance of 7000 AU. |
| In the text | |
 |
Fig. 6 Relative abundances (absolute molecular density with respect to the hydrogen density) of gaseous C18O (black solid line), frozen-out C18O (dashed black line) and gaseous N2H+ (gray solid line) in the final models. At the outer radii of the emission profiles derived from the observations, the lines turn from a solid into a dotted line shape, indicating that these parts of the profiles are not constrained by observations. |
| In the text | |
 |
Fig. 7 Top row: the ratio of icy-to-total C18O abundance of the best-fit models is plotted against the core radius, the hydrogen number density, the column density, and the dust temperature. Bottom row: the N2H+ abundance (relative to the hydrogen density) is plotted against the same quantities. The dashed lines indicate the results of the individual globules. Where the models cannot be compared to observations (because the line radiation is too weak), the dashed lines turn into dotted lines. The bold solid lines mark the mean values. The gray area indicates one standard deviation. |
| In the text | |
 |
Fig. 8 Correlation of C18O freezeout and hydrogen density in the core centers. The horizontal error bars on the hydrogen density represent the fitting uncertainty of the ray-tracing modeling (i.e., excluding systematic uncertainties from, e.g., the dust opacity model; see Sect. 3.1). The vertical error bars represent a 20% uncertainty in the amount of icy CO in the chemical model. |
| In the text | |
 |
Fig. 9 Relative gas phase abundance of C18O against that of N2H+. At X(C18O)≈ 2 × 10-8 the correlations turn into an anti-correlation. While at high X(C18O), the N2H+ molecules are destroyed by reactions with CO, at low X(C18O) (and high densities) freezeout of nitrogen is the dominant reason for depletion of N2H+. |
| In the text | |
 |
Fig. 10 We plot the parameters Av, out of the best models over the measured values of Av, NIR from the NIR extinction maps. The dashed line is a linear fit to the data points, which is only meant to illustrate the trend. The dotted line indicates Av, out = Av, NIR. We interpret the anti-correlation as an indication of increasing decoupling of gas and dust temperatures towards lower extinction. |
| In the text | |
 |
Fig. A.1 Observations of CB4. Digitized Sky Survey (DSS) red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2. The white circles indicate the regions of which 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.2 Observations of CB17. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.3 Observations of CB26. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.4 Observations of CB27. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.5 Observations of B68. DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.6 Observations of CB130: DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the position of the Class I YSO. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. A.7 Observations of CB244: DSS red, Herschel SPIRE 250 μm, 12CO (J = 2−1), 13CO (J = 2−1), C18O (J = 2−1), and N2H+ (J = 1−0). The gray circles in the lower right corners indicate the respective beam sizes. The square marker indicates the center of the starless core, the asterisk the center of the Class 0 protostellar core. The dashed contour marks NH = 1021 cm-2, the solid contour NH = 1022 cm-2. The white circles indicate the regions where 1D-profiles were obtained by azimuthally averaging. |
| In the text | |
 |
Fig. B.1 Dust temperature map of CB4 overlaid with contours of the hydrogen density. They mark densities of 102, 103, and 104 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.2 Dust temperature map of CB17 overlaid with contours of the hydrogen density. They mark densities of 102, 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.3 Dust temperature map of CB26 overlaid with contours of the hydrogen density. They mark densities of 103, and 104 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.4 Dust temperature map of CB27 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.5 Dust temperature map of B68 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.6 Dust temperature map of CB130 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. B.7 Dust temperature map of CB244 overlaid with contours of the hydrogen density. They mark densities of 103, 104, and 105 cm-3. The square indicates the center of the starless core. |
| In the text | |
 |
Fig. C.1 Results from the LTE-analysis. Plotted are a) the relative column densities of 13CO against radius b) and against the hydrogen column density, c) the relative column densities of C18O against radius d) and against the hydrogen column density, e) the ratios of N(13CO)/N(C18O) are plotted against radius f) and against the hydrogen column density, g) the relative column densities of N2H+against radius, h) and against the hydrogen column density. The column densities of N2H+ in CB 4 and CB 26 could not be derived, since the emission in these globules is too weak and so are missing in the plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


