| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201321397 | |
| Published online | 16 December 2013 | |
The age structure of stellar populations in the solar vicinity
Clues of a two-phase formation history of the Milky Way disk
1
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot,
5 place Jules Janssen,
92190
Meudon,
France
e-mail:
Misha.Haywood@obspm.fr
2
Institut d’Astrophysique de Paris, Université Pierre et Marie
Curie/CNRS, 98 bis Bd
Arago, 75014
Paris,
France
Received: 4 March 2013
Accepted: 19 July 2013
We analyze a sample of solar neighborhood stars that have high-quality abundance determinations and show that there are two distinct regimes of [α/Fe] versus age, which we identify as the epochs of the thick and thin disk formation. A tight correlation between metallicity and [α/Fe] versus age is clearly identifiable for thick disk stars, implying that this population formed from a well mixed interstellar medium, probably initially in starburst and then more quiescently, over a time scale of 4−5 Gyr. Thick disk stars have vertical velocity dispersions which correlate with age, with the youngest objects of this population having small scale heights similar to those of thin disk stars. A natural consequence of these two results is that a vertical metallicity gradient is expected in this population. We suggest that the youngest thick disk set the initial conditions from which the inner thin disk started to form about 8 Gyr ago, at [Fe/H] in the range of (−0.1, +0.1) dex and [α/Fe] ~ 0.1 dex. This also provides an explanation for the apparent coincidence between the existence of a step in metallicity at 7−10 kpc in the thin disk and the confinement of the thick disk within R < 10 kpc. We suggest that the outer thin disk developed outside the influence of the thick disk, giving rise to a separate structure, but also that the high alpha-enrichment of those regions may originate from a primordial pollution of the outer regions by the gas expelled from the forming thick disk. Metal-poor thin disk stars ([Fe/H] < −0.4 dex) in the solar vicinity, whose properties are best explained by them originating in the outer disk, are shown to be as old as the youngest thick disk (9−10 Gyr). This implies that the outer thin disk started to form while the thick disk was still forming stars in the inner parts of the Galaxy. Hence, while the overall inner (thick+thin) disk is comprised of two structures with different scale lengths and whose combination may give the impression of an inside-out formation process, the thin disk itself probably formed its first stars in its outskirts. Moreover, we point out that, given the tight age−metallicity and age–[α/Fe] relations that exist in the thick disk, an inside-out process would give rise to a radial gradient in metallicity and α-elements in this population, which is not observed. Finally, we argue that our results leave little room for radial migration (in the sense of churning) either to have contaminated the solar vicinity, or, on a larger scale, to have redistributed stars in significant proportion across the solar annulus.
Key words: stars: abundances / stars: kinematics and dynamics / solar neighborhood / Galaxy: disk / Galaxy: formation / Galaxy: evolution
© ESO, 2013
1. Introduction
A stellar population is commonly viewed as an ensemble of stars that share some observable properties (Baade 1944; McCarthy 1959). A subtler definition would allow us to link some observable quantities to properties that we think uniquely define the conditions of the formation of the population. Hopefully, such an approach would aid us in finding out how the formation of individual stellar populations relates to the evolution of the galaxies generally. In practice, however, such link is difficult to tease out because there is no simple way to define unambiguously a single population of stars. An example of this failure is epitomized by the recent discussion about the existence of a thick disk as a separate population in its own right (e.g. Bovy et al. 2012a,b). Structural parameters may give us a hint of the existence of such a population in the Milky Way (Gilmore & Reid 1983) as well as in external galaxies (Burstein 1979; Dalcanton & Bernstein 2002; Pohlen et al. 2004; Comerón et al. 2011), but no clue as to its origin or to its link to the other populations. Kinematics are also often used to segregate thin and thick disk stars (e.g. Soubiran et al. 2003; Bensby et al. 2003), but have currently offered few insights beyond simple classification, and may even represent a loss of information if it is used to group all the kinematic data. Finally, chemical characteristics have been proposed as a way to parametrize the properties of various stellar populations in the Milky Way (scale height, scale length, kinematics, etc., see Bovy et al. 2012b), or for setting limits on the characteristics of the thin and thick disks (see Navarro et al. 2011), but defined in an arbitrary way, and with no direct evidence that these definitions correspond to the properties of the interstellar medium (ISM) at a particular epoch. Up to now, no clear picture has emerged as to where to put boundaries or even if boundaries exist between the thick and thin disk populations (Norris 1987; Bovy et al. 2012b).
In the present study, we analyze the properties of a sample of FGK stars within the solar vicinity. We show that the formation of stars within the thick disk is clearly identifiable as a phase of steady and monotonic variation in the chemical properties over a period of about 4−5 Gyr. We suggest that the processes that occurred during the formation of the thick disk set the initial conditions for the formation of the inner thin disk, while the outer disk may have built up independently but certainly over a longer time scale.
In the following section, we describe the sample used for this analysis. In Sect. 3, we give a description of the “age structure” of the two disk populations through an inspection of Hertzsprung-Russell (HR) diagrams and the determination of individual ages. We outline the implications of our results in Sect. 4, propose a scenario for the formation of the Milky Way disk in Sect. 5, and discuss some critical aspects of disk formation in the light of our findings. Finally, we summarize our results in Sect. 6.
2. Sample characteristics and derived ages
 |
Fig. 1 [α/Fe] vs. [Fe/H] for stars in the sample of Adibekyan et al. (2012). α is defined as the mean of the abundances of magnesium, silicon and titanium. The thick and thin disk sequences are distinguished by whether they lie above or below the three segments of the solid line respectively. The two double circles at [Fe/H] < −1.0 dex and [α/Fe] < 0.1 dex are HIP 74234 and HIP 100568, while the two solid dot-and-circle symbols represent HIP 54641 and HIP 57360 (see text). |
The sample used in this study was originally designed for the detection of planets through radial velocity measurements (see Adibekyan et al. 2012 for a description). It comprises 1111 FGK stars with spectra at a resolution of R = 110 000 and excellent signal-to-noise ratio (S/N) for most objects (the authors report a S/N better than 200 for 55% of the sample). The sample is composed of various subsamples defined on the basis of spectral type range (FGK), limiting distance (see Udry et al. 2000; Lo Curto et al. 2010), low rotational velocity, and low atmospheric activity. 97 stars in the sample were selected to have photometric metallicities between −0.5 and −1.5 and b−y > 0.33. To our knowledge, no other cut in colour or kinematics were made in the selection of the stars.
Atmospheric parameters (Teff, [Fe/H], [α/Fe]) are adopted from Adibekyan et al. (2012), while absolute magnitudes were calculated from the parallaxes presented in van Leeuwen (2007)1. Note that we have defined the α element abundance as the mean of magnesium, silicon and titanium, while excluding calcium, as recommended in Adibekyan et al. (2012). We adopt galactic space UVW velocities (corrected for the solar motion using the values from Schönrich et al. 2010) from the study of Adibekyan et al. (2012). Further, we determined the orbital parameters from orbits calculated in a Galactic axisymmetric potential (Allen & Santillan 1991). We show the sample of stars in the [α/Fe] vs. [Fe/H] plane in Fig. 1. The upper sequence (above the line) is usually classified as containing thick disk stars, and stars in the lower sequence are classified as thin disk. However, in such a scheme, the classification of the most metal-rich stars on the thick disk sequence is not clear. Note that the two deficient stars ([Fe/H] < −1.0 dex) with low alpha content ([α/Fe] < +0.1 dex) are stars which are counter rotating with respect to the disk. The two other deficient stars identified in Fig. 1 and which have [α/Fe] ≈ +0.2 dex, HIP 54641 and HIP 57360, have a strong U component and are significantly younger (see Fig. 9) than typical stars of similar metallicity. All four stars are possible members of the so-called accreted halo (see Nissen & Schuster 2010)2.
We derived individual ages using the bayesian method of Jørgensen & Lindegren (2005), adopting the Yonsei-Yale (Y2) set of isochrones (version 2, Demarque et al. 2004). Atmospheric parameters were taken from the study of Adibekyan et al. (2012), including [α/Fe] values, as defined in the previous paragraph.
2.1. Uncertainties on ages due to atmospheric parameters
Formal errors in the individual atmospheric parameters (Adibekyan et al. 2012) are less than 70 K in the effective temperature (<25 K for solar-type stars), <0.05 dex for [Fe/H] (<0.02 dex for solar-like stars) and <0.1 dex in [α/Fe] (<0.03 dex for solar-type stars). Adopting such small uncertainties in the atmospheric parameters would imply unrealistically robust ages, so we adopted conservative uncertainties of 50 K in temperature, 0.1 dex in metallicity and 0.1 mag in absolute magnitude. These uncertainties in the atmospheric parameters translate into uncertainties of about 0.8 Gyr for the younger stars (age < 5 Gyr) and 1.5 Gyr for the oldest (age > 9 Gyr). While random errors can be important for individual objects, systematic uncertainties that can affect these parameters (or stellar models) may result in very significant biases in the derived ages and perhaps lead to spurious trends (Haywood 2006). Sousa et al. (2011) compared stars that are in common with this sample and various other samples (Edvardsson et al. 1993; Bensby et al. 2003; Valenti & Fischer 2005), showing that there is no systematic difference in these analyses for [Fe/H] or Teff for stars with Teff < 6000 K, but found a significant offset of about 100 K above this Teff limit for stars in common with the Valenti & Fischer (2005) sample.
 |
Fig. 2 Upper plot: difference between effective temperatures from Adibekyan et al. (2012) and those derived from the V − K indices and calibration from Casagrande et al. (2010) for the whole sample. The lower curve is the mean of the difference calculated over 75 points, the upper curve is the dispersion. Lower plot: difference in age resulting from the two scales, as a function of age (based on Adibekyan et al. (2012) spectroscopic scale) for stars with “good” ages (see text). |
Since systematic uncertainties that affect the temperature scale can produce the most significant effects on the age determinations (Haywood 2006), we compared the spectroscopic temperatures (Adibekyan et al. 2012) with those derived from the V − K color index plus a state-of-the-art calibration (Casagrande et al. 2010). The comparison (Fig. 2) shows that the mean of the differences (running average calculated over 75 stars) between the spectroscopically-derived and the V − K color temperature is always lower than 56 K. These differences are in the sense that spectroscopic temperatures are higher. The agreement is remarkable given that the two scales are entirely independent and suggests that the systematic uncertainties in the effective temperatures are actually quite low.
In order to illustrate the effect of these minor offsets and random uncertainties in effective temperatures, we derived ages using temperatures from the V − K color. Figure 2 (bottom plot) shows the age difference (age on Adibekyan Teff − age from V − KTeff scale) between the two determinations as a function of age (on Adibekyan et al. Teff scale). 70% of the stars have an age difference lower than 1 Gyr, and below 0.5 Gyr for 50% of the cases. For stars with ages greater than 5 Gyr, 50% have an age difference lower than 0.5 Gyr.
2.2. Uncertainties on ages due to the method and to the stellar physics
As a final test to the robustness of our ages, we did two additional checks: we first derived ages applying a simple χ2 minimization between the position of the star and the nearest isochrone (at the metallicity and [α/Fe] of the star) in the (effective temperature, absolute magnitude) plane, following the prescription from Ng & Bertelli (1998) and using Y2 isochrones. The result is shown in Fig. 3 (left), with χ2-ages as a function of bayesian ages. There is a trend in the sense that χ2 minimization gives greater ages than the bayesian method for the older stars, reaching a difference of about 1.5 Gyr at ages > 13 Gyr. We think this is due to the fact that the χ2 minimization favors older isochrones, which are more closely spaced for a fixed age step. While the relative merit of each method is beyond the scope of the present analysis, we note that apart from this systematic shift, small random uncertainty (on the order of 0.7 Gyr) also arises due to difference in the way the “best” age is defined in each method. In particular, the stretch of stars which deviate gradually from the diagonal starting at 4 Gyr upward, is due to the stars in the hook region, and whose bayesian age shows a doubled-peaked probability distribution function.
The second check is made deriving new ages using the χ2 minimization and the set of isochrones from Dotter et al. (2007; Dartmouth isochrones). The two age scales are compared in Fig. 3 (right panel). The plot illustrates that uncertainties in stellar physics add both a systematic and “random” error to the ages: in addition to the shift due to the method, Dartmouth isochrones give systematically older ages by about 1 Gyr. A “random” uncertainty also adds up, which amounts to almost 1 Gyr. Therefore, we expect the absolute age scale used in this study to be uncertain by about 1 to 1.5 Gyr, while relative ages have uncertainties of about 1 Gyr, due to stellar physics.
 |
Fig. 3 Left: χ2 vs. bayesians ages, using the same set of isochrones. Right: χ2 (Dartmouth isochrones) vs. bayesians ages (Y2 isochrones). |
From the initial sample of 1111 stars, about half could be age dated. After taking into account stars with a well defined probability distribution function together with absolute magnitude Mv < 4.75, the final subsample with meaningful ages has 363 stars, a rather severe pruning, but which ensures robust age estimates.
3. Results
For convenience, hereafter we adopt the terms thin and thick disk sequences to designate stars that are below or above the line in Fig. 1. This definition will be then compared to that of thin and thick disk populations, introduced in Sect. 3.2.
3.1. General trends in age: HR diagrams
 |
Fig. 4 HR diagrams for stars in various metallicity ranges and [α/Fe] content (given explicitly in the legend at the bottom left corner of each plot). The lines in each plot are isochrones of various ages (Demarque et al. 2004). Isochrones shown as solid dark blue lines have ages of 5, 10 and 15 Gyr (from left to right). The open and solid red circles are the same as defined in Fig. 1. Stars that have been dated are above the grey area. |
 |
Fig. 5 HR diagrams for stars selected in the thick disk sequence for various ranges in metallicity. The exact range in [Fe/H] is indicated in the legend in the bottom left corner of each plot. The isochrones are the same as in Fig. 4. Stars that have been dated are above the grey area. |
Before presenting the relations between age, chemistry and kinematics, in this section we investigate the trends in the variation of [α/Fe] with age by simple inspection of HR diagrams (Fig. 4). Such a simple approach has the advantage of not relying on methods used to determine individual ages and their concomitant systematic uncertainties. At [α/Fe] < 0.0 dex, most objects are younger than 3 Gyr, while they lie between 3 and 6 Gyr for 0.01 < [α/Fe] < 0.03 dex and 5−7 Gyr for [α/Fe] > 0.06 dex (Fig. 4). The middle row of Fig. 4 shows a similar sequence for stars in the metallicity range ~−0.4 < [Fe/H] < −0.1 dex. Note that there is no significant number of stars with such metallicities and [α/Fe] < 0.0 dex. At 0.00 < [α/Fe] < 0.05, stars are grouped around 4−5 Gyr, as in the upper row, middle plot. In the range 0.05<[α/Fe]<0.1, stars are bracketed between the isochrones of 5 and 10 Gyr as it is the case for stars with the same range of alpha abundance and higher metallicities (upper row, Fig. 4). Finally, in the last plot of the middle row, only a few stars with [α/Fe] > 0.1 are seen which lie around the 10 Gyr isochrone. The bottom row shows stars at −0.6 < [Fe/H] < −0.4 dex, which mostly lie between the 5 and 8 Gyr isochrones for 0.05 <[α/Fe] < 0.12, and beyond the 10 Gyr isochrone for [α/Fe] > 0.18 dex. Clearly, there is a good qualitative relationship between α enhancement and age over the various metallicity intervals.
We now repeat that same exercise but selecting the objects that lie along the sequence of the thick disk stars (i.e., above the separating line in Fig. 1). The upper row in Fig. 5 shows first the position of the stars in the HR diagram as a function of metallicity, while the bottom row shows the positions of stars in the HR diagram for three different alpha abundance intervals. Interestingly, both variations in metallicity and in [α/Fe] abundance show a variation with age in the sense that the most metal-rich stars have ages around 7−8 Gyr, shifting to about 10 Gyr around [α/Fe] = 0.15 dex and [Fe/H] = −0.15 dex, and 11−13 Gyr at [α/Fe] > 0.25 dex. These results indicate a real correlation between age and both [α/Fe] and metallicity for stars in the thick disk sequence. Whether all these stars belong to a “thick disk population” is the subject we will discuss subsequently.
3.2. The age–[α/Fe] relation: towards defining the thin and thick disk populations from ages
A logical place to start when attempting to define stellar populations is by investigating relationships with their ages and other characteristics that may act like chronometers, such as the relative alpha enhancement, [α/Fe]. The upper panel of Fig. 6 shows a correlation between [α/Fe] and age such that the [α/Fe] enhancement of stars decreases with the stellar age. Interestingly, the relation suggests that the rate at which the alpha enhancement declines, Δ [α/Fe] /Δt, has a break at an age of ~8 Gyr. Δ [α/Fe] /Δt is a factor of 5 higher for stars older than ~8 Gyr compared to stars which are younger. There are few outliers in the age–[α/Fe] relation that lie on the thick disk sequence according to their position in the [α/Fe]−[Fe/H] plane but lie above the thick or thin disk sequences in the age–[α/Fe] plane. Their age may of course be underestimated or their enhancements overestimated. However, there is no indication of binarity for these stars nor do there appear to be problems with the determination of their atmospheric parameters. Despite any worries about outliers, it is worth noting how remarkably tight the relation age–[α/Fe] is for stars we have classified as part of the “thin disk” (ages < 8 Gyr). At any given age within the thin disk, the dispersion in [α/Fe] is always less than 0.04 dex. Even more surprising is that, given the difficulty to derive ages for old stars, the relationship between age and [α /Fe] is still very tight for stars we have classified as “thick disk” (i.e., ages ≳ 8 Gyr). The bottom panel of Fig. 6 represents the age–[α/Fe] distribution with the color coding the absolute magnitude of the stars, showing that the faintest stars in our sample introduce no bias in the distribution.
While obviously there are complexities that are underlying this relation, which we will discuss later, we emphasize that the age–[α/Fe] distribution gives us the opportunity to propose a definition of the thick and thin disk populations that actually corresponds to two different epochs of star formation. These two epochs in the Milky Way appear to be neatly demarcated at an age of ~8 Gyr. Hence, from now on, we refer to the thin and thick disk population as stars formed in these two distinct phases of the Milky Way disk(solar neighborhood to be more precise), as manifested in the stellar age–[α/Fe] relation. The appropriateness of this definition when other parameters are taken into account and how it fits into a more general view of the disk assembly will be discussed in Sects. 4 and 5.
It is first natural to ask how the thin and thick disk stars, often defined on the basis of their membership to one of the two sequences in the [α/Fe]−[Fe/H] plane (Fig. 1), redistribute along this new relation. This is done in the top panel of Fig. 7, where the same stars already present in Fig. 6 are shown, but with symbols now representing objects situated on the thick disk (solid red circles) and thin disk (open red circles) sequences, as defined in Fig. 1. Figure 7, top panel, shows that:
-
1.
the thin disk sequence, as defined in the [α/Fe] − [Fe/H] plane (open circles), mostly overlaps with the thin disk population – the majority of its stars having ages ≤ 8 Gyr – but some stars have ages between ~8−10 Gyr consistent with the thick disk population. However, over the whole time interval from 0 to 10 Gyr, the thin disk sequence maintains approximately the same Δ [α/Fe] /Δt slope. We will comment on these important points in the following sections.
-
2.
the thick disk sequence, as defined in the [α/Fe] − [Fe/H] plane, is mostly coincident with the thick disk population, but some of these stars have ages younger than 8 Gyr, and, as a consequence, contaminate the thin disk population. Half of these stars clearly have all characteristics of thin disk objects and fall into the thick disk sequence only due to the arbitrary definition of this sequence at [α/Fe] > 0.05 dex. The other half have above average [α/Fe] content (0.05−0.1 dex) at these high metallicities, and kinematics more akin to thick disk objects.
Conversely, it is interesting to see how stars in the two segments of the age–[α/Fe] relation are distributed within the [α/Fe]–[Fe/H] plane. This is shown in Fig. 8, which shows (top panel) the two thick and thin disk populations separated by a (somewhat arbitrary) diagonal line. The yellow symbols represent the old metal-poor thin disk stars which mix with thick disk stars in the [α/Fe]–[Fe/H] plane (shown in the bottom panel). We conclude that:
-
1.
Given the remaining uncertainties in the age determination, and the fact that there is some arbitrariness in the positioning of the separating line – and apart from the specific problem of the metal-poor thin disk stars which we address below – our classification for the age–[α/Fe] plane corresponds to a remarkable separation of the two populations in the [α/Fe]−[Fe/H] plane.
-
2.
The oldest metal-poor thin disk stars are responsible for the contamination of the thick disk population by thin disk objects in the age–[α/Fe] distribution. Haywood (2008) proposed that thin disk stars with metallicities below about ~−0.3 dex (of almost all ages: as young as 2 Gyr and up to the stars discuss here with ages > 8 Gyr, see Fig. 9) originate from the outer thin disk. We contend that they have no direct connection with the thick disk (but see Sect. 5.2), despite having similar ages and [α/Fe] content, neither are they progenitors of the younger (age < 8 Gyr) inner disk stars. The following arguments favors an outer disk origin for these objects. Several of these stars have apocenters reaching galactocentric distances larger than 9 kpc, being the only disk population in the solar vicinity showing this characteristic. This was demonstrated in Haywood (2008) for stars in the solar vicinity, and is also clearly visible in Fig. 7 of Bovy et al. (2012b) for a more spatially extended sample. While these metal-poor stars represent only a few per cent of the local disk, objects with similar chemical properties dominate the disk at R > 9−10 kpc, or about 1−2 kpc outside the solar orbit. With a dispersion in the U-component of about 50 km s-1, one derives an epicycle radial excursion of 1−2 kpc (e.g, Roškar et al. 2011), which is sufficient to explain that some of these objects contaminate local samples. Further arguments and a discussion of the status of these stars and how they fit in our general scheme are presented in Sect. 5.1.
 |
Fig. 6 Top panel: the general [α/Fe] vs. age distribution for stars in the sample, for all stars having an absolute magnitude Mv < 4.75. Open circles indicate stars which have alpha enhancements consistent with the thick disk but have ages indicative of the thin disk and also lie on the thick disk sequence in the [α/Fe]–[Fe/H] plane. The line divides the thick and thin disk populations. Bottom panel: same stars, the color coding the absolute magnitude of stars is described by the vertical scale. |
3.3. The age–metallicity relation
In light of the insights gained in investigating the relationship between age and α-enhancement, it is interesting to look at the age–metallicity ([Fe/H]) relation. The age–metallicity relation confirms that stars in the thick disk show a much tighter correlation between age and metallicity than thin disk stars (Fig. 9). Moreover, the increase in metallicity in the thick disk phase (~0.15 dex Gyr-1) is much steeper than in the thin disk (0.025 dex Gyr-1), also implying a decrease by a factor of 5−6 in the production of iron after 8 Gyr. Moreover, metal-poor thin disk stars are not degenerate in the age–[Fe/H] as they are in the [α/Fe]–age plane. Once they are identified in the age–metallicity distribution, the correlation between age and metallicity for thick disk stars becomes much clearer. Note the four outliers to the thick disk age–metallicity relation. Two of them have no particular characteristics, and seem to be standard thick disk objects. We can offer no particular explanation for their “young” ages. The two others (circled symbols on Fig. 9) are HIP 54641 and HIP 57360, two stars with slightly low alpha abundances (see Fig. 1), and significant U velocity (respectively +84 and +100 km s-1). Taken together, these arguments suggest that these two stars have been accreted.
 |
Fig. 7 Top panel: same as Fig. 6, but the open and solid circles represent stars on the thin and thick disks sequences as classified from their distribution in Fig. 1, respectively. Bottom panel: same as above, but color coding based on the metallicity of the stars is indicated by the color bar. |
At ages less than about 8 Gyr, in the thin disk regime, the dispersion in metallicity increases sharply. This is in agreement with a number of previous studies (e.g. Edvardsson et al. 1993; Nordström et al. 2004; Haywood 2006). This may be mainly an effect of radial migration of the stars through “churning” or “blurring”3. However, it is unclear which type of mixing is responsible for the dispersion in metallicity measured in the solar vicinity, because it is known that the Sun is near the dividing line between the inner disk, which is enriched in metals (mean [Fe/H] ~ +0.2 dex at R < 7 kpc, see Hill et al. 2012), and the outer disk which is depleted in metals (mean [Fe/H] ~ −0.3 dex at R > 10 kpc, field stars: Bensby et al. (2011) and references therein; open clusters: Jacobson et al. (2011) and references therein). As a result of the Sun lying near this dividing line, it is possible that the solar neighborhood has contamination from stars with a relatively wide range of metallicities but which did not originate very far from the solar orbit. We comment further on this point and the importance of radial migration in the Milky Way in Sects. 3.5.2 and 5.2.
 |
Fig. 8 Top panel: [α/Fe] vs. age for stars in the sample. The solid black line separates the thin and thick disk populations. The yellow dots represent the oldest stars that are on the thin disk sequence in the [α/Fe]–[Fe/H] plane (see the lower panel), and for which age could be determined. These objects fall in the part of the age–[α/Fe] distribution that corresponds to the thick disk (above the line). Bottom panel: [α/Fe] vs. [Fe/H] for the same sample and with the symbols indicating the same population of stars as above. This illustrates how the two sequences are separated in this plane. |
 |
Fig. 9 Metallicity as a function of age for stars in the sample. Symbols as in the top panel of Fig. 8. When thin disk metal-poor stars (yellow dots) are not considered, the age–metallicity relation of thick disk stars (blue solid circles) is obvious. The two objects at [Fe/H] < −1.0 dex and age ~ 9 Gyr are HIP 54641 and HIP 57360. See text for details. |
 |
Fig. 10 [α/Fe] vs. [Fe/H] for the stars in the sample of Adibekyan et al. for which a robust age could be derived. The color and the size of the symbols both code the age of the stars, to emphasize the age stratification of the distribution of stars within this plane. |
3.4. The age structure within the [α/Fe]–[Fe/H] distribution
We have investigated the [α/Fe]–age and age–metallicity relations separately, but does there exist a temporal sequence within the [α/Fe]–[Fe/H] plane? Any possible relationship is shown in Fig. 10, where the [α/Fe]−[Fe/H] distribution is shown for those stars in the sample which have well-determined ages. The main findings from this investigation are:
-
1.
There is a clear tendency of ages to decrease with [α/Fe], no matter what the metallicity.
-
2.
For the thick disk population, because of the tight relation between metallicity and age, this tendency reflects into a clear temporal sequence: the thick disk evolved with time from a metal poor ([Fe/H] ~ −0.8 dex), α-enriched population with ages ~13 Gyr, to a younger (ages ~ 8 Gyr), metal-rich population with metallicities around solar and an mild α-enhancement ([α/Fe] ~ 0.1 dex). Adibekyan et al. (2011, 2013) have discussed the status of the most metal-rich stars at the end of the thick disk sequence as being a mix of thin and thick disk stars. With the new definition of thin and thick disks introduced in Sect. 3.2, most objects are classified as thin disk. Out of 28 stars with [Fe/H] > −0.1 dex, [α/Fe] > 0.05 dex and for which age has been obtained, 9 are in the thick disk regime.
-
3.
Unsurprisingly, within the thin disk, the age sequence becomes much less evident. There is still a tendency for stellar population to move with decreasing age from lower metallicities and higher α abundances towards higher metallicities and solar and sub-solar α abundances. However, as already known, the dispersion in [Fe/H] is large, whatever the [α/Fe] or age. However, the metallicity dispersion is expected to increase with the relative alpha element abundance as it does with age, due to dynamical effects which progressively radially mix stars in the disk. This is confirmed in our study of this sample: the dispersion in the metallicity increases with increasing age from about 0.14 dex at [α/Fe] < 0.0 dex to 0.25 dex at [α/Fe] = 0.1 dex.
3.5. Kinematics
3.5.1. Age–vertical velocity dispersions
Figure 11 shows the W velocity component as a function of [α/Fe] and age, for the stars in the sample. The two curves in each panel are the running dispersion in the W velocity calculated over 50 points. The dispersion along the thin disk sequence increases from about 9 ± 1.5 km s-1 to 35 ± 6 km s-1, while in the thick disk sequence, the dispersion varies from 22 ± 3.7 km s-1 to 50 ± 8.3 km s-1. It is interesting to note that it is the group of old, metal-poor thin disk stars that is responsible for the higher dispersion of 35 km s-1 in the thin disk sequence. When these objects are discarded by selecting thin disk sequence stars with [Fe/H] > −0.3 dex (−0.4 dex), the vertical dispersion rises to only 22 km s-1 (27 km s-1). This is confirmed by the data shown in the right panel, where the vertical dispersion rises to about the same values at age ~ 8 Gyr.
The zmax values corresponding to the vertical velocities are plotted as a function of [α/Fe] and age in Fig. 12, clearly illustrating the decrease in scale height within the thick disk population.
 |
Fig. 11 Left panel: W component of velocity as a function of [α/Fe] for the stars in the sample (open red circles represent stars on the thin disk sequence; solid red circles represent stars on the thick disk sequence). The two thin and thick black curves are running dispersions for the W component of the velocity of the thin and thick disk sequence stars, calculated as a function of [α/Fe] (over 50 stars). Right panel: W component of velocity as a function of age. Open blue circles represent thin disk stars and solid blue circles represent thick disk stars as defined in Fig. 5. The curve is a running dispersion calculated on 50 stars. |
 |
Fig. 12 Maximum distance from the galactic plane as function of [α/Fe] abundance (upper plot) and age (lower plot). Open (red or blue) circles represent thin disk stars and solid (red or blue) circles represent thick disk stars as defined in Fig. 5. |
The so-called age–σW relation, which has been investigated intensely in the hope of measuring a saturation value or a step that would indicate a transition from the thick to the thin disk, mixes stars of different provenance and which for a given age, have different vertical dispersions. In mixing stars of different provenance, finding a transition may be spurious. We note that stars along the thin disk population with ages of ~8 Gyr have similar dispersion as stars along the thick disk sequence with ages of ~9−10 Gyr, probably due to the same process of vertical heating. Paradoxically, stars of the metal-poor thin disk, also being 9−10 Gyr old, have a dispersion higher than that of the thick disk of the same age. Therefore, we should not be surprised that samples comprising different amount of metal-poor thin disk, “young” thick disk, and old thin disk, would produce different overall σW at a given age, being a mix of stars of different populations with different vertical energies. We emphasize that discussing an age–σW relation is meaningful only if the contributions of the different components are properly disentangled.
The fact that metal-poor thin disk stars have higher vertical velocity dispersions, together with their probable outer disk origin, suggests the intervention of some dynamical mechanism operating in the outskirts of the disk that may add some extra vertical kinetic energy. A warp could produce an increase in the velocity dispersion. Specific signatures, as an asymmetry in the distribution of vertical velocities, have been searched on local data, with contradictory results (Dehnen 1998; Seabroke & Gilmore 2007). The mean of the vertical velocities of our metal-deficient thin disk stars is 2 km s-1, compatible with no asymmetry. Flat profiles of the vertical velocity dispersion in external parts of spirals have been found in a number of objects (Herrmann et al. 2009), and a flaring of the disk has been suggested to be responsible for such effect.
Figure 13 shows the U velocity component as a function of age and [α/Fe]. The left panel shows that the velocity dispersion reaches 50 km s-1 for the metal-poor (alpha-rich) thin disk stars, significantly higher than the standard thin disk (30−40 km s-1). Overall, the outer thin disk appears to be significantly hotter than the old, local, thin disk, with values not far from stars of intermediate age in the thick disk, while maintaining a substantial rotation velocity. By virtue of the asymmetric drift relation, this implies that the scale length of metal-poor thin disk stars must be substantially larger than the one of the inner thin disk. In the disk decomposition made by Bovy et al. (2012b) using the SEGUE data, it is noticeable that the low-metallicity, low-alpha abundance component, has the longest scale length measured of all thin disk components, with hR = 4.3 kpc. By comparison, the most metal-rich components have scale lengths on the order of 2.3−2.8 kpc.
 |
Fig. 13 Left panel: U component of velocity as a function of [α/Fe] for the stars in the sample (open red circles represent stars on the thin disk sequence; solid red circles represent stars on the thick disk sequence). The two thin and thick curves are running dispersions for U component of the velocity of the thin and thick disk sequence stars, calculated as a function of [α/Fe] (over 50 stars). Right panel: U component of velocity as a function of age. Open blue circles represent thin disk stars and solid blue circles represent thick disk stars as defined in Fig. 5. |
3.5.2. Rotational velocities versus [Fe/H], [α/Fe] and ages
 |
Fig. 14 Top panel: V component of the velocity as a function of [Fe/H] for the thick disk (solid circles) and thin disk (open circles) populations, as defined in Fig. 6. Middle panel: V component of the velocity as a function of [Fe/H] for thick disk sequence stars in the sample. Bottom panel: V component of the velocity as a function of [Fe/H] for thin disk sequence stars in the sample. In the middle and bottom panels, stars without age determinations are shown as solid grey circles. For stars with age determinations, the color and the size of the symbols indicate the age using the scale given in the color bars shown on the right of each plot. Solid black lines represent the best fit linear regression to the data, with the fit coefficient indicated. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
 |
Fig. 15 Top panel: V component of the velocity as a function of [α/Fe] for the thick disk (filled circles) and thin disk (open circles) populations, as defined in Fig. 6. Middle panel: V component of the velocity as a function of [αFe] for thick disk sequence stars in the sample. Bottom panel: V component of the velocity as a function of [αFe] for thin disk sequence stars in the sample. In the middle and bottom panels, stars without age determinations are shown as solid grey circles. For stars with age determinations, the color and the size of the symbols indicate the age using the scale given in the color bars shown on the right within each plot. Solid black lines represent the best fit linear regression to the data, with the fit coefficient indicated. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
 |
Fig. 16 Top panel: V component of the velocity as a function of age for thick and thin disks population stars, as defined in Fig. 6. Middle panel: V component of the velocity as a function of age for thick disk sequence stars. Bottom panel: V component of the velocity as a function of age for thin disk sequence stars. In all panels, the color and the size of the symbols are a function of the star’s [Fe/H] value as indicated by the color bar in each plot. Solid lines represent the best fit linear regression to the data. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
The relation between the rotational support, V, of stars and their chemical properties has been extensively studied as a way to measure the Galactic disk evolution. However, the introduction of the concept of radial migration in the last years has lead to conflicting results both in the predictions of models and in the data analysis and interpretation (see, for example, Ivezić et al. 2008; Schönrich & Binney 2009b; Spagna et al. 2010; Navarro et al. 2011; Loebman et al. 2011; Lee et al. 2011; Curir et al. 2012). Loebman et al. (2011) claimed that such correlation should be erased in the presence of substantial mixing. Note, however, that starting from rather different, opposing assumptions, Navarro et al. (2011) interpreted the absence of a V–[Fe/H] relation in the local thin disk as an absence of migration processes. On the contrary, Schönrich & Binney (2009b), suggested that this correlation may subsist even in the presence of substantial mixing, because stars coming from the inner disk will still dominate the low angular momentum values even though they have migrated through churning. In their picture, it is the strength (or weakness) of the observed V–[Fe/H] relation at the solar vicinity which constrains the amount of churning in the disk. If stars did not experience any angular momentum change (e.g. mixing only by blurring), the conservation of angular momentum for stars coming from several kpc − as suggested by their extreme metallicities, and in the hypothesis of a linear gradient − would imply extreme rotational velocities that are not seen in the solar vicinity metallicity gradient. We shall discuss actual evidence of radial migration in Sect. 5.2.
There is also a lot of confusion as to how samples are defined and interpreted. Loebman et al. (2011), for example, pointed out the absence of a V–[Fe/H] correlation among old disk stars in the Geneva-Copenhagen Survey sample (GCS, Holmberg et al. 2009). But Loebman et al. (2011) use undistinguished old disk stars, without classifying them as either belonging to the thin and thick disk populations. As pointed out by Haywood (2012), the mix of lagging thick disk stars and fast rotating metal-poor thin disk stars could erase a correlation in the thin disk. Navarro et al. (2011) concluded also on the absence of such a correlation among thin disk stars, defining a sample using a single limit in [α/Fe] over the whole range of metallicities, but which has the effect of mixing the thick and thin disks. These results seems in contradiction with the results of Spagna et al. (2010), and Lee et al. (2011), who both reported the existence of a rotational velocity-metallicity gradient in the thick disk.
In this context, we have analyzed the trends in rotational velocity versus metallicity for the stars in our sample. The top panel in Fig. 14 shows the V −[Fe/H] relation for stars in the thin and thick disk population. We remind the reader that since the membership of stars to one of these two populations is defined according to their location in the [α/Fe]–age relation (Fig. 6), in this panel only a subset of the whole sample is shown. The data show a flat trends for stars of the thin disk population, with a slight decrease of the rotational velocity only for the less metal poor thin disk stars ([Fe/H] < −0.5 dex). Stars belonging to the thick disk population show a more complex trend, characterized by the absence of a V −[Fe/H] gradient for [Fe/H] > −0.5 and a positive V −[Fe/H] correlation for more metal poor stars ([Fe/H] < −0.5 dex). Overall the two populations show a continuity in the rotational velocity-metallicity trend, with thick disk stars at [Fe/H] > −0.5 dex having a slightly lower rotational support than thin disk stars of the same metallicity. When separating stars in the thick and thin sequences (as defined in Fig. 1), rather than in the two populations, similar trends are found. Thick disk stars show an overall increase in the rotational velocity with metallicity, the gradient of the relation being ΔV−Fe/H = 53.9 km s-1/dex (central panel, Fig. 14). To evaluate the gradient all the stars of the thick disk sequence have been included, e.g. those with ages estimates (colored point in the plot) and those without (grey points). Only few stars in retrograde motion (V < −220 km s-1) have been excluded from the linear fit. Note however that while the overall sample of thick disk sequence stars can be represented by a single linear fit, we notice the same tendency already found for the thick disk population, i.e. a flattening of the relation for [Fe/H] > −0.5 dex. This trend, already noticed by Spagna et al. (2010) for metallicity as high as [Fe/H] = −0.3 dex, is maintained all along the metal rich thick disk sequence, up to supersolar metallicities. The existence of a double gradient in the V −[Fe/H] relation for thick disk stars may reconcile the apparent contradictory results, as those by Lee et al. (2011) and Loebman et al. (2011). Indeed, the first focused their analysis on thick disk stars with metallicities lower than [Fe/H] = −0.5−0.3 dex, while the second evaluated the gradient for old disk stars, with Fe/H] > −0.5 dex, but note that with this selection, thick disk stars must have remained a minority.
Figures 15, 16 show similar trends:
-
α-enriched, old stars tend to rotate slower than α-poor, young stars;
-
there is a continuity in the evolution of V with α elements and ages;
-
the thick disk sequence shows a positive correlation between V and α (or age), while the thin disk sequence shows a flat gradient;
-
the evolution of the rotational support with age proceeds more than ten times faster among thick disk sequence stars (ΔV−age = −5.5 km s-1 Gyr) than for the thin disk counterpart (ΔV − age = −0.4 km s-1 Gyr).
4. Implications
Before discussing the implications, it is worthwhile to summarize the results from the previous section. We enumerate our results as follows:
-
(1)
There are two distinct regimes in the decline of [α/Fe] and theincrease in [Fe/H] with age. One regime, at early epochs, shows[α/Fe] decreasing 5 times faster and also [Fe/H] increasing morethan 10 times faster than in the second regime, at later times. Thetwo regimes separate rather cleanly at ages around8 Gyr.
-
(2)
The age–metallicity and age–[α/Fe] correlations in the thick disk regime have small scatter.
-
(3)
The vertical velocity dispersion decreases with decreasing [α/Fe] (or age) for stars along the thick disk sequence.
-
(4)
The oldest stars in the thin disk have metallicities around −0.6 dex and ages ≈ 10 Gyr. Although these objects have similar age and [α/Fe] content as the youngest thick disk stars, they have very different metallicities and have a higher rotational component in their velocities. Both these points can be considered as indicating that these stars originated in the outer disk (Haywood 2008).
Point (1) provides evidence for the existence of two different epochs of star formation in the Galaxy, which we have defined as the epochs of thick disk and thin disk formation. The change between these two epochs is well segregated in time, and suggests that the conditions under which stars formed were significantly different before and after ~8 Gyr. However, this should not be taken to imply that there was a discontinuity between the formation of the two disks. The marked change of slope in the age–metallicity relation shows that it is the decrease in the production of iron at ~8 Gyr that is mainly responsible for the slowing down in the decrease of [α/Fe] at that same epoch.
Point (2) implies that stars in the thick disk were formed in an ISM that was well-mixed at any given time. It suggests that the thick disk formed its stars in a turbulent ISM for several Gyr, confined to the inner parts of the Galaxy (compatible with a short scale length, Bovy et al. 2012b). This well-mixed gas was progressively enriched, giving rise to a monotonic and well defined age–metallicity–[α/Fe] relation. The result that the ISM at the epoch of the thick disk formation was well mixed is supported by the fact that no radial gradient has been detected in the α-enriched population, over a spatial scale of about 10 kpc (see Cheng et al. 2012a). Moreover, if the α-enriched population had an initial gradient that was subsequently erased, we should find a significant increase of the metallicity dispersion with age (Minchev et al. 2013), especially at ages greater than 8 Gyr, which is not observed. It implies that even in the presence of stellar migration, no change in the age–chemistry relation is expected, since the enrichment has been similar throughout the thick disk. The small scatter in the age-chemistry relation of the thick disk also leaves not much room for a component resulting from a mixture of satellite-accreted and in situ stars. The present dataset is not adequate to sample the metal-poor end of the age–chemistry relation, and to see how it behaves at the thick disk-halo interface. At the metal-rich end of the correlation however (at about 8 Gyr), it can be seen that thick disk objects reach solar metallicity and [α/Fe] ≈ 0.1, suggesting that they provide the chemical initial conditions of the thin disk formation. Since the ISM is well mixed during the thick disk phase, these initial conditions may be common to the whole inner thin disk. Given that the radial extension of the high [α/Fe] population seems to have a limit at about 10 kpc from the Galactic center (Cheng et al. 2012a), we consider this is also the limit at which the thick disk provided significant material to set up the initial conditions from which the thin disk formed. Note that this explains the apparent coincidence between the step at 10 kpc in metallicity between the inner and outer part of the thin disk and the extent in radius of the α-rich population. We contend that the thin disk inside 10 kpc is in direct filiation with the thick disk, while outer parts of the thin disk had a different and separate history.
Point (3) implies that the “thick disk” population is not only thick, it has a thin component, or, more precisely, is a continuum of components from a thick to a thinner disk, as measured from the decrease of the vertical velocity dispersion from [α/Fe] = 0.3 to 0.12 dex. Note that a continuity in the [α/Fe]−[Fe/H] plane for the inner (thin+thick) disks, as evidenced by Bovy et al. (2012a), does not imply necessarily a unique star formation regime all along the disk sequence. Bovy et al. excluded the presence of a separate thick disk component on the basis of the continuity in the chemical properties of their stars. Our analysis shows that even if these properties draw a continuum, their related star formation history does not, as evidenced by the different slopes in the [α/Fe]–age and [Fe/H]–age sequences. Note also that an age–metallicity correlation in the thick disk, together with an age–σW relation is expected to give a vertical gradient: older and metal weaker stars will reach higher distances from the galactic plane. Hence the thick disk has a vertical (see Katz et al. 2011, and references therein), but no radial metallicity gradient.
Point (4) suggests that the metal-poor thin disk and the thick disk stars must have formed in two different parts of the disk, because they have similar ages and [α/Fe] abundances, but different metallicity and different rotation speeds. It also suggests that, at the onset of the thin disk formation (at ages of about 8−10 Gyr), stars started to form first in the outer parts (R > 10 kpc), while the thick disk was still forming stars in the inner parts. At around 8 Gyr, the formation ceases in the thick disk altogether, and after some time, starts in the inner thin disk, following different paths of metallicity increase, and decrease in α enhancement, and of course, different intrinsic dispersion in the vertical disk direction.
We note also that the similar amount of [α/Fe] abundance at 8−10 Gyr in the thick disk and in the outer thin disk stars suggests that the material out of which metal-poor thin disk has formed may have been contaminated by the thick disk nucleosynthesis, but diluted in the outer disk gas reservoir. Finally, the presence of these metal-poor thin disk stars with similar characteristics in age and α elements as the thick disk goes against the suggestion that these objects could have formed also in the inner disk and then migrated to the outer disk: being formed at similar times, they must originate from a different lower metallicity environment.
5. Discussion
In this section, we first review some critical points: the status of the metal-poor thin disk stars, the weak evidence for significant radial migration and inside-out formation of the disk. We then sketch a scenario of the formation of the Milky Way disk based on our results and discuss how this scenario fits into a broader context.
5.1. The status of metal-poor thin disk stars and the outer thin disk
Different interpretations of the presence of metal-poor thin disk stars have been envisaged, based on similar data of solar neighbourhood stars. Reddy et al. (2003) or Bensby & Feltzing (2012) proposed that the hiatus in metallicity between metal-rich thick disk objects (at [Fe/H] ~ 0.0 dex) and thin disk metal-poor stars (at [Fe/H] ~ −0.6 dex) was caused by accretion of lower metallicity gas which diluted the ISM at the end of the thick disk phase. We think this is unlikely for two reasons. First, young thick disk stars have similar age as the oldest metal-poor thin disk objects. Being both formed at the same time, and since the thick disk is a population confined to the inner parts of the Galaxy, it is most likely that these objects originated from the outer disk. Second, the kinematics and orbital parameters of some of these stars is highly suggestive of an external origin: several of these objects have large apocenter (Rapo > 10 kpc), with their V-component overtaking the LSR (V > 0 km s-1), see Haywood (2008). In the SEGUE sample, metal-poor thin disk stars share the same properties, having mean galactocentric radii above 9 kpc (see Bovy et al. 2012b, Fig. 7), and a clear positive V-component (see Liu & van de Ven 2012, Fig. 3).
These properties have to be combined with the fact that, starting at RGC = 9−10 kpc, the disk mean metallicity drops below [Fe/H] ≈ −0.3 dex, with an apparent flat distribution beyond this distance. In particular, this is observed for open clusters, which exhibit a (possibly) steeper drop in metallicity for older clusters (ages > 4 Gyr; see Bragaglia et al. 2012,Fig. 7), while field giants have mean metallicities of −0.48 dex and [α/Fe] = +0.12 (Bensby et al. 2011), in good agreement with Adibekyan et al. (2012) for similar stars. Hence, local metal-poor thin disk stars have mean orbital radii of about 9−10 kpc and stars at 9−10 kpc have metallicities and alpha-element abundances similar to their local counterparts. Since stars of such metallicities and alpha abundances seem dominant beyond R = 9 kpc, it suggests that metal-poor local counterparts originated in the outer disk. Moreover, while vertical motions of field stars in the outer disk have not yet been measured, some open clusters are found at distances of several hundred parsecs from the galactic plane, which seems in line with the rather hot kinematics of local metal-poor thin disk stars (see Sect. 3.5.2.). There is therefore strong similarities of the properties of these stars with those of the outer disk as a whole. It is this relationship, together with the fact that local metal-poor thin disk objects can have ages up to ~10 Gyr, which suggests that the outer thin disk must have started to form stars before the inner thin disk. Figure 17 highlights the position of metal-poor thin disk stars having metallicities below [Fe/H] = −0.3 dex on the thin disk sequence (see Fig. 1). These objects form a sequence parallel to that of the local thin disk, but at higher relative α abundance, connecting to the thick disk at ages of 9−10 Gyr.
 |
Fig. 17 Age–metallicity and age–[α/Fe] distributions, with stars in the metal-poor tail of the thin disk sequence (see Fig. 1) at [Fe/H] < −0.3 dex shown as white dots. The metal-poor thin disk stars draw a sequence parallel to the local thin disk, joining the thick disk at 9−10 Gyr and [α/Fe] in [0.1,0.15]. |
Note that a number of extragalactic studies show the presence of old stars in the outskirts of disks (Ferguson & Johnson 2001; Vlajić 2010; Barker et al. 2011; Yoachim et al. 2012; among other studies). These stars may have been formed in the outskirts of galaxy disks, without necessarily having migrated from the inner disk regions (see, for example, the discussion in Sánchez-Blázquez et al. 2009; Gibson et al. 2012). Several studies also have shown the change in metallicity profile that occurs in the outskirts of disks (Bresolin et al 2012 and references therein). In the case of M33, it seems particularly clear that the increase in mean age beyond the break radius is accompanied by a very significant decrease in metallicity (Barker et al. 2011). A behavior which ressembles very much what is observed in the Milky Way.
To some extent, we confirm the viability of [α/Fe] as a proxy for age used by Bovy et al. (2012b): [α/Fe] correlates well with age, but this correlation is stronger for the thick disk population (Fig. 6). However, the specific status of metal-poor thin disk stars is not discussed in the study of Bovy et al. (2012b). Metal-poor thin disk stars do not fit into their scheme because they result from different conditions during their formation. At [α/Fe] ~ 0.1 dex, they have higher vertical velocity dispersion, hence higher scale height, than local thin disk stars with similar relative alpha element content. In the Bovy et al. (2012b) decomposition, these objects are outliers to the scale height–scale length anti-correlation, and possibly results in the point that can be seen at (4.3 kpc, 440 pc; their Fig. 5). Furthermore, it is tempting to suggest that it is the presence of these metal-poor thin disk stars that leads Bovy et al. (2012a) to conclude on the absence of a dip between alpha-poor and alpha-rich stars: these objects have alpha abundance intermediate between the local disk and the thick disk, and kinematics hotter than standard thin disk. They will contribute to fill the dip between the thin and thick disks, although they cannot be considered an intermediate phase between the two, and should not be counted undistinguished when estimating surface densities. Hence, we infer that the dip probably is real, although confirmation would require to properly disentangle the different stellar populations in the SEGUE data.
While we discuss the conditions of the ISM in which stars may have formed in the outer disk in Sect. 5.4.2, we note that such stars, having, at similar ages, the same level of alpha abundance ratios, may be related to the thick disk population. In a highly turbulent disk, like the one that may have formed the thick disk, a significant amount of gas is expected to be expelled outwards, likely contaminating the outer regions (Sect. 5.4.2). Combined with metal-poor accreted gas, this gas could have provided the mixture from which these stars formed resulting in their observed chemical composition. This would provide a natural explanation of the high abundance ratios found in the outer regions for which only adhoc solutions have been proposed until now.
5.2. Radial migration
5.2.1. Thin disk
While the “contamination” or “pollution” of the solar vicinity by stars originating from other radii hampers direct deciphering of the evolution of our Galaxy from simple correlations between ages and chemical properties of ensembles of stars, such contaminants do convey crucial information about the formation of the disk on larger scales. Since the suggestion by Sellwood & Binney (2002) that migration could play a significant role in redistributing stars in disks, there has been several studies suggesting that migration is necessary to explain patterns observed in the solar neighbourhood (Haywood 2008; Schönrich & Binney 2009a,b; Loebman et al. 2011).
We distinguish two cases:
-
Limited migration, in which case we consider that only the tails of the solar neighborhood metallicity distribution (at [Fe/H] < −0.2 dex and [Fe/H] > +0.2 dex) are populated by stars that come from other radii. In this case, which mechanism (churning/blurring) is more likely to have produced such contamination? These contaminating stars have metallicities similar to stars found at 2−3 kpc from the Sun, and which have a mean metallicity of +0.2 dex at just 2 kpc towards the galactic center (Hill et al. 2012), and −0.3 dex at 10 kpc (Bensby et al. 2011). Simple estimates of radial excursions due to epicycle oscillations give of the order of 1−2 kpc at the solar galactocentric radii, which put stars of the inner or outer disk within reach of the solar vicinity. These stars are found in limited amounts in the solar neighborhood (a few per cent), and certainly does not require significant radial migration across the solar circle. If only the tails require pollution by objects born outside the solar circle, then probably epicycle oscillation could bring a few per cent of stars that dominate the disk at just 2 kpc from the solar radius. We consider that blurring (which we know to occur in disks) would be sufficient to explain most of these tails, even though we do not exclude that a limited amount of churning may have contributed. Orbital parameters of metal-poor thin disk stars support this conclusion.
-
Strong migration, where it has been suggested that the mean metallicity of solar neighborhood stars is dominated by objects that have migrated from the inner disk (see, e.g Loebman et al. 2011). This argument has been proposed in particular to explain how the mean metallicity at the solar radius had already reached [Fe/H] ~ −0.1 dex, 8−10 Gyr ago. However, our results show that the thick disk stars set the chemical initial conditions for the formation of the thin disk, hence there is no need to invoke the action of radial migration to explain the metallicity of the old thin disk (i.e., by bringing stars with [Fe/H] ~ −0.1 dex into the solar neighborhood). Moreover, the fact that the outer disk is dominated by stars with a metallicity significantly lower than that of the youngest thick disk means that no inner disk stars (either thin or thick disk) have migrated to the outer disk in significant numbers over the last 10 Gyr.
Finally, it is interesting to speculate about the radial age-profile which arises from the picture outlined in Sect. 5.1 and from the results discussed in Sect. 4. In the inner disk (R < 10 kpc), the superposition of an old thick disk with a short scale length (2 kpc; Bovy et al. 2012b) and a thinner and younger component with a long scale length (3.6 kpc) will naturally give rise to a decreasing mean age outward. In the outer regions (R > 10 kpc) where stars older than local thin disk stars can be found, the mean age could be higher than that within the solar neighborhood, giving rise to a U-shape age profile, without invoking any significant mixing (Roškar et al. 2008). Of course, this conclusion depends on the way star formation proceeded in the outer disk of the Milky Way, but at least suggests the possibility that U-shaped age profile could exist in disks where there has been no substantial redistribution of stars due to migration. This reinforces the fact that, even in ΛCDM scenarios for galaxy formation and evolution, old stars may have been formed in the outskirts of galaxy disks, without necessarily having migrated from the inner disk regions (see also the discussion in Sánchez-Blázquez et al. 2009). Understanding where these stars have formed is crucial in shedding light on the early epochs of thin disk formation.
5.2.2. Thick disk
It is also interesting to discuss the impact that radial migration may have had in forming the Milky Way thick disk population, in light of our age estimates of thick disk stars. The possibility that the thick disk is the result of secular processes instead of more violent ones has been extensively debated in the last couple of years (Schönrich & Binney 2009b; Loebman et al. 2011; Minchev et al. 2013). The first consideration to make is that radial migration, as it has been discussed in the literature (Sellwood & Binney 2002; Schönrich & Binney 2009a; Roškar et al. 2008; Minchev & Famaey 2010; Minchev et al. 2011, 2012a,b; Di Matteo et al. 2013) is the result of a secular process related to the presence of stellar asymmetries likes bars and spiral arms in galaxy disks. Similar structures in disks are almost absent from the progenitors of present-day spirals at z > 1.5 and they generally remain rare up to z ~ 1 (e.g., Sheth et al. 2008). This epoch is perhaps the transition between an early violent phase of disk formation to a more quiescent one (e.g., Martig et al. 2012; Kraljic et al. 2012). The redshift evolution of the bar fraction seems to agree with this scenario, indicating that the bar fraction drops by a factor of about three from z = 0 to z = 0.8 (Sheth et al. 2008). If stellar asymmetries were rare above z ~ 1, redshifts higher than this do not correspond to a secular evolution phase for galaxy disks, we have to conclude that if radial migration formed thick disks, this can have been possible only in the last 8 Gyr of galaxy evolution. Within this context, it is perhaps surprising then to see that thick disk stars in the solar neighborhood are all older than 8 Gyr (as indicated for example by the zmax −age and W −age relations). If radial migration only started to affect galaxy disks during the last 8 Gyr, producing the observed thickening of the disk at the solar vicinity, we should expect to find a significant fraction of stars with ages less than 8 Gyr with high zmax and W. There is no trace of these stars within the solar vicinity. All stars with ages younger than 8 Gyr are redistributed in a thin configuration (zmax < 0.5 kpc). This, in our opinion, rules out the possibility that migration may have been a major contributor to the thickening of the galactic disk. Moreover, during the evolution of the thick disk there was a decrease in the disk scale height which is not accompanied by an increase in the disk scale length (Bovy et al. 2012b). This favors scenarios which cool the disk vertically without substantially heating it radially. Once again, radial migration seems incompatible with these findings – migration is usually accompanied by an increase in the disk scale lengths, with a net outward flow of stars (i.e. radial heating).
Apart from the thickening of a pre-existing thin disk component, cosmological numerical simulations have often claimed that radial migration is a fundamental mechanism in driving the evolution of a thick disk because, in these models, thick disk stars within the solar neighborhood are found with a variety of formation radii, frequently smaller than 4 kpc (Brook et al. 2012; Minchev et al. 2013). A small formation radius is thus associated with subsequent radial migration which would carry those inner thick disk stars out to the solar annulus. Note however that if thick disk stars formed already in a thick disk configuration with high velocity dispersions and an angular momentum content lower than that of the thin disk (Figs. 12, 13, 14), they must have had eccentric orbits already at the time of their formation. An eccentricity e = 0.3 would be sufficient to allow a star born at R = 4 kpc, for example, to reach the solar annulus, without any need to invoke strong subsequent migration. In Brook et al. (2012) for example, most thick disk objects have formation radii in the inner disk (see their Fig. 9), but moderate eccentricities would be sufficient to bring a substantial number of these objects out to the solar radius. The recent models by Bird et al. (2013) seem to support this scenario: their thick disk stars have small formation radii, and their guiding centers do not change significantly over time, thus indicating that thick disk stars had already eccentric orbits at the time of their formation. In Brook et al. (2012) also, the thick disk forms with a scale length of 1.7 kpc, very near to the observed value of 1.8 kpc (Bovy et al. 2012b). Thus one may wonder if any substantial migration is needed to explain the observed properties of the thick disk in the Milky Way.
5.3. Inside-out formation of the disk
An interesting consequence of the proposed scenario concerns the so-called inside-out paradigm that has been proposed for the formation of disks (Larson 1976, and e.g. Sommer-Larsen et al. 2003; Rahimi et al. 2011; Brook et al. 2012), and which received support from the analysis of Bovy et al. (2012b). How much of that picture is due to the superposition of two components that have different scale lengths and ages, and how much to the effect of a real inside-out process?
Combining our results with those of Bovy et al. (2012b), one can see that the formation of the thick disk, which lasted 4−5 Gyr (Fig. 6), did not produce any significant increase in scale length – the scale length remains <2 kpc down to [α/Fe] ~ 0.25, which, in their α abundance scale, is the beginning of the thin disk regime (see their Fig. 5). At the same time, the thick disk scale height decreased by a factor of 2 to 3. Moreover, a tight age–metallicity relation as found here, combined with an inside-out scenario, should produce a radial metallicity, or [α/Fe], gradient in the thick disk, which is not observed (Cheng et al. 2012b).
Within the (inner) thin disk itself, whose formation lasted 8 Gyr, one can hardly see any trend in support of an inside-out formation (blue and cyan points in the upper panel of Fig. 5, or orange and red points in the lower panel, Bovy et al. 2012b): several points with the lowest [α/Fe] (<0.05 dex), and high metallicities, which ought to be young and to have long scale length in the scheme of Bovy et al., have indeed scale lengths as short as 2.1 or 2.8 kpc, while some others, at the limit between the thick and thin disk in terms of [α/Fe], have scale lengths greater than 4 kpc.
It is clearly the combination of the two structures that gives Bovy et al. the impetus to favor an inside-out formation scenario, but this is much less supported once one looks more carefully into the details of the age structure of the population.
Finally, it is worth commenting on some of the implications that result from assuming that the formation of the disk proceeded inside-out. Bovy et al. (2012b) proposed that the outer disk formed after the inner disk because of it’s larger scale length and lower metallicity, which were interpreted as a signature of younger ages (from the model of Schönrich & Binney 2009b). Similarly, Roškar et al. (2013) predict that the outer disk should be essentially younger than 2 Gyr following Bovy et al. (2012b). Clearly, the observations are in conflict with these predictions: open clusters older than 4−5 Gyr are seen beyond 11 kpc (Berkeley 17, 32, 36, 39) and out to at least 15 kpc (Berkeley 20, 29), while metal-poor thin disk stars seen in local samples are older than the general population of local thin disk stars. All these arguments suggest a more complex star formation history than that predicted until now − simple inside-out formation scenarios and radial-mixing alone do not alleviate this tension between models and observations.
5.4. Proposed scenario and context
5.4.1. Qualitative outline of the evolution of the MW
From the results presented in Sects. 3 and 4 we outline the following qualitative scenario: the first stars in the thick disk started to form out of a turbulent gaseous disk at redshift z > 3. This gaseous disk was characterized by high velocity dispersions, had a short scale length (Bovy et al. 2012b) and large scale height (deduced from the zmax vs. age and σW vs. age relations; Fig. 11), and a low rotational velocity. The strong feedback associated with an active phase of intense star formation at that epoch was likely responsible of an efficient mixing of metals in the ISM as suggested by the tight age–metallicity relation found in local thick disk (Sect. 3.3), and in the absence of a radial gradient among thick disk stars over several kpc (Cheng et al. 2012b). We suggest that the increase in the stellar velocity dispersion that the data show for ages greater than ~8 Gyr is related to the fact that, at those times, the Milky Way disk had high star-formation intensities, similar to local starburst galaxies, i.e. with star formation rate densities ΣSFR > 0.01 M⊙ kpc-2 yr-1 (e.g. Lehnert & Heckman 1996; Meurer 1996).
We concluded the star formation in the early Milky Way must have been intense through the following considerations. Bovy et al. (2012b) found a thick disk scale length of the order of 1.8 kpc. Assuming that the thick disk has an exponential density distribution, and a local volume density ratio between thick and thin disk stars of 0.05 (which is at the lower end of possible values, see Chang et al. 2011), then, the thick disk mass is no less than two tenths of the thin disk mass. We assumed the scale height ratio between the two populations is 1/4 and that both disks have similar scale lengths, but the thick disk mass could be much higher (perhaps up to the thin disk mass ~1011 M⊙), depending on the exact scale length of the thin disk. Thick disks with comparable masses to that of their thin disks have been found recently in some external galaxies (Comerón et al. 2011). In case of a thick disk with just two tenths of thin disk mass (which we believe to be a very conservative choice) and which formed over ~4 Gyr leads to an average star formation rate ⟨ SFR ⟩ ~ 5 M⊙ yr-1 or an average star-formation rate per unit area4 ΣSFR ~ 0.05 M⊙ yr-1 kpc-2. Such a value for the star formation intensity, which is likely a lower limit, would imply that Milky Way would have a star formation intensity similar to that of nearby starbursts and distant intensely star-forming galaxies at z ~ 2−3 (e.g. Lehnert & Heckman 1996; Dib et al. 2006; Lehnert et al. 2009, 2013) Above these values, there is a sharp increase in the velocity dispersion of the ISM with ΣSFR. We thus suggest that the relations found between stellar vertical velocity (or zmax) and age reflects similar relations in the ISM: stars formed in a thick ISM, whose high dispersions were sustained for several Gyr by intense star formation (but notice not necessarily high star formation rates overall).
Several processes may have contributed creating an initial gas rich phase and/or in maintaining such high SFRs over several Gyr in the Milky Way disk: multiple accretion of gas-rich companions (Brook et al. 2004; House et al. 2011), gas accretion from filaments (Kereš et al. 2009), gravitational instabilities (Forbes et al. 2012), gas cooling in the halo, and recycling of the gas from outflows. Heating during the merger epoch (Quinn et al. 1993; Qu et al. 2011; House et al. 2011), or scattering of stars by massive clumps (Bournaud et al. 2009) may have caused additional thickening of the already formed thick stellar component (Quinn et al. 1993; Qu et al. 2011).
The star formation must have continued for 4−5 Gyr with each new generation of stars forming in thinner and thinner layers, and increasingly supported by rotation. During this phase turbulent mixing of the gas maintains a homogeneous ISM, and permits a monotonic chemical enrichment as the stellar population evolves and enriches the ISM with metals. The steep gradient in the Fe enrichment with time indicates that star formation proceeded at a sustained rate in the inner parts, but the star formation in the outer parts must have been less intense and reached more moderate metallicities and α-enrichment compared to the inner parts. At the end of the thick disk phase (~8 Gyr), the inner disk is left with a metallicity ~−0.1 ± 0.1 dex. There may be an age gap in the star formation possibly causing the gap in α element enrichment (Adibekyan et al. 2012), after which, star formation proceeds in a thin disk. The forming thin disk inherited its metallicity and α element enrichment level from (approximately) the end of the formation of the thick disk. The growth of the thin disk must have had characteristics somewhat different from that of the thick disk as there is a change in the chemical enrichment rate in the inner disk. During these periods of formation, the star formation continues in the outer disk, as revealed by the presence of metal-poor stars (−0.7 < [Fe/H] < −0.3) at all ages between 2−10 Gyr in the solar vicinity. Being at the edge of the inner disk, the solar vicinity is dominated by objects formed along the evolutionary path followed by the inner disk, and is only weakly contaminated by objects that formed in the outer disk, and which have metallicities [Fe/H] < −0.3 dex.
5.4.2. Scenario within the context of distant galaxies
As explained in the previous section, if the thick disk was formed in the Galaxy, as our results suggest, most probably the Milky Way was in starburst mode at z = 2−3. Actively star forming galaxies at high redshift are known to be both gas rich, have high gas mass surface densities (Daddi et al. 2010; Aravena et al. 2010; Dannerbauer et al. 2009; Tacconi et al. 2010; Combes et al. 2011), have high velocity dispersions in their gas and intense star formation (Lehnert et al. 2009, 2013; Swinbank et al. 2011). Within the context of gas rich distant intensely star forming galaxies, global disk instabilities may have played an important role in regulating star formation in the early universe.
In this spirit, the Toomre criterion may provide a simple way to understand the early evolution of disk of galaxies and their global star formation properties. The effective Toomre criterion is given by 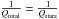 +
+ 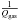 (Wang & Silk 1994; Jog 1996; Romeo & Wiegert 2011), where for the gas, Qgas = κσgas/πGΣgas and similarly for the stars, where κ is the epicyclic frequency, Σgas is the gas mass surface density, G is the gravitational constant, and σgas is the velocity dispersion of the gas. The line of stability against star-formation is Qtotal ~ 1 where values higher than about 1 imply that a disk is stable against star formation. In the early evolution of galaxies, the surface mass densities of the disks may be dominated by the gas and are much higher than local galaxies (cf. Daddi et al. 2010; Tacconi et al. 2010; Kennicutt & Evans 2012, and references therein). This suggests that to maintain galaxies at about Q ~ 1 requires higher dispersions than local galaxies. The thickness of the disk is proportional to σ2/Σtotal. With the higher dispersions necessary to keep the disk near the line of stability suggests that the disks are generally thicker than disks in the local universe as perhaps observed (e.g. Elmegreen et al. 2009; Epinat et al. 2012).
(Wang & Silk 1994; Jog 1996; Romeo & Wiegert 2011), where for the gas, Qgas = κσgas/πGΣgas and similarly for the stars, where κ is the epicyclic frequency, Σgas is the gas mass surface density, G is the gravitational constant, and σgas is the velocity dispersion of the gas. The line of stability against star-formation is Qtotal ~ 1 where values higher than about 1 imply that a disk is stable against star formation. In the early evolution of galaxies, the surface mass densities of the disks may be dominated by the gas and are much higher than local galaxies (cf. Daddi et al. 2010; Tacconi et al. 2010; Kennicutt & Evans 2012, and references therein). This suggests that to maintain galaxies at about Q ~ 1 requires higher dispersions than local galaxies. The thickness of the disk is proportional to σ2/Σtotal. With the higher dispersions necessary to keep the disk near the line of stability suggests that the disks are generally thicker than disks in the local universe as perhaps observed (e.g. Elmegreen et al. 2009; Epinat et al. 2012).
To sustain the galaxies for the necessary length of time as observed in the thick disk of the MW, approximately a few Gyr, some process or processes must regulate the star formation to either equilibrate with the gas supply, say from cosmological gas accretion or mergers, or have star-formation self-regulated through its own energy output or combinations of all of the above (e.g. Elmegreen & Burkert 2010). Processes which may drive the large scale turbulence in the ISM whether it be gravitational collapse and instabilities on large scales, shearing from large scale motions, energy injection from massive stars, or cosmological gas accretion, the velocity of the cold molecular gas out of which stars form, will tend to moderate such that galaxies are near the line of instability in gas rich disks. If the dispersions are too low and Q ≪ 1, the star formation intensities will grow rapidly, consuming all the gas in few rotational or crossing times or the young stars will inject sufficient energy to increase the dispersions in the gas tending to stabilize the disk. If Q ≫ 1, star formation will be strongly suppressed globally, allowing the gas content to grow until the disk again becomes unstable. The homogeneity in the stars and the smooth growth in the metallicity and decline in the α-enhancement suggests that thick disk must have been mostly near the line of instability throughout its evolution, maintaining a high level of turbulence, and supporting a thick disk whose thickness decreased with time.
The high dispersions necessary to maintain this equilibrium in a thick disk also has the advantage of leading to a short mixing time. The turnover time of large scale turbulence is H/σgas which in the case of a 1 kpc thick disk and a dispersion of 100 km s-1 (which are rough characteristics of high redshift star forming galaxies; Lehnert et al. 2009, 2013), leads to a timescale of 10 Myrs which is a about a tenth of a rotation time, for a rotation speed of 150 km s-1 and at re = 2.5 kpc (about the rotation speed and half light radius of the thick disk; Förster Schreiber et al. 2006, 2009) and similar to the evolutionary timescale of massive stars that enrich the ISM with metals through stellar winds and supernovae. Thus the metals lost to the ISM by massive stars will mix very quickly with some being lost to outflows because of the intense star formation (e.g. Kornei et al. 2012).
As the gas mass surface densities drops due to the gas being consummed by star formation and as the mass surface density of the thick stellar disk increases, we would expect the gas disk to grow thinner – at lower gas mass surface densities, the velocity dispersion of the gas necessary to maintain the gas along the line of stability drops and naturally leads to a shorter scale height (which is proportional to σ2). In other words, the increasing (both in absolute terms and in terms of declining gas fraction) stellar mass tends to stabilize the disk against intense star formation. This stabilization is what leads to a declining scale height with time and likely leads to greater inhomogeneities in the abundances of the stars forming in progressively lower scale heights.
In addition, such a scenario might explain why the outer disk appears to have characteristics of the younger stars in the thick disk. In the outer disk both the gas mass surface densities are lower, the gas surface fractions (Σgas/Σtotal) are likely higher, and the orbital time much longer. The star formation rate per unit area is probably also low in the outer disks (as is observed both in local and distant galaxies, e.g. Kennicutt & Evans 2012; Lehnert et al. 2013). Thus both the enrichment and the mixing timescales will be much longer since the star formation occurs at a much lower intensity. This will naturally lead to less energy injection from massive stars, the accretion rate per unit area is likely lower, and the impact on a gas rich outer portion of the disk may be less (mostly driving the gas inwards) than in the inner disk where the gas is stabilized by the higher stellar mass surface densities. In addition, the intense star formation in the inner region during the early evolution of the thick disk will disperse metal-rich, alpha-enhanced gas into the halo which then can subsequently cool and rain back down on the disk. This would account for the enhanced alpha-element ratios of the stars in the outer disk despite their relatively inefficient star formation.
6. Summary
We summarize our results and conclusions as follows:
-
(1)
The thick disk arose from a well mixed turbulent gaseous diskwhich gave rise to a steep and monotonic chemical enrichmentlasting 4−5 Gyr.
-
(2)
The vertical velocity dispersion progressively decreased in the thick disk, from about 50 km s-1 to 25 km s-1, suggesting that star formation proceeded in progressively thinner layers.
-
(3)
The inner thin disk (<10 kpc) inherited from the chemical conditions left at the end of the thick disk phase, some 8 Gyr ago. The transition between the two disks is imprinted in the fossil signature left by the change of regime that can be seen in the rate of [α/Fe] variation as a function of time (Fig. 6). This is the only discontinuity that we can detect between the two populations.
-
(4)
Combined with the scale length and scale height measurements from Bovy et al. (2012b), these results do not support a continuous inside-out formation of the disk. We advocate that it is only the combination of two structures with different scale lengths that gives the impression of an inside-out process, but that there is hardly any trace of such process in each population, although their formation lasted several Gyr.
-
(5)
The outer thin disk started to form stars while the thick disk phase was still on-going in the inner disk, 9−10 Gyr ago, possibly from a mixture of enriched material expelled from the thick disk, and accreted gas depleted of metals. However, the evolution of the outer disk remained essentially disconnected from that of the inner disk afterwards.
-
Combination of points (1−4) leaves little room for radial migration, in the sense of churning, to have played a substantial role in redistributing stars seen in the solar vicinity, or across the solar annulus. Other factual results have been obtained:
-
(7)
The rate iron enrichment in the thick disk was about 5 times higher as compared to the thin disk phase.
-
(8)
The vertical velocity dispersion of old disk stars is a mixture of objects of different origin: the local thin disk (~8 Gyr) and the young thick disk (9−10 Gyr), which, although being of different ages, have the same vertical velocity dispersion (around 22−27 km s-1), probably due to being heated by the same process, and the old metal-poor thin disk (9−10 Gyr), which although having the same age as the young thick disk, have higher vertical velocity dispersion (~35 km s-1). It is the mixture of different amount of each of these populations in studied samples which have conducted to varying results.
Finally, we conclude with a point of nomenclature. The search for a parameter most closely related to the defining properties and limits of a stellar population has questioned galactic astronomy for at least fifty years (e.g. Schwarzschild 1958). With this work we went one step further in this direction by linking the gross characteristics of a population to properties that reflect the ISM in which it was formed at an identifiable epoch. In doing so however, we pulled the old labelling of “thin” and “thick” disks further away from their original meaning. In our new definition, the thick disk is not only thick, it has a thin component, it is not only older than, but also coeval with the (outer) thin disk. The “thin” outer disk, as sampled in the solar vicinity, shows kinematics more akin to a conventional “thick” disk. While we have maintained throughout the paper the conventional designation of thick and thin disks, other designations could be more appropriate. There is perhaps more continuity between the thin and thick disks than between the inner thin disk and outer thin disk. The inner thin disk and the thick disk seem to be more like the same structure and could be designated as the young and old inner disk, while the outer disk appear more like a separate component.
Following the terminology introduced by Schönrich & Binney (2009a), we use the term “churning” to characterise a change of guiding center with no kinematic heating, as proposed by Sellwood & Binney (2002), and “blurring” for the increase in eccentricity, or epicycle radial oscillation of the orbit.
ΣSFR = ⟨ SFR ⟩ /Area. Following Dib et al. (2006), we have evaluated the galactic surface area as Area = π(3rd)2, with rd being the thick disk scale length, i.e. rd = 1.8 kpc (Bovy et al. 2012b).
Acknowledgments
M.H. wish to thank Vardan Adibekyan for his kind advice on the use of the data, and Poul Nissen for interesting comments on the first version of this article. The authors acknowledge support from the French Agence Nationale de la Recherche (ANR) under contract ANR-10-BLAN-0508 (Galhis project) and wish to thank the referee for helpful and constructive comments which greatly improved this paper. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France
References
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 554, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, C., & Santillan, A. 1991, Rev. Mex. Astron. Astrofis., 22, 255 [NASA ADS] [Google Scholar]
- Aravena, M., Carilli, C., Daddi, E., et al. 2010, ApJ, 718, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W. 1944, ApJ, 100, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, M. K., Ferguson, A. M. N., Cole, A. A., et al. 2011, MNRAS, 410, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2012, EPJ Web Conf., 19, 4001 [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2011, ApJ, 735, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2012, Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, ASP Conf. Ser., 458, 171 [NASA ADS] [Google Scholar]
- Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., & Hogg, D. W. 2012a, ApJ, 751, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012b, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Gratton, R. G., Carretta, E., et al. 2012, A&A, 548, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., & Ryan-Weber, E. 2012, ApJ, 750, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Kawata, D., Gibson, B. K., & Freeman, K. C. 2004, ApJ, 612, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D. 1979, ApJ, 234, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, C.-K., Ko, C.-M., & Peng, T.-H. 2011, ApJ, 740, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., Morrison, H. L., et al. 2012a, ApJ, 752, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., Morrison, H. L., et al. 2012b, ApJ, 746, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., García-Burillo, S., Braine, J., et al. 2011, A&A, 528, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S., Elmegreen, B. G., Knapen, J. H., et al. 2011, ApJ, 741, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Curir, A., Lattanzi, M. G., Spagna, A., et al. 2012, A&A, 545, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., & Bernstein, R. A. 2002, AJ, 124, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- Dannerbauer, H., Daddi, E., Riechers, D. A., et al. 2009, ApJ, 698, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1998, AJ, 115, 2384 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Bell, E., & Burkert, A. 2006, ApJ, 638, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2007, AJ, 134, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Elmegreen, B. G., & Burkert, A. 2010, ApJ, 712, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Marcus, M. T., et al. 2009, ApJ, 701, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, A. M. N., & Johnson, R. A. 2001, ApJ, 559, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, J., Krumholz, M., & Burkert, A. 2012, ApJ, 754, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Lehnert, M. D., et al. 2006, ApJ, 645, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2011, MNRAS, 414, 2893 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Courty, S., Cunnama, D., & Molla, M. 2012 [arXiv:1204.1399] [Google Scholar]
- Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2006, MNRAS, 371, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2012, EPJ Web Conf., 19, 5001 [CrossRef] [Google Scholar]
- Herrmann, K. A., Ciardullo, R., & Sigurdsson, S. 2009, ApJ, 693, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Babusiaux, C., Gómez, A., et al. 2012, EPJ Web Conf., 19, 6001 [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- House, E. L., Brook, C. B., Gibson, B. K., et al. 2011, MNRAS, 415, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Sesar, B., Jurić, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobson, H. R., Pilachowski, C. A., & Friel, E. D. 2011, AJ, 142, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Jog, C. J. 1996, MNRAS, 278, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Soubiran, C., Cayrel, R., et al. 2011, A&A, 525, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Fardal, M., Davé, R., & Weinberg, D. H. 2009, MNRAS, 395, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K. A., Shapley, A. E., Martin, C. L., et al. 2012, ApJ, 758, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kraljic, K., Bournaud, F., & Martig, M. 2012, ApJ, 757, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1976, MNRAS, 176, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Law, D. R., Shapley, A. E., Steidel, C. C., et al. 2012, Nature, 487, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., An, D., et al. 2011, ApJ, 738, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 462, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Le Tiran, L., et al. 2009, ApJ, 699, 1660 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Tiran, L. L., Nesvadba, N. P. H., et al. 2013, A&A, 555, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, C., & van de Ven, G. 2012, MNRAS, 425, 2144 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Curto, G., Mayor, M., Benz, W., et al. 2010, A&A, 512, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loebman, S. R., Roškar, R., Debattista, V. P., et al. 2011, ApJ, 737, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Bournaud, F., Croton, D. J., Dekel, A., & Teyssier, R. 2012, ApJ, 756, 26 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. F. 1959, J.R. Astron. Soc. Can., 53, 211 [NASA ADS] [Google Scholar]
- Meurer, G. R. 1996, New Light on Galaxy Evolution (Kluwer Academic Publishers), IAU Symp., 171, 421 [NASA ADS] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012a, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012b, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moster, B. P., Macciò, A. V., Somerville, R. S., Naab, T., & Cox, T. J. 2012, MNRAS, 423, 2045 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Abadi, M. G., Venn, K. A., Freeman, K. C., & Anguiano, B. 2011, MNRAS, 412, 1203 [NASA ADS] [Google Scholar]
- Ng, Y. K., & Bertelli, G. 1998, A&A, 329, 943 [NASA ADS] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J. 1987, ApJ, 314, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., Balcells, M., Lütticke, R., & Dettmar, R.-J. 2004, A&A, 422, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qu, Y., Di Matteo, P., Lehnert, M. D., & van Driel, W. 2011, A&A, 530, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Rahimi, A., Kawata, D., Allen de Prieto, C., et al. 2011, MNRAS, 415, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., & Lambert, D. L. 2008, MNRAS, 391, 95 [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Romeo, A. B., & Wiegert, J. 2011, MNRAS, 416, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Loebman, S. R., Ivezić, Z., & Quinn, T. R. 2011, Cool Stars, Stellar Systems, and the Sun, ASP Conf. Ser., 448, 371 [NASA ADS] [Google Scholar]
- Roškar, R., Debattista, V. P., & Loebman, S. R. 2013, MNRAS, 433, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009a, MNRAS, 399, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009b, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M. 1958, Ric. Astron. Specola Vaticana, 5, 204 [Google Scholar]
- Seabroke, G. M., & Gilmore, G. 2007, MNRAS, 380, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Sommer-Larsen, J., Götz, M., & Portinari, L. 2003, ApJ, 596, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spagna, A., Lattanzi, M. G., Re Fiorentin, P., & Smart, R. L. 2010, A&A, 510, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swinbank, A. M., Papadopoulos, P. P., Cox, P., et al. 2011, ApJ, 742, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Udry, S., Mayor, M., Naef, D., et al. 2000, A&A, 356, 590 [NASA ADS] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlajić, M. 2010, PASA, 27, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2008, ApJ, 682, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2012, ApJ, 752, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Silk, J. 1994, ApJ, 427, 759 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 [α/Fe] vs. [Fe/H] for stars in the sample of Adibekyan et al. (2012). α is defined as the mean of the abundances of magnesium, silicon and titanium. The thick and thin disk sequences are distinguished by whether they lie above or below the three segments of the solid line respectively. The two double circles at [Fe/H] < −1.0 dex and [α/Fe] < 0.1 dex are HIP 74234 and HIP 100568, while the two solid dot-and-circle symbols represent HIP 54641 and HIP 57360 (see text). |
| In the text | |
 |
Fig. 2 Upper plot: difference between effective temperatures from Adibekyan et al. (2012) and those derived from the V − K indices and calibration from Casagrande et al. (2010) for the whole sample. The lower curve is the mean of the difference calculated over 75 points, the upper curve is the dispersion. Lower plot: difference in age resulting from the two scales, as a function of age (based on Adibekyan et al. (2012) spectroscopic scale) for stars with “good” ages (see text). |
| In the text | |
 |
Fig. 3 Left: χ2 vs. bayesians ages, using the same set of isochrones. Right: χ2 (Dartmouth isochrones) vs. bayesians ages (Y2 isochrones). |
| In the text | |
 |
Fig. 4 HR diagrams for stars in various metallicity ranges and [α/Fe] content (given explicitly in the legend at the bottom left corner of each plot). The lines in each plot are isochrones of various ages (Demarque et al. 2004). Isochrones shown as solid dark blue lines have ages of 5, 10 and 15 Gyr (from left to right). The open and solid red circles are the same as defined in Fig. 1. Stars that have been dated are above the grey area. |
| In the text | |
 |
Fig. 5 HR diagrams for stars selected in the thick disk sequence for various ranges in metallicity. The exact range in [Fe/H] is indicated in the legend in the bottom left corner of each plot. The isochrones are the same as in Fig. 4. Stars that have been dated are above the grey area. |
| In the text | |
 |
Fig. 6 Top panel: the general [α/Fe] vs. age distribution for stars in the sample, for all stars having an absolute magnitude Mv < 4.75. Open circles indicate stars which have alpha enhancements consistent with the thick disk but have ages indicative of the thin disk and also lie on the thick disk sequence in the [α/Fe]–[Fe/H] plane. The line divides the thick and thin disk populations. Bottom panel: same stars, the color coding the absolute magnitude of stars is described by the vertical scale. |
| In the text | |
 |
Fig. 7 Top panel: same as Fig. 6, but the open and solid circles represent stars on the thin and thick disks sequences as classified from their distribution in Fig. 1, respectively. Bottom panel: same as above, but color coding based on the metallicity of the stars is indicated by the color bar. |
| In the text | |
 |
Fig. 8 Top panel: [α/Fe] vs. age for stars in the sample. The solid black line separates the thin and thick disk populations. The yellow dots represent the oldest stars that are on the thin disk sequence in the [α/Fe]–[Fe/H] plane (see the lower panel), and for which age could be determined. These objects fall in the part of the age–[α/Fe] distribution that corresponds to the thick disk (above the line). Bottom panel: [α/Fe] vs. [Fe/H] for the same sample and with the symbols indicating the same population of stars as above. This illustrates how the two sequences are separated in this plane. |
| In the text | |
 |
Fig. 9 Metallicity as a function of age for stars in the sample. Symbols as in the top panel of Fig. 8. When thin disk metal-poor stars (yellow dots) are not considered, the age–metallicity relation of thick disk stars (blue solid circles) is obvious. The two objects at [Fe/H] < −1.0 dex and age ~ 9 Gyr are HIP 54641 and HIP 57360. See text for details. |
| In the text | |
 |
Fig. 10 [α/Fe] vs. [Fe/H] for the stars in the sample of Adibekyan et al. for which a robust age could be derived. The color and the size of the symbols both code the age of the stars, to emphasize the age stratification of the distribution of stars within this plane. |
| In the text | |
 |
Fig. 11 Left panel: W component of velocity as a function of [α/Fe] for the stars in the sample (open red circles represent stars on the thin disk sequence; solid red circles represent stars on the thick disk sequence). The two thin and thick black curves are running dispersions for the W component of the velocity of the thin and thick disk sequence stars, calculated as a function of [α/Fe] (over 50 stars). Right panel: W component of velocity as a function of age. Open blue circles represent thin disk stars and solid blue circles represent thick disk stars as defined in Fig. 5. The curve is a running dispersion calculated on 50 stars. |
| In the text | |
 |
Fig. 12 Maximum distance from the galactic plane as function of [α/Fe] abundance (upper plot) and age (lower plot). Open (red or blue) circles represent thin disk stars and solid (red or blue) circles represent thick disk stars as defined in Fig. 5. |
| In the text | |
 |
Fig. 13 Left panel: U component of velocity as a function of [α/Fe] for the stars in the sample (open red circles represent stars on the thin disk sequence; solid red circles represent stars on the thick disk sequence). The two thin and thick curves are running dispersions for U component of the velocity of the thin and thick disk sequence stars, calculated as a function of [α/Fe] (over 50 stars). Right panel: U component of velocity as a function of age. Open blue circles represent thin disk stars and solid blue circles represent thick disk stars as defined in Fig. 5. |
| In the text | |
 |
Fig. 14 Top panel: V component of the velocity as a function of [Fe/H] for the thick disk (solid circles) and thin disk (open circles) populations, as defined in Fig. 6. Middle panel: V component of the velocity as a function of [Fe/H] for thick disk sequence stars in the sample. Bottom panel: V component of the velocity as a function of [Fe/H] for thin disk sequence stars in the sample. In the middle and bottom panels, stars without age determinations are shown as solid grey circles. For stars with age determinations, the color and the size of the symbols indicate the age using the scale given in the color bars shown on the right of each plot. Solid black lines represent the best fit linear regression to the data, with the fit coefficient indicated. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
| In the text | |
 |
Fig. 15 Top panel: V component of the velocity as a function of [α/Fe] for the thick disk (filled circles) and thin disk (open circles) populations, as defined in Fig. 6. Middle panel: V component of the velocity as a function of [αFe] for thick disk sequence stars in the sample. Bottom panel: V component of the velocity as a function of [αFe] for thin disk sequence stars in the sample. In the middle and bottom panels, stars without age determinations are shown as solid grey circles. For stars with age determinations, the color and the size of the symbols indicate the age using the scale given in the color bars shown on the right within each plot. Solid black lines represent the best fit linear regression to the data, with the fit coefficient indicated. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
| In the text | |
 |
Fig. 16 Top panel: V component of the velocity as a function of age for thick and thin disks population stars, as defined in Fig. 6. Middle panel: V component of the velocity as a function of age for thick disk sequence stars. Bottom panel: V component of the velocity as a function of age for thin disk sequence stars. In all panels, the color and the size of the symbols are a function of the star’s [Fe/H] value as indicated by the color bar in each plot. Solid lines represent the best fit linear regression to the data. For the thick disk sequence, only stars in prograde orbits (V > −220 km s-1) have been included in the fit. For thin disk sequence stars, the two points with V < −200 km s-1 have not been included when evaluating the best fit linear regression of the data. |
| In the text | |
 |
Fig. 17 Age–metallicity and age–[α/Fe] distributions, with stars in the metal-poor tail of the thin disk sequence (see Fig. 1) at [Fe/H] < −0.3 dex shown as white dots. The metal-poor thin disk stars draw a sequence parallel to the local thin disk, joining the thick disk at 9−10 Gyr and [α/Fe] in [0.1,0.15]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


