| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321160 | |
| Published online | 28 August 2013 | |
Planck intermediate results. XII: Diffuse Galactic components in the Gould Belt system ⋆
1
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3,
CEA/lrfu, Observatoire de Paris,
Sorbonne Paris Cité, 10 rue Alice Domon et Léonie
Duquet,
75205
Paris Cedex 13,
France
2
Aalto University Metsähovi Radio Observatory,
Metsähovintie 114, 02540
Kylmälä,
Finland
3
African Institute for Mathematical Sciences,
6-8 Melrose Road, Muizenberg,
Cape Town, South
Africa
4
Agenzia Spaziale Italiana Science Data Center, c/o ESRIN, via
Galileo Galilei, Frascati, Italy
5
Agenzia Spaziale Italiana, Viale Liegi 26,
Roma,
Italy
6
Astrophysics Group, Cavendish Laboratory, University of
Cambridge, J J Thomson
Avenue, Cambridge
CB3 0HE,
UK
7
CITA, University of Toronto, 60 St. George St., Toronto, ON
M5S 3H8,
Canada
8
CNR – ISTI, Area della Ricerca, via G. Moruzzi 1,
Pisa,
Italy
9
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
10
California Institute of Technology, Pasadena, California, USA
11
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza
San Juan, 1, planta 2, 44001
Teruel,
Spain
12
Computational Cosmology Center, Lawrence Berkeley National
Laboratory, Berkeley,
California,
USA
13
Consejo Superior de Investigaciones Científicas
(CSIC), Madrid,
Spain
14
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
15
DTU Space, National Space Institute, Technical University of
Denmark, Elektrovej
327, 2800
Kgs. Lyngby,
Denmark
16
Département de Physique Théorique, Université de
Genève, 24 Quai E.
Ansermet, 1211
Genève 4,
Switzerland
17
Departamento de Física Fundamental, Facultad de Ciencias,
Universidad de Salamanca, 37008
Salamanca,
Spain
18
Departamento de Física, Universidad de Oviedo,
Avda. Calvo Sotelo s/n,
Oviedo,
Spain
19
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
20
Department of Electrical Engineering and Computer Sciences,
University of California, Berkeley, California, USA
21
Department of Physics & Astronomy, University of
British Columbia, 6224 Agricultural
Road, Vancouver, British
Columbia, Canada
22
Department of Physics and Astronomy,Dana and David Dornsife
College of Letter, Arts and Sciences, University of Southern California,
Los Angeles, CA
90089,
USA
23
Department of Physics, Gustaf Hällströmin katu 2a, University of
Helsinki, Helsinki,
Finland
24
Department of Physics, University of California,
Santa Barbara, California, USA
25
Department of Physics, University of Illinois at
Urbana-Champaign, 1110 West Green
Street, Urbana,
Illinois,
USA
26
Dipartimento di Fisica e Astronomia G. Galilei, Università degli
Studi di Padova, via Marzolo
8, 35131
Padova,
Italy
27
Dipartimento di Fisica e Scienze della Terra, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
28
Dipartimento di Fisica, Università La Sapienza,
P. le A. Moro 2, Roma, Italy
29
Dipartimento di Fisica, Università degli Studi di
Milano, via Celoria
16, Milano,
Italy
30
Dipartimento di Fisica, Università degli Studi di
Trieste, via A. Valerio
2, Trieste,
Italy
31
Dipartimento di Fisica, Università di Roma Tor
Vergata, via della Ricerca
Scientifica 1, Roma, Italy
32
Dipartimento di Matematica, Università di Roma Tor
Vergata, via della Ricerca
Scientifica 1, Roma, Italy
33
Discovery Center, Niels Bohr Institute,
Blegdamsvej 17, Copenhagen, Denmark
34
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206 La Laguna, Tenerife, Spain
35
European Space Agency, ESAC, Planck Science Office, Camino bajo
del Castillo, s/n, Urbanización Villafranca del Castillo, Villanueva de la
Cañada, Madrid,
Spain
36
European Space Agency, ESTEC, Keplerlaan 1,
2201 AZ
Noordwijk, The
Netherlands
37
Helsinki Institute of Physics, Gustaf Hällströmin katu 2,
University of Helsinki, Helsinki, Finland
38
INAF – Osservatorio Astronomico di Padova, Vicolo
dell’Osservatorio 5, Padova, Italy
39
INAF – Osservatorio Astronomico di Roma, via di Frascati
33, Monte Porzio
Catone, Italy
40
INAF – Osservatorio Astronomico di Trieste, via G.B. Tiepolo
11, Trieste,
Italy
41
INAF Istituto di Radioastronomia, via P. Gobetti
101, 40129
Bologna,
Italy
42
INAF/IASF Bologna, via Gobetti, 101, Bologna, Italy
43
INAF/IASF Milano, via E. Bassini 15, Milano, Italy
44
INFN, Sezione di Bologna, via Irnerio 46,
40126
Bologna,
Italy
45
INFN, Sezione di Roma 1, Universit‘a di Roma
Sapienza, Piazzale Aldo Moro
2, 00185
Roma,
Italy
46
IUCAA, Post Bag 4, Ganeshkhind, Pune University
Campus, 411 007
Pune,
India
47
Imperial College London, Astrophysics group, Blackett
Laboratory, Prince Consort
Road, London,
SW7 2AZ,
UK
48
Infrared Processing and Analysis Center, California Institute of
Technology, Pasadena,
CA
91125,
USA
49
Institut Néel, CNRS, Université Joseph Fourier Grenoble
I, 25 rue des
Martyrs, Grenoble,
France
50
Institut Universitaire de France, 103 bd Saint-Michel, 75005
Paris,
France
51
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, Orsay,
France
52
Institut d’Astrophysique de Paris, CNRS (UMR 7095),
98 bis Boulevard Arago,
75014
Paris,
France
53
Institute for Space Sciences, Bucharest-Magurale,
Romania
54
Institute of Astronomy and Astrophysics, Academia
Sinica, Taipei,
Taiwan
55
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
56 Institute of Theoretical Astrophysics, University of Oslo,
Blindern, Oslo, Norway
57
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, Tenerife, Spain
58
Instituto de Física de Cantabria (CSIC-Universidad de
Cantabria), Avda. de los Castros
s/n, Santander,
Spain
59
Jet Propulsion Laboratory, California Institute of
Technology, 4800 Oak Grove
Drive, Pasadena,
California,
USA
60
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13
9PL, UK
61
Kavli Institute for Cosmology Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
62
Kavli Institute for Theoretical Physics, University of
California, Santa Barbara Kohn
Hall, Santa
Barbara, CA
93106,
USA
63
LAL, Université Paris-Sud, CNRS/IN2P3,
Orsay,
France
64
LERMA, CNRS, Observatoire de Paris, 61 Avenue de
l’Observatoire, Paris, France
65
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
66
Laboratoire Traitement et Communication de l’Information, CNRS
(UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634
Paris Cedex 13,
France
67
Laboratoire de Physique Subatomique et de Cosmologie,Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble cedex,
France
68
Laboratoire de Physique Théorique, Université Paris-Sud 11
& CNRS, Bâtiment
210, 91405
Orsay,
France
69
Lawrence Berkeley National Laboratory,
Berkeley, California, USA
70
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
71
MilliLab, VTT Technical Research Centre of Finland, Tietotie
3, Espoo,
Finland
72
National University of Ireland, Department of Experimental
Physics, Maynooth,
Co. Kildare,
Ireland
73
Niels Bohr Institute, Blegdamsvej 17, Copenhagen, Denmark
74
Optical Science Laboratory, University College
London, Gower
Street, London,
UK
75
SISSA, Astrophysics Sector, via Bonomea 265,
34136
Trieste,
Italy
76
School of Physics and Astronomy, Cardiff University,
Queens Buildings, The Parade,
Cardiff, CF24 3AA, UK
77
Space Sciences Laboratory, University of California,
Berkeley, California, USA
78
Special Astrophysical Observatory, Russian Academy of
Sciences, Nizhnij Arkhyz,
Zelenchukskiy region, 369167
Karachai-Cherkessian Republic,
Russia
79
Stanford University, Dept of Physics, Varian Physics Bldg, 382 via Pueblo
Mall, Stanford,
California,
USA
80
UPMC Univ Paris 06, UMR 7095, 98bis Boulevard Arago, 75014
Paris,
France
81
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
82
Universities Space Research Association, Stratospheric Observatory
for Infrared Astronomy, MS
232-11, Moffett
Field, CA
94035,
USA
83
University of Granada, Departamento de Física Teórica y del
Cosmos, Facultad de Ciencias, Granada, Spain
84
University of Miami, Knight Physics Building, 1320
Campo Sano Dr. Coral Gables,
Florida,
USA
85
Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478
Warszawa,
Poland
Received:
24
January
2013
Accepted:
31
May
2013
We perform an analysis of the diffuse low-frequency Galactic components in the southern part of the Gould Belt system (130° ≤ l ≤ 230° and −50° ≤ b ≤ −10°). Strong ultra-violet flux coming from the Gould Belt super-association is responsible for bright diffuse foregrounds that we observe from our position inside the system and that can help us improve our knowledge of the Galactic emission. Free-free emission and anomalous microwave emission (AME) are the dominant components at low frequencies (ν < 40 GHz), while synchrotron emission is very smooth and faint. We separated diffuse free-free emission and AME from synchrotron emission and thermal dust emission by using Planck data, complemented by ancillary data, using the correlated component analysis (CCA) component-separation method and we compared our results with the results of cross-correlation of foreground templates with the frequency maps. We estimated the electron temperature Te from Hα and free-free emission using two methods (temperature-temperature plot and cross-correlation) and obtained Te ranging from 3100 to 5200K for an effective fraction of absorbing dust along the line of sight of 30% (fd = 0.3). We estimated the frequency spectrum of the diffuse AME and recovered a peak frequency (in flux density units) of 25.5 ± 1.5 GHz. We verified the reliability of this result with realistic simulations that include biases in the spectral model for the AME and in the free-free template. By combining physical models for vibrational and rotational dust emission and adding the constraints from the thermal dust spectrum from Planck and IRAS, we are able to present a good description of the AME frequency spectrum for plausible values of the local density and radiation field.
Key words: Galaxy: general / radio continuum: ISM / radiation mechanisms: general
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The wide frequency coverage of the Planck1 data provides a unique opportunity of studying the main four Galactic foregrounds, namely free-free emission, synchrotron emission, anomalous microwave emission (AME), and thermal (vibrational) dust emission. The different frequency spectra of the components and their different spatial morphologies provide a means for separating the emission components. In this paper we apply the correlated component analysis method (CCA, Bonaldi et al. 2006; Ricciardi et al. 2010), which uses the spatial morphology of the components to perform the separation. The local Gould Belt system of current star formation is chosen as a particularly interesting area in which to make an accurate separation of the four foregrounds because of the different morphologies of the components. Gould (1879) first noted this concentration of prominent OB associations inclined at 20° to the Galactic plane. It was next identified as an Hi feature (Davies 1960; Lindblad 1967). Along with velocity data from Hi and CO combined with stellar distances from Hipparcos, the total system appears to be a slowly expanding and rotating ring of gas and dust surrounding a system of OB stars within 500pc of the Sun (Lindblad et al. 1997). A recent modelling of the Gould Belt system by Perrot & Grenier (2003) gives semi-axes of 373 × 233pc inclined at 17° with an ascending node at l = 296° and a centre 104pc distant from us lying at l = 180°. The Gould Belt thickness is 60pc. The stars defining the system have ages younger than 30 × 106yr.
The free-free emission from ionized hydrogen is well-understood (Dickinson et al. 2003). Hα is a good indicator of the emission measure in regions of low dust absorption. Elsewhere a correction has to be applied, which depends on where the absorbing dust lies relative to the Hα emission. The conversion of an emission measure value to a radio brightness temperature at a given frequency requires a knowledge of the electron temperature. Alternatively, an electron temperature can be derived by assuming a value for the dust absorption. Values for the electron temperature of 4000–8000K are found in similar studies (Banday et al. 2003; Davies et al. 2006; Ghosh et al. 2012). Radio recombination-line observations on the Galactic plane (Alves et al. 2012) give values that agree with those of individual Hii regions, having temperatures that rise with increasing distance from the Galactic centre; the value at the solar distance where the current study applies is 7000–8000K.
The spectrum of synchrotron emission reflects the spectrum of the cosmic-ray electrons trapped in the Galactic magnetic field. At frequencies below a few GHz the brightness temperature spectral index, βs, is ranging from −2.5 to −2.7 (Broadbent et al. 1989). Between 1.0 GHz and WMAP and Planck frequencies, the spectral index steepens to values from −2.9 to −3.1 (Banday et al. 2003; Davies et al. 2006; Kogut et al. 2011).
Thermal dust dominates the Galactic emission at Planck frequencies above 100 GHz. The spectrum is well-defined here with temperature Td ≈ 18K and spectral index βd ranging from 1.5 to 1.8 (Planck Collaboration 2011c). In the frequency range 60–143 GHz the dust emission overlaps that of the free-free emission and AME, making it a critical range for component separation.
The AME component is highly correlated with the far infra-red dust emission (Kogut 1996; Leitch et al. 1997; Banday et al. 2003; Lagache 2003; de Oliveira-Costa et al. 2004; Finkbeiner et al. 2004a; Davies et al. 2006; Dobler & Finkbeiner 2008a; Miville-Deschênes et al. 2008; Ysard et al. 2010; Gold et al. 2011; Planck Collaboration 2011d) and is believed to be the result of electric dipole radiation from small spinning dust grains (Erickson 1957; Draine & Lazarian 1998) in a range of environments (Ali-Haïmoud et al. 2009; Ysard & Verstraete 2010). AME is seen in individual dust clouds associated with molecular clouds, photo-dissociation regions, reflection nebulae and Hii regions (e.g., Finkbeiner et al. 2002, 2004b; Watson et al. 2005; Casassus et al. 2006, 2008; Dickinson et al. 2006, 2007, 2009; Scaife et al. 2007, 2010; AMI Consortium et al. 2009; Todorović et al. 2010; Murphy et al. 2010; Planck Collaboration 2011d; Dickinson 2013). In the present study we examine the AME spectrum in more extended regions.
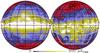 |
Fig.1 Orthographic projection (looking towards the Galactic centre in the left panel and the Galactic anti-centre in the right panel) of the Planck CMB-subtracted 30 GHz channel showing the Gould Belt and the region of interest for this paper (defined by 130° ≤ l ≤ 230° and −50° ≤ b ≤ −10°). |
 |
Fig.2 Gnomonic projections of the region of interest. Top panels: Haslam et al. (1982) 408 MHz map (left); Hα map from Dickinson et al. (2003) (middle); and 100 map from Schlegel et al. (1998) (right) at native resolution. Middle panels (left to right): Planck CMB-subtracted 30, 44, and 70 GHz maps at 1° resolution. Bottom panels (left to right): Planck CMB-subtracted 143, 353, and 857 GHz at 1° resolution. |
2. Definition of the region of interest and aim of the work
The projection of the Gould Belt disc on the sky is a strip that is superimposed on the Galactic plane, except towards the Galactic centre (northern Gould Belt) and around l = 180° (southern Gould Belt). In this work we consider the southern Gould Belt, which can be approximately defined by Galactic coordinates 130° ≤ l ≤ 230° and −50° ≤ b ≤ −10° (see Fig. 1). This choice gives us a cleaner view of the Gould Belt, because the background emission from the Galactic plane is weaker here than towards the Galactic centre. Notable structures within the region are the Orion complex, Barnard’s arc and the Taurus, Eridanus, and Perseus star-forming complexes. All these emitting regions, including the diffuse emission from the Eridanus shell at −50° < b < −30°, are at a distance within 500pc from us and thus they belong to the local inter-stellar medium (ISM) associated with the Gould Belt (e.g. Reynolds & Ogden 1979; Boumis et al. 2001).
In Fig. 2 we show the CMB-subtracted Planck data at 1° resolution, compared with the Haslam et al. (1982) 408 MHz map, which mostly traces the synchrotron component, the Dickinson et al. (2003) Hα map, tracing free-free emission, and the 100 map from Schlegel et al. (1998), tracing the dust emission. The visual inspection reveals dust-correlated features at low frequency, which could be attributed to AME. There is also prominent free-free emission, especially strong in the Barnard’s arc region (towards l = 207°,b = −18°). The synchrotron component appears to be sub-dominant with respect to the free-free emission and the AME.
This work aims at separating and studying the diffuse low-frequency foregrounds, in particular AME and free-free emission, in the region of interest. This requires estimating the spectral behaviour of the AME (carried out in Sect. 4). We compare this spectrum with predictions for spinning dust emission, one of the mechanisms that is most often invoked to explain AME (Sect. 7). After reconstructing the free-free emission, we estimate the free-free electron temperature (Sect. 6), which relates free-free brightness to emission measure, and investigate the dependence of this result on the dust absorption fraction.
3. Description of the analysis
3.1. Input data
Planck (Tauber et al. 2010; Planck Collaboration 2011a) is the third-generation space mission that measures the anisotropy of the cosmic microwave background (CMB). It observes the sky in nine frequency bands covering 30–857 GHz with high sensitivity and angular resolution from 31′ to 5′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1K. Polarization is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration 2011b). Two data-processing centres (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for galactic and extragalactic astrophysics as well as cosmology. Early astrophysics results are given in Planck Collaboration 2011c,d,e,f, 2013b, based on data taken between 13 August 2009 and 7 June 2010. Intermediate astrophysics results are now being presented in a series of papers based on data taken between 13 August 2009 and 27 November 2010.
The Planck data used throughout this paper are an internal data set known as DX7, whose properties are described in appendices to the LFI and HFI data processing papers (Planck Collaboration 2013a,b). However, we have tested the analysis to the extent that the results will not change if carried out on the maps that have been released to the public in March 2013.
Summary of Planck data.
The specifications of the Planck maps are reported in Table 1. The dataset used for the analysis consists of full-resolution frequency maps and the corresponding noise information. We indicate whenever the CMB-removed version of this dataset was used for display purposes.
When analysing the results, we applied a point source mask based on blind detection of sources above 5σ in each Planck map, as described in Zacchei et al. (2011) and Planck HFI Core Team (2011b). Ancillary data were used throughout the paper for component-separation purposes, to simulate the sky and data, or to analyse our results. The full list of ancillary data is reported in Table 2 with the main specifications.
Summary of ancillary data.
3.2. Components
The main diffuse components present in the data are CMB and Galactic synchrotron emission, free-free emission, thermal dust emission, and AME. The frequency spectrum of the CMB component is well-known: it is accurately described by a black-body with a temperature TCMB = 2.7255K (Fixsen 2009).
Thermal dust emission dominates at high frequencies. Its spectral behaviour is a
superposition of modified black-body components identified by temperature
Tdust and emissivity index βd:
![\begin{eqnarray} T_{\rm RJ,dust} (\nu)\propto \nu^{\hbox{\hglue0.7pt}{\beta_{\rm d}+1}}/[\exp(h\nu/kT_{\rm dust})-1] \label{dust}, \end{eqnarray}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq32.png) (1)where
k is the Boltzmann constant and h is the Planck
constant. In the approximation of a single component, over most of the sky we have
Tdust ≈ 18K and βd of 1.5–1.8
(Finkbeiner et al. 1999; Planck Collaboration 2011c,f).
(1)where
k is the Boltzmann constant and h is the Planck
constant. In the approximation of a single component, over most of the sky we have
Tdust ≈ 18K and βd of 1.5–1.8
(Finkbeiner et al. 1999; Planck Collaboration 2011c,f).
The frequency spectrum of the free-free component is often described by a power-law with
spectral index −2.14 in RJ units. A more accurate description (see, e.g. Planck Collaboration 2011d) is given by 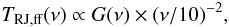 (2)where
G = 3.96(T4)0.21(ν/40)-0.14
is the Gaunt factor, which is responsible for the departure from a pure power-law
behaviour. T4 is the electron temperature
Te in units of 104K
(Te can range over 2000–20000K, but for most of the ISM it
is 4000–15000K).
(2)where
G = 3.96(T4)0.21(ν/40)-0.14
is the Gaunt factor, which is responsible for the departure from a pure power-law
behaviour. T4 is the electron temperature
Te in units of 104K
(Te can range over 2000–20000K, but for most of the ISM it
is 4000–15000K).
The spectral behaviour of synchrotron radiation can be described to first order by a power-law model with spectral index βs that typically assumes values from −2.5 to −3.2, depending on the position in the sky. Steepening of the synchrotron spectral index with frequency is expected due to energy losses of the electrons.
The frequency scaling of the AME component is the most poorly constrained. The distinctive feature is a peak around 20–40 GHz (Draine & Lazarian 1998; Dobler & Finkbeiner 2008b; Dobler et al. 2009; Hoang et al. 2011). However, a power-law behaviour is compatible with most detections above 23 GHz (Banday et al. 2003; Davies et al. 2006; Ghosh et al. 2012). This could be the result of a superposition of several peaked components along the line of sight or could indicate a peak frequency lower than 23 GHz. The most recent WMAP 9-yr results quote a peak frequency at low latitudes ranging from 10 to 20 GHz for the spectrum in KR−J units, which means 20–30 GHz when considering flux density units.
3.3. Component separation pipeline
Several component-separation methods adopt the linear-mixture data model (see
Appendix A for a full derivation). For each line
of sight we write  (3)where
x and n contain the data
and the noise signals. They are vectors of dimension Nd, which
is the number of frequency channels considered. The vector
s, with the dimension Nc,
contains the Nc unknown astrophysical components (e.g. CMB,
dust emission, synchrotron emission, free-free emission, AME) and the
Nd × Nc matrix
H, called the mixing matrix, contains the frequency scaling of
the components for all frequencies. The elements of the mixing matrix are computed by
integrating the source emission spectra within the instrumental bandpass. When working in
the pixel domain, Eq. (3) holds under the
assumption that the instrumental beam is the same for all frequency channels. In the
general case, this is achieved by equalizing the resolution of the data maps to the lowest
one. When working in the harmonic or Fourier domain, the convolution for the instrumental
beam is a multiplication and is linearized without assuming a common resolution.
(3)where
x and n contain the data
and the noise signals. They are vectors of dimension Nd, which
is the number of frequency channels considered. The vector
s, with the dimension Nc,
contains the Nc unknown astrophysical components (e.g. CMB,
dust emission, synchrotron emission, free-free emission, AME) and the
Nd × Nc matrix
H, called the mixing matrix, contains the frequency scaling of
the components for all frequencies. The elements of the mixing matrix are computed by
integrating the source emission spectra within the instrumental bandpass. When working in
the pixel domain, Eq. (3) holds under the
assumption that the instrumental beam is the same for all frequency channels. In the
general case, this is achieved by equalizing the resolution of the data maps to the lowest
one. When working in the harmonic or Fourier domain, the convolution for the instrumental
beam is a multiplication and is linearized without assuming a common resolution.
Within the linear model, we can obtain an estimate ŝ of the
components s through a linear mixture of the data:
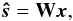 (4)where
W is called the reconstruction matrix. Suitable reconstruction
matrices can be obtained from the mixing matrix H. For example,
(4)where
W is called the reconstruction matrix. Suitable reconstruction
matrices can be obtained from the mixing matrix H. For example,
![\begin{eqnarray} \label{gls} {\bf W}=[{\bf H}^{\rm T}{\bf C}_{\rm n}^{-1}{\bf H}]^{-1}{\bf H}^{\rm T}{\bf C}_{\rm n}^{-1} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq54.png) (5)is
called the generalized least-squares (GLS) solution and only depends on the mixing matrix
and on the noise covariance Cn.
(5)is
called the generalized least-squares (GLS) solution and only depends on the mixing matrix
and on the noise covariance Cn.
The mixing matrix is the key ingredient of component separation. However, as discussed in Sect. 3.2, the frequency spectra of the components are not known with sufficient precision to perform an accurate separation. To overcome this problem, our component-separation pipeline implements a first step in which the mixing matrix is estimated from the data and a second one in which this result is exploited to reconstruct the amplitudes of the components.
3.3.1. Estimating the mixing matrix
To estimate the mixing matrix we relied on the CCA (Bonaldi et al. 2006; Ricciardi et al. 2010), which exploits second-order statistics of the data to estimate the frequency scaling of the components on defined regions of the sky (sky patches). We used the harmonic-domain version of the CCA, whose basic principles of operation are reported in Appendix A. This code works on square sky patches using Fourier transforms. It exploits the data auto- and cross-spectra to estimate a set of parameters describing the frequency scaling of the components. The patch-by-patch estimation prevents the detection of small-scale spatial variations of the spectral properties. On the other hand, by using a large number of samples we retain more information, which provides good constraints, even when the components have similar spectral behaviour. The CCA has been successfully used to separate the synchrotron, free-free and AME components from WMAP data in Bonaldi et al. (2007).
We used a patch size of 20° × 20°, obtained as a trade-off between having enough statistics for a robust computation of the data cross-spectra and limited spatial variability of the foreground properties. Given the dimension of the region of interest, we have ten independent sky patches. However, exploiting a redundant number of patches, widely overlapping each other, enables us to eradicate the gaps between them and obtain a result that is independent of any specific selection of patches. We covered the region of interest with patches spaced by 2° in both latitude and longitude. By re-projecting the results of the CCA on a sphere and averaging the outputs for each line of sight, we can synthesize smooth, spatially varying maps of the spectral parameters (see Ricciardi et al. 2010 for more details).
3.3.2. Reconstruction of the component amplitudes
The amplitudes were reconstructed in pixel space at 1° resolution using
Eqs. (4) and (5), exploiting the output of the previous
step. To equalize the resolution of the data maps, the
aℓm of each map were multiplied by a
window function, 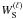 ,
given by a 1° Gaussian beam divided by the instrumental beam of the
corresponding channel (assumed to be Gaussian with a full width half maximum (FWHM) as
specified in Table 1). This corresponds, in real space, to a convolution with a beam
BS. To obtain an estimate of the corresponding noise after
smoothing, the noise variance maps should be convolved with
BN = (BS)2. We did
this again in harmonic-space, after obtaining the window function
,
given by a 1° Gaussian beam divided by the instrumental beam of the
corresponding channel (assumed to be Gaussian with a full width half maximum (FWHM) as
specified in Table 1). This corresponds, in real space, to a convolution with a beam
BS. To obtain an estimate of the corresponding noise after
smoothing, the noise variance maps should be convolved with
BN = (BS)2. We did
this again in harmonic-space, after obtaining the window function
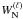 ,
corresponding to BN, by Legendre-transforming
,
corresponding to BN, by Legendre-transforming
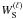 ,
squaring the result, and Legendre-transforming back.
,
squaring the result, and Legendre-transforming back.
The smoothing process also correlates noise between different pixels, which means that the rms per pixel obtained as detailed above is not a complete description of the noise properties. However, estimating of the full covariance of noise (and its propagation through the separation in Eqs. (4) and (5)) is very computationally demanding. In this work we took into account only the diagonal noise covariance and neglected any correlation between noise in different pixels. In a signal-dominated case, such as the one considered here, the errors on the noise model have only a weak impact on the results.
4. AME frequency spectrum
We modelled the mixing matrix to account for five components: the CMB, the synchrotron emission, the thermal dust emission, the free-free emission, and the AME. We neglected the CO component by excluding the 100 and 217 GHz Planck channels from the analysis, which are significantly contaminated by the CO lines J = 1 → 0 and J = 2 → 1, respectively (Planck HFI Core Team 2011b). CO is also present at 353 GHz, where it can contaminate the dust emission by up to 3% in the region of interest, and at 545 and 857 GHz, where the contamination is negligible. To estimate the mixing matrix we used the following datasets
-
the Planck 30, 44, 70, 143 and353 GHz channels,
-
the WMAP 7-yr K band (23 GHz),
-
the Haslam et al. 408MHz map,
-
the predicted free-free emission at 23 GHz based on the HαDickinson et al. (2003) template corrected for dust absorption with the Schlegel et al. (1998)E(B − V) map by assuming a dust absorption fraction of 0.33.
We verified that including the WMAP Ka-W bands in this analysis did not produce appreciable changes in the results. The explored frequency range is now covered by Planck data with higher angular resolution and sensitivity. Caution is needed when using Hα as a free-free tracer: dust absorption (Dickinson et al. 2003) and scattering of Hα photons from dust grains (Wood & Reynolds 1999; Dong & Draine 2011) cause dust-correlated errors in the free-free template, which could bias the AME spectrum. The impact of such biases was assessed through simulations as described in Sect. 4.1.
For dust emission we used the model of Eq. (1) with Td = 18K and estimated the dust spectral index βd. The reason why we fixed the dust temperature is that this parameter is mostly constrained by high-frequency data, which we do not include in this analysis. In fact, a single modified black-body model with constant βd only poorly describes the dust spectrum across the frequency range covered by Planck. In particular, βd is derived to be flatter in the microwave (ν ≤ 353 GHz) than in the millimetre range (ν > 353 GHz).
The temperature Td = 18K we adopted is consistent with the
one-component dust model by Finkbeiner et al. (1999)
and agrees well with the median temperature of 17.7K estimated at
|b| > 10° by Planck Collaboration (2011c). For the dust spectral index we obtained
βd = 1.73 ± 0.09. For synchrotron radiation we adopted a
power-law model with a fixed spectral index βs = −2.9 (e.g.,
Miville-Deschênes et al. 2008), because the
weakness of the signal prevented a good estimation of this parameter. We verified that
different choices for βs (up to a 10% variation,
βs from –2.6 to –3.2) changed the results for the other
parameters only by about 1%, due to the weakness of the synchrotron component with respect
to the AME and thermal dust. As a spectral model for the AME we adopted the best-fit model
of Bonaldi et al. (2007), which is a parabola in the
log (S)-log (ν) plane parametrized in terms of peak
frequency νp2 and slope at
60 GHz m60: 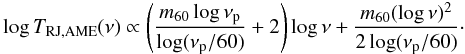 (6)Details
of the model and justification of this choice are given in Appendix B. We also tested a pure power-law model
(TRJ,AME(ν) ∝ να)
for AME, fitting for the spectral index α, but we were unable to obtain
valid estimates in this case. This is what we expect when the true spectrum presents some
curvature, as verified through simulations (see Sect. 4.1 and Appendix C).
(6)Details
of the model and justification of this choice are given in Appendix B. We also tested a pure power-law model
(TRJ,AME(ν) ∝ να)
for AME, fitting for the spectral index α, but we were unable to obtain
valid estimates in this case. This is what we expect when the true spectrum presents some
curvature, as verified through simulations (see Sect. 4.1 and Appendix C).
 |
Fig.3 CCA estimates of the AME frequency spectrum in the region of interest for real data (left panels) and simulated data (right panels). Top: estimated spectra including 1σ errors. Middle and bottom: histograms of the spectral parameters m60 and νp on Nside = 16 estimated spectral index maps. For the simulated case (right panels) we considered two convex spectra peaking at 19 GHz and 26 GHz and a power-law model. Top right: the true inputs are shown as solid black lines (power-law) with triangles (19 GHz peak) and squares (26 GHz peak) and the estimates as shaded areas. The blue and red colours show estimates derived by exploiting the free-free templates FF1 and FF2 described in Appendix C. Middle and bottom-right panels: the true inputs are shown as solid and dotted vertical lines for the simulations peaking at 26 GHz and 19 GHz respectively; the blue dot-dashed and red solid histograms show the estimates obtained using the FF1 and FF2 templates, and the black dashed lines show the estimates for the 19 GHz input spectrum. |
Our results for the AME spectrum are shown in the left panels of Fig. 3. On average, the AME peaks at 25.5 GHz, with a standard deviation of 0.6 GHz, which is within estimation errors (1.5 GHz). This means we find no significant spatial variations of the spectrum of the AME in the region of the sky considered here. However, we recall that this only applies to diffuse AME, because our pipeline cannot detect small-scale spatial variations, and we are restricted to a limited area of the sky.
Our results on the peak frequency of the AME are similar to those of Planck Collaboration (2011d) for Perseus and ρ Ophiuchi. The WMAP 9-yr MEM analysis (Bennett et al. 2012) measures the position of the peak for the spectrum in KR−J units and finds a typical value of 14.4 GHz for diffuse AME at low latitudes, which roughly corresponds to 27 GHz when the spectrum is in flux density units. According to previous work, at higher latitudes the peak frequency is probably lower (see e.g. Banday et al. 2003; Davies et al. 2006; Ghosh et al. 2012). Interestingly, the same CCA method used in this paper yields νp around 22 GHz when applied to the North Celestial Pole region (towards l = 125°, b = 25°, Bonaldi & Ricciardi 2012). Spatial variations of the physical properties of the medium could explain these differences.
In the hypothesis of spinning dust emission, there are many ways to achieve a shift in the peak frequency. Because the available data do not allow us to distinguish between them, we just mention two main possibilities. The first is a change in the density of the medium, lower densities being associated with lower peak frequencies (see also Table B.1). Indeed, the AME spectrum is modelled with densities of 0.2–0.4cm-3 in Bonaldi & Ricciardi (2012), while it requires higher densities in the Gould Belt region, as discussed in Sect. 7. The second possibility is a change in the size distribution of the dust grains, smaller sizes yielding higher peak frequencies. We return to these aspects in Sect. 7.
4.1. Assessment through simulations
The reliability of our results has been tested with simulations. The main purposes of this assessment are
-
to verify the ability of our procedure to accurately recover theAME spectrum for different input models and
-
to investigate how the use of foreground templates – free-free in particular – can bias the results.
We assessed this by applying the procedure described in Sect. 4 to sets of simulated data, whose true inputs are known. For the first target, we performed three separate simulations including a different AME model: two spinning-dust models, peaking at 19 GHz and 26 GHz, and a spatially varying power-law. For the second target, we introduced dust-correlated biases in the free-free template and quantified their impact on the estimated parameters. The full description of the simulations and of the tests performed is given in Appendix C.
The results are displayed in the right panels of Fig. 3. In the top panel we show the true spectrum (solid line) and the estimated spectrum with errors (shaded area) for each of the three tested input models. The red and blue areas distinguish between two free-free templates (referred to as FF1 and FF2), which are biased in a different way with respect to the simulated free-free component. In the middle and bottom panels we show the histograms of the recovered spectral parameters compared with the true inputs (vertical lines); the red and blue colours are as before. We conclude the following:
-
If the input AME is a convex spectrum, we are able to accuratelyrecover the peak frequency, νp, for both the 19 and26 GHz input values. Our pipeline is able todistinguish very clearly between the two input models; biases inthe free-free template do not affect the recovery of the peakfrequency.
-
The estimated spectrum can be slightly biased above 40–50 GHz, where the AME is faint, as a result of limitations of the spectral model we used (see Appendix B) and errors in the free-free template. The systematic error on m60 is quantified as 0.5–0.6.
-
If the input AME spectrum is a power-law, we obtain a good recovery when fitting for a spectral index.
When the AME is a power-law, the parabolic model is clearly wrong, because the parameter describing the position of the peak is completely unconstrained and the model steepens considerably with frequency. Similarly, when the AME is a curved spectrum, the power-law model is too inaccurate to describe it. As expected, both these estimates fail to converge. We note that the distribution of m60 recovered on real data is quite different from that obtained from the simulation. This could indicate spatial variability of the true spectrum, which is not included in the simulation. It could also indicate that the systematic errors on m60 predicted by simulations, as we just described, are different in different regions of the sky, thus creating a non-uniform effect.
5. Reconstruction of the amplitudes
 |
Fig.4 1° resolution reconstruction at 30 GHz of (from left to right): synchrotron emission; free-free emission; AME; and thermal dust emission. These reconstructions are performed as described in Sect. 3.3.2. Rows from top to bottom: component amplitudes; noise rms; predicted rms of component separation error due to the estimation of AME and thermal dust spectra; and predicted rms of component separation error including a random error on βs = −2.9 ± 0.1. |
 |
Fig.5 Validation of the reconstructed components shown in Fig. 4. Left panels: sum of the components vs frequency maps at 30, 44, and 70 GHz (from top to bottom). The line is the x = y relation. Right panels: pixel distribution of the residual (frequency map-sum of the components) maps compared with the best-fit Gaussian distribution. |
We reconstructed the amplitude of the components on the 1° resolution version of the dataset. We used the same frequencies as for estimating the mixing matrix, except for the free-free template, which was excluded to avoid possible biases in the reconstruction. The results are shown in Fig. 4. The first and second rows show the components reconstructed at 30 GHz (from left to right: synchrotron emission, free-free emission, AME, and thermal dust emission) and the corresponding noise rms maps. Thanks to the linearity of the problem, the noise variance maps can be obtained by combining the noise variance maps of the channels at 1° degree resolution with the squared reconstruction matrix W. The noise on the synchrotron and thermal dust maps is low compared with that for free-free and AME. This is because the 408MHz map and the Planck 353 GHz channel constrain well the amplitudes of synchrotron and thermal dust emission.
The AME component is correlated at about 60% and 70% with the 100 and the E(B − V) dust templates by Schlegel et al. (1998), at about 40% with Haslam et al. (1982) 408 MHz and at about 20% with Hα. This favours emission mechanisms based on dust over other hypotheses, such as curved synchrotron emission and free-free emission. The E(B − V) template correlates better with thermal dust emission than the 100 map (the correlation coefficients are 0.73 ± 0.01 and 0.96 ± 0.01, respectively). This is expected if AME is dust emission. In fact, both spinning dust and thermal dust emission are proportional to the column density, for which E(B − V) is a better estimator than the 100 emission, which is strongly affected by the dust temperature.
 |
Fig.6 Estimated spectra of synchrotron emission (dashed line), free-free emission (solid line), thermal dust emission (dash-dotted line), and AME (dotted line) for average local properties (top) and for Barnard’s region (bottom). |
The errors due to the separation process (third and fourth row of Fig. 4) are obtained by propagating via a Monte-Carlo simulation the uncertainties on the mixing matrix estimated by CCA to the reconstruction of the components (see Ricciardi et al. 2010, for more details). Essentially, the mixing matrix parameters are randomized according to their posterior distributions; the component separation error on the amplitudes is estimated to be the variance of GLS reconstructions for different input mixing matrices.
One complication is that we did not estimate the synchrotron spectral index, but fixed it at βs = −2.9. Thus, we do not have errors on the synchrotron spectral index from our analysis. We therefore considered two cases: one in which we propagated only the errors on the AME and thermal dust spectral parameters, thus assuming no error on βs (third row of Fig. 4), and another in which we included an indicative random error Δβs = 0.1 (last row of Fig. 4).
The predicted error due to separation is generally higher than noise and on average of about 15–20% of the component amplitude for AME, free-free, and dust emission. Once we allow some scatter on βs, the predicted error on synchrotron emission becomes about 50%: this indicates that the reconstruction of this component is essentially prior-driven. The inclusion of Δβs has some effect on the error prediction for free-free emission, while AME and dust emission are mostly unaffected.
To evaluate the quality of the separation we compared the frequency maps with the sum of the reconstructed components at the same frequency. In the left panels of Fig. 5 we plot the sum of the components for 30, 44, and 70 GHz against the amplitude of the frequency map. The comparison is made at 1° resolution with Nside = 128 pixels. The dashed line indicates the x = y relation, which corresponds to the ideal case in which the two maps are identical.
The agreement between data and predictions is in general very good. The scatter of the points does not measure the quality of the separation, but the signal-to-noise ratio of the maps. It increases from 30 to 70 GHz, as the foreground signal becomes weaker. The errors in the component separation show up as systematic departures of the data from the prediction. Because those are not apparent, we also show on the right panels of Fig. 5 the pixel distribution of the residual map compared with the best-fit Gaussian distribution. At 44 and 70 GHz the scatter, though quite small, dominates the residual and covers the systematic effects, with the exception of a few outliers, mostly due to compact sources. At 30 GHz the scatter is low enough to reveal a feature: a sub-sample of pixels in which the reconstructed signal is higher than the true one, thus creating a negative in the residual.
This kind of systematic effect is very difficult to avoid when separating many bright components, because small errors in the mixing matrix cause bright features in the residual maps. Our Monte Carlo approach is able to propagate these errors however. At 30 GHz the brightest components are AME and free-free emission, for which the predicted component separation error is on average 0.04–0.05mKCMB, in agreement with the level of the non-Gaussian residuals. Coherent structures in the residual maps are induced by the low resolution of the maps of spectral parameters, which means that over nearby pixels the error in the mixing matrix, and thus on the separation, is similar.
In Fig. 6 we show the amplitude of the components as a function of frequency. The top panel represents the typical behaviour in the Gould Belt, while the bottom one refers to a particular case, Barnard’s region, where free-free emission is particularly strong. The points are the average amplitude of the components at each frequency within the selected regions of the sky. The scaling of the amplitudes with frequency is, by construction, given by the spectral model estimated with CCA. The error bars measure the scatter induced on the amplitudes by the errors on the spectral parameters (also including Δβs = 0.1).
6. Free-free electron temperature
The intensity of the free-free emission at a given frequency with respect to
Hα can be expressed as ![\begin{eqnarray} \frac{T_{\rm ff}(\nu)[\mu {\rm K}_{\rm R-J}]}{\rm{H}{\alpha}[\rm Rayleighs]}=14\, T_4^{0.517} \times 10^{0.029/T_4}\times 1.08 \, G(\nu)(\nu/10)^{-2}, \label{ff2halpha} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq93.png) (7)where
G(ν) is the Gaunt factor already introduced in Sect. 3.2 and T4 is the electron temperature
Te in units of 104K. In the previous equation,
Hα has been corrected for dust absorption. Following Dickinson et al. (2003), the correction depends on
fd, the effective dust fraction in the line of sight that
absorbs the Hα. Therefore fd and
Te are degenerate parameters.
(7)where
G(ν) is the Gaunt factor already introduced in Sect. 3.2 and T4 is the electron temperature
Te in units of 104K. In the previous equation,
Hα has been corrected for dust absorption. Following Dickinson et al. (2003), the correction depends on
fd, the effective dust fraction in the line of sight that
absorbs the Hα. Therefore fd and
Te are degenerate parameters.
The ratio Tff(ν)/Hα can be obtained by comparing the Hα and free-free emission from component separation through a temperature-temperature plot (T-T analysis). We made free-free versus Hα plots by using the CCA free-free solution at 30 GHz and both the Dickinson et al. (2003) and the Finkbeiner (2003) Hα templates corrected for dust absorption for different values of fd. We considered 3° resolution maps, sampled with Nside = 64 pixels. In addition to point sources, we excluded from the analysis the region most affected by dust absorption based on the Schlegel et al. (1998)E(B − V) map, as shown in the top panel of Fig. 7. The electron temperature Te was inferred by fitting the data points with a linear relation and converting the best-fit slope to Te through Eq. (7). The error on Te was derived from the error on the best-fit slope given by the fitting procedure through error propagation. In the bottom panel of Fig. 7 we show the T-T plots for the Dickinson et al. (2003) Hα template corrected for fd = 0.3 (red points), and the best-fit linear relations to the T-T plots for different values of fd = 0.3 (lines). The electron temperatures are reported in the top part of Table 3. We obtain Te = 5900–3900K with fd = 0–0.5 for the Dickinson template; the Finkbeiner template yields generally higher, but consistent, values (Te = 5800–4300K with fd = 0–0.5).
 |
Fig.7 T-T analysis for the estimation of Te. Top: gnomonic projection showing the mask used (masked pixels are in black, while pixels used in the analysis are in white). Bottom: T-T plot comparing the CCA free-free solution with the Hα template for fd = 0.3 (points) and linear fits to the T-T plots for different values of fd (lines). |
Inferred Te [K] for the T-T and C-C analysis using different Hα templates and dust absorption fractions fd.
 |
Fig.8 Comparison between correlation coefficients (symbols with error bars) and component separation results (shaded areas) for free-free emission (top) and dust emission (bottom). For free-free emission we show the Dickinson et al. (2003) Hα correlation coefficients and for dust emission the Finkbeiner et al. (1999) correlation coefficients. The grey area in the bottom panel is the sum of the AME (blue) and thermal dust (red) components. The dash-dotted line in both panels shows the 1σ error due to the chance correlation of CMB with foreground templates, estimated using simulations. |
6.1. Comparison of the cross-correlation with templates
An alternative way of computing Tff(ν)/Hα and Te is through cross-correlation of the Hα template with frequency maps (C-C analysis). We simultaneously cross-correlated the templates for free-free, dust, and synchrotron emission, as described in Ghosh et al. (2012). We used the 408MHz map from Haslam et al. (1982) as a tracer of synchrotron emission, the Dickinson et al. (2003) Hα as a tracer of free-free emission, and the Finkbeiner et al. (1999) model eight 94 GHz prediction as a tracer of dust emission. We used the same resolution, pixel size, and sky mask as adopted for the T-T analysis (3° and Nside = 64). As pointed out by Ghosh et al. (2012), at this resolution the template-fitting analysis is more reliable than at 1° because the smoothing reduces artefacts in the templates. The correlation coefficients were computed for each emission process at a given frequency by minimizing the generalized χ2 expression. We also fitted for an additional monopole term that can account for offset contributions in all templates and the data in a way that does not bias the results (Macellari et al. 2011). The chance correlation of the templates with the CMB component in the data causes a systematic error in the correlated coefficients and was estimated using simulations. We generated 1000 random realizations of the CMB using the WMAP best-fit ΛCDM model3 and cross-correlated each of them using the templates with the same procedure applied to the data. The amplitude of the predicted chance correlation, given by the rms over the 1000 realizations, is 1.13μKCMB/μKCMB for the dust template, 1.12μKCMB/R for the free-free template and 3.8μKCMB/K for the synchrotron template.
In the top panel of Fig. 8 we compare the Hα correlation coefficients (points with error bars) with the component separation results for free-free emission obtained in Sect. 5 (shaded area). The flux for both the component separation and cross-correlation was computed as the standard deviation of the maps (the separated free-free map and the scaled Hα template, respectively) because this is not affected by possible offsets between the Planck data and the Hα template. The two results generally agree well; in the frequency range 40–60 GHz there is an excess in the correlated coefficients, which could be indicative of a contribution from the AME component (similar to that found by Dobler & Finkbeiner 2008b). Flattening of the C-C coefficients for ν > 60GHz is consistent with positive chance correlation between the CMB and the Hα template.
The dust-correlated coefficients are compared with the component separation results in the bottom panel of Fig. 8. The agreement is very good for ν < 40 GHz and ν > 100 GHz, where AME and thermal dust emission are strong. In the 40–70 GHz range the C-C results are higher than the component separation results. As discussed in Appendix B, the parametric fit to the AME spectrum implemented by CCA could be inaccurate in this frequency range, where the AME is faint. Alternatively, a similar effect could be explained by the presence of a secondary AME peak, around 40 GHz (e.g. Planck Collaboration 2011d; Ghosh et al. 2012) or flattening of the dust spectral index towards low frequencies, which are not included in our spectral model. Distinguishing between these hypotheses is not possible given the large error bars.
To determine the free-free electron temperature, the Hα correlation coefficients were fitted with a combination of power-law free-free radiation (with a fixed spectral index of −2.14) and a CMB chance correlation term (which is constant in thermodynamic units). The amplitude of the free-free component with respect to Hα resulting from the fit, and its uncertainty, yield Te and the corresponding error bar. The results for the Gould Belt region outside the adopted sky mask are reported in the bottom part of Table 3. We found Te = 5300–2400K for fd = 0–0.5 with the Dickinson et al. (2003) template, and Te = 7000–3800K for fd = 0–0.5 with the Finkbeiner (2003) template.
With respect to the T-T analysis, these results are more sensitive to the choice of the template and the fd correction. Similarly, we expect the C-C analysis to be more sensitive to the other systematic uncertainties on the templates, such as the contribution of scattered light to the Hα map (Witt et al. 2010; Brandt & Draine 2012).
The sensitivity of the C-C analysis to differences between the Dickinson et al. and Finkbeiner templates – the former yielding lower Te than the latter – is a known problem (see Ghosh et al. 2012 for a detailed analysis). The different processing of the two maps results in residuals at the 1R level over large regions of the sky, and of more than 20R near very bright regions. The adopted χ2 estimator, which contains the square of the template in the denominator, tends to amplify the differences.
For this analysis we adopted a 3° resolution, as advised by Ghosh et al. (2012) to reduce artefacts in the templates due to beam effects, and we masked the most discrepant pixels. Still, the best-fit electron temperatures yielded by the two templates may differ by 30%, whereas for the T-T analysis this difference is 10% at most. In fact, the fit of the T-T plot is determined by large samples of pixels, on which the two templates are generally more similar, while the C-C method is more sensitive to bright features, on which they may be more different. We verified that by enlarging the mask to exclude the brightest pixels, the numbers we obtain for the two templates agree better.
The C-C results are always consistent with the T-T ones within the error bars, but they are systematically lower for the Dickinson et al. template. In addition to systematic errors related to methods and templates, a difference between T-T and C-C results could also indicate spatial variability of Te within the region, since the two methods have different sensitivity to different features in the map. This confirms that estimating the free-free electron temperature is a difficult problem and that caution is needed when interpreting the results.
7. AME as spinning-dust emission
An explanation that is often invoked for the AME is electric dipole radiation from small, rapidly spinning, polycyclic aromatic hydrocarbon (PAHs) dust grains (Erickson 1957; Draine & Lazarian 1998; Dobler & Finkbeiner 2008b; Dobler et al. 2009; Hoang et al. 2011).
Alternatively, the AME could be generated by synchrotron radiation with a flat (hard) spectral index (e.g. Bennett et al. 2003). The presence of such a hard spectrum synchrotron component could be highlighted by comparing the 408MHz map of Haslam et al. (1982), which would predominantly trace steep spectrum radiation, with the 2.3 GHz map by Jonas et al. (1998), which would be more sensitive to flat spectrum radiation. This question has been studied in detail by Peel et al. (2012) using a cross-correlation of WMAP 7-yr data with foreground templates. They analysed the region defined by 170° ≤ l ≤ 210°, −55° ≤ b ≤ −25° and found that the dust-correlated coefficients are mostly unaffected by the use of the 2.3 GHz template instead of the 408MHz template. This indicates that hard synchrotron radiation cannot account for most of the dust-correlated component at low frequencies.
To check the hypothesis of spinning dust emission we applied the method proposed by Ysard et al. (2011), which exploits the SpDust (Ali-Haïmoud et al. 2009; Silsbee et al. 2011) and DustEM (Compiègne et al. 2011) codes, to model the frequency spectra of thermal and anomalous dust emission from the microwaves to the IR. The dust populations and properties are assumed to be the same as in the diffuse interstellar medium at high Galactic latitude (DHGL), defined in Compiègne et al. (2010). This model includes three dust populations: PAHs; amorphous carbonaceous grains; and amorphous silicates. For PAHs, it assumes a log-normal size distribution with centroid a0 = 0.64nm and width σ = 0.4, with a dust-to-gas mass ratio MPAH/MH = 7.8 × 10-4.
By fitting the thermal dust spectrum with DustEM we determined the local intensity of the interstellar radiation field, G0 (the scaling factor with respect to a UV flux of 1.6 × 10-3ergs-1cm-2 integrated between 6 and 13.6eV), and the hydrogen column density, NH. We then fitted the AME spectrum with SpDust, the only free parameter being the local hydrogen density nH. We assumed a cosmic-ray ionization rate ζCR = 5 × 10-17s-1H-1, and took the electric dipole moment to be the same as in Draine & Lazarian (1998), a prescription also shown to be compatible with the AME extracted from WMAP data (Ysard et al. 2010). It is worth noticing that there is a degeneracy with the size of the grains (smaller size yields higher peak frequency and intensity of the AME). However, the size distribution can only be constrained using shorter-wavelength data (typically 3–8). The size we adopted (0.64nm) was motivated by its ability to reproduce the data in the mid-IR (Compiègne et al. 2011); other models adopted different sizes (e.g. 0.54nm and 0.5nm in Draine & Li 2001 and 2007 respectively).
Because the Gould Belt region contains strong foreground-emission components, which are significantly correlated with each-other, we expect different environments to be mixed in a complex way. To obtain meaningful results for the physical modelling we tried to isolate sub-regions where single environments dominate. To first order, we can use the free-free emission as a tracer of the ionized gas environment, CO emission as a tracer of molecular gas, and associate the rest of the emission with the diffuse ISM. In Fig. 9 we schematically map the different environments by setting a threshold on the free-free emission coming from component separation, the CO emission from Planck, and the total foreground emission at 30 GHz. We identified two relatively big sub-regions (shown as circles in Fig. 9) as selections that are dominated by ionized gas and diffuse ISM environments. It would not be meaningful to consider smaller areas because of the patch-by-patch estimation of the AME frequency scalings, which means that our AME spectra are averaged over relatively large areas of the sky. Due to the clumpiness of the molecular gas environment it was not possible to select a region for this case. It is worth noting that some molecular gas may be contained in the diffuse ISM region.
 |
Fig.9 Partitioning of the Gould Belt region based on thresholds over free-free emission (red), CO emission (blue), and total emission at 30 GHz (yellow), used as tracers of Hii gas, molecular gas, and diffuse ISM environments, respectively, and the rest of the Gould Belt region (white). Circled regions are those selected for computing the spectra and have been labelled Hii-gas (Barnard’s arc) and diffuse ISM (centred on l = 190°, b = −35°) regions, respectively. |
 |
Fig.10 Frequency spectra (black points with error bars) for thermal dust emission and AME compared, respectively, with DustEM and SpDust (dashed lines) for the diffuse ISM (top) and ionized gas (middle and bottom) regions within the Gould Belt. The solid line is the sum of the DustEM and SpDust models. The grey area in the top and middle panels corresponds to the ± 1σ variations on the best-fit nH values when fitting for a single phase. In the bottom panel we consider a mixture of two phases (nH = 0.1cm-3 and nH = 55cm-3, in the proportion of 46% and 54%, respectively), which marginally improves the fit for the ionized gas region at 23 GHz (the error is 0.3σ instead of 0.9σ ). |
The spectra of the AME and thermal dust in the 20–353 GHz frequency range are based on component-separation results. The frequency scaling is that estimated with CCA and the normalization is given by the average of the reconstructed amplitude map in the region of the sky considered. The error bars on the data points include the rms of the amplitude in the same region (considered as the error in the normalization) and the errors on the estimated spectral parameters. The thermal dust spectra were complemented with higher-frequency data points computed directly from the frequency maps: Planck 545 GHz and 857 GHz; IRIS 100 map; and the IRIS 12 map corrected for zodiacal light emission used in Ysard et al. (2010).
The results of the modelling for the ionized gas and diffuse ISM regions within the Gould Belt are shown in Fig. 10. The empirical spectra of AME coming from component separation can be successfully modelled as spinning-dust emission for both regions. The match between data and model becomes poorer at higher frequencies, where the AME spectrum could be biased (see Sect. C and Appendix B).
The joint fit of thermal and spinning-dust models yields plausible physical descriptions of the two environments. In the top panel of Fig. 10 the diffuse ISM region is modelled with NH = 2.46 × 1021Hcm-2, G0 = 0.55 and nH = 50cm-3. The ionized region (middle panel) is modelled with NH = 5.73 × 1021 Hcm-2, G0 = 0.90 and nH = 25cm-3.
We tested the stability of these results against calibration errors on the high-frequency Planck (545 and 857 GHz) and IRIS (100 and 12) data (the remaining data points come from the component-separation procedure and their error bars include systematic uncertainties).
The total calibration uncertainty on the Planck 545 and 857 GHz channels is estimated to be 10% (Planck Collaboration 2013c), that on the IRIS data is of the order of 10% or larger, especially at 12, where it also includes errors on the zodiacal light subtraction. We verified that very conservative uncertainties up to 20% both on Planck and IRIS data have a negligible impact on G0, while they may affect NH and nH (up to a level of about 10%). The overall picture does not change however: the ionized region is less dense and is illuminated by a stronger radiation field than the diffuse region (which is expected to contain mostly neutral gas). Both spectra can be modelled as spinning-dust emission arising from regions with densities characteristic of the cold neutral medium (CNM, a few tens of H per cm3). This confirms the results of Planck Collaboration (2011d) and Planck Collaboration (2011e), showing that most of the observed AME could be explained by spinning dust in dense gas. In fact, whenever we have a mixture of warm neutral medium (WNM), warm ionized medium (WIM), and CNM, the spinning dust spectrum is dominated by the denser phase, which emits more strongly.
In the bottom panel of Fig. 10 we consider for the ionized region a mixture of two phases, one with a lower density (nH = 0.1cm-3, 46%) and one with a higher density (nH = 55cm-3, 54%), illuminated by the same G0 as in the middle panel. This mixture fits the data somewhat better at 23 GHz than the one-phase model considered previously (the error in the fit at this frequency is 0.3σ instead of 0.9σ). To fully isolate and study different ISM phases (ionized/neutral, dense/diffuse), both the observations and the analysis should be carried out at high angular resolution.
8. Conclusions
We performed an analysis of the diffuse low-frequency Galactic foregrounds as seen by Planck in the southern part (130° ≤ l ≤ 230° and −50° ≤ b ≤ −10°) of the Gould Belt system, a local star-forming region emitting bright diffuse foreground emission. In addition to Planck data, our analysis included WMAP 7-yr data and foreground ancillary data as specified in Table 2.
We used the CCA (Bonaldi et al. 2006; Ricciardi et al. 2010) component separation method to separate the diffuse Galactic foregrounds. In the region of interest the synchrotron component is smooth and faint.
The free-free emission is strong and clearly dominates in the Orion-Barnard region. We inferred the free-free electron temperature both by cross-correlation (C-C) of channel maps with foreground templates and temperature-temperature (T-T) plots comparing the CCA free-free emission with Hα maps. We obtained Te ranging from 3100 to 5200K for fd = 0.3, which broadens to 2400–7000K when we allowed fd to range within 0–0.5. The Finkbeiner (2003) Hα template yielded systematically higher Te than the Dickinson et al. (2003) one. For the T-T analysis the difference is at most 500K (<1σ), while for the C-C analysis it can reach 2000K (within 2σ). The C-C results for the Dickinson et al. template are also systematically lower than the T-T ones, yet consistent within 1σ.
The AME is the dominant foreground emission at the lowest frequencies of Planck over most of the region considered. We estimated the AME peak frequency in flux density units to be 25.5 ± 1.5 GHz, almost uniformly over the region of interest. This agrees with AME spectra measured in compact dust clouds (e.g. Planck Collaboration 2011d) and WMAP 9-yr results at low latitudes (once the same convention is adopted, e.g. their AME spectrum is converted from KR−J to flux density, Bennett et al. 2012). For diffuse AME at higher latitudes a lower peak frequency is favoured (Banday et al. 2003; Davies et al. 2006; Ghosh et al. 2012; Bonaldi & Ricciardi 2012). Spatial variability of the AME peak frequency is expected for spinning dust emission as a result of changes in the local physical conditions. For instance, the observed differences can be modelled in terms of a different density of the medium (lower density at high latitudes causes lower peak frequency) or a different size of the grains (smaller size giving higher peak frequency). The ability of our method to correctly recover the peak frequency of the AME, νp, was verified through realistic simulations. We also considered the effect of systematic errors in the spectral model and in the free-free template and demonstrated that they have only a negligible impact on νp.
Following Peel et al. (2012), a hard (flat spectrum) synchrotron component would not be sufficient to account for the dust-correlated low-frequency emission in this region. In support of the spinning dust mechanism, we performed a joint modelling of vibrational and rotational emission from dust grains as described by Ysard et al. (2011) and obtained a good description of the data from microwaves to the IR. The fit, which we performed separately for the ionized area near to Barnard’s arc and the diffuse emission towards the centre of our region, in both cases yields plausible values for the local density and radiation field. This indicates that the spinning-dust mechanism can explain the AME in the Gould Belt reasonably.
Online material
Appendix A: Harmonic-domain CCA
The sky radiation,  ,
from direction r at frequency ν results from the
superposition of signals coming from Nc different physical
processes
,
from direction r at frequency ν results from the
superposition of signals coming from Nc different physical
processes 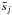 :
:
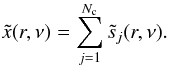 (A.1)The
signal
(A.1)The
signal 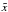 is observed through a telescope, the beam pattern of which can be modelled at each
frequency as a spatially invariant point spread function
B(r,ν). For each value of ν, the
telescope convolves the physical radiation map with B. The
frequency-dependent convolved signal is input to an
Nd-channel measuring instrument, which integrates the signal
over frequency for each of its channels and adds noise to its outputs. The output of the
measurement channel at a generic frequency ν is
is observed through a telescope, the beam pattern of which can be modelled at each
frequency as a spatially invariant point spread function
B(r,ν). For each value of ν, the
telescope convolves the physical radiation map with B. The
frequency-dependent convolved signal is input to an
Nd-channel measuring instrument, which integrates the signal
over frequency for each of its channels and adds noise to its outputs. The output of the
measurement channel at a generic frequency ν is 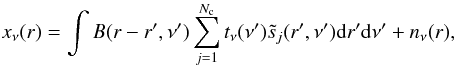 (A.2)where
tν(ν′) is the
frequency response of the channel and
nν(r) is the noise map.
The data model in Eq. (A.2) can be
simplified by virtue of the following assumptions:
(A.2)where
tν(ν′) is the
frequency response of the channel and
nν(r) is the noise map.
The data model in Eq. (A.2) can be
simplified by virtue of the following assumptions:
-
Each source signal is a separable func-tion of direction and frequency, i.e.,
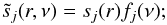 (A.3)
(A.3) -
B(r,ν) = Bν(r)is constant within the bandpass of the measurement channel.
These two assumptions lead us to a new data model: 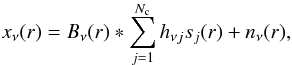 (A.4)where
∗ denotes convolution, and
(A.4)where
∗ denotes convolution, and 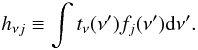 (A.5)For
each location, r, we define
(A.5)For
each location, r, we define
-
the Nc-vector s (sources vector), whose elements are sj(r);
-
the Nd-vector x (data vector), whose elements are xν(r);
-
the Nd-vector n (noise vector), whose elements are nν(r);
-
the diagonal Nd-matrix B, whose elements are Bν(r);
-
the Nd × Nc matrix H, containing all hνj elements.
Then, we can rewrite Eq. (A.4) in
vector form: +\vec{n}(r).\label{vect_m1} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq168.png) (A.6)The
matrix H is called the mixing matrix and contains the frequency
scaling of the components for all the data maps involved.
(A.6)The
matrix H is called the mixing matrix and contains the frequency
scaling of the components for all the data maps involved.
Under the assumption that B does not depend on the frequency,
when working in the pixel domain, we can simplify Eq. (A.6) to  (A.7)where
the components in the source vector s are now convolved
with the instrumental beam.
(A.7)where
the components in the source vector s are now convolved
with the instrumental beam.
Equation (A.6) can be translated into
the harmonic domain, where for each transformed mode it becomes  (A.8)where
X, S, and
N are the transforms of
x, s, and
n, respectively, and
(A.8)where
X, S, and
N are the transforms of
x, s, and
n, respectively, and
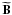 is the
transform of matrix B. Relying on this data model, we can
derive the following relation between the cross-spectra of the data
is the
transform of matrix B. Relying on this data model, we can
derive the following relation between the cross-spectra of the data
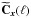 ,
sources
,
sources
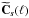 and
noise,
and
noise,
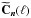 , all
depending on the multipole ℓ:
, all
depending on the multipole ℓ:
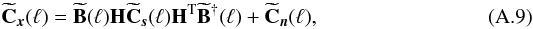 (A.9)where
the dagger superscript denotes the adjoint matrix. To reduce the number of unknowns, the
mixing matrix is parametrized through a parameter vector p
(such that
H = H(p)),
using the fact that its elements are proportional to the spectra of astrophysical
sources (see Sect. 3.2).
(A.9)where
the dagger superscript denotes the adjoint matrix. To reduce the number of unknowns, the
mixing matrix is parametrized through a parameter vector p
(such that
H = H(p)),
using the fact that its elements are proportional to the spectra of astrophysical
sources (see Sect. 3.2).
Since the foreground properties are expected to be spatially variable, we work on relatively small square patches of data. This allows us to use the 2D Fourier transform to approximate the harmonic spectra (see, e.g., Bond & Efstathiou 1987).
The HEALPix (Górski et al. 2005) data on the
sphere are projected on the plane tangential to the centre of the patch and are
re-gridded with a suitable number of bins to correctly sample the original resolution.
Each pixel in the projected image is associated with a specific vector normal to the
tangential plane and assumes the value of the HEALPix pixel nearest to the corresponding
position on the sphere. Clearly, the projection and re-gridding process will create some
distortion in the image at small scales and will modify the noise properties. However,
we verified that this has only a negligible impact on the spectra in Eq. (A.9) for the scales considered in this work
and, therefore, on the spectral parameters. If
x(i,j) contains the data projected on
the planar grid and X(i,j) is its
two-dimensional discrete Fourier transform, the energy of the signal at a certain scale,
which corresponds to the power spectrum, can be obtained as the average of
X(i,j)X†(i,j)
over annular bins 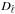 ,
,
 (Bedini & Salerno 2007):
(Bedini & Salerno 2007): 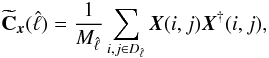 (A.10)where
(A.10)where
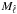 is the number of pairs (i,j) contained in the spectral bin denoted by
is the number of pairs (i,j) contained in the spectral bin denoted by
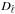 .
Every spectral bin
.
Every spectral bin 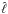 is related to a specific ℓ in the spherical harmonic domain by
is related to a specific ℓ in the spherical harmonic domain by
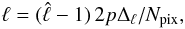 (A.11)where
p is the thickness of the annular bin,
Δℓ = 180/Ldeg(Npix − 1),
and Ldeg, Npix are the size in
degrees and the number of pixels on the side of the square patch, respectively.
(A.11)where
p is the thickness of the annular bin,
Δℓ = 180/Ldeg(Npix − 1),
and Ldeg, Npix are the size in
degrees and the number of pixels on the side of the square patch, respectively.
If we reorder the matrices  and
and  into vectors
into vectors 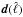 and
and 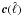 ,
respectively, we can rewrite Eq. (A.9)
as
,
respectively, we can rewrite Eq. (A.9)
as 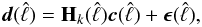 (A.12)where
(A.12)where
![\hbox{${\bf H}_{k}(\hat \ell) = [\widetilde{{\bf B}}(\hat \ell){\bf H}]\otimes[\widetilde{{\bf B}}(\hat \ell){\bf H}]$}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq207.png) , and the symbol ⊗ denotes the
Kronecker product. The vector
, and the symbol ⊗ denotes the
Kronecker product. The vector 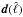 is now computed using the approximated data cross-spectrum matrix in Eq. (A.10) and
is now computed using the approximated data cross-spectrum matrix in Eq. (A.10) and
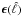 represents the error on the noise power spectrum.
represents the error on the noise power spectrum.
The parameter vector p and the source cross-spectra are
finally obtained by minimizing the functional ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{hcca_objective} \!\!&&\vec{\Phi}[\vec{p},\vec{c}_V]=\\ \!\!&&\!\!\!\![\vec{d}_V-{\bf H}_{kB}(\vec{p})\cdot \vec{c}_V]^{\rm T} {\bf N}_{\epsilon B}^{-1} [\vec{d}_V-{\bf H}_{kB}(\vec{p})\cdot \vec{c}_V]+\lambda \vec{c}_V^{\rm T}{\bf C}\vec{c}_V. \nonumber \end{eqnarray}](/articles/aa/full_html/2013/09/aa21160-13/aa21160-13-eq211.png) (A.13)The
vectors dV and
cV contain the elements
(A.13)The
vectors dV and
cV contain the elements
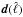 and
and 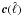 ,
respectively, and the diagonal matrices
HkB and
Nϵ the elements
,
respectively, and the diagonal matrices
HkB and
Nϵ the elements
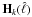 and the covariance of error
and the covariance of error 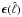 for all relevant spectral bins. The term
for all relevant spectral bins. The term 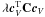 is a quadratic
stabilizer for the source power cross-spectra: the matrix C is
in our case the identity matrix, and the parameter λ must be tuned to
balance the effects of data fit and regularization in the final solution. The functional
in Eq. (A.13) can be considered as a
negative joint log-posterior for p and
cV, where the first
quadratic form represents the log-likelihood, and the regularization term can be viewed
as a log-prior density for the source power cross-spectra.
is a quadratic
stabilizer for the source power cross-spectra: the matrix C is
in our case the identity matrix, and the parameter λ must be tuned to
balance the effects of data fit and regularization in the final solution. The functional
in Eq. (A.13) can be considered as a
negative joint log-posterior for p and
cV, where the first
quadratic form represents the log-likelihood, and the regularization term can be viewed
as a log-prior density for the source power cross-spectra.
Appendix B: Spectral model for AME
Theoretical spinning-dust models predict a variety of spectra that can be substantially different in shape, depending on a large number of parameters describing the physics of the medium. The number of these physical parameters is too large to be constrained by the data in the available frequency range. For the purpose estimating the spectral behaviour of the AME we adopted a simple formula depending on only a few parameters. The CCA component-separation method used in this work implements the parametric relation proposed by Bonaldi et al. (2007) (Eq. (6)), depending on the peak frequency, νp, and slope at 60 GHz, m60. To verify the adequacy of this parametrization we produced spinning-dust spectra for different input physical parameters with the SpDust code and fitted each of them with the proposed relation by minimizing the χ2 for the set of frequencies used in this work. The input models we considered are weak neutral medium (WNM), cold neutral medium (CNM), weak ionized medium (WIM), and molecular cloud (MC). Both the input SpDust parameters and the best-fit m60, νp parameters for each model are reported in Table B.1. For comparison, we also considered alternative parametric relations and in particular
-
the model implemented in the Commander componentseparation method (Pietrobonet al. 2012; PlanckCollaboration 2013d) which is a Gaussian in the TCMB − ln(ν)plane, parametrized in terms of central frequency and width;
-
the Tegmark et al. (2000) model, which is a modified black-body relation (Eq. (1)) with a temperature of around 0.25K and an emissivity index of about 2.4;
Because this test neither accounts for the presence of the other components and includes any data simulation, it verifies the intrinsic ability of the parametric model to reproduce the actual spectra. Realistic estimation errors for the CCA model are derived through simulations in Appendix C.
Figure B.1 compares the input spectra with the best-fit models for the different parametrizations. In general, the fits are accurate at least up to ν = 50–60 GHz, while at higher frequencies the parametric relations may not be able to reproduce the input spectra in detail. This is a consequence of fitting complex spectra with only a few parameters. The fit tends to fail where the AME signal is weaker.
Over the frequency range considered, CCA and Commander models fit the input spectrum generally better than the Tegmark et al. (2000) model (which decreases too rapidly at high frequencies). When adding lower frequency data, however, CCA and Commander models will be increasingly inaccurate, because they are symmetric with respect to the peak of the emission. The models implemented by CCA and Commander perform quite similarly, despite the different formulation. As a result, these methods are able to give consistent answers, which ensures consistency between different analyses within Planck (e.g. Planck Collaboration 2013d).
The CCA model used in this work provides a reasonable fit to theoretical spinning-dust models for a variety of physical conditions. The best-fit parameters that we obtain, reported in Table B.1, vary significantly from one input model to another and have a straightforward interpretation in terms of the spectrum.
 |
Fig.B.1 Theoretical spinning dust models produced with SpDust (solid lines) and fitted with CCA (triangles), Commander (diamonds), and Tegmark et al. (2000) (asterisks) models. Input SpDust parameters and best-fit parameters for the CCA model are provided in Table B.1. |
Appendix C: Description of the simulations
 |
Fig.C.1 Free-free templates at 23 GHz used for the analysis. The reference template FFREF is in the upper left corner; the other columns (left to right) are FF1, FF2 and FF3, respectively. The differences in the lower panels (FFi − FFREF)/FFREF are on average of the order of 10%, but reach 50% in regions of strong dust emission. |
We simulated Planck and WMAP 7-yr data by assuming monochromatic bandpasses positioned at the central frequency of the bands, Gaussian beams at the nominal values indicated in Tables 1 and 2, and Gaussian noise generated according to realistic, spatially varying noise rms. Our model of the sky consists of the following components:
-
CMB emission given by the best-fit power spectrum model fromWMAP 7-yr analyses;
-
synchrotron emission given by the Haslam et al. (1982) template scaled in frequency with a power-law model with a spatially varying synchrotron spectral index βs, as modelled by Giardino et al. (2002);
-
free-free emission given by the Dickinson et al. (2003) Hα corrected for dust absorption with the E(B − V) map from Schlegel et al. (1998) with a dust absorption fraction fd = 0.33, and scaled in frequency according to Eq. (2) with Te = 7000K;
-
thermal dust emission modelled with the 100 map from Schlegel et al. (1998), scaled in frequency according to Eq. (1) with Td = 18K and a spatially varying βd with an average value of 1.7;
-
AME modelled by the E(B − V) map from Schlegel et al. (1998) with the intensity at 23 GHz calibrated using the results of Ghosh et al. (2012) for the same region of the sky.
We adopted more than one spectral model for the AME. We first considered two convex spectra, generated with the SpDust code: one peaking around 26 GHz and the other peaking around 19 GHz. We also tested a spatially varying power-law model (with spectral index of −3.6 ± 0.6, Ghosh et al. 2012), which could result from the superposition of multiple convex components along the line of sight.
It is worth noting that the simulated sky is more complex than the model assumed in the
component separation. This has been done intentionally, to reflect a more realistic
situation. Another realistic feature we included are errors in the synchrotron and
free-free templates. The spatial variability of the synchrotron spectral index modifies
the morphology of the component with respect to that traced by the 408MHz map from Haslam et al. (1982). The use of Hα
as a tracer of free-free emission is affected by even larger uncertainties. Our
uncertainties on the dust absorption fraction fd (estimated
to be 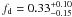 at intermediate latitudes by Dickinson et al.
2003) and on the scattering of Hα photons from dust grains can
create dust-correlated biases in the template. This is illustrated in Fig. C.1, where we compare different versions of the
free-free template. FFREF is our reference template, adopted for the analysis
of real data and for simulating the component, which is corrected for
fd = 0.33 as described in Dickinson et al. (2003). Two more templates (FF1 and
FF2) were obtained by correcting Hα for
fd = 0.33−0.15 and
fd = 0.33 + 0.1 (± 1σ according to Dickinson et al. 2003). A final template
(FF3) was obtained by correcting FFREF for scattered light at
the 15% level by subtracting from the free-free map the 1 map of Schlegel et al. (1998) multiplied by a suitable constant factor
(Witt et al. 2010). Difference maps
(FFi − FFREF)/FFREF, presented in
the lower panels of Fig. C.1, are on average of
order of 10%, but can be much higher (up to 50–60%) in regions of strong dust emission.
at intermediate latitudes by Dickinson et al.
2003) and on the scattering of Hα photons from dust grains can
create dust-correlated biases in the template. This is illustrated in Fig. C.1, where we compare different versions of the
free-free template. FFREF is our reference template, adopted for the analysis
of real data and for simulating the component, which is corrected for
fd = 0.33 as described in Dickinson et al. (2003). Two more templates (FF1 and
FF2) were obtained by correcting Hα for
fd = 0.33−0.15 and
fd = 0.33 + 0.1 (± 1σ according to Dickinson et al. 2003). A final template
(FF3) was obtained by correcting FFREF for scattered light at
the 15% level by subtracting from the free-free map the 1 map of Schlegel et al. (1998) multiplied by a suitable constant factor
(Witt et al. 2010). Difference maps
(FFi − FFREF)/FFREF, presented in
the lower panels of Fig. C.1, are on average of
order of 10%, but can be much higher (up to 50–60%) in regions of strong dust emission.
When analysing the simulated data, we used both FF1 and FF2 as free-free templates in place of FFREF, which corresponds to the simulated component. For synchrotron emission the morphological mismatch between the simulated component and the template was achieved by scaling the component from 23 GHz to 408MHz with a spatially varying spectral index. The comparison between component and template is presented in Fig. C.2; the differences are of the order of 10%.
 |
Fig.C.2 Upper panel: simulated synchrotron component (left) and synchrotron template (right) at 23 GHz. Lower panel: difference map divided by the simulated component. |
The simulated data-sets described above were analysed with the CCA method using the same procedure as applied to the real data; the results of this assessment are presented in Sect. 4.1. As a separate test, we verified the impact of the CMB component on the results for νp and m60. We generated 100 sets of mock data with the same foreground emission and different realizations of CMB and instrumental noise, and repeated the estimation of the AME frequency scaling. For this test we used the simulation with a spatially constant AME spectrum peaking at 26 GHz. As this analysis is computationally demanding, the CCA estimation was performed only on the ten independent patches covering the Gould Belt region (centred on latitudes −20° and −40° and longitudes of 140°, 160°, 180°, 200°, and 220°). In Fig. C.3 we show the average (diamonds) and rms (error bars) νp and m60 over the 100 realizations for each
patch for different patches on the x-axis. The scatter between the results obtained for different patches (indicated by the grey area in the plots) is typically larger than the error bars, measuring the scatter due to different CMB realizations. This means that the foreground emission generally dominates over the CMB as a source of error. Larger error bars associated with the CMB are obtained for three patches with faint foreground emission. For these patches the estimated errors on νp and m60 are consistently larger. The CMB variation results on average in Δνp = 0.1 GHz and Δm60 = 0.3, which reach 0.3 GHz and 0.8, respectively, for the poorest sky patch. These values are below the error bars resulting from the analysis of the data, which amount to 1–1.5 GHz for νp and 1.5–2 for m60. The CMB has limited impact on the results because this component is modelled in the mixing matrix. Having a known frequency scaling, the statistical constraint used by CCA is able to trace the pattern of the CMB through the frequencies with good precision and hence identify it correctly.
 |
Fig.C.3 Average and rms of νp and m60 estimated over simulations with different CMB and noise realizations for different patches on the x-axis. The grey area is the average and rms over different patches, which is typically larger than that due to noise and CMB. |
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Acknowledgments
Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and the development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php ?project=planck&page=Planck_Collaboration. We acknowledge the use of the HEALPix (Górski et al. 2005) package and of the LAMBDA website http://lambda.gsfc.nasa.gov.
References
- Ali-Haïmoud, Y., Hirata, C. M., & Dickinson, C. 2009, MNRAS, 395, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, M. I. R., Davies, R. D., Dickinson, C., et al. 2012, MNRAS, 422, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- AMI Consortium, Scaife, A. M. M., Hurley-Walker, N., et al. 2009, MNRAS, 400, 1394 [NASA ADS] [CrossRef] [Google Scholar]
- Banday, A. J., Dickinson, C., Davies, R. D., Davis, R. J., & Górski, K. M. 2003, MNRAS, 345, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Bedini, L., & Salerno, E. 2007, Lecture Notes in Artificial Intelligence, 4964, 9 [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2012, ApJS, submitted [arXiv:1212.5225] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonaldi, A., & Ricciardi, S. 2012, Adv. Astron., 2012, id. 853927 [Google Scholar]
- Bonaldi, A., Bedini, L., Salerno, E., Baccigalupi, C., & de Zotti, G. 2006, MNRAS, 373, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaldi, A., Ricciardi, S., Leach, S., et al. 2007, MNRAS, 382, 1791 [NASA ADS] [Google Scholar]
- Bond, J. R., & Efstathiou, G. 1987, MNRAS, 226, 655 [NASA ADS] [Google Scholar]
- Boumis, P., Dickinson, C., Meaburn, J., et al. 2001, MNRAS, 320, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., & Draine, B. T. 2012, ApJ, 744, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Broadbent, A., Osborne, J. L., & Haslam, C. G. T. 1989, MNRAS, 237, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Cabrera, G. F., Förster, F., et al. 2006, ApJ, 639, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Dickinson, C., Cleary, K., et al. 2008, MNRAS, 391, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Flagey, N., Noriega-Crespo, A., et al. 2010, ApJ, 724, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. D. 1960, MNRAS, 120, 483 [NASA ADS] [Google Scholar]
- Davies, R. D., Dickinson, C., Banday, A. J., et al. 2006, MNRAS, 370, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira-Costa, A., Tegmark, M., Davies, R. D., et al. 2004, ApJ, 606, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C. 2013, Adv. Astron., 2013, id. 162478 [Google Scholar]
- Dickinson, C., Davies, R. D., & Davis, R. J. 2003, MNRAS, 341, 369 [Google Scholar]
- Dickinson, C., Casassus, S., Pineda, J. L., et al. 2006, ApJ, 643, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., Bronfman, L., et al. 2007, MNRAS, 379, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Davies, R. D., Allison, J. R., et al. 2009, ApJ, 690, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008a, ApJ, 680, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008b, ApJ, 680, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Draine, B., & Finkbeiner, D. P. 2009, ApJ, 699, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., & Draine, B. T. 2011, ApJ, 727, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lazarian, A. 1998, ApJ, 508, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Erickson, W. C. 1957, ApJ, 126, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Schlegel, D. J., Frank, C., & Heiles, C. 2002, ApJ, 566, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Langston, G. I., & Minter, A. H. 2004a, ApJ, 617, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Langston, G. I., & Minter, A. H. 2004b, ApJ, 617, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Ghosh, T., Banday, A. J., Jaffe, T., et al. 2012, MNRAS, 422, 3617 [NASA ADS] [CrossRef] [Google Scholar]
- Giardino, G., Banday, A. J., Górski, K. M., et al. 2002, A&A, 387, 82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, B. A. 1879, Resultados del Observatorio Nacional Argentino, 1, 1 [NASA ADS] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hoang, T., Lazarian, A., & Draine, B. T. 2011, ApJ, 741, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Jarosik, N., Bennett, C. L., Dunkley, J., et al. 2011, ApJS, 192, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jonas, J. L., Baart, E. E., & Nicolson, G. D. 1998, MNRAS, 297, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A. 1996, in BAAS, 28, 1295 [Google Scholar]
- Kogut, A., Fixsen, D. J., Levin, S. M., et al. 2011, ApJ, 734, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G. 2003, A&A, 405, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitch, E. M., Readhead, A. C. S., Pearson, T. J., & Myers, S. T. 1997, ApJ, 486, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, P. O. 1967, Bull. Astron. Inst. Netherlands, 19, 34 [Google Scholar]
- Lindblad, P. O., Palous, J., Loden, K., & Lindegren, L. 1997, in Hipparcos – Venice ’97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA SP, 402, 507 [NASA ADS] [Google Scholar]
- Macellari, N., Pierpaoli, E., Dickinson, C., & Vaillancourt, J. E. 2011, MNRAS, 418, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Mennella, A., Bersanelli, M., Butler, R. C., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2006, in ASP Conf. Ser., 357, eds. L. Armus, & W. T. Reach, 167 [Google Scholar]
- Miville-Deschênes, M.-A., Ysard, N., Lavabre, A., et al. 2008, A&A, 490, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, E. J., Helou, G., Condon, J. J., et al. 2010, ApJ, 709, L108 [NASA ADS] [CrossRef] [Google Scholar]
- Peel, M. W., Dickinson, C., Davies, R. D., et al. 2012, MNRAS, 424, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Perrot, C. A., & Grenier, I. A. 2003, A&A, 404, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrobon, D., Górski, K. M., Bartlett, J., et al. 2012, ApJ, 755, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration. 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2011b, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2011c, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2011d, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2011e, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2011f, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration. 2013a, A&A, submitted [arXiv:1303.5063] [Google Scholar]
- Planck Collaboration. 2013b, A&A, submitted [arXiv:1303.5067] [Google Scholar]
- Planck Collaboration. 2013c, A&A, submitted [arXiv:1303.5070] [Google Scholar]
- Planck Collaboration. 2013d, A&A, 554, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team. 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team. 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, R. J., & Ogden, P. M. 1979, ApJ, 229, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Ricciardi, S., Bonaldi, A., Natoli, P., et al. 2010, MNRAS, 406, 1644 [NASA ADS] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scaife, A., Green, D. A., Battye, R. A., et al. 2007, MNRAS, 377, L69 [NASA ADS] [Google Scholar]
- Scaife, A. M. M., Nikolic, B., Green, D. A., et al. 2010, MNRAS, 406, L45 [NASA ADS] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Silsbee, K., Ali-Haïmoud, Y., & Hirata, C. M. 2011, MNRAS, 411, 2750 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tegmark, M., Eisenstein, D. J., Hu, W., & de Oliveira-Costa, A. 2000, ApJ, 530, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Todorović, M., Davies, R. D., Dickinson, C., et al. 2010, MNRAS, 406, 1629 [NASA ADS] [Google Scholar]
- Watson, R. A., Rebolo, R., Rubiño-Martín, J. A., et al. 2005, ApJ, 624, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., Gold, B., Barnes, III, F. S., et al. 2010, ApJ, 724, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., & Reynolds, R. J. 1999, ApJ, 525, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., & Verstraete, L. 2010, A&A, 509, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Miville-Deschênes, M. A., & Verstraete, L. 2010, A&A, 509, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Juvela, M., & Verstraete, L. 2011, A&A, 535, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Inferred Te [K] for the T-T and C-C analysis using different Hα templates and dust absorption fractions fd.
All Figures
 |
Fig.1 Orthographic projection (looking towards the Galactic centre in the left panel and the Galactic anti-centre in the right panel) of the Planck CMB-subtracted 30 GHz channel showing the Gould Belt and the region of interest for this paper (defined by 130° ≤ l ≤ 230° and −50° ≤ b ≤ −10°). |
| In the text | |
 |
Fig.2 Gnomonic projections of the region of interest. Top panels: Haslam et al. (1982) 408 MHz map (left); Hα map from Dickinson et al. (2003) (middle); and 100 map from Schlegel et al. (1998) (right) at native resolution. Middle panels (left to right): Planck CMB-subtracted 30, 44, and 70 GHz maps at 1° resolution. Bottom panels (left to right): Planck CMB-subtracted 143, 353, and 857 GHz at 1° resolution. |
| In the text | |
 |
Fig.3 CCA estimates of the AME frequency spectrum in the region of interest for real data (left panels) and simulated data (right panels). Top: estimated spectra including 1σ errors. Middle and bottom: histograms of the spectral parameters m60 and νp on Nside = 16 estimated spectral index maps. For the simulated case (right panels) we considered two convex spectra peaking at 19 GHz and 26 GHz and a power-law model. Top right: the true inputs are shown as solid black lines (power-law) with triangles (19 GHz peak) and squares (26 GHz peak) and the estimates as shaded areas. The blue and red colours show estimates derived by exploiting the free-free templates FF1 and FF2 described in Appendix C. Middle and bottom-right panels: the true inputs are shown as solid and dotted vertical lines for the simulations peaking at 26 GHz and 19 GHz respectively; the blue dot-dashed and red solid histograms show the estimates obtained using the FF1 and FF2 templates, and the black dashed lines show the estimates for the 19 GHz input spectrum. |
| In the text | |
 |
Fig.4 1° resolution reconstruction at 30 GHz of (from left to right): synchrotron emission; free-free emission; AME; and thermal dust emission. These reconstructions are performed as described in Sect. 3.3.2. Rows from top to bottom: component amplitudes; noise rms; predicted rms of component separation error due to the estimation of AME and thermal dust spectra; and predicted rms of component separation error including a random error on βs = −2.9 ± 0.1. |
| In the text | |
 |
Fig.5 Validation of the reconstructed components shown in Fig. 4. Left panels: sum of the components vs frequency maps at 30, 44, and 70 GHz (from top to bottom). The line is the x = y relation. Right panels: pixel distribution of the residual (frequency map-sum of the components) maps compared with the best-fit Gaussian distribution. |
| In the text | |
 |
Fig.6 Estimated spectra of synchrotron emission (dashed line), free-free emission (solid line), thermal dust emission (dash-dotted line), and AME (dotted line) for average local properties (top) and for Barnard’s region (bottom). |
| In the text | |
 |
Fig.7 T-T analysis for the estimation of Te. Top: gnomonic projection showing the mask used (masked pixels are in black, while pixels used in the analysis are in white). Bottom: T-T plot comparing the CCA free-free solution with the Hα template for fd = 0.3 (points) and linear fits to the T-T plots for different values of fd (lines). |
| In the text | |
 |
Fig.8 Comparison between correlation coefficients (symbols with error bars) and component separation results (shaded areas) for free-free emission (top) and dust emission (bottom). For free-free emission we show the Dickinson et al. (2003) Hα correlation coefficients and for dust emission the Finkbeiner et al. (1999) correlation coefficients. The grey area in the bottom panel is the sum of the AME (blue) and thermal dust (red) components. The dash-dotted line in both panels shows the 1σ error due to the chance correlation of CMB with foreground templates, estimated using simulations. |
| In the text | |
 |
Fig.9 Partitioning of the Gould Belt region based on thresholds over free-free emission (red), CO emission (blue), and total emission at 30 GHz (yellow), used as tracers of Hii gas, molecular gas, and diffuse ISM environments, respectively, and the rest of the Gould Belt region (white). Circled regions are those selected for computing the spectra and have been labelled Hii-gas (Barnard’s arc) and diffuse ISM (centred on l = 190°, b = −35°) regions, respectively. |
| In the text | |
 |
Fig.10 Frequency spectra (black points with error bars) for thermal dust emission and AME compared, respectively, with DustEM and SpDust (dashed lines) for the diffuse ISM (top) and ionized gas (middle and bottom) regions within the Gould Belt. The solid line is the sum of the DustEM and SpDust models. The grey area in the top and middle panels corresponds to the ± 1σ variations on the best-fit nH values when fitting for a single phase. In the bottom panel we consider a mixture of two phases (nH = 0.1cm-3 and nH = 55cm-3, in the proportion of 46% and 54%, respectively), which marginally improves the fit for the ionized gas region at 23 GHz (the error is 0.3σ instead of 0.9σ ). |
| In the text | |
 |
Fig.B.1 Theoretical spinning dust models produced with SpDust (solid lines) and fitted with CCA (triangles), Commander (diamonds), and Tegmark et al. (2000) (asterisks) models. Input SpDust parameters and best-fit parameters for the CCA model are provided in Table B.1. |
| In the text | |
 |
Fig.C.1 Free-free templates at 23 GHz used for the analysis. The reference template FFREF is in the upper left corner; the other columns (left to right) are FF1, FF2 and FF3, respectively. The differences in the lower panels (FFi − FFREF)/FFREF are on average of the order of 10%, but reach 50% in regions of strong dust emission. |
| In the text | |
 |
Fig.C.2 Upper panel: simulated synchrotron component (left) and synchrotron template (right) at 23 GHz. Lower panel: difference map divided by the simulated component. |
| In the text | |
 |
Fig.C.3 Average and rms of νp and m60 estimated over simulations with different CMB and noise realizations for different patches on the x-axis. The grey area is the average and rms over different patches, which is typically larger than that due to noise and CMB. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


