| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321031 | |
| Published online | 11 September 2013 | |
The IRAM-30 m line survey of the Horsehead PDR
III. High abundance of complex (iso-)nitrile molecules in UV-illuminated gas⋆,⋆⋆
1 Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint Martin d’Hères, France
e-mail: gratier@iram.fr; pety@iram.fr
2 LERMA, UMR 8112, CNRS and Observatoire de Paris, 61 avenue de l’Observatoire, 75014 Paris, France
3 Centro de Astrobiología, CSIC-INTA, Carretera de Ajalvir, Km 4, Torrejón de Ardoz, 28850 Madrid, Spain
4 LUTH UMR 8102, CNRS and Observatoire de Paris, Place J. Janssen, 92195 Meudon Cedex, France
5 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
Received: 2 January 2013
Accepted: 7 May 2013
Context. Complex (iso-)nitrile molecules, such as CH3CN and HC3N, are relatively easily detected in our Galaxy and in other galaxies.
Aims. We aim at constraining their chemistry through observations of two positions in the Horsehead edge: the photo-dissociation region (PDR) and the dense, cold, and UV-shielded core just behind it.
Methods. We systematically searched for lines of CH3CN, HC3N, C3N, and some of their isomers in our sensitive unbiased line survey at 3, 2, and 1 mm. We stacked the lines of C3N to improve the detectability of this species. We derived column densities and abundances through Bayesian analysis using a large velocity gradient radiative transfer model.
Results. We report the first clear detection of CH3NC at millimeter wavelength. We detected 17 lines of CH3CN at the PDR and 6 at the dense core position, and we resolved its hyperfine structure for 3 lines. We detected 4 lines of HC3N, and C3N is clearly detected at the PDR position. We computed new electron collisional rate coefficients for CH3CN, andwe found that including electron excitation reduces the derived column density by 40% at the PDR position, where the electron density is 1–5 cm-3. While CH3CN is 30 times more abundant in the PDR (2.5 × 10-10) than in the dense core (8 × 10-12), HC3N has similar abundance at both positions (8 × 10-12). The isomeric ratio CH3NC/CH3CN is 0.15 ± 0.02.
Conclusions. The significant amount of complex (iso-)nitrile molecule in the UV illuminated gas is puzzling as the photodissociation is expected to be efficient. This is all the more surprising in the case of CH3CN, which is 30 times more abundant in the PDR than in the dense core. In this case, pure gas phase chemistry cannot reproduce the amount of CH3CN observed in the UV-illuminated gas. We propose that CH3CN gas phase abundance is enhanced when ice mantles of grains are destroyed through photo-desorption or thermal-evaporation in PDRs, and through sputtering in shocks.
Key words: astrochemistry / ISM: clouds / ISM: molecules / ISM: individual objects: Horsehead / radiative transfer
Based on observations obtained with the IRAM-30 m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Complex nitriles like CH3CN and HC3N are easily detected in (massive) star-forming regions (Araya et al. 2005; Bottinelli et al. 2004; Purcell et al. 2006).CH3CN and HC3N were detected in the Mon R2 ultracompact H ii region (Ginard et al. 2012). Mauersberger et al. (1991) reported the first detection of CH3CN in M 82 and NGC 253. Lindberg et al. (2011) detected HC3N in 13 local universe galaxies. These molecules are often used to constrain the physical conditions of the host gas. In particular, CH3CN is thought to be a good thermometer because it exhibits sets of metastable transitions, which are only coupled through collisions, but not radiatively (Guesten et al. 1985).
Moreover, CH3CN is easily detected towards hot molecular cores (Olmi et al. 1996a,b; Hatchell et al. 1998; Purcell et al. 2006). In particular, Purcell et al. (2006) detect 3 mm lines of CH3CN in 58 candidate hot molecular cores on a sample of 83 methanol maser-selected star-forming regions. They detect CH3CN in isolated methanol maser sites and find that CH3CN is more prevalent and brighter when an ultracompact H ii region is present, independent of the distance to the source. The inferred CH3CN abundances are higher than can be accounted for by current pure gas phase chemical modeling (e.g. Olmi et al. 1996b; Hatchell et al. 1998). Mackay (1999) proposed that the CH3CN abundance could be explained if the abundances of the gas phase precursors of CH3CN, i.e. CH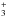 and HCN, are enhanced by evaporation from grain ices and by further photo-processing of methanol and ammonia.
and HCN, are enhanced by evaporation from grain ices and by further photo-processing of methanol and ammonia.
The mane of the Horsehead nebula is an ideal source to test the excitation and chemistry of nitriles. Indeed, it is viewed nearly edge-on (Abergel et al. 2003) at a distance of 400 pc (implying that 10′′ correspond to 0.02 pc). It has a steep density gradient, from nH ~ 100 cm-3 in the UV illuminated outer layers rising to nH ~ 2 × 105 cm-3 in less than 10′′ (Habart et al. 2005). Gerin et al. (2009) show that the HCO emission delineates the UV illuminated edge of the nebula. Less than 40′′ away from the HCO peak emission where the gas is warm (Tkin ~ 60 K), there is a UV-shielded, dense, and cold condensation (Tkin ≤ 20 K), where HCO+ is highly deuterated (Pety et al. 2007). For simplicity, the HCO and DCO+ emission peaks are hereafter referred to as the PDR and dense core positions. The moderate illumination (χ ~ 60 Abergel et al. 2003; Draine 1978) translates into dust temperatures low enough that thermal evaporation of complex molecules is negligible. In the Horsehead nebula one can thus isolate photo-desorption effects for complex molecules like formaldehyde, which can form on the grain ice mantles before being photo-desorbed into gas phase, as was shown by Guzmán et al. (2011).
 |
Fig. 1 Overview of the Horsehead mane photodissociation region showing the two observed positions. Left: DCO+ map (Pety et al. 2007), right: HCO emission map (Gerin et al. 2009). In both maps, The HCO emission peak (PDR position) at RA = 05h40m53.9s, Dec = −02°28′00′′ is shown with a green cross, and the DCO+ emission peak (dense core position) at RA = 05h40m55.7s, Dec = −02°28′22′′ with a blue one. The maps have been rotated 14 degree anti clockwise around the position RA = 05h40m54.27s, Dec = −02°28′00′′ and shifted 20′′ to the east to align the PDR front (vertical red line) with the horizontal 0 offset of the map. |
In this work, we report the detection of CH3CN, CH3NC, HC3N, and C3N in the PDR and/or the dense core positions of the Horsehead edge. Determining the isomeric abundance ratio is an important tool for constraining the chemical routes to form the molecules. Indeed, the observed column density ratios often differ significantly from the ones expected by the energies of the molecules at thermodynamic equilibrium. One such example related to the CH3CN/CH3NC ratio is the ratio between HNC and HCN which is found in the interstellar medium to be close to 1 (Sarrasin et al. 2010; Mendes et al. 2012), even though HNC is less stable than HCN by 0.5 eV. This gives constraints on the mechanisms of formation and destruction of these species. We thus also searched for emission of CH3NC and HC2NC. Table 1 shows that all these species have similar dipole moments.
Section 2 presents the observations and the spectroscopy of the observed molecules. Section 3 summarizes the observed line properties. Section 4 explains how the column densities are computed and it presents the inferred abundances. The implications of these results for the chemistry of CH3CN and HC3N are discussed in Sect. 5. Appendix A summarizes the line properties (integrated intensity, line width, systemic velocity) for observed lines and derived upper limits for undetected lines. Appendix B details the Bayesian approach used to infer the abundances from the line brightnesses. Finally, Appendix C discusses the shortcoming of the rotational diagram method in the subthermal excitation conditions found in the PDR position. Larger versions of Figs. 3 and 4 are presented in Appendix D.
2. Observations and spectroscopy
After a short description of the Horsehead WHISPER unbiased line survey, this section presents the spectroscopy of the different molecules studied here, including their hyperfine structure.
Dipole moments for the observed species.
2.1. Horsehead WHISPER: an unbiased line survey
The data1 presented in this paper are extracted from the Horsehead Wideband High-resolution Iram-30 m Surveys at two Positions with Emir Receivers (WHISPER project, PI: J. Pety), an unbiased line survey of the 3, 2 and 1 mm band, which is currently completed with the IRAM-30 m telescope. This project was observed in 2011 and 2012. Two positions are observed: 1) the HCO peak that is characteristics of the photo-dissociation region at the surface of the Horsehead nebula (Gerin et al. 2009); and 2) the DCO+ peak that belongs to the nearby cold dense core at high visual extinction (Pety et al. 2007). The combination of the new EMIR receivers and the Fourier Transform Spectrometers yield a spectral survey with unprecedented bandwidth (36 GHz at 3 mm, 34 GHz at 2 mm, and 76 GHz at 1 mm), spectral resolution (49 kHz at 3 and 2 mm and 195 kHz at 1 mm, this corresponds a velocity resolution between 0.1 and 0.3 km s-1), and sensitivity (median noises of 8.0 mK, 18.5 mK, and 8.3 mK respectively). This allowed us to detect ~150 lines from ~30 species and their isotopologues. Each sky frequency was observed with two different frequency tunings. The Horsehead PDR and dense core positions (see Fig. 1) were alternatively observed every 15 minutes in position switching mode with a common fixed off position (offset: −100′′, 0′′ from RA = 05h40m54.27s, Dec = −02°28′00′′). The total observing time amounted to one hour per frequency setup and position. This observing strategy allows us to remove potential ghost lines resulting from the incomplete attenuation of strong spectral features in the image side band (the typical rejection of the EMIR sideband separating mixers is 13dB or a factor 20). A detailed presentation of the observing strategy and data reduction process will be given in another paper. Table 2 summarizes the beamwidths and noise levels for the frequency ranges of the survey corresponding to the lines discussed in this paper.
Observation parameters for the observed lines.
 |
Fig. 2 CH3CN energy diagram of levels which contribute to the J = 5 → 4, J = 6 → 5, J = 7 → 6, and J = 8 → 7 transitions in the 3 and 2 mm frequency ranges, i.e. for K levels from 0 to 7 and J levels from 4 to 8, other levels are displayed in dotted line. The E (K = 3n ± 1) and A (K = 3n) states are displayed in black and red, respectively. |
2.2. CH3CN and CH3NC: two symmetric top species
2.2.1. Energy diagrams
Figure 2 displays the CH3CN energy diagram. The CH3NC energy diagram has a similar structure. Indeed, as prolate symmetric top molecules, their rotational energy (EJ,K) is derived (Gordy & Cook 1984) from the moments of inertia and angular momentum through 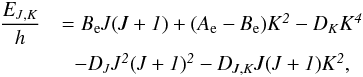 where 1) the J and K quantum numbers describe respectively the total angular momentum and its projection along the molecule symmetry axis; 2) Ae and Be are the rotational constants, characteristics of the moments of inertia along and perpendicular to the symmetry axes; and 3) the DJ, DK and DJ,K are the centrifugal stretching constants. As a symmetric top, the degeneracy on the symmetry axis is removed, giving a splitting of each rotational J level into doubly degenerate K components, with K = 0,...,J (except when K = 0).
where 1) the J and K quantum numbers describe respectively the total angular momentum and its projection along the molecule symmetry axis; 2) Ae and Be are the rotational constants, characteristics of the moments of inertia along and perpendicular to the symmetry axes; and 3) the DJ, DK and DJ,K are the centrifugal stretching constants. As a symmetric top, the degeneracy on the symmetry axis is removed, giving a splitting of each rotational J level into doubly degenerate K components, with K = 0,...,J (except when K = 0).
2.2.2. Transitions
Using the rules for allowed rotational transitions (Gordy & Cook 1984) 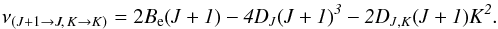 (1)the frequencies of a (J,K) transition can then be derived as
(1)the frequencies of a (J,K) transition can then be derived as 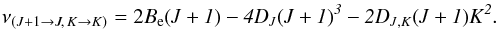 A set of (J + 1 → J, K = const.) lines is named a J-ladder, and a set of (J = const., K + 1 → K) lines is named a K-ladder.
A set of (J + 1 → J, K = const.) lines is named a J-ladder, and a set of (J = const., K + 1 → K) lines is named a K-ladder.
For a given J, the probed energy range is mainly determined by (Ae − Be)K2 (a first order effect), while the frequencies are separated by 2DJ,K(J + 1)K2 (a second order effect due to the centrifugal distortion). Hence, each J-ladder can be observed simultaneously in a relatively narrow frequency band, while they probe a wide range of energies, typically from 10 to a few 100 K. This is why the excitation of symmetric top molecules are good thermometers when the lines are thermalized.
 |
Fig. 3 Spectrum of the CH3NC 3 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum), the spectrum towards the HCO peak has been shifted vertically by 0.1 K for clarity. The panel displays the K set of lines for the given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
2.3. HC3N, HC2NC, HNC3 and C3N: four rigid rotors
HC3N, HC2NC and HNC3 are linear species with a 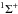 electronic state. Their spectroscopy is thus much simpler than the symmetric top ones. Their rotational spectrum is well described by the rigid rotor approximation with lines separated by 9.1 GHz, 9.9 GHz, 9.3 GHz respectively. HC2NC and HNC3 are isomers of HC3N, which can also be described as rigid rotors. C3N has a more complex 2Σ ground state electronic structure, which exhibits doublets of nearby frequencies.
electronic state. Their spectroscopy is thus much simpler than the symmetric top ones. Their rotational spectrum is well described by the rigid rotor approximation with lines separated by 9.1 GHz, 9.9 GHz, 9.3 GHz respectively. HC2NC and HNC3 are isomers of HC3N, which can also be described as rigid rotors. C3N has a more complex 2Σ ground state electronic structure, which exhibits doublets of nearby frequencies.
2.4. Hyperfine splitting
All of the observed N species exhibit a hyperfine structure, although that of the 15N species are not resolved due to the small magnetic dipole coupling term. The NC isomers have lower hyperfine splitting values than the CN isomers. This comes from the fact that the electric field gradient, which creates the hyperfine splitting through interaction with the nuclear electric quadrupole moment of 14N, is stronger for outermost N positions. This is well known for HCN and HNC (see Bechtel et al. 2006).
As the Horsehead PDR is seen edge-on, the lines are narrow with typical full width at half maximum values of 0.6−0.8 km s-1. This enables us to resolve the hyperfine splitting when it is large enough. In the case of symmetric top molecules, the hyperfine splitting increases with increasing K levels and decreasing J level. In practice, the hyperfine splitting is resolved only for the (J = 5 → 4, K = 2), (J = 5 → 4, K = 3), and (J = 6 → 5, K = 3) lines of CH3CN in our observations (see Fig. 4).
We wish to estimate the correct integrated intensities for each (ΔJ,K) line even though hyperfine components can be blended. To do this, we fitted together multiple Gaussian profiles over all of the hyperfine levels for each (ΔJ = 1,K = cst) transition. In this global fit, we fixed 1) the relative intensities of the hyperfine levels to the optically thin values and 2) the frequency offsets of all the lines to the CDMS catalog values (Müller et al. 2005). There remains J + 2 free parameters, namely a global linewidth, a global velocity shift and a multiplicative amplitude factor for each of the hyperfine set of lines in the (ΔJ = 1,K = const.), with K = 0,...,J − 1. The integrated intensity of each (ΔJ,K) transition is then obtained by summing the integrated intensities of the individual Gaussian functions fitted to the hyperfine structure. This method is only correct for optically thin lines. Section 4.2.1 shows that this is case for the spectral lines we analyze in this paper.
 |
Fig. 4 Spectrum of the CH3CN 3 mm and 2 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.2 K for clarity. The panel displays the K set of lines for a given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars, whose heights indicate their relative hyperfine intensities in the optically thin regime applicable to these observations. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
3. Observational results
3.1. First clear detection of CH3NC in the millimeter domain
Figure 3 shows the 3 lines of CH3NC detected in the Horsehead PDR. They belong to the 5 lines of the J = 5−4 K-ladder of CH3NC. None of them were detected in the UV-shielded dense core. As the hyperfine splitting is not resolved for any of these lines, we simultaneously fitted a single Gaussian profile at each frequency found in the JPL database (Pickett et al. 1998). Moreover, we required a common linewidth for the different lines. The fit results are displayed in Table A.1. The line intensity modeling carried out in Sect. 4 predicts line intensities for the other CH3NC lines in the 1, 2 and 3 mm bands well below our detection limit.
This is the first clear detection of this molecule in the millimeter domain. A detection of the J = 1−0 line of CH3NC at centimeter wavelengths (i.e., 20.1 GHz) has been reported by Irvine & Schloerb (1984) in TMC-1 and Remijan et al. (2005) in SgrB2. At millimeter wavelengths, Cernicharo et al. (1988) reported a tentative detection of the J = 4−3, J = 5−4 and J = 7−6 lines in SgrB2 but the large linewidths (20 km s-1 FWHM) and contamination from numerous other lines prevented a robust identification.
3.2. CH3CN lines are brighter in the PDR than in the dense core
In our line survey, four J + 1 → JK-ladders are detected: the J = 5 → 4, J = 6 → 5 K-ladders in the 3 mm atmospheric window at 91.9 GHz and 110.3 GHz respectively and, the J = 7 → 6 and J = 8 → 7 K-ladders in the 2 mm window at 128.7 GHz and 147.1 GHz. Figure 4 displays the 17 and 6 detected lines at the PDR and dense core positions, respectively. Lines from the additional 5 J + 1 → JK-ladders (from J = 11−10 to J = 15−14), whose wavelengths lie at 1mm, remain undetected in our survey. The corresponding noise levels for these undetected lines are 15–30 mK per 200 kHz channel.
The derived line properties are synthesized in Table A.2. Not only are there many more detected lines of CH3CN in the PDR than in the dense core, but the detected lines are also brighter in the less dense, UV-illuminated PDR position. Moreover, when the lines are detected in both environment, they systematically show a narrower linewidth in the PDR than in the core.
3.3. CH3NC/CH3CN isomeric line ratios
The value of the ratios of the CH3NC/CH3CN integrated intensities for the J = 5 − 4K-ladder are given in Table 3 for both the PDR and dense core positions. The weighted average line ratio is 0.15 ± 0.02 at the PDR position. The individual ratios exhibit a small scatter around this value.
 |
Fig. 5 Spectrum of the HC3N 3 mm lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.3 K for clarity. |
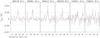 |
Fig. 6 Observed spectra (black line) of the three 3 mm C3N doublets at the PDR peak. The green horizontal lines are the ± 3σ levels. The red spectrum is the LTE model for a 6′′ × 50′′ filament centered at the PDR positions, a 10 K excitation temperature, and a column density of 2 × 1012 cm-2. |
3.4. HC3N lines have similar brigthnesses in the PDR and the dense core
Four HC3N lines lie in the 3 mm, 2 in the 2 mm and 8 in the 1 mm band we have observed. All four 3 mm lines of HC3N are detected at both observed positions, no detection were obtained at 2 and 1 mm. Independent Gaussian profiles were fitted for each detected line. Figure 5 displays the HC3N lines, which are detected in our survey and Table A.3 summarizes the fit results. In contrast with the results for CH3CN, HC3N lines are slightly more luminous in the UV-shielded dense core.
HC2NC has three lines in the 3 mm band. None of these are detected in any of the two observed positions. HNC3 has four lines in the 3 mm band, none of them are detected. Table A.5 gives the derived upper limits for both species. Stacking with the method presented in Sect. 3.5 did not reveal any detection. For reference, HC2NC and HNC3 have both been detected in dark clouds (Kawaguchi et al. 1992a,b), while only HC2NC has been detected in circumstellar envelopes (Gensheimer 1997).
CH3NC/CH3CN line ratio for different K levels of J = 5 − 4.
3.5. C3N is twice as bright in the PDR than in the dense core
Because of its 2Σ ground state electronic structure, and of the hyperfine splitting due to the Nitrogen atom, the energy radiated by C3N is spread over a large number of lines. This implies that individual lines of C3N are less easily detected than, e.g., that of CH3CN in the same conditions of noise. We thus have coadded the spectral regions where individual lines from C3N were expected to show up. This method can be applied to any species expected to present a rich spectrum with numerous weak spectral lines of similar intensity.
Using the list of transitions observable in our survey from public catalogs, we averaged the intensities of each potential line after 1) aligning each spectral window to the same LSR velocity, and 2) resampling each line spectrum to the same velocity resolution. In this process, we reject all partss of the original spectrum which could be contaminated by a line from another already detected species. We first tried a simple noise-weighted average, i.e., 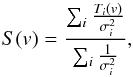 (2)where v is the velocity, Ti(v), and σi the brightness temperature and noise of the ith transition, and S(v) the stacked spectra. This is however a too simple approach because the searched species have complex hyperfine structures with expected line intensities which vary over several orders of magnitude. Hence, the signal can easily be drowned in noise. It is thus important to also weight the different lines according to their expected integrated intensities, Wi,
(2)where v is the velocity, Ti(v), and σi the brightness temperature and noise of the ith transition, and S(v) the stacked spectra. This is however a too simple approach because the searched species have complex hyperfine structures with expected line intensities which vary over several orders of magnitude. Hence, the signal can easily be drowned in noise. It is thus important to also weight the different lines according to their expected integrated intensities, Wi, 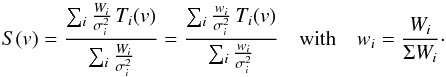 (3)The relative integrated intensities, wi, are computed with a simple local thermodynamic equilibrium (LTE) approach. In the optically thin regime, only the excitation temperature fixes the wi, because the normalization cancels the contribution of the total column density.
(3)The relative integrated intensities, wi, are computed with a simple local thermodynamic equilibrium (LTE) approach. In the optically thin regime, only the excitation temperature fixes the wi, because the normalization cancels the contribution of the total column density.
 |
Fig. 7 Top: cumulative distribution function of computed integrated intensities for C3N in the optically thin LTE regime with Tex = 10 K, and normalized to the intensity of the brightest line. Only 10% of all the 1, 2 and 3 mm lines have intensities brighter than a fifth of the brightest line. The transitions are color coded by bands, black: 3mm, orange: 2 mm, blue: 1 mm. Bottom C3N spectra resulting from the stacking of 38 individual lines at 3 mm. The stacked spectra are shown both for the PDR and dense core positions. The red curve is a gaussian fit to the stacked spectra, the green lines are ± 3σ levels. |
We explored a range of excitation temperatures and we kept the stacked spectra corresponding to the highest derived peak temperature. This strategy was checked against a spectrum simulated with a LTE code, assuming a typical excitation temperature of 10 K, consistent with our previous studies of complex molecules in the Horsehead edge, which showed that they are subthermally excited (Guzmán et al. 2011; Pety et al. 2012). The proposed strategy recovered the right excitation temperature.
There are 7+4+3 C3N doublets in the 1, 2, and 3 mm bands, each one split by hyperfine interaction into a total of 211 lines. Observationally, this results into six marginal detections (i.e., a peak signal-to-noise ratio (S/N) lower or close to 3) at the PDR position (see Fig. 6).
Figure 7 shows 1) the distribution of C3N line brightnesses modeled assuming optically thin LTE emission with Tex = 10 K, and 2) the C3N spectra obtained by stacking the 383 mm lines at the PDR and dense core position. The contributions from all 173 lines at 1 mm and 2 mm is negligible in our case, as none of them are brighter than 20% of the brightest 3 mm band line. Including the 1 mm and 2 mm lines would have reduced the spectral resolution of the stacked spectrum as individual spectra must first be resampled to the coarsest velocity resolution (0.282 km s-1).
C3N is twice as bright in the PDR than in the dense core. The brightest C3N line corresponds to a telescope half primary beam width of 27.7′′, the proportion of the line intensity observed towards the dense core that arises from beam pickup from the PDR position is less than 8%. The remaining emission could arise in the lower density skin of the dense core, already detected in HCO (Gerin et al. 2009) and CF+ (Guzmán et al. 2012a,b).
4. Column densities and abundances
4.1. Tools
4.1.1. Local thermodynamic equilibrium vs. escape probability radiative transfer
Detailed excitation and radiative transfer calculations are needed to estimate the line intensities of interstellar species from the source physical properties (gas density, temperature and source size) and the species column density. The inverse problem of deriving physical conditions and column densities for observed line intensities needs assumptions. For instance, the rotation diagram analysis can be used when the populations of the energy levels are in LTE (see Goldsmith & Langer 1999, for a detailed description of non LTE and optical thickness effects on the rotational diagram method). The critical densities for the methylcyanide lines are typically 105 − 106 cm-3, while the typical gas density and temperatures are 6 × 104 cm-3 and 60 K in the Horsehead PDR, and 1 × 105 cm-3 and 25 K in the dense core.
The lines detected in the Horsehead are thus subthermally excited. In this case, both collisional and radiative (de)excitation must be taken into account. For instance, escape probability methods (Sobolev 1960; Castor 1970; Goldreich & Kwan 1974) correctly treat the radiative transfer micro-physics. However, they suppose the presence of a large velocity gradient so that photons escape their local environment, i.e., radiative transfer is only local. RADEX (van der Tak et al. 2007) is one such method. We use it here and we compare the results with those obtained in LTE.
4.1.2. Hydrogen vs. electron excitation
In order to correctly treat the micro-physics, radiative transfer methods need collisional (de)excitation coefficients as inputs. In general, only collisions with the most abundant gas species, i.e. ortho and para H2 and helium, are taken into account. However, excitation by electrons are expected to play a significant role when the electron fraction reaches [e−] = ne/nH2 ~ 10-5 − 10-4. The importance of the collisional exception with these two families of partners are similar when neCe ~ nH2CH2. While collisional coefficients with neutral are typically 10-11 − 10-10 cm3 s-1, those with electrons are around 10-6. Goicoechea et al. (2009) determined an electron fraction of 10-4 at the PDR position, implying that electrons contribute significantly to the excitation. In contrast, the same study derived an electron fraction of a few 10-9 in the dense core, where the electron excitation is thus negligible.
We have computed the CH3CN-e− and HC3N-e− collisional coefficients within the dipolar Born approximation (e.g. Itikawa 1971). Owing to the large dipole of both species (3.73 D for HC3N and 3.92 D for CH3CN), dipole-allowed cross sections are indeed expected to be dominant and entirely determined by the long-range electron-dipole interaction (see e.g. Faure et al. 2007). In this approximation, cross sections are proportional to line strengths (and the square of the dipole) and therefore strictly obey the dipolar selection rule (see Eq. (1)). Line strengths and dipoles were taken from the CDMS catalog (Müller et al. 2005). Excitation cross sections were computed in the energy range 0.1 meV−1 eV and rate coefficients were deduced in the range 10−1000 K, for the lowest 251 levels of CH3CN (238 transitions) and the lowest 31 levels of HC3N (30 transitions). The CH3CN–e− and HC3N–e− collisional rates are available online through the BASECOL2 database.
4.1.3. Beam dilution
Beam dilution arises when the source does not fill the beam. In our observations, the half primary beam width of the IRAM-30 m varies from 30′′ at the low end of the 3 mm band to 10′′ at the high end of 1 mm band. Moreover, a PDR lies by definition at the interface between fully ionized and molecular gas. Previous PDR modeling of the Horsehead edge implies that the physical and chemical typical angular scales ranges from 1 to 50′′. It thus is likely that the beam dilution will affect the line luminosities and then the derivation of column densities. Beam dilution can be more easily disentangled from excitation effects when several lines of different energy levels and critical densities happen at close by frequencies so that the beam dilution is identical for these lines. However, we cannot derive source properties below the lowest measured angular resolution without an a priori analytical model of the source spatial distribution. The derived column densities are thus beam-averaged to the lowest observed angular resolution i.e. 16.8′′ for CH3CN and 22.7′′ for HC3N. A beam dilution factor is applied to transistions corresponding to a larger beam. The derived column densities will then be lower limits, because lower beam filling factors translate to higher column densities.
Quantitative informations of the distribution functions used as priors in the Bayesian fitting.
4.1.4. The Bayesian framework
In the case of subthermal excitation and optically thin lines, the main parameters controlling the line intensities (gas density, column density, temperature, beam dilution) cannot be independently retrieved without additional information. As stated in Sect. 1, our previous studies of the Horsehead edge implies a knowledge of the H2 gas density and the gas temperature for each observed position.
We wish to combine these previously known information about the source with the observed line shapes in order to determine robust estimates of the column densities. The formulation of the inverse problem in the Bayesian framework is the best way to reach our goal. The principles of Bayesian inference can be found in (Press et al. 1992; Feigelson & Jogesh Babu 2012), and a technical description is available in Appendix B. In short, the information on the source physical properties is taken into account by defining informative priors, i.e. peaked distributions of the parameters. In our case, we use standard normal and lognormal distributions respectively for the temperature and density parameters. Lognormal laws allow us to span several orders of magnitude for, e.g. the density.
We have no a priori information for the column densities and the beam dilution. In the Bayesian framework, we used “uninformative” distributions (named Jeffreys prior), i.e. uniform distributions in a given plausible parameter range. RADEX has hard coded limits of 5 and 25 for log 10N. It is safe to use a smaller interval for the considered species in the Horsehead case. The chosen statistical law for the column density was thus taken as a uniform distribution of the logarithm of the column density with 9 and 17 as boundaries. For the beam dilution, we chose a uniform distribution between 0 and 1. Table 4 summarizes the quantitative information characterizing the used distributions.
Beam dilution for CH3CN determined from the radiative transfer modeling.
Best fit parameters for the radiative transfer modeling.
4.2. Derived results
4.2.1. CH3CN abundance, beam dilution and line opacities
We used the collisional coefficients from Green (1986). These coefficients were computed for collisions with He and scaled to H2. They are computed for 251 levels (31 375 coefficients) with upper level energies up to 1150 K. We restricted our computation to the first 185 levels (16 650 coefficients) up to upper level energies of 580 K in order to limit the computation time. We then checked that using the full set of coefficients for the best fit parameters yields the same integrated intensities.
The main remaining uncertainty is the quality of the used collisional rate as the potential energy surface and the dynamical method employed by Green (1986) were approximate. The rate coefficients of Green (1986), computed for Helium in the infinite sudden order (IOS) approximation, and then scaled by a factor 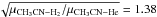 to obtain the value for H2 are expected to be lower than the actual H2 rate coefficients by up to an order of magnitude. We thus checked the sensitivity of these results to the variation of the collisional rate coefficients by multiplying them by one order of magnitude. The absolute abundances varies by less than a factor 3 and the abundance ratio between the PDR and the dense core positions varies by at most 50%. Both results are thus robust.
to obtain the value for H2 are expected to be lower than the actual H2 rate coefficients by up to an order of magnitude. We thus checked the sensitivity of these results to the variation of the collisional rate coefficients by multiplying them by one order of magnitude. The absolute abundances varies by less than a factor 3 and the abundance ratio between the PDR and the dense core positions varies by at most 50%. Both results are thus robust.
As the hyperfine structure of some CH3CN lines were resolved, there are two independent ways to measure the line opacities. The first one explicitly fits the hyperfine structure using the GILDAS HFS fitting method3. In our observations, the (J = 5 − 4,K = 2) set of hyperfine lines at the PDR position features the best compromise between signal-to-noise ratio and separation of the hyperfine components to enable a meaningful fit. The derived opacity is τ = 1.3 ± 1.1. The low opacity of CH3CN is consistent with the non-detection of 13CH3CN and CH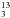 CN. The second method is based on opacities modeled by RADEX. For the same line, the derived opacity is 0.22 ± 0.05. None of the lines modeled by RADEX have opacities higher than 0.6 (see Fig. B.2). Given the large uncertainties of the HFS method in the estimate of the line opacities, this value is not taken into account in the analysis. Nevertheless, from the radiative transfer analysis, we derive that the CH3CN lines are optically thin.
CN. The second method is based on opacities modeled by RADEX. For the same line, the derived opacity is 0.22 ± 0.05. None of the lines modeled by RADEX have opacities higher than 0.6 (see Fig. B.2). Given the large uncertainties of the HFS method in the estimate of the line opacities, this value is not taken into account in the analysis. Nevertheless, from the radiative transfer analysis, we derive that the CH3CN lines are optically thin.
The beam filling factors for CH3CN are summarized in Table 5. At the PDR position, the beam dilution factors are compatible with a source structure that is small (<10″) in only one dimension. In the dense core, only the two lower frequency lines are detected and the beam dilutions have similar values, larger than 0.5, implying the emission is more extended than at the PDR position.
The best fit results, which take the excitation by collision with electrons into account, are summarized in Table 6. The associated CH3CN column densities for the PDR and core positions, are NCH3CN = (6 − 15) × 1012 cm-2 and NCH3CN = (3 − 8) × 1011 cm-2, respectively these values correspond to the smallest observed beam for each molecule. This translates into abundances of (2 − 4) × 10-10 for the HCO peak and (5 − 12) × 10-12 for the DCO+ peak. CH3CN is therefore 30 times more abundant in the PDR than in the dense core.
4.2.2. CH3NC abundances and CH3NC/CH3CN isomeric ratio
Only 3 CH3NC lines are detected at the HCO peak and none at the DCO+ peak. Including the beam dilution factors, more than 3 unknowns must be constrained forbidding a complete modeling of the physical parameters of the source without additional a priori assumptions. In addition to the same prior on the gas density and temperature as for CH3CN, we assumed that the two molecules are cospatial, which translates into identical beam dilutions. In addition, we do not know about any computation of the CH3NC collisional coefficients. We thus used the CH3CN ones.
With these hypotheses, we derived a column density of NCH3NC = (6 − 25) × 1011 cm-2 at the PDR position and NCH3NC ≤ 5 × 1011 cm-2 as the 2 sigma upper limit in the dense core.
The CH3NC/CH3CN abundance ratio is 0.15 ± 0.02 and <0.15 at the PDR and the dense core position, respectively. This value is similar to the ratio of the integrated intensities. This points towards optically thin lines.
4.2.3. HC3N and HC2NC abundances and isomeric ratio
We used the collisional coefficients computed by Wernli et al. (2007) for para-H2 and Faure et al. (in prep.) for ortho-H2. The derived critical densities for collisions of HC3N with H2 are 4 × 105 − 1 × 106 cm-3. In this modeling, we used the standard RADEX prescription, i.e. the determination of the ortho-H2/para-H2 from the gas kinetic temperature (0.01 and 0.52 for Tkin = 25 and 60 K, respectively).
However, we checked that using a fixed ortho-H2/para-H2 ratio of 3 does not influence the results above the derived uncertainties.
For HC3N, all 4 lines were detected at 3 mm at both positions, while neither the 2 lines at 2 mm nor the 8 lines at 1 mm were detected. The derived column densities and abundances of HC3N are similar at the PDR and dense core positions with values of (1−5) × 1011 cm-2 and (5−12) × 10-12, respectively.
For HC2NC, none of the millimetric lines were detected in either of the observed positions. Assuming the same priors on the gas temperature and density and cospatial emission of HC2NC and HC3N, the derived 2 sigma upper limits of the column densities of HC2NC are NHC2NC ≤ 2 × 1010 cm-2 at both position positions.
Since the opacities of all observed lines are low for HC3N, the abundance ratio is similar to the observed intensity ratio. The 2 sigma upper limit for the HC2NC/HC3N abundance ratio thus is 0.1.
Column density and abundances for C3N.
4.2.4. C3N abundance
Three doublets of C3N are marginally detected at the PDR position in the 3 mm band. As the collision rates for C3N are not available, we used the CLASS/WEEDS (Maret et al. 2011) LTE engine to model these lines. Based on previous experience (Guzmán et al. 2012a; Pety et al. 2012), we used an excitation temperature of 10 K, and a source structure corresponding to a 6′′ × 50′′ filament centered on the PDR position. This yields a column density of (2 ± 1) × 1012 cm-3 at the PDR position, i.e., an abundance of (5 ± 2.5) × 10-11. No individual line of C3N is detected at the dense core position, even though stacking yields a 5σ detection. We thus report an 2σ upper limit on the column density at the dense core position of 1 × 1012 cm-3, i.e., a 2σ upper limit on the abundance of 1.5 × 10-11.
4.3. Comments
4.3.1. H2H2 vs. electron excitation
Table 6 compare the best fit parameters obtained either without electron excitation or with a fixed electron fraction of 10-4 as derived for the PDR position by Goicoechea et al. (2009). Including electron excitation reduces the derived column density by 40% for CH3CN, but by less than the uncertainty on the column density (i.e., ≤25%) for HC3N. This difference between the two molecules is due to a higher critical densities of CH3CN lines (~106 cm-3) compared to those of HC3N (~105 cm-3).
4.3.2. Shortcomings of rotational diagrams in the case of CH3CN
CH3CN is a relatively complex species. It is often assumed to exist only in dense environments where it is thermalized. In such environments, rotational diagrams (Goldsmith & Langer 1999) are then the tool of choice to derive the column density of CH3CN. However, we find that CH3CN is brighter and much more abundant in UV-illuminated relatively low density gas than in the UV-shielded dense core. In Appendix C, we discuss the use of rotational diagrams in the case of moderately subthermal excitation such as in the PDR position. The determination of the column density through the use of a rotational diagram would have been underestimated by a factor 6 to 33, depending on the observed K-ladder, at the PDR position compared to the escape probability computations. The density being higher at the dense core position, the rotational diagram yield the same column density as the escape probability method.
5. Discussion
Even when taking the excitation by electrons into account, which is significant in the UV-illuminated gas, CH3CN is 30 times more abundant in the PDR (2.5 × 10-10) than in the UV-shielded dense core (8 × 10-12). In contrast, HC3N has similar abundance at both positions (8 × 10-12), while C3N is only abundant in the PDR (5 × 10-11). In this section, we discuss the chemistry of CH3CN and the values of the isomeric ratios.
5.1. CH3CN and CH3NC chemistry
The major gas phase route to CH3CN and CH3NC is thought to be a radiative association (Huntress & Mitchell 1979; Bates 1983; Leung et al. 1984) 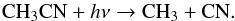 (4)with a reaction constant kra, followed by the ion-electron dissociative recombination reaction
(4)with a reaction constant kra, followed by the ion-electron dissociative recombination reaction 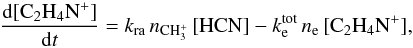 (5)The main destruction route in presence of UV illumination is
(5)The main destruction route in presence of UV illumination is 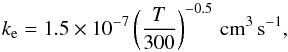 (6)In this simplified view, the abundance of CH3CN is given by
(6)In this simplified view, the abundance of CH3CN is given by ![\begin{equation} \frac{{\rm d}[\metcy]}{{\rm d}t} = \kdr \, \nel \, [\chem{C_{2}H_{4}N^{+}}] - \chi \, \kdiss \, [\metcy], \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq204.png) (7)where the rate of the dissociative recombination to CH3CN (Vigren et al. 2008)
(7)where the rate of the dissociative recombination to CH3CN (Vigren et al. 2008) 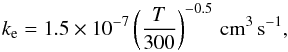 (8)the photodissociation rate (van Dishoeck et al. 2006) is
(8)the photodissociation rate (van Dishoeck et al. 2006) is 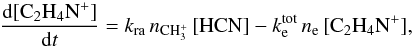 (9)and χ is the UV illumination at the PDR edge. The abundance of C2H4N+ is given by
(9)and χ is the UV illumination at the PDR edge. The abundance of C2H4N+ is given by ![\begin{equation} \frac{{\rm d}[\chem{C_{2}H_{4}N^{+}}]}{{\rm d}t} = \kra \, n_\chem{CH_{3}^{+}} \, [\chem{HCN}] -\kdrtot \, \nel \, [\chem{C_{2}H_{4}N^{+}}], \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq208.png) (10)where the value of the radiative association rate is typically 2 × 10-8 cm-3 s-1 at 50 K (Bates 1983), and ktote is the total rate of the dissociative recombination to CH3CN, CH3NC, and possibly other products. The steady-state solution is
(10)where the value of the radiative association rate is typically 2 × 10-8 cm-3 s-1 at 50 K (Bates 1983), and ktote is the total rate of the dissociative recombination to CH3CN, CH3NC, and possibly other products. The steady-state solution is
![\begin{equation} [\metcy] = \frac{\kdr}{\kdrtot}\frac{\kra \, n_\chem{CH_{3}^{+}} \, [\chem{HCN}]}{\chi \, \kdiss}\cdot \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq210.png) (11)
The UV illumination for the Horsehead PDR is χ ~ 60 (Abergel et al. 2003; Draine 1978). Using the known density profile, we derive a visual extinction of Av ~ 2 mag (see Fig. 4 Guzmán et al. 2012a). At the PDR position, the (pure gas phase) Meudon PDR code indicates that [HCN] ~ 10-9, and
(11)
The UV illumination for the Horsehead PDR is χ ~ 60 (Abergel et al. 2003; Draine 1978). Using the known density profile, we derive a visual extinction of Av ~ 2 mag (see Fig. 4 Guzmán et al. 2012a). At the PDR position, the (pure gas phase) Meudon PDR code indicates that [HCN] ~ 10-9, and 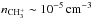 . With these normalizing factors, we deduce
. With these normalizing factors, we deduce
![\begin{equation} [\metcy] = 10^{-13}\, \bracket{\frac{\kdr}{\kdrtot} \, \frac{\kra}{2\times10^{-8}} \, \frac{n_\chem{CH_{3}^{+}} \, [\chem{HCN}]}{10^{-14}} \, \frac{1.21}{\chi \, \exp(-\gamma\,\Av)}}\cdot \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq214.png) (12)So the predicted abundance of CH3CN is ~10-13 at the PDR position. This is an upper limit as
(12)So the predicted abundance of CH3CN is ~10-13 at the PDR position. This is an upper limit as 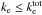 . As the measured abundance of CH3CN is ~2400 times larger than this predicted abundance, this route does not seem efficient enough to produce the observed amount of CH3CN at the PDR position.
. As the measured abundance of CH3CN is ~2400 times larger than this predicted abundance, this route does not seem efficient enough to produce the observed amount of CH3CN at the PDR position.
A potential alternative to pure gas phase chemistry is the formation of CH3CN on ices through ice photo-processing followed by photo-desorption in the UV-illuminated part of the Horsehead edge. Danger et al. (2011) have studied the formation of CH3CN by the UV photolysis of ethylamine (CH3CH3NH2) ices. They determined that methyl cyanide could be formed at 20 K with a yield of 4%. Photo-desorption of small molecules like H2CO (Guzmán et al. 2011; Noble et al. 2012) is efficient even at low grain temperatures (20 K) where thermal desorption is absent. Larger molecules created on the ices have higher photo-desorption thresholds and would stay on the grains.
CH3CN has also been observed in shocks (e.g. L1157-B1 Arce et al. 2008; Codella et al. 2009). In this case, sputtering of grains by impacting gas evaporates the CH3CN formed in ices. However, high abundances of CH3CN is not a specific tracer of shock, as shown by the example of the Horsehead PDR.
5.2. Isomeric ratios
5.2.1. CH3NC/CH3CN
Defrees et al. (1985) argued that the CH3NC/CH3CN isomeric ratio depends on the isomerisation equilibrium which happens when the C2H4N+ ⋆ unstable molecule or “complex” radiatively loses its energy, provided that the dissociative recombination does not modify the molecule backbone. From consideration on the energies of the different isomers of C2H4N+, they deduced an CH3NC/CH3CN isomeric ratio in the 0.1−0.4 range, i.e. very different from the typical HCN/HNC isomeric ratio value of 1 found in the interstellar medium (Sarrasin et al. 2010; Mendes et al. 2012).
From their tentative detection of the J = 4 → 3, J = 5 → 4, and J = 7 → 6 lines of CH3NC in Sgr B2, Cernicharo et al. (1988) found a CH3NC/CH3CN abundance ratio of ≃0.05. Also in Sgr B2, Remijan et al. (2005) deduced an even smaller CH3NC/CH3CN abundance ratio of 0.02 ± 0.02 from their detection of the CH3CN and CH3NC J = 1 → 0 lines. The value we derive for this abundance ratio in the Horsehead PDR is 0.15 ± 0.02, i.e. 2–5 times higher than these previous results. Our value falls directly in the range (0.1–0.4) predicted by Defrees et al. (1985).
5.2.2. HC2NC/HC3N
HC2NC was first detected in TMC-1 by Kawaguchi et al. (1992a), they find a HC2NC/HC3N abundance ratio of 0.02−0.05. In CRL618 (a circumstellar envelope affected by strong UV fields from the central star) Pardo & Cernicharo (2007) derive an abundance ratio of 0.025−0.03. Our derived upper limit for this abundance ratio is compatible with these results.
6. Summary
While CH3CN is a complex nitrile molecule (more than 6 atoms), its lines are brighter in the PDR than in the dense core. Its linewidths are also narrower in the PDR than in the dense core. Due to the lower density at the PDR position, the lines are subthermally excited, implying that a rotational diagram analysis underestimates the column density by a factor 6−33 depending on the observed K-ladder. In other words, bright CH3CN lines do not necessarily imply high densities (nH ≳ 106 cm-3) and LTE.
Large velocity gradient radiative transfer methods implies that CH3CN is 30 times more abundant in the UV illuminated gas than in the UV shielded dense core. The overabundance of CH3CN in the PDR compared to the dense core position is surprising because the photodissociation of this complex molecule is expected to be efficient. A simple pure gas phase chemical model underestimates the abundance of CH3CN in the PDR by a factor of at least a few thousand.We propose that CH3CN gas phase abundance is enhanced when ice mantles of grains are destroyed (photo-desorption or thermal-evaporation in PDRs, sputtering in shocks).
We also report the first clear detection of 4 CH3NC lines in the millimeter bands at the PDR position. The CH3NC/CH3CN isomeric ratio of 0.15 is compatible with the theoretical range of 0.1−0.4 from Defrees et al. (1985).
In sharp contrast to CH3CN and its isomer, HC3N lines are stronger in the dense core than in the PDR. The HC3N abundance is similar at both positions. No lines of its isomer HC2NC were detected in either position. The pure gas phase chemistry of HC3N is more complex than the CH3CN one, requiring a detail chemical modeling to understand these results.
Online material
Appendix A: Observational tables
This section gathers the observational fit obtained for all the lines studied in this paper. The line parameters are taken from the CDMS (Müller et al. 2005) for CH3CN, HC3N and C3N, and from the JPL (Pickett et al. 1998) for CH3NC, HC2NC and HNC3. Original spectroscopic data come from Müller et al. (2009) for CH3CN, Thorwirth et al. (2000) for HC3N, Gottlieb et al. (1983) for C3N, Bauer & Bogey (1970) for CH3NC, Guarnieri et al. (1992) for HC2NC, and Hirahara et al. (1993) for HNC3. The accuracy is excellent for CH3CN, HC3N, HC2NC and C3N and moderate for CH3NC (~0.09 MHz or 0.27 km s-1 at 100 GHz), and HNC3 (~0.12 MHz or 0.42 km s-1 at 84 GHz).
Line properties for CH3NC in Tmb.
Observed line properties for CH3CN.
Line properties for HC3N in Tmb.
Stacked line properties for C3N.
Line properties for HC2NC in Tmb.
Line properties for HNC3 in Tmb.
Appendix B: Bayesian radiative transfer modeling
 |
Fig. B.1 Distributions of the posterior probability for three parameters, i.e. gas density (nH2), kinetic temperature (TK) and CH3CN column density (N), at the PDR position. Along the diagonal, the one dimensional probability distribution functions are integrations of the two dimension probability distribution functions displayed below. The color coding of the two dimensional histograms runs from 0% (white) to 100% of the peak value(black). The contours correspond to 68% (1σ) and 95% (2σ) of cumulated posterior probability. |
 |
Fig. B.2 Distribution of modeled integrated intensities (top 4 panels) and line opacities (bottom 4 panels) as a function of the K number. Each panel presents the results for a different (J + 1 → J) K-ladder. The 3 different gray levels corresponds to 3 different uncertainty intervals, i.e., 68% (1σ), 95% (2σ), and 99.9% (3σ) from dark to light gray. For the 4 top panels, the observed line intensities with their 1σ uncertainty intervals are plotted as red segments The dashed horizontal black line displays the 2σ upper limits for the undetected lines. |
The inputs of the RADEX code are the kinetic temperature (TK), the volume density of the collisional partner4 (nH2) and the column density of the computed species (N). Given a set of energy levels and the radiative and collisional transitions linking them (both from the LAMBDA database Schöier et al. 2005), the LVG code computes for each line, its opacity, excitation temperature and flux assuming a Gaussian profile of a given fixed linewidth. We combined this LVG model with a Bayesian fitting method to determine the optimal physical parameters of the source. We assume that the observation uncertainties are centered Gaussians. The observed data D is thus represented by a set of N integrated intensity and its associated measurement uncertainty, D = { Ii,σi } i = 1..N.
With the hypothesis of independent Gaussian centered noise, the likelihood of having observing the data D given the model parameters θ = { θi } is given by ![\appendix \setcounter{section}{2} \begin{equation} L(D|{\bm{\theta}}) = \prod_{i=1}^{N}\left[\frac{1}{\sqrt{2\pi\sigma_{i}}}\exp\left(-\frac{[I^\emr{obs}_ {i}-I^\emr{mod}_{i}(\bm{\theta})]^{2}}{2\sigma_{i}^{2}}\right)\right], \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq348.png) (B.1)where i is an index over the N channels. Taking the logarithm, the equation becomes
(B.1)where i is an index over the N channels. Taking the logarithm, the equation becomes ![\appendix \setcounter{section}{2} \begin{equation} \ln L(D|{\bm{\theta}}) = -\frac{1}{2}\sum_{i=1}^{N}\ln\,(2 \pi\sigma_{i})-\sum_{i=1}^{N}\frac{[I^\emr{obs}_{i}-I^\emr{mod}_{i}(\bm{\theta})]^ {2}}{2\sigma_{i}^{2}}, \end{equation}](/articles/aa/full_html/2013/09/aa21031-13/aa21031-13-eq350.png) (B.2)where Imod are derived from the parameters θ through the RADEX model. In the Bayesian framework, the posterior probability distribution of the parameters p(θ | D) is obtained through the Bayes rule
(B.2)where Imod are derived from the parameters θ through the RADEX model. In the Bayesian framework, the posterior probability distribution of the parameters p(θ | D) is obtained through the Bayes rule  (B.3)where p(θ) is the prior probability distribution of the θ parameter. Through the use of informative prior distribution of the model parameters, it is possible to break model degeneracies. The posterior probability function can have a complicated surface with more than one maxima, in order to identify the best set of parameters (i.e., the posterior probability function around the global maxima) numerous tools have been developed. We use a Markov Chain Monte Carlo (MCMC) method for sampling the posterior probability function, specifically emcee (Foreman-Mackey et al. 2013), a MCMC Python implementation using the affine-invariant ensemble sampler presented in Goodman & Weare (2010). This sampling method enables us to have the posterior probability distribution as an equilibrium-sampling distribution. With the set of sampling values of the parameters it is then possible to compute marginalized one dimension probability distribution functions for each individual parameters. A central tendency (i.e. mean, median or histogram maximum) gives the most probable a posteriori parameter value and a confidence interval can be directly computed from the probability distribution of the parameters.
(B.3)where p(θ) is the prior probability distribution of the θ parameter. Through the use of informative prior distribution of the model parameters, it is possible to break model degeneracies. The posterior probability function can have a complicated surface with more than one maxima, in order to identify the best set of parameters (i.e., the posterior probability function around the global maxima) numerous tools have been developed. We use a Markov Chain Monte Carlo (MCMC) method for sampling the posterior probability function, specifically emcee (Foreman-Mackey et al. 2013), a MCMC Python implementation using the affine-invariant ensemble sampler presented in Goodman & Weare (2010). This sampling method enables us to have the posterior probability distribution as an equilibrium-sampling distribution. With the set of sampling values of the parameters it is then possible to compute marginalized one dimension probability distribution functions for each individual parameters. A central tendency (i.e. mean, median or histogram maximum) gives the most probable a posteriori parameter value and a confidence interval can be directly computed from the probability distribution of the parameters.
As an example, Figs. B.1 and B.2 shows the results of the modeling of the CH3CN emission at the PDR position. Figure B.1 shows 2d posterior distributions of the model parameters. The marginalized 1d probability distribution functions of each parameter, which are displayed along the diagonal, are integrated over all the other parameter axes. Figure B.2 gathers the 1d probability distribution functions of the RADEX results: 1) the integrated intensity; and 2) the line opacity as a function of the K number for different (J + 1 → J) K-ladder.
Appendix C: Shortcomings of rotational diagrams in the case of CH3CN
 |
Fig. C.1 Rotational diagrams for CH3CN at the HCO peak, in each of the 4 top panels, the solid lines correspond to fits restricted to to observed K transitions for a given J − J − 1 set, the fitted line is of the same color as the fitted points. The final panel shows, in a dotted line, the result of fitting all lines simultaneously. Each panel shows the rotational temperature and column density derived from the fit. |
In this section, we quantify the error made when using rotational diagrams to derive column densities and abundances in moderately sub thermal excitation regimes such as those found in the PDR position (~6 × 104 cm-3). We built the rotational diagrams assuming that the line emission is optically thin, i.e. we did not correct the measured column densities of the upper levels for opacity. Figures C.1 and C.2 shows the results. Two points
stand out. First, the rotational temperatures derived from a fit of all the lines are lower than the kinetic temperature. However, the derived temperatures gets closer to the kinetic temperature when fitting the transitions with different J levels separately (one fit per panel in Figs. C.1 and C.2). This comes from the fact that different K-levels at constant J are not radiatively coupled (cf. Eq. (1)).
When fitting all the lines simultaneously, the rotational diagram derived column densities are underestimated by a factor 20 compared to the LVG derived ones for the PDR and a factor 2.5 for the dense core. When the K-ladders are fitted independently, the column densities increase when the associated J level decreases. Indeed, the high J levels are more difficult to thermalize because their critical densities are higher. As a consequence, the derived column densities is more and more underestimated as J increases. In the Horsehead PDR case, the column density derived from the rotational diagram for the lowest J level (5−4) is still six times lower than the column density derived by the escape probability radiative transfer modeling. In contrast, the rotational diagram and the RADEX methods yields the same column density at the dense core position. This is expected as the CH3CN level population will be closer to thermal equilibrium in the higher density core.
Three different situations happen when using the rotational diagram method to determine the column density of CH3CN and/or the gas kinetic temperature.
-
1.
When the level populations follow an LTE distribution (e.g. the gas density is higher than a few 105 cm-3 for the J = 5–4 K-ladder) both the gas kinetic temperature and the CH3CN column density can be derived accurately. This approximately corresponds to the case of the dense core position in our study.
-
2.
When the excitation is slightly subthermal (e.g. the gas density is in the range (4 − 8) × 104 cm-3 for the J = 5–4 K-ladder), the gas kinetic temperature can be obtained by fitting only the corresponding K-ladder lines that are close to thermalization. However, the column density will be underestimated. This corresponds to the case of the PDR position in our study.
-
3.
When the excitation is strongly subthermal (e.g. the gas density is lower than 4 × 104 cm-3 for the J = 5–4 K-ladder), both the gas kinetic temperature and the CH3CN are underestimated. It is then necessary to study the excitation with more advanced methods like escape probability methods.
Appendix D: Methyl cyanide and isocyanide spectra
 |
Fig. D.1 Spectrum of the CH3CN 3 mm and 2 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.2 K for clarity. The panel displays the K set of lines for a given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars, whose heights indicate their relative hyperfine intensities in the optically thin regime applicable to these observations. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
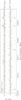 |
Fig. D.2 Spectrum of the CH3NC 3mm detected lines at the HCO peak (i.e., the PDR position, top spectrum) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum), the spectrum towards the HCO peak has been shifted vertically by 0.1 K for clarity. The panel displays the K set of lines for the given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
Published WHISPER data are available on the project website: http://www.iram.fr/~horsehead/
The HFS fitting method is described in the documentation of the GILDAS/CLASS software at http://www.iram.fr/IRAMFR/GILDAS
Acknowledgments
This work has been funded by the grant ANR-09-BLAN-0231-01 from the French Agence Nationale de la Recherche as part of the SCHISM project (http://schism.ens.fr/). J.R.G. thanks the Spanish MINECO for funding support through grants AYA2009-07304 and CSD2009-00038. J.R.G. is supported by a Ramón y Cajal research contract from the MINECO. V.G. acknowledges support from the Chilean Government through the Becas Chile scholarship program.
References
- Abergel, A., Teyssier, D., Bernard, J. P., et al. 2003, A&A, 410, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araya, E., Hofner, P., Kurtz, S., Bronfman, L., & DeDeo, S. 2005, ApJS, 157, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H. G., Santiago-García, J., Jørgensen, J. K., Tafalla, M., & Bachiller, R. 2008, ApJ, 681, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D. R. 1983, ApJ, 270, 564 [Google Scholar]
- Bauer, A., & Bogey, M. 1970, C. R. Acad. Sc. Ser. B, 271, 892 [Google Scholar]
- Bechtel, H. A., Steeves, A. H., & Field, R. W. 2006, ApJ, 649, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Lefloch, B., et al. 2004, ApJ, 615, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I. 1970, MNRAS, 149, 111 [NASA ADS] [Google Scholar]
- Cernicharo, J., Kahane, C., Guelin, M., & Gomez-Gonzalez, J. 1988, A&A, 189, L1 [NASA ADS] [Google Scholar]
- Codella, C., Benedettini, M., Beltrán, M. T., et al. 2009, A&A, 507, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danger, G., Bossa, J.-B., de Marcellus, P., et al. 2011, A&A, 525, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Defrees, D. J., McLean, A. D., & Herbst, E. 1985, ApJ, 293, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Deleon, R. L., & Muenter, J. S. 1985, J. Chem. Phys., 82, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Varambhia, H. N., Stoecklin, T., & Tennyson, J. 2007, MNRAS, 382, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Jogesh Babu, G. 2012, Modern Statistical Methods for Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gadhi, J., Lahrouni, A., Legrand, J., & Demaison, J. 1995, J. Chim. Phys., 92, 1984 [Google Scholar]
- Gensheimer, P. D. 1997, ApJ, 479, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Goicoechea, J. R., Pety, J., & Hily-Blant, P. 2009, A&A, 494, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginard, D., González-García, M., Fuente, A., et al. 2012, A&A, 543, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., Hily-Blant, P., & Le Bourlot, J. 2009, A&A, 498, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5 [Google Scholar]
- Gordy, W., & Cook, R. 1984, Microwave molecular spectra, Techniques of chemistry (Wiley) [Google Scholar]
- Gottlieb, C. A., Gottlieb, E. W., Thaddeus, P., & Kawamura, H. 1983, ApJ, 275, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, S. 1986, ApJ, 309, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Guarnieri, A., Hinze, R., Krüger, M., & Zerbe-Foese, H. 1992, J. Mol. Spect. 156, 39 [Google Scholar]
- Guesten, R., Walmsley, C. M., Ungerechts, H., & Churchwell, E. 1985, A&A, 142, 381 [NASA ADS] [Google Scholar]
- Guzmán, V., Pety, J., Goicoechea, J. R., Gerin, M., & Roueff, E. 2011, A&A, 534, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, V., Pety, J., Gratier, P., et al. 2012a, A&A, 543, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, V., Roueff, E., Gauss, J., et al. 2012b, A&A, 548, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Abergel, A., Walmsley, C. M., Teyssier, D., & Pety, J. 2005, A&A, 437, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&A, 133, 29 [Google Scholar]
- Hirahara, Y., Ohshima, Y., & Endo, Y. 1993, ApJ, 403, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Huntress, Jr., W. T., & Mitchell, G. F. 1979, ApJ, 231, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., & Schloerb, F. P. 1984, ApJ, 282, 516 [Google Scholar]
- Itikawa, Y. 1971, J. Phys. Soc. Japan, 30, 835 [Google Scholar]
- Kawaguchi, K., Ohishi, M., Ishikawa, S.-I., & Kaifu, N. 1992a, ApJ, 386, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Takano, S., Ohishi, M., et al. 1992b, ApJ, 396, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, M., Dreizler, H., Preugschat, D., & Lentz, D. 1991, Angewandte Chemie International Edition in English, 30, 1644 [Google Scholar]
- Leung, C. M., Herbst, E., & Huebner, W. F. 1984, ApJS, 56, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lindberg, J. E., Aalto, S., Costagliola, F., et al. 2011, A&A, 527, A150 [Google Scholar]
- Mackay, D. D. S. 1999, MNRAS, 304, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., Bardeau, S., & Reynier, E. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauersberger, R., Henkel, C., Walmsley, C. M., Sage, L. J., & Wiklind, T. 1991, A&A, 247, 307 [NASA ADS] [Google Scholar]
- McCarthy, M. C., Gottlieb, C. A., Thaddeus, P., Horn, M., & Botschwina, P. 1995, J. Chem. Phys., 103, 7820 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes, M. B., Buhr, H., Berg, M. H., et al. 2012, ApJ, 746, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Drouin, B. J., & Pearson, J. C. 2009, A&A, 506, 1487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noble, J. A., Theule, P., Mispelaer, F., et al. 2012, A&A, 543, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olmi, L., Cesaroni, R., Neri, R., & Walmsley, C. M. 1996a, A&A, 315, 565 [NASA ADS] [Google Scholar]
- Olmi, L., Cesaroni, R., & Walmsley, C. M. 1996b, A&A, 307, 599 [NASA ADS] [Google Scholar]
- Pardo, J. R., & Cernicharo, J. 2007, ApJ, 654, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Goicoechea, J. R., Hily-Blant, P., Gerin, M., & Teyssier, D. 2007, A&A, 464, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing [Google Scholar]
- Purcell, C. R., Balasubramanyam, R., Burton, M. G., et al. 2006, MNRAS, 367, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., Plusquellic, D. F., & Jewell, P. R. 2005, ApJ, 632, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Sarrasin, E., Abdallah, D. B., Wernli, M., et al. 2010, MNRAS, 404, 518 [NASA ADS] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sobolev, V. V. 1960, Moving envelopes of stars (Harvard University Press) [Google Scholar]
- Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2000, J. Mol. Spectrosc., 204, 133 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discuss., 133, 231 [Google Scholar]
- Vigren, E., Kaminska, M., Hamberg, M., et al. 2008, Phys. Chem. Chem. Phys., 10, 4014 [Google Scholar]
- Wernli, M., Wiesenfeld, L., Faure, A., & Valiron, P. 2007, A&A, 464, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Quantitative informations of the distribution functions used as priors in the Bayesian fitting.
All Figures
 |
Fig. 1 Overview of the Horsehead mane photodissociation region showing the two observed positions. Left: DCO+ map (Pety et al. 2007), right: HCO emission map (Gerin et al. 2009). In both maps, The HCO emission peak (PDR position) at RA = 05h40m53.9s, Dec = −02°28′00′′ is shown with a green cross, and the DCO+ emission peak (dense core position) at RA = 05h40m55.7s, Dec = −02°28′22′′ with a blue one. The maps have been rotated 14 degree anti clockwise around the position RA = 05h40m54.27s, Dec = −02°28′00′′ and shifted 20′′ to the east to align the PDR front (vertical red line) with the horizontal 0 offset of the map. |
| In the text | |
 |
Fig. 2 CH3CN energy diagram of levels which contribute to the J = 5 → 4, J = 6 → 5, J = 7 → 6, and J = 8 → 7 transitions in the 3 and 2 mm frequency ranges, i.e. for K levels from 0 to 7 and J levels from 4 to 8, other levels are displayed in dotted line. The E (K = 3n ± 1) and A (K = 3n) states are displayed in black and red, respectively. |
| In the text | |
 |
Fig. 3 Spectrum of the CH3NC 3 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum), the spectrum towards the HCO peak has been shifted vertically by 0.1 K for clarity. The panel displays the K set of lines for the given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| In the text | |
 |
Fig. 4 Spectrum of the CH3CN 3 mm and 2 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.2 K for clarity. The panel displays the K set of lines for a given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars, whose heights indicate their relative hyperfine intensities in the optically thin regime applicable to these observations. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| In the text | |
 |
Fig. 5 Spectrum of the HC3N 3 mm lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.3 K for clarity. |
| In the text | |
 |
Fig. 6 Observed spectra (black line) of the three 3 mm C3N doublets at the PDR peak. The green horizontal lines are the ± 3σ levels. The red spectrum is the LTE model for a 6′′ × 50′′ filament centered at the PDR positions, a 10 K excitation temperature, and a column density of 2 × 1012 cm-2. |
| In the text | |
 |
Fig. 7 Top: cumulative distribution function of computed integrated intensities for C3N in the optically thin LTE regime with Tex = 10 K, and normalized to the intensity of the brightest line. Only 10% of all the 1, 2 and 3 mm lines have intensities brighter than a fifth of the brightest line. The transitions are color coded by bands, black: 3mm, orange: 2 mm, blue: 1 mm. Bottom C3N spectra resulting from the stacking of 38 individual lines at 3 mm. The stacked spectra are shown both for the PDR and dense core positions. The red curve is a gaussian fit to the stacked spectra, the green lines are ± 3σ levels. |
| In the text | |
 |
Fig. B.1 Distributions of the posterior probability for three parameters, i.e. gas density (nH2), kinetic temperature (TK) and CH3CN column density (N), at the PDR position. Along the diagonal, the one dimensional probability distribution functions are integrations of the two dimension probability distribution functions displayed below. The color coding of the two dimensional histograms runs from 0% (white) to 100% of the peak value(black). The contours correspond to 68% (1σ) and 95% (2σ) of cumulated posterior probability. |
| In the text | |
 |
Fig. B.2 Distribution of modeled integrated intensities (top 4 panels) and line opacities (bottom 4 panels) as a function of the K number. Each panel presents the results for a different (J + 1 → J) K-ladder. The 3 different gray levels corresponds to 3 different uncertainty intervals, i.e., 68% (1σ), 95% (2σ), and 99.9% (3σ) from dark to light gray. For the 4 top panels, the observed line intensities with their 1σ uncertainty intervals are plotted as red segments The dashed horizontal black line displays the 2σ upper limits for the undetected lines. |
| In the text | |
 |
Fig. C.1 Rotational diagrams for CH3CN at the HCO peak, in each of the 4 top panels, the solid lines correspond to fits restricted to to observed K transitions for a given J − J − 1 set, the fitted line is of the same color as the fitted points. The final panel shows, in a dotted line, the result of fitting all lines simultaneously. Each panel shows the rotational temperature and column density derived from the fit. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1 for the dense core. |
| In the text | |
 |
Fig. D.1 Spectrum of the CH3CN 3 mm and 2 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.2 K for clarity. The panel displays the K set of lines for a given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars, whose heights indicate their relative hyperfine intensities in the optically thin regime applicable to these observations. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| In the text | |
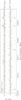 |
Fig. D.2 Spectrum of the CH3NC 3mm detected lines at the HCO peak (i.e., the PDR position, top spectrum) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum), the spectrum towards the HCO peak has been shifted vertically by 0.1 K for clarity. The panel displays the K set of lines for the given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


