| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321031 | |
| Published online | 11 September 2013 | |
Online material
Appendix A: Observational tables
This section gathers the observational fit obtained for all the lines studied in this paper. The line parameters are taken from the CDMS (Müller et al. 2005) for CH3CN, HC3N and C3N, and from the JPL (Pickett et al. 1998) for CH3NC, HC2NC and HNC3. Original spectroscopic data come from Müller et al. (2009) for CH3CN, Thorwirth et al. (2000) for HC3N, Gottlieb et al. (1983) for C3N, Bauer & Bogey (1970) for CH3NC, Guarnieri et al. (1992) for HC2NC, and Hirahara et al. (1993) for HNC3. The accuracy is excellent for CH3CN, HC3N, HC2NC and C3N and moderate for CH3NC (~0.09 MHz or 0.27 km s-1 at 100 GHz), and HNC3 (~0.12 MHz or 0.42 km s-1 at 84 GHz).
Line properties for CH3NC in Tmb.
Observed line properties for CH3CN.
Line properties for HC3N in Tmb.
Stacked line properties for C3N.
Line properties for HC2NC in Tmb.
Line properties for HNC3 in Tmb.
Appendix B: Bayesian radiative transfer modeling
 |
Fig. B.1
Distributions of the posterior probability for three parameters, i.e. gas density (nH2), kinetic temperature (TK) and CH3CN column density (N), at the PDR position. Along the diagonal, the one dimensional probability distribution functions are integrations of the two dimension probability distribution functions displayed below. The color coding of the two dimensional histograms runs from 0% (white) to 100% of the peak value(black). The contours correspond to 68% (1σ) and 95% (2σ) of cumulated posterior probability. |
| Open with DEXTER | |
 |
Fig. B.2
Distribution of modeled integrated intensities (top 4 panels) and line opacities (bottom 4 panels) as a function of the K number. Each panel presents the results for a different (J + 1 → J) K-ladder. The 3 different gray levels corresponds to 3 different uncertainty intervals, i.e., 68% (1σ), 95% (2σ), and 99.9% (3σ) from dark to light gray. For the 4 top panels, the observed line intensities with their 1σ uncertainty intervals are plotted as red segments The dashed horizontal black line displays the 2σ upper limits for the undetected lines. |
| Open with DEXTER | |
The inputs of the RADEX code are the kinetic temperature (TK), the volume density of the collisional partner4 (nH2) and the column density of the computed species (N). Given a set of energy levels and the radiative and collisional transitions linking them (both from the LAMBDA database Schöier et al. 2005), the LVG code computes for each line, its opacity, excitation temperature and flux assuming a Gaussian profile of a given fixed linewidth. We combined this LVG model with a Bayesian fitting method to determine the optimal physical parameters of the source. We assume that the observation uncertainties are centered Gaussians. The observed data D is thus represented by a set of N integrated intensity and its associated measurement uncertainty, D = { Ii,σi } i = 1..N.
With the hypothesis of independent Gaussian centered noise, the likelihood of having observing the data D given the model parameters θ = { θi } is given by  (B.1)where i is an index over the N channels. Taking the logarithm, the equation becomes
(B.1)where i is an index over the N channels. Taking the logarithm, the equation becomes 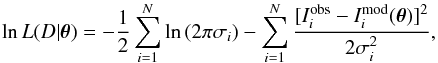 (B.2)where Imod are derived from the parameters θ through the RADEX model. In the Bayesian framework, the posterior probability distribution of the parameters p(θ | D) is obtained through the Bayes rule
(B.2)where Imod are derived from the parameters θ through the RADEX model. In the Bayesian framework, the posterior probability distribution of the parameters p(θ | D) is obtained through the Bayes rule 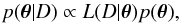 (B.3)where p(θ) is the prior probability distribution of the θ parameter. Through the use of informative prior distribution of the model parameters, it is possible to break model degeneracies. The posterior probability function can have a complicated surface with more than one maxima, in order to identify the best set of parameters (i.e., the posterior probability function around the global maxima) numerous tools have been developed. We use a Markov Chain Monte Carlo (MCMC) method for sampling the posterior probability function, specifically emcee (Foreman-Mackey et al. 2013), a MCMC Python implementation using the affine-invariant ensemble sampler presented in Goodman & Weare (2010). This sampling method enables us to have the posterior probability distribution as an equilibrium-sampling distribution. With the set of sampling values of the parameters it is then possible to compute marginalized one dimension probability distribution functions for each individual parameters. A central tendency (i.e. mean, median or histogram maximum) gives the most probable a posteriori parameter value and a confidence interval can be directly computed from the probability distribution of the parameters.
(B.3)where p(θ) is the prior probability distribution of the θ parameter. Through the use of informative prior distribution of the model parameters, it is possible to break model degeneracies. The posterior probability function can have a complicated surface with more than one maxima, in order to identify the best set of parameters (i.e., the posterior probability function around the global maxima) numerous tools have been developed. We use a Markov Chain Monte Carlo (MCMC) method for sampling the posterior probability function, specifically emcee (Foreman-Mackey et al. 2013), a MCMC Python implementation using the affine-invariant ensemble sampler presented in Goodman & Weare (2010). This sampling method enables us to have the posterior probability distribution as an equilibrium-sampling distribution. With the set of sampling values of the parameters it is then possible to compute marginalized one dimension probability distribution functions for each individual parameters. A central tendency (i.e. mean, median or histogram maximum) gives the most probable a posteriori parameter value and a confidence interval can be directly computed from the probability distribution of the parameters.
As an example, Figs. B.1 and B.2 shows the results of the modeling of the CH3CN emission at the PDR position. Figure B.1 shows 2d posterior distributions of the model parameters. The marginalized 1d probability distribution functions of each parameter, which are displayed along the diagonal, are integrated over all the other parameter axes. Figure B.2 gathers the 1d probability distribution functions of the RADEX results: 1) the integrated intensity; and 2) the line opacity as a function of the K number for different (J + 1 → J) K-ladder.
Appendix C: Shortcomings of rotational diagrams in the case of CH3CN
 |
Fig. C.1
Rotational diagrams for CH3CN at the HCO peak, in each of the 4 top panels, the solid lines correspond to fits restricted to to observed K transitions for a given J − J − 1 set, the fitted line is of the same color as the fitted points. The final panel shows, in a dotted line, the result of fitting all lines simultaneously. Each panel shows the rotational temperature and column density derived from the fit. |
| Open with DEXTER | |
 |
Fig. C.2
Same as Fig. C.1 for the dense core. |
| Open with DEXTER | |
In this section, we quantify the error made when using rotational diagrams to derive column densities and abundances in moderately sub thermal excitation regimes such as those found in the PDR position (~6 × 104 cm-3). We built the rotational diagrams assuming that the line emission is optically thin, i.e. we did not correct the measured column densities of the upper levels for opacity. Figures C.1 and C.2 shows the results. Two points
stand out. First, the rotational temperatures derived from a fit of all the lines are lower than the kinetic temperature. However, the derived temperatures gets closer to the kinetic temperature when fitting the transitions with different J levels separately (one fit per panel in Figs. C.1 and C.2). This comes from the fact that different K-levels at constant J are not radiatively coupled (cf. Eq. (1)).
When fitting all the lines simultaneously, the rotational diagram derived column densities are underestimated by a factor 20 compared to the LVG derived ones for the PDR and a factor 2.5 for the dense core. When the K-ladders are fitted independently, the column densities increase when the associated J level decreases. Indeed, the high J levels are more difficult to thermalize because their critical densities are higher. As a consequence, the derived column densities is more and more underestimated as J increases. In the Horsehead PDR case, the column density derived from the rotational diagram for the lowest J level (5−4) is still six times lower than the column density derived by the escape probability radiative transfer modeling. In contrast, the rotational diagram and the RADEX methods yields the same column density at the dense core position. This is expected as the CH3CN level population will be closer to thermal equilibrium in the higher density core.
Three different situations happen when using the rotational diagram method to determine the column density of CH3CN and/or the gas kinetic temperature.
-
1.
When the level populations follow an LTE distribution (e.g. the gas density is higher than a few 105 cm-3 for the J = 5–4 K-ladder) both the gas kinetic temperature and the CH3CN column density can be derived accurately. This approximately corresponds to the case of the dense core position in our study.
-
2.
When the excitation is slightly subthermal (e.g. the gas density is in the range (4 − 8) × 104 cm-3 for the J = 5–4 K-ladder), the gas kinetic temperature can be obtained by fitting only the corresponding K-ladder lines that are close to thermalization. However, the column density will be underestimated. This corresponds to the case of the PDR position in our study.
-
3.
When the excitation is strongly subthermal (e.g. the gas density is lower than 4 × 104 cm-3 for the J = 5–4 K-ladder), both the gas kinetic temperature and the CH3CN are underestimated. It is then necessary to study the excitation with more advanced methods like escape probability methods.
Appendix D: Methyl cyanide and isocyanide spectra
 |
Fig. D.1
Spectrum of the CH3CN 3 mm and 2 mm detected lines at the HCO peak (i.e., the PDR position, top spectrum of each panel) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum of each panel), each spectrum towards the HCO peak has been shifted vertically by 0.2 K for clarity. The panel displays the K set of lines for a given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars, whose heights indicate their relative hyperfine intensities in the optically thin regime applicable to these observations. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| Open with DEXTER | |
 |
Fig. D.2
Spectrum of the CH3NC 3mm detected lines at the HCO peak (i.e., the PDR position, top spectrum) and the DCO+ peak (i.e., inside the cold dense core, bottom spectrum), the spectrum towards the HCO peak has been shifted vertically by 0.1 K for clarity. The panel displays the K set of lines for the given ΔJ set of lines. The frequencies corresponding to each transitions are displayed as vertical bars. The best fit model is overplotted in red. The green horizontal lines display the ± 3σ significance levels. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


