| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220669 | |
| Published online | 04 June 2013 | |
Mass-metallicity relation explored with CALIFA
I. Is there a dependence on the star-formation rate?⋆
1 Instituto de Astrofísica de Andalucía (CSIC), Glorieta de la Astronomía s/n, Aptdo. 3004, 18080-, Granada, Spain
e-mail: sanchez@iaa.es
2 Centro Astronómico Hispano Alemán, Calar Alto, (CSIC − MPG), C/Jesús Durbán Remón 2-2, 04004 Almería, Spain
3 Astronomical Institute, Academy of Sciences of the Czech Republic, Boční II 1401/1a, 141 00 Prague, Czech Republic
4 Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
5 Instituto Nacional de AstrofísicaÓptica y Electrónica, Luis E. Erro 1 72840 Tonantzintla Puebla Mexico
6 CEI Campus Moncloa, UCM-UPM, Departamento de Astrofísica y CC. de la Atmósfera, Facultad de CC. Físicas, Universidad Complutense de Madrid, Avda. Complutense s/n, 28040 Madrid, Spain
7 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
8 Departamento de Física, Universidade Federal de Santa Catarina, PO Box 476, 88040-900 Florianópolis, SC, Brazil
9 CENTRA − Instituto Superior Tecnico, Av. Rovisco Pais, 1, 1049-001 Lisbon, Portugal
10 Max-Planck-Institut für Astronomie, 69117 Heidelberg, Germany
11 Laboratoire Galaxies Étoiles Physique et Instrumentation, Observatoire de Paris, 5 place Jules Janssen, 92195 Meudon, France
12 Sydney Institute for Astronomy, School of Physics A28, University of Sydney, NSW 2006, Australia
13 Australian Astronomical Observatory, PO box 296, Epping, NSW 1710, Australia
14 Departamento de Investigación Básica, CIEMAT, Avda. Complutense 40, 28040 Madrid, Spain
15 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
16 Centro de Astrofísica and Faculdade de Ciencias, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
17 University of Sheffield, Department of Physics and Astronomy, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
18 Dpto. de Física Teórica y del Cosmos, University of Granada, Facultad de Ciencias (Edificio Mecenas), 18071 Granada, Spain
19 Depto. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
20 Instituto de Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
21 University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
22 Landessternwarte, Zentrum für Astronomie der Universitát Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
23 Astronomical Institute of the Ruhr-University Bochum Universitaetsstr. 150, 44801 Bochum, Germany . ⋆⋆
Received: 30 October 2012
Accepted: 8 April 2013
We studied the global and local ℳ-Z relation based on the first data available from the CALIFA survey (150 galaxies). This survey provides integral field spectroscopy of the complete optical extent of each galaxy (up to 2−3 effective radii), with a resolution high enough to separate individualH ii regions and/or aggregations. About 3000 individualH ii regions have been detected. The spectra cover the wavelength range between [OII]3727 and [SII]6731, with a sufficient signal-to-noise ratio to derive the oxygen abundance and star-formation rate associated with each region. In addition, we computed the integrated and spatially resolved stellar masses (and surface densities) based on SDSS photometric data. We explore the relations between the stellar mass, oxygen abundance and star-formation rate using this dataset.
We derive a tight relation between the integrated stellar mass and the gas-phase abundance, with a dispersion lower than the one already reported in the literature (σΔlog (O/H) = 0.07 dex). Indeed, this dispersion is only slightly higher than the typical error derived for our oxygen abundances. However, we found no secondary relation with the star-formation rate other than the one induced by the primary relation of this quantity with the stellar mass. The analysis for our sample of ~3000 individualH ii regions confirms (i) a local mass-metallicity relation and (ii) the lack of a secondary relation with the star-formation rate. The same analysis was performed with similar results for the specific star-formation rate.
Our results agree with the scenario in which gas recycling in galaxies, both locally and globally, is much faster than other typical timescales, such like that of gas accretion by inflow and/or metal loss due to outflows. In essence, late-type/disk-dominated galaxies seem to be in a quasi-steady situation, with a behavior similar to the one expected from an instantaneous recycling/closed-box model.
Key words: Galaxy: abundances / galaxies: ISM / galaxies: fundamental parameters / galaxies: spiral / galaxies: structure / galaxies: evolution
Table 1 and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Metals form in stars as a by-product of the thermonuclear reactions that are the central engine of stellar activity. Once they have completed their life cycle, stars eject metals into the interstellar medium, polluting the gas, which is the fuel for the new generation of stars. Therefore, the star-formation rate (SFR), the stellar mass, the metal content and the overall star-formation history of galaxies are strongly interconnected quantities. The details of these interconnections (are they local or global? Are both intristic or a consequence of the evolution?) and their dependence on other properties of galaxies (are they affected by the environment, and if so, how? How does the merging history of the small interactions affect them?) are still not well understood.
The strong correlation between stellar mass and gas-phase metallicity in galaxies is well known (Lequeux et al. 1979; Skillman 1992). These parameters are two of the most fundamental physical properties of galaxies, both directly related to the process of galaxy evolution. The mass-metallicity (ℳ-Z) relation is consistent with more massive galaxies being more metal-enriched. This was confirmed observationally by Tremonti et al. (2004,hereafter T04), who found a tight correlation spanning over 3 orders of magnitude in mass and a factor of 10 in metallicity, using a large sample of star-forming galaxies up to z ~ 0.1 from the Sloan Digital Sky Survey (SDSS). The ℳ-Z relation appears to be independent of large-scale (Mouhcine et al. 2007) and local environment (Hughes et al. 2013), although it has been observed that in high-density environments metallicities are higher than expected (e.g. Mateus et al. 2007; Petropoulou et al. 2012), and in lower density environments satellites have higher metallicities than central galaxies (e.g. Pasquali et al. 2010, 2012). Finally, the relation has been confirmed at all accessible redshifts (e.g. Savaglio et al. 2005; Erb et al. 2006; Maiolino et al. 2008).
Considerable work has been devoted to understanding the physical mechanisms underlying the ℳ-Z relation. The scenarios proposed to explain its origin can be broadly categorized as 1) the loss of enriched gas by outflows (T04; Kobayashi et al. 2007); 2) the accretion of pristine gas by inflows (Finlator & Davé 2008); 3) variations of the initial mass function with galaxy mass (Köppen et al. 2007); 4) selective star-formation efficiency or downsizing (Brooks et al. 2007; Ellison et al. 2008; Calura et al. 2009; Vale Asari et al. 2009); or a combination of them.
Despite the local nature of the star-formation processes, it has only recently become possible to analyze the ℳ-Z relation for spatially resolved, external galaxies. Early precedents with more limited data include Edmunds & Pagel (1984) and Vila-Costas & Edmunds (1992), who noticed a correlation between mass surface-density and gas metallicity in a number of galaxies. Moran et al. (2012) recently reported a correlation between the local stellar mass density and the metallicity that was valid for all galaxies in their sample. This result was derived by analyzing the individualH ii regions of a sample of 174 star-forming galaxies, based on slit spectroscopy. We independently confirmed this relation (Rosales-Ortega et al. 2012), using a statistically complete sample of ~2500H ii regions extracted from a sample of 38 galaxies, using integral field spectroscopy (IFS), described in Sánchez et al. (2012b).
This local relation is a scaled version of the ℳ-Z relation. This new relation is explained as a simple effect of the inside-out mass/metallicity growth that dominates the secular evolution of late-type galaxies (e.g. Matteucci & Francois 1989; Boissier & Prantzos 1999), combined with the fact that more massive regions form stars faster (i.e., at higher SFRs), thus earlier in cosmological times, which can be considered a local downsizing effect, similar to the one observed in individual galaxies (e.g. Pérez-González et al. 2008). This explanation does not require a strong effect of inflows/outflows in shaping the ℳ-Z relation, which can be naturally explained by secular evolution processes.
Recently, evidence has been reported for a dependence of the ℳ-Z relation on the SFR. Different authors found that these three quantities define either a surface or a plane in the corresponding 3D space, i.e., the so-called fundamental mass-metallicity relation (FMR) and/or ℳ-Z-fundamental plane, depending on the authors (Lara-López et al. 2010; Mannucci et al. 2010; Yates et al. 2012). Irrespective of the actual shape of this relation (Lara-Lopez et al. 2012), its existence is still controversial. The described relationship implies that (i) for the same mass, galaxies with stronger SFRs have lower metallicities; and (ii) for low-mass galaxies, the dependence on the SFR is stronger. Metallicity is a parameter that depends on (i) the star-formation (which enriches galaxies); (ii) inflows (which dilute and reduce the metallicity); and (iii) outflows (which eject metals out of the galaxy). Thus, the reported relation imposes restrictions on the ratio between the chemical enrichment, produced by the SFR, and dynamical timescales that regulate the dilution due to inflows (e.g. Quillen & Bland-Hawthorn 2008). On the other hand, it also restricts the dependence between the amount of metals ejected by an outflow and the strength of the SFR (Mannucci et al. 2010, and references therein). In a stable situation, described by a simple instantaneous recycling model, no dependence on the SFR is expected.
So far, all studies reporting a dependence between the ℳ-Z relation and the SFR are based on single aperture spectroscopic data, such as the one provided by the SDSS (York et al. 2000). In spite of the impressive dataset provided by these surveys, with tens or hundreds of thousands of individual measurements, they present some well-known drawbacks: (i) single-aperture spectroscopic data have a fundamental aperture bias that restricts the derived parameters to different scale-lengths of the galaxies at different redshifts (e.g. Ellis et al. 2005). This is a strong limitation for these studies, considering that both the oxygen abundance and the SFR shows strong gradients within galaxies (e.g. Sánchez et al. 2012b). Therefore, the derived parameters may not be representative of the integrated (or characteristic) ones; (ii) the fact that most of these surveys sample galaxies at a wide range of redshifts implies that the derived parameters correspond to different physical scales for similar galaxies at different redshift, because of an aperture bias. This may induce secondary correlations difficult to address, in particular, if some of these parameters present a cosmological evolution and/or spatial gradients within each galaxy; (iii) while the spectroscopic information (oxygen abundance and SFR) is derived from this aperture-limited dataset, the third analyzed parameter, the mass, is derived mostly based on integrated photometric data. Moreover, in some cases it is derived using the information comprised in the spectroscopic data to estimate the corresponding M/L-ratio (Mannucci et al. 2010; Kauffmann et al. 2003a). Contrary to what is often claimed, we recall that these systematic effects cannot be reduced by the large statistical number of data encompassed in the considered dataset.
 |
Fig. 1 Top panels: IFS-based Hα maps, in units of 10-16 erg s-1 cm-2 arcsec-2, derived for two representative galaxies of the sample (color images), together with the detectedH iiregions shown as black segmented contours. Bottom panels: radial distribution of the oxygen abundance derived for the individualH iiregions with abundace errors below 0.15 dex, as a function of the deprojected distance (i.e., corrected for inclination), normalized to the effective radius, for the same galaxies. The size of the circles is proportional to the Hα intensity. |
Some of these issues are partially solved when a large aperture is used to derive the spectra of each galaxy, as in the case of drift-scan observations (e.g. Moustakas et al. 2010; Hughes et al. 2013). In this case, the derived abundance (basically luminosity weighted across the optical extent of the galaxies) has a better correspondence with the characteristic one (i.e., the value at 0.4ρ25, where ρ25 is the radius at a surface brightness of 25 mag/arcsec2, Zaritsky et al. 1994; Garnett 2002), as demonstrated by Moustakas & Kennicutt (2006). On the other hand, the SFR can be directly derived from the integrated Hα emission across the considered aperture. However, these observations also have some limitations: (i) in many cases they do not cover the entire optical extent of the galaxies, and the covered fraction is different from galaxy to galaxy, which again introduces an aperture uncertainty (Fig. 3 of Sánchez et al. 2011, for example); (ii) because of the lack of spatially resolved spectroscopic information, they mix regions with different ionization properties and/or ionization sources, which could change substantially at different locations even within quiescent spiral galaxies (e.g. Sánchez et al. 2012b). This introduces uncertainties in both the derived abundances and the estimated SFR.
In spite of these limitations, Hughes et al. (2013) explored in a recent study the dependence of the ℳ-Z relation on the SFR, using drift-scan observations of 135 nearby late-type galaxies in the Local Universe. As expected, their dispersion around the ℳ-Z relation is similar or even slightly higher than the one reported by T04. Although they cannot reproduce the results by Mannucci et al. (2010) and Lara-López et al. (2010), and in fact the scatter increases when they introduced a dependence on the SFR, they found a strong depedence of the metallicity with the gas fraction. This dependece could induce a correlation with the SFR in a large sample of galaxies.
More recently, Pérez-Montero et al. (2013) and Cresci et al. (2012) studied the ℳ-Z relation in a wide range of redshifts both using the zCOSMOS data, and those of the SDSS in the first case. They found either a negative trend of the metallicity with the SFR for a fixed galaxy mass, in the first case, or a distribution of masses, metallicities, and SFRs consistent with the FMR, in the latter one, both in agreement with Mannucci et al. (2010) and Lara-López et al. (2010). Despite this agreement, Pérez-Montero et al. (2013) noted that the dispersion around the ℳ-Z relation is only reduced by 0.01 dex at all stellar masses when a secondary relation with the SFR is introduced, for an initial dispersion of ~ 0.1 dex. As a comparison, the decrease of the dispersion reported by Mannucci et al. (2010) was nearly half the original value when they introduced the same relation. Pérez-Montero et al. (2013) considered that the lack of extreme SFR values in their SDSS galaxies might explain this effect.
At higher redshifts the situation is more complicated. Wuyts et al. (2012) found that the distribution of their data agreed with the local FMR relation presented by Mannucci et al. (2010). However, they found no correlation between metallicity and SFR at a fixed mass. In contrast, Richard et al. (2011) interpreted the highest metallicities found at the low-mass range as a consequence of the FMR in combination with a lower SFR of these objects. In a similar way, Nakajima et al. (2012) showed that the lower limit to the average metallicities found for a sample of Lyα emitters at z ~ 2.2, after stacking the individual spectra, is roughly consistent with the FMR relation. Finally, Magrini et al. (2012) supported the idea that the scaling relation between the mass, metallicity, and SFR has a different origin (and shape) for “active” starbursts, which are more common at high redshifts, and quiescent galaxies, which are more frequent at lower redshifts. The fact that in most cases only the N2 indicator is accesible at high redshift may introduce biases difficult to quantify.
To explore the ℳ-Z relation in the Local Universe, and to bring light to its dependence on the SFR, while minimizing the bias effects previously described, we used the integral-field spectroscopic (IFS) data provided by the CALIFA survey (Sánchez et al. 2012a)1. CALIFA is an ongoing exploration of the spatially resolved spectroscopic properties of galaxies in the Local Universe (z < 0.03) using wide-field IFS to cover the full optical extent (up to ~ 2.5 re) of ~ 600 galaxies of any morphological type, distributed across the entire color–magnitude diagram (Walcher et al., in prep.), and sampling the wavelength range 3650 − 7500 Å. So far, the survey has completed ~ 1/3 of its observations, and the first data release, comprising 100 galaxies, has been delivered recently (Husemann et al. 2013).
The layout of this article is as follows: in Sect. 2 we summarize the main properties of the sample and data used in this study; in Sect. 3, we present the main analysis and the derivation of the parameters analyzed in the article: the mass, metallicity, and SFR for each individual galaxy andH ii region; the global ℳ-Z relation and its dependence with the SFR is explored in Sects. 3.2 and 3.3; a similar analysis for the local ℳ-Z (or Σ-Z) relation is presented in Sect. 3.4; we explore the possible dependence on the specific SFR (sSFR) in Sect. 3.5; our results and conclusions are summarized in Sect. 4.
2. Sample of galaxies and data
The galaxies were selected from the CALIFA observed sample1. Since CALIFA is an ongoing survey, whose observations are scheduled on a monthly basis (i.e., dark nights), the list of objects increases regularly. The current results are based on the 150 galaxies observed using the low-resolution setup until July 2012. At that point, most of the color–magnitude diagram had been sampled by the survey with at least one or two targets per bin of magnitude and color, including galaxies of any morphological type. The CALIFA mother sample becomes incomplete below Mr > −19 mag, which corresponds to a stellar mass of ~109.5 M⊙. Therefore, it does not sample low-mass and/or dwarf galaxies. Most of these galaxies are part of the 1st CALIFA Data Release (Husemann et al. 2013), and therefore the datacubes are accesible from the DR1 webpage2. Table 1 shows the list of the galaxies analyzed in the current study, including for each galaxy (i) its name; (ii) redshift; (iii) V-band magnitudes and B − V color and visual morphological classification (extracted from Walcher et al., in prep.). In addition, we include the main properties derived along this article, as explained below: (i) the integrated stellar mass; (ii) characteristic oxygen abundance; and (iii) the integrated star-formation.
 |
Fig. 2 Distribution of the stellar masses derived using the average M/L ratios described in Bell & de Jong (2001) and the B- and V-band photometry (Y axis in all panels) along the stellar masses derived using other procedures (X axis in all panels): top-left panel: stellar masses derived using the entire five-bands SDSS photometry and the M/L ratio provided by the SED analysis performed using PARADISE; top-right panel: stellar masses derived using the 2MASS K-band photometry and the M/L ratio provided in Longhetti & Saracco (2009); bottom-left panel: stellar masses derived using the CALIFA datacube spectrophotometry and the M/L ratio provided by PyCASSO/Starlight; and bottom-right panel: stellar Masses derived from CALIFA datacube spectrophotometry and the M/L ratio provided by FIT3D. |
The details of the survey, sample, observational strategy, and reduction are explained in Sánchez et al. (2012a). All galaxies were observed using PMAS (Roth et al. 2005) in the PPAK configuration (Kelz et al. 2006), covering a hexagonal field-of-view of 74″ × 64″, sufficient to cover the full optical extent of the galaxies up to 2 − 3 effective radii. This is possible because of the diameter selection of the sample (Walcher et al., in prep.). The observing strategy guarantees a complete coverage of the FoV, with a final spatial resolution of FWHM ~ 3″, i.e., ~1 kpc at the average redshift of the survey. The sampled wavelength range and spectroscopic resolution (3745 − 7500 Å, λ/Δλ ~ 850, for the low-resolution setup) are more than sufficient to explore the most prominent ionized gas emission lines, from [OII]λ3727 to [SII]λ6731, on one hand, and to deblend and subtract the underlying stellar population, on the other hand (e.g. Sánchez et al. 2012a; Kehrig et al. 2012; Cid Fernandes et al. 2013). The dataset was reduced using version 1.3c of the CALIFA pipeline, whose modifications with respect to the one presented in Sánchez et al. (2012a) are described in detail in Husemann et al. (2013). In summary, the data fulfill the predicted quality-control requirements, with a spectrophotometric accuracy better than 15% everywhere within the wavelength range, both absolute and relative, and a depth that allows us to detect emission lines in individualH ii regions as weak as ~ 10-17 erg s-1 cm-2 Å-1, with a signal-to-noise ratio of S/N ~ 3 − 5.
The final product of the data-reduction is a regular-grid datacube, with x and y coordinates indicating the right-ascension and declination of the target and z being a common step in wavelength. The CALIFA pipeline also provides the propagated error cube, a proper mask cube of bad pixels, and a prescription of how to handle the errors when performing spatial binning (due to covariance between adjacent pixels after image reconstruction). These datacubes, together with the ancillary data described in Walcher et al. (in prep.), are the basic starting point of our analysis.
In addition to these galaxies, we have included 31 out of the 38 face-on spirals analyzed in Sánchez et al. (2012b). This sample comprises face-on spiral galaxies extracted from the CALIFA feasibility studies (Mármol-Queraltó et al. 2011). All these galaxies were observed with PPAK, using a setup similar to the one used for CALIFA, with slightly different spectral resolutions and wavelength coverage (see Mármol-Queraltó et al. 2011, for details). They cover the same redshift range, optical size, and the extent covered by CALIFA. On the other hand, the remaining seven spirals were extracted from the PINGS survey (Rosales-Ortega et al. 2010). These galaxies are located at lower redshift, because they are larger in projected sizes, and in some cases they have not been completely covered by the IFS data. Therefore, we chose to exclude them from this analysis.
3. Analysis and results
3.1. Derivation of the analyzed parameters
The three main quantities to derive for each galaxy are (i) the integrated stellar mass; (ii) the characteristic oxygen abundance; and (iii) the integrated SFR. These parameters were derived following the procedure described in Sánchez et al. (2012b), developed for a similar set of data. In the following we briefly outline the most important aspects of their derivation.
3.1.1. Stellar masses
We derived the stellar masses using the integrated V-band magnitudes and B − V colors listed in Table 1 and the average mass-luminosity (M/L) ratio described in Bell & de Jong (2001). The B- and V-band magnitudes were derived using the Petrosian magnitudes provided the SDSS photometric catalog3, and transformed using the equations by Jester et al. (2005). The errors provided by the SDSS catalog were propagated to derive the corresponding errors for the B- and V-band magnitudes. The expected systematic error of the transformation, of ~0.02 mag, was not taken into account since it equally affects all listed values. A direct comparison with our own derived magnitudes, based on a growth-curve analysis and a detailed subtraction of the local background of the SDSS images, shows that the errors could be at most ~0.07 mag (Walcher et al., in prep.) The integrated luminosities and colors were corrected for the effect of dust attenuation, where the internal extinction was derived from the multi-SSP analysis of the stellar continuum summarized in Sánchez et al. (2012a), prior to deriving the stellar masses.
This procedure of deriving the stellar masses is robust and straight forward, and it only requires a few assumptions on the properties of the galaxies. We adopted the Bell & de Jong (2001)M/L ratios instead of the more recent ones provided by Bell et al. (2003) for the SDSS colors, for consistency with the derivation performed in Sánchez et al. (2012b). Indeed, Bell et al. (2003) showed that the two M/L ratios are consistent with each other.
We performed a sanity check to test the robustness of the derived stellar masses. To do so, we derived the masses using four additional methods: (i) we used the full spectral energy distrubution (SED) provided by the SDSS photometry and derived the masses using the stellar population analysis provided by the PARADISE code (Walcher et al. 2011). This derivation is less affected by possible color biases, since it includes the whole optical SEDs. However, the dust attenuation affecting the stellar populations was not taken into account. (ii) We derived the stellar masses using the K-band photometry extracted from the 2MASS photometric catalog4, applying a global aperture correction, and adopting the M/L ratio described by Longhetti & Saracco (2009). This derivation is clearly the one that is less affected by any possible color biases, the effect of young stellar populations, and dust effects, a priori. However, it presents its own problems, in particular the uncertainties in the M/L ratio related to the unknown contribution of the TP-AGB stars in this wavelength regime (e.g. Walcher et al. 2011). Only 128 objects of those considered here have photometry in the 2MASS catalog. (iii) We collected the stellar masses recently published by Pérez et al. (2013), extracted from the CALIFA datacubes, using pycasso (Cid Fernandes et al. 2013), the 3D implementation of the Starlight code (Cid Fernandes et al. 2005), for the galaxies in common (75 objects). These masses are the most self-consistent with the other parameters presented in this article, but they rely on a less straight forward stellar population decomposition. The analysis takes into account the dust attenuation. Finally, (iv) we derived the stellar masses provided by the stellar population decomposition method used to remove the underlying stellar population pixel by pixel, using FIT3D. This method is, in principle, similar to the previous one. However, FIT3D uses a much smaller library of stellar populations, and therefore it provides, a priori, less accurate M/L ratios and stellar masses.
Figure 2 illustrates the results of this analysis. For each panel, it shows the comparison between the stellar mass derived using the Bell & de Jong (2001) relation, and those described before. Throughout we find a very good agreement, close to a one-to-one relation in most cases. The best agreement is achieved with the stellar masses derived using only photometric information, either the full SDSS SED, or the 2MASS K-band data, with a standard deviation of the difference of σ ~ 0.15 dex. The masses derived using only the SDSS photometry are slightly lower, in particular in the low-mass regime, which is expected because they are not corrected by dust attenuation. For the stellar masses derived using the CALIFA spectroscopic information, the best agreement is found with those provided by pycasso. The standard deviation of the difference is σ ~ 0.14 dex, which is consistent with a spectrophotometric accuracy of the CALIFA datacubes of ~10% with respect to the SDSS one. Finally, the highest dispersion is found when comparing the adopted stellar masses with those derived from the multi-SSP analysis provided by FIT3D (σ ~ 0.24 dex), as expected.
Similar results are found when comparing the masses derived with the total stellar masses listed in the MPA/JHU catalog (Kauffmann et al. 2003b). Therefore, if there is a systematic effect in the derivation of the stellar masses, which is at most of about the typical error estimated based on the propagation of the photometric errors (~0.15 dex).
3.1.2. Star-formation rate
The SFR was derived for each galaxy based on the properties of the ionized gas emission. By construction, CALIFA IFS data sample most of the optical extent of galaxies, which allows one to derive the total SFR minimizing any aperture effect. The SFR was derived from the integrated Hα luminosity. To do so, we first performed a spectroscopic decomposition analysis between the underlying stellar population and the ionized gas emission lines described using FIT3D (Sánchez et al. 2007; Rosales-Ortega et al. 2011; Sánchez et al. 2012a,b). The analysis was performed spaxel by spaxel, following Sánchez et al. (2011). Each spectrum in the datacube was then decontaminated by the underlying stellar continuum using the multi-SSP model derived. Then, we selected the spaxels whose ionization was dominated by star-formation based on emission line ratios (e.g. Sánchez et al. 2012b), i.e., theH ii regions described below. The areas dominated by diffuse gas emission were excluded on purpose, since their nature is still unclear (e.g. Thilker et al. 2002; Iglesias-Páramo et al., in prep.). This does not affect the results, since diffuse gas comprises less than 5% of the total integrated dust corrected flux of Hα for our galaxies. We repeated all calculations using the SFR integrating over the whole FoV, instead of just only theH ii regions without any significant difference. The observed Hα intensities were corrected for reddening using the Balmer decrement (Hα/Hβ) according to the reddening function of Cardelli et al. (1989), assuming R ≡ AV/E(B − V) = 3.1. The theoretical value for the intrinsic Balmer line ratios were taken from Osterbrock (1989), assuming case B recombination (optically thick in all Lyman lines), an electron density of ne = 100 cm-3, and an electron temperature Te = 104 K, which are reasonable assumptions for typical star-forming regions. The values of the SFR were derived for each galaxy adopting the classical relations by Kennicutt (1998), based on the dust-corrected Hα luminosities.
The corresponding errors for the SFR were derived for each galaxy by propagating through the equations the errors provided by the fitting procedure for the derivation of Hα and Hβ emission lines spaxel to spaxel (FIT3D, Sánchez et al. 2011, 2012b). These errors do not include the possible zero-point calibration errors in the CALIFA datacubes, which are estimated to be lower than ~ 15% throughout the wavelength range (Husemann et al. 2013).
3.1.3. Oxygen abundance
The characteristic oxygen abundance was defined in Zaritsky et al. (1994) as the abundance at 0.4ρ25, which is representative of the average value across the galaxy, as we indicated before. This distance corresponds basically to one effective radius for galaxies in the Local Universe. We demonstrated in Sánchez et al. (2012b) that the effective radius is a convenient parameter to normalize the abundance gradients in galaxies at different redshifts. We study the abundance gradients and the relation between the integrated and characteristic oxygen abundance in a forthcoming article (Sánchez et al., in prep.). Thus, we redefine the characteristic or effective oxygen abundance as the corresponding value at the effective radius.
To derive this parameter we analyzed the radial gradients of the oxygen abundance in all galaxies of our sample, using the procedures detailed in Sánchez et al. (2012b). In a companion article we will describe the procedure for this particular dataset, summarizing the main properties of the ionized regions across the galaxies (Sanchez, in prep.). We present here just a brief summary of the different steps included in the overall process: (i) First we created a narrow-band image of 120 Å width, centered on the wavelength of Hα shifted at the redshift of the targets. The narrow-band image is properly corrected for the contamination of the adjacent continuum. (ii) The narrow-band image is used as an input for HIIexplorer5, an automaticH iiregion detection code created for this kind of analysis (Sánchez et al. 2012b; Rosales-Ortega et al. 2012). The code provides a segmentation map that identifies each detected ionized region. Then, it extracts the integrated spectra corresponding to each segmented region. Figure 1 illustrates the process, showing the Hα intensity maps and the corresponding segmentations for two objects. A total of 3435 individual ionized regions are detected in a total of 137 galaxies from the sample. (iii) Each extracted spectrum is then decontaminated by the underlying stellar continuum using the multi-SSP fitting routines included in FIT3D, as described before. (iv) Each emission line within the considered wavelength range is fitted with a Gaussian function to recover the line intensities and ratios. (v) These line ratios are used to distinguish between different ionization conditions and to derive the oxygen abundances for each particular ionized region. Basically, we selected the clumpy ionized regions with a strong blue underlying stellar population that contributes at least 20% of the flux in the V-band, to ensure that they are located below the Kewley & Ellison (2008) demarcation line in the classical [OIII]/Hβ vs. [NII]/Hα diagnostic diagram (Baldwin et al. 1981). A total of 2846H iiregions were extracted for a total of 134 galaxies. (vi) Finally, in combination with a morphological analysis of the galaxy, we can recover the abundance gradients for each particular galaxy, and derive the corresponding value at the effective radius. To do so, we fit the radial distribution of the oxygen abundance between 0.2 and 2.1 effective radius with a linear regression, and used the derived zero-point and slope to determine the oxygen abundance at one effective radius. This procedure increses the accuracy of the derived abundance, since it uses the full radial distribution of individual estimates. We used only (1) the regions for which the oxygen abundance was derived with a nominal error lower than < 0.2 dex, which corresponds to emission lines with a S/N > 5 in all considered emission lines ([OII]3727, Hβ, [OIII]5007, Hα and [NII]6583), and (2) the galaxies with at least threeH ii regions covering at least between 0.3 and 2.1 effective radii. This comprises a total of 2061H iiregions and associations, distributed in 113 galaxies. This sample comprises galaxies of any type, mostly spirals (both early- and late-type), with and without bars, and with different inclinations. We note that although the detectability ofH ii regions is affected by inclination, i.e., fewer accesible and detected, we notice no other difference in their properties (abundance, radial distribution, luminosity, etc.).
The oxygen abundance was derived using different strong-line indicators, such as the R23 fit derived by T04, the N2 and O3N2 calibrators by Pettini & Pagel (2004), and the recent counterpart-method by Pilyugin et al. (2012). Interestingly, despite the differences in the derived estimates, all values show a trend with the stellar mass (e.g. Kewley & Ellison 2008). In fact, there is a clear correspondence not only with the calibrators (e.g. López-Sánchez et al. 2012), but also between the line ratios used to derive them (e.g. Sánchez et al. 2012b). Therefore, for simplicity, we show here only the results based on the O3N2-calibrator, which is among the most straight forward methods.
The results of this analysis are listed in Table 1, including the final number ofH iiregions considered for each galaxy and the derived parameters, i.e., the integrated stellar mass and SFR, and characteristic oxygen abundance, together with their corresponding errors. In addition to these characteristic values for each individual galaxy, we derived similar parameters for each individualH iiregion: the mass surface density (Σ) and the surface SFR density (μSFR). These quantities were derived using the same procedures as described in Sects. 3.1.1 and 3.1.2, but using as observables (i.e., the photometric values and the Hα fluxes) those corresponding to each particularH ii region. Finally, the derived values were divided by the corresponding encircled area.
3.2. Mass metallicity relation
We first explore the ℳ-Z relation following T04 and Mannucci et al. (2010). Figure 4 shows the distribution of the characteristic oxygen abundances as a function of the stellar masses for the galaxies of our sample (blue circles). In addition, we included the values corresponding to the galaxies analyzed in Sánchez et al. (2012b) from the CALIFA feasibility studies (red squares). As expected, there is a clear trend in both quantities, following basically the shape described in Kewley & Ellison (2008) for the considered abundance calibrator. The correlation coefficient of both quantities is r = 0.769, indicating that there is a positive trend. From the formal point of view, this coefficient should be used only for linear relations. However, it is still valid as an indication of a trend between two parameters.
For comparison purposes, we include the density distribution of galaxies within the ℳ-Z plane for the SDSS galaxies corresponding to the redshift range studied by Lara-López et al. (2010) (dashed black contours) and Mannucci et al. (2010) (solid gray contours). The first contour encircles ~ 95% of the total number of galaxies, with a 20% decrease in each consecutive one.We calculated the oxygen abundances for these galaxies using the O3N2 indicator, instead of adopting published metallicities, which will force us to adopt a correction. To do this, the stellar masses and emission line ratios were directly extracted from the Max-Planck-Institute for Astrophysics-John Hopkins University (MPA-JHU) emission-line analysis database6. The contours show that the CALIFA data cover a similar range of masses and metallicities similar to the two previous studies. However, it is important to note here that Lara-López et al. (2010) sampled a lower mass and higher metallicity range than Mannucci et al. (2010), which is a clear effect of the redshift range covered by these studies and the SDSS selection function.
Instead of the classical polynomial function adopted by most previous studies for this relation (e.g., T04, Kewley & Ellison 2008; Mannucci et al. 2010; Rosales-Ortega et al. 2012; Hughes et al. 2013), we chose to adopt an asymptotic function to describe the relation between both parameters following Moustakas et al. (2011): ![\begin{equation} \label{eq1} {y}=a+b({\rm x}-c)\exp[-({x}-c)], \end{equation}](/articles/aa/full_html/2013/06/aa20669-12/aa20669-12-eq51.png) (1)where y = 12 + log (O/H), and x is the logarithm of the stellar mass in units of 108 M⊙. This functional form tries to describe the distribution of parameters defining a maximum abundance for large masses (a). Although the adopted formula is slightly different for computational convenience than the one adopted by Moustakas et al. (2011), the main motivations and interpretation are the same. Obviously, due to the sample construction, we do not have enough data in the low-mass/low-metallicity range toexplore this second range.
(1)where y = 12 + log (O/H), and x is the logarithm of the stellar mass in units of 108 M⊙. This functional form tries to describe the distribution of parameters defining a maximum abundance for large masses (a). Although the adopted formula is slightly different for computational convenience than the one adopted by Moustakas et al. (2011), the main motivations and interpretation are the same. Obviously, due to the sample construction, we do not have enough data in the low-mass/low-metallicity range toexplore this second range.
The derived parameters for the CALIFA data are a = 8.74 ± 0.01, b = 0.018 ± 0.007 and c = 3.5 ± 0.3. The two latter parameters govern the increase in metallicity with mass, while the first one is the asymptotic oxygen abundance for large masses at the effective radius of the galaxies. The derived values cannot be extrapolated to masses lower than 109 M⊙, which are not covered by the CALIFA mother sample. A recent compilation by Kudritzki et al. (2012) of the characteristic metallicities of a set of Local Universe galaxies indicates that while at high mass they reach an asymptotic value, at low masses the relation is almost linear, consistent with previous derivations (e.g. Skillman et al. 1989; Skillman 1992). With the adopted formula it is possible to reproduce this behavior, although the parameters need to be adjusted.
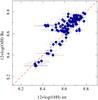 |
Fig. 3 Distribution of the oxygen abundances estimated for each galaxy at the effective radius (Re), using the radial gradients, and the oxygen abundances derived directly from the spectra integrated over the entire field-of-view (int). |
 |
Fig. 4 . Top-left panel: distribution of the oxygen abundances at the effective radii as a function of the integrated stellar masses for the CALIFA galaxies (113, blue solid circles). For comparison purposes, we show similar values for the galaxies observed in the CALIFA feasibility studies (31, red solid squares) included in theH ii regions catalog described in Sánchez et al. (2012b). The size of the symbols is proportional to the integrated SFR. The solid line represents the best-fitted curve, as described in the text. We also included the distribution of abundaces as a function of the stellar masses for the SDSS data corresponding to the redshift ranges sampled by Lara-López et al. (2010), dashed black contours, and Mannucci et al. (2010), solid grey contours. In both cases, the first contour encircles the 95% of the objects, and 20% less objects in each consecutive contour. Top-right panel: distribution of the integrated SFR as a function of the stellar masses. The size of the symbols is proportional to the oxygen abundance shown in previous panel. The solid line represents the best fitted linear regression to the CALIFA data.Like in the previos panel the contours represent the distribution of both parameters corresponding to the redshift ranges sampled by Lara-López et al. (2010), dashed black contours, and Mannucci et al. (2010), solid grey contours Bottom-left panel: same distribution shown in the top-left panel, for the CALIFA and feasibility-studies objects. The colors represent the logarithm of the integrated SFR for each galaxy. Bottom-right Panel: distribution of the differential oxygen abundances at the effective radii, once the dependency with the stellar mass has been subtracted, as a function of the integrated SFR for the CALIFA galaxies (113, blue solid circles). The size of the symbols is proportional to the oxygen abundances shown in Fig. 4. The histogram shows the same distribution of differential oxygen abundances. The solid line represents a Gaussian function with the same central value (0.01 dex) and standard deviation (0.07 dex) as the represented distribution, scaled to match the histogram. |
From a theoretical point of view, an asymptotic value is predicted, as proceeding from the production of elements in stars and a given IMF, that is, the stellar true yield for a single stellar population, which will be reached when all stars die. An abundance at the effective radius of ~8.74 dex corresponds to a maximum abundance of ~8.84 in the central regions, in agreement with theoretical expectations. For example, Mollá & Díaz (2005) found a saturation level in 12 + log (O/H) = 8.80. They used a grid of chemical evolution models for spiral and irregular galaxies, the stellar yields by Woosley & Weaver (1995) for oxygen, and the IMF by Ferrini et al. (1992). If a different combination of IMF and stellar yield set is used, differences of a factor two may be found. An average value of 8.80 ± 0.15 would be the highest oxygen abundance predicted theoretically, which also agrees with more recent estimations (Pilyugin et al. 2007).
Since abundance is a relative parameter (amount of oxygen relative to the amount of hydrogen), this value can also be interpreted as the maximum abundance of the universe at a certain redshift. As shown by Moustakas et al. (2011), this parameter evolves with redshift at about 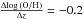 . The functional form describes the considered data well, as can be appreciated in Fig. 4. The dispersion of the abundance values along this curve is σΔlog (O/H) = 0.07 dex, much lower than previous reported values by (e.g., ~ 0.1 dex, T04 Mannucci et al. 2010; Hughes et al. 2013). It is important to note here that this dispersion is not much higher than the estimated errors for the characteristic abundances (elog (O/H) ~ 0.06 dex). Although the dispersion around the correlation depends on the actual form adopted for the ℳ-Z relation, the derived value is always low. If instead of the considered functional form we adopt a third or fourth order polynomial function, as considered by Kewley & Ellison (2008), the dispersion is just 0.084 dex, lower than the value reported in that publication for SDSS data using the same calibrator. However, our adopted functional form has a more straighforward physical interpretation than the pure polynomial functions adopted in the literature.
. The functional form describes the considered data well, as can be appreciated in Fig. 4. The dispersion of the abundance values along this curve is σΔlog (O/H) = 0.07 dex, much lower than previous reported values by (e.g., ~ 0.1 dex, T04 Mannucci et al. 2010; Hughes et al. 2013). It is important to note here that this dispersion is not much higher than the estimated errors for the characteristic abundances (elog (O/H) ~ 0.06 dex). Although the dispersion around the correlation depends on the actual form adopted for the ℳ-Z relation, the derived value is always low. If instead of the considered functional form we adopt a third or fourth order polynomial function, as considered by Kewley & Ellison (2008), the dispersion is just 0.084 dex, lower than the value reported in that publication for SDSS data using the same calibrator. However, our adopted functional form has a more straighforward physical interpretation than the pure polynomial functions adopted in the literature.
The results do not vary significantly when using the oxygen abundance derived from the integrated spectra across the covered FoV. However, both the dispersion around the derived ℳ-Z relation (~0.1 dex) and the estimated errors for the abundances are slightly larger (~0.07 dex). This is expected since for the integrated spectra we coadded regions with different ionization sources (e.g. Sánchez et al. 2012b), on one hand, and we have a single estimate of the abundance per object, not a value derived from the analysis of a well-defined gradient (which reduces the error in the derivation of the oxygen abundance). Figure 3 illustrates this effect, showing the distribution of the oxygen abundances estimated for each galaxy at the effective radius using the radial gradients with the oxygen abundances derived directly from the spectra integrated over the entire field-of-view. As expected, both parameters shows a tight correlation (σ ~ 0.06 dex). The errors estimated for the integrated abundance are larger, and they are directly transferred to the dispersion along the one-to-one relation, and thus, to the corresponding ℳ-Z distribution.
Once this functional form had been derived, we determined the offset and dispersion for the data corresponding to the galaxies analyzed in Sánchez et al. (2012b). Based also on IFS, and covering the full optical extent of the galaxies, the only possible differences would be either the details of the sample selection and/or the redshift range. The galaxies from the feasibility studies considered here are all face-on spiral galaxies, with an average redshift similar to that of the CALIFA data (z ~ 0.016), and only slightly higher projected sizes (red squares in Fig. 4). They present a minor offset with respect to the derived ℳ-Z relation (Δlog (O/H) = − 0.003 dex) and a slightly broader dispersion (σΔlog (O/H) = 0.084 dex). Considering that the spectrophotometric calibration of the data is not that accurate (~20%, Mármol-Queraltó et al. 2011), the slightly larger redshift range covered by this sample (Sánchez et al. 2012b), and considering that the sample is smaller (31 objects), the difference is not significant. If we consider this dataset and the CALIFA one described before, the derived dispersion is just σΔlog (O/H) = 0.07.
3.3. Dependence of the ℳ-Z relation on the SFR
The main goal of this study is to explore whether there is a dependence of the ℳ-Z relation on the SFR. Before doing that, it is important to understand the possible additional dependence of the SFR on other properties of the galaxies, in particular on the stellar mass. The SFR of blue/star-forming galaxies has a well-known relation with the stellar mass, which has been described not only in the Local Universe (e.g. Brinchmann et al. 2004), but also at different redshifts (e.g. Elbaz et al. 2007,and references therein). Its nature is still under debate (e.g. Davé 2008; Vulcani et al. 2010), but it is most probably related to the ability of a certain galaxy to acquire neutral gas, together with the well-known Schmidt-Kennicutt law (Kennicutt 1998). Irrespective of its nature, this relation together with the ℳ-Z relation may induce a secondary correlation between the SFR and the oxygen abundance.
Figure 4, top-right panel, shows the distribution of the SFR as a function of the stellar mass for the CALIFA galaxies analyzed here and the galaxies extracted from the feasibility studies. As expected, both parameters show a clear correlation, with a strong correlation coefficient (r = 0.77). The slope of this relation for our galaxies is α = 0.63, only slightly lower than the value reported for the Local Universe based on SDSS data (~0.77, Elbaz et al. 2007). This value is somewhat lower than the value near to one expected from the simulations (Elbaz et al. 2007). The limited number of low-SFR objects in our sample may explain the difference in slope. Nevertheless, it is clear that we reproduce the expected correlation. To investigate whether the selection criteria of the CALIFA galaxies, or the limited number of observed galaxies, have induced any spurious correlation that may affect the distribution of the two quantities and/or the described trend, we compared these distribution with those of the complete SDSS sample for the redshift ranges covered by Lara-López et al. (2010) and Mannucci et al. (2010). To do so, we used the MPA-JHU catalog described in the previous section and extracted the same stellar masses and aperture-corrected SFR for the two redshift ranges. The distribution of the two parameters are represented in Fig. 4, top-right panel, using similar density contours as the ones shown in the top-left panel. It is clear that the ranges of the two quantities and the distribution along the Mass-SFR plane agree between the three samples. In particular, the agreement is remarkable between our analyzed CALIFA sample and the one studied by Lara-López et al. (2010), which is the one at the more similar redshift range. Indeed, the described correlation agrees completely with the SDSS data corresponding to this redshift range. Thus, the selection criteria do not seem to affect the range of parameters or the correlation between the two quantities.
Figure 4, bottom-left panel, shows the ℳ-Z relation, but with a different color-coding that indicates the integrated SFR of each particular galaxy. The trend of the SFR with metallicity follows the trend of the SFR with mass. Thus, more massive galaxies have a higher SFR and are more metal rich. To determine which is the dominant correlation, we derived the correlation coefficient between the SFR and the oxygen abundance, obtaining a value of r = 0.54. This indicates that while the strength of the ℳ-Z and the SFR-Mass relations are indistinguishable statistically, the SFR-abundance is weaker and seems to be induced by the other two.
We found no trend between the SFR and the oxygen abundance for a given mass similar to the one described in Lara-López et al. (2010) and Mannucci et al. (2010). For a given mass, the galaxies with stronger star formation do not seem to have a lower metal content. To investigate this in more detail, we derived the differential oxygen abundance with respect to the considered ℳ-Z relation, to search for any correlation with the SFR.
Figure 4, bottom-right panel, shows the distribution of the oxygen abundance residual after subtracting the ℳ-Z relation as a function of the SFR. The data are consistent with being randomly distributed around the zero value, with no correlation between both parameters (r = 0.08). The histogram of the differential oxygen abundances shows a distribution compatible with a Gaussian function. We recall here that the dispersion around the ℳ-Z relation was just ~ 0.07 dex, a markedly small error considering the nominal errors of the parameters involved. In summary, we cannot confirm the dependency of the ℳ-Z relation on the SFR with the current CALIFA data.
A possible concern regarding this result may be that the limited number of objects in the current CALIFA sample may hamper the detection of a significant correlation. We performed a simple Monte-Carlo simulation to test this possibility. For this, we assumed that the ℳ-Z -SFR distribution follows the analytical formulae described by Mannucci et al. (2010). Then, we extracted a random subsample of 100 objects covering a similar range of the parameters as covered by the CALIFA sample, and we added a Gaussian noise of 0.05 dex (i.e., the value reported by Mannucci et al. 2010). For this subsample, we subtracted the ℳ-Z relation predicted by the same authors, and analyzed the possible correlation between the residual of the abundance and the SFR. After 1000 realizations we found in all the cases a clear correlation (r ~ 0.7), with an slope compatible with the one predicted by the FMR relation. Thus, the number of objects does not affect the result.
 |
Fig. 5 . Top-left panel: distribution of the oxygen abundances for the 3000 individualH ii regions extracted from the CALIFA data as a function of the surface mass density, represented with a density contour-plot. The first contour encircles 95% of the total number ofH ii regions, with ~ 20% less in each consecutive contour. The solid-yellow points represent the average oxygen abundances, with their corresponding standard deviations indicated as error bars for consecutive bins of 0.1 dex in surface mass density. The dot-dashed line represents the best-fitted curve for these points. Top-right panel: distribution of the SFR surface density as a function of the stellar mass density of each individualH ii region. The contour plots represent the density of points in the distribution of oxygen abundances as a function of the surface SFR densities, with the same encircled numbers as in the previous panel. Bottom-left panel: same distribution shown in the top-left panel, for the CALIFA and feasibility-studies objects. The colors represent the logarithm of the integrated surface density of the SFR for eachH ii region. Bottom-right panel: distribution of the differential oxygen abundance, once the dependency with the surface mass density has been subtracted, for individualH ii regions. The contour plots represent the density of points in the distribution of differential oxygen abundances, once subtracted the dependence on the surface masses densities, as a function of the surface SFR densities, with the same encircled numbers as in the previous panel. The solid-yellow points represent the average values for the abundance offsets, with their corresponding standard deviations indicated as error bars, for consecutive bins of 0.1 dex in surface SFR density. |
3.4. Dependence of the Σ-Z relation on the SFR
In Rosales-Ortega et al. (2012) we presented a new scaling relation between the oxygen abundance and the surface mass density for individualH ii regions (Σ-Z relation)7.This relation is a local version of the global ℳ-Z relation, and indeed, it is possible to recover this latter one from the former by integrating over a certain aperture (Rosales-Ortega et al. 2012). We proposed that this relation is the real fundamental one and the ℳ-Z relation is a natural consequence. Following this reasoning, it is important to test if there is a secondary relation between the local-ℳ-Z relation and the SFR. An additional advantage of this exploration is the increased statistical significance of the results, because of the much larger number of sampled objects here (~3000 H ii regions).
Figure 5, top-left panel, shows the Σ-Z relation for theH ii regions of the CALIFA galaxies explored so far. As a first result, we reproduce the relation described in Rosales-Ortega et al. (2012), using a completely different dataset (the catalog ofH ii regions extracted from 38 face-on spirals, using IFS data, from Sánchez et al. 2012b). Both quantities have a strong correlation, with a correlation coefficient of r = 0.98. As in the case of the global ℳ-Z relation, we adopted the asymptotic Eq. (1). In this case, the x parameter represents the logarithm of the stellar mass surface density in units of M⊙ pc-2. The a, b, and c parameters have the same interpretation as those derived for the global relation, and we derive similar values when fitting the data: a = 8.86 ± 0.01, b = 0.97 ± 0.07 and c = 2.80 ± 0.21, which reinforces our hypothesis that the two relations are strongly linked. In general, the global-ℳ-Z relation has the same shape as the local one but shifted arbitrarily in mass (to match them to the corresponding mass densities).
Like in the case of the integrated properties of the galaxies, there is a tight correlation between the stellar surface mass density and the surface star-formation density (Fig. 5, top-right panel). The correlation is a clear (r = 0.66) and is well described by a simple linear regression. The surface star-formation density scales with the surface mass density with a slope of α = 0.66 ± 0.18, again, below the expected value derived in semi-analytical simulations for the mass-SFR relation. Note that a comparison with a simulation taking into account the described local relationship is not feasible at present, since no such simulation exists to our knowledge.
This relation indicates that the HII regions with stronger star-formation are located in more massive areas of the galaxies (i.e., towards the center). We explored if our result is affected by young stars that biases our mass derivation. However, we found that our surface-brightness and colors (the two parameters used to derive the masses) are not strongly correlated with either the age of the underlying stellar population or the fraction of young stars. Even more, the SFR density presents a positive weak trend with the B − V color, not the other way round.
 |
Fig. 6 Left panel: same distribution of the characteristic oxygen abundance as a function of the stellar mass as shown in the bottom panel of Fig. 4. Right panel: same distribution of the oxygen abundances as a function of the stellar surface density for the individualH ii regions as shown in the bottom panel of Fig. 5. In both cases, the color code indicates the logarithm of the specific star formation rate. |
Like in the global case, these two relations between the oxygen abundance and the surface SFR with the surface mass density may induce a third relation between the two former parameters. In fact, there is a trend between the two parameters, much weaker than the other two described here (r = 0.59), as expected from an induced correlation. Figure 5 bottom-left panel illustrates this dependence, showing the local-ℳ-Z relation, color-coded by the mean surface SFR per bin of oxygen abundance and surface mass density. There is a clear gradient in the surface SFR that mostly follows the local-ℳ-Z relation. In this figure we can see a deviation from this global trend in agreement with the results by Lara-López et al. (2010) and Mannucci et al. (2010), in the sense that there are a fewH ii regions with a low metal content and high SFR for their corresponding mass surface density (bottom-right edge of the figure). However, all together they represent less than a 2 − 3% of the total sampled regions, and therefore cannot explain a global effect as described in these publications. Furthermore, the stochastic fluctuations around the average values at this low number statistics may clearly produce this effect, since there are otherH ii regions in the same location of the diagram with much lower surface SFR.
Following the same procedure as outlined in Sect. 3.3, we removed the dependence of the oxygen abundance on the surface mass density by subtracting the derived relation between the two parameters. Then, we explored possible dependencies on the surface density SFR. Figure 5, bottom-right panel, illustrates the result of this analysis. It shows the distribution of the differential oxygen abundance along the surface SFR for the individual H ii regions. No correlation is found between the two for the individual values (r = 0.17). However, the dispersion around the zero-value is higher than that reported for the similar residual distribution for the global relation (σlocal = 0.11 dex). The distribution seems to show some tail toward higher abundances for weaker SFRs and lower for stronger ones. Therefore, to explore possible dependencies even more, we derived the average differential oxygen abundance for equal ranges of surface SFR of 0.2 dex width and determined the correlation coefficient. In this case we found a clearer trend (r = 0.67) in the sense thatH ii regions with higher surface SFR shows slightly lower abundances for similar masses. However, the slope of the derived regression α = − 0.0155 ± 0.217 is incompatible with any trend, and it is far below the reported value of α ~ − 0.3 for the dependence of the ℳ-Z relation and the SFR Mannucci et al. (2010) or α ~ − 0.4 by Lara-López et al. (2010). Applying any of these correlations (i.e., adding α·log (SFR) to the mass) does not reduce the dispersion found around the zero value at all (σlocal,SFR = 0.108 dex). In summary, we find no correlation between the local-ℳ-Z relation with the SFR in the way described by other authors for the global one. Our results for the local and global ℳ-Z relations are therefore fully consistent.
3.5. Dependence of the ℳ-Z relation on the sSFR
Following Mannucci et al. (2010), we have explored the possible dependence of the ℳ-Z relation on the sSFR, a measurement of the current star-formation activity of the galaxy in comparison with the past one. It is known to exhibit a smooth dependence on the stellar mass (sSFR ∝ M-1), which has been described at different redshifts (e.g. Elbaz et al. 2007). Many properties of galaxies depend on this parameter. In particular, Mannucci et al. (2010) found that there was an apparent threshold in the sSFR at about 10-10 yr-1 that diminishes the effect of the SFR on the ℳ-Z relation in the sense that the depence is stronger for higher values of the sSFR. In this section we explore the possible dependence of the ℳ-Z on sSFR.
Figure 6 shows the global and local ℳ-Z relations for the galaxies andH ii regions discussed in this article. In this case the color code indicates the sSFR, determined by dividing the SFR and stellar masses described before. In both cases the sSFR seems to follow the dependence of the abundance with the mass, without a significant deviation from the trend along this relation. Thus, we do not identify either a clear secondary dependence on the sSFR, or a clear threshold at which the global and local ℳ-Z relation show a change in the trend or an offset with respect to the average relation.
In the case of the Σ-Z relation, the data seem to follow a smooth surface in 3D space, with the three parameters clearly correlated. This surface was already discussed in Rosales-Ortega et al. (2012), who, instead of using the sSFR, used the equivalent width of Hα, a well-known proxy for the former parameter (e.g. Kennicutt 1998). Figure 7 shows the empirical relation for the two parameters based on the individualH ii regions. The correlation is very strong (r = 0.84), and well described with a simple linear regression, with a dispersion 0.26 dex: 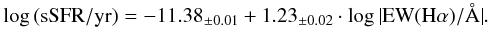 (2)Adopting this relation, the described curve is basically the same as discussed in Rosales-Ortega et al. (2012), considering the reparametrization of one of the axes. We note here that it is required to take the absolute value of the equivalent width of Hα, which has always negative values for strong emission line regions.
(2)Adopting this relation, the described curve is basically the same as discussed in Rosales-Ortega et al. (2012), considering the reparametrization of one of the axes. We note here that it is required to take the absolute value of the equivalent width of Hα, which has always negative values for strong emission line regions.
 |
Fig. 7 Distribution of the specific star formation as a function of the absolute equivalent width of Hα for the individualH ii regions. The solid yellow circles indicate the location of the average values in bins of 0.2 dex of the equivalent width of Hα. The solid line shows the best-fitted linear regression line. |
4. Discussion and conclusions
In this study we have explored the global and local ℳ-Z relations and their possible dependence on the SFR and sSFR based on the ionized gas properties of the first 150 galaxies observed by the CALIFA survey. So far, we found no dependence on the SFR and sSFR other than that induced by the well known relation of both parameters with the stellar mass. In addition, we explored similar dependencies for the sample of ~ 3000 individualH ii regions extracted from the IFS data. We confirm the Σ-Z relation described in Rosales-Ortega et al. (2012). However, no secondary dependence was found between this relation and the SFR (or sSFR), other than that induced by their dependences on the stellar mass.
Our results contradict those of Mannucci et al. (2010) and Lara-López et al. (2010), who described a trend for which galaxies with stronger star-formation show lower oxygen abundances for the same mass range. Similar results were already presented in Hughes et al. (2013), using a sample of galaxies observed using drift-scan techniques. The main difference between the two datasets is that while Mannucci et al. (2010) and Lara-López et al. (2010) used the spectroscopic data provided by the SDSS (i.e., single aperture, with a strong aperture bias), both Hughes et al. (2013) and the results presented here are based on integrated (and spatially resolved) properties of the galaxies. Shen et al. (2003) showed that the physical size of galaxies in the SDSS comprises a range of values between a few kpcs to a few tens of kpcs. This means that the SDSS fiber covers a range between ~ 0.3 and ~ 10 times the effective radii of galaxies at the redshift range covered by Mannucci et al. (2010) and Lara-López et al. (2010), depending on their intrinsic properties and the involved cosmological distances. This aperture bias mostly affects the derived SFR (depending on the aperture corretion applied, which are under debate, e.g. Gerssen et al. 2012) and the oxygen abundances (e.g. Sánchez et al. 2012a,b), but in some cases it may also affect the mass derivation (if the spectroscopic information is used to derive the mass-to-light ratio).
In addition, the redshift ranges covered by these studies are also different. The data presented in Hughes et al. (2013) and here are focused on relatively nearby galaxies (D < 120 Mpc), with a narrow range of distances in both cases. In contrast, SDSS data used by Mannucci et al. (2010) and Lara-López et al. (2010) also differ (0.07 < z < 0.30 and 0.04 < z < 0.1, respectively), but they both correspond to a much wider redshift range than that covered by us. In both cases the aperture biases of the SDSS spectra have two effects: (i) They cover a larger portion of the galaxies at higher redshifts for the same masses, which affects their abundance estimates (decreasing the value at higher redshifts) and the SFR (increasing the value at higher redshifts too). (ii) Due to the reported redshift evolution of the ℳ-Z relation, these authors derived a lower abundance for higher redshift galaxies than for lower redshift ones for the same mass, even in the absence of any aperture bias.This second effect may be less important, since it would be at most of about of 0.06 dex for Mannucci et al. (2010), but just ~ 0.02 dex for Lara-López et al. (2010). The first effect is also stronger for the study by Mannucci et al. (2010). We can reproduce qualitatively the secondary trend with the SFR of the ℳ-Z relation by taking our IFS data and simulating different SDSS aperture spectra corresponding to different projected distances (see Appendix A). However, the derived slope is not reliable because of the uncertainties involved (different sample selections, different methods of deriving the metallicity, unclear evolution of ℳ-Z relation with the redshift). Although we cannot unambiguously prove that aperture effects are inducing this relation, qualitatively there is certainly an agreement.
As described in Mannucci et al. (2010), oxygen abundance is a rather simple parameter, that is governed by three processes: (i) star-formation, which transforms gas into stellar mass, increasing the metal content; (ii) gas accretion, or inflows, which dilutes the oxygen abundance (assuming accretion of more or less pristine gas); and (iii) gas outflows, induced by the star-formation. However, none of these processes is simple, and their interdependence is unclear.
Based on the Schmidt-Kennicutt law, the surface SFR depends on the surface mass density, 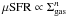 (Kennicutt 1998), with a slope larger than one (n ~ 1.4 − 1.5). This means that the integrated SFR of a galaxy should depend on the gas inflow rate (e.g. Mannucci et al. 2010). However, this does not necessarily mean a global dilution and a decrease in the average oxygen abundance, since inflow is a radial process while star-formation is a local one. Gas that falls into the inner regions may be polluted by star formation farther out if the latter process is fast enough. Therefore, if the typical timescale of gas recycling is shorter than the inflow timescale (e.g. Silk 1993), no SFR dependence is expected.On the other hand, if the timescales for the feedback and global gas recycling are much longer than the typical length of a star-formation episode (~1 Gyr for L∗ galaxies Quillen & Bland-Hawthorn 2008), there will be a loses of connection between the starformation and the global metal enrichment, too.
(Kennicutt 1998), with a slope larger than one (n ~ 1.4 − 1.5). This means that the integrated SFR of a galaxy should depend on the gas inflow rate (e.g. Mannucci et al. 2010). However, this does not necessarily mean a global dilution and a decrease in the average oxygen abundance, since inflow is a radial process while star-formation is a local one. Gas that falls into the inner regions may be polluted by star formation farther out if the latter process is fast enough. Therefore, if the typical timescale of gas recycling is shorter than the inflow timescale (e.g. Silk 1993), no SFR dependence is expected.On the other hand, if the timescales for the feedback and global gas recycling are much longer than the typical length of a star-formation episode (~1 Gyr for L∗ galaxies Quillen & Bland-Hawthorn 2008), there will be a loses of connection between the starformation and the global metal enrichment, too.
On the other hand, outflows induced by strong star-formation and the subsequent winds due to SN explosions are known to eject metals into the intergalactic medium, and hence regulate the metal content of galaxies (e.g. Larson 1974; Prieto et al. 2008; Palacios et al. 2005). It is therefore expected that the strength of the outflows, and the fraction of metals lost, depends on the SFR. However, the detailed relation is difficult to assess, since the ability of an outflow to eject metals could be counter-balanced by the gravitational field of the galaxy, which makes metals fall back into the disk in a back-rain process. The high metallicity of the diffuse IGM in galaxy groups and clusters is indirect evidence that at least some fraction of the metals in these winds is lost to the environment (e.g. Renzini et al. 1993).
Although it is hard to study with only the integrated properties of galaxies, the spatial distribution of metals and, in particular, the dispersion of the oxygen abundance at a certain distance from the center could be used to constrain the strength of these (and other) diffusion processes. Our preliminary results, Sánchez et al. (2012b), indicate that this dispersion is rather low. Therefore, either metals are really expelled and lost and/or the net effect is not very strong. The lack of a clear secondary dependence of the oxygen abundance, both globally or locally on the SFR and the μSFR, also suggests that this is not the dominant process.
Following the formalism presented in Mannucci et al. (2010), the fraction of metals ejected from outflows has to be compensated for by the metals produced by the star-formation process. If, instead of the reported dependence of the abundance on the SFR of ~ − 0.32·log (SFR), we consider no dependence at all, and using their formulae, the amount of metals lost by this process should be Δlog (O/H) ∝ SFR0.33, i.e., much smaller than that required to reproduce their results.
In summary, our results are consistent with those previously presented in Sánchez et al. (2012b) and Rosales-Ortega et al. (2012). In general, the properties of the ionized gas in late-type galaxies are consistent with a quiescent evolution, where gas recycling is faster than other timescales involved (Silk 1993). This would imply that the galaxies seem to behave locally in a similar manner as globally, dominated by a radial mass distribution following the potential well of the matter, with an inside-out growth that is regulated by gas inflow and local down-sizing star-formation. Therefore, the dominant parameter that defines the amount of metals is the stellar mass, since both parameters are the consequence of an (almost) closed-box star-formation process. However, our results are only valid for galaxies with stellar masses higher than ~109.5 M⊙, where the CALIFA sample becomes complete.
Online material
Properties of the galaxy sample.
Appendix A: Dependence of ℳ-Z relation with the SFR: Apperture effects
 |
Fig. A.1 Top-right panel: distribution of the oxygen abundance along the stellar mass for the ~50,000 simulated aperture measurements, as described in the text. The contours indicate the same encircled fraction of object than in precendent figures (e.g., Fig. 5). The solid yellow circles indicate the average abundances for consecutive bins of 0.2 dex in stellar mass. Only those binned values with a significant number of objects are shown. Top-left panel: distribution of the integrated star-formation rate along the stellar mass for the simulated galaxies. Contours and symbols represent the same as in previous panel. The solid line shows the regression line between the two parameters. Bottom-left panel: Distribution of the differential oxygen abundance with respect to the derived ℳ-Z relation along the SFR for the simulated galaxies, when only the aperture effect is considered. Bottom-right panel: distribution of the differential oxygen abundance with respect to the derived ℳ-Z relation along the SFR for the simulated galaxies, when both the aperture effect and the evolution of the ℳ-Z relation with redshift is taken into account. In both panels the contours and sybmols represent similar concepts like in previous figures and panels. The solid line shows the best derived fit using a simple linear regression method. |
We showed in the main text our results of the study of a possible dependence of the ℳ-Z relation with the SFR. Using the IFS data provided by the CALIFA survey, we were able to derive the ℳ-Z relation with abundances unaffected by aperture effects. In a similar way we derived the complete integrated SFR for these galaxies. In contrast to previous results in the literature (e.g. Mannucci et al. 2010; Lara-López et al. 2010), we found no secondary dependence of the abundance with the SFR once we considered the dependence of these parameters with the mass. The only similar result found in the literature where no dependence on the SFR is described used a sample of integrated spectra taken using drift-scan observations (e.g. Hughes et al. 2013). In summary, when the biases due to aperture are minimized, the dependence on the SFR seems to disappear.
It is beyond the scope of this article to explain why other studies found a correlation that we cannot reproduce, in particular when we used a less biased and more detailed estimate of the considered quantities. However, as a sanity check and to provide a suitable explanation, we performed a test of the aperture effects. The oxygen abundance and the SFR are potentially affected by this aperture effect. However, the stellar mass is the less affected, in particular if only photometric data are considered. With CALIFA we are in the unique situation of being able to reproduce the aperture effects present in single aperture observations by simulating the considered apertures and re-analyzing the corresponding simulated spectra.
It is important to use a sample as our starting dataset for the simulations of which we know a priori that it does not show any secondary correlation between the abundance and the SFR when the dependency with the mass is removed. That way we can be sure that the induced correlation was not present as an input ingredient of the simulation.
For each galaxy in our dataset with well-defined characteristic oxygen abundance, we extracted a set of aperture spectra centred on the peak emission of the galaxy and with consecutive apertures corresponding to the distance of each of the detectedH ii regions from our catalog. This ensures that there is a clear change in the ionization conditions between consecutive apertures. Each of these aperture spectra corresponds to the same galaxy observed at different redshifts. To be consistent with the redshift ranges adopted in Mannucci et al. (2010) and Lara-López et al. (2010), we restricted our apertures to diameters larger than 12″. This roughly corresponds to the projected size of a SDSS fiber at the lower redshift adopted by this study (z ~ 0.07). After extracting the spectra, we repeated the same analysis as we performed for the individualH ii regions, described in Sect. 3.1, deriving the oxygen abundance and integrated SFR. Together with the integrated stellar masses, we had with ~ 2500 individual simulations of the three quantities analyzed in this study.
Finally, we performed a Monte-Carlo simulation to take into account possible effects of the noise in the overall process. For each of the three considered quantities 20 individual realizations were derived, taking into account the corresponding propagated errors (including also those of the stellar masses). We obtained with ~ 50 000 simulated aperture biased quantities.
Figure A.1 shows the results of this simulation. In the top-left panel we show the derived ℳ-Z relation for the simulated
spectra. As expected, it follows the observed relation presented in Fig. 4.This result was previously shown by Rosales-Ortega et al. (2012), who reproduced the global ℳ-Z from the local one (derived from the abundance gradients), based purely on simulated galaxies. However, a more detailed comparison shows that although both relations are very similar, there are slightly differences: (i) the asymptotic oxygen abundance for large masses is ~ 0.05 dex larger in the simulated relation and (ii) the dispersion of oxygen abundances along the average value is higher (σlog (O/H) ~ 0.1 dex, similar to the one reported by T04). Both results are expected: (1) we are including more central estimates of the abundance for the same range of masses. In the center of the galaxies the abundance is larger than in the outer parts by ~ 0.1 dex (e.g. Sánchez et al. 2012b). Thus, the net effect is an increase of the upper envelope of the abundance; (2) we are including measurements of different abundances for the same mass range because we enlarge the covered area of the galaxy, simulating the effect of the redshift. Therefore, the dispersion at a certain mass range is increased.
Figure A.1, top-right panel, shows the distribution of the simulated SFRs along the stellar masses. As expected, we reproduce the relation between the two quantities in a similar way as described in Fig. 4. The main differences are that (1) the dispersion is slightly higher: σlog (SFR) ~ ~ 0.35 dex, compared to σlog (SFR) ~ 0.18 dex; (2) there is a tail to lower values of the SFR at a given mass. This is in particular evident for the low-mass range of the figure (M ~ 109.5 M⊙). Again, these effects are clearly explained by the aperture bias, since at a given mass we are sampling areas of lower integrated SFR than the real one (i.e., the central regions), which is an upper limit.
Finally, we derived the differential oxygen abundance with respect to the considered ℳ-Z relation for the simulated data. We aimed to determine whether there is any correlation with the SFR, following the analysis in Sect. 3.3. Figure A.1, bottom-left panel shows the distribution of these two parameters. There is a clear correlation (r = 0.92) in a similar sense as described in Mannucci et al. (2010) and Lara-López et al. (2010), i.e., galaxies with lower SFR seem to be more metal poor. After applying this correlation, we recovered the initial dispersion of the ℳ-Z relation described for our original dataset (σΔlog (O/H) ~ 0.07 dex), a decrease similar to the one reported by these two authors. The dependence of the SFR is Δlog (O/H) ∝ − 0.1 log (SFR), just slightly weaker than the linear term of Eq. (2) in Mannucci et al. (2010), − 0.14 dex/log (SFR), or the combination of Eqs. (3) and (4) of the same authors.
To investigate this problem in more detail, we included in our simulation the reported ℳ-Z evolution with redshift as described in Moustakas et al. (2011). To do this, we determined which redshift corresponds to each of the simulated apertures and applied the described correction to the corresponding derived abundance. Results are shown in Fig. A.1, bottom-right panel. Taking into account the possible redshift dependence, the new differential oxygen abundance depends more strongly on the SFR, Δlog (O/H) ∝ − 0.2log (SFR).
Although this is a very simplistic simulation, based on a reduced number of input galaxies, in general we have shown that aperture effects, together with other evolutionary properties of galaxies, may induce the secondary correlations between the ℳ-Z and the SFR that we were unable to reproduce using our IFS data.
An online animated version of this relation for the current analysed data is available at http://www.youtube.com/watch?v=F7JCX-d7uPY
Acknowledgments
We thank the director of CEFCA, M. Moles, for his sincere support of this project. This study makes uses of the data provided by the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). CALIFA is the first legacy survey being performed at Calar Alto. The CALIFA collaboration would like to thank the IAA-CSIC and MPIA-MPG as major partners of the observatory, and CAHA itself, for the unique access to telescope time and support in manpower and infrastructures. The CALIFA collaboration also thanks the CAHA staff for the dedication to this project. Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck-Institut für Astronomie and the Instituto de Astrofísica de Andalucia (CSIC). We thank the Viabilidad, Diseño, Acceso y Mejorafunding program, ICTS-2009-10, for supporting the initial developement of this project. S.F.S., F.F.R.O. and D. Mast thank the Plan Nacional de Investigación y Desarrollo funding programs, AYA2010-22111-C03-03 and AYA2010-10904E, of the Spanish Ministerio de Ciencia e Innovación, for the support given to this project. S.F.S. thanks the Ramón y Cajal project RyC-2011-07590 of the spanish Ministerio de Economía y Competitividad, for the support giving to this project. S.F.S. and B.J. acknowledge suuport by the grants No. M100031241 and M100031201 of the Academy of Sciences of the Czech Republic (ASCR Internal support program of international cooperation projects − PIPPMS) and by the Czech Republic program for the long-term development of the research institution No. RVO67985815. R.G.D., E.P. and R.G.B. thank the Plan Nacional de Investigación y Desarrollo funding program AYA2010-15081. F.F.R.O. acknowledges the Mexican National Council for Science and Technology (CONACYT) for financial support under the programme Estancias Posdoctorales y Sabáticas al Extranjero para la Consolidación de Grupos de Investigación, 2010-2011 J.M. and J.P. acknowledge financial support from the Spanish grant AYA2010-15169 and Junta de Andalucía TIC114 and Excellence Project P08-TIC-03531. D. M. and A. M.-I. are supported by the Spanish Research Council within the program JAE-Doc, Junta para la Ampliación de Estudios, co-funded by the FSE. R.A. Marino was also funded by the spanish programme of International Campus of Excellence Moncloa (CEI). J.I.-P., J.M.V., A.M.-I. and C.K. have been partially funded by the projects AYA2010-21887 from the Spanish PNAYA, CSD2006 − 00070 “1st Science with GTC” from the CONSOLIDER 2010 programme of the Spanish MICINN, and TIC114 Galaxias y Cosmología of the Junta de Andalucía (Spain). M.A.P.T. acknowledges support by the Spanish MICINN through grant AYA2012-38491-C02-02, and by the Autonomic Government of Andalusia through grants P08-TIC-4075 and TIC-126. Polychronis Papaderos is supported by a Ciencia 2008 contract, funded by FCT/MCTES (Portugal) and POPH/FSE (EC). Jean-Michel Gomes is supported by grant SFRH/BPD/66958/2009 from FCT (Portugal). This paper makes use of the Sloan Digital Sky Survey data. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., et al. 2013, submitted [Google Scholar]
- Cresci, G., Mannucci, F., Sommariva, V., et al. 2012, MNRAS, 421, 262 [NASA ADS] [Google Scholar]
- Davé, R. 2008, MNRAS, 385, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Edmunds, M. G., & Pagel, B. E. J. 1984, MNRAS, 211, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellis, S. C., Driver, S. P., Allen, P. D., et al. 2005, MNRAS, 363, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, ApJ, 672, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrini, F., Matteucci, F., Pardi, C., & Penco, U. 1992, ApJ, 387, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gerssen, J., Wilman, D. J., & Christensen, L. 2012, MNRAS, 420, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jester, S., Schneider, D. P., Richards, G. T., et al. 2005, AJ, 130, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kehrig, C., Monreal-Ibero, A., Papaderos, P., et al. 2012, A&A, 540, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Springel, V., & White, S. D. M. 2007, MNRAS, 376, 1465 [Google Scholar]
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Gazak, Z., et al. 2012, ApJ, 747, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, 521, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-Lopez, M. A., Lopez-Sanchez, A. R., & Hopkins, A. M. 2012, ApJ, submitted, ArXiv e-prints [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Longhetti, M., & Saracco, P. 2009, MNRAS, 394, 774 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R., Dopita, M. A., Kewley, L. J., et al. 2012, MNRAS, 426, 2630 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Hunt, L., Galli, D., et al. 2012, MNRAS, 427, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Mármol-Queraltó, E., Sánchez, S. F., Marino, R. A., et al. 2011, A&A, 534, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateus, A., Sodré, L., Cid Fernandes, R., & Stasińska, G. 2007, MNRAS, 374, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Moran, S. M., Heckman, T. M., Kauffmann, G., et al. 2012, ApJ, 745, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Mouhcine, M., Baldry, I. K., & Bamford, S. P. 2007, MNRAS, 382, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., & Kennicutt, R. C. Jr. 2006, ApJ, 651, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C. Jr., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Zaritsky, D., Brown, M., et al. 2011, ApJ, submitted [arXiv:1112.3300] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2012, ApJ, 745, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (University Science Books) [Google Scholar]
- Palacios, A., Meynet, G., Vuissoz, C., et al. 2005, A&A, 429, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquali, A., Gallazzi, A., Fontanot, F., et al. 2010, MNRAS, 407, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquali, A., Gallazzi, A., & van den Bosch, F. C. 2012, MNRAS, 425, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, E., Cid Fernandes, R., González Delgado, R. M., et al. 2013, ApJ, 764, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Villar, V., et al. 2008, ApJ, 675, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Montero, E., Contini, T., Lamareille, F., et al. 2013, A&A, 549, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petropoulou, V., Vílchez, J., & Iglesias-Páramo, J. 2012, ApJ, 749, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Thuan, T. X., & Vílchez, J. M. 2007, MNRAS, 376, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Mattsson, L. 2012, MNRAS, 424, 2316 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, J. L., Stanek, K. Z., & Beacom, J. F. 2008, ApJ, 673, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., & Bland-Hawthorn, J. 2008, MNRAS, 386, 2227 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., Ciotti, L., D’Ercole, A., & Pellegrini, S. 1993, ApJ, 419, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Jones, T., Ellis, R., et al. 2011, MNRAS, 413, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Kennicutt, R. C., Sánchez, S. F., et al. 2010, MNRAS, 405, 735 [NASA ADS] [Google Scholar]
- Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Sánchez, S. F., Iglesias-Páramo, J., et al. 2012, ApJ, 756, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Cardiel, N., Verheijen, M. A. W., Pedraz, S., & Covone, G. 2007, MNRAS, 376, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Kennicutt, R. C., et al. 2011, MNRAS, 410, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012a, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012b, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1993, Proc. Nat. Acad. Sci., 90, 4835 [Google Scholar]
- Skillman, E. D. 1992, in Elements and the Cosmos, eds. M. G. Edmunds, & R. Terlevich, 246 [Google Scholar]
- Skillman, E. D., Kennicutt, R. C., & Hodge, P. W. 1989, ApJ, 347, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Walterbos, R. A. M., Braun, R., & Hoopes, C. G. 2002, AJ, 124, 3118 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vale Asari, N., Stasińska, G., Cid Fernandes, R., et al. 2009, MNRAS, 396, L71 [NASA ADS] [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Finn, R. A., et al. 2010, ApJ, 710, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, J., Groves, B., Budavári, T., & Dale, D. 2011, Ap&SS, 331, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, E., Rigby, J. R., Sharon, K., & Gladders, M. D. 2012, ApJ, 755, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Yates, R. M., Kauffmann, G., & Guo, Q. 2012, MNRAS, 422, 215 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr. et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zaritsky, D., Kennicutt, R. C. Jr., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top panels: IFS-based Hα maps, in units of 10-16 erg s-1 cm-2 arcsec-2, derived for two representative galaxies of the sample (color images), together with the detectedH iiregions shown as black segmented contours. Bottom panels: radial distribution of the oxygen abundance derived for the individualH iiregions with abundace errors below 0.15 dex, as a function of the deprojected distance (i.e., corrected for inclination), normalized to the effective radius, for the same galaxies. The size of the circles is proportional to the Hα intensity. |
| In the text | |
 |
Fig. 2 Distribution of the stellar masses derived using the average M/L ratios described in Bell & de Jong (2001) and the B- and V-band photometry (Y axis in all panels) along the stellar masses derived using other procedures (X axis in all panels): top-left panel: stellar masses derived using the entire five-bands SDSS photometry and the M/L ratio provided by the SED analysis performed using PARADISE; top-right panel: stellar masses derived using the 2MASS K-band photometry and the M/L ratio provided in Longhetti & Saracco (2009); bottom-left panel: stellar masses derived using the CALIFA datacube spectrophotometry and the M/L ratio provided by PyCASSO/Starlight; and bottom-right panel: stellar Masses derived from CALIFA datacube spectrophotometry and the M/L ratio provided by FIT3D. |
| In the text | |
 |
Fig. 3 Distribution of the oxygen abundances estimated for each galaxy at the effective radius (Re), using the radial gradients, and the oxygen abundances derived directly from the spectra integrated over the entire field-of-view (int). |
| In the text | |
 |
Fig. 4 . Top-left panel: distribution of the oxygen abundances at the effective radii as a function of the integrated stellar masses for the CALIFA galaxies (113, blue solid circles). For comparison purposes, we show similar values for the galaxies observed in the CALIFA feasibility studies (31, red solid squares) included in theH ii regions catalog described in Sánchez et al. (2012b). The size of the symbols is proportional to the integrated SFR. The solid line represents the best-fitted curve, as described in the text. We also included the distribution of abundaces as a function of the stellar masses for the SDSS data corresponding to the redshift ranges sampled by Lara-López et al. (2010), dashed black contours, and Mannucci et al. (2010), solid grey contours. In both cases, the first contour encircles the 95% of the objects, and 20% less objects in each consecutive contour. Top-right panel: distribution of the integrated SFR as a function of the stellar masses. The size of the symbols is proportional to the oxygen abundance shown in previous panel. The solid line represents the best fitted linear regression to the CALIFA data.Like in the previos panel the contours represent the distribution of both parameters corresponding to the redshift ranges sampled by Lara-López et al. (2010), dashed black contours, and Mannucci et al. (2010), solid grey contours Bottom-left panel: same distribution shown in the top-left panel, for the CALIFA and feasibility-studies objects. The colors represent the logarithm of the integrated SFR for each galaxy. Bottom-right Panel: distribution of the differential oxygen abundances at the effective radii, once the dependency with the stellar mass has been subtracted, as a function of the integrated SFR for the CALIFA galaxies (113, blue solid circles). The size of the symbols is proportional to the oxygen abundances shown in Fig. 4. The histogram shows the same distribution of differential oxygen abundances. The solid line represents a Gaussian function with the same central value (0.01 dex) and standard deviation (0.07 dex) as the represented distribution, scaled to match the histogram. |
| In the text | |
 |
Fig. 5 . Top-left panel: distribution of the oxygen abundances for the 3000 individualH ii regions extracted from the CALIFA data as a function of the surface mass density, represented with a density contour-plot. The first contour encircles 95% of the total number ofH ii regions, with ~ 20% less in each consecutive contour. The solid-yellow points represent the average oxygen abundances, with their corresponding standard deviations indicated as error bars for consecutive bins of 0.1 dex in surface mass density. The dot-dashed line represents the best-fitted curve for these points. Top-right panel: distribution of the SFR surface density as a function of the stellar mass density of each individualH ii region. The contour plots represent the density of points in the distribution of oxygen abundances as a function of the surface SFR densities, with the same encircled numbers as in the previous panel. Bottom-left panel: same distribution shown in the top-left panel, for the CALIFA and feasibility-studies objects. The colors represent the logarithm of the integrated surface density of the SFR for eachH ii region. Bottom-right panel: distribution of the differential oxygen abundance, once the dependency with the surface mass density has been subtracted, for individualH ii regions. The contour plots represent the density of points in the distribution of differential oxygen abundances, once subtracted the dependence on the surface masses densities, as a function of the surface SFR densities, with the same encircled numbers as in the previous panel. The solid-yellow points represent the average values for the abundance offsets, with their corresponding standard deviations indicated as error bars, for consecutive bins of 0.1 dex in surface SFR density. |
| In the text | |
 |
Fig. 6 Left panel: same distribution of the characteristic oxygen abundance as a function of the stellar mass as shown in the bottom panel of Fig. 4. Right panel: same distribution of the oxygen abundances as a function of the stellar surface density for the individualH ii regions as shown in the bottom panel of Fig. 5. In both cases, the color code indicates the logarithm of the specific star formation rate. |
| In the text | |
 |
Fig. 7 Distribution of the specific star formation as a function of the absolute equivalent width of Hα for the individualH ii regions. The solid yellow circles indicate the location of the average values in bins of 0.2 dex of the equivalent width of Hα. The solid line shows the best-fitted linear regression line. |
| In the text | |
 |
Fig. A.1 Top-right panel: distribution of the oxygen abundance along the stellar mass for the ~50,000 simulated aperture measurements, as described in the text. The contours indicate the same encircled fraction of object than in precendent figures (e.g., Fig. 5). The solid yellow circles indicate the average abundances for consecutive bins of 0.2 dex in stellar mass. Only those binned values with a significant number of objects are shown. Top-left panel: distribution of the integrated star-formation rate along the stellar mass for the simulated galaxies. Contours and symbols represent the same as in previous panel. The solid line shows the regression line between the two parameters. Bottom-left panel: Distribution of the differential oxygen abundance with respect to the derived ℳ-Z relation along the SFR for the simulated galaxies, when only the aperture effect is considered. Bottom-right panel: distribution of the differential oxygen abundance with respect to the derived ℳ-Z relation along the SFR for the simulated galaxies, when both the aperture effect and the evolution of the ℳ-Z relation with redshift is taken into account. In both panels the contours and sybmols represent similar concepts like in previous figures and panels. The solid line shows the best derived fit using a simple linear regression method. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


