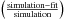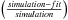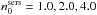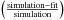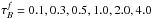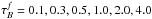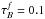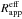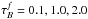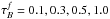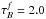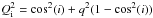| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220962 | |
| Published online | 14 May 2013 | |
The effects of dust on the derived photometric parameters of disks and bulges in spiral galaxies⋆
1 Jeremiah Horrocks Institute, University of Central Lancashire, PR1 2HE, Preston, UK
e-mail: bapastrav@uclan.ac.uk; cpopescu@uclan.ac.uk; aesansom@uclan.ac.uk
2 Max Planck Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
e-mail: Richard.Tuffs@mpi-hd.mpg.de
Received: 19 December 2012
Accepted: 21 January 2013
We present results of a study made to quantify the effects of dust on the derived photometric parameters of disks (old and young stellar disks) and bulges: disk scale-lengths, axis-ratios, central surface-brightness, bulge effective radii, and Sérsic indices. The changes in the derived photometric parameters from their intrinsic values (as would be seen in the absence of dust) were obtained by fitting simulated images of disks and bulges produced using radiative transfer calculations. The simulations were fitted with the GALFIT 3.0.2 data analysis algorithm and the fitted models were the commonly used infinitely thin disks described by exponential, general Sérsic and de Vaucouleurs distributions. We find the young stellar disks to suffer the most severe variation in the photometric parameters due to dust effects. In this context we also present corrections for narrow line (Balmer line) images. Old stellar disks are also significantly affected by dust, in particular when fits are performed with exponential functions. The photometric parameters of bulges are to a lesser extent affected by dust. We also find that the variation of dust corrections with face-on dust opacity and inclination is similar for bulges with different intrinsic stellar emissivities (different Sérsic index), with differences manifesting only close to edge-on orientations of the disk. Dust corrections for bulges are found to be insensitive to the choice of the truncation radius and ellipticity of the bulge. All corrections are listed in the appendices and made available in electronic format.
Key words: galaxies: spiral / galaxies: bulges / galaxies: photometry / galaxies: structure / dust, extinction / radiative transfer
Appendices are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A80
© ESO, 2013
1. Introduction
In recent years deep wide-field spectroscopic and photometric surveys of galaxies (e.g. Sloan Digital Sky Survey − SDSS, York et al. 2000; The Galaxy and Mass Assembly − GAMA, Driver et al. 2011) are providing us with large statistical samples of galaxies for which major morphological components can be resolved out to z = 0.1. This trend will continue with the advent of VISTA/VST (Emerson & Sutherland 2010; Arnaboldi et al. 2012), which will provide wide-field imaging surveys with sub-arcsec resolution, and will culminate in the wide-field diffraction-limited space-borne surveys made with Euclid (Laureijs et al. 2010). In parallel, automatic routines like GALFIT (Peng et al. 2002, 2010), GIM2D (Simard et al. 2002), BUDDA (Gadotti 2008) or MegaMorph (Bamford et al. 2013) have been developed to address the need of fitting large numbers of images of galaxies with 1D analytic functions to characterise the surface brightness distribution of their stellar components. In particular, Sérsic functions are the most common distributions used to describe and fit the observed profiles of galaxies and their constituent morphological components (e.g. Hoyos et al. 2011; Simard et al. 2011; Kelvin et al. 2012; Häußler et al. 2013). The derived Sérsic indices are then used (either by themselves or in combination with other photometric parameters) to classify galaxies as being disk- or spheroid-dominated (e.g. Kelvin et al. 2012; Grootes et al. 2013) or in terms of a bulge-to-disk ratio when bulge/disk decomposition is performed (Allen et al. 2006; Simard et al. 2011; Lackner & Gunn 2012).
One potential problem in interpreting the results of Sérsic fits is that the measured Sérsic parameters differ from the intrinsic ones (that would be derived in the absence of dust). This is because real galaxies, in particular spiral galaxies, contain large amounts of dust (e.g. Stickel et al. 2000, 2004; Tuffs et al. 2002; Popescu et al. 2002; Vlahakis et al. 2005; Driver et al. 2007; Dariush et al. 2011; Rowlands et al. 2012; Bourne et al. 2012; Dale et al. 2012; Grootes et al. 2013) and this dust changes their appearance from what would be predicted to be seen in projection based on only their intrinsic stellar distributions (e.g. Tuffs et al. 2004; Möllenhoff et al. 2006; Gadotti et al. 2010). Determining the changes due to dust is thus essential when characterising and classifying galaxies based on their fitted Sérsic indices (Pastrav et al. 2012). In addition it is, for a variety of reasons, essential to quantitatively understand and correct for the effects of dust on all photometric parameters derived from Sérsic fits, such as scale-lengths, effective radii, axis-ratios, surface-brightnesses, and integrated luminosities.
Thus, knowledge of the scale-length of disks of galaxies is essential for understanding how these systems were assembled over cosmic time. If the disks of spiral galaxies grow from the inside out, as predicted by semi-analytical hierarchical models for galaxy formation (e.g. Mo et al. 1998), one would predict the stellar populations to be younger and have a lower metallicity in the outer disk than in the inner disk, such that local universe galaxies would be intrinsically larger at the shorter wavelengths where light from the young stellar population is more prominent. For the same reason one would expect the intrinsic sizes of spiral disks to be larger at the current epoch than at higher redshift. Observationally, these predictions can be tested in two ways. One way is to compare the spatial distribution of the constituent stellar populations at different wavelengths for local Universe galaxies. Another way is to look for structural differences in galaxies observed at different cosmological epochs at the same rest-frame wavelength. Both methods require knowledge of the scale-length of disks, as measured at different wavelengths or at different redshifts (and therefore potentially for different dust opacities in disks). Since the effect of dust on the measured scale-lengths varies as a function of wavelength and disk opacity (e.g. Möllenhoff et al. 2006), it is imperative to quantify these effects on the derived scale-lengths. Accurate knowledge of the intrinsic scale-lengths of disks is also important for modelling radiation fields in galaxies based on self-consistent calculations of the transfer of radiation in galaxy disks, since any scaling of solutions will depend on the surface area of the disk, and therefore on the square of the scale-length.
Another photometric parameter derived from surface-brightness photometry is the axis-ratio of the disk, which traditionally has been used as a proxy for estimating disk inclinations (Hubble 1926). Here again it is important to quantify the effects of dust on the derived ratios, in particular in studies that require precise knowledge of inclination, as for example in radiative transfer modelling of spiral disks. In the future high-precision measurements of axis-ratios of galaxies will be the main tool at quantifying the weak-lensing effects in experiments aimed at understanding the nature of dark energy in the Universe (Peacock 2008; Jouvel et al. 2011; Cimatti & Scaramella 2012) or at constraining modified gravitational theories (Martinelli et al. 2011). In these studies even small systematic deviations introduced by dust could prove important when estimating weak-lensing effects.
Surface brightness measurements are an integral part of resolved studies of stellar populations, and quantitative corrections for dust are required for a proper analysis that removes degeneracies caused by dust. Studies of bulges in galaxies also require their effective radii and surface brightness distributions to be corrected for the effects of dust. This is because, although bulges themselves may be largely devoid of dust, they are seen through copious amounts of dust in the interstellar medium in the central regions of disks (Tuffs et al. 2004; Driver et al. 2007). Finally, measurements of scale-lengths and luminosities of narrow band images, like those of Balmer lines or of nebular lines, are also important for understanding the extent to which star-formation is distributed in galaxies. Again, these studies will rely on proper corrections for dust.
While a long list of reasons for the importance of proper dust corrections on the derived photometric parameters of galaxies can be still continued, we should mention one last topic, the scaling relations of galaxies (see Graham 2011, for a review on this topic). These relations are extremely important because they provide direct insights into the physical mechanisms of how galaxies assemble over cosmic time. Graham & Worley (2008) used the radiative transfer model of Popescu et al. (2000) and the predictions for dust corrections for brightness and scale-length of disks from Möllenhoff et al. (2006) to analyse the intrinsic (dust-corrected) luminosity-size and (surface-brightness)-size relations for disks and bulges. Recently, Grootes et al. (2013) found a strong relation between dust opacity and stellar surface mass density, a relation that was derived using dust corrections (Pastrav et al., in prep.) calculated from simulations produced with radiative transfer models (Popescu et al. 2011). The work of Graham & Worley (2008) and of Grootes et al. (2013) demonstrated the crucial importance of proper dust corrections for the analysis of scaling relations of galaxies.
At this point one could ask the rhetorical question of why we should not try to do a proper job from the beginning, and fit images of galaxies with realistic surface distributions that, from the outset, take into account the distortions caused by dust. The first answer to this question is that no analytic functions exist to describe the complex modifications to surface brightness distributions induced by dust. Nonetheless, such modified surface brightness distributions can be calculated with radiative transfer codes, and indeed such simulations already exist in the literature (e.g. Tuffs et al. 2004; Popescu et al. 2011) or could be potentially produced. The problem is, however, that instead of fitting one or two analytic functions with a few free parameters, as usually done by the observers, one would need to find the best-fit distribution from a large data set of simulations corresponding to all combinations of parameters describing dust effects. When knowing that even simple function fitting is computationally a difficult task when dealing with large samples of galaxies, it becomes immediately apparent that complex distribution-fitting, though desirable, is computationally impractical. The goal of this paper is therefore not to provide a better description of “nature”, but to use realistic descriptions to provide observers with a means of correcting their simplistic − but necessary − approach to the quantification of the appearance of galaxies.
The approach of providing corrections for dust is not new, and has already been used in the past to quantify these effects on the photometric parameters derived from surface brightness photometry, especially for disks (Byun et al. 1994; Evans et al. 1994; Cunow 2001; Möllenhoff et al. 2006; Gadotti et al. 2010). While there is overall consistency in the general trends found in these studies, the amplitude of the effects depend on the details of the geometrical model and/or of the optical properties of the grains used in the radiative transfer simulations, and, to some extent, on the fitting algorithm used to compare these simulations with the commonly used analytic functions. In some cases simplifying assumptions in the calculations of simulations can also account for differences in results (e.g. ignoring scattered light; Evans et al. 1994).
This paper follows-on from our previous study from Möllenhoff et al. (2006), where we quantified the effects of dust on the derived photometric parameters of disks only, seen at low- to- intermediate inclinations. In keeping with our previous approach we used simulations based on a model that can simultaneously account for both dust-attenuation in the ultraviolet (UV)/optical range and dust emission in the mid-infrared (MIR)/far-infrared (FIR)/submillimeter (sub-mm) range. Most of the simulations come from the library of Popescu et al. (2011), while additional simulations were created for the purpose of this paper. In particular, we quantify here the effects of dust on all morphological components of spirals, including bulges of different Sérsic indices and young stellar disks seen in the ultraviolet. We also consider corrections for photometric parameters on narrow-line imaging. Another goal of this paper is to quantify the effects of dust when fits are made with general Sérsic functions with variable Sérsic indices, even for exponential disks, since, as we show in this paper, dust can even alter the type of function (the Sérsic index) that provides the best fits to dust-attenuated images. In addition, we disentangle in this paper dust effects from projection effects of the combined radial and vertical distribution of stellar emissivity, and give detailed corrections for both effects, to be used individually or in conjuction, as may better serve the purpose of observers. We provide a comprehensive data set of corrections that cover the whole parameter space in dust opacity, inclination, and wavelength for all morphological components in spiral disks. All corrections are publically available at the CDS database. These corrections describe the effect of dust on each morphological component taken individually, as seen through a common distribution of dust. When more morphological components need to be decomposed, dust may introduce an extra effect on the decomposition itself. We do not attempt to describe this latter effect here. The effect of dust on bulge-disk decomposition has been previously discussed by Gadotti et al. (2010) and will be the object of a future study (Pastrav et al., in prep.).
This paper is organised as follows. In Sect. 2, we briefly describe the stellar emissivity and dust distributions used in the simulations. The method and general approach used to fit the simulated images and to derive the apparent photometric parameters is explained in Sect. 3, while the technical details of the whole fitting process are presented in Sect. 4. The projection effects are presented and discussed in Sect. 5, while in Sect. 6 we show and comment on the results for dust effects on the derived photometric parameters, for each morphological component. In Sect. 7, we discuss the effect of changing some of the geometrical parameters of our model on the dust and projection corrections. In Sect. 8 we compare the predictions of our model with recent observational data from the GAMA survey and in Sect. 9 we summarise the results and present our conclusions.
2. Simulated images
Since the philosophy of this paper is to provide corrections to observers, our approach is to follow as closely as possible the procedures and algorithms observers use to perform surface brightness photometry of real images of galaxies. It is just that instead of using observations of galaxies we use simulations for which the input parameters describing the distributions of stellar emissivity and dust are known. By comparing the input values of the parameters describing the simulations with the values of the measured parameters describing simplified distributions, as used by the observers, we can then quantify the degree to which observers underestimate or overestimate the intrinsic parameters of galaxies, under the assumption that the simulations are a good representation of observed galaxies.
Our simulations were produced as part of the large library of dust- and polycyclic aromatic hydrocarbon (PAH)-emission spectral energy distributions (SEDs) and corresponding dust attenuations presented in Popescu et al. (2011). The details of these calculations are described at length in Popescu et al. (2011). Here we only briefly mention their main characteristics. All simulations were calculated using a modified version of the ray-tracing radiative transfer code of Kylafis & Bahcall (1987), which includes a full treatment of anisotropic scattering, and the dust model from Weingartner & Draine (2001) and Draine & Li (2007), incorporating a mixture of silicates, graphites, and PAH molecules.
 |
Fig. 1 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from pure exponentials due to projection effects. Solid upper curves are for B-band dust-free images, dashed curves are for corresponding exponential fits, while absolute residuals (simulation-fit) are represented by solid lower curves. The fits were made by fixing the position of the intensity peak of the fitted image to the geometrical centre of the map, which, in this case, corresponds to the intensity peak in the simulated image. The cuts were taken parallel and perpendicular to the major-axis of the disk images, through their geometrical centres, at inclinations 1 − cos(i) = 0.3,0.7,0.9 (i = 46°,73°,84°). Lower row: corresponding relative residuals |
The simulations were produced separately for old stellar disks, bulges, and young stellar disks, all seen through a common distribution of dust. The geometrical model of Popescu et al. (2011) consists both of a large-scale distribution of diffuse dust and stars, as well as of a clumpy component physically associated with the star-forming complexes. For the purpose of this study only the large-scale distribution of diffuse dust is considered, as it is this that affects the large-scale distribution of UV/optical light determining the values of parameters typically used in fitting surface-brightness distributions (as listed in Sects. 3 and 4).
The intrinsic volume stellar distributions were described by exponential functions in both radial and vertical direction for the disks and by deprojected de Vaucouleurs functions for the bulges. The corresponding dust distributions were described by double (radial and vertical) exponential functions for the two dust disks of the model. The length parameters of the model describing the volume emissivity for stars and dust − scale-lengths, scale-heights and effective radii − are listed in Table 1 in Tuffs et al. (2004). The relevant information for this work is that the old stellar disk component has a scale-length that decreases with increasing optical/near-infrared (NIR) wavelength, as given in Table 2 in Tuffs et al. (2004), while the scale-height remains constant over this wavelength range. Similarly, the effective radius of the bulge does not vary with optical/NIR wavelength. The bulge is an oblate ellipsoid with an axis-ratio (thickness) of 0.6. To test the effects of changing the ellipticity of the bulge on the derived corrections, we also produced a few simulations for spherical bulges. The young stellar disk has a much smaller scale-height than the older stellar disk (by a factor of 4.6), while its scale-length is constant over wavelength and is equal to that of the old stellar disk in the B band. The scale-length of the dust disk associated with the old stellar population is larger (by a factor of 1.4) than that of the corresponding stellar disk, while its scale-height is smaller (by a factor of 1.5) than the scaleheight of the old stellar disk. In contrast, the young stellar disk spatially coincides with its associated dust disk (same scale-heights and -lengths). The physical interpretation of this model and the way some of the geometrical parameters have been empirically constrained from data are also described at length in Tuffs et al. (2004) and Popescu et al. (2011). A schematic representation of the geometrical model can be found in Fig. 1 in Popescu et al. (2011).
Apart from these already existing simulations additional ones have been produced for the purpose of this study. These are simulations of bulges corresponding to general Sérsic functions with various Sérsic indices. Since there is no exact analytical deprojection of Sérsic functions, the simulations were created with volume emissivities that, for the case of untruncated distributions, will reproduce Sérsic distributions of various Sérsic indices.
All simulated images have 34.54 pc/pixel. The disks were produced with a truncation radius at 5 exponential scale-lengths of the volume stellar emissivities. For bulges we produced two sets of simulations, with truncations at 3 and 10 effective radii. The truncation at 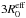 was chosen because it avoids the problem of having a disk-bulge system dominated by the bulge light at high galactocentric radii for large values of the Sérsic index. The truncation at
was chosen because it avoids the problem of having a disk-bulge system dominated by the bulge light at high galactocentric radii for large values of the Sérsic index. The truncation at 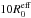 is essentially representative of a bulge without any truncation, since at this galactocentric radius almost all the light inside the profile has been accounted for.
is essentially representative of a bulge without any truncation, since at this galactocentric radius almost all the light inside the profile has been accounted for.
Here we note that the simulations for old stellar disks presented in this paper slightly differ from the disk simulations from our previous study in Möllenhoff et al. (2006). This is due to the updates in the dust model used in Popescu et al. (2011), which included the incorporation of PAH molecules. Thus, though both the old dust model (from Popescu et al. 2000, as used in the simulations from Möllenhoff et al. 2006) and the new one can simultaneously account for the extinction and emission properties of the diffuse dust in the Milky Way, the relative contribution of scattering and absorption to the total extinction differs between the two models. This produces some small differences in the simulations.
The simulations used in this paper span the whole parameter space of the model of Popescu et al. (2011). Thus, simulations were produced for seven values of central face-on B-band optical depth  , 21 values for the disk inclination, five standard optical/NIR bands B, V, I, J, K (for disk, thin disk, and bulge) and nine far-UV (FUV) to near-UV (NUV) wavebands (for the thin disk, corresponding to wavelengths of 912 Å, 1350 Å, 1500 Å, 1650 Å, 2000 Å, 2200 Å, 2500 Å, 2800 Å, and 3650 Å). The values of the dust opacity cover a wide range, from almost dust-free to extremely optically thick cases,
, 21 values for the disk inclination, five standard optical/NIR bands B, V, I, J, K (for disk, thin disk, and bulge) and nine far-UV (FUV) to near-UV (NUV) wavebands (for the thin disk, corresponding to wavelengths of 912 Å, 1350 Å, 1500 Å, 1650 Å, 2000 Å, 2200 Å, 2500 Å, 2800 Å, and 3650 Å). The values of the dust opacity cover a wide range, from almost dust-free to extremely optically thick cases, 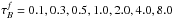 . The inclination values were chosen in such a way that △ cos(i) = 0.05, with 1 − cos(i) ∈ [0,1], resulting in 21 values. For each case corresponding dust-free simulations were produced to provide the reference point for quantifying the effects of dust and also to assess projection effects of the stellar distributions (see Sect. 3).
. The inclination values were chosen in such a way that △ cos(i) = 0.05, with 1 − cos(i) ∈ [0,1], resulting in 21 values. For each case corresponding dust-free simulations were produced to provide the reference point for quantifying the effects of dust and also to assess projection effects of the stellar distributions (see Sect. 3).
3. Method and general approach
Following the approach taken by observers on real images, all simulated images were fitted with infinitely thin disks described by exponential (Eq. (1)), Sérsic (Eq. (2)), or de Vaucouleurs (Eq. (3)) distributions: ![\begin{eqnarray} \label{eq:exp} \Sigma(r)&=&\Sigma_{0}~\exp\left(-\frac{r}{r_{\rm s}}\right) \\[1mm]\label{eq:sersic} \Sigma(r)&=&\Sigma_{0}~\exp\left[-\kappa_{n} \left(\frac{r}{r_{\rm e}}\right)^{1/n}\right] \\[1mm]\label{eq:devauc} \Sigma(r)&=&\Sigma_{0}~\exp\left[-\kappa_{4} \left(\frac{r}{r_{\rm e}}\right)^{1/4}\right] , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq17.png) where Σ0 is the central surface brightness of the infinitely thin disk, rs and re is the scale-length and effective radius1 of the infinitely thin disk respectively, n is the Sérsic index, while κn is a variable, coupled with n (e.g. Ciotti & Bertin 1999; Graham & Driver 2005).
where Σ0 is the central surface brightness of the infinitely thin disk, rs and re is the scale-length and effective radius1 of the infinitely thin disk respectively, n is the Sérsic index, while κn is a variable, coupled with n (e.g. Ciotti & Bertin 1999; Graham & Driver 2005).
From the formulation of the fitting functions it is clear that, even in the absence of dust, these simple distributions would differ from those of real galaxies because they describe infinitely thin disks, while disks and bulges have a thickness. This means that in real life there would be an additional vertical distribution of stars superimposed on the corresponding radial distribution. This would produce isophotal shapes which are different from those predicted by an infinitely thin disk. We call these effects projection effects.
The approach adopted in this paper is to separate projection effects from dust effects. Therefore, we first derive the projection effects by calculating the change between the intrinsic parameters of the volume stellar emissivity and those measured on dust-free images. Subsequently, we derive the dust effects by calculating the change between the parameters measured on dust-free and dusty images, respectively, for the same inclination and wavelength. In this way the total change in parameter values between those measured on dusty images and the corresponding parameters of the volume stellar emissivity can be written as a chain of corrections. In the case that the parameter is either the exponential scale-length R or the Sérsic effective radius Reff of the surface-brightness distribution of the measured object, the total correction can be written as 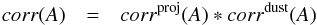 (4)with
(4)with  where A is either R or Reff, A0 is the corresponding parameter describing the volume stellar emissivity (which we call “intrinsic parameter of the volume stellar emissivity”), Ai is the corresponding fitted parameter of the dust-free simulated image (which we simply call “intrinsic” parameter), and Aapp is the fitted parameter of the dust-attenuated simulated image (which we call “apparent” parameter).
where A is either R or Reff, A0 is the corresponding parameter describing the volume stellar emissivity (which we call “intrinsic parameter of the volume stellar emissivity”), Ai is the corresponding fitted parameter of the dust-free simulated image (which we simply call “intrinsic” parameter), and Aapp is the fitted parameter of the dust-attenuated simulated image (which we call “apparent” parameter).
Equations (4)–(6) also apply to the fitted axis-ratio Q, except that the meaning of the quantities defining corrproj in Eq. (5) is different, since, as we will see later, it only makes sense to express corrections with respect to an infinitely thin disk case.
In the case that the fitted parameter is the Sérsic index nsers, the corrections are additive, since they are expressed as differences instead of ratios. The corresponding formulas for them become: 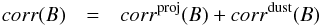 (7)with
(7)with ![\begin{eqnarray} \label{eq:corr0B} corr^{ \rm proj}(B) & = & B_{\rm i} - B_0 \\[2mm] \label{eq:corr1B} corr^{\rm dust}(B) & = & B_{\rm app} - B_{\rm i} . \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq35.png) Equations (7)–(9) also apply to the fitted parameter surface-brightness, except that the term corrproj in Eq. (8) is again not taken with respect to the volume stellar emissivity. This is because surface-brightness is by definition a projected quantity (describing a surface). We define this correction with respect to the simulated dust-free image.
Equations (7)–(9) also apply to the fitted parameter surface-brightness, except that the term corrproj in Eq. (8) is again not taken with respect to the volume stellar emissivity. This is because surface-brightness is by definition a projected quantity (describing a surface). We define this correction with respect to the simulated dust-free image.
One advantage of separating projection from dust effects is that this provides observers with more flexibility in using these corrections, according to different needs. In some cases observers may be only interested in the pure dust effects (corrdust), in other cases the interest may be in deriving the intrinsic parameters of the volume stellar emissivity (e.g. corrdust ∗ corrproj).
Another advantage of this approach is that it provides a more robust quantification of the dust effects. As we will show in this paper, the term related to projection effects corrproj is affected by variations in the geometrical parameters of the volume stellar emissivity, including the truncation radius, while the term related to dust effects corrdust is relatively insensitive to such factors. This of course is true as long as both terms are derived from simulations produced with the same geometrical parameters: e.g. truncation radius.
Finally, the approach of chain corrections allows further corrections to be added to the formula if more complex cases are to be considered. The best example of the generalisation of this formula is for multicomponent fits. Thus, when bulge-disk decomposition is to be performed, an additional correction would need to be calculated. This is the correction between the fitted parameters obtained from bulge-disk decomposition in the presence of dust, and the fitted parameters of the same bulge and disk, if they were to be observed alone through the same distribution of dust. If we were to use the example from Eqs. (4) and (7), the generalisation of these formulae for the case of bulge/disk decomposition would be: ![\begin{eqnarray} \label{eq:corr2A} corr(A) & = & corr^{ \rm proj}(A) * corr^{\rm dust}(A) * corr^{B/D}(A) \\[2mm] \label{eq:corr2B} corr(B) & = & corr^{ \rm proj}(B) + corr^{\rm dust}(B) + corr^{B/D}(B) , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq38.png) where the additional terms are
where the additional terms are ![\begin{eqnarray} \label{eq:corr3A} corr^{B/D}(A) & = & \frac{A^{B/D}_{\rm app}}{A_{\rm app}} \\[2mm] \label{eq:corr3B} corr^{B/D}(B) & = & B^{B/D}_{\rm app} - B_{\rm app} . \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq39.png) The additional term corrB/D will be quantified in a separate paper (Pastrav et al., in prep.) for all photometric parameters, and will be related to the effects described here through equations like Eqs. (10) and (11).
The additional term corrB/D will be quantified in a separate paper (Pastrav et al., in prep.) for all photometric parameters, and will be related to the effects described here through equations like Eqs. (10) and (11).
All corrections are presented in terms of polynomial fits. Most of the fits are of the form 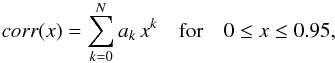 (14)where x = 1 − cos(i) and N has a maximum value of 5. In the case of the axis-ratio of disks Q, a combination of a polynomial and a constant was necessary, according to different ranges in inclination (see Sects. 5.1 and 6.1).
(14)where x = 1 − cos(i) and N has a maximum value of 5. In the case of the axis-ratio of disks Q, a combination of a polynomial and a constant was necessary, according to different ranges in inclination (see Sects. 5.1 and 6.1).
4. Fitting procedure
For the fitting routine we used the commonly used GALFIT (version 3.0.2) data analysis algorithm (Peng et al. 2002, 2010). GALFIT uses a non-linear least-squares fitting based on the Levenberg-Marquardt algorithm. Through this, the goodness of the fit is checked by computing the χ2 between the simulated image (for observations, the real galaxy image) and the model image (created by GALFIT to fit the galaxy image). This is an iterative process, and the free parameters corresponding to each component are adjusted after each interation to minimimise the normalised (reduced) value of χ2 (χ2/Nd.o.f., with Nd.o.f. = number of pixels − number of free parameters, the number of degrees of freedom).
Since in our simulated images we do not have noise, we used as input to GALFIT a “sigma” image (error/weight image) which is constant for all pixels, except for points outside the physical extent of our simulated images. The latter points were set to a very high number, to act as a mask. This was necessary since our simulations are truncated in their volume stellar and dust emissivities while the fitting functions extend to infinity. We did not try to use the truncation functions from GALFIT, as this would only work properly for truncations made on surface stellar brightnesses. The simulated images have no background (by construction, unlike real images); this is why the sky value was set to zero during the fitting procedure for all morphological components.
To fit the simulated images we used the exponential (“expdisk”), the Sérsic (“sersic”) and the de Vaucouleurs (“devauc”) functions available in GALFIT. As explained in Sect. 3, these functions represent the distribution of an infinitely thin disk, and their mathematical description is given by Eqs. (1)–(3)
Since our simulations were produced with high resolution and were not convolved with any instrumental point spread function (PSF), there was no need to use the PSF component available in GALFIT during the fitting procedure. However, for lower resolution observations, where deconvolution from PSF is essential, an extra correction needs to be added to the corrections presented here. This is because the deconvolution itself is affected by dust. This effect will be analysed in future papers. Here we only note that such a correction, when available, could simply be added in our formulation of chain corrections. Equations (4) and (7) would then become ![\begin{eqnarray} \label{eq:corr4A} corr(A) & = & corr^{ \rm proj}(A) * corr^{\rm dust}(A) * corr^{\rm PSF}(A) \\[2mm] corr(B) & = & corr^{ \rm proj}(B) + corr^{\rm dust}(B) + corr^{\rm PSF}(B) , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq47.png) where the additional terms are
where the additional terms are
![\begin{eqnarray} \label{eq:corr5A} corr^{\rm PSF}(A) & = & \frac{A^{\rm PSF}_{\rm app}}{A_{\rm app}} \\[2mm] corr^{\rm PSF}(B) & = & B^{\rm PSF}_{\rm app} - B_{\rm app} . \end{eqnarray}](/articles/aa/full_html/2013/05/aa20962-12/aa20962-12-eq48.png) The terms
The terms 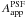 or
or 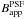 represent the measured values of the photometric parameters A or B, which would be derived from fits made on dust-attenuated simulations convolved with PSFs. In this case the corrections will be a function of resolution.
represent the measured values of the photometric parameters A or B, which would be derived from fits made on dust-attenuated simulations convolved with PSFs. In this case the corrections will be a function of resolution.
 |
Fig. 2 Projection effects corrproj on the derived B-band photometric parameters of disks fitted with exponential functions (black) and with Sérsic functions (red): scale-lengths, axis-ratios, and central surface brightnesses. The symbols represent the measurements while the solid lines are polynomial fits to the measurements.The plots represent the inclination dependence of left − the ratio between the intrinsic scale-lengths, Ri, and the intrinsic (radial) scale-length of the volume stellar emissivity, R0; middle − the ratio between the intrinsic axis-ratio, Qi, and the axis-ratio of an infinitely thin disk, Q0; with the dashed line we overplotted the analytic formula from Driver et al. (2007), which is a modification of the Hubble formula from Hubble (1926), to take into acount the thickness of the disk; right − the ratio between the central surface brightness of the fitted images and of the coresponding simulated images, ΔSB0, expressed in magnitudes. In the case of a Sérsic fit, Ri (left panel) is the equivalent intrinsic scale-length, calculated from the derived intrinsic Sérsic effective radius, |
Coming back to our fully sampled simulations, for the measurements presented in this paper the free parameters of the fit are: the X and Y coordinates of the centre of the galaxy in pixels, the integrated magnitude of the image, the scale-length R (for exponential)/ effective radius Reff (for Sérsic and de Vaucouleurs functions), axis-ratios Q, Sérsic index nsers (for Sérsic functions) and the position angle. The axis-ratio Q is defined as the ratio between the semi-minor and semi-major axis of the projected image. The position angle is the angle between the semi-major axis and the Y axis which increases anti-clockwise. For all our simulated images, the position angle was fixed to − 90° (semi-major axis perpendicular to the Y axis).
5. Projection effects
The main goal of this work, that of quantifying the changes due to dust on the derived photometric parameters of the main morphological components of spiral galaxies, is achievable due to the fact that, as mentioned before, the intrinsic parameters of the volume stellar emissivity are known, since they are input to the simulations. However, even in the absence of dust, the derived photometric parameters of the images measured from fitting infinitely thin disk distributions would differ from the intrinsic parameters of the volume stellar emissivity due to the thickness of real galaxies, which we call projection effects. Quantifying projection effects allows us to derive the change between the intrinsic parameters of the volume stellar emissivity and those measured on dust-free images, which, subsequently, can be used to measure the changes between the parameters of the dust-free and dusty images, respectively.
5.1. The disk
Disks are fairly thin objects; their vertical extent is significantly smaller than their radial extent (by a factor of about 10 in our model; Tuffs et al. 2004). This means that projection effects will only start to be visible close to edge-on orientations, when the vertical distribution of stars becomes apparent.
5.1.1. Exponential fits to the disk
To quantify the projection effects we first fitted the dust-free simulated images with an infinitely thin exponential disk, as available in GALFIT. To observe the accuracy of the fits, we analysed both the profiles and the relative residual maps, between the simulated and the fitted images. In the upper and middle rows of Fig. 1, we present the major- and minor-axis profiles for the B-band images for three orientations of the disk. At lower inclinations the exponential fits are a good representation of the profiles, while at higher inclinations deviations from a pure exponential start to appear due to the above-mentioned projection effects. In particular, these deviations can be seen in the central part of the disks − the flattening of the simulated profiles. At higher inclinations, projection effects produce deviations from a pure exponential also at intermediate radii, with stronger effects in the minor-axis direction. For example, at an inclination of 84°, Fig. 1 (lower row, right panel) shows a deviation of up to 15% in the minor-axis direction (the yellow wings; see also the corresponding double peak in the minor-axis profile residuals in Fig. 1, second row). The black area that surrounds the disk, corresponding to very large relative residuals, appears because the simulated images are truncated, while the fitted images extend to infinity (as explained in Sect. 4, we did not attempt to use the truncation features of GALFIT).
To understand the cause of all these deviations we need to remember that what we try to do is to fit the projection of two exponential distributions (radial and vertical) with one single exponential, which will inevitably result in an imperfect fit. As long as the vertical extent of the disk will project within the predicted elliptical shape of the infinitely thin disk, meaning as long as the axis-ratios of the measured isophotes correspond to the predicted cos(i) inclination of the infinitely thin disk, the projected stellar distribution will be dominated by the radial exponential distribution of the disk, and the fit will accurately reproduce this radial distribution. At higher inclinations the vertical extent of the disk will increase the measured axis-ratio of the projected elliptical isophotes (from the predicted cos(i) ratio). This means that the measured axis-ratio will not be a good representation of the inclination of the disk. This also means that the fit with an infinitely thin exponential disk will try to account for the extra thickness of the measured elliptical isophotes by trying to force a solution with a larger scale-length. This will produce the deviations from a pure exponential seen in the plots and will systematically overestimate the radial scale-length of the disk and underestimate the inclination of the disk on the basis of an infinitely thin disk approximation only.
 |
Fig. 3 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from Sérsic functions due to projection effects. Solid upper curves are for B-band dust-free images, dashed curves are for corresponding variable-index Sérsic fits, while absolute residuals (simulation − fit) are represented by solid lower curves. The fits were made by fixing the position of the intensity peak of the fitted image to the geometrical centre of the map. The cuts were taken parallel and perpendicular to the major-axis of the dust-free disk images, through their geometrical centres, at inclinations 1 − cos(i) = 0.3,0.7,0.9 (i = 46°,73°,84°). Lower row: corresponding relative residuals |
The results on this analysis allows us to derive projection effects corrproj on stellar disks using Eq. (5) for the exponential scale-length and axis-ratio and Eq. (8) for the central surface brightness. The inclination dependence of these corrections are shown in Fig. 2. As explained above, the disk scale-length is relatively insensitive to projection effects at low-to-intermediate inclinations (left panel, Fig. 2), while for close to edge-on orientations it increases with inclination with respect to the radial scale-length of the volume stellar emissivity. We note here that the amplitude of these results slightly varies with the wavelength at which the measurements are taken. This happens because the simulations originate from a volume stellar emissivity whose radial scale-length varies with wavelength (for a fixed scale-height), as prescribed in the model of Popescu et al. (2011). Here we only show the results for the B-band, as the overall trend in the variation of the derived scale-lengths with inclination is the same for all wavebands. The results for all wavebands are given in the form of polynomial fits (Eq. (14)) and are listed in Table A.1.
The deviation of the derived disk axis-ratios from the corresponding axis-ratio of an infinitely thin exponential disk (corrproj(Q)) is plotted in the middle panel of Fig. 2 as a function of inclination. As expected, at low inclination the thin disk approximation works very well, while at high inclination the vertical distribution of stars introduces an extra thickness, which cannot be taken into account by the infinitely thin approximation. To account for the steep increase in the measured axis-ratio with respect to that of an infinitely thin disk, at high inclination, we had to fit the measurements with a combination of a fifth order polynomial and a constant, of the form: 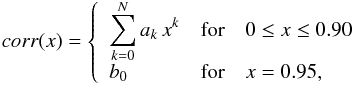 (19)where x = 1 − cos(i). The coefficients of these polynomial fits are listed in Table A.2 for the B, V, I, J, K bands.
(19)where x = 1 − cos(i). The coefficients of these polynomial fits are listed in Table A.2 for the B, V, I, J, K bands.
Here we also checked that the analytical formula used in Driver et al. (2007)2 to account for the finite thickness of the disk is a good representation of the dependence of the measured axis-ratios on inclination (see overplotted dashed line in Fig. 2, middle).
Finally, we looked at the distortions introduced by the projection effects on the derived central surface brightness ratios (corrproj(SB)). Here we considered two measurements. The first one is the measurement for the central pixel, where we calculated the ratio between the central surface brightness for the fitted dust-free images of the old stellar disk and the central surface brightness for the corresponding simulated images, ΔSB0 (Fig. 2, right). The ratios are expressed in magnitudes. A second measurement is to consider an average of the surface brightness over an elliptical aperture. This second measurement is necessary as a reference for measurements of surface brightness in simulations that include dust. As we will see in Sect. 6, dust introduces asymmetries in the surface-brightness distribution, therefore it only make sense to take an average measurement in the central region. Furthermore, in real observations central regions may be affected by resolution effects, which result in essentially an averaging of the signal. For this reason we define the average central surface brightness ratio as ΔSB0 = −2.5log (Fi/Fs): the ratio of the average central surface brightness (Fi) of the fitted dust-free disk images, and the average central surface brightness of the simulated dust-free disk images (Fs). Both Fi and Fs were calculated as an average over an elliptical aperture centred on the position of the geometrical centre of the simulated image, with a semi-major axis of Ri/10 and an axis-ratio of Qi. In this case the geometrical centre coincides with the coordinates of the intensity peak of the fitted image and of the simulated image.
As expected for the dust-free case, the trends in the corrections for the central pixel ΔSB are the same as for the average ΔSB. These corrections are tabulated in Table A.1 in the form of polynomial fits (Eq. (14)). Overall, the distortions in the surface brightness due to projection effects are negligible at face-on orientation and increase with inclination, producing up to 0.5 mag. difference for an edge-on galaxy. As already noted from Fig. 1, the derived surface brightness from the exponential fit is always brighter than the corresponding one in the simulated images due to the flattening of their brightnesses in the central regions.
5.1.2. Sérsic fits to the disk
To quantify the deviation of the simulated images from pure exponentials we also fitted these images with a variable-index general Sérsic function to see if a better fit to the images can be obtained. We followed the same approach as in the previous case, plotting major- and minor-axis profiles (Fig. 3, upper and middle rows) and generating relative residual maps (lower row, same figure) for various inclinations.
Overall the variable-index Sérsic functions provide better fits to the simulated images at higher inclinations than pure exponentials. Thus, the reduced-χ2 shows a 63% decrease at an inclination of 73° and a 73% decrease at an inclination of 84°. This is a significant improvement in the goodness-of-fit for the inclinations where projection effects play a role. In particular, one can see from the profiles in Fig. 3 that GALFIT tries to mimick the departure from exponentiality in the centre of the disks by fitting the simulated images with a Sérsic index lower than 1. This can also be seen from Fig. 4, where we plotted the inclination dependence of the derived Sérsic index of the fitted disk images. At high inclinations, the best fits correspond to output values for the Sérsic indices as low as 0.8.
As expected, at lower inclinations Sérsic fits recover the results from pure exponentials, since no projection effects are manifested by face-on disks. Thus, the reduced-χ2 is similar for exponential and Sérsic fits. For example, the reduced-χ2 shows a 0.0004% decrease at an inclination of 46°. Similarly, the fitted Sérsic index is 1 (exponential) for face-on disks.
 |
Fig. 4 Inclination dependence of the Sérsic index |
We fitted the variation of 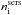 index with inclination using a fourth order polynomial (Eq. (14)). The fit for the B band is shown by the solid line in Fig. 4, while the coefficients of the fits in all wavebands are listed in Table A.3. By applying Eq. (8) for the specific case of the Sérsic index, we define the departure from exponentiality due to projection effects,
index with inclination using a fourth order polynomial (Eq. (14)). The fit for the B band is shown by the solid line in Fig. 4, while the coefficients of the fits in all wavebands are listed in Table A.3. By applying Eq. (8) for the specific case of the Sérsic index, we define the departure from exponentiality due to projection effects, 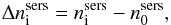 (20)where
(20)where 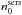 is the Sérsic index of the volume stellar emissivity (for disks
is the Sérsic index of the volume stellar emissivity (for disks 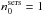 ; exponential). From the definition, it follows that
; exponential). From the definition, it follows that 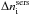 varies with inclination from 0 to up to −0.2. Though Sérsic functions provide better fits to the disk images, in particular in the centre and at intermediate distances from the centre, they are poorer fits to the outer disks, where relative residuals can be high (e.g. 35−40% at 84°; see Fig. 3). The reason for this is that the surface brightness distribution in the outer parts is still decreasing according to an exponential distribution, while the fitted distribution − described by a Sérsic index lower than 1.0 (mainly determined by the brightest pixels in the centre) is falling faster at large radii, thus underpredicting the luminosity profiles in the outer parts. However, outer disks of galaxies are in real life subject to additional truncation/anti-truncation effects, and may in any case require additional components to be fitted. We therefore conclude that variable index Sérsic functions are better representations of the disk images corresponding to pure exponential distributions of the volume stellar emissivity.
varies with inclination from 0 to up to −0.2. Though Sérsic functions provide better fits to the disk images, in particular in the centre and at intermediate distances from the centre, they are poorer fits to the outer disks, where relative residuals can be high (e.g. 35−40% at 84°; see Fig. 3). The reason for this is that the surface brightness distribution in the outer parts is still decreasing according to an exponential distribution, while the fitted distribution − described by a Sérsic index lower than 1.0 (mainly determined by the brightest pixels in the centre) is falling faster at large radii, thus underpredicting the luminosity profiles in the outer parts. However, outer disks of galaxies are in real life subject to additional truncation/anti-truncation effects, and may in any case require additional components to be fitted. We therefore conclude that variable index Sérsic functions are better representations of the disk images corresponding to pure exponential distributions of the volume stellar emissivity.
The resulting variation of the derived Sérsic effective radius 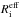 is compared with the corresponding derived exponential scale-length (from an exponential fit) by using the linear transformation
is compared with the corresponding derived exponential scale-length (from an exponential fit) by using the linear transformation 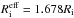 (which is exact only for nsers = 1.0) and by overplotting the variation of the equivalent intrinsic scale-length Ri in Fig. 2, with a red line (left panel). One can see an opposite trend in the two variations. At face-on inclinations the exponential and the Sérsic fit are identical (nsers = 1.0). As the inclination increases, the equivalent scale-length of the Sérsic fit decreases with respect to the radial scale-length of the volume stellar emissivity (while the intrinsic exponential scale-length increases). This is due to the decrease in the fitted Sérsic index with increasing inclination, resulting in an equivalent scale-length that continuously decreases from the
(which is exact only for nsers = 1.0) and by overplotting the variation of the equivalent intrinsic scale-length Ri in Fig. 2, with a red line (left panel). One can see an opposite trend in the two variations. At face-on inclinations the exponential and the Sérsic fit are identical (nsers = 1.0). As the inclination increases, the equivalent scale-length of the Sérsic fit decreases with respect to the radial scale-length of the volume stellar emissivity (while the intrinsic exponential scale-length increases). This is due to the decrease in the fitted Sérsic index with increasing inclination, resulting in an equivalent scale-length that continuously decreases from the 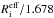 transformation. The results of the polynomial fits (Eq. (14)) to the corrproj(Reff) for all wavebands are listed in Table A.3.
transformation. The results of the polynomial fits (Eq. (14)) to the corrproj(Reff) for all wavebands are listed in Table A.3.
Though the derived effective radius shows a different behaviour with inclination with respect to the exponential fit, the variation in axis-ratios seems to be insensitive to whether the fit is made with an exponential or with a variable-index Sérsic function (see Fig. 2, middle panel). In other words, the axis-ratio seems to be a more robust quantity against projection effects. Irrespectively of the fitting function, the variation with inclination of Qi only shows the departure from an infinitively thin disk variation because of the vertical distribution of stars. The corrproj(Q) for the Sérsic fits are therefore the same as for the exponential fits. The coefficients of the polynomial fits (Eq. (19)) for all wavebands can be found in Table A.2.
Finally, the departure of the fitted central surface brightness from that of the simulated images is minimal compared with the exponential fit case (see right hand panel in Fig. 2), another proof that Sérsic fits are better representations of images corresponding to exponential distributions of volume stellar emissivity, especially in the central regions of the disks. The slight overestimation of the central surface brightnesses in the fit as compared to that of the simulations for the high inclinations can also be seen in the radial profiles from Fig. 3. The overall departure of the fit from the simulation is ±0.1 mag, as compared to the 0.5 mag departure in the exponential fit. The coefficients of the polynomial fits (Eq. (14)) to corrproj(ΔSB) for all wavebands are listed in Table A.3.
5.2. The thin disk
For the thin disk (young stellar disk), the projection effects are insignificant even at very high inclinations. This is due to the different geometry of the young stellar disk where the ratio between the scale-height and the scale-length of the thin disk is very small (63 in our model; Tuffs et al. 2004). In other words, the approximation of the infinite thin disk is a very good one for this stellar component.
 |
Fig. 5 Derived Sérsic index |
5.3. The bulge
The problem of projection effects for bulges is very different from that encountered in disks. The difference does not have an intrinsic, physical cause, but originates from the different way astrophysicists use to characterise the distribution of stellar emissivity in these two types of objects, and therefore in the two different ways our simulations are built. In disks the exact mathematical formulation of the stellar emissivity happens at the level of the volume emisivity, where we expect disks to be described by a double exponential, one for the radial distribution and one for the vertical distribution. When projecting this double exponential and fitting the resulting image with a single exponential distribution corresponding to an infinitely thin disk, we are obviously unable to exactly fit the surface brightness distribution. So this will result in a projection effect. In bulges the situation is reversed. The exact mathematical formulation is for the surface brightness distribution of the images, as given by the Sérsic functions. By construction, the simulations were produced for a volume emissivity that, when projected, at any inclination will reproduce the Sérsic function for a bulge that extends to infinity. So by construction, the simulations incorporate the projection effects. The caveat is, however, that this is only true if bulges were to extend to infinity. Since in real life truncations must occur at some distance from the centre (whether this is at a shorter or a longer distance), distortions from the expected Sérsic distributions will also occur. Accordingly, we expect projection effects in our simulations solely because of the missing light beyond the truncation radius. This would be a constant with inclination, because the missing light will always be the same at any given inclination. It will, however, strongly depend on the truncation radius, and on the type of Sérsic distribution considered (the Sérsic index).
Since real-life bulges can be described by Sérsic functions characterized by different Sérsic indices, 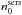 , and, since real bulges could be either truncated or extend to high galactocentric radii (see Maltby et al. 2012), we need to consider all these extra dimensions to the problem. Therefore, we made simulations of bulges whose volume stellar emissivities correspond to (deprojected) Sérsic functions with four different values of the Sérsic index
, and, since real bulges could be either truncated or extend to high galactocentric radii (see Maltby et al. 2012), we need to consider all these extra dimensions to the problem. Therefore, we made simulations of bulges whose volume stellar emissivities correspond to (deprojected) Sérsic functions with four different values of the Sérsic index 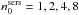 . For each of these the bulges were truncated in the first case at three effective radii and in the second one at ten effective radii. As mentioned in Sect. 2, the truncation at
. For each of these the bulges were truncated in the first case at three effective radii and in the second one at ten effective radii. As mentioned in Sect. 2, the truncation at 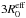 was chosen as this avoids the problem of having a disk-bulge system dominated by the bulge light at high galactocentric radii for large values of the Sérsic index. The truncation at
was chosen as this avoids the problem of having a disk-bulge system dominated by the bulge light at high galactocentric radii for large values of the Sérsic index. The truncation at 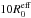 is essentially representative of a bulge without any truncation, since at this galactocentric radius almost all light inside the profile has been accounted for.
is essentially representative of a bulge without any truncation, since at this galactocentric radius almost all light inside the profile has been accounted for.
The results for the projection effects of bulges are calculated using Eqs. (8) and (5) for the derived Sérsic indices and corresponding effective radii for different types of volume stellar emissivities (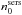 ) and different truncations.
) and different truncations.
In Fig. 5 we show that, as expected, the derived Sérsic index 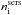 does not depend on inclination. This is true irrespectively of the
does not depend on inclination. This is true irrespectively of the 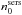 index of the corresponding volume stellar emissivity and of the truncation radius. For high values of the
index of the corresponding volume stellar emissivity and of the truncation radius. For high values of the 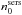 index (
index (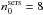 ) the constancy of
) the constancy of 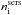 with inclination is strongly affected by noise in the measurements. This is not caused by any physical effect, but instead is produced by insufficient spatial resolution in the radiative transfer calculations in the inner parts of these bulges. Our simulations were optimised to properly sample the volume emissivity for bulges up to
with inclination is strongly affected by noise in the measurements. This is not caused by any physical effect, but instead is produced by insufficient spatial resolution in the radiative transfer calculations in the inner parts of these bulges. Our simulations were optimised to properly sample the volume emissivity for bulges up to 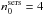 . For higher values of
. For higher values of 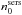 , the steep rise in volume emissivity profiles near the centre would require even finer sampling, which would make these calculations prohibitively time consuming. We believe that for the purpose of this paper the benefit of increasing the resolution in these simulations is limited, and we instead opted to fit all measurements with a first order polynomial function (Eq. (14)) with a slope equal to zero. The results of the fits are overplotted in Fig. 5 and are listed in Table A.4.
, the steep rise in volume emissivity profiles near the centre would require even finer sampling, which would make these calculations prohibitively time consuming. We believe that for the purpose of this paper the benefit of increasing the resolution in these simulations is limited, and we instead opted to fit all measurements with a first order polynomial function (Eq. (14)) with a slope equal to zero. The results of the fits are overplotted in Fig. 5 and are listed in Table A.4.
From these results one can also see that the derived Sérsic index is always smaller than the Sérsic index corresponding to the volume stellar emissivity. This is because of the missing light outside the truncation radius. The difference between the Sérsic indices of the deprojected and projected distribution, 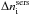 increases (in absolute value) with increasing
increases (in absolute value) with increasing 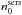 , as seen in Fig. 5, due to the stronger variation in the light intensity between the inner and outer radii for large values of
, as seen in Fig. 5, due to the stronger variation in the light intensity between the inner and outer radii for large values of 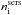 (more peaky and steep profiles).
(more peaky and steep profiles).
In the case of bulges truncated at 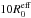 , the fitted values of
, the fitted values of 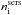 are closer to those of
are closer to those of 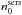 , since in this case bulges are closer to a bulge whose emissivity extends to infinity (where, as explained before, by construction
, since in this case bulges are closer to a bulge whose emissivity extends to infinity (where, as explained before, by construction 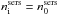 ).
).
The constancy of projection effects with inclination is also visible in Fig. 6, for corrproj(Reff). As for the case of 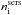 , we fitted the derived ratios with a constant, as listed in Table A.4. Fig. 6 also shows that the derived effective radius of truncated bulges decreases with increasing
, we fitted the derived ratios with a constant, as listed in Table A.4. Fig. 6 also shows that the derived effective radius of truncated bulges decreases with increasing 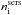 . As expected, the decrease is minimal for bulges truncated at
. As expected, the decrease is minimal for bulges truncated at 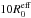 . Another aspect that can be noticed from this figure is that for any
. Another aspect that can be noticed from this figure is that for any 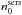 the effective radii for the bulges truncated at
the effective radii for the bulges truncated at 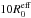 are always higher than those for bulges truncated at
are always higher than those for bulges truncated at 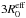 . This happens because in the former case more stellar emissivity will contribute to the corresponding Sérsic distribution than in the latter. Therefore, half of the total stellar emissivity will be enclosed in a larger region for bulges truncated at
. This happens because in the former case more stellar emissivity will contribute to the corresponding Sérsic distribution than in the latter. Therefore, half of the total stellar emissivity will be enclosed in a larger region for bulges truncated at 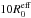 , with a corresponding higher effective radius.
, with a corresponding higher effective radius.
Since in many cases bulges are fitted by observers with de Vaucouleurs functions, we also consider this case, but only for de Vaucouleurs bulges (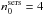 ) truncated at 3Reff. The results of the polynomial fits to the
) truncated at 3Reff. The results of the polynomial fits to the 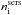 are given in Table A.5 and are very similar to those obtained using Sérsic functions (for the same
are given in Table A.5 and are very similar to those obtained using Sérsic functions (for the same 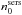 and truncation radius).
and truncation radius).
In the following section, when we quantify dust effects for bulges with different Sérsic functions and/or truncation, we apply Eqs. (6) and (9) as well as the chain corrections from Eqs. (4) and (7), by using dust-free and dusty simulations with a common 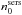 and truncation radius.
and truncation radius.
 |
Fig. 6 Projection effects corrproj on the derived effective radius of the bulge. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the ratio between the intrinsic Sérsic effective radii, |
6. Dust effects
The quantification of projection effects corrproj allows the subsequent derivation of dust effects corrdust. To do this, the simulated dusty images of disks and bulges were fitted, in order to derive the apparent (dust-affected) values for the photometric parameters. corrdust were then derived using Eqs. (6) and (9), by relating these apparent values of the photometric parameters with the corresponding intrinsic ones, determined from our previous analysis of projection effects. Dust effects were quantified for various values of the central B-band face-on dust optical depth  .
.
In our previous work (Möllenhoff et al. 2006) we did not attempt to disentangle dust and projection effects, neither did we attempt to analyse the simulations at high inclinations. As we will see in this section, the changes induced by dust in the values of the photometric parameters of the components of spiral galaxies, corrdust, are far more important than the projection effects corrproj. We present here dust effects for each morphological component and discuss the results.
6.1. The disk
Dust affects the appearance of the galaxy disks because its opacity is higher in the central parts of the disks and decreases exponentially with radius (e.g. Boissier et al. 2004; Popescu et al. 2005). As a consequence, the central parts of the disks will be more attenuated than the outer parts. This will alter the distribution of stellar emissivity as would be seen in the absence of dust.
Dust can also induce asymmetries in the surface brightness profiles at high to edge-on inclinations. This happens because of the difference in the attenuation between the two halves of the disk (separated by the dust disk). At face-on and low inclinations, this effect is negligible, because at each radial position we see the distribution of stellar emissivity through dust columns of the same scale-height. At high inclinations of the disk (seen through the associated dust disk), the half of the disk seen above the dust layer will suffer less attenuation than the half behind it. In addition, anisotropic scattering will also introduce asymmetries, that work in the same direction as the effect of absorption. This results in asymmetric minor-axis profiles for inclined disks, with the half of the disk nearest to the observer appearing brighter. These asymmetries cannot be properly taken into account when fitting the images with symmetric analytical functions – exponential distribution and variable index Sérsic function.
Because of these dust-induced asymmetries for the simulated images the position of the intensity peak will generally not coincide with the geometrical centre. As a consequence, better fits are provided when the position of the peak intensity is left as a free parameter. The asymmetries induced by dust are particularly visible for higher values of  and at higher inclinations.
and at higher inclinations.
 |
Fig. 7 Major and minor-axis disk profiles (upper and middle rows) showing the deviations from pure exponentials due to the combination of dust and projection effects. Solid upper curves are for B-band dusty disk images, for |
6.1.1. Exponential fits to the disk
When fitting disks with exponential functions, a main problem is, as mentioned before, the appearance of dust-induced asymmetries at higher values of  and i. A good illustration of this effect can be seen from the minor-axis profiles in Fig. 7 (middle row, for
and i. A good illustration of this effect can be seen from the minor-axis profiles in Fig. 7 (middle row, for 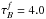 case), where the position of the intensity peak is shifted with respect to the position of the geometrical centre, marked by the light green line. Moreover, in the corresponding residual maps on the lower row of Fig. 7 one can notice asymmetric residuals. For example, at 73° inclination the fit underpredicts the lower half of the simulated image by 10−15% (see the yellow lower feature in the residual maps) while at 84°, the residuals are as high as 30−35% (the lower yellow-red feature from Fig. 7; see also the minor-axis profiles in the same figure, middle row, right panel).
case), where the position of the intensity peak is shifted with respect to the position of the geometrical centre, marked by the light green line. Moreover, in the corresponding residual maps on the lower row of Fig. 7 one can notice asymmetric residuals. For example, at 73° inclination the fit underpredicts the lower half of the simulated image by 10−15% (see the yellow lower feature in the residual maps) while at 84°, the residuals are as high as 30−35% (the lower yellow-red feature from Fig. 7; see also the minor-axis profiles in the same figure, middle row, right panel).
It is also interesting to note that the residual maps exhibit a ring-like structure at intermediate inclinations (see the yellow ring in the middle row, left panel of Fig. 7). This feature appears because the fit underpredicts the simulated dusty images at intermediate radii (see also the left column of plots in Fig. 7) (first two rows), where both the fit and the simulated image contain only smooth (diffuse) distributions of stellar emissivity. In other words, dust can induce feature-like structures in the residual maps which have no connection with real structures like rings, spiral arms or clumpiness. In view of the fact that it is common practice to use residual maps in observations of galaxies to assess the degree of clumpiness of an object, or even to assess the morphological type (spiral type), we caution that the reliability of the method is limited by the above-mentioned dust effects.
Figure 8 shows the inclination dependence of the ratio between the apparent and intrinsic scale-lengths (corrdust(R); Eq. (6)) for different values of the central face-on optical depth,  . As previously found (e.g. Möllenhoff et al. 2006), the scale-length ratios increase with opacity and are always greater than 1. As noticed before from Fig. 7, this is due to the dust-induced flattening of the intrinsic stellar emissivity profiles. An additional feature of the plots for the B-band is that, for low values of
. As previously found (e.g. Möllenhoff et al. 2006), the scale-length ratios increase with opacity and are always greater than 1. As noticed before from Fig. 7, this is due to the dust-induced flattening of the intrinsic stellar emissivity profiles. An additional feature of the plots for the B-band is that, for low values of  , there is a monotonic increase in scale-length with inclination, while at high opacities, when the disk becomes optically thick along all lines of sight, the increase flattens asymptotically (Fig. 8, left panel; see also Möllenhoff et al. 2006). However, this is not the case for the K band, where even at high
, there is a monotonic increase in scale-length with inclination, while at high opacities, when the disk becomes optically thick along all lines of sight, the increase flattens asymptotically (Fig. 8, left panel; see also Möllenhoff et al. 2006). However, this is not the case for the K band, where even at high  we see a monotonic increase in scale-length ratios with inclination (Fig. 8, right panel). This is because in the K band the disk is still optically thin along most of the lines of sight, at all inclinations. The results of the polynomial fits (Eq. (14)) to corrdust(R), for all opacities considered, are listed in Tables B.1 to B.5 for the B, V, I, J, K bands.
we see a monotonic increase in scale-length ratios with inclination (Fig. 8, right panel). This is because in the K band the disk is still optically thin along most of the lines of sight, at all inclinations. The results of the polynomial fits (Eq. (14)) to corrdust(R), for all opacities considered, are listed in Tables B.1 to B.5 for the B, V, I, J, K bands.
Figure 9 shows the inclination dependence of the ratio between the apparent and intrinsic average central surface-brightness, expressed in magnitudes ΔSB = −2.5log (Fapp/Fi) (corrdust(SB); Eq. (9)). As already noted in Sect. 5, these are calculated as averages in elliptical apertures. Fapp was calculated as an average over an elliptical aperture centred on the position of the geometrical centre of the fitted dusty images, with a semi-major axis of Rapp/10 and an axis-ratio of Qapp.
 |
Fig. 8 Dust effects corrdust on the derived scale-length of disks fitted with exponential functions. The symbols represent the measurements while the solid line are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic scale-lengths Rapp and Ri respectively, as a function of inclination (1 − cos(i)), for the B and K optical bands. From bottom to top, the curves are plotted for |
The surface brightness ratios are always positive at any inclination and for all values of  , meaning the apparent average central surface brightnesses are always fainter than the intrinsic ones. At high opacities, and close to edge-on inclinations, when the lines of sight pass through the longest columns of dust, the attenuation of central surface brightness is very strong (up to 8 mag for the B band and up to 5 mag for the K band at
, meaning the apparent average central surface brightnesses are always fainter than the intrinsic ones. At high opacities, and close to edge-on inclinations, when the lines of sight pass through the longest columns of dust, the attenuation of central surface brightness is very strong (up to 8 mag for the B band and up to 5 mag for the K band at 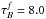 ). As for corrdust(R), the results of the polynomial fits (Eq. (14)) to corrdust(ΔSB) for all opacities considered are given in Tables B.1 to B.5 for the B, V, I, J, K bands.
). As for corrdust(R), the results of the polynomial fits (Eq. (14)) to corrdust(ΔSB) for all opacities considered are given in Tables B.1 to B.5 for the B, V, I, J, K bands.
The change in the disk axis-ratio due to dust (corrdust(Q); Eq. (6)) is fitted by a combination of two polynomials of the form: 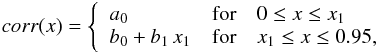 (21)where x = 1 − cos(i) and x1 = 0.95 for
(21)where x = 1 − cos(i) and x1 = 0.95 for 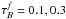 , x1 = 0.90 for
, x1 = 0.90 for 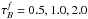 and x1 = 0.65 for
and x1 = 0.65 for 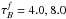 . At low to intermediate inclinations, up to 1 − cos(i) = 0.65, the derived axis-ratio in the presence of dust, Qapp, is the same as the intrinsic axis-ratio, Qi, which, in turn, is the same as the axis-ratio of the infinitely thin disk, Q0 = cos(i). It is only at higher inclinations and higher dust opacities that the dust starts to affect the derived axis-ratios, in the sense that the measured ratios are lower than the corresponding intrinsic values. This means that dust causes disks to appear slightly thinner than they are in reality. Nonetheless, even at higher inclinations and dust opacities, the effects due to dust, corrdust(Q), are weaker than projection effects, corrproj(Q). Thus, the decrease in the axis-ratio due to dust is at most 10%, while the increase in the intrinsic axis-ratio with respect to the axis-ratio of the infinitely thin disk is up to 50%. Overall, the correction from the cos(i) term is dominated by the increase in the axis-ratio due to the vertical distribution of stars. The resulting coefficients of the polynomial fits to corrdust(Q) are given for all opacities considered in Tables B.6 to B.10 for B, V, I, J, K bands.
. At low to intermediate inclinations, up to 1 − cos(i) = 0.65, the derived axis-ratio in the presence of dust, Qapp, is the same as the intrinsic axis-ratio, Qi, which, in turn, is the same as the axis-ratio of the infinitely thin disk, Q0 = cos(i). It is only at higher inclinations and higher dust opacities that the dust starts to affect the derived axis-ratios, in the sense that the measured ratios are lower than the corresponding intrinsic values. This means that dust causes disks to appear slightly thinner than they are in reality. Nonetheless, even at higher inclinations and dust opacities, the effects due to dust, corrdust(Q), are weaker than projection effects, corrproj(Q). Thus, the decrease in the axis-ratio due to dust is at most 10%, while the increase in the intrinsic axis-ratio with respect to the axis-ratio of the infinitely thin disk is up to 50%. Overall, the correction from the cos(i) term is dominated by the increase in the axis-ratio due to the vertical distribution of stars. The resulting coefficients of the polynomial fits to corrdust(Q) are given for all opacities considered in Tables B.6 to B.10 for B, V, I, J, K bands.
6.1.2. Sérsic fits to the disk
As with projection effects, to quantify the deviations of the simulated images from pure exponentials we also fitted the dusty disk images with general Sérsic functions. The corresponding major- and minor-axis profiles for 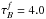 (as displayed in the upper and middle rows of Fig. 10 at three inclinations) show that overall general Sérsic functions are a better representation of the dusty disks. This can also be noticed from the the residual maps (same figure, lower row) where the residuals are very low at most inclinations and radii. A reduced-χ2 test for the case presented in Fig. 10 (B band and
(as displayed in the upper and middle rows of Fig. 10 at three inclinations) show that overall general Sérsic functions are a better representation of the dusty disks. This can also be noticed from the the residual maps (same figure, lower row) where the residuals are very low at most inclinations and radii. A reduced-χ2 test for the case presented in Fig. 10 (B band and 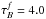 ) shows a decrease of 94% at an inclination of 46° with respect to the exponential case. However, at higher inclinations the dust-induced asymmetries still remain, as both Sérsic and exponential are symmetric distributions. Correspondingly, the reduced-χ2 shows a deterioration in the advantage of the Sérsic fit over the exponential fit as the inclination increases. Thus, the improvement in the goodness-of-fit is only 42% for i = 73° and reaches 1.9% at i = 84°.
) shows a decrease of 94% at an inclination of 46° with respect to the exponential case. However, at higher inclinations the dust-induced asymmetries still remain, as both Sérsic and exponential are symmetric distributions. Correspondingly, the reduced-χ2 shows a deterioration in the advantage of the Sérsic fit over the exponential fit as the inclination increases. Thus, the improvement in the goodness-of-fit is only 42% for i = 73° and reaches 1.9% at i = 84°.
 |
Fig. 9 Dust effects corrdust on the derived central surface brightnesses of disks fitted with exponential functions. The symbols represent the measurements while the solid line are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic average central surface-brightness, ΔSB, expressed in magnitudes, versus inclination (1 − cos(i)), for the B and K optical bands. From bottom to top, the curves are plotted for |
The general trend for the derived Sérsic index is to decrease from the value 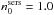 (characteristic for an exponential distribution) with the increase of
(characteristic for an exponential distribution) with the increase of  and inclination, for lower values of
and inclination, for lower values of  (see Fig. 11, left panels). This comes as a result of the flattening in the central regions due to the higher attenuation at small galactocentric radii. For higher
(see Fig. 11, left panels). This comes as a result of the flattening in the central regions due to the higher attenuation at small galactocentric radii. For higher  values the trend reverts, with
values the trend reverts, with 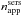 now increasing with inclination (see in particular the blue and red curves in the left panels from Fig. 11). This non-monotonic behaviour is caused by the fact that for larger
now increasing with inclination (see in particular the blue and red curves in the left panels from Fig. 11). This non-monotonic behaviour is caused by the fact that for larger  the optical thick core increases in size, moving outwards towards large radii, thus flattening the profile at increasingly large radii. This will eventually revert to an exponential. The results of the polynomial fits to the
the optical thick core increases in size, moving outwards towards large radii, thus flattening the profile at increasingly large radii. This will eventually revert to an exponential. The results of the polynomial fits to the 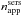 , for all opacities considered, are listed in Tables B.11 to B.15 for the B, V, I, J, K bands.
, for all opacities considered, are listed in Tables B.11 to B.15 for the B, V, I, J, K bands.
 |
Fig. 10 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from a general Sersic profile due to the combination of dust and projection effects. Solid upper curves are for B-band dusty disk images, for |
 |
Fig. 11 Left panels: the inclination dependence of the derived Sérsic index for disks fitted with Sérsic functions, due to combined dust and projection effects. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Right panels: the same but corrected for projection effects ( |
Since the trends seen in the plots for 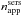 are due to both dust and projection effects, we correct for the latter by subtracting
are due to both dust and projection effects, we correct for the latter by subtracting 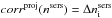 – the corrections defined in Sect. 5.1.2 − from the derived values of
– the corrections defined in Sect. 5.1.2 − from the derived values of 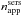 . The results are plotted in the right-hand panels of Fig. 11. It is reassuring to note that in the K-band, after correcting for projection effects, we recover the intrinsic value of unity for the Sérsic index, for all inclinations except the edge-on ones, and for most values of dust opacities, except for the very high ones. It is also apparent that at low inclinations the deviations from exponentiality are mainly due to dust effects while at higher inclinations, both dust and projection effects affect the derived Sérsic index. The resulting effective radius will always be larger than the corresponding one in the absence of dust, with the ratio of these two increasing with inclination, as already noted from Fig. 12. The coefficients of the polynomial fits are listed in the same tables as the
. The results are plotted in the right-hand panels of Fig. 11. It is reassuring to note that in the K-band, after correcting for projection effects, we recover the intrinsic value of unity for the Sérsic index, for all inclinations except the edge-on ones, and for most values of dust opacities, except for the very high ones. It is also apparent that at low inclinations the deviations from exponentiality are mainly due to dust effects while at higher inclinations, both dust and projection effects affect the derived Sérsic index. The resulting effective radius will always be larger than the corresponding one in the absence of dust, with the ratio of these two increasing with inclination, as already noted from Fig. 12. The coefficients of the polynomial fits are listed in the same tables as the 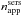 .
.
The effects of dust on the derived axis-ratios Qapp/Qi are the same for the Sérsic and exponential fits, so the results are only listed once in the tables corresponding to the exponential fits.
6.2. The thin disk
The dust affects the perceived distribution of stellar emissivity in the young stellar disk in a stronger way than in the old stellar disk, as we will see in this section, although the overall trend is similar. This is because the young stellar disk is, in our model, completely embedded in the dust distribution, and therefore suffers more attenuation effects than the old stellar disk. By contrast, as already noted in Sect. 5.2, projection effects are negligible for the thin disk, and therefore can be safely ignored.
The main application of our dust corrections to the derived photometric parameters of thin disks are for the UV range, as it is in this spectral range that the young stellar disk is prominent. In the optical range, the young stellar disk cannot be distinguished from the old stellar disk, based on optical images alone. Therefore, in the optical, the measured structural parameters are indicative of the old stellar disk. In analysing optical images of galaxies it is recommended to use dust corrections for the “disk” component. We nevertheless quantify dust corrections in the optical for the “thin disk” as well, as these are useful for deriving corrections for Balmer line/nebular line emission. Dust corrections on line emission can be derived by interpolating between the optical wavelength tabulated in this paper. As an example we only show dust corrections for the Hα line emission.
6.2.1. Exponential fits to the thin disk
In Fig. 13, we show major-axis profiles for the dusty young stellar disk images for two UV bands at face-on inclination. One can see that for intermediate values of the optical depth, even at face-on inclinations, the profiles deviate from pure exponentials, because dust strongly alters the shape of the profile, making it extremely flat in the central part (see the third column plots in Fig. 13). In the central regions we can also observe high residuals between the simulated and the fitted profiles, another indication that the fits are imperfect. With increasing opacity and inclinations, the fits become more imperfect. At a certain point, exponential fits become completely inadequate to represent the surface-brightness distribution of thin disks. For this reason, we present here dust effects only at inclinations and opacity values for which an exponential profile is still a good representation of the stellar emissivity distribution in the young stellar disk. For example, in the UV range we present corrections only up to a dust opacity of 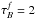 .
.
 |
Fig. 12 Dust effects corrdust on the derived effective radius of disks fitted with Sérsic functions. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic Sérsic effective radii, |
Figure 14 shows the inclination dependence of the ratio between the apparent and intrinsic scale-lengths of the thin disk (corrdust(R); Eq. (6)) for different values of the B-band central face-on optical depth,  , for various UV wavelengths. As we can observe from these plots, the strongest distortion dust exerts over the stellar emissivity distribution is, as expected, at the shortest UV wavelengths. The dust effects decrease non-monotonically with increasing UV wavelength, due to the bump in the extinction curve at 2200 Å. Overall, the dust effects are quite severe for this morphological component, in particular in the UV range.
, for various UV wavelengths. As we can observe from these plots, the strongest distortion dust exerts over the stellar emissivity distribution is, as expected, at the shortest UV wavelengths. The dust effects decrease non-monotonically with increasing UV wavelength, due to the bump in the extinction curve at 2200 Å. Overall, the dust effects are quite severe for this morphological component, in particular in the UV range.
But even in the optical range the thin disk is strongly affected by dust. This can be seen in Fig. 15, where we plotted the same quantities as in Fig. 14, this time for the longer optical wavelengths. The strong dust effects arise because, as mentioned before, the young stellar disk has a smaller scale-height than the old stellar disk, and therefore it has a stronger spatial coupling with the dust. By comparing Fig. 8 on one hand (old stellar disk) with Fig. 15 (young stellar disk) on the other hand, one can see that, for the same wavelength and  , the amplitude of the changes in the apparent scale-lengths is higher for the young stellar disk. We note however that the trend is similar for both stellar components.
, the amplitude of the changes in the apparent scale-lengths is higher for the young stellar disk. We note however that the trend is similar for both stellar components.
 |
Fig. 13 Face-on major-axis profiles for the thin disk showing the deviations from pure exponentials due to dust effects. Solid upper curves are for the face-on dusty images, the corresponding exponential fits are represented by dashed curves, while the solid lower curves denote the residuals. The upper plots correspond to the 912 Å UV wavelength and |
 |
Fig. 14 Dust effects corrdust on the derived scale-length of thin disks fitted with exponential functions. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the inclination dependence of the ratio between the apparent and intrinsic scale-lengths, Rapp and Ri respectively. From left to right, the plots corresponds to increasing UV wavelengths: 912 Å, 1500 Å, 2200 Å, and 2800 Å. From bottom to top the black curves are plotted for |
 |
Fig. 15 Same as in Fig. 14, for the optical bands and the Hα line. From bottom to top the black curves are plotted for |
 |
Fig. 16 Upper row: inclination dependence of the derived Sérsic index for the dusty images of thin disks fitted with Sérsic functions. Lower row: same, for the ratio between the apparent and intrinsic Sérsic effective radii, |
In addition to the continuum optical emission we also show an example for the Hα line (Fig. 15), as it is the young stellar disk component from which the recombination lines originate (the star-forming regions). Dust corrections for other Balmer lines can be obtained by interpolating the corrections for the thin disk between the relevant optical wavelengths. All corrections corrdust, both in the UV range and in the optical, including those for the Hα line, are listed in terms of coefficients of polynomial fits in Tables B.16 to B.30.
6.2.2. Sérsic fits to the thin disk
As for the old stellar disk, in order to quantify the deviations of the stellar emissivity profiles from pure exponentials we also performed Sérsic fits for the thin disk images. In Fig. 16 we present the inclination dependence of the derived Sérsic index (upper row) and the Sérsic effective radii ratios (lower row) for the same UV wavelengths we used when fitting with an exponential. Even for low values of  , at high inclinations the effects of dust are significant and increase towards shorter wavelengths. At higher values of
, at high inclinations the effects of dust are significant and increase towards shorter wavelengths. At higher values of  the deviations of the derived Sérsic indices from its exponential value can be dramatic, with values decreasing to
the deviations of the derived Sérsic indices from its exponential value can be dramatic, with values decreasing to 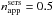 (Gaussian) or even lower, to
(Gaussian) or even lower, to 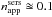 . Since there are no significant projection effects (
. Since there are no significant projection effects (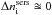 ) for the thin disk (as mentioned in Sect. 5.2), the deviations of the Sérsic index from an exponential are in this case caused only by the dust effects. At high inclinations and for extremely opaque thin disks even Sérsic fits become poor representations of the profiles, therefore these cases were omitted from the plots in Fig. 16.
) for the thin disk (as mentioned in Sect. 5.2), the deviations of the Sérsic index from an exponential are in this case caused only by the dust effects. At high inclinations and for extremely opaque thin disks even Sérsic fits become poor representations of the profiles, therefore these cases were omitted from the plots in Fig. 16.
In the optical range we proceeded in a similar way to the UV range, by fitting variable Sérsic index functions to the simulated images of the young stellar disk. In Figs. 17 and 18 we display the corresponding Sérsic index and effective-radii ratios variation as a function of inclination for various optical bands and also for the Hα line. By comparing the derived Sérsic indices for the old stellar disk (Fig. 11, right hand panel) and the young stellar disk (Fig. 17), at the same wavelength,  and inclination, we can see that the dust-induced changes in the derived Sérsic index are more pronounced in the latter case. We also see that for high values of
and inclination, we can see that the dust-induced changes in the derived Sérsic index are more pronounced in the latter case. We also see that for high values of  (
(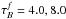 ) the trend for the two morphological components is not the same. Thus, for the old stellar disk the derived Sérsic index increases with increasing inclination, while for the young stellar disk an opposite trend is observed.
) the trend for the two morphological components is not the same. Thus, for the old stellar disk the derived Sérsic index increases with increasing inclination, while for the young stellar disk an opposite trend is observed.
Our analysis of the dust effects on the derived thin disk axis-ratios (corrdust(Q); Eq. (6)) shows that these are negligible, therefore we do not present these. All the other results for corrdust, both in the UV and in the optical range, including the Hα line, are listed in terms of coefficients of polynomial fits in Tables B.31 to B.45.
6.3. The bulge
 |
Fig. 19 Left: inclination dependence of the derived Sérsic index of bulges due to combined dust and projection effects, in the B-band, for simulations having volume stellar emissivities described by different Sérsic indices, |
The analysis of the effect of dust on bulges is the most novel aspect of this study, as, unlike disks, there is very little work based on radiation transfer simulations on this topic. As for the case of dust-free bulges, we used simulations of dusty bulges with volume stellar emissivity distributions described by various Sérsic indices, 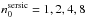 . Accordingly, for each of these cases we used variable-index Sérsic distributions as fitting functions. For
. Accordingly, for each of these cases we used variable-index Sérsic distributions as fitting functions. For 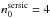 we also used de Vaucouleurs functions to fit the simulations. We considered simulations for bulges truncated at three and ten effective radii, respectively.
we also used de Vaucouleurs functions to fit the simulations. We considered simulations for bulges truncated at three and ten effective radii, respectively.
We have already seen in Sect. 5.3 that projection effects corrproj on bulges strongly depend on the intrinsic Sérsic index of the volume stellar emissivity 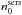 , and on the presence or absence of a truncation radius. Accordingly, it is important to assess whether dust effects corrdust also have these extra dimensions in parameter space.
, and on the presence or absence of a truncation radius. Accordingly, it is important to assess whether dust effects corrdust also have these extra dimensions in parameter space.
We first tested whether the corrections depend on the choice of the Sérsic index used as input in the simulations (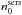 ). To do this we analysed bulges produced with four different values of the Sérsic indices,
). To do this we analysed bulges produced with four different values of the Sérsic indices, 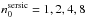 , for the same
, for the same 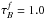 , for bulges truncated at
, for bulges truncated at 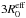 , and at different inclinations. Subsequently, we fitted these bulges with variable-index Sérsic functions. The variation of the derived Sérsic indices with inclination is displayed in Fig. 19. After correcting for projection effects (right panel in Fig. 19), we see that for low to intermediate inclinations the variation of the derived Sérsic index (
, and at different inclinations. Subsequently, we fitted these bulges with variable-index Sérsic functions. The variation of the derived Sérsic indices with inclination is displayed in Fig. 19. After correcting for projection effects (right panel in Fig. 19), we see that for low to intermediate inclinations the variation of the derived Sérsic index (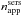 ) with inclination does not depend on the input Sérsic index in the simulation,
) with inclination does not depend on the input Sérsic index in the simulation, 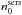 . In particular for this value of
. In particular for this value of  , we broadly recover the values of the parameter
, we broadly recover the values of the parameter 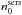 . It is only for high values of
. It is only for high values of 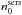 and closer to edge-on inclinations that the measured Sérsic index starts to fall significantly from its intrinsic value. As mentioned in Sect. 5.3, the noisier curves at
and closer to edge-on inclinations that the measured Sérsic index starts to fall significantly from its intrinsic value. As mentioned in Sect. 5.3, the noisier curves at 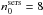 are not caused by real physical effects, but are inherent to the limited resolution of our radiative transfer calculations for this high value of Sérsic index. As a result of these tests performed for simulations with different
are not caused by real physical effects, but are inherent to the limited resolution of our radiative transfer calculations for this high value of Sérsic index. As a result of these tests performed for simulations with different 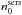 , we decided, because the differences are small, to only consider dust effects for two different values of the Sérsic index,
, we decided, because the differences are small, to only consider dust effects for two different values of the Sérsic index, 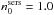 (exponential bulge) and
(exponential bulge) and 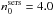 (de Vaucouleurs bulge).
(de Vaucouleurs bulge).
 |
Fig. 20 Inclination dependence of the derived Sérsic index of bulges due to dust effects only (corrected for projection effects), for bulges truncated at three effective radii (black curves) and at ten effective radii (red curves). The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Results are for the B-band and for simulations corresponding to a volume stellar emissivity described by a (deprojected) Sérsic function with |
 |
Fig. 21 Left: simulated image of a bulge in the B band, seen through the dust disks, having |
Secondly, we tested whether truncation radius affects the dust corrections corrdust. In Fig. 20 we show the effect of dust for bulges truncated at 3 Reff and at 10 Reff, for two values of 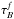 . This test indicates that, unlike for the projection effects, truncation radius does not affect the results on dust effects. Therefore there was no need to present our dust corrections as a function of truncation radius.
. This test indicates that, unlike for the projection effects, truncation radius does not affect the results on dust effects. Therefore there was no need to present our dust corrections as a function of truncation radius.
When performing fits to simulations, one of the main problems was related to the dust-induced asymmetries in the surface brightness distribution profiles at high inclinations (of the dust disk) and large values of  . As an illustration of this effect, we show in Fig. 21 two dusty bulge-simulated images, one at 73° inclination (left) and one edge-on (right). We can easily see from the image on the left that a bulge observed in B-band at 73° inclination, for
. As an illustration of this effect, we show in Fig. 21 two dusty bulge-simulated images, one at 73° inclination (left) and one edge-on (right). We can easily see from the image on the left that a bulge observed in B-band at 73° inclination, for 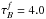 , would be half obscured by dust. This issue produces difficulties when fitting such images with a symmetrical analytic function like a Sérsic distribution. Similar problems can arise for bulges seen at edge-on inclinations, where the dust lanes block the bulge stellar emissivity in the plane of the disk3 (see right panel of Fig. 21 for an edge-on orientation). For this reason it is not feasible to perform Sérsic fits on bulges at high inclinations and high
, would be half obscured by dust. This issue produces difficulties when fitting such images with a symmetrical analytic function like a Sérsic distribution. Similar problems can arise for bulges seen at edge-on inclinations, where the dust lanes block the bulge stellar emissivity in the plane of the disk3 (see right panel of Fig. 21 for an edge-on orientation). For this reason it is not feasible to perform Sérsic fits on bulges at high inclinations and high  .
.
To quantify the dust effects on the bulge photometric parameters, we fitted both exponential ( ) and de Vaucouleurs (
) and de Vaucouleurs ( ) bulges with variable-index Sérsic functions. We plotted the inclination dependence of the Sérsic index only for the values of
) bulges with variable-index Sérsic functions. We plotted the inclination dependence of the Sérsic index only for the values of  and at inclinations for which the derived fit was reasonable. The combined dust and projection effects on the Sérsic index of exponential bulges can be seen in the left-hand panels of Fig. 22, for the B- and K-bands. For large values of
and at inclinations for which the derived fit was reasonable. The combined dust and projection effects on the Sérsic index of exponential bulges can be seen in the left-hand panels of Fig. 22, for the B- and K-bands. For large values of  the distortions in the derived Sérsic index are strong, with observed trends looking similar, and with
the distortions in the derived Sérsic index are strong, with observed trends looking similar, and with 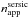 decreasing with inclination and
decreasing with inclination and  . For example, for
. For example, for 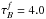 , i = 78°,
, i = 78°, 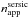 decreases to 0.45. The decrease of the measured Sérsic index of bulges with increasing opacity and inclination has also been found by Gadotti et al. (2010), though a direct comparison is not possible, since the latter trends were derived from bulges obtained from bulge/disk decomposition, which, in addition to the effects of dust, also contain the effect of dust on the bulge/disk decomposition itself, which we refer to in this paper as corrB/D, given by Eqs. (12) and (13).
decreases to 0.45. The decrease of the measured Sérsic index of bulges with increasing opacity and inclination has also been found by Gadotti et al. (2010), though a direct comparison is not possible, since the latter trends were derived from bulges obtained from bulge/disk decomposition, which, in addition to the effects of dust, also contain the effect of dust on the bulge/disk decomposition itself, which we refer to in this paper as corrB/D, given by Eqs. (12) and (13).
Since the trends seen in our plots for 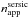 of exponential bulges are caused both by dust and by projection effects, we correct for the latter by subtracting
of exponential bulges are caused both by dust and by projection effects, we correct for the latter by subtracting 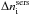 − the corrections defined in Sects. 5.1 and 5.3, to the derived values of
− the corrections defined in Sects. 5.1 and 5.3, to the derived values of 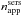 . The results are plotted in the right panels of Fig. 22. The derived values of Sérsic index are now closer to the values of the
. The results are plotted in the right panels of Fig. 22. The derived values of Sérsic index are now closer to the values of the 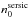 parameter input in the simulations. At very high inclinations and large values of
parameter input in the simulations. At very high inclinations and large values of  , the deviations in the B-band are still very strong. The plots also show that at all inclinations the deviations from the intrinsic distributions are due to both dust and projection effects, with projection effects being constant with inclination (see Fig. 5).
, the deviations in the B-band are still very strong. The plots also show that at all inclinations the deviations from the intrinsic distributions are due to both dust and projection effects, with projection effects being constant with inclination (see Fig. 5).
 |
Fig. 22 Left panels: inclination dependence of the derived Sérsic index for the exponential bulges ( |
In Fig. 23 we show the inclination dependence of the ratio between the apparent and intrinsic bulge effective radii of exponential bulges for different values of  . The effect of dust on the effective ratios is small, even for large values of
. The effect of dust on the effective ratios is small, even for large values of  , and has a weak dependence on inclination.
, and has a weak dependence on inclination.
 |
Fig. 23 Dust effects corrdust on the derived effective radius of exponential ( |
Overall, looking at the effects dust has on the bulge photometric parameters, we noted an overestimation of the effective radii and an underestimation of the Sérsic indices when fitting bulges with variable-index Sérsic functions. The overestimation of the effective radii is more pronounced for de Vaucouleurs bulges than for exponential bulges, while the underestimation of the Sérsic indices is more pronounced for exponential bulges than for de Vaucouleurs bulges. In particular at high inclination and opacities the ratio of the apparent to intrinsic effective radius increases with inclination for de Vaucouleurs bulges and decreases with inclination for exponential bulges.
All the corrections corrdust, for both exponential and de Vaucouleurs bulges, are presented in form of coefficients of polynomial fits in Tables B.46 to B.55. For de Vaucouleurs bulges, the fits at higher inclinations were quite poor, therefore we restricted our measurements to inclinations of up to 1 − cos(i) = 0.7. Consequently, only the flat trend with inclination was recovered. In addition, we also give results for de Vaucouleurs fits to de Vaucouleurs bulges (constrained Sérsic functions). These are listed in Tables B.56 to B.60.
7. Discussion
The corrections presented in this paper, both for projection and dust effects, assume a fixed geometry for the underlying components of spiral galaxies. In particular, the relative ratios between scale-lengths and scale-heights of stars and dust are fixed to the reproducible trends found from modelling edge-on galaxies with radiative transfer calculations, as described in length in Tuffs et al. (2004) and Popescu et al. (2011). Nonetheless, one can expect some scatter from these trends, and a logical question to ask is to what extent the corrections presented in this paper are affected by such a variation. While it is beyond the scope of this paper to quantify this effect, as indeed the whole power and reliability of the calculations based on radiative transfer calculations rely on the existence of these constant trends in geometrical parameters, we can discuss some simple plausible variations from these trends and consequences for the dust and projection effects.
One geometrical parameter that could vary is the thickness of the old stellar disk relative to its scale-length. As long as the ratio of the scale-height of the stellar disk to the dust disk remains the same, the dust corrections will not change much. However, there will be a visible effect on the projection effects. In particular, this can be seen from our existing calculations at various optical/NIR wavelengths, since our geometrical model assumes that the scale-length of the stellar disk decreases with increasing wavelength, which is the same, from the point of view of projection effects, as having a thicker stellar disk with increasing wavelength. The main effect is the departure from the cos(i) law of an infinitely thin disk (see Sect. 5.1 and Fig. 2). Because the stellar disk has a larger scale-height, the departure from the infinitely thin approximation starts at lower inclinations, and the amplitude of the effect is more pronounced. Thus, corrproj(Q), the ratio between the intrinsic axis-ratio Qi, and the axis-ratio of an infinitely thin disk, Q0, will increase (at higher inclinations) for galaxies having a thicker stellar disk. Consequently, the overestimation of the exponential scalelength of the disk will start at lower inclinations, and the amplitude of the effect will increase for thicker stellar disks (corrproj(R) will increase). When fitting thicker stellar disks with Sérsic functions, the underestimation of the Sérsic index will also be larger. Overall thicker stellar disks will produce the same trends for projection effects, but with a larger amplitude of the effect.
A more complex problem to address is when an increase in thickness of the stellar disk is also accompanied by an increase in the ratio between the scale-height of stars and that of dust. This will produce not only changes in projection effects but also changes in the dust corrections. An extreme case of such a change can be seen from the differences in dust corrections between the “thin disk” and the “disk”. The stellar emissivity in the thin disk is completely embedded in the dust disk, while the disk has a layer of stars extending above the dust layer. Consequently, the dust corrections are less severe for the disk than for the thin disk. Thus, when fitting a galaxy having a larger ratio of the scale-height of stars-to-dust, we will obtain smaller corrections for corrdust(R), corrdust(Reff), and Δnsersic, for the same dust opacity and inclination.
 |
Fig. 24 Inclination dependence of the derived Sérsic index of bulges due to dust effects only (corrected for projection effects), for spherical bulges (axis-ratios of 1.0; black curves) and for our standard bulges with axis-ratios of 0.6 (red curves). The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Results are for the B-band and for simulations corresponding to a volume stellar emissivity described by a (deprojected) Sérsic function with |
In the case of bulges there are only two parameters defining the geometry: the effective radius and the ellipticity of the bulge. The effective radius in our model was taken to be much smaller than the radial scalelength of the stellar disk (and of the dust disk). Essentially, much of the stellar light from the bulge is strongly attenuated by the higher optical depth in the centre of the disks. As long as the size of the bulge remains within these constraints, not much change in the dust corrections is foreseen due to changes in the radial distribution. It is more likely that any effects would be due to changes in the vertical distribution controlling the amount of stars seen above the dust layer. This can be caused by either a larger effective radius of the bulge or by a more spherical bulge. We test the latter effect by producing a few simulations for bulges with axis-ratios equal to unity (spherical bulge). In Fig. 24 we show the results for exponential bulges, for two cases of dust opacity, 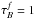 and
and 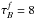 . The curves showing the inclination dependence of the corrected (for projection effects) Sérsic index are very similar for both spherical and ellipsoidal bulges, for both optically thin and optically thick cases. We therefore conclude that the ellipticity of the bulge does not significantly affect the corrections for dust effects of the derived structural parameters of bulges.
. The curves showing the inclination dependence of the corrected (for projection effects) Sérsic index are very similar for both spherical and ellipsoidal bulges, for both optically thin and optically thick cases. We therefore conclude that the ellipticity of the bulge does not significantly affect the corrections for dust effects of the derived structural parameters of bulges.
8. Application: the wavelength dependence of dust effects
 |
Fig. 25 The wavelength dependence of the Sérsic index (top) and effective radius (bottom) predicted to be measured on a disk population, due to the effect of dust only (black). The recent measurements from the GAMA survey, from Kelvin et al. (2012), are overplotted in red. All the plots are normalised to the corresponding measurement in the r band. |
One important application of our modelling is the predictions for the wavelength dependence of the effects of dust. Recent observational work (Kelvin et al. 2012; Häußler et al. 2013) has shown that for a population of disk-dominated galaxies there is a distinctive trend of increasing Sérsic index and effective radius with increasing wavelength. In the case of Kelvin et al. (see the red curves in Fig. 25) the results have been obtained using single-Sérsic fits to 167 600 galaxies measured independently in the ugrizYJHK bandpasses using reprocessed Sloan Sky Survey Data Release Seven and UKIRT Infrared Deep Sky Survey Large Area Survey imaging data available from the Galaxy and Mass Assembly (GAMA; Driver et al. 2011). The measured galaxies were further divided into early-type and late-type galaxies, according to the K-band Sérsic index/u-r colour relation. The averaged trends for late-type galaxies are compared with the predictions of our models (black curves in Fig. 25). For this purpose we considered our corrdust obtained for simulations of disks with 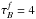 and an average inclination of 60°. The choice of
and an average inclination of 60°. The choice of 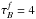 was motivated by the analysis of the attenuation-inclination relation by Driver et al. (2007), who found an average dust opacity for local-universe disk galaxies of
was motivated by the analysis of the attenuation-inclination relation by Driver et al. (2007), who found an average dust opacity for local-universe disk galaxies of 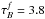 . A similar average value for comparable stellar masses was also found by Grootes et al. (2013). Moreover, the radiative transfer analysis of the UV to FIR SEDs of individual edge-on galaxies by Misiriotis et al. (2001) and Popescu et al. (2004) found similar values for
. A similar average value for comparable stellar masses was also found by Grootes et al. (2013). Moreover, the radiative transfer analysis of the UV to FIR SEDs of individual edge-on galaxies by Misiriotis et al. (2001) and Popescu et al. (2004) found similar values for 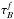 .
.
The comparison between data and model predictions for effective radii indicates that in both cases there is a trend of decreasing radius with increasing wavelength, with the data showing a more pronounced decrease than the models. This could potentially indicate that, in addition to the dust effects, there is an intrinsic stellar gradient, with disks being smaller at longer than at shorter wavelength, as predicted from theories of disk growth from inside out. This preliminary result would need to be followed-up with more accurate determinations of disk sizes, which are performed on disk/bulge decomposition. The caveat of our interpretation is that, although a population of disk-dominated galaxies has been isolated in Kelvin et al. (2012), we cannot exclude contamination from bulges in late-type spirals. This would bias the results towards smaller effective radii at longer wavelength, where bulges are more prominent (see also Häußler et al. 2013), resulting in the same qualitative trend as the effect of intrinsic stellar gradients. Thus, a quantitative interpretation of these trends still awaits for more accurate determinations of disk sizes and disk opacities.
The comparison between data and model predictions for Sérsic indices shows again that dust effects can account for most of the trends shown in the data, with a small difference towards the K band. As before, we note that a quantitative comparison of these trends would require disk measurements obtained from bulge-disk decomposition on higher resolution data.
9. Summary and conclusions
We presented the results of a study to quantify the effects of dust on the derived photometric parameters of pure disks and bulges in spiral galaxies. In our approach we followed the same path observers do, but instead of real images we used simulated ones, produced by radiative transfer techniques.
The simulations were produced as part of the large library of dust and PAH emission SEDs and corresponding dust attenuations presented in Popescu et al. (2011). All simulations were calculated using a modified version of the ray-tracing radiative transfer code of Kylafis & Bahcall (1987), which includes a full treatment of anisotropic scattering. The simulations were produced separately for old stellar disks, bulges, and young stellar disks, all seen through a common distribution of dust.
The intrinsic volume stellar distributions were described by exponential functions in both radial and vertical directions for the disks and by deprojected de Vaucouleurs functions for the bulges. The corresponding dust distributions were described by double (radial and vertical) exponential functions for the two dust disks of the model. Apart from these already existing simulations additional ones have been produced for the purpose of this study. These are simulations of bulges corresponding to general Sérsic functions with various Sérsic indices.
We fitted the simulated images of disks and bulges with 1D analytic functions available in GALFIT, the same ones observers use when fitting real galaxy images (exponentials/variable index Sérsic functions or de Vaucouleurs distributions). We showed that, even in the absence of dust, these simple distributions would differ from those of real galaxies due to the fact that they describe infinitely thin disks, while disks and bulges have a thickness. We called these effects projection effects.
The approach adopted in this paper was to separate projection from dust effects. Thus, we first derived the projection effects, by calculating the change between the intrinsic parameters of the volume emissivity and those measured on dust-free images. Subsequently, we derived the dust effects by calculating the change between the parameters measured on dust-free and dusty images, respectively, for the same inclination and wavelength. The total change in parameter values between the measured ones on dusty images and the corresponding parameters of the volume stellar emissivity was written as a chain of corrections (Eqs. (4)−(6) or Eqs. (7)–(9)).
We showed that one advantage of this approach is that it provides a more robust quantification of the dust effects. In particular, we showed that the term related to projection effects is affected by variations in the geometrical parameters of the volume stellar emissivity, including the truncation radius, while the term related to dust effects is relatively insensitive to these factors.
The main results on the dust effects are as follows:
Disks
-
The derived scale-length of dusty disks fitted with exponentialfunctions is always greater than that obtained in the absence ofdust, with the amplitude of the effect increasing with the centralface-on dust opacity
 of the disk and with inclination, and with decreasing wavelength. The increase is very small for low values of
of the disk and with inclination, and with decreasing wavelength. The increase is very small for low values of  or longer wavelengths, steepens for intermediate values of
or longer wavelengths, steepens for intermediate values of  or higher inclinations, and flattens again for very high values of
or higher inclinations, and flattens again for very high values of  and shorter wavelengths.
and shorter wavelengths. -
The derived central surface-brightness of dusty disks fitted with exponential functions is always fainter than that obtained in the absence of dust, with the amplitude of the effect increasing with
 of the disk and with inclination, and with decreasing wavelength.
of the disk and with inclination, and with decreasing wavelength. -
At low to intermediate inclinations, up to 1 − cos(i) = 0.65, the derived axis-ratio in the presence of dust is the same as the intrinsic axis-ratio, which, in turn, is the same as the axis-ratio of the infinitely thin disk, cos(i). It is only at higher inclinations and higher dust opacities that the dust starts to affect the derived axis-ratios, in the sense that the measured ratios are lower than the corresponding intrinsic values. This means that dust makes disks appear slightly thinner than they are in reality. Nonetheless, even at higher inclinations and dust opacities, the effects due to dust are smaller than projection effects. Overall, the correction from the cos(i) term is dominated by the increase in the axis-ratio due to the vertical distribution of stars.
-
The derived Sérsic index of dusty disks fitted with Sérsic functions is, for a broad range of
 and inclinations, smaller than that obtained in the absence of dust. The trend is for the Sérsic index to decrease with increasing inclination and
and inclinations, smaller than that obtained in the absence of dust. The trend is for the Sérsic index to decrease with increasing inclination and  . Only at very high opacitites (
. Only at very high opacitites (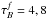 ) and close to the edge-on view is the derived Sérsic index larger than that obtained in the absence of dust, and the trend with inclination is reversed. At low inclinations the deviations from exponentiality are mainly due to dust effects while at higher inclinations, both dust and projection effects affect the derived Sérsic index.
) and close to the edge-on view is the derived Sérsic index larger than that obtained in the absence of dust, and the trend with inclination is reversed. At low inclinations the deviations from exponentiality are mainly due to dust effects while at higher inclinations, both dust and projection effects affect the derived Sérsic index. -
The derived effective radius of disks fitted with Sérsic functions is always greater than that obtained in the absence of dust, with the amplitude of the effect increasing with
 of the disk and with inclination, and with decreasing wavelength.
of the disk and with inclination, and with decreasing wavelength. -
The effects of dust on the derived axis-ratios are the same for the Sérsic and exponential fits.
Thin disks
-
The trends in the derived scale-length and effective radius of thindisks fitted with exponential and Sérsic functions, respectively,are similar to those obtained for disks. However, the amplitude ofthe effect is more pronounced, even when the comparison is madeat the same optical wavelength. In the UV range the trend withwavelength is non-monotonic, due to the bump in the extinctioncurve at the 2200 Å. The derivedSérsic index is always smaller than that obtained in the absence ofdust, and has a monotonic decrease with increasing inclinationand
 .
. -
We also showed corrections for the Hα line, both for the case of exponential and Sérsic fits.
Bulges
-
The effects of dust do not seem to strongly depend on the exactvalue of the Sérsic index corresponding to the intrinsic volumestellar emissivity,
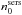 . Only at very high values of
. Only at very high values of 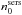 and close to the edge-on view do the effects of dust start to deviate from the trends seen at lower
and close to the edge-on view do the effects of dust start to deviate from the trends seen at lower 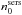 .
. -
The effects of dust are completely insensitive to the truncation radius of the bulge, in strong contrast to projection effects, which critically depend on the choice of truncation radius.
-
The effects of dust are also insensitive to the ellipticity of the bulge. In particular, spherical or ellipsoidal bulges seem to require the same corrections for the effects of dust.
-
Dust does not significantly change the derived Sérsic index of bulges, for a wide range of
 and inclinations. Only at very high
and inclinations. Only at very high  and close to the edge-on view is the derived Sérsic index of bulges smaller that that obtained in the absence of dust (the Sérsic index is underestimated). The trend is for the Sérsic index to decrease with inclination and
and close to the edge-on view is the derived Sérsic index of bulges smaller that that obtained in the absence of dust (the Sérsic index is underestimated). The trend is for the Sérsic index to decrease with inclination and  .
. -
Similarly, dust only induces small changes in the derived effective radius of bulges. The radii are higher than that obtained in the absence of dust. The trend is for the effective radius to increase with
 .
. -
The overestimation of the effective radii is more pronounced for de Vaucouleurs bulges than for exponential bulges, while the underestimation of the Sérsic indices is more pronounced for exponential bulges than for de Vaucouleurs bulges.
We used our derived corrections to compare our model predictions for the wavelength dependence of dust effects with similar trends seen in recent observational data from the GAMA survey (Kelvin et al. 2012). The results of this comparison for Sérsic indices and effective radii show that dust effects can account for most of the trends seen in the data, with some additional room for intrinsic gradients in the stellar populations.
All corrections for dust, for all opacities considered in this paper and at different wavelengths, are listed in the tables given in the appendix. The corrections are provided in the form of coefficients of polynomial fits to the corrections as a function of inclination. In the optical range, where both a disk and a thin disk are emitting, we recommend the following. To correct the structural parameters of optical images in broad-band continuum light, dust corrections for the “disk” (and “bulge”) component should be used. The corrections for the thin disk in the optical should only be used to correct narrow-band optical images of line emission (Balmer or nebular lines), by interpolating between the optical wavelengths tabulated in this paper (except for the Hα line, for which corrections are already explicitly listed in tables). The main application of our dust corrections for the thin disk is for UV broad-band imaging, where this morphological component dominates the bolometric output and appearance of the spiral galaxy images.
This study was done for pure disks and bulges. Because real spiral galaxies have both a bulge and a disk one first needs to decompose their images into its components through bulge-disk decompositions, and only then correct for dust and projection effects to recover the intrinsic photometric parameters. Performing bulge-disk decompositions on real dusty spiral galaxy images has proved to be a difficult task as the derived photometric parameters for disks and bulges can be biased through the decomposition process itself. In this respect, a mixing between stellar emissivity from disks and bulges can occur, with a fraction of the disk stellar emissivity being transferred to the bulge stellar emissivity as a result of the decompositions (and vice versa). Therefore one needs to quantify the dust effects when performing bulge-disk decompositions. In our future work we will assess the dust effects on bulge-disk decompositions through multi-component fits of simulated galaxy images. This new set of corrections will be added to those for projection and dust effects to provide a means to accurately recover the intrinsic photometric parameters of disk and bulges in spiral galaxies.
Acknowledgments
We thank the referee for his/her careful reading of the text, for the useful suggestions and for pointing out an omission from the original manuscript. C.C. Popescu thanks the Max Planck Institute für Kernphysik for support during a sabbatical, when this work was completed.
References
- Allen, P. D., Driver, S. P., Graham, A. W., et al. 2006, MNRAS, 371, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Rejkuba, M., Retzlaff, J., et al. 2012, Msngr, 149, 7 [Google Scholar]
- Baes, M., Davies, J. I., Dejonghe, H., et al. 2003, MNRAS, 343, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., et al. 2013, submitted [Google Scholar]
- Boissier, S., Boselli, A., Buat, V., et al. 2004, A&A, 424, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourne, N., Maddox, S. J., Dunne, L., et al. 2012, MNRAS, 421, 3027 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, Y. I., Freeman, K. C., & Kylafis, N. D. 1994, ApJ, 432, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., & Scaramella, R. 2012, MSAIS, 19, 31 [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Cunow, B. 2001, MNRAS, 323, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, R. 1994, MNRAS, 266, 511 [NASA ADS] [Google Scholar]
- Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Cortese, L., Eales, S., et al. 2011, MNRAS, 418, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Popescu, C. C., Tuffs, R. J., et al. 2007, MNRAS, 379, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Hill, D. K., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Emerson, J. P., & Sutherland, W. J. 2010, SPIE Conf. Ser., 7733, 4 [NASA ADS] [Google Scholar]
- Gadotti, A. D. 2008, MNRAS, 384, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, A. D., Baes, M., & Falony, S. 2010, MNRAS, 403, 2053 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W. 2011, Planets Stars Stell. Systems, 6, 91 [Google Scholar]
- Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Worley, C. C. 2008, MNRAS, 388, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Grootes, M., Tuffs, R. J., Popescu, C. C., et al. 2013, ApJ, 766, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Häußler, B., Bamford, S. P., Vika, M., et al. 2013, MNRAS, 430, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyos, C., den Brok, M., Verdoes, K. G., et al. 2011, MNRAS, 411, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. 1926, ApJ, 64, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Jouvel, S., Kneib, J.-P., Bernstein, G., et al. 2011, A&A, 532, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2012, MNRAS, 421, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., & Bahcall, J. N. 1987, ApJ, 317, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Lackner, C. N., & Gunn, J. E. 2012, MNRAS, 421, 2277 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R. J., Duvet, L., Escudero, S. I., et al. 2010, SPIE, 7731, 40 [NASA ADS] [Google Scholar]
- Maltby, D. T., Hoyos, C., Gray, M. E., Aragón-Salamanca, A., & Wolf, C. 2012, MNRAS, 420, 2475 [NASA ADS] [CrossRef] [Google Scholar]
- Martinelli, M., Calabrese, E., de Bernardis, F., et al. 2011, Phys. Rev. D, 83, 023012 [NASA ADS] [CrossRef] [Google Scholar]
- Misiriotis, A., Popescu, C. C., Tuffs, R., & Kylafis, N. D. 2001, A&A, 372, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mo, H., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Möllenhoff, C., Popescu, C. C., & Tuffs, R. J. 2006, A&A, 456, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pastrav, B. A., Popescu, C. C., Tuffs, R. J., & Sansom, A. E. 2012, in The Spectral Energy Distribution of Galaxies, eds. R. J. Tuffs, & C. C. Popescu, Proc. IAU Symp., 284, 306 [Google Scholar]
- Peacock, J. 2008, in A Decade of Dark Energy, eds. N. Pirzkal, & H. Ferguson [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Pierini, D., Gordon, K. D., Witt, A. N., & Madsen, G. J. 2004, ApJ, 617, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Misiriotis, A., Kylafis, N. D., Tuffs, R. J., & Fischera, J. 2000, A&A, 362, 138 [NASA ADS] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Völk, H. J., Pierini, D., & Madore, B. F. 2002, ApJ, 567, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Kylafis, N. D., & Madore, B. F. 2004, A&A, 414, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Madore, B. F., et al. 2005, ApJ, 619, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Dopita, M. A., et al. 2011, A&A, 527, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowlands, K., Dunne, L., Maddox, S., et al. 2012, MNRAS, 419, 2545 [NASA ADS] [CrossRef] [Google Scholar]
- Simard, L., Willmer, C. N. A., Vogt, N. P., et al. 2002, ApJS, 142, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Simard, L., Mendel, J. T., Patton, D. R., et al. 2011, ApJS, 196, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Stickel, M., Lemke, D., Klaas, U., et al. 2000, A&A, 359, 865 [NASA ADS] [Google Scholar]
- Stickel, M., Lemke, D., Klaas, U., Krause, O., & Egner, S. 2004, A&A, 422, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuffs, R. J., Popescu, C. C., Pierini, D., et al. 2002, ApJS, 139, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Tuffs, R. J., Popescu, C. C., Völk, H. J., Kylafis, N. D., & Dopita, M. A. 2004, A&A, 419, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlahakis, C., Dunne, L., & Eales, S. 2005, MNRAS, 364, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
All Figures
 |
Fig. 1 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from pure exponentials due to projection effects. Solid upper curves are for B-band dust-free images, dashed curves are for corresponding exponential fits, while absolute residuals (simulation-fit) are represented by solid lower curves. The fits were made by fixing the position of the intensity peak of the fitted image to the geometrical centre of the map, which, in this case, corresponds to the intensity peak in the simulated image. The cuts were taken parallel and perpendicular to the major-axis of the disk images, through their geometrical centres, at inclinations 1 − cos(i) = 0.3,0.7,0.9 (i = 46°,73°,84°). Lower row: corresponding relative residuals |
| In the text | |
 |
Fig. 2 Projection effects corrproj on the derived B-band photometric parameters of disks fitted with exponential functions (black) and with Sérsic functions (red): scale-lengths, axis-ratios, and central surface brightnesses. The symbols represent the measurements while the solid lines are polynomial fits to the measurements.The plots represent the inclination dependence of left − the ratio between the intrinsic scale-lengths, Ri, and the intrinsic (radial) scale-length of the volume stellar emissivity, R0; middle − the ratio between the intrinsic axis-ratio, Qi, and the axis-ratio of an infinitely thin disk, Q0; with the dashed line we overplotted the analytic formula from Driver et al. (2007), which is a modification of the Hubble formula from Hubble (1926), to take into acount the thickness of the disk; right − the ratio between the central surface brightness of the fitted images and of the coresponding simulated images, ΔSB0, expressed in magnitudes. In the case of a Sérsic fit, Ri (left panel) is the equivalent intrinsic scale-length, calculated from the derived intrinsic Sérsic effective radius, |
| In the text | |
 |
Fig. 3 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from Sérsic functions due to projection effects. Solid upper curves are for B-band dust-free images, dashed curves are for corresponding variable-index Sérsic fits, while absolute residuals (simulation − fit) are represented by solid lower curves. The fits were made by fixing the position of the intensity peak of the fitted image to the geometrical centre of the map. The cuts were taken parallel and perpendicular to the major-axis of the dust-free disk images, through their geometrical centres, at inclinations 1 − cos(i) = 0.3,0.7,0.9 (i = 46°,73°,84°). Lower row: corresponding relative residuals |
| In the text | |
 |
Fig. 4 Inclination dependence of the Sérsic index |
| In the text | |
 |
Fig. 5 Derived Sérsic index |
| In the text | |
 |
Fig. 6 Projection effects corrproj on the derived effective radius of the bulge. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the ratio between the intrinsic Sérsic effective radii, |
| In the text | |
 |
Fig. 7 Major and minor-axis disk profiles (upper and middle rows) showing the deviations from pure exponentials due to the combination of dust and projection effects. Solid upper curves are for B-band dusty disk images, for |
| In the text | |
 |
Fig. 8 Dust effects corrdust on the derived scale-length of disks fitted with exponential functions. The symbols represent the measurements while the solid line are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic scale-lengths Rapp and Ri respectively, as a function of inclination (1 − cos(i)), for the B and K optical bands. From bottom to top, the curves are plotted for |
| In the text | |
 |
Fig. 9 Dust effects corrdust on the derived central surface brightnesses of disks fitted with exponential functions. The symbols represent the measurements while the solid line are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic average central surface-brightness, ΔSB, expressed in magnitudes, versus inclination (1 − cos(i)), for the B and K optical bands. From bottom to top, the curves are plotted for |
| In the text | |
 |
Fig. 10 Major- and minor-axis disk profiles (upper and middle rows) showing the deviations from a general Sersic profile due to the combination of dust and projection effects. Solid upper curves are for B-band dusty disk images, for |
| In the text | |
 |
Fig. 11 Left panels: the inclination dependence of the derived Sérsic index for disks fitted with Sérsic functions, due to combined dust and projection effects. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Right panels: the same but corrected for projection effects ( |
| In the text | |
 |
Fig. 12 Dust effects corrdust on the derived effective radius of disks fitted with Sérsic functions. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the ratio between the apparent and intrinsic Sérsic effective radii, |
| In the text | |
 |
Fig. 13 Face-on major-axis profiles for the thin disk showing the deviations from pure exponentials due to dust effects. Solid upper curves are for the face-on dusty images, the corresponding exponential fits are represented by dashed curves, while the solid lower curves denote the residuals. The upper plots correspond to the 912 Å UV wavelength and |
| In the text | |
 |
Fig. 14 Dust effects corrdust on the derived scale-length of thin disks fitted with exponential functions. The symbols represent the measurements while the solid lines are polynomial fits to the measurements. The plots represent the inclination dependence of the ratio between the apparent and intrinsic scale-lengths, Rapp and Ri respectively. From left to right, the plots corresponds to increasing UV wavelengths: 912 Å, 1500 Å, 2200 Å, and 2800 Å. From bottom to top the black curves are plotted for |
| In the text | |
 |
Fig. 15 Same as in Fig. 14, for the optical bands and the Hα line. From bottom to top the black curves are plotted for |
| In the text | |
 |
Fig. 16 Upper row: inclination dependence of the derived Sérsic index for the dusty images of thin disks fitted with Sérsic functions. Lower row: same, for the ratio between the apparent and intrinsic Sérsic effective radii, |
| In the text | |
 |
Fig. 17 Same as in Fig. 16 top, for the optical bands and the Hα line. |
| In the text | |
 |
Fig. 18 Same as in Fig. 16 bottom, for the optical bands and the Hα line. |
| In the text | |
 |
Fig. 19 Left: inclination dependence of the derived Sérsic index of bulges due to combined dust and projection effects, in the B-band, for simulations having volume stellar emissivities described by different Sérsic indices, |
| In the text | |
 |
Fig. 20 Inclination dependence of the derived Sérsic index of bulges due to dust effects only (corrected for projection effects), for bulges truncated at three effective radii (black curves) and at ten effective radii (red curves). The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Results are for the B-band and for simulations corresponding to a volume stellar emissivity described by a (deprojected) Sérsic function with |
| In the text | |
 |
Fig. 21 Left: simulated image of a bulge in the B band, seen through the dust disks, having |
| In the text | |
 |
Fig. 22 Left panels: inclination dependence of the derived Sérsic index for the exponential bulges ( |
| In the text | |
 |
Fig. 23 Dust effects corrdust on the derived effective radius of exponential ( |
| In the text | |
 |
Fig. 24 Inclination dependence of the derived Sérsic index of bulges due to dust effects only (corrected for projection effects), for spherical bulges (axis-ratios of 1.0; black curves) and for our standard bulges with axis-ratios of 0.6 (red curves). The symbols represent the measurements while the solid lines are polynomial fits to the measurements. Results are for the B-band and for simulations corresponding to a volume stellar emissivity described by a (deprojected) Sérsic function with |
| In the text | |
 |
Fig. 25 The wavelength dependence of the Sérsic index (top) and effective radius (bottom) predicted to be measured on a disk population, due to the effect of dust only (black). The recent measurements from the GAMA survey, from Kelvin et al. (2012), are overplotted in red. All the plots are normalised to the corresponding measurement in the r band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.