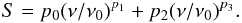| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201220517 | |
| Published online | 16 May 2013 | |
Long-term variability of extragalactic radio sources in the Planck Early Release Compact Source Catalogue⋆
1 Infrared Processing and Analysis Centre, California Institute of Technology, Pasadena, CA 91125, USA
e-mail: xchen@ipac.caltech.edu
2 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
3 Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, Santander, Spain
4 Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
5 California Institute of Technology, Pasadena, California, USA
6 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
7 Haverford College Astronomy Department, 370 Lancaster Avenue, Haverford, Pennsylvania, USA
8 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received: 8 October 2012
Accepted: 18 January 2013
Combining measurements taken using the Wilkinson Microwave Anisotropy Probe (WMAP) from 2001 to 2008 with measurements taken using Planck from 2009 to 2010, we investigate the long-term flux density variability of extragalactic radio sources selected from the Planck Early Release Compact Source Catalogue. The single-year, single-frequency WMAP maps are used to estimate yearly-averaged flux densities of the sources in the four WMAP bands: Ka (33 GHz), Q (41 GHz), V (61 GHz), and W (94 GHz). We identify 82, 67, 32, and 15 sources respectively as variable at greater than 99% confidence level in these four bands. The amplitudes of variation are comparable between bands, and are not correlated with either the flux densities or the spectral indices of the sources. The number counts of WMAP Ka-band sources are stable from year to year despite the fluctuation caused by individual source variability. Most of our sources show strong correlation in variability between bands. Almost all the sources that show variability are blazars. We have attempted to fit two simple, four-parameter models to the time-series of 32 sources showing correlated variability at multiple frequencies – a long-term flaring model and a rotating-jet model. We find that 19 sources (60%) can be fit with the simple rotating-jet model, and ten of these also fit the simple long-term flaring model. The remaining 13 sources (40%) show more complex variability behaviour that is not consistent with either model. Extended radio galaxies in our sample show no sign of variability, as expected, with the exception of Pictor A for which we report evidence for a millimetre flare lasting between 2002 and 2010.
Key words: surveys / radio continuum: galaxies / BL Lacertae objects: general / quasars: general / galaxies: individual
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A107
© ESO, 2013
1. Introduction
Compact radio sources are the most significant contaminant at small angular scales in high-precision cosmic microwave background (CMB) experiments such as the Wilkinson Microwave Anisotropy Probe (WMAP, Bennett et al. 2003a) and the Planck1 satellite (Planck Collaboration 2011a). In the frequency range 20–100 GHz, which includes all the WMAP bands and the lower-frequency Planck channels, the radio source population is dominated by compact, flat-spectrum sources (Bennett et al. 2003b; Hinshaw et al. 2007; Wright et al. 2009; Planck Collaboration 2011c), many of which are variable on time-scales ranging from days to years (Planck Collaboration 2011d,e). The Planck Early Release Compact Source Catalogue (ERCSC, Planck Collaboration 2011b) lists bright sources detected by the Planck satellite during the first 1.6 sky surveys at all nine frequency channels. For some of the extragalactic radio sources, the spectral shape at Planck frequencies suggests that they have been caught in a bright, flaring stage (Planck Collaboration 2011d). Knowledge of variability is thus essential in order to correctly account for the contamination of the CMB measurements by radio sources.
Characteristics of relevant WMAP and Planck bands in this study.
Most variable extragalactic sources are active galactic nuclei (AGN), and the most extreme variability is seen in blazars. Relativistically beamed, non-thermal emission dominates the spectral energy distribution (SED) of blazars over other components such as dust emission from the galaxy or unbeamed synchrotron emission from radio galaxy lobes. Relativistically beamed sources are prone to variability for two reasons: (a) the emission is strongly Doppler boosted, so small changes of the Doppler factor caused by variations of the bulk Lorentz factor or the viewing angle can lead to strong variability; (b) in a relativistic jet, any small perturbation at the origin of the jet can cause the formation of shocks (e.g., Begelman et al. 1984). Variability caused by changes in Doppler boosting, also called geometric variability, changes the spectrum only slowly if at all (e.g., Begelman et al. 1980; Camenzind & Krockenberger 1992; Steffen et al. 1995; Villata & Raiteri 1999). Flares produced by shocks in the plasma flow can lead to strongly frequency-dependent variability on shorter time scales, while also contribute to largely achromatic variability on longer time scales (e.g., Marscher & Gear 1985; Valtaoja et al. 1988).
Studies of radio source variability in the radio-to-millimetre regime on time-scales up to several decades have been facilitated by monitoring programmes targeting medium or large source samples selected by known variability (Aller et al. 1996; Tornikoski et al. 1996; Aller et al. 1999; Stevens et al. 1994), radio spectrum (Valtaoja et al. 1992; Teraesranta et al. 1998; Nieppola et al. 2007), or gamma-ray brightness (Fuhrmann et al. 2007, and in prep.). Discussions of blazar variability have mostly been focused on understanding the characteristics of flares, which are observed on time scales ranging from one day or less (Wagner et al. 1995) to weeks or months (e.g., Angelakis et al. 2012) to several years (Hovatta et al. 2009), and their interpretation in the framework of jet models (e.g., Valtaoja et al. 1999; Lähteenmäki et al. 1999; Lähteenmäki & Valtaoja 1999; Türler et al. 2000; Ciaramella et al. 2004; Hovatta et al. 2009; Angelakis et al. 2012). While it is generally accepted that shock-produced flares dominate the variability on very short time scales (days to weeks), geometric variability should have an effect on longer time scales because rotation or precession, as suggested by VLBI observations of many jets (e.g., Kellermann et al. 2004), would inevitably lead to changes in Doppler boosting of the radiative zones in the jet. Indeed, Bach et al. (2006) have modelled optical and radio time-series of blazars observed in the monitoring campaigns of the Whole Earth Blazar Telescope (WEBT, Villata et al. 2002, 2004) in the framework of inhomogeneous, rotating helical jets (Villata et al. 1998; Villata & Raiteri 1999; Ostorero et al. 2004), and have suggested that all variability down to time scales of ~ 100 days can be explained by geometric effects alone.
In this paper, we report results on long-term flux density variations of a sample of sources selected from the Planck ERCSC. We primarily use data collected by WMAP and Planck. WMAP started its observations at the second Sun-Earth Lagrange point (L2) in August 2001, and ended the collection of science data on 19 August 2010. Planck started its observation at L2 on 13 August 2009 and is still taking data. Both telescopes take about 6 months to complete a single sky survey. Since the lower four frequency bands of Planck overlap with the upper four frequency bands of WMAP, and both telescopes have the powerful ability to make near-simultaneous measurements at multiple frequency bands, combining the observations from the two experiments across an interval of nearly ten years provides the best opportunity to track the long-term variations of radio sources at frequencies between 30 and 100 GHz. Table 1 lists the central frequencies and beam-widths of the WMAP and Planck bands that are of interest here.
We describe the selection of our sample from the Planck ERCSC in Sect. 2. In Sect. 3 we introduce the WMAP data used in our analysis and the method of estimating source flux densities from the WMAP maps. Source variability is quantified and studied statistically in Sect. 4. In Sect. 5, we analyse the long-term averaged variability patterns of strongly variable blazars in our sample. We then discuss the interesting case of long-term variability in unbeamed radio sources in Sect. 6. The results are put into perspective with other studies in Sect. 7, and we conclude in Sect. 8.
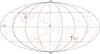 |
Fig. 1 Map in Galactic coordinates showing the locations of the 198 extragalactic sources selected from the Planck ERCSC. The north ecliptic pole (NEP) and the south ecliptic pole (SEP) are indicated by crosses. Source densities are higher near the ecliptic poles, where Planck has longer integration time. |
2. Sample selection and Planck data
The Planck ERCSC (Planck Collaboration 2011b) is a catalogue of highly reliable sources (with ≥ 90% cumulative reliability), both Galactic and extragalactic, detected over the entire sky in the first 1.6 Planck sky surveys. This catalogue provides separate lists of sources detected in each of the nine Planck frequency channels (30 to 857 GHz). We restricted our sample selection to the Planck 30, 44, 70, and 100 GHz channels that overlap with the WMAP Ka to W bands, and excluded sources close to the Galactic plane ( | b | < 5°). We first collated the lists at these four frequencies and constructed a “band-merged” catalogue listing the sources detected in all four channels. The band-merging process was based on positions only. No brightness information was used, to avoid biasing towards or against any class of sources. The source list at each frequency was used as the seed catalogue and counterparts were sought in the candidate catalogues, i.e., the source lists at the other frequencies. The matching radius was always defined as half of the full width at half maximum (FWHM) of whichever band (seed or candidate) has lower resolution. A confusion check was then performed to ensure a one-to-one reciprocal relation between matches across all four bands. Due to the change in resolution, there was one case in which the 44 GHz source could be matched with two sources at 100 GHz; we excluded this source. We then cross-checked this list with both the NASA/IPAC Extragalactic Database (NED2) and the SIMBAD Astronomical Database3 to remove any Galactic objects (H ii regions, planetary nebulae, supernova remnants, etc.). This process yielded a final list of 198 extragalactic sources, including 135 flat-spectrum radio quasars (FSRQs), 26 BL Lacertae objects (BLLs), 28 non-blazar active galaxies (AGNs, including many extended radio galaxies), 1 starburst galaxy (SBG), 1 normal galaxy (GAL), and 7 radio sources of uncertain type. The classification of the active galaxies was taken from the Candidate Gamma-Ray Blazar Survey (CGRaBS, Healey et al. 2008), the third edition of the Roma-BZCAT blazar catalogue (Massaro et al. 2011), and the twelfth edition of the Catalogue of Quasars and Active Nuclei (Véron-Cetty & Véron 2006). Figure 1 shows the distribution of the sources on the sky. We emphasize that there is no guarantee that the sample is complete. In addition, requiring that a source be seen in all the Planck bands between 30 and 100 GHz will inevitably favour flat-spectrum radio sources.
The calibration of the Planck 30–100 GHz maps is currently based on the CMB dipole (Zacchei et al. 2011; Planck HFI Core Team 2011). Since the ERCSC flux densities were calculated directly from the maps and are therefore only correct if the source has a CMB spectrum, colour corrections are needed for sources with different spectra. To determine the spectra, we looked for the counterparts of our sources in the higher-frequency (143 − 857 GHz) ERCSC source lists. We then fit the SED of each source over all the frequencies at which it was detected, using three simple models, when there were enough data points for fitting:
Here pi (i = 0,1,2,3) denote parameters that are different in each model. Since the Planck 100 GHz data can be significantly contaminated by the CO (J = 1 → 0) line at 115 GHz (Planck HFI Core Team 2011), we did not include the 100 GHz flux densities in the SED fitting. A model fit was accepted when the χ2 values indicated that the model was compatible with 95% of the data. In cases when more than one model was acceptable, we always selected the model with fewest parameters unless an additional parameter significantly improved the value of the reduced χ2 (as described in Bevington & Robinson 2003). A few examples of the source SEDs and our fitted models are given in Fig. 2. For sources with a good fit (144 out of the 198 sources), we used the model to estimate the spectral index α (S ∝ ν α) at the Planck central frequencies. For sources that could not be reasonably fit by any of the models, flux densities in the adjacent bands were used to estimate the spectral indices. We then applied the corresponding colour corrections given in Zacchei et al. (2011) and Planck HFI Core Team (2011). These range from almost no change to 5.7%, depending on frequency and source spectral shape. The absolute calibration errors are at the 1% level for the Planck 30–70 GHz channels, and 2% level for the 100 GHz channel. We conservatively assumed an overall calibration uncertainty of 3% and added it in quadrature with the ERCSC flux density errors prior to modelling the spectra.
 |
Fig. 2 Examples of source SEDs and fitted models (grey solid line). The reduced χ2 values are indicated. |
3. WMAP data
The WMAP individual-year maps from 2001 to 2008 and the flux measurements of our sources from these maps constitute the main dataset of this paper, which is described in this section. To support our analysis, we have also used some ground-based data from the Effelsberg 100-m telescope, the IRAM 30-m telescope, and the Metsähovi 14-m telescope. We defer the description of these data to the sections where they are used.
3.1. WMAP maps and photometry
The high-resolution (Nside = 1024 in the HEALPix scheme, Górski et al. 2005) WMAP single-year, single differencing-assembly (DA) maps4 from 2001 to 2008 are the basis of this study. Since the ERCSC was derived from single-frequency Planck maps, we performed a weighted, pixel-by-pixel, mean of the single DA maps from each year to generate single-year maps at each WMAP frequency. The number of observations per pixel was used as the weight. The average temperature outside the WMAP seven-year KQ85 mask (Gold et al. 2011) was subtracted from the single DA maps before the weighted mean was calculated.
For consistency with the ERCSC flux density measurements, we used aperture photometry to obtain flux densities for the Planck-detected sources from the WMAP maps. The source position was taken from the ERCSC 100 GHz catalogue as this band has the highest resolution of the four bands considered here. We measured the flux density in a circular aperture with radius equal to 1.1 times the nominal FWHM of the WMAP beam at each frequency, and subtracted an estimate of the local background, computed as the median intensity within a concentric annulus. The size of the aperture is chosen to include ≳ 95% of the source power in the K- to V-bands, which was calculated from the WMAP seven-year beam radial profile5. Due to a significant shoulder in the W-band beam profile at 0 2–0
2–0 5 (Page et al. 2003), this aperture only includes ~ 85% of the source flux in the W-band. To have ≳ 95% of the source power in the aperture, we would have to adopt an aperture radius of 2 × FWHM in this band, which would then include too much noise from the background. We therefore decided to stay with an aperture radius of 1.1 × FWHM for the W-band, and correct for the flux loss using Monte Carlo simulations (see the next paragraph). Similarly, we calculated at each band the radial distance from the center of the beam that includes 97.5% of the source power (~1.3, 1.3, 1.4, 1.7, or 2.4 times the corresponding beam FWHM at K, Ka, Q, V, or W band), and used this for the inner radius of the annulus to avoid over-subtraction of the source. We then chose the outer radius to make the area of the annulus approximately the same as the aperture.
5 (Page et al. 2003), this aperture only includes ~ 85% of the source flux in the W-band. To have ≳ 95% of the source power in the aperture, we would have to adopt an aperture radius of 2 × FWHM in this band, which would then include too much noise from the background. We therefore decided to stay with an aperture radius of 1.1 × FWHM for the W-band, and correct for the flux loss using Monte Carlo simulations (see the next paragraph). Similarly, we calculated at each band the radial distance from the center of the beam that includes 97.5% of the source power (~1.3, 1.3, 1.4, 1.7, or 2.4 times the corresponding beam FWHM at K, Ka, Q, V, or W band), and used this for the inner radius of the annulus to avoid over-subtraction of the source. We then chose the outer radius to make the area of the annulus approximately the same as the aperture.
For studying variability, it is important to have unbiased flux density measurements and reliable estimates of their uncertainties. Since we do not know whether the aperture is perfectly centered on each source and we do not have precise estimates of the background, we estimated aperture corrections using a Monte Carlo method. We injected fake point sources into the WMAP maps at random positions and compared the extracted flux densities with the input. The flux densities of the artificial sources had a flat dlog N/dlog S distribution (equal numbers of sources per decade of S) in the range 100 mJy < S < 200 Jy. The sources were first injected into single pixels in an empty Nside = 4096 map, which was then smoothed with the WMAP beam profile appropriate for the chosen frequency and degraded to Nside = 1024 before being added to the WMAP single-year maps at that frequency. We then performed the same aperture photometry at the input source locations, excluding those at | b | < 5° and those within 2° of other fake sources or sources in the WMAP seven-year source catalogue (Gold et al. 2011). To minimize collisions of fake sources, we injected 1000 sources in each map and iterated five times to get a sample of ~ 5000 fake measurements. We used the distribution of the ratio of extracted to input flux density to estimate a bias correction factor, which was typically ~ 10–20% except at the W-band.
We estimated the uncertainties in the flux densities obtained from the aperture photometry by error propagation in the formula for the aperture flux density, assuming white uncorrelated noise. This assumption is justified for instrumental noise, but not for noise in the background. We therefore used Monte Carlo simulations to test our error estimates, by injecting 1000 sources with the same flux density (from 1 Jy to 20 Jy in 1 Jy steps) in each map, and using the dispersion of the recovered flux densities as an indicator of the “true” uncertainty. We found that the flux density uncertainties from the white noise model were always less than those returned from Monte Carlo simulations, as expected. However, when repeating the same process on CMB-subtracted maps (subtracting the WMAP seven-year internal linear combination CMB map at | b | > 30°), the simulation results agree well with the white-noise estimates, showing that the correlated noise is mostly CMB. Since CMB noise is constant from year to year and therefore will not affect the variability analysis, we decided to use the flux density uncertainty returned directly from the white-noise model in our study.
The absolute calibration of WMAP data is based on the CMB monopole temperature and the velocity-dependent dipole resulting from WMAP’s orbit about the solar system barycentre, and has an absolute calibration uncertainty of 0.2% (Jarosik et al. 2011). The aperture correction error measured from simulations varied between 0.4% and 1.3% in the K to W bands. We therefore assumed an overall 2% error from aperture correction and calibration, and added it in quadrature with the flux density uncertainty to constitute the final error term for the flux density of each source.
We fit the SED of each source at each year with a single power law (Eq. (1)), and applied colour corrections to the central frequencies, following the recipe of Jarosik et al. (2003). The WMAP single-year maps are generally much noisier than the Planck maps, especially at the V and W bands where even the seven-year co-added maps are less sensitive than the one-year Planck maps (see Planck Collaboration 2011b, Fig. 5). As a result, the flux density estimates can sometimes be negative for faint sources at certain frequencies in some years. In the SED fitting, we only used the good quality (defined as S > 3σ) flux density measurements. A 3σ threshold (~99.7% probability that the signal is truly positive assuming the background is Gaussian) is adopted and considered sufficient in our case as we look for a positive signal at the location of a known source. We do, however, caution that in non-Gaussian backgrounds a 3σ threshold raises the risk of deriving incorrect flux density and error estimates. Although the WMAP K-band (23 GHz) flux densities were not used in the variability study because there is no corresponding channel in Planck, we included them in the SED fitting to obtain more accurate spectral indices.
The WMAP single-year flux densities for our sources, together with the Planck ERCSC flux densities extrapolated to the WMAP centre frequencies (using the SED models described in Sect. 2), are listed in Table 2. These flux density values are used to construct light curves for all the sources in our sample. The full set of light curves is available in Fig. D.1, arranged in ascending order of Right Ascension. Only light curves that have four or more good quality measurements in the seven years of WMAP data are plotted (see Sect. 4 for detailed discussion). For sources that are specifically discussed in the paper, individual light curves are presented where they are discussed. We show all the flux density measurements with S > 2σ, with dash-dot lines indicating 3σ noise level at each frequency. Since the flux measurements here are generally averages over a fraction of a year (see Sect. 3.2), all the data points are plotted at a nominal epoch in February of each year, as both WMAP and Planck single year observations start in mid-August. The effective epoch of each observation may differ by a few months from the nominal epoch.
Flux densities at WMAP Ka, Q, V, and W band for the 198 extragalactic radio sources selected from the ERCSC.
3.2. Difference between WMAP and Planck flux density measurements
WMAP and Planck employ different scanning strategies, and when comparing flux density measurements from the two telescopes it is important to understand how they are affected by the scanning strategy.
The WMAP satellite is a differential experiment, and its optical system consists of two back-to-back telescopes that measure the difference in temperature between two points separated by 141deg on the sky. The satellite spins around its symmetry axis once every 2.2 min while the spin axis precesses at 22.5deg h-1 about the Sun-WMAP line. Since each telescope line of sight is ~70deg off the symmetry axis, the combined motion of spin and precession causes the observing beams to fill an annulus centered on the local solar vector, with inner and outer radii of ~48deg and ~93deg, respectively6. Although this complex scanning strategy provides many repeated observations (WMAP observes more than 30% of the sky each day), the coverage is not uniform. For example, in one year, a source on the ecliptic plane can be seen continuously for 1.5 months, then off for 3 months, then on for another 1.5 months, then off for 6 months; while a source at 48deg ecliptic latitude or higher can be seen for 6 months straight, and then not seen for another 6 months. Sources close to the ecliptic poles are seen continuously throughout the year. Therefore, flux densities estimated from a single-year map are averages over a different fraction of the year for each source.
The Planck satellite spins around its axis at a rate of one rotation per minute. The focal plane is oriented at an angle of 85deg to the spin axis, which tracks the direction of the Sun at ~1deg per day (Planck Collaboration 2011a). This scan pattern also results in inhomogeneous integration time, and areas near the ecliptic poles are observed with greater depth than the rest of the sky. Most sources are seen for a few days every six months. Since the data included in the ERCSC amount to 1.6 full-sky surveys (Planck Collaboration 2011b), some of the sources in our sample have been covered twice with a time separation of ~6 months. Therefore, with the exception of sources close to the ecliptic poles, the flux densities given in the ERCSC are mostly from a single snapshot or an average of two passes, rather than an average over a substantial fraction of a year.
Because of these differences, we treat the WMAP single-year flux densities and the ERCSC flux densities differently in our analysis. To avoid systematic errors, we include only the WMAP flux densities in the statistical studies of the source variability. The ERCSC flux densities, extrapolated to the WMAP frequencies, while helpful in confirming the long-term trend for sources exhibiting long-term variability, are more sensitive to short-term variability (e.g., flares). An example is given in Fig. 3, where the top panel shows that the highly variable source 3C 273 maintains a steep spectrum in the WMAP year 1 to year 7 observations, but its spectrum suddenly becomes flat in the ERCSC. This is because this source was undergoing a strong flare during the time Planck observed it (1–10 January 2010). Ground-based observations with the Effelsberg 100-m and IRAM 30-m telescopes (obtained within the framework of the F-GAMMA programme; Fuhrmann et al. 2007, and in prep.) show that this source has undergone a few flares in the years 2007–2008 while generally preserving a steep spectrum (Fig. 3, bottom panel). The January 2010 observation at the Effelsberg telescope was obtained near-simultaneously with the Planck data, and confirms the flaring activity captured by Planck.
Variable sources in our sample (198 sources in total).
 |
Fig. 3 Top: WMAP/Planck light curves of 3C 273. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols. Bottom: spectra of 3C 273 from Planck, Effelsberg, and IRAM observations at several epochs. The 201001 Effelsberg 100-m observation is nearly simultaneous with the Planck observation, and confirms the flare seen by Planck. |
4. Flux density variability
In this section we quantify and discuss the variability properties of the sources in our sample. We first define and discuss different measures of variability in accordance with those used in the literature, then investigate possible effects of variability on source number counts, and finally discuss correlation between variability found in different bands. In all steps of our analysis, we define incremental quality cuts to select sources which are included in the analysis. These cuts are chosen in order to maximize the number of sources included while keeping the results robust. We discuss qualitative statistical trends found in our sample, but emphasize that no quantitative significance levels can be assigned to them owing to the incompleteness of the sample.
4.1. Quantifying variability
We define the fractional variability index, Vrms, by 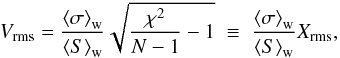 (4)where
(4)where  (5)is the mean of the N individual flux measurements Si, weighted by their individual inverse variances corresponding to the measurement error σi, and
(5)is the mean of the N individual flux measurements Si, weighted by their individual inverse variances corresponding to the measurement error σi, and 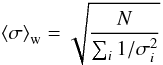 (6)is the average error of the measurements contributing to the weighted mean. The quantity χ2 is defined as
(6)is the average error of the measurements contributing to the weighted mean. The quantity χ2 is defined as 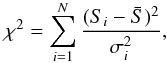 (7)where
(7)where  , and χ2/(N − 1) is the reduced χ2 of the sample for N − 1 degrees of freedom (assuming Gaussian errors). The term Xrms gives the variability amplitude in units of the average measurement error. As explained in Appendix A.1, our Vrms is equivalent to the quantity used by Sadler et al. (2006), but generalised for the case of small sample size and unequal measurement errors.
, and χ2/(N − 1) is the reduced χ2 of the sample for N − 1 degrees of freedom (assuming Gaussian errors). The term Xrms gives the variability amplitude in units of the average measurement error. As explained in Appendix A.1, our Vrms is equivalent to the quantity used by Sadler et al. (2006), but generalised for the case of small sample size and unequal measurement errors.
As defined in Eq. (4), Vrms naturally connects the variability amplitude of a source with the statistical significance of its being variable (see Appendix A.2). Following Bolton et al. (2006) and Franzen et al. (2009), χ2 is used to test the null hypothesis that each source is non-variable (i.e., having constant flux density) at each frequency. We classify a source as strongly variable when the χ2 value indicates that the probability of the null hypothesis is less than 1% (i.e., source is variable at > 99% confidence level). For N = 7 (corresponding to seven years of WMAP measurements), we have N − 1 = 6 degrees of freedom, which requires χ2 > 16.8 or Vrms > 1.34⟨σ⟩w/⟨S⟩w in order to claim a source strongly variable. Additionally, we use Vrms > ⟨σ⟩w/⟨S⟩w (or Xrms > 1), corresponding to a confidence level of ~ 95%, to classify a source as moderately variable. Other sources are not considered to be significantly variable. Since the sampling of WMAP and Planck are different (see Sect. 3.2), we have used only the WMAP flux density measurements in the calculations here to avoid systematic errors.
For many sources, especially at higher frequencies, we do not have good quality (i.e., Si > 3σi) measurements for all years. We require at least four good data points (i.e., N3σ ≥ 4) at a given frequency to include a timeline in our variability analysis, and use Si = 3σi as fiducial data points to fill in the years without good measurements. As discussed in Appendix A.2, this leads to true lower limits for χ2 and Vrms. This approach also ensures that we have no variation in the sampling frequency of our data and formally have N = 7 in all cases. We include all the available Vrms values in Table 2 (expressed as a percentage), and flag strongly variable sources with a “V” and moderately variable sources with a “v” in the notes column.
Table 3 summarizes, for each band, the total number of sources qualified for variability analysis, the number (and fraction) of strongly variable sources with their median fractional variability index Vrms (expressed as a percentage), and the number (and fraction) of all the variable sources (both strongly and moderately variable) with their median Vrms. The percentage of variable sources decreases with increasing frequency, while the level of variability, indicated by median Vrms, increases with frequency. A similar trend has been reported by Franzen et al. (2009) who suggested that it arises because sources tend to have larger flux density uncertainties and smaller flux densities at higher frequencies. Therefore only the sources with the strongest fractional variability can still be found to be variable at high significance at these frequencies. Our definition of Vrms makes this explicit: ⟨ Vrms ⟩ ∝ ⟨ ⟨σ⟩w/⟨S⟩w ⟩ when calculated on a set of sources limited by variability significance (i.e., with a fixed threshold on χ2 and hence Xrms). Since the flux density errors tend to increase and flux densities tend to decrease with frequency in our sample, ⟨ Vrms ⟩ will inevitably increase with frequency even when no true correlation of physical variability and frequency is present. To further test our hypothesis, we selected a subset of sources in our sample that are limited by a minimum 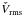 instead of Xrms. We define
instead of Xrms. We define  so that all the sources (across all the frequencies) with
so that all the sources (across all the frequencies) with  would have Xrms > 1. We find
would have Xrms > 1. We find 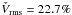 in our sample, which leaves us a subsample of 56, 50, 31, and 20 sources at Ka, Q, V, and W bands, respectively. The median variability indices for this subsample are found to be comparable in all four bands: 30.5% (Ka); 33.0% (Q); 31.4% (V); and 33.0% (W). Although our sample is not statistically complete, this confirms qualitatively the proposed explanation of Franzen et al. (2009) that the trend of increasing variability with frequency may be caused entirely by systematics in source selection, and suggests that on the time scales and the frequency range we are probing, there is no significant increase of physical variability with frequency. Since different physical processes may dominate variability at short and long time scales (see Sect. 5), our finding is not necessarily inconsistent with the conflicting results found on shorter time scales (e.g., Angelakis et al. 2012).
in our sample, which leaves us a subsample of 56, 50, 31, and 20 sources at Ka, Q, V, and W bands, respectively. The median variability indices for this subsample are found to be comparable in all four bands: 30.5% (Ka); 33.0% (Q); 31.4% (V); and 33.0% (W). Although our sample is not statistically complete, this confirms qualitatively the proposed explanation of Franzen et al. (2009) that the trend of increasing variability with frequency may be caused entirely by systematics in source selection, and suggests that on the time scales and the frequency range we are probing, there is no significant increase of physical variability with frequency. Since different physical processes may dominate variability at short and long time scales (see Sect. 5), our finding is not necessarily inconsistent with the conflicting results found on shorter time scales (e.g., Angelakis et al. 2012).
 |
Fig. 4 Dependence of fractional variability index Vrms on mean spectral index ⟨ α ⟩ in Ka, Q, V, and W bands for variable sources. BLLs are shown by filled circles, FSRQs by open circles, and all the other sources by plus signs. The dashed lines indicate the level of |
 |
Fig. 5 Dependence of fractional variability index Vrms on mean flux density ⟨ Sν ⟩ in Ka, Q, V, and W bands for variable sources. BLLs are shown by filled circles, FSRQs by open circles, and all the other sources by plus signs. The dashed lines indicate the level of |
We also tested for possible dependences of variability index on source spectral index and total flux density. For all the variable sources, we calculated the two-point spectral indices (i.e.,  ,
,  ,
, 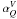 , and
, and 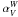 ) for the years when good quality data points were available. Figure 4 plots the fractional variability index of each source against the time-averaged spectral index in each band. We use
) for the years when good quality data points were available. Figure 4 plots the fractional variability index of each source against the time-averaged spectral index in each band. We use  to approximate the spectral index at Ka-band,
to approximate the spectral index at Ka-band,  for Q-band,
for Q-band, 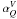 for V-band, and
for V-band, and 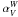 for W-band. The variable sources are clearly dominated by flat-spectrum sources. Unlike Bolton et al. (2006) and Franzen et al. (2009), we do not find that sources with rising spectrum are more variable. We have also plotted the variability indices of all variable sources against their time-averaged flux densities at each frequency (Fig. 5). The apparent tendency for fainter sources to be more variable is not a physical trend, and is caused by the fact that fainter sources have larger relative flux density errors, and thus have a lower Vrms when applying a significance cut (e.g., Xrms > 1). As can be seen from Fig. 5, when only sources with a fractional variability above
for W-band. The variable sources are clearly dominated by flat-spectrum sources. Unlike Bolton et al. (2006) and Franzen et al. (2009), we do not find that sources with rising spectrum are more variable. We have also plotted the variability indices of all variable sources against their time-averaged flux densities at each frequency (Fig. 5). The apparent tendency for fainter sources to be more variable is not a physical trend, and is caused by the fact that fainter sources have larger relative flux density errors, and thus have a lower Vrms when applying a significance cut (e.g., Xrms > 1). As can be seen from Fig. 5, when only sources with a fractional variability above 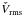 are considered, no significant correlation is found between the amplitude of variability and flux density.
are considered, no significant correlation is found between the amplitude of variability and flux density.
As mentioned in Sect. 2, most of the sources in our sample can be classified as either luminous broad-line FSRQs or continuum-dominated BLLs. In Fig. 6 we plot the distribution of fractional variability index for the sources that are classified as variable in each band. There is no evidence that one class is more variable than the other.
 |
Fig. 6 Histograms of fractional variability index for variable sources; FSRQs are shown in white and BLLs in grey. |
4.2. Modification of source number counts due to variability?
The number of sources with good quality (S > 3σ) data across all seven years of WMAP observations is greatest at the WMAP Ka-band (33 GHz), with ~ 168 ± 12 sources in each year. The number decreases with frequency because most sources have flat or falling spectra, and flux uncertainties are also higher at higher frequencies due to the sensitivities of the maps. We therefore study the influence of source variability on number counts only in the Ka-band. In Fig. 7, we plot the differential number counts of the whole sample at the Ka-band in each year, including the ERCSC observation period. The ERCSC data points displayed here are again the ERCSC 30 GHz flux densities extrapolated to the Ka-band central frequency. Although they vary from year to year, our source counts are largely consistent with the prediction of extragalactic radio source evolutionary models from de Zotti et al. (2005) and Tucci et al. (2011). The departure of the data from the models suggests that our sample is incomplete below 2 Jy. We thus model the source count distribution dN/dS in Ka band as a power law κ(S/Jy)β in each year, with a flux density cut of 2 Jy, using least-squares. The values we obtain are presented in Table 4. We apply a completeness correction to account for the Galactic cut of |b| > 5deg that we used in selecting our sample. The slopes are close to Euclidean. It is clear that although the number counts fluctuate from year to year, they are consistent within the uncertainty. We therefore conclude that individual source variability does not have a significant effect on the source number counts, i.e., the counts are statistically stable, and so the contamination by unresolved sources in the CMB power spectrum that are estimated from the counts will also be stable.
 |
Fig. 7 Euclidean normalised differential number counts at WMAP Ka-band (33 GHz) in each year. The solid curve shows the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) evolution model, and the dashed line represents the total number counts from the Tucci et al. (2011) model. |
WMAP Ka-band source counts in the flux density range 2−20 Jy.
4.3. Correlation analysis
As mentioned in Sect. 1 (see also Sect. 5) geometric variability or low-peaked flares are likely responsible for the variability at the time scales and frequencies probed in our study. Both physical processes predict that the average radio-millimetre spectral shape should remain nearly unchanged during flux variations. We thus expect flux density variations in different bands to be directly correlated. To quantify this correlation, we calculate the Pearson product correlation coefficient, r, between bands for each source. We note that this method quantifies the instantaneous correlation between flux density changes, but is less sensitive to correlated changes with time lags between bands. The existence of significant time lags would reduce the correlation coefficient in our analysis. However, it is our intention in this study to distinguish between long-term ( ≳ 3 yr), frequency independent patterns, and short-term ( ≲ 1 yr), high-peaked flares (see Sect. 5.1). We do not employ more sophisticated methods such as discrete correlation function analysis to quantify possible time lags, as this is not meaningful for a sample containing only seven data points in each timeline.
We analyse the correlations between Ka-band and each of the other bands (Q, V, and W). We restrict our analysis to sources which have been classified as strongly variable in the Ka-band, and satisfy the requirement of N3σ ≥ 4 and N2σ = 7 in each band; we do not require that the source to be classified as variable in the Q, V, or W bands. We include all data points with S > 2σ here to ensure that we have no missing data points in the time lines. Unlike in Sect. 4.1, we cannot use upper limits for flux densities here as this would not lead to any useful limits on r, and the more restrictive requirement N3σ = 7 would leave us with too few time lines to analyse. We regard the variability between two bands as “strongly correlated” if r > 0.875, which corresponds to a probability of less than ~ 1% that the null hypothesis of an uncorrelated variability is true (see Appendix A.3). We regard a value r < 0.3 as indication of no correlation, i.e., a 50% probability to reject perfect correlation. Sources with 0.3 < r < 0.875 are considered “moderately” correlated.
Our criteria select 55, 39, and 21 sources in the Q, V, and W band, respectively, for correlation analysis. Of these sources, 58%, 46%, and 28% show strong correlation with the Ka band, and 40%, 49%, and 57% show moderate correlation. The majority of our sources show correlated variability between Ka and Q band, which confirms a similar finding by Franzen et al. (2009) between 15 and 32 GHz. Although there may be a moderate trend towards less correlated variability at higher frequencies, this should not be overstated as it may be due to the larger error bars affecting these bands. In general we find that very few variable sources show no direct correlation between Ka and higher-frequency bands. This result may suggest that variability in these frequencies on long time scales is less frequency-dependent than on short time scales (e.g., Angelakis et al. 2012).
5. Variability patterns in blazars
In this section we describe the variability patterns expected in simple models motivated by current understanding of AGNs and extragalactic jets, and search for the signatures of these patterns in the time series of sources in our sample.
5.1. Physics of blazars and models for variability
The term blazar was introduced in the late 1970s to denote the combined class of optical violent variable (OVV) quasars and BL Lac objects (Angel & Stockman 1980). In the radio-to-millimetre range, blazars show featureless, often highly polarised, continuum spectra which are attributed to partially self-absorbed synchrotron emission from relativistically boosted, compact jets emerging from AGN at a small angle θ to the line of sight (e.g., Begelman et al. 1984). If 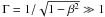 is the bulk Lorentz factor of the relativistic jet plasma, the Doppler boosting factor D = [Γ(1 − β cosθ)] -1 is ~ Γ for θ ≲ Γ-1. This causes the flux density of the synchrotron emission to dominate over unboosted thermal components of the AGN, as Sν ∝ D3 + α. The Doppler factor, bulk Lorentz factor and inclination angle of the jets can be estimated by several methods. Firstly, by comparing number counts of blazars with those of unboosted radio galaxies (Urry & Padovani 1995). Secondly, from superluminal apparent speeds of VLBI components (e.g., Blandford et al. 1977; Ghisellini et al. 1993; Zensus 1997; Kellermann et al. 2004). And thirdly, by exploiting physical constraints on models of radiative emission (Ghisellini et al. 1998; Lähteenmäki et al. 1999; Lähteenmäki & Valtaoja 1999; Hovatta et al. 2009). All these methods allow a consistent estimate of D ~ Γ ~ 10 and θ ~ 5°. Estimates of individual Doppler factors and viewing angles, however, are too model-dependent to be considered reliable (e.g., Hovatta et al. 2009).
is the bulk Lorentz factor of the relativistic jet plasma, the Doppler boosting factor D = [Γ(1 − β cosθ)] -1 is ~ Γ for θ ≲ Γ-1. This causes the flux density of the synchrotron emission to dominate over unboosted thermal components of the AGN, as Sν ∝ D3 + α. The Doppler factor, bulk Lorentz factor and inclination angle of the jets can be estimated by several methods. Firstly, by comparing number counts of blazars with those of unboosted radio galaxies (Urry & Padovani 1995). Secondly, from superluminal apparent speeds of VLBI components (e.g., Blandford et al. 1977; Ghisellini et al. 1993; Zensus 1997; Kellermann et al. 2004). And thirdly, by exploiting physical constraints on models of radiative emission (Ghisellini et al. 1998; Lähteenmäki et al. 1999; Lähteenmäki & Valtaoja 1999; Hovatta et al. 2009). All these methods allow a consistent estimate of D ~ Γ ~ 10 and θ ~ 5°. Estimates of individual Doppler factors and viewing angles, however, are too model-dependent to be considered reliable (e.g., Hovatta et al. 2009).
Blazars are strongly variable down to time scales of ~ 1 day or less. Such rapid variability is usually attributed to the presence of shocks in the jets, which are expected to arise from instabilities inside the jet or from interactions of the jet with an external medium (Begelman et al. 1984). Several phenomenological approaches to the formation and evolution of shocks in jets have been suggested, ranging from persistent moving or standing shock waves (Marscher & Gear 1985; Marscher et al. 2008) to rapid sequences of shocks formed over a large range of scales in the jet (Spada et al. 2001; Guetta et al. 2004; Rachen et al. 2010). Shocks in AGN jets can also provide the sites for efficient particle acceleration (e.g., Biermann & Strittmatter 1987) needed to produce the observed high energy gamma-ray emission (see, e.g., Böttcher 2012).
Another type of variability, usually called geometric variability, is expected in a number of phenomenological models describing helical or precessing motion in jets (Camenzind & Krockenberger 1992; Steffen et al. 1995; Valtaoja et al. 1989; Wagner et al. 1995; Villata & Raiteri 1999; Ostorero et al. 2004; Valtonen et al. 2009, 2011). Because of the strong dependence of the beamed flux on the Doppler factor ( ∝ D3 + α), small changes of the inclination angle θ or the bulk Lorentz factor Γ of the jet will induce large changes in the observed flux. For example, in a source with Γ = 10, θ = 5°, and α = 1, a change of inclination angle by one degree towards the observer increases the measured flux by a factor of two.
These two types of variations are expected to affect the spectrum of the source differently: while shocks naturally produce spectral changes by injecting a new population of energetic particles, geometric effects should not have a large effect on the emitted spectrum. Detailed modelling, however, shows that this simple criterion has to be used with care. For example, the strongly inverted “edges” often seen in the radio-millimetre spectra of variable blazars (Valtaoja et al. 1988; Brown et al. 1989; Krichbaum et al. 2008; Planck Collaboration 2011d,e) can be explained both by synchrotron self-absorbed emission from a compact, shocked region with temporarily enhanced emission compared to the surrounding jet (e.g., Valtaoja et al. 1988; Brown et al. 1989; Türler et al. 2000; Rachen et al. 2010), and by decreasing inclination angle in a steady but rotating helical jet (Ostorero et al. 2004). The same ambiguity affects the interpretation of helically moving VLBI components (Savolainen et al. 2002; Bach et al. 2006; Rastorgueva et al. 2009; Jorstad et al. 2010). On the other hand, achromatic variability, canonically expected from geometric effects, can also be explained by shock-induced flares if they are observed only above their peak-frequency (so-called low-peaked flares, Valtaoja et al. 1988). Thus, although the overall properties of variability from shocks and from geometric effects can be quite different, the spectral behaviour during flares may not be a reliable way to distinguish the processes.
5.2. Short-term vs. long-term variability
A major difference between geometric and shock induced variability is the observed time scale. In a relativistically boosted emitter, all intrinsic time scales of variability are compressed by the Doppler factor, τobs = τint/D ≪ τint. This applies in particular to the time scales connected to the formation and propagation of shocks in the jet, and allows emission regions of sub-parsec size to produce variability on observed time scales down to a few days. In contrast, the physical time scale of geometric changes are not Doppler compressed, as the rotation is transverse to the jet propagation (τobs ~ τint). If indeed both processes contribute to variability with comparable intrinsic time scale and amplitude, geometric variability should then dominate the amplitude on long time scales. We illustrate below how this affects the patterns observed in long-term averaged data.
 |
Fig. 8 Upper panels: WMAP/Planck light curves for the sources that are better fit by the rotating jet model. The WMAP data are shown by filled symbols and the later Planck data are shown by open symbols. Lower panels: residuals between the normalised WMAP flux densities (Eq. (11)) and the rotating jet model. Grey dash-dot lines indicate the zero level. |
Let 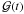 and ℱ(t,ν) denote the time structure of geometric and shock induced (flare) variability respectively, with the total flux of the source being
and ℱ(t,ν) denote the time structure of geometric and shock induced (flare) variability respectively, with the total flux of the source being 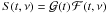 . The WMAP data used in this paper provide regularly sampled 1-year averages, i.e.,
. The WMAP data used in this paper provide regularly sampled 1-year averages, i.e., 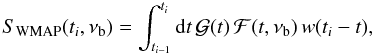 (8)where ti is the end-time of operation year i, νb is the central frequency of the appropriate WMAP band, and w is the exposure function of WMAP in this band (which we assume is approximately the same in every operation year). Equation (8) describes a low-pass filter, suppressing all fluctuations in S(t,νb) on time scales τ ≪ Δt ≡ ti − ti − 1 ~ 1 yr. This is typically the case for the flare process ℱ(t,νb), but not for the geometric process
(8)where ti is the end-time of operation year i, νb is the central frequency of the appropriate WMAP band, and w is the exposure function of WMAP in this band (which we assume is approximately the same in every operation year). Equation (8) describes a low-pass filter, suppressing all fluctuations in S(t,νb) on time scales τ ≪ Δt ≡ ti − ti − 1 ~ 1 yr. This is typically the case for the flare process ℱ(t,νb), but not for the geometric process 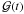 , as its characteristic time scale is not Doppler compressed. Therefore, although large amplitudes of ℱ(t,νb) may cause an irregular structure in S(t,νb), characteristic patterns of
, as its characteristic time scale is not Doppler compressed. Therefore, although large amplitudes of ℱ(t,νb) may cause an irregular structure in S(t,νb), characteristic patterns of 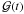 may become more evident when using averaged data. We note that these considerations apply to the WMAP data, but not to the Planck ERCSC data in general. Most ERCSC flux densities represent averages of one or two snapshots, except for a few sources near the ecliptic poles which were observed more often. The flux densities thus retain a significant fraction of the short-term variability amplitude. We therefore discuss the WMAP and ERCSC data separately.
may become more evident when using averaged data. We note that these considerations apply to the WMAP data, but not to the Planck ERCSC data in general. Most ERCSC flux densities represent averages of one or two snapshots, except for a few sources near the ecliptic poles which were observed more often. The flux densities thus retain a significant fraction of the short-term variability amplitude. We therefore discuss the WMAP and ERCSC data separately.
5.3. Test for variability patterns
Geometric variability is not bound to specific simple patterns, as the direction of jet emission can change in potentially chaotic ways. However, a major motivation for proposing geometric variability is the possible connection to helical jet structures shown by VLBI monitoring (see Sect. 7.1), which are thought to originate in a rotating jet base. As discussed in Appendix C, a simple rotating relativistic jet will produce a flux variability pattern of the form ![\begin{equation} \label{eq:rotpattern} S_{\rm rot}(t) = \frac{S_0}{\big( 1 + A \cos[\omega(t-t_0)]\big)^{3+\alpha}} \cdot \end{equation}](/articles/aa/full_html/2013/05/aa20517-12/aa20517-12-eq146.png) (9)Assuming the amplitude A and frequency ω of the oscillation are time-independent, this model involves four free parameters (the spectral index α is determined from the data).
(9)Assuming the amplitude A and frequency ω of the oscillation are time-independent, this model involves four free parameters (the spectral index α is determined from the data).
 |
Fig. 9 Top panels: WMAP/Planck light curves for the sources that are well fit by both the VLTL-flare model and the rotating jet model. The WMAP data are shown by filled symbols and the later Planck data are shown by open symbols. Middle panels: residuals between the normalised WMAP flux densities (Eq. (11)) and the VLTL-flare model. Bottom panels: residuals between the normalised WMAP flux densities and the rotating jet model. Grey dash dot lines indicate the zero level in the residual plots. |
A similarly simple phenomenological description of the time evolution of flares caused by shocks has been introduced by Valtaoja et al. (1999, hereafter VLTL), based on observed flare properties and a generalisation of the “shock in jet” model (Marscher & Gear 1985; Valtaoja et al. 1988). It has been successfully applied to decompose single-frequency blazar light-curves into a constant background and a number of separate exponential flares (see also Nieppola et al. 2009). In the original VLTL model, a flare is described by an exponential rise with time constant τr followed by an exponential decay with time constant τf ≈ 1.3τr. The time scales of such flares can vary between a few months and ~10 yr, with a median of ~3 yr (Nieppola et al. 2009), which is comparable to the time scales probed in this paper. This motivates a four-parameter VLTL pattern as a heuristic description of a single flare or activity phase: 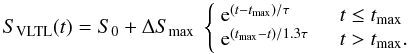 (10)Both models are clearly simplified. Realistic models of helical jets involve complex dependencies on more parameters (Camenzind & Krockenberger 1992; Steffen et al. 1995; Villata & Raiteri 1999), and may potentially include static inhomgenities in the jets (Ostorero et al. 2004). For the VLTL model, Nieppola et al. (2009) showed that the relation τf ≈ 1.3τr holds only as a gross average, while the individual flare decay-to-rise time scale ratio varies between 0.3 and 5. Moreover, it is likely that more than one flare appears during the decade probed by our data. We therefore emphasize that our quest is not to provide fits to the data with realistic models, but to test how well our data can be represented by the simplified models discussed here.
(10)Both models are clearly simplified. Realistic models of helical jets involve complex dependencies on more parameters (Camenzind & Krockenberger 1992; Steffen et al. 1995; Villata & Raiteri 1999), and may potentially include static inhomgenities in the jets (Ostorero et al. 2004). For the VLTL model, Nieppola et al. (2009) showed that the relation τf ≈ 1.3τr holds only as a gross average, while the individual flare decay-to-rise time scale ratio varies between 0.3 and 5. Moreover, it is likely that more than one flare appears during the decade probed by our data. We therefore emphasize that our quest is not to provide fits to the data with realistic models, but to test how well our data can be represented by the simplified models discussed here.
 |
Fig. 9 continued. |
We limit our analysis to sources that show strong correlated variability between Ka band and at least one other band (Sect. 4.3), which ensures a better detection of common patterns between bands. In order to use information from all the bands to determine the best fit parameters of a pattern and its fit quality, we normalize all the data points to a common level at 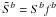 , where
, where 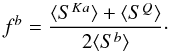 (11)This normalization is somewhat arbitrary, and was chosen mainly for comparability with external data (see Sect. 5.4.3). Using an initial guess for both the VLTL and rotating patterns, we minimize the residual χ2 with respect to the model using the Nelder-Meade simplex method implemented in the GNU scientific library7. We then calculate the residual Xres, defined as
(11)This normalization is somewhat arbitrary, and was chosen mainly for comparability with external data (see Sect. 5.4.3). Using an initial guess for both the VLTL and rotating patterns, we minimize the residual χ2 with respect to the model using the Nelder-Meade simplex method implemented in the GNU scientific library7. We then calculate the residual Xres, defined as 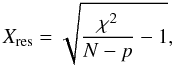 (12)where p = 4 is the number of fitted parameters. We accept a model fit if Xres < 1, or if it reduces the mean of Xrms (defined as in Eq. (4)) from all the bands by a significant factor, i.e.,
(12)where p = 4 is the number of fitted parameters. We accept a model fit if Xres < 1, or if it reduces the mean of Xrms (defined as in Eq. (4)) from all the bands by a significant factor, i.e., 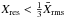 .
.
The one-year averaged WMAP flux densities have equal weighting in each year, and therefore it is correct to space the points by exactly one year when fitting models, even if the exact epoch of each (and hence the reference time of the fit) is uncertain by a few months. We do not use the Planck ERCSC flux densities in the fitting as they have different weighting, and the time spacing relative to the WMAP observations is difficult to determine.
5.4. Results
Among the 32 sources in our sample that show strong correlated variability between Ka-band and at least another band, we find 19 (60%) whose long-term averaged variability pattern is well represented by a simple four-parameter model. The other 13 sources show more complex variability patterns.
5.4.1. Simple patterns
A preference for a rotating jet pattern is found for sources J0428−3756, J0457−2324, J0721+7120, J1159+2914, J1310+3220, J1337−1257, J1733 − 1305, J1924−2914, and J2235−4835. Most of these sources show strongly correlated variability in more than two bands. The rotation periods found are in the range 3–5 yr. The shortest rotation period of 3 yr is found for J1337−1257, which showed more than two complete oscillations within our observing period. The WMAP/Planck light curves of these sources, as well as the fitted pattern, are shown in Fig. 8. Although the fitting is done on the scaled WMAP flux densities, we plot the original WMAP flux densities to demonstrate that the model traces the variation trend of the original data very well. The residuals shown in the bottom panels are, however, the differences between the normalised flux densities and the fit.
 |
Fig. 10 WMAP/Planck light curves for the sources J0538 − 4405, 3C 273 and 3C 279. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. The dashed lines indicate the 3σ level at each band if in the plotted range. |
 |
Fig. 11 WMAP/Planck light curves for the sources J1058+0134, J1549+0236, BL Lac, 3C 446, J2232+1143 and 3C 454.3. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. The dashed lines indicate the 3σ level at each band if in the plotted range. |
For sources J0106−4034, J0253−5441, J0403−3605, J0423−0120, J0440−4333, J0530+1332, J1613+3412, J1635+3807, J1743−0350, and J2258−2757, both the rotating jet model and the VLTL-flare model yield a reasonable match to the long-term flux variation pattern. Figure 9 gives their WMAP/Planck light curves, together with the pattern fit. With the exception of J0423−0120, the rotation periods of these sources in the rotating jet model are found to be ≥7 yr, and the flare time scales in the VLTL-flare model are ~0.5−2 yr. For five sources with rotation periods >10 yr (τ > 1.4 yr) we mostly see only the increasing or decreasing part of the pattern in the time window of our observations.
The Planck ERCSC flux densities, though not used in the fitting, are found to agree well with the model fits in some cases, e.g., J0457−2324, J1310+3220. When both models fit the WMAP data, the Planck flux densities sometimes prefer one model over the other, e.g., J0403−3605 for the rotating-jet pattern, and J2258−2757 for the VLTL-flare pattern. In about 50% of the cases, the Planck data are in disagreement with the fitted pattern. This is likely due to the unmodelled short-term variability and the difference between the actual Planck observation times and the referenced time (set to be exactly 2 yr later than the last WMAP data point).
5.4.2. Sources with complex variability
There are 13 sources for which neither the VLTL-flare model nor the rotating jet model fits the variation pattern well. These sources can be divided into two classes: (1) those showing highly-correlated variability across all bands; and (2) those showing significant differences between the variability patterns at different bands.
In the first category, we find bright FSRQs like 3C 273, 3C 279, and J0538−4405 (Fig. 10). These sources would probably be fitted by a correlated pattern comprising several VLTL flares, or a rotating pattern plus long-term flares. Sources in the second category all show moderately correlated, partially inverted spectra at higher frequencies. A famous example is 3C 454.3, for which our data capture the well-studied millimetre flare from 2005 (Krichbaum et al. 2008). A very strong inversion in the V–W spectral index is also found in source J2232+1143 between 2002 and 2004. In addition, the light curves of BL Lac, 3C 446, J1058+0134, and J1549+0236 all display similar spectral behaviour (see Fig. 11). Such signatures of spectral dependence of variability are well known at shorter time scales, and are expected from physical models of both shock-induced flares and geometric effects in rotating helical jets (Villata & Raiteri 1999; Ostorero et al. 2004).
5.4.3. Comparison with long-term monitoring data
A limitation of our analysis is the small dynamic range in time scales within which our method can distinguish between different patterns; time scales smaller than one year are not resolved, and for time scales longer than a few years our fits become ambiguous, as discussed above.
For the three sources J0423-0120, J0721+7120, and J1310+3220 that are included in the 37 GHz long-term monitoring programme on the Metsähovi radio telescope (Lähteenmäki, priv. comm., see also Teraesranta et al. 1998), we can test the validity of our finding over a long time period (>20 yr). To make the Metsähovi data comparable to our WMAP data, we averaged them into one year bins (see Appendix B). Figure 12 shows the the WMAP Ka and Q band light curves along with the binned Metsähovi 37 GHz data. In all three cases, we find excellent agreement between the Metsähovi binned data and the WMAP data. This confirms that long-term averaged data provide a good and consistent representation of the long-term variability trends, regardless of the details of the averaging method.
The three examples both highlight the potential strengths and reveal the various problems of our approach. For source J0423−0120, neither the Metsähovi data nor the Planck data support the rotating-jet pattern that is compatible with the WMAP data; rather, the binned Metsähovi data suggest that the source underwent a single, strong activity phase between 2001 and 2005, well fitted by a VLTL flare profile with τ ≈ 0.5 yr, superimposed on a flux density which remained roughly constant between 1980 and 2010. For source J0721+7120, both the Metsähovi and the Planck data are consistent with the fitted rotational pattern between 2002 and 2010, but before 1998 the long-term average flux density of the source was continuously in a low state. This could be interpreted as the onset of a new rotating pattern as expected, e.g., in lighthouse scenarios (Steffen et al. 1995). An alternative explanation would be to assume two consecutive long-term flares (or flaring phases) of τ ~ 1 yr in the years after 2002. Finally, for source J1310+3220, the Metsähovi and Planck data are consistent with a continuation of the rotating pattern fitted to the WMAP data alone at least for the period 1998–2010, covering almost two full oscillations. Additionally, the long-term averaged 37 GHz light curve observed between 1983 and 1990 fits the same pattern, with a consistent phase, as expected of geometric variability from stable rotating jet; the departure from the pattern between 1990 and 1998 could be explained by a single superimposed flare (τ ~ 1 yr).
 |
Fig. 12 WMAP/Planck light curves for the sources J0423 − 0120, J0721+7120, and J1310+3220 at 33 GHz (black filled circles) and 41 GHz (red filled triangles), with the Metsähovi 37 GHz long-term monitoring data added (grey stars). For J1310+3220, the residuals between the Metsähovi data and the best fit model are shown. |
6. Variability in unbeamed sources
Our sample includes some bright radio galaxies, which in the standard unification model (e.g., Urry & Padovani 1995) are the unbeamed counterparts of blazars. We note that for a source with inclination angle θ ≫ Γ-1, the contribution of the compact, highly relativistic jets is not only unbeamed, but deboosted with a Doppler factor D ~ 0.1 if the source is exactly viewed from the side. This suppresses its contribution to the total emission of the source by a factor ≳ 106 relative to a beamed blazar. Therefore, in such sources all the emission must come from the extended jets and lobes, which are subdominant in highly beamed blazars.
The extended radio galaxies in our sample, most notably Cen A, Cyg A, and M 87, are all classified as non-variable at all frequencies, which is expected because the emission regions in these sources extend over several kiloparsecs, too large to show significant variability on the time scales we probe. This is a consistency check on the reliability of our photometry.
6.1. A millimetre-wavelength flare in the giant radio galaxy Pictor A
The giant radio galaxy Pic A, however, is an exception: it shows moderate to strong variability in the Ka, Q, and V bands, with χ2 values of 17.0, 18.3, and 15.6, respectively. The flux densities in the WMAP Ka, Q, and V band were generally increasing until 2008. Planck ERCSC data suggest that in 2010 the flux density returned to its 2002 value for all bands (Fig. 13). The χ2 values suggest a combined probability of ~10-6 for constant flux density in all bands, so the variation is highly significant. From the shape of the variation, which is essentially coherent in all bands, we can estimate an observed flare time scale of ~3 yr, assuming an exponential rise, and a somewhat shorter decay time scale.
 |
Fig. 13 WMAP/Planck light curves of the FR II radio galaxy Pic A. |
Pic A is a Fanaroff-Riley class II (FR II) radio galaxy at a redshift z = 0.035. It shows two prominent radio lobes, with bright hot spots terminating the jets at distances of about 140 kpc from the central AGN. They are connected to the AGN by extended jets, which appear to propagate with mildly relativistic speeds (Meisenheimer et al. 1989). Within these central jets, at a distance of ~30 kpc from the AGN, Chandra observations provided evidence for a transient X-ray knot, which apparently decayed within the time scale of ~1 yr (Marshall et al. 2010). Assuming that the X-ray radiation was produced by synchrotron radiating electrons, Marshall et al. (2010) concluded that the magnetic field in the emission region must have been ~2 mG, about 100 times larger than the canonical estimates for the jets of radio galaxies. This magnetic field, however, is still too weak to explain the time scales of the flare observed by WMAP at millimetre wavelengths (also assuming synchrotron origin), therefore we consider it unlikely that the two flares originate in the same region of the jet.
An alternative explanation is that the increase in millimetre flux density is not from the extended jet, but from the central flat-spectrum core, which is almost as bright as the dominant western hot spot at 20 GHz (Perley et al. 1997; Burke-Spolaor et al. 2009; Sajina et al. 2011). Interpreting the variable component as unboosted (D ~ 1) emission from a central blazar, and assuming standard jet parameters, the emission region would have an inclination angle to the line of sight of θ ≈ 25°, and the observed factor-of-two increase in flux density within three years could be explained by a change of inclination angle by ≈ 3° towards the observer. However, this would require a rotational speed significantly larger than that inferred from VLBI observations of the central jet of Pic A, if these are interpreted in a precessing jet model (Tingay et al. 2000). An interpretation of the flare in Pic A as due to a shock in the jet would be more consistent with the misaligned-blazar picture: with a Doppler factor D ~ 10 the Pic A flare would be comparable in intrinsic time scale and peak frequency with the exceptional outburst in 3C 454.3 observed in 2005.
7. Discussion
7.1. Geometric variability and helical jets
Rotating jet patterns have been discussed in the literature in connection with VLBI observations of morphologically “curved” or “bent” jets, and of apparent helical motion of parsec-scale jet components (Zensus 1997; Kellermann et al. 2004). Among the sources for which we find a variability pattern matched with the rotating jet model, curved and potentially helical VLBI jets have been observed in J0423 − 0120 (Wagner et al. 1995; Britzen et al. 2001), J0530+1332 (Pohl et al. 1996; Cai et al. 2006), J0721+7120 (Bach et al. 2005), J1159+2914 (Hong et al. 2004; Zhao et al. 2011), J1337 − 1257 (Lister et al. 2009), J1613+3412 (Piner & Kingham 1997), and J1924 − 2914 (Shen et al. 1999; Lister et al. 2009). Helical structures have also been found in the VLBI jet of FSRQ J1310+3220 (Cassaro et al. 2002), for which a rotating pattern with essentially constant period is largely consistent with the flux variation pattern shown in the Metsähovi 37 GHz data (Sect. 5.4.3).
Although our data are consistent with geometric variability, all the above-mentioned sources also show flaring behaviour on short time scales. An extreme example is the BL Lac object J0721+7120, which showed rapid variability on time scales of a day or less (Ostorero et al. 2006). In some sources this flaring activity may have obscured an underlying rotating jet pattern, or in some cases our geometric model may be too simple. For example, BL Lac shows complex long-term variability in our data, but its variations have been sucessfully modelled over much longer time scales as a purely geometric effect, assuming a rotating inhomogeneous helical jet (Bach et al. 2006; Villata et al. 2009).
Long-term rotation cycles have been identified in VLBI observations of 3C 454.3 (Qian et al. 2007) and 3C 279 (Carrara et al. 1993); both sources show strong variability correlation between bands, but a complex variability pattern in our data (Sect. 5.4.2). Source J0423 − 0120 shows a pattern compatible with the rotating jet model in the WMAP data, but the 25-year Metsähovi 37 GHz light curve does not support a rotational pattern.
There are a few helical jet candidates that are not included in our variability pattern test due to weak correlation of variability between WMAP bands. These include 3C 84 (NGC 1275, Krichbaum et al. 1992), 3C 345 (Steffen et al. 1995; Qian et al. 2009), J1800+7828 (Cassaro et al. 2002), and the famous binary black hole candidate OJ 287 (Sillanpää et al. 1988; Villata et al. 1998; Valtonen et al. 2009, 2011). The FSRQ J1833 − 2103 is a gravitationally lensed rotating jet source (Guirado et al. 1999; Nair et al. 2005) that is also excluded from our pattern test, owing to the lack of correlation between flux variations in the W-band and the other WMAP bands, although visual inspection suggests a rotating-jet pattern with a period of < 10 yr.
In summary, rotating jets are common features in AGN, but only some of them display a characteristic sinusoidal pattern in the long-term averaged WMAP light curves.
7.2. Relation to other frequency bands
The long-term variability and possible periodic behaviour of AGN have been studied using many methods (e.g., structure function, wavelet, periodogram, DCCF; see Sect. 5.1). Evidence for periodic behaviour has mostly come from optical data, in particular for bright sources where archival optical data provide time series extending over many decades (Villata et al. 1998; Fan & Lin 2000). These periodicities have generally been interpreted as resulting from geometric effects, potentially in connection with shocks (Lainela et al. 1999). Whilst large samples of radio time series spanning more than 20 yr have not provided strong support for periodicities, WEBT campaigns on BL Lac and AO 0235+16 (J0238+1637) have shown that time lags between radio and optical variability can be explained as a geometric effect, where rotation successively moves regions emitting at different frequencies into positions of maximal Doppler boosting (Ostorero et al. 2004; Bach et al. 2006; Villata et al. 2009).
Gamma-ray emission in blazars is likely to a have a different origin from the radio emission (e.g., Ghisellini et al. 1998; Rachen 2000; Böttcher 2012), so comparison of the long-term variability in radio and gamma-ray data could provide an important cross-check for the geometric interpretation, which predicts that these data should show long-term correlations like those seen in the radio and optical data. Among our sources, 133 are present in the second source catalogue from the Fermi Large Area Telescope (2FGL, Ackermann et al. 2011), 105 of which show significant variability in gamma-rays. The uniform sampling of Fermi-GST makes it an ideal instrument for such study.
7.3. Caveats
We find simple, sinusoidal patterns on time scales < 10 yr in only nine out of 198 sources, i.e., 4.5% of the full sample. This is consistent with the results of Ciaramella et al. (2004), who found periodic behaviour in about 4% of their irregularly sampled blazar light curves spanning several decades. For most sources, the time scales are too long or the variability is too complex to fit our simple models. More complex, physically motivated models are possible, and have been used to model selected blazar light curves. However, the added flexibility of the more complex models allows both geometric models (Villata & Raiteri 1999; Ostorero et al. 2004; Bach et al. 2006) and shock-based models (Hovatta et al. 2008; Nieppola et al. 2009) to fit the data. For example, the exceptional outburst observed during 2005 in 3C 454.3, has been modelled successfully in both geometric (Villata et al. 2007) and shock-based scenarios (Rachen et al. 2010). One approach to discriminate between models of different complexity is to adopt Bayesian classification methods (Rachen 2013). It is possible that such methods, in conjunction with more data and better models, may eventually elucidate the true cause of long-term variability in blazars.
The present data merely demonstrate that a surprisingly simple sinusoidal pattern, indicative of geometric variability, is a good representation of the long-term averaged variability behaviour for more than half of the sources in our selected sample of 32 sources. It is not yet possible to exclude any of the more complex explanations for blazar variability that have been proposed.
8. Conclusions
We have used data obtained from the WMAP and Planck satellites to analyse the long-term flux-density variations of a sample of extragalactic radio sources selected from the Planck ERCSC. We have used flux densities averaged over one-year periods, which suppresses short-term variability and makes the data set particularly suitable for studying underlying, long-term variability patterns.
At WMAP Ka, Q, V, and W band, we found 82, 67, 32, and 15 sources to be variable at > 99% confidence level. The number of variable sources decreases at higher frequencies owing to the higher flux density uncertainties at these frequencies. The amplitudes of variation are found to be comparable in the different bands, and are not correlated with either the flux densities or the spectral indices of the sources. At Ka band, we modelled the source number counts in each year, and found that although the fitted parameters for the model vary from year to year as a consequence of individual source variability, the variation is within the uncertainty of the fitted parameters, and therefore the number counts derived from the source sample remain stable over the years. Almost all of our sources show correlated variability between bands. Essentially all of the sources in our sample are radio loud AGNs, and most of them are blazars. We do not find any significant difference between the two subclasses of blazars, FSRQs and BLLs.
As expected from theory and VLBI observations, both shock induced flares and geometric variability due to helical or precession jet motion may contribute to the total variability at long time scales. In more than half of the sources that show strong correlated variability between Ka and another band, the long-term averaged variability shows the sinusoidal patterns expected from simple jet rotation, with periods greater than ≈ 3 yr. A simple exponential flare model is less successful in representing our data, but definite conclusions on the nature of variability cannot be drawn because more complex models cannot be ruled out.
Most extended radio galaxies in our sample show no sign of variability. An exception is the extended radio galaxy Pic A, for which we found significant changes in the flux density between 2002 and 2010, which could arise from the central “misaligned blazar” nucleus if the inner jet has a small angle to the line of sight.
The unexpected observation of a millimetre-flare in an extended radio galaxy underlines the potential of cosmology probes and other multi-survey instruments for research on variability and transient phenomena, as they allow comparisons between many, identically sampled full sky surveys.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
All the maps are available from NASA’s Legacy Archive for Microwave Background Data Analysis (LAMBDA) at http://lambda.gsfc.nasa.gov/
See the WMAP mission site (http://wmap.gsfc.nasa.gov/) for more details of scanning strategy.
Acknowledgments
We thank Dave Clements, Joaquin González-Nuevo, Anne Lähteenmäki, Anthony Lasenby, Luigi Toffolatti, and the anonymous referee for useful comments and discussion. We gratefully acknowledge the use of partially unpublished observation data from the Metsähovi telescope 37 GHz long-term blazar monitoring programme. We also make use of data obtained with the 100-m telescope of the Max-Planck-Institut für Radioastronomie (MPIfR) at Effelsberg, and the 30 m telescope of the Institut de Radioastronomie Millimétrique (IRAM) at Pico Veleta. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and the SIMBAD database, operated at CDS, Strasbourg, France. We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA). Support for LAMBDA is provided by the NASA Office of Space Science. Some of the results in this paper have been derived using the HEALPix package. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and DEISA (EU). A full description of the Planck Collaboration and a list of its members, indicating which technical or scientific activities they have been involved in, can be found at http://www.rssd.esa.int/Planck. M.L.C. thanks the Spanish Ministerio de Economía y Competitividad for a Juan de la Cierva fellowship and acknowledges partial financial support from projects AYA2010-21766-C03-01 and CSD2010-00064. C.D. acknowledges an STFC Advanced Fellowship and an EU IRG grant under the FP7.
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, ApJ, 743, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, H. D., Aller, M. F., & Hughes, P. A. 1996, in Blazar Continuum Variability, eds. H. R. Miller, J. R. Webb, & J. C. Noble, ASP Conf. Ser., 110, 208 [Google Scholar]
- Aller, M. F., Aller, H. D., Hughes, P. A., & Latimer, G. E. 1999, ApJ, 512, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Angel, J. R. P., & Stockman, H. S. 1980, ARA&A, 18, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Angelakis, E., Fuhrmann, L., Nestoras, I., et al. 2012, J. Phys. Conf. Ser., 372, 012007 [NASA ADS] [CrossRef] [Google Scholar]
- Bach, U., Krichbaum, T. P., Ros, E., et al. 2005, A&A, 433, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bach, U., Villata, M., Raiteri, C. M., et al. 2006, A&A, 456, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1984, Rev. Mod. Phys., 56, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003a, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003b, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences (Boston: McGraw-Hill) [Google Scholar]
- Biermann, P. L., & Strittmatter, P. A. 1987, ApJ, 322, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., McKee, C. F., & Rees, M. J. 1977, Nature, 267, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, R. C., Chandler, C. J., Cotter, G., et al. 2006, MNRAS, 370, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M. 2012 [arXiv:1205.0539] [Google Scholar]
- Britzen, S., Roland, J., Laskar, J., et al. 2001, A&A, 374, 784 [Google Scholar]
- Brown, L. M. J., Robson, E. I., Gear, W. K., et al. 1989, ApJ, 340, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Burke-Spolaor, S., Ekers, R. D., Massardi, M., et al. 2009, MNRAS, 395, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, H.-B., Shen, Z.-Q., Chen, X., & Shang, L.-L. 2006, A&A, 458, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camenzind, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Carrara, E. A., Abraham, Z., Unwin, S. C., & Zensus, J. A. 1993, A&A, 279, 83 [NASA ADS] [Google Scholar]
- Cassaro, P., Stanghellini, C., Dallacasa, D., Bondi, M., & Zappalà, R. A. 2002, A&A, 381, 378 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciaramella, A., Bongardo, C., Aller, H. D., et al. 2004, A&A, 419, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Zotti, G., Ricci, R., Mesa, D., et al. 2005, A&A, 431, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, J. H., & Lin, R. G. 2000, ApJ, 537, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Franzen, T. M. O., Davies, M. L., Davies, R. D., et al. 2009, MNRAS, 400, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, L., Zensus, J. A., Krichbaum, T. P., Angelakis, E., & Readhead, A. C. S. 2007, in The First GLAST Symposium, AIP Conf. Proc., 921, 249 [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Guetta, D., Ghisellini, G., Lazzati, D., & Celotti, A. 2004, A&A, 421, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guirado, J. C., Jones, D. L., Lara, L., et al. 1999, A&A, 346, 392 [NASA ADS] [Google Scholar]
- Healey, S. E., Romani, R. W., Cotter, G., et al. 2008, ApJS, 175, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Nolta, M. R., Bennett, C. L., et al. 2007, ApJS, 170, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, X. Y., Jiang, D. R., Gurvits, L. I., et al. 2004, A&A, 417, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Tornikoski, M., Lehto, H. J., et al. 2008, in Blazar Variability across the Electromagnetic Spectrum, Workshop, Palaiseau [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarosik, N., Barnes, C., Bennett, C. L., et al. 2003, ApJS, 148, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Jarosik, N., Bennett, C. L., Dunkley, J., et al. 2011, ApJS, 192, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Larionov, V. M., et al. 2010, ApJ, 715, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Krichbaum, T. P., Witzel, A., Graham, D. A., et al. 1992, A&A, 260, 33 [NASA ADS] [Google Scholar]
- Krichbaum, T. P., Lee, S. S., Lobanov, A. P., Marscher, A. P., & Gurwell, M. A. 2008, in Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, eds. T. A. Rector, & D. S. De Young, ASP Conf. Ser., 386, 186 [Google Scholar]
- Lähteenmäki, A., & Valtaoja, E. 1999, ApJ, 521, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Lähteenmäki, A., Valtaoja, E., & Wiik, K. 1999, ApJ, 511, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lainela, M., Takalo, L. O., Sillanpää, A., et al. 1999, ApJ, 521, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marshall, H. L., Hardcastle, M. J., Birkinshaw, M., et al. 2010, ApJ, 714, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Giommi, P., Leto, C., et al. 2011, Multifrequency Catalogue of Blazars, 3rd ed., eds. E. Massaro, P. Giommi, C. Leto, et al. (Rome: Aracne editrice) [Google Scholar]
- Meisenheimer, K., Roser, H.-J., Hiltner, P. R., et al. 1989, A&A, 219, 63 [NASA ADS] [Google Scholar]
- Nair, S., Jin, C., & Garrett, M. A. 2005, MNRAS, 362, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Nieppola, E., Tornikoski, M., Lähteenmäki, A., et al. 2007, AJ, 133, 1947 [NASA ADS] [CrossRef] [Google Scholar]
- Nieppola, E., Hovatta, T., Tornikoski, M., et al. 2009, AJ, 137, 5022 [NASA ADS] [CrossRef] [Google Scholar]
- Ostorero, L., Villata, M., & Raiteri, C. M. 2004, A&A, 419, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostorero, L., Wagner, S. J., Gracia, J., et al. 2006, A&A, 451, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, L., Barnes, C., Hinshaw, G., et al. 2003, ApJS, 148, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Roser, H.-J., & Meisenheimer, K. 1997, A&A, 328, 12 [NASA ADS] [Google Scholar]
- Piner, B. G., & Kingham, K. A. 1997, ApJ, 479, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011e, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team 2011, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M., Reich, W., Schlickeiser, R., Reich, P., & Ungerechts, H. 1996, A&AS, 120, C529 [NASA ADS] [Google Scholar]
- Qian, S.-J., Kudryavtseva, N. A., Britzen, S., et al. 2007, Chin. J. Astron. Astrophys., 7, 364 [Google Scholar]
- Qian, S.-J., Witzel, A., Zensus, J. A., et al. 2009, Res. Astron. Astrophys., 9, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rachen, J. P. 2000, in GeV-TeV Gamma Ray Astrophysics Workshop: Towards a Major Atmospheric Cherenkov Detector VI, eds. B. L. Dingus, M. H. Salamon, & D. B. Kieda, AIP Conf. Ser., 515, 41 [Google Scholar]
- Rachen, J. P. 2013, in 32nd International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, eds. U. V. Toussaint, et al., AIP Conf. Ser., in print [Google Scholar]
- Rachen, J. P., Häberlein, M., Reimold, F., & Krichbaum, T. 2010, in Fermi meets Jansky: AGN in Radio and Gamma Rays, eds. T. Savolainen, E. Ros, R. W. Porcas, & J. A. Zensus, MPIfR Bonn [Google Scholar]
- Rastorgueva, E. A., Wiik, K., Savolainen, T., et al. 2009, A&A, 494, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2006, MNRAS, 371, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Sajina, A., Partridge, B., Evans, T., et al. 2011, ApJ, 732, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., Jorstad, S. G., & Marscher, A. P. 2002, A&A, 394, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Z.-Q., Edwards, P. G., Lovell, J. E. J., et al. 1999, PASJ, 51, 513 [NASA ADS] [Google Scholar]
- Sillanpää, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, M., Ghisellini, G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, W., Zensus, J. A., Krichbaum, T. P., Witzel, A., & Qian, S. J. 1995, A&A, 302, 335 [Google Scholar]
- Stevens, J. A., Litchfield, S. J., Robson, E. I., et al. 1994, ApJ, 437, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Teraesranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tingay, S. J., Jauncey, D. L., Reynolds, J. E., et al. 2000, AJ, 119, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Tornikoski, M., Valtaoja, E., Teraesranta, H., et al. 1996, A&AS, 116, 157 [NASA ADS] [Google Scholar]
- Tucci, M., Toffolatti, L., de Zotti, G., & Martínez-González, E. 2011, A&A, 533, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Türler, M., Courvoisier, T. J.-L., & Paltani, S. 2000, A&A, 361, 850 [NASA ADS] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Valtaoja, E., Haarala, S., Lehto, H., et al. 1988, A&A, 203, 1 [NASA ADS] [Google Scholar]
- Valtaoja, L., Valtonen, M. J., & Byrd, G. G. 1989, ApJ, 343, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Valtaoja, E., Lähteenmäki, A., & Teräsranta, H. 1992, A&AS, 95, 73 [NASA ADS] [Google Scholar]
- Valtaoja, E., Lähteenmäki, A., Teräsranta, H., & Lainela, M. 1999, ApJS, 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M. J., Nilsson, K., Villforth, C., et al. 2009, ApJ, 698, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M. J., Lehto, H. J., Takalo, L. O., & Sillanpää, A. 2011, ApJ, 729, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 [NASA ADS] [Google Scholar]
- Villata, M., Raiteri, C. M., Sillanpää, A., & Takalo, L. O. 1998, MNRAS, 293, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., Raiteri, C. M., Tosti, G., et al. 2002, Mem. Soc. Astron. Italiana, 73, 1191 [NASA ADS] [Google Scholar]
- Villata, M., Raiteri, C. M., Aller, H. D., et al. 2004, A&A, 424, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Aller, M. F., et al. 2007, A&A, 464, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2009, A&A, 501, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, S. J., Camenzind, M., Dreissigacker, O., et al. 1995, A&A, 298, 688 [NASA ADS] [Google Scholar]
- Wright, E. L., Chen, X., Odegard, N., et al. 2009, ApJS, 180, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zensus, J. A. 1997, ARA&A, 35, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, W., Hong, X.-Y., An, T., et al. 2011, A&A, 529, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Quantifying variability in astronomical data sets
A.1. Statistical significance and variability index
To quantify significant changes in the measured flux density of a source, recent astronomical literature has adopted a so-called de-biased variability index, 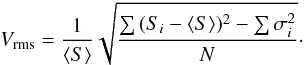 (A.1)The expression is usually attributed to Akritas & Bershady (1996), but the form of Eq. (A.1) was first applied to time series by Sadler et al. (2006). For the special case that all measurement errors are equal, σi = σ, Vrms can be written as
(A.1)The expression is usually attributed to Akritas & Bershady (1996), but the form of Eq. (A.1) was first applied to time series by Sadler et al. (2006). For the special case that all measurement errors are equal, σi = σ, Vrms can be written as 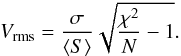 (A.2)Assuming N is large and the bias through diminishing one degree of freedom is small, this equation relates to the statistical significance of variability in a plausible way: it shows that for χ2/N > 1, i.e., an average scatter in excess of the measurements error, Vrms is positive, and is given as a fraction of the average total flux density by scaling with σ/ ⟨ S ⟩ . For χ2/N < 1, Vrms becomes imaginary, indicating that the data scatter is less than expected. Data sets showing a large fraction of sources with imaginary Vrms are likely to have overestimated the measurement errors and thus underestimated the fraction of truly variable sources.
(A.2)Assuming N is large and the bias through diminishing one degree of freedom is small, this equation relates to the statistical significance of variability in a plausible way: it shows that for χ2/N > 1, i.e., an average scatter in excess of the measurements error, Vrms is positive, and is given as a fraction of the average total flux density by scaling with σ/ ⟨ S ⟩ . For χ2/N < 1, Vrms becomes imaginary, indicating that the data scatter is less than expected. Data sets showing a large fraction of sources with imaginary Vrms are likely to have overestimated the measurement errors and thus underestimated the fraction of truly variable sources.
From the derivation of this expression in Akritas & Bershady (1996), we note that, in spite of the notation of individual errors, Eq. (A.1) is based on a valid statistical estimator only for the case of equal errors. Moreover, it has been derived under an assumption of large sample sizes (see also Franzen et al. 2009). Comparing with Eq. (A.2), we immediately see where this constraint comes from: (a) the failure to reduce the degrees of freedom in the normalised χ2; and (b) the use of the arithmetic mean σ/ ⟨ S ⟩ , which does not minimize χ2 except in case of equal errors. Correcting for this, i.e., doing the transformations 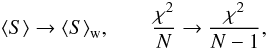 (A.3)and introducing ⟨σ⟩w as an estimate for the average error in the scaling factor, we obtain Eq. (4).
(A.3)and introducing ⟨σ⟩w as an estimate for the average error in the scaling factor, we obtain Eq. (4).
A.2. Dealing with incomplete data
In this paper, we are limited not only by the small sample size, but also by the small fraction of above 3σ detections in a time line in many cases. However, given that enough “good” ( > 3σ) data are available to achieve a reasonable estimate for the mean source flux density, and upper limits in the years in between can provide valuable information on the variability of the source, we chose to treat all upper limits as data points with Si = 3σnoise and σi = σnoise, and use Eq. (7) to calculate χ2. Since a reasonable estimate on the average source flux density Sabove the noise level is vital for a meaningful analysis, we require more good data than upper limits in order to include a time line in our analysis, i.e., N3σ ≥ 4. We also note that the value obtained in this way for variability strength and significance is a lower limit, as the distribution is cut on one end by our noise level, which reduces the scatter.
A.3. Pearson product correlation coefficient
For our correlation analysis, we calculated the Pearson product correlation coefficient, defined as 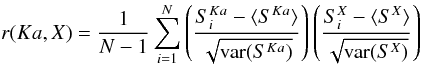 (A.4)between the Ka band and other bands X = Q,V,W showing significant variability. As all errors in the same band for the same source are approximately equal, we took ⟨ S ⟩ and var(S) as the straight, unweighted arithmetic mean and variance of the data in each time line. For approximate Gaussian distributions of S in each band, and large enough samples, the variable
(A.4)between the Ka band and other bands X = Q,V,W showing significant variability. As all errors in the same band for the same source are approximately equal, we took ⟨ S ⟩ and var(S) as the straight, unweighted arithmetic mean and variance of the data in each time line. For approximate Gaussian distributions of S in each band, and large enough samples, the variable
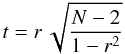 follows Student’s t-distribution for N − 2 degrees of freedom. We note that none of the above assumptions really holds for our data sets, but more exact derivations of correlation confidence do not help as they also depend on the assumption of Gaussianity.
follows Student’s t-distribution for N − 2 degrees of freedom. We note that none of the above assumptions really holds for our data sets, but more exact derivations of correlation confidence do not help as they also depend on the assumption of Gaussianity.
Appendix B: Binning and de-biasing Metsähovi monitoring data
To assure compatibility with the WMAP results, we need to bin the Metsähovi data to match WMAP operation years, starting from August of a given year through July of the next year. We have to consider that, unlike WMAP with its fixed scanning pattern, monitoring programmes like Metsähovi do not sample data in an unbiased way. Telescope time is usually focused on sources that show rapid flaring; sources that are not in an active phase are observed less frequently. Therefore, we have more data points in high states than in low states of a source, leading to strong bias in simple averages. To reduce the bias, we bin the data using a weighted average 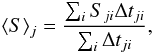 (B.1)where j denotes the number of the bin, and the sum runs over all data points included in the bin with individual flux densities Sji. Here, Δti = ti + 1 − ti represents the time difference between adjacent flux density measurements in the monitoring, and is used as the weight factor in the average to compensate the bias introduced by the irregular sampling rate. In a similar way, we determine a weighted average of squared flux density ⟨ S2 ⟩ j, and obtain the standard deviation
(B.1)where j denotes the number of the bin, and the sum runs over all data points included in the bin with individual flux densities Sji. Here, Δti = ti + 1 − ti represents the time difference between adjacent flux density measurements in the monitoring, and is used as the weight factor in the average to compensate the bias introduced by the irregular sampling rate. In a similar way, we determine a weighted average of squared flux density ⟨ S2 ⟩ j, and obtain the standard deviation 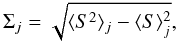 (B.2)which describes the amount of variation of the source flux density within the one-year bin. We note that this should not be confused with a measurement error; rather it reflects the standard deviation of the distribution of data points within the bin. It may therefore be regarded as a measure of the strength of short-term variability during the respective one-year period.
(B.2)which describes the amount of variation of the source flux density within the one-year bin. We note that this should not be confused with a measurement error; rather it reflects the standard deviation of the distribution of data points within the bin. It may therefore be regarded as a measure of the strength of short-term variability during the respective one-year period.
Appendix C: Brightness variation in relativistically beamed rotating emitters
We consider a beamed emitter rotating with angular velocity ω around a cone of opening angle Φ about a central axis of a jet. Let Θ be the angle of the line of sight to the central axis of the cone. The inclination angle of the jet at time t to the line of sight is then given by  (C.1)which can be simply written as a + bcosωt. For a beamed emitter, a ≈ 1 and b ≪ 1. Inserting this into the definition of the Doppler factor and setting a = 1, we obtain
(C.1)which can be simply written as a + bcosωt. For a beamed emitter, a ≈ 1 and b ≪ 1. Inserting this into the definition of the Doppler factor and setting a = 1, we obtain 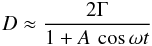 (C.2)with A = bβ/(1 − β) < 1, where we used 1 − β2 = 1/Γ2, and eventually set β = 1. As Sν ∝ D3 + α, this leads to Eq. (9).
(C.2)with A = bβ/(1 − β) < 1, where we used 1 − β2 = 1/Γ2, and eventually set β = 1. As Sν ∝ D3 + α, this leads to Eq. (9).
If we consider a combined variability process which comprises both flare and geometric variability (see Sect. 5.2), Doppler boosting acts as a multiplicative factor on the light curve describing the flare-induced process. For a rotating jet, this means that Eq. (9) not only describes the oscillation of the average flux density of the jet, but also a modulation of the amplitude ΔS of all short-term flares in it. For the special case of (1 − A)3 + α < ⟨ σ ⟩ / ⟨ ΔS ⟩ , this can lead to a pattern in which short term variability, clearly detectable in the high states of boosting, becomes insignificant in the low states. For a more detailed treatment of rotating patterns with superimposed inhomogenities we refer to Ostorero et al. (2004), and references therein.
Appendix D: WMAP/Planck light curves
 |
Fig. D.1 WMAP/Planck light curves for sources with at least one good timeline (i.e., four or more > 3σ data points in seven years of WMAP observation) in our sample. For each good timeline, all > 2σ data points are plotted, with dash-dot lines indicating the 3σ level. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. |
 |
Fig. D.1 continued. |
 |
Fig. D.1 continued. |
 |
Fig. D.1 continued. |
 |
Fig. D.1 continued. |
 |
Fig. D.1 continued. |
All Tables
Flux densities at WMAP Ka, Q, V, and W band for the 198 extragalactic radio sources selected from the ERCSC.
All Figures
 |
Fig. 1 Map in Galactic coordinates showing the locations of the 198 extragalactic sources selected from the Planck ERCSC. The north ecliptic pole (NEP) and the south ecliptic pole (SEP) are indicated by crosses. Source densities are higher near the ecliptic poles, where Planck has longer integration time. |
| In the text | |
 |
Fig. 2 Examples of source SEDs and fitted models (grey solid line). The reduced χ2 values are indicated. |
| In the text | |
 |
Fig. 3 Top: WMAP/Planck light curves of 3C 273. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols. Bottom: spectra of 3C 273 from Planck, Effelsberg, and IRAM observations at several epochs. The 201001 Effelsberg 100-m observation is nearly simultaneous with the Planck observation, and confirms the flare seen by Planck. |
| In the text | |
 |
Fig. 4 Dependence of fractional variability index Vrms on mean spectral index ⟨ α ⟩ in Ka, Q, V, and W bands for variable sources. BLLs are shown by filled circles, FSRQs by open circles, and all the other sources by plus signs. The dashed lines indicate the level of |
| In the text | |
 |
Fig. 5 Dependence of fractional variability index Vrms on mean flux density ⟨ Sν ⟩ in Ka, Q, V, and W bands for variable sources. BLLs are shown by filled circles, FSRQs by open circles, and all the other sources by plus signs. The dashed lines indicate the level of |
| In the text | |
 |
Fig. 6 Histograms of fractional variability index for variable sources; FSRQs are shown in white and BLLs in grey. |
| In the text | |
 |
Fig. 7 Euclidean normalised differential number counts at WMAP Ka-band (33 GHz) in each year. The solid curve shows the total number counts of extragalactic radio sources predicted by the de Zotti et al. (2005) evolution model, and the dashed line represents the total number counts from the Tucci et al. (2011) model. |
| In the text | |
 |
Fig. 8 Upper panels: WMAP/Planck light curves for the sources that are better fit by the rotating jet model. The WMAP data are shown by filled symbols and the later Planck data are shown by open symbols. Lower panels: residuals between the normalised WMAP flux densities (Eq. (11)) and the rotating jet model. Grey dash-dot lines indicate the zero level. |
| In the text | |
 |
Fig. 9 Top panels: WMAP/Planck light curves for the sources that are well fit by both the VLTL-flare model and the rotating jet model. The WMAP data are shown by filled symbols and the later Planck data are shown by open symbols. Middle panels: residuals between the normalised WMAP flux densities (Eq. (11)) and the VLTL-flare model. Bottom panels: residuals between the normalised WMAP flux densities and the rotating jet model. Grey dash dot lines indicate the zero level in the residual plots. |
| In the text | |
 |
Fig. 9 continued. |
| In the text | |
 |
Fig. 10 WMAP/Planck light curves for the sources J0538 − 4405, 3C 273 and 3C 279. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. The dashed lines indicate the 3σ level at each band if in the plotted range. |
| In the text | |
 |
Fig. 11 WMAP/Planck light curves for the sources J1058+0134, J1549+0236, BL Lac, 3C 446, J2232+1143 and 3C 454.3. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. The dashed lines indicate the 3σ level at each band if in the plotted range. |
| In the text | |
 |
Fig. 12 WMAP/Planck light curves for the sources J0423 − 0120, J0721+7120, and J1310+3220 at 33 GHz (black filled circles) and 41 GHz (red filled triangles), with the Metsähovi 37 GHz long-term monitoring data added (grey stars). For J1310+3220, the residuals between the Metsähovi data and the best fit model are shown. |
| In the text | |
 |
Fig. 13 WMAP/Planck light curves of the FR II radio galaxy Pic A. |
| In the text | |
 |
Fig. D.1 WMAP/Planck light curves for sources with at least one good timeline (i.e., four or more > 3σ data points in seven years of WMAP observation) in our sample. For each good timeline, all > 2σ data points are plotted, with dash-dot lines indicating the 3σ level. The WMAP flux densities are shown by filled symbols and the Planck flux densities are shown by open symbols of the same shape. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.