| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201218789 | |
| Published online | 15 May 2013 | |
Hα3: an Hα imaging survey of HI selected galaxies from ALFALFA⋆
II. Star formation properties of galaxies in the Virgo cluster and surroundings
1 Università degli Studi di Milano-Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
e-mail: giuseppe.gavazzi@mib.infn.it
2 Carnegie Observatories, 813 Santa Barbara Street, Pasadena, CA 91101, USA
e-mail: mfumagalli@obs.carnegiescience.edu
3 Department of Astrophysics, Princeton University, Princeton, NJ 08544-1001, USA
4 Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching, Germany
e-mail: mfossati@mpe.mpg.de
5 Laboratoire d’Astrophysique de Marseille, UMR 6110 CNRS, 38 rue F. Joliot-Curie, 13388 Marseille, France
e-mail: alessandro.boselli@oamp.fr
6 Center for Radiophysics and Space Research, Space Science Building, Ithaca, NY, 14853, USA
e-mail: haynes@astro.cornell.edu; riccardo@astro.cornell.edu
Received: 8 January 2012
Accepted: 11 March 2013
Context. We present the analysis of Hα3, an Hα narrow-band imaging follow-up survey of 409 galaxies selected from the HI Arecibo Legacy Fast ALFA Survey (ALFALFA) in the Local Supercluster, including the Virgo cluster, in the region 11h < RA < 16h ; 4o < Dec < 16°; 350 < cz < 2000 km s-1.
Aims. Taking advantage of Hα3, which provides the complete census of the recent massive star formation rate (SFR) in HI-rich galaxies in the local Universe and of ancillary optical data from SDSS we explore the relations between the stellar mass, the HI mass, and the current, massive SFR of nearby galaxies in the Virgo cluster. We compare these with those of isolated galaxies in the Local Supercluster, and we investigate the role of the environment in shaping the star formation properties of galaxies at the present cosmological epoch.
Methods. By using the Hα hydrogen recombination line as a tracer of recent star formation, we investigated the relationships between atomic neutral gas and newly formed stars in different environments (cluster and field), for many morphological types (spirals and dwarfs), and over a wide range of stellar masses (107.5 to 1011.5 M⊙). To quantify the degree of environmental perturbation, we adopted an updated calibration of the HI deficiency parameter which we used to divide the sample into three classes: unperturbed galaxies (DefHI ≤ 0.3), perturbed galaxies (0.3 < DefHI < 0.9), and highly perturbed galaxies (DefHI ≥ 0.9).
Results. Studying the mean properties of late-type galaxies in the Local Supercluster, we find that galaxies in increasing dense local galaxy conditions (or decreasing projected angular separation from M 87) show a significant decrease in the HI content and in the mean specific SFR, along with a progressive reddening of their stellar populations. The gradual quenching of the star formation occurs outside-in, consistently with the predictions of the ram pressure model. Once considered as a whole, the Virgo cluster is effective in removing neutral hydrogen from galaxies, and this perturbation is strong enough to appreciably reduce the SFR of its entire galaxy population.
Conclusions. An estimate of the present infall rate of 300–400 galaxies per Gyr in the Virgo cluster is obtained from the number of existing HI-rich late-type systems, assuming 200–300 Myr as the time scale for HI ablation. If the infall process has been acting at a constant rate, this would imply that the Virgo cluster has formed approximately 2 Gyr ago, consistently with the idea that Virgo is in a young state of dynamical evolution.
Key words: galaxies: clusters: individual: Virgo / galaxies: fundamental parameters / galaxies: ISM
© ESO, 2013
1. Introduction
A deeper understanding of the basic processes that regulate the life of galaxies, i.e., the conversion of gas into new stars and their progressive aging, is becoming a reality owing to the recent multi-wavelength surveys that are providing a wealth of information on the different phases of the interstellar medium (ISM), the stellar content, and the current star formation rate (SFR) in nearby galaxies. This observational effort is complemented by new progress in numerical simulations and theory in modeling the processes that regulate the formation of new stars in galaxies (e.g. Somerville & Primack 1999).
ALFALFA (Giovanelli et al. 2005) is a blind survey that just ended at Arecibo (October 2012), aimed at obtaining a census of HI sources within 7000 sq degrees of the sky accessible from Arecibo (including the Virgo cluster), with a sensitivity of about 21 mJy km s-1, corresponding to 107.7 M⊙ of HI at the distance of Virgo. A catalog listing 40% of the whole ALFALFA sources (α.40 catalog) has been published by Haynes et al. (2011). The Sloan Digital Sky Survey (SDSS, York et al. 2000) revolutionized our knowledge on the stellar content of galaxies in the local Universe. The GALEX mission (Martin et al. 2005) with its all-sky survey (and other smaller but deeper surveys, such as GUVICS by Boselli et al. 2011) disclosed our view of the ultraviolet sky, thereby providing quantitative knowledge on the massive, recent star formation in galaxies.
 |
Fig. 1 Sky distribution of 409 HI-selected galaxies in Hα3, coded according to their morphology (E-S0-S0a: circles; giant spirals Sa-Sm: squares; Irr-BCD: triangles) The two vertical dashed lines mark the adopted boundaries of the Virgo cluster. Red symbols refer to galaxies considered as part of the Virgo cluster, blue are galaxies considered as isolated. Superposed are the X-ray contours from ROSAT (Böhringer et al. 1994). |
Based on these datasets Huang et al. (2012) were able to determine the scaling relations between the atomic hydrogen content, the stellar content, and the SFR in HI selected galaxies over a range of mass approaching one million (from 106 to 1012 M⊙). Similar analyses from optically selected surveys were carried out in the local volume (Lee et al. 2007, 2009; Bothwell et al. 2009) and beyond (e.g. GASS, the GALEX Arecibo SDSS Survey, Catinella et al. 2010; Schiminovich et al. 2010), limited to galaxies with stellar masses in excess of 1010 M⊙ however.
Huang et al. (2012) based their study on the star formation rate estimated by fitting spectral energy distributions (SEDs) obtained by combining optical (SDSS) and UV (GALEX) photometry. This technique requires that extinction in the UV is properly accounted for (Cortese et al. 2006, 2008b) and depends on the assumed star formation history (SFH) and metallicity. On the other hand the UV or Hα luminosity alone (see Kennicutt 1998) provides a more instantaneous estimate of the SFR and requires that the SFH of galaxies has remained stationary over the time scale typical of A (108 yr) or OB stars (107 yr). This approach is more suitable when it is necessary to determine the SFR of galaxies that are subject to abrupt changes in their SFH, e.g., when they suffer from environmental disturbances, such as quenching by ram pressure. Vollmer et al. (2004) and Boselli et al. (2006) have shown that in massive galaxies, such as NGC 4569, ram pressure can produce complete quenching of the star formation on a timespan as short as 100–300 Myr, and even shorter in dwarf galaxies (Boselli et al. 2008).
The SFR determined from UV magnitudes has been compared to that from recombination lines by Boselli et al. (2009), who arrived at the conclusion that the accuracy of SFR based on UV (GALEX) luminosity critically depends on the quality of the data used, i.e., whether they come from the shallow (100 s exposure) All-sky-survey (AIS) or from the deeper MIS survey (typically 1500 s integration). Huang et al. (2012) reported that 25% of the α.4 targets do not have a counterpart in GALEX, 52.2% of the remaining match to UV sources found in the AIS, and only 23.1% matches those in the MIS. This severely hampers an unbiased comparison of the star formation properties of galaxies in the Virgo cluster with respect to isolated galaxies in the Local Supercluster, i.e., the main goal of the present investigation using UV data, because the large majority of Virgo galaxies have been observed in the MIS (owing to GUViCS by Boselli et al. 2011), whereas the remaining objects in the local field have only AIS data. One more source of uncertainty in determining the SFR using SED fitting is connected with the large errors introduced by the SDSS pipeline on the photometry of large nearby galaxies due to “shredding” in multiple pieces, which leads to wrong magnitude determinations.
Given these considerations, we decided to make a new estimate of the “instantaneous” SFR based on our own measurements of the hydrogen recombination lines using the data from the Hα3 narrow-band imaging survey of nearby galaxies selected from ALFALFA in the spring sky of the Local Supercluster (Gavazzi et al. 2012, Paper I), including the Virgo cluster.
Virgo is the cluster of galaxies nearest to us, which, in spite of the enormous angular extent of about 6x10 square degrees, lies in the footprint of both ALFALFA and Hα3. Already in early studies Virgo appeared to be a cluster in the early stage of dynamical evolution. Its general appearance is highly irregular (Abell et al. 1989), and it is classified as Bautz-Morgan type III (Bautz & Morgan 1970). Owing to the intensive optical survey by Binggeli et al. (1985), its velocity dispersion was found to be 760 ± 45 km s-1, lower than that of evolved clusters, indicating a shallow gravitational potential. The spiral fraction is 48% compared to 16% of Coma. As seen by ROSAT (Böhringer et al. 1994), the Virgo cluster is known to have an irregular X-ray morphology. These features provide evidence that the Virgo cluster is currently undergoing dynamical evolution (Forman & Jones 1982).
The role of the environment in shaping the star formation properties of galaxies in the local Universe is still an open question. As early as in the Las Campanas redshift survey (Hashimoto et al. 1998), or in the DR3 release of the SDSS (Gómez et al. 2003), evidence has built that suppression of the SFR of galaxies in dense environments takes place at z = 0, up to z = 0.8 (Patel et al. 2009; see a review by Boselli & Gavazzi 2006). By comparing the statistical HI properties of galaxies in nine nearby clusters with those of “field” objects of similar type and luminosity, Giovanelli & Haynes (1985) showed that clusters contain a high percentage of HI deficient galaxies. The mechanism that most likely contributes to significant gas depletion in clusters is ram-pressure stripping (Gunn & Gott 1972). Since then the HI deficiency parameter has been used as a proxy for the degree of the perturbation that galaxies experience in the harsh environment of rich galaxy clusters.
Taking advantage of the presence of the Virgo cluster in Hα3, the first goal of the present work is to quantify, in addition to the HI content, how the SFR is affected by the environment of an evolving cluster such as Virgo, following the line traced by the pioneering work of Kennicutt (1983). We approach this question by studying a possible residual correlation between the SFR, the gas content and the gas deficiency after the first-order scaling law from the stellar mass have been removed.
The dataset used in this paper has been presented in Paper I of the present series, which illustrates Hα3, the ongoing imaging survey at the 2.1 m telescope of the San Pedro Martir (SPM) Observatory, the details of the sample selection, completeness, the Hα observations, data reduction and analysis, which gives access to the integrated extinction-free measurements of the SFR for 233 galaxies observed at SPM between 2006 and 2009. The present Paper II contains the analysis of the integrated SFR obtained using Hα3. After a brief introduction to the galaxy sample (Sect. 2), we derive an updated calibration of the HI deficiency parameter valid for dwarf gas-rich systems such as those that dominate Hα3 (Sect. 3). The main results of the present analysis are given in Sect. 4, where we analyze the relations between the mean optical colors and the extent of the star formation regions of galaxies in the present survey as a function of their HI content. The scaling relations between gas and stellar masses and current SFR in the Local Supercluster are analyzed (Sect. 5). The overall perturbation on the gas content and star formation properties of galaxies in the Local Supercluster due to the Virgo cluster is quantified in Sect. 6. The results are discussed in Sect. 7, where some conclusions on the present evolutionary stage of the Virgo cluster are drawn, and we summarize our results in Sect. 8.
Two companion papers continue this series. Paper III (Gavazzi et al. 2013) carries an analysis similar to the one reported in the present paper, focused on the properties of galaxies in the Great Wall, including the Coma cluster. Paper IV (Fossati et al. 2013) contains the analysis of the structural properties of galaxies in the local and Coma superclusters. The CAS parameters (concentration, asymmetry, and clumpiness developed by Conselice 2003) are determined on both the r band and the Hα images to study the morphology of the star-forming regions and compare it with that of older stars at arcsec resolution (unachievable on GALEX UV data which have a resolution of 4–5 arcsec).
Throughout the paper we adopt a flat ΛCDM cosmology, with H0 = 73 km s-1 Mpc-1 and ΩΛ = 0.7. All magnitudes are given in the AB system unless explicitly noted.
2. Sample
 |
Fig. 2 Sky distribution of galaxies around the Virgo cluster. ETGs (from the VCC with mp < 18.0 mag) are given with small black dots. HI-selected LTG galaxies, coded according to their HI deficiency parameter (red dots: DefHI > 0.9; green dots: 0.3 < DefHI < 0.9; blue dots DefHI ≤ 0.3). The empty red circles represent the 26 LTGs undetected by ALFALFA listed in Table 1. Superposed are the X-ray contours from ROSAT (Böhringer et al. 1994). The position of cluster A (M 87), B (M 49) and of clouds M, N and W are given. Clouds M and N coincide in position but have significantly different distance moduli. |
The sample analyzed in this work is drawn from the 900 square degree region 11h < RA < 16h; 4° < Dec < 16°, covering the Local Supercluster, including the Virgo cluster. This region has been fully mapped by ALFALFA which provides us with a complete sample of HI-selected galaxies with gas masses as low as 107.7 M⊙ (Haynes et al. 2011).
Hα3 is a follow-up survey consisting of Hα imaging observations of ALFALFA targets with high signal-to-noise (typically S/N > 6.5) and a good match between two independent polarizations (code = 1 sources; Giovanelli et al. 2005; Haynes et al. 2011). Hα observations of members of the Virgo cluster were given in Gavazzi et al. (2002a,b, 2006), Boselli & Gavazzi (2002), and Boselli et al. (2002b). Images and fluxes are also publicly available via the GOLDMine web server (Gavazzi et al. 2003). Hα data for galaxies in low-density regions of the Local Supercluster are given in Paper I. Outside Virgo the redshift window of Hα3 is 350 < cz < 2000 km s-1, and we limited the study to objects with HI fluxes FHI > 0.7 Jy km s-1, while in the Virgo cluster the velocity interval is extended to 350 < cz < 3000 km s-1 to map the cluster in its full extent we did not restrict ourselves to FHI > 0.7 Jy km s-1. At the distance of 17 Mpc, assumed for the Virgo subcluster A (Gavazzi et al. 1999), a flux limit S21 = 0.7 Jy km s-1 corresponds to an HI mass MHI = 107.7 M⊙, while Hα3 is complete to MHI > 108 M⊙ (see Paper I). Figure 1 illustrates the sky region covered by Hα3, which contains 409 galaxies.
The basic quantities extensively used in this paper, i.e., the HI mass, the stellar mass, and the extinction-free SFR were derived in Paper I. The HI mass is defined by MHI = 2.36 × 105 × S21 × D2, where D is the distance to the source in Mpc and S21 is the integrated flux of the HI profile in units of Jy km s-1 from ALFALFA.
As explained in Paper I, the g and i band total magnitudes of galaxies detected by ALFALFA were measured by us on SDSS images (DR7, Abazajian et al. 2009) using IRAF. This ensured proper foreground star-subtraction and overcomes the “shredding” problem generated by the automatic SDSS pipeline.
Inside the Virgo cluster we obtained an optically selected sample (see Sect. 4) of 640 objects based on the VCC catalog by Binggeli et al. (1985) (including objects of all morphological types with B < 18 mag between 4° < Dec < 16° and excluding those detected by ALFALFA and galaxies in the background of Virgo with cz > 3000 km s-1). For this large sample we computed the integrated magnitudes using an automatic procedure. Starting from the SDSS images that are available from the GOLDMine web site, we produced deep “white” images by stacking frames in five filters. Using Sextractor (Bertin & Arnouts 1996), we separated the galaxies of interest from foreground stars and background galaxies. After masking these objects, we computed the integrated magnitudes using elliptical apertures, the parameters of which were computed on the white images. As a test, we compared the photometry derived with this automatic procedure with a subset of galaxies that were measured manually on i and g images (Paper I) and we obtained very consistent results.
g − i colors were corrected for internal extinction using the empirical transformation dependent on stellar mass and galaxy inclination, derived in Appendix A of Paper III: ![\begin{equation} (g-i)_{\rm o} = (g-i) - \left\{ +0.17 [1-\cos(incl)] \left[\log\left(\frac{M_*}{M_\odot}\right)-8.19\right]\right\}, \end{equation}](/articles/aa/full_html/2013/05/aa18789-12/aa18789-12-eq47.png) (1)where incl is the galaxy inclination (computed for disk galaxies (from Sa to Sdm) following Solanes et al. (1996).
(1)where incl is the galaxy inclination (computed for disk galaxies (from Sa to Sdm) following Solanes et al. (1996).
The stellar mass was derived from the i magnitudes and (g − i)o color using the transformation 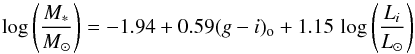 (2)consistent with the mass determination of MPA-JHU2, where log Li is the i band luminosity in solar units (log Li = (I − 4.56)/− 2.5).
(2)consistent with the mass determination of MPA-JHU2, where log Li is the i band luminosity in solar units (log Li = (I − 4.56)/− 2.5).
The extinction-free SFR was computed from the luminosity of the Hα line after correcting for Galactic and internal dust extinction and deblending from [NII] emission. Details on these quantities are given in Paper I.
Following a similar procedure as in Gavazzi et al. (2010, 2011) and Paper III, the local surface density Σ around each galaxy was computed within a circle of 1 Mpc radius. Around each galaxy we computed the density contrast as 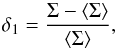 where Σ is the local surface density and ⟨Σ⟩ = 1.3 gal (Mpc)-2 represents the mean surface density measured in the whole region.
where Σ is the local surface density and ⟨Σ⟩ = 1.3 gal (Mpc)-2 represents the mean surface density measured in the whole region.
3. HI content of Virgo galaxies
The Virgo cluster is well known for its unrelaxed structure (Forman & Jones 1982) and for its irregular morphology, elongated in the N-S direction. Figure 2 shows an enlargement of Fig. 1, highlighting the zone that contains the Virgo cluster, with the early-type galaxies (hereafter ETGs) added to emphasize the global density of galaxies in this region. Following Gavazzi et al. (1999), we assume that Virgo is composed of the main cluster A, which contains the bulk of the X-ray emission centered on M 87, and a secondary cluster B centered on M49, infalling into A at about 750 km s-1. These subcomponents are at a distance of about 17 Mpc. Clouds M and W are twice more distant and are probably infalling into the main cluster along with cloud N, which is in the process of merging with cluster A. Virgo is a spiral-rich cluster. The Virgo Cluster catalog (VCC, Binggeli et al. 1985) lists 48% (36%) galaxies of type later than S0a for mp < 18 mag (mp < 20). Restricting this to mp < 13.9 mag, corresponding to the completeness limit of the spectroscopic SDSS g < 17.75 at Coma, the spiral fraction increases to 60%, i.e., four times more than in the Coma cluster (16%) at similar depth.
It might well be that some of the late-type galaxies (hereafter LTGs) that contribute to the large spiral fraction in Virgo are LTGs seen projected on Virgo, but that are distributed along the line of sight on a filament connecting the local group to Virgo, similar to some of the elongated filaments that exist in the Coma supercluster (see Paper III). However, we estimate that if we were to look at Coma from an angle such that we integrate along one of these filaments, the number of LTGs projected on Coma would increase from 16% to about 30%. Although significant, this is not enough to explain the high fraction of LTGs seen in Virgo in terms of projection effects.
The parameter that is best suited to disentangle galaxies that physically belong to the Virgo cluster from either projected on it or belonging to clouds not yet fully processed by the cluster potential is perhaps the HI-deficiency parameter (DefHI). High-resolution HI maps of Virgo galaxies, such as those obtained by the VIVA survey of Chung et al. (2009), confirm earlier claims (Cayatte et al. 1990) that the perturbed spiral/Irr galaxies in the Virgo cluster have a high DefHI and their HI morphology shows evidence of truncation/one-sidedness, consistent with the hypothesis that they are suffering from ram-pressure stripping by the dense cluster ICM.
The DefHI parameter has been defined by Haynes & Giovanelli (1984) as the logarithmic difference between the HI mass observed in a galaxy and the expected value in isolated and unperturbed objects of similar morphological type T and linear diameter dL: DefHI = ⟨log MHI(T,dL)⟩ − log MHI(obs). Here, ⟨log MHI(T,dL)⟩ = C1 + C2 × 2log (dL), where dL (in kpc) is determined in the g band at the 25th mag arcsec-2 isophote. The coefficients C1 and C2 were determined by Haynes & Giovanelli (1984) by studying a control sample of isolated objects, and later, on a larger sample by Solanes et al. (1996). Both samples are composed almost exclusively of giant spirals however. The HI-deficiency parameter was therefore poorly calibrated for dwarf objects.
 |
Fig. 3 Histogram of the DefHI parameter separately for the isolated and W, N clouds (black) and for members of the Virgo A and B subclusters (red). The bulk of HI-deficient galaxies is located within the two subclusters. |
The problem is re-addressed here using ALFALFA by assuming as isolated the galaxies outside the Virgo cluster (outside the interval 12h08m00s < RA < 12h48m00s), excluding a few more objects that appear to be clustered in small groups. We took these objects (the blue symbols in Fig. 1) as a reference sample of nearly isolated objects, representative of local normal and unperturbed galaxies. Scd-BCD dwarf systems dominate this sub-sample.
The coefficients C1 and C2 obtained by us for the giant galaxies (Sa-Sc) are similar to those of Solanes (1996) and of Boselli & Gavazzi (2009). Consistent values are found in our sample for Scd-BCD. For this reason, we decided to adopt C1 = 7.51 and C2 = 0.68 for all LTGs (Sa-BCD), obtained by combining all late-type galaxies. The resulting DefHI are plotted in Fig. 3, where we display the frequency distribution of DefHI in the isolated sample mixed with members of Virgo clouds M and W (black histogram), separately from Virgo members of sub-clusters A and B (red). For the isolated and M, W clouds, we find a mean deficiency ⟨DefHI⟩ = 0.01 ± 0.35, consistent with normal HI content, while for sub-clusters A and B this is ⟨DefHI⟩ = 0.33 ± 0.39.
Unfortunately, the two distributions have overlapping tails, which reflect the difficulty of spatially separating in 3-D) galaxies that belong to the real cluster from those that are just projected on it. For example (see Fig. 2) there are many perfectly HI-normal LTGs projected within 2 degrees from M 87, while there are several highly deficient objects up to 4 degrees away from M 87 or outside the X-ray contours. However, the large majority of LTGs outside the X-ray contours are non-deficient (blue symbols). Thus the assumption that the HI-deficiency parameter is a reliable tracer of the degree of perturbation suffered by LTG by the cluster medium, allows us to adopt in the rest of this paper a conservative threshold of DefHI = 0.3 (1σ above the mean deficiency of the normal sample) to separate normal from deficient galaxies. There are approximately 30 galaxies in the bin 0.2 < DefHI < 0.3 that we consider normal, because they are projected onto the N and W cloud. In reality they might belong to the outskirts of the A cluster, which would justify their slightly positive deficiency. Throughout this paper we adopt DefHI = 0.3 as a threshold below which (270) galaxies can be considered as normal or unperturbed by the cluster environment, while those with DefHI > 0.3 are treated as environmentally perturbed. The abundant number statistics allows us to further sub-divide the deficient sample into 0.3 < DefHI < 0.9 (115 perturbed), and DefHI ≥ 0.9 (24 highly perturbed).
4. Radio versus optical selection
The comparison between the star formation properties of galaxies selected with radio vs optical criteria helps to shed some light on the relation between the star formation properties (both global and nuclear) of LTGs and their HI content in various environments.
 |
Fig. 4 Top panel: (g − i)o color (corrected for internal extinction) vs. stellar mass diagram of Hα3 galaxies detected by ALFALFA (isolated+Virgo), color–coded by morphology (red = ETGs, blue+cyan = LTGs). Bottom panel: color–mass diagram of galaxies not in Hα3 (undetected by ALFALFA). They have been optically selected from NED among isolated objects, and from the VCC within the Virgo cluster (red = ETG; green = LTG). In both panels the diagonal dashed red lines mark the loci of the red sequence. The 26 LTGs in the VCC, undetected by ALFALFA, with log M∗ > 9.0 are listed in Table 1. |
As already stressed in Paper I, the radio selection biases Hα3 toward gas-rich, late-type galaxies (see also Gavazzi et al. 2008). The color (g − i)o versus stellar mass diagram composed of galaxies in Hα3 (top panel of Fig. 4) contains no well-developed red sequence (as emphasized by the red dashed line that marks the loci potentially occupied by the red sequence). This disagrees with similar diagrams derived from optically selected samples (e.g. Hogg et al. 2004). The census of Hα3 is made almost exclusively of LTG galaxies in the blue sequence. Only 15 ETG galaxies are detected in the radio in our survey (see Fig. 4, top panel). Interestingly, there is a minor (0.13 mag) but significant difference in the mean (g − i)o color between LTGs with normal HI content (blue symbols in Fig. 4, top panel) and LTGs with deficient HI content (cyan symbols in Fig. 4, top panel).
Furthermore, not all LTGs are detected by ALFALFA. To demonstrate this point one would like to be able to extract a priori an optical catalog of galaxies in the sky covered by ALFALFA. A similar exercise was carried out by Cortese et al. (2008a) in their HI survey of the cluster A1367 and in Paper III for the Coma cluster.
Owing to the notorious limitations that affects the completeness of SDSS for z ≪ 0.05 due to the shredding problem (Blanton et al. 2005), a similar exercise cannot easily be repeated for the Local Supercluster and Virgo. Alternatively, we proceeded in two steps as follows. Out of the boundaries of the Virgo cluster we searched in NED all galaxies with cz < 2000 km s-1 in the footprint of Hα3. At their position we searched the SDSS navigator and we took the i and g Petrosian magnitudes. After selecting those with i < 17.0 mag, we were left with 50 objects, 35 of late and 15 of early type. It is not surprising that the 15 ETGs are not detected by ALFALFA. The 35 LTG have stellar mass log M∗ < 8.5, thus it is not surprising that they remain undetected by ALFALFA because, owing to the relation log MHI = 0.55 × log M∗ + 3.85 that exists for unperturbed galaxies (see Sect. 8 and Gavazzi et al. 2008), they lie below the survey limiting sensitivity.
Inside the Virgo cluster a reliable optical selection was obtained using the VCC catalog by Binggeli et al. (1985) (including objects of all morphological type with B < 18 mag (Vega) between 4° < Dec < 16° and excluding those detected by ALFALFA and galaxies in the background of Virgo with cz > 3000 km s-1).
For this large-sample we computed the integrated magnitudes using the automatic procedure described in Sect. 2. In the surveyed region we count 640 optically selected galaxies with r < 17.5 mag (in addition to 509 HI selected galaxies). The color-mass relation of optical selected galaxies is plotted in the bottom panel of Fig. 4 separately for early (red symbols) and late types (green symbols). The 26 massive LTG Virgo members (log (M∗/M⊙) > 9) undetected LTGs even though they are in the footprint of ALFALFA3 are listed in Table 1. They are well-known high-HI-deficiency objects from previous deep pointed observations taken at Arecibo by Helou et al. (1984), Haynes & Giovanelli (1986), Hoffman et al. (1987, 1989), and Gavazzi et al. (2005). The interesting new fact is that the undetected LTGs have redder colors than the corresponding HI-detected galaxies (see bottom panel of Fig. 4), and are approximately 0.2 mag bluer than galaxies in the red sequence, which fill the “green valley” (see also Cortese & Hughes 2009).
26 LTG VCC galaxies in the Virgo cluster with log M∗ > 9.0 not detected by ALFALFA, with detections or more stringent upper limits from previous pointed observations.
All fits have a consistent slope of 0.10 and the intercepts are: 0.18 for ETGs; − 0.05 for undetected LTGs (0.23 mag bluer); − 0.24 for detected LTGs with DefHI > 0.3 (0.19 mag bluer); and − 0.37 (0.13 mag bluer) for detected LTGs with DefHI < 0.3. A consistent increase of the specific star formation rate (SSFR) in steps of decreasing DefHI is also visible in Fig. 8c. The above exercise, although it should be taken with a grain of salt because of NED incompleteness, confirms the result of Cortese et al. (2008a) (A1367) and of Paper III (Coma): given the sensitivity of ALFALFA at the distance of the Local Supercluster, only LTGs are detected. Among them, however, ALFALFA misses objects that are the most HI-anemic.
 |
Fig. 5 Corrected (g − i)o color of galaxies of all morphological types as a function of the local galaxy density (top panel) and of the projected angular separation from M 87 (bottom panel). HI-rich LTGs are depicted with blue symbols; HI-poor LTGs are plotted with cyan symbols; LTGs undetected by ALFALFA are given with green symbols; ETGs are marked with red symbols. |
Another way to show how the morphological/HI-content mix of galaxies depends on the environment in and around the Virgo cluster is offered in Fig. 5. Here we plot the corrected color of galaxies of all morphological types regardless of their HI properties (i.e., including objects undetected by ALFALFA) as a function of the projected separation from M 87 (bottom panel) and of the local galaxy density (top panel). We use the same symbols as in Fig. 4. The Virgo cluster (which lies within 10 degrees from M 87) is visible because it causes a strong color and morphology segregation, i.e., all ETGs (in the red sequence) are confined into its boundaries. Moreover, it also segregates LTGs with a low HI content from their HI-rich counterparts, which are mostly found outside its boundaries. These families also appear to be significantly segregated as far as their specific star formation is concerned, as indicated by their different color.
 |
Fig. 6 Cumulative distribution of the ratio of total Hα flux in the imaging material to the Hα flux measured in a central aperture of 10, 15, 30 or 45 arcsec diameter for galaxies of major axis 0–100, 100–200, 200–300 and >300 arcsec. The blue histogram refers to LTG-in ALFALFA with DefHI ≤ 0.3 and the red one includes LTGs with DefHI > 0.9 and LTGs undetected by ALFALFA. |
The properties of the studied galaxies on nuclear/circumnuclear scales are investigated in Fig. 6 and in Table 2. The figure gives the cumulative distribution of the ratio of total Hα flux (measured in the imaging material) to the Hα flux measured in a central aperture of variable size according to the total size of the galaxy, separately for LTGs-in ALFALFA with DefHI ≤ 0.3 (blue) and for LTGs with DefHI > 0.9 mixed with LTGs undetected by ALFALFA (red). A Kolmogorov-Smirnov test indicates that the probability that the two samples are drawn from the same parent population is 0.03%, i.e., that they significantly differ. In other words, the Hα sources associated with HI-rich galaxies are extended, while those of strongly deficient/undetected objects are predominantly nuclear/circumnuclear, see also Koopmann & Kenney (2004a,b).
Table 2 summarizes the classification of the available nuclear SDSS spectra of LTG galaxies in this work in three bins of DefHI (the LTG galaxies undetected by ALFALFA are included in the highest deficiency bin). It shows that the fraction of star-forming nuclei decreases significantly with increasing DefHI, although some signs of nuclear star formation remain in 46% of the most HI-poor systems. The fraction of passive spectra is relevant only in the highest DefHI bin, while the fraction of AGNs (including LINERS) does not significantly change with DefHI (consistently with Gavazzi et al. 2011).
Altogether we find evidence that
-
there is a mild gradual progression toward redder colors from (1)LTGs detected by ALFALFA with normal HI content;(2) LTGs detected by ALFALFA with deficient HIcontent; (3) LTGs undetected by ALFALFA and (4) ETGs;
-
the same morphology/HI-content sequence depends on the ambient density;
-
the extent of the star formation region in HI-rich (1) LTGs is statistically larger than in their HI-poor (2+3) counterparts.
In other words, we confirm the finding of Paper III (Coma) that the environmental conditions not only affect the HI content of galaxies, but also govern the average color (specific star formation rate) of galaxies. Moreover, whatever ablation mechanism is causing this pattern, it must proceed outside-in, in agreement with Boselli et al. (2008).
5. Scaling relations
The study of the scaling relations among the barionic constituents of (gas rich) galaxies has made a significant step forward with the work of Huang et al. (2012), who analyzed α.40 (Haynes et al. 2011), the most updated ALFALFA catalog available so far. Here we compare our local data with the results of Huang et al. (2012), whereas in Paper III we compare Virgo with Coma.
We begin by comparing in Fig. 7 the star formation estimates obtained in the present work from the Hα corrected luminosities taken from Paper I, with the estimates of Huang et al. (2012) computed by fitting UV, u,g,r,i,z SEDs. The correlation coefficient is 0.65, implying that the two quantities have a probability higher than 99% of being correlated. The bottom panel shows the distribution of the differences of the two quantities. The Gaussian fitted to the data was obtained after sigma clipping of the most deviant points. Two most extremes outlier galaxies (VCC 131 and VCC 1932) merit a more detailed comment. These are both bright edge-on galaxies with significant Hα flux (see GOLDMine) (log F = −12.68 and − 12.32 erg cm-2 s-1 respectively), therefore with consistent SFR as computed in this work (− 1.15 and − 0.37 M⊙ yr-1). Furthermore the SFR derived by directly converting the FUV magnitudes (corrected following Cortese et al. 2006, 2008b, assuming balance between the absorbed UV photons and the total FIR energy) into SFR are found to be (− 0.44 and 0.31) within a factor of 5 from each other. Conversely, the SFR found by Huang et al. (2012) (1.11, − 4.42) differs by more than five orders of magnitude, revealing some problems that are probably connected to the SED fitting procedure. Similarly, the galaxy VCC 785 is discrepant in Fig. 7, the SFR by SED fitting is approximately two orders of magnitude above the linear correlation. This is a face-on galaxy surrounded by a faint outer disk (as revealed in a deep 1500 s NUV image by GALEX not accompanied by a similar length FUV exposure). However, as explicitly mentioned by Huang et al. (2012), when deep GALEX images are not available in both NUV and FUV bands, the single long exposure is discarded and the SED fitting is performed with available FUV and NUV data of similar exposures, albeit shorter. For VCC 785 the GALEX database reports a FUV magnitude of 19.5 mag compared with a NUV of 15.4 mag (as derived from 200 s exposures). The SED fitting routine probably assumes an overestimated extinction correction to allow for such a large discrepancy in magnitude, hence it overestimates the SFR. In summary, we conclude that, albeit the large scatter, the two sets of SFR measurements are consistent, which makes the comparison between the scaling relations obtained from the two SFR estimators meaningful.
 |
Fig. 7 Top: correlation between the SFR used in this work (from Hα) and those adopted by Huan et al. (2012) (computed from SED fitting) The one-to-one relation is given with a dotted line. Some outliers marked with their VCC names are commented on in the text. Bottom: the distribution of the residual of the two star formation indicators, with a Gaussian of mean μ and σ fitted to it. |
The scaling relations relevant to our study are given in Figs. 8a through c, and the linear regression parameters are listed in Table 34.
We consider the relation between the HI and stellar mass by showing in Fig. 8a the HI gas fraction MHI/M∗ as a function of the stellar mass. The diagonal dot-dashed line represents the sensitivity limit of ALFALFA, computed for galaxies with an inclination of 45 deg in the plane of the sky5. By slicing the Hα3 sample in three subsamples of increasing DefHI: DefHI ≤ 0.3 (normal; blue symbols); 0.3 < DefHI < 0.9 (moderate deficiency; green symbols), and DefHI ≥ 0.9 (high deficiency; red symbols) we explore the whole range of environmental perturbations exhibited by galaxies in the Local Supercluster, an aspect that was not examined by Huang et al. (2012).
Consistently with the results of Gavazzi et al. (2008) and Huang et al (2012), the gas to stars fraction decreases by approximately 4 orders of magnitude by increasing galaxy mass, from log M∗ ~ 7 M⊙ to ~11.5 M⊙, independently of the HI deficiency parameter. This basic result seems to be independent of the fact that Hα3 is an HI-selected survey. Indeed our scaling relation perfectly agrees with the one found in the GASS survey by Catinella et al. (2010, see the black symbols in Fig. 8a). Similarly, over a broader interval of stellar mass 108.5 < M∗ < 1011.5 M⊙ there is also a good agreement with the relation found by Cortese et al. (2011) among HI-normal galaxies in a near-infrared selected sample derived from the Herschel Reference Survey (HRS; Boselli et al. 2010, see the large magenta squares in Fig. 8a)6. This result is consistent with the downsizing scenario (Gavazzi 1993; Gavazzi et al. 1996; Gavazzi & Scodeggio 1996; Boselli et al. 2001; Fontanot et al. 2009), where progressively more massive galaxies have less gas/star at z = 0 because they have transformed most of their gas into stars at higher z, while late-type dwarf galaxies retain large quantities of hydrogen capable of sustaining the star formation at some significant rate at the present cosmological epoch.
 |
Fig. 8 Scaling relations of HI mass, stellar mass and SFR for galaxies in three classes of increasing DefHI blue: DefHI ≤ 0.3 (normal); green: 0.3 < DefHI < 0.9 (perturbed), red: DefHI ≥ 0.9 (highly perturbed). Symbols are assigned according to the morphology. E-S0-S0a: circles; giant spirals (Sa-Sm): squares; Irr-BCD: triangles; AGN: asterisks. Panel a): gas fraction (MHI/M∗) versus M∗. The diagonal dot-dashed line represents the limiting sensitivity of ALFALFA at the distance of Virgo. The black symbols give the representative – sample extracted from GASS by Catinella et al. (2010), the large magenta squares represent the HI-normal sample and the large red squares the Virgo sample from Cortese et al. (2011). Across the stellar mass range in common there is an almost perfect agreement, but the present sample extends the correlation to two orders of magnitude fainter. Panel b): SFR versus M∗. Panel c): specific SFR versus M∗. The blue and red solid lines reproduce the relations plotted in Fig. 8 of Schiminovich et al. (2010) for the star-forming sequence (blue) and the non-star forming locus of red galaxies (red). |
The log SFR versus log M∗ relation (Fig. 8b) obtained at z = 0 is near the direct proportionality (slope = 0.97). A nearly exponential mass growth has also been obtained at redshift up to 3 by, e.g., Grützbauch et al. (2011) and beyond, e.g. Labbé et al. (2010). The specific star formation rate (SFR/M∗) (Fig. 8c) is thus unsurprisingly flat, or marginally decreasing with increasing mass.
In none of Figs. 8 there is compelling evidence that the relations shown have a significant change of slope in the considered interval of stellar mass, in contrast to the one found by Huang et al. (2012) near log M∗ ~ 9 M⊙. This is probably because the Local Supercluster lacks high mass galaxies due to the small sampled volume compared to α.40. However, a change of slope cannot be excluded in the present data set because of the paucity of data at high stellar mass.
Good agreement is found between Hα3 and HRS (Cortese et al. 2011) by comparing our deficient (green dots) or strongly deficient (red dots) objects with the Virgo HRS subsample (large red squares in Fig. 8a). Altogether, there is full agreement with previous surveys that on the common mass range there is a primary scaling relation between HI and the stellar mass, but Hα3 extends the studied range of mass to one order of magnitude fainter.
High-deficiency galaxies (see Fig. 8a) are found exclusively among the most massive systems and lie dangerously near to the ALFALFA detection limit already at the distance of Virgo (this lack of sensitivity is at the origin of the LTGs undetected by ALFALFA considered in Sect. 4). More highly HI-deficient galaxies exist at low stellar mass, but they require deeper HI observations than ALFALFA to be detected. Indeed when the optically selected galaxies (see Sect. 4) are considered and their deeper available HI observations are used to complement the ALFALFA data in Fig. 8a, several objects with severe HI depletion are detected at all stellar masses, including objects as faint as 107 M⊙. This is consistent with the idea that hydrogen depletion occurs more easily in dwarf galaxies within a cluster like Virgo (Boselli et al. 2008). The time scale for gas depletion is short enough (~100 Myr) to quickly transform them into anemics that become gas-free, passive dEs. This is precisely the mechanism invoked by Boselli et al. (2008) and by Gavazzi et al. (2010) to migrate dwarf star-forming systems into dEs in the neighborhood of rich galaxy clusters.
In our sample the specific star formation is found to depend only mildly on the stellar mass (Fig. 8d, compared with Huang et al. (2012) or with optical selected samples (Gavazzi et al. 2002b; Schiminovich et al. 2010).
The most remarkable feature of the specific star formation vs. stellar mass relation is the enormous scatter, as noted by other authors (Lee et al. 2007; Bothwell et al. 2009), particularly evident at low mass, where the scatter reaches 2 orders of magnitude. The faintest dwarfs are amorphous objects composed of few HII regions. Some of these are outliers with respect to the trends in Figs. 8, with a high SFR for a given HI mass and M∗. It is debated (Boselli et al. 2009; Fumagalli et al. 2011a; Weisz et al. 2011) whether sporadic bursts of SFR occurring in the individual HII regions in a stochastic manner could produce 100% variations in the integrated SSFR, hence a spread similar to the one observed in Fig. 8c. The same relation was also studied by Bothwell et al. (2009) and by Schiminovich et al. (2010, see their Fig. 8) in the (optically selected) GASS survey, limited to galaxies with 1010 < M∗ < 1011.5 M⊙. In this mass range our data agree with their high SFE objects (see the blue line in Fig. 8c), but in addition to these, Bothwell et al. (2009) and Schiminovich et al. (2010) have many low SFE objects at log SSFR ~ − 12 yr-1 (see the red line in Fig. 8c) that are simply not sampled in Hα3, which makes the overall relation steeper than in Hα3. Boselli et al. (2001) also found a correlation steeper than in Fig. 8c.
Summarizing, our analysis has highlighted in agreement with previous studies (e.g., Vulcani et al. 2010; Sobral et al. 2011) that the stellar mass is a fundamental parameter in driving the observed scaling relations. The effect of the environment is then superimposed on this scaling relations and is more evident in the relations that involve the mass of neutral hydrogen, which more easily prone to the effects of the environment when quantified using the HI deficiency.
 |
Fig. 9 Top panel: the sky distribution of LTGs within seven annuli of increasing radius from M 87. Galaxies in each ring are given with a different color. b) SSFR; c) SFR per unit HI mass; d) HI-deficiency as function of the projected angular separation from M 87. Bottom panel: same as above in bins of local galaxy density. This analysis is limited to galaxies with projected distance <45° from M 87, i.e., 20 objects in the interval 15:00:00 < RA < 16:00:00) were excluded because they do not constitute a statistically meaningful subset. |
6. Overview of the SFR in the Local Volume
We now illustrate the global role of the Virgo cluster on the star formation properties of the Local Supercluster as a whole, as shown in Fig. 9. Only the population of LTGs is considered, meaning we disregard ETGs that would obviously trace the phenomenon of morphology segregation in the Virgo cluster. The top panel shows the celestial distribution of LTGs in the present work. Annuli centered on M 87 are drawn with dashed lines, chosen to contain approximately an equal number of galaxies7. After discarding galaxies that do not properly belong to cluster A or B (background groups, such as clouds M, W), within each annulus we compute the median specific SFR (SFR per unit stellar mass) (second panel). The depletion or Robert’s time (HI mass divided by SFR) shown in the third panel gives the duration of the remaining star formation activity at the present rate for the available HI content. The inverse of the latter quantity is sometime called the star formation efficiency. The HI deficiency is given in the bottom panels. These quantities are plotted in bins of projected distance from M 87 (top panels) and in bins of local galaxy density (bottom panels).
There is a significant radial dependence of the HI content (the strongest of all), of the specific star formation rate, and therefore of the depletion time. LTGs in the Local Supercluster located up to 20 degrees away from Virgo have a life expectation longer than 1010 yr (i.e., almost one Hubble time) if they continue to burn their hydrogen at the present rate, while galaxies near to M 87 will remain active 109.3 yr (less than 2 Gyr). This derives from the reduced gas reservoir of galaxies in the cluster environment (HI-deficiency) and appears to be associated with a significant suppression of the star formation rate.
7. Discussion
The scaling relations between the gaseous (HI) mass and the star formation rate as a function of the stellar mass, in intervals of HI deficiency are analyzed in Fig. 8 and are found to be consistent with previous determinations based on HI and on optically selected samples.
The environmental conditions occurring in a young, still evolving cluster of galaxies such as the Virgo cluster have profound consequences on the morphological composition of its member galaxies, producing the well known phenomenon named morphology segregation (Dressler 1980). Moreover, it induces observable modifications to the population of LTGs, even when they are considered alone: their HI content and to a lesser extent their specific star formation are significantly reduced compared to LTGs found in relative isolation. To quantify the quenching introduced by the environment on the gas content and on the SFR independently of the stellar mass, we plot in the central panel of Figs. 10a, b the relation of the specific star formation versus gas fraction. This figure was obtained by dividing both the SFR and the HI mass by the stellar mass, so that both axes contain normalized quantities. In other words, this figure contains the residual correlation excluding the scaling law with stellar mass. The symbols are color-coded according to the DefHI parameter. The histograms in the side panels enable to estimate the average gas fraction and SSFR in three bins of HI deficiency. While the left panel contains only giant galaxies (log M∗ > 9 M⊙), the right panel shows all galaxies. Both panels show that even after subtracting the scaling law with stellar mass, a significant residual (second-order) dependence of the SSFR on the HI-deficiency remains: gas-rich objects that contain as much mass in HI and stars (log MHI/M∗ = 0) have SSFR ten times higher than galaxies that contain 100 times less HI relative to stars. The gas-rich, high SSFR systems are exclusively found among unperturbed galaxies (DefHI ≤ 0.3), while gas-poor objects with a lower SSFR are exclusively highly perturbed (DefHI ≥ 0.9) members of Virgo. The comparison between the two panels emphasizes the large scatter in the SSFR of low mass objects mentioned earlier. These faint systems preferentially have a high gas fraction, normal or intermediate HI-deficiency and an erratic specific star formation rate over 2 dex, in contrast to high stellar mass systems, whose specific star formation correlates better with the gas fraction (see Boselli et al. 2009). In summary, once the scaling relation with stellar mass is neutralized, it is found that by decreasing the gas fraction by 2 dex, the specific star formation rate decreases by one dex, i.e., the effect of the environment is ten times as effective at removing the HI gas than at quenching the star formation.
 |
Fig. 10 Left panel: relation between the specific star formation rate and the gas fraction in three classes of increasing DefHI, excluding objects fainter than M∗ = 109M⊙. Right panel: same as in the left panel, but including fainter objects. The histograms drawn on top and to the right show the counts of galaxies with given HI gas fraction and SSFR, with the mean values given in three bins of DefHI. |
This is consistent with the finding of Fig. 9, which shows that the star formation efficiency (MHI/SFR) decreases going toward the Virgo cluster, i.e., MHI decrease more than SFR, implying that the cluster produces a significant perturbation to the Local Supercluster, even on its member late-type galaxies, particularly efficient at reducing their HI content and to a lesser extent at quenching their present star formation rate.
In Sect. 4 we showed that there is evidence of a continuous sequence of transformations that make LTGs gradually gas-poorer and redder in their disk components while they approach the Virgo cluster. Meanwhile, their star formation shrinks to the circumnuclear or even nuclear scale. The last feature calls for a truncation process of the star formation that is inconsistent with the so-called strangulation (Boselli et al. 2006, 2008) and consistent with ram pressure.
HI ablation occurs on very brief time scales of 100–200 Myr for low-mass galaxies and 300 Myr for massive galaxies. An example is NGC 4569, analyzed by Boselli et al. (2006). In spite of being very HI-poor (85% of the HI gas has been removed from this galaxy by ram-pressure), neverless it is only marginally H2 deficient (Fumagalli et al. 2009) and its global star formation is only reduced by a factor of two. This is consistent with the fact that most of the gas has been removed from the outer disk, while in the inner regions the star formation continues sustained by copious H2, coexistent with an inner HI shell. The time-scales for ram-pressure stripping in this massive galaxy is consistently estimated to be ~300 Myr by Vollmer et al. (2004) and between 100 and 400 Myr by Boselli et al. (2006). Estimates of 200 Myr were derived for two dwarf galaxies in the Virgo cluster: VCC 1217 (Fumagalli et al. 2011b) and VCC 1249 in the M49 group (Arrigoni Battaia et al. 2012).
The ongoing infall rate of galaxies on the Virgo cluster can be obtained by dividing the number of HI rich LTGs that still exist in the Virgo cluster by the time scale of the HI stripping mechanism. Table 4 contains two estimates: for >107 M⊙ and for >109 M⊙ (the second interval is to compare our estimate with a similar estimate obtained for the Coma cluster in Paper III). In the two cases we obtain a current infall rate of 400–100 galaxy Gyr-1 in the two mass bins (the former consistent with 300 galaxy Gyr-1 found by Boselli et al. (2008) for Virgo and the latter consistent with the estimate for Coma).
Build-up of the Virgo cluster from various estimators.
An alternative method for estimating the infall rate can be achieved using the number of LTGs that are currently in the HI-poor phase divided by the time scale for complete hydrogen exhaust: 0.5 Gyr for low-mass galaxies (Boselli et al. 2008) and somewhat longer for massive systems. This time scale is estimated assuming that a complete HI and H2 ablation will occur during the second passage through the cluster center. This is considerably shorter than ~2 ± 1 Gyr (Bigiel et al. 2008): the time scale for complete consumption of the H2 due to star formation in intermediate HI deficiency galaxies, i.e., without an extended reservoir of atomic hydrogen that can replenish the inner HI fuel consumed by the star formation (Fumagalli et al. 2009). The derived infall rates adopting these figures are consistent with the previous estimates.
Finally, assuming that all galaxies (LTGs+ETGs) were accreted by the Virgo cluster at a rate that remained approximately constant in time, and that massive galaxies require an additional 1–2 Gyr after a stripping event to migrate from the blue cloud to the transition region and to the red sequence (Boselli et al. 2008; Cortese & Hughes 2009; Gavazzi et al. 2010), we infer that the age of the Virgo cluster is roughly 2 Gyr, implying a cluster formation at z ~ 0.2, much later than z ~ 1 derived using similar arguments for the Coma cluster in Paper III. Of course, these are just order-of-magnitude estimates of the accretion rate on the Virgo cluster. For example, cluster B (M49) will soon merge with cluster A (M 87) to form an even more relaxed and rich Virgo cluster, contributing with many galaxies that have been pre-processed in the group itself. The significant age difference found between Virgo and Coma is consistent with the high contrast in the observed X-ray properties of the two clusters (Forman & Jones 1982), suggesting a marked difference in their evolutionary stages.
8. Summary and conclusions
The wealth of data provided by ALFALFA in the stretch of the Local Supercluster visible in spring, which contains the Virgo cluster, which were followed-up with Hα imaging observations, enabled us to analyze the relations between the HI gas, the stellar content and the rate at which the gas is currently fueling the formation of new stars in spiral galaxies.
Given the sensitivity of ALFALFA and of Hα3 at the distance of Virgo, our analysis comprises galaxies with a stellar mass in the range 107.5 < M∗ < 1011.5 M⊙, a gas mass 107.7 < MHI < 1010 M⊙ and a star formation rate in excess of 10-3 M⊙ yr-1. The main results of the present investigation can be summarized as follows:
-
In addition to morphology segregation, the Virgo clusterrepresents a significant perturbation on the Local Superclusterfor the gas content and the star formation properties of its membergalaxies of late-type, such that on average theHI content is reduced by a factor of four and thespecific star formation rate by a factor of two.
-
LTGs in the Local Supercluster have progressively redder color with decreasing HI gas content, from normal deficient galaxies to objects that are undetected by ALFALFA. The gas-ablation mechanism also governs the star formation properties.
-
Highly HI deficient and undetected LTGs have ongoing nuclear and circumnuclear (truncated) star formation, while HI-rich LTGs show star formation extended on the disk scale. We propose that the quenching mechanism responsible for these features is ram pressure.
-
The fundamental scaling relation (studied in Sect. 8) between the HI mass and the stellar mass in normal spiral galaxies is such that
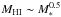 . This implies that increasingly more massive galaxies have progressively lower HI gas fraction, consistent with the idea that they have transformed most of their gas into stars at higher z, in agreement with the downsizing scenario.
. This implies that increasingly more massive galaxies have progressively lower HI gas fraction, consistent with the idea that they have transformed most of their gas into stars at higher z, in agreement with the downsizing scenario. -
The scaling relation between MHI and M∗ followed by galaxies in the Virgo cluster is significantly offset toward lower gas content, compared to that of HI-normal galaxies.
-
Once the scaling law with stellar mass is removed by analyzing the correlation between the specific star formation and the gas fraction, it is found that a residual second-order correlation exists between these quantities. The effect of the environment is ten times stronger at producing the gas depletion than at quenching the star formation.
-
The present infall rate of ~400 galaxies per Gyr (of ≥107 M⊙ objects), inferred by the number of healthy spirals present in the Virgo cluster, is consistent with the number of galaxies of all types (of similar mass) if the infall process has been acting for approximately 2 Gyr, about three times shorter than on the Coma cluster (Paper III). This is consistent with the idea that Virgo is a young cluster caught in an early evolutionary stage.
2 mJy is the noise per channel after Hanning smoothing to 10 km s-1 (see Haynes et al. 2011).
http://www.mpa-garching.mpg.de/SDSS/DR7/, see Salim et al. (2007).
Six additional VCC objects are undetected by ALFALFA, not because the are HI-poor, but because they are confused among each-other or with other sources: i.e., VCC 386, 483, 497, 1673, 1676, and 1972; see Hallenbeck et al. (2012).
Linear regressions are obtained in this work using the “bisector” method by Isobe et al. (1990) (mean coefficients of the direct and the inverse relation).
As introduced in Giovanelli et al. (2005), ALFALFA is a noise-limited survey rather than a flux-limited one. At any given integrated HI mass the 21 cm flux per velocity channel is inversely proportional to the width of the HI profile, hence to the galaxy inclination. The completeness and sensitivity of ALFALFA are clearly defined and discussed in detail in Saintonge (2007), Martin at al. (2010) and Haynes et al. (2011).
The GASS and HRS points plotted in Fig. 8a are binned averages, thus the error-bars do not represent the dispersion of the distribution.
Figure 9 was obtained adding to the ALFALFA-detected LTGs the undetected LTGs that were optically selected with HI and Hα measurements taken from GOLDMine.
Acknowledgments
We thank Luca Cortese and Barbara Catinella for their comments on an early version of the manuscript, and Massimo Dotti and Emanuele Ripamonti for useful discussions. We also thank Silvia Fabello for her contribution to the observations and Shan Huang for providing original data. The authors would like to acknowledge the work of the entire ALFALFA collaboration team in observing, flagging, and extracting the catalog of galaxies used in this work. This research has made use of the GOLDMine database (Gavazzi et al. 2003) and of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We wish to thank the anonymous referee, whose criticism helped us to improve the manuscript. Funding for the Sloan Digital Sky Survey (SDSS) and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, and the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, The University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. G.G. acknowledges financial support from the italian MIUR PRIN contract 200854ECE5. R.G. and M.P.H. are supported by US NSF grants AST-0607007 and AST-1107390 and by a Brinson Foundation grant. Support for M.Fumagalli was provided by NASA through Hubble Fellowship grant HF-51305.01-A awarded by the Space Telescope Science Insititute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abell, G. O., Corwin, H. G., Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arrigoni Battaia, F., Gavazzi, G., Fumagalli, M., et al. 2012, A&A, 543, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautz, L. P., & Morgan, W. W. 1970, ApJ, 162, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & de Vaucouleurs, G. 1981, MNRAS, 194, 679 [NASA ADS] [Google Scholar]
- Blanton, M. R., Schlegel, D. J., Strauss, M. A., et al. 2005, AJ, 129, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Briel, U. G., Schwarz, R. A., et al. 1994, Nature, 368, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2002, A&A, 386, 124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2009, A&A, 508, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Gavazzi, G., Donas, J., & Scodeggio, M. 2001, AJ, 121, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Lequeux, J., & Gavazzi, G. 2002a, A&A, 384, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Iglesias, J., Vílchez, J. M., & Gavazzi, G. 2002b, A&A, 386, 134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2006, ApJ, 651, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., & Gavazzi, G. 2008, ApJ, 674, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2009, ApJ, 706, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Eales, S., Cortese, L., et al. 2010, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Heinis, S., et al. 2011, A&A, 528, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Kennicutt, R. C., & Lee, J. C. 2009, MNRAS, 400, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Schiminovich, D., Kauffmann, G., et al. 2010, MNRAS, 403, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Cayatte, V., van Gorkom, J. H., Balkowski, C., & Kotanyi, C. 1990, AJ, 100, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Chung, A., van Gorkom, J. H., Kenney, J. D. P., Crowl, H., & Vollmer, B. 2009, AJ, 138, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2003, ApJS, 147, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., & Hughes, T. M. 2009, MNRAS, 400, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Boselli, A., Buat, V., et al. 2006, ApJ, 637, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Minchin, R. F., Auld, R. R., et al. 2008a, MNRAS, 383, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Boselli, A., Franzetti, P., et al. 2008b, MNRAS, 386, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Catinella, B., Boissier, S., et al. 2011, MNRAS, 415, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Decarli, R., Gavazzi, G., Arosio, I., et al. 2007, MNRAS, 381, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., De Lucia, G., Monaco, P., Somerville, R. S., & Santini, P. 2009, MNRAS, 397, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Forman, W., & Jones, C. 1982, ARA&A, 20, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, M., Gavazzi, G., Savorgnan, G., et al. 2013, A&A, 553, A91 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fumagalli, M., & Gavazzi, G. 2008, A&A, 490, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fumagalli, M., Krumholz, M. R., Prochaska, J. X., Gavazzi, G., & Boselli, A. 2009, ApJ, 697, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., da Silva, R. L., & Krumholz, M. R. 2011a, ApJ, 741, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Gavazzi, G., Scaramella, R., et al. 2011b, A&A, 528, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G. 1993, ApJ, 419, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., & Scodeggio, M. 1996, A&A, 312, L29 [NASA ADS] [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Scodeggio, M., Pierini, D., & Belsole, E. 1999, MNRAS, 304, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Boselli, A., Pedotti, P., Gallazzi, A., et al. 2002a, A&A, 386, 114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Boselli, A., Pedotti, P., Gallazzi, A., et al. 2002b, A&A, 396, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Boselli, A., Donati, A., Franzetti, P., et al. 2003, A&A, 400, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Boselli, A., van Driel, W., & O’Neil, K. 2005, A&A, 429, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Boselli, A., Cortese, L., et al. 2006, A&A, 446, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Giovanelli, R., Haynes, M. P., et al. 2008, A&A, 482, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Fumagalli, M., Cucciati, O., & Boselli, A. 2010, A&A, 517, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Savorgnan, G., & Fumagalli, M. 2011, A&A, 534, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Fumagalli, M., Galardo, V., et al. 2012, A&A, 545, A16 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., Savorgnan, G., Fossati, M., et al. 2013, A&A, 553, A90 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giovanelli, R., & Haynes, M. P. 1985, ApJ, 292, 404 [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Kent, B. R., et al. 2005, AJ, 130, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Grützbauch, R., Conselice, C. J., Bauer, A. E., et al. 2011, MNRAS, 418, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hallenbeck, G., Papastergis, E., Huang, S., et al. 2012, AJ, 144, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, Y., Oemler, A., Jr., Lin, H., & Tucker, D. L. 1998, ApJ, 499, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., & Giovanelli, R. 1984, AJ, 89, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., & Giovanelli, R. 1986, ApJ, 306, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., Giovanelli, R., Martin, A. M., et al. 2011, AJ, 142, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Hoffman, G. L., & Salpeter, E. E. 1984, ApJS, 55, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, G. L., Glosson, J., Helou, G., Salpeter, E. E., & Sandage, A. 1987, ApJS, 63, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, G. L., Williams, B. M., Lewis, B. M., Helou, G., & Salpeter, E. E. 1989, ApJS, 69, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Blanton, M. R., Brinchmann, J., et al. 2004, ApJ, 601, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Haynes, M. P., Giovanelli, R., & Brinchmann, J. 2012, ApJ, 756, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, P. A., Shane, N. S., Beckman, J. E., et al. 2004, A&A, 414, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr. 1983, AJ, 88, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Lee, J. C., Funes, S. J., et al. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmann, R. A., & Kenney, J. D. P. 2004a, ApJ, 613, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmann, R. A., & Kenney, J. D. P. 2004b, ApJ, 613, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmann, R. A., Kenney, J. D. P., & Young, J. 2001, ApJS, 135, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 716, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Kennicutt, R. C., Funes, S. J., José, G., et al. 2007, ApJ, 671, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Meurer, G. R., Hanish, D. J., Ferguson, H. C., et al. 2006, ApJS, 165, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, S. G., Holden, B. P., Kelson, D. D., Illingworth, G. D., & Franx, M. 2009, ApJ, 705, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A. 2007, AJ, 133, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Catinella, B., Kauffmann, G., et al. 2010, MNRAS, 408, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Smail, I., et al. 2011, MNRAS, 411, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Solanes, J. M., Giovanelli, R., & Haynes, M. P. 1996, ApJ, 461, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., & Primack, J. R. 1999, MNRAS, 310, 1087 [CrossRef] [Google Scholar]
- Vollmer, B., Balkowski, C., Cayatte, V., et al. 2004, A&A, 419, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Finn, R. A., et al. 2010, ApJ, 710, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002, ApJ, 568, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Weisz, D. R., Dalcanton, J. J., Williams, B. F., et al. 2011, ApJ, 739, 5 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
26 LTG VCC galaxies in the Virgo cluster with log M∗ > 9.0 not detected by ALFALFA, with detections or more stringent upper limits from previous pointed observations.
All Figures
 |
Fig. 1 Sky distribution of 409 HI-selected galaxies in Hα3, coded according to their morphology (E-S0-S0a: circles; giant spirals Sa-Sm: squares; Irr-BCD: triangles) The two vertical dashed lines mark the adopted boundaries of the Virgo cluster. Red symbols refer to galaxies considered as part of the Virgo cluster, blue are galaxies considered as isolated. Superposed are the X-ray contours from ROSAT (Böhringer et al. 1994). |
| In the text | |
 |
Fig. 2 Sky distribution of galaxies around the Virgo cluster. ETGs (from the VCC with mp < 18.0 mag) are given with small black dots. HI-selected LTG galaxies, coded according to their HI deficiency parameter (red dots: DefHI > 0.9; green dots: 0.3 < DefHI < 0.9; blue dots DefHI ≤ 0.3). The empty red circles represent the 26 LTGs undetected by ALFALFA listed in Table 1. Superposed are the X-ray contours from ROSAT (Böhringer et al. 1994). The position of cluster A (M 87), B (M 49) and of clouds M, N and W are given. Clouds M and N coincide in position but have significantly different distance moduli. |
| In the text | |
 |
Fig. 3 Histogram of the DefHI parameter separately for the isolated and W, N clouds (black) and for members of the Virgo A and B subclusters (red). The bulk of HI-deficient galaxies is located within the two subclusters. |
| In the text | |
 |
Fig. 4 Top panel: (g − i)o color (corrected for internal extinction) vs. stellar mass diagram of Hα3 galaxies detected by ALFALFA (isolated+Virgo), color–coded by morphology (red = ETGs, blue+cyan = LTGs). Bottom panel: color–mass diagram of galaxies not in Hα3 (undetected by ALFALFA). They have been optically selected from NED among isolated objects, and from the VCC within the Virgo cluster (red = ETG; green = LTG). In both panels the diagonal dashed red lines mark the loci of the red sequence. The 26 LTGs in the VCC, undetected by ALFALFA, with log M∗ > 9.0 are listed in Table 1. |
| In the text | |
 |
Fig. 5 Corrected (g − i)o color of galaxies of all morphological types as a function of the local galaxy density (top panel) and of the projected angular separation from M 87 (bottom panel). HI-rich LTGs are depicted with blue symbols; HI-poor LTGs are plotted with cyan symbols; LTGs undetected by ALFALFA are given with green symbols; ETGs are marked with red symbols. |
| In the text | |
 |
Fig. 6 Cumulative distribution of the ratio of total Hα flux in the imaging material to the Hα flux measured in a central aperture of 10, 15, 30 or 45 arcsec diameter for galaxies of major axis 0–100, 100–200, 200–300 and >300 arcsec. The blue histogram refers to LTG-in ALFALFA with DefHI ≤ 0.3 and the red one includes LTGs with DefHI > 0.9 and LTGs undetected by ALFALFA. |
| In the text | |
 |
Fig. 7 Top: correlation between the SFR used in this work (from Hα) and those adopted by Huan et al. (2012) (computed from SED fitting) The one-to-one relation is given with a dotted line. Some outliers marked with their VCC names are commented on in the text. Bottom: the distribution of the residual of the two star formation indicators, with a Gaussian of mean μ and σ fitted to it. |
| In the text | |
 |
Fig. 8 Scaling relations of HI mass, stellar mass and SFR for galaxies in three classes of increasing DefHI blue: DefHI ≤ 0.3 (normal); green: 0.3 < DefHI < 0.9 (perturbed), red: DefHI ≥ 0.9 (highly perturbed). Symbols are assigned according to the morphology. E-S0-S0a: circles; giant spirals (Sa-Sm): squares; Irr-BCD: triangles; AGN: asterisks. Panel a): gas fraction (MHI/M∗) versus M∗. The diagonal dot-dashed line represents the limiting sensitivity of ALFALFA at the distance of Virgo. The black symbols give the representative – sample extracted from GASS by Catinella et al. (2010), the large magenta squares represent the HI-normal sample and the large red squares the Virgo sample from Cortese et al. (2011). Across the stellar mass range in common there is an almost perfect agreement, but the present sample extends the correlation to two orders of magnitude fainter. Panel b): SFR versus M∗. Panel c): specific SFR versus M∗. The blue and red solid lines reproduce the relations plotted in Fig. 8 of Schiminovich et al. (2010) for the star-forming sequence (blue) and the non-star forming locus of red galaxies (red). |
| In the text | |
 |
Fig. 9 Top panel: the sky distribution of LTGs within seven annuli of increasing radius from M 87. Galaxies in each ring are given with a different color. b) SSFR; c) SFR per unit HI mass; d) HI-deficiency as function of the projected angular separation from M 87. Bottom panel: same as above in bins of local galaxy density. This analysis is limited to galaxies with projected distance <45° from M 87, i.e., 20 objects in the interval 15:00:00 < RA < 16:00:00) were excluded because they do not constitute a statistically meaningful subset. |
| In the text | |
 |
Fig. 10 Left panel: relation between the specific star formation rate and the gas fraction in three classes of increasing DefHI, excluding objects fainter than M∗ = 109M⊙. Right panel: same as in the left panel, but including fainter objects. The histograms drawn on top and to the right show the counts of galaxies with given HI gas fraction and SSFR, with the mean values given in three bins of DefHI. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


