| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220859 | |
| Published online | 01 March 2013 | |
Panchromatic spectral energy distributions of Herschel sources⋆,⋆⋆,⋆⋆⋆
1 Max-Planck-Institut für Extraterrestrische Physik (MPE), Postfach 1312, 85741 Garching, Germany
e-mail: berta@mpe.mpg.de
2 INAF – Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
3 Center for Radiophysics and Space Research, Cornell University, Ithaca, NY 14853, USA
4 Dept. of Physics & Astronomy, University of California, CA 92697, Irvine, USA
5 Dipartimento di Astronomia, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
6 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
7 ESO, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
8 Smithsonian Astrophysical Observatory, 60 Garden Street, MA 02138, Cambridge, USA
9 Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service d’Astrophysique, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
10 School of Physics and Astronomy, The Raymond and Beverly Sackler Faculty of Exact Sciences, Tel-Aviv University, 69978 Tel-Aviv, Israel
11 Astronomy Centre, Department of Physics and Astronomy, University of Sussex, Brighton BN1 9QH, UK
12 Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
13 Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
14 Astrophysics Branch, NASA – Ames Research Center, MS 245-6, CA 94035, Moffett Field, USA
15 Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, EH9 3 HJ Edinburgh, UK
16 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, BC V6T 1Z1, Vancouver, Canada
17 Herschel Science Centre, ESAC, ESA, PO Box 78, Villanueva de la Canãda, 28691 Madrid, Spain
18 California Institute of Technology, 1200 E. California Blvd., CA 91125, Pasadena, USA
Received: 6 December 2012
Accepted: 16 January 2013
Combining far-infrared Herschel photometry from the PACS Evolutionary Probe (PEP) and Herschel Multi-tiered Extragalactic Survey (HerMES) guaranteed time programs with ancillary datasets in the GOODS-N, GOODS-S, and COSMOS fields, it is possible to sample the 8–500 μm spectral energy distributions (SEDs) of galaxies with at least 7–10 bands. Extending to the UV, optical, and near-infrared, the number of bands increases up to 43. We reproduce the distribution of galaxies in a carefully selected restframe ten colors space, based on this rich data-set, using a superposition of multivariate Gaussian modes. We use this model to classify galaxies and build median SEDs of each class, which are then fitted with a modified version of the magphys code that combines stellar light, emission from dust heated by stars and a possible warm dust contribution heated by an active galactic nucleus (AGN). The color distribution of galaxies in each of the considered fields can be well described with the combination of 6–9 classes, spanning a large range of far- to near-infrared luminosity ratios, as well as different strength of the AGN contribution to bolometric luminosities. The defined Gaussian grouping is used to identify rare or odd sources. The zoology of outliers includes Herschel-detected ellipticals, very blue z ~ 1 Ly-break galaxies, quiescent spirals, and torus-dominated AGN with star formation. Out of these groups and outliers, a new template library is assembled, consisting of 32 SEDs describing the intrinsic scatter in the restframe UV-to-submm colors of infrared galaxies. This library is tested against L(IR) estimates with and without Herschel data included, and compared to eightother popular methods often adopted in the literature. When implementing Herschel photometry, these approaches produce L(IR) values consistent with each other within a median absolute deviation of 10–20%, the scatter being dominated more by fine tuning of the codes, rather than by the choice of SED templates. Finally, the library is used to classify 24 μm detected sources in PEP GOODS fields on the basis of AGN content, L(60)/L(100) color and L(160)/L(1.6) luminosity ratio. AGN appear to be distributed in the stellar mass (M∗) vs. star formation rate (SFR) space along with all other galaxies, regardless of the amount of infrared luminosity they are powering, with the tendency to lie on the high SFR side of the “main sequence”. The incidence of warmer star-forming sources grows for objects with higher specific star formation rates (sSFR), and they tend to populate the “off-sequence” region of the M∗ − SFR − z space.
Key words: infrared: galaxies / galaxies: statistics / galaxies: star formation / galaxies: active / galaxies: evolution
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendix A is available in electronic form at http://www.aanda.org
Galaxy SED templates are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A100
© ESO, 2013
1. Introduction
The advent of wide-field surveys on the one hand, and deep pencil-beam observation of selected blank fields on the other, have produced, in recent years, extensive multiwavelength photometric information for very large numbers of galaxies. Optical and near-infrared (NIR) surveys such as the Sloan Digital Sky Survey (SDSS, York et al. 2000), the Two Degree Field survey (Colless 1999), the Two Micron All Sky Survey (2MASS, Kleinmann et al. 1994), the Cosmic Evolution Survey (COSMOS, Scoville et al. 2007), the Great Observatories Origins Deep Survey (GOODS, Dickinson et al. 2001), the All-wavelength Extended Groth Strip International Survey (Aegis, Davis et al. 2007) survey, the Spitzer Wide-Area Infrared Extragalactic (SWIRE) Legacy survey (Lonsdale et al. 2003, 2004), among many others, include now millions of galaxies spanning across all epochs, to z > 4 in the deepest cases, and covering the whole electromagnetic spectrum from X-rays to radio wavelengths.
At long wavelengths, extragalactic surveys with the Infrared Astronomical Satellite (IRAS, Neugebauer et al. 1984), Infrared Space Observatory (ISO, e.g. ELAIS, Rowan-Robinson et al. 2004), Spitzer (e.g. Frayer et al. 2009; Le Floc’h et al. 2009; Magnelli et al. 2009; Lonsdale et al. 2003, 2004; Dickinson et al. 2001) and AKARI (e.g. Matsuura et al. 2009; Matsuhara et al. 2006) revealed the mid- and far-infrared (MIR, FIR) counterparts of local galaxies first, and of several thousands of distant sources up to z ~ 3 in the latest incarnation of 80-cm class IR space telescopes.
While detailed spectroscopic studies are still very demanding in terms of observing time, and include a relatively limited number of sources, especially at z > 1.0−1.5 and at the faint end of the luminosity function, a variety of techniques has been developed to extract the wealth of information stored in photometric data. Fitting the broad band spectral energy distribution (SED) of each source by adopting a library of galaxy templates can provide a classification, together with an estimate of luminosity (in the desired bands), stellar mass and other possible parameters. However, success depends on the predefined templates being representative of the galaxies under consideration.
Basic approaches to SED fitting follow different paths, depending on goals and wavelength coverage. Evolutionary and mixed stellar population synthesis, including global or age-selective extinction corrections (e.g. Bruzual & Charlot 2003; Poggianti et al. 2001; Bressan et al. 1994; Renzini & Buzzoni 1986), has proven to be very successful in the optical and NIR to study galaxy properties such as stellar mass, star formation rate and history, and has been sometimes extended to longer wavelengths by means of energy balance arguments (e.g. da Cunha et al. 2008; Berta et al. 2004). Modeling from the ultraviolet (UV) to FIR, making use of radiative transfer and ray tracing techniques (e.g. Siebenmorgen & Krügel 2007; Piovan et al. 2006; Dopita et al. 2005; Efstathiou et al. 2000; Silva et al. 1998), provides extensive information on the physical properties of star-forming regions, molecular clouds, and the diffuse dust component, as well as of stellar populations. Finally semi-empirical libraries (e.g. Polletta et al. 2007; Kirkpatrick et al. 2012; and this work) offer flexible templates to be compared in a fast manner to large observed catalogs for quick classification and derivation of basic properties.
The semi-empirical library built by Polletta et al. (2007) spans from the UV to submm, and covers a wide range of spectral types, from elliptical galaxies to spirals and irregulars, and includes templates of prototype starbursts, ultra-luminous infrared galaxies (ULIRGs), and objects with different amounts of an active galactic nucleus (AGN) power (both type-1 and type-2).
Alternatives in the infrared domain focus on star-forming objects and are based on locally determined properties such as the local luminosity-temperature relation, implying that a single SED shape is associated with each value of L(IR) (e.g. Chary & Elbaz 2001; Dale & Helou 2002; Elbaz et al. 2010; Nordon et al. 2010, the latter two already pointing out weaknesses of this approach). Recent works indicate that the SED shape of infrared galaxies is more naturally explained in relation to their distance from the so-called “main sequence” of star formation (Elbaz et al. 2011; Nordon et al. 2012; see also Magnelli et al., in prep.). Defined in the M∗ − SFR plane, this main sequence (MS) represents the “secular” and dominant mode of baryon transformation into stars (e.g. Elbaz et al. 2011, 2007; Rodighiero et al. 2011; Wuyts et al. 2011b; Daddi et al. 2009, 2007), likely supported by accretion of gas from the intergalactic medium (e.g. Davé et al. 2010, and references therein). In this picture, galaxies lying above the MS would be undergoing powerful, starbursting events, possibly triggered by major mergers.
The above-mentioned SED libraries, as well as others not listed, have not only been employed to derive properties of individual sources, but have also been widely used in describing the statistical properties of galaxy populations, for example while interpreting and modeling observed number counts (e.g. Berta et al. 2011, 2010; Béthermin et al. 2011; Franceschini et al. 2010) or assessing luminosity functions at different wavelengths (e.g. Gruppioni et al. 2013, 2010; Rodighiero et al. 2010b).
Most of the templates adopted in the literature have actually been built using local galaxies (e.g. Rieke et al. 2009; Polletta et al. 2007; Dale & Helou 2002; Chary & Elbaz 2001), and although they have proven to reproduce the SEDs of high-z galaxies reasonably well, their applicability can be subject to criticism. Gruppioni et al. (2010) have shown, for example, that the observed SEDs of Herschel detected galaxies are in general well reproduced by the Polletta et al. (2007) library, but very bright FIR emitters, or objects intermediate between spirals and starburst, are actually poorly represented.
After three years of operation, the Herschel Space Observatory (Pilbratt et al. 2010) has proven to be the ultimate machine to build detailed FIR SEDs of galaxies up to z > 3, without being limited to very luminous sources. The sensitivity reached by the Photodetector Array Camera and Spectrometer (PACS, Poglitsch et al. 2010) and the Spectral and Photometric Imaging REceiver (SPIRE, Griffin et al. 2010) instruments aboard Herschel has guaranteed the detection not only of the most extreme star-forming galaxies, with star formation time scales on the order of ~0.1 Gyr or less (e.g. Magnelli et al. 2010, 2012; Rodighiero et al. 2011), but also objects lying on the MS of star formation up to z ~ 2. In addition, the variety of Herschel detections includes objects with MIR power-law spectra, dominated by an AGN torus emission, but with optical stellar SEDs (e.g. Hatziminaoglou et al. 2010), as well as type-1 AGN.
This paper is based on Herschel FIR observations carried out in the framework of the PACS Evolutionary Probe (PEP, Lutz et al. 2011) and the Herschel Multi-tiered Extragalactic Survey (HerMES, Oliver et al. 2012) in three of the most popular extragalactic “blank fields”: GOODS-N, GOODS-S, and COSMOS (Dickinson et al. 2001; Scoville et al. 2007). Combining Herschel and Spitzer data, it is now possible to sample the 8–500 μm SEDs of galaxies with 7 to 10 bands, thus accurately probing the shape of the dust emission peak, as well as MIR light dominated by warmer dust. Extending to the UV, optical, and NIR, the number of bands increases up to 43 in the most favorable case (COSMOS, including intermediate bands).
We take advantage of this rich multiwavelength data-sets to build a new set of semi-empirical templates, based on the observed UV to FIR photometry of galaxies detected by Herschel (but not only), without any restriction in redshift.
The objects are going to be grouped on the basis of their UV-FIR restframe colors: following the inspiring work of Davoodi et al. (2006), we model the multicolor distribution of galaxies with a mixture of multivariate Gaussians (Connolly et al. 2000; Nichol et al. 2001a). This technique is independent of the predetermined galaxy template libraries, and provides the identification, classification, and characterization of both existing and new object types, a compact description of the data, and a recipe for the identification of outliers. Each source is then classified as belonging to one of these Gaussian modes, and a median SED is derived for all identified groups.
These SEDs are going to be fitted using a custom, modified version of magphys (da Cunha et al. 2008), combining stellar light, emission from dust heated by stellar populations and a possible AGN contribution. Our main product is a robust library of templates which can cope with the very large scatter in observed colors of infrared galaxies over the full UV, optical, NIR, MIR and FIR spectral range, thus discriminating between different classes of galaxies, including AGN-harboring objects, and other obscured sources.
This paper is structured as follows. Section 2 describes the available data-sets and the simple procedure adopted to derive restframe colors; Sect. 3 deals with the classification scheme, based on the parametric description of the multivariate distribution in the chosen N-dimensional color space. Interpolation of median SEDs by means of a multicomponent fit is presented in Sect. 4. In Sect. 5 we use the results of the previous decomposition of the restframe multicolor distribution to identify outliers and very rare sources. Finally, Sect. 6 applies the new library to the derivation of infrared luminosities, comparing results to eight other popular methods often adopted in the literature. The newly derived UV-to-submm templates are used to classify MIPS 24 μm detected objects in the GOODS fields. Throughout our analysis, we adopt a standard ΛCDM cosmology with H0 = 71 [km s-1 Mpc-1], Ωm = 0.27, and ΩΛ = 0.73.
2. Building color catalogs
The PACS Evolutionary Probe survey (PEP1, Lutz et al. 2011) observed the most popular and widely studied extragalactic blank fields (The Lockman Hole, EGS, ECDFS, COSMOS, GOODS-N, and GOODS-S) with the PACS (Poglitsch et al. 2010) instrument aboard Herschel (Pilbratt et al. 2010) at 70, 100 and 160 μm. In parallel, the HerMES survey (Oliver et al. 2012) covered the same (and additional) fields at longer wavelengths (250, 350, 500 μm) with the SPIRE instrument (Griffin et al. 2010). We first describe the multiwavelength data-sets available in the adopted fields, and then enter into the details of source selection, which is mostly driven by the need to derive restframe colors of galaxies.
2.1. Available data
Here we exploit PEP and HerMES data in the Great Observatories Origins Deep Survey (GOODS, Dickinson et al. 2001) northern and southern fields, as well as in COSMOS (Scoville et al. 2007). Herschel data are combined with ancillary catalogs covering the electromagnetic spectrum from UV to FIR wavelengths. Table 1 summarizes Herschel depths reached in the three fields considered.
We defer to dedicated publications for details on reduction, map making and simulations for PACS (Lutz et al. 2011; Popesso et al. 2012; Berta et al. 2010) and SPIRE (Levenson et al. 2010; Viero et al. 2012) datasets.
MIPS and Herschel 3σ depth [mJy] reached in the three selected fields.
Herschel photometry was performed through point spread function (PSF) fitting, adopting Spitzer MIPS 24 μm detected sources as positional priors. This approach maximizes depth, optimizes deblending, and facilitates the match of the FIR photometry to ancillary data, because 24 μm catalogs are linked to Spitzer/IRAC (3.6 to 8.0 μm) and then optical bands, either through prior extraction (e.g. see Magnelli et al. 2009 for GOODS fields) or PSF-matching (e.g. see Berta et al. 2011). PACS priors source extraction followed the method described by Magnelli et al. (2009), while SPIRE fluxes were obtained with the Roseboom et al. (2010) recipe. Images at all Herschel wavelengths have undergone extractions using the same MIPS prior catalogs, i.e. those presented by Magnelli et al. (2009, 2011) in the GOODS fields and by Le Floc’h et al. (2009) in COSMOS.
 |
Fig. 1 Redshift distribution of GOODS-S (left), GOODS-N (center) and COSMOS (right) sources, obtained by applying single-band cuts at local S/N = 3, and while adopting the restframe interpolation scheme described in the text. For each field, the top-left panel includes all sources in the adopted optical-NIR catalogs, i.e. those built by Grazian et al. (2006), Berta et al. (2011), and Capak et al. (2007). |
In GOODS-S we make use of the MUSIC (Grazian et al. 2006) photometric catalog, with the addition of GALEX and Spitzer IRS 16 μm (Teplitz et al. 2011) data, matched to the 24–500 μm catalog via a simple closest neighbor algorithm. Spectroscopic redshifts were collected for more than 3000 sources (see Berta et al. 2011, and references therein).
A PSF-matched catalog2 was created in GOODS-N, including photometry from GALEX UV to Spitzer IRAC and MIPS 24 μm (see Berta et al. 2011, 2010, for further details). This catalog includes the collection of spectroscopic redshifts by Barger et al. (2008) and new photometric redshifts derived with the eazy (Brammer et al. 2008) code. To these, we add the Spitzer IRS 16 μm photometry by Teplitz et al. (2011).
Finally, in COSMOS we adopt the public3 UV-optical catalog, including U to K broad and intermediate bands (Capak et al. 2007; Ilbert et al. 2009), combined with public spectroscopic (Lilly et al. 2009; Trump et al. 2009) redshifts. New photometric redshifts have been computed with eazy, including all available UV-optical-NIR bands up to 4.5 μm (see Berta et al. 2011).
We defer to Lutz et al. (2011) and Roseboom et al. (2010) for further details on PACS and SPIRE catalogs, and to Berta et al. (2011) and Nguyen et al. (2010) for a derivation of the respective confusion noise. A thorough description of photometric redshifts incidence and accuracy in the three fields considered is provided in Berta et al. (2011). Finally, Berta et al. (2011, 2010) provide additional information about ancillary catalogs.
2.2. Restframe colors and source selection
We are going to group galaxies in an N-dimensional color space, using a parametric, multidimensional technique; here we describe the choice of bands and colors that will be adopted in this analysis.
Avoiding restrictions in redshift space or galaxy type, we opted to apply the classification technique to restframe colors. This approach has the advantage of maximizing the number of available sources; moreover a classification process in the observed frame would be dominated by color-redshift dependences.
Adopting a library of SED templates, one could in principle derive restframe luminosities, by integrating through the desired passbands, but the results would depend on the models/templates adopted. Alternative methods, such as the one described in Rudnick et al. (2003), still imply a hybrid of templates and interpolation, which include some dependence on models and the need for a priori SED fitting.
We hence derive restframe colors by simply interpolating between bands – once redshift is known – excluding any model assumption. This might be a dangerous approximation in some wavelength ranges, where the gap between available bands is wide (e.g. in the MIR). To avoid this problem, the choice of restframe bands to be used is optimized to be fully covered by observed photometry, once redshift is taken into account. Moreover, when performing interpolation, we impose the conditions that no more than two adjacent observed bands around each restframe filter miss a detection. The chosen restframe colors are: 1400−1700 Å; 2200−2700 Å; U − V; V − J; J − Ks; Ks − 3.6 μm; Ks − 8.0 μm; Ks − 60 μm; 8.0−60 μm; 60−100 μm.
This approach does not strictly require a detection in each band, but only that each restframe filter (in the range between 1400 Å and 100 μm) is bracketed by two observed bands having detections, with any gap – due to nondetections – not larger than two observed bands. This allows more sources to take part in the grouping, but significantly complicates the selection function. Figure 1 shows the redshift distribution of sources in the three fields obtained from Herschel, Spitzer or GALEX brightness cuts and resulting from our restframe interpolation scheme. The gap around redshift z ≃ 1.5 is mainly due to the combination of Herschel (or 24 μm, to sample MIR-FIR wavelengths) and GALEX (sampling the UV), with blue optical bands covering the ultraviolet regime on the high redshift side. A total of 234, 343 and 4498 sources from GOODS-N, GOODS-S and COSMOS are included, out of 540, 782, and 22659 Herschel-detected objects, respectively.
To fulfill the aim of grouping and defining new templates, we need to construct a sample representative of the bulk of galaxy populations in color space. Nevertheless, because of the requirement to cover as wide a wavelength range as possible, the risk of missing some part of color space cannot be fully avoided. In fact, by imposing a restframe FIR and UV coverage, over a wide range of redshifts, we incur into losses of sources mainly due to the limited sensitivity of Herschel and GALEX surveys. In particular, un-obscured galaxies with faint FIR emission might slip away from the selection, and passive galaxies are likely poorly represented. In Sect. 5 rare objects, outliers of the parametric grouping used to define templates, will be identified, thus partially recovering parts of color space not sampled otherwise. Finally, in Sect. 6.2 we will compare the new templates – based on the median SEDs of the selected sources – to observed objects, regardless of selection cuts, showing that most of the observed UV-FIR color-redshift space is effectively covered.
3. Parametric description of multicolor data
We describe galaxies by means of their colors, as derived from our multiwavelength catalogs, i.e. their position in an N-dimensional color space. Our aim is to identify structures in the N-dimensional distribution of galaxies, thus identifying potentially different galaxy populations.
We assume that the N-dimensional color distribution function of these sources can be reproduced as the superposition of M multivariate Gaussians. In what follows, we will refer to these Gaussian components also as “groups”, “modes” or “classes”, without distinction. As we are reasoning in restframe, each Gaussian mode would then represent a different population of galaxies, and can be used to define median colors, to be later fit with SED synthesis codes.
The M components are sought using the code by Connolly et al. (2000), further developed and distributed by the Auton Lab4 Team, and now called FastEM. The code fits the n datapoints, representing our galaxies in the N-dimensional space, with M multivariate Gaussian distributions. FastEM uses an expectation-minimization algorithm for parameter estimation and a Bayesian information criterion to decide how many components are statistically justified by the data (Connolly et al. 2000; Nichol et al. 2001b,a), i.e. the number M of Gaussians to be used is a free parameter and is optimized by FastEM on the basis of the actual amount and distribution of datapoints. For each jth Gaussian component, the code provides its mean coordinates μj and an N × N covariance matrix Σj describing its N-dimensional shape (including cross terms).
Assuming that the distribution of sources in our N-dimensional color-space are described by the superposition of the M multivariate normal distributions, the probability of the ith object to belong to the jth multivariate Gaussian is given by ![\begin{equation} \label{eq:probability1} P\left( x_i , \mu_j , \Sigma_j \right) = A_j \frac{1}{\sqrt{{\left( 2\pi\right)}^N \left|\Sigma_j\right|}} \exp\left[ -\frac{1}{2}{\left(x_i-\mu_j\right)}^T \Sigma_j^{-1}\left(x_i-\mu_j\right)\right]\textnormal{,} \end{equation}](/articles/aa/full_html/2013/03/aa20859-12/aa20859-12-eq47.png) (1)where xi is the position of the given object in the N-dimensional space, Σj is the covariance matrix of the jth multivariate Gaussian group, μj is its barycenter (mean coordinate), Aj is its amplitude (probability normalization), and the superscript T represent matrix transposition. Note that x and μ are N-dimensional arrays and the rank of Σ is N × N.
(1)where xi is the position of the given object in the N-dimensional space, Σj is the covariance matrix of the jth multivariate Gaussian group, μj is its barycenter (mean coordinate), Aj is its amplitude (probability normalization), and the superscript T represent matrix transposition. Note that x and μ are N-dimensional arrays and the rank of Σ is N × N.
We define as total probability that the ith source belongs to any of the Gaussian groups, the sum 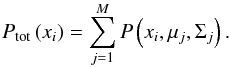 (2)This quantity integrates to unity and is therefore a probability density function (PDF), describing the probability for a single ith object in the sample to lie at the position xi = (xi,1, xi,2, ..., xi,N) (see Davoodi et al. 2006).
(2)This quantity integrates to unity and is therefore a probability density function (PDF), describing the probability for a single ith object in the sample to lie at the position xi = (xi,1, xi,2, ..., xi,N) (see Davoodi et al. 2006).
Given Eq. (1), the PDF determines the relative probability for any galaxy in the sample to come from any of the M components. We assign each galaxy to the mode that maximizes its probability density. Davoodi et al. (2006) demonstrated that an alternative choice, consisting in randomly assigning each galaxy to one of the modes with a probability proportional to the PDF value at its position, gives equivalent results.
3.1. Grouping in PEP fields
The three fields adopted for this analysis (GOODS-S, GOODS-N and COSMOS) have been observed by PACS and SPIRE down to very different depths (see Table 1) and over different areas (~200 arcmin2 in the GOODS fields and ~2 deg2 in COSMOS). As a consequence, different luminosities as a function of redshift are covered, potentially probing different regimes with respect to the so-called “main sequence of star formation” (MS) at different redshifts in different fields.
We therefore chose to keep the three fields separate for classification, in order not to dilute the information available. In this way we would like to avoid objects which may be peculiar to deep fields (e.g. MS galaxies at high redshift) from getting lost in the plethora of COSMOS sources. Furthermore, this choice will lead to a wider variety of SED shapes and a better sampling of the observed scatter in the colors.
As a result of the parametric grouping, the color distributions of sources in GOODS-S and COSMOS are reproduced by the superposition of nine Gaussian modes, while only six components are required in GOODS-N. The latter misses those groups with bluer MIR-FIR colors. These are missed also in the large, shallow COSMOS field, where – on the other hand – a larger population of NIR-MIR power-law sources is detected.
Through Monte Carlo simulations, it is possible to estimate the chance that one source effectively belonging to a given group is nevertheless assigned by FastEM to a different one because of scatter. Based on the groups defined using observed data, we build an artificial data-set (see Sect. 5.1), which is then evaluated by running FastEM using the known set of multivariate Gaussians. The incidence of mis-classifications – defined as the fraction of sources in a given class being assigned to any other group belonging to the same data-set/field – turns out to vary depending on classes, with a maximum of 15% in the worst cases. Mis-classifications happen in the regions of color space where there are overlapping modes with similar amplitudes.
Filters adopted to produce rest-frame weighted-median SEDs for each Gaussian mode.
Overlap of classes between different fields exists. This is evident in subspaces of reduced dimensions, especially due to the large dispersion in some colors (see Fig. A.1 for error bars on median SEDs), but becomes difficult to trace when working in the full 10-dimensional set. In this context, Table A.1 lists a subset of colors derived after fitting the median SEDs of each Gaussian mode (see next section). Keeping fields separate results in a finer sampling of multicolor space.
4. Fitting SEDs
Once that Gaussian modes have been identified, we derive the weighted-median5 restframe SEDs of each group. This is done by shifting all objects to restframe wavelengths and normalizing at a common wavelength: 1.6 μm in our case. Different normalization wavelengths have been attempted, but the NIR turned out to be the most effective choice, as it is well covered by the observed bands (i.e. there are no large gaps in wavelength), and it lies in a relatively central position of the covered frequency range. Therefore normalizing at 1.6 μm minimizes both uncertainties in interpolation at the normalization wavelength itself and scatter at the extremes of the covered spectral range.
Median SEDs are computed through a set of passbands, aimed at optimizing spectral coverage, as listed in Table 2. When computing weighted medians, weights are given by photometric uncertainties combined to passbands (i.e. we take the position of de-redshifted points within the filter transmission curve into account), and are propagated into uncertainties on median fluxes by means of an unbiased variance estimator.
Figure 2 shows the SEDs of all Gaussian modes in the three fields, including de-redshifted photometry of all sources belonging to each group (colored points) and median photometry (black squares).
The median SEDs thus obtained are discretized in passbands (Table 2), and therefore need to be fit with an SED synthesis code to provide a reliable “interpolation” and description of the whole spectrum.
 |
Fig. 2 Rest-frame spectral energy distributions of the Gaussian modes found in the three fields. Black squares represent median SEDs obtained through restframe filters (see Table 2). Colored dots trace the de-redshifted photometry of individual sources. The number of objects contributing to each group is quoted in the respective panel. |
4.1. Fitting with magphys
Among the numerous codes available for SED fitting, we adopt the magphys software (da Cunha et al. 2008), because of a number of features:
-
it covers the whole wavelength range from UV toFIR and submm;
-
it links the energy absorbed by dust in the UV-optical domain to dust emission in the MIR and FIR in a self-consistent way;
-
it is user friendly and simple to use; moreover the code is structured in such a way that it can be easily modified, if desired.
magphys combines the Bruzual & Charlot (2003, BC03, see also Bruzual 2007) optical/NIR stellar library, including the effects of dust attenuation as prescribed by Charlot & Fall (2000), with MIR/FIR dust emission computed as in da Cunha et al. (2008). The optical and infrared libraries are linked together, taking into account energy balance (no radiation transfer involved). The total energy absorbed by dust in stellar birth clouds and in the ambient interstellar medium (ISM) is re-distributed at infrared wavelengths. The main assumptions are that the energy re-radiated by dust is equal to that absorbed, and that starlight is the only significant source of dust heating.
It is worth to note that, since we are fitting the median photometry of several galaxies, possible variations of the effective attenuation law (e.g. Buat et al. 2012; Reddy et al. 2012, 2006; Wild et al. 2011) are diluted. Such variations would mainly influence star formation histories and thus the ages of the dominant stellar populations in the magphys modeling. Nevertheless, our results on infrared luminosities and AGN fractions (see next Sections) would not be affected by this effect.
We defer to da Cunha et al. (2008) for a thorough formal description of how galaxy SEDs are built (see also Smith et al. 2012, for an application to Herschel-selected z < 0.5 galaxies). Here we only recall that the SED of the power re-radiated by dust in stellar birth clouds is computed as the sum of three components: polycyclic aromatic hydrocarbons (PAHs); a mid-infrared continuum describing the emission of hot grains with temperatures T = 130–250 K; and grains in thermal equilibrium with T = 30–60 K. The “ambient” ISM is modeled by fixing the relative proportions of these three components to reproduce the cirrus emission of the Milky Way, and adding a component of cold grains in thermal equilibrium, with adjustable temperature in the range T = 15–25 K.
Different combinations of star formation histories, metallicities and dust content can lead to similar amounts of energy absorbed by dust in the stellar birth clouds, and these energies can be distributed in wavelength using different combinations of dust parameters. Consequently, in the process of fitting, a wide range of optical models is associated with a wide range of infrared spectra and compared to observed photometry, seeking for χ2 minimization. The number of possible combinations is on the order of 109 at z = 0.
Figure A.1 in Appendix A presents the best fits, and Table A.1 summarizes the results.
4.2. Adding an AGN component
As mentioned above, one of the main underlying assumptions of the magphys code is that starlight is the only significant source of dust heating, i.e. so far a possible AGN component has been ignored while fitting our median SEDs. We have therefore developed a modified version of the magphys code, adding a warm dust component to the modeled SED emission. This represents dust surrounding the active nucleus, often assumed to be distributed in a toroidal region (hence hereafter referred as “torus” for simplicity).
The da Cunha et al. (2008) original code is now combined with the Fritz et al. (2006) AGN torus library (see also Feltre et al. 2012). The quest for a best fit is still based on χ2 minimization; the stars+dust model is freely normalized and subtracted from the observed photometry; the torus emission is then added to reproduce what is left out from this subtraction. Thanks to the magphys structure, dust emission – no more limited to single templates as in some older attempts – is linked to the stellar optical component. Allowing the normalization of stars+dust to be free, i.e. not strictly anchored to the observed photometry but simply randomly picked from a grid of values, the torus is effectively fit to the data in a simultaneous 3-component model (see also Fritz et al. 2006; Berta et al. 2007; Noll et al. 2009; Santini et al. 2012; Lusso et al. 2012; Bongiorno et al. 2012, for alternative implementations).
The torus/AGN library of Fritz et al. spans several geometries of the dust distribution around the central AGN nucleus, varying the ratio between outer and inner radii (Rout/Rin = 20–300), and the aperture angle of the torus (measured starting from the equatorial plane, Θ = 40°–140°). The optical depth at the equator covers the range τ = 0.1−10.0 at 9.7 μm. The spectrum emitted by the central engine is modeled with a broken power-law λ L(λ) ∝ λα, with indexes α1 = 1.2, α2 = 0.0, α3 = −0.5 or −1.0, in the ranges λ1 = 0.001–0.03, λ2 = 0.03–0.125, and λ3 = 0.125–20 μm, respectively. Two different sets of models are included, differing for the UV-optical-IR slope of this power law, α3. When visible along the line of sight, the direct AGN light is included in these SED models. The full library comprises a total of roughly 700 models, each one computed at 10 different lines of sight angles Φ, but we limit the fit to Rout/Rin ≤ 100, as extreme values have so far not been confirmed by observations (e.g. Mullaney et al. 2011; Hatziminaoglou et al. 2008; Netzer et al. 2007). See Fritz et al. (2006) for more details on this model.
In terms of computational time, the performance of our modified code is comparable to the original magphys code. On an Intel XeonTM 3.2 GHz CPU, 1010 model combinations are sampled in roughly 80–100 min, to be compared to 10–15 min spent for ~109 evaluations in magphys.
Best fits obtained with magphys+AGN are shown in Fig. A.1 in Appendix A, and results are summarized in Table A.1. A description of all physical parameters involved in the fit, and their marginalized likelihood distributions (with or without AGN) goes beyond the scope of this work. Here we limit to describe the fraction of infrared luminosity, L(8–1000 μm) powered by the torus component (see Table A.1). When sampling the wide parameter space in searching for a best fit, the code registers the details of all attempted model combinations and builds the probability distribution function of a wide number of physical quantities. In this way degeneracies in the fit are taken into account and are translated into uncertainty ranges. Table A.1 includes the AGN fraction of the best fit, as well as its 2.5th, 50th and 97.5th percentiles, and gives a short description in terms of their main properties (AGN component, star formation strength, colors, etc).
5. Rare sources
The probability of a given object to belong to any of the Gaussian modes found by FastEM and its total probability to belong to any of these groups is described by Eqs. (1) and (2). We build the cumulative total probability distribution function over all objects in each field and perform Monte Carlo simulations in order to identify a potential excess of observed objects at the low probability end.
Such an excess can be used to define potential outliers, or rare sources which cannot be categorized in any of the Gaussian modes found. Figure 3 shows the cumulative Ptot distribution in COSMOS (red dashed line).
 |
Fig. 3 Cumulative distribution of probability densities in COSMOS. The red dashed line is for the observed sources, and is compared to simulated results (blue dotted line). The excess of observed sources, with respect to expectations from simulations, at the low probability side is due to rare objects, not complying with the restframe colors of Gaussian groups. |
 |
Fig. 4 SEDs of outliers (black symbols), grouped in classes, and compared to the rest of FastEM-based templates (grey), normalized to 1.6 μm. |
5.1. Simulations
Given the M multivariate normal distributions that build up our N-dimensional color-space, we run a Monte Carlo simulation aimed at constructing the expected total probability distribution function PDFexp. The code designed for this goal, produces a set of n random points for each jth N-dimensional multivariate normal distribution, where n is the actual number of real sources belonging to the jth group. Then the artificial catalogs thus built are “evaluated” by FastEM using the multivariate normal groups previously found on real catalogs, and already used to build the random artificial catalogs themselves. The probability of each artificial object to belong to any of the j = 1, ..., M multivariate distributions (i.e. including all others that were not used to build the random sample) is thus computed in the same way as for real objects (Eq. (2)). The M probabilities are summed together for each of the i = 1, ...,n × M random points in the N-dimensional space. The expected cumulative distribution of probability densities expected from simulations (using all random points) is then compared to the “observed” one in Fig. 3 (blue dotted line).
The analysis of these simulations is not straightforward. In principle, we would like to define a probability threshold Pthresh, below which a source can be considered an outlier (see Davoodi et al. 2006). In practice, in the COSMOS case, the observed and simulated curves intersect each other at roughly Ptot ≃ 10-4. In our case N(obs) = 2 × N(exp) holds at Ptot ≃ 10-5. Simulations for the GOODS fields (not shown here for simplicity) have a different behavior: the observed and simulated PDFs do not cross each other, but are roughly parallel, with PDFexp ≳ PDFtot. The two GOODS fields include a rather limited number of sources, i.e. our N-dimensional space is rather sparsely sampled. In such a small-number limit, simulated and real probabilities follow the same trend, but real catalogs are missing a fraction of sources. On the other hand, the large COSMOS (Fig. 3) indeed contains some significant fraction of unexpected objects at the low-probability end. To be conservative, we adopt Pthresh = 10-5 as threshold for all fields.
5.2. Outliers
Using the probability threshold defined above, we identify outlier candidates in the N-dimensional color space. In this way, 5, 21, and 32 potential outliers are identified in GOODS-N, GOODS-S and COSMOS, respectively.
The SEDs of selected objects are checked individually against photometric oddities (e.g. glitches, cosmic ray hits, etc.) and multiwavelength images (in the F814W or F850LP ACS bands, together with 3.6 μm, 24 μm, 100 μm, 250 μm, and others if needed) are visually inspected. Several outlier candidates turn out to be sources affected by potential photometric problems in some band, mostly due to blending, wrong associations, and (consequently) also wrong photometric redshifts. These cases are often related to each other. For example a faint galaxy in the vicinity of a bright star would have an optical SED resembling that of a passive object, but would be also bright in the FIR. The warning bell in such a case would be rung by the fact that the 1.6 μm stellar peak would appear to lie at the wrong wavelength, with respect to the tabulated redshift. Another exemplary case is an object appearing isolated in the optical, but double at 24 μm and finally being the blend of two components in Herschel maps.
In addition, objects at the edge of a given FastEM group definition might be identified as outlier candidates, but it might happen that they are reproduced by the SED of a neighboring mode. Since we are here searching for objects not covered by any of the SEDs defined so far, these cases are not considered as real outliers.
After these individual checks, 12 definite outliers are left. Their SEDs are shown in Fig. 4, and compared to the median SEDs of FastEM groups (see Sects. 3 and 4). We have assigned them to eight new groups, according to their SEDs and visual inspection of ACS images.
Outliers of the group 1 are two GOODS-S and one COSMOS sources with torus-dominated, almost featureless SEDs. They are characterized by moderate FIR emission, a prominent MIR excess and red optical colors. All three are known X-ray sources (Luo et al. 2008, 2010; Brusa et al. 2010; Cappelluti et al. 2009) and two are detected at radio frequencies (Miller et al. 2008; Schinnerer et al. 2010).
Galaxies in groups 2 and 3 have featureless continua from the UV to the MIR and their IRAC-MIPS emission is likely dominated by an AGN component. The two differ from each other in their optical colors. Both SEDs have flat power-law like shape, while group 1 is convex in the NIR-MIR regime. Both are detected in the X-rays (Luo et al. 2008). The prototype galaxy of group 3 is a bright radio emitter with a 1.4 GHz flux of ~3.31 ± 0.01 mJy at z ≃ 1.6, while the other is not detected at radio frequencies (Miller et al. 2008).
Group 4 includes two z ~ 3 galaxies with very bright FIR and far- to mid-infrared flux ratio much redder than any class found by FastEM.
Outliers of class 5 represent bright FIR emitters with very red optical SEDs. With an observed flux ratio Sν(100)/Sν(24) = 90 and a redshift z ~ 1.8, this outlier is similar to the high redshift “silicate break” galaxies described by Magdis et al. (2011), although no 16 μm information is available in our case.
Outliers of class 6 are represented by a z ~ 1.1 Lyman break galaxy, detected well in the near-UV band by GALEX, but barely seen in the far-UV. The optical emission is very blue and does not comply with any previously defined SED.
Class 7 includes a nice and isolated spiral galaxy at z = 0.11, with no MIR emission and very weak FIR.
Finally, group 8 comprises two large nearby spheroidal galaxies at redshifts z = 0.10 and z = 0.38. They both are characterized by a slight MIR excess, with respect to a pure old stellar population Rayleigh-Jeans spectrum and faint FIR emission, which can be interpreted as circumstellar dust of AGB stars and emission from diffuse dust even in these passive systems (see, for example, Bressan et al. 2006; Panuzzo et al. 2011).
As in the case of the Gaussian modes, the SEDs of outliers have been fit using the original magphys (da Cunha et al. 2008) and our modified version including an AGN component. Results are shown in Appendix A and summarized in Table A.1.
6. Discussion
Combining the modeled SEDs of multivariate Gaussian modes and outliers, a library of new templates spanning from the ultraviolet to submillimiter spectral domains is now defined.
Here we apply this new library to full multiwavelength data sets in GOODS-N and GOODS-S, with the aim of testing its performance in evaluating infrared luminosities of galaxies and classifying 24 μm-selected objects on the basis of their AGN content, FIR colors and far-to-near infrared flux ratios.
6.1. Deriving infrared luminosities
We would now like to compare the new library of templates to other existing templates and methods, focusing our attention on the estimate of infrared (8–1000 μm) luminosity.
Figure 5 shows all templates, as in Table A.1, normalized to 1.6 μm and color coded by their L(8–1000 μm)/L(1.6 μm) color. A normalization in correspondence of the NIR stellar emission peak stresses color differences and highlights the wide variety of FIR SEDs describing real sources.
 |
Fig. 5 SEDs of all templates, belonging to all groups and outliers. Color coding is based on the infrared bolometric (8–1000 μm) to NIR (1.6 μm) luminosity ratio. |
 |
Fig. 6 Testing L(IR) estimates using 8 different methods, and including Herschel data. The employed methods and templates are: Wuyts et al. (2008, W08); Chary & Elbaz (2001, CE01); Polletta et al. (2007, P07) fitted using hyper-z; Siebenmorgen & Krügel (2007, SK07) fitted with a custom code; Dale & Helou (2002, DH02); Elbaz et al. (2011, E11); Nordon et al. (2012, N12); and this work (B13). Elbaz et al. (2011) adopt two different templates (“main sequence”, shown in black, and “starburst”, in blue). See text for more detail about each method. Red diagonal lines simply mark the one to one relation. The large bottom left panel shows the distribution of the relative spread per object, computed as M.A.D./median using the 8 different L(IR) estimates per object. The large upper left panel, instead, depicts the distribution of scatter computed for each pair of methods as M.A.D. of the quantity (y − x)/x. In this case, x and y denote pairs of L(IR) estimates on the abscissa and ordinate axes, for each pair of methods. |
 |
Fig. 7 Comparison of infrared luminosities, as obtained with and without Herschel data included in the fit. In the latter case, 24 μm flux densities are used. The methods and templates used are: Wuyts et al. (2008, W08); Chary & Elbaz (2001, CE01); Polletta et al. (2007, P07) fitted using hyper-z; Siebenmorgen & Krügel (2007, SK07) fitted with a custom code; Dale & Helou (2002, DH02); Elbaz et al. (2011, E11); Nordon et al. (2012, N12); Rujopakarn et al. (2011, R11); and this work (B13). The fit obtained with SK07 templates was designed to work with multiband photometry, hence was not tested on 24 μm data alone and is not shown here. Rujopakarn et al. (2011) provide an estimate of L(TIR) using 24 μm only, but no Herschel information, therefore it is here compared to the results obtained with the new templates (B13) including Herschel data. A correction to transform L(TIR,5 − 1000 μm) into L(IR,8–1000 μm) has been computed by integrating Rieke et al. (2009) templates, as used in Rujopakarn et al. (2011); this correction ranges between 8% and 1% depending on luminosity. Red diagonal lines simply mark the one to one relation. |
The PEP team defined a test case catalog, extracted semi-randomly from the GOODS-S MUSIC+PEP source list (Lutz et al. 2011; Berta et al. 2010, 2011; Grazian et al. 2006), aimed at comparing different L(IR) estimators. The list of sources was designed to cover as wide a redshift and PACS flux range as possible, and includes 200 entries. No SPIRE data were included at this stage. In this analysis, the following approaches are being tested:
-
1.
the luminosity-independent conversion between observedflux density and luminosity by Wuytset al. (2008,, based on a singletemplate, constructed by averaging the logarithm of Dale &Helou (2002, templates. In terms of localanalogs, its mid- to far-infrared SED shape is reminiscent of M82.
-
2.
fit of FIR SEDs with the Chary & Elbaz (2001, CE01) luminosity-dependent template library (see also Nordon et al. 2010; Elbaz et al. 2010; Hwang et al. 2010).
-
3.
standard UV-to-FIR SED fitting using the hyper-z code (Bolzonella et al. 2000) and Polletta et al. (2007, P07) templates, allowing for extinction with AV = 0–3.
-
4.
maximum likelihood analysis using a custom code and the starburst SED library by Siebenmorgen & Krügel (2007, SK07), which is based on radiative transfer and spans a three dimensional parameter grid of luminosity, nuclear radius, and visual extinction.
-
5.
fit of PACS flux densities using DH02 templates, normalized to an IR luminosity (8–1000 μm) using the Marcillac et al. (2006) relation between L(IR) and the F(60)/F(100) color, and corrected on the basis of Papovich et al. (2007) recipe to account for the overestimation of 24 μm-based L(IR) (see Santini et al. 2009).
-
6.
rescaling of the two Elbaz et al. (2011, E11) templates of “main sequence” (MS) and “starburst” (SB) galaxies to observed FIR data.
-
7.
the Nordon et al. (2012, N12) recipe, based on the offset from the star-forming “main sequence”, Δ(sSFR)MS, to re-calibrate CE01 templates.
-
8.
fit of UV-FIR data, using hyper-z and the templates defined in this work (hereafter labeled B13).
In all cases, redshifts have been fixed to known values (see Sect. 2 for details). Estimations of L(IR) with each method have been performed both including and excluding Herschel data. In the latter case, 24 μm data were used in the estimation of infrared luminosities. Most approaches are based on χ2 minimization while fitting the data. Methods number 6 and 7 need additional knowledge of stellar mass (and SFR). Ideally, method 6 would also require an estimate of either IR8 (i.e. LIR/L8 μm) or compactness, in order to distinguish between the MS and SB templates. Since these pieces of information are not available in our case, we apply both templates to all objects, thus deriving two L(IR) values for each source.
In addition to the above listed techniques, when excluding Herschel data we also applied to our test case the recipe by Rujopakarn et al. (2011, R11), mapping 24 μm fluxes into total infrared luminosities L(TIR). This method was defined by parameterizing galaxy SEDs as a function of luminosity surface density, ΣL(TIR), and adopting the Rieke et al. (2009) templates. The correction needed to transform L(TIR,5 − 1000 μm) into L(IR,8–1000 μm) has been computed by integrating these templates; this correction ranges between 8% and 1%, depending on luminosity.
Figure 6 shows the direct comparison of L(IR) estimates based on the different techniques. Infrared luminosities derived including Herschel data are globally very consistent with each other. When computing the dispersion of all 8 determinations around their median value for each object (i.e. computing the median absolute deviation, M.A.D., per object), it turns out that the relative uncertainties peak at ~10% with a tail extending to >50% for a few cases only (large bottom-left panel in Fig. 6). In other words, by implementing Herschel photometry in SED fitting, it is possible to estimate L(IR) within ~10% (M.A.D.), regardless of the adopted technique. No trends of M.A.D. as a function of redshift or infrared luminosity are detected.
To quantify the scatter in each possible combination of two methods shown in Fig. 6, the upper large panel on the left presents the distribution of the M.A.D. of the quantity (y − x)/x, computed for each pair of methods using all sources. In this case x and y simply represent the L(IR) values computed with methods in the abscissa or ordinate axis. When comparing two methods, the scatter over all objects ranges between a few percent to ~20% (in M.A.D. terms again). Most of the adopted techniques present only few catastrophic outliers, defined as those sources having 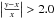 , when compared to other methods.
, when compared to other methods.
In some cases the scatter between two methods is remarkably small, pointing to their similarities. The Chary & Elbaz (2001), Elbaz et al. (2011) and Nordon et al. (2012) approaches are conceptually very similar and produce the lowest scatter when compared to each other. Also the Wuyts et al. (2008) approach produces scatter lower than 10%, when compared to the above mentioned three techniques. These four L(IR) estimates practically reduce to fitting a single template to the observed photometry, either chosen from a library on the basis of luminosity itself or the offset from the “main sequence” of star formation Δ(sSFR)MS (CE01, N12), or simply being the only available choice (W08, E11).
As the complexity of fits increases, the scatter also grows: techniques employing a variety of templates with free normalization, and/or extending the wavelength range all the way to the NIR, optical or UV, naturally produce a larger scatter, when compared to others. It is worth pointing out (not shown for the sake of conciseness) that, in UV-to-FIR SED fitting, scatter seems to be dominated more by the choice of code and its setup, rather than specific templates. Fitting SEDs with the new template library or with Polletta’s, but adopting hyper-z (Bolzonella et al. 2000), eazy (Brammer et al. 2008), or Le Phare (Arnouts et al. 1999; Ilbert et al. 2006) produces significantly different amounts of scatter. Determining the source of this effect is not trivial, because tuning these codes so that the adopted configurations are equivalent is not straightforward. To give an idea of the size of this effect, when considering these three codes with standard setup and employing the same template library, the peak of the distribution of relative M.A.D. scatter per source (see the large bottom-left panel in Fig. 6 for comparison) can shift to values as high as 20%.
Deep Spitzer blank field observations at 24 μm contain a large number of objects not detected by Herschel. It is thus important to verify how reliable the L(IR) derivation will be in the absence of FIR photometry. This is particularly relevant in light of the short Herschel lifetime and because of the spectral range covered by other current/future space missions (e.g. WISE, 3–25 μm; JWST, 0.6–28 μm), before the launch of next generation projects extending to the FIR again (e.g. SPICA).
Figure 7 compares L(IR) estimates obtained with and without the inclusion of Herschel data, for each approach. The well known bending in luminosity-dependent, locally-calibrated (e.g. CE01-based) approaches (see Elbaz et al. 2010; Nordon et al. 2010) and its correction (Elbaz et al. 2011; Nordon et al. 2012) can be seen here. It is worth noting that – since higher luminosity objects tend to lie at a higher redshift because of Malmquist bias – the deviation from the one to one line affects mainly distant galaxies (z ≥ 1.5, see also Elbaz et al. 2010, 2011), while all methods show self consistency below L(IR) ≃ 1012L⊙, i.e. at lower redshift. We warn that since the knowledge of IR8 (i.e. LIR/L8 μm) or compactness is not available, a proper choice between the Elbaz et al. (2011) MS or SB templates is not possible; thus a direct comparison between the two should not necessarily be taken at face value for this test case. Classical SED-fitting methods, allowing for template luminosity rescaling, seem to be less affected by this problem at the high luminosity end, highlighting conceptual differences between linear and nonlinear L(IR) derivations/corrections. Nordon et al. (2012) analyze in detail the systematics in L(IR,160)/L(IR,24) affecting luminosity-dependent methods at z ~ 2, showing that N12 seems to be the most effective one in reducing trends, at the expense of a 1.2–1.5 times larger scatter with respect to other approaches. For comparison, when extending to all redshifts (Fig. 7 here), the scatter in L(IR,Herschel)/L(IR,24) is ~0.3 dex (in terms of σ) for most methods, with the exception of CE01 and N12 (~0.45 dex).
Summarizing, when including Herschel photometry, all libraries and methods provide L(IR) estimates within a ~10−20% scatter, modulo tuning subtleties; known caveats (see, e.g., Elbaz et al. 2010; Nordon et al. 2010) apply to derivations limited to MIR wavelengths. The latter are still affected by a large scatter, when compared to FIR-based L(IR) estimates, thus pointing out the importance of Herschel-based surveys and future upcoming FIR missions.
6.2. Classification of MIR and FIR sources
 |
Fig. 8 Trends of colors as a function of redshift for the new FastEM templates (left) and Polletta et al. (2007) templates (right), compared to GOODS-S data. In each panel, only sources detected in the two bands needed to build the given color are taken into account. We plot the density of sources in each color-redshift bin, using a logarithmic color scale ranging from magenta (lowest density) to light green (highest density). |
 |
Fig. 8 continued. |
The newly generated SED templates were obtained on a limited selection of sources drawn from GOODS-N/S and COSMOS multiwavelength catalogs (see Sect. 2). Thus, it is worth comparing them against the photometry of all sources detected in any band. In the left panels of Fig. 8, we show the color tracks as a function of redshift, computed for the new set of templates (dark blue, solid lines). These are plotted onto the position of all real sources in the GOODS-S field (roughly 18 000 sources in total), with the sole requirement that a detection in the two bands giving each color is guaranteed. To avoid confusion due to the plethora of points, in this figure we actually draw the density of objects in small color-redshift bins, logarithmically color-coded from magenta (lowest density) to light green.
The right-hand panels of Fig. 8 show the same color-redshift tracks for the Polletta et al. (2007) template set.
The main advantage of our new library, based on actual Herschel data, is that it spans a wider color range, with respect to the Polletta et al. (2007) one, both on the blue and red MIR-FIR color sides. The same applies also to the optical and NIR domains, with slight differences varying from case to case. When comparing to observed data, the new library based on Herschel sources covers most of the observed colors, with the exception of the bluest side of the NIR color space. This can be due to a combination of the large scatter in the IRAC observed photometry and a possible missing set of passive templates (remember that the library was defined on Herschel-detected objects). However note that the Polletta library spans a similar NIR color range, although it contains a number of elliptical galaxy templates of different ages, obtained with GraSil (Silva et al. 1998).
The SEDs of all 24 μm objects in the GOODS-N/S catalogs are then fit with the same B13 setup as in Sect. 6.1, with the purpose of classifying the whole population of infrared galaxies with the information provided by the new library. The list of sources detected by MIPS in the MIR (see Table 1) comprises 2575 objects in GOODS-N and 1712 in GOODS-S.
Three main parameters are examined: the fraction of infrared luminosity L(8–1000 μm) contributed by the possible AGN component, the L(60)/L(100) restframe FIR color, and the ratio L(160)/L(1.6) between FIR and NIR restframe luminosities. For ease of interpretation, templates are grouped in three classes for each of the parameters considered:
-
(a)
f(AGN) = 0.0, 0.0 < f(AGN) ≤ 0.3, f(AGN) > 0.3;
-
(b)
L(60)/L(100) ≤ 0.5, 0.5 < L(60)/L(100) ≤ 1.0, L(60)/L(100) > 1.0;
-
(c)
L(160)/L(1.6) ≤ 10, 10 < L(160)/L(1.6) ≤ 100, L(160)/L(1.6) > 100.
In what follows we analyze GOODS-S data; similar results are obtained in GOODS-N. Figure 9 reports on the relative distribution of sources at all redshifts in each bin of f(AGN), L(60)/L(100) and L(160)/L(1.6), grouped in 1 dex wide bins of IR luminosity. When analyzing classes (b) and (c) objects hosting an AGN (on the basis of our SED fitting) have been excluded, because of the contamination of MIR and NIR fluxes by the torus component.
 |
Fig. 9 Relative distribution of GOODS-S sources as a function of AGN L(IR) fraction, L(60)/L(100) and L(160)/L(1.6), as indicated by the labeling in the right-hand panels, in different IR luminosity bins. Histograms are normalized to the number of sources in each L(IR) bin. Left/right panels refer to a 24 μm selection and sources detected by Herschel, respectively. Infrared luminosity bins are 1 dex wide, i.e. they cover ranges 108 − 109, 109 − 1010, etc. |
As infrared luminosity increases, the fraction of detected objects hosting an AGN with respect to the total number in the given L(IR) bin tends to increase. This is particularly true for extreme sources, with f(AGN) > 0.30. Nevertheless, their incidence over the whole detected sample is well below 10%.
As far as the L(60)/L(100) color is concerned, the classification based on SED fitting shows how the relative number of bluer objects increases as a function of luminosity, at the expense of L(60)/L(100) ≤ 0.5 sources. At the same time, FIR emission becomes more prominent, with respect to NIR, and L(160)/L(1.6) > 100 galaxies dominate the bright end. Results obtained including (right hand panels) and excluding (left panels) Herschel bands in the fit are remarkably similar, but one should keep in mind that roughly 75% of the sources in the analysis benefit from a Herschel detection. The reader is thus warned that results based on L(60)/L(100) and 24 μm detections only (left panels) should be taken with care, if a higher fraction of objects is missing a FIR detection.
The L(160)/L(1.6) ratio is a proxy for the specific star formation rate (sSFR), while L(60)/L(100) has often been adopted as a tracer of dust temperature (e.g. Dale & Helou 2002). Figure 10 shows the M∗–SFR–z space for GOODS-S 24 μm detected sources. Star formation rates are based on our estimate of L(IR) and the Kennicutt (1998) conversion to SFR. An independent estimate, obtained through a ladder of SFR tracers, and calibrated on SFRUV+IR (Wuyts et al. 2011a,b) produces similar results. Stellar masses M∗ are based on Bruzual & Charlot (2003) models, as applied to our data by Wuyts et al. (2011b). Note that, if the Maraston (2005) models with enhanced emission by TP-AGB (thermally pulsating asymptotic giant branch) stars would have been adopted, best fits would correspond to younger, less massive (and more actively starforming) systems than inferred with BC03 (Wuyts et al. 2011a; Santini et al. 2009; Salimbeni et al. 2009). When the two color classification schemes are adopted (middle and bottom panels), we exclude sources with an AGN component. The incidence of warmer sources (larger 60 to 100 μm luminosity ratio) grows for objects with larger FIR “excess”. This is in line with what is found by Magnelli et al. (in prep.) studying the dependence of dust temperature Tdust as a function of position in the M∗–SFR–z space and distance from the so-called “main sequence” of star formation, and by Symeonidis et al. (2013) studying the L − T relation of Herschel-selected IR-luminous galaxies. For reference, the MS locus defined by stacking 4.5 μm selected galaxies (Rodighiero et al. 2010a) is shown by dashed lines (obtained by interpolating between Rodighiero’s redshift bins), and the levels of MS +0.6 and +1.0 dex are marked with dotted lines. Rodighiero et al. (2011) used a +0.6 dex threshold to isolate off-sequence galaxies at 1.5 < z < 2.5. Note that, when limiting the analysis to Herschel-detected sources only, objects lying below the main sequence at z ≥ 0.5 are excluded.
 |
Fig. 10 Position of GOODS-S 24 μm sources in the M∗–SFR–z space. Top, middle, and bottom panels depict objects color coded on the basis of L(IR) AGN fraction, L(60)/L(100) luminosity ratio and L(160)/L(1.6) color, respectively. Color coding is the same as in Fig. 9. Dashed lines represent the position of the “main sequence” of star formation, as derived by Rodighiero et al. (2010a) by stacking 4.5 μm-selected sources. Dotted lines trace the MS +0.6 and +1.0 dex, respectively. |
Segregation on the basis of L(60)/L(100) or L(160)/L(1.6) is clearly seen, although it becomes gradually diluted at larger cosmic distances, possibly because an increasing incompleteness affects the locus of MS galaxies (see e.g. Magnelli et al., in prep.). The L(160)/L(1.6) < 10 bin is hardly sampled by MIR-FIR detections: the few sources belonging to this class indeed turn out to lie off-sequence, in the locus occupied by passive galaxies in the M∗ − SFR plane, and are characterized by our outlier quiescent templates. Finally, in the M∗–SFR diagram, above M∗ ~ 1010M⊙, AGN appear to be distributed along with all other galaxies (see also Santini et al. 2012). They have a tendency to lie on the high SFR side of the source distribution across the “main sequence”, but with no evident dependence on the fraction of infrared luminosity – f(AGN) – they are powering.
7. Summary
Starting from FIR detected sources and including multiwavelength information from the ultraviolet to optical, NIR and MIR, we have grouped a subsample of sources in the deepest and in the widest fields observed by Herschel within the overlapping PEP plus HerMES dataset: GOODS-S, GOODS-N and COSMOS. Following the work by Davoodi et al. (2006), the color distribution of galaxies has been modeled as the superposition of multivariate Gaussian modes. The chosen parameter space, consisting of 10 restframe colors in the wavelength range between 1400 Å and 100 μm, covers galaxy properties such as the UV slope, D4000 break, 1.6 μm stellar peak, PAH and warm dust emission, possible AGN contamination and cold dust contribution.
A modified version of the magphys (da Cunha et al. 2008) code has been developed, aimed at reproducing galaxy SEDs with the combination of three emitting components: stellar emission, thermal emission from dust heated by stellar UV-optical radiation, and a possible AGN torus. The median SEDs of each Gaussian mode have been fit with this code and with the original magphys code, thus providing a reliable interpolation over a continuous wavelength range. A new library of SED templates has thus been defined.
The main results of this grouping and SED fitting classification are:
-
the distribution of Herschel-detected galaxies in the 10 restframecolor space can be reproduced by six to nine multivariateGaussian modes in the three fields considered, with somedifferences due to depth of data, wavelength coverage, and howfine the grid of observed bands is.
-
the classification thus obtained has been used to identify rare objects, so-called “outliers” in the grouping scheme. The main classes of outliers identified are torus-dominated objects, type-1 AGN with featureless SEDs, and very bright FIR emitters. Two low redshift elliptical and one passively evolving spiral, well detected by Herschel, provide the completion of the classification picture.
-
fitting the median SED of each group and outlier with multicomponent SED synthesis, a new set of templates has been defined6. Among others, it includes five type-1 AGN models, and five type-2, characterized by different AGN torus contributions to total infrared (8–1000 μm) luminosity.
-
the new set of templates has been compared to other libraries and methods often adopted in the literature to derive infrared luminosities of galaxies (see Sect. 6.1 for a list). When including FIR data, the L(IR) estimates obtained with the different methods are consistent with each other to within 10–20%. Scatter in comparing different derivations of L(IR) strongly depends on the choice of codes and their fine tuning.
-
comparing L(IR) derived with or without the inclusion of Herschel data, all methods are affected by a significant scatter. Luminosity-dependent approaches, calibrated on local galaxies, turn out to be affected by more critical problems (e.g. Elbaz et al. 2010; Nordon et al. 2010) than simple SED fitting allowing for free rescaling, but appropriate corrections account for most systematics (e.g. Elbaz et al. 2011; Nordon et al. 2012).
-
when compared to full catalogs, independently from any selection cut, the new templates cover most of the color range occupied by real sources at all wavelengths.
-
24 μm sources in the two GOODS fields have been classified on the basis of their L(IR) AGN fraction, L(60)/L(100) color and L(160)/L(1.6) flux ratio, as derived by SED fitting with our new library. The incidence of warmer sources grows for objects with higher sSFR, in line with what is found by Magnelli et al. (in prep.) through a detailed study of Tdust in the M∗–SFR plane, and with results on the L − T relation of IR SEDs by Symeonidis et al. (2013). AGN appear to be distributed along with all other galaxies, above M∗ ~ 1010M⊙, with the tendency to lie on the high SFR side of the “main sequence”, but with no evident dependence on the fraction of infrared luminosity they are powering.
The new library of semi-empirical SEDs describes the actual scatter of FIR detected sources in color space, from the UV to the FIR itself. Direct applications can span from deriving the contribution of AGN and various populations to mid and FIR luminosity functions and L(IR) or SFR density as a function of look-back time (see also Gruppioni et al. 2013), to describing the SEDs of individual sources.
Online material
Appendix A: Results of SED fitting
In this Appendix, the results of SED fitting are presented. For each median SED or outlier, only the best fit solution is shown, either with or without the AGN component added.
We recall (see Sect. 4) that the magphys code (da Cunha et al. 2008) was adopted to reproduce SEDs. It combines BC03 optical/NIR stellar models, including the effects of dust attenuation as prescribed by Charlot & Fall (2000), to MIR/FIR dust emission computed as in da Cunha et al. (2008), linking the two components through energy balance: the total energy absorbed by dust in stellar birth clouds and in the ambient interstellar medium is re-distributed at infrared wavelengths.
The code has then been modified to include the possible contribution of an AGN torus component, using the Fritz et al. (2006) library, in order to overcome one of magphys main assumptions, implying that the only source of dust heating is starlight.
Figure A.1 shows our best fit solutions (i.e. those with minimum χ2). Table A.1 summarizes results, including a brief description of each template, restframe colors spanning from the u band to 160 μm, and AGN contribution to the infrared (8−1000 μm) luminosity. The latter is reported only for objects that require an AGN component, while sources best reproduced by the original magphys code have a L(IR) AGN fraction <1%.
Restframe colors have been obtained by convolving best fit models with filter transmission curves. Descriptions provided in Table A.1 highlight the main features of templates, e.g. optical colors (red/blue), position of the FIR peak (warm/cold), intensity of PAH emission, optical extinction, AGN contribution, as well as additional known properties of individual outliers. Type-1 and Type-2 AGN labels refer simply to the best fit solution and are defined such that in “type-2” models the line of sight intersects the torus dust distribution (Φ > 90°−Θ/2, with Φ defined starting from the polar axis, see Fritz et al. 2006), and vice versa in “type-1” cases.
Description of new templates, including colors [mag] in the optical to FIR wavelength range and the contribution of a possible AGN to the 8–1000 μm luminosity.
 |
Fig. A.1 Best fit to median SEDs, as obtained either with the magphys code (da Cunha et al. 2008) or with the modified version including a torus component (using the Fritz et al. 2006 library). Blue dotted lines represent the un-absorbed stellar component, while red dashed lines trace the combination of extinguished stars and dust infrared emission. The torus component is depicted with long-dashed green lines, and black solid lines are the total emission, in those cases for which an AGN is needed. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
The multiwavelength GOODS-N catalog is available on the PEP web page at the URL http://www.mpe.mpg.de/ir/Research/PEP/public_data_releases.php.
A weighted percentile is defined as the percentage in the total weight is counted, instead of the total number. The weighted median corresponds to the 50th weighted percentile. In practice, having N values v1, v2, ..., vN and their corresponding weights w1, w2, ..., wN, they are first sorted in order of ascending v, and then the partial sum of the weights 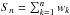 is computed for each nth (sorted) value. The weighted median is defined as the value vn having
is computed for each nth (sorted) value. The weighted median is defined as the value vn having 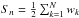 .
.
The new library can be retrieved at http://www.mpe.mpg.de/ir/Research/PEP/uvfir_templ, normalized by L(IR), L(1.6 μm), and M∗ (based on the results of SED fitting).
Acknowledgments
The authors wish to thank Dr. Jacopo Fritz for providing his library of AGN torus emission models, and the anonymous referee for her/his useful comments. This work made use of the code FastEM, distributed by the Auton Lab, and developed by Andrew Moore, Paul Hsiung, Peter Sand, point of contact Saswati Ray. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including University of Lethbridge (Canada), NAOC (PR China), CEA, LAM (France), IFSI, University of Padua (Italy), IAC (Spain), Stockholm Observatory (Sweden), Imperial College London, RAL, UCL-MSSL, UKATC, University of Sussex (UK), Caltech, JPL, NHSC, University of Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (PR China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK) and NASA (USA).
References
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., & Wang, W. 2008, ApJ, 689, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Fritz, J., Franceschini, A., Bressan, A., & Lonsdale, C. 2004, A&A, 418, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Lonsdale, C. J., Siana, B., et al. 2007, A&A, 467, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Magnelli, B., Lutz, D., et al. 2010, A&A, 518, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, S., Magnelli, B., Nordon, R., et al. 2011, A&A, 532, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Dole, H., Lagache, G., Le Borgne, D., & Penin, A. 2011, A&A, 529, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bongiorno, A., Merloni, A., Brusa, M., et al. 2012, MNRAS, 427, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Chiosi, C., & Fagotto, F. 1994, ApJS, 94, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Panuzzo, P., Buson, L., et al. 2006, ApJ, 639, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Civano, F., Comastri, A., et al. 2010, ApJ, 716, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G. 2007, in IAU Symp. 241, eds. A. Vazdekis, & R. F. Peletier, 125 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Brusa, M., Hasinger, G., et al. 2009, A&A, 497, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M. 1999, Roy. Soc. London Phil. Trans. Ser. A, 357, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Connolly, A. J., Genovese, C., Moore, A. W., et al. 2000, unpublished [arXiv:astro-ph/0008187] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H., Stern, D., et al. 2009, ApJ, 694, 1517 [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Finlator, K., Oppenheimer, B. D., et al. 2010, MNRAS, 404, 1355 [NASA ADS] [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Davoodi, P., Oliver, S., Polletta, M. d. C., et al. 2006, AJ, 132, 1818 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, M., & GOODS Legacy Team. 2001, BAAS, 33, 820 [NASA ADS] [Google Scholar]
- Dopita, M. A., Groves, B. A., Fischera, J., et al. 2005, ApJ, 619, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, A., Rowan-Robinson, M., & Siebenmorgen, R. 2000, MNRAS, 313, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elbaz, D., Hwang, H. S., Magnelli, B., et al. 2010, A&A, 518, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., Rodighiero, G., Vaccari, M., et al. 2010, A&A, 517, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frayer, D. T., Sanders, D. B., Surace, J. A., et al. 2009, AJ, 138, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Franceschini, A., & Hatziminaoglou, E. 2006, MNRAS, 366, 767 [Google Scholar]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gruppioni, C., Pozzi, F., Andreani, P., et al. 2010, A&A, 518, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruppioni, C., Pozzi, F., Rodighiero, G., et al. 2013, A&A, submitted [Google Scholar]
- Hatziminaoglou, E., Fritz, J., Franceschini, A., et al. 2008, MNRAS, 386, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Hatziminaoglou, E., Omont, A., Stevens, J. A., et al. 2010, A&A, 518, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hwang, H. S., Elbaz, D., Magdis, G., et al. 2010, MNRAS, 409, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kirkpatrick, A., Pope, A., Alexander, D. M., et al. 2012, ApJ, 759, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kleinmann, S. G., Lysaght, M. G., Pughe, W. L., et al. 1994, Ap&SS, 217, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Aussel, H., Ilbert, O., et al. 2009, ApJ, 703, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Levenson, L., Marsden, G., Zemcov, M., et al. 2010, MNRAS, 409, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C., Polletta, M. d. C., Surace, J., et al. 2004, ApJS, 154, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Bauer, F. E., Brandt, W. N., et al. 2008, ApJS, 179, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2010, ApJS, 187, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E., Elbaz, D., Dickinson, M., et al. 2011, A&A, 534, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Lutz, D., Berta, S., et al. 2010, A&A, 518, L28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2011, A&A, 528, A35 [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Marcillac, D., Elbaz, D., Chary, R. R., et al. 2006, A&A, 451, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuhara, H., Wada, T., Matsuura, S., et al. 2006, PASJ, 58, 673 [NASA ADS] [Google Scholar]
- Matsuura, S., Shirahata, M., Kawada, M., Takeuchi, T. T., & Akari/Mp-Fbsep Team. 2009, in ASP Conf. Ser. 418, AKARI, a Light to Illuminate the Misty Universe, eds. T. Onaka, G. J. White, T. Nakagawa, & I. Yamamura, 347 [Google Scholar]
- Miller, N. A., Fomalont, E. B., Kellermann, K. I., et al. 2008, ApJS, 179, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., Lutz, D., Schweitzer, M., et al. 2007, ApJ, 666, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Nguyen, H. T., Schulz, B., Levenson, L., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nichol, R. C., Connolly, A. J., Moore, A. W., et al. 2001a, in Virtual Observatories of the Future, eds. R. J. Brunner, S. G. Djorgovski, & A. S. Szalay, ASP Conf. Ser., 225, 265 [Google Scholar]
- Nichol, R. C., Miller, C., Connolly, A. J., et al. 2001b, in Mining the Sky, eds. A. J. Banday, S. Zaroubi, & M. Bartelmann, 613 [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordon, R., Lutz, D., Shao, L., et al. 2010, A&A, 518, L24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordon, R., Lutz, D., Genzel, R., et al. 2012, ApJ, 745, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panuzzo, P., Rampazzo, R., Bressan, A., et al. 2011, A&A, 528, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papovich, C., Rudnick, G., Le Floc’h, E., et al. 2007, ApJ, 668, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Piovan, L., Tantalo, R., & Chiosi, C. 2006, MNRAS, 370, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Bressan, A., & Franceschini, A. 2001, ApJ, 550, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Magnelli, B., Buttiglione, S., et al. 2012, A&A, submitted [arXiv:1211.4257] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N., Dickinson, M., Elbaz, D., et al. 2012, ApJ, 744, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Buzzoni, A. 1986, in Spectral Evolution of Galaxies, eds. C. Chiosi, & A. Renzini, Astrophys. Space Sci. Lib., 122, 195 [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Cimatti, A., Gruppioni, C., et al. 2010a, A&A, 518, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Vaccari, M., Franceschini, A., et al. 2010b, A&A, 515, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Roseboom, I. G., Oliver, S. J., Kunz, M., et al. 2010, MNRAS, 409, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Lari, C., Perez-Fournon, I., et al. 2004, MNRAS, 351, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, G., Rix, H.-W., Franx, M., et al. 2003, ApJ, 599, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Rujopakarn, W., Rieke, G. H., Weiner, B. J., et al. 2011, ApJ, submitted [arXiv:1107.2921] [Google Scholar]
- Salimbeni, S., Fontana, A., Giallongo, E., et al. 2009, in AIP Conf. Ser. 111, eds. G. Giobbi, A. Tornambe, G. Raimondo, et al., 207 [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santini, P., Rosario, D. J., Shao, L., et al. 2012, A&A, 540, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., & Krügel, E. 2007, A&A, 461, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Dunne, L., da Cunha, E., et al. 2012, MNRAS, 427, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Symeonidis, M., Vaccari, M., Berta, S., et al. 2013, MNRAS, submitted [Google Scholar]
- Teplitz, H. I., Chary, R., Elbaz, D., et al. 2011, AJ, 141, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trump, J. R., Impey, C. D., Elvis, M., et al. 2009, ApJ, 696, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2012, ApJ, submitted [arXiv:1208.5049] [Google Scholar]
- Wild, V., Charlot, S., Brinchmann, J., et al. 2011, MNRAS, 417, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Labbé, I., Schreiber, N. M. F., et al. 2008, ApJ, 682, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Lutz, D., et al. 2011a, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011b, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
All Tables
Filters adopted to produce rest-frame weighted-median SEDs for each Gaussian mode.
Description of new templates, including colors [mag] in the optical to FIR wavelength range and the contribution of a possible AGN to the 8–1000 μm luminosity.
All Figures
 |
Fig. 1 Redshift distribution of GOODS-S (left), GOODS-N (center) and COSMOS (right) sources, obtained by applying single-band cuts at local S/N = 3, and while adopting the restframe interpolation scheme described in the text. For each field, the top-left panel includes all sources in the adopted optical-NIR catalogs, i.e. those built by Grazian et al. (2006), Berta et al. (2011), and Capak et al. (2007). |
| In the text | |
 |
Fig. 2 Rest-frame spectral energy distributions of the Gaussian modes found in the three fields. Black squares represent median SEDs obtained through restframe filters (see Table 2). Colored dots trace the de-redshifted photometry of individual sources. The number of objects contributing to each group is quoted in the respective panel. |
| In the text | |
 |
Fig. 3 Cumulative distribution of probability densities in COSMOS. The red dashed line is for the observed sources, and is compared to simulated results (blue dotted line). The excess of observed sources, with respect to expectations from simulations, at the low probability side is due to rare objects, not complying with the restframe colors of Gaussian groups. |
| In the text | |
 |
Fig. 4 SEDs of outliers (black symbols), grouped in classes, and compared to the rest of FastEM-based templates (grey), normalized to 1.6 μm. |
| In the text | |
 |
Fig. 5 SEDs of all templates, belonging to all groups and outliers. Color coding is based on the infrared bolometric (8–1000 μm) to NIR (1.6 μm) luminosity ratio. |
| In the text | |
 |
Fig. 6 Testing L(IR) estimates using 8 different methods, and including Herschel data. The employed methods and templates are: Wuyts et al. (2008, W08); Chary & Elbaz (2001, CE01); Polletta et al. (2007, P07) fitted using hyper-z; Siebenmorgen & Krügel (2007, SK07) fitted with a custom code; Dale & Helou (2002, DH02); Elbaz et al. (2011, E11); Nordon et al. (2012, N12); and this work (B13). Elbaz et al. (2011) adopt two different templates (“main sequence”, shown in black, and “starburst”, in blue). See text for more detail about each method. Red diagonal lines simply mark the one to one relation. The large bottom left panel shows the distribution of the relative spread per object, computed as M.A.D./median using the 8 different L(IR) estimates per object. The large upper left panel, instead, depicts the distribution of scatter computed for each pair of methods as M.A.D. of the quantity (y − x)/x. In this case, x and y denote pairs of L(IR) estimates on the abscissa and ordinate axes, for each pair of methods. |
| In the text | |
 |
Fig. 7 Comparison of infrared luminosities, as obtained with and without Herschel data included in the fit. In the latter case, 24 μm flux densities are used. The methods and templates used are: Wuyts et al. (2008, W08); Chary & Elbaz (2001, CE01); Polletta et al. (2007, P07) fitted using hyper-z; Siebenmorgen & Krügel (2007, SK07) fitted with a custom code; Dale & Helou (2002, DH02); Elbaz et al. (2011, E11); Nordon et al. (2012, N12); Rujopakarn et al. (2011, R11); and this work (B13). The fit obtained with SK07 templates was designed to work with multiband photometry, hence was not tested on 24 μm data alone and is not shown here. Rujopakarn et al. (2011) provide an estimate of L(TIR) using 24 μm only, but no Herschel information, therefore it is here compared to the results obtained with the new templates (B13) including Herschel data. A correction to transform L(TIR,5 − 1000 μm) into L(IR,8–1000 μm) has been computed by integrating Rieke et al. (2009) templates, as used in Rujopakarn et al. (2011); this correction ranges between 8% and 1% depending on luminosity. Red diagonal lines simply mark the one to one relation. |
| In the text | |
 |
Fig. 8 Trends of colors as a function of redshift for the new FastEM templates (left) and Polletta et al. (2007) templates (right), compared to GOODS-S data. In each panel, only sources detected in the two bands needed to build the given color are taken into account. We plot the density of sources in each color-redshift bin, using a logarithmic color scale ranging from magenta (lowest density) to light green (highest density). |
| In the text | |
 |
Fig. 8 continued. |
| In the text | |
 |
Fig. 9 Relative distribution of GOODS-S sources as a function of AGN L(IR) fraction, L(60)/L(100) and L(160)/L(1.6), as indicated by the labeling in the right-hand panels, in different IR luminosity bins. Histograms are normalized to the number of sources in each L(IR) bin. Left/right panels refer to a 24 μm selection and sources detected by Herschel, respectively. Infrared luminosity bins are 1 dex wide, i.e. they cover ranges 108 − 109, 109 − 1010, etc. |
| In the text | |
 |
Fig. 10 Position of GOODS-S 24 μm sources in the M∗–SFR–z space. Top, middle, and bottom panels depict objects color coded on the basis of L(IR) AGN fraction, L(60)/L(100) luminosity ratio and L(160)/L(1.6) color, respectively. Color coding is the same as in Fig. 9. Dashed lines represent the position of the “main sequence” of star formation, as derived by Rodighiero et al. (2010a) by stacking 4.5 μm-selected sources. Dotted lines trace the MS +0.6 and +1.0 dex, respectively. |
| In the text | |
 |
Fig. A.1 Best fit to median SEDs, as obtained either with the magphys code (da Cunha et al. 2008) or with the modified version including a torus component (using the Fritz et al. 2006 library). Blue dotted lines represent the un-absorbed stellar component, while red dashed lines trace the combination of extinguished stars and dust infrared emission. The torus component is depicted with long-dashed green lines, and black solid lines are the total emission, in those cases for which an AGN is needed. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


