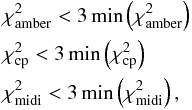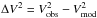| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219282 | |
| Published online | 25 February 2013 | |
Amorphous carbon in the disk around the post-AGB binary HR 4049
Discerning dust species with featureless opacity curves⋆
1 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: bram@ster.kuleuven.be
2 Belgian Institute for Space Aeronomy, Ringlaan 3, 1180 Brussels, Belgium
3 European Southern Observatory, Karl Schwarzschildstrasse 2, Garching 85748, Germany
Received: 26 March 2012
Accepted: 8 January 2013
Context. Infrared spectroscopy has been extensively used to determine the mineralogy of circumstellar dust. The identification of dust species with featureless opacities, however, is still ambiguous. Here we present a method to lift the degeneracy using the combination of infrared spectroscopy and interferometry.
Aims. The binary post-AGB star HR 4049 is surrounded by a circumbinary disk viewed at a high inclination angle. Apart from gaseous emission lines and molecular emission bands of polycyclic aromatic hydrocarbons (PAH), diamonds, and fullerenes, the 2–25 μm infrared spectrum is featureless. The goal of the paper is to identify the dust species responsible for the smooth spectrum.
Methods. We gathered high-angular-resolution measurements in the near- and mid-infrared with the VLTI interferometric instruments AMBER and MIDI. The data set is expanded with archival Geneva optical photometry, ISO-SWS and Spitzer-IRS infrared spectroscopy, and VISIR N-band images and spectroscopy. We computed a grid of radiative-transfer models of the circumbinary disk of HR 4049 using the radiative-transfer code MCMax. We searched for models that provide good fits simultaneously to all available observations.
Results. We find that the variable optical extinction towards the primary star is consistent with the presence of very small (0.01 μm) iron-bearing dust grains or amorphous carbon grains. The combination of the interferometric constraint on the disk extent and the shape of the infrared spectrum points to amorphous carbon as the dominant source of opacity in the circumbinary disk of HR 4049. The disk is optically thick to the stellar radiation in the radial direction. At infrared wavelengths it is optically thin. The PAH emission is spatially resolved in the VISIR data and emanates from a region with an extent of several hundreds of AU, with a projected photocenter displacement of several tens of AU from the disk center. The PAHs most likely reside in a bipolar outflow.
Conclusions. Dust species with featureless opacity curves, such as metallic iron and amorphous carbon, can be identified by combining infrared spectroscopy and high-angular-resolution measurements. In essence, this is because the temperatures of the dust species are notably different at the same physical distance to the star.
Key words: stars: AGB and post-AGB / binaries: spectroscopic / circumstellar matter / techniques: interferometric / techniques: spectroscopic / radiative transfer
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The post-asymptotic giant branch (AGB) star HR 4049 is a single-lined spectroscopic binary, surrounded by a circumbinary disk rich in dust and gas. The secondary star has not been detected at any wavelength, but its presence is inferred from the radial-velocity variations of the primary. HR 4049 is a remarkable object in several respects. First, it is the prototype of a group of evolved binaries in which the primary star has an extremely metal-depleted photosphere ([Fe/H] = −4.8 dex, Van Winckel et al.1995). The photospheric abundance pattern resembles that of the interstellar medium, where chemical elements with high condensation temperatures have formed dust grains and are underabundant in the gas phase. Mathis & Lamers (1992) and Waters et al. (1992) have proposed a scenario to explain the selective depletion in these post-AGB binaries. A fraction of the mass lost by the primary star during its AGB phase is captured in a stable circumbinary disk. The process of disk formation around post-AGB stars is not well understood, but binarity is a necessary condition (Van Winckel 2003; Gielen et al. 2008). When the disk has formed and the strong AGB wind has ceased, gas in the disk can be re-accreted from the disk onto the primary star. Dust grains, however, experience radiation pressure and are prevented from falling in. Since refractive elements easily condense into dust grains, the accreted gas is chemically peculiar, which gives rise to the observed photospheric abundance pattern. The photosphere of HR 4049, therefore, became extremely depleted in iron. The selective re-accretion hypothesis thus holds the promise of a high abundance of iron-rich dust in the circumbinary environment.
Second, HR 4049 has a peculiar infrared spectrum. The infrared excess is large (LIR/L⋆ = 1/3, Dominik et al. 2003). The spectrum, shown in Fig. 1, displays strong features of polycyclic aromatic hydrocarbon molecules (PAHs) and even diamond emission bands, which indicates the presence of carbon-rich material in the system (Geballe et al. 1989; Guillois et al. 1999). Recently, the detection of Buckminsterfullerene (C60) was reported (Roberts et al. 2012). The strong gaseous emission lines of H2O, OH, CO, and CO2, on the other hand, point to oxygen-rich gas-phase chemistry (Cami & Yamamura 2001; Hinkle et al. 2007). The rest of the spectrum is featureless. In particular, the 10-μm silicate emission feature, which is common in disks around evolved binaries (Gielen et al. 2008), is absent. The spectrum has a shape that closely matches that of a 1200 K blackbody. Dominik et al. (2003) propose two models to fit the spectral energy distribution: the emission is produced by large (≫1 μm) grains, or the disk is very optically thick. The authors favor the second option. In this paper, we will propose another alternative: the emission is produced by (small) dust grains with a smooth opacity curve.
 |
Fig. 1 Infrared spectrum of HR 4049 (black: ISO-SWS, blue: Spitzer-IRS). The prominent features between 6 and 13 μm are caused by PAHs. The band between 4 and 5.3 μm is the result of a forest of CO, OH, and H2O molecular emission lines (Hinkle et al. 2007). Emission lines of CO2 are visible longward of 13 μm (Cami & Yamamura 2001). |
Furthermore, HR 4049 is an attractive observational target. The circumbinary disk is viewed at a large inclination angle, close to edge-on. Waelkens et al. (1991) have published Geneva optical photometry of HR 4049. The Geneva photometric system comprises seven bands, U,B1,B,B2,V1,V, and G, with effective wavelengths ranging from 346 nm to 581 nm1. Waelkens et al. (1991) found that the target is variable in all seven filters. The largest-amplitude variability is synchronous with the 430-day orbital period of the binary and ascribed to variable extinction in the line of sight towards the primary star by matter in the circumbinary disk. Due to its orbital motion, the primary hides behind the inner rim of the disk at phases of minimal brightness, when it is closest to the observer, and returns to maximal brightness roughly half an orbit later. The Geneva color–magnitude diagrams of HR 4049 contain information on the material that attenuates the primary star. Waelkens et al. (1991) show that the observed extinction law is roughly consistent with interstellar extinction, although notable differences are present.
In this paper we attempt to identify the dust species which produces the featureless infrared spectrum of HR 4049. We search for the dominant source of opacity in the circumbinary disk at optical-to-infrared wavelengths. We will show that the combination of infrared spectroscopy with spatially resolved observations is a powerful tool to discern between dust species with featureless opacities. The method described in this paper can potentially be applied to solve other astronomical questions, such as the iron-to-carbon dust content of winds around AGB stars.
2. Observations and data reduction
2.1. Interferometry
Interferometric measurements of HR 4049 were obtained within the Belgian Guaranteed Time on the European Southern Observatory’s (ESO) Very Large Telescope Interferometer (VLTI) Sub-Array (VISA). We made observations in the near-infrared H and K bands on nine baseline triangles with AMBER (Petrov et al. 2007) in the low spectral-resolution mode (LR-HK). Medium-resolution AMBER observations were obtained on four baseline triangles; two centered around 2.1 μm (MR–2.1) and two around 2.3 μm (MR-2.3). When the weather conditions allowed, the AMBER observations were obtained with the aid of the fringe tracker FINITO. This instrument uses 70% of the H-band flux to stabilize the fringes on the AMBER detector. Mid-infrared interferometry of HR 4049 was obtained with MIDI (Leinert et al. 2003) in the HIGH-SENS prism mode (HSP) on two baselines. The observing log is shown in Table 1. The corresponding spatial-frequency coverage is shown in Fig. 2. The interferometric observations were made at binary orbital phases φ ∈ [0,0.2], where φ = 0 corresponds to periastron passage. This is around the photometric minimum of the primary star in the optical (φ = 0.13, Bakker et al. 1998).
Log of the AMBER and MIDI interferometric observations.
2.1.1. AMBER data reduction
The AMBER data were reduced using the data processing software amdlib version 3 (Tatulli et al. 2007; Chelli et al. 2009). The calibrator star is HD 91964, a K4/K5 III giant with a stellar diameter of 1.27 mas (Mérand et al. 2005). For both science target and calibrator, the 25% fringe measurements with the highest signal-to-noise were selected to compute and calibrate the squared visibilities. The data are of very good quality and an increase in the percentage of selected frames does not significantly alter the outcome of the reduction procedure. For the closure phases, 90% of the best frames were selected. The closure phase was estimated by adding phasors in the complex plane (Tatulli et al. 2007). The closure phase of the science target was calibrated by subtracting the measured closure phase of the calibrator.
 |
Fig. 2 Spatial-frequency coverage of the interferometric measurements. Black dots refer to AMBER data, red dots to MIDI data. |
2.1.2. MIDI data reduction
The MIDI data reduction was performed using the MIA+EWS package2. Despite the fact that HR 4049 is a rather faint target for VISA+MIDI, the signal-to-noise of the correlated-flux (CF) measurements is high (~25). The total flux (F) is disentangled from the strong mid-infrared sky background by chopping to an off-target position on the sky and subtracting the on- and off-target spectra. For faint targets this leads to noisy spectra. This technique is not employed to determine the correlated flux. The background in the two interferometric channels is uncorrelated, while the interferometric signals are in phase opposition. Subtraction of both channels effectively removes the background while maintaining the correlated flux (see MIDI manual3). This results in correlated-flux spectra with much better signal-to-noise than the total-flux spectrum. Because HR 4049 is a faint target, F could not be measured reliably and we cannot compute the calibrated visibility (V)  (1)Here, the indices sci and cal refer to the uncalibrated measurements of science target and calibrator. However, the ratio of the visibilities at two given baselines is equal to the ratio of the calibrated correlated fluxes
(1)Here, the indices sci and cal refer to the uncalibrated measurements of science target and calibrator. However, the ratio of the visibilities at two given baselines is equal to the ratio of the calibrated correlated fluxes 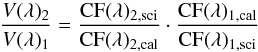 (2)where the indices refer to baselines 1 and 2. We cannot determine the absolute visibilities V15 m and V29 m because of the low-quality total spectrum, but the ratio of the visibilities at the two baselines V29 m/V15 m can be recovered from the observations. We will use the latter quantity in our analysis and refer to it as the MIDI relative visibility.
(2)where the indices refer to baselines 1 and 2. We cannot determine the absolute visibilities V15 m and V29 m because of the low-quality total spectrum, but the ratio of the visibilities at the two baselines V29 m/V15 m can be recovered from the observations. We will use the latter quantity in our analysis and refer to it as the MIDI relative visibility.
2.2. Archival observations
The analysis presented here also makes use of archival observations of HR 4049. For the optical analysis, we have used the Geneva photometry published by Waelkens et al. (1991). Optical spectroscopy of HR 4049 indicates Teff = 7500 K, log g = 1 dex, and an iron depletion of [Fe/H] = −4.8 dex for the primary star, while the secondary is undetected (Lambert et al. 1988; Waelkens et al. 1991; Van Winckel et al. 1995; Bakker et al. 1996). A fit to the optical photometry with a Kurucz (1993) model with these parameters yields a stellar angular diameter of 0.45 ± 0.03 mas. The interstellar reddening towards the binary was determined to be E(B − V) = 0.17 mag from fits to the data at photometric maximum. We used the interstellar extinction law of Cardelli et al. (1989) with RV = 3.1.
Two infrared spectra of HR 4049 have been obtained with the Short-Wavelength Spectrograph (SWS, de Graauw et al. 1996) aboard the Infrared Space Observatory (ISO, Kessler et al. 1996). We use the spectrum that was taken on 6 May 1996 at an orbital phase φ = 0.04, which is within the orbital-phase range covered by the interferometric observations. We downloaded the highly processed data products (HPDP) from the ISO archive in the reduction of Frieswijk et al.4. These authors started from data products produced with the off-line processing pipeline version 10.1. The Infrared Spectrograph (IRS, Houck et al. 2004) aboard the Spitzer Space Telescope (Werner et al. 2004) has also obtained a spectrum of HR 4049 in the short-high (SH) mode. We reduced the spectrum with pipeline version S15.3.0. It is reassuring that this spectrum, albeit obtained with a different instrument on a different satellite, is very similar to the ISO-SWS spectrum, both in shape and in absolute flux level. We show both infrared spectra in Fig. 1.
Ground-based mid-infrared observations of HR 4049 were obtained with VLT/VISIR (Lagage et al. 2004) mounted on UT3. The VISIR data were retrieved from the ESO data archive5. Images were obtained in one broad-band and three narrow-band photometric filters: SiC (λcen = 11.85 μm, Δλ = 2.34 μm), PAH2 (λcen = 11.25 μm, Δλ = 0.59 μm), PAH2_2 (λcen = 11.88 μm, Δλ = 0.37 μm), and Q1 (λcen = 17.65 μm, Δλ = 0.83 μm). The filter at 11.25 μm is centered on the PAH 11.3 μm feature. The PAH flux contribution in this band, estimated from the ISO-SWS spectrum, is 25%. The other two narrow-band filters (at 11.88 and 17.65 μm) capture almost no PAH emission. The PAH flux contribution in the broad-band filter at 11.85 μm is 5%. VISIR also obtained spectroscopy of HR 4049 in the N band. Due to the poor quality of the calibrator measurements, we could not extract a calibrated VISIR spectrum. However, VISIR is a slit spectrograph. The spatial information in the direction of the slit (north-south in this case) is therefore preserved. We performed astrometry on the spectral order in the raw 2D CCD images of HR 4049. This yields the spatial extent (full width at half maximum, FWHM) and relative photocenter position of the target at each wavelength. We discuss the VISIR data in Sect. 4.
The Hipparcos parallax of HR 4049 is 1.23 ± 0.36 mas, which places the object at a distance of 800 pc (Van Leeuwen 2007). Remarkably, Hipparcos did not flag HR 4049 as a binary. The spectroscopically determined semi-major axis of the primary orbit is asini = 0.60 ± 0.01 AU (Bakker et al. 1998). If the object is at a distance of 800 pc, the photocenter displacement of the primary on the sky due to the binary orbit is at least 0.75 mas, of the same order of magnitude as the measured parallax. In fact, this is true for any distance to the source; the dimensions of the binary are similar to the major axis of Earth’s orbit around the Sun. Although not detected by Hipparcos, the binarity of HR 4049 must have influenced the parallax measurement. We will come back to this issue and solve it in Sect. 6.
3. Optical extinction
3.1. The dust model
We re-analysed the Geneva photometry published by Waelkens et al. (1991). We tested which dust species can produce the observed extinction law towards the primary star. To this end, we computed opacities, i.e., mass absorption and scattering coefficients κ, for a set of common astronomical dust species in the JENA database (Jäger et al. 1994, 1998; Dorschner et al. 1995; Henning et al. 1995; Henning & Stognienko 1996; Scott & Duley 1996). We selected the species for which refractive indices are available from UV to infrared wavelengths, covering at least 0.2–100 μm. Because of the remarkably featureless infrared spectrum of HR 4049, we also focused on the dust species which have smooth infrared opacities. This excludes a priori small crystalline silicates, for example.
To convert optical constants to absorption and scattering opacities, a dust grain size and morphology needs to be assumed. Here, we tested a range of grain sizes covering 0.01 μm to 10 μm, and three grain shape models: solid spherical particles (Mie grains), a distribution of hollow spheres (DHS), and a continuous distribution of ellipsoids (CDE). The DHS model assumes that grains are spherical, but may include a large volume fraction of vacuum, mimicking grain porosity. We varied the maximum vacuum fraction between fmax = 0 (i.e., Mie grains) and fmax = 0.8. The CDE model assumes a distribution of ellipsoidal grains, ranging from spheres to needles. Opacities are computed in the Rayleigh limit, i.e., for grains with sizes a that obey 2πa/λ ≪ 1, with λ the wavelength. Because the computed opacities are used here at optical wavelengths, the CDE model is only valid for small grains with sizes below 0.1 μm. Both DHS and CDE are able to represent grain morphologies that deviate strongly from spherical (Min et al. 2003, 2005). Table 2 lists the dust species, adopted grain sizes, and shape distributions, for which absorption and scattering opacities were computed.
3.2. Extinction law
We reddened the Kurucz model atmosphere for the primary star according to the opacity curve of each of the dust species. We assumed isotropic scattering. The stellar light was attenuated by gradually increasing the dust column density until the maximal observed optical attenuation of AV ≈ 0.3 mag was reached. We then computed synthetic Geneva magnitudes and colors for the reddened atmosphere models. Because of the logarithmic magnitude scale, the synthetic color–magnitude diagrams are straight lines.
Tested dust species, sizes, and shapes.
 |
Fig. 3 Six independent Geneva color–magnitude diagrams of HR 4049. The linear-regression fit to the data is shown in black. The other curves show the color/magnitudes of the Kurucz model, reddened with the interstellar extinction law of Cardelli et al. (1989, foreground extinction) and with different dust species with a grain size of 0.01 μm and an appropriate range of column densities (variable circumstellar extinction). The grain shape distribution is DHS with fmax = 0.8, except for amorphous carbon (Mie, i.e., DHS with fmax = 0). Top left panel: the discrepancy between the observed and the modeled U − B color may be due to a UV-excess in the binary system. |
We turned back to the observations and performed a linear-regression fit to six independent color–magnitude diagrams of HR 4049: U − B, B1 − B, B2 − B, V1 − B, V − B, and G − B vs. V (Fig. 3). All other color–magnitude diagrams are linear combinations of these six and thus contain the same information. The residual scatter around the linear fit may have different causes, including intrinsic brightness variations of the primary star, activity in the binary system, density variations in the circumbinary dust that attenuates the primary starlight, and also observational uncertainties. We defined a chi-square variable  (3)with di the perpendicular distance of a point in the color–magnitude diagram to the linear fit and ⟨ d ⟩ the average distance of the points to the line. The latter is zero because of the linear regression. An analoguous value
(3)with di the perpendicular distance of a point in the color–magnitude diagram to the linear fit and ⟨ d ⟩ the average distance of the points to the line. The latter is zero because of the linear regression. An analoguous value  was computed for the reddened atmosphere models. In the latter case, ⟨ d ⟩ is non-zero. An offset between the location of the linear fit to the model data and the photometric observations can occur because of differences between the modeled and the true spectrum of the target, or between the modeled and true interstellar extinction law. This is clear in the U − B vs. V color–magnitude diagram (Fig. 3, upper left panel). However, here we focused on the extinction law in the line of sight and hence only on the slope of the variations in the color–magnitude diagrams. We defined
was computed for the reddened atmosphere models. In the latter case, ⟨ d ⟩ is non-zero. An offset between the location of the linear fit to the model data and the photometric observations can occur because of differences between the modeled and the true spectrum of the target, or between the modeled and true interstellar extinction law. This is clear in the U − B vs. V color–magnitude diagram (Fig. 3, upper left panel). However, here we focused on the extinction law in the line of sight and hence only on the slope of the variations in the color–magnitude diagrams. We defined  (4)A model with X2 = 1 provides a match to the slopes of the extinction curve equivalent to a linear regression fit, given the residual spread on the data.
(4)A model with X2 = 1 provides a match to the slopes of the extinction curve equivalent to a linear regression fit, given the residual spread on the data.
 |
Fig. 4 a) ISO-SWS spectrum in the N-band range. The PAH features at 8.6, 11.3, 12.0, and 12.7 μm are indicated, the dashed line represents the continuum. b) Spatial extent along the slit north-south direction of VISIR. The dashed line indicates the width of the spatially unresolved continuum, which increases with wavelength. c) Relative spatial position with respect to the continuum along the slit direction of VISIR. The PAH emission region is extended on a scale of several 100 s of AU and its photocenter is located towards the south of the continuum emission region. |
Because of the extreme iron depletion in the primary photosphere and the hypothetical selective re-accretion, one may expect that the circumbinary disk contains detectable amounts of iron-bearing dust. DHS-shaped iron oxides, magnetite, and metallic iron grains reproduce the observed extinction law reasonably well; however, 0.01 μm-sized Mie amorphous-carbon opacities provide the best fit. The fit with 0.01 μm-sized DHS-shaped (i.e., fmax > 0) amorphous carbon grains is also acceptable. A summary is presented in Table 3. We cannot unambiguously differentiate between these different dust species based on the optical extinction data alone. All other tested dust species, including amorphous silicates and Fe2O3, can be rejected (X2 ≫ 3). Grain sizes larger than 0.1 μm can be excluded as well, because the corresponding opacities are too grey to match the steep observed extinction law.
4. PAH emission
We now focus on the appearance of the system at infrared wavelengths. Menut et al. (2009) analyzed early MIDI observations of HR 4049. They find that the emission region of the PAH 7.7, 8.6, and 11.3 μm features is more extended than that of the underlying continuum. Our new MIDI measurements confirm this. The correlated fluxes show no sign of the PAH features. This indicates that the PAH emission region is fully resolved by the interferometer, even on the short baseline of 15 m. We estimated a lower limit to the extent of the PAH emission region of 100 mas (64 AU at 640 pc). In line with Menut et al. (2009), we conclude that the PAH emission region is not only situated in the disk, although a contribution from the disk is still possible.
We turn to the VISIR data to locate the PAH emission. In all four VISIR images, HR 4049 appears as a point source. Closer inspection of the point spread function (PSF), however, shows that it is 15% broader than the calibrator PSF in the photometric band that covers the PAH 11.3 μm feature, while both PSFs are almost identical in the broad-band filter. This indicates that the PAH emission region is slightly resolved on a scale comparable to that of the VISIR PSF, i.e., several 100 mas.
Confirmation comes from the VISIR slit spectroscopy. Figure 4 shows the mid-infrared ISO-SWS spectrum, the spatial extent (FWHM), and the relative spatial position of HR 4049 projected onto the slit direction (i.e., north-south) from VISIR. The PAH emission region is marginally, but convincingly, resolved with respect to the unresolved emission of the circumbinary disk. Moreover, the photocenter of the PAH emission region, projected onto the slit north-south direction, is located towards the south of the continuum emission region. The PAH emission is therefore not centered on HR 4049, consistent with the idea of a bipolar outflow in which the receding lobe (towards the north) is partially obscured by the circumbinary disk.
5. The circumbinary disk: an optically thick wall?
 |
Fig. 5 Spectral energy distribution of HR 4049. The ISO-SWS spectrum (grey line), and IRAS 25, 60, and 100 μm, and SCUBA 850 μm photometry (grey boxes). The green line is the fit with a single blackbody (1200 K, in accordance with Dominik et al. 2003). The spectral energy distribution of our model (blue) underestimates the flux at λ > 20 μm. The red line shows our model plus a 200 K blackbody, scaled to the SCUBA 850 μm flux. See Sect. 7 for details. |
Based on the shape of the infrared spectral energy distribution (Fig. 5), Dominik et al. (2003) argue that the disk around HR 4049 is optically very thick. In their model, the disk is a vertical wall with a large scale height, 1/3 of the inner disk radius. We have compared this geometry to our interferometric observations.
Our wall model consists of a vertical wall of uniform brightness with an inner radius Rin ∈ [5,25] mas, a height H = Rin/3, an inclination i ∈ [40°,70°], and a disk position angle on the sky PA ∈ [0°,360°]. We define PA = 0° when the far side of the inclined disk, projected on the sky, is oriented towards the north6. Only the inside of the wall, which faces the binary, is bright. Because a high optical depth is assumed, the backside is dark and blocks the light from the inside. The flux contribution of the primary star at near-infrared wavelengths is estimated from the spectral energy distribution and the stellar atmosphere model. We construct wall model images and compute near-infrared visibilities and closure phases as explained in Appendices A and B.
The best wall models have PA = 130 ± 10°, i = 60 ± 10°, Rin> 15 mas, and reduced chi-square values of ~20 for the AMBER visibilities and ~8 for the AMBER closure phases. The wall model images have by definition very sharp edges and they deviate strongly from point symmetry because of the high inclination. As a result, the model closure phases have large amplitudes, which is inconsistent with the moderate closure phases observed. Nonetheless, the orientation of the disk on the sky is well established. Specifically, it is the progression of the zero points in the closure phase as a function of baseline position angle, well sampled by the observation sequence (c) to (g) listed in Table 1, that provides a strong constraint on the disk position angle.
The disk extent is less well determined; the simple geometric model provides only a lower limit to the inner radius of the wall. At long baselines, the circumbinary disk is almost fully resolved, while the primary star remains spatially unresolved. In other words, the measurements at long baselines provide only information on the wavelength-dependent flux ratio of the star and the disk in the near-infrared. As a reference, a basic model with an unresolved star (V⋆ = 1) surrounded by a fully resolved disk (Vdisk = 0) provides a fit to the AMBER visibilities with a reduced chi-square of ~40. The corresponding closure phases are obviously zero in this case, inconsistent with the observations.
Following the reasoning of Dominik et al. (2003, their Sect. 5), one obtains for the optically thick wall that 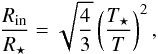 (5)an equation that is valid irrespective of the distance to HR 4049. Dominik et al. (2003) derive T = 1200 K for a fit to the spectral energy distribution with a single blackbody, a value that we confirm here in Fig. 5. This temperature corresponds to Rin/R⋆ = 45. All our best wall models have Rin/R⋆ larger than 67 ± 4, using a stellar angular diameter of 0.45 mas (Sect. 2.2), and hence T < 1000 K. The assumption of an optically thick vertical wall producing blackbody emission is not consistent with the interferometric measurements. We therefore reject this hypothesis.
(5)an equation that is valid irrespective of the distance to HR 4049. Dominik et al. (2003) derive T = 1200 K for a fit to the spectral energy distribution with a single blackbody, a value that we confirm here in Fig. 5. This temperature corresponds to Rin/R⋆ = 45. All our best wall models have Rin/R⋆ larger than 67 ± 4, using a stellar angular diameter of 0.45 mas (Sect. 2.2), and hence T < 1000 K. The assumption of an optically thick vertical wall producing blackbody emission is not consistent with the interferometric measurements. We therefore reject this hypothesis.
The presence of very small dust particles in the upper layers of the circumbinary disk is evidenced by the optical extinction towards the primary. We investigate an alternative model in which the featureless infrared spectrum is produced by small grains with smooth opacities. We present this new model in Sect. 7. First, however, we discuss the distance to HR 4049.
6. The distance to HR 4049
The distance to HR 4049 is highly uncertain because the Hipparcos parallax measurement is influenced by the binary motion. Strangely enough, Hipparcos did not recognize HR 4049 as a binary star and also a detailed inspection of the Hipparcos data did not reveal the binary signature (D. Pourbaix, priv. comm.). This means that, due to the specific combination of orbital parameters and the distance to HR 4049, the Hipparcos measurements resemble that of a single star at a distance of 800 pc.
The optical spectroscopy constrains all orbital parameters of the primary (epoch of periastron passage T0, period P, projected semi-major axis asini, eccentricity e, and argument of periastron ω; Bakker et al. 1998), apart from the longitude of the ascending node Ω and the inclination of the orbital plane i. The interferometric measurements, and specifically the closure phase measurements, constrain the orientation angle of the disk’s major axis on the sky. If the orbital plane of the binary coincides with the disk plane, this angle is equivalent to Ω. This assumption is justified: although the formation process of the disk is unknown, binary interaction is most likely a key ingredient and the plane of the disk is expected to be identical to the orbital plane.
The far side of the disk in the wall models presented in Sect. 5 is located at a position angle PA = 130° ± 10° E of N. The longitude of the ascending node Ω is either PA + 90° or PA − 90°, depending on the orbital direction of the binary: if the binary revolves counterclockwise in the plane of the sky, then Ω = 40°. Otherwise Ω is 220°. We have computed the apparent parallax of HR 4049, which is a combination of the binary orbit and the intrinsic, distance-related parallax, for Ω and i consistent with the results of the interferometric modeling and for any distance to the source d. To mimic the Hipparcos measurements, we have computed the offset of the primary on the sky at the times of the Hipparcos observations. An ellipse was fitted to these offsets to determine the simulated parallax.
We find that for Ω = 40°, the computed parallax agrees within uncertainties with the observed value of 1.23 ± 0.36 mas, if the distance to HR 4049 is 1050 ± 320 pc. In this case, the combination of the binary orbit and Earth’s orbit projected on the sky increases the parallax signal. Hence, the measured Hipparcos parallax appears larger than that expected for a single star at a distance of 1050 pc. For Ω = 220°, we find a distance of 640 ± 190 pc. In the latter case, the binary motion on the sky counteracts the distance-induced parallax and the target is closer than the combined parallax appears to suggest.
7. Radiative-transfer modeling
7.1. A priori considerations
The optical attenuation AV of the primary due to the circumbinary matter varies between 0 and 0.3 mag. The line of sight towards the primary intersects with the upper layers of the inner disk. The optical analysis indicates that the dust in this region is either iron-bearing dust or amorphous carbon. It also proves that very small (0.01 μm) grains are present and that these grains are the dominant source of opacity in the upper layers of the disk at optical wavelengths.
The goal of this paper is to identify the dust species which establishes the appearance of the HR 4049 system from optical to mid-infrared wavelengths. We stress that our investigation does not aim to determine the dust component that dominates the disk in terms of mass or abundance, but in opacity.
For this purpose, we use the radiative-transfer modeling code MCMax (Min et al. 2009). The code computes the temperature and density structure of a dust- and gas-rich disk around a central illuminating source. The detection of strong gaseous emission lines indicates that the circumbinary disk around HR 4049 is indeed rich in gas (Cami & Yamamura 2001; Hinkle et al. 2007). The dust provides the opacity and is heated by the star. The gas is assumed to be thermally coupled to the dust and thus has the same temperature structure. The prime assumption of the model is that the disk is in vertical hydrostatic equilibrium. The disk scale height is set by the balance between gas pressure and gravitational pull of the central object perpendicular to the disk midplane. In the case of HR 4049, the central source is a binary. The estimated semi-major axis of the binary is of the order of a few primary stellar radii (Bakker et al. 1998). It is clear from our simple geometric model presented above in Sect. 5, that the dimensions of the binary are much smaller than the dimensions of the disk. Therefore, we can approximate the binary by a single central star, which has the temperature and luminosity of the primary star of HR 4049, but with a stellar mass representing both stars.
Radiative-transfer modeling of circumstellar disks has shown that the smallest dust grains provide the bulk of the opacity, both in terms of absorption in the optical and thermal emission in the near- and mid-infrared, even when these grains represent only a tiny fraction of the total disk mass (e.g., Meijer et al. 2008; Acke et al. 2009). The appearance of the disk in the mid-infrared is almost exclusively dominated by this small-grain component, regardless of the presence of larger grains with lower opacities. A radiative-transfer model with a content of only small grains, or with a mixture of large and small grains, will produce similar spectra and images. Therefore, for the purpose of our investigation, it is viable to assume that the entire circumbinary dust disk fully consists of small grains. Furthermore, guided by our analysis of the attenuation of the stellar light by the disk at optical wavelengths, we assume the disk contains only one of the species mentioned above. The opacities of the four tested dust species are plotted in Fig. 6. As described in Sect. 6, the distance to HR 4049 is either 640 pc or 1050 pc. We computed radiative-transfer models for both distances.
A downside of our approach is that our model cannot produce a satisfying match to the spectral energy distribution at far-infrared and millimeter wavelengths. At long wavelengths, 0.01 μm-sized grains have no opacity and hence produce no emission. The inclusion of large dust grains in the model would significantly improve the match to the spectral energy distribution. However, this strongly increases the complexity of the model in terms of free parameters (e.g., grain size distribution, vertical settling and mixing) and is beyond the scope of this paper.
7.2. The model grid
 |
Fig. 6 Opacity curves of the four dust species that satisfy the optical extinction law towards HR 4049, normalized by κV (at 0.55 μm). The grain size is 0.01 μm, the grain shape distribution is either DHS with fmax = 0.8, or Mie (fmax = 0). |
The computational time needed to calculate a single model is approximately 1 min. We opted for a grid approach instead of applying a minimization fitting routine. Each of the grid models is compared a posteriori to the available data (see Sect. 7.3). The free input parameters of the radiative-transfer model are limited to the following: the opacity table of the dust species under consideration, the total stellar mass of the binary (M⋆ ⋆), the inner and outer radius of the disk (Rin, Rout), the total mass in the small dust grains (Mdust), and the surface density power law ![\begin{equation} \Sigma(R) = \Sigma_\mathrm{in} \left(\frac{R}{R_\mathrm{in}}\right)^{-p}\ \mathrm{with}\ R \in [R_{\rm in},R_{\rm out}], \end{equation}](/articles/aa/full_html/2013/03/aa19282-12/aa19282-12-eq144.png) (6)where p is a free parameter and Σin is fixed by
(6)where p is a free parameter and Σin is fixed by 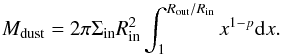 (7)The orientation of the disk in space is fixed by two angles: the inclination (i) and the position angle on the sky (PA). Again, we define PA = 0° when the far side of the inclined disk, projected on the sky, is oriented towards the north. The grid parameter ranges are summarized in Table 4.
(7)The orientation of the disk in space is fixed by two angles: the inclination (i) and the position angle on the sky (PA). Again, we define PA = 0° when the far side of the inclined disk, projected on the sky, is oriented towards the north. The grid parameter ranges are summarized in Table 4.
Grid parameters of the radiative-transfer models.
7.3. Comparing the models to the observations
In the search for the model in the grid which best reproduces the observations, we have defined five chi-square variables.
-
 . The modeled infrared spectrum is compared to the ISO-SWSspectrum of HR 4049 at wavelengths outside ofthe PAH features (see Fig. 7).
. The modeled infrared spectrum is compared to the ISO-SWSspectrum of HR 4049 at wavelengths outside ofthe PAH features (see Fig. 7). -
 and
and  . From the model images at 2.2 μm, squared visibilities and closure phases are computed (see Appendices A and B). We compute a chi-square for both the squared visibilities
. From the model images at 2.2 μm, squared visibilities and closure phases are computed (see Appendices A and B). We compute a chi-square for both the squared visibilities 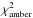 and the closure phases
and the closure phases  . The latter is defined using phasors
. The latter is defined using phasors  (8)\begin{lxirformule}$\Phi_{j}$\end{lxirformule} are the observed closure phases, σj the corresponding errors, Φmod,j the modeled closure phases, and N = 2152 the number of closure phase measurements.
(8)\begin{lxirformule}$\Phi_{j}$\end{lxirformule} are the observed closure phases, σj the corresponding errors, Φmod,j the modeled closure phases, and N = 2152 the number of closure phase measurements. -
 . From the image at 10 μm, model visibilities are computed. Because the MIDI data reduction only provides good estimates of the relative visibilities on the two baselines, we define a chi-square
. From the image at 10 μm, model visibilities are computed. Because the MIDI data reduction only provides good estimates of the relative visibilities on the two baselines, we define a chi-square 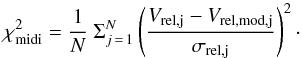 (9)Herein, Vrel,j = V29m,j/V15m,j are the MIDI relative visibilities, σrel,j the corresponding errors, Vrel,mod,j the model visibility ratios, and N = 30 the number of MIDI relative visibilities.
(9)Herein, Vrel,j = V29m,j/V15m,j are the MIDI relative visibilities, σrel,j the corresponding errors, Vrel,mod,j the model visibility ratios, and N = 30 the number of MIDI relative visibilities. -
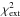 . All interferometric observations were taken near the photometric minimum, when the primary of HR 4049 is most obscured. The optical attenuation at that phase is AV = 0.3 ± 0.1 mag. The attenuation of the model is computed by comparing the model spectrum to the input Kurucz model at 0.55 μm. Because the tested dust species are selected to provide a good fit to the extinction curve in the optical wavelength range, radiative-transfer models with the right optical attenuation have the right optical colors as well.
. All interferometric observations were taken near the photometric minimum, when the primary of HR 4049 is most obscured. The optical attenuation at that phase is AV = 0.3 ± 0.1 mag. The attenuation of the model is computed by comparing the model spectrum to the input Kurucz model at 0.55 μm. Because the tested dust species are selected to provide a good fit to the extinction curve in the optical wavelength range, radiative-transfer models with the right optical attenuation have the right optical colors as well.
An acceptable model should provide a good fit to all observations simultaneously. First, we select models based on their ability to reproduce the interferometric observations, that is, models that satisfy simultaneously
where the minimum is taken over the entire grid of models. We then pick the models that satisfy  (11)with the minimum taken over the selected subset. Finally, the best model is defined as the one with the lowest value in
(11)with the minimum taken over the selected subset. Finally, the best model is defined as the one with the lowest value in 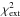 .
.
7.4. Modeling results
We discuss the modeling results for the four dust species that satisfy the optical extinction law.
Iron oxide. The opacities of the magnesium/iron oxides show a lack of opacity in the near-infrared and a smooth, broad band around 20 μm. The models that best reproduce the interferometric data therefore have spectra with a strong excess at mid-infrared wavelengths and a moderate near-infrared excess. The observed infrared spectrum of HR 4049 clearly does not have this shape. Magnesium/iron oxides are excluded as the dominant opacity source in the circumbinary disk.
Magnetite. None of the models in the computed grid satisfies the interferometric criterium (Eq. (10)) and reproduces both visibilities and closure phases simultaneously. Ignoring the bad fit to the interferometry, some models have spectra that match the observed infrared spectrum well. However, like the iron oxides, the magnetite opacities have structured spectra in the 10–30 μm range. This results in a clear feature at 17 μm in the model spectra, which is not seen in the observations of HR 4049 (see Fig. 7). We reject magnetite.
Metallic iron. While the interferometric observations can be reproduced relatively well, not a single one of the models in the grid with metallic iron produces an infrared spectrum that is compatible with the observed spectrum. All the model disks are optically thin at infrared wavelengths. The spectrum is therefore proportional to a gradient of blackbody curves, multiplied with the opacity. Due to the steep decline of the opacity curve of metallic iron towards long wavelengths, the infrared spectra of all metallic-iron models are skewed, with a strong shoulder at near-infrared wavelengths (1–2 μm). This is inconsistent with the observed infrared spectrum.
To reduce the strong near-IR bump and get the peak of the emission at 4–5 μm, as observed in the spectrum of HR 4049, the metallic iron has to be cooler than ~600 K. Even in model disks with the largest inner radii (30 AU), however, the iron grains are too hot (1100 K) because of the high optical-to-infrared opacity ratio of metallic iron. Expanding the grid to even larger inner disk radii would improve the spectral match, but the interferometric data do not allow for a larger angular extent of the disk on the sky. Metallic iron is removed from the shortlist of dominant opacity sources in the disk around HR 4049.
Amorphous carbon. The disk models with amorphous carbon provide significantly better fits to the infrared observations. A few dozen grid models satisfy both the interferometric criterium (Eq. (10)) and the spectral criterium (Eq. (11)). The parameters of the best model are listed in Table 5. The error bars represent the spread around the best model parameters of those grid models that satisfy the criteria.
The spectrum of the best amorphous-carbon model is plotted in Fig. 7. The match between the shape of the modeled spectrum and the observed infrared spectrum is remarkable. The fit to the interferometric data is shown in Figs. 8 to 12. The low-resolution AMBER visibilities (Fig. 8) span the H and K bands. The relative flux contribution of the spatially unresolved primary star to the total flux decreases towards longer wavelengths, from ~0.6 at the blue end of the H band to ~0.2 at the red end of the K band. We take this effect into account (see Appendix B). It leads to higher visibilities at short wavelengths.
 |
Fig. 7 Model fit to the ISO-SWS spectrum of HR 4049. The spectrum of the best amorphous-carbon model is shown (red), along with the best magnetite model (cyan) and the best fit with a single blackbody (T = 1200 K, green). |
 |
Fig. 8 Low-resolution (LR-HK) squared visibilities of HR 4049 as a function of spatial frequency. Top to bottom: observed squared visibilities |
Deviations between the observed and modeled visibilities are largest in the H band. The AMBER observations were obtained using the fringe tracker FINITO when the weather conditions allowed (see Sect. 2.1). Only 30% of the H-band flux of HR 4049, intrinsically an already faint AMBER target, is transmitted to the science detector. Even when the weather conditions were worse, and FINITO could not be used, the H-band flux was low. As a result, the uncertainties on the H-band correlated fluxes are large. Moreover, systematic calibration errors may occur. Decreasing quality of the fringe measurements generally leads to a loss of coherence, reducing the calibrated visibilities if the measurements of the calibrator are of better quality than those of the science target. In Fig. 8, it can be seen that the model visibilities systematically exceed the observations, which may point to this effect. It is also possible that the flux ratio of the star and disk deviates from the model in the H band. However, this flux ratio is constrained by the Kurucz stellar atmosphere model, fit to the optical photometry, and the ISO-SWS infrared spectrum, and fixed in the radiative transfer modeling (see Appendix B). This approach is self-consistent, and comparison of the data sets at different wavelengths and with different instruments, which is necessary for our investigation, remains possible.
 |
Fig. 9 Medium-resolution (MR-2.1 and MR-2.3) squared visibilities of HR 4049. Colors refer to different baselines: respectively blue, red, and green for the first, second and third baseline of observations (k) to (n) in the order listed in Table 1. Top to bottom in each panel: observed |
 |
Fig. 10 Low-resolution (LR-HK) closure phase measurements of HR 4049. Each panel refers to a baseline triangle. The letter in the top corner refers to the corresponding entry in Table 1. Measurements are indicated by black dots with error bars; the red line represents the model. |
 |
Fig. 11 Medium-resolution (MR-2.1 and MR-2.3) closure phase measurements of HR 4049. Symbols are similar to those in Fig. 10. |
 |
Fig. 12 MIDI relative visibilities V29m/V15m. Black dots are the data; the red line is the model. |
Because of the large uncertainties of the H-band visibilities, the interferometric model is mostly constrained by the low- and medium-resolution K-band measurements. The latter are reproduced well: the two local minima seen in the low-resolution K-band visibilities (at spatial frequencies around 60 and 150 cycles/arcsec; Fig. 8) and the relative shape of the medium-resolution visibilities (Fig. 9).
The orientation of the disk on the sky is mostly constrained by the LR-HK closure phase series (c) to (g) (see Table 1). These observations were obtained consecutively on a single baseline triangle. Due to the Earth’s rotation, the baseline lengths and orientations on the sky change during the night. The model reproduces nicely the observed trend of the closure phases with time (Fig. 10). Also the medium-resolution closure phases are matched by the model (Fig. 11). The MIDI relative visibilities, shown in Fig. 12, are reproduced perfectly.
The model disk density and temperature structure are shown in Fig. 13. Model images at 2.2 μm and 10 μm are displayed in Fig. 14. Note that the disk is moderately optically thick at optical wavelengths but optically thin at infrared wavelengths, in contrast to the very optically thick wall model of Dominik et al. (2003).
 |
Fig. 13 Density and temperature structure of the best model. R is the radial distance to the primary, z the vertical height above the disk midplane. The color scale and black contours indicate the local temperature of the amorphous carbon in Kelvin. White contours indicate the local density with respect to the maximal density at R = Rin and z = 0. The dotted line is the line of sight towards the primary. |
7.5. The distance to HR 4049 revisited
We may be able to differentiate between the two possible distances to HR 4049 found in Sect. 6. Our best models have a binary stellar mass of 1.1 ± 0.1 M⊙ and 2.8 ± 0.3 M⊙ for a distance of 640 and 1050 pc, respectively. By means of the mass function of the primary, derived from optical spectroscopy (0.158 ± 0.004 M⊙, Bakker et al. 1998), and the now known inclination of the system, the binary mass can be converted to the masses of the individual stars. For a distance of 1050 pc, the primary and secondary mass are 1.6 ± 0.2 M⊙ and 1.1 ± 0.1 M⊙, respectively. Such a primary mass is excessively high for a white dwarf, which makes a distance of 1050 pc unlikely. At a distance of 640 pc, the primary and secondary have a lower mass of 0.4 ± 0.1 M⊙ and 0.7 ± 0.1 M⊙, respectively. This primary mass is within the expected range for a post-AGB star. We conclude that the most likely distance to HR 4049 is 640 pc.
With an effective temperature of 7500 ± 200 K and an angular diameter of 0.45 ± 0.03 mas at a distance of 640 ± 190 pc, the primary has a radius of 31 ± 9 R⊙ and a luminosity of 2800 ± 1700 L⊙ for a stellar mass of 0.4 ± 0.1 M⊙. This is close to what is expected from Paczyński’s core mass-luminosity relation: a luminosity of 2800 L⊙ corresponds to a stellar mass of ~0.55 M⊙ (Paczyński 1970a,b). The inferred surface gravity log g is 1.1 ± 0.3 dex, consistent with the spectroscopic value of 1.0 ± 0.5 dex.
At a distance of 1050 ± 320 pc, the primary’s radius and luminosity would be 50 ± 15 R⊙ and 8000 ± 4000 L⊙, for an (unlikely) mass of 1.6 ± 0.2 M⊙. Also in this case, log g = 1.2 ± 0.3 dex is consistent with the spectroscopic value, but, again according to the mass-luminosity relation, the luminosity corresponds to that of a post-AGB star that is only half as massive.
Parameters of the best model.
8. Conclusions
8.1. Discerning metallic iron and amorphous carbon
With our case study of HR 4049, we have shown that the combination of infrared spectroscopy and interferometry is a powerful tool for discriminating between dust species with featureless opacities. While the spectrum is related to the temperature structure of the circumstellar dust, the high-angular-resolution data constrain the physical location of the material. Dust species that are not in thermal contact have different temperatures at the same physical location from the illuminating source because of their different absorption/emission properties.
In general, by measuring the temperature of the dust and its location, one can constrain the type of dust under consideration. This is specifically true for small metallic iron and amorphous carbon grains. Both species are expected to be abundant in different astrophysical environments, e.g., AGB winds and circumstellar disks, but their identification based on the infrared spectrum alone is impossible. Fortunately, the opacity of metallic iron decreases more quickly towards longer wavelengths than that of amorphous carbon (Fig. 6). This makes metallic iron grains much hotter than amorphous carbon grains under the same optical irradiation. Spatially resolved observations lift the ambiguity. The combination of spectroscopy and interferometry is therefore a very promising tool for identifying these dust species in a wide range of astrophysical environments.
8.2. A consistent image of HR 4049
The system HR 4049 consists of a binary located at a distance of 640 pc, surrounded by a circumbinary dust- and gas-rich disk. It contains an evolved, 0.4 ± 0.1 M⊙, 7500 ± 200 K star, and an undetected 0.7 ± 0.1 M⊙ secondary. Under the assumption that the latter is on the main sequence, this mass corresponds to that of a K-type star.
 |
Fig. 14 Best-model image at 2.2 and 10 μm. North is up, east is left. At a distance of 640 pc, 1 mas corresponds to 0.64 AU. The dashed line in the right panel indicates the photocenter location of the PAH 11.3 μm emission region relative to the disk center, projected on the N − S axis (xns). The photocenter position in the E − W direction is not constrained (see Sect. 8.2.2). |
8.2.1. The circumbinary disk
The binary is surrounded by a circumbinary disk, rich in gas and dust. Our model indicates that small amorphous carbon grains are the dominant source of opacity. The total dust mass in these grains required to reproduce the near- to mid-infrared observations is only 10% of a Moon mass.
The radial extent of the disk seen in the near- and mid-infrared is limited to a few tens of AU. The disk is optically thick to the stellar radiation in radial direction, but almost optically thin at infrared wavelengths. The ratio of the total infrared excess luminosity and the stellar luminosity of the best model is 25%, lower than the observed 33% (Dominik et al. 2003). The difference between the thermal emission of the model and the photometric observations occurs at wavelengths beyond the mid-infrared, where our model fails (as explained in Sect. 7.1). This discrepancy at long wavelengths can be phenomenologically solved by including large (>several μm) and cold dust grains either in the midplane of the disk or at larger distances from the star. Inclusion of a dust component of this kind results in additional emission at long wavelengths, while the appearance of the disk at optical and mid-infrared wavelengths remains similar.
The spectral energy distribution of HR 4049 is shown in Fig. 5. While our model provides a satisfying fit at short wavelengths, it underestimates the flux beyond 20 μm. A fit with a 200 K blackbody representing the cold dust component in the disk provides an ad hoc solution to this problem. We scaled the blackbody so that the SCUBA 850 μm flux is matched. The radiating surface of the blackbody is 740 mas2 (i.e., 30% of the midplane surface of our model projected on the sky). We note that a single-temperature blackbody fit (1200 K) does not fully grasp the shape of the spectral energy distribution either (Fig. 5).
The optical spectrum of HR 4049 shows the [O i] 6300 Å emission line. The position and width of the line profile do not change with orbital period, which made Bakker et al. (1996) conclude that the emission region is located in the circumbinary disk. This is not uncommon for early-type stars surrounded by a disk; also pre-main-sequence stars display disk [O i] emission (Acke et al. 2005). The broadening of the line is due to the Keplerian velocity of the line formation region in orbit around the star/binary. With our value for the binary stellar mass of HR 4049 we derive a Keplerian velocity at the inner radius of the circumbinary disk of vin = 9 ± 1 km s-1, in perfect agreement with the feature’s full width at half maximum of 20 km s-1 (Bakker et al. 1996). Hinkle et al. (2007) have determined the widths of the infrared CO lines to be in the range of 16–18 km s-1. Adopting our model parameters, this broadening is consistent with a disk origin of the CO emission as well7.
8.2.2. PAH outflow
The far side of the circumbinary disk is oriented towards PA = 130°. The VISIR spectroscopy indicates that the photocenter of the PAH emission, projected onto a N − S axis, is located south of the photocenter of the disk emission. These observations are consistent with a bipolar outflow, perpendicular to the disk midplane, along the rotation axis of the disk. The receding lobe is oriented towards PA = 310°. Compensating for the PAH-to-total flux ratio (fpah = Fpah/Ftotal) and taking into account the orientation of the disk (PA), one can compute the photocenter displacement of the PAH emission region on the sky x from the photocenter displacement measured in the N − S direction by VISIR xns using  (12)The photocenter of the PAH 11.3 μm emission region on the sky is located 40 ± 10 mas (26 AU at 640 pc) from the disk center, comparable to the extent of the disk at these wavelengths (Fig. 14). This again shows that the emission region is much larger than the circumbinary disk and is most likely a bipolar outflow.
(12)The photocenter of the PAH 11.3 μm emission region on the sky is located 40 ± 10 mas (26 AU at 640 pc) from the disk center, comparable to the extent of the disk at these wavelengths (Fig. 14). This again shows that the emission region is much larger than the circumbinary disk and is most likely a bipolar outflow.
8.2.3. Diamonds
HR 4049 is one of the very few astronomical sources that displays the near-infrared emission bands of hydrogenated diamonds (Geballe et al. 1989; Guillois et al. 1999). The pre-main-sequence star HD 97048 is also surrounded by a disk containing diamonds (Acke & van den Ancker 2006). The infrared spectrum of HD 97048 shows strong PAH emission emanating from the disk and no sign of silicate emission. The geometry of the disk is remarkable as well: mid-infrared imaging has shown that it is an extremely flared, i.e., bowl-shaped, disk (Lagage et al. 2006). Carbonaceous grains provide a straightforward explanation for the featureless continuum, while the large disk opening angle may reflect strong heating via hydrocarbon molecules and very small grains. Here, we report that also the circumbinary disk around HR 4049 is rich carbonaceous dust.
Acke & van den Ancker (2006) searched for observational characteristics that set apart diamond sources from others, but found none. Here, we suggest that a carbon-dominated dust chemistry is a necessary condition to form the diamonds and/or make their features appear in the infrared spectrum.
9. Discussion
HR 4049 belongs to a fairly large group of evolved binary stars surrounded by a circumbinary disk (Van Winckel 2003). The orbital parameters are such that the evolved objects must have been subject to severe binary interaction processes when at giant dimensions. The systems managed to avoid the strong spiral-in and reveal themselves as long-period (>100 days), mainly eccentric binaries, often still surrounded by a stable dusty disk (e.g., Van Winckel et al. 2009). A recent study of optically bright objects in the Large Magellanic Cloud has shown that disk sources are also rather common there among the post-AGB population. Because of the known distance to the LMC, their location in the Hertzsprung-Russell diagram is better constrained. The primary stars in these systems display a wide range in luminosities and hence in initial mass (van Aarle et al. 2011). This indicates that disk formation does not depend vitally on the primary’s initial mass, but rather on the dimensions of the binary system and of the primary during the thermally pulsing AGB phase.
Investigation of the infrared spectra of circumbinary disks around evolved binaries has indicated an oxygen-rich dust mineralogy in most systems. Amorphous and crystalline silicate features are dominant (Gielen et al. 2008, 2011a). The evolutionary scenario (Waters et al. 1998; Molster et al. 1999; Van Winckel 2003) assumes that the circumbinary disk is a relic of the strong binary interaction process and hence contains the chemical footprint of the former giant envelope out of which it was formed. The dominant occurance of purely oxygen-rich material shows that the interaction processes occured prior to the evolutionary phase when enough thermal pulses with dredge-up would have made the star carbon-rich. Only a few objects display PAH emission features, and some even fullerene emission features, on top of the dust spectra which are dominated by (crystalline) silicate features (Gielen et al. 2011a,b).
In this context, HR 4049 is an exception to the rule. The emission bands in the infrared spectrum are all attributed to carbonaceous species and we have shown in this paper that the continuum emission is also produced by carbon grains. There is no sign of silicates. We stress, however, that large (≫10 μm) silicate grains may be present in the disk. These grains have a smooth spectral signature, that would be veiled by the spectrum of the small carbon grain component. The presence of large grains may be suggested by the strong far-infrared excess, not reproduced by our model. The particular nature of HR 4049 is highlighted by the contrasting oxygen-rich chemistry of the circumbinary gas.
The mass of the secondary star in HR 4049 does not exclude it from being a compact object, which may have been a source of circumbinary material as well. If indeed the current companion is a white dwarf, it does not show symbiotic activity and it should be cool and hence old (Jorissen et al. 1998). It is therefore unlikely that circumstellar matter from the now cool white dwarf would still be present in a dust and gas-rich environment. The disk would then have survived the vast energy releases and dimensional increases of the current primary during its thermal pulses. Moreover, old mass loss from a carbon star cannot explain the oxygen-rich chemistry of the circumbinary gas. We conclude that the current circumstellar matter most likely comes from the current, luminous primary.
We describe our interpretation of the observed dust and gas chemistry in the circumbinary disk. The primary is losing mass, as evidenced by the P-Cygni profile of the Hα line (Bakker et al. 1998). This mass loss bears the chemical signature of the photospheric abundance pattern. The primary photosphere has a C/O ratio below or close to unity (Lambert et al. 1988) and is strongly depleted in refractory elements such as iron, but also silicon. Because of this depletion, silicates cannot form in the current outflow of HR 4049. The outflowing material is still oxygen-rich, but the oxygen atoms cannot form dust because of the absence of refractory elements. The oxygen therefore only forms molecules with the abundantly available hydrogen and carbon: OH, H2O, CO, and CO2. The carbon atoms, on the other hand, are able to form large molecules (PAHs, fullerenes) and very small dust grains (diamonds and amorphous carbon grains). In other words, because of the lack of refractory elements in the current mass loss of the primary, only carbonaceous dust can be formed, despite the intrinsically oxygen-rich chemistry.
The carbonaceous dust is confined to the circumbinary disk, while the outflow contains carbon-rich molecules. This is consistent with our hypothesis: the spherical outflow of the primary is probably too tenuous to form dust grains and so only (large) molecules are formed. However, the gas-rich disk intercepts and slows down the wind in the binary plane. There, the densities become large enough for dust to condense. The amorphous carbon grains form a veil over the pre-existing disk.
The question remains why only HR 4049 displays this particular circumstellar chemistry among the evolved binaries with disks. The answer is probably linked to the extreme depletion pattern of the primary photosphere. The re-accretion of metal-poor gas in the previous evolutionary phases apparently was so efficient, that subsequent mass loss from this photosphere became completely depleted of refractory elements. If this hypothesis holds, the disk around HR 4049 must contain silicates and iron-bearing dust, but their spectral signature is overwhelmed by that of the amorphous carbon. In this context, HD 52961 is an interesting target for a similar study to the one presented here. The primary in this evolved binary also displays an extreme depletion pattern and the infrared spectrum indicates the presence of PAH molecules, fullerenes, and CO2 (Gielen et al. 2011b). However, silicate emission is also detected. The current outflow in HD 52961 is similar in composition to the one in HR 4049. We therefore expect that carbonaceous grains are currently forming in this circumbinary disk as well.
Online material
Appendix A: From images to complex visibilities
The radiative-transfer code MCMax produces images on a predefined grid of pixels on the sky. We chose a 256 × 256 grid covering a field-of-view of 100 mas × 100 mas. This results in an angular resolution of 0.39 mas per pixel.
The model image produced by MCMax for a given set of parameters (M⋆ ⋆, Rin, Rout, Mdust, p, i) has a default disk orientation angle on the sky of 0° E of N. That is, the far side of the inclined disk is oriented towards the north. This image is rotated according to the grid disk PA under consideration to yield the model image corresponding to (M⋆ ⋆, Rin, Rout, Mdust, p, i, PA).
For a specific observational setting with baseline length b, baseline orientation angle θ, and at wavelength λ, the van Cittert-Zernicke theorem gives the complex normalized visibility  (A.1)where (u = bsinθ/λ,v = bcosθ/λ) are the spatial frequencies, (α,β) the angular coordinates, and B(α, β) the brightness distribution (i.e., the image) of the source on the sky, normalized to a total intensity of unity.
(A.1)where (u = bsinθ/λ,v = bcosθ/λ) are the spatial frequencies, (α,β) the angular coordinates, and B(α, β) the brightness distribution (i.e., the image) of the source on the sky, normalized to a total intensity of unity.
To compute  , the image is rotated through the angle θ. This is equivalent to a coordinate transform such that (u′,v′) = (0,b/λ) and (α′,β′) = (αcosθ − βsinθ,αsinθ + βcosθ). Equation (A.1) becomes
, the image is rotated through the angle θ. This is equivalent to a coordinate transform such that (u′,v′) = (0,b/λ) and (α′,β′) = (αcosθ − βsinθ,αsinθ + βcosθ). Equation (A.1) becomes ![\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{V}(u,v) &=& \iint {\rm d}\alpha^\prime {\rm d}\beta^\prime\ B(\alpha^\prime,\beta^\prime)\ {\rm e}^{-2 \pi i\ (\alpha^\prime u^\prime + \beta^\prime v^\prime)} \\[-2.5mm] &=& \int {\rm d} \beta^\prime\ \left( \int {\rm d}\alpha^\prime B(\alpha^\prime,\beta^\prime) \right) \ {\rm e}^{-2 \pi i\ \beta^\prime v^\prime}. \label{vCZred} \end{eqnarray}](/articles/aa/full_html/2013/03/aa19282-12/aa19282-12-eq229.png) Numerically, the integration over α′ reduces to a sum over the first dimension of the rotated image B(α′,β′). The second integration is a one-dimensional Fourier transform and can be done quickly with the fast Fourier transform (FFT) algorithm. However, FFT converts the 256-array with a pixel step of 0.39 mas into a 256-array with a spatial-frequency step of 10 cycles/arcsec. Since the observations are obtained at spatial frequencies in the range 25−370 cycles/arcsec, the default FFT resolution is too coarse for direct comparison. To increase the resolution in spatial frequency, the 256-array (i.e., ∫dα′B(α′,β′)) is placed in a 1024-array, which is zero outside the image. The FFT of the latter array yields a spatial-frequency step of 2.5 cycles/arcsec. This higher resolution makes the FFT result smooth enough to allow interpolation at the exact spatial frequencies of the observations.
Numerically, the integration over α′ reduces to a sum over the first dimension of the rotated image B(α′,β′). The second integration is a one-dimensional Fourier transform and can be done quickly with the fast Fourier transform (FFT) algorithm. However, FFT converts the 256-array with a pixel step of 0.39 mas into a 256-array with a spatial-frequency step of 10 cycles/arcsec. Since the observations are obtained at spatial frequencies in the range 25−370 cycles/arcsec, the default FFT resolution is too coarse for direct comparison. To increase the resolution in spatial frequency, the 256-array (i.e., ∫dα′B(α′,β′)) is placed in a 1024-array, which is zero outside the image. The FFT of the latter array yields a spatial-frequency step of 2.5 cycles/arcsec. This higher resolution makes the FFT result smooth enough to allow interpolation at the exact spatial frequencies of the observations.
The method was tested on images of simple geometries (point source, binary with unresolved components, uniform disk, uniform ellipse), for which analytic formulae of the complex visibility exist. Good agreement was found. For a uniform disk with a diameter of 10 mas, the absolute difference between the analytic and image-based squared visibilities is 0.002 on average, and always below 0.01. The absolute difference between the analytic closure phase (i.e., 0° or 180° for a uniform disk) and the image closure phase is 1° on average, but can increase to 10° at the longest baselines. At these high spatial frequencies, pixelation effects start to play a role for the closure phases, while they do not affect the visibilities to a measurable level9.
The obtained accuracy of the model is sufficient for the goals of this paper. An increase of the spatial resolution of the model image is possible, but would lead to an increase of the grid computation time from days to weeks.
Appendix B: Stellar contribution in the near-infrared
In the near-IR, the flux contribution of the central star to the total flux can be large. The stellar flux contribution of the primary of HR 4049 drops from ~0.6 at 1.6 μm to ~0.2 at 2.5 μm. The intensity-normalized image of the disk, on the other hand, is similar in the H and K band. We therefore took the following approach to compute squared visibilities and closure phases in the near-IR:
-
1.
From the radiative-transfer model, we computed a2.2 μm image. The central2 × 2 pixels in this image contain the primary star. We removed the star from the image by replacing these central pixel values by interpolated values. Hence, we created a star-less image, which provides a representative disk image at all wavelengths between 1.6 and 2.5 μm.
-
2.
We computed the disk complex visibilities
 from the star-less image as described in Appendix A.
from the star-less image as described in Appendix A. -
3.
From the model infrared spectrum and the input Kurucz model for the primary star, the stellar-to-total flux contribution f was estimated at all AMBER wavelengths.
-
4.
The final model visibilities were computed from the disk visibilities and the flux ratio f, according to
 (B.1)From this complex quantity, squared visibilities (per baseline and wavelength) and closure phases (per baseline triangle and wavelength) were computed. Given its angular diameter (0.45 ± 0.03 mas, determined from the Kurucz model fit to the optical photometry), the primary star is unresolved at the spatial resolution of the observations. Moreover, we assumed the primary star is at the disk’s center and hence
(B.1)From this complex quantity, squared visibilities (per baseline and wavelength) and closure phases (per baseline triangle and wavelength) were computed. Given its angular diameter (0.45 ± 0.03 mas, determined from the Kurucz model fit to the optical photometry), the primary star is unresolved at the spatial resolution of the observations. Moreover, we assumed the primary star is at the disk’s center and hence 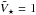 . Note that we neglected the possible offset of the primary star with respect to the disk center due to binary motion. However, given the dimensions of the disk (~15 mas) and of the binary (~1 mas), the effect of such an offset on visibilities and closure phases is expected to be small. Moreover, the interferometric observations were taken close to minimal brightness, when the primary star was close to the observer. The primary was therefore close to projected minor axis of the disk and close to the disk center on the sky.
. Note that we neglected the possible offset of the primary star with respect to the disk center due to binary motion. However, given the dimensions of the disk (~15 mas) and of the binary (~1 mas), the effect of such an offset on visibilities and closure phases is expected to be small. Moreover, the interferometric observations were taken close to minimal brightness, when the primary star was close to the observer. The primary was therefore close to projected minor axis of the disk and close to the disk center on the sky.
In the mid-IR, the relative flux contribution of the primary star to the total flux is less than a few percent. Moreover, it is constant over the N band because of the near-blackbody shape of both the stellar flux and the excess. The intensity-normalized model image of HR 4049 at 8 μm is therefore the same as at 13 μm. The variations in (relative) visibility over the N band are exclusively due to a change in spatial frequency and not due to a change in disk geometry or stellar flux contribution with wavelength.
Hinkle et al. (2007) assumed an inner dust-disk radius of 10 AU and mention that the CO gas is located at the inner radius if the total binary mass is 0.9 M⊙. Our models constrain both parameters, and place the disk at a slighly larger distance from the binary, but also indicate a slightly higher binary mass.
Available at http://www.jmmc.fr/amberdrs
Acknowledgments
This research has made use of the AMBER data reduction package of the Jean-Marie Mariotti Center8. The authors thank D. Pourbaix for his much appreciated help with the Hipparcos data and the anonymous referee for helpful comments.
References
- Acke, B., & van den Ancker, M. E. 2006, A&A, 457, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acke, B., van den Ancker, M. E., & Dullemond, C. P. 2005, A&A, 436, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acke, B., Min, M., van den Ancker, M. E., et al. 2009, A&A, 502, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakker, E. J., van der Wolf, F. L. A., Lamers, H. J. G. L. M., et al. 1996, A&A, 306, 924 [NASA ADS] [Google Scholar]
- Bakker, E. J., Lambert, D. L., Van Winckel, H., et al. 1998, A&A, 336, 263 [NASA ADS] [Google Scholar]
- Cami, J., & Yamamura, I. 2001, A&A, 367, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chelli, A., Utrera, O. H., & Duvert, G. 2009, A&A, 502, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Haser, L. N., Beintema, D. A., et al. 1996, A&A, 315, L49 [NASA ADS] [Google Scholar]
- Dominik, C., Dullemond, C. P., Cami, J., & Van Winckel, H. 2003, A&A, 397, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Geballe, T. R., Noll, K. S., Whittet, D. C. B., & Waters, L. B. F. M. 1989, ApJ, 340, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Gielen, C., Van Winckel, H., Min, M., Waters, L. B. F. M., & Lloyd Evans, T. 2008, A&A, 490, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., Bouwman, J., Van Winckel, H., et al. 2011a, A&A, 533, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., Cami, J., Bouwman, J., Peeters, E., & Min, M. 2011b, A&A, 536, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillois, O., Ledoux, G., & Reynaud, C. 1999, ApJ, 521, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., & Stognienko, R. 1996, A&A, 311, 291 [NASA ADS] [Google Scholar]
- Henning, T., Begemann, B., Mutschke, H., & Dorschner, J. 1995, A&AS, 112, 143 [NASA ADS] [Google Scholar]
- Hinkle, K. H., Brittain, S. D., & Lambert, D. L. 2007, ApJ, 664, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Jäger, C., Mutschke, H., Begemann, B., Dorschner, J., & Henning, T. 1994, A&A, 292, 641 [NASA ADS] [Google Scholar]
- Jäger, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1993, VizieR Online Data Catalog, VI/039 [Google Scholar]
- Lagage, P. O., Pel, J. W., Authier, M., et al. 2004, The Messenger, 117, 12 [NASA ADS] [Google Scholar]
- Lagage, P., Doucet, C., Pantin, E., et al. 2006, Science, 314, 621 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lambert, D. L., Hinkle, K. H., & Luck, R. E. 1988, ApJ, 333, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Graser, U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., & Lamers, H. J. G. L. M. 1992, A&A, 259, L39 [NASA ADS] [Google Scholar]
- Meijer, J., Dominik, C., de Koter, A., et al. 2008, A&A, 492, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menut, J., Chesneau, O., Bakker, E., et al. 2009, A&A, 496, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé Du Foresto, V. 2005, A&A, 433, 1155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2003, A&A, 404, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., Trams, N. R., et al. 1999, A&A, 350, 163 [NASA ADS] [Google Scholar]
- Paczyński, B. 1970a, Acta Astron., 20, 47 [NASA ADS] [Google Scholar]
- Paczyński, B. 1970b, Acta Astron., 20, 195 [NASA ADS] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, K. R. G., Smith, K. T., & Sarre, P. J. 2012, MNRAS, 421, 3277 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, A., & Duley, W. W. 1996, ApJS, 105, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Aarle, E., Van Winckel, H., Lloyd Evans, T., et al. 2011, A&A, 530, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Van Winckel, H., Waelkens, C., & Waters, L. B. F. M. 1995, A&A, 293, L25 [NASA ADS] [Google Scholar]
- Van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waelkens, C., Lamers, H. J. G. L. M., Waters, L. B. F. M., et al. 1991, A&A, 242, 433 [NASA ADS] [Google Scholar]
- Waters, L. B. F. M., Trams, N. R., & Waelkens, C. 1992, A&A, 262, L37 [NASA ADS] [Google Scholar]
- Waters, L. B. F. M., Cami, J., de Jong, T., et al. 1998, Nature, 391, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Infrared spectrum of HR 4049 (black: ISO-SWS, blue: Spitzer-IRS). The prominent features between 6 and 13 μm are caused by PAHs. The band between 4 and 5.3 μm is the result of a forest of CO, OH, and H2O molecular emission lines (Hinkle et al. 2007). Emission lines of CO2 are visible longward of 13 μm (Cami & Yamamura 2001). |
| In the text | |
 |
Fig. 2 Spatial-frequency coverage of the interferometric measurements. Black dots refer to AMBER data, red dots to MIDI data. |
| In the text | |
 |
Fig. 3 Six independent Geneva color–magnitude diagrams of HR 4049. The linear-regression fit to the data is shown in black. The other curves show the color/magnitudes of the Kurucz model, reddened with the interstellar extinction law of Cardelli et al. (1989, foreground extinction) and with different dust species with a grain size of 0.01 μm and an appropriate range of column densities (variable circumstellar extinction). The grain shape distribution is DHS with fmax = 0.8, except for amorphous carbon (Mie, i.e., DHS with fmax = 0). Top left panel: the discrepancy between the observed and the modeled U − B color may be due to a UV-excess in the binary system. |
| In the text | |
 |
Fig. 4 a) ISO-SWS spectrum in the N-band range. The PAH features at 8.6, 11.3, 12.0, and 12.7 μm are indicated, the dashed line represents the continuum. b) Spatial extent along the slit north-south direction of VISIR. The dashed line indicates the width of the spatially unresolved continuum, which increases with wavelength. c) Relative spatial position with respect to the continuum along the slit direction of VISIR. The PAH emission region is extended on a scale of several 100 s of AU and its photocenter is located towards the south of the continuum emission region. |
| In the text | |
 |
Fig. 5 Spectral energy distribution of HR 4049. The ISO-SWS spectrum (grey line), and IRAS 25, 60, and 100 μm, and SCUBA 850 μm photometry (grey boxes). The green line is the fit with a single blackbody (1200 K, in accordance with Dominik et al. 2003). The spectral energy distribution of our model (blue) underestimates the flux at λ > 20 μm. The red line shows our model plus a 200 K blackbody, scaled to the SCUBA 850 μm flux. See Sect. 7 for details. |
| In the text | |
 |
Fig. 6 Opacity curves of the four dust species that satisfy the optical extinction law towards HR 4049, normalized by κV (at 0.55 μm). The grain size is 0.01 μm, the grain shape distribution is either DHS with fmax = 0.8, or Mie (fmax = 0). |
| In the text | |
 |
Fig. 7 Model fit to the ISO-SWS spectrum of HR 4049. The spectrum of the best amorphous-carbon model is shown (red), along with the best magnetite model (cyan) and the best fit with a single blackbody (T = 1200 K, green). |
| In the text | |
 |
Fig. 8 Low-resolution (LR-HK) squared visibilities of HR 4049 as a function of spatial frequency. Top to bottom: observed squared visibilities |
| In the text | |
 |
Fig. 9 Medium-resolution (MR-2.1 and MR-2.3) squared visibilities of HR 4049. Colors refer to different baselines: respectively blue, red, and green for the first, second and third baseline of observations (k) to (n) in the order listed in Table 1. Top to bottom in each panel: observed |
| In the text | |
 |
Fig. 10 Low-resolution (LR-HK) closure phase measurements of HR 4049. Each panel refers to a baseline triangle. The letter in the top corner refers to the corresponding entry in Table 1. Measurements are indicated by black dots with error bars; the red line represents the model. |
| In the text | |
 |
Fig. 11 Medium-resolution (MR-2.1 and MR-2.3) closure phase measurements of HR 4049. Symbols are similar to those in Fig. 10. |
| In the text | |
 |
Fig. 12 MIDI relative visibilities V29m/V15m. Black dots are the data; the red line is the model. |
| In the text | |
 |
Fig. 13 Density and temperature structure of the best model. R is the radial distance to the primary, z the vertical height above the disk midplane. The color scale and black contours indicate the local temperature of the amorphous carbon in Kelvin. White contours indicate the local density with respect to the maximal density at R = Rin and z = 0. The dotted line is the line of sight towards the primary. |
| In the text | |
 |
Fig. 14 Best-model image at 2.2 and 10 μm. North is up, east is left. At a distance of 640 pc, 1 mas corresponds to 0.64 AU. The dashed line in the right panel indicates the photocenter location of the PAH 11.3 μm emission region relative to the disk center, projected on the N − S axis (xns). The photocenter position in the E − W direction is not constrained (see Sect. 8.2.2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.