| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118609 | |
| Published online | 31 October 2012 | |
Solar flare hard X-ray spikes observed by RHESSI: a case study
1 Department of Physics, Montana State University, Bozeman, MT 59717-3840, USA
2 School of Astronomy & Space Science, Nanjing University, 210093 Nanjing, PR China
e-mail: chengjx@shao.ac.cn
3 Shanghai Astronomical Observatory, Chinese Academy of Sciences, 200030 Shanghai, PR China
4 Space Sciences Lab, University of California, Berkeley, CA 94720-7450, USA
5 New Jersey Institute of Technology, 323 Martin Luther Kind Blvd., Newark, NJ 07102, USA
Received: 8 December 2011
Accepted: 14 September 2012
Context. Fast-varying hard X-ray spikes of subsecond time scales were discovered by space telescopes in the 70s and 80s, and are also observed by the Ramaty High Energy Solar Spectroscopic Imager (RHESSI). These events indicate that the flare energy release is fragmented.
Aims. In this paper, we analyze hard X-ray spikes observed by RHESSI to understand their temporal, spectral, and spatial properties.
Methods. A recently developed demodulation code was applied to hard X-ray light curves in several energy bands observed by RHESSI. Hard X-ray spikes were selected from the demodulated flare light curves. We measured the spike duration, the energy-dependent time delay, and count spectral index of these spikes. We also located the hard X-ray source emitting these spikes from RHESSI mapping that was coordinated with imaging observations in visible and UV wavelengths.
Results. We identify quickly varying structures of ≤ 1 s during the rise of hard X-rays in five flares. These hard X-ray spikes can be observed at photon energies over 100 keV. They exhibit sharp rise and decay with a duration (FWHM) of less than 1 s. Energy-dependent time lags are present in some spikes. It is seen that the spikes exhibit harder spectra than underlying components, typically by 0.5 in the spectral index when they are fitted to power-law distributions.
RHESSI clean maps at 25–100 keV with an integration of 2 s centered on the peak of the spikes suggest that hard X-ray spikes are primarily emitted by double foot-point sources in magnetic fields of opposite polarities. With the RHESSI mapping resolution of ~4′′, the hard X-ray spike maps do not exhibit detectable difference in the spatial structure from sources emitting underlying components. Coordinated high-resolution imaging UV and infrared observations confirm that hard X-ray spikes are produced in magnetic structures embedded in the same magnetic environment of the underlying components. The coordinated high-cadence TRACE UV observations of one event possibly reveal new structures on spatial scales ≤1–2′′ at the time of the spike superposed on the underlying component. They are probably sources of hard X-ray spikes.
Key words: Sun: flares / Sun: X-rays, gamma rays
© ESO, 2012
1. Introduction
Solar flare emission on fine time scales of fewer than a few seconds were first reported in hard X-ray observations from the S-100 solar hard X-ray spectrometer aboard the ESRO TD-1A satellite over the period from 1972 March 12 to 1973 October 1 (van Beek et al. 1974, 1976; Hoyng et al. 1976; de Jager & de Jonger 1978). Numerous short-lived hard X-ray spikes were found with the rise and decay time as low as 1.2 s, approaching the time resolution of the instrument. These are called “elementary bursts” (de Jager & de Jonger 1978). A few years later, fast-varying spikes with even shorter time scales were discovered in microwave and hard X-ray observations (Kiplinger et al. 1983, 1984, 1989; Kaufmann et al. 1980, 1984, 2001; Aschwanden et al. 1993, 1995a,b, 1998). Using observations by the hard X-ray burst spectrometer on the Solar Maximum Mission (SMM) at a time resolution of 128 ms and 10 ms, Kiplinger et al. (1983) identified 53 out of nearly 3000 flares to exhibit one or more fast spikes with durations less than 1 s. Among these spikes, the shortest time scale, i.e., rise and decay time and spike full width at half maximum (FWHM) duration, were several tens of ms. In recent years, efforts to search for small-scale structures have also been made in high-cadence and high-resolution imaging observations in optical wavelengths such as Hα and white light (Neidig et al. 1993; Wang et al. 2000; Trottet et al. 2000; Kurt et al. 2000). For example, Wang et al. (2000) explored high cadence imaging observations in the far blue wing of Hα line and found 300–700 ms bursts at flare foot-point kernels, which are correlated with BATSE hard X-ray peaks. Qiu & Wang (2006) furthermore compared the fine temporal and spatial structures of flare emissions observed in hard X-rays and Hα offband. These observations confirm that flare energy release is fragmented, and the hard X-ray spikes are likely due to thick-target nonthermal emissions.
Discovery of flare bursts on very short time scales have led scientists to consider that magnetic energy release primarily occurs on small scales. The observed fast-varying spikes may reflect single magnetic reconnection and/or particle acceleration events (Sturrock 1989; Parker 1989; Bastian & Vlahos 1997). The bursts’ time scales may depend on the characteristic size of the elementary flux tubes (e.g., Sturrock et al. 1984; LaRosa & Moore 1993) or the turbulent dynamics of the reconnecting current sheets (eg., Litvinenko 1996). Specifically, spikes with very short time scales reported in hard X-ray and microwave observations will provide diagnostics of the acceleration of nonthermal particles in flare environment. To unravel the physical mechanisms that govern energy release and particle acceleration in these short-scale events requires quality observations that push to the limit of the existing temporal, spatial, and spectral-resolving capabilities.
The Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI Lin et al. 2002) launched in early 2002 has unprecedented resolution to further the study of the temporal, spectral, and spatial properties of hard X-ray spikes. In this paper, we present five flares, all exhibiting ≤1 s structures in hard X-ray light curves during the rise of the flares. In some events, high-cadence imaging infrared observations by the National Solar Observatory (NSO) and UV observations from Transition Region and Corona Explorer (TRACE) are compared with spatial structures of these spikes.
2. Observations and data analysis
The RHESSI imaging spectrometer is based on a set of nine rotating modulation collimators (RMCs). Their angular resolutions ranges logarithmically from 2.3 to 183 arcsec. Each RMC consists of a high spectral resolution germanium detector located behind a pair of widely separated grids. As the spacecraft rotates (15 rpm), the grids transmit a rapidly time modulated fraction of the incident flux so that the imaging information is encoded in the time profiles of the detected flux.
Since the telemetry includes the energy and arrival time of each detected photon, in principle, the time resolution for light curves is only limited by photon statistics; however, the rapidly time-varying transmission of the grids imposes temporal artifacts of the observed count rates so that the raw count rates from any given detector represent a convolution of solar variations and the effect of the rotating grids. The latter occurs on three time scales: rapid modulation (which encodes imaging information) on a grid-dependent time scale from 4 to 500 ms; slower modulation with a period equal to the 4 s rotation period; and a component with half of the rotation period. The last two terms are due to the variations in transmission of individual grids.
 |
Fig. 1 Demodulated RHESSI hard X-ray light curves (dark) in comparison with summed raw data counts (gray). The light curves are acquired at 25–100 keV. Top panel shows 2002 March 17 event that exhibits fast-varying spikes and bottom panel shows 2005 January 19 event without significant fast-varying spikes. The scales of the demodulated (in units of counts per second per detector) and raw (in units of counts) light curves are indicated on the left and right y-axes, respectively. |
There are four known methods to suppress the effects of modulation (demodulation). The first and most widely used is to just make light curves with 4 s time resolution and so average over all the modulation terms. A second approach is to sum the light curves from individual detectors each of which modulates with different frequencies or phases. This helps, but typically leaves residual artifacts of 20% rms. A third alternative is an algorithm developed by Arzner (2002) that can estimate a smoothed light curve with higher time resolution, but since the resulting data points are not statistically independent, quantitative evaluation of temporal features in the output can be problematic.
The demodulation algorithm used here is based on the fact that for sources within a few arc-minutes of the (known) flare location, the instantaneous modulation period and average grid transmission for each RMC is both known and independent of flare morphology. The algorithm may be used to recover time structures with the user-chosen interval in the range of 0.05 to 0.25 s. Shorter time limits systematically exclude additional coarse detectors, whereas longer time limits begin to violate the important assumption that the modulation period be constant during the interval. For each time interval (0.125 s in this paper), the count rates in each detector for which the modulation period is less than this interval is fitted with the sum of a sinusoid plus a constant offset. After dividing by the average grid transmission for that grid and time, the offset represents a modulation-free estimate of the (pre-grid) incident count rate over a 0.125 s interval in this case. Corresponding estimates from all grids with sufficiently rapid modulation are averaged to yield the best estimate of the incident count rates at that time. Additional minor corrections to compensate for residual calibration uncertainties are also applied. It is important to note that the incident flux estimates for each time interval and for each energy interval are statistically independent. As we shall see, this helps with the evaluation of temporal features in the resulting demodulated light curves.
Figure 1 shows examples of high-cadence hard X-ray light curves of flares that are demodulated from the raw data with this recently developed algorithm. A large number of fluctuations are present in the raw data set, most of which are removed in the demodulated light curves with real hard X-ray spikes standing out. However, hard X-ray spikes are not found in all flares. Figure 1a shows an event with evident fast-varying structures, such as the spike at 19:27:43 UT. While for the event in Fig. 1b, no outstanding fast-varying spikes can be recognized in the demodulated light curves. Kiplinger et al. (1988) found that about 20% SMM bursts exhibit subsecond structures.
Since analyzing RHESSI data is a time and disk-space consuming job and it is not our primary goal in this present paper to compare statistics with previous studies, we have not analyzed enough events that are statistically significant. In this study, we analyze RHESSI observations of a few flares ranging from C- to X-class in GOES classification. Most of these events emit impulsive hard X-rays with significant count rates ( ≥ 100 counts s-1 detector-1) at 50–100 keV, making them viable candidates for hosting hard X-ray spikes at high energies. Analysis of these events with the demodulation algorithm shows that five events exhibit fast-varying hard X-ray spikes, which are visible at photon energies of ≥ 100 keV. The analysis results show that hard X-ray spikes are not necessarily present in all impulsive hard X-ray events. A more thorough statistical survey will be presented in Cheng et al. (2012, Paper II). In this paper, we only present, as listed in Table 1, the five flares exhibiting hard X-ray spikes. We analyzed the data during the rise phase of these events when impulsive hard X-ray structures are most pronounced. For each of these events, RHESSI observations are selected in a two to four minute duration without switching attenuators and decimators for the consistency in calibration.
3. Selection of hard X-ray spikes
Figures 2a–e show the demodulated light curves of the five events at varying energies from 25 to 300 keV during the rise of the flare. The designated time bin is 0.125 s. These events all exhibit fast-varying structures on a time scale of 1 s or less in most of the energy bins above 20 keV. Signals up to 100 keV are significant and are likely real features. Some of these spikes are also visible in 100–300 keV, though less significant because of reduced counts level. The inset frames in Fig. 2 give a close look at the most pronounced spikes picked out by a combination of visual inspection and automatic selection algorithms.
We identify fast varying structures by subtracting a slow-varying component (Is) from the demodulated light curves (I), leaving the residual signals as Ir = I − Is. The slow-varying component Is is obtained with three different methods. First, Is can be derived as the running mean of the light curve I. Second, Is is obtained by applying a low-pass filter to I. Third, Is at time t can be derived as an integration of emission components before t, which decay exponentially,thus 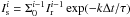 , where τ is the burst decay time scale. The time scale of a running-mean or low-pass filter used in this study is 4 to 8 s. The exponential decay time scale in the third method strongly depends on properties of bursts and the duration of analysis, which can be adjusted to achieve a reasonable fit to the data.
, where τ is the burst decay time scale. The time scale of a running-mean or low-pass filter used in this study is 4 to 8 s. The exponential decay time scale in the third method strongly depends on properties of bursts and the duration of analysis, which can be adjusted to achieve a reasonable fit to the data.
Flares with hard X-ray spikes.
Derivation of Is and Ir and selection of hard X-ray spikes by these algorithms is illustrated in Fig. 3 using the 2005 January 17 event as an example. The left hand panels in the figure show the demodulated light curve at 60–100 keV, superposed on the slow component Is derived with the three methods. The residuals Ir are also plotted at the bottom of each panel. Significant residuals over 3σ level are marked in the plots. The right hand panels illustrate the times (x-axis) and energy bands (y-axis: see figure caption) of significant residuals. We decide that only significant residuals, i.e., above the 3σ level, that span several consecutive time bins and are present in a few, though not necessarily all, energies can be safely regarded as real hard X-ray spikes. (However, we note an exceptional case in the selection of S5 and S6 in the 2003 October 29 event. The demodulated light curves are full of structures, which raises the σ level of the residual signals, therefore, significant residuals at S5 and S6 do not span over more than one time bin. In this case, significant residuals are defined as residuals over 2σ). Abiding by this principle, several spikes can be recognized at the times of around 24 s (S10), 30 s, and marginally at 43 s and 48 s as well.
We applied the spike recognition algorithms to demodulated light curves of the selected events and generated diagrams as shown in Fig. 3. Hard X-ray spikes were picked out by visually inspecting these diagrams. In general, we empirically required that a spike should span at least three consecutive time bins in at least three energy channels, and should be identified by at least two methods. Furthermore, to derive the temporal properties of spikes such as their rise, decay, and duration, we fit these spikes to Gaussian profiles as shown in the following section. For this purpose, we need to clearly separate spikes from each other and from their background. Therefore, we discard spikes that appear to reside in a cluster of spikes, such as the spikes at around 30 s in Fig. 3, because they pose significant difficulty in the fitting procedure. Eventually, only the ten most prominent spikes with the best Gaussian fitting results are reported in this paper (Table 2 and Fig. 2).
Seen from Fig. 2, some spikes, like S1 and S2, appear to have a rather symmetric sharp rise and decay. The time interval between the maximum and the background in both the rise and decay phases is about half a second, and the duration (FWHM) is below 1 s. Some of these bursts, such as S1 and S10, consist of more than one spike each, which may be resolved if higher temporal resolution can be reliably achieved. We also note that the most pronounced spikes occur in the early rising phase of hard X-ray emissions. In the maximum phase, though emission gets stronger, it is more difficult to recognize spiky structures from the underlying background, perhaps because of a cumulative effect by clusters of spikes.
 |
Fig. 2 Demodulated RHESSI hard X-ray light curves at varying energies for the five flares. Then inset frame gives magnified view of some pronounced spikes. Note that y-axis gives the units of the 25–100 keV light curve, and light curves at other energies are scaled arbitrarily. |
4. Temporal and spectral properties of fast-varying spikes
We investigated the temporal and spectral properties of the ten most pronounced spikes, S1 to S10, identified in the five studied events. The peak time, duration (FWHM), and peak count rates of the spikes are measured in a few energy bins. We also derived and compared the count rates of different energies, for the spikes and their underlying components.
Since most spikes reside on top of a gradually varying background, and many of them exhibit symmetric rise and decay, as judged from a visual inspection of the spike light curves (also see similar conclusions by Kiplinger et al. 1984; Wang et al. 2000), we fit the spike light curves in time intervals of 20 s to Gaussian profiles with a quadratic background in the form of ![\hbox{$I(t) = (A_0 + A_1 t + A_2 t^2) +\Sigma_i \left[I_i \exp\left(-\frac{(t-t_i)^2}{2\tau_i^2}\right)\right]$}](/articles/aa/full_html/2012/11/aa18609-11/aa18609-11-eq17.png) , where the first three items on the righthand side represent the quadratic background, and Ii, ti, and τi represent the peak intensity, peak time, and FWHM of each identified spike, respectively. The Gaussian FWHM gives a measure of the duration of the spike. Figure 4 shows an example of fitting the spike S1 and its background at different energies.
, where the first three items on the righthand side represent the quadratic background, and Ii, ti, and τi represent the peak intensity, peak time, and FWHM of each identified spike, respectively. The Gaussian FWHM gives a measure of the duration of the spike. Figure 4 shows an example of fitting the spike S1 and its background at different energies.
Using a Gaussian fit implies symmetric rising and decaying profiles, which is not too far from reality, judged from a visual inspection of the spike light curves. Earlier studies have also revealed that the hard X-ray spikes have fairly symmetric time profiles (Kiplinger et al. 1984; Wang et al. 2000).
The fitting procedure is applied to demodulated light curves at a few energies, when applicable, in order to examine the energy dependence of the fitting parameters. Table 2 lists these parameters for light curves at 25–100 keV and 100–300 keV of the ten spikes indicated in Fig. 2. Taking S1 and S10 as examples, we also plot in Fig. 5 the peak time and FWHM from the fit at energies 15–25, 25–40, 40–60, 60–100, and 100–300 keV. The fitting results suggest that the detected hard X-ray spikes have a typical time scale (FWHM) of ≤ 1 s (Fig. 5a and Table 2). With the data resolution and uncertainties in fitting, we do not find any energy-dependent duration in hard X-ray spikes. Readers should call that the presented time scales are an upper limit set by our selection criterion. Spikes on shorter time scales probably exist in reality, but they are likely to be filtered out by the selection criterion, which requires significant residuals spanning a few time bins. We also note that, since this paper focuses on seeking hard X-ray spikes on very short time scales, bursts on longer time scales are often regarded as multiple spikes residing in clusters and are hence left out by the selection criterion.
For some spikes, e.g., S1 and S10, the fitting results suggest energy-dependent lags in the peaking time. Figure 5b shows that, for S1 and S10, emission at higher energies peaks earlier. The time lag between 20 and 100 keV photon energies is less than half a second. If we assume that such time lags result from time-of-flight (TOF; Aschwanden et al. 1996) of directly precipitating electrons, the upper limit of the loop length L can be derived from the TOF measurements by 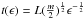 , where t(ϵ) is the energy-dependent TOF, L the loop length, and m the electron mass. For S1 and S10, L is estimated to be about 60′′ and 40′′, respectively. These are plausible values of coronal loop size, as RHESSI maps show the separation of the foot points to be about 50′′ and 40′′, respectively, for the two spikes (see Fig. 8 and Sect. 4). These values are upper limits of the loop length, because realistically, electrons spiral down along the loops with nonzero pitch angles (Krucker et al. 1999).
, where t(ϵ) is the energy-dependent TOF, L the loop length, and m the electron mass. For S1 and S10, L is estimated to be about 60′′ and 40′′, respectively. These are plausible values of coronal loop size, as RHESSI maps show the separation of the foot points to be about 50′′ and 40′′, respectively, for the two spikes (see Fig. 8 and Sect. 4). These values are upper limits of the loop length, because realistically, electrons spiral down along the loops with nonzero pitch angles (Krucker et al. 1999).
We further analyzed the spectra of the spikes and their evolution, in comparison with the spectra of slow-varying underlying components. We assumed a power-law distribution of hard X-ray emissions, i.e., 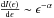 , and make least-squares fit to the count rates at ≥ 30 keV, as indicated by the straight lines in Fig. 6. The fit yields the power-law index α of the count spectrum. The illustrated spectra in Fig. 6 are not fully calibrated photon spectra but are count rates spectra, which, however, can still reflect some properties, such as the hardness, of the hard X-ray photon spectrum.
, and make least-squares fit to the count rates at ≥ 30 keV, as indicated by the straight lines in Fig. 6. The fit yields the power-law index α of the count spectrum. The illustrated spectra in Fig. 6 are not fully calibrated photon spectra but are count rates spectra, which, however, can still reflect some properties, such as the hardness, of the hard X-ray photon spectrum.
 |
Fig. 3 Example of spike detection algorithm using 3 methods (see text) for the 2005 January 19 event. Left panels show the demodulated light curves (dark) at 60–100 keV, the slow-varying component (gray) determined by 3 methods, and the residuals (bottom of each panel), with the significant residuals marked (plus symbols). Right panels show the times (x-axis) and energies (y-axis) of significant residuals recognized by the algorithms. The numbers 1 to 7 along the y-axis indicate energy bands of 10–15, 15–25, 25–40, 40–60, 60–100, 100–300, 25–100 keV, respectively. The two arrows in the top right panel indicate the most pronounced spikes standing out in the diagrams. |
Properties of RHESSI hard X-ray elementary bursts.
First, we fit the count spectra at the rise, peak, and decay of each spike (not shown in the paper) to investigate evolution of the spike spectra. Within fitting accuracies that are mostly limited by the designated energy resolution, no significant variation is found in the values of the power-law exponent α at the rise, peak, and decay of a spike. This pattern is different from the soft-hard-soft spectral evolution usually seen in large bursts.
We then compared the spike spectra with their underlying components. Figure 6 displays some examples of integrated spike flux from the Gaussian fit with respect to photon energy, i.e., the spike counts spectrum. Also plotted is the directly measured count rates spectra of the underlying components adjacent to the spikes. Comparison of the power-law exponents between the spikes and their underlying components is illustrated in the scatter plot in Fig. 7. It is seen that the α value derived from the count rates spectrum of the underlying component is systematically greater than the α value derived from the spike spectrum by about 0.5. This result indicates that hard X-ray count spectrum of the spike is in general harder than the spectrum of underlying component.
We are aware of the fact that background subtraction is key to spectral fitting. The hard X-ray spike intensity is derived as the integrated flux of the Gaussian component from the fit with contribution from the underlying component removed. For the underlying component, we take the pre-flare emission as the background for most of the events, and post-flare emission for the 2002 August 30 event as pre-flare data are not satisfactory. The RHESSI quick-look light curves show that during the events in the study, the background is not subject to modulations by electron events, thus the treatment of subtracting a mean pre-flare background is appropriate in general. For two events, at energies below 25 keV, pre-flare emission during the selected background period is already high. This indicates that at low energies, the background is over subtracted from the underlying components, and the spectra of the properly background-subtracted underlying components would be still steeper than illustrated in Table 2. Overall, the fast-varying spikes have a significantly harder spectra than underlying components. This result agrees with the general notation that hard X-ray photon or electron spectrum is harder at emission peaks than at valleys or underlying components (e.g. Kiplinger et al. 1983).
Readers are also reminded of the effect of the spike selection principle on the distinct spectral properties between the spikes and underlying components. As stated in the previous section, the selection rule requires that significant residuals be present in a few energy bands, which usually leads to preference to selecting signals with more pronounced emission, with respect to backgrounds, at high energies (e.g., ≥ 100 keV in this study) than underlying components. To examine whether the data counts at higher energies, which also carry the larger statistical uncertainties, are crucial to the different spectral properties, we fit the counts spectra again by eliminating the 100–300 keV energy bin. This is a very crude test, though, since fitting accuracies are severely degenerated in such experiment, which uses only three points in a nonlinear fitting procedure to determine three variables. Still, except for the 2003 October 29 event when the exponents of the spike spectra become nearly identical to those of the underlying components, the experiment produces comparable or even greater difference in the power-law exponents between the spikes and underlying components.
 |
Fig. 4 Demodulated light curves of spike S1 at four energy channels, 25–40, 40–60, 60–100, and 100–300 keV from top to bottom, superimposed with the fitted curves (solid lines). Count light curves from 40–300 keV are arbitrarily normalized for clarity of display. |
 |
Fig. 5 Examples of durations and peaking times of the spikes S1 and S10 at varying energies, derived from fitting the spike light curves to Gaussian profiles. Horizontal bars in the bottom panels indicate the widths of the energy bins, and vertical bars indicate 1σ fitting uncertainties. Lines in the bottom panel give the time-of-flight fit (see text). |
 |
Fig. 6 In each panel, the symbols and solid lines show examples of hard X-ray photon count spectra of integrated spike flux from the Gaussian fitting, in comparison with the count rates spectra of underlying components. Solid lines show the least-squares fit of the spectra to a power-law distribution, and the exponents and their uncertainties from the fit are noted in the figures. The y-axis gives the units of the spike intensities, and the intensities of the underlying component are divided by four for clarity. The three panels from top to bottom illustrate the count spectra for spikes S1, S5, and S8, respectively, and the underlying components. |
 |
Fig. 7 Scatter plot of power index (αy) of the spike spectra and index (αx) of underlying components. The dotted guide line outlines αy = αx. |
In general, with limitations in the spectral analysis procedures, a conservative conclusion may still be reached that the hard X-ray spike spectrum is harder than the spectrum of the underlying component. The distinctive spectral properties of spikes from underlying components may suggest that underlying components are not an unresolved collection of fast-varying spikes. In other words, the different spectral characters between fast-varying hard X-ray spikes and underlying components are very likely the result of specific physical mechanisms to generate nonthermal emissions in such a way that the spectral properties are closely related to the burst time scales.
 |
Fig. 8 RHESSI hard X-ray clean maps at 25–100 keV of spikes S1 to S10 (gray scale) superimposed on the maps of underlying components (contours) in the same energy range. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of the image. Axis labels indicate the E-W and N-S coordinates in arcsec. |
5. Imaging of hard X-ray spikes
The spatial structure of hard X-ray spikes can be studied through high-resolution imaging observations. In this section, we explore RHESSI hard X-ray, TRACE UV, and NSO infrared imaging observations to understand the morphological properties of hard X-ray spikes.
We constructed RHESSI maps of the ten spikes studied in this paper. The adjacent underlying components are also mapped to compare with the spatial structures of the spikes. Figure 8 shows the RHESSI hard X-ray clean maps at 25–100 keV at the times of the spikes. Each map is constructed with a 2 s integration centered at the peak of the spike. Also shown are maps of immediate underlying components. They are also constructed by integrating data counts over 2 s immediately before or after the spike. In principle, for maps above 25 keV, all collimators can be used. We attempted maps including collimator 1, which is supposed to yield the best possible resolution of 2′′. However, with the finest grid, for all events studied, stronger sources are usually over-resolved while weaker sources are not uncovered. Therefore, in this study, we use the collimators 2 to 9 for optimal mapping resolution (3.92′′).
In Table 2, we point out the morphology of the ten spikes based on the mapping results. Most spikes and their immediate underlying components are primarily emitted by double sources (see Fig. 8), likely conjugate footpoints of flare loops. The FWHM of these sources are all close to 10′′, which may be the result of the limited RHESSI imaging resolution. The 2002 August 30 flare exhibits a single source in hard X-rays throughout the evolution. For this event, TRACE EUV images show small flaring loop arcade with a separation of about 10′′. Given the RHESSI image resolution, it is very likely that in the 2002 August 30 event, the spikes are also emitted by double foot-point sources not resolved in RHESSI maps. Maps of some spikes in other events suggest more than two sources, but the third source is usually very weak, with the intensity about one tenth of the maximum source intensity.
 |
Fig. 9 RHESSI hard X-ray clean maps (dark contours) at 25–100 keV of spikes b) S1 and d) S2 and the pre-spike underlying components (a) and c)) on 2002 March 17 superposed on the longitudinal magnetogram taken at 19:46:01.11 UT by MDI. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of all the images, which is 0.57 photons cm-2 s-1 asec-2. White contours indicate the polarity inversion line of longitudinal magnetic fields. |
 |
Fig. 10 RHESSI hard X-ray clean maps (dark contours) at 25–100 keV a) of spike S5 and b) at the maximum of the 2003 October 29 flare superposed on the longitudinal magnetogram taken by MDI. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of each image, which is noted in each plot in the unit of photons cm-2 s-1 asec-2. c) A snapshot of an infrared image around the flare maximum revealing two bright kernels coincident with RHESSI hard X-ray sources (white contours). The white box in b) defines the FOV of c). |
To study the detailed morphology of these spikes, in Figs. 9–11, we compared the images of a few spikes with coordinated observations of the magnetic field obtained by MichelsonDopplerImager (MDI; Scherrer et al. 1995), UV images by TRACE, and infrared images from NSO. The RHESSI images are conveniently co-aligned with the MDI longitudinal magnetogram using the satellite-pointing information. We then co-aligned UV and optical images with the MDI magnetogram by registering features, such as sunspots, pores, and plages, which are observed in all these images. The co-alignment accuracy is limited by the instrument resolution, which is about 1–2′′.
Figure 9 shows the maps of spikes S1 and S2, and the pre-spike underlying components for the 2002 March 17 event. S1 and S2 are both emitted by double sources about 50′′ apart in opposite polarity magnetic fields. S1 primarily stems from the source in the east, while S2 is contributed more by the source in the west. This is different from previous studies (e.g. Wang et al. 1995), suggesting that flare footpoints in weaker magnetic fields emit stronger hard X-rays as a result of magnetic mirroring effects. The spatial variation between S1 and S2 suggests that the magnetic structures that emit S1 and S2 rapidly evolve during 20 s, although they are embedded in the same magnetic environment.
As shown in Fig. 9, the images of the spikes have nearly identical morphologies to the images of the underlying components. In general, for each of the events analyzed in this paper, when we compare the RHESSI map constructed at the spike with the map of the underlying component, no detectable difference is found in the spatial structure between the two, although emission of the spike is enhanced with respect to the underlying component. We note that the RHESSI map constructed over 2 s is a combination of both the spike source and the underlying component. As the spike duration is less than 1 s, and the net spike emission is comparable to the underlying component, the spike source would contribute about 20% to the 2 s map. This may be an important reason that the spike source is not distinguished from the underlying component. We also note that the RHESSI hard X-ray source size (FWHM) is around 10′′, rendering it difficult to uncover the real spatial structure of hard X-ray spikes. Alternatively, we have sought other high-resolution imaging observations to compare with RHESSI data.
For the 2003 October 29 flare, high-resolution infrared observations were taken at National Solar Observatory (NSO) around the maximum phase of the flare. The image scale of the infrared observations is around 0.1′′, yielding a resolution approaching the diffraction limit of 0.2′′. In Fig. 10, we compare infrared images with RHESSI maps. The infrared observations cover only the maximum of the flare, while RHESSI hard X-ray spikes S5 and S6 occurred a minute earlier. The infrared images show double sources coincident with the hard X-ray sources (Fig. 10c; also see Xu et al. 2004) around the maximum of the flare (Figs. 10b and c). In infrared images, the source in the north of the sunspot can be recognized as two patches of less than 2′′ in size, which cannot be resolved in RHESSI maps. Figure 10a shows that hard X-ray spikes S5 an S6 have a similar structure to sources at the maximum, though emission in the southern footpoint is stronger. Unfortunately, no infrared observations were taken at the times of S5 and S6 to uncover the spatial structure of these spikes. However, we point out that the scale of infrared emission sources is similar to the size of a granule clearly shown in the high-resolution images, which may be comparable to the size of an elementary burst, as elementary bursts are thought to reflect reconnection events between single flux tubes (Sturrock 1989).
 |
Fig. 11 Bottom panel: RHESSI hard X-ray maps (white contours) at 25–100 keV around the times of spikes b) S7-S8 and d) S9, and pre-spike times (a) and c)) on 2005 January 19, superposed on the longitudinal magnetogram taken at 09:36:02.32 UT by MDI. The integration time of each image is 2 s. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of the images, which is 2.52 photons cm-2 s-1 asec-2. Top panel: snapshots of TRACE 1600 Å images around the times of RHESSI maps. The inset gray-scale images in c) and d) are magnified images of two kernels, the FOV being indicated by the white boxes in c). The over plotted dark contours in b) and d) show the difference between the spike image and pre-spike background image by TRACE, the contour level being 0.3, 0.5, 0.7 of the maximum of each difference image. Gray contours indicate the polarity inversion line of longitudinal magnetic fields. |
For the 2005 January 19 event, high cadence (2 s) observations at UV 1600 Å were obtained by TRACE with an image scale of 0.5′′, which covers the entire period of interest. Figure 11 shows a series of TRACE UV images in comparison with RHESSI maps at 25–100 keV. Specifically we compare the RHESSI and TRACE images at spikes S7-S8, S9 and the underlying components. The RHESSI maps in the lower panel in Fig. 11 reveals little spatial variation between the spike images and the underlying component images, except for stronger emission at the times of the spikes. TRACE UV 1600 Å images in the upper panel in Fig. 11 were obtained within 1 s of RHESSI hard X-ray spikes and their underlying components. They also show nearly identical spike and pre-spike images, all exhibiting three bright patches in magnetic fields of opposite polarities. Spatially resolved UV light curves reveal enhanced emission correlated with hard X-ray spikes at a few sites in magnetic fields of opposite polarities, suggesting that hard X-ray spikes be emitted by footpoint pairs rather than a single polarity footpoint or a loop top source.
To detect the locality of hard X-ray spikes, we plot the contours of the TRACE difference images between the spike time and pre-spike time in Fig. 11. For S7–S8, excess emission at the time of the spike is exactly from the location of the peak emission of the kernels, confirming that these spikes are emitted by magnetic structures embedded in the same magnetic environment of underlying emissions. For S9, the situation is slightly different: some part of excess emission is located in new spot-like structures extended from the edges of the background kernels. This is most evident in the magnified images of two kernels shown in Fig. 11. The centers of these new structures are displaced from the peak of the background emission by 1′′–2′′, and the FWHM size of the new structures is about 1′′–2′′, which should set the upper limit for the spatial scale of the spikes if we believe that these structures truly reflect the sources of the spikes.
To summarize, RHESSI mapping results suggest that the sources emitting hard X-ray spikes are the same as or very closely attached to sources that emit their underlying components, and they are footpoint sources located in magnetic fields of opposite polarities. This is confirmed by coordinated observations with comparable time cadence and better spatial resolutions by other imaging instruments. Such a result indicates that reconnection and acceleration events that produce hard X-ray spikes take place in the same magnetic environment of the underlying sources. Here the word “same” is accurate within the RHESSI mapping resolution, or ~ 4′′.
6. Conclusions
We present the results in search of fast-varying hard X-ray emissions from RHESSI observations. Spikes on time scales ≤ 1 s are found in hard X-ray emissions at photon energies from 20 to over 100 keV during the rise of hard X-rays in five flare events. These spikes exhibit fairly symmetric sharp rise and decay, and the duration (FWHM) of the spike is from 0.5–1 s. Energy-dependent time lags are present in a few spikes, suggesting time-of-flight effects. The photon count spectra of hard X-ray spikes are generally harder than the spectra of underlying components, typically by 0.5 in the spectral index. This result implies that underlying components might not be an unresolved collection of fast-varying spikes and that hard X-ray emissions in these events might be produced by physical mechanisms linking time scales to spectral hardness. Future observations holding a greater promise for precise spectral analysis should be conducted to examine this point with more confidence.
RHESSI clean maps at 25–100 keV with an integration of 2 s centered on the peak of spikes reveal that hard X-ray spikes are primarily emitted by double foot-point sources in magnetic fields of opposite polarities, which are likely superposed on, rather than at a very different location from, the sources emitting underlying components. With the RHESSI mapping integration time of 2 s, mapping resolution of 4′′, and source FWHM size of nearly 10′′, it is hard to distinguish the spatial structure of ≤ 1 s spikes from the underlying components. Complementary high-resolution imaging UV and infrared observations confirm that hard X-ray spikes are produced in magnetic structures embedded in the same magnetic environment as the underlying components, and the scale of a spike source is likely below 1′′–2′′.
In spite of the limitations of existing capabilities and analysis approaches as discussed above, our present study poses an intriguing question: what physical mechanisms are responsible for producing fast-varying hard X-ray spikes superposed on the temporally and spectrally different underlying components in the same magnetic environment? An analog to this result is the well-known distinctive tempo-spectral behaviors between impulsive and gradual hard X-ray and microwave bursts on much longer time scales and usually in different flares. We also stress that the very pronounced hard X-ray spikes reported in this paper are conceptually different from “elementary bursts”, which the overall flare emission is believed to be comprised of, such as the one described in the flare “avalanche” model (e.g. Lu & Hamilton 1991). This study is not focused on decomposing the entire flare light curve into a sum of short-scale bursts, as practic by Aschwanden et al. (1998). These outstanding hard X-ray spikes are only found in a number of flares, as first remarked by Kiplinger et al. (1983), which indicates of specific physical environment or mechanisms that generate them. To explore this subject further, demodulated RHESSI observations aided by substantially improved spectral and imaging resolving capabilities or techniques (e.g., the visibility imaging by Hurford et al. 2005) are needed. The demodulation algorithm itself can be improved with the explicit calculation of statistical errors and more sophisticated normalization corrections. Study of the particle acceleration associated with fast-varying spikes may be conducted further with the next generation of hard X-ray and/or microwave observing facilities such as the Spectrometer/Telescope for Imaging X-rays (STIX) and Expanded Owens Valley Solar Array (EOVSA).
Acknowledgments
We thank the referee for constructive comments that helped improve the presentation. We acknowledge Mrs. Nora Harrington for editing the language. This work is supported by NASA grant NNX08AE44G, NSF grant AGS-1153424, and NSFC under grants 10878002, 10933003, 11133004 and 11103008 and by the Chinese Academy of Sciences (KZZD-EW-01-3). J.Q. acknowledges the hospitality of RHESSI group at the Space Science Laboratory in University California at Berkeley, where part of the work was conducted during her visit.
References
- Arzner, K. 2002, Sol. Phys., 210, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Benz, A. O., & Schwartz, R. A. 1993, ApJ, 417, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Benz, A. O., Dennis, B. R., & Schwartz, R. A. 1995a, ApJ, 455, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Schwartz, R. A., & Alt, D. M. 1995b, ApJ, 447, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Wills, M. J., Hudson, H. S., Kosugi, T., & Schwartz, R. A. 1996, ApJ, 468, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Kliem, B., Schwarz, U., et al. 1998, ApJ, 505, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, T. S., & Vlahos, L. 1997, in Coronal Physics and Space Observations, ed. G. Trottet, 68 [Google Scholar]
- Cheng, J. X., Qiu, J., Ding, M. D., & Wang, H. M. 2012, A&A, 547, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jager, C., & de Jonge, G. 1978, Sol. Phys., 58, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyng, P., van Beek, H. F., & Brown, J. C. 1976, Sol. Phys., 48, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Hurford, G. J., Schmahl, E. J., & Schwartz, R. A. 2005, AGU Spring Meeting, #SP21A-12 [Google Scholar]
- Kaufmann, P., Strauss, F. M., Laporte, C., & Opher, R. 1980, A&A, 87, 58. [NASA ADS] [Google Scholar]
- Kaufmann, P., Correia, E., Costa, J. E. R., et al. 1984, Sol. Phys., 91, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufmann, P., Raulin, J.-P., Correia, E., et al. 2001, ApJ, 548, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., Frost, K. J., Orwig, L. E., & Emslie, A. G. 1983, ApJ, 265, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., Frost, K. J., & Orwig, L. E. 1984, ApJ, 287, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., Orwig, L. E., & Chen, P. C. 1988, in Proc. First Max’91 Workshop, Kansas City, 214 [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., & Orwig, L. E. 1989, in Max ’91 Workshop 2: Developments in Observations and Theory for Solar Cycle 22, eds. R. M. Winglee, & B. R. Dennis (Greenbelt: NASA), 346 [Google Scholar]
- Krucker, S., Larson, D. E., Lin, R. P., & Thompson, B. J. 1999, ApJ, 519, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Kurt, V. G., Akimov, V. V., Hagyard, M. J., & Hathaway, D. H. 2000, in High Energy Solar Physics: Anticipating HESSI, eds. R. Ramaty, & N. Mandzhavidze, ASP Conf. Ser., 206, 426 [Google Scholar]
- LaRosa, T. N., & Moore, R. L. 1993, ApJ, 418, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Litvinenko, R. E. 1996, Sol. Phys., 167, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Neidig, D. F., Kiplinger, A. L., Cohl, H. S., & Wiborg, P. H. 1993, ApJ, 406, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1989, Sol. Phys., 121, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, J., & Wang, H. 2006, Sol. Phys., 236, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Sturrock, P. A. 1989, in Proc. Max’91 Workshop, ed. R. M. Winglee, & B. R. Dennis (Greenbelt: NASA), 1 [Google Scholar]
- Sturrock, P. A., Kaufman, P., Moore, R. L., & Smith, D. F. 1984, Sol. Phys., 94, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Trottet, G., Rolli, E., Magun, A., et al. 2000, A&A, 356, 1067 [NASA ADS] [Google Scholar]
- van Beek, H. F., de Feiter, L. D., & de Jager, C. 1974, in Space research XIV, Proc. of the Sixteenth Plenary Meeting (Berlin: Akademie-Verlag GmbH), 447 [Google Scholar]
- van Beek, H. F., de Feiter, L. D., & de Jager, C. 1976, in Space research XVI; Proc. of the Open Meetings of Working Groups on Physical Sciences (Berlin: Akademie-Verlag GmbH), 819 [Google Scholar]
- Wang, H., Gary, D. E., Zirin, H., et al. 1995, ApJ, 453, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Qiu, J., Denker, C., et al. 2000, ApJ, 542, 1080 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Cao, W., Liu, C., et al. 2004, ApJ, 607, L131 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Demodulated RHESSI hard X-ray light curves (dark) in comparison with summed raw data counts (gray). The light curves are acquired at 25–100 keV. Top panel shows 2002 March 17 event that exhibits fast-varying spikes and bottom panel shows 2005 January 19 event without significant fast-varying spikes. The scales of the demodulated (in units of counts per second per detector) and raw (in units of counts) light curves are indicated on the left and right y-axes, respectively. |
| In the text | |
 |
Fig. 2 Demodulated RHESSI hard X-ray light curves at varying energies for the five flares. Then inset frame gives magnified view of some pronounced spikes. Note that y-axis gives the units of the 25–100 keV light curve, and light curves at other energies are scaled arbitrarily. |
| In the text | |
 |
Fig. 3 Example of spike detection algorithm using 3 methods (see text) for the 2005 January 19 event. Left panels show the demodulated light curves (dark) at 60–100 keV, the slow-varying component (gray) determined by 3 methods, and the residuals (bottom of each panel), with the significant residuals marked (plus symbols). Right panels show the times (x-axis) and energies (y-axis) of significant residuals recognized by the algorithms. The numbers 1 to 7 along the y-axis indicate energy bands of 10–15, 15–25, 25–40, 40–60, 60–100, 100–300, 25–100 keV, respectively. The two arrows in the top right panel indicate the most pronounced spikes standing out in the diagrams. |
| In the text | |
 |
Fig. 4 Demodulated light curves of spike S1 at four energy channels, 25–40, 40–60, 60–100, and 100–300 keV from top to bottom, superimposed with the fitted curves (solid lines). Count light curves from 40–300 keV are arbitrarily normalized for clarity of display. |
| In the text | |
 |
Fig. 5 Examples of durations and peaking times of the spikes S1 and S10 at varying energies, derived from fitting the spike light curves to Gaussian profiles. Horizontal bars in the bottom panels indicate the widths of the energy bins, and vertical bars indicate 1σ fitting uncertainties. Lines in the bottom panel give the time-of-flight fit (see text). |
| In the text | |
 |
Fig. 6 In each panel, the symbols and solid lines show examples of hard X-ray photon count spectra of integrated spike flux from the Gaussian fitting, in comparison with the count rates spectra of underlying components. Solid lines show the least-squares fit of the spectra to a power-law distribution, and the exponents and their uncertainties from the fit are noted in the figures. The y-axis gives the units of the spike intensities, and the intensities of the underlying component are divided by four for clarity. The three panels from top to bottom illustrate the count spectra for spikes S1, S5, and S8, respectively, and the underlying components. |
| In the text | |
 |
Fig. 7 Scatter plot of power index (αy) of the spike spectra and index (αx) of underlying components. The dotted guide line outlines αy = αx. |
| In the text | |
 |
Fig. 8 RHESSI hard X-ray clean maps at 25–100 keV of spikes S1 to S10 (gray scale) superimposed on the maps of underlying components (contours) in the same energy range. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of the image. Axis labels indicate the E-W and N-S coordinates in arcsec. |
| In the text | |
 |
Fig. 9 RHESSI hard X-ray clean maps (dark contours) at 25–100 keV of spikes b) S1 and d) S2 and the pre-spike underlying components (a) and c)) on 2002 March 17 superposed on the longitudinal magnetogram taken at 19:46:01.11 UT by MDI. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of all the images, which is 0.57 photons cm-2 s-1 asec-2. White contours indicate the polarity inversion line of longitudinal magnetic fields. |
| In the text | |
 |
Fig. 10 RHESSI hard X-ray clean maps (dark contours) at 25–100 keV a) of spike S5 and b) at the maximum of the 2003 October 29 flare superposed on the longitudinal magnetogram taken by MDI. Each map is constructed with 2 s integration. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of each image, which is noted in each plot in the unit of photons cm-2 s-1 asec-2. c) A snapshot of an infrared image around the flare maximum revealing two bright kernels coincident with RHESSI hard X-ray sources (white contours). The white box in b) defines the FOV of c). |
| In the text | |
 |
Fig. 11 Bottom panel: RHESSI hard X-ray maps (white contours) at 25–100 keV around the times of spikes b) S7-S8 and d) S9, and pre-spike times (a) and c)) on 2005 January 19, superposed on the longitudinal magnetogram taken at 09:36:02.32 UT by MDI. The integration time of each image is 2 s. The contour levels are 0.25, 0.4, 0.55, 0.7, and 0.85 of the maximum count rates of the images, which is 2.52 photons cm-2 s-1 asec-2. Top panel: snapshots of TRACE 1600 Å images around the times of RHESSI maps. The inset gray-scale images in c) and d) are magnified images of two kernels, the FOV being indicated by the white boxes in c). The over plotted dark contours in b) and d) show the difference between the spike image and pre-spike background image by TRACE, the contour level being 0.3, 0.5, 0.7 of the maximum of each difference image. Gray contours indicate the polarity inversion line of longitudinal magnetic fields. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


