| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201016235 | |
| Published online | 27 July 2012 | |
International observational campaigns of the last two eclipses in EE Cephei: 2003 and 2008/9⋆,⋆⋆
1
Toruń Centre for Astronomy, Nicolaus Copernicus
University, ul. Gagarina
11, 87-100
Toruń,
Poland
e-mail: cgalan@astri.uni.torun.pl; mamiko@astri.uni.torun.pl; tomtom@astri.uni.torun.pl
2
Olsztyn Planetarium and Astronomical Observatory,
Al. Marszałka J. Piłsudskiego 38,
10-450
Olsztyn,
Poland
3
Universidad de Concepción, Departamento de
Astronomia, Casilla
160-C, Concepción,
Chile
4
Institute of Physics, Faculty of Science, Ss. Cyril and Methodius
University, PO Box
162, 1000
Skopje, FYROM,
Macedonia
5
Institute of Astronomy and National Astronomical Observatory,
Bulgarian Academy of Sciences, 72
Tsarigradsko Shose Blvd., 1784
Sofia,
Bulgaria
6
Institute for Astronomy, Astrophysics, Space Applications and
Remote Sensing, NOA PO Box
20048, 11810
Athens,
Greece
7
Dept. of Physics and Earth Science, University of North
Alabama, Florence,
35632
AL,
USA
8
David Dunlap Observatory, Department of Astronomy and
Astrophysics, University of Toronto, 50 St. George St., Toronto, ON
M5S 3H4,
Canada
9
International Centre for Astronomical and Medico-Ecological
Research, Terskol,
Russia
10
Variable Star and Exoplanet Section ofCzech Astronomical
Society, Czech Republic
11
Altan Observatory, Velka Upa 193, Pec pod Snezkou, Czech
Republic
12
Tadeusz Banachiewicz Astronomical Observatory,
Wȩglówka, 32-412
Wiśniowa,
Poland
13
Max Planck Institute for Astronomy, Königstuhl 17, 69117
Heidelberg,
Germany
14
Department of Earth and Space Sciences, University of California
at Los Angeles, 595, Charles E.
Young Dr. East
CA
90095,
USA
15
Mt. Suhora Observatory, Pedagogical Univ.,
ul. Podchora¸żych 2,
30-084
Kraków,
Poland
16
Rolling Hills Observatory Clermont, FL,
USA
17
University of Hawaii Maui College, Kahului, Hawaii
18
Instituto de Astronomia, Universidad Catolica del
Norte, Av. Angamos
0610, Antofagasta,
Chile
19
Department of Astrophysics, Astronomy and Mechanics, National and
Kapodistrian University of Athens, 157 84 Zografos, Athens, Greece
20
Instituto de Astronomá, Universidad Nacional Autónoma de México
Apdo. postal 70264, Ciudad Universitaria, México
D.F. 04510,
México
21
Department of Experimental Physics and Astronomical Observatory,
University of Szeged, Dom ter
9, 6720
Szeged,
Hungary
22
Pulkovo Astronomical Observatory, Russian Academy of
Sciences, Pulkovskoe sh.
65, 196140
St. Petersburg,
Russia
23
Space Research Centre, Polish Academy of Sciences,
Bartycka 18A, 00-716
Warsaw,
Poland
24
Nicolaus Copernicus Astronomical Center,
Rabiańska 8, 87-100
Toruń,
Poland
25
Observatorio Astronómico “Las Pegueras”, NAVAS DE ORO
(Segovia), Spain
26
Hopkins Phoenix Observatory, 7812 West Clayton Drive, Phoenix, 85033-2439
Arizona,
USA
27
Observatory and Planetarium of Johann Palisa, VŠB – Technical
University of Ostrava, 17.
listopadu 15, 708
33
Ostrava-Poruba, Czech
Republic
28
Instytut Astronomiczny, Uniwersytet Wrocławski,
Kopernika 11, 51-622
Wrocław,
Poland
29
Astronomical Observatory, Jagiellonian Univ.,
ul. Orla 171, 30-244
Kraków,
Poland
30
Las Cumbres Observatory, 6740 Cortona Drive Suite 102, Goleta, CA
93117,
USA
31
National Centre for Nuclear Research, 00-681
Warsaw,
Poland
32
Leiden Observatory, PO Box 9513, 2300 RA
Leiden, The
Netherlands
33
Furzehill House, Ilston, Swansea, SA2 7LE, UK
34
Variable Star Section of the British Astronomical Association,
Furzehill House, Ilston, Swansea, SA2
7LE, UK
35
INAF, Osservatorio Astronomico di Padova,
via dell Osservatorio 8, 36012
Asiago ( VI), Italy
36
Special Astrophysical Observatory of the Russian AS,
369167
Nizhnij Arkhyz,
Russia
37
GRAS Observatory, Mayhill, New
Mexico, USA
38
Department of Physics and Space Sciences, 150 W. University Blvd,
Florida Institute of Technology, Melbourne, FL
32901,
USA
39 Green Island Observatory (B34),
North Cyprus
40
Hankasalmi Observatory, Jyvaskylan Sirius ry, Vertaalantie 419,
40270
Palokka,
Finland
41
Nicolaus Copernicus Astronomical Center, Bartycka 18,
00-716
Warsaw,
Poland
42 Sonoita Research Observatory/AAVSO, USA
43
Department of Physics and Astronomy, Box 516, 751 20
Uppsala,
Sweden
44
Centrum Hewelianum, PKFM “Twierdza Gdańsk”, ul. 3 Maja 9a,
80-802
Gdańsk,
Poland
45
University of Ljubljana, Faculty of Mathematics and Physics,
Jadranska 19,
1000
Ljubljana,
Slovenia
Received:
30
November
2010
Accepted:
17
April
2012
Context. EE Cep is an unusual long-period (5.6 yr) eclipsing binary discovered during the mid-twentieth century. It undergoes almost-grey eclipses that vary in terms of both depth and duration at different epochs. The system consists of a Be type star and a dark dusty disk around an invisible companion. EE Cep together with the widely studied ε Aur are the only two known cases of long-period eclipsing binaries with a dark, dusty disk component responsible for periodic obscurations.
Aims. Two observational campaigns were carried out during the eclipses of EE Cep in 2003 and 2008/9 to verify whether the eclipsing body in the system is indeed a dark disk and to understand the observed changes in the depths and durations of the eclipses.
Methods. Multicolour photometric data and spectroscopic observations performed at both low and high resolutions were collected with several dozen instruments located in Europe and North America. We numerically modelled the variations in brightness and colour during the eclipses. We tested models with different disk structure, taking into consideration the inhomogeneous surface brightness of the Be star. We considered the possibility of disk precession.
Results. The complete set of observational data collected during the last three eclipses are made available to the astronomical community. The 2003 and 2008/9 eclipses of EE Cep were very shallow. The latter is the shallowest among all observed. The very high quality photometric data illustrate in detail the colour evolution during the eclipses for the first time. Two blue maxima in the colour indices were detected during these two eclipses, one before and one after the photometric minimum. The first (stronger) blue maximum is simultaneous with a “bump” that is very clear in all the UBV(RI)C light curves. A temporary increase in the I-band brightness at the orbital phase ~0.2 was observed after each of the last three eclipses. Variations in the spectral line profiles seem to be recurrent during each cycle. The Na i lines always show at least three absorption components during the eclipse minimum and strong absorption is superimposed on the Hα emission.
Conclusions. These observations confirm that the eclipsing object in
EE Cep system is indeed a dark, dusty disk around a low luminosity object. The primary
appears to be a rapidly rotating Be star that is strongly darkened at the equator and
brightened at the poles. Some of the conclusions of this work require verification in
future studies: (i) a complex, possibly multi-ring structure of the disk in EE Cep; (ii)
our explanation of the “bump” observed during the last two eclipses in terms of the
different times of obscuration of the hot polar regions of the Be star by the disk; and
(iii) our suggested period of the disk precession
(~11–12 Porb) and predicted depth of about
2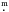 for the
forthcoming eclipse in 2014.
for the
forthcoming eclipse in 2014.
Key words: binaries: eclipsing / circumstellar matter / stars: emission-line, Be / planetary systems
Appendix A is available in electronic form at http://www.aanda.org
Tables B.1–B.36 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/544/A53
© ESO, 2012
1. Introduction
The 11th magnitude star EE Cep is a unique object
among the about 40 well-known eclipsing systems with orbital periods longer than one year.
The primary B5 III star is obscured by an invisible, dark secondary component of very low
luminosity every 5.6 yr. The variability of the star was discovered in 1952 (epoch
E = 0) by Romano (1956) and soon
confirmed by Weber (1956), who reported observations
obtained during a previous eclipse in 1947 (E = −1). Since then, ten
consecutive primary eclipses have been observed, while a secondary eclipse has never been
detected. The depths of the eclipses vary across a wide range of magnitudes from about
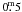 to
to
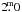 (see Graczyk et al. 2003). However, all of them seem to have the same features:
they are almost grey and have a similar asymmetric shape (the descending branch of every
eclipse has a longer duration than the ascending one). In the light curves of all the
eclipses, it is possible to distinguish five characteristic phases (shown in Fig. 1): ingress (1-2) and egress (3-4) are preceded and
followed, respectively, by extended atmospheric eclipse parts (1a-1 and 4-4a), and in the
middle of the eclipses a bottom phase of variable slope (2-3) occurs.
(see Graczyk et al. 2003). However, all of them seem to have the same features:
they are almost grey and have a similar asymmetric shape (the descending branch of every
eclipse has a longer duration than the ascending one). In the light curves of all the
eclipses, it is possible to distinguish five characteristic phases (shown in Fig. 1): ingress (1-2) and egress (3-4) are preceded and
followed, respectively, by extended atmospheric eclipse parts (1a-1 and 4-4a), and in the
middle of the eclipses a bottom phase of variable slope (2-3) occurs.
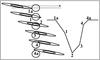 |
Fig. 1 Schematic representation of the eclipse geometry in the EE Cep system. The inner opaque and outer semi-transparent regions of the disk are separated. The characteristic positions of the disk and the star configuration during the eclipses (left) correspond to the contact times (1a, 1, 2, 3, 4, 4a) distinguished in the light curve (right). The figure shows a highly simplified case that ignores a number of issues such as e.g. possible inhomogeneities in the distribution of brightness on the star’s surface or of the actual size of the disk. |
The most plausible hypothesis to explain the observed shape of the light curve, as well as
the changes in the eclipse depth during successive conjunctions and their weak dependence on
the photometric band was proposed by Mikołajewski &
Graczyk (1999). Their model considers the eclipses of a hot B5-type primary by an
invisible, dark companion, which is most probably a dusty disk around a low-luminosity
central object. The disk is slightly inclined to the orbital plane. The obscurations of the
star by the opaque interior of the disk can explain the deep central parts of the eclipses,
while the semi-transparent exterior areas are responsible for the observed external wings,
which are similar to wings caused by atmospheric eclipses in ζ Aur type
variable stars. The projection of the inclined disk onto the sky plane produces oblong shape
of an obscuring body, which is tilted with respect to the direction of motion during most of
the occultations. Since the eclipses are not central (the impact parameter is non-zero), the
light curves observed during the eclipses have an asymmetric shape (Fig. 1). A possible precession of the disk can change both the
inclination of the disk to the line of sight and the tilt of its cross-section to the
transit direction. This leads to changes in the depth and the duration of the eclipses. The
model briefly described above can explain the shallow
(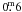 ), flat-bottomed eclipse observed
in 1969, if we assume a nearly edge-on and non-tilted projection of the disk (Graczyk et al. 2003). This very specific configuration in
1969 is very similar to the geometry of the eclipses in the ε Aur system (see Mikołajewski & Graczyk 1999). Wide eclipsing binaries of this kind, i.e.
those containing a nearly edge-on dusty disk as an eclipsing object, are very rare and apart
from the two above-mentioned cases we know of only about one additional system – M2-29 – that may show some similarities (Hajduk et al. 2008).
), flat-bottomed eclipse observed
in 1969, if we assume a nearly edge-on and non-tilted projection of the disk (Graczyk et al. 2003). This very specific configuration in
1969 is very similar to the geometry of the eclipses in the ε Aur system (see Mikołajewski & Graczyk 1999). Wide eclipsing binaries of this kind, i.e.
those containing a nearly edge-on dusty disk as an eclipsing object, are very rare and apart
from the two above-mentioned cases we know of only about one additional system – M2-29 – that may show some similarities (Hajduk et al. 2008).
In this paper, we present the results of two observational campaigns organized for the eclipses that occured in 2003 and 2008/9, mainly to test the hypothesis of a precessing disk. The results of the second campaign were systematically presented during the eclipse at a web page1.
2. Observations
2.1. The 1997 eclipse
During the 1997 eclipse (epoch E = 8), the first multicolour
UBVRCi
(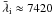 Å)
photometric observations were made using a 60 cm Cassegrain telescope at the Piwnice
Observatory near Toruń (Poland) equipped with a one-channel photometer (Mikołajewski & Graczyk 1999). This eclipse was
one of the deepest eclipses of all those observed in EE Cep. However, the amplitude of the
minimum changes quite weakly with wavelength from about
Å)
photometric observations were made using a 60 cm Cassegrain telescope at the Piwnice
Observatory near Toruń (Poland) equipped with a one-channel photometer (Mikołajewski & Graczyk 1999). This eclipse was
one of the deepest eclipses of all those observed in EE Cep. However, the amplitude of the
minimum changes quite weakly with wavelength from about
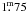 in the U
passband to about
in the U
passband to about 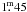 in i
(Fig. 2). These observations thus provided the
first evidence that the eclipsing body cannot be an ordinary evolved cool star, motivating
us to organize a special international observational campaign for the next two minima.
A complete set of UBVRCi
photometry obtained in 1997 is shown in Table B.1.
in i
(Fig. 2). These observations thus provided the
first evidence that the eclipsing body cannot be an ordinary evolved cool star, motivating
us to organize a special international observational campaign for the next two minima.
A complete set of UBVRCi
photometry obtained in 1997 is shown in Table B.1.
 |
Fig. 2 U (dots) and i (crosses) light curves obtained during the 1997 eclipse of EE Cep. |
Overview of instruments and their involvement in photometric observations of the EE Cep eclipses since 1997.
2.2. International photometric campaigns in 2003 and 2008/9
Observers from four European countries responded to the appeal of Mikołajewski et al. (2003) to perform a precise monitoring of the
subsequent eclipse of EE Cep anticipated in 2003 (epoch E = 9). During
the organized campaign, ten telescopes were used to acquire the photometric observations
(Table 1). Very high quality photometric
UBV(RI)C data were obtained with very fine
sampling. The eclipse turned out to be quite shallow and in accordance with the
expectations, almost grey. The eclipse reached depths from about
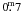 in U to
in U to
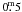 in
IC. The preliminary photometric results of the 2003 campaign
were described by Mikołajewski et al. (2005a). The
results of this fruitful campaign in 2003 did not however significantly constrain the
precessing disk model, and the nature of the central part of the disk and its contribution
to the total flux remained uncertain. The next opportunity for resolving these
uncertainties came with the most recent eclipse, which took place at the turn of 2008
(epoch E = 10), with a minimum on January 10, 2009. An invitation to
participate in an observational campaign (Gałan et al.
2008) attracted strong interest. Twenty telescopes located in Europe and North
America were involved in the photometric observations (Table 1), which provided a more comprehensive multicolour and temporal
photometric coverage than for any previous eclipse. The first results and the
UBV(RI)C light curves in graphical form
were published by Gałan et al. (2009). Surprisingly,
the last eclipse turned out to be the shallowest in the observing history of EE Cep,
reaching a depth of only ~
in
IC. The preliminary photometric results of the 2003 campaign
were described by Mikołajewski et al. (2005a). The
results of this fruitful campaign in 2003 did not however significantly constrain the
precessing disk model, and the nature of the central part of the disk and its contribution
to the total flux remained uncertain. The next opportunity for resolving these
uncertainties came with the most recent eclipse, which took place at the turn of 2008
(epoch E = 10), with a minimum on January 10, 2009. An invitation to
participate in an observational campaign (Gałan et al.
2008) attracted strong interest. Twenty telescopes located in Europe and North
America were involved in the photometric observations (Table 1), which provided a more comprehensive multicolour and temporal
photometric coverage than for any previous eclipse. The first results and the
UBV(RI)C light curves in graphical form
were published by Gałan et al. (2009). Surprisingly,
the last eclipse turned out to be the shallowest in the observing history of EE Cep,
reaching a depth of only ~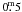 in U and
nearly ~
in U and
nearly ~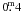 in
IC.
in
IC.
 |
Fig. 3 All of the approximately 800 individual photometric UBV(RI)C measurements obtained during the 2003 eclipse (left; Tables B.2–B.11) and all of the more than 1600 observations obtained during the 2008/9 eclipse (right; Tables B.12–B.32). |
Overview of the instruments involved in the spectroscopic observations during the three last eclipses at epochs E = 8, E = 9, and E = 10.
The strong interest inspired by Mikołajewski et al.
(2003) and Gałan et al. (2008) resulted in
many observations. The original data and the observatories that sent them are presented in
Tables B.2–B.11 for the 2003 eclipse (E = 9) and Tables B.12–B.32 for the
2008/9 (E = 10) eclipse, respectively. The three standard stars
“a” = BD +55°2690, “b” = GSC-3973:2150, and
“c” = BD +55°2691 have been recommended by Mikołajewski et al. (2003). Most magnitudes were evaluated with respect
to either the standard star “a” (Tables B.2–B.20) or all three standard
stars “a”, “b”, and “c” independently
(Tables B.24–B.32). One set of data (Table B.21) were obtained only with respect to
standard star “c” because of the small field of view of the instrument
used. The data in Tables B.2–B.21 and B.24–B.32 are shown in differential form. Two sets
of data, from Sonoita Research Observatory (Tables B.22–B.23), were obtained partly with
respect to other standard stars (see Table B.22), and we show them as apparent magnitudes.
They were transformed to a differential form using the known brightness of star
“a” from Mikołajewski et al.
(2003). The original differential magnitudes obtained with the three standard
stars were calculated with respect to star “a”, using the average
differences between the standard stars 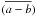 and
and
 . All of the mean values in
Tables B.24–B.32 for variable star “v” were calculated according to the
expression
. All of the mean values in
Tables B.24–B.32 for variable star “v” were calculated according to the
expression ![\hbox{$[(v-a) + (v-b)-(\overline{a-b}) + (v-c)-(\overline{a-c})]/3$}](/articles/aa/full_html/2012/08/aa16235-10/aa16235-10-eq55.png) for each filter, excluding
ΔV and ΔRC data in Table B.25. For this
last set of data, the differences (v − a) were not
recorded by the observers, hence the reduced average values were calculated using the
expression
for each filter, excluding
ΔV and ΔRC data in Table B.25. For this
last set of data, the differences (v − a) were not
recorded by the observers, hence the reduced average values were calculated using the
expression ![\hbox{$[(v-b)-(\overline{a-b}) + (v-c)-(\overline{a-c})]/2$}](/articles/aa/full_html/2012/08/aa16235-10/aa16235-10-eq59.png) , where the
, where the
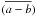 and
and
 VR magnitudes
were adopted from Mikołajewski et al. (2003). All
data were corrected for the differences between the particular photometric systems. The
CCD data from Kraków were adopted as a zero-point, owing to their high quality and good
coverage during both the eclipses. Original individual data points obtained close to the
eclipses are presented in Fig. 3, which is composed
of about 2500 measurements. The phases were calculated with ephemeris (Mikołajewski & Graczyk 1999)
VR magnitudes
were adopted from Mikołajewski et al. (2003). All
data were corrected for the differences between the particular photometric systems. The
CCD data from Kraków were adopted as a zero-point, owing to their high quality and good
coverage during both the eclipses. Original individual data points obtained close to the
eclipses are presented in Fig. 3, which is composed
of about 2500 measurements. The phases were calculated with ephemeris (Mikołajewski & Graczyk 1999)
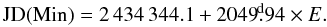 (1)
The photometric observational data were further processed
by averaging the groups of neighbouring points. In the case of the previous eclipse at
E = 9, for which the photometric measurements were obtained only in
Europe, each point in the light curves represents the average of all measurements obtained
in a given passband during a single night. The V light curve constructed
in this way was complemented by the data obtained independently for this eclipse by Samolyk & Dvorak (2004), which we shifted by
(1)
The photometric observational data were further processed
by averaging the groups of neighbouring points. In the case of the previous eclipse at
E = 9, for which the photometric measurements were obtained only in
Europe, each point in the light curves represents the average of all measurements obtained
in a given passband during a single night. The V light curve constructed
in this way was complemented by the data obtained independently for this eclipse by Samolyk & Dvorak (2004), which we shifted by
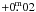 onto the reference system. The
last eclipse at E = 10 was observed from two continents, Europe and North
America. The measurements obtained during each day form groups of points separated by
about one-third of a day and should not be averaged together. In the light curves of this
eclipse, each point represents the average of all measurements obtained in a given filter
during the first or second part of a particular Julian day. The accuracy of the photometry
obtained in this way is excellent, reaching a few mmag. The resulting mean points of the
average light curves, together with the formal standard deviations for particular
observations, are shown in Table B.35.
onto the reference system. The
last eclipse at E = 10 was observed from two continents, Europe and North
America. The measurements obtained during each day form groups of points separated by
about one-third of a day and should not be averaged together. In the light curves of this
eclipse, each point represents the average of all measurements obtained in a given filter
during the first or second part of a particular Julian day. The accuracy of the photometry
obtained in this way is excellent, reaching a few mmag. The resulting mean points of the
average light curves, together with the formal standard deviations for particular
observations, are shown in Table B.35.
 |
Fig. 4 Average points from Table B.35 of the 2003 eclipse (left) and the 2008/9 eclipse (right). The B light curves (top) and three colour indices (bottom) are presented. Arrows denote times of blue maxima. |
2.3. Spectroscopic data collected in 2003 and 2008/9
For several decades until the eclipse at epoch E = 9 in 2003, changes in EE Cep’s spectrum outside and during eclipses had been poorly studied, whereas the photometric behaviour during the eclipses had been relatively well characterized. The situation improved significantly after the observational campaign in 2003. Seven observatories located in Europe and North America took part in the observations (using the instruments listed in Table 2), collecting spectra at low and high resolution. The spectral observations covered various phases of the eclipse, revealing changes in the line profiles (mainly Hα, Na i, Hβ, and Fe ii) not only during the photometric eclipse but even more than two months before and after the minimum (Mikołajewski et al. 2005b). Unfortunately, during the last campaign at the turn of 2008 (epoch E = 10) only a small number of spectra were obtained, with only three instruments. The new spectra complement those obtained during the previous epoch, because a significant number of these spectra were acquired during orbital phases that had not been previously covered.
With this paper, we make available a large number (100) of spectra, most of which were, however, obtained with moderate resolution and/or cover a narrow spectral range, containing mainly Hα or Na i spectral lines. In addition, they were clustered near the eclipse – the spectroscopic observations have insufficient temporal coverage throughout the orbital phase to use them in studying changes in the radial velocities. The list of spectra and instruments together with some additional information are given in Table B.36. All these spectra were heliocentric corrected and some of them (obtained at Rozhen Observatory and DDO), which cover a narrow spectral range (~100–200 Å), were normalized to the continuum. The low resolution spectra obtained at Piwnice Observatory were flux calibrated. All spectra are available as FITS files at the CDS2.
3. Results
3.1. Light and colour changes during the last two eclipses
Thanks to the aforementioned observational campaigns, it has been possible for the first
time to analyse colour evolution during the eclipses. In Fig. 4, the mean B light curves and the colour indices for
both of the last eclipses are presented. The 2003 and 2008/9 eclipses reached their minima
on Julian days JD = 2 452 795 and JD = 2 454 842, respectively. The small timing
residuals (O–C, observations minus calculations) 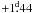 and
and 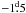 with respect to the ephemeris
(Eq. (1)) did not change this significantly. The Mikołajewski & Graczyk (1999) ephemeris was
used (unchanged) for orbital phasing to produce all the observational data in this paper.
The colour indices for the 2003 eclipse show two blue maxima, about nine days before and
after the mid-eclipse. Two weak maxima in the B light curve are also
clearly visible. Similar features also occur in the 2008/9 eclipse but the “bump” (at
JD 2 454 836) preceding the minimum (Figs. 3
and 4) is much more pronounced than previously. The
differences in the phase and strength of these features can be caused, such as the depth
of eclipses, by changes in the spatial orientation of the disk.
with respect to the ephemeris
(Eq. (1)) did not change this significantly. The Mikołajewski & Graczyk (1999) ephemeris was
used (unchanged) for orbital phasing to produce all the observational data in this paper.
The colour indices for the 2003 eclipse show two blue maxima, about nine days before and
after the mid-eclipse. Two weak maxima in the B light curve are also
clearly visible. Similar features also occur in the 2008/9 eclipse but the “bump” (at
JD 2 454 836) preceding the minimum (Figs. 3
and 4) is much more pronounced than previously. The
differences in the phase and strength of these features can be caused, such as the depth
of eclipses, by changes in the spatial orientation of the disk.
 |
Fig. 5 Differential I magnitudes of EE Cep obtained at Piwnice
Observatory during the 13 years from 1996 to 2010. The zero value corresponds to the
level of the average brightness outside (phases 0.4–0.8) eclipses. Below
+0 |
The observed variations in the I passband after the eclipses could give additional support to this idea. In Fig. 5, the I-band light curve obtained over 13 years, from 1996 to 2010, is shown. About one year after each eclipse, near the orbital phase ~0.2, an increase in I-band brightness appears. The recurrence and rapid variation during these events allow us to speculate that this increase may be caused by proximity effects when the components are close to periastron. If this is true, then the orbit in the EE Cep system must be significantly eccentric. An interesting correlation – the brightening events appear to be stronger when the eclipses are deeper – may indicate that there are changes in the disk projection and this may be an additional observational argument for precession of the disk. The quite large amplitude of variability outside the eclipse in the I passband (which is not clearly visible at shorter wavelengths) also indicates that the contribution of a dark component (disk or/and central object) to this band has to be significant. The cool component becomes readily noticeable at the red edge of the visible spectrum, and in the near infrared (the JHK bands) it might dominate the observed fluxes.
3.2. Variations in the spectrum
 |
Fig. 6 Hβ and Fe ii line profiles in the spectra obtained during the 2008/9 eclipse with the Nordic Optical Telescope (NOT, La Palma). The spectra are vertically offset for clarity. |
 |
Fig. 7 Balmer H10 and H11 line profiles in the spectrum of EE Cep taken on 11 Aug. 2003 with an Echelle spectrograph on the 2.12 m telescope in SPM Observatory in Mexico. The best fit was obtained for a synthetic spectrum with: Teff = 15 000 K, log g = 3.5, [Fe/H] = 0, and vsini = 350 km s-1 (solid line). Two poorer fits calculated with different values of the rotational velocity, vsini = 300 km s-1 (dashed line) and vsini = 400 km s-1 (dash-dotted line), are shown for comparison purposes. |
 |
Fig. 8 Representative examples of Hα line profiles in the spectra obtained near the eclipses at epochs E = 10, E = 9, and E = 8 (in the electronic version of this paper, the profiles have different colours: red, blue, and green, respectively). The spectra are vertically offset for clarity. |
The most important results of the spectroscopic observations obtained during the 2003 campaign seem to be the conclusions regarding the nature of the hot component. The emission and absorption components of the Balmer and Fe ii line profiles in the spectra obtained around the 2003 eclipse imply that the hot component is a rapidly rotating Be star surrounded by a highly inclined emitting gaseous ring (Mikołajewski et al. 2005b). These line profiles show the same pattern during the 2008/9 eclipse (compare Fig. 6 with Fig. 2 of Mikołajewski et al. 2005b). A comparison of the Balmer H8-H11 absorption lines in the spectrum of EE Cep with theoretical profiles (Fig. 7) gives vsini ≈ 350 km s-1 (Gałan et al. 2008), which implies that there has been a strong equatorial gravitational darkening. The rotational velocity of the Be star in the EE Cep system is very close to the critical value. It must lead to a continuously strong radial outflow of the gas stream from the equator, which is confirmed by the existence of the gaseous ring – a characteristic feature of Be-type stars (Mikołajewski et al. 2005b).
 |
Fig. 9 Representative examples of Na i doublet line profiles in the spectra obtained near the eclipses at epochs E = 10, E = 9, and E = 8 (in the electronic version of this paper, the profiles have different colours: red, blue, and green, respectively). The spectra are vertically offset for clarity. |
Figures 8–10 show the evolution of the Hα and Na i line profiles in which additional absorption components appeared during both of the last two eclipses. Towards the mid-eclipse, an absorption component in the Hα profile grows, and during the minimum it is very deep and broad. The sodium doublet line profiles in the minimum show a multi-component structure and we can discern at least two additional absorption components shifted towards blue wavelengths, first at a velocity of about −40 km s-1 and then at about −70 km s-1 (Fig. 11).
In a few high-resolution spectra from the Rozhen, NOT, Asiago, and Terskol observatories, we can see Hα and Hβ lines. The spectra from NOT and Terskol contain higher order Balmer lines, which are, however, underexposed, permitting us to see only that the emission is weakening and the broad and strong absorption features of the Be star begin to dominate. The only spectrum displaying absorption from Hα to H13-H14 is the SPM spectrum (see Table 2) obtained during the 2003 eclipse. In this spectrum, strong absorption in the Be star dominates and the higher order emission Balmer lines are absent (see Fig. 7). In the case of other lines of the Be star, in a few spectra, the He i 5876 Å, 4471 Å, and Mg ii 4481 Å lines appear to be present but are barely visible. In the spectra from CCS and Asiago, the emission triplet Ca ii (8498 Å 8542 Å 8662 Å) and the O i 8446 Å line are visible. Because of the small number of lines in the Be star spectrum and their weakness and large width, it was impossible to extract reliable information about changes in the radial velocities of the hot component.
The spectra obtained during the two most recent eclipses suggest that the behaviour of the spectral line profiles might not change between eclipses. A unique spectrum was obtained at phase ~− 0.025 before the 2003 eclipse when both lines of the Na i doublet showed a P Cyg profile. If this is a sign of outflow from the Be star, then this implies that the eclipses occur relatively close to periastron. At orbital phases far from the eclipses, absorption structures are indeed sometimes appear imposed on the emission lines indicating that there are large amounts of loose gaseous clouds in the system, which could support such a scheme (see e.g. Fig. 8 – Hα line profiles at phases ~0.17 and ~0.25). On the other hand, these structures are observed during the brightening event observed in the I band at an orbital phase ~0.2.
The changes of the spectral line profiles during phases close to the photometric eclipses allowed us to estimate the sizes of the eclipsing dusty disk and gaseous ring around the Be star (Mikołajewski et al. 2005b). The disappearance of the bluest component of the Na i doublet at a phase of about 0.011 suggests that the radius of the eclipsing cloud producing the Na i lines is at least 6RBe. The shell absorption in Hα rapidly decays about 2.5 months after minimum (at phase ~0.036), which suggests that the gaseous ring around the Be star producing the Hα emission is almost twice the size of the eclipsing cloud, i.e. ≳ 10RBe.
4. Modelling of the eclipse light curves, precession of the disk, and discussion
4.1. Numerical code and basic assumptions
Although similar to ε Aur and maybe even M2-29, EE Cep is nevertheless quite a unique system, and existing tools do not seem to be suitable for analysing this system. To model the brightness and colour variations during the eclipses and changes from epoch to epoch, possibly depending on precession, it was necessary to develop our own, original numerical code.
 |
Fig. 10 B and B − V light curves of the 2003 (bottom) and 2008/9 (top) eclipses. In the middle panel, we present all available line profiles of the Na i doublet and Hα for epoch 9 (superposition of two lines: thick dashed with thin solid) and 10 (solid line). The positions of the continuum levels refer to the orbital phases. The right-hand panels show a zoom of the central part of left-hand panels as indicated by vertical dashed lines. The arrows indicate the shallow minima in the external parts of the eclipses observed about 35 days before and after mid-eclipse at both last epochs (both last eclipses seem to be longer than expected and lasted about 90 days). |
 |
Fig. 11 Radial velocities of the three components of the sodium doublet Na i lines obtained from the spectra of five observatories (NOT, SPM, DDO, Asiago, and Rozhen). The main stellar component is shown with filled circles, and two components from the disk blue-shifted by about −40 and −70 km s-1 are shown with open circles and filled diamonds, respectively. |
The models require the adoption of some quite simplistic assumptions. An axially symmetric, circular, flat disk with an r−n density profile was assumed in all cases. The disk was considered to be geometrically thin, although we highlight that two different approaches are possible with our code. One is to assume a disk thickness H and integrate the density of the matter in the disk. The second approach, which is more efficient for the calculation, is to assume that the disk has a negligible thickness (in reality zero thickness in the model). Changes in the optical depth depending on the disk inclination could also be taken into account (τ ~ |cosid-1|). The outer disk radius was assumed to be six times the equatorial radius of the Be star (Rd0 = 63.4 R⊙), i.e. approximately the minimal possible radius that can be estimated from the contact times in the eclipse light curves (Mikołajewski et al. 2005a). A possible additional contribution of radiation from the eclipsing body (disk and/or its central object) to the total flux (commonly called “the third light”) and scattering of Be star radiation off the disk particles have been neglected. We assumed that the matter of the disk absorbs radiation selectively in accordance with interstellar extinction. The passband-dependent absorption coefficients were estimated based on the total value of the reddening, which increased by ΔEB − V ≈ 0.05 during mid-eclipse in 2003.
The Be star parameters that could not be reliably calculated during the modelling process
had to be entered as inputs into the model. Our spectra show that the hot component has an
effective temperature Teff = 15 000 K and
log g = 3.5, implying that it is a B5III or B4II type star. With the
spectral type and luminosity class, the stellar effective temperature and luminosity
L = 3500 L⊙ can be determined using the
statistical relations of de Jager & Nieuwenhuijzen
(1987). Comparing the resulting values with the theoretical evolutionary models
for stars with moderate and high masses (Claret
2004), via interpolation, the mass range
MBe = 8.0 ± 2.2 M⊙ was
estimated for the mass of the Be star in EE Cep. A mean stellar radius was estimated with
the Stefan-Boltzmann law. For a description of the star’s surface, its shape and
radiation, we used the model described by Cranmer &
Owocki (1995) and Owocki et al. (1994) in
our program. The model takes into account both the oblateness of the star and gravity
darkening using a Roche model and a von Zeipel
(F ~ g → Teff ~ g0.25)
law. By comparing of the critical rotational velocities that characterize each pair of
mass and radius with the observed rotational velocity, which for the adopted inclination
i = 90° is v = 350 ± 50 km s-1, we
constrained the possible masses to the range
5.9 M⊙ ≲ MBe ≲ 7.9 M⊙,
i.e. the range in which stars do not disintegrate as a result of rapid rotation. We
eventually decided to fix the basic parameters of the Be star in our model to a mass
M = 6.7 M⊙, mean radius
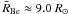 (with equatorial to polar radius ratio
(with equatorial to polar radius ratio 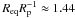 , giving equatorial and
polar radii, respectively,
Req ≈ 10.57 R⊙ and
Rp ≈ 7.34 R⊙), luminosity
L = 3500 L⊙, and rotational velocity at
the equator Veq = 325 km s-1. To perform
a χ2 minimization, our numerical code was equipped with the
simplex algorithm. This procedure used the method described in Brandt (1998) and the flowchart of Kallrath & Milone (1999).
, giving equatorial and
polar radii, respectively,
Req ≈ 10.57 R⊙ and
Rp ≈ 7.34 R⊙), luminosity
L = 3500 L⊙, and rotational velocity at
the equator Veq = 325 km s-1. To perform
a χ2 minimization, our numerical code was equipped with the
simplex algorithm. This procedure used the method described in Brandt (1998) and the flowchart of Kallrath & Milone (1999).
 |
Fig. 12 Schematical explanation of the geometrical parameters in the special case when the precession axis of the disk (the symmetry axis of the conical surface over which the rotation axis of the disk moves cyclically with the precession period Pprec) is parallel to the Y axis of the coordinate system (i.e. it is perpendicular to the orbital plane). Our code allows this axis to be inclined by angles θprec and φprec in a similar way to the inclination of the rotation axis. |
The solutions were carried out using the UBV(RI)C light curves. In general, several parameters were treated as free parameters: the impact parameter D, the mid-eclipse moment T0 (in the sense of the minimum proximity of the star and the disk centres in the projection on the sky plane), the relative tangential velocity of the star and the disk Vt, the inclination of the disk (90° − θd), an angle related to the disk precession phase φd, the absorption coefficient κs representing the contribution by the grey extinction and the central disk density ρc expressed in arbitrary units. The geometrical parameters (D, θd, φd, Rd0, Rd1, and Rd2) describing the disk sizes and orientation in the models are presented in Fig. 12. The code allows additional disk radii Rdi for i ≤ 5 to be defined, making it possible to take into account the presence of one or two gaps in the disk and the central opening.
4.2. A solid or a gapped disk model?
We used our code to model the last two eclipses with a solid disk causing the eclipses. This model is consistent with the global changes in the light curves and colours (it fits the depth and the shape of the eclipses), especially for the 2003 eclipse (see Fig. A.1). However, this model has trouble in explaining the two blue maxima in the colour evolution that appeared during the last two eclipses, roughly symmetrically a few days before and after the photometric minimum.
We tried to explain these blue maxima based on a hot star being rotationally darkened at the equator and brightened at the poles, and assuming that the eclipsing disk is divided into two parts by a gap. For a hot Be star such as EE Cep, convection is impossible in the envelope and we can expect the darkening effect to occur in pure von Zeipel (1924) form. Since the star rotates with a velocity very close to the critical value, the gravity darkening effect can result in a difference between the polar and the equatorial temperatures of as much as 5–6 thousand Kelvins. Thus, the appearance of the hot polar area in the gap could be observed as the blue maxima. Gałan et al. (2008) considered and briefly described a model with a disk that has a concentric gap for the 2003 eclipse. In the current work, an attempt has been made to create a similar model for the last two eclipses together, by taking into account the precession period Pprec as an additional free parameter. Although this model seemed to be appropriate when the 2003 eclipse alone is considered, it does not work well when we consider the two eclipses together (see Fig. A.2). The model indeed generates colour changes and blue maxima of the same order as observed during the 2003 eclipse. However, its predictions are inconsistent with the observations, because the shallower eclipses should be accompanied by a less pronounced “bump” and associated blue maximum, in contradiction to the case of the 2003 and 2008/9 eclipses taken together. The “bump” at JD 2 454 836 in the last eclipse (E = 10) seems to be too strong to be explained entirely by a gap in the disk.
 |
Fig. 13 Schematic explanation for the formation of the bump in the light curves. The configurations of the star and the disk at the first and second minima are shown at the top. |
 |
Fig. 14 Modelling of the eclipses of a rapidly rotating Be star by a solid disk, considering both the 2003 (left) and 2008/9 (right) eclipses. The precession period is a free parameter. The top panels show projections of the system onto the plane of the sky. The polar (hot) and equatorial (cool) areas of the star are shown by changing shades. The inner (opaque) and outer (semi-transparent) areas of the disk are shown by dark and light shades, respectively. The sizes are expressed in solar radii. The lower panels show the B light curve (middle) and the B − IC colour index (bottom) together with the synthetic fits (lines). The Julian day in the upper right corner represents the moment at which (according to the model) the spatial configuration of the system is the same as shown in the relevant panel. |
After many attempts to model the light changes during the eclipses, especially the shallow ones, we realized that another mechanism, connected with the flattening of the Be star, could be helpful in explaining the “bump”. For example, we consider the case when the disk has an inclination close to 90 degrees (when the eclipse is shallow) and the tilt with respect to the direction of motion is high (we expect that this could occur for the eclipses at epochs E = 9, E = 10). The temporal superposition of the two minima should be observed, corresponding to the successive obscuration of the two hot poles separately, at significantly different times (see Fig. 13). The first minimum is shallower and the second deeper, because of the non-zero value of the impact parameter, which reduces the obscuration of one of the poles, and because the outer part of the disk is more transparent than the inner part. The condition for the occurrence of the “bump” is a sufficiently long temporal separation of the two minima. Models generated using our numerical code at various precession phases suggest that the “bump” would disappear in the deep eclipses and be stronger in the shallow ones, matching what we observe. Although this scenario is very promising, it may not match the observed colour changes. The main problem is the second blue maximum, which appears in both of the last eclipses (during 2003 and 2008/9), although it is already very weak during the last one. We speculate that the reason for the occurrence of the second blue maximum may be (i) a concentric gap (or a local, concentric depression of the density) or (ii) a central opening in the disk structure. The former would be adequate for eclipse models similar to those presented here, i.e. in which the impact parameter is small enough for both sides of the entire disk to be involved in the eclipses. The latter would require the impact parameter to be larger, so that the eclipses could be caused by about half of the disk. Which of these two cases is true? We are unable to establish this based on the photometric observations. The behaviour of the Na i sodium doublet lines suggests that case (ii) may be correct. In this case, the disk would be about twice as large as in case (i) and it would move on an orbit with an appropriately higher speed.
4.3. Precession solutions from the 2003 and 2008/9 eclipses
As stated above, we propose that the precession of the disk is responsible for the observed differences between the eclipses from epoch to epoch. Since the number of eclipses observed is small, the constraints on precession are weak, so other processes, perhaps connected with changes in the disk size and/or its internal structure, might be needed to explain the rapid changes. Nevertheless, we decided to study our hypothesis of precession as the most likely hypothesis that can presently be constrained.
In one approach, we used the highest quality photometric data obtained during the last two eclipses, when the disk was nearly edge-on, so that its optical thickness was high, but it projected to a small solid angle at that time. Using our code, we determined the best-fit solution for the solid disk for the two last eclipses, taking precession into account. The basic assumptions about the nature of the Be star, and the both fixed and free parameters were the same as those in Sect. 4.1. The disk was treated as having negligible thickness (infinitesimally small with all its mass concentrated in the plane) with an r-2 density profile. The precession period of the disk Pprec was adopted as an additional free parameter. For simplicity, the precession axis was assumed to be perpendicular to the orbital plane. The resulting model is presented in Fig. 14 and its parameters are shown in Table 3. The best-fit solution was obtained for the precession period Pprec ≈ 61.94 yr (about 11 Porb) for which the angle related to the disk precession phase φd changes from 34.88°at epoch E = 9 to 67.5°at epoch E = 10. Such a fast precession seems to be necessary to explain the observed rapid changes in the eclipse depths at consecutive epochs. For example, the very shallow eclipse at E = 3 occurred very close in time to two very deep eclipses at E = 2 and E = 4, and the deep minimum at E = 8 was followed by two shallow ones at E = 9 and 10. An alternative solution exists according to which the disk would achieve, at epoch E = 10, the precession phase φd = 112.5°with about half the precession period of the former solution, Pprec ≈ 26.03 yr (~5 Porb). Since we are only able to observe a projection of the disk, we are unable to distinguish between these two cases using only the photometric data of these two eclipses.
Parameters obtained from the solution of the solid disk model when applied to the last two eclipses together, taking into account disk precession.
4.4. Precession solutions using all the eclipses
However, although the precession period in EE Cep should indeed be rather short, its lower limit of about five orbital periods inferred from colour variations during two successive eclipses, as presented in Sect. 4.3, seems unrealistic. One credible argument for a longer period of precession is the following, which favours a Pprec of the order of 14Porb (≈ 78.5 yr). If the shallow minimum with a flat bottom observed in 1969 was indeed caused by an edge-on, non-tilted disk (Mikołajewski & Graczyk 1999), then the precession axis is not perpendicular to the orbital plane. For perpendicular orientations, two edge-on positions with opposite tilt angles should be observed. More generally, two edge-on positions can occur when the precession axis lies nearly in the sky plane and is inclined with respect to the orbital plane. One of these positions may be non-tilted with respect to the orbital motion, but both should produce similar (shallow) eclipse depths, despite the very different tilt angles, because an edge-on disk obscures at most only a small part of the Be star. This situation might have arisen in 1969 (E = 3) and 2008/9 (E = 10), if the time interval between these minima was about half a precession period. This hypothesis provides a solution what may satisfy the data of all the eclipses. Thus, we propose this as a possible way of explaining the seemingly chaotic changes that occur in successive eclipses. The next key step in understanding this system was to realize that the deepest eclipses are not necessarily those that occur when the projected disk size is greatest (as we assumed at first); the deepest eclipses must instead be those where the column density in the disk and the projected disk size are together high enough to obscure most of the Be star surface. This situation must occur close in time to the most shallow eclipses in order to be consistent with the rapid changes in the eclipse depths. According to this line of reasoning, during the shallowest eclipses, the projection of the disk becomes small so that there is very little obscuration of the stellar flux, even though the column density in the disk is greatest at that time. Similarly, the eclipses should have intermediate depths at those precession phases at which the projected disk size is largest, since, despite the eclipsing of nearly the whole surface of the star, this eclipsing is performed by the highly transparent part of the disk.
We tested this hypothesis using our numerical code for the case with a precession axis inclined relative to the normal of the orbital plane by several different small values of θprec. We found that as a first approximation, φprec should be around 70°–80° (see Fig. 12 for the definition of θprec and φprec). When θprec is non-zero (i.e. the precession axis is inclined), the value of φprec determines how unequal the time intervals between the two shallowest minima in the precession cycle will be and how different the eclipse depths will be between these two intervals. We define II as the time interval from the eclipse with the minimal tilt of the projected disk (as in 1969) to the eclipse with a maximal disk tilt (as in 2008/9) and vice versa, III as the time interval from the eclipse with maximal disk tilt to the eclipse with minimal disk tilt. When φprec = 90°, the time intervals II and III are equal and the changes in eclipse depth as a function of precession phase proceed symmetrically with respect to the times of the shallowest eclipses. In general, however, φprec differs from 90°, in which case asymmetry appears. For example, when φprec < 90°, the time interval III is shorter than II and the eclipses during III are deeper, especially during the central parts of this interval. This seems to be the case for EE Cep. We know that II ~ 7Porb and that III seems to be shorter. Hence, if this scenario were correct, we would have succeeded in constraining the full precession period Pprec ≲ 14Porb.
 |
Fig. 15 Dependence of the depths of eclipses in EE Cep system on precession. Photometry obtained during epochs 0–10 is shown as circular symbols. The solid and dashed lines delineate two models of the changes in eclipse depth as a function of orbital phase, generated using our numerical code. In these two cases, the precession periods Pprec are 10.8 Porb and 11.8 Porb, respectively. At the bottom, the spatial configurations of the disk and the star in four special cases, denoted by the letters a, b, c, and d, are shown. |
Subjective (“eye”) and quantitative (“fit”) optimal solutions of our precession model using all the eclipses.
We considered many combinations of sets of parameters, for different disk sizes, starting from the large (Rd0 ~ 200 R⊙) and geometrically thick (H ~ Rp) disks. Because the adopted artificial density distribution does not provide a good solutions for the external parts of the light curves during the eclipses, we concentrated on their central parts, i.e. we searched for the set of parameters that could explain the dependence of eclipse depth on precession phase. By visual inspection of plots comparing the synthetic curves that represent the dependence of the eclipse depth on precession with the observational data, we chose subjectively a few optimal sets of parameters. One of these fits, perhaps the best of them, is shown in Table 4 (left) and Fig. 15 (dashed line). Using the simplex algorithm, we performed a χ2 minimization over the parameter space of the system input parameters. The best-fit solution is that shown in Table 4 (right) and the synthetic fit is presented as the solid line in Fig. 15. Our solutions were obtained for a disk radius Rd0 ≈ 75 R⊙ and a geometrically very thin disk H = 0.6 R⊙. We cannot exclude, however, the possibility that a smaller or larger disk could provide more reliable results. On the other hand, the disk thickness in the optimal solution equals the spatial resolution adopted in the model (which represents the grid size) and in reality, the disk could be even thinner. The disk must be extremely thin in order for this model to work correctly at times close to the shallow minima. Some of the eclipses in the EE Cep system could be even shallower than those in 2008/9 (the disk could sometimes almost completely disappear, as happens with Saturn’s rings when they have an edge-on orientation).
Thus, our model (Table 4) suggests that the value
of the precession period should be about 11–12 Porb. Is it
possible that the precession period is really so short? The development of a mechanical
model of a precessing circumstellar disk would be a useful follow-up study to this paper
to test our preferred solution theoretically. Empirically, at least one binary system that
appears to have a similarly short precession period exists. This system, SS433, is very different from EE Cep – it is far more
compact and the disk has to be smaller and perhaps more massive. Margon et al. (1980) suggested that the SS433 system,
with Porb ≈ 13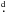 1, has an
accretion disk that can precess with a period of
164
1, has an
accretion disk that can precess with a period of
164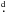 , which is just
12.5 times its orbital period.
, which is just
12.5 times its orbital period.
Applying our model of precession to predict the depth of the next EE Cep minimum, we find
that it should be similar to the deepest of the previous eclipses, reaching about
2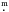 . According to
the ephemeris (Eq. (1)), this minimum should occur on
23 Aug. 2014. To some degree, this tests our proposed model, although this model has
a serious problem. The existing set of observations span a time interval that is almost
identical to the expected precession period. A statistically more significant test would
require much more than one full precession cycle, and preferably at least two cycles.
Several more decades of observations would be required. Nevertheless, there is some hope
that old photographic surveys might contain a sufficient amount of extra data. For
example, the database of the DASCH3 (Digital Access
to a Sky Century at Harvard) project (see Grindlay et al.
2009) provides data from more than 5000 old Harvard photographic plates obtained
between JD 2 411 556 and JD 2 447 823 (nearly exactly 100 years) that contain EE Cep in
their field of view. By checking the Julian dates when these photographs were obtained
using EE Cep’s ephemeris, it seems likely that we may be able to extract data for the
eclipses from epochs E = −9 to E = −1, with which we
can test our model.
. According to
the ephemeris (Eq. (1)), this minimum should occur on
23 Aug. 2014. To some degree, this tests our proposed model, although this model has
a serious problem. The existing set of observations span a time interval that is almost
identical to the expected precession period. A statistically more significant test would
require much more than one full precession cycle, and preferably at least two cycles.
Several more decades of observations would be required. Nevertheless, there is some hope
that old photographic surveys might contain a sufficient amount of extra data. For
example, the database of the DASCH3 (Digital Access
to a Sky Century at Harvard) project (see Grindlay et al.
2009) provides data from more than 5000 old Harvard photographic plates obtained
between JD 2 411 556 and JD 2 447 823 (nearly exactly 100 years) that contain EE Cep in
their field of view. By checking the Julian dates when these photographs were obtained
using EE Cep’s ephemeris, it seems likely that we may be able to extract data for the
eclipses from epochs E = −9 to E = −1, with which we
can test our model.
4.5. On the similarity of EE Cep and ε Aur
Our observations show that the disk in the EE Cep system may be similar to (though smaller than) the multi-ring structure observed in ε Aurigae. Leadbeater & Stencel (2010) found that the equivalent width of the K i potassium line at 7699 Å increased step-wise during the ingress of the last ε Aur eclipse. They interpreted this pattern as a manifestation of the complex structure of the disk as an alternating series of concentric rings and gaps, which had already been suggested based on the observations of the previous eclipse during the 1980’s (Ferluga 1990). According to what until recently has been the dominant interpretation, based on ε Aur observations during the eclipse of the 1980’s, a quite close binary system should exist at the disk centre (Lissauer & Backman 1984). On the basis of their spectral energy distribution (SED) analysis, Hoard et al. (2010) suggested that the ε Aur system is composed of a massive B5V type primary embedded in a dusty disk with a radius of about 3.8 AU and an F type post-AGB secondary of about half the mass of the primary. In this model, the disk has to be a byproduct of mass transfer from the initially more massive star (currently an F type post-AGB) to what was initially the secondary (and is now a more massive B5V star). Kloppenborg et al. (2010), via interferometric observations during the ingress of the 2009 eclipse, detected and measured movement of the disk with respect to the F star. They confirmed the existence of an optically thick, inclined disk in the system and provided the first direct evidence that the disk is geometrically thin. The mass of the disk is dynamically negligible (≲ 15 M ⊕ ), but is sufficient to cause eclipses. Hoard et al. (2010) pointed out that the dust content of the disk must be largely confined to grains larger than ~10 μm to explain the grey nature of eclipses, from the optical range up to the infrared, and the lack of broad dust emission features in the mid-infrared spectra. Owing to the important role that grey extinction plays in our models, we can conclude that the disk in the EE Cep system should also be dominated by particles of quite large diameters – a mixture of grains and dust, and our results concerning our precession model also suggest that this disk should be geometrically very thin.
In both cases, ε Aur and EE Cep, the disks are inclined to the orbital plane. The presence of a binary system at the disk centre might help to explain the inclination of the disk and the rapid precession. However, the statistical likelihood of a binary system at the centre of the disk in the case of ε Aur is low, and for EE Cep even lower. Another possible way of explaining the inclination of the disk is that since the main component in EE Cep is a rapidly rotating Be star, it is very probable that it is the donor star that supports a disk around its companion. Therefore, to explain the inclination of this disk relative to the orbit, we have to assume that the orbital plane is not coplanar with the equatorial plane of the Be star. In this case, the disk around the companion will also not be coplanar with the orbit. In principle, to introduce disk precession into the system in a way in which the precession axis is inclined to the orbital plane, it is sufficient to add a third body as the perturber if it satisfies two conditions: (i) its orbit should not be coplanar with the orbital plane of the disk, and (ii) it should have a high enough mass (and/or the disk should have a low enough mass). In the light of these two conditions, we have many possibilities as to what could constitute a third body. It could be an object orbiting the Be star, either closer to or further away from than the eclipsing object, but it might also be an object on an orbit around the body at the disk centre, either outside or within the disk. The latter case would be equivalent to the presence of a binary system at the disk centre. At the moment, we probably do not have enough observations of the system to decide which of these possibilities is most likely to be correct.
In addition to the differences in the sizes of the systems, there are additional indications that the geometries of the eclipses could be very different. While the consecutive eclipses in ε Aur are nearly identical in terms of their depth (see e.g. Stencel 2009), the eclipse depths in EE Cep are highly variable. Some variations in the durations of the entire eclipse and the various stages of the eclipse (ingress, totality, and egress) in ε Aur (see Hopkins & Stencel 2008) are observed. Perhaps these changes could be explained in terms of disk precession. In this case, the large differences between the eclipse depths of EE Cep and ε Aur would be explained by variations in the direction of the rotation axis due to the strong precession in the case of EE Cep and a small θprec (of Fig. 12 caption) in ε Aur. There are also interesting differences between the Na i doublet line profiles observed during the eclipses of these systems. During the last eclipse of ε Aur, an additional component appeared, which was redshifted during the first part of the eclipse and blueshifted during the second part (see Tomov et al. 2012), in contrast to EE Cep, where only blueshifted additional components were observed. This may indicate that in the case of EECep, the impact parameter may be so large that roughly only half of the disk is involved in the eclipses.
5. Conclusions
We have presented our observational data obtained during the last three eclipses of EE Cep. We release these data for use by the astronomical community. For the two latest minima, our investigations were carried out as international campaigns that provided data of unprecedented quality for this object, especially in the case of the photometry, where an accuracy of a few thousandths of a magnitude was achieved. These minima turned out to be the shallowest EE Cep eclipses observed. The grey character of these eclipses, i.e. the weak dependence of the eclipses’ depth on the photometric band, reinforces our belief that the eclipsing object is indeed a dark, dusty debris-disk around a low-luminosity central body that is visible in neither the spectra nor photometry.
The results of these campaigns shed new light on our understanding of the EE Cep system. Our spectroscopic data have demonstrated that the main component of the system is a rapidly rotating (vsini ≈ 350 km s-1) Be-type star. The oblateness of the star leads, via the von Zeipel effect, to a highly inhomogeneous temperature distribution across its surface. The spectra obtained during the last two eclipses suggest that the absorption lines change in the same way during each eclipse. During the minima of both eclipses, we were able to detect at least three absorption components in the Na i lines and the same strong absorption superimposed on the Hα emission.
By analysing all the photometric and spectroscopic data together, we have proposed several hypotheses that provide predictions for future eclipses.
Using high quality photometry, it was possible to detect two blue maxima in the colour indices during the 2003 and 2008/9 eclipses, that occurred from about six to nine days before and after the photometric minimum. The first (stronger) blue maximum occurred simultaneously with a “bump” in the light curves, which is very clear in all the UBV(RI)C photometric bands. This “bump” seems to be caused by a temporal offset between the two minima in a single eclipse, which can be explained by the non-simultaneous obscuration of the hot polar regions of the Be star by the elliptical, tilted shape of the projected disk.
The durations of the last two eclipses were longer than expected (both lasting about 90 days). In the external parts of these long minima, two shallow minima were observed about 35 days before and after mid-eclipse during both epochs (arrows in Fig. 10). This could be explained by the presence of a gap near the outer border of the disk. The second blue maximum, which could not be explained by the mechanism proposed for the “bump”, may indicate the existence of either an inner gap or a central opening. Thus, the disk in the EE Cep system could have a complex, possibly multi-ring structure. The behaviour of the Na i line profiles gives some support to this idea. Another hypothesis that follows from the behaviour of these lines and the recurrent asymmetry of the eclipses is that maybe only half the disk is involved in the eclipses.
Considering all the eclipses together, from the 1950’s to the present, we estimated the
duration of the disk precession period to be about 62–67 years
(~11–12 Porb). Using our new model of precession, we predict
that the depth of the forthcoming eclipse in 2014 should be one of its deepest, reaching
about 2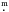 .
.
More spectroscopic observations during the next eclipse would be needed to more clearly
understand the nature of the EE Cep system. Photometry in the infrared JHK
bands during and after the eclipse would be very useful. This could make it
possible to detect the secondary companion of EE Cep (disk and/or central star/stars), as it
seems to make a significant contribution to the total flux at the red edge of the visible
spectrum (a brightening event by about 0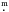 05 at the phase
~0.2 was observed). The radial velocity variations of the hot component, which would be
a real challenge to obtain, may be of crucial importance in constraining the parameters of
this system.
05 at the phase
~0.2 was observed). The radial velocity variations of the hot component, which would be
a real challenge to obtain, may be of crucial importance in constraining the parameters of
this system.
Online material
Appendix A: The models of eclipses with a solid or a gapped disk
Using our numerical code, we fitted models of the last two eclipses separately, using a solid disk as the eclipsing object. We made the same assumptions about the nature of the Be star, and we used the same fixed and free parameters as in Sect. 4.1. The disk was treated as having negligible thickness (infinitesimally small with all the mass concentrated in the plane) and an r-2 density profile. For simplicity, the precession axis was assumed to be perpendicular to the orbital plane. The resulting solution is shown in Table A.1 together with the error estimates. In Fig. A.1, we present models of two eclipses using a solid disk, for the 2003 eclipse on the left and for the 2008/9 eclipse on the right. The models containing a solid disk provide quite a good fit to the light curve and the global colour changes, reproducing both the depth and the shape of the eclipses, especially for the 2003 eclipse. This model, however, cannot explain the two maxima in the colour evolution during the eclipses.
Parameters of the solutions obtained for the solid disk model, derived independently for the 2003 eclipse (left) and the 2008/9 eclipse (right).
In the present study, we adopted a model containing a disk that has a concentric gap for the two last eclipses, taking into account the precession of the disk. We assumed the same disk diameter, disk density distribution, and orthogonality of the precession axis to the orbital plane, and the same Be star parameters
as in the case of the solid disk. This model was based solely on the B − IC, V − IC, and V − RC colour indices. We chose the same free parameters as in the case of the solid disk model for the 2008/9 eclipse (the tangential velocity was fixed at Vt = 1.57 R⊙ day-1) but added three more free parameters: the precession period Pprec and two parameters specifying the outer Rd1 and inner Rd2 radii of the gap. The resulting model is presented in Fig. A.2 and Table A.2. The best results were obtained for the precession period Pprec ≈ 31.91yr (about 5–6 Porb), for which the angle related to the disk precession phase φd changes from 50.00°at epoch E = 9 to 113.32°at epoch E = 10. An alternative solution was found to exist in which the precession phase φd = 66.68°at epoch E = 10 has a precession period Pprec ≈ 121.13 yr, which is almost four times longer (being about 22 Porb). In the light of the results of Sects. 4.3 and 4.4, both these periods of precession seem to be unrealistic. Comparison of this model with the Gałan et al. (2008) model for the 2003 eclipse alone reveals a problem. The gapped disk model seemed to be very promising for explaining the colour changes that occurred during the 2003 eclipse, but fails in the case of the 2008/9 eclipse, since it cannot explain either the colour changes during an eclipse or the strong “bump” in the light curve.
Parameters of the solution of the gapped disk model when applied to the last two eclipses together, taking into account disk precession.
 |
Fig. A.1 Modelling of the eclipse of a rapidy rotating Be star as a solid disk during the 2003 eclipse (left) and the 2008/9 eclipse (right). The top panels show the system projected onto the plane of the sky. The polar (hot) and equatorial (cool) areas of the star are shown by different shades. The inner (opaque) and outer (semi-transparent) areas of the disk are shown by dark and light shades, respectively. The sizes are expressed in solar radii. The lower panels show the B light curve (middle) and the B − IC colour index (bottom) together with the synthetic fits (lines). The Julian day in the upper right corner represents a moment at which (according to the model) the spatial configuration of the system is the same as that shown in the relevant panel. |
 |
Fig. A.2 Modelling of the last two eclipses together with the precession period taken as an additional free parameter, when a gapped disk is considered. The sky plane projections of the system during the last two eclipses (at E = 9 and E = 10) (top), the B light curve (middle), and the B − IC colour index (bottom), together with the synthetic fits (lines) are shown. The symbols and the shades of colour have the same meaning as those in Fig. A.1. |
Acknowledgments
E. Semkov would like to thank the Director of Skinakas Observatory, Prof. I. Papamastorakis, and Dr. I. Papadakis for granting telescope time. We thank T. Karmo, Stefan Mochnacki, and G. Conidis for contributing their data. Some of the observations used here were taken courtesy of the AAVSO and the Sonoita Research Observatory. This study was supported by MNiSW grant No. N203 018 32/2338.
References
- Brandt, S. 1998, Data Analysis, Statistical and Computational Methods, Polish edition (Polish Scientific Publishers PWN) [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cranmer, S. R., & Owocki, S. P. 1995, ApJ, 440, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Ferluga, S. 1990, A&A, 238, 278 [Google Scholar]
- Gałan, C., Mikołajewski, M., Tomov, T., et al. 2008, IBVS, 5866 [Google Scholar]
- Gałan, C., Mikołajewski, M., Tomov, T., et al. 2009, in Binaries – Key to Comprehension of the Universe, eds. A. Prsa, & M. Zejda, ASP Conf. Ser., 435, 423 [Google Scholar]
- Graczyk, D., Mikołajewski, M., Tomov, T., et al. 2003, A&A, 403, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grindlay, J., Tang, S., Simcoe, R., et al. 2009, in Preserving Astronomys Photographic Legacy, ed. W. Osborn, & L. Robbins, ASP Conf. Ser., 410, 101 [Google Scholar]
- Hajduk, M., Zijlstra, A. A., & Gȩsicki, K. 2008, A&A, 490, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoard, D.W., Howell, S. B., & Stencel, R. E. 2010, AJ, 714, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, J. L., & Stencel, E. R. 2008, Epsilon Aurigae – a mysterious star system, Phoenix Observatory, 2008, 67 [Google Scholar]
- de Jager, C., & Nieuwenhuijzen, H. 1987, A&A, 177, 217 [NASA ADS] [Google Scholar]
- Kallrath, J., & Milone, E. F. 1999, Eclipsing binary stars – modeling and analysis (New York: Springer) [Google Scholar]
- Kloppenborg, B., Stencel, R., Monnier, J., et al. 2010, Nature, 464, 870 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leadbeater, R., & Stencel, R. 2010 [arXiv:1003.3617] [Google Scholar]
- Lissauer, J. J., & Backman, D. E. 1984, ApJ, 286, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Margon, B., Grandi, S. A., & Downes, R. A. 1980, ApJ, 241, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewski, M., & Graczyk, D. 1999, MNRAS, 303, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewski, M., Tomov, T., Graczyk, D., et al. 2003, IBVS, 5412 [Google Scholar]
- Mikołajewski, M., Gałan, C., Gazeas, K., et al. 2005a, Ap&SS, 296, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewski, M., Tomov, T., Hajduk, M., et al. 2005b, Ap&SS, 296, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., Cranmer, S. R., & Blondin, J. M. 1994, ApJ, 424, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, G. 1956, Coelum, 24, 135 [Google Scholar]
- Samolyk, G., & Dvorak, S. 2004, JAAVSO, 33, 42 [NASA ADS] [Google Scholar]
- Stencel, R. E. 2009, Sky Telesc., 58 [Google Scholar]
- Tomov, T., Wychudzki, P., Mikołajewski, M., et al. 2012, BlgAJ, in press [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, R. 1956, Doc. des Obs. Circ., No. 9 [Google Scholar]
All Tables
Overview of instruments and their involvement in photometric observations of the EE Cep eclipses since 1997.
Overview of the instruments involved in the spectroscopic observations during the three last eclipses at epochs E = 8, E = 9, and E = 10.
Parameters obtained from the solution of the solid disk model when applied to the last two eclipses together, taking into account disk precession.
Subjective (“eye”) and quantitative (“fit”) optimal solutions of our precession model using all the eclipses.
Parameters of the solutions obtained for the solid disk model, derived independently for the 2003 eclipse (left) and the 2008/9 eclipse (right).
Parameters of the solution of the gapped disk model when applied to the last two eclipses together, taking into account disk precession.
All Figures
 |
Fig. 1 Schematic representation of the eclipse geometry in the EE Cep system. The inner opaque and outer semi-transparent regions of the disk are separated. The characteristic positions of the disk and the star configuration during the eclipses (left) correspond to the contact times (1a, 1, 2, 3, 4, 4a) distinguished in the light curve (right). The figure shows a highly simplified case that ignores a number of issues such as e.g. possible inhomogeneities in the distribution of brightness on the star’s surface or of the actual size of the disk. |
| In the text | |
 |
Fig. 2 U (dots) and i (crosses) light curves obtained during the 1997 eclipse of EE Cep. |
| In the text | |
 |
Fig. 3 All of the approximately 800 individual photometric UBV(RI)C measurements obtained during the 2003 eclipse (left; Tables B.2–B.11) and all of the more than 1600 observations obtained during the 2008/9 eclipse (right; Tables B.12–B.32). |
| In the text | |
 |
Fig. 4 Average points from Table B.35 of the 2003 eclipse (left) and the 2008/9 eclipse (right). The B light curves (top) and three colour indices (bottom) are presented. Arrows denote times of blue maxima. |
| In the text | |
 |
Fig. 5 Differential I magnitudes of EE Cep obtained at Piwnice
Observatory during the 13 years from 1996 to 2010. The zero value corresponds to the
level of the average brightness outside (phases 0.4–0.8) eclipses. Below
+0 |
| In the text | |
 |
Fig. 6 Hβ and Fe ii line profiles in the spectra obtained during the 2008/9 eclipse with the Nordic Optical Telescope (NOT, La Palma). The spectra are vertically offset for clarity. |
| In the text | |
 |
Fig. 7 Balmer H10 and H11 line profiles in the spectrum of EE Cep taken on 11 Aug. 2003 with an Echelle spectrograph on the 2.12 m telescope in SPM Observatory in Mexico. The best fit was obtained for a synthetic spectrum with: Teff = 15 000 K, log g = 3.5, [Fe/H] = 0, and vsini = 350 km s-1 (solid line). Two poorer fits calculated with different values of the rotational velocity, vsini = 300 km s-1 (dashed line) and vsini = 400 km s-1 (dash-dotted line), are shown for comparison purposes. |
| In the text | |
 |
Fig. 8 Representative examples of Hα line profiles in the spectra obtained near the eclipses at epochs E = 10, E = 9, and E = 8 (in the electronic version of this paper, the profiles have different colours: red, blue, and green, respectively). The spectra are vertically offset for clarity. |
| In the text | |
 |
Fig. 9 Representative examples of Na i doublet line profiles in the spectra obtained near the eclipses at epochs E = 10, E = 9, and E = 8 (in the electronic version of this paper, the profiles have different colours: red, blue, and green, respectively). The spectra are vertically offset for clarity. |
| In the text | |
 |
Fig. 10 B and B − V light curves of the 2003 (bottom) and 2008/9 (top) eclipses. In the middle panel, we present all available line profiles of the Na i doublet and Hα for epoch 9 (superposition of two lines: thick dashed with thin solid) and 10 (solid line). The positions of the continuum levels refer to the orbital phases. The right-hand panels show a zoom of the central part of left-hand panels as indicated by vertical dashed lines. The arrows indicate the shallow minima in the external parts of the eclipses observed about 35 days before and after mid-eclipse at both last epochs (both last eclipses seem to be longer than expected and lasted about 90 days). |
| In the text | |
 |
Fig. 11 Radial velocities of the three components of the sodium doublet Na i lines obtained from the spectra of five observatories (NOT, SPM, DDO, Asiago, and Rozhen). The main stellar component is shown with filled circles, and two components from the disk blue-shifted by about −40 and −70 km s-1 are shown with open circles and filled diamonds, respectively. |
| In the text | |
 |
Fig. 12 Schematical explanation of the geometrical parameters in the special case when the precession axis of the disk (the symmetry axis of the conical surface over which the rotation axis of the disk moves cyclically with the precession period Pprec) is parallel to the Y axis of the coordinate system (i.e. it is perpendicular to the orbital plane). Our code allows this axis to be inclined by angles θprec and φprec in a similar way to the inclination of the rotation axis. |
| In the text | |
 |
Fig. 13 Schematic explanation for the formation of the bump in the light curves. The configurations of the star and the disk at the first and second minima are shown at the top. |
| In the text | |
 |
Fig. 14 Modelling of the eclipses of a rapidly rotating Be star by a solid disk, considering both the 2003 (left) and 2008/9 (right) eclipses. The precession period is a free parameter. The top panels show projections of the system onto the plane of the sky. The polar (hot) and equatorial (cool) areas of the star are shown by changing shades. The inner (opaque) and outer (semi-transparent) areas of the disk are shown by dark and light shades, respectively. The sizes are expressed in solar radii. The lower panels show the B light curve (middle) and the B − IC colour index (bottom) together with the synthetic fits (lines). The Julian day in the upper right corner represents the moment at which (according to the model) the spatial configuration of the system is the same as shown in the relevant panel. |
| In the text | |
 |
Fig. 15 Dependence of the depths of eclipses in EE Cep system on precession. Photometry obtained during epochs 0–10 is shown as circular symbols. The solid and dashed lines delineate two models of the changes in eclipse depth as a function of orbital phase, generated using our numerical code. In these two cases, the precession periods Pprec are 10.8 Porb and 11.8 Porb, respectively. At the bottom, the spatial configurations of the disk and the star in four special cases, denoted by the letters a, b, c, and d, are shown. |
| In the text | |
 |
Fig. A.1 Modelling of the eclipse of a rapidy rotating Be star as a solid disk during the 2003 eclipse (left) and the 2008/9 eclipse (right). The top panels show the system projected onto the plane of the sky. The polar (hot) and equatorial (cool) areas of the star are shown by different shades. The inner (opaque) and outer (semi-transparent) areas of the disk are shown by dark and light shades, respectively. The sizes are expressed in solar radii. The lower panels show the B light curve (middle) and the B − IC colour index (bottom) together with the synthetic fits (lines). The Julian day in the upper right corner represents a moment at which (according to the model) the spatial configuration of the system is the same as that shown in the relevant panel. |
| In the text | |
 |
Fig. A.2 Modelling of the last two eclipses together with the precession period taken as an additional free parameter, when a gapped disk is considered. The sky plane projections of the system during the last two eclipses (at E = 9 and E = 10) (top), the B light curve (middle), and the B − IC colour index (bottom), together with the synthetic fits (lines) are shown. The symbols and the shades of colour have the same meaning as those in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


