| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117838 | |
| Published online | 17 February 2012 | |
Star-formation laws in luminous infrared galaxies
New observational constraints on models⋆
1 Observatorio Astronómico Nacional (OAN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
e-mail: s.gburillo@oan.es
2 Centro de Astrobiología (CSIC-INTA), Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
3 Instituto de Física de Cantabria, CSIC-UC, Avenida de los Castros s/n, 39005 Santander, Spain
4 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
5 ESO & Joint ALMA Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
Received: 5 August 2011
Accepted: 28 November 2011
Context. The observational study of star-formation relations in galaxies is central for unraveling the related physical processes that are at work on local and global scales. It is still debated whether star formation can be described by a universal law that remains valid in different populations of galaxies.
Aims. We aim to expand the sample of extreme starbursts, represented by local luminous and ultra-luminous infrared galaxies (LIRGs and ULIRGs), with high-quality observations in the 1–0 line of HCN, which is taken as a proxy for the dense molecular gas content. The new data presented in this work allow us to enlarge in particular the number of LIRGs studied in HCN by a factor 3 compared to previous works. The chosen LIRG sample has a range of HCN luminosities that partly overlaps with that of the normal galaxy population. We study if a universal law can account for the star-formation relations observed for the dense molecular gas in normal star-forming galaxies and extreme starbursts and explore the validity of different theoretical prescriptions of the star-formation law.
Methods. We have used the IRAM 30 m telescope to observe a sample of 19 LIRGs in the 1–0 lines of CO, HCN and HCO+. The galaxies were extracted from a sample of local LIRGs with available high-quality and high-resolution images obtained at optical, near and mid IR wavelengths, which probe the star-formation activity. We therefore derived the star-formation rates using different tracers and determined the sizes of the star-forming regions of all targets.
Results. The analysis of the new data proves that the efficiency of star formation in the dense molecular gas (SFEdense) of extreme starbursts is a factor 3–4 higher compared to normal galaxies. Kennicutt-Schmidt (KS) power laws were also derived. We find a duality in KS laws that is further reinforced if we account for the likely different conversion factor for HCN (αHCN) in extreme starbursts and for the unobscured star-formation rate in normal galaxies. This result extends the more extreme bimodal behavior of star-formation laws that was derived from CO molecular lines by two recent surveys to the higher molecular densities probed by HCN lines.
Conclusions. We compared our observations with the predictions of theoretical models in which the efficiency of star formation is determined by the ratio of a constant star-formation rate per free-fall time (SFRff) to the local free-fall time (tff). We find that it is possible to fit the observed differences in the SFEdense between normal galaxies and LIRGs/ULIRGs using a common constant SFRff and a set of physically acceptable HCN densities, but only if SFRff ~ 0.005–0.01 and/or if αHCN is a factor of ~a few lower than our favored values. Star-formation recipes that explicitly depend on the galaxy global dynamical time scales do not significantly improve the fit to the new HCN data presented in this work.
Key words: galaxies: ISM / radio lines: ISM / galaxies: starburst / galaxies: star formation / radio lines: galaxies
© ESO, 2012
1. Introduction
The quest for a quantitative description of the star-formation rate dependence on a set of galaxy parameters (gas and stellar content, gas kinematics, environment) is a fundamental, though not fully understood problem. Observational constraints are central to understanding the role that small-scale (local) and large-scale (global) galaxy properties play in star-formation relations. This is a requisite to validating the recipes of star formation used in numerical simulations of galaxy evolution.
Based on simple theoretical grounds, Schmidt (1959) proposed that the star-formation rate (SFR) per unit volume (ρSFR) should be a power law of index N of the gas volume density (ρgas): 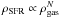 . Schmidt (1959) predicted that N should be around 2. If we suppose that the relevant time scale for star formation is the local free-fall time (tff), in this case ρSFR ∝ ρgas/
. Schmidt (1959) predicted that N should be around 2. If we suppose that the relevant time scale for star formation is the local free-fall time (tff), in this case ρSFR ∝ ρgas/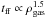 . If the gas scale-height is constant among galaxies, a non-trivial additional assumption, the equivalent of the Schmidt law in terms of the corresponding surface densities of SFR (ΣSFR) and gas (Σgas) is
. If the gas scale-height is constant among galaxies, a non-trivial additional assumption, the equivalent of the Schmidt law in terms of the corresponding surface densities of SFR (ΣSFR) and gas (Σgas) is 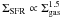 .
.
Krumholz & McKee (2005, see also Krumholz et al. 2009) developed a model that successfully describes how star formation takes place in a highly turbulent molecular medium. Their scenario pictures star formation as a very inefficient process that takes place in small subregions of supersonic turbulent and virialized molecular clouds. The surface density of the star-formation rate is in any case expected to scale as a power law of the mean density of the gas with an index close to 1.5. Star formation in Krumholz & McKee’s formulation is regulated by processes mostly within the clouds. The relevant time scale for these models, the free-fall time for cloud collapse, consequently is a local time scale. In this type of formulation, star-formation laws should not depend explicitly on global dynamical time scales or be determined by galactic-scale phenomena. Instead, large-scale processes are thought to be responsible for making the gas assembly prior to star formation in galaxies. Alternatively, other forms of the star-formation laws adduce the importance of including explicitly global dynamical time scales tdyn (Elmegreen 1997; Silk 1997; Kennicutt 1998; Elmegreen 2002; Boissier et al. 2003; Tasker & Tan 2009; Tan 2010; Genzel et al. 2010). The star-formation rate density ΣSFR should then scale as ∝ Σgas/tdyn. It is unclear as yet if the two forms of star-formation laws are fully equivalent in normal galaxies and in mergers. Kennicutt (1998) found that if tdyn is the average orbital dynamical time scale, both formulations are equally successful at describing star-formation laws in the disks of normal galaxies. The physical framework for this equivalence relies on the fact that normal galaxy disks, viewed as dynamically relaxed stable systems, fulfill the Toomre stability criterion (Toomre 1964). It is questionable, nevertheless, if this equivalence should also hold in extreme starbursts, which are often hosted by merging systems.
During the last decades observers have been using different proxies for ΣSFR and Σgas to validate the predictions of star-formation law models. These observations have been conducted on different galaxy samples, including normal galaxies and extreme starbursts at different redshifts. They also encompass a wide range of spatial resolutions, which allow not only global measurements but also studies of spatially resolved objects. The different observers do not find a single exponent fitting the entire star-formation relation. Kennicutt (1998) finds an index n = 1.40 ± 0.15 using CO and HI as gas tracers and a ~100 galaxy sample that includes normal galaxies, nuclear starbursts and a few luminous infrared galaxies (LIRGs) (~5) at z = 0. Yao et al. (2003) find an index n = 1.40 ± 0.30 in their CO survey of IR luminous galaxies. Bouché et al. (2007), by including submillimeter galaxies (SMGs) and using a lower CO conversion factor in z = 0 ultra-luminous infrared galaxies (ULIRGs), determines a higher index for the Kennicutt-Schmidt (KS) law n ~ 1.7. The high-resolution survey of 18 normal galaxies published by Bigiel et al. (2008) and Leroy et al. (2008) found a linear KS relation above a gas surface density threshold of 10 M⊙ pc-2, which determines the transition from atomic to molecular gas, here traced by CO lines.
More recently the CO surveys of Daddi et al. (2010) and Genzel et al. (2010) presented evidence that normal galaxies and mergers (LIRGs, ULIRGs and SMGs) occupy different regions in the molecular gas mass versus star-formation rate plane. These results suggest the existence of a bimodality in star-formation laws, where normal galaxies show 4–10 longer depletion time-scales compared to mergers. While the KS relation remains mostly linear inside each galaxy population, bimodality introduces a discontinuity in the two-function power law. These authors discussed that when global dynamical time scales are included, a universal star-formation law is obtained. Based on a study of far-infrared fine structure lines, Graciá-Carpio et al. (2011) concluded that extreme starbursts display significantly enhanced line deficits. The results of Graciá-Carpio et al. (2011) provide additional support for the existence of different properties of the interstellar medium in normal star-forming galaxies and extreme starburst systems.
Krumholz & Thompson (2007; see also Narayanan et al. 2008) studied how the power index of KS laws determined from observations should change depending on the critical density of the tracer used to probe the star-forming gas, a prediction confirmed by observations conducted in several dense gas tracers (Narayanan et al. 2005; Bussmann et al. 2008; Bayet et al. 2009; Juneau et al. 2009). In the particular case of HCN(1–0), only in galaxies where the average gas density exceeds a few 104 cm-3 (i.e., the effective critical density of the HCN J = 1–0 line), we would start to recover the expected superlinear behavior of the universal KS law derived by Krumholz & McKee (2005).
Observations of HCN lines have been used to study dense molecular gas properties in samples of normal spirals, LIRGs, ULIRGs, quasi-stellar objects (QSOs) and molecular gas-rich high-z galaxies (e.g., Gao & Solomon 2004a,b; Solomon & Vanden Bout 2005; Wagg et al. 2005; Riechers et al. 2007; Graciá-Carpio et al. 2006; 2008). In contrast to CO line observations, which are sensitive to the global molecular gas content, HCN observations are a much better tracer of the dense molecular phase, which is more directly related to star formation, and can therefore put stringent constraints on star-formation models. The most important result presented by Gao & Solomon in their seminal papers is the discovery of a tight correlation between the infrared and the HCN(1–0) luminosities over three orders of magnitude in LIR. This result was interpreted as evidence that star formation is the main power source in ULIRGs. The linearity of the tight correlation between the IR and the HCN(1–0) luminosities implies that the star-formation efficiency measured with respect to the dense molecular gas content (SFE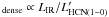 ) is constant in all galaxies, independently of LIR.
) is constant in all galaxies, independently of LIR.
More recent results have partly questioned this picture, however. Graciá-Carpio et al. (2008) published observations made with the IRAM 30 m telescope of the J = 1–0 and 3–2 lines of HCN and HCO+ used to probe the dense molecular gas content of a sample of 17 LIRGs and ULIRGs. These observations were also used to derive a new version of the power law describing the correlation between LFIR and 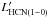 from normal galaxies (LIR < 1011 L⊙) to high-z galaxies. The results of Graciá-Carpio et al. (2008) indicated that the
from normal galaxies (LIR < 1011 L⊙) to high-z galaxies. The results of Graciá-Carpio et al. (2008) indicated that the 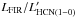 ratio, taken as proxy for SFEdense, is a factor ~ 2–3 higher in IR luminous targets compared to normal galaxies. Furthermore, Graciá-Carpio et al. (2008) found, based on a multiline analysis of HCN and HCO+ data, that XHCN is probably about three times lower at high LFIR. Taken together, these findings suggest that SFEdense may be up to an order of magnitude higher in extreme starbursts (LIRGs, ULIRGs) than in normal galaxies.
ratio, taken as proxy for SFEdense, is a factor ~ 2–3 higher in IR luminous targets compared to normal galaxies. Furthermore, Graciá-Carpio et al. (2008) found, based on a multiline analysis of HCN and HCO+ data, that XHCN is probably about three times lower at high LFIR. Taken together, these findings suggest that SFEdense may be up to an order of magnitude higher in extreme starbursts (LIRGs, ULIRGs) than in normal galaxies.
Compared to normal galaxies and the most extreme starbursts represented by ULIRGs, LIRGs can constitute the transition point in the star-formation laws of galaxies. The main purpose of this paper is to enlarge the sample of LIRGs with high-quality HCN(1–0) observations. This is a key requirement for testing if the observed bimodality of star-formation laws in galaxies derived from CO can be extended to the higher density regime probed by HCN. We used these results to explore the validity of different star-formation law theoretical prescriptions that are currently debated. To this aim we have used the 30 m telescope to observe a sample of 19 LIRGs in the 1–0 lines of CO, HCN and HCO+. Most of the targets were extracted from the complete sample of local (d < 78 Mpc) LIRGs studied by Alonso-Herrero et al. (2006). All targets in this sample have high-quality and high-resolution imaging at optical, near infrared (NIR) and mid infrared (MIR) wavelengths (obtained with HST, VLT, CAHA and Spitzer). This allows us to accurately derive the sizes of the star-forming regions and the star-formation rates for all the targets. The new data presented in this work allow us to expand the number of LIRGs studied in HCN-HCO+ lines by more than a factor 3 compared to previous works (nine LIRGs in Graciá-Carpio et al.’s sample).
2. The sample of LIRGs
We obtained new observations for a sample of 19 LIRGs. Out of these, fourteen were extracted from the sample of nearby LIRGs studied by Alonso-Herrero et al. (2006). This is a volume-limited sample (v < 5200 km s-1, distances of between 35 and 78 Mpc) drawn from the IRAS Revised Bright Galaxy Sample (RBGS) analyzed by Sanders et al. (2003). Alonso-Herrero et al. (2006) required the logarithm of the total IR luminosity to be ≥11.05 L⊙ and the galaxies to be at Galactic latitude b > 10°. The remaining five LIRGs were selected to populate the high end of the IR luminosity distribution of LIRGs. For the Alonso-Herrero et al. LIRGs we obtained HST/NICMOS Paα imaging (Alonso-Herrero et al. 2001; 2002; 2006), as well as ground-based optical integral field spectroscopy using CAHA/PMAS and VLT/VIMOS covering the Hα spectral region (Alonso-Herrero et al. 2009; Rodríguez Zaurín et al. 2011). In addition there are MIR Spitzer imaging observations for the entire sample from the GOALS sample (Armus et al. 2009). This means that the SFRs of the sample are very well characterized from hydrogen recombination lines (Hα, Paα) and MIR (24 μm) luminosities on the same angular scales probed by the IRAM observations. We also have a good estimate of the typical size of the star-forming regions in all galaxies of our sample, thanks to the available high-resolution imaging (Hα, Paα). This minimizes the errors when both ΣSFR and Σdense, required to derive KS laws, are evaluated. The estimated sizes are typically < 10″ in all sources, equivalent to 1.7–3.6 kpc for the given range of distances. This guarantees that the total emission of the molecular gas is contained in the 30 m beam (~28″ at the frequency of the HCN(1–0) line).
Additionally, we used a compiled sample of 108 galaxies with published far infrared (FIR) and HCN(1–0) observations in the literature. When available, we also included HCO+(1–0) data. In addition to the new data obtained in LIRGs for this work we include the data of normal galaxies, LIRGs and ULIRGs of Gao & Solomon (2004a), data from the sample of infrared-excess Palomar-Green QSOs (Evans et al. 2006) and data from high-z galaxies with available HCN observations (see Gao et al 2007, and references therein). Following the same approach as adopted by Graciá-Carpio et al. (2008), in those high-z sources where HCN(1–0) are not available, 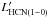 was derived assuming that their rotational line luminosity ratios are
was derived assuming that their rotational line luminosity ratios are 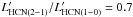 , similar to the mean value measured by Krips et al. (2008). For the z ≃ 4 quasar APM 08279+5255 we adopted
, similar to the mean value measured by Krips et al. (2008). For the z ≃ 4 quasar APM 08279+5255 we adopted 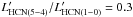 , assuming the physical conditions derived in García-Burillo et al. (2006).
, assuming the physical conditions derived in García-Burillo et al. (2006).
 |
Fig. 1 a) CO(1–0) spectra observed with the IRAM 30 m telescope in a sample of 19 LIRGs. Spectra appear from top to bottom and from left to right in order of increasing right ascension of the source. For clarity some of the line intensities were scaled by the factor indicated in the panel. Gray-filled histograms highlight the velocity range used to calculate the baseline fitting and the line areas. |
 |
Fig. 1 b) Same as a) but showing the HCN(1–0) spectra. |
 |
Fig. 1 c) Same as a) but showing the HCO+(1–0) spectra. |
3. Observations
The new molecular line observations of the sample of 19 LIRGs described in Sect. 2 were carried out in one observing run in June 2008 with the IRAM 30 m telescope at Pico de Veleta (Spain). We tuned the 3 mm and 1 mm SIS receivers of the 30 m telescope to the redshifted frequencies of the HCN(1–0), HCO+(1–0), CO(1–0) and CO(2–1) lines. The beam sizes of the 30 m telescope range from FWHM ~ 28″ at 88 GHz to ~11″ at 230 GHz). We covered a velocity range 1300−1800 km s-1 for the 3 mm lines and 1200 km s-1 for the 1 mm lines. We used the wobbler switching mode to make baselines flatter. System temperatures during the observations were typically ~100–130 K at 3 mm and ~300–500 K at 1 mm. Receivers were used in single side-band mode (SSB), with a high rejection of the image band: >12 dB at 1 mm and >20 dB at 3 mm. The calibration accuracy is estimated to be better than 20%. We checked the pointing of the telescope every 1.5 h by observing nearby continuum sources; the average rms pointing error was 2″ during the observing run.
Throughout the paper, velocity-integrated line intensities (I) are given in antenna temperature scale, 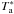 . The
. The 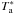 scale relates to the main beam temperature scale, Tmb, by the equation
scale relates to the main beam temperature scale, Tmb, by the equation 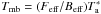 , where Feff and Beff are the forward and beam efficiencies of the telescope at a given frequency. For the IRAM 30 m telescope Feff/Beff = 1.22 (1.57) at 87–88 GHz (230 GHz) and S/Tmb = 4.95 Jy K-1. The velocity windows used to derive IHCO + and IHCN were defined from the corresponding higher signal-to-noise CO line profiles. We subtracted linear baselines to the individual scans and eliminated those showing instabilities requiring higher order baselines. We show in Fig. 1 the ensemble of HCN(1–0), HCO+(1–0) and CO(1–0) spectra used in this work. Molecular line luminosities (L′) were computed in units of L′ = K km s-1 pc2 as defined by Gao & Solomon (2004a). Luminosity distances were derived assuming a flat Λ-dominated cosmology described by H0 = 71 km s-1 Mpc-1 and Ωm = 0.27. Observational parameters and results are summarized in Tables 1 and 2.
, where Feff and Beff are the forward and beam efficiencies of the telescope at a given frequency. For the IRAM 30 m telescope Feff/Beff = 1.22 (1.57) at 87–88 GHz (230 GHz) and S/Tmb = 4.95 Jy K-1. The velocity windows used to derive IHCO + and IHCN were defined from the corresponding higher signal-to-noise CO line profiles. We subtracted linear baselines to the individual scans and eliminated those showing instabilities requiring higher order baselines. We show in Fig. 1 the ensemble of HCN(1–0), HCO+(1–0) and CO(1–0) spectra used in this work. Molecular line luminosities (L′) were computed in units of L′ = K km s-1 pc2 as defined by Gao & Solomon (2004a). Luminosity distances were derived assuming a flat Λ-dominated cosmology described by H0 = 71 km s-1 Mpc-1 and Ωm = 0.27. Observational parameters and results are summarized in Tables 1 and 2.
 |
Fig. 2 a) (Left panel) We plot the |
 |
Fig. 3 a) (Left panel) LFIR- |
4. Star-formation laws of the dense gas
In Sects. 4.1 and 4.2 we study the star-formation efficiency of the dense gas (SFEdense) and the KS laws in the different populations of galaxies compiled for this work, including the new sample of LIRGs. Following the same approach as adopted by Graciá-Carpio et al. (2008), we derive an SFR [M⊙ yr-1] from 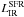 defined as
defined as 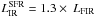 (40–500 μm). This aims at minimizing the possible active galactic nucleus (AGN) contribution to LIR(8–1000 μm). The AGN contribution to LIR in the population of local LIRGs with AGN detections is nonetheless known to be small, with a median value of Lbol(AGN)/LIR = 0.05 (Alonso-Herrero et al. 2012).
(40–500 μm). This aims at minimizing the possible active galactic nucleus (AGN) contribution to LIR(8–1000 μm). The AGN contribution to LIR in the population of local LIRGs with AGN detections is nonetheless known to be small, with a median value of Lbol(AGN)/LIR = 0.05 (Alonso-Herrero et al. 2012).
In this section we adopt the common assumptions regarding conversion factors used to derive SFR from 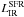 and Mdense from
and Mdense from 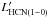 . We first adopt the same universal factor used by Kennicutt (1998):
. We first adopt the same universal factor used by Kennicutt (1998): ![\begin{equation} {\rm SFR}\ \left[M_{\sun}\,{\rm yr^{-1}}\right] = 1.7 \times 10^{-10}\,L^{\rm SFR}_{\rm IR}\ [L_{\sun}]. \end{equation}](/articles/aa/full_html/2012/03/aa17838-11/aa17838-11-eq83.png) (1)Similarly, Mdense is obtained in the following from
(1)Similarly, Mdense is obtained in the following from 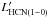 assuming a universal conversion factor (αHCN) similar to that of Gao & Solomon (2004a):
assuming a universal conversion factor (αHCN) similar to that of Gao & Solomon (2004a): ![\begin{equation} M_{\rm dense}\ [M_{\sun}] = 10\,L'_{\rm HCN(1-0)}\ [\rm K\,km\,s^{-1}\,pc^{2}]. \end{equation}](/articles/aa/full_html/2012/03/aa17838-11/aa17838-11-eq84.png) (2)We nevertheless question the grounds for these two working assumptions and their consequences in Sect. 6.
(2)We nevertheless question the grounds for these two working assumptions and their consequences in Sect. 6.
4.1. Star-formation efficiency (SFEdense)
Figure 2 shows the 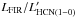 luminosity ratio versus LFIR for the different populations of galaxies in this compilation, defined in Sect. 2. We adopt here the common assumption that the
luminosity ratio versus LFIR for the different populations of galaxies in this compilation, defined in Sect. 2. We adopt here the common assumption that the 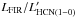 luminosity ratio is a good proxy for the star-formation efficiency of the dense gas (SFE
luminosity ratio is a good proxy for the star-formation efficiency of the dense gas (SFE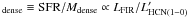 ). We estimate that the total uncertainty on both LFIR and
). We estimate that the total uncertainty on both LFIR and 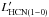 (and related quantities), with an equal contribution of statistical and systematic errors, amounts to ± 30% ( ± 0.13 dex). The corresponding total uncertainty on
(and related quantities), with an equal contribution of statistical and systematic errors, amounts to ± 30% ( ± 0.13 dex). The corresponding total uncertainty on 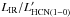 is ± 42% ( ± 0.19 dex).
is ± 42% ( ± 0.19 dex).
In Fig. 2 we can see that SFEdense increases with LFIR from normal galaxies to extreme starbursts, represented by LIRGs, ULIRGs and high-z objects. In particular, the orthogonal regression fit to the full sample of objects gives a power law index for SFEdense significantly different from zero:  The location of the new sample of LIRGs in the SFEdense diagrams of Figs. 2 and 3b corroborates on a more solid statistical basis, compared to the results of Graciá-Carpio et al. (2008), that SFEdense is on average a factor ~2–3 higher in LIRGs/ULIRGs compared to normal galaxies ( ⟨ SFEdense ⟩ (LIRGs/ULIRGs) ~ 1400 ± 100 L⊙ L′-1; ⟨ SFEdense ⟩ (normal) ~ 600 ± 70 L⊙ L′-1). This difference is a factor of 2 larger than the total uncertainty on individual data points in Fig. 2. The total change in SFEdense expands an order of magnitude from normal galaxies to LIRGs/ULIRGs. Interestingly, two objects of the new sample, NGC 1614 and II Zw96, show the highest SFEdense values (≥3500 L⊙ L′-1) thus far reported in a galaxy. These values are close to the upper limit imposed by the maximum efficiencies measured in Galactic star-forming cores (~3900 L⊙ L′-1; Wu et al. 2005). The resulting index derived for the SFEdense law (0.29 ± 0.04) is higher than that obtained by Graciá-Carpio et al. (2008) (0.24 ± 0.04).
The location of the new sample of LIRGs in the SFEdense diagrams of Figs. 2 and 3b corroborates on a more solid statistical basis, compared to the results of Graciá-Carpio et al. (2008), that SFEdense is on average a factor ~2–3 higher in LIRGs/ULIRGs compared to normal galaxies ( ⟨ SFEdense ⟩ (LIRGs/ULIRGs) ~ 1400 ± 100 L⊙ L′-1; ⟨ SFEdense ⟩ (normal) ~ 600 ± 70 L⊙ L′-1). This difference is a factor of 2 larger than the total uncertainty on individual data points in Fig. 2. The total change in SFEdense expands an order of magnitude from normal galaxies to LIRGs/ULIRGs. Interestingly, two objects of the new sample, NGC 1614 and II Zw96, show the highest SFEdense values (≥3500 L⊙ L′-1) thus far reported in a galaxy. These values are close to the upper limit imposed by the maximum efficiencies measured in Galactic star-forming cores (~3900 L⊙ L′-1; Wu et al. 2005). The resulting index derived for the SFEdense law (0.29 ± 0.04) is higher than that obtained by Graciá-Carpio et al. (2008) (0.24 ± 0.04).
 |
Fig. 4 LFIR- |
 |
Fig. 5 Dense molecular gas depletion or exhaustion time scale, tdep ≡ 1/SFEdense in Myr, derived for normal galaxies and LIRGs/ULIRGs. Symbols are as in Fig. 3. We highlight the location of NGC 1614 and II Zw 96 in the diagram. Errorbars show total uncertainties: ± 42% in tdep and ± 30% in LFIR. |
Figure 3a shows the LFIR-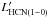 correlation plot obtained for the full sample of galaxies. The orthogonal fit to the data points gives a superlinear correlation:
correlation plot obtained for the full sample of galaxies. The orthogonal fit to the data points gives a superlinear correlation: 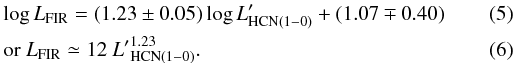 The fit is similar to that found by Graciá-Carpio et al. (2008). With the addition of the new LIRG sample we therefore confirm that the
The fit is similar to that found by Graciá-Carpio et al. (2008). With the addition of the new LIRG sample we therefore confirm that the 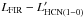 correlation is significantly superlinear. This partly contradicts the first findings of Gao & Solomon (2004a,b), who determined a power index about 1 for the
correlation is significantly superlinear. This partly contradicts the first findings of Gao & Solomon (2004a,b), who determined a power index about 1 for the 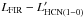 scatter plot and a correspondingly constant SFEdense independent of galaxy type.
scatter plot and a correspondingly constant SFEdense independent of galaxy type.
Figure 4 shows the LFIR-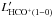 correlation plot obtained for the sample of 34 LIRGs/ULIRGs for which we obtained data in the HCO+ line1 (data from this work and from Graciá-Carpio et al. 2006; 2008). The orthogonal fit to the data points gives a close to linear correlation:
correlation plot obtained for the sample of 34 LIRGs/ULIRGs for which we obtained data in the HCO+ line1 (data from this work and from Graciá-Carpio et al. 2006; 2008). The orthogonal fit to the data points gives a close to linear correlation: 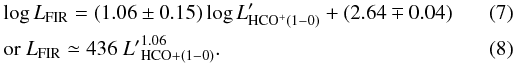 We note that a similar fit using HCN(1–0) data but restricted to the sample of LIRGs/ULIRGs also gives a close to linear power law (n = 1.10 ± 0.10). A similar fit of the
We note that a similar fit using HCN(1–0) data but restricted to the sample of LIRGs/ULIRGs also gives a close to linear power law (n = 1.10 ± 0.10). A similar fit of the 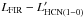 relation restricted to normal galaxies also gives a power index compatible with unity: n = 0.95 ± 0.20. Altogether this is an indication that the inclusion of both normal galaxies and LIRGs/ULIRGs in the fit of Eq. (5) is the reason that the relation between LFIR and
relation restricted to normal galaxies also gives a power index compatible with unity: n = 0.95 ± 0.20. Altogether this is an indication that the inclusion of both normal galaxies and LIRGs/ULIRGs in the fit of Eq. (5) is the reason that the relation between LFIR and 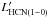 becomes superlinear.
becomes superlinear.
Main properties of the new sample of LIRGs.
Results derived from the IRAM 30 m telescope observations.
Figure 5 shows the dense molecular gas depletion or exhaustion time scale tdep in Myr units, defined as tdep ≡ SFE![\hbox{$_{\rm dense}^{-1} \equiv M_{\rm dense}\ [M_{\sun}]$}](/articles/aa/full_html/2012/03/aa17838-11/aa17838-11-eq120.png) /SFR [M⊙ yr-1] , as a function of LFIR. NGC 1614 and II Zw96 lie at the lower end of the tdep distribution and are characterized by significantly short depletion time scales ≃ 10 Myr. This is an indication that they represent extreme starburst systems that will exhaust their dense molecular gas content on time scales comparable to the typical dynamical time scales for these sources (see discussion in Sect. 7.3 and in Sect. 3.6 of Alonso-Herrero et al. 2001, for NGC 1614).
/SFR [M⊙ yr-1] , as a function of LFIR. NGC 1614 and II Zw96 lie at the lower end of the tdep distribution and are characterized by significantly short depletion time scales ≃ 10 Myr. This is an indication that they represent extreme starburst systems that will exhaust their dense molecular gas content on time scales comparable to the typical dynamical time scales for these sources (see discussion in Sect. 7.3 and in Sect. 3.6 of Alonso-Herrero et al. 2001, for NGC 1614).
4.2. Kennicutt-Schmidt power laws
Figure 6 shows the KS law obtained for the different populations of galaxies compiled for this work., i.e., the star-formation rate surface density ΣSFR as a function of dense molecular gas surface density as traced by the HCN(1–0) line, Σdense. In order to derive ΣSFR and Σdense we adopted the molecular gas size estimates from published CO or HCN interferometer maps, which are available for most of the sources culled from the literature. For the new sample of LIRGs, we estimated the size of the central star-forming region from the high-resolution Hα and/or Paα images of the galaxies published by Alonso-Herrero et al. (2006) and adopted those as representative of the typical sizes of the actively star-forming molecular gas complexes.
In Fig. 6a we represented the derived KS law. The two surface densities, ΣSFR and Σdense, follow a correlation over more than 4 orders of magnitude in Σdense. An orthogonal regression fit to the data results in a KS-law of the dense molecular gas with a power index N = 1.12 ± 0.04: 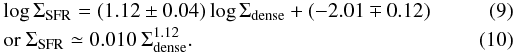 The location of the new sample of LIRGs in the KS diagram of Fig. 6a helps visualize that extreme starbursts (LIRGs/ULIRGs) and normal galaxies are not fully overlapping in this scatter plot. In order to quantify if a two-function power law significantly improves the overall fit, we split the sample into normal (LIR < 1011 L⊙) and IR luminous galaxies (LIR > 1011 L⊙). Figure 6b shows the result of the two-function fit, which can be expressed as
The location of the new sample of LIRGs in the KS diagram of Fig. 6a helps visualize that extreme starbursts (LIRGs/ULIRGs) and normal galaxies are not fully overlapping in this scatter plot. In order to quantify if a two-function power law significantly improves the overall fit, we split the sample into normal (LIR < 1011 L⊙) and IR luminous galaxies (LIR > 1011 L⊙). Figure 6b shows the result of the two-function fit, which can be expressed as 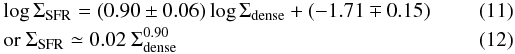 for galaxies with LIR < 1011 L⊙, and:
for galaxies with LIR < 1011 L⊙, and: 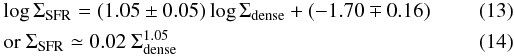 for local and high-z IR luminous galaxies with LIR ≥ 1011 L⊙.
for local and high-z IR luminous galaxies with LIR ≥ 1011 L⊙.
 |
Fig. 6 a) (Left panel) Star-formation rate surface density ΣSFR as a function of dense molecular gas surface density as traced by the HCN(1–0) line, Σdense, in different populations of galaxies for which we have an estimate of the molecular disk size. Symbols are as in Fig. 3. The solid black line is the orthogonal regression fit to the full sample of galaxies. b) (Right panel) Same as a), but showing the two-function power law fit to normal galaxies (gray line) and IR luminous galaxies (black line). Here, normal galaxies (LIR < 1011 L⊙) are represented by open squares and IR luminous galaxies (LIR > 1011 L⊙) by black filled squares as referred to in text. Errorbars show ± 30% uncertainties in ΣSFR and Σdense. |
Whereas the index of the power law is not substantially different in normal galaxies (N = 0.90 ± 0.06) and LIRGs/ULIRGs (N = 1.05 ± 0.05), this fit reinforces the idea of duality hinted at in the solution that Graciá-Carpio et al. (2008) found using a smaller sample of LIRGs/ULIRGs. As illustrated in Fig. 6b, the extrapolation of the KS law fitting normal galaxies to the highest values of Σdense (~a few104 M⊙ pc-2) underpredicts the ΣSFR in IR luminous galaxies by up to a factor ~5. This is a factor ~4 larger than the total uncertainty on ΣSFR. Within the range of gas surface densities shared by normal galaxies and LIRGs/ULIRGs, Σdense ~ 102–2 × 103 M⊙ pc-2, the disagreement between the two laws stays within a factor 2 to 3, i.e., still a factor ~2–2.5 larger than the total uncertainty on ΣSFR.
We have evaluated the goodness of the two-function power law fit by a standard χ2 analysis. We find that χ2 decreases by a factor of 1.4 in the dual fit compared to the single power law, an indication that the dual KS law for the dense gas qualifies as a better description of the data. This result is reminiscent of the bimodality found in star-formation laws derived in normal star-forming galaxies and mergers (LIRGs, ULIRGs and SMGs) from CO line data (Genzel et al. 2010; Daddi et al. 2010). We nevertheless analyze in Sect. 5 the potential biases of the two-function fit of Eqs. (11)–(14), motivated by the division of our sample at LIR = 1011 L⊙.
In our derivation of KS laws we used different methods to derive the typical sizes assumed to be common for the actively star-forming regions and the dense molecular gas disks. This is certainly a source of uncertainty, already included in our error budget. We note, however, that a possible bias will affect the estimated ΣSFR and Σdense to the same extent. These uncertainties would shift all data points along trajectories that correspond to straight lines of slope unity. The fits found for the KS laws are very close to the linear behavior and the described uncertainties associated to source sizes therefore cannot create a fake segregation.
 |
Fig. 7 Histograms of depletion times for the dense gas in the whole sample of galaxies (solid line) and in the populations of LIRGs/ULIRGs (gray filled) and of normal galaxies (hatched). The depletion times in the left-hand panel are calculated assuming the same FIR-to-SFR and HCN-to-mass conversion factors for the two populations. In the middle panel, the two conversion factors are modified (see Sect. 6), whereas in the right-hand panel only the HCN-to-mass factor is changed. |
5. Statistical assessment of the two-function fit
The results found in the previous section suggest that the KS law for the dense gas in LIRGs/ULIRGs differs from that in normal star-forming galaxies. In this section we quantify this conclusion by addressing the statistical biases inherent to these results.
5.1. Bimodality
We first analyze if the star-formation laws derived from HCN qualify as bimodal. The definition of bimodality is very strict because it requires the existence of two distinct populations within a given sample with few if any objects connecting the two populations, reflecting two different modes. We can assess if the star-formation laws derived from HCN qualify as strictly bimodal by inspecting the distribution of depletion times. Figure 7 shows histograms of tdep in the whole sample and in the groups of LIRGs/ULIRGs and of normal galaxies derived using different approaches of the assumed conversion factors. As expected from the difference in the mean values derived in Sect. 4, LIRGs/ULIRGs and normal galaxies tend to populate different regions of the joint histogram. This suggests a bimodal distribution with two unequally populated peaks. Assuming the non-universal conversion factors discussed in Sect. 6 certainly increases the spread in tdep between normal galaxies and LIRGs/ULIRGs (Fig. 7).
Hartigan & Hartigan (1985) proposed a test that measures the goodness of unimodality as the best description of a statistical sample. The test measures the dip of a sample, defined as the maximum distance between a given empirical distribution and its corresponding best-fitting unimodal distribution. For a given sample size, the deeper the dip, the less likely it is that the distribution is unimodal. An updated version of the Hartigan dip test is implemented in the R package, a free software environment for statistical computing2. We applied it to our sample of galaxies to evaluate if the set of depletion times is compatible with an unimodal distribution. The test indicates that the dip of an unimodal distribution could be as deep as measured for the depletion times in ~90% of the cases, which otherwise implies that unimodality is far from being rejected. These admittedly high probabilities decrease to ~80% if we assume the revised conversion factors for ΣSFR and Σdense discussed in Sect. 6, and could reach ~20% if we only changed the conversion factor for Σdense, i.e., if we adopted a similar approach to that of Genzel et al. (2010).
We conclude that we cannot claim that the star-formation process is strictly bimodal on the basis of the depletion timescale distribution. This conclusion holds particularly where universal conversion factors are adopted.
 |
Fig. 8 Results from testing the null hypotheses of a single KS law (left column) and of a double KS law (right column). Each panel shows the 2.5%,25%,50%,75% and 97.5% percentiles of σ1fit (top), Δlog (tdep) (middle) and SSR2fit/SSR1fit (bottom) as a function of σrand. The measured values are indicated by dashed horizontal lines. A gray rectangle represents the 95% confidence interval for σrand derived in each panel from the measured value. Dotted lines show the confidence intervals derived from σ1fit (top panels). |
5.2. Universality of the KS law for the dense gas
That the two-function fit is a significant improvement over the one-function fit nevertheless suggests an underlying duality in the distribution. Because of our previous arbitrary splitting of the galaxy sample into two groups, defined by the dividing line at LIR = 1011 L⊙, the evaluation of average galaxy properties in the two subsamples is subject to potential biases, however. The underlying reason is that the selection cut used to separate the populations is not orthogonal to the variables that are being fit.
Below we test the null hypothesis that a single KS law with a fixed power law index for both LIRGs/ULIRGs and normal galaxies (e.g., Eq. (9)) is a suitable representation of our data. This hypothesis can be rejected if, on the assumption that it holds true, the measured values of three chosen observables are unlikely to result from pure random scatter. The observables used as constraints are
-
The scatter of the data with respect to the one-functionpower law fitted to the data (Eq. (9))
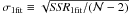 . SSR1fit is the sum of squared residuals and
. SSR1fit is the sum of squared residuals and 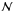 is the number of sources. The observable σ1fit tells us the amount of random scatter we can plausibly assume. The value derived for σ1fit is 0.20 dex.
is the number of sources. The observable σ1fit tells us the amount of random scatter we can plausibly assume. The value derived for σ1fit is 0.20 dex. -
The difference, in median, between the logarithms of the depletion times of the two populations Δlog (tdep) ≡ median { log (tdep) } normal − median { log (tdep) } (U)LIRG. The measured value for Δlog (tdep) is 0.45 dex. The parameter Δlog (tdep) measures the difference between LIRGs/ULIRGs and normal galaxies, although it is biased toward positive values. The reason is that ΣSFR is essentially proportional to LIR, so that a positive noise-driven error in the LIR of a galaxy simultaneously underestimates its tdep and increases the probability that the object is classified as LIRG/ULIRG. Superlinear KS laws as that of Eq. (9) (slope ~ 1.12) enhance this bias.
-
The ratio of SSR2fit/SSR1fit, where SSR2fit is the sum of squared residuals when using two functions to fit the data as in Sect. 4.2. The measured value for this ratio is about 0.70. This ratio measures the improvement in the fit when separate KS laws are adopted for the two populations. SSR2fit/SSR1fit is always smaller than or equal to one, since a two-function fit can always match or even improve the solution of the one-function fit.
To calculate the corresponding probability distributions of the observables, we proceeded as follows:
-
We assumed that the intrinsic distribution of data in the (log Σdense,log ΣSFR) plane is given by the corrected values that result from the orthogonal least-squares fit to our observations derived in Sect. 4.2. These points follow Eq. (9) by construction.
-
We evaluated the effect of the scatter of the distribution on the definition of the subsamples by scrambling our sample independently along the Σdense and ΣSFR axes with a Gaussian scatter, hereafter denoted as σrand. The galaxies were then re-classified either as LIRG/ULIRG or as normal after rescaling the IR luminosity of each object by the randomized-to-observed ratio of ΣSFR. This mimics the effect of errors on the classification.
-
The scatter parameter σrand appears as a free parameter in our analysis, since there may be sources of random scatter other than the observational error (0.13 dex). We chose 10 values of σrand from ~0 dex to 0.9 dex and performed 5 × 103 randomizations for each value. Each randomized set of data was analyzed in the same way as the observed data to derive the probability distributions of our observables as a function of σrand.
The left column of Fig. 8 shows the 2.5%,25%,50%,75% and 97.5% percentiles of σ1fit (top), Δlog (tdep) (middle) and SSR2fit/SSR1fit (bottom) as a function of σrand assuming the null hypothesis. From each panel we can derive a 95% confidence interval for σrand (gray bands in the plots) by requiring that the probability to obtain the measured value lies within the 2.5%−97.5% range. As shown in the top panel, σrand should lie in the range 0.18−0.24 dex to be compatible with our measurement of σ1fit at the 95% confidence level. Outside that range, σ1fit would be either lower or higher than measured (0.20 dex) in 97.5% of the cases. Comparing the three panels, we clearly see that this confidence interval is formally incompatible with those derived from the measured Δlog (tdep) (0.25−0.81 dex) and SSR2fit/SSR1fit (>0.42 dex).
We can therefore conclude that the universal one-function fit is not the best description of the data. Although the (ΣSFR, Σdense) distribution does not qualify as strictly bimodal according to the dip test, the two-function fit to the data qualifies as a better description of the star-formation laws derived from HCN. None of the biases related to the intrinsic non-linearity of the law or to the a priori arbitrary cut in LIR to divide the sample are able to account for the observed differences between normal galaxies and LIRGs/ULIRGs discussed in Sects. 4.1 and 4.2.
Furthermore, following a similar proof by contradiction approach, we carried out a similar test assuming a double KS law determined by the best two-function fit of Eqs. (11)–(14) discussed in Sect. 4.2. Equivalent plots to those discussed above are shown in the right column of Fig. 8. These plots clearly show that the hypothesis of a double KS law formally agrees with the measured values. Therefore, although the test cannot prove that the hypothesis of a double KS law is the only solution, we can conclude that it is a better description of the star-formation laws derived from HCN than a single KS law. We note that it might be possible to save the single KS law model by assuming that a significant fraction of the measured scatter is not random, but is caused by hidden variables relevant to the star-formation process such as global dynamical time scales. This alternative is explored in Sect. 7.3.
6. Conversion factors and star-formation laws
We discuss in Sect. 6.1 the validity of the Mdense – 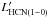 conversion factor adopted above for LIRGs/ULIRGs and consider in Sect. 6.2 the biases in estimating the SFR for normal galaxies from
conversion factor adopted above for LIRGs/ULIRGs and consider in Sect. 6.2 the biases in estimating the SFR for normal galaxies from 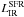 . The consequences of revising conversion factors for the star-formation laws obtained are discussed in Sect. 6.3.
. The consequences of revising conversion factors for the star-formation laws obtained are discussed in Sect. 6.3.
 |
Fig. 9 HCN to CO luminosity ratios as function of LIR for the full sample of galaxies. Here, normal galaxies (LIR < 1011 L⊙) are represented by open squares and IR luminous galaxies (LIR > 1011 L⊙) by filled squares. Red markers highlight those galaxies showing over-luminous HCN lines (HCN/CO ≥ 0.1). With the exception of one normal galaxy, all galaxies in this category are IR luminous. |
6.1. The HCN-to-Mdense conversion factor in LIRGs/ULIRGs
It is currently accepted that the conversion factor between the CO luminosity (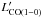 ) and the mass of molecular gas (Mgas) is lower in mergers than in the Milky Way (MW) (
) and the mass of molecular gas (Mgas) is lower in mergers than in the Milky Way (MW) (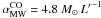 ). The first conclusive evidence of a different conversion factor in mergers was found by Downes & Solomon (1998). These authors derived that the Mgas –
). The first conclusive evidence of a different conversion factor in mergers was found by Downes & Solomon (1998). These authors derived that the Mgas – 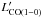 conversion factor in ULIRGs is ~1/5 of the MW’s value (this lowering factor is 1/10 for Arp220). More generally, the analysis of CO line emission by radiative transfer models indicates that the physical conditions found in the CO clouds of mergers and nuclear starbursts (densities n(H2) ≃ 103–104 cm-3 and brightness temperatures TR ≃ 20–50 K) imply that the CO conversion factor, which scales as n(H2)1/2/TR, is typically about (1/2–1/4) ×
conversion factor in ULIRGs is ~1/5 of the MW’s value (this lowering factor is 1/10 for Arp220). More generally, the analysis of CO line emission by radiative transfer models indicates that the physical conditions found in the CO clouds of mergers and nuclear starbursts (densities n(H2) ≃ 103–104 cm-3 and brightness temperatures TR ≃ 20–50 K) imply that the CO conversion factor, which scales as n(H2)1/2/TR, is typically about (1/2–1/4) × 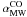 (Solomon et al. 1997; Scoville et al. 1997). A clear-cut argument in favor of a lower CO conversion factor in mergers is that the canonical MW value of αCO applied to
(Solomon et al. 1997; Scoville et al. 1997). A clear-cut argument in favor of a lower CO conversion factor in mergers is that the canonical MW value of αCO applied to 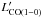 predicts gas masses that are larger than the dynamical masses in many LIRGs/ULIRGs at different redshift ranges (Tacconi et al. 2008; Daddi et al. 2010; Genzel et al. 2010)
predicts gas masses that are larger than the dynamical masses in many LIRGs/ULIRGs at different redshift ranges (Tacconi et al. 2008; Daddi et al. 2010; Genzel et al. 2010)
There have also been claims in the literature that the MW value of the Mdense – 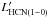 conversion factor, initially adopted in Sect. 4, does not apply to mergers either (Gao & Solomon 2004a; Graciá-Carpio et al. 2008). The high HCN to CO ratios measured in some ULIRGs/LIRGs ( ≃ 0.1) make the requirement that
conversion factor, initially adopted in Sect. 4, does not apply to mergers either (Gao & Solomon 2004a; Graciá-Carpio et al. 2008). The high HCN to CO ratios measured in some ULIRGs/LIRGs ( ≃ 0.1) make the requirement that 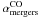 ≤ (1/2–1/4) ×
≤ (1/2–1/4) × 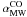 mostly incompatible with the basic prescription that Mdense should not in all likelihood exceed 0.5 × Mgas (Gao & Solomon 2004a).
mostly incompatible with the basic prescription that Mdense should not in all likelihood exceed 0.5 × Mgas (Gao & Solomon 2004a).
The case of the ULIRG Arp 220 is paradigmatic in this respect. Downes & Solomon (1998) derived from the lower conversion factor for CO a total gas mass for the system Mgas ~ 5 × 109 M⊙. The mass of dense gas derived from our HCN observations if we use the standard conversion version factor for HCN (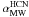 ) is Mdense ~ 1.2 × 1010 M⊙, i.e., ~(2–3) × Mgas. This result indicates that
) is Mdense ~ 1.2 × 1010 M⊙, i.e., ~(2–3) × Mgas. This result indicates that 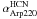 should be ≤ (1/2–1/3)
should be ≤ (1/2–1/3)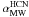 even in the extreme limit case where Mdense = Mgas. The new data obtained in our work for other IR luminous galaxies corroborates this picture. Figure 9 shows the HCN to CO ratios as a function of LIR derived for the full sample of galaxies used in this paper. This diagram is used to single out overluminous HCN line targets in our sample, characterized by HCN/CO ≥ 0.1 within the errors. About 50% of the LIRGs/ULIRGs in our sample are overluminous HCN galaxies, identified by the red filled square symbols in Fig. 9. By contrast, only one normal galaxy in our sample is overluminous in HCN. In these galaxies αHCN has to be lowered by a similar factor as
even in the extreme limit case where Mdense = Mgas. The new data obtained in our work for other IR luminous galaxies corroborates this picture. Figure 9 shows the HCN to CO ratios as a function of LIR derived for the full sample of galaxies used in this paper. This diagram is used to single out overluminous HCN line targets in our sample, characterized by HCN/CO ≥ 0.1 within the errors. About 50% of the LIRGs/ULIRGs in our sample are overluminous HCN galaxies, identified by the red filled square symbols in Fig. 9. By contrast, only one normal galaxy in our sample is overluminous in HCN. In these galaxies αHCN has to be lowered by a similar factor as 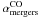 relative to the MW canonical values.
relative to the MW canonical values.
 |
Fig. 10 a) (Left panel) Same as Fig. 6a, but showing the revised two-function power law fit to normal galaxies (gray line) and luminous infrared galaxies (black line) discussed in Sect. 6.3. Symbols and errorbars as in Fig. 6. b) (Right panel) We show the revised depletion time scale as a function of |
Following a similar approach to that employed to constrain the value of 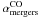 , Graciá-Carpio et al. (2008) used the data obtained in a multiline survey of HCN and HCO+ of 17 LIRGs and ULIRGs to fit αHCN with large velocity gradient (LVG) radiative transfer codes. The main outcome of Graciá-Carpio et al.’s study also backs up the claim that αHCN is ~3 times lower at high LFIR. Lower conversion factor for HCN in extreme starbursts can be related to the particular chemical environment of the dense molecular gas in these sources where a hot-core like type of chemistry may prevail and enhance HCN abundances (e.g., Lintott et al. 2005). In addition, non-collisional excitation could also be responsible for the surprising strength of HCN lines in some IR luminous systems (e.g.; Aalto et al. 1995; García-Burillo et al. 2006; Guélin et al. 2007; Weiß et al. 2007). In either case, the HCN conversion factor should be lowered.
, Graciá-Carpio et al. (2008) used the data obtained in a multiline survey of HCN and HCO+ of 17 LIRGs and ULIRGs to fit αHCN with large velocity gradient (LVG) radiative transfer codes. The main outcome of Graciá-Carpio et al.’s study also backs up the claim that αHCN is ~3 times lower at high LFIR. Lower conversion factor for HCN in extreme starbursts can be related to the particular chemical environment of the dense molecular gas in these sources where a hot-core like type of chemistry may prevail and enhance HCN abundances (e.g., Lintott et al. 2005). In addition, non-collisional excitation could also be responsible for the surprising strength of HCN lines in some IR luminous systems (e.g.; Aalto et al. 1995; García-Burillo et al. 2006; Guélin et al. 2007; Weiß et al. 2007). In either case, the HCN conversion factor should be lowered.
The independent lines of evidence mentioned above indicate that for a sizeable fraction of the IR luminous galaxies in our sample, the HCN conversion factor should be lowered. It remains to be proved that a similar correction should be applied to all the galaxies in our sample that qualify as IR luminous mergers. With this caveat in mind we rederive the KS laws in Sect. 6.3 adopting 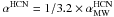 in LIRGs/ULIRGs. This is the same rescaling factor generally adopted for mergers in the CO study of Genzel et al. (2010). We note that about 70% of the LIRGs/ULIRGs analyzed in our paper have LIR > 1011.5 L⊙, the limit beyond which mergers and strongly interacting systems start to dominate over less disturbed disk systems (Sanders & Ishida 2004; Alonso-Herrero et al. 2009).
in LIRGs/ULIRGs. This is the same rescaling factor generally adopted for mergers in the CO study of Genzel et al. (2010). We note that about 70% of the LIRGs/ULIRGs analyzed in our paper have LIR > 1011.5 L⊙, the limit beyond which mergers and strongly interacting systems start to dominate over less disturbed disk systems (Sanders & Ishida 2004; Alonso-Herrero et al. 2009).
6.2. The LFIR-to-SFR conversion factor in normal galaxies
In Sect. 4 we used the IR luminosity of the galaxies as a proxy for their SFR. While this approach is valid for dusty galaxies, it has now become clear that in normal star-forming galaxies one needs to account for both the obscured (traced by the IR luminosity) and the unobscured SFRs (Pérez-González et al. 2006; Calzetti et al. 2007; Kennicutt et al. 2009). In particular, combinations of an IR tracer (e.g., the 24 μm luminosity) with the observed Hα luminosities are shown to work well. In this section we evaluate the corrections needed to account for all the SFR (obscured+unobscured) in our sample of galaxies.
For the normal star-forming galaxies in our sample we used the SINGS sample data. We have eight galaxies in common with the SINGS survey. We used the integrated observed (that is, not corrected for extinction) Hα and 24 μm luminosities given by Kennicutt et al. (2009) to compute the total SFR using the prescriptions given in their paper. As described in Kennicutt et al. (2009), the use of total IR or monochromatic IR luminosities work equally well to derive the total (obscured+unobscured) SFR. On average we find that SFR(24 μm)/SFR(tot) = 0.5−0.6. This indicates that SFR based on an IR tracer underestimates the true SFR roughly by a factor of 2 in normal star-forming galaxies (see also Kennicutt et al. 2009, and references therein).
In LIRGs and ULIRGs, as mentioned above, the IR-based SFR indicators account for most of the total SFR. This was shown by recent integral field spectroscopy studies of a sample of more than 50 LIRGs and ULIRGs (García-Marín et al. 2009; Rodríguez-Zaurín et al. 2011). Therefore no corrections were applied to derive the SFR surface density for LIRGs and ULIRGs.
We therefore adopt in Sect. 6.3 a correction factor of 2 to derive ΣSFR from 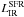 in normal star-forming galaxies. This is likely an upper limit to the true correction factor in normal galaxies, because we expect that the attenuation will vary more continuously as a function of the FIR luminosity. We note, however, that applying a lower correction factor for normal galaxies would further reinforce the dual behavior of star-formation laws discussed in Sect. 6.3 (see Fig. 7).
in normal star-forming galaxies. This is likely an upper limit to the true correction factor in normal galaxies, because we expect that the attenuation will vary more continuously as a function of the FIR luminosity. We note, however, that applying a lower correction factor for normal galaxies would further reinforce the dual behavior of star-formation laws discussed in Sect. 6.3 (see Fig. 7).
6.3. Revised star-formation laws
We have fitted a new two-function power law to the whole sample of galaxies using the revised values of Σdense (in LIRGs/ULIRGs) and ΣSFR (in normal galaxies) derived according to Sects. 6.1 and 6.2. Figure 10a visualizes the new star-formation relation in normal galaxies and LIRGs/ULIRGs. The best orthogonal fit solution can be expressed as 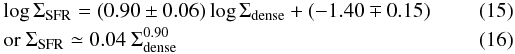 for galaxies with LIR < 1011 L⊙, and
for galaxies with LIR < 1011 L⊙, and 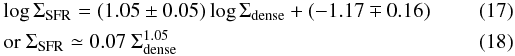 for local and high-z IR luminous galaxies with LIR ≥ 1011 L⊙.
for local and high-z IR luminous galaxies with LIR ≥ 1011 L⊙.
An inspection of Fig. 10a indicates that compared to Fig. 6b, the dual behavior is significantly reinforced in the new version of the KS laws. At the high end of Σdense values (~a few 104 M⊙ pc-2) the normal galaxy law underpredicts ΣSFR in IR luminous galaxies by about an order of magnitude, a factor ~8 larger than the typical uncertainty on ΣSFR. Furthermore, within the range of gas surface densities shared by normal galaxies and LIRGs/ULIRGs, Σdense ~ 2 × 101–2 × 103 M⊙ pc-2, the factor 3 to 5 disagreement between the two laws is statistically significant, being a factor ~3–4 larger than the typical uncertainty on ΣSFR. Instead, if we try to fit all the observations shown in Fig. 10a with a one-parameter law over the whole range of IR luminosities, we obtain 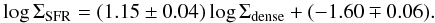 (19)This solution has a 2.2 times higher χ2 than the two-function fit found above.
(19)This solution has a 2.2 times higher χ2 than the two-function fit found above.
Figure 10b shows the revised depletion time scales of the dense molecular gas in normal galaxies and LIRGs/ULIRGs. A similar reinforcement of the duality in star-formation laws can be identified if we compare the new estimates of tdep with those shown in Fig. 5. The value of tdep is on average a factor ~3–4 lower in LIRGs/ULIRGs (tdep ~ 14 ± 1.4 Myr) compared to normal galaxies (tdep ~ 50 ± 5 Myr). This difference is a factor of 2–3 larger than the total uncertainty of individual data points.
As extensively discussed in Sect. 5, the revised star-formation laws of Eqs. (15)–(18), by increasing the spread between normal galaxies and LIRGs/ULIRGs, make the two-function fit as the best description of the data more plausible.
 |
Fig. 11 a) (Left panel) Star-formation rate per free-fall time (SFRff; shown in the left Y axis) derived from the observed SFEdense in different populations of galaxies assuming a characteristic gas density for the HCN cloud nHCN(H2) = 3 × 104 cm-3. We show on the right Y axis the value of nHCN(H2) derived from SFEdense assuming a constant SFRff = 0.02. This value lies within the most likely range for SFRff ~ 0.011–0.028 as determined by the star-formation model of Krumholz & McKee (2005). We also highlight the average value of SFRff ~ 0.0058 as determined by Krumholz & Tan (2007) from a compilation of galactic and extragalactic HCN observations. Symbols are as in Fig. 3. Errorbars on SFRff (±42%) and LFIR (±30%) are shown. b) (Right panel) Same as a) but obtained based on the revised values of Σdense (in LIRGs/ULIRGs) and ΣSFR (in normal galaxies) discussed in Sect. 6. |
7. Star-formation models: local vs. global
The evidence of bimodality in star-formation laws derived from CO line data is a challenge for star-formation models relying only on local processes (e.g., Genzel et al. 2010). Our findings of a similar yet admittedly less extreme duality in the star-formation laws derived from HCN, a better tracer of the dense molecular phase, and thus more directly related to star formation, can put stringent constraints on models. In contrast with the highly scattered CO diagram, the lower intrinsic dispersion in the HCN star-formation laws helps assess the verisimilitude of duality with a higher statistical significance. We discuss in Sect. 7.1 to what extent our results based on the HCN observations can be used to test one of the key predictions of the star-formation model of Krumholz & McKee (2005): the constancy of the star-formation rate per free-fall time (SFRff). We study in Sect. 7.2 the values predicted by Krumholz et al.’s models for the 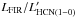 luminosity ratios in different galaxy populations and use our data to benchmark the models. Furthermore, we study in Sect. 7.3 whether the inclusion of “global” dynamical time scales offers a better description of the star-formation laws derived for the dense gas.
luminosity ratios in different galaxy populations and use our data to benchmark the models. Furthermore, we study in Sect. 7.3 whether the inclusion of “global” dynamical time scales offers a better description of the star-formation laws derived for the dense gas.
7.1. Observations vs. models: is the star-formation rate per free-fall time constant?
Krumholz &McKee (2005) developed an analytic prescription for the star-formation laws that are valid for different galactic environments. In their model star formation is globally very inefficient because it only takes place in a small subregion of a supersonic turbulent virialized molecular cloud. In this overdense subregion, known as the cloud core(s), gravitational pull is able to take over kinetic energy and the collapse starts. If SFR is the total star-formation rate in a galaxy, the star-formation rate per free-fall time in objects of class X, SFRff−X, can be obtained as a function of SFR and the total mass of X objects, MX, (or of their associated variables SFE or tdep), as well as of the fraction of star formation occurring in these objects, fX and the free-fall time, tff − X: 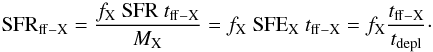 (20)The star-formation rate per free-fall time is a function of two parameters: the ratio of the kinetic energy (thermal plus turbulent) to the gravitational energy of the cloud (αVIR) and the Mach number of the region (ℳ) where ℳ2 is roughly the ratio of the kinetic energy to the thermal energy. One of the key predictions of these models is that the dimensionless SFRff is expected to be low and lie within a quite restricted range ≤3% (~0.011–0.028) for the entire span of plausible values of αVIR (~1–2) and ℳ (~20–80). This offers a quantitative description for why star formation is so inefficient in a highly turbulent molecular medium.
(20)The star-formation rate per free-fall time is a function of two parameters: the ratio of the kinetic energy (thermal plus turbulent) to the gravitational energy of the cloud (αVIR) and the Mach number of the region (ℳ) where ℳ2 is roughly the ratio of the kinetic energy to the thermal energy. One of the key predictions of these models is that the dimensionless SFRff is expected to be low and lie within a quite restricted range ≤3% (~0.011–0.028) for the entire span of plausible values of αVIR (~1–2) and ℳ (~20–80). This offers a quantitative description for why star formation is so inefficient in a highly turbulent molecular medium.
If we take HCN clouds as representative objects, then SFEX ≡ SFEdense ≡ 1/tdep as defined in Sect. 4.1. We can therefore estimate SFRff using Eq. (20) directly from observations, provided that we assume a typical density for HCN clouds and suppose a value for fX. It is reasonable to assume that fX is about unity because all star formation in galaxies is likely taking place at densities exceeding the critical densities of the HCN(1–0) line (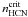 (H2) ~ 3 × 104 cm-3/τ, where τ is the opacity of the 1–0 line of HCN; e.g., Gao & Solomon 2004a). The actual value of tff − HCN depends on the density of clouds emitting HCN. All in all, observations can be used to verify/falsify the prediction of Krumholz & McKee (2005)’s model about the behavior of SFRff.
(H2) ~ 3 × 104 cm-3/τ, where τ is the opacity of the 1–0 line of HCN; e.g., Gao & Solomon 2004a). The actual value of tff − HCN depends on the density of clouds emitting HCN. All in all, observations can be used to verify/falsify the prediction of Krumholz & McKee (2005)’s model about the behavior of SFRff.
Krumholz & Tan (2007) used galactic and extragalactic observations of a variety of objects to derive SFRff−X as a function of the characteristic ISM densities, which are probed by different molecular tracers (i.e., X-objects) in their compilation. A key outcome of their work is that SFRff−X seems to stay roughly constant with density. However, the results obtained from HCN suggest a significant deviation of SFRff−X from this general trend. The average value of SFRff derived from the HCN observations used in their paper (SFRff − HCN ~ 0.0058) lies below the range predicted by Krumholz & McKee (2005)’s model. Krumholz & Tan (2007) nevertheless assigned a large error bar to SFRff−HCN, implicitly assuming that the scattered distribution of SFRff derived from HCN data is mostly random3.
We use below the HCN data discussed in this work to study the distribution of SFRff values derived in our sample of galaxies. Our goal is to check if the new observations are compatible with the prediction of a constant SFRff. In this comparison we use the two versions of the star-formation laws derived using the standard conversion factors (Case-I below) and the revised conversion factors discussed in Sect. 6 (Case-II below). As discussed below, exploring different conversion factors is paramount if we are to probe the plausible range of values for SFRff, because these two quantities are interconnected through Eq. (20).
7.1.1. Case-I: standard conversion factors
If we assume that all HCN clouds have densities equal to 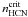 = 3 × 104 cm-3 (i.e., we take τ = 1) we can obtain SFRff from Eq. (20). Figure 11a represents SFRff as a function of LFIR obtained from the SFEdense values derived in Sect. 4, i.e., prior to the correction of conversion factors discussed in Sect. 6. We note that the distribution of SFRff lies noticeably below the range predicted by the model, as shown in Fig. 11a. In addition to this conspicuous downward shift, the deduced SFRff distribution shows a systematic trend with LFIR and thus cannot be described as random. The order of magnitude increase in SFRff from normal galaxies to LIRGs/ULIRGs is statistically significant and it is about a factor of 7 higher than the typical uncertainty of individual data points (42%). The SFRff progression echoes the SFEdense trend with LFIR discussed in Sect. 4.1.
= 3 × 104 cm-3 (i.e., we take τ = 1) we can obtain SFRff from Eq. (20). Figure 11a represents SFRff as a function of LFIR obtained from the SFEdense values derived in Sect. 4, i.e., prior to the correction of conversion factors discussed in Sect. 6. We note that the distribution of SFRff lies noticeably below the range predicted by the model, as shown in Fig. 11a. In addition to this conspicuous downward shift, the deduced SFRff distribution shows a systematic trend with LFIR and thus cannot be described as random. The order of magnitude increase in SFRff from normal galaxies to LIRGs/ULIRGs is statistically significant and it is about a factor of 7 higher than the typical uncertainty of individual data points (42%). The SFRff progression echoes the SFEdense trend with LFIR discussed in Sect. 4.1.
To render a constant SFRff compatible with the order of magnitude increase in SFEdense, the density of HCN clouds has to change notably from normal galaxies to LIRGs/ULIRGs, as nHCN(H2) scales as ~SFE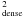 . We represent in the right Y axis of Fig. 11a the value of nHCN(H2) required to fit observations, assuming a fixed SFRff = 0.02 for all galaxies, which is close to the average value predicted by the star-formation model of Krumholz & McKee (2005). The required nHCN(H2) densities span two orders of magnitude from normal galaxies (~102 cm-3) to LIRGs/ULIRGs (~104 cm-3). These densities are exceedingly low compared to
. We represent in the right Y axis of Fig. 11a the value of nHCN(H2) required to fit observations, assuming a fixed SFRff = 0.02 for all galaxies, which is close to the average value predicted by the star-formation model of Krumholz & McKee (2005). The required nHCN(H2) densities span two orders of magnitude from normal galaxies (~102 cm-3) to LIRGs/ULIRGs (~104 cm-3). These densities are exceedingly low compared to 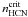 ; this poses a problem for the standard scenario of collisional excitation of HCN lines. Extreme and therefore unrealistic high opacities for HCN would be required to compensate for the low densities: τHCN = 3–300. As an additional relevant constraint, we would need to assume that opacities are a factor 10–100 higher in normal galaxies compared to LIRGs/ULIRGs. This requirement is at odds with the commonly measured higher molecular abundances of extreme starbursts (Combes 1991; Wild et al. 1992; Nguyen et al. 1992; Krips et al. 2008; Graciá-Carpio et al. 2008). The current observational evidence contradicts the existence of these abnormally low HCN densities, at least in the galaxies for which reliable estimates of nHCN(H2) exist (e.g., Tacconi et al. 1994; Sternberg et al. 1994; Usero et al. 2004; Krips et al. 2008; Graciá-Carpio et al. 2008).
; this poses a problem for the standard scenario of collisional excitation of HCN lines. Extreme and therefore unrealistic high opacities for HCN would be required to compensate for the low densities: τHCN = 3–300. As an additional relevant constraint, we would need to assume that opacities are a factor 10–100 higher in normal galaxies compared to LIRGs/ULIRGs. This requirement is at odds with the commonly measured higher molecular abundances of extreme starbursts (Combes 1991; Wild et al. 1992; Nguyen et al. 1992; Krips et al. 2008; Graciá-Carpio et al. 2008). The current observational evidence contradicts the existence of these abnormally low HCN densities, at least in the galaxies for which reliable estimates of nHCN(H2) exist (e.g., Tacconi et al. 1994; Sternberg et al. 1994; Usero et al. 2004; Krips et al. 2008; Graciá-Carpio et al. 2008).
Based on the new HCN observations presented in this work and the use of standard conversion factors, we derive values for SFRff and/or nHCN(H2) that are well below the theoretical expectations both for normal galaxies and LIRGs/ULIRGs. Furthermore, the different densities required to fit the two populations of galaxies with a common constant SFRff ~ 0.02 are far from the values derived in observations.
7.1.2. Case-II: revised conversion factors
Figure 11b is similar to Fig. 11a but here SFRff values have been obtained from the revised estimates of the conversion factors discussed in Sect. 6 for Σdense (in LIRGs/ULIRGs) and ΣSFR (in normal galaxies). Not surprisingly, by adopting the revised conversion factors the global distribution of SFRff is shifted upward and, at the same time, the difference between normal galaxies and LIRGs/ULIRGs is increased. Most of the LIRGs/ULIRGs in Fig. 11b show now values of SFRff that lie within the range predicted by Krumholz & McKee (2005) with HCN densities very close to 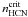 . The problem persists in the fit of normal galaxies, however, where the predicted values for SFRff and/or nHCN(H2) are still well below the expected range. The paradigm of a common constant SFRff in all galaxies can only be saved if we allow this parameter to be as low as ~0.0035. In this scenario the HCN densities fitting the observed efficiencies would range from
. The problem persists in the fit of normal galaxies, however, where the predicted values for SFRff and/or nHCN(H2) are still well below the expected range. The paradigm of a common constant SFRff in all galaxies can only be saved if we allow this parameter to be as low as ~0.0035. In this scenario the HCN densities fitting the observed efficiencies would range from 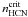 in normal galaxies to ~106 cm-3 in LIRGs/ULIRGs. The fit in densities nevertheless requires us to assume a value for SFRff that is a factor of 5–6 lower than expected by Krumholz & McKee’ s models or derived from CO observations (Krumholz & Tan 2007).
in normal galaxies to ~106 cm-3 in LIRGs/ULIRGs. The fit in densities nevertheless requires us to assume a value for SFRff that is a factor of 5–6 lower than expected by Krumholz & McKee’ s models or derived from CO observations (Krumholz & Tan 2007).
We can therefore conclude that the paradigm of a constant SFRff predicted by models within the range covered by the new HCN observations of normal galaxies and LIRGs/ULIRGs is not supported. The use of revised conversion factors alleviates the problem especially in LIRGs/ULIRGs. However, within the framework of local models it is not possible to fit the observed differences in the SFEdense between normal galaxies and LIRGs/ULIRGs using a common constant SFRff ~ 0.02 and a set of physically acceptable HCN densities.
7.2. Observations vs. models: the LFIR/L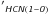 luminosity ratio
luminosity ratio
Based on the ISM model developed by Krumholz & McKee (2005), Krumholz & Thompson (2007) predicted how the 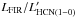 luminosity ratios should change as a function of the galaxy mean gas density
luminosity ratios should change as a function of the galaxy mean gas density 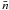 for three different object classes: normal galaxies, intermediate galaxies and starbursts. In Krumholz & Thompson’s formulation, molecular clouds in normal galaxies are characterized by low kinetic temperatures (TK = 10 K), as well as moderate-to-low Mach numbers (ℳ = 30), HCN abundances (X(HCN) = 1 × 10-8), and HCN(1–0) opacities (τHCN = 0.5). These molecular cloud parameters are expected to be boosted to higher values in starburst galaxies: TK = 50 K, ℳ = 80, X(HCN) = 4 × 10-8, τHCN = 2 (see Table 1 of Krumholz & Thompson 2007, for details). The common envelope to normal and starburst systems is that molecular clouds are characterized by a roughly constant dimensionless star-formation efficiency measured by SFRff.
for three different object classes: normal galaxies, intermediate galaxies and starbursts. In Krumholz & Thompson’s formulation, molecular clouds in normal galaxies are characterized by low kinetic temperatures (TK = 10 K), as well as moderate-to-low Mach numbers (ℳ = 30), HCN abundances (X(HCN) = 1 × 10-8), and HCN(1–0) opacities (τHCN = 0.5). These molecular cloud parameters are expected to be boosted to higher values in starburst galaxies: TK = 50 K, ℳ = 80, X(HCN) = 4 × 10-8, τHCN = 2 (see Table 1 of Krumholz & Thompson 2007, for details). The common envelope to normal and starburst systems is that molecular clouds are characterized by a roughly constant dimensionless star-formation efficiency measured by SFRff.
One key prediction of this model is that for mean densities 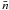 ≤ 104 cm-3, normal galaxies are expected to show higher SFEdense than galaxies classified as starbursts. Another key prediction is that the
≤ 104 cm-3, normal galaxies are expected to show higher SFEdense than galaxies classified as starbursts. Another key prediction is that the 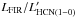 luminosity ratio should remain roughly constant in a diagram that simultaneously contains data from normal galaxies (characterized by low
luminosity ratio should remain roughly constant in a diagram that simultaneously contains data from normal galaxies (characterized by low 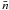 ) and starburst galaxies (characterized by high
) and starburst galaxies (characterized by high 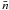 ) up to densities
) up to densities 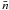 ≤ 104 cm-3. A different (less flat) appearance of SFEdense as a function of
≤ 104 cm-3. A different (less flat) appearance of SFEdense as a function of 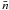 can be predicted at higher densities, however. Figure 12, a modified version of Fig. 2 of Krumholz & Thompson (2007), purposely explores the predicted SFEdense in the high-density regime: 104 cm-3 <
can be predicted at higher densities, however. Figure 12, a modified version of Fig. 2 of Krumholz & Thompson (2007), purposely explores the predicted SFEdense in the high-density regime: 104 cm-3 < 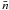 < 107 cm-3. Following the convention of Krumholz & Thompson (2007), we represent the
< 107 cm-3. Following the convention of Krumholz & Thompson (2007), we represent the 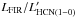 and SFR/
and SFR/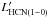 ratios as a function of the mean gas density
ratios as a function of the mean gas density 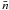 for normal (dot-dashed line), intermediate (solid line) and starburst (dashed line) galaxies4. As argued by Krumholz & Thompson (2007), the models for normal galaxies and starbursts are seen to converge in the high-density regime (
for normal (dot-dashed line), intermediate (solid line) and starburst (dashed line) galaxies4. As argued by Krumholz & Thompson (2007), the models for normal galaxies and starbursts are seen to converge in the high-density regime (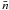 ≥ 105 cm-3).
≥ 105 cm-3).
 |
Fig. 12 We show the model-predicted ratio of the star-formation rate or IR luminosity to the HCN(1–0) luminosity as a function of the mean gas density |
As discussed in Sect. 4.1, the observations presented in this paper show that the LFIR/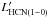 ratio is not constant inside our combined sample: SFEdense is a factor ~2–3 higher in LIRGs/ULIRGs compared to normal galaxies (⟨SFEdense⟩ (LIRGs/ULIRGs) ~ 1400 ± 100 L⊙ L′-1; ⟨ SFEdense ⟩ (normal) ~ 600 ± 70 L⊙ L′-1). These data can be used to benchmark the predictions of the model shown in Fig. 12. Two conclusions can be drawn from this comparison. First, in relative terms, the model is able to reproduce the increase in the SFEdense derived from observations as being caused by a dramatic increase in the average gas densities. According to Fig. 12, if we assume that normal galaxies are characterized by
ratio is not constant inside our combined sample: SFEdense is a factor ~2–3 higher in LIRGs/ULIRGs compared to normal galaxies (⟨SFEdense⟩ (LIRGs/ULIRGs) ~ 1400 ± 100 L⊙ L′-1; ⟨ SFEdense ⟩ (normal) ~ 600 ± 70 L⊙ L′-1). These data can be used to benchmark the predictions of the model shown in Fig. 12. Two conclusions can be drawn from this comparison. First, in relative terms, the model is able to reproduce the increase in the SFEdense derived from observations as being caused by a dramatic increase in the average gas densities. According to Fig. 12, if we assume that normal galaxies are characterized by 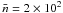 cm-3, extreme starbursts (LIRGs/ULIRGs) should be in a
cm-3, extreme starbursts (LIRGs/ULIRGs) should be in a 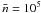 cm-3 regime to fit the observed change in SFEdense. In absolute terms, the model predicts values of SFEdense for normal galaxies and extreme starbursts that are marginally a factor ~1.5 above the observed values5. This success of the model would be in apparent contradiction with the scenario described in the previous section, where we concluded that the star-formation efficiency per free-fall time SFRff in the model, supposed to be ~0.02, has to be lowered by a factor 5–6 to fit the observations (after the revision of conversion factors discussed in Sect. 7.1.2). As argued below, there is no contradiction, however. Based on the output of the model of Krumholz & Thompson, we can estimate the implicit value of αHCN for the model molecular clouds at densities higher than
cm-3 regime to fit the observed change in SFEdense. In absolute terms, the model predicts values of SFEdense for normal galaxies and extreme starbursts that are marginally a factor ~1.5 above the observed values5. This success of the model would be in apparent contradiction with the scenario described in the previous section, where we concluded that the star-formation efficiency per free-fall time SFRff in the model, supposed to be ~0.02, has to be lowered by a factor 5–6 to fit the observations (after the revision of conversion factors discussed in Sect. 7.1.2). As argued below, there is no contradiction, however. Based on the output of the model of Krumholz & Thompson, we can estimate the implicit value of αHCN for the model molecular clouds at densities higher than 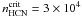 cm-3. The HCN conversion factor depends, for each galaxy class, on
cm-3. The HCN conversion factor depends, for each galaxy class, on  . Assuming the best fit values for
. Assuming the best fit values for  reported above, we derive that αHCN ~ 1–2 M⊙ L′-1 in starbursts and ~3–4 M⊙ L′-1 in normal galaxies in the model, i.e., a factor ~2–3 lower than the values of αHCN adopted in Sect. 6.1. Taking into account that the best compromise solution for
reported above, we derive that αHCN ~ 1–2 M⊙ L′-1 in starbursts and ~3–4 M⊙ L′-1 in normal galaxies in the model, i.e., a factor ~2–3 lower than the values of αHCN adopted in Sect. 6.1. Taking into account that the best compromise solution for 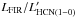 implies ratios that are still ~50% too high (Fig. 12), we conclude that the model (with SFRff ~ 0.02 and our preferred values for αHCN) is a factor of ~4 off. This is similar to the factor of ~5–6 disagreement found in Sect. 7.1.2.
implies ratios that are still ~50% too high (Fig. 12), we conclude that the model (with SFRff ~ 0.02 and our preferred values for αHCN) is a factor of ~4 off. This is similar to the factor of ~5–6 disagreement found in Sect. 7.1.2.
The conclusion common to the present section and Sect. 7.1 is that a rough agreement between the HCN observations presented in this paper and the predictions of local models can only be reached if SFRff ~ 0.005–0.01 and/or if αHCN is still a factor of ~ a few lower than our favored values for normal galaxies and starbursts (LIRGs/ULIRGs). In qualitative agreement with this picture, the recent paper of Krumholz et al. (2012) has presented conclusive evidence that the best correspondence between the prediction of local models and the results of CO galaxy surveys requires lowering SFRff to 0.01, i.e., a factor of 1.5–3 below the value previously assumed by Krumholz & McKee (2005). Dib (2011) recently came to similar conclusions that also point to lower values of SFRff based on a different formulation of the star-formation process, which is regulated in his model by stellar feedback.
7.3. Observations vs. models: is “global” dynamical time scale a key parameter?
We have provided evidence that the conversion of dense molecular gas into stars is more efficient in LIRGs/ULIRGs than in normal galaxies. Although this has been ascribed to the existence of very different local physical properties (densities) of the clouds in these two populations of galaxies, we have seen in Sects. 7.1 and 7.2 that this hypothesis has difficulties in explaining the HCN results discussed in this paper (unless significantly lower SFRff and/or αHCN are assumed). Alternatively, the star-formation rates could be regulated by the global large-scale dynamics of the ISM, more perturbed in strongly interacting galaxies (in our sample most of them are LIRGs/ULIRGs) than in normal galaxies. In this scenario we expect that the differences in SFEdense (or equivalently in tdep) between the two populations of galaxies can be reproduced by similar differences in tdyn, as SFEdense ≡ 1/tdep ∝ 1/tdyn. To explore this possibility, we compare in this section the distribution of dynamical time scales and depletion time scales of the dense molecular gas in our sample.
Figure 13 represents log(tdep) versus log(tdyn) for normal galaxies and LIRGs/ULIRGs. Depletion time scales of the dense gas tdep are derived as defined in Sect. 4.1. Dynamical time scales tdyn are defined as a crossing time scale unit determined by the ratio between the radius of the star-forming region, where the HCN emitting gas is expected to lie, and half the full width of the HCN line. When available, we corrected tdyn for the value of the inclination of the galaxies. Whereas there is a clear segregation between the two populations of galaxies as to the values of tdep, the corresponding differences in tdyn are less significant.
Figure 14 shows a histogram representation of the number density of galaxies as a function of tdep, tdyn and the tdep/tdyn ratio. We split our sample into normal galaxies (LIR < 1011 L⊙, gray filled histograms) and luminous infrared galaxies (LIR > 1011 L⊙, empty histograms). Depletion times (top panel) roughly span an order of magnitude in each subsample. They peak around ~10 Myr for LIRGs/ULIRGs and around ~50 Myr for normal galaxies. The clear separation between the two histograms highlights the higher star-formation efficiency of LIRGs/ULIRGs. The middle panel shows the dynamical time scales of the studied galaxies. The two histograms extend across a common range of ~1.5 orders of magnitude, although the dynamical time scales in LIRGs/ULIRGs are about a factor of 2 lower on average. These differences between the two populations of galaxies can be expected, because many LIRGs/ULIRGs are mergers where the interaction has brought most of the molecular gas to smaller radii. We note, however, that the differences reported for tdyn fall short of explaining the factor 5 difference in tdep.
 |
Fig. 13 We represent log(tdep) versus log(tdyn) for normal galaxies (LIR < 1011 L⊙, open symbols) and luminous infrared galaxies (LIR > 1011 L⊙, filled symbols). |
 |
Fig. 14 a) (Upper panel) Histograms showing the number density of galaxies (number of galaxies per unit interval, as shown) as a function of log(tdep) for normal galaxies (LIR < 1011 L⊙, gray filled histogram) and luminous infrared galaxies (LIR > 1011 L⊙, empty histogram). b) (Middle panel) Same as a) but representing the number density of galaxies as a function of log (tdyn). c) (Lower panel) Same as a) but representing the number density of galaxies as a function of log (tdep/tdyn). |
 |
Fig. 15 Three-dimensional representation of the bi-parametric star-formation law giving the star-formation rate density ΣSFR as a function of the dense molecular gas surface density Σdense and the dynamical time tdyn. |
We represent in the lower panel of Fig. 14 the histograms of the tdep/tdyn ratio. This is equivalent to the ratio between the mass of dense molecular gas and the mass of stars formed in one dynamical time scale. Although the shape (intrinsic dispersion) of the two histograms is similar, tdep/tdyn ratios in LIRGs/ULIRGs are typically a factor of 2 lower than in normal galaxies. Taken at face value, this suggests that the amount of dense gas converted into stars per unit of dynamical time is somewhat higher in LIRGs/ULIRGs. This result would contradict the idea that star formation is governed mainly by global dynamical time scales, because in this case we expect that the tdep/tdyn ratio is roughly constant, and consequently shows no significant differences between the two galaxy populations.
The inability of “global” star-formation models to fully explain the KS law derived from HCN, anticipated above, is better illustrated in Fig. 15. We show in this figure the three-dimensional representation of the bi-parametric star-formation law that expresses the star-formation rate density ΣSFR as a function of the dense molecular gas surface density Σdense and the dynamical time tdyn. The best fit to the HCN data is given by 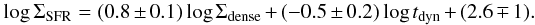 (21)While the power law index for Σdense (0.8 ± 0.1) is not far from unity within the errors, the corresponding index for tdyn (–0.5 ± 0.2) is not compatible with –1. This is against the theoretical expected power law index for Σdense/tdyn ratio that should be about ~1 (Kennicutt 1998). Furthermore, the goodness of the fit of Eq. (21), estimated by a standard χ2 analysis, indicates a meager 12% improvement with respect to the value of χ2 obtained in the single parameter fit of Eq. (19). With the inclusion of “global” dynamical time scales we are unable to significantly improve the fit of star-formation laws derived from HCN.
(21)While the power law index for Σdense (0.8 ± 0.1) is not far from unity within the errors, the corresponding index for tdyn (–0.5 ± 0.2) is not compatible with –1. This is against the theoretical expected power law index for Σdense/tdyn ratio that should be about ~1 (Kennicutt 1998). Furthermore, the goodness of the fit of Eq. (21), estimated by a standard χ2 analysis, indicates a meager 12% improvement with respect to the value of χ2 obtained in the single parameter fit of Eq. (19). With the inclusion of “global” dynamical time scales we are unable to significantly improve the fit of star-formation laws derived from HCN.
Several biases in the way the dynamical time scales are derived could explain why the tdep/tdyn histograms shown in Fig. 14 are not coincident for the two populations of galaxies. In particular, dynamical time scales in normal galaxies, where star formation is typically much more widely spread in the disks compared to LIRG/ULIRGs, could be underestimated. However, LIRGs/ULIRGs do not behave as a monolithic family in this respect: some LIRGs, especially in the range LIR ≤ 1011.4 L⊙ can have spread-out star formation (Hattori et al. 2004; Alonso-Herrero et al. 2006; Rodríguez-Zahurín et al. 2011).
8. Summary and conclusions
We have used the IRAM 30 m telescope to observe a sample of 19 LIRGs in the 1–0 lines of CO, HCN and HCO+. The galaxies were extracted from a sample of local LIRGs with available high-quality and high-resolution images obtained at optical, near- and mid-IR wavelengths, which probe the star-formation activity. The new data presented in this work allow us to expand the number of LIRGs studied in HCN-HCO+ lines by more than a factor 3 compared to previous works. The chosen LIRG sample has a range of HCN luminosities that overlaps to a significant extent with that of normal galaxies. This is a key requirement for testing if LIRGs represent a transition point in star-formation laws between normal galaxies and ULIRGs. In particular, we studied if the observed bimodality of star-formation laws in galaxies derived from CO line data in previous surveys can be extended to the higher density regime probed by HCN. We used these results to explore the validity of different theoretical prescriptions for star-formation laws where local and/or global dynamical time scales are explicitly included.
We summarize below the main results and conclusions of this work:
We find that the star-formation efficiency of the dense gas (SFEdense) estimated by
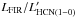 luminosity ratios is on average a factor ~2–3 higher in LIRGs/ULIRGs (~1400 ± 100 L⊙ L′-1) compared to normal galaxies (~600 ± 70 L⊙ L′-1). With the addition of the new LIRG sample we confirm on a more solid statistical basis that the LFIR-
luminosity ratios is on average a factor ~2–3 higher in LIRGs/ULIRGs (~1400 ± 100 L⊙ L′-1) compared to normal galaxies (~600 ± 70 L⊙ L′-1). With the addition of the new LIRG sample we confirm on a more solid statistical basis that the LFIR-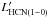 correlation is significantly superlinear (power law ~1.23 ± 0.05) when we include normal galaxies and LIRGs/ULIRGs in the fit.
correlation is significantly superlinear (power law ~1.23 ± 0.05) when we include normal galaxies and LIRGs/ULIRGs in the fit. We derived KS laws relating the two surface densities, ΣSFR and Σdense in normal galaxies and LIRGs/ULIRGs. A fit to the full sample yielded a power index N = 1.12 ± 0.04. However, LIRGs/ULIRGs and normal galaxies are not fully overlapping in this scatter plot. In order to quantify if a dual fit applies to the power law, we split the sample into normal and IR luminous galaxies. While the (ΣSFR, Σdense) distribution cannot be described as strictly bimodal, we found that a two-function power law fit with indices close to unity qualifies as a much better description of the star-formation relation for the dense gas. This result is seen to be solid against the statistical biases inherent to this analysis.
If we account for the different conversion factors for HCN in extreme starbursts and for the unobscured star-formation rate in normal galaxies, for which we find new evidence in these observations, the duality in star-formation laws is enhanced. This result extends the more extreme bimodal behavior of star-formation laws, derived from CO molecular lines by two recent surveys (Daddi et al. 2010; Genzel et al. 2010), to the higher molecular densities probed by HCN lines. The revised depletion time scales for the dense molecular gas show a significant difference between LIRGs/ULIRGs (tdep ~ 14 ± 1.4 Myr) and normal galaxies (tdep ~ 50 ± 5 Myr).
-
We compared the results of the new HCN observations with the predictions of theoretical models in which the efficiency of star formation is determined by the ratio of a constant star-formation rate per free-fall time (SFRff) to the local free-fall time (tff) (Krumholz &McKee 2005). Within the framework of these models we found that it is possible to fit the observed differences in the SFEdense between normal galaxies and LIRGs/ULIRGs using a common constant SFRff and a set of physically acceptable HCN densities, but only if SFRff ~ 0.005–0.01 and/or if αHCN is still a factor of ~ a few lower than our favored values.
We studied whether the inclusion of “global” dynamical time scales offers a better description of the star-formation relations derived for the dense gas. This approach helps finding a marginally better universal relation for the dense molecular gas. In the best-fit solution for ΣSFR ∝
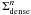
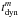 , the power law index for Σdense (n = 0.8 ± 0.1) is not far from unity within the errors, i.e., in agreement with the theoretical expected value. Nevertheless, the corresponding index for tdyn (m = −0.5 ± 0.2) is not compatible with –1, a result whose theoretical implications remain to be understood.
, the power law index for Σdense (n = 0.8 ± 0.1) is not far from unity within the errors, i.e., in agreement with the theoretical expected value. Nevertheless, the corresponding index for tdyn (m = −0.5 ± 0.2) is not compatible with –1, a result whose theoretical implications remain to be understood.
A fit of the SF laws similar to the one discussed in Sect. 7.3 was first explored by Genzel et al. (2010), who used CO line data in a sample of normal SF galaxies and extreme starbursts at different redshift ranges. The two-parameter (Mgas, tdyn) SFR law derived by Genzel et al. (2010) (SFR ∝ 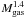
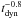 ) is successful at providing a universal SF relation. Remarkably, the power law indices in their fitted SF relation are also found to deviate from the theoretical expected values (SFR ∝
) is successful at providing a universal SF relation. Remarkably, the power law indices in their fitted SF relation are also found to deviate from the theoretical expected values (SFR ∝ 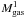
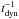 ), however. Altogether the SF relation obtained in Eq. (21) from HCN data and the one obtained by Genzel et al. (2010) from CO are very similar to the KS laws obtained, respectively, by Gao & Solomon (2004b) and Kennicutt (1998) provided that we remain in the ΣSFR − Σ(dense)gas projection of the SF laws.
), however. Altogether the SF relation obtained in Eq. (21) from HCN data and the one obtained by Genzel et al. (2010) from CO are very similar to the KS laws obtained, respectively, by Gao & Solomon (2004b) and Kennicutt (1998) provided that we remain in the ΣSFR − Σ(dense)gas projection of the SF laws.
The bottom line, however, is that the different dynamical time scale ranges found for normal galaxies and extreme starbursts are not sufficient to dissolve the duality observed in the ΣSFR − Σ(dense)gas projection of the SF laws (see also Krumholz et al. 2012). A possible explanation for this failure can be searched for in the uncertainties that plague the definition and the observational determination of tdyn. This is paramount if we are to compare systems that are known to be in very different dynamical states. So far, the most widely accepted definition for tdyn, also used in this work, is equivalent to that of a crossing or orbit time scale for the system, which is determined from observations. However, while normal galaxies can be described as dynamically relaxed rotating disks, mergers are strongly interacting and dynamically very disturbed. In this context using a common definition for tdyn is questionable. High-spatial resolution observations can help to disentangle the role of large-scale dynamics in the small-scale spatially resolved SF laws both in normal galaxies and in extreme starbursts (e.g. Boquien et al. 2011).
Alternatively, the inclusion of global dynamical time scales may not be the key for estimating the correct scaling of the SF relation and thus for determining the absolute value of the SFR for different galaxy populations. From the observational point of view there is ample room for improvement in our understanding of how conversion factors for different tracers of molecular gas may differ in galaxies. As discussed above, this is a prerequisite for accurately calibrating SF relations and exploring their differences between galaxies. So far, the evidence for different conversion factors in normal galaxies and extreme starbursts is limited to CO and HCN lines. Multi-transition studies for different molecular tracers will be paramount for tackling this problem.
In addition to providing a better handle of conversion factors, which are required to convert intensities (I) into gas surface densities (Σgas), multi-line observations can yield an estimate of volume gas densities (ρgas). This will facilitate a more direct comparison between observations and models that predict how the SFR volume density should depend on ρgas, rather than on Σgas. In this context we mention that Krumholz et al. (2012) have recently argued that a simple, local, volumetric star-formation law with SFRff ~ 0.01 can dissolve the apparent bimodality found by Genzel et al. (2010) if different scale-heights are assumed for the gas disks (hgas) in normal galaxies and extreme starbursts. While this is a plausible explanation, we note that the observational constraints on how hgas might differ in different galaxy populations are currently scarce. The change in hgas required to make duality/bimodality disappear in SF laws consequently remains to be observationally validated.
Krumholz & Tan (2007) claim that uncertainties in observations translate into an order of magnitude errorbar.
This figure has been produced using the code of the model made publicly available by Mark Krumholz at http://www.ucolick.org/~krumholz/
We note that the absolute scale along the right Y axis of Fig. 2 of Krumholz & Thompson (2007) seems to be incorrect. A re-evaluation of this scale, derived from the output of the model, indicates that the predicted 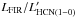 ratios are a factor of 2–3 lower than shown in the figure. Of particular note, this change helps finding a better agreement between observations and the model.
ratios are a factor of 2–3 lower than shown in the figure. Of particular note, this change helps finding a better agreement between observations and the model.
Acknowledgments
We acknowledge the IRAM staff at 30 m telescope for their help during the observations data reduction. S.G.B. acknowledges support from MICIN within program CONSOLIDER INGENIO 2010, under grant “Molecular Astrophysics: The Herschel and ALMA Era-ASTROMOL” (Ref. CSD2009-00038). A.A.H., M.P.S., L.C. and S.A. acknowledge support from AYA2010-21161-C02-1. M.P.S. also acknowledges support from the CSIC under grant JAE-Predoc-2007. We also thank the anonymous referee for his/her insightful and constructive report.
References
- Aalto, S., Booth, R. S., Black, J. H., & Johansson, L. E. B. 1995, A&A, 300, 369 [NASA ADS] [Google Scholar]
- Alonso-Herrero, A., Engelbracht, C. W., Rieke, M. J., Rieke, G. H., & Quillen, A. C. 2001, ApJ, 546, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Scoville, N. Z. 2002, AJ, 124, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 650, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Monreal-Ibero, A., et al. 2009, A&A, 506, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., Rieke, G. H., & Rigopoulou, D. 2012, ApJ, in press [arXiv:1109.1372] [Google Scholar]
- Armus, L., Mazzarella, J. M., Evans, A. S., et al. 2009, PASP, 121, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Bayet, E., Gerin, M., Phillips, T. G., & Contursi, A. 2009, MNRAS, 399, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., Prantzos, N., Boselli, A., & Gavazzi, G. 2003, MNRAS, 346, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Lisenfeld, U., Duc, P.-A., et al. 2011, A&A, 533, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouché, N., Cresci, G., Davies, R., et al. 2007, ApJ, 671, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Bussmann, R. S., Narayanan, D., Shirley, Y. L., et al. 2008, ApJ, 681, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 1991, ARA&A, 29, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- Dib, S. 2011, ApJ, 737, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1997, Rev. Mex. Astron. Astrofis. Conf. Ser., 6, 165 [Google Scholar]
- Elmegreen, B. G. 2002, ApJ, 577, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A. S., Solomon, P. M., Tacconi, L. J., Vavilkin, T., & Downes, D. 2006, AJ, 132, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004a, ApJS, 152, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004b, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., Carilli, C. L., Solomon, P. M., & Van den Bout, P. A. 2007, ApJ, 660, L93 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., Graciá-Carpio, J., Guélin, M., et al. 2006, ApJ, 645, L17 [NASA ADS] [CrossRef] [Google Scholar]
- García-Marín, M., Colina, L., & Arribas, S. 2009, A&A, 505, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., & Colina, L. 2006, ApJ, 640, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., et al. 2008, A&A, 479 [Google Scholar]
- Graciá-Carpio, J., Sturm, E., Hailey-Dunsheath, S., et al. 2011, ApJ, 728, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Guélin, M., Salomé, P., Neri, R., et al. 2007, A&A, 462, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, J. A., & Hartigan, P. M. 1985, Ann. Stat., 13, 70 [CrossRef] [MathSciNet] [Google Scholar]
- Hattori, T., Yoshida, M., Ohtani, H., et al. 2004, AJ, 127, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Juneau, S., Narayanan, D. T., Moustakas, J., et al. 2009, ApJ, 707, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Neri, R., García-Burillo, S., et al. 2008, ApJ, 677, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Thompson, T. A. 2007, ApJ, 669, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 699, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Groppi, C. E., Kulesa, C. A., & Walker, C. K. 2005, ApJ, 630, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Cox, T. J., Shirley, Y., et al. 2008, ApJ, 684, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, Q.-R., Jackson, J. M., Henkel, C., Truong, B., & Mauersberger, R. 1992, ApJ, 399, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Kennicutt, R. C., Jr., Gordon, K. D., et al. 2006, ApJ, 648, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Walter, F., Carilli, C. L., & Bertoldi, F. 2007, ApJ, 671, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Zaurín, J., Arribas, S., Monreal-Ibero, A., et al. 2011, A&A, 527, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D., & Ishida, C. 2004, The Neutral ISM in Starburst Galaxies (ASP), ed. S. Aalto, S. Huttemeister, & A. Pedlar, 320, 230 [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., et al. 2003, AJ, 126, 1607 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Yun, M. S., & Bryant, P. M. 1997, ApJ, 484, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1997, ApJ, 481, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Van den Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Genzel, R., & Tacconi, L. 1994, ApJ, 436, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Blietz, M., et al. 1994, ApJ, 426, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tan, J. C. 2010, ApJ, 710, L88 [NASA ADS] [CrossRef] [Google Scholar]
- Tasker, E. J., & Tan, J. C. 2009, ApJ, 700, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Usero, A., García-Burillo, S., Fuente, A., et al. 2004, A&A, 419, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lintott, C. J., Viti, S., Williams, D. A., Rawlings, J. M. C., & Ferreras, I. 2005, MNRAS, 360, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Wagg, J., Wilner, D. J., Neri, R., Downes, D., & Wiklind, T. 2005, ApJ, 634, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Weiß, A., Downes, D., Neri, R., et al. 2007, A&A, 467, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wild, W., Harris, A. I., Eckart, A., et al. 1992, A&A, 265, 447 [NASA ADS] [Google Scholar]
- Wu, J., Evans, N. J., II, Gao, Y., et al. 2005, ApJ, 635, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, L., Seaquist, E. R., Kuno, N., & Dunne, L. 2003, ApJ, 588, 771 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) CO(1–0) spectra observed with the IRAM 30 m telescope in a sample of 19 LIRGs. Spectra appear from top to bottom and from left to right in order of increasing right ascension of the source. For clarity some of the line intensities were scaled by the factor indicated in the panel. Gray-filled histograms highlight the velocity range used to calculate the baseline fitting and the line areas. |
| In the text | |
 |
Fig. 1 b) Same as a) but showing the HCN(1–0) spectra. |
| In the text | |
 |
Fig. 1 c) Same as a) but showing the HCO+(1–0) spectra. |
| In the text | |
 |
Fig. 2 a) (Left panel) We plot the |
| In the text | |
 |
Fig. 3 a) (Left panel) LFIR- |
| In the text | |
 |
Fig. 4 LFIR- |
| In the text | |
 |
Fig. 5 Dense molecular gas depletion or exhaustion time scale, tdep ≡ 1/SFEdense in Myr, derived for normal galaxies and LIRGs/ULIRGs. Symbols are as in Fig. 3. We highlight the location of NGC 1614 and II Zw 96 in the diagram. Errorbars show total uncertainties: ± 42% in tdep and ± 30% in LFIR. |
| In the text | |
 |
Fig. 6 a) (Left panel) Star-formation rate surface density ΣSFR as a function of dense molecular gas surface density as traced by the HCN(1–0) line, Σdense, in different populations of galaxies for which we have an estimate of the molecular disk size. Symbols are as in Fig. 3. The solid black line is the orthogonal regression fit to the full sample of galaxies. b) (Right panel) Same as a), but showing the two-function power law fit to normal galaxies (gray line) and IR luminous galaxies (black line). Here, normal galaxies (LIR < 1011 L⊙) are represented by open squares and IR luminous galaxies (LIR > 1011 L⊙) by black filled squares as referred to in text. Errorbars show ± 30% uncertainties in ΣSFR and Σdense. |
| In the text | |
 |
Fig. 7 Histograms of depletion times for the dense gas in the whole sample of galaxies (solid line) and in the populations of LIRGs/ULIRGs (gray filled) and of normal galaxies (hatched). The depletion times in the left-hand panel are calculated assuming the same FIR-to-SFR and HCN-to-mass conversion factors for the two populations. In the middle panel, the two conversion factors are modified (see Sect. 6), whereas in the right-hand panel only the HCN-to-mass factor is changed. |
| In the text | |
 |
Fig. 8 Results from testing the null hypotheses of a single KS law (left column) and of a double KS law (right column). Each panel shows the 2.5%,25%,50%,75% and 97.5% percentiles of σ1fit (top), Δlog (tdep) (middle) and SSR2fit/SSR1fit (bottom) as a function of σrand. The measured values are indicated by dashed horizontal lines. A gray rectangle represents the 95% confidence interval for σrand derived in each panel from the measured value. Dotted lines show the confidence intervals derived from σ1fit (top panels). |
| In the text | |
 |
Fig. 9 HCN to CO luminosity ratios as function of LIR for the full sample of galaxies. Here, normal galaxies (LIR < 1011 L⊙) are represented by open squares and IR luminous galaxies (LIR > 1011 L⊙) by filled squares. Red markers highlight those galaxies showing over-luminous HCN lines (HCN/CO ≥ 0.1). With the exception of one normal galaxy, all galaxies in this category are IR luminous. |
| In the text | |
 |
Fig. 10 a) (Left panel) Same as Fig. 6a, but showing the revised two-function power law fit to normal galaxies (gray line) and luminous infrared galaxies (black line) discussed in Sect. 6.3. Symbols and errorbars as in Fig. 6. b) (Right panel) We show the revised depletion time scale as a function of |
| In the text | |
 |
Fig. 11 a) (Left panel) Star-formation rate per free-fall time (SFRff; shown in the left Y axis) derived from the observed SFEdense in different populations of galaxies assuming a characteristic gas density for the HCN cloud nHCN(H2) = 3 × 104 cm-3. We show on the right Y axis the value of nHCN(H2) derived from SFEdense assuming a constant SFRff = 0.02. This value lies within the most likely range for SFRff ~ 0.011–0.028 as determined by the star-formation model of Krumholz & McKee (2005). We also highlight the average value of SFRff ~ 0.0058 as determined by Krumholz & Tan (2007) from a compilation of galactic and extragalactic HCN observations. Symbols are as in Fig. 3. Errorbars on SFRff (±42%) and LFIR (±30%) are shown. b) (Right panel) Same as a) but obtained based on the revised values of Σdense (in LIRGs/ULIRGs) and ΣSFR (in normal galaxies) discussed in Sect. 6. |
| In the text | |
 |
Fig. 12 We show the model-predicted ratio of the star-formation rate or IR luminosity to the HCN(1–0) luminosity as a function of the mean gas density |
| In the text | |
 |
Fig. 13 We represent log(tdep) versus log(tdyn) for normal galaxies (LIR < 1011 L⊙, open symbols) and luminous infrared galaxies (LIR > 1011 L⊙, filled symbols). |
| In the text | |
 |
Fig. 14 a) (Upper panel) Histograms showing the number density of galaxies (number of galaxies per unit interval, as shown) as a function of log(tdep) for normal galaxies (LIR < 1011 L⊙, gray filled histogram) and luminous infrared galaxies (LIR > 1011 L⊙, empty histogram). b) (Middle panel) Same as a) but representing the number density of galaxies as a function of log (tdyn). c) (Lower panel) Same as a) but representing the number density of galaxies as a function of log (tdep/tdyn). |
| In the text | |
 |
Fig. 15 Three-dimensional representation of the bi-parametric star-formation law giving the star-formation rate density ΣSFR as a function of the dense molecular gas surface density Σdense and the dynamical time tdyn. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.