| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 41 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117562 | |
| Published online | 23 February 2012 | |
The optical-UV spectral energy distribution of the unabsorbed AGN population in the XMM-Newton Bright Serendipitous Survey⋆,⋆⋆
1 INAF-Osservatorio Astronomico di Brera, via Brera 28, 20121 Milano, Italy
e-mail: elena.marchese@brera.inaf.it; roberto.dellaceca@brera.inaf.it
2 Università Milano Bicocca, Dipartimento di Fisica G. Occhialini, Piazza della Scienza 3, 20126 Milano, Italy
Received: 24 June 2011
Accepted: 17 November 2011
Context. Active galactic nuclei (AGN) emit radiation over a wide range of wavelengths, with a peak of emission in the far-UV region of the electromagnetic spectrum, a spectral region that is historically difficult to observe.
Aims. Using optical, GALEX UV, and XMM-Newton data we derive the spectral energy distribution (SED) from the optical/UV to X-ray regime of a sizeable sample of AGN. The principal motivation is to investigate the relationship between the optical/UV emission and the X-ray emission and provide bolometric corrections to the hard X-ray (2–10 keV) energy range, kbol, the latter being a fundamental parameter in current physical cosmology.
Methods. We construct and study the X-ray to optical SED of a sample of 195 X-ray selected Type 1 AGN belonging to the XMM-Newton bright serendipitous survey (XBS). The optical-UV luminosity was computed using data from the Sloan Digital Sky Survey (SDSS), from our own dedicated optical spectroscopy and the satellite GALaxy evolution EXplorer (GALEX), while the X-ray luminosity was computed using XMM-Newton data. Because it covers a wide range of redshift (0.03 < z ≲ 2.2), X-ray luminosities (41.8 < log L[2−10] keV < 45.5 erg/s) and because it is composed of “bright objects”, this sample is ideal for this kind of investigation.
Results. We confirm a highly significant correlation between the accretion disc luminosity Ldisc and the hard X-ray luminosity L[2−10] keV, in the form Ldisc ∝ Lβ[2-10] keV, where β = 1.18 ± 0.05. We find a very shallow dependence of kbol on the X-ray luminosity with respect to the broad distribution of values of kbol. We find a correlation between kbol and the hard X-ray photon index Γ2−10 keV and a tight correlation between the optical-to-X-ray spectral index αox and kbol, so we conclude that both Γ2−10 keV and αox can be used as a proxy for kbol.
Key words: galaxies: active / galaxies: nuclei / accretion, accretion disks / cosmology: observations / methods: statistical
The XMM-Newton Bright Serendipitous Survey is part of the follow-up program being conducted by the XMM-Newton Survey Science Centre (SSC), http://xmmssc-www.star.le.ac.uk/
Table 2 and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
A large fraction of the active galactic nuclei (AGN) bolometric luminosity is emitted in a strong, broad feature that begins to dominate the spectral energy distribution (SED) at the bluest optical wavelengths, and appears to extend short-wards of the current limits of UV satellite data (~100 Å). This feature of the continuum, also known as the Big Blue Bump (Sanders et al. 1989), is most likely thermal emission arising from a geometrically thin, optically thick accretion disc (Shields 1978; Malkan & Sargent 1982; Ward et al. 1987). Another large fraction of the total luminosity in AGN is also emitted in the X-ray band, which is more likely arising from the inverse Compton scattering of the disc’s photons by a corona of hot plasma surrounding the central regions of the disc, therefore X-ray and optical/UV observations are critical probes of the physics of the innermost regions of AGN, and investigating the relationship between the UV and X-ray emission is an important step towards better understanding the physics involved. Indeed the study of the correlation between X-ray and UV luminosities has in the past been the subject of many works on optically or X-ray selected samples of AGN (see Sect. 5).
In this paper we investigate the SEDs of a sample of 195 AGNs belonging to the XMM-Newton Bright Serendipitous Survey (XBS, Della Ceca et al. 2001) having UV observations from the satellite GALaxy evolution EXplorer (GALEX), optical magnitudes from the Sloan Digital Sky Survey (SDSS, complemented with optical data reported in Caccianiga et al. 2008) and X-ray observations from XMM-Newton (see Corral et al. 2011, hereafter referred as C11). The main goals of this work are:
-
a)
to derive accretion disc luminosities for a significant andrepresentative sample of AGN;
-
b)
to investigate the correlations between the accretion disc and the X-ray luminosity;
-
c)
to evaluate the bolometric luminosity (computed as the contribution of X-ray, UV and optical emission) and thus the bolometric correction to the hard X-ray (2–10 keV), defined as
![\begin{equation} k_{\rm bol}=\frac{L_{\rm bol}}{L_{\rm [2{-}10]~keV}} \label{kbol} \end{equation}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq13.png) (1)for a sample of AGN spanning a wide range in X-ray luminosities and redshifts. We stress that the infrared emission is not taken into account in the computation of the bolometric luminosity, since it is known to be re-processed emission mainly from the ultraviolet (see Antonucci et al. 1993); indeed its inclusion would mean counting part of the emission twice, overestimating the derived bolometric luminosities.
(1)for a sample of AGN spanning a wide range in X-ray luminosities and redshifts. We stress that the infrared emission is not taken into account in the computation of the bolometric luminosity, since it is known to be re-processed emission mainly from the ultraviolet (see Antonucci et al. 1993); indeed its inclusion would mean counting part of the emission twice, overestimating the derived bolometric luminosities.
The paper is organised as follows: in Sect. 2 we discuss the sample selection and the procedure used in cross-matching the sources in the XBS database with the GALEX and SDSS catalogues; Sect. 3 covers the construction of reliable SEDs for each source in the sample, taking into account intrinsic extinction and host galaxy contamination to the observed emission, as well as the emission lines contribution and absorption from Lyman α systems along the line of sight. In Sect. 4 we describe the results obtained in this work, focusing on the correlation analysis between the accretion disc luminosity and the X-ray luminosity, and the relation between bolometric correction and the X-ray luminosity. Our results are discussed within the context of previous works in Sect. 5 while in Sect. 6 summary and conclusions are presented. As done for other papers on the XBS survey we assume here the cosmological model H0 = 65 km s-1 Mpc-1, Ωλ = 0.7 and ΩM = 0.3 throughout this paper.
2. Data sources
2.1. XMM-Newton bright serendipitous survey
The XMM-Newton bright serendipitous survey (XBS survey) is a wide-angle (~28 sq. deg) high Galactic latitude (|b| > 20°) survey based on the XMM-Newton archival data. It is composed of two flux-limited serendipitous samples of X-ray selected sources: the XMM bright source sample (BSS, 0.5–4.5 keV band, 389 sources) and the XMM Hard bright source sample (HBSS, 4.5–7.5 keV band, 67 sources, with 56 sources in common with the BSS sample), having a flux limit of ~7 × 10-14 erg cm-2 s-1 in both energy selection bands. The details on the XMM-Newton fields selection strategy and the source selection criteria of the XMM BSS and HBSS samples are discussed in Della Ceca et al. (2004) and Della Ceca et al. (2008).
To date, the spectroscopic identification level has reached 93% and 97% for the BSS and the HBSS samples, respectively. The current classification of the XBS sample is as follows: 305 AGN (including 5 BL Lacs), 8 clusters of galaxies, 2 normal galaxies and 58 X-ray emitting stars (Caccianiga et al. 2008; Corral et al. 2011). The large majority of the still unidentified objects are expected to be absorbed AGN and BL Lac objects, so the sample of Type 1 AGN in the XBS can be considered complete at a confidence level approaching 100%. The analysis of the optical data, along with the relevant classification scheme and the optical properties of the extragalactic sources are presented in Caccianiga et al. (2007) and Caccianiga et al. (2008); the optical and X-ray properties of the galactic population are discussed in Lopez-Santiago et al. (2007).
The availability of good XMM-Newton data for the sources in the XBS sample, spanning the energy range between ~0.3 and ~10 keV, allowed us to perform a reliable X-ray spectral analysis for almost every AGN of the sample. The X-ray spectral analysis of the complete XBS AGN sample is presented in C11, which provide reliable X-ray photon indices, intrinsic column densities NH, and X-ray luminosities, which are necessary to derive bolometric luminosities.
The following work is focused on Type 1 AGN, in order to limit uncertainties due to obscuration in the determination of the intrinsic SED shape. Furthermore, in the source selection, we applied a cut in intrinsic column density NH, selecting only Type 1 AGN with NH < 4 × 1021 cm-2, resulting in a sample of 262 sources (7 AGN have been excluded). From this sample we excluded 14 sources, classified as radio loud AGN (Galbiati et al. 2005), because we do not know the orientation of the relativistic jet respect to the line of sight, and thus we can not quantify its contamination on the X-ray observed spectrum (Zamorani et al. 1981; Wilkes & Elvis 1987; Galbiati et al. 2005). We note that selecting X-ray unabsorbed (NH < 4 × 1021 cm-2) AGN also mitigate the possible “contamination” due to broad absorption line quasars (BALQSOs). Indeed BALQSOs seem to be characterised by the same intrinsic underlying X-ray continuum as the majority of the AGN population but their X-ray emission is often depressed by large amounts of intrinsic absorption (Streblyanska et al. 2010; Giustini et al. 2008; Gallagher et al. 2006). An X-ray to optical investigation of optically selected samples of Type 1 AGN without taking into account this contamination could lead to misleading results, since BALQSOs can cause an “artificial” steepening of the optical to X-ray correlation. To our knowledge there are no BALQSOs in our Type 1 AGN sample.
Thus the starting sample of our analysis is composed of 248 X-ray selected Type 1 AGN. We remark that the exclusion of obscured sources from our analysis does not necessarily mean that the conclusions we will outline further on are valid for unobscured sources only. Our results are still applicable to obscured AGNs if the obscuration is a line-of-sight orientation effect and does not affect the emission process at work in AGN.
2.2. Cross correlation with GALEX
The GALEX satellite is performing the first large-scale UV imaging survey (Martin et al. 2005; Morrisey et al. 2007). Most images are taken simultaneously in two broad bands, the near UV (NUV, ~1770–2850 Å) and the far UV (FUV, ~1350–1780 Å) at a resolution of ~5′′ full width at half maximum (FWHM). Three nested GALEX imaging surveys have been defined: the All-Sky Survey (AIS) expected to cover a large fraction (~85%) of the high Galactic latitude (|b| > 20°) sky to mAB ~ 21, the Medium Imaging Survey (MIS) reaching mAB ~ 23 on 1000 deg2, and the Deep Imaging Survey (DIS) extending to mAB ~ 25 on 80 deg2. These main surveys are complemented by guest investigator programs.
Here we used the GALEX data from the officially distributed Data Release 4 (GR4), which has been homogeneously reduced and analysed by a dedicated software pipeline. A previous version of this pipeline used for the earlier GR3 data release is described in detail by Morrisey et al. (2007). For details about the changes between GR3 and GR4 and on the GALEX mission see respectively http://galex.stsci.edu/GR4/ and http://www.galex.caltech.edu/.
2.2.1. GALEX detections
The cross correlation of the 248 Type 1 XBS AGN with the GALEX catalogue GR4 was performed by using the coordinates of the optical counterparts of the X-ray sources (reported in Caccianiga et al. 2008), with an impact parameter of 2.6′′. This latter value was derived by Trammell et al. (2007) cross-correlating a sample of 6371 quasar from the SDSS with GALEX; they find that 99% of the matches is recovered with a search radius of 2.6′′.
The cross-correlation produced (multiple or single) matches for 182 X-ray sources. We now describe how these matches were analysed. In the case of multiple matches (115 X-ray sources) the duplicates were removed with the following procedure. If two GALEX sources were within 2.6′′, but had the same “photoextractid” (i.e. they were both from the same observation) they were considered as two independent sources. In these cases (6 matches: XBSJ003418.9-115940, XBSJ012000.0-110429, XBSJ120359.1+443715, XBSJ120413.7+443149, XBSJ141809.1+250040, XBSJ163309.8+571039) the brightest source was selected as the best candidate to be the counterpart of the XBS source. Otherwise, if the multiple matches were from different observations, they were assumed to be multiple observations of the same source. In these cases the observation with the longest exposure time was retained. In the cases of almost equal exposure times we chose the observation where the source was closer to the centre of the field of view (that is the source with the smallest “fov-radius” from the “photoobjall” table), as generally the photometric quality is better in the central part of the field (Bianchi et al. 2011). All the selected sources, with the exception of two (XBSJ210355.3-121858, XBSJ165406.6+142123) have photometric errors (based on Poissonian source counts statistics, see also Sect. 3.3.1) on the UV magnitudes lower than 0.5 mag, in agreement with the selection procedure used by Bianchi et al. (2011). The two exceptions reported above, having respectively errors on NUV magnitudes of 0.56 mag and 0.58 mag, were still considered in our analysis.
From this sample of 182 Type 1 AGN we excluded two sources (XBSJ031851.9-441815 and XBSJ062134.8-643150) from the analysis, due to huge (up to a factor 1000) uncertainties in the estimate of the UV-optical fluxes, once the corrections discussed in Sect. 3 were taken into account. This procedure allowed us to define 180 X-ray/UV matches, from the original sample of 248 AGN; about 98% of the sources have at least a NUV detection, ~2% were detected in the FUV band only, and about 75% of these sources were detected both in the NUV and in the FUV band.
In order to estimate the reliability of these matches we computed the expected number of random matches within 2.6′′. This was done by performing the same cross-correlation after shifting the X-ray catalogue (along the right ascension and the declination) so that only chance coincidences are expected. To account for the non-uniform distribution of the sources in the sky we repeated several times the cross-correlation with different offsets and computed the average number of random sources found in each cross-correlation. Thus we derived that the probability of finding a GALEX UV spurious source within 2.6′′ is 0.015, which correspond to ~4 chance matches over the original sample of 248 sources.
2.2.2. Upper limits on GALEX fluxes
In this section we will discuss how the remaining 66 sources (for which we do not have GALEX photometric data) were treated. Forty six of these 66 sources (~18.5% of the original sample of 248 sources) do not fall in the area of sky covered by GALEX (Data Release 4), thus the lack of UV data does not depend on the properties of the sources in this sub-sample. It is worth noting that, as the sources contained in the XBS catalogue have a serendipitous distribution in the sky (at |b| > 20°), we expect that a fraction of them will be “not covered” with GALEX data since the AIS survey is not covering the whole sky. Indeed, the total sky area at |b| > 20° covered from AIS (GALEX DR4) is ~23 000 square degrees (Karl Forster, mission planner, private communication), i.e. ~85% of the sky at |b| > 20°. Therefore the fact that 18.5% of the original sample of sources is not covered by GALEX is fully consistent with the “missing” GALEX coverage of the |b| > 20° sky (~15%).
 |
Fig. 1 Distribution in the mUV − mr plane of the final sample of Type 1 AGN analysed. The red crosses represent the sources with UV upper limits, the black circles are the sources detected by GALEX. |
The remaining 20 sources are indeed located in sky regions covered by GALEX observations. A visual inspection of the regions near these sources lead to the following conclusions: 3 sources (XBSJ002707.5+170748, XBSJ022253.0-044515, XBSJ220320.8+184930) were not detected since each of them lies in the wings of a very bright UV source in the sky, while 17 sources were simply too faint to be detected with the exposure time of the GALEX data along their line of sight. The former three sources were removed from the sample, while for the latter 17 sources we decided to use as an upper limit on the NUV flux (since 98% of the sources have at least a NUV detection) the one corresponding to the faintest detected source (with photometric error <0.5 mag, see Bianchi et al. 2011) within ~2 arcmin from the position of our undetected target. In order to investigate if these sources have different properties from the detected ones we compare (see Fig. 1) the optical r magnitude against the magnitude in the NUV band for the final sample of GALEX detected sources (black circles) and the sources with GALEX upper limits (red crosses, in the electronic form only); as expected, the latter ones are on average fainter than the detections in the r magnitude too. We also investigated the distribution in the L[2−10] keV − z plane of these two samples (see Fig. 2). It is evident that the undetected sources do not show any difference in the X-ray luminosity distribution as compared to the detected ones.
From this sub-sample of 17 source we excluded from the following analysis 2 sources (XBSJ014109.9-675639 and XBSJ050453.4-284532): the reason is that only one optical flux (in the red band) is available and it corresponds to an intrinsic rest-frame λ > 5000 Å, a wavelength range we did not consider in the SED fitting (see Sect. 3.1 for further details). At this stage, the sample is composed of 195 sources: 180 GALEX detections and 15 sources with GALEX upper limits.
2.3. Cross correlation with the Sloan Digital Sky Survey
All the sources of the XBS sample have a measured optical magnitude (mainly in the red optical band, Caccianiga et al. 2008). In order to have more reliable SEDs we need more than one optical point, preferably of the same epoch, to avoid variability effects. Thus we searched for optical information from the SDSS. This is one of the most ambitious surveys, which over eight years of operations (SDSS-I, 2000–2005; SDSS-II, 2005–2008) obtained deep, multi-colour images covering more than a quarter of the sky and created three-dimensional maps containing more than 930 000 galaxies and more than 120 000 quasars. The SDSS uses a dedicated 2.5-m wide-angle optical telescope at Apache Point Observatory (New Mexico), and takes images using photometric system of five filters (named u, g, r, i and z). For more information see http://www.sdss.org).
We cross-matched the optical positions of the resulting sample of 195 sources (including both the 180 XBS-GALEX detected sources and the 15 sources with GALEX upper limits) with the SDSS DR7 catalogue. This has produced 101 matches, i.e. 101 sources with a measured fluxes in the X-ray, UV (detection or upper limit) and at least one of the optical SDSS (u,g,r,i,z) bands; for the remaining 94 sources we used the optical magnitudes reported in Caccianiga et al. (2008).
To summarise, the final sample of Type 1 unabsorbed AGN (NH < 4 × 1021 cm-2) used in the analysis reported here is composed of 195 sources; their distribution in the LX − z and in the mUV − mr planes are shown in Figs. 1 and 2. The sample covers a range of redshift between 0.03 and ~2 and a wide range of X-ray luminosities, i.e. from 6 × 1041 to 3 × 1045 erg/s. Besides the X-ray information (e.g. spectral slope, flux), which are available for all the sources, we have a) optical magnitudes (from SDSS and/or from the XBS project) for all the 195 sources analysed and b) GALEX detections for 180 sources and GALEX upper limits for 15 sources.
 |
Fig. 2 Distribution in the LX − z plane of the final sample of Type 1 AGN. Black circles: GALEX detections; red crosses: upper limits. |
3. Construction of SEDs
3.1. Exclusion of data at λrest > 5000 Å
In order to study the intrinsic emission produced by the accretion disc it is necessary to consider wavelength ranges which are free from contamination due to different spectral components (e.g. stellar emission from the host galaxy). Vanden Berk et al. (2001), studying the composite spectra of a sample of SDSS quasars, showed that the slope of the continuum changes abruptly at a rest-frame wavelength of about 5000 Å, becoming steeper (optical spectral index αν changing from −0.44 to −2.45) at longer rest-frame wavelengths (see Fig. 5 in Vanden Berk et al. 2001). The authors hypothesise that this behaviour can be partly due to the host-galaxy starlight contamination, as suggested from the presence of stellar absorption lines in the composite spectrum. Nevertheless, they also theorise that this contribution of emission at wavelengths beyond 5000 Å could be caused by an intrinsic change in the quasar continuum (e.g. emission from hot dust). As the emission from the accretion disc is concentrated at wavelengths lower than 5000 Å (we expect a peak of emission in the Far-UV), we did not consider in the fit of the accretion disc emission the rest-frame wavelengths longer than 5000 Å. For this reason two sources (XBSJ014109.9-675639 and XBSJ050453.4-284532) having only GALEX upper limits and optical magnitudes corresponding to a rest-frame wavelength λ > 5000 Å were already from our analysis (see Sect. 2.2.2). However, since a contamination from the host-galaxy (although weaker) is expected also for wavelength below 5000 Å we have developed a method (see Sect. 3.2.2) to take into account this possible contamination.
3.2. Corrections to measured fluxes
The radiation emitted from an astronomical source has obviously undergone various interactions during its journey, depending on different factors (redshift, environment, etc.). For this reason, in order to reliably study the intrinsic luminosity of our sources, the potential effects on the primary radiation have to be considered. First of all, Galactic reddening: for our sample this effect was estimated from the extinction law computed by Allen (1976), with RV = 3.1, adopting the values of the Galactic colour excess EB − V available for each source in the GALEX database.
3.2.1. Lyman α forest
Even if the large majority (97%) of the sources in our sample lies at z < 1.6, we decided to account for the potential attenuation given by absorption of neutral hydrogen in intervening Lyman-α absorption systems. For our sample this is possible only adopting a statistical approach, to produce an estimate of the attenuation τeff = −ln ⟨ e − τ ⟩ , where the average is taken over all possible lines of sights. In order to account for this effect we considered the results reported in Ghisellini et al. (2010), where a relation between the attenuation and redshift has been estimated for the six central wavelengths of the UV filters of the instrument UVOT on board of the satellite Swift. We extrapolated the average attenuation corresponding to the effective wavelengths of the GALEX filters FUV and NUV and we found that for z < 1 (~75% of the sources) the attenuation produces a flux reduction lower than 15% (5%) in the FUV (NUV) band while, for 1 < z < 1.6 (~22% of the sources) the reduction in flux is between 15–50% (5–20%) in the FUV (NUV) band. Only 3% of our sources have 1.6 < z < 2.3, implying corrections between 50–80% (20–70%) in the FUV (NUV). We applied these corrections to the UV fluxes of the whole sample of 195 sources with GALEX detections, even if they are negligible for ~75% of them.
3.2.2. Host Galaxy contamination
A first look at the SEDs obtained after these first corrections to the observed fluxes highlighted out that ~20% of the sources shows a steepening of the SED at the optical wavelengths, in evident disagreement with the expected accretion disc emission continuum (see Fig. 3).
 |
Fig. 3 Example of the rest-frame SED of one source showing the optical fluxes (empty squares) contaminated by the emission contribution of the host galaxy. The solid line represents the accretion disc emission model described in Sect. 3.4. |
We also noted that all these sources are characterised by a value of the 4000 Å break1 (also known as calcium break Δ) higher than ~17%. This strongly suggests a not negligible contribution of the stellar emission of the host galaxy to the total observed continuum.
In order to subtract this contribution and to constrain the SED shape at optical wavelengths, we assumed a first approximation model of a host galaxy composed by a step function having a calcium break of 50%. This value was chosen as an intermediate value between 45% and 55%, enclosing the 4000 Å breaks computed using the templates reported in Polletta et al. (2007), for elliptical galaxies and spirals S0, Sa, Sb. The AGN is instead represented by a power law with a mean spectral index αν = −0.44 in the wavelength region 1500–5000 Å (Vanden Berk et al. 2001). Superimposing these two components we derived an empirical relation between the observed 4000 Å break and the relative normalization of the AGN component with respect to the host galaxy component. This procedure allowed us to derive an empirical correction for the contamination of the host-galaxy for all the sources with measured values of the 4000 Å break.
In Fig. 4 we report the ratio between the fluxes of AGN and host galaxy in the wavelength range 4050–4250 Å as a function of the intensity of the calcium break Δ measured for the sources in our sample (blue points).
The data points have been fitted by a best fit relation described by the polynomial: 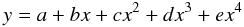 (2)where
(2)where 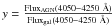 , x = Δ, a = 3.09, b = −15.23, c = 20.96, d = 12.34 and e = −36.64. This plot and the relative best fit relation represent a tool to derive an estimate of the contribution of the host galaxy to the AGN emission, once the intensity of the 4000 Å break is known. We also show the expected relation when the intensity of the host-galaxy 4000 Å break takes values in the range between 45% (lower dashed line) and 55% (upper dashed line). A variation from 45% to 55% of the assumed host-galaxy calcium break implies a variation on the accretion disc luminosity of ~45% at 2σ, with a mean variation of ~14%. Observing the empirical relations plotted in Fig. 4 we can infer that the relative optical flux ratio AGN/host galaxy changes from ~15% (for observed Δ less than ~15%) up to a maximum of 60% (for observed Δ ~ 40%). We also tested that the results obtained in this work (discussed in Sect. 4) were not statistically affected by a change in the range 45–55% of our assumed Δgalaxy = 50%.
, x = Δ, a = 3.09, b = −15.23, c = 20.96, d = 12.34 and e = −36.64. This plot and the relative best fit relation represent a tool to derive an estimate of the contribution of the host galaxy to the AGN emission, once the intensity of the 4000 Å break is known. We also show the expected relation when the intensity of the host-galaxy 4000 Å break takes values in the range between 45% (lower dashed line) and 55% (upper dashed line). A variation from 45% to 55% of the assumed host-galaxy calcium break implies a variation on the accretion disc luminosity of ~45% at 2σ, with a mean variation of ~14%. Observing the empirical relations plotted in Fig. 4 we can infer that the relative optical flux ratio AGN/host galaxy changes from ~15% (for observed Δ less than ~15%) up to a maximum of 60% (for observed Δ ~ 40%). We also tested that the results obtained in this work (discussed in Sect. 4) were not statistically affected by a change in the range 45–55% of our assumed Δgalaxy = 50%.
Furthermore we also checked if a variation of the AGN spectral index could lead to different results: considering the uncertainty of ≈ 0.1 on the spectral index, reported by Vanden Berk et al. (2001), we found that the accretion disc luminosities are affected by less then 1%.
 |
Fig. 4 Plot of the ratio between the fluxes of AGN and host galaxy in the wavelength range 4050–4250 Å as a function of the intensity of the calcium break Δ for the sources in our sample. The relations obtained assuming a host galaxy calcium break of respectively 45% or 55% are shown as dashed lines. |
3.2.3. Intrinsic extinction
The shape of the Big Blue Bump in the optical-UV region of AGN spectra is notoriously prone to effects of reddening: it is thus of great importance to account for intrinsic extinction (at the source redshift) at these wavelengths, in order to constrain the effective energy output. The effect is stronger in type 2 objects but a weaker effect is likely to be present in Type 1 objects as well. These corrections are not trivial, as the exact shape of the extinction curve in the far-UV for AGN is still a matter of debate.
We adopted the results of Gaskell & Benker (2007), who derived a mean extinction curve for 17 AGN with data from FUSE and HST.
We also verified “a posteriori” that these corrections are in good agreement with the expected SED shapes.
The extinction curve obtained by Gaskell & Benker (2007) is only valid in the range 1216 Å–6565 Å. To apply the intrinsic absorption correction below 1216 Å, we extrapolated this curve by preserving the flat trend that characterises the UV emission at short wavelengths.
The intrinsic colour excess EB − V for each source was derived from the values of intrinsic column density NH measured from the X-ray spectral analysis, assuming a Galactic gas-to-dust ratio NH/EB − V = 4.8 × 1021 cm-2 mag-1 (Bohlin et al. 1978). We recall that there are claims in the literature of a non-Galactic gas-to-dust ratio for some AGN (e.g. Maiolino et al. 2001), thus there could be objects where this assumption cannot be fulfilled. However, from the analysis of the optical and X-ray spectra of the AGN of the XBS sample, we found good consistency between the optical and the X-ray classifications, with very few exceptions (Caccianiga et al. 2004; Corral et al. 2011) thus supporting the idea of using the Galactic gas-to-dust ratio. Despite having reliable X-ray spectral information, we only have upper limits on NH for ~68% of the sources in the sample.
To derive the best guess for the intrinsic NH for each source we made use of the survival analysis, an efficient tool to work with censored data (Isobe et al. 1986, 1990). By using this statistical approach we could estimate a cumulative and a differential distribution of NH for the whole sample of AGN.
The differential distribution was then fitted with a gaussian curve, deriving values for the mean and the sigma of the NH distribution. Thus, for each source with NH upper limits, we produced a series of 100 random values between the minimum 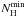 of the distribution and the upper limit relative to the individual source. Finally, we adopted the average of these 100 values as the estimated
of the distribution and the upper limit relative to the individual source. Finally, we adopted the average of these 100 values as the estimated 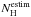 of the source; the 1σ confidence interval on this average encloses the 68% of the values of NH computed for each source around
of the source; the 1σ confidence interval on this average encloses the 68% of the values of NH computed for each source around 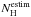 . The derived
. The derived 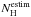 (and the relative 68% confidence error) for each source was used to derive the corresponding EB − V using the equation reported above.
(and the relative 68% confidence error) for each source was used to derive the corresponding EB − V using the equation reported above.
3.2.4. Emission lines contribution
The presence of broad emission lines within the bandpass of a given filter contributes significantly to the observed photometric magnitudes.
It is thus important to correct for the presence of the emission lines to obtain magnitudes closer to the continuum emission alone.
The “redshift dependent” magnitude correction is given by (“Allen’s Astrophysical Quantities”, 1990): 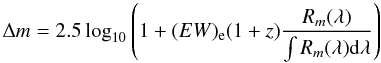 (3)where (EW)e is the rest-frame equivalent width of the emission line, λ = λe(1 + z) is the observed wavelength of the line and Rm is the response of the filter (Å-1)2.
(3)where (EW)e is the rest-frame equivalent width of the emission line, λ = λe(1 + z) is the observed wavelength of the line and Rm is the response of the filter (Å-1)2.
Only the most prominent AGN emission lines in the wavelengths of interest were considered: Lyα+NV, CIV, MgII, OIV+Lyβ and CIII+SiIII. The rest frame equivalent widths assumed to derive these corrections were taken from Telfer et al. (2002), and these equivalent widths were based on the investigations of 184 QSOs at z > 0.33 having HST spectra. The line that produces the higher contamination to the measured continuum is the Lyα emission line. This line contribution to the computed magnitudes can amount to 0.4–0.5 mag in the FUV, for objects in the 0.1–0.4 redshift range, and to 0.2–0.3 mag in the NUV, for objects in the 0.6–1.2 redshift range. The equivalent width of the Lyα line used here is in very good agreement with the average one computed from the composite quasar spectra of the SDSS (Vanden Berk et al. 2001). Another significant contribution is produced by the CIV emission line (e.g. ~0.2 mag for sources at 1.1 < z < 1.5 in the u band of the SDSS). In this case the equivalent width of the CIV emission line considered here (54 Å) is quite different from the one computed by Vanden Berk et al. (2001) (24 Å); we stress that in the last case the variation in magnitude would be ~0.1 mag.
3.3. Errors on fluxes
3.3.1. GALEX Photometric errors
The GR4 UV source extractor of the GALEX image processing pipeline reports photometric uncertainties for each object by assuming the observations are limited by Poisson noise. Therefore, the magnitude errors given in the GR4 object tables do not take additional sources of noise into account, including unknown variances of the detector background level and flat-field maps, or any other systematic errors present in the data. To account for these errors we referred to the work of Trammell et al. (2007). Assuming that the bulk of the stars observed in a GALEX field are non-variable, Trammell et al. (2007) used fields with multi-epoch observations as a tool for analysing the repeatability of the GALEX UV photometry for the same objects, using a large number of objects to empirically estimate the true photometric uncertainties. They derived an empirical relation between the NUV (FUV) magnitude and the corresponding true photometric error for both the AIS and DIS surveys. Applying this empirical relation to the GALEX magnitudes of our sources we find that the actual photometric errors are on average ~0.2 mag (in the FUV band) and ~0.11 (in the NUV band) larger than the Poissonian errors quoted in the GR4 tables.
3.3.2. Errors due to long-term variability
To account for the the lack of simultaneity in the optical and UV data it is necessary to have an estimate of the average uncertainties on optical and UV fluxes, due to long term variability. De Vries et al. (2005), in a study on optical long term variability of a sample of 41 391 quasars, derived a distribution of the quasar variability as a function of the time-lag between observations. In this work De Vries et al. (2005) found that in a time-lag of years the magnitude difference given by long term variability is ~0.35 mag; consequently, we associated this value to the long term variability for each source.
3.3.3. Total errors
The asymmetric 1σ total errors on the corrected fluxes that were adopted hereafter are given by the quadratic sum of the 1σ errors due to long term variability, the 1σ errors due to the photometric errors, and 1σ errors related to the corrections for the intrinsic extinction.
3.4. The accretion disc emission model
We described the optical-UV data points with a simple multicolour disc model (diskpn in the xspec12 package, Arnaud 1996). The parameters of this model are kTmax (maximum temperature of the accretion disc), Rin (inner radius of the accretion disc), and the normalization K (for details on this model see Gierlinski et al. 1999). In our study the inner radius Rin was set at 6.0 gravitational radii, and the normalization K was left as a free parameter. We created a grid of models corresponding to values of kTmax in the range between kT ≈ 1 eV and kT ≈ 10 eV, and we fitted these models to the photometric data with our routines.
For the 15 sources with only an upper limit from GALEX, we assumed a fixed average temperature of the accretion disc (kTmax ≈ 4 eV, as derived from the best-fit temperature computed for the 180 sources with detected GALEX fluxes) or a lower value of Tmax, in case of inconsistency of the UV upper limits with the fit with kTmax ≈ 4 eV. In these cases the SED normalization was determined using only the optical data.
3.5. Resulting SEDs
One example of the optical-UV-Xray spectral energy distribution obtained applying the correction discussed so far is shown in Fig. 5. The SEDs for all the remaining 194 objects are reported in the appendix. We also show the best-fit power-law model in the X-ray energy range 2–10 keV obtained from the X-ray spectral analysis (for more details see C11).
The optical/UV SED was carried out using the model and the grid of kTmax quoted in Sect. 3.4 leaving the normalization as free parameter. For each kTmax the best fit normalization was established by calculating an asymmetric weighted mean that uses the asymmetric errors as weights in the computation. Finally for each source, we chose the model whose Tmax minimises the value of the reduced χ2. Given this best fit Tmax, the asymmetric range of 1σ errors on the disc luminosity reported hereafter is given by the normalization range corresponding to 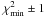 .
.
 |
Fig. 5 Example of the optical-UV-Xray spectral energy distribution obtained by applying the correction discussed so far. The filled blue squares are the fluxes in the GALEX NUV/FUV bands, while the empty squares represent the optical data. The fit used the model quoted in Sect. 3.4 (blue curve in the electronic form). The magenta curve is the best-fit power-law model in the X-ray energy range 2–10 keV obtained from the X-ray spectral analysis (see C11) The dashed magenta lines represent the errors on the best-fit model of the X-ray data, given by the errors on the spectral index Γ. |
3.6. Bolometric luminosities
In Fig. 6 we report the distribution of the accretion disc luminosities, which were computed by integrating over the optical-UV continuum spectra of each source. The accretion disc luminosity covers a luminosity range 42.4 < log (Ldisc) < 47.3 erg/s with a median value log (Ldisc)med ≅ 45.4 erg/s.
The bolometric luminosities were obtained as the sum of the accretion disc luminosity and the 0.1–500 keV X-ray luminosity, and the distribution is reported in Fig. 6. We computed this with the photon indices Γ available from the X-ray spectral analysis (C11) and introduced an exponential cut-off at 200 keV (Dadina 2008), F(E) ∝ E − Γe − E/200. The values of L [2 − 10] keV and Γ used hereafter are reported in Table 2.
Since the largest part of the bolometric luminosity is given by the accretion disc luminosity we obtained a very similar distribution, covering the range 42.8 < log (Lbol) < 47.3 erg/s with median value log (Lbol)med ≅ 45.5 erg/s.
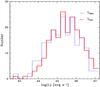 |
Fig. 6 Distribution of the AGN accretion disc luminosities (dotted blue line), computed by integrating over the optical-UV continuum spectra of each source and distribution of the bolometric luminosities (solid red line), obtained as a sum of the accretion disc luminosities and the 0.1–500 keV X-ray luminosities. |
4. Results
We derived the accretion disc luminosities, the X-ray luminosities, and the bolometric luminosities for a significant sample of Type 1 AGN covering a wide range of redshift (0.03 < z ≲ 2.2) and a wide range of X-ray luminosities (41.8 < log L[2−10] keV < 45.5 erg/s). The next step is to investigate the correlations between Ldisc, L[2−10] keV, and the bolometric correction ![\hbox{$\kbol = \frac{L_{\rm bol}}{L_{\rm [2{-}10]~keV}}$}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq115.png) .
.
We computed the slope of the relation between two linearly correlated variables using two different methods
-
1.
a linear least squares regression method choosing: a) X as independent variable (LSQ(y|x)); b) Y as independent variable (LSQ(x|y));
-
2.
a symmetric approach (i.e. without fixing one of the variables as independent and the other as dependent) that computes the bisector between the two least squares regression lines obtained by interchanging the choice of the independent variable (hereafter the “bisector method”, Isobe et al. 1990).
The study of correlations between outputs at different wavelengths is better done by directly comparing luminosities rather than fluxes, since any correlation in the luminosity space will be distorted in the flux space unless the luminosities are linearly correlated (Feigelson & Berg 1983; Padovani 1992). However, the use of luminosities instead of fluxes always introduces a redshift bias in flux limited samples, as luminosities are strongly correlated with redshift. It is therefore crucial to estimate the influence of this effect on the correlations in order to draw reliable conclusions on the true physical relationship between two redshift-dependent variables.
A way of dealing with this problem is via a partial-correlation analysis, i.e. computing the correlation between two variables (e.g. Ldisc, L[2−10] keV) and checking the effect of additional parameters (in this case the redshift) that the two variables depend on. The procedure used here is based on the Spearman rank-order correlation coefficient rS,z (and the two-sided probability of no correlation P, computed given the degrees of freedom and the t-value) as modified by Kendall & Stuart (1979) and Padovani (1992), in order to take the dependence on z into account. We assumed the correlation to be marginally significant if the probability P of no correlation is less than 10%, significant if P ≤ 5%, and highly significant if P ≤ 1%.
Finally, to check the stability of our results, the analysis was done for the main sample of 195 sources and for a sub-sample of 176 sources (Low-err sample hereafter) obtained by excluding the 19 sources with the highest uncertainties (i.e. those sources having an uncertainty (1σ) on kbol of more than a factor 1.5).
4.1. L[2−10] keV − Ldisc
The of the correlation between X-ray and UV luminosities has been, in the past, the subject of many works on optically or X-ray selected samples of AGNs (see Sect. 5.1 for an account of these works). For our sources, the Spearman correlation coefficient is rS,z = 0.34, giving a highly significant correlation (P < 10-3) according to our criteria, and a similar highly significant correlation is obtained for the sub-sample Low-err.
Treating L[2−10] keV as the independent variable, we found ![\begin{equation} \log L_{\rm disc}=(1.009\pm0.05)\log L_{\rm [2{-}10]~keV}+ 0.84 , \label{eq1_LDLX} \end{equation}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq130.png) (4)and while treating Ldisc as the independent variable we found
(4)and while treating Ldisc as the independent variable we found ![\begin{equation} \log L_{\rm disc}=(1.38\pm0.06)\log L_{\rm [2{-}10]~keV}- 15.71 . \label{eq2_LDLX} \end{equation}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq131.png) (5)Computing the bisector of the two regression lines as described by Isobe et al. (1990) the best-fit relation is
(5)Computing the bisector of the two regression lines as described by Isobe et al. (1990) the best-fit relation is ![\begin{equation} \log L_{\rm disc}=(1.18\pm 0.05)\log L_{\rm [2{-}10]~keV} -6.68 . \label{eq3_LDLX} \end{equation}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq132.png) (6)In Fig. 7 we display the relations (4), (5), and (6), between L[2−10] keV and Ldisc.
(6)In Fig. 7 we display the relations (4), (5), and (6), between L[2−10] keV and Ldisc.
A similar relation was obtained for the Low err sub-sample. Using the “bisector method” we obtain log Ldisc = (1.20 ± 0.05)log L[2−10] keV−7.65.
 |
Fig. 7 Plot of Ldisc vs. X-ray luminosity L[2−10] keV for our sample of sources. The two green lines represent the best-fit regression lines, given by Eqs. (4) and (5), obtained by interchanging the independent and dependent variable; the red line is the bisector of these two lines, parametrised by Eq. (6). |
It is worth noting that the correlation between the disc and the X-ray luminosity has often been studied in the literature by using the monochromatic optical luminosity, L2500 Å, and the monochromatic X-ray luminosity at 2 keV, L2 keV. For completeness, we also adopted this approach. For each source, L2500 Å was computed using the intrinsic best-fit SED discussed in Sect. 3.5, while L2 keV was derived from the intrinsic X-ray spectrum (C11). If we use these two quantities for our sample we obtain
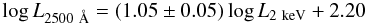 (7)if treating L2 keV as the independent variable,
(7)if treating L2 keV as the independent variable, 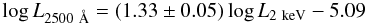 (8)when treating L2500 Å as the independent variable, and
(8)when treating L2500 Å as the independent variable, and 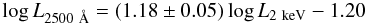 (9)using the “bisector” method. The derived slopes are in very good agreement with those derived using log Ldisc and log L [2 − 10] keV, confirming the equivalence of the two approaches.
(9)using the “bisector” method. The derived slopes are in very good agreement with those derived using log Ldisc and log L [2 − 10] keV, confirming the equivalence of the two approaches.
Finally, we also tried to evaluate whether β (![\hbox{$L_{\rm disc}\propto L_{\rm [2{-}10]~keV}^{\beta}$}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq145.png) ) could change as a function of the redshift, by splitting the sample in two sub-samples containing almost the same number of sources (having z above and below 0.6, respectively). We found marginal (2σ) evidence of an evolution of the slope with redshift, because it is steeper for the high z sub-sample.
) could change as a function of the redshift, by splitting the sample in two sub-samples containing almost the same number of sources (having z above and below 0.6, respectively). We found marginal (2σ) evidence of an evolution of the slope with redshift, because it is steeper for the high z sub-sample.
 |
Fig. 8 Plot of bolometric correction vs. X-ray luminosity L[2−10] keV for our sample of sources. The red line represents the best fit relation obtained assuming L[2−10] keV as independent variable. |
4.2. kbol − L[2−10] keV
A fundamental parameter for cosmological studies of AGN is the bolometric correction to the hard X-ray (2–10 keV), kbol, defined in Eq. (1). In Fig. 8 we display kbol against the 2–10 keV X-ray luminosity. Since the dependence of Ldisc from L [2−10] keV is very close to (although statistically different from) linear, the “slope” in the correlation between kbol and L [2−10] keV (that was found to be highly significant when the redshift is considered) is expected to be close to 0. Indeed, using the data shown in Fig. 8 we derived a best fit relation (assuming this time L[2−10] keV as the independent variable since kbol and L[2−10] keV are related, see Eq. (1)) with a flat slope3, log kbol ∝ − (0.01 ± 0.04) × log LX.
This flat slope (Fig. 8) implies a variation of less than 10% in kbol over about five order of magnitude in luminosities. This said, and given the very large dispersion observed, kbol could be therefore considered practically independent from L[2−10] keV. It is worth noting that the bulk of this large dispersion is intrinsic; i.e., the measurement errors do not constitute the dominant source of dispersion. In Fig. 9 we report the histogram of the bolometric corrections derived using the Low-err sample (176 objects), in order to give a “representative” distribution of kbol for the AGN population.
 |
Fig. 9 Histogram of the bolometric corrections for the AGN population (obtained using the Low-err sample composed of 176 objects). |
Spearman rank correlation coefficients (rS,z) and probabilities of null correlation (P) for the samples considered in this work.
5. Discussion
5.1. The X-ray to optical/UV correlation
The study of the correlation between X-ray and UV luminosities has been subject of many works on optically or X-ray selected samples of AGNs. This correlation is found to be 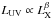 , with β ranging, in most studies, from 1.2 to 1.6 (Avni & Tananbaum 1982, 1986; Kriss & Canizares 1985; Anderson & Margon 1987; Wilkes et al. 1994; Yuan et al. 1998; Vignali et al. 2003; Strateva et al. 2005; Steffen et al. 2006; Just et al. 2007; Young et al. 2009; Lusso et al. 2010; Grupe et al. 2010; Stalin et al. 2010). This correlation provides a strong constraint on the physical processes at work, since it tells us that the fraction of power in the accretion disc corona, emitted in the X-rays, decreases/increases as a function of the accretion disc power (mainly emitted in the UV).
, with β ranging, in most studies, from 1.2 to 1.6 (Avni & Tananbaum 1982, 1986; Kriss & Canizares 1985; Anderson & Margon 1987; Wilkes et al. 1994; Yuan et al. 1998; Vignali et al. 2003; Strateva et al. 2005; Steffen et al. 2006; Just et al. 2007; Young et al. 2009; Lusso et al. 2010; Grupe et al. 2010; Stalin et al. 2010). This correlation provides a strong constraint on the physical processes at work, since it tells us that the fraction of power in the accretion disc corona, emitted in the X-rays, decreases/increases as a function of the accretion disc power (mainly emitted in the UV).
A direct comparison between our results and previous works is not very straightforward since different samples (each one with its selection effects that should be carefully evaluated) and different fitting methods (LSQ(y|x)), LSQ(x|y), or else the bisector method, have been used in the past. Furthermore, as also stressed by Green et al. (2009), different regression methods can yield very different results in samples with large dispersions.
As discussed in Isobe et al. (1990) when the physics (or the question to be solved) does not clearly indicate which variable depends on the other, a symmetric approach (such as the bisector method) should provide the best guess for the intrinsic relationship between the two variables (e.g. the X-ray and the disc luminosities in this case). Using the bisector method we found a slope that is different from linear at ~ 3.6σ, i.e. ![\hbox{$L_{\rm disc} \propto L_{\rm [2{-}10]~keV}^{(1.18\,\pm\, 0.05)}$}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq161.png) , and this result can now be compared with those obtained from other authors using a similar symmetric approach.
, and this result can now be compared with those obtained from other authors using a similar symmetric approach.
Statistically we found that our best-fit slope differs ~2.8σ from the slope obtained by Lusso et al. (2010, β = 1.32 ± 0.04), 4.6σ from Just et al. (2007, β = 1.41 ± 0.01), and 5.6σ from Green et al. (2009, β = 0.90 ± 0.02). However, there are a number of differences between our analysis and those reported above that can alleviate these differences.
First of all, as mentioned above, we are dealing with a statistically representative sample of X-ray selected, spectroscopically confirmed, Type 1 AGN. For all the studied objects we have an X-ray spectrum allowing us to measure the intrinsic X-ray luminosity; UV data from GALEX are available for about 93% of the sample. Finally we also tried to account for the factors contaminating or absorbing the primary radiation emitted from the AGN.
For the optically selected sample of SDSS AGN used in Green et al. (2009), the result quoted above refers to what is obtained with their “Main” sample (~2300 sources) having an X-ray detection fraction of only about 50%. When using their “zLxBox” sample, with a detection fraction of 100%, Green et al. (2009) obtain β = 1.19 ± 0.02, in excellent agreement with our results. Just et al. (2007) combine a sample of 26 optically selected, X-ray-observed AGN, at high z (between 1.5 and 4.5) with an homogeneous sample of 333 optically selected AGN from Steffen et al. (2006). Most of the Type 1 unabsorbed AGN have been classified as such using only photometric data. Finally Lusso et al. (2010) use a sample of X-ray selected Type 1 AGN from the COSMOS survey (545 objects) with about 40% of the objects with a photometric redshift and a classification based on their multi-band SED. All considered, it is difficult to say whether these differences in sample selections have any influence on the best-fit relationship. We aimed at obtaining the most accurate result by adopting a new large (195 objects), statistically complete sample of X-ray selected Type 1 AGN, spanning a wide range of redshift (0.03 < z ≲ 2.2) and X-ray luminosities (41.8 < log L[2−10] keV < 45.5 erg/s), with complete spectroscopic identifications and accurate X-ray spectral analysis (C11); furthermore, we also accounted for the factors contaminating or absorbing the primary radiation emitted from the AGN. Because statistically representative and composed of “X-ray bright” sources, this sample is ideal for this kind of investigation.
5.2. The bolometric correction, kbol
The bolometric correction kbol, used to derive the bolometric luminosities (laborious to obtain) from the measured X-ray luminosity, is a fundamental parameter for much important research in current physical cosmology, including the study of the accretion rate (e.g., Marconi et al. 2004), measurement of SMBH densities in the universe (e.g., Marconi et al. 2004), estimation of the active accretion lifetimes or duty cycles (e.g., Hopkins et al. 2005; Adelberger & Steidel 2005), and the conversion the energy density of the X-ray background (which is produced by the integrated X-ray emission of AGN) into a mass density of SMBHs in the local Universe (Soltan 1982).
In Sect. 4.2 we discussed our kbol values, where we had a very shallow dependence with the X-ray luminosity if compared with its very broad distribution (ranging from kbol ~ 5 up to kbol ~ few hundred). Similar results were obtained by Vasudevan & Fabian (2007) with a sample of 54 nearby AGN, where they also found a significant spread in kbol (ranging from ~5 up to ~100 when Radio Loud objects are removed). It is clear that this rather broad and “flat” distribution implies a very large distribution in the SED of AGN, preventing the use of a single value for the total population. Given the importance of kbol in a cosmological context, many authors investigated the possibility of deriving it from correlations with other simpler observables to compute. After already showing that we cannot use the X-ray luminosities, we discuss below two other observables recently proposed in literature.
In a recent paper, Lusso et al. (2010) have reported a very tight correlation between kbol and the X-ray to optical-UV luminosity ratio αox4, which is expected since both quantities are sensitive to the strength of the optical/UV part of the AGN spectrum compared with the X-ray part . However, to compute αox ideally, only two measurements are needed, one in a proximity of 2500 Å and another of 2 keV (both rest frame). Because of the good correlation between kbol and αox, Lusso et al. (2010) state that αox can be used as an accurate estimate (~20% at 1σ) of kbol. After studying an independent sample of Type 1 AGN using a different analysis to derive the bolometric output, we can now test the validity of this suggestion.
In Fig. 10 we show kbol against αox for our sample of sources, where a tight correlation is clearly present. However we found a steeper correlation with respect to the best fit in Lusso et al. (2010). Fitting our data with a quadratic polynomial we found the following best-fit relation: 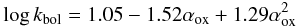 (11)(see Fig. 10 upper panel). In the bottom panel we also show the residual Δkbol from our best-fit relation: about 68% (≃1σ) of the objects are contained within 14% of the best-fit relationship while the maximum deviation of the data points from the expected relation is ~60%. Provided that measurements around 2500 Å and around 2 keV (rest frame) are available and that all the discussed corrections to these measurements are applied, we confirm that αox could be used as a proxy of kbol. In particular, using the relation (11) the value of kbol can be estimated with a mean accuracy of 0.14 dex (~30%).
(11)(see Fig. 10 upper panel). In the bottom panel we also show the residual Δkbol from our best-fit relation: about 68% (≃1σ) of the objects are contained within 14% of the best-fit relationship while the maximum deviation of the data points from the expected relation is ~60%. Provided that measurements around 2500 Å and around 2 keV (rest frame) are available and that all the discussed corrections to these measurements are applied, we confirm that αox could be used as a proxy of kbol. In particular, using the relation (11) the value of kbol can be estimated with a mean accuracy of 0.14 dex (~30%).
 |
Fig. 10 Upper panel: plot of kbol against αox for our sample of Type 1 AGN. The solid line and dotted lines represent our best fit and the range of variation with respect to the best-fit, including 68% of the sources. The dashed line represent the best fit relation computed by Lusso et al. (2010); in the bottom panel we show the residuals with respect to our best-fit relationship. |
A correlation between the hard X-ray photon index Γ2−10keV and the bolometric correction has been recently proposed by Zhou & Zhao (2010) based on the data on 29 optically selected low-redshift (z < 0.33) AGN. They propose that the rest frame Γ2−10keV can be used as a proxy for the bolometric correction with a mean uncertainty of a factor 2–3. The AGN sample discussed here is ideal for testing this correlation, since a detailed X-ray spectral analysis was carried out for all the sources in the sample (see C11). In Fig. 11 we report the relation between the hard X-ray photon index Γ2 − 10keV and the bolometric correction for our sample of AGN.
A highly significant correlation between the two quantities is clearly present (rS = 0.37,P < 10-6), confirming the results of Zhou & Zhao (2010); for comparison, we also show in Fig. 11 the best-fit relationship reported by Zhou & Zhao (2010), obtained using a symmetric approach (log kbol = (1.12 ± 0.30)Γ2−10 keV − (0.63 ± 0.53)). For our sample, the best-fit relation, obtained assuming Γ2−10 keV as independent variable, is 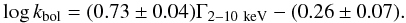 (12)The divergence between the best-fit relation derived for our data set and the Zhou & Zhao (2010) relationship can be attributed to the different statistical approach and to selection effects arising when comparing X-ray and optically selected samples. We conclude that Eq. (12) can be adopted to derive kbol from Γ2−10 keV with a mean error of ~0.34 dex (i.e. ~80%).
(12)The divergence between the best-fit relation derived for our data set and the Zhou & Zhao (2010) relationship can be attributed to the different statistical approach and to selection effects arising when comparing X-ray and optically selected samples. We conclude that Eq. (12) can be adopted to derive kbol from Γ2−10 keV with a mean error of ~0.34 dex (i.e. ~80%).
The physical justification of the observed kbol − Γ2−10keV relation could be related to the common dependence of these two quantities to the same physical parameter, namely the Eddington ratio (λEdd). Indeed, evidence for a direct dependence of both kbol and Γ on λEdd have recently been found by different authors (e.g. Vasudevan 2009; Risaliti et al. 2009; Lusso et al. 2010; Shemmer et al. 2009; Grupe et al. 2010; Caccianiga et al. 2011; Grupe et al. 2011). This common dependence on λEdd may naturally lead to a mutual correlation between these two quantities. A more detailed investigation of these correlations, using the AGN of the XBS, is currently in progress.
 |
Fig. 11 Plot of kbol vs. the 2–10 keV photon index Γ2 − 10keV. We show our best-fit relation (red solid line) and the best-fit relation computed by Zhou & Zhao (2010) (blue dashed line). |
6. Summary and conclusions
In this paper we have presented the analysis of the optical-UV-X-ray SEDs of a complete and representative sample of 195 X-ray selected, spectroscopically identified, Type 1 AGN, with intrinsic absorbing column densities NH < 4 × 1021 cm-2. The adopted sample, spanning a wide range of redshift 0.03 < z ≲ 2.2 and X-ray luminosity, 6 × 1041 erg/s < L [2 − 10] keV < 3 × 1045 erg/s, is composed of relatively bright AGN and thus ideal for this study. The optical-UV SED was investigated using data from the SDSS, from our own dedicated optical spectroscopy and photometry and from the satellite GALEX, while the X-ray part was studied using data from XMM-Newton.
While the X-ray spectra was presented and discussed in C11, we derived here the intrinsic optical-UV SED, trying to take all the factors contaminating or absorbing the primary optical-UV radiation emitted from the AGN into account. In particular we applied correction for
-
the Galactic extinction;
the potential attenuation given by absorption of neutral hydrogen in intervening Lyman-α absorption systems;
the contamination from the stellar emission of the host galaxy of the AGN;
the intrinsic extinction, using the mean extinction curve computed by Gaskell & Benker (2007), a galactic gas-to-dust ratio, and the measured values (or upper limits) of intrinsic column density NH available from the X-ray spectral analysis;
the contribution of the emission lines Lyman α+NV, CIV, MgII, OIV+Lyβ and CIII+SiIII.
We investigated here the correlations between the physical parameters inferred from the optical to X-ray SEDs, such as accretion disc luminosity, bolometric luminosity, bolometric correction, and X-ray photon index. We recall that our results are also applicable to Type 2 (obscured) AGNs if the obscuration is a line-of-sight orientation effect and does not affect the intrinsic energy generation mechanisms within AGNs (i.e. if the unified model of AGNs is valid). The main results of this work are the following
-
1.
Using a symmetric fitting approach (the bisector method) we found a highly significant intrinsic correlation between the accretion disc luminosity Ldisc and the X-ray luminosity L [2 − 10] keV, in the form
![\hbox{$L_{\rm disc} \propto L_{\rm [2{-}10]~ keV}^{\beta}$}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq195.png) , where β = 1.18 ± 0.05. The
non-linearity of this relation implies that the fraction of X-ray emission decreases
with increasing accretion disc luminosity. We also found marginal evidence that this
relationship depends on redshift;
, where β = 1.18 ± 0.05. The
non-linearity of this relation implies that the fraction of X-ray emission decreases
with increasing accretion disc luminosity. We also found marginal evidence that this
relationship depends on redshift; - 2.
We found a very shallow dependence of the bolometric correction on the X-ray luminosity if compared with its very broad distribution (ranging from kbol ~ 5 up to kbol ~ few hundred). This rather broad and “flat” distribution (mainly intrinsic, i.e. it is not caused by the measurement errors) implies a very large distribution of the SED in AGN, preventing the use of a single value for the total AGN family. Furthermore, this implies that the X-ray luminosities are not a useful proxy to derive bolometric corrections.
- 3.
We confirm a tight correlation between kbol and αox and a correlation between kbol and the hard-X-ray photon index. The first correlation could be used to derive a relatively good estimate of kbol, with a mean error of ~30% (providing that all the main corrections discussed here are applied). The second correlation, despite its higher dispersion, can also be adopted (with a mean error of ~80%) to estimate kbol once the photon index is known.
A correlation analysis of Ldisc, L[2−10] keV, and kbol with the physical parameters of the central supermassive black-hole (e.g. black hole mass and Eddington ratio) for the AGN sample belonging to the XBS survey will be reported in a forthcoming paper. Expanding the analysis to include these parameters may provide a fundamental tool for constraining AGN models (see e.g. Sobolewska et al. 2004a,b).
Online material
Main properties of the sample of 195 Type 1 AGN analysed in this work.
Appendix A
We present here the optical-UV-X-ray SEDs obtained applying the correction discussed in Sect. 3.2, for all the 195 sources analysed in this paper. The filled blue squares represent the fluxes in the GALEX NUV/FUV bands, while the empty squares represent the optical data. The upper limits on the NUV/FUV fluxes are represented as downward arrays. The fit has been done using the model quoted in Sect. 3.4 (blue curve). We also show the slope of the best-fit model in the rest-frame energy range 1–10 keV (magenta curve) obtained from the X-ray spectral analysis (for further details see Corral et al. 2011). The dashed magenta lines represent the errors on the best-fit model of the X-ray data, given by the errors on the spectral index Γ.
This slope is very close to what is expected from the relationship ![\hbox{$L_{\rm disc}\propto L_{\rm [2{-}10]~keV}^{\beta}$}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq145.png) when we apply the same fitting method (i.e. assuming L [2 − 10] keV as the independent variable) as requested from a statistical point of view (see Andreon & Hurn 2010, for a discussion of this point). In this case, if β = 1.009 (see Eq. (4)), and if we assume that Lbol ~ Ldisc, we expect log kbol ∝ 0.01 × log LX, well within the errors (0.04) on the slope derived from the fit (β = −0.01).
when we apply the same fitting method (i.e. assuming L [2 − 10] keV as the independent variable) as requested from a statistical point of view (see Andreon & Hurn 2010, for a discussion of this point). In this case, if β = 1.009 (see Eq. (4)), and if we assume that Lbol ~ Ldisc, we expect log kbol ∝ 0.01 × log LX, well within the errors (0.04) on the slope derived from the fit (β = −0.01).
Acknowledgments
We thank Luciana Bianchi for help with the GALEX data, Stefano Andreon for the useful suggestions about the statistical issues, Valentina Braito, Cristian Vignali and the anonymous referee for many useful suggestions and comments that significantly improved the paper. The authors acknowledge financial support from ASI (grant No. I/088/06/0, COFIS contract and ASI-INAF grant No. I/009/10/0).
References
- Adelberger, K. L., & Steidel, C. C. 2005, ApJ, 630, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, C. W. 1976, Astrophysical Quantities, Univ. of London (The Athlone Press), 264 [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Anderson, S. F., & Margon, B. 1987, ApJ, 314, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, ed. G. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Avni, Y., & Tananbaum, H. 1982, ApJ, 262, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Tananbaum, H. 1986, ApJ, 305, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, L., Efremova, B., Herald, J., et al. 2011, MNRAS, 411, 2770 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Buckley, J., & James, I. 1979, Biometrika, 66, 429 [CrossRef] [Google Scholar]
- Caccianiga, A., Severgnini, P., Braito, V., et al. 2004, A&A, 416, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Della Ceca, R., et al. 2007, A&A, 470, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Della Ceca, R., et al. 2008, A&A, 477, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Della Ceca, R., et al. 2011, Narrow-Line Seyfert 1 Galaxies and their Place in the Universe, Milano, Italy [Google Scholar]
- Corral, A., Della Ceca, R., Caccianiga, A., et al. 2011, A&A, 530, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dadina, M. 2008, A&A, 485, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dempster, A. P., Laird, N. M., & Rubin, D. B. 1977, J. Roy. Stat. Soc. Ser. B, 39, 1 [Google Scholar]
- Della Ceca, R., Pellegrini, S., Bassani, L., et al. 2001, A&A, 375, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Maccacaro, T., Caccianiga, A., et al. 2004, A&A, 428, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Caccianiga, A., Severgnini, P., et al. 2008, A&A, 487, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Vries, W. H., Becker, R. H., White, R. L., & Loomis, C. 2005, AJ, 129, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. S., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Berg, C. J. 1983, ApJ, 269, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Galbiati, E., Caccianiga, A., Maccacaro, T., et al. 2005, A&A, 430, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Chartas, G., et al. 2006, ApJ, 644, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., & Benker, A. J. 2007 [arXiv:0711.1013] [Google Scholar]
- Ghisellini, G., Della Ceca, R., Volonteri, M., et al. 2010, MNRAS, 405, 387 [NASA ADS] [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Giustini, M., Cappi, M., & Vignali, C. 2008, A&A, 491, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Green, P. J., Aldcroft, T. L., Richards, G. T., et al. 2009, ApJ, 690, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K., & Gallo, L. 2011, Narrow-Line Seyfert 1 Galaxies and their Place in the Universe, Milano, Italy [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Martini, P., et al. 2005, ApJ, 625, L71 [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Just, D., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
- Kelly, B. C., Bechtold, J., Trump, J. R., Vestergaard, M., & Siemiginowska, A. 2008, ApJS, 176, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, M., & Stuart, A. 1979, The advanced theory of statistics, Vol. 2, Griffin, London, 4th edition [Google Scholar]
- Kriss G. A., & Canizares C. R. 1985, ApJ, 297, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley, M., Isobe, T., & Feigelson, E. 1992, Astronomical Data Analysis Software and Systems I, ASP Conf. Ser., 25, 1, 245 [Google Scholar]
- Lopez-Santiago, J., Micela, G., Sciortino, S., et al. 2007, A&A, 463, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Marconi, A., Salvati, M., et al. 2001, A&A, 365, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malkan, M. A., & Sargent, W. L. W. 1982, ApJ, 254, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Morrissey, P., Conrow, T., Barlow, T. A., et al. 2007, ApJS, 173, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 1992, A&A, 256, 399 [NASA ADS] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Young, M., & Elvis, M. 2009, ApJ, 700, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Severgnini, P., Caccianiga, A., Braito, V., et al. 2003, A&A, 406, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shemmer, O., Brandt, W. N., Anderson, S. F., et al. 2009, ApJ, 696, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A. 1978, Nature, 272, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., Siemiginowska, A., & Zycki, P. T. 2004a, ApJ, 608, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., Siemiginowska, A., & Zycki, P. T. 2004b, ApJ, 617, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Stalin, C. S., Petitjean, P., Srianand, R., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I. V., Brandt, W. N., Schneider, D. P., Vanden Berk, D. G., & Vignali, C. 2005, AJ, 130, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Soltan, A. 1982, MNRAS, 200, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Streblyanska, A., Barcons, X., Carrera, F. J., & Gil-Merino, R. 2010, A&A, 515, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., & Davidsen, A. F. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Trammell, G. B., Van den Berk, D. E., Schneider, D. P., et al. 2007, AJ, 133, 1780 [Google Scholar]
- Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2007, MNRAS, 381, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Mushotzky, R. F., Winter, L. M., & Fabian, A. C. 2009, MNRAS, 399, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, M., Elvis, M., Fabbiano, G., et al. 1987, ApJ, 315, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., & Elvis, M. S. 1987, ApJ, 323, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., Tananbaum, H., Worrall, D. M., et al. 1994, ApJS, 92, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G., 2009, ApJS, 185, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Siebert, J., Tananbaum, H., Worrall, D. M., & Brinkmann, W. 1998, A&A, 334, 498 [NASA ADS] [Google Scholar]
- Zamorani, G., Henry, J. P., Maccacaro, T., et al. 1981, ApJ, 245, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Kriss, G. A., Telfer, R. C., Grimes, J. P., & Davidsen, A. F. 1997, ApJ, 475, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X.-L., & Zhao, Y. H. 2010, ApJ, 720, L206 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spearman rank correlation coefficients (rS,z) and probabilities of null correlation (P) for the samples considered in this work.
All Figures
 |
Fig. 1 Distribution in the mUV − mr plane of the final sample of Type 1 AGN analysed. The red crosses represent the sources with UV upper limits, the black circles are the sources detected by GALEX. |
| In the text | |
 |
Fig. 2 Distribution in the LX − z plane of the final sample of Type 1 AGN. Black circles: GALEX detections; red crosses: upper limits. |
| In the text | |
 |
Fig. 3 Example of the rest-frame SED of one source showing the optical fluxes (empty squares) contaminated by the emission contribution of the host galaxy. The solid line represents the accretion disc emission model described in Sect. 3.4. |
| In the text | |
 |
Fig. 4 Plot of the ratio between the fluxes of AGN and host galaxy in the wavelength range 4050–4250 Å as a function of the intensity of the calcium break Δ for the sources in our sample. The relations obtained assuming a host galaxy calcium break of respectively 45% or 55% are shown as dashed lines. |
| In the text | |
 |
Fig. 5 Example of the optical-UV-Xray spectral energy distribution obtained by applying the correction discussed so far. The filled blue squares are the fluxes in the GALEX NUV/FUV bands, while the empty squares represent the optical data. The fit used the model quoted in Sect. 3.4 (blue curve in the electronic form). The magenta curve is the best-fit power-law model in the X-ray energy range 2–10 keV obtained from the X-ray spectral analysis (see C11) The dashed magenta lines represent the errors on the best-fit model of the X-ray data, given by the errors on the spectral index Γ. |
| In the text | |
 |
Fig. 6 Distribution of the AGN accretion disc luminosities (dotted blue line), computed by integrating over the optical-UV continuum spectra of each source and distribution of the bolometric luminosities (solid red line), obtained as a sum of the accretion disc luminosities and the 0.1–500 keV X-ray luminosities. |
| In the text | |
 |
Fig. 7 Plot of Ldisc vs. X-ray luminosity L[2−10] keV for our sample of sources. The two green lines represent the best-fit regression lines, given by Eqs. (4) and (5), obtained by interchanging the independent and dependent variable; the red line is the bisector of these two lines, parametrised by Eq. (6). |
| In the text | |
 |
Fig. 8 Plot of bolometric correction vs. X-ray luminosity L[2−10] keV for our sample of sources. The red line represents the best fit relation obtained assuming L[2−10] keV as independent variable. |
| In the text | |
 |
Fig. 9 Histogram of the bolometric corrections for the AGN population (obtained using the Low-err sample composed of 176 objects). |
| In the text | |
 |
Fig. 10 Upper panel: plot of kbol against αox for our sample of Type 1 AGN. The solid line and dotted lines represent our best fit and the range of variation with respect to the best-fit, including 68% of the sources. The dashed line represent the best fit relation computed by Lusso et al. (2010); in the bottom panel we show the residuals with respect to our best-fit relationship. |
| In the text | |
 |
Fig. 11 Plot of kbol vs. the 2–10 keV photon index Γ2 − 10keV. We show our best-fit relation (red solid line) and the best-fit relation computed by Zhou & Zhao (2010) (blue dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




























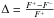
![\begin{equation} \alpha_{\rm ox}=-0.384 \log \left[\frac{L_{\rm 2~keV}}{L_{2500~\AA} }\right]\cdot \end{equation}](/articles/aa/full_html/2012/03/aa17562-11/aa17562-11-eq173.png)