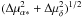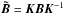| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 47 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117905 | |
| Published online | 08 February 2012 | |
The astrometric core solution for the Gaia mission
Overview of models, algorithms, and software implementation
1 Lund Observatory, Lund University, Box 43, 22100 Lund, Sweden
e-mail: Lennart.Lindegren@astro.lu.se; David.Hobbs@astro.lu.se
2 European Space Agency (ESA), European Space Astronomy Centre (ESAC), PO Box (Apdo. de Correos) 78, 28691 Villanueva de la Cañada, Madrid, Spain
e-mail: Uwe.Lammers@sciops.esa.int; William.OMullane@sciops.esa.int; Jose.Hernandez@sciops.esa.int
3 Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12–14, 69120 Heidelberg, Germany
e-mail: bastian@ari.uni-heidelberg.de
Received: 17 August 2011
Accepted: 25 November 2011
Context. The Gaia satellite will observe about one billion stars and other point-like sources. The astrometric core solution will determine the astrometric parameters (position, parallax, and proper motion) for a subset of these sources, using a global solution approach which must also include a large number of parameters for the satellite attitude and optical instrument. The accurate and efficient implementation of this solution is an extremely demanding task, but crucial for the outcome of the mission.
Aims. We aim to provide a comprehensive overview of the mathematical and physical models applicable to this solution, as well as its numerical and algorithmic framework.
Methods. The astrometric core solution is a simultaneous least-squares estimation of about half a billion parameters, including the astrometric parameters for some 100 million well-behaved so-called primary sources. The global nature of the solution requires an iterative approach, which can be broken down into a small number of distinct processing blocks (source, attitude, calibration and global updating) and auxiliary processes (including the frame rotator and selection of primary sources). We describe each of these processes in some detail, formulate the underlying models, from which the observation equations are derived, and outline the adopted numerical solution methods with due consideration of robustness and the structure of the resulting system of equations. Appendices provide brief introductions to some important mathematical tools (quaternions and B-splines for the attitude representation, and a modified Cholesky algorithm for positive semidefinite problems) and discuss some complications expected in the real mission data.
Results. A complete software system called AGIS (Astrometric Global Iterative Solution) is being built according to the methods described in the paper. Based on simulated data for 2 million primary sources we present some initial results, demonstrating the basic mathematical and numerical validity of the approach and, by a reasonable extrapolation, its practical feasibility in terms of data management and computations for the real mission.
Key words: astrometry / methods: data analysis / methods: numerical / space vehicles: instruments
© ESO, 2012
1. Introduction
The space astrometry mission Gaia, planned to be launched by the European Space Agency (ESA) in 2013, will determine accurate astrometric data for about one billion objects in the magnitude range from 6 to 20. Accuracies of 8–25 micro-arcsec (μas) are typically expected for the trigonometric parallaxes, positions at mean epoch, and annual proper motions of simple (i.e., apparently single) stars down to 15th magnitude. The astrometric data are complemented by photometric and spectroscopic information collected with dedicated instruments on board the Gaia satellite. The mission will result in an astronomical database of unprecedented scope, accuracy and completeness becoming available to the scientific community around 2021.
The original interferometric concept for a successor mission to Hipparcos, called GAIA (Global Astrometric Interferometer for Astrophysics), was described by Lindegren & Perryman (1996) but has since evolved considerably by the incorporation of novel ideas (Høg 2008) and as a result of industrial studies conducted under ESA contracts (Perryman et al. 2001). The mission, now in the final integration phase with EADS Astrium as prime contractor, is no longer an interferometer but has retained the name Gaia, which is thus no acronym. For some brief but up-to-date overviews of the mission, see Lindegren et al. (2008) and Lindegren (2010). The scientific case is most comprehensively described in the proceedings of the conference The Three-Dimensional Universe with Gaia (Turon et al. 2005).
In parallel with the industrial development of the satellite, the Gaia Data Processing and Analysis Consortium (DPAC; Mignard et al. 2008) is charged with the task of developing and running a complete data processing system for analysing the satellite data and constructing the resulting database (“Gaia Catalogue”). This task is extremely difficult due to the large quantities of data involved, the complex relationships between different kinds of data (astrometric, photometric, spectroscopic) as well as between data collected at different epochs, the need for complex yet efficient software systems, and the interaction and sustained support of many individuals and groups over an extended period of time.
A fundamental part of the data processing task is the astrometric core solution, currently under development in DPAC’s Coordination Unit 3 (CU3), “Core Processing”. Mathematically, the astrometric core solution is a simultaneous determination of a very large number of unknowns representing three kinds of information: (i) the astrometric parameters for a subset of the observed stars, representing the astrometric reference frame; (ii) the instrument attitude, representing the accurate celestial pointing of the instrument axes in that reference frame as a function of time; and (iii) the geometric instrument calibration, representing the mapping from pixels on the CCD detectors to angular directions relative to the instrument axes. Although the astrometric core solution is only made for a subset of the stars, the resulting celestial reference frame, attitude and instrument calibration are fundamental inputs for the processing of all observations. Optionally, a fourth kind of unknowns, the global parameters, may be introduced to describe for example a hypothetical deviation from General Relativity.
We use the term “source” to denote any astronomical object that Gaia detects and observes as a separate entity. The vast majority of the Gaia sources are ordinary stars, many of them close binaries or the components of wide systems, but some are non-stellar (for example asteroids and quasars). Nearly everywhere in this paper, one can substitute “star” for “source” without distortion; however, for consistency with established practice in the Gaia community we use “source” throughout.
While the total number of distinct sources that will be observed by Gaia is estimated to slightly more than one billion, only a subset of them shall be used in the astrometric core solution. This subset, known as the “primary sources”, is selected to be astrometrically well-behaved (see Sect. 6.2) and consists of (effectively) single stars and extragalactic sources (quasars and AGNs) that are sufficiently stable and point-like. We assume here that the number of primary sources is about 108, i.e., roughly one tenth of the total number of objects, although in the end it is possible that an even larger number will be used.
In comparison with many other parts of the Gaia data processing, the astrometric core solution is in principle simple, mainly because it only uses a subset of the observations (namely, those of the primary sources), which can be accurately modelled in a relatively straightforward way. In practice, the problem is however formidable: the total number of unknowns is of the order of 5 × 108, the solution uses some 1011 individual observations extracted from some 70 Terabyte (TB) of raw satellite data, and the entangled nature of the data excludes a direct solution. A feasible approach has nevertheless been found, including a precise mathematical formulation, practical solution method, and efficient software implementation. It is the aim of this paper to provide a comprehensive overview of this approach.
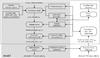 |
Fig. 1 Schematic representation of the main elements of the astrometric data analysis. In the shaded area is the mathematical model that allows to calculate the position of the stellar image in pixel coordinates, and hence the expected CCD data, for any given set of model parameters. To the right are the processes that fit this model to the observed CCD data by adjusting the parameters in the rectangular boxes along the middle. This paper is primarily concerned with the geometrical part of the analysis contained in the dashed box. However, a brief outline of the CCD data modelling and processing (bottom part of the diagram) is given in Sect. 3.5 and Appendix D.2. |
Concerning notations we have followed the usual convention to denote all non-scalar entities (vectors, tensors, matrices, quaternions) by boldfaced characters. Lower-case bold italics (a) are used for vectors and one-dimensional column matrices; upper-case bold italics (A) usually denote two-dimensional matrices. Following Murray (1983) the prime ( ′) signifies both matrix transpose (a′, A′) and scalar multiplication of vectors; thus ∥ a ∥ = (a′a)1/2 defines the magnitude of the vector a as well as the Euclidean norm of the column matrix a. Angular brackets denote normalization to unit length, as in ⟨ x ⟩ = x ∥ x ∥ -1. In this notation, no special distinction is thus made between vectors as physical entities (also known as geometric, spatial or Euclidean vectors) on one hand, and their numerical representations in some coordinate system as column matrices (also known as list vectors) on the other hand. Moreover, list vectors can of course have any dimension: a ∈ Rn. In the coordinate system whose axes are aligned with unit vectors x, y, and z, the components of the arbitrary vector a are given by ax = x′a, ay = y′a, and az = z′a; if the coordinate system is represented by the vector triad S = [x y z], these components are given by the column matrix S′a (cf. Appendix A in Murray 1983). This notation, although perhaps unfamiliar to many readers, provides a convenient and unambiguous framework for representing and transforming spatial vectors in different coordinate systems. For a vector-valued function f(x), ∂f/∂x′ denotes the dim(f) × dim(x) matrix whose (i,j)th element is ∂fi/∂xj. Quaternions follow their own algebra (see Appendix A for a brief introduction) and must not be confused with vectors/matrices; quaternions are therefore denoted by bold Roman characters (a). When taking a derivative with respect to the quaternion a, ∂x/∂a denotes the 4 × 1 matrix of derivatives with respect to the quaternion components; ∂x/∂a′ is the transposed matrix. Tables of acronyms and variables are provided in Appendix E.
2. Outline of the approach
The astrometric principles for Gaia were outlined already in the Hipparcos Catalogue (ESA 1997, Vol. 3, Ch. 23) where, based on the accumulated experience of the Hipparcos mission, a view was cast to the future. The general principle of a global astrometric data analysis was succinctly formulated as the minimization problem: 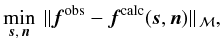 (1)with a slight change of notation to adapt to the present paper. Here s is the vector of unknowns (parameters) describing the barycentric motions of the ensemble of sources used in the astrometric solution, and n is a vector of “nuisance parameters” describing the instrument and other incidental factors which are not of direct interest for the astronomical problem but are nevertheless required for realistic modelling of the data. The observations are represented by the vector fobs which could for example contain the measured detector coordinates of all the stellar images at specific times. fcalc(s,n) is the observation model, e.g., the expected detector coordinates calculated as functions of the astrometric and nuisance parameters. The norm is calculated in a metric ℳ defined by the statistics of the data; in practice the minimization will correspond to a weighted least-squares solution with due consideration of robustness issues (see Sect. 3.6).
(1)with a slight change of notation to adapt to the present paper. Here s is the vector of unknowns (parameters) describing the barycentric motions of the ensemble of sources used in the astrometric solution, and n is a vector of “nuisance parameters” describing the instrument and other incidental factors which are not of direct interest for the astronomical problem but are nevertheless required for realistic modelling of the data. The observations are represented by the vector fobs which could for example contain the measured detector coordinates of all the stellar images at specific times. fcalc(s,n) is the observation model, e.g., the expected detector coordinates calculated as functions of the astrometric and nuisance parameters. The norm is calculated in a metric ℳ defined by the statistics of the data; in practice the minimization will correspond to a weighted least-squares solution with due consideration of robustness issues (see Sect. 3.6).
While Eq. (1) encapsulates the global approach to the data analysis problem, its actual implementation will of course depend strongly on the specific characteristics of the Gaia instrument and mission as well as on the practical constraints on the data processing task.
At the heart of the problem is the modelling of data represented by the function fcalc(s,n) in Eq. (1). This is schematically represented in the shaded part of the diagram in Fig. 1. It shows the main steps for calculating the expected CCD output in terms of the various parameters. The data processing, effecting the minimization in Eq. (1), is represented in the right part of the diagram. In subsequent sections we describe in some detail the main elements depicted in Fig. 1. The astrometric (source) parameters are represented by the vector s, while the nuisance parameters are of three kinds: the attitude parameters a, the geometric calibration parameters c, and the global parameters g. The observables f are represented by the pixel coordinates (κ,μ) of point source images on Gaia’s CCDs. (In the actual implementation of the approach, the minimization problem is formulated in terms of the field angles η, ζ rather than in the directly measured pixel coordinates κ, μ; see Sects. 3.3 and 3.4.)
The various elements of the astrometric solution are described in some detail in the subsequent sections. Section 3 provides the mathematical framework needed to model the Gaia observations and setting up the least-squares equations for the astrometric solution. In the interest of clarity and overview we omit in this description certain complications that need to be considered in the final data processing system; these are instead briefly discussed in Appendix D. In Sect. 4 we describe the iterative solution method in general terms, and then provide, in Sects. 5 and 6, the mathematical details of the most important procedures. Section 7 outlines the existing implementation of the solution and presents the results of a demonstration run based on simulated observations of about 2 million primary sources. Appendices A to C provide brief introductions to three mathematical tools that are particularly important for the subsequent development, namely the use of quaternions for representing the instantaneous satellite attitude, the B-spline formalism used to model the attitude as a function of time, and a modified Cholesky algorithm for the decomposition of positive semidefinite normal matrices.
3. Mathematical formulation of the basic observation model
3.1. Reference systems
The high astrometric accuracy aimed for with Gaia makes it necessary to use general relativity for modelling the data. This implies a precise and consistent formulation of the different reference systems used to describe the motion of the observer (Gaia), the motion of the observed object (source), the propagation of light from the source to the observer, and the transformations between these systems. The formulation adopted for Gaia (Klioner 2003, 2004) is based on the parametrized post-Newtonian (PPN) version of the relativistic framework adopted in 2000 by the International Astronomical Union (IAU); see Soffel et al. (2003). In this section only some key concepts from this formulation are introduced.
The orbit of Gaia and the light propagation from the source to Gaia are entirely modelled in the Barycentric Celestial Reference System (BCRS) whose spatial axes are aligned with the International Celestial Reference System (ICRS, Feissel & Mignard 1998). The associated time coordinate is the barycentric coordinate time (TCB). Throughout this paper, all time variables denoted t (with various subscripts) must be interpreted as TCB. The ephemerides of solar-system bodies (including the Sun and the Earth) are also expressed in this reference system. Even the motions of the stars and extragalactic objects are formally modelled in this system, although for practical reasons certain effects of the light-propagation time are conventionally ignored in this model (Sect. 3.2).
In order to model the rotation (attitude) of Gaia and the celestial direction of the light rays as observed by Gaia, it is expedient to introduce also a co-moving celestial reference system having its origin at the centre of mass of the satellite and a coordinate time equal to the proper time at Gaia. This is known as the Centre-of-Mass Reference System (CoMRS) and the associated time coordinate is Gaia Time (TG). Klioner (2004) demonstrates how the CoMRS can be constructed in the IAU 2000 framework in exact analogy with the Geocentric Celestial Reference System (GCRS), only for a massless particle (Gaia) instead of the Earth. Like the BCRS and GCRS, the CoMRS is kinematically non-rotating, and its spatial axes are aligned with the ICRS. The celestial reference system (either the CoMRS or the ICRS depending on whether the origin is at Gaia or the solar-system barycentre) will in the following be represented by the vector triad C = [ X Y Z ] , where X, Y, and Z are orthogonal unit vectors aligned with the axes of the celestial reference system. That is, X points towards the origin (α = δ = 0), Z towards the north celestial pole (δ = + 90°), and Y = Z × X points to (α = 90°,δ = 0).
In the CoMRS the attitude of the satellite is a spatial rotation in three dimensions, and can therefore be described purely classically, for example using quaternions (Sect. 3.3 and Appendix A). The rotated reference system, aligned with the instrument axes, is known as the Scanning Reference System (SRS). Its spatial x, y, z axes (Fig. 2) are defined in terms of the two viewing directions of Gaia fP (in the centre of the preceding field of view, PFoV) and fF (in the centre of the following field of view, FFoV) as 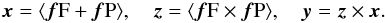 (2)(The precise definition of fP and fF is implicit in the geometric instrument model; see Sect. 3.4.) The SRS is represented by the vector triad S = [ x y z ] .
(2)(The precise definition of fP and fF is implicit in the geometric instrument model; see Sect. 3.4.) The SRS is represented by the vector triad S = [ x y z ] .
For determining the orbit of Gaia and calibrating the on-board clock, it is also necessary to model the radio ranging and other ground-based observations of the Gaia spacecraft in the same relativistic framework. For this, we also need the GCRS. These aspects of the Gaia data processing are, however, not discussed in this paper.
3.2. Astrometric model
The astrometric model is a recipe for calculating the proper direction ui(t) to a source (i) at an arbitrary time of observation (t) in terms of its astrometric parameters si and various auxiliary data, assumed to be known with sufficient accuracy. The auxiliary data include an accurate barycentric ephemeris of the Gaia satellite, bG(t), including its coordinate velocity dbG/dt, and ephemerides of all other relevant solar-system bodies.
For the astrometric core solution every source is assumed to move with uniform space velocity relative to the solar-system barycentre. In the BCRS its spatial coordinates at time t∗ are therefore given by 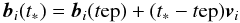 (3)where tep is an arbitrary reference epoch and bi(tep), vi define six kinematic parameters for the motion of the source. The six astrometric parameters in si are merely a transformation of the kinematic parameters into an equivalent set better suited for the analysis of the observations. The six astrometric parameters are:
(3)where tep is an arbitrary reference epoch and bi(tep), vi define six kinematic parameters for the motion of the source. The six astrometric parameters in si are merely a transformation of the kinematic parameters into an equivalent set better suited for the analysis of the observations. The six astrometric parameters are:
-
α
i
the barycentric right ascension at the adopted reference epoch tep;
-
δ
i
the barycentric declination at epoch tep;
-
ϖ
i
the annual parallax at epoch tep;
-
μα ∗ i = (dαi/dt)cosδi
the proper motion in right ascension at epoch tep;
-
μδi = dδi/dt
the proper motion in declination at epoch tep;
-
μri = vriϖi/Au
the “radial proper motion” at epoch tep, i.e., the radial velocity of the source (vri) expressed in the same unit as the transverse components of proper motion (Au = astronomical unit).
As explained in Sect. 3.1, the astrometric parameters refer to the ICRS and the time coordinate used is TCB. The reference epoch tep is preferably chosen to be near the mid-time of the mission in order to minimize statistical correlations between the position and proper motion parameters.
The transformation between the kinematic and the astrometric parameters is non-trivial (Klioner 2003), mainly as a consequence of the practical need to neglect most of the light-propagation time t − t∗ between the emission of the light at the source (t∗) and its reception at Gaia (t). This interval is typically many years and its value, and rate of change (which depends on the radial velocity of the source), will in general not be known with sufficient accuracy to allow modelling of the motion of the source directly in terms of its kinematic parameters according to Eq. (3). The proper motion components μα ∗ i, μδi and radial velocity vri correspond to the “apparent” quantities discussed by Klioner (2003, Sect. 8).
The coordinate direction to the source at time t is calculated with the same “standard model” as was used for the reduction of the Hipparcos observations (ESA 1997, Vol. 1, Sect. 1.2.8), namely 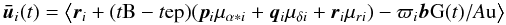 (4)where the angular brackets signify vector length normalization, and [ pi qi ri ] is the “normal triad” of the source with respect to the ICRS (Murray 1983). In this triad, ri is the barycentric coordinate direction to the source at time tep, pi = ⟨ Z × ri ⟩ , and qi = ri × pi. The components of these unit vectors in the ICRS are given by the columns of the matrix
(4)where the angular brackets signify vector length normalization, and [ pi qi ri ] is the “normal triad” of the source with respect to the ICRS (Murray 1983). In this triad, ri is the barycentric coordinate direction to the source at time tep, pi = ⟨ Z × ri ⟩ , and qi = ri × pi. The components of these unit vectors in the ICRS are given by the columns of the matrix ![\begin{equation} \label{eq:normal-triad} \tens{C}'[\vec{p}_i~\vec{q}_i~\vec{r}_i] = \begin{bmatrix} -\sin\alpha_i &~ -\sin\delta_i\cos\alpha_i &~ \cos\delta_i\cos\alpha_i \\ \phantom{-}\cos\alpha_i &~ -\sin\delta_i\sin\alpha_i &~ \cos\delta_i\sin\alpha_i \\ 0 &~ \cos\delta_i &~ \sin\delta_i \end{bmatrix}. \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq83.png) (5)bG(t) is the barycentric position of Gaia at the time of observation, and Au the astronomical unit. tB is the barycentric time obtained by correcting the time of observation for the Römer delay; to sufficient accuracy it is given by
(5)bG(t) is the barycentric position of Gaia at the time of observation, and Au the astronomical unit. tB is the barycentric time obtained by correcting the time of observation for the Römer delay; to sufficient accuracy it is given by 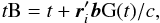 (6)where c is the speed of light.
(6)where c is the speed of light.
In Eq. (4) the term containing μri accounts for the relative rate of change of the barycentric distance to the source. This term may produce secular variations of the proper motions and parallaxes of some nearby stars, which in principle allow their radial velocities to be determined astrometrically (Dravins et al. 1999). However, for the vast majority of these stars, μri can be more accurately calculated by combining the spectroscopically measured radial velocities with the astrometric parallaxes. Thus, although all six astrometric parameters are taken into account when computing the coordinate direction, usually only five of them are considered as unknowns in the astrometric solution.
The standard model can be derived by considering the uniform motion of the source in a purely classical framework, using Euclidean coordinates and neglecting the light propagation time from the source to the observer (except for the Römer delay). To the accuracy of Gaia, relativistic and light-propagation effects are by no means negligible, but it can be shown that this model is nevertheless accurate enough to model the observations to sub-microarcsec accuracy. It is adopted for this purpose because it closely corresponds to the conventional interpretation of the astrometric parameters. However, when the astrometric parameters are to be interpreted in terms of the barycentric space velocity of the source, some of these effects may come into play (Lindegren & Dravins 2003).
The transformation from 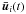 to the observable (proper) direction ui(t) involves taking into account gravitational light deflection by solar-system bodies and the Lorentz transformation to the co-moving frame of the observer (stellar aberration); the relevant formulae are given by Klioner (2003). This transformation therefore depends also on the global parameters g, for example the PPN parameter γ which measures the strength of the gravitational light deflection. The calculation uses some auxiliary data, not subject to improvement by the solution, and which are here denoted h; normally they include for example the barycentric ephemerides of the Gaia satellite and of solar-system bodies, along with their masses. The complete transformation can therefore be written symbolically as:
to the observable (proper) direction ui(t) involves taking into account gravitational light deflection by solar-system bodies and the Lorentz transformation to the co-moving frame of the observer (stellar aberration); the relevant formulae are given by Klioner (2003). This transformation therefore depends also on the global parameters g, for example the PPN parameter γ which measures the strength of the gravitational light deflection. The calculation uses some auxiliary data, not subject to improvement by the solution, and which are here denoted h; normally they include for example the barycentric ephemerides of the Gaia satellite and of solar-system bodies, along with their masses. The complete transformation can therefore be written symbolically as: 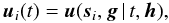 (7)where the vertical bar formally separates the (updatable) parameters si and g from the (fixed) given data t and h. Strictly speaking, the function u returns the coordinates of the proper direction in the CoMRS, that is the column matrix C′ui(t). The source parameter vector s is the concatenation of the sub-vectors si for all the primary sources.
(7)where the vertical bar formally separates the (updatable) parameters si and g from the (fixed) given data t and h. Strictly speaking, the function u returns the coordinates of the proper direction in the CoMRS, that is the column matrix C′ui(t). The source parameter vector s is the concatenation of the sub-vectors si for all the primary sources.
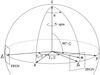 |
Fig. 2 The Scanning Reference System (SRS) [ x y z ] is defined by the viewing directions fP and fF according to Eq. (2). The instrument angles (ϕ,ζ) are the spherical coordinates in the SRS of the observed (proper) direction u towards the object. See Fig. 4 for further definition of the viewing directions. The field sizes are greatly exaggerated in this drawing; in reality the astrometrically useful field is 0.72° × 0.69° (along × across scan) for each viewing direction. The basic angle is Γc = arccos(fP′fF), nominally equal to 106.5°. |
3.3. Attitude model
The attitude specifies the instantaneous orientation of the Gaia instrument in the celestial reference frame, that is the transformation from C = [X Y Z] (more precisely, the CoMRS) to S = [x y z] (Sect. 3.1) as a function of time. The spacecraft is controlled to follow a specific attitude as a function of time, for example the so-called Nominal Scanning Law (NSL; de Bruijne et al. 2010), designed to provide good coverage of the whole celestial sphere while satisfying a number of other requirements. The NSL is analytically defined for arbitrarily long time intervals by just a few free parameters.
However, the actual attitude will deviate from the intended (nominal) scanning law by up to ~1 arcmin in all three axes, and these deviations vary on time scales from seconds to minutes depending on the level of physical perturbations and the characteristics of the real-time attitude measurements and control law (cf. Appendix D.4). The CCD integration time of (usually) 4.42 s means that the true (physical) attitude cannot be observed, but only a smoothed version of it, corresponding to the convolution of the physical attitude with the CCD exposure function (Appendix D.3). This “effective” attitude must however be a posteriori estimable, at any instant, to an accuracy compatible with the astrometric goals, i.e., at sub-mas level. For this purpose the effective attitude is modelled in terms of a finite number of attitude parameters, for which it is necessary to choose a suitable mathematical representation of the instantaneous transformation, as well as of its time dependence. For the Gaia data processing, we have chosen to use quaternions (Appendix A) for the former, and B-splines (Appendix B) for the latter representation.
At any time the orientation of the SRS (S) with respect to the CoMRS (C) may be represented by the attitude matrix 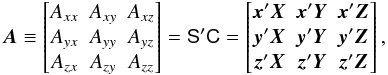 (8)which is a proper orthonormal matrix, AA′ = I, det(A) = + 1. This is also called the direction cosine matrix, since the rows are the direction cosines of x, y and z in the CoMRS, and the columns are the direction cosines of X, Y and Z in the SRS.
(8)which is a proper orthonormal matrix, AA′ = I, det(A) = + 1. This is also called the direction cosine matrix, since the rows are the direction cosines of x, y and z in the CoMRS, and the columns are the direction cosines of X, Y and Z in the SRS.
The orthonormality of A implies that the matrix elements satisfy six constraints, leaving three degrees of freedom for the attitude representation. Although one could parametrize each of the nine matrix elements as a continuous function of time, for example using splines, it would in practice not be possible to guarantee that the orthonormality constraints hold at any time. The adopted solution is to represent the instantaneous attitude by a unit quaternion q, which has only four components, {qx,qy,qz,qw}, satisfying the single constraint 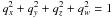 . This is easily enforced by normalization.
. This is easily enforced by normalization.
The attitude quaternion q(t) gives the rotation from the CoMRS (C) to the SRS (S). Using quaternions, their relation is defined by the transformation of the coordinates of the arbitrary vector v in the two reference systems, 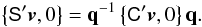 (9)In the terminology of Appendix A.3 this is a frame rotation of the vector from C to S. The inverse operation is {C′v,0} = q{S′v,0}q-1.
(9)In the terminology of Appendix A.3 this is a frame rotation of the vector from C to S. The inverse operation is {C′v,0} = q{S′v,0}q-1.
Using the B-spline representation in Appendix B, we have 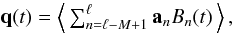 (10)where an (n = 0...N − 1) are the coefficients of the B-splines Bn(t) of order M defined on the knot sequence
(10)where an (n = 0...N − 1) are the coefficients of the B-splines Bn(t) of order M defined on the knot sequence 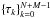 . The function Bn(t) is non-zero only for τn < t < τn + M, which is why the sum in Eq. (10) only extends over the M terms ending with n = ℓ. Here, ℓ is the so-called left index of t satisfying τℓ ≤ t < τℓ + 1. The normalization operator ⟨ ⟩ guarantees that q(t) is a unit quaternion for any t in the interval [ τM − 1,τN ] over which the spline is completely defined. Although the coefficients an are formally quaternions, they are not of unit length. The attitude parameter vector a consists of the components of the whole set of quaternions an.
. The function Bn(t) is non-zero only for τn < t < τn + M, which is why the sum in Eq. (10) only extends over the M terms ending with n = ℓ. Here, ℓ is the so-called left index of t satisfying τℓ ≤ t < τℓ + 1. The normalization operator ⟨ ⟩ guarantees that q(t) is a unit quaternion for any t in the interval [ τM − 1,τN ] over which the spline is completely defined. Although the coefficients an are formally quaternions, they are not of unit length. The attitude parameter vector a consists of the components of the whole set of quaternions an.
Cubic splines (M = 4) are currently used in this attitude model. Each component of the quaternion (before the normalization in Eq. (10)) is then a piecewise cubic polynomial with continuous value, first, and second derivative for any t; the third derivative is discontinuous at the knots. When initializing the solution, it is possible to select any desired order of the spline. Using a higher order, such as M = 5 (quartic) or 6 (quintic), provides improved smoothness but also makes the spline fitting less local, and therefore more prone to undesirable oscillatory behaviour. The flexibility of the spline is in principle only governed by the number of degrees of freedom (that is, in practice, the knot frequency), and is therefore independent of the order. One should therefore not choose a higher order than is warranted by the smoothness of the actual effective attitude, which is difficult to model a priori (cf. Appendix D.4). Determining the optimal order and knot frequency may in the end only be possible through analysis of the real mission data.
Equation (7) returns the observed direction to the source relative to the celestial reference system, or C′u = [uX, uY, uZ] ′. In order to compute the position of the image in the field of view, we need to express this direction in the Scanning Reference System, SRS (Sect. 3.1), or S′u = [ux, uy, uz]′. The required transformation is obtained by a frame rotation according to Eq. (9), 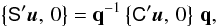 (11)whereupon the instrument angles (ϕ,ζ) are obtained from
(11)whereupon the instrument angles (ϕ,ζ) are obtained from ![\begin{equation} \label{eq:srsprop1} \tens{S}'\vec{u} \equiv \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix} = \begin{bmatrix} \cos\zeta\cos\varphi \\ \cos\zeta\sin\varphi \\ \sin\zeta \end{bmatrix} \quad\Leftrightarrow\quad \left\{\begin{array}{l} \varphi = \text{atan2}\bigl(u_y,u_x\bigr)\\[3pt] \zeta = \text{atan2}\Bigl(u_z,\,\sqrt{u_x^2+u_y^2}\,\Bigr) \end{array}\right. \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq132.png) (12)(Fig. 2), where we adopt the convention that − π ≤ ϕ < π. The field index f and the along-scan field angle η are finally obtained as
(12)(Fig. 2), where we adopt the convention that − π ≤ ϕ < π. The field index f and the along-scan field angle η are finally obtained as 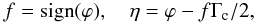 (13)where the basic angle, Γc, is here a purely conventional value (as suggested by the subscript). The field-of-view limitations imply that |η| ≲ 0.5° and |ζ| ≲ 0.5° for any observation.
(13)where the basic angle, Γc, is here a purely conventional value (as suggested by the subscript). The field-of-view limitations imply that |η| ≲ 0.5° and |ζ| ≲ 0.5° for any observation.
Given the time of observation t and the set of source parameters s, attitude parameters a, and global parameters g, the field index f and the field angles (η,ζ) can thus be computed by application of Eqs. (7), (10)–(13). The resulting computed field angles are concisely written η(t | s,a,g), ζ(t | s,a,g).
 |
Fig. 3 Layout of the CCDs in Gaia’s focal plane. The star images move from right to left in the diagram. The along-scan (AL) and across-scan (AC) directions are indicated in the top left corner. The skymappers (SM1, SM2) provide source image detection, two-dimensional position estimation and field-of-view discrimination. The astrometric field (AF1–AF9) provides accurate AL measurements and (sometimes) AC positions. Additional CCDs used in the blue and red photometers (BP, RP), the radial-velocity spectrometer (RVS), for wavefront sensing (WFS) and basic-angle monitoring (BAM) are not further described in this paper. One of the rows (AF3) illustrates the system for labelling individual CCDs (AF3_1, etc.). The nominal paths of two star images, one in the preceding field of view (PFoV) and one in the following field of view (FFoV) are indicated. For purely technical reasons the origin of the field angles (η,ζ) corresponds to different physical locations on the CCDs in the two fields. The physical size of each CCD is 45 × 59 mm2. |
3.4. Geometric instrument model
The geometric instrument model defines the precise layout of the CCDs in terms of the field angles (η,ζ). This layout depends on several different factors, including: the physical geometry of each CCD; its position and alignment in the focal-plane assembly; the optical system including its scale value, distortion and other aberrations; and the adopted (conventional) value of the basic angle Γc. Some of these (notably the optical distortion) are different in the two fields of view and may evolve slightly over the mission; on the other hand these variations are expected to be very smooth as a function of the field angles. Other factors, such as the detailed physical geometry of the pixel columns, may be extremely stable but possibly quite irregular on a small scale. As a result, the geometric calibration model must be able to accommodate both smooth and irregular patterns evolving on different time scales in the two fields of view.
In the following it should be kept in mind that the astrometric instrument of Gaia is optimised for one-dimensional measurements in the along-scan direction, i.e., of the field angle η, while the requirements in the perpendicular direction (ζ) are much relaxed. This feature of Gaia (and Hipparcos) is a consequence of fundamental considerations derived from the requirements to determine a global reference frame and absolute parallaxes (Lindegren & Bastian 2011). In principle the measurement accuracy in the ζ direction, as well as the corresponding instrument modelling and calibration accuracies, may be relaxed by up to a factor given by the inverse angular size of the field of view (Lindegren 2005), or almost two orders of magnitude for a field of 0.7°. In practice a ratio of the order of 10 may be achieved, in which case the across-scan measurement and calibration errors have a very marginal effect on the overall astrometric accuracy.
The focal plane of Gaia contains a total of 106 CCDs (Laborie et al. 2007), of which only the 14 CCDs in the skymappers (SM1 and SM2) and the 62 in the astrometric field (AF1 through AF9) are used for the astrometric solution (Fig. 3). The CCDs have 4500 pixel lines in the along-scan (AL, constant ζ, decreasing η) direction and 1966 pixel columns in the across-scan (AC, constant η, increasing ζ) direction. They are operated in the Time, Delay and Integrate (TDI) mode (also known as drift-scanning), an imaging technique well-known in astronomy from ground-based programmes such as the Sloan Digital Sky Survey (Gunn et al. 1998). Effectively, the charges are clocked along the CCD columns at the same (average) speed as the motion of the optical images, i.e., 60 arcsec s-1 for Gaia. The exposure (integration) time is thus set by the time it takes the image to move across the CCD, or nominally T ≃ 4.42 s, if no gate is activated. At this exposure time the central pixels will be saturated for sources brighter than magnitude G ≃ 121. Gate activation, or “gating” for short, is the adopted method to obtain valid measurements of brighter sources. Gating temporarily inhibits charge transfer across a certain TDI line (row of pixels AC), thus effectively zeroing the charge image and reducing the exposure time in proportion to the number of TDI lines following the gate. A range of discrete exposure times is thus available, the shortest one, according to current planning, using only 16 TDI lines (15.7 ms). Gate selection is made by the on-board software based on the measured brightness of the source in relation to the calibrated full-well capacity of the relevant section of the CCD. Measurement errors and the spread in full-well capacities make the gate-activation thresholds somewhat fuzzy, and a given bright source is not necessarily always observed using the same gate. Moreover, a quasi-random selection of the observations of fainter sources will also be gated, viz., if they happen to be read out at about the same time, and on the same CCD, as a gated bright star. The skymappers are operated in a permanently gated mode, so that in practice only the last 2900 TDI lines are used in SM1 and SM2.
The skymappers are crucial for the real-time operation of the instrument, since they detect the sources as they enter the field of view, and allow determination of an approximate two-dimensional position of the images and (together with data from AF1) their speed across the CCDs. This information is used by the on-board attitude computer, in order to determine which CCD pixels should be read out and transmitted to ground (Sect. 3.5). The skymappers also allow to discriminate between the two viewing directions, since sources in the preceding field of view (PFoV) are only seen by SM1 and sources in the following field of view (FFoV) are only seen by SM2. In the astrometric field (as well as in BP, RP and RVS) the two fields of view are superposed.
Most observations acquired in the astrometric field (AF) are purely one-dimensional through the on-chip AC binning of data (Sect. 3.5). However, sources brighter than magnitude G ≃ 13 are always observed as two-dimensional images, providing accurate information about the AC pixel coordinate (μ) as well. Some randomly selected fainter images are also observed two-dimensionally (“Calibration Faint Stars”, CFS). The bright sources, CFS and SM data provide the AC information necessary for the on-ground three-axis attitude determination.
Because of the TDI mode of observation, AL irregularities of the pixel geometry are smeared out and need not be calibrated, and any measurement of the AL or AC position must effectively be referred back to an “observation time” half-way through the integration. Correspondingly, the pixel geometry can be represented by a fiducial “observation line” [η(μ), ζ(μ)] traced out in the field angles η, ζ as functions of the AC pixel coordinate μ (Fig. 4). The AC pixel coordinate is defined as a continuous variable with μ = 14 when the image is centred on the first pixel column, μ = 15 at the second pixel column, and so on until μ = 1979 at the last (1966th) pixel column. The offset by 13 pixels allows for the presence of pre-scan pixel data in some observations.
Nominally, the observation line corresponds to the (K/2)th pixel line projected backwards through the optical instrument onto the Scanning Reference System on the sky, where K is the number of active AL pixel lines in the observation (normally K = 4500)2. For a gated observation K is much smaller and the observation line is therefore correspondingly displaced towards the CCD readout register. A separate set of geometrical calibration parameters is therefore needed for each gate being used. In the calibration updating (Sect. 5.3) all the calibration parameters are however solved together, with the overlap due to the fuzzy gate-activation thresholds providing the necessary connection between the different gates.
 |
Fig. 4 Schematic illustration of how the field angles (η,ζ) are defined in terms of the CCD layout in Fig. 3. For simplicity only the projections of two CCDs, AF8_3 and AF8_4, into the Scanning Reference System (SRS) are shown (not to scale). The field angles have their origins at the respective viewing direction fP or fF (Fig. 2), which are defined in relation to the nominal centres of the CCDs (crosses); the actual configuration of the detectors is described by fiducial observation lines according to Eq. (15). The dashed curve shows the apparent path of a stellar image across the two fields of view. Its intersections with the observation lines define the instants of observations. |
Let n be an index identifying the different CCDs used for astrometry, i.e., for each of the 76 CCDs in the SM and AF part of the focal plane. Furthermore, let g be a gate index such that g = 0 is used for non-gated observations and g = 1, ..., 12 for gated observations of progressively brighter sources. In each field of view (index f) the nominal observation lines ![\hbox{$\left[\eta^0_{fng}(\mu),\,\zeta^0_{fng}(\mu)\right]$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq160.png) could in principle be calculated from the nominal characteristics of the focal plane assembly (FPA) and ray tracing through the nominal optical system. However, since the nominal observation lines are only used as a reference for the calibration of the actual observation lines, a very simplistic transformation from linear coordinates to angles can be used without introducing approximation errors in the resulting calibration model. The nominal observation lines are therefore defined by the transformation
could in principle be calculated from the nominal characteristics of the focal plane assembly (FPA) and ray tracing through the nominal optical system. However, since the nominal observation lines are only used as a reference for the calibration of the actual observation lines, a very simplistic transformation from linear coordinates to angles can be used without introducing approximation errors in the resulting calibration model. The nominal observation lines are therefore defined by the transformation ![\begin{equation} \label{eq:etazeta0} \left. \begin{aligned} \eta^0_{fng}(\mu) &\equiv \eta^0_{ng} = -Y{\rm FPA}[n,g]/F \\ \zeta^0_{fng}(\mu) &= -\left(X{\rm FPA}[n]-(\mu-\mu{\rm c})p{\rm AC} -X{\rm FPA}^\text{centre}[f]\right)/F \end{aligned} \right\} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq161.png) (14)where XFPA, YFPA are physical coordinates (in mm) in the focal plane3, XFPA [ n ] is the physical AC coordinate of the nominal centre of the nth CCD, YFPA [ n,g ] the physical AL coordinate of the nominal observation line for gate g on the nth CCD, and XFPAcentre [f] the physical AC coordinate of the nominal field centre for field index f. μc = 996.5 is the AC pixel coordinate of the CCD centre, pAC = 30 μm the physical AC pixel size, and F = 35 m the nominal equivalent focal length of the telescope. While
(14)where XFPA, YFPA are physical coordinates (in mm) in the focal plane3, XFPA [ n ] is the physical AC coordinate of the nominal centre of the nth CCD, YFPA [ n,g ] the physical AL coordinate of the nominal observation line for gate g on the nth CCD, and XFPAcentre [f] the physical AC coordinate of the nominal field centre for field index f. μc = 996.5 is the AC pixel coordinate of the CCD centre, pAC = 30 μm the physical AC pixel size, and F = 35 m the nominal equivalent focal length of the telescope. While 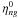 is independent of f, in the AC direction the origins are offset by about ± 221 arcsec between the two fields of view, corresponding to the physical coordinates XFPAcentre [ f ] = ( − 37.5 mm)f. It is emphasized that the nominal observation lines are purely conventional reference quantities, and need not be recomputed, e.g., once a more accurate estimate of F becomes available.
is independent of f, in the AC direction the origins are offset by about ± 221 arcsec between the two fields of view, corresponding to the physical coordinates XFPAcentre [ f ] = ( − 37.5 mm)f. It is emphasized that the nominal observation lines are purely conventional reference quantities, and need not be recomputed, e.g., once a more accurate estimate of F becomes available.
Because of possible changes in the instrument during the mission, the actual observation lines will be functions of time. The time dependence is quantified by introducing independent sets of calibration parameters for successive, non-overlapping time intervals. Different groups of parameters may develop on different time scales, and the resulting formulation can be quite complex. For the sake of illustration, let us distinguish between three categories of geometric calibration parameters:
-
1.
Large-scale AL calibration, Δη. This may (minutely but importantly) change due to thermal variations in the optics, the detectors, and their supporting mechanical structure. These variations could occur on short time scales (of the order of a day), and would in general be different in the two fields of view. They are modelled as low-order polynomials in the across-scan pixel coordinate μ.
-
2.
Small-scale AL calibration, δη. This is mainly related to physical defects or irregularities in the CCDs themselves, for example “stitching errors” introduced by the photolithography process used to manufacture the CCDs. These irregularities are expected to be stable over very long time scales, possibly throughout the mission, and should be identical in both fields of view. They require a spatially detailed modelling, perhaps with a resolution of just one or a few AC pixels.
-
3.
Large-scale AC calibration, Δζ. Although the physical origin is the same as for Δη, the AC components can be assumed to be constant on long time scales, since the calibration requirement in the AC direction is much more relaxed than in the AL direction. They are modelled as low-order polynomials in the field angles, separately in each field of view.
Let index j identify the “short” time intervals needed for the large-scale AL calibration, and index k identify the “long” time intervals applicable to the small-scale AL calibration and large-scale AC calibration. That is, an observation at time t belongs to some short time interval j and some long time interval k, where j and k are readily computed from the known t and the corresponding sequences of division times4. Assuming that quadratic polynomials in μ are sufficient for the large-scale calibrations, and that full AC pixel resolution is required for the small-scale AL calibration, the observation lines at time t are modelled as 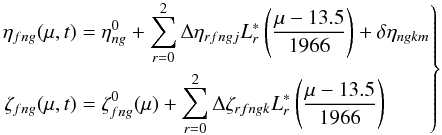 (15)where
(15)where 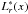 is the shifted Legendre polynomial of degree r (orthogonal on [ 0,1 ] ), i.e.,
is the shifted Legendre polynomial of degree r (orthogonal on [ 0,1 ] ), i.e., 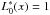 ,
, 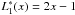 ,
, 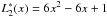 , etc.; Δηrfngj are the large-scale AL parameters, δηngkm the small-scale AL parameters (with m = round(μ) the index of the nearest pixel column), and Δζrfngk the large-scale AC parameters.
, etc.; Δηrfngj are the large-scale AL parameters, δηngkm the small-scale AL parameters (with m = round(μ) the index of the nearest pixel column), and Δζrfngk the large-scale AC parameters.
In order to render all the geometric calibration parameters uniquely determinable, a number of constraints are rigorously enforced by the astrometric solution. Effectively, they define the origins of the field angles, i.e., the viewing directions fP and fF, to coincide with the average nominal field angles of the CCD centres. The necessary constraints are: 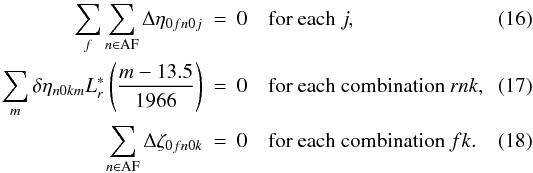 Note that g = 0 throughout in Eqs. (16)–(18). That the constraints are only defined in terms of the non-gated observations (g = 0) implies that the observation lines for the gated observations must be calibrated relative to the non-gated observations. This is possible since any given bright source will not always be observed with the same gate.
Note that g = 0 throughout in Eqs. (16)–(18). That the constraints are only defined in terms of the non-gated observations (g = 0) implies that the observation lines for the gated observations must be calibrated relative to the non-gated observations. This is possible since any given bright source will not always be observed with the same gate.
Constraint (16) effectively defines the zero point of the AL field angle η by requiring that 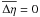 when averaging over the CCDs and between the two fields of view. Constraint (17) implies that the small-scale AL corrections δη do not have any components that could be described by Δη instead; it therefore ensures a unique division between the large-scale and small-scale components. Constraint (18) effectively defines the zero point of the AC field angle ζ by requiring that
when averaging over the CCDs and between the two fields of view. Constraint (17) implies that the small-scale AL corrections δη do not have any components that could be described by Δη instead; it therefore ensures a unique division between the large-scale and small-scale components. Constraint (18) effectively defines the zero point of the AC field angle ζ by requiring that 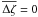 , separately in each field of view, when averaged over the CCDs. The sums over n in Eqs. (16) and (18) are restricted to the CCDs in the astrometric field (AF), since the skymapper (SM) measurements are less accurate.
, separately in each field of view, when averaged over the CCDs. The sums over n in Eqs. (16) and (18) are restricted to the CCDs in the astrometric field (AF), since the skymapper (SM) measurements are less accurate.
The basic angle Γc introduced in Sect. 3.3 is a fixed reference value, and any real variations of the angle between the two lines of sight will therefore show up as a variation in Δη with opposite signs in the two fields of view. The offset of the actual basic angle with respect to the conventional value Γc may be defined as the average difference of Δη between the two fields of view, where the average is computed over the astrometric CCDs, for gate g = 0, and over μ; the result for time period j is 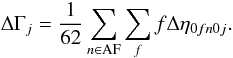 (19)Although this is obviously a useful quantity to monitor, it does not appear as a parameter in the geometric calibration model. A number of additional quantities representing the mean scale offset, the mean field orientation, etc., can similarly be computed from the large-scale calibration parameters for the purpose of monitoring.
(19)Although this is obviously a useful quantity to monitor, it does not appear as a parameter in the geometric calibration model. A number of additional quantities representing the mean scale offset, the mean field orientation, etc., can similarly be computed from the large-scale calibration parameters for the purpose of monitoring.
Equation (15) encapsulates a specific formulation of the geometric instrument model, with certain assumptions about the shape, dependencies, and time scales of possible variations. While this particular model is currently believed to be sufficient to describe the behaviour of the actual instrument to the required accuracy, it is very likely that modifications will be needed after a first analysis of the flight data. Moreover, in the course of the data analysis one may want to try out alternative models, or examine possible systematics resulting from the pre-processing (location estimator). In order to facilitate this, a much more flexible generic calibration model has been implemented. In the generic model, the “observed” field angles (representing the true observation lines) for any observation l are written 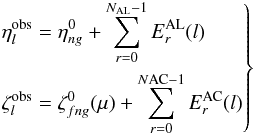 (20)where each of the Er(l) (for brevity dropping superscript AL/AC) represents a basic calibration effect, being a linear combination of elemental calibration functions Φrs:
(20)where each of the Er(l) (for brevity dropping superscript AL/AC) represents a basic calibration effect, being a linear combination of elemental calibration functions Φrs: 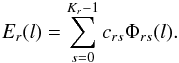 (21)NAL and NAC are the number of effects considered along and across scan. The whole set of coefficients crs forms the calibration vector c.
(21)NAL and NAC are the number of effects considered along and across scan. The whole set of coefficients crs forms the calibration vector c.
In the generic formulation, the multiple indices f, n, g and the variables μ and t are replaced by the single observation index l. This allows maximum flexibility in terms of how the calibration model is implemented in the software. The functions Φrs receive the observation index l, and it is assumed that this index suffices to derive from it all quantities needed to evaluate the calibration functions for this observation. Examples of quantities that can be derived from the observation index are: the FoV index f, the CCD and gate indices n and g, the AC pixel coordinate μ, time t, and any relevant astrometric, photometric or spectroscopic parameter of the source (magnitude, colour index, etc.). Intrinsically real-valued quantities such as t can be subdivided into non-overlapping intervals with different sets of calibration parameters applicable to each interval. The basic calibration model (15) can therefore be implemented as a particular instance of the generic model, with for example 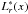 (r = 0, 1, 2) constituting three of the calibration functions (with μ derived from l). Once the calibration functions have been coded, the entire calibration model can be conveniently specified (and changed) through an external configuration file alone using, e.g., XML structures.
(r = 0, 1, 2) constituting three of the calibration functions (with μ derived from l). Once the calibration functions have been coded, the entire calibration model can be conveniently specified (and changed) through an external configuration file alone using, e.g., XML structures.
Some elemental calibration functions may be introduced for diagnostic purposes rather than actual calibration. An example of this is any function depending on the colour or magnitude of the source. The origin of such effects is briefly explained in Appendices D.1 and D.2. Magnitude- and colour-dependent variations of the instrument response are expected to be fully taken into account by the signal modelling on the CCD data level, as outlined in Sect. 3.5 (notably by the LSF and CDM calibrations), and should not show up in the astrometric solution. Thus, non-zero results for such “non-geometric” diagnostic calibration parameters indicate that the signal modelling should be improved. In the final solution the diagnostic calibration parameters should ideally be zero.
The parameters of the generic calibration model must satisfy a number of constraints similar to Eqs. (16)–(18). These can be cast in the general form 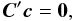 (22)where the matrix C contains one column, with known coefficients, for each constraint. The columns are, by design, linearly independent.
(22)where the matrix C contains one column, with known coefficients, for each constraint. The columns are, by design, linearly independent.
3.5. Signal (CCD data) model
As suggested in Fig. 1, the modelling of CCD data at the level of individual pixels (i.e., the photon counts) is not part of the geometrical model of the observations with which we are concerned in this paper. However, the processing of the photon counts, effectively by fitting the CCD data model, produces the “observations” that are the input to the astrometric core solution. In order to clarify the exact meaning of these observations we include here a brief overview of the signal model.
The pixel size, 10 μm ≃ 59 mas in the along-scan (AL) direction and 30 μm ≃ 177 mas in the across-can (AC) direction, roughly matches the theoretical diffraction image for the 1.45 × 0.50 m2 telescope pupil of Gaia (effective wavelength ~ 650 nm). Around each detected object, only a small rectangular window (typically 6–18 pixels long in the AL direction and 12 pixels wide in the AC direction) is actually read out and transmitted to the ground. Moreover, for most of the observations in the astrometric field (AF), on-chip binning in the serial register is used to sum the charges over the window in the AC direction. This effectively results in a one-dimensional image of 6–18 AL “samples”, where the signal (Nk) in each sample k is the sum of 12 AC pixels. The exact time tk when a sample was transferred to the serial register, expressed on the TCB scale, is in principle known from the time correlation of the on-board clock with ground-based time signals. Because of the known one-to-one relation between the TDI period counter k and tk, we may use k as a proxy for tk in subsequent calculations.
For single stars, and in the absence of the effects discussed in Appendix D.2, the sample values in the window are modelled as a stochastic variable (Poisson photon noise plus electronic readout noise) with expected value 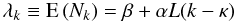 (23)where β, α and κ are the so-called image parameters representing the (uniform) background level, the amplitude (or flux) of the source, and the AL location (pixel coordinate) of the image centroid. The continuous, non-negative function L(x) is the Line Spread Function (LSF) appropriate for the observation. L(x) depends, for example, on the spectrum of the source and on the position of the image in the focal plane. The (in general non-integer) pixel coordinate κ is expressed on the same scale as the (integer) TDI index k, and may be translated to the equivalent TCB t(κ) by means of the known relation between k and tk. The CCD observation time is defined as t(κ − K/2), where K is the number of TDI periods used for integrating the image (see Appendix D.3). Formally, the CCD observation time is the instant of time at which the centre of the source image passed across the CCD fiducial line halfway between the first and the last TDI line used in the integration (this will depend on the gating).
(23)where β, α and κ are the so-called image parameters representing the (uniform) background level, the amplitude (or flux) of the source, and the AL location (pixel coordinate) of the image centroid. The continuous, non-negative function L(x) is the Line Spread Function (LSF) appropriate for the observation. L(x) depends, for example, on the spectrum of the source and on the position of the image in the focal plane. The (in general non-integer) pixel coordinate κ is expressed on the same scale as the (integer) TDI index k, and may be translated to the equivalent TCB t(κ) by means of the known relation between k and tk. The CCD observation time is defined as t(κ − K/2), where K is the number of TDI periods used for integrating the image (see Appendix D.3). Formally, the CCD observation time is the instant of time at which the centre of the source image passed across the CCD fiducial line halfway between the first and the last TDI line used in the integration (this will depend on the gating).
Fitting the CCD signal model to the one-dimensional sample values Nk thus gives, as the end result of observation l, an estimate of the AL pixel coordinate κ of the image in the pixel stream, which is then transformed to the observation time tl. The fitting procedure also provides an estimate of the uncertainty in κ, which can be expressed in angular measure as a formal standard deviation of the AL measurement, 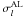 . It is derived by error propagation through the fitted signal model, taking into account the dominant noise sources, photon noise and readout noise.
. It is derived by error propagation through the fitted signal model, taking into account the dominant noise sources, photon noise and readout noise.
For some observations, AC information is also provided through two-dimensional sampling of the pixel window around the detected object. This applies to all SM observations, AF observations of bright (G ≲ 13) sources, and AF observations of Calibration Faint Stars (Sect. 3.4). The modelling of the two-dimensional images follows the same principles as outlined above for the one-dimensional (AL only) case, only that the LSF is replaced by a two-dimensional Point Spread Function (PSF) and that there is one more location parameter to estimate, namely the AC pixel coordinate μ. The astrometric result in this case consists of the observation time tl, the observed AC coordinate μl, and their formal standard uncertainties 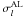 and
and 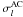 (both expressed as angles).
(both expressed as angles).
The estimation errors for different images are, for the subsequent analysis, assumed to be statistically independent (and therefore uncorrelated). This is a very good approximation to the extent that they only depend on the photon and readout noises. However, modelling errors at the various stages of the processing (in particular CTI effects in the signal modelling [Appendix D.3] and attitude irregularities [Appendix D.4]) are likely to introduce errors that are correlated at least over the nine AF observations in a field transit. The resulting correlations as such are not taken into account in the astrometric solution (i.e., the weight matrix of the least-squares equations is taken to be diagonal), but the sizes of the modelling errors are estimated, and are employed to reduce the statistical weights of the observations as described in Sect. 3.6. The AL and AC estimates of a given (two-dimensional) image are roughly independent at least in the limit of small optical aberrations.
3.6. Synthesis model
By synthesis of the models described in the preceding sections, we are now in a position to formulate very precisely the core astrometric data analysis problem as outlined in Sect. 2. The unknowns are represented by the vectors s, a, c, and g of respectively the source, attitude, calibration, and global parameters. For any observation l the observed quantities are the observation time tl and, where applicable, the observed AC pixel coordinate μl, with their formal uncertainties 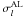 ,
, 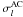 . We then have the global minimization problem
. We then have the global minimization problem 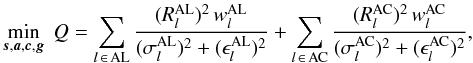 (24)where
(24)where ![\begin{eqnarray} R_l^\text{AL}(\vec{s},\vec{a},\vec{c},\vec{g}) &=& \eta_{fng}(\mu_l,t_l\,|\,\vec{c})- \eta(t_l\,|\,\vec{s},\vec{a},\vec{g})\label{eq:resAL},\\[3pt] R_l^\text{AC}(\vec{s},\vec{a},\vec{c},\vec{g}) &=& \zeta_{fng}(\mu_l,t_l\,|\,\vec{c})- \zeta(t_l\,|\,\vec{s},\vec{a},\vec{g})\label{eq:resAC} \end{eqnarray}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq222.png) are the residuals in the field angles, taken as functions of the unknowns5, and l ∈ AL refers to observations with a valid AL component, etc. The applicable indices f, n, g are of course known for every observation l. In Eq. (24),
are the residuals in the field angles, taken as functions of the unknowns5, and l ∈ AL refers to observations with a valid AL component, etc. The applicable indices f, n, g are of course known for every observation l. In Eq. (24), 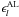 and
and 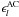 represent all AL and AC error sources extraneous to the formal uncertainties; they include in particular modelling errors in the source behaviour (e.g., for unrecognized binaries), attitude and calibration, which have to be estimated as functions of time and source in the course of the data analysis process.
represent all AL and AC error sources extraneous to the formal uncertainties; they include in particular modelling errors in the source behaviour (e.g., for unrecognized binaries), attitude and calibration, which have to be estimated as functions of time and source in the course of the data analysis process. 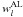 and
and 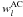 are weight factors, always in the range 0 to 1; for most observations they are equal to 1, but “bad” data (outliers) are assigned smaller weight factors. The determination of these factors is discussed in Sect. 5.1.2.
are weight factors, always in the range 0 to 1; for most observations they are equal to 1, but “bad” data (outliers) are assigned smaller weight factors. The determination of these factors is discussed in Sect. 5.1.2.
For the sake of conciseness we shall hereafter consider the AL and AC components of an observation to have separate observation indices l, so that for example Rl stands for either 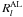 or
or 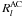 , as the case may be. This allows the two sums in Eq. (24) to be contracted and written concisely as
, as the case may be. This allows the two sums in Eq. (24) to be contracted and written concisely as 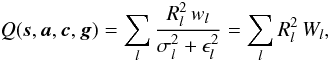 (27)where
(27)where 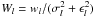 is the statistical weight of the observation.
is the statistical weight of the observation.
The excess noise ϵl represents modelling errors and should ideally be zero. However, it is unavoidable that some sources do not behave exactly according to the adopted astrometric model (Sect. 3.2), or that the attitude sometimes cannot be represented by the spline model in Sect. 3.3 to sufficient accuracy. The excess noise term in Eq. (27) is introduced to allow these cases to be handled in a reasonable way, i.e., by effectively reducing the statistical weight of the observations affected. It should be noted that these modelling errors are assumed to affect all the observations of a particular star, or all the observations in a given time interval. (By contrast, the downweighting factor wl is intended to take care of isolated outliers, for example due to a cosmic-ray hit in one of the CCD samples.) This is reflected in the way the excess noise is modelled as the sum of two components, 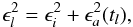 (28)where ϵi is the excess noise associated with source i (if l ∈ i, that is, l is an observation of source i), and ϵa(t) is the excess attitude noise, being a function of time. For a “good” primary source, we should have ϵi = 0, and for a “good” stretch of attitude data we may have ϵa(t) = 0. Calibration modelling errors are not explicitly introduced in Eq. (28), but could be regarded as a more or less constant part of the excess attitude noise. The estimation of ϵi is described in Sect. 5.1.2, and the estimation of ϵa(t) in Sect. 5.2.5.
(28)where ϵi is the excess noise associated with source i (if l ∈ i, that is, l is an observation of source i), and ϵa(t) is the excess attitude noise, being a function of time. For a “good” primary source, we should have ϵi = 0, and for a “good” stretch of attitude data we may have ϵa(t) = 0. Calibration modelling errors are not explicitly introduced in Eq. (28), but could be regarded as a more or less constant part of the excess attitude noise. The estimation of ϵi is described in Sect. 5.1.2, and the estimation of ϵa(t) in Sect. 5.2.5.
Three separate functions are needed to describe the excess attitude noise, corresponding to AL observations, AC observations in the preceding field of view (ACP), and AC observations in the following field of view (ACF). We distinguish between these functions by letting the subscript a in ϵa(t) stand for either AL, ACP or ACF.
4. Solving the global minimization problem
Assuming 108 primary sources, the number of unknowns in the global minimization problem, Eq. (24), is about 5 × 108 for the sources (s), 4 × 107 for the attitude (a, assuming a knot interval of 15 s for the 5 yr mission; cf. Sect. 5.2.1), 106 for the calibration c, and less than 100 global parameters (g). The number of elementary observations (l) considered is about 8 × 1010. However, the size of the data set, and the large number of parameters, would not by themselves be a problem if the observations, or sources, could be processed sequentially. The difficulty is caused by the strong connectivity among the observations: each source is effectively observed relative to a large number of other sources simultaneously in the field of view, or in the complementary field of view some 106.5° away on the sky, linked together by the attitude and calibration models. The complexity of the astrometric solution in terms of the connectivity between the sources provided by the attitude modelling was analysed by Bombrun et al. (2010), who concluded that a direct solution is infeasible, by many orders of magnitude, with today’s computational capabilities. The study neglected the additional connectivity due to the calibration model, which makes the problem even more unrealistic to attack by a direct method. Note that this impossibility is not a defect, but a virtue of the mathematical system under consideration: it guarantees that a unique, coherent and completely independent global solution for the whole sky can be derived from the system.
The natural alternative to a direct solution is to use some iterative method. This is in fact the standard way to deal with large, sparse systems of equations. The literature in the field is vast and a plethora of methods exist for various kinds of applications. However, the iterative method adopted for Gaia did not spring from a box of ready-made algorithms. Rather, it was developed over several years in parallel with the software system in which it could be implemented and tested. Originally based on an intuitive and somewhat simplistic approach, the algorithm has developed through a series of experiments, insights and improvements into a rigorous, efficient and well-understood procedure, completely adapted to its particular application. In this section we first describe the approach in broad outline, then provide the mathematical background for its better understanding and further development.
4.1. Outline of the iterative solution
The numerical approach to the Gaia astrometry is a block-iterative least-squares solution, referred to as the Astrometric Global Iterative Solution (AGIS). In its simplest form, four blocks are evaluated in a cyclic sequence until convergence. The blocks map to the four different kinds of unknowns outlined in Sect. 3, namely:
-
S:
the source (star) update, in which the astrometric parameterss of the primary sources are improved;
-
A:
the attitude update, in which the attitude parameters a are improved;
-
C:
the calibration update, in which the calibration parameters c are improved;
-
G:
the global update, in which the global parameters g are improved.
The G block is optional, and will perhaps only be used in some of the final solutions, since the global parameters can normally be assumed to be known a priori to high accuracy.
The blocks must be iterated because each one of them needs data from the three other processes. For example, when computing the astrometric parameters in the S block, the attitude, calibration and global parameters are taken from the previous iteration. The resulting (updated) astrometric parameters are used the next time the A block is run, and so on. This iterative approach to the astrometric solution was proposed early on in the Hipparcos project as an alternative to the “three-step method” subsequently adopted for the original Hipparcos reductions; see ESA (1997, Vol. 3, p. 488) and references therein. Indeed, the later re-reduction of the Hipparcos raw data by van Leeuwen (2007) used a very similar iterative method, and yielded significantly improved results mainly by virtue of the much more elaborate attitude modelling implemented as part of the approach.
While the block-iterative solution as outlined above is intuitive and appealing in its simplicity, it is from a mathematical standpoint not obvious that it must converge; and if it does indeed converge, it is not obvious how many iterations are required, whether the order of the blocks in each iteration matter, and whether the converged results do in fact constitute a solution to the global minimization problem. These are fundamental questions for the validity of the adopted iterative approach, and we therefore take some care in the following subsections to establish its theoretical foundations (Sects. 4.2–4.5). Section 5 then describes each of the S, A, C and G blocks in some detail. In addition to these blocks, separate processes are required for the alignment of the astrometric solution with the ICRS, the selection of primary sources, and the calculation of standard uncertainties; these auxiliary processes are discussed in Sect. 6.
4.2. Least-squares approach
Strictly speaking, Eq. (24) is not a least-squares problem, because of the weight factors 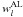 ,
, 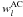 (as well as the excess noises
(as well as the excess noises 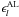 ,
, 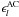 ), which depend on the AL and AC residuals and hence on the unknowns (s,a,c,g). In Eq. (1) this dependence is formally included in the unspecified metric ℳ, which therefore is not simply a (weighted) Euclidean norm.
), which depend on the AL and AC residuals and hence on the unknowns (s,a,c,g). In Eq. (1) this dependence is formally included in the unspecified metric ℳ, which therefore is not simply a (weighted) Euclidean norm.
In principle, the minimization problem (24) can be solved by finding a point where the partial derivatives of the objective function Q with respect to all the unknowns are simultaneously zero. In practice, however, the partial derivatives are not computed completely rigorously, and the problem solved is therefore a slightly different one from what is outlined above. In order to understand precisely the approximations involved, it is necessary to consider how different kinds of non-linearities enter the problem.
The functions ηfng(μ,t | c) and ζfng(μ,t | c) appearing in Eqs. (25), (26) are strictly linear in the calibration parameters c, by virtue of the basic geometric calibration model in Eq. (15) or the generic model in Eqs. (20), (21). On the other hand, the functions η(t | s,a,g) and ζ(t | s,a,g) are non-linear in s, a, and g due to the complex transformations involved (Sects. 3.2, 3.3). However, thanks to the data processing prior to the astrometric solution, the initial errors in these parameters are already so small that the corresponding errors in η and ζ are only some 0.1 arcsec (~10-6 rad). Second-order terms are therefore typically less than 10-12 rad ≃ 0.2 μas, that is negligible in comparison with the noise of a single AL observation (some 100 μas). This means that the partial derivatives of the residuals 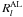 and
and 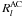 with respect to all the unknowns do not change in the course of the solution. (In practice they are in fact recomputed in each iteration, although that is mainly done because it is more convenient than to store and retrieve the values; nevertheless, this takes care of any remaining non-linearity, however small.) The non-linearities of the underlying astrometric, attitude, calibration and global models are therefore not an issue for the minimization problem as such.
with respect to all the unknowns do not change in the course of the solution. (In practice they are in fact recomputed in each iteration, although that is mainly done because it is more convenient than to store and retrieve the values; nevertheless, this takes care of any remaining non-linearity, however small.) The non-linearities of the underlying astrometric, attitude, calibration and global models are therefore not an issue for the minimization problem as such.
The weight factors wl represent a different kind of non-linearity, potentially much more important for the final solution. These factors are introduced to make the solution robust against outliers, by reducing their influence on Q and hence on the estimated parameter values (Sect. 5.1.2). Ideally, outlying observations should not contribute at all to the solution (by having wl = 0), while “normal” observations should receive full weight (wl = 1). In reality there will however be a transition region where the weight factors are between 0 and 1. Since the weight factors are in practice determined by the normalized residuals, 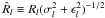 , which in turn depend on the parameter values (s,a,c,g), it follows that the partial derivatives contain extra terms of the form
, which in turn depend on the parameter values (s,a,c,g), it follows that the partial derivatives contain extra terms of the form 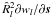 ,
, 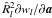 , etc., that are non-zero for some observations. Analogous considerations apply to the excess noise terms ϵl: they too are estimated by means of the residuals (Sects. 5.1.2 and 5.2.5), and therefore in principle introduce additional terms in the partial derivatives.
, etc., that are non-zero for some observations. Analogous considerations apply to the excess noise terms ϵl: they too are estimated by means of the residuals (Sects. 5.1.2 and 5.2.5), and therefore in principle introduce additional terms in the partial derivatives.
We take the somewhat pragmatic approach of neglecting the terms depending on the partial derivatives of wl and ϵl with respect to the unknowns when seeking the solution to the global minimization problem. The consequences of this approximation can be appreciated by observing that the down-weighting (wl < 1) only kicks in when the absolute value of the residual exceeds a few times the total standard uncertainty, or some 0.5–1 mas for typical observations of bright sources. Similarly the estimated ϵl are only sensitive to changes of the residuals of a similar size. Experience with AGIS runs on simulated data show that the typical changes of the residuals fall below this level already in the first few iterations. Thereafter the weight factors and the estimated excess noises do not change significantly. Neglecting the derivatives of wl and ϵl in the global minimization problem is therefore equivalent to solving the weighted least-squares problem with wl and ϵl fixed at whatever values they settle to after the initial iterations. This is a reasonable assumption given that the statistical weight of any observation, and the size of the modelling errors, are not a priori expected to depend on the actual values of the parameters. The precise solution does of course depend on how wl and ϵl are estimated, but that is an unavoidable consequence of any practical data analysis approach.
4.3. Normal equations
The minimization of Q in Eq. (27) is thus solved by the weighted least-squares method, assuming fixed weights Wl that are however determined as part of the solution. The normal equations for the sources are given by 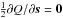 , and similarly for the other unknowns. Linearising around any reference point (sref,aref,cref,gref) within the linear regime of parameter space, i.e., setting s = sref + xs, and similarly for the other unknowns, and expanding to first order in the differential vector
, and similarly for the other unknowns. Linearising around any reference point (sref,aref,cref,gref) within the linear regime of parameter space, i.e., setting s = sref + xs, and similarly for the other unknowns, and expanding to first order in the differential vector 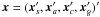 , we find the normal equations as
, we find the normal equations as ![\begin{equation} \label{eq:norm} \left[ \sum_l \frac{\partial R_l}{\partial\vec{x}}\frac{\partial R_l}{\partial\vec{x}'} W_l\right]\vec{x} = -\sum_l \frac{\partial R_l}{\partial\vec{x}} R_l(\vec{s}^\text{ref},\vec{a}^\text{ref},\vec{c}^\text{ref},\vec{g}^\text{ref})W_l . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq264.png) (29)This can be written in matrix form as
(29)This can be written in matrix form as 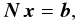 (30)where N is a symmetric matrix. We now proceed to analyse the structure of this linear system of equations in terms of the previously mentioned block updates S, A, C, G.
(30)where N is a symmetric matrix. We now proceed to analyse the structure of this linear system of equations in terms of the previously mentioned block updates S, A, C, G.
The matrix N and the vectors (column matrices) x, b can be partitioned into sub-matrices and sub-vectors corresponding to the different parameter vectors s, a, c, and g: 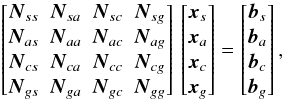 (31)where
(31)where 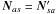 , etc. Of importance here is that Nss and Naa have a particularly simple structure. Since s is sub-divided into vectors si of length 5 for the individual primary sources (i), it is natural to sub-divide Nss into blocks of 5 × 5 elements. From Eq. (29) it follows that the (i,j)th such block is given by
, etc. Of importance here is that Nss and Naa have a particularly simple structure. Since s is sub-divided into vectors si of length 5 for the individual primary sources (i), it is natural to sub-divide Nss into blocks of 5 × 5 elements. From Eq. (29) it follows that the (i,j)th such block is given by ![\begin{equation} \label{eq:Nss} \left[\vec{N}_{ss}\right]_{ij} = \sum_l \frac{\partial R_l}{\partial\vec{s}_i}\frac{\partial R_l}{\partial\vec{s}'_{\!j}} W_l = \begin{cases}\displaystyle \sum_{l\,\in\,i} \frac{\partial R_l}{\partial\vec{s}_i}\frac{\partial R_l}{\partial\vec{s}'_{\!i}} W_l & \text{if }i=j,\\[12pt] \vec{0} & \text{if }i\ne j, \end{cases} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq273.png) (32)where l ∈ i signifies that the sum is taken over the observations of source i. The result for i ≠ j follows because no observation l is associated with more than one primary source. Nss is consequently block-diagonal, and
(32)where l ∈ i signifies that the sum is taken over the observations of source i. The result for i ≠ j follows because no observation l is associated with more than one primary source. Nss is consequently block-diagonal, and 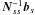 can trivially be computed for arbitrary vector bs by looping through the sources and solving the corresponding 5 × 5 system for each source6. This is exactly what is done in the source update block (S).
can trivially be computed for arbitrary vector bs by looping through the sources and solving the corresponding 5 × 5 system for each source6. This is exactly what is done in the source update block (S).
The vector of attitude unknowns is naturally sub-divided into vectors an of length 4, containing the elements of the quaternions an that serve as coefficients in the B-spline representation, Eq. (10). If Naa is correspondingly sub-divided into blocks of 4 × 4 elements, it follows from Eq. (29) that the (n,m)th such block is given by ![\begin{equation} \label{eq:Naa} \left[\vec{N}_{aa}\right]_{nm} = \sum_l \frac{\partial R_l}{\partial\vec{a}_n}\frac{\partial R_l}{\partial\vec{a}'_{m}} W_l . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq280.png) (33)With ℓ denoting the left index of tl (Sect. 3.3), we have ∂Rl/∂an = 0 whenever n < ℓ − M + 1 or n > ℓ, where M is the order of the spline. It follows that [Naa]nm = 0 if |n − m| > M − 1 (cf. Appendix B.1). The non-zero blocks in Naa are therefore confined to the diagonal and M − 1 blocks above and below the diagonal (Fig. 5). Thus,
(33)With ℓ denoting the left index of tl (Sect. 3.3), we have ∂Rl/∂an = 0 whenever n < ℓ − M + 1 or n > ℓ, where M is the order of the spline. It follows that [Naa]nm = 0 if |n − m| > M − 1 (cf. Appendix B.1). The non-zero blocks in Naa are therefore confined to the diagonal and M − 1 blocks above and below the diagonal (Fig. 5). Thus, 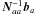 can be efficiently computed for arbitrary ba since the Cholesky decomposition of the matrix does not produce any additional fill-in (Appendix C). This system is solved in the attitude update block (A).
can be efficiently computed for arbitrary ba since the Cholesky decomposition of the matrix does not produce any additional fill-in (Appendix C). This system is solved in the attitude update block (A).
In the geometric instrument model (Sect. 3.4), each CCD/gate and time interval combination (index ngk for example in Eq. (15)) has its own set of unknowns. Moreover, a given observation l can only refer to one CCD/gate combination. By the same reasoning as above, the sub-matrix Ncc is therefore block-diagonal, and 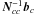 can be computed for arbitrary bc by looping over the CCD/gates combinations. This is done in the calibration update block (C). Although the number of calibration parameters per CCD/gate combination can be fairly large (~104), the resulting systems are well within the bounds that can readily be handled by direct matrix methods, even without taking into account their sparseness.
can be computed for arbitrary bc by looping over the CCD/gates combinations. This is done in the calibration update block (C). Although the number of calibration parameters per CCD/gate combination can be fairly large (~104), the resulting systems are well within the bounds that can readily be handled by direct matrix methods, even without taking into account their sparseness.
By definition all the global parameters affect each observation, and the sub-matrix Ngg is therefore full. However, since the number of global parameters is never large, 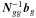 can easily be computed, which is done in the global update block (G).
can easily be computed, which is done in the global update block (G).
In the description above we have implicitly assumed that each of the diagonal blocks Nss, Naa, Ncc, and Ngg is non-singular, and even well-conditioned in order to avoid numerical instability. This is equivalent to the statement that each of the blocks S, A, C and G is a well-posed problem: for example, that the determination of the source parameters is “easy” if we assume that we know the attitude, calibration and global parameters. This will in practice be guaranteed by the choice of primary sources (which will make ![\hbox{$[\vec{N}_{ss}]_{ii}$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq296.png) well-conditioned for every i) for the S block, and by the adopted attitude, calibration and global parametrizations, including the constraints necessary to render the updates unique – in particular the quaternion length normalization in Eq. (10) for the attitude model, and Eq. (22) for the calibration model.
well-conditioned for every i) for the S block, and by the adopted attitude, calibration and global parametrizations, including the constraints necessary to render the updates unique – in particular the quaternion length normalization in Eq. (10) for the attitude model, and Eq. (22) for the calibration model.
Turning now to the off-diagonal sub-matrices of N, it is natural to sub-divide for example the sub-matrix Nas into blocks of 4 × 5 elements corresponding to the 4 components of the quaternion and the 5 astrometric parameters. The (n,i)th block, ![\begin{equation} \label{eq:Nas} \left[\vec{N}_{as}\right]_{ni} = \sum_l \frac{\partial R_l}{\partial\vec{a}_n}\frac{\partial R_l}{\partial\vec{s}'_{\!i}} W_l , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq300.png) (34)is non-zero only if source i was observed in the time interval [ τn,τn + M ] , which is the support of the B-spline Bn(t). Nas is therefore very sparse, but it also has no simple structure because the distribution of the non-zero blocks is linked to the scanning law. Fortunately, as will be explained in Sect. 4.5, there is no need to explicitly compute, much less store, this sub-matrix, nor any of the other off-diagonal sub-matrices in Eq. (31).
(34)is non-zero only if source i was observed in the time interval [ τn,τn + M ] , which is the support of the B-spline Bn(t). Nas is therefore very sparse, but it also has no simple structure because the distribution of the non-zero blocks is linked to the scanning law. Fortunately, as will be explained in Sect. 4.5, there is no need to explicitly compute, much less store, this sub-matrix, nor any of the other off-diagonal sub-matrices in Eq. (31).
4.4. Rank of the normal equations
From the nature of the astrometric observations, which are in effect differential within the (combined) field of view, and the modelling of the primary sources, which does not assume that any of their positions or proper motions are known a priori, it is clear that there is no unique astrometric solution to the problem as outlined above. The fundamental reason for this is that any (small) change in the orientation of the celestial reference system, as well as the introduction of a (small) inertial spin of the system, would leave all observations invariant. In principle the non-uniqueness of the solution is not a problem as such, since the resulting system of positions and proper motions are afterwards aligned with the ICRS by a special process (Sect. 6.1). However, it does imply that the normal matrix N is in principle singular7, which may have consequences for the numerical solution of the normal equations. We say singular “in principle” because arithmetic rounding errors will in practice prevent it from becoming truly singular, although it remains extremely ill-conditioned.
More precisely, we expect N to have rank n − 6, if n = dim(N) is the total number of unknowns. The null space of the matrix, 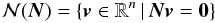 (35)therefore has rank six. Indeed, it is easy to find six linearly independent vectors v0, ..., v5 that span the null space: the first three are found by introducing small changes in the orientation of the celestial reference system around each of its principal axes, and deriving the corresponding changes in s and a (c and g being independent of the reference system); the last three are correspondingly found by introducing a small inertial spin of the reference system around each axis (see Sect. 6.1.5 for details). Introducing the n × 6 matrix V = (v0, ..., v5) we have
(35)therefore has rank six. Indeed, it is easy to find six linearly independent vectors v0, ..., v5 that span the null space: the first three are found by introducing small changes in the orientation of the celestial reference system around each of its principal axes, and deriving the corresponding changes in s and a (c and g being independent of the reference system); the last three are correspondingly found by introducing a small inertial spin of the reference system around each axis (see Sect. 6.1.5 for details). Introducing the n × 6 matrix V = (v0, ..., v5) we have 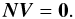 (36)The singularity can in principle be removed by adding the six constraints V′x = 0, but in practice that is not necessary. It suffices to derive one particular solution
(36)The singularity can in principle be removed by adding the six constraints V′x = 0, but in practice that is not necessary. It suffices to derive one particular solution 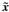 to the normal equations, then the whole solution space can be written
to the normal equations, then the whole solution space can be written 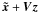 for arbitrary z ∈ R6. The vector z is effectively determined by the frame rotator (Sect. 6.1), yielding the unique solution that best agrees with the adopted definition of the ICRS.
for arbitrary z ∈ R6. The vector z is effectively determined by the frame rotator (Sect. 6.1), yielding the unique solution that best agrees with the adopted definition of the ICRS.
Quite apart from numerical rounding errors, it is not completely true that N is mathematically singular. Stellar aberration and parallax introduce some absolute knowledge about the reference system via the barycentric ephemeris of Gaia, which is expressed in ICRS and is not part of the adjustment process. However, since stellar aberration is at most 10-4 rad, the orientation error would have to be of the order of 1 mas for the aberration effect to change by 0.1 μas (say). So, although absent in principle, the indeterminacy of the reference frame orientation and spin exists in practice. Since the orientation can be determined to much higher accuracy than 1 mas (by means of the optical counterparts of radio sources), the contribution of stellar aberration to the absolute frame knowledge can be neglected in practice. The same holds, a fortiori, for the much smaller parallax effect.
4.5. The simple iteration step
Consider the system 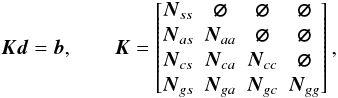 (37)where b is the same right-hand side as in Eq. (30), and each ∅ stands for a zero-filled sub-matrix of the appropriate dimensions. Although this system is of the same size as Eq. (30), it is fundamentally different in that it can be directly solved through a sequence of smaller systems,
(37)where b is the same right-hand side as in Eq. (30), and each ∅ stands for a zero-filled sub-matrix of the appropriate dimensions. Although this system is of the same size as Eq. (30), it is fundamentally different in that it can be directly solved through a sequence of smaller systems, 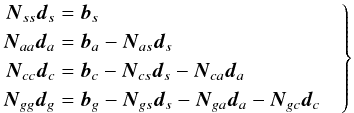 (38)where each sub-system is of the form S, A, C, G described above, allowing it to be solved with relative ease. (Naturally, the resulting solution d is also quite different from the x in Eq. (30) !) By means of Eqs. (29) and (34) the right-hand side in the second sub-system becomes
(38)where each sub-system is of the form S, A, C, G described above, allowing it to be solved with relative ease. (Naturally, the resulting solution d is also quite different from the x in Eq. (30) !) By means of Eqs. (29) and (34) the right-hand side in the second sub-system becomes ![\begin{eqnarray} \vec{b}_a-\vec{N}_{as}\vec{d}_s &=& -\sum_l \frac{\partial R_l}{\partial\vec{a}} \left[ R_l(\vec{s}^\text{ref},\vec{a}^\text{ref},\vec{c}^\text{ref},\vec{g}^\text{ref}) +\frac{\partial R_l}{\partial\vec{s}'}\vec{d}_s\right]W_l \nonumber \\ &=& -\sum_l \frac{\partial R_l}{\partial\vec{a}} R_l(\vec{s}^\text{ref}+\vec{d}_s,\vec{a}^\text{ref},\vec{c}^\text{ref},\vec{g}^\text{ref})W_l ,\label{eq:precond2} \end{eqnarray}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq319.png) (39)where the linearity of Rl(s,a,c,g) has been used in a Taylor expansion around the reference values. This shows that the off-diagonal matrix Nas is not needed in order to compute the right-hand side of the second sub-system in Eq. (38), if only the residuals are computed after the source parameters have been updated by the solution of the first sub-system. Similarly, we find that the right-hand side in the third sub-system can be obtained from the residuals after updating both the source and attitude parameters, and so on. The off-diagonal sub-matrices in K are therefore not needed, provided that the sub-vectors of unknowns are successively updated before the new right-hand sides are computed.
(39)where the linearity of Rl(s,a,c,g) has been used in a Taylor expansion around the reference values. This shows that the off-diagonal matrix Nas is not needed in order to compute the right-hand side of the second sub-system in Eq. (38), if only the residuals are computed after the source parameters have been updated by the solution of the first sub-system. Similarly, we find that the right-hand side in the third sub-system can be obtained from the residuals after updating both the source and attitude parameters, and so on. The off-diagonal sub-matrices in K are therefore not needed, provided that the sub-vectors of unknowns are successively updated before the new right-hand sides are computed.
From the above it is clear that a single AGIS iteration, consisting of the successive application of the four update blocks S, A, C and G, is mathematically equivalent to an updating of the unknowns by d = K-1b. In the context of iterative solution algorithms, the matrix K is referred to as the preconditioner of the normal equations system (Axelsson 1996).
As previously noted, we assume that the block-diagonal matrices Nss, Naa, Ncc, Ngg are all non-singular, and in fact positive definite, for a proper formulation of the S, A, C, and G blocks. This ensures that the preconditioner K is non-singular, even though N is not.
In the course of the iterations, new right-hand sides of the normal equations will be computed, while the matrix remains essentially unchanged. From now on, let us express the residuals Rl not as functions of the parameter values s, a, c, g but in terms of the differential parameter vector x relative to the reference values. The original right-hand side, denoted b(0), corresponds to the initial differential parameter vector x(0) = 0. If x (without a superscript) denotes the exact solution of Eq. (30), the initial error vector is e(0) = x(0) − x = −x. Although this vector is of course not known, we do know − Ne(0) = Nx = b(0). Solving the preconditioner system (37) gives d(0) = K-1b(0) and the updated parameter vector x(1) = x(0) + d(0). The new error vector e(1) = x(1) − x is again not known, but − Ne(1) = b(0) − Nd(0) = b(1) is obtained by inserting the updated parameters in the right-hand side of Eq. (29), by the same argument as in Eq. (39). Generalizing, we have the so-called simple iteration scheme 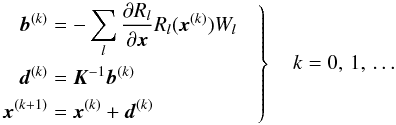 (40)For the successive right-hand sides we find by recursion
(40)For the successive right-hand sides we find by recursion 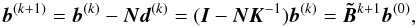 (41)where
(41)where 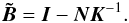 (42)For the successive updates and errors we find
(42)For the successive updates and errors we find 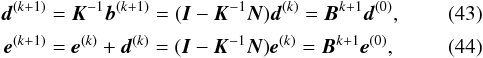 where
where 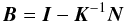 (45)is called the iteration matrix (Axelsson 1996). Equations (41)–(45) are of great theoretical interest, as explained below, although none of them is used in the actual computations.
(45)is called the iteration matrix (Axelsson 1996). Equations (41)–(45) are of great theoretical interest, as explained below, although none of them is used in the actual computations.
The convergence behaviour of the simple iteration scheme can largely be understood by means of these relations and especially in terms of the properties of the iteration matrix B governing the sequence of updates d and errors e, and the adjunct matrix  governing the sequence of right-hand sides. It is well known (e.g., Axelsson 1996) that the simple iteration scheme in Eq. (40) converges (that is x(k) → x) for arbitrary starting approximation if and only if ρ(B) < 1. Here, ρ(B) is the spectral radius of B, i.e., the largest absolute value of its eigenvalues. Under this condition we have d(k) → 0 and e(k) → 0 for k → ∞. Also the right-hand side b(k) = Kd(k) → 0 under the same condition8.
governing the sequence of right-hand sides. It is well known (e.g., Axelsson 1996) that the simple iteration scheme in Eq. (40) converges (that is x(k) → x) for arbitrary starting approximation if and only if ρ(B) < 1. Here, ρ(B) is the spectral radius of B, i.e., the largest absolute value of its eigenvalues. Under this condition we have d(k) → 0 and e(k) → 0 for k → ∞. Also the right-hand side b(k) = Kd(k) → 0 under the same condition8.
As discussed in Sect. 4.4, the normal matrix N is singular and its null space spanned by the n × 6 matrix V. Therefore, 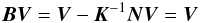 (46)which shows that B has a six-fold eigenvalue equal to 1, with the corresponding eigenvectors spanning
(46)which shows that B has a six-fold eigenvalue equal to 1, with the corresponding eigenvectors spanning  . The spectral radius of B is therefore not less than 1, and the simple iteration scheme does not converge for arbitrary initial errors.
. The spectral radius of B is therefore not less than 1, and the simple iteration scheme does not converge for arbitrary initial errors.
This is not a real problem, for the following reason. First, let us note that B is not a full-rank matrix. Indeed, a direct calculation of Eq. (45) using the expression for K in Eq. (37) shows that the first ns columns of B are zero9. Thus (at least) ns of its eigenvalues are identically zero. A corresponding set of orthogonal unit vectors is given by the columns of the n × ns matrix ![\begin{equation} \label{eq:eigenZ} \vec{Z}= \left[\begin{array}{c} \vec{I} \\[3pt] \vec{\varnothing} \end{array}\right] \quad\begin{array}{cl} \} & n_s~\text{rows}\\[3pt] \} & n-n_s~\text{rows}, \end{array} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq351.png) (47)so that BZ = 0. We assume that the remaining n − ns − 6 eigenvalues satisfy 0 < |λ| < 1. Thus, if Λ is the diagonal matrix containing these eigenvalues and U a matrix of size n × (n − ns − 6) whose columns are made up of the corresponding eigenvectors, we have BU = UΛ. The columns of Z, U and V together span Rn, and it is therefore possible to decompose the solution vector as
(47)so that BZ = 0. We assume that the remaining n − ns − 6 eigenvalues satisfy 0 < |λ| < 1. Thus, if Λ is the diagonal matrix containing these eigenvalues and U a matrix of size n × (n − ns − 6) whose columns are made up of the corresponding eigenvectors, we have BU = UΛ. The columns of Z, U and V together span Rn, and it is therefore possible to decompose the solution vector as 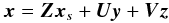 (48)where xs ∈ Rns is the “source” part of x, y ∈ Rn − ns − 6 and z ∈ R6. Since − e(0) = x we find
(48)where xs ∈ Rns is the “source” part of x, y ∈ Rn − ns − 6 and z ∈ R6. Since − e(0) = x we find 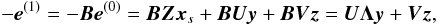 (49)and by recursion
(49)and by recursion 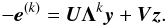 (50)The first term clearly vanishes for k → ∞ if ρ(Λ) < 1, as we have assumed. The second term, which is the projection of x on the null space of N, remains unchanged by the iterations. The update vector can be written
(50)The first term clearly vanishes for k → ∞ if ρ(Λ) < 1, as we have assumed. The second term, which is the projection of x on the null space of N, remains unchanged by the iterations. The update vector can be written 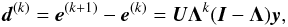 (51)which vanishes under the same condition. The same is then true for the right-hand side b(k) = Kd(k). Effectively, this means that we can ignore the singularity of N in the simple iteration scheme; it will converge to some valid solution of the (singular) normal equations, and the convergence process can be monitored by means of the vectors d(k) and b(k). After convergence, the required null-space components can be found and added by means of the frame rotator.
(51)which vanishes under the same condition. The same is then true for the right-hand side b(k) = Kd(k). Effectively, this means that we can ignore the singularity of N in the simple iteration scheme; it will converge to some valid solution of the (singular) normal equations, and the convergence process can be monitored by means of the vectors d(k) and b(k). After convergence, the required null-space components can be found and added by means of the frame rotator.
To summarize, we have shown that the simple iteration scheme converges in the desired way, provided that the spectral radius of B, not counting the eigenvalues related to the null space of N, is less than 1. It is well known (e.g., Golub & van Loan 1996) that this condition is satisfied for any symmetric positive definite N, using the Gauss-Seidel preconditioner. However, the spectral radius may be very close to 1, implying very slow convergence. In the case of AGIS the situation is more complex, and convergence is in practice demonstrated through simulations (Sect. 7), but the theoretical background outlined above is of great help when interpreting the results.
4.6. Order of the block processes
In the preceding sections we have assumed that the four blocks are always executed in the sequence SACG, and that the updated parameters resulting from each block is used in the subsequent blocks. The particular preconditioner K in Eq. (37) incorporates these assumptions. We will now discuss variants of this scheme and show that they can be mathematically represented by different preconditioners.
Each AGIS iteration always starts with the source update block (S). The main reason for starting with S rather than A, for example, is that the observations can be inspected and analysed one source at a time in order to estimate the quality of the data, identify possible outliers, and check whether the source is suitable as a primary source. The identification of outliers, in particular, requires several “inner” iterations of the source observation equations (Sect. 5.1.2), which can be done with relative ease because of the small number of data points involved.
The order of the remaining blocks ACG adopted in the preceding sections is more or less arbitrary. It is easy to see through an analogy with Eqs. (37), (38) that the sequence SCAG (for example) is mathematically represented by the alternative preconditioner 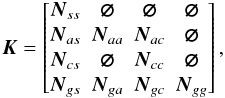 (52)and that other permutations of the sequence are similarly obtained by transposing the corresponding off-diagonal blocks. Changing the preconditioner means changing the iteration matrix (45) and therefore possibly also its eigenvalues, which in turn govern the rate of convergence.
(52)and that other permutations of the sequence are similarly obtained by transposing the corresponding off-diagonal blocks. Changing the preconditioner means changing the iteration matrix (45) and therefore possibly also its eigenvalues, which in turn govern the rate of convergence.
From a mathematical viewpoint, the choice of the starting block (S in our case) determines the initial update d(0) (cf. footnote 9) and therefore influences all subsequent updates. However, this particular choice is not expected to have much influence on the convergence rate after a number of iterations, since the S block has no special status in the periodically repeated sequence ... SACGSACGSACGSA... . Thus we may surmise that the different iteration matrices for the cyclically permuted sequences SACG, ACGS, CGSA and GSAC do in fact have the same set of eigenvalues. For symmetry reasons it can also be surmised that the reversed sequences GCAS, SGCA, ASGC and CASG have the same eigenvalues as the original sequences. Thus, there are in fact only three sets of sequences with possibly distinct convergence behaviour, represented by SACG (or SGCA), SAGC (or SCGA), and SCAG (or SGAC) if we take S to be the starting block. There is no obvious way of knowing a priori which of the three possibilities is to be preferred, or even if they are significantly different.
Apart from the various permutations discussed above, there is another way to modify the AGIS iteration scheme, which can also be described in terms of the preconditioner. This modification is related to the practical organization of the flow of data to the different block processes. The current implementation of the simple iteration scheme differs somewhat from the description in Sect. 4.5, and the block updates are in fact practically organized as follows:
-
1.
Initialize the iteration counter, k = 0.
-
2.
Choose starting values for all unknowns: s(0), a(0), c(0), g(0).
-
3.
Estimate s(k + 1) using a(k), c(k), g(k).
-
4.
Estimate a(k + 1) using s(k + 1), c(k), g(k).
-
5.
Estimate c(k + 1) using s(k + 1), a(k), g(k).
-
6.
Estimate g(k + 1) using s(k + 1), a(k), c(k).
-
7.
Increment k and go to Step 3.
The crucial difference compared with Eq. (38) is that the C block in Step 5 does not use the updated attitude but the old one, and that the G block in Step 6 similarly uses the “old” attitude and calibration parameters. This has the practical advantage that the A, C and G blocks can be carried out in parallel, with big savings in terms of the amounts of data that have to be exchanged between the processes (see Sect. 7). Schematically, this can be represented as S[ACG], where the blocks in brackets are (or can be) executed in parallel (and so the order of the bracketed blocks does not matter). The corresponding preconditioner is 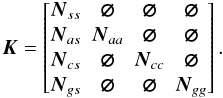 (53)Yet other variants may be considered, for example S[AC]G, where Step 6 uses the updated attitude and calibration parameters, with preconditioner
(53)Yet other variants may be considered, for example S[AC]G, where Step 6 uses the updated attitude and calibration parameters, with preconditioner 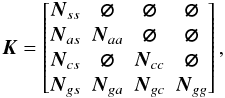 (54)and [SACG], for which
(54)and [SACG], for which 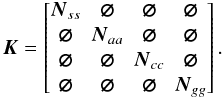 (55)This last case is known as the (block) Jacobi method, while the use of a full triangular preconditioner as in Eq. (37) is known as the (block) Gauss-Seidel method (Axelsson 1996). As we have seen, the currently implemented simple iteration scheme is intermediate between the Jacobi and Gauss-Seidel methods.
(55)This last case is known as the (block) Jacobi method, while the use of a full triangular preconditioner as in Eq. (37) is known as the (block) Gauss-Seidel method (Axelsson 1996). As we have seen, the currently implemented simple iteration scheme is intermediate between the Jacobi and Gauss-Seidel methods.
Intuitively, we expect the Gauss-Seidel method to converge more quickly than the Jacobi or any intermediate method, simply because each block then uses the most recent (and, presumably, best) estimates of the parameters. However, our practical experience with AGIS shows that the “difficult” part of the problem is to disentangle the source and attitude parameters. For example, the calibration parameters are generally found to converge much faster than the source and attitude parameters. Thus it does not seem to matter much if Step 5 above uses a(k + 1) or a(k), i.e., whether the sub-matrix Nca is included or not in the preconditioner. A similar argument can be made concerning the G block, provided some measures are taken to decorrelate the global parameters from the source parameters (Sect. 5.4). Thus, the various intermediate methods are probably nearly as good as the Gauss-Seidel method, in terms of the convergence rate, and the precise scheme may then rather be determined by practical considerations. With the present data processing architecture, the favoured scheme is S[ACG] as described above.
4.7. Accelerated iteration, conjugate gradients and the hybrid iteration scheme
The “simple iteration” (SI) scheme described above was the starting point for a long development towards a fully functional scheme with much improved convergence properties. The main stages in this development were the “accelerated simple iteration” (ASI), the conjugate gradients (CG), and finally the fully flexible “hybrid scheme” (A/SI-CG) to be used in the final implementation of AGIS. As much of this development has at most historical interest, only a brief outline is given here.
Already in the very early implementation of the simple iteration scheme it was observed that convergence was slower than (naively) expected, and that after some iterations, the updates always seemed to go in the same direction, forming a geometrically (exponentially) decreasing series. With the hindsight of the analysis in Sect. 4.5 this behaviour is very easily understood: the persistent pattern of updates is roughly proportional to the eigenvector of the largest eigenvalue of the iteration matrix, and the (nearly constant) ratio of the sizes of successive updates is the corresponding eigenvalue. From this realization it was natural to test an acceleration method based on a Richardson-type extrapolation of the updates. The idea is simply that if the updates in two successive iterations are roughly proportional to each other, d(k + 1) ≃ λd(k), with |λ| < 1, then we can infer that the next update is again a factor λ smaller than d(k + 1), and so on. The sum of all the updates after iteration k can therefore be estimated as d(k + 1) + λd(k + 1) + λ2d(k + 1) + ··· = (1 − λ)-1d(k + 1). Thus, in iteration k + 1 we apply an acceleration factor 1/(1 − λ) based on the current estimate of the ratio λ. This accelerated simple iteration (ASI) scheme is seen to be a variant of the well-known successive overrelaxation method (Axelsson 1996). The factor λ is estimated by statistical analysis of the parallax updates for a small fraction of the sources; the parallax updates are used for this analysis, since they are unaffected by a possible change in the frame orientation between successive iterations. With this simple device, the number of iterations for full convergence was reduced roughly by a factor 2.
Both the simple iteration and the accelerated simple iteration belongs to a much more general class of solution methods known as Krylov subspace approximations. The sequence of updates d(k), k = 0...K − 1 generated by the first K simple iterations constitute the basis for the K-dimensional subspace of the solution space, known as the Krylov subspace for the given matrix and right-hand side (e.g., Greenbaum 1997; van der Vorst 2003). Krylov methods compute approximations that, in the kth iteration, belongs to the k-dimensional Krylov subspace. But whereas the simple and accelerated iteration schemes, in the kth iteration, use updates that are just proportional to the kth basis vector, more efficient algorithms generate approximations that are (in some sense) optimal linear combinations of all k basis vectors. Conjugate gradients (CG) is one of the best-known such methods, and possibly the most efficient one for general symmetric positive-definite matrices. (e.g., Axelsson 1996; Björck 1996; van der Vorst 2003). Its implementation within the AGIS framework is more complicated, but has been considered in detail by Bombrun et al. (2012). As it provides significant advantages over the SI and ASI schemes in terms of convergence speed, this algorithm has been chosen as the baseline method for the astrometric core solution of Gaia (see below however). From practical experience, we have found that CG is roughly a factor 2 faster than ASI, or a factor 4 faster than the SI scheme. Like SI, the CG algorithm uses a preconditioner and can be formulated in terms of the S, A, C and G blocks, so the subsequent description of these blocks remains valid. In the terminology of Bombrun et al. (2012) the process of solving the preconditioner system Kd = b is the kernel operation common to all these solution methods, which only differ in how the updates are applied according to the various iteration schemes.
The CG algorithm assumes that the normal matrix is constant in the course of the iterations. This is not strictly true if the observation weights are allowed to change as functions of the residuals, as will be required for efficient outlier elimination (Sect. 5.1.2). Using the CG algorithm together with the weight-adjustment scheme described below could therefore lead to instabilities, i.e., a reduced convergence rate or even non-convergence. On the other hand, the SI scheme is extremely stable with respect to all such modifications in the course of the iterations, as can be expected from the interpretation of the SI scheme as the successive and independent application of the different solution blocks. The finally adopted algorithm is therefore a hybrid scheme combining SI (or ASI) and CG, where SI is used initially, until the weights have settled, after which CG is turned on. A temporary switch back to SI, with an optional re-adjustment of the weights, may be employed after a certain number of CG iterations; this could avoid some problems due to the accumulation of numerical rounding errors in CG.
5. Updating processes
In this section we describe in some detail each of the updating blocks S, A, C and G that form the basis (or kernel process) for the AGIS iteration loop.
5.1. Source updating (S)
5.1.1. The normal equations
The astrometric model for the sources is given in Sect. 3.2. In the source update block (S) the source parameters s are improved by solving the first line in Eq. (38). According to Eqs. (29) and (32) this can be done for one source (i) at a time by solving the following system of equations for the update di of the five astrometric parameters in si: ![\begin{equation} \label{eq:normS} \left[ \sum_{l\,\in\,i} \frac{\partial R_l}{\partial\vec{s}_i} \frac{\partial R_l}{\partial\vec{s}'_{\!i}}W_l \right]\,\vec{d}_i = -\sum_{l\,\in\,i} \frac{\partial R_l}{\partial\vec{s}_i} R_l(\vec{s}_i)W_l . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq401.png) (56)Here
(56)Here 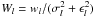 , with σl denoting the given formal standard uncertainty of observation l, expressed as an angle. wl and ϵl are, respectively, the downweighting factor and excess noise introduced in Sect. 3.6. In Eq. (56) the dependence of Rl on a, c and g has been suppressed, since the system is solved with these parameters fixed.
, with σl denoting the given formal standard uncertainty of observation l, expressed as an angle. wl and ϵl are, respectively, the downweighting factor and excess noise introduced in Sect. 3.6. In Eq. (56) the dependence of Rl on a, c and g has been suppressed, since the system is solved with these parameters fixed.
In matrix notation, the normal Eqs. (56) can be written 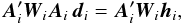 (57)where
(57)where ![\begin{equation} \label{eq:designS} \vec{A}_i=\left[ -\frac{\partial R_l}{\partial\vec{s}'_{\!i}} \right]_{l\in i} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq404.png) (58)is an ni × 5 matrix with ni = ∑ l ∈ i1 the number of observations of source i (typically ni ~ 800),
(58)is an ni × 5 matrix with ni = ∑ l ∈ i1 the number of observations of source i (typically ni ~ 800), ![\begin{equation} \label{eq:designSrhs} \vec{h}_i=\left[ R_l(\vec{s}_i) \right]_{l\in i} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq408.png) (59)is a column matrix of length ni, and Wi is a diagonal matrix containing the weight factors Wl. Although the residuals Rl are in principle non-linear functions of si, this non-linearity can be neglected if the parameters are close enough to the final solution, i.e., if the resulting update di is small enough. The partial derivatives in Ai can then be regarded as fixed throughout the updating process, and Ai and hi can immediately be computed when entering the source updating. The weight matrix Wi, on the other hand, depends on wl and ϵl, which are modified as part of the process as explained below.
(59)is a column matrix of length ni, and Wi is a diagonal matrix containing the weight factors Wl. Although the residuals Rl are in principle non-linear functions of si, this non-linearity can be neglected if the parameters are close enough to the final solution, i.e., if the resulting update di is small enough. The partial derivatives in Ai can then be regarded as fixed throughout the updating process, and Ai and hi can immediately be computed when entering the source updating. The weight matrix Wi, on the other hand, depends on wl and ϵl, which are modified as part of the process as explained below.
For given Wi the system of Eq. (57) is solved using the Cholesky algorithm (Appendix C). At the end of the source updating, the full (5 × 5) inverse matrix is computed, providing a first-order estimate of the covariance of the astrometric parameters in si (see Sect. 6.3).
We note that Eq. (57) corresponds to the overdetermined system of observation equations 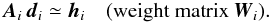 (60)After solution, the updated residuals are contained in the vector Ri = hi − Aidi, and the contribution of the source to the objective function Q is given by
(60)After solution, the updated residuals are contained in the vector Ri = hi − Aidi, and the contribution of the source to the objective function Q is given by 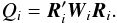 (61)
(61)
5.1.2. The inner iteration: identifying outliers and estimating the excess source noise
Since the weight matrix Wi depends on the downweighting factors wl and the excess noises ϵl, which in turn depend on the updated residuals Ri, the normal Eqs. (57) are non-linear and must be solved by iteration. We refer to this as the inner iteration of the source update, to distinguish it from the AGIS iteration discussed in Sect. 4.5.
Using Eq. (28) we can write 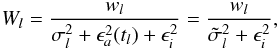 (62)where
(62)where ![\hbox{$\tilde{\sigma}_l=\left[\sigma_l^2+\epsilon_a^2(t_l)\right]^{1/2}$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq418.png) is the formal standard uncertainty of the observation adjusted for the excess attitude noise, which, when entering the source update, is assumed to be known from a previous attitude update (Sect. 5.2.5). In the very first source update the excess attitude noise must be set to the mean errors of the pre-AGIS attitude parameter estimates which are used for starting up the iterations. The downweighting factors depend on the normalized residuals, i.e.,
is the formal standard uncertainty of the observation adjusted for the excess attitude noise, which, when entering the source update, is assumed to be known from a previous attitude update (Sect. 5.2.5). In the very first source update the excess attitude noise must be set to the mean errors of the pre-AGIS attitude parameter estimates which are used for starting up the iterations. The downweighting factors depend on the normalized residuals, i.e., 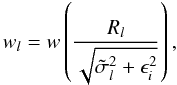 (63)where the function w(z) is such that w(z) = 1 for |z| ≲ 3 and gradually decreasing to 0 for larger |z| (see Eq. (66)).
(63)where the function w(z) is such that w(z) = 1 for |z| ≲ 3 and gradually decreasing to 0 for larger |z| (see Eq. (66)).
The inner iteration actually consists of two nested procedures: an outer one which determines the downweighting factors wl, and an inner one which determines the excess source noise ϵi for a fixed set of wl. We begin by considering the inner procedure.
For fixed downweighting factors, the source update aims to minimize Qi in Eq. (61) with respect to the unknown di and ϵi. But it is immediately seen that Qi can be made arbitrarily small just by making ϵi large enough. Consequently, we cannot use unconstrained minimization to solve this problem. The necessary constraint is provided by the condition that Qi, under the assumption that the excess noises have been correctly estimated and the outliers properly removed, should follow the chi-square distribution with ν = ni − nout − 5 degrees of freedom. Here ni is the number of observations of source i, nout the number of outliers and 5 the number of astrometric parameters estimated. In particular, the expected value is E(Qi) = ν. The number of outliers nout is estimated by counting the number of observations with wl < 0.2. This limit was empirically found to give a reasonable estimate of the actual number of outliers in a variety of simulated cases.
For given ϵi the weight matrix is now known, Eq. (57) can be trivially solved and the residuals Ri computed. We thus define the function 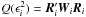 . The excess source variance is then taken to be
. The excess source variance is then taken to be 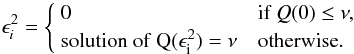 (64)In the second case, the non-linear equation Q(y) = ν is iteratively solved by a series of improvements Δy = (1 − Q(y)/ν)Q(y)/Q′(y), starting from y = 0. Typically, 2–3 iterations are sufficient10.
(64)In the second case, the non-linear equation Q(y) = ν is iteratively solved by a series of improvements Δy = (1 − Q(y)/ν)Q(y)/Q′(y), starting from y = 0. Typically, 2–3 iterations are sufficient10.
This procedure returns a positive ϵi as soon as Q(0) > ν. If the resulting ϵi is much smaller than the typical σl of the source, it is probably not significant. The significance of the ϵi can more easily be judged from an auxiliary statistic that can be computed almost for free. Under the null hypothesis (ϵi = 0) we know that 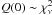 , so the expected value is ν and the variance 2ν. Thus we may take
, so the expected value is ν and the variance 2ν. Thus we may take 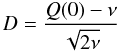 (65)as a measure of the significance of the estimated ϵi, with D > 2 indicating a probably significant value.
(65)as a measure of the significance of the estimated ϵi, with D > 2 indicating a probably significant value.
Having determined ϵi, and a corresponding set of residuals Ri, the downweighting factors can immediately be computed from Eq. (63). However, having changed the downweighting factors (and possibly ν) it is now necessary to repeat the estimation of ϵi and di with the new set wl. Typically, four such iterations are found to be sufficient. The only remaining problem is how to start the iterations, that is the initial selection of the downweights wl. It is not possible to start by assuming wl = 1 for all the observations, since we must take into account that some small fraction of the data could be utterly wrong. Such gross outliers, if not removed already from the start, would severely slow down or even prevent the convergence of the inner iterations. The adopted solution is to make an extremely robust estimation of the standard deviation of the initial residuals (contained in hi), from which the initial downweightings are obtained. This robust standard deviation ςi is calculated as half the intersextile range of the elements in hi, whereupon the initial wl = w(hl/ςi).
After convergence of the inner iteration, the statistical weight of the source Wi is computed according to Eq. (119). This quantity, together with ϵi and the magnitude, are the most important indicators for the selection of primary sources (Sect. 6.2.2).
The weight function w(z) currently used is the following: 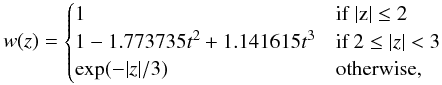 (66)where t = |z| − 2 and the numerical constants have been chosen to make a smooth transition at |z| = 3. The exponential decay for |z| > 3 provides a dramatic weight reduction for large residuals; e.g., at 10 sigmas we have w(10) ≃ 0.036, while at 100 sigmas we have w(100) ≃ 3 × 10-15.
(66)where t = |z| − 2 and the numerical constants have been chosen to make a smooth transition at |z| = 3. The exponential decay for |z| > 3 provides a dramatic weight reduction for large residuals; e.g., at 10 sigmas we have w(10) ≃ 0.036, while at 100 sigmas we have w(100) ≃ 3 × 10-15.
Among the many different weight functions proposed in the literature, the so-called Huber estimator (Huber 1981) using 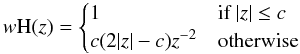 (67)has been considered as an alternative to Eq. (66), e.g., with c = 2. This gives a much slower weight decay for large residuals, e.g., wH(10) = 0.36 and wH(100) = 0.0396. Future experiments may decide which weight function will finally be used for AGIS.
(67)has been considered as an alternative to Eq. (66), e.g., with c = 2. This gives a much slower weight decay for large residuals, e.g., wH(10) = 0.36 and wH(100) = 0.0396. Future experiments may decide which weight function will finally be used for AGIS.
5.1.3. Calculation of partial derivatives
The calculation of the partial derivatives in Eq. (58) is done as follows. From Eqs. (25) and (26) we have, by means of (13), 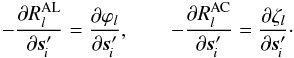 (68)In analogy with Eq. (5) we introduce the auxiliary vectors ml = ⟨ z × ul ⟩ and nl = ul × ml, which together with ul form the normal triad [ ml nl ul ] with respect to the SRS; its components in the SRS are given by the columns of the matrix
(68)In analogy with Eq. (5) we introduce the auxiliary vectors ml = ⟨ z × ul ⟩ and nl = ul × ml, which together with ul form the normal triad [ ml nl ul ] with respect to the SRS; its components in the SRS are given by the columns of the matrix ![\begin{equation} \label{eq:srspqr} \tens{S}'[\vec{m}_l~\vec{n}_l~\vec{u}_l] = \begin{bmatrix} -\sin\varphi_l &~ -\sin\zeta_l\cos\varphi_l &~ \cos\zeta_l\cos\varphi_l \\ \phantom{-}\cos\varphi_l &~ -\sin\zeta_l\sin\varphi_l &~ \cos\zeta_l\sin\varphi_l \\ 0 &~ \cos\zeta_l &~ \sin\zeta_l \end{bmatrix}. \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq458.png) (69)By differentiation of the last column we obtain
(69)By differentiation of the last column we obtain 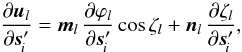 (70)and thus
(70)and thus 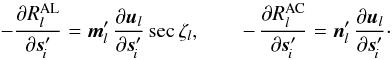 (71)These expressions can be evaluated in any coordinate system, but perhaps most conveniently in the SRS using S′ml and S′nl from Eq. (69), and
(71)These expressions can be evaluated in any coordinate system, but perhaps most conveniently in the SRS using S′ml and S′nl from Eq. (69), and 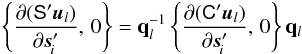 (72)from Eq. (11). To compute the partial derivatives of C′ui, we first obtain from Eq. (4) the derivatives11 of the coordinate direction as:
(72)from Eq. (11). To compute the partial derivatives of C′ui, we first obtain from Eq. (4) the derivatives11 of the coordinate direction as: ![\begin{eqnarray} \label{eq:ubardiff} \frac{\partial\vec{\bar{u}}_l}{\partial\alpha_{*i}} &=& \vec{p}_i, \quad\quad \frac{\partial\vec{\bar{u}}_l}{\partial\delta_{i}} = \vec{q}_i , \quad \frac{\partial\vec{\bar{u}}_l}{\partial\varpi_{i}} = (\vec{I}-\vec{r}_i\vec{r}'_i)\vec{b}{\rm G}(t_l)/A{\rm u}, \nonumber\\[1mm] \frac{\partial\vec{\bar{u}}_l}{\partial\mu_{\alpha *i}} &=& \vec{p}_i\tau_l,\quad \frac{\partial\vec{\bar{u}}_l}{\partial\mu_{\delta i}} = \vec{q}_i\tau_l, \nonumber\\[1mm] \frac{\partial\vec{\bar{u}}_l}{\partial\mu_{r i}} &=& (\vec{I}-\vec{r}_i\vec{r}'_i)\vec{b}{\rm G}(t_l)\varpi_i\tau_l/A{\rm u} - (\vec{p}_i\mu_{\alpha *i}+\vec{q}_i\mu_{\delta i})\tau_l^2, \end{eqnarray}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq465.png) (73)where τl = tBl − tep for brevity, and we have used the normal triad in the celestial reference system, Eq. (5). Although usually only the first five derivatives are needed (see however Sect. 6.3), the last equation gives, for completeness, the derivative with respect to the sixth astrometric parameter μri: the first term corresponds to the secular change in parallax and the second to the perspective acceleration.
(73)where τl = tBl − tep for brevity, and we have used the normal triad in the celestial reference system, Eq. (5). Although usually only the first five derivatives are needed (see however Sect. 6.3), the last equation gives, for completeness, the derivative with respect to the sixth astrometric parameter μri: the first term corresponds to the secular change in parallax and the second to the perspective acceleration.
The rigorous transformation from 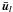 to ul is quite complex, but by far the largest difference (~10-4 rad) is due to stellar aberration. By comparison, gravitational light deflection by the Sun is ~2 × 10-8 rad. While the rigorous transformation is required to compute the vector ul itself, some simplifications can be accepted when computing the partial derivatives. Indeed, for this purpose it is sufficient to consider the classical stellar aberration formula,
to ul is quite complex, but by far the largest difference (~10-4 rad) is due to stellar aberration. By comparison, gravitational light deflection by the Sun is ~2 × 10-8 rad. While the rigorous transformation is required to compute the vector ul itself, some simplifications can be accepted when computing the partial derivatives. Indeed, for this purpose it is sufficient to consider the classical stellar aberration formula, 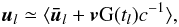 (74)accurate to first order in vG/c, where vG = dbG/dt is the barycentric coordinate velocity of Gaia and c the speed of light. To a relative precision better than 10-6 we then have
(74)accurate to first order in vG/c, where vG = dbG/dt is the barycentric coordinate velocity of Gaia and c the speed of light. To a relative precision better than 10-6 we then have ![\begin{equation} \label{eq:duds} \frac{\partial\vec{u}_l}{\partial\vec{s}'_{\!i}} \simeq \left[\left(1-\frac{\vec{\bar{u}}'_l\vec{v}{\rm G}}{c}\right)\vec{I} -\frac{\vec{\bar{u}}_l\vec{v}{\rm G}'}{c}\right] \frac{\partial\vec{\bar{u}_l}}{\partial\vec{s}'_{\!i}} , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq472.png) (75)where I is the 3 × 3 identity matrix.
(75)where I is the 3 × 3 identity matrix.
5.2. Attitude updating (A)
5.2.1. The normal equations
The attitude model using B-splines to represent the components of the attitude quaternion as functions of time is described in Sect. 3.3. (For reference purposes, conventions for notation and some important properties of splines and B-splines are explained in Appendix B.1.) In the attitude update process (A) the attitude parameters a are improved by solving the second sub-system in Eq. (38). Recalling that a is divided into sub-vectors of length 4, representing the quaternions an in Eq. (10), the nth set of four equations can be written, using Eqs. (29) and (33), ![\begin{equation} \label{eq:normA} \sum_{m=n-M+1}^{n+M-1} \left[ \sum_{l\,\in\, L_n\cap L_m} \frac{\partial R_l}{\partial\quat{a}_n} \frac{\partial R_l}{\partial\quat{a}'_{\!m}}W_l \right]\,\vec{d}_m = -\sum_{l\,\in\, L_n} \frac{\partial R_l}{\partial\quat{a}_n} R_l(\vec{s},\vec{a},\vec{c},\vec{g})W_l . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq475.png) (76)Here Ln stands for the set of observations occurring within the support of Bn(t), i.e., Ln = { l | τn ≤ tl < τn + M } , where M is the order of the spline. On the right-hand side, it is understood that the residuals Rl are calculated for the most recent source parameters s (i.e., from the preceding source updating), while the attitude, calibration and global parameters are the not-yet-updated ones, as explained in Sect. 4.6. The weights Wl are the ones calculated in the source updating.
(76)Here Ln stands for the set of observations occurring within the support of Bn(t), i.e., Ln = { l | τn ≤ tl < τn + M } , where M is the order of the spline. On the right-hand side, it is understood that the residuals Rl are calculated for the most recent source parameters s (i.e., from the preceding source updating), while the attitude, calibration and global parameters are the not-yet-updated ones, as explained in Sect. 4.6. The weights Wl are the ones calculated in the source updating.
The structure of the symmetric matrix Naa is shown in Fig. 5. If each quaternion component is represented by a spline of order M with N degrees of freedom (so n = 0...N − 1), the total number of unknowns is 4N and the average bandwidth of Naa (counting non-zero elements from the diagonal up) is 4(M − 1) + 2.5. Including the right-hand side, the total number of reals that need to be stored for the normal equations is therefore ≃ (16M − 2)N or 62N for cubic splines. With a knot interval of about 15 s, about 3 MB is required to store the attitude normal equations for one day of observations. Thus it is completely realistic to store the attitude normal equations for the entire mission in primary memory. Cholesky factorization of the normal equations does not produce any more non-zero elements in the matrix; the factorization and solution can therefore use the same storage as the normal equations. Moreover, since the number of arithmetic operations grows only linearly with N, it is computationally feasible to solve the normal equations for any stretch of data.
5.2.2. Segmentation of the data
Even though it is feasible to treat the complete set of normal equations for the attitude updating as a single system, it is desirable for several reasons to divide up the data temporally. This allows one to set up a very straightforward and efficient distributed attitude updating, simply by handing out the processing of different time segments to different computing nodes. Also the inspection of residuals in order to detect stretches of bad fit (caused, for example, by micrometeoroid impacts), and the subsequent reprocessing of these stretches, is greatly facilitated if it can be done on shorter data segments.
The spline model is capable of interpolating sensibly (if not accurately) over short data gaps. However, if the data gap contains at least M knots (with M = 4 for cubic splines), the two splines on each side of the gap become completely disconnected. This is illustrated in Fig. 6, where n and m are the left indices of, respectively, the last observation before the gap (tlast) and the first observation after the gap (tfirst). Bn(t) and Bm − M + 1(t) are the last and first B-splines whose coefficients depend on the observations before and after the gap. Clearly the two segments of the attitude spline are disconnected if n < m − M + 1 or m − n ≥ M. We call this a natural attitude break.
 |
Fig. 5 Structure of the attitude normal equations matrix Naa for a cubic spline (order M = 4). The blocks of size 4 × 4 are indexed by (n,m) as in Eq. (33). The grey cells represent non-zero elements. Since the matrix is symmetric, the elements below the diagonal (in lighter grey) need not be stored. |
 |
Fig. 6 A natural break in the definition of the attitude spline occurs if there is a gap in the observations containing at least M knots, where M is the order of the spline. tlast is the time of the last observation before the gap, tfirst the time of the first observation after the gap. |
 |
Fig. 7 Illustrating the assignment of knots for the attitude update solutions in two consecutive segments K and K + 1, with a breakpoint at knot index x and using 2L overlapping knot intervals. |
In the absence of natural breaks, artificial ones can be introduced at suitable intervals by a simple method and without any significant loss of accuracy. The idea is to make separate solutions for overlapping segments, as illustrated in Fig. 7. The segments use a common knot sequence { τk } that may extend over the whole length of the mission. Each segment K defines an attitude spline in the interval [ tbeg(K),tend(K) ] , based on data with observation times in that same interval. The endpoints coincide with certain knots in such a way that tend(K) = τx + L and tbeg(K + 1) = τx − L, where τx is the cross-over knot between segments K and K + 1 and 2L the number of overlapping knot intervals. The anterior and posterior knots for each segment are also taken from the common knot sequence. The local character of the splines means that the resulting fit around τx is practically the same for the two segments, provided L is large enough. For cubic splines (M = 4) it is found that L = 12 is sufficient.
Each segment gives a system of normal Eqs. (76) for the updates dn to the attitude parameters an for a certain range of index n. For example, with reference to Fig. 7, in segment K updates are computed up to and including n = x + L − 1, while in segment K + 1 updates are computed starting with n = x − L − M + 1. At least in the middle part of the overlap region, the updates for a given n should be essentially the same in the two segments. It therefore does not matter much which of the results is chosen. The mid-point is at index n = x − M/2 if M is even, or half-way between x − (M + 1)/2 and x − (M − 1)/2 if M is odd. We may therefore agree to use the solution from segment K to update an up to and including index n = x − ⌊ M/2 ⌋ , while the solution from segment K + 1 is used starting with n = x − ⌊ M/2 ⌋ + 1. The important thing is that no n is missed by the updating, nor updated twice.
Once all the coefficients an have been updated from the different segmented solutions, the segmentation loses its meaning and can in principle be forgotten. For example, when evaluating the attitude at a specific time t, it does not matter to which segment that instant belonged. In the next iteration of the attitude update, a different segmentation can in principle be used.
The overlapping segments mean that a fraction of the observations need to be processed twice in the attitude updating. The fraction equals the ratio of the overlap length to the mean length of the segment, and increases the shorter the segments are made. For example, with a segment length of one day (it would not seem reasonable to have shorter segments) and a mean knot interval of 15 s, the fractional overlap for L = 12 is only 0.4%.
5.2.3. Calculation of partial derivatives
For the partial derivatives we obtain in analogy with Eq. (71) 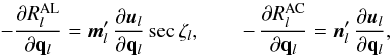 (77)where the derivatives with respect to the attitude quaternion should be interpreted componentwise. Differentiating Eq. (11) and using that d(C′ul) = 0, we have
(77)where the derivatives with respect to the attitude quaternion should be interpreted componentwise. Differentiating Eq. (11) and using that d(C′ul) = 0, we have 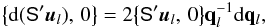 (78)which after some manipulation gives
(78)which after some manipulation gives 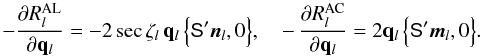 (79)The derivatives with respect to the spline coefficients an are obtained after multiplying the above expressions by Bn(tl), assuming that the normalization factor in Eq. (10) is close to unity (Sect. 5.2.4).
(79)The derivatives with respect to the spline coefficients an are obtained after multiplying the above expressions by Bn(tl), assuming that the normalization factor in Eq. (10) is close to unity (Sect. 5.2.4).
5.2.4. Constraining the attitude updating
Since the attitude is represented by a unit quaternion, its components should at all times satisfy 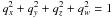 . All four components are nevertheless needed, for while the magnitude of any of them can be inferred from the other three components, its sign cannot. The redundancy of the representation manifests itself in that the length of the quaternion cannot be determined from the observations. Indeed, as can be seen from Eqs. (11), (12), applying an arbitrary non-zero scale factor to the attitude quaternion q has no effect on the computed instrument angles, and is therefore unobservable. The attitude parameters an are therefore also undefined with respect to a certain scale value. As a consequence, the normal matrix Naa computed from Eq. (76) is singular, and constraints are needed for computing a unique solution.
. All four components are nevertheless needed, for while the magnitude of any of them can be inferred from the other three components, its sign cannot. The redundancy of the representation manifests itself in that the length of the quaternion cannot be determined from the observations. Indeed, as can be seen from Eqs. (11), (12), applying an arbitrary non-zero scale factor to the attitude quaternion q has no effect on the computed instrument angles, and is therefore unobservable. The attitude parameters an are therefore also undefined with respect to a certain scale value. As a consequence, the normal matrix Naa computed from Eq. (76) is singular, and constraints are needed for computing a unique solution.
The normalization in Eq. (10) was introduced to guarantee that the calculated quaternion is always of unit length, although, as we have seen, this is not strictly necessary for some of the subsequent calculations12.
Naively, one might expect that the coefficients an could be scaled independently for each B-spline, i.e., that different scale factors could apply to each index n. This is not the case, however. At any time, the (non-normalized) attitude quaternion is a linear combination of M adjacent coefficients an, and unless all four coefficients are scaled by exactly the same factor, the result will not be a simple scaling of the quaternion13. Applying this argument to every observation time tl, it is readily seen that the same scaling factor must be used for all the coefficients in any attitude segment without natural or artificial breaks. In principle, therefore, the attitude normal matrix for such a segment has a rank defect of 1 (that is, the rank is one less than the number of attitude parameters), and would only need a single constraint equation to become non-singular.
Numerical experiments, using Singular Value Decomposition (SVD; see, e.g., Golub & van Loan 1996) of the matrix Naa computed from simulated observations over successively longer time intervals, indeed show the expected rank defect of 1 for intervals up to several hundred knots. That is, there is a clear gap (of several orders of magnitude) between the smallest singular value and the second smallest one. For longer time intervals the gap gradually closes and the problem thus becomes ill-posed (Hansen 1998). Thus, any reasonably long time interval will in practice require some form of regularization rather than the application of just a single constraint.
The adopted solution method is a variant of the well known Tikhonov regularization (Hansen 1998). The objective function in Eq. (27) is modified to include a term depending on the deviation of the normalization factor in Eq. (10) from unity for each observation. We write the deviation as 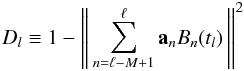 (80)and the modified objective function as
(80)and the modified objective function as 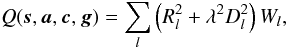 (81)where λ is a small but non-zero regularization parameter. We have found that λ = 10-3 to 10-2 gives a solution that is always numerically stable, and quite insensitive to the precise value of λ. As a result, the normal Eqs. (76) become
(81)where λ is a small but non-zero regularization parameter. We have found that λ = 10-3 to 10-2 gives a solution that is always numerically stable, and quite insensitive to the precise value of λ. As a result, the normal Eqs. (76) become ![\begin{eqnarray} \label{eq:normAmod} \sum_{m=n-M+1}^{n+M-1} \left[ \sum_{l\,\in\, L_n\cap L_m} \left( \frac{\partial R_l}{\partial\quat{a}_n}\frac{\partial R_l}{\partial\quat{a}'_{\!m}} + \lambda^2 \frac{\partial D_l}{\partial\quat{a}_n}\frac{\partial D_l}{\partial\quat{a}'_{\!m}} \right)W_l \right]\,\vec{d}_m = \nonumber\\ -\sum_{l\,\in\, L_n} \left( \frac{\partial R_l}{\partial\quat{a}_n}R_l + \lambda^2 \frac{\partial D_l}{\partial\quat{a}_n}D_l \right)W_l . \end{eqnarray}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq518.png) (82)The required partial derivatives, obtained from Eq. (80), are
(82)The required partial derivatives, obtained from Eq. (80), are 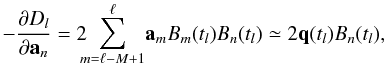 (83)where the approximation makes use of the fact that the normalization factor in Eq. (10) is close to unity.
(83)where the approximation makes use of the fact that the normalization factor in Eq. (10) is close to unity.
5.2.5. Estimating the excess attitude noise
The excess attitude noise ϵa(t) introduced in Eq. (28) accounts for modelling errors in the attitude representation. Such errors could be caused for example by (unmodelled) micrometeoroid impacts, “clanks” due to sudden redistributions of satellite inertia, propellant sloshing, thruster noise, or mechanical vibrations (Appendix D.4). Due to the cubic spline representation, any localized effect that cannot be fitted by the spline will result in systematic residuals that span over a few consecutive knot intervals. Indeed, discontinuities in the rate (e.g., from micrometeoroid impacts) or angle (e.g., from clanks) produce characteristic patterns of residuals that can be used to identify such events. A significant effort will be devoted to the possibly semi-manual and interactive process of finding these events. When identified, they can be handled for example by modifying the knot sequence (Sect. 5.2.6). But even after this process, the model will be imperfect due to for example high-frequency thruster noise14. Similarly, there will be a large number of impacts that are too small to be individually recognized; collectively they add some unmodelled attitude errors, which ϵa(t) may account for. However, it should be noted that ϵa(t) does not include any component of the observation noise (principally from CCD photon noise), nor is it an estimation of the attitude uncertainty (cf. Sect. 6.3).
Three components of the excess noise, designated ϵAL(t), ϵACP(t), and ϵACF(t), need to be derived independently of each other, representing modelling errors in the AL attitude, the AC attitude of the preceding field of view, and the AC attitude in the following field of view. The three components are statistically nearly independent thanks to the way the attitude measurements are made, and the fact that the basic angle is not far from 90°.
The algorithm to estimate ϵa(t) (for a = AL, ACP or ACF) is based on a simple statistical processing of the residuals Rl derived in the source updating. The time line t is divided into “buckets” [ tj, tj + 1) such that each bucket (j) will contain a sufficient number of observations, also in the AC direction. The size (duration) of a bucket should be several knot intervals for the attitude spline, but the boundaries tj need not in any other way be related to the attitude knot sequence. One set of buckets is needed for each attitude component (AL, ACP, ACF). Let l ∈ ja signify that observation l belongs to bucket j and attitude component a. After having completed the source updating for all primary sources, the excess attitude noise in bucket j is estimated as 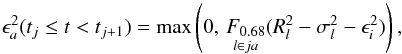 (84)where F0.68() is the 68% quantile (68th percentile) of the argument values. It is important to note that the downweighting factors wl determined during the source updating are not used here to eliminate possible outliers; this function is instead taken care of by using the quantile to compute a robust estimate of the typical excess variance in the attitude bucket. This means that if the “outliers” detected by the source update were actually caused by a stretch of bad attitude, then this will be recognized by a large value of the quantile in Eq. (84), and consequently by an increased
(84)where F0.68() is the 68% quantile (68th percentile) of the argument values. It is important to note that the downweighting factors wl determined during the source updating are not used here to eliminate possible outliers; this function is instead taken care of by using the quantile to compute a robust estimate of the typical excess variance in the attitude bucket. This means that if the “outliers” detected by the source update were actually caused by a stretch of bad attitude, then this will be recognized by a large value of the quantile in Eq. (84), and consequently by an increased 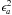 .
.
In the subsequent attitude update, the downweighting factors wl are re-computed based on the residual from the previous source update but with a value for the total variance,  , using the newly estimated
, using the newly estimated 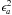 . Thus, only the “true” outliers – that are not due to the bad attitude – are now downweighted. The data may thus contribute to the attitude updating even if they had been flagged as outliers in the preceding source updating.
. Thus, only the “true” outliers – that are not due to the bad attitude – are now downweighted. The data may thus contribute to the attitude updating even if they had been flagged as outliers in the preceding source updating.
The functions ϵa(t) are obviously an extremely useful diagnostic for the progress of the AGIS iterations as well as (after convergence) for the quality of the attitude modelling and data. They can be plotted as a function of time, and the quantity of data is such that human inspection is feasible. They are also needed for setting the detection threshold for micrometeoroid impacts.
The accumulation of statistics in the buckets is best done in parallel with the source updating, when the residuals are readily at hand. One remaining problem is how to compute the quantile in Eq. (84) in an efficient way, without having to store billions of residuals. Indeed, exact calculation of quantiles would require to store all the values 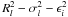 in a bucket before the quantile can be computed. However, if we are content with an approximate estimate of the quantile, there are a number of sequential estimation algorithms available that only need to store a much smaller amount of data per bucket, see for example Greenwald & Khanna (2001), Gilbert et al. (2002) and references therein. We have chosen to use the Incremental Quantile estimation algorithm due to Chambers et al. (2006).
in a bucket before the quantile can be computed. However, if we are content with an approximate estimate of the quantile, there are a number of sequential estimation algorithms available that only need to store a much smaller amount of data per bucket, see for example Greenwald & Khanna (2001), Gilbert et al. (2002) and references therein. We have chosen to use the Incremental Quantile estimation algorithm due to Chambers et al. (2006).
5.2.6. Initialization of the attitude parameters
An approximate estimate of the attitude is already provided by the initial data treatment (IDT) preceding the astrometric solution. This may be given as a discrete time series, for example one quaternion every second of time. The first time the attitude update is executed for a certain time interval, a regular knot sequence is set up and the B-spline coefficients an in Eq. (10) are determined by a least-squares fit. For a given time series of attitude estimates, this is a linear problem and therefore easily solved. The resulting initial attitude a(0) is used in the first source update (S) and subsequently improved by the attitude update process (A) as part of the AGIS iteration scheme.
By default, a regular knot sequence is adopted, i.e., the knot interval Δτ = τn + 1 − τn is taken to be more or less constant. Given the endpoints tbeg, tend of a data segment, the knots are set up at regular intervals respecting a given maximum value of Δτ (of the order of 5 to 20 s). The assignment of knots must also take into account the need for anterior and posterior knots, as discussed in Appendix B, and in the case of segmented data, the overlapping knots as discussed in Sect. 5.2.2.
Occasionally the knot sequence needs to be redefined as a result of the adjustment process. Possible causes could be:
-
If the spline is not flexible enough to accurately model the data, itmay be necessary to decrease the maximum allowed Δτ.
-
Conversely, overfitting of the data may require the maximum allowed Δτ to be increased.
-
Locally, a scarcity of accurate data or a short gap could make it necessary to remove some knots or introduce a natural break in the attitude representation (Sect. 5.2.2).
-
Very locally, a bad fit may result from a micrometeoroid hit causing an almost instantaneous change in the angular velocity of the satellite. This may be dealt with by introducing multiple knots at the appropriate instants (Appendices D.4 and B.3).
Having redefined the knot sequence, it is necessary to re-initialize the spline coefficients an, which must now refer to the new knot sequence. This is most easily done by evaluating q(t) for a regular time series, with a sampling interval much smaller than Δτ (e.g., 1 s), and fitting the new spline to the time series.
5.3. Calibration updating (C)
The geometric instrument model is given in Sect. 3.4. We assume here the generic calibration model in Eqs. (20), (21), in which the parameters are indexed by rs. In the calibration update block (C) the calibration parameters c are improved by solving the third sub-system in Eq. (38), i.e., the normal equations ![\begin{equation} \label{eq:normC} \left[\sum_l \frac{\partial R_l}{\partial\vec{c}} \frac{\partial R_l}{\partial\vec{c}'} W_l \right]\,\vec{d}_c = -\sum_l \frac{\partial R_l}{\partial\vec{c}} R_l(\vec{s},\vec{a},\vec{c},\vec{g}) W_l . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq538.png) (85)The residuals in the right-hand side are computed from the parameter values in the current or preceding iteration according to the discussion in Sect. 4.6. Because the calibration model is linear, the partial derivatives are uniquely determined by the observation index l,
(85)The residuals in the right-hand side are computed from the parameter values in the current or preceding iteration according to the discussion in Sect. 4.6. Because the calibration model is linear, the partial derivatives are uniquely determined by the observation index l, 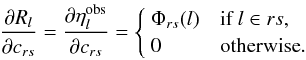 (86)In the normal matrix, the element with subscripts (rs)1 and (rs)2 is non-zero only if there is at least one observation l such that l ∈ (rs)1 and l ∈ (rs)2. Depending on how the calibration parameters are grouped into sets with no common observations (for example according to the CCD/gate combination; cf. Sect. 4.3), the normal matrix will therefore be block-diagonal, which the calibration updating takes advantage of in order to save computations. It also facilitates distributed processing.
(86)In the normal matrix, the element with subscripts (rs)1 and (rs)2 is non-zero only if there is at least one observation l such that l ∈ (rs)1 and l ∈ (rs)2. Depending on how the calibration parameters are grouped into sets with no common observations (for example according to the CCD/gate combination; cf. Sect. 4.3), the normal matrix will therefore be block-diagonal, which the calibration updating takes advantage of in order to save computations. It also facilitates distributed processing.
Since the weights Wl are fixed from the preceding source and attitude updating processes, the update dc can be calculated in a single direct solution, using the robust Cholesky decomposition (Appendix C). However, due to the degeneracy between for example the large-scale and small-scale AL calibration parameters, this will produce an arbitrary feasible solution  , which does not necessarily satisfy the constraints in Eq. (22). The constrained update is obtained as
, which does not necessarily satisfy the constraints in Eq. (22). The constrained update is obtained as 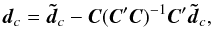 (87)whereupon the updated c can be computed.
(87)whereupon the updated c can be computed.
The above-mentioned degeneracy among the calibration parameters means that the normal matrix calculated according to Eq. (85) is singular, which seems to contradict our assumption (Sect. 4.3) that Ncc is positive-definite. However, if C spans the null space of Ncc, as it should for a properly formulated set of constraints, then it can be seen that Eq. (87) gives the same result as solving the updates with the modified normal matrix Ncc + λ2CC′, which is positive definite for any λ ≠ 0. Thus, the procedure outlined above is equivalent to solving the constrained system with positive-definite matrix.
5.4. Global updating
An arbitrary number of global parameters may be solved for in the AGIS system. Global parameters should be defined in such a way that their default values, equal to zero, correspond to the baseline solution. By not solving for the globals, we implicitly set them to zero, resulting in the baseline solution. For example, we have a very high confidence in General Relativity, which in the parametrized post-Newtonian (PPN) formalism implies the parameter γ = 1. The global parameter related to the gravitational deflection of light should therefore not be γ itself, but for example the parameter g0 in 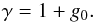 (88)That is, g0 = 0 corresponds to the baseline case of General Relativity. The global parameter vector is g = (g0, g1, ... )′.
(88)That is, g0 = 0 corresponds to the baseline case of General Relativity. The global parameter vector is g = (g0, g1, ... )′.
The normal equations for the update dg to the global parameter vector are ![\begin{equation} \label{eq:normG} \left[ \sum_l \frac{\partial R_l}{\partial\vec{g}} \frac{\partial R_l}{\partial\vec{g}'} W_l \right]\,\vec{d}_g = -\sum_l \frac{\partial R_l}{\partial\vec{g}} R_l(\vec{s},\vec{a},\vec{c},\vec{g})W_l , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq555.png) (89)where the sums are taken over all the observations l, and the statistical weights Wl follow from the preceding source and attitude updates. The partial derivatives in Eq. (89) are computed in exact analogy with Eqs. (71), (72) for the source updating, only with g replacing si. The calculation of ∂ul/∂g′ is not detailed here.
(89)where the sums are taken over all the observations l, and the statistical weights Wl follow from the preceding source and attitude updates. The partial derivatives in Eq. (89) are computed in exact analogy with Eqs. (71), (72) for the source updating, only with g replacing si. The calculation of ∂ul/∂g′ is not detailed here.
In the simple iteration scheme (Sect. 4.5), the inclusion of g0 representing the PPN parameter γ considerably slows down the convergence of the astrometric solution. As explained by Hobbs et al. (2010), this behaviour is caused by the relatively strong correlation between the gravitational light deflection by the Sun (proportional to 1 + γ, and directed away from the Sun) and trigonometric parallax (directed towards the solar-system barycentre, never far from the Sun). Hobbs et al. (2010) found that the convergence rate could be restored by the introduction of a pseudo-parameter g1 representing a global shift of all parallaxes. (The update to this parameter is solved in each iteration but never applied – its value remains at zero and the converged values of all the other parameters are unaffected; hence the prefix “pseudo”.) It was later found that this artefact is not needed when using the conjugate gradients scheme, which gives roughly the same rate of convergence whether or not g1 is included.
6. Auxiliary processes
In this section we describe some auxiliary processes that are not necessarily part of the astrometric solution as such, but nevertheless needed in order to construct the astrometric catalogue. They concern the definition of the reference system for the source positions and proper motions by means of the frame rotator (Sect. 6.1), the selection of primary sources (Sect. 6.2), and the computation of the standard uncertainties and correlations of the astrometric parameters (Sect. 6.3).
6.1. Frame rotator
As explained in Sect. 4.4, the measurement principle of Gaia results in a system of positions and proper motions that is essentially undefined with respect to an arbitrary (small) offset in the orientation and spin of the reference frame. As a consequence, the normal matrix N is in principle singular with a rank defect of 6.
While the solution of rank-deficient problems in general requires special attention to the singularities, for example by adding constraints to avoid numerical instability, no such complication arises here because of the way AGIS works. Basically, a solution is found by iterating between the source and attitude updatings (the calibration and global updatings play no role here because they are to first order independent of the reference frame). When the sources are updated, the reference frame is in reality set by the (then assumed) attitude; similarly, when the attitude is updated, the frame is set by the (then assumed) source parameters. In terms of the matrix formulation of Sect. 4.5 this is equivalent to the statement that the preconditioner K is non-singular. The end result is that AGIS converges to a solution with both the source and attitude parameters expressed in the same, but largely arbitrary, reference frame.
The intention is however that the final source parameters (positions and proper motions) shall be expressed in a celestial reference frame that represents, as closely as possible, the International Celestial Reference System (ICRS). For consistency, it is moreover necessary that the attitude parameters are expressed in exactly the same frame as the source parameters. It is the task of the frame rotator to accomplish this. A similar process was used to align the Hipparcos Catalogue with the extragalactic reference frame (Lindegren & Kovalevsky 1995).
In the following we start with the rigorous definition of the rotation correction, then derive a linear approximation applicable to the small corrections that we have in practice. Finally, we discuss the determination of the rotation parameters and their application in the AGIS iteration scheme.
6.1.1. Relation between the ICRS and AGIS frames
Ideally, the astrometric solution should result in parameters that are expressed in the BCRS (Sect. 3.1), whose axes are aligned with the ICRS here represented by C = [X Y Z]. However, due to the in principle undefined reference frame of AGIS, the astrometric solution is in effect expressed relative to a slightly different triad, which we denote ![\hbox{$\tilde{\tens{C}}=\left[ \vec{\tilde{X}}~\vec{\tilde{Y}}~\vec{\tilde{Z}} \right]$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq560.png) . The two reference systems, which for simplicity will be referred to as the ICRS and AGIS frames, are related by a time-dependent spatial rotation given by the quaternion f(t); thus the coordinates of the arbitrary (fixed) vector v are transformed according to the frame rotation formula
. The two reference systems, which for simplicity will be referred to as the ICRS and AGIS frames, are related by a time-dependent spatial rotation given by the quaternion f(t); thus the coordinates of the arbitrary (fixed) vector v are transformed according to the frame rotation formula 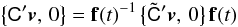 (90)(cf. Eq. (A.15)). Due to the kinematical constraints of the AGIS solution, f(t) describes a uniform spin motion of the two frames with respect to each other.
(90)(cf. Eq. (A.15)). Due to the kinematical constraints of the AGIS solution, f(t) describes a uniform spin motion of the two frames with respect to each other.
For consistency with Lindegren & Kovalevsky (1995) we parametrize f(t) by means of two vectors ε and ω representing corrections to the orientation and spin of the AGIS frame. More precisely, the parameters of the frame rotator are the six coordinates of the vectors in the AGIS frame at some adopted frame rotator epoch tfr (not necessarily the same as the reference epoch tep of the astrometric parameters). These coordinates are denoted  ,
, 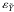 ,
, 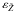 ,
, 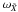 ,
, 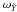 , and
, and 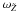 ; according to our kinematical assumption they are strictly constant numbers. For the arbitrary epoch t the frame rotator quaternion is, therefore,
; according to our kinematical assumption they are strictly constant numbers. For the arbitrary epoch t the frame rotator quaternion is, therefore, ![\begin{equation} \label{eq:fr1} \quat{f}(t) = \quat{Q}\big[(t-t{\rm fr})\tilde{\tens{C}}'\vec{\omega}\big] \quat{Q}\big(\tilde{\tens{C}}'\vec{\varepsilon}\big) , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq572.png) (91)where Q is the function introduced by Eq. (A.12). Equations (90) and (91) provide the basis for the rigorous transformation of any data between the two frames, given the rotation parameters
(91)where Q is the function introduced by Eq. (A.12). Equations (90) and (91) provide the basis for the rigorous transformation of any data between the two frames, given the rotation parameters ![\hbox{$\tilde{\tens{C}}'\vec{\varepsilon}=\left[ \varepsilon_{\tilde{X}}~\varepsilon_{\tilde{Y}}~\varepsilon_{\tilde{Z}}\right]'$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq574.png) and
and ![\hbox{$\tilde{\tens{C}}'\vec{\omega}=\left[ \omega_{\tilde{X}}~\omega_{\tilde{Y}}~\omega_{\tilde{Z}}\right]'$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq575.png) .
.
While the above expressions are strictly valid for arbitrarily large rotation parameters, we have in practice ∥ ε ∥ , ∥ (t − tfr)ω ∥ < 20 mas ≃ 10-7 rad, at least in the final iterations of AGIS. This means that second-order terms are completely negligible (<0.002 μas). To first order we have ![\begin{equation} \label{eq:fr2} \quat{f}(t) \simeq \quat{Q}\big[\tilde{\tens{C}}'\vec{\varepsilon} + (t-t{\rm fr})\tilde{\tens{C}}'\vec{\omega}\big] , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq579.png) (92)and the vector part of Eq. (90) becomes, to the same approximation,
(92)and the vector part of Eq. (90) becomes, to the same approximation, 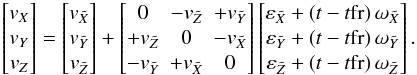 (93)
(93)
6.1.2. Transformation of the astrometric parameters
Let 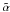 ,
, 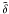 ,
, 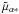 ,
, 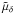 be the position and proper motion parameters for a source as derived in AGIS, that is referring to
be the position and proper motion parameters for a source as derived in AGIS, that is referring to 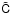 . For brevity we omit here the source index (i), and do not consider the parallax ϖi and radial proper motion μri which are independent of the frame orientation. In analogy with Eq. (5) we have the normal triad
. For brevity we omit here the source index (i), and do not consider the parallax ϖi and radial proper motion μri which are independent of the frame orientation. In analogy with Eq. (5) we have the normal triad ![\hbox{$[\vec{\tilde{p}}~\vec{\tilde{q}}~\vec{r}]$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq587.png) with respect to the AGIS frame, where r is the barycentric direction to the source at time tep,
with respect to the AGIS frame, where r is the barycentric direction to the source at time tep, 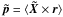 and
and 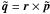 ; its coordinates in the AGIS frame are given by the columns of the matrix
; its coordinates in the AGIS frame are given by the columns of the matrix ![\begin{equation} \label{eq:normal-triad-AGIS} \tilde{\tens{C}}'\left[\vec{\tilde{p}}~~\vec{\tilde{q}}~~\vec{r}\right] = \begin{bmatrix} -\sin\tilde{\alpha} &~ -\sin\tilde{\delta}\cos\tilde{\alpha} &~ \cos\tilde{\delta}\cos\tilde{\alpha}~ \\ \phantom{-}\cos\tilde{\alpha} &~ -\sin\tilde{\delta}\sin\tilde{\alpha} &~ \cos\tilde{\delta}\sin\tilde{\alpha}~ \\ 0 &~ \cos\tilde{\delta} &~ \sin\tilde{\delta}~ \end{bmatrix}. \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq591.png) (94)At the source reference epoch tep the direction cosines of r are related by the frame rotation in Eq. (91); thus
(94)At the source reference epoch tep the direction cosines of r are related by the frame rotation in Eq. (91); thus 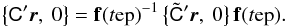 (95)From C′r = [ rx ry rz ] ′ the position parameters in the ICRS frame are obtained as
(95)From C′r = [ rx ry rz ] ′ the position parameters in the ICRS frame are obtained as 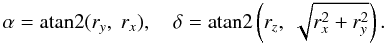 (96)The transformation of the proper motion components is a bit more complicated, as they are expressed with respect to axes that are physically (slightly) different in the two frames, viz.,
(96)The transformation of the proper motion components is a bit more complicated, as they are expressed with respect to axes that are physically (slightly) different in the two frames, viz., 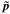 ,
, 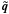 in the AGIS frame, and p, q in the ICRS frame. However, the time derivative (at epoch tep) of the barycentric direction to the source is a fixed vector in space, known as the proper motion vector. In a kinematically non-rotating system it can be written
in the AGIS frame, and p, q in the ICRS frame. However, the time derivative (at epoch tep) of the barycentric direction to the source is a fixed vector in space, known as the proper motion vector. In a kinematically non-rotating system it can be written 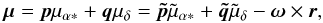 (97)where the last term is the correction for the spin of the AGIS frame. The coordinates of the proper motion vector in the two frames,
(97)where the last term is the correction for the spin of the AGIS frame. The coordinates of the proper motion vector in the two frames, 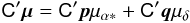 (98)and
(98)and 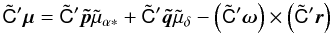 (99)are related by a frame rotation analogous to Eq. (95),
(99)are related by a frame rotation analogous to Eq. (95), 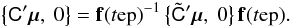 (100)From Eq. (97) the proper motion components in the ICRS frame are then
(100)From Eq. (97) the proper motion components in the ICRS frame are then 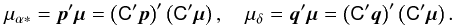 (101)For given
(101)For given  and
and  , the sequence of calculations is therefore:
, the sequence of calculations is therefore:
-
1.
calculate f(tep) by Eq. (91);
-
2.
calculate
![\hbox{$\tilde{\tens{C}}'[\vec{\tilde{p}}~\vec{\tilde{q}}~\vec{r}]$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq607.png) by Eq. (94);
by Eq. (94); - 3.
- 4.
-
5.
calculate μα ∗ and μδ by Eq. (101).
As we have not employed the approximations in Eqs. (92), (93), these transformations are rigorous.
6.1.3. Transformation of the attitude parameters
In analogy with Eq. (9) the attitude quaternion 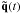 derived in AGIS defines the transformation from the AGIS frame
derived in AGIS defines the transformation from the AGIS frame 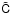 to the SRS S as a function of time; thus for the arbitrary vector v
to the SRS S as a function of time; thus for the arbitrary vector v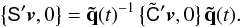 (102)Solving
(102)Solving 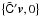 and inserting into Eq. (90) yields
and inserting into Eq. (90) yields 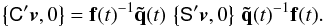 (103)Comparison with Eq. (9) shows that the corrected attitude is given by
(103)Comparison with Eq. (9) shows that the corrected attitude is given by 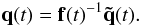 (104)In practice the AGIS attitude
(104)In practice the AGIS attitude 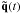 is expressed in terms of B-splines by means of coefficients
is expressed in terms of B-splines by means of coefficients 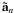 as in Eq. (10). The result of the time-dependent transformation by f(t)-1 in Eq. (104) cannot, in general, be exactly represented by means of B-splines. However, since the transformation is changing extremely slowly in comparison with the duration of the support of each B-spline (~1 min), and also the changes of a from knot to knot are very small, we make a negligible error by transforming the coefficients instead of the attitude quaternion. Thus we use
as in Eq. (10). The result of the time-dependent transformation by f(t)-1 in Eq. (104) cannot, in general, be exactly represented by means of B-splines. However, since the transformation is changing extremely slowly in comparison with the duration of the support of each B-spline (~1 min), and also the changes of a from knot to knot are very small, we make a negligible error by transforming the coefficients instead of the attitude quaternion. Thus we use 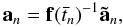 (105)where
(105)where 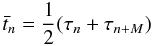 (106)is the time half-way through the support of Bn(t).
(106)is the time half-way through the support of Bn(t).
6.1.4. Determination of the frame rotator parameters
The parameters ![\hbox{$\tilde{\tens{C}}'\vec{\varepsilon}=\left[ \varepsilon_{\tilde{X}},~\varepsilon_{\tilde{Y}},~\varepsilon_{\tilde{Z}}\right]'$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq624.png) and
and ![\hbox{$\tilde{\tens{C}}'\vec{\omega}=\left[ \omega_{\tilde{X}},~\omega_{\tilde{Y}},~\omega_{\tilde{Z}}\right]'$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq625.png) are determined by a weighted least-squares solution, using as input the differences in positions and proper motions, for a subset of the sources, between the AGIS results and a priori data. Three kinds of sources may be used for this purpose:
are determined by a weighted least-squares solution, using as input the differences in positions and proper motions, for a subset of the sources, between the AGIS results and a priori data. Three kinds of sources may be used for this purpose:
-
A subset SNR of the primary sources can be assumed to define akinematically non-rotating celestial frame. Typically this subsetwill contain some 105 to 106 quasars and point-likegalactic nuclei, mainly identified from ground-based surveysand photometric criteria. This subset effectively determines ω.
-
A subset SP of SNR in addition have positions
 accurately determined with respect to the ICRS by means that are completely independent of Gaia. Typically it will contain the optical counterparts of extragalactic objects with accurate positions from radio interferometry (VLBI). Due to the cosmological acceleration effect described below it is necessary to assign an epoch tP to each such position. This subset effectively determines ε.
accurately determined with respect to the ICRS by means that are completely independent of Gaia. Typically it will contain the optical counterparts of extragalactic objects with accurate positions from radio interferometry (VLBI). Due to the cosmological acceleration effect described below it is necessary to assign an epoch tP to each such position. This subset effectively determines ε. -
The third subset SPM consists of primary sources that do not a priori belong to the non-rotating subset, but have positions and/or proper motions that are accurately determined with respect to the ICRS independent of Gaia. This could include radio stars observed by VLBI, or stars whose absolute proper motions have been determined by some other means. The astrometric parameters of a source in this subset are denoted
 ,
, 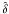 ,
, 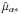 ,
, 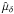 and refer to the epoch tPM (the parallax is irrelevant here, as it is identical in both frames). It is not expected that this subset will contribute very significantly to the determination of ε and/or ω, but they are included in the discussion below since they may provide important consistency checks.
and refer to the epoch tPM (the parallax is irrelevant here, as it is identical in both frames). It is not expected that this subset will contribute very significantly to the determination of ε and/or ω, but they are included in the discussion below since they may provide important consistency checks.
In the following we derive the appropriate observation equations for the different kinds of sources. The derivation assumes that the frame rotator parameters are numerically small so that the linear approximation in Eq. (93) applies. For the (weighted) least-squares estimation of the frame rotator parameters it is, furthermore, necessary to assign the appropriate statistical weights to the observations and to have procedures for identifying and handling outliers. These issues are however not discussed here.
In the frame rotator solution, the six parameters must be complemented by three more parameters aX, aY, aZ taking into account the acceleration of the solar-system barycentre in a cosmological frame (Bastian 1995; Gwinn et al. 1997; Kopeikin & Makarov 2006). Such an acceleration, by the vector α, will cause a systematic “streaming” (dipole) pattern of the apparent proper motions of extragalactic objects, described by 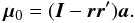 (107)Here r is the direction to the source and a = α/c to first order in c-1, where c is the speed of light. The galactocentric acceleration of the solar-system barycentre by ∥α∥ ≃ 2 × 10-10 m s-2 is expected to produce a proper motion pattern with an amplitude of ∥a∥ ≃ 4 μas yr-1, which Gaia should be able to detect given a sufficient number of quasars among the primary sources15. The additional parameters introduced in the frame rotator solution are the components of a in the ICRS, or [aX aY aZ] = C′a; they may be expressed in the same unit as the proper motions.
(107)Here r is the direction to the source and a = α/c to first order in c-1, where c is the speed of light. The galactocentric acceleration of the solar-system barycentre by ∥α∥ ≃ 2 × 10-10 m s-2 is expected to produce a proper motion pattern with an amplitude of ∥a∥ ≃ 4 μas yr-1, which Gaia should be able to detect given a sufficient number of quasars among the primary sources15. The additional parameters introduced in the frame rotator solution are the components of a in the ICRS, or [aX aY aZ] = C′a; they may be expressed in the same unit as the proper motions.
Observation equations for a source in SNR.
A kinematically non-rotating source should only have an apparent proper motion due to the cosmological acceleration. Equating μ in (97) with μ0 from Eq. (107) and taking the scalar products with 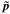 and
and 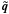 results in the two observation equations
results in the two observation equations ![\begin{equation} \label{eq:cond-mu1} \left. \begin{aligned} \vec{\tilde{p}}'\vec{a} + \vec{\tilde{q}}'\vec{\omega} &= \tilde{\mu}_{\alpha*} \\[3pt] \vec{\tilde{q}}'\vec{a} - \vec{\tilde{p}}'\vec{\omega} &= \tilde{\mu}_{\delta} \end{aligned} \quad\right\} , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq650.png) (108)where we have used the scalar triple product rule16 for the terms including ω. These equations are linear in the unknown acceleration and spin parameters, and the coefficients are the known coordinates of
(108)where we have used the scalar triple product rule16 for the terms including ω. These equations are linear in the unknown acceleration and spin parameters, and the coefficients are the known coordinates of  and
and  in either
in either  or C (to the adopted approximation the coefficients are the same in the two frames).
or C (to the adopted approximation the coefficients are the same in the two frames).
Observation equations for a source in SP.
In order to compare positions it is necessary to choose an epoch at which to make the comparison. At the chosen epoch of comparison, t, the barycentric coordinate direction of the source is, to first order in the proper motion, ![\begin{eqnarray} \label{eq:fr-ubar} \vec{\bar{u}}{\rm B}(t) &=& \vec{r}(t{\rm P})+(t-t{\rm P})\vec{\mu}_0 \nonumber \\[3pt] &=&\vec{r}(t{\rm ep})+(t-t{\rm ep}) \left(\vec{\tilde{p}}\tilde{\mu}_{\alpha*} + \vec{\tilde{q}}\tilde{\mu}_\delta - \vec{\omega}\times\vec{r}\right) . \end{eqnarray}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq652.png) (109)In the first equality we have made the assumption that the source has the apparent proper motion μ0 when observed in the ICRS frame; the second uses the same proper motion vector derived from the AGIS data according to Eq. (97). If we now compute the coordinates of
(109)In the first equality we have made the assumption that the source has the apparent proper motion μ0 when observed in the ICRS frame; the second uses the same proper motion vector derived from the AGIS data according to Eq. (97). If we now compute the coordinates of  in C (using the first equality) and
in C (using the first equality) and  (using the second equality), they must be related according to Eq. (93). Resolving the coordinate differences along α and δ we obtain the observation equations
(using the second equality), they must be related according to Eq. (93). Resolving the coordinate differences along α and δ we obtain the observation equations ![\begin{equation} \label{eq:cond-Delta} \left. \begin{aligned} (t-t{\rm P})\vec{\tilde{p}}'\vec{a}+ \vec{\tilde{q}}'\big(\vec{\varepsilon}+(t-t{\rm fr})\vec{\omega}\big) &= \Delta\alpha^* \\[3pt] (t-t{\rm P})\vec{\tilde{q}}'\vec{a}- \vec{\tilde{p}}'\big(\vec{\varepsilon}+(t-t{\rm fr})\vec{\omega}\big) &= \Delta\delta \end{aligned} \quad\right\} , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq654.png) (110)where
(110)where 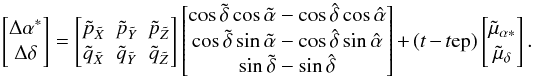 (111)The observation equations in proper motion are of course the same as in Eq. (108).
(111)The observation equations in proper motion are of course the same as in Eq. (108).
Returning to the choice of comparison epoch t, it is clear that the result in terms of the estimated frame rotator parameters should in principle not depend on this choice. However, that will only be the case if the statistical correlations among the data are taken into account in the least-squares estimation. Otherwise one should choose t to minimize these correlations. From Eq. (111) it is seen that the right-hand sides of Eq. (108) and (110) are uncorrelated if t = tep, provided that the position and proper motion errors in AGIS are also uncorrelated (which is generally the case if tep is appropriately chosen, i.e., close to mid-mission). Consequently we suggest using t = tep.
Observation equations for a source in SPM.
Here it will be necessary to distinguish two cases depending on how the proper motions have been measured. If 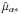 ,
, 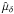 are the proper motion components of a source measured relative to background quasars, then the observation equations are simply
are the proper motion components of a source measured relative to background quasars, then the observation equations are simply ![\begin{equation} \label{eq:cond-mu2} \left. \begin{aligned} \vec{\tilde{p}}'\vec{a} + \vec{\tilde{q}}'\vec{\omega} &= \tilde{\mu}_{\alpha*} - \hat{\mu}_{\alpha*}\\[3pt] \vec{\tilde{q}}'\vec{a} - \vec{\tilde{p}}'\vec{\omega} &= \tilde{\mu}_{\delta} -\hat{\mu}_{\delta} \end{aligned} \quad\right\} . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq658.png) (112)As expected, the equations simplify to Eq. (108) in case the measured proper motion is zero. The observation equations obtained from the comparison of positions are the same as in Eq. (110), but with right-hand side
(112)As expected, the equations simplify to Eq. (108) in case the measured proper motion is zero. The observation equations obtained from the comparison of positions are the same as in Eq. (110), but with right-hand side 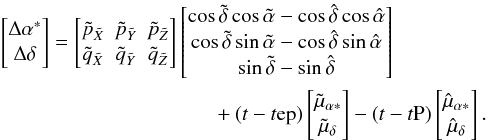 (113)If, on the other hand, the proper motion is not measured relative to the local extragalactic background, but in a global non-rotating frame, then it already includes a contribution from μ0 and the appropriate observation equations are obtained by deleting the terms depending on a:
(113)If, on the other hand, the proper motion is not measured relative to the local extragalactic background, but in a global non-rotating frame, then it already includes a contribution from μ0 and the appropriate observation equations are obtained by deleting the terms depending on a: ![\begin{equation} \label{eq:cond-mu3} \left. \begin{aligned} \vec{\tilde{q}}'\vec{\omega} &= \tilde{\mu}_{\alpha*}-\hat{\mu}_{\alpha*}\\[3pt] -\vec{\tilde{p}}'\vec{\omega} &= \tilde{\mu}_{\delta}-\hat{\mu}_{\delta}\\[3pt] \vec{\tilde{q}}'\big(\vec{\varepsilon}+(t-t{\rm fr})\vec{\omega}\big) &= \Delta\alpha^* \\[3pt] -\vec{\tilde{p}}'\big(\vec{\varepsilon}+(t-t{\rm fr})\vec{\omega}\big) &= \Delta\delta \end{aligned} \quad\right\} . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq660.png) (114)
(114)
6.1.5. The null space vectors
In Sect. 4.4 we introduced the n × 6 matrix V whose columns span the null space of the normal matrix N. For completeness we give here the explicit expressions for one such set of null vectors. Any small change in the unknowns x, by a linear combination of the columns in V, will leave the calculated residuals unchanged. Applying the frame rotator for arbitrary ε and ω obviously leaves the residuals unchanged, and we can therefore compute the columns of V as the partial derivatives of x with respect to the six frame rotator parameters. Since we are concerned with infinitesimal changes, the distinction between the AGIS and ICRS frames is no longer necessary. If V is partitioned similarly to x and b in Eq. (31), or ![\hbox{$\vec{V}=\big[\vec{V}'_s,\,\vec{V}'_a,\,\vec{V}'_c,\,\vec{V}'_g\big]'$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq661.png) , we find by means of Eq. (114),
, we find by means of Eq. (114), ![\begin{equation} \left[\vec{V}_s\right]_i = \begin{bmatrix} \phantom{-}q_X & \phantom{-}q_Y & \phantom{-}q_Z & \phantom{-}\tau q_X & \phantom{-}\tau q_Y & \phantom{-}\tau q_Z \\ -p_X & -p_Y & -p_Z & -\tau p_X & -\tau p_Y & -\tau p_Z \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \phantom{-}q_X & \phantom{-}q_Y & \phantom{-}q_Z \\ 0 & 0 & 0 & -p_X & -p_Y & -p_Z \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq662.png) (115)where τ = tep − tfr and we have omitted the source index i on the matrix elements. The order of the astrometric parameters is (α ∗ , δ, ϖ, μα ∗ , μδ). From Eqs. (92) and (105) we similarly obtain for the attitude parameters an = {ax, ay, az, aw},
(115)where τ = tep − tfr and we have omitted the source index i on the matrix elements. The order of the astrometric parameters is (α ∗ , δ, ϖ, μα ∗ , μδ). From Eqs. (92) and (105) we similarly obtain for the attitude parameters an = {ax, ay, az, aw}, ![\begin{equation} \left[\vec{V}_a\right]_n = \frac{1}{2} \begin{bmatrix} -a_w & -a_z & \phantom{-}a_y & -\tau_n a_w & -\tau_n a_z & \phantom{-}\tau_n a_y \\ \phantom{-}a_z & -a_w & -a_x & \phantom{-}\tau_n a_z & -\tau_n a_w & -\tau_n a_x \\ -a_y & \phantom{-}a_x & -a_w & -\tau_n a_y & \phantom{-}\tau_n a_x & -\tau_n a_w \\ \phantom{-}a_x & \phantom{-}a_y & \phantom{-}a_z & \phantom{-}\tau_n a_x & \phantom{-}\tau_n a_y & \phantom{-}\tau_n a_z \\ \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq666.png) (116)where
(116)where 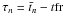 . The calibration and global parameters are not affected by the frame rotator, so Vc = 0 and Vg = 0.
. The calibration and global parameters are not affected by the frame rotator, so Vc = 0 and Vg = 0.
Let 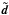 be a vector of small changes to the unknowns x, as for example the update computed in one of the AGIS iterations. In some situations it is desirable to remove from
be a vector of small changes to the unknowns x, as for example the update computed in one of the AGIS iterations. In some situations it is desirable to remove from 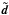 its component in the null space, i.e., to project it on the row space of N. This will for example ensure that the orientation and spin of the AGIS frame is not, on the average, changed by the update. In principle, we could achieve this by a process analogous to Eq. (87):
its component in the null space, i.e., to project it on the row space of N. This will for example ensure that the orientation and spin of the AGIS frame is not, on the average, changed by the update. In principle, we could achieve this by a process analogous to Eq. (87): 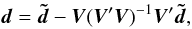 (117)where d is the projection of the update on the row space of N. This is equivalent to solving the unweighted least-squares problem
(117)where d is the projection of the update on the row space of N. This is equivalent to solving the unweighted least-squares problem 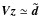 , yielding the orientation and spin components as
, yielding the orientation and spin components as 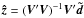 , followed by the subtraction of the null space component Vẑ. In practice, this can equivalently be achieved by means of the frame rotator, without the need to compute V explicitly.
, followed by the subtraction of the null space component Vẑ. In practice, this can equivalently be achieved by means of the frame rotator, without the need to compute V explicitly.
6.1.6. Role of the frame rotator in AGIS
The frame rotator process consists of the three steps: (i) determine the frame rotator parameters according to Sect. 6.1.4; (ii) correct the astrometric parameters for all sources according to Sect. 6.1.2; (iii) correct the attitude parameters according to Sect. 6.1.3. In principle, this process only needs to be run after convergence of the AGIS iterations; nevertheless, there may be a case for running it after each AGIS iteration, preventing a progressive deviation from the ICRS in the course of the iterations.
In particular, for the simulation experiments described in Sect. 7 it was found necessary to run the frame rotator after each iteration, in order to be able to compare the results of each iteration with the “true” astrometric parameters (used as input to the simulations). Without this correction, the differences between the “estimated” and “true” parameters for the source positions and proper motions would have been grossly distorted by frame errors originating from the starting values of the attitude parameters. In this case all the primary sources were treated as belonging to the subset SPM, for which Eq. (114) is appropriate.
6.2. Selection of primary sources
The astrometric core solution does not use all the sources observed by Gaia, but only a subset of them known as the primary sources. The selection of this subset is made iteratively, based on the results of earlier astrometric solutions and other processes such as double-star and variability analysis (not discussed in this paper). The main criterion for a primary source is that its proper direction, at all times when it is observed by Gaia, is adequately modelled by the standard astrometric model outlined in Sect. 3.2. Examples of sources that should be excluded based on this criterion are solar-system objects, short-period astrometric binaries with a significant size of the photocentre orbit, long-period astrometric binaries with a significant curvature of the photocentre orbit, certain unresolved binaries where one or both of the components are variable, and active galactic nuclei (AGNs) with significant variation of their photocentre positions. Variable stars, long-period resolved binaries, eclipsing and spectroscopic binaries need not be excluded a priori from the set of primary sources, although many of them are potentially problematic from an astrometric modelling viewpoint (e.g., a variable star might be part of an unresolved double or multiple star, resulting in a variable photocentre position). On the other hand, partially resolved double/multiple stars and other extended sources will be problematic even if their photocentres strictly adhere to the basic astrometric model, Eq. (3), because technically the determination of the photocentre becomes more difficult and less precise.
For the calibrations there are other requirements on the primary sources, in particular that there are enough of them at various magnitudes and colours, while their sky distribution is less important. Securing a sufficient number of primary sources for the calibrations will tend to include many more primary sources in some areas, such as the galactic plane, resulting in a very non-uniform distribution across the celestial sphere.
6.2.1. The number of sources needed for AGIS
The number of sources required for the Astrometric Global Iterative Solution is driven by the calibration needs of having representative numbers of sources of different magnitudes, and the attitude needs of having a sufficient number of sources in every knot interval.
Let us consider first the requirements for the geometric small-scale calibration of the CCDs (Sect. 3.4). The angular extent of a single CCD in the across-scan direction is about 0.1°. It scans the celestial sphere at a rate of 1° min-1 and therefore covers about 2000 deg2 per week, if both fields of view are counted. Since there are 1966 pixel columns across the CCD, we have the convenient rule of thumb that each pixel column covers 1 deg2 per week. Thus, if the average density of suitable primary sources is D deg-2 and we require a minimum of N observations of such sources per pixel column for its calibration, then the minimum time needed is N/D weeks. For example, with 108 primary sources we have D = 2400 deg-2, and it is then reasonable that the small-scale calibration can be made, at a resolution of one or a few pixels, in a matter of weeks. However, for the gated observations of bright sources (G ≲ 12 mag), the available numbers are much smaller and it will be necessary to sacrifice resolution in time, number of pixels, or both in order to have a sufficient number of observations per calibration cell. For example, the gate used for the brightest sources will perhaps mainly be used for G ≃ 5.7 to 8.8; the total number of such stars is about 130 000 (from the Tycho-2 Catalogue; Høg et al. 2000) or D ≃ 3 deg-2, of which only a fraction will be suitable as primary sources. Thus, even over the whole five-year mission there will only be a few hundred observations per pixel column. From these considerations it is clear that as many as possible of the bright stars should be selected as primary sources.
Consider next the requirements for the attitude determination. The minimum reasonable knot interval is of the same order as the transit time over a CCD, or about 5 s. Since we require both along-scan and across-scan measurements, and the latter are normally only provided by the SM and some of the AF1 observations, we assume conservatively one observation in each coordinate per field-of-view transit. There are seven CCDs across the width of the field of view; the area scanned is therefore 1000 deg2 per day in each field of view, or 0.06 deg2 per 5 s interval. If we require, say, 100 transits per knot interval for a reliable attitude determination, then the minimum density of primary sources is D = 1700 deg-2, or some 70 million sources in total. To achieve this density in the galactic pole regions requires that stars as faint as G ≃ 19 are included among the primary sources. Thus it is clear that the design aim of ≃ 108 primary sources is quite reasonable, and that these will have to include both very bright and very faint stars, as well as many quasars down to G = 20 for the extragalactic link.
Apart from these minimum requirements, it must be maintained that the quality of the solution will only improve, the more (good) primary sources are included. Stated in the negative sense, the solution quality cannot improve by removing good-quality primary sources. From this viewpoint one should aim to include as many primary sources as possible in the final solution.
On the other hand, one should not forget that it is possible to run AGIS with much fewer primary sources by disabling short-term small-scale calibrations and using longer knot intervals for the attitude. This will increase modelling errors, which however is acceptable for initial runs where the input data have not yet been properly calibrated.
6.2.2. Selection criteria
As outlined above a source has to pass several tests, derived from different processes, in order to qualify as a primary source. The most important test is derived from the AGIS solution itself, and is based on how well the standard astrometric model (Sect. 3.2) fits the data. However, if initially we want to limit the number of primary sources, a somewhat more sophisticated selection procedure is needed to guarantee the minimum requirements.
Each source carries an attribute representing the “relegation factor” U, which is a floating-point number ranging from about 1 to infinity. U ≃ 1 implies the source is perfect for use in the astrometric solution, while successively larger values indicate less suitable sources. The relegation factor may incorporate the results of several different tests, and therefore provides a continuous variable for use in the selection process. The name derives from the need to “relegate” a primary source into a secondary one when U exceeds a predefined value, which may happen for example in the course of the AGIS iterations, or from one solution to the next. On the other hand, a secondary source may be promoted to a primary if its U value decreases below the set threshold. This suggests that all potential primary sources should be processed through the source update (Sect. 5.1), after which its status as primary/secondary may be decided.
The excess source noise ϵi estimated during the source updating (Sect. 5.1.2) may be a good starting point for calculating the relegation factor, e.g.: ![\begin{equation} \label{eq:relegFac} U_i = \sqrt{1 + \left[\epsilon_i / e(G_i)\right]^2}, \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq689.png) (118)where e(G) is a normalization factor depending on the magnitude. The choice of the function e(G) determines the balance between absolute and relative contributions to the modelling error budget. With the choice
(118)where e(G) is a normalization factor depending on the magnitude. The choice of the function e(G) determines the balance between absolute and relative contributions to the modelling error budget. With the choice 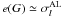 (the formal along-scan observational standard uncertainty for a source of magnitude G), Ui approximates the rms normalized residual of the source. Selecting sources based on this Ui tends to discriminate against bright stars where modelling errors may dominate over photon-noise errors. On the other hand, choosing e(G) = const. means that only sources with the smallest ϵi are accepted; this may remove too many of the faint sources, where ϵi is still small in comparison with
(the formal along-scan observational standard uncertainty for a source of magnitude G), Ui approximates the rms normalized residual of the source. Selecting sources based on this Ui tends to discriminate against bright stars where modelling errors may dominate over photon-noise errors. On the other hand, choosing e(G) = const. means that only sources with the smallest ϵi are accepted; this may remove too many of the faint sources, where ϵi is still small in comparison with 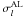 . A reasonable compromise between these two extreme cases should be found. The value from Eq. (118) can later be combined with other factors indicating for example photometric variability, or some other potentially problematic property, so that in general the relegation factor can be determined with some formula using a combination of the source attributes.
. A reasonable compromise between these two extreme cases should be found. The value from Eq. (118) can later be combined with other factors indicating for example photometric variability, or some other potentially problematic property, so that in general the relegation factor can be determined with some formula using a combination of the source attributes.
Apart from the relegation factor, which indicates whether a source is at all suitable as a primary source, the general principle should be to maximize the total weight of the primary sources. The weight of a source i is defined as 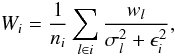 (119)where the average is taken over the ni = ∑ l ∈ i1 accepted AL observations of the source. Note that we do not use the more obvious definition Wi = ∑ l ∈ iWl with Wl from Eq. (62), since we do not want to penalize a source by the excess attitude noise in some of its observations, nor favour a source because it is observed many times due to the scanning law.
(119)where the average is taken over the ni = ∑ l ∈ i1 accepted AL observations of the source. Note that we do not use the more obvious definition Wi = ∑ l ∈ iWl with Wl from Eq. (62), since we do not want to penalize a source by the excess attitude noise in some of its observations, nor favour a source because it is observed many times due to the scanning law.
Having defined the relegation factor and weight per source, the selection of primary sources can be made to maximize the total weight with due regard to sky uniformity (for attitude determination) and magnitude distribution (for instrument calibration). A possible procedure is the following.
We start by specifying the minimum density Dmin (deg-2) required for the attitude determination, the targeted total number Ntot of primary sources, with Ntot ≥ (129 600/π)Dmin, and the maximum acceptable relegation factor Umax. For the geometric calibration of gated observations we may also specify minimum numbers { Ng } for several intervals in G. Then:
-
1.
Using a coarse-grained tessellation of the celestial sphere (seebelow), select in each pixel the Np sources with the largest Wi that satisfy Ui ≤ Umax, where Np is the minimum number per pixel that will ensure Dmin.
-
2.
For each magnitude bin with a required minimum number Ng, count the actual number of primary sources already selected; if it is less than Ng add sources with Ui ≤ Umax based on Wi.
-
3.
If the total number after Step 1 and 2 is less than Ntot, add sources with Ui ≤ Umax based on Wi. If the total number exceeds Ntot, reduce Umax and repeat the process.
If the required number cannot be reached in a particular pixel or magnitude bin, then it is necessary to increase Umax locally for that pixel or bin.
For the tessellation in Step 1 in principle any reasonable way to divide up the sphere into cells of approximately the same area could be used, but for statistical operations the HEALPix scheme (Górski et al. 2005) has some advantages (O’Mullane et al. 2001). The cell size is determined by the choice of HEALPix parameter NSIDE and is important as it predicts the level of homogeneity over the sphere. A cell area of about 1/3 of the field of view might be close to optimal, and is achieved with NSIDE = 128 yielding 196 608 cells.
For the first run with real data some selection must be made using the initial star catalogue. In this case the relegation factor may be set to 1 for all sources and the selection based entirely on their spatial distribution and magnitudes. This will reduce the input to the first run of the astrometric solution, after which the relegation factor will be updated as described above. The secondary-source update step runs on all sources not included in AGIS; hence this will set a relegation factor for all sources observed by Gaia.
6.3. Computation of standard uncertainties and correlations
It is mandatory that the catalogue of astrometric parameters resulting from the astrometric core solution includes complete and reliable information about the expected error statistics. The most important quantity is the estimated standard uncertainty of each astrometric parameter. However, the statistical correlation between the different astrometric parameters – both between the different parameters of the same source and between the parameters of different sources – is also important and should be quantified. Such correlations are produced both by attitude modelling errors (Sect. 5.2.5) and the statistical uncertainty due to the finite astrometric weight of the sources contributing to the attitude determination. More generally, we need a method to estimate the 5 × 5 covariance matrix Cov(si,sj) of the astrometric parameters of any two sources i, j (including the case i = j). In principle, these are sub-matrices of the upper-left ns × ns part of , the pseudo-inverse of the complete normal equations matrix in Eq. (30). (The pseudo-inverse should be used since the matrix is singular.) Although there are methods to compute selected elements in that may be feasible even for a system as large as this, it is utterly impossible to produce any significant fraction of the covariances by a direct computation. Instead, it will be necessary to rely on approximations and statistical estimates. A first approximation is obtained by ignoring the statistical uncertainty contributed by the errors of the attitude, calibration and global parameters; in this case we can ignore all parts of N in Eq. (31) except Nss and find ![\begin{equation}\label{eq:cov}\text{Cov}(\vec{s}_i,\vec{s}_j) \equiv \left[\big(\vec{N}^\dagger\big)_{ss}\right]_{ij}\simeq\left\{\begin{array}{ll}~\left[\vec{N}_{ss}\right]_{ii}^{-1} & \text{if }i=j,\\[3pt] ~\vec{0} & \text{if }i\ne j,\end{array}\right.\end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq712.png) where the inverse of
where the inverse of ![\hbox{$\left[\vec{N}_{ss}\right]_{ii}=\vec{A}_i' \vec{W}_i \vec{A}_i$}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq713.png) is regularly computed as part of the source updating using Eq. (57). However, in this approximation we clearly cannot estimate the covariance between sources (i ≠ j), which is unacceptable; moreover, we underestimate the within-source covariance (i = j) because of the neglected attitude and calibration errors. Refining this estimate is a very important problem which however is addressed elsewhere (Holl et al. 2010; Holl et al., in prep.).
is regularly computed as part of the source updating using Eq. (57). However, in this approximation we clearly cannot estimate the covariance between sources (i ≠ j), which is unacceptable; moreover, we underestimate the within-source covariance (i = j) because of the neglected attitude and calibration errors. Refining this estimate is a very important problem which however is addressed elsewhere (Holl et al. 2010; Holl et al., in prep.).
A somewhat related problem is the need to be able to transform the astrometric results, without loss of information, to an arbitrary epoch different from the tep used in the astrometric solution. The standard model in Eq. (4) allows the astrometric parameters to be transformed in a completely reversible manner, based on the assumption of uniform space motion relative to the solar-system barycentre. In this process it is necessary to include the sixth astrometric parameter μri, even if it is (partially) derived from a spectroscopic radial velocity. Similarly, the transformation of the covariance matrix must consider all six parameters. The relevant formulae are given in Vol. 1, Sect. 1.5.5 of The Hipparcos and Tycho Catalogues (ESA 1997) and are not repeated here17. Indeed, the normal equations for the six parameters contain the full information of the Gaia observations of a particular source with respect to the standard astrometric model, and for this reason it is desirable to compute and store these normals even if only a subset of them is used in the actual source update (cf. Sect. 5.1.3).
7. Software implementation and demonstration solutions
The practical realisation of the AGIS scheme as outlined in the preceding sections is contained in software that is being developed, since early 2006, jointly by teams at the European Space Astronomy Centre (ESAC) and Lund Observatory within the Gaia Data Processing and Analysis Consortium (DPAC). It is a central software module embedded into a complex, overall data processing system (O’Mullane et al. 2007), whose ultimate goal is the creation of the final Gaia catalogue with a targeted release date around 2021.
This section gives a concise overview of the architectural design of the AGIS software (Sect. 7.1) on the one hand, and on the other presents some selected results from a recently (June-November 2011) conducted large-scale astrometric solution (Sect. 7.2) using as input simulated data for more than 2 million sources. While this number is still a factor 50 smaller than the number of primary sources foreseen in the final AGIS runs (around 2018–2020), and the present simulations are much simplified especially with respect to the attitude modelling, we believe that this proof-of-concept run demonstrates the practical validity and correctness of the key theoretical concepts described in this paper. Future tests will involve simulated data sets that are both larger and more realistic, with a parallel further development of the algorithms and software in view of the added new complexities.
7.1. AGIS software overview
The term AGIS is subsequently often used to refer to the actual software implementation of the scheme. Like virtually all Gaia data processing software, AGIS is entirely written in the object-oriented Java programming language (O’Mullane et al. 2010). The implementation has been briefly outlined in Lammers et al. (2009) and more comprehensively in O’Mullane et al. (2011), to which the interested reader is referred for more details. In this section, some key classes are briefly described; following Java naming conventions their names (given in italics) are concatenated capitalized nouns, as in RunManager.
Owing to the number of sources and the associated large data volumes that have to be handled (see Sect. 1) it is clear that a well-performing system must be distributable on modern, multi-node, multi-core processing hardware environments and make optimal use of parallelism as far as permitted by the AGIS scheme. Another elementary consideration is that inherently slow disk input-output operations should be minimized and never allowed to be a bottleneck for any of the computing processes.
These basic requirements have led to the system schematically depicted in Fig. 8 with its main components and data flow. The central elements are DataTrains, Servers, a RunManager, and a ConvergenceMonitor. When an AGIS run starts the RunManager splits the entire processing task of the first iteration into separate and independent jobs which are then taken and executed in parallel by DataTrains that have been started on the different CPUs of the processing system. Each such job involves the processing of all observations for a group of sources (with typically 100–1000 sources per group), which is done by looping over the sources, one at a time. Before the loop is entered all the data that are needed for the processing (observations, as well as all source, attitude, and calibration data) have been loaded into memory and are passed on to the core algorithms. This is a key design aspect which, together with a suitable grouping of the data on the storage system, ensures that the system is never input/output limited and that it has a constantly high utilization of the CPUs (typically at the 90% level).
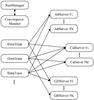 |
Fig. 8 Simplified architectural design diagram of AGIS. The rounded boxes are independent Java processes running in parallel on different nodes of a multi-CPU processing cluster. The arrows indicate main data exchanges between the various processes. Input/output-related data flow from/to the storage system is not shown, and likewise some important but conceptually irrelevant interactions between some elements (e.g., the Servers and the RunManager). |
Each AGIS iteration starts with the updating of the respective sources (see Sect. 5.1). Computed provisional updates are then written to the storage system and, finally, the observations together with the updated source data are sent to attitude, calibration, and global servers via the CPU-interconnecting network. The servers themselves are distributed in different ways (see, e.g., Sect. 5.2.2 for attitude), but all are similar in that they accumulate normal equations by adding observation equations as outlined in Sects. 5.2.1, 5.3, and 5.4, respectively. When all DataTrain jobs are finished, the RunManager signals to the servers that all observations have been sent. This triggers that a Cholesky decomposition (Appendix C) is made of the accumulated normals matrices in every server, that the partial results on different servers are combined where necessary (e.g., the attitude segments are joined), and finally that the results are persisted in the storage system. That marks the end of an iteration. Subsequent iterations are then started in the same manner as the first one, viz., through the creation of a set of processing jobs.
Iteration k uses the computed updates from iteration k − 1 and generates updated parameters for use in the following iteration k + 1. This progress is monitored by the ConvergenceMonitor through the accumulation of a selected list of statistical quantities in the form of graphical plots (e.g., histograms of the updates of all the astrometric parameters) accessible in real time through a web interface. Naively, one may expect that the system can be considered converged if the updates become smaller than a pre-defined limit; however, finding an unambiguous and automatically verifiable convergence criterion has proven to be a surprisingly complex problem (see Sect. 4.4 in Bombrun et al. 2012). We believe now that human inspection is indispensable to assess the convergence status of the system reliably and, ultimately, decide on the termination of the iterative loop.
An important feature of the RunManager is the ability to use different algebraic solution methods by selecting among different available iteration schemes. The description above explains the “kernel” computation of provisional updates to the unknowns employing the Gauss-Seidel-type preconditioner approximation (Eq. (53) in Sect. 4.6) to the full normal matrix of the system (Sect. 4.5). How these provisional updates are actually combined at the end of an iteration to form the final updates to the unknowns depends on the chosen iteration scheme. AGIS can use all four schemes outlined in Sect. 4.7, viz., the simple iteration (SI), accelerated simple iteration (ASI), conjugate gradients (CG), and hybrid scheme (A/SI-CG). The previous description essentially refers to SI; in the other schemes there are a few extra steps which however are immaterial for understanding the software system.
AGIS is controlled through a list of a few hundred key-value parameters (“properties”) which are configured before a run starts. Examples are: the numbers of servers and threads, the size of DataTrain jobs, the starting values for the unknowns, and the employed solution method. Also, which update blocks are active during a run is controlled via properties. Any combination that involves at least a source update is possible, e.g., SACG, SA, SCG.
The optimum number of data trains in a run is a complex trade-off between the available number of CPUs and memory, usable network bandwidth (more trains create more inter-CPU traffic), and the given maximum storage system throughput. By design of the system, the run time should scale inversely with the number of data trains (assuming there are enough CPUs), i.e., doubling the number of DataTrains should halve the run time. In the tests done until now, the run times are very satisfactory; however, more work remains for achieving the desired optimal scaling behaviour. A first AGIS run using simulated data for a 5 yr mission with 50 million primary sources was successfully completed in June 2011. This being only a factor 2 less than the baseline 100 million sources envisaged in the final AGIS run towards the end of the mission, it marks an important milestone in the development of the operational system.
7.2. Demonstration solution
7.2.1. Data simulation and model assumptions
Since the start of the development in early 2006, AGIS has been tested continuously using simulated datasets of varying complexity and size generated by the Gaia System Simulator (Masana et al. 2005) created by DPAC’s dedicated coordination unit for Data Simulations (CU2; Mignard et al. 2008; Luri & Babusiaux 2011). In the following we present the results of a test solution using 5 years of simulated astrometric observations for about 2 million well-behaved (single) stars with a realistic distribution both in magnitude and coordinates, based on the Besançon galaxy model (Robin et al. 2003). Figure 9 (top) shows the spatial source density of the data set in equatorial coordinates. Of particular interest for the AGIS run is the stark density contrast between ~1 and 5000 deg-2 mainly depending on galactic latitude, resulting in similarly high ratios in the total astrometric weight of the sources in Gaia’s two fields of view. In Bombrun et al. (2012) it was shown (using simulations on a smaller scale) that a high weight contrast tends to reduce the convergence rate of the astrometric solution compared to a situation where the weights are more balanced; however, the solution always converges to the correct solution provided that enough CG iterations are carried out. We will show that this key result is confirmed in the demonstration solution.
 |
Fig. 9 All-sky projections of (from top to bottom) the total stellar density in the input data to the demonstration solution, the number of AL observations per source, and the resulting spatial density of AL observations. These and all subsequent sky maps use the Hammer-Aitoff equal-area projection in equatorial coordinates, with α running from − 180° to + 180° right to left. Top: the simulated sky contains some 2 million single stars covering the Gaia magnitude range 6 ≤ G ≤ 20. The density ranges from less than 1 deg-2 around the galactic poles to a maximum of about 4800 deg-2 near the galactic centre in the bottom-right quadrant of the map. Middle: the number of along-scan observations per source reflects the scanning law of Gaia, which is roughly symmetric around the ecliptic plane and gives an over-abundance of observations at ecliptic latitudes ± 45°. Bottom: the combination of the source density and the scanning law gives the displayed density of along-scan observations. |
The input data were generated using a fully-relativistic model of the observed (proper) directions ui(t) in Eq. (7), including gravitational light deflection for PPN parameter γ = 1, assuming the Nominal Scanning Law (Sect. 3.3), the nominal geometrical instrument model (Sect. 3.4) and nominal performance of the instrument (in particular the centroiding accuracies 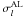 ,
, 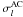 as functions of G; see Table 1). However, in order to test the capability to recover a varying basic angle, a step-wise perturbation was introduced corresponding to the sinusoidal variation of ΔΓj in Eq. (19) with a period of 2.5 yr and an (unrealistically large) amplitude of 500 μas. In the astrometric solution, the large-scale AL calibration interval was set to 30 days, matching the step width of the perturbation signal. The solution used only one global parameter, viz., g0 = γ − 1 as described in Sect. 5.4. Table 1 lists some statistics of the data and solution, while the middle and bottom maps in Fig. 9 show how the number of observations varies across the sky.
as functions of G; see Table 1). However, in order to test the capability to recover a varying basic angle, a step-wise perturbation was introduced corresponding to the sinusoidal variation of ΔΓj in Eq. (19) with a period of 2.5 yr and an (unrealistically large) amplitude of 500 μas. In the astrometric solution, the large-scale AL calibration interval was set to 30 days, matching the step width of the perturbation signal. The solution used only one global parameter, viz., g0 = γ − 1 as described in Sect. 5.4. Table 1 lists some statistics of the data and solution, while the middle and bottom maps in Fig. 9 show how the number of observations varies across the sky.
Characteristics of the simulated input data and demonstration solution.
Not all elements of the numerical algorithms described in this paper have as yet been integrated into the running software system which otherwise implements the basic model described in Sect. 3. In particular, the estimation of source and attitude excess noise (Sects. 5.1.2 and 5.2.5) were not activated in the present solution. This was not a problem for the demonstration run, as the applied observation noise is well-behaved, purely Gaussian. Further development of the AGIS software will to a large extent focus on making the solution robust against all kinds of unexpected input data.
 |
Fig. 10 Map of the parallax errors in iteration 1. The iterative astrometric solution starts off with spatially correlated errors in the astrometric parameters, generated as described in the text. These (initial) parallax errors have amplitudes of a few tens of mas. The number at the top-right corner of this (and subsequent) maps is the maximum value of the displayed range in μas. |
 |
Fig. 11 Top: evolution of the typical parallax error (crosses) and parallax update (circles) as functions of the iteration number. The typical error settles at around 146 μas. Bottom: evolution of the typical attitude error (crosses) and update (circles) as functions of the iteration number, for the three principal SRS axes x (red), y (blue), and z (black). The errors settle at around 167, 224, and 20 μas, respectively. In both these plots the typical errors and updates are given by the Robust Scatter Estimate (RSE), similar to an rms value (see footnote 18). |
The demonstration solution was run with all four update blocks (S, A, C, G) enabled, using starting values for the attitude, calibration and global parameters that were erroneous on the mas level. (As explained in Sect. 4.5 and footnote 9, the results of the subsequent iterations are independent of the initial values for the source parameters, because the updating always starts with the source block.) These initial values were created by adding Gaussian, uncorrelated errors to the true attitude parameters, with a standard deviation of 50 mas, using the nominal calibration parameters (i.e., excluding the sinusoidal modulation of the basic angle), and a value of g0 ≡ γ − 1 = 0.1 (Sect. 5.4). An attitude knot interval of 240 s was used in order to have a sufficient number of observations per degree of freedom even at the galactic poles. This interval is short enough that the attitude splines are able to represent the true attitude (i.e., the analytical nominal scanning law) with an rms error of less than 9 μas. Although this is larger than the modelling errors aimed at in the real data analysis, it is sufficiently small in comparison with the typical attitude estimation errors ( ≥ 20 μas; see Fig. 11) to have a negligible impact on the overall astrometric accuracy of the present solution.
 |
Fig. 12 Maps (in equatorial coordinates) of the parallax errors in the three selected iterations k = 5, 20, 135 (top to bottom). The left column shows the median of the parallax error ϖ(k) − ϖtrue, while the right column shows the median of the absolute error |ϖ(k) − ϖtrue|; each map cell (of about 0.84 deg2) shows the colour-coded value computed for the sources located in that cell. Empty cells are shown in black. On every map plot the top left label indicates the iteration number and the top right label is the maximum value of the displayed range in μas. See text for further details. |
During the source update in the very first iteration, the initial errors in the attitude, calibration parameters and γ propagate to the sources, creating astrometric errors of a few tens of mas (Fig. 10) that are spatially correlated on a scale comparable to the attitude knot interval (~4°). These errors are quite hard to remove in subsequent iterations, but may be representative of the situation encountered by AGIS when processing the real mission data based on a fairly uncertain initial attitude and instrument calibration.
With these starting conditions, 135 iterations were carried out using the conjugate gradients (CG) scheme. A re-initialisation of the CG scheme was made after the first 40 iterations to avoid the development of a much slower convergence phase observed in some previous runs; after this, no further re-initialisation was made. At iteration 135 the typical updates of, for example, the parallaxes and the along-scan attitude were at or below a level of 5 × 10-4 μas (Fig. 11). This is still slightly above the numerical noise floor set by the double-precision arithmetic (~10-16 rad or ~10-5 μas). As discussed by Bombrun et al. (2012), truncating the iterations before the numerical noise floor has been reached implies the presence of spatially correlated “truncation errors” having an amplitude of a few times the typical updates, or ~10-3 μas in the present case. We now proceed with a more detailed analysis of the results.
7.2.2. Source results
In this section we focus on the results for the parallax (ϖ), which is arguably the most interesting parameter from an astrophysical viewpoint; moreover, as a scalar quantity independent of epoch and reference frame, its statistics can be summarized compactly and without ambiguity. However, the behaviour of the position and proper motion parameters is qualitatively similar, and some results are given in Table 2 and Fig. 14.
The top diagram in Fig. 11 shows the typical sizes of the errors and updates in parallax versus iteration number, as measured by the Robust Scatter Estimate18 (RSE). The parallax errors settle relatively quickly (around iteration 25) at a level of 146 μas and remain stable till the end of the run with updates becoming successively smaller, reaching the level of 10-3 μas around iteration 120. The actual error distribution is symmetric but strongly non-Gaussian (in fact more like a Laplace distribution) due to the variation of star numbers and observational standard uncertainties with magnitude (cf. Tables 1 and 2). The overall parallax error RSE of ~150 μas is therefore representative for the median magnitude, G ≃ 19, in good agreement with current accuracy predictions (Lindegren 2010). The overall sizes of the errors and updates shown in Fig. 11 should however be complemented by more detailed statistics as functions of coordinate and magnitude.
 |
Fig. 13 Same as Fig. 12 but showing the updates in parallax, i.e., the median values of ϖ(k) − ϖ(k − 1) (left column) and |ϖ(k) − ϖ(k − 1)| (right column). |
Figure 12 shows the spatial distribution of the parallax errors at a few selected iterations. The left column shows the median error in each cell, while the right column shows the median absolute value of the error. These quantities serve as robust proxies for the mean and rms values (the RSE is not used for the latter as many cells have too few sources for this measure), and therefore may suggest the levels of systematic and random errors as function of position. Figure 13 shows the corresponding maps for the parallax updates. After a few iterations, when the overall parallax errors are already below the 1 mas level, very significant systematic (i.e., spatially correlated) errors of a few mas remain, especially in the high-density areas of the galactic plane. These are damped in the subsequent iterations, but still remain at a level of several hundred μas in the galactic centre region around iteration 20, when the overall parallax errors start to settle at their final value according to Fig. 11. At iteration 135 the regional errors have virtually disappeared, and the error map shows a characteristic pattern with the solution being seemingly better around the galactic equator than in the polar regions. This is purely an effect of number statistics: in the galactic pole areas the cells contain rather few sources (often just a single source, in which case the displayed values are simply the individual parallax errors), while closer to the galactic plane the scatter from one cell to the next is reduced by the median-averaging over many sources.
The sequence of error maps for iterations 5, 20, and 135 corroborates a key result of Bombrun et al. (2012), viz., that by iterating long enough the system can cope with large spatial imbalances in the astrometric weights, provided that the minimum source density allows a good attitude determination at all points.
 |
Fig. 14 Maps of the error (left) and update (right) in proper motion for iteration 135. Each cell shows the colour-coded median error/update in units of μas yr-1, where the individual error/update is computed in terms of the equatorial components as |
The median absolute values of the parallax errors shown in the right column of Fig. 12 quickly settle in a large-scale pattern that mainly reflects the expected variation of parallax accuracy with ecliptic latitude (see, e.g., Table 3 in Lindegren 2010). This, in turn, depends on the scanning law, i.e., on a combination of the number of observations per source (see Fig. 9, middle) and the geometric configuration of the scans – for example, the over-density of observations at ± 45° ecliptic latitude does little to improve the parallaxes, which are then mainly producing shifts in the AC direction, while Gaia is primarily sensitive to the AL displacement. Number statistics reduce the between-cell scatter of the median absolute values as well, which accounts for the smoother appearance along the galactic equator.
The update maps in Fig. 13 conform with expectations and the preceding discussion. Of particular interest from a diagnostic viewpoint is the observation that the amplitude and spatial distribution of the median updates in the non-converged solution give a fair indication of the (systematic) truncation errors. This is obviously useful for assessing the state of convergence, as the update maps can be constructed for the real mission data as well (whereas the error maps are of course unknown). For example, based on the median updates in iteration 20 (middle left map of Fig. 13) one might correctly conclude that truncation errors of a few hundred μas remain, especially in the galactic centre region, as shown in the middle left map of Fig. 12. By the same reasoning it appears that truncation errors at iteration 135 should be well below 1 μas.
In tests using other datasets with lower density contrasts we have seen a more rapid convergence. A similar slowdown in convergence for a non-uniform weight distribution was observed and discussed in Bombrun et al. (2012) based on small-scale simulations. A likely mechanism for this slowdown is related to the weight contrast problem discussed by van Leeuwen (2005) in connection with the new reduction of the Hipparcos data. Any of the fields of view scanning through a high-density area (or an area with many bright stars) creates a strong astrometric weight imbalance between the two viewing directions, as the other field usually points to an area of the sky with much lower source density (or fainter stars). Errors in the along-scan attitude create correlated errors in the parameters of all sources observed at that time, whether they are in the preceding or following field of view. If these source parameters are then used to correct the attitude, with little counterbalancing effect from the (relatively few) sources in the other field, the attitude may get only marginally improved, with the net effect of slowing down the damping and de-correlation of the errors in the high-density areas. Thus, more iterations are needed compared to a more weight-balanced situation19.
Figure 14 shows the error and update maps of the proper motions at iteration 135. Since proper motions are vectors, the displayed quantities are the median lengths of the vectorial differences, which are non-negative by definition. The maps are in expected agreement with the corresponding parallax ones concerning visible patterns and structures. A prominent feature absent in the case of the parallaxes is the lighter bands of relatively smaller proper motion errors around ecliptic latitudes ± 45° caused by the oversampling of these parallels by the scanning law (cf. Fig. 9). In contrast to the parallax case, these observations do contribute to the determination of the proper motion, especially for the component in ecliptic longitude.
RSE of the errors in the astrometric parameters and of the normalized errors (i.e., after division by the formal standard deviations) for different magnitude ranges. See text for further explanations.
All spatial maps in Figs. 12–14 show median values computed from distributions with stars of all magnitudes. A lot more information is contained in the magnitude-resolved versions of the maps, which are not presented here for brevity. Instead, Table 2 shows the RSEs (see footnote 18) of the errors and normalized errors (see below) of all the astrometric parameters in iteration 135, subdivided according to magnitude. The normalized error is defined as the error (in the case of right ascension, Δα ∗ ≡ Δαcosδ) divided by the corresponding formal standard uncertainty obtained from the inverse of the source normal matrix, i.e., by using the approximation in Eq. (120). As discussed in Sect. 6.3 this approximation underestimates the true standard uncertainties of the astrometric parameters by neglecting the contribution from the attitude uncertainty, which may be particularly important for the bright stars where the photon noise is relatively less important.
The RSE of the errors in Table 2 are in reasonable agreement with recent mission accuracy assessments. For example, compared with Eqs. (5.2)–(5.5) in Lindegren (2010) the present values are a few per cent larger for G < 15, and up to some 20% smaller for the fainter stars. This suggests a more conservative photon-statistical error budget in Lindegren (2010), combined with a larger-than-nominal contribution from the attitude uncertainty in the present solution. The latter effect, further discussed in Sect. 7.2.3, is indeed to be expected in the present demonstration solution using far fewer primary stars than planned for the real mission.
A more stringent test of the quality of the solution is obtained by considering the RSE of the normalized errors (i.e., after division by the formal standard uncertainties as described above), which is here denoted ϱ. Ideally we should have ϱ ≃ 1 for any parameter and any magnitude. As shown in Table 2, this is very nearly the case in all parameters for G > 15, meaning that the actual errors are roughly consistent with the standard uncertainties computed from Eq. (120). For the brighter stars ϱ becomes progressively larger, supporting the interpretation that the attitude uncertainty has a significant impact on the accuracy of the bright stars in this solution. For example, the value ϱ = 1.369 obtained for the parallaxes of stars brighter than G = 13 suggests a quadratic attitude contribution to the parallax errors for these stars of [7.52 − (7.5/1.369)2] 1/2 = 5.1 μas, while a similar computation for the next three magnitude bins gives 5.7, 5.1 and 5.4 μas (with a rapidly increasing uncertainty). Thus it appears that the values ϱ > 1 found for the parallaxes of the brighter stars can be accounted for by assuming a constant contribution, by about 5–6 μas rms, to the parallax errors from attitude and/or calibration errors. For the other astrometric parameters we similarly find a constant rms contribution to the positional errors of about 4–5 μas, and to the proper motion errors of about 3–4 μas yr-1. It will be shown below that these numbers are consistent with the actual attitude errors found in the solution.
It should be noted that the reference epoch for the astrometric parameters was set to exactly half-way into the mission, i.e., te = 2014.5 for the simulated mission interval 2012.0–2017.0. This is optimal in the sense that the positional uncertainties are minimized for approximately this epoch, and that the errors in position and proper motion are nearly uncorrelated. A reference epoch half-way through the mission was also assumed for the accuracy assessment in Lindegren (2010), with which the present results have been compared.
In this solution, the median value of the parallax errors of all the 2.2 million sources was not significantly different from zero (the actual value was + 0.004 μas). This shows that, in the absence of systematic observational errors, the astrometric solution is able to determine the absolute parallaxes of the sources, as could be expected from the basic principles of the mission. It is especially worth noting that this was achieved while simultaneously determining the PPN γ parameter, known to be strongly correlated with the parallaxes (cf. Sect. 5.4).
7.2.3. Attitude results
The bottom diagram in Fig. 11 shows the RSE attitude errors and updates as a functions of the iteration number, where the small differences of the attitude quaternions have been transformed into small rotations along the SRS axes (x, y, z) according to Sect. A.6 and expressed in μas. The error component around the z axis corresponds to the AL attitude error, while the x and y components are linear combinations of the AC attitude errors in the PFoV and FFoV20. The z (AL) errors settle at an overall level of 20 μas around iteration 60, while the updates continue to decrease in a similar manner as for the parallaxes (Fig. 11, top). The RSE values of the x and y errors converge to 167 μas and 224 μas, i.e., an order of magnitude larger than in z, reflecting the larger observational errors in the AC direction (Table 1) and the smaller number of AC observations. The ratio of the errors about y and x, 224/167 ≃ 1.34 is in perfect agreement with the value expected from the geometry of the observations (Fig. 2), viz., tan(Γc/2) ≃ 1.34 for a basic angle of Γc = 106.5°.
The converged AL attitude error of 20 μas is completely consistent with the previously inferred constant rms contribution, by 5–6 μas, to the parallax errors (see Sect. 7.2.2), as can be seen from the following considerations. For most stars, the propagation of random observational errors from individual AL observations to the parallaxes (say) is largely governed by geometrical factors and the total number of observations per star, and can be statistically described by a “coefficient of improvement” which can be estimated to 207.6/2300 ≃ 0.09 using the RSE of the parallax errors for the faintest bin in Table 2 combined with the typical AL observational error at G ≃ 19.6 (cf. Table 1). This factor assumes that the individual observational errors (at each CCD) are uncorrelated, which is a very good approximation for the photon-statistical centroiding errors, but not for the attitude errors, which have a correlation length determined by the knot interval of the attitude spline. In the demonstration solution, the knot interval was 240 s, which is much longer than the time it takes an image to cross the nine CCDs in the astrometric field (≃40 s). Therefore it is a much better approximation to assume a constant attitude error for the whole field crossing, corresponding to nine AL observations. As a result, the coefficient of improvement relevant for the attitude error should be a factor three larger, or ≃ 0.27. The AL attitude uncertainty of 20 μas therefore corresponds to 20 × 0.27 ≃ 5.4 μas in the parallax, in very good agreement with the empirical result of 5–6 μas. For the other astrometric parameters a corresponding calculation yields a contribution of about 4 μas in position and 3 μas yr-1 in proper motion. Although these numbers are somewhat smaller than the empirical estimates in Sect. 7.2.2 (possibly indicating an additional contribution from the calibration errors), the overall agreement is striking.
The attitude errors obtained in the solution ultimately come from the observational errors of the individual observations, through the process of fitting the attitude spline functions to these observations. If more observations (of the same quality) are added, the attitude errors are expected to diminish inversely with the square root of the number of observations (as long as the modelling errors are not a limiting factor). The present AL attitude error of 20 μas is roughly what can be expected from the density and magnitudes of primary sources in the demonstration solution, as can be seen from the following simple calculation. The AL attitude has essentially one degree of freedom per knot interval (240 s). The average number of AL observations per degree of freedom is therefore about 2500 (Table 1). From the magnitude distribution in Table 2 and the AL observational uncertainties in Table 1 one can estimate that the average AL observation carries a statistical weight (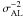 ) corresponding to an AL standard uncertainty of σAL ≃ 650 μas (taking into account the weight reduction by ϱ-2 for the bright stars). The mean flow of observations therefore should allow the AL attitude to be pinned down with an uncertainty of about 650 × 2500 − 1/2 ≃ 13 μas. However, this rough calculation assumes uniform distribution of the stars across the sky, with the same mean density (55 deg-2) as in the demonstration run. Considering that large parts of the sky have a much lower density (typically 5–10 deg-2; see Fig. 9, top), which implies a less precise attitude at the corresponding times, and that we have also neglected the attitude modelling errors, which here amount to at most 9 μas rms (Sect. 7.2.1), it is not unreasonable that the overall AL attitude uncertainty is about 50% larger than according to the above calculation.
) corresponding to an AL standard uncertainty of σAL ≃ 650 μas (taking into account the weight reduction by ϱ-2 for the bright stars). The mean flow of observations therefore should allow the AL attitude to be pinned down with an uncertainty of about 650 × 2500 − 1/2 ≃ 13 μas. However, this rough calculation assumes uniform distribution of the stars across the sky, with the same mean density (55 deg-2) as in the demonstration run. Considering that large parts of the sky have a much lower density (typically 5–10 deg-2; see Fig. 9, top), which implies a less precise attitude at the corresponding times, and that we have also neglected the attitude modelling errors, which here amount to at most 9 μas rms (Sect. 7.2.1), it is not unreasonable that the overall AL attitude uncertainty is about 50% larger than according to the above calculation.
The demonstration run uses only 2% of the stars envisaged for the final AGIS solution, and the majority of them are faint, whereas the real primary stars are preferentially selected among the brighter stars when possible (cf. the discussion in Sect. 6.2.2). For a model distribution of 108 primary sources similar to the one described by Hobbs et al. (2010), the AL observational uncertainty corresponding to the average statistical weight is more like 200 μas, rather than the 650 μas in the present data. On the other hand, the attitude knot interval will also be much shorter than the 240 s used in the present run, perhaps even as short as 5 s, which is about the shortest knot interval that can reasonably be used in view of the normal CCD integration time of 4.42 s. Combining these numbers we estimate that the final AGIS run on the real Gaia data might obtain an AL attitude uncertainty, due to the photon noise, of about (20 μas) × (200/650) × [0.02 × (240/5)] 1/2 ≃ 6 μas. To this should be added the attitude modelling error (i.e., how well the spline can represent the effective attitude), which is difficult to estimate without more reliable information about attitude irregularities (Appendix D.4). Generally speaking, the optimum knot interval will roughly balance the estimation and modelling uncertainties, so that the total uncertainty is less than twice the estimation uncertainty. Assuming a total AL attitude error of 12 μas rms, this would give less than 4 μas rms to be added quadratically to the parallax uncertainties. Thus, the attitude contribution to the final astrometric parameters appears to be relatively small even for the bright stars. However, this does not take into account the additional complications caused by the gated observations (Appendix D.3) and residual calibration errors due to, for example, CTI effects (Appendix D.2).
 |
Fig. 15 Variation of the AL large-scale calibration parameters (averaged over all CCDs) in the preceding field of view (PFoV), as a function of the time since the beginning of the mission. The step-sinusoidal curve is the expected variation due to the simulated basic-angle variation having a period of 2.5 yr and an amplitude of 500 μas, but constant within each 30 day interval. The asterisks show the results of the solution (one value per 30 day interval), and the circles show the differences on the magnified scale to the right. Thanks to the constraint in Eq. (16), the mean calibration parameters in the following field of view (FFoV) exactly mirror the displayed ones, and are therefore not shown. |
7.2.4. Calibration results
The calibration model used for the run merely contained one effect (NAL = 1 in Eq. (20)), viz., the large-scale calibration Δη in Eq. (15) accounting for geometric distortions of the CCDs and optical effects which are indistinguishable from geometric irregularities of the focal plane. On this account, we expect the simulated basic angle signal (see beginning of Sect. 7.2) to manifest itself through a corresponding time-dependence of the AL large-scale calibration parameters Δη0fn0j. The asterisks in Fig. 15 show, for f = PFoV and for each time interval j, the calibration parameter values of the demonstration solution averaged over the 62 CCDs (n). The solid line depicts the step-sinusoidal input basic-angle signal applicable for PFoV. As anticipated, the estimated calibration parameters are in very good agreement with the input signal: the rms value of the differences is 0.20 μas, corresponding to an rms error of 0.40 μas for the basic angle offsets ΔΓj per calibration time interval (cf. Eq. (19)). This is reasonably consistent with the expected precision of the large-scale calibration based on the total weight of the observations, as shown by the following calculation. The mean number of AL observations per calibration time interval and field of view is 1.33 × 107 (cf. Table 1). Assuming, as we did in Sect. 7.2.3, that an AL observation of average weight corresponds to a standard uncertainty of σAL ≃ 650 μas, the expected precision of the basic angle determination is 21/2 × (650 μas) × [1.33 × 107] − 1/2 ≃ 0.25 μas. The observed scatter, 0.40 μas, is larger by roughly the same factor as found for the AL attitude errors.
The good agreement between the input calibration signal and the recovered parameters demonstrates the correct functioning of the generic calibration model (see Sect. 3.4) in this simple case. We expect that many more validation runs will be needed to confirm this result in more complex circumstances, i.e., with more calibration effects of different functional compositions and dependencies. A further important aspect is the practical study of possible hidden correlations and degeneracies of calibration with source, attitude, and global parameters which may not be fully obvious at the mathematical level.
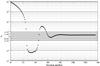 |
Fig. 16 Evolution of the estimated global parameter g0 = γ − 1 (where γ is the PPN parameter) as a function of the iteration number. g0 settles at a level of 2.6 × 10-5 from a starting value of g0 = 0.1. The formal uncertainty of g0 in this solution is 2.15 × 10-5. Note that a linear scale is used for |g0| < 10-4 (the grey area), while a logarithmic scale is used outside of this interval. |
7.2.5. Global results
Starting the iterations from a PPN γ value of 1.1, the purpose of running with the Global block was to see how such a grossly wrong initial value would affect the (overall) convergence rate and to what level the correct value could be recovered (recall that the input data were simulated using γ = 1).
Figure 16 presents the evolution of g0 = γ − 1 during the run. In iteration 135 the parameter had settled on the value g0 = 2.62 × 10-5, with a formal standard uncertainty21 of 2.15 × 10-5. At + 1.2 standard deviations, this value of g0 is not significantly different from 0. The run shows that the system is capable of recovering the “correct” value with an error compatible with the statistical uncertainty, which in this case is set by the photon noise of the individual observations.
The total astrometric weight of the AL observations in the demonstration run is ≃ 4000 μas-2. According to Hobbs et al. (2010) this should yield an rms uncertainty in γ of about 3 × 10-5, in reasonable agreement with the formal standard uncertainty given above and the parameter value obtained in the solution.
7.3. Processing times
The demonstration solution was run on an IBM cluster at ESAC using 14 nodes (out of 32 available), each node having two processors22 with four cores each; thus in total 112 CPUs were engaged. This configuration of 14 nodes is estimated to have a total floating point performance of 0.65 Tflop s-1 (0.65 × 1012 floating point operations per second). One iteration took about 1 h (with high CPU occupancy, typically 90%), so the total run time for 135 iterations was nearly 6 days, corresponding to about 3 × 1017 floating point operations (flop).
Scaled up to the projected 108 primary sources of the final AGIS run this would amount to 1.5 × 1019 flop. Using a more conservative estimate of 5 × 1019 flop to account for additional features not included in the demonstration run, this will require some 60 days on a typically targeted 10 Tflop s-1 machine. On the other hand, there could also be a significant saving in computing time due to the fact that the final solution will start off from a previous solution, already very close to the final one; a smaller number of iterations might therefore suffice. In summary, the estimated processing time is clearly within the feasible range.
8. Conclusions
A fundamental part of the scientific data processing for the Gaia mission is the astrometric core solution, which will be run during and after the mission (ca. 2013–2020) with successively larger datasets and eventually encompassing at least some 100 million primary sources. This solution is central to the performance of the mission as a whole, since it not only provides the astrometric results for these primary sources, but also the reference frame (in the form of the instrument attitude as a function of time) and the geometric calibration of the instrument, for use by a large number of other processes in the overall scientific reduction of the Gaia data.
In order to accomplish the astrometric core solution, a software system known as AGIS (Astrometric Global Iterative Solution) is being built within Coordination Unit 3 (CU3) of the Gaia Data Processing and Analysis Consortium (DPAC). As detailed in this paper, the necessary mathematical models and numerical algorithms are well understood, and have been developed with sufficient rigour to allow the potential accuracy of Gaia to be fully exploited. Most critical parts of this system have been implemented, and numerous test runs have demonstrated the theoretical validity of the global iterative approach, as well as its practical feasibility in terms of data management and computations. While a number of additional features will have to be included in the software before it can be considered ready for the flight data, and many more complications will undoubtedly be discovered during the actual analysis of these data, all the fundamental parts of AGIS are already in place.
In 2011, with roughly two years left until the launch of the satellite and time to mature the concepts and software presented here into a robust operational system, we have no reason to doubt that AGIS will be able to compute an accurate astrometric solution, consistent with the ambitious goals of the Gaia mission.
G is the broad-band magnitude measured on Gaia’s unfiltered CCDs. G ≃ V for unreddened early-type stars, while G ≃ V − 2 for M stars. See Jordi et al. (2010) for a precise characterization of G.
Technically, the use of independent parameter values in successive time intervals represents a spline of order 1 (i.e., degree 0), the separation times constitute the knot sequence, and j or k correspond to the “left index” (Appendix B.2).
Note that in Eq. (25) the quantity μl is just a given value (observed or computed); in the case of one-dimensional images the observed μl is replaced by an approximate value derived from current knowledge on the source and attitude.
That the first ns columns in the iteration matrix are zero means that the results of the next iteration are independent of the current source parameters 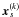 . This may seem surprising at first, but is a simple consequence of the fact that each iteration starts with the source update block (S). In this block, the updated source parameters depend on the previous attitude, calibration and global parameters, but not on the previous source parameters.
. This may seem surprising at first, but is a simple consequence of the fact that each iteration starts with the source update block (S). In this block, the updated source parameters depend on the previous attitude, calibration and global parameters, but not on the previous source parameters.
This iteration formula can be derived by matching the rational approximation Q(y) ≃ a/(b + y) to the value and derivative of Q(y) at the current point y. Compared with the standard Newton-Raphson method, which uses a linear approximation around the current y, the present formula converges much quicker due to the more reasonable behaviour of the rational approximation especially for large y.
On the other hand we have implicitly assumed , for example in deriving Eq. (79).
Note that the normalization in Eq. (10) is effected by applying a normalization factor that is a continuous function of time. Since any given spline coefficient is used in a finite time interval (namely, the support of the corresponding B-spline), one cannot obtain a correct normalization for all by scaling the spline coefficients by some value depending on .
The expected acceleration due to, for example, the Andromeda galaxy or the Shapley Supercluster (Proust et al. 2006) are at most ~10-3 of the galactocentric acceleration. On the other hand, nearby massive galactic objects and large-scale deviations of the galactic potential from axisymmetry could conceivably produce a larger deviation in the direction of the total acceleration.
The sixth parameter μr is denoted ζ in ESA (1997).
In the new reduction of the Hipparcos data by van Leeuwen (2007) the weight ratio was artificially damped in order to improve the connectivity between the two fields of view in high-contrast situations. We have found that this is not required for Gaia provided that the solution is iterated to convergence; see Bombrun et al. (2012).
The attitude errors discussed here must not be confused with the excess attitude noise ϵa introduced in Sect. 3.6. The latter represents modelling errors, which are practically absent in the demonstration solution.
The formal uncertainty of g0 was calculated as 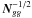 (Eq. (31)) times the factor (1 − ρ) − 1/2 = cot(ξ/2) = 2.414, where ξ = 45° is the constant angle between Gaia’s spin axis (z) and the direction to the Sun; as explained by Hobbs et al. (2010), this factor takes into account the statistical correlation (ρ) between PPN γ and the parallaxes. The correction factor would not have been required, had the solution included the pseudo-parameter g1 (Sect. 5.4).
(Eq. (31)) times the factor (1 − ρ) − 1/2 = cot(ξ/2) = 2.414, where ξ = 45° is the constant angle between Gaia’s spin axis (z) and the direction to the Sun; as explained by Hobbs et al. (2010), this factor takes into account the statistical correlation (ρ) between PPN γ and the parallaxes. The correction factor would not have been required, had the solution included the pseudo-parameter g1 (Sect. 5.4).
When the spline is used for interpolation, it is typically chosen to go exactly through the K + 1 values S(tk) for k = 0...K. This leaves (K + M − 1) − (K + 1) = M − 2 degrees of freedom. Thus, for a cubic spline (M = 4), two more conditions must be imposed for the spline to become unique. The most common choice is to make the second derivative vanish at tbeg and tend. This defines the “natural” interpolating spline. By contrast, when splines are least-squares fitted to data, as in the attitude determination problem, there are typically many data points per sub-interval, and no need for special endpoint conditions.
In the attitude determination problem, each of the four components of the quaternion is represented by a spline, so the number of parameters is actually 4N and the normal matrix is of dimension 4N × 4N. Alternatively, we may take the elements of N to be sub-matrices of dimension 4 × 4. The indices i and j used below refer to these sub-matrices.
“Centroid” should here not be understood as the centre of gravity of the optical image; rather, it is a non-trivial function of the light distribution, similar to the estimation of the image location κ in Sect. 3.5. For the sake of illustration, the centroid could for example be the point obtained by fitting a Gaussian PSF to the image.
A further complication is that most AF observations are binned in the AC direction before read-out, while the CTI effects operate independently on each pixel column. Thus the CDM should ideally be applied to the two-dimensional charge image, and the distorted charge image then binned for comparison with the one-dimensional data. This requires the use of a PSF replacing the LSF in Eq. (23).
The corresponding expression in Bastian & Biermann (2005) is their Eq. (6), in which k(t) is the (integer) index of the last TDI clock stroke before time t. Thus their κ∗(t) oscillates with an amplitude of ± 0.5 unit for every TDI period. The continuous approximation adopted in our Eq. (D.3) is acceptable since we are always considering integrals covering a whole number of oscillations.
The effective attitude is then the physical attitude convolved with the (average) exposure function for maximum T. It corresponds closely to the “astrometric attitude” introduced by Bastian & Biermann (2005).
Acknowledgments
The constant work of the Gaia Data Processing and Analysis Consortium (DPAC) has played an important part in this work. We are particularly indebted to CU2 for the production of independently simulated Gaia-like data for use in the system. The data simulations have been done in the supercomputer Mare Nostrum at Barcelona Supercomputing Center – Centro Nacional de Supercomputación (The Spanish National Supercomputing Center). Research and development in Sweden is kindly supported by the Swedish National Space Board (SNSB). Gaia work in Germany is supported by BMFT through DLR. The successful development of concepts, algorithms and software incorporated in AGIS over a number of years, as well as the drafting of this manuscript, has benefited from the interaction with numerous colleagues, of which we especially wish to mention Sergei Klioner, Alex Bombrun, Alexey Butkevich, Jos de Bruijne, Berry Holl, Floor van Leeuwen, and François Mignard. We thank the referee, Dr. F. van Leeuwen, for numerous constructive comments which helped to improve the original version of the manuscript. Our special thanks go to Gaia’s former Project Scientist Michael Perryman, whose vision, leadership, and enthusiasm in the early years of the project laid the foundations for the excellent progress that is today seen throughout DPAC and with AGIS in particular.
References
- Axelsson, O. 1996, Iterative Solution Methods (Cambridge University Press) [Google Scholar]
- Bastian, U. 1995, in Future Possibilities for astrometry in Space, ed. M. A. C. Perryman, & F. van Leeuwen, ESA Spec. Publ., 379, 99 [Google Scholar]
- Bastian, U., & Biermann, M. 2005, A&A, 438, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Björck, Å. 1996, Numerical Methods for Least Squares Problems (Society for Industrial and Applied Mathematics) [Google Scholar]
- Bombrun, A., Lindegren, L., Holl, B., & Jordan, S. 2010, A&A, 516, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bombrun, A., Lindegren, L., Hobbs, D., et al. 2012, A&A, 538, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J., James, D., Lambert, D., & Van der Wiel, S. 2006, Stat. Sci., 21, 463 [CrossRef] [Google Scholar]
- de Boor, C. 2001, A Practical Guide to Splines, Rev. edn., Appl. Math. Sci., 27 (Springer) [Google Scholar]
- de Bruijne, J., Siddiqui, H., Lammers, U., et al. 2010, in IAU Symposium, 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 331 [Google Scholar]
- Dongarra, J., Bunch, J., Moler, C., & Stewart, G. 1979, LINPACK Users’ Guide (Philadelphia, PA, USA: Society for Industrial and Applied Mathematics), 367 [Google Scholar]
- Dravins, D., Lindegren, L., & Madsen, S. 1999, A&A, 348, 1040 [NASA ADS] [Google Scholar]
- ESA. 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Feissel, M., & Mignard, F. 1998, A&A, 331, L33 [Google Scholar]
- Gilbert, A. C., Kotidis, Y., Muthukrishnan, S., & Strass, M. J. 2002, in Proc. 28th International Conference on Very Large Data Bases, Hong Kong, China, 454 [Google Scholar]
- Golub, G. H., & van Loan, C. F. 1996, Matrix computations, 3rd edn. (Baltimore: The Johns Hopkins University Press) [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Greenbaum, A. 1997, Iterative Methods for Solving Linear Systems (Society for Industrial and Applied Mathematics) [Google Scholar]
- Greenwald, M., & Khanna, S. 2001, in Proc. ACM SIGMOD International Conference on Management of Data, Santa Barbara, CA, 58 [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gwinn, C. R., Eubanks, T. M., Pyne, T., Birkinshaw, M., & Matsakis, D. N. 1997, ApJ, 485, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, W. R. 1843, in Proceedings of the Royal Irish Academy, 2, 424 [Google Scholar]
- Hansen, P. C. 1998, Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion, Monographs on Mathematical Modeling and Computation 4 (SIAM) [Google Scholar]
- Higham, N. 1990, in Reliable Numerical Computation, ed. M. G. Cox & S. J. Hammarling (Oxford University Press), 161 [Google Scholar]
- Higham, N. J. 2002, Accuracy and Stability of Numerical Algorithms, 2nd edn. (Philadelphia, PA, USA: Society for Industrial and Applied Mathematics), 680 [Google Scholar]
- Hobbs, D., Holl, B., Lindegren, L., et al. 2010, in IAU Symp., 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 315 [Google Scholar]
- Høg, E. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 300 [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Holl, B., Hobbs, D., & Lindegren, L. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 320 [Google Scholar]
- Huber, P. 1981, Robust Statistics (Wiley) [Google Scholar]
- Janesick, J. R. 2001, Scientific charge-coupled devices (SPIE Optical Engineering Press) [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kane, T. R., Likins, P. W., & Levinson, D. A. 1983, Spacecraft dynamics (McGraw Hill Book Company) [Google Scholar]
- Klioner, S. A. 2003, AJ, 125, 1580 [Google Scholar]
- Klioner, S. A. 2004, Phys. Rev. D, 69, 124001 [NASA ADS] [CrossRef] [Google Scholar]
- Klumpp, A. R. 1976, J. Spacecraft, 13, 754 [CrossRef] [Google Scholar]
- Kopeikin, S. M., & Makarov, V. V. 2006, AJ, 131, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Laborie, A., Davancens, R., Pouny, P., et al. 2007, in SPIE Conf. Ser., 6690 [Google Scholar]
- Lammers, U., Lindegren, L., O’Mullane, W., & Hobbs, D. 2009, in Astronomical Data Analysis Software and Systems XVIII, ed. D. A. Bohlender, D. Durand, & P. Dowler, ASPC Ser., 411, 55 [Google Scholar]
- Lawson, C. L., & Hanson, R. J. 1974, Solving Least Squares Problems (New Jersey: Prentice-Hall) [Google Scholar]
- Lindegren, L. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA Spec. Publ., 576, 29 [Google Scholar]
- Lindegren, L. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 296 [Google Scholar]
- Lindegren, L., & Bastian, U. 2011, in EAS Publ. Ser., 45, 109 [Google Scholar]
- Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., & Kovalevsky, J. 1995, A&AS, 304, 189 [NASA ADS] [Google Scholar]
- Lindegren, L., & Perryman, M. A. C. 1996, A&A, 116, 579 [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 217 [Google Scholar]
- Luri, X., & Babusiaux, C. 2011, in EAS Publ. Ser., 45, 25 [Google Scholar]
- Masana, E., Luri, X., Anglada-Escudé, G., & Llimona, P. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA Spec. Publ., 576, 457 [Google Scholar]
- Mignard, F., Bailer-Jones, C., Bastian, U., et al. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 224 [Google Scholar]
- Murray, C. A. 1983, Vectorial astrometry (Bristol: Adam Hilger) [Google Scholar]
- O’Mullane, W., Banday, A. J., Górski, K. M., Kunszt, P., & Szalay, A. S. 2001, in Mining the Sky, ed. A. J. Banday, S. Zaroubi, & M. Bartelmann, 638 [Google Scholar]
- O’Mullane, W., Lammers, U., Bailer-Jones, C., et al. 2007, in Astronomical Data Analysis Software and Systems XVI, ed. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 99 [Google Scholar]
- O’Mullane, W., Lammers, U., Hernández, J., et al. 2010, in Astronomical Data Analysis Software and Systems XIX, ed. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 135 [Google Scholar]
- O’Mullane, W., Luri, X., Parsons, P., et al. 2011, Exp. Astron., 1, 10.1007/s10686-011-9241-6 [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 2007, Numerical Recipes: The Art of Scientific Computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Prod’Homme, T., Weiler, M., Brown, S. W., Short, A. D. T., & Brown, A. G. A. 2010, in SPIE Conf. Ser., 7742 [Google Scholar]
- Prod’homme, T., Brown, A. G. A., Lindegren, L., Short, A. D. T., & Brown, S. W. 2011, MNRAS, 414, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Proust, D., Quintana, H., Carrasco, E. R., et al. 2006, A&A, 447, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnabel, R. B., & Eskow, E. 1999, SIAM J. Optim., 9, 1135 [CrossRef] [Google Scholar]
- Seabroke, G. M., Holland, A. D., Burt, D., & Robbins, M. S. 2009, in SPIE, Conf. Ser., 7439 [Google Scholar]
- Short, A., Prod’homme, T., Weiler, M., Brown, S., & Brown, A. 2010, in SPIE Conf., 7742 [Google Scholar]
- Soffel, M., Klioner, S. A., Petit, G., et al. 2003, AJ, 126, 2687 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, G. 1998, Matrix Algorithms: Basic decompositions (Society for Industrial and Applied Mathematics) [Google Scholar]
- Turon, C., O’Flaherty, K. S., & Perryman, M. A. C. 2005, The Three-Dimensional Universe with Gaia, ESA Spec. Publ., 576 [Google Scholar]
- van der Vorst, H. 2003, Iterative Krylov Methods for Large Linear Systems (Cambridge University Press) [Google Scholar]
- van Leeuwen, F. 2005, A&A, 439, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data (Springer), Astrophys. Space Sci. Lab. 350 [Google Scholar]
- Wertz, J. R. 1978, Spacecraft Attitude Determination and Control (Kluwer Academic Publishers) [Google Scholar]
Appendix A: Quaternions
Quaternions form a non-commutative algebra in R4. Invented by Hamilton in 1843 as an extension of the complex numbers (Hamilton 1843), their most common usage today is for representing spatial rotations in a particularly compact and convenient way, with applications for example in computer graphics and spacecraft attitude control. Quaternions can be introduced and understood in many different ways, with a correspondingly confusing multitude of notations and conventions. Here we give just a brief introduction to the subject, stating only the minimum results needed for our applications. For more details, see for example Wertz (1978) and Kane et al. (1983).
A.1. Quaternion algebra
A quaternion is a quadruple of real numbers for which the following algebraic operations are defined. For any quaternions a = {ax, ay, az, aw} and b = {bx, by, bz, bw} we have addition 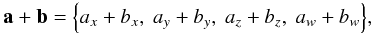 (A.1)multiplication
(A.1)multiplication 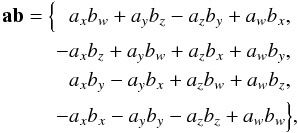 (A.2)and scalar multiplication
(A.2)and scalar multiplication 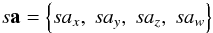 (A.3)for scalar s. Subtraction is analogous to addition, as derived from a − b = a + ( − 1)b. The conjugate of a is
(A.3)for scalar s. Subtraction is analogous to addition, as derived from a − b = a + ( − 1)b. The conjugate of a is 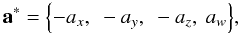 (A.4)the norm (length) is
(A.4)the norm (length) is 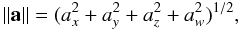 (A.5)and the inverse (provided ∥ a ∥ > 0) is
(A.5)and the inverse (provided ∥ a ∥ > 0) is 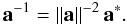 (A.6)We have
(A.6)We have 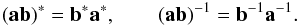 (A.7)Any non-zero quaternion can be normalized to unit length. In analogy with the notation for vector normalization, we use angular brackets for this operation:
(A.7)Any non-zero quaternion can be normalized to unit length. In analogy with the notation for vector normalization, we use angular brackets for this operation: 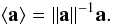 (A.8)The triplet of real numbers (ax, ay, az) can be regarded as the coordinates of the vector a in some reference system S = [ x y z ] (where x, y, z is a right-handed set of orthogonal unit vectors). Thus, we can write a = {S′a, aw}, where S′a = [ ax ay az ] ′ constitutes the so-called vector part of the quaternion, and aw the scalar part. Both scalars and vectors (in R3) can thus be seen as special cases of quaternions, namely, when the vector or the scalar part is zero. This allows us to write for example ∥ a ∥ 2 = aa ∗ = a ∗ a. In terms of the usual vector-scalar operations the quaternion multiplication can also be written as
(A.8)The triplet of real numbers (ax, ay, az) can be regarded as the coordinates of the vector a in some reference system S = [ x y z ] (where x, y, z is a right-handed set of orthogonal unit vectors). Thus, we can write a = {S′a, aw}, where S′a = [ ax ay az ] ′ constitutes the so-called vector part of the quaternion, and aw the scalar part. Both scalars and vectors (in R3) can thus be seen as special cases of quaternions, namely, when the vector or the scalar part is zero. This allows us to write for example ∥ a ∥ 2 = aa ∗ = a ∗ a. In terms of the usual vector-scalar operations the quaternion multiplication can also be written as 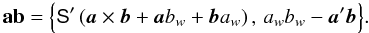 (A.9)Note that the vector part of a quaternion only makes sense when expressed in some coordinate system (S in this example); a physical vector cannot be part of a quaternion.
(A.9)Note that the vector part of a quaternion only makes sense when expressed in some coordinate system (S in this example); a physical vector cannot be part of a quaternion.
A.2. Spatial rotations
Unit quaternions (of unit length) are convenient for representing orientations and spins of objects in three-dimensional space. This is compacter, numerically more stable and requires fewer arithmetic operations than the use of rotation matrices. Compared with the use of Euler angles, much fewer or no trigonometric functions need to be evaluated, and singularities are avoided.
According to Euler’s rotation theorem any change in the orientation of an object can be described as a rotation by a certain angle around some fixed axis. Let this axis be represented by the unit vector u and the rotation angle by φ, reckoned in the positive sense around the vector. In the given reference system S = [x y z] , the rotation is then represented by the unit quaternion 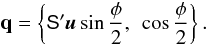 (A.10)The useful property here is that a sequence of rotations is represented by the product of the corresponding unit quaternions (see Sect. A.3).
(A.10)The useful property here is that a sequence of rotations is represented by the product of the corresponding unit quaternions (see Sect. A.3).
From Eq. (A.6) it follows that the inverse of a unit quaternion equals its conjugate, so 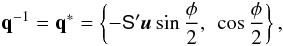 (A.11)which represents a rotation by − φ around u.
(A.11)which represents a rotation by − φ around u.
A rotation by the angle 2π around any axis is represented by the unit quaternion {0,0,0, − 1}. Since this operation is physically equivalent to no rotation at all, it implies a sign ambiguity in the quaternion representation of any given rotation (modulo 2π). This is potentially a problem only when the quaternion is used to represent a continuously changing orientation as a function of time, as is the case for the Gaia attitude (Sect. 3.3). It is then necessary to ensure that no sign flips occur, e.g., when converting from some other representation of the orientations.
Equation (A.10) suggests an alternative, non-redundant, way of representing spatial rotation, namely by means of the components of the vector φ = uφ. For any continuous rotation the three components could be continuous functions of time. This formalism is mainly useful for small rotations ( ∥ φ ∥ ≪ 1); when applied for example to a spinning satellite the length of the vector may grow indefinitely, causing unacceptable numerical errors in finite arithmetic. For the arbitrary vector φ we nevertheless introduce the special notation Q(S′φ) for the unit quaternion, in the reference system S, representing a spatial rotation by the angle φ = ∥ φ ∥ about an axis parallel to φ: ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:qrot} \quat{Q}(\tens{S}'\vec{\phi}) = \begin{cases} \quad\displaystyle\left\{ \tens{S}'\langle\vec{\phi}\rangle \sin\frac{\phi}{2},~\cos\frac{\phi}{2}\right\} &\text{if }\phi>0,\\[6pt] \quad\displaystyle\left\{0,0,0,1\right\} &\text{if }\phi=0. \end{cases} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq841.png) (A.12)This notation is here only used when discussing the small rotational offset between the ICRS and AGIS frames in Sect. 6.1.1.
(A.12)This notation is here only used when discussing the small rotational offset between the ICRS and AGIS frames in Sect. 6.1.1.
A.3. Vector and frame rotations
Vector rotation and frame rotation are not standard notions in vector or quaternion calculus, but we have found them helpful in order to clarify the relations between vectors and their representations in different reference systems.
Vector rotation.
Let {S′r0, 0} be the quaternion representation in the reference system S of the arbitrary vector r0. Rotating the vector an angle φ around unit vector u results in a new vector r1, whose coordinates in S can be calculated by two successive quaternion multiplications, 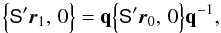 (A.13)where q is given by Eq. (A.10) and q-1 = q ∗ . We call the operation in Eq. (A.13) for the vector rotation of r0 by the quaternion q. This calculation requires the use of a particular reference system (S in this example) in which to express the vectors and the quaternion; the resulting physical vector r1 is however independent of the reference system.
(A.13)where q is given by Eq. (A.10) and q-1 = q ∗ . We call the operation in Eq. (A.13) for the vector rotation of r0 by the quaternion q. This calculation requires the use of a particular reference system (S in this example) in which to express the vectors and the quaternion; the resulting physical vector r1 is however independent of the reference system.
Applying n successive vector rotations, specified by the quaternions q1, q2, ...,qn, gives the vector rn in 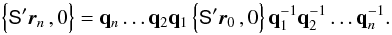 (A.14)This is equivalent to a single vector rotation by q = qn···q2q1. All the quaternions are here expressed in the fixed reference system S, and the order of multiplication is from right to left.
(A.14)This is equivalent to a single vector rotation by q = qn···q2q1. All the quaternions are here expressed in the fixed reference system S, and the order of multiplication is from right to left.
Frame rotation.
A more common application in astrometry is where the reference system itself is rotated, say from S0 = [x0 y0 z0] to S1 = [x1 y1 z1] , by the quaternion q. Given the coordinates 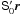 of the arbitrary vector r in reference system S0, we want to compute the coordinates
of the arbitrary vector r in reference system S0, we want to compute the coordinates 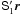 of the same physical vector in the rotated reference system. By applying a vector rotation to each of the basis vectors we find
of the same physical vector in the rotated reference system. By applying a vector rotation to each of the basis vectors we find 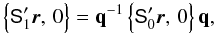 (A.15)which we refer to as the frame rotation of r by the quaternion q.
(A.15)which we refer to as the frame rotation of r by the quaternion q.
It is important to note that the numerical representation of the quaternion q, representing a frame rotation from S0 to S1, is the same in the two frames. This follows because the components of the vector u are invariant under a frame rotation about the vector itself, i.e., 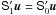 . In Eq. (A.10) the vector part of q can therefore be expressed in either of the two reference systems, i.e., we may take S = S0 or S = S1. The scalar part cos(φ/2) is of course independent of the reference system.
. In Eq. (A.10) the vector part of q can therefore be expressed in either of the two reference systems, i.e., we may take S = S0 or S = S1. The scalar part cos(φ/2) is of course independent of the reference system.
Successive frame rotations can therefore be accomplished by referring each rotation to the current set of axes, which is usually precisely what is needed. Let q1, q2, ...,qn be a sequence of frame rotations, from S0 to S1, and then from S1 to S2, etc.; here q1 is expressed in S0 (or S1), q2 in S1 (or S2), and so on. The corresponding transformation of the coordinates of the vector r is given by 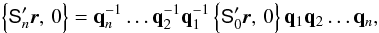 (A.16)equivalent to a single frame rotation by q = q1q2...qn. The quaternions are here expressed in the concurrent reference system, and the order of multiplication is from left to right.
(A.16)equivalent to a single frame rotation by q = q1q2...qn. The quaternions are here expressed in the concurrent reference system, and the order of multiplication is from left to right.
A.4. Angular velocity
Let q be a unit quaternion, expressed in the non-rotating reference system C, and let us assume that q is a differentiable function of time. The angular velocity Ω associated with the time-dependent vector rotation by q is the same for all vectors, and given by 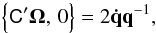 (A.17)where the dot signifies the time derivative. This result can be derived by taking the time derivative of the vector rotation formula for arbitrary vector r, using
(A.17)where the dot signifies the time derivative. This result can be derived by taking the time derivative of the vector rotation formula for arbitrary vector r, using  and Eq. (A.9).
and Eq. (A.9).
Let S be the reference system obtained after rotation by q. The coordinates of the angular velocity vector in the new system are found by performing a frame rotation of Eq. (A.17) by q; thus 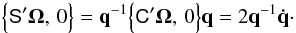 (A.18)These expressions show, for example, how the instantaneous angular velocity of Gaia can be calculated either in the celestial reference system (CoMRS), using Eq. (A.17), or in the instrument system (SRS), using Eq. (A.18), from a knowledge of the attitude q and its time derivative
(A.18)These expressions show, for example, how the instantaneous angular velocity of Gaia can be calculated either in the celestial reference system (CoMRS), using Eq. (A.17), or in the instrument system (SRS), using Eq. (A.18), from a knowledge of the attitude q and its time derivative 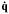 .
.
A.5. The attitude matrix
For completeness, we give here the full relations between the attitude matrix defined in Sect. 3.3 and the quaternion representation of the attitude. Let C = [ X Y Z ] be the celestial reference system (CoMRS; Sect. 3.1) and S = [ x y z ] the instrument system (SRS). The attitude matrix A is defined by Eq. (8). The attitude quaternion q = {qx, qy, qz, qw} gives the rotation from the CoMRS to the SRS, i.e., {C′x,0} = q {C′X,0} q-1, etc. Then 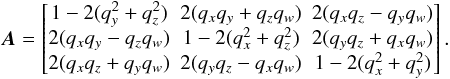 (A.19)The conversion from A to q is less straightforward if we want to avoid numerical problems for certain attitudes. A stable algorithm was given by Klumpp (1976). In our notation, using pseudo-code, it is given by Algorithm A.1. Note that {qx, qy, qz, qw} and { − qx, − qy, − qz, − qw} correspond to the same A, while the algorithm always returns a quaternion with qw ≥ 0; a reversal of the signs may therefore sometimes be required to ensure the temporal continuity of the quaternion components.
(A.19)The conversion from A to q is less straightforward if we want to avoid numerical problems for certain attitudes. A stable algorithm was given by Klumpp (1976). In our notation, using pseudo-code, it is given by Algorithm A.1. Note that {qx, qy, qz, qw} and { − qx, − qy, − qz, − qw} correspond to the same A, while the algorithm always returns a quaternion with qw ≥ 0; a reversal of the signs may therefore sometimes be required to ensure the temporal continuity of the quaternion components.

A.6. Differential rotation
Up until now, the quaternion formulae given in this Appendix hold rigorously for arbitrary rotations. We now derive a useful result, which however is only valid to first order in the (small) rotation angles. It can be used, for example, to compute the attitude error angles about the SRS axes, as was done in Sect. 7.2.3.
Let q0 and q1 be given unit quaternions, representing the two nearly co-aligned reference systems S0 = [x0 y0 z0 ] and S1 = [x1 y1 z1 ] with respect to some third (common) reference system such as the ICRS. It is required to express the difference between S1 and S0 by means of three small angles φx, φy, φz representing rotations about the axes in either system. More precisely, let φ = [ φx φy φz ] ′ be the spatial rotation that brings S0 into coincidence with S1. Assuming that ∥ φ ∥ ≪ 1 and neglecting terms of order ∥ φ ∥ 2, we have S1 ≃ S0 + φ × S0, or  (A.20)According to Eq. (8) this matrix describes the orientation of S1 with respect to S0. If d is the quaternion representing a frame rotation from S0 to S1, we have (Sect. A.3) q1 = q0d and hence
(A.20)According to Eq. (8) this matrix describes the orientation of S1 with respect to S0. If d is the quaternion representing a frame rotation from S0 to S1, we have (Sect. A.3) q1 = q0d and hence  (A.21)Given that ∥ φ ∥ is small, dx, dy and dz are also small quantities, while |dw| ≃ 1. Due to the sign ambiguity of the quaternion representation (Sect. A.2), dw could however have either sign. Comparing Eqs. (A.19) and (A.20) we find, to first order in the small quantities,
(A.21)Given that ∥ φ ∥ is small, dx, dy and dz are also small quantities, while |dw| ≃ 1. Due to the sign ambiguity of the quaternion representation (Sect. A.2), dw could however have either sign. Comparing Eqs. (A.19) and (A.20) we find, to first order in the small quantities, 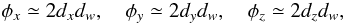 (A.22)where the factor dw (being close to ± 1) guarantees that the angles obtain their correct signs. Equations (A.21), (A.22) provide the required transformation from (q0, q1) to (φx, φy, φz).
(A.22)where the factor dw (being close to ± 1) guarantees that the angles obtain their correct signs. Equations (A.21), (A.22) provide the required transformation from (q0, q1) to (φx, φy, φz).
Appendix B: Splines
A spline is a piecewise polynomial function S(t) defined on some interval [ tbeg,tend ] . That is, if the interval is divided into K > 0 sub-intervals by means of the instants tk (called knots), such that tbeg = t0 < t1 < ... < tK = tend, then in the sub-interval tk ≤ t < tk + 1 the spline function S(t) equals some polynomial Pk(t), k = 0...K − 1. The splines of interest here consist of polynomials of some fixed order M (or degree M − 1); typically M = 4, corresponding to cubic splines. Moreover, the splines are usually maximally smooth, i.e., S(m)(t) ≡ dmS/dtm is continuous for tbeg < t < tend and m = 0...M − 2.
The K polynomials of order M require KM coefficients for their specification. For a maximally smooth spline, there are M − 1 continuity conditions for each interior knot, namely S(m)(tk − ) = S(m)(tk + ) for m = 0...M − 2 and k = 1...K − 1; thus a total of (K − 1)(M − 1) constraints. The spline consequently has KM − (K − 1)(M − 1) = K + M − 1 degrees of freedom23. In the context of least-squares fitting, this equals the number of unknowns (parameters to fit), which we denote by N. In the following we take N and M to be the characteristic numbers of the spline, rather than K and M. For a maximally smooth spline we have K = N − M + 1.
 |
Fig. B.1 The first six B-splines of order M = 4 (cubic) defined on the regular knot sequence τ0, τ1, ... For better visibility, each B-spline is vertically displaced by one unit, and the non-zero parts are drawn in thick lines. |
B.1. B-splines
There are many different ways in which a spline could be represented (parametrized). The approach taken here is to consider S(t) as a linear combination of some basis functions Bn(t), 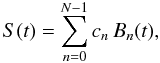 (B.1)where cn are coefficients to be determined. Choosing the basis functions to have minimal support (see below) for the given order and smoothness leads to the so-called B-splines (de Boor 2001).
(B.1)where cn are coefficients to be determined. Choosing the basis functions to have minimal support (see below) for the given order and smoothness leads to the so-called B-splines (de Boor 2001).
The B-splines are uniquely defined by the adopted knot sequence. In the following we shall use τn (rather than tn) to denote the knots associated with the B-splines. The reason is that the knot sequence for the B-splines has a slightly more general interpretation than just the simple division of [ tbeg,tend ] considered above. Moreover, when fitting the spline to given data points, this allows us to use tk (for example) to denote the time associated with the kth data point, without ambiguity.
The knot sequence must be non-decreasing, τ0 ≤ τ1 ≤ τ2 ≤ ..., and at least two knots must be different. Very often we use a regular knot sequence in which τn + 1 = τn + Δτ for some Δτ > 0 (the knot interval). Figure B.1 shows the first six cubic B-splines defined on a regular knot sequence. Note that the non-zero part of each B-spline, shown in heavy line, stretches over M consecutive knot intervals. We use the convention that the B-splines are labelled with the same index as the left-most knot of its non-zero part; therefore, the support of Bn(t) is (τn,τn + M).
It is not possible to construct a maximally smooth spline function of order M that is non-zero over less than M consecutive knot intervals. This is what we mean by the statement that B-splines have minimal support: they could not be shortened without loosing some smoothness. This is an important property for the least-squares fitting, as shown by the following consideration. Least-squares fitting of (B.1) to a given set of data points (tk,zk) (where tk ∈ [ tbeg,tend ] for each k) will be done by forming normal equations. The normal equations matrix N is a symmetric, positive definite matrix of dimension24N × N. Since N may be very large, it is desirable that the matrix is sparse, i.e., that most elements are zero. It is easy to see that element Nij will be non-zero as soon as Bi(tk)Bj(tk) ≠ 0 for some data point k. To make the matrix maximally sparse, we should therefore choose basis functions with minimal support. B-splines have minimal support and are therefore ideal for least-squares fitting using sparse matrix algebra.
Since the support of a B-spline of order M extends over at most M consecutive knot intervals, we have Nij = 0 for |i − j| > M − 1. This shows that N is a symmetric banded matrix with (half-) bandwidth equal to M − 1. Cholesky decomposition preserves the band structure of the matrix and is therefore ideal for solving the normals; it is also numerically very efficient.
B.2. Calculation of B-splines
At any given point t there are at most M non-zero B-splines, namely Bℓ − M + 1(t), Bℓ − M + 2, ... Bℓ(t), where ℓ is the “left index” of t, such that τℓ ≤ t < τℓ + 1. They can be computed simultaneously in a numerically stable way by means of de Boor’s algorithm (de Boor 2001), which is given as pseudo-code in Algorithm B.1. If needed, the derivatives of the B-splines with respect to t can be computed simultaneously with little additional effort.

By inspection of the algorithm it is found that the knots used for computing the B-spline values in the interval [ τℓ, τℓ + 1) are τℓ − M + 2 through τℓ + M − 1. For example, with reference to Fig. B.1 (with M = 4), the B-splines between τ3 and τ4 (i.e., for left index ℓ = 3) depend on { τ1, τ2, ..., τ6 } , but not on τ0 or τ7, even though B0(t) in general depends on τ0 and B3(t) depends on τ7.
B.3. Use of multiple knots
Algorithm B.1 works also in the case when several consecutive knots are placed at the same t coordinate. Having a knot of multiplicity m (i.e., m knots at the same t) removes the continuity for derivatives of order M − m and higher. The normal situation is that the knots have multiplicity 1, which means that the spline is continuous at the knots up to and including its (M − 2)th derivative, but discontinuous in its (M − 1)th derivative. By inserting multiple knots at some specific instant, one allows the spline to become less smooth at this point. For example, in a cubic spline (M = 4) a triple knot (m = 3) allows the first derivative to become discontinuous at that point, while leaving the spline function itself continuous. In the Gaia attitude processing, multiple knots will be used for modelling the effects of micrometeoroid impacts, which cause (almost) instantaneous changes in the angular velocity, corresponding to discontinuities in the first derivative of the attitude spline.
Multiple knots may also be used at the endpoints of the spline interval [ tbeg,tend ] . At any point in this interval, there must be exactly M non-zero B-splines in order that a linear combination of them should to be able to represent an arbitrary spline of order M. Again, with reference to Fig. B.1 (for M = 4), we see that this is the case to the right of τ3 (or τM − 1 in general). Thus we should put τM − 1 = tbeg. The first M − 1 knots can in principle be placed anywhere, as long as τ0 ≤ τ1 ≤ ... ≤ τM − 1: any such arrangement will produce M non-zero B-splines in the next sub-interval (τM − 1,τM), and although the B-splines are different depending on the arrangement of the knots, they are always linearly independent and therefore can be used as a basis for the spline. In particular, it is possible to put the first M knots at the same point, i.e., τ0 = τ1 = ... = τM − 1 = tbeg.
Corresponding considerations apply to the right limit of the spline interval: with N degrees of freedom, the support of the last B-spline BN − 1(t) extends from τN − 1 to τN + M − 1. The spline interval must end at τN = tend, and the remaining M − 1 knots can be placed anywhere provided that τN ≤ τN + 1 ≤ ··· ≤ τN + M − 1. In particular, it is possible to have an M-fold knot at the endpoint of the spline interval, i.e., tend = τN = τN + 1 = ··· = τN + M − 1. Figure B.2 summarizes the placement of knots in relation to a given spline interval for given order M and degrees of freedom N (number of spline coefficients).
 |
Fig. B.2 Illustration of the knot placement for a spline of order M (e.g., M = 4 for a cubic spline) with N degrees of freedom. [tbeg,tend ] is the spline interval over which the spline is fitted to given data points. The end knots τM − 1 and τN are at the endpoints of the spline interval. The N − M interior knots are chosen to give the spline the desired flexibility, including multiple knots where required. The placement of the anterior (τ ≤ tbeg) and posterior knots (τ ≥ tend) is in principle arbitrary: it does not change the fitted spline in [ tbeg,tend ] , but may affect the condition number of the least-squares fit. The parameters of the fitted spline are the coefficients c0, ... cN − 1 of the B-splines B0(t) through BN − 1(t). |
Although the placement of the first and last M − 1 knots is arbitrary, and does not change the resulting spline between tbeg and tend, their placement does affect the numerical stability of the resulting least-squares system. Butkevich & Klioner (unpublished technical note) has pointed out that collapsing the anterior and posterior knots into the end knots, so that τ0 = τ1 = ··· = τM − 1 = tbeg and tend = τN = τN + 1 = ··· = τN + M − 1 results in a system with much smaller condition number than a regular sequence extending beyond the endpoints. For a cubic spline (M = 4) the spline interval then begins and ends with 4-fold knots as illustrated in Fig. B.3. However, the use of data segmentation, as described in Sect. 5.2.2, may not permit this device.
 |
Fig. B.3 Definition of a regular knot sequence for fitting a cubic spline (order M = 4) in the interval [ tbeg,tend ] . The spline interval is divided into N − 3 knot intervals of equal length Δτ = (tend − tbeg)/(N − 3). |
Appendix C: A robust Cholesky algorithm for positive semidefinite matrices without pivoting
C.1. The use of normal equations
The least-squares problems considered in this paper are solved by the method of normal equations (here denoted Nx = b), using the Cholesky algorithm to decompose the symmetric normal matrix N. This method is known to be computationally efficient and accurate for well-conditioned problems (e.g., Stewart 1998), and is moreover well adapted to in-place manipulation of sparse matrices such as the band matrix obtained when fitting B-splines (Fig. 5).
The method of normal equations for the general least-squares problem is usually discouraged in the literature, due to the much superior stability and accuracy of alternative methods operating directly on the observation equations Ax ≃ h (where N = A′A and b = A′h), e.g., using Householder orthogonal transformations (e.g., Björck 1996). However, when working with very large problems that are inherently well-posed, thanks to a good design of experiment and reduction model, our experience is that the method of normal equations is nearly always adequate in terms of accuracy, and then has the edge over other methods in terms of speed, storage and simplicity of the code. Moreover, in these problems, iterative improvement of the solution is usually required for other reasons (non-linearity, elimination of outliers), which partly compensates for the loss of precision when forming the normal equations.

C.2. The Cholesky algorithm
The standard Cholesky algorithm (e.g., Björck 1996; Golub & van Loan 1996) requires that N is positive definite, which is always the case for a well-conditioned least-squares problem. Given N and b, the solution of the system Nx = b proceeds in three steps:
-
C1.
Use the Cholesky algorithm to find the unique upper-diagonal matrix U, with positive diagonal entries, such that N = U′U.
-
C2.
Solve the lower-triangular system U′y = b.
-
C3.
Solve the upper-triangular system Ux = y.
The matrix U (or its transpose) is known as the Cholesky factor or square root of N. As all the computations can be made in-place, we have symbolically ![\appendix \setcounter{section}{3} \begin{equation} \label{eq:chol1} \left[~\vec{N}~|~\vec{b}~\right] \xrightarrow{\text{C1}} \left[~\vec{U}~|~\vec{b}~\right] \xrightarrow{\text{C2}} \left[~\vec{U}~|~\vec{y}~\right] \xrightarrow{\text{C3}} \left[~\vec{U}~|~\vec{x}~\right] . \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq978.png) (C.1)The extension to an arbitrary number of right-hand sides (to the right of the vertical line) is trivial. For example, the inverse N-1 can be obtained by inserting the identity matrix for b. We also note that C1 and C2 are mathematically equivalent to pre-multiplying the matrix and right-hand side, respectively, by
(C.1)The extension to an arbitrary number of right-hand sides (to the right of the vertical line) is trivial. For example, the inverse N-1 can be obtained by inserting the identity matrix for b. We also note that C1 and C2 are mathematically equivalent to pre-multiplying the matrix and right-hand side, respectively, by  . Performing C2 on the unit vector ei = [ 0,0,...,1,...,0 ] ′ (with 1 in position i) thus produces
. Performing C2 on the unit vector ei = [ 0,0,...,1,...,0 ] ′ (with 1 in position i) thus produces  such that
such that 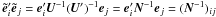 . Selected elements or sub-matrices of N-1 can thus be obtained without computing the full matrix.
. Selected elements or sub-matrices of N-1 can thus be obtained without computing the full matrix.
The above three steps are accomplished by Algorithms C.1–C.3 for arbitrary symmetric positive definite N. (Actually, these algorithms include the non-standard modification discussed below in order to handle semidefinite matrices gracefully.) A few remarks should be made concerning its practical implementation. First, the matrices U and N in C1, y and b in C2, and x and y in C3 can share the same memory if it is acceptable that U overwrites N, etc. (in-place calculation). Second, since N is symmetric, only the upper-diagonal part of it (Nij for i ≤ j) is used in C1, and similarly for U. For large systems one can therefore save roughly half the memory by storing only the upper-diagonal parts of N and U, e.g., as one-dimensional arrays. The code in lines 19–21 of Algorithm C.1 is then irrelevant. Third, if N is a “skyline matrix” with envelope Ej (i.e., Nij = 0 for i < Ej) then U has the same envelope: the Cholesky decomposition gives no fill-in above the envelope. This allows to store and decompose certain sparse matrices very efficiently, such as the band matrix in Fig. 5.

C.3. Application to semidefinite systems
In several of our applications the normal matrix is however not positive definite, either from a lack of observations (e.g., data gaps in the attitude spline representation) or by design (e.g., for the calibration parameters). Application of the standard Cholesky algorithm in such cases results in an exception which may be non-trivial to handle (for example, by changing the knot sequence of the attitude spline) and which may leave the partially solved system in an undefined state. However, that the Cholesky algorithm fails does not mean that there is no solution to the normal equations: on the contrary, there is an infinitude of solutions and the problem is rather which one to pick. Indeed, in many situations we could in principle accept any valid solution; for example, when the null space of the problem is known a priori, and we are prepared to handle the associated non-uniqueness of the solution (cf. Sect. 6.1). For these and several other reasons it is advantageous if the computation can be continued in some sensible way, while of course noting the detected rank deficiency.
A number of methods are available to handle rank-deficient or ill-conditioned least-squares problems. Singular Value Decomposition (SVD; e.g., Björck 1996; Golub & van Loan 1996; Press et al. 2007) is the method often recommended; it provides the unique “pseudo-solution” with the smallest Euclidean norm. However, SVD is computationally expensive and the pseudo-solution is not necessarily better than any other valid solution to the singular least-squares problem.
By construction, the normal matrix N = A′A is positive semidefinite: x′Nx = ∥ Ax ∥ 2 ≥ 0 for any x (cf. footnote 7). A modification of the standard Cholesky algorithm allows the decomposition in C1 to be made also for such matrices, although U is no longer unique; similarly C2 and C3 can be modified to produce a valid (if non-unique) solution to the normal equations Nx = b. For example, the LINPACK routine xCHDC (Dongarra et al. 1979) implements a robust version of the Cholesky algorithm, using complete pivoting (i.e., a simultaneous permutation of the rows and columns of N) to generate the unique square root with non-zero elements only in the first r rows, if r < n is the rank of the matrix (for a detailed analysis, see Higham 2002). Other modifications of the Cholesky algorithm (e.g., Schnabel & Eskow 1999) also uses pivoting.
Permuting the rows and/or columns of the matrix is highly undesirable in the present applications. For example, when applied to a band matrix (such as Fig. 5) it likely destroys the band structure, and in general prevents the envelope-based storing of the sparse matrices N and U outlined above. While pivoting is never needed for the Cholesky factorization of a positive definite matrix, it is thought to be an essential ingredient in modified algorithms aimed at more general symmetric matrices. A simple modification of the Cholesky algorithm, which makes it applicable to the semidefinite case without pivoting was described by Lawson & Hanson (1974, Eq. (19.5)); see also Golub & van Loan (1996, Eq. (4.2.11)), who however warn that “it may be preferable to incorporate pivoting”. Nevertheless we have implemented the corresponding modifications in Algorithms C.1–C.3 without pivoting, and find that they work quite well in our applications. Algorithm C.1 includes a rough estimation of the rank defect d = n − r.
The numerical accuracy of the decomposition in Algorithm C.1 was tested in MATLAB for a range of rank-deficient random positive semidefinite matrices N (patterned after Higham 1990) by computing the quantity ρN = ∥ N − U′U ∥ F/(u ∥ N ∥ F) as a measure of the relative error in units of the floating point precision. Here ∥ N ∥ F = [ trace(N′N) ] 1/2 is the Frobenius norm of N, and u = 2-52 is the unit roundoff (Golub & van Loan 1996) of the double precision floating point arithmetic used. We find that the present algorithm, without pivoting, performs almost as well as LINPACK’s xCHDC with complete pivoting, as judged from the statistics of our ρN compared with the corresponding quantity ρk reported by Higham. However, C.1 is much less useful as a rank-revealing algorithm – the estimated rank defect is often much too small.
Similarly, in order to check the numerical validity of the solution to the rank-deficient normal equations computed by C.1–C.3, we made the following experiments, using the same matrices as above. For random vectors x we first computed b = Nx, then used C.1–C.3 to recover a solution 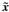 (usually very different from x). Finally we computed
(usually very different from x). Finally we computed 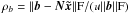 . We find that our algorithm performs almost as well as MATLAB’s basic solution xtilde = N \ b, and much better than the minimum norm solution xtilde = pinv(N)*b (with default tolerance). For example, the 99th percentile of ρb was ~104 for C.1–C.3, ~103 for MATLAB’s backslash (\) operator, and ~1011 (!) when using pinv.
. We find that our algorithm performs almost as well as MATLAB’s basic solution xtilde = N \ b, and much better than the minimum norm solution xtilde = pinv(N)*b (with default tolerance). For example, the 99th percentile of ρb was ~104 for C.1–C.3, ~103 for MATLAB’s backslash (\) operator, and ~1011 (!) when using pinv.
We conclude from these limited experiments that the present version of the Cholesky algorithm is a useful, simple and efficient substitute for much more sophisticated algorithms applicable in the semidefinite case. Since it does not use pivoting, it preserves the envelope of the matrix and is therefore especially suited for banded matrices and envelope-based sparse matrix methods. It provides an estimate of the rank of the matrix, which however is rather unreliable. In the positive definite case the algorithm is equivalent to the standard Cholesky method.

Appendix D: Complexities beyond the basic modelling
Section 3 describes a set of baseline models for the sources, attitude, and geometrical instrument, which are believed to be realistic enough to serve as an acceptable first-order approximation of the actual data for primary sources. Due to the many complexities of the real satellite and its operation, as well as the physical environment in space, there are however many additional effects that may affect the astrometric results at the μas level, and which have to be considered in the final modelling. In this appendix we discuss some of the known effects that will be addressed in future versions of the astrometric solution.
D.1. Chromaticity
Although the Gaia telescopes are all-reflective, with no refractive elements in the optical paths to the astrometric field, they are nevertheless not completely achromatic. In the presence of odd wavefront errors, such as coma, the centroids of the optical images do in fact depend on the wavelength, and hence on the spectral energy distributions of the observed sources25. For the typical wavefront errors expected in the astrometric field of Gaia (about 50 nm rms), the AL centroid shift from an early-type star to a late spectral type could amount to several mas. This systematic effect, known as chromaticity, can therefore be many times larger than the photon-statistical uncertainty of the estimated image location (cf. Table 1). It is thus essential to have a very good calibration of the chromaticity, for which it is necessary to know the spectral energy distribution of every observed source. This is obtained from the photometric observations in the BP and RP fields (see Fig. 3).
Chromaticity is eliminated in the CCD signal analysis by using a Line Spread Function (LSF), L(x) in Eq. (23), which is correspondingly shifted depending on the (known) spectrum of the source. The resulting AL pixel coordinate κ is therefore in principle achromatic, and the effect need not be further considered in the astrometric solution. However, as mentioned in Sect. 3.4, it is envisaged to have diagnostic colour-dependent terms in the geometric instrument model of the astrometric solution. These calibration parameters should obtain negligible values in the solution if the chromaticity has been correctly accounted for in the calibration of L(x). Conversely, non-zero values can be used to improve the LSF calibration in the next processing cycle.
D.2. Charge transfer inefficiency of the CCDs
The CCD signal model in Eq. (23) assumes a perfectly linear detector, which is not exactly the case for the real detectors and especially not in the presence of radiation damage on the CCDs. Traps in the silicon substrate, produced by particle radiation in the space environment, will capture charges during the TDI operation of the CCDs, and release them with delays ranging from a fraction of the TDI period to minutes. The charge capture and release processes introduce a number of phenomena, collectively referred to as Charge Transfer Inefficiency (CTI = 1 − CTE, where CTE is the Charge Transfer Efficiency; Janesick 2001). CTI will affect all kinds of observations in Gaia (astrometric, photometric, spectroscopic). The most important phenomena for the astrometric observations are the apparent charge loss (because part of the charges are released outside the observed window) and centroid shift (because some charges are released with a delay of one or a few TDI periods). These and more general effects of the radiation damage are the subject of extensive theoretical and experimental studies within the Gaia community (e.g., Seabroke et al. 2009; Prod’Homme et al. 2010, 2011). The adopted method to handle these effects in the Gaia data processing is by means of forward modelling using a so-called Charge Distortion Model (CDM; Short et al. 2010). In the context of the CCD signal model of Sect. 3.5, the CDM may be represented by the (non-linear) operator D: ![\appendix \setcounter{section}{4} \begin{equation} \lambda_k \equiv \mbox{E}\left( N_k \right) = D \left[ \left\{ \lambda_{k'}^0\right\} _{k'\le k}\, | \, \Psi\right], \label{eq:signal02} \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq1003.png) (D.1)where
(D.1)where  is the signal model at sample k in the absence of radiation-damage effects, e.g., according to Eq. (23). The variable Ψ represents the state of the CCD, e.g., in terms of how much radiation damage it has suffered. Note that the expected value of sample k depends on the CCD illumination history up to and including sample k, which is expressed by the CDM taking as input the (undamaged) value not only for sample k but also for the preceding samples (k′ ≤ k)26. One of the methods employed for mitigating CTI effects in Gaia is through a periodic (e.g., once per second) electronic injection of charges in a few consecutive TDI lines. As the lines of charges travel across the CCD, most of the harmful traps are temporarily filled, thus reducing the CTI of subsequent charge transfers (Laborie et al. 2007). The method has the additional benefit of periodically resetting the illumination history of the pixels, so that in Eq. (D.1) only the samples since the previous charge injection need to be considered (Short et al. 2010).
is the signal model at sample k in the absence of radiation-damage effects, e.g., according to Eq. (23). The variable Ψ represents the state of the CCD, e.g., in terms of how much radiation damage it has suffered. Note that the expected value of sample k depends on the CCD illumination history up to and including sample k, which is expressed by the CDM taking as input the (undamaged) value not only for sample k but also for the preceding samples (k′ ≤ k)26. One of the methods employed for mitigating CTI effects in Gaia is through a periodic (e.g., once per second) electronic injection of charges in a few consecutive TDI lines. As the lines of charges travel across the CCD, most of the harmful traps are temporarily filled, thus reducing the CTI of subsequent charge transfers (Laborie et al. 2007). The method has the additional benefit of periodically resetting the illumination history of the pixels, so that in Eq. (D.1) only the samples since the previous charge injection need to be considered (Short et al. 2010).
The CDM depends on a moderate number of parameters that will be estimated in parallel with the LSF (or PSF) calibration prior to the astrometric solution (the “Instrument response parameters” in Fig. 1). In principle, the subsequently estimated image location κ should then not only be achromatic, as discussed in Appendix D.1, but also free of CTI effects, so that the astrometric solution can use a purely geometric instrument model, as required by the primary source model. Although this is obviously a highly idealised condition, it it nevertheless what the final data analysis must aim to achieve.
For the simple image of a primary source, the centroid shift due to the CTI depends mainly on the magnitude of the source, the time since the previous charge injection, and the accumulated radiation dose experienced by the CCD (Prod’homme et al. 2011). It is expected that imperfections in the CDM calibration will likewise show up in systematic shifts depending primarily on these (known) quantities, and can be represented by a set of diagnostic calibration functions in the generic calibration model of Sect. 3.4. Non-negligible values of the diagnostic parameters in the astrometric solution indicate that the CDM is not doing its job properly, and they can then be used to improve the model. The reader is referred to the cited papers for quantitative information on the expected level of CTI effects in Gaia data, the effectiveness of different mitigation strategies, and the associated performance degradations.
D.3. Effects of the finite CCD integration time
Up until now we have regarded the astrometric observations of Gaia as instantaneous measurements of the crossings of the source images over the fiducial “observation line” (Fig. 4) at the centre of the CCD (or of the gated portion of the CCD) in the AL direction. In reality, due to the finite integration time (T) of the CCD observations, any measurement clocked into the CCD readout register at time t actually depends on the average attitude and source position over the preceding integration time interval, [ t − T,t ] . The time delay is, to first order, taken into account by associating the measurement with the observation time t − T/2 (Sect. 3.5). Following Bastian & Biermann (2005) we should, more precisely, assume that the observed location κ of the image centre in the pixel stream is a weighted mean of the instantaneous location κ∗(t) of the optical image relative to the charge image during the preceding integration interval: 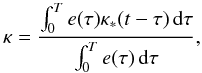 (D.2)where e(τ) is the (nominally flat) “exposure function” for look-back time τ, i.e., the rate at which electrons are produced, and transported to the read-out register, for constant illumination. The instantaneous location is given by
(D.2)where e(τ) is the (nominally flat) “exposure function” for look-back time τ, i.e., the rate at which electrons are produced, and transported to the read-out register, for constant illumination. The instantaneous location is given by ![\appendix \setcounter{section}{4} \begin{equation} \label{eq:kappa-ast} \kappa_*(t) = s\left[ \eta_*(t) - \eta_{fng} \right] + k(t), \end{equation}](/articles/aa/full_html/2012/02/aa17905-11/aa17905-11-eq1014.png) (D.3)where s is the local scale factor (pixels per radian), η∗(t) the instantaneous AL field angle of the optical image centre, and ηfgn the AL coordinate of the fiducial observation line for the appropriate AC coordinate, field of view, etc. The function k(t) is the inverse of tk, relating the time coordinate to the TDI period index k. For the present discussion k(t) is regarded as a continuous function, ignoring the step-wise transportation of the charge image in TDI mode27.
(D.3)where s is the local scale factor (pixels per radian), η∗(t) the instantaneous AL field angle of the optical image centre, and ηfgn the AL coordinate of the fiducial observation line for the appropriate AC coordinate, field of view, etc. The function k(t) is the inverse of tk, relating the time coordinate to the TDI period index k. For the present discussion k(t) is regarded as a continuous function, ignoring the step-wise transportation of the charge image in TDI mode27.
Recalling that η∗(t) is decreasing with time (cf. Fig. 3), while k(t) is increasing, it is seen that κ∗(t) remains approximately constant throughout the integration. Let us denote by tc the exact time when the centre of the optical image crosses the fiducial observation line, so that η∗(tc) = ηfng, and let κc = k(tc) be the corresponding pixel coordinate. If the speed of the optical image exactly matches the speed of the charge image, or 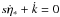 , it is seen that κ∗(t) is indeed constant and equal to κc. Let us now consider what happens if there is a mismatch between the speeds. This could be caused by (i) a deviation in the local scale value s due to optical distortion; (ii) a non-nominal local scan rate; and (iii) that the object itself has significant motion (e.g., an asteroid). Assuming that
, it is seen that κ∗(t) is indeed constant and equal to κc. Let us now consider what happens if there is a mismatch between the speeds. This could be caused by (i) a deviation in the local scale value s due to optical distortion; (ii) a non-nominal local scan rate; and (iii) that the object itself has significant motion (e.g., an asteroid). Assuming that 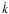 is constant and adopting a Taylor series expansion for the AL field angle over the exposure time, we have
is constant and adopting a Taylor series expansion for the AL field angle over the exposure time, we have 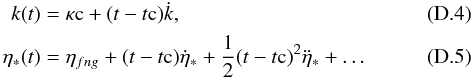 Inserting in Eq. (D.3), and assuming that s is constant across the section of the CCD in question, we obtain by means of Eq. (D.2)
Inserting in Eq. (D.3), and assuming that s is constant across the section of the CCD in question, we obtain by means of Eq. (D.2) 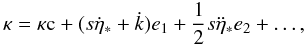 (D.6)where
(D.6)where 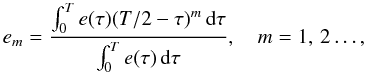 (D.7)are the normalized moments of e(τ) relative to the exposure mid-time at τ = T/2. For a constant and matching image speed we recover κ = κc as expected. In the general case of imperfect speed matching and non-constant scan rate there is a difference which should be taken into account in the astrometric solution. If we assume that s is known, the speed mismatch
(D.7)are the normalized moments of e(τ) relative to the exposure mid-time at τ = T/2. For a constant and matching image speed we recover κ = κc as expected. In the general case of imperfect speed matching and non-constant scan rate there is a difference which should be taken into account in the astrometric solution. If we assume that s is known, the speed mismatch 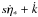 can be computed for every observation, and the factor e1 can then be estimated as an instrument calibration parameter using the generic calibration model in Sect. 3.4. e1 will depend (at least) on the CCD and gate used; but due to the accumulating radiation damage it is likely to evolve with time and could possibly have a magnitude-dependent component as well. In the next (quadratic) term we may know
can be computed for every observation, and the factor e1 can then be estimated as an instrument calibration parameter using the generic calibration model in Sect. 3.4. e1 will depend (at least) on the CCD and gate used; but due to the accumulating radiation damage it is likely to evolve with time and could possibly have a magnitude-dependent component as well. In the next (quadratic) term we may know 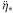 (from the attitude) and e2 ≃ T2/12 (for constant exposure function) to sufficient accuracy that it might be applied as a correction to the observed κ. However, since most observations are ungated (giving maximum T), it may be better to adopt the uncorrected κ for this maximum T as defining the effective attitude28, and only correct the gated observations for the difference in e2; hence they, too, will refer to the effective attitude. A complication is that
(from the attitude) and e2 ≃ T2/12 (for constant exposure function) to sufficient accuracy that it might be applied as a correction to the observed κ. However, since most observations are ungated (giving maximum T), it may be better to adopt the uncorrected κ for this maximum T as defining the effective attitude28, and only correct the gated observations for the difference in e2; hence they, too, will refer to the effective attitude. A complication is that 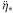 in Eq. (D.6) should be computed from the (unknown) physical attitude, but to first order it can be obtained from the effective attitude. Attitude irregularities on time scales shorter than T add further complications (see Appendix D.4), but it is unlikely that higher-order terms in Eq. (D.6) can profitably be accounted for.
in Eq. (D.6) should be computed from the (unknown) physical attitude, but to first order it can be obtained from the effective attitude. Attitude irregularities on time scales shorter than T add further complications (see Appendix D.4), but it is unlikely that higher-order terms in Eq. (D.6) can profitably be accounted for.
D.4. Attitude irregularities
The basic attitude model described in Sect. 3.3 uses a spline representation which is (normally) continuous in the angles specifying the instantaneous orientation of the instrument, as well as in the first M − 2 derivatives of the angles, where M is the order of the spline (typically cubic splines are used, for which M = 4). The actual (physical) attitude is much more complex and in particular there may be discontinuities and irregularities on time scales that are too short to be adequately represented by a spline with the knot separations considered in the basic model. Low-frequency perturbations ( ≲ 0.01 Hz) are of no concern here, as they can be perfectly represented by splines. The most important contributors to perturbations at higher frequencies are thruster noise in the micro-propulsion system used for the attitude control; the discrete and partially stochastic nature of the control system (for example that the commanded thrusts are updated once per second); micrometeoroid impacts on the satellite; and various dynamical effects such as fuel sloshing and structural vibrations.
The high-frequency perturbations due to the thruster noise and control system generate angular jitter of the physical attitude that has a significant amplitude relative to the astrometric accuracies ultimately aimed at, but still small in comparison with the AL pixel size ( ≃ 59 mas). Thanks to the TDI integration this high-frequency jitter is largely removed from the effective attitude by the averaging over the exposure time T. As a result, the shortest knot interval needed to accurately represent the effective attitude is also of the order of the exposure time, or about 5 s. The optimum knot interval may be longer, depending on the number and magnitudes of the primary sources available for the attitude determination, and on the actual level of perturbations.
The expected frequency of micrometeoroid impacts of various sizes can be predicted from the known velocity and mass spectrum of interplanetary particles. Each impact produces a quasi-instantaneous change in the angular velocity of the satellite, while the attitude angles are continuous across the impact time. It is expected that a few hundred impacts will occur every year producing a change in the AL angular velocity exceeding 1 mas s-1 (which should be easily detectable), with the frequency roughly inversely proportional to the minimum change considered. Discontinuities in the physical attitude rate can be represented in the spline model by inserting multiple knots at the estimated times of impact, ti (Sect. 5.2.6). However, the effective attitude will instead see a linear change in the attitude rates over an interval equal to the exposure time T, centred on ti, which requires that multiple knots are inserted both at ti − T/2 and ti + T/2. (This treatment becomes more problematic in connection with gated observations, when T is non-nominal.) Impacts will be detected by inspecting the observation residuals in connection with the attitude updating (Sect. 5.2.5).
The detailed re-examination of the Hipparcos attitude by van Leeuwen (2005, 2007) revealed numerous discontinuities of the along-scan attitude angle (scan phase) of several tens of mas. A large fraction of them could be linked to the beginning or end of eclipses experienced by Hipparcos in its highly elliptic orbit around the Earth. A likely cause is thermal re-adjustment of the solar-panel hinges, following a sudden change in temperature. As there is no change in the net angular momentum, but only a re-distribution of inertia, the attitude rates are the same before and after a discontinuity. For Gaia it is estimated that such “clanks” will be negligible, but the attitude processing should nevertheless be capable of identifying instances, should they occur, and to take appropriate measures. Due to the finite CCD integration time, the apparent effects of a clank will be two discontinuities in the attitude rates, equal but of opposite sign, and separated by the integration time T. Again, this can be handled by suitable modification of the knot sequence of the attitude spline. Like the micrometeoroid impacts, clanks will be detected during the attitude updating by means of the characteristic patterns that they generate in the observation residuals versus time.
Appendix E: Tables of acronyms and variables
Table E.1 is a list of acronyms used in the paper. Table E.2 lists the most important variables, with a short description and a reference to where it is introduced or explained.
List of acronyms.
List of mathematical variables.
All Tables
RSE of the errors in the astrometric parameters and of the normalized errors (i.e., after division by the formal standard deviations) for different magnitude ranges. See text for further explanations.
All Figures
 |
Fig. 1 Schematic representation of the main elements of the astrometric data analysis. In the shaded area is the mathematical model that allows to calculate the position of the stellar image in pixel coordinates, and hence the expected CCD data, for any given set of model parameters. To the right are the processes that fit this model to the observed CCD data by adjusting the parameters in the rectangular boxes along the middle. This paper is primarily concerned with the geometrical part of the analysis contained in the dashed box. However, a brief outline of the CCD data modelling and processing (bottom part of the diagram) is given in Sect. 3.5 and Appendix D.2. |
| In the text | |
 |
Fig. 2 The Scanning Reference System (SRS) [ x y z ] is defined by the viewing directions fP and fF according to Eq. (2). The instrument angles (ϕ,ζ) are the spherical coordinates in the SRS of the observed (proper) direction u towards the object. See Fig. 4 for further definition of the viewing directions. The field sizes are greatly exaggerated in this drawing; in reality the astrometrically useful field is 0.72° × 0.69° (along × across scan) for each viewing direction. The basic angle is Γc = arccos(fP′fF), nominally equal to 106.5°. |
| In the text | |
 |
Fig. 3 Layout of the CCDs in Gaia’s focal plane. The star images move from right to left in the diagram. The along-scan (AL) and across-scan (AC) directions are indicated in the top left corner. The skymappers (SM1, SM2) provide source image detection, two-dimensional position estimation and field-of-view discrimination. The astrometric field (AF1–AF9) provides accurate AL measurements and (sometimes) AC positions. Additional CCDs used in the blue and red photometers (BP, RP), the radial-velocity spectrometer (RVS), for wavefront sensing (WFS) and basic-angle monitoring (BAM) are not further described in this paper. One of the rows (AF3) illustrates the system for labelling individual CCDs (AF3_1, etc.). The nominal paths of two star images, one in the preceding field of view (PFoV) and one in the following field of view (FFoV) are indicated. For purely technical reasons the origin of the field angles (η,ζ) corresponds to different physical locations on the CCDs in the two fields. The physical size of each CCD is 45 × 59 mm2. |
| In the text | |
 |
Fig. 4 Schematic illustration of how the field angles (η,ζ) are defined in terms of the CCD layout in Fig. 3. For simplicity only the projections of two CCDs, AF8_3 and AF8_4, into the Scanning Reference System (SRS) are shown (not to scale). The field angles have their origins at the respective viewing direction fP or fF (Fig. 2), which are defined in relation to the nominal centres of the CCDs (crosses); the actual configuration of the detectors is described by fiducial observation lines according to Eq. (15). The dashed curve shows the apparent path of a stellar image across the two fields of view. Its intersections with the observation lines define the instants of observations. |
| In the text | |
 |
Fig. 5 Structure of the attitude normal equations matrix Naa for a cubic spline (order M = 4). The blocks of size 4 × 4 are indexed by (n,m) as in Eq. (33). The grey cells represent non-zero elements. Since the matrix is symmetric, the elements below the diagonal (in lighter grey) need not be stored. |
| In the text | |
 |
Fig. 6 A natural break in the definition of the attitude spline occurs if there is a gap in the observations containing at least M knots, where M is the order of the spline. tlast is the time of the last observation before the gap, tfirst the time of the first observation after the gap. |
| In the text | |
 |
Fig. 7 Illustrating the assignment of knots for the attitude update solutions in two consecutive segments K and K + 1, with a breakpoint at knot index x and using 2L overlapping knot intervals. |
| In the text | |
 |
Fig. 8 Simplified architectural design diagram of AGIS. The rounded boxes are independent Java processes running in parallel on different nodes of a multi-CPU processing cluster. The arrows indicate main data exchanges between the various processes. Input/output-related data flow from/to the storage system is not shown, and likewise some important but conceptually irrelevant interactions between some elements (e.g., the Servers and the RunManager). |
| In the text | |
 |
Fig. 9 All-sky projections of (from top to bottom) the total stellar density in the input data to the demonstration solution, the number of AL observations per source, and the resulting spatial density of AL observations. These and all subsequent sky maps use the Hammer-Aitoff equal-area projection in equatorial coordinates, with α running from − 180° to + 180° right to left. Top: the simulated sky contains some 2 million single stars covering the Gaia magnitude range 6 ≤ G ≤ 20. The density ranges from less than 1 deg-2 around the galactic poles to a maximum of about 4800 deg-2 near the galactic centre in the bottom-right quadrant of the map. Middle: the number of along-scan observations per source reflects the scanning law of Gaia, which is roughly symmetric around the ecliptic plane and gives an over-abundance of observations at ecliptic latitudes ± 45°. Bottom: the combination of the source density and the scanning law gives the displayed density of along-scan observations. |
| In the text | |
 |
Fig. 10 Map of the parallax errors in iteration 1. The iterative astrometric solution starts off with spatially correlated errors in the astrometric parameters, generated as described in the text. These (initial) parallax errors have amplitudes of a few tens of mas. The number at the top-right corner of this (and subsequent) maps is the maximum value of the displayed range in μas. |
| In the text | |
 |
Fig. 11 Top: evolution of the typical parallax error (crosses) and parallax update (circles) as functions of the iteration number. The typical error settles at around 146 μas. Bottom: evolution of the typical attitude error (crosses) and update (circles) as functions of the iteration number, for the three principal SRS axes x (red), y (blue), and z (black). The errors settle at around 167, 224, and 20 μas, respectively. In both these plots the typical errors and updates are given by the Robust Scatter Estimate (RSE), similar to an rms value (see footnote 18). |
| In the text | |
 |
Fig. 12 Maps (in equatorial coordinates) of the parallax errors in the three selected iterations k = 5, 20, 135 (top to bottom). The left column shows the median of the parallax error ϖ(k) − ϖtrue, while the right column shows the median of the absolute error |ϖ(k) − ϖtrue|; each map cell (of about 0.84 deg2) shows the colour-coded value computed for the sources located in that cell. Empty cells are shown in black. On every map plot the top left label indicates the iteration number and the top right label is the maximum value of the displayed range in μas. See text for further details. |
| In the text | |
 |
Fig. 13 Same as Fig. 12 but showing the updates in parallax, i.e., the median values of ϖ(k) − ϖ(k − 1) (left column) and |ϖ(k) − ϖ(k − 1)| (right column). |
| In the text | |
 |
Fig. 14 Maps of the error (left) and update (right) in proper motion for iteration 135. Each cell shows the colour-coded median error/update in units of μas yr-1, where the individual error/update is computed in terms of the equatorial components as |
| In the text | |
 |
Fig. 15 Variation of the AL large-scale calibration parameters (averaged over all CCDs) in the preceding field of view (PFoV), as a function of the time since the beginning of the mission. The step-sinusoidal curve is the expected variation due to the simulated basic-angle variation having a period of 2.5 yr and an amplitude of 500 μas, but constant within each 30 day interval. The asterisks show the results of the solution (one value per 30 day interval), and the circles show the differences on the magnified scale to the right. Thanks to the constraint in Eq. (16), the mean calibration parameters in the following field of view (FFoV) exactly mirror the displayed ones, and are therefore not shown. |
| In the text | |
 |
Fig. 16 Evolution of the estimated global parameter g0 = γ − 1 (where γ is the PPN parameter) as a function of the iteration number. g0 settles at a level of 2.6 × 10-5 from a starting value of g0 = 0.1. The formal uncertainty of g0 in this solution is 2.15 × 10-5. Note that a linear scale is used for |g0| < 10-4 (the grey area), while a logarithmic scale is used outside of this interval. |
| In the text | |
 |
Fig. B.1 The first six B-splines of order M = 4 (cubic) defined on the regular knot sequence τ0, τ1, ... For better visibility, each B-spline is vertically displaced by one unit, and the non-zero parts are drawn in thick lines. |
| In the text | |
 |
Fig. B.2 Illustration of the knot placement for a spline of order M (e.g., M = 4 for a cubic spline) with N degrees of freedom. [tbeg,tend ] is the spline interval over which the spline is fitted to given data points. The end knots τM − 1 and τN are at the endpoints of the spline interval. The N − M interior knots are chosen to give the spline the desired flexibility, including multiple knots where required. The placement of the anterior (τ ≤ tbeg) and posterior knots (τ ≥ tend) is in principle arbitrary: it does not change the fitted spline in [ tbeg,tend ] , but may affect the condition number of the least-squares fit. The parameters of the fitted spline are the coefficients c0, ... cN − 1 of the B-splines B0(t) through BN − 1(t). |
| In the text | |
 |
Fig. B.3 Definition of a regular knot sequence for fitting a cubic spline (order M = 4) in the interval [ tbeg,tend ] . The spline interval is divided into N − 3 knot intervals of equal length Δτ = (tend − tbeg)/(N − 3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.