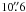| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117849 | |
| Published online | 15 February 2012 | |
A (sub)millimetre study of dense cores in Orion B9⋆,⋆⋆
1 Department of Physics, PO Box 64, 00014 University of Helsinki, Finland
e-mail: oskari.miettinen@helsinki.fi
2 Finnish Centre for Astronomy with ESO (FINCA), University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
Received: 8 August 2011
Accepted: 16 December 2011
Context. Studies of dense molecular-cloud cores at (sub)millimetre wavelengths are needed to understand the early stages of star formation.
Aims. We aim to further constrain the properties and evolutionary stages of dense cores in Orion B9. The prime objective of this study is to examine the dust emission of the cores near the peak of their spectral energy distributions, and to determine the degrees of CO depletion, deuterium fractionation, and ionisation.
Methods. The central part of Orion B9 was mapped at 350 μm with APEX/SABOCA. A sample of nine cores in the region were observed in C17O(2−1), H13CO+(4−3) (towards 3 sources), DCO+(4−3), N2H+(3−2), and N2D+(3−2) with APEX/SHFI. These data are used in conjunction with our previous APEX/LABOCA 870-μm dust continuum data.
Results. All the LABOCA cores in the region covered by our SABOCA map were detected at 350 μm. The strongest 350 μm emission is seen towards the Class 0 candidate SMM 3. Many of the LABOCA cores show evidence of substructure in the higher-resolution SABOCA image. In particular, we report on the discovery of multiple very low-mass condensations in the prestellar core SMM 6. Based on the 350-to-870 μm flux density ratios, we determine dust temperatures of Tdust ≃ 7.9−10.8 K, and dust emissivity indices of β ~ 0.5−1.8. The CO depletion factors are in the range fD ~ 1.6−10.8. The degree of deuteration in N2H+ is ≃0.04−0.99, where the highest value (seen towards the prestellar core SMM 1) is, to our knowledge, the most extreme level of N2H+ deuteration reported so far. The level of HCO+ deuteration is about 1–2%. The fractional ionisation and cosmic-ray ionisation rate of H2 could be determined only towards two sources with the lower limits of ~2−6 × 10-8 and ~2.6 × 10-17−4.8 × 10-16 s-1, respectively. We also detected D2CO towards two sources.
Conclusions. The detected protostellar cores are classified as Class 0 objects, in agreement with our previous SED results. The detection of subcondensations within SMM 6 shows that core fragmentation can already take place during the prestellar phase. The origin of this substructure is likely caused by thermal Jeans fragmentation of the elongated parent core. Varying levels of fD and deuteration among the cores suggest that they are evolving chemically at different rates. A low fD value and the presence of gas-phase D2CO in SMM 1 suggest that the core chemistry is affected by the nearby outflow. The very high N2H+ deuteration in SMM 1 is likely to be remnant of the earlier CO-depleted phase.
Key words: astrochemistry / stars: formation / ISM: abundances / ISM: clouds / ISM: molecules / submillimeter: ISM
This publication is based on data acquired with the Atacama Pathfinder EXperiment (APEX) under programmes 079.F-9313A, 084.F-9304A, and 084.F-9312A. APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
Our SABOCA map shown in Fig. 2 is available electronically in FITS format at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/538/A137
© ESO, 2012
1. Introduction
New stars in our Galaxy form predominantly in the so-called giant molecular clouds (GMCs). The nearest GMC to the Sun is the Orion molecular cloud complex1. This cloud complex contains a number of star-forming regions, one example being the Orion B9 region in the central part of Orion B molecular cloud. Orion B9 represents a very early stage of star formation which is manifest in the fact that most “dense cores” in the cloud are either prestellar or contain Class 0 protostars. These objects are cold, and their study requires observations at (sub)millimetre wavelengths.
 |
Fig. 1 Spitzer/MIPS 24-μm image of the central part of Orion B9 overlaid with contours showing the LABOCA 870-μm dust continuum emission. The contours go from 0.1 (~3.3σ) to 1.0 Jy beam-1 in steps of 0.1 Jy beam-1. The 24-μm image is shown with a logarithmic scaling to improve the contrast between bright and faint features. The colour bar indicates the 24-μm intensity scale in units of MJy sr-1. The green plus signs show the target positions of our molecular-line observations (i.e., the submm peak positions of the LABOCA map before adjusting the pointing; see text). The green line shows the base and northwest tip of the HH 92 jet driven by IRAS 05399-0121 (Bally et al. 2002). The 0.2-pc scale bar and the effective LABOCA beam HPBW (~20″) are shown in the bottom left (Paper I). |
Using the LABOCA bolometer array on APEX (Atacama Pathfinder EXperiment), we mapped that region at 870 μm (Miettinen et al. 2009, hereafter Paper I). The dust continuum mapping resulted in the discovery of twelve dense cores of which four were found to be associated with IRAS point sources, and eight of them appeared previously unknown sources. Of the newly discovered cores, two (we called SMM 3 and 4) were found to be associated with Spitzer 24- and 70-μm sources, and were tentatively classified as Class-0 protostellar candidates. Six cores showed no signs of embedded infrared emission, and were thus classified as starless. Figure 1 shows the 870 μm emission as contours overlaid on the Spitzer/MIPS 24-μm image of the central part of Orion B92. In Paper I, we also derived the degree of deuteration, or the N(N2D+)/N(N2H+) column density ratio, towards selected positions and found the values in the range 0.03–0.04, comparable to those seen in other low-mass star-forming regions (e.g., Crapsi et al. 2005; Emprechtinger et al. 2009; Friesen et al. 2010b). Taking advantage of the H2D+ data from Harju et al. (2006), the ionisation degree and the cosmic-ray ionisation rate of H2 towards the same target positions were estimated to be x(e) ~ 10-7 and ζH2 ~ 1−2 × 10-16 s-1, respectively.
The physical properties of dense cores in Orion B9 were studied further by Miettinen et al. (2010, hereafter Paper II). Using the observations of the NH3 (1, 1) and (2, 2) inversion transitions performed with the Effelsberg 100-m telescope, we determined the gas kinetic temperature, kinematical properties, and dynamical state of the cores. The gas kinetic temperature of the cores were found to be Tkin ~ 9.4−13.9 K, and the internal non-thermal motions in the cores appeared to be subsonic, or at most transonic. The virial-parameter analysis showed that the starless cores in the region are likely to be gravitationally bound, and thus prestellar objects. Interestingly, some of the cores were found to have significantly (by ~5−7.5 km s-1) lower radial velocity than the systemic velocity of the region (vLSR ~ 9 km s-1). This suggests that they belong to the “low-velocity part” of Orion B which is likely to originate from the feedback from the massive stars of the nearby Ori OB 1b association.
In this paper, we present the results of our new APEX observations of the Orion B9 region. These include the dust continuum mapping with the SABOCA (Submillimetre APEX BOlometer CAmera) bolometer array at 350 μm, and observations of the molecular-line transitions C17O(2−1), H13CO+(4−3), DCO+(4−3), N2H+(3−2), and N2D+(3−2). The SABOCA 350-μm observations allow us to probe the peak of the core’s spectral energy distributions (SEDs). We also aim to study the degrees of CO depletion and deuterium fractionation, and the fractional ionisation in the cores. These are useful parameters to further constrain the physical and chemical properties of the sources, and their evolutionary stages.
This paper is structured as follows. The observations and data-reduction procedures are described in Sect. 2. The direct observational results are presented in Sect. 3. In Sect. 4, we describe the analysis and present the results of the physical and chemical properties of the cores. Discussion of our results is presented in Sect. 5, and in Sect. 6, we summarise the main conclusions of this study.
Source list.
Observed spectral-line transitions and observational parameters.
2. Observations and data reduction
2.1. Submillimetre dust continuum observations
The central 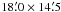 part of Orion B9 was mapped with SABOCA (Siringo et al. 2010) on the APEX 12-m telescope (Güsten et al. 2006) at Llano de Chajnantor (Chilean Andes). SABOCA is a 37-channel on-sky bolometer array operating at 350 μm, with a nominal resolution of ~
part of Orion B9 was mapped with SABOCA (Siringo et al. 2010) on the APEX 12-m telescope (Güsten et al. 2006) at Llano de Chajnantor (Chilean Andes). SABOCA is a 37-channel on-sky bolometer array operating at 350 μm, with a nominal resolution of ~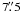 (HPBW). The effective field of view of the array is 1
(HPBW). The effective field of view of the array is 1 5. The SABOCA passband has an equivalent width of about 120 GHz centred on an effective frequency of 852 GHz.
5. The SABOCA passband has an equivalent width of about 120 GHz centred on an effective frequency of 852 GHz.
The observations were carried out on 5 October and 10 November 2009. The atmospheric zenith opacity at 350 μm was measured using the sky-dip method, and was found to be in the range 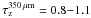 . The amount of precipitable water vapour (PWV) was in the range 0.4–0.6 mm. The telescope pointing and focus checks were made at regular intervals using the planets Mars, Jupiter, and Uranus, and several secondary calibrators (e.g., CRL618, N2071IR, and CW Leo). The absolute calibration uncertainty for SABOCA is 25–30%. Mapping was performed using a “fast-scanning” method without chopping the secondary mirror (Reichertz et al. 2001). The mosaic was constructed by combining 147 individual fast-scanning (typically 1
. The amount of precipitable water vapour (PWV) was in the range 0.4–0.6 mm. The telescope pointing and focus checks were made at regular intervals using the planets Mars, Jupiter, and Uranus, and several secondary calibrators (e.g., CRL618, N2071IR, and CW Leo). The absolute calibration uncertainty for SABOCA is 25–30%. Mapping was performed using a “fast-scanning” method without chopping the secondary mirror (Reichertz et al. 2001). The mosaic was constructed by combining 147 individual fast-scanning (typically 1 2 s-1) maps. The total integration time spent on the area was 9.7 h.
2 s-1) maps. The total integration time spent on the area was 9.7 h.
Data reduction was done with the CRUSH-2 (Comprehensive Reduction Utility for SHARC-2) (version 2.03-2) software package (Kovács 2008), which includes calibration data covering the period of our SABOCA observations. We used the pipeline iterations with specifying the “deep” option, which is appropriate for point-like sources. To improve the image appearance and increase the signal-to-noise (S/N) ratio, a beam-smoothing was applied, i.e., the map was smoothed with a Gaussian kernel of the size 7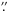 5 (FWHM). Therefore, the angular resolution of the final image is 10
5 (FWHM). Therefore, the angular resolution of the final image is 10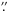 6 (0.02 pc at 450 pc). The gridding was done with a cell size of 1
6 (0.02 pc at 450 pc). The gridding was done with a cell size of 1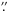 5. The resulting 1σ rms noise level in the final co-added map is ~0.06 Jy beam-1.
5. The resulting 1σ rms noise level in the final co-added map is ~0.06 Jy beam-1.
2.2. Molecular-line observations
The spectral-line observations of C17O(2−1), DCO+(4−3), N2H+(3−2), and N2D+(3−2) towards nine Orion B9 cores, and H13CO+(4−3) observations towards three cores, were carried out on 2–3, 8–9, and 11–12 September, and 13 and 18–19 November 2009 with APEX. The target cores with their physical properties derived in Paper II are listed in Table 1. In Table 1 we give the LABOCA submm peak positions of the cores after adjusting the pointing by 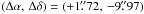 . The target positions of our molecular-line observations can be found in Table 1 of Paper II. The observed transitions, their spectroscopic properties, and observational parameters are listed in Table 2. The critical densities, ncrit, listed in Col. (4) of Table 2 were calculated at T = 10 K using the collisional-rate data available in the Leiden Atomic and Molecular Database (LAMDA; Schöier et al. 2005)3. To calculate ncrit for N2D+, we used the Einstein A-coefficient from Pagani et al. (2009b) and the same collisional rate as for N2H+. The N2H+(3−2) observations were already presented in Paper II, but are re-analysed in the present paper.
. The target positions of our molecular-line observations can be found in Table 1 of Paper II. The observed transitions, their spectroscopic properties, and observational parameters are listed in Table 2. The critical densities, ncrit, listed in Col. (4) of Table 2 were calculated at T = 10 K using the collisional-rate data available in the Leiden Atomic and Molecular Database (LAMDA; Schöier et al. 2005)3. To calculate ncrit for N2D+, we used the Einstein A-coefficient from Pagani et al. (2009b) and the same collisional rate as for N2H+. The N2H+(3−2) observations were already presented in Paper II, but are re-analysed in the present paper.
As frontend for the C17O(2−1) and N2D+(3−2) observations, we used APEX-1 of the SHFI (Swedish Heterodyne Facility Instrument; Belitsky et al. 2007; Vassilev et al. 2008a,b). APEX-1 operates in single-sideband (SSB) mode using sideband separation mixers, and it has a sideband rejection ratio >10 dB. The SHFI sidebands are separated by 12 GHz, i.e., ± 6 GHz around the local oscillator (LO) frequency. Therefore, the centre frequency for the image band is 12 GHz above or below the observing frequency depending on whether the receiver tuning is optimised for operation in the upper or lower sideband (USB or LSB), respectively. For the H13CO+(4−3), DCO+(4−3), and N2H+(3−2) observations the frontend used was APEX-2, which has similar characteristics as APEX-1. The backend for all observations was the Fast Fourier Transfrom Spectrometer (FFTS; Klein et al. 2006) with two 1 GHz units. Both units were divided into 8192 channels. The two units were connected to one receiver each, thus providing 1 GHz bandwidth for two receivers simultaneously.
The observations were performed in the wobbler-switching mode with a 100″ azimuthal throw (symmetric offsets) and a chopping rate of 0.5 Hz. The telescope pointing and focus corrections were checked by continuum scans on the planets Mars and Uranus, and the pointing was found to be accurate to ~3″. Calibration was done by the chopper-wheel technique, and the output intensity scale given by the system is 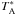 , the antenna temperature corrected for atmospheric attenuation. The observed intensities were converted to the main-beam brightness temperature scale by
, the antenna temperature corrected for atmospheric attenuation. The observed intensities were converted to the main-beam brightness temperature scale by 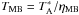 , where ηMB = Beff/Feff is the main beam efficiency, and Beff and Feff are the beam and forward efficiencies, respectively. The absolute calibration uncertainty is estimated to be 10%.
, where ηMB = Beff/Feff is the main beam efficiency, and Beff and Feff are the beam and forward efficiencies, respectively. The absolute calibration uncertainty is estimated to be 10%.
The spectra were reduced using the CLASS90 programme of the IRAM’s GILDAS software package4. The individual spectra were averaged and the resulting spectra were Hanning-smoothed in order to improve the S/N ratio of the data. A first- or third-order polynomial was applied to correct the baseline in the final spectra. The resulting 1σ rms noise levels are ~20−80 mK at the smoothed resolutions. As shown in the second last column of Table 2, the on-source integration times were different between different sources. This is particularly the case for C17O(2−1), N2D+(3−2), and H13CO+(4−3) where tint varies by a factor of ~3−7. This explains the variations in the rms noise values (up to a factor of 2.4 in the C17O data).
The J = 2−1 transition of C17O contains nine hyperfine (hf) components. We fitted this hf structure using “method hfs” of CLASS90 to derive the LSR velocity (vLSR) of the emission, and FWHM linewidth (Δv). The hf line fitting can also be used to derive the line optical thickness, τ. However, in all spectra the hf components are mostly blended together and thus the optical thickness could not be reliably determined. For the rest frequencies of the hf components, we used the values from Ladd et al. (1998, Table 6 therein). The adopted central frequency, 224 714.199 MHz, is that of the JF = 29/2 → 17/2 hf component which has a relative intensity of 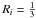 .
.
Also, rotational lines of H13CO+ and DCO+ also have hf structure (e.g., Schmid-Burgk et al. 2004; Caselli & Dore 2005). The J = 4 − 3 transition of DCO+ is split up into six hf components. To fit this hf structure, we used the rest frequencies from the CDMS database (Müller et al. 2005). The adopted central frequency of DCO+(4−3), 288 143.855 MHz, is that of the JF = 45 → 34 hf component which has a relative intensity of 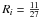 . We note that this frequency is 2.7 kHz lower than the value determined by Caselli & Dore (2005, their Table 5). The frequency interval of the hf components for DCO+(4−3) is very small. Therefore, the lines overlap significantly which causes the hf structure to be heavily blended. In general, for the Jupper ≥ 3 lines of DCO+ the hf components are so heavily blended that, even determined through a single Gaussian fit, the linewidth is not expected to be significantly overestimated (Caselli & Dore 2005). The hf structure of H13CO+ lines is more complicated because both the 1H and 13C nuclei have a nuclear spin of I = 1/2, and the nuclear magnetic spin couples to rotation. To our knowledge, the rest frequencies of the H13CO+(4 − 3) hf components have not been published. We thus fitted these lines using a single Gaussian fit to derive the values of vLSR and Δv. As in the case of DCO+(Jupper ≥ 3), the Δv thus determined is not expected to be significantly overestimated because of the strong blending of the hf components. The central frequency used was 346 998.344 MHz (CDMS), which is 3.0 kHz lower than the value determined by Schmid-Burgk et al. (2004; Table 3 therein).
. We note that this frequency is 2.7 kHz lower than the value determined by Caselli & Dore (2005, their Table 5). The frequency interval of the hf components for DCO+(4−3) is very small. Therefore, the lines overlap significantly which causes the hf structure to be heavily blended. In general, for the Jupper ≥ 3 lines of DCO+ the hf components are so heavily blended that, even determined through a single Gaussian fit, the linewidth is not expected to be significantly overestimated (Caselli & Dore 2005). The hf structure of H13CO+ lines is more complicated because both the 1H and 13C nuclei have a nuclear spin of I = 1/2, and the nuclear magnetic spin couples to rotation. To our knowledge, the rest frequencies of the H13CO+(4 − 3) hf components have not been published. We thus fitted these lines using a single Gaussian fit to derive the values of vLSR and Δv. As in the case of DCO+(Jupper ≥ 3), the Δv thus determined is not expected to be significantly overestimated because of the strong blending of the hf components. The central frequency used was 346 998.344 MHz (CDMS), which is 3.0 kHz lower than the value determined by Schmid-Burgk et al. (2004; Table 3 therein).
The J = 3−2 transitions of both N2H+ and N2D+ contain 38 hf components. The hf lines were fitted using the rest frequencies from Pagani et al. (2009b, Tables 4 and 10 therein). The adopted central frequencies of N2H+(3−2) and N2D+(3−2), 279 511.832 and 231 321.912 MHz, are those of the JF1F = 345 → 234 hf component which has a relative intensity of 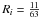 . Also in these cases, the hf components are blended and thus the value of τ could not be reliably determined through hf fitting.
. Also in these cases, the hf components are blended and thus the value of τ could not be reliably determined through hf fitting.
 |
Fig. 2 SABOCA 350-μm image (smoothed to |
The 350-μm core properties.
3. Observational results
3.1. SABOCA 350-μm emission
The 350-μm SABOCA map is shown in Fig. 2. Almost all the cores detected with LABOCA show also clear 350 μm emission. The exceptions are SMM 5 and Ori B9 N for which the 350-μm peak flux densities are at the levels 3.5σ (210 mJy) and 3σ (180 mJy), respectively. With the peak flux density of 60.5σ (3630 mJy), SMM 3 is by far the strongest 350-μm source in the region. Four of the cores are resolved into at least two emission peaks in the SABOCA image. In the case of SMM 3, there is a 350-μm condensation, we call SMM 3b (4.2σ or 250 mJy), at about 36″ east of the “main” source. At about 17″ from SMM 3b, there is another 4σ (240 mJy) emission peak, designated here as SMM 3c. The 870 μm emission of SMM 3 extends to the direction of the subcondensations SMM 3b and 3c, and both of them lie either within or at the borderline of the 3.3σ (99 mJy) 870-μm contour. SMM 4 is resolved into two condensations. The western condensation coincides with the LABOCA peak position, whereas the eastern one, SMM 4b, is coincident with a Spitzer 24-μm source near SMM 4 (see Sect. 5.7.2). The elongated core SMM 6 is resolved into at least three subcondensations. The northwesternmost condensation corresponds to LABOCA peak of SMM 6. Finally, SMM 7 shows a hint of substructure in the western part of the core, where the 870 μm emission is above 3.3σ (99 mJy) level. SMM 3, 4, 6, 7, and their substructure will be discussed further in Sect. 5.7. There are also two 4−4.5σ (240–270 mJy) emission peaks at α2000.0 = 05h42m47.4s, δ2000.0 = −01°17′15″ (south of SMM 3b) and α2000.0 = 05h43m24.7s, δ2000.0 = −01°14′35″ (southeast of SMM 7), and a few 3.5−4σ (210–240 mJy) peaks to the east of SMM 6 at α2000.0 = 05h43m16.5s, δ2000.0 ≃ −01°19′00″. There is some weak LABOCA emission just slightly north of the latter peaks. However, because these “additional” sources are below 5σ (300 mJy), were not detected by LABOCA at 870 μm, and were not identified by the SIMBAD Astronomical Database5, they may well be unreal and are not discussed further in this paper.
To identify and extract the cores from the SABOCA map, we employed the commonly used two-dimensional clumpfind algorithm, clfind2d, developed by Williams et al. (1994). The clfind2d routine determines the peak position, the FWHM size (not corrected for beam size), and the peak and total integrated flux density of the source based on specified contour levels. The algorithm requires two configuration parameters: i) the intensity threshold, i.e., the lowest contour level, Tlow, which determines the minimum emission to be included into the source; and ii) the contour level spacing, ΔT, which determines the required “contrast” between two sources to be considered as different objects. We set both parameters to 3σ (180 mJy). The selected 3σ contour levels turned out to give the best agreement with the identification by eye. With these parameter settings, the SMM 6c and 6d condensations are treated as a single source by clumpfind.
The J2000.0 coordinates of the peak 350 μm emission, source effective radius (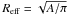 , where A is the projected area within the 3σ contour), and peak and integrated flux densities are listed in Cols. (2)–(6) of Table 3. In Col. (7), we also list the flux densities measured in a 40″ diameter aperture from the SABOCA map smoothed to the resolution of our LABOCA data. These flux densities were determined using the CRUSH-2 programme. The effective radius is only given for sources which are larger than the beam size. The total flux density uncertainty was derived from
, where A is the projected area within the 3σ contour), and peak and integrated flux densities are listed in Cols. (2)–(6) of Table 3. In Col. (7), we also list the flux densities measured in a 40″ diameter aperture from the SABOCA map smoothed to the resolution of our LABOCA data. These flux densities were determined using the CRUSH-2 programme. The effective radius is only given for sources which are larger than the beam size. The total flux density uncertainty was derived from 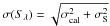 , where σcal is the absolute calibration error (adopted to be 30% of flux density), and σS is the uncertainty in the flux-density determination based on the rms noise near the source area. The 1σ rms noise in the smoothed SABOCA map, σ = 0.08 Jy beam-1, is slightly higher than in the original map. We note that the data reduction produces negative artefacts (“holes”) around regions of bright emission, most notably around SMM 3. This decreases the source’s peak intensity, introducing an additional uncertainty in the flux density. The uncertainties due to negative bowls are neglected in the subsequent analysis.
, where σcal is the absolute calibration error (adopted to be 30% of flux density), and σS is the uncertainty in the flux-density determination based on the rms noise near the source area. The 1σ rms noise in the smoothed SABOCA map, σ = 0.08 Jy beam-1, is slightly higher than in the original map. We note that the data reduction produces negative artefacts (“holes”) around regions of bright emission, most notably around SMM 3. This decreases the source’s peak intensity, introducing an additional uncertainty in the flux density. The uncertainties due to negative bowls are neglected in the subsequent analysis.
3.2. Spectra
The Hanning-smoothed spectra are shown in Fig. 3. The C17O(2 − 1) line is clearly detected towards all sources except SMM 4 where only a low-velocity component is observed at vLSR ≃ 1.7 km s-1 (hereafter, SMM 4-LVC, where LVC stands for low-velocity component). We note that SMM 4 shows strong NH3(1, 1) emission at about 9.1 km s-1 (Paper II). IRAS 05405-0117 (henceforth, IRAS 05405 etc.) shows two additional velocity components at ~1.3 and 3.0 km s-1, and Ori B9 N shows an additional and wide C17O(2−1) line at ~1.9 km s-1. There is also a hint of C17O(2−1) emission at the systemic velocity of the region (~9 km s-1) in the spectrum towards SMM 7, although the radial velocity of SMM 7, as determined from NH3(1, 1) measurements in Paper II, is 3.6 km s-1. The hf-structure of the C17O(2−1) line is partially resolved in IRAS 05399, SMM 1 and 3, and Ori B9 N.
The H13CO+(4−3) observations were carried out only towards three sources (IRAS 05399, SMM 1, and SMM 4). The line is only detected in IRAS 05399 and SMM 4-LVC. The DCO+(4−3) line is detected towards all the other sources except IRAS 05405, SMM 4, and SMM 5. The line is also quite weak (4σ) in Ori B9 N. Again, clear emission from an additional velocity component can be seen towards SMM 4 and Ori B9 N.
As already presented in Paper II, N2H+(3−2) emission is clearly seen in all sources with the exception of target position near Ori B9 N where the line is very weak. It should be noted, however, that towards SMM 4 only the LVC is detected. Ori B9 N shows an additional velocity component at about 1.8 km s-1. Finally, the N2D+(3−2) line was detected in IRAS 05399, SMM 1, SMM 3, IRAS 05405, SMM 4-LVC, and SMM 6. In addition, the line appears at ~3 km s-1 towards IRAS 05405.
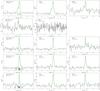 |
Fig. 3 Smoothed C17O(2−1), H13CO+(4−3), DCO+(4−3), N2H+(3−2), and N2D+(3−2) spectra. Overlaid on the C17O, DCO+, N2H+, and N2D+ spectra are the hf-structure fits. The relative velocities of individual hf components in these transitions are labelled with a short bar on the spectra towards IRAS 05399. The H13CO+ spectra are overlaid with a single Gaussian fit. The fits to the lines at the systemic velocity ~9 km s-1 are shown as green lines, whereas the red lines show fits to the lines at lower velocities. Note that H13CO+(4 − 3) observations were carried out only towards three sources and the line is detected only towards IRAS 05399 and SMM 4 (at ~1.5 km s-1). |
 |
Fig. 3 continued. |
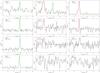 |
Fig. 3 continued. |
3.2.1. Other line detections
All the observed sources except SMM 5 show additional spectral lines in the frequency band covering the N2D+(3 − 2) transition. The line identification was done by using Weeds, which is an extension of CLASS (Maret et al. 2011), and the JPL and CDMS spectroscopic databases. We used the LTE modelling application of Weeds to check if all predicted lines of a candidate molecule are present in the observed spectrum. In some cases, we were able to reject some line candidates on the basis of non-detection of other transitions expected at nearby frequencies.
The JKa,Kc = 40,4−30,3 transition6 of ortho-D2CO at ~231.4 GHz was detected towards IRAS 05399 and SMM 1 in the LSB (see Fig. 4). Also, the J = 2−1 transition of C18O at ~219.56 GHz (LSB) was detected in the image sideband towards all sources except SMM 5 [marked with “(i)”; Fig. 5]. An additional velocity component is detected towards IRAS 05405 and SMM 4. Moreover, in the spectrum towards Ori B9 N several distinct velocity components are detected. The possible fourth velocity component of C18O could, in principle, be blended with the line at ~231.06 GHz, which can be assigned to either OCS(J = 19−18) (231 060.9830 MHz, Eu/kB = 110.9 K) or CH3NH2-E(JKa,Kc = 72,5−71,5) (231 060.6041 MHz, Eu/kB = 75.6 K) because these two transitions are also blended. However, these can almost certainly be excluded because of the high transition energies involved, and because both species are expected to be formed by grain-surface chemistry. Detection of these species in a cold core is therefore very unlikely. Note that the lines “leaking” from the rejected image band are heavily attenuated by the sideband filter. Therefore, we cannot establish the correct intensity scale for the C18O(2−1) lines.
In Table 4 we list the detected extra transitions, their rest frequencies, and upper-state energies. The rest frequencies and upper-state energies were assigned using JPL, CDMS, and Splatalogue7 (Remijan et al. 2007) spectroscopic databases. The D2CO detections are discussed further in Sect. 5.6.
3.3. Spectral-line parameters
The spectral line parameters are given in Table 5. In this table we give the radial velocity (vLSR), FWHM linewidth (Δv), peak intensity (TMB), integrated intensity (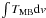 ), peak optical thickness of the line (τ0), and excitation temperature (Tex). For non-detections, the 3σ upper limit on the line intensity is given. The values of vLSR and Δv for C17O, DCO+, N2H+, and N2D+ were derived through fitting the hf structure. For the other lines these parameters were derived by fitting a single Gaussian to the line profile. Also, the values of TMB and
), peak optical thickness of the line (τ0), and excitation temperature (Tex). For non-detections, the 3σ upper limit on the line intensity is given. The values of vLSR and Δv for C17O, DCO+, N2H+, and N2D+ were derived through fitting the hf structure. For the other lines these parameters were derived by fitting a single Gaussian to the line profile. Also, the values of TMB and 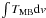 were determined from Gaussian fits. The integrated C17O(2 − 1) line intensities of IRAS 05399, SMM 1, 3, and 7, and Ori B9 N were calculated over the velocity range given in Col. (6) of Table 5 because the hf structure of the line is partially resolved in these cases. The uncertainties reported in vLSR and Δv represent the formal 1σ errors determined by the fitting routine, whereas those in TMB and
were determined from Gaussian fits. The integrated C17O(2 − 1) line intensities of IRAS 05399, SMM 1, 3, and 7, and Ori B9 N were calculated over the velocity range given in Col. (6) of Table 5 because the hf structure of the line is partially resolved in these cases. The uncertainties reported in vLSR and Δv represent the formal 1σ errors determined by the fitting routine, whereas those in TMB and 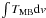 also include the 10% calibration uncertainty. We used RADEX8 (van der Tak et al. 2007) to determine the values of τ0 and Tex for the lines of C17O, H13CO+, DCO+, and N2H+. RADEX modelling is described in more detail in Sect. 4.4 where we discuss the determination of molecular column densities. For the rest of the lines, τ0 was determined through Weeds modelling (Sect. 4.4), and the associated error was estimated from the 10% calibration uncertainty. The lines appear to be optically thin in most cases, except that the N2H+ lines are mostly optically thick (τ0 > 1). The Tex values for C17O(2−1) are close to Tkin, indicating that the lines are nearly thermalised. The Tex [H13CO+(4−3)] values are found to be similar to Tex [DCO+(4−3)] . We note that the Tex values obtained for the J = 3−2 transition of N2H+ (3.8–5.0 K) are mostly comparable to the values Tex = 4.6−5.5 K determined or assumed in Paper II. For N2D+(3−2) we adopt as Tex the value derived for N2H+(3−2).
also include the 10% calibration uncertainty. We used RADEX8 (van der Tak et al. 2007) to determine the values of τ0 and Tex for the lines of C17O, H13CO+, DCO+, and N2H+. RADEX modelling is described in more detail in Sect. 4.4 where we discuss the determination of molecular column densities. For the rest of the lines, τ0 was determined through Weeds modelling (Sect. 4.4), and the associated error was estimated from the 10% calibration uncertainty. The lines appear to be optically thin in most cases, except that the N2H+ lines are mostly optically thick (τ0 > 1). The Tex values for C17O(2−1) are close to Tkin, indicating that the lines are nearly thermalised. The Tex [H13CO+(4−3)] values are found to be similar to Tex [DCO+(4−3)] . We note that the Tex values obtained for the J = 3−2 transition of N2H+ (3.8–5.0 K) are mostly comparable to the values Tex = 4.6−5.5 K determined or assumed in Paper II. For N2D+(3−2) we adopt as Tex the value derived for N2H+(3−2).
4. Analysis and results
4.1. Core properties derived from 350 μm emission
We used the 350-μm dust continuum data to determine the mass, peak beam-averaged column density of H2, and volume-averaged H2 number density of the cores and their condensations. The formulas for the mass and H2 column density can be found in Paper I [Eqs. (2) and (3) therein]. Note that in Eq. (3) of Paper I, the peak surface brightness is 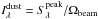 , where Ωbeam is the solid angle of the telescope beam. As the dust temperature of the sources, we used the gas kinetic temperatures listed in Col. (4) of Table 1, and assumed that Tdust = Tkin. For the subcondensations, such as SMM 6b, 6c, etc., it was assumed that Tdust is the same as in the “main” core. This assumption may not be valid, however, because in most cases the subcondensations lie outside the 40″ beam of the NH3 measurements used to derive Tkin in the main cores. Moreover, the temperature of an individual small condensation may be lower than the temperature of the parent core because of more effective shielding from the external radiation field. If the temperature is lower than assumed the mass and column density will be underestimated. As the dust opacity per unit dust mass at 350 μm, κ350 μm, we used the value 1.0 m2 kg-1 which was extrapolated from the Ossenkopf & Henning (1994, hereafter OH94) model describing graphite-silicate dust grains that have coagulated and accreted thick ice mantles over a period of 105 yr at a gas density of nH = n(H) + 2n(H2) ≃ 2n(H2) = 105 cm-3. The same dust model was adopted in Paper I (κ870 μm ≃ 0.17 m2 kg-1), and is expected to be a reasonable model for cold, dense molecular cloud cores9. We note that the sub-mm opacities recently calculated by Ormel et al. (2011) are comparable to the OH94 values (after 105 yr of coagulation). However, the dust opacities are likely to be uncertain by a factor of ≳ 2 (e.g., OH94; Motte & André 2001; Ormel et al. 2011). For the average dust-to-gas mass ratio, Rd ≡ ⟨ Mdust/Mgas ⟩ , we adopted the canonical value 1/100. Finally, we assumed a He/H abundance ratio of 0.1, which leads to the mean molecular weight per H2 molecule of μH2 = 2.8.
, where Ωbeam is the solid angle of the telescope beam. As the dust temperature of the sources, we used the gas kinetic temperatures listed in Col. (4) of Table 1, and assumed that Tdust = Tkin. For the subcondensations, such as SMM 6b, 6c, etc., it was assumed that Tdust is the same as in the “main” core. This assumption may not be valid, however, because in most cases the subcondensations lie outside the 40″ beam of the NH3 measurements used to derive Tkin in the main cores. Moreover, the temperature of an individual small condensation may be lower than the temperature of the parent core because of more effective shielding from the external radiation field. If the temperature is lower than assumed the mass and column density will be underestimated. As the dust opacity per unit dust mass at 350 μm, κ350 μm, we used the value 1.0 m2 kg-1 which was extrapolated from the Ossenkopf & Henning (1994, hereafter OH94) model describing graphite-silicate dust grains that have coagulated and accreted thick ice mantles over a period of 105 yr at a gas density of nH = n(H) + 2n(H2) ≃ 2n(H2) = 105 cm-3. The same dust model was adopted in Paper I (κ870 μm ≃ 0.17 m2 kg-1), and is expected to be a reasonable model for cold, dense molecular cloud cores9. We note that the sub-mm opacities recently calculated by Ormel et al. (2011) are comparable to the OH94 values (after 105 yr of coagulation). However, the dust opacities are likely to be uncertain by a factor of ≳ 2 (e.g., OH94; Motte & André 2001; Ormel et al. 2011). For the average dust-to-gas mass ratio, Rd ≡ ⟨ Mdust/Mgas ⟩ , we adopted the canonical value 1/100. Finally, we assumed a He/H abundance ratio of 0.1, which leads to the mean molecular weight per H2 molecule of μH2 = 2.8.
 |
Fig. 4 Ortho-D2CO(40,4 − 30,3) spectra towards IRAS 05399 and SMM 1. |
The integrated flux densities used to calculate the masses refer to core areas, A. Thus, in order to properly calculate the volume-average H2 number density, ⟨ n(H2) ⟩ , we use the effective radius, 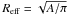 , in the formula
, in the formula 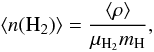 (1)where
(1)where 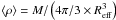 is the mass density, and mH is the mass of a hydrogen atom.
is the mass density, and mH is the mass of a hydrogen atom.
The results of the above calculations are presented in Table 6. The uncertainties in the derived parameters were propagated from the uncertainties in Tkin. We note that the 1σ rms noise on our SABOCA map, ~ 0.06 Jy beam-1, corresponds to a 3σ mass detection limit of ~ 0.1 M⊙ assuming Tdust = 10 K. In terms of column density, the 3σ detection limit is about 2.8 × 1021 cm-2.
Other detected species/transitions.
 |
Fig. 5 C18O(2−1) lines at 219 560.3568 MHz (JPL) arising from the image sideband. The x-axis range is different in the spectrum towards Ori B9 N, and the lines are overlaid with Gaussian fits for a better illustration. The blended OCS and CH3NH2 lines at ~231.06 GHz marked on the spectrum towards Ori B9 N can be excluded on the basis of high upper-state energies and formation chemistry of the species (see text). The line is likely to be caused by an additional C18O(2 − 1) velocity component. |
Spectral-line parameters.
4.2. Dust properties determined from 350 and 870 μm data
We can use our observations at two submm wavelengths, 350 and 870 μm, to estimate the dust colour temperature, Tdust, and dust emissivity spectral index, β [κλ = κ0(λ0/λ)β]. Note that according to the Wien displacement law, the wavelength of the peak of the blackbody radiation curve is about 290 μm at 10 K. Therefore, the Rayleigh-Jeans (R-J) approximation, hν ≪ kBT, is not valid for our 350 and 870 μm data.
In the following analysis, it is assumed that Tdust and β are constant across the source. We first smoothed the SABOCA map to the resolution of our LABOCA data, and then calculated the flux densities at both wavelengths in a fixed 40″ diameter aperture [Col. (7) of Table 3]. The resulting flux density ratios, 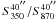 , are given in Col. (2) of Table 7. A dust colour temperature can be determined by fixing the value of β (see, e.g., Eq. (3) of Shetty et al. 2009). The value of β in the OH94 thick-ice dust model we adopted earlier is about 1.9 over the wavelength range λ ∈ [250, 1300 μm] (see also Shirley et al. 2005). By adopting the value β = 1.9, we derive the Tdust values in the range ~7.9−10.8 K (see Col. (3) of Table 7).
, are given in Col. (2) of Table 7. A dust colour temperature can be determined by fixing the value of β (see, e.g., Eq. (3) of Shetty et al. 2009). The value of β in the OH94 thick-ice dust model we adopted earlier is about 1.9 over the wavelength range λ ∈ [250, 1300 μm] (see also Shirley et al. 2005). By adopting the value β = 1.9, we derive the Tdust values in the range ~7.9−10.8 K (see Col. (3) of Table 7).
To calculate β from the ratio of two flux densities at different wavelengths, an estimate for the dust temperature is needed. We assumed that Tdust = Tkin, and applied Eq. (5) of Shetty et al. (2009). The resulting values, β ≃ 0.5 − 1.8, are listed in Col. (4) of Table 7. We note that Tkin measurements were obtained with a 40″ resolution, whereas the above flux density ratio was determined at about 20″ resolution. However, flux densities were measured in a 40″ aperture, which matches the resolution of our NH3 data.
4.3. SEDs
With the aid of our new 350 μm data, we were able to refine some of the protostellar SEDs presented in Paper I. As in Paper I, the SEDs constructed from the 24, 70, 350, and 870-μm flux densities were fitted by the sum of two modified blackbody curves of cold and warm temperatures (the original version of the fitting routine was written by Steinacker). Again, the dust model used to fit the SEDs is the OH94 model of thick ice mantles as adopted earlier in Sect. 4.1, incorporating a dust-to-gas mass ratio of 1/100. The SEDs of SMM 3, IRAS 05405, and SMM 4 are shown in Fig. 6. Note that in Paper I we utilised the IRAS flux densities to build the SED of IRAS 05405. In the present paper we have ignored the IRAS data from the fit because the ~arcminute resolution of the IRAS observations also includes emission from the nearby core SMM 4, confusing the emission from IRAS 05405. This probably explains why the 100-μm flux density of IRAS 05405 appears so high (~19.7 Jy).
 |
Fig. 6 Spectral energy distributions of three protostellar cores in Orion B9 built from Spitzer 24 and 70 μm, SABOCA 350 μm, and LABOCA 870-μm flux densities. Open circles in the middle panel represent IRAS data points at 12, 25, 60, and 100 μm (not used in the fit). The solid lines correspond to the two-temperature model fits to the data. Error bars (1σ) are indicated for all data points, but are mostly smaller than the symbol size. Note the appearance of a 10-μm silicate absorption feature in the SED of IRAS 05405, and the absorption “knee” at ~30 μm (most notably towards IRAS 05405) where a considerable change of κν occurs at the dust model used (OH94 and references therein). |
The SED fitting results are shown in Table 8. Column (2) of Table 8 gives the mass of the cold component, which represents the mass of the cold envelope, Mcold ≡ Menv. In Cols. (3)–(5), we list the luminosities of the cold and warm component, and the bolometric luminosity, Lbol = Lcold + Lwarm. The temperature of the cold component, Tcold, is given in Col. (6). Columns (7) and (8) give the Lcold/Lbol and Lsubmm/Lbol ratios, where the submm luminosity, Lsubmm, is defined to be the luminosity longward of 350 μm. In the last column of Table 8 we give the normalised envelope mass, 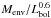 (Bontemps et al. 1996). The latter parameter, which is related to the outflow activity, decreases with time and can be used to further constrain the core evolutionary stage. We do not report the temperature and mass of the warm component, because i) the OH94 dust model of grains covered by thick ice mantles we have adopted may not be appropriate for the warm dust component; and ii) dust emission may not be optically thin at 24 and 70 μm, so the masses and temperatures of the warm component are not well constrained. In contrast, the luminosity of the warm component is not affected by these opacity effects.
(Bontemps et al. 1996). The latter parameter, which is related to the outflow activity, decreases with time and can be used to further constrain the core evolutionary stage. We do not report the temperature and mass of the warm component, because i) the OH94 dust model of grains covered by thick ice mantles we have adopted may not be appropriate for the warm dust component; and ii) dust emission may not be optically thin at 24 and 70 μm, so the masses and temperatures of the warm component are not well constrained. In contrast, the luminosity of the warm component is not affected by these opacity effects.
4.4. Molecular column densities and fractional abundances
The beam-averaged column densities of C17O, H13CO+, DCO+, and N2H+ were derived using a one-dimensional spherically symmetric non-LTE radiative transfer code called RADEX (see Sect. 3.3). RADEX uses the method of mean escape probability for an isothermal and homogeneous medium. The molecular data files (collisional rates) used in the RADEX excitation analysis were taken from the LAMDA database (Schöier et al. 2005). The C17O, H13CO+, DCO+, and N2H+ transitions are treated as a hypothetical unsplit transition. The input parameters in the off-line mode of RADEX are the gas kinetic temperature, H2 number density, and the width (FWHM) and intensity of the spectral line. We used the values of Tkin and ⟨ n(H2) ⟩ listed in Table 1. However, we multiplied the densities by 1.2 (He/H2 = 0.2) to take the collisions with He into account (see Sect. 4.1 of the RADEX manual10). As the input line intensity we used the main-beam brightness temperature, TMB. When the source is resolved, TMB is equal to the R-J equivalent radiation temperature, TR. The simulations aim to reproduce the observed line intensity and yield the values of τ0 and Tex, and the total column density of the molecule (Ntot). We varied Tkin and ⟨ n(H2) ⟩ according to their errors to estimate the uncertainties associated with τ0, Tex, and Ntot. The uncertainties in TMB and Δv were not taken into account, but test calculations showed that they lead to errors in column density that are comparable to those derived from the errors in temperature and density. We also note that the use of higher H2 densities for the cores derived from the SABOCA map [Col. (4), Table 6] would lead to lower column densities of the molecules because then the excitation would be closer to thermalisation.
Effective radius, mass, H2 column density, and volume-averaged H2 density derived from the 350 μm emission.
Dust colour temperature and emissivity index derived from 350-to-870 μm flux density ratio.
For N2D+ and o-D2CO there are no molecular data files available in the LAMDA database. The line optical thicknesses and total beam-averaged column densities of these molecules were determined through LTE modelling with CLASS/Weeds. The input parameters for a Weeds model are Ntot, Tex, source size (θs), linewidth (FWHM), and offset from the reference-channel velocity. The linewidth is directly determined from the observed line profile, so there are basically three free parameters left (Ntot, Tex, θs). Some of the model parameters may be degenerate, and cannot be determined independently (Schilke et al. 2006; Maret et al. 2011). The source size is degenerate with excitation temperature in the case of completely optically thick lines (τ ≫ 1), and with column density if the lines are completely optically thin (τ ≪ 1). We assumed that the source fills the telescope beam, i.e., that the beam filling factor is unity11, and thus the line brightness temperature is TB ≃ TMB (see Eqs. (1) and (2) in Maret et al. 2011). For N2D+, we used as Tex the values obtained for N2H+ from RADEX simulations. For the asymmetric top rotor o-D2CO we adopted the value Tex = 2/3 × Eu/kB, which gives a lower limit to the column density (Hatchell et al. 1998). The input Ntot was then varied until a reasonable fit to the line was obtained (see Fig. 7). The associated error estimate is based on the 10% calibration uncertainty. In the derivation of column densities, the line-strength contribution of hf components within the detected lines was taken into account, i.e., the column densities were corrected for the fraction of the total line strength given in brackets in Col. (6) of Table 5.
Fitting results of the SEDs.
We also determined the HCO+ column density from the column density of H13CO+. For this calculation, it was assumed that the carbon-isotope ratio is [12C] / [13C] = 60 (Hatchell et al. 1998; Savage et al. 2002). This value has been used in several previous studies, e.g., by Bergin et al. (1999) in their study of dense cores in Orion (including IRAS 05399)12.
We calculated the fractional abundances of the molecules by dividing the molecular column density by the H2 column density: x(mol) = N(mol)/N(H2). For this purpose, the values of N(H2) were derived from the LABOCA dust continuum map smoothed to the corresponding resolution of the line observations. The resolution of the H13CO+ observations (18′′) is slightly better, but comparable, to that of the original LABOCA data, and thus no smoothing was done in this case. The derived column densities and abundances are listed in Table 9. We stress that the reported uncertainties are formal and optimistic, and probably underestimate the true uncertainties. A stock chart showing the fractional abundances (excluding the additional velocity components) is presented in Fig. 8. The abundance errors were derived by propagating the errors in N(mol) and N(H2).
 |
Fig. 7 Example of the Weeds LTE modelling outlined in Sect. 4.4. The synthetic model spectrum is overlaid as a red line. |
Molecular column densities and fractional abundances with respect to H2.
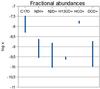 |
Fig. 8 A bar representation of fractional abundances on a logarithmic scale. The H13CO+ and HCO+ abundances derived towards IRAS 05399 are shown by a slightly stretch stock for a better illustration. |
4.5. CO depletion and deuterium fractionation
To estimate the amount of CO depletion in the cores, we calculated the CO depletion factor, fD. If x(CO)can is the “canonical” (undepleted) abundance, and x(CO)obs is the observed CO abundance, fD is given by 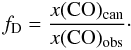 (2)We adopted the standard value x(CO)can = 9.5 × 10-5 (Frerking et al. 1982). To calculate the “canonical” C17O abundance we assumed the oxygen-isotopic ratio of [16O] / [18O] = 500 (e.g., Hatchell et al. 1998; Williams et al. 1998). When this is combined with the [18O] / [17O] ratio, for which we use the standard value 3.52 (Frerking et al. 1982), the value of x(C17O)can can be calculated as
(2)We adopted the standard value x(CO)can = 9.5 × 10-5 (Frerking et al. 1982). To calculate the “canonical” C17O abundance we assumed the oxygen-isotopic ratio of [16O] / [18O] = 500 (e.g., Hatchell et al. 1998; Williams et al. 1998). When this is combined with the [18O] / [17O] ratio, for which we use the standard value 3.52 (Frerking et al. 1982), the value of x(C17O)can can be calculated as ![\begin{equation} x({\rm C^{17}O})_{\rm can} = \frac{x({\rm CO})_{\rm can}}{[^{18}{\rm O}]/[^{17}{\rm O}]\times [^{16}{\rm O}]/[^{18}{\rm O}]}= \frac{x({\rm CO})_{\rm can}}{1760}\cdot \end{equation}](/articles/aa/full_html/2012/02/aa17849-11/aa17849-11-eq597.png) (3)The depletion factor fD is then calculated from fD = x(C17O)can/x(C17O)obs. The results are listed in Col. (2) of Table 10, where the ± -errors quoted were calculated by propagating the uncertainty in x(C17O)obs.
(3)The depletion factor fD is then calculated from fD = x(C17O)can/x(C17O)obs. The results are listed in Col. (2) of Table 10, where the ± -errors quoted were calculated by propagating the uncertainty in x(C17O)obs.
Degree of CO depletion and deuterium fractionation.
The degree of deuterium fractionation in HCO+ and N2H+ was calculated by dividing the column density of the deuterated isotopologue by its normal hydrogen-bearing form as RD(HCO+) ≡ N(DCO+)/N(HCO+) and RD(N2H+) ≡ N(N2D+)/N(N2H+). The error in RD was derived from the errors in the corresponding column densities (see Cols. (3) and (4) of Table 10). We note that the N2H+ and N2D+ column densities were calculated using the non-LTE and LTE models, respectively. Although not taken into account here, this may introduce an additional error of a factor of a few in RD, which should be bear in mind. Note, however, that in all cases the normal and deuterated forms of the molecule show line emission at similar radial velocities and with similar linewidths. Therefore, the two transitions are probably tracing the same gas which makes the derived deuteration levels reasonable.
4.6. Fractional ionisation
Fractional abundances of all the observed ionic species and their different isotopologues could be determined only towards IRAS 05399 and SMM 4-LVC. Therefore, the fractional ionisation and cosmic-ray ionisation rate of H2 were estimated only for these two sources. A rough estimate of the lower limit to the ionisation degree can be obtained by simply summing up the abundances of the ionic species (e.g., Caselli et al. 2002a; Paper I): 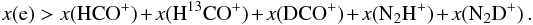 (4)This is based on the gas quasi-neutrality: the electron abundance equals the difference between the total abundances of the cations and anions. The resulting values are x(e) > 1.5 × 10-8 for IRAS 05399, and x(e) > 6.1 × 10-8 for SMM 4-LVC. In the outer envelope where CO is not heavily depleted, HCO+ is expected to be the main molecular ion. On the other hand, we do not have observational constraints on the abundances of H+, H
(4)This is based on the gas quasi-neutrality: the electron abundance equals the difference between the total abundances of the cations and anions. The resulting values are x(e) > 1.5 × 10-8 for IRAS 05399, and x(e) > 6.1 × 10-8 for SMM 4-LVC. In the outer envelope where CO is not heavily depleted, HCO+ is expected to be the main molecular ion. On the other hand, we do not have observational constraints on the abundances of H+, H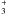 (and its deuterated isotopologues), H3O+, and metal ions (such as C+), all of which could play an important role in the ionisation level.
(and its deuterated isotopologues), H3O+, and metal ions (such as C+), all of which could play an important role in the ionisation level.
When the fractional ionisation in the source is determined, the abundance ratio RH ≡ [HCO+] / [CO] can be used to infer the cosmic-ray ionisation rate of H2, ζH2. By deriving a steady-state equation for the H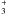 abundance, and applying it in the corresponding equation for HCO+, it can be shown that
abundance, and applying it in the corresponding equation for HCO+, it can be shown that ![\begin{equation} \label{eq:RH} R_{\rm H}=\frac{[\zeta_{\rm H_2}/n({\rm H_2})]k_{\rm H_3^+}}{\left[\beta_{\rm H_3^+} x({\rm e}) + k_{\rm H_3^+} x({\rm CO})+k_{\rm gr,\,H_3^+} x({\rm g})\right]\left [\beta_{\rm HCO^+} x({\rm e})+k_{\rm gr,\,HCO^+}x({\rm g}) \right]} \, , \end{equation}](/articles/aa/full_html/2012/02/aa17849-11/aa17849-11-eq626.png) (5)where
(5)where 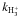 is the rate coefficient for the reaction
is the rate coefficient for the reaction 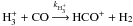 ,
, 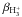 and βHCO+ are the dissociative recombination rate coefficients of H
and βHCO+ are the dissociative recombination rate coefficients of H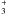 and HCO+, and
and HCO+, and 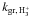 and kgr, HCO+ are the rate coefficients for the recombination of H
and kgr, HCO+ are the rate coefficients for the recombination of H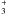 and HCO+ onto dust grains. The values of
and HCO+ onto dust grains. The values of 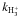 and βHCO+ were taken from the UMIST database13 (Woodall et al. 2007), whereas
and βHCO+ were taken from the UMIST database13 (Woodall et al. 2007), whereas 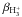 ,
, 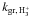 , and kgr, HCO+ were interpolated from Pagani et al. (2009a; Tables A.1 and B.1 therein). For the grain abundance, x(g), we used the value 2.64 × 10-12, which is based on the grain radius a = 0.1 μm, density ρgrain = 3 g cm-3, and the dust-to-gas mass ratio Rd = 1/100 (see, e.g., Eq. (15) in Pagani et al. 2009a). To calculate ζH2, we adopted as x(e) the summed abundance of ionic species. As n(H2) of SMM 4-LVC, we used the density of SMM 4. The obtained values are ζH2 ~ 2.6 × 10-17 s-1 towards IRAS 05399, and ~ 4.8 × 10-16 s-1 towards SMM 4-LVC. These values should be taken as lower limits in the sense that we have used the lower limits to x(e).
, and kgr, HCO+ were interpolated from Pagani et al. (2009a; Tables A.1 and B.1 therein). For the grain abundance, x(g), we used the value 2.64 × 10-12, which is based on the grain radius a = 0.1 μm, density ρgrain = 3 g cm-3, and the dust-to-gas mass ratio Rd = 1/100 (see, e.g., Eq. (15) in Pagani et al. 2009a). To calculate ζH2, we adopted as x(e) the summed abundance of ionic species. As n(H2) of SMM 4-LVC, we used the density of SMM 4. The obtained values are ζH2 ~ 2.6 × 10-17 s-1 towards IRAS 05399, and ~ 4.8 × 10-16 s-1 towards SMM 4-LVC. These values should be taken as lower limits in the sense that we have used the lower limits to x(e).
5. Discussion
5.1. Dust properties
By fixing the value of β to 1.9, we derived the dust temperatures in the range ~7.9−10.8 K. These are about 0.5–5.5 K lower than the gas temperatures in the same objects as derived from NH3. Due to the large uncertainties associated with Tdust, the near equality Tkin ≃ Tdust seems possible, as expected at high densities where collisional coupling between the gas and dust becomes efficient. Theoretical models have shown that in the dense interiors of starless cores [n(H2) ≳ 3 × 104 cm-3], the gas and dust temperatures are similar, although the gas can be slightly warmer due to cosmic-ray heating (e.g., Galli et al. 2002).
Some of the dust temperatures we derived are very low. In particular, for SMM 6 we obtained 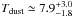 K. Theoretical models (e.g., Evans et al. 2001) and previous observational studies (e.g., Schnee et al. 2007a; Crapsi et al. 2007; Harju et al. 2008) have indicated that very low gas and dust temperatures (~6–7 K) can be reached in the dense interiors of dense cores.
K. Theoretical models (e.g., Evans et al. 2001) and previous observational studies (e.g., Schnee et al. 2007a; Crapsi et al. 2007; Harju et al. 2008) have indicated that very low gas and dust temperatures (~6–7 K) can be reached in the dense interiors of dense cores.
The dust emissivity spectral indices we derived, β ~ 0.5−1.8, are physically reasonable, and suggest that the assumption Tdust = Tkin is valid (cf. Schnee & Goodman 2005). Furthermore, the β values derived towards SMM 3, 5, and 7 are close to 1.9. We note that the dense gas and dust associated with the additional velocity components along the line of sight also affect the observed dust continuum properties (e.g., SMM 4). Therefore, the derived β values for these sources should be taken with caution.
We note, however, that a decrease of β from the “fiducial” value 2 to a shallower emissivity spectral index could be related to dust grain coagulation in the inner parts of dense cores (e.g., Miyake & Nakagawa 1993; OH94). Observational studies have found evidence that β decreases as a result of grain growth at high densities (e.g., Goldsmith et al. 1997; Visser et al. 1998). More recently, Kwon et al. (2009) found that β ≲ 1 for their sample of three Class 0 sources, resembling the values we found towards the Class 0 candidates IRAS 05405 and SMM 4. These results suggest that dust grains in the envelopes of Class 0 protostars can grow in size leading to a shallower spectral index of dust emissivity. Based on Herschel observations of cold interstellar clouds detected with the Planck satellite, Juvela et al. (2011) found that β decreases down to ~1 near internal heating sources. Radiative transfer modelling, however, suggests that such a decrement is due to line-of-sight temperature variations rather than changes in the grain properties. On the other hand, some studies of low-mass dense cores suggest that β could be larger than 2 (e.g., Shirley et al. 2005; Schnee et al. 2010a; Shirley et al. 2011). Also, recent studies of Planck-detected cold Galactic clumps indicate that β > 2 (Planck Collaboration et al. 2011). It is possible that β is anticorrelated with Tdust, so that in cold, dense cores the emissivity spectral index is steeper than 2.
5.2. Refined SEDs
Inclusion of the new 350 μm data to the source SEDs confirmed our earlier protostellar classifications. In Paper I, we classified the sources SMM 3, SMM 4, and IRAS 05405 as Class 0 objects. For such objects, the bolometric temperature is Tbol < 70 K, Lsubmm/Lbol ratio is >0.005, and they are characterised by the ratio 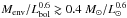 (André et al. 1993; Bontemps et al. 1996; André et al. 2000). All these conditions are fulfilled after the refined SED analysis.
(André et al. 1993; Bontemps et al. 1996; André et al. 2000). All these conditions are fulfilled after the refined SED analysis.
The SED models presented in Paper I suggested 350-μm flux densities of 21.7 Jy for SMM 3, 13.5 Jy for IRAS 05405, and 11.1 Jy for SMM 4 – much higher than determined in the present work. Compared to the SED results in Paper I, the envelope mass of SMM 3 and 4 is 1.0 M⊙ higher and 1.8 M⊙ lower, respectively; the mass of IRAS 05405 remains the same. The refined luminosity is lower by a factor of ~3 in all three cases. The temperature of the envelope, Tcold, resulting from the new SEDs is only 8 K for all sources. This is much lower than the values 11.6–16.1 K derived in Paper I. The Lcold/Lbol ratios derived here are also much smaller than estimated previously. Unlike deduced in Paper I, the cold component does not appear to dominate the total source luminosity. The Lsubmm/Lbol and 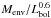 ratios derived here are mostly comparable to those obtained in Paper I.
ratios derived here are mostly comparable to those obtained in Paper I.
The angular resolution of the Spitzer images used is about 6″ at 24 μm, and 18″ at 70 μm. Photometry was done by point-source fitting, and the aperture size for photometry was 13″ at 24 μm, and 35″ at 70 μm (Paper I). The submm data points used in the SEDs were obtained at about 20″ resolution within a 40″ aperture. Therefore, the 70, 350, and 870-μm flux densities refer to a similar spatial scale (~0.09 pc). Direct comparison of these data with the 24 μm data is reasonable because we are dealing with 24-μm point sources. Our model SEDs therefore produce an approximation to the core parameters on ~0.09 pc spatial scale. Note that the sources SMM 4 and 4b are treated as one source and thus the corresponding SED should be taken with caution (Sect. 5.7.2).
5.3. Molecular column densities and abundances
The present N2H+ column densities are about 0.6–5 times the corresponding LTE column densities presented in Paper II; within the errors, the two values are comparable in the case of IRAS 05399, SMM 1, 3, and 7. Bergin et al. (1999) found the column densities N(N2H+) ~4.0 ± 0.3 × 1012 cm-2, N(H13CO+) ~6.9 ± 1.3 × 1011 cm-2, and N(DCO+) ~1.4 ± 0.2 × 1012 cm-2 towards IRAS 05399 using a statistical equilibrium model. Our values, which are derived towards a position of about 12″ northeast from the target position of Bergin et al. (1999), are about 3.8 ± 0.8, 9.3 ± 2.3, and 5.4 ± 1.0 times higher, respectively. Moreover, the C18O column density of ~5.8 ± 0.2 × 1015 cm-2 derived by Bergin et al. (1999) towards IRAS 05399 implies the value N(C17O) ~1.6 ± 0.1 × 1015 cm-2. The latter value is 4.7 ± 0.3 times higher than the value we have obtained. Besides a slightly different target position, these discrepancies are likely caused by the fact that Bergin et al. (1999) assumed optically thin emission, and the values n(H2) ~105 cm-3 and Tkin = 15 K in their non-LTE excitation analysis.
The C17O column densities and abundances we have derived are comparable to those found by Bacmann et al. (2002) for their sample of seven prestellar cores, and by Schnee et al. (2007b) towards the starless core TMC-1C. The N2H+ column densities are also comparable to those determined towards several other low-mass starless cores and Class 0 protostellar objects (Caselli et al. 2002b; Crapsi et al. 2005; Roberts & Millar 2007; Daniel et al. 2007; Emprechtinger et al. 2009; Friesen et al. 2010a,b). On the other hand, the N2D+ column densities we have obtained are generally larger than those derived for other low-mass cores in the studies mentioned above. Also, the H13CO+ and DCO+ column densities and abundances we derive are higher than those obtained by Anderson et al. (1999) in the R CrA region, and by Frau et al. (2010) for a sample of starless cores in the Pipe Nebula.
The HCO+ abundance of ~1.4 × 10-8 we have derived towards IRAS 05399 is relatively high. HCO+ could, in principle, increase in abundance at later evolutionary stages, when the CO gas-phase abundance is enhanced, and the reaction 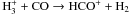 becomes efficient. However, the derived CO depletion factor in IRAS 05399 is relatively large, fD ~ 3.2, and thus the high HCO+ abundance may be the result of an alternative production pathway, C+ + H2O → HCO+ + H, viable in the shocks (Rawlings et al. 2000; Viti et al. 2002). We note that IRAS 05399 drives the HH92 jet, which lies close to the plane of the sky, and the presence of shock is therefore plausible (Gredel et al. 1992; Bally et al. 2002).
becomes efficient. However, the derived CO depletion factor in IRAS 05399 is relatively large, fD ~ 3.2, and thus the high HCO+ abundance may be the result of an alternative production pathway, C+ + H2O → HCO+ + H, viable in the shocks (Rawlings et al. 2000; Viti et al. 2002). We note that IRAS 05399 drives the HH92 jet, which lies close to the plane of the sky, and the presence of shock is therefore plausible (Gredel et al. 1992; Bally et al. 2002).
5.4. Depletion and deuteration
The CO depletion factors we have derived are in the range fD ~ 1.6 ± 0.5 − 10.8 ± 2.2 (fD = 3.6 ± 1.2 for SMM4-LVC and 0.8 ± 0.3 for Ori B9 N-LVC). Interestingly, the strongest depletion is observed towards the protostellar core SMM 3, and the lowest fD value is found in the starless core SMM 7. This could be caused by the fact that we do not observe exactly towards the submm peak of SMM 7, whereas we probe the dense envelope of SMM 3 (see Figs. 1 and 2). The second lowest fD value, 1.9 ± 0.3, is seen towards the starless core SMM 1. Bergin et al. (1999) mapped the IRAS 05399/SMM 1-system in C18O, CS, H13CO+, and DCO+, and found that the emission peaks coincide with the position of SMM 1, in agreement with our finding of low CO depletion. In general, the gas-phase CO abundance is expected to decrease during the prestellar phase of core evolution as a result of freeze out onto grain surfaces. During the protostellar phase, on the other hand, CO is expected to be released back into the gas phase via ice-mantle sublimation in the warmer envelope surrounding the protostar.
Caselli et al. (2008) estimated the value fD(CO) = 3.6 towards a position at the edge of Ori B9 N using the data from Caselli & Myers (1995) and Harju et al. (2006). This is higher than the value 2.1 ± 0.8 we have derived towards our target position near Ori B9 N (also at the core edge). For comparison, Bacmann et al. (2002) studied the level of CO depletion in prestellar cores, and found the values in the range 4.5–15.5. These are comparable to the values we have obtained. Moreover, Bacmann et al. (2002) found a positive correlation between fD and n(H2) of the form fD ∝ n(H2)0.4 − 0.8. No correlation was found between fD and n(H2) in the present study. Emprechtinger et al. (2009) derived the values fD ~ 0.3−4.4 towards a sample of Class 0 protostars.
We note that in the depletion analysis we used the value 9.5 × 10-5 for the undepleted CO abundance. However, this value is known to vary by a factor of ~2−3 between different star-forming regions. For example, Lacy et al. (1994) determined the CO abundance of ~2.7 × 10-4 towards NGC 2024 in Orion B. Adopting the latter value would result in ~2.8 times larger depletion factors.
The N2H+ deuteration degree in the Orion B9 cores is found to be in the range RD(N2H+) ≃ 0.035−0.992. The extreme value of 0.992 measured towards SMM 1 is, to our knowledge, the highest level of deuteration in N2H+ observed so far. This suggests that the core is chemically highly evolved but is in contradiction with the low fD value which points towards a younger evolutionary stage. SMM 1 could have been affected by the outflow driven by IRAS 05399, releasing CO into the gas phase and effectively resetting the chemical clock. In this case, the very high RD(N2H+) value would be remnant of the earlier CO-depleted phase, and not yet affected by the gas-phase CO which destroys N2H+ and N2D+. An opposite situation was found by Crapsi et al. (2004) towards the chemically evolved dense core L1521F which harbours a very low luminosity object or VeLLO (Bourke et al. 2006), where fD ~ 15 but RD(N2H+) is only ~0.1. For comparison, Crapsi et al. (2005) derived the values of RD(N2H+) in the range ≲ 0.02 − 0.44 for their sample of starless cores, and Daniel et al. (2007) derived comparable values of RD(N2H+) ~ 0.07−0.53 towards another sample of starless cores. Also, Roberts & Millar (2007) found RD(N2H+) values of < 0.01 − 0.31 for low-mass cores. Emprechtinger et al. (2009) found the values RD(N2H+) < 0.029−0.271 towards Class 0 objects. Pagani et al. (2009a) and Fontani et al. (2011) derived the value RD(N2H+) ~ 0.7 at the centre of the starless core L183 and towards the high-mass prestellar core candidate G034-G2 MM2, respectively, which were the highest fractionations reported before the present work.
The degree of deuterium fractionation in HCO+ could be derived only towards IRAS 05399 and SMM 4-LVC with the values RD(HCO+) ≃ 0.020 and 0.010, respectively. These are significantly lower than the corresponding RD(N2H+) values, in agreement with the results by Roberts & Millar (2007) and Emprechtinger et al. (2009). Such a trend is believed to be caused by the role of CO, which is the parent species of HCO+ and DCO+, but the main destroyer of H2D+, N2H+, and N2D+ molecules. Therefore, molecular deuteration proceeds most efficiently in regions where CO is depleted. In the warmer envelope layers where CO is not depleted, HCO+ can have a relatively high abundance, resulting in a lower line-of-sight average value of RD(HCO+) compared to that of N2H+ (Emprechtinger et al. 2009). Note that we have employed the DCO+(4−3) transition, which is expected to trace the inner part of the high-density envelope, where heating by the embedded protostar may affect the deuterium chemistry [by lowering the RD(HCO+) ratio]. For comparison, Jørgensen et al. (2004) determined similar RD(HCO+) values of ≲ 0.001 − 0.05 for a sample of 18 low-mass pre- and protostellar cores.
Previous studies of low-mass starless and protostellar cores have found correlations between the degree of CO depletion and deuterium fractionation (Bacmann et al. 2003; Jørgensen et al. 2004; Crapsi et al. 2005; Emprechtinger et al. 2009). No correlation was found between fD and RD(N2H+) in the present study. However, the values of fD and RD(N2H+) for the protostellar cores SMM 3 and IRAS 05399 are in rough agreement with the finding of Emprechtinger et al. (2009), i.e., that deuteration in the envelopes of Class 0 protostars increases as a function of fD.
5.5. Fractional ionisation
In Paper I, we determined the lower limits to x(e) of a few times 10-8, and upper limits of about six times 10-7 towards two target positions near the clump associated with IRAS 05405. The lower limits to x(e) derived in the present work are comparable to those from Paper I.
The standard relation between the electron abundance and the H2 number density is x(e) ~ 1.3 × 10-5n(H2)−1/2 (McKee 1989). This is based on the pure cosmic-ray ionisation with the rate 1.3 × 10-17 s-1 and includes no depletion of heavy elements. The standard relation yields the values x(e) ≃ 5.5 × 10-8 for IRAS 05399, and ≃ 6.7 × 10-8 for SMM 4-LVC. These are roughly comparable to the estimated lower limits to x(e). The values of ζH2 were found in Paper I to be ~1−2 × 10-16 s-1. These resemble the value derived here towards SMM 4-LVC, but are an order of magnitude higher than obtained for IRAS 05399. Instead, the value ζH2 ~ 2.6 × 10-17 s-1 derived towards IRAS 05399 is within a factor of two of the standard value. For comparision, observations of the Horsehead Nebula in Orion B by Goicoechea et al. (2009) could only be reproduced with ζH2 = 7.7 ± 4.6 × 10-17 s-1.
Caselli et al. (1998) determined x(e) in a sample of 24 low-mass cores consisting of both starless and protostellar objects. Their analysis was based on observations of CO, HCO+, and DCO+, and the resulting values were in the range 10-8 to 10-6, bracketing the values for the Orion B9 cores. They argued that the variation in x(e) among the sources is due to variations in metal abundance and ζH2; the latter was found to span a range of two orders of magnitude between 10-18 − 10-16 s-1. Some of this variation could be due to different cosmic-ray flux in the source regions. Williams et al. (1998) used observations of C18O, H13CO+, and DCO+ to determine the values 10-7.5 ≲ x(e) ≲ 10-6.5 in a similar sample of low-mass cores as Caselli et al. (1998), but using a slightly different analysis. They deduced a mean value of ζH2 = 5 × 10-17 s-1. Applying the same analysis as Williams et al. (1998), Bergin et al. (1999) found the ionisation levels of 10-7.3 ≲ x(e) ≲ 10-6.9 towards more massive cores (in Orion) than to those studied by Williams et al. (1998); Bergin et al. (1999) determined the fractional ionisation towards IRAS 05399 to lie in the range x(e) ~ 9.3 × 10-8 − 1.8 × 10-7. The lower limit we have derived, x(e) ~ 1.5 × 10-8, is about six times lower than the corresponding value derived by Bergin et al. (1999).
Recently, Padovani & Galli (2011) suggested that the magnetic field threading the core affects the penetration of cosmic rays, and can decrease the ionisation rate by a factor of ~3−4. The values of ζH2 determined through observations (so far) would then underestimate the inter-core values by the above factor, making the ζH2 values more comparable with those measured in diffuse clouds.
5.6. Deuterated formaldehyde
We have detected the ortho form of doubly deuterated formaldehyde, D2CO, towards the prestellar core SMM 1 and the protostellar core IRAS 05399. We derived the column densities and abundances of this molecule to be 1−2 × 1012 cm-2 and ~5−10 × 10-11, respectively. We note that the high-temperature statistical ortho/para ratio of D2CO is 2, and appears to be similar even in cold star-forming cores (see Roberts & Millar 2007).
Using the IRAM 30-m telescope, Ceccarelli et al. (1998) detected D2CO towards IRAS 16293-2422. It was the first reported detection of D2CO towards a low-mass star-forming core. A lower limit to the D2CO column density they obtained, ~1014 cm-2, is much higher than in our sources. Ceccarelli et al. (1998) speculated that such a high D2CO column density requires evaporation of D2CO from the grain mantles, where it is expected to be formed during the prestellar phase. Later, Ceccarelli et al. (2001) demonstrated that heating by the central protostar in IRAS 16293-2422 is responsible for the mantle evaporation, and injection of D2CO into the gas phase. Loinard et al. (2002) detected D2CO towards 19 low-mass protostellar cores, and found the D2CO/H2CO abundance ratios of ~0.02−0.4. Bacmann et al. (2003) and Roberts & Millar (2007) found D2CO column densities of ~0.5−2.7 × 1012 cm-2 towards a sample of low-mass prestellar and protostellar cores. These column densities are similar to those we have derived. However, the D2CO abundances derived by Bacmann et al. (2003) are somewhat lower than those we have derived. Recently, Bergman et al. (2011) found the D2CO column densities of ~2 × 1012 cm-2 towards a few positions in ρ Oph A, which are very similar to our values; towards the D-peak of ρ Oph A, however, they derived a high value of ~3.2 × 1013 cm-2.
D2CO is expected to evaporate from the CO-rich grain mantles when the dust temperature exceeds about 25 K (Ceccarelli et al. 2001). This would agree with the low CO depletion factor of 1.9 derived towards SMM 1, because the CO sublimation temperature is about 20 K (e.g., Aikawa et al. 2008). It is uncertain, however, why we see higher degree of CO depletion towards the nearby protostellar core IRAS 05399. Moreover, the gas kinetic temperature is only 11.9 K in SMM 1 and 13.5 K in IRAS 05399. It is possible, that the presence of gas-phase D2CO in these two sources is due to a non-thermal desorption mechanism (Roberts & Millar 2007). Bergman et al. (2011) suggested that cosmic-ray heating and the formation energy of the newly formed species could play an important role in the release of D2CO from the grain mantles in starless cores. In addition to these two mechanisms, shocks caused by the protostellar outflow driven by IRAS 05399 could be responsible in releasing D2CO from the icy grain mantles in the IRAS 05399/SMM 1-region. Towards IRAS 05399 the emission is perhaps dominated by the cool envelope whereas in SMM 1 we might see a component which is interacting with the outflow (causing the high gas-phase CO abundance).
5.7. Fragmentation in the Orion B9 cores
5.7.1. SMM 6 – a fragmented prestellar core
Figure 9 shows the SABOCA 350-μm image of the prestellar core SMM 6 overlaid with the LABOCA 870-μm contours. The core is filamentary in shape, and it is resolved into three to four subcondensations at 350 μm. The projected linear extent of core’s long axis is about 1 9 or 0.25 pc, and the core’s mass-per-length is Mline ≃ 33 M⊙ pc-1. The length-to-width ratio increases from about 1.9 at the NW end to about 7.4 at the SE end. The projected separation between the condensations is ~29″ or ~0.06 pc, where the sources 6c and 6d are treated as a single fragment. The measured separations should be taken as lower limits because of the possible projection effects.
9 or 0.25 pc, and the core’s mass-per-length is Mline ≃ 33 M⊙ pc-1. The length-to-width ratio increases from about 1.9 at the NW end to about 7.4 at the SE end. The projected separation between the condensations is ~29″ or ~0.06 pc, where the sources 6c and 6d are treated as a single fragment. The measured separations should be taken as lower limits because of the possible projection effects.
 |
Fig. 9 Detailed 350-μm SABOCA image of the fragmented prestellar core SMM 6 with power-law scaling. The contours are as in Fig. 2. The green plus sign indicates the position of our molecular-line observations. The colour-bar scale corresponds to Jy beam-1. |
To analyse the fragmentation of SMM 6 in more detail, we calculate its thermal Jeans length from 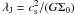 , where
, where 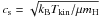 is the isothermal sound speed (at Tkin = 11 K), G is the gravitational constant, and Σ0 = μmHN(H2) is the surface density; μ is the mean molecular weight per free particle (2.33 for He/H = 0.1), and N(H2) refers to the central column density for which we use the value ~1022 cm-2 (see Col. (3) of Table 6). The resulting Jeans length is ~0.05 pc, very similar to the observed separation between the condensations. In Paper II, we found from NH3 measurements that turbulent motions within SMM 6 are subsonic, so their contribution to the effective sound speed would not increase the calculated Jeans length much. Assuming spherical geometry, the local Jeans mass of SMM 6 is MJ = 4π/3 × ⟨ ρ ⟩ (λJ/2)3 ~ 2.2 M⊙. The corresponding Jeans number is nJ = M/MJ ~ 4, which is similar to the number of observed subfragments. If the core substructure is caused by gravitational fragmentation, nJ is expected to give an approximate number of subfragments within the core (e.g., Rathborne et al. 2007).
is the isothermal sound speed (at Tkin = 11 K), G is the gravitational constant, and Σ0 = μmHN(H2) is the surface density; μ is the mean molecular weight per free particle (2.33 for He/H = 0.1), and N(H2) refers to the central column density for which we use the value ~1022 cm-2 (see Col. (3) of Table 6). The resulting Jeans length is ~0.05 pc, very similar to the observed separation between the condensations. In Paper II, we found from NH3 measurements that turbulent motions within SMM 6 are subsonic, so their contribution to the effective sound speed would not increase the calculated Jeans length much. Assuming spherical geometry, the local Jeans mass of SMM 6 is MJ = 4π/3 × ⟨ ρ ⟩ (λJ/2)3 ~ 2.2 M⊙. The corresponding Jeans number is nJ = M/MJ ~ 4, which is similar to the number of observed subfragments. If the core substructure is caused by gravitational fragmentation, nJ is expected to give an approximate number of subfragments within the core (e.g., Rathborne et al. 2007).
The measured radii of the individual condensations, ~0.01−0.02 pc, and their masses, ~ 0.1−0.2 M⊙, are smaller than the Jeans lengths of 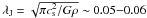 pc14, and Jeans masses of ~0.8−0.9 M⊙ (assuming Tkin = 11 K and densities from Col. (4) of Table 6). Because the subcondensations are presumably colder than 11 K, their masses and densities are likely to be higher. For instance, using the dust temperature Tdust = 7.9 K derived earlier for SMM 6 would result in about 4.4 times higher masses and densities. Lower temperature would also cause the Jeans length and mass to be smaller. At 7.9 K, these would be ~0.02 pc and ~0.2−0.3 M⊙, respectively. Therefore, the observed condensation properties can well be comparable to the corresponding Jeans values.
pc14, and Jeans masses of ~0.8−0.9 M⊙ (assuming Tkin = 11 K and densities from Col. (4) of Table 6). Because the subcondensations are presumably colder than 11 K, their masses and densities are likely to be higher. For instance, using the dust temperature Tdust = 7.9 K derived earlier for SMM 6 would result in about 4.4 times higher masses and densities. Lower temperature would also cause the Jeans length and mass to be smaller. At 7.9 K, these would be ~0.02 pc and ~0.2−0.3 M⊙, respectively. Therefore, the observed condensation properties can well be comparable to the corresponding Jeans values.
The above analysis suggests that thermal Jeans instability is the dominant process responsible for the core fragmentation. Moreover, the process of Jeans-fragmentation appears to have reached its final state at scale of the observed subcondensations. Thus, the condensations are potential sites to give birth to individual stars or small stellar systems. The condensations can grow in mass through (competitive) accretion from the parent core. In general, core fragmentation is believed to be the principal mechanism for the formation of binary and multiple stellar systems (e.g., Tohline 2002; Goodwin et al. 2007).
Besides the Jeans analysis, it is interesting to examine whether SMM 6, owing to its filamentary shape, is unstable to axisymmetric perturbations. For an unmagnetised isothermal filament the instability is reached if its Mline value exceeds the critical equilibrium value of 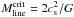 (e.g., Ostriker 1964; Inutsuka & Miyama 1992). For SMM 6,
(e.g., Ostriker 1964; Inutsuka & Miyama 1992). For SMM 6, 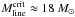 pc-1, and
pc-1, and 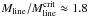 . Thus, SMM 6 appears to be a thermally supercritical filament susceptible to fragmentation, in agreement with the detected substructure. We note that in the case of a magnetised molecular-cloud filament,
. Thus, SMM 6 appears to be a thermally supercritical filament susceptible to fragmentation, in agreement with the detected substructure. We note that in the case of a magnetised molecular-cloud filament, 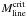 differs by only a factor of order unity from that of an unmagnetised case (Fiege & Pudritz 2000).
differs by only a factor of order unity from that of an unmagnetised case (Fiege & Pudritz 2000).
The three-dimensional velocity dispersion in SMM 6 is σ3D = 0.384 km s-1 (from the NH3 data in Paper II). This can be used to estimate the perturbation timescale, or the signal crossing time, τcross ≡ D/σ3D, where the diameter is D = 0.25 pc for SMM 6. The value of τcross is about 6.3 × 105 yr or ~2.8 times the free-fall timescale, τff. This timescale is comparable to the lifetime of the prestellar phase of core evolution of a few times τff (see Papers I and II and references therein).
The observed substructure within SMM 6 shows that core fragmentation can take place already during the early prestellar phase of evolution, i.e., before the formation of embedded protostar(s). Recently, Chen & Arce (2010) suggested that the three subcondensations in the prestellar core R CrA SMM 1A were formed through the fragmentation of the elongated parent core in the isothermal phase. It seems likely that SMM 6 has undergone a similar fragmentation process. The universality of fragmentation of the starless cores is unclear, however. For example, Schnee et al. (2010b) found that none of their 11 starless cores in Perseus are fragmented into smaller subunits. This is important knowledge when comparing the core mass function (CMF) to the stellar initial mass function (IMF), because the presence of substructure is believed to be one reason for the mass shift between the CMF and the IMF.
5.7.2. SMM 3, 4, and 7
The SABOCA 350-μm images of SMM 3, 4, and 7 overlaid with 870-μm contours are shown in more detail in Fig. 10. In SMM 3, there is a subcondensation, we called SMM 3b, at about 36″ from the protostar position. Next to that, at the borderline of the 3.3σ LABOCA 870-μm contour, there is another subcondensation, SMM 3c. The projected separation between SMM 3 and 3b is about 0.08 pc. This is very close to the thermal Jeans length for the whole SMM 3 core of 0.07 pc. In SMM 7, the subcondensation SMM 7b is at ~26″ or 0.06 pc from the “main” submm peak. Again, this is quite close to the local Jeans length of 0.09 pc. It thus seems possible, that the substructure within SMM 3 and 7 is caused by thermal Jeans fragmentation. We note that the SMM 3/3b-system is qualitatively similar to L1448 IRS2/2E, where there is a dust condensation (IRS 2E) next to a Class 0 protostar; L1448 IRS2E is the most promising candidate of the “first hydrostatic core” detected so far (Chen & Arce 2010).
 |
Fig. 10 Zoom-in views of Fig. 2 with linear scaling towards SMM 3, 4, and 7. The box symbols mark the positions of the Spitzer 24-μm point sources. The green plus signs show the positions of our molecular-line observations. In each panel, the colour-bar scale corresponds to Jy beam-1. |
SMM 4 is resolved into two fragments at 350 μm. The eastern one, SMM 4b, is associated with a Spitzer source at 24 and 70 μm. In Papers I and II, we proposed that N2H+ could be depleted in the dense envelope of SMM 4. This was based on two observational results: i) the N2H+(1−0) map of Caselli & Myers (1994) shows no emission peaks near SMM 4; and ii) the N2H+(3−2) line was not detected towards SMM 4 at the systemic velocity ~9 km s-1 (see also Fig. 3). The NH3 lines, on the other hand, can be seen at ~9 km s-1 with an additional velocity component at about 1.6 km s-1 (Paper II). The present molecular-line observations, however, revealed a somewhat surprising result: all the observed lines are at an LSR velocity of about 1.5–1.7 km s-1, not at ~9 km s-1. The absence of molecular-line emission at ~9 km s-1 is probably not due to chemistry, because it is not reasonable to think that all the observed species, in particular DCO+ and N2D+, would have been depleted (e.g., Lee et al. 2003). Instead, it seems that SMM 4 is a member of the low-velocity part of Orion B discussed in Paper II. Such a chance line-of-sight alignment is surprising, because the nearby sources SMM 5, IRAS 05405, and Ori B9 N show line emission at ~9 km s-1. The reason why we detected the 9-km s-1 NH3 lines towards SMM 4 could be due to the large beam size (40′′) of the observations; NH3 emission could have been captured from the nearby cores by the beam. Also, the morphology of the N2H+ integrated intensity map of Caselli & Myers (1994) can be understood if the velocity range used to construct the map only covers emission near 9 km s-1; SMM 4 emits at lower velocity and does not show up on the map. The dust properties of SMM 4, such as its SED, should be taken with caution as the core consists of subcondensations. It also seems possible that the emission from the clump near SMM 4 is “contaminated” by an unrelated object(s) along the line of sight.
6. Summary and conclusions
We have carried out a (sub)mm study of dense cores in Orion B9. We used APEX to map the region at 350 μm, and to observe the transitions of C17O, H13CO+, DCO+, N2H+, and N2D+. These data were compared with our previous LABOCA 870-μm data. The principal aim of this study was to investigate the dust emission of the cores near the peak of their SEDs, and the degrees of CO depletion, deuterium fractionation, and ionisation in the sources. Our primary results are summarised as follows:
-
1.
All the 870-μm cores within the boundaries of our SABOCA map were detected at 350 μm. The strongest 350-μm source in the region is SMM 3, a candidate Class-0 protostellar core.
-
2.
Four of the 870-μm cores, namely SMM 3, 4, 6, and 7, were resolved into at least two condensations at 350 μm. In particular, the elongated prestellar core SMM 6 was resolved into three to four very low-mass subcondensations, showing that core fragmentation can take place during the prestellar phase of evolution. In all cases, the origin of substructure can be explained by thermal Jeans-type fragmentation.
-
3.
The dust temperatures derived from the 350-to-870-μm flux density ratio are very low, only
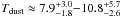 K. The corresponding gas temperatures are typically a few kelvins higher. We also derived the submm dust emissivity spectral indices using the assumption Tdust = Tgas, and they are in the range β ≈ 0.5 ± 0.8 − 1.8 ± 0.6. The uncertainties in β are large, and within the errors the values are comparable to the fiducial value β = 2.
K. The corresponding gas temperatures are typically a few kelvins higher. We also derived the submm dust emissivity spectral indices using the assumption Tdust = Tgas, and they are in the range β ≈ 0.5 ± 0.8 − 1.8 ± 0.6. The uncertainties in β are large, and within the errors the values are comparable to the fiducial value β = 2. -
4.
We refined some of the protostellar SEDs presented in Paper I by adding the observed 350-μm flux densities. No radical changes were found, and the sources IRAS 05405-0117 and SMM 3 and 4 are classified as Class 0 objects, in agreement with our previous results.
-
5.
The CO depletion factors were found to lie in the range fD ~ 1.6 ± 0.5 − 10.8 ± 2.2. We found no systematic difference in fD between the starless and protostellar cores. In accordance with previous observations and theoretical predictions the most severe CO depletion is seen towards the core with highest average density, SMM 3. The degree of deuteration in N2H+ was found to be in the range N(N2D+)/N(N2H+) ≃ 0.035 ± 0.006 − 0.992 ± 0.267. The N(DCO+)/N(HCO+) ratio was found to be about 1–2%, comparable to those seen in other low-mass star-forming regions.
-
6.
The fractional ionisation could only be derived towards IRAS 05399-0121 and SMM 4-LVC with the lower limits of x(e) > 1.5 × 10-8 and > 6.1 × 10-8, respectively. These values are comparable to the fractional ionisations we derived earlier towards a few target positions near IRAS 05405-0117 and SMM 4. The cosmic-ray ionisation rate of H2 implied by the derived lower x(e) limit is ζH2 ~ 2.6 × 10-17 s-1 towards IRAS 05399-0121, and ~4.8 × 10-16 s-1 towards SMM 4-LVC. The former value, which does not suffer from line-of-sight contamination, is within a factor of two of the “standard” value 1.3 × 10-17 s-1.
-
7.
The highest degree of deuteration in N2H+, ~0.99, was derived towards the prestellar core SMM 1. To our knowledge, this is the most extreme level of N2H+ deuteration reported so far. We also detected D2CO emission towards SMM 1 with an abundance of several times 10-11. Because D2CO is expected to be formed through the grain-surface chemistry, its presence in the gas phase in SMM 1 could be due to shocks driven by the jet from IRAS 05399-0121, resulting in the release of D2CO from the grain mantles. This conforms to the low CO depletion factor of 1.9 derived towards SMM 1. The very high N2H+ deuteration could be remnant of the earlier CO-depleted phase, and not yet affected by the destroying effect of gas-phase CO.
-
8.
It seems likely that the elongated clump associated with IRAS 05405-0117 and SMM 4 consists of physically independent objects that form a single clump only in projection along the line of sight.
In Papers I and II we discussed the origin of dense cores in Orion B9. The region could have been affected by the feedback from the nearby Ori OB1b subgroup of the Orion OB1 association (resembling the process termed “cloud shuffling” by Elmegreen 1979). This feedback process may have played a role in sweeping up the gas into dense shells and filaments out of which the dense cores were later fragmented. This picture is supported by the kinematics of Orion B9 (low-velocity line-of-sight components). The present observational results suggest that the further fragmentation of cores into smaller condensations is caused by the thermal Jeans instability. The observations presented in this paper also reveal the intricate chemistry of the cores, such as heterogeneous depletion and deuteration among the cores. This suggests that the individual Orion-B9 cores, though possibly formed collectively in the parent filaments, are evolving chemically at different rates.
Comparison of our LABOCA map to the new SABOCA map together with Spitzer images showed that the LABOCA observations were not well-pointed. The SABOCA peaks appeared to systematically lie southeast from the LABOCA peak positions. The difference in angular resolution between SABOCA and LABOCA data did not appear to be the cause of the offset in peak positions; by smoothing the SABOCA map to correspond the resolution of our LABOCA data, and regridding the maps onto the same grid, the offsets still remained. We used the brightest SABOCA 350-μm source in the region, SMM3, as a reference to adjust the pointing of our LABOCA map. The pointing of the LABOCA map was shifted by 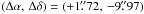 . Unfortunately, the target positions of our molecular-line observations, which were chosen to be the LABOCA peak positions from our previous map, are now slightly offset from the dust maxima (but still within the beam size for most line observations).
. Unfortunately, the target positions of our molecular-line observations, which were chosen to be the LABOCA peak positions from our previous map, are now slightly offset from the dust maxima (but still within the beam size for most line observations).
For asymmetric top molecules such as D2CO, Ka and Kc refer to the projection of the angular momentum along the a and c principal axes. The detected o-D2CO transition exhibits a-type selection rules (ΔKa = 0, ± 2,... and ΔKc = ± 1, ± 3,...) (Gordy & Cook 1984).
For comparison, for dust grains covered by thin ice mantles at a density 105 cm-3, κ350 μm ≃ 0.78 m2 kg-1. The κ350 μm value we have adopted is the same as in the OH94 model of grains with thin ice mantles at a density 106 cm-3. At 106 cm-3 with thick ice mantles κ350 μm rises to about 1.1 m2 kg-1.
The 27″ beam of our N2D+ observations is comparable to the extent of the strongest dust emission region within the cores. On the other hand, N2D+ emission has been found to trace dust emission very well in low-mass dense cores (e.g., Crapsi et al. 2005). Therefore, the assumption of unity beam filling factor is reasonable. For o-D2CO, the beam filling factor may be < 1. For example, Bergman et al. (2011), using the same resolution as we (27″), derived the filling factor of ≃ 0.5 for the o-D2CO(40, 4 − 30, 3) emission region in ρ Oph A. Moreover, the filling factor is lower if the cores contain unresolved small-scale structure.
Spectral lines of 12C-isotopologue of HCO+ are likely to be optically thick. Therefore, the HCO+ deuteration can be better investigated through the DCO+/H13CO+ column density ratio. However, a caveat should be noted here. The HCO+ molecules are produced directly from CO (Sect. 4.6). On the other hand, at low temperature, CO is susceptible to the exothermic isotopic charge exchange reaction 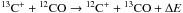 , where ΔE/kB = 35 K (Watson et al. 1976). This is expected to cause considerable 13C-fractionation in cold and dense gas, which complicates the deuteration analysis.
, where ΔE/kB = 35 K (Watson et al. 1976). This is expected to cause considerable 13C-fractionation in cold and dense gas, which complicates the deuteration analysis.
Acknowledgments
We acknowledge the staff at the APEX telescope for performing the service-mode observations presented in this paper. We would also like to thank the people who maintain the CDMS and JPL molecular spectroscopy databases, and the Splatalogue Database for Astronomical Spectroscopy. The authors would like to thank the anonymous referee for useful comments. We acknowledge support from the Academy of Finland through grants 127015 and 132291. This work makes use of observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory (JPL), California Institute of Technology under a contract with NASA. Moreover, this research has made use of NASA’s Astrophysics Data System and the NASA/IPAC Infrared Science Archive, which is operated by the JPL, California Institute of Technology, under contract with the NASA.
References
- Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, I. M., Caselli, P., Haikala, L. K., & Harju, J. 1999, A&A, 347, 983 [NASA ADS] [Google Scholar]
- André, Ph., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- André, Ph., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russell (Tuscon, AZ: Univ. Arizona Press), 59 [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2003, ApJ, 585, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bally, J., Reipurth, B., & Aspin, C. 2002, ApJ, 574, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Belitsky, V., Lapkin, I., Vassilev, V., et al. 2007, in Proceedings of joint 32nd International Conference on Infrared Millimeter Waves and 15th International Conference on Terahertz Electronics, September 3–7, City Hall, Cardiff, Wales, UK, 326 [Google Scholar]
- Bergin, E. A., Plume, R., Williams, J. P., & Myers, P. C. 1999, ApJ, 512, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Bergman, P., Parise, B., Liseau, R., & Larsson, B. 2011, A&A, 527, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bontemps, S., André, Ph., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 [NASA ADS] [Google Scholar]
- Bourke, T. L., Myers, P. C., Evans, N. J., II, et al. 2006, ApJ, 649, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Dore, L. 2005, A&A, 433, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., & Myers, P. C. 1994, in Clouds, Cores, and Low Mass Stars, ed. D. P. Clemens, & R. Barvainis, 65, 52 [Google Scholar]
- Caselli, P., & Myers, P. C. 1995, ApJ, 446, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002a, ApJ, 565, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002b, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Vastel, C., Ceccarelli, C., et al. 2008, A&A, 492, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Castets, A., Loinard, L., et al. 1998, A&A, 338, L43 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., et al. 2001, A&A, 372, 998 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, X., & Arce, H. G. 2010, ApJ, 720, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Arce, H. G., Zhang, Q., et al. 2010, ApJ, 715, 1344 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2004, A&A, 420, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daniel, F., Cernicharo, J., Roueff, E., et al. 2007, ApJ, 667, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1979, ApJ, 231, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Emprechtinger, M., Caselli, P., Volgenau, N. H., et al. 2009, A&A, 493, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, N. J., II, Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000, MNRAS, 311, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Palau, A., Caselli, P., et al. 2011, A&A, 529, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frau, P., Girart, J. M., Beltrán, M. T., et al. 2010, ApJ, 723, 1665 [NASA ADS] [CrossRef] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shimajiri, Y., & Takakuwa, S. 2010a, ApJ, 708, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Myers, P. C., et al. 2010b, ApJ, 718, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., & Stutzki, J. 1989, ARA&A, 27, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2009, A&A, 498, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Bergin, E. A., & Lis, D. C. 1997, ApJ, 491, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., Kroupa, P., Goodman, A., & Burkert, A. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tuscon, AZ: Univ. Arizona Press), 133 [Google Scholar]
- Gordy, W., & Cook, R. L. 1984, Microwave Molecular Spectroscopy (New York: Wiley) [Google Scholar]
- Gredel, R., Reipurth, B., & Heathcote, S. 1992, A&A, 266, 439 [NASA ADS] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harju, J., Haikala, L. K., Lehtinen, K., et al. 2006, A&A, 454, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harju, J., Juvela, M., Schlemmer, S., et al. 2008, A&A, 482, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&AS, 133, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S.-I., & Miyama, S. M. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Rosolowsky, E., Tafalla, M., & Kirk, H. 2010, ApJ, 711, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pelkonen, V.-M., et al. 2011, A&A, 527, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Philipp, S. D., Krämer, I., et al. 2006, A&A, 454, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, A. 2008, Proc. SPIE, 7020, 45 [NASA ADS] [Google Scholar]
- Kwon, W., Looney, L. W., Mundy, L. G., et al. 2009, ApJ, 696, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, J. H., Knacke, R., Geballe, T. R., & Tokunaga, A. T. 1994, ApJ, 428, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Ladd, E. F., Fuller, G. A., & Deane, J. R. 1998, ApJ, 495, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Evans, N. J., II, Shirley, Y. L., & Tatematsu, K. 2003, ApJ, 583, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Castets, A., Ceccarelli, C., et al. 2002, Planet. Space Sci., 50, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., et al. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKee, C. F. 1989, ApJ, 345, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., et al. 2009, A&A, 500, 845 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miettinen, O., Harju, J., Haikala, L. K., & Juvela, M. 2010, A&A, 524, A91 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Min, M., Tielens, A. G. G. M., et al. 2011, A&A, 532, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 (OH94) [NASA ADS] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009a, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Daniel, F., & Dubernet, M.-L. 2009b, A&A, 494, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, I. R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Planck Collaboration, Ade, P. A. R., Aghanim, N., Arnaud, M., et al. 2011, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathborne, J. M., Simon, R., & Jackson, J. M. 2007, ApJ, 662, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, J. M. C., Taylor, S. D., & Williams, D. A. 2000, MNRAS, 313, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Reichertz, L. A., Weferling, B., Esch, W., & Kreysa, E. 2001, A&A, 379, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remijan, A. J., Markwick-Kemper, A., & ALMA Working Group on Spectral Line Frequencies 2007, BAAS, 38, 963 [NASA ADS] [Google Scholar]
- Roberts, H., & Millar, T. J. 2007, A&A, 471, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, C., Apponi, A. J., Ziurys, L. M., & Wyckoff, S. 2002, ApJ, 578, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Comito, C., Thorwirth, S., et al. 2006, A&A, 454, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid-Burgk, J., Muders, D., Müller, H. S. P., & Brupbacher-Gatehouse, B. 2004, A&A, 419, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schnee, S., & Goodman, A. 2005, ApJ, 624, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Kauffmann, J., Goodman, A., & Bertoldi, F. 2007a, ApJ, 657, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Caselli, P., Goodman, A., et al. 2007b, ApJ, 671, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Enoch, M., Noriega-Crespo, A., et al. 2010a, ApJ, 708, 127 [Google Scholar]
- Schnee, S., Enoch, M., Johnstone, D., et al. 2010b, ApJ, 718, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., et al. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, Y. L., Nordhaus, M. K., Grcevich, J. M., et al. 2005, ApJ, 632, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, Y. L., Huard, T. L., Pontoppidan, K. M., et al. 2011, ApJ, 728, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., De Breuck, C., et al. 2010, The Messenger, 139, 20 [NASA ADS] [Google Scholar]
- Tohline, J. E. 2002, ARA&A, 40, 349 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., et al. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008a, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassilev, V., Henke, D., Lapkin, I., et al. 2008b, IEEE Microwave and Wireless Components Letters, 55, 18, 1 [Google Scholar]
- Visser, A. E., Richer, J. S., Chandler, C. J., & Padman, R. 1998, MNRAS, 301, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Natarajan, S., & Williams, D. A. 2002, MNRAS, 336, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, W. D., Anicich, V. G., & Huntress, W. T., Jr. 1976, ApJ, 205, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., Bergin, E. A., Caselli, P., et al. 1998, ApJ, 503, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Effective radius, mass, H2 column density, and volume-averaged H2 density derived from the 350 μm emission.
Dust colour temperature and emissivity index derived from 350-to-870 μm flux density ratio.
All Figures
 |
Fig. 1 Spitzer/MIPS 24-μm image of the central part of Orion B9 overlaid with contours showing the LABOCA 870-μm dust continuum emission. The contours go from 0.1 (~3.3σ) to 1.0 Jy beam-1 in steps of 0.1 Jy beam-1. The 24-μm image is shown with a logarithmic scaling to improve the contrast between bright and faint features. The colour bar indicates the 24-μm intensity scale in units of MJy sr-1. The green plus signs show the target positions of our molecular-line observations (i.e., the submm peak positions of the LABOCA map before adjusting the pointing; see text). The green line shows the base and northwest tip of the HH 92 jet driven by IRAS 05399-0121 (Bally et al. 2002). The 0.2-pc scale bar and the effective LABOCA beam HPBW (~20″) are shown in the bottom left (Paper I). |
| In the text | |
 |
Fig. 2 SABOCA 350-μm image (smoothed to |
| In the text | |
 |
Fig. 3 Smoothed C17O(2−1), H13CO+(4−3), DCO+(4−3), N2H+(3−2), and N2D+(3−2) spectra. Overlaid on the C17O, DCO+, N2H+, and N2D+ spectra are the hf-structure fits. The relative velocities of individual hf components in these transitions are labelled with a short bar on the spectra towards IRAS 05399. The H13CO+ spectra are overlaid with a single Gaussian fit. The fits to the lines at the systemic velocity ~9 km s-1 are shown as green lines, whereas the red lines show fits to the lines at lower velocities. Note that H13CO+(4 − 3) observations were carried out only towards three sources and the line is detected only towards IRAS 05399 and SMM 4 (at ~1.5 km s-1). |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 Ortho-D2CO(40,4 − 30,3) spectra towards IRAS 05399 and SMM 1. |
| In the text | |
 |
Fig. 5 C18O(2−1) lines at 219 560.3568 MHz (JPL) arising from the image sideband. The x-axis range is different in the spectrum towards Ori B9 N, and the lines are overlaid with Gaussian fits for a better illustration. The blended OCS and CH3NH2 lines at ~231.06 GHz marked on the spectrum towards Ori B9 N can be excluded on the basis of high upper-state energies and formation chemistry of the species (see text). The line is likely to be caused by an additional C18O(2 − 1) velocity component. |
| In the text | |
 |
Fig. 6 Spectral energy distributions of three protostellar cores in Orion B9 built from Spitzer 24 and 70 μm, SABOCA 350 μm, and LABOCA 870-μm flux densities. Open circles in the middle panel represent IRAS data points at 12, 25, 60, and 100 μm (not used in the fit). The solid lines correspond to the two-temperature model fits to the data. Error bars (1σ) are indicated for all data points, but are mostly smaller than the symbol size. Note the appearance of a 10-μm silicate absorption feature in the SED of IRAS 05405, and the absorption “knee” at ~30 μm (most notably towards IRAS 05405) where a considerable change of κν occurs at the dust model used (OH94 and references therein). |
| In the text | |
 |
Fig. 7 Example of the Weeds LTE modelling outlined in Sect. 4.4. The synthetic model spectrum is overlaid as a red line. |
| In the text | |
 |
Fig. 8 A bar representation of fractional abundances on a logarithmic scale. The H13CO+ and HCO+ abundances derived towards IRAS 05399 are shown by a slightly stretch stock for a better illustration. |
| In the text | |
 |
Fig. 9 Detailed 350-μm SABOCA image of the fragmented prestellar core SMM 6 with power-law scaling. The contours are as in Fig. 2. The green plus sign indicates the position of our molecular-line observations. The colour-bar scale corresponds to Jy beam-1. |
| In the text | |
 |
Fig. 10 Zoom-in views of Fig. 2 with linear scaling towards SMM 3, 4, and 7. The box symbols mark the positions of the Spitzer 24-μm point sources. The green plus signs show the positions of our molecular-line observations. In each panel, the colour-bar scale corresponds to Jy beam-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.