| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117458 | |
| Published online | 30 January 2012 | |
A quantitative study of O stars in NGC 2244 and the Monoceros OB2 association⋆
1 LUPM–UMR 5299, CNRS & Université Montpellier II, Place Eugène Bataillon, 34095 Montpellier Cedex 05, France
e-mail: fabrice.martins@univ-montp2.fr
2 Institut d’Astrophysique et de Géophysique, Université de Liège, Bât. B5C, Allée du 6 Août 17, 4000 Liége, Belgium
3 Department of Physics and Astronomy, University of Pittsburgh, 3941 O’Hara Street, Pittsburgh, PA 15260, USA
Received: 10 June 2011
Accepted: 13 October 2011
Aims. Our goal is to determine the stellar and wind properties of seven O stars in the cluster NGC 2244 and three O stars in the OB association Mon OB2. These properties give us insight into the mass loss rates of O stars. They allow us to both check the validity of rotational mixing in massive stars and to better understand the effects of the ionizing flux and wind mechanical energy release on the surrounding interstellar medium and its influence on triggered star formation.
Methods. We collected optical and UV spectra of the target stars that we analyzed by means of atmosphere models computed with the code CMFGEN. The spectra of binary stars were disentangled and the components studied separately.
Results. All stars have an evolutionary age less than 5 million years, with the most massive stars being among the youngest. Nitrogen surface abundances show no clear relation with projected rotational velocities. Binaries and single stars show the same range of enrichment. This is attributed to the youth and/or wide separation of the binary systems in which the components have not (yet) experienced strong interaction. A clear trend toward greater enrichment in higher luminosity objects is observed, consistent with what evolutionary models with rotation predict for a population of O stars at any given age. We confirm the weakness of winds in late O dwarfs. In general, mass loss rates derived from UV lines are lower than mass loss rates obtained from Hα. The UV mass loss rates are even lower than the single-line driving limit in the latest type dwarfs. These issues are discussed in the context of the structure of massive stars winds. The evolutionary and spectroscopic masses are in agreement above 25 M⊙, but the uncertainties are large. Below this threshold, the few late-type O stars studied here indicate that the mass discrepancy still seems to hold.
Key words: stars: fundamental parameters / stars: winds, outflows / stars: early-type / Hii regions
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Massive stars play key roles in various fields of astrophysics thanks to their strong ionizing fluxes, powerful winds and extreme stellar properties. They have been recognized as the precursors of long-soft gamma-ray bursts. Population III stars are thought to consist of very massive stars with exceptionally hard UV luminosity. As they live rapidly, they are excellent tracers of star formation. But they also trigger the formation of new generations of stars through their feedback effects. The heavy elements produced in their cores are injected into the interstellar medium by stellar winds and supernovae ejecta, contributing to the chemical evolution of galaxies. Constraining their properties and understanding quantitatively their evolution and feedback effects is thus of interest for fields well beyond pure stellar physics.
Sample stars and photometry.
In addition to their mass, the evolution of massive stars is governed by two main parameters: mass loss (Chiosi & Maeder 1986) and rotation (Maeder & Meynet 2000). The accurate determination of mass-loss rates relies mainly on two types of methods. First, the infrared-millimeter-radio excess emission is measured and converted to mass-loss rate (Wright & Barlow 1975; Barlow & Cohen 1977; Leitherer & Robert 1991). This method suffers from few approximations but requires stars to be relatively nearby to be detected with the current generation of instruments. Second, spectroscopic features sensitive to the wind extension (such as P-Cygni profiles or emission lines) are fitted by atmosphere models (Puls et al. 1996; Hillier & Miller 1999). This method allows analysis of larger samples of massive stars, but relies on the physics and approximations included in atmosphere models. The main uncertainty in mass-loss rate determinations (which affects both types of methods) is the non homogeneity of massive stars winds (clumping). Direct (Eversberg et al. 1998) and indirect (e.g. Hillier 1991; Bouret et al. 2005) evidence exists that there are inhomogeneities in O and Wolf-Rayet stars winds. Although theoretically expected (MacGregor et al. 1979; Owocki & Rybicki 1984, 1985; Runacres & Owocki 2002), clumping is currently not fully understood and characterized, although work is in progress (e.g. Puls et al. 2006; Sundqvist et al. 2010). This is a severe problem for stellar evolution since mass loss is a key parameter. This means that having as many stars as possible studied quantitatively is desirable in order to understand their outflows. In this context, the late O-type main-sequence stars represent a puzzle of their own, since they display very weak winds with mass-loss rates down to a few 10-10 M⊙ yr-1 (Martins et al. 2004, 2005b; Marcolino et al. 2009). The origin of such a weakness is not known.
Rotation has several effects on the appearance and evolution of massive stars. In addition to shaping the surface of the star and modifying the surface temperature (poles being hotter than the equator), it triggers internal mixing processes (mainly meridional circulation and shear turbulence) that affect the transport of angular momentum and chemical species. Consequently, the timescales (such as main-sequence lifetime) and surface abundances depend on the rotation rate (Maeder & Meynet 2000). Hunter et al. (2008, 2009) have questioned the role of rotational mixing in the surface chemical enrichment of B stars in the Magellanic Clouds and the Galaxy. They found both slowly rotating N-rich and rapidly rotating unenriched stars that, according to the authors, cannot be accounted for by single-star evolution with rotation. However, Maeder et al. (2009) argued that when care is taken in disentangling the various parameters on which the surface nitrogen content depends, 80% of the population of B stars is explained by normally rotating single stars. Of particular importance is the age of the population: it is crucial to build samples of stars of the same age to avoid too wide a spread in nitrogen surface abundances. So far, the relation between chemical enrichment and rotation has not been looked at in more massive O stars. Since they evolve more rapidly and produce more enrichment than B stars, they are important objects to analyze.
The region of the Rosette nebula is especially interesting in this context. It harbors the ionizing cluster NGC 2244 at the core of the nebula itself, as well as several more widely spread massive stars in the Mon OB2 association. NGC 2244 contains seven O stars covering the entire range of spectral types, from O4 to O9. All of them have main-sequence luminosity classes (see Table 1). The stars of Mon OB2 have similar spectral types. As a result, this region contains a homogeneous sample of O stars with different masses and luminosities, but most likely the same age. Binaries are also present (Mahy et al. 2009). As such, this sample is well suited to investigating the effects of rotation on massive stars surface abundances. The Rosette nebula is also famous for the numerous young stellar objects and embedded clusters in the so-called Rosette molecular cloud (Phelps & Lada 1997; di Francesco et al. 2010). Triggered star formation is thought to be at work in this region, owing to the ionizing radiation and powerful winds of the NGC 2244 O stars. Recent results obtained by the Herschel Space Observatory reveal the presence of younger objects farther away from the HII region center, as well as temperature gradients (di Francesco et al. 2010; Motte et al. 2010; Schneider et al. 2010). Constraining the mechanical energy release and ionizing flux of the massive star population is thus important in order to quantitatively study the process of star formation triggering.
In this paper, we analyze nine O stars and one supposed B star in the Rosette nebula region. Seven are located in NGC 2244 and three in Mon OB2. Our study encompasses six out of the seven O stars powering the Rosette HII region1. Two confirmed binaries (HD 46149 and HD 46573) and one binary candidate (HD 46150) are included. This work complements and extends the analysis of HD 48099 (Mahy et al. 2010), also a binary member of the Mon OB2 association. In Sect. 2 we present the observations of the targets. Their analysis by means of atmosphere models is described in Sect. 3. The results are given in Sect. 4 and discussed in Sect. 5. Finally, our conclusions are drawn in Sect. 6.
Journal of optical observations.
List of IUE UV spectra retrieved from the archive and used for the analysis.
2. Observations and data reduction
Table 1 summarizes the main observational properties of our sample stars. Photometry is taken from the Galactic O star Catalog of Maíz-Apellániz et al. (2004). We have adopted a distance of 1.55 ± 0.15 kpc for the Mon OB2 association and NGC 2244. Photometric distances range between 1.4 and 1.7 kpc according to the summary of Hensberge et al. (2000). We simply adopt the average of these values in the present work (see also Mahy et al. 2009).
Spectroscopic data were obtained at the Observatoire de Haute-Provence (OHP, France) with the Aurélie spectrograph mounted on the 1.52 m telescope. Several observing runs from 2006 to 2008 allowed us to collect spectra in two different wavelength domains: [4450–4900] and [5500–5920] Å. In the adopted configuration, the Aurélie spectrograph offers a resolving power of about R = 8000 in the blue domain while R = 10 000 is reached in the red band. The exposure times, needed to reach a signal-to-noise ratio higher than 150, were typically 10 to 45 min. We also retrieved 13 spectra from the Elodie (R = 42 000) archives taken from November 1999 to November 2005 with the 1.93 m telescope at the OHP. The exposure times of these data ranged from 10 min to 1 h.
In April 2007 and March 2008, another set of spectra was obtained at Observatorio Astronómico Nacional of San Pedro Màrtir (SPM) in Mexico with the Espresso spectrograph mounted on the 2.10 m telescope (R = 27 000). This échelle spectrograph covers the wavelength domain [3780–6950] Å with 27 orders. We used a typical exposure time from 5 to 15 min. Several consecutive spectra of a given night were added to improve the signal-to-noise ratio of our data.
We have also retrieved 11 spectra from the ESO archives (PI: Casassus, run 076.C-0431(A) and PI: Lo Curto, run 076.C-0164(A)) taken with the Fiber-fed Extended Range Optical Spectrograph (FEROS) mounted on the ESO/MPG 2.20 m telescope at La Silla (Chile). The wavelength region covered by this instrument is [3550–9200] Å and the spectral resolution is about R = 48 000. The data reduction was done with an improved version of the FEROS pipeline as described in Sana (2009).
Finally, to model the winds of the O-type stars with more accuracy, we retrieved a total of 40 high-resolution IUE spectra (SWP with a dispersion of 0.2 Å). Such data are available for all targets of our sample, except HD 46573. These data were taken between September 1978 and February 1987 with exposure times between 539 and 18 000 s. These spectra cover the [1200–1800] Å spectral band, which is particularly interesting for the UV P-Cygni profiles (C iv1548 − 1550 and N v1240).
A full description of the optical instruments used, as well as the reduction procedure was given in Mahy et al. (2009). Tables 2 and 3 present the main characteristics of the observed optical spectra. For the single stars, we have selected the spectra of Mahy et al. (2009) with the widest wavelength coverage, highest spectral resolution, and highest signal-to-noise ratio. Table 3 provides the IUE spectra used for our analysis. For HD 48279, we used the average of the two spectra listed in the table since they were obtained in the same mode (high aperture), with the same exposure time and do not show any variability. For the other stars, we chose the spectra with the highest exposure time in the high aperture mode.
Derived stellar properties of the sample stars.
3. Modeling
We used the code CMFGEN (Hillier & Miller 1998) for the quantitative analysis of the optical and UV spectra. CMFGEN provides non-LTE atmosphere models including winds and line-blanketing. An exhaustive description can be found in Hillier & Miller (1998) and a summary of the main characteristics is given in Hillier et al. (2003). CMFGEN needs input from an estimate of the hydrodynamical structure that we constructed from TLUSTY models (taken from the OSTAR2002 grid of Lanz & Hubeny 2003) connected to a β velocity law of the form v = v∞(1 − R/r)β where v∞ is the wind terminal velocity. We adopted β = 0.8 since this is the typical value for O dwarfs (e.g. Repolust et al. 2004). Once the model was reasonably converged, the radiative acceleration was computed and used to iterate on the initial hydrodynamical structure in the inner atmosphere. The radiation field and level populations were then converged once again. Two to five of these global hydrodynamical iterations were performed before the atmosphere model finally converged.
Our final models include H, He, C, N, O, Ne, Mg, Si, S, and Fe with the solar composition of Grevesse et al. (2007) unless otherwise stated. The super-level approach is used to reduce the amount of memory requirements. On average, we include 1600 super levels for a total of 8000 levels. For the formal solution of the radiative transfer equation leading to the emergent spectrum, a microturbulent velocity varying linearly (with velocity) from 10 km s-1 to 0.1 × v∞ was used.
We included X-ray emission in the wind since this can affect the ionization balance and the strength of key UV diagnostic lines. In practice, we adopted a temperature of three million degrees and adjusted the flux level so that the X-ray flux coming out of the atmosphere matches the observed LX/Lbol ratio. This ratio was computed from the observed X-ray fluxes of Wang et al. (2008) and our derived luminosities. In case no X-ray flux was detected, we simply adopted the canonical value LX/Lbol = 10-7 (Sana et al. 2006; Nazé 2009).
Summary of various mass loss rates for our sample stars.
In practice we proceeded as follows to derive the stellar and wind parameters.
-
Effective temperature: we used the classical ratio of He i to He ii lines to constrain Teff. The main indicators were He i 4471 and He ii 4542. Additional diagnostics are He i 4026 (blended with He ii 4026), He i 4388, He i 4713, He i 4921, He i 5876, He ii 4200, and He ii 5412. The typical uncertainty on the Teff determination is 1000 K.
-
Gravity: the wings of the Balmer lines Hβ, Hγ, and Hδ are the main log g indicators. An accuracy of about 0.1 dex on log g is achieved.
-
Luminosity: we fitted the flux-calibrated IUE spectra and UBVJHK fluxes to derive both the luminosity and the extinction. For this, we adopted a distance of 1.55 ± 0.15 kpc (see discussion in Mahy et al. 2009). The Galactic extinction law of Seaton (1979) and Howarth (1983) was used. We adjusted the stellar luminosity and E(B − V) to reproduce the UV-optical-infrared SED. In those cases where no UV spectra were available, we simply derived the extinction from E(B − V) and adjusted the luminosity to reproduce the V magnitude.
-
Wind terminal velocity: the blueward extension of P-Cygni lines observed in the UV provides v∞ with an accuracy of 100 km s-1.
-
Mass-loss rate: we used two diagnostic lines to constrain the mass loss rate: the UV P-Cygni profiles and Hα. A single value of Ṁ should allow a good fit of both types of lines. However in practice, several recent studies have shown that this was not the case. To be as complete as possible, we thus provide both values: the “UV mass loss rate” (ṀUV, given in Table 4) and the “Hα mass loss rates” (ṀHα, given in Table 5).
The projected rotational velocities were derived by direct comparison of our synthetic spectra to observed line profiles for fast-rotating stars (i.e., those with V sin i ≥ 150 km s-1). The rotationally broadened synthetic line profiles usually provided a good match to the observed profile. In the case of moderately to slowly rotating objects, some amount of macroturbulence had to be introduced to correctly reproduce the line profiles of several features (e.g., He i 4713, C iv 5812, He i 5876). The need for extra broadening is well documented (Howarth et al. 1997; Ryans et al. 2002; Howarth et al. 2007; Nieva & Przybilla 2007; Martins et al. 2010; Fraser et al. 2010) but its origin is unclear. Aerts et al. (2009) have recently suggested that non radial pulsations could trigger large-scale motions (hence macroturbulence), but this needs to be confirmed by a study covering a wider parameter space. A recent study by Simón-Díaz et al. (2010) shows that the amplitude of macroturbulence was correlated to the amplitude of line profile variability in a sample of OB supergiants. In practice, we introduced macroturbulence by convolving our (rotationally broadened) synthetic spectra with a Gaussian profile (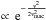 where vmac is the macroturbulent velocity), thus mimicking isotropic turbulence. This is obviously a very simple approach, but it significantly improves the quality of the fits. Given the present limitations, we restricted ourselves to rough estimates of the amount of macroturbulence by judging the fit quality by eye. In practice, we used He i 4713 as the main indicator of macroturbulence since it is present with sufficient SNR in all our sample stars. Secondary indicators were the C iv doublet at 5801–5812 Å and He i 5876. V sin i was also obtained from the Fourier transform method (Simón-Díaz & Herrero 2007). For the moderately to slowly rotating stars, we obtained upper limits from the absence of zero and the position of the noise level in the FT.
where vmac is the macroturbulent velocity), thus mimicking isotropic turbulence. This is obviously a very simple approach, but it significantly improves the quality of the fits. Given the present limitations, we restricted ourselves to rough estimates of the amount of macroturbulence by judging the fit quality by eye. In practice, we used He i 4713 as the main indicator of macroturbulence since it is present with sufficient SNR in all our sample stars. Secondary indicators were the C iv doublet at 5801–5812 Å and He i 5876. V sin i was also obtained from the Fourier transform method (Simón-Díaz & Herrero 2007). For the moderately to slowly rotating stars, we obtained upper limits from the absence of zero and the position of the noise level in the FT.
We also determined the nitrogen content of our sample stars. We relied mainly on the N iii lines between 4500 and 4520 Å. They are present in absorption in all the stars, and are not affected by winds and are strong enough for abundance determination. The uncertainties are on the order of 50%. They were estimated from the comparison of the selected N iii lines to models with various N content. The errors do not take any systematics related to atomic data into account.
When possible, the degree of inhomogeneities of the winds of our sample stars was determined. Clumping is implemented in CMFGEN by means of a volume filling factor f following the law f = f∞ + (1 − f∞)e − v/vcl where f∞ is the maximum clumping factor at the top of the atmosphere and vcl a parameter indicating the position where the wind starts to be significantly clumped. As shown by Bouret et al. (2005), O v 1371 and N iv 1720 are two UV features especially sensitive to wind inhomogeneities in early O stars. We have used these lines to constrain f∞ in the earliest O stars of our sample. In mid to late O stars, no UV clumping diagnostic has been identified. This is confirmed by our study. For the O7–O9 stars of our sample, we computed models with several values of f∞ (scaling Ṁ so that 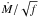 is constant) and found no difference in the UV wind sensitive lines. Hence, we decided to adopt f∞ = 1 (i.e. homogeneous model). Our mass-loss rates for those objects should thus be regarded as upper limits.
is constant) and found no difference in the UV wind sensitive lines. Hence, we decided to adopt f∞ = 1 (i.e. homogeneous model). Our mass-loss rates for those objects should thus be regarded as upper limits.
4. Results
The derived stellar and wind parameters of the sample stars are gathered in Table 4. The values of the Hα mass loss rates are given in Table 5. We show the best optical fits for HD 46223 and HD 48279 in Figs. 1. The optical fits for the other stars are gathered in Appendix A. The fits to the UV spectra for all stars are shown in Fig. 2. Below, we briefly comment on each star.
HD 46223: a clumped wind (f = 0.1) is required to fit O v 1371. The nitrogen content is difficult to estimate given the weakness of the N iii 4500–4520 features. A value of N/H = 7.0 × 10-4 is preferred. It also provides a good fit to the N iv 1720 feature. The parameters are similar to those of Martins et al. (2005b) within the uncertainties. The better quality and wider wavelength coverage of the present optical spectra explains the refined effective temperature estimate.
HD 46150: this is a binary candidate. We thus derive upper limits on the luminosity and mass loss rate. A clumping factor of 0.1 is needed to correctly reproduce the O v 1371 Å line profile. Models with higher (lower) clumping factor yield too strong (weak) an absorption in the blue part of the profile. See also Sect. 5.2 for further discussion.
HD 46485: this is the second fastest rotator of our sample, with V sin i = 300 km s-1. The fit of the optical and UV spectra is of excellent quality. The only notable exceptions are the C III line complex at 4640 Å, C iv 5801–5812 Å, and He i 5876 Å. The C iii 4650 line complex is slightly too weak in our best-fit model. However, we found out that this transition is sensitive to detailed line-blanketing effects. The lower level of these transitions is connected to the C iii ground level by a transition at 538 Å. This transition is blended with Fe iv transitions. The interaction between these UV lines thus affects the strength of the C iii 4650 lines, in a manner similar to what is described by Najarro et al. (2006) for the He i singlet lines.
HD 46056: this is the fastest rotator of our sample, and no macroturbulence is necessary to reproduce the line profiles. The fit is good with the exception of the C iii 4650 line complex, which is underpredicted. The C iii 4650 lines suffer from the same problem as for HD 46485.
 |
Fig. 1 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46223 (top), HD 48279 (bottom). The models have the mass loss rate best reproducing the UV features. The unfitted feature around 4425 Å is a DIB. |
 |
Fig. 2 Best CMFGEN fits (red) of the UV spectra (black) of the sample stars. |
HD 46149: this is a binary (Mahy et al. 2009). The spectra were disentangled using the method described in Mahy et al. (2010). They were subsequently used to classify the two components of the system. The classical diagnostic log  led to a spectral type O8 for the primary and O8.5–O9 for the secondary. Similarly, a luminosity class V was assigned based on the values of log
led to a spectral type O8 for the primary and O8.5–O9 for the secondary. Similarly, a luminosity class V was assigned based on the values of log  (Conti & Alschuler 1971). These classifications are slightly different from those derived by Mahy et al. (2009), although it remains in the error range for the primary. However, such a discrepancy for the secondary could come from the disentangling process, making the disentangled spectra uncertain. Indeed, they were computed from a sample of observed spectra taken essentially at similar phases where the separation between the radial velocities of both components (RVS − RVP) are of about − 30, 0, and + 140 km s-1. Moreover, the orientation and the high eccentricity of the orbit imply an asymmetric excursion in radial velocity, which could also affect the accuracy of the broadest lines. We thus caution that the disentangling process does not provide perfect results and should be refined in the future when more data taken at different phases has been obtained. This is especially true for the wings of broad lines, which need to be correctly sampled and fully separated in the observed spectrum (at maximum separation) to be reconstructed (see below – HD 48099). Consequently, the gravity and spectroscopic masses in Table 4 are highly uncertain. The effective temperature and nitrogen content also have larger error bars than the other sample stars: 2000 K (3000 K) on Teff for the primary (secondary) and ~ 70% on N/H. In addition, given the poor quality of the spectrum of the secondary, we adopted log g = 4.0. Using the calibrations of Martins & Plez (2006), we find that the V-band flux ratio between an O8V and an O9V star is ≈ 1.3. Optical photometry of HD 46149 indicates E(B − V) = 0.45, leading to AV = 1.40. For the adopted distance, the absolute V-band magnitude of the system is thus MV = −4.75. Given the V-band flux ratio of the two components, we have
(Conti & Alschuler 1971). These classifications are slightly different from those derived by Mahy et al. (2009), although it remains in the error range for the primary. However, such a discrepancy for the secondary could come from the disentangling process, making the disentangled spectra uncertain. Indeed, they were computed from a sample of observed spectra taken essentially at similar phases where the separation between the radial velocities of both components (RVS − RVP) are of about − 30, 0, and + 140 km s-1. Moreover, the orientation and the high eccentricity of the orbit imply an asymmetric excursion in radial velocity, which could also affect the accuracy of the broadest lines. We thus caution that the disentangling process does not provide perfect results and should be refined in the future when more data taken at different phases has been obtained. This is especially true for the wings of broad lines, which need to be correctly sampled and fully separated in the observed spectrum (at maximum separation) to be reconstructed (see below – HD 48099). Consequently, the gravity and spectroscopic masses in Table 4 are highly uncertain. The effective temperature and nitrogen content also have larger error bars than the other sample stars: 2000 K (3000 K) on Teff for the primary (secondary) and ~ 70% on N/H. In addition, given the poor quality of the spectrum of the secondary, we adopted log g = 4.0. Using the calibrations of Martins & Plez (2006), we find that the V-band flux ratio between an O8V and an O9V star is ≈ 1.3. Optical photometry of HD 46149 indicates E(B − V) = 0.45, leading to AV = 1.40. For the adopted distance, the absolute V-band magnitude of the system is thus MV = −4.75. Given the V-band flux ratio of the two components, we have 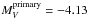 and
and 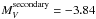 .
.
HD 46202: the parameters derived for HD 46202 are very similar to those of Martins et al. (2005b). The fit to the optical spectrum is of excellent quality. A combination of a low rotation rate (20 km s-1) and a macroturbulent velocity of 17 km s-1 correctly reproduces the photospheric line profiles. See also Sect. 5.2 for further discussion.
HD 46573: this is a binary candidate. No UV spectra are available for that star, so that our analysis is restricted to the optical range. A very good fit is achieved. Only the core of the Balmer lines is too deep in our synthetic spectra. The line profiles show that macroturbulence is important. We found that a combination of V sin i in the range 40–60 km s-1 with a macroturbulent velocity of 40 to 50 km s-1 leads to much better fits than do purely rotationally broadened profiles.
HD 48279: our synthetic spectrum provides a good fit of most optical and UV lines. The singlet lines He i 4388 Å and He i 4921 Å are too weak in our spectrum. They are known to be sensitive to details of line blanketing (Najarro et al. 2006).
HD 46966: the fit of the optical and UV spectra is one of the best in the present work. The only problem is observed in He ii 4686 Å for which our synthetic profile is too deep. A projected rotational velocity of 40–50 km s-1 combined with a macroturbulent velocity ~30–40 km s-1 provided better fits than models with only rotationally broadened profiles.
HD 48099: this star is a binary and has been studied by Mahy et al. (2010). We did not re-analyze the two components, and we simply adopted the parameters derived by Mahy et al. However, we add a few words of caution. The spectra used in the disentangling process of this binary system sample the full orbital cycle, so do not suffer from the same limitations as in the case of HD 46149. But while we expect narrow spectral features to be reliably reconstructed in the disentangled spectra of both the primary and secondary stars, the reconstruction of the broad features is more uncertain. Indeed, given the rather low orbital inclination of HD 48099 (Mahy et al. 2010), the maximum radial velocity excursions of the stars remain small (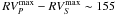 km s-1 –
km s-1 – 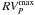 and
and  being the maximum radial velocities of the primary and secondary components) compared to the possible widths of broad Balmer lines ( ± 950 km s-1 for Hγ). This poor sampling of the broadest lines can lead to poor reconstruction of the wings of the Balmer lines especially for the fainter secondary component. As a result, the gravity of the latter is very likely underestimated. There is unfortunately no way to remedy to this situation, and as a result, the spectroscopic masses for this system are unreliable as becomes clear for instance when comparing the spectroscopic mass ratio from Table 4 (M1/M2 ~ 30) with the dynamical mass ratio (M1/M2 = 1.77) from the orbital solution of Mahy et al. (2010). In view of this discussion, we chose to adopt the same error bars on Teff and log g as for HD 46149 (i.e. 2000 K on Teff–3000 K for the secondary – and 0.2 dex on log g). The error bars are thus larger than in Mahy et al. (2010). They are also realistic, since reducing log g by 0.25 dex, we find that we need an effective temperature lower by 1000–2000 K to correctly reproduce the He i and He ii lines of the primary.
being the maximum radial velocities of the primary and secondary components) compared to the possible widths of broad Balmer lines ( ± 950 km s-1 for Hγ). This poor sampling of the broadest lines can lead to poor reconstruction of the wings of the Balmer lines especially for the fainter secondary component. As a result, the gravity of the latter is very likely underestimated. There is unfortunately no way to remedy to this situation, and as a result, the spectroscopic masses for this system are unreliable as becomes clear for instance when comparing the spectroscopic mass ratio from Table 4 (M1/M2 ~ 30) with the dynamical mass ratio (M1/M2 = 1.77) from the orbital solution of Mahy et al. (2010). In view of this discussion, we chose to adopt the same error bars on Teff and log g as for HD 46149 (i.e. 2000 K on Teff–3000 K for the secondary – and 0.2 dex on log g). The error bars are thus larger than in Mahy et al. (2010). They are also realistic, since reducing log g by 0.25 dex, we find that we need an effective temperature lower by 1000–2000 K to correctly reproduce the He i and He ii lines of the primary.
 |
Fig. 3 HR diagram of NGC 2244. The evolutionary tracks and isochrones are from Meynet & Maeder (2003). They are computed for an initial rotational velocity of 300 km s-1. Triangles are the components of the binaries HD 48099 (cyan) and HD 6149 (pink). Stars belonging to NGC 2244 are shown in red/pink and stars from the Mon OB2 association are shown in blue/cyan. Arrows indicate upper limits on luminosities for SB1 and binary candidates. |
5. Discussion
5.1. HR diagram and evolutionary status
The HR diagram of the stars analyzed in the present study is shown in Fig. 3, with colors used for the stars of NGC 2244 (Mon OB2 respectively). The stars of NGC 2244 have an age less than 5 Myr. The most massive stars of the cluster, namely HD 46223 and HD 46150, are less than 2 Myr old. There is no significant age difference between these two stars, contrary to what Wang et al. (2008) suspected. Whether the trend for the most massive stars to be younger than the lower mass O stars is real or an artifact of the parameter determination is unclear. It is known that the stellar parameters of an average early O star indicate a younger age than that of late-type O stars (e.g. Fig. 12 of Martins et al. 2005a). An explanation for this trend is that late-type O stars have lower ionizing fluxes and weaker winds than early-type O stars. Consequently, they remain hidden in their parental cloud for a longer time, so that on average late-type O stars appear older. In the present case, since both early and late-type stars are visible at the same time, one needs another explanation. One possibility is that the most massive stars were the last to form. Alternatively, there might be a bias in determining the effective temperature of the hottest O stars. It would have to be 2000–3000 K lower in order to lead to a similar age to the late-type O stars.
Such a reduction is difficult to explain. Line-blanketing, when included in model atmospheres, leads to a downward revision of effective temperatures by several thousand K. But as shown by Martins et al. (2002), C, N, O, Si, S, and Fe are the main contributors to opacities in O star atmospheres. Since our present models include all these elements and additional ones, it is unlikely that we overestimate Teff by 2000–3000 K. Since we are using clumped models for the hottest stars and homogeneous winds for the coolest ones, one might wonder whether this affects the temperature determination. However, the photospheric lines used to constrain Teff are unaffected by clumping since they form deep in the atmosphere where the wind is still homogeneous even in clumped models. Another speculative hypothesis is that the most massive O stars have, on average, higher rotation rates. If so, the use of the same set of evolutionary tracks (i.e., computed with the same initial rotational velocity) for early and late-type O stars is inappropriate. Indeed for faster rotation, the main-sequence lifetime is increased. Maeder & Meynet (2000) conclude that the use of non rotating tracks could lead to an underestimate of the actual age of stars by about 25%. Brott et al. (2011a) show the effect of rotation on isochrones (see their Fig. 7) and confirm that fast-rotating massive stars stay closer to the zero-age main sequence compared to moderately rotating lower mass stars of the same age.
This could partly explain the age difference we observe between early and late O stars. But this relies on the assumption that rotation is faster for larger masses among O stars. So far, there has been no detailed study of the evolution of rotational velocities with spectral type among O stars. An average V sin i of 129 ± 82 km s-1 results from the work of Penny (1996), consistent with the more recent result of Penny et al. (2004) – 131 ± 93 km s-1. Howarth et al. (1997) found that the distribution of V sin i peaked at about 100 km s-1. Concerning B stars, Abt et al. (2002) found values of 100–130 km s-1 for B0–B5V stars. It is thus not clear whether there is a trend toward higher rotation rate between B and O stars (and consequently not clear whether such a trend continues within the O class).
The stars in the Mon OB2 association appear to have an age of about 1–5 Myr, with a preferred value between 2 and 4 Myr. The only exception is the primary of the binary system HD 48099. As already discussed by Mahy et al. (2010), several factors can explain the apparently younger age of this star: rapid rotation, mass and angular momentum transfer, inappropriate evolutionary tracks. Rapid rotation is the favored explanation. The present study confirms that the secondary star has a similar age to the other stars of the association, making the primary peculiar. It is thus very likely that the position of the primary in the HR diagram is due to a rapid rotation and that comparison with normal (i.e. moderate rotation) evolutionary tracks is not appropriate.
5.2. Wind properties
In Table 5, we gather the mass loss rates derived from our quantitative analysis (ṀUV and ṀHα), as well as the theoretical mass loss rates of Vink et al. (2001) and the values L/c2. The last corresponds to the mass loss rates obtained if the driving is due to a single line located at the emission peak of the SED. They are thus a lower limit to the mass loss rate expected by the radiation-driven wind theory. From Table 5 we can draw the following conclusions:
-
1.
all stars have ṀUV < ṀHα. The difference is between a factor of ten and a factor of a few 100!;
-
2.
the theoretical mass-loss rates of Vink et al. (2001) are systematically higher than the UV mass-loss rates. The discrepancy reaches two orders of magnitudes in the latest type O stars, as usually seen (Martins et al. 2005b; Marcolino et al. 2009). The Hα mass loss rates usually fairly well agrees with the theoretical predictions (when comparisons are made for unclumped Ṁ for the early O dwarfs);
-
3.
for all late type O dwarfs, the UV mass loss rates are lower than the single line driving limit. This is a serious puzzle. If the UV mass loss rates are the correct ones, this implies that line driving is less efficient than thought. It could mean that the line absorbs only at discrete values of velocities in the range 0–v∞ (i.e., that absorbing material is only present at specific velocities, see below). For the earliest O dwarfs, the UV mass loss rates are only a factor three to four more than this limit.
The results of Table 5 raise the question of the validity of our mass-loss rate determinations. We list a few reasons why they could be biased:
-
the mass-loss rates are based on a few features, and sometimesbased on only a single line (although the absence of other windfeatures provides upper limits);
-
the inferred mass-loss rate requires that the wind ionization structure derived by CMFGEN is accurate. Since CMFGEN provides a good fit to the photospheric spectrum, there is no a priori reason that CMFGEN should get the ionization structure dramatically wrong. Studies of H ii regions generally find that the far-UV spectrum predicted by CMFGEN is generally consistent with what is required to ionize the nebulae (Morisset et al. 2004; Simón-Díaz & Stasińska 2008);
-
CMFGEN does not compute the wind properties from first principles (see Sect. 3). The mass loss rate and velocity law are adopted to compute the atmosphere structure and the emerging spectra. However, the results can be used to check the consistency between the adopted mass-loss rate/velocity law and the momentum absorbed by the wind. Knowledge of the atmospheric structure allows the computation of the radiative forces;
-
recent developments in understanding the clumping properties of O stars have shown that porosity (and its effect on the velocity structure, called vorosity) could alter the shape of key diagnostic lines (e.g. Sundqvist et al. 2010). Neglecting this effect could thus bias our determination.
In the following we investigate the last two points in more detail. To check the hydrodynamics of our models, we ran several tests on HD 46202, which is typical of the late type O stars with only weak evidence of winds in C iv 1548–1550 (and perhaps N v 1240). We derived a UV mass-loss rate of 1.0 × 10-9 M⊙ yr-1. This is a factor of five lower than the single-line limit (4.8 × 10-9 M⊙ yr-1), and a factor of 190 lower than what is derived using Vink’s prescription for estimating the mass-loss rate (which gives Ṁ = 1.9 × 10-7 M⊙ yr-1), and is primarily based on the strength of the absorption associated with the C iv 1548–1550 doublet. As noted previously, the single line limit is greater than the derived UV mass loss rate. To check the hydrodynamics, we ran additional models with as many elements/lines as allowed by our computational resources (the models include H, He, C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, Ni, and a total of about 10 000 atomic levels) to be able to calculate the radiative force as accurately as possible.
 |
Fig. 4 Comparison between the best-fit models of the UV spectrum (red lines) and models with higher mass-loss rates (blue lines). The solid lines are the observed spectra. The left panel shows the comparison for HD 46150, the right panel for HD 46202. The narrow absorption features in the C iv 1548–1550 profiles are interstellar. |
The momentum equation can be written as 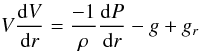 (1)where
(1)where 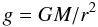 (2)and, gr, the radiative acceleration, is given by
(2)and, gr, the radiative acceleration, is given by  (3)
(3)
Once gr has been computed, we can thus check whether Eq. (1) is satisfied or not.
When clumping is important we utilize the same equation, but this is only an approximation. First we note that the presence of clumps implies a dynamic flow, but the above equation is for a steady flow. Second, it is unclear how to handle the pressure term when clumping is important; in practice, this is not crucial for O stars since we assume the clumping to be initiated close to, or above the sonic point where the gas pressure term can be neglected. The expression for gr, ρ and χν are evaluated in the clumps.
In our best-fit model of the UV lines, the radiation field exceeds the one required to drive the wind everywhere – at most locations by over an order of magnitude. This result is not unexpected, since our derived mass-loss rate is lower than the single-line limit. As a check of the consistency of the calculations we computed a model using a mass loss rate of 4.0 × 10-8 M⊙ yr-1 – this is a factor five below Vink’s estimate, but a factor of 40 above what we derived. As shown in Fig. 4 (right panel), the predicted UV spectrum shows some crucial disagreements with observation. Particularly noteworthy is the presence of a saturated C iv profile and two high-velocity wind features due to Si iv. In the observed spectrum, Si iv shows only photospheric components2. The high mass loss rate model shown has no X-rays, and when we include X-rays N v 1240, unlike the observations, shows a strong P Cygni profile. The weakness of the N v profile relative to C iv is consistent with the late spectral class of HD 46202 and argues against a shift in the wind to high ionization stages.
For a mass-loss rate of 4 × 10-8 M⊙ yr-1, the wind momentum deposited is close to what is needed to drive the wind for velocities in excess of 700 km s-1, and for a standard β = 1 velocity law. Below 700 km s-1 there is insufficient line force, sometimes by a large factor, to drive the flow. This is an important issue, because for a steady flow the momentum balance must be satisfied at all depths, not just globally. Clearly we have an inconsistency. Either the derived UV mass-loss rate is wrong or there is an additional retarding force that needs to be included in the momentum balance equation.
For early type O dwarfs, mass loss rates are higher and closer to the theoretical predictions. However, problems still occur. We take HD 46150 as an illustrative case. For that star, we derive a mass-loss rate of 5.0 × 10-8 M⊙ yr-1 from UV diagnostics. This gives a C iv profile in reasonable agreement with observation, but the N v doublet is overestimated. Surprisingly, both the C iv and N v profile do not reach zero intensity (C iv has a residual intensity of 15%, while the residual intensity for N v is 35%).
On the other hand, the mass-loss rate derived from Hα (assuming f = 0.1, Vcl = 100 km s-1) is nearly an order of magnitude larger, 4.0 × 10-7 M⊙ yr-1. This mass-loss rate also provides a better fit to the cores of Hβ and Hδ. The optically derived mass-loss rate is inconsistent with the O iv 1339, 1343, and O v 1371 lines. The theoretical spectra show noticeable perturbations by the wind whereas the observed profiles are only photospheric (see Fig. 4). The fit to C iv is somewhat worse, although definitive statements are impossible since C iv shows a strong P Cygni profile that is insensitive to Ṁ.
Clumping, and more precisely porosity, might be a way to partly solve the issues mentioned above. Porosity comes in two flavors: spatial and velocity. Spatial porosity has been invoked to help explain the observed X-ray profiles, which tend to show much more symmetric profiles than expected on the basis of Hα derived mass-loss rates (Oskinova et al. 2007). An alternative explanation is that Hα mass-loss rates are too high – by a factor of a few (Cohen et al. 2010). The need for spatial porosity and its importance are controversial. Cohen et al. (2010) argue that the X-ray profiles in ζ Pup are explained much better by a simple reduction in mass loss. In addition, Owocki & Cohen (2006) argue that the wind clumping structure is inconsistent with what is required to give rise to a significant porosity effect.
Vorosity (i.e. porosity in velocity space) can arise in a clumped medium because the clump velocities are discrete: not all velocities may be present along a given sight line. Since continuum transfer is unaffected by the presence of velocity fields, vorosity, unlike spatial porosity, only affects line profiles3. As shown by Prinja & Massa (2010), vorosity could explain that the ratio of optical depth in the two components of Si iv 1393, 1403 in B supergiants is not equal to the ratio of oscillator strengths, as expected in the case of homogeneous flows.
Recent simulations by Sundqvist et al. (2010, 2011) have highlighted the importance of vorosity (among others) for the formation of strong UV lines. They show that when accounting for vorosity, UV line profiles can be strongly reduced for a given mass-loss rate. At the same time, Hα is less affected. This tends to bring the optical and UV mass-loss rates into better agreement when fitting oberved spectra. But these results also indicate that, if vorosity is important, it implies that the winds are clumped. Consequently, the Hα mass loss rates derived using homogeneous models (such as most values in Table 5) are upper limits. These computations are still exploratory (there is no detailed radiative transfer or feedback on the atmosphere structure), but they appear to be a way of solving the issues presented above.
Aside from this, the effect of porosity and vorosity on theoretical mass-loss rates is unclear. If it begins beyond the critical point we would expect a reduction in the line force, hence a reduction in the terminal velocity of the wind, with no change in the mass-loss rate. The reduction in line force occurs because thick lines would absorb less continuum flux, owing to the presence of absorbing material only at specific velocities and not all over the entire 0 – v∞ velocity range. The radiation force from thin lines would not alter since only the column density, not the velocity field, is important. Of course the definition of which lines are thin and which are optically thick may be affected by the wind structure. If vorosity is important below the critical point we might expect a reduction in the mass-loss rate.
Clearly, the structure, properties, and dynamics of O star winds is complex and requires improvements in both spectroscopic analysis and theoretical predictions. But vorosity appears as a valid way of solving (at least partly) some of the issues raised above.
Regardless of the exact nature of these winds, some qualitative features can be obtained directly from the observations. This is what we show in Fig. 5. Most of the results presented above rely directly or indirectly on atmosphere models. In Fig. 5 we show a direct comparison between the observed spectra of two stars: HD 46966 and HD 48279. According to Table 4, they have very similar Teff and gravities. This is mirrored in Fig. 5 by the perfect match of the He i and He ii features and the wings of Balmer lines. However, N v 1240 and C iv 1548–1550 show a smaller blueward extent in HD 48279 indicating a lower terminal velocity. In addition, C iv 1548–1550 is clearly weaker in HD 48279, while the N v 1240 profile have a similar strength (slightly weaker in HD 48279 though). The Hα profiles are barely differentiated. From the C iii optical features, we tentatively estimate the carbon abundance (C/H) of HD 48279 (respectively HD 46966) to be 1.0 × 10-4 (resp. 2.0 × 10-4). Consequently, HD 48279 exhibits a higher N/C ratio than HD 46966. If the mass loss rate were the same in both stars, one would expect a weaker C iv 1548–1550 line but also a much stronger N v 1240 line (the profile is not saturated) since the nitrogen overabundance in HD 48279 is much larger than its carbon depletion (see Table 4 and above). This is not what we see. We thus conclude that the wind of HD 48279 is weaker than for HD 46966. The value of the mass loss rate is low enough that the Hα profiles are photospheric in both stars, and thus similar since Teff and log g are the same. HD 46966 has a luminosity L = 105.20 L⊙, while for HD 48279, L = 104.95 L⊙. It is thus natural to have a weaker wind in HD 48279. This is what both the UV diagnostics and Hα indicate. We note, however, the difference in mass-loss rate between the two stars is 0.8 dex if the former are used, while it is only 0.4 dex in the case of Hα. This raises once again the question of the origin of the differences between the UV and optical wind sensitive lines. Regardless of the reason, we see that two stars with very similar effective temperature and gravity can have different wind properties with only a difference in luminosity by less than a factor of two.
 |
Fig. 5 Comparison between the observed spectra of HD 46966 (blue) and HD 48279 (red). The spectra of HD 46966 have been convolved to the same rotational velocity as HD 48279. |
5.3. Chemical evolution and rotation
Rotation is known to affect the angular momentum and chemical elements transport through mixing processes (meridional circulation and shear turbulence, see Maeder & Meynet 2000). The first analysis of surface CNO abundances of O stars and B supergiants tends to confirm the theoretical predictions qualitatively: more evolved stars have a higher N content as a result of CNO processing and mixing (Hillier et al. 2003; Heap et al. 2006; Crowther et al. 2006); however, the role of rotation in explaining the chemical patterns of B stars in the Magellanic Clouds has been questioned by the results of the first ESO/VLT Large Programme dedicated to massive stars (Evans et al. 2005, 2006). Hunter et al. (2008) showed that 60% of their sample of B main-sequence stars in the Large Magellanic Cloud displayed the nitrogen surface abundances expected by evolutionary models including rotational mixing, but the remaining 40% escaped such an agreement. These outliers are divided in two groups with approximately the same number of members: one with highly enriched but slowly rotating stars, the other with barely enriched fast rotators. The former group was also identified in the SMC (Hunter et al. 2009). In the Galaxy, the results of Hunter et al. (2009) point to a lack of surface nitrogen enrichment in all main-sequence objects, probably due to the relatively unevolved status of most stars. In contrast, Morel et al. (2006, 2008) report detecting N-rich non-supergiant Galactic B stars with low rotation rates, lending support to the idea that rotational mixing cannot explain the surface abundances of a significant number of massive stars also in the Galaxy.
However, Maeder et al. (2009) argued that surface chemical enrichment is a multivariate function that does not depend only on projected rotational velocity. The higher the mass of a star, the larger the nitrogen enrichment. Similarly, lower metallicity stars have greater surface enrichment at a given evolutionary state. In addition, more evolved stars show higher N/H ratios, so a combination of ages, masses, metallicities and rotational velocities can lead to various surface enrichments. It is important to disentangle the different effects to draw reliable conclusions. According to Maeder et al. (2009), if this is done, rotational mixing explains most of the observed abundance patterns. Twenty per cent of the sample of Hunter et al. (2008) might escape this scenario due to binary evolution. Brott et al. (2011b) have built population synthesis models to take all these effects into account. They investigated the properties of a population of seven to 60 M⊙ stars (with a Salpeter IMF) formed continuously for the past 30 Myr and with rotational velocities drawn from the distribution of Hunter et al. (2008). They confirm that about 35% of the stars observed by Hunter et al. (2008) cannot be explained by single star evolutionary models with rotation. But the rest – and majority – of the population is well accounted for by rotating evolutionary models. Przybilla et al. (2010) also confirm the role of rotational mixing by showing a tight correlation between N/C and N/O in main sequence and supergiants stars. However, the theoretical enrichments are too strong compared to observations.
Most of the results summarized above have been obtained from the analysis of surface abundances of B main-sequence stars. In this paper, we present results for main-sequence O stars. Our sample is smaller than those of Morel et al. (2008) or Hunter et al. (2008) but it allowed us to identify some trends, and extend their work to the most massive stars. Figure 6 shows the nitrogen surface abundance as a function of rotational velocity. The results of Morel et al. (2008), Hunter et al. (2008) and Przybilla et al. (2010) have been added for comparison (small symbols). The following comments can be made.
 |
Fig. 6 Nitrogen surface abundance (in units of 12 + log(N/H)) as a function of projected rotational velocity. Single O stars are the blue squares and binaries the red triangles. The small black triangles (pentagons, open circles) are the Galactic B stars of (Hunter et al. 2009; Morel et al. 2008; Przybilla et al. 2010) with log g larger than 3.5 (i.e. comparable to our sample). The grey area corresponds to the range of solar values from studies of the Sun, B stars and HII regions (see Table 3 of Hunter et al. 2009). |
-
Up to about 120 km s-1 a possible trend toward larger N/H with larger V sin i is emerging among O stars, although a significant scatter exists and more stars are definitely needed to draw firm conclusions. We note that our sample is relatively homogeneous in age and metallicity. On the other hand it covers a relatively wide mass range (15–60 M⊙). Both binaries and single stars seem to follow this trend.
-
The components of the binaries studied in this paper have surface N/H values that are consistent with those of single stars. This conclusion applies only to the binaries studied here and should not be generalized.
-
The two fastest rotators show very little enrichment if any.
-
On the main-sequence, in the Galaxy, O stars show on average higher values of N/H than B stars.
These results confirm some of the expectations of stellar evolution with rotation. First, more massive stars display greater surface nitrogen enrichment. This is even more clearly illustrated in Fig. 7 where the ratio N/H is shown as a function of luminosity. A clear trend toward higher N content for more luminous stars is observed. At any given age, this is what evolutionary models predict. The dotted lines in Fig. 7 show isochrones for 2 and 4 Myr, which are typical of the age of our sample stars. They indicate faster evolution and consequently faster chemical enrichment for more luminous and thus more massive stars. Interestingly, the two fast rotators do not appear as outliers in this plot, but fall perfectly in the sequence followed by most of the stars. This means that given their mass, these objects are too young to have experienced a strong enrichment in spite of their large rotational velocity. This confirms the conclusion of Maeder et al. (2009) that it is important to disentangle the various effects at work in the surface enrichment of massive stars to pin down the true role of rotation.
 |
Fig. 7 Nitrogen surface abundance (in units of 12+log(N/H)) as a function of luminosity. Single O stars are the blue squares and binaries the red triangles. Evolutionary tracks – shown by the solid, dot-long dashed, dot-dashed, dashed lines for M = 15, 20, 25, and 40 M⊙ – are from Meynet & Maeder (2003). The dotted lines are isochrones for 2 and 4 Myr. |
Our sample includes binaries. In Figs. 6 and 7 they do not show any peculiar property in terms of chemical enrichment compared to single O stars. This does not mean that binarity has no effect on the history of surface enrichment, but that it depends on the binary properties. In particular, not all binaries have experienced mass transfer which would affect both the rotational speed and surface composition (Linder et al. 2008; de Mink et al. 2009). With the exception of HD 48099, all the binaries of our sample have orbital periods longer than three days. According to de Mink et al. (2011), it takes more than 8 Myr for Roche-lobe overflow to occur in such systems. This result is valid for binaries of about 20 M⊙, and it obviously depends on masses and mass ratios. The binaries of our sample are thus most likely too young and/or too separated to have experienced significant mass transfer. This conclusion only applies to the systems included in our sample and should not be generalized to all binary stars. Once mass transfer has occurred, it is likely that additional mixing processes take place and affect the surface composition. Further analysis of such interacting systems should shed more light on the exact role of binarity on the chemical appearance of O stars.
In Fig. 7, the only clear outlier is star HD 48279 with a very strong enrichment in spite of a moderate luminosity. To a lesser extent, HD 46573 can also be considered rather enriched compared to the expectations of single star evolutionary models thanks to the upper limit on its luminosity. For HD 48279, it does not seem possible that rotation only can explain the large N content. According to Fig. 1 of Maeder et al. (2009), an increase in the rotational velocity from 150 km s-1 to 300 km s-1 leads to an extra enrichment on the order of 0.5 dex. HD 48279 is 0.7 dex more N-rich than the other stars of the same luminosity in Fig. 7. Binarity is excluded for that object (Mahy et al. 2009). The only possible explanation for the strong N enrichment is that HD 48279 was member of a binary system in the past and experienced mass transfer and/or tidal interaction. Either the binary has been disrupted (by supernova kick, for instance) or the companion is a low-mass compact object rendering any radial velocity variation undetectable (see de Mink et al. 2011). In the case of HD 46573, a high initial velocity or binarity can explain the possible slightly higher N/H ratio than stars in the same luminosity range (HD 46573 has been classified as SB1 by Mahy et al. 2009). Finally, HD 46150 also only has an upper limit on its luminosity. But even accounting for an extreme reduction by 0.3 dex, the N/H content would still be consistent with single star evolutionary tracks.
5.4. Stellar masses
 |
Fig. 8 Ratio of spectroscopic to evolutionary masses versus spectroscopic masses for the sample stars. The dotted line is the one to one relation. Black circles are single stars, red squares are members of binary systems. The insert shows the position of the primary component of HD 48099. |
How to determine stellar masses is a long-standing problem. The so-called “mass discrepancy” (Groenewegen et al. 1989; Herrero et al. 1992) refers to the systematic overestimate of evolutionary masses compared to spectroscopic masses. The former are masses derived from the HR diagram and evolutionary tracks. The latter are the masses resulting from the knowledge of the gravity and radius obtained from spectroscopic analysis with atmosphere models. The revision of the effective temperature scale of O stars (Martins et al. 2002) has lead to improvements (see Gies 2003). However, differences of up to a factor of three still exist in some cases. Massey et al. (2005) and Mokiem et al. (2007) report a mass discrepancy for LMC stars. The latter paper indicates that part of the discrepancy could be caused by fast rotation in He-rich stars. Fast rotating stars tend to evolve toward higher luminosities for the same initial mass as non-rotating stars. Consequently, using non-rotating tracks to analyze them leads to overestimating their evolutionary masses. However, even unenriched objects (hence not likely to rotate rapidly) show the mass discrepancy.
In Fig. 8 we show the ratio between spectroscopic (Mspec) and evolutionary (Mev) masses for our sample of Galactic stars. The spectroscopic masses have been computed from the effective gravity (that we determine through line fitting) corrected from the effect of centrifugal forces. However, because of the high uncertainty on the gravity of the SB2 systems, we do not include the components of HD 46149 and HD 48099 in this discussion. In spite of the small number of objects, the trend toward a mass discrepancy at low masses (M < 25 M⊙) is present. At higher masses, a good agreement is observed, but the error bars are large. These results are qualitatively consistent with those of Repolust et al. (2004), who show that stars with masses lower than about 50 M⊙ seem to follow a relation parallel to the 1:1 relation in the Mev versus Mspec diagram.
Recently, Weidner & Vink (2010) have conducted a study of a sample of Galactic O stars and conclude that the mass discrepancy was solved. In their analysis, they mainly focuse on binary components. They establishe the evolutionary masses of their stars by using a spectral type – mass relation. They use the Teff-scale of Martins et al. (2005a) to determine an effective temperature and luminosity for each star and subsequently use the evolutionary tracks of Meynet & Maeder (2003) to assign an evolutionary mass. They then compare these estimates to dynamical masses resulting from fits to velocity and light curves of binary systems. They find good agreement between both types of masses (see their Fig. 3). However, the comparison with spectroscopic masses (not shown directly by Weidner & Vink but available from their Table 3) still reveals that evolutionary masses are higher. It therefore seems that at least part of the origin of the discrepancy is rooted in an underestimate of gravities.
6. Conclusion
We analyzed ten OB stars (nine O stars and one B star) in the NGC 2244 cluster and Mon OB2 association, including two bona-fide binaries and one candidate. Optical and UV spectroscopy were obtained. Atmosphere models computed with the code CMFGEN were used to derive the main stellar and wind parameters of the target stars. The main results are the following:
-
All stars have an age between 1 and 5 Myr, with a trend toward lower age for the most massive stars. Whether this is a real effect or an artifact of the method used to derive the stellar parameters is not clear at present.
-
We confirm the existence of weak winds in the latest type stars of our sample. For those stars, UV mass loss rates are lower than the single line driving limit. UV mass loss rates are systematically lower than Hα mass loss rates. Vorosity might be a solution to these issues, although its effects on dynamics are still unclear.
-
Nitrogen surface abundances in O stars indicate a wider range of enrichment compared to B stars. A clear trend toward more enrichment in higher mass stars is observed, consistent with the prediction of evolutionary models for a population of stars of the same age. There is no clear difference between single and binary stars in our sample, most likely because the latter have not (yet) experienced mass transfer or very severe tidal effects. Fast rotating, unenriched O stars are understood as too young to have had time to bring enough fresh nitrogen to their surface.
-
The so-called “mass discrepancy” still exists for the latest type O dwarfs. Above 25 M⊙, evolutionary and spectroscopic masses agree within the uncertainties. Part of the discrepancy seems related to underestimates of the spectroscopic masses.
We need to analyze more stars of the same age to confirm the trends observed, especially concerning the surface nitrogen enrichment. Winds of massive stars are complex, and a better understanding of clumping, both observationally and theoretically, is necessary to quantify their properties.
Online material
Appendix A: Best fit to the observed spectra
Figures A.1 to A.4 show the observed spectra in black together with the best fit CMFGEN models in red.
 |
Fig. A.1 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46573 (top), HD 46485 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
 |
Fig. A.2 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46056 (top), HD 46966 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
 |
Fig. A.3 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46223 (top), HD 46202 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
 |
Fig. A.4 Best CMFGEN fits (red) of the optical spectra (black) of the primary (top) and secondary (bottom) components of HD 46149. The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
Acknowledgments
We thank the referee, Artemio Hererro, for useful comments. L.M. and G.R. are supported by the FNRS (Belgium), by a PRODEX XMM/Integral contract (Belspo) and by the Communauté Française de Belgique Action de recherche concertée (ARC) Académie Wallonie Europe. L.M. and G.R. acknowledge the Ministère de l’Enseignement Supérieur et de la Recherche de la Communauté Française for supporting their travels to O.H.P. D.J.H. acknowledges support from STScI theory grant HST-AR-11756.01.A. We also thank the staff of Observatoire de Haute-Provence and of La Silla ESO Observatory for their technical support.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Puls, J., Godart, M., & Dupret, M. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barlow, M. J., & Cohen, M. 1977, ApJ, 213, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011a, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., Evans, C. J., Hunter, I., et al. 2011b, A&A, 530, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiosi, C., & Maeder, A. 1986, ARA&A, 24, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D. H., Leutenegger, M. A., Wollman, E. E., et al. 2010, MNRAS, 405, 2391 [NASA ADS] [Google Scholar]
- Conti, P. S., & Alschuler, W. R. 1971, ApJ, 170, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., & Izzard, R. G. 2011, Bulletin de la Societe Royale des Sciences de Liege, 80, 543 [Google Scholar]
- di Francesco, J., Sadavoy, S., Motte, F., et al. 2010, A&A, 518, L91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Smartt, S. J., Lee, J., et al. 2005, A&A, 437, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Lennon, D. J., Smartt, S. J., & Trundle, C. 2006, A&A, 456, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eversberg, T., Lepine, S., & Moffat, A. F. J. 1998, ApJ, 494, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., & Ryans, R. S. I. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Gies, D. R. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, ed. K. van der Hucht, A. Herrero, & C. Esteban (Cambridge: University Press), IAU Symp., 212, 91 [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Groenewegen, M. A. T., Lamers, H. J. G. L. M., & Pauldrach, A. W. A. 1989, A&A, 221, 78 [NASA ADS] [Google Scholar]
- Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Hillier, D. J. 1991, A&A, 247, 455 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1999, ApJ, 519, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., Lanz, T., Heap, S. R., et al. 2003, ApJ, 588, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D. 1983, MNRAS, 203, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Walborn, N. R., Lennon, D. J., et al. 2007, MNRAS, 381, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., & Robert, C. 1991, ApJ, 377, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, N., Rauw, G., Martins, F., et al. 2008, A&A, 489, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacGregor, K. B., Hartmann, L., & Raymond, J. C. 1979, ApJ, 231, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., Meynet, G., Ekström, S., & Georgy, C. 2009, Comm. Asteroseismol., 158, 72 [Google Scholar]
- Mahy, L., Nazé, Y., Rauw, G., et al. 2009, A&A, 502, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahy, L., Rauw, G., Martins, F., et al. 2010, ApJ, 708, 1537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz-Apellániz, J., Walborn, N. R., Galué, H. Á., & Wei, L. H. 2004, ApJS, 151, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolino, W. L. F., Bouret, J., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., & Plez, B. 2006, A&A, 457, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2002, A&A, 382, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., & Heydari-Malayeri, M. 2004, A&A, 420, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005a, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005b, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Donati, J., Marcolino, W. L. F., et al. 2010, MNRAS, 407, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Puls, J., Pauldrach, A. W. A., et al. 2005, ApJ, 627, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Evans, C. J., et al. 2007, A&A, 465, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Butler, K., Aerts, C., Neiner, C., & Briquet, M. 2006, A&A, 457, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Hubrig, S., & Briquet, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morisset, C., Schaerer, D., Bouret, J., & Martins, F. 2004, A&A, 415, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najarro, F., Hillier, D. J., Puls, J., Lanz, T., & Martins, F. 2006, A&A, 456, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y. 2009, A&A, 506, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2007, A&A, 467, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P., & Cohen, D. H. 2006, ApJ, 648, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1984, ApJ, 284, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1985, ApJ, 299, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Penny, L. R. 1996, ApJ, 463, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Penny, L. R., Sprague, A. J., Seago, G., & Gies, D. R. 2004, ApJ, 617, 1316 [NASA ADS] [CrossRef] [Google Scholar]
- Phelps, R. L., & Lada, E. A. 1997, ApJ, 477, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Prinja, R. K., & Massa, D. L. 2010, A&A, 521, L55 [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Kudritzki, R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryans, R. S. I., Dufton, P. L., Rolleston, W. R. J., et al. 2002, MNRAS, 336, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H. 2009, A&A, 501, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., Rauw, G., Nazé, Y., Gosset, E., & Vreux, J. 2006, MNRAS, 372, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Motte, F., Bontemps, S., et al. 2010, A&A, 518, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seaton, M. J. 1979, MNRAS, 187, 73P [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2008, MNRAS, 389, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., Uytterhoeven, K., Herrero, A., Castro, N., & Puls, J. 2010, Astron. Nachr., 331, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Feldmeier, A. 2010, A&A, 510, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Puls, J., Feldmeier, A., & Owocki, S. P. 2011, A&A, 528, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J., Townsley, L. K., Feigelson, E. D., et al. 2008, ApJ, 675, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Vink, J. S. 2010, A&A, 524, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, A. E., & Barlow, M. J. 1975, MNRAS, 170, 41 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46223 (top), HD 48279 (bottom). The models have the mass loss rate best reproducing the UV features. The unfitted feature around 4425 Å is a DIB. |
| In the text | |
 |
Fig. 2 Best CMFGEN fits (red) of the UV spectra (black) of the sample stars. |
| In the text | |
 |
Fig. 3 HR diagram of NGC 2244. The evolutionary tracks and isochrones are from Meynet & Maeder (2003). They are computed for an initial rotational velocity of 300 km s-1. Triangles are the components of the binaries HD 48099 (cyan) and HD 6149 (pink). Stars belonging to NGC 2244 are shown in red/pink and stars from the Mon OB2 association are shown in blue/cyan. Arrows indicate upper limits on luminosities for SB1 and binary candidates. |
| In the text | |
 |
Fig. 4 Comparison between the best-fit models of the UV spectrum (red lines) and models with higher mass-loss rates (blue lines). The solid lines are the observed spectra. The left panel shows the comparison for HD 46150, the right panel for HD 46202. The narrow absorption features in the C iv 1548–1550 profiles are interstellar. |
| In the text | |
 |
Fig. 5 Comparison between the observed spectra of HD 46966 (blue) and HD 48279 (red). The spectra of HD 46966 have been convolved to the same rotational velocity as HD 48279. |
| In the text | |
 |
Fig. 6 Nitrogen surface abundance (in units of 12 + log(N/H)) as a function of projected rotational velocity. Single O stars are the blue squares and binaries the red triangles. The small black triangles (pentagons, open circles) are the Galactic B stars of (Hunter et al. 2009; Morel et al. 2008; Przybilla et al. 2010) with log g larger than 3.5 (i.e. comparable to our sample). The grey area corresponds to the range of solar values from studies of the Sun, B stars and HII regions (see Table 3 of Hunter et al. 2009). |
| In the text | |
 |
Fig. 7 Nitrogen surface abundance (in units of 12+log(N/H)) as a function of luminosity. Single O stars are the blue squares and binaries the red triangles. Evolutionary tracks – shown by the solid, dot-long dashed, dot-dashed, dashed lines for M = 15, 20, 25, and 40 M⊙ – are from Meynet & Maeder (2003). The dotted lines are isochrones for 2 and 4 Myr. |
| In the text | |
 |
Fig. 8 Ratio of spectroscopic to evolutionary masses versus spectroscopic masses for the sample stars. The dotted line is the one to one relation. Black circles are single stars, red squares are members of binary systems. The insert shows the position of the primary component of HD 48099. |
| In the text | |
 |
Fig. A.1 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46573 (top), HD 46485 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
| In the text | |
 |
Fig. A.2 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46056 (top), HD 46966 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
| In the text | |
 |
Fig. A.3 Best CMFGEN fits (red) of the optical spectra (black) of stars HD 46223 (top), HD 46202 (bottom). The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
| In the text | |
 |
Fig. A.4 Best CMFGEN fits (red) of the optical spectra (black) of the primary (top) and secondary (bottom) components of HD 46149. The models have the mass-loss rate that best reproduces the UV features. The unfitted feature around 4425 Å is a DIB. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


