| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 17 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201117150 | |
| Published online | 13 December 2011 | |
HYPERION: an open-source parallelized three-dimensional dust continuum radiative transfer code
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street,
Cambridge,
MA
02138,
USA
e-mail: trobitaille@cfa.harvard.edu
Received:
27
April
2011
Accepted:
16
September
2011
Hyperion is a new three-dimensional dust continuum Monte-Carlo radiative transfer code that is designed to be as generic as possible, allowing radiative transfer to be computed through a variety of three-dimensional grids. The main part of the code is problem-independent, and only requires an arbitrary three-dimensional density structure, dust properties, the position and properties of the illuminating sources, and parameters controlling the running and output of the code. Hyperion is parallelized, and is shown to scale well to thousands of processes. Two common benchmark models for protoplanetary disks were computed, and the results are found to be in excellent agreement with those from other codes. Finally, to demonstrate the capabilities of the code, dust temperatures, SEDs, and synthetic multi-wavelength images were computed for a dynamical simulation of a low-mass star formation region. Hyperion is being actively developed to include new features, and is publicly available⋆⋆.
Key words: methods: numerical / radiative transfer / scattering / polarization
© ESO, 2011
1. Introduction
The investigation of astrophysical sources via multi-wavelength observations requires understanding the transfer of radiation through dust and gas in order to reliably derive geometrical, physical, and chemical properties. While a small subset of problems can be solved analytically, most require a numerical solution.
A variety of techniques have been developed to this effect, and until recently, most relied on a direct numerical solution to the differential equation of radiative transfer. Examples include 2nd order finite differences (Steinacker et al. 2003), 5th order Runge-Kutta integration (Steinacker et al. 2006), and variable Eddington tensors (Dullemond & Turolla 2000; Dullemond 2002).
While these techniques can often provide results accurate to arbitrary precision, and have been very successful for one-dimensional problems, they become increasingly complex when applied to two- and three-dimensional problems. Within the last decade, the Monte-Carlo technique applied to radiative transfer has become an increasingly popular alternative that is well suited to arbitrary three-dimensional density distributions. Rather than solving the equation of radiative transfer directly, this method relies on random sampling of probability distribution functions to propagate photon packets through a grid of constant density and temperature cells.
In its simplest implementation, Monte-Carlo radiative transfer considers single-frequency photon packets that are emitted by sources, and are propagated through a grid of constant density cells. Each photon packet travels a certain optical depth, before being either scattered, or absorbed and immediately re-emitted (to conserve energy). These photon packets can then continue to travel and interact until they escape the grid. The optical depth, type of interaction, and frequency of re-emitted photon packets, as well as scattering/re-emission directions are all sampled from probability distribution functions. Photon packets escaping from the grid can be used to compute synthetic observations, such as spectral energy distributions (SEDs) and images. By repeating this process for large numbers of photon packets, the signal-to-noise of the synthetic observations can be increased.
In cases where local thermodynamic equilibrium (LTE) can be assumed, the energy absorbed in each cell can be used to compute the equilibrium temperature. Since the emissivity depends on the temperature, the radiative transfer has to be run iteratively to obtain a self-consistent solution for the temperature.
Various methods have been developed to improve the performance of Monte-Carlo radiative transfer codes, which would otherwise be inefficient in many cases. For example, rather than simply using discrete absorptions in cells to compute the equilibrium temperature, Lucy (1999) suggested summing the optical depth to absorption of photon packet paths through each grid cell, requiring far fewer photons to achieve a comparable signal-to-noise in the derived temperatures. Bjorkman & Wood (2001) developed an algorithm whereby the temperature of a cell is updated immediately each time a photon is absorbed, and the frequency of the re-emitted photon is sampled from a difference emissivity function that introduces a correction to account for the fact that previous photons were sampled from emissivities for different temperatures. This algorithm is sometimes referred to simply as “immediate re-emission”, but this is a misnomer since other algorithms also immediately re-emit a photon following an absorption to conserve energy (e.g., Lucy 1999); instead, what this algorithm introduces is the immediate temperature correction aspect.
For synthetic observations, the peeling-off technique (Yusef-Zadeh et al. 1984) greatly improves the signal-to-noise of SEDs and images: every time a photon packet is emitted, scattered, or re-emitted after an absorption, the probability that the emitted or scattered photon would reach the observer is used to build up the observations. Thus each photon contributes multiple times to the SEDs or images. Another example is that of forced first scattering (e.g. Mattila 1970; Wood & Reynolds 1999), which can be used in optically thin cases to force photon packets to interact with the dust (this requires weighting the photons accordingly to avoid any bias due to the forcing).
In standard Monte-Carlo, the number of interactions a photon packet will undergo before traveling a certain distance increases approximately with the square of the density, so that in very optically thick cells, photon packets may become effectively trapped. This problem can be avoided by locally making use of the diffusion approximation to solve the radiative transfer in these regions. For example, Min et al. (2009) developed a modified random walk procedure based on the diffusion approximation that can dramatically reduce the number of steps required for a photon to escape from a grid cell of arbitrarily large optical depth.
A large collection of dust continuum Monte-Carlo radiative transfer codes has been developed (e.g. Wolf et al. 1999; Harries 2000; Gordon et al. 2001; Misselt et al. 2001; Wood et al. 2001, 2002a,b; Wolf 2003; Stamatellos & Whitworth 2003; Whitney et al. 2003a,b, 2004; Dullemond & Dominik 2004; Jonsson 2006; Pinte et al. 2006; Min et al. 2009), each including some or all of the above optimizations, as well as other optimizations not mentioned here. While some of the early codes assumed spherical or axis-symmetric geometries for simplicity, many have since been adapted to compute fully arbitrary three-dimensional distributions. In addition to dust continuum radiative transfer, some codes can also compute non-LTE line transfer (Carciofi & Bjorkman 2006, 2008), or photoionization (e.g. Ercolano et al. 2003, 2005, 2008).
This paper presents Hyperion, a new dust-continuum Monte-Carlo radiative transfer code that is designed to be applicable to a wide range of problems. Hyperion implements many of the recent optimizations to the Monte-Carlo technique discussed above, was written from the start to be a parallel code that can scale to thousands of processes, and is written in a modular and extensible way so as to be easily improved in future. It can treat the emission from an arbitrary number of sources, can include multiple dust types, and can compute the anisotropic scattering of polarized radiation using fully numerical scattering phase functions. It uses the Lucy (1999) iterative method to determine the radiative equilibrium temperature, but does not use the Bjorkman & Wood (2001) temperature correction technique, as the latter is much more challenging to parallelize efficiently. Thanks to the modular nature of the code, the radiative transfer can be computed on a number of different three-dimensional grid types, and additional grid types can be added in future. Hyperion can compute SEDs and multi-wavelength images and polarization maps. The code is released under an open source license, and is hosted on a service that allows members of the community to easily contribute to the code and documentation.
Section 2 gives an overview of the implementation of the code. Section 3 discusses the efficiency of the parallelized code. Section 4 presents the results for two benchmark models of protoplanetary disks. Finally, Sect. 5 demonstrates the capabilities of the code by computing temperatures, SEDs, and synthetic images for a simulation of a star-formation region. The availability of the code and plans for the future are discussed in Sect. 6.
2. Code overview
The code is split into two main components. The first, which carries out the core of the radiative transfer calculation, is implemented in Fortran 95/2003 for high performance. This part of the code is problem-independent: the input (bundled into a single file) consists of an arbitrary three-dimensional density structure as well as dust properties, a list of sources, and output parameters. This input is used by the Monte-Carlo radiative transfer code to compute temperatures, SEDs, and images. Therefore, it is possible to use either gridded analytical density structures, or arbitrary density grids from simulations. At the moment, Hyperion supports several types of three-dimensional grids (Sect. 2.1.2) and the modular nature of the code will make it easy to add support for additional grid types in the future. It is possible to specify an arbitrary number of dust types (within computational limits), which allows models to have different effective grain size distributions and compositions in different grid cells.
The second component of the code consists of an object-oriented Python library that makes it easy to set up the input file for arbitrary problems from a single script. This library includes pre-defined analytical density structures for common problems such as flared disks and rotationally flattened envelopes and will also include scripts to import density structures from simulations. Post-processing tools are also provided in the Python library to analyze the results of radiative transfer models.
The present section describes the algorithm for the main radiative transfer code. The code first reads in the inputs (Sect. 2.1), then propagates photon packets through the grid (Sect. 2.2) for multiple iterations to compute the energy absorbed in each cell (Sect. 2.3). Once the absorbed energy calculation has converged (Sect. 2.4), the code computes SEDs and images (Sect. 2.6).
2.1. Inputs to the code
2.1.1. Sources
A model can include any number of sources of emission (within computational limits). Each source is characterized by a bolometric luminosity, and the frequencies of the emitted photon packets are randomly sampled such that the emergent frequency distribution of the packets reproduces a user-defined spectrum. The total number of photons to emit from sources is set by the user. A number of different source types can be used – at the moment, the code supports:
-
isotropic point sources;
-
spherical sources with or without limb darkening. These can include arbitrary numbers of cool or hot spots, each with different positions, sizes, and with their own spectrum;
-
diffuse sources where flux is emitted from within grid cells according to a three-dimensional probability distribution function (this can be useful for unresolved stellar populations in galaxy models, or for accretion luminosity emitted via viscous energy dissipation in protoplanetary disks);
-
external isotropic sources, which can be used to simulate an interstellar or intergalactic radiation field.
Each photon packet emitted is characterized by a position, direction vector, frequency, and a Stokes vector (I, Q, U, V) that describes the total intensity and the linear and circular polarization.
2.1.2. Dust density grid
The code is written in a modular way that allows support for different grid geometries to be easily added. At the moment, three-dimensional Cartesian, spherical-polar, and cylindrical-polar grids can be used, as well as two types of adaptive Cartesian grids. The first is a standard octree grid, in which each cubic cell can be recursively split equally into eight smaller cubic cells. The second is the type of grid commonly used in adaptive mesh refinement (AMR) hydrodynamical codes. Here, a coarse grid is first defined on the zero-th level of refinement, and with increasing levels, increasingly finer grids can be used in areas where high resolution is needed. Because they concentrate the resolution where it is needed, variable resolution grids such as octrees and AMR allow radiation transfer to be computed on density grids with effective resolutions that would be prohibitive with regular Cartesian grids.
2.1.3. Dust properties
The dust properties required are the frequency-dependent mass extinction coefficient
χν and albedo
ων, as well as the scattering
properties of the dust. At this time, Hyperion supports anisotropic
wavelength-dependent scattering of randomly oriented grains, using a 4-element Mueller
matrix (Chandrasekhar 1960; Code & Whitney 1995):
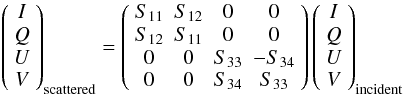 (1)Support
for aligned non-spherical dust grains, which are described by a full 16-element matrix,
will be implemented in future (e.g. Whitney &
Wolff 2002).
(1)Support
for aligned non-spherical dust grains, which are described by a full 16-element matrix,
will be implemented in future (e.g. Whitney &
Wolff 2002).
To keep the Fortran code as general as possible, the mean opacities and emissivities of the dust are pre-computed by the Python library as a function of the specific energy absorption rate of the dust rather than the dust temperature (cf. Sect. 2.3). For dust in LTE, the emissivities are given by jν = κν Bν(T), and the mean opacities are the usual Planck and Rosseland mean opacities to extinction and absorption. However, it is also possible to specify mean opacities and emissivities that do not assume LTE (e.g. Sect. 2.5). Thus, assumptions about LTE are made at the level of the dust files, rather than in the radiative transfer code itself.
2.2. Photon packet propagation
The code implements the propagation of photon packets in the following way: a photon packet is emitted from a source, randomly selected from a probability distribution function defined by the relative luminosity of the different sources. This sampling can be done either in the standard way to give a number of photon packets proportional to the source luminosity, or to give equal numbers of photons to each source, which requires weighting the energy of the photons. The direction and frequency of the photon packet are randomly sampled accordingly for the type and the spectrum of the source it originates from, using standard sampling with no weighting. A random optical depth to extinction τ is sampled from the probability distribution function exp(− τ) by sampling a random number ζ uniformly between 0 and 1, and taking τ = −lnζ. The photon packet is then propagated along a ray until it either escapes the grid, or reaches the sampled optical depth, whichever happens first. If the photon packet has not escaped the grid, it will then interact with the dust. A random number ζ is sampled uniformly between 0 and 1, and if it is larger than the albedo of the dust, the photon packet is absorbed; otherwise it is scattered. Once the photon packet is scattered or re-emitted, a new optical depth is sampled, and the process is repeated until the photon packet escapes from the grid.
Very optically thick regions are an issue in basic Monte-Carlo radiative transfer, as photon packets can get trapped in these regions and require in some cases millions of absorptions/re-emissions and scatterings to escape. Recently, Min et al. (2009) proposed a modified random walk (MRW) algorithm that allows photon packets to propagate efficiently in very optically thick regions by grouping many scatterings and absorptions/re-emissions into single larger steps. The photon packet propagation described previously is done in a grid made up of cells of constant density and temperature. Therefore if the mean optical depth to the edge of a cell is much larger than unity, one can set up a sphere whose radius is smaller than the distance to the closest wall, inside which the density will be constant, and travel to the edge of a sphere in a single step using the diffusion approximation, thus avoiding the need to compute millions of interactions. Hyperion includes the implementation of the MRW algorithm described in Robitaille (2010).
2.3. Temperature/energy absorption rate calculation
Hyperion uses the iterative continuous absorption method proposed by Lucy (1999): in the first iteration, the specific
energy absorption rate of the dust is computed in each cell using
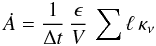 (2)where
Δt is the time over which photon packets are emitted (taken to be 1 s
in the code), V is the cell volume, ϵ is the energy of a
photon packet, ℓ is the path length traveled – which depends on the
density, as does the number of path lengths being added – and
κν is the mass absorption coefficient. The
temperature T of the dust can be found from Ȧ by
balancing absorbed and emitted energy, assuming LTE:
(2)where
Δt is the time over which photon packets are emitted (taken to be 1 s
in the code), V is the cell volume, ϵ is the energy of a
photon packet, ℓ is the path length traveled – which depends on the
density, as does the number of path lengths being added – and
κν is the mass absorption coefficient. The
temperature T of the dust can be found from Ȧ by
balancing absorbed and emitted energy, assuming LTE:
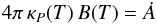 (3)where
κP(T) is the Planck mean
mass absorption coefficient, and
B(T) = (σ/π) T4
is the integral of the Planck function. As mentioned in Sect. 2.1.3, Hyperion does not compute temperatures, but instead the
mean opacities and emissivities of the dust, which are pre-computed, are tabulated as a
function of Ȧ rather than T. In cases where the
temperature is needed (for example if requested as output from the user), the temperature
is computed on the fly using the pre-computed Planck mean opacities.
(3)where
κP(T) is the Planck mean
mass absorption coefficient, and
B(T) = (σ/π) T4
is the integral of the Planck function. As mentioned in Sect. 2.1.3, Hyperion does not compute temperatures, but instead the
mean opacities and emissivities of the dust, which are pre-computed, are tabulated as a
function of Ȧ rather than T. In cases where the
temperature is needed (for example if requested as output from the user), the temperature
is computed on the fly using the pre-computed Planck mean opacities.
For high optical depth problems, such as protoplanetary disks, some regions in the grid may see few or no photon packets, and reliable values for Ȧ or T can therefore not be directly computed. In this case, one can formally solve the diffusion approximation for the cells that see fewer than a given threshold of photon packets, using cells that do have reliable values as boundary conditions (see Appendix A). This is referred to as the partial diffusion approximation (PDA) in Min et al. (2009).
2.4. Convergence
The emissivity of the dust depends on Ȧ, which depends on the
propagation of the photon packets and the frequency of the photon packets, which in turn
depends on the emissivity of the dust, so one needs to compute the radiative transfer for
several iterations before the values of Ȧ in each cell converge. A simple
algorithm to determine convergence is included in the code. The main function used in the
convergence algorithm is 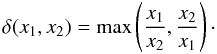 (4)This measures how
different x2 is from x1 and does
not depend on the direction of the change. For example, a value of δ = 2
means that the quantity has changed by a factor of 2. Because the change is expressed as a
ratio, this means that large changes can be more easily expressed than using a simple
fractional difference.
(4)This measures how
different x2 is from x1 and does
not depend on the direction of the change. For example, a value of δ = 2
means that the quantity has changed by a factor of 2. Because the change is expressed as a
ratio, this means that large changes can be more easily expressed than using a simple
fractional difference.
At each iteration i, the code determines by how much the energy absorbed
Ȧ has changed by computing for each cell j the change
in the energy absorbed in each cell j,
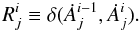 (5)The quantile value
Qi at the pth percentile
of the Rj values is then computed and
compared to the value found during the previous iteration,
Qi−1. Finally, the change in this
quantile is calculated using
(5)The quantile value
Qi at the pth percentile
of the Rj values is then computed and
compared to the value found during the previous iteration,
Qi−1. Finally, the change in this
quantile is calculated using 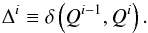 (6)The specific energy
absorption rate is considered to be converged once
Qi and Δi
have fallen below user specified values Qthres and
Δthres. As an example, setting p = 99.9%,
Qthres = 2., and Δthres = 1.1 means that
convergence is achieved once 99.9% of the differences in specific energy absorption rates
between iterations are less than a factor of 2, and once the 99.9% percentile value of the
difference changes by less than a factor of 1.1 (~ 10%).
(6)The specific energy
absorption rate is considered to be converged once
Qi and Δi
have fallen below user specified values Qthres and
Δthres. As an example, setting p = 99.9%,
Qthres = 2., and Δthres = 1.1 means that
convergence is achieved once 99.9% of the differences in specific energy absorption rates
between iterations are less than a factor of 2, and once the 99.9% percentile value of the
difference changes by less than a factor of 1.1 (~ 10%).
Using this techniques is more robust to noise in the specific energy values than simply requiring that all cells vary less than a given threshold, since it allows the user to ignore outliers by setting the percentile value appropriately. Of course, there is no guarantee that the criteria set by the user will be met at any iteration if the noise is too large, but in this case the user will see that there is not convergence, and can increase the number of photon packets, the maximum number of iterations, or use less stringent requirements for convergence. In any case, this method allows users to set quantitative requirements that are necessary to meet their scientific problem and that are more flexible than a single threshold on all values.
2.5. PAH/VSG emission
In addition to dust continuum radiative transfer, the code can also take into account any population where the opacity is independent of temperature or density, and for which the emissivity depends only on the specific energy absorbed (Ȧ) inside each cell (Sect. 2.1.3). While this does not permit arbitrary non-LTE radiative transfer, it does allow one to use an approximation of the emission from stochastically heated polycyclic aromatic hydrocarbons (PAHs) and very small non-thermal grains (VSGs) using a similar prescription to that given in Wood et al. (2008).
The idea behind the algorithm is to pre-compute the average emissivity of an ensemble of PAHs and VSGs, as a function of the energy deposited by radiation into the PAHs and VSGs – the specific energy absorption rate Ȧ for the PAH and VSG populations – for a given irradiating spectrum, and to then use these emissivities as look-up tables in the radiative transfer code.
Since the opacities of PAHs and VSGs are typically strongly peaked in the UV and optical, this means that the UV and optical will dominate the energy exciting and being reprocessed by the PAHs and VSGs, and the emissivities are then being chosen based on the total strength of the UV and optical emission relative to the original template spectrum. The shape of the template spectrum does have a small impact on the pre-computed emissivities, but to first order, simply using the ratio of the total energy absorbed should be adequate for estimating the importance of PAHs and VSGs as absorbers and emitters, and allows the impact on the SEDs and images to be studied. While the strength of the PAH features and VSG continuum in SEDs should be accurate to first order, the shape of the PAH features should be treated with caution.
Note that the implementation discussed here differs in one respect from the Wood et al. (2008) prescription: the latter uses the mean intensity, rather than the energy intercepted by the PAHs and VSGs, to determine which emissivity file to use. Using the energy absorbed by the PAHs and VSGs may be more appropriate than using the mean intensity, since the latter would predict the same excitation for a fixed mean intensity, whether this intensity peaked in the UV or the millimeter, while using Ȧ would give a higher excitation for a spectrum peaking in the UV compared to one peaking in the mm.
2.6. SEDs and images
Once the specific energy absorption rate calculation has converged, SEDs and images can be computed. There are several methods to do this, and all of the following are implemented in the code.
2.6.1. Photon binning
The easiest and most inefficient method to compute SEDs and images is to propagate the photon packets as for the initial iterations, and bin them all into viewing angles as they escape from the grid. This is very inefficient, because each photon packet only contributes once to the SEDs and images, and only to one viewing angle. Furthermore, the viewing angle bins cannot be arbitrarily small, and therefore the SEDs and images resulting from this are averaged over viewing angle.
2.6.2. Peeling-off
Yusef-Zadeh et al. (1984) introduced the concept of peeling-off, whereby at each scattering or re-emission, the probability p of the photon packet being scattered or re-emitted towards the observer immediately after the interaction is computed, and a photon packet with weight p exp(− τ) is added to the SED and images, where τ is the optical depth to reach the observer from the interaction. This results in much higher signal-to-noise than photon packet binning, because each photon packet contributes several times to the SEDs and images at each viewing angle.
2.6.3. Raytracing
By far the most efficient method of computing SEDs and images is raytracing, which essentially consists of determining the source function at each position in the grid, and solving – in post-processing – the equation of radiative transfer along lines of sight to the observer through the dust geometry. For thermal emission, this is relatively straightforward, because the source function in each cell is simply related to the mass and temperature or energy in the cell. For scattered light, unless the scattering phase function is isotropic, one needs to retain information about the angular and frequency dependence of the incident or scattered light. As discussed in Pinte et al. (2009), this is either computationally very expensive in terms of memory, or results in a loss of accuracy for strongly peaked scattering phase functions. In the current implementation of Hyperion, raytracing can be used for the source and dust emission, allowing excellent signal-to-noise to be achieved at long wavelengths where traditional Monte-Carlo only produces very few photon packets. Raytracing for scattered light will be implemented as an option in future since – if adequate computational resources are available – it can provide excellent signal-to-noise significantly faster than conventional peeling-off as for source and dust emission.
2.6.4. Monochromatic radiative transfer
The default mode of the binning (Sect. 2.6.1), peeling-off (Sect. 2.6.2), and raytracing (Sect. 2.6.3) algorithms is to produce SEDs and images with finite width wavelength/frequency bins. However, in some cases it is desirable to compute SEDs or images at exact wavelengths/frequencies. When this is the case, the peeling-off algorithm for computing the scattered light contribution to the SED or images has to be modified. In this case, the scattered light is separated into two contributions, namely the scattered light from the sources, and the scattered dust emission. To compute the scattered light from the sources, photon packets are emitted by all the sources at the fixed wavelengths/frequencies required. Each time a photon packet scatters, a photon packet is peeled-off, and each time a photon packet is absorbed, it is terminated. Thus, there is no immediate re-emission following an absorption. The next step is to compute the scattered dust emission. The specific energy absorption rate is used to compute the emissivity at the fixed wavelengths/frequencies inside each cell. To emit a photon packet, a random cell is selected in the grid, and the photon packet is emitted randomly within the cell, carrying an amount of energy proportional to the local emissivity. The photon packet is then propagated, and a photon packet is peeled-off at each scattering. As before, the photon packet is terminated once it is absorbed. This algorithm ensures conservation of the total scattered light contribution.
 |
Fig. 1 The main panels show the wall clock speedup relative to serial execution for a model of a protoplanetary disk. The right panel shows the same model as that in the left panel, but with 10 times more photon packets for every iteration. The open circles show the average values of 10 executions of the code, and the uncertainties in these values derived from the scatter are not shown as they are smaller than the data points. The dashed curves show the speedup expected from a perfectly parallelized code. The solid curves show the best fit to the speedup curve assuming Amdahl’s law (described in text). The gray shaded areas around the curves show the 68.3% confidence interval. The maximum speedups derived from the best fits are shown as horizontal dotted lines. The inset panels show the probability of different P values, with the 68.3% confidence intervals shown in shaded gray. |
2.7. Additional user options
2.7.1. Uncertainties
When computing SEDs and images, Hyperion allows the user to compute uncertainties, which uses the scatter in the photon packet flux values to derive errors in the flux at each wavelength/frequency and in each aperture or pixel. The fact that a given SED or image can be constructed using a combination of techniques, such as peeling-off and raytracing – which can produce very different signal-to-noise – is properly taken into account by computing the uncertainties for the contribution from each technique to the final SEDs or images separately and then combining them.
2.7.2. Photon tracking
Hyperion offers the option for the user to track the origin of each photon packet to split SEDs and images into different components. A basic mode allows SEDs and images to be split into contributions from sources and from dust, while a more detailed mode allows the flux to be split into individual sources and dust types. In both cases, the flux can be split further into photon packets reaching the observer directly, and photon packets having been scattered since the last emission/re-emission and before reaching the observer.
2.7.3. Dust sublimation
Users have the option to specify a dust sublimation specific energy absorption rate for each dust type, and three different dust sublimation modes are possible:
-
the specific energy absorption rate can simply be cappedto the maximum value, without changing thedensity;
-
the dust can be completely removed from cells exceeding the maximum specific energy absorption rate;
-
the dust density can be reduced but not set to zero. This can be useful because in optically thick cells, if radiation originates from the cell (for example luminosity from viscous dissipation), the specific energy absorption rate can be high because the radiation is trapped. If the density had been lower but non-zero, the specific energy absorption rate might not have exceeded the maximum specified. In this situation, the dust density should be reduced but not set to zero.
2.7.4. Forced first scattering
As mentioned in Section 1, forced first scattering (e.g. Mattila 1970; Wood & Reynolds 1999) can be used to improve the signal-to-noise of scattered radiation in optically thin dust. Hyperion includes an implementation of this algorithm.
3. Parallelized performance
The reason for not using the Bjorkman & Wood (2001) immediate temperature correction method in Hyperion is that each time a photon gets absorbed and re-emitted, the specific energy absorption rate grid has to be updated. Thus, it is not possible to compute the propagation of multiple photons simultaneously and to then combine the results, and codes using this method can therefore not easily be parallelized. By simply using an iterative approach to computing the specific energy absorption rate using the Lucy (1999) continuous absorption method, one has the advantage that within an iteration, the problem is “embarrassingly parallel”. Each process can propagate photon packets independently, and at the end of the iteration, the energy absorbed in each cell is synchronized over processes. Similarly, when SEDs, images, or polarization maps are computed, these can be computed by separate processes, and combined at the end of the calculation.
The code has been parallelized using the Message Passing Interface (MPI). Since different cores or nodes can have inhomogeneous performance, rather than dividing the total number of photon packets equally between processes, the task is divided into chunks of photon packets that are small enough that there are many more chunks than total number of processes, but large enough that the processes do not communicate too often. Each process then computes one batch of photon packets, and reports back to the main process to find out whether to process another batch or whether to stop. This incurs a very small overhead, since the request consists essentially of a single number both ways. Only at the end of the iteration, once all processes have received the signal to stop, are the results combined. This last step incurs an overhead, which scales with the number of processes and the grid, image, or SED resolution. However, in most cases, the overhead is negligible compared to the main computation.
The parallel efficiency of the code depends on the particular model being computed and the
number of photon packets requested. One way to quantify the speedup for a given model is to
compare the fraction of time spent in the serial execution of the code, such as the startup
phase where the data is read in from the input file, or the time between iterations, to the
fraction of time spent in the “embarrassingly parallel” photon packet propagation. If one
writes the fraction of the code that is truly parallel as P, then the
speedup obtained by running the code on N parallel processes is:
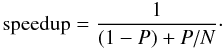 (7)This is often
referred to as Amdahl’s law (Amdahl 1967). One
consequence of Eq. (7) is that as
N tends to infinity, the speedup tends to a finite maximum
(7)This is often
referred to as Amdahl’s law (Amdahl 1967). One
consequence of Eq. (7) is that as
N tends to infinity, the speedup tends to a finite maximum
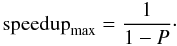 (8)In this case, the
parallelized part of the code runs infinitely fast, and the execution time is given purely
by the serial portion of the code.
(8)In this case, the
parallelized part of the code runs infinitely fast, and the execution time is given purely
by the serial portion of the code.
 |
Fig. 2 Temperature results for the Pascucci et al. (2004) disk benchmark, for the τV = 100 model. The left panel shows a radial temperature profile close to the mid-plane (θ = 2.5°), both in absolute terms (top) and relative to the reference code RADICAL (bottom). The right panel shows a vertical cut through the disk at a cylindrical radius of 2 AU. The black lines show the results from Hyperion, while the gray lines show the results from the codes tested in Pascucci et al. (2004) |
 |
Fig. 3 SED results for the Pascucci et al. (2004) disk benchmark, for the four disk masses used. In each panel, the top section shows the SED obtained using Hyperion (black line), compared to the reference code from Pascucci et al. (2004) (RADICAL; gray circles), for the three viewing angles used (12.5, 42.5, and 77.5°). The dashed line shows the blackbody spectrum of the central source. The bottom three sections in each panel show the fractional difference between Hyperion and RADICAL (black line), and between the other codes in Pascucci et al. (2004) and RADICAL (gray lines). |
 |
Fig. 4 Temperature results for the Pinte et al. (2009) disk benchmark. The top-left and top-right panels shows the radial temperature profile at the disk mid-plane for the lowest and highest disk mass models. The bottom panels shows two vertical cuts through the disk for the highest disk mass model, at cylindrical radii of 0.2 and 200 AU respectively. In each panel, the top section shows the temperature profile in absolute terms, while the bottom section shows the results relative to the reference result from Pinte et al. (2009), which is the average of the results from MCFOST, MCMAX, and TORUS. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, and TORUS. |
 |
Fig. 5 SED results for the Pinte et al. (2009) disk benchmark, for the four disk masses used. In each panel, the top section shows the SED obtained using Hyperion (black line), compared to the average result of the codes used in Pinte et al. (2009) (gray circles), for four of the viewing angles (18.2, 75.5, 81.4, 87.1°). The dashed line shows the blackbody spectrum of the central source. The bottom four sections in each panel show the fractional difference between Hyperion and the reference result (black line), and between the other codes compared in Pinte et al. (2009) and the reference result (gray lines). |
 |
Fig. 6 Image results for the Pinte et al. (2009) disk benchmark. The top two rows show the results for the i = 69.5° model, while the bottom two rows show the results for the i = 87.1° model. For each viewing angle, the resulting image is shown on the left on a power-law stretch (with power 1/4), while the remaining plots show various cuts (indicated on the images), in absolute flux units, as well as relative to the reference result in Pinte et al. (2009), which is the average of the MCFOST, MCMAX, TORUS, and Pinball codes. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, TORUS, and Pinball. As in Pinte et al. (2009), the cuts are 11 pixels wide to improve the signal-to-noise of the profiles. |
 |
Fig. 7 Linear polarization map results for the Pinte et al. (2009) disk benchmark. The top two rows show the results for the i = 69.5° model, while the bottom two rows show the results for the i = 87.1° model. For each viewing angle, the resulting linear polarization map is shown on the left on a linear stretch, while the remaining plots show various cuts (indicated on the maps, and identical to those in Fig. 6), both in absolute terms, and relative to the reference result in Pinte et al. (2009), which is the average of the MCFOST, MCMAX, and Pinball codes. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, and Pinball. As in Pinte et al. (2009), the cuts are 11 pixels wide to improve the signal-to-noise of the profiles. |
 |
Fig. 8 Three-color unconvolved synthetic images of the simulation, from the near-infrared
(top left) and mid-infrared (top right) to the
far-infrared (bottom left and right). The wavelengths and colors used
are 1.25 μm (blue), 1.65 μm (green), and
2.15 μm (red) for the JHK image,
3.6 μm (blue), 4.5 μm (green), and
8.0 μm (red) for the Spitzer/IRAC image,
70 μm (blue), 110 μm (green), and
170 μm (red) for the Herschel/PACS image, and
250 μm (blue), 350 μm (green), and
500 μm (red) for the Herschel/SPIRE image. All
images are shown on an arcsinh stretch which allows a larger dynamic range to be shown
by reducing the intensity of the brightest regions. The exact transformation is given
by |
 |
Fig. 9 Three-color synthetic images of the simulation, from the near-infrared (top left) and mid-infrared (top right) to the far-infrared (bottom left and right). The images are binned to the pixel resolutions appropriate for ground based observations (JHK) and for Spitzer and Herschel observations respectively. The images were convolved with the appropriate instrumental PSFs, and include Gaussian noise with realistic levels. The wavelengths, stretches, and levels used for the images are identical to those used in Fig. 8. |
The value of P is dependent on the choice of the model being computed and
number of photon packets. This is demonstrated here with a model of a protoplanetary disk
(taken from Sect. 4.2) computed on different numbers
of cores, ranging from N = 1 to N = 512 in powers of 2.
The wall clock times of the parallel computations are compared to the true serial runtime
rather than the parallel version running with one process, since these will have slightly
different runtimes. The times used are wall clock times1, rather than CPU times. For each number of cores, the model was run ten times to
obtain a mean speedup and a measure of the scatter from one run to the next. The results are
shown in Fig. 1 for two instances of the model – one
with ten times more photon packets than the other. The models were run on the Harvard
Odyssey cluster, allowing N up to 512. For the model with the lower number
of photon packets2, the speedups obtained are well fit
by P = 0.99658 ± 0.00014, while the speedups for the model with the higher
number of photon packets were well fit by P = 0.999373 ± 0.00006 where the
uncertainties were derived as a formal confidence interval using the
χ2 surface. The reduced χ2 values
for the fits were 1.01 and 3.25 respectively, indicating good fits. The P
values translate into maximum speedups of 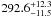 and
and
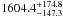 respectively. These values differ by almost an order of magnitude, which is expected, since
the only difference between the two models is that the CPU time of the parallel section of
the code was increased by a factor of ten, while the serial part of the code remained
identical (same input/output and synchronization overheads). In other words, both models
tend to the same runtime, since the serial portion of the code is the same in both cases.
respectively. These values differ by almost an order of magnitude, which is expected, since
the only difference between the two models is that the CPU time of the parallel section of
the code was increased by a factor of ten, while the serial part of the code remained
identical (same input/output and synchronization overheads). In other words, both models
tend to the same runtime, since the serial portion of the code is the same in both cases.
The speedup values presented here are purely illustrative, and should not be assumed to hold for all models, but they serve to show that the efficiency of the code does have a finite limit which depends on the model set-up. As for most parallel codes, beyond a certain number of parallel processes, the wall clock runtime is completely dominated by the time to execute the serial part of the code (typically input/output and calculations between iterations such as the PDA). Users are encouraged to determine the optimal number of processes for the problem they are considering.
4. Benchmarks
4.1. Pascucci et al. (2004) benchmark
4.1.1. Definition
Pascucci et al. (2004) defined a benchmark
problem for 2D radiative transfer, consisting of a flared disk around a point source.
The central source is a point source with a 5800 K blackbody spectrum, and a luminosity
of 1.016 L⊙. The disk extends from 1 to 1000 AU, and has a
density structure given by: ![\begin{equation} \label{eq:disk} \rho(r, z) = \rho_0\,\left(\frac{r}{r_0}\right)^{-\alpha}\,\exp{\left[-\frac{1}{2}\,\left(\frac{z}{h_0 \left(r/r_0\right)^{\beta}}\right)^2\right]}, \end{equation}](/articles/aa/full_html/2011/12/aa17150-11/aa17150-11-eq68.png) (9)where
r is the cylindrical polar radius,
r0 = 500 AU,
(9)where
r is the cylindrical polar radius,
r0 = 500 AU, 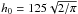 AU,
α = 1., and β = 1.125. The disk is made up of dust
grains with a single size of 0.12 μm, a density of
3.6 g/cm3, and composed of astronomical silicates with properties given by
Draine & Lee (1984). Scattering is
assumed to be isotropic.
AU,
α = 1., and β = 1.125. The disk is made up of dust
grains with a single size of 0.12 μm, a density of
3.6 g/cm3, and composed of astronomical silicates with properties given by
Draine & Lee (1984). Scattering is
assumed to be isotropic.
The benchmark consists of four cases, with visual (λ = 550 nm) optical depths, measured radially along the disk mid-plane, of τV = 0.1, 1, 10, and 100. These correspond to disk (dust) masses of 1.1138 × 10-7, 1.1138 × 10-6, 1.1138 × 10-5, and 1.1138 × 10-4 M⊙ respectively. The corresponding maximum optical depths perpendicular to the disk are of the order of τV = 0.01, 0.1, 1, and 10 respectively. SEDs are computed at three viewing angles in each case: 12.5, 42.5, and 77.5°.
4.1.2. Results
The benchmark models were computed using a spherical polar grid with dimensions (nr,nθ,nφ) = (499,399,1) and extending out to 1300 AU. The SEDs were computed at specific wavelengths using the monochromatic radiative transfer described in Sect. 2.6. The MieX code (Wolf & Voshchinnikov 2004) was used to compute the optical properties of the dust. The convergence algorithm discussed in Sect. 2.4 was used, with p = 99%, Qthres = 2, and Δthres = 1.02. The models were run with enough photon packets to provide very high signal-to-noise in the temperatures and SEDs3, and were run using the parallel version of the code on a single machine with 8 cores, requiring a wall clock time of under 20 min for each model. The τV = 0.1 and 1 models converged after 3 iterations, while the τV = 10 and 100 models converged after 4 iterations.
Figure 2 shows for the most optically thick case (τV = 100) the temperature profile for a fixed polar angle (θ = 2.5°) as a function of radius r, and the temperature profile for a fixed radius (r = 2 AU) as a function of polar angle θ. The temperatures found by Hyperion are within the dispersion of the results from the other codes.
Figures 3 shows the SEDs for the Hyperion code and the reference code in Pascucci et al. (RADICAL) for the four disk masses and three viewing angles, and the fractional difference between the SEDs is shown in each case. Also shown in gray are the differences for other codes presented in Pascucci et al. The SEDs from Hyperion are within the dispersion of results from the other codes.
4.2. Pinte et al. (2009) benchmark
4.2.1. Definition
While the Pascucci et al. (2004) benchmark includes a case with fairly high visual optical depth through the mid-plane of the disk, the optical depths through realistic protoplanetary disks are much higher (τV > 106 in some cases), and are such that computing temperatures in the disk mid-plane becomes computationally challenging and requires approximations to be made (e.g. Sects. 2.2 and 2.3). Pinte et al. (2009) developed a complementary benchmark problem consisting of more massive disks with a more extreme radial density profile to test codes in the limit of very optically thick disks. In addition, the benchmark also tests the ability to compute anisotropic scattering, and to reproduce images and polarization maps at various viewing angles.
The benchmark case consists once again of a central star surrounded by a disk. The central star has a radius of 2 R⊙ and a temperature of 4000 K, with a blackbody spectrum. The disk extends from 0.1 to 400 AU (with cylindrical edges), and the density is given by Eq. (9), with r0 = 100 AU, h0 = 10 AU, α = 2.625, and β = 1.125. The disk is made up of dust grains with a single size of 1 μm, a density of 3.5 g/cm3, and composed of astronomical silicates with properties given by Weingartner & Draine (2001).
The benchmark consists of four cases, with disk (dust) masses of 3 × 10-8, 3 × 10-7, 3 × 10-6, and 3 × 10-5 M⊙. While the disk masses are comparable to that of the Pascucci et al. benchmark problem, the smaller inner radius (0.1 vs. 1 AU) and the much steeper surface density profile make this a more computationally challenging problem. In fact, the I-band (λ = 810 nm) optical depths, measured radially along the disk mid-plane, are of the order of τI = 103, 104, 105, and 106 for the four disk masses respectively, orders of magnitude higher than for the Pascucci et al. benchmark. The corresponding maximum optical depths perpendicular to the disk are of the order of τI = 100, 103, 104, and 105 respectively.
The benchmark test compares SEDs, images and polarization maps at 10 viewing angles corresponding to cosi = 0.05 to 0.95 in steps of 0.10, corresponding to viewing angles from 18.2 (almost pole-on) to 87.1° (almost edge-on). The images and polarization maps are computed at 1 μm, and span 251 × 251 pixels, and a physical size of 900 × 900 AU. Due to the single grain size, the scattering phase function oscillates strongly around 1 μm and at shorter wavelengths. Thus, these oscillations have a direct impact on scattered-light images computed at these wavelengths. While a single grain size, and therefore these oscillations, would not be seen in a real disk, this allows codes to test whether they correctly compute the scattering of photon packets.
4.2.2. Results
The benchmark models were computed using a cylindrical polar grid with dimensions (nr,nz,nφ) = (499,399,1) extending out to the outer disk radius. The SEDs were computed at exact wavelengths using the monochromatic radiative transfer described in Sect. 2.6. As before, the MieX code was used to compute the optical properties of the dust. The convergence algorithm discussed in Sect. 2.4 was used, with p = 99%, Qthres = 2, and Δthres = 1.02. The MRW (with γ = 2) and PDA approximations were used due to the high optical depths. The models were run with enough photon packets to provide very high signal-to-noise in the temperatures, SEDs, and images4, and were run using the parallel version of the code on 32 cores, requiring a wall clock time of 12 to 17 hours to compute the temperature and SEDs for the τI = 103 to 106 models, and an additional 11 h for the images and polarization maps. The temperatures converged after 7, 9, 9, and 10 iterations for the τI = 103, 104, 105, and 106 models respectively.
Figure 4 compares the mid-plane temperature profile in two of the models (τI = 103 and τI = 106), as well as two vertical cuts in the most optically thick model (τI = 106). Figure 5 compares the SEDs for the four models at four of the viewing angles (18.2, 75.5, 81.4, 87.1°). Finally, Figs. 6 and 7 compare the total intensity and polarization fraction maps for the most optically thick model (τI = 106). In all cases, the results produced by Hyperion are within the dispersion of results obtained from the other codes.
5. Case study: simulated observations of a low-mass star-forming region
5.1. The simulation
To demonstrate the capabilities of the code, a radiative transfer calculation on a simulation of a low-mass star forming cloud was carried out in order to produce synthetic observations from near-infrared to sub-milimeter wavelengths.
The demonstration uses a simulation of low-mass star formation computed with the ORION AMR three-dimensional gravito-radiation-hydrodyamics code (Offner et al. 2009, and references therein). The simulation contains 185 M⊙ of gas and dust in a box of side 0.65 pc, and resolves size-scales down to 32 AU, with an effective resolution of 40963. Offner et al. studied the effects of heating from protostars on the formation of stars, and therefore ran a simulation including radiative heating, and a control case with no radiation heating. The simulation used here is a snapshot of the one including radiative heating, for t ~ tff, where tff is the free-fall time.
 |
Fig. 10 Spectral Energy Distributions for the three sources labelled in Fig. 8. Each panel shows SEDs for 20 different viewing angles. The black lines show the minimum and maximum values as a function of wavelength, the light gray shows the range of values, and the dark gray shows the individual SEDs. |
5.2. The radiative transfer model
The radiative transfer through the star-forming region was simulated by taking into account both the luminosity from the forming stars (cf. Appendix B of Offner et al. 2009), represented by sink particles in the simulation, and the interstellar radiation field at the solar neighborhood from Porter & Strong (2005), which includes contributions from the stellar emission, PAH emission, and far-infrared thermal emission5. The simulation was embedded at the center of a cube of side 1.95 pc and a uniform density of 10-22 g/cm to simulate an ambient medium. The dust properties were taken from Draine (2003a,b) using the Weingartner & Draine (2001) Milky Way grain size distribution A for RV = 5.5 and C/H = 30 ppm renormalized to C/H = 42.6 ppm. In order to compute the full Mie scattering properties of this dust model, the bhmie routine from (Bohren & Huffman 1983) and modified by B. Draine6 was used.
The radiative equilibrium temperatures were first computed, followed by images at 12 wavelengths ranging from 1.25 microns to 500 microns7. The wavelengths were chosen to produce synthetic images in common bands, including JHK (1.25, 1.65, and 2.15 μm), Spitzer/IRAC 3.6, 4.5, and 8.0 μm, Herschel/PACS (70, 110, and 170 μm), and Herschel/SPIRE (250, 350, and 500 μm). A distance of 300 pc was used to simulate a nearby low-mass star-formation region. The images were computed at a viewing angle of (θ,φ) = (45°,45°), and are shown in Fig. 8 at a common resolution of 1′′/pix.
The near-infrared (JHK) image shows emission from the diffuse cloud, which is scattered light from the interstellar radiation field, as well as bright features corresponding to light from the forming stars scattered in the circumstellar dust. The near-infrared images are entirely dominated by direct and scattered stellar light, and there is no contribution from thermal emission. The mean colors of the near-infrared emission are J − H = 0.387 ± 0.280 and H − K = −0.214 ± 0.273 where the uncertainties indicate the scatter in the values rather than the error in the mean.
The IRAC image also shows (in blue) the scattered light from some of the sources, and a couple of the sources show a bipolar structure. This is noteworthy because the simulation does not include outflows. The bipolar structures seen here are instead due to beaming of the radiation by the three-dimensional structure of the accretion flows and the presence of protostellar disks. These cause the density to be lower along the rotation axis, and the radiation to preferentially escape in those directions. Thus, bipolar scattered light structures in the near- and mid-infrared are not necessarily evidence for actual outflows.
The IRAC image also shows the bright PAH background from the interstellar radiation field, which causes the cloud to appear in absorption as an infrared-dark cloud (IRDC). The column density of the filaments is typical of IRDCs: for instance, 10% of the area shown in Figure 8 has Σ > 0.10 g/cm2 or AV > 34.6 mag and 1% of the area has Σ > 0.27 g/cm2 or AV > 90.7 mag. In contrast, the far-infrared images show the cloud in emission. The color gradients across the PACS image trace gradients in the dust temperature, with the regions immediately surrounding the protostars being warmer than the rest of the cloud. Finally, the SPIRE image traces most of the mass, but does not show very strong color gradients, as most of the emission is in the Rayleigh-Jeans part of the spectrum.
5.3. Synthetic observations
Synthetic observations were produced by resampling the pixel resolution of the images to values typical of ground based observations for JHK (1′′), and of Spitzer and Herschel observations for the other bands (1.2′′ for IRAC, 3.2′′ for PACS, and 6′′ for SPIRE). The observations were convolved with the appropriate instrumental PSFs and Gaussian noise with typical values (listed in Table 1) was added to the images. The resulting synthetic observations are shown in Fig. 9.
The near-infrared (JHK) image does not change, since the pixel resolution is the same as before, and the PSF full-width at half maximum (1′′) is the same as the pixel resolution. The IRAC image shows many of the protostars appearing as strong 8 μm point sources. These were not seen in Fig. 8 since only one pixel contained this bright emission for each source. The PACS and SPIRE images are severely degraded, with only the brightest diffuse emission seen in the PACS image. Nevertheless, the PACS image shows very strong compact emission associated with the protostars. The SPIRE image does show bright point sources for a few of the protostars, but the remainder are confused with the cloud.
5.4. Spectral energy distributions
For three sources, indicated in Fig. 8, SEDs were computed inside 20 apertures, with a central circular aperture 5000 AU in radius, and the remaining apertures consisting of annuli logarithmically spaced between 5000 AU to 20 000 AU. The SEDs were directly computed by binning photon packets into apertures in the radiative transfer code (rather than using the images). In reality, measuring SEDs from convolved and noisy images is going to affect the resulting SEDs, but since this is highly dependent on the convolution and noise parameters, we do not take this into account here as we are interested in the “intrinsic” SEDs. The SEDs were computed for 20 viewing angles regularly distributed in three dimensions around the sources8.The innermost circular aperture was used to compute the SED, and the median of the SEDs in the 19 surrounding annular apertures was used as an estimate of the wavelength-dependent background that was subtracted from the central aperture SED.
The resulting SEDs are shown in Fig. 10. The three sources were chosen as they were expected to produce different SEDs based on the images shown in Fig. 8, and indeed the three sources show SEDs with varying amounts of near- and mid-infrared emission. The dependence of the near- and mid-infrared emission on viewing angle is very large, and is a consequence of the three-dimensional structure of the circumstellar material. The basic evolutionary properties of the sources are listed in Table 2. Source 2 is actually composed of a pair of sink particles, so these are listed as 2a and 2b in the table. Sources 1, 2a, and 2b have similar masses, of the order or 0.5−2 M⊙. Source 3 in contrast has a much lower mass, around 0.06 M⊙. By looking at the accretion rate of the sources relative to the sink particle masses, one can see that the relative accretion rate increases from Source 1 to 3, which is consistent with the average behavior of the near- to far-infrared ratio in the SEDs. However, the evolutionary stage of the sources – both relative to each other and in absolute terms – may be derived incorrectly in reality, when only one viewing angle is available.
6. Future
The code will be actively developed in the future to improve existing features and add new capabilities. Some of the planned capabilities include:
-
Scattering and absorption by non-spherical grains aligned along magnetic fields. The main effect of aligned grains is to produce linear and polarization polarization signatures that trace the magnetic fields (Whitney & Wolff 2002).
-
Continuum and line gas radiative transfer, including photoionization. This will be very useful for modeling ionization and dynamics in a wide range of environments.
-
Support for unstructured meshes, where each cell is an irregular polyhedron, and which are commonly constructed from a Voronoi tessellation of space. They allow a more precise sampling of arbitrary three-dimensional density structures than other types of adaptive grids for a fixed number of cells. Unstructured meshes are now being used in hydrodynamical simulations (e.g. Springel 2011; Greif et al. 2011), and support for these in Hyperion would allow radiative transfer post-processing of the simulations without the need for re-gridding the density structures.
-
Raytracing for scattered light, which – while memory intensive – would provide high signal-to-noise for both images and SEDs efficiently at wavelengths dominated by scattered light faster than the peeling-off algorithm (Pinte et al. 2009).
-
Temperature dependent opacities for dust, since the composition of dust often depends on the temperature, especially when including ices.
7. Summary
Hyperion is a new radiative transfer code that has been designed to be applicable to a wide range of problems. Radiative transfer can be carried out through a variety of three-dimensional grids, including Cartesian, cylindrical and spherical polar, and adaptive Cartesian grids. The algorithms used by the code, including the photon packet propagation, raytracing, convergence detection, and diffusion approximations are described in detail (Sect. 2).
The code is parallelized and scales well to hundreds or thousands of processes. As expected, the maximum speedup depends on the fraction of the execution time spent in the serial part of the code (such as file input/output), which in turn depends on the problem being computed (Sect. 3).
The code was tested against the Pascucci et al. (2004) and Pinte et al. (2009) benchmarks for circumstellar disks and was found to be in excellent agreement with the respective published benchmark results (Sect. 4).
As a case study, Hyperion was used to predict near-infrared to sub-millimeter observations of a star formation region using a dynamical simulation of a region of low-mass star formation (Offner et al. 2009). One interesting finding was that despite the absence of outflows in the simulation, three-dimensional accretion flows caused beaming of radiation that produced fairly symmetric structures usually associated with bipolar outflow cavities.
Hyperion is published under an open-source license at http://www.hyperion-rt.org, using a version control hosting website that makes it easy for users to contribute to the code and documentation.
108 photons for each specific energy iteration, 107 and 2 × 108 photons per wavelength for the monochromatic peeling-off for scattering of source and dust emission respectively (for SEDs; 100 times more for the images and polarization maps), and 107 photons for the raytracing for both the source and dust emission.
Truly regular non-random three-dimensional spacing of points on a sphere is only possible for 4, 6, 8, 12, and 20 points, and the position of the points corresponds to the vertices of regular polyhedra. In the current section, the regular spacing is achieved by using the 20 vertices of a dodecahedron.
Acknowledgments
I wish to thank the referee for a careful review and for comments that helped improve this paper. I also wish to thank C. Pinte and I. Pascucci for assistance with their respective disk benchmark problems, Stella Offner for providing the star formation simulation and for useful discussions and comments, and Barbara Whitney and Kenneth Wood for helpful discussions and comments. The computations in this paper were run on the Odyssey cluster supported by the FAS Sciences Division Research Computing Group. The parallel performance tests were run using 0.7.7 of the code, while the benchmarks problems and the case study model were computed using version 0.8.4. Support for this work was provided by NASA through the Spitzer Space Telescope Fellowship Program, through a contract issued by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research has made use of NASA’s Astrophysics Data System. No photon packets were harmed in the making of this paper.
References
- Amdahl, G. M. 1967, in Proc. April 18–20, 1967, spring joint computer conference, AFIPS ’67 (Spring) (New York, NY, USA: ACM), 483 [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (New York: Wiley) [Google Scholar]
- Carciofi, A. C., & Bjorkman, J. E. 2006, ApJ, 639, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Carciofi, A. C., & Bjorkman, J. E. 2008, ApJ, 684, 1374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1960, Radiat. trans., ed. S. Chandrasekhar [Google Scholar]
- Code, A. D., & Whitney, B. A. 1995, ApJ, 441, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003a, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003b, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Dullemond, C. P. 2002, A&A, 395, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Turolla, R. 2000, A&A, 360, 1187 [NASA ADS] [Google Scholar]
- Ercolano, B., Barlow, M. J., Storey, P. J., & Liu, X.-W. 2003, MNRAS, 340, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Barlow, M. J., & Storey, P. J. 2005, MNRAS, 362, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Young, P. R., Drake, J. J., & Raymond, J. C. 2008, ApJS, 175, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Misselt, K. A., Witt, A. N., & Clayton, G. C. 2001, ApJ, 551, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Springel, V., White, S. D. M., et al. 2011, ApJ, 737, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J. 2000, MNRAS, 315, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Jonsson, P. 2006, MNRAS, 372, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1999, A&A, 344, 282 [NASA ADS] [Google Scholar]
- Mattila, K. 1970, A&A, 9, 53 [NASA ADS] [Google Scholar]
- Min, M., Dullemond, C. P., Dominik, C., de Koter, A., & Hovenier, J. W. 2009, A&A, 497, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misselt, K. A., Gordon, K. D., Clayton, G. C., & Wolff, M. J. 2001, ApJ, 551, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Klein, R. I., McKee, C. F., & Krumholz, M. R. 2009, ApJ, 703, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Wolf, S., Steinacker, J., et al. 2004, A&A, 417, 793 [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Harries, T. J., Min, M., et al. 2009, A&A, 498, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porter, T. A., & Strong, A. W. 2005, in Int. Cosm Ray Conf. 4, 77 [Google Scholar]
- Robitaille, T. P. 2010, A&A, 520, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V. 2011, in IAU Symp. 270, ed. J. Alves, B. G. Elmegreen, J. M. Girart, & V. Trimble, 203 [Google Scholar]
- Stamatellos, D., & Whitworth, A. P. 2003, A&A, 407, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinacker, J., Henning, T., Bacmann, A., & Semenov, D. 2003, A&A, 401, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinacker, J., Bacmann, A., & Henning, T. 2006, ApJ, 645, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, B. A., & Wolff, M. J. 2002, ApJ, 574, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, B. A., Wood, K., Bjorkman, J. E., & Cohen, M. 2003a, ApJ, 598, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, B. A., Wood, K., Bjorkman, J. E., & Wolff, M. J. 2003b, ApJ, 591, 1049 [Google Scholar]
- Whitney, B. A., Indebetouw, R., Bjorkman, J. E., & Wood, K. 2004, ApJ, 617, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S. 2003, Comp. Phys. Commun., 150, 99 [Google Scholar]
- Wolf, S., & Voshchinnikov, N. V. 2004, Comp. Phys. Commun., 162, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Henning, T., & Stecklum, B. 1999, A&A, 349, 839 [NASA ADS] [Google Scholar]
- Wood, K., & Reynolds, R. J. 1999, ApJ, 525, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., Smith, D., Whitney, B., et al. 2001, ApJ, 561, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., Lada, C. J., Bjorkman, J. E., et al. 2002a, ApJ, 567, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., Wolff, M. J., Bjorkman, J. E., & Whitney, B. 2002b, ApJ, 564, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, K., Whitney, B. A., Robitaille, T., & Draine, B. T. 2008, ApJ, 688, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Morris, M., & White, R. L. 1984, ApJ, 278, 186 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The partial diffusion approximation (PDA)
The diffusion approximation is described by
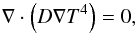 (A.1)\pagebreak\newpagewhere
(A.1)\pagebreak\newpagewhere
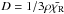 is the diffusion coefficient. This equation can be written as a system of linear
equations. Since Hyperion stores the specific energy absorption rate of the dust
rather than the temperature, the PDA is actually solved using:
is the diffusion coefficient. This equation can be written as a system of linear
equations. Since Hyperion stores the specific energy absorption rate of the dust
rather than the temperature, the PDA is actually solved using:
![\appendix \setcounter{section}{1} \begin{equation} \nabla\cdot\left[D\nabla \left(\frac{\dot{A}}{\kappa_P(\dot{A})}\right)\right] = 0. \end{equation}](/articles/aa/full_html/2011/12/aa17150-11/aa17150-11-eq149.png) (A.2)In spherical polar
coordinates, the diffusion equation is
(A.2)In spherical polar
coordinates, the diffusion equation is
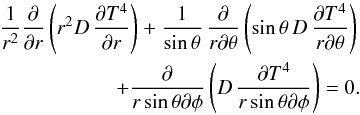 (A.3)This
equation can be written for a discrete spherical polar grid as
(A.3)This
equation can be written for a discrete spherical polar grid as
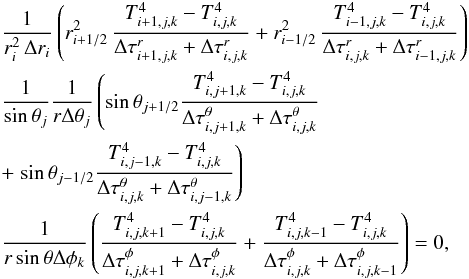 (A.4)where
i, j, and k are the indices of the
grid cells, r, θ and φ are the
coordinates of the center of the cell, Δri,
rΔθj, and
rsinθΔφk
are the spatial extent of the cell along each coordinate, and the Δτ
terms are the Rosseland optical depth across the cell along each coordinate. This equation
can be written down for all the cells in which the PDA is required. In some cases, the T
value will be well determined if they neighbor the diffusion region – these values act as
boundary conditions. The result is a system of linear equations that can be formally
solved.
(A.4)where
i, j, and k are the indices of the
grid cells, r, θ and φ are the
coordinates of the center of the cell, Δri,
rΔθj, and
rsinθΔφk
are the spatial extent of the cell along each coordinate, and the Δτ
terms are the Rosseland optical depth across the cell along each coordinate. This equation
can be written down for all the cells in which the PDA is required. In some cases, the T
value will be well determined if they neighbor the diffusion region – these values act as
boundary conditions. The result is a system of linear equations that can be formally
solved.
All Tables
All Figures
 |
Fig. 1 The main panels show the wall clock speedup relative to serial execution for a model of a protoplanetary disk. The right panel shows the same model as that in the left panel, but with 10 times more photon packets for every iteration. The open circles show the average values of 10 executions of the code, and the uncertainties in these values derived from the scatter are not shown as they are smaller than the data points. The dashed curves show the speedup expected from a perfectly parallelized code. The solid curves show the best fit to the speedup curve assuming Amdahl’s law (described in text). The gray shaded areas around the curves show the 68.3% confidence interval. The maximum speedups derived from the best fits are shown as horizontal dotted lines. The inset panels show the probability of different P values, with the 68.3% confidence intervals shown in shaded gray. |
| In the text | |
 |
Fig. 2 Temperature results for the Pascucci et al. (2004) disk benchmark, for the τV = 100 model. The left panel shows a radial temperature profile close to the mid-plane (θ = 2.5°), both in absolute terms (top) and relative to the reference code RADICAL (bottom). The right panel shows a vertical cut through the disk at a cylindrical radius of 2 AU. The black lines show the results from Hyperion, while the gray lines show the results from the codes tested in Pascucci et al. (2004) |
| In the text | |
 |
Fig. 3 SED results for the Pascucci et al. (2004) disk benchmark, for the four disk masses used. In each panel, the top section shows the SED obtained using Hyperion (black line), compared to the reference code from Pascucci et al. (2004) (RADICAL; gray circles), for the three viewing angles used (12.5, 42.5, and 77.5°). The dashed line shows the blackbody spectrum of the central source. The bottom three sections in each panel show the fractional difference between Hyperion and RADICAL (black line), and between the other codes in Pascucci et al. (2004) and RADICAL (gray lines). |
| In the text | |
 |
Fig. 4 Temperature results for the Pinte et al. (2009) disk benchmark. The top-left and top-right panels shows the radial temperature profile at the disk mid-plane for the lowest and highest disk mass models. The bottom panels shows two vertical cuts through the disk for the highest disk mass model, at cylindrical radii of 0.2 and 200 AU respectively. In each panel, the top section shows the temperature profile in absolute terms, while the bottom section shows the results relative to the reference result from Pinte et al. (2009), which is the average of the results from MCFOST, MCMAX, and TORUS. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, and TORUS. |
| In the text | |
 |
Fig. 5 SED results for the Pinte et al. (2009) disk benchmark, for the four disk masses used. In each panel, the top section shows the SED obtained using Hyperion (black line), compared to the average result of the codes used in Pinte et al. (2009) (gray circles), for four of the viewing angles (18.2, 75.5, 81.4, 87.1°). The dashed line shows the blackbody spectrum of the central source. The bottom four sections in each panel show the fractional difference between Hyperion and the reference result (black line), and between the other codes compared in Pinte et al. (2009) and the reference result (gray lines). |
| In the text | |
 |
Fig. 6 Image results for the Pinte et al. (2009) disk benchmark. The top two rows show the results for the i = 69.5° model, while the bottom two rows show the results for the i = 87.1° model. For each viewing angle, the resulting image is shown on the left on a power-law stretch (with power 1/4), while the remaining plots show various cuts (indicated on the images), in absolute flux units, as well as relative to the reference result in Pinte et al. (2009), which is the average of the MCFOST, MCMAX, TORUS, and Pinball codes. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, TORUS, and Pinball. As in Pinte et al. (2009), the cuts are 11 pixels wide to improve the signal-to-noise of the profiles. |
| In the text | |
 |
Fig. 7 Linear polarization map results for the Pinte et al. (2009) disk benchmark. The top two rows show the results for the i = 69.5° model, while the bottom two rows show the results for the i = 87.1° model. For each viewing angle, the resulting linear polarization map is shown on the left on a linear stretch, while the remaining plots show various cuts (indicated on the maps, and identical to those in Fig. 6), both in absolute terms, and relative to the reference result in Pinte et al. (2009), which is the average of the MCFOST, MCMAX, and Pinball codes. The black lines show the results from Hyperion, while the gray lines show the results from MCFOST, MCMAX, and Pinball. As in Pinte et al. (2009), the cuts are 11 pixels wide to improve the signal-to-noise of the profiles. |
| In the text | |
 |
Fig. 8 Three-color unconvolved synthetic images of the simulation, from the near-infrared
(top left) and mid-infrared (top right) to the
far-infrared (bottom left and right). The wavelengths and colors used
are 1.25 μm (blue), 1.65 μm (green), and
2.15 μm (red) for the JHK image,
3.6 μm (blue), 4.5 μm (green), and
8.0 μm (red) for the Spitzer/IRAC image,
70 μm (blue), 110 μm (green), and
170 μm (red) for the Herschel/PACS image, and
250 μm (blue), 350 μm (green), and
500 μm (red) for the Herschel/SPIRE image. All
images are shown on an arcsinh stretch which allows a larger dynamic range to be shown
by reducing the intensity of the brightest regions. The exact transformation is given
by |
| In the text | |
 |
Fig. 9 Three-color synthetic images of the simulation, from the near-infrared (top left) and mid-infrared (top right) to the far-infrared (bottom left and right). The images are binned to the pixel resolutions appropriate for ground based observations (JHK) and for Spitzer and Herschel observations respectively. The images were convolved with the appropriate instrumental PSFs, and include Gaussian noise with realistic levels. The wavelengths, stretches, and levels used for the images are identical to those used in Fig. 8. |
| In the text | |
 |
Fig. 10 Spectral Energy Distributions for the three sources labelled in Fig. 8. Each panel shows SEDs for 20 different viewing angles. The black lines show the minimum and maximum values as a function of wavelength, the light gray shows the range of values, and the dark gray shows the individual SEDs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.