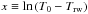| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117814 | |
| Published online | 22 November 2011 | |
Type Ia supernovae and the 12C+12C reaction rate
1
Dept. Física i Enginyeria Nuclear, Univ. Politècnica de Catalunya, Carrer Pere Serra 1-15, 08173 Sant Cugal del Vallès, Spain
e-mail: eduardo.bravo@upc.edu
2 INAF – Osservatorio Astronomico di Teramo, via mentore Maggini snc, 64100 Teramo, Italy
e-mail: piersanti@oa-teramo.inaf.it; straniero@oa-teramo.inaf.it
3
INFN Sezione di Napoli, 80126 Napoli, Italy
4
Departamento de Física Teórica y del Cosmos, Universidad de Granada, 18071 Granada, Spain
e-mail: inma@ugr.es
5
Institut de Ciències de l’Espai (CSIC), Campus UAB, 08193 Bellaterra, Spain
e-mail: isern@aliga.ieec.uab.es
6
Institut d’Estudis Espacials de Catalunya, Ed. Nexus-201, c/Gran Capita 2-4, 08034 Barcelona, Spain
7
Dept. Física i Enginyeria Nuclear, Univ. Politècnica de Catalunya, Carrer Comte d’Urgell 187, 08036 Barcelona, Spain
e-mail: jose.antonio.escartin@upc.edu
Received: 3 August 2011
Accepted: 4 September 2011
Context. Even if the 12C+12C reaction plays a central role in the ignition of type Ia supernovae (SNIa), the experimental determination of its cross-section at astrophysically relevant energies (E ≲ 2 MeV) has never been made. The profusion of resonances throughout the measured energy range has led to speculation that there is an unknown resonance at E0 ~ 1.5 MeV possibly as strong as the one measured for the resonance at 2.14 MeV, i.e. (ωγ)R = 0.13 meV.
Aims. We study the implications that such a resonance would have for our knowledge of the physics of SNIa, paying special attention to the phases that go from the crossing of the ignition curve to the dynamical event.
Methods. We use one-dimensional hydrostatic and hydrodynamic codes to follow the evolution of accreting white dwarfs until they grow close to the Chandrasekhar mass and explode as SNIa. In our simulations, we account for a low-energy resonance by exploring the parameter space allowed by experimental data.
Results. A change in the 12C+12C rate similar to the one explored here would have profound consequences for the physical conditions in the SNIa explosion, namely the central density, neutronization, thermal profile, mass of the convective core, location of the runaway hot spot, or time elapsed since crossing the ignition curve. For instance, with the largest resonance strength we use, the time elapsed since crossing the ignition curve to the supernova event is shorter by a factor ten than for models using the standard rate of 12C+12C, and the runaway temperature is reduced from ~8.14 × 108 K to ~ 4.26 × 108 K. On the other hand, a resonance at 1.5 MeV, with a strength ten thousand times smaller than the one measured at 2.14 MeV, but with an α/p yield ratio substantially different from 1 would have a sizeable impact on the degree of neutronization of matter during carbon simmering.
Conclusions. A robust understanding of the links between SNIa properties and their progenitors will not be attained until the 12C+12C reaction rate is measured at energies ~1.5 MeV.
Key words: nuclear reactions, nucleosynthesis, abundances / supernovae: general / white dwarfs
© ESO, 2011
1. Introduction
The idea that type Ia supernovae (SNIa) are triggered by explosive carbon burning in degenerate material dates back to the seminal paper of Hoyle & Fowler (1960): “Pure carbon is explosive through 12C(12C,α)20Ne and 12C(12C,p)23Na at a temperature somewhat less than 1.5 × 109 degrees, even on a timescale as short as 1 second”. Since that time, the paradigm of SNIa has changed from carbon detonation (Arnett 1969), first, to carbon deflagration (Nomoto et al. 1976), and, finally, to the currently favoured paradigm: a delayed detonation starting as a carbon deflagration (Khokhlov 1991, delayed-detonation model). Shortly after the formulation of the delayed-detonation paradigm, Höflich et al. (1995) and Höflich & Khokhlov (1996) showed that this kind of model can account for the basic observational properties (brightness, light curves) of normal and subluminous SNIa. Nowadays, sofisticated three-dimensional simulations of SNIa based on different flavours of the delayed-detonation model (e.g. Gamezo et al. 2003; Meakin et al. 2009; Bravo et al. 2009; Röpke et al. 2011) are confronted with data in order to explain increasingly subtle observational details (Mazzali et al. 2007; Kasen et al. 2009; Maeda et al. 2010). These numerical simulations have taught us that the outcome of the explosion is very sensitive to the runaway conditions (e.g. Seitenzahl et al. 2011), which are set during the so-called carbon simmering phase, the pre-explosive period that begins when carbon starts burning at a slow pace and ends when the nuclear timescale becomes comparable to the white dwarf (WD) sound crossing time, tsound ≃ 0.1 s (Piro & Chang 2008). The evolution of the progenitor WD during the simmering phase (which is difficult to address because it is on the borderline between hydrostatic and hydrodynamic phenomena) is controlled by the competition between cooling processes (neutrino emission and convection) and heating by a dominant nuclear reaction: the fusion of two 12C nuclei at temperatures in the range 2 × 108 − 109 K.
The experimental measurement of the cross-section of the 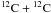 reaction (carbon fusion reaction) at low energies has advanced slowly in the past few decades. At the time of formulation of the carbon detonation model for SNIa (Arnett 1969), the latest known experimental results extended down to a center of mass energy Ecm = 3.23 MeV (Patterson et al. 1969). Seven years later, when the deflagration model was proposed, the reference
reaction (carbon fusion reaction) at low energies has advanced slowly in the past few decades. At the time of formulation of the carbon detonation model for SNIa (Arnett 1969), the latest known experimental results extended down to a center of mass energy Ecm = 3.23 MeV (Patterson et al. 1969). Seven years later, when the deflagration model was proposed, the reference 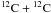 reaction rate evaluated by Fowler et al. (1975, hereafter FCZ75) was based on experimental measurements at Ecm > 2.45 MeV (Mazarakis & Stephens 1973). When Khokhlov (1991) formulated the delayed detonation paradigm, the calculation of the carbon fusion rate was based on the Caughlan & Fowler (1988, hereafter CF88) fit to experimental cross-sections down to the same energy Ecm (~2.5 MeV), although with higher resolution (e.g. Becker et al. 1981). The rate from CF88 differs from that of FCZ75 by less than 20% at T ≳ 109 K, and by less than a factor 2.5 at T ≳ 108 K. In the past 30 years, the lower limit to Ecm reached experimentally has decreased to only 2.10 MeV (Aguilera et al. 2006; Barrón-Palos et al. 2006; Spillane et al. 2007), because of experimental difficulties in reducing the background related to secondary reactions induced by hydrogen and deuterium contamination in the carbon targets. Present-day data exhibit pronounced resonances throughout the measured energy range. Spillane et al. (2007), indeed, found a strong resonance at ER = 2.14 MeV, close to the low-energy limit of their measurements. It turns out that the Gamow energies relevant to the carbon fusion reaction during the simmering process lie far below the lower energy tested experimentally. For instance, for temperatures in the range 2 × 108 − 109 K, the Gamow energies go from EG ± ΔEG = 0.82 ± 0.14 MeV to EG ± ΔEG = 2.4 ± 0.5 MeV. Even though the most recent low-energy measurements give an average astrophysical factor ~ 2–4 times smaller than the value recommended by CF88, the cross-sections measured at Ecm ≲ 3 MeV are rather uncertain, which explains why the
reaction rate evaluated by Fowler et al. (1975, hereafter FCZ75) was based on experimental measurements at Ecm > 2.45 MeV (Mazarakis & Stephens 1973). When Khokhlov (1991) formulated the delayed detonation paradigm, the calculation of the carbon fusion rate was based on the Caughlan & Fowler (1988, hereafter CF88) fit to experimental cross-sections down to the same energy Ecm (~2.5 MeV), although with higher resolution (e.g. Becker et al. 1981). The rate from CF88 differs from that of FCZ75 by less than 20% at T ≳ 109 K, and by less than a factor 2.5 at T ≳ 108 K. In the past 30 years, the lower limit to Ecm reached experimentally has decreased to only 2.10 MeV (Aguilera et al. 2006; Barrón-Palos et al. 2006; Spillane et al. 2007), because of experimental difficulties in reducing the background related to secondary reactions induced by hydrogen and deuterium contamination in the carbon targets. Present-day data exhibit pronounced resonances throughout the measured energy range. Spillane et al. (2007), indeed, found a strong resonance at ER = 2.14 MeV, close to the low-energy limit of their measurements. It turns out that the Gamow energies relevant to the carbon fusion reaction during the simmering process lie far below the lower energy tested experimentally. For instance, for temperatures in the range 2 × 108 − 109 K, the Gamow energies go from EG ± ΔEG = 0.82 ± 0.14 MeV to EG ± ΔEG = 2.4 ± 0.5 MeV. Even though the most recent low-energy measurements give an average astrophysical factor ~ 2–4 times smaller than the value recommended by CF88, the cross-sections measured at Ecm ≲ 3 MeV are rather uncertain, which explains why the 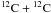 reaction rate formulated by CF88 is still nowadays the reference rate for astrophysical applications.
reaction rate formulated by CF88 is still nowadays the reference rate for astrophysical applications.
There has been lively discussion about the extrapolation of the 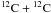 rate throughout the Gamow energy range. On the one hand, theoretical phenomenological models predicting the behavior of the non-resonant astrophysical factor at low energies, based on different approaches, differ by up to ~2–3 orders of magnitude at Ecm ~ 1–1.5 MeV (Gasques et al. 2005; Aguilera et al. 2006; Jiang et al. 2007). Most of these predictions give rates well below the standard rate of CF88 (see, e.g., Fig. 3 in Strieder 2008). On the other hand, the profusion of measured resonances has led to speculation about the hypothetical presence of a resonance within the Gamow energy range, say at Ecm ~ 1.5 MeV, that could completely dominate the reaction rate at the densities and temperatures characteristic of the carbon simmering phase of SNIa.
rate throughout the Gamow energy range. On the one hand, theoretical phenomenological models predicting the behavior of the non-resonant astrophysical factor at low energies, based on different approaches, differ by up to ~2–3 orders of magnitude at Ecm ~ 1–1.5 MeV (Gasques et al. 2005; Aguilera et al. 2006; Jiang et al. 2007). Most of these predictions give rates well below the standard rate of CF88 (see, e.g., Fig. 3 in Strieder 2008). On the other hand, the profusion of measured resonances has led to speculation about the hypothetical presence of a resonance within the Gamow energy range, say at Ecm ~ 1.5 MeV, that could completely dominate the reaction rate at the densities and temperatures characteristic of the carbon simmering phase of SNIa.
Our aim is to explore the consequences that a resonance in the 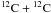 reaction near Ecm ~ 1.5 MeV would have for the physics of SNIa. As a strong resonance at this energy is expected to dominate the rate, we can disregard the uncertainties in the behavior of the non-resonant part of the astrophysical factor at low energies, and adopt for it the CF88 rate. This kind of speculation about a hypothetical low-energy resonance in the carbon fusion reaction rate has been addressed in several works. Cooper et al. (2009) studied the changes induced by such a resonance on the physics of superburst ignition on accreting neutron star crusts. Bennett et al. (2010a) and Bennett et al. (2010b) explored the impact on the s-process induced by an increase in the carbon fusion reaction rate up to a factor 50 000 at T = 5 × 108 K. Finally, Iapichino & Lesaffre (2010) analyzed the influence of uncertainties in the
reaction near Ecm ~ 1.5 MeV would have for the physics of SNIa. As a strong resonance at this energy is expected to dominate the rate, we can disregard the uncertainties in the behavior of the non-resonant part of the astrophysical factor at low energies, and adopt for it the CF88 rate. This kind of speculation about a hypothetical low-energy resonance in the carbon fusion reaction rate has been addressed in several works. Cooper et al. (2009) studied the changes induced by such a resonance on the physics of superburst ignition on accreting neutron star crusts. Bennett et al. (2010a) and Bennett et al. (2010b) explored the impact on the s-process induced by an increase in the carbon fusion reaction rate up to a factor 50 000 at T = 5 × 108 K. Finally, Iapichino & Lesaffre (2010) analyzed the influence of uncertainties in the 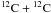 reaction at T ≲ 5 × 108 K on the ignition of the WD core. They found that the ignition density depends slightly on the presence of a low-energy resonance while the ignition temperature is almost unaffected. However, their results are influenced by the small value of the resonance strength they assumed, which implied that their reaction rate exceeded that from CF88 by only a factor of two.
reaction at T ≲ 5 × 108 K on the ignition of the WD core. They found that the ignition density depends slightly on the presence of a low-energy resonance while the ignition temperature is almost unaffected. However, their results are influenced by the small value of the resonance strength they assumed, which implied that their reaction rate exceeded that from CF88 by only a factor of two.
As there exists no theoretical framework that allows us to predict the location and strength of the resonances in the 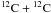 reaction, the best approach to studying their consequences is an exploration of the parameter space of a low-energy resonance. In the next section, we determine the resonance energy and strength that are compatible with the available cross-section data, and discuss the expected implications for our understanding of SNIa. In Sect. 3, we present the results of our simulations of the evolution of a WD from mass accretion to supernova explosion. These simulations have been obtained with the use of one-dimensional hydrostatic, hydrodynamic, and nucleosynthetic codes where the
reaction, the best approach to studying their consequences is an exploration of the parameter space of a low-energy resonance. In the next section, we determine the resonance energy and strength that are compatible with the available cross-section data, and discuss the expected implications for our understanding of SNIa. In Sect. 3, we present the results of our simulations of the evolution of a WD from mass accretion to supernova explosion. These simulations have been obtained with the use of one-dimensional hydrostatic, hydrodynamic, and nucleosynthetic codes where the 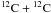 reaction rate was computed consistently assuming different resonance properties. To cover a wider range of evolutionary scenarios (in particular, a wider range of accretion rates that would lead to different density-temperature tracks), we adopt in Sect. 4 a somewhat different approach: we follow the evolution of a homogeneous region through the latest stages of accretion until the dynamical instability with different physico-chemical parameters. In this section, we study the dependence of the global neutronization of the convective core of the WD during carbon simmering, and the runaway temperature of convective bubbles. Finally, we present our conclusions in Sect. 5.
reaction rate was computed consistently assuming different resonance properties. To cover a wider range of evolutionary scenarios (in particular, a wider range of accretion rates that would lead to different density-temperature tracks), we adopt in Sect. 4 a somewhat different approach: we follow the evolution of a homogeneous region through the latest stages of accretion until the dynamical instability with different physico-chemical parameters. In this section, we study the dependence of the global neutronization of the convective core of the WD during carbon simmering, and the runaway temperature of convective bubbles. Finally, we present our conclusions in Sect. 5.
2. Low-energy resonance
We explore the consequences of a resonance in the neighborhood of E0 = 1.5 ± 0.2 MeV with a strength limited by the measured cross-sections at low energy. The low-energy measurements that have provided the tightest constraints to date are those obtained by Spillane et al. (2007, hereafter S07), who explored energies E > 2.10 MeV and found that the resonance structure continues down to this energy limit. They also found a resonance at Ecm = 2.14 MeV, although this resonance has a quite limited impact on carbon burning: it speeds up slightly the carbon fusion rate at temperatures in the range T ~ 6 × 108–1.2 × 109 K (e.g., by a factor 1.8 at T = 8 × 108 K). On the other hand, the α-channel yield of this resonance is larger than the p-channel by a factor ~5, at variance with the standard formulation of CF88, in which both channels have similar strength.
Our 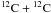 reaction rate is given by the sum of the nonresonant contribution (that we calculate following CF88) plus a resonant one that accounts for the resonance found by S07 at Ecm = 2.14 MeV, and the assumed low-energy ghost resonance (LER). We compute the contribution of both resonances to the carbon fusion reaction rate as (see, for instance, S07):
reaction rate is given by the sum of the nonresonant contribution (that we calculate following CF88) plus a resonant one that accounts for the resonance found by S07 at Ecm = 2.14 MeV, and the assumed low-energy ghost resonance (LER). We compute the contribution of both resonances to the carbon fusion reaction rate as (see, for instance, S07): ![\begin{eqnarray} \langle\sigma v\rangle^\mathrm{R} & = & 2.28\times10^{-24}T_9^{-3/2}\bigg[\exp\left(-24.8/T_9\right) \nonumber \\ & & + \frac{\left(\omega\gamma\right)_\mathrm{R}}{0.13~\mathrm{meV}}\exp\left(-11.6E_\mathrm{R} /T_9\right)\bigg] ~\mathrm{cm}^3~\mathrm{s}^{-1} , \label{eqres} \end{eqnarray}](/articles/aa/full_html/2011/11/aa17814-11/aa17814-11-eq36.png) (1)where ER is the energy, in MeV, at which a resonance is assumed, and (ωγ)R is the ghost resonance strength.
(1)where ER is the energy, in MeV, at which a resonance is assumed, and (ωγ)R is the ghost resonance strength.
Although there exist in the literature some discussions of the properties of such a resonance that are compatible with current experimental data, different authors allow for different limits. Hence, we repeat here the derivation of the maximum possible strength of a LER (e.g. Cooper et al. 2009).
As a first approach, we demand that the ghost resonance at ER contributes to the cross-section at Ecm = 2.10 MeV less than 10% of the value measured by S07 at the same energy, σexp(2.1 MeV) < 0.8 nb. Assuming a narrow resonance, as are all known resonances of the carbon fusion reaction, ΓR ≈ 40–100 keV (Aguilera et al. 2006), the energy dependent cross-section is given by the Breit-Wigner formula (e.g. Clayton 1968; Rolfs & Rodney 1988): 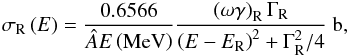 (2)where  = 6 is the reduced baryon number. Substituting E = 2.10 MeV, ΓR = 100 keV, and σR < 0.08 nb we get
(2)where  = 6 is the reduced baryon number. Substituting E = 2.10 MeV, ΓR = 100 keV, and σR < 0.08 nb we get ![\begin{eqnarray} \left(\omega\gamma\right)_\mathrm{R} & < & 7.3\times10^{-10} E\left(\mathrm{MeV}\right) \frac{\left(E-E_\mathrm{R}\right)^2+\Gamma_\mathrm{R}^2/4}{\Gamma_\mathrm{R}} \nonumber\\ & = & 15.4\left[\left(2.10-E_\mathrm{R}\right)^2+2.5\times10^{-3}\right]~\mathrm{meV} , \end{eqnarray}](/articles/aa/full_html/2011/11/aa17814-11/aa17814-11-eq47.png) (3)where ER is in MeV. Thus, the resonance strength is limited to be less than 9.9, 5.6, and 2.5 meV for ER = 1.3, 1.5, and 1.7 MeV, respectively. We note that a smaller value of the resonance width, ΓR < 100 keV, would result in still higher upper limits to the resonance strength.
(3)where ER is in MeV. Thus, the resonance strength is limited to be less than 9.9, 5.6, and 2.5 meV for ER = 1.3, 1.5, and 1.7 MeV, respectively. We note that a smaller value of the resonance width, ΓR < 100 keV, would result in still higher upper limits to the resonance strength.
A second, similar, approach to the determination of the maximum possible strength of the ghost resonance makes use of the recommended value of the modified astrophysical factor, S∗, defined as 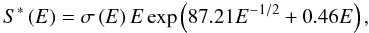 (4)where E is in MeV. The average experimental S∗ at the lowest energies is ~0.7 × 1016 MeV b (Strieder 2008), while the value recommended by CF88 is 3 × 1016 MeV b. Taking an approximate value of the experimental modified astrophysical factor
(4)where E is in MeV. The average experimental S∗ at the lowest energies is ~0.7 × 1016 MeV b (Strieder 2008), while the value recommended by CF88 is 3 × 1016 MeV b. Taking an approximate value of the experimental modified astrophysical factor 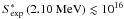 MeV b, and using Eq. (2) for the energy-dependent cross-section due to the ghost resonance, we obtain
MeV b, and using Eq. (2) for the energy-dependent cross-section due to the ghost resonance, we obtain 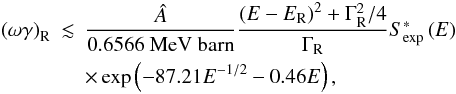 (5)which, after substituting E = 2.10 MeV and ΓR = 100 keV, gives
(5)which, after substituting E = 2.10 MeV and ΓR = 100 keV, gives ![\begin{equation} \left(\omega\gamma\right)_\mathrm{R} \lesssim 2.54\left[\left(2.10-E_\mathrm{R}\right)^2+2.5\times10^{-3}\right]~\mathrm{meV} , \end{equation}](/articles/aa/full_html/2011/11/aa17814-11/aa17814-11-eq57.png) (6)again with ER in MeV. In this case, the resonance strength is limited to 1.6, 0.92, and 0.41 meV for ER = 1.3, 1.5, and 1.7 MeV, respectively. These limits increase by a factor ~10 if the resonance width is ΓR = 10 keV.
(6)again with ER in MeV. In this case, the resonance strength is limited to 1.6, 0.92, and 0.41 meV for ER = 1.3, 1.5, and 1.7 MeV, respectively. These limits increase by a factor ~10 if the resonance width is ΓR = 10 keV.
A quite different approach, found in the literature, consists in assuming that the modified astrophysical factor remains constant at energies below 2 MeV. This assumption leads to much lower resonance strengths at the resonance energies we explore. However, we note that these are not upper limits to the resonance strength compatible with experimental data.
In Fig. 1 (top panel), we show the modified astrophysical factor of the 12C+12C reaction as a function of energy assuming a strong LER, compatible with the limits derived above, S∗(2.10 MeV) ≲ 1016 MeV b. As might be expected, the farther the energy of the assumed resonance is from the measured energies, the larger is the maximum resonance strength that is compatible with the data. We can see that a shift of −0.2 MeV in ER allows us to increase the peak of the astrophysical factor by approximately two orders of magnitude. The bottom panel of Fig. 1 shows the ratio of our 12C+12C rate, which we calculated as the sum of the CF88 rate and the resonant rate given by Eq. (1), to the non-resonant rate (CF88), as a function of temperature. The assumption of a strong ghost resonance of the aforementioned characteristics leads to a substantial enhancement of the carbon fusion rate in the temperature range 2 × 108–2 × 109 K. While this temperature range depends scarcely on the assumed ER (the peak of the rate ratio shifts from 3.9 × 108 K to 5.8 × 108 K when the resonance energy changes from ER = 1.3 MeV to 1.7 MeV), the maximum ratio changes by as much as four orders of magnitude between the extreme explored values of ER.
 |
Fig. 1 Astrophysical factor and rate of the 12C+12C reaction due to a resonance at an energy ER = 1.3 MeV (dashed line), 1.5 MeV (solid line), and 1.7 MeV (dot-dashed line), with resonance strengths of 16 meV, 9.2 meV, and 4.1 meV, respectively. Top: modified astrophysical factor as a function of energy. The bar at the bottom right shows the maximal astrophysical factor measured by S07 at an energy of ~2.1 MeV (σ < 0.8 nb), which is the most constraining low energy measurement to date. The quoted strengths of the resonances would be compatible with a σ two orders of magnitude smaller than that measured by S07 (if the resonance width is ΓR ≈ 10 keV). Bottom: ratio of our 12C+12C reaction, accounting for a LER, to the CF88 reaction rate, as a function of temperature. The dotted line close to the horizontal axis is the ratio of the rate accounting for the resonance found by S07 to the CF88 rate. The arrows mark the temperature ranges relevant to carbon ignition, carbon simmering, and the explosive burning in a subsonic flame or a detonation. The gap between carbon simmering and flames reflects the dominance of thermal conduction and shock heating over nuclear energy release in stationary explosive burning fronts. |
We can gain some insight into the impact of a ghost resonance on the physics of SNIa by analyzing the different phases involved in the process of explosive carbon burning:
-
at first, carbon competes with neutrino emission, until thetemperature is high enough to ensure that nuclear heating cannotbe balanced by neutrino cooling (ignition condition). In thiswork, we define the ignition curve as the local ρ-T conditions for which the nuclear timescale equals the neutrino cooling timescale (see Fig. 2 for the definition of the nuclear timescale). Typically, this occurs at T ~ 2 × 108 K, just at the border of the temperature range where the resonance begins to noticeably increase the carbon fusion rate. The evolution of the white dwarf during this phase determines the place where carbon ignites: either at the center or close to the white dwarf surface, the latter giving rise to an accretion-induced collapse of the white dwarf rather than a supernova event;
when the neutrino cooling is negligible, relative to the nuclear energy release, convection becomes the dominant energy-transport mechanism. An adiabatic thermal profile is imprinted in the white dwarf as long as the convective timescale ~10–100 s remains below the nuclear timescale. If the carbon fusion rate is just given by the non-resonant contribution, the maximum temperature at which convection is able to remove the excess nuclear heat is ~7−9 × 108 K. When neither neutrinos nor convection can equilibrate the nuclear heating, a flame starts to propagate through the white dwarf. Here, we define the dynamical curves as the local ρ-T conditions for which the nuclear timescale equals the (global) convective timescale. In general, the convective timescale is difficult to determine and may change over time. However, for the purposes of studying the effects of a LER, it is enough to use an approximate, constant value, which we have taken to be tconv = 10 s1.
-
The (microscopic) thermal structure of a subsonic flame(deflagration) is determined by heat diffusion from hot ashes tocool fuel until the temperature of the last one is as high as2 − 5 × 109 K (depending on fuel density). At higher temperatures, the flux of heat released by nuclear reactions is higher than that of the heat diffusion.
-
Detonations are supersonic combustion waves where ignition is triggered by an initial temperature jump due to a shock front. In the conditions of thermonuclear supernovae, this jump raises the fuel temperature well above ~2 × 109 K. Later on, the heat released by thermonuclear reactions determines the thermal profile.
As can be seen in Fig. 1, the range of temperatures for which nuclear reactions control the thermal evolution of thermonuclear combustion fronts in SNIa is above the range of temperatures at which a ghost resonance significantly affects the rate of the carbon fusion reaction. Thus, we expect that the largest effect of such a resonance will take place during the carbon simmering phase.
In this work, we systematically explore the effects of a LER at different values of the resonance energy, ER, and with different resonance strengths, (ωγ)R. Moreover, motivated by the experimental finding of an alpha-to-proton yield ratio, α/p, substantially different from one at the lowest measured energy (S07), we further study the effects of varying this ratio. As we demonstrate in Sect. 4.1, varying α/p has an interesting effect on the level of neutronization attained during the carbon simmering phase. In Table 1, we summarize the combinations of the resonance parameters we have considered. Model CF88 is a reference model in which the 12C+12C rate is given just by the non-resonant CF88 rate. The rate of all the other models is given by the sum of the CF88 rate and the experimentally known resonance at 2.14 MeV plus a ghost resonance (Eq. (1)).
Summary of 12C+12C rates explored in this paper.
 |
Fig. 2 Nuclear timescale vs. temperature. The nuclear timescale has been computed as τnuc = (2ρNAY12 ⟨ σv ⟩ )-1, where NA is Avogadro’s number, Y12 = 0.5/12 mol g-1 is the molar fraction of 12C, and ⟨ σv ⟩ is the rate of the 12C+12C reaction. There are shown curves belonging to the CF88 non-resonant rate, the non-resonant plus the resonance at 2.1 MeV measured by S07, and the non-resonant plus the 2.1 MeV resonance plus a LER. For the last, the curves are labeled with the values of the resonance energy, ER in MeV, and the resonance strength, (ωγ)R in meV. The hatched region shows the range of the convective timescales. In this plot, the density is ρ = 2 × 109 g cm-3 and the carbon mass fraction is 0.5. Note that a lower carbon abundance would imply a longer nuclear timescale. |
A first quantitative evaluation of the impact of the ghost resonance parameters assumed in Table 1 can be made by comparing the nuclear timescale to relevant timescales of the white dwarf. Figure 2 shows the nuclear timescale for the different models, as functions of temperature, compared to typical values of the convective turnover timescale (tconv ≈ 10–100 s). We see that the experimental resonance at 2.14 MeV with no ghost resonance (S07) has a small effect on the nuclear timescale. On the other hand, a resonance at ER = 1.5 MeV with a strength 100 times smaller than that measured at 2.14 MeV (i.e., with (ωγ)R = 0.001 meV) can reduce the runaway temperature by ~2 × 108 K, if the density is kept fixed at ρ = 2 × 109 g cm-3. Increasing the resonance strength by two orders of magnitude translates into an approximate reduction in the runaway temperature by ~108 K. The same reduction in the runaway temperature can be achieved by decreasing the resonance energy by ~0.2 MeV.
Similar conclusions would result from using the thermal timescale instead of the nuclear timescale. In general, the thermal timescale is shorter than the nuclear timescale by a factor τth/τnuc ≃ 2cpT/QNAY12, where cp is the specific heat at constant pressure and Q is the effective heat release per carbon fusion reaction, Q ≃ 9.1 MeV (Chamulak et al. 2008). For instance, at T = 6 × 108 K, τth/τnuc ≃ 0.06 but, owing to the steep slope of the τnuc vs. T curves (see Fig. 2), such a reduction in the timescale only slightly affects the values of the runaway temperatures.
The utility of Fig. 2 is limited by the use of a fixed density, independent of temperature and of the parameters adopted for the ghost resonance. In reality, both the temperature and density evolve during the simmering phase and depend on the assumed 12C+12C rate. In the calculations reported in the next section, we address both dependences.
3. White dwarf evolution from accretion to explosion
We now discuss the evolution of a non-rotating WD from the beginning of accretion to explosion. We have followed the WD with an hydrostatic code until the first crossing of the dynamical curve at any zone within the WD. The structure so obtained was then fed into a hydrodynamic supernova code, where the structure evolved until the star was completely disintegrated (maximum density ≲ 0.2 g cm-3). Both codes are one-dimensional and assume spherical symmetry. Strictly speaking, the onset of the dynamical event takes place when the evolutionary timescale becomes shorter than the sound crossing timescale, tsound ≃ 0.1 s, which occurs slightly later than the crossing of the dynamical curve. However, when the nuclear timescale is shorter than the convective timescale the runaway becomes local, hence the heat released before attaining tsound remains small relative to the WD binding energy, and the WD structure does not change appreciably in the interim.
3.1. Methods
Our initial model is the same as in Piersanti et al. (2003), i.e. a CO WD with M = 0.8 M⊙, on which we accrete directly CO-rich matter at a rate of Ṁ = 5 × 10-7 M⊙ yr-1. The hydrostatic evolution is performed using the FRANEC evolutionary code (Chieffi & Straniero 1989) with the same input physics as in Piersanti et al. (2003). The main difference of our approach concerns the neutrino energy losses, which are computed according to Esposito et al. (2002) and Esposito et al. (2003). Moreover, to properly describe the late part of the hydrostatic evolution, composition changes produced by convective mixing are modeled by adding diffusion terms to the nuclear burning terms in the composition equations.
White dwarf properties at the crossing of the ignition and dynamical curves.
 |
Fig. 3 Changes in the physics of the accretion phase owing to a LER: ignition curves (dashed lines), dynamical curve (dot-dashed lines), and track of central ρ vs. T during the hydrostatic evolution (solid lines). The top left panel shows the results obtained when the 12C+12C rate was computed following CF88, the other panels show the results adding a LER to that rate (see Table 1). For comparison purposes, in all the panels we have drawn the CF88 curves as thin lines. In the panels belonging to the LER-1.5-10.-1.0 and LER-1.3-0.1-1.0 rates, the track belongs to the evolution of the shell that first crosses the dynamical curve. We assumed a chemical composition made of 50% 12C and 50% 16O for both curves, while the hydrostatic ρ-T tracks were computed with the realistic chemical composition obtained from full stellar evolutionary calculations (FRANEC code). |
The supernova hydrodynamic code used in the present work is the same as in Badenes et al. (2003), in addition to both Bravo et al. (1996) and Bravo et al. (2011). The present models are based on the delayed-detonation paradigm (Khokhlov 1991), with a fixed deflagration-detonation transition density, ρDDT = 1.6 × 107 g cm-3.
3.2. Results
The results of the hydrostatic simulation of the accretion phase up to the crossing of the dynamical curve are shown in Figs. 3 and 4 and Table 2. Figure 3 shows the ignition and dynamical curves obtained using the reference CF88 rate for the 12C+12C reaction and the changes introduced by the different sets of resonance parameters that we have explored. The different ignition curves converge towards the CF88 ignition curve at high densities, whereas the dynamical curves follow the opposite trend, i.e. they diverge from the CF88 dynamical curve as the density increases. In all cases, as expected, the temperature defined by these curves, at any given density, decreases when a resonance is included. The effect, however, depends significantly on the resonance strength and energy. For instance, a resonance strength of (ωγ)R = 0.001 meV at ER = 1.5 MeV (model LER-1.5-0.001-1.0) scarcely affects either the ignition or the dynamical curves. On the other extreme, the combinations of (ωγ)R = 0.1 meV at ER = 1.3 MeV, as well as (ωγ)R = 10. meV at ER = 1.5 MeV (models LER-1.3-0.1-1.0 and LER-1.5-10.-1.0, respectively), result in a decrease in the temperature of the ignition curve by ≃ 2.5 × 108 K at low densities, and a decrease in the temperature of the dynamical curve by ≃ 4 × 108 K at high densities.
The time elapsed since the beginning of accretion until the supernova explosion is about the same for all the 12C+12C rates, tacc ≃ 1.11–1.15 Myr, because all the models need to arrive close to the Chandrasekhar mass before destabilization. Models LER-1.3-0.1-1.0 and LER-1.5-10.-1.0 are the ones that differ most from the reference model, for which tacc is approximately 40,000 yr shorter than that of CF88. On the other hand, the time elapsed between the crossing of the ignition and the dynamical curves (simmering time, last column of Table 2) is quite different from model to model. Even for model LER-1.5-0.1-1.0, whose strength is similar to that of the experimental resonance at 2.14 MeV, the simmering time is just ~13% of that of model CF88.
Figure 3 shows the tracks followed by the runaway zone in the ρ-T plane. For models igniting at the center, the track is exactly the same as in CF88 up to the crossing of the ignition curve, as expected from the discussion in Sect. 2. In models LER-1.5-0.001-1.0 and LER-1.7-0.1-1.0, the ρ-T tracks are hardly distinguishable from CF88, even up to the crossing of the dynamical curve. However, as the dynamical curve of the ghost resonance models lies systematically below that of CF88, the dynamical curve is reached at a different temperature and density than the reference model. On the other hand, model LER-1.5-0.1-1.0 diverges away from that of CF88 after crossing the ignition curve, which results again in both a substantially lower temperature and a slightly higher density at runaway (see Table 2).
The most interesting cases are those of models LER-1.5-10.-1.0 and LER-1.3-0.1-1.0, which are characterized by either a large resonance strength or a low resonance energy. As can be seen in Table 2, in both cases the dynamical curve is first reached off-center, at radii 149 and 233 km, respectively. The off-center ignition is caused by the compressional heating timescale of the WD being slightly longer than the thermal diffusion timescale, so that the WD is not completely isothermal at carbon ignition. A somewhat different accretion rate would provide off-center ignitions for different combinations of the resonance parameters. The igniting zones are located in the ρ-T plane to the left of the track of the center of the WD, and reach the dynamical curve at a much lower temperature and density than model CF88. Thus, although the presence of a LER always results in a smaller temperature at the crossing of the dynamical curve, the density can be either lower or higher than in model CF88 depending on the resonance properties. This lack of monotonicity reflects as well in other details of the outcome of the supernova explosion, as we later discuss.
Table 2 provides additional properties of the WD at runaway, that are worth discussing. The size of the convective core determines the degree of dissemination of the products of carbon simmering throughout the WD prior to the SNIa explosion, with consequences for the chemical stratification of supernova remnants and the interpretation of their X-ray spectra (Badenes et al. 2008). In general, the mass of the convective core, Mconv, decreases monotonically with increasing resonance strength or decreasing resonance energy. For the extreme case, model LER-1.5-10.-1.0, Mconv is 30% lower than for model CF88.
Results of the hydrodynamic explosion models plus post-processing nucleosynthesis.
Another interesting quantity provided in Table 2 is the total mass of 12C that is burned during the simmering phase, ΔM(12C). This mass varies strongly from model to model, again monotonically decreasing with either increasing resonance strength or decreasing resonance energy, because of their lower temperature at runaway, which implies a smaller thermal content of the WD. The value of ΔM(12C) has a significant effect on the amount of neutronization during carbon simmering, as we discuss in Sect. 4.1.
The thermal and 12C mass fraction profiles through the WD at the dynamical curve are shown in Fig. 4, where the range of the convective core can be clearly appreciated. In all the models, there is a temperature spike close to the surface that is caused by the high accretion rate, but this spike has no practical consequences for the supernova explosion. The temperature peaks at the center in all the models apart from LER-1.3-0.1-1.0 and LER-1.5-10.-1.0. In these models, even though convection extends all the way down to the very center of the WD, the 12C+12C rate increases so steeply with temperature that time-dependent, convective mixing is at late times only efficient in the neighborhood of the runaway zone.
 |
Fig. 4 Thermal and chemical profiles at the crossing of the dynamical curves. The line types used for the models from Table 1 are the same as those used in Fig. 2. Top panel: temperature profiles. From top to bottom (at M ~ 0.2 M⊙) the curves belong to models CF88, LER-1.5-0.001-1.0, LER-1.7-0.1-1.0, LER-1.5-0.1-1.0, LER-1.3-0.1-1.0, and LER-1.5-10.-1.0. Note that the last two models run away off-center. Bottom panel: 12C mass fraction profiles. For comparison purposes, we have plotted with a thin solid line the profile of model CF88 at the crossing of the ignition curve. As can be easily appreciated, the extension of the convective core is very sensitive to the inclusion of a LER in the 12C+12C reaction rate. |
The chemical profile of 12C at the crossing of the ignition curve, shown as a thin line in the bottom panel of Fig. 4, reflects the previous history of the WD. Above 0.8 M⊙, the carbon mass fraction is 0.5, which is the value we adopted for the accreting carbon mass fraction, while the central ~0.4 M⊙ have a homogeneous composition with a smaller carbon mass fraction, Xc(12C) = 0.24, as results from hydrostatic He-burning. At runaway, the chemical profile is the result of the competition between convective mixing and carbon burning. When the dynamical curve is approached, burning consumes carbon more efficiently than convection can supply fresh fuel, and there is a drop in the carbon mass fraction at the burning place. The main impact of a LER on the chemical profile is a lower abundance of carbon in the convective core, owing to the smaller size of the convective region than for model CF88. On the other hand, models igniting carbon off-center maintain the original 12C abundance at the center, because there is neither mixing nor burning there. However, the differences in the carbon mass fractions and profiles that we have found do not have a significant impact on the SNIa outcome.
 |
Fig. 5 Chemical profile in the outer layers of models CF88 and LER-1.5-10.-1.0. The mass coordinate measures the mass within the white dwarf surface, i.e. the surface is at the right end of the horizontal axis. The thicker unlabeled line shows the maximum temperature achieved in each layer during the explosion (right axis). |
There is currently no successful theoretical model able to predict the properties of SNIa explosions univocally, starting from a given presupernova structure. In other words, all current SNIa models rely on a more or less large number of free parameters, either related to the ignition configuration (usually in two and three dimensional models), or to the nuclear front propagation (in models of any dimensionality), or to both of them. It turns out that the explosion properties are mainly sensitive to these free, uncertain, parameters rather than to the details of the presupernova structure. In our study, the adoption of the delayed-detonation paradigm with a fixed transition density, ρDDT, and the use of a one-dimensional model implies that all the details of the presupernova are lost apart from the central density, and the chemical composition profile, whose most relevant byproduct is the profile of the neutron excess. As a result, the kinetic energy of the computed SNIa (Table 3) changes by less than ~5% among our set of models. On the other hand, the mass of radioactive 56Ni synthesized in the explosion varies by as much as ~17%. Rather surprisingly, the largest difference in the 56Ni mass ejected, ΔM(56Ni) ~ 0.06 M⊙, belongs to two models that have quite similar properties during the accretion phase: LER-1.3-0.1-1.0 and LER-1.5-10.-1.0. In any case, the synthesized masses of 56Ni are well within the values usually accepted for normal SNIa, so that the presence of a LER would not change our basic picture of the formation of the light curve of these standard candles.
In Table 3, we report the yields of some elements that might be affected by a change in the rate of carbon burning: carbon, oxygen, magnesium, and silicon. We note, in particular, that oxygen is destroyed by the flame but partially regenerated in the outer shells of the supernova by explosive carbon burning. The most interesting characteristic is the monotonic dependence of the yield of carbon on resonance strength and energy. Although, in general, the variation in the carbon yield with respect to model CF88 is quite modest, it is largest in the two models igniting off-center (LER-1.3-0.1-1.0 and LER-1.5-10.-1.0). However, the reason for the smaller carbon yield of these two models does not rely on the off-center location of the igniting spot. We have checked it by computing a mixed model in which the pre-supernova structure was that belonging to model LER-1.5-10.-1.0, but the supernova (and the nucleosynthesis) was computed with the CF88 rate, the result being that the yield of carbon amounted to 5.4 × 10-3 M⊙, i.e. close to the value obtained for the CF88 model. Hence, the reason for the small yield of carbon obtained in the two models with the strongest and with the lowest energy resonance has to be found in the higher 12C+12C rate in the outer layers of the star, where carbon burning is incomplete. A higher carbon fusion rate implies a smaller flame width (Timmes & Woosley 1992), which is crucial for completing the carbon burning process when the flame width becomes comparable to the WD radius (Domínguez & Khokhlov 2011).
Figure 5 shows the chemical profiles in the outer layers of models CF88 and LER-1.5-10.-1.0 (note that the mass coordinate in this figure starts at the surface of the ejecta and increases radially inwards, i.e. to the left of the plot). While the chemical profile is quite similar in both models within the inner ~0.03 M⊙, carbon is burned more efficiently in the outermost ~0.01 M⊙ of model LER-1.5-10.-1.0, producing as well a higher yield of magnesium, neon, and silicon. Unfortunately, the yields of the elements most sensitive to the 12C+12C reaction rate are small and are located in the lowest density regions of the ejecta, which implies that they can only be detected at a significant level during the few days following the supernova explosion.
4. Physical conditions at thermal runaway
The structure of massive non-rotating white dwarfs at carbon runaway is determined by a few basic properties of the star: 1) its central density, ρc; 2) the electron mole number, Ye, or the neutron excess, η = 1 − 2Ye; and 3) the number and distribution of hot spots at which the temperature first runs away. We have discussed in the previous section the dependence of the first factor, the central density at runaway, on the presence of a LER. The second factor, the electron mole number, is determined by the weak interactions taking place during carbon simmering and by convective mixing. Even if we use a time-dependent mixing scheme coupled to the nuclear burning, the adopted nuclear network is not complete enough to describe the evolution of Ye with the required precision. In addition, as we now demonstrate, the final value of Ye depends critically on α/p. The third factor, namely the number and distribution of runaway centers, also known as hot spots or igniting bubbles, is intrinsically multidimensional, so that it cannot be determined with our one-dimensional hydrostatic code. Hence, we consider alternative ways of addressing both the dependence of the neutronization during carbon simmering (Chamulak et al. 2008; Piro & Bildsten 2008) and the number and distribution of hot spots, on the presence of a LER in the 12C+12C reaction (Woosley et al. 2004).
We note that there is another potential effect of the presupernova structure on the SNIa outcome that we have not accounted for: the possible dependence of the deflagration-detonation transition density on the WD chemical profile. Although this dependence has already been addressed elsewhere (Bravo et al. 2010; Jackson et al. 2010), it is somewhat speculative and we prefer not to mix it with the already hypothetical character of our ghost resonance.
Neutronization during carbon simmering for different 12C+12C rates.
4.1. Neutronization during carbon simmering
The progenitor metallicity sets a ceiling on the fraction of the incinerated mass that can be in the form of radioactive 56Ni, and thus influences the supernova luminosity, with profound implications for supernova cosmology. Timmes et al. (2003) proposed a linear relationship between the mass of 56Ni and metallicity: M(56Ni) ∝ 1−0.057Z/Z⊙. Later, Chamulak et al. (2008) argued that even a zero metallicity progenitor is subject to neutronization through electron captures during the time that elapses between the crossing of the carbon ignition curve and the onset of the dynamical event, i.e. until the timescale becomes on the order of 1–10 s. The neutronization during the simmering phase would affect mainly SNIa from low metallicity progenitors, and the relationship between M(56Ni) and Z would change slightly, to become M(56Ni) ∝ 0.965−0.057Z/Z⊙. Existing methods to determine the progenitor metallicity from the supernova properties depend on the degree of neutronization during carbon simmering (Lentz et al. 2000; Taubenberger et al. 2008; Badenes et al. 2008).
The final neutron excess at runaway is a result of several chains of reactions taking place during carbon simmering, all of them primed by the 12C+12C reaction. The main reaction chain is activated by the release of a proton by the carbon fusion reaction 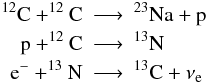 with the result that there is one electron capture for each proton delivered in the 12C + 12C reaction. This sequence of reactions is fast enough relative to the fusion of 12C to ensure that every time a proton is released it is followed by an electron capture onto 13N2.
with the result that there is one electron capture for each proton delivered in the 12C + 12C reaction. This sequence of reactions is fast enough relative to the fusion of 12C to ensure that every time a proton is released it is followed by an electron capture onto 13N2.
Another significant contributor to the neutronization of matter during carbon simmering is the electron capture onto 23Na 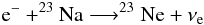 that is activated also by the proton channel of the 12C+12C reaction. However, in this case the electron capture timescale is longer than the convective timescale implying that, as the temperature rises approaching the runaway, the strong interactions become faster than these electron captures. A direct consequence is that the abundance of 23Ne freezes out at high temperatures.
that is activated also by the proton channel of the 12C+12C reaction. However, in this case the electron capture timescale is longer than the convective timescale implying that, as the temperature rises approaching the runaway, the strong interactions become faster than these electron captures. A direct consequence is that the abundance of 23Ne freezes out at high temperatures.
 |
Fig. 6 Evolution of the chemical composition at the center of the white dwarf as a function of temperature for different 12C+12C rates: CF88 rate (top left), LER-1.5-0.1-1.0 model (top right), and α/p: LER-1.5-0.1-5.0 with α/p = 5.0 (bottom left), and LER-1.5-0.1-0.2 with α/p = 0.2 (bottom right). To improve the readability, the upper limit to the vertical axis has been set at a mass fraction of 0.01, hence the curves of 12C and 16O (both with mass fractions > 0.1) lie out of the plot (the relative variations in their mass fractions are very tiny within the temperature range shown). The thick curve gives the electron molar fraction. The abundance of 23Ne reflects the amount of electron captures on 23Na: it grows quickly with increasing temperature at low temperatures but levels out at T ~ 5.5 × 108 K for the CF88 model and T ~ 3.5 × 108 K for the rest of the models shown. The sum of the abundances of 17O and 14C reflect the electron captures on 13N: the sum grows steadily but is always smaller than the abundance of 23Ne, except at very high temperatures. The top axes of the plots belonging to models CF88 and LER-1.5-0.1-1.0 are labeled with the time to runaway. |
Assuming the proton yield estimated by CF88, i.e. 0.43 protons per reaction, gives 0.14 electron captures for every 12C nuclei consumed in the above chains. At densities in excess of 109 g cm-3, other electron captures become energetically feasible and the ratio of electron captures per 12C nuclei destroyed increases to a typical value of ~0.3 (Chamulak et al. 2008). On the other hand, a proton yield as low as that found by S07 for the 2.14 MeV resonance can modify substantially the ratio of electron captures per 12C nuclei destroyed. For instance, a yield of 0.16 protons per reaction would give 0.055 electron captures for every 12C nuclei consumed in the above chains, i.e. approximately a factor of three reduction in the amount of electrons captured for a given reduction in the carbon mass fraction.
A reduction in the amount of electron captures activated by the proton channel allows other reactions to contribute significantly to the neutronization. The initial presence of 22Ne opens up another route for electron captures activated by the alpha channel of the carbon fusion reaction 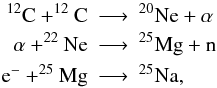 which has to be taken into account in the calculations of neutronization during carbon simmering.
which has to be taken into account in the calculations of neutronization during carbon simmering.
4.1.1. Impact of a low-energy resonance
To evaluate the impact of a ghost resonance on the degree of neutronization during carbon simmering we post-processed, with our nucleosynthetic code, the central ρ-T tracks obtained with the hydrostatic code (Fig. 3) until they crossed the dynamic curve. We did not account for convective mixing, because the changes in the chemical composition we consider are so moderate that the contribution of fresh fuel would not have a significant effect on the nuclear network.
Table 4 shows the results obtained for our reference model, CF88, and two different resonance strengths with ER = 1.5 MeV, (ωγ)R = 0.1 and 0.001 meV (first three rows). We also computed models that differ from LER-1.5-0.1-1.0 in terms of the α to proton yield ratios (last two rows). The second column gives dYe/dY12, which is actually the average, during carbon simmering, of the ratio of the reduction in the electron mole number to the reduction in the 12C molar fraction. The presence of the ghost resonance, clearly does not affect the average number of electron captures per carbon nuclei destroyed unless the α or proton channels contribute to the carbon fusion rate in significantly different proportions. An increase (decrease) in α/p by a factor five translates into a ~50% decrease (increase) of dYe/dY12. The third column of Table 4 gives the average derivative of the mean molar fraction with respect to the carbon molar fraction, which reflects the progress of the nuclear network to increasingly bound and heavy nuclei. This quantity depends strongly on neither the presence of the ghost resonance nor α/p. The small decrement in dYb/dY12 for α/p = 0.2 is due to the destruction of a third 12C nuclei, for each carbon fusion reaction, by a radiative proton capture, which depends directly on the strength of the proton channel in the 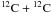 reaction.
reaction.
 |
Fig. 7 Evolution of the decrement in the electron mole number vs. the decrement in the carbon molar fraction for models: CF88, LER-1.5-0.1-1.0, LER-1.5-0.1-5.0, and LER-1.5-0.1-0.2. |
The main conclusion from Table 4 is the definite dependence of the final neutron excess on the output channel of the carbon fusion reaction. In Fig. 6, we show details of the chemical evolution of the reference model, CF88, and the models with ER = 1.5 MeV and (ωγ)R = 0.1 meV and different α/p. In this figure, the different roles played by the electron captures on 13N and 23Na with respect to neutronization can be appreciated.
The abundance of 23Ne directly reflects the electron captures on 23Na, it increases steadily at low temperatures but freezes out as soon as the nuclear timescale becomes smaller than its electron capture timescale. This condition is achieved at T ~ 5.5 × 108 K with the CF88 rate, and at T ~ 3.5 × 108 K with the (low-energy) resonant rate. After peaking at these temperatures, the abundance of 23Ne slightly decreases as a consequence of the reaction 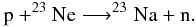 This last reaction, which leads to a stronger decrease in the 23Ne abundance in the models as α/p decreases, does not change the electron mole number. Hence, the peak of the abundance of 23Ne gives the measure of the contribution of the electron captures on 23Na to the global neutronization of matter.
This last reaction, which leads to a stronger decrease in the 23Ne abundance in the models as α/p decreases, does not change the electron mole number. Hence, the peak of the abundance of 23Ne gives the measure of the contribution of the electron captures on 23Na to the global neutronization of matter.
The evolution of the electron captures on 13N can be monitored by adding the abundances of 14C and 17O. Following each electron capture on 13N, to give 13C, this last nucleus captures any available α particle and unties a chain of reactions 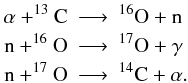 Owing to the large abundance of 16O, the last neutron capture is only significant after the mass fraction of 17O has grown to X(17O) ~ 4 × 10-4–10-3. As can be seen by comparing the peak abundance of 23Ne with the sum of the abundances of 14C and 17O, the largest contributors to neutronization in all the models are the electron captures onto 23Na.
Owing to the large abundance of 16O, the last neutron capture is only significant after the mass fraction of 17O has grown to X(17O) ~ 4 × 10-4–10-3. As can be seen by comparing the peak abundance of 23Ne with the sum of the abundances of 14C and 17O, the largest contributors to neutronization in all the models are the electron captures onto 23Na.
Electron captures onto 25Mg only contribute significantly to neutronization in model LER-1.5-0.1-5.0, with α/p = 5. Even in a model with such a reduced proton yield, their contribution to neutronization, as measured by the peak abundance of 25Na, is less than half the contribution of the electron captures onto 23Na.
Figure 7 shows the evolution of the decrement in the electron mole number as a function of the decrement in the carbon molar fraction, for the same models as above. Each curve displays two parts with different slopes. The knee of the curves belongs to the time at which electron captures on 23Na freeze-out and, thereafter matter is less efficiently neutronized. The plot clearly shows that the models with the same α/p (CF88 and LER-1.5-0.1-1.0) are characterized by the same rate of neutronization relative to the rate of consumption of 12C, while a different weight of proton and α channels implies different slopes in both parts of the corresponding curves. Another interesting feature in Fig. 7 is that the total consumption of 12C in the resonant models is far less than in the CF88 model, and the same applies to the total decrease in the electron mole number.
To evaluate the consequences of any dependence of − ΔYe on the resonance properties, we have to take into account the total mass of 12C destroyed before reaching the dynamic curve, ΔM(12C), and the size of the convective core, Mconv (Table 1). The total decrement in the 12C molar fraction within the convective core, − (ΔY12)core (third column in Table 4) is given by 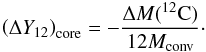 (7)The total decrement in the electron mole number within the WD core during carbon simmering is
(7)The total decrement in the electron mole number within the WD core during carbon simmering is 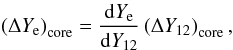 (8)which is given in the last column of Table 4. Accounting for all these factors results in a significant reduction in the neutronization when there is a LER in the carbon fusion reaction. The largest reduction in (ΔYe)core belongs to the model assuming α/p = 5.0, in which case the reduction in the electron mole number in the convective core is only ~13% of the reduction obtained with the CF88 model.
(8)which is given in the last column of Table 4. Accounting for all these factors results in a significant reduction in the neutronization when there is a LER in the carbon fusion reaction. The largest reduction in (ΔYe)core belongs to the model assuming α/p = 5.0, in which case the reduction in the electron mole number in the convective core is only ~13% of the reduction obtained with the CF88 model.
We note that the reduction in the electron mole number within the convective core is the result of different factors, some of which depend on α/p, while others depend on the resonance energy and strength. However, for α/p = 5, even a small strength of LER (for which ΔM(12C) and Mconv were similar to the CF88 model) would be enough to reduce the neutronization during carbon simmering by a factor ≲ 0.5.
Runaway conditions for different 12C+12C rates.
4.1.2. Variations in either central density or accretion rate
In realistic evolutionary models, the central density at carbon ignition is determined mainly by the accretion rate. However, a variation in Ṁ also affects the thermal profile along the whole WD, hence the mass coordinate where carbon runs away (e.g. Piersanti et al. 2003). While it is impractical to explore with our hydrostatic code the whole space of accretion rates together with all the resonance parameters, we can gain some indirect insight into the consequences of different accretion rates by computing the evolution during the simmering phase with our post-processing code at different constant densities. Hence, we repeated the calculations described in Sect. 4.1.1 following, at constant density, the thermal and chemical evolution between the temperatures of the ignition and dynamic curves. Our results are summarized in Fig. 8, where we use four different densities in the range 109–4 × 109 g cm-3.
The results show that the impact of the resonance strength (or even of the existence of a LER) is minimal. The points belonging to models with ER = 1.5 MeV and resonance strengths differing by four orders of magnitude are indeed indistinguishable (blue triangles and green stars at ρ = 2 × 109 g cm-3). In contrast, the most influencing parameter is the ratio of the yields of protons to alphas in the 12C+12C reaction, whose impact on the variation in the electron molar fraction is by far higher than that of the density. It is remarkable that the impact of the α/p ratio on the electron captures is about the same at high densities as at ρ = 109 g cm-3, even though in this case the only electron captures allowed are those onto 13N.
 |
Fig. 8 Average derivative of the electron molar fraction with respect to the 12C molar fraction during carbon simmering, as a function of density for different carbon fusion rates: CF88 (black asterisks), LER-1.5-0.1-1.0 (blue triangles), LER-1.5-0.001-1.0 and LER-1.5-10.-1.0 (green stars), and LER-1.5-0.1-5.0 and LER-1.5-0.1-0.2 (red and magenta circles, respectively). All the models shown in this panel were computed at constant density. The models with the extreme resonance strengths were computed only at ρ = 2 × 109 g cm-3. |
4.2. Runaway bubbles
The thermal structure of the white dwarf, and thus the distribution of hot spots, at thermal runaway is set during the last seconds before the crossing of the dynamical curve, when the nuclear timescale becomes of the same order as the convective turnover time, ~10–100 s (Woosley et al. 2004, hereafter WWK04). At this point, the timescale is so short that the temperature of the central region of the WD is no longer uniform. Hot spots originate, instead at random locations near the center and are moved by the convective cells across the turbulent core. During their trip, these bubbles are subject to thermal stresses of different sign: on the one hand, nuclear reactions release heat efficiently while, on the other hand, thermal exchange with the background cools them. If the thermal fluctuations induced by convection are large enough, the heat release by nuclear reactions dominates over adiabatic cooling and a bubble can run away in a time shorter than the turnover timescale. Although this process is intrinsically three-dimensional, we can model it following the ideas of WWK04.
To determine the runaway temperature, Trw, of the convective bubbles, we use the same nucleosynthetic code as before. Now, however, the evolution of the bubble temperature is integrated together with the nuclear network, and takes into account both the nuclear reactions and the convective cooling 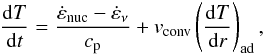 (9)where cp is again the heat capacity at constant pressure,
(9)where cp is again the heat capacity at constant pressure, 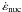 is the rate of energy release by nuclear reactions including electron captures,
is the rate of energy release by nuclear reactions including electron captures, 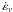 is the rate of neutrino energy loss (although it is not relevant near runaway, we have included it for completeness), vconv is the convective velocity, which we take here as a free parameter, and (dT/dr)ad is the adiabatic thermal gradient. The last term in Eq. (9) models the loss of heat from the bubble to the background caused by convection (WWK04). Equation (9) can be easily integrated for a given initial temperature, T0, and bubble distance to the center, r0, which we take as the radius of the zone that first crosses the dynamical curve. As we adopt a constant vconv, we can easily calculate the position of the bubble at any time, t, as r = r0 + vconvt. Using these approximations, the initial bubble temperature, T0 = Trw, above which the integration of Eq. (9) diverges and the radius, rrw, at the time of runaway can be computed for a given central density, ρ0, and convective velocity.
is the rate of neutrino energy loss (although it is not relevant near runaway, we have included it for completeness), vconv is the convective velocity, which we take here as a free parameter, and (dT/dr)ad is the adiabatic thermal gradient. The last term in Eq. (9) models the loss of heat from the bubble to the background caused by convection (WWK04). Equation (9) can be easily integrated for a given initial temperature, T0, and bubble distance to the center, r0, which we take as the radius of the zone that first crosses the dynamical curve. As we adopt a constant vconv, we can easily calculate the position of the bubble at any time, t, as r = r0 + vconvt. Using these approximations, the initial bubble temperature, T0 = Trw, above which the integration of Eq. (9) diverges and the radius, rrw, at the time of runaway can be computed for a given central density, ρ0, and convective velocity.
Table 5 allows a comparison between the runaway temperature, Trw, obtained with a LER and the one achieved with the CF88 rate. The resonance leads to a lower ignition temperature, from Trw ~ 8 × 108 K to Trw ~ 4–6 × 108 K. The runaway radius, rrw, is not as sensitive to the presence of the ghost resonance, as it stays in a narrow range of rrw ≃ 180–240 km for most models. The runaway radius for model LER-1.3-0.1-1.0 is larger because of the off-center crossing of the dynamical curve.
We have explored the sensitivity of the bubble runaway conditions of model LER-1.5-0.1-1.0 to the assumed physico-chemical parameters: convective velocity, vconv, density, and 12C mass fraction, and present the results in Table 6. As can be seen, for the chosen combination of parameters, the runaway temperature remains much lower than that of the CF88 model, and is mostly sensitive to the central density of the WD (we recall that the mass accretion rates that differ from those we assumed would lead to different central densities at runaway). On the other hand, a decrease in the convective velocity from 80 km s-1 to 20 km s-1 changes Trw by only 0.2 × 108 K. The value of the central density of the WD also affects substantially the runaway radius, which changes by a factor of two between our extreme densities. However, it is the convective velocity that has the strongest influence on rrw. If vconv is as small as 20 km s-1, the bubble runs away just at 90 km from the center of the WD.
Sensitivity of the runaway conditions of model LER-1.5-0.1-1.0 with respect to physico-chemical parameters.
Tables 5 and 6 give the time, trw it takes for the bubble to run away after the temperature reaches T = Trw. In all cases, the runaway time is short enough to allow for the survival of the hot bubbles against disruption by the Rayleigh-Taylor instability, which is on the order of tRT ~ 5 s (Iapichino et al. 2006). The survival time of the bubbles against disruption sets a limit to the maximum distance a bubble can travel from its birthplace before running away. For instance, for our adopted convective velocity of vconv = 80 km s-1, this distance is rmax ~ 400 km.
Some examples of the temperature evolution of the bubbles are shown in Fig. 9, for different initial temperatures, T0, and carbon fusion rates. As can be seen, the radius at which a bubble runs away depends sensitively on its initial temperature (i.e. on the level of thermal fluctuations in the convective core). As might be expected, the larger the excess of the initial temperature of a bubble over Trw, the closer it burns towards its initial location.
 |
Fig. 9 Evolution of the temperature of a burning convective bubble as a function of the distance to the center of the white dwarf, for different initial temperatures, T0, and prescriptions for the 12C+12C rate. From top to bottom: CF88 (short-long dashed line), LER-1.5-0.001-1.0 (dot-long dashed line), LER-1.5-0.1-1.0 (solid line), and LER-1.5-10.-1.0 (long-dashed line). For each reaction rate, we followed the evolution of the bubbles starting at the center, r = 0, with different trial initial temperatures, until we found the minimum initial temperature leading to runaway of the bubble before reaching the end of the convective core. The distance to the center varies linearly with the elapsed time, r = r0 + vconvt, where vconv = 80 km s-1 is the convective velocity. To test the impact of the off-center ignition (at Rrw ~ 149 km) in model LER-1.5-10.-1.0, we computed the bubble evolution with the same rate but starting from the center. The runaway temperature, shown by the thin long-dashed line, is nearly the same as in the off-center calculation of the same model. |
4.2.1. Multispot runaway
Once a bubble runs away, the time available for other sparks to ignite, δt, is limited by the time it takes for a conductive flame to cross the whole region where hot spots dwell, d ~ 2rmax. As the conductive flame speed at the densities of interest is vflame ≃ 40 km s-1 (Timmes & Woosley 1992), the formation of multiple flame centers is possible during a time ~20 s. Thus, a multispot runaway scenario is a reasonable assumption for SNIa, and its properties are an important ingredient for multidimensional SNIa models.
Because the induction of local peaks of temperature by convection is a stochastic process, we have to rely on a statistical approach to the multispot scenario. Indeed, WWK04 studied the distribution of thermal fluctuations in the convective core of an igniting WD and proposed that there is an exponential probability density function (EPDF) of temperatures 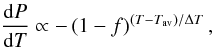 (10)where f is a parameter correlated to convective mixing efficiency, which following WWK04 we assume to be f ≃ 0.9, Tav is the average temperature, which we take without loss of generality as the runaway temperature, Tav = Trw, and ΔT ~ 0.1 × 108 K or slightly lower (WWK04). To derive a distribution function for the runaway radii (distance to the center of the WD) of the bubbles, we need the relationship between rrw and the initial temperature excess over Tav. We computed, for both model CF88 and model LER-1.5-0.1-1.0, the temperature evolution of bubbles with an initial temperature, T0, above the runaway temperature, from which we found the corresponding runaway radii, and we fit an empirical relationship between T0 and rrw (Fig. 10). A second-order polynomial provides a good description of
(10)where f is a parameter correlated to convective mixing efficiency, which following WWK04 we assume to be f ≃ 0.9, Tav is the average temperature, which we take without loss of generality as the runaway temperature, Tav = Trw, and ΔT ~ 0.1 × 108 K or slightly lower (WWK04). To derive a distribution function for the runaway radii (distance to the center of the WD) of the bubbles, we need the relationship between rrw and the initial temperature excess over Tav. We computed, for both model CF88 and model LER-1.5-0.1-1.0, the temperature evolution of bubbles with an initial temperature, T0, above the runaway temperature, from which we found the corresponding runaway radii, and we fit an empirical relationship between T0 and rrw (Fig. 10). A second-order polynomial provides a good description of 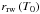 and allows us to find the probability density function of runaway radii
and allows us to find the probability density function of runaway radii 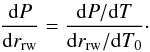 (11)The results are shown in the bottom panel of Fig. 10. The distributions of runaway radii for both carbon fusion rates are qualitatively similar in shape and width, but with the LER the peak of the distribution is ~50 km closer to the center of the WD. Such a displacement of the runaway radius can have important consequences for SNIa models such as the gravitationally confined detonation model (see, e.g., Röpke et al. 2007).
(11)The results are shown in the bottom panel of Fig. 10. The distributions of runaway radii for both carbon fusion rates are qualitatively similar in shape and width, but with the LER the peak of the distribution is ~50 km closer to the center of the WD. Such a displacement of the runaway radius can have important consequences for SNIa models such as the gravitationally confined detonation model (see, e.g., Röpke et al. 2007).
 |
Fig. 10 Distribution of runaway radii. Top: runaway radius as a function of the temperature above the runaway temperature (Trw, see Table 5): stars belong to model CF88, and triangles to model LER-1.5-0.1-1.0. The lines are quadratic fits to the dependence of runaway radii on temperature: r = ax2 + bx + c, where r is in km and |
5. Conclusions
We have systematically explored the consequences that a hypothetical low-energy resonance in the carbon fusion rate would have for the physics and outcome of thermonuclear supernovae. We have considered resonance energies in the range ER = 1.3–1.7 MeV, with strengths limited by the available experimental cross-section data at Ecm > 2.10 MeV. We have also studied different ratios of the yields of α to protons, α/p = 0.2–5.0. Within these limits, the phase of the supernova that is most affected by the presence of a LER is carbon simmering. In particular, the degree of neutronization of the white dwarf prior to the explosion can be reduced by a large factor even for a LER with a strength much smaller, say by four-six orders of magnitude, than that measured for the resonance with the lowest experimental energy (ER = 2.14 MeV, S07).
The main changes induced by a LER with respect to the model that uses the standard carbon fusion rate, CF88, are:
-
The central density of the white dwarf at runaway can increase by ~25–30%, for a given mass accretion rate. However, a strong enough resonance gives an off-center ignition, in which case the density is lower than that obtained with the CF88 rate.
-
The minimum neutron excess of thermonuclear supernova ejecta, determined by the progenitor initial metallicity and by several electron capture reactions synchronized with carbon simmering, is quite sensitive to the relative α to proton yield of the carbon fusion reaction The presence of a small resonance at 1.5 MeV (1.3 MeV) with a strength ≳ 13 neV ( ≳ 0.12 neV) and an alpha/p yield ratio substantially different from unity would dominate over the non-resonant contribution at the relevant Gamow energies and, hence, would have a non-negligible impact on the neutronization of matter during carbon simmering.
-
The mass of the convective core is also affected by a LER. In general, the lower the resonance energy and/or the stronger the resonance, the smaller the convective core. The neutronization produced during carbon simmering erases the imprint of the initial metallicity of the supernova progenitor, and convection homogenizes the core composition before the thermal runaway. Hence, the smaller the convective core the higher the mass of the supernova that bears a record of the initial metallicity.
-
The time it takes the WD to cover the path from the ignition curve to the dynamic curve (simmering time) is substantially shorter (by up to a factor ten) if there is a strong LER.
-
The runaway temperature is strongly affected by the presence of a LER, which could lower Trw by as much as 2–4 × 108 K.
-
In a multispot runaway scenario, the distribution of igniting bubbles changes quantitatively in the presence of a LER. With such a resonance, even of moderate strength, bubbles run away closer to the center than predicted by using the CF88 rate (see also Iapichino & Lesaffre 2010). On the other hand, if the resonance were strong enough to provoke an off-center ignition, it would have the opposite effect.
-
At the present level of theoretical understanding of the physics of thermonuclear supernovae, it is difficult to predict the true impact of an increase in the rate of carbon fusion on the nucleosynthesis and energetics of the explosive event. Such an study would require a completely parameter-free successful SNIa model, which is currently not available. Within the one-dimensional delayed-detonation paradigm, we have found quite small variations in the kinetic energy of the supernova, K, mild variations in the yield of 56Ni (but still well within the observationally allowed range), and a ratio of K to the mass of unburned carbon ejected that is quite sensitive to the existence of a LER.
Finally, we briefly discuss some potential (even though speculative) implications of the distributions of the runaway radii of the ignition bubbles that we have found for the different models with/without a LER. We have shown that both the runaway radius, rrw, is affected by a LER (Table 5), and the runaway bubbles cluster around rrw (Fig. 10). However, although a LER may influence the outcome of the explosion, it is impossible at present to make a more specific prediction. On the other hand, we have shown that rrw is a sensitive function of the central density (Table 6), with the result that at a higher density the igniting bubbles would be concentrated toward smaller runaway radii, which can have important consequences for the subsequent development of the explosion. The effects of the distribution of hot spots in the WD at runaway has been explored just recently with the aid of multidimensional SNIa models. For instance, Seitenzahl et al. (2011) searched for the systematic effects of the central density on SNIa luminosity by simulating WD explosions starting from hot bubbles randomly located within a radius independent of ρc. As we have shown, it would be advisable to use a density-dependent distribution of the bubble positions in these studies, even if the carbon fusion rate is that of CF88.
We conclude that a robust understanding of the links between SNIa properties and their progenitors will not be attained until the 12C+12C reaction rate is measured at energies ~1.5 MeV.
In the literature, the term ignition is often used to describe the conditions (density, temperature, chemical composition, and geometry of the runaway kernels) when the white dwarf evolution becomes dynamical. This should not be confused with our use of the term ignition, referred to in the ignition curve, which takes place tens, or even hundreds, of years before the actual explosion.
Acknowledgments
This work has been partially supported by the Spanish Ministry for Science and Innovation projects AYA2008-04211-C02-02, AYA08–1839/ESP, and EUI2009–04170, by European Union FEDER funds, by the Generalitat de Catalunya, and by the ASI-INAF I/016/07/0. J.A.E. research is funded by the Comissionat per a Universitats i Recerca of the DIUE of the Generalitat de Catalunya, and by ESF.
References
- Aguilera, E. F., Rosales, P., Martinez-Quiroz, E., et al. 2006, Phys. Rev. C, 73, 064601 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1969, Ap&SS, 5, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Bravo, E., Borkowski, K. J., & Domínguez, I. 2003, ApJ, 593, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Bravo, E., & Hughes, J. P. 2008, ApJ, 680, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Barrón-Palos, L., Aguilera, E. F., Aspiazu, J., et al. 2006, Nucl. Phys. A, 779, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, H. W., Kettner, K.-U., Rolfs, C., & Trautvetter, H. P. 1981, Zeitschrift fur Physik A Hadrons and Nuclei, 303, 305 [NASA ADS] [Google Scholar]
- Bennett, M. E., Hirschi, R., Pignatari, M., et al. 2010a [arXiv:1012.3258] [Google Scholar]
- Bennett, M. E., Hirschi, R., Pignatari, M., et al. 2010b, J. Phys. Conf. Ser., 202, 012023 [Google Scholar]
- Bravo, E., Tornambe, A., Dominguez, I., & Isern, J. 1996, A&A, 306, 811 [NASA ADS] [Google Scholar]
- Bravo, E., García-Senz, D., Cabezón, R. M., & Domínguez, I. 2009, ApJ, 695, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E., Domínguez, I., Badenes, C., Piersanti, L., & Straniero, O. 2010, ApJ, 711, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E., Althaus, L. G., García-Berro, E., & Domínguez, I. 2011, A&A, 526, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tab., 40, 283 [Google Scholar]
- Chamulak, D. A., Brown, E. F., Timmes, F. X., & Dupczak, K. 2008, ApJ, 677, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Chieffi, A., & Straniero, O. 1989, ApJS, 71, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D. 1968, Principles of stellar evolution and nucleosynthesis, ed. D. D. Clayton [Google Scholar]
- Cooper, R. L., Steiner, A. W., & Brown, E. F. 2009, ApJ, 702, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., & Khokhlov, A. 2011, ApJ, 730, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, S., Mangano, G., Miele, G., Picardi, I., & Pisanti, O. 2002, Mod. Phys. Lett. A, 17, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, S., Mangano, G., Miele, G., Picardi, I., & Pisanti, O. 2003, Nucl. Phys. B, 658, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, W. A., Caughlan, G. R., & Zimmerman, B. A. 1975, ARA&A, 13, 69 [Google Scholar]
- Gamezo, V. N., Khokhlov, A. M., Oran, E. S., Chtchelkanova, A. Y., & Rosenberg, R. O. 2003, Science, 299, 77 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gasques, L. R., Afanasjev, A. V., Aguilera, E. F., et al. 2005, Phys. Rev. C, 72, 025806 [Google Scholar]
- Höflich, P., & Khokhlov, A. 1996, ApJ, 457, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Khokhlov, A. M., & Wheeler, J. C. 1995, ApJ, 444, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iapichino, L., & Lesaffre, P. 2010, A&A, 512, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iapichino, L., Brüggen, M., Hillebrandt, W., & Niemeyer, J. C. 2006, A&A, 450, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, A. P., Calder, A. C., Townsley, D. M., et al. 2010, ApJ, 720, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C. L., Rehm, K. E., Back, B. B., & Janssens, R. V. F. 2007, Phys. Rev. C, 75, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Khokhlov, A. M. 1991, A&A, 245, 114 [NASA ADS] [Google Scholar]
- Lentz, E. J., Baron, E., Branch, D., Hauschildt, P. H., & Nugent, P. E. 2000, ApJ, 530, 966 [Google Scholar]
- Maeda, K., Benetti, S., Stritzinger, M., et al. 2010, Nature, 466, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mazarakis, M. G., & Stephens, W. E. 1973, Phys. Rev. C, 7, 1280 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Röpke, F. K., Benetti, S., & Hillebrandt, W. 2007, Science, 315, 825 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meakin, C. A., Seitenzahl, I., Townsley, D., et al. 2009, ApJ, 693, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Sugimoto, D., & Neo, S. 1976, Ap&SS, 39, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. R., Winkler, H., & Zaidins, C. S. 1969, ApJ, 157, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Gagliardi, S., Iben, Jr., I., & Tornambé, A. 2003, ApJ, 583, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2008, ApJ, 673, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Chang, P. 2008, ApJ, 678, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Rolfs, C. E., & Rodney, W. S. 1988, Cauldrons in the cosmos: Nuclear astrophysics (University of Chicago Press) [Google Scholar]
- Röpke, F. K., Woosley, S. E., & Hillebrandt, W. 2007, ApJ, 660, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., Seitenzahl, I. R., Benitez, S., et al. 2011, Progress in Particle and Nuclear Physics, 66, 309 [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., & Röpke, F. K. 2011, MNRAS, 414, 2709 [NASA ADS] [CrossRef] [Google Scholar]
- Spillane, T., Raiola, F., Rolfs, C., et al. 2007, Phys. Rev. Lett., 98, 122501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strieder, F. 2008, J. Phys. G Nucl. Phys., 35, 014009 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Hachinger, S., Pignata, G., et al. 2008, MNRAS, 385, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Woosley, S. E. 1992, ApJ, 396, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wunsch, S., & Kuhlen, M. 2004, ApJ, 607, 921 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Results of the hydrodynamic explosion models plus post-processing nucleosynthesis.
Sensitivity of the runaway conditions of model LER-1.5-0.1-1.0 with respect to physico-chemical parameters.
All Figures
 |
Fig. 1 Astrophysical factor and rate of the 12C+12C reaction due to a resonance at an energy ER = 1.3 MeV (dashed line), 1.5 MeV (solid line), and 1.7 MeV (dot-dashed line), with resonance strengths of 16 meV, 9.2 meV, and 4.1 meV, respectively. Top: modified astrophysical factor as a function of energy. The bar at the bottom right shows the maximal astrophysical factor measured by S07 at an energy of ~2.1 MeV (σ < 0.8 nb), which is the most constraining low energy measurement to date. The quoted strengths of the resonances would be compatible with a σ two orders of magnitude smaller than that measured by S07 (if the resonance width is ΓR ≈ 10 keV). Bottom: ratio of our 12C+12C reaction, accounting for a LER, to the CF88 reaction rate, as a function of temperature. The dotted line close to the horizontal axis is the ratio of the rate accounting for the resonance found by S07 to the CF88 rate. The arrows mark the temperature ranges relevant to carbon ignition, carbon simmering, and the explosive burning in a subsonic flame or a detonation. The gap between carbon simmering and flames reflects the dominance of thermal conduction and shock heating over nuclear energy release in stationary explosive burning fronts. |
| In the text | |
 |
Fig. 2 Nuclear timescale vs. temperature. The nuclear timescale has been computed as τnuc = (2ρNAY12 ⟨ σv ⟩ )-1, where NA is Avogadro’s number, Y12 = 0.5/12 mol g-1 is the molar fraction of 12C, and ⟨ σv ⟩ is the rate of the 12C+12C reaction. There are shown curves belonging to the CF88 non-resonant rate, the non-resonant plus the resonance at 2.1 MeV measured by S07, and the non-resonant plus the 2.1 MeV resonance plus a LER. For the last, the curves are labeled with the values of the resonance energy, ER in MeV, and the resonance strength, (ωγ)R in meV. The hatched region shows the range of the convective timescales. In this plot, the density is ρ = 2 × 109 g cm-3 and the carbon mass fraction is 0.5. Note that a lower carbon abundance would imply a longer nuclear timescale. |
| In the text | |
 |
Fig. 3 Changes in the physics of the accretion phase owing to a LER: ignition curves (dashed lines), dynamical curve (dot-dashed lines), and track of central ρ vs. T during the hydrostatic evolution (solid lines). The top left panel shows the results obtained when the 12C+12C rate was computed following CF88, the other panels show the results adding a LER to that rate (see Table 1). For comparison purposes, in all the panels we have drawn the CF88 curves as thin lines. In the panels belonging to the LER-1.5-10.-1.0 and LER-1.3-0.1-1.0 rates, the track belongs to the evolution of the shell that first crosses the dynamical curve. We assumed a chemical composition made of 50% 12C and 50% 16O for both curves, while the hydrostatic ρ-T tracks were computed with the realistic chemical composition obtained from full stellar evolutionary calculations (FRANEC code). |
| In the text | |
 |
Fig. 4 Thermal and chemical profiles at the crossing of the dynamical curves. The line types used for the models from Table 1 are the same as those used in Fig. 2. Top panel: temperature profiles. From top to bottom (at M ~ 0.2 M⊙) the curves belong to models CF88, LER-1.5-0.001-1.0, LER-1.7-0.1-1.0, LER-1.5-0.1-1.0, LER-1.3-0.1-1.0, and LER-1.5-10.-1.0. Note that the last two models run away off-center. Bottom panel: 12C mass fraction profiles. For comparison purposes, we have plotted with a thin solid line the profile of model CF88 at the crossing of the ignition curve. As can be easily appreciated, the extension of the convective core is very sensitive to the inclusion of a LER in the 12C+12C reaction rate. |
| In the text | |
 |
Fig. 5 Chemical profile in the outer layers of models CF88 and LER-1.5-10.-1.0. The mass coordinate measures the mass within the white dwarf surface, i.e. the surface is at the right end of the horizontal axis. The thicker unlabeled line shows the maximum temperature achieved in each layer during the explosion (right axis). |
| In the text | |
 |
Fig. 6 Evolution of the chemical composition at the center of the white dwarf as a function of temperature for different 12C+12C rates: CF88 rate (top left), LER-1.5-0.1-1.0 model (top right), and α/p: LER-1.5-0.1-5.0 with α/p = 5.0 (bottom left), and LER-1.5-0.1-0.2 with α/p = 0.2 (bottom right). To improve the readability, the upper limit to the vertical axis has been set at a mass fraction of 0.01, hence the curves of 12C and 16O (both with mass fractions > 0.1) lie out of the plot (the relative variations in their mass fractions are very tiny within the temperature range shown). The thick curve gives the electron molar fraction. The abundance of 23Ne reflects the amount of electron captures on 23Na: it grows quickly with increasing temperature at low temperatures but levels out at T ~ 5.5 × 108 K for the CF88 model and T ~ 3.5 × 108 K for the rest of the models shown. The sum of the abundances of 17O and 14C reflect the electron captures on 13N: the sum grows steadily but is always smaller than the abundance of 23Ne, except at very high temperatures. The top axes of the plots belonging to models CF88 and LER-1.5-0.1-1.0 are labeled with the time to runaway. |
| In the text | |
 |
Fig. 7 Evolution of the decrement in the electron mole number vs. the decrement in the carbon molar fraction for models: CF88, LER-1.5-0.1-1.0, LER-1.5-0.1-5.0, and LER-1.5-0.1-0.2. |
| In the text | |
 |
Fig. 8 Average derivative of the electron molar fraction with respect to the 12C molar fraction during carbon simmering, as a function of density for different carbon fusion rates: CF88 (black asterisks), LER-1.5-0.1-1.0 (blue triangles), LER-1.5-0.001-1.0 and LER-1.5-10.-1.0 (green stars), and LER-1.5-0.1-5.0 and LER-1.5-0.1-0.2 (red and magenta circles, respectively). All the models shown in this panel were computed at constant density. The models with the extreme resonance strengths were computed only at ρ = 2 × 109 g cm-3. |
| In the text | |
 |
Fig. 9 Evolution of the temperature of a burning convective bubble as a function of the distance to the center of the white dwarf, for different initial temperatures, T0, and prescriptions for the 12C+12C rate. From top to bottom: CF88 (short-long dashed line), LER-1.5-0.001-1.0 (dot-long dashed line), LER-1.5-0.1-1.0 (solid line), and LER-1.5-10.-1.0 (long-dashed line). For each reaction rate, we followed the evolution of the bubbles starting at the center, r = 0, with different trial initial temperatures, until we found the minimum initial temperature leading to runaway of the bubble before reaching the end of the convective core. The distance to the center varies linearly with the elapsed time, r = r0 + vconvt, where vconv = 80 km s-1 is the convective velocity. To test the impact of the off-center ignition (at Rrw ~ 149 km) in model LER-1.5-10.-1.0, we computed the bubble evolution with the same rate but starting from the center. The runaway temperature, shown by the thin long-dashed line, is nearly the same as in the off-center calculation of the same model. |
| In the text | |
 |
Fig. 10 Distribution of runaway radii. Top: runaway radius as a function of the temperature above the runaway temperature (Trw, see Table 5): stars belong to model CF88, and triangles to model LER-1.5-0.1-1.0. The lines are quadratic fits to the dependence of runaway radii on temperature: r = ax2 + bx + c, where r is in km and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.